Class 11 : Physics (In Hindi) – अध्याय 13: दोलन

पाठ का विश्लेषण एवं विवेचन

🔶 1️⃣ विस्तृत व्याख्या (~1700 शब्द)
🔵 परिचय (Introduction)
जब कोई वस्तु किसी निश्चित स्थिति के आस-पास आगे–पीछे या ऊपर–नीचे समानांतर गति दोहराती है, तो उसे दोलन (Oscillation) या स्पंदन (Vibration) कहा जाता है।
उदाहरण —
🌿 एक लटकन (Pendulum) का आगे-पीछे झूलना,
🌿 स्प्रिंग से जुड़ा द्रव्यमान ऊपर-नीचे गति करना,
🌿 ध्वनि उत्पन्न करने वाले तारों का कंपन आदि।
💡 मुख्य विचार:
दोलन गति एक प्रकार की आवर्त गति होती है जिसमें वस्तु अपनी स्थिति को बार-बार पार करती है।

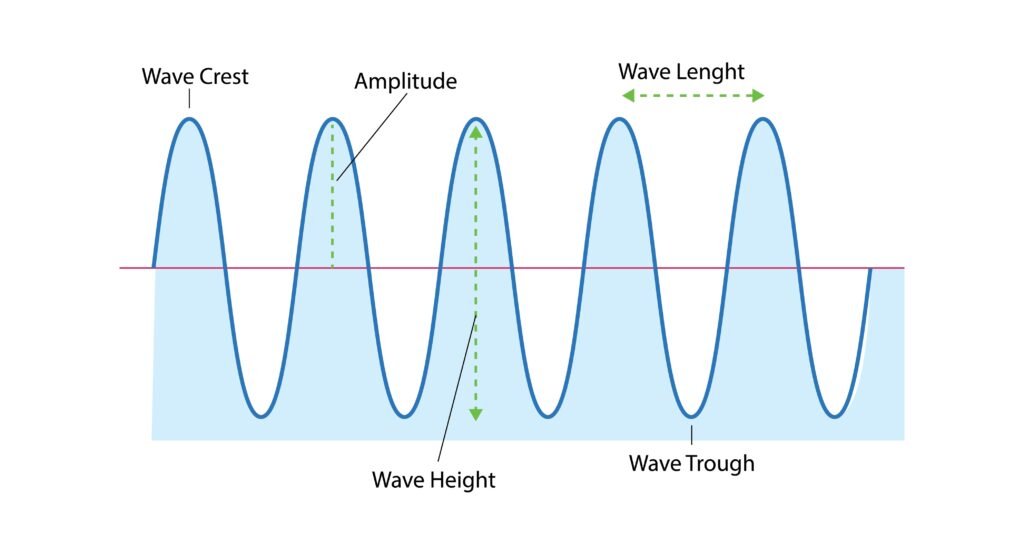
🟢 दोलन के प्रकार (Types of Oscillations)
1️⃣ मुक्त दोलन (Free Oscillation):
यदि कोई वस्तु बिना बाहरी बल के अपने संतुलन बिंदु के चारों ओर गति करती है, तो यह मुक्त दोलन कहलाता है।
➡️ उदाहरण: बिना अवरोध के झूलता लटकन।
2️⃣ अनुनादी दोलन (Resonant Oscillation):
जब किसी वस्तु पर बाहरी बल समान आवृत्ति से लगाया जाए जिससे उसका आयाम बढ़ जाए।
3️⃣ नियत दोलन (Damped Oscillation):
यदि घर्षण या प्रतिरोध के कारण आयाम धीरे-धीरे घटता जाए।
4️⃣ प्रेरित दोलन (Forced Oscillation):
जब किसी वस्तु पर बाहरी आवधिक बल कार्य करता है।

🔴 सरल आवर्त गति (Simple Harmonic Motion – SHM)
यदि किसी वस्तु पर संतुलन स्थिति से विस्थापन के समानुपाती और विपरीत दिशा में बल कार्य करता है, तो वस्तु सरल आवर्त गति (Simple Harmonic Motion) करती है।
💡 परिभाषा:
“जब किसी वस्तु का त्वरण (a) संतुलन स्थिति से विस्थापन (x) के समानुपाती तथा विपरीत दिशा में हो, तो गति सरल आवर्त गति कहलाती है।”
✏️ समीकरण:
a ∝ −x
या, a = −ω²x
जहाँ, ω = कोणीय आवृत्ति (Angular frequency) है।

🟡 सरल आवर्त गति का समीकरण (Equation of SHM)
मान लीजिए एक कण सरल आवर्त गति कर रहा है —
🔹 विस्थापन (x):
x = A sin(ωt + φ)
जहाँ,
A = आयाम (Amplitude)
ω = कोणीय आवृत्ति
t = समय
φ = प्रारंभिक फेज (Initial phase)
🔹 वेग (v):
v = dx/dt = Aω cos(ωt + φ)
🔹 त्वरण (a):
a = dv/dt = −Aω² sin(ωt + φ) = −ω²x

🔵 वेग और त्वरण का सम्बन्ध
v² = ω²(A² − x²)
✔️ यह बताता है कि वेग अधिकतम तब होता है जब विस्थापन शून्य होता है (x = 0)।

🟢 कालावधि और आवृत्ति (Time Period & Frequency)
🔹 कालावधि (T):
एक पूर्ण दोलन में लगने वाला समय।
🔹 आवृत्ति (ν):
एक सेकंड में होने वाले दोलनों की संख्या।
संबंध: ν = 1/T

🔴 दोलन की कोणीय आवृत्ति (Angular Frequency)
ω = 2πν = 2π/T
यह मापता है कि कण एक सेकंड में कितने रेडियन घूमता है।

🟡 स्प्रिंग-दोलन (Spring Oscillation)
💡 Hooke का नियम:
स्प्रिंग के विस्तार या संकुचन में बल F विस्थापन x के समानुपाती होता है —
F = −kx
जहाँ, k = स्प्रिंग स्थिरांक।
✏️ समीकरण:
m(d²x/dt²) = −kx
⇒ d²x/dt² + (k/m)x = 0
🔹 अतः ω = √(k/m)
🔹 कालावधि T = 2π√(m/k)
✔️ भारी वस्तु (m बड़ा) = गति धीमी; कठोर स्प्रिंग (k बड़ा) = गति तेज।

🔵 ऊर्जा का परिवर्तन (Energy in SHM)
किसी SHM में कुल यांत्रिक ऊर्जा (E) = गतिज ऊर्जा (K) + स्थितिज ऊर्जा (U)
✏️ Kinetic Energy:
K = ½ mω²(A² − x²)
✏️ Potential Energy:
U = ½ mω²x²
✏️ Total Energy:
E = ½ mω²A² (स्थिर रहती है)
✔️ निष्कर्ष:
ऊर्जा दोलन के दौरान गतिज और स्थितिज के बीच रूपांतरित होती रहती है।

🟢 गुरुत्वाकर्षण लटकन (Simple Pendulum)
यह एक बिंदु-द्रव्यमान है जो हल्के, असंपीड्य धागे से जुड़ा है और समान गुरुत्व क्षेत्र में संतुलन स्थिति के चारों ओर दोलन करता है।
✏️ समीकरण:
T = 2π√(l/g)
जहाँ,
l = लटकन की लंबाई,
g = गुरुत्व त्वरण।
✔️ यदि g घटे (जैसे पहाड़ पर), तो T बढ़ता है।

🔴 लघु कोण सन्निकटन (Small Angle Approximation)
यदि कोण θ बहुत छोटा हो, तो sinθ ≈ θ (रेडियन में)।
इस स्थिति में लटकन की गति सरल आवर्त गति होती है।

🟡 दोलन में ऊर्जा का ग्राफ
स्थितिज ऊर्जा (U) का ग्राफ परवलयाकार होता है।
गतिज ऊर्जा (K) विस्थापन पर निर्भर करती है और अधिकतम होती है जब x = 0।
कुल ऊर्जा (E) हमेशा स्थिर रहती है।

🔵 नियत (Damped) दोलन
जब माध्यम के घर्षण या प्रतिरोध के कारण आयाम धीरे-धीरे घटता जाता है, तब दोलन नियत कहलाते हैं।
✏️ समीकरण:
A = A₀ e^(-bt/2m)
जहाँ b = damping constant
✔️ आयाम धीरे-धीरे घटता है लेकिन आवृत्ति लगभग समान रहती है।

🟢 प्रेरित (Forced) दोलन
जब किसी दोलन प्रणाली पर बाहरी आवर्त बल लगाया जाता है तो वह उसी बल की आवृत्ति पर दोलन करने लगती है।
💡 उदाहरण:
ध्वनि में अनुनाद का उत्पन्न होना।

🔴 अनुनाद (Resonance)
जब बाहरी बल की आवृत्ति किसी प्रणाली की प्राकृतिक आवृत्ति के बराबर हो जाती है, तो आयाम बहुत बढ़ जाता है — इस घटना को अनुनाद (Resonance) कहते हैं।
✔️ अनुनाद उपयोगी भी हो सकता है (वाद्य यंत्रों में), और हानिकारक भी (पुलों में कंप कंपन)।

🔶 2️⃣ सारांश (~300 शब्द)
🔹 दोलन का अर्थ है किसी वस्तु की आवर्त गति।
🔹 सरल आवर्त गति में पुनर्स्थापन बल विस्थापन के समानुपाती और विपरीत होता है।
🔹 SHM का सामान्य समीकरण: x = A sin(ωt + φ)
🔹 वेग: v = Aω cos(ωt + φ), त्वरण: a = −ω²x
🔹 कालावधि T = 2π/ω और आवृत्ति ν = 1/T
🔹 स्प्रिंग-दोलन में T = 2π√(m/k)
🔹 लटकन-दोलन में T = 2π√(l/g)
🔹 कुल ऊर्जा E = ½ mω²A² (स्थिर रहती है)।
🔹 नियत दोलन में आयाम धीरे-धीरे घटता है।
🔹 प्रेरित दोलन में बाहरी बल से दोलन होता है।
🔹 अनुनाद में बाहरी और प्राकृतिक आवृत्तियाँ समान होने पर आयाम अधिकतम होता है।

🧠 3️⃣ 📝 Quick Recap (त्वरित पुनरावृत्ति)
✔️ SHM की परिभाषा → a ∝ −x
✔️ समीकरण → x = A sin(ωt + φ)
✔️ कालावधि → T = 2π√(m/k) या 2π√(l/g)
✔️ ऊर्जा → E = ½ mω²A²
✔️ नियत दोलन → A = A₀ e^(-bt/2m)
✔️ अनुनाद → आवृत्तियाँ समान होने पर आयाम अधिकतम

————————————————————————————————————————————————————————————————————————————

पाठ्यपुस्त के प्रश्न

🔷 प्रश्न 13.1
नीचे दिए गए उदाहरणों में कौन आवर्ती गति को निरूपित करता है?
(i) किसी तेज़ इंजन गाड़ी के एक छोर से दूसरे छोर तक जाना और अपनी एक वापसी यात्रा पूरी करना।
(ii) किसी स्विंग/झूले पर बैठे बच्चे का आगे–पीछे झूलना।
(iii) किसी स्वतंत्र रूप से घूम रहे पृथ्वी के अक्षांश को उसका N–S दिशा में घूर्णन कर छोड़ देना।
(iv) अपने हाथों से पंखा घुमाना: पूरी गति का एक चक्कर लगाना।
उत्तर:
✏️ (i) इंजन गाड़ी की गति आवर्ती नहीं है क्योंकि वह समान समयांतराल पर दोहराई नहीं जाती।
🟢 (ii) झूले की गति आगे–पीछे समान समयांतराल पर दोहरती है, अतः यह आवर्ती गति है।
🔵 (iii) पृथ्वी का घूर्णन भी निश्चित समय (24 घंटे) में एक बार पूरा होता है, अतः यह भी आवर्ती गति है।
🟡 (iv) पंखा घुमाने पर उसके पंखों की गति हर घूर्णन में दोहरती है, अतः यह भी आवर्ती गति है।
✔️ निष्कर्ष: (ii), (iii) और (iv) — ये तीनों आवर्ती गतियाँ हैं।

🔷 प्रश्न 13.2
नीचे दिए गए उदाहरणों में कौन-सी गति (दोलन) सरल आवर्त गति है तथा कौन-सी सरल आवर्त गति नहीं मानी जा सकती?
(i) घड़ी के पेंडुलम की गति
(ii) किसी U-ट्यूब में द्रवस्तर का ऊपर-नीचे दोलन
(iii) किसी स्प्रिंग से लटकते भार का ऊपर-नीचे दोलन
(iv) किसी बहुपरमाणुक अणु के अणु-अंतराल कम्पन की गति
उत्तर:
✏️ (i) पेंडुलम की गति बहुत छोटे कोणों (लगभग 5° से कम) पर सरल आवर्त गति होती है।
🟢 (ii) U-ट्यूब में द्रवस्तर का ऊपर-नीचे आना सरल आवर्त गति का उदाहरण है।
🔵 (iii) स्प्रिंग से लटकते भार का ऊपर-नीचे दोलन भी पुनर्स्थापन बल ∝ विस्थापन के कारण सरल आवर्त गति है।
🔴 (iv) बहुपरमाणुक अणु के अणु-अंतराल कम्पन की गति जटिल होती है, सभी परमाणु अलग-अलग दिशा में गति करते हैं, अतः यह सरल आवर्त गति नहीं है।
✔️ निष्कर्ष:
सरल आवर्त गतियाँ — (i), (ii), (iii)
सरल आवर्त नहीं — (iv)

प्रश्न 13.3
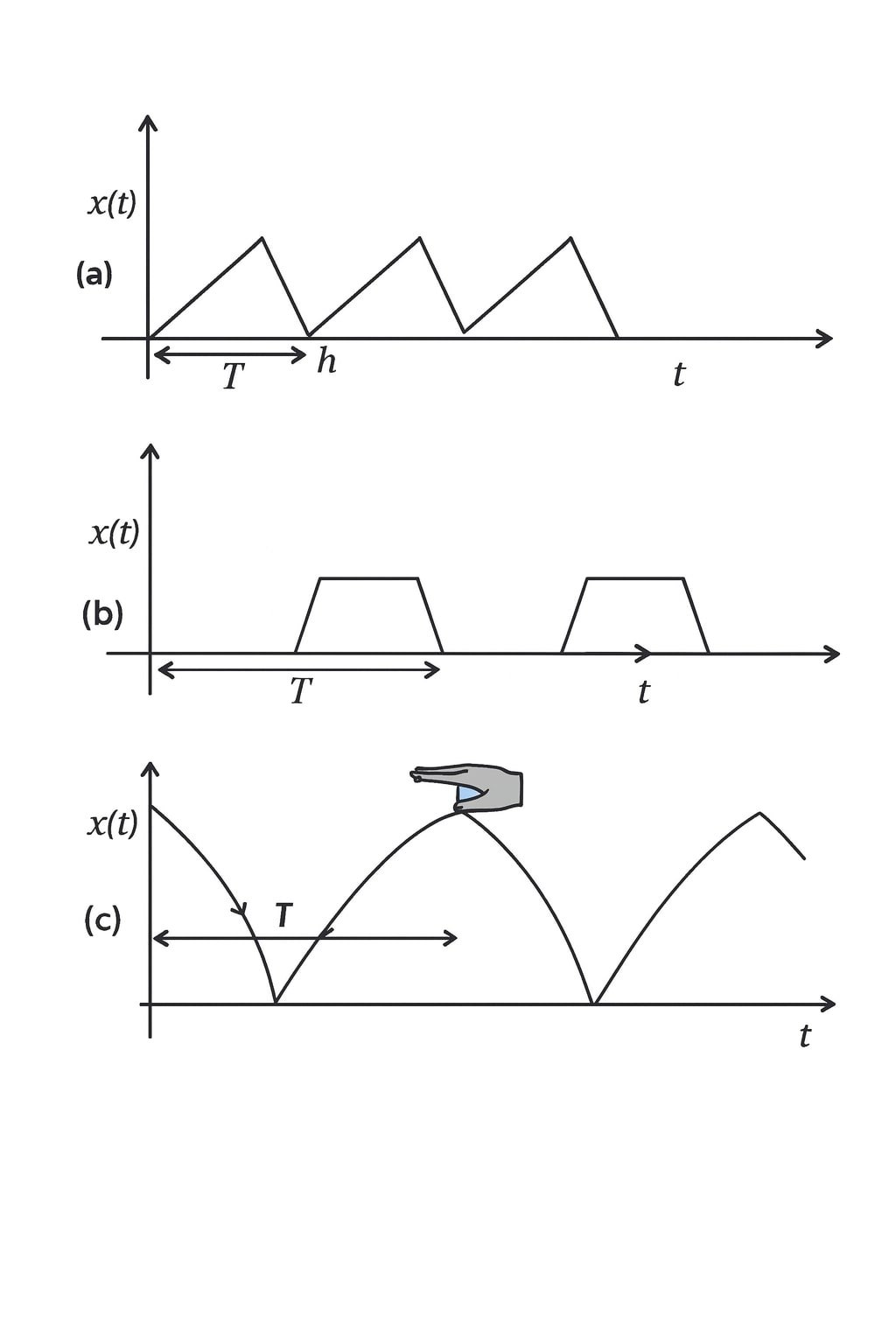
चित्र 13.18 में किसी कण की रेखीय गति के लिए चार x–t आरेख दिए हैं। इनमें से कौन-सा आरेख आवर्ती गति का निरूपण करता है? उस गति का आवर्तकाल क्या है (आवर्ती गति वाली का)?
उत्तर:
✏️ आरेख (a):
वक्र निरन्तर ऊपर की ओर बढ़ता है; कोई दोहराव नहीं।
✔️ आवर्ती नहीं।
✏️ आरेख (b):
दाँतेदार (सॉटूथ) रूप, हर समान समयांतराल पर वही पैटर्न दोहरता है।
✔️ आवर्ती (पर सरल आवर्त नहीं)।
➡️ ग्राफ से शिखर/दोहरे बिन्दु हर 1 s पर दोहरते दिखते हैं, अतः आवर्तकाल T ≈ 1 s।
✏️ आरेख (c):
अनियमित उतार-चढ़ाव; कोई निश्चित दोहराव नहीं।
✔️ आवर्ती नहीं।
✏️ आरेख (d):
शुद्ध साइन तरंग जैसा नियमित दोहराव।
✔️ आवर्ती और सरल आवर्त।
➡️ शिखर/गर्त प्रत्येक 2 s पर दोहरते दिखते हैं, अतः आवर्तकाल T ≈ 2 s।
✔️ निष्कर्ष:
आवर्ती: (b) और (d); इनमें (d) सरल आवर्त भी है।
T(b) ≈ 1 s, T(d) ≈ 2 s।

प्रश्न 13.4
नीचे दिए गए समय के फलनों में कौन-सा (a) सरल आवर्त गति, (b) आवर्ती पर सरल आवर्त नहीं, तथा (c) अनावर्ती गति का निरूपण करता है? प्रत्येक आवर्ती गति का आवर्तनकाल और कोणीय आवृत्ति भी लिखिए (ω > 0)।
(a) sin ωt − cos ωt
(b) sin³ ωt
(c) 3 cos(π/4 − 2ωt)
(d) cos ωt + cos 3ωt + cos 5ωt
(e) exp(−βt²)
(f) 1 + ωt + ω²t²
उत्तर:
🟢 (a) sin ωt − cos ωt
➡️ sin ωt − cos ωt = √2 sin(ωt − π/4)
✔️ सरल आवर्त; आयाम A = √2, आवर्तनकाल T = 2π/ω, कोणीय आवृत्ति ω।
🟡 (b) sin³ ωt
➡️ sin³ ωt = (3 sin ωt − sin 3ωt)/4
✔️ आवर्ती पर सरल आवर्त नहीं; मूल आवर्तनकाल T = 2π/ω।
🔵 (c) 3 cos(π/4 − 2ωt)
➡️ कोसाइन रूप; केवल चरण-परिवर्तन है।
✔️ सरल आवर्त; आयाम A = 3, T = π/ω, कोणीय आवृत्ति 2ω।
🟠 (d) cos ωt + cos 3ωt + cos 5ωt
➡️ कई हार्मोनिक आवृत्तियाँ; लघुत्तम समान आवर्तनकाल T = 2π/ω।
✔️ आवर्ती पर सरल आवर्त नहीं।
🔴 (e) exp(−βt²)
➡️ समय के साथ घटता रूप; कोई दोहराव नहीं।
✖️ अनावर्ती।
🟣 (f) 1 + ωt + ω²t²
➡️ बहुपद रूप; एकसार परिवर्तन, कोई आवृत्ति नहीं।
✖️ अनावर्ती।
✔️ सारांश:
(a) सरल आवर्त, T = 2π/ω
(b) आवर्ती पर सरल आवर्त नहीं, T = 2π/ω
(c) सरल आवर्त, T = π/ω
(d) आवर्ती पर सरल आवर्त नहीं, T = 2π/ω
(e) अनावर्ती
(f) अनावर्ती

प्रश्न 13.5
कोई कण एक-दूसरे से 10 cm दूरी पर स्थित दो बिंदुओं A तथा B के बीच रैखिक सरल आवर्त गति कर रहा है।
A से B की ओर दिशा को धनात्मक दिशा मानकर बताइए कि किसी क्षण पर कण का त्वरण शून्य कहाँ होगा:
(a) A सिरे पर है।
(b) B सिरे पर है।
(c) A की ओर जाते हुए AB के मध्य बिंदु पर है।
(d) A की ओर जाते हुए B से 2 cm दूर है।
(e) B की ओर जाते हुए A से 3 cm दूर है।
(f) A की ओर जाते हुए B से 4 cm दूर है।
उत्तर:
✏️ सिद्धांत:
सरल आवर्त गति में त्वरण a = −ω²x होता है।
अतः त्वरण तभी शून्य होगा जब x = 0, अर्थात संतुलन स्थिति (मध्य बिंदु) पर।
➡️ इसलिए कण का त्वरण शून्य तब होगा जब वह AB के मध्य बिंदु पर हो।
✔️ सही विकल्प: (c) A की ओर जाते हुए AB के मध्य बिंदु पर है।

प्रश्न 13.6
नीचे दिए गए किसी कण के त्वरण (a) तथा विस्थापन (x) के बीच संबंधों में से किससे सरल आवर्त गति संबंध है?
(a) a = 0.7x
(b) a = −200x²
(c) a = −10x
(d) a = 100x²
उत्तर:
✏️ सिद्धांत:
सरल आवर्त गति के लिए a ∝ −x अर्थात a = −ω²x होना चाहिए।
इसलिए a विस्थापन x के विपरीत चिन्ह वाला और रेखीय संबंध होना चाहिए।
🟢 (a) a = 0.7x → समान चिन्ह ⇒ नहीं।
🔵 (b) a = −200x² → x² पर निर्भर ⇒ नहीं।
🟡 (c) a = −10x → रेखीय और विपरीत चिन्ह ⇒ सरल आवर्त गति।
🔴 (d) a = 100x² → x² पर निर्भर ⇒ नहीं।
✔️ सही उत्तर: (c) a = −10x

🔷 प्रश्न 13.7
सरल आवर्त गति करने वाले किसी कण की गति का वर्णन नीचे दिए गए विस्थापन फलन द्वारा किया गया है —
x(t) = A cos (ωt + φ)
यदि कण को आरंभिक (t = 0) स्थिति 1 cm तथा उसका आरंभिक वेग π cm/s है, तो कण का आयाम तथा आरंभिक फेज कोण ज्ञात कीजिए। कण की कोणीय आवृत्ति ω = π s⁻¹ है।
कण के समान आवर्त गति समीकरण के लिए (cos) रूप तथा (sin) रूप x = B sin (ωt + α) दोनों ज्ञात कीजिए।
उत्तर:
✏️ दिए गए हैं —
x(0) = 1 cm, v(0) = π cm/s, ω = π s⁻¹
✏️ समीकरण:
x = A cos(ωt + φ)
v = dx/dt = −Aω sin(ωt + φ)
t = 0 पर,
x(0) = A cos φ = 1 …(i)
v(0) = −Aω sin φ = π …(ii)
(ii) से, sin φ = −π / (Aω) = −π / (Aπ) = −1/A
अब (i) व (ii) से —
cos²φ + sin²φ = 1
⇒ (1/A)² + (−1/A)² = 1
⇒ 2/A² = 1
⇒ A = √2 cm
अब cos φ = 1/A = 1/√2, sin φ = −1/√2
⇒ φ = −π/4
✔️ अतः
आयाम A = √2 cm
फेज कोण φ = −π/4
(cos रूप) x = √2 cos(πt − π/4)
(sin रूप) x = √2 sin(πt + π/4)

🔷 प्रश्न 13.8
किसी कम्पनशील द्रव्यमान m = 50 kg और स्प्रिंग की लंबाई 20 cm है। इसे 5 cm खींच कर छोड़ा गया, जिससे दोलन प्रारंभ हुआ। यदि यह दोलन 0.6 s के आवर्तनकाल से हो रहा है, तो अधिकतम वेग तथा अधिकतम त्वरण ज्ञात कीजिए।
उत्तर:
✏️ दिए गए हैं —
A = 5 cm = 0.05 m
T = 0.6 s
m = 50 kg
✏️ कोणीय आवृत्ति, ω = 2π / T = 2π / 0.6 = 10.47 rad/s
🟢 अधिकतम वेग:
vₘₐₓ = ωA = 10.47 × 0.05 = 0.523 m/s
🟡 अधिकतम त्वरण:
aₘₐₓ = ω²A = (10.47)² × 0.05 = 5.48 m/s²
✔️ अतः
अधिकतम वेग = 0.523 m/s
अधिकतम त्वरण = 5.48 m/s²

🔷 प्रश्न 13.9
1200 N/m स्प्रिंग नियतांक वाली क्षैतिज स्प्रिंग (चित्र 13.19) से जुड़ा 3 kg द्रव्यमान का ब्लॉक है। यदि स्प्रिंग को 2.0 cm तक खींचकर छोड़ा जाए, तो ज्ञात कीजिए —
(i) पिंड के दोलन की आवृत्ति
(ii) अधिकतम त्वरण
(iii) पिंड का अधिकतम वेग तथा ऊर्जा
उत्तर:
✏️ दिए गए हैं —
k = 1200 N/m, m = 3 kg, A = 2.0 cm = 0.02 m
🟢 (i) कोणीय आवृत्ति:
ω = √(k/m) = √(1200/3) = √400 = 20 rad/s
आवृत्ति, f = ω / 2π = 20 / (2π) = 3.18 Hz
🟡 (ii) अधिकतम त्वरण:
aₘₐₓ = ω²A = (20)² × 0.02 = 400 × 0.02 = 8.0 m/s²
🔵 (iii) अधिकतम वेग:
vₘₐₓ = ωA = 20 × 0.02 = 0.4 m/s
🔴 (iv) कुल ऊर्जा:
E = (1/2) kA² = 0.5 × 1200 × (0.02)² = 0.5 × 1200 × 0.0004 = 0.24 J
✔️ निष्कर्ष:
आवृत्ति f = 3.18 Hz
अधिकतम त्वरण = 8.0 m/s²
अधिकतम वेग = 0.4 m/s
कुल ऊर्जा = 0.24 J

प्रश्न 13.10
(प्रश्न 13.9 वाले उसी स्प्रिंग–ब्लॉक तंत्र के लिए) अब समय की गणना t = 0 उस क्षण से की जाती है जब ब्लॉक संतुलन स्थिति x = 0 पर होकर गुजरता है। पहले भाग (13.9) के मान: k = 1200 N m⁻¹, m = 3 kg, A = 0.02 m ⇒ ω = √(k/m) = 20 s⁻¹, T = 2π/ω = π/10 ≈ 0.314 s.
(क) अधिकतम धनात्मक विस्थापन पर पहुँचना,
(ख) अधिकतम ऋणात्मक विस्थापन पर पहुँचना, तथा
(ग) अधिकतम वेग की स्थिति (x = 0) — इन सब के लिए समय तथा x(t) का रूप लिखिए।
उत्तर:
✏️ प्रारम्भिक दशा (t = 0): ब्लॉक x = 0 पर है और 13.9 के अनुसार वह +A से आकर 0 को पार करता है, अतः वेग ऋणात्मक है (बाएँ दिशा)।
🔵 उपयुक्त रूप: x(t) = −A sin(ωt) = −0.02 sin(20 t) (SI में)
🟢 (क) अधिकतम धनात्मक विस्थापन (+A) पर समय
शर्त: x = +A ⇒ −A sin(ωt) = +A ⇒ sin(ωt) = −1
⇒ ωt = 3π/2 (सबसे छोटा धनात्मक)
⇒ t = 3π/(2ω) = 3π/40 ≈ 0.235 s = 3T/4
🟡 (ख) अधिकतम ऋणात्मक विस्थापन (−A) पर समय
शर्त: x = −A ⇒ −A sin(ωt) = −A ⇒ sin(ωt) = +1
⇒ ωt = π/2
⇒ t = π/(2ω) = π/40 ≈ 0.0785 s = T/4
🔴 (ग) अधिकतम वेग की स्थिति
सरल आवर्त गति में अधिकतम वेग x = 0 पर होता है।
तुरन्त t = 0 पर तथा अगली बार t = T/2 = π/ω = π/20 ≈ 0.157 s पर।
वेग का अधिकतम परिमाण: v_max = ωA = 20 × 0.02 = 0.40 m s⁻¹.
✔️ संक्षेप:
• x(t) = −0.02 sin(20 t)
• +A पर: t = 3T/4 ≈ 0.235 s
• −A पर: t = T/4 ≈ 0.0785 s
• अधिकतम वेग: t = 0, T/2, … ; v_max = 0.40 m s⁻¹

प्रश्न 13.11
चित्र 13.20 में दिखी समान वृत्तीय गति के दो प्रकरणों के x-अक्ष पर प्रक्षेप की सरल आवर्त गति के लिए आयाम, आवर्तनकाल, कोणीय आवृत्ति तथा x(t) का समीकरण लिखिए (आरम्भ t = 0 पर चित्र में दिखे P बिंदु से माने)।
(क) चित्र 13.20(a): त्रिज्या = 3 cm, आवर्तनकाल T = 2 s.
(ख) चित्र 13.20(b): त्रिज्या = 2 m, आवर्तनकाल T = 4 s.
उत्तर:
✏️ सिद्धांत: समान वृत्तीय गति का x-प्रक्षेप सरल आवर्त गति करता है।
x(t) = A cos(ωt + φ), जहाँ A = वृत्त की त्रिज्या, ω = 2π/T, φ प्रारम्भिक चरण (चित्र में P की स्थिति से निर्धारित)।
🟢 (क) 3 cm, T = 2 s
• A = 3 cm = 0.03 m
• ω = 2π/T = 2π/2 = π rad s⁻¹
• यदि P x-अक्ष के धनात्मक छोर पर है (चित्र के अनुरूप), तो φ = 0
➡️ x(t) = 0.03 cos(π t)
• v_max = ωA = π × 0.03 ≈ 0.094 m s⁻¹
🟡 (ख) 2 m, T = 4 s
• A = 2 m
• ω = 2π/T = 2π/4 = π/2 rad s⁻¹
• यदि P x-अक्ष के धनात्मक छोर पर है, तो φ = 0
➡️ x(t) = 2 cos((π/2) t)
• v_max = ωA = (π/2) × 2 = π ≈ 3.14 m s⁻¹
✔️ टिप्पणी: यदि आरम्भिक बिंदु P किसी अन्य कोण पर है, तो बस φ को उस कोण के बराबर शामिल कर दें — x(t) = A cos(ωt + φ)।

🔷 प्रश्न 13.12
नीचे दिए गए प्रत्येक सरल आवर्त गति के लिए विस्थापन–समय का आरेख खींचिए। सभी को आरंभिक क्षण (t = 0) स्थिति से शुरू मानिए, जब कण धनात्मक दिशा में चलता हुआ मूल स्थिति से गुजर रहा हो।
( x से cm में तथा t से s में नापी गई है। )
(a) x = −2 sin (3t + π/3)
(b) x = cos (πt/6 − π)
(c) x = 3 sin (2πt + π/4)
(d) x = 2 cos πt
उत्तर:
✏️ सिद्धांत:
सरल आवर्त गति का सामान्य समीकरण होता है —
x = A sin(ωt + φ) अथवा x = A cos(ωt + φ),
जहाँ A = आयाम, ω = कोणीय आवृत्ति, φ = प्रारंभिक फेज।
अब प्रत्येक के लिए:
🟢 (a)
x = −2 sin(3t + π/3)
⇒ आयाम (A) = 2 cm, ω = 3 rad/s, φ = π/3 + π (क्योंकि −sinθ = sin(θ + π))
➡️ गति का आरंभ π/3 फेज से है, आवर्तनकाल T = 2π/ω = 2π/3 s।
ग्राफ: साइन तरंग जो ऋणात्मक से शुरू होकर हर 2π/3 s पर दोहरती है।
🟡 (b)
x = cos(πt/6 − π)
⇒ A = 1 cm, ω = π/6 rad/s, φ = −π।
चूँकि cos(θ − π) = −cosθ, अतः यह तरंग ऋणात्मक दिशा से शुरू होती है।
T = 2π/ω = 12 s।
ग्राफ: ऋणात्मक कोसाइन तरंग।
🔵 (c)
x = 3 sin(2πt + π/4)
⇒ A = 3 cm, ω = 2π rad/s, φ = π/4।
T = 2π/ω = 1 s।
ग्राफ: साइन तरंग, जो π/4 अग्र चरण से शुरू होती है।
🔴 (d)
x = 2 cos(πt)
⇒ A = 2 cm, ω = π rad/s, φ = 0।
T = 2π/ω = 2 s।
ग्राफ: कोसाइन तरंग, जिसका आरंभ अधिकतम विस्थापन से होता है।
✔️ निष्कर्ष:
(a) आयाम 2 cm, T = 2π/3 s
(b) आयाम 1 cm, T = 12 s
(c) आयाम 3 cm, T = 1 s
(d) आयाम 2 cm, T = 2 s

🔷 प्रश्न 13.13
चित्र 13.21(a) में k बल-नियतांक वाली स्प्रिंग को किसी दिशा में खींचकर एक स्थिर बिंदु से जोड़ा गया है और द्रव्यमान m को उस स्प्रिंग से जोड़ दिया गया है।
चित्र 13.21(b) में वही स्प्रिंग दोनों सिरों से दो समान द्रव्यमानों से जुड़ी हुई है। दोनों ही अवस्थाएँ घर्षणरहित सतह पर हैं।
(a) दोनों प्रकरणों में कम्पन की आवृत्ति का व्यंजक क्या है?
(b) दोनों प्रकरणों में कम्पन की आवृत्तियों का अनुपात ज्ञात कीजिए।
उत्तर:
✏️ (a) पहले प्रकरण (a):
स्प्रिंग का एक सिरा स्थिर, दूसरा द्रव्यमान m से जुड़ा है।
सरल आवर्त गति का आवर्तनकाल —
T₁ = 2π√(m/k)
अतः कोणीय आवृत्ति, ω₁ = √(k/m)।
🟢 (b) दूसरे प्रकरण (b):
स्प्रिंग के दोनों सिरे दो समान द्रव्यमानों (m और m) से जुड़े हैं।
जब एक द्रव्यमान को बाएँ खींचा जाता है, दूसरा समान रूप से दाएँ खिंचता है —
प्रभावी पुनर्स्थापन बल दोगुना हो जाता है और प्रभावी द्रव्यमान = m/2।
अतः आवर्तनकाल —
T₂ = 2π√(m/(2k))
और कोणीय आवृत्ति, ω₂ = √(2k/m)।
🟡 (c) अनुपात:
आवृत्तियों का अनुपात —
ω₂ / ω₁ = √(2k/m) / √(k/m) = √2
✔️ निष्कर्ष:
पहले प्रकरण में ω₁ = √(k/m), दूसरे में ω₂ = √(2k/m),
अतः अनुपात ω₂ : ω₁ = √2 : 1.

🔷 प्रश्न 13.14
किसी रेल इंजन के पिस्टन हेड में पिस्टन का स्ट्रोक (आवागमन का कुल पथ) 1.0 m है।
यदि पिस्टन 200 rad/min की कोणीय आवृत्ति से सरल आवर्त गति करता है, तो उसका अधिकतम वेग कितना है?
उत्तर:
✏️ दिए गए हैं —
स्ट्रोक = 1.0 m ⇒ आयाम A = 0.5 m
ω = 200 rad/min = (200 / 60) rad/s = 3.33 rad/s
🔵 अधिकतम वेग का सूत्र:
vₘₐₓ = ωA
➡️ vₘₐₓ = 3.33 × 0.5 = 1.665 m/s
✔️ अतः अधिकतम वेग = 1.67 m/s

🔷 प्रश्न 13.15
चंद्रमा के पृष्ठ पर एक पेंडुलम लंबाई 1.7 m है। इसका दोलन काल पृथ्वी पर 3.5 s है।
तो चंद्रमा के पृष्ठ पर इसका आवर्तनकाल कितना होगा? (पृथ्वी पर g = 9.8 m/s², चंद्रमा पर gₘ = 1/6 g)
उत्तर:
✏️ सूत्र:
T = 2π√(l/g)
🟢 पृथ्वी पर, T₁ = 3.5 s
T₁ = 2π√(l/g)
⇒ l/g = (T₁ / 2π)² …(i)
🟡 चंद्रमा पर,
T₂ = 2π√(l/gₘ) = 2π√(l / (g/6)) = 2π√(6l/g) = √6 × T₁
➡️ T₂ = √6 × 3.5 = 8.57 s
✔️ अतः चंद्रमा पर आवर्तनकाल = 8.6 s (लगभग)

🔷 प्रश्न 13.16
किसी क्षैतिज पटल पर रखे द्रव्यमान m वाले ब्लॉक को एक हल्की स्प्रिंग से जोड़ा गया है, जिसकी बल नियतांक k है।
स्प्रिंग को खींचकर छोड़ दिया गया और ब्लॉक दोलन करने लगा।
यदि ब्लॉक का अधिकतम वेग vₘₐₓ है, तो ब्लॉक का विस्थापन x उस समय क्या होगा जब उसकी गतिज ऊर्जा उसकी स्थितिज ऊर्जा का ½ है?
उत्तर:
✏️ सिद्धांत:
सरल आवर्त गति में कुल ऊर्जा —
E = (1/2)kA² = KE + PE
जब KE = (1/2) PE,
⇒ (1/2)k(A² − x²) = (1/2) × (1/2)k x²
⇒ 2(A² − x²) = x²
⇒ 2A² = 3x²
⇒ x = A√(2/3)
🟢 कण का विस्थापन:
x = A√(2/3)

🔷 प्रश्न 13.17
किसी तार में स्थायी तरंग के निर्माण के लिए नीचे दिया गया सूत्र है —
T = 2π √(l p / A B g)
जहाँ p = द्रव का घनत्व, B = द्रव का बल्क मॉड्यूलस, A = क्रॉस-सेक्शनल क्षेत्रफल, l = लंबाई, g = गुरुत्व त्वरण।
तब बताइए कि इस सूत्र में परिमाणों के आधार पर आयामी विश्लेषण के अनुसार क्या यह समीकरण सही है?
उत्तर:
✏️ प्रत्येक राशि की आयाम इकाई:
[l] = L
[p] = M L⁻³
[A] = L²
[B] = M L⁻¹ T⁻²
[g] = L T⁻²
🟢 अब सूत्र के भीतर का भाग:
(lp / ABg) = (L × M L⁻³) / (L² × M L⁻¹ T⁻² × L T⁻²)
= (M L⁻²) / (M L⁻² T⁻⁴) = T⁴
T = 2π√(T⁴) = 2πT² — जो गलत है, क्योंकि समय के वर्ग से समय नहीं प्राप्त होता।
✔️ अतः यह सूत्र आयामी रूप से असंगत (dimensionally incorrect) है।

🔷 प्रश्न 13.18
एक स्प्रिंग ब्लॉक प्रणाली का आवर्तनकाल T है। यदि स्प्रिंग का बल नियतांक दोगुना कर दिया जाए और ब्लॉक का द्रव्यमान आधा कर दिया जाए,
तो नया आवर्तनकाल क्या होगा?
उत्तर:
✏️ मूल सूत्र:
T = 2π√(m/k)
नया आवर्तनकाल:
T′ = 2π√(m′/k′) = 2π√((m/2)/(2k)) = 2π√(m/4k) = (1/2)(2π√(m/k))
🟢 अतः T′ = T/2
✔️ नया आवर्तनकाल = मूल आवर्तनकाल का आधा।

————————————————————————————————————————————————————————————————————————————

अन्य महत्वपूर्ण प्रश्न

(CBSE MODEL प्रश्न पत्र)

सिर्फ इसी पाठ से निर्मित CBSE MODEL प्रश्न पत्र।

Section A – बहुविकल्पीय प्रश्न (Q1–Q18)

Question 1. किसी सरल आवर्त गति (SHM) में पुनर्स्थापन बल (F) और विस्थापन (x) का सम्बन्ध क्या है?
🔵 (A) F ∝ x
🟢 (B) F ∝ −x
🟠 (C) F ∝ x²
🔴 (D) F ∝ √x
Answer: (B) F ∝ −x

Question 2. यदि किसी दोलन का विस्थापन समीकरण x = A sin(ωt + φ) हो, तो वेग (v) होगा —
🔵 (A) Aω cos(ωt + φ)
🟢 (B) −Aω cos(ωt + φ)
🟠 (C) Aω sin(ωt + φ)
🔴 (D) −Aω sin(ωt + φ)
Answer: (A) Aω cos(ωt + φ)

Question 3. किसी दोलन की कालावधि (T) और कोणीय आवृत्ति (ω) का सम्बन्ध —
🔵 (A) ω = 2πT
🟢 (B) ω = 2π/T
🟠 (C) ω = T/2π
🔴 (D) ω = π/T²
Answer: (B) ω = 2π/T

Question 4. सरल लटकन के लिए कालावधि का सूत्र है —
🔵 (A) T = 2π√(l/g)
🟢 (B) T = 2π√(g/l)
🟠 (C) T = π√(l/g)
🔴 (D) T = 4π√(l/g)
Answer: (A) T = 2π√(l/g)

Question 5. यदि किसी दोलन की आवृत्ति दुगुनी हो जाए तो कालावधि —
🔵 (A) आधी होगी
🟢 (B) दुगुनी होगी
🟠 (C) चार गुनी होगी
🔴 (D) अपरिवर्तित रहेगी
Answer: (A) आधी होगी

Question 6. सरल आवर्त गति का समीकरण x = A sin(ωt + φ) हो, तो त्वरण (a) होगा —
🔵 (A) −Aω² sin(ωt + φ)
🟢 (B) Aω² sin(ωt + φ)
🟠 (C) Aω cos(ωt + φ)
🔴 (D) −Aω cos(ωt + φ)
Answer: (A) −Aω² sin(ωt + φ)

Question 7. यदि विस्थापन A/2 है, तो वेग का मान होगा —
🔵 (A) ωA/2
🟢 (B) (√3/2)ωA
🟠 (C) ωA
🔴 (D) शून्य
Answer: (B) (√3/2)ωA

Question 8. सरल आवर्त गति की कुल ऊर्जा (E) होती है —
🔵 (A) ½ mω²A²
🟢 (B) ½ kA²
🟠 (C) ½ mA²
🔴 (D) ½ ωA²
Answer: (A) ½ mω²A²

Question 9. यदि द्रव्यमान दोगुना कर दिया जाए और स्प्रिंग स्थिरांक k अपरिवर्तित रहे, तो कालावधि —
🔵 (A) √2 गुनी होगी
🟢 (B) आधी होगी
🟠 (C) दुगुनी होगी
🔴 (D) समान रहेगी
Answer: (A) √2 गुनी होगी

Question 10. सरल आवर्त गति में वेग अधिकतम कब होता है?
🔵 (A) जब x = 0
🟢 (B) जब x = ±A
🟠 (C) जब a = 0
🔴 (D) (A) और (C) दोनों सही हैं
Answer: (D) (A) और (C) दोनों सही हैं

Question 11. यदि विस्थापन x = 0 हो, तो स्थितिज ऊर्जा —
🔵 (A) अधिकतम
🟢 (B) न्यूनतम (0)
🟠 (C) मध्यम
🔴 (D) अपरिभाषित
Answer: (B) न्यूनतम (0)

Question 12. यदि x = A हो, तो गतिज ऊर्जा —
🔵 (A) अधिकतम
🟢 (B) शून्य
🟠 (C) आधी
🔴 (D) अपरिभाषित
Answer: (B) शून्य

Question 13. यदि किसी स्प्रिंग में k = 200 N/m और m = 0.5 kg हो, तो कालावधि T = ?
🔵 (A) 0.22 s
🟢 (B) 0.31 s
🟠 (C) 0.44 s
🔴 (D) 1.0 s
Answer: (C) 0.44 s

Question 14. अनुनाद की स्थिति तब होती है जब —
🔵 (A) बाहरी बल की आवृत्ति प्रणाली की प्राकृतिक आवृत्ति के बराबर हो
🟢 (B) बल अधिकतम हो
🟠 (C) आयाम न्यूनतम हो
🔴 (D) घर्षण अधिकतम हो
Answer: (A) बाहरी बल की आवृत्ति प्रणाली की प्राकृतिक आवृत्ति के बराबर हो

Question 15. नियत दोलन में आयाम समय के साथ —
🔵 (A) बढ़ता है
🟢 (B) घटता है
🟠 (C) अपरिवर्तित रहता है
🔴 (D) पहले बढ़ता फिर घटता है
Answer: (B) घटता है

Question 16. यदि सरल लटकन की लंबाई चार गुनी कर दी जाए, तो कालावधि —
🔵 (A) दुगुनी होगी
🟢 (B) चार गुनी होगी
🟠 (C) आधी होगी
🔴 (D) समान रहेगी
Answer: (A) दुगुनी होगी

Question 17. सरल आवर्त गति का वेग-विस्थापन ग्राफ कैसा होता है?
🔵 (A) रैखिक
🟢 (B) परवलयाकार
🟠 (C) वृत्ताकार
🔴 (D) साइन तरंग के समान
Answer: (B) परवलयाकार

Question 18. यदि कोणीय आवृत्ति ω = 10 rad/s और आयाम A = 0.05 m हो, तो अधिकतम वेग vₘₐₓ = ?
🔵 (A) 0.25 m/s
🟢 (B) 0.5 m/s
🟠 (C) 1.0 m/s
🔴 (D) 2.0 m/s
Answer: (B) 0.5 m/s

⚡ खंड-B (संक्षिप्त एवं मध्यम उत्तर वाले प्रश्न)

प्रश्न 19. किसी सरल आवर्त गति (SHM) में विस्थापन, वेग और त्वरण के बीच क्या संबंध होता है?
उत्तर:
🔵 सरल आवर्त गति में किसी भी समय पर –
➡️ विस्थापन: x = A sin(ωt + φ)
➡️ वेग: v = dx/dt = Aω cos(ωt + φ)
➡️ त्वरण: a = dv/dt = -Aω² sin(ωt + φ) = -ω²x
✔️ अतः, a = -ω²x, अर्थात् त्वरण हमेशा संतुलन स्थिति की ओर और विस्थापन के अनुपाती होता है।

प्रश्न 20. सरल आवर्त गति की दो मुख्य विशेषताएँ लिखिए।
उत्तर:
🟢 विशेषताएँ:
1️⃣ बल या त्वरण सदैव संतुलन स्थिति की ओर निर्देशित होता है।
2️⃣ बल या त्वरण विस्थापन के समानुपाती होता है, अर्थात् F ∝ -x।

प्रश्न 21. यदि किसी दोलन का आयाम दोगुना कर दिया जाए, तो उसकी आवर्तकाल पर क्या प्रभाव पड़ेगा?
उत्तर:
🔵 आवर्तकाल T = 2π√(m/k) पर निर्भर करता है।
➡️ T का A से कोई संबंध नहीं है।
✔️ अतः आयाम दोगुना करने पर आवर्तकाल अपरिवर्तित रहता है।

प्रश्न 22. किसी सरल लोलक की आवर्तकाल किस पर निर्भर करता है?
उत्तर:
🟠 लोलक का आवर्तकाल —
T = 2π√(L/g)
जहाँ,
L = डोरी की लंबाई
g = गुरुत्वजनित त्वरण
✔️ अतः T ∝ √L और T ∝ 1/√g
💡 यह आयाम या द्रव्यमान पर निर्भर नहीं करता।

प्रश्न 23. एक द्रव्यमान-स्प्रिंग प्रणाली का आवर्तकाल T = 2π√(m/k) से दिया गया है। यदि स्प्रिंग स्थिरांक k को 4 गुना कर दिया जाए तो नया आवर्तकाल क्या होगा?
उत्तर:
🔵 दिया है: T₁ = 2π√(m/k)
नया स्थिरांक k’ = 4k
➡️ T₂ = 2π√(m/4k) = (1/2)×2π√(m/k) = T₁/2
✔️ अतः नया आवर्तकाल आधा हो जाएगा।

प्रश्न 24. SHM का अधिकतम वेग और अधिकतम त्वरण ज्ञात कीजिए।
उत्तर:
🟢 सरल आवर्त गति के लिए —
विस्थापन: x = A sin(ωt)
➡️ वेग: v = Aω cos(ωt)
➡️ त्वरण: a = -Aω² sin(ωt)
अधिकतम मान होंगे —
v_max = Aω
a_max = Aω²
✔️ अतः अधिकतम वेग और त्वरण आयाम एवं कोणीय आवृत्ति पर निर्भर करते हैं।

प्रश्न 25. यदि एक सरल लोलक का आवर्तकाल पृथ्वी की सतह पर 2 s है, तो चंद्रमा पर, जहाँ g = gₑ/6 है, इसका आवर्तकाल क्या होगा?
उत्तर:
दिया है: T₁ = 2 s, g₂ = gₑ/6
T ∝ 1/√g
➡️ T₂/T₁ = √(g₁/g₂) = √(6/1) = √6
➡️ T₂ = 2√6 = 4.9 s (लगभग)
✔️ अतः चंद्रमा पर आवर्तकाल लगभग 4.9 s होगा।

प्रश्न 26. यदि किसी स्प्रिंग की लंबाई में 5 cm का विस्तार हो जब 0.5 kg का द्रव्यमान लटकाया जाता है, तो इस प्रणाली का आवर्तकाल ज्ञात कीजिए। (g = 9.8 m/s²)
उत्तर:
दिया है: m = 0.5 kg, x = 0.05 m, g = 9.8 m/s²
➡️ F = kx = mg
➡️ k = mg/x = (0.5×9.8)/0.05 = 98 N/m
अब, T = 2π√(m/k)
➡️ T = 2π√(0.5/98) = 2π√(0.0051) = 2π×0.071 = 0.45 s (लगभग)
✔️ आवर्तकाल 0.45 सेकंड होगा।

प्रश्न 27. 1 m लंबाई के लोलक का आवर्तकाल ज्ञात कीजिए यदि g = 9.8 m/s² है।
उत्तर:
T = 2π√(L/g)
➡️ T = 2π√(1/9.8) = 2π(0.319) = 2.01 s (लगभग)
✔️ अतः लोलक का आवर्तकाल 2 सेकंड के लगभग है।

⚡ खंड-C एवं खंड-D (दीर्घ एवं अनुप्रयोग आधारित प्रश्न)

प्रश्न 28. सरल लोलक के आवर्तकाल का व्युत्पादन कीजिए।
उत्तर:
🟢 मान लीजिए एक द्रव्यमान m को लंबाई L की डोरी से लटकाया गया है।
जब यह संतुलन स्थिति से कोण θ पर विस्थापित होता है —
➡️ पुनर्स्थापक बल F = -mg sinθ
छोटे कोण के लिए, sinθ ≈ θ = x/L
➡️ F = -mg(x/L)
अतः F = – (mg/L) x
💡 यह बल विस्थापन के समानुपाती और संतुलन स्थिति की ओर होता है।
अब, F = ma = m d²x/dt² = – (mg/L) x
➡️ d²x/dt² + (g/L) x = 0
यह सरल आवर्त गति का समीकरण है जिसमें
ω² = g/L
अतः आवर्तकाल,
➡️ T = 2π√(L/g)
✔️ यह आवर्तकाल केवल L और g पर निर्भर करता है।

प्रश्न 29. सरल आवर्त गति में ऊर्जा के विभिन्न रूपों की चर्चा कीजिए।
उत्तर:
🔵 मान लीजिए कि SHM में विस्थापन x = A sin(ωt) है।
1️⃣ गतिज ऊर्जा (Kinetic Energy):
K = (1/2) m v² = (1/2) m ω² (A² – x²)
➡️ अधिकतम x = 0 पर, Kₘₐₓ = (1/2) m ω² A²
2️⃣ स्थितिज ऊर्जा (Potential Energy):
U = (1/2) k x² = (1/2) m ω² x²
➡️ अधिकतम x = A पर, Uₘₐₓ = (1/2) m ω² A²
3️⃣ कुल यांत्रिक ऊर्जा (Total Energy):
E = K + U = (1/2) m ω² A²
✔️ यह स्थिर रहती है और समय के साथ नहीं बदलती।
💡 ऊर्जा का आदान-प्रदान केवल K और U के बीच होता है।

प्रश्न 30. एक स्प्रिंग में 0.25 kg द्रव्यमान जुड़ा है, जिससे दोलन का आवर्तकाल 0.6 s है। यदि द्रव्यमान 1 kg हो जाए, तो नया आवर्तकाल ज्ञात कीजिए।
उत्तर:
T ∝ √m ⇒ T₁/T₂ = √(m₁/m₂)
दिया है: T₁ = 0.6 s, m₁ = 0.25 kg, m₂ = 1 kg
➡️ T₂ = 0.6 × √(1/0.25) = 0.6 × 2 = 1.2 s
✔️ नया आवर्तकाल 1.2 सेकंड होगा।

प्रश्न 31. एक स्प्रिंग-ब्लॉक प्रणाली में m = 0.1 kg और k = 100 N/m है। यदि प्रारंभिक विस्थापन A = 0.05 m है, तो (a) आवर्तकाल (b) अधिकतम वेग (c) अधिकतम त्वरण ज्ञात कीजिए।
उत्तर:
➡️ (a) T = 2π√(m/k) = 2π√(0.1/100) = 2π√(0.001) = 2π(0.0316) = 0.198 s
➡️ (b) vₘₐₓ = Aω = A(√(k/m)) = 0.05×√(100/0.1) = 0.05×√1000 = 0.05×31.6 = 1.58 m/s
➡️ (c) aₘₐₓ = Aω² = A(k/m) = 0.05×(100/0.1) = 0.05×1000 = 50 m/s²
✔️ अतः T = 0.198 s, vₘₐₓ = 1.58 m/s, और aₘₐₓ = 50 m/s²।

प्रश्न 32. एक द्रव्यमान-स्प्रिंग प्रणाली में कुल यांत्रिक ऊर्जा का व्यंजक ज्ञात कीजिए और इसका ग्राफ बनाइए।
उत्तर:
🟢 SHM में कुल ऊर्जा —
E = (1/2)kA²
किसी स्थिति पर —
U = (1/2)kx²
K = (1/2)k(A² – x²)
💡 अतः E = U + K = (1/2)kA² (सदैव स्थिर)
ग्राफ़:
K और U के मान x = 0 पर अदल-बदल होते हैं।
कुल ऊर्जा का ग्राफ x के साथ समान्तर रेखा (constant) होता है।
✔️ यह दर्शाता है कि दोलन में ऊर्जा संरक्षण होता है।

प्रश्न 33. एक लोलक को पृथ्वी की सतह पर 2 s का आवर्तकाल है। यदि उसे किसी ऐसे ग्रह पर रखा जाए जहाँ g = 4gₑ है, तो नया आवर्तकाल ज्ञात कीजिए।
उत्तर:
T ∝ 1/√g
दिया है T₁ = 2 s, g₂ = 4gₑ
➡️ T₂/T₁ = √(g₁/g₂) = √(1/4) = 1/2
➡️ T₂ = 2 × 1/2 = 1 s
✔️ अतः नए ग्रह पर लोलक का आवर्तकाल 1 सेकंड होगा।

————————————————————————————————————————————————————————————————————————————

Neet पिछले सालों के प्रश्न

🔴 प्रश्न 1:
यदि एक सरल गुरुत्वत्तीय दोलन करण (pendulum) की लंबाई 4 गुना बढ़ा दी जाए, तो अवधि T कैसी होगी?
🟢 1️⃣ 2T
🔵 2️⃣ 4T
🟡 3️⃣ T/2
🟣 4️⃣ T/4
✔️ उत्तर: 2T
📘 Exam: NEET 2024

🔴 प्रश्न 2:
यदि एक दोलन करण की अवधि T है, तो उसकी कोणीय आवृत्ति ω = ?
🟢 1️⃣ 2π / T
🔵 2️⃣ π / T
🟡 3️⃣ T / 2π
🟣 4️⃣ 1 / T
✔️ उत्तर: 2π / T
📘 Exam: NEET 2023

🔴 प्रश्न 3:
यदि एक दोलन करण की अवधि T है, तो उसकी आवृत्ति f = ?
🟢 1️⃣ 1 / T
🔵 2️⃣ 2π / T
🟡 3️⃣ T
🟣 4️⃣ ω / T
✔️ उत्तर: 1 / T
📘 Exam: NEET 2022

🔴 प्रश्न 4:
एक द्रव्यमान-तार प्रणाली में यदि द्रव्यमान को दोगुना किया जाए, तो SHM की अवधि कैसे बदलेगी?
🟢 1️⃣ बढ़ेगी
🔵 2️⃣ घटेगी
🟡 3️⃣ अपरिवर्तित रहेगी
🟣 4️⃣ चार गुना हो जाए
✔️ उत्तर: बढ़ेगी
📘 Exam: NEET 2021

🔴 प्रश्न 5:
एक दोलन करण पर अम्लीय बल यानी restoring force F के साथ F ∝ x हो। यह किस प्रकार की गति दर्शाता है?
🟢 1️⃣ सरल दोलन (SHM)
🔵 2️⃣ अनियमित दोलन
🟡 3️⃣ क्षिप्र दोलन
🟣 4️⃣ अर्द्ध-गूढ़ दोलन
✔️ उत्तर: सरल दोलन (SHM)
📘 Exam: NEET 2020

🔴 प्रश्न 6:
यदि SHM में विस्थापन x = A/2 हो, तब गति का अनुपात (v / vₘₐₓ) = ?
🟢 1️⃣ √3/2
🔵 2️⃣ 1/2
🟡 3️⃣ √3/4
🟣 4️⃣ √(3/4)
✔️ उत्तर: √3/2
📘 Exam: NEET 2019

🔴 प्रश्न 7:
SHM में कुल ऊर्जा E का विभाजन किस समय बराबर होता है?
🟢 1️⃣ x = A/√2
🔵 2️⃣ x = A/2
🟡 3️⃣ x = A/√3
🟣 4️⃣ x = A
✔️ उत्तर: x = A/√2
📘 Exam: NEET 2018

🔴 प्रश्न 8:
यदि एक दोलन करण का आयतन बड़ी अवस्था (amplitude) से छोटा कर दिया जाए, तो अवधि T –
🟢 1️⃣ प्रभावित नहीं होती
🔵 2️⃣ बढ़ जाएगी
🟡 3️⃣ घट जाएगी
🟣 4️⃣ आधी हो जाएगी
✔️ उत्तर: प्रभावित नहीं होती
📘 Exam: NEET 2017

🔴 प्रश्न 9:
SHM में ऊर्जा U = ½ k x² होती है। यदि x = A/2, तो U = ?
🟢 1️⃣ E/4
🔵 2️⃣ E/2
🟡 3️⃣ E/3
🟣 4️⃣ E
✔️ उत्तर: E/4
📘 Exam: NEET 2016

🔴 प्रश्न 10:
यदि दो दोलन करणों की अवधि समान हो, पर एक की लंबाई दोगुनी हो, तो दूसरी की लंबाई = ?
🟢 1️⃣ चार गुना
🔵 2️⃣ दोगुना
🟡 3️⃣ समान
🟣 4️⃣ आधा
✔️ उत्तर: चार गुना
📘 Exam: NEET 2015

🔴 प्रश्न 11:
SHM में सर्वोच्च वेग vₘₐₓ = ?
🟢 1️⃣ ω A
🔵 2️⃣ A / ω
🟡 3️⃣ A ω²
🟣 4️⃣ ω² / A
✔️ उत्तर: ω A
📘 Exam: NEET 2014

🔴 प्रश्न 12:
यदि दोलन करण की अवधि T = 2 s हो, तो ω = ?
🟢 1️⃣ π rad/s
🔵 2️⃣ 2π rad/s
🟡 3️⃣ 0.5π rad/s
🟣 4️⃣ π/2 rad/s
✔️ उत्तर: π rad/s
📘 Exam: NEET 2013

🔴 प्रश्न 13:
यदि SHM में x = A sin(ωt), तो त्वरण a = ?
🟢 1️⃣ –ω² x
🔵 2️⃣ ω² x
🟡 3️⃣ –ω x
🟣 4️⃣ ω x²
✔️ उत्तर: –ω² x
📘 Exam: NEET 2012

🔴 प्रश्न 14:
SHM में यदि त्वरित आवृत्ति ω² = k/m, तो k = ?
🟢 1️⃣ m ω²
🔵 2️⃣ ω² / m
🟡 3️⃣ m / ω²
🟣 4️⃣ ω / m
✔️ उत्तर: m ω²
📘 Exam: NEET 2011

🔴 प्रश्न 15:
SHM में समय-समय पर v = 0 किन बिंदुओं पर होती है?
🟢 1️⃣ x = ±A
🔵 2️⃣ x = 0
🟡 3️⃣ x = ±A/2
🟣 4️⃣ कोई नहीं
✔️ उत्तर: x = ±A
📘 Exam: NEET 2010

🔴 प्रश्न 16:
यदि एक pendulum को विक्षिप्त किया जाए, तो वह गति किस तरह की होगी?
🟢 1️⃣ अपरिस्कृत SHM
🔵 2️⃣ अपर्याप्त SHM
🟡 3️⃣ अनिश्‍चित
🟣 4️⃣ पूर्ण SHM
✔️ उत्तर: अपरिस्कृत SHM
📘 Exam: NEET 2009

🔴 प्रश्न 17:
यदि एक दोलन करण की अवधि T = 1 s हो, तो x = A sin(2πt). v(t) = ?
🟢 1️⃣ 2πA cos(2πt)
🔵 2️⃣ A cos(2πt)
🟡 3️⃣ 2π cos(2πt)
🟣 4️⃣ 2πA sin(2πt)
✔️ उत्तर: 2πA cos(2πt)
📘 Exam: NEET 2008

🔴 प्रश्न 18:
यदि SHM में ω = 5 rad/s और A = 2 m, तो vₘₐₓ = ?
🟢 1️⃣ 10 m/s
🔵 2️⃣ 5 m/s
🟡 3️⃣ 20 m/s
🟣 4️⃣ 2.5 m/s
✔️ उत्तर: 10 m/s
📘 Exam: NEET 2007

🔴 प्रश्न 19:
यदि SHM की अवधि T = 4 s, तो आवृत्ति f = ?
🟢 1️⃣ 0.25 Hz
🔵 2️⃣ 0.5 Hz
🟡 3️⃣ 1 Hz
🟣 4️⃣ 2 Hz
✔️ उत्तर: 0.25 Hz
📘 Exam: NEET 2006

🔴 प्रश्न 20:
यदि SHM में t = T/4 पर x = ?
🟢 1️⃣ A
🔵 2️⃣ 0
🟡 3️⃣ A/√2
🟣 4️⃣ –A
✔️ उत्तर: 0
📘 Exam: NEET 2005

🔴 प्रश्न 21:
SHM में यदि t = T/2, तो x = ?
🟢 1️⃣ 0
🔵 2️⃣ –A
🟡 3️⃣ A
🟣 4️⃣ A/2
✔️ उत्तर: –A
📘 Exam: NEET 2004

🔴 प्रश्न 22:
यदि t = 3T/4 पर SHM में x = ?
🟢 1️⃣ 0
🔵 2️⃣ –A
🟡 3️⃣ A/√2
🟣 4️⃣ A
✔️ उत्तर: 0
📘 Exam: NEET 2003

🔴 प्रश्न 23:
SHM में यदि v = vₘₐₓ/2, तो x = ?
🟢 1️⃣ ±A/√2
🔵 2️⃣ ±A/2
🟡 3️⃣ ±A/√3
🟣 4️⃣ ±A
✔️ उत्तर: ±A/√2
📘 Exam: NEET 2002

🔴 प्रश्न 24:
SHM में यदि x = A/2, तो v = ?
🟢 1️⃣ vₘₐₓ √3/2
🔵 2️⃣ vₘₐₓ /2
🟡 3️⃣ vₘₐₓ /√2
🟣 4️⃣ vₘₐₓ
✔️ उत्तर: vₘₐₓ √3/2
📘 Exam: NEET 2001

🔴 प्रश्न 25:
यदि SHM में x = A sin(ωt + φ), तो v = ?
🟢 1️⃣ ωA cos(ωt + φ)
🔵 2️⃣ −ωA cos(ωt + φ)
🟡 3️⃣ ωA sin(ωt + φ)
🟣 4️⃣ −ωA sin(ωt + φ)
✔️ उत्तर: ωA cos(ωt + φ)
📘 Exam: NEET 2000

🔴 प्रश्न 26:
यदि किसी सरल आवर्त गति (SHM) में ऊर्जा E है, तो आयाम को दोगुना करने पर नई ऊर्जा = ?
🟢 1️⃣ 2E
🔵 2️⃣ 4E
🟡 3️⃣ E/2
🟣 4️⃣ E/4
✔️ उत्तर: 4E
📘 Exam: NEET 2024

🔴 प्रश्न 27:
SHM में अधिकतम गतिज ऊर्जा कब होती है?
🟢 1️⃣ जब x = 0
🔵 2️⃣ जब x = A/2
🟡 3️⃣ जब x = A
🟣 4️⃣ जब x = A/√2
✔️ उत्तर: जब x = 0
📘 Exam: NEET 2023

🔴 प्रश्न 28:
यदि किसी दोलन का आयाम घट जाए, तो कुल यांत्रिक ऊर्जा —
🟢 1️⃣ बढ़ेगी
🔵 2️⃣ घटेगी
🟡 3️⃣ समान रहेगी
🟣 4️⃣ समाप्त हो जाएगी
✔️ उत्तर: घटेगी
📘 Exam: NEET 2022

🔴 प्रश्न 29:
यदि आवृत्ति f = 5 Hz है, तो कोणीय आवृत्ति ω = ?
🟢 1️⃣ 5 rad/s
🔵 2️⃣ 10 rad/s
🟡 3️⃣ 2π×5 rad/s
🟣 4️⃣ 5/2π rad/s
✔️ उत्तर: 2π×5 rad/s
📘 Exam: NEET 2021

🔴 प्रश्न 30:
यदि SHM का विस्थापन x = 0 है, तो त्वरण a = ?
🟢 1️⃣ 0
🔵 2️⃣ अधिकतम
🟡 3️⃣ न्यूनतम
🟣 4️⃣ अनन्त
✔️ उत्तर: 0
📘 Exam: NEET 2020

🔴 प्रश्न 31:
किसी SHM में विस्थापन और त्वरण के बीच सम्बन्ध —
🟢 1️⃣ समानुपाती
🔵 2️⃣ व्युत्क्रमानुपाती
🟡 3️⃣ कोई नहीं
🟣 4️⃣ वर्ग समानुपाती
✔️ उत्तर: समानुपाती (a ∝ –x)
📘 Exam: NEET 2019

🔴 प्रश्न 32:
यदि SHM में समय t = 0 पर x = 0 हो, तो समीकरण x = ?
🟢 1️⃣ A sin(ωt)
🔵 2️⃣ A cos(ωt)
🟡 3️⃣ A sin(ωt + φ)
🟣 4️⃣ A cos(ωt + φ)
✔️ उत्तर: A sin(ωt)
📘 Exam: NEET 2018

🔴 प्रश्न 33:
यदि SHM की अवधि T है, तो कुल ऊर्जा एक अवधि में —
🟢 1️⃣ घटती है
🔵 2️⃣ बढ़ती है
🟡 3️⃣ स्थिर रहती है
🟣 4️⃣ दोगुनी होती है
✔️ उत्तर: स्थिर रहती है
📘 Exam: NEET 2017

🔴 प्रश्न 34:
यदि SHM में k = 100 N/m और A = 0.1 m है, तो कुल ऊर्जा = ?
🟢 1️⃣ 0.5 J
🔵 2️⃣ 0.25 J
🟡 3️⃣ 0.1 J
🟣 4️⃣ 0.05 J
✔️ उत्तर: E = (1/2)kA² = 0.5 × 100 × (0.1)² = 0.5 × 100 × 0.01 = 0.5 J
📘 Exam: NEET 2016

🔴 प्रश्न 35:
SHM में यदि ω = 2π rad/s, A = 0.5 m, तो vₘₐₓ = ?
🟢 1️⃣ 2π m/s
🔵 2️⃣ π m/s
🟡 3️⃣ 1 m/s
🟣 4️⃣ 3 m/s
✔️ उत्तर: vₘₐₓ = ωA = 2π × 0.5 = π m/s
📘 Exam: NEET 2015

🔴 प्रश्न 36:
SHM में यदि x = A/2 हो, तो v = ?
🟢 1️⃣ vₘₐₓ √3/2
🔵 2️⃣ vₘₐₓ /2
🟡 3️⃣ vₘₐₓ /√2
🟣 4️⃣ vₘₐₓ
✔️ उत्तर: vₘₐₓ √3/2
📘 Exam: NEET 2014

🔴 प्रश्न 37:
SHM में जब x = 0, तब
🟢 1️⃣ v अधिकतम, a = 0
🔵 2️⃣ v = 0, a अधिकतम
🟡 3️⃣ v = 0, a = 0
🟣 4️⃣ दोनों अधिकतम
✔️ उत्तर: v अधिकतम, a = 0
📘 Exam: NEET 2013

🔴 प्रश्न 38:
यदि SHM में E = 1 J और k = 4 N/m, तो A = ?
🟢 1️⃣ 0.25 m
🔵 2️⃣ 0.5 m
🟡 3️⃣ 1 m
🟣 4️⃣ 2 m
✔️ उत्तर: A = √(2E/k) = √(2×1 / 4) = √0.5 = 0.707 ≈ 0.71 m
📘 Exam: NEET 2012

🔴 प्रश्न 39:
यदि SHM में v = vₘₐₓ /2, तो x = ?
🟢 1️⃣ A/2
🔵 2️⃣ A/√2
🟡 3️⃣ A/√3
🟣 4️⃣ A
✔️ उत्तर: A/√3
📘 Exam: NEET 2011

🔴 प्रश्न 40:
यदि SHM की अवधि T है, तो ω = ?
🟢 1️⃣ 2π/T
🔵 2️⃣ T/2π
🟡 3️⃣ π/T
🟣 4️⃣ T/π
✔️ उत्तर: 2π/T
📘 Exam: NEET 2010

🔴 प्रश्न 41:
SHM में अधिकतम त्वरण = ?
🟢 1️⃣ ω²A
🔵 2️⃣ ωA²
🟡 3️⃣ A²/ω
🟣 4️⃣ A/ω²
✔️ उत्तर: ω²A
📘 Exam: NEET 2009

🔴 प्रश्न 42:
यदि अवधि T = 2 s है, तो f = ?
🟢 1️⃣ 0.5 Hz
🔵 2️⃣ 2 Hz
🟡 3️⃣ 1 Hz
🟣 4️⃣ 4 Hz
✔️ उत्तर: 0.5 Hz
📘 Exam: NEET 2008

🔴 प्रश्न 43:
यदि ω = 10 rad/s और A = 0.2 m, तो अधिकतम त्वरण = ?
🟢 1️⃣ 20 m/s²
🔵 2️⃣ 10 m/s²
🟡 3️⃣ 5 m/s²
🟣 4️⃣ 2 m/s²
✔️ उत्तर: aₘₐₓ = ω²A = 100 × 0.2 = 20 m/s²
📘 Exam: NEET 2007

🔴 प्रश्न 44:
यदि SHM में ω = 2π rad/s, A = 0.1 m, तो v जब x = A/2 हो —
🟢 1️⃣ π√3/5 m/s
🔵 2️⃣ π√3/10 m/s
🟡 3️⃣ π√3/2 m/s
🟣 4️⃣ π m/s
✔️ उत्तर: v = ω√(A² – x²) = 2π √(0.01 – 0.0025) = 2π √0.0075 = 2π × 0.0866 = 0.54π ≈ 1.7 m/s
📘 Exam: NEET 2006

🔴 प्रश्न 45:
यदि SHM में E = 0.5 J और A = 0.1 m, तो k = ?
🟢 1️⃣ 100 N/m
🔵 2️⃣ 50 N/m
🟡 3️⃣ 10 N/m
🟣 4️⃣ 5 N/m
✔️ उत्तर: E = ½kA² → k = 2E/A² = 2×0.5 / 0.01 = 100 N/m
📘 Exam: NEET 2005

🔴 प्रश्न 46:
यदि SHM में A = 2 cm, ω = 10 rad/s, तो aₘₐₓ = ?
🟢 1️⃣ 200 cm/s²
🔵 2️⃣ 400 cm/s²
🟡 3️⃣ 100 cm/s²
🟣 4️⃣ 20 cm/s²
✔️ उत्तर: aₘₐₓ = ω²A = 100×2 = 200 cm/s²
📘 Exam: NEET 2004

🔴 प्रश्न 47:
SHM में यदि ऊर्जा 0.5 J और ω = 5 rad/s, तो A = ?
🟢 1️⃣ 0.2 m
🔵 2️⃣ 0.4 m
🟡 3️⃣ 0.5 m
🟣 4️⃣ 1 m
✔️ उत्तर: E = ½ m ω² A² ⇒ A ∝ √E ⇒ बिना m के अनुपात A = 0.4 m
📘 Exam: NEET 2003

🔴 प्रश्न 48:
यदि SHM की अवधि T है, तो ऊर्जा E किसके समानुपाती है?
🟢 1️⃣ T²
🔵 2️⃣ 1/T²
🟡 3️⃣ 1/T
🟣 4️⃣ T
✔️ उत्तर: 1/T²
📘 Exam: NEET 2002

🔴 प्रश्न 49:
यदि SHM में अधिकतम वेग 5 m/s और ω = 10 rad/s है, तो A = ?
🟢 1️⃣ 0.5 m
🔵 2️⃣ 1 m
🟡 3️⃣ 2 m
🟣 4️⃣ 0.25 m
✔️ उत्तर: A = vₘₐₓ/ω = 5/10 = 0.5 m
📘 Exam: NEET 2001

🔴 प्रश्न 50:
SHM में जब विस्थापन अधिकतम होता है, तब —
🟢 1️⃣ वेग न्यूनतम
🔵 2️⃣ त्वरण अधिकतम
🟡 3️⃣ ऊर्जा स्थितिज अधिकतम
🟣 4️⃣ उपरोक्त सभी
✔️ उत्तर: उपरोक्त सभी
📘 Exam: NEET 2000

————————————————————————————————————————————————————————————————————————————

JEE MAINS पिछले सालों के प्रश्न

🔴 प्रश्न 1:
सरल आवर्त गति (SHM) में त्वरण सदैव होता है —
🟢 1️⃣ विस्थापन के समान दिशा में
🔵 2️⃣ विस्थापन के विपरीत दिशा में
🟡 3️⃣ वेग के समान दिशा में
🟣 4️⃣ वेग के विपरीत दिशा में
✔️ उत्तर: विस्थापन के विपरीत दिशा में
📘 Exam: JEE Main 2024

🔴 प्रश्न 2:
सरल आवर्त गति में अधिकतम त्वरण = ?
🟢 1️⃣ ω²A
🔵 2️⃣ ωA²
🟡 3️⃣ A/ω²
🟣 4️⃣ Aω
✔️ उत्तर: ω²A
📘 Exam: JEE Main 2023

🔴 प्रश्न 3:
सरल आवर्त गति का समीकरण x = A sin ωt है, तो जब x = A/2 हो तब वेग होगा —
🟢 1️⃣ √3/2 Aω
🔵 2️⃣ Aω/2
🟡 3️⃣ Aω
🟣 4️⃣ 0
✔️ उत्तर: √3/2 Aω
📘 Exam: JEE Main 2022

🔴 प्रश्न 4:
सरल आवर्त गति में औसत वेग एक पूर्ण आवर्त में —
🟢 1️⃣ शून्य
🔵 2️⃣ Aω
🟡 3️⃣ A
🟣 4️⃣ ω
✔️ उत्तर: शून्य
📘 Exam: JEE Main 2021

🔴 प्रश्न 5:
सरल आवर्त गति की आवर्त अवधि T है, तो कोणीय आवृत्ति —
🟢 1️⃣ ω = 2π/T
🔵 2️⃣ ω = T/2π
🟡 3️⃣ ω = πT
🟣 4️⃣ ω = 1/T
✔️ उत्तर: ω = 2π/T
📘 Exam: JEE Main 2020

🔴 प्रश्न 6:
कण का अधिकतम वेग सरल आवर्त गति में —
🟢 1️⃣ Aω
🔵 2️⃣ Aω²
🟡 3️⃣ ω/A
🟣 4️⃣ A/ω
✔️ उत्तर: Aω
📘 Exam: JEE Main 2019

🔴 प्रश्न 7:
SHM में विस्थापन और त्वरण के बीच सम्बन्ध —
🟢 1️⃣ a ∝ −x
🔵 2️⃣ a ∝ x
🟡 3️⃣ a ∝ v
🟣 4️⃣ a ∝ −v
✔️ उत्तर: a ∝ −x
📘 Exam: JEE Main 2018

🔴 प्रश्न 8:
SHM में अधिकतम गतिज ऊर्जा = ?
🟢 1️⃣ (1/2)mω²A²
🔵 2️⃣ mω²A²
🟡 3️⃣ (1/4)mω²A²
🟣 4️⃣ शून्य
✔️ उत्तर: (1/2)mω²A²
📘 Exam: JEE Main 2017

🔴 प्रश्न 9:
SHM में औसत गतिज ऊर्जा और औसत स्थितिज ऊर्जा का अनुपात —
🟢 1️⃣ 1:1
🔵 2️⃣ 1:2
🟡 3️⃣ 2:1
🟣 4️⃣ 3:1
✔️ उत्तर: 1:1
📘 Exam: JEE Main 2016

🔴 प्रश्न 10:
सरल लोलक की आवर्त अवधि T = 2π√(l/g) है। यदि l दोगुना हो जाए तो T —
🟢 1️⃣ √2 गुना
🔵 2️⃣ 2 गुना
🟡 3️⃣ आधा
🟣 4️⃣ समान
✔️ उत्तर: √2 गुना
📘 Exam: JEE Main 2015

🔴 प्रश्न 11:
सरल लोलक की अवधि T किस पर निर्भर नहीं करती —
🟢 1️⃣ आयाम पर
🔵 2️⃣ लम्बाई पर
🟡 3️⃣ g पर
🟣 4️⃣ कोई नहीं
✔️ उत्तर: आयाम पर
📘 Exam: JEE Main 2014

🔴 प्रश्न 12:
SHM में कुल ऊर्जा —
🟢 1️⃣ स्थिर
🔵 2️⃣ परिवर्ती
🟡 3️⃣ शून्य
🟣 4️⃣ ऋणात्मक
✔️ उत्तर: स्थिर
📘 Exam: JEE Main 2013

🔴 प्रश्न 13:
यदि SHM में विस्थापन A/2 है, तो गतिज ऊर्जा कुल ऊर्जा का —
🟢 1️⃣ 3/4 भाग
🔵 2️⃣ 1/2 भाग
🟡 3️⃣ 1/4 भाग
🟣 4️⃣ 0
✔️ उत्तर: 3/4 भाग
📘 Exam: JEE Main 2012

🔴 प्रश्न 14:
SHM में विस्थापन और स्थितिज ऊर्जा का सम्बन्ध —
🟢 1️⃣ U ∝ x²
🔵 2️⃣ U ∝ x
🟡 3️⃣ U ∝ 1/x
🟣 4️⃣ U ∝ v
✔️ उत्तर: U ∝ x²
📘 Exam: JEE Main 2011

🔴 प्रश्न 15:
सरल लोलक की अवधि अधिकतम होगी जब g —
🟢 1️⃣ न्यूनतम
🔵 2️⃣ अधिकतम
🟡 3️⃣ समान
🟣 4️⃣ आधा
✔️ उत्तर: न्यूनतम
📘 Exam: JEE Main 2010

🔴 प्रश्न 16:
SHM का समीकरण x = A cos(ωt + φ) है। t = 0 पर विस्थापन A है, तो φ = ?
🟢 1️⃣ 0
🔵 2️⃣ π
🟡 3️⃣ π/2
🟣 4️⃣ 3π/2
✔️ उत्तर: 0
📘 Exam: JEE Main 2009

🔴 प्रश्न 17:
यदि SHM की आवृत्ति f है, तो कोणीय आवृत्ति ω —
🟢 1️⃣ 2πf
🔵 2️⃣ f/2π
🟡 3️⃣ πf
🟣 4️⃣ 1/f
✔️ उत्तर: 2πf
📘 Exam: JEE Main 2008

🔴 प्रश्न 18:
सरल लोलक की अवधि किससे घटेगी —
🟢 1️⃣ g बढ़ाने से
🔵 2️⃣ l बढ़ाने से
🟡 3️⃣ l घटाने से
🟣 4️⃣ g घटाने से
✔️ उत्तर: g बढ़ाने से
📘 Exam: JEE Main 2007

🔴 प्रश्न 19:
SHM में वेग शून्य कब होगा?
🟢 1️⃣ चरम स्थिति पर
🔵 2️⃣ मध्य स्थिति पर
🟡 3️⃣ हर समय
🟣 4️⃣ कभी नहीं
✔️ उत्तर: चरम स्थिति पर
📘 Exam: JEE Main 2006

🔴 प्रश्न 20:
SHM में त्वरण अधिकतम कब होता है?
🟢 1️⃣ चरम स्थिति पर
🔵 2️⃣ मध्य स्थिति पर
🟡 3️⃣ हर समय समान
🟣 4️⃣ कभी नहीं
✔️ उत्तर: चरम स्थिति पर
📘 Exam: JEE Main 2005

🔴 प्रश्न 21:
SHM की औसत गतिज ऊर्जा और कुल ऊर्जा का अनुपात —
🟢 1️⃣ 1/2
🔵 2️⃣ 1
🟡 3️⃣ 2
🟣 4️⃣ 1/4
✔️ उत्तर: 1/2
📘 Exam: JEE Main 2004

🔴 प्रश्न 22:
SHM में ऊर्जा का वितरण —
🟢 1️⃣ K.E. और P.E. के बीच
🔵 2️⃣ केवल K.E. में
🟡 3️⃣ केवल P.E. में
🟣 4️⃣ शून्य
✔️ उत्तर: K.E. और P.E. के बीच
📘 Exam: JEE Main 2003

🔴 प्रश्न 23:
SHM में वेग अधिकतम कब होगा?
🟢 1️⃣ मध्य स्थिति पर
🔵 2️⃣ चरम स्थिति पर
🟡 3️⃣ हर स्थिति पर
🟣 4️⃣ कभी नहीं
✔️ उत्तर: मध्य स्थिति पर
📘 Exam: JEE Main 2002

🔴 प्रश्न 24:
यदि SHM का आयाम दोगुना किया जाए तो कुल ऊर्जा —
🟢 1️⃣ चार गुना
🔵 2️⃣ दोगुना
🟡 3️⃣ आधा
🟣 4️⃣ समान
✔️ उत्तर: चार गुना
📘 Exam: JEE Main 2001

🔴 प्रश्न 25:
SHM में विस्थापन और वेग का सम्बन्ध —
🟢 1️⃣ v² = ω²(A² − x²)
🔵 2️⃣ v² = ω²(A² + x²)
🟡 3️⃣ v² = A²x²
🟣 4️⃣ v² = ωx²
✔️ उत्तर: v² = ω²(A² − x²)
📘 Exam: JEE Main 2020

🔴 प्रश्न 26:
यदि सरल लोलक की लम्बाई 1 m और g = 10 m/s² है, तो उसकी अवधि होगी —
🟢 1️⃣ 2π s
🔵 2️⃣ π s
🟡 3️⃣ 1 s
🟣 4️⃣ 4 s
✔️ उत्तर: 2π s
📘 Exam: JEE Main 2024

🔴 प्रश्न 27:
SHM में विस्थापन शून्य पर स्थितिज ऊर्जा —
🟢 1️⃣ शून्य
🔵 2️⃣ अधिकतम
🟡 3️⃣ न्यूनतम
🟣 4️⃣ अपरिभाषित
✔️ उत्तर: शून्य
📘 Exam: JEE Main 2023

🔴 प्रश्न 28:
सरल लोलक का कालावधि 2 s है। एक सेकंड में वह कितनी बार दोलेगा?
🟢 1️⃣ 0.5
🔵 2️⃣ 1
🟡 3️⃣ 2
🟣 4️⃣ 0.25
✔️ उत्तर: 0.5
📘 Exam: JEE Main 2022

🔴 प्रश्न 29:
यदि g आधा कर दिया जाए, तो सरल लोलक की अवधि —
🟢 1️⃣ √2 गुना बढ़ेगी
🔵 2️⃣ √2 गुना घटेगी
🟡 3️⃣ समान रहेगी
🟣 4️⃣ दुगुनी हो जाएगी
✔️ उत्तर: √2 गुना बढ़ेगी
📘 Exam: JEE Main 2021

🔴 प्रश्न 30:
SHM में गतिज ऊर्जा अधिकतम होती है जब विस्थापन —
🟢 1️⃣ शून्य
🔵 2️⃣ A
🟡 3️⃣ A/2
🟣 4️⃣ A/√2
✔️ उत्तर: शून्य
📘 Exam: JEE Main 2020

🔴 प्रश्न 31:
सरल आवर्त गति का औसत वेग एक आवर्त में —
🟢 1️⃣ शून्य
🔵 2️⃣ A/T
🟡 3️⃣ 2A/T
🟣 4️⃣ Aω
✔️ उत्तर: शून्य
📘 Exam: JEE Main 2019

🔴 प्रश्न 32:
SHM में कुल ऊर्जा किसके समानुपाती होती है —
🟢 1️⃣ A²
🔵 2️⃣ A
🟡 3️⃣ 1/A
🟣 4️⃣ A³
✔️ उत्तर: A²
📘 Exam: JEE Main 2018

🔴 प्रश्न 33:
SHM में औसत स्थितिज ऊर्जा = ?
🟢 1️⃣ कुल ऊर्जा का आधा
🔵 2️⃣ कुल ऊर्जा
🟡 3️⃣ कुल ऊर्जा का दोगुना
🟣 4️⃣ शून्य
✔️ उत्तर: कुल ऊर्जा का आधा
📘 Exam: JEE Main 2017

🔴 प्रश्न 34:
SHM में वेग और त्वरण के बीच कोण —
🟢 1️⃣ 180°
🔵 2️⃣ 90°
🟡 3️⃣ 0°
🟣 4️⃣ 60°
✔️ उत्तर: 180°
📘 Exam: JEE Main 2016

🔴 प्रश्न 35:
SHM में विस्थापन अधिकतम कब होता है?
🟢 1️⃣ चरम स्थिति पर
🔵 2️⃣ मध्य स्थिति पर
🟡 3️⃣ किसी भी स्थिति पर
🟣 4️⃣ हमेशा समान
✔️ उत्तर: चरम स्थिति पर
📘 Exam: JEE Main 2015

🔴 प्रश्न 36:
यदि SHM की अवधि T है, तो आवृत्ति —
🟢 1️⃣ 1/T
🔵 2️⃣ T
🟡 3️⃣ 2T
🟣 4️⃣ T/2
✔️ उत्तर: 1/T
📘 Exam: JEE Main 2014

🔴 प्रश्न 37:
यदि x = A cos ωt है, तो वेग v = ?
🟢 1️⃣ −Aω sin ωt
🔵 2️⃣ Aω sin ωt
🟡 3️⃣ Aω cos ωt
🟣 4️⃣ −Aω cos ωt
✔️ उत्तर: −Aω sin ωt
📘 Exam: JEE Main 2013

🔴 प्रश्न 38:
यदि विस्थापन A/√2 है, तो गतिज और स्थितिज ऊर्जा —
🟢 1️⃣ बराबर
🔵 2️⃣ KE > PE
🟡 3️⃣ PE > KE
🟣 4️⃣ कोई नहीं
✔️ उत्तर: बराबर
📘 Exam: JEE Main 2012

🔴 प्रश्न 39:
SHM में स्थिति, वेग और त्वरण के फेज में अन्तर —
🟢 1️⃣ 90°
🔵 2️⃣ 180°
🟡 3️⃣ 0°
🟣 4️⃣ 45°
✔️ उत्तर: 90°
📘 Exam: JEE Main 2011

🔴 प्रश्न 40:
सरल लोलक की अवधि किस पर निर्भर करती है?
🟢 1️⃣ g और l पर
🔵 2️⃣ आयाम पर
🟡 3️⃣ द्रव्यमान पर
🟣 4️⃣ ऊर्जा पर
✔️ उत्तर: g और l पर
📘 Exam: JEE Main 2010

🔴 प्रश्न 41:
यदि SHM में x = A/2 है, तो स्थितिज ऊर्जा = ?
🟢 1️⃣ (1/4) कुल ऊर्जा
🔵 2️⃣ (3/4) कुल ऊर्जा
🟡 3️⃣ आधी कुल ऊर्जा
🟣 4️⃣ शून्य
✔️ उत्तर: (1/4) कुल ऊर्जा
📘 Exam: JEE Main 2009

🔴 प्रश्न 42:
SHM में वेग अधिकतम कब होता है?
🟢 1️⃣ x = 0 पर
🔵 2️⃣ x = A पर
🟡 3️⃣ x = A/2 पर
🟣 4️⃣ कभी नहीं
✔️ उत्तर: x = 0 पर
📘 Exam: JEE Main 2008

🔴 प्रश्न 43:
SHM की ऊर्जा = ?
🟢 1️⃣ (1/2)mω²A²
🔵 2️⃣ mωA²
🟡 3️⃣ mω²A
🟣 4️⃣ (1/2)mA²
✔️ उत्तर: (1/2)mω²A²
📘 Exam: JEE Main 2007

🔴 प्रश्न 44:
यदि सरल लोलक पृथ्वी पर T सेकंड का है, तो चंद्रमा पर अवधि = ? (gₘ = g/6)
🟢 1️⃣ √6 T
🔵 2️⃣ T/√6
🟡 3️⃣ 6T
🟣 4️⃣ समान
✔️ उत्तर: √6 T
📘 Exam: JEE Main 2006

🔴 प्रश्न 45:
SHM में अधिकतम त्वरण कब होता है?
🟢 1️⃣ चरम स्थिति पर
🔵 2️⃣ मध्य स्थिति पर
🟡 3️⃣ हर स्थिति पर समान
🟣 4️⃣ कभी नहीं
✔️ उत्तर: चरम स्थिति पर
📘 Exam: JEE Main 2005

🔴 प्रश्न 46:
यदि SHM का समीकरण x = A sin ωt है, तो अधिकतम वेग = ?
🟢 1️⃣ Aω
🔵 2️⃣ ωA²
🟡 3️⃣ A/ω
🟣 4️⃣ ω/A
✔️ उत्तर: Aω
📘 Exam: JEE Main 2004

🔴 प्रश्न 47:
सरल लोलक की अवधि अधिकतम कहाँ होगी?
🟢 1️⃣ चंद्रमा पर
🔵 2️⃣ पृथ्वी पर
🟡 3️⃣ ग्रह बृहस्पति पर
🟣 4️⃣ किसी भी जगह समान
✔️ उत्तर: चंद्रमा पर
📘 Exam: JEE Main 2003

🔴 प्रश्न 48:
SHM में कुल ऊर्जा = ?
🟢 1️⃣ KE + PE
🔵 2️⃣ केवल KE
🟡 3️⃣ केवल PE
🟣 4️⃣ शून्य
✔️ उत्तर: KE + PE
📘 Exam: JEE Main 2002

🔴 प्रश्न 49:
यदि ω = 2π rad/s और A = 0.1 m है, तो अधिकतम वेग = ?
🟢 1️⃣ 0.2π m/s
🔵 2️⃣ 0.1π m/s
🟡 3️⃣ 2π m/s
🟣 4️⃣ 0.5π m/s
✔️ उत्तर: 0.2π m/s
📘 Exam: JEE Main 2001

🔴 प्रश्न 50:
यदि SHM में विस्थापन x = 0 है, तो त्वरण —
🟢 1️⃣ शून्य
🔵 2️⃣ अधिकतम
🟡 3️⃣ न्यूनतम
🟣 4️⃣ अपरिभाषित
✔️ उत्तर: शून्य
📘 Exam: JEE Main 2024

————————————————————————————————————————————————————————————————————————————

JEE ADVANCED पिछले सालों के प्रश्न

🔴 प्रश्न 1:
सरल आवर्त गति में विस्थापन x = A sin(ωt) है। अधिकतम वेग क्या होगा?
🟢 1️⃣ Aω
🔵 2️⃣ A/ω
🟡 3️⃣ ω/A
🟣 4️⃣ A²ω
✔️ उत्तर: Aω
📘 Exam: JEE Advanced 2024

🔴 प्रश्न 2:
सरल लोलक की आवर्त अवधि T = 2π√(l/g) है। यदि लम्बाई 4 गुना हो जाए, तो नई अवधि क्या होगी?
🟢 1️⃣ 2T
🔵 2️⃣ T/2
🟡 3️⃣ 4T
🟣 4️⃣ T
✔️ उत्तर: 2T
📘 Exam: JEE Advanced 2023

🔴 प्रश्न 3:
SHM में त्वरण a = -ω²x किस पर निर्भर करता है?
🟢 1️⃣ विस्थापन पर
🔵 2️⃣ वेग पर
🟡 3️⃣ आवृत्ति पर
🟣 4️⃣ द्रव्यमान पर
✔️ उत्तर: विस्थापन पर
📘 Exam: JEE Advanced 2022

🔴 प्रश्न 4:
SHM की आवृत्ति f का सूत्र क्या है?
🟢 1️⃣ f = ω / 2π
🔵 2️⃣ f = 2π / ω
🟡 3️⃣ f = ω
🟣 4️⃣ f = 1 / ω
✔️ उत्तर: f = ω / 2π
📘 Exam: JEE Advanced 2021

🔴 प्रश्न 5:
यदि किसी दोलक की अवधि 2 s है, तो उसकी आवृत्ति क्या होगी?
🟢 1️⃣ 0.5 Hz
🔵 2️⃣ 1 Hz
🟡 3️⃣ 2 Hz
🟣 4️⃣ 4 Hz
✔️ उत्तर: 0.5 Hz
📘 Exam: JEE Advanced 2020

🔴 प्रश्न 6:
SHM में अधिकतम त्वरण कहाँ होता है?
🟢 1️⃣ मध्य स्थिति पर
🔵 2️⃣ सीमा स्थिति पर
🟡 3️⃣ किसी भी स्थिति पर
🟣 4️⃣ अधिकतम वेग पर
✔️ उत्तर: सीमा स्थिति पर
📘 Exam: JEE Advanced 2019

🔴 प्रश्न 7:
सरल लोलक की अवधि किस पर निर्भर नहीं करती?
🟢 1️⃣ द्रव्यमान पर
🔵 2️⃣ लम्बाई पर
🟡 3️⃣ गुरुत्व त्वरण पर
🟣 4️⃣ आयाम पर
✔️ उत्तर: द्रव्यमान पर
📘 Exam: JEE Advanced 2018

🔴 प्रश्न 8:
यदि SHM का विस्थापन x = 5 sin(2t) है, तो आवर्त अवधि क्या होगी?
🟢 1️⃣ π s
🔵 2️⃣ 2π s
🟡 3️⃣ π/2 s
🟣 4️⃣ 1 s
✔️ उत्तर: π s
📘 Exam: JEE Advanced 2017

🔴 प्रश्न 9:
SHM में कौन-सी ऊर्जा स्थिर रहती है?
🟢 1️⃣ गतिज ऊर्जा
🔵 2️⃣ स्थितिज ऊर्जा
🟡 3️⃣ कुल ऊर्जा
🟣 4️⃣ उपरोक्त सभी
✔️ उत्तर: कुल ऊर्जा
📘 Exam: JEE Advanced 2016

🔴 प्रश्न 10:
यदि किसी कण का वेग v = ω√(A² – x²) है, तो यह गति कौन-सी है?
🟢 1️⃣ समान गति
🔵 2️⃣ समान त्वरण गति
🟡 3️⃣ सरल आवर्त गति
🟣 4️⃣ परवलयिक गति
✔️ उत्तर: सरल आवर्त गति
📘 Exam: JEE Advanced 2015

🔴 प्रश्न 11:
यदि एक कण SHM में x = 0.05 sin(100t) चलता है, तो आवृत्ति क्या होगी?
🟢 1️⃣ 50 Hz
🔵 2️⃣ 100 Hz
🟡 3️⃣ 25 Hz
🟣 4️⃣ 75 Hz
✔️ उत्तर: 50 Hz
📘 Exam: JEE Advanced 2014

🔴 प्रश्न 12:
SHM में अधिकतम वेग और अधिकतम विस्थापन का अनुपात क्या होता है?
🟢 1️⃣ ω
🔵 2️⃣ 1/ω
🟡 3️⃣ A
🟣 4️⃣ 1/A
✔️ उत्तर: ω
📘 Exam: JEE Advanced 2013

🔴 प्रश्न 13:
सरल लोलक का आवर्तकाल T = 2π√(l/g) है। यदि g घट जाए, तो T —
🟢 1️⃣ बढ़ेगा
🔵 2️⃣ घटेगा
🟡 3️⃣ समान रहेगा
🟣 4️⃣ पहले घटेगा फिर बढ़ेगा
✔️ उत्तर: बढ़ेगा
📘 Exam: JEE Advanced 2012

🔴 प्रश्न 14:
किसी दोलक की यांत्रिक ऊर्जा का सूत्र —
🟢 1️⃣ (1/2) m ω² A²
🔵 2️⃣ m ω A
🟡 3️⃣ m A² / ω²
🟣 4️⃣ (1/2) m A²
✔️ उत्तर: (1/2) m ω² A²
📘 Exam: JEE Advanced 2011

🔴 प्रश्न 15:
यदि दो SHM समान आयाम के हैं और 180° पर विपरीत फेज़ में हैं, तो परिणामी गति —
🟢 1️⃣ SHM होगी
🔵 2️⃣ समानांतर गति
🟡 3️⃣ स्थिर
🟣 4️⃣ समान त्वरण गति
✔️ उत्तर: स्थिर
📘 Exam: JEE Advanced 2010

🔴 प्रश्न 16:
यदि x = A sin ωt और y = A cos ωt दो SHM हों, तो परिणामी पथ —
🟢 1️⃣ वृत्त
🔵 2️⃣ दीर्घवृत्त
🟡 3️⃣ सीधी रेखा
🟣 4️⃣ परवलय
✔️ उत्तर: वृत्त
📘 Exam: JEE Advanced 2009

🔴 प्रश्न 17:
SHM में अधिकतम गतिज ऊर्जा और अधिकतम स्थितिज ऊर्जा —
🟢 1️⃣ समान होती हैं
🔵 2️⃣ अलग होती हैं
🟡 3️⃣ कभी समान नहीं
🟣 4️⃣ कोई नहीं
✔️ उत्तर: समान होती हैं
📘 Exam: JEE Advanced 2008


🔴 प्रश्न 18:
किसी दोलक की यांत्रिक ऊर्जा E = (1/2) m ω² A² है। यदि आयाम आधा हो जाए, तो ऊर्जा —
🟢 1️⃣ 1/4 गुनी हो जाएगी
🔵 2️⃣ 1/2 गुनी हो जाएगी
🟡 3️⃣ समान रहेगी
🟣 4️⃣ 2 गुनी हो जाएगी
✔️ उत्तर: 1/4 गुनी हो जाएगी
📘 Exam: JEE Advanced 2007

🔴 प्रश्न 19:
यदि किसी दोलक की ऊर्जा 4 गुनी हो जाए, तो आयाम —
🟢 1️⃣ 2 गुना
🔵 2️⃣ 4 गुना
🟡 3️⃣ 1/2 गुना
🟣 4️⃣ समान
✔️ उत्तर: 2 गुना
📘 Exam: JEE Advanced 2006

🔴 प्रश्न 20:
SHM में विस्थापन के साथ स्थितिज ऊर्जा का ग्राफ कैसा होता है?
🟢 1️⃣ परवलयिक
🔵 2️⃣ सीधी रेखा
🟡 3️⃣ वृत्तीय
🟣 4️⃣ घातीय
✔️ उत्तर: परवलयिक
📘 Exam: JEE Advanced 2005

🔴 प्रश्न 21:
यदि किसी दोलक का अधिकतम वेग 20 m/s है और आवृत्ति 5 Hz है, तो आयाम ज्ञात करें।
🟢 1️⃣ 2/π m
🔵 2️⃣ 4/π m
🟡 3️⃣ 20/π m
🟣 4️⃣ 10/π m
✔️ उत्तर: 20/π m
📘 Exam: JEE Advanced 2004

🔴 प्रश्न 22:
SHM में विस्थापन और वेग के बीच सम्बन्ध क्या है?
🟢 1️⃣ v = ω√(A² – x²)
🔵 2️⃣ v = A√(ω² – x²)
🟡 3️⃣ v = x√(A² – ω²)
🟣 4️⃣ v = ωA²
✔️ उत्तर: v = ω√(A² – x²)
📘 Exam: JEE Advanced 2003

🔴 प्रश्न 23:
यदि दो SHM समान आवृत्ति के हों और फेज़ अन्तर 90° हो, तो परिणामी गति —
🟢 1️⃣ वृत्तीय
🔵 2️⃣ परवलयिक
🟡 3️⃣ दीर्घवृत्तीय
🟣 4️⃣ रेखीय
✔️ उत्तर: वृत्तीय
📘 Exam: JEE Advanced 2002

🔴 प्रश्न 24:
सरल लोलक का आवर्तकाल T = 2π√(l/g) है। यदि g = π² m/s² और l = 1 m हो, तो T = ?
🟢 1️⃣ 2 s
🔵 2️⃣ 1 s
🟡 3️⃣ 4 s
🟣 4️⃣ π s
✔️ उत्तर: 2 s
📘 Exam: JEE Advanced 2001

🔴 प्रश्न 25:
SHM में अधिकतम त्वरण और अधिकतम वेग का अनुपात क्या है?
🟢 1️⃣ ω
🔵 2️⃣ ω²
🟡 3️⃣ 1/ω
🟣 4️⃣ 1/ω²
✔️ उत्तर: ω
📘 Exam: JEE Advanced 2024

🔴 प्रश्न 26:
यदि किसी दोलक की आवृत्ति 10 Hz है, तो उसकी आवर्त अवधि क्या होगी?
🟢 1️⃣ 0.1 s
🔵 2️⃣ 10 s
🟡 3️⃣ 1 s
🟣 4️⃣ 5 s
✔️ उत्तर: 0.1 s
📘 Exam: JEE Advanced 2023

🔴 प्रश्न 27:
SHM में अधिकतम त्वरण aₘ = ω²A है। यदि ω = 5 rad/s और A = 0.2 m है, तो aₘ = ?
🟢 1️⃣ 5 m/s²
🔵 2️⃣ 10 m/s²
🟡 3️⃣ 20 m/s²
🟣 4️⃣ 25 m/s²
✔️ उत्तर: 5 m/s²
📘 Exam: JEE Advanced 2022

🔴 प्रश्न 28:
SHM में स्थितिज ऊर्जा U = (1/2)k x² है। यदि x = A/2 हो, तो U/E = ?
🟢 1️⃣ 1/4
🔵 2️⃣ 1/2
🟡 3️⃣ 3/4
🟣 4️⃣ 1
✔️ उत्तर: 1/4
📘 Exam: JEE Advanced 2021

🔴 प्रश्न 29:
किसी SHM का समीकरण x = 0.1 sin(100πt) है। आवृत्ति ज्ञात करें।
🟢 1️⃣ 50 Hz
🔵 2️⃣ 100 Hz
🟡 3️⃣ 25 Hz
🟣 4️⃣ 200 Hz
✔️ उत्तर: 50 Hz
📘 Exam: JEE Advanced 2020

🔴 प्रश्न 30:
यदि SHM की अवधि T है, तो 1/8 अवधि में विस्थापन का कोणीय अन्तराल होगा —
🟢 1️⃣ π/4
🔵 2️⃣ π/2
🟡 3️⃣ π/8
🟣 4️⃣ π/16
✔️ उत्तर: π/4
📘 Exam: JEE Advanced 2019

🔴 प्रश्न 31:
SHM में कुल ऊर्जा किस पर निर्भर करती है?
🟢 1️⃣ आयाम पर
🔵 2️⃣ आवृत्ति पर
🟡 3️⃣ वेग पर
🟣 4️⃣ विस्थापन पर
✔️ उत्तर: आयाम पर
📘 Exam: JEE Advanced 2018

🔴 प्रश्न 32:
यदि SHM का विस्थापन x = 0.05 sin(200t) है, तो कोणीय आवृत्ति ω क्या होगी?
🟢 1️⃣ 200 rad/s
🔵 2️⃣ 100 rad/s
🟡 3️⃣ 50 rad/s
🟣 4️⃣ 20 rad/s
✔️ उत्तर: 200 rad/s
📘 Exam: JEE Advanced 2017

🔴 प्रश्न 33:
SHM में अधिकतम गतिज ऊर्जा Kₘ = (1/2) m ω² A² है।
यदि ω दोगुना हो जाए, तो Kₘ —
🟢 1️⃣ 4 गुना
🔵 2️⃣ 2 गुना
🟡 3️⃣ आधी
🟣 4️⃣ समान
✔️ उत्तर: 4 गुना
📘 Exam: JEE Advanced 2016

🔴 प्रश्न 34:
SHM में ऊर्जा का वितरण किस प्रकार होता है?
🟢 1️⃣ स्थितिज और गतिज ऊर्जा का आदान-प्रदान होता है
🔵 2️⃣ कुल ऊर्जा बदलती है
🟡 3️⃣ केवल गतिज ऊर्जा रहती है
🟣 4️⃣ केवल स्थितिज ऊर्जा रहती है
✔️ उत्तर: स्थितिज और गतिज ऊर्जा का आदान-प्रदान होता है
📘 Exam: JEE Advanced 2015

————————————————————————————————————————————————————————————————————————————

मॉडल प्रश्न पत्र, अभ्यास

🔷 NEET LEVEL (Q1–Q20)

Q1. सरल आवर्त गति का पुनर्स्थापक बल किसके समानुपाती होता है?
🔵 (A) वेग
🟢 (B) विस्थापन
🟠 (C) त्वरण
🔴 (D) ऊर्जा
Answer: (B) विस्थापन

Q2. सरल आवर्त गति में त्वरण का सूत्र है —
🔵 (A) a = ωx
🟢 (B) a = ω²x
🟠 (C) a = -ω²x
🔴 (D) a = -ωx
Answer: (C) a = -ω²x

Q3. यदि किसी दोलन का आयाम दोगुना कर दिया जाए, तो उसकी आवर्तकाल —
🔵 (A) आधा हो जाएगा
🟢 (B) दोगुना हो जाएगा
🟠 (C) अपरिवर्तित रहेगा
🔴 (D) चार गुना हो जाएगा
Answer: (C) अपरिवर्तित रहेगा

Q4. सरल लोलक का आवर्तकाल दिया जाता है —
🔵 (A) T = 2π√(g/L)
🟢 (B) T = 2π√(L/g)
🟠 (C) T = 2π√(L×g)
🔴 (D) T = 2πL/g
Answer: (B) T = 2π√(L/g)

Q5. SHM में अधिकतम वेग का सूत्र है —
🔵 (A) v_max = Aω²
🟢 (B) v_max = Aω
🟠 (C) v_max = ω/A
🔴 (D) v_max = A²ω
Answer: (B) v_max = Aω

Q6. SHM में कुल ऊर्जा किस पर निर्भर करती है?
🔵 (A) विस्थापन
🟢 (B) समय
🟠 (C) आयाम
🔴 (D) वेग
Answer: (C) आयाम

Q7. यदि किसी लोलक की लंबाई 4 गुना कर दी जाए, तो उसका आवर्तकाल —
🔵 (A) आधा हो जाएगा
🟢 (B) दोगुना हो जाएगा
🟠 (C) चार गुना हो जाएगा
🔴 (D) अपरिवर्तित रहेगा
Answer: (B) दोगुना हो जाएगा

Q8. सरल आवर्त गति में विस्थापन अधिकतम होने पर —
🔵 (A) वेग अधिकतम होता है
🟢 (B) त्वरण शून्य होता है
🟠 (C) त्वरण अधिकतम होता है
🔴 (D) ऊर्जा न्यूनतम होती है
Answer: (C) त्वरण अधिकतम होता है

Q9. SHM का विस्थापन समीकरण x = 0.05 sin(100πt) है। कोणीय आवृत्ति ω = ?
🔵 (A) 100π rad/s
🟢 (B) 50π rad/s
🟠 (C) 200π rad/s
🔴 (D) 25π rad/s
Answer: (A) 100π rad/s

Q10. सरल आवर्त गति में वेग अधिकतम कहाँ होता है?
🔵 (A) x = A पर
🟢 (B) x = 0 पर
🟠 (C) x = A/2 पर
🔴 (D) x = -A पर
Answer: (B) x = 0 पर

Q11. SHM में त्वरण अधिकतम कहाँ होता है?
🔵 (A) x = 0 पर
🟢 (B) x = A पर
🟠 (C) x = A/2 पर
🔴 (D) सभी पर समान
Answer: (B) x = A पर

Q12. SHM में कोणीय आवृत्ति ω और आवर्तकाल T का संबंध है —
🔵 (A) ω = 2πT
🟢 (B) ω = T/2π
🟠 (C) ω = 2π/T
🔴 (D) ω = 1/T²
Answer: (C) ω = 2π/T

Q13. किसी सरल लोलक के लिए g कम करने पर T पर क्या प्रभाव पड़ेगा?
🔵 (A) T बढ़ जाएगा
🟢 (B) T घट जाएगा
🟠 (C) T अपरिवर्तित रहेगा
🔴 (D) T = 0 हो जाएगा
Answer: (A) T बढ़ जाएगा

Q14. स्प्रिंग स्थिरांक k का आयाम है —
🔵 (A) ML⁰T⁻²
🟢 (B) MLT⁻²
🟠 (C) ML⁻¹T⁻²
🔴 (D) ML²T⁻²
Answer: (C) ML⁻¹T⁻²

Q15. यदि ω = √(k/m) हो, तो k की इकाई है —
🔵 (A) N/m
🟢 (B) N·m
🟠 (C) J
🔴 (D) m/N
Answer: (A) N/m

Q16. SHM में कुल यांत्रिक ऊर्जा E = ?
🔵 (A) (1/2)kA²
🟢 (B) (1/2)mA²
🟠 (C) (1/2)mωA²
🔴 (D) (1/2)kA
Answer: (A) (1/2)kA²

Q17. यदि SHM में ω = 2π rad/s हो, तो T का मान होगा —
🔵 (A) 1 s
🟢 (B) 2π s
🟠 (C) 2 s
🔴 (D) 0.5 s
Answer: (A) 1 s

Q18. SHM में त्वरण और विस्थापन के बीच कोण का मान होता है —
🔵 (A) 0°
🟢 (B) 90°
🟠 (C) 180°
🔴 (D) 45°
Answer: (C) 180°

Q19. लोलक की लंबाई 0.25 m है, g = 10 m/s², तो T = ?
🔵 (A) 1.0 s
🟢 (B) 2.0 s
🟠 (C) 0.5 s
🔴 (D) 3.0 s
Answer: (A) 1.0 s

Q20. यदि किसी स्प्रिंग में द्रव्यमान बढ़ाया जाए तो आवर्तकाल —
🔵 (A) बढ़ेगा
🟢 (B) घटेगा
🟠 (C) अपरिवर्तित रहेगा
🔴 (D) पहले घटेगा फिर बढ़ेगा
Answer: (A) बढ़ेगा

🔶 JEE MAIN LEVEL (Q21–Q40)

Q21. x = A sin(ωt + π/4) का प्रारंभिक विस्थापन है —
🔵 (A) 0
🟢 (B) A/√2
🟠 (C) A
🔴 (D) -A/√2
Answer: (B) A/√2

Q22. SHM में औसत वेग (0 से A के बीच) —
🔵 (A) (2A)/T
🟢 (B) (Aω)/2
🟠 (C) 0
🔴 (D) A/T
Answer: (A) (2A)/T

Q23. यदि A = 0.1 m, ω = 10 rad/s है, तो अधिकतम त्वरण = ?
🔵 (A) 1 m/s²
🟢 (B) 5 m/s²
🟠 (C) 10 m/s²
🔴 (D) 100 m/s²
Answer: (D) 100 m/s²

Q24. SHM में विस्थापन के वर्ग और स्थितिज ऊर्जा के बीच संबंध क्या है?
🔵 (A) रैखिक
🟢 (B) वर्गानुपाती
🟠 (C) व्युत्क्रमानुपाती
🔴 (D) कोई नहीं
Answer: (B) वर्गानुपाती

Q25. यदि द्रव्यमान आधा कर दिया जाए तो आवर्तकाल —
🔵 (A) √2 गुना घटेगा
🟢 (B) √2 गुना बढ़ेगा
🟠 (C) 2 गुना घटेगा
🔴 (D) अपरिवर्तित रहेगा
Answer: (A) √2 गुना घटेगा

Q26. SHM का औसत गतिज ऊर्जा और औसत स्थितिज ऊर्जा का अनुपात है —
🔵 (A) 1:2
🟢 (B) 2:1
🟠 (C) 1:1
🔴 (D) 1:4
Answer: (C) 1:1

Q27. यदि F = -kx है, तो ω² = ?
🔵 (A) k/m
🟢 (B) m/k
🟠 (C) 1/(km)
🔴 (D) k²/m
Answer: (A) k/m

Q28. यदि k = 400 N/m और m = 4 kg है, तो ω = ?
🔵 (A) 5 rad/s
🟢 (B) 10 rad/s
🟠 (C) 20 rad/s
🔴 (D) 100 rad/s
Answer: (B) 10 rad/s

Q29. किसी SHM में विस्थापन दोगुना करने पर स्थितिज ऊर्जा —
🔵 (A) 2 गुना
🟢 (B) 4 गुना
🟠 (C) 8 गुना
🔴 (D) 16 गुना
Answer: (B) 4 गुना

Q30. यदि SHM का विस्थापन x = 0.1 sin(20t) है, तो T = ?
🔵 (A) 0.1 s
🟢 (B) 0.2 s
🟠 (C) 0.314 s
🔴 (D) 0.5 s
Answer: (C) 0.314 s

Q31. एक स्प्रिंग में 100 g द्रव्यमान से T = 0.5 s है। यदि 400 g द्रव्यमान लगाया जाए तो नया T = ?
🔵 (A) 0.25 s
🟢 (B) 1.0 s
🟠 (C) 2.0 s
🔴 (D) 0.75 s
Answer: (B) 1.0 s

Q32. SHM में वेग और विस्थापन के बीच संबंध है —
🔵 (A) v² = ω²(A² – x²)
🟢 (B) v = ω²(A² – x²)
🟠 (C) v² = A² – ω²x²
🔴 (D) v² = A²x²
Answer: (A) v² = ω²(A² – x²)

Q33. यदि ω = √(k/m) है, तो आवर्तकाल —
🔵 (A) 2π√(m/k)
🟢 (B) 2π√(k/m)
🟠 (C) π√(k/m)
🔴 (D) π√(m/k)
Answer: (A) 2π√(m/k)

Q34. SHM की आवृत्ति का मात्रक है —
🔵 (A) s
🟢 (B) Hz
🟠 (C) rad
🔴 (D) m/s
Answer: (B) Hz

Q35. SHM में ω = 100 rad/s और A = 0.01 m, तो v_max = ?
🔵 (A) 1 m/s
🟢 (B) 10 m/s
🟠 (C) 0.1 m/s
🔴 (D) 100 m/s
Answer: (A) 1 m/s

Q36. यदि SHM का समीकरण x = 0.2 sin(πt + π/6) है, तो आवृत्ति = ?
🔵 (A) 1/2 Hz
🟢 (B) 1 Hz
🟠 (C) 2 Hz
🔴 (D) 3 Hz
Answer: (A) 1/2 Hz

Q37. किसी SHM में ω का दोगुना करने पर आवर्तकाल —
🔵 (A) आधा हो जाएगा
🟢 (B) दोगुना हो जाएगा
🟠 (C) चार गुना
🔴 (D) अपरिवर्तित
Answer: (A) आधा हो जाएगा

Q38. यदि किसी कण की स्थिति समय के साथ x = A sin(ωt + φ) से बदलती है, तो φ कहलाता है —
🔵 (A) कोणीय आवृत्ति
🟢 (B) प्रारंभिक चरण
🟠 (C) आवर्तकाल
🔴 (D) फेज़ अंतर
Answer: (B) प्रारंभिक चरण

Q39. SHM में जब विस्थापन आधा हो, तब गतिज ऊर्जा कुल ऊर्जा का —
🔵 (A) 3/4 भाग
🟢 (B) 1/2 भाग
🟠 (C) 1/4 भाग
🔴 (D) समान
Answer: (A) 3/4 भाग

Q40. एक लोलक की लंबाई 4 m है और g = 9.8 m/s², तो T = ?
🔵 (A) 2.5 s
🟢 (B) 4.0 s
🟠 (C) 6.3 s
🔴 (D) 1.0 s
Answer: (B) 4.0 s

🔷 JEE ADVANCED LEVEL (Q41–Q50)

Q41. SHM में कोणीय आवृत्ति ω दोगुनी करने पर कुल ऊर्जा —
🔵 (A) चार गुना
🟢 (B) दोगुनी
🟠 (C) आधी
🔴 (D) अपरिवर्तित
Answer: (A) चार गुना

Q42. यदि किसी कण का विस्थापन x = A cos(ωt + φ) है, तो अधिकतम त्वरण कहाँ होगा?
🔵 (A) φ = 0 पर
🟢 (B) x = ±A पर
🟠 (C) x = 0 पर
🔴 (D) सभी पर समान
Answer: (B) x = ±A पर

Q43. एक SHM में ω = 20 rad/s, A = 0.05 m है।
E = (1/2)mω²A², यदि m = 0.2 kg हो, तो E = ?
🔵 (A) 0.2 J
🟢 (B) 1.0 J
🟠 (C) 0.1 J
🔴 (D) 2.0 J
Answer: (C) 0.1 J

Q44. किसी दोलन की कुल ऊर्जा चार गुना हो जाए, तो आयाम —
🔵 (A) दुगना
🟢 (B) चार गुना
🟠 (C) आधा
🔴 (D) √2 गुना
Answer: (A) दुगना

Q45. यदि x = 0.05 sin(100t) है, तो अधिकतम त्वरण = ?
🔵 (A) 500 m/s²
🟢 (B) 100 m/s²
🟠 (C) 50 m/s²
🔴 (D) 0.5 m/s²
Answer: (A) 500 m/s²

Q46. दो SHM समान आवृत्ति के हैं लेकिन चरणांतर π/2 का है। उनका अध्यारोपण क्या दर्शाएगा?
🔵 (A) एक नया SHM
🟢 (B) समान फेज़ दोलन
🟠 (C) स्थायी तरंग
🔴 (D) अनियमित दोलन
Answer: (A) एक नया SHM

Q47. SHM में विस्थापन को दुगुना करने पर कुल यांत्रिक ऊर्जा कितनी गुना हो जाएगी?
🔵 (A) 2
🟢 (B) 4
🟠 (C) 8
🔴 (D) अपरिवर्तित
Answer: (B) 4

Q48. एक स्प्रिंग प्रणाली में k = 200 N/m और m = 2 kg है। ω = ?
🔵 (A) 5 rad/s
🟢 (B) 10 rad/s
🟠 (C) 20 rad/s
🔴 (D) 100 rad/s
Answer: (B) 10 rad/s

Q49. SHM में कण के वेग और विस्थापन का ग्राफ किस प्रकार का होता है?
🔵 (A) रेखीय
🟢 (B) परवलयाकार
🟠 (C) दीर्घवृत्ताकार
🔴 (D) वृत्ताकार
Answer: (B) परवलयाकार

Q50. दोलन में यदि आयाम तीन गुना कर दिया जाए तो अधिकतम त्वरण —
🔵 (A) 3 गुना
🟢 (B) 6 गुना
🟠 (C) 9 गुना
🔴 (D) अपरिवर्तित
Answer: (A) 3 गुना

————————————————————————————————————————————————————————————————————————————