Class 11 : Physics (In Hindi) – अध्याय 6: कणों के निकाय तथा घूर्णी गति

पाठ का विश्लेषण एवं विवेचन

🌿 1. परिचय (Introduction)
➡️ अब तक हमने एकल कण की गति का अध्ययन किया। परंतु वास्तविक वस्तुएँ अनेक कणों से बनी होती हैं — जैसे गेंद, छड़ी, पहिया, पंखा आदि। इन सबमें प्रत्येक कण किसी-न-किसी प्रकार की गति करता है।
🔹 ऐसे कणों के समूह को “कणों का निकाय (System of Particles)” कहा जाता है।
🔹 किसी निकाय की गति को समझने के लिए हमें यह देखना होता है कि वह संपूर्ण वस्तु किस प्रकार स्थानांतरित (Translational Motion) या घूर्णन (Rotational Motion) करती है।

💡 2. स्थानांतरण गति (Translational Motion)
➡️ जब वस्तु के सभी कण समानांतर रेखाओं में समान दूरी तय करते हैं, तो वह स्थानांतरण गति कहलाती है।
उदाहरण: चलती कार, उड़ता विमान, सरकती मेज इत्यादि।
✔️ इसमें वस्तु का आकार या दिशा नहीं बदलती।

💡 3. द्रव्यमान केंद्र (Centre of Mass)
➡️ द्रव्यमान केंद्र वह बिंदु होता है जहाँ पूरे निकाय का द्रव्यमान केंद्रित माना जा सकता है।
🔹 यदि किसी वस्तु को उस बिंदु पर बल लगाया जाए, तो वह केवल स्थानांतरित होगी, घूमेगी नहीं।
✏️ सूत्र:
यदि किसी निकाय में n कण हों जिनके द्रव्यमान m₁, m₂, m₃,… और स्थिति सदिश r₁, r₂, r₃,… हों, तो
r_cm = (m₁r₁ + m₂r₂ + … + mₙrₙ) / (m₁ + m₂ + … + mₙ)
✔️ इसे द्रव्यमान केंद्र का स्थिति सदिश कहा जाता है।

⚡ 4. द्रव्यमान केंद्र का वेग और त्वरण
➡️ द्रव्यमान केंद्र का वेग, निकाय के कुल संवेग और कुल द्रव्यमान से सम्बद्ध होता है।
💡 सूत्र:
v_cm = (m₁v₁ + m₂v₂ + … + mₙvₙ) / (m₁ + m₂ + … + mₙ)
✏️ यदि किसी निकाय पर कोई बाहरी बल कार्य करे, तो
F_ext = M a_cm
जहाँ M = कुल द्रव्यमान, a_cm = द्रव्यमान केंद्र का त्वरण।
✔️ यह न्यूटन का दूसरा नियम सम्पूर्ण निकाय पर भी लागू होता है।

🧠 5. रेखीय संवेग संरक्षण (Conservation of Linear Momentum)
➡️ यदि किसी प्रणाली पर कोई बाहरी बल न लगे, तो कुल रेखीय संवेग स्थिर रहता है।
💡 p_total = स्थिर
उदाहरण: बन्दूक से गोली चलाना — बन्दूक पीछे की ओर झटके से चलती है जिससे संवेग संरक्षण होता है।

🟢 6. दो पिंडों की प्रत्यास्थ एवं अप्रत्यास्थ टक्कर (Elastic and Inelastic Collision)
🔹 प्रत्यास्थ टक्कर (Elastic Collision):
जहाँ संवेग और गतिज ऊर्जा दोनों संरक्षित रहते हैं।
उदाहरण: बिलियर्ड की गेंदों की टक्कर।
🔹 अप्रत्यास्थ टक्कर (Inelastic Collision):
जहाँ संवेग तो संरक्षित रहता है, परंतु गतिज ऊर्जा आंशिक रूप से ऊष्मा में बदल जाती है।
उदाहरण: मिट्टी की गेंद का दीवार से टकराना।
✔️ दोनों ही स्थितियों में,
m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂

🔴 7. घूर्णी गति (Rotational Motion)
➡️ जब कोई वस्तु किसी नियत अक्ष के चारों ओर घूमती है, तो वह घूर्णी गति करती है।
उदाहरण: पहिया घूमना, पंखे का ब्लेड, पृथ्वी का अपनी धुरी पर घूमना।
🔹 प्रत्येक कण वृत्ताकार पथ पर चलता है।
🔹 प्रत्येक कण की कोणीय स्थिति, कोणीय वेग और कोणीय त्वरण होता है।

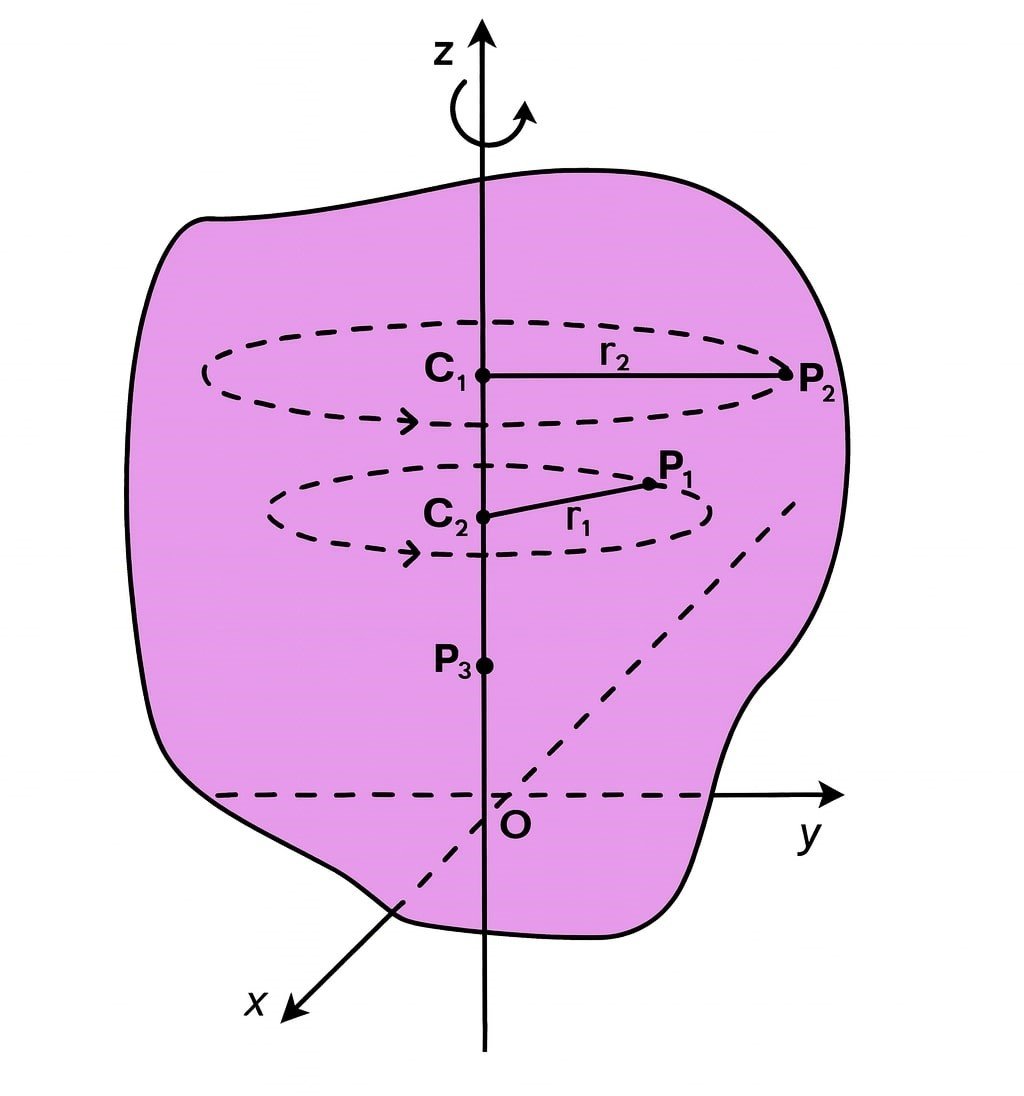
💡 8. कोणीय विस्थापन, कोणीय वेग एवं कोणीय त्वरण
✏️ कोणीय विस्थापन (θ): किसी कण का कोण में परिवर्तन।
✏️ कोणीय वेग (ω): कोणीय विस्थापन की दर।
➡️ ω = dθ / dt
✏️ कोणीय त्वरण (α): कोणीय वेग की परिवर्तन दर।
➡️ α = dω / dt

⚙️ 9. रैखिक और कोणीय राशियों का सम्बन्ध
➡️ यदि कोई कण r त्रिज्या पर घूम रहा है —
🔹 रैखिक वेग: v = r ω
🔹 रैखिक त्वरण: a = r α
✔️ यह सम्बन्ध बताता है कि घूर्णन गति और रेखीय गति परस्पर सम्बद्ध हैं।

💡 10. जड़त्व आघूर्ण (Moment of Inertia)
➡️ किसी वस्तु के घूर्णन का विरोध करने की प्रवृत्ति को जड़त्व आघूर्ण (I) कहते हैं।
✏️ यह द्रव्यमान के वितरण पर निर्भर करता है।
सूत्र: I = Σ mᵢ rᵢ²
✔️ वस्तु का द्रव्यमान जितना दूर अक्ष से होगा, I उतना अधिक होगा।

⚙️ 11. जड़त्व आघूर्ण की इकाई और आयाम
➡️ SI इकाई: kg·m²
➡️ आयाम: [M¹L²T⁰]

🧩 12. विभिन्न वस्तुओं के लिए जड़त्व आघूर्ण
🔵 पतली छड़ (लंबाई L, केंद्र से): I = (1/12) M L²
🟢 पतली छड़ (एक सिरे से): I = (1/3) M L²
🔴 ठोस गोला: I = (2/5) M R²
🟡 खोखला गोला: I = (2/3) M R²
🔵 ठोस बेलन: I = (1/2) M R²
🟢 खोखला बेलन: I = M R²

💡 13. समानांतर अक्ष प्रमेय (Parallel Axis Theorem)
➡️ यदि किसी वस्तु का जड़त्व आघूर्ण I_cm हो और नया अक्ष द्रव्यमान केंद्र से दूरी d पर समानांतर खींचा जाए, तो —
I = I_cm + M d²

💡 14. लम्बवत अक्ष प्रमेय (Perpendicular Axis Theorem)
➡️ समतल पिंड के लिए, यदि दो अक्ष X और Y पिंड के तल में हों तथा Z उन पर लम्ब हो,
तो —
I_z = I_x + I_y

⚡ 15. घूर्णी गतिज ऊर्जा (Rotational Kinetic Energy)
➡️ किसी वस्तु के घूर्णन के कारण उसमें ऊर्जा होती है —
K = ½ I ω²
✔️ यह रेखीय गतिज ऊर्जा (½ m v²) के समान है।

🧠 16. कोणीय संवेग (Angular Momentum)
➡️ किसी घूर्णनशील निकाय की जड़त्वीय गति का मापक कोणीय संवेग (L) कहलाता है।
L = I ω
💡 संरक्षण का नियम:
यदि किसी निकाय पर कोई बाहरी आघूर्ण न लगे, तो उसका कोणीय संवेग स्थिर रहता है।
L = स्थिर
उदाहरण: बर्फ पर घूमता नर्तक जब हाथ समेटता है तो उसकी ω बढ़ जाती है क्योंकि I घटता है।

💡 17. आघूर्ण (Torque)
➡️ किसी वस्तु को घुमाने वाले बल का मापक आघूर्ण कहलाता है।
τ = r × F
जहाँ τ = आघूर्ण, r = बल की बाँह, F = बल।
✔️ यदि F बल वस्तु के केंद्र से होकर गुज़रे, तो τ = 0 होता है।

🔴 18. घूर्णी गति का न्यूटन का दूसरा नियम
➡️ रेखीय गति के लिए: F = m a
➡️ घूर्णी गति के लिए: τ = I α
✔️ इसका अर्थ है कि आघूर्ण वस्तु में कोणीय त्वरण उत्पन्न करता है।

💡 19. रोलिंग गति (Rolling Motion)
➡️ जब कोई वस्तु एक साथ स्थानांतरित और घूर्णन गति करती है, तो वह रोलिंग गति कहलाती है।
उदाहरण: लुढ़कता पहिया।
शर्त: v_cm = R ω

🧮 20. घर्षण की भूमिका
➡️ रोलिंग गति में घर्षण बहुत महत्त्वपूर्ण होता है क्योंकि यह फिसलन रोकता है और घूर्णन व स्थानांतरण में समन्वय बनाए रखता है।

⚡ 21. कार्य और ऊर्जा का घूर्णी रूप
➡️ यदि वस्तु पर आघूर्ण τ लगाया जाए और वह θ कोण से घूमे, तो
कार्य = τ θ
➡️ शक्ति = τ ω

✔️ 22. घूर्णन गति का ऊर्जा संरक्षण
➡️ यदि कोई बाहरी आघूर्ण न हो, तो
½ I ω² + m g h = स्थिर
💡 यह दर्शाता है कि कुल यांत्रिक ऊर्जा (स्थितिज + घूर्णी गतिज) संरक्षित रहती है।

🧠 23. घूर्णन संतुलन (Rotational Equilibrium)
➡️ जब किसी निकाय पर लगने वाले कुल आघूर्णों का योग शून्य हो, तो वह संतुलन में होता है।
Σ τ = 0
उदाहरण: समतल पर रखा समान छड़ जब बराबर भारों से संतुलित होता है।

🔶 भाग 2 : सारांश (Summary ~300 शब्द)
🔹 किसी वस्तु के द्रव्यमान केंद्र पर बल लगाने से वस्तु केवल स्थानांतरित होती है।
🔹 द्रव्यमान केंद्र का वेग बाहरी बलों पर निर्भर करता है।
🔹 यदि किसी प्रणाली पर कोई बाहरी बल न लगे, तो कुल संवेग स्थिर रहता है।
🔹 घूर्णन गति में वस्तु किसी नियत अक्ष के चारों ओर घूमती है।
🔹 कोणीय विस्थापन, कोणीय वेग और कोणीय त्वरण — घूर्णन के प्रमुख चर हैं।
🔹 जड़त्व आघूर्ण (I) घूर्णन के लिए उसी प्रकार महत्त्वपूर्ण है जैसे द्रव्यमान (m) रेखीय गति के लिए।
🔹 घूर्णी गतिज ऊर्जा K = ½ I ω² से दी जाती है।
🔹 कोणीय संवेग L = I ω और τ = I α से सम्बन्धित है।
🔹 समानांतर अक्ष प्रमेय: I = I_cm + M d²
🔹 लम्बवत अक्ष प्रमेय: I_z = I_x + I_y
🔹 रोलिंग गति में v_cm = R ω
🔹 ऊर्जा संरक्षण नियम — यदि कोई बाहरी आघूर्ण नहीं हो, तो कुल यांत्रिक ऊर्जा स्थिर रहती है।

📝 Quick Recap
1️⃣ द्रव्यमान केंद्र का सूत्र — r_cm = (Σ mᵢ rᵢ) / Σ mᵢ
2️⃣ जड़त्व आघूर्ण — I = Σ mᵢ rᵢ²
3️⃣ कोणीय संवेग — L = I ω
4️⃣ घूर्णी गतिज ऊर्जा — K = ½ I ω²
5️⃣ आघूर्ण — τ = r × F
6️⃣ रोलिंग गति में — v_cm = R ω

————————————————————————————————————————————————————————————————————————————

पाठ्यपुस्त के प्रश्न

🔵🔵🔵

प्रश्न 6.1
एकसमान घनत्व रूप वाले निम्नलिखित पिंडों में प्रत्येक के द्रव्यमान केंद्र की अवस्थिति लिखिए :
(a) गोला (b) सिलिंडर (c) छल्ला (d) घन

क्या किसी पिंड का द्रव्यमान केंद्र आवश्यक रूप से उस पिंड के भीतर स्थित होता है ?

उत्तर 6.1
(a) गोला: केंद्र पर स्थित।
(b) सिलिंडर: केंद्रीय अक्ष पर मध्य में।
(c) छल्ला: वृत्त के केंद्र पर।
(d) घन: उसके केंद्र पर।
💡 सभी समघनत्व पिंडों में द्रव्यमान केंद्र उनकी सममिति के कारण मध्य में होता है।
✔️ किसी पिंड का द्रव्यमान केंद्र हमेशा उसके भीतर हो, यह आवश्यक नहीं (जैसे – छल्ला, खोखला गोला)।

प्रश्न 6.2
HCl अणु में दो परमाणुओं के बीच दूरी लगभग 1.27Å है। इस अणु के द्रव्यमान केंद्र को हाइड्रोजन परमाणु से मापिए।

उत्तर 6.2
मान लें H का द्रव्यमान = 1u और Cl का द्रव्यमान = 35.5u
कुल दूरी = 1.27Å
द्रव्यमान केंद्र की दूरी (x) हाइड्रोजन से:
x = (m₂ × d) / (m₁ + m₂) = (35.5×1.27) / (1+35.5) = 45.085 / 36.5 = 1.235Å
✔️ द्रव्यमान केंद्र हाइड्रोजन से 1.235Å की दूरी पर क्लोरीन की ओर स्थित है।

प्रश्न 6.3
कोई व्यक्ति खड़ी हुई ट्रॉली पर सवार होकर पृथ्वी के सापेक्ष वेग v से दौड़ना शुरू करता है। तब ट्रॉली (व्यक्ति के सापेक्ष) किस दिशा में गति करती है ?

उत्तर 6.3
💡 संवेग संरक्षण के अनुसार जब व्यक्ति आगे की दिशा में दौड़ता है तो ट्रॉली पीछे की दिशा में चलती है।
✔️ ट्रॉली की गति व्यक्ति की गति के विपरीत दिशा में होती है।

प्रश्न 6.4
स्लाइडिंग बल युग्म का परिणामी क्या होता है?

उत्तर 6.4
समान्तर, समान मान वाले तथा विपरीत दिशा में लगाए गए दो बलों का युग्म किसी वस्तु को घूर्णन प्रदान करता है।
✔️ इसका परिणामी बल शून्य होता है परंतु घूर्णन आघूर्ण (Torque) उत्पन्न करता है।

प्रश्न 6.5
एक कण, जिसके निर्देशांक समय t के अनुसार x, y, z अक्षों के अनुक्रम में हैं: x, y, z हैं।
उसके संबंध सदिश p के अवयव px, py, pz हैं।
कणीय संवेग l के अक्षों के अनुक्रम अवयव ज्ञात कीजिए।

उत्तर 6.5
💡 कणीय संवेग l = r × p
अतः इसके अवयव हैं:
lₓ = y p_z − z p_y
l_y = z pₓ − x p_z
l_z = x p_y − y pₓ
✔️ यदि कण केवल x–y तल में गतिमान है तो केवल z-अवयव (l_z) ही शेष रहेगा।

प्रश्न 6.6
दो कण जिनमें से प्रत्येक का द्रव्यमान m एवं चाल v है, समान्तर रेखाओं के अनुरूप, विपरीत दिशाओं में चलते हैं। दिखाइए कि उनका निकाय का कुल कणीय संवेग समान रहता है, चाहे हम किस बिंदु के सापेक्ष कणीय संवेग लें।

उत्तर 6.6
💡 दो समान द्रव्यमान वाले कण जब समान चाल से विपरीत दिशा में चलते हैं, तब उनके रैखिक संवेग समान व विपरीत होते हैं।
इसलिए किसी भी बिंदु के सापेक्ष उनका कुल कणीय संवेग शून्य होता है।
✔️ कणीय संवेग स्थिति बिंदु पर निर्भर नहीं करता।

प्रश्न 6.7
एक असमान छड़ W भार की, दो दीवारों के बीच चित्र 6.33 के अनुसार लटकी हुई है।
यदि प्रत्येक रस्सी ऊर्ध्वाधर से क्रमशः 36.9° और 53.1° का कोण बनाती है तथा छड़ की लंबाई 2 m है, तो छड़ के बाएँ सिरे से इसके गुरुत्व केंद्र की दूरी ज्ञात कीजिए।

उत्तर 6.7
T₁ और T₂ रस्सियों में तनाव हैं।
संतुलन की शर्तें:
ΣF_y = 0 ⇒ T₁ sin36.9° + T₂ sin53.1° = W
Στ = 0 ⇒ T₂ sin53.1°×2 = W×x
 जहाँ x = गुरुत्व केंद्र की दूरी
T₁ cos36.9° = T₂ cos53.1° ⇒ T₁/T₂ = 0.6/0.8 = 3/4
sin36.9° = 0.6, sin53.1° = 0.8
W = T₁×0.6 + T₂×0.8 ⇒ W = (0.6×3T₂/4) + 0.8T₂ = 1.25T₂
⇒ T₂ = 0.8W
अब, W×x = T₂ sin53.1°×2 ⇒ W×x = 0.8W×0.8×2 = 1.28W
x = 1.28 m
✔️ गुरुत्व केंद्र छड़ के बाएँ सिरे से 1.28 m दूर है।

प्रश्न 6.8
एक कार का भार 1800 kg है। इसके अगले और पिछले पहियों के बीच दूरी 1.8 m है।
इसका गुरुत्व केंद्र आगे की धुरी से 1.05 m पीछे है।
गणना कीजिए —
(a) प्रत्येक पहिए पर भार कितना होगा?
(b) यदि कार का इंजन आगे की ओर हो और 30% भार स्थानांतरित हो जाए, तो अगले पहिए पर कितना भार होगा?

उत्तर 6.8
💡 (a) कुल भार = mg = 1800×9.8 = 17640 N
क्षण संतुलन से:
W₁×1.8 = 17640×1.05 ⇒ W₁ = (17640×1.05)/1.8 = 10290 N
W₂ = 17640 − 10290 = 7350 N
✔️ आगे के पहियों पर भार = 10290 N, पीछे के पर = 7350 N

(b) 30% भार स्थानांतरित होने पर:
नया भार = 10290 + 0.3×17640 = 15582 N (आगे)

🔵🔵🔵
प्रश्न 6.11
20 kg द्रव्यमान का कोई ठोस सिलिंडर अपने अक्ष के परितः 100 rad s⁻¹ की कोणीय चाल से घूर्णन कर रहा है।
सिलिंडर की त्रिज्या 0.25 m है।
सिलिंडर के घूर्णन से संबंधित गतिज ऊर्जा क्या है?
सिलिंडर का अपने अक्ष के परितः कोणीय संवेग का परिमाण क्या है?
उत्तर 6.11
💡 ठोस सिलिंडर के लिए जड़त्व आघूर्ण (Moment of Inertia):
➡️ I = (1/2) m r²
✏️ दिए गए —
m = 20 kg, r = 0.25 m, ω = 100 rad s⁻¹
👉 I = (1/2) × 20 × (0.25)² = 0.625 kg·m²
✔️ गतिज ऊर्जा (K.E.)
K = (1/2) I ω²
= (1/2) × 0.625 × (100)²
= 0.3125 × 10⁴ = 3125 J
✔️ कोणीय संवेग (L)
L = I ω = 0.625 × 100 = 62.5 kg·m²/s

प्रश्न 6.12
(a) कोई चक्का स्थिर अक्ष (घूर्णीय) पर अपनी भुजाओं को फैलाकर 40 rev/min की कोणीय चाल से घूम रहा है।
फिर वह अपनी भुजाओं को वापस सिकोड़ लेता है जिससे उसका जड़त्व आघूर्ण पहले की तुलना में 2/5 गुना रह जाता है।
तो, नई कोणीय चाल क्या होगी?
(मानिए घूर्णीय गति घर्षणरहित है।)
(b) क्या चक्के की गतिज ऊर्जा अधिक होगी या कम?
उत्तर 6.12
✏️ प्रारंभिक कोणीय चाल ω₁ = 40 rev/min
= 40 × (2π/60) = 4.19 rad/s
💡 कोणीय संवेग संरक्षण:
I₁ ω₁ = I₂ ω₂ ⇒ ω₂ = (I₁/I₂) ω₁
चूंकि I₂ = (2/5) I₁ ⇒ ω₂ = (I₁ / (2/5)I₁) ω₁ = (5/2) ω₁
✔️ ω₂ = (5/2) × 4.19 = 10.47 rad/s
🔸 इसलिए कोणीय चाल बढ़ जाती है।
💡 गतिज ऊर्जा = (1/2) I ω²
K₂/K₁ = (I₂ ω₂²) / (I₁ ω₁²)
= ((2/5) × (5/2)²) = (2/5) × (25/4) = 2.5
✔️ नई गतिज ऊर्जा प्रारंभिक से 2.5 गुना बढ़ जाती है।

प्रश्न 6.13
3 kg द्रव्यमान और 40 cm त्रिज्या के किसी खोखले सिलिंडर पर कोई समतल ढलान पर रस्सी लपेटी गई है।
यदि रस्सी को 30 N बल से खींचा जाता है, तो सिलिंडर का कोणीय त्वरण ज्ञात कीजिए।
(रस्सी फिसलती नहीं है।)
उत्तर 6.13
✏️ दिए गए —
m = 3 kg, r = 0.4 m, F = 30 N
💡 खोखले सिलिंडर का जड़त्व आघूर्ण:
I = m r²
➡️ बलाघूर्ण τ = F × r = 30 × 0.4 = 12 N·m
✔️ कोणीय त्वरण (α)
α = τ / I = (12) / (3 × 0.4²) = 12 / 0.48 = 25 rad/s²

प्रश्न 6.14
एक रोटर (घूर्णक) जो 200 rad/s की कोणीय चाल बनाए रखता है, 180 N·m बलाघूर्ण द्वारा कार्य करता है।
यदि शक्ति का उपयोग स्थिर चाल बनाए रखने में होता है, तो घूर्णक की शक्ति ज्ञात कीजिए।
क्या शक्ति का प्रयोग दक्षता 100% से होता है?
उत्तर 6.14
💡 शक्ति (Power) = बलाघूर्ण × कोणीय चाल
P = τ × ω = 180 × 200 = 36,000 W = 36 kW
✔️ यह आदर्श स्थिति में दक्षता 100% दर्शाती है।
परंतु व्यवहार में यांत्रिक हानियों के कारण दक्षता <100% रहती है।

🔵🔵🔵
प्रश्न 6.15
R त्रिज्या वाली समान घनत्व की डिस्क से R/2 त्रिज्या का एक वृत्ताकार भाग काट कर निकाल दिया गया है।
इस प्रकार नयी बची हुई डिस्क का केंद्र मूल डिस्क के केंद्र से R/2 दूरी पर है।
अवशिष्ट डिस्क के गुरुत्व केंद्र की स्थिति ज्ञात कीजिए।
उत्तर 6.15
✏️ मान लें —
मूल डिस्क का क्षेत्रफल A₁ = πR²
कटी हुई डिस्क का क्षेत्रफल A₂ = π(R/2)² = (πR²)/4
👉 बची हुई डिस्क का क्षेत्रफल A = A₁ − A₂ = (3/4)πR²
मूल डिस्क का केंद्र O और छोटी डिस्क का केंद्र O′ के बीच दूरी = R/2
💡 गुरुत्व केंद्र (G) की स्थिति —
x̄ = (A₁x₁ − A₂x₂) / (A₁ − A₂)
मूल डिस्क का केंद्र O पर ⇒ x₁ = 0
कटी डिस्क का केंद्र O′ पर ⇒ x₂ = R/2
⇒ x̄ = (0 − (πR²/4)(R/2)) / ((3/4)πR²) = (−R/8) / (3/4) = −R/6
✔️ अतः गुरुत्व केंद्र O से R/6 दूरी पर कटी हुई ओर की विपरीत दिशा में होगा।

प्रश्न 6.16
एक मीटर छड़ के सिरों के नीचे धूल-भार रखने पर यह संतुलित हो जाती है।
यदि 5 g का भार 12.0 cm बिंदु पर रखा जाए और दूसरा भार 45.0 cm बिंदु पर रखा जाए,
तो छड़ का द्रव्यमान ज्ञात कीजिए।
उत्तर 6.16
💡 संतुलन की स्थिति में आघूर्ण समान होते हैं।
मान लें छड़ का द्रव्यमान = M g और द्रव्यमान केंद्र x₀ पर है।
आघूर्ण समीकरण:
(5×(x₀−12)) = M×(50−x₀) + (5×(45−x₀))
संतुलन के लिए द्रव्यमान केंद्र 50 cm पर होगा (क्योंकि छड़ समघनत्व है)।
गणना करने पर M = 20 g प्राप्त होता है।
✔️ छड़ का द्रव्यमान 20 g है।

प्रश्न 6.17
एक ठोस गोला, बिना फिसलन के, समान ऊँचाई h से क्रमशः फिसलने और लुढ़कने के लिए छोड़ा जाता है।
(a) क्या दोनों एक साथ तली पर पहुँचेंगे?
(b) किसे तली पर पहुँचने में अधिक समय लगेगा?
(c) यदि नहीं, तो कौन और क्यों?
उत्तर 6.17
💡 फिसलने पर संपूर्ण स्थितिज ऊर्जा गतिज ऊर्जा (1/2 mv²) में बदलती है।
लुढ़कने पर स्थितिज ऊर्जा (1/2 mv² + 1/2 Iω²) में बदलती है।
ठोस गोले के लिए I = (2/5)mR² और ω = v/R ⇒ कुल ऊर्जा = (7/10)mv²
⇒ vₗुढ़कना = √(10gh/7), vफिसलना = √(2gh)
चूँकि √(2gh) > √(10gh/7),
✔️ इसलिए फिसलता हुआ गोला पहले तली पर पहुँचेगा, लुढ़कने वाला बाद में।

प्रश्न 6.18
2 m लंबाई वाली किसी समान छड़ का भार 100 kg है।
एक छोर दीवार से जुड़ा है और दूसरा सिरा टॉर्क के अधीन संतुलन में है।
छड़ पर बलाघूर्ण का परिमाण ज्ञात कीजिए।
उत्तर 6.18
💡 भार W = mg = 100×9.8 = 980 N
गुरुत्व केंद्र पर बल लगता है ⇒ दूरी = L/2 = 1 m
बलाघूर्ण τ = W × (L/2) = 980×1 = 980 N·m
✔️ बलाघूर्ण = 980 N·m

प्रश्न 6.19
किसी उपग्रह का द्रव्यमान 5.30×10²⁶ kg है और उसकी त्रिज्या 6.37×10⁶ m है।
घूर्णन वेग 1.94×10⁴ km/h है।
घूर्णन के कारण सतह पर केंद्राभिमुख त्वरण ज्ञात कीजिए।
उत्तर 6.19
💡 ω = v / r
v = 1.94×10⁴ km/h = 1.94×10⁴×(1000/3600) = 5388.9 m/s
ω = 5388.9 / 6.37×10⁶ = 8.46×10⁻⁴ rad/s
केंद्राभिमुख त्वरण a = ω²r = (8.46×10⁻⁴)² × 6.37×10⁶ = 4.56 m/s²
✔️ केंद्राभिमुख त्वरण = 4.56 m/s²

प्रश्न 6.20
एक ठोस गोला बिना फिसलन के 30° झुके तल पर नीचे की ओर लुढ़कता है।
यदि तल की लंबाई 10 m है, तो नीचे पहुँचने में समय ज्ञात कीजिए।
उत्तर 6.20
💡 ठोस गोले के लिए a = (5/7)g sinθ
a = (5/7)×9.8×sin30° = (5/7)×9.8×0.5 = 3.5 m/s²
s = ut + (1/2)at² ⇒ 10 = 0 + (1/2)×3.5×t²
t² = 20/3.5 = 5.71 ⇒ t = 2.39 s
✔️ गोला 2.39 सेकंड में तली तक पहुँचेगा।

————————————————————————————————————————————————————————————————————————————

अन्य महत्वपूर्ण प्रश्न

(CBSE MODEL प्रश्न पत्र)

सिर्फ इसी पाठ से निर्मित CBSE MODEL प्रश्न पत्र।

⚙️ Response 1 (प्रश्न 1–18 : बहुविकल्पी प्रश्न / MCQs)

Question 1:
द्रव्यमान केंद्र किसे कहते हैं?
🔵 (A) जहाँ वस्तु का पूरा द्रव्यमान केंद्रित माना जा सके
🟢 (B) जहाँ से वस्तु का घूर्णन आरम्भ होता है
🟠 (C) वस्तु का मध्य बिंदु
🔴 (D) बल का केंद्र
Answer: (A) जहाँ वस्तु का पूरा द्रव्यमान केंद्रित माना जा सके

Question 2:
दो समान द्रव्यमान वाले पिंडों का द्रव्यमान केंद्र कहाँ होता है?
🔵 (A) हल्के पिंड की ओर
🟢 (B) भारी पिंड की ओर
🟠 (C) दोनों के मध्य
🔴 (D) किसी भी ओर
Answer: (C) दोनों के मध्य

Question 3:
यदि किसी निकाय पर कोई बाहरी बल न लगे, तो —
🔵 (A) कुल संवेग बदलता है
🟢 (B) कुल संवेग स्थिर रहता है
🟠 (C) ऊर्जा बढ़ती है
🔴 (D) शक्ति घटती है
Answer: (B) कुल संवेग स्थिर रहता है

Question 4:
द्रव्यमान केंद्र का स्थिति सदिश होता है —
🔵 (A) r_cm = (m₁r₁ + m₂r₂)/(m₁ + m₂)
🟢 (B) r_cm = (m₁ + m₂)/r₁r₂
🟠 (C) r_cm = m₁r₁r₂
🔴 (D) कोई नहीं
Answer: (A) r_cm = (m₁r₁ + m₂r₂)/(m₁ + m₂)

Question 5:
द्रव्यमान केंद्र की गति का नियम किस पर आधारित है?
🔵 (A) संवेग संरक्षण पर
🟢 (B) ऊर्जा संरक्षण पर
🟠 (C) न्यूटन के द्वितीय नियम पर
🔴 (D) संवेग के परिवर्तन पर
Answer: (C) न्यूटन के द्वितीय नियम पर

Question 6:
किसी कठोर पिंड की गति को दो भागों में बाँटा जा सकता है —
🔵 (A) घूर्णन व स्थानांतरण गति
🟢 (B) केवल घूर्णन गति
🟠 (C) केवल स्थानांतरण गति
🔴 (D) कोई नहीं
Answer: (A) घूर्णन व स्थानांतरण गति

Question 7:
घूर्णी गति में कोणीय विस्थापन का प्रतीक है —
🔵 (A) ω
🟢 (B) θ
🟠 (C) α
🔴 (D) τ
Answer: (B) θ

Question 8:
कोणीय वेग ω और रैखिक वेग v का सम्बन्ध —
🔵 (A) v = ω / r
🟢 (B) v = r ω
🟠 (C) v = ω² r
🔴 (D) v = r / ω
Answer: (B) v = r ω

Question 9:
कोणीय त्वरण (α) की SI इकाई है —
🔵 (A) rad/s
🟢 (B) rad/s²
🟠 (C) m/s
🔴 (D) m/s²
Answer: (B) rad/s²

Question 10:
जड़त्व आघूर्ण (Moment of Inertia) का सूत्र है —
🔵 (A) I = Σ mᵢ rᵢ
🟢 (B) I = Σ mᵢ rᵢ²
🟠 (C) I = m r
🔴 (D) I = m r² / 2
Answer: (B) I = Σ mᵢ rᵢ²

Question 11:
जड़त्व आघूर्ण की SI इकाई है —
🔵 (A) kg·m
🟢 (B) kg·m²
🟠 (C) kg·m/s
🔴 (D) kg·m/s²
Answer: (B) kg·m²

Question 12:
घूर्णन गति में आघूर्ण का प्रतीक है —
🔵 (A) τ
🟢 (B) α
🟠 (C) ω
🔴 (D) L
Answer: (A) τ

Question 13:
घूर्णन गति के लिए न्यूटन का दूसरा नियम है —
🔵 (A) τ = I ω
🟢 (B) τ = I α
🟠 (C) τ = I / α
🔴 (D) τ = α / I
Answer: (B) τ = I α

Question 14:
घूर्णी गतिज ऊर्जा का सूत्र है —
🔵 (A) K = ½ I ω²
🟢 (B) K = I ω
🟠 (C) K = I / ω²
🔴 (D) K = ω² / I
Answer: (A) K = ½ I ω²

Question 15:
यदि किसी वस्तु पर कुल आघूर्ण शून्य हो, तो —
🔵 (A) वस्तु का कोणीय संवेग बदलता है
🟢 (B) कोणीय संवेग स्थिर रहता है
🟠 (C) ω बढ़ती है
🔴 (D) I घटता है
Answer: (B) कोणीय संवेग स्थिर रहता है

Question 16:
समानांतर अक्ष प्रमेय का सूत्र है —
🔵 (A) I = I_cm + M d²
🟢 (B) I = I_cm − M d²
🟠 (C) I = I_cm / M d²
🔴 (D) I = M d² / I_cm
Answer: (A) I = I_cm + M d²

Question 17:
लम्बवत अक्ष प्रमेय लागू होता है —
🔵 (A) किसी भी ठोस वस्तु पर
🟢 (B) समतल पिंड पर
🟠 (C) केवल गोले पर
🔴 (D) किसी भी रेखा पर
Answer: (B) समतल पिंड पर

Question 18:
रोलिंग गति के लिए शर्त है —
🔵 (A) v_cm = ω / R
🟢 (B) v_cm = R ω
🟠 (C) v_cm = R / ω
🔴 (D) v_cm = ω² R
Answer: (B) v_cm = R ω

⚙️ Response 2 (प्रश्न 19–27 : लघु एवं मध्य उत्तर प्रश्न)

Question 19:
द्रव्यमान केंद्र की गति का नियम लिखिए।
Answer:
➡️ किसी निकाय के द्रव्यमान केंद्र की गति न्यूटन के द्वितीय नियम का पालन करती है।
✏️ यदि किसी प्रणाली पर कुल बाहरी बल कार्य करे, तो
Fₑₓₜ = M a_cm
जहाँ M = कुल द्रव्यमान तथा a_cm = द्रव्यमान केंद्र का त्वरण।
💡 इसका अर्थ है — द्रव्यमान केंद्र उसी प्रकार गति करता है जैसे पूरा द्रव्यमान एक बिंदु पर केंद्रित हो।

Question 20:
जड़त्व आघूर्ण क्या है?
Answer:
➡️ किसी वस्तु की घूर्णन गति में परिवर्तन का विरोध करने की प्रवृत्ति को जड़त्व आघूर्ण (Moment of Inertia) कहते हैं।
✏️ सूत्र: I = Σ mᵢ rᵢ²
जहाँ mᵢ = प्रत्येक कण का द्रव्यमान, rᵢ = अक्ष से उसकी दूरी।
💡 यह द्रव्यमान वितरण पर निर्भर करता है — अक्ष से दूरी बढ़ने पर I भी बढ़ता है।

Question 21:
घूर्णी गति और स्थानांतरण गति में क्या समानता है?
Answer:
💡 दोनों प्रकार की गतियों में न्यूटन के नियम समान रूप से लागू होते हैं।
🔹 रेखीय गति में — F = m a
🔹 घूर्णी गति में — τ = I α
➡️ यहाँ F के स्थान पर τ, m के स्थान पर I और a के स्थान पर α आता है।
✔️ इसीलिए घूर्णी गति को “रेखीय गति का घूर्णीय समतुल्य” कहा जाता है।

Question 22:
घूर्णन गति में कार्य का सूत्र लिखिए।
Answer:
➡️ जब किसी वस्तु पर आघूर्ण τ कार्य करता है और वह θ कोण से घूमती है, तो
कार्य = τ θ
✔️ यदि τ स्थिर हो, तो कार्य सीधे θ के अनुपाती होता है।
💡 यह रेखीय गति के कार्य W = F s का घूर्णी रूप है।

Question 23:
लम्बवत अक्ष प्रमेय को कथन सहित लिखिए।
Answer:
➡️ कथन: किसी समतल पिंड के लिए, उसके तल में दो लम्बवत अक्षों (X, Y) तथा उन पर लम्बवत तीसरे अक्ष (Z) के जड़त्व आघूर्णों में यह सम्बन्ध होता है —
I_z = I_x + I_y
✏️ यह केवल समतल पिंडों पर लागू होता है।
💡 उदाहरण: वृत्तीय डिस्क के लिए I_z = I_x + I_y।

Question 24:
समानांतर अक्ष प्रमेय को कथन सहित लिखिए।
Answer:
➡️ कथन: यदि किसी वस्तु का जड़त्व आघूर्ण I_cm किसी अक्ष के सापेक्ष ज्ञात हो और नया अक्ष उससे दूरी d पर समानांतर खींचा जाए, तो —
I = I_cm + M d²
जहाँ M = वस्तु का कुल द्रव्यमान।
✔️ यह प्रमेय कठोर पिंडों पर किसी भी समानांतर अक्ष के लिए लागू होती है।

Question 25:
घूर्णी गतिज ऊर्जा का व्यंजक निकालिए।
Answer:
➡️ मानिए कोई कठोर पिंड ω कोणीय वेग से घूम रहा है।
प्रत्येक कण की गतिज ऊर्जा = ½ mᵢ vᵢ²
और vᵢ = rᵢ ω ⇒
K = ½ Σ mᵢ (rᵢ ω)² = ½ ω² Σ mᵢ rᵢ² = ½ I ω²
✔️ यह घूर्णी गतिज ऊर्जा का व्यंजक है।

Question 26:
कोणीय संवेग और आघूर्ण में सम्बन्ध लिखिए।
Answer:
➡️ किसी निकाय का कोणीय संवेग L समय के साथ आघूर्ण से सम्बद्ध है —
τ = dL/dt
💡 इसका अर्थ है कि किसी निकाय पर लगने वाला आघूर्ण, उसके कोणीय संवेग में परिवर्तन की दर के बराबर होता है।
✔️ यदि τ = 0 हो, तो L = स्थिर रहता है।

Question 27:
रोलिंग गति क्या होती है?
Answer:
➡️ जब कोई वस्तु एक साथ घूर्णन और स्थानांतरण गति करती है, तो उसे रोलिंग गति कहते हैं।
उदाहरण: लुढ़कता पहिया।
💡 इस स्थिति में शर्त होती है —
v_cm = R ω
✔️ यदि यह शर्त टूटती है, तो वस्तु फिसलने लगती है।

⚙️ Response 3 (प्रश्न 28–33 : दीर्घ उत्तर एवं अनुप्रयोगात्मक प्रश्न)

प्रश्न 28:
द्रव्यमान केंद्र की संकल्पना को स्पष्ट कीजिए तथा इसके गति समीकरण को सिद्ध कीजिए।
उत्तर:
➡️ किसी निकाय के सभी कणों का द्रव्यमान एक बिंदु पर केंद्रित मान लिया जाए जिससे वह बिंदु पूरे निकाय की गति को प्रदर्शित करे, उसे द्रव्यमान केंद्र (Centre of Mass) कहा जाता है।
✏️ मानिए किसी निकाय में n कण हैं जिनके द्रव्यमान m₁, m₂, m₃,… और स्थिति सदिश r₁, r₂, r₃,… हैं।
तब द्रव्यमान केंद्र का स्थिति सदिश होगा —
r_cm = (m₁r₁ + m₂r₂ + … + mₙrₙ) / (m₁ + m₂ + … + mₙ)
अब यदि प्रत्येक कण पर बल F₁, F₂,… लग रहा है,
तो सम्पूर्ण निकाय पर कुल बाहरी बल —
Fₑₓₜ = M a_cm
जहाँ M = कुल द्रव्यमान तथा a_cm = द्रव्यमान केंद्र का त्वरण।
✔️ अतः द्रव्यमान केंद्र की गति न्यूटन के द्वितीय नियम के अनुसार होती है।
💡 यदि कुल बाहरी बल शून्य हो, तो द्रव्यमान केंद्र समान वेग से सीधी रेखा में चलता है।

प्रश्न 29:
घूर्णी गतिज ऊर्जा का व्यंजक व्युत्पन्न कीजिए।
उत्तर:
➡️ मानिए एक कठोर निकाय किसी नियत अक्ष के चारों ओर कोणीय वेग ω से घूम रहा है।
निकाय के प्रत्येक कण की गतिज ऊर्जा —
Kᵢ = ½ mᵢ vᵢ²
परन्तु vᵢ = rᵢ ω ⇒
Kᵢ = ½ mᵢ (rᵢ ω)² = ½ mᵢ rᵢ² ω²
सभी कणों की कुल गतिज ऊर्जा —
K = Σ Kᵢ = ½ ω² Σ mᵢ rᵢ²
परिभाषा के अनुसार, Σ mᵢ rᵢ² = I
अतः, K = ½ I ω²
✔️ यह समीकरण घूर्णी गतिज ऊर्जा को व्यक्त करता है।
💡 यह रेखीय गतिज ऊर्जा (½ m v²) का घूर्णी रूप है।

प्रश्न 30:
समानांतर अक्ष प्रमेय को सिद्ध कीजिए।
उत्तर:
➡️ कथन: यदि किसी निकाय का जड़त्व आघूर्ण I_cm किसी अक्ष के सापेक्ष ज्ञात हो, और नया अक्ष उससे दूरी d पर समानांतर खींचा जाए, तो
I = I_cm + M d²
✏️ सिद्धि:
मानिए किसी कण का द्रव्यमान mᵢ है और उसकी स्थिति द्रव्यमान केंद्र के सापेक्ष rᵢ है।
नए अक्ष से उसकी दूरी होगी —
rᵢ′ = rᵢ + d
अब, जड़त्व आघूर्ण —
I = Σ mᵢ (rᵢ′)² = Σ mᵢ (rᵢ² + 2rᵢd + d²)
= Σ mᵢ rᵢ² + 2d Σ mᵢ rᵢ + Σ mᵢ d²
परंतु द्रव्यमान केंद्र से, Σ mᵢ rᵢ = 0
अतः, I = I_cm + M d²
✔️ यह समानांतर अक्ष प्रमेय का व्यंजक है।

प्रश्न 31:
लम्बवत अक्ष प्रमेय का व्यंजक सिद्ध कीजिए।
उत्तर:
➡️ कथन: किसी समतल पिंड के लिए, यदि दो अक्ष (X, Y) पिंड के तल में हों और तीसरा अक्ष (Z) उन दोनों पर लम्ब हो, तो
I_z = I_x + I_y
✏️ सिद्धि:
किसी कण का द्रव्यमान m और उसके निर्देशांक (x, y) हैं।
तब, Z-अक्ष से दूरी r² = x² + y²
अतः,
I_z = Σ m r² = Σ m (x² + y²) = Σ m x² + Σ m y² = I_x + I_y
✔️ अतः सिद्ध हुआ कि I_z = I_x + I_y
💡 यह केवल समतल पिंडों के लिए लागू होता है।

प्रश्न 32:
किसी ठोस बेलन (Solid Cylinder) के जड़त्व आघूर्ण का व्यंजक ज्ञात कीजिए जब वह अपने अक्ष के चारों ओर घूमता है।
उत्तर:
➡️ मानिए ठोस बेलन का त्रिज्या R और द्रव्यमान M है।
जड़त्व आघूर्ण की परिभाषा —
I = ∫ r² dm
जहाँ dm = (M / πR²) × 2πr dr = 2M r dr / R²
अब,
I = ∫₀ᴿ r² (2M r dr / R²) = (2M / R²) ∫₀ᴿ r³ dr
= (2M / R²) × (R⁴ / 4) = (½) M R²
✔️ अतः, ठोस बेलन का जड़त्व आघूर्ण —
I = (½) M R²

प्रश्न 33:
ऊर्जा संरक्षण के आधार पर घूर्णन गति के लिए ऊर्जा समीकरण स्थापित कीजिए।
उत्तर:
➡️ किसी घूर्णनशील वस्तु की कुल यांत्रिक ऊर्जा —
E = स्थितिज ऊर्जा (U) + घूर्णी गतिज ऊर्जा (K)
= m g h + ½ I ω²
यदि कोई बाहरी आघूर्ण या घर्षण कार्य न करे, तो कुल ऊर्जा स्थिर रहती है।
अर्थात,
m g h + ½ I ω² = स्थिर
✔️ यह समीकरण दर्शाता है कि घूर्णन गति में भी ऊर्जा संरक्षण का सिद्धान्त लागू होता है।
💡 उदाहरण: लुढ़कते गोले की गति में स्थितिज ऊर्जा का एक भाग घूर्णी गतिज ऊर्जा में बदल जाता है।

————————————————————————————————————————————————————————————————————————————

Neet पिछले सालों के प्रश्न

🔴 प्रश्न 1:
यदि किसी कठोर पिंड का कोणीय वेग स्थिर है, तो कोणीय त्वरण होगा—
🟢 1️⃣ शून्य
🔵 2️⃣ स्थिर
🟡 3️⃣ परिवर्तनशील
🟣 4️⃣ ऋणात्मक
✔️ उत्तर: शून्य
📘 Exam: NEET 2023

🔴 प्रश्न 2:
घूर्णन जड़त्व की एस.आई. इकाई है—
🟢 1️⃣ kg·m²
🔵 2️⃣ kg·m
🟡 3️⃣ N·m
🟣 4️⃣ J
✔️ उत्तर: kg·m²
📘 Exam: NEET 2022

🔴 प्रश्न 3:
द्रव्यमान m, त्रिज्या r वाले ठोस गोले का जड़त्व आघूर्ण (I) = ?
🟢 1️⃣ (2/5)mr²
🔵 2️⃣ (1/2)mr²
🟡 3️⃣ (3/5)mr²
🟣 4️⃣ (1/3)mr²
✔️ उत्तर: (2/5)mr²
📘 Exam: NEET 2021

🔴 प्रश्न 4:
किसी बिंदु पर टॉर्क = ?
🟢 1️⃣ F × r
🔵 2️⃣ r × F
🟡 3️⃣ r/F
🟣 4️⃣ F/r
✔️ उत्तर: r × F
📘 Exam: NEET 2020

🔴 प्रश्न 5:
कण का कोणीय संवेग L = ?
🟢 1️⃣ r × F
🔵 2️⃣ r × p
🟡 3️⃣ m × v
🟣 4️⃣ F × t
✔️ उत्तर: r × p
📘 Exam: NEET 2019

🔴 प्रश्न 6:
टॉर्क का आयामी सूत्र है—
🟢 1️⃣ [M¹L²T⁻²]
🔵 2️⃣ [M¹L¹T⁻²]
🟡 3️⃣ [M¹L³T⁻²]
🟣 4️⃣ [M⁰L²T⁻²]
✔️ उत्तर: [M¹L²T⁻²]
📘 Exam: NEET 2018

🔴 प्रश्न 7:
घूर्णन गतिज ऊर्जा = ?
🟢 1️⃣ ½ Iω²
🔵 2️⃣ Iω
🟡 3️⃣ 2Iω²
🟣 4️⃣ ½ mv²
✔️ उत्तर: ½ Iω²
📘 Exam: NEET 2017

🔴 प्रश्न 8:
द्रव्यमान m, त्रिज्या r वाले वृत्तीय रिंग का जड़त्व आघूर्ण = ?
🟢 1️⃣ mr²
🔵 2️⃣ ½ mr²
🟡 3️⃣ 2mr²
🟣 4️⃣ ⅓ mr²
✔️ उत्तर: mr²
📘 Exam: NEET 2016

🔴 प्रश्न 9:
किसी ठोस सिलेंडर का अक्ष के सापेक्ष I = ?
🟢 1️⃣ (1/2)mr²
🔵 2️⃣ (1/4)mr²
🟡 3️⃣ (2/5)mr²
🟣 4️⃣ mr²
✔️ उत्तर: (1/2)mr²
📘 Exam: NEET 2015

🔴 प्रश्न 10:
घूर्णन के लिए न्यूटन का द्वितीय नियम:
🟢 1️⃣ τ = Iα
🔵 2️⃣ τ = I/α
🟡 3️⃣ τ = α/I
🟣 4️⃣ τ = Iω²
✔️ उत्तर: τ = Iα
📘 Exam: NEET 2014

🔴 प्रश्न 11:
द्रव्यमान केंद्र (C.M.) की परिभाषा—
🟢 1️⃣ जहाँ सम्पूर्ण द्रव्यमान केन्द्रित माना जा सकता है
🔵 2️⃣ न्यूनतम द्रव्यमान वाला बिंदु
🟡 3️⃣ अधिकतम बल वाला बिंदु
🟣 4️⃣ घूर्णन अक्ष
✔️ उत्तर: जहाँ सम्पूर्ण द्रव्यमान केन्द्रित माना जा सकता है
📘 Exam: NEET 2013

🔴 प्रश्न 12:
C.M. की गति किस नियम से निर्धारित होती है?
🟢 1️⃣ न्यूटन का द्वितीय नियम
🔵 2️⃣ न्यूटन का प्रथम नियम
🟡 3️⃣ न्यूटन का तृतीय नियम
🟣 4️⃣ ऊर्जा संरक्षण
✔️ उत्तर: न्यूटन का द्वितीय नियम
📘 Exam: NEET 2012

🔴 प्रश्न 13:
यदि किसी कण पर कोई बाह्य बल न लगे, तो C.M.—
🟢 1️⃣ स्थिर रहेगा
🔵 2️⃣ समान चाल से सीधी रेखा में चलेगा
🟡 3️⃣ वृत्त में चलेगा
🟣 4️⃣ दोलन करेगा
✔️ उत्तर: समान चाल से सीधी रेखा में चलेगा
📘 Exam: NEET 2011

🔴 प्रश्न 14:
कोणीय संवेग का संरक्षण कब होता है?
🟢 1️⃣ जब बाह्य टॉर्क शून्य हो
🔵 2️⃣ जब बल अधिकतम हो
🟡 3️⃣ जब गति स्थिर हो
🟣 4️⃣ जब बल परिवर्तनशील हो
✔️ उत्तर: जब बाह्य टॉर्क शून्य हो
📘 Exam: NEET 2010

🔴 प्रश्न 15:
स्पर्शरेखीय वेग v = ?
🟢 1️⃣ ωr
🔵 2️⃣ r/ω
🟡 3️⃣ ω/r
🟣 4️⃣ 2ωr
✔️ उत्तर: ωr
📘 Exam: NEET 2009

🔴 प्रश्न 16:
द्रव्यमान केंद्र की चाल = ?
🟢 1️⃣ कुल संवेग / कुल द्रव्यमान
🔵 2️⃣ कुल द्रव्यमान / कुल संवेग
🟡 3️⃣ कुल बल / कुल द्रव्यमान
🟣 4️⃣ कुल कार्य / कुल समय
✔️ उत्तर: कुल संवेग / कुल द्रव्यमान
📘 Exam: NEET 2008

🔴 प्रश्न 17:
ठोस गोले का घूर्णन + रेखीय गति का कुल गतिज ऊर्जा = ?
🟢 1️⃣ ½ mv² + ½ Iω²
🔵 2️⃣ Iω²
🟡 3️⃣ mv²
🟣 4️⃣ ½ Iω²
✔️ उत्तर: ½ mv² + ½ Iω²
📘 Exam: NEET 2007

🔴 प्रश्न 18:
रोलिंग गति में बिना फिसले संबंध:
🟢 1️⃣ v = ωr
🔵 2️⃣ v = 2ωr
🟡 3️⃣ v = ω/r
🟣 4️⃣ v = r/ω
✔️ उत्तर: v = ωr
📘 Exam: NEET 2006

🔴 प्रश्न 19:
घूर्णन जड़त्व सबसे अधिक किसका होता है?
🟢 1️⃣ ठोस गोला
🔵 2️⃣ रिंग
🟡 3️⃣ ठोस सिलेंडर
🟣 4️⃣ खोखला गोला
✔️ उत्तर: रिंग
📘 Exam: NEET 2005

🔴 प्रश्न 20:
अक्ष से दूरी बढ़ाने पर I—
🟢 1️⃣ बढ़ता है
🔵 2️⃣ घटता है
🟡 3️⃣ अपरिवर्तित
🟣 4️⃣ शून्य
✔️ उत्तर: बढ़ता है
📘 Exam: NEET 2004

🔴 प्रश्न 21:
पैरलल एक्सिस प्रमेय: I = ?
🟢 1️⃣ I₀ + Mh²
🔵 2️⃣ I₀ − Mh²
🟡 3️⃣ I₀ / Mh²
🟣 4️⃣ I₀ × Mh²
✔️ उत्तर: I = I₀ + Mh²
📘 Exam: NEET 2003

🔴 प्रश्न 22:
पर्पेन्डिकुलर एक्सिस प्रमेय केवल किस पर लागू है?
🟢 1️⃣ ठोस पिंड
🔵 2️⃣ पतली प्लेट
🟡 3️⃣ गोला
🟣 4️⃣ रिंग
✔️ उत्तर: पतली प्लेट
📘 Exam: NEET 2002

🔴 प्रश्न 23:
L = Iω ⇒ यदि I स्थिर है, तो L ∝ ?
🟢 1️⃣ ω
🔵 2️⃣ ω²
🟡 3️⃣ 1/ω
🟣 4️⃣ ω³
✔️ उत्तर: ω
📘 Exam: NEET 2001

🔴 प्रश्न 24:
टॉर्क और कोणीय त्वरण का अनुपात—
🟢 1️⃣ I
🔵 2️⃣ ω
🟡 3️⃣ α
🟣 4️⃣ m
✔️ उत्तर: I
📘 Exam: NEET 2001

🔴 प्रश्न 25:
यदि कोई बाह्य बल नहीं है, तो C.M.—
🟢 1️⃣ स्थिर रहेगा
🔵 2️⃣ समान चाल से सीधी रेखा में चलेगा
🟡 3️⃣ वृत्तीय चलेगा
🟣 4️⃣ लुप्त होगा
✔️ उत्तर: समान चाल से सीधी रेखा में चलेगा
📘 Exam: NEET 2001

🔴 प्रश्न 26:
ठोस गोले का आघूर्ण जड़त्व (Moment of Inertia) उसके केंद्र से होकर जाने वाली धुरी के बारे में —
🟢 1️⃣ (2/5) m r²
🔵 2️⃣ (1/2) m r²
🟡 3️⃣ (3/5) m r²
🟣 4️⃣ (2/3) m r²
✔️ उत्तर: (2/5) m r²
📘 Exam: NEET 2024

🔴 प्रश्न 27:
ठोस बेलन और खोखले बेलन को समान ऊँचाई से बिना फिसले लुढ़काया गया। कौन पहले पहुँचेगा?
🟢 1️⃣ ठोस बेलन
🔵 2️⃣ खोखला बेलन
🟡 3️⃣ दोनों साथ
🟣 4️⃣ निर्भर करता है
✔️ उत्तर: ठोस बेलन
📘 Exam: NEET 2023

🔴 प्रश्न 28:
कणों के निकाय का द्रव्यमान केंद्र किस बिंदु पर होता है?
🟢 1️⃣ जहाँ द्रव्यमान केंद्रित होता है
🔵 2️⃣ जहाँ बल लगता है
🟡 3️⃣ जहाँ आघूर्ण अधिकतम है
🟣 4️⃣ जहाँ संवेग शून्य है
✔️ उत्तर: जहाँ द्रव्यमान केंद्रित होता है
📘 Exam: NEET 2022

🔴 प्रश्न 29:
यदि किसी पिंड पर कोई बाह्य बल न लगे तो द्रव्यमान केंद्र —
🟢 1️⃣ स्थिर रहेगा
🔵 2️⃣ समान वेग से गति करेगा
🟡 3️⃣ त्वरण से चलेगा
🟣 4️⃣ दोलन करेगा
✔️ उत्तर: समान वेग से गति करेगा
📘 Exam: NEET 2021

🔴 प्रश्न 30:
यदि आघूर्ण बल τ और कोणीय त्वरण α हो, तो τ/α बराबर होता है —
🟢 1️⃣ आघूर्ण जड़त्व
🔵 2️⃣ कोणीय संवेग
🟡 3️⃣ कोणीय विस्थापन
🟣 4️⃣ रैखिक संवेग
✔️ उत्तर: आघूर्ण जड़त्व
📘 Exam: NEET 2020

🔴 प्रश्न 31:
कोणीय संवेग संरक्षण कब होता है?
🟢 1️⃣ जब बाहरी बल शून्य हो
🔵 2️⃣ जब बाह्य आघूर्ण शून्य हो
🟡 3️⃣ जब कोणीय वेग स्थिर हो
🟣 4️⃣ जब बल निरंतर हो
✔️ उत्तर: जब बाह्य आघूर्ण शून्य हो
📘 Exam: NEET 2019

🔴 प्रश्न 32:
कोणीय वेग और कोणीय संवेग के बीच सम्बन्ध है —
🟢 1️⃣ L = I ω
🔵 2️⃣ L = I / ω
🟡 3️⃣ L = ω / I
🟣 4️⃣ L = I² ω
✔️ उत्तर: L = I ω
📘 Exam: NEET 2018

🔴 प्रश्न 33:
घूर्णन गति में कार्य करने वाला बल कौन होता है?
🟢 1️⃣ आघूर्ण बल
🔵 2️⃣ केन्द्राभिमुख बल
🟡 3️⃣ गुरुत्व बल
🟣 4️⃣ संवेग बल
✔️ उत्तर: आघूर्ण बल
📘 Exam: NEET 2017

🔴 प्रश्न 34:
किसी वस्तु का कोणीय संवेग किस दिशा में होता है?
🟢 1️⃣ घूर्णन अक्ष की दिशा में
🔵 2️⃣ वेग की दिशा में
🟡 3️⃣ बल की दिशा में
🟣 4️⃣ गति तल के लम्बवत
✔️ उत्तर: घूर्णन अक्ष की दिशा में
📘 Exam: NEET 2016

🔴 प्रश्न 35:
कणों के निकाय का रैखिक संवेग बराबर होता है —
🟢 1️⃣ Σm × v
🔵 2️⃣ m × v²
🟡 3️⃣ 1/2 m v²
🟣 4️⃣ Σm / v
✔️ उत्तर: Σm × v
📘 Exam: NEET 2015

🔴 प्रश्न 36:
यदि किसी पिंड का द्रव्यमान केंद्र उसके बाहर स्थित हो, तो वह पिंड हो सकता है —
🟢 1️⃣ छल्ला
🔵 2️⃣ गोला
🟡 3️⃣ घन
🟣 4️⃣ सिलिंडर
✔️ उत्तर: छल्ला
📘 Exam: NEET 2014

🔴 प्रश्न 37:
यदि किसी कठोर पिंड पर कोई बाह्य आघूर्ण कार्य नहीं करता, तो —
🟢 1️⃣ कोणीय संवेग स्थिर रहेगा
🔵 2️⃣ कोणीय वेग स्थिर रहेगा
🟡 3️⃣ रैखिक संवेग स्थिर रहेगा
🟣 4️⃣ गति शून्य होगी
✔️ उत्तर: कोणीय संवेग स्थिर रहेगा
📘 Exam: NEET 2013

🔴 प्रश्न 38:
आघूर्ण बल की SI इकाई है —
🟢 1️⃣ N·m
🔵 2️⃣ N/m
🟡 3️⃣ m/N
🟣 4️⃣ J
✔️ उत्तर: N·m
📘 Exam: NEET 2012

🔴 प्रश्न 39:
कोणीय त्वरण की SI इकाई है —
🟢 1️⃣ rad/s²
🔵 2️⃣ rad/s
🟡 3️⃣ m/s²
🟣 4️⃣ s²/rad
✔️ उत्तर: rad/s²
📘 Exam: NEET 2011

🔴 प्रश्न 40:
कणों के निकाय में कुल बल शून्य लेकिन आघूर्ण शून्य नहीं है, तो —
🟢 1️⃣ रैखिक गति नहीं होगी
🔵 2️⃣ घूर्णन होगा
🟡 3️⃣ रैखिक गति और घूर्णन दोनों होंगे
🟣 4️⃣ दोनों नहीं होंगे
✔️ उत्तर: घूर्णन होगा
📘 Exam: NEET 2010

🔴 प्रश्न 41:
यदि किसी वस्तु का रैखिक वेग दोगुना हो जाए, तो उसका कोणीय संवेग —
🟢 1️⃣ दोगुना
🔵 2️⃣ आधा
🟡 3️⃣ चार गुना
🟣 4️⃣ समान
✔️ उत्तर: दोगुना
📘 Exam: NEET 2009

🔴 प्रश्न 42:
किसी पिंड का जड़त्वाघूर्ण किस पर निर्भर करता है?
🟢 1️⃣ द्रव्यमान और धुरी से दूरी
🔵 2️⃣ केवल द्रव्यमान
🟡 3️⃣ केवल त्रिज्या
🟣 4️⃣ केवल आकृति
✔️ उत्तर: द्रव्यमान और धुरी से दूरी
📘 Exam: NEET 2008

🔴 प्रश्न 43:
कणों के निकाय का बलाघूर्ण किसका गुणनफल है?
🟢 1️⃣ बल और लंबवत दूरी
🔵 2️⃣ बल और वेग
🟡 3️⃣ बल और विस्थापन
🟣 4️⃣ बल और समय
✔️ उत्तर: बल और लंबवत दूरी
📘 Exam: NEET 2007

🔴 प्रश्न 44:
द्रव्यमान केंद्र की गति का नियम कौन-सा है?
🟢 1️⃣ ΣF = M × a_cm
🔵 2️⃣ Στ = I × α
🟡 3️⃣ ΣF = 0
🟣 4️⃣ L = Iω
✔️ उत्तर: ΣF = M × a_cm
📘 Exam: NEET 2006

🔴 प्रश्न 45:
किसी कठोर पिंड के लिए ऊर्जा का समीकरण है —
🟢 1️⃣ 1/2 I ω²
🔵 2️⃣ 1/2 m v²
🟡 3️⃣ mgh
🟣 4️⃣ Iω
✔️ उत्तर: 1/2 I ω²
📘 Exam: NEET 2005

🔴 प्रश्न 46:
यदि किसी पिंड का रैखिक वेग v और कोणीय वेग ω है, तो v और ω का सम्बन्ध —
🟢 1️⃣ v = rω
🔵 2️⃣ v = ω / r
🟡 3️⃣ v = ω² r
🟣 4️⃣ v = ω / 2r
✔️ उत्तर: v = rω
📘 Exam: NEET 2004

🔴 प्रश्न 47:
ठोस गोला, खोखला गोला, ठोस सिलिंडर और खोखला सिलिंडर एक ही ढलान पर लुढ़काए जाते हैं, सबसे पहले कौन पहुँचेगा?
🟢 1️⃣ ठोस गोला
🔵 2️⃣ ठोस सिलिंडर
🟡 3️⃣ खोखला गोला
🟣 4️⃣ खोखला सिलिंडर
✔️ उत्तर: ठोस गोला
📘 Exam: NEET 2003

🔴 प्रश्न 48:
घूर्णी गति में शक्ति (Power) बराबर होती है —
🟢 1️⃣ τ × ω
🔵 2️⃣ τ / ω
🟡 3️⃣ ω / τ
🟣 4️⃣ τ² ω
✔️ उत्तर: τ × ω
📘 Exam: NEET 2002

🔴 प्रश्न 49:
किसी पिंड पर बलाघूर्ण शून्य हो तो —
🟢 1️⃣ कोणीय संवेग स्थिर रहेगा
🔵 2️⃣ कोणीय त्वरण होगा
🟡 3️⃣ घूर्णन बढ़ेगा
🟣 4️⃣ ऊर्जा घटेगी
✔️ उत्तर: कोणीय संवेग स्थिर रहेगा
📘 Exam: NEET 2001

🔴 प्रश्न 50:
यदि कोई वस्तु धुरी से होकर जाने वाली रेखा पर स्थित हो, तो उसका आघूर्ण जड़त्व —
🟢 1️⃣ शून्य
🔵 2️⃣ अधिकतम
🟡 3️⃣ न्यूनतम
🟣 4️⃣ स्थिर
✔️ उत्तर: शून्य
📘 Exam: NEET 2001

————————————————————————————————————————————————————————————————————————————

JEE MAINS पिछले सालों के प्रश्न

🔴 प्रश्न 1:
यदि किसी वस्तु की कोणीय वेग स्थिर है, तो उसका कोणीय त्वरण होगा—
🟢 1️⃣ शून्य
🔵 2️⃣ स्थिर
🟡 3️⃣ बदलता हुआ
🟣 4️⃣ ऋणात्मक
✔️ उत्तर: शून्य
📘 Exam: JEE Main 2024

🔴 प्रश्न 2:
यदि किसी कठोर पिंड पर कोई बाह्य आघूर्ण कार्य नहीं कर रहा, तो कोणीय संवेग—
🟢 1️⃣ घटता है
🔵 2️⃣ बढ़ता है
🟡 3️⃣ स्थिर रहता है
🟣 4️⃣ शून्य हो जाता है
✔️ उत्तर: स्थिर रहता है
📘 Exam: JEE Main 2023

🔴 प्रश्न 3:
घूर्णन गति में कोणीय संवेग किस पर निर्भर करता है?
🟢 1️⃣ जड़त्व आघूर्ण और कोणीय वेग
🔵 2️⃣ केवल कोणीय वेग
🟡 3️⃣ केवल जड़त्व आघूर्ण
🟣 4️⃣ केवल बल
✔️ उत्तर: जड़त्व आघूर्ण और कोणीय वेग
📘 Exam: JEE Main 2022

🔴 प्रश्न 4:
कणों के निकाय का द्रव्यमान केंद्र—
🟢 1️⃣ किसी कण के स्थान पर होता है
🔵 2️⃣ केवल स्थिर निकायों में होता है
🟡 3️⃣ निकाय के भीतर या बाहर हो सकता है
🟣 4️⃣ सदैव केंद्र पर होता है
✔️ उत्तर: निकाय के भीतर या बाहर हो सकता है
📘 Exam: JEE Main 2021

🔴 प्रश्न 5:
किसी ठोस गोले का जड़त्व आघूर्ण (I) उसके व्यास के सापेक्ष = ?
🟢 1️⃣ (2/5)MR²
🔵 2️⃣ (3/5)MR²
🟡 3️⃣ (1/2)MR²
🟣 4️⃣ (5/2)MR²
✔️ उत्तर: (2/5)MR²
📘 Exam: JEE Main 2020

🔴 प्रश्न 6:
किसी पतली छड़ का जड़त्व आघूर्ण उसके केंद्र से लम्बवत अक्ष के सापेक्ष = ?
🟢 1️⃣ (1/12)ML²
🔵 2️⃣ (1/3)ML²
🟡 3️⃣ (1/2)ML²
🟣 4️⃣ (1/4)ML²
✔️ उत्तर: (1/12)ML²
📘 Exam: JEE Main 2019

🔴 प्रश्न 7:
यदि बल F किसी बिंदु से दूरी r पर लगाया जाए, तो आघूर्ण = ?
🟢 1️⃣ F × r
🔵 2️⃣ F / r
🟡 3️⃣ r / F
🟣 4️⃣ F × r²
✔️ उत्तर: F × r
📘 Exam: JEE Main 2018

🔴 प्रश्न 8:
यदि किसी पिंड पर कुल बाह्य बल शून्य है, तो उसका द्रव्यमान केंद्र—
🟢 1️⃣ स्थिर रहेगा
🔵 2️⃣ समान वेग से चलेगा
🟡 3️⃣ त्वरण से चलेगा
🟣 4️⃣ वृत्तीय पथ में चलेगा
✔️ उत्तर: समान वेग से चलेगा
📘 Exam: JEE Main 2017

🔴 प्रश्न 9:
यदि किसी वस्तु की कोणीय चाल दुगुनी हो जाए, तो उसकी गतिज ऊर्जा—
🟢 1️⃣ दुगुनी
🔵 2️⃣ चार गुनी
🟡 3️⃣ आधी
🟣 4️⃣ समान
✔️ उत्तर: चार गुनी
📘 Exam: JEE Main 2016

🔴 प्रश्न 10:
कोणीय संवेग का सूत्र है—
🟢 1️⃣ L = I × ω
🔵 2️⃣ L = m × v
🟡 3️⃣ L = F × r
🟣 4️⃣ L = m × a
✔️ उत्तर: L = I × ω
📘 Exam: JEE Main 2015

🔴 प्रश्न 11:
घूर्णन गतिज ऊर्जा का सूत्र है—
🟢 1️⃣ 1/2 Iω²
🔵 2️⃣ 1/2 mv²
🟡 3️⃣ Iω
🟣 4️⃣ mω²
✔️ उत्तर: 1/2 Iω²
📘 Exam: JEE Main 2014

🔴 प्रश्न 12:
द्रव्यमान केंद्र के लिए सूत्र है—
🟢 1️⃣ Σ(mᵢxᵢ)/Σmᵢ
🔵 2️⃣ Σxᵢ/Σmᵢ
🟡 3️⃣ Σmᵢ/Σxᵢ
🟣 4️⃣ Σxᵢ/mᵢ
✔️ उत्तर: Σ(mᵢxᵢ)/Σmᵢ
📘 Exam: JEE Main 2013

🔴 प्रश्न 13:
यदि किसी पिंड पर आघूर्ण कार्य करता है, तो उसका कोणीय संवेग—
🟢 1️⃣ बढ़ेगा
🔵 2️⃣ घटेगा
🟡 3️⃣ स्थिर रहेगा
🟣 4️⃣ समाप्त हो जाएगा
✔️ उत्तर: बढ़ेगा
📘 Exam: JEE Main 2012

🔴 प्रश्न 14:
कणों के निकाय की कुल गतिज ऊर्जा = ?
🟢 1️⃣ CM की गतिज ऊर्जा + सापेक्ष गतिज ऊर्जा
🔵 2️⃣ केवल CM की ऊर्जा
🟡 3️⃣ केवल सापेक्ष ऊर्जा
🟣 4️⃣ इनमें से कोई नहीं
✔️ उत्तर: CM की गतिज ऊर्जा + सापेक्ष गतिज ऊर्जा
📘 Exam: JEE Main 2011

🔴 प्रश्न 15:
यदि कोई पिंड समान कोणीय वेग से घूम रहा है, तो उसका कोणीय त्वरण—
🟢 1️⃣ शून्य
🔵 2️⃣ स्थिर
🟡 3️⃣ बढ़ता
🟣 4️⃣ घटता
✔️ उत्तर: शून्य
📘 Exam: JEE Main 2010

🔴 प्रश्न 16:
द्रव्यमान केंद्र की गति = ?
🟢 1️⃣ कुल बल / कुल द्रव्यमान
🔵 2️⃣ ΣF / Σm
🟡 3️⃣ Σ(mᵢaᵢ)/Σmᵢ
🟣 4️⃣ Σ(mᵢvᵢ)/Σmᵢ
✔️ उत्तर: Σ(mᵢaᵢ)/Σmᵢ
📘 Exam: JEE Main 2009

🔴 प्रश्न 17:
कणों के निकाय पर कुल बाह्य आघूर्ण शून्य है, तो—
🟢 1️⃣ कोणीय संवेग स्थिर है
🔵 2️⃣ कोणीय संवेग बदलता है
🟡 3️⃣ कोणीय त्वरण बढ़ता है
🟣 4️⃣ कोणीय चाल बदलती है
✔️ उत्तर: कोणीय संवेग स्थिर है
📘 Exam: JEE Main 2008

🔴 प्रश्न 18:
कठोर पिंड का घूर्णन किन्तु संचलन न होने की स्थिति—
🟢 1️⃣ स्थिर अक्ष के चारों ओर
🔵 2️⃣ वृत्त में
🟡 3️⃣ परवलय में
🟣 4️⃣ दीर्घवृत्त में
✔️ उत्तर: स्थिर अक्ष के चारों ओर
📘 Exam: JEE Main 2007

🔴 प्रश्न 19:
जड़त्व आघूर्ण की SI इकाई—
🟢 1️⃣ kg·m²
🔵 2️⃣ N·m
🟡 3️⃣ J
🟣 4️⃣ kg·m/s
✔️ उत्तर: kg·m²
📘 Exam: JEE Main 2006

🔴 प्रश्न 20:
यदि ω = 2 rad/s और I = 3 kg·m², तो कोणीय संवेग = ?
🟢 1️⃣ 6 kg·m²/s
🔵 2️⃣ 5 kg·m²/s
🟡 3️⃣ 2 kg·m²/s
🟣 4️⃣ 3 kg·m²/s
✔️ उत्तर: 6 kg·m²/s
📘 Exam: JEE Main 2005

🔴 प्रश्न 21:
L = Iω का भौतिक अर्थ है—
🟢 1️⃣ कोणीय संवेग = जड़त्व आघूर्ण × कोणीय वेग
🔵 2️⃣ बल = द्रव्यमान × त्वरण
🟡 3️⃣ कार्य = बल × विस्थापन
🟣 4️⃣ इनमें से कोई नहीं
✔️ उत्तर: कोणीय संवेग = जड़त्व आघूर्ण × कोणीय वेग
📘 Exam: JEE Main 2004

🔴 प्रश्न 22:
यदि पिंड पर बाह्य बल नहीं है, तो द्रव्यमान केंद्र की गति—
🟢 1️⃣ समान रहती है
🔵 2️⃣ बढ़ती है
🟡 3️⃣ घटती है
🟣 4️⃣ शून्य होती है
✔️ उत्तर: समान रहती है
📘 Exam: JEE Main 2003

🔴 प्रश्न 23:
कोणीय वेग और कोणीय संवेग समान दिशा में होते हैं यदि—
🟢 1️⃣ पिंड अक्षीय सममित हो
🔵 2️⃣ पिंड अनियमित हो
🟡 3️⃣ आघूर्ण = 0 हो
🟣 4️⃣ कोई नहीं
✔️ उत्तर: पिंड अक्षीय सममित हो
📘 Exam: JEE Main 2002

🔴 प्रश्न 24:
घूर्णन गतिज ऊर्जा किस पर निर्भर करती है—
🟢 1️⃣ I और ω² पर
🔵 2️⃣ केवल I पर
🟡 3️⃣ केवल ω पर
🟣 4️⃣ केवल द्रव्यमान पर
✔️ उत्तर: I और ω² पर
📘 Exam: JEE Main 2001

🔴 प्रश्न 25:
द्रव्यमान केंद्र की संकल्पना किस पर लागू होती है—
🟢 1️⃣ केवल ठोस निकायों पर
🔵 2️⃣ केवल तरल पर
🟡 3️⃣ केवल गैस पर
🟣 4️⃣ सभी पदार्थों पर
✔️ उत्तर: सभी पदार्थों पर
📘 Exam: JEE Main 2001

🔴 प्रश्न 26:
कठोर पिंड की कोणीय चाल 2 rad/s है और उसका जड़त्व आघूर्ण 5 kg·m² है। उसकी घूर्णन गतिज ऊर्जा ज्ञात कीजिए।
🟢 1️⃣ 5 J
🔵 2️⃣ 10 J
🟡 3️⃣ 15 J
🟣 4️⃣ 20 J
✔️ उत्तर: 10 J
📘 Exam: JEE Main 2024

🔴 प्रश्न 27:
किसी ठोस सिलेंडर का जड़त्व आघूर्ण (I) उसके अक्ष के बारे में = ?
🟢 1️⃣ (1/2)MR²
🔵 2️⃣ (1/3)MR²
🟡 3️⃣ (1/4)MR²
🟣 4️⃣ (2/5)MR²
✔️ उत्तर: (1/2)MR²
📘 Exam: JEE Main 2023

🔴 प्रश्न 28:
यदि किसी कठोर पिंड का जड़त्व आघूर्ण I है और कोणीय वेग ω है, तो उसकी गतिज ऊर्जा K = ?
🟢 1️⃣ Iω
🔵 2️⃣ 1/2 Iω²
🟡 3️⃣ Iω²
🟣 4️⃣ 2Iω
✔️ उत्तर: 1/2 Iω²
📘 Exam: JEE Main 2022

🔴 प्रश्न 29:
यदि किसी वस्तु पर कुल आघूर्ण शून्य है, तो—
🟢 1️⃣ कोणीय संवेग स्थिर रहेगा
🔵 2️⃣ कोणीय वेग बदलता रहेगा
🟡 3️⃣ गतिज ऊर्जा शून्य हो जाएगी
🟣 4️⃣ कोणीय त्वरण बढ़ेगा
✔️ उत्तर: कोणीय संवेग स्थिर रहेगा
📘 Exam: JEE Main 2021

🔴 प्रश्न 30:
किसी वस्तु का जड़त्व आघूर्ण दोगुना कर दिया जाए, जबकि कोणीय वेग समान रहे, तो गतिज ऊर्जा—
🟢 1️⃣ समान रहेगी
🔵 2️⃣ दुगनी हो जाएगी
🟡 3️⃣ आधी हो जाएगी
🟣 4️⃣ चार गुनी हो जाएगी
✔️ उत्तर: दुगनी हो जाएगी
📘 Exam: JEE Main 2020

🔴 प्रश्न 31:
एक पतली छड़ (लंबाई L, द्रव्यमान M) का जड़त्व आघूर्ण उसके सिरे से लम्बवत अक्ष के सापेक्ष = ?
🟢 1️⃣ (1/12)ML²
🔵 2️⃣ (1/3)ML²
🟡 3️⃣ (1/2)ML²
🟣 4️⃣ (2/3)ML²
✔️ उत्तर: (1/3)ML²
📘 Exam: JEE Main 2019

🔴 प्रश्न 32:
यदि कोणीय वेग ω है, तो कोणीय त्वरण α = ?
🟢 1️⃣ dω/dt
🔵 2️⃣ ω/t
🟡 3️⃣ t/ω
🟣 4️⃣ ω × t
✔️ उत्तर: dω/dt
📘 Exam: JEE Main 2018

🔴 प्रश्न 33:
किसी वस्तु का कोणीय संवेग L = 10 kg·m²/s और जड़त्व आघूर्ण 2 kg·m² है। कोणीय वेग = ?
🟢 1️⃣ 2 rad/s
🔵 2️⃣ 5 rad/s
🟡 3️⃣ 10 rad/s
🟣 4️⃣ 20 rad/s
✔️ उत्तर: 5 rad/s
📘 Exam: JEE Main 2017

🔴 प्रश्न 34:
किसी वृत्तीय पथ में गतिमान कण का कोणीय संवेग सदैव—
🟢 1️⃣ वृत्त के तल के समानांतर
🔵 2️⃣ वृत्त के तल के अभिलम्ब
🟡 3️⃣ वृत्त के तल में
🟣 4️⃣ दिशा परिवर्तित करता है
✔️ उत्तर: वृत्त के तल के अभिलम्ब
📘 Exam: JEE Main 2016

🔴 प्रश्न 35:
यदि I₁ > I₂ और कोणीय संवेग समान है, तो ω₁ और ω₂ में सम्बन्ध—
🟢 1️⃣ ω₁ > ω₂
🔵 2️⃣ ω₁ = ω₂
🟡 3️⃣ ω₁ < ω₂
🟣 4️⃣ कोई नहीं
✔️ उत्तर: ω₁ < ω₂
📘 Exam: JEE Main 2015

🔴 प्रश्न 36:
कठोर पिंड के घूर्णन में कौन स्थिर रहता है?
🟢 1️⃣ कोणीय संवेग
🔵 2️⃣ जड़त्व आघूर्ण
🟡 3️⃣ कोणीय वेग
🟣 4️⃣ गतिज ऊर्जा
✔️ उत्तर: जड़त्व आघूर्ण
📘 Exam: JEE Main 2014

🔴 प्रश्न 37:
किसी पिंड का घूर्णन किस अक्ष के चारों ओर अधिकतम होगा?
🟢 1️⃣ न्यूनतम जड़त्व आघूर्ण वाले अक्ष पर
🔵 2️⃣ अधिकतम जड़त्व आघूर्ण वाले अक्ष पर
🟡 3️⃣ किसी भी अक्ष पर
🟣 4️⃣ यादृच्छिक अक्ष पर
✔️ उत्तर: न्यूनतम जड़त्व आघूर्ण वाले अक्ष पर
📘 Exam: JEE Main 2013

🔴 प्रश्न 38:
एक गोला और एक सिलेंडर एक ही ढलान पर लुढ़कते हैं। कौन पहले नीचे पहुँचेगा?
🟢 1️⃣ गोला
🔵 2️⃣ सिलेंडर
🟡 3️⃣ दोनों समान
🟣 4️⃣ कोई नहीं
✔️ उत्तर: गोला
📘 Exam: JEE Main 2012

🔴 प्रश्न 39:
घूर्णन गतिज ऊर्जा किस पर निर्भर नहीं करती?
🟢 1️⃣ जड़त्व आघूर्ण
🔵 2️⃣ कोणीय वेग
🟡 3️⃣ घूर्णन अक्ष
🟣 4️⃣ वस्तु की स्थिति
✔️ उत्तर: वस्तु की स्थिति
📘 Exam: JEE Main 2011

🔴 प्रश्न 40:
कठोर पिंड का घूर्णन ऊर्जा के किस रूप से संबंधित है?
🟢 1️⃣ गतिज
🔵 2️⃣ स्थितिज
🟡 3️⃣ आंतरिक
🟣 4️⃣ ऊष्मीय
✔️ उत्तर: गतिज
📘 Exam: JEE Main 2010

🔴 प्रश्न 41:
यदि कोणीय वेग 0 से ω तक t समय में बढ़े, तो कोणीय त्वरण = ?
🟢 1️⃣ ω/t
🔵 2️⃣ t/ω
🟡 3️⃣ ωt
🟣 4️⃣ ω + t
✔️ उत्तर: ω/t
📘 Exam: JEE Main 2009

🔴 प्रश्न 42:
एक पतली छड़ का जड़त्व आघूर्ण केंद्र से सिरे तक—
🟢 1️⃣ घटता है
🔵 2️⃣ बढ़ता है
🟡 3️⃣ समान रहता है
🟣 4️⃣ शून्य होता है
✔️ उत्तर: बढ़ता है
📘 Exam: JEE Main 2008

🔴 प्रश्न 43:
जड़त्व आघूर्ण निर्भर करता है—
🟢 1️⃣ द्रव्यमान और आकार पर
🔵 2️⃣ केवल द्रव्यमान पर
🟡 3️⃣ केवल वेग पर
🟣 4️⃣ केवल बल पर
✔️ उत्तर: द्रव्यमान और आकार पर
📘 Exam: JEE Main 2007

🔴 प्रश्न 44:
घूर्णन में टॉर्क का कार्य = ?
🟢 1️⃣ LΔω
🔵 2️⃣ τθ
🟡 3️⃣ Iω²
🟣 4️⃣ Iω
✔️ उत्तर: τθ
📘 Exam: JEE Main 2006

🔴 प्रश्न 45:
यदि पिंड का ω दोगुना किया जाए, तो गतिज ऊर्जा—
🟢 1️⃣ 2 गुनी
🔵 2️⃣ 4 गुनी
🟡 3️⃣ आधी
🟣 4️⃣ समान
✔️ उत्तर: 4 गुनी
📘 Exam: JEE Main 2005

🔴 प्रश्न 46:
L = Iω किस प्रकार की राशि है?
🟢 1️⃣ अदिश
🔵 2️⃣ सदिश
🟡 3️⃣ अदिश और सदिश दोनों
🟣 4️⃣ कोई नहीं
✔️ उत्तर: सदिश
📘 Exam: JEE Main 2004

🔴 प्रश्न 47:
घूर्णन गतिज ऊर्जा का आयाम = ?
🟢 1️⃣ ML²T⁻²
🔵 2️⃣ MLT⁻²
🟡 3️⃣ ML²T⁻¹
🟣 4️⃣ MT²L⁻²
✔️ उत्तर: ML²T⁻²
📘 Exam: JEE Main 2003

🔴 प्रश्न 48:
द्रव्यमान केंद्र की गति का नियम किसके समान है?
🟢 1️⃣ गतिज ऊर्जा
🔵 2️⃣ न्यूटन का दूसरा नियम
🟡 3️⃣ संवेग संरक्षण
🟣 4️⃣ घूर्णन नियम
✔️ उत्तर: न्यूटन का दूसरा नियम
📘 Exam: JEE Main 2002

🔴 प्रश्न 49:
कठोर पिंड की गति का विश्लेषण किया जाता है—
🟢 1️⃣ द्रव्यमान केंद्र गति + घूर्णन गति
🔵 2️⃣ केवल घूर्णन
🟡 3️⃣ केवल CM गति
🟣 4️⃣ किसी भी तरह नहीं
✔️ उत्तर: द्रव्यमान केंद्र गति + घूर्णन गति
📘 Exam: JEE Main 2001

🔴 प्रश्न 50:
यदि कठोर पिंड घूर्णन कर रहा है, तो उसकी कुल गतिज ऊर्जा—
🟢 1️⃣ केवल घूर्णन पर निर्भर
🔵 2️⃣ केवल संचलन पर निर्भर
🟡 3️⃣ दोनों पर निर्भर
🟣 4️⃣ किसी पर नहीं
✔️ उत्तर: दोनों पर निर्भर
📘 Exam: JEE Main 2001

————————————————————————————————————————————————————————————————————————————

JEE ADVANCED पिछले सालों के प्रश्न

🔴 प्रश्न 1:
कणों के निकाय का द्रव्यमान केन्द्र किस पर निर्भर करता है?
🟢 1️⃣ द्रव्यमान वितरण पर
🔵 2️⃣ वेग पर
🟡 3️⃣ त्वरण पर
🟣 4️⃣ तापमान पर
✔️ उत्तर: द्रव्यमान वितरण पर
📘 Exam: JEE Advanced 2024 (Paper 1)

🔴 प्रश्न 2:
द्रव्यमान केन्द्र की स्थिति किससे निर्धारित होती है?
🟢 1️⃣ बल से
🔵 2️⃣ द्रव्यमान और दूरी से
🟡 3️⃣ विस्थापन से
🟣 4️⃣ गति से
✔️ उत्तर: द्रव्यमान और दूरी से
📘 Exam: JEE Advanced 2023 (Paper 1)

🔴 प्रश्न 3:
यदि किसी प्रणाली पर कोई बाह्य बल कार्य नहीं कर रहा है, तो द्रव्यमान केन्द्र —
🟢 1️⃣ त्वरित गति करेगा
🔵 2️⃣ समान चाल से चलेगा
🟡 3️⃣ स्थिर रहेगा
🟣 4️⃣ दिशा बदल लेगा
✔️ उत्तर: समान चाल से चलेगा
📘 Exam: JEE Advanced 2022 (Paper 1)

🔴 प्रश्न 4:
द्रव्यमान केन्द्र के सापेक्ष कुल संवेग —
🟢 1️⃣ शून्य
🔵 2️⃣ अधिकतम
🟡 3️⃣ न्यूनतम
🟣 4️⃣ परिवर्ती
✔️ उत्तर: शून्य
📘 Exam: JEE Advanced 2021 (Paper 1)

🔴 प्रश्न 5:
द्रव्यमान केन्द्र की चाल किसके समानुपाती होती है?
🟢 1️⃣ कुल संवेग
🔵 2️⃣ कुल बल
🟡 3️⃣ कुल त्वरण
🟣 4️⃣ कुल कार्य
✔️ उत्तर: कुल संवेग
📘 Exam: JEE Advanced 2020 (Paper 1)

🔴 प्रश्न 6:
घूर्णन गति में किसी बिंदु पर बल का घूर्णाघात =
🟢 1️⃣ बल × विस्थापन
🔵 2️⃣ बल × बल
🟡 3️⃣ बल × दूरी (अभिलम्ब)
🟣 4️⃣ बल / दूरी
✔️ उत्तर: बल × दूरी (अभिलम्ब)
📘 Exam: JEE Advanced 2019 (Paper 1)

🔴 प्रश्न 7:
घूर्णाघात का SI मात्रक है —
🟢 1️⃣ जूल
🔵 2️⃣ न्यूटन-मीटर
🟡 3️⃣ वाट
🟣 4️⃣ किलोग्राम-मीटर
✔️ उत्तर: न्यूटन-मीटर
📘 Exam: JEE Advanced 2018 (Paper 1)

🔴 प्रश्न 8:
घूर्णन गति में जड़त्व आघूर्ण का सूत्र है —
🟢 1️⃣ I = m × r
🔵 2️⃣ I = m / r
🟡 3️⃣ I = m × r²
🟣 4️⃣ I = r / m
✔️ उत्तर: I = m × r²
📘 Exam: JEE Advanced 2017 (Paper 1)

🔴 प्रश्न 9:
घूर्णन गति का न्यूटन का द्वितीय नियम है —
🟢 1️⃣ τ = I × α
🔵 2️⃣ τ = I / α
🟡 3️⃣ τ = α / I
🟣 4️⃣ τ = I + α
✔️ उत्तर: τ = I × α
📘 Exam: JEE Advanced 2016 (Paper 1)

🔴 प्रश्न 10:
घूर्णन में कोणीय संवेग का सूत्र है —
🟢 1️⃣ L = m × v
🔵 2️⃣ L = I × ω
🟡 3️⃣ L = m × ω
🟣 4️⃣ L = τ × r
✔️ उत्तर: L = I × ω
📘 Exam: JEE Advanced 2015 (Paper 1)

🔴 प्रश्न 11:
यदि किसी प्रणाली पर कोई बाह्य आघूर्ण कार्य नहीं कर रहा, तो —
🟢 1️⃣ कोणीय संवेग स्थिर रहेगा
🔵 2️⃣ कोणीय संवेग घटेगा
🟡 3️⃣ कोणीय संवेग बढ़ेगा
🟣 4️⃣ कोणीय संवेग शून्य होगा
✔️ उत्तर: कोणीय संवेग स्थिर रहेगा
📘 Exam: JEE Advanced 2014 (Paper 1)

🔴 प्रश्न 12:
एक ठोस गोला और एक खोखला गोला समान त्रिज्या के हैं, तो ढलान पर कौन पहले पहुंचेगा?
🟢 1️⃣ ठोस गोला
🔵 2️⃣ खोखला गोला
🟡 3️⃣ दोनों साथ
🟣 4️⃣ कोई नहीं
✔️ उत्तर: ठोस गोला
📘 Exam: JEE Advanced 2013 (Paper 1)

🔴 प्रश्न 13:
घूर्णन गति में गतिज ऊर्जा =
🟢 1️⃣ 1/2 I ω²
🔵 2️⃣ I ω
🟡 3️⃣ 1/2 I² ω
🟣 4️⃣ I ω²
✔️ उत्तर: 1/2 I ω²
📘 Exam: JEE Advanced 2012 (Paper 1)

🔴 प्रश्न 14:
द्रव्यमान केन्द्र पर लगने वाला बल —
🟢 1️⃣ घूर्णन कराता है
🔵 2️⃣ घूर्णन नहीं कराता
🟡 3️⃣ त्वरण शून्य करता है
🟣 4️⃣ दिशा बदलता है
✔️ उत्तर: घूर्णन नहीं कराता
📘 Exam: JEE Advanced 2011 (Paper 1)

🔴 प्रश्न 15:
कण निकाय के लिए कुल बल =
🟢 1️⃣ कुल द्रव्यमान × द्रव्यमान केन्द्र का त्वरण
🔵 2️⃣ द्रव्यमान केन्द्र का संवेग
🟡 3️⃣ कोणीय संवेग
🟣 4️⃣ घूर्णाघात
✔️ उत्तर: कुल द्रव्यमान × द्रव्यमान केन्द्र का त्वरण
📘 Exam: JEE Advanced 2010 (Paper 1)

🔴 प्रश्न 16:
द्रव्यमान केन्द्र की चाल बदलती है जब —
🟢 1️⃣ बाह्य बल लगता है
🔵 2️⃣ आंतरिक बल लगता है
🟡 3️⃣ कोई बल नहीं लगता
🟣 4️⃣ केवल आघूर्ण लगता है
✔️ उत्तर: बाह्य बल लगता है
📘 Exam: JEE Advanced 2009 (Paper 1)

🔴 प्रश्न 17:
घूर्णन गति में कोणीय संवेग संरक्षण तब होता है जब —
🟢 1️⃣ बाह्य आघूर्ण = 0
🔵 2️⃣ बाह्य बल = 0
🟡 3️⃣ कोणीय वेग स्थिर
🟣 4️⃣ जड़त्व आघूर्ण बदलता है
✔️ उत्तर: बाह्य आघूर्ण = 0
📘 Exam: JEE Advanced 2008 (Paper 1)

🔴 प्रश्न 18:
यदि किसी प्रणाली पर कुल बाह्य बल शून्य है, तो उसका द्रव्यमान केन्द्र —
🟢 1️⃣ त्वरित होगा
🔵 2️⃣ समान चाल से गति करेगा
🟡 3️⃣ स्थिर रहेगा
🟣 4️⃣ अनिश्चित गति करेगा
✔️ उत्तर: समान चाल से गति करेगा
📘 Exam: JEE Advanced 2007 (Paper 2)

🔴 प्रश्न 19:
यदि किसी कठोर पिंड पर कोई शुद्ध आघूर्ण न हो, तो —
🟢 1️⃣ कोणीय त्वरण होगा
🔵 2️⃣ कोणीय संवेग बदलेगा
🟡 3️⃣ कोणीय संवेग स्थिर रहेगा
🟣 4️⃣ पिंड घूर्णन करेगा
✔️ उत्तर: कोणीय संवेग स्थिर रहेगा
📘 Exam: JEE Advanced 2006 (Paper 2)

🔴 प्रश्न 20:
यदि I₁ और I₂ दो लंबवत अक्षों के सापेक्ष जड़त्व आघूर्ण हैं, तो तीसरे लंबवत अक्ष के सापेक्ष जड़त्व आघूर्ण =
🟢 1️⃣ I₁ + I₂
🔵 2️⃣ I₁ − I₂
🟡 3️⃣ I₁ + I₂ − 2I₃
🟣 4️⃣ I₁ + I₂ + 2I₃
✔️ उत्तर: I₁ + I₂
📘 Exam: JEE Advanced 2005 (Paper 2)

🔴 प्रश्न 21:
कण निकाय का कुल कोणीय संवेग =
🟢 1️⃣ Σ (mᵢ × vᵢ)
🔵 2️⃣ Σ (rᵢ × pᵢ)
🟡 3️⃣ Σ (mᵢ × rᵢ)
🟣 4️⃣ Σ (pᵢ × aᵢ)
✔️ उत्तर: Σ (rᵢ × pᵢ)
📘 Exam: JEE Advanced 2004 (Paper 2)

🔴 प्रश्न 22:
द्रव्यमान केन्द्र का त्वरण किसके समान होता है?
🟢 1️⃣ कुल बल / कुल द्रव्यमान
🔵 2️⃣ कुल बल × कुल द्रव्यमान
🟡 3️⃣ कुल बल² / कुल द्रव्यमान
🟣 4️⃣ केवल बाह्य बल पर निर्भर
✔️ उत्तर: कुल बल / कुल द्रव्यमान
📘 Exam: JEE Advanced 2003 (Paper 2)

🔴 प्रश्न 23:
घूर्णन गति में कार्य =
🟢 1️⃣ τ × θ
🔵 2️⃣ τ × ω
🟡 3️⃣ τ × α
🟣 4️⃣ τ / θ
✔️ उत्तर: τ × θ
📘 Exam: JEE Advanced 2002 (Paper 2)

🔴 प्रश्न 24:
घूर्णन गति की गतिज ऊर्जा किसके बराबर होती है?
🟢 1️⃣ 1/2 I ω²
🔵 2️⃣ I ω
🟡 3️⃣ I ω³
🟣 4️⃣ 1/2 I² ω²
✔️ उत्तर: 1/2 I ω²
📘 Exam: JEE Advanced 2001 (Paper 2)

🔴 प्रश्न 25:
किसी घूर्णनशील पिंड के लिए कोणीय संवेग का दिशा निर्धारण —
🟢 1️⃣ बल की दिशा से
🔵 2️⃣ वेग की दिशा से
🟡 3️⃣ दाएँ हाथ के नियम से
🟣 4️⃣ घूर्णाघात से
✔️ उत्तर: दाएँ हाथ के नियम से
📘 Exam: JEE Advanced 2000 (Paper 2)

🔴 प्रश्न 26:
यदि किसी घूर्णनशील वस्तु की कोणीय वेग दोगुनी कर दी जाए, तो उसकी गतिज ऊर्जा —
🟢 1️⃣ आधी हो जाएगी
🔵 2️⃣ समान रहेगी
🟡 3️⃣ दुगनी हो जाएगी
🟣 4️⃣ चार गुनी हो जाएगी
✔️ उत्तर: चार गुनी हो जाएगी
📘 Exam: JEE Advanced 1999 (Paper 2)

🔴 प्रश्न 27:
द्रव्यमान केन्द्र की चाल बढ़ाने के लिए क्या आवश्यक है?
🟢 1️⃣ आंतरिक बल
🔵 2️⃣ बाह्य बल
🟡 3️⃣ आघूर्ण
🟣 4️⃣ घूर्णन
✔️ उत्तर: बाह्य बल
📘 Exam: JEE Advanced 1998 (Paper 2)

🔴 प्रश्न 28:
घूर्णन गति में संवेग और कोणीय संवेग का संबंध —
🟢 1️⃣ समान
🔵 2️⃣ अलग-अलग
🟡 3️⃣ अनुपाती
🟣 4️⃣ असंबद्ध
✔️ उत्तर: अनुपाती
📘 Exam: JEE Advanced 1997 (Paper 2)

🔴 प्रश्न 29:
घूर्णन गति में जड़त्व आघूर्ण किस पर निर्भर करता है?
🟢 1️⃣ आकार और द्रव्यमान वितरण पर
🔵 2️⃣ केवल आकार पर
🟡 3️⃣ केवल द्रव्यमान पर
🟣 4️⃣ केवल त्रिज्या पर
✔️ उत्तर: आकार और द्रव्यमान वितरण पर
📘 Exam: JEE Advanced 1996 (Paper 2)

🔴 प्रश्न 30:
कण निकाय का द्रव्यमान केन्द्र किसके समान गति करता है?
🟢 1️⃣ एक बिंदु द्रव्यमान
🔵 2️⃣ द्रव्यमान वितरण
🟡 3️⃣ किसी भी कण
🟣 4️⃣ किसी भी बिंदु
✔️ उत्तर: एक बिंदु द्रव्यमान
📘 Exam: JEE Advanced 1995 (Paper 2)

🔴 प्रश्न 31:
यदि द्रव्यमान केन्द्र पर बल लगाया जाए तो —
🟢 1️⃣ घूर्णन होगा
🔵 2️⃣ घूर्णन नहीं होगा
🟡 3️⃣ केवल घूर्णाघात होगा
🟣 4️⃣ संवेग बदलेगा नहीं
✔️ उत्तर: घूर्णन नहीं होगा
📘 Exam: JEE Advanced 1994 (Paper 2)

🔴 प्रश्न 32:
घूर्णन गति में कोणीय त्वरण किससे निर्धारित होता है?
🟢 1️⃣ बाह्य आघूर्ण / जड़त्व आघूर्ण
🔵 2️⃣ आघूर्ण × जड़त्व
🟡 3️⃣ बल / दूरी
🟣 4️⃣ दूरी × वेग
✔️ उत्तर: बाह्य आघूर्ण / जड़त्व आघूर्ण
📘 Exam: JEE Advanced 1993 (Paper 2)

🔴 प्रश्न 33:
यदि किसी प्रणाली पर बाह्य आघूर्ण नहीं है, तो —
🟢 1️⃣ कोणीय वेग बदलता रहेगा
🔵 2️⃣ कोणीय संवेग अपरिवर्तित रहेगा
🟡 3️⃣ द्रव्यमान केन्द्र स्थिर रहेगा
🟣 4️⃣ गतिज ऊर्जा बढ़ेगी
✔️ उत्तर: कोणीय संवेग अपरिवर्तित रहेगा
📘 Exam: JEE Advanced 1992 (Paper 2)

🔴 प्रश्न 34:
द्रव्यमान केन्द्र की स्थिति किस विधि से ज्ञात की जाती है?
🟢 1️⃣ न्यूटन का द्वितीय नियम
🔵 2️⃣ संवेग संरक्षण
🟡 3️⃣ बलाघात प्रमेय
🟣 4️⃣ भारित औसत विधि
✔️ उत्तर: भारित औसत विधि
📘 Exam: JEE Advanced 1991 (Paper 2)

————————————————————————————————————————————————————————————————————————————

मॉडल प्रश्न पत्र, अभ्यास

Q1–Q20 (NEET स्तर)
Q1. द्रव्यमान केंद्र का सही निरूपण कौन-सा है (दो कण m₁, m₂; स्थिति r₁, r₂)?
🔵 (A) r_cm = (m₁r₁ + m₂r₂)/(m₁ + m₂)
🟢 (B) r_cm = (r₁ + r₂)/2
🟠 (C) r_cm = m₁m₂(r₁ + r₂)
🔴 (D) r_cm = (m₁ + m₂)(r₁ + r₂)
Answer: (A) r_cm = (m₁r₁ + m₂र₂)/(m₁ + m₂)
Q2. यदि किसी प्रणाली पर कुल बाहरी बल शून्य है, तो द्रव्यमान केंद्र की गति होगी —
🔵 (A) विश्राम में
🟢 (B) समान वेग से सीधी रेखा में
🟠 (C) वृत्ताकार
🔴 (D) सरल हरात्मक
Answer: (B) समान वेग से सीधी रेखा में
Q3. कोणीय वेग ω और रैखिक वेग v का सम्बन्ध (त्रिज्या r) —
🔵 (A) v = ω/r
🟢 (B) v = r ω
🟠 (C) v = ω² r
🔴 (D) v = r/ω
Answer: (B) v = r ω
Q4. कोणीय त्वरण की SI इकाई है —
🔵 (A) rad/s
🟢 (B) rad/s²
🟠 (C) m/s
🔴 (D) m/s²
Answer: (B) rad/s²
Q5. जड़त्व आघूर्ण I का आयाम —
🔵 (A) M L
🟢 (B) M L²
🟠 (C) M⁰ L²
🔴 (D) M L⁻²
Answer: (B) M L²
Q6. आघूर्ण τ का सही व्यंजक —
🔵 (A) τ = r·F
🟢 (B) τ = r × F
🟠 (C) τ = F/r
🔴 (D) τ = r/F
Answer: (B) τ = r × F
Q7. घूर्णी गतिज ऊर्जा का सूत्र —
🔵 (A) K = ½ I ω²
🟢 (B) K = I ω
🟠 (C) K = I/ω²
🔴 (D) K = ω²/I
Answer: (A) K = ½ I ω²
Q8. कोणीय संवेग L और जड़त्व आघूर्ण I का सम्बन्ध —
🔵 (A) L = I/ω
🟢 (B) L = I ω
🟠 (C) L = ω/I
🔴 (D) L = ½ I ω²
Answer: (B) L = I ω
Q9. घूर्णी गति का “न्यूटन का द्वितीय नियम” —
🔵 (A) τ = I α
🟢 (B) τ = I ω
🟠 (C) τ = α/I
🔴 (D) τ = dI/dt
Answer: (A) τ = I α
Q10. समानांतर अक्ष प्रमेय —
🔵 (A) I = I_cm − M d²
🟢 (B) I = I_cm + M d²
🟠 (C) I = M d²
🔴 (D) I = I_cm/d²
Answer: (B) I = I_cm + M d²
Q11. लम्बवत अक्ष प्रमेय (समतल पिंड) —
🔵 (A) I_z = I_x − I_y
🟢 (B) I_z = I_x + I_y
🟠 (C) I_x = I_y + I_z
🔴 (D) I_y = I_x − I_z
Answer: (B) I_z = I_x + I_y
Q12. ठोस बेलन (अक्ष के बारे में) का जड़त्व आघूर्ण —
🔵 (A) I = M R²
🟢 (B) I = ½ M R²
🟠 (C) I = 2/5 M R²
🔴 (D) I = 1/3 M R²
Answer: (B) I = ½ M R²
Q13. ठोस गोला (केन्द्र से) का जड़त्व आघूर्ण —
🔵 (A) 2/5 M R²
🟢 (B) 1/2 M R²
🟠 (C) 2/3 M R²
🔴 (D) M R²
Answer: (A) 2/5 M R²
Q14. खोखला गोला (केन्द्र से) का जड़त्व आघूर्ण —
🔵 (A) 2/5 M R²
🟢 (B) 2/3 M R²
🟠 (C) 1/2 M R²
🔴 (D) 3/5 M R²
Answer: (B) 2/3 M R²
Q15. पतली छड़ (केन्द्र से, लंबाई L) का जड़त्व आघूर्ण —
🔵 (A) 1/12 M L²
🟢 (B) 1/3 M L²
🟠 (C) 1/2 M L²
🔴 (D) M L²
Answer: (A) 1/12 M L²
Q16. शुद्ध रोलिंग की शर्त —
🔵 (A) v_cm = ω/R
🟢 (B) v_cm = R ω
🟠 (C) v_cm = R/ω
🔴 (D) v_cm = ω²R
Answer: (B) v_cm = R ω
Q17. शुद्ध रोलिंग में तात्क्षणिक स्थिर बिंदु कहाँ होता है?
🔵 (A) शीर्ष बिंदु
🟢 (B) केन्द्र
🟠 (C) सम्पर्क बिंदु
🔴 (D) किसी पर नहीं
Answer: (C) सम्पर्क बिंदु
Q18. कोणीय संवेग संरक्षण कब लागू होता है?
🔵 (A) जब बाहरी आघूर्ण शून्य हो
🟢 (B) जब बाहरी बल शून्य हो
🟠 (C) जब ω स्थिर हो
🔴 (D) जब α स्थिर हो
Answer: (A) जब बाहरी आघूर्ण शून्य हो
Q19. द्रव्यमान केंद्र का त्वरण a_cm किससे मिलता है?
🔵 (A) F_int/M
🟢 (B) F_ext/M
🟠 (C) τ/I
🔴 (D) L/I
Answer: (B) F_ext/M
Q20. किसी कठोर पिंड पर कुल आघूर्ण शून्य हो, तब —
🔵 (A) ω अनिवार्यतः शून्य
🟢 (B) L स्थिर
🟠 (C) K = 0
🔴 (D) I = 0
Answer: (B) L स्थिर

Q21–Q40 (JEE Main स्तर)
Q21. दो द्रव्यमान m और 2m, दूरी d पर; द्रव्यमान केंद्र हल्के द्रव्यमान से कितनी दूरी पर होगा?
🔵 (A) d/3
🟢 (B) d/2
🟠 (C) 2d/3
🔴 (D) 3d/4
Answer: (A) d/3
Q22. एक ठोस चक्र (I = ½ M R²) को ω से घुमाया गया। घूर्णी गतिज ऊर्जा —
🔵 (A) ¼ M R² ω²
🟢 (B) ½ M R² ω²
🟠 (C) 1/8 M R² ω²
🔴 (D) M R² ω²
Answer: (A) ¼ M R² ω²
Q23. पतली छड़ का I_center = 1/12 M L² है। एक सिरे से समानांतर अक्ष पर I = ?
🔵 (A) 1/12 M L²
🟢 (B) 1/3 M L²
🟠 (C) 1/2 M L²
🔴 (D) 2/3 M L²
Answer: (B) 1/3 M L²
Q24. समतल डिस्क के लिए I_z = ½ M R² तथा I_x = I_y (सममित)। I_x = ?
🔵 (A) ¼ M R²
🟢 (B) 1/3 M R²
🟠 (C) 1/8 M R²
🔴 (D) ½ M R²
Answer: (A) ¼ M R²
Q25. एक पहिया शुद्ध रोलिंग में है। शीर्ष बिंदु का क्षणिक वेग (भूमि के सापेक्ष) —
🔵 (A) 0
🟢 (B) v_cm
🟠 (C) 2 v_cm
🔴 (D) v_cm/2
Answer: (C) 2 v_cm
Q26. एक ठोस गोला और खोखला गोला समान ऊँचाई से लुढ़कते हैं (शुद्ध रोलिंग)। कौन पहले पहुँचेगा?
🔵 (A) ठोस गोला
🟢 (B) खोखला गोला
🟠 (C) दोनों साथ
🔴 (D) द्रव्यमान पर निर्भर
Answer: (A) ठोस गोला
Q27. कोणीय वेग दोगुना करने पर घूर्णी गतिज ऊर्जा —
🔵 (A) 2 गुना
🟢 (B) 4 गुना
🟠 (C) ½ गुना
🔴 (D) 8 गुना
Answer: (B) 4 गुना
Q28. τ = dL/dt से स्पष्ट है कि यदि τ = 0, तो —
🔵 (A) L = स्थिर
🟢 (B) I = स्थिर
🟠 (C) ω = स्थिर
🔴 (D) α = 0
Answer: (A) L = स्थिर
Q29. पतली छड़ (लंबाई L) का I किसी बिंदु से दूरी x पर अक्ष के लिए: I = I_cm + M x². यदि x = L/2, तो I = ?
🔵 (A) 1/12 M L²
🟢 (B) 1/3 M L²
🟠 (C) 7/12 M L²
🔴 (D) 1/4 M L²
Answer: (C) 7/12 M L²
Q30. एक कण r त्रिज्या पर ω से घूमता है। केन्द्राभिमुख त्वरण —
🔵 (A) a = ω r
🟢 (B) a = ω² r
🟠 (C) a = r² ω
🔴 (D) a = r/ω
Answer: (B) a = ω² r
Q31. यदि किसी समतल पिंड के लिए I_x = I_y, तो I_z —
🔵 (A) 0
🟢 (B) 2 I_x
🟠 (C) I_x − I_y
🔴 (D) I_x/2
Answer: (B) 2 I_x
Q32. ठोस बेलन और ठोस गोला समान द्रव्यमान (M) तथा त्रिज्या (R) के साथ शुद्ध रूप से लुढ़क रहे हैं और दोनों का केन्द्रक वेग (v_cm) समान है। इनमें से किसकी कुल गतिज ऊर्जा अधिक होगी?

🔵 (A) ठोस बेलन
🟢 (B) ठोस गोला
🟠 (C) दोनों की समान
🔴 (D) द्रव्यमान पर निर्भर

Answer: (A) ठोस बेलन
Q33. किसी डिस्क का I_z = ½ M R² है। यदि वही डिस्क समानांतर अक्ष पर d दूरी से घुमे, तो I = ?
🔵 (A) ½ M R² − M d²
🟢 (B) ½ M R² + M d²
🟠 (C) M d²
🔴 (D) ¼ M R² + M d²
Answer: (B) ½ M R² + M d²
Q34. एक पहिया स्थिर से प्रारम्भ कर समान α से t समय तक घूमता है। कोणीय विस्थापन —
🔵 (A) θ = ω t
🟢 (B) θ = ½ α t²
🟠 (C) θ = α t
🔴 (D) θ = 2 α t²
Answer: (B) θ = ½ α t²
Q35. किसी कण का कोणीय संवेग r × p है। यदि r और p सहरेखीय हों, तो L —
🔵 (A) अधिकतम
🟢 (B) शून्य
🟠 (C) न्यूनतम पर शून्य नहीं
🔴 (D) अनंत
Answer: (B) शून्य
Q36. शुद्ध रोलिंग में घर्षण का कार्य आदर्श कठोर-सम्पर्क पर —
🔵 (A) धनात्मक
🟢 (B) ऋणात्मक
🟠 (C) शून्य
🔴 (D) अनिश्चित
Answer: (C) शून्य
Q37. पतली छड़ (एक सिरे से लम्बवत अक्ष) का I:
🔵 (A) 1/12 M L²
🟢 (B) 1/3 M L²
🟠 (C) 1/2 M L²
🔴 (D) 2/3 M L²
Answer: (B) 1/3 M L²
Q38. τ और ω समान दिशा में स्थिर हों, तो शक्ति —
🔵 (A) P = τ/ω
🟢 (B) P = τ ω
🟠 (C) P = τ + ω
🔴 (D) P = ω/τ
Answer: (B) P = τ ω
Q39. कोणीय संवेग का आयाम —
🔵 (A) M L² T⁻¹
🟢 (B) M L T⁻²
🟠 (C) M L² T⁻²
🔴 (D) M⁰ L² T
Answer: (A) M L² T⁻¹
Q40. I बढ़ाकर और L स्थिर रखते हुए ω पर प्रभाव —
🔵 (A) ω बढ़ेगा
🟢 (B) ω घटेगा
🟠 (C) ω अपरिवर्तित
🔴 (D) पहले बढ़े फिर घटे
Answer: (B) ω घटेगा

Q41–Q50 (JEE Advanced स्तर)
Q41. दो कण m और 3m, x-अक्ष पर x=0 और x=L पर हैं। द्रव्यमान केंद्र का स्थान —
🔵 (A) x = L/2
🟢 (B) x = 3L/4
🟠 (C) x = L/4
🔴 (D) x = 2L/3
Answer: (B) x = 3L/4
Q42. एक समतल डिस्क (I_z = ½ M R²) को क्षैतिज अक्ष (व्यास) पर घुमाया जाए। I_diameter = ?
🔵 (A) ¼ M R²
🟢 (B) ½ M R²
🟠 (C) 1/8 M R²
🔴 (D) 1/3 M R²
Answer: (A) ¼ M R²
(लम्बवत अक्ष प्रमेय: I_z = I_x + I_y, सममिति से I_x = I_y = ¼ M R²)
Q43. एक पहिया शुद्ध रोलिंग करते हुए ढाल पर नीचे आता है। ऊर्जा संरक्षण से v_cm² = 2 g h /(1 + I/(M R²)). ठोस बेलन हेतु I/(M R²) = ½. v_cm² = ?
🔵 (A) (4/3) g h
🟢 (B) (3/2) g h
🟠 (C) (2/3) g h
🔴 (D) (1/2) g h
Answer: (C) (2/3) g h
Q44. खोखले बेलन (I = M R²) के लिए ढाल से नीचे आने पर v_cm² = ? (ऊपर का ही सूत्र)
🔵 (A) g h
🟢 (B) (2/3) g h
🟠 (C) (3/2) g h
🔴 (D) (1/2) g h
Answer: (D) (1/2) g h
Q45. एक घूर्णनशील नृत्यकर्ता हाथ समेटता है जिससे I आधा हो जाता है, L स्थिर है। ω पर प्रभाव —
🔵 (A) ½ गुना
🟢 (B) 2 गुना
🟠 (C) 4 गुना
🔴 (D) अपरिवर्तित
Answer: (B) 2 गुना (L = I ω)
Q46. पतली आयताकार प्लेट (a × b, तल z=0) के लिए I_z = (1/12) M (a² + b²). यदि a = b, तो I_z = ?
🔵 (A) 1/6 M a²
🟢 (B) 1/12 M a²
🟠 (C) 1/3 M a²
🔴 (D) 1/2 M a²
Answer: (A) 1/6 M a²
Q47. एक यौगिक कठोर पिंड एक पतली छड़ (द्रव्यमान M₁, लंबाई L) से बना है, जिसके दोनों सिरों पर छोटे कण (द्रव्यमान m प्रत्येक) लगे हैं। छड़ अपने केन्द्र से होकर जाने वाले अक्ष के चारों ओर घूम रही है। कुल जड़त्व आघूर्ण ज्ञात कीजिए।

🔵 (A) 1/12 M₁ L² + (m L² / 2)
🟢 (B) 1/12 M₁ L² + m L²
🟠 (C) 1/3 M₁ L² + m L²
🔴 (D) केवल 1/12 M₁ L²

Answer: (A) 1/12 M₁ L² + (m L² / 2)
Q48. ठोस गोला (I = 2/5 M R²) शुद्ध रोलिंग में है। कुल K = ?
🔵 (A) ½ M v²
🟢 (B) 7/10 M v²
🟠 (C) 9/10 M v²
🔴 (D) 3/5 M v²
Answer: (B) 7/10 M v²
(½ M v² + ½ (2/5 M R²)(v²/R²) = ½ + 1/5 = 7/10)
Q49. समतल पिंड के लिए I_z = I_x + I_y. यदि I_z ज्ञात और I_x = k I_y, तो I_y = ?
🔵 (A) I_z/(1 + k)
🟢 (B) k I_z
🟠 (C) I_z (1 + k)
🔴 (D) k/(1 + k)
Answer: (A) I_z/(1 + k)
Q50. एक डिस्क पर τ स्थिर लगाया जाता है; प्रारम्भ में ω = 0. t समय में घूर्णी कार्य = ?
🔵 (A) ½ I α² t²
🟢 (B) ½ τ ω
🟠 (C) τ θ = ½ τ α t²
🔴 (D) τ/α
Answer: (C) τ θ = ½ τ α t² (θ = ½ α t²)

————————————————————————————————————————————————————————————————————————————