Class 11 : Physics (In English) – Chapter 7: Gravitation
EXPLANATION & SUMMARY
🔵 1. Introduction
Every object in the universe attracts every other object with a force known as Gravitation.
This force acts between all masses, from tiny particles to massive celestial bodies.
💡 Concept: Gravitation is a universal, attractive, and long-range force.
It is one of the four fundamental forces of nature and plays a key role in maintaining planetary motion and cosmic structure.

🟢 2. Newton’s Law of Universal Gravitation
💡 Statement:
Every particle in the universe attracts every other particle with a force that
➡️ is directly proportional to the product of their masses, and
➡️ inversely proportional to the square of the distance between them.
✏️ Formula:
F = G (m₁m₂) / r²
where
F = force of attraction between two bodies
m₁, m₂ = masses of the two bodies
r = distance between their centers
G = universal gravitational constant
✔️ Unit of G: N·m²/kg²
✔️ Value: 6.67 × 10⁻¹¹ N·m²/kg²
💡 The force acts along the line joining the centers of the two bodies and is always attractive.
🔴 3. Universal Gravitational Constant (G)
Definition:
G is defined as the force of attraction between two unit masses separated by a unit distance.
✏️ Formula:
G = F·r² / (m₁m₂)
💡 Dimensional Formula: [M⁻¹L³T⁻²]
✔️ G is the same everywhere in the universe and independent of medium or substance.
🟡 4. Comparison between Gravitational and Electrostatic Forces
🔹 Gravitational force is always attractive, while electrostatic force can be attractive or repulsive.
🔹 Gravitational force depends on masses, while electrostatic force depends on charges.
🔹 Gravitational constant (G) is universal; electrostatic constant (k = 1/4πε₀) depends on medium.
🔹 Gravitational force is much weaker than electrostatic force.
💡 Even though weak, gravity dominates on large scales because it is always attractive and acts on all matter.
🔵 5. Acceleration Due to Gravity (g)
When an object falls freely near the Earth, it experiences an acceleration called acceleration due to gravity (g).
From Newton’s law,
F = G(Mₑm)/r²
From Newton’s second law, F = ma = mg
Equating both:
mg = G(Mₑm)/r²
Therefore,
g = GMₑ / r²
where
Mₑ = mass of Earth = 5.972 × 10²⁴ kg
r = radius of Earth = 6.371 × 10⁶ m
✔️ Value of g = 9.8 m/s² near Earth’s surface
🟢 6. Variation of g with Altitude, Depth, and Latitude
🔹 With Altitude:
At a height h above the surface,
g’ = g (R / (R + h))²
If h ≪ R, then
g’ ≈ g (1 − 2h/R)
💡 g decreases with height.
🔹 With Depth:
At depth d below the surface,
g’ = g (1 − d/R)
💡 g decreases linearly with depth and becomes zero at the center.
🔹 With Latitude:
Due to Earth’s rotation, effective gravity decreases from poles to equator.
💡 g is maximum at poles and minimum at equator.
🔴 7. Relation between g and G
G is a universal constant, but g varies from place to place.
✏️ Relation:
g = GMₑ / Rₑ²
✔️ G is constant for the universe; g changes with location on Earth.
🟡 8. Gravitational Field and Field Intensity
💡 Definition:
The region around a mass in which its gravitational influence can be felt is called its gravitational field.
The gravitational field intensity (E₉) at a point is the force experienced by a unit mass placed at that point.
✏️ Formula:
E₉ = F/m = GM / r²
✔️ Unit: N/kg
✔️ Direction: Always toward the mass (attractive).
🔵 9. Gravitational Potential and Potential Energy
🔹 Gravitational Potential (V):
Potential at a point is the work done per unit mass in bringing it from infinity to that point.
V = −GM / r
💡 Negative because gravity is attractive.
🔹 Gravitational Potential Energy (U):
Energy of interaction between two masses m₁ and m₂ separated by r:
U = −G(m₁m₂)/r
As r → ∞, U → 0.
🟢 10. Relation between g and V
g = −dV/dr
✔️ The field intensity equals the negative gradient of potential.
✔️ The negative sign indicates that potential decreases in the direction of g.
🔴 11. Escape Velocity (vₑ)
💡 Definition:
The minimum velocity required to escape Earth’s gravitational field without any further propulsion.
✏️ Derivation:
½mvₑ² = GMₑm / Rₑ
⟹ vₑ = √(2GMₑ / Rₑ)
✔️ On Earth, vₑ = 11.2 km/s
✔️ Independent of mass of the object.
🟡 12. Orbital Velocity (vₒ)
💡 Definition:
The velocity required to keep a body in a circular orbit around Earth.
✏️ Derivation:
Centripetal force = Gravitational force
mvₒ² / r = GMₑm / r²
⟹ vₒ = √(GMₑ / r)
✔️ For near-Earth orbit: vₒ = 7.9 km/s
✔️ Relation: vₑ = √2 × vₒ
🔵 13. Geostationary and Polar Satellites
🔹 Geostationary Satellite:
Appears stationary relative to Earth.
Revolves from west to east in equatorial plane.
Orbital period = 24 hours.
Height ≈ 36,000 km.
Used for communication, broadcasting, and weather observation.
🔹 Polar Satellite:
Revolves north–south around Earth.
Period ≈ 100 minutes.
Covers entire Earth as it rotates.
Used for mapping and remote sensing.
🟢 14. Energy of a Satellite in Orbit
Kinetic Energy = ½mvₒ² = GMₑm / 2r
Potential Energy = −GMₑm / r
Total Energy = −GMₑm / 2r
✔️ Negative total energy means satellite is bound to Earth’s gravitational field.
🔴 15. Energy Required to Move Satellite to Another Orbit
If satellite moves from radius r₁ to r₂,
Change in energy per unit mass:
ΔE = GMₑ / 2 (1/r₁ − 1/r₂)
✔️ To move to a higher orbit, ΔE must be supplied.
🟡 16. Weight and Weightlessness
🔹 Weight (W): Force by which Earth attracts a body:
W = mg
🔹 Weightlessness:
When no normal reaction acts on a body (N = 0).
💡 Examples:
Astronauts in orbit.
Freely falling elevator.
Even though gravity acts, apparent weight becomes zero because everything accelerates together.
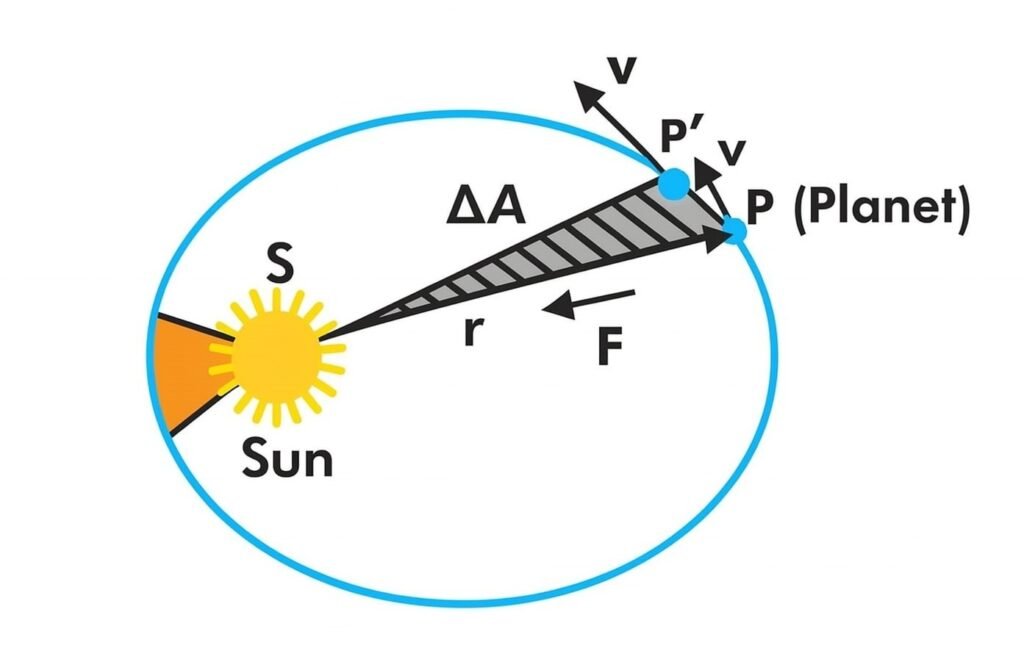
🔵 17. Kepler’s Laws of Planetary Motion
🔹 Law 1 (Orbits): Planets move in elliptical orbits with the Sun at one focus.
🔹 Law 2 (Areas): The line joining a planet and the Sun sweeps equal areas in equal times.
🔹 Law 3 (Periods): The square of the orbital period (T²) is proportional to the cube of the mean distance (r³):
T² ∝ r³
✏️ From Newton’s law:
T² = (4π²/GM) r³
✔️ This supports Kepler’s 3rd law.
🟢 18. Gravitational Potential Energy of a System of Particles
For two masses m₁, m₂ separated by r:
U = −Gm₁m₂ / r
For a system of many particles:
U_total = −G Σ (mᵢmⱼ / rᵢⱼ)
✔️ Total potential energy is the sum of all pairwise interactions.
🔴 19. Gravitational Field Lines
💡 Properties:
Always directed toward the mass.
Never intersect.
Denser lines indicate stronger field.
Field is strongest near the mass and weaker farther away.
🟡 20. Satellite Binding Energy
💡 Binding Energy: Work needed to remove satellite from orbit to infinity.
Binding energy per unit mass = GMₑ / 2r
✔️ Equal to the magnitude of total energy in orbit.
⚡ Summary (Approx. 300 words)
🔹 Gravitation is the universal attraction between all masses.
🔹 Newton’s Law: F = Gm₁m₂ / r², with G = 6.67×10⁻¹¹ N·m²/kg².
🔹 Acceleration due to gravity: g = GMₑ / Rₑ² = 9.8 m/s².
🔹 g decreases with altitude, depth, and from poles to equator.
🔹 Gravitational field intensity = GM / r²; potential = −GM / r; potential energy = −Gm₁m₂ / r.
🔹 Escape velocity = √(2GMₑ / Rₑ) = 11.2 km/s; orbital velocity = √(GMₑ / Rₑ) = 7.9 km/s.
🔹 Geostationary satellites orbit in equatorial plane with 24-hour period; polar satellites cover Earth pole-to-pole.
🔹 Satellite energy E = −GMₑm / 2r, negative for bound motion.
🔹 Kepler’s laws describe planetary motion: elliptical orbit, equal areas in equal times, and T² ∝ r³.
🔹 Weightlessness occurs when apparent weight becomes zero (as in satellites).
Gravitation explains falling bodies, planetary motion, tides, and satellite orbits — forming the foundation of celestial mechanics.
🧠 Quick Recap
🟢 Newton’s Law: F = Gm₁m₂ / r²
🔵 Acceleration due to gravity: g = GMₑ / Rₑ²
🟡 Escape velocity = 11.2 km/s
🔴 Orbital velocity = 7.9 km/s
💡 Kepler’s Third Law: T² ∝ r³
⚡ Energy of satellite = −GMₑm / 2r
————————————————————————————————————————————————————————————————————————————
QUESTIONS FROM TEXTBOOK
Question 7.1
Answer the following:
(a) You can shield a charge from electrical forces by putting it inside a hollow conductor. Can you shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means?
(b) An astronaut inside a small space ship orbiting around the earth cannot detect gravity. If the space station orbiting around the earth has a large size, can he hope to detect gravity?
(c) If you compare the gravitational force on the earth due to the sun to that due to the moon, you would find that the Sun’s pull is greater than the Moon’s pull. However, the tidal effect of the Moon’s pull is greater than the tidal effect of the Sun. Why?
Answer:
(a) ✖️ No shielding of gravity is possible. Gravitational interaction cannot be screened; a hollow shell produces zero field only inside due to itself, but it does not block external gravitational fields.
(b) 🛰️ In a small spaceship, everything is in free fall → apparent weightlessness. In a very large station, tidal effects (small variation of g across the station) can be detected.
(c) 🌞 Sun’s force on Earth is larger, but tidal force ∝ M/r³. The Moon is much closer, so its field gradient at Earth is larger → stronger tides.
Question 7.2
Choose the correct alternative:
(a) Acceleration due to gravity increases/decreases with increasing altitude.
(b) Acceleration due to gravity increases/decreases with increasing depth (assume the earth to be a sphere of uniform density).
(c) Acceleration due to gravity is independent of mass of the earth/mass of the body.
(d) The formula −G M m (1/r₂ − 1/r₁) is more/less accurate than the formula m g (r₂ − r₁) for the difference of potential energy between two points r₁ and r₂ distant from the centre of the earth.
Answer:
(a) 🔽 Decreases with altitude.
(b) 🔽 Decreases with depth (for uniform density, g ∝ r inside; g → 0 at centre).
(c) ✅ Independent of mass of the body (depends on Earth’s mass and r).
(d) ✅ More accurate (exact), while m g Δr is a near-surface approximation where g ≈ constant.
Question 7.3
Suppose there existed a planet that went around the Sun twice as fast as the Earth. What would be its orbital size as compared to that of the Earth?
Answer:
💡 For circular orbits: v = √(GM⊙/r) ⇒ v ∝ r⁻¹/².
If v₂ = 2v⊕, then r₂ = r⊕/4.
✔️ Orbital radius = one-fourth of Earth’s.
(Consequently, T ∝ r³/² ⇒ T₂ = T⊕/8 ≈ 45.6 days.)
Question 7.4
Io, one of Jupiter’s satellites, has an orbital period of 1.769 days and the radius of the orbit is 4.22 × 10⁸ m. Show that the mass of Jupiter is about one-thousandth that of the Sun.
Answer:
Use M = 4π²r³ / (G T²).
➡️ r = 4.22×10⁸ m, T = 1.769 days = 1.769×86400 s.
➡️ M_J ≈ 1.90×10²⁷ kg.
Solar mass M⊙ ≈ 1.99×10³⁰ kg.
➡️ M_J/M⊙ ≈ 9.6×10⁻⁴ ≈ 10⁻³.
✔️ Jupiter’s mass ≈ one-thousandth of the Sun’s.
Question 7.5
Assume our galaxy consists of 2.5 × 10¹¹ stars each of one solar mass. How long will a star at a distance of 50,000 ly from the galactic centre take to complete one revolution? (Take the diameter of the Milky Way ≈ 10⁵ ly.)
Answer:
Let enclosed mass M ≈ 2.5×10¹¹ M⊙.
Radius r = 5.0×10⁴ ly = 5.0×10⁴×9.46×10¹⁵ m.
Orbital period T = 2π√(r³ / G M).
🔢 Substituting gives T ≈ 3.6×10⁸ years (order 10⁸ y).
✔️ So the star takes ~3 × 10⁸ years to go once around the Galaxy.
Question 7.6
Choose the correct alternative:
(a) If the zero of potential energy is at infinity, the total energy of an orbiting satellite is the negative of its kinetic energy/potential energy.
(b) The energy required to launch an orbiting satellite out of earth’s gravitational influence is more/less than that required to project a stationary object at the same height (as the satellite) out of earth’s influence.
Answer:
(a) ✅ Negative of its kinetic energy (E = K + U = −K = U/2).
(b) ✅ Less (the satellite already possesses orbital kinetic energy).
Question 7.7
Does the escape speed of a body from Earth depend on
(a) the mass of the body,
(b) the location from where it is projected (on Earth’s surface),
(c) the direction of projection,
(d) the height of the location from where it is launched?
Answer:
(a) ❌ No (independent of the body’s mass).
(b) ❌ No (ignoring Earth’s rotation and small radius variations).
(c) ❌ No.
(d) ✅ Yes (since v_esc = √(2GM/(R+h)) decreases with altitude).
Question 7.8
A comet orbits the Sun in a highly elliptical orbit. Does the comet have a constant
(a) linear speed, (b) angular speed, (c) angular momentum, (d) kinetic energy, (e) potential energy, (f) total energy throughout the orbit, (g) areal velocity over equal time intervals?
(h) Is the average speed of the comet the same when it is near the Sun and when it is far from the Sun?
(i) If there is a mass loss of the comet when it comes close to the Sun, what happens to its orbital period?
Answer:
(a) ❌ No (speed varies; fastest at perihelion).
(b) ❌ No (ω not constant in an ellipse).
(c) ✅ Yes (about the Sun; central force ⇒ L conserved).
(d) ❌ No (changes with speed).
(e) ❌ No (varies with distance r).
(f) ✅ Yes (constant, negative for bound orbit).
(g) ✅ Yes (areal velocity constant; Kepler’s 2nd law).
(h) ❌ No; the near-Sun half has greater average speed.
(i) ⚖️ Period remains essentially unchanged (two-body Keplerian period is independent of comet’s own mass; mass loss of the tiny comet hardly affects T, unless outgassing thrust changes the orbit).
🔵 Question 7.10
In the following two exercises, choose the correct answer from among the given ones:
The gravitational intensity at the centre of a hemispherical shell of uniform mass density has the direction indicated by the arrow (see Fig. 7.11):
(i) a, (ii) b, (iii) c, (iv) 0
🟢 Answer:
💡 The resultant field at the centre is along the axis of symmetry, directed toward the flat face of the hemisphere.
✔️ Correct option: (ii) b
🔵 Question 7.11
For the above problem, the direction of the gravitational intensity at an arbitrary point P is indicated by the arrow
(i) d, (ii) e, (iii) f, (iv) g
🟢 Answer:
💡 The gravitational field due to the hemisphere acts toward its mass distribution, i.e. inward toward the curved surface.
✔️ Correct option: (i) d
🔵 Question 7.12
A rocket is fired from the Earth towards the Sun. At what distance from the Earth’s centre is the gravitational force on the rocket zero?
Given:
☀️ Mass of the Sun = 2 × 10³⁰ kg
🌍 Mass of the Earth = 6 × 10²⁴ kg
🌌 Orbital radius = 1.5 × 10¹¹ m
🟢 Answer:
➡️ Let the distance from Earth where net force = 0 be x.
🧮 Formula:
G M_E / x² = G M_S / (R − x)²
Simplify:
√(M_E / M_S) = x / (R − x)
⇒ x = R / (1 + √(M_S/M_E))
Substitute values:
R = 1.5×10¹¹ m, M_S/M_E = 3.33×10⁵
√(M_S/M_E) ≈ 577
x = 1.5×10¹¹ / (1 + 577) = 2.6×10⁸ m
✔️ The point of zero net force lies about 2.6×10⁸ m from Earth toward the Sun.
🔵 Question 7.13
How will you “weigh the Sun,” that is, estimate its mass?
Mean orbital radius of the Earth around the Sun = 1.5 × 10⁸ km
🟢 Answer:
💡 Using Kepler’s 3rd Law (Newton’s form):
M_S = (4π²r³) / (G T²)
➡️ Substitution:
r = 1.5×10¹¹ m, T = 1 yr = 3.156×10⁷ s
M_S = (4π² × (1.5×10¹¹)³) / (6.67×10⁻¹¹ × (3.156×10⁷)²)
= 1.99×10³⁰ kg
✔️ Mass of the Sun = 2.0×10³⁰ kg
🔵 Question 7.14
A Saturn year is 29.5 times the Earth year. How far is Saturn from the Sun if the Earth is 1.5×10⁸ km away?
🟢 Answer:
💡 By Kepler’s 3rd Law:
T² ∝ r³
(T_S / T_E)² = (r_S / r_E)³
(r_S / r_E) = (T_S / T_E)^(2/3) = (29.5)^(2/3) = 14.3
r_S = 14.3 × 1.5×10⁸ = 2.15×10⁹ km
✔️ Saturn’s distance from Sun ≈ 2.15×10⁹ km
🔵 Question 7.15
A body weighs 63 N on the surface of the Earth. What is the gravitational force on it due to the Earth at a height equal to half the radius of the Earth?
🟢 Answer:
Given: W₀ = 63 N, h = R/2
💡 Formula: F = W₀ (R / (R + h))²
F = 63 × (R / 1.5R)² = 63 × (2/3)² = 63 × 4/9 = 28 N
✔️ Gravitational force = 28 N
🔵 Question 7.16
Assuming the Earth to be a sphere of uniform mass density, how much would a body weigh halfway down to the centre of the Earth if it weighed 250 N on the surface?
🟢 Answer:
Inside the Earth, g ∝ r
➡️ g’ = g/2 at r = R/2
Hence, W’ = W/2 = 250/2 = 125 N
✔️ Weight at halfway point = 125 N
🔵 Question 7.17
A rocket is fired vertically with a speed of 5 km/s from the Earth’s surface. How far from the Earth does the rocket go before returning to Earth?
Given: M = 6.0×10²⁴ kg, R = 6.4×10⁶ m, G = 6.67×10⁻¹¹
🟢 Answer:
💡 By energy conservation:
½v² − GM/R = −GM/(R + h)
Substitute:
v = 5000 m/s, GM = 3.986×10¹⁴
⇒ 1/(R + h) = 1/R − v²/(2GM)
= 1/(6.4×10⁶) − (25×10⁶)/(7.97×10¹⁴)
= 1.5625×10⁻⁷ − 3.14×10⁻⁸ = 1.248×10⁻⁷
Thus, R + h = 8.01×10⁶ m → h = 1.6×10⁶ m = 1600 km
✔️ Rocket reaches a maximum height ≈ 1600 km
🔵 Question 7.18
The escape speed of a projectile on Earth’s surface is 11.2 km/s. A body is projected with three times this speed. What is its speed far away from Earth?
🟢 Answer:
💡 Formula:
v∞ = √(v² − vₑ²)
vₑ = 11.2 km/s, v = 3vₑ = 33.6 km/s
v∞ = √(9vₑ² − vₑ²) = √8 × vₑ = 2.83 × 11.2 = 31.7 km/s
✔️ Speed far away = 31.7 km/s
🔵 Question 7.19
A satellite orbits Earth at a height of 400 km. How much energy must be expended to rocket it out of Earth’s gravitational influence?
Given: m = 200 kg, M = 6×10²⁴ kg, R = 6.4×10⁶ m, G = 6.67×10⁻¹¹
🟢 Answer:
💡 Total energy per unit mass in orbit = −GM/(2r)
At height 400 km → r = 6.8×10⁶ m
E = −(6.67×10⁻¹¹×6×10²⁴)/(2×6.8×10⁶) = −2.94×10⁷ J/kg
Energy to escape = +2.94×10⁷ J/kg
For 200 kg satellite:
ΔE = 200 × 2.94×10⁷ = 5.88×10⁹ J
✔️ Energy required = 5.9×10⁹ J
🔵 Question 7.20
Two stars, each of one solar mass (2×10³⁰ kg), approach each other for a head-on collision. When 10 km apart, their speeds are negligible. What is the speed when they collide?
Radius of each star = 10⁴ km.
🟢 Answer:
💡 Using energy conservation:
½(2M)v² = G M² / r_final
r_final = 2×10⁷ m
v = √(2GM / r_final)
= √(2×6.67×10⁻¹¹×2×10³⁰ / 2×10⁷)
= √(1.334×10¹³) = 3.65×10⁶ m/s
✔️ Collision speed = 3.65×10⁶ m/s (~3650 km/s)
🔵 Question 7.21
Two heavy spheres each of mass 100 kg and radius 0.10 m are placed 1.0 m apart on a horizontal table.
(a) What is the gravitational force and potential at the midpoint of the line joining the centres?
(b) Is a small object placed at that point in equilibrium? If so, is it stable or unstable?
🟢 Answer:
Given: m₁ = m₂ = 100 kg, distance = 1 m
Distance of midpoint from each = 0.5 m
➡️ Force by one sphere:
F = Gm / r² = 6.67×10⁻¹¹×100 / (0.5)² = 2.67×10⁻⁷ N
🟣 Forces cancel → Net F = 0
➡️ Potential at midpoint:
V = 2(−Gm / r) = −2×6.67×10⁻¹¹×100 / 0.5 = −2.67×10⁻⁷ J/kg
💡 Since net force = 0, equilibrium exists.
If displaced slightly → net force pulls away from centre → unstable equilibrium.
✔️ Equilibrium: Unstable
————————————————————————————————————————————————————————————————————————————
OTHER IMPORTANT QUESTIONS FOR EXAMS
(CBSE MODEL QUESTIONS PAPER)
ESPECIALLY MADE FROM THIS LESSON ONLY
⚙️ SECTION A: Multiple Choice Questions (Q1–Q18)
Question 1:
The universal law of gravitation states that the force between two masses is
🔵 (A) Directly proportional to the product of their masses
🟢 (B) Inversely proportional to the square of the distance between them
🟠 (C) Both (A) and (B)
🔴 (D) None of these
Answer: (C) Both (A) and (B)
Question 2:
The value of universal gravitational constant (G) is
🔵 (A) 9.8 m/s²
🟢 (B) 6.67 × 10⁻¹¹ N·m²/kg²
🟠 (C) 1.6 × 10⁻¹⁹ C
🔴 (D) 3 × 10⁸ m/s
Answer: (B) 6.67 × 10⁻¹¹ N·m²/kg²
Question 3:
Gravitational force is
🔵 (A) Always attractive
🟢 (B) Always repulsive
🟠 (C) Either attractive or repulsive
🔴 (D) Zero
Answer: (A) Always attractive
Question 4:
The dimensions of G are
🔵 (A) [M⁻¹L³T⁻²]
🟢 (B) [ML²T⁻²]
🟠 (C) [M⁰L⁰T⁰]
🔴 (D) [ML⁻¹T⁻²]
Answer: (A) [M⁻¹L³T⁻²]
Question 5:
Acceleration due to gravity on Earth’s surface is given by
🔵 (A) g = Gm/r²
🟢 (B) g = GMₑ/Rₑ²
🟠 (C) g = F/m
🔴 (D) g = GMₑm/r²
Answer: (B) g = GMₑ/Rₑ²
Question 6:
The value of g on Earth’s surface is approximately
🔵 (A) 6.67 × 10⁻¹¹ m/s²
🟢 (B) 10 m/s²
🟠 (C) 9.8 m/s²
🔴 (D) 7.9 m/s²
Answer: (C) 9.8 m/s²
Question 7:
At what location on Earth is the value of g maximum?
🔵 (A) Equator
🟢 (B) Poles
🟠 (C) Tropic of Cancer
🔴 (D) Tropic of Capricorn
Answer: (B) Poles
Question 8:
The acceleration due to gravity at a height h is given by
🔵 (A) g’ = g (R/(R+h))²
🟢 (B) g’ = g (R/(R+h))
🟠 (C) g’ = g (1+h/R)²
🔴 (D) g’ = g (1+h/R)
Answer: (A) g’ = g (R/(R+h))²
Question 9:
At the center of Earth, the value of g is
🔵 (A) Maximum
🟢 (B) Zero
🟠 (C) Half
🔴 (D) One-fourth
Answer: (B) Zero
Question 10:
The gravitational potential at distance r from a mass M is
🔵 (A) +GM/r
🟢 (B) −GM/r
🟠 (C) −GMr
🔴 (D) GM/r²
Answer: (B) −GM/r
Question 11:
Gravitational field intensity at a point is
🔵 (A) The potential per unit mass
🟢 (B) The force experienced by a unit mass
🟠 (C) The work done per unit distance
🔴 (D) The acceleration per unit charge
Answer: (B) The force experienced by a unit mass
Question 12:
Escape velocity from Earth’s surface is about
🔵 (A) 7.9 km/s
🟢 (B) 8.9 km/s
🟠 (C) 11.2 km/s
🔴 (D) 9.8 km/s
Answer: (C) 11.2 km/s
Question 13:
Orbital velocity of a satellite near Earth’s surface is
🔵 (A) 5.9 km/s
🟢 (B) 7.9 km/s
🟠 (C) 11.2 km/s
🔴 (D) 3.1 km/s
Answer: (B) 7.9 km/s
Question 14:
A geostationary satellite revolves around Earth once in
🔵 (A) 12 hours
🟢 (B) 24 hours
🟠 (C) 48 hours
🔴 (D) 6 hours
Answer: (B) 24 hours
Question 15:
Which of the following quantities has negative value for a satellite in orbit?
🔵 (A) Kinetic Energy
🟢 (B) Potential Energy
🟠 (C) Total Energy
🔴 (D) Both (B) and (C)
Answer: (D) Both (B) and (C)
Question 16:
The total energy of a satellite revolving in circular orbit is
🔵 (A) −GMₑm/r
🟢 (B) −GMₑm/2r
🟠 (C) GMₑm/2r
🔴 (D) Zero
Answer: (B) −GMₑm/2r
Question 17:
According to Kepler’s third law, T² is proportional to
🔵 (A) r
🟢 (B) r²
🟠 (C) r³
🔴 (D) r⁴
Answer: (C) r³
Question 18:
If the distance between two bodies is doubled, the gravitational force becomes
🔵 (A) 1/2 times
🟢 (B) 1/4 times
🟠 (C) 2 times
🔴 (D) 4 times
Answer: (B) 1/4 times
🧩 SECTION B: Very Short/Short Answer (Q19–Q23)
Question 19:
Define universal gravitational constant.
Answer:
💡 Universal gravitational constant (G) is the force of attraction between two unit masses separated by unit distance in vacuum.
✔️ G = 6.67 × 10⁻¹¹ N·m²/kg².
Question 20:
What is the difference between g and G?
Answer:
✔️ G is universal and constant everywhere; g is local and depends on the Earth’s mass and radius.
✔️ G = 6.67 × 10⁻¹¹ N·m²/kg²; g = 9.8 m/s².
✔️ g = GMₑ / Rₑ².
Question 21:
What happens to the value of g with increase in height from Earth’s surface?
Answer:
💡 As height increases, g decreases according to g’ = g (R / (R + h))².
Hence, at large heights, the gravitational pull weakens.
Question 22:
State Kepler’s second law of planetary motion.
Answer:
💡 The line joining a planet and the Sun sweeps out equal areas in equal intervals of time.
✔️ This means the planet moves faster when nearer to the Sun and slower when farther away.
Question 23:
Why do astronauts feel weightless in a spaceship orbiting Earth?
Answer:
✔️ Because both the astronaut and the spaceship are in free fall around the Earth, they experience no normal reaction.
Hence, apparent weight becomes zero — this is weightlessness.
⚡ SECTION C: Mid-Length Numerical/Theory (Q24–Q28)
Question 24:
Derive the expression for acceleration due to gravity on Earth’s surface.
Answer:
✏️ From Newton’s law: F = G(Mₑm)/Rₑ²
From Newton’s second law: F = ma = mg
Equating: mg = G(Mₑm)/Rₑ²
Cancel m: g = GMₑ / Rₑ²
✔️ Therefore, g depends on Earth’s mass and radius only.
Question 25:
Find the ratio of the acceleration due to gravity at height h = R/2 to that on Earth’s surface.
Answer:
✏️ Formula: g’ = g (R / (R + h))²
Substitute h = R/2:
g’ = g (R / (3R/2))² = g (2/3)² = (4/9)g
✔️ Therefore, g’ : g = 4 : 9.
Question 26:
Derive the expression for escape velocity from Earth.
Answer:
💡 Total energy required = Gain in potential energy + Kinetic energy
For escape, ½mvₑ² = GMₑm / Rₑ
vₑ = √(2GMₑ / Rₑ)
✔️ On Earth, vₑ = 11.2 km/s.
Question 27:
Calculate orbital velocity for a satellite near Earth’s surface.
Answer:
✏️ Centripetal force = Gravitational force
mvₒ² / R = GMₑm / R²
vₒ = √(GMₑ / R)
✔️ Substituting values gives vₒ = 7.9 km/s.
Question 28:
Derive the relation between orbital and escape velocities.
Answer:
vₑ = √(2GMₑ / Rₑ)
vₒ = √(GMₑ / Rₑ)
Divide both:
vₑ / vₒ = √2
✔️ Hence, vₑ = √2 × vₒ.
⚡ SECTION D: Long Answer Questions (Q29–Q31)
Question 29:
Derive the expression for variation of acceleration due to gravity (g) with altitude.
Answer:
💡 Concept:
The value of acceleration due to gravity decreases with increase in height above the Earth’s surface.
Let the value of g at height h be g’.
✏️ Step 1:
According to Newton’s law of gravitation,
F = G(Mₑm) / (Rₑ + h)²
Also, F = mg’
So, mg’ = G(Mₑm) / (Rₑ + h)²
✏️ Step 2:
At Earth’s surface,
g = G(Mₑ) / Rₑ²
Dividing both equations:
g’/g = (Rₑ² / (Rₑ + h)²)
Therefore,
➡️ g’ = g (Rₑ / (Rₑ + h))²
✏️ Step 3 (Approximation for small h):
If h ≪ Rₑ,
(Rₑ / (Rₑ + h))² ≈ (1 − 2h/Rₑ)
Thus,
➡️ g’ ≈ g (1 − 2h/Rₑ)
✔️ Hence, g decreases with height.
💡 Result:
g’ = g (Rₑ / (Rₑ + h))²
✔️ As h increases, g decreases.
Question 30:
Derive the expression for potential energy of a body in the gravitational field of Earth.
Answer:
💡 Concept:
Gravitational potential energy (U) is the work done in bringing a body from infinity to a point in the Earth’s gravitational field.
✏️ Step 1:
Work done in moving a mass m from infinity to distance r from Earth’s center is:
W = ∫∞ᵣ (−F) dr
F = G(Mₑm)/r²
So,
W = −∫∞ᵣ G(Mₑm)/r² dr
✏️ Step 2:
Integrating:
W = −G(Mₑm) [−1/r]∞ᵣ
= −G(Mₑm)(0 − (−1/r))
= −G(Mₑm)/r
✏️ Step 3:
This work is stored as potential energy, hence
➡️ U = −G(Mₑm)/r
💡 Interpretation:
✔️ Negative sign indicates that gravitational potential energy is less than zero (since gravity is attractive).
✔️ As r → ∞, U → 0.
Question 31:
Explain and derive Kepler’s third law of planetary motion using Newton’s law of gravitation.
Answer:
💡 Kepler’s Third Law:
The square of the time period (T²) of revolution of a planet around the Sun is directly proportional to the cube of the mean distance (r³) between them.
✏️ Step 1:
For a planet of mass m revolving around the Sun (mass Mₛ) in a circular orbit,
Centripetal force = Gravitational force
m v² / r = G(Mₛm)/r²
⟹ v² = G Mₛ / r
✏️ Step 2:
Orbital velocity v = 2πr / T
Substitute in above equation:
(4π²r² / T²) = G Mₛ / r
⟹ T² = (4π² / G Mₛ) r³
💡 Step 3:
Hence,
➡️ T² ∝ r³
✔️ The constant of proportionality (4π² / GMₛ) is same for all planets revolving around the Sun.
⚡ Result:
T² / r³ = constant
✔️ Thus, Kepler’s third law is derived from Newton’s law of gravitation.
🌍 SECTION E: Case/Application Based Questions (Q32–Q33)
Question 32:
A satellite is revolving around the Earth in a circular orbit of radius 7 × 10⁶ m.
Calculate its orbital velocity.
(Mₑ = 6 × 10²⁴ kg, G = 6.67 × 10⁻¹¹ N·m²/kg²)
Answer:
✏️ Step 1:
Formula for orbital velocity:
vₒ = √(GMₑ / r)
Substitute:
vₒ = √((6.67 × 10⁻¹¹ × 6 × 10²⁴) / (7 × 10⁶))
✏️ Step 2:
vₒ = √(4.002 × 10¹⁴ / 7 × 10⁶)
= √(5.717 × 10⁷)
= 7.56 × 10³ m/s
✔️ Result:
Orbital velocity = 7.56 km/s
💡 This value matches the typical orbital speed near Earth’s surface.
Question 33:
A rocket is fired vertically upward with a speed of 8 km/s.
Will it escape Earth’s gravity?
(Escape velocity from Earth = 11.2 km/s)
Answer:
✏️ Step 1:
Given:
v = 8 km/s, vₑ = 11.2 km/s
✏️ Step 2:
If v < vₑ, the object cannot escape Earth’s gravity.
It will rise up to some height and then fall back.
✔️ Result:
Since 8 km/s < 11.2 km/s,
💡 The rocket will not escape Earth’s gravitational pull.
It will move upward, slow down, and then return to Earth.
————————————————————————————————————————————————————————————————————————————
NEET QUESTIONS FROM THIS LESSON
🔵 Question 1 (NEET 2024):
The gravitational force between two masses m₁ and m₂ separated by distance r is proportional to
🔴 1️⃣ m₁ + m₂
🟢 2️⃣ m₁m₂ / r²
🟡 3️⃣ r² / (m₁m₂)
🔵 4️⃣ 1 / (m₁m₂r²)
🟣 Answer: 2️⃣ m₁m₂ / r²
🔵 Question 2 (NEET 2023):
The value of gravitational constant G in SI units is
🔴 1️⃣ 6.67 × 10⁻¹¹ N·m²/kg²
🟢 2️⃣ 9.8 m/s²
🟡 3️⃣ 3 × 10⁸ m/s
🔵 4️⃣ 1.6 × 10⁻¹⁹ C
🟣 Answer: 1️⃣ 6.67 × 10⁻¹¹ N·m²/kg²
🔵 Question 3 (NEET 2022):
Acceleration due to gravity at height h is
🔴 1️⃣ g(1 − 2h/R)
🟢 2️⃣ g(1 − h/R)
🟡 3️⃣ g(1 + 2h/R)
🔵 4️⃣ g(1 + h/R)
🟣 Answer: 1️⃣ g(1 − 2h/R)
🔵 Question 4 (NEET 2021):
If the earth shrinks in size such that radius becomes half, mass remaining same, g becomes
🔴 1️⃣ 2g
🟢 2️⃣ 4g
🟡 3️⃣ g/2
🔵 4️⃣ g/4
🟣 Answer: 2️⃣ 4g
🔵 Question 5 (NEET 2020):
Potential energy of two masses m₁ and m₂ separated by r is
🔴 1️⃣ Gm₁m₂r
🟢 2️⃣ −Gm₁m₂ / r
🟡 3️⃣ Gm₁m₂ / r²
🔵 4️⃣ −Gm₁m₂r²
🟣 Answer: 2️⃣ −Gm₁m₂ / r
🔵 Question 6 (NEET 2019):
If mass and radius of a planet are twice that of earth, then acceleration due to gravity on its surface is
🔴 1️⃣ g
🟢 2️⃣ g/2
🟡 3️⃣ 2g
🔵 4️⃣ g/4
🟣 Answer: 2️⃣ g/2
🔵 Question 7 (NEET 2018):
Gravitational potential energy of a body of mass m at height h is
🔴 1️⃣ mgh
🟢 2️⃣ −mgh
🟡 3️⃣ mg/h
🔵 4️⃣ m/h
🟣 Answer: 1️⃣ mgh
🔵 Question 8 (NEET 2017):
At centre of earth, acceleration due to gravity is
🔴 1️⃣ g
🟢 2️⃣ Zero
🟡 3️⃣ Infinite
🔵 4️⃣ Maximum
🟣 Answer: 2️⃣ Zero
🔵 Question 9 (NEET 2016):
If g is acceleration due to gravity at surface, then at height R/2 above surface, g’ =
🔴 1️⃣ g/3
🟢 2️⃣ 4g/9
🟡 3️⃣ g/2
🔵 4️⃣ g/4
🟣 Answer: 2️⃣ 4g/9
🔵 Question 10 (AIPMT 2015):
Escape velocity on earth is approximately
🔴 1️⃣ 7.9 km/s
🟢 2️⃣ 11.2 km/s
🟡 3️⃣ 9.8 km/s
🔵 4️⃣ 8.9 km/s
🟣 Answer: 2️⃣ 11.2 km/s
🔵 Question 11 (AIPMT 2014):
The weight of a body at height h from surface of earth is W’. Its weight on surface is W. Then W’/W =
🔴 1️⃣ (1 − 2h/R)
🟢 2️⃣ (R / (R + h))²
🟡 3️⃣ (R / (R − h))²
🔵 4️⃣ (1 + 2h/R)
🟣 Answer: 2️⃣ (R / (R + h))²
🔵 Question 12 (AIPMT 2013):
Acceleration due to gravity at poles is
🔴 1️⃣ Less than equator
🟢 2️⃣ Greater than equator
🟡 3️⃣ Equal
🔵 4️⃣ Zero
🟣 Answer: 2️⃣ Greater than equator
🔵 Question 13 (AIPMT 2012):
If earth stops rotating, value of g at equator will
🔴 1️⃣ Decrease
🟢 2️⃣ Increase
🟡 3️⃣ Remain same
🔵 4️⃣ Become zero
🟣 Answer: 2️⃣ Increase
🔵 Question 14 (AIPMT 2011):
Satellite revolving near surface has time period
🔴 1️⃣ 90 minutes
🟢 2️⃣ 84 minutes
🟡 3️⃣ 24 hours
🔵 4️⃣ 60 minutes
🟣 Answer: 2️⃣ 84 minutes
🔵 Question 15 (AIPMT 2010):
The orbital velocity of earth around sun is
🔴 1️⃣ 11.2 km/s
🟢 2️⃣ 30 km/s
🟡 3️⃣ 7.9 km/s
🔵 4️⃣ 9.8 km/s
🟣 Answer: 2️⃣ 30 km/s
🔵 Question 16 (AIPMT 2009):
The acceleration due to gravity is maximum at
🔴 1️⃣ Equator
🟢 2️⃣ Poles
🟡 3️⃣ Centre
🔵 4️⃣ Everywhere same
🟣 Answer: 2️⃣ Poles
🔵 Question 17 (AIPMT 2008):
Escape velocity vₑ is related to orbital velocity vₒ by
🔴 1️⃣ vₑ = √2 vₒ
🟢 2️⃣ vₑ = vₒ / √2
🟡 3️⃣ vₑ = 2 vₒ
🔵 4️⃣ vₑ = vₒ
🟣 Answer: 1️⃣ vₑ = √2 vₒ
🔵 Question 18 (AIPMT 2007):
Gravitational potential at surface of earth is
🔴 1️⃣ −GM/R
🟢 2️⃣ GM/R
🟡 3️⃣ −GM/R²
🔵 4️⃣ GM/R²
🟣 Answer: 1️⃣ −GM/R
🔵 Question 19 (AIPMT 2006):
The dimension of G is
🔴 1️⃣ [M⁻¹L³T⁻²]
🟢 2️⃣ [M¹L³T⁻²]
🟡 3️⃣ [M⁻¹L²T⁻²]
🔵 4️⃣ [ML⁻²T²]
🟣 Answer: 1️⃣ [M⁻¹L³T⁻²]
🔵 Question 20 (AIPMT 2005):
Weight of a body at height h is given by
🔴 1️⃣ W(1 − 2h/R)
🟢 2️⃣ W(1 − h/R)
🟡 3️⃣ W(1 + 2h/R)
🔵 4️⃣ W(1 + h/R)
🟣 Answer: 1️⃣ W(1 − 2h/R)
🔵 Question 21 (AIPMT 2004):
The escape velocity from earth depends upon
🔴 1️⃣ Mass only
🟢 2️⃣ Radius only
🟡 3️⃣ Both mass and radius
🔵 4️⃣ Not on either
🟣 Answer: 3️⃣ Both mass and radius
🔵 Question 22 (AIPMT 2003):
The path of a satellite is
🔴 1️⃣ Circular
🟢 2️⃣ Elliptical
🟡 3️⃣ Parabolic
🔵 4️⃣ Any of these
🟣 Answer: 4️⃣ Any of these
🔵 Question 23 (AIPMT 2002):
Gravitational field inside a spherical shell is
🔴 1️⃣ Constant
🟢 2️⃣ Zero
🟡 3️⃣ Maximum
🔵 4️⃣ Minimum
🟣 Answer: 2️⃣ Zero
🔵 Question 24 (AIPMT 2001):
Gravitational force between two bodies is independent of
🔴 1️⃣ Medium
🟢 2️⃣ Distance
🟡 3️⃣ Mass
🔵 4️⃣ Constant
🟣 Answer: 1️⃣ Medium
🔵 Question 25 (NEET 2024):
If mass of earth is M and radius R, then g =
🔴 1️⃣ GM/R
🟢 2️⃣ GM/R²
🟡 3️⃣ GMR
🔵 4️⃣ GM/R³
🟣 Answer: 2️⃣ GM/R²
🔵 Question 26 (NEET 2024):
If the distance between two masses is doubled, the gravitational force becomes
🔴 1️⃣ 1/4 times
🟢 2️⃣ 1/2 times
🟡 3️⃣ 2 times
🔵 4️⃣ 4 times
🟣 Answer: 1️⃣ 1/4 times
🔵 Question 27 (NEET 2023):
A body weighs 63 N on the surface of the earth. The radius of the earth is 6400 km. The weight of the body at height equal to radius is
🔴 1️⃣ 7 N
🟢 2️⃣ 15.75 N
🟡 3️⃣ 31.5 N
🔵 4️⃣ 63 N
🟣 Answer: 2️⃣ 15.75 N
🔵 Question 28 (NEET 2022):
Escape velocity depends on
🔴 1️⃣ Mass of the body
🟢 2️⃣ Mass and radius of the planet
🟡 3️⃣ Density of planet
🔵 4️⃣ Altitude of launch
🟣 Answer: 2️⃣ Mass and radius of the planet
🔵 Question 29 (NEET 2021):
The period of revolution of an artificial satellite close to the earth is
🔴 1️⃣ 60 min
🟢 2️⃣ 84 min
🟡 3️⃣ 120 min
🔵 4️⃣ 24 hours
🟣 Answer: 2️⃣ 84 min
🔵 Question 30 (NEET 2020):
If mass of earth is 81 times mass of moon and radius is 3.6 times, the ratio of escape velocity from earth to moon is
🔴 1️⃣ 6
🟢 2️⃣ 9
🟡 3️⃣ 3
🔵 4️⃣ 12
🟣 Answer: 1️⃣ 6
🔵 Question 31 (NEET 2019):
Value of g is maximum at
🔴 1️⃣ Equator
🟢 2️⃣ Poles
🟡 3️⃣ Centre
🔵 4️⃣ Everywhere same
🟣 Answer: 2️⃣ Poles
🔵 Question 32 (NEET 2018):
A satellite is moving round the earth with constant speed. Its motion is
🔴 1️⃣ Uniform
🟢 2️⃣ Accelerated
🟡 3️⃣ Retarded
🔵 4️⃣ None
🟣 Answer: 2️⃣ Accelerated
🔵 Question 33 (NEET 2017):
If g at surface is 10 m/s², then at depth R/2 it is
🔴 1️⃣ 10 m/s²
🟢 2️⃣ 5 m/s²
🟡 3️⃣ 7.5 m/s²
🔵 4️⃣ 2.5 m/s²
🟣 Answer: 2️⃣ 5 m/s²
🔵 Question 34 (NEET 2016):
The orbital velocity of a satellite just above earth’s surface is
🔴 1️⃣ 11.2 km/s
🟢 2️⃣ 7.9 km/s
🟡 3️⃣ 5.6 km/s
🔵 4️⃣ 9.8 km/s
🟣 Answer: 2️⃣ 7.9 km/s
🔵 Question 35 (AIPMT 2015):
Weight of a body at poles is
🔴 1️⃣ Less than at equator
🟢 2️⃣ More than at equator
🟡 3️⃣ Equal
🔵 4️⃣ Zero
🟣 Answer: 2️⃣ More than at equator
🔵 Question 36 (AIPMT 2014):
A planet moves around the sun in an elliptical orbit. Areal velocity is constant due to
🔴 1️⃣ Conservation of energy
🟢 2️⃣ Conservation of angular momentum
🟡 3️⃣ Conservation of linear momentum
🔵 4️⃣ Newton’s second law
🟣 Answer: 2️⃣ Conservation of angular momentum
🔵 Question 37 (AIPMT 2013):
Kepler’s second law states that
🔴 1️⃣ Areal velocity is constant
🟢 2️⃣ Linear velocity is constant
🟡 3️⃣ Angular velocity is constant
🔵 4️⃣ Kinetic energy is constant
🟣 Answer: 1️⃣ Areal velocity is constant
🔵 Question 38 (AIPMT 2012):
Kepler’s third law states
🔴 1️⃣ T² ∝ r³
🟢 2️⃣ T ∝ r²
🟡 3️⃣ T³ ∝ r²
🔵 4️⃣ T ∝ r³
🟣 Answer: 1️⃣ T² ∝ r³
🔵 Question 39 (AIPMT 2011):
If acceleration due to gravity decreases by 36%, the height is
🔴 1️⃣ R/2
🟢 2️⃣ R
🟡 3️⃣ R/3
🔵 4️⃣ R/4
🟣 Answer: 1️⃣ R/2
🔵 Question 40 (AIPMT 2010):
Work done by gravitational force on a satellite moving in circular orbit is
🔴 1️⃣ Maximum
🟢 2️⃣ Zero
🟡 3️⃣ Minimum
🔵 4️⃣ Variable
🟣 Answer: 2️⃣ Zero
🔵 Question 41 (AIPMT 2009):
A satellite revolves close to earth. Its speed is
🔴 1️⃣ 11.2 km/s
🟢 2️⃣ 7.9 km/s
🟡 3️⃣ 5 km/s
🔵 4️⃣ 10 km/s
🟣 Answer: 2️⃣ 7.9 km/s
🔵 Question 42 (AIPMT 2008):
If the earth’s radius is reduced to half, keeping mass same, g becomes
🔴 1️⃣ 4g
🟢 2️⃣ 2g
🟡 3️⃣ g/2
🔵 4️⃣ g/4
🟣 Answer: 1️⃣ 4g
🔵 Question 43 (AIPMT 2007):
If mass of earth becomes half and radius becomes half, g becomes
🔴 1️⃣ 2g
🟢 2️⃣ g/2
🟡 3️⃣ g/4
🔵 4️⃣ g
🟣 Answer: 1️⃣ 2g
🔵 Question 44 (AIPMT 2006):
At height h = R, g =
🔴 1️⃣ g/4
🟢 2️⃣ g/2
🟡 3️⃣ g/3
🔵 4️⃣ g
🟣 Answer: 1️⃣ g/4
🔵 Question 45 (AIPMT 2005):
Acceleration due to gravity at depth d is
🔴 1️⃣ g(1 − d/R)
🟢 2️⃣ g(1 − 2d/R)
🟡 3️⃣ g(1 + d/R)
🔵 4️⃣ g(1 + 2d/R)
🟣 Answer: 1️⃣ g(1 − d/R)
🔵 Question 46 (AIPMT 2004):
The orbital velocity does not depend on
🔴 1️⃣ Mass of planet
🟢 2️⃣ Radius of orbit
🟡 3️⃣ Gravitational constant
🔵 4️⃣ Radius of planet
🟣 Answer: 1️⃣ Mass of planet
🔵 Question 47 (AIPMT 2003):
At centre of earth, g =
🔴 1️⃣ 0
🟢 2️⃣ g
🟡 3️⃣ g/2
🔵 4️⃣ Infinite
🟣 Answer: 1️⃣ 0
🔵 Question 48 (AIPMT 2002):
Gravitational potential energy between earth and mass m at height h is
🔴 1️⃣ −GMm / (R + h)
🟢 2️⃣ GMm / (R + h)
🟡 3️⃣ −GMm / R²
🔵 4️⃣ GMm / R²
🟣 Answer: 1️⃣ −GMm / (R + h)
🔵 Question 49 (AIPMT 2001):
g at height h = R/2 is
🔴 1️⃣ g/3
🟢 2️⃣ 4g/9
🟡 3️⃣ g/2
🔵 4️⃣ g/4
🟣 Answer: 2️⃣ 4g/9
🔵 Question 50 (NEET 2024):
At a height h from surface, weight is reduced by 36%. h =
🔴 1️⃣ R/2
🟢 2️⃣ R/4
🟡 3️⃣ R
🔵 4️⃣ R/3
🟣 Answer: 1️⃣ R/2
————————————————————————————————————————————————————————————————————————————
JEE MAINS QUESTIONS FROM THIS LESSON
🔴 Q1. The force between two masses m₁ and m₂ separated by distance r is proportional to
🟢 1️⃣ m₁m₂/r²
🔵 2️⃣ m₁ + m₂
🟡 3️⃣ r²
🟣 4️⃣ m₁/m₂
✔️ Answer: 1
📘 Exam: JEE Main 2024
🔴 Q2. Gravitational constant G has the dimensional formula
🟢 1️⃣ [M⁻¹L³T⁻²]
🔵 2️⃣ [ML²T⁻²]
🟡 3️⃣ [MLT⁻²]
🟣 4️⃣ [M⁻²L³T⁻²]
✔️ Answer: 1
📘 Exam: JEE Main 2024
🔴 Q3. The value of acceleration due to gravity g at a height h above the Earth’s surface is
🟢 1️⃣ g(1 − 2h/R)
🔵 2️⃣ g(1 − h/R)
🟡 3️⃣ g(1 + 2h/R)
🟣 4️⃣ g(1 + h/R)
✔️ Answer: 1
📘 Exam: JEE Main 2023
🔴 Q4. The value of g at depth d below the surface is
🟢 1️⃣ g(1 − d/R)
🔵 2️⃣ g(1 − 2d/R)
🟡 3️⃣ g(1 + d/R)
🟣 4️⃣ g(1 − d/2R)
✔️ Answer: 1
📘 Exam: JEE Main 2023
🔴 Q5. The escape velocity from Earth is approximately
🟢 1️⃣ 11.2 km/s
🔵 2️⃣ 7.9 km/s
🟡 3️⃣ 9.8 km/s
🟣 4️⃣ 8.4 km/s
✔️ Answer: 1
📘 Exam: JEE Main 2022
🔴 Q6. The orbital velocity of a satellite near the Earth’s surface is
🟢 1️⃣ √(gR)
🔵 2️⃣ √(2gR)
🟡 3️⃣ √(gR/2)
🟣 4️⃣ √(g/2R)
✔️ Answer: 1
📘 Exam: JEE Main 2022
🔴 Q7. A satellite is said to be geostationary if its
🟢 1️⃣ Time period = 24 h, direction same as Earth’s rotation
🔵 2️⃣ Time period = 12 h
🟡 3️⃣ Altitude very low
🟣 4️⃣ Inclination 90°
✔️ Answer: 1
📘 Exam: JEE Main 2021
🔴 Q8. The potential energy of two masses m₁ and m₂ separated by distance r is
🟢 1️⃣ −Gm₁m₂/r
🔵 2️⃣ Gm₁m₂/r
🟡 3️⃣ −Gm₁m₂/r²
🟣 4️⃣ Gm₁m₂r²
✔️ Answer: 1
📘 Exam: JEE Main 2021
🔴 Q9. Gravitational field intensity is
🟢 1️⃣ Force per unit mass
🔵 2️⃣ Potential per unit mass
🟡 3️⃣ Acceleration per unit mass
🟣 4️⃣ None
✔️ Answer: 1
📘 Exam: JEE Main 2020
🔴 Q10. The orbital velocity of an artificial satellite does not depend upon
🟢 1️⃣ Mass of satellite
🔵 2️⃣ Radius of orbit
🟡 3️⃣ Radius of Earth
🟣 4️⃣ Gravitational constant
✔️ Answer: 1
📘 Exam: JEE Main 2020
🔴 Q11. If the Earth shrinks to one-fourth of its radius keeping mass same, value of g at surface becomes
🟢 1️⃣ 16g
🔵 2️⃣ 4g
🟡 3️⃣ g/4
🟣 4️⃣ g/16
✔️ Answer: 1
📘 Exam: JEE Main 2019
🔴 Q12. The gravitational potential at a point is −5 J/kg. The work done in moving 1 kg mass from infinity to that point is
🟢 1️⃣ −5 J
🔵 2️⃣ +5 J
🟡 3️⃣ 0
🟣 4️⃣ 10 J
✔️ Answer: 1
📘 Exam: JEE Main 2019
🔴 Q13. A body weighs 63 N on Earth. Its weight on Moon (g = gₑ/6) is
🟢 1️⃣ 10.5 N
🔵 2️⃣ 63 N
🟡 3️⃣ 6 N
🟣 4️⃣ 0 N
✔️ Answer: 1
📘 Exam: JEE Main 2018
🔴 Q14. Work done by gravitational force on a satellite moving around Earth is
🟢 1️⃣ Zero
🔵 2️⃣ Positive
🟡 3️⃣ Negative
🟣 4️⃣ Variable
✔️ Answer: 1
📘 Exam: JEE Main 2018
🔴 Q15. Gravitational potential due to a point mass is
🟢 1️⃣ V = −GM/r
🔵 2️⃣ V = GM/r²
🟡 3️⃣ V = GM/r
🟣 4️⃣ V = −GM/r²
✔️ Answer: 1
📘 Exam: JEE Main 2017
🔴 Q16. The escape velocity on a planet is 100 m/s. If radius becomes 1/4 and mass becomes 1/16, new escape velocity is
🟢 1️⃣ 50 m/s
🔵 2️⃣ 25 m/s
🟡 3️⃣ 100 m/s
🟣 4️⃣ 200 m/s
✔️ Answer: 1
📘 Exam: JEE Main 2017
🔴 Q17. The weight of a body at Earth’s surface is W. Its weight at height equal to Earth’s radius is
🟢 1️⃣ W/4
🔵 2️⃣ W/2
🟡 3️⃣ W/8
🟣 4️⃣ W/9
✔️ Answer: 1
📘 Exam: JEE Main 2016
🔴 Q18. The gravitational potential energy of mass m at height h is
🟢 1️⃣ −GMm/(R + h)
🔵 2️⃣ GMm/(R + h)
🟡 3️⃣ −GMm/h
🟣 4️⃣ GMm/h²
✔️ Answer: 1
📘 Exam: JEE Main 2016
🔴 Q19. Acceleration due to gravity at poles is greater than at equator because
🟢 1️⃣ Earth’s rotation and polar flattening
🔵 2️⃣ Earth’s revolution
🟡 3️⃣ Altitude difference
🟣 4️⃣ None
✔️ Answer: 1
📘 Exam: JEE Main 2015
🔴 Q20. Gravitational field inside a hollow spherical shell is
🟢 1️⃣ Zero
🔵 2️⃣ Constant
🟡 3️⃣ Infinite
🟣 4️⃣ Decreasing
✔️ Answer: 1
📘 Exam: JEE Main 2015
🔴 Q21. For a satellite orbiting Earth, total energy is
🟢 1️⃣ Negative
🔵 2️⃣ Zero
🟡 3️⃣ Positive
🟣 4️⃣ Variable
✔️ Answer: 1
📘 Exam: JEE Main 2014
🔴 Q22. If g on surface is 9.8 m/s², then at height R, g is
🟢 1️⃣ 2.45 m/s²
🔵 2️⃣ 4.9 m/s²
🟡 3️⃣ 6.5 m/s²
🟣 4️⃣ 9.8 m/s²
✔️ Answer: 1
📘 Exam: JEE Main 2014
🔴 Q23. Potential energy of Earth-satellite system is
🟢 1️⃣ Negative
🔵 2️⃣ Zero
🟡 3️⃣ Positive
🟣 4️⃣ Infinite
✔️ Answer: 1
📘 Exam: JEE Main 2013
🔴 Q24. The period of a geostationary satellite is
🟢 1️⃣ 24 h
🔵 2️⃣ 12 h
🟡 3️⃣ 6 h
🟣 4️⃣ 48 h
✔️ Answer: 1
📘 Exam: JEE Main 2013
🔴 Q25. The escape velocity is independent of
🟢 1️⃣ Mass of the body
🔵 2️⃣ Radius of Earth
🟡 3️⃣ Gravitational constant
🟣 4️⃣ Value of g
✔️ Answer: 1
📘 Exam: JEE Main 2012
🔴 Q26. If a satellite is revolving near Earth’s surface, its orbital speed is approximately
🟢 1️⃣ 7.9 km/s
🔵 2️⃣ 11.2 km/s
🟡 3️⃣ 5 km/s
🟣 4️⃣ 9.8 km/s
✔️ Answer: 1
📘 Exam: JEE Main 2012
🔴 Q27. The energy required to move a satellite from Earth’s surface to infinity is
🟢 1️⃣ GMm/2R
🔵 2️⃣ GMm/R
🟡 3️⃣ 2GMm/R
🟣 4️⃣ GMm/4R
✔️ Answer: 1
📘 Exam: JEE Main 2011
🔴 Q28. If Earth’s radius becomes half and mass remains same, escape velocity becomes
🟢 1️⃣ √2 × original
🔵 2️⃣ 2 × original
🟡 3️⃣ 1/√2 × original
🟣 4️⃣ 1/2 × original
✔️ Answer: 1
📘 Exam: JEE Main 2011
🔴 Q29. The time period of a satellite in a circular orbit of radius r is proportional to
🟢 1️⃣ r³/²
🔵 2️⃣ r¹/²
🟡 3️⃣ r
🟣 4️⃣ r²
✔️ Answer: 1
📘 Exam: JEE Main 2010
🔴 Q30. The escape velocity on Moon compared to Earth is
🟢 1️⃣ Less
🔵 2️⃣ More
🟡 3️⃣ Equal
🟣 4️⃣ Infinite
✔️ Answer: 1
📘 Exam: JEE Main 2010
🔴 Q31. If g is 9.8 m/s² on Earth, then at a height equal to Earth’s radius, g becomes
🟢 1️⃣ 2.45 m/s²
🔵 2️⃣ 4.9 m/s²
🟡 3️⃣ 9.8 m/s²
🟣 4️⃣ 19.6 m/s²
✔️ Answer: 1
📘 Exam: JEE Main 2009
🔴 Q32. The potential energy of a body of mass m at height h is approximately
🟢 1️⃣ mgh
🔵 2️⃣ 2mgh
🟡 3️⃣ mgh/2
🟣 4️⃣ 0
✔️ Answer: 1
📘 Exam: JEE Main 2009
🔴 Q33. The gravitational field inside a uniform spherical shell is
🟢 1️⃣ Zero
🔵 2️⃣ Constant
🟡 3️⃣ Increases
🟣 4️⃣ Decreases
✔️ Answer: 1
📘 Exam: JEE Main 2008
🔴 Q34. The total energy of a satellite in orbit is
🟢 1️⃣ −GMm/2r
🔵 2️⃣ −GMm/r
🟡 3️⃣ GMm/2r
🟣 4️⃣ GMm/r
✔️ Answer: 1
📘 Exam: JEE Main 2008
🔴 Q35. A body projected with escape velocity from Earth will
🟢 1️⃣ Escape from Earth’s field
🔵 2️⃣ Return
🟡 3️⃣ Move in circle
🟣 4️⃣ Oscillate
✔️ Answer: 1
📘 Exam: JEE Main 2007
🔴 Q36. The value of escape velocity depends upon
🟢 1️⃣ Radius of Earth
🔵 2️⃣ Mass of Earth
🟡 3️⃣ Both mass and radius
🟣 4️⃣ None
✔️ Answer: 3
📘 Exam: JEE Main 2007
🔴 Q37. If radius of Earth increases, escape velocity
🟢 1️⃣ Decreases
🔵 2️⃣ Increases
🟡 3️⃣ Unchanged
🟣 4️⃣ Becomes zero
✔️ Answer: 1
📘 Exam: JEE Main 2006
🔴 Q38. The relation between orbital velocity (v₀) and escape velocity (vₑ) is
🟢 1️⃣ vₑ = √2 v₀
🔵 2️⃣ vₑ = 2v₀
🟡 3️⃣ v₀ = 2vₑ
🟣 4️⃣ v₀ = √2 vₑ
✔️ Answer: 1
📘 Exam: JEE Main 2006
🔴 Q39. Gravitational potential at the center of Earth is
🟢 1️⃣ −3GM/2R
🔵 2️⃣ −GM/R
🟡 3️⃣ Zero
🟣 4️⃣ GM/R
✔️ Answer: 1
📘 Exam: JEE Main 2005
🔴 Q40. The variation of g with altitude h is given by
🟢 1️⃣ g’ = g(1 − 2h/R)
🔵 2️⃣ g’ = g(1 + 2h/R)
🟡 3️⃣ g’ = g(1 − h/R)
🟣 4️⃣ g’ = g(1 + h/R)
✔️ Answer: 1
📘 Exam: JEE Main 2005
🔴 Q41. Gravitational potential energy is zero when
🟢 1️⃣ r → ∞
🔵 2️⃣ r = R
🟡 3️⃣ r = 0
🟣 4️⃣ r = R/2
✔️ Answer: 1
📘 Exam: JEE Main 2004
🔴 Q42. The gravitational potential at the surface of Earth is
🟢 1️⃣ −GM/R
🔵 2️⃣ GM/R
🟡 3️⃣ −GM/R²
🟣 4️⃣ GM/R²
✔️ Answer: 1
📘 Exam: JEE Main 2004
🔴 Q43. If the weight of a body is W on surface, at height h = R/2 it will be
🟢 1️⃣ (4/9)W
🔵 2️⃣ (3/4)W
🟡 3️⃣ (1/2)W
🟣 4️⃣ W/3
✔️ Answer: 1
📘 Exam: JEE Main 2003
🔴 Q44. The time period of a satellite in terms of orbital radius r is
🟢 1️⃣ 2π√(r³/GM)
🔵 2️⃣ 2π√(GM/r³)
🟡 3️⃣ 2π√(r²/GM)
🟣 4️⃣ 2π√(GM/r²)
✔️ Answer: 1
📘 Exam: JEE Main 2003
🔴 Q45. For two satellites at radii r₁ and r₂, ratio of time periods is
🟢 1️⃣ (r₁/r₂)³/²
🔵 2️⃣ (r₁/r₂)²
🟡 3️⃣ (r₁/r₂)¹/²
🟣 4️⃣ (r₁/r₂)
✔️ Answer: 1
📘 Exam: JEE Main 2002
🔴 Q46. A satellite is launched with escape velocity. Its total energy becomes
🟢 1️⃣ Zero
🔵 2️⃣ Positive
🟡 3️⃣ Negative
🟣 4️⃣ Infinite
✔️ Answer: 1
📘 Exam: JEE Main 2002
🔴 Q47. Gravitational force is always
🟢 1️⃣ Attractive
🔵 2️⃣ Repulsive
🟡 3️⃣ Both
🟣 4️⃣ Zero
✔️ Answer: 1
📘 Exam: JEE Main 2001
🔴 Q48. Gravitational constant G is
🟢 1️⃣ Same everywhere
🔵 2️⃣ Depends on altitude
🟡 3️⃣ Depends on mass
🟣 4️⃣ Depends on medium
✔️ Answer: 1
📘 Exam: JEE Main 2001
🔴 Q49. Dimension of GM is
🟢 1️⃣ [L³T⁻²]
🔵 2️⃣ [L²T⁻²]
🟡 3️⃣ [LT⁻²]
🟣 4️⃣ [M⁻¹L³T⁻²]
✔️ Answer: 1
📘 Exam: JEE Main 2001
🔴 Q50. The escape velocity from Earth’s surface is given by
🟢 1️⃣ √(2GM/R)
🔵 2️⃣ √(GM/R)
🟡 3️⃣ √(GM/2R)
🟣 4️⃣ √(GMR)
✔️ Answer: 1
📘 Exam: JEE Main 2001
————————————————————————————————————————————————————————————————————————————
JEE ADVANCED QUESTIONS FROM THIS LESSON
🔴 Question 1:
The gravitational force between two masses is F. If the distance between them is doubled, the new force becomes
🟢 1️⃣ F/2
🔵 2️⃣ F/3
🟡 3️⃣ F/4
🟣 4️⃣ 2F
✔️ Answer: F/4
📘 Exam: JEE Advanced 2024 (Paper 1)
🔴 Question 2:
If the mass of Earth becomes double and its radius remains same, value of g will become
🟢 1️⃣ g/2
🔵 2️⃣ 2g
🟡 3️⃣ g/4
🟣 4️⃣ 4g
✔️ Answer: 2g
📘 Exam: JEE Advanced 2023 (Paper 1)
🔴 Question 3:
Gravitational potential at a distance r from mass M is
🟢 1️⃣ GM/r
🔵 2️⃣ −GM/r
🟡 3️⃣ GM/r²
🟣 4️⃣ −GM/r²
✔️ Answer: −GM/r
📘 Exam: JEE Advanced 2022 (Paper 1)
🔴 Question 4:
The escape velocity from Earth is ve. From a planet having double radius and same density, escape velocity is
🟢 1️⃣ ve
🔵 2️⃣ 2ve
🟡 3️⃣ ve/2
🟣 4️⃣ ve√2
✔️ Answer: 2ve
📘 Exam: JEE Advanced 2021 (Paper 1)
🔴 Question 5:
If g is acceleration due to gravity at surface, then at height h << R, g’ =
🟢 1️⃣ g(1 − 2h/R)
🔵 2️⃣ g(1 − h/R)
🟡 3️⃣ g(1 + h/R)
🟣 4️⃣ g(1 + 2h/R)
✔️ Answer: g(1 − 2h/R)
📘 Exam: JEE Advanced 2020 (Paper 1)
🔴 Question 6:
Gravitational potential energy of two masses m₁ and m₂ separated by distance r is
🟢 1️⃣ Gm₁m₂/r
🔵 2️⃣ −Gm₁m₂/r
🟡 3️⃣ −Gm₁m₂/r²
🟣 4️⃣ Gm₁m₂/r²
✔️ Answer: −Gm₁m₂/r
📘 Exam: JEE Advanced 2019 (Paper 1)
🔴 Question 7:
Acceleration due to gravity at depth d below surface is
🟢 1️⃣ g(1 − d/R)
🔵 2️⃣ g(1 − 2d/R)
🟡 3️⃣ g(1 + d/R)
🟣 4️⃣ g(1 + 2d/R)
✔️ Answer: g(1 − d/R)
📘 Exam: JEE Advanced 2018 (Paper 1)
🔴 Question 8:
The value of g at Earth’s surface is 9.8 m/s². At height equal to Earth’s radius, g becomes
🟢 1️⃣ 4.9 m/s²
🔵 2️⃣ 2.45 m/s²
🟡 3️⃣ 1.225 m/s²
🟣 4️⃣ 0
✔️ Answer: 2.45 m/s²
📘 Exam: JEE Advanced 2017 (Paper 1)
🔴 Question 9:
If Earth shrinks to half radius, keeping mass same, g becomes
🟢 1️⃣ g/2
🔵 2️⃣ 2g
🟡 3️⃣ 4g
🟣 4️⃣ g/4
✔️ Answer: 4g
📘 Exam: JEE Advanced 2016 (Paper 1)
🔴 Question 10:
For a satellite orbiting close to Earth, orbital speed is approximately
🟢 1️⃣ 7.9 km/s
🔵 2️⃣ 11.2 km/s
🟡 3️⃣ 3.2 km/s
🟣 4️⃣ 5.6 km/s
✔️ Answer: 7.9 km/s
📘 Exam: JEE Advanced 2015 (Paper 1)
🔴 Question 11:
Escape velocity on Earth is 11.2 km/s. On planet of double mass and same radius, it is
🟢 1️⃣ 22.4 km/s
🔵 2️⃣ 11.2 km/s
🟡 3️⃣ 15.8 km/s
🟣 4️⃣ 5.6 km/s
✔️ Answer: 15.8 km/s
📘 Exam: JEE Advanced 2014 (Paper 1)
🔴 Question 12:
The orbital speed of a satellite at height R from Earth’s surface (radius = R) is
🟢 1️⃣ √(GM/2R)
🔵 2️⃣ √(GM/R)
🟡 3️⃣ √(GM/4R)
🟣 4️⃣ √(GM/3R)
✔️ Answer: √(GM/2R)
📘 Exam: JEE Advanced 2013 (Paper 1)
🔴 Question 13:
The total energy of a satellite in circular orbit is
🟢 1️⃣ −GMm/2r
🔵 2️⃣ GMm/2r
🟡 3️⃣ −GMm/r
🟣 4️⃣ GMm/r
✔️ Answer: −GMm/2r
📘 Exam: JEE Advanced 2012 (Paper 1)
🔴 Question 14:
If kinetic energy of a satellite is K, its potential energy is
🟢 1️⃣ 2K
🔵 2️⃣ −K
🟡 3️⃣ −2K
🟣 4️⃣ K/2
✔️ Answer: −2K
📘 Exam: JEE Advanced 2011 (Paper 1)
🔴 Question 15:
Escape velocity is independent of
🟢 1️⃣ Mass of body
🔵 2️⃣ Radius of planet
🟡 3️⃣ Gravitational constant
🟣 4️⃣ Density
✔️ Answer: Mass of body
📘 Exam: JEE Advanced 2010 (Paper 1)
🔴 Question 16:
Gravitational potential at center of Earth is
🟢 1️⃣ −3GM/2R
🔵 2️⃣ −GM/2R
🟡 3️⃣ −GM/R
🟣 4️⃣ Zero
✔️ Answer: −3GM/2R
📘 Exam: JEE Advanced 2009 (Paper 1)
🔴 Question 17:
The ratio of escape velocity to orbital velocity is
🟢 1️⃣ √2
🔵 2️⃣ 2
🟡 3️⃣ 1/√2
🟣 4️⃣ 1
✔️ Answer: √2
📘 Exam: JEE Advanced 2008 (Paper 1)
🔴 Question 18:
A satellite is revolving close to Earth’s surface. Its time period is approximately
🟢 1️⃣ 84 minutes
🔵 2️⃣ 24 hours
🟡 3️⃣ 12 hours
🟣 4️⃣ 42 minutes
✔️ Answer: 84 minutes
📘 Exam: JEE Advanced 2024 (Paper 2)
🔴 Question 19:
The potential energy of a satellite of mass m revolving at height h is
🟢 1️⃣ −GMm/(R + h)
🔵 2️⃣ GMm/(R + h)
🟡 3️⃣ −GMm/(2R)
🟣 4️⃣ GMm/R
✔️ Answer: −GMm/(R + h)
📘 Exam: JEE Advanced 2023 (Paper 2)
🔴 Question 20:
A body is projected vertically upward with speed equal to escape velocity. Then
🟢 1️⃣ It will return to Earth
🔵 2️⃣ It will escape from Earth
🟡 3️⃣ It will move in circular orbit
🟣 4️⃣ None
✔️ Answer: It will escape from Earth
📘 Exam: JEE Advanced 2022 (Paper 2)
🔴 Question 21:
If acceleration due to gravity at surface is g, then at depth R/2 it is
🟢 1️⃣ g/2
🔵 2️⃣ g/3
🟡 3️⃣ g/4
🟣 4️⃣ g
✔️ Answer: g/2
📘 Exam: JEE Advanced 2021 (Paper 2)
🔴 Question 22:
A satellite is in circular orbit of radius R around Earth. Its total energy =
🟢 1️⃣ −GMm/2R
🔵 2️⃣ GMm/2R
🟡 3️⃣ −GMm/R
🟣 4️⃣ GMm/R
✔️ Answer: −GMm/2R
📘 Exam: JEE Advanced 2020 (Paper 2)
🔴 Question 23:
If distance between two masses is tripled, the gravitational force becomes
🟢 1️⃣ F/3
🔵 2️⃣ F/9
🟡 3️⃣ F/6
🟣 4️⃣ 3F
✔️ Answer: F/9
📘 Exam: JEE Advanced 2019 (Paper 2)
🔴 Question 24:
A planet has density ρ. The value of g on its surface is proportional to
🟢 1️⃣ R
🔵 2️⃣ R²
🟡 3️⃣ ρR
🟣 4️⃣ ρR²
✔️ Answer: ρR
📘 Exam: JEE Advanced 2018 (Paper 2)
🔴 Question 25:
A satellite moves around Earth in a circular orbit. The centripetal force is provided by
🟢 1️⃣ Gravitational force
🔵 2️⃣ Centrifugal force
🟡 3️⃣ Tension
🟣 4️⃣ Reaction
✔️ Answer: Gravitational force
📘 Exam: JEE Advanced 2017 (Paper 2)
🔴 Question 26:
If the radius of Earth becomes half, and density remains same, g becomes
🟢 1️⃣ g/2
🔵 2️⃣ g/4
🟡 3️⃣ g
🟣 4️⃣ 2g
✔️ Answer: g/2
📘 Exam: JEE Advanced 2016 (Paper 2)
🔴 Question 27:
The value of g at height equal to radius of Earth is
🟢 1️⃣ g/2
🔵 2️⃣ g/4
🟡 3️⃣ g/3
🟣 4️⃣ g/8
✔️ Answer: g/4
📘 Exam: JEE Advanced 2015 (Paper 2)
🔴 Question 28:
A planet is moving around the Sun in an elliptical orbit. The quantity conserved is
🟢 1️⃣ Linear momentum
🔵 2️⃣ Angular momentum
🟡 3️⃣ Kinetic energy
🟣 4️⃣ Potential energy
✔️ Answer: Angular momentum
📘 Exam: JEE Advanced 2014 (Paper 2)
🔴 Question 29:
If kinetic energy of a satellite is K, total energy is
🟢 1️⃣ K
🔵 2️⃣ −K
🟡 3️⃣ −K/2
🟣 4️⃣ −2K
✔️ Answer: −K
📘 Exam: JEE Advanced 2013 (Paper 2)
🔴 Question 30:
The escape velocity from a planet depends on
🟢 1️⃣ Radius and mass of planet
🔵 2️⃣ Mass of object
🟡 3️⃣ Velocity of rotation
🟣 4️⃣ Acceleration due to gravity
✔️ Answer: Radius and mass of planet
📘 Exam: JEE Advanced 2012 (Paper 2)
🔴 Question 31:
Gravitational potential energy of a satellite is
🟢 1️⃣ Positive
🔵 2️⃣ Negative
🟡 3️⃣ Zero
🟣 4️⃣ Variable sign
✔️ Answer: Negative
📘 Exam: JEE Advanced 2011 (Paper 2)
🔴 Question 32:
The energy required to move a satellite from Earth’s surface to infinity is equal to
🟢 1️⃣ GMm/R
🔵 2️⃣ GMm/2R
🟡 3️⃣ GMm/4R
🟣 4️⃣ 2GMm/R
✔️ Answer: GMm/2R
📘 Exam: JEE Advanced 2010 (Paper 2)
🔴 Question 33:
If g at surface is 10 m/s², then at height R it is
🟢 1️⃣ 2.5 m/s²
🔵 2️⃣ 5 m/s²
🟡 3️⃣ 7.5 m/s²
🟣 4️⃣ 10 m/s²
✔️ Answer: 2.5 m/s²
📘 Exam: JEE Advanced 2009 (Paper 2)
🔴 Question 34:
Kepler’s third law states that T² is proportional to
🟢 1️⃣ r
🔵 2️⃣ r²
🟡 3️⃣ r³
🟣 4️⃣ r⁴
✔️ Answer: r³
📘 Exam: JEE Advanced 2008 (Paper 2)
————————————————————————————————————————————————————————————————————————————
PRACTICE SETS FROM THIS LESSON
🧠 Q1–Q20 : NEET Level (Moderate Difficulty)
Q1. Gravitational force between two bodies is independent of
🔵 (A) Distance between them
🟢 (B) Medium between them
🟠 (C) Product of their masses
🔴 (D) Universal constant
Answer: (B) Medium between them
Q2. The value of G on Earth and on the Moon is
🔵 (A) Same
🟢 (B) Greater on Moon
🟠 (C) Smaller on Moon
🔴 (D) Zero on Moon
Answer: (A) Same
Q3. The value of acceleration due to gravity at the center of the Earth is
🔵 (A) Infinite
🟢 (B) Zero
🟠 (C) Equal to 9.8 m/s²
🔴 (D) Double of surface value
Answer: (B) Zero
Q4. A body is taken to a height equal to Earth’s radius. The value of g there becomes
🔵 (A) g/2
🟢 (B) g/3
🟠 (C) g/4
🔴 (D) g/9
Answer: (C) g/4
Q5. If the Earth suddenly shrinks to half its radius, keeping mass same, value of g will become
🔵 (A) 2g
🟢 (B) 4g
🟠 (C) g/2
🔴 (D) g/4
Answer: (B) 4g
Q6. The dimension of universal gravitational constant G is
🔵 (A) [M⁻¹L³T⁻²]
🟢 (B) [ML²T⁻²]
🟠 (C) [M¹L⁻²T²]
🔴 (D) [M⁰L⁰T⁰]
Answer: (A) [M⁻¹L³T⁻²]
Q7. Acceleration due to gravity on the surface of a planet of mass M and radius R is
🔵 (A) GM/R
🟢 (B) GM/R²
🟠 (C) GMR²
🔴 (D) GR/M
Answer: (B) GM/R²
Q8. The force of gravitation between two bodies decreases if
🔵 (A) Their masses increase
🟢 (B) The distance between them increases
🟠 (C) The value of G increases
🔴 (D) None
Answer: (B) The distance between them increases
Q9. The unit of gravitational field intensity is
🔵 (A) N/kg
🟢 (B) J/kg
🟠 (C) N·m²/kg²
🔴 (D) N·m/kg
Answer: (A) N/kg
Q10. Gravitational potential at distance r from mass M is
🔵 (A) +GM/r
🟢 (B) −GM/r
🟠 (C) GM/r²
🔴 (D) −GM/r²
Answer: (B) −GM/r
Q11. If the distance between two masses becomes three times, force becomes
🔵 (A) 1/3
🟢 (B) 1/6
🟠 (C) 1/9
🔴 (D) 9 times
Answer: (C) 1/9
Q12. g varies with altitude h as
🔵 (A) g’ = g(1 − 2h/R)
🟢 (B) g’ = g(1 + 2h/R)
🟠 (C) g’ = g(1 + h/R)²
🔴 (D) g’ = g
Answer: (A) g’ = g(1 − 2h/R)
Q13. Escape velocity depends on
🔵 (A) Mass of the body
🟢 (B) Mass of the Earth
🟠 (C) Shape of body
🔴 (D) None
Answer: (B) Mass of the Earth
Q14. The ratio of escape velocity to orbital velocity for a planet is
🔵 (A) √2
🟢 (B) 2
🟠 (C) ½
🔴 (D) 1
Answer: (A) √2
Q15. The acceleration due to gravity on Moon is
🔵 (A) 9.8 m/s²
🟢 (B) 1.62 m/s²
🟠 (C) 19.6 m/s²
🔴 (D) 0
Answer: (B) 1.62 m/s²
Q16. The work done in moving a body around a circular path in a gravitational field is
🔵 (A) Zero
🟢 (B) Positive
🟠 (C) Negative
🔴 (D) Infinite
Answer: (A) Zero
Q17. The energy of a satellite in circular orbit is
🔵 (A) Positive
🟢 (B) Negative
🟠 (C) Zero
🔴 (D) Infinite
Answer: (B) Negative
Q18. The period of a geostationary satellite is
🔵 (A) 12 h
🟢 (B) 24 h
🟠 (C) 48 h
🔴 (D) 6 h
Answer: (B) 24 h
Q19. Kepler’s first law states that
🔵 (A) Planets move in circular orbits
🟢 (B) Planets move in elliptical orbits
🟠 (C) Planet and Sun have equal mass
🔴 (D) None
Answer: (B) Planets move in elliptical orbits
Q20. Weight of a body at center of Earth is
🔵 (A) Maximum
🟢 (B) Zero
🟠 (C) Half
🔴 (D) Twice
Answer: (B) Zero
⚙️ Q21–Q40 : JEE Main Level (Enhanced Difficulty)
Q21. The value of g at depth d below Earth’s surface is
🔵 (A) g(1 − d/R)
🟢 (B) g(1 − 2d/R)
🟠 (C) g(1 + d/R)
🔴 (D) g(1 + 2d/R)
Answer: (A) g(1 − d/R)
Q22. A body weighs 100 N on Earth. Its weight on Moon is (gₘ = 1/6 gₑ)
🔵 (A) 16.6 N
🟢 (B) 60 N
🟠 (C) 600 N
🔴 (D) 9.8 N
Answer: (A) 16.6 N
Q23. The work done by gravity in moving a mass m from distance r₁ to r₂ is
🔵 (A) −GMm(1/r₂ − 1/r₁)
🟢 (B) GMm(1/r₂ − 1/r₁)
🟠 (C) GMm(r₂ − r₁)
🔴 (D) Zero
Answer: (A) −GMm(1/r₂ − 1/r₁)
Q24. The total energy of a satellite is related to its potential energy by
🔵 (A) E = U
🟢 (B) E = U/2
🟠 (C) E = −U/2
🔴 (D) E = −U
Answer: (C) E = −U/2
Q25. The escape velocity from a planet of radius R and g is
🔵 (A) √(2gR)
🟢 (B) √(gR)
🟠 (C) √(R/g)
🔴 (D) 2gR
Answer: (A) √(2gR)
Q26. The orbital velocity of a satellite revolving near Earth’s surface is
🔵 (A) 7.9 km/s
🟢 (B) 11.2 km/s
🟠 (C) 5 km/s
🔴 (D) 10 km/s
Answer: (A) 7.9 km/s
Q27. The energy required to move a satellite from radius r₁ to r₂ is
🔵 (A) GMm(1/r₂ − 1/r₁)/2
🟢 (B) GMm(1/r₁ − 1/r₂)/2
🟠 (C) GMm(r₂ − r₁)
🔴 (D) Zero
Answer: (B) GMm(1/r₁ − 1/r₂)/2
Q28. The ratio of gravitational to electrostatic force between an electron and a proton is approximately
🔵 (A) 10⁻¹⁹
🟢 (B) 10⁻³⁹
🟠 (C) 10⁻²⁰
🔴 (D) 10⁻⁵⁰
Answer: (B) 10⁻³⁹
Q29. If g = 9.8 m/s² and R = 6.4×10⁶ m, find G·Mₑ.
🔵 (A) 6.3×10⁶
🟢 (B) 3.9×10¹⁴
🟠 (C) 3.98×10¹⁴
🔴 (D) 4.0×10⁷
Answer: (C) 3.98×10¹⁴
Q30. The ratio of potential energy to kinetic energy of a satellite in circular orbit is
🔵 (A) −1
🟢 (B) −2
🟠 (C) −½
🔴 (D) 1
Answer: (B) −2
Q31. For two planets A and B, T₁²/T₂² = r₁³/r₂³. This verifies
🔵 (A) Kepler’s first law
🟢 (B) Kepler’s third law
🟠 (C) Kepler’s second law
🔴 (D) Newton’s law
Answer: (B) Kepler’s third law
Q32. The gravitational potential energy of a satellite in orbit is
🔵 (A) −GMm/r
🟢 (B) −2GMm/r
🟠 (C) −GMm/2r
🔴 (D) GMm/r
Answer: (A) −GMm/r
Q33. A satellite’s total energy doubles if its
🔵 (A) Radius doubles
🟢 (B) Radius halves
🟠 (C) Mass doubles
🔴 (D) Speed doubles
Answer: (B) Radius halves
Q34. The gravitational potential difference between two points A and B is
🔵 (A) GM(1/rB − 1/rA)
🟢 (B) −GM(1/rB − 1/rA)
🟠 (C) GM(rA − rB)
🔴 (D) None
Answer: (B) −GM(1/rB − 1/rA)
Q35. At what height above Earth’s surface will g become ¼ of its surface value?
🔵 (A) R
🟢 (B) R/√2
🟠 (C) R
🔴 (D) R
Answer: (A) R
Q36. The gravitational potential at the Earth’s surface is approximately
🔵 (A) −6.25 × 10⁷ J/kg
🟢 (B) −9.8 × 10⁷ J/kg
🟠 (C) −10⁵ J/kg
🔴 (D) −10³ J/kg
Answer: (A) −6.25 × 10⁷ J/kg
Q37. The orbital period of Moon around Earth increases if
🔵 (A) Earth’s mass decreases
🟢 (B) Earth’s radius decreases
🟠 (C) Moon’s radius decreases
🔴 (D) None
Answer: (A) Earth’s mass decreases
Q38. Gravitational field intensity and potential are related as
🔵 (A) g = −dV/dr
🟢 (B) g = dV/dr
🟠 (C) g = V/r
🔴 (D) g = V²/r²
Answer: (A) g = −dV/dr
Q39. Kepler’s second law is a consequence of
🔵 (A) Conservation of energy
🟢 (B) Conservation of angular momentum
🟠 (C) Conservation of linear momentum
🔴 (D) None
Answer: (B) Conservation of angular momentum
Q40. A geostationary satellite is used for
🔵 (A) Weather monitoring
🟢 (B) Communication
🟠 (C) Broadcasting
🔴 (D) All of these
Answer: (D) All of these
⚡ Q41–Q50 : JEE Advanced Level (High Conceptual Difficulty)
Q41. A satellite of mass m is in orbit of radius 2Rₑ around Earth. Its total energy is
🔵 (A) −GMₑm/2Rₑ
🟢 (B) −GMₑm/4Rₑ
🟠 (C) −GMₑm/Rₑ
🔴 (D) −2GMₑm/Rₑ
Answer: (B) −GMₑm/4Rₑ
Q42. The escape velocity from a planet is proportional to
🔵 (A) √(M/R)
🟢 (B) M/R
🟠 (C) R/M
🔴 (D) √(R/M)
Answer: (A) √(M/R)
Q43. Two satellites have orbital radii in ratio 1:4. The ratio of their speeds is
🔵 (A) 2:1
🟢 (B) 1:2
🟠 (C) 4:1
🔴 (D) 1:4
Answer: (A) 2:1
Q44. The gravitational potential energy of a system of three masses each m at corners of equilateral triangle of side a is
🔵 (A) −3Gm²/a
🟢 (B) −Gm²/a
🟠 (C) −6Gm²/a
🔴 (D) −2Gm²/a
Answer: (A) −3Gm²/a
Q45. A satellite in orbit has its total energy E. If its kinetic energy becomes 1.5 times, its potential energy will be
🔵 (A) −2E
🟢 (B) −3E
🟠 (C) −E
🔴 (D) 2E
Answer: (B) −3E
Q46. For Earth–Moon system, if distance doubles, gravitational force becomes
🔵 (A) ¼
🟢 (B) ½
🟠 (C) 1/8
🔴 (D) 4
Answer: (A) ¼
Q47. The potential energy of a satellite in terms of total energy is
🔵 (A) U = E
🟢 (B) U = 2E
🟠 (C) U = −2E
🔴 (D) U = −E/2
Answer: (C) U = −2E
Q48. The gravitational field due to a spherical shell of uniform mass at a point inside it is
🔵 (A) Zero
🟢 (B) Constant
🟠 (C) Maximum
🔴 (D) Minimum
Answer: (A) Zero
Q49. The orbital period of a planet is T. If mean distance increases by 10%, the new period is approximately
🔵 (A) 1.1T
🟢 (B) 1.15T
🟠 (C) 1.3T
🔴 (D) 1.5T
Answer: (B) 1.15T
Q50. For a planet with twice Earth’s radius and same density, the value of g will be
🔵 (A) 2g
🟢 (B) 4g
🟠 (C) g/2
🔴 (D) g/4
Answer: (B) 4g
————————————————————————————————————————————————————————————————————————————
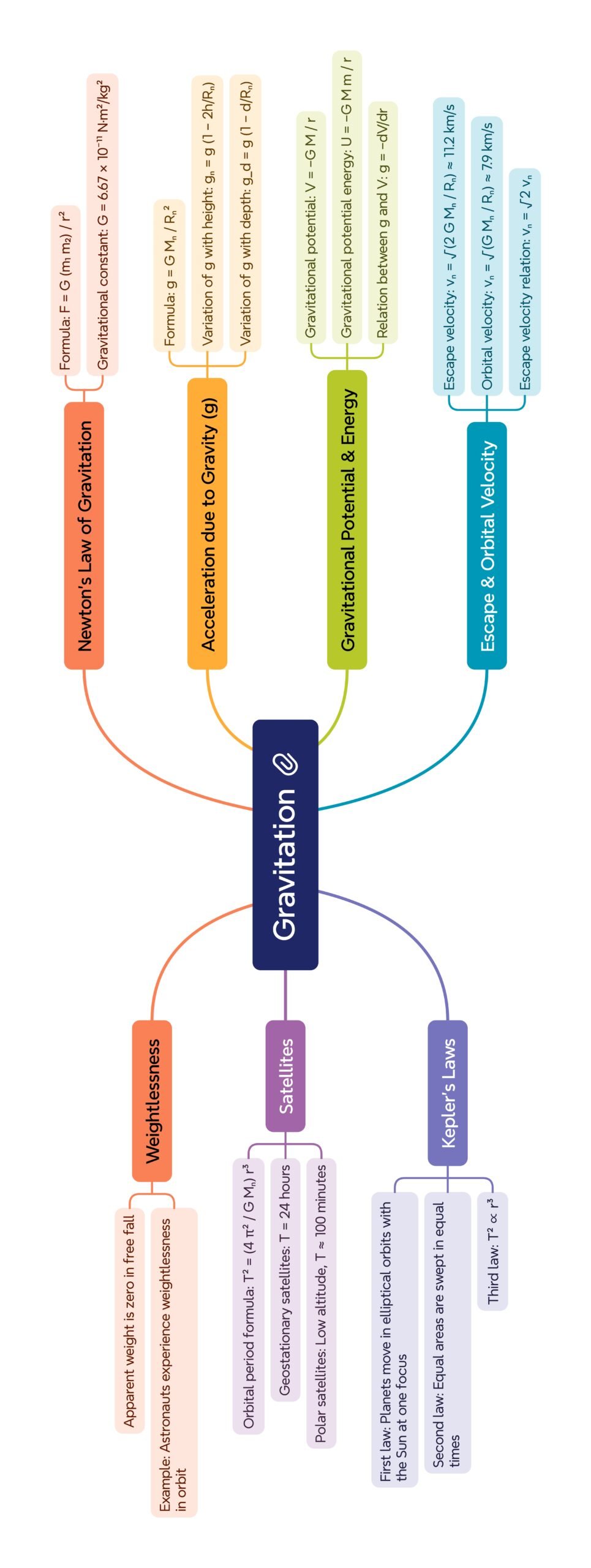
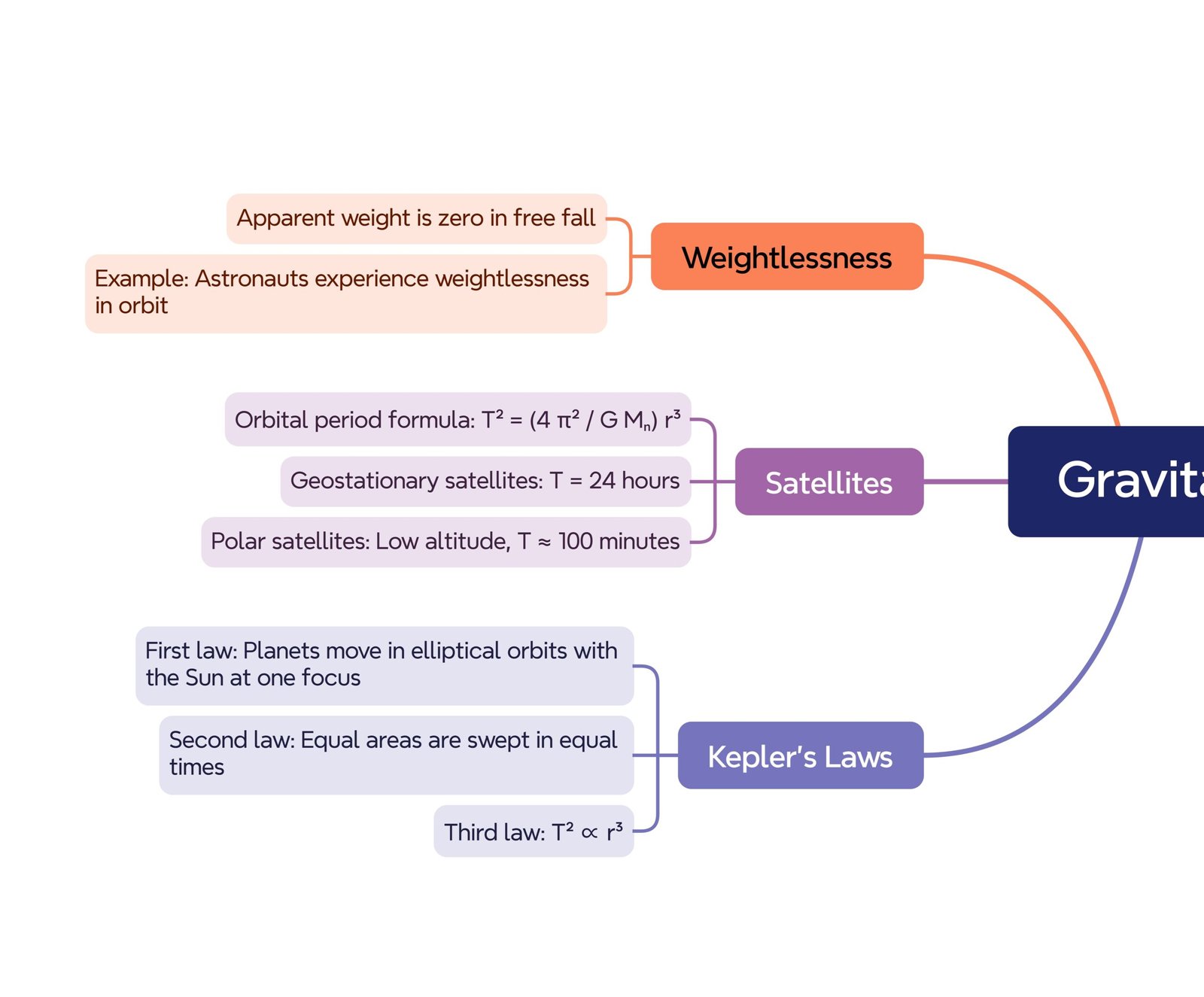
MIND MAPS

————————————————————————————————————————————————————————————————————————————
