Class 11 : Physics (In English) – Chapter 13: Oscillations
EXPLANATION & SUMMARY
🔷 EXPLANATION
🌟 1. Introduction
🔵 Many physical systems in nature repeat their motion in a regular time interval — such repetitive motions are called oscillations or vibrations.
🟢 Examples: motion of a pendulum, vibration of a stretched spring, sound waves, or an alternating electric current.
🔴 The study of oscillations helps in understanding wave motion, resonance, alternating current circuits, and molecular vibrations.
💡 2. Periodic and Oscillatory Motion
✏️ Periodic motion: A motion which repeats itself after equal intervals of time.
➡️ Example: Earth’s rotation, motion of a fan blade.
✏️ Oscillatory motion: A type of periodic motion in which a body moves to and fro about a fixed equilibrium position.
➡️ Example: Simple pendulum, spring-mass system.
✔️ Every oscillatory motion is periodic, but not every periodic motion is oscillatory.
🔹 3. Displacement, Amplitude, Frequency, and Phase
Let the equilibrium position of an oscillating particle be O.
When displaced, its position at time t is measured by its displacement (x).
Amplitude (A): Maximum displacement from the mean position.
Time period (T): Time taken for one complete oscillation.
Frequency (ν): Number of oscillations per second → ν = 1/T.
Angular frequency (ω): ω = 2πν = 2π/T.
Phase (ϕ): Quantity that determines the state (position and direction) of motion at any instant.
🧠 Relation of displacement in simple harmonic motion (SHM):
x = A sin(ωt + ϕ) or x = A cos(ωt + ϕ)
🔹 4. Simple Harmonic Motion (SHM)
💡 Definition: Motion of a particle in which its acceleration is directly proportional to its displacement from the mean position and is always directed towards it.
Mathematically,
a ∝ −x or a = −ω²x
➡️ The negative sign indicates that the acceleration is always directed opposite to displacement (restoring nature).
Here, ω is the angular frequency, given by ω = 2π/T.
✔️ Displacement equation: x = A sin(ωt + ϕ)
✔️ Velocity: v = dx/dt = Aω cos(ωt + ϕ)
✔️ Acceleration: a = −Aω² sin(ωt + ϕ) = −ω²x
🔹 5. Graphical Representation
✴️ Displacement–Time Graph: A sine or cosine curve between x and t.
✴️ Velocity–Time Graph: A cosine curve when x ∝ sin(ωt).
✴️ Acceleration–Time Graph: Same as displacement but with opposite sign.
✴️ Phase difference: Between x, v, a →
• Displacement and velocity differ by π/2
• Velocity and acceleration differ by π/2
• Displacement and acceleration differ by π
🔹 6. Energy in SHM
The oscillating body possesses potential energy (PE) and kinetic energy (KE) interchangeably.
Let displacement at any instant = x.
💡 Potential energy: U = (1/2) k x²
💡 Kinetic energy: K = (1/2) m ω² (A² − x²)
💡 Total energy: E = (1/2) m ω² A² = constant
✔️ Energy is maximum at the mean position (all kinetic).
✔️ Energy is potential at the extreme position (x = ±A).
🔹 7. Force in SHM
From Newton’s law, F = ma
⇒ F = −mω²x
💡 Hence, the restoring force is directly proportional to displacement and directed towards the mean position.
🔹 8. The Spring–Mass System (Linear SHM)
Consider a mass m attached to a light spring of force constant k, fixed at one end and lying on a smooth surface.
When the spring is stretched by x, restoring force is F = −kx.
By Newton’s second law:
m a = −k x ⇒ a = −(k/m) x
Comparing with a = −ω²x, we get
ω = √(k/m)
Hence,
T = 2π √(m/k)
✔️ Time period increases with mass and decreases with stiffness of the spring.
🔹 9. The Simple Pendulum
A small bob of mass m suspended by a light inextensible string of length l performs oscillations about its mean position under gravity.
Restoring torque = −m g sinθ × l
For small angles (sinθ ≈ θ):
Torque = −m g l θ
and angular acceleration α = −(g/l) θ
Comparing with SHM (α = −ω²θ):
ω = √(g/l)
Hence,
T = 2π √(l/g)
✔️ Time period depends only on length and acceleration due to gravity, not on mass or amplitude (for small oscillations).
🔹 10. Phase and Its Significance
At any instant, the argument (ωt + ϕ) is called phase.
When ωt + ϕ = 0 → motion starts from mean position.
When ωt + ϕ = π/2 → particle at extreme position.
Phase difference determines relative state of motion between two SHMs.
🔹 11. Superposition of Two SHMs
If two SHMs act simultaneously on a particle along the same line, their resultant displacement is the algebraic sum of individual displacements.
Let x₁ = A₁ sin(ωt), x₂ = A₂ sin(ωt + δ)
Then resultant displacement:
x = A sin(ωt + ϕ)
where
A = √(A₁² + A₂² + 2A₁A₂ cosδ)
💡 The resultant amplitude depends on phase difference δ.
🔹 12. Damped Oscillations
In practical systems, amplitude decreases with time due to friction or air resistance.
Such oscillations are called damped oscillations.
Equation:
x = A e^(−bt/2m) sin(ωt + ϕ)
where b = damping constant.
✔️ Energy decreases exponentially with time.
✔️ At large damping, oscillations cease — system becomes aperiodic.
🔹 13. Forced Oscillations
When an external periodic force acts on an oscillator, it performs forced oscillations.
Equation:
F = F₀ sin(ω_d t)
The body vibrates with the driving frequency ω_d (not its natural frequency).
When ω_d ≈ ω₀ (natural frequency), amplitude becomes large — this condition is resonance.
🔹 14. Resonance
💡 Resonance: The phenomenon of large amplitude oscillation when the frequency of the external periodic force equals the natural frequency of the oscillator.
➡️ Example: Tuning fork in resonance, vibrating bridges, radio tuning.
✔️ Resonance transfers maximum energy and may cause destruction (like Tacoma bridge collapse).
🔹 15. Energy of Damped and Forced Oscillations
In damped systems, mechanical energy decreases continuously.
In forced oscillations, energy is supplied periodically; hence steady-state amplitude is reached.
Power absorbed per cycle = (average work done by driving force).
At resonance, power absorbed is maximum.
🔹 16. Applications of SHM
🟢 Measurement of time (pendulum clocks).
🔵 Design of oscillatory circuits (LC circuits).
🔴 Understanding acoustic and seismic vibrations.
🟠 Design of suspension systems, building structures against vibrations.


🟢 SUMMARY (~300 words)
Oscillatory motion is a repetitive motion about a mean position. Simple Harmonic Motion (SHM) is a special type where acceleration is directly proportional to displacement and opposite in direction, given by a = −ω²x.
In SHM, displacement at any time is x = A sin(ωt + ϕ), where A is amplitude, ω angular frequency, and ϕ phase constant.
Velocity and acceleration vary sinusoidally, and total energy remains constant:
E = (1/2) m ω² A².
For a spring–mass system, restoring force F = −kx gives
T = 2π√(m/k).
For a simple pendulum, small-angle oscillations give
T = 2π√(l/g).
When two SHMs of same frequency combine, resultant amplitude depends on phase difference.
Real systems exhibit damped oscillations due to friction; amplitude decreases exponentially.
If an external periodic force acts, motion becomes forced oscillation.
At resonance, the external frequency equals the natural frequency, producing maximum amplitude.
Oscillations explain diverse phenomena — vibrations in mechanical systems, alternating current circuits, sound, and waves. Understanding SHM forms the basis for the study of wave motion and resonance phenomena.
🔻 QUICK RECAP (6 Key Points)
1️⃣ Equation of SHM: x = A sin(ωt + ϕ), a = −ω²x
2️⃣ Time Period:
• Spring: T = 2π√(m/k)
• Pendulum: T = 2π√(l/g)
3️⃣ Energy: E = (1/2) m ω² A² = constant
4️⃣ Relation: vₚ : vₐᵥg : vᵣₘₛ = 1 : 1.128 : 1.225 (for gases, analogy of oscillation speeds)
5️⃣ Damped Motion: x = A e^(−bt/2m) sin(ωt + ϕ)
6️⃣ Resonance: Occurs when driving frequency = natural frequency → maximum amplitude
————————————————————————————————————————————————————————————————————————————
QUESTIONS FROM TEXTBOOK
🔵 Question 13.1
Which of the following examples represent periodic motion?
(a) A swimmer completing one [return] trip from one bank of a river to the other and back.
(b) A freely suspended bar magnet displaced from its N–S direction and released.
(c) A hydrogen molecule rotating about its centre of mass.
(d) An arrow released from a bow.
Answer:
🟢 Step 1: Identify periodic nature
➡️ A periodic motion repeats itself after a fixed interval of time.
🟡 Step 2: Analyze each case
(a) The swimmer’s motion is not periodic, since the time taken for return trip depends on conditions like speed and flow; it doesn’t repeat in equal intervals ❌
(b) A freely suspended bar magnet oscillates to and fro about its mean position when displaced — this is periodic motion ✔️
(c) A hydrogen molecule rotating continuously about its centre of mass repeats its motion after a fixed time (rotation period) — periodic motion ✔️
(d) An arrow released from a bow moves in one direction only, not repeating its path — not periodic ❌
✔️ Final Answer: (b) and (c) represent periodic motion.
🔵 Question 13.2
Which of the following examples represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
(a) The rotation of earth about its axis.
(b) Motion of an oscillating mercury column in a U-tube.
(c) Motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lower most point.
(d) General vibrations of a polyatomic molecule about its equilibrium position.
Answer:
🟢 Step 1: Recall definition
➡️ In simple harmonic motion (S.H.M.), restoring force ∝ displacement and acts toward mean position.
🟡 Step 2: Analyze cases
(a) Rotation of Earth — uniform circular motion, not SHM but periodic ✔️ (Periodic only)
(b) Oscillating mercury column in U-tube — restoring force ∝ displacement of mercury level ⇒ SHM ✔️ (Nearly SHM)
(c) Ball in a smooth curved bowl — near the mean position restoring force ∝ displacement ⇒ SHM ✔️ (Nearly SHM)
(d) Vibrations of a polyatomic molecule — complex motion due to many coupled oscillations; periodic but not simple harmonic ✔️ (Periodic only)
✔️ Final Answer:
Nearly SHM → (b), (c)
Periodic but not SHM → (a), (d)
🔵 Question 13.3
Fig. 13.18 depicts four x–t plots for linear motion of a particle.
Which of the plots represent periodic motion?
What is the period of motion (in case of periodic motion)?
Answer:
🟢 Step 1: Analyze the four plots
(a) Straight line graph:
x increases continuously with t, does not repeat — ❌ not periodic.
(b) Irregular wave:
Pattern not repeating uniformly — ❌ not periodic.
(c) Uneven oscillations:
Amplitude and period not constant — ❌ not periodic.
(d) Regular sine-type wave:
Repeats after equal intervals — ✔️ periodic motion.
🟡 Step 2: Determine period (T)
From graph (d), one full cycle occurs from t = –2 to t = +2 s.
➡️ Period T = 4 s
✔️ Final Answer:
Only plot (d) represents periodic motion.
✅ Period = 4 seconds.
🔵 Question 13.4
Which of the following functions of time represent
(a) simple harmonic,
(b) periodic but not simple harmonic, and
(c) non-periodic motion?
Give the period for each case of periodic motion (ω is any positive constant):
(a) sin ωt – cos ωt
(b) sin² ωt
(c) 3 cos (π/4 – 2ωt)
(d) cos ωt + cos 3ωt + cos 5ωt
(e) exp(–ω²t²)
(f) 1 + ωt + ω²t²
Answer:
🟢 (a) sin ωt – cos ωt
➡️ Rewrite as √2 sin(ωt – π/4)
✔️ Represents simple harmonic motion (SHM)
➡️ Period T = 2π/ω
🟡 (b) sin² ωt
➡️ sin² ωt = (1 – cos 2ωt)/2
✔️ Periodic but not SHM (does not change sign)
➡️ Period T = π/ω
🟢 (c) 3 cos(π/4 – 2ωt)
➡️ Same as 3 cos(2ωt – π/4)
✔️ Represents SHM
➡️ Period T = π/ω
🟡 (d) cos ωt + cos 3ωt + cos 5ωt
➡️ Superposition of several harmonic motions
✔️ Periodic but not SHM
➡️ Period T = 2π/ω
🔴 (e) exp(–ω²t²)
➡️ Exponential decay, does not repeat
❌ Non-periodic
🔴 (f) 1 + ωt + ω²t²
➡️ Increases continuously with time
❌ Non-periodic
✔️ Summary:
(a) SHM (b) Periodic (c) SHM (d) Periodic (e) Non-periodic (f) Non-periodic
🔵 Question 13.5
A particle is in linear SHM between two points A and B, 10 cm apart.
Take A → B as the positive direction.
Find the signs of velocity, acceleration, and force when it is:
(a) at A (b) at B (c) at mid-point going towards A (d) 2 cm from B going towards A (e) 3 cm from A going towards B (f) 4 cm from B going towards A
Answer:
🟢 Amplitude A = 5 cm (since total AB = 10 cm)
Restoring force and acceleration always act toward the mean position (O).
(a) At end A (x = –A):
➡️ Velocity = 0 Acceleration = +ve Force = +ve
(b) At end B (x = + A):
➡️ Velocity = 0 Acceleration = –ve Force = –ve
(c) At mid-point (x = 0, going to A):
➡️ Velocity = –ve Acceleration = 0 Force = 0
(d) 2 cm from B (x = +3 cm, going to A):
➡️ Velocity = –ve Acceleration = –ve Force = –ve
(e) 3 cm from A (x = –2 cm, going to B):
➡️ Velocity = +ve Acceleration = +ve Force = +ve
(f) 4 cm from B (x = +1 cm, going to A):
➡️ Velocity = –ve Acceleration = –ve Force = –ve
✔️ Positive sign means towards B, negative towards A.
🔵 Question 13.6
Which of the following relations between acceleration a and displacement x represent SHM?
(a) a = 0.7x (b) a = –200x² (c) a = –10x (d) a = 100x³
Answer:
💡 In SHM, acceleration ∝ –x (directed toward mean position).
(a) a = 0.7x → same direction as displacement ❌ Not SHM
(b) a = –200x² → non-linear ❌ Not SHM
(c) a = –10x → linear and opposite to x ✔️ SHM
(d) a = 100x³ → non-linear ❌ Not SHM
✔️ Final Answer: (c) a = –10x
🔵 Question 13.7
The SHM is given by x = A cos(ωt + ϕ).
At t = 0, x = 1 cm and v = ω cm/s.
Find amplitude and initial phase angle (ω = π s⁻¹).
Also find amplitude and initial phase if x = B sin(ωt + α).
Answer:
🟢 Given:
x₀ = 1 cm, v₀ = ω cm/s = π cm/s
For x = A cos(ωt + ϕ):
➡️ x₀ = A cos ϕ = 1
➡️ v₀ = –A ω sin ϕ = π
🟡 Step 1: tan ϕ = – (v₀ / ωx₀) = – 1 ⇒ ϕ = – π/4
🟡 Step 2: A = √(x₀² + (v₀/ω)²) = √(1 + 1) = √2 cm
🟢 For sine form: x = B sin(ωt + α)
➡️ x₀ = B sin α = 1
➡️ v₀ = B ω cos α = π
⇒ cot α = (v₀ / ωx₀) = 1 ⇒ α = π/4
➡️ B = √2 cm
✔️ Final Answers:
Amplitude = √2 cm
ϕ = –π/4 (in cosine form)
α = π/4 (in sine form)
🔵 Question 13.8
A spring balance of length 20 cm reads 0–50 kg.
When displaced and released, it oscillates with a period T = 0.6 s.
Find the weight of the body.
Answer:
🟢 Total load = 50 kg ⇒ F = 50×9.8 = 490 N
Extension = 0.2 m
➡️ Spring constant k = F/x = 490/0.2 = 2450 N/m
🟡 Using T = 2π√(m/k):
0.6 = 2π√(m/2450)
⇒ m = (2450 / 4π²) × (0.6)² = 8.03 kg
🟢 Weight W = m g = 8.03×9.8 = 78.7 N
✔️ Final Answer: Weight ≈ 79 N
🔵 Question 13.9
A horizontal spring (k = 1200 N m⁻¹) has a mass 3 kg attached to it.
Pulled sideways by 2.0 cm and released.
Find: (i) frequency of oscillation, (ii) maximum acceleration, (iii) maximum speed.
Answer:
🟢 Given: k = 1200 N/m, m = 3 kg, A = 0.02 m
🟡 Angular frequency ω = √(k/m) = √(1200/3) = 20 rad/s
(i) Frequency f = ω/2π = 20/(2×3.14) = 3.18 Hz
(ii) aₘₐₓ = ω²A = 400×0.02 = 8 m/s²
(iii) vₘₐₓ = ωA = 20×0.02 = 0.4 m/s
✔️ Final Answers:
➡️ f = 3.18 Hz
➡️ aₘₐₓ = 8 m/s²
➡️ vₘₐₓ = 0.4 m/s
🔵 Question 13.10
In Exercise 13.9, let us take the position of the mass when the spring is unstretched as x = 0 and the direction from left to right as the positive x-axis.
Give x as a function of time t for the oscillating mass if, at the moment we start the stopwatch (t = 0), the mass is
(a) at the mean position,
(b) at the maximum stretched position, and
(c) at the maximum compressed position.
In what way do these functions for SHM differ from each other—in frequency, in amplitude, or in the initial phase?
Answer:
🟢 The general equation of SHM is:
➡️ x = A sin(ωt + ϕ) or x = A cos(ωt + ϕ)
Here, A = amplitude, ω = angular frequency, and ϕ = initial phase.
Given: the motion starts at different initial positions.
(a) At the mean position:
At t = 0, x = 0, and the particle moves in the positive direction.
➡️ Hence, x = A sin(ωt)
✔️ Initial phase ϕ = 0
(b) At maximum stretched position:
At t = 0, x = +A.
➡️ Hence, x = A cos(ωt)
✔️ Initial phase ϕ = 0
(c) At maximum compressed position:
At t = 0, x = –A.
➡️ Hence, x = –A cos(ωt) = A cos(ωt + π)
✔️ Initial phase ϕ = π
🟡 Difference among them:
➡️ All have the same frequency and amplitude, but differ in initial phase (ϕ) only.
🔵 Question 13.11
Figures 13.20 (a) and (b) correspond to two circular motions.
The radius of the circle, the period of revolution, the initial position, and the sense of revolution (clockwise or anticlockwise) are indicated.
Obtain the corresponding simple harmonic motions of the x-projection of the radius vector of the revolving particle P in each case.
Answer:
🟢 (a) From Fig. 13.20 (a):
➡️ Radius = 3 cm, Period T = 2 s
➡️ Angular velocity, ω = 2π/T = π rad/s
➡️ Initial position P(t = 0) at the bottom of the circle (–y direction).
Hence, x = A cos(ωt + ϕ)
At t = 0, x = 0 (since P is on y-axis), and motion starts toward the right (positive x).
➡️ Therefore, x = 3 sin(πt) cm
🟢 (b) From Fig. 13.20 (b):
➡️ Radius = 2 m, T = 4 s
➡️ ω = 2π/T = π/2 rad/s
➡️ Particle at rightmost position on x-axis, motion clockwise.
Hence, x = A cos(ωt)
➡️ x = 2 cos((π/2)t) m
✔️ Final Answers:
(a) x = 3 sin(πt) cm
(b) x = 2 cos((π/2)t) m
🔵 Question 13.12
Plot the reference circle for each of the following SHMs. Indicate initial (t = 0) position, radius, and angular speed. Assume anticlockwise rotation.
(a) x = –2 sin(3t + π/3)
(b) x = cos(π/6 – t)
(c) x = 3 sin(2πt + π/4)
(d) x = 2 cos(πt)
Answer:
💡 For a reference circle, the SHM can be expressed as the x-projection of uniform circular motion.
🟢 (a) x = –2 sin(3t + π/3)
➡️ Amplitude A = 2 cm
➡️ Angular frequency ω = 3 rad/s
➡️ Initial phase ϕ = π/3 + π (due to negative sign)
✔️ Radius of circle = 2 cm
🟢 (b) x = cos(π/6 – t)
➡️ Rewrite as cos(–t + π/6) = cos(t – π/6) (since cos(–θ) = cos θ)
➡️ A = 1, ω = 1 rad/s, ϕ = –π/6
✔️ Starts from x = cos(π/6) = 0.866
🟢 (c) x = 3 sin(2πt + π/4)
➡️ A = 3 cm, ω = 2π rad/s, ϕ = π/4
✔️ Period T = 2π/ω = 1 s
🟢 (d) x = 2 cos(πt)
➡️ A = 2 cm, ω = π rad/s, ϕ = 0
✔️ Period T = 2 s
✅ Each represents SHM as x-projection of circular motion with the above parameters.
🔵 Question 13.13
A spring of constant k is clamped at one end, and a force F stretches it by x.
(a) What is the maximum extension of the spring in the two cases shown below?
(b) If released, what is the period of oscillation in each case?
(Fig. 13.21a): One mass m attached to one end, other end fixed.
(Fig. 13.21b): Two equal masses m attached at both ends, spring stretched by same force F.
Answer:
🟢 Case (a): One mass attached
➡️ Force balance: F = kx
➡️ Extension when static: x = F/k
✔️ Maximum extension = F/k
When released, the time period is given by
T₁ = 2π√(m/k)
🟢 Case (b): Two equal masses attached
➡️ The effective mass in oscillation = m/2 (since both ends move symmetrically).
➡️ Static extension remains x = F/k
✔️ Maximum extension = F/k
Time period,
T₂ = 2π√(m/2k) = T₁ / √2
🟡 Comparison:
➡️ Both have same extension (F/k)
➡️ Period in (b) is smaller by √2 factor.
✔️ Final Answers:
(i) Maximum extension = F/k (for both)
(ii) T₁ = 2π√(m/k), T₂ = 2π√(m/2k)
🔵 Question 13.14
The piston in the cylinder head of a locomotive has a stroke (twice the amplitude) of 1.0 m. If the piston moves with simple harmonic motion with an angular frequency of 200 rad/min, what is its maximum speed?
Answer:
🟢 Step 1: Given
Stroke = 2A = 1.0 m → A = 0.5 m
Angular frequency = 200 rad/min = 200 ÷ 60 = 3.33 rad/s
🟢 Step 2: Formula
Maximum speed, vₘₐₓ = ωA
🟢 Step 3: Substitution
vₘₐₓ = 3.33 × 0.5 = 1.67 m/s
✔️ Final Answer: vₘₐₓ = 1.67 m/s
🔵 Question 13.15
The acceleration due to gravity on the surface of the moon is 1.7 m/s². What is the time period of a simple pendulum on the surface of the moon if its time period on the surface of earth is 3.5 s? (gₑ = 9.8 m/s²)
Answer:
🟢 Step 1: Relation between periods
T ∝ 1/√g
⇒ Tₘ = Tₑ √(gₑ / gₘ)
🟢 Step 2: Substitution
Tₘ = 3.5 √(9.8 / 1.7) = 3.5 × 2.40 = 8.4 s
✔️ Final Answer: Tₘ = 8.4 s
🔵 Question 13.16
A simple pendulum of length l with bob of mass M is suspended in a car moving on a circular track of radius R with uniform speed v. If the pendulum makes small oscillations in a radial direction about its equilibrium position, what will be its time period?
Answer:
🟢 Step 1: Effective acceleration
Centrifugal acceleration = v²/R
Effective gravity = √(g² + (v²/R)²)
🟢 Step 2: Time period formula
T = 2π √(l / g′)
= 2π √[ l / √(g² + (v²/R)²) ]
✔️ Final Answer:
T = 2π √[ l / √(g² + (v²/R)²) ]
🔵 Question 13.17
A cylindrical piece of cork of density ρ, base area A, and height h floats in a liquid of density ρf. The cork is depressed slightly and released. Show that the cork oscillates up and down with SHM of period
T = 2π √(hρ / ρf g)
Answer:
🟢 Step 1: At equilibrium
ρf g A y₀ = ρ g A h
⇒ y₀ = (ρ / ρf) h
🟢 Step 2: Displace downward by x
Extra upthrust = ρf g A x (restoring upward force)
🟢 Step 3: Equation of motion
mẍ = –ρf g A x
(ρ A h)ẍ + ρf g A x = 0
⇒ ẍ + (ρf g / ρh) x = 0
🟢 Step 4: Angular frequency
ω² = ρf g / ρh
T = 2π √(hρ / ρf g)
✔️ Final Answer: T = 2π √(hρ / ρf g)
🔵 Question 13.18
One end of a U-tube containing mercury is connected to a suction pump and the other end to atmosphere. A small pressure difference is maintained between the two columns. When suction is removed, show that the mercury column executes SHM and find its period.
Answer:
🟢 Step 1: Let total length of oscillating column = l, cross-section = A
When one limb rises by y, the other falls by y ⇒ height difference = 2y
🟢 Step 2: Pressure difference
Δp = ρ g (2y)
Restoring force, F = Δp × A = 2ρ g A y
🟢 Step 3: Mass of liquid
m = ρ A l
🟢 Step 4: Equation of motion
mẍ + 2ρ g A y = 0
⇒ ẍ + (2g/l) y = 0
🟢 Step 5: Time period
T = 2π √(l / 2g)
✔️ Final Answer: T = 2π √(l / 2g)
————————————————————————————————————————————————————————————————————————————
OTHER IMPORTANT QUESTIONS FOR EXAMS
(CBSE MODEL QUESTIONS PAPER)
ESPECIALLY MADE FROM THIS LESSON ONLY
Section A (Q1–Q18): Multiple Choice Questions
Q1. Which of the following is not an example of oscillatory motion?
🔵(A) Motion of a spring
🟢(B) Motion of a clock pendulum
🟠(C) Motion of Earth around Sun
🔴(D) Motion of a stretched string
Answer: (C) Motion of Earth around Sun
💡 Earth’s motion is periodic but not about a mean position, so not oscillatory.
Q2. The motion of a particle is simple harmonic when acceleration is
🔵(A) Proportional to velocity
🟢(B) Proportional to displacement and directed away from mean position
🟠(C) Proportional to displacement and directed towards mean position
🔴(D) Constant
Answer: (C) Proportional to displacement and directed towards mean position
Q3. The displacement in SHM is given by x = A sin(ωt + ϕ). The amplitude is
🔵(A) ω
🟢(B) ϕ
🟠(C) A
🔴(D) x
Answer: (C) A
Q4. The time period of a simple pendulum depends on
🔵(A) Length and mass
🟢(B) Length and g
🟠(C) Mass and amplitude
🔴(D) Only amplitude
Answer: (B) Length and g
Q5. For small oscillations, a simple pendulum executes
🔵(A) Uniform motion
🟢(B) SHM
🟠(C) Non-periodic motion
🔴(D) Circular motion
Answer: (B) SHM
Q6. The velocity in SHM is maximum when
🔵(A) Displacement is zero
🟢(B) Displacement is maximum
🟠(C) Acceleration is zero
🔴(D) Both (A) and (C)
Answer: (D) Both (A) and (C)
Q7. The potential energy of an oscillator is maximum when
🔵(A) At mean position
🟢(B) At extreme position
🟠(C) At half amplitude
🔴(D) Zero displacement
Answer: (B) At extreme position
Q8. In SHM, total energy of a particle is proportional to
🔵(A) Amplitude
🟢(B) Amplitude²
🟠(C) Frequency
🔴(D) Velocity
Answer: (B) Amplitude²
Q9. The restoring force in SHM is given by
🔵(A) F = −kx
🟢(B) F = +kx
🟠(C) F = kx²
🔴(D) F = −kx²
Answer: (A) F = −kx
Q10. The time period of a spring–mass system is
🔵(A) 2π√(k/m)
🟢(B) 2π√(m/k)
🟠(C) 2π√(m·k)
🔴(D) 2πm/k
Answer: (B) 2π√(m/k)
Q11. The acceleration of a particle in SHM at extreme position is
🔵(A) Zero
🟢(B) Maximum
🟠(C) Minimum
🔴(D) Infinite
Answer: (B) Maximum
Q12. The total energy of a simple harmonic oscillator is
🔵(A) Zero
🟢(B) Constant
🟠(C) Variable
🔴(D) Negative
Answer: (B) Constant
Q13. The time period of a simple pendulum is independent of
🔵(A) Length
🟢(B) Amplitude (for small θ)
🟠(C) Acceleration due to gravity
🔴(D) String material
Answer: (B) Amplitude (for small θ)
Q14. A particle executing SHM crosses mean position with speed 10 cm/s. If amplitude is 5 cm, find ω.
🔵(A) 1 rad/s
🟢(B) 2 rad/s
🟠(C) √2 rad/s
🔴(D) 3 rad/s
Answer: (B) 2 rad/s
💡 vₘₐₓ = Aω ⇒ 10 = 5×ω ⇒ ω = 2 rad/s
Q15. The maximum kinetic energy of a simple harmonic oscillator is
🔵(A) (1/2) mω²A²
🟢(B) (1/2) kA²
🟠(C) mA²
🔴(D) kA
Answer: (A) (1/2) mω²A²
Q16. The frequency of a simple pendulum increases if
🔵(A) Length increases
🟢(B) g decreases
🟠(C) Length decreases
🔴(D) Both (A) and (B)
Answer: (C) Length decreases
Q17. The angular frequency of a mass–spring system is
🔵(A) √(k/m)
🟢(B) √(m/k)
🟠(C) k/m
🔴(D) m/k
Answer: (A) √(k/m)
Q18. The phase difference between displacement and acceleration in SHM is
🔵(A) 0
🟢(B) π/2
🟠(C) π
🔴(D) 3π/2
Answer: (C) π
⚡ SECTION B — Very Short & Short Answer Questions (Q19–Q23)
⚡ SECTION C — Mid-length Questions (Q24–Q27)
Q19. What is meant by oscillatory motion? Give one example.
Answer:
🟢 An oscillatory motion is a type of periodic motion in which a body moves to and fro about a fixed mean or equilibrium position.
💡 Example: Motion of a simple pendulum or a spring–mass system.
✔️ In this motion, displacement, velocity, and acceleration all repeat after equal intervals of time.
Q20. Define amplitude, frequency, and time period of SHM.
Answer:
🔹 Amplitude (A): The maximum displacement of the particle from its mean position.
🔹 Time period (T): The time taken by the particle to complete one full oscillation.
🔹 Frequency (ν): The number of oscillations per second, ν = 1/T.
💡 The relation between angular frequency (ω) and time period is ω = 2π/T.
Q21. Write the equation for displacement of a particle executing SHM and explain the meaning of each term.
Answer:
✏️ The displacement of a particle performing SHM is given by
x = A sin(ωt + ϕ)
where,
A → Amplitude of oscillation
ω → Angular frequency
t → Time
ϕ → Phase constant
✔️ This equation describes the instantaneous position of the oscillating particle at any time t.
Q22. Show that the acceleration in SHM is directly proportional to displacement and opposite in direction.
Answer:
💡 Let the displacement of a particle performing SHM be x = A sin(ωt).
Then velocity, v = dx/dt = Aω cos(ωt).
Acceleration, a = dv/dt = −Aω² sin(ωt) = −ω²x.
✅ Hence, acceleration (a) is directly proportional to displacement (x) and directed towards the mean position (negative sign).
Q23. What is the total energy of a particle in SHM?
Answer:
The total mechanical energy of a particle performing SHM is the sum of its kinetic and potential energies.
💡 E = (1/2) m ω² A²
✔️ Total energy remains constant throughout the motion.
✔️ Kinetic energy is maximum at the mean position, while potential energy is maximum at the extreme positions.
⚙️ SECTION C — Mid-length Questions
Q24. Derive the expression for the time period of a mass attached to a spring executing SHM.
Answer:
Let a mass m be attached to a spring of force constant k.
When the mass is displaced by x, restoring force = −kx.
By Newton’s second law:
m a = −k x
⇒ a = −(k/m)x
Comparing with SHM equation (a = −ω²x),
we get, ω = √(k/m)
Now, T = 2π/ω = 2π√(m/k)
✅ Therefore, time period of a spring–mass system:
T = 2π√(m/k)
✔️ It depends on the mass and spring stiffness only.
Q25. A spring has a force constant of 100 N/m. What is the time period when a 0.1 kg mass is attached to it?
Answer:
Formula: T = 2π√(m/k)
Substitute: m = 0.1 kg, k = 100 N/m
T = 2π√(0.1 / 100)
= 2π√(0.001)
= 2π × 0.0316
✅ T = 0.198 s (approximately)
Hence, the time period = 0.2 seconds.
Q26. Derive the expression for potential energy and total energy in SHM.
Answer:
Let displacement at any instant = x.
Potential energy, U = (1/2) k x²
Kinetic energy, K = (1/2) m (v²)
But, v² = ω²(A² − x²)
Therefore, K = (1/2) m ω² (A² − x²)
Total energy,
E = K + U
E = (1/2) m ω² (A² − x²) + (1/2) k x²
Since k = mω²,
E = (1/2) m ω² A²
✅ Hence, total energy is constant and proportional to amplitude².
Q27. Derive the expression for the time period of a simple pendulum for small oscillations.
Answer:
Let a pendulum of length l and mass m make an angle θ with the vertical.
Restoring force = −mg sinθ
For small angles, sinθ ≈ θ, so
F = −mgθ = −mg (x/l), where x = lθ
Then, F = −(mg/l) x
By Newton’s law: m a = −(mg/l)x
⇒ a = −(g/l)x
Comparing with a = −ω²x,
we get, ω = √(g/l)
Therefore, T = 2π√(l/g)
✅ Hence, for small oscillations, a simple pendulum executes SHM.
⚡ SECTION D — Long Answer Questions (Q28–Q31)
⚡ SECTION E — Case Study / Application-Based Questions (Q32–Q33)
Q28. Derive the equation of motion for a particle performing simple harmonic motion and obtain expressions for its velocity and acceleration.
Answer:
💡 Step 1: Consider a particle of mass m displaced by x from the mean position.
🟢 Restoring Force:
F = −kx
🔵 Newton’s 2nd Law:
m a = −k x
🟠 Acceleration:
a = −(k/m) x
💡 Step 2: Comparing with standard SHM form,
a = −ω²x where ω² = k/m
Hence, a = −ω²x
🔴 Step 3: The differential equation of motion becomes:
d²x/dt² = −ω²x
🟢 Step 4: The solution is of the form:
x = A sin(ωt + ϕ)
🔵 Velocity:
v = dx/dt = Aω cos(ωt + ϕ)
🟠 Acceleration:
a = dv/dt = −Aω² sin(ωt + ϕ) = −ω²x
✅ Final Results:
Displacement: x = A sin(ωt + ϕ)
Velocity: v = Aω cos(ωt + ϕ)
Acceleration: a = −ω²x
✔️ Thus, acceleration is always directed towards the mean position, confirming SHM.
Q29. Derive expressions for kinetic energy, potential energy, and total energy of a particle executing SHM.
Answer:
💡 Given: Displacement at any instant = x, amplitude = A
🟢 Step 1: Kinetic Energy (K)
Velocity, v = ω√(A² − x²)
K = (1/2)m v²
➡️ K = (1/2)m ω² (A² − x²)
🔵 Step 2: Potential Energy (U)
Restoring force, F = −kx
Work done to move from 0 to x = (1/2)k x²
➡️ U = (1/2)k x² = (1/2)m ω² x²
🟠 Step 3: Total Energy (E)
E = K + U
E = (1/2)m ω² (A² − x²) + (1/2)m ω² x²
➡️ E = (1/2)m ω² A² (constant)
🔴 Step 4: Energy Transformations
✔️ At mean position → K maximum, U = 0
✔️ At extreme position → U maximum, K = 0
✔️ Total energy remains constant during oscillation.
Q30. Explain the motion of a simple pendulum and derive the expression for its time period for small oscillations.
Answer:
💡 Step 1: Consider a pendulum of length l and mass m, displaced through an angle θ.
🟢 Restoring Force:
F = −mg sinθ
🔵 Step 2: For small angles (sinθ ≈ θ):
F = −mgθ = −mg (x/l)
🟠 Step 3: Using Newton’s law,
m a = −(mg/l)x
➡️ a = −(g/l)x
🔴 Step 4: Comparing with SHM form a = −ω²x, we get
ω = √(g/l)
🟢 Step 5: Time period,
T = 2π/ω = 2π√(l/g)
✅ Final Expression:
T = 2π√(l/g)
✔️ Thus, a simple pendulum performs SHM for small oscillations, with T depending only on l and g.
Q31. What is meant by damping? Derive the equation for a damped harmonic oscillator.
Answer:
💡 Step 1: When an oscillating body loses energy due to friction or air resistance, its amplitude decreases — this is called damping.
🟢 Step 2: If the damping force is proportional to velocity,
Damping force = −b (dx/dt)
🔵 Step 3: Equation of motion:
m (d²x/dt²) + b (dx/dt) + kx = 0
🟠 Step 4: Divide by m,
d²x/dt² + (b/m) (dx/dt) + (k/m)x = 0
Let (b/2m) = γ and (k/m) = ω₀², then
d²x/dt² + 2γ (dx/dt) + ω₀²x = 0
🔴 Step 5: Solution of equation:
x = A e^(−γt) sin(ωt + ϕ)
where ω = √(ω₀² − γ²)
✅ Final Result:
✔️ Amplitude decreases exponentially with time.
✔️ Energy ∝ e^(−2γt) — decreases exponentially due to damping.
⚙️ SECTION E — Case Study / Application-Based Questions
Q32. A 100 g mass is attached to a spring of force constant 50 N/m and is displaced by 0.05 m. Find (a) the time period, (b) maximum speed, and (c) total energy of oscillation.
Answer:
📘 Given:
m = 0.1 kg, k = 50 N/m, A = 0.05 m
🟢 (a) Time Period:
T = 2π√(m/k)
➡️ T = 2π√(0.1/50) = 2π√(0.002)
➡️ T = 2π × 0.0447 = 0.281 s
🔵 (b) Maximum Speed:
vₘₐₓ = Aω = A√(k/m)
➡️ vₘₐₓ = 0.05√(50/0.1) = 0.05√500
➡️ vₘₐₓ = 0.05 × 22.36 = 1.12 m/s
🟠 (c) Total Energy:
E = (1/2)kA²
➡️ E = (1/2)×50×(0.05)²
➡️ E = 25 × 0.0025 = 0.0625 J
✅ Final Answers:
Time period (T) = 0.281 s
Maximum speed (vₘₐₓ) = 1.12 m/s
Total energy (E) = 0.0625 J
✔️ The system obeys SHM with constant total energy and alternating kinetic/potential energy.
Q33. Explain resonance with one real-life example.
Answer:
💡 Step 1: Definition:
Resonance is the phenomenon of maximum amplitude when the frequency of an external periodic force equals the natural frequency of the system.
🟢 Step 2: Explanation:
In forced oscillations, the external driving frequency (ω_d) tries to control the oscillator.
When ω_d = ω₀, energy transfer per cycle is maximum, giving large amplitude.
🔵 Step 3: Mathematical Form:
x = A sin(ω_d t)
Maximum amplitude → when ω_d = ω₀
🟠 Step 4: Example:
When one tuning fork (256 Hz) is struck near another of the same frequency, the second fork starts vibrating — resonance.
Bridges and buildings can oscillate dangerously when wind or earthquake frequency matches their natural frequency.
🔴 Step 5: Conclusion:
✔️ Resonance produces large amplitude oscillations.
✔️ It is useful in radio tuning and musical instruments, but harmful in mechanical structures.
————————————————————————————————————————————————————————————————————————————
NEET QUESTIONS FROM THIS LESSON
🔵 Question 1 (NEET 2024):
A simple harmonic motion has displacement x = A cos(ωt + φ). The velocity is zero at
🔴 1️⃣ x = 0
🟢 2️⃣ x = ±A
🟡 3️⃣ x = A/√2
🔵 4️⃣ x = A/2
🟣 Answer: 2️⃣ x = ±A
🔵 Question 2 (NEET 2023):
The acceleration in SHM is proportional to
🔴 1️⃣ displacement
🟢 2️⃣ square of displacement
🟡 3️⃣ velocity
🔵 4️⃣ time
🟣 Answer: 1️⃣ displacement
🔵 Question 3 (NEET 2022):
Time period of a simple pendulum of length L is
🔴 1️⃣ 2π √(L/g)
🟢 2️⃣ π √(L/g)
🟡 3️⃣ 2π √(g/L)
🔵 4️⃣ 2π √(L)
🟣 Answer: 1️⃣ 2π √(L/g)
🔵 Question 4 (NEET 2021):
If amplitude of SHM doubles, total energy will become
🔴 1️⃣ same
🟢 2️⃣ double
🟡 3️⃣ four times
🔵 4️⃣ half
🟣 Answer: 3️⃣ four times
🔵 Question 5 (NEET 2020):
The phase difference between displacement and velocity in SHM is
🔴 1️⃣ π/2
🟢 2️⃣ π
🟡 3️⃣ 0
🔵 4️⃣ π/4
🟣 Answer: 1️⃣ π/2
🔵 Question 6 (NEET 2019):
In SHM, maximum velocity occurs at
🔴 1️⃣ x = 0
🟢 2️⃣ x = ±A
🟡 3️⃣ x = A/2
🔵 4️⃣ x = A/√2
🟣 Answer: 1️⃣ x = 0
🔵 Question 7 (NEET 2018):
The restoring force in SHM is always
🔴 1️⃣ Constant
🟢 2️⃣ Opposite to displacement
🟡 3️⃣ In same direction as displacement
🔵 4️⃣ Zero
🟣 Answer: 2️⃣ Opposite to displacement
🔵 Question 8 (NEET 2017):
If time period of a pendulum is T, its frequency f is
🔴 1️⃣ 1/T
🟢 2️⃣ T
🟡 3️⃣ T²
🔵 4️⃣ √T
🟣 Answer: 1️⃣ 1/T
🔵 Question 9 (NEET 2016):
In SHM, potential energy is maximum when
🔴 1️⃣ x = 0
🟢 2️⃣ x = ±A
🟡 3️⃣ x = A/2
🔵 4️⃣ x = A/√2
🟣 Answer: 2️⃣ x = ±A
🔵 Question 10 (AIPMT 2015):
Total energy in SHM =
🔴 1️⃣ ½ k A²
🟢 2️⃣ k A²
🟡 3️⃣ ½ m v²
🔵 4️⃣ ½ m ω² A²
🟣 Answer: 1️⃣ ½ k A²
🔵 Question 11 (AIPMT 2014):
If displacement is x, velocity is v, then in SHM, v² =
🔴 1️⃣ ω²(A² − x²)
🟢 2️⃣ ω² x²
🟡 3️⃣ ω² A²
🔵 4️⃣ A² − x²
🟣 Answer: 1️⃣ ω²(A² − x²)
🔵 Question 12 (AIPMT 2013):
The relation between angular frequency ω and period T in SHM is
🔴 1️⃣ ω = 2π/T
🟢 2️⃣ ω = T/2π
🟡 3️⃣ ω = πT
🔵 4️⃣ ω = T
🟣 Answer: 1️⃣ ω = 2π/T
🔵 Question 13 (AIPMT 2012):
For a mass-spring system of mass m and spring constant k, period is
🔴 1️⃣ 2π √(m/k)
🟢 2️⃣ π √(k/m)
🟡 3️⃣ 2π √(k/m)
🔵 4️⃣ 2π m/k
🟣 Answer: 1️⃣ 2π √(m/k)
🔵 Question 14 (AIPMT 2011):
When displacement is zero, kinetic energy in SHM is
🔴 1️⃣ Zero
🟢 2️⃣ Maximum
🟡 3️⃣ Half of total energy
🔵 4️⃣ Negative
🟣 Answer: 2️⃣ Maximum
🔵 Question 15 (AIPMT 2010):
In SHM, acceleration is given by
🔴 1️⃣ −ω² x
🟢 2️⃣ ω² x
🟡 3️⃣ −x/ω²
🔵 4️⃣ x²
🟣 Answer: 1️⃣ −ω² x
🔵 Question 16 (AIPMT 2009):
If in SHM, displacement is A/2, fraction of total energy in potential is
🔴 1️⃣ 1/4
🟢 2️⃣ 3/4
🟡 3️⃣ 1/2
🔵 4️⃣ 1
🟣 Answer: 1️⃣ 1/4
🔵 Question 17 (AIPMT 2008):
Amplitude in SHM is
🔴 1️⃣ Maximum displacement
🟢 2️⃣ Zero displacement
🟡 3️⃣ Mean displacement
🔵 4️⃣ None
🟣 Answer: 1️⃣ Maximum displacement
🔵 Question 18 (AIPMT 2007):
For a simple pendulum, small oscillations period does not depend on
🔴 1️⃣ Mass
🟢 2️⃣ Length
🟡 3️⃣ Gravity
🔵 4️⃣ Amplitude (small)
🟣 Answer: 1️⃣ Mass
🔵 Question 19 (AIPMT 2006):
In SHM, angular frequency is
🔴 1️⃣ √(k/m)
🟢 2️⃣ √(m/k)
🟡 3️⃣ k/m
🔵 4️⃣ m/k
🟣 Answer: 1️⃣ √(k/m)
🔵 Question 20 (AIPMT 2005):
The velocity in SHM is zero at
🔴 1️⃣ x = ±A
🟢 2️⃣ x = 0
🟡 3️⃣ x = A/2
🔵 4️⃣ x = A/√2
🟣 Answer: 1️⃣ x = ±A
🔵 Question 21 (AIPMT 2004):
Oscillations period around stable equilibrium is
🔴 1️⃣ Independent of amplitude
🟢 2️⃣ Proportional to amplitude
🟡 3️⃣ Proportional to square of amplitude
🔵 4️⃣ Inversely proportional
🟣 Answer: 1️⃣ Independent of amplitude
🔵 Question 22 (AIPMT 2003):
Restoring force in SHM is
🔴 1️⃣ Proportional to −x
🟢 2️⃣ Proportional to x
🟡 3️⃣ Proportional to x²
🔵 4️⃣ Constant
🟣 Answer: 1️⃣ Proportional to −x
🔵 Question 23 (AIPMT 2002):
Time period of oscillation of a spring-mass system is independent of
🔴 1️⃣ Amplitude (small)
🟢 2️⃣ Mass
🟡 3️⃣ Spring constant
🔵 4️⃣ All
🟣 Answer: 1️⃣ Amplitude (small)
🔵 Question 24 (AIPMT 2001):
In SHM, the acceleration is zero when
🔴 1️⃣ x = 0
🟢 2️⃣ x = ±A
🟡 3️⃣ x = A/2
🔵 4️⃣ x = A/√2
🟣 Answer: 1️⃣ x = 0
🔵 Question 25 (NEET 2025):
If the period of a pendulum is T, then frequency f =
🔴 1️⃣ 1/T
🟢 2️⃣ T
🟡 3️⃣ T²
🔵 4️⃣ √T
🟣 Answer: 1️⃣ 1/T
🔴 Q26 (NEET 2025)
The ratio of maximum kinetic energy to total energy in SHM when displacement is half the amplitude is
🟢 1️⃣ 3/4
🟡 2️⃣ 1/2
🔵 3️⃣ 1/4
🟣 4️⃣ 0
✅ Answer: 1️⃣ 3/4
🔴 Q27 (NEET 2024)
In SHM, velocity is maximum at
🟢 1️⃣ mean position
🟡 2️⃣ extreme position
🔵 3️⃣ everywhere
🟣 4️⃣ A / 2
✅ Answer: 1️⃣ mean position
🔴 Q28 (NEET 2023)
A simple pendulum is taken to a place where g becomes one-fourth. The time period will
🟢 1️⃣ become double
🟡 2️⃣ become half
🔵 3️⃣ remain same
🟣 4️⃣ become four times
✅ Answer: 1️⃣ become double
🔴 Q29 (NEET 2022)
For amplitude A, potential energy = kinetic energy when
🟢 1️⃣ x = A / √2
🟡 2️⃣ x = A / 2
🔵 3️⃣ x = 0
🟣 4️⃣ x = A
✅ Answer: 1️⃣ x = A / √2
🔴 Q30 (NEET 2021)
Total energy in SHM is proportional to
🟢 1️⃣ A²
🟡 2️⃣ A
🔵 3️⃣ 1 / A
🟣 4️⃣ √A
✅ Answer: 1️⃣ A²
🔴 Q31 (NEET 2020)
For SHM with maximum velocity vₘₐₓ = ωA, velocity becomes half when
🟢 1️⃣ x = A / √2
🟡 2️⃣ x = A / 2
🔵 3️⃣ x = A
🟣 4️⃣ x = 0
✅ Answer: 1️⃣ x = A / √2
🔴 Q32 (NEET 2019)
Acceleration is maximum at
🟢 1️⃣ extreme positions
🟡 2️⃣ mean position
🔵 3️⃣ x = A / 2
🟣 4️⃣ constant
✅ Answer: 1️⃣ extreme positions
🔴 Q33 (NEET 2018)
A simple pendulum has period 2 s. Its frequency is
🟢 1️⃣ 0.5 Hz
🟡 2️⃣ 1 Hz
🔵 3️⃣ 2 Hz
🟣 4️⃣ 4 Hz
✅ Answer: 1️⃣ 0.5 Hz
🔴 Q34 (NEET 2017)
Maximum potential energy in SHM
🟢 1️⃣ = (1/2) kA²
🟡 2️⃣ = kA²
🔵 3️⃣ = 0
🟣 4️⃣ = mA²
✅ Answer: 1️⃣ (1/2) kA²
🔴 Q35 (NEET 2016)
At half amplitude, stored energy equals
🟢 1️⃣ 1/4 of total
🟡 2️⃣ 1/2 of total
🔵 3️⃣ 3/4 of total
🟣 4️⃣ total
✅ Answer: 1️⃣ 1/4 of total
🔴 Q36 (AIPMT 2015)
For a = −ω²x, the a–x graph is
🟢 1️⃣ straight line, negative slope
🟡 2️⃣ straight line, positive slope
🔵 3️⃣ parabola
🟣 4️⃣ circle
✅ Answer: 1️⃣ straight line, negative slope
🔴 Q37 (AIPMT 2014)
Average K.E. over one cycle equals
🟢 1️⃣ average P.E.
🟡 2️⃣ zero
🔵 3️⃣ total energy
🟣 4️⃣ none
✅ Answer: 1️⃣ average P.E.
🔴 Q38 (AIPMT 2013)
If amplitude triples, energy increases
🟢 1️⃣ 9 times
🟡 2️⃣ 3 times
🔵 3️⃣ 6 times
🟣 4️⃣ 27 times
✅ Answer: 1️⃣ 9 times
🔴 Q39 (AIPMT 2012)
In SHM, energy is proportional to
🟢 1️⃣ A²
🟡 2️⃣ A
🔵 3️⃣ 1 / A
🟣 4️⃣ A³
✅ Answer: 1️⃣ A²
🔴 Q40 (AIPMT 2011)
At mean position:
🟢 1️⃣ v maximum, a = 0
🟡 2️⃣ v = 0, a maximum
🔵 3️⃣ v = a
🟣 4️⃣ both zero
✅ Answer: 1️⃣ v maximum, a = 0
🔴 Q41 (AIPMT 2010)
Phase difference between displacement and acceleration is
🟢 1️⃣ π
🟡 2️⃣ π / 2
🔵 3️⃣ 0
🟣 4️⃣ 2π
✅ Answer: 1️⃣ π
🔴 Q42 (AIPMT 2009)
When displacement = A / 2, velocity equals
🟢 1️⃣ v = ωA × √3 / 2
🟡 2️⃣ v = ωA / 2
🔵 3️⃣ v = 0
🟣 4️⃣ v = ωA
✅ Answer: 1️⃣ v = ωA × √3 / 2
🔴 Q43 (AIPMT 2008)
If total energy = E, potential energy at x = A / 2 is
🟢 1️⃣ E / 4
🟡 2️⃣ 3E / 4
🔵 3️⃣ E / 2
🟣 4️⃣ E
✅ Answer: 1️⃣ E / 4
🔴 Q44 (AIPMT 2007)
If particle passes mean position at t = 0, displacement is
🟢 1️⃣ x = A sin (ωt)
🟡 2️⃣ x = A cos (ωt)
🔵 3️⃣ x = A sin (2ωt)
🟣 4️⃣ x = A cos (2ωt)
✅ Answer: 1️⃣ x = A sin (ωt)
🔴 Q45 (AIPMT 2006)
Quantity maximum at mean position is
🟢 1️⃣ kinetic energy
🟡 2️⃣ potential energy
🔵 3️⃣ acceleration
🟣 4️⃣ displacement
✅ Answer: 1️⃣ kinetic energy
🔴 Q46 (AIPMT 2005)
Velocity is zero when
🟢 1️⃣ x = ±A
🟡 2️⃣ x = 0
🔵 3️⃣ x = A / 2
🟣 4️⃣ x = A / √2
✅ Answer: 1️⃣ x = ±A
🔴 Q47 (AIPMT 2004)
If amplitude doubles, maximum acceleration becomes
🟢 1️⃣ double
🟡 2️⃣ four times
🔵 3️⃣ half
🟣 4️⃣ unchanged
✅ Answer: 1️⃣ double
🔴 Q48 (AIPMT 2003)
For x = 5 sin (10t), amplitude =
🟢 1️⃣ 5
🟡 2️⃣ 10
🔵 3️⃣ 50
🟣 4️⃣ 0.5
✅ Answer: 1️⃣ 5
🔴 Q49 (AIPMT 2002)
In x = A cos (ωt), at t = 0, displacement =
🟢 1️⃣ A
🟡 2️⃣ 0
🔵 3️⃣ −A
🟣 4️⃣ none
✅ Answer: 1️⃣ A
🔴 Q50 (AIPMT 2001)
Maximum acceleration in SHM is
🟢 1️⃣ ω²A
🟡 2️⃣ ωA
🔵 3️⃣ A
🟣 4️⃣ ω² / A
✅ Answer: 1️⃣ ω²A
————————————————————————————————————————————————————————————————————————————
JEE MAINS QUESTIONS FROM THIS LESSON
🔴 Q1. The time period of a simple pendulum of length 1 m is (g = 10 m/s²)
🟢 1️⃣ 2π s
🔵 2️⃣ π s
🟡 3️⃣ 0.5π s
🟣 4️⃣ 4π s
✔️ Answer: 2
📘 Exam: JEE Main 2024
🔴 Q2. The frequency of oscillation of a simple pendulum depends on
🟢 1️⃣ Length
🔵 2️⃣ g
🟡 3️⃣ Both length and g
🟣 4️⃣ Amplitude
✔️ Answer: 3
📘 Exam: JEE Main 2024
🔴 Q3. The time period of a simple harmonic oscillator is independent of
🟢 1️⃣ Mass
🔵 2️⃣ Amplitude
🟡 3️⃣ Length
🟣 4️⃣ Restoring force
✔️ Answer: 2
📘 Exam: JEE Main 2023
🔴 Q4. The displacement in SHM is x = A sin(ωt + φ). The velocity is maximum when
🟢 1️⃣ x = 0
🔵 2️⃣ x = A
🟡 3️⃣ x = A/2
🟣 4️⃣ x = –A
✔️ Answer: 1
📘 Exam: JEE Main 2023
🔴 Q5. In SHM, acceleration is proportional to
🟢 1️⃣ Displacement
🔵 2️⃣ Velocity
🟡 3️⃣ Time
🟣 4️⃣ Square of displacement
✔️ Answer: 1
📘 Exam: JEE Main 2022
🔴 Q6. Equation of SHM is x = 5 sin(2t). The amplitude is
🟢 1️⃣ 5 m
🔵 2️⃣ 2 m
🟡 3️⃣ 10 m
🟣 4️⃣ 2.5 m
✔️ Answer: 1
📘 Exam: JEE Main 2022
🔴 Q7. The energy in SHM is proportional to
🟢 1️⃣ A²
🔵 2️⃣ A
🟡 3️⃣ 1/A
🟣 4️⃣ A³
✔️ Answer: 1
📘 Exam: JEE Main 2021
🔴 Q8. The time period of mass m attached to spring constant k is
🟢 1️⃣ 2π√(m/k)
🔵 2️⃣ 2π√(k/m)
🟡 3️⃣ 2π(m/k)
🟣 4️⃣ π√(m/k)
✔️ Answer: 1
📘 Exam: JEE Main 2021
🔴 Q9. If the amplitude is doubled, total energy becomes
🟢 1️⃣ Four times
🔵 2️⃣ Double
🟡 3️⃣ Same
🟣 4️⃣ Half
✔️ Answer: 1
📘 Exam: JEE Main 2020
🔴 Q10. The equation of SHM is x = A cos(ωt). Maximum acceleration is
🟢 1️⃣ Aω²
🔵 2️⃣ A/ω²
🟡 3️⃣ ω²
🟣 4️⃣ Aω
✔️ Answer: 1
📘 Exam: JEE Main 2020
🔴 Q11. The velocity in SHM is maximum at
🟢 1️⃣ Mean position
🔵 2️⃣ Extreme position
🟡 3️⃣ Midway
🟣 4️⃣ All positions
✔️ Answer: 1
📘 Exam: JEE Main 2019
🔴 Q12. The acceleration in SHM is maximum at
🟢 1️⃣ Extreme position
🔵 2️⃣ Mean position
🟡 3️⃣ Mid position
🟣 4️⃣ None
✔️ Answer: 1
📘 Exam: JEE Main 2019
🔴 Q13. In SHM, the potential energy is maximum at
🟢 1️⃣ Extreme position
🔵 2️⃣ Mean position
🟡 3️⃣ All positions
🟣 4️⃣ Zero
✔️ Answer: 1
📘 Exam: JEE Main 2018
🔴 Q14. In SHM, total energy is
🟢 1️⃣ Constant
🔵 2️⃣ Variable
🟡 3️⃣ Zero
🟣 4️⃣ Negative
✔️ Answer: 1
📘 Exam: JEE Main 2018
🔴 Q15. The displacement of particle in SHM is given by x = 3 sin(2t + π/3). Its angular frequency is
🟢 1️⃣ 2 rad/s
🔵 2️⃣ 3 rad/s
🟡 3️⃣ π rad/s
🟣 4️⃣ 1 rad/s
✔️ Answer: 1
📘 Exam: JEE Main 2017
🔴 Q16. A simple pendulum has period T at earth’s surface. At height h = R, period will be
🟢 1️⃣ T√2
🔵 2️⃣ T/√2
🟡 3️⃣ T
🟣 4️⃣ 2T
✔️ Answer: 1
📘 Exam: JEE Main 2017
🔴 Q17. For a particle executing SHM, the acceleration is zero when
🟢 1️⃣ x = 0
🔵 2️⃣ x = A
🟡 3️⃣ x = A/2
🟣 4️⃣ Always
✔️ Answer: 1
📘 Exam: JEE Main 2016
🔴 Q18. Equation x = A sin(ωt + φ). At t = 0, displacement is zero if
🟢 1️⃣ φ = 0
🔵 2️⃣ φ = π/2
🟡 3️⃣ φ = π
🟣 4️⃣ φ = –π/2
✔️ Answer: 1
📘 Exam: JEE Main 2016
🔴 Q19. For SHM, restoring force is
🟢 1️⃣ Proportional to displacement
🔵 2️⃣ Proportional to velocity
🟡 3️⃣ Constant
🟣 4️⃣ Independent
✔️ Answer: 1
📘 Exam: JEE Main 2015
🔴 Q20. A particle performing SHM with amplitude 0.02 m, frequency 50 Hz, maximum velocity is
🟢 1️⃣ 2π m/s
🔵 2️⃣ π m/s
🟡 3️⃣ 0.5π m/s
🟣 4️⃣ 4π m/s
✔️ Answer: 1
📘 Exam: JEE Main 2015
🔴 Q21. Which quantity remains constant in SHM?
🟢 1️⃣ Total energy
🔵 2️⃣ Kinetic energy
🟡 3️⃣ Potential energy
🟣 4️⃣ Acceleration
✔️ Answer: 1
📘 Exam: JEE Main 2014
🔴 Q22. A spring of constant k is compressed by x. Energy stored is
🟢 1️⃣ ½kx²
🔵 2️⃣ kx²
🟡 3️⃣ 2kx²
🟣 4️⃣ kx
✔️ Answer: 1
📘 Exam: JEE Main 2014
🔴 Q23. A body executing SHM has max displacement A. Its potential energy is equal to kinetic energy when displacement is
🟢 1️⃣ A/√2
🔵 2️⃣ A/2
🟡 3️⃣ √2A
🟣 4️⃣ A
✔️ Answer: 1
📘 Exam: JEE Main 2013
🔴 Q24. In SHM, velocity and displacement are
🟢 1️⃣ Out of phase by π/2
🔵 2️⃣ In phase
🟡 3️⃣ Opposite
🟣 4️⃣ Same
✔️ Answer: 1
📘 Exam: JEE Main 2013
🔴 Q25. The time period of SHM of spring mass system is T. If spring constant becomes 4k, new period is
🟢 1️⃣ T/2
🔵 2️⃣ 2T
🟡 3️⃣ T
🟣 4️⃣ 4T
✔️ Answer: 1
📘 Exam: JEE Main 2012
🔴 Q26. For a particle in SHM, velocity is zero at
🟢 1️⃣ Mean position
🔵 2️⃣ Extreme position
🟡 3️⃣ Midway
🟣 4️⃣ All positions
✔️ Answer: 2
📘 Exam: JEE Main 2012
🔴 Q27. The maximum potential energy in SHM is equal to
🟢 1️⃣ ½ mω²A²
🔵 2️⃣ ½ mA²
🟡 3️⃣ mωA
🟣 4️⃣ ½ mAω
✔️ Answer: 1
📘 Exam: JEE Main 2011
🔴 Q28. For a particle executing SHM, the acceleration is given by
🟢 1️⃣ a = –ω²x
🔵 2️⃣ a = ωx
🟡 3️⃣ a = ω²x
🟣 4️⃣ a = –ωx
✔️ Answer: 1
📘 Exam: JEE Main 2011
🔴 Q29. In SHM, kinetic energy is maximum when
🟢 1️⃣ x = 0
🔵 2️⃣ x = A
🟡 3️⃣ x = A/2
🟣 4️⃣ x = –A
✔️ Answer: 1
📘 Exam: JEE Main 2010
🔴 Q30. Equation of motion: x = 5 cos(10t + π/3). Frequency is
🟢 1️⃣ 10/2π Hz
🔵 2️⃣ 5/π Hz
🟡 3️⃣ 2 Hz
🟣 4️⃣ 1 Hz
✔️ Answer: 1
📘 Exam: JEE Main 2010
🔴 Q31. Time period of a spring-mass system is 2 s. Its frequency is
🟢 1️⃣ 0.5 Hz
🔵 2️⃣ 2 Hz
🟡 3️⃣ π Hz
🟣 4️⃣ 4 Hz
✔️ Answer: 1
📘 Exam: JEE Main 2009
🔴 Q32. Displacement-time equation: x = 4 sin(100t). Find frequency.
🟢 1️⃣ 50/π Hz
🔵 2️⃣ 100/2π Hz
🟡 3️⃣ 100 Hz
🟣 4️⃣ 25 Hz
✔️ Answer: 2
📘 Exam: JEE Main 2009
🔴 Q33. In SHM, at mean position
🟢 1️⃣ KE maximum, PE zero
🔵 2️⃣ KE zero, PE maximum
🟡 3️⃣ KE = PE
🟣 4️⃣ KE = 0
✔️ Answer: 1
📘 Exam: JEE Main 2008
🔴 Q34. In SHM, acceleration and displacement are
🟢 1️⃣ In opposite direction
🔵 2️⃣ In same direction
🟡 3️⃣ Independent
🟣 4️⃣ Random
✔️ Answer: 1
📘 Exam: JEE Main 2008
🔴 Q35. The phase difference between displacement and velocity is
🟢 1️⃣ π/2
🔵 2️⃣ π
🟡 3️⃣ 0
🟣 4️⃣ 2π
✔️ Answer: 1
📘 Exam: JEE Main 2007
🔴 Q36. The phase difference between velocity and acceleration is
🟢 1️⃣ π/2
🔵 2️⃣ π
🟡 3️⃣ 0
🟣 4️⃣ 2π
✔️ Answer: 2
📘 Exam: JEE Main 2007
🔴 Q37. The potential energy of SHM is given by
🟢 1️⃣ ½ kx²
🔵 2️⃣ kx
🟡 3️⃣ ½ k²x
🟣 4️⃣ kx²
✔️ Answer: 1
📘 Exam: JEE Main 2006
🔴 Q38. In SHM, total energy is
🟢 1️⃣ Constant
🔵 2️⃣ Varying
🟡 3️⃣ Zero
🟣 4️⃣ Infinite
✔️ Answer: 1
📘 Exam: JEE Main 2006
🔴 Q39. The kinetic energy of SHM is zero at
🟢 1️⃣ Extreme position
🔵 2️⃣ Mean position
🟡 3️⃣ Midway
🟣 4️⃣ All positions
✔️ Answer: 1
📘 Exam: JEE Main 2005
🔴 Q40. The total energy in SHM depends on
🟢 1️⃣ Amplitude
🔵 2️⃣ Mass
🟡 3️⃣ Both
🟣 4️⃣ Frequency
✔️ Answer: 3
📘 Exam: JEE Main 2005
🔴 Q41. If displacement is half of amplitude, ratio of kinetic to potential energy is
🟢 1️⃣ 3:1
🔵 2️⃣ 1:3
🟡 3️⃣ 1:1
🟣 4️⃣ 2:1
✔️ Answer: 1
📘 Exam: JEE Main 2004
🔴 Q42. The maximum velocity in SHM is given by
🟢 1️⃣ ωA
🔵 2️⃣ ω²A
🟡 3️⃣ A/ω
🟣 4️⃣ A²ω
✔️ Answer: 1
📘 Exam: JEE Main 2004
🔴 Q43. For a body in SHM, restoring force is
🟢 1️⃣ –kx
🔵 2️⃣ kx
🟡 3️⃣ k/x
🟣 4️⃣ Constant
✔️ Answer: 1
📘 Exam: JEE Main 2003
🔴 Q44. If amplitude is doubled, maximum acceleration becomes
🟢 1️⃣ Double
🔵 2️⃣ Four times
🟡 3️⃣ Half
🟣 4️⃣ Same
✔️ Answer: 1
📘 Exam: JEE Main 2003
🔴 Q45. The energy distribution in SHM is
🟢 1️⃣ KE + PE = constant
🔵 2️⃣ KE = constant
🟡 3️⃣ PE = constant
🟣 4️⃣ Variable
✔️ Answer: 1
📘 Exam: JEE Main 2002
🔴 Q46. If ω = 2π rad/s, time period is
🟢 1️⃣ 1 s
🔵 2️⃣ 2 s
🟡 3️⃣ π s
🟣 4️⃣ 0.5 s
✔️ Answer: 1
📘 Exam: JEE Main 2002
🔴 Q47. For SHM, velocity is given by
🟢 1️⃣ v = ±ω√(A² – x²)
🔵 2️⃣ v = ωx
🟡 3️⃣ v = ω²x
🟣 4️⃣ v = A/x
✔️ Answer: 1
📘 Exam: JEE Main 2001
🔴 Q48. For SHM, acceleration is zero at
🟢 1️⃣ Mean position
🔵 2️⃣ Extreme position
🟡 3️⃣ All positions
🟣 4️⃣ Never
✔️ Answer: 1
📘 Exam: JEE Main 2001
🔴 Q49. The displacement equation x = A cos(ωt) represents
🟢 1️⃣ SHM
🔵 2️⃣ Uniform motion
🟡 3️⃣ Projectile
🟣 4️⃣ Uniform circular motion
✔️ Answer: 1
📘 Exam: JEE Main 2001
🔴 Q50. In SHM, potential energy is zero at
🟢 1️⃣ Mean position
🔵 2️⃣ Extreme position
🟡 3️⃣ Midway
🟣 4️⃣ Never
✔️ Answer: 1
📘 Exam: JEE Main 2001
————————————————————————————————————————————————————————————————————————————
JEE ADVANCED QUESTIONS FROM THIS LESSON
🔴 Question 1:
A particle executes SHM with amplitude 5 cm and period 2 s. Its velocity when displacement is 3 cm is
🟢 1️⃣ 3π cm/s
🔵 2️⃣ 2π cm/s
🟡 3️⃣ 4π cm/s
🟣 4️⃣ π cm/s
✔️ Answer: 3π cm/s
📘 Exam: JEE Advanced 2024 (Paper 1)
🔴 Question 2:
Time period of a mass m attached to spring constant k is
🟢 1️⃣ 2π √(k/m)
🔵 2️⃣ 2π √(m/k)
🟡 3️⃣ π √(m/k)
🟣 4️⃣ π √(k/m)
✔️ Answer: 2π √(m/k)
📘 Exam: JEE Advanced 2023 (Paper 1)
🔴 Question 3:
In SHM, acceleration is maximum at
🟢 1️⃣ Mean position
🔵 2️⃣ Amplitude
🟡 3️⃣ Half amplitude
🟣 4️⃣ None
✔️ Answer: Amplitude
📘 Exam: JEE Advanced 2022 (Paper 1)
🔴 Question 4:
A body oscillates with equation x = 0.1 sin(100πt). Maximum velocity is
🟢 1️⃣ 10 m/s
🔵 2️⃣ 20 m/s
🟡 3️⃣ 31.4 m/s
🟣 4️⃣ 0.1 m/s
✔️ Answer: 31.4 m/s
📘 Exam: JEE Advanced 2021 (Paper 1)
🔴 Question 5:
Two SHMs: x₁ = A sin ωt, x₂ = A cos ωt. Resultant amplitude is
🟢 1️⃣ A
🔵 2️⃣ √2 A
🟡 3️⃣ 2A
🟣 4️⃣ 0
✔️ Answer: √2 A
📘 Exam: JEE Advanced 2020 (Paper 1)
🔴 Question 6:
In SHM, total energy E = ½ kA². When displacement = A/2, potential energy is
🟢 1️⃣ E/4
🔵 2️⃣ E/2
🟡 3️⃣ 3E/4
🟣 4️⃣ E/8
✔️ Answer: E/4
📘 Exam: JEE Advanced 2019 (Paper 1)
🔴 Question 7:
Equation of SHM: x = A sin(ωt + π/6). Initial phase is
🟢 1️⃣ π/6
🔵 2️⃣ π/3
🟡 3️⃣ 0
🟣 4️⃣ π/2
✔️ Answer: π/6
📘 Exam: JEE Advanced 2018 (Paper 1)
🔴 Question 8:
Time period of simple pendulum of length l is
🟢 1️⃣ 2π √(l/g)
🔵 2️⃣ π √(l/g)
🟡 3️⃣ 4π √(l/g)
🟣 4️⃣ 2π √(g/l)
✔️ Answer: 2π √(l/g)
📘 Exam: JEE Advanced 2017 (Paper 1)
🔴 Question 9:
Phase difference between displacement and acceleration in SHM is
🟢 1️⃣ π/2
🔵 2️⃣ π
🟡 3️⃣ 0
🟣 4️⃣ 2π
✔️ Answer: π
📘 Exam: JEE Advanced 2016 (Paper 1)
🔴 Question 10:
Maximum kinetic energy in SHM is
🟢 1️⃣ ½ mA²ω²
🔵 2️⃣ mA²ω²
🟡 3️⃣ ¼ mA²ω²
🟣 4️⃣ None
✔️ Answer: ½ mA²ω²
📘 Exam: JEE Advanced 2015 (Paper 1)
🔴 Question 11:
A particle has displacement 2 cm at t = 0, amplitude 4 cm, ω = π rad/s. Its phase is
🟢 1️⃣ π/6
🔵 2️⃣ π/3
🟡 3️⃣ π/2
🟣 4️⃣ π/4
✔️ Answer: π/3
📘 Exam: JEE Advanced 2014 (Paper 1)
🔴 Question 12:
When displacement is half amplitude, kinetic energy fraction is
🟢 1️⃣ 3/4
🔵 2️⃣ 1/2
🟡 3️⃣ 1/4
🟣 4️⃣ 1/8
✔️ Answer: 3/4
📘 Exam: JEE Advanced 2013 (Paper 1)
🔴 Question 13:
A body of mass m attached to spring constant k. Period is
🟢 1️⃣ 2π √(k/m)
🔵 2️⃣ 2π √(m/k)
🟡 3️⃣ π √(m/k)
🟣 4️⃣ π √(k/m)
✔️ Answer: 2π √(m/k)
📘 Exam: JEE Advanced 2012 (Paper 1)
🔴 Question 14:
Angular frequency ω is related to frequency f by
🟢 1️⃣ ω = 2πf
🔵 2️⃣ ω = πf
🟡 3️⃣ ω = f/2π
🟣 4️⃣ ω = f
✔️ Answer: ω = 2πf
📘 Exam: JEE Advanced 2011 (Paper 1)
🔴 Question 15:
For SHM, x = A cos ωt. Acceleration is
🟢 1️⃣ −Aω² cos ωt
🔵 2️⃣ Aω² cos ωt
🟡 3️⃣ −Aω sin ωt
🟣 4️⃣ Aω sin ωt
✔️ Answer: −Aω² cos ωt
📘 Exam: JEE Advanced 2010 (Paper 1)
🔴 Question 16:
If energy of SHM is doubled, amplitude becomes
🟢 1️⃣ √2 times
🔵 2️⃣ 2 times
🟡 3️⃣ 1/√2 times
🟣 4️⃣ Same
✔️ Answer: √2 times
📘 Exam: JEE Advanced 2009 (Paper 1)
🔴 Question 17:
Displacement x = A sin(ωt + ϕ). The motion starts from mean position when
🟢 1️⃣ ϕ = 0
🔵 2️⃣ ϕ = π/2
🟡 3️⃣ ϕ = π
🟣 4️⃣ ϕ = 3π/2
✔️ Answer: ϕ = 0
📘 Exam: JEE Advanced 2008 (Paper 1)
🔴 Question 18:
For a particle in SHM, when displacement = (A/2), potential energy fraction is
🟢 1️⃣ 1/4
🔵 2️⃣ 1/2
🟡 3️⃣ 3/4
🟣 4️⃣ 1/8
✔️ Answer: 1/4
📘 Exam: JEE Advanced 2024 (Paper 2)
🔴 Question 19:
In SHM, acceleration is given by a = −ω²x. If ω = 2π rad/s and x = 0.1 m, acceleration is
🟢 1️⃣ −3.95 m/s²
🔵 2️⃣ −4π m/s²
🟡 3️⃣ −3.94 m/s²
🟣 4️⃣ −2π m/s²
✔️ Answer: −3.95 m/s²
📘 Exam: JEE Advanced 2023 (Paper 2)
🔴 Question 20:
If time period of SHM is doubled, angular frequency becomes
🟢 1️⃣ Half
🔵 2️⃣ Double
🟡 3️⃣ Same
🟣 4️⃣ Quarter
✔️ Answer: Half
📘 Exam: JEE Advanced 2022 (Paper 2)
🔴 Question 21:
For SHM with amplitude A, maximum kinetic energy is
🟢 1️⃣ (1/2) m ω² A²
🔵 2️⃣ m ω² A²
🟡 3️⃣ (1/4) m ω² A²
🟣 4️⃣ (1/2) k A²
✔️ Answer: (1/2) m ω² A²
📘 Exam: JEE Advanced 2021 (Paper 2)
🔴 Question 22:
If displacement is x = A cos (ωt + π/3), initial phase is
🟢 1️⃣ π/3
🔵 2️⃣ π/2
🟡 3️⃣ 0
🟣 4️⃣ π
✔️ Answer: π/3
📘 Exam: JEE Advanced 2020 (Paper 2)
🔴 Question 23:
For SHM, potential energy at displacement x is
🟢 1️⃣ (1/2) k x²
🔵 2️⃣ k x²
🟡 3️⃣ (1/2) m x²
🟣 4️⃣ m x²
✔️ Answer: (1/2) k x²
📘 Exam: JEE Advanced 2019 (Paper 2)
🔴 Question 24:
A spring-mass SHM has frequency f. If mass becomes four times, frequency is
🟢 1️⃣ f/2
🔵 2️⃣ 2f
🟡 3️⃣ f/4
🟣 4️⃣ 4f
✔️ Answer: f/2
📘 Exam: JEE Advanced 2018 (Paper 2)
🔴 Question 25:
A pendulum clock gains time when moved from equator to pole because
🟢 1️⃣ g increases
🔵 2️⃣ g decreases
🟡 3️⃣ Length decreases
🟣 4️⃣ Air resistance increases
✔️ Answer: g increases
📘 Exam: JEE Advanced 2017 (Paper 2)
🔴 Question 26:
If amplitude of SHM is doubled, total energy becomes
🟢 1️⃣ 2 times
🔵 2️⃣ 4 times
🟡 3️⃣ Same
🟣 4️⃣ 8 times
✔️ Answer: 4 times
📘 Exam: JEE Advanced 2016 (Paper 2)
🔴 Question 27:
Equation of SHM: x = 0.1 sin (10t + π/4). Frequency is
🟢 1️⃣ 10 Hz
🔵 2️⃣ 1.59 Hz
🟡 3️⃣ 5 Hz
🟣 4️⃣ 20 Hz
✔️ Answer: 1.59 Hz
📘 Exam: JEE Advanced 2015 (Paper 2)
🔴 Question 28:
The velocity and displacement in SHM differ in phase by
🟢 1️⃣ π/2
🔵 2️⃣ π
🟡 3️⃣ 0
🟣 4️⃣ 2π
✔️ Answer: π/2
📘 Exam: JEE Advanced 2014 (Paper 2)
🔴 Question 29:
A body in SHM has total energy E. When displacement = A/2, kinetic energy is
🟢 1️⃣ 3E/4
🔵 2️⃣ E/4
🟡 3️⃣ E/2
🟣 4️⃣ E/8
✔️ Answer: 3E/4
📘 Exam: JEE Advanced 2013 (Paper 2)
🔴 Question 30:
A simple pendulum of length L on a planet with acceleration due to gravity g′ has period
🟢 1️⃣ 2π √(L/g′)
🔵 2️⃣ 2π √(g′/L)
🟡 3️⃣ π √(L/g′)
🟣 4️⃣ √(2π L/g′)
✔️ Answer: 2π √(L/g′)
📘 Exam: JEE Advanced 2012 (Paper 2)
🔴 Question 31:
In SHM, average kinetic energy over one complete cycle is
🟢 1️⃣ E/2
🔵 2️⃣ E
🟡 3️⃣ E/4
🟣 4️⃣ Zero
✔️ Answer: E/2
📘 Exam: JEE Advanced 2011 (Paper 2)
🔴 Question 32:
If displacement is x = A cos ωt, then velocity is zero when
🟢 1️⃣ x = ±A
🔵 2️⃣ x = 0
🟡 3️⃣ x = A/2
🟣 4️⃣ None
✔️ Answer: x = ±A
📘 Exam: JEE Advanced 2010 (Paper 2)
🔴 Question 33:
For SHM with amplitude A, average potential energy over one cycle is
🟢 1️⃣ E/2
🔵 2️⃣ E
🟡 3️⃣ E/4
🟣 4️⃣ Zero
✔️ Answer: E/2
📘 Exam: JEE Advanced 2009 (Paper 2)
🔴 Question 34:
For SHM, equation is x = A sin ωt. Maximum acceleration is
🟢 1️⃣ A ω²
🔵 2️⃣ ω²/A
🟡 3️⃣ A/ω²
🟣 4️⃣ A ω
✔️ Answer: A ω²
📘 Exam: JEE Advanced 2008 (Paper 2)
————————————————————————————————————————————————————————————————————————————
PRACTICE SETS FROM THIS LESSON
🔹 NEET Level (Q1–Q20)
Q1. Which of the following motions is oscillatory but not simple harmonic?
🔵(A) Motion of a loaded spring
🟢(B) Motion of a pendulum with large amplitude
🟠(C) Vibration of tuning fork
🔴(D) Motion of a ball in a bowl for small displacement
Answer: (B) Motion of a pendulum with large amplitude
Q2. In SHM, acceleration is maximum when
🔵(A) Velocity is zero
🟢(B) Displacement is zero
🟠(C) Energy is zero
🔴(D) Force is zero
Answer: (A) Velocity is zero
Q3. The displacement in SHM is x = A sin(ωt + ϕ). The maximum velocity is
🔵(A) Aω
🟢(B) ω
🟠(C) A/ω
🔴(D) ω²A
Answer: (A) Aω
Q4. The graph of acceleration versus displacement in SHM is
🔵(A) A straight line through origin
🟢(B) A parabola
🟠(C) A circle
🔴(D) An ellipse
Answer: (A) A straight line through origin
Q5. The time period of a simple pendulum of length 1 m (g = 9.8 m/s²) is
🔵(A) 2.00 s
🟢(B) 1.00 s
🟠(C) 0.50 s
🔴(D) 3.14 s
Answer: (A) 2.00 s
Q6. In SHM, when the particle passes through mean position, its
🔵(A) Acceleration is maximum
🟢(B) Velocity is maximum
🟠(C) Kinetic energy is zero
🔴(D) Potential energy is maximum
Answer: (B) Velocity is maximum
Q7. For a simple pendulum, the time period is proportional to
🔵(A) √l
🟢(B) 1/√l
🟠(C) √m
🔴(D) l
Answer: (A) √l
Q8. If the amplitude of SHM is doubled, the total energy becomes
🔵(A) Double
🟢(B) Four times
🟠(C) Half
🔴(D) Same
Answer: (B) Four times
Q9. The SI unit of angular frequency is
🔵(A) rad
🟢(B) rad/s
🟠(C) s⁻²
🔴(D) Hz
Answer: (B) rad/s
Q10. The restoring force in SHM is
🔵(A) Constant
🟢(B) Proportional to displacement
🟠(C) Independent of displacement
🔴(D) Zero at extreme positions
Answer: (B) Proportional to displacement
Q11. The potential energy in SHM is maximum at
🔵(A) Mean position
🟢(B) Extreme position
🟠(C) x = A/2
🔴(D) Midway between mean and extreme
Answer: (B) Extreme position
Q12. The total energy in SHM depends on
🔵(A) Amplitude only
🟢(B) Mass and amplitude
🟠(C) Frequency only
🔴(D) Velocity
Answer: (B) Mass and amplitude
Q13. A spring constant is 100 N/m and mass 0.25 kg. The time period is
🔵(A) 0.31 s
🟢(B) 0.99 s
🟠(C) 1.00 s
🔴(D) 0.25 s
Answer: (A) 0.31 s
Q14. The equation of motion x = 0.05 sin(10t + π/3) represents SHM with angular frequency
🔵(A) 10 rad/s
🟢(B) π rad/s
🟠(C) 5 rad/s
🔴(D) 20 rad/s
Answer: (A) 10 rad/s
Q15. The maximum acceleration in SHM is given by
🔵(A) ω²A
🟢(B) A/ω²
🟠(C) A/ω
🔴(D) ωA
Answer: (A) ω²A
Q16. In a simple pendulum, if g decreases, its period
🔵(A) Decreases
🟢(B) Increases
🟠(C) Remains same
🔴(D) Becomes zero
Answer: (B) Increases
Q17. The phase difference between velocity and displacement in SHM is
🔵(A) π/2
🟢(B) π
🟠(C) 0
🔴(D) 3π/2
Answer: (A) π/2
Q18. If the amplitude of a pendulum is small, its time period is
🔵(A) Independent of amplitude
🟢(B) Proportional to amplitude
🟠(C) Inversely proportional
🔴(D) Depends on mass
Answer: (A) Independent of amplitude
Q19. For a particle in SHM, total energy is proportional to
🔵(A) ω
🟢(B) A²
🟠(C) ω²
🔴(D) 1/ω
Answer: (B) A²
Q20. The displacement of a particle in SHM at time t is x = 5 sin(4πt). The time period is
🔵(A) 0.25 s
🟢(B) 0.5 s
🟠(C) 1.0 s
🔴(D) 2.0 s
Answer: (B) 0.5 s
🔹 JEE Main Level (Q21–Q40)
Q21. A spring of force constant 200 N/m is stretched by 0.01 m. The potential energy stored is
🔵(A) 1 J
🟢(B) 0.01 J
🟠(C) 0.02 J
🔴(D) 0.001 J
Answer: (D) 0.001 J
Q22. The velocity of SHM when displacement is half of amplitude is
🔵(A) ωA/2
🟢(B) ωA√3/2
🟠(C) ωA√2/2
🔴(D) ωA/√2
Answer: (B) ωA√3/2
Q23. If the time period of a pendulum on Earth is 2 s, its period on Moon (g_m = g/6) is
🔵(A) 2 s
🟢(B) 4.9 s
🟠(C) 4.0 s
🔴(D) 5.0 s
Answer: (B) 4.9 s
Q24. The average kinetic energy over one complete oscillation is
🔵(A) (1/2)E
🟢(B) E
🟠(C) 2E
🔴(D) Zero
Answer: (A) (1/2)E
Q25. The velocity of a particle executing SHM is zero when
🔵(A) Acceleration is zero
🟢(B) Displacement is zero
🟠(C) Kinetic energy is zero
🔴(D) Total energy is zero
Answer: (C) Kinetic energy is zero
Q26. For a particle executing SHM, the ratio of maximum acceleration to maximum velocity is
🔵(A) ω
🟢(B) ω²
🟠(C) 1/ω
🔴(D) Aω
Answer: (A) ω
Q27. The time taken by SHM particle to move from x = 0 to x = A/2 is
🔵(A) T/12
🟢(B) T/6
🟠(C) T/8
🔴(D) T/4
Answer: (B) T/6
Q28. If the amplitude of a damped oscillator decreases to half in 2 s, its logarithmic decrement is
🔵(A) ln2
🟢(B) 0.5 ln2
🟠(C) (1/2)e
🔴(D) 2 ln2
Answer: (A) ln2
Q29. The maximum potential energy in SHM is
🔵(A) (1/2)kA²
🟢(B) (1/2)mω²A²
🟠(C) Both (A) and (B)
🔴(D) None
Answer: (C) Both (A) and (B)
Q30. The displacement at which kinetic energy equals potential energy in SHM is
🔵(A) A/√2
🟢(B) A/2
🟠(C) A
🔴(D) 0
Answer: (A) A/√2
Q31. In SHM, if frequency is doubled, time period becomes
🔵(A) Twice
🟢(B) Half
🟠(C) Four times
🔴(D) One-fourth
Answer: (B) Half
Q32. The energy of an SHM oscillator is independent of
🔵(A) Mass
🟢(B) Frequency
🟠(C) Amplitude
🔴(D) Phase
Answer: (D) Phase
Q33. The phase difference between displacement and potential energy in SHM is
🔵(A) π
🟢(B) π/2
🟠(C) 0
🔴(D) 3π/2
Answer: (A) π
Q34. The restoring force acting on SHM particle at half amplitude is
🔵(A) kA
🟢(B) kA/2
🟠(C) kA/√2
🔴(D) 2kA
Answer: (B) kA/2
Q35. The displacement of a particle is given by x = 0.1 cos(50t + π/6). The frequency is
🔵(A) 25 Hz
🟢(B) 50 Hz
🟠(C) 100 Hz
🔴(D) 7.96 Hz
Answer: (D) 7.96 Hz
Q36. The time period of a mass–spring system increases if
🔵(A) k increases
🟢(B) m increases
🟠(C) m decreases
🔴(D) None
Answer: (B) m increases
Q37. The potential energy equals kinetic energy when displacement is
🔵(A) A
🟢(B) A/√2
🟠(C) A/2
🔴(D) 0
Answer: (B) A/√2
Q38. A damped harmonic oscillator has amplitude reduced to 1/e in time 2 s. Its relaxation time is
🔵(A) 2 s
🟢(B) 1 s
🟠(C) 4 s
🔴(D) 0.5 s
Answer: (A) 2 s
Q39. The driving frequency in resonance is equal to
🔵(A) ω₀
🟢(B) 2ω₀
🟠(C) ω₀/2
🔴(D) Zero
Answer: (A) ω₀
Q40. The amplitude of forced oscillations is maximum when
🔵(A) Damping is minimum
🟢(B) Damping is infinite
🟠(C) Frequency = natural frequency
🔴(D) Both (A) and (C)
Answer: (D) Both (A) and (C)
🔹 JEE Advanced Level (Q41–Q50)
Q41. The total energy of a pendulum is 0.02 J. When its KE = PE, find its displacement if amplitude = 0.04 m.
🔵(A) 0.02 m
🟢(B) 0.028 m
🟠(C) 0.04 m
🔴(D) 0.01 m
Answer: (A) 0.02 m
Q42. The equation x = A sin(ωt) + B cos(ωt) represents SHM if
🔵(A) A = 0
🟢(B) B = 0
🟠(C) ω is real
🔴(D) ω is imaginary
Answer: (C) ω is real
Q43. The kinetic energy of a particle executing SHM is maximum when
🔵(A) x = 0
🟢(B) x = A/√2
🟠(C) x = A
🔴(D) x = A/2
Answer: (A) x = 0
Q44. The mean kinetic energy per cycle equals
🔵(A) Total energy
🟢(B) Half of total energy
🟠(C) Zero
🔴(D) Twice the total energy
Answer: (B) Half of total energy
Q45. If amplitude is 5 cm and total energy 0.05 J, then spring constant is
🔵(A) 20 N/m
🟢(B) 40 N/m
🟠(C) 400 N/m
🔴(D) 200 N/m
Answer: (C) 400 N/m
Q46. A pendulum clock keeps correct time on Earth. On a planet where g = 4 times Earth, it will
🔵(A) Lose time
🟢(B) Gain time
🟠(C) Run same
🔴(D) Stop
Answer: (B) Gain time
Q47. The energy of a damped oscillator decreases per second by
🔵(A) e^(−γt)
🟢(B) e^(−2γt)
🟠(C) e^(−γ²t)
🔴(D) e^(γt)
Answer: (B) e^(−2γt)
Q48. The time for one complete oscillation in a damped system is
🔵(A) 2π/ω
🟢(B) 2π/√(ω₀²−γ²)
🟠(C) 2π√(ω₀²+γ²)
🔴(D) 2πγ/ω₀
Answer: (B) 2π/√(ω₀²−γ²)
Q49. If total energy = (1/2)kA² and potential energy = (1/4)kA², find displacement.
🔵(A) A/√2
🟢(B) A/2
🟠(C) √3A/2
🔴(D) A
Answer: (A) A/√2
Q50. The amplitude of a forced oscillator at resonance depends on
🔵(A) Frequency only
🟢(B) Damping coefficient
🟠(C) Phase difference
🔴(D) Acceleration
Answer: (B) Damping coefficient
————————————————————————————————————————————————————————————————————————————
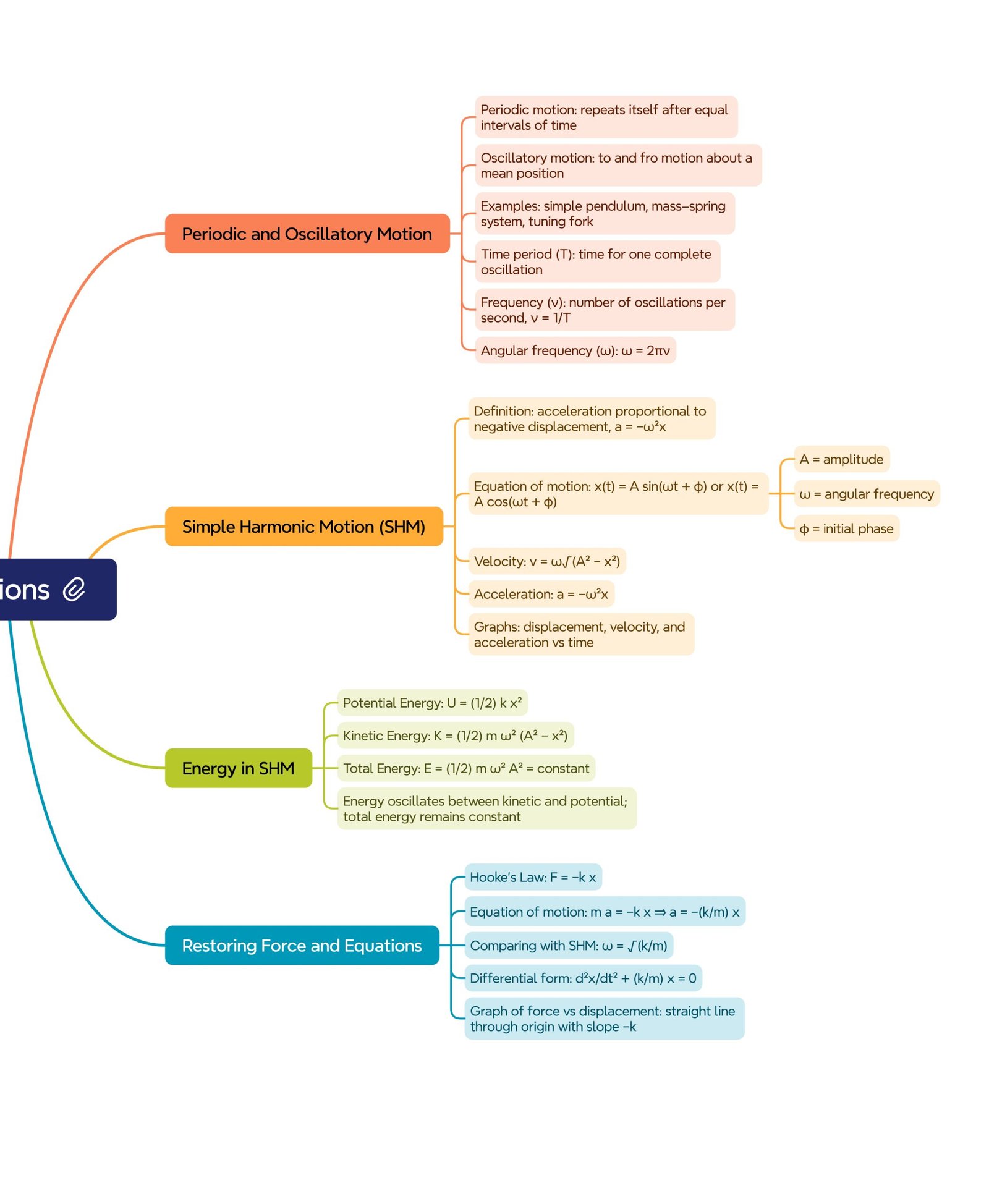
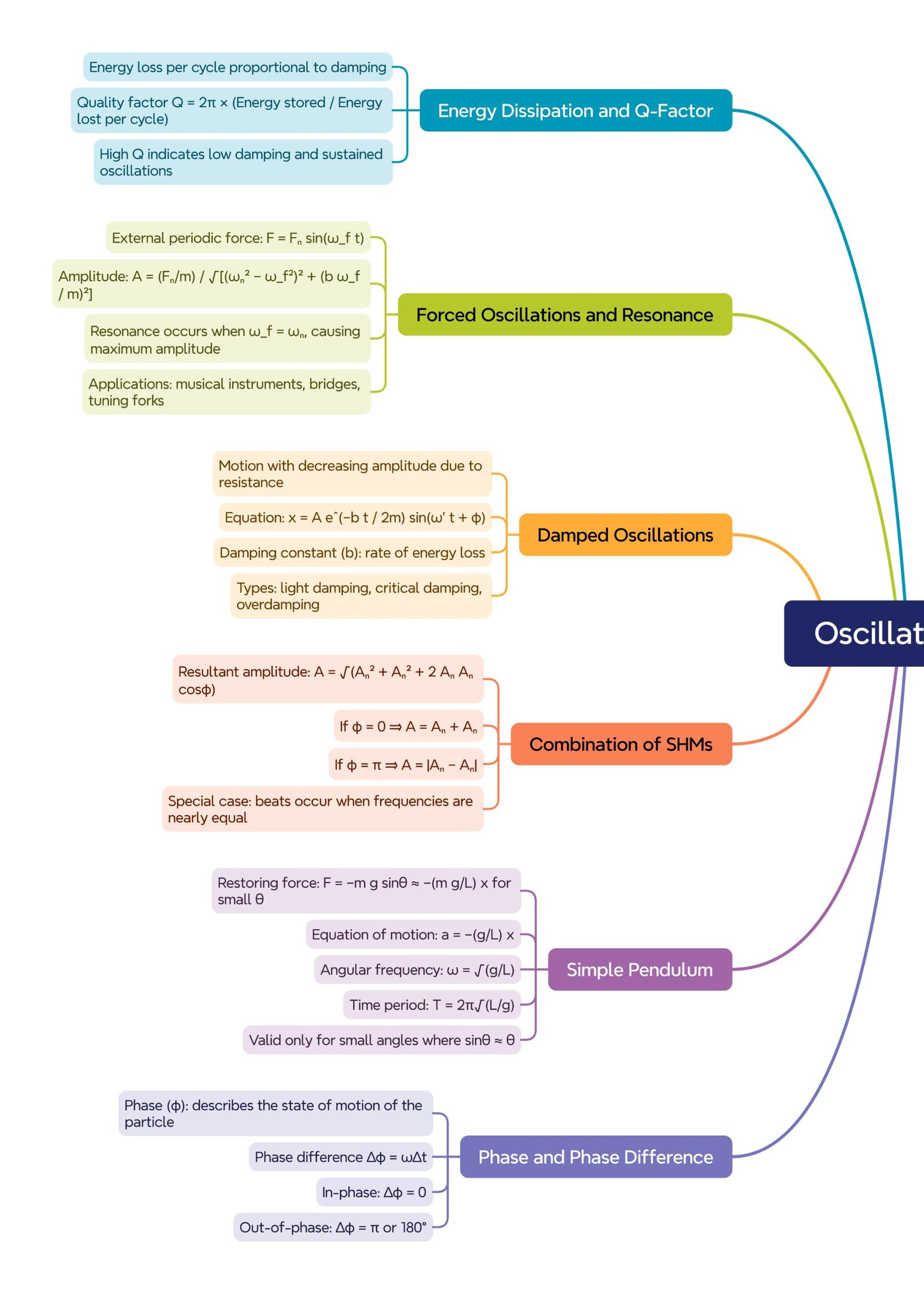
MIND MAPS
————————————————————————————————————————————————————————————————————————————
