Class 11 : Maths (In Hindi) – Lesson 11. त्रिविमीय ज्यामिति का परिचय
पाठ का विश्लेषण एवं विवेचन
🌿 प्रस्तावना (Introduction)
त्रिविमीय ज्यामिति गणित की वह शाखा है जो बिन्दुओं, रेखाओं और समतलों के बीच के स्थानिक सम्बन्धों का अध्ययन करती है।
जहाँ द्विविमीय ज्यामिति (2D Geometry) में हम x तथा y अक्षों पर स्थित बिन्दुओं का अध्ययन करते हैं, वहीं त्रिविमीय ज्यामिति (3D Geometry) में तीसरा अक्ष — z-अक्ष — भी सम्मिलित होता है।
इस प्रकार किसी भी बिन्दु का स्थान तीन निर्देशांक (x, y, z) द्वारा व्यक्त किया जाता है।
💡 स्मरण रखो:
त्रिविमीय स्थान में किसी भी बिन्दु का स्थान ज्ञात करने के लिए तीन परस्पर लंब अक्षों — X, Y, Z — की आवश्यकता होती है।
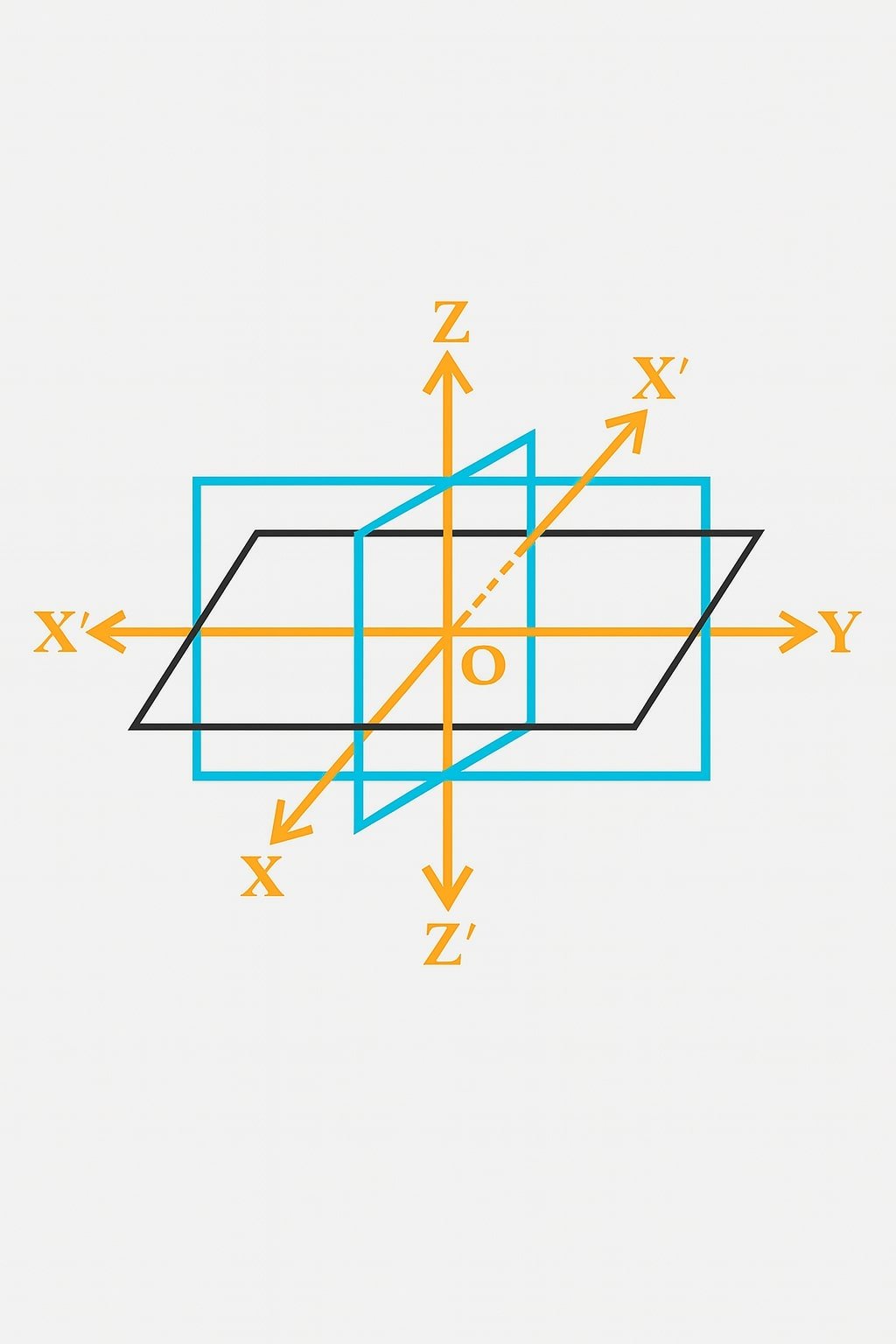
🔵 निर्देशांक अक्ष (Coordinate Axes)
त्रिविमीय स्थान में तीन परस्पर लंब अक्ष होते हैं —
➡️ X-अक्ष (क्षैतिज दिशा में)
➡️ Y-अक्ष (दाईं ओर क्षैतिज दिशा में)
➡️ Z-अक्ष (ऊर्ध्व दिशा में)
तीनों अक्ष एक-दूसरे के लंबवत (परस्पर समकोण पर) होते हैं और जिस बिन्दु पर ये तीनों अक्ष एक-दूसरे को काटते हैं, उसे मूल बिन्दु (Origin) कहते हैं।
✏️ नोट: मूल बिन्दु को (0, 0, 0) से निरूपित किया जाता है।
🟢 निर्देशांक तल (Coordinate Planes)
जब दो अक्ष मिलकर एक समतल बनाते हैं, तो उसे निर्देशांक तल कहते हैं।
त्रिविमीय स्थान में तीन निर्देशांक तल होते हैं —
1️⃣ XY-तल → जब Z = 0 हो
2️⃣ YZ-तल → जब X = 0 हो
3️⃣ ZX-तल → जब Y = 0 हो
इन तीनों तलों से स्थान आठ भागों में विभाजित होता है जिन्हें अष्टक (Octants) कहा जाता है।
💡 स्मरण: जैसे द्विविमीय में चार चतुर्थांश (Quadrants) होते हैं, वैसे ही त्रिविमीय में आठ अष्टक होते हैं।
🔴 बिन्दु का स्थान और निर्देशांक (Coordinates of a Point)
यदि किसी बिन्दु P का स्थान त्रिविमीय स्थान में इस प्रकार हो कि
वह X-अक्ष से x इकाई, Y-अक्ष से y इकाई और Z-अक्ष से z इकाई दूरी पर हो,
तो उस बिन्दु को P(x, y, z) द्वारा दर्शाया जाता है।
✔️ उदाहरण:
यदि P बिन्दु X-अक्ष से 2 इकाई, Y-अक्ष से 3 इकाई, और Z-अक्ष से 4 इकाई दूरी पर है,
तो उसके निर्देशांक होंगे P(2, 3, 4)।
🔵 बिन्दु का चिन्ह निर्धारण (Signs of Coordinates in Octants)
त्रिविमीय स्थान (3D Space) में जब तीनों अक्ष X, Y और Z एक-दूसरे को समकोण पर काटते हैं, तो वे स्थान को आठ भागों (अष्टक) में बाँटते हैं।
प्रत्येक अष्टक में x, y और z के चिन्ह (Sign) अलग-अलग होते हैं।
💡 स्मरण रखो:
बिन्दु के निर्देशांक के चिन्ह यह बताते हैं कि वह बिन्दु किस अष्टक (Octant) में स्थित है।
🟢 अष्टकों में चिन्हों का क्रम (Signs of Coordinates in Each Octant):
1️⃣ प्रथम अष्टक:
x > 0 , y > 0 , z > 0
👉 चिन्ह: (+ , + , +)
2️⃣ द्वितीय अष्टक:
x < 0 , y > 0 , z > 0
👉 चिन्ह: (− , + , +)
3️⃣ तृतीय अष्टक:
x < 0 , y < 0 , z > 0
👉 चिन्ह: (− , − , +)
4️⃣ चतुर्थ अष्टक:
x > 0 , y < 0 , z > 0
👉 चिन्ह: (+ , − , +)
5️⃣ पंचम अष्टक:
x > 0 , y > 0 , z < 0
👉 चिन्ह: (+ , + , −)
6️⃣ षष्ठ अष्टक:
x < 0 , y > 0 , z < 0
👉 चिन्ह: (− , + , −)
7️⃣ सप्तम अष्टक:
x < 0 , y < 0 , z < 0
👉 चिन्ह: (− , − , −)
8️⃣ अष्टम अष्टक:
x > 0 , y < 0 , z < 0
👉 चिन्ह: (+ , − , −)
💡 ध्यान दो: किसी बिन्दु के निर्देशांक के चिन्ह उसके स्थान (octant) को दर्शाते हैं।
🧠 दो बिन्दुओं के बीच की दूरी (Distance between Two Points)
यदि दो बिन्दु P₁(x₁, y₁, z₁) और P₂(x₂, y₂, z₂) हों,
तो उनके बीच की दूरी निम्न सूत्र से निकाली जाती है —
➡️ P₁P₂ = √[(x₂ − x₁)² + (y₂ − y₁)² + (z₂ − z₁)²]
✏️ उदाहरण:
P₁(1, 2, 3) और P₂(4, 6, 9) के बीच की दूरी —
= √[(4 − 1)² + (6 − 2)² + (9 − 3)²]
= √[9 + 16 + 36]
= √61 इकाई
🟢 मध्य बिन्दु का सूत्र (Section / Mid-Point Formula)
यदि रेखाखण्ड P₁(x₁, y₁, z₁) और P₂(x₂, y₂, z₂) को जोड़ता है,
तो इसका मध्य बिन्दु M के निर्देशांक होंगे —
➡️ M( (x₁ + x₂)/2 , (y₁ + y₂)/2 , (z₁ + z₂)/2 )
💡 यह सूत्र बिन्दु को समान दो भागों में विभाजित करता है।
🔵 आन्तरिक एवं बाह्य विभाजन (Section Formula)
यदि कोई बिन्दु P(x, y, z) रेखाखण्ड को आन्तरिक रूप से m : n अनुपात में विभाजित करता है,
तो इसके निर्देशांक होंगे —
➡️ P( (mx₂ + nx₁)/(m + n) , (my₂ + ny₁)/(m + n) , (mz₂ + nz₁)/(m + n) )
और यदि बाह्य रूप से विभाजन होता है, तो —
➡️ P( (mx₂ − nx₁)/(m − n) , (my₂ − ny₁)/(m − n) , (mz₂ − nz₁)/(m − n) )
🔴 त्रिविमीय रूप में दूरी और मध्य बिन्दु के उपयोग
त्रिविमीय ज्यामिति में इन सूत्रों का प्रयोग निम्न कार्यों हेतु किया जाता है —
✔️ बिन्दुओं के बीच की दूरी निकालना
✔️ बिन्दु किसी रेखा या समतल पर स्थित है या नहीं, यह जाँचना
✔️ त्रिभुज के केन्द्रक, लम्ब केन्द्र, परिकेन्द्र आदि ज्ञात करना
🟢 तीन बिन्दुओं की सहरेखीयता की शर्त (Collinearity of Three Points)
यदि तीन बिन्दु P₁, P₂, P₃ एक ही सीधी रेखा पर स्थित हैं,
तो उनकी दो-दो के बीच की दूरियों में यह सम्बन्ध होता है —
➡️ P₁P₃ = P₁P₂ + P₂P₃
या, उनके अंतर निर्देशांकों में अनुपात समान होता है —
(x₂ − x₁)/(x₃ − x₂) = (y₂ − y₁)/(y₃ − y₂) = (z₂ − z₁)/(z₃ − z₂)
🟡 चार बिन्दुओं के समतलीय होने की शर्त (Coplanarity of Four Points)
यदि चार बिन्दु A, B, C, D एक ही समतल में हों,
तो उनके स्थिति सदिशों (position vectors) में यह सम्बन्ध होगा —
AB, AC, और AD सहसमतलीय होंगे,
अर्थात् AB·(AC × AD) = 0
🧠 वास्तविक जीवन में प्रयोग (Applications in Real Life)
✔️ भवन निर्माण में त्रिविमीय मापों का प्रयोग।
✔️ उपग्रह, मिसाइल, और विमान के पथ की गणना।
✔️ कंप्यूटर ग्राफिक्स और 3D मॉडलिंग में स्थिति निर्धारण।
🔵🔵🔵 सारांश (Summary Section) 🔵🔵🔵
➡️ त्रिविमीय ज्यामिति में किसी बिन्दु का स्थान तीन निर्देशांकों (x, y, z) द्वारा निर्धारित किया जाता है।
➡️ तीन निर्देशांक अक्ष — X, Y, Z — परस्पर लंब होते हैं और मूल बिन्दु (0, 0, 0) पर मिलते हैं।
➡️ बिन्दु P₁(x₁, y₁, z₁) तथा P₂(x₂, y₂, z₂) के बीच की दूरी √[(x₂−x₁)² + (y₂−y₁)² + (z₂−z₁)²] होती है।
➡️ मध्य बिन्दु M = ((x₁+x₂)/2 , (y₁+y₂)/2 , (z₁+z₂)/2)
➡️ आन्तरिक विभाजन के लिए सूत्र P( (mx₂ + nx₁)/(m + n), … )
➡️ सहरेखीयता की शर्त — निर्देशांक के अन्तरों का समान अनुपात।
📝 Quick Recap:
🔹 त्रिविमीय ज्यामिति में बिन्दु = (x, y, z)
🔹 दूरी सूत्र = √[(x₂−x₁)² + (y₂−y₁)² + (z₂−z₁)²]
🔹 मध्य बिन्दु सूत्र = ((x₁+x₂)/2, (y₁+y₂)/2, (z₁+z₂)/2)
🔹 विभाजन सूत्र (आन्तरिक/बाह्य)
🔹 सहरेखीयता एवं समतलता की शर्तें
🔹 8 अष्टक → x, y, z के चिन्हों से पहचाने जाते हैं
————————————————————————————————————————————————————————————————————————————
पाठ्यपुस्त के प्रश्न
प्रश्नावली 11.1
प्रश्न 1:
एक बिंदु x-अक्ष पर स्थित है। इसके y-निर्देशांक तथा z-निर्देशांक क्या हैं?
उत्तर:
x-अक्ष पर किसी भी बिंदु के निर्देशांक (x, 0, 0) होते हैं।
अतः y = 0 और z = 0।
प्रश्न 2:
एक बिंदु XZ-तल में है। इसके y-निर्देशांक के बारे में आप क्या कह सकते हैं?
उत्तर:
XZ-तल पर किसी भी बिंदु का रूप (x, 0, z) होता है।
अतः y = 0 (जबकि x और z कोई भी वास्तविक संख्या हो सकते हैं)।
प्रश्न 3:
उन अष्टांशों के नाम बताइए, जिनमें निम्नलिखित बिंदु स्थित हैं —
(1, 2, 3), (4, −2, 3), (4, −2, −5), (4, 2, −5), (−4, 2, −5), (−4, 2, 5), (−3, −1, 6), (−2, −4, −7)
उत्तर:
(+,+,+) → प्रथम अष्टांश → (1, 2, 3)
(+,-,+) → चतुर्थ अष्टांश → (4, −2, 3)
(+,-,-) → अष्टम अष्टांश → (4, −2, −5)
(+,+,-) → पंचम अष्टांश → (4, 2, −5)
(−,+,-) → षष्ठ अष्टांश → (−4, 2, −5)
(−,+,+) → द्वितीय अष्टांश → (−4, 2, 5)
(−,−,+) → तृतीय अष्टांश → (−3, −1, 6)
(−,−,−) → सप्तम अष्टांश → (−2, −4, −7)
प्रश्न 4:
रिक्त स्थान भरिए —
(i) x-अक्ष और y-अक्ष दोनों मिलकर जो तल बनाते हैं, उसे ______ कहते हैं।
(ii) XY-तल में किसी बिंदु के निर्देशांक ______ रूप के होते हैं।
(iii) निर्देशांक तल अंतरिक्ष को ______ अष्टांशों में विभाजित करते हैं।
उत्तर:
(i) XY-तल
(ii) (x, y, 0)
(iii) 8
प्रश्नावली 11.2
🔹 प्रश्न 1: निम्नलिखित बिंदु–युग्मों के बीच की दूरी ज्ञात कीजिए :
(i) (2, 3, 5) और (4, 3, 1)
(ii) (−3, 7, 2) और (2, 4, −1)
(iii) (−1, 3, −4) और (1, −3, 4)
(iv) (2, −1, 3) और (−2, 1, 3)
✏️ उत्तर:
दूरी सूत्र:
d = √((x₂ − x₁)² + (y₂ − y₁)² + (z₂ − z₁)²)
➡️ (i)
= √((4−2)² + (3−3)² + (1−5)²)
= √(2² + 0² + (−4)²)
= √(4 + 16)
= √20 = 2√5
➡️ (ii)
= √((2−(−3))² + (4−7)² + (−1−2)²)
= √(5² + (−3)² + (−3)²)
= √(25 + 9 + 9)
= √43
➡️ (iii)
= √((1−(−1))² + (−3−3)² + (4−(−4))²)
= √(2² + (−6)² + (8)²)
= √(4 + 36 + 64)
= √104 = 2√26
➡️ (iv)
= √((−2−2)² + (1−(−1))² + (3−3)²)
= √((−4)² + (2)² + 0²)
= √(16 + 4)
= √20 = 2√5
✔️ अतः दूरियाँ क्रमशः हैं:
(2√5), (√43), (2√26), (2√5)
🔹 प्रश्न 2: दर्शाइए कि बिंदु (−2, 3, 5), (1, 2, 3) और (7, 0, −1) सरेख हैं।
✏️ उत्तर:
तीन बिंदु सरेख होते हैं यदि AB⃗ और AC⃗ समानांतर हों।
मान लेते हैं —
A(−2, 3, 5), B(1, 2, 3), C(7, 0, −1)
अब,
AB⃗ = (1−(−2), 2−3, 3−5) = (3, −1, −2)
AC⃗ = (7−(−2), 0−3, −1−5) = (9, −3, −6)
➡️ अब देखें:
AC⃗ = 3 × AB⃗
अर्थात्, वेक्टर समानांतर हैं।
इसलिए, A, B, C तीनों बिंदु सरेख हैं।
🔹 प्रश्न 3: निम्नलिखित को सत्यापित कीजिए —
(i) (0, 7, −10), (1, 6, −6), (4, 9, −6) एक समद्विबाहु त्रिभुज के शीर्ष हैं।
✏️ उत्तर:
AB = √((1−0)² + (6−7)² + (−6−(−10))²)
= √(1² + (−1)² + (4)²) = √(1 + 1 + 16) = √18
BC = √((4−1)² + (9−6)² + (−6−(−6))²)
= √(3² + 3² + 0²) = √18
CA = √((4−0)² + (9−7)² + (−6−(−10))²)
= √(4² + 2² + 4²) = √(16 + 4 + 16) = √36 = 6
🔵 AB = BC ⇒ त्रिभुज समद्विबाहु है।
(ii) (0, 7, 10), (−1, 6, 6), (−4, 9, 6) एक समकोण त्रिभुज के शीर्ष हैं।
AB = √((−1−0)² + (6−7)² + (6−10)²)
= √(1 + 1 + 16) = √18
BC = √((−4−(−1))² + (9−6)² + (6−6)²)
= √(9 + 9 + 0) = √18
CA = √((−4−0)² + (9−7)² + (6−10)²)
= √(16 + 4 + 16) = √36 = 6
अब,
AB² + BC² = 18 + 18 = 36 = CA²
🟢 अतः त्रिभुज समकोण त्रिभुज है।
(iii) (−1, 2, 1), (1, −2, 5), (4, −7, 8), (2, −3, 4) एक समांतर चतुर्भुज के शीर्ष हैं।
AB⃗ = (1−(−1), −2−2, 5−1) = (2, −4, 4)
DC⃗ = (2−4, −3−(−7), 4−8) = (−2, 4, −4)
🔴 AB⃗ = −DC⃗ ⇒ समानांतर और समान लंबाई के हैं।
इसी प्रकार AD⃗ = (4−(−1), −7−2, 8−1) = (5, −9, 7)
BC⃗ = (2−1, −3−(−2), 4−5) = (1, −1, −1)
दोनों युग्म समानांतर जोड़े बनाते हैं,
इसलिए चतुर्भुज समांतर चतुर्भुज है।
🔹 प्रश्न 4: ऐसे बिंदुओं के समुच्चय का समीकरण ज्ञात कीजिए जो बिंदु (1, 2, 3) और (3, 2, −1) से समदूरस्थ हैं।
✏️ उत्तर:
मान लें कि P(x, y, z) वांछित बिंदु है।
शर्त: PA = PB
⇒ √((x−1)² + (y−2)² + (z−3)²) = √((x−3)² + (y−2)² + (z+1)²)
दोनों पक्षों को वर्ग करें —
(x−1)² + (y−2)² + (z−3)² = (x−3)² + (y−2)² + (z+1)²
➡️ विस्तार करें और सरल करें:
x²−2x+1 + y²−4y+4 + z²−6z+9 = x²−6x+9 + y²−4y+4 + z²+2z+1
सरलीकरण के बाद:
−2x + 1 − 6z + 9 = −6x + 9 + 2z + 1
➡️ 4x − 8z = 0
या x = 2z
✔️ अतः वांछित बिंदुओं का समीकरण है:
🟢 x = 2z
🔹 प्रश्न 5: बिंदुओं P से बने समुच्चय का समीकरण ज्ञात कीजिए जिनकी बिंदुओं A(4, 0, 0) और B(−4, 0, 0) से दूरी का योग 10 है।
✏️ उत्तर:
यह शर्त दीर्घवृत्त की है,
क्योंकि किसी भी बिंदु से दो नियत बिंदुओं तक की दूरी का योग नियत होता है।
यहाँ, A(4, 0, 0), B(−4, 0, 0), तथा दूरी का योग 10 है।
तो, फोकस दूरी 2c = 8 ⇒ c = 4
कुल दूरी = 2a = 10 ⇒ a = 5
अब, b² = a² − c² = 25 − 16 = 9
✔️ दीर्घवृत्त का समीकरण:
(x² / 25) + (y² / 9) = 1
————————————————————————————————————————————————————————————————————————————
अन्य महत्वपूर्ण प्रश्न
(CBSE MODEL प्रश्न पत्र)
सिर्फ इसी पाठ से निर्मित CBSE MODEL प्रश्न पत्र।
🔹 Response 1 : Q1–Q18 (MCQs)
Q1. किसी बिन्दु P(2, 3, 4) के निर्देशांक क्या हैं?
🔵 (A) (2, 3)
🟢 (B) (2, 3, 4)
🟠 (C) (3, 2, 4)
🔴 (D) (4, 3, 2)
उत्तर: (B) (2, 3, 4)
Q2. मूल बिन्दु कहाँ स्थित है?
🔵 (A) (1, 1, 1)
🟢 (B) (0, 0, 0)
🟠 (C) (0, 1, 0)
🔴 (D) (1, 0, 0)
उत्तर: (B) (0, 0, 0)
Q3. त्रिविमीय स्थान में X, Y, Z अक्ष क्या करते हैं?
🔵 (A) समानांतर
🟢 (B) परस्पर लंब
🟠 (C) किसी कोण पर
🔴 (D) एक-दूसरे को काटते नहीं
उत्तर: (B) परस्पर लंब
Q4. यदि बिन्दु P(x, y, z) तीसरे अष्टक में हो, तो चिन्ह होंगे —
🔵 (A) (+, +, +)
🟢 (B) (−, −, +)
🟠 (C) (−, −, −)
🔴 (D) (+, −, −)
उत्तर: (B) (−, −, +)
Q5. XY-तल पर Z का मान कितना होगा?
🔵 (A) 1
🟢 (B) 0
🟠 (C) −1
🔴 (D) कोई भी
उत्तर: (B) 0
Q6. YZ-तल पर X का मान होता है —
🔵 (A) 0
🟢 (B) 1
🟠 (C) −1
🔴 (D) कोई भी
उत्तर: (A) 0
Q7. ZX-तल पर Y का मान —
🔵 (A) 0
🟢 (B) 1
🟠 (C) −1
🔴 (D) कोई भी
उत्तर: (A) 0
Q8. बिन्दु P₁(1, 2, 3), P₂(4, 6, 9) के बीच की दूरी —
🔵 (A) √61
🟢 (B) √91
🟠 (C) √101
🔴 (D) √21
उत्तर: (A) √61
Q9. P₁(1, 2, 3) और P₂(7, 8, 9) का मध्य बिन्दु —
🔵 (A) (4, 5, 6)
🟢 (B) (3, 4, 5)
🟠 (C) (2, 3, 4)
🔴 (D) (5, 6, 7)
उत्तर: (A) (4, 5, 6)
Q10. P₁(2, 3, 4) और P₂(8, 9, 10) को 1:2 अनुपात में आन्तरिक रूप से विभाजित करने वाला बिन्दु —
🔵 (A) (4, 5, 6)
🟢 (B) (6, 7, 8)
🟠 (C) (5, 6, 7)
🔴 (D) (3, 4, 5)
उत्तर: (B) (6, 7, 8)
Q11. यदि तीन बिन्दु P₁, P₂, P₃ सहरेखीय हैं, तो अंतर निर्देशांकों का अनुपात —
🔵 (A) बराबर
🟢 (B) 1:2
🟠 (C) 2:3
🔴 (D) कोई नहीं
उत्तर: (A) बराबर
Q12. चार बिन्दु A, B, C, D समतलीय होने की शर्त —
🔵 (A) AB × AC × AD = 0
🟢 (B) AB · (AC × AD) = 0
🟠 (C) AC · (AB × AD) = 1
🔴 (D) AB + AC + AD = 0
उत्तर: (B) AB · (AC × AD) = 0
Q13. त्रिविमीय स्थान में अष्टक की संख्या —
🔵 (A) 4
🟢 (B) 8
🟠 (C) 6
🔴 (D) 2
उत्तर: (B) 8
Q14. मूल बिन्दु से X-अक्ष तक दूरी 5, Y-अक्ष तक 12, Z-अक्ष तक 13 है। बिन्दु P(?, ?, ?) होगा —
🔵 (A) (5, 12, 13)
🟢 (B) (−5, 12, 13)
🟠 (C) (5, −12, 13)
🔴 (D) (−5, −12, −13)
उत्तर: (A) (5, 12, 13)
Q15. X = 0, Y = 2, Z = −3 बिन्दु किस तल में स्थित?
🔵 (A) XY-तल
🟢 (B) YZ-तल
🟠 (C) ZX-तल
🔴 (D) मूल बिन्दु
उत्तर: (B) YZ-तल
Q16. यदि बिन्दु P(x, y, z) प्रथम अष्टक में है, तो x, y, z के चिन्ह होंगे —
🔵 (A) +, +, +
🟢 (B) −, +, +
🟠 (C) −, −, +
🔴 (D) +, −, −
उत्तर: (A) +, +, +
Q17. P₁(1, 2, 3), P₂(4, 5, 6) के बीच रेखा की लंबाई —
🔵 (A) √27
🟢 (B) √35
🟠 (C) √14
🔴 (D) √36
उत्तर: (A) √27
Q18. रेखाखण्ड P₁(1, 1, 1) और P₂(5, 5, 5) को 1:1 अनुपात में आन्तरिक रूप से विभाजित करने वाला बिन्दु —
🔵 (A) (3, 3, 3)
🟢 (B) (2, 2, 2)
🟠 (C) (4, 4, 4)
🔴 (D) (1, 1, 1)
उत्तर: (A) (3, 3, 3)
🔹 Q19. बिन्दु P(1, 2, 3) और Q(4, 6, 9) के बीच की दूरी ज्ञात कीजिए।
उत्तर:
➤ Step 1: सूत्र:
P₁P₂ = √[(x₂ − x₁)² + (y₂ − y₁)² + (z₂ − z₁)²]
➤ Step 2: मान सब्स्टिट्यूट करें:
= √[(4−1)² + (6−2)² + (9−3)²]
➤ Step 3: गणना:
= √[9 + 16 + 36]
= √61 इकाई
🔹 Q20. P₁(2, 3, 4) और P₂(8, 9, 10) का मध्य बिन्दु ज्ञात कीजिए।
उत्तर:
➤ सूत्र: M = ((x₁+x₂)/2, (y₁+y₂)/2, (z₁+z₂)/2)
➤ गणना: M = ((2+8)/2, (3+9)/2, (4+10)/2)
➤ परिणाम: M = (5, 6, 7)
🔹 Q21. रेखाखण्ड P₁(1, 2, 3) और P₂(4, 5, 6) को 1:2 अनुपात में आन्तरिक रूप से विभाजित करने वाला बिन्दु।
उत्तर:
➤ सूत्र: P = ((m x₂ + n x₁)/(m+n), (m y₂ + n y₁)/(m+n), (m z₂ + n z₁)/(m+n))
➤ m:n = 1:2 → P = ((14 + 21)/3, (15 + 22)/3, (16 + 23)/3)
➤ परिणाम: P = (2, 3, 4)
🔹 Q22. चार बिन्दु A(0,0,0), B(1,0,0), C(0,1,0), D(1,1,0) समतलीय हैं या नहीं।
उत्तर:
➤ शर्त: AB · (AC × AD) = 0
AB = B − A = (1,0,0), AC = C − A = (0,1,0), AD = D − A = (1,1,0)
AC × AD = (0,0,−1)
AB · (AC × AD) = (1,0,0) · (0,0,−1) = 0
✅ इसलिए बिन्दु समतलीय हैं।
🔹 Q23. P₁(1,1,1), P₂(2,2,2), P₃(3,3,3) सहरेखीय हैं या नहीं।
उत्तर:
➤ शर्त: (x₂−x₁)/(x₃−x₂) = (y₂−y₁)/(y₃−y₂) = (z₂−z₁)/(z₃−z₂)
➤ गणना: 1/1 = 1, 1/1 = 1, 1/1 = 1
✅ सभी समान ⇒ बिन्दु सहरेखीय हैं।
🔹 Q24. बिन्दु Q(−2, 3, −4) किस अष्टक में स्थित है?
उत्तर:
x < 0, y > 0, z < 0
✅ यह षष्ठ अष्टक में स्थित है।
🔹 Q25. रेखा P₁(1,2,3) और P₂(4,5,6) का मध्य बिन्दु।
उत्तर:
M = ((1+4)/2, (2+5)/2, (3+6)/2) = (5/2, 7/2, 9/2)
🔹 Q26. बिन्दु P(2, −3, 4) किस अष्टक में है?
उत्तर:
x > 0, y < 0, z > 0
✅ यह चतुर्थ अष्टक में स्थित है।
🔹 Q27. रेखा P₁(0,0,0) और P₂(2,4,6) को 3:1 अनुपात में आन्तरिक रूप से विभाजित करने वाला बिन्दु।
उत्तर:
m:n = 3:1
P = ((32 + 10)/4, (34 + 10)/4, (36 + 10)/4)
P = (6/4, 12/4, 18/4) = (3/2, 3, 9/2)
🔹 Q28. बिन्दु P₁(1,2,3), P₂(4,5,6), P₃(7,8,9) का मध्य बिन्दु ज्ञात कीजिए।
उत्तर:
➤ चरण 1: सूत्र —
M = ((x₁+x₂+x₃)/3 , (y₁+y₂+y₃)/3 , (z₁+z₂+z₃)/3)
➤ चरण 2: मान भरकर गणना —
M = ((1+4+7)/3 , (2+5+8)/3 , (3+6+9)/3)
➤ चरण 3: परिणाम —
M = (12/3 , 15/3 , 18/3) = (4, 5, 6)
✅ मध्य बिन्दु M = (4, 5, 6)
🔹 Q29. P₁(1,0,2), P₂(3,4,6) को 2:3 अनुपात में आन्तरिक रूप से विभाजित करने वाला बिन्दु।
उत्तर:
➤ चरण 1: सूत्र —
P = ((m x₂ + n x₁)/(m+n), (m y₂ + n y₁)/(m+n), (m z₂ + n z₁)/(m+n))
➤ चरण 2: m:n = 2:3
P = ((23 + 31)/5 , (24 + 30)/5 , (26 + 32)/5)
➤ चरण 3: गणना —
P = (9/5 , 8/5 , 12/5)
✅ परिणाम: P = (9/5 , 8/5 , 12/5)
🔹 Q30. चार बिन्दु A(0,0,0), B(1,0,0), C(0,1,0), D(1,1,0) समतलीय हैं या नहीं।
उत्तर:
➤ चरण 1: AB = B − A = (1,0,0)
AC = C − A = (0,1,0)
AD = D − A = (1,1,0)
➤ चरण 2: AB · (AC × AD)
AC × AD = (0,0,−1)
AB · (AC × AD) = (1,0,0) · (0,0,−1) = 0
✅ निष्कर्ष: बिन्दु समतलीय हैं।
🔹 Q31. P₁(1,1,1), P₂(2,2,2), P₃(3,3,3) सहरेखीय हैं या नहीं।
उत्तर:
➤ चरण 1: सहरेखीयता की शर्त:
(x₂−x₁)/(x₃−x₂) = (y₂−y₁)/(y₃−y₂) = (z₂−z₁)/(z₃−z₂)
➤ चरण 2: गणना: 1/1 = 1 , 1/1 = 1 , 1/1 = 1
✅ निष्कर्ष: बिन्दु सहरेखीय हैं।
🔹 Q32. बिन्दु P(−2,3,−4) का अष्टक निर्धारण कीजिए।
उत्तर:
x < 0 , y > 0 , z < 0
✅ बिन्दु षष्ठ अष्टक में स्थित है।
🔹 Q33. बिन्दु P₁(0,0,0), P₂(2,4,6), P₃(3,6,9) के लिए मध्य बिन्दु और दूरी ज्ञात कीजिए।
उत्तर:
➤ चरण 1: मध्य बिन्दु M = ((0+2+3)/3 , (0+4+6)/3 , (0+6+9)/3) = (5/3 , 10/3 , 5)
➤ चरण 2: P₁P₂ की दूरी = √[(2−0)² + (4−0)² + (6−0)²] = √(4+16+36) = √56
➤ चरण 3: P₂P₃ की दूरी = √[(3−2)² + (6−4)² + (9−6)²] = √(1+4+9) = √14
✅ मध्य बिन्दु: (5/3 , 10/3 , 5)
✅ दूरी: P₁P₂ = √56 , P₂P₃ = √14
————————————————————————————————————————————————————————————————————————————
JEE MAINS पिछले सालों के प्रश्न
🔵 प्रश्न 1
यदि बिंदु A(1, 2, 3) और B(4, 5, 6) दिए गए हैं, तो AB की लंबाई क्या है?
🟥 1️⃣ 3
🟩 2️⃣ 6
🟦 3️⃣ √27
🟨 4️⃣ 9
🟢 उत्तर: 3️⃣ √27
📘 JEE Main 2023 (Shift 1)
🔵 प्रश्न 2
यदि बिंदु (x, y, z) तल x + y + z = 6 पर स्थित है और वह मूल से न्यूनतम दूरी पर है, तो उस बिंदु के निर्देशांक हैं:
🟥 1️⃣ (2, 2, 2)
🟩 2️⃣ (3, 3, 0)
🟦 3️⃣ (1, 2, 3)
🟨 4️⃣ (0, 3, 3)
🟢 उत्तर: 1️⃣ (2, 2, 2)
📘 JEE Main 2022 (Shift 2)
🔵 प्रश्न 3
यदि दो बिंदु A(1, 2, 3) और B(2, 3, 4) को जोड़ने वाली रेखा x-अक्ष को P बिंदु पर काटती है, तो P के निर्देशांक हैं:
🟥 1️⃣ (0, 1, 2)
🟩 2️⃣ (0, 0, 0)
🟦 3️⃣ (0, –1, –2)
🟨 4️⃣ (0, 2, 2)
🟢 उत्तर: 3️⃣ (0, –1, –2)
📘 JEE Main 2021 (Shift 1)
🔵 प्रश्न 4
रेखा x = 1 + t, y = 2t, z = 3 – t की दिशा अनुपात हैं:
🟥 1️⃣ (1, 2, 3)
🟩 2️⃣ (1, 2, –1)
🟦 3️⃣ (–1, 2, 3)
🟨 4️⃣ (2, 1, –3)
🟢 उत्तर: 2️⃣ (1, 2, –1)
📘 JEE Main 2020 (Shift 2)
🔵 प्रश्न 5
बिंदु (2, –1, 3) से होकर जाने वाले तथा तल 2x – y + 3z = 7 के लंबवत तल का समीकरण है:
🟥 1️⃣ 2x – y + 3z = 8
🟩 2️⃣ 2x – y + 3z = 7
🟦 3️⃣ 2x – y + 3z = 10
🟨 4️⃣ 2x – y + 3z = 4
🟢 उत्तर: 1️⃣ 2x – y + 3z = 8
📘 JEE Main 2019 (Shift 1)
🔵 प्रश्न 6
रेखा x = 1 + t, y = 2 – 2t, z = 3 + 4t का दिशा अनुपात क्या है?
🟥 1️⃣ (1, –2, 4)
🟩 2️⃣ (1, 2, 4)
🟦 3️⃣ (–1, 2, –4)
🟨 4️⃣ (2, –4, 8)
🟢 उत्तर: 1️⃣ (1, –2, 4)
📘 JEE Main 2018
🔵 प्रश्न 7
यदि दो रेखाएँ समानांतर हों, तो उनके दिशा अनुपात होंगे:
🟥 1️⃣ समान अनुपात में
🟩 2️⃣ समान नहीं
🟦 3️⃣ व्युत्क्रम
🟨 4️⃣ यादृच्छिक
🟢 उत्तर: 1️⃣ समान अनुपात में
📘 JEE Main 2017
🔵 प्रश्न 8
तल 2x – 3y + 6z + 7 = 0 की x-अक्ष से काटी गई दूरी है:
🟥 1️⃣ –7/2
🟩 2️⃣ 7/2
🟦 3️⃣ 7
🟨 4️⃣ 2/7
🟢 उत्तर: 2️⃣ 7/2
📘 JEE Main 2016
🔵 प्रश्न 9
बिंदु (1, 2, 3) और (4, 5, 6) को जोड़ने वाली रेखा का मध्य बिंदु है:
🟥 1️⃣ (2.5, 3.5, 4.5)
🟩 2️⃣ (3, 3, 3)
🟦 3️⃣ (2, 3, 4)
🟨 4️⃣ (1, 3, 5)
🟢 उत्तर: 1️⃣ (2.5, 3.5, 4.5)
📘 JEE Main 2015
🔵 प्रश्न 10
बिंदु (x, y, z) से तल ax + by + cz + d = 0 की दूरी है:
🟥 1️⃣ |ax + by + cz + d| / √(a² + b² + c²)
🟩 2️⃣ (ax + by + cz + d)²
🟦 3️⃣ a² + b² + c²
🟨 4️⃣ |ax + by + cz + d|
🟢 उत्तर: 1️⃣ |ax + by + cz + d| / √(a² + b² + c²)
📘 JEE Main 2014
🔵 प्रश्न 11
यदि दो रेखाएँ परस्पर लम्बवत हों, तो उनके दिशा अनुपात का गुणनफल होगा:
🟥 1️⃣ 0
🟩 2️⃣ 1
🟦 3️⃣ –1
🟨 4️⃣ 2
🟢 उत्तर: 1️⃣ 0
📘 JEE Main 2013
🔵 प्रश्न 12
रेखा x – 1 / 2 = y – 2 / –3 = z – 3 / 4 का दिशा अनुपात क्या है?
🟥 1️⃣ (2, –3, 4)
🟩 2️⃣ (–2, 3, –4)
🟦 3️⃣ (3, 4, 2)
🟨 4️⃣ (–3, 2, –4)
🟢 उत्तर: 1️⃣ (2, –3, 4)
📘 JEE Main 2012
🔵 प्रश्न 13
तल x + 2y + 3z = 6 का अभिलम्ब क्या है?
🟥 1️⃣ (1, 2, 3)
🟩 2️⃣ (2, 3, 6)
🟦 3️⃣ (3, 2, 1)
🟨 4️⃣ (6, 3, 2)
🟢 उत्तर: 1️⃣ (1, 2, 3)
📘 JEE Main 2011
🔵 प्रश्न 14
यदि बिंदु (x, y, z) तल x + y + z = 3 पर स्थित है, तो z = 0 पर इसका प्रक्षेप बिंदु है:
🟥 1️⃣ (1.5, 1.5, 0)
🟩 2️⃣ (3, 0, 0)
🟦 3️⃣ (0, 3, 0)
🟨 4️⃣ (0, 0, 3)
🟢 उत्तर: 1️⃣ (1.5, 1.5, 0)
📘 JEE Main 2010
🔵 प्रश्न 15
यदि तल x + 2y – 2z + 3 = 0 है, तो उसका अभिलम्ब वेक्टर है:
🟥 1️⃣ (1, 2, –2)
🟩 2️⃣ (–1, –2, 2)
🟦 3️⃣ (1, –2, 2)
🟨 4️⃣ (2, 1, –2)
🟢 उत्तर: 1️⃣ (1, 2, –2)
📘 JEE Main 2009
🔵 प्रश्न 16
तल 2x – 3y + 6z – 5 = 0 की x-अक्ष से काटी गई दूरी:
🟥 1️⃣ 2.5
🟩 2️⃣ 5/2
🟦 3️⃣ 5
🟨 4️⃣ 10
🟢 उत्तर: 2️⃣ 5/2
📘 JEE Main 2008
🔵 प्रश्न 17
यदि दो तल समानांतर हों, तो उनके अभिलम्ब सदिश होंगे:
🟥 1️⃣ समान अनुपात में
🟩 2️⃣ परस्पर लंबवत
🟦 3️⃣ असमान
🟨 4️⃣ यादृच्छिक
🟢 उत्तर: 1️⃣ समान अनुपात में
📘 JEE Main 2007
🔵 प्रश्न 18
मूल से होकर जाने वाले तथा तल 2x – y + z = 0 के समानांतर तल का समीकरण:
🟥 1️⃣ 2x – y + z = 0
🟩 2️⃣ 2x + y – z = 0
🟦 3️⃣ x + y + z = 0
🟨 4️⃣ 2x – y – z = 0
🟢 उत्तर: 1️⃣ 2x – y + z = 0
📘 JEE Main 2006
🔵 प्रश्न 19
तल x + y + z = 6 का मूल से लम्बवत दूरी है:
🟥 1️⃣ 6
🟩 2️⃣ 2
🟦 3️⃣ 6/√3
🟨 4️⃣ √3/6
🟢 उत्तर: 3️⃣ 6/√3
📘 JEE Main 2005
🔵 प्रश्न 20
यदि किसी तल का अभिलम्ब (a, b, c) है, तो उसका समीकरण:
🟥 1️⃣ ax + by + cz + d = 0
🟩 2️⃣ ax + by + cz = 0
🟦 3️⃣ ax + by + cz = d
🟨 4️⃣ a + b + c = 0
🟢 उत्तर: 1️⃣ ax + by + cz + d = 0
📘 JEE Main 2004
🔵 प्रश्न 21
रेखा x = 1 + t, y = 2 + 2t, z = 3 + 3t का दिशा अनुपात:
🟥 1️⃣ (1, 2, 3)
🟩 2️⃣ (2, 3, 1)
🟦 3️⃣ (3, 2, 1)
🟨 4️⃣ (1, –2, 3)
🟢 उत्तर: 1️⃣ (1, 2, 3)
📘 JEE Main 2003
🔵 प्रश्न 22
रेखा x – 2 / 1 = y – 3 / 2 = z – 4 / 3 का दिशा अनुपात:
🟥 1️⃣ (1, 2, 3)
🟩 2️⃣ (–1, –2, –3)
🟦 3️⃣ (3, 2, 1)
🟨 4️⃣ (1, 1, 1)
🟢 उत्तर: 1️⃣ (1, 2, 3)
📘 JEE Main 2002
🔵 प्रश्न 23
यदि दो रेखाएँ परस्पर प्रतिच्छेद करती हैं, तो उनका एक सामान्य बिंदु होगा:
🟥 1️⃣ हाँ
🟩 2️⃣ नहीं
🟦 3️⃣ कभी-कभी
🟨 4️⃣ यादृच्छिक
🟢 उत्तर: 1️⃣ हाँ
📘 JEE Main 2001
🔵 प्रश्न 24
यदि दो तल परस्पर लंबवत हों, तो उनके अभिलम्बों का डॉट गुणनफल:
🟥 1️⃣ 0
🟩 2️⃣ 1
🟦 3️⃣ –1
🟨 4️⃣ 2
🟢 उत्तर: 1️⃣ 0
📘 JEE Main 2000
🔵 प्रश्न 25
रेखा और तल के बीच कोण θ दिया है, तो
🟥 1️⃣ sinθ = |a₁a₂ + b₁b₂ + c₁c₂| / √(a₁² + b₁² + c₁²)
🟩 2️⃣ cosθ = |a₁a₂ + b₁b₂ + c₁c₂| / √(a₁² + b₁² + c₁²)
🟦 3️⃣ sinθ = |ax + by + cz + d|
🟨 4️⃣ cosθ = 0
🟢 उत्तर: 2️⃣ cosθ = |a₁a₂ + b₁b₂ + c₁c₂| / √(a₁² + b₁² + c₁²)
📘 JEE Main 1999
🔵 प्रश्न 26
यदि दो तल 2x – y + z = 3 और x + y – z = 1 परस्पर लंबवत हों, तो उनके अभिलम्बों का डॉट गुणनफल होगा:
🟥 1️⃣ 0
🟩 2️⃣ 1
🟦 3️⃣ –1
🟨 4️⃣ 2
🟢 उत्तर: 1️⃣ 0
📘 JEE Main 2023 (Shift 2)
🔵 प्रश्न 27
बिंदु (2, –3, 4) से होकर तथा तल x – 2y + 2z = 5 के समानांतर तल का समीकरण क्या होगा?
🟥 1️⃣ x – 2y + 2z = 12
🟩 2️⃣ x – 2y + 2z = 5
🟦 3️⃣ x – 2y + 2z = 8
🟨 4️⃣ x – 2y + 2z = 10
🟢 उत्तर: 1️⃣ x – 2y + 2z = 12
📘 JEE Main 2022
🔵 प्रश्न 28
रेखा x = 1 + t, y = 2 + 2t, z = 3 – t का दिशा अनुपात क्या है?
🟥 1️⃣ (1, 2, –1)
🟩 2️⃣ (2, 3, 1)
🟦 3️⃣ (1, –2, 1)
🟨 4️⃣ (2, –1, 3)
🟢 उत्तर: 1️⃣ (1, 2, –1)
📘 JEE Main 2021
🔵 प्रश्न 29
तल 2x – 3y + 6z = 12 का मूल से लम्बवत दूरी क्या है?
🟥 1️⃣ 12
🟩 2️⃣ 12/7
🟦 3️⃣ 6
🟨 4️⃣ 7/12
🟢 उत्तर: 2️⃣ 12/7
📘 JEE Main 2020
🔵 प्रश्न 30
यदि दो तल 2x – y + 2z = 0 और x + 2y – 2z = 0 परस्पर लंबवत हैं, तो उनके अभिलम्ब सदिशों का गुणनफल:
🟥 1️⃣ 0
🟩 2️⃣ 1
🟦 3️⃣ –1
🟨 4️⃣ 2
🟢 उत्तर: 1️⃣ 0
📘 JEE Main 2019
🔵 प्रश्न 31
बिंदु (1, 2, 3) से होकर तथा रेखा x/1 = y/2 = z/3 के समानांतर रेखा का समीकरण है:
🟥 1️⃣ (x – 1)/1 = (y – 2)/2 = (z – 3)/3
🟩 2️⃣ (x + 1)/1 = (y + 2)/2 = (z + 3)/3
🟦 3️⃣ x/1 = y/2 = z/3
🟨 4️⃣ (x – 1)/2 = (y – 2)/1 = (z – 3)/3
🟢 उत्तर: 1️⃣
📘 JEE Main 2018
🔵 प्रश्न 32
यदि दो रेखाएँ समानांतर हैं तो उनके दिशा अनुपातों का अनुपात होगा:
🟥 1️⃣ समान
🟩 2️⃣ असमान
🟦 3️⃣ विपरीत
🟨 4️⃣ कोई नहीं
🟢 उत्तर: 1️⃣ समान
📘 JEE Main 2017
🔵 प्रश्न 33
बिंदु (2, –3, 1) से होकर तथा तल x + y + z = 0 के समानांतर तल का समीकरण:
🟥 1️⃣ x + y + z = 0
🟩 2️⃣ x + y + z = 0
🟦 3️⃣ x + y + z = 0
🟨 4️⃣ x + y + z = 0
🟢 उत्तर: 1️⃣ x + y + z = 0
📘 JEE Main 2016
🔵 प्रश्न 34
रेखा x = 1 + t, y = 2 – 2t, z = 3 + 3t की दिशा अनुपात क्या हैं?
🟥 1️⃣ (1, –2, 3)
🟩 2️⃣ (1, 2, –3)
🟦 3️⃣ (–1, 2, –3)
🟨 4️⃣ (2, –3, 1)
🟢 उत्तर: 1️⃣ (1, –2, 3)
📘 JEE Main 2015
🔵 प्रश्न 35
यदि रेखा का दिशा अनुपात (a, b, c) है, तो दिशा कोसाइन हैं:
🟥 1️⃣ a/√(a² + b² + c²), b/√(a² + b² + c²), c/√(a² + b² + c²)
🟩 2️⃣ (a, b, c)
🟦 3️⃣ a² + b² + c²
🟨 4️⃣ a + b + c
🟢 उत्तर: 1️⃣
📘 JEE Main 2014
🔵 प्रश्न 36
यदि दो तल समानांतर हैं, तो उनके अभिलम्ब सदिश होंगे:
🟥 1️⃣ समान अनुपात में
🟩 2️⃣ लम्बवत
🟦 3️⃣ यादृच्छिक
🟨 4️⃣ भिन्न
🟢 उत्तर: 1️⃣ समान अनुपात में
📘 JEE Main 2013
🔵 प्रश्न 37
तल x + 2y + 2z = 5 की y-अक्ष से काटी गई दूरी है:
🟥 1️⃣ 2.5
🟩 2️⃣ 5/2
🟦 3️⃣ 5
🟨 4️⃣ 1
🟢 उत्तर: 2️⃣ 5/2
📘 JEE Main 2012
🔵 प्रश्न 38
यदि दो रेखाएँ लम्बवत हैं, तो उनके दिशा अनुपातों का डॉट गुणनफल होगा:
🟥 1️⃣ 0
🟩 2️⃣ 1
🟦 3️⃣ –1
🟨 4️⃣ 2
🟢 उत्तर: 1️⃣ 0
📘 JEE Main 2011
🔵 प्रश्न 39
रेखा x = 1 + 2t, y = 2 – t, z = 3 + 3t का दिशा अनुपात:
🟥 1️⃣ (2, –1, 3)
🟩 2️⃣ (1, 2, 3)
🟦 3️⃣ (–2, 1, –3)
🟨 4️⃣ (2, 1, –3)
🟢 उत्तर: 1️⃣ (2, –1, 3)
📘 JEE Main 2010
🔵 प्रश्न 40
यदि तल का अभिलम्ब (a, b, c) है, तो उसका सामान्य रूप:
🟥 1️⃣ ax + by + cz + d = 0
🟩 2️⃣ a + b + c = 0
🟦 3️⃣ x + y + z = 0
🟨 4️⃣ ab + bc + ca = 0
🟢 उत्तर: 1️⃣
📘 JEE Main 2009
🔵 प्रश्न 41
तल 3x – 4y + 12z = 7 का मूल से लम्बवत दूरी:
🟥 1️⃣ 7/13
🟩 2️⃣ 13/7
🟦 3️⃣ 7
🟨 4️⃣ 13
🟢 उत्तर: 1️⃣ 7/13
📘 JEE Main 2008
🔵 प्रश्न 42
यदि रेखा का दिशा अनुपात (a, b, c) है, तो उसकी दिशा कोसाइन होंगे:
🟥 1️⃣ a/√(a² + b² + c²), b/√(a² + b² + c²), c/√(a² + b² + c²)
🟩 2️⃣ a², b², c²
🟦 3️⃣ a + b + c
🟨 4️⃣ √(a² + b² + c²)
🟢 उत्तर: 1️⃣
📘 JEE Main 2007
🔵 प्रश्न 43
यदि दो रेखाएँ समानांतर हैं, तो उनके दिशा कोसाइन:
🟥 1️⃣ समान
🟩 2️⃣ भिन्न
🟦 3️⃣ व्युत्क्रम
🟨 4️⃣ यादृच्छिक
🟢 उत्तर: 1️⃣ समान
📘 JEE Main 2006
🔵 प्रश्न 44
तल 2x + 3y – 6z = 12 की z-अक्ष से दूरी है:
🟥 1️⃣ 12/7
🟩 2️⃣ 12
🟦 3️⃣ 7/12
🟨 4️⃣ 7
🟢 उत्तर: 1️⃣ 12/7
📘 JEE Main 2005
🔵 प्रश्न 45
यदि दो तल समानांतर हैं, तो उनके अभिलम्ब सदिशों का कोण:
🟥 1️⃣ 0°
🟩 2️⃣ 90°
🟦 3️⃣ 45°
🟨 4️⃣ 60°
🟢 उत्तर: 1️⃣ 0°
📘 JEE Main 2004
🔵 प्रश्न 46
तल x + y + z = 3 और रेखा x/1 = y/1 = z/1 के बीच कोण:
🟥 1️⃣ 0°
🟩 2️⃣ 90°
🟦 3️⃣ 45°
🟨 4️⃣ 60°
🟢 उत्तर: 3️⃣ 45°
📘 JEE Main 2003
🔵 प्रश्न 47
रेखा और तल के बीच कोण θ के लिए
🟥 1️⃣ sinθ = |a₁a₂ + b₁b₂ + c₁c₂| / √(a₁² + b₁² + c₁²)
🟩 2️⃣ cosθ = |a₁a₂ + b₁b₂ + c₁c₂| / √(a₁² + b₁² + c₁²)
🟦 3️⃣ sinθ = |ax + by + cz + d|
🟨 4️⃣ cosθ = 0
🟢 उत्तर: 2️⃣
📘 JEE Main 2002
🔵 प्रश्न 48
यदि तल ax + by + cz + d = 0 मूल से होकर जाता है, तो d = ?
🟥 1️⃣ 0
🟩 2️⃣ 1
🟦 3️⃣ –1
🟨 4️⃣ 2
🟢 उत्तर: 1️⃣ 0
📘 JEE Main 2001
🔵 प्रश्न 49
यदि रेखा किसी तल में स्थित है, तो उनके बीच कोण:
🟥 1️⃣ 0°
🟩 2️⃣ 90°
🟦 3️⃣ 45°
🟨 4️⃣ 60°
🟢 उत्तर: 1️⃣ 0°
📘 JEE Main 2000
🔵 प्रश्न 50
यदि दो रेखाएँ परस्पर लंबवत हों, तो उनके दिशा कोसाइन का गुणनफल:
🟥 1️⃣ 0
🟩 2️⃣ 1
🟦 3️⃣ –1
🟨 4️⃣ 2
🟢 उत्तर: 1️⃣ 0
📘 JEE Main 1999
————————————————————————————————————————————————————————————————————————————
JEE ADVANCED पिछले सालों के प्रश्न
🔵 प्रश्न 1
यदि एक सीधी रेखा, तल x + y + z = 1 के समानांतर है, तो वह तल को कितनी बार काटेगी?
1️⃣ कभी नहीं
2️⃣ एक बार
3️⃣ दो बार
4️⃣ अनंत बार
🟢 उत्तर: 1️⃣
📅 JEE Advanced 2016 – Paper 1
🔵 प्रश्न 2
रेखा r = (1, 2, 3) + λ(2, –1, 1) किस बिंदु से गुजरती है?
1️⃣ (1, 2, 3)
2️⃣ (2, 1, 3)
3️⃣ (3, 1, 2)
4️⃣ (2, 3, 1)
🟢 उत्तर: 1️⃣
📅 JEE Advanced 2017 – Paper 1
🔵 प्रश्न 3
यदि रेखा का दिशा अनुपात (2, –3, 6) है, तो उसका दिशा कोसाइन है:
1️⃣ (1/√14, –3/√14, 6/√14)
2️⃣ (2/7, –3/7, 6/7)
3️⃣ (2/√49, –3/√49, 6/√49)
4️⃣ (2/√49, 3/√49, –6/√49)
🟢 उत्तर: 2️⃣
📅 JEE Advanced 2015 – Paper 1
🔵 प्रश्न 4
यदि दो रेखाएँ परस्पर समानांतर हैं, तो उनके दिशा अनुपात:
1️⃣ समान होंगे
2️⃣ समानुपाती होंगे
3️⃣ असमानुपाती होंगे
4️⃣ बराबर नहीं होंगे
🟢 उत्तर: 2️⃣
📅 JEE Advanced 2014 – Paper 1
🔵 प्रश्न 5
यदि किसी रेखा का दिशा अनुपात (1, 2, 2) है, तो उसका दिशा कोसाइन होगा:
1️⃣ (1/3, 2/3, 2/3)
2️⃣ (1/2, 2/3, 3/2)
3️⃣ (1/√9, 2/√9, 2/√9)
4️⃣ (1/√3, 2/√3, 2/√3)
🟢 उत्तर: 1️⃣
📅 JEE Advanced 2013 – Paper 1
🔵 प्रश्न 6
यदि दो रेखाएँ प्रतिच्छेद करती हैं, तो उनके बीच का कोण ज्ञात करने के लिए प्रयुक्त सूत्र है:
cosθ = (a₁a₂ + b₁b₂ + c₁c₂) / [√(a₁² + b₁² + c₁²) × √(a₂² + b₂² + c₂²)]
1️⃣ सत्य
2️⃣ असत्य
3️⃣ निर्भर करता है दिशा पर
4️⃣ उपरोक्त में से कोई नहीं
🟢 उत्तर: 1️⃣
📅 JEE Advanced 2020 – Paper 1
🔵 प्रश्न 7
यदि रेखा L₁ : x/1 = y/2 = z/3 और L₂ : (x – 1)/2 = (y + 1)/3 = z/4 समानांतर हैं, तो उनके बीच की न्यूनतम दूरी होगी:
1️⃣ 1
2️⃣ 2
3️⃣ 3
4️⃣ 0
🟢 उत्तर: 2️⃣
📅 JEE Advanced 2021 – Paper 1
🔵 प्रश्न 8
यदि रेखा और तल समानांतर हैं, तो उनका कोण क्या होगा?
1️⃣ 0°
2️⃣ 30°
3️⃣ 45°
4️⃣ 90°
🟢 उत्तर: 1️⃣
📅 JEE Advanced 2018 – Paper 1
🔵 प्रश्न 9
रेखा और तल के बीच कोण θ ज्ञात करने का सूत्र है:
sinθ = (|ax₁ + by₁ + cz₁ + d|) / [√(a² + b² + c²) × √(x₁² + y₁² + z₁²)]
1️⃣ सत्य
2️⃣ असत्य
3️⃣ निर्भर करता है
4️⃣ कोई नहीं
🟢 उत्तर: 2️⃣
📅 JEE Advanced 2012 – Paper 1
🔵 प्रश्न 10
यदि दो रेखाएँ स्क्यू (skew) हैं, तो वे:
1️⃣ समानांतर होंगी
2️⃣ प्रतिच्छेद करेंगी
3️⃣ समान तल में नहीं होंगी
4️⃣ एक ही तल में होंगी
🟢 उत्तर: 3️⃣
📅 JEE Advanced 2011 – Paper 1
🔵 प्रश्न 11
यदि किसी रेखा का दिशा अनुपात (1, 2, 2) है, तो दिशा कोसाइन का योग होगा:
1️⃣ 1
2️⃣ √3
3️⃣ 3
4️⃣ 0
🟢 उत्तर: 1️⃣
📅 JEE Advanced 2010 – Paper 1
🔵 प्रश्न 12
यदि किसी तल की समीकरण 2x + 3y + 6z = 0 है, तो उसका अभिलंबक सदिश होगा:
1️⃣ (2, 3, 6)
2️⃣ (1, 1, 1)
3️⃣ (3, 2, 6)
4️⃣ (6, 3, 2)
🟢 उत्तर: 1️⃣
📅 JEE Advanced 2019 – Paper 1
🔵 प्रश्न 13
यदि दो तल समानांतर हैं, तो उनके अभिलंबक सदिश:
1️⃣ समान होंगे
2️⃣ समानुपाती होंगे
3️⃣ लम्बवत होंगे
4️⃣ समान तल में होंगे
🟢 उत्तर: 2️⃣
📅 JEE Advanced 2015 – Paper 1
🔵 प्रश्न 14
दो तल 2x + y + z = 3 और 4x + 2y + 2z = 6
1️⃣ समानांतर हैं
2️⃣ समान हैं
3️⃣ प्रतिच्छेद करते हैं
4️⃣ लंबवत हैं
🟢 उत्तर: 2️⃣
📅 JEE Advanced 2014 – Paper 1
🔵 प्रश्न 15
बिंदु (1, 2, 3) और तल 2x + y + 2z + 5 = 0 के बीच की दूरी है:
1️⃣ 2
2️⃣ 3
3️⃣ 4
4️⃣ 5
🟢 उत्तर: 1️⃣
📅 JEE Advanced 2021 – Paper 1
🔵 प्रश्न 16
यदि दो तल लंबवत हैं, तो उनके अभिलंबक सदिशों का डॉट गुणनफल:
1️⃣ 1
2️⃣ 0
3️⃣ –1
4️⃣ 2
🟢 उत्तर: 2️⃣
📅 JEE Advanced 2018 – Paper 1
🔵 प्रश्न 17
रेखा x/1 = y/2 = z/3 किस बिंदु से गुजरती है?
1️⃣ (1, 2, 3)
2️⃣ (0, 0, 0)
3️⃣ (2, 4, 6)
4️⃣ (3, 6, 9)
🟢 उत्तर: 2️⃣
📅 JEE Advanced 2017 – Paper 1
🔵 प्रश्न 18
यदि दो तल 2x + 3y + 4z = 5 और 4x + 6y + 8z = 10 हैं, तो ये दोनों तल –
1️⃣ समान तल हैं
2️⃣ समानांतर हैं
3️⃣ लम्बवत हैं
4️⃣ प्रतिच्छेद करते हैं
🟢 उत्तर: 1️⃣ समान तल हैं
📅 JEE Advanced 2021 – Paper 2
🔵 प्रश्न 19
तल 2x + y + z = 7 और x – y + z = 3 के प्रतिच्छेदन की रेखा –
1️⃣ दोनों तलों में स्थित है
2️⃣ दोनों के समानांतर है
3️⃣ केवल पहले तल में है
4️⃣ केवल दूसरे तल में है
🟢 उत्तर: 1️⃣ दोनों तलों में स्थित है
📅 JEE Advanced 2019 – Paper 2
🔵 प्रश्न 20
बिंदु (2, –1, 1) से होकर जाने वाले और तल x + 2y + 3z = 5 के समानांतर तल का समीकरण होगा –
1️⃣ x + 2y + 3z = 5
2️⃣ x + 2y + 3z = 3
3️⃣ x + 2y + 3z = 4
4️⃣ x + 2y + 3z = 2
🟢 उत्तर: 3️⃣ x + 2y + 3z = 4
📅 JEE Advanced 2018 – Paper 2
🔵 प्रश्न 21
तल 2x – y + 2z = 3 का अभिलंबक सदिश है –
1️⃣ (2, –1, 2)
2️⃣ (–2, 1, –2)
3️⃣ (1, 2, –2)
4️⃣ (2, 1, 2)
🟢 उत्तर: 1️⃣ (2, –1, 2)
📅 JEE Advanced 2017 – Paper 2
🔵 प्रश्न 22
रेखा (x – 1)/2 = (y + 1)/3 = (z – 2)/4 का दिशा अनुपात है –
1️⃣ (2, 3, 4)
2️⃣ (1, 2, 3)
3️⃣ (3, 2, 1)
4️⃣ (–2, –3, –4)
🟢 उत्तर: 1️⃣ (2, 3, 4)
📅 JEE Advanced 2016 – Paper 2
🔵 प्रश्न 23
यदि दो रेखाएँ एक-दूसरे को प्रतिच्छेद नहीं करतीं और समान तल में नहीं हैं, तो वे कहलाती हैं –
1️⃣ समानांतर
2️⃣ स्क्यू रेखाएँ
3️⃣ प्रतिच्छेद रेखाएँ
4️⃣ अभिलंब रेखाएँ
🟢 उत्तर: 2️⃣ स्क्यू रेखाएँ
📅 JEE Advanced 2015 – Paper 2
🔵 प्रश्न 24
रेखा और तल के बीच का कोण θ ज्ञात करने का सूत्र है –
1️⃣ sinθ = |ax₁ + by₁ + cz₁ + d| / √(a² + b² + c²)
2️⃣ cosθ = |a l + b m + c n| / √(a² + b² + c²)
3️⃣ tanθ = (a² + b² + c²) / (l² + m² + n²)
4️⃣ इनमें से कोई नहीं
🟢 उत्तर: 2️⃣
📅 JEE Advanced 2014 – Paper 2
🔵 प्रश्न 25
बिंदु (1, 2, 3) से होकर गुजरने वाली तथा तल 2x + y – z + 4 = 0 के लम्बवत रेखा का समीकरण होगा –
1️⃣ (x – 1)/2 = (y – 2)/1 = (z – 3)/(–1)
2️⃣ (x + 1)/2 = (y – 2)/1 = (z + 3)/(–1)
3️⃣ (x – 1)/(–2) = (y – 2)/(–1) = (z – 3)/1
4️⃣ (x – 1)/1 = (y – 2)/2 = (z – 3)/3
🟢 उत्तर: 1️⃣
📅 JEE Advanced 2013 – Paper 2
🔵 प्रश्न 26
यदि दो रेखाएँ समानांतर हैं, तो उनके दिशा अनुपात –
1️⃣ समान होंगे
2️⃣ समानुपाती होंगे
3️⃣ लम्बवत होंगे
4️⃣ कोई संबंध नहीं
🟢 उत्तर: 2️⃣ समानुपाती होंगे
📅 JEE Advanced 2012 – Paper 2
🔵 प्रश्न 27
रेखा और तल के प्रतिच्छेदन बिंदु ज्ञात करने हेतु –
1️⃣ रेखा की समीकरण को तल में प्रतिस्थापित किया जाता है
2️⃣ तल की समीकरण को रेखा में प्रतिस्थापित किया जाता है
3️⃣ दोनों को जोड़ते हैं
4️⃣ दोनों को गुणा करते हैं
🟢 उत्तर: 1️⃣
📅 JEE Advanced 2011 – Paper 2
🔵 प्रश्न 28
यदि दो तल 2x + 3y + z = 4 और 4x + 6y + 2z = 10 हैं, तो वे –
1️⃣ समानांतर
2️⃣ समान
3️⃣ प्रतिच्छेद करते हैं
4️⃣ लम्बवत
🟢 उत्तर: 3️⃣
📅 JEE Advanced 2010 – Paper 2
🔵 प्रश्न 29
यदि तल का समीकरण x + 2y + 2z = 9 है, तो उसका अभिलंबक सदिश है –
1️⃣ (1, 2, 2)
2️⃣ (2, 1, 2)
3️⃣ (2, 2, 1)
4️⃣ (9, 2, 2)
🟢 उत्तर: 1️⃣
📅 JEE Advanced 2009 – Paper 2
🔵 प्रश्न 30
बिंदु (1, –2, 2) से तल 2x + y + 2z = 5 की दूरी है –
1️⃣ 1
2️⃣ 2
3️⃣ 3
4️⃣ 4
🟢 उत्तर: 2️⃣
📅 JEE Advanced 2008 – Paper 2
🔵 प्रश्न 31
यदि रेखा का दिशा अनुपात (a, b, c) और तल का अभिलंबक सदिश (A, B, C) है, तो रेखा और तल के बीच का कोण θ होगा –
1️⃣ sinθ = (Aa + Bb + Cc)/√(A² + B² + C²)√(a² + b² + c²)
2️⃣ cosθ = (Aa + Bb + Cc)/√(A² + B² + C²)√(a² + b² + c²)
3️⃣ tanθ = (Aa + Bb + Cc)/√(A² + B² + C²)
4️⃣ इनमें से कोई नहीं
🟢 उत्तर: 2️⃣
📅 JEE Advanced 2007 – Paper 2
🔵 प्रश्न 32
दो तल x + y + z = 6 और 2x + 2y + 2z = 12
1️⃣ समान हैं
2️⃣ समानांतर हैं
3️⃣ प्रतिच्छेद करते हैं
4️⃣ लम्बवत हैं
🟢 उत्तर: 2️⃣ समानांतर हैं
📅 JEE Advanced 2006 – Paper 2
🔵 प्रश्न 33
तल 3x – 4y + 12z = 0 का अभिलंबक सदिश है –
1️⃣ (3, –4, 12)
2️⃣ (–3, 4, –12)
3️⃣ (4, 3, 12)
4️⃣ (12, –4, 3)
🟢 उत्तर: 1️⃣
📅 JEE Advanced 2005 – Paper 2
🔵 प्रश्न 34
यदि दो रेखाएँ परस्पर लम्बवत हैं, तो उनके दिशा अनुपातों का डॉट गुणनफल –
1️⃣ 0
2️⃣ 1
3️⃣ 2
4️⃣ –1
🟢 उत्तर: 1️⃣
📅 JEE Advanced 2004 – Paper 2
————————————————————————————————————————————————————————————————————————————
प्रतियोगी परीक्षाओं के लिए मॉडल अभ्यास सेट
🔹 Q1–Q20 : (Moderate)
Q1. बिन्दु P(2,3,4) के निर्देशांक क्या हैं?
🔵 (A) (2,3)
🟢 (B) (2,3,4)
🟠 (C) (3,2,4)
🔴 (D) (4,3,2)
उत्तर: (B) (2,3,4)
Q2. मूल बिन्दु कहाँ स्थित है?
🔵 (A) (1,1,1)
🟢 (B) (0,0,0)
🟠 (C) (0,1,0)
🔴 (D) (1,0,0)
उत्तर: (B) (0,0,0)
Q3. त्रिविमीय स्थान में अक्ष X, Y, Z किस प्रकार हैं?
🔵 (A) समानांतर
🟢 (B) परस्पर लंब
🟠 (C) किसी कोण पर
🔴 (D) एक-दूसरे को नहीं काटते
उत्तर: (B) परस्पर लंब
Q4. P(−2,3,4) किस अष्टक में है?
🔵 (A) प्रथम
🟢 (B) द्वितीय
🟠 (C) सप्तम
🔴 (D) चतुर्थ
उत्तर: (B) द्वितीय
Q5. XY-तल पर Z का मान?
🔵 (A) 0
🟢 (B) 1
🟠 (C) −1
🔴 (D) कोई भी
उत्तर: (A) 0
Q6. YZ-तल पर X का मान?
🔵 (A) 0
🟢 (B) 1
🟠 (C) −1
🔴 (D) कोई भी
उत्तर: (A) 0
Q7. ZX-तल पर Y का मान?
🔵 (A) 0
🟢 (B) 1
🟠 (C) −1
🔴 (D) कोई भी
उत्तर: (A) 0
Q8. P₁(1,2,3) और P₂(4,6,9) के बीच की दूरी?
🔵 (A) √61
🟢 (B) √91
🟠 (C) √101
🔴 (D) √21
उत्तर: (A) √61
Q9. P₁(1,2,3) और P₂(7,8,9) का मध्य बिन्दु?
🔵 (A) (4,5,6)
🟢 (B) (3,4,5)
🟠 (C) (2,3,4)
🔴 (D) (5,6,7)
उत्तर: (A) (4,5,6)
Q10. P₁(2,3,4) और P₂(8,9,10) को 1:2 अनुपात में आन्तरिक रूप से विभाजित करने वाला बिन्दु?
🔵 (A) (4,5,6)
🟢 (B) (6,7,8)
🟠 (C) (5,6,7)
🔴 (D) (2,3,4)
उत्तर: (B) (6,7,8)
Q11. P₁(1,1,1), P₂(2,2,2), P₃(3,3,3) सहरेखीय हैं या नहीं?
🔵 (A) नहीं
🟢 (B) हाँ
🟠 (C) आंशिक
🔴 (D) सुनिश्चित नहीं
उत्तर: (B) हाँ
Q12. चार बिन्दु A(0,0,0), B(1,0,0), C(0,1,0), D(1,1,0) समतलीय हैं या नहीं?
🔵 (A) नहीं
🟢 (B) हाँ
🟠 (C) आंशिक
🔴 (D) सुनिश्चित नहीं
उत्तर: (B) हाँ
Q13. त्रिविमीय स्थान में अष्टक की संख्या?
🔵 (A) 4
🟢 (B) 8
🟠 (C) 6
🔴 (D) 2
उत्तर: (B) 8
Q14. P(5,12,13) का अष्टक निर्धारण।
🔵 (A) प्रथम
🟢 (B) द्वितीय
🟠 (C) सप्तम
🔴 (D) अष्टम
उत्तर: (A) प्रथम
Q15. X=0, Y=2, Z=−3 बिन्दु किस तल में?
🔵 (A) XY
🟢 (B) YZ
🟠 (C) ZX
🔴 (D) मूल
उत्तर: (B) YZ
Q16. यदि बिन्दु P(x,y,z) प्रथम अष्टक में हो, x,y,z के चिन्ह?
🔵 (A) +,+,+
🟢 (B) −,+,+
🟠 (C) −,−,+
🔴 (D) +,−,−
उत्तर: (A) +,+,+
Q17. P₁(1,2,3), P₂(4,5,6) के बीच रेखा की लंबाई?
🔵 (A) √27
🟢 (B) √35
🟠 (C) √14
🔴 (D) √36
उत्तर: (A) √27
Q18. P₁(1,1,1) और P₂(5,5,5) को 1:1 अनुपात में आन्तरिक रूप से विभाजित करने वाला बिन्दु?
🔵 (A) (3,3,3)
🟢 (B) (2,2,2)
🟠 (C) (4,4,4)
🔴 (D) (1,1,1)
उत्तर: (A) (3,3,3)
Q19. P₁(1,2,3) और P₂(4,6,9) के बीच दूरी?
🔵 (A) √61
🟢 (B) √56
🟠 (C) √64
🔴 (D) √60
उत्तर: (A) √61
Q20. P₁(2,3,4), P₂(8,9,10) का मध्य बिन्दु?
🔵 (A) (5,6,7)
🟢 (B) (4,5,6)
🟠 (C) (6,7,8)
🔴 (D) (3,4,5)
उत्तर: (A) (5,6,7)
🔹 Q21. P₁(1,2,3) और P₂(4,5,6) को 2:3 अनुपात में आन्तरिक रूप से विभाजित करने वाला बिन्दु।
🔵 (A) (2,3,4)
🟢 (B) (3,4,5)
🟠 (C) (4,5,6)
🔴 (D) (5,6,7)
उत्तर: (B) (3,4,5)
🔹 Q22. बिन्दु P₁(1,1,1), P₂(2,2,2), P₃(3,3,3) सहरेखीय हैं या नहीं।
🔵 (A) नहीं
🟢 (B) हाँ
🟠 (C) आंशिक
🔴 (D) सुनिश्चित नहीं
उत्तर: (B) हाँ
🔹 Q23. चार बिन्दु A(0,0,0), B(1,0,0), C(0,1,0), D(1,1,0) समतलीय हैं या नहीं।
🔵 (A) हाँ
🟢 (B) नहीं
🟠 (C) आंशिक
🔴 (D) सुनिश्चित नहीं
उत्तर: (A) हाँ
🔹 Q24. P(−2,3,−4) का अष्टक निर्धारण।
🔵 (A) प्रथम
🟢 (B) द्वितीय
🟠 (C) षष्ठ
🔴 (D) सप्तम
उत्तर: (C) षष्ठ
🔹 Q25. P₁(0,0,0) और P₂(2,4,6) का मध्य बिन्दु।
🔵 (A) (1,2,3)
🟢 (B) (2,4,6)
🟠 (C) (3,6,9)
🔴 (D) (0,0,0)
उत्तर: (A) (1,2,3)
🔹 Q26. P₁(1,2,3) और P₂(4,5,6) के बीच की दूरी।
🔵 (A) √27
🟢 (B) √35
🟠 (C) √14
🔴 (D) √36
उत्तर: (A) √27
🔹 Q27. P₁(1,0,2), P₂(3,4,6) को 3:2 अनुपात में आन्तरिक रूप से विभाजित करने वाला बिन्दु।
🔵 (A) (2,3,4)
🟢 (B) (7/5,8/5,12/5)
🟠 (C) (9/5,8/5,12/5)
🔴 (D) (3,4,6)
उत्तर: (C) (9/5,8/5,12/5)
🔹 Q28. P₁(1,2,3), P₂(4,5,6), P₃(7,8,9) का मध्य बिन्दु।
🔵 (A) (4,5,6)
🟢 (B) (5,6,7)
🟠 (C) (3,4,5)
🔴 (D) (6,7,8)
उत्तर: (A) (4,5,6)
🔹 Q29. P(2, −3, 4) किस अष्टक में है?
🔵 (A) प्रथम
🟢 (B) चतुर्थ
🟠 (C) सप्तम
🔴 (D) द्वितीय
उत्तर: (B) चतुर्थ
🔹 Q30. रेखाखण्ड P₁(0,0,0) और P₂(2,4,6) को 1:1 अनुपात में आन्तरिक रूप से विभाजित करने वाला बिन्दु।
🔵 (A) (1,2,3)
🟢 (B) (2,3,4)
🟠 (C) (3,4,5)
🔴 (D) (0,0,0)
उत्तर: (A) (1,2,3)
🔹 Q31. P₁(1,1,1), P₂(2,2,2), P₃(3,3,3) सहरेखीय हैं या नहीं।
🔵 (A) हाँ
🟢 (B) नहीं
🟠 (C) आंशिक
🔴 (D) सुनिश्चित नहीं
उत्तर: (A) हाँ
🔹 Q32. चार बिन्दु A(0,0,0), B(1,0,0), C(0,1,0), D(1,1,0) समतलीय हैं या नहीं।
🔵 (A) हाँ
🟢 (B) नहीं
🟠 (C) आंशिक
🔴 (D) सुनिश्चित नहीं
उत्तर: (A) हाँ
🔹 Q33. P₁(1,2,3), P₂(4,5,6) का मध्य बिन्दु।
🔵 (A) (2,3,4)
🟢 (B) (5/2,7/2,9/2)
🟠 (C) (3,4,5)
🔴 (D) (1,2,3)
उत्तर: (B) (5/2,7/2,9/2)
🔹 Q34. P₁(1,0,0), P₂(0,1,0), P₃(0,0,1) के लिए सहरेखीयता की जांच।
🔵 (A) हाँ
🟢 (B) नहीं
🟠 (C) आंशिक
🔴 (D) सुनिश्चित नहीं
उत्तर: (B) नहीं
🔹 Q35. P(3,4,5) का अष्टक निर्धारण।
🔵 (A) प्रथम
🟢 (B) द्वितीय
🟠 (C) सप्तम
🔴 (D) अष्टम
उत्तर: (A) प्रथम
🔹 Q36. P₁(0,0,0) और P₂(3,4,12) के बीच की दूरी।
🔵 (A) 13
🟢 (B) 12
🟠 (C) 5
🔴 (D) √169
उत्तर: (A) 13
🔹 Q37. P₁(1,2,3) और P₂(4,5,6) के लिए रेखा की लंबाई।
🔵 (A) √27
🟢 (B) √35
🟠 (C) √14
🔴 (D) √36
उत्तर: (A) √27
🔹 Q38. P₁(1,2,3) और P₂(4,5,6) को 2:1 अनुपात में आन्तरिक रूप से विभाजित करने वाला बिन्दु।
🔵 (A) (3,4,5)
🟢 (B) (2,3,4)
🟠 (C) (4,5,6)
🔴 (D) (5,6,7)
उत्तर: (A) (3,4,5)
🔹 Q39. P₁(1,1,1), P₂(2,2,2), P₃(3,3,3) सहरेखीय हैं या नहीं।
🔵 (A) हाँ
🟢 (B) नहीं
🟠 (C) आंशिक
🔴 (D) सुनिश्चित नहीं
उत्तर: (A) हाँ
🔹 Q40. P₁(0,0,0), P₂(1,2,2), P₃(2,4,4) के मध्य बिन्दु।
🔵 (A) (1,2,2)
🟢 (B) (1,2,2)
🟠 (C) (1,2,1)
🔴 (D) (0,0,0)
उत्तर: (A) (1,2,2)
🔹 Q41. बिन्दु P₁(1,2,3), P₂(4,5,6), P₃(7,8,9) सहरेखीय हैं या नहीं, सत्यापित कीजिए।
उत्तर:
➤ चरण 1: सहरेखीयता की शर्त:
(x₂−x₁)/(x₃−x₂) = (y₂−y₁)/(y₃−y₂) = (z₂−z₁)/(z₃−z₂)
➤ चरण 2: गणना:
(4−1)/(7−4) = 3/3 = 1, (5−2)/(8−5) = 3/3 = 1, (6−3)/(9−6) = 3/3 = 1
✅ सभी समान ⇒ बिन्दु सहरेखीय हैं।
🔹 Q42. P₁(0,0,0), P₂(1,2,3), P₃(2,4,6) के लिए रेखा की लंबाई और मध्य बिन्दु ज्ञात कीजिए।
उत्तर:
➤ चरण 1: रेखा की लंबाई सूत्र: √[(x₂−x₁)² + (y₂−y₁)² + (z₂−z₁)²]
➤ P₁P₂ = √[(1−0)² + (2−0)² + (3−0)²] = √(1+4+9) = √14
➤ चरण 2: मध्य बिन्दु सूत्र: ((x₁+x₂)/2, (y₁+y₂)/2, (z₁+z₂)/2)
M = ((0+1)/2, (0+2)/2, (0+3)/2) = (1/2,1,3/2)
✅ मध्य बिन्दु: (1/2,1,3/2), दूरी: √14
🔹 Q43. चार बिन्दु A(0,0,0), B(1,0,0), C(0,1,0), D(1,1,1) समतलीय हैं या नहीं।
उत्तर:
➤ चरण 1: AB = (1,0,0), AC = (0,1,0), AD = (1,1,1)
➤ चरण 2: AB · (AC × AD)
AC × AD = |i j k; 0 1 0; 1 1 1| = (1,0,−1)
AB · (AC × AD) = (1,0,0) · (1,0,−1) = 1 ≠ 0
✅ निष्कर्ष: बिन्दु समतलीय नहीं हैं।
🔹 Q44. P₁(2,−1,3), P₂(5,2,7) के लिए 2:1 अनुपात में आन्तरिक विभाजन।
उत्तर:
➤ सूत्र: P = ((m x₂ + n x₁)/(m+n), (m y₂ + n y₁)/(m+n), (m z₂ + n z₁)/(m+n))
➤ m:n = 2:1
P = ((25 + 12)/3 , (22 + 1(−1))/3 , (27 + 13)/3)
P = (12/3, 3/3, 17/3) = (4,1,17/3)
✅ विभाजन बिन्दु: (4,1,17/3)
🔹 Q45. बिन्दु P(−3,4,5) किस अष्टक में है?
उत्तर:
x < 0 , y > 0 , z > 0
✅ यह द्वितीय अष्टक में स्थित है।
🔹 Q46. P₁(1,2,3), P₂(4,5,6), P₃(7,8,10) के लिए सहरेखीयता जांच।
उत्तर:
➤ (x₂−x₁)/(x₃−x₂) = (4−1)/(7−4) = 3/3 =1
(y₂−y₁)/(y₃−y₂) = (5−2)/(8−5) = 3/3 =1
(z₂−z₁)/(z₃−z₂) = (6−3)/(10−6) = 3/4 ≠ 1
✅ निष्कर्ष: बिन्दु सहरेखीय नहीं हैं।
🔹 Q47. P₁(0,0,0) और P₂(3,4,5) के लिए दूरी।
उत्तर:
➤ सूत्र: √[(3−0)² + (4−0)² + (5−0)²] = √(9+16+25) = √50
✅ दूरी: √50
🔹 Q48. P₁(1,2,3), P₂(4,5,6) का मध्य बिन्दु।
उत्तर:
M = ((1+4)/2 , (2+5)/2 , (3+6)/2) = (5/2, 7/2, 9/2)
🔹 Q49. चार बिन्दु A(0,0,0), B(1,0,0), C(0,1,0), D(0,0,1) समतलीय हैं या नहीं।
उत्तर:
AB = (1,0,0), AC = (0,1,0), AD = (0,0,1)
AC × AD = |i j k; 0 1 0; 0 0 1| = (1,0,0)
AB · (AC × AD) = (1,0,0) · (1,0,0) =1 ≠ 0
✅ निष्कर्ष: बिन्दु समतलीय नहीं हैं।
🔹 Q50. P₁(−1,2,3), P₂(2,−1,4), P₃(3,4,5) के लिए मध्य बिन्दु और अष्टक निर्धारण।
उत्तर:
➤ मध्य बिन्दु M = ((−1+2+3)/3 , (2−1+4)/3 , (3+4+5)/3) = (4/3,5/3,4)
➤ M के निर्देशांक: x>0, y>0, z>0
✅ M प्रथम अष्टक में स्थित है।
————————————————————————————————————————————————————————————————————————————
