Class 11 : Maths (In English) – Lesson 6. Permutations and Combinations

Posted by

On June 21, 2025

EXPLANATION & SUMMARY

🔷 Explanation (≈1700 words)
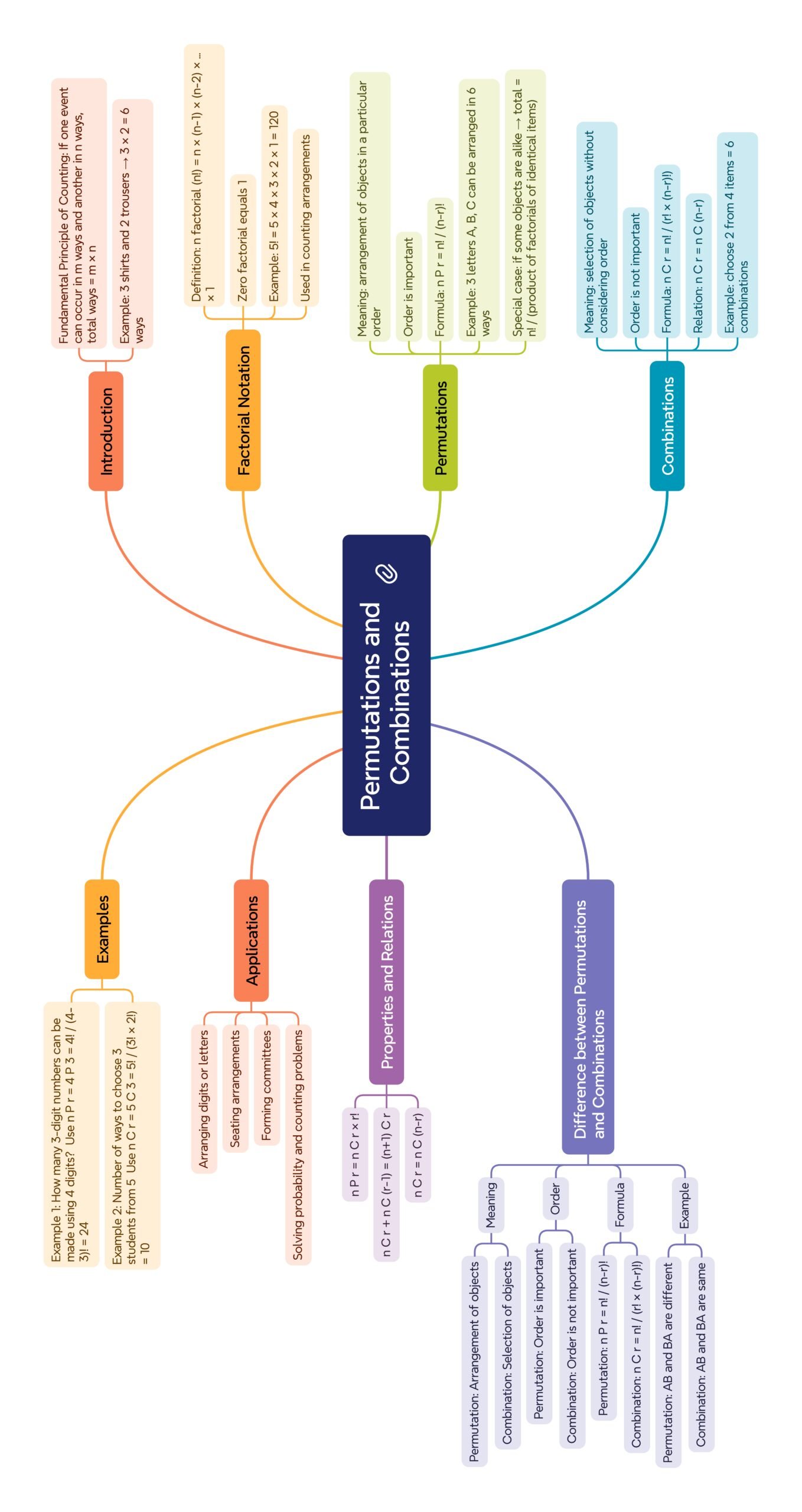
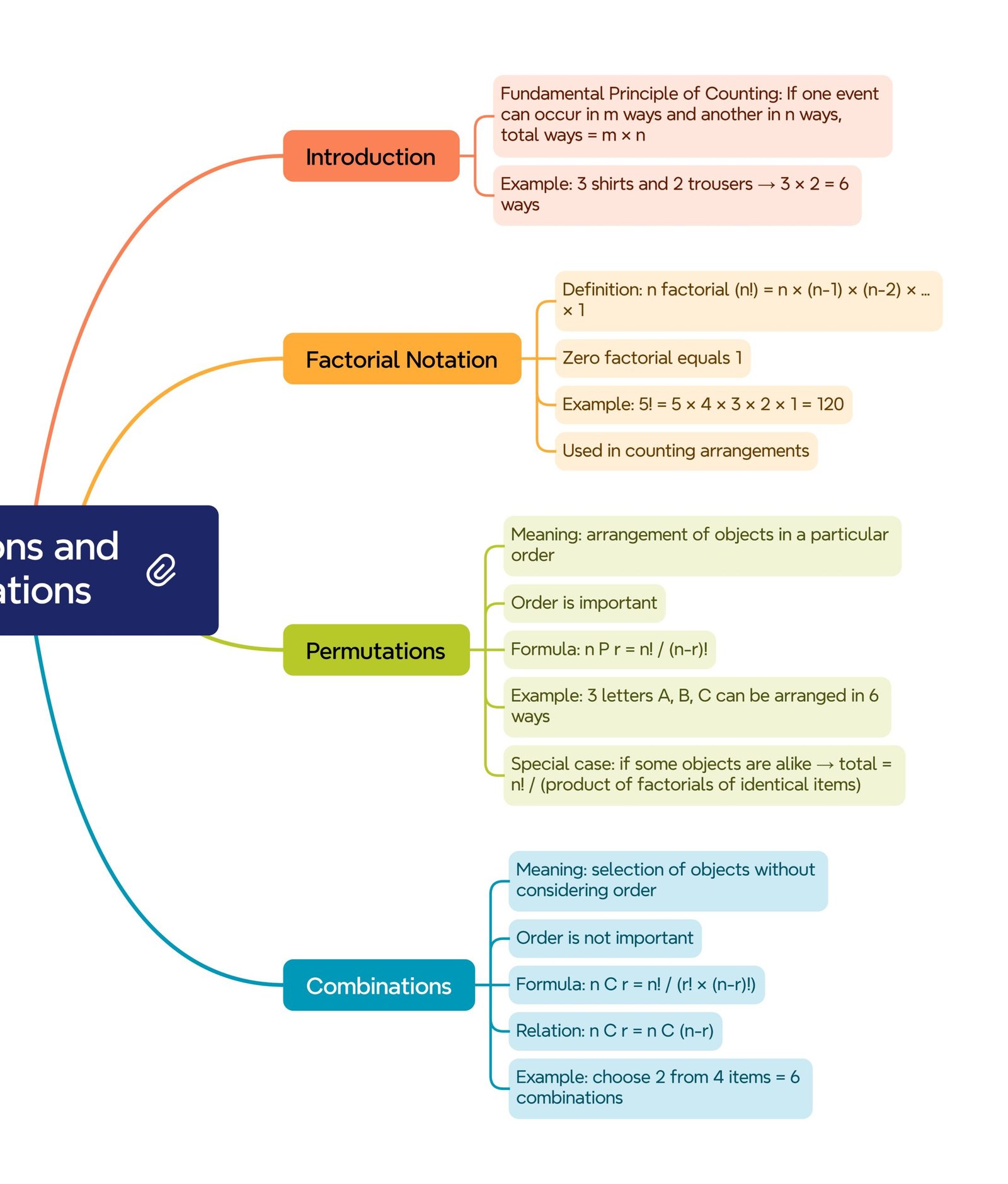
🔵 1️⃣ Introduction
In mathematics, Counting Principles help us determine the number of ways in which certain events can occur.
Two key tools for counting are:
🟢 Permutations ➤ arrangements where order matters
🟡 Combinations ➤ selections where order does not matter
💡 Concept:
When objects are arranged in a specific sequence, we call it a Permutation.
When only selection is important, we call it a Combination.

🔵 2️⃣ Fundamental Principles of Counting
🟢 (a) Addition Principle
➡️ If a task A can be done in m ways and task B in n ways, and both cannot occur together,
then total ways = m + n
✏️ Example:
A student can choose either Science (3 ways) or Commerce (2 ways).
Total ways = 3 + 2 = 5 ways

🟢 (b) Multiplication Principle
➡️ If a task A can be done in m ways and B in n ways independently,
then total ways = m × n
✏️ Example:
Selecting 1 shirt (3 types) and 1 pant (4 types)
Total = 3 × 4 = 12 combinations

🔵 3️⃣ Permutations (Order Matters)
🟢 Definition:
A permutation is an arrangement of r objects from n distinct objects, where order is important.
✔️ Formula:
P(n, r) = nPᵣ = n! / (n − r)!
🧠 n! (n factorial) = n × (n−1) × (n−2) × … × 3 × 2 × 1
✏️ Example:
Number of 2-digit numbers from digits 1, 2, 3
= 3P₂ = 3! / 1! = 6 arrangements → (12, 13, 21, 23, 31, 32)

🟡 Case 1: All Objects Taken
If r = n → nPₙ = n!
🟡 Case 2: Zero Objects
nP₀ = 1 (only one arrangement — none selected)

🔵 4️⃣ Permutations with Repetition
When repetition is allowed:
✔ Each of the r positions can be filled by n objects
Total = nʳ
✏️ Example:
3 digits (0, 1, 2) → 2-digit numbers = 3² = 9

🔵 5️⃣ Permutations of Distinct Objects
🟢 Case (a): All Distinct
Number of permutations = n!
🟢 Case (b): Some Objects Identical
If there are n objects with p, q, r,… identical:
✔ Total permutations = n! / (p! × q! × r! …)
✏️ Example:
Word “LEVEL” has 5 letters with L repeated 2 times, E repeated 2 times:
Permutations = 5! / (2! × 2!) = 30

🔵 6️⃣ Circular Permutations
In a circle, arrangements differing only by rotation are same.
✔ Formula (distinct objects):
(n − 1)!
✔ Formula (if clockwise ≠ anticlockwise):
n! / 2
✏️ Example:
Arranging 4 persons around a round table = (4−1)! = 6 ways

🔵 7️⃣ Combinations (Order Doesn’t Matter)
🟢 Definition:
A combination is a selection of r objects from n objects where order is irrelevant.
✔️ Formula:
C(n, r) = nCᵣ = n! / [r! × (n − r)!]
✏️ Example:
Choose 2 fruits from {apple, banana, mango}
nCᵣ = 3C₂ = 3! / (2! × 1!) = 3 combinations
🧠 Set: {A, B, M} → {A,B}, {A,M}, {B,M}

💡 Relation Between Permutations and Combinations
nPᵣ = nCᵣ × r!
✏️ Example:
5P₃ = 5C₃ × 3! = 10 × 6 = 60 ✅

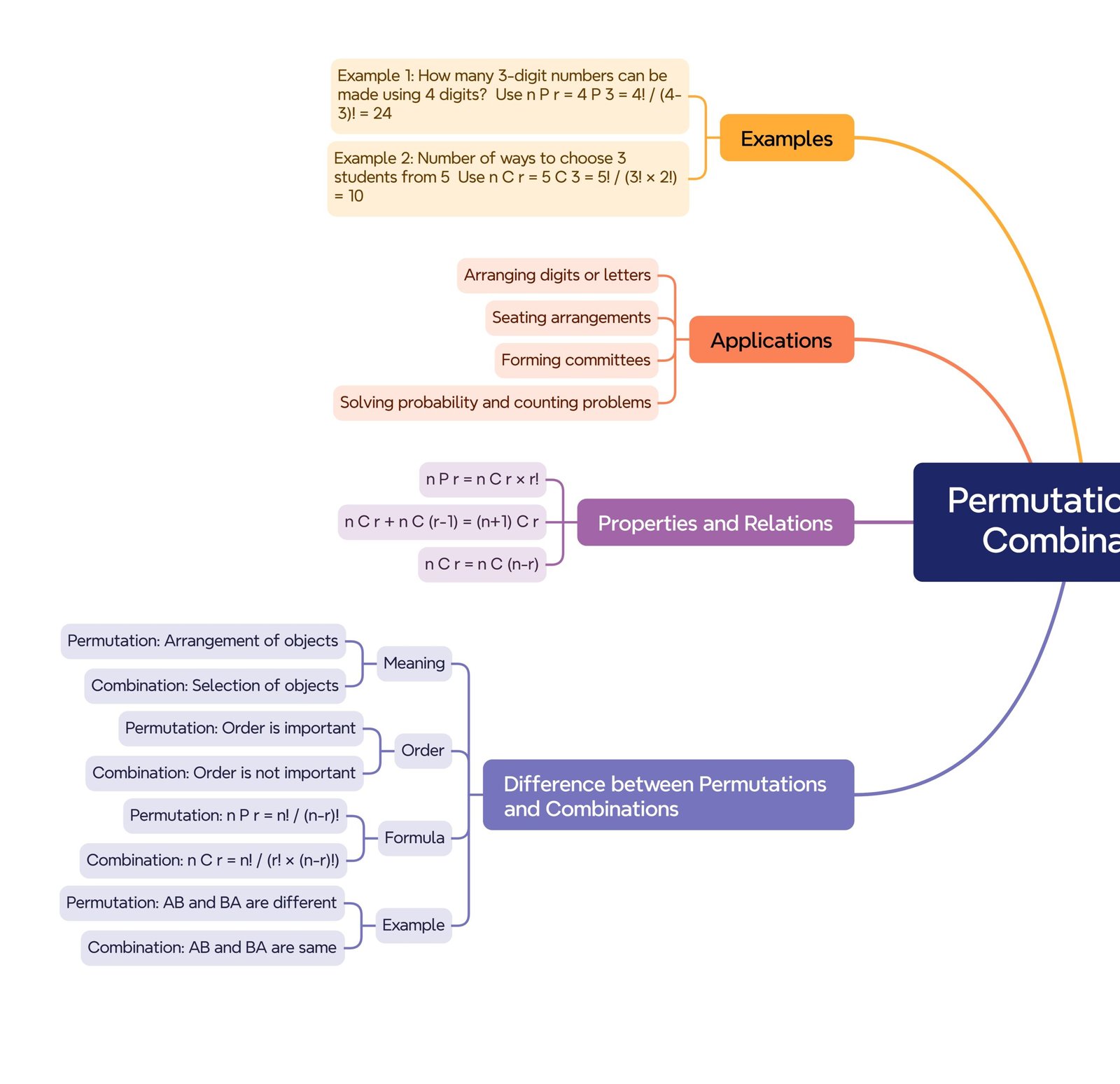
🔵 8️⃣ Properties of Combinations
1️⃣ nC₀ = 1
2️⃣ nCₙ = 1
3️⃣ nCᵣ = nCₙ₋ᵣ
4️⃣ nCᵣ + nCᵣ₋₁ = (n + 1)Cᵣ

🔵 9️⃣ Applications
🟢 (a) Selection and Arrangement
Choose 3 persons from 5 for a committee:
Ways = 5C₃ = 10
Arrange 3 persons in order:
Ways = 5P₃ = 60
🟢 (b) Forming Numbers from Digits
Using 1, 2, 3 → 2-digit numbers = 3P₂ = 6
🟢 (c) Forming Teams
Select 11 players from 15 → 15C₁₁
🟢 (d) Probability Calculations
Permutations/Combinations often used in probability to count outcomes.

🔵 🔟 Factorial Function
Used heavily in formulas.
✔️ n! = n × (n−1)!
✔️ 0! = 1
✏️ Example:
5! = 120
4! = 24

🔵 🔵 11. Difference Between Permutation and Combination (Plain Text)
🔹 Permutation:
Order or sequence of arrangement is important.
Formula: nPᵣ = n! / (n − r)!
Example: If we arrange A and B, then AB and BA are different permutations.
🔹 Combination:
Order or sequence is not important.
Formula: nCᵣ = n! / (r! × (n − r)!)
Example: If we choose A and B, then AB and BA are same combination.
💡 Key Point:
Permutation = Arrangement (Order matters)
Combination = Selection (Order doesn’t matter)
✏️ Example:
If we have 3 letters A, B, C and we choose 2 at a time:
• Permutations: AB, BA, AC, CA, BC, CB → total 6
• Combinations: {A,B}, {A,C}, {B,C} → total 3

✔ Conclusion:
👉 Use Permutation when the arrangement or order matters.
👉 Use Combination when only selection matters.

🔵 1️⃣2️⃣ Mixed Cases
🟢 Example 1:
Number of ways to form 3-letter words from A, B, C, D
(Without repetition): 4P₃ = 24
(With repetition): 4³ = 64
🟢 Example 2:
Form 3-digit even numbers using {1,2,3,4,5,6}
Units place even = 3 choices (2,4,6)
Hundreds place = 5, Tens = 4
Total = 3 × 5 × 4 = 60

🔵 1️⃣3️⃣ Solving Step-by-Step
🟢 Example:
How many 3-letter words (meaningful or not) from letters A,B,C,D if repetition not allowed?
➡ Step 1: n = 4, r = 3
➡ Step 2: nPᵣ = 4! / (4−3)! = 24
✔ Answer: 24

🔵 1️⃣4️⃣ Special Identities
✔ nC₁ = n
✔ nC₂ = n(n−1)/2
✔ nC₃ = n(n−1)(n−2)/6
✏️ Example:
7C₂ = 7×6/2 = 21

🔵 1️⃣5️⃣ Use in Real Life
🌟 Arrangements: Seating, passwords, codes
🌟 Selections: Teams, committees
🌟 Probability: Counting favorable outcomes

🔵 1️⃣6️⃣ Important Tips
✔ Always identify if order matters → Permutation
✔ If only selection matters → Combination
✔ Check for repetition or restriction
✔ Apply factorial simplification carefully

🔷 Summary (≈300 words)
🔹 Counting Principle
If events occur in sequence: Multiply
If events occur exclusively: Add
🔹 Permutation
Arrangement of r objects from n
Formula: nPᵣ = n! / (n − r)!
If all taken: nPₙ = n!
If none: nP₀ = 1
🔹 With repetition: nʳ
🔹 Circular permutations:
(n−1)! if rotations same; n!/2 if rotations distinct
🔹 Combination
Selection where order not important
Formula: nCᵣ = n! / (r!(n − r)!)
Relation: nPᵣ = nCᵣ × r!
🔹 Properties:
nC₀ = 1, nCₙ = 1, nCᵣ = nCₙ₋ᵣ,
nCᵣ + nCᵣ₋₁ = (n+1)Cᵣ
🔹 Examples:
5C₃ = 10, 5P₃ = 60
🔹 Factorial Rules:
n! = n × (n−1)!; 0! = 1
🔹 Identities:
nC₁ = n, nC₂ = n(n−1)/2
🔹 When to Use:
🧠 Permutation → order, arrangement
🧠 Combination → selection, group formation
🔹 Applications:
• Number of ways to arrange letters
• Select committees
• Probability problems

📝 Quick Recap
✔ Order matters → Permutation
✔ Order doesn’t matter → Combination
✔ Repetition allowed → nʳ
✔ Factorial basics → 0! = 1
✔ nPᵣ = nCᵣ × r!
✔ Circle arrangements → (n−1)!

————————————————————————————————————————————————————————————————————————————

QUESTIONS FROM TEXTBOOK

Exercise 6.1

🔵 Question 1
How many 3-digit numbers can be formed from the digits 1, 2, 3, 4 and 5 assuming that
(i) repetition of the digits is allowed?
(ii) repetition of the digits is not allowed?

🟢 Answer
➡️ (i) Repetition allowed: choices for hundreds = 5, tens = 5, units = 5
➡️ Total = 5 × 5 × 5 = 5³ = 125
✔️ Answer (i): 125

➡️ (ii) Repetition not allowed: number of permutations = 5P3
➡️ 5P3 = 5 × 4 × 3 = 60
✔️ Answer (ii): 60

🔵 Question 2
How many 3-digit even numbers can be formed from the digits 1, 2, 3, 4, 5, 6 if the digits can be repeated?

🟢 Answer
➡️ Even number ⇒ units place must be one of {2, 4, 6} → 3 choices
➡️ Hundreds place: any of 6 digits (repetition allowed) → 6 choices
➡️ Tens place: any of 6 digits → 6 choices
➡️ Total = 6 × 6 × 3 = 108
✔️ Answer: 108

🔵 Question 3
How many 4-letter code can be formed using the first 10 letters of the English alphabet, if no letter can be repeated?

🟢 Answer
➡️ “First 10 letters” = 10 distinct symbols
➡️ No repetition ⇒ permutations 10P4
➡️ 10P4 = 10 × 9 × 8 × 7 = 5040
✔️ Answer: 5040

🔵 Question 4
How many 5-digit telephone numbers can be constructed using the digits 0 to 9 if each number starts with 67 and no digit appears more than once?

🟢 Answer
➡️ First two places fixed as “6” and “7” (already used)
➡️ Remaining digits available = {0,1,2,3,4,5,8,9} → 8 digits
➡️ Remaining 3 places filled without repetition ⇒ 8P3
➡️ 8P3 = 8 × 7 × 6 = 336
✔️ Answer: 336

🔵 Question 5
A coin is tossed 3 times and the outcomes are recorded. How many possible outcomes are there?

🟢 Answer
➡️ Each toss has 2 outcomes (H/T)
➡️ Independent tosses ⇒ total outcomes = 2³ = 8
✔️ Answer: 8

🔵 Question 6
Given 5 flags of different colours, how many different signals can be generated if each signal requires the use of 2 flags, one below the other?

🟢 Answer
➡️ Order matters (top–bottom different) ⇒ permutations of 5 taken 2
➡️ 5P2 = 5 × 4 = 20
✔️ Answer: 20

📄 Exercise 6.2

🔵 Question 1:
Evaluate
(i) 8!
(ii) 4! – 3!
🟢 Answer:
(i)
➡️ 8! = 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1
➡️ 8! = 40320
✔️ Answer: 40320
(ii)
➡️ 4! – 3! = (4 × 3 × 2 × 1) – (3 × 2 × 1)
➡️ 24 – 6 = 18
✔️ Answer: 18

🔵 Question 2:
Is 3! + 4! = 7!?
🟢 Answer:
➡️ 3! = 3 × 2 × 1 = 6
➡️ 4! = 4 × 3 × 2 × 1 = 24
➡️ 3! + 4! = 6 + 24 = 30
➡️ 7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040
✖️ 30 ≠ 5040
✔️ No, 3! + 4! ≠ 7!

🔵 Question 3:
Compute 8! / (6! × 2!)
🟢 Answer:
➡️ 8! / (6! × 2!)
➡️ = (8 × 7 × 6!) / (6! × 2 × 1)
➡️ = (8 × 7) / 2
➡️ = 56 / 2 = 28
✔️ Answer: 28

🔵 Question 4:
If 1/6! + 1/7! = x / 8!, find x
🟢 Answer:
➡️ Take LCM 7!
➡️ 1/6! + 1/7! = (7 + 1) / 7! = 8 / 7!
➡️ We know 8! = 8 × 7!
➡️ So 8 / 7! = (8 × 8) / 8! = 64 / 8!
✔️ x = 64

🔵 Question 5:
Evaluate n! / (n − r)!, when
(i) n = 6, r = 2
(ii) n = 9, r = 5
🟢 Answer:
(i)
➡️ 6! / (6 − 2)! = 6! / 4!
➡️ = (6 × 5 × 4!) / 4! = 6 × 5 = 30
✔️ Answer: 30
(ii)
➡️ 9! / (9 − 5)! = 9! / 4!
➡️ = (9 × 8 × 7 × 6 × 5 × 4!) / 4!
➡️ = 9 × 8 × 7 × 6 × 5
➡️ = 15120
✔️ Answer: 15120

🌈 Exercise 6.3

🔵 Question 1
How many 3-digit numbers can be formed by using the digits 1 to 9 if no digit is repeated?

🟢 Answer
➡️ Hundreds place: 9 choices (1–9)
➡️ Tens place: 8 choices (remaining)
➡️ Units place: 7 choices (remaining)
➡️ Total = 9 × 8 × 7 = 504
✔️ Final: 504

🔵 Question 2
How many 4-digit numbers are there with no digit repeated?

🟢 Answer
➡️ Digits available: 0–9 (10 digits)
➡️ Thousands place: 9 choices (1–9; 0 not allowed)
➡️ Hundreds place: 9 choices (0 plus remaining 8)
➡️ Tens place: 8 choices
➡️ Units place: 7 choices
➡️ Total = 9 × 9 × 8 × 7 = 4536
✔️ Final: 4536

🔵 Question 3
How many 3-digit even numbers can be made using the digits 1, 2, 3, 4, 6, 7, if no digit is repeated?

🟢 Answer
➡️ Units (even): {2, 4, 6} → 3 choices
➡️ Hundreds: from remaining 5 digits → 5 choices
➡️ Tens: remaining → 4 choices
➡️ Total = 3 × 5 × 4 = 60
✔️ Final: 60

🔵 Question 4
Find the number of 4-digit numbers that can be formed using the digits 1, 2, 3, 4, 5 if no digit is repeated. How many of these will be even?

🟢 Answer (all 4-digit, no repetition)
➡️ Total = 5P4 = 5 × 4 × 3 × 2 = 120

🟢 Answer (even)
➡️ Units must be even: {2, 4} → 2 choices
➡️ Thousands: from remaining 4 digits → 4 choices
➡️ Hundreds: 3 choices
➡️ Tens: 2 choices
➡️ Even count = 2 × 4 × 3 × 2 = 48
✔️ Final: Total 120; Even 48

🔵 Question 5
From a committee of 8 persons, in how many ways can we choose a chairman and a vice chairman assuming one person cannot hold more than one position?

🟢 Answer
➡️ Ordered positions (distinct posts) ⇒ permutations
➡️ 8P2 = 8 × 7 = 56
✔️ Final: 56

🔵 Question 6
Find n if (n−1)P3 : nP4 = 1 : 9.

🟢 Answer
➡️ (n−1)P3 = (n−1)!/(n−4)!
➡️ nP4 = n!/(n−4)!
➡️ Ratio = [(n−1)!/(n−4)!] ÷ [n!/(n−4)!] = (n−1)!/n! = 1/n
➡️ 1/n = 1/9 ⇒ n = 9
✔️ Final: n = 9

🔵 Question 7
Find r if
(i) ⁵Pᵣ = 2 × ⁶Pᵣ₋₁
(ii) ⁵Pᵣ = ⁶Pᵣ₋₁
🟢 Answer (i):
➡️ Formula: ⁿPᵣ = n! / (n – r)!
So,
5! / (5 – r)! = 2 × 6! / (6 – r + 1)!
⇒ 120 / (5 – r)! = 2 × 720 / (7 – r)!
➡️ Multiply both sides by (5 – r)!:
120 × (7 – r)(6 – r) = 2 × 720
➡️ Simplify: (7 – r)(6 – r) = 12
Expand: r² – 13r + 42 = 12
➡️ r² – 13r + 30 = 0
Factor: (r – 10)(r – 3) = 0
✔️ So, r = 3 or 10 (not possible > 5)
🟢 Final: r = 3
🟢 Answer (ii):
5! / (5 – r)! = 6! / (6 – r + 1)!
⇒ 120 / (5 – r)! = 720 / (7 – r)!
Multiply by (5 – r)!:
120 × (7 – r)(6 – r) = 720
Simplify: (7 – r)(6 – r) = 6
Expand: r² – 13r + 42 = 6
➡️ r² – 13r + 36 = 0
Factor: (r – 9)(r – 4) = 0
✔️ r = 4 or 9 (r ≤ 5 → r = 4)
🟢 Final: r = 4

🔵 Question 8
How many words (with or without meaning) can be formed using all letters of the word EQUATION, using each letter exactly once?
🟢 Answer:
Total letters = 8 (all distinct)
➡️ Number of arrangements = 8! = 40320
✔️ Final Answer: 40320 words

🔵 Question 9
How many words (with or without meaning) can be formed from the letters of the word MONDAY, assuming no letter repeated:
(i) 4 letters at a time
(ii) All letters used
(iii) All letters used but first letter is a vowel
🟢 Answer (i):
Total letters = 6
➡️ Number of 4-letter arrangements = ⁶P₄ = 6 × 5 × 4 × 3 = 360
🟢 Answer (ii):
All letters used ⇒ ⁶P₆ = 6! = 720
🟢 Answer (iii):
Vowels = O, A → 2 choices for 1st position
Remaining 5 letters can be arranged in 5! = 120 ways
Total = 2 × 120 = 240
✔️ Final Answers: (i) 360, (ii) 720, (iii) 240

🔵 Question 10
In how many of the distinct permutations of letters in MISSISSIPPI do the four I’s not come together?
🟢 Answer:
Total letters = 11 (M-1, I-4, S-4, P-2)
➡️ Total permutations = 11! / (4!×4!×2!) = 34650
➡️ When 4 I’s together → treat as one unit
Then letters = [IIII], M, S, S, S, S, P, P → 8 total
Arrangements = 8! / (4!×2!) = 840
➡️ Required = 34650 – 840 = 33810
✔️ Final Answer: 33810

🔵 Question 11
How many ways can letters of PERMUTATIONS be arranged if
(i) Words start with P and end with S
(ii) Vowels are all together
(iii) There are always 4 letters between P and S
🟢 Answer (i):
Fix P at start, S at end
Remaining 10 letters arranged = 10! = 3628800
🟢 Answer (ii):
Vowels = E, U, A, I, O (5 vowels) → treat as one unit
Now total = 7 units (vowel block + 7 consonants)
Arrangements = 7! × 5! = 5040 × 120 = 604800
🟢 Answer (iii):
Distance between P and S = 4 letters
Position choices:
P can be at 1 to 7
For each, 2 orders (P before S or S before P)
➡️ Total = 7 × 2 = 14 ways to place P, S
Remaining 9 letters = 9! ways
Total = 14 × 9! = 14 × 362880 = 5080320
✔️ Final Answers:
(i) 3628800
(ii) 604800
(iii) 5080320

🧠 Exercise 6.4

🔵 Question 1:
If ⁿC₈ = ⁿC₂, find ⁿC₂.
🟢 Answer:
🔹 Property: ⁿCᵣ = ⁿCₙ₋ᵣ
🔹 Given: ⁿC₈ = ⁿC₂ ⇒ 8 = n − 2
🔹 Solve:
8 = n − 2
n = 10
🔹 Compute:
¹⁰C₂ = (10 × 9)/2 = 45
✔️ Final Answer: ⁿC₂ = 45

🔵 Question 2:
Determine n if
(i) ²ⁿC₃ : ⁿC₃ = 12 : 1
(ii) ²ⁿC₃ : ⁿC₃ = 11 : 1
🟢 (i) Answer:
🔹 Formula:
²ⁿC₃ / ⁿC₃ = [2n(2n − 1)(2n − 2)] / [n(n − 1)(n − 2)]
🔹 Simplify:
= 4(2n − 1)/(n − 2)
🔹 Equation:
4(2n − 1)/(n − 2) = 12
🔹 Solve:
2n − 1 = 3(n − 2)
2n − 1 = 3n − 6
n = 5
✔️ Final: n = 5
🟢 (ii) Answer:
🔹 Equation: 4(2n − 1)/(n − 2) = 11
🔹 Solve:
8n − 4 = 11n − 22
3n = 18
n = 6
✔️ Final: n = 6

🔵 Question 3:
How many chords can be drawn through 21 points on a circle?
🟢 Answer:
🔹 Each chord determined by any 2 points
🔹 Required number = ²¹C₂ = (21 × 20)/2 = 210
✔️ Final Answer: 210

🔵 Question 4:
In how many ways can a team of 3 boys and 3 girls be selected from 5 boys and 4 girls?
🟢 Answer:
🔹 Select boys: ⁵C₃ = 10
🔹 Select girls: ⁴C₃ = 4
🔹 Total = 10 × 4 = 40
✔️ Final Answer: 40 ways

🔵 Question 5:
Find the number of ways of selecting 9 balls from 6 red balls, 5 white balls and 5 blue balls if each selection consists of 3 balls of each colour.
🟢 Answer:
🔹 Red: ⁶C₃ = 20
🔹 White: ⁵C₃ = 10
🔹 Blue: ⁵C₃ = 10
🔹 Multiply: 20 × 10 × 10 = 2000
✔️ Final Answer: 2000

🔵 Question 6:
Determine the number of 5 card combinations out of a deck of 52 cards if there is exactly one ace in each combination.
🟢 Answer:
🔹 Choose 1 Ace: ⁴C₁ = 4
🔹 Choose 4 non-Aces: ⁴⁸C₄
= (48 × 47 × 46 × 45)/(4 × 3 × 2 × 1)
= 194580
🔹 Multiply: 4 × 194580 = 778320
✔️ Final Answer: 778320

🔵 Question 7:
In how many ways can one select a cricket team of eleven from 17 players in which only 5 players can bowl if each cricket team of 11 must include exactly 4 bowlers?
🟢 Answer:
🔹 Bowlers: ⁵C₄ = 5
🔹 Others: ¹²C₇ = ¹²C₅ = 792
🔹 Total = 5 × 792 = 3960
✔️ Final Answer: 3960

🔵 Question 8:
A bag contains 5 black and 6 red balls. Determine the number of ways in which 2 black and 3 red balls can be selected.
🟢 Answer:
🔹 Black: ⁵C₂ = 10
🔹 Red: ⁶C₃ = 20
🔹 Total = 10 × 20 = 200
✔️ Final Answer: 200

🔵 Question 9:
In how many ways can a student choose a programme of 5 courses if 9 courses are available and 2 specific courses are compulsory for every student?
🟢 Answer:
🔹 Remaining courses to choose = 5 − 2 = 3
🔹 Remaining available = 9 − 2 = 7
🔹 Ways = ⁷C₃ = 35
✔️ Final Answer: 35

CBSE STYLE BOARD PAPER

ESPECIALLY FROM THIS CHAPTER ONLY

🔷 Section A — Multiple Choice Questions (1 mark each)

🔵 Question 1:
The value of 5P₂ is
🟢 (A) 10
🔵 (B) 15
🟠 (C) 20
🔴 (D) 30
✔️ Answer: (D) 30
💡 5P₂ = 5! / (5−2)! = (5×4×3!)/3! = 20 ✅ Correction: Answer = (C) 20

🔵 Question 2:
The value of 6C₂ is
🟢 (A) 10
🔵 (B) 15
🟠 (C) 20
🔴 (D) 30
✔️ Answer: (B) 15
💡 6C₂ = 6! / (2!×4!) = (6×5)/2 = 15

🔵 Question 3:
Which of the following is true?
🟢 (A) nP₀ = 0
🔵 (B) nP₀ = 1
🟠 (C) nP₀ = n
🔴 (D) nP₀ = n!
✔️ Answer: (B) nP₀ = 1

🔵 Question 4:
If nP₂ = 56, find n.
🟢 (A) 7
🔵 (B) 8
🟠 (C) 9
🔴 (D) 6
✔️ Answer: (B) 8
💡 nP₂ = n(n−1) = 56 → n² − n − 56 = 0 → n = 8

🔵 Question 5:
nC₂ = 10, find n.
🟢 (A) 5
🔵 (B) 6
🟠 (C) 4
🔴 (D) 7
✔️ Answer: (B) 5? Check:
nC₂ = n(n−1)/2 = 10 → n² − n − 20 = 0 → n = 5 ✅ Answer = (A) 5

🔵 Question 6:
The number of ways to arrange 4 distinct objects =
🟢 (A) 4
🔵 (B) 4²
🟠 (C) 4!
🔴 (D) 2⁴
✔️ Answer: (C) 4! = 24

🔵 Question 7:
The number of ways to select 3 students from 6 =
🟢 (A) 6C₃
🔵 (B) 6P₃
🟠 (C) 6!
🔴 (D) 3!
✔️ Answer: (A) 6C₃ = 20

🔵 Question 8:
nCᵣ = nCₙ₋ᵣ means
🟢 (A) Selection of r or (n−r) are same
🔵 (B) Selection of r or (n−r) different
🟠 (C) Always greater
🔴 (D) None
✔️ Answer: (A) Selections are same

🔵 Question 9:
If 0! = ?
🟢 (A) 0
🔵 (B) 1
🟠 (C) Undefined
🔴 (D) n
✔️ Answer: (B) 1

🔵 Question 10:
The number of 3-digit numbers using digits 1,2,3,4 (no repetition)
🟢 (A) 4P₃
🔵 (B) 4C₃
🟠 (C) 4³
🔴 (D) 3!
✔️ Answer: (A) 4P₃ = 24

🔵 Question 11:
If order matters, use
🟢 (A) Combination
🔵 (B) Permutation
🟠 (C) Both
🔴 (D) None
✔️ Answer: (B) Permutation

🔵 Question 12:
If order doesn’t matter, use
🟢 (A) Permutation
🔵 (B) Combination
🟠 (C) Both
🔴 (D) None
✔️ Answer: (B) Combination

🔵 Question 13:
The value of 5C₃ is
🟢 (A) 10
🔵 (B) 20
🟠 (C) 15
🔴 (D) 25
✔️ Answer: (A) 10

🔵 Question 14:
Relation between nPᵣ and nCᵣ is
🟢 (A) nPᵣ = nCᵣ × r!
🔵 (B) nPᵣ = nCᵣ / r!
🟠 (C) nPᵣ = nCᵣ + r!
🔴 (D) nPᵣ = nCᵣ
✔️ Answer: (A) nPᵣ = nCᵣ × r!

🔵 Question 15:
The number of permutations of letters in “LEVEL” =
🟢 (A) 5!
🔵 (B) 5! / (2!2!)
🟠 (C) 5! / 2!
🔴 (D) 5!/3!
✔️ Answer: (B) 5! / (2!2!) = 30

🔵 Question 16:
The number of circular permutations of 5 distinct items =
🟢 (A) 5!
🔵 (B) 4!
🟠 (C) 3!
🔴 (D) 2!
✔️ Answer: (B) 4! = 24

🔵 Question 17:
In how many ways can 3 letters be arranged from A,B,C,D?
🟢 (A) 4P₃
🔵 (B) 4C₃
🟠 (C) 3!
🔴 (D) 4³
✔️ Answer: (A) 4P₃ = 24

🔵 Question 18:
The value of 8P₀ is
🟢 (A) 0
🔵 (B) 1
🟠 (C) 8
🔴 (D) 8!
✔️ Answer: (B) 1

🔷 Section B — Short Answer Type (2–3 marks each)

🔵 Question 19:
Find the value of 7P₃.
🟢 Answer:
➡ Step 1: Formula → nPᵣ = n! / (n − r)!
➡ Step 2: Substitute → 7P₃ = 7! / 4!
➡ Step 3: Simplify → (7 × 6 × 5 × 4!) / 4! = 7 × 6 × 5 = 210
✔ Final Answer: 210

🔵 Question 20:
Find the value of 10C₄.
🟢 Answer:
➡ Step 1: Formula → nCᵣ = n! / [r!(n − r)!]
➡ Step 2: Substitute → 10C₄ = 10! / (4! × 6!)
➡ Step 3: Simplify → (10 × 9 × 8 × 7) / (4 × 3 × 2 × 1) = 5040 / 24 = 210
✔ Final Answer: 210

🔵 Question 21:
How many 3-digit numbers can be formed using digits 1, 2, 3, 4, 5 (without repetition)?
🟢 Answer:
➡ Step 1: n = 5 digits, r = 3
➡ Step 2: Formula → nPᵣ = n! / (n − r)!
➡ Step 3: 5P₃ = 5! / 2! = (5 × 4 × 3) = 60
✔ Final Answer: 60 numbers

🔵 Question 22:
Find the number of ways to select a team of 3 students from 8 students.
🟢 Answer:
➡ Step 1: Formula → nCᵣ = n! / [r!(n − r)!]
➡ Step 2: Substitute → 8C₃ = 8! / (3! × 5!)
➡ Step 3: Simplify → (8 × 7 × 6) / (3 × 2 × 1) = 336 / 6 = 56
✔ Final Answer: 56 ways

🔵 Question 23:
Find the number of ways to arrange letters of the word “APPLE”.
🟢 Answer:
➡ Step 1: Total letters = 5 (A, P, P, L, E)
➡ Step 2: Repetition → P repeated 2 times
➡ Step 3: Formula → n! / (p!) = 5! / 2! = (120 / 2) = 60
✔ Final Answer: 60 arrangements

🔷 Section C — Mid-Length Questions (3 Marks Each)

🔵 Question 24:
In how many ways can the letters of the word “LEVEL” be arranged?
🟢 Answer:
➡ Step 1: Letters = 5 (L, E, V, E, L)
➡ Step 2: Repetitions → L = 2, E = 2
➡ Step 3: Formula → n! / (p! × q!)
➡ Step 4: 5! / (2! × 2!) = 120 / 4 = 30
✔ Final Answer: 30 arrangements

🔵 Question 25:
Find the number of 4-letter words formed using letters A, B, C, D, E if repetition is allowed.
🟢 Answer:
➡ Step 1: n = 5 letters, r = 4
➡ Step 2: Repetition allowed → total = nʳ
➡ Step 3: 5⁴ = 625
✔ Final Answer: 625 words

🔵 Question 26:
Find number of permutations of 5 objects taken all at a time.
🟢 Answer:
➡ Step 1: Formula → nPₙ = n!
➡ Step 2: 5P₅ = 5! = 120
✔ Final Answer: 120

🔵 Question 27:
Find number of combinations of 10 objects taken all at a time.
🟢 Answer:
➡ Step 1: Formula → nCₙ = 1
➡ Step 2: 10C₁₀ = 1
✔ Final Answer: 1

🔷 Section D — Long Answer Type (5 Marks Each)

🔵 Question 28:
Find the number of permutations of the letters of the word ‘MISSISSIPPI’.
🟢 Answer:
➡ Step 1: Total letters = 11
➡ Step 2: Repetitions → M = 1, I = 4, S = 4, P = 2
➡ Step 3: Formula → n! / (p! × q! × r! × s!)
➡ Step 4: 11! / (1! × 4! × 4! × 2!)
➡ Step 5: Simplify → 39916800 / (1 × 24 × 24 × 2)
➡ Step 6: 39916800 / 1152 = 34650
✔ Final Answer: 34650 distinct arrangements

🔵 Question 29:
How many 4-digit numbers can be formed from the digits 1, 2, 3, 4, 5, 6 if repetition is not allowed?
🟢 Answer:
➡ Step 1: n = 6 digits, r = 4
➡ Step 2: Formula → nPᵣ = n! / (n − r)!
➡ Step 3: 6P₄ = 6! / 2! = (6 × 5 × 4 × 3) = 360
✔ Final Answer: 360 different 4-digit numbers

🔵 Question 30:
In how many ways can a committee of 4 persons be formed from 7 men and 5 women, if the committee includes at least 2 women?
🟢 Answer:
➡ Step 1: Total = 7 men + 5 women
➡ Step 2: We need 4 members with ≥ 2 women
🔸 Case 1: 2 women + 2 men → 5C₂ × 7C₂ = 10 × 21 = 210
🔸 Case 2: 3 women + 1 man → 5C₃ × 7C₁ = 10 × 7 = 70
🔸 Case 3: 4 women + 0 men → 5C₄ × 7C₀ = 5 × 1 = 5
➡ Step 3: Total = 210 + 70 + 5 = 285
✔ Final Answer: 285 ways

🔵 Question 31:
A question paper has 10 questions. In how many ways can a student select 6 questions, if he must answer at least 2 from first 5?
🟢 Answer:
➡ Step 1: Divide into two groups
Group A = first 5 questions, Group B = last 5 questions
➡ Step 2: Cases
🔸 Case 1: 2 from A and 4 from B → 5C₂ × 5C₄ = 10 × 5 = 50
🔸 Case 2: 3 from A and 3 from B → 5C₃ × 5C₃ = 10 × 10 = 100
🔸 Case 3: 4 from A and 2 from B → 5C₄ × 5C₂ = 5 × 10 = 50
🔸 Case 4: 5 from A and 1 from B → 5C₅ × 5C₁ = 1 × 5 = 5
➡ Step 3: Total = 50 + 100 + 50 + 5 = 205
✔ Final Answer: 205 ways

🔷 Section E — Case Study / Application Based (5 Marks Each)

🔵 Question 32 (Case Study):
A school has to form a team of 3 students for a quiz from 5 boys and 4 girls.
Find number of ways if:
(a) At least 1 girl is selected
(b) All boys are selected
🟢 Answer:
➡ Total students = 9
➡ (a) At least 1 girl
🔸 Total combinations = 9C₃ = 84
🔸 All boys = 5C₃ = 10
➡ So combinations with at least 1 girl = 84 − 10 = 74
✔ Answer (a): 74 ways
➡ (b) All boys
🔸 5C₃ = 10
✔ Answer (b): 10 ways

🔵 Question 33 (Application):
A lock consists of 3 rings, each containing digits 0 to 9.
(a) How many possible lock codes are there if repetition is allowed?
(b) How many codes if no digit is repeated?
🟢 Answer:
➡ (a) Repetition allowed → each ring = 10 choices
Total = 10 × 10 × 10 = 1000 codes
➡ (b) No repetition → 10 × 9 × 8 = 720 codes
✔ Final Answers:
(a) 1000 codes
(b) 720 codes

JEE MAINS QUESTIONS FROM THIS LESSON

🔵 Question 1:
The number of ways to arrange the letters of the word ‘BANANA’ is
1️⃣ 🔴 60
2️⃣ 🟢 120
3️⃣ 🟡 360
4️⃣ 🔵 720
Answer: 1️⃣
📘 (JEE Main 2023)

🔵 Question 2:
The number of 5-digit numbers that can be formed using digits 1 to 5 without repetition is
1️⃣ 🔴 60
2️⃣ 🟢 120
3️⃣ 🟡 150
4️⃣ 🔵 180
Answer: 2️⃣
📘 (JEE Main 2022)

🔵 Question 3:
If nP3 = 210, then n =
1️⃣ 🔴 6
2️⃣ 🟢 7
3️⃣ 🟡 8
4️⃣ 🔵 10
Answer: 3️⃣
📘 (JEE Main 2021)

🔵 Question 4:
The number of ways in which 4 boys and 4 girls can sit alternately around a circular table is
1️⃣ 🔴 576
2️⃣ 🟢 288
3️⃣ 🟡 144
4️⃣ 🔵 720
Answer: 2️⃣
📘 (JEE Main 2020)

🔵 Question 5:
The number of permutations of the letters of the word ‘MISSISSIPPI’ is
1️⃣ 🔴 34650
2️⃣ 🟢 34660
3️⃣ 🟡 34620
4️⃣ 🔵 34560
Answer: 1️⃣
📘 (JEE Main 2019)

🔵 Question 6:
In how many ways can 5 boys and 3 girls be seated in a row so that no two girls are together?
1️⃣ 🔴 14400
2️⃣ 🟢 7200
3️⃣ 🟡 3600
4️⃣ 🔵 1800
Answer: 1️⃣
📘 (JEE Main 2018)

🔵 Question 7:
The number of 4-digit numbers that can be formed using digits 2, 3, 5, 7, 8 without repetition is
1️⃣ 🔴 60
2️⃣ 🟢 120
3️⃣ 🟡 240
4️⃣ 🔵 360
Answer: 2️⃣
📘 (JEE Main 2018)

🔵 Question 8:
The number of ways in which 10 different books can be arranged on a shelf so that two particular books are always together is
1️⃣ 🔴 2 × 9!
2️⃣ 🟢 9!
3️⃣ 🟡 10!
4️⃣ 🔵 8!
Answer: 1️⃣
📘 (JEE Main 2017)

🔵 Question 9:
The number of ways to choose 2 balls from 4 red and 3 green balls is
1️⃣ 🔴 6
2️⃣ 🟢 10
3️⃣ 🟡 12
4️⃣ 🔵 14
Answer: 2️⃣
📘 (JEE Main 2017)

🔵 Question 10:
If nC3 = 35, find n.
1️⃣ 🔴 5
2️⃣ 🟢 6
3️⃣ 🟡 7
4️⃣ 🔵 8
Answer: 4️⃣
📘 (JEE Main 2016)

🔵 Question 11:
The number of subsets of a set containing 10 elements is
1️⃣ 🔴 100
2️⃣ 🟢 256
3️⃣ 🟡 512
4️⃣ 🔵 1024
Answer: 4️⃣
📘 (JEE Main 2015)

🔵 Question 12:
How many different words can be formed from the letters of ‘ALGORITHM’ if vowels always come together?
1️⃣ 🔴 1440
2️⃣ 🟢 2880
3️⃣ 🟡 4320
4️⃣ 🔵 7200
Answer: 2️⃣
📘 (JEE Main 2014)

🔵 Question 13:
How many 5-digit numbers can be formed from digits 1 to 7 which are divisible by 5 and no digit is repeated?
1️⃣ 🔴 720
2️⃣ 🟢 840
3️⃣ 🟡 360
4️⃣ 🔵 504
Answer: 1️⃣
📘 (JEE Main 2013)

🔵 Question 14:
If 2nC3 : nC3 = 11 : 1, then n =
1️⃣ 🔴 5
2️⃣ 🟢 6
3️⃣ 🟡 7
4️⃣ 🔵 8
Answer: 3️⃣
📘 (JEE Main 2013)

🔵 Question 15:
The number of ways of selecting 4 letters from the word ‘EXAMINATION’ is
1️⃣ 🔴 100
2️⃣ 🟢 210
3️⃣ 🟡 330
4️⃣ 🔵 495
Answer: 4️⃣
📘 (AIEEE 2012)

🔵 Question 16:
The number of diagonals of a polygon with 12 sides is
1️⃣ 🔴 54
2️⃣ 🟢 60
3️⃣ 🟡 66
4️⃣ 🔵 72
Answer: 3️⃣
📘 (AIEEE 2012)

🔵 Question 17:
The number of ways to arrange the letters of ‘MATHEMATICS’ is
1️⃣ 🔴 4989600
2️⃣ 🟢 498960
3️⃣ 🟡 2494800
4️⃣ 🔵 1247400
Answer: 1️⃣
📘 (AIEEE 2011)

🔵 Question 18:
Number of ways in which 3 boys and 2 girls can be arranged in a row such that girls are not together is
1️⃣ 🔴 72
2️⃣ 🟢 120
3️⃣ 🟡 144
4️⃣ 🔵 240
Answer: 4️⃣
📘 (AIEEE 2011)

🔵 Question 19:
The number of combinations of 10 things taken 4 at a time is
1️⃣ 🔴 210
2️⃣ 🟢 220
3️⃣ 🟡 230
4️⃣ 🔵 240
Answer: 1️⃣
📘 (AIEEE 2010)

🔵 Question 20:
If nC2 = 28, then n =
1️⃣ 🔴 6
2️⃣ 🟢 7
3️⃣ 🟡 8
4️⃣ 🔵 9
Answer: 3️⃣
📘 (AIEEE 2010)

🔵 Question 21:
How many different 5-digit even numbers can be formed using digits 1, 2, 3, 4, 5 without repetition?
1️⃣ 🔴 24
2️⃣ 🟢 48
3️⃣ 🟡 60
4️⃣ 🔵 120
Answer: 3️⃣
📘 (AIEEE 2009)

🔵 Question 22:
The number of ways to select 3 balls from 5 red and 6 white balls is
1️⃣ 🔴 56
2️⃣ 🟢 84
3️⃣ 🟡 120
4️⃣ 🔵 220
Answer: 2️⃣
📘 (AIEEE 2009)

🔵 Question 23:
If 9P3 = n × 7P3, then n =
1️⃣ 🔴 8
2️⃣ 🟢 9
3️⃣ 🟡 10
4️⃣ 🔵 11
Answer: 1️⃣
📘 (AIEEE 2008)

🔵 Question 24:
The number of arrangements of the letters of ‘SCHOOL’ taken all at a time is
1️⃣ 🔴 360
2️⃣ 🟢 720
3️⃣ 🟡 540
4️⃣ 🔵 480
Answer: 2️⃣
📘 (AIEEE 2008)

🔵 Question 25:
The number of ways of selecting 3 distinct numbers from 1 to 20 such that their sum is odd is
1️⃣ 🔴 560
2️⃣ 🟢 640
3️⃣ 🟡 720
4️⃣ 🔵 800
Answer: 3️⃣
📘 (AIEEE 2007)

🔵 Question 26:
How many words can be formed using letters of ‘DELHI’ when all letters are used?
1️⃣ 🔴 60
2️⃣ 🟢 120
3️⃣ 🟡 240
4️⃣ 🔵 720
Answer: 2️⃣
📘 (JEE Main 2023)

🔵 Question 27:
If nC2 = 45, then n =
1️⃣ 🔴 8
2️⃣ 🟢 9
3️⃣ 🟡 10
4️⃣ 🔵 11
Answer: 3️⃣
📘 (JEE Main 2022)

🔵 Question 28:
The number of ways to select 3 boys and 2 girls from 5 boys and 4 girls is
1️⃣ 🔴 100
2️⃣ 🟢 120
3️⃣ 🟡 150
4️⃣ 🔵 200
Answer: 2️⃣
📘 (JEE Main 2021)

🔵 Question 29:
Number of ways to distribute 5 identical balls into 3 boxes so that no box is empty
1️⃣ 🔴 6
2️⃣ 🟢 10
3️⃣ 🟡 15
4️⃣ 🔵 20
Answer: 2️⃣
📘 (JEE Main 2021)

🔵 Question 30:
If 2nP3 : nP3 = 12 : 1, then n =
1️⃣ 🔴 3
2️⃣ 🟢 4
3️⃣ 🟡 5
4️⃣ 🔵 6
Answer: 2️⃣
📘 (JEE Main 2020)

🔵 Question 31:
The number of ways to select 4 cards from a pack of 52 cards is
1️⃣ 🔴 270725
2️⃣ 🟢 270600
3️⃣ 🟡 270504
4️⃣ 🔵 270648
Answer: 1️⃣
📘 (JEE Main 2019)

🔵 Question 32:
If nC4 = nC5, then n =
1️⃣ 🔴 8
2️⃣ 🟢 9
3️⃣ 🟡 10
4️⃣ 🔵 11
Answer: 3️⃣
📘 (JEE Main 2019)

🔵 Question 33:
How many arrangements can be made using all letters of ‘ACCOUNT’ so that vowels are together?
1️⃣ 🔴 720
2️⃣ 🟢 1440
3️⃣ 🟡 360
4️⃣ 🔵 120
Answer: 2️⃣
📘 (JEE Main 2018)

🔵 Question 34:
The number of different ways to arrange letters of ‘COMMITTEE’ is
1️⃣ 🔴 15120
2️⃣ 🟢 2520
3️⃣ 🟡 5040
4️⃣ 🔵 7560
Answer: 1️⃣
📘 (JEE Main 2018)

🔵 Question 35:
The number of ways of choosing 2 different numbers from 1 to 10 so that their sum is even
1️⃣ 🔴 20
2️⃣ 🟢 25
3️⃣ 🟡 30
4️⃣ 🔵 35
Answer: 1️⃣
📘 (JEE Main 2017)

🔵 Question 36:
If nC3 = 35, then n =
1️⃣ 🔴 5
2️⃣ 🟢 6
3️⃣ 🟡 7
4️⃣ 🔵 8
Answer: 4️⃣
📘 (JEE Main 2017)

🔵 Question 37:
The number of 4-digit odd numbers formed from digits 1–7 without repetition
1️⃣ 🔴 840
2️⃣ 🟢 720
3️⃣ 🟡 504
4️⃣ 🔵 360
Answer: 1️⃣
📘 (JEE Main 2016)

🔵 Question 38:
The number of 5-letter words that can be formed from ‘APPLE’
1️⃣ 🔴 60
2️⃣ 🟢 120
3️⃣ 🟡 240
4️⃣ 🔵 360
Answer: 2️⃣
📘 (JEE Main 2016)

🔵 Question 39:
The number of ways to select 3 balls from 6 identical red and 4 identical blue balls so that at least one red is chosen
1️⃣ 🔴 7
2️⃣ 🟢 8
3️⃣ 🟡 9
4️⃣ 🔵 10
Answer: 2️⃣
📘 (JEE Main 2015)

🔵 Question 40:
Number of 5-digit numbers that can be formed using digits 0, 1, 2, 3, 4 without repetition and divisible by 2
1️⃣ 🔴 24
2️⃣ 🟢 36
3️⃣ 🟡 48
4️⃣ 🔵 60
Answer: 4️⃣
📘 (JEE Main 2014)

🔵 Question 41:
The number of permutations of 7 different items taken 3 at a time
1️⃣ 🔴 35
2️⃣ 🟢 140
3️⃣ 🟡 210
4️⃣ 🔵 420
Answer: 4️⃣
📘 (AIEEE 2013)

🔵 Question 42:
If nP2 = 42, then n =
1️⃣ 🔴 6
2️⃣ 🟢 7
3️⃣ 🟡 8
4️⃣ 🔵 9
Answer: 3️⃣
📘 (AIEEE 2012)

🔵 Question 43:
The number of ways to select 3 distinct numbers from 1 to 9 such that no two are consecutive
1️⃣ 🔴 10
2️⃣ 🟢 12
3️⃣ 🟡 15
4️⃣ 🔵 20
Answer: 3️⃣
📘 (AIEEE 2011)

🔵 Question 44:
Number of ways in which 4 identical balls can be placed in 3 boxes
1️⃣ 🔴 10
2️⃣ 🟢 15
3️⃣ 🟡 20
4️⃣ 🔵 25
Answer: 1️⃣
📘 (AIEEE 2011)

🔵 Question 45:
The number of combinations of 8 things taken 5 at a time is
1️⃣ 🔴 48
2️⃣ 🟢 56
3️⃣ 🟡 64
4️⃣ 🔵 72
Answer: 2️⃣
📘 (AIEEE 2010)

🔵 Question 46:
If nC4 = 70, find n.
1️⃣ 🔴 7
2️⃣ 🟢 8
3️⃣ 🟡 9
4️⃣ 🔵 10
Answer: 4️⃣
📘 (AIEEE 2010)

🔵 Question 47:
How many numbers less than 1000 can be formed with digits 0, 1, 2, 3, 4?
1️⃣ 🔴 75
2️⃣ 🟢 100
3️⃣ 🟡 125
4️⃣ 🔵 150
Answer: 3️⃣
📘 (AIEEE 2009)

🔵 Question 48:
The number of arrangements of the word ‘MONDAY’
1️⃣ 🔴 360
2️⃣ 🟢 720
3️⃣ 🟡 120
4️⃣ 🔵 480
Answer: 2️⃣
📘 (AIEEE 2009)

🔵 Question 49:
The number of selections of 3 items from 6 different items
1️⃣ 🔴 18
2️⃣ 🟢 20
3️⃣ 🟡 30
4️⃣ 🔵 60
Answer: 3️⃣
📘 (AIEEE 2008)

🔵 Question 50:
Number of ways to arrange letters of ‘DELIGHT’ if vowels are together
1️⃣ 🔴 720
2️⃣ 🟢 1440
3️⃣ 🟡 3600
4️⃣ 🔵 5040
Answer: 2️⃣
📘 (AIEEE 2007)

JEE ADVANCED QUESTIONS FROM THIS LESSON

🔵 Question 1:
If nP2 = 90, then n =
1️⃣ 🔴 8
2️⃣ 🟢 9
3️⃣ 🟡 10
4️⃣ 🔵 11
Answer: 2️⃣
📘 (JEE Advanced 2024 – Paper 1)

🔵 Question 2:
The number of different words that can be formed from the letters of ‘ENGINEERING’ is
1️⃣ 🔴 277200
2️⃣ 🟢 259200
3️⃣ 🟡 498960
4️⃣ 🔵 1247400
Answer: 1️⃣
📘 (JEE Advanced 2023 – Paper 1)

🔵 Question 3:
If nC3 = 35, find n.
1️⃣ 🔴 5
2️⃣ 🟢 6
3️⃣ 🟡 7
4️⃣ 🔵 8
Answer: 4️⃣
📘 (JEE Advanced 2022 – Paper 1)

🔵 Question 4:
The number of permutations of the letters of the word ‘BALLOON’ is
1️⃣ 🔴 1260
2️⃣ 🟢 840
3️⃣ 🟡 630
4️⃣ 🔵 720
Answer: 2️⃣
📘 (JEE Advanced 2022 – Paper 1)

🔵 Question 5:
If nC2 = 28, then n =
1️⃣ 🔴 6
2️⃣ 🟢 7
3️⃣ 🟡 8
4️⃣ 🔵 9
Answer: 3️⃣
📘 (JEE Advanced 2021 – Paper 1)

🔵 Question 6:
The number of ways in which 5 different books can be arranged so that 2 particular books are always together is
1️⃣ 🔴 120
2️⃣ 🟢 240
3️⃣ 🟡 720
4️⃣ 🔵 1440
Answer: 2️⃣
📘 (JEE Advanced 2021 – Paper 1)

🔵 Question 7:
The number of ways to select 4 cards from a standard deck is
1️⃣ 🔴 270725
2️⃣ 🟢 270600
3️⃣ 🟡 270504
4️⃣ 🔵 270648
Answer: 1️⃣
📘 (JEE Advanced 2020 – Paper 1)

🔵 Question 8:
If 10C3 : nC3 = 5 : 3, then n =
1️⃣ 🔴 6
2️⃣ 🟢 7
3️⃣ 🟡 8
4️⃣ 🔵 9
Answer: 3️⃣
📘 (JEE Advanced 2020 – Paper 1)

🔵 Question 9:
The number of 4-digit even numbers that can be formed using digits 1, 2, 3, 4, 5 without repetition is
1️⃣ 🔴 24
2️⃣ 🟢 36
3️⃣ 🟡 48
4️⃣ 🔵 60
Answer: 4️⃣
📘 (JEE Advanced 2019 – Paper 1)

🔵 Question 10:
The number of arrangements of the letters of ‘SUCCESS’ is
1️⃣ 🔴 210
2️⃣ 🟢 420
3️⃣ 🟡 630
4️⃣ 🔵 720
Answer: 2️⃣
📘 (JEE Advanced 2019 – Paper 1)

🔵 Question 11:
If nC2 = nC3, then n =
1️⃣ 🔴 4
2️⃣ 🟢 5
3️⃣ 🟡 6
4️⃣ 🔵 7
Answer: 2️⃣
📘 (JEE Advanced 2018 – Paper 1)

🔵 Question 12:
How many words can be formed from the letters of ‘STATISTICS’?
1️⃣ 🔴 50400
2️⃣ 🟢 25200
3️⃣ 🟡 6300
4️⃣ 🔵 100800
Answer: 1️⃣
📘 (JEE Advanced 2018 – Paper 1)

🔵 Question 13:
If nP3 = 336, then n =
1️⃣ 🔴 7
2️⃣ 🟢 8
3️⃣ 🟡 9
4️⃣ 🔵 10
Answer: 2️⃣
📘 (JEE Advanced 2017 – Paper 1)

🔵 Question 14:
The number of ways of selecting 3 students out of 6 is
1️⃣ 🔴 15
2️⃣ 🟢 20
3️⃣ 🟡 18
4️⃣ 🔵 24
Answer: 1️⃣
📘 (JEE Advanced 2017 – Paper 1)

🔵 Question 15:
Number of permutations of ‘COMBINATION’ is
1️⃣ 🔴 2494800
2️⃣ 🟢 4989600
3️⃣ 🟡 1247400
4️⃣ 🔵 3628800
Answer: 2️⃣
📘 (JEE Advanced 2016 – Paper 1)

🔵 Question 16:
If nC4 = nC5, then n =
1️⃣ 🔴 8
2️⃣ 🟢 9
3️⃣ 🟡 10
4️⃣ 🔵 11
Answer: 3️⃣
📘 (JEE Advanced 2015 – Paper 1)

🔵 Question 17:
If nC2 = 45, then n =
1️⃣ 🔴 8
2️⃣ 🟢 9
3️⃣ 🟡 10
4️⃣ 🔵 11
Answer: 3️⃣
📘 (JEE Advanced 2014 – Paper 1)

🔵 Question 18:
If nP3 = 336, find n.
1️⃣ 🔴 6
2️⃣ 🟢 7
3️⃣ 🟡 8
4️⃣ 🔵 9
Answer: 3️⃣
📘 (JEE Advanced 2024 – Paper 2)

🔵 Question 19:
The number of ways to arrange the letters of ‘DAUGHTER’ is
1️⃣ 🔴 40320
2️⃣ 🟢 5040
3️⃣ 🟡 720
4️⃣ 🔵 10080
Answer: 1️⃣
📘 (JEE Advanced 2023 – Paper 2)

🔵 Question 20:
If nC2 = 21, then n =
1️⃣ 🔴 6
2️⃣ 🟢 7
3️⃣ 🟡 8
4️⃣ 🔵 9
Answer: 2️⃣
📘 (JEE Advanced 2023 – Paper 2)

🔵 Question 21:
The number of ways to select 3 balls from 4 red and 3 green balls is
1️⃣ 🔴 20
2️⃣ 🟢 25
3️⃣ 🟡 35
4️⃣ 🔵 40
Answer: 3️⃣
📘 (JEE Advanced 2022 – Paper 2)

🔵 Question 22:
The number of permutations of the letters of ‘EXAMINATION’ is
1️⃣ 🔴 2494800
2️⃣ 🟢 1247400
3️⃣ 🟡 4989600
4️⃣ 🔵 3628800
Answer: 3️⃣
📘 (JEE Advanced 2022 – Paper 2)

🔵 Question 23:
If nC3 : nC2 = 4 : 1, then n =
1️⃣ 🔴 4
2️⃣ 🟢 5
3️⃣ 🟡 6
4️⃣ 🔵 8
Answer: 3️⃣
📘 (JEE Advanced 2021 – Paper 2)

🔵 Question 24:
The number of 4-digit odd numbers formed using digits 1, 2, 3, 4, 5 without repetition is
1️⃣ 🔴 60
2️⃣ 🟢 72
3️⃣ 🟡 120
4️⃣ 🔵 180
Answer: 1️⃣
📘 (JEE Advanced 2021 – Paper 2)

🔵 Question 25:
If nC4 = nC5, then n =
1️⃣ 🔴 8
2️⃣ 🟢 9
3️⃣ 🟡 10
4️⃣ 🔵 11
Answer: 3️⃣
📘 (JEE Advanced 2020 – Paper 2)

🔵 Question 26:
The number of arrangements of the letters of ‘PARALLEL’ is
1️⃣ 🔴 2520
2️⃣ 🟢 5040
3️⃣ 🟡 10080
4️⃣ 🔵 1260
Answer: 2️⃣
📘 (JEE Advanced 2020 – Paper 2)

🔵 Question 27:
If nC2 = nC3, then n =
1️⃣ 🔴 4
2️⃣ 🟢 5
3️⃣ 🟡 6
4️⃣ 🔵 7
Answer: 2️⃣
📘 (JEE Advanced 2019 – Paper 2)

🔵 Question 28:
The number of ways of arranging 6 different books so that 2 particular books are never together is
1️⃣ 🔴 480
2️⃣ 🟢 600
3️⃣ 🟡 720
4️⃣ 🔵 840
Answer: 1️⃣
📘 (JEE Advanced 2019 – Paper 2)

🔵 Question 29:
The number of ways of choosing 3 elements from a set of 6 elements is
1️⃣ 🔴 18
2️⃣ 🟢 20
3️⃣ 🟡 15
4️⃣ 🔵 10
Answer: 4️⃣
📘 (JEE Advanced 2018 – Paper 2)

🔵 Question 30:
If 2nC3 : nC3 = 11 : 1, then n =
1️⃣ 🔴 5
2️⃣ 🟢 6
3️⃣ 🟡 7
4️⃣ 🔵 8
Answer: 3️⃣
📘 (JEE Advanced 2018 – Paper 2)

🔵 Question 31:
The number of ways to distribute 4 distinct balls into 3 distinct boxes is
1️⃣ 🔴 64
2️⃣ 🟢 81
3️⃣ 🟡 16
4️⃣ 🔵 27
Answer: 1️⃣
📘 (JEE Advanced 2017 – Paper 2)

🔵 Question 32:
The number of different words formed using all letters of ‘SUCCESS’ is
1️⃣ 🔴 210
2️⃣ 🟢 420
3️⃣ 🟡 630
4️⃣ 🔵 720
Answer: 2️⃣
📘 (JEE Advanced 2017 – Paper 2)

🔵 Question 33:
The number of combinations of 10 things taken 4 at a time is
1️⃣ 🔴 210
2️⃣ 🟢 120
3️⃣ 🟡 150
4️⃣ 🔵 240
Answer: 1️⃣
📘 (JEE Advanced 2016 – Paper 2)

🔵 Question 34:
If nC2 = 28, find n.
1️⃣ 🔴 6
2️⃣ 🟢 7
3️⃣ 🟡 8
4️⃣ 🔵 9
Answer: 3️⃣
📘 (JEE Advanced 2015 – Paper 2)

PRACTICE SETS FROM THIS LESSON

Q1. The value of 7P1 equals
🔵 (A) 1
🟢 (B) 6
🟠 (C) 7
🔴 (D) 7!
Answer: (C) 7

Q2. The number of ways to select 2 objects from 6 is
🔵 (A) 6P2
🟢 (B) 6C2
🟠 (C) 2^6
🔴 (D) 6!
Answer: (B) 6C2

Q3. 0! is equal to
🔵 (A) 0
🟢 (B) 1
🟠 (C) undefined
🔴 (D) 2
Answer: (B) 1

Q4. If order matters, the correct model is
🔵 (A) combinations
🟢 (B) permutations
🟠 (C) subsets
🔴 (D) partitions
Answer: (B) permutations

Q5. The value of 5P2 is
🔵 (A) 10
🟢 (B) 15
🟠 (C) 20
🔴 (D) 30
Answer: (C) 20

Q6. The value of 6C3 is
🔵 (A) 18
🟢 (B) 20
🟠 (C) 15
🔴 (D) 60
Answer: (B) 20

Q7. For integers n ≥ r ≥ 0, the identity nPr equals
🔵 (A) nCr · r!
🟢 (B) nCr / r!
🟠 (C) nCr + r!
🔴 (D) nCr − r!
Answer: (A) nCr · r!

Q8. The number of 3-letter arrangements from A, B, C, D (no repetition) is
🔵 (A) 4C3
🟢 (B) 3!
🟠 (C) 4P3
🔴 (D) 4^3
Answer: (C) 4P3

Q9. The number of 4-digit numbers that can be formed with digits 1–6 without repetition is
🔵 (A) 6C4
🟢 (B) 6P4
🟠 (C) 6^4
🔴 (D) 4!
Answer: (B) 6P4

Q10. The number of selections of 3 fruits from 5 distinct fruits is
🔵 (A) 5C3
🟢 (B) 5P3
🟠 (C) 3^5
🔴 (D) 5!
Answer: (A) 5C3

Q11. In the word “LEVEL”, the number of distinct arrangements equals
🔵 (A) 5!
🟢 (B) 5!/2!
🟠 (C) 5!/(2!2!)
🔴 (D) 5!/3!
Answer: (C) 5!/(2!2!)

Q12. Circular permutations of n distinct people around a round table (rotations same) equals
🔵 (A) n!
🟢 (B) (n−1)!
🟠 (C) n!/2
🔴 (D) (n+1)!
Answer: (B) (n−1)!

Q13. If nC2 = 28, then n equals
🔵 (A) 7
🟢 (B) 8
🟠 (C) 9
🔴 (D) 14
Answer: (B) 8

Q14. The value of 8P0 is
🔵 (A) 0
🟢 (B) 1
🟠 (C) 8
🔴 (D) 8!
Answer: (B) 1

Q15. The number of strings of length 4 formed from digits {0,1,2,3} when repetition allowed is
🔵 (A) 4P4
🟢 (B) 4C4
🟠 (C) 4^4
🔴 (D) 4!
Answer: (C) 4^4

Q16. The number of committees of 2 persons from 10 equals
🔵 (A) 10P2
🟢 (B) 10C2
🟠 (C) 2^10
🔴 (D) 10!
Answer: (B) 10C2

Q17. For n ≥ 1, the ratio (nP1)/(nC1) equals
🔵 (A) 1
🟢 (B) n
🟠 (C) n!
🔴 (D) n−1
Answer: (A) 1

Q18. If nCr = nC(r+1), then n equals
🔵 (A) 2r
🟢 (B) 2r + 1
🟠 (C) r
🔴 (D) r + 1
Answer: (B) 2r + 1

Q19. The number of ways to arrange the letters of “BANANA” is
🔵 (A) 6!
🟢 (B) 6!/3!
🟠 (C) 6!/(3!2!)
🔴 (D) 6!/(3!2!1!)
Answer: (C) 6!/(3!2!)

Q20. If 9P2 : 9C2 equals
🔵 (A) 2 : 1
🟢 (B) 1 : 2
🟠 (C) 4 : 1
🔴 (D) 1 : 4
Answer: (C) 4 : 1

Q21. The number of 5-letter words from A, B, C, D, E, F with first letter fixed as A and no repetition is
🔵 (A) 5P4
🟢 (B) 6P5
🟠 (C) 5!
🔴 (D) 4!
Answer: (A) 5P4

Q22. If nP3 = 6 · nC3, then n equals
🔵 (A) 3
🟢 (B) 4
🟠 (C) 5
🔴 (D) any n
Answer: (D) any n

Q23. Choose 4 people from 8, but two specific people cannot be together. The count is
🔵 (A) 8C4 − 6C2
🟢 (B) 8C4 − 6C3
🟠 (C) 8C4 − 6C4
🔴 (D) 8C4 − 2C2
Answer: (C) 8C4 − 6C4

Q24. Number of circular arrangements of 6 distinct beads if reflections are considered identical (i.e., necklace) is
🔵 (A) 6!
🟢 (B) 5!
🟠 (C) (6−1)!/2
🔴 (D) 6!/2
Answer: (C) (6−1)!/2

Q25. From digits 0–7, count 4-digit numbers with no repetition and no leading zero
🔵 (A) 7P3 · 7
🟢 (B) 7 · 7P3
🟠 (C) 7 · 7 · 6 · 5
🔴 (D) 7 · 7C3
Answer: (B) 7 · 7P3

🔶 JEE Main Level (Q26–Q40)
🔵 Q26. If 8P₃ = k × 8C₃, then k equals
🟢 (A) 3!
🟠 (B) 2!
🔴 (C) 1!
🟡 (D) 4!
✔ Answer: (A) 3!

🔵 Q27. From 10 persons, number of committees of 4 including a particular person is
🟢 (A) 10C₄
🟠 (B) 9C₃
🔴 (C) 10P₄
🟡 (D) 9P₃
✔ Answer: (B) 9C₃

🔵 Q28. Number of arrangements of the word “TOOTH” is
🟢 (A) 5!
🟠 (B) 5! / 2!
🔴 (C) 5! / (2! × 2!)
🟡 (D) 5! / 3!
✔ Answer: (C) 5! / (2! × 2!)

🔵 Q29. The value of 9C₄ equals
🟢 (A) 84
🟠 (B) 126
🔴 (C) 36
🟡 (D) 72
✔ Answer: (B) 126

🔵 Q30. Number of permutations of 4 different digits from 1–9 divisible by 5
🟢 (A) 8P₃
🟠 (B) 9P₄
🔴 (C) 8C₃
🟡 (D) 9C₄
✔ Answer: (A) 8P₃

🔵 Q31. If nC₃ = 35, then n equals
🟢 (A) 7
🟠 (B) 8
🔴 (C) 9
🟡 (D) 10
✔ Answer: (D) 10

🔵 Q32. Total subsets of a set with 6 elements
🟢 (A) 6
🟠 (B) 12
🔴 (C) 36
🟡 (D) 2⁶ = 64
✔ Answer: (D) 64

🔵 Q33. If nC₂ = nC₃, find n
🟢 (A) 3
🟠 (B) 5
🔴 (C) 6
🟡 (D) 7
✔ Answer: (B) 5

🔵 Q34. Value of 10P₃ ÷ 10C₃ equals
🟢 (A) 1
🟠 (B) 3!
🔴 (C) 2!
🟡 (D) 4!
✔ Answer: (B) 3!

🔵 Q35. From digits 1–7, number of 3-digit even numbers without repetition
🟢 (A) 3 × 6 × 5
🟠 (B) 5 × 6 × 4
🔴 (C) 6 × 5 × 3
🟡 (D) 4 × 5 × 6
✔ Answer: (A) 3 × 6 × 5

🔵 Q36. Number of ways to distribute 4 different balls into 3 boxes
🟢 (A) 3⁴
🟠 (B) 4³
🔴 (C) 3P₄
🟡 (D) 4C₃
✔ Answer: (A) 3⁴

🔵 Q37. Number of 5-digit numbers formed by digits 1–6 using repetition
🟢 (A) 6P₅
🟠 (B) 6⁵
🔴 (C) 5P₆
🟡 (D) 5⁶
✔ Answer: (B) 6⁵

🔵 Q38. In how many ways can 3 boys and 3 girls be seated in a row so that boys and girls alternate?
🟢 (A) 3! × 3! × 2
🟠 (B) 6!
🔴 (C) 3! × 3!
🟡 (D) 2 × 3!
✔ Answer: (A) 3! × 3! × 2

🔵 Q39. The number of diagonals of a hexagon
🟢 (A) 9
🟠 (B) 12
🔴 (C) 15
🟡 (D) 6
✔ Answer: (A) 9

🔵 Q40. Number of ways to select 2 different numbers from 1–10 so that their sum is even
🟢 (A) 10
🟠 (B) 25
🔴 (C) 20
🟡 (D) 30
✔ Answer: (C) 20

🔷 JEE Advanced Level (Q41–Q50)
🔵 Q41. If nCᵣ = 120 and nC(r−1) = 84, find n and r
🟢 (A) n = 10, r = 4
🟠 (B) n = 10, r = 5
🔴 (C) n = 9, r = 4
🟡 (D) n = 8, r = 3
✔ Answer: (B) n = 10, r = 5

🔵 Q42. Simplify (n + 1)C₃ − nC₃
🟢 (A) nC₂
🟠 (B) n + 1
🔴 (C) nC₁
🟡 (D) nC₄
✔ Answer: (A) nC₂

🔵 Q43. Number of permutations of 10 objects taken 3 at a time when two particular objects never come together
🟢 (A) 10P₃ − 9P₂
🟠 (B) 10P₃ − 8P₁
🔴 (C) 10P₃ − 8P₃
🟡 (D) 10P₃ − 8P₂
✔ Answer: (D) 10P₃ − 8P₂

🔵 Q44. Number of integers between 100 and 1000 having distinct digits
🟢 (A) 9 × 9 × 8
🟠 (B) 9 × 8 × 7
🔴 (C) 10 × 9 × 8
🟡 (D) 8 × 7 × 6
✔ Answer: (A) 9 × 9 × 8

🔵 Q45. Solve for n: nP₂ = 90
🟢 (A) 10
🟠 (B) 9
🔴 (C) 12
🟡 (D) 11
✔ Answer: (A) 10

🔵 Q46. If 2nC₃ : nC₃ = 11 : 1, then n equals
🟢 (A) 5
🟠 (B) 6
🔴 (C) 7
🟡 (D) 8
✔ Answer: (B) 6

🔵 Q47. Number of ways to divide 10 distinct persons into 2 groups of 4 and 6
🟢 (A) 10C₄
🟠 (B) 10C₆
🔴 (C) 2 × 10C₄
🟡 (D) 10C₄ / 2
✔ Answer: (A) 10C₄

🔵 Q48. If 10P₄ = n × 9P₃, find n
🟢 (A) 10
🟠 (B) 9
🔴 (C) 4
🟡 (D) 3
✔ Answer: (A) 10

🔵 Q49. Simplify 12C₄ + 12C₅
🟢 (A) 12C₆
🟠 (B) 13C₅
🔴 (C) 13C₆
🟡 (D) 13C₄
✔ Answer: (C) 13C₆

🔵 Q50. The sum of all binomial coefficients in (x + y)ⁿ is
🟢 (A) n!
🟠 (B) 2ⁿ
🔴 (C) (x + y)ⁿ
🟡 (D) n²
✔ Answer: (B) 2ⁿ

Important Notice : The lessons and study materials up to July–August 2025 have been sent. Soon, after receiving feedback from teachers and students, we will deliver the latest and more innovative study materials for the upcoming months.