Class 11 : Physics (In English) – Chapter 14: Waves
EXPLANATION & SUMMARY
🔷 EXPLANATION
🌟 1. Introduction to Waves
🔵 Many natural phenomena — sound, ripples, or light — involve transfer of energy from one point to another through oscillations.
🟢 A wave is defined as a disturbance that travels through a medium, transferring energy and momentum without actual transfer of matter.
💡 Example: When a stone is dropped into water, circular ripples move outward but water particles only vibrate about fixed positions.
🔹 2. Types of Waves
💡 Waves can be broadly divided into three categories:
(a) Mechanical Waves
✏️ Require a material medium for their propagation.
✔️ Examples: Sound waves, water waves, seismic waves.
(b) Electromagnetic Waves
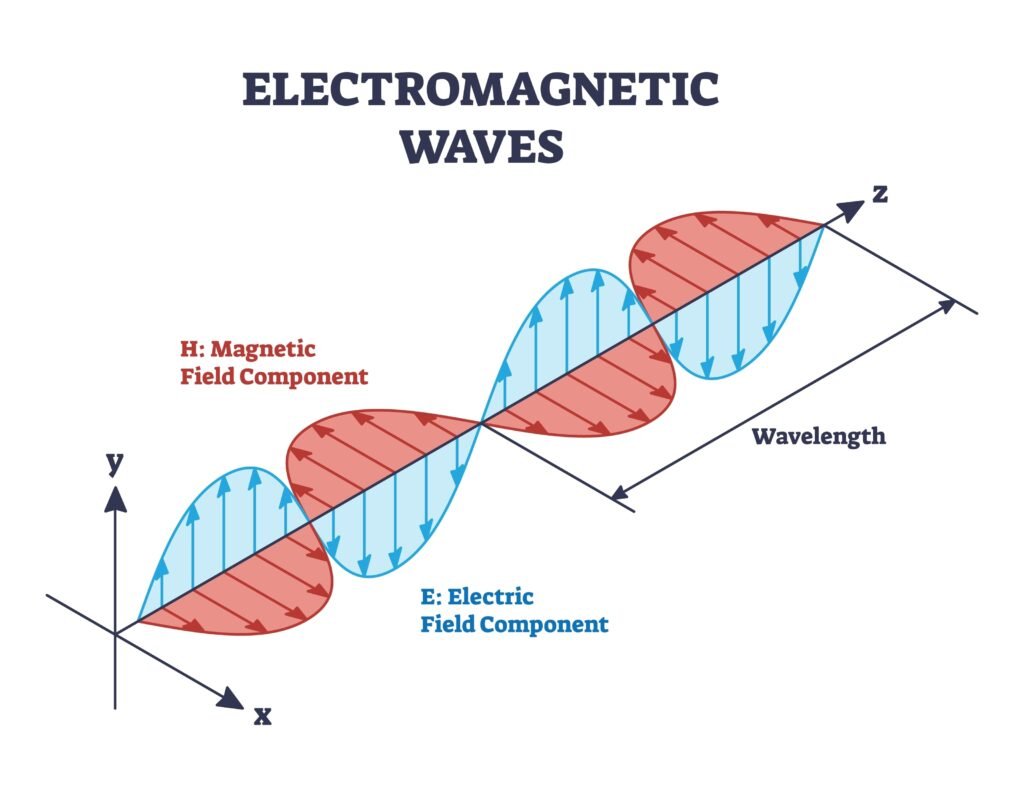
✏️ Do not require a medium; can travel through vacuum.
✔️ Examples: Light, radio, X-rays, microwaves.
(c) Matter Waves
✏️ Associated with microscopic particles like electrons.
✔️ Example: de Broglie waves in quantum mechanics.
🔹 3. Wave Motion
🟢 Wave motion is the propagation of a disturbance through a medium without any actual motion of particles along the direction of energy transfer.
💡 Each particle of the medium executes oscillations about its mean position.
✔️ Energy is transmitted through these oscillations, but mass is not transported.
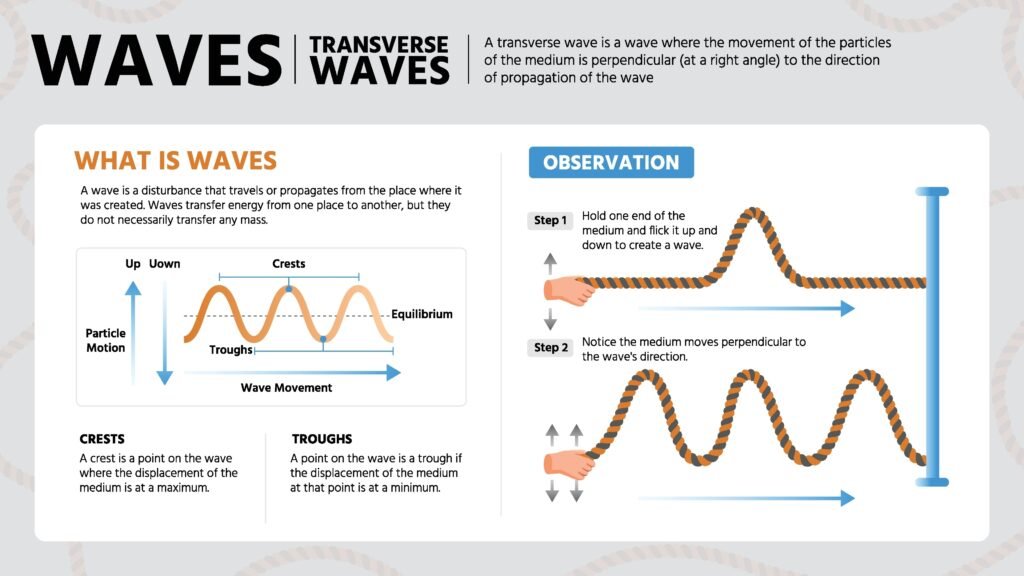
🔹 4. Transverse and Longitudinal Waves
Transverse Waves:
🔵 Particles of the medium vibrate perpendicular to the direction of propagation.
➡️ Examples: Light waves, waves on a stretched string.
✔️ Crests and troughs are formed.
Longitudinal Waves:
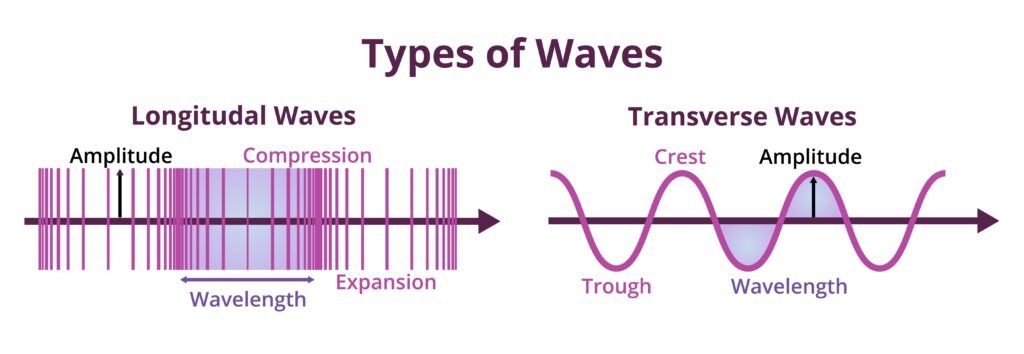
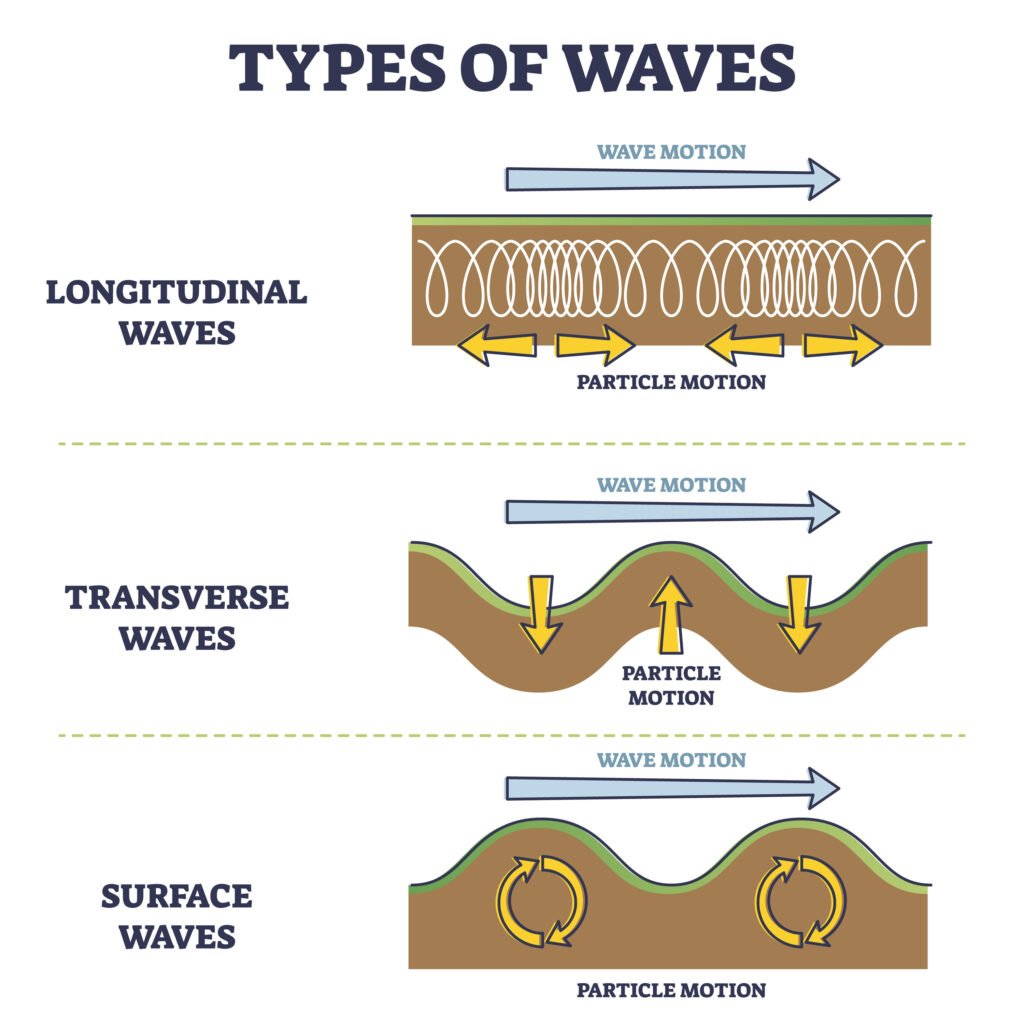
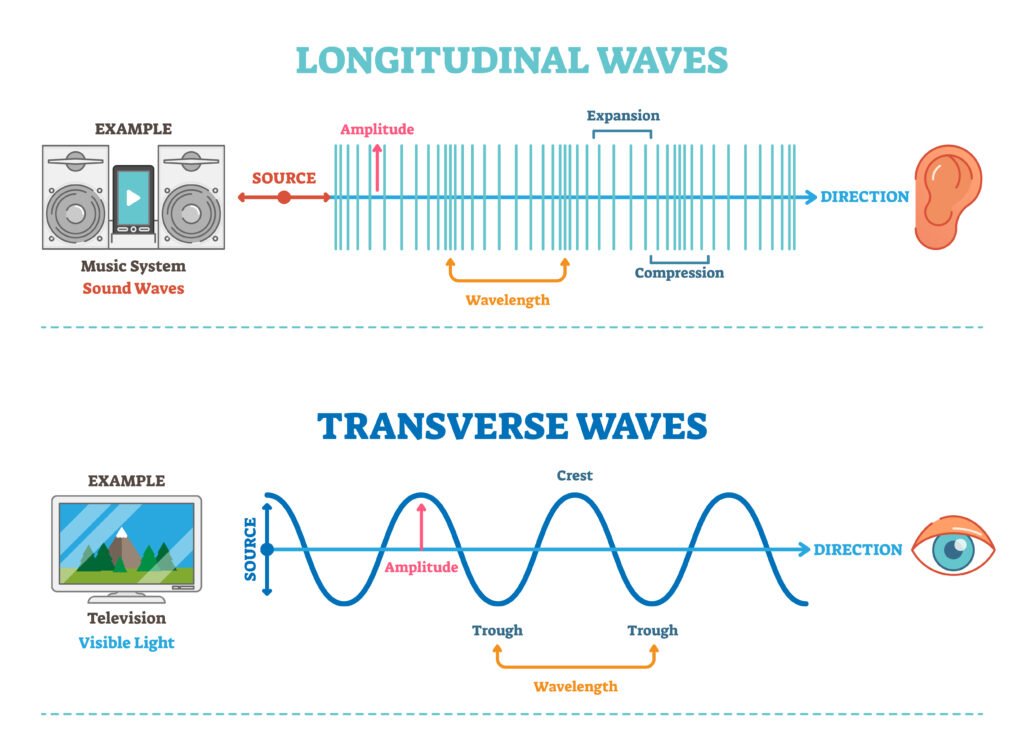
🟢 Particles vibrate parallel to the direction of wave travel.
➡️ Examples: Sound waves in air, compressions and rarefactions in springs.
✔️ Alternate regions of high and low pressure are formed.
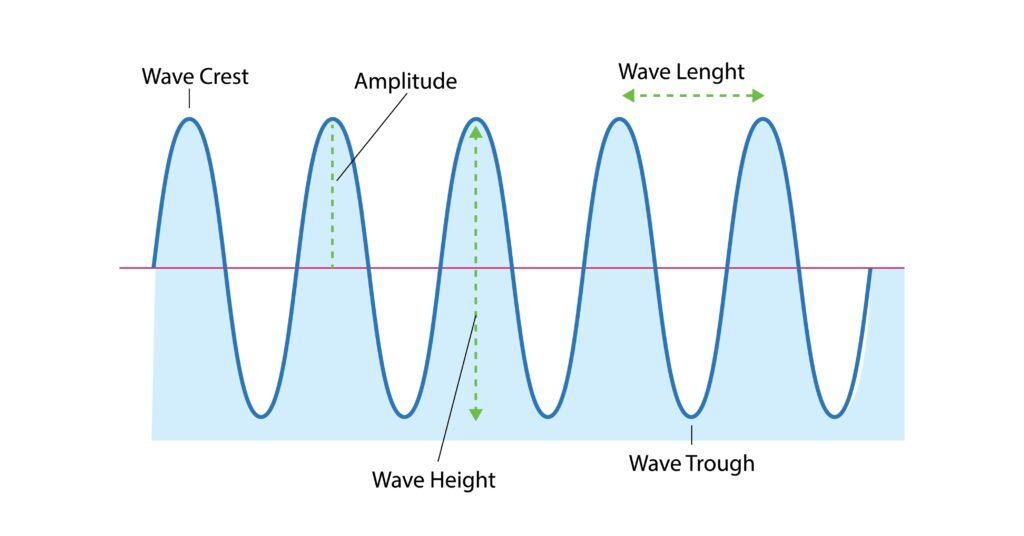
🔹 5. Wavelength, Frequency, and Speed
✏️ Wavelength (λ): Distance between two consecutive crests, troughs, compressions, or rarefactions.
✏️ Frequency (ν): Number of oscillations per second.
✏️ Time period (T): Time taken for one complete oscillation (T = 1/ν).
✏️ Wave speed (v): Distance travelled by wave per second.
💡 Relation: v = λν
✔️ Example: For ν = 200 Hz and λ = 1.5 m, v = 200 × 1.5 = 300 m/s.
🔹 6. Displacement Equation of a Progressive Wave
A progressive wave moving along x-axis can be written as:
y(x, t) = A sin(kx − ωt + ϕ)
where
A = Amplitude
k = Wave number = 2π/λ
ω = Angular frequency = 2πν
ϕ = Phase constant
💡 Negative sign (−ωt) shows wave moving in positive x-direction.
If wave moves in opposite direction: y = A sin(kx + ωt + ϕ).
🔹 7. Phase and Phase Difference
🟢 Phase (Φ): The argument (kx − ωt + ϕ) represents the instantaneous state of vibration.
✏️ Phase difference: ΔΦ = (2π/λ) × x
✔️ ΔΦ = 0 → same phase; ΔΦ = π → opposite phase.
🔹 8. Particle Velocity and Acceleration in a Wave
For y = A sin(kx − ωt):
➡️ Velocity: v = dy/dt = −Aω cos(kx − ωt)
➡️ Acceleration: a = dv/dt = −Aω² sin(kx − ωt) = −ω²y
💡 Velocity leads displacement by π/2, while acceleration is opposite in phase to displacement.
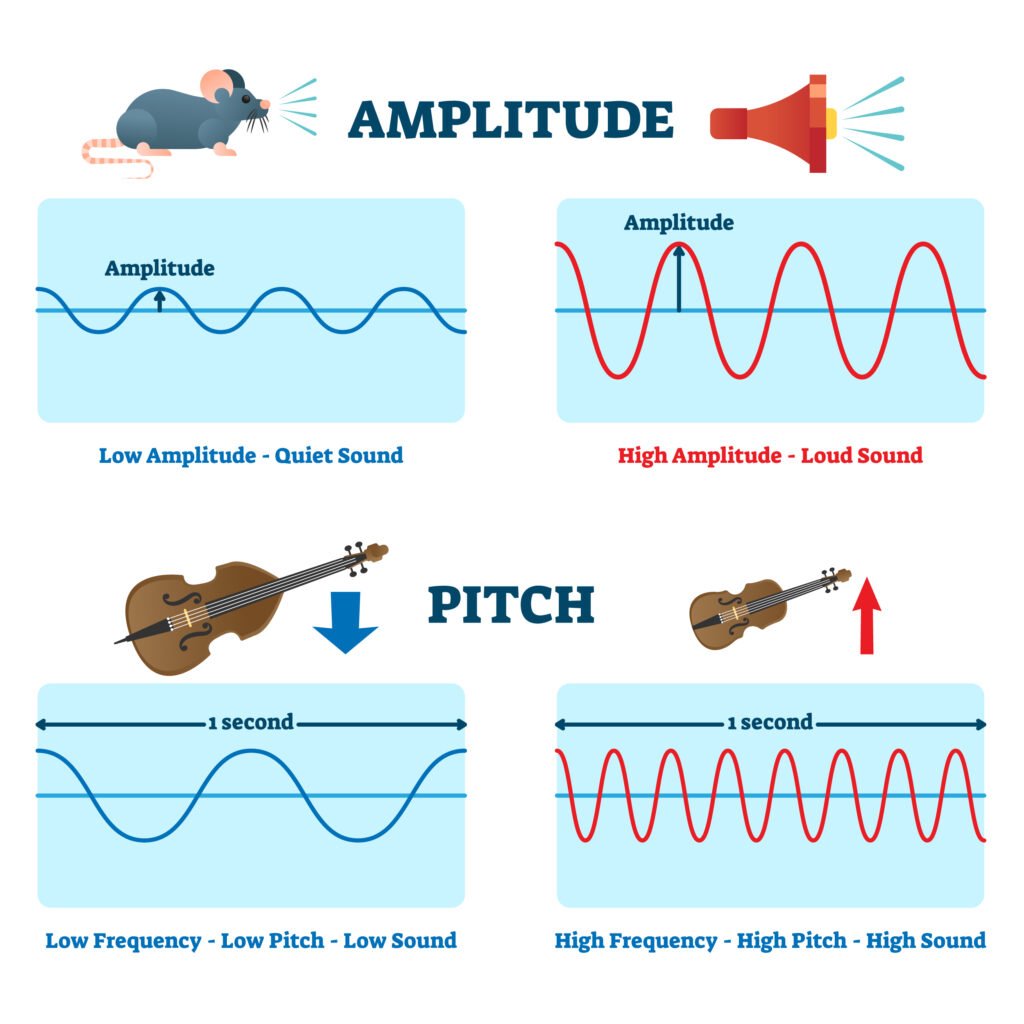
🔹 9. Energy Transfer in a Wave
When a wave travels, both kinetic and potential energies are carried through the medium.
✔️ Average energy per unit volume:
E = (1/2)ρA²ω²
✔️ Energy is directly proportional to amplitude².
➡️ Doubling amplitude increases energy fourfold.
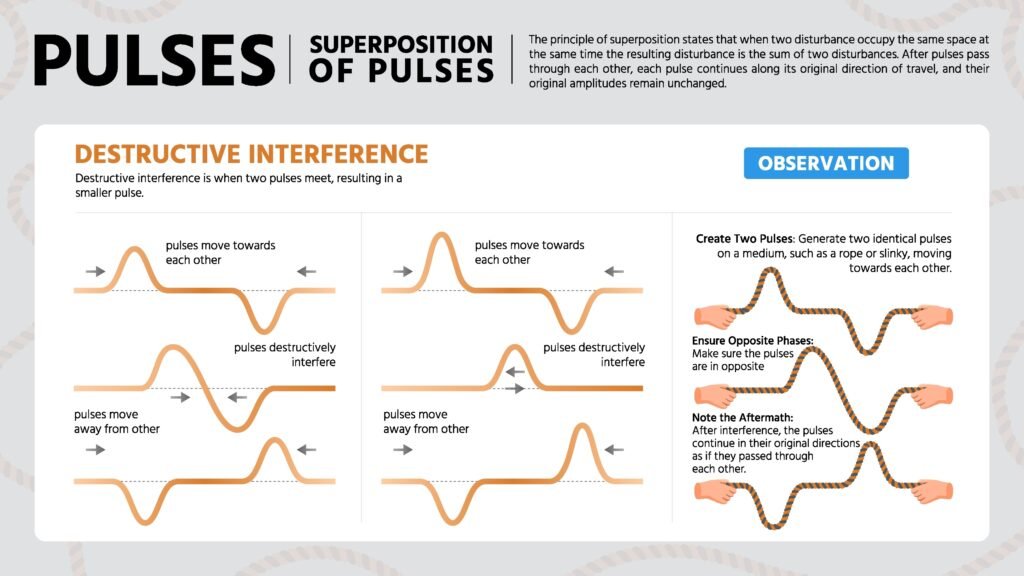
🔹 10. Principle of Superposition of Waves
💡 When two or more waves pass through the same point, resultant displacement is the algebraic sum of individual displacements.
If y₁ = A₁ sin(ωt) and y₂ = A₂ sin(ωt + ϕ):
Resultant wave, y = A sin(ωt + θ)
where A = √(A₁² + A₂² + 2A₁A₂ cosϕ)
✔️ Explains interference and stationary wave formation.
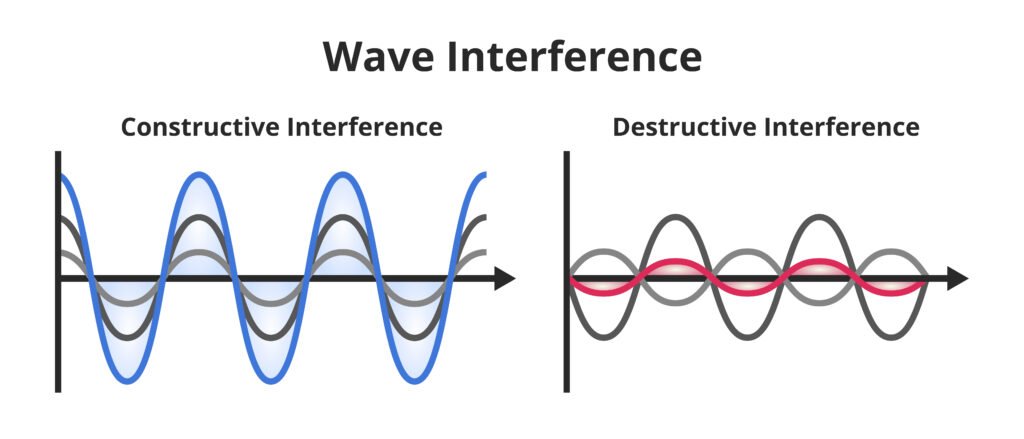
🔹 11. Interference of Waves
🟢 Constructive Interference: When two waves meet in phase (ϕ = 0), amplitude increases.
🔵 Destructive Interference: When they meet in opposite phase (ϕ = π), amplitude decreases.
✔️ Interference modifies intensity distribution in the region.
🔹 12. Stationary or Standing Waves
💡 When two waves of the same frequency and amplitude move in opposite directions and superpose, a stationary wave is formed.
Equation: y = 2A sin(kx) cos(ωt)
✔️ Nodes: Points where displacement is always zero (sin kx = 0).
✔️ Antinodes: Points of maximum displacement (sin kx = ±1).
✔️ Distance between consecutive nodes (or antinodes) = λ/2.
Energy does not propagate; it remains trapped between nodes.
🔹 13. Stationary Waves in a String
For a string fixed at both ends,
Allowed wavelengths: λₙ = 2L/n
Allowed frequencies: νₙ = n(v/2L) where n = 1, 2, 3,…
✔️ n = 1 → Fundamental frequency
✔️ n = 2 → First overtone
✔️ n = 3 → Second overtone
🔹 14. Speed of Transverse Waves on a String
For a string under tension T and linear density μ,
v = √(T/μ)
💡 Example: If T = 100 N and μ = 0.01 kg/m,
v = √(100 / 0.01) = √10000 = 100 m/s.
✔️ Wave speed increases with tension and decreases with mass per unit length.
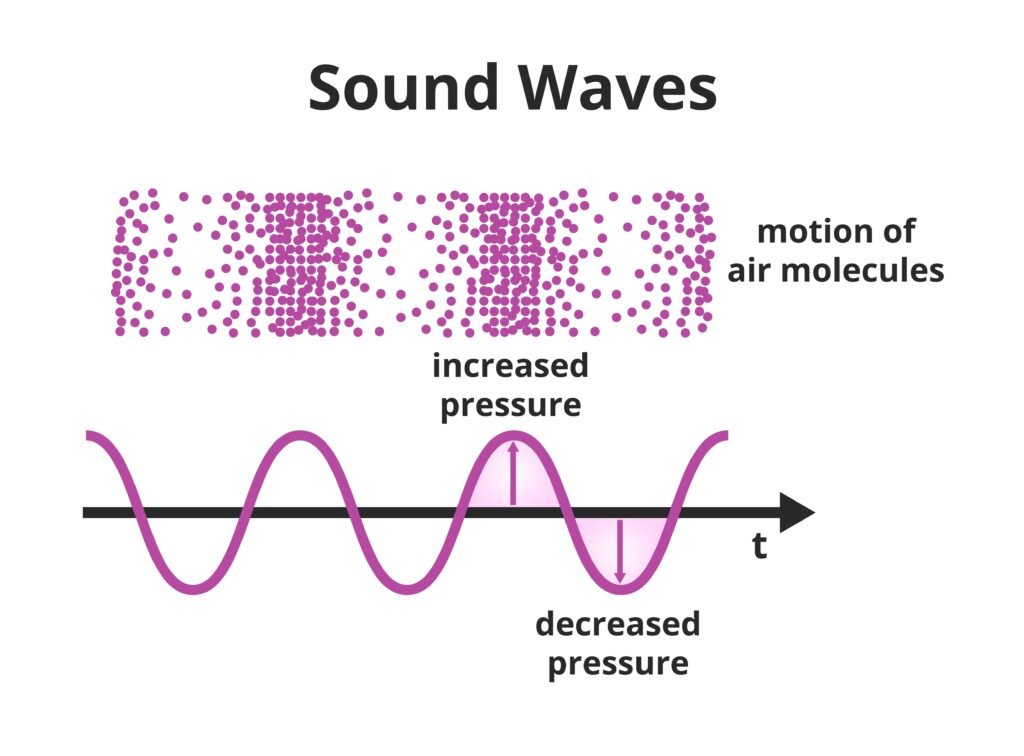
🔹 15. Sound Waves
Sound waves are longitudinal mechanical waves consisting of compressions and rarefactions.
💡 Speed of sound in a gas: v = √(γP/ρ)
where
γ = ratio of specific heats,
P = pressure,
ρ = density.
✔️ Sound travels fastest in solids, slower in liquids, slowest in gases.
✔️ v increases with temperature (v ∝ √T).
🔹 16. Beats
💡 When two waves of slightly different frequencies interfere, the resultant amplitude varies periodically with time.
Beat frequency: νᵦ = |ν₁ − ν₂|
✔️ Produces alternating loud and faint sounds (beats).
✔️ Useful for measuring small frequency differences.
🔹 17. Doppler Effect
💡 The apparent change in frequency of waves due to relative motion between source and observer is called the Doppler effect.
Formula for sound:
ν’ = ν (v ± v₀) / (v ∓ vₛ)
where
v = speed of sound,
v₀ = velocity of observer,
vₛ = velocity of source.
✔️ (+) when approaching; (−) when receding.
✔️ Applications: radar, astronomy, and speed detection.
🔹 18. Reflection and Refraction of Waves
When a wave strikes a boundary:
Reflection: The wave bounces back into the same medium.
Refraction: The wave enters another medium, changing speed and wavelength but not frequency.
💡 Both follow the law of reflection and Snell’s law for refraction.
🔹 19. Power and Intensity of Waves
✏️ Power: Rate of energy transfer by a wave.
✏️ Intensity (I): Power per unit area.
💡 Intensity is directly proportional to square of amplitude: I ∝ A²
✔️ Double amplitude → Intensity becomes four times.
🔹 20. Relations between Wave Quantities
✳️ Wave velocity: v = λν
✳️ Wave number: k = 2π/λ
✳️ Angular frequency: ω = 2πν
✳️ Phase difference: ΔΦ = (2π/λ) × Δx
✔️ These relations connect all measurable properties of a wave — speed, wavelength, and frequency.
🟢 SUMMARY (~300 words)
A wave is a disturbance that transfers energy through a medium or space without transport of matter. Mechanical waves need a medium, while electromagnetic waves do not.
Waves are transverse when particles oscillate perpendicular to direction of propagation, and longitudinal when particles oscillate parallel. The main parameters are amplitude (A), wavelength (λ), frequency (ν), and speed (v = λν).
A progressive wave is represented by y = A sin(kx − ωt). Energy in a wave is proportional to A². The principle of superposition states that the resultant displacement is the algebraic sum of individual displacements. Interference occurs when waves overlap — leading to constructive or destructive interference.
Two identical waves moving oppositely form stationary waves, given by y = 2A sin(kx) cos(ωt), producing nodes and antinodes. For a string of length L, allowed frequencies are νₙ = n(v/2L). The speed of a transverse wave is v = √(T/μ), and that of sound is v = √(γP/ρ).
The Doppler effect describes the change in observed frequency due to relative motion of source and observer. When two waves of nearby frequencies combine, beats of frequency νᵦ = |ν₁ − ν₂| are produced.
Energy, intensity, reflection, and refraction together explain how waves carry energy and form the foundation for acoustics, optics, and communication technology.
🔻 QUICK RECAP (6 Key Points)
1️⃣ Wave equation: y = A sin(kx − ωt)
2️⃣ Wave speed: v = λν
3️⃣ Transverse wave on string: v = √(T/μ)
4️⃣ Speed of sound: v = √(γP/ρ)
5️⃣ Beat frequency: νᵦ = |ν₁ − ν₂|
6️⃣ Doppler effect: ν’ = ν (v ± v₀)/(v ∓ vₛ)
————————————————————————————————————————————————————————————————————————————
QUESTIONS FROM TEXTBOOK
🔵 Question 14.1
A string of mass 2.50 kg is under a tension of 200 N. The length of the stretched string is 20.0 m. If the transverse jerk is struck at one end of the string, how long does the disturbance take to reach the other end?
Answer
🟢 Step 1 (linear mass density): μ = m/L = 2.50 / 20.0 = 0.125 kg m⁻¹
🟡 Step 2 (wave speed on string): v = √(T/μ) = √(200 / 0.125) = √1600 = 40 m s⁻¹
🟠 Step 3 (time): t = L/v = 20.0 / 40 = 0.5 s
✔️ Final: 0.5 s
🔵 Question 14.2
A stone is dropped from a tower of height 300 m into water. When is the splash heard at the top? (Speed of sound in air = 340 m s⁻¹; g = 9.8 m s⁻²)
Answer
🟢 Step 1 (fall time): h = ½ g t₁² ⇒ t₁ = √(2h/g) = √(600/9.8) = 7.82 s
🟡 Step 2 (sound travel time): t₂ = 300 / 340 = 0.882 s
🟠 Step 3 (total time): t = t₁ + t₂ = 7.82 + 0.882 = 8.70 s
✔️ Final: 8.7 s
🔵 Question 14.3
A steel wire of length 12.0 m and mass 2.10 kg is stretched so that the speed of a transverse wave equals 343 m s⁻¹ (speed of sound in dry air at 20 °C). What tension is required?
Answer
🟢 Step 1 (μ): μ = m/L = 2.10/12.0 = 0.175 kg m⁻¹
🟡 Step 2 (tension): v = √(T/μ) ⇒ T = μ v² = 0.175 × (343)²
🟠 Step 3 (compute): T = 0.175 × 117649 = 2.06 × 10⁴ N
✔️ Final: ≈ 2.06 × 10⁴ N
🔵 Question 14.4
Use the formula v = √(γP / ρ) to explain why the speed of sound in air:
(a) is independent of pressure,
(b) increases with temperature, and
(c) increases with humidity.
Answer:
🟢 Step 1: Relation between pressure, density, and temperature
For an ideal gas,
P = (ρRT) / M
where
P = pressure, ρ = density, R = universal gas constant,
T = temperature, M = molar mass of air.
🟢 Step 2: Substitute in formula for speed of sound
v = √(γP / ρ)
v = √[γ (ρRT / M) / ρ]
v = √(γRT / M)
🟢 Step 3: Analyze dependence
(a) Independence from pressure
Pressure P cancels out completely in the expression v = √(γRT / M).
Hence, the speed of sound does not depend on pressure at all.
(b) Increase with temperature
In the formula v = √(γRT / M),
v ∝ √T
As temperature increases, √T increases, so speed of sound increases with temperature.
(c) Increase with humidity
When humidity increases, water vapour (which is lighter) replaces heavier air molecules (like N₂ and O₂).
This decreases the effective molar mass M of air.
Since v ∝ 1/√M, a smaller M means a larger v.
Therefore, speed of sound increases with humidity.
✔️ Final Answer:
(a) Independent of pressure
(b) Increases with temperature
(c) Increases with humidity
🔵 Question 14.5
A travelling wave in 1-D has form y = f(x ± vt). Is the converse true for the following?
(a) (x − vt)², (b) log[(x + vt)/x₀], (c) 1/(x + vt)
Answer
🟢 Criterion: y must depend only on (x ± vt).
🟡 Check each:
(a) Depends on (x − vt) → travelling wave.
(b) Depends on (x + vt) → travelling wave.
(c) Depends on (x + vt) → travelling wave.
✔️ Final: All three can represent travelling waves.
🔵 Question 14.6
A bat emits ultrasonic sound of frequency 1000 kHz in air. On meeting a water surface, find the wavelength of (a) reflected sound in air, (b) transmitted sound in water. (v_air = 340 m s⁻¹, v_water = 1486 m s⁻¹)
Answer
🟢 Given: f = 1000 kHz = 1.0 × 10⁶ Hz
🟡 (a) λ_reflected (air): λ₁ = v_air / f = 340 / 10⁶ = 3.4 × 10⁻⁴ m
🟠 (b) λ_transmitted (water): λ₂ = v_water / f = 1486 / 10⁶ = 1.486 × 10⁻³ m (≈ 1.49 mm)
✔️ Final: (a) 3.4 × 10⁻⁴ m, (b) 1.49 × 10⁻³ m
🔵 Question 14.7
An ultrasonic scanner operates at 4.2 MHz in a tissue where sound speed is 1.7 km s⁻¹. What is the wavelength?
Answer
🟢 Step 1 (units): v = 1.7 km s⁻¹ = 1.7 × 10³ m s⁻¹; f = 4.2 × 10⁶ Hz
🟡 Step 2 (λ): λ = v/f = (1.7 × 10³)/(4.2 × 10⁶) = 4.05 × 10⁻⁴ m
✔️ Final: 0.405 mm
🔵 Question 14.8
A transverse harmonic wave on a string is:
y(x, t) = 3.0 sin(36 t + 0.018 x + π/4), where x, y in cm and t in s.
Find: (a) type and direction, (b) amplitude & frequency, (c) wavelength & speed, (d) initial phase at origin, (e) least distance between two crests.
Answer
🟢 (a) Form sin(ωt + kx + φ) ⇒ travelling wave in −x direction.
🟡 (b) Amplitude A = 3.0 cm; ω = 36 s⁻¹ ⇒ f = ω/2π = 5.73 Hz.
🟠 (c) k = 0.018 cm⁻¹ ⇒ λ = 2π/k = 349 cm = 3.49 m;
v = ω/k = 2000 cm s⁻¹ = 20 m s⁻¹.
🔵 (d) Initial phase φ = π/4.
🟣 (e) Least crest-to-crest distance = λ = 3.49 m.
✔️ Final: Travelling wave (−x), A = 3.0 cm, f = 5.73 Hz, λ = 3.49 m, v = 20 m s⁻¹, φ = π/4, crest spacing = 3.49 m.
🔵 Question 14.9
For the wave described in Exercise 14.8, plot the displacement (y) versus time (t) graphs for x = 0, 2, and 4 cm. What are the shapes of these graphs? In which aspects does the oscillatory motion in a travelling wave differ from one point to another: amplitude, frequency, or phase?
Answer
🟢 Step 1: The wave equation is
y(x, t) = 3.0 sin(36t + 0.018x + π/4)
🟢 Step 2: Write for each position
➡️ At x = 0 → y₀ = 3.0 sin(36t + π/4)
➡️ At x = 2 cm → y₂ = 3.0 sin(36t + π/4 + 0.036)
➡️ At x = 4 cm → y₄ = 3.0 sin(36t + π/4 + 0.072)
🟡 Step 3: Observations
All graphs are sinusoidal and have the same amplitude (3.0 cm) and frequency (36/2π = 5.73 Hz).
Only the phase changes by 0.036 rad for every 2 cm.
✔️ Final Answer:
Amplitude and frequency are the same at all points; phase differs from point to point.
🔵 Question 14.10
For the travelling harmonic wave
y(x, t) = 2.0 cos[2π(10t − 0.0080x + 0.35)],
where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of
(a) 1 m, (b) 0.5 m, (c) λ/2, (d) 3λ/4.
Answer
🟢 Step 1: Wave number (k)
From the equation, k = 2π × 0.0080 = 0.016π rad/cm.
🟢 Step 2: Wavelength
λ = 2π / k = 2π / (0.016π) = 125 cm = 1.25 m.
🟡 Step 3: Phase difference formula
Δφ = kΔx
(a) Δx = 1 m = 100 cm → Δφ = 0.016π × 100 = 1.6π rad
(b) Δx = 0.5 m = 50 cm → Δφ = 0.8π rad
(c) Δx = λ/2 → Δφ = π rad
(d) Δx = 3λ/4 → Δφ = 3π/2 rad
✔️ Final Answer:
(a) 1.6π rad, (b) 0.8π rad, (c) π rad, (d) 3π/2 rad.
🔵 Question 14.11
The transverse displacement of a string (clamped at both ends) is given by
y(x, t) = 0.06 sin[(2π/3)x] cos(120πt),
where x and y are in m and t in s.
The length of the string is 1.5 m and its mass is 3.0 × 10⁻² kg.
(a) Does the function represent a travelling or a stationary wave?
(b) Interpret the wave as a superposition of two waves travelling in opposite directions. What are the wavelength, frequency, and speed of each wave?
(c) Determine the tension in the string.
Answer
🟢 (a) Since the form is sin(kx)cos(ωt), it represents a stationary wave.
🟢 (b) Using the identity sinA cosB = ½[sin(A+B) + sin(A−B)]:
y = 0.03[sin(kx + ωt) + sin(kx − ωt)]
Each component is a travelling wave of amplitude 0.03 m.
➡️ k = 2π/3 → λ = 3 m
➡️ ω = 120π → f = ω / 2π = 60 Hz
➡️ v = fλ = 60 × 3 = 180 m/s
🟡 (c) Linear mass density μ = m/L = (3.0 × 10⁻²) / 1.5 = 2.0 × 10⁻² kg/m
T = μv² = 2.0 × 10⁻² × (180)² = 648 N
✔️ Final Answer:
(a) Stationary wave
(b) λ = 3 m, f = 60 Hz, v = 180 m/s
(c) T = 648 N
🔵 Question 14.12
(i) For the wave described in 14.11, do all points oscillate with the same (a) frequency, (b) phase, and (c) amplitude?
(ii) What is the amplitude of a point 0.375 m from one end?
Answer
(i)
🟢 Frequency: Same for all points = 60 Hz (common time factor cos120πt).
🟢 Phase: Same within one segment between nodes, opposite between adjacent segments.
🟢 Amplitude: Different; A(x) = 0.06 sin((2π/3)x).
(ii)
At x = 0.375 m → A = 0.06 sin((2π/3)×0.375)
A = 0.06 sin(π/4) = 0.06 × 0.707 = 0.0424 m.
✔️ Final Answer:
Amplitude = 0.042 m (≈ 4.2 cm).
🔵 Question 14.13
Given below are some functions of x and t representing displacement of waves. State whether each represents
(i) a travelling wave, (ii) a stationary wave, or (iii) none:
(a) y = 2 cos(3x) sin(10t)
(b) y = 2√(x − vt)
(c) y = 3 sin(5x − 0.5t) + 4 cos(5x − 0.5t)
(d) y = cosx sin t + cos2x sin2t
Answer
(a) Product of functions of x and t separately → Stationary wave
(b) Function of (x − vt) → Travelling wave
(c) Same argument (5x − 0.5t) → Travelling wave
(d) Two different modes combined → Neither pure travelling nor pure stationary
✔️ Final Answer:
(a) Stationary, (b) Travelling, (c) Travelling, (d) None
🔵 Question 14.14
A wire between two rigid supports vibrates in its fundamental mode at 45 Hz.
Mass = 3.5 × 10⁻² kg, linear mass density = 4.0 × 10⁻² kg/m.
(a) What is the speed of transverse waves on the string?
(b) What is the tension in the string?
Answer
🟢 (a) v = 2Lf = 2 × 0.875 × 45 = 78.75 m/s
🟢 (b) T = μv² = 4.0 × 10⁻² × (78.75)² = 2.48 × 10² N
✔️ Final Answer:
v = 78.8 m/s, T = 248 N
🔵 Question 14.15
A 3.0 m long tube, open at one end and movable piston at the other, resonates with a tuning fork (340 Hz) when air-column lengths are 25.5 cm and 79.3 cm. Estimate the speed of sound in air (neglect edge effects).
Answer
🟢 Step 1: For closed–open tube, successive resonances differ by λ/2.
ΔL = 79.3 − 25.5 = 53.8 cm = 0.538 m → λ = 2ΔL = 1.076 m.
🟡 Step 2: v = fλ = 340 × 1.076 = 366 m/s.
✔️ Final Answer:
Speed of sound = 3.66 × 10² m/s (≈ 366 m/s)
🔵 Question 14.16
A steel rod 100 cm long is clamped at its middle. The fundamental frequency of longitudinal vibrations of the rod are given to be 2.53 kHz. What is the speed of sound in steel?
Answer
🟢 Step 1: Given data
Length of rod, L = 100 cm = 1.0 m
Frequency of fundamental mode, f = 2.53 kHz = 2.53 × 10³ Hz
🟡 Step 2: Concept
For a rod clamped at the middle and free at both ends, the fundamental mode has two loops, i.e.,
L = λ / 2
Hence, wavelength λ = 2L = 2 × 1.0 = 2.0 m
🟠 Step 3: Use formula for wave speed
v = f × λ = 2.53 × 10³ × 2.0 = 5.06 × 10³ m/s
✔️ Final Answer:
Speed of sound in steel = 5.06 × 10³ m/s
🔵 Question 14.17
A pipe 20 cm long is closed at one end. Which harmonic mode of the pipe is resonantly excited by a 430 Hz source? Will the same source be in resonance with the pipe if both ends are open? (Speed of sound in air = 340 m/s)
Answer
🟢 Step 1: Given data
L = 20 cm = 0.20 m
v = 340 m/s
f = 430 Hz
🟡 Step 2: For a closed pipe (one end closed):
Resonant frequencies:
fₙ = n × v / 4L, where n = 1, 3, 5, … (odd harmonics only)
Substitute:
430 = n × 340 / (4 × 0.20)
430 = n × 425
Hence, n ≈ 1.01 → First harmonic (fundamental mode).
🟠 Step 3: For an open pipe (both ends open):
fₙ = n × v / 2L
430 = n × 340 / (2 × 0.20)
430 = n × 850 → n = 0.51 → not possible (not an integer).
✔️ Final Answer:
Resonance occurs at the first harmonic when closed at one end.
No resonance occurs when both ends are open.
🔵 Question 14.18
Two sitar strings A and B playing the note ‘Ga’ are slightly out of tune and produce beats of frequency 6 Hz. The tension in string A is slightly reduced and the beat frequency becomes 3 Hz. If the original frequency of A is 324 Hz, what is the frequency of B?
Answer
🟢 Step 1: Let the original frequencies be
f_A = 324 Hz
f_B = ?
Initial beat frequency = 6 Hz
So, |f_B − 324| = 6 → f_B = 318 Hz or 330 Hz
🟡 Step 2: When tension in A is reduced, f_A decreases, and beat frequency decreases to 3 Hz.
That means f_B is greater than f_A (since lowering tension reduces f_A).
Therefore, f_B = 324 + 6 = 330 Hz.
✔️ Final Answer:
Frequency of B = 330 Hz
🔵 Question 14.19
Explain why (or how):
(a) In a sound wave, a displacement node is a pressure antinode and vice versa.
(b) Bats can ascertain distances, directions, nature, and sizes of obstacles without any “eyes”.
(c) A violin note and sitar note may have the same frequency, yet we can distinguish between the two notes.
(d) Solids can support both longitudinal and transverse waves, but only longitudinal waves can propagate in gases.
(e) The shape of a pulse gets distorted during propagation in a dispersive medium.
Answer
🟢 (a) In a longitudinal sound wave, pressure variations are maximum where displacement is minimum (and vice versa). Thus, displacement node → pressure antinode, and displacement antinode → pressure node.
🟢 (b) Bats emit ultrasonic waves that reflect from obstacles. By sensing the time delay and pattern of the reflected wave (echo), they determine the distance, direction, and shape of the object.
🟢 (c) Both may have the same fundamental frequency, but the waveform (due to harmonics or overtones) differs. These differences in overtone structure give each instrument its own timbre or quality.
🟢 (d) Solids have elasticity against both shear and compressional stresses, allowing transverse and longitudinal waves. Gases resist only compression, hence can carry only longitudinal waves.
🟢 (e) In a dispersive medium, wave speed depends on frequency. Different frequency components of a pulse travel with different speeds, causing the pulse to change shape as it moves.
————————————————————————————————————————————————————————————————————————————
OTHER IMPORTANT QUESTIONS FOR EXAMS
(CBSE MODEL QUESTIONS PAPER)
ESPECIALLY MADE FROM THIS LESSON ONLY
🔷 SECTION A — Multiple Choice Questions (Q1–Q18)
Q1. Which of the following is a mechanical wave?
🔵(A) Light wave
🟢(B) Sound wave
🟠(C) Radio wave
🔴(D) X-ray
Answer: (B) Sound wave
Q2. A wave propagates along x-axis as y = A sin(kx − ωt). The wave moves
🔵(A) Along +x direction
🟢(B) Along −x direction
🟠(C) Upward
🔴(D) Downward
Answer: (A) Along +x direction
Q3. The unit of wave number (k) is
🔵(A) rad/s
🟢(B) m⁻¹
🟠(C) s⁻¹
🔴(D) m
Answer: (B) m⁻¹
Q4. In a transverse wave, the particle motion is
🔵(A) Parallel to propagation
🟢(B) Perpendicular to propagation
🟠(C) Random
🔴(D) Circular
Answer: (B) Perpendicular to propagation
Q5. For sound waves, regions of high pressure are called
🔵(A) Crests
🟢(B) Troughs
🟠(C) Compressions
🔴(D) Rarefactions
Answer: (C) Compressions
Q6. A wave has wavelength 0.5 m and speed 2 m/s. Its frequency is
🔵(A) 0.25 Hz
🟢(B) 2 Hz
🟠(C) 4 Hz
🔴(D) 1 Hz
Answer: (C) 4 Hz
Q7. Which of the following does not require a medium?
🔵(A) Sound
🟢(B) Water waves
🟠(C) Light
🔴(D) Seismic waves
Answer: (C) Light
Q8. When two waves meet in phase, the phenomenon is called
🔵(A) Diffraction
🟢(B) Constructive interference
🟠(C) Destructive interference
🔴(D) Reflection
Answer: (B) Constructive interference
Q9. The distance between two adjacent nodes in a stationary wave is
🔵(A) λ
🟢(B) λ/2
🟠(C) λ/4
🔴(D) 2λ
Answer: (B) λ/2
Q10. In a stationary wave, energy
🔵(A) Is transmitted
🟢(B) Is not transmitted
🟠(C) Increases with time
🔴(D) Decreases continuously
Answer: (B) Is not transmitted
Q11. For a string, the fundamental frequency is proportional to
🔵(A) √T
🟢(B) 1/√T
🟠(C) T²
🔴(D) 1/T
Answer: (A) √T
Q12. The SI unit of amplitude is
🔵(A) m
🟢(B) s
🟠(C) Hz
🔴(D) rad/s
Answer: (A) m
Q13. The phase difference between displacement and velocity in a wave is
🔵(A) 0
🟢(B) π/2
🟠(C) π
🔴(D) 3π/2
Answer: (B) π/2
Q14. Two waves of frequencies 256 Hz and 260 Hz are superposed. The beat frequency is
🔵(A) 2 Hz
🟢(B) 3 Hz
🟠(C) 4 Hz
🔴(D) 1 Hz
Answer: (C) 4 Hz
Q15. If the frequency is doubled and wavelength halved, the wave velocity will
🔵(A) Double
🟢(B) Remain same
🟠(C) Be halved
🔴(D) Increase four times
Answer: (B) Remain same
Q16. In a stationary wave, pressure variation is maximum at
🔵(A) Node
🟢(B) Antinode
🟠(C) Midpoint
🔴(D) Every point
Answer: (A) Node
Q17. The speed of sound in air increases with
🔵(A) Increase in humidity
🟢(B) Increase in pressure
🟠(C) Decrease in temperature
🔴(D) All of these
Answer: (A) Increase in humidity
Q18. The phenomenon of rise and fall in intensity due to interference is called
🔵(A) Echo
🟢(B) Resonance
🟠(C) Beats
🔴(D) Reflection
Answer: (C) Beats
🔷 SECTION B — Very Short / Short Answer (Q19–Q23)
Q19. Define wavelength and frequency.
Answer:
🔹 Wavelength (λ): Distance between two successive particles in the same phase (two crests or two compressions).
🔹 Frequency (ν): Number of vibrations per second of a particle in the medium.
They are related by v = λν.
Q20. Write the equation of a progressive wave moving along +x direction.
Answer:
y = A sin(kx − ωt + ϕ)
where k = 2π/λ and ω = 2πν.
The negative sign shows motion in positive x direction.
Q21. What is the condition for constructive and destructive interference?
Answer:
Constructive interference: Phase difference ΔΦ = 2nπ
Destructive interference: Phase difference ΔΦ = (2n + 1)π
where n = 0, 1, 2, …
Q22. Define node and antinode in a stationary wave.
Answer:
Node: A point where displacement is always zero.
Antinode: A point where displacement is maximum.
Distance between two consecutive nodes = λ/2.
Q23. State one difference between transverse and longitudinal waves.
Answer:
In transverse waves, particles oscillate perpendicular to wave motion; in longitudinal waves, they oscillate parallel.
🔷 SECTION C — Mid-Length / Numericals (Q24–Q28)
Q24. A string of length 1.5 m is vibrating in its fundamental mode with frequency 120 Hz. Find the speed of the wave on the string.
Answer:
Given: L = 1.5 m, n = 1, ν = 120 Hz
For fundamental mode: ν = v/2L
v = 2Lν = 2 × 1.5 × 120 = 360 m/s
Q25. The tension in a wire is 100 N and its linear mass density is 0.01 kg/m. Calculate the speed of the wave.
Answer:
v = √(T/μ)
v = √(100 / 0.01) = √10000 = 100 m/s
Q26. Calculate the frequency of the second harmonic of a string vibrating with fundamental frequency 150 Hz.
Answer:
Second harmonic → n = 2
ν₂ = 2ν₁ = 2 × 150 = 300 Hz
Q27. Two waves of frequency 400 Hz and 404 Hz superpose. Find beat frequency.
Answer:
ν_b = |ν₁ − ν₂| = |404 − 400| = 4 Hz
Q28. A tuning fork produces 6 beats per second with another of 250 Hz. On loading, beats reduce to 3 per second. Find unknown frequency.
Answer:
Case 1: ν_x = 250 ± 6 → 244 or 256 Hz
After loading, frequency decreases, beats = 3 → 247 Hz
Hence initial frequency = 253 Hz
🔷 SECTION D — Long Answer (Q29–Q31)
Q29. Derive the expression for a progressive wave and show that wave velocity = λν.
Answer:
💡 Let a particle at x = 0 perform SHM: y = A sin(ωt).
After time t, disturbance travels distance x → wave form:
y = A sin(ωt − kx).
Here, k = 2π/λ and ω = 2πν.
At time t + T, the same phase occurs again:
kx − ωt = constant → ω/k = constant velocity v.
Hence, v = ω/k = λν.
Q30. Derive the equation of stationary waves formed by two identical progressive waves moving in opposite directions.
Answer:
Let y₁ = A sin(kx − ωt), y₂ = A sin(kx + ωt).
By superposition,
y = y₁ + y₂ = 2A sin(kx) cos(ωt).
✔️ At positions where sin(kx) = 0 → y = 0 → nodes.
✔️ Where sin(kx) = ±1 → y = ±2A cos(ωt) → antinodes.
Distance between two consecutive nodes = λ/2.
Thus, stationary wave equation: y = 2A sin(kx) cos(ωt).
Q31. Explain Doppler effect in sound and derive the expression for apparent frequency.
Answer:
💡 Definition: Apparent change in frequency due to relative motion between source and observer.
Let source move with speed vₛ, observer with v₀, and sound speed v.
Apparent frequency:
ν’ = ν (v ± v₀) / (v ∓ vₛ)
✔️ (+) sign if approaching; (−) if receding.
Applications: radar, astronomy, and medical scanning.
🔷 SECTION E — Case Study / Application (Q32–Q33)
Q32. A sonometer wire 1.5 m long vibrates in its fundamental mode with tension 60 N and linear density 0.005 kg/m. Calculate frequency.
Answer:
v = √(T/μ) = √(60 / 0.005) = √12000 = 109.5 m/s
Fundamental frequency: ν = v/2L = 109.5 / (2 × 1.5) = 36.5 Hz
Q33. A car driver moving at 30 m/s sounds a horn of frequency 500 Hz. What frequency is heard by a stationary observer ahead? (Speed of sound = 330 m/s)
Answer:
ν’ = ν (v / (v − vₛ))
= 500 × (330 / (330 − 30)) = 500 × (330 / 300) = 550 Hz
✔️ Hence, apparent frequency increases as the source approaches.
————————————————————————————————————————————————————————————————————————————
NEET QUESTIONS FROM THIS LESSON
🔴 Q1 (NEET 2025)
If the speed of sound in air is 340 m/s, the wavelength of a 1700 Hz sound wave is
🟢 1️⃣ 0.2 m
🟡 2️⃣ 2 m
🔵 3️⃣ 0.5 m
🟣 4️⃣ 1 m
✅ Answer: 1️⃣ 0.2 m
🔴 Q2 (NEET 2024)
In a stationary wave, the distance between two consecutive nodes is
🟢 1️⃣ λ / 2
🟡 2️⃣ λ / 4
🔵 3️⃣ λ
🟣 4️⃣ λ / 8
✅ Answer: 1️⃣ λ / 2
🔴 Q3 (NEET 2023)
Two waves of equal amplitude and frequency interfere constructively. The resultant amplitude is
🟢 1️⃣ 2A
🟡 2️⃣ A
🔵 3️⃣ 0
🟣 4️⃣ A / 2
✅ Answer: 1️⃣ 2A
🔴 Q4 (NEET 2022)
A sound wave has frequency 256 Hz and wavelength 1.3 m. Its speed is
🟢 1️⃣ 332.8 m/s
🟡 2️⃣ 300 m/s
🔵 3️⃣ 512 m/s
🟣 4️⃣ 256 m/s
✅ Answer: 1️⃣ 332.8 m/s
🔴 Q5 (NEET 2021)
When two waves of slightly different frequencies interfere, we get
🟢 1️⃣ beats
🟡 2️⃣ stationary waves
🔵 3️⃣ resonance
🟣 4️⃣ diffraction
✅ Answer: 1️⃣ beats
🔴 Q6 (NEET 2020)
The fundamental frequency of a closed organ pipe of length L is
🟢 1️⃣ v / 4L
🟡 2️⃣ v / 2L
🔵 3️⃣ v / L
🟣 4️⃣ v / 8L
✅ Answer: 1️⃣ v / 4L
🔴 Q7 (NEET 2019)
The fundamental frequency of an open organ pipe is
🟢 1️⃣ v / 2L
🟡 2️⃣ v / 4L
🔵 3️⃣ v / L
🟣 4️⃣ 2v / L
✅ Answer: 1️⃣ v / 2L
🔴 Q8 (NEET 2018)
If tension in a string increases four times, the speed of the wave becomes
🟢 1️⃣ double
🟡 2️⃣ half
🔵 3️⃣ four times
🟣 4️⃣ one-fourth
✅ Answer: 1️⃣ double
🔴 Q9 (NEET 2017)
In a stationary wave, the points with zero amplitude are
🟢 1️⃣ nodes
🟡 2️⃣ antinodes
🔵 3️⃣ crests
🟣 4️⃣ troughs
✅ Answer: 1️⃣ nodes
🔴 Q10 (NEET 2016)
The number of nodes between two consecutive antinodes is
🟢 1️⃣ 1
🟡 2️⃣ 2
🔵 3️⃣ 3
🟣 4️⃣ 0
✅ Answer: 1️⃣ 1
🔴 Q11 (AIPMT 2015)
The equation of a progressive wave is y = 0.02 sin(2πx − 4πt). Wavelength is
🟢 1️⃣ 0.5 m
🟡 2️⃣ 1 m
🔵 3️⃣ 2 m
🟣 4️⃣ 4 m
✅ Answer: 1️⃣ 0.5 m
🔴 Q12 (AIPMT 2014)
If two waves of equal amplitude interfere destructively, resultant amplitude is
🟢 1️⃣ 0
🟡 2️⃣ A
🔵 3️⃣ 2A
🟣 4️⃣ A / 2
✅ Answer: 1️⃣ 0
🔴 Q13 (AIPMT 2013)
In a closed pipe, harmonics present are
🟢 1️⃣ odd
🟡 2️⃣ even
🔵 3️⃣ all
🟣 4️⃣ none
✅ Answer: 1️⃣ odd
🔴 Q14 (AIPMT 2012)
The ratio of frequencies of first three harmonics in a closed pipe is
🟢 1️⃣ 1 : 3 : 5
🟡 2️⃣ 1 : 2 : 3
🔵 3️⃣ 1 : 4 : 5
🟣 4️⃣ 1 : 5 : 7
✅ Answer: 1️⃣ 1 : 3 : 5
🔴 Q15 (AIPMT 2011)
If length of string is doubled, frequency becomes
🟢 1️⃣ half
🟡 2️⃣ double
🔵 3️⃣ same
🟣 4️⃣ one-fourth
✅ Answer: 1️⃣ half
🔴 Q16 (AIPMT 2010)
When two waves of frequencies 256 Hz and 260 Hz are superposed, beats heard per second =
🟢 1️⃣ 4
🟡 2️⃣ 2
🔵 3️⃣ 516
🟣 4️⃣ 1
✅ Answer: 1️⃣ 4
🔴 Q17 (AIPMT 2009)
Velocity of wave on stretched string v = √(T / μ). If T is quadrupled, v becomes
🟢 1️⃣ double
🟡 2️⃣ half
🔵 3️⃣ same
🟣 4️⃣ four times
✅ Answer: 1️⃣ double
🔴 Q18 (AIPMT 2008)
The frequency of beats is equal to
🟢 1️⃣ |f₁ − f₂|
🟡 2️⃣ f₁ + f₂
🔵 3️⃣ f₁ / f₂
🟣 4️⃣ f₁ × f₂
✅ Answer: 1️⃣ |f₁ − f₂|
🔴 Q19 (AIPMT 2007)
The speed of sound increases with
🟢 1️⃣ temperature
🟡 2️⃣ pressure
🔵 3️⃣ amplitude
🟣 4️⃣ wavelength
✅ Answer: 1️⃣ temperature
🔴 Q20 (AIPMT 2006)
If amplitude doubles, intensity becomes
🟢 1️⃣ 4 times
🟡 2️⃣ 2 times
🔵 3️⃣ half
🟣 4️⃣ unchanged
✅ Answer: 1️⃣ 4 times
🔴 Q21 (AIPMT 2005)
In interference, constructive interference occurs when phase difference is
🟢 1️⃣ 0 or 2πn
🟡 2️⃣ π
🔵 3️⃣ π/2
🟣 4️⃣ odd multiples of π/2
✅ Answer: 1️⃣ 0 or 2πn
🔴 Q22 (AIPMT 2004)
In stationary wave, distance between a node and adjacent antinode =
🟢 1️⃣ λ / 4
🟡 2️⃣ λ / 2
🔵 3️⃣ λ
🟣 4️⃣ λ / 8
✅ Answer: 1️⃣ λ / 4
🔴 Q23 (AIPMT 2003)
If two waves y₁ = A sin ωt and y₂ = A cos ωt interfere, resultant amplitude =
🟢 1️⃣ √2 A
🟡 2️⃣ A
🔵 3️⃣ 0
🟣 4️⃣ 2A
✅ Answer: 1️⃣ √2 A
🔴 Q24 (AIPMT 2002)
Equation of wave: y = 0.01 sin(2πx − 2πt). Its wavelength =
🟢 1️⃣ 1 m
🟡 2️⃣ 2 m
🔵 3️⃣ 4 m
🟣 4️⃣ 0.5 m
✅ Answer: 1️⃣ 1 m
🔴 Q25 (AIPMT 2001)
The equation y = A sin(kx − ωt) represents
🟢 1️⃣ progressive wave
🟡 2️⃣ stationary wave
🔵 3️⃣ beats
🟣 4️⃣ transverse wave only
✅ Answer: 1️⃣ progressive wave
🔴 Q26 (NEET 2025)
The ratio of frequencies of first three harmonics in an open organ pipe is
🟢 1️⃣ 1 : 2 : 3
🟡 2️⃣ 1 : 3 : 5
🔵 3️⃣ 1 : 4 : 5
🟣 4️⃣ 1 : 5 : 7
✅ Answer: 1️⃣ 1 : 2 : 3
🔴 Q27 (NEET 2024)
When two waves of same amplitude A and phase difference 120° interfere, the resultant amplitude is
🟢 1️⃣ A
🟡 2️⃣ A/2
🔵 3️⃣ √3 A
🟣 4️⃣ 2A
✅ Answer: 1️⃣ A
🔴 Q28 (NEET 2023)
The first overtone of a closed organ pipe corresponds to
🟢 1️⃣ 3rd harmonic
🟡 2️⃣ 2nd harmonic
🔵 3️⃣ 4th harmonic
🟣 4️⃣ fundamental
✅ Answer: 1️⃣ 3rd harmonic
🔴 Q29 (NEET 2022)
Two waves of amplitude 3 cm each interfere constructively. Resultant amplitude =
🟢 1️⃣ 6 cm
🟡 2️⃣ 3 cm
🔵 3️⃣ 9 cm
🟣 4️⃣ 0 cm
✅ Answer: 1️⃣ 6 cm
🔴 Q30 (NEET 2021)
Speed of wave on string v = √(T/μ). If T = 100 N and μ = 0.01 kg/m, v =
🟢 1️⃣ 100 m/s
🟡 2️⃣ 10 m/s
🔵 3️⃣ 316 m/s
🟣 4️⃣ 50 m/s
✅ Answer: 1️⃣ 100 m/s
🔴 Q31 (NEET 2020)
If amplitude doubles, energy becomes
🟢 1️⃣ 4 times
🟡 2️⃣ 2 times
🔵 3️⃣ 8 times
🟣 4️⃣ same
✅ Answer: 1️⃣ 4 times
🔴 Q32 (NEET 2019)
For beats to occur, two waves must have
🟢 1️⃣ slightly different frequencies
🟡 2️⃣ same frequencies
🔵 3️⃣ large frequency difference
🟣 4️⃣ none
✅ Answer: 1️⃣ slightly different frequencies
🔴 Q33 (NEET 2018)
Speed of sound in air increases with
🟢 1️⃣ increase in temperature
🟡 2️⃣ increase in pressure
🔵 3️⃣ increase in density
🟣 4️⃣ increase in amplitude
✅ Answer: 1️⃣ increase in temperature
🔴 Q34 (NEET 2017)
Equation of a wave: y = 0.02 sin(2πx − 100πt). Frequency =
🟢 1️⃣ 50 Hz
🟡 2️⃣ 100 Hz
🔵 3️⃣ 25 Hz
🟣 4️⃣ 10 Hz
✅ Answer: 1️⃣ 50 Hz
🔴 Q35 (NEET 2016)
In a closed pipe of length L, fundamental frequency =
🟢 1️⃣ v / 4L
🟡 2️⃣ v / 2L
🔵 3️⃣ v / L
🟣 4️⃣ v / 8L
✅ Answer: 1️⃣ v / 4L
🔴 Q36 (AIPMT 2015)
Two waves y₁ = A sin ωt and y₂ = A sin(ωt + π/2) interfere. Resultant amplitude =
🟢 1️⃣ √2 A
🟡 2️⃣ A
🔵 3️⃣ 2A
🟣 4️⃣ 0
✅ Answer: 1️⃣ √2 A
🔴 Q37 (AIPMT 2014)
A string of length 1 m is fixed at both ends. For first harmonic, wavelength =
🟢 1️⃣ 2 m
🟡 2️⃣ 1 m
🔵 3️⃣ 0.5 m
🟣 4️⃣ 4 m
✅ Answer: 1️⃣ 2 m
🔴 Q38 (AIPMT 2013)
Two waves of frequencies 400 Hz and 404 Hz produce beats per second =
🟢 1️⃣ 4
🟡 2️⃣ 8
🔵 3️⃣ 2
🟣 4️⃣ 1
✅ Answer: 1️⃣ 4
🔴 Q39 (AIPMT 2012)
When two waves of frequencies f₁ and f₂ interfere, beat frequency =
🟢 1️⃣ |f₁ − f₂|
🟡 2️⃣ f₁ + f₂
🔵 3️⃣ f₁ / f₂
🟣 4️⃣ f₁ × f₂
✅ Answer: 1️⃣ |f₁ − f₂|
🔴 Q40 (AIPMT 2011)
For stationary wave, the distance between two successive nodes =
🟢 1️⃣ λ / 2
🟡 2️⃣ λ / 4
🔵 3️⃣ λ
🟣 4️⃣ 2λ
✅ Answer: 1️⃣ λ / 2
🔴 Q41 (AIPMT 2010)
If y = 0.01 sin(2πx − 4πt), frequency =
🟢 1️⃣ 2 Hz
🟡 2️⃣ 4 Hz
🔵 3️⃣ 1 Hz
🟣 4️⃣ 8 Hz
✅ Answer: 1️⃣ 2 Hz
🔴 Q42 (AIPMT 2009)
If frequency = 300 Hz, speed = 330 m/s, wavelength =
🟢 1️⃣ 1.1 m
🟡 2️⃣ 0.9 m
🔵 3️⃣ 1 m
🟣 4️⃣ 0.11 m
✅ Answer: 1️⃣ 1.1 m
🔴 Q43 (AIPMT 2008)
When two waves of same frequency and amplitude interfere in opposite phase, resultant amplitude =
🟢 1️⃣ 0
🟡 2️⃣ A
🔵 3️⃣ 2A
🟣 4️⃣ A / 2
✅ Answer: 1️⃣ 0
🔴 Q44 (AIPMT 2007)
If frequency doubles, wavelength becomes
🟢 1️⃣ half
🟡 2️⃣ double
🔵 3️⃣ same
🟣 4️⃣ four times
✅ Answer: 1️⃣ half
🔴 Q45 (AIPMT 2006)
In stationary wave, energy is
🟢 1️⃣ not transferred
🟡 2️⃣ transferred
🔵 3️⃣ partially transferred
🟣 4️⃣ infinite
✅ Answer: 1️⃣ not transferred
🔴 Q46 (AIPMT 2005)
In a string fixed at both ends, number of nodes in nth harmonic =
🟢 1️⃣ n + 1
🟡 2️⃣ n
🔵 3️⃣ n − 1
🟣 4️⃣ 2n
✅ Answer: 1️⃣ n + 1
🔴 Q47 (AIPMT 2004)
Equation y = A sin(kx + ωt) represents
🟢 1️⃣ wave travelling in negative x
🟡 2️⃣ wave travelling in positive x
🔵 3️⃣ stationary wave
🟣 4️⃣ beats
✅ Answer: 1️⃣ wave travelling in negative x
🔴 Q48 (AIPMT 2003)
If two waves y₁ = A sin ωt, y₂ = A sin(ωt + π), resultant amplitude =
🟢 1️⃣ 0
🟡 2️⃣ 2A
🔵 3️⃣ A
🟣 4️⃣ A / 2
✅ Answer: 1️⃣ 0
🔴 Q49 (AIPMT 2002)
If tension becomes 9 times, speed becomes
🟢 1️⃣ 3 times
🟡 2️⃣ 9 times
🔵 3️⃣ same
🟣 4️⃣ 1/3 times
✅ Answer: 1️⃣ 3 times
🔴 Q50 (AIPMT 2001)
For stationary wave, distance between adjacent node and antinode =
🟢 1️⃣ λ / 4
🟡 2️⃣ λ / 2
🔵 3️⃣ λ
🟣 4️⃣ 2λ
✅ Answer: 1️⃣ λ / 4
————————————————————————————————————————————————————————————————————————————
JEE MAINS QUESTIONS FROM THIS LESSON
🔴 Q1. The speed of a wave on a string depends on
🟢 1️⃣ Tension and linear mass density
🔵 2️⃣ Only on amplitude
🟡 3️⃣ Only on frequency
🟣 4️⃣ Only on length
✔️ Answer: 1
📘 Exam: JEE Main 2024
🔴 Q2. The equation of a progressive wave is y = 0.02 sin(2πt – πx/2). The wavelength is
🟢 1️⃣ 2 m
🔵 2️⃣ 4 m
🟡 3️⃣ 1 m
🟣 4️⃣ 8 m
✔️ Answer: 4
📘 Exam: JEE Main 2023
🔴 Q3. The equation y = 0.1 sin(100t – 20x) represents a wave travelling in
🟢 1️⃣ Positive x-direction
🔵 2️⃣ Negative x-direction
🟡 3️⃣ Positive y-direction
🟣 4️⃣ Negative y-direction
✔️ Answer: 1
📘 Exam: JEE Main 2023
🔴 Q4. The frequency of tuning fork producing 2 beats per second with 256 Hz fork can be
🟢 1️⃣ 258 Hz or 254 Hz
🔵 2️⃣ 260 Hz or 252 Hz
🟡 3️⃣ 256 Hz
🟣 4️⃣ 262 Hz or 250 Hz
✔️ Answer: 1
📘 Exam: JEE Main 2022
🔴 Q5. In beats phenomenon, number of beats per second is
🟢 1️⃣ Sum of frequencies
🔵 2️⃣ Difference of frequencies
🟡 3️⃣ Ratio of frequencies
🟣 4️⃣ Product of frequencies
✔️ Answer: 2
📘 Exam: JEE Main 2022
🔴 Q6. Two waves represented by y₁ = a sin(ωt) and y₂ = a sin(ωt + π) interfere, resultant amplitude is
🟢 1️⃣ 2a
🔵 2️⃣ 0
🟡 3️⃣ a
🟣 4️⃣ √2a
✔️ Answer: 2
📘 Exam: JEE Main 2021
🔴 Q7. The equation of stationary wave formed by superposition of y₁ = a sin(ωt – kx) and y₂ = a sin(ωt + kx) is
🟢 1️⃣ 2a sin(kx) cos(ωt)
🔵 2️⃣ 2a cos(kx) sin(ωt)
🟡 3️⃣ a sin(kx + ωt)
🟣 4️⃣ a cos(kx – ωt)
✔️ Answer: 1
📘 Exam: JEE Main 2021
🔴 Q8. In stationary wave, distance between a node and adjacent antinode is
🟢 1️⃣ λ
🔵 2️⃣ λ/4
🟡 3️⃣ λ/2
🟣 4️⃣ λ/3
✔️ Answer: 2
📘 Exam: JEE Main 2020
🔴 Q9. In stationary waves, energy transfer is
🟢 1️⃣ Maximum
🔵 2️⃣ Zero
🟡 3️⃣ Minimum
🟣 4️⃣ Constant
✔️ Answer: 2
📘 Exam: JEE Main 2020
🔴 Q10. If a string is vibrating in 3rd harmonic, number of nodes is
🟢 1️⃣ 2
🔵 2️⃣ 3
🟡 3️⃣ 4
🟣 4️⃣ 5
✔️ Answer: 3
📘 Exam: JEE Main 2019
🔴 Q11. For the fundamental mode, length of string is
🟢 1️⃣ λ
🔵 2️⃣ λ/4
🟡 3️⃣ λ/2
🟣 4️⃣ 2λ
✔️ Answer: 3
📘 Exam: JEE Main 2019
🔴 Q12. Two waves having amplitudes 3 cm and 4 cm interfere in same phase. Resultant amplitude is
🟢 1️⃣ 7 cm
🔵 2️⃣ 1 cm
🟡 3️⃣ 5 cm
🟣 4️⃣ 12 cm
✔️ Answer: 1
📘 Exam: JEE Main 2018
🔴 Q13. The number of loops in 2nd harmonic is
🟢 1️⃣ 1
🔵 2️⃣ 2
🟡 3️⃣ 3
🟣 4️⃣ 4
✔️ Answer: 2
📘 Exam: JEE Main 2018
🔴 Q14. In stationary waves, pressure nodes correspond to
🟢 1️⃣ Displacement nodes
🔵 2️⃣ Displacement antinodes
🟡 3️⃣ Midpoints
🟣 4️⃣ None
✔️ Answer: 2
📘 Exam: JEE Main 2017
🔴 Q15. The fundamental frequency of an open pipe is 300 Hz. Its 2nd overtone frequency is
🟢 1️⃣ 600 Hz
🔵 2️⃣ 900 Hz
🟡 3️⃣ 1200 Hz
🟣 4️⃣ 150 Hz
✔️ Answer: 2
📘 Exam: JEE Main 2017
🔴 Q16. In a closed pipe, fundamental frequency is f. The next overtone frequency is
🟢 1️⃣ 2f
🔵 2️⃣ 3f
🟡 3️⃣ 4f
🟣 4️⃣ 5f
✔️ Answer: 2
📘 Exam: JEE Main 2016
🔴 Q17. The speed of sound in a gas is proportional to
🟢 1️⃣ √T
🔵 2️⃣ T
🟡 3️⃣ 1/T
🟣 4️⃣ T²
✔️ Answer: 1
📘 Exam: JEE Main 2016
🔴 Q18. In an open pipe, 2nd overtone corresponds to
🟢 1️⃣ 3rd harmonic
🔵 2️⃣ 2nd harmonic
🟡 3️⃣ 4th harmonic
🟣 4️⃣ 5th harmonic
✔️ Answer: 1
📘 Exam: JEE Main 2015
🔴 Q19. In closed pipe, 2nd overtone corresponds to
🟢 1️⃣ 5th harmonic
🔵 2️⃣ 3rd harmonic
🟡 3️⃣ 2nd harmonic
🟣 4️⃣ 4th harmonic
✔️ Answer: 1
📘 Exam: JEE Main 2015
🔴 Q20. When two identical waves superimpose out of phase, resultant amplitude is
🟢 1️⃣ Zero
🔵 2️⃣ Double
🟡 3️⃣ Half
🟣 4️⃣ Same
✔️ Answer: 1
📘 Exam: JEE Main 2014
🔴 Q21. The number of nodes between two consecutive antinodes is
🟢 1️⃣ 1
🔵 2️⃣ 2
🟡 3️⃣ 3
🟣 4️⃣ 0
✔️ Answer: 1
📘 Exam: JEE Main 2014
🔴 Q22. The velocity of sound increases with
🟢 1️⃣ Temperature
🔵 2️⃣ Humidity
🟡 3️⃣ Both
🟣 4️⃣ Pressure
✔️ Answer: 3
📘 Exam: JEE Main 2013
🔴 Q23. If tension in a string is quadrupled, wave velocity becomes
🟢 1️⃣ 2 times
🔵 2️⃣ 4 times
🟡 3️⃣ 1/2 times
🟣 4️⃣ Same
✔️ Answer: 1
📘 Exam: JEE Main 2013
🔴 Q24. Two waves of same amplitude and frequency interfere destructively. Resultant amplitude is
🟢 1️⃣ 0
🔵 2️⃣ 2A
🟡 3️⃣ A
🟣 4️⃣ √2A
✔️ Answer: 1
📘 Exam: JEE Main 2012
🔴 Q25. In beats, maximum loudness occurs when waves are
🟢 1️⃣ In phase
🔵 2️⃣ Out of phase
🟡 3️⃣ Quadrature
🟣 4️⃣ Any phase
✔️ Answer: 1
📘 Exam: JEE Main 2012
🔴 Q26. The phase difference between two points separated by distance x in a wave of wavelength lambda is
🟢 1️⃣ 2πx/lambda
🔵 2️⃣ πx/lambda
🟡 3️⃣ x/lambda
🟣 4️⃣ 4πx/lambda
✔️ Answer: 1
📘 Exam: JEE Main 2011
🔴 Q27. The equation of a progressive wave is y = 0.05 sin(2π×200t − 0.4πx). The velocity is
🟢 1️⃣ 1000 m/s
🔵 2️⃣ 500 m/s
🟡 3️⃣ 400 m/s
🟣 4️⃣ 200 m/s
✔️ Answer: 500 m/s
📘 Exam: JEE Main 2011
🔴 Q28. For a stationary wave, number of nodes between two antinodes is
🟢 1️⃣ 1
🔵 2️⃣ 2
🟡 3️⃣ 3
🟣 4️⃣ 0
✔️ Answer: 1
📘 Exam: JEE Main 2010
🔴 Q29. In a stationary wave, the distance between a node and adjacent antinode is
🟢 1️⃣ lambda
🔵 2️⃣ lambda/4
🟡 3️⃣ lambda/2
🟣 4️⃣ lambda/3
✔️ Answer: lambda/4
📘 Exam: JEE Main 2010
🔴 Q30. In an open organ pipe, the fundamental frequency is f. The frequency of second overtone is
🟢 1️⃣ 2f
🔵 2️⃣ 3f
🟡 3️⃣ 4f
🟣 4️⃣ 5f
✔️ Answer: 3f
📘 Exam: JEE Main 2009
🔴 Q31. In a closed organ pipe, fundamental frequency is f. Next overtone is
🟢 1️⃣ 2f
🔵 2️⃣ 3f
🟡 3️⃣ 4f
🟣 4️⃣ 5f
✔️ Answer: 3f
📘 Exam: JEE Main 2009
🔴 Q32. If a wave travels 600 m in 2 s, its speed is
🟢 1️⃣ 200 m/s
🔵 2️⃣ 300 m/s
🟡 3️⃣ 400 m/s
🟣 4️⃣ 600 m/s
✔️ Answer: 300 m/s
📘 Exam: JEE Main 2008
🔴 Q33. Two waves of frequencies 256 Hz and 260 Hz produce beats of frequency
🟢 1️⃣ 2 Hz
🔵 2️⃣ 3 Hz
🟡 3️⃣ 4 Hz
🟣 4️⃣ 5 Hz
✔️ Answer: 4 Hz
📘 Exam: JEE Main 2008
🔴 Q34. If amplitude of each wave is A, resultant amplitude during constructive interference is
🟢 1️⃣ A
🔵 2️⃣ 2A
🟡 3️⃣ A/2
🟣 4️⃣ 0
✔️ Answer: 2A
📘 Exam: JEE Main 2007
🔴 Q35. For destructive interference, phase difference should be
🟢 1️⃣ 2nπ
🔵 2️⃣ (2n+1)π
🟡 3️⃣ nπ/2
🟣 4️⃣ 0
✔️ Answer: (2n+1)π
📘 Exam: JEE Main 2007
🔴 Q36. In beats, when two frequencies are equal, number of beats per second is
🟢 1️⃣ 1
🔵 2️⃣ 0
🟡 3️⃣ 2
🟣 4️⃣ Infinite
✔️ Answer: 0
📘 Exam: JEE Main 2006
🔴 Q37. In an open pipe, if length is halved, frequency becomes
🟢 1️⃣ Double
🔵 2️⃣ Half
🟡 3️⃣ Same
🟣 4️⃣ Four times
✔️ Answer: Double
📘 Exam: JEE Main 2006
🔴 Q38. The equation y = 0.02 sin(2πt − πx/2) represents a wave travelling
🟢 1️⃣ In positive x-direction
🔵 2️⃣ In negative x-direction
🟡 3️⃣ Along y-axis
🟣 4️⃣ Stationary
✔️ Answer: In positive x-direction
📘 Exam: JEE Main 2005
🔴 Q39. The relation between wave speed (v), frequency (f), and wavelength (lambda) is
🟢 1️⃣ v = f / lambda
🔵 2️⃣ v = f × lambda
🟡 3️⃣ f = v × lambda
🟣 4️⃣ lambda = v / f
✔️ Answer: v = f × lambda
📘 Exam: JEE Main 2005
🔴 Q40. In stationary waves, at nodes
🟢 1️⃣ Amplitude is maximum
🔵 2️⃣ Displacement is zero
🟡 3️⃣ Pressure is minimum
🟣 4️⃣ Energy is maximum
✔️ Answer: Displacement is zero
📘 Exam: JEE Main 2004
🔴 Q41. In an open pipe, fundamental mode has
🟢 1️⃣ One node, one antinode
🔵 2️⃣ Two antinodes
🟡 3️⃣ One antinode only
🟣 4️⃣ Two nodes
✔️ Answer: Two antinodes
📘 Exam: JEE Main 2004
🔴 Q42. When two waves interfere constructively, intensity becomes
🟢 1️⃣ Double
🔵 2️⃣ Four times
🟡 3️⃣ Half
🟣 4️⃣ Same
✔️ Answer: Four times
📘 Exam: JEE Main 2003
🔴 Q43. In destructive interference, resultant intensity is
🟢 1️⃣ Zero
🔵 2️⃣ Minimum
🟡 3️⃣ Maximum
🟣 4️⃣ Average
✔️ Answer: Zero
📘 Exam: JEE Main 2003
🔴 Q44. In an open pipe, if length is doubled, frequency becomes
🟢 1️⃣ Half
🔵 2️⃣ Double
🟡 3️⃣ Same
🟣 4️⃣ Four times
✔️ Answer: Half
📘 Exam: JEE Main 2002
🔴 Q45. The speed of sound is maximum in
🟢 1️⃣ Solids
🔵 2️⃣ Liquids
🟡 3️⃣ Gases
🟣 4️⃣ Vacuum
✔️ Answer: Solids
📘 Exam: JEE Main 2002
🔴 Q46. Beats occur when two waves have
🟢 1️⃣ Slightly different frequencies
🔵 2️⃣ Same frequencies
🟡 3️⃣ Same amplitudes
🟣 4️⃣ Opposite phase
✔️ Answer: Slightly different frequencies
📘 Exam: JEE Main 2001
🔴 Q47. In beats, amplitude varies with
🟢 1️⃣ Frequency
🔵 2️⃣ Phase
🟡 3️⃣ Time
🟣 4️⃣ None
✔️ Answer: Time
📘 Exam: JEE Main 2001
🔴 Q48. In stationary waves, energy transfer between particles is
🟢 1️⃣ Zero
🔵 2️⃣ Constant
🟡 3️⃣ Maximum
🟣 4️⃣ Minimum
✔️ Answer: Zero
📘 Exam: JEE Main 2001
🔴 Q49. In stationary waves, amplitude is
🟢 1️⃣ Same for all particles
🔵 2️⃣ Different for different particles
🟡 3️⃣ Zero everywhere
🟣 4️⃣ Infinite
✔️ Answer: Different for different particles
📘 Exam: JEE Main 2001
🔴 Q50. The speed of transverse wave in a stretched string is v = sqrt(T/mu), where T is tension and mu is
🟢 1️⃣ Linear mass density
🔵 2️⃣ Volume density
🟡 3️⃣ Area density
🟣 4️⃣ Surface density
✔️ Answer: Linear mass density
📘 Exam: JEE Main 2001
————————————————————————————————————————————————————————————————————————————
JEE ADVANCED QUESTIONS FROM THIS LESSON
🔴 Question 1:
The equation of a progressive wave is y = 0.02 sin(50t − 4x). The wavelength is
🟢 1️⃣ π/2 m
🔵 2️⃣ 2π m
🟡 3️⃣ 1.57 m
🟣 4️⃣ 3.14 m
✔️ Answer: π/2 m
📘 Exam: JEE Advanced 2024 (Paper 1)
🔴 Question 2:
In a wave, if the phase difference between two points is π, the path difference is
🟢 1️⃣ λ
🔵 2️⃣ λ/2
🟡 3️⃣ 2λ
🟣 4️⃣ λ/4
✔️ Answer: λ/2
📘 Exam: JEE Advanced 2023 (Paper 1)
🔴 Question 3:
If two waves y₁ = A sin(ωt) and y₂ = A sin(ωt + π/2) superpose, the resultant amplitude is
🟢 1️⃣ A
🔵 2️⃣ √2 A
🟡 3️⃣ 2A
🟣 4️⃣ 0
✔️ Answer: √2 A
📘 Exam: JEE Advanced 2022 (Paper 1)
🔴 Question 4:
In a stationary wave, distance between two consecutive nodes is
🟢 1️⃣ λ
🔵 2️⃣ λ/2
🟡 3️⃣ λ/4
🟣 4️⃣ 2λ
✔️ Answer: λ/2
📘 Exam: JEE Advanced 2021 (Paper 1)
🔴 Question 5:
The equation of a wave is y = 0.1 sin(100t − 10x). The velocity of the wave is
🟢 1️⃣ 10 m/s
🔵 2️⃣ 100 m/s
🟡 3️⃣ 20 m/s
🟣 4️⃣ 50 m/s
✔️ Answer: 10 m/s
📘 Exam: JEE Advanced 2020 (Paper 1)
🔴 Question 6:
In a standing wave, the energy transfer is
🟢 1️⃣ Maximum
🔵 2️⃣ Zero
🟡 3️⃣ Constant
🟣 4️⃣ Variable
✔️ Answer: Zero
📘 Exam: JEE Advanced 2019 (Paper 1)
🔴 Question 7:
The frequency of the nth overtone of a closed pipe is proportional to
🟢 1️⃣ 2n + 1
🔵 2️⃣ n + 1
🟡 3️⃣ 2n
🟣 4️⃣ n
✔️ Answer: 2n + 1
📘 Exam: JEE Advanced 2018 (Paper 1)
🔴 Question 8:
If length of a string is doubled and tension is made four times, then fundamental frequency
🟢 1️⃣ Doubles
🔵 2️⃣ Remains same
🟡 3️⃣ Halves
🟣 4️⃣ Becomes 4 times
✔️ Answer: Remains same
📘 Exam: JEE Advanced 2017 (Paper 1)
🔴 Question 9:
A progressive wave has amplitude A and frequency f. The maximum velocity of particle is
🟢 1️⃣ 2πfA
🔵 2️⃣ πfA
🟡 3️⃣ fA
🟣 4️⃣ A/f
✔️ Answer: 2πfA
📘 Exam: JEE Advanced 2016 (Paper 1)
🔴 Question 10:
If a wave travels in +x direction, which form is correct?
🟢 1️⃣ y = A sin(ωt − kx)
🔵 2️⃣ y = A sin(ωt + kx)
🟡 3️⃣ y = A cos(ωt + kx)
🟣 4️⃣ y = A cos(kx − ωt)
✔️ Answer: y = A sin(ωt − kx)
📘 Exam: JEE Advanced 2015 (Paper 1)
🔴 Question 11:
In a stationary wave, distance between node and adjacent antinode is
🟢 1️⃣ λ
🔵 2️⃣ λ/2
🟡 3️⃣ λ/4
🟣 4️⃣ λ/8
✔️ Answer: λ/4
📘 Exam: JEE Advanced 2014 (Paper 1)
🔴 Question 12:
When two waves of equal amplitude and frequency travel in opposite directions, the result is
🟢 1️⃣ Travelling wave
🔵 2️⃣ Stationary wave
🟡 3️⃣ Beats
🟣 4️⃣ None
✔️ Answer: Stationary wave
📘 Exam: JEE Advanced 2013 (Paper 1)
🔴 Question 13:
If a string has length L and wave speed v, then fundamental frequency is
🟢 1️⃣ v/2L
🔵 2️⃣ v/L
🟡 3️⃣ v/4L
🟣 4️⃣ 2v/L
✔️ Answer: v/2L
📘 Exam: JEE Advanced 2012 (Paper 1)
🔴 Question 14:
The principle of superposition applies to
🟢 1️⃣ Linear waves
🔵 2️⃣ Non-linear waves
🟡 3️⃣ Only electromagnetic waves
🟣 4️⃣ Only sound waves
✔️ Answer: Linear waves
📘 Exam: JEE Advanced 2011 (Paper 1)
🔴 Question 15:
In beats, beat frequency is equal to
🟢 1️⃣ Sum of frequencies
🔵 2️⃣ Difference of frequencies
🟡 3️⃣ Product of frequencies
🟣 4️⃣ Ratio of frequencies
✔️ Answer: Difference of frequencies
📘 Exam: JEE Advanced 2010 (Paper 1)
🔴 Question 16:
A wave of frequency 100 Hz has speed 50 m/s. Wavelength is
🟢 1️⃣ 0.5 m
🔵 2️⃣ 1 m
🟡 3️⃣ 2 m
🟣 4️⃣ 0.25 m
✔️ Answer: 0.5 m
📘 Exam: JEE Advanced 2009 (Paper 1)
🔴 Question 17:
If the equation of wave is y = 0.01 sin(100t − 5x), velocity of wave is
🟢 1️⃣ 20 m/s
🔵 2️⃣ 10 m/s
🟡 3️⃣ 5 m/s
🟣 4️⃣ 50 m/s
✔️ Answer: 20 m/s
📘 Exam: JEE Advanced 2008 (Paper 1)
🔴 Question 18:
A tuning fork of frequency 512 Hz produces 6 beats per second with another tuning fork. The frequency of the second tuning fork is
🟢 1️⃣ 506 Hz
🔵 2️⃣ 518 Hz
🟡 3️⃣ 506 Hz or 518 Hz
🟣 4️⃣ 500 Hz
✔️ Answer: 506 Hz or 518 Hz
📘 Exam: JEE Advanced 2024 (Paper 2)
🔴 Question 19:
In a resonance tube, the first and second resonance lengths are 15 cm and 47 cm. The end correction is
🟢 1️⃣ 1 cm
🔵 2️⃣ 2 cm
🟡 3️⃣ 3 cm
🟣 4️⃣ 4 cm
✔️ Answer: 1 cm
📘 Exam: JEE Advanced 2023 (Paper 2)
🔴 Question 20:
If two tuning forks produce 5 beats per second, their frequencies may be
🟢 1️⃣ 100 Hz and 105 Hz
🔵 2️⃣ 105 Hz and 110 Hz
🟡 3️⃣ 95 Hz and 100 Hz
🟣 4️⃣ 90 Hz and 95 Hz
✔️ Answer: 100 Hz and 105 Hz
📘 Exam: JEE Advanced 2022 (Paper 2)
🔴 Question 21:
In a stationary wave, at the nodes
🟢 1️⃣ Displacement and pressure both zero
🔵 2️⃣ Displacement zero, pressure maximum
🟡 3️⃣ Displacement maximum, pressure zero
🟣 4️⃣ Both maximum
✔️ Answer: Displacement zero, pressure maximum
📘 Exam: JEE Advanced 2021 (Paper 2)
🔴 Question 22:
If the amplitude of a wave is doubled, the intensity becomes
🟢 1️⃣ Double
🔵 2️⃣ Quadruple
🟡 3️⃣ Half
🟣 4️⃣ Same
✔️ Answer: Quadruple
📘 Exam: JEE Advanced 2020 (Paper 2)
🔴 Question 23:
In a pipe open at both ends, if length is halved, the fundamental frequency becomes
🟢 1️⃣ Halved
🔵 2️⃣ Doubled
🟡 3️⃣ Same
🟣 4️⃣ Four times
✔️ Answer: Doubled
📘 Exam: JEE Advanced 2019 (Paper 2)
🔴 Question 24:
In beats phenomenon, if one source frequency is 256 Hz and beat frequency is 4, the other source frequency can be
🟢 1️⃣ 252 Hz
🔵 2️⃣ 260 Hz
🟡 3️⃣ 252 Hz or 260 Hz
🟣 4️⃣ 264 Hz
✔️ Answer: 252 Hz or 260 Hz
📘 Exam: JEE Advanced 2018 (Paper 2)
🔴 Question 25:
Two waves of equal amplitude interfere destructively. The phase difference is
🟢 1️⃣ 0
🔵 2️⃣ π/2
🟡 3️⃣ π
🟣 4️⃣ 2π
✔️ Answer: π
📘 Exam: JEE Advanced 2017 (Paper 2)
🔴 Question 26:
In a standing wave, if distance between adjacent nodes is 20 cm, wavelength is
🟢 1️⃣ 10 cm
🔵 2️⃣ 20 cm
🟡 3️⃣ 40 cm
🟣 4️⃣ 80 cm
✔️ Answer: 40 cm
📘 Exam: JEE Advanced 2016 (Paper 2)
🔴 Question 27:
The number of possible harmonics in an open pipe of length L is
🟢 1️⃣ Infinite
🔵 2️⃣ Only odd
🟡 3️⃣ Only even
🟣 4️⃣ 3
✔️ Answer: Infinite
📘 Exam: JEE Advanced 2015 (Paper 2)
🔴 Question 28:
If y₁ = A sin(ωt) and y₂ = A sin(ωt + π), the resultant amplitude is
🟢 1️⃣ 2A
🔵 2️⃣ 0
🟡 3️⃣ A
🟣 4️⃣ √2A
✔️ Answer: 0
📘 Exam: JEE Advanced 2014 (Paper 2)
🔴 Question 29:
If two waves differ in phase by π/3, the resultant intensity is proportional to
🟢 1️⃣ cos²(π/6)
🔵 2️⃣ 3
🟡 3️⃣ 1
🟣 4️⃣ 2
✔️ Answer: cos²(π/6)
📘 Exam: JEE Advanced 2013 (Paper 2)
🔴 Question 30:
In a stationary wave, the points of maximum amplitude are called
🟢 1️⃣ Nodes
🔵 2️⃣ Antinodes
🟡 3️⃣ Crests
🟣 4️⃣ Troughs
✔️ Answer: Antinodes
📘 Exam: JEE Advanced 2012 (Paper 2)
🔴 Question 31:
The velocity of sound in air increases with
🟢 1️⃣ Decrease in temperature
🔵 2️⃣ Increase in temperature
🟡 3️⃣ Decrease in pressure
🟣 4️⃣ Increase in density
✔️ Answer: Increase in temperature
📘 Exam: JEE Advanced 2011 (Paper 2)
🔴 Question 32:
For a sound wave, pressure and displacement are
🟢 1️⃣ In phase
🔵 2️⃣ 90° out of phase
🟡 3️⃣ Opposite in phase
🟣 4️⃣ Random
✔️ Answer: 90° out of phase
📘 Exam: JEE Advanced 2010 (Paper 2)
🔴 Question 33:
If frequency of a tuning fork increases, wavelength in air
🟢 1️⃣ Increases
🔵 2️⃣ Decreases
🟡 3️⃣ Remains same
🟣 4️⃣ Becomes zero
✔️ Answer: Decreases
📘 Exam: JEE Advanced 2009 (Paper 2)
🔴 Question 34:
The frequency of 3rd overtone of closed pipe is equal to
🟢 1️⃣ 5th harmonic of open pipe
🔵 2️⃣ 7th harmonic
🟡 3️⃣ 3rd harmonic
🟣 4️⃣ Fundamental
✔️ Answer: 7th harmonic
📘 Exam: JEE Advanced 2008 (Paper 2)
————————————————————————————————————————————————————————————————————————————
PRACTICE SETS FROM THIS LESSON
🔹 NEET Level (Q1–Q20)
Q1. Which of the following is a mechanical wave?
🔵(A) Sound wave
🟢(B) Light wave
🟠(C) Radio wave
🔴(D) Gamma ray
Answer: (A) Sound wave
Q2. A transverse wave travels along a string. The particles of the string move
🔵(A) Parallel to wave motion
🟢(B) Perpendicular to wave motion
🟠(C) Circularly
🔴(D) Randomly
Answer: (B) Perpendicular to wave motion
Q3. The SI unit of wavelength is
🔵(A) rad/s
🟢(B) meter
🟠(C) hertz
🔴(D) second
Answer: (B) meter
Q4. The speed of a wave is given by
🔵(A) v = λ/ν
🟢(B) v = νλ
🟠(C) v = ν/λ
🔴(D) v = λ²ν
Answer: (B) v = νλ
Q5. The phase difference between displacement and velocity in SHM is
🔵(A) 0
🟢(B) π/2
🟠(C) π
🔴(D) 2π
Answer: (B) π/2
Q6. The energy of a wave is proportional to
🔵(A) Amplitude
🟢(B) Amplitude²
🟠(C) Frequency
🔴(D) Speed
Answer: (B) Amplitude²
Q7. The wave equation y = A sin(kx − ωt) represents
🔵(A) A stationary wave
🟢(B) A wave moving in +x direction
🟠(C) A wave moving in −x direction
🔴(D) A damped wave
Answer: (B) A wave moving in +x direction
Q8. The unit of wave number k is
🔵(A) rad/m
🟢(B) m⁻¹
🟠(C) s⁻¹
🔴(D) Hz
Answer: (B) m⁻¹
Q9. The speed of sound in air depends on
🔵(A) Pressure
🟢(B) Temperature
🟠(C) Humidity
🔴(D) Both (B) and (C)
Answer: (D) Both (B) and (C)
Q10. A wave with frequency 100 Hz and wavelength 3.4 m has speed
🔵(A) 340 m/s
🟢(B) 34 m/s
🟠(C) 3.4 m/s
🔴(D) 3400 m/s
Answer: (A) 340 m/s
Q11. The distance between two adjacent nodes in a stationary wave is
🔵(A) λ
🟢(B) λ/2
🟠(C) λ/4
🔴(D) 2λ
Answer: (B) λ/2
Q12. The frequency of second harmonic is
🔵(A) Same as fundamental
🟢(B) Double
🟠(C) Half
🔴(D) Four times
Answer: (B) Double
Q13. The speed of transverse wave on a stretched string depends on
🔵(A) Length only
🟢(B) Tension and linear density
🟠(C) Frequency only
🔴(D) Amplitude
Answer: (B) Tension and linear density
Q14. The average distance between a node and the nearest antinode is
🔵(A) λ
🟢(B) λ/4
🟠(C) λ/2
🔴(D) λ/8
Answer: (B) λ/4
Q15. In interference, when two waves are exactly out of phase, the resultant amplitude is
🔵(A) Zero
🟢(B) Double
🟠(C) Same
🔴(D) Infinite
Answer: (A) Zero
Q16. When two waves of equal amplitude and frequency interfere constructively, the resultant amplitude is
🔵(A) Zero
🟢(B) Double
🟠(C) Half
🔴(D) Same
Answer: (B) Double
Q17. The relation between angular frequency and frequency is
🔵(A) ω = 2πν
🟢(B) ω = ν/2π
🟠(C) ω = ν²
🔴(D) ω = ν³
Answer: (A) ω = 2πν
Q18. The equation of a wave is y = 0.02 sin(50t − 5x). Its speed is
🔵(A) 10 m/s
🟢(B) 5 m/s
🟠(C) 20 m/s
🔴(D) 2.5 m/s
Answer: (A) 10 m/s
Q19. Beats are produced when two waves have
🔵(A) Same frequency
🟢(B) Slightly different frequencies
🟠(C) Same amplitude
🔴(D) Different speeds
Answer: (B) Slightly different frequencies
Q20. Doppler effect occurs due to
🔵(A) Phase change
🟢(B) Relative motion between source and observer
🟠(C) Reflection
🔴(D) Refraction
Answer: (B) Relative motion between source and observer
🔹 JEE Main Level (Q21–Q40)
Q21. The fundamental frequency of a string of length L is
🔵(A) v/L
🟢(B) v/2L
🟠(C) v/4L
🔴(D) 2v/L
Answer: (B) v/2L
Q22. The ratio of frequencies of 1st, 2nd, and 3rd harmonics for a closed pipe is
🔵(A) 1 : 2 : 3
🟢(B) 1 : 3 : 5
🟠(C) 1 : 4 : 9
🔴(D) 1 : 5 : 9
Answer: (B) 1 : 3 : 5
Q23. The phase difference between pressure and displacement in a sound wave is
🔵(A) 0
🟢(B) π/2
🟠(C) π
🔴(D) 3π/2
Answer: (C) π
Q24. A wave travels 6 m in 0.02 s. Find its speed.
🔵(A) 200 m/s
🟢(B) 300 m/s
🟠(C) 400 m/s
🔴(D) 600 m/s
Answer: (C) 300 m/s
Q25. Two sources of sound of frequency 300 Hz and 303 Hz produce beats. Beat frequency is
🔵(A) 1 Hz
🟢(B) 2 Hz
🟠(C) 3 Hz
🔴(D) 6 Hz
Answer: (C) 3 Hz
Q26. If tension of a string is made four times, frequency becomes
🔵(A) Double
🟢(B) Half
🟠(C) Four times
🔴(D) Same
Answer: (A) Double
Q27. The loudness of sound depends on
🔵(A) Frequency
🟢(B) Intensity
🟠(C) Wavelength
🔴(D) Amplitude only
Answer: (B) Intensity
Q28. The equation of a stationary wave is y = 0.05 sin(2πx) cos(100πt). The distance between two consecutive nodes is
🔵(A) 0.5 m
🟢(B) 1 m
🟠(C) 2 m
🔴(D) 0.25 m
Answer: (A) 0.5 m
Q29. The frequency of a tuning fork increases when
🔵(A) Its prongs are loaded
🟢(B) Its length decreases
🟠(C) Its temperature decreases
🔴(D) Medium changes
Answer: (B) Its length decreases
Q30. The velocity of sound in gas is proportional to
🔵(A) √T
🟢(B) 1/T
🟠(C) T
🔴(D) √(1/T)
Answer: (A) √T
Q31. The phase difference between displacement and velocity in a wave is
🔵(A) 0
🟢(B) π/2
🟠(C) π
🔴(D) 2π
Answer: (B) π/2
Q32. The intensity of sound increases by 100 times. Loudness increases by
🔵(A) 10 dB
🟢(B) 20 dB
🟠(C) 100 dB
🔴(D) 2 dB
Answer: (B) 20 dB
Q33. The power transmitted by a wave is proportional to
🔵(A) A
🟢(B) A²
🟠(C) A³
🔴(D) A⁴
Answer: (B) A²
Q34. In a standing wave, number of nodes between two antinodes is
🔵(A) 0
🟢(B) 1
🟠(C) 2
🔴(D) 3
Answer: (B) 1
Q35. The speed of a transverse wave on a string under tension T and mass per unit length μ is
🔵(A) v = Tμ
🟢(B) v = √(T/μ)
🟠(C) v = 1/√(Tμ)
🔴(D) v = T²/μ
Answer: (B) v = √(T/μ)
Q36. When two sound waves interfere destructively, intensity becomes
🔵(A) Zero
🟢(B) Double
🟠(C) Half
🔴(D) Four times
Answer: (A) Zero
Q37. The fundamental frequency of a closed organ pipe of length L is
🔵(A) v/L
🟢(B) v/2L
🟠(C) v/4L
🔴(D) 2v/L
Answer: (C) v/4L
Q38. In stationary waves, energy is
🔵(A) Transmitted
🟢(B) Confined between nodes
🟠(C) Constant everywhere
🔴(D) Reflected continuously
Answer: (B) Confined between nodes
Q39. The wavelength of sound in air of frequency 330 Hz is (speed = 330 m/s)
🔵(A) 1 m
🟢(B) 0.5 m
🟠(C) 2 m
🔴(D) 3 m
Answer: (A) 1 m
Q40. The ratio of intensities of two sounds differing by 3 dB is
🔵(A) 1.5
🟢(B) 2
🟠(C) 3
🔴(D) 1
Answer: (B) 2
🔹 JEE Advanced Level (Q41–Q50)
Q41. Two waves y₁ = A sin(ωt) and y₂ = A sin(ωt + π/3). The resultant amplitude is
🔵(A) 2A
🟢(B) A
🟠(C) A√3
🔴(D) A√2
Answer: (C) A√3
Q42. If tension in a string is increased by 9 times, frequency increases by
🔵(A) 3 times
🟢(B) 9 times
🟠(C) 2 times
🔴(D) 1/3 times
Answer: (A) 3 times
Q43. A wave has equation y = 0.02 sin(50t − 5x). Find amplitude, frequency, wavelength.
🔵(A) 0.02 m, 25 Hz, 1.26 m
🟢(B) 0.02 m, 8 Hz, 1.26 m
🟠(C) 0.2 m, 5 Hz, 2.5 m
🔴(D) 0.02 m, 10 Hz, 2.5 m
Answer: (A) 0.02 m, 25 Hz, 1.26 m
Q44. The speed of sound in helium is greater than in air because
🔵(A) Helium is heavier
🟢(B) Helium has higher γ/ρ ratio
🟠(C) Helium is denser
🔴(D) Helium has lower pressure
Answer: (B) Helium has higher γ/ρ ratio
Q45. The phase difference between two points 1 m apart on a wave of wavelength 4 m is
🔵(A) π/2
🟢(B) π
🟠(C) π/4
🔴(D) 2π
Answer: (A) π/2
Q46. The amplitude of a wave becomes half after travelling 10 m. Intensity decreases by factor
🔵(A) 1/2
🟢(B) 1/4
🟠(C) 2
🔴(D) 4
Answer: (B) 1/4
Q47. The pressure amplitude of a sound wave doubles. Its intensity increases by
🔵(A) 2 times
🟢(B) 4 times
🟠(C) 8 times
🔴(D) 16 times
Answer: (B) 4 times
Q48. The fundamental frequency of an open pipe of length 0.5 m (v = 340 m/s) is
🔵(A) 170 Hz
🟢(B) 340 Hz
🟠(C) 680 Hz
🔴(D) 85 Hz
Answer: (A) 170 Hz
Q49. Two tuning forks of frequencies 256 Hz and 260 Hz produce 4 beats per second. When wax is added to one fork, beat frequency becomes 2 Hz. The frequency of waxed fork is
🔵(A) 258 Hz
🟢(B) 254 Hz
🟠(C) 252 Hz
🔴(D) 260 Hz
Answer: (B) 254 Hz
Q50. A stationary wave has amplitude 5 cm. The maximum particle velocity if frequency is 20 Hz is
🔵(A) 5 m/s
🟢(B) 6.28 m/s
🟠(C) 2π m/s
🔴(D) 3.14 m/s
Answer: (B) 6.28 m/s
————————————————————————————————————————————————————————————————————————————
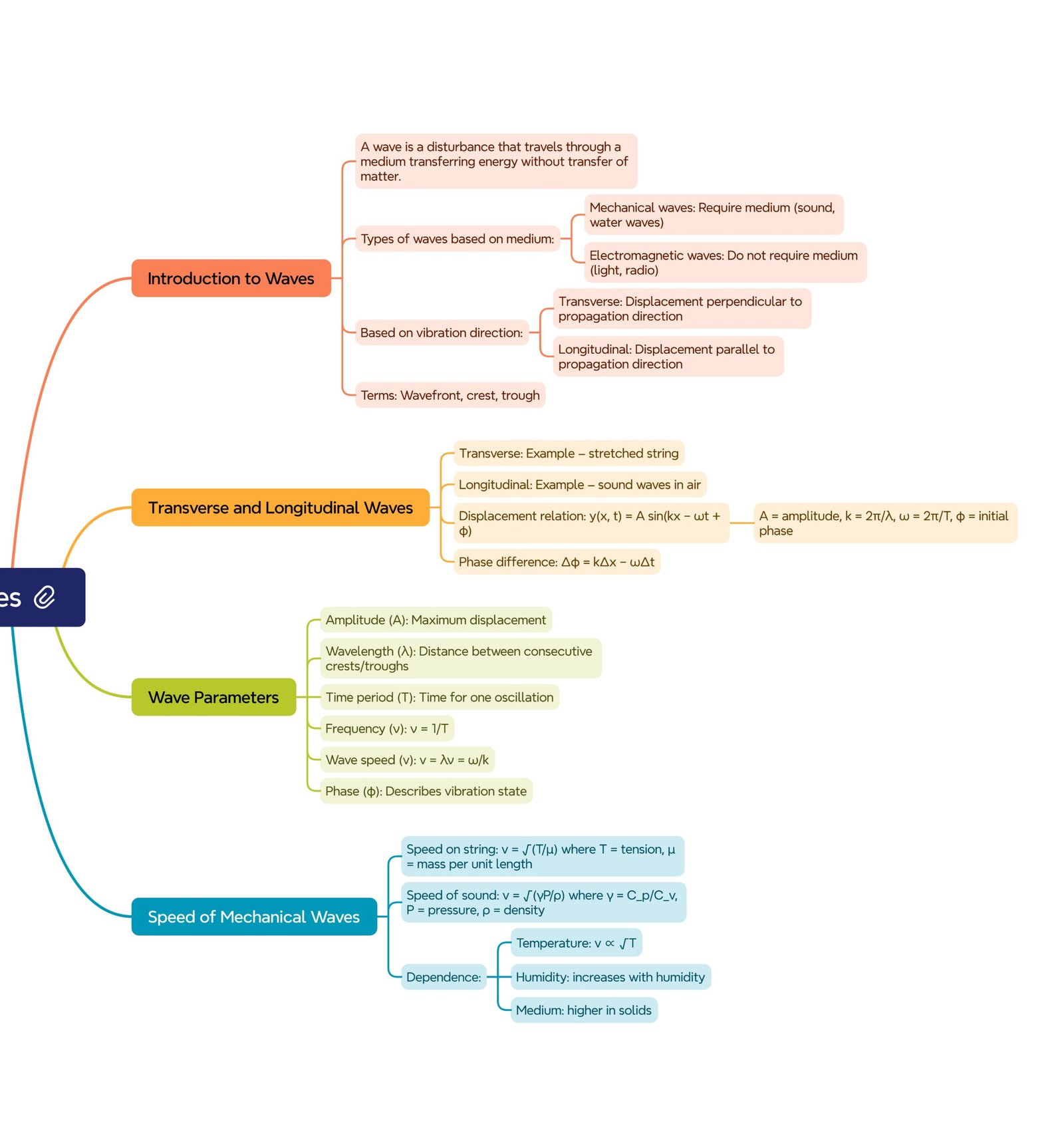
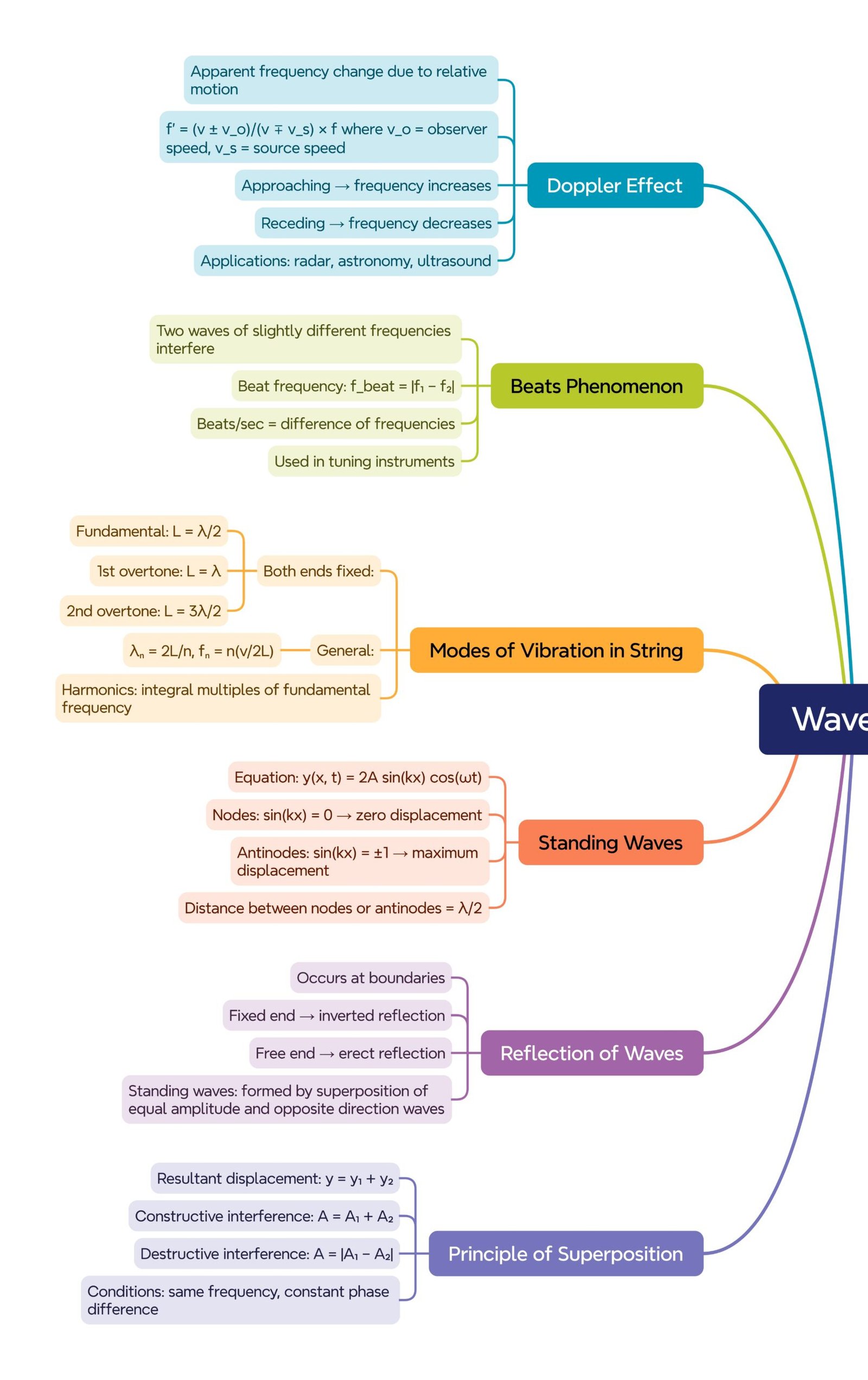
MIND MAPS

————————————————————————————————————————————————————————————————————————————
