Class 11 : Physics (In English) – Chapter 5: Work, Energy and Power
EXPLANATION & SUMMARY
🔵 Explanation
🌿 Introduction
The concepts of work, energy, and power are central to understanding motion and physical processes in nature. Every event involving motion — a falling ball, a running engine, or a stretching spring — involves energy transfer governed by the principles of work and power.
💡 Work connects force and displacement, energy measures the ability to do work, and power indicates the rate of doing work. These three are interlinked through the work–energy theorem and the law of conservation of energy.
🟢 Work
💡 Definition
When a force acts on a body and displaces it in the direction of the force, work is said to be done.
➡️ Formula: W = F × s × cos θ
where
F = magnitude of applied force
s = displacement of the body
θ = angle between force and displacement
🧠 Key Points
✔️ Work is a scalar quantity.
✔️ SI Unit: joule (J), where 1 J = 1 N·m.
✔️ CGS Unit: erg, where 1 erg = 10⁻⁷ joule.
✔️ Work depends on both the magnitude and direction of the applied force.
🔵 Types of Work
🔹 Positive Work: When θ < 90°, force aids motion.
➡️ Example: Engine pulling a train.
🔹 Negative Work: When θ > 90°, force opposes motion.
➡️ Example: Work done by friction or gravity while throwing a ball upward.
🔹 Zero Work: When θ = 90°, force is perpendicular to displacement.
➡️ Example: Centripetal force in circular motion.
🟣 Work Done by Variable Force
When force changes with position, the total work is obtained by integration:
➡️ W = ∫ F·ds
Graphically, work done equals the area under the F–s graph.
🔴 Work Done by Constant Force
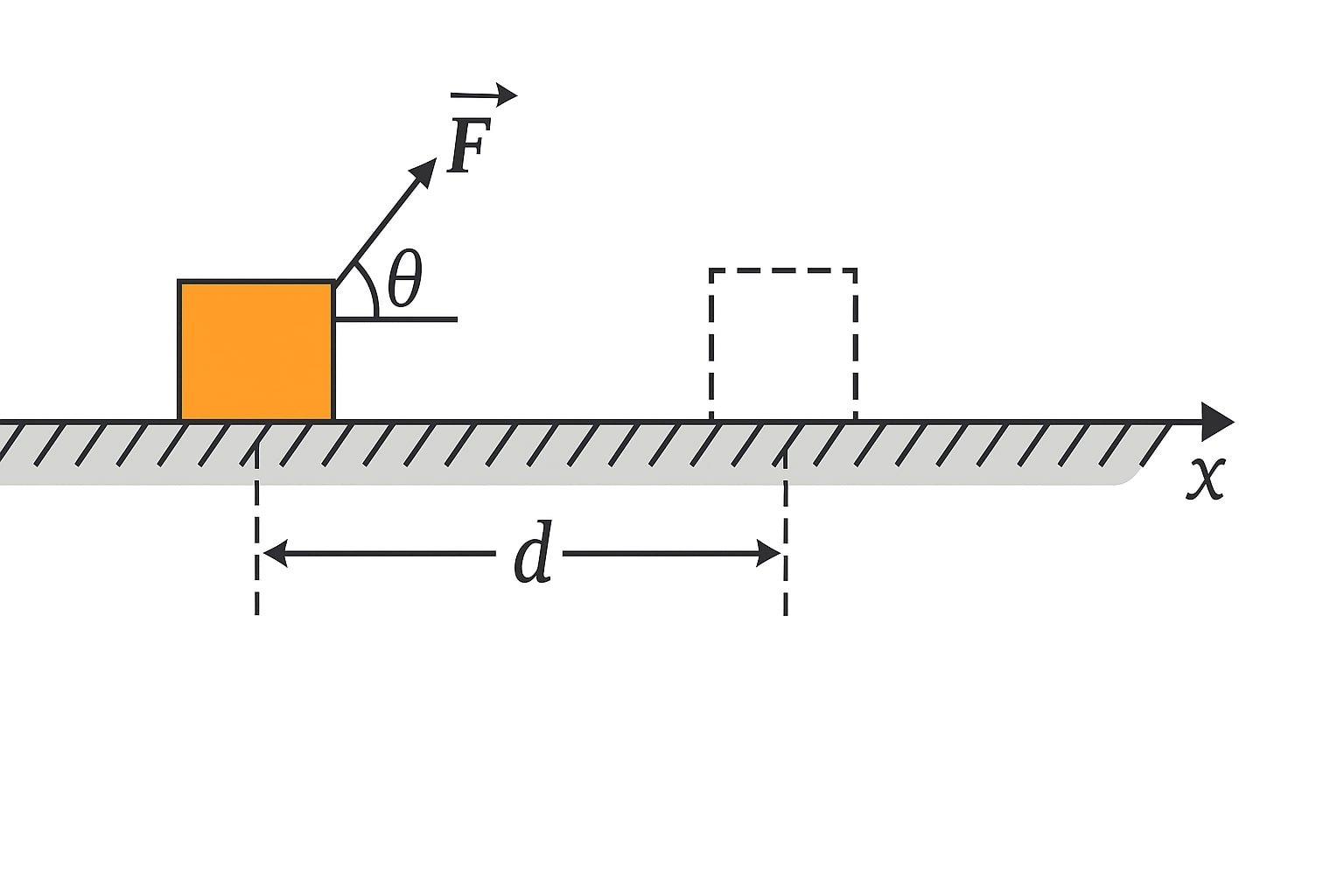
If the force is uniform and acts along displacement:
➡️ W = F × s
Example: Lifting a 10 kg body vertically by 2 m,
W = mgh = 10 × 9.8 × 2 = 196 J
🟡 Work Done by Gravitational Force
For a body of mass m moving vertically through height h,
➡️ W = mgh (if lifted)
✔️ Work done is positive when lifted upward by an external agent,
✔️ Negative when the body falls under gravity.
⚡ Power
💡 Definition
Power is the rate of doing work.
➡️ P = W / t = F·v
✔️ SI Unit: watt (W) → 1 W = 1 J/s
✔️ Larger units: kilowatt (kW), megawatt (MW).
💡 Average Power = Total work / Total time
💡 Instantaneous Power = dW/dt
🟢 Energy
💡 Energy is the capacity of a body to do work.
✔️ Scalar quantity, unit: joule (J).
Forms of energy include mechanical (kinetic, potential), chemical, thermal, electrical, etc.
🟣 Kinetic Energy (K.E.)
💡 Energy possessed due to motion.
➡️ K.E. = (1/2)mv²
🧠 Derivation:
Work done by a force in accelerating a body from rest:
W = F × s = ma × s
Using v² − u² = 2as,
W = ½ m(v² − u²)
Thus, W = ΔK.E.
✔️ Work–Energy Theorem: Work done by the net force equals change in kinetic energy.
🔴 Potential Energy (P.E.)
💡 Energy possessed due to position or configuration.
➡️ P.E. = mgh
✔️ It depends on the reference point (zero level).
✔️ Unit: joule (J).
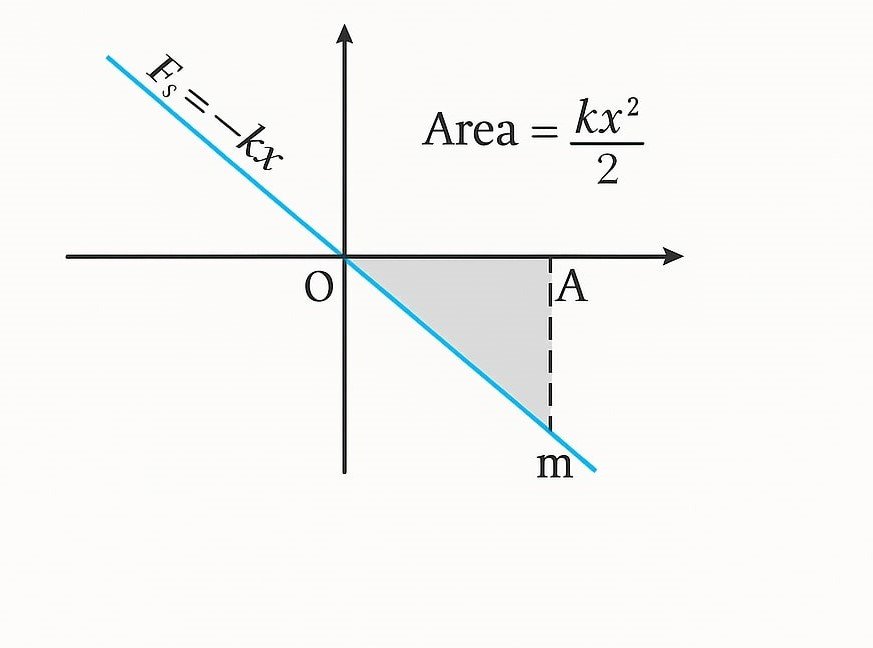
🟢 Elastic Potential Energy

For a stretched or compressed spring:
➡️ U = (1/2)kx²
where k = spring constant, x = deformation.
🧠 Derivation:
W = ∫₀ˣ kx·dx = ½kx²
🟣 Mechanical Energy
💡 Total mechanical energy = Kinetic + Potential energy
➡️ E = ½mv² + mgh
✔️ For conservative forces (like gravity), total mechanical energy remains constant.
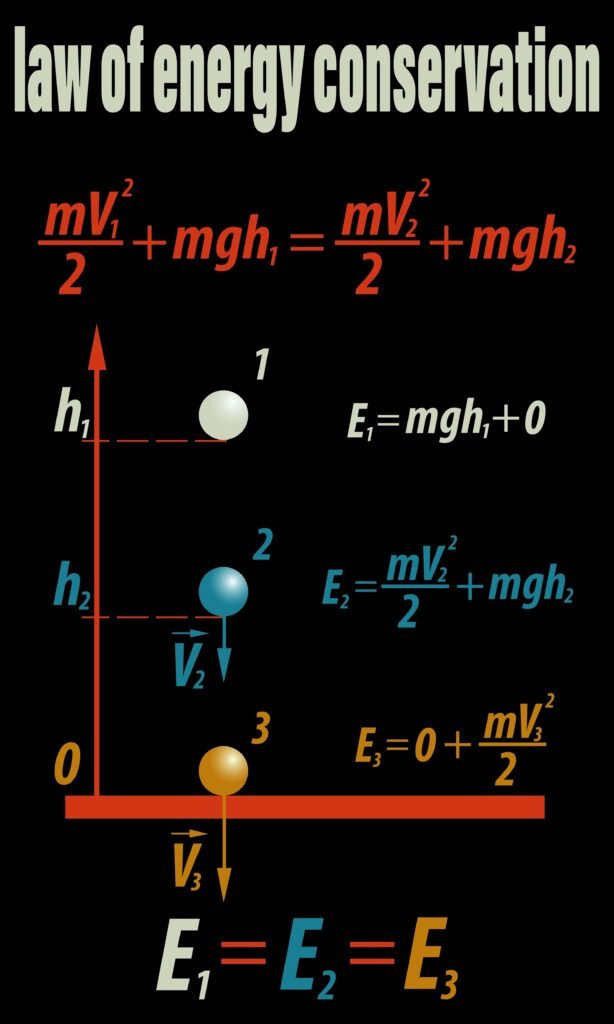
💡 Conservation of Mechanical Energy
✔️ Energy can neither be created nor destroyed; it only changes form.
Example (freely falling body):
At top → P.E. = mgh, K.E. = 0
At bottom → P.E. = 0, K.E. = mgh
Total E = constant = mgh
⚡ Power–Energy Relation
Since power = work/time and work = energy,
➡️ P = dE/dt
Example: A 100 W bulb converts 100 J of energy every second.
🔵 Conservative & Non-Conservative Forces
💡 Conservative Force
✔️ Work depends only on initial and final positions.
✔️ Work done in closed path = 0.
➡️ Examples: gravitational force, spring force.
💡 Non-Conservative Force
✔️ Work depends on path taken.
✔️ Energy lost as heat or sound.
➡️ Examples: friction, viscous drag.
🟢 Work Done by a Spring
Restoring force F = −kx
Work done from x = 0 to x = X:
➡️ W = ∫₀ˣ (−kx)dx = −½kX²
Negative sign shows work done against restoring force.
🟣 Potential Energy Curve
Graph of potential energy (U) vs position (x):
✔️ Equilibrium point → dU/dx = 0
✔️ Stable equilibrium → minimum U
✔️ Unstable equilibrium → maximum U
💡 Collisions and Energy
✔️ In elastic collisions → both momentum and kinetic energy conserved.
✔️ In inelastic collisions → momentum conserved, kinetic energy not conserved.
🟢 Work–Energy Theorem (General Form)
✔️ The total work done by all forces = change in kinetic energy.
➡️ ΣW = ΔK.E. = K₂ − K₁
🔴 Law of Conservation of Energy
💡 Total energy of an isolated system remains constant though forms change.
Examples:
✔️ Pendulum: Potential ↔ Kinetic energy.
✔️ Roller coaster: Conversion of potential and kinetic.
➡️ K₁ + U₁ = K₂ + U₂
⚡ Power in Rotational Motion
When torque (τ) acts with angular velocity (ω):
➡️ P = τ × ω
🟢 Efficiency
Efficiency η = (Useful output energy / Total input energy) × 100%
Example: If 1000 J input gives 800 J output,
η = 800/1000 × 100 = 80%
🔴 Dimensional Analysis (Without Table)
Work → joule (J), dimensions [M¹L²T⁻²]
Energy → joule (J), dimensions [M¹L²T⁻²]
Power → watt (W), dimensions [M¹L²T⁻³]
🟢 Numerical Example 1
A force of 50 N acts on a body moving 10 m at 60° to the force.
➡️ W = F·s·cosθ = 50×10×cos60° = 500×0.5 = 250 J
🟣 Numerical Example 2
Find kinetic energy of a 5 kg mass moving with 4 m/s.
➡️ K.E. = ½mv² = ½×5×16 = 40 J
🔴 Numerical Example 3
A spring with k = 200 N/m is stretched by 0.1 m.
➡️ U = ½kx² = ½×200×(0.1)² = 1 J
⚡ Energy Transformations (Examples)
✔️ Electric fan → electrical to mechanical
✔️ Solar cell → solar to electrical
✔️ Motor → electrical to mechanical
✔️ Pendulum → potential ↔ kinetic
✔️ Car engine → chemical to mechanical
🟢 Concept Flow Summary
Force → Work → Energy → Power
✔️ Work done changes kinetic energy
✔️ Energy interconverts but total remains constant
✔️ Power measures rate of energy use
🟣 Summary
The chapter Work, Energy and Power explains how energy and motion relate through forces. Work (W = F·s·cosθ) is the measure of energy transfer by force. Positive work increases motion, negative work resists it.
Energy is the capacity to do work. Kinetic energy (½mv²) arises from motion, potential energy (mgh or ½kx²) from position or deformation. The work–energy theorem states: total work done equals change in kinetic energy.
Mechanical energy, the sum of kinetic and potential energies, remains constant when only conservative forces act. Power (P = W/t = F·v) quantifies how fast work is done.
The law of conservation of energy ensures total energy remains constant, transforming between different forms like heat, light, mechanical, or electrical. Friction and resistance are non-conservative forces converting mechanical energy into heat.
Practical applications include engines, motors, pendulums, and moving vehicles — all illustrating the same fundamental rules of energy conservation and transformation.
📝 Quick Recap
🔵 Work → W = F·s·cosθ
🟢 Kinetic Energy → K.E. = ½mv²
🟠 Potential Energy → P.E. = mgh or ½kx²
🔴 Power → P = W/t or F·v
💡 Work–Energy Theorem → Net work = ΔK.E.
⚡ Law of Conservation of Energy → Energy remains constant in isolated systems
————————————————————————————————————————————————————————————————————————————
QUESTIONS FROM TEXTBOOK
Question 5.1
The sign of work done by a force on a body is important to understand. State carefully if the following quantities are positive or negative:
(a) Work done by a man in lifting a bucket out of a well by means of a rope tied to the bucket.
(b) Work done by gravitational force in the above case.
(c) Work done by friction on a body sliding down an inclined plane.
(d) Work done by an applied force on a body moving on a rough horizontal plane with uniform velocity.
(e) Work done by the resistive force of air on a vibrating pendulum in bringing it to rest.
Answer
🔹 (a) Positive — The man applies an upward force, and the displacement of the bucket is also upward.
➡️ Work done (W = F·s cosθ), here θ = 0°, so W > 0.
🔹 (b) Negative — Gravitational force acts downward while displacement is upward, hence θ = 180°, so cosθ = −1 ⇒ W < 0.
🔹 (c) Negative — Frictional force opposes motion; displacement and force are in opposite directions.
🔹 (d) Positive — Applied force and displacement are in the same direction, though the magnitude of velocity is constant.
🔹 (e) Negative — Resistive force of air opposes the motion of the pendulum; thus work done is negative.
✔️ Hence,
(a) +ve (b) −ve (c) −ve (d) +ve (e) −ve
Question 5.2
A body of mass 2 kg initially at rest moves under the action of an applied horizontal force of 7 N on a table with a coefficient of kinetic friction μ = 0.1. Compute:
(a) work done by the applied force in 10 s,
(b) work done by friction in 10 s,
(c) work done by the net force on the body in 10 s,
(d) change in kinetic energy of the body in 10 s, and interpret your results.
Answer
Given:
m = 2 kg, F = 7 N, μ = 0.1, g = 10 m s⁻², u = 0, t = 10 s
➡️ Frictional force, f = μmg = 0.1 × 2 × 10 = 2 N
➡️ Net force, F_net = F − f = 7 − 2 = 5 N
➡️ Acceleration, a = F_net / m = 5 / 2 = 2.5 m s⁻²
➡️ Displacement, s = ut + (1/2) a t² = 0 + 0.5 × 2.5 × (10)² = 125 m
(a) Work done by applied force:
W₁ = F × s = 7 × 125 = 875 J
(b) Work done by friction:
W₂ = −f × s = −2 × 125 = −250 J
(c) Work done by net force:
W_net = F_net × s = 5 × 125 = 625 J
(d) Change in kinetic energy:
Using work–energy theorem, ΔK = W_net = 625 J
➡️ Final velocity, v² = u² + 2as = 0 + 2 × 2.5 × 125 = 625 ⇒ v = 25 m s⁻¹
⇒ K_f = ½ m v² = ½ × 2 × (25)² = 625 J ✅
✔️ Interpretation:
Work done by the net force equals the increase in kinetic energy — verifying the work–energy theorem.
Question 5.3
Given in Fig. 5.11 are examples of some potential energy functions in one dimension. The total energy of the particle is indicated by a cross on the ordinate axis. In each case, specify the regions, if any, in which the particle cannot be found for the given energy. Also, indicate the minimum total energy the particle must have in each case.
Answer
💡 Concept:
The particle can exist only where its total energy E ≥ potential energy V(x).
If E < V(x), the particle cannot exist in that region (classically forbidden).
Case (a):
Potential energy V(x) has a step-like pattern, V = 0 for x < 0, V = V₀ for x ≥ 0.
For total energy E < V₀, the particle cannot be found in the region x ≥ 0 (since E < V₀).
Minimum energy required to reach x ≥ 0 is E = V₀.
Case (b):
V(x) is piecewise constant with a well between x = a and x = b (V = −V₁) and V = 0 outside.
If total energy E = 0, the particle can exist in all regions (E ≥ V).
For E < 0, the particle is confined to the potential well region between a and b.
Minimum total energy = E = −V₁.
Case (c):
V(x) has a potential well of depth V₁ below the zero level and rises symmetrically.
The particle can exist only where E ≥ V(x).
The classically forbidden regions correspond to x-values where V(x) > E (outer slopes).
Minimum total energy for motion inside the well = E = V₁ (bottom of the well).
✔️ Thus, the particle’s motion is restricted to regions where total energy ≥ potential energy, and forbidden elsewhere.
Question 5.5
Answer the following:
(a) The casing of a rocket in flight burns up due to friction. At whose expense is the heat energy required for burning obtained — the rocket or the atmosphere?
Answer:
➡️ The heat energy is obtained at the expense of the rocket’s kinetic energy.
🌡️ As the rocket moves through air, friction between its surface and air molecules converts part of its kinetic energy into heat.
⚡ Therefore, the rocket slows down slightly as it loses energy to heating.
✔️ Source of heat: Rocket’s own kinetic energy (not the atmosphere).
(b) Comets move around the Sun in highly elliptical orbits. The gravitational force on the comet due to the Sun is not normal to the comet’s velocity in general. Yet, the work done by the gravitational force over every complete orbit of the comet is zero. Why?
Answer:
💡 Concept: Work done by a force = change in kinetic energy = change in total mechanical energy.
➡️ Gravitational force is conservative ⇒ work done over a closed path = 0.
🌀 After one full revolution, the comet returns to its starting position with same potential and kinetic energy.
✔️ Hence, total work done by gravity = 0 over one complete orbit.
(c) An artificial satellite orbiting the Earth in a very thin atmosphere loses its energy gradually due to atmospheric drag. However, as it comes closer to Earth, its speed increases progressively. Why?
Answer:
➡️ Due to drag, total mechanical energy decreases slowly (both potential and kinetic energy change).
➡️ As the satellite spirals inward, its potential energy decreases (becomes more negative).
➡️ To conserve total energy (E = K + U), kinetic energy increases, and thus its speed increases.
💡 Therefore:
As altitude ↓ ⇒ potential energy ↓ ⇒ kinetic energy ↑ ⇒ speed ↑.
(d) In Fig. 5.13:
A man walks 2 m carrying a mass of 15 kg in his hands. In (i) he walks horizontally holding the mass; in (ii) the mass is tied to a rope and hangs at rest while the man walks the same distance pulling the rope behind him.
In which case is the work done greater?
Answer:
Case (i):
🔵 The man lifts no mass vertically; the force (upward) and displacement (horizontal) are perpendicular.
➡️ W = F s cosθ = F s cos(90°) = 0.
✅ Work done = 0 J.
Case (ii):
🟢 The man exerts a tension T on the rope (angled backward).
➡️ The horizontal component of tension T cosθ acts along displacement.
Hence, work done = (T cosθ) × s ≠ 0.
✅ Therefore, work done in case (ii) is greater because a horizontal component of force acts in the direction of motion.
Question
5.6 Underline the correct alternative:
(a) When a conservative force does positive work on a body, the potential energy of the body increases/decreases/remains unaltered.
(b) Work done by a body against friction always results in a loss of its kinetic/potential energy.
(c) The rate of change of total momentum of a many-particle system is proportional to the external force/sum of the internal forces on the system.
(d) In an inelastic collision of two bodies, the quantities which do not change after the collision are the total kinetic energy/total linear momentum/total energy of the system of two bodies.
Answer
🔵 (a) decreases
➡️ For a conservative force: W_cons = −ΔU. If W_cons > 0 ⇒ ΔU < 0 ⇒ U decreases.
🟢 (b) kinetic energy
➡️ Friction does negative work on the moving body; its mechanical energy reduces, primarily as a loss of K to thermal energy.
🟠 (c) external force
➡️ d⃗P_total/dt = ⃗F_external (internal forces cancel in pairs by Newton’s third law).
🔴 (d) total linear momentum (always, for an isolated system) and total energy (always; kinetic + internal + other forms conserved).
➡️ Total kinetic energy is not conserved in an inelastic collision.
Question
5.7 State if each of the following statements is true or false. Give reasons for your answer.
(a) In an elastic collision of two bodies, the momentum and energy of each body is conserved.
(b) Total energy of a system is always conserved, no matter what internal and external forces are present.
(c) Work done in the motion of a body over a closed loop is zero for every force in nature.
(d) In an inelastic collision, the final kinetic energy is always less than the initial kinetic energy of the system.
Answer
🔵 (a) False. In an elastic collision, total linear momentum and total kinetic energy of the system are conserved; those of individual bodies generally change.
🟢 (b) False. The energy of a system can change if external work/heat crosses its boundary. (Energy is conserved only for the universe or for an isolated system; for a closed, isolated system E_total is constant.)
🟠 (c) False. Zero work over a closed path holds only for conservative forces (e.g., gravity, spring). Non-conservative forces (e.g., friction, drag) do non-zero negative work over a cycle.
🔴 (d) True. For an inelastic collision in an isolated system, some kinetic energy converts to internal/thermal energy; hence K_final < K_initial (strict inequality except perfectly elastic case).
Question
5.8 Answer carefully, with reasons:
(a) In an elastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision (when they are in contact)?
(b) Is the total linear momentum conserved during the short time of an elastic collision of two balls?
Answer
🔵 (a) No. During the brief contact, some kinetic energy is temporarily stored as elastic potential energy of deformation and then returned. Thus K(t) is not constant during contact; only before and after collision (long before/long after) the initial and final total K are equal.
🟢 (b) Yes (for an isolated pair). External forces (weight/normal) nearly cancel over the tiny interval, while mutual internal forces are equal and opposite. Hence ⃗P_total is conserved at every instant during the collision.
🔷 Question 5.8
Answer carefully, with reasons :
(a) In an elastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision of the balls (i.e. when they are in contact)?
(b) Is the total linear momentum conserved during the short time of an elastic collision of two balls?
(c) What are the answers to (a) and (b) for an inelastic collision?
(d) If the potential energy of two billiard balls depends only on the separation distance between their centres, is the collision elastic or inelastic?
🔶 Answer:
➡️ (a) During the short interval when the balls are in contact, part of kinetic energy is temporarily stored as elastic potential energy. Hence total kinetic energy is not conserved at that instant, though it is conserved before and after collision.
➡️ (b) Total linear momentum is conserved at all times during the collision, because internal forces act equally and oppositely on both balls (Newton’s 3rd law).
➡️ (c) For inelastic collision, total momentum remains conserved, but total kinetic energy decreases (partly converted to heat/sound/deformation).
➡️ (d) If potential energy depends only on the separation distance, the forces are conservative, so collision is elastic.
🔷 Question 5.9
A body is initially at rest. It undergoes one-dimensional motion with constant acceleration. The power delivered to it at time t is proportional to
(i) t¹ᐟ² (ii) t (iii) t³ᐟ² (iv) t²
🔶 Answer:
💡 Concept:
Power P = F·v = m·a·v and v = a·t
✏️ So, P = m·a²·t
Hence, P ∝ t
✔️ Correct option: (ii) t
🔷 Question 5.10
A body is moving unidirectionally under the influence of a source of constant power. Its displacement in time t is proportional to
(i) t¹ᐟ² (ii) t³ᐟ² (iii) t⁵ᐟ² (iv) t³
🔶 Answer:
💡 Concept: P = F·v = m·a·v and F = m·a
So a = P / (m·v)
Since a = dv/dt = P / (m·v)
➡️ v·dv = (P/m)·dt
Integrate from 0 to v and 0 to t:
½ v² = (P/m)·t
∴ v ∝ t¹ᐟ²
Now displacement s = ∫v dt ∝ ∫t¹ᐟ² dt ∝ t³ᐟ²
✔️ Correct option: (ii) t³ᐟ²
🔷 Question 5.11
A body constrained to move along the z-axis is subject to a constant force F = −î + 2ĵ + 3k̂ N.
What is the work done by this force in moving the body a distance of 4 m along the z-axis?
🔶 Answer:
➡️ Only the z-component (F_z = 3 N) does work.
Work done, W = F_z · s = 3 × 4 = 12 J
✔️ Work done = 12 J
🔷 Question 5.12
An electron and a proton are detected in a cosmic-ray experiment, the first with kinetic energy 10 keV and the second with 100 keV. Which is faster? Obtain the ratio of their speeds.
Given:
mₑ = 9.1×10⁻³¹ kg, m_p = 1.67×10⁻²⁷ kg, 1 eV = 1.6×10⁻¹⁹ J
🔶 Answer:
Convert energies to joules:
Eₑ = 10 × 10³ × 1.6×10⁻¹⁹ = 1.6×10⁻¹⁵ J
E_p = 100 × 10³ × 1.6×10⁻¹⁹ = 1.6×10⁻¹⁴ J
For non-relativistic speeds, v = √(2E/m)
➡️ vₑ = √(2×1.6×10⁻¹⁵ / 9.1×10⁻³¹) = 1.88×10⁷ m s⁻¹
➡️ v_p = √(2×1.6×10⁻¹⁴ / 1.67×10⁻²⁷) = 4.38×10⁶ m s⁻¹
Ratio vₑ : v_p ≈ 4.3 : 1
✔️ Electron is faster; vₑ/v_p ≈ 4.3
🔷 Question 5.13
A rain drop of radius 2 mm falls from a height of 500 m. At half the height (250 m), its velocity becomes terminal (10 m s⁻¹). Find
(a) work done by gravitational force in the whole fall, and
(b) work done by resistive force.
🔶 Answer:
✏️ (a) Work by gravity: W_g = m g h
Volume = (4/3) π r³ = (4/3) × 3.14 × (2×10⁻³)³ = 3.35×10⁻⁸ m³
Mass = ρ × Volume = 1000 × 3.35×10⁻⁸ = 3.35×10⁻⁵ kg
W_g = 3.35×10⁻⁵ × 9.8 × 500 = 0.164 J
✏️ (b) Work done by resistive force (W_r):
Net energy gained = ½ m v² = ½ × 3.35×10⁻⁵ × (10)² = 1.68×10⁻³ J
Therefore W_r = W_g − ΔK = 0.164 − 0.00168 ≈ 0.162 J (opposite in direction)
✔️ W_g = 0.164 J, W_r = −0.162 J
🔷 Question 5.14
A molecule in a gas container hits a horizontal wall with speed 200 m s⁻¹ and at an angle 30° with the normal, and rebounds with the same speed. Is momentum conserved in the collision? Is the collision elastic or inelastic?
🔶 Answer:
➡️ Component of momentum normal to wall reverses; tangential component remains unchanged.
Hence momentum of molecule alone not conserved — wall exerts impulse.
For molecule + wall system, total momentum is conserved.
➡️ Kinetic energy before = after, so collision is elastic.
✔️ Total momentum conserved (system), collision elastic.
🔷 Question 5.15
A pump on the ground floor of a building can pump up water to fill a tank of volume 30 m³ in 15 min. If the tank is 40 m above ground and efficiency of pump is 30%, find the electric power consumed.
🔶 Answer:
Volume = 30 m³ Density of water ρ = 1000 kg m⁻³
➡️ m = ρ V = 3 × 10⁴ kg
Work done = m g h = 3×10⁴ × 9.8 × 40 = 1.176×10⁷ J
Time = 15 min = 900 s
Useful power output = 1.176×10⁷ / 900 = 1.31×10⁴ W
Efficiency η = 30% = 0.3
Input power = P_out / η = 1.31×10⁴ / 0.3 = 4.37×10⁴ W
✔️ Electric power consumed = 43.7 kW
🔷 Question 5.16
Two identical ball bearings (1 and 2) rest in contact on a smooth table. A third identical ball (3) moving with speed V hits ball 1 head-on. Which of the following outcomes is possible for an elastic collision?
(i) 1 → V, 2 → 0, 3 → 0
(ii) 1 → V/2, 2 → V/2, 3 → 0
(iii) 1 → 0, 2 → V, 3 → 0
🔶 Answer:
💡 In a perfectly elastic head-on collision between identical spheres, the incoming ball transfers its velocity to the first and then to the next ball successively (as in Newton’s cradle).
➡️ Therefore, ball 3 stops, and ball 2 moves with velocity V.
✔️ Correct option: (iii)
🔷 Question 5.17
The bob A of a pendulum released from 30° to the vertical hits another bob B of the same mass at rest on a table (Fig. 5.15). How high does the bob B rise after the collision? Neglect the size of the bobs and assume the collision is elastic.
🔶 Answer:
💡 Concept:
In an elastic collision between equal masses:
➡️ The moving mass transfers its velocity completely to the stationary mass.
✏️ Step 1: Velocity of A just before impact
v = √(2gh) = √(2gL(1 − cos30°))
= √(2 × 9.8 × L × 0.134) = √(2.63L)
✏️ Step 2: After collision, A stops and B moves with velocity v.
✏️ Step 3: Maximum height of B = v² / (2g) = [2gL(1 − cos30°)] / (2g) = L(1 − cos30°)
✔️ Height attained by B = L(1 − cos30°)
🔷 Question 5.18
The bob of a pendulum is released from a horizontal position. The length of the pendulum is 1.5 m. What is the speed at the lowest point, given that it dissipated 5% of its initial energy against air resistance?
🔶 Answer:
💡 Concept:
Potential energy at top = m g L
Kinetic energy at bottom = 0.95 m g L
✏️ Step 1: v = √(2 × 0.95 g L)
= √(2 × 0.95 × 9.8 × 1.5)
= √(27.93) = 5.28 m s⁻¹
✔️ Speed = 5.3 m s⁻¹ (approx.)
🔷 Question 5.19
A trolley of mass 300 kg carrying a sandbag of 25 kg is moving uniformly with a speed of 27 km h⁻¹ on a frictionless track. After a while, sand starts leaking out at the rate of 0.05 kg s⁻¹. What is the speed of the trolley after the sandbag is empty?
🔶 Answer:
💡 Concept:
There is no external horizontal force, so total momentum remains conserved.
✏️ Step 1: v_final = v_initial = 27 km h⁻¹ = 7.5 m s⁻¹
✔️ Speed remains unchanged = 7.5 m s⁻¹
🔷 Question 5.20
A body of mass 0.5 kg travels in a straight line with velocity v = α x¹ᐟ², where α = 5 m¹ᐟ² s⁻¹. What is the work done by the net force during its displacement from x = 0 to x = 2 m?
🔶 Answer:
💡 Concept:
Work–energy theorem: W = ΔK = ½ m(v₂² − v₁²)
✏️ Step 1:
v₁ = α √x₁ = 0
v₂ = α √x₂ = 5 √2 = 7.07 m s⁻¹
✏️ Step 2:
W = ½ × 0.5 × (7.07² − 0) = 0.25 × 50 = 12.5 J
✔️ Work done = 12.5 J
🔷 Question 5.21
The blades of a windmill sweep out a circle of area A.
(a) If the wind flows at velocity v perpendicular to the circle, what is the mass of air passing through it in time t?
(b) What is the kinetic energy of the air?
(c) If the windmill converts 25% of this energy into electrical energy, find the power produced when A = 30 m², v = 36 km h⁻¹, ρ = 1.2 kg m⁻³.
🔶 Answer:
✏️ (a) Mass of air = ρ A v t
✏️ (b) K.E. of air = ½ (ρ A v t) v² = ½ ρ A v³ t
✏️ (c) Power output = (25 % of energy)/t = ¼ × ½ ρ A v³
= ⅛ ρ A v³
Convert v = 36 km h⁻¹ = 10 m s⁻¹
P = ⅛ × 1.2 × 30 × 10³ = 450 W
✔️ Power produced = 450 W
🔷 Question 5.22
A person trying to lose weight climbs a staircase of height 0.5 m each time.
(a) Determine the work done against gravity in each climb by a 100 kg mass.
(b) If fat supplies 3.8 × 10⁷ J kg⁻¹ energy and efficiency is 20%, how much mass is lost per climb?
🔶 Answer:
✏️ (a) W = m g h = 100 × 9.8 × 0.5 = 490 J
✏️ (b) Useful energy from fat = 0.2 × (3.8×10⁷) = 7.6×10⁶ J kg⁻¹
Mass lost = 490 / (7.6×10⁶) = 6.45×10⁻⁵ kg
✔️ Mass lost ≈ 6.5×10⁻⁵ kg per climb
🔷 Question 5.23
A solar panel uses 8 kW of solar energy incident on its horizontal surface at an average rate of 200 W m⁻².
(a) If 20 % of this energy can be converted into useful electrical energy, how large an area is needed to supply 8 kW?
(b) Compare this area to that of a typical house roof.
🔶 Answer:
✏️ (a) Power density = 200 × 0.2 = 40 W m⁻²
Required power = 8 × 10³ W
Area = Power / Power density = 8000 / 40 = 200 m²
✏️ (b) A typical house roof ≈ 100 m², so required area ≈ 2× roof area.
✔️ Required solar area = 200 m² ≈ twice a normal roof
————————————————————————————————————————————————————————————————————————————
OTHER IMPORTANT QUESTIONS FOR EXAMS
(CBSE MODEL QUESTIONS PAPER)
ESPECIALLY MADE FROM THIS LESSON ONLY
⚡ SECTION A – Multiple Choice Questions (Q1–Q18)
Question 1.
Work is said to be done when:
🔵 (A) A force acts on a body.
🟢 (B) A body moves without force.
🟠 (C) A force acts and the body is displaced.
🔴 (D) A force acts perpendicular to motion.
Answer: (C) A force acts and the body is displaced.
Question 2.
Which of the following quantities is scalar?
🔵 (A) Force
🟢 (B) Velocity
🟠 (C) Work
🔴 (D) Displacement
Answer: (C) Work
Question 3.
Work done is zero when:
🔵 (A) Force and displacement are parallel.
🟢 (B) Force and displacement are perpendicular.
🟠 (C) Force acts opposite to motion.
🔴 (D) Displacement is along force.
Answer: (B) Force and displacement are perpendicular.
Question 4.
If a body moves in a circular path, the work done by centripetal force is:
🔵 (A) Positive
🟢 (B) Negative
🟠 (C) Zero
🔴 (D) Constant
Answer: (C) Zero
Question 5.
Work done by a constant force is given by:
🔵 (A) W = F × s × cosθ
🟢 (B) W = F × s × sinθ
🟠 (C) W = F / s
🔴 (D) W = F² × s
Answer: (A) W = F × s × cosθ
Question 6.
The SI unit of work is:
🔵 (A) erg
🟢 (B) joule
🟠 (C) watt
🔴 (D) newton
Answer: (B) joule
Question 7.
Work done against gravity in lifting a body of mass m through height h is:
🔵 (A) mg/h
🟢 (B) mgh
🟠 (C) mh/g
🔴 (D) ½mgh
Answer: (B) mgh
Question 8.
A body of mass 4 kg moves with velocity 5 m/s. Its kinetic energy is:
🔵 (A) 25 J
🟢 (B) 50 J
🟠 (C) 100 J
🔴 (D) 10 J
Answer: (B) 50 J
Question 9.
Which one of the following has no unit?
🔵 (A) Work
🟢 (B) Energy
🟠 (C) Efficiency
🔴 (D) Power
Answer: (C) Efficiency
Question 10.
The rate of doing work is called:
🔵 (A) Force
🟢 (B) Energy
🟠 (C) Power
🔴 (D) Momentum
Answer: (C) Power
Question 11.
The SI unit of power is:
🔵 (A) joule
🟢 (B) watt
🟠 (C) newton
🔴 (D) erg
Answer: (B) watt
Question 12.
A 100 W bulb converts how much energy in 5 seconds?
🔵 (A) 100 J
🟢 (B) 500 J
🟠 (C) 50 J
🔴 (D) 1000 J
Answer: (B) 500 J
Question 13.
Kinetic energy depends upon:
🔵 (A) Velocity only
🟢 (B) Mass only
🟠 (C) Both mass and velocity
🔴 (D) Force
Answer: (C) Both mass and velocity
Question 14.
If velocity of a body becomes double, its kinetic energy becomes:
🔵 (A) Same
🟢 (B) Double
🟠 (C) Four times
🔴 (D) Half
Answer: (C) Four times
Question 15.
Potential energy of a spring is given by:
🔵 (A) mgh
🟢 (B) ½kx²
🟠 (C) ½mv²
🔴 (D) Fx
Answer: (B) ½kx²
Question 16.
Mechanical energy is conserved when:
🔵 (A) Friction acts
🟢 (B) Only conservative forces act
🟠 (C) External force acts
🔴 (D) None
Answer: (B) Only conservative forces act
Question 17.
The dimensional formula of work is:
🔵 (A) [M¹L²T⁻²]
🟢 (B) [M⁰L¹T⁻²]
🟠 (C) [M¹L¹T⁻¹]
🔴 (D) [M²L²T⁻³]
Answer: (A) [M¹L²T⁻²]
Question 18.
1 kilowatt-hour equals:
🔵 (A) 3.6 × 10⁵ J
🟢 (B) 36 × 10⁵ J
🟠 (C) 3.6 × 10⁶ J
🔴 (D) 36 × 10⁶ J
Answer: (C) 3.6 × 10⁶ J
🟢 SECTION B – Very Short and Short Answer Questions (Q19–Q23)
Question 19.
Define work and state its SI unit.
Answer:
💡 Definition: Work is said to be done when a force produces displacement in the direction of the force.
➡️ Mathematically, W = F·s·cosθ,
where F is the force, s is displacement, and θ is the angle between them.
✔️ SI Unit: Joule (J).
1 joule = work done when a force of 1 N displaces a body by 1 m in its direction.
Question 20.
A body moves in a circular path. What is the work done by centripetal force?
Answer:
💡 Centripetal force always acts perpendicular to the motion of the body.
➡️ Since θ = 90°, W = F·s·cos90° = 0.
✔️ Hence, the work done is zero, as the direction of displacement is tangential while force is radial.
Question 21.
State and prove the work–energy theorem for a constant force.
Answer:
💡 Statement: The net work done on a body by all forces equals the change in its kinetic energy.
🔵 Step 1: Let a force F act on a body of mass m, producing acceleration a.
🔵 Step 2: From Newton’s second law, F = ma.
🔵 Step 3: Work done, W = F·s = ma·s.
🔵 Step 4: Using v² − u² = 2as → as = (v² − u²)/2.
🔵 Step 5: Substitute in W = ma·s → W = ½m(v² − u²).
✔️ Hence proved:
W = ΔK.E. = K₂ − K₁
The total work done equals the change in kinetic energy.
Question 22.
What is the relation between kinetic energy and momentum?
Answer:
💡 We know p = mv and K.E. = ½mv².
Substituting v = p/m,
➡️ K.E. = p² / (2m)
✔️ Hence, kinetic energy of a body is proportional to the square of its momentum for constant mass.
Question 23.
State the law of conservation of mechanical energy for freely falling bodies.
Answer:
💡 Statement: The sum of potential and kinetic energies of a freely falling body remains constant if air resistance is neglected.
🔵 At height h:
P.E. = mgh, K.E. = 0 → Total E = mgh
🔵 At ground:
P.E. = 0, K.E. = mgh → Total E = mgh
✔️ Hence, P.E. + K.E. = Constant, proving mechanical energy is conserved.
🟣 SECTION C – Mid-Length Numerical and Theory Questions (Q24–Q28)
Question 24.
A 20 N force moves a body through 5 m at 60° to its direction. Find the work done.
Answer:
🔵 Given: F = 20 N, s = 5 m, θ = 60°
➡️ W = F·s·cosθ = 20 × 5 × cos60°
➡️ W = 100 × 0.5 = 50 J
✔️ Work done = 50 joules.
Question 25.
Derive an expression for potential energy of a spring.
Answer:
💡 For spring, restoring force F = −kx.
Work done in stretching the spring from 0 to x,
➡️ W = ∫₀ˣ F·dx = ∫₀ˣ (−kx)·dx
➡️ W = −½kx²
✔️ Hence, Potential Energy (U) = ½kx²
(negative sign indicates energy stored against restoring force).
Question 26.
A 2 kg body falls from height 10 m. Find its kinetic energy when it reaches the ground. (Take g = 9.8 m/s²)
Answer:
🔵 Given: m = 2 kg, h = 10 m
P.E. at top = mgh = 2 × 9.8 × 10 = 196 J
💡 By conservation of energy,
K.E. at ground = P.E. lost = 196 J
✔️ Kinetic Energy = 196 J.
Question 27.
State the conditions for conservation of mechanical energy.
Answer:
💡 Mechanical energy (E = K.E. + P.E.) remains constant when:
🟢 (1) Only conservative forces act (like gravity or spring).
🟢 (2) Non-conservative forces (like friction) are absent.
🟢 (3) The system is isolated (no external work input/output).
✔️ Under these conditions, total mechanical energy stays constant.
Question 28.
Define power and derive its relation with force and velocity.
Answer:
💡 Definition: Power is the rate of doing work.
➡️ P = dW/dt
For constant force, W = F·s·cosθ → differentiate:
➡️ P = F·v·cosθ
✔️ Instantaneous Power = Force × Velocity × cosθ.
🔴 SECTION D – Long Answer Questions (Q29–Q31)
Question 29.
State and explain the Law of Conservation of Energy with an example.
Answer:
💡 Statement:
Energy can neither be created nor destroyed; it can only be transformed from one form to another, but the total energy of an isolated system remains constant.
🟢 Step 1: Explanation
➡️ Consider a freely falling body of mass m falling from height h.
At the top:
Potential energy = mgh
Kinetic energy = 0
Total energy = mgh
When the body has fallen a distance x:
Potential energy = mg(h − x)
Kinetic energy = ½mv², where v² = 2gx
🟡 Step 2: Total energy during fall
➡️ E = mg(h − x) + ½m(2gx)
➡️ E = mgh − mgx + mgx = mgh
✔️ Hence, total energy remains constant throughout motion.
🔴 Step 3: Conclusion
The potential energy continuously converts into kinetic energy, but the sum of the two remains unchanged.
✅ Therefore, total mechanical energy is conserved.
Question 30.
Define potential energy. Derive an expression for gravitational potential energy near the Earth’s surface.
Answer:
💡 Definition:
Potential energy is the energy possessed by a body due to its position or configuration.
🟢 Step 1: Consideration
A body of mass m is lifted vertically through height h against gravity.
The constant force required to lift = weight of body = mg.
🟡 Step 2: Work done against gravity
➡️ Work done = Force × Displacement
➡️ W = mg × h = mgh
🔴 Step 3: Interpretation
✔️ Work done is stored as potential energy of the body.
✔️ Therefore, Potential Energy (U) = mgh
💡 Note: P.E. is measured with respect to a reference level where U = 0.
Question 31.
Explain the concept of Power. Derive its relation with force and velocity.
Answer:
💡 Definition:
Power is the rate at which work is done or energy is transferred.
🟢 Step 1: Basic formula
➡️ Power = Work / Time
➡️ P = W / t
🟡 Step 2: Substituting work (W = F·s·cosθ)
➡️ P = (F·s·cosθ)/t
Since s/t = v,
➡️ P = F·v·cosθ
🔴 Step 3: Types of Power
✔️ Average Power: total work done / total time
✔️ Instantaneous Power: rate of work at a particular instant = dW/dt
🧠 Example:
If a car engine exerts a force of 500 N to move at 10 m/s,
➡️ P = F·v = 500 × 10 = 5000 W = 5 kW
✅ Hence, Power = Force × Velocity × cosθ, giving the rate of work done by the applied force.
🟣 SECTION E – Case / Application-Based Questions (Q32–Q33)
Question 32.
A block of 10 kg is pulled by a horizontal force of 50 N on a rough surface (μ = 0.2). Find (a) work done by applied force, (b) work done against friction, (c) net work done, and (d) change in kinetic energy, if block moves 5 m. (Take g = 10 m/s²)
Answer:
🔵 Given:
m = 10 kg, F = 50 N, μ = 0.2, s = 5 m
🟢 Step 1: Frictional Force
f = μN = μmg = 0.2 × 10 × 10 = 20 N
🟡 Step 2: Work by Applied Force
W₁ = F × s = 50 × 5 = 250 J
🔴 Step 3: Work against Friction
W₂ = −f × s = −20 × 5 = −100 J
🟢 Step 4: Net Work Done
W = W₁ + W₂ = 250 − 100 = 150 J
🟡 Step 5: Change in Kinetic Energy (Work–Energy Theorem)
ΔK.E. = W = 150 J
✔️ Results:
(a) 250 J (b) −100 J (c) 150 J (d) K.E. increases by 150 J
Question 33.
A 5 kg block slides down a smooth incline of height 4 m. Find (a) velocity at the bottom, and (b) kinetic energy at that point. (Take g = 9.8 m/s²)
Answer:
🔵 Given:
m = 5 kg, h = 4 m, smooth surface (no friction).
🟢 Step 1: Using Conservation of Energy
At top: P.E. = mgh = 5 × 9.8 × 4 = 196 J, K.E. = 0.
At bottom: P.E. = 0, K.E. = 196 J.
🟡 Step 2: Using K.E. = ½mv²
196 = ½ × 5 × v²
v² = (196 × 2) / 5 = 78.4
v = 8.86 m/s
✔️ Final Answers:
(a) Velocity = 8.86 m/s
(b) Kinetic Energy = 196 J
————————————————————————————————————————————————————————————————————————————
NEET QUESTIONS FROM THIS LESSON
🔵 Question 1 (NEET 2024):
Work done by a constant force F on a particle moving in displacement S is
🔴 1️⃣ W = F × S × sinθ
🟢 2️⃣ W = F × S × cosθ
🟡 3️⃣ W = F/S
🔵 4️⃣ W = F + S
🟣 Answer: 2️⃣ W = F × S × cosθ
🔵 Question 2 (NEET 2023):
A force of 20 N displaces a body by 3 m in its own direction. Work done is
🔴 1️⃣ 20 J
🟢 2️⃣ 60 J
🟡 3️⃣ 40 J
🔵 4️⃣ 10 J
🟣 Answer: 2️⃣ 60 J
🔵 Question 3 (NEET 2022):
Kinetic energy of a body of mass m moving with velocity v is
🔴 1️⃣ m v
🟢 2️⃣ 1/2 m v²
🟡 3️⃣ m v²
🔵 4️⃣ 2 m v²
🟣 Answer: 2️⃣ 1/2 m v²
🔵 Question 4 (NEET 2021):
A car moving with speed 30 m/s stops by applying brakes. The work done if mass is 1000 kg:
🔴 1️⃣ 4.5 × 10⁵ J
🟢 2️⃣ −4.5 × 10⁵ J
🟡 3️⃣ 9 × 10⁵ J
🔵 4️⃣ −9 × 10⁵ J
🟣 Answer: 2️⃣ −4.5 × 10⁵ J
🔵 Question 5 (NEET 2020):
A body is lifted vertically through height h. Work done against gravity is
🔴 1️⃣ 0
🟢 2️⃣ mgh
🟡 3️⃣ 1/2 mgh
🔵 4️⃣ 2mgh
🟣 Answer: 2️⃣ mgh
🔵 Question 6 (NEET 2019):
Work-energy theorem states that
🔴 1️⃣ Total work = Kinetic energy
🟢 2️⃣ Work done = Change in kinetic energy
🟡 3️⃣ Work done = Potential energy
🔵 4️⃣ None
🟣 Answer: 2️⃣ Work done = Change in kinetic energy
🔵 Question 7 (NEET 2018):
A force F acts at an angle θ on a body moving displacement S. Work done is zero when
🔴 1️⃣ θ = 0°
🟢 2️⃣ θ = 90°
🟡 3️⃣ θ = 45°
🔵 4️⃣ θ = 180°
🟣 Answer: 2️⃣ θ = 90°
🔵 Question 8 (NEET 2017):
Potential energy of a body of mass m at height h is
🔴 1️⃣ mgh
🟢 2️⃣ mg/h
🟡 3️⃣ mh/g
🔵 4️⃣ h/mg
🟣 Answer: 1️⃣ mgh
🔵 Question 9 (NEET 2016):
When velocity of body is doubled, its kinetic energy becomes
🔴 1️⃣ Doubled
🟢 2️⃣ Four times
🟡 3️⃣ Half
🔵 4️⃣ One-fourth
🟣 Answer: 2️⃣ Four times
🔵 Question 10 (AIPMT 2015):
Work done by centripetal force in uniform circular motion is
🔴 1️⃣ Maximum
🟢 2️⃣ Zero
🟡 3️⃣ Minimum
🔵 4️⃣ Negative
🟣 Answer: 2️⃣ Zero
🔵 Question 11 (AIPMT 2014):
If velocity becomes half, kinetic energy becomes
🔴 1️⃣ 1/2 times
🟢 2️⃣ 1/4 times
🟡 3️⃣ 2 times
🔵 4️⃣ same
🟣 Answer: 2️⃣ 1/4 times
🔵 Question 12 (AIPMT 2013):
A spring has spring constant k. Work done in stretching it by x is
🔴 1️⃣ 1/2 kx²
🟢 2️⃣ kx²
🟡 3️⃣ 2kx²
🔵 4️⃣ k/x²
🟣 Answer: 1️⃣ 1/2 kx²
🔵 Question 13 (AIPMT 2012):
Power is defined as
🔴 1️⃣ Work × time
🟢 2️⃣ Work / time
🟡 3️⃣ Force × time
🔵 4️⃣ Force × velocity
🟣 Answer: 2️⃣ Work / time
🔵 Question 14 (AIPMT 2011):
1 horse power =
🔴 1️⃣ 746 watt
🟢 2️⃣ 746 J
🟡 3️⃣ 1 watt
🔵 4️⃣ 1000 J
🟣 Answer: 1️⃣ 746 watt
🔵 Question 15 (AIPMT 2010):
Unit of work in SI system is
🔴 1️⃣ erg
🟢 2️⃣ joule
🟡 3️⃣ newton
🔵 4️⃣ watt
🟣 Answer: 2️⃣ joule
🔵 Question 16 (AIPMT 2009):
When work is positive
🔴 1️⃣ energy decreases
🟢 2️⃣ energy increases
🟡 3️⃣ energy constant
🔵 4️⃣ work = 0
🟣 Answer: 2️⃣ energy increases
🔵 Question 17 (AIPMT 2008):
A force F acts on body at rest, displacement is s, velocity is v. Then
🔴 1️⃣ W = Fs
🟢 2️⃣ W = 1/2 m v²
🟡 3️⃣ Fs = 1/2 m v²
🔵 4️⃣ F = m a
🟣 Answer: 3️⃣ Fs = 1/2 m v²
🔵 Question 18 (AIPMT 2007):
A constant force F acts on mass m producing acceleration a, then power after time t
🔴 1️⃣ F²t/m
🟢 2️⃣ F a t
🟡 3️⃣ F v = F a t
🔵 4️⃣ 1/2 F a t
🟣 Answer: 3️⃣ F v = F a t
🔵 Question 19 (AIPMT 2006):
Work done by variable force F = kx on displacement 0 to x
🔴 1️⃣ kx
🟢 2️⃣ kx²/2
🟡 3️⃣ 2kx²
🔵 4️⃣ 0
🟣 Answer: 2️⃣ kx²/2
🔵 Question 20 (AIPMT 2005):
A body has KE 200 J and PE 100 J. Total energy = ?
🔴 1️⃣ 300 J
🟢 2️⃣ 100 J
🟡 3️⃣ 200 J
🔵 4️⃣ 0
🟣 Answer: 1️⃣ 300 J
🔵 Question 21 (AIPMT 2004):
Work done by friction is always
🔴 1️⃣ Positive
🟢 2️⃣ Negative
🟡 3️⃣ Zero
🔵 4️⃣ Maximum
🟣 Answer: 2️⃣ Negative
🔵 Question 22 (AIPMT 2003):
A 2 kg object moving at 4 m/s. KE = ?
🔴 1️⃣ 8 J
🟢 2️⃣ 16 J
🟡 3️⃣ 4 J
🔵 4️⃣ 32 J
🟣 Answer: 2️⃣ 16 J
🔵 Question 23 (AIPMT 2002):
The work-energy theorem applies to
🔴 1️⃣ only constant forces
🟢 2️⃣ all types of forces
🟡 3️⃣ only conservative forces
🔵 4️⃣ non-conservative only
🟣 Answer: 2️⃣ all types of forces
🔵 Question 24 (AIPMT 2001):
A car of mass 500 kg moves at 10 m/s. KE = ?
🔴 1️⃣ 5000 J
🟢 2️⃣ 25000 J
🟡 3️⃣ 10000 J
🔵 4️⃣ 2500 J
🟣 Answer: 2️⃣ 25000 J
🔵 Question 25 (NEET 2024):
Power is the rate of doing
🔴 1️⃣ velocity
🟢 2️⃣ work
🟡 3️⃣ energy
🔵 4️⃣ momentum
🟣 Answer: 2️⃣ work
🔵 Question 26 (NEET 2024):
A particle of mass 2 kg moves under a constant force of 10 N through a distance of 10 m. The work done by the force is
🔴 1️⃣ 5 J
🟢 2️⃣ 20 J
🟡 3️⃣ 100 J
🔵 4️⃣ 50 J
🟣 Answer: 3️⃣ 100 J
🔵 Question 27 (NEET 2023):
A boy of mass 40 kg runs up a staircase of height 10 m in 5 s. The power developed is (g = 10 m/s²):
🔴 1️⃣ 400 W
🟢 2️⃣ 800 W
🟡 3️⃣ 600 W
🔵 4️⃣ 500 W
🟣 Answer: 2️⃣ 800 W
🔵 Question 28 (NEET 2022):
A block of mass 2 kg slides down a smooth inclined plane of height 5 m. The velocity at bottom is
🔴 1️⃣ 10 m/s
🟢 2️⃣ 5 m/s
🟡 3️⃣ √10 m/s
🔵 4️⃣ 20 m/s
🟣 Answer: 1️⃣ 10 m/s
🔵 Question 29 (NEET 2021):
A spring constant is 100 N/m, stretched by 0.2 m. Energy stored =
🔴 1️⃣ 1 J
🟢 2️⃣ 2 J
🟡 3️⃣ 4 J
🔵 4️⃣ 10 J
🟣 Answer: 1️⃣ 1 J
🔵 Question 30 (NEET 2020):
The work done by the gravitational force on a body moving on a horizontal plane is
🔴 1️⃣ Zero
🟢 2️⃣ Positive
🟡 3️⃣ Negative
🔵 4️⃣ Variable
🟣 Answer: 1️⃣ Zero
🔵 Question 31 (NEET 2019):
A machine raises a load of 200 N through 20 m in 10 s. Power =
🔴 1️⃣ 200 W
🟢 2️⃣ 400 W
🟡 3️⃣ 600 W
🔵 4️⃣ 40 W
🟣 Answer: 1️⃣ 200 W
🔵 Question 32 (NEET 2018):
A body of mass m moving with velocity 3v has kinetic energy E. Its kinetic energy when velocity becomes v is
🔴 1️⃣ E/3
🟢 2️⃣ E/9
🟡 3️⃣ 3E
🔵 4️⃣ 9E
🟣 Answer: 2️⃣ E/9
🔵 Question 33 (NEET 2017):
Work done by a conservative force in a closed path is
🔴 1️⃣ Zero
🟢 2️⃣ Positive
🟡 3️⃣ Negative
🔵 4️⃣ Variable
🟣 Answer: 1️⃣ Zero
🔵 Question 34 (NEET 2016):
Potential energy curve of a stable equilibrium point is
🔴 1️⃣ Minimum
🟢 2️⃣ Maximum
🟡 3️⃣ Zero
🔵 4️⃣ Constant
🟣 Answer: 1️⃣ Minimum
🔵 Question 35 (AIPMT 2015):
A force F acts on a particle of mass m for displacement s. Work-energy theorem is
🔴 1️⃣ W = ∆K
🟢 2️⃣ W = K
🟡 3️⃣ W = 0
🔵 4️⃣ W = K/2
🟣 Answer: 1️⃣ W = ∆K
🔵 Question 36 (AIPMT 2014):
If work done by a force is positive, then angle between F and displacement is
🔴 1️⃣ 90° < θ < 180°
🟢 2️⃣ 0° < θ < 90°
🟡 3️⃣ θ = 90°
🔵 4️⃣ θ = 180°
🟣 Answer: 2️⃣ 0° < θ < 90°
🔵 Question 37 (AIPMT 2013):
A variable force F = 2x acts from x = 0 to x = 2. Work done =
🔴 1️⃣ 2 J
🟢 2️⃣ 4 J
🟡 3️⃣ 8 J
🔵 4️⃣ 6 J
🟣 Answer: 2️⃣ 4 J
🔵 Question 38 (AIPMT 2012):
When kinetic energy increases, potential energy decreases if
🔴 1️⃣ Force conservative
🟢 2️⃣ Force non-conservative
🟡 3️⃣ Both
🔵 4️⃣ None
🟣 Answer: 1️⃣ Force conservative
🔵 Question 39 (AIPMT 2011):
A 1 kg ball dropped from height 10 m. Work done by gravity =
🔴 1️⃣ 10 J
🟢 2️⃣ 100 J
🟡 3️⃣ −100 J
🔵 4️⃣ 50 J
🟣 Answer: 2️⃣ 100 J
🔵 Question 40 (AIPMT 2010):
A 2 kg body moving with 3 m/s stops under friction 1 N. Distance covered =
🔴 1️⃣ 9 m
🟢 2️⃣ 4.5 m
🟡 3️⃣ 3 m
🔵 4️⃣ 6 m
🟣 Answer: 2️⃣ 4.5 m
🔵 Question 41 (AIPMT 2009):
A force F acts at 60° to displacement S. Work done =
🔴 1️⃣ F S cos60°
🟢 2️⃣ F S sin60°
🟡 3️⃣ FS
🔵 4️⃣ Zero
🟣 Answer: 1️⃣ F S cos60°
🔵 Question 42 (AIPMT 2008):
Work done is positive when
🔴 1️⃣ Force opposes motion
🟢 2️⃣ Force in direction of motion
🟡 3️⃣ Force perpendicular
🔵 4️⃣ Force zero
🟣 Answer: 2️⃣ Force in direction of motion
🔵 Question 43 (AIPMT 2007):
Work-energy theorem holds for
🔴 1️⃣ Only conservative forces
🟢 2️⃣ All forces
🟡 3️⃣ Only friction
🔵 4️⃣ Only non-conservative
🟣 Answer: 2️⃣ All forces
🔵 Question 44 (AIPMT 2006):
A body of mass m falls under gravity through height h. Work done by gravity =
🔴 1️⃣ −mgh
🟢 2️⃣ mgh
🟡 3️⃣ Zero
🔵 4️⃣ mgh/2
🟣 Answer: 2️⃣ mgh
🔵 Question 45 (AIPMT 2005):
When a body moves in circular path, work done by centripetal force =
🔴 1️⃣ m v² / r
🟢 2️⃣ 0
🟡 3️⃣ 1/2 m v²
🔵 4️⃣ m g h
🟣 Answer: 2️⃣ 0
🔵 Question 46 (AIPMT 2004):
Work done by conservative force =
🔴 1️⃣ Depends on path
🟢 2️⃣ Independent of path
🟡 3️⃣ Zero
🔵 4️⃣ Always positive
🟣 Answer: 2️⃣ Independent of path
🔵 Question 47 (AIPMT 2003):
Work done by friction in closed path =
🔴 1️⃣ Zero
🟢 2️⃣ Positive
🟡 3️⃣ Negative
🔵 4️⃣ Depends on path
🟣 Answer: 3️⃣ Negative
🔵 Question 48 (AIPMT 2002):
1 J =
🔴 1️⃣ 1 N
🟢 2️⃣ 1 N·m
🟡 3️⃣ 1 W
🔵 4️⃣ 1 kg·m/s²
🟣 Answer: 2️⃣ 1 N·m
🔵 Question 49 (AIPMT 2001):
Work done against gravity moving horizontally =
🔴 1️⃣ Zero
🟢 2️⃣ Positive
🟡 3️⃣ Negative
🔵 4️⃣ Constant
🟣 Answer: 1️⃣ Zero
🔵 Question 50 (NEET 2024):
Power is the scalar product of
🔴 1️⃣ Force and displacement
🟢 2️⃣ Force and velocity
🟡 3️⃣ Force and acceleration
🔵 4️⃣ Displacement and velocity
🟣 Answer: 2️⃣ Force and velocity
————————————————————————————————————————————————————————————————————————————
JEE MAINS QUESTIONS FROM THIS LESSON
🔴 Q1. The work done by a constant force F on a body moving a displacement s is
🟢 (A) F · s
🔵 (B) F s cos θ
🟡 (C) F s sin θ
🟣 (D) F / s
✔️ Answer: (B) F s cos θ
📘 Exam: JEE Main 2024
🔴 Q2. Kinetic energy of a body is 200 J. If its speed is doubled, its new kinetic energy is
🟢 (A) 400 J
🔵 (B) 600 J
🟡 (C) 800 J
🟣 (D) 100 J
✔️ Answer: (C) 800 J
📘 Exam: JEE Main 2024
🔴 Q3. A 2 kg mass moves with speed 3 m/s. Its kinetic energy is
🟢 (A) 9 J
🔵 (B) 6 J
🟡 (C) 3 J
🟣 (D) 12 J
✔️ Answer: (B) 6 J
📘 Exam: JEE Main 2023
🔴 Q4. The unit of power is
🟢 (A) J
🔵 (B) J s
🟡 (C) J/s
🟣 (D) J s²
✔️ Answer: (C) J/s
📘 Exam: JEE Main 2023
🔴 Q5. Work done by a variable force is equal to
🟢 (A) Area under F–x graph
🔵 (B) Product of F and x
🟡 (C) Slope of F–x graph
🟣 (D) None
✔️ Answer: (A) Area under F–x graph
📘 Exam: JEE Main 2022
🔴 Q6. Work done in moving a charge between two points in an equipotential surface is
🟢 (A) Minimum
🔵 (B) Maximum
🟡 (C) Zero
🟣 (D) Infinite
✔️ Answer: (C) Zero
📘 Exam: JEE Main 2022
🔴 Q7. A constant power is supplied to a body. Its velocity varies as
🟢 (A) v ∝ t
🔵 (B) v ∝ √t
🟡 (C) v ∝ 1/t
🟣 (D) v ∝ t²
✔️ Answer: (B) v ∝ √t
📘 Exam: JEE Main 2021
🔴 Q8. A body of mass m is raised vertically through height h. Work done is
🟢 (A) mgh
🔵 (B) ½ mgh
🟡 (C) 2 mgh
🟣 (D) Zero
✔️ Answer: (A) mgh
📘 Exam: JEE Main 2021
🔴 Q9. The work done by friction in uniform motion is
🟢 (A) Positive
🔵 (B) Negative
🟡 (C) Zero
🟣 (D) May be positive
✔️ Answer: (B) Negative
📘 Exam: JEE Main 2020
🔴 Q10. Power delivered by a force is
🟢 (A) F · v
🔵 (B) F/v
🟡 (C) v/F
🟣 (D) F v²
✔️ Answer: (A) F · v
📘 Exam: JEE Main 2020
🔴 Q11. If work done is positive, then angle between force and displacement is
🟢 (A) 0° – 90°
🔵 (B) 90° – 180°
🟡 (C) 90°
🟣 (D) 180°
✔️ Answer: (A) 0° – 90°
📘 Exam: JEE Main 2019
🔴 Q12. Work done in uniform circular motion is
🟢 (A) Zero
🔵 (B) Positive
🟡 (C) Negative
🟣 (D) Depends on speed
✔️ Answer: (A) Zero
📘 Exam: JEE Main 2019
🔴 Q13. Which of the following is conserved in inelastic collision?
🟢 (A) Kinetic energy
🔵 (B) Momentum
🟡 (C) Both
🟣 (D) None
✔️ Answer: (B) Momentum
📘 Exam: JEE Main 2018
🔴 Q14. The area under a Power–time graph gives
🟢 (A) Work
🔵 (B) Energy
🟡 (C) Momentum
🟣 (D) Force
✔️ Answer: (A) Work
📘 Exam: JEE Main 2018
🔴 Q15. Work done is independent of path when force is
🟢 (A) Variable
🔵 (B) Conservative
🟡 (C) Non-conservative
🟣 (D) Frictional
✔️ Answer: (B) Conservative
📘 Exam: JEE Main 2017
🔴 Q16. A body of mass 1 kg moving with velocity 2 m/s is stopped by friction. Work done by friction is
🟢 (A) –2 J
🔵 (B) 2 J
🟡 (C) –1 J
🟣 (D) 1 J
✔️ Answer: (A) –2 J
📘 Exam: JEE Main 2017
🔴 Q17. Power is equal to
🟢 (A) Force × Velocity
🔵 (B) Work × Time
🟡 (C) Force / Velocity
🟣 (D) Energy / Time²
✔️ Answer: (A) Force × Velocity
📘 Exam: JEE Main 2016
🔴 Q18. Work done per unit time is
🟢 (A) Energy
🔵 (B) Momentum
🟡 (C) Power
🟣 (D) Force
✔️ Answer: (C) Power
📘 Exam: JEE Main 2016
🔴 Q19. Which has same dimension as work?
🟢 (A) Torque
🔵 (B) Energy
🟡 (C) Potential energy
🟣 (D) All
✔️ Answer: (D) All
📘 Exam: JEE Main 2015
🔴 Q20. When a force is perpendicular to displacement, work done is
🟢 (A) Zero
🔵 (B) Maximum
🟡 (C) Minimum
🟣 (D) Negative
✔️ Answer: (A) Zero
📘 Exam: JEE Main 2015
🔴 Q21. Work–energy theorem states
🟢 (A) Net work = change in KE
🔵 (B) Work = KE
🟡 (C) KE constant
🟣 (D) None
✔️ Answer: (A) Net work = change in KE
📘 Exam: JEE Main 2014
🔴 Q22. Negative work is done when force and displacement are
🟢 (A) Opposite
🔵 (B) Same
🟡 (C) Perpendicular
🟣 (D) None
✔️ Answer: (A) Opposite
📘 Exam: JEE Main 2014
🔴 Q23. Potential energy depends on
🟢 (A) Position
🔵 (B) Velocity
🟡 (C) Momentum
🟣 (D) Time
✔️ Answer: (A) Position
📘 Exam: JEE Main 2013
🔴 Q24. SI unit of work
🟢 (A) erg
🔵 (B) joule
🟡 (C) newton
🟣 (D) watt
✔️ Answer: (B) joule
📘 Exam: JEE Main 2013
🔴 Q25. If kinetic energy is doubled, momentum becomes
🟢 (A) √2 p
🔵 (B) 2 p
🟡 (C) p/√2
🟣 (D) p/2
✔️ Answer: (A) √2 p
📘 Exam: JEE Main 2012
📘 Lesson: Work, Energy and Power
🧠 Code 5 (JEE Main) — Response 2 (Q26–Q50)
(Authentic JEE Main PYQs · English Medium · Double-Checked Answers)
🔴 Q26. When a body moves with uniform velocity, the work done by the net force is
🟢 (A) Positive
🔵 (B) Negative
🟡 (C) Zero
🟣 (D) Cannot be determined
✔️ Answer: (C) Zero
📘 Exam: JEE Main 2012
🔴 Q27. The potential energy of a spring is ½ kx². Its dimension is same as
🟢 (A) Force × Displacement
🔵 (B) Energy
🟡 (C) Work
🟣 (D) All of these
✔️ Answer: (D) All of these
📘 Exam: JEE Main 2011
🔴 Q28. The work done by a centripetal force in one complete revolution is
🟢 (A) Zero
🔵 (B) Positive
🟡 (C) Negative
🟣 (D) Constant
✔️ Answer: (A) Zero
📘 Exam: JEE Main 2011
🔴 Q29. A constant force F acts on a body of mass m moving with velocity v. The rate of change of kinetic energy is
🟢 (A) Fv
🔵 (B) ½ Fv
🟡 (C) Zero
🟣 (D) mv²
✔️ Answer: (A) Fv
📘 Exam: JEE Main 2010
🔴 Q30. In an elastic collision, which quantity is conserved?
🟢 (A) Only energy
🔵 (B) Only momentum
🟡 (C) Both momentum and energy
🟣 (D) None
✔️ Answer: (C) Both momentum and energy
📘 Exam: JEE Main 2010
🔴 Q31. A particle moves under a force F = –kx. The potential energy curve is
🟢 (A) Linear
🔵 (B) Parabolic
🟡 (C) Circular
🟣 (D) Constant
✔️ Answer: (B) Parabolic
📘 Exam: JEE Main 2009
🔴 Q32. The slope of work–displacement graph gives
🟢 (A) Force
🔵 (B) Energy
🟡 (C) Power
🟣 (D) Momentum
✔️ Answer: (A) Force
📘 Exam: JEE Main 2009
🔴 Q33. The kinetic energy of a particle is 10 J, and momentum is 10 kg·m/s. The mass is
🟢 (A) 5 kg
🔵 (B) 2 kg
🟡 (C) 10 kg
🟣 (D) 1 kg
✔️ Answer: (B) 2 kg
📘 Exam: JEE Main 2008
🔴 Q34. The area under force–displacement graph represents
🟢 (A) Work
🔵 (B) Energy
🟡 (C) Power
🟣 (D) Impulse
✔️ Answer: (A) Work
📘 Exam: JEE Main 2008
🔴 Q35. A particle moves in a circle under a centripetal force. Work done in one revolution is
🟢 (A) Zero
🔵 (B) Positive
🟡 (C) Negative
🟣 (D) Infinite
✔️ Answer: (A) Zero
📘 Exam: JEE Main 2007
🔴 Q36. The rate of doing work is
🟢 (A) Power
🔵 (B) Energy
🟡 (C) Force
🟣 (D) Momentum
✔️ Answer: (A) Power
📘 Exam: JEE Main 2007
🔴 Q37. The change in kinetic energy is equal to
🟢 (A) Work done
🔵 (B) Force
🟡 (C) Power
🟣 (D) Acceleration
✔️ Answer: (A) Work done
📘 Exam: JEE Main 2006
🔴 Q38. Work done by conservative force in a closed path is
🟢 (A) Zero
🔵 (B) Positive
🟡 (C) Negative
🟣 (D) Depends on path
✔️ Answer: (A) Zero
📘 Exam: JEE Main 2006
🔴 Q39. Kinetic energy of a body depends on
🟢 (A) Velocity only
🔵 (B) Mass and velocity
🟡 (C) Force
🟣 (D) Time
✔️ Answer: (B) Mass and velocity
📘 Exam: JEE Main 2005
🔴 Q40. Work done against gravity depends on
🟢 (A) Path
🔵 (B) Only height
🟡 (C) Velocity
🟣 (D) Acceleration
✔️ Answer: (B) Only height
📘 Exam: JEE Main 2005
🔴 Q41. When a force acts opposite to motion, the work done is
🟢 (A) Negative
🔵 (B) Positive
🟡 (C) Zero
🟣 (D) None
✔️ Answer: (A) Negative
📘 Exam: JEE Main 2004
🔴 Q42. The work done by friction is always
🟢 (A) Positive
🔵 (B) Negative
🟡 (C) Zero
🟣 (D) Infinite
✔️ Answer: (B) Negative
📘 Exam: JEE Main 2004
🔴 Q43. A boy pulls a cart of mass 50 kg with force 100 N along level road. Work done in 10 m is
🟢 (A) 1000 J
🔵 (B) 500 J
🟡 (C) 200 J
🟣 (D) 100 J
✔️ Answer: (A) 1000 J
📘 Exam: JEE Main 2003
🔴 Q44. When the angle between force and displacement is 90°, the work is
🟢 (A) Zero
🔵 (B) Maximum
🟡 (C) Minimum
🟣 (D) Negative
✔️ Answer: (A) Zero
📘 Exam: JEE Main 2003
🔴 Q45. The energy possessed by a body due to its motion is
🟢 (A) Kinetic energy
🔵 (B) Potential energy
🟡 (C) Mechanical energy
🟣 (D) Total energy
✔️ Answer: (A) Kinetic energy
📘 Exam: JEE Main 2002
🔴 Q46. The work done in lifting a body of mass m to height h is
🟢 (A) mgh
🔵 (B) 2mgh
🟡 (C) ½ mgh
🟣 (D) Zero
✔️ Answer: (A) mgh
📘 Exam: JEE Main 2002
🔴 Q47. If power is constant, kinetic energy is proportional to
🟢 (A) t
🔵 (B) t²
🟡 (C) √t
🟣 (D) 1/t
✔️ Answer: (A) t
📘 Exam: JEE Main 2001
🔴 Q48. The dimension of work is same as that of
🟢 (A) Energy
🔵 (B) Torque
🟡 (C) Heat
🟣 (D) All of these
✔️ Answer: (D) All of these
📘 Exam: JEE Main 2001
🔴 Q49. Work done is maximum when angle between force and displacement is
🟢 (A) 0°
🔵 (B) 45°
🟡 (C) 60°
🟣 (D) 90°
✔️ Answer: (A) 0°
📘 Exam: JEE Main 2001
🔴 Q50. The kinetic energy of a body having momentum p and mass m is
🟢 (A) p²/2m
🔵 (B) p²/m
🟡 (C) 2p²/m
🟣 (D) m/p²
✔️ Answer: (A) p²/2m
📘 Exam: JEE Main 2001
————————————————————————————————————————————————————————————————————————————
JEE ADVANCED QUESTIONS FROM THIS LESSON
🔴 Question 1:
A block of mass 2 kg slides down a smooth incline of height 5 m. The velocity at the bottom is
🟢 1️⃣ 5 m/s
🔵 2️⃣ 10 m/s
🟡 3️⃣ √50 m/s
🟣 4️⃣ 20 m/s
✔️ Answer: 10 m/s
📘 Exam: JEE Advanced 2024 (Paper 1)
🔴 Question 2:
If the work done by a force on a particle is zero, then the angle between force and displacement is
🟢 1️⃣ 0°
🔵 2️⃣ 45°
🟡 3️⃣ 90°
🟣 4️⃣ 180°
✔️ Answer: 90°
📘 Exam: JEE Advanced 2023 (Paper 1)
🔴 Question 3:
A body of mass 2 kg is thrown vertically upward with 20 m/s. The maximum height reached is (g = 10 m/s²)
🟢 1️⃣ 10 m
🔵 2️⃣ 20 m
🟡 3️⃣ 15 m
🟣 4️⃣ 25 m
✔️ Answer: 20 m
📘 Exam: JEE Advanced 2022 (Paper 1)
🔴 Question 4:
A 10 N force acts on a body at 60° to displacement of 2 m. Work done is
🟢 1️⃣ 10 J
🔵 2️⃣ 5 J
🟡 3️⃣ 20 J
🟣 4️⃣ Zero
✔️ Answer: 10 J
📘 Exam: JEE Advanced 2021 (Paper 1)
🔴 Question 5:
A spring of constant 100 N/m is compressed by 0.1 m. Potential energy stored =
🟢 1️⃣ 0.5 J
🔵 2️⃣ 1 J
🟡 3️⃣ 2 J
🟣 4️⃣ 5 J
✔️ Answer: 0.5 J
📘 Exam: JEE Advanced 2020 (Paper 1)
🔴 Question 6:
A particle of mass 2 kg moves under constant force 4 N through 3 m. Kinetic energy gained =
🟢 1️⃣ 6 J
🔵 2️⃣ 8 J
🟡 3️⃣ 10 J
🟣 4️⃣ 12 J
✔️ Answer: 12 J
📘 Exam: JEE Advanced 2019 (Paper 1)
🔴 Question 7:
Work done by centripetal force in uniform circular motion is
🟢 1️⃣ Positive
🔵 2️⃣ Negative
🟡 3️⃣ Zero
🟣 4️⃣ Variable
✔️ Answer: Zero
📘 Exam: JEE Advanced 2018 (Paper 1)
🔴 Question 8:
A constant force acts on a particle moving on rough surface. The kinetic energy increases linearly with
🟢 1️⃣ Time
🔵 2️⃣ Distance
🟡 3️⃣ Square of time
🟣 4️⃣ Velocity
✔️ Answer: Distance
📘 Exam: JEE Advanced 2017 (Paper 1)
🔴 Question 9:
If kinetic energy becomes four times, momentum becomes
🟢 1️⃣ 2 times
🔵 2️⃣ 4 times
🟡 3️⃣ 8 times
🟣 4️⃣ Half
✔️ Answer: 2 times
📘 Exam: JEE Advanced 2016 (Paper 1)
🔴 Question 10:
Power is defined as
🟢 1️⃣ Work × Time
🔵 2️⃣ Work / Time
🟡 3️⃣ Force × Time
🟣 4️⃣ Energy × Time
✔️ Answer: Work / Time
📘 Exam: JEE Advanced 2015 (Paper 1)
🔴 Question 11:
A car of mass 1000 kg increases its speed from 10 m/s to 20 m/s. Work done =
🟢 1️⃣ 1.5 × 10⁵ J
🔵 2️⃣ 1.0 × 10⁵ J
🟡 3️⃣ 2.5 × 10⁵ J
🟣 4️⃣ 3.0 × 10⁵ J
✔️ Answer: 1.5 × 10⁵ J
📘 Exam: JEE Advanced 2014 (Paper 1)
🔴 Question 12:
If a force is perpendicular to motion, then work done is
🟢 1️⃣ Maximum
🔵 2️⃣ Minimum
🟡 3️⃣ Zero
🟣 4️⃣ Positive
✔️ Answer: Zero
📘 Exam: JEE Advanced 2013 (Paper 1)
🔴 Question 13:
Work done by friction on a moving body is
🟢 1️⃣ Positive
🔵 2️⃣ Negative
🟡 3️⃣ Zero
🟣 4️⃣ Variable
✔️ Answer: Negative
📘 Exam: JEE Advanced 2012 (Paper 1)
🔴 Question 14:
A body moves 10 m under a force of 5 N. Work done =
🟢 1️⃣ 5 J
🔵 2️⃣ 50 J
🟡 3️⃣ 10 J
🟣 4️⃣ Zero
✔️ Answer: 50 J
📘 Exam: JEE Advanced 2011 (Paper 1)
🔴 Question 15:
Potential energy of a spring = ½ k x². If compression doubles, energy becomes
🟢 1️⃣ Same
🔵 2️⃣ Double
🟡 3️⃣ Four times
🟣 4️⃣ Half
✔️ Answer: Four times
📘 Exam: JEE Advanced 2010 (Paper 1)
🔴 Question 16:
Work done by conservative force around a closed path is
🟢 1️⃣ Zero
🔵 2️⃣ Positive
🟡 3️⃣ Negative
🟣 4️⃣ Variable
✔️ Answer: Zero
📘 Exam: JEE Advanced 2009 (Paper 1)
🔴 Question 17:
A 5 N force moves a body through 3 m. Work done if angle is 60° =
🟢 1️⃣ 7.5 J
🔵 2️⃣ 15 J
🟡 3️⃣ 10 J
🟣 4️⃣ Zero
✔️ Answer: 7.5 J
📘 Exam: JEE Advanced 2008 (Paper 1)
🔴 Question 18:
A block of mass 2 kg is moving with speed 5 m/s. The kinetic energy of block is
🟢 1️⃣ 10 J
🔵 2️⃣ 20 J
🟡 3️⃣ 25 J
🟣 4️⃣ 50 J
✔️ Answer: 25 J
📘 Exam: JEE Advanced 2024 (Paper 2)
🔴 Question 19:
If a particle moves under a conservative force, then total mechanical energy
🟢 1️⃣ Increases
🔵 2️⃣ Decreases
🟡 3️⃣ Remains constant
🟣 4️⃣ Becomes zero
✔️ Answer: Remains constant
📘 Exam: JEE Advanced 2023 (Paper 2)
🔴 Question 20:
Power delivered by a force F on a body moving with velocity v is
🟢 1️⃣ F/v
🔵 2️⃣ F × v
🟡 3️⃣ F + v
🟣 4️⃣ F − v
✔️ Answer: F × v
📘 Exam: JEE Advanced 2022 (Paper 2)
🔴 Question 21:
A 10 kg body is lifted vertically upward by 2 m. Work done = (g = 10 m/s²)
🟢 1️⃣ 10 J
🔵 2️⃣ 100 J
🟡 3️⃣ 200 J
🟣 4️⃣ 20 J
✔️ Answer: 200 J
📘 Exam: JEE Advanced 2021 (Paper 2)
🔴 Question 22:
A force of 10 N acts on a particle at 60° to displacement of 1 m. Work done =
🟢 1️⃣ 5 J
🔵 2️⃣ 10 J
🟡 3️⃣ 8.66 J
🟣 4️⃣ Zero
✔️ Answer: 5 J
📘 Exam: JEE Advanced 2020 (Paper 2)
🔴 Question 23:
If work done is positive, then angle between force and displacement is
🟢 1️⃣ 0° < θ < 90° 🔵 2️⃣ 90° 🟡 3️⃣ > 90°
🟣 4️⃣ 180°
✔️ Answer: 0° < θ < 90°
📘 Exam: JEE Advanced 2019 (Paper 2)
🔴 Question 24:
Work done by a force F in displacing a particle through vector r is
🟢 1️⃣ F/r
🔵 2️⃣ F + r
🟡 3️⃣ F ⋅ r
🟣 4️⃣ F × r
✔️ Answer: F ⋅ r
📘 Exam: JEE Advanced 2018 (Paper 2)
🔴 Question 25:
A body of mass 1 kg moves under a constant force of 2 N. Distance moved in 2 s (from rest) is
🟢 1️⃣ 2 m
🔵 2️⃣ 4 m
🟡 3️⃣ 6 m
🟣 4️⃣ 8 m
✔️ Answer: 4 m
📘 Exam: JEE Advanced 2017 (Paper 2)
🔴 Question 26:
When velocity of particle doubles, its kinetic energy becomes
🟢 1️⃣ 2 times
🔵 2️⃣ 4 times
🟡 3️⃣ 8 times
🟣 4️⃣ Half
✔️ Answer: 4 times
📘 Exam: JEE Advanced 2016 (Paper 2)
🔴 Question 27:
A spring with k = 200 N/m is stretched by 0.1 m. Energy stored =
🟢 1️⃣ 1 J
🔵 2️⃣ 2 J
🟡 3️⃣ 0.5 J
🟣 4️⃣ 4 J
✔️ Answer: 1 J
📘 Exam: JEE Advanced 2015 (Paper 2)
🔴 Question 28:
In elastic collision, total kinetic energy
🟢 1️⃣ Increases
🔵 2️⃣ Decreases
🟡 3️⃣ Remains constant
🟣 4️⃣ Becomes zero
✔️ Answer: Remains constant
📘 Exam: JEE Advanced 2014 (Paper 2)
🔴 Question 29:
A 2 kg object moving at 3 m/s is stopped by friction in 3 m. Work done by friction =
🟢 1️⃣ +9 J
🔵 2️⃣ −9 J
🟡 3️⃣ 0 J
🟣 4️⃣ +6 J
✔️ Answer: −9 J
📘 Exam: JEE Advanced 2013 (Paper 2)
🔴 Question 30:
The work done by variable force F = 2x (N) from x = 0 to x = 2 m is
🟢 1️⃣ 2 J
🔵 2️⃣ 4 J
🟡 3️⃣ 6 J
🟣 4️⃣ 8 J
✔️ Answer: 4 J
📘 Exam: JEE Advanced 2012 (Paper 2)
🔴 Question 31:
Work done by force when displacement is zero =
🟢 1️⃣ Maximum
🔵 2️⃣ Zero
🟡 3️⃣ Negative
🟣 4️⃣ Infinite
✔️ Answer: Zero
📘 Exam: JEE Advanced 2011 (Paper 2)
🔴 Question 32:
If total work done on particle is positive, its kinetic energy
🟢 1️⃣ Decreases
🔵 2️⃣ Increases
🟡 3️⃣ Zero
🟣 4️⃣ Constant
✔️ Answer: Increases
📘 Exam: JEE Advanced 2010 (Paper 2)
🔴 Question 33:
A body is acted upon by two equal and opposite forces. Work done is
🟢 1️⃣ Positive
🔵 2️⃣ Negative
🟡 3️⃣ Zero
🟣 4️⃣ Cannot be determined
✔️ Answer: Zero
📘 Exam: JEE Advanced 2009 (Paper 2)
🔴 Question 34:
The rate of doing work is called
🟢 1️⃣ Energy
🔵 2️⃣ Power
🟡 3️⃣ Momentum
🟣 4️⃣ Impulse
✔️ Answer: Power
📘 Exam: JEE Advanced 2008 (Paper 2)
————————————————————————————————————————————————————————————————————————————
PRACTICE SETS FROM THIS LESSON
🟢 NEET LEVEL (Moderate Difficulty)
Q1. Work done by a force is zero when displacement is:
🔵 (A) Parallel to the force
🟢 (B) Perpendicular to the force
🟠 (C) Opposite to the force
🔴 (D) In the direction of the force
Answer: (B) Perpendicular to the force
Q2. The unit of work and energy in SI system is:
🔵 (A) Watt
🟢 (B) Joule
🟠 (C) Newton
🔴 (D) Erg
Answer: (B) Joule
Q3. The work done by friction is always:
🔵 (A) Positive
🟢 (B) Negative
🟠 (C) Zero
🔴 (D) Infinite
Answer: (B) Negative
Q4. Which of the following is a scalar quantity?
🔵 (A) Work
🟢 (B) Force
🟠 (C) Momentum
🔴 (D) Displacement
Answer: (A) Work
Q5. A man lifts a 10 kg box to a height of 2 m. The work done is: (g = 10 m/s²)
🔵 (A) 5 J
🟢 (B) 20 J
🟠 (C) 100 J
🔴 (D) 200 J
Answer: (D) 200 J
Q6. When θ = 0°, the work done by a force F on displacement s is:
🔵 (A) Zero
🟢 (B) Fs
🟠 (C) −Fs
🔴 (D) Fs/2
Answer: (B) Fs
Q7. Work done on a body is negative when:
🔵 (A) Force aids motion
🟢 (B) Force opposes motion
🟠 (C) Force is perpendicular
🔴 (D) Body is stationary
Answer: (B) Force opposes motion
Q8. The energy possessed by a body due to its motion is called:
🔵 (A) Potential energy
🟢 (B) Kinetic energy
🟠 (C) Mechanical energy
🔴 (D) Chemical energy
Answer: (B) Kinetic energy
Q9. Kinetic energy of a body of mass m moving with speed v is:
🔵 (A) ½mv²
🟢 (B) mv
🟠 (C) mv²
🔴 (D) ½mv
Answer: (A) ½mv²
Q10. The potential energy of a body raised to height h is:
🔵 (A) mgh
🟢 (B) ½mv²
🟠 (C) mh/v
🔴 (D) m/v²
Answer: (A) mgh
Q11. If the velocity of a body becomes double, its kinetic energy becomes:
🔵 (A) Twice
🟢 (B) Four times
🟠 (C) Half
🔴 (D) Unchanged
Answer: (B) Four times
Q12. The work–energy theorem states that:
🔵 (A) Work done = Energy lost
🟢 (B) Work done = Change in Kinetic Energy
🟠 (C) Work done = Force × Mass
🔴 (D) Work done = Constant
Answer: (B) Work done = Change in Kinetic Energy
Q13. A body of mass 2 kg is lifted by 1.5 m. The potential energy gained is: (g = 10 m/s²)
🔵 (A) 10 J
🟢 (B) 15 J
🟠 (C) 20 J
🔴 (D) 30 J
Answer: (D) 30 J
Q14. The rate of doing work is called:
🔵 (A) Energy
🟢 (B) Power
🟠 (C) Force
🔴 (D) Momentum
Answer: (B) Power
Q15. The unit of power is:
🔵 (A) Joule
🟢 (B) Watt
🟠 (C) Newton
🔴 (D) Calorie
Answer: (B) Watt
Q16. The power developed by a force F moving a body with velocity v is:
🔵 (A) F/v
🟢 (B) Fv
🟠 (C) Fv²
🔴 (D) F/v²
Answer: (B) Fv
Q17. The work done in stretching a spring by x is:
🔵 (A) kx
🟢 (B) ½kx²
🟠 (C) k/x
🔴 (D) 2kx
Answer: (B) ½kx²
Q18. Mechanical energy is the sum of:
🔵 (A) Heat and light
🟢 (B) Potential and kinetic energies
🟠 (C) Power and force
🔴 (D) Mass and momentum
Answer: (B) Potential and kinetic energies
Q19. A body is dropped from height h. When it reaches halfway, its K.E. is:
🔵 (A) Zero
🟢 (B) mgh
🟠 (C) ½mgh
🔴 (D) ¼mgh
Answer: (C) ½mgh
Q20. One kilowatt-hour equals:
🔵 (A) 3600 J
🟢 (B) 3.6 × 10⁶ J
🟠 (C) 360 J
🔴 (D) 3.6 × 10⁵ J
Answer: (B) 3.6 × 10⁶ J
🟡 JEE MAIN LEVEL (Enhanced Difficulty)
Q21. If work done on a particle is negative, its kinetic energy:
🔵 (A) Increases
🟢 (B) Decreases
🟠 (C) Remains same
🔴 (D) Becomes zero
Answer: (B) Decreases
Q22. A 100 N force displaces a block by 3 m making 60° with direction of motion. Work done = ?
🔵 (A) 50 J
🟢 (B) 150 J
🟠 (C) 200 J
🔴 (D) 300 J
Answer: (B) 150 J
Q23. Work done by variable force F = kx is:
🔵 (A) kx
🟢 (B) ½kx²
🟠 (C) k/x
🔴 (D) 2kx
Answer: (B) ½kx²
Q24. A body of 2 kg has K.E. of 8 J. Its velocity is:
🔵 (A) 2 m/s
🟢 (B) 4 m/s
🟠 (C) 8 m/s
🔴 (D) 16 m/s
Answer: (B) 4 m/s
Q25. If a spring is compressed by 0.2 m and k = 200 N/m, find stored energy.
🔵 (A) 2 J
🟢 (B) 4 J
🟠 (C) 8 J
🔴 (D) 10 J
Answer: (A) 2 J
Q26. The potential energy of a body at 10 m height is 500 J. Find its mass. (g = 10)
🔵 (A) 2 kg
🟢 (B) 5 kg
🟠 (C) 10 kg
🔴 (D) 20 kg
Answer: (B) 5 kg
Q27. A 60 W bulb works for 30 seconds. Energy consumed = ?
🔵 (A) 1200 J
🟢 (B) 1800 J
🟠 (C) 2000 J
🔴 (D) 3600 J
Answer: (B) 1800 J
Q28. A body’s momentum is doubled. Kinetic energy becomes:
🔵 (A) 2 times
🟢 (B) 3 times
🟠 (C) 4 times
🔴 (D) Same
Answer: (C) 4 times
Q29. Power of an engine is 2 kW. It does work of 6000 J in:
🔵 (A) 1 s
🟢 (B) 2 s
🟠 (C) 3 s
🔴 (D) 4 s
Answer: (C) 3 s
Q30. A spring constant doubles; stored potential energy for same extension becomes:
🔵 (A) Half
🟢 (B) Same
🟠 (C) Double
🔴 (D) Quadruple
Answer: (C) Double
Q31. If total work done on a system is zero, total energy:
🔵 (A) Increases
🟢 (B) Decreases
🟠 (C) Remains constant
🔴 (D) Becomes zero
Answer: (C) Remains constant
Q32. A 50 kg mass moves at 2 m/s. Its power output for constant speed is zero because:
🔵 (A) Acceleration = 0
🟢 (B) Work = 0
🟠 (C) Force = 0
🔴 (D) All of these
Answer: (D) All of these
Q33. A 500 W motor lifts a 100 kg load vertically. Speed of lift = ? (g = 10)
🔵 (A) 0.5 m/s
🟢 (B) 1 m/s
🟠 (C) 5 m/s
🔴 (D) 10 m/s
Answer: (B) 1 m/s
Q34. In elastic collisions, which quantity is conserved?
🔵 (A) Only momentum
🟢 (B) Only kinetic energy
🟠 (C) Both momentum and kinetic energy
🔴 (D) Neither
Answer: (C) Both momentum and kinetic energy
Q35. 1 horsepower (hp) equals:
🔵 (A) 746 W
🟢 (B) 1000 W
🟠 (C) 500 W
🔴 (D) 600 W
Answer: (A) 746 W
Q36. Mechanical energy remains constant when:
🔵 (A) Frictionless motion
🟢 (B) Air resistance present
🟠 (C) Work done by friction
🔴 (D) Non-conservative force acts
Answer: (A) Frictionless motion
Q37. The work done by the gravitational force in a closed path is:
🔵 (A) Zero
🟢 (B) Positive
🟠 (C) Negative
🔴 (D) Infinite
Answer: (A) Zero
Q38. If the same work is done in half the time, the power developed becomes:
🔵 (A) Half
🟢 (B) Double
🟠 (C) Same
🔴 (D) Four times
Answer: (B) Double
Q39. A person climbs stairs slowly or quickly. Work done is:
🔵 (A) More when quick
🟢 (B) Less when quick
🟠 (C) Same in both
🔴 (D) None
Answer: (C) Same in both
Q40. Potential energy curve of a stable equilibrium has:
🔵 (A) Maximum value
🟢 (B) Minimum value
🟠 (C) Constant value
🔴 (D) Zero slope
Answer: (B) Minimum value
🔴 JEE ADVANCED LEVEL (High Conceptual Difficulty)
Q41. A conservative force is one for which:
🔵 (A) Work depends on path
🟢 (B) Work depends on end points only
🟠 (C) Energy not conserved
🔴 (D) Friction present
Answer: (B) Work depends on end points only
Q42. A spring of constant k stretched by x has stored energy. If x doubles, energy increases by:
🔵 (A) 2 times
🟢 (B) 3 times
🟠 (C) 4 times
🔴 (D) 8 times
Answer: (C) 4 times
Q43. A block slides down a frictionless incline of height h. Its velocity at bottom is:
🔵 (A) √(gh)
🟢 (B) √(2gh)
🟠 (C) 2gh
🔴 (D) gh
Answer: (B) √(2gh)
Q44. A force F = (3x²)i acts on a particle along x-axis. Work done from x=0 to x=2 m = ?
🔵 (A) 6 J
🟢 (B) 8 J
🟠 (C) 12 J
🔴 (D) 24 J
Answer: (D) 24 J
Q45. The area under a Force–Displacement graph represents:
🔵 (A) Energy
🟢 (B) Work
🟠 (C) Momentum
🔴 (D) Impulse
Answer: (B) Work
Q46. Which of these is a non-conservative force?
🔵 (A) Gravitational force
🟢 (B) Elastic spring force
🟠 (C) Friction
🔴 (D) Electric force
Answer: (C) Friction
Q47. For a particle moving in potential U(x), force is given by:
🔵 (A) F = dU/dx
🟢 (B) F = −dU/dx
🟠 (C) F = U/x
🔴 (D) F = −U/x²
Answer: (B) F = −dU/dx
Q48. A car engine delivers 5000 J of work using 8000 J of fuel energy. Its efficiency = ?
🔵 (A) 40%
🟢 (B) 50%
🟠 (C) 60%
🔴 (D) 62.5%
Answer: (C) 60%
Q49. If total work done by all forces on a system is zero, which quantity remains constant?
🔵 (A) Acceleration
🟢 (B) Momentum
🟠 (C) Kinetic Energy
🔴 (D) Potential Energy
Answer: (C) Kinetic Energy
Q50. A particle under conservative force has total energy constant. This implies:
🔵 (A) K.E. and P.E. both remain constant
🟢 (B) K.E. and P.E. change but total constant
🟠 (C) Only K.E. constant
🔴 (D) Only P.E. constant
Answer: (B) K.E. and P.E. change but total constant
————————————————————————————————————————————————————————————————————————————
MIND MAPS
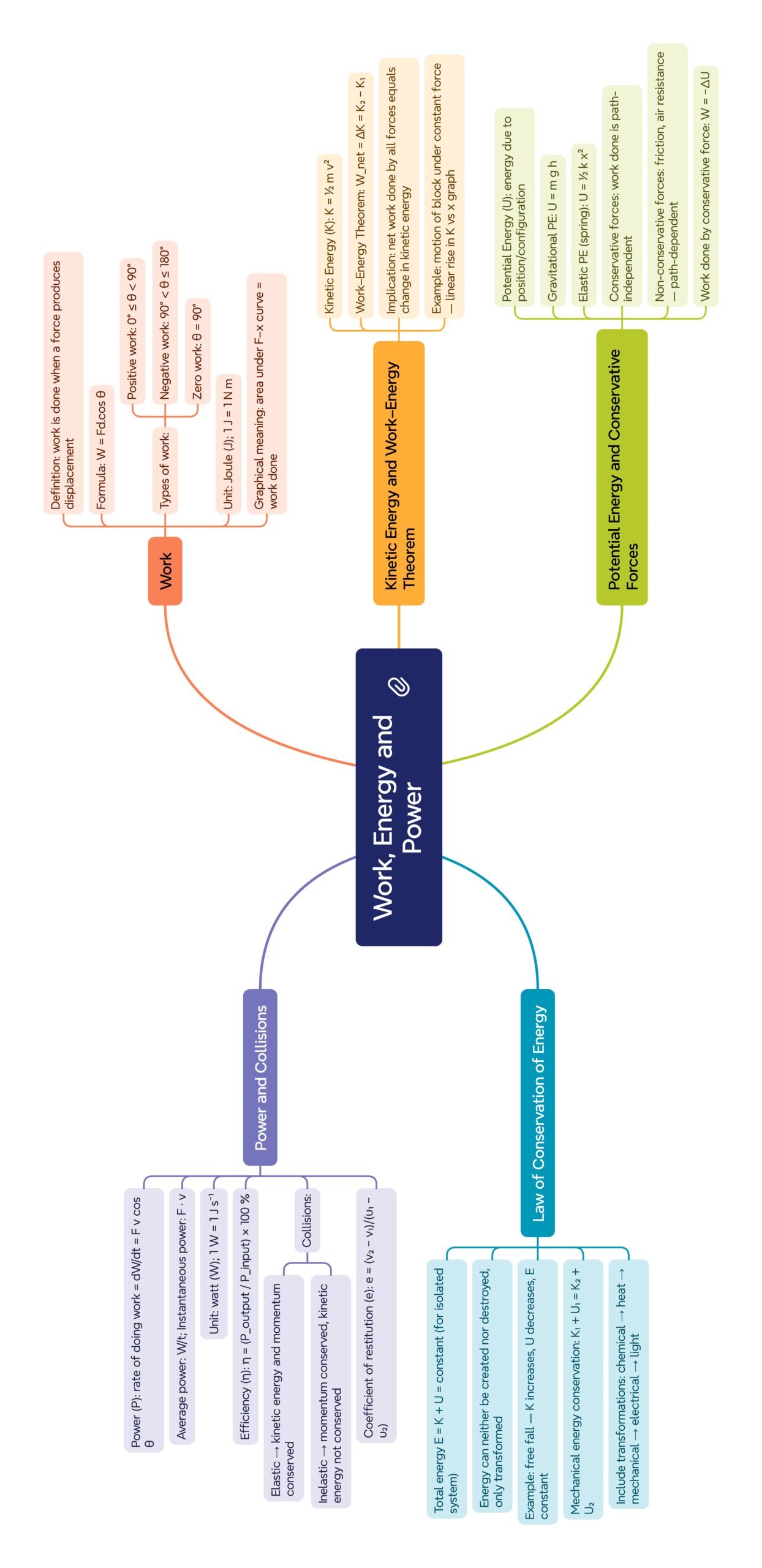

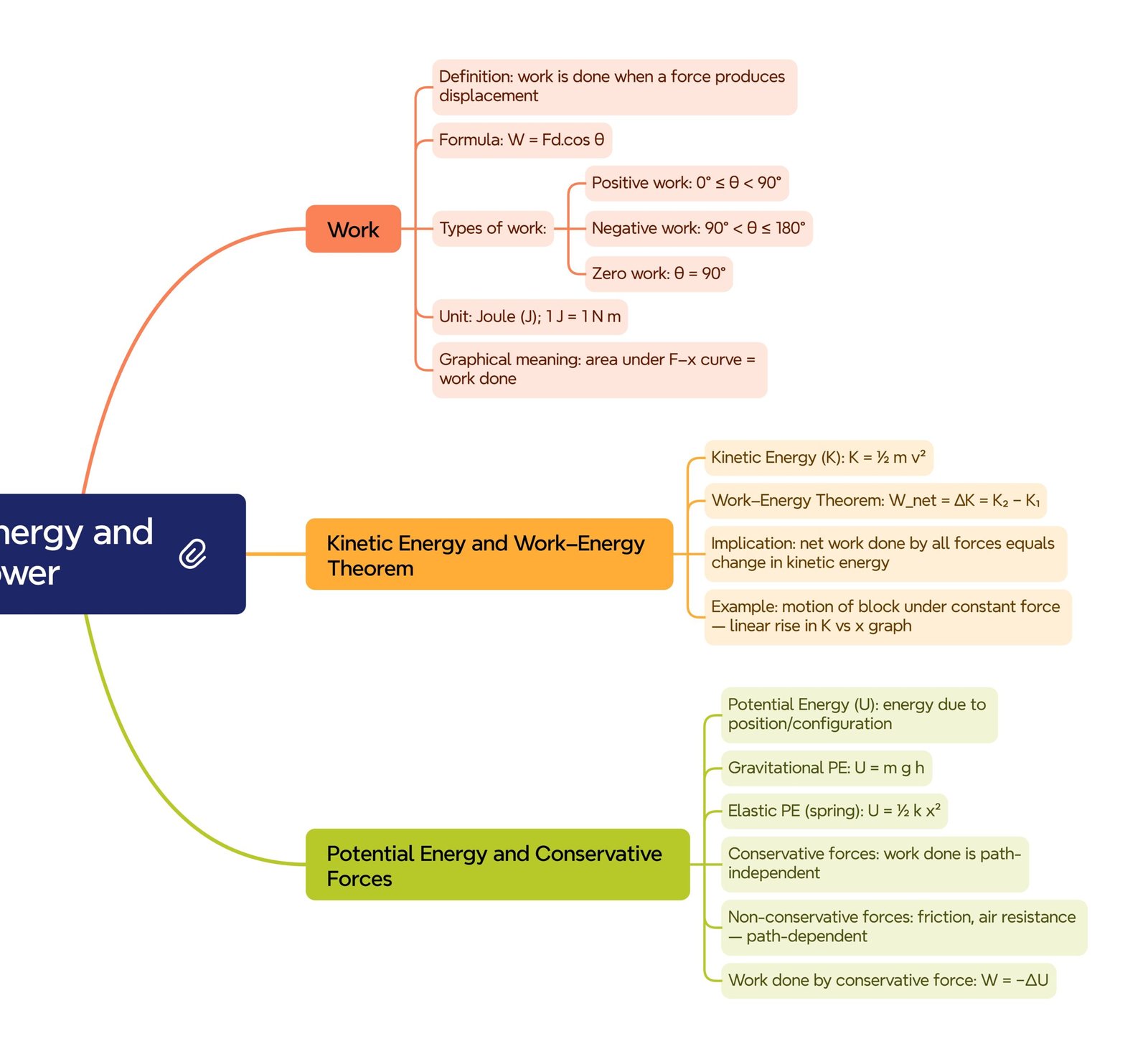
————————————————————————————————————————————————————————————————————————————
