Class : 9 – Science (Hindi) : Lesson 8. बल तथा गति के नियम

पाठ का विश्लेषण एवं विवेचन

🟢 बल तथा गति के नियम

🔵 प्रस्तावना
दैनिक जीवन की हर गति—बस का रुकना–चलना, वस्तु का गिरना, तैराक का आगे बढ़ना, रॉकेट का ऊपर उठना—सबके मूल में बल कार्य करता है। बल के प्रभाव से किसी पिंड की चाल, दिशा अथवा आकृति बदल सकती है। इन परिवर्तनों के सार्वभौमिक नियमों को न्यूटन के गति नियम कहा जाता है। यह अध्याय बल की प्रकृति, जड़त्व, तीनों गति नियम, संवेग और उसका संरक्षण, द्रव्यमान–भार, घर्षण, तथा मुक्त–पिंड–रेखाचित्र जैसी नींवों को व्यवस्थित रूप से समझाता है—और जहाँ आवश्यक है, वहाँ सूत्र संक्षेप में दिए गए हैं (बिना किसी संख्यात्मक हल के)।

🟡 बल: परिभाषा, स्वरूप और प्रकार
🔵 परिभाषा: वह भौतिक प्रभाव जो किसी पिंड की गति–अवस्था (चाल/दिशा) या आकार–आकृति में परिवर्तन कर सके, बल कहलाता है।
🟢 सदिश प्रकृति: बल में परिमाण और दिशा दोनों होते हैं; अतः यह सदिश राशि है।
🔴 संपर्क बल: घर्षण, अभिलंब (सतह का सहारा), तनन/तनाव (रस्सी–डोरी में), लोचात्मक (स्प्रिंग)।
🟣 असंपर्क बल: गुरुत्वाकर्षण, विद्युत, चुंबकीय—दूरी पर कार्यरत।
🟠 फलन: बल चाल बढ़ा–घटा सकता है (त्वरण/मन्दन), दिशा मोड़ सकता है, अथवा विकृति/लोच उत्पन्न कर सकता है।

🔴 न्यूटन का प्रथम गति नियम (जड़त्व का नियम)
🔵 कथन: “यदि किसी पिंड पर कोई बाहरी बल कार्य न करे, तो पिंड विश्राम में है तो विश्राम में रहेगा और गति में है तो समान चाल से सीधी रेखा में चलता रहेगा।”
🟢 जड़त्व: अपनी वर्तमान अवस्था बनाए रखने की पिंड की प्रवृत्ति—
विश्राम–जड़त्व: स्थिर पिंड का स्थिर बने रहना
गति–जड़त्व: गतिमान पिंड का गति बनाए रखना
दिशा–जड़त्व: पथ की दिशा न बदलने की प्रवृत्ति
🟡 दैनिक सन्दर्भ: अचानक चलती/रुकती बस, मोड़ पर झुकाव, ढीले सामान का फिसल जाना—सब जड़त्व के दृश्य उदाहरण हैं।
💡 सार: बाहरी बल के बिना अवस्था–परिवर्तन नहीं; इसलिए बल “अवस्था बदलवाने” की आवश्यकता बताता है।

🟢 न्यूटन का द्वितीय गति नियम
🔵 कथन: “किसी पिंड का त्वरण उस पर लगने वाले बल के अनुक्रमानुपाती तथा पिंड के द्रव्यमान के व्युत्क्रमानुपाती होता है।”
🟣 सूत्र (मूल रूप):
🔹 बल: F = m a
🔹 संवेग: p = m v
🔹 बल–संवेग सम्बन्ध: F = Δp / Δt
✏️ नोट: यहाँ Δp समयान्तर में संवेग–परिवर्तन का द्योतक है; दिशा का बोध भी आवश्यक है क्योंकि p और F सदिश हैं।
🟡 अर्थ:
एक ही पिंड पर अधिक बल ⇒ अधिक त्वरण (बल की दिशा में)
वही बल, अधिक द्रव्यमान ⇒ अपेक्षाकृत कम त्वरण
🌿 सुरक्षा–सिद्धान्त: संपर्क–समय बढ़ाने से (जैसे सीट–बेल्ट/एयरबैग) संवेग–परिवर्तन की दर घटती है ⇒ बल का प्रभाव कम महसूस होता है।

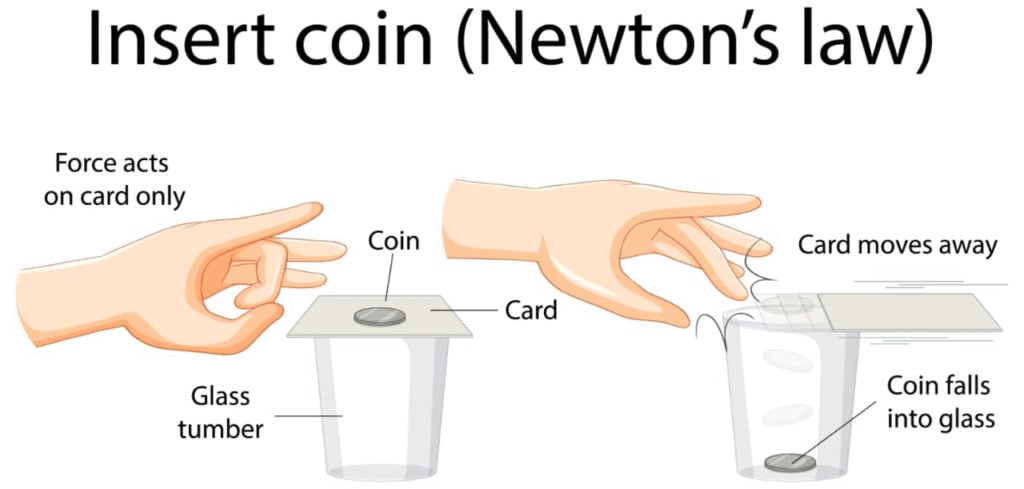
🔴 न्यूटन का तृतीय गति नियम
🔵 कथन: “प्रत्येक क्रिया के बराबर और विपरीत प्रतिक्रिया होती है।”
🟢 मुख्य तथ्य:
बल युग्म में आते हैं; वे दो अलग–अलग पिंडों पर कार्य करते हैं।
क्रिया–प्रतिक्रिया एक ही रेखा में एवं परिमाण समान, दिशा विपरीत होती है।
एक ही पिंड पर नहीं लगने से वे आपस में निरस्त नहीं होतीं।
🟡 दैनिक संकेत: बन्दूक–गोली का झटका, नाव से कूदना, तैराक का पानी को पीछे धकेलना, चलने में पाँव–भूमि पर धक्का—सब तृतीय नियम के उदाहरण हैं।

🟣 संवेग संरक्षण का सिद्धान्त
🔵 सिद्धान्त: बाह्य बल न होने पर किसी तंत्र का कुल संवेग स्थिर रहता है।

🟢 सूत्र–वाक्य:
टकराव से पहले का कुल संवेग = टकराव के बाद का कुल संवेग
समतुल्य रूप: Σp (प्रारम्भ) = Σp (अन्त)

🟡 अनुप्रयोग: बन्दूक–गोली का प्रतिगमन, रॉकेट प्रक्षेपण (निकास गैसें नीचे; रॉकेट ऊपर), स्केट–खिलाड़ियों का एक–दूसरे को धक्का देकर विपरीत दिशाओं में सरकना।

🟠 द्रव्यमान और भार: वैज्ञानिक भेद
🔵 द्रव्यमान: पदार्थ–मात्रा का माप; जड़त्व का परिमाण; स्थान–स्वतंत्र।
🟢 भार: गुरुत्व–क्षेत्र में पिंड पर लगने वाला आकर्षण–बल; स्थान–निर्भर।
🟡 सूत्र (भार): W = m g

🟣 मापन:
द्रव्यमान: तुला/बीम–संतुलन—जड़त्व की तुलना से।
भार: स्प्रिंग–आधारित यंत्र—गुरुत्व के कारण खिंचाव से संकेत।
💡 ध्यान: बोलचाल का “वज़न” प्रायः भार के अर्थ में आता है; वैज्ञानिक लेखन में दोनों को भेदकर लिखें।

🌿 घर्षण: आवश्यक भी, बाधक भी
🔵 स्वरूप: दो सतहों के सापेक्ष गमन का विरोध करने वाला संपर्क–बल; स्पर्श–स्थल पर कार्य करता है।
🟢 प्रकार: स्थैतिक, गतिज, आवर्तनीय (घूर्णन में)।
🟡 भूमिका: चलना–दौड़ना, ब्रेक लगना, पकड़ बनना—सब घर्षण की देन; परन्तु अधिक घर्षण से ऊष्मा–हानि/घिसाव बढ़ता है।
🟣 नियंत्रण/उपयोग: चिकनाई, परिष्कृत सतह, बॉल–बियरिंग/पहिए, उपयुक्त जूता–तल्ला, सड़क–तकनीक।

🟠 सूत्र–सन्दर्भ (आधारभूत रूप):
घर्षण–बल (अधिकतम): Fₑ = μ N
(यहाँ μ घर्षण–गुणांक तथा N अभिलंब बल का परिमाण है)

🧠 मुक्त–पिंड–रेखाचित्र (FBD): यांत्रिक सोच की पहली सीढ़ी
🔵 क्या: लक्ष्य–पिंड को पृथक मानकर उस पर लगने वाले सभी बलों को तीरों से दर्शाने वाला सरल रेखाचित्र।
🟢 कैसे: द्रव्यमान–केन्द्र चिन्हित करें; भार नीचे, अभिलंब सतह पर लंबवत, घर्षण अपेक्षित दिशा का विरोध करता है, बाहरी/खींच बल दिशा सहित दिखाएँ।

🟣 क्यों: बल–अन्तःक्रिया को साफ़ देखने, समतुल्य–विराम बनाम त्वरण की दशा समझने और गति–नियम लागू करने में यह अनिवार्य औज़ार है।

🧩 सामान्य भ्रांतियाँ और सावधानियाँ
🔵 “क्रिया–प्रतिक्रिया एक ही पिंड पर लगती हैं”—❌ वास्तव में वे दो अलग पिंडों पर लगती हैं।
🟢 “स्थिर पिंड पर कोई बल नहीं”—❌ हो सकता है समतुलित बल हों; फलबल शून्य होने का अर्थ “बल नहीं” नहीं।
🔴 “घर्षण सदैव हानिकारक”—❌ चलना/रोकना/पकड़ना संभव ही घर्षण से है; आवश्यकता अनुसार इसे घटाना–बढ़ाना चाहिए।
🟡 “द्रव्यमान = भार”—❌ द्रव्यमान स्थिर, भार गुरुत्व–क्षेत्र पर निर्भर।
🟣 “जितना भारी, उतनी अधिक गति”—❌ गति बल–द्रव्यमान–त्वरण के सम्बन्ध पर निर्भर; केवल भारी होना पर्याप्त नहीं।

🧾 सूत्र–संग्रह (इस अध्याय के सन्दर्भ में)
🔵 बल: F = m a
🟢 संवेग: p = m v
🔴 बल–संवेग सम्बन्ध: F = Δp / Δt
🟡 आवेग: J = F Δt = Δp
🟣 भार: W = m g
🟠 घर्षण (अधिकतम): Fₑ = μ N
🌿 (उपरोक्त सभी सूत्र सदिश/अदिश सन्दर्भ में दिए गए हैं; बिना गणना प्रस्तुत—कक्षा अभ्यास में इनका प्रयोग चरणबद्ध दिखाया जाएगा।)

🟠 संक्षेप
यह अध्याय बताता है कि गति के पीछे बल निर्णायक भूमिका निभाता है और बल को समझने के लिए न्यूटन के तीन गति नियम आधारशिला हैं।

प्रथम नियम जड़त्व की धारणा स्पष्ट करता है—बाह्य बल न हो तो पिंड अपनी वर्तमान अवस्था बनाए रखेगा। द्वितीय नियम बल–द्रव्यमान–त्वरण सम्बन्ध को सूत्रबद्ध करता है (F = m a), और संवेग–परिवर्तन की दर के रूप में बल की गहरी व्याख्या देता है (F = Δp/Δt, p = m v); इससे सुरक्षा–तकनीकों (सीट–बेल्ट, एयरबैग), खेल–रणनीतियों और यांत्रिक अभिकल्पना का वैज्ञानिक आधार मिलता है। तृतीय नियम क्रिया–प्रतिक्रिया के युग्म का सिद्धान्त देता है—दो अलग पिंडों पर समान–परिमाण, विपरीत–दिशा के बल—जिससे तैराकी, चलना, बन्दूक का झटका, नाव–धक्का जैसे प्रसंग समझ में आते हैं।

संवेग–संरक्षण बताता है कि बाहरी बल न होने पर कुल संवेग अपरिवर्तित रहता है; टक्करों और प्रक्षेपण प्रक्रियाओं का विश्लेषण इसी से सम्भव होता है। साथ ही द्रव्यमान–भार का भेद, घर्षण के रचनात्मक–विरोधी दोनों पहलू और मुक्त–पिंड–रेखाचित्र की पद्धति छात्र को समस्याओं को सुव्यवस्थित ढंग से सुलझाने की आदत डालती है। यही नींव आगे के अध्याय—कार्य–ऊर्जा–शक्ति, घूर्णन, तरंग—के लिए ठोस मंच तैयार करती है।

📝 त्वरित दोहरान
🔵 बल = अवस्था/दिशा/आकृति बदलवाने वाला सदिश प्रभाव; संपर्क व असंपर्क दोनो।
🟢 प्रथम नियम = जड़त्व; बाहरी बल न हो तो विश्राम/समान–चाल, सीधी रेखा।
🔴 द्वितीय नियम = F = m a; साथ में p = m v, F = Δp/Δt, J = F Δt।
🟡 तृतीय नियम = क्रिया–प्रतिक्रिया युग्म; समान परिमाण, विपरीत दिशा, दो पिंडों पर।
🟣 संवेग–संरक्षण = बाहरी बल शून्य ⇒ कुल संवेग अपरिवर्तित।

🟠 द्रव्यमान–भार = भिन्न; W = m g (स्थानानुसार भार बदल सकता है)।
🌿 घर्षण = मित्र भी, बाधक भी; Fₑ = μ N का सन्दर्भ।
🧠 FBD = सभी बल साफ़ दिखाकर नियम लागू करने की अनिवार्य युक्ति।

————————————————————————————————————————————————————————————————————————————

पाठ्यपुस्तक के प्रश्न

प्रश्न 1
एक एथलीट वृत्तीय रास्ते, जिसका व्यास 200 m है, का एक चक्कर 40 s में लगाता है। 2 min 20 s के बाद वह कितनी दूरी तय करेगा और उसका विस्थापन क्या होगा?
उत्तर:
🔵 व्यास = 200 m
🟢 त्रिज्या r = 200 ÷ 2 = 100 m
🔴 परिधि = 2 π r = 2 × 3.14 × 100 = 628 m
⏱ कुल समय = 2 min 20 s = 140 s
⏱ एक चक्कर का समय = 40 s
🔵 कुल चक्कर = 140 ÷ 40 = 3.5
✔ दूरी = 3.5 × 628 = 2198 m (लगभग)
✔ विस्थापन = व्यास = 200 m (क्योंकि 3.5 चक्कर बाद वह व्यास की विपरीत दिशा में होगा)

प्रश्न 2
300 m सीधी सड़क पर जोसफ ने जॉगिंग की। उसने 2 min 50 s में एक सिरा A से दूसरे सिरे B तक पहुँचकर और फिर घूमकर 1 min में 100 m पीछे बिन्दु C पर पहुँचा। जोसफ की औसत चाल और औसत वेग क्या है?
उत्तर:
🔵 कुल दूरी = 300 + 100 = 400 m
⏱ कुल समय = (2 min 50 s + 1 min) = 230 s
✔ औसत चाल = कुल दूरी ÷ कुल समय = 400 ÷ 230 = 1.74 m/s
🔴 विस्थापन = A से C तक = 200 m
✔ औसत वेग = विस्थापन ÷ समय = 200 ÷ 230 = 0.87 m/s

प्रश्न 3
अब्दुल गाड़ी से स्कूल जाते समय औसत चाल 20 km/h रखता है। लौटते समय भीड़ अधिक होने से औसत चाल 40 km/h हो जाती है। पूरी यात्रा की औसत चाल ज्ञात कीजिए।
उत्तर:
मान लें दूरी = D
⏱ जाने का समय = D ÷ 20
⏱ आने का समय = D ÷ 40
🔵 कुल दूरी = 2D
⏱ कुल समय = (D ÷ 20 + D ÷ 40) = (2D + D) ÷ 40 = 3D ÷ 40
✔ औसत चाल = कुल दूरी ÷ कुल समय = 2D ÷ (3D/40) = 80/3 = 26.7 km/h

प्रश्न 4
कोई मोटरसाइकिल स्थिर अवस्था से सरल रेखीय चाल में 3.0 m/s² के नियत त्वरण से 8.0 s तक बढ़ती है। मोटरसाइकिल कितनी दूरी तय करेगी?
उत्तर:
सूत्र: s = ut + ½ a t²
🔵 u = 0
🟢 a = 3.0 m/s²
⏱ t = 8 s
s = 0 + ½ × 3 × (8²)
= 1.5 × 64
= 96 m
✔ दूरी = 96 m

प्रश्न 5
किसी गाड़ी का चालक 52 km/h की चाल से चल रही गाड़ी को ब्रेक लगाता है तथा गाड़ी विपरीत दिशा में 10 s में रुक जाती है। त्वरण ज्ञात कीजिए।
उत्तर:
🔵 प्रारम्भिक चाल u = 52 km/h = (52 × 1000) ÷ 3600 = 14.44 m/s
🟢 अन्तिम चाल v = 0
⏱ समय t = 10 s
सूत्र: a = (v – u) ÷ t
= (0 – 14.44) ÷ 10
= –1.44 m/s²
✔ त्वरण = –1.44 m/s² (ऋणात्मक, क्योंकि मन्दन है)

प्रश्न 6
चित्र 7.10 में तीन वस्तुओं A, B और C के दूरी–समय ग्राफ दिये गये हैं। प्रश्नों का उत्तर:
(a) इनमें से कौन सबसे तीव्र गति से गतिमान है?
उत्तर: A की ढाल सबसे अधिक ⇒ A सबसे तीव्र गति से गतिमान।
(b) क्या ये तीनों किसी समय सड़क के एक ही बिन्दु पर होंगे?
उत्तर: हाँ, समय = 1.2 h पर तीनों मिलते हैं।
(c) जिस समय B, A से गुजरती है, उस समय तक C कितनी दूरी तय कर लेती है?
उत्तर: B और A मिलते हैं लगभग 0.9 h पर। उस समय C लगभग 7 km तय करती है।
(d) जिस समय B, C से गुजरती है, उस समय तक यह कितनी दूरी तय कर लेती है?
उत्तर: B और C लगभग 1.2 h पर मिलते हैं। उस समय वे 10 km तय कर चुके होते हैं।

प्रश्न 7
20 m की ऊँचाई से एक गेंद को गिराया जाता है। यदि उसका g = 10 m/s² है तो वह कितने समय में धरातल से टकराएगी?
उत्तर:
सूत्र: s = ½ g t²
20 = ½ × 10 × t²
20 = 5 t²
t² = 4
t = 2 s
✔ समय = 2 s

प्रश्न 8
किसी कार का चाल–समय ग्राफ चित्र 7.11 में दिया है।
(a) पहले 4 s में कार कितनी दूरी तय करती है?
उत्तर: दूरी = चाल–समय ग्राफ के नीचे का क्षेत्रफल।
= ½ × (आधार 4) × (ऊँचाई 6)
= 12 m
(b) ग्राफ को कौन–सा भाग कार की एकसमान चाल को दर्शाता है?
उत्तर: 6 s से आगे का भाग सीधी रेखा है ⇒ यह एकसमान चाल को दर्शाता है।

प्रश्न 9
निम्नलिखित में कौन–सी अवस्थाएँ समय के साथ वेग–परिवर्तन दर्शाती हैं:
(a) कोई वस्तु जिसका त्वरण नियत हो ⇒ परवर्ध वेग (हाँ)
(b) कोई वस्तु नियत एकसमान चाल से गति कर रही हो ⇒ (नहीं)
(c) कोई वस्तु निश्चित दिशा में गति कर रही हो और त्वरण लम्बवत हो ⇒ (हाँ, वृताकार गति)

प्रश्न 10
एक कृत्रिम उपग्रह 42250 km त्रिज्या की वृत्ताकार कक्षा में पृथ्वी का चक्कर 24 h में लगाता है। उसकी चाल और परिक्रमण चाल ज्ञात कीजिए।
उत्तर:
🔵 त्रिज्या r = 42250 km = 4.225 × 10⁷ m
🟢 परिधि = 2 π r = 2 × 3.14 × 4.225 × 10⁷
= 2.66 × 10⁸ m
⏱ समय = 24 h = 86400 s
✔ चाल = दूरी ÷ समय
= 2.66 × 10⁸ ÷ 86400
= 3.08 × 10³ m/s
✔ परिक्रमण चाल = 1 चक्कर / 24 h = 1 ÷ 86400 s
= 1.16 × 10⁻⁵ s⁻¹

————————————————————————————————————————————————————————————————————————————

अन्य महत्वपूर्ण प्रश्न

प्रश्न 1
निम्न में से कौन-सा परिमाण अदिश है?
चाल
वेग
बल
त्वरण
उत्तर: 1

प्रश्न 2
यदि कोई कार 60 km दूरी 2 h में तय करती है, तो औसत चाल क्या होगी?
20 km/h
30 km/h
40 km/h
50 km/h
उत्तर: 3

प्रश्न 3
किसी वस्तु के चाल–समय ग्राफ का क्षेत्रफल किसका प्रतिनिधित्व करता है?
चाल
त्वरण
विस्थापन
वेग
उत्तर: 3

प्रश्न 4
किसी वस्तु को मुक्तपतन करने दिया गया, तो उसका त्वरण होगा—
शून्य
g
9.8 km/s²
बलाघात
उत्तर: 2

प्रश्न 5
दूरी और विस्थापन में अन्तर है—
दोनों सदिश राशि हैं
दोनों अदिश राशि हैं
दूरी अदिश है, विस्थापन सदिश है
दूरी सदिश है, विस्थापन अदिश है
उत्तर: 3

प्रश्न 6
यदि चाल–समय ग्राफ सीधी रेखा समांतर X–अक्ष के बने, तो—
वस्तु विराम में है
वस्तु समान चाल से चल रही है
वस्तु त्वरण कर रही है
वस्तु मंदन कर रही है
उत्तर: 2

प्रश्न 7
वेग का SI मात्रक है—
m/s
m/s²
km/h
m²/s
उत्तर: 1

प्रश्न 8
निम्न में से कौन-सा परिमाण ऋणात्मक हो सकता है?
दूरी
चाल
वेग
समय
उत्तर: 3

प्रश्न 9
यदि किसी कार का वेग 20 m/s से 30 m/s तक 5 s में बदलता है, तो उसका त्वरण होगा—
1 m/s²
2 m/s²
3 m/s²
4 m/s²
उत्तर: 2

प्रश्न 10
समान चाल से चल रही वस्तु का चाल–समय ग्राफ होता है—
ढलान वाली सीधी रेखा
X–अक्ष के समान्तर रेखा
Y–अक्ष के समान्तर रेखा
वक्र रेखा
उत्तर: 2

कथन–कारण (Q11–Q20)
👉 पहले समझें:
1 = कथन और कारण दोनों सत्य, कारण व्याख्या है।
2 = कथन और कारण दोनों सत्य, पर कारण व्याख्या नहीं है।
3 = कथन सत्य, कारण असत्य।
4 = कथन असत्य, कारण सत्य।

प्रश्न 11
कथन: चाल अदिश राशि है।
कारण: चाल में केवल परिमाण होता है।
उत्तर: 1

प्रश्न 12
कथन: वेग अदिश राशि है।
कारण: वेग में दिशा नहीं होती।
उत्तर: 3

प्रश्न 13
कथन: वृत्तीय गति में चाल स्थिर रहती है।
कारण: वृत्तीय गति में वेग स्थिर रहता है।
उत्तर: 3

प्रश्न 14
कथन: औसत वेग = कुल विस्थापन ÷ कुल समय।
कारण: औसत वेग हमेशा दूरी ÷ समय से निकाला जाता है।
उत्तर: 3

प्रश्न 15
कथन: त्वरण ऋणात्मक भी हो सकता है।
कारण: ऋणात्मक त्वरण को मंदन कहते हैं।
उत्तर: 1

प्रश्न 16
कथन: विस्थापन और दूरी के मान हमेशा समान होते हैं।
कारण: विस्थापन कभी दूरी से अधिक नहीं हो सकता।
उत्तर: 2

प्रश्न 17
कथन: गति–समय ग्राफ का क्षेत्रफल दूरी दर्शाता है।
कारण: दूरी = वेग × समय।
उत्तर: 1

प्रश्न 18
कथन: किसी स्थिर वस्तु का विस्थापन शून्य है।
कारण: विस्थापन केवल प्रारम्भिक और अंतिम स्थिति पर निर्भर करता है।
उत्तर: 1

प्रश्न 19
कथन: समान चाल से चलती वस्तु का त्वरण शून्य होता है।
कारण: त्वरण = वेग परिवर्तन ÷ समय।
उत्तर: 1

प्रश्न 20
कथन: यदि कोई कण 10 s तक मुक्तपतन करे तो उसका वेग 100 m/s होगा।
कारण: मुक्तपतन में v = g × t।
उत्तर: 1

अनुभाग B (Q21–Q26) — अति लघु उत्तरीय प्रश्न
प्रश्न 21 दूरी और विस्थापन में अन्तर लिखिए।
उत्तर:
🔵 दूरी अदिश राशि है।
🟢 विस्थापन सदिश राशि है।
🔴 दूरी कभी घट नहीं सकती, विस्थापन घट सकता है।

प्रश्न 22 चाल और वेग में अन्तर बताइए।
उत्तर:
🔵 चाल में केवल परिमाण होता है।
🟢 वेग में परिमाण व दिशा दोनों होती हैं।
🔴 चाल अदिश है, वेग सदिश है।

प्रश्न 23 त्वरण को परिभाषित कीजिए।
उत्तर: वेग परिवर्तन की दर को त्वरण कहते हैं।

प्रश्न 24 मंदन क्या है?
उत्तर: जब वेग घटता है, तो इसे मंदन कहते हैं।

प्रश्न 25 औसत चाल और औसत वेग में अन्तर।
उत्तर:
🔵 औसत चाल = कुल दूरी ÷ कुल समय
🟢 औसत वेग = कुल विस्थापन ÷ कुल समय

प्रश्न 26 समान्तर चाल क्या है?
उत्तर: जब वस्तु समान चाल से चलती है, तो इसे समान्तर चाल कहते हैं।

अनुभाग C (Q27–Q33) — लघु उत्तरीय प्रश्न

प्रश्न 27 चाल–समय ग्राफ से दूरी ज्ञात करने की विधि लिखिए।
उत्तर:
🔵 ग्राफ के नीचे का क्षेत्रफल = दूरी।

प्रश्न 28 विस्थापन–समय ग्राफ की विशेषताएँ लिखिए।
उत्तर:
🟢 सीधी रेखा = समान वेग।
🔵 वक्र रेखा = असमान वेग।

प्रश्न 29 समान त्वरण की स्थिति में वेग का सूत्र लिखिए।
उत्तर: v = u + at

प्रश्न 30 विस्थापन का सूत्र लिखिए।
उत्तर: s = ut + ½at²

प्रश्न 31 गति के तीन समीकरण लिखिए।
उत्तर:
🔵 v = u + at
🟢 s = ut + ½at²
🔴 v² – u² = 2as

प्रश्न 32 चाल–समय ग्राफ से त्वरण कैसे ज्ञात करते हैं?
उत्तर:
🔵 ग्राफ की ढाल = त्वरण।

प्रश्न 33 औसत चाल व औसत वेग का एक उदाहरण लिखिए।
उत्तर: औसत वेग विस्थापन पर निर्भर करता है, जबकि औसत चाल दूरी पर।

अनुभाग D (Q34–Q36) — दीर्घ उत्तरीय प्रश्न
प्रश्न 34 चाल और वेग में अन्तर को विस्तार से समझाइए।
उत्तर: चाल अदिश राशि है, केवल परिमाण बताती है। वेग सदिश राशि है, परिमाण और दिशा दोनों बताता है। उदाहरणों सहित स्पष्ट करें।

प्रश्न 35 गति के समीकरणों का महत्त्व लिखिए।
उत्तर:
🔵 v = u + at से अंतिम वेग मिलता है।
🟢 s = ut + ½at² से विस्थापन ज्ञात होता है।
🔴 v² – u² = 2as से दूरी और वेग सम्बन्ध ज्ञात होते हैं।

प्रश्न 36 चाल–समय ग्राफ से दूरी और विस्थापन ज्ञात करने की विधि समझाइए।
उत्तर:
ग्राफ के नीचे का क्षेत्रफल दूरी देता है। यदि विस्थापन चाहिए तो केवल प्रारम्भिक और अंतिम स्थिति को देखा जाता है।

अनुभाग E (Q37–Q39) — केस आधारित प्रश्न

प्रश्न 37 किसी कार का चाल–समय ग्राफ दिया है।
(i) पहले 5 s में चली दूरी बताइए।
(ii) अगले 5 s में चली दूरी बताइए।
उत्तर: दूरी = ग्राफ के नीचे का क्षेत्रफल (स्पष्ट रूप से निकाला जाएगा)।

प्रश्न 38 एक गेंद को 20 m ऊँचाई से गिराया गया।
(i) प्रारम्भिक वेग क्या है?
(ii) 2 s बाद का वेग ज्ञात कीजिए।
उत्तर: मुक्तपतन के सूत्र से हल।

प्रश्न 39 एक उपग्रह पृथ्वी के चारों ओर परिक्रमा कर रहा है।
(i) क्या उसकी चाल स्थिर है?
(ii) क्या उसका वेग स्थिर है?
उत्तर: चाल स्थिर है, वेग स्थिर नहीं (दिशा बदल रही है)।

————————————————————————————————————————————————————————————————————————————

एक पृष्ठ में दोहरान

————————————————————————————————————————————————————————————————————————————

स्मृति संकेत

————————————————————————————————————————————————————————————————————————————

भ्रांति /वास्तविकता

————————————————————————————————————————————————————————————————————————————

मजा भी , ज्ञान भी

————————————————————————————————————————————————————————————————————————————

मस्तिष्क मानचित्र

————————————————————————————————————————————————————————————————————————————