Class : 9 – Science (English) : Lesson 8. Force and Laws of Motion

EXPLANATION & SUMMARY

🔵 Introduction
The motion of bodies cannot be explained only by describing how they move; we must also understand why they move.
The concept of force explains the cause of motion.
Sir Isaac Newton formulated three fundamental laws which form the foundation of classical mechanics.

🟢 Force
Definition: A force is a push or pull acting on an object that can change its state of rest or motion.
It can:
Change speed
Change direction
Change shape/size
💡 Examples: Kicking a football (changes motion), stretching a rubber band (changes shape).

🟡 Balanced and Unbalanced Forces
Balanced forces
Equal in magnitude, opposite in direction.
Net force = 0.
No change in state of motion.
Example: Tug of war when both teams pull equally.
Unbalanced forces
Unequal forces act.
Net force ≠ 0.
Object accelerates in direction of greater force.
Example: Tug of war when one team is stronger.

🟣 Newton’s First Law of Motion (Law of Inertia)

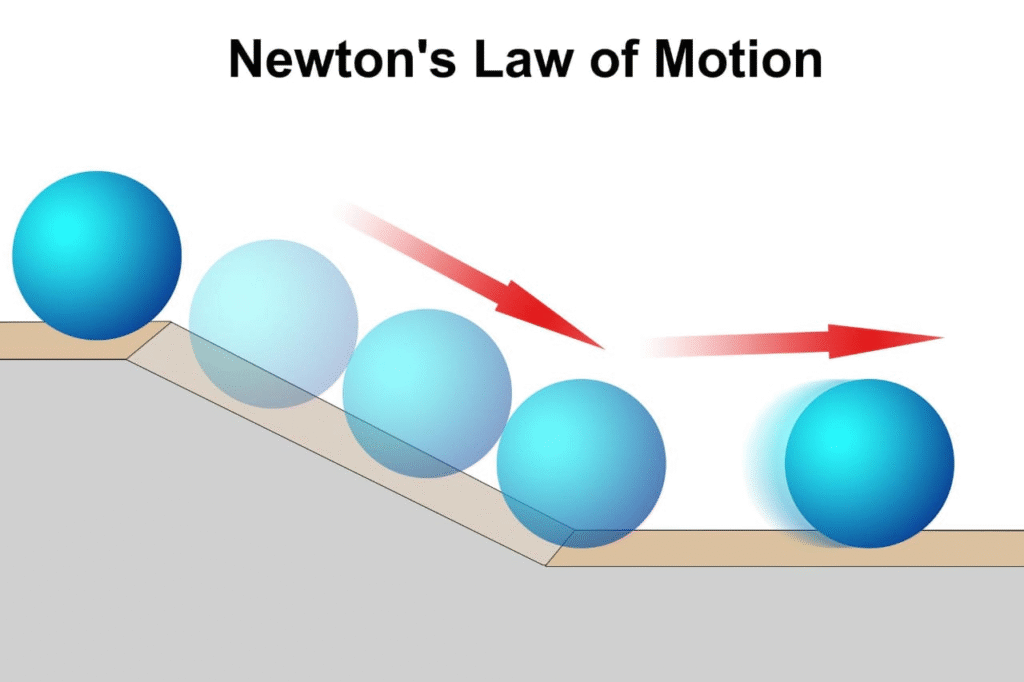
“An object continues to be in its state of rest or uniform motion in a straight line unless acted upon by an external unbalanced force.”
Inertia = tendency of a body to resist change in its state.

Types:
Inertia of rest (object at rest remains so).
Inertia of motion (moving object keeps moving).
Inertia of direction (object keeps same direction).
💡 Example: Passengers jerk forward when bus stops suddenly (inertia of motion).
✏️ Note: This law gives the concept of force — force is needed only to change motion, not to sustain it.

🔴 Momentum
Definition: Momentum = mass × velocity
Formula: p = m × v
Vector quantity, direction = direction of velocity.
Unit: kg m s⁻¹
💡 Example: A moving truck has more momentum than a car at same speed due to greater mass.

🟤 Newton’s Second Law of Motion
“The rate of change of momentum of a body is directly proportional to the applied force and takes place in the direction of force.”
Formula: F = m × a (when mass constant).
Explains how force is measured.

💡 Applications:
Catching a ball by moving hands backward → increases time, decreases force.
Seat belts in cars increase stopping time, reduce force on passengers.

🟠 Newton’s Third Law of Motion
“For every action, there is an equal and opposite reaction.”
Action and reaction act on different bodies, are equal in magnitude, opposite in direction.

💡 Examples:
A gun recoils backward when fired.
A swimmer pushes water backward, moves forward.
Rocket propulsion works on this principle.

🟣 Law of Conservation of Momentum
Total momentum of a system remains constant if no external force acts.
Proof (two bodies colliding):
Before collision: total momentum = m₁u₁ + m₂u₂
After collision: total momentum = m₁v₁ + m₂v₂
Hence: m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂
Momentum conserved in explosions, collisions, rocket launches.

🟢 Real-Life Applications
Sports: Moving bats backward while catching or hitting ball.
Transport: Seat belts, airbags (increase time of impact).
Space: Rocket motion → gases pushed backward, rocket moves forward.
Safety: Sand beds on highways stop vehicles by reducing acceleration.

🟡 Summary
Force: push/pull that changes motion.
Balanced forces → no motion change; Unbalanced forces → motion change.
Newton’s First Law → inertia, need of external force.
Newton’s Second Law → F = m a, defines force.
Newton’s Third Law → action–reaction pair.
Momentum conserved in all isolated systems.

📝 Quick Recap
🔵 Force = push/pull.
🟢 Inertia = resistance to change of state.
🟡 1st Law → rest/motion continues unless unbalanced force acts.
🔴 2nd Law → F = m a.
🟣 3rd Law → action = reaction.
🟠 Momentum conserved in collisions, explosions.

————————————————————————————————————————————————————————————————————————————

QUESTIONS FROM TEXTBOOK

Question 1
An object experiences a net zero external unbalanced force. Is it possible for the object to be travelling with a non-zero velocity? If yes, state the conditions that must be placed on the object.
Answer
🔵 Yes. If no unbalanced external force acts, an object can move with constant velocity in a straight line (Newton’s First Law).
🟢 Condition: velocity must remain constant in magnitude and direction (no acceleration); surfaces and forces must balance so that the net force = 0.

Question 2
When a carpet is beaten with a stick, dust comes out of it. Explain.
Answer
🟡 Due to inertia of rest: beating gives the carpet a sudden acceleration but dust particles tend to remain at rest and get left behind, so they separate and come out.

Question 3
Why is it advised to tie any luggage kept on the roof of a bus with a rope?
Answer
🔴 Because of inertia. During sudden starts, stops or turns, luggage tends to keep its state of motion; tying provides an external force to prevent sliding or toppling.

Question 4
A batsman hits a cricket ball which then rolls on a level ground. After covering a short distance, the ball comes to rest. The ball slows to a stop because
(a) the batsman did not hit the ball hard enough.
(b) velocity is proportional to the force exerted on the ball.
(c) there is a force on the ball opposing the motion.
(d) there is no unbalanced force on the ball, so the ball would want to come to rest.
Answer
✔️ (c) there is a force on the ball opposing the motion (mainly rolling friction and air resistance).

Question 5
A truck starts from rest and rolls down a hill with a constant acceleration. It travels a distance of 400 m in 20 s. Find its acceleration. Find the force acting on it if its mass is 7 tonnes (Hint: 1 tonne = 1000 kg.)
Answer
Given: u = 0 m s⁻¹, s = 400 m, t = 20 s, m = 7 tonnes = 7000 kg.
Step 1 (equation): s = ut + ½ a t²
Step 2 (substitute): 400 = 0 × 20 + ½ × a × (20)²
Step 3 (square time): 400 = ½ × a × 400
Step 4 (multiply): 400 = 200 a
Step 5 (solve a): a = 400 ÷ 200 = 2 m s⁻²
Step 6 (force): F = m a = 7000 × 2 = 14 000 N
Final: acceleration = 2 m s⁻²; force = 1.4 × 10⁴ N. 🟢

Question 6
A stone of 1 kg is thrown with a velocity of 20 m s⁻¹ across the frozen surface of a lake and comes to rest after travelling a distance of 50 m. What is the force of friction between the stone and the ice?
Answer
Given: m = 1 kg, u = 20 m s⁻¹, v = 0 m s⁻¹, s = 50 m.
Step 1 (equation): v² = u² + 2 a s
Step 2 (substitute): 0² = (20)² + 2 × a × 50
Step 3 (rearrange): 0 = 400 + 100 a
Step 4 (solve a): a = −400 ÷ 100 = −4 m s⁻²
Step 5 (force): F = m a = 1 × (−4) = −4 N
Final: friction force = 4 N opposite to motion. 🔵

Question 7
A 8000 kg engine pulls a train of 5 wagons, each of 2000 kg, along a horizontal track. If the engine exerts a force of 40 000 N and the track offers a friction force of 5000 N, then calculate:
(a) the net accelerating force and
(b) the acceleration of the train.
Answer
Given: mass of engine = 8000 kg; wagons = 5 × 2000 = 10 000 kg; total mass M = 18 000 kg.
Step 1 (net force): F_net = 40 000 − 5 000 = 35 000 N
Step 2 (acceleration): a = F_net ÷ M = 35 000 ÷ 18 000 m s⁻²
Step 3 (divide): a ≈ 1.9444 m s⁻²
Final: net accelerating force = 35 000 N; acceleration ≈ 1.94 m s⁻². 🟡

Question 8
An automobile vehicle has a mass of 1500 kg. What must be the force between the vehicle and road if the vehicle is to be stopped with a negative acceleration of 1.7 m s⁻²?
Answer
Given: m = 1500 kg, a = −1.7 m s⁻².
Step 1 (force): F = m a = 1500 × (−1.7) N
Step 2 (multiply): F = −2550 N
Final: required retarding force = 2550 N opposite to motion. 🔴

Question 9
What is the momentum of an object of mass m, moving with a velocity v?
(a) (mv)²
(b) m v²
(c) ½ m v²
(d) m v
Answer
✔️ (d) m v (definition of momentum p = m v). 🟣

Question 10
Using a horizontal force of 200 N, we intend to move a wooden cabinet across a floor at a constant velocity. What is the friction force that will be exerted on the cabinet?
Answer
🌿 For constant velocity, acceleration = 0, so net force = 0.
Therefore friction force = 200 N opposite to the applied force.

Question 11
According to the third law of motion when we push on an object, the object pushes back on us with an equal and opposite force. If the object is a massive truck parked along the roadside, it will probably not move. A student justifies this by answering that the two opposite and equal forces cancel each other. Comment on this logic and explain why the truck does not move.
Answer
🔵 Action–reaction forces act on different bodies (your hands and the truck), so they do not cancel for the same body.
🟢 The truck remains at rest because your applied force is not enough to overcome static friction and the truck’s inertia; the road–tyre static friction provides an opposing force up to a limit.
🟡 Resultant force on the truck is effectively zero (your push balanced by friction at the tyres), hence no acceleration, so it does not move.

Question 12
A hockey ball of mass 200 g travelling at 10 m s⁻¹ is struck by a hockey stick so as to return it along its original path with a velocity at 5 m s⁻¹. Calculate the magnitude of change of momentum occurred in the motion of the hockey ball by the force applied by the hockey stick.
Answer
Given: m = 200 g = 0.2 kg, u = +10 m s⁻¹ (toward the stick), v = −5 m s⁻¹ (returned along same line).
Step 1 (change in momentum): Δp = m (v − u)
Step 2 (substitute): Δp = 0.2 × (−5 − 10) kg m s⁻¹
Step 3 (simplify): Δp = 0.2 × (−15) = −3.0 kg m s⁻¹
Step 4 (magnitude): |Δp| = 3.0 kg m s⁻¹
Final: magnitude of change of momentum = 3.0 N s. 🟠

Question 13
A bullet of mass 10 g travelling horizontally with a velocity of 150 m s⁻¹ strikes a stationary wooden block and comes to rest in 0.03 s. Calculate the distance of penetration of the bullet into the block. Also calculate the magnitude of the force exerted by the wooden block on the bullet.
Answer
Given: m = 10 g = 0.01 kg, u = 150 m s⁻¹, v = 0 m s⁻¹, t = 0.03 s.
Step 1 (acceleration): a = (v − u) ÷ t = (0 − 150) ÷ 0.03 m s⁻²
Step 2 (divide): a = −150 ÷ 0.03 = −5000 m s⁻²
Step 3 (distance): s = u t + ½ a t² = 150 × 0.03 + ½ × (−5000) × (0.03)² m
Step 4 (compute ut): 150 × 0.03 = 4.5 m
Step 5 (compute t²): (0.03)² = 0.0009
Step 6 (triangle term): ½ × (−5000) × 0.0009 = −2.25 m
Step 7 (add): s = 4.5 + (−2.25) = 2.25 m
Step 8 (force magnitude): F = m |a| = 0.01 × 5000 = 50 N
Final: penetration distance = 2.25 m; force magnitude on bullet = 50 N (opposite to motion). 🔵

Question 14
An object of mass 1 kg travelling in a straight line with a velocity of 10 m s⁻¹ collides with, and sticks to, a stationary wooden block of mass 5 kg. Then they both move off together in the same straight line. Calculate the total momentum just before the impact and just after the impact. Also, calculate the velocity of the combined object.
Answer
Given: m₁ = 1 kg, u₁ = 10 m s⁻¹; m₂ = 5 kg, u₂ = 0 m s⁻¹.
Step 1 (momentum before): p_before = m₁u₁ + m₂u₂ = 1×10 + 5×0 = 10 kg m s⁻¹
Step 2 (combined mass): M = m₁ + m₂ = 1 + 5 = 6 kg
Step 3 (momentum conservation): p_after = p_before = 10 kg m s⁻¹
Step 4 (velocity after): v = p_after ÷ M = 10 ÷ 6 = 1.6667 m s⁻¹
Final: momentum before = 10 kg m s⁻¹; momentum after = 10 kg m s⁻¹; combined velocity ≈ 1.67 m s⁻¹. 🟢

Question 15
An object of mass 100 kg is accelerated uniformly from a velocity of 5 m s⁻¹ to 8 m s⁻¹ in 6 s. Calculate the initial and final momentum of the object. Also, find the magnitude of the force exerted on the object.
Answer
Given: m = 100 kg, u = 5 m s⁻¹, v = 8 m s⁻¹, t = 6 s.
Step 1 (initial momentum): p_i = m u = 100 × 5 = 500 kg m s⁻¹
Step 2 (final momentum): p_f = m v = 100 × 8 = 800 kg m s⁻¹
Step 3 (acceleration): a = (v − u) ÷ t = (8 − 5) ÷ 6 = 3 ÷ 6 = 0.5 m s⁻²
Step 4 (force): F = m a = 100 × 0.5 = 50 N
Final: p_i = 500 kg m s⁻¹; p_f = 800 kg m s⁻¹; force magnitude = 50 N. 🟣

Question 16
Akhtar, Kiran and Rahul were riding in a motorcar at high velocity on an expressway when an insect hit the windshield and got stuck on the windscreen. Kiran suggested that the insect suffered a greater change in momentum as compared to the change in momentum of the motorcar (because the change in the velocity of the insect was much more than that of the motorcar). Akhtar said that since the motorcar was moving with a larger velocity, it exerted a larger force on the insect. And as a result the insect died. Rahul, while putting an entirely new explanation, said that both the motorcar and the insect experienced the same force and a change in their momentum. Comment on these suggestions.
Answer
🔵 Rahul is correct. During the very short collision time, the interaction forces on insect and car are equal in magnitude and opposite in direction (Newton’s Third Law).
🟢 Therefore the impulse (change in momentum) of both is equal in magnitude and opposite in sign.
🟡 However, because the insect’s mass is tiny, the same impulse produces a huge acceleration and large fractional change in velocity for the insect, which causes its death; the car’s velocity changes negligibly.

Question 17
How much momentum will a dumb-bell of mass 10 kg transfer to the floor if it falls from a height of 80 cm? Take its downward acceleration to be 10 m s⁻².
Answer
Given: m = 10 kg, h = 80 cm = 0.80 m, g = 10 m s⁻².
Step 1 (final speed before impact): v² = u² + 2 g h
Step 2 (substitute): v² = 0² + 2 × 10 × 0.80 = 16
Step 3 (root): v = √16 = 4 m s⁻¹ (downward)
Step 4 (momentum just before impact): p = m v = 10 × 4 = 40 kg m s⁻¹
Step 5 (momentum transferred if it comes to rest): Δp = 40 kg m s⁻¹
Final: momentum transferred to the floor = 40 N s. 🔴

————————————————————————————————————————————————————————————————————————————

OTHER IMPORTANT QUESTIONS FOR EXAMS

🔵 Section A – MCQs (Q1–Q10, 1 mark each)
Question 1
Force is required to
keep a body moving with uniform velocity
stop a moving body
change the direction of motion
both 2 and 3
Answer: 4

Question 2
Momentum of an object depends on
only mass
only velocity
both mass and velocity
neither mass nor velocity
Answer: 3

Question 3
Which of the following is correct for balanced forces?
They change the state of motion
They cannot bring acceleration
They always act on different bodies
They always produce rotation
Answer: 2

Question 4
The SI unit of momentum is
kg m s⁻²
kg m s⁻¹
N m
J
Answer: 2

Question 5
If force is doubled on a body of constant mass, acceleration becomes
halved
doubled
unchanged
four times
Answer: 2

Question 6
A man of mass 60 kg runs with velocity 5 m s⁻¹. His momentum is
300 N
300 kg m s⁻¹
12 N s
65 kg m s⁻¹
Answer: 2

Question 7
Newton’s third law of motion explains
walking
recoil of a gun
swimming
all of the above
Answer: 4

Question 8
When no external force acts on a system, total momentum remains constant. This is
conservation of energy
conservation of momentum
inertia
work–energy theorem
Answer: 2

Question 9
Rate of change of momentum gives
velocity
force
acceleration
energy
Answer: 2

Question 10
A car of mass 1000 kg moving at 20 m s⁻¹ has momentum
20 000 kg m s⁻¹
200 kg m s⁻¹
2 × 10⁴ N
5 × 10³ kg m s⁻¹
Answer: 1

🟢 Section A – Assertion–Reason (Q11–Q20, 1 mark each)
Question 11
A: Inertia of motion means resistance to change of uniform motion.
R: A moving ball continues to move until stopped by friction.
Answer: 1

Question 12
A: A person jumps from a boat to shore, the boat moves backward.
R: For every action there is equal and opposite reaction.
Answer: 1

Question 13
A: Balanced forces can change the shape of a body.
R: Stretching of rubber band is an example.
Answer: 1

Question 14
A: Momentum has direction same as force.
R: Momentum is product of mass and velocity.
Answer: 3

Question 15
A: A heavy truck and a small car with same momentum have same kinetic energy.
R: Momentum and kinetic energy are proportional.
Answer: 3

Question 16
A: Rocket propulsion works on Newton’s third law.
R: Gases pushed backward exert equal opposite force on rocket.
Answer: 1

Question 17
A: Action and reaction cancel each other.
R: They act on different bodies.
Answer: 4

Question 18
A: A cricketer lowers hands while catching ball.
R: It increases time of impact, reduces force.
Answer: 1

Question 19
A: Momentum conserved if no external force acts.
R: Total kinetic energy always conserved.
Answer: 3

Question 20
A: Friction opposes relative motion.
R: Friction is self-adjusting.
Answer: 1

🟡 Section B – Very Short Answer (Q21–Q26, 2 marks)
Question 21
Define momentum.
Answer
🔵 Momentum = mass × velocity
🟢 Formula: p = m v
🔴 SI unit = kg m s⁻¹

Question 22
State Newton’s first law with example.
Answer
Body remains at rest/uniform motion until unbalanced force acts.
💡 Example: Passenger jerk forward when bus stops suddenly.

Question 23
Give 2 differences between balanced & unbalanced forces.
Answer
🟠 Balanced: Net force = 0 → no acceleration.
🟣 Unbalanced: Net force ≠ 0 → causes acceleration.

Question 24
Why are seat belts provided?
Answer
🌿 They increase stopping time.
⚡ This reduces force on passenger → prevents injury.

Question 25
What is inertia? Types?
Answer
🔵 Inertia = resistance to change of state.
Types: Rest, Motion, Direction.

Question 26
Give 2 examples of Newton’s 3rd law.
Answer
🚀 Rocket propulsion.
🔫 Recoil of gun.

🔴 Section C – Short Answer (Q27–Q33, 3 marks)
Question 27
State Newton’s 2nd law and derive F = ma.
Answer
🟢 Law: Force ∝ rate of change of momentum.
Δp = m (v − u)
F = Δp / t = m a
✔️ Hence F = m a

Question 28
Force 200 N acts on mass 50 kg. Find acceleration.
Answer
Formula: F = m a
a = F ÷ m
a = 200 ÷ 50 = 4 m s⁻²

Question 29
Explain conservation of momentum.
Answer
Total momentum before = total momentum after, if no external force.
💡 Example: Two colliding carts conserve momentum.

Question 30
Bullet 20 g at 300 m/s hits 2 kg block and stays inside. Find velocity.
Answer
m₁ = 0.02, u₁ = 300, m₂ = 2, u₂ = 0
Initial momentum = 0.02 × 300 = 6
Final mass = 2.02
v = 6 ÷ 2.02 ≈ 2.97 m/s

Question 31
Boy 40 kg runs at 2 m/s, jumps on 60 kg cart at 1 m/s. Find final velocity.
Answer
Momentum before = (40×2) + (60×1) = 140
Total mass = 100
v = 140 ÷ 100 = 1.4 m/s

Question 32
Why does a gun recoil?
Answer
🔫 Bullet forward momentum = gun backward momentum.
v_gun = − (m_bullet v_bullet / m_gun).

Question 33
Stone 1 kg dropped from 20 m. Find momentum before hitting ground. g = 10.
Answer
v² = u² + 2 g h = 0 + 2 × 10 × 20 = 400
v = √400 = 20 m/s
p = m v = 1 × 20 = 20 kg m/s

🟠 Section D – Long Answer (Q34–Q36, 5 marks)
Question 34
State Newton’s 3 laws with examples.
Answer
🟢 First: Inertia – bus jerk.
🔴 Second: F = ma – harder kick accelerates more.
🟣 Third: Action–reaction – rocket, swimming.

Question 35
Derive law of conservation of momentum.
Answer
Two bodies A & B collide.
Force on A = − Force on B.
Change momentum A = − Change momentum B.
Net change = 0.
🌍 Hence total momentum conserved.

Question 36
Car 1200 kg, u = 20 m/s, v = 0 in 5s. Find force, distance.
Answer
a = (v − u)/t = (0 − 20)/5 = −4 m/s²
F = m a = 1200 × (−4) = −4800 N
s = u t + ½ a t² = 20×5 + ½×(−4)×25 = 100 − 50 = 50 m
✔️ Force = 4800 N; Distance = 50 m

🟣 Section E – Case-Based (Q37–Q39, 4 marks)
Question 37
Case: Ball 0.15 kg, u = 20 m/s stopped in 0.05s. Find force.
Answer
p_i = 0.15×20 = 3
p_f = 0
Δp = −3
F = Δp ÷ Δt = −3 ÷ 0.05 = −60 N

Question 38
Case: Two bodies collide and stick. Explain principle.
Answer
🔵 Principle: Conservation of momentum.
v = (m₁u₁ + m₂u₂) ÷ (m₁+m₂).

Question 39
Case: Person throws stone backward from boat, boat moves forward.
Answer
🌍 Law: Newton’s 3rd law.
Action: Person pushes stone backward.
Reaction: Stone pushes boat forward.
🚀 Used in rockets.

————————————————————————————————————————————————————————————————————————————

MIND MAPS

————————————————————————————————————————————————————————————————————————————