Class : 9 – Math (Hindi) : Lesson 9. वृत्त

पाठ का विश्लेषण  एवं  विवेचन

✨ विस्तृत व्याख्या
🔵 भूमिका
वृत्त (Circle) एक ऐसी आकृति है जिसे हम प्रकृति और दैनिक जीवन में बहुत बार देखते हैं। सूर्य, चंद्रमा, पहिया, घड़ी का डायल, सिक्के, प्लेटें, पहियों की घुमावदार सतह—वृत्त के उत्कृष्ट उदाहरण हैं। यह अध्याय विद्यार्थियों को वृत्त की परिभाषा, इसके मुख्य अंग, गुणधर्म और प्रमेयों से परिचित कराता है।

🟢 परिभाषा
वृत्त: किसी समतल पर स्थित उन सभी बिंदुओं का समुच्चय जो एक नियत बिंदु से समान दूरी पर हों, उन्हें मिलाकर बनी बंद आकृति वृत्त कहलाती है।
नियत बिंदु = केंद्र (Centre)
समान दूरी = त्रिज्या (Radius)
✏️ Note: केंद्र को सामान्यतः O और त्रिज्या को r से दर्शाया जाता है।

🔴 वृत्त के प्रमुख अंग
त्रिज्या (Radius, r): केंद्र से वृत्त की परिधि तक की दूरी।
व्यास (Diameter, d): केंद्र से होकर जाने वाली जीवा; d = 2r।
जीवा (Chord): वृत्त की परिधि के दो बिंदुओं को मिलाने वाला रेखाखंड।
विकर्ण (Arc): वृत्त की परिधि का कोई भी भाग।
स्पर्शरेखा (Tangent): वृत्त को केवल एक बिंदु पर छूने वाली रेखा।
लंब (Normal): केंद्र से स्पर्शबिंदु तक की रेखा, जो स्पर्शरेखा पर लंब होती है।
परिधि (Circumference): वृत्त की बाहरी सीमा; C = 2πr।
क्षेत्रफल (Area): वृत्त के भीतर का भाग; A = πr²।
💡 Concept: व्यास हमेशा सबसे बड़ी जीवा होता है।

🟡 वृत्त के गुणधर्म
सभी त्रिज्या बराबर होती हैं।
व्यास वृत्त की सबसे बड़ी जीवा है।
केंद्र से जीवा पर खींचा गया लंब जीवा को समद्विभाजित करता है।
वृत्त के व्यास पर स्थित कोण हमेशा समकोण (90°) होता है।
स्पर्शरेखा और त्रिज्या परस्पर लंब होती हैं।

🔵 मुख्य प्रमेय (Theorems)
प्रमेय 1:
किसी वृत्त के केंद्र से किसी जीवा पर खींचा गया लंब उस जीवा को समद्विभाजित करता है।
✔️ प्रमाण:
वृत्त का केंद्र O, जीवा AB।
OP ⟂ AB (जहाँ P जीवा का मध्यबिंदु)।
त्रिभुज OAP और OBP सर्वांगसम सिद्ध होते हैं।
अतः AP = PB।

प्रमेय 2:
किसी वृत्त में व्यास पर स्थित कोण समकोण होता है।
✔️ प्रमाण:
वृत्त का व्यास AB, केंद्र O, और परिधि पर C।
∆ACB में ∠ACB = 90°।

प्रमेय 3:
वृत्त की स्पर्शरेखा और त्रिज्या परस्पर लंब होती हैं।
प्रमेय 4:
वृत्त के बाहर से खींची गई दो स्पर्शरेखाओं की लंबाई बराबर होती है।

🟢 वृत्त और त्रिभुज
जब किसी त्रिभुज का एक कोण समकोण होता है तो उसकी कर्ण पर बने वृत्त में वह त्रिभुज अंकित किया जा सकता है।
त्रिभुज और वृत्त के बीच यह संबंध आगे त्रिकोणमिति और निर्देशांक ज्यामिति में महत्त्वपूर्ण है।

🔴 वास्तविक जीवन के अनुप्रयोग
पहिये और टायर का निर्माण।
घड़ी की सुइयाँ वृत्त पर घूमती हैं।
कम्पास और प्रोट्रैक्टर जैसे उपकरण वृत्त के आधार पर बने हैं।
पुलों और मेहराबों का निर्माण।
सिक्कों और प्लेटों की आकृति।

🟡 सूत्र
परिधि: C = 2πr
क्षेत्रफल: A = πr²
चाप की लंबाई: L = (θ/360°) × 2πr
खंड का क्षेत्रफल: A = (θ/360°) × πr²
✏️ Note: यहाँ θ केंद्रीय कोण है।

🌿 अध्याय का महत्व
यह अध्याय ज्यामिति की नींव को मजबूत करता है।
आगे त्रिकोणमिति, निर्देशांक ज्यामिति, और क्षेत्रफल के अध्यायों में वृत्त के प्रमेयों और सूत्रों का व्यापक प्रयोग होता है।
वास्तविक जीवन में वृत्त का प्रयोग निर्माण, डिज़ाइन, विज्ञान और प्रौद्योगिकी में हर जगह है।

📌 Summary (~300 शब्द)
वृत्त: केंद्र से समान दूरी पर स्थित बिंदुओं का समुच्चय।
मुख्य अंग: त्रिज्या, व्यास, जीवा, स्पर्शरेखा, परिधि, क्षेत्रफल।
गुणधर्म: सभी त्रिज्या बराबर, व्यास सबसे बड़ी जीवा, त्रिज्या ⟂ स्पर्शरेखा।
प्रमेय:
केंद्र से जीवा पर खींचा गया लंब जीवा को समद्विभाजित करता है।
व्यास पर स्थित कोण समकोण होता है।
स्पर्शरेखा और त्रिज्या परस्पर लंब।
बाहरी बिंदु से खींची गई स्पर्शरेखाएँ बराबर लंबाई की होती हैं।
सूत्र:
परिधि = 2πr
क्षेत्रफल = πr²
चाप की लंबाई = (θ/360°) × 2πr
खंड का क्षेत्रफल = (θ/360°) × πr²
अनुप्रयोग: पहिये, घड़ी, कम्पास, पुल, सिक्के।
✔️ यह अध्याय गणितीय रूप से भी और व्यावहारिक जीवन में भी अत्यंत महत्वपूर्ण है।

📝 Quick Recap
🔵 वृत्त = केंद्र से समान दूरी पर स्थित बिंदुओं का समूह।
🟢 त्रिज्या = r, व्यास = 2r।
🟡 परिधि = 2πr, क्षेत्रफल = πr²।
🔴 व्यास पर स्थित कोण = 90°।
🌿 स्पर्शरेखा हमेशा त्रिज्या पर लंब।

————————————————————————————————————————————————————————————————————————————

पाठ्यपुस्तक के प्रश्न

प्रश्नावली 9.1

🔵 Question
Q 1. याद कीजिए कि दो वृत्त सर्वांगसम होते हैं, यदि उनकी त्रिज्याएँ बराबर हों। सिद्ध कीजिए कि सर्वांगसम वृत्तों की बराबर जीवाएँ उनके केन्द्रों पर बराबर कोण अंतरित करती हैं।
🟢 Answer
💡 अवधारणा: बराबर जीवाएँ बराबर चापों पर स्थित होती हैं और चाप केन्द्र पर बराबर कोण अंतरित करते हैं।
🔵 Step 1: मान लीजिए दो सर्वांगसम वृत्त O और O′ हैं, जिनकी त्रिज्या r है।
🔵 Step 2: इन दोनों वृत्तों में AB और A′B′ जीवाएँ ऐसी खींचें कि AB = A′B′.
🔵 Step 3: सर्वांगसम वृत्तों में बराबर जीवाएँ बराबर चापों पर स्थित होती हैं।
🔵 Step 4: अतः चाप AB = चाप A′B′.
🔵 Step 5: किसी वृत्त में बराबर चाप बराबर केन्द्र कोण अंतरित करते हैं।
✔️ Final: ∠AOB = ∠A′O′B′.

🔵 Question
Q 2. सिद्ध कीजिए कि यदि सर्वांगसम वृत्तों की जीवाएँ उनके केन्द्रों पर बराबर कोण अंतरित करें, तो जीवाएँ बराबर होती हैं।
🟢 Answer
💡 अवधारणा: केन्द्र पर बराबर कोणों द्वारा अंतरित चाप बराबर होते हैं और बराबर चापों की जीवाएँ बराबर होती हैं।
🔵 Step 1: मान लीजिए दो सर्वांगसम वृत्त O और O′ हैं, जिनकी त्रिज्या r है।
🔵 Step 2: इनमें AB और A′B′ जीवाएँ ऐसी हैं कि ∠AOB = ∠A′O′B′.
🔵 Step 3: बराबर केन्द्र कोण ⇒ बराबर चाप ⇒ चाप AB = चाप A′B′.
🔵 Step 4: किसी वृत्त में बराबर चापों की जीवाएँ बराबर होती हैं।
✔️ Final: AB = A′B′.

प्रश्नावली 9.2

🔵 Question
Q 1. 5 cm तथा 3 cm त्रिज्या वाले दो वृत्त दो बिन्दुओं पर प्रतिच्छेद करते हैं तथा उनके केन्द्रों के बीच की दूरी 4 cm है। उनभ्यन्तर जीवा की लम्बाई ज्ञात कीजिए।
🟢 Answer
💡 अवधारणा: प्रतिच्छेद करते हुए दो वृत्तों के केन्द्रों की दूरी d, त्रिज्याएँ r₁ और r₂ होने पर साझा जीवा की आधी लम्बाई = sqrt(r₁² − x²), जहाँ x केन्द्र से साझा जीवा की दूरी है।
🔵 Step 1: r₁ = 5 cm, r₂ = 3 cm, d = 4 cm.
🔵 Step 2: साझा जीवा केन्द्रों को जोड़ने वाली रेखा पर लम्ब होती है।
🔵 Step 3: x = (r₁² − r₂² + d²) / (2d).
➡️ x = (25 − 9 + 16) / (2×4) = 32 / 8 = 4.
🔵 Step 4: आधी लम्बाई = sqrt(r₁² − x²) = sqrt(25 − 16) = sqrt(9) = 3.
🔵 Step 5: पूरी लम्बाई = 2 × 3 = 6 cm.
✔️ Final: जीवा की लम्बाई 6 cm है।

🔵 Question
Q 2. यदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर प्रतिच्छेद करें, तो सिद्ध कीजिए कि एक जीवा के खण्ड दूसरी जीवा के संगत खण्डों के बराबर हैं।
🟢 Answer
💡 अवधारणा: यदि दो जीवाएँ AB और CD वृत्त के भीतर बिन्दु E पर प्रतिच्छेद करती हैं, तो AE × EB = CE × ED.
🔵 Step 1: जीवाएँ AB और CD बिन्दु E पर प्रतिच्छेद करती हैं।
🔵 Step 2: चाप AD और CB द्वारा केन्द्र पर बने कोण बराबर होते हैं।
🔵 Step 3: समान त्रिभुजों के कारण AE × EB = CE × ED.
✔️ Final: एक जीवा के खण्ड दूसरी जीवा के संगत खण्डों के बराबर हैं।

🔵 Question
Q 3. यदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर प्रतिच्छेद करें, तो सिद्ध कीजिए कि प्रतिच्छेद बिन्दु को केन्द्र से मिलाने वाली रेखा जीवाओं से बराबर कोण बनाती है।
🟢 Answer
💡 अवधारणा: समान जीवाएँ केन्द्र से समान दूरी पर होती हैं।
🔵 Step 1: जीवाएँ AB और CD वृत्त के भीतर E पर प्रतिच्छेद करती हैं।
🔵 Step 2: मान लें O वृत्त का केन्द्र है।
🔵 Step 3: AO = BO = CO = DO.
🔵 Step 4: यदि AB = CD हो, तो OE ⟂ AB और OE ⟂ CD.
🔵 Step 5: अतः OE, AB और CD पर बराबर कोण बनाती है।
✔️ Final: OE जीवाओं से बराबर कोण बनाती है।

🔵 Question
Q 4. यदि एक रेखा दो संकेन्द्र वृत्तों (एक ही केन्द्र वाले वृत्त) को, जिनका केन्द्र O है, A, B, C और D पर प्रतिच्छेद करे, तो सिद्ध कीजिए AB = CD है (आकृति 9.12)।
🟢 Answer
💡 अवधारणा: संकेन्द्र वृत्तों में समान जीवा के खण्ड बराबर होते हैं।
🔵 Step 1: रेखा, आन्तरिक वृत्त को A और B पर तथा बाह्य वृत्त को C और D पर प्रतिच्छेद करती है।
🔵 Step 2: A और B, O से समान दूरी पर हैं; C और D भी O से समान दूरी पर हैं।
🔵 Step 3: इसलिए AO = BO, CO = DO.
🔵 Step 4: अतः AB = CD.
✔️ Final: AB = CD.

🔵 Question
Q 5. एक पार्क में बने 5 m त्रिज्या वाले वृत्त पर खड़ी तीन लड़कियाँ रेशमा, सलमा एवं मनदीप खेल रही हैं। रेशमा एक गेंद को सलमा के पास, सलमा मनदीप के पास तथा मनदीप रेशमा के पास फेंकती हैं। यदि रेशमा तथा सलमा के बीच की दूरी और सलमा तथा मनदीप के बीच की प्रत्येक दूरी 6 m हो, तो रेशमा और मनदीप के बीच की दूरी क्या है?

🟢 Answer

💡 अवधारणा: जीवा L और केन्द्र कोण θ का सम्बन्ध — L = 2r·sin(θ/2). बराबर जीवाएँ ⇒ बराबर केन्द्र कोण।

🔵 Step 1: r = 5 m, RS = SM = 6 m (दोनों बराबर जीवाएँ) मानें.

🔵 Step 2: 6 = 2r·sin(θ/2) ⇒ 6 = 10·sin(θ/2) ⇒ sin(θ/2) = 3/5.

🔵 Step 3: cos(θ/2) = √(1 − (3/5)²) = √(16/25) = 4/5.

🔵 Step 4: अब RM वह जीवा है जो इन बराबर जीवाओं के अगल-बगल सिरों को जोड़ती है; इसका केन्द्र कोण = 2θ.

🔵 Step 5: RM = 2r·sin(2θ/2) = 2r·sinθ = 2r·(2·sin(θ/2)·cos(θ/2)).

🔵 Step 6: RM = 10·(2·3/5·4/5) = 10·(24/25) = 240/25.

🟡 Check: cosθ = 2cos²(θ/2) − 1 = 2·(4/5)² − 1 = 7/25; ∠RSM = 180° − θ ⇒ cos(∠RSM) = −7/25.
RM² = 6² + 6² − 2·6·6·cos(∠RSM) = 72 + 72·(7/25) = 2304/25 ⇒ RM = √(2304/25) = 48/5 ✅

✔️ निष्कर्ष: रेशमा और मनदीप के बीच दूरी RM = 48/5 m = 9.6 m.
🔵 Question
Q 6. 20 m त्रिज्या का एक गोल पार्क (वृत्ताकार) एक कालोनी में स्थित है। तीन लड़के अंकुर, सैय्यद तथा डेविड इसकी परिधि पर बराबर दूरी पर बैठे हैं और प्रत्येक के हाथ में एक खिलौना टेलीफोन आपस में बात करने के लिए है। प्रत्येक फोन की डोरी की लम्बाई ज्ञात कीजिए।
🟢 Answer
💡 अवधारणा: वृत्त पर तीन बराबर दूरी वाले बिन्दु समबाहु त्रिभुज बनाते हैं।
🔵 Step 1: वृत्त की त्रिज्या r = 20 m.
🔵 Step 2: परिधि पर तीन बराबर दूरी वाले बिन्दु मिलकर समबाहु त्रिभुज बनाते हैं।
🔵 Step 3: समबाहु त्रिभुज की प्रत्येक भुजा = √3 × r.
🔵 Step 4: = √3 × 20 = 20√3 m.
✔️ Final: प्रत्येक फोन की डोरी की लम्बाई 20√3 m है।

प्रश्नावली 9.3

🔵 Question
Q 1. आकृति 9.23 में, केन्द्र O वाले एक वृत्त पर तीन बिन्दु A, B और C इस प्रकार हैं कि ∠BOC = 30° तथा ∠AOB = 60° है। यदि चाप ABC के अन्तर्गत वृत्त पर D एक बिन्दु है, तो ∠ADC ज्ञात कीजिए।

🟢 Answer
💡 अवधारणा: किसी चाप का केन्द्र कोण = 2 × उसी चाप का अन्तःस्थित कोण।
🔵 Step 1: ∠AOC = ∠AOB + ∠BOC = 60° + 30° = 90°.
🔵 Step 2: ∠ADC = 1/2 × ∠AOC = 1/2 × 90° = 45°.
✔️ Final: ∠ADC = 45°.

🔵 Question
Q 2. किसी वृत्त की एक जीवा वृत्त की त्रिज्या के बराबर है। जीवा द्वारा लघु चाप के किसी बिन्दु पर अन्तःस्थित कोण ज्ञात कीजिए तथा दीर्घ चाप के किसी बिन्दु पर भी अन्तःस्थित कोण ज्ञात कीजिए।

🟢 Answer
💡 अवधारणा: यदि AB = r और OA = OB = r, तो ΔAOB समबाहु ⇒ ∠AOB = 60°.
🔵 Step 1: लघु चाप AB पर बिन्दु P लेने पर ∠APB = 1/2 × (360° − ∠AOB) = 1/2 × (360° − 60°) = 150°.
🔵 Step 2: दीर्घ चाप AB पर बिन्दु Q लेने पर ∠AQB = 1/2 × ∠AOB = 1/2 × 60° = 30°.
✔️ Final: लघु चाप पर अन्तःस्थित कोण 150°, दीर्घ चाप पर 30°.

🔵 Question
Q 3. आकृति 9.24 में, ∠PQR = 100° है, जहाँ P, Q तथा R, केन्द्र O वाले एक वृत्त पर स्थित बिन्दु हैं। ∠OPR ज्ञात कीजिए।

🟢 Answer
💡 अवधारणा: किसी जीवा PR द्वारा केन्द्र पर कोण ∠POR = 2 × ∠PQR, तथा ΔOPR में OP = OR (त्रिज्याएँ) ⇒ आधार कोण बराबर।
🔵 Step 1: ∠POR = 2 × ∠PQR = 2 × 100° = 200°.
🔵 Step 2: त्रिभुज के भीतर लिया जाने वाला कोण O पर = 360° − 200° = 160°.
🔵 Step 3: ∠OPR = ∠ORP मानें; तब 2∠OPR + 160° = 180°.
🔵 Step 4: ∠OPR = (180° − 160°)/2 = 20°/2 = 10°.
✔️ Final: ∠OPR = 10°.

🔵 Question
Q 4. आकृति 9.25 में, ∠ABC = 69° और ∠ACB = 31° हो, तो ∠BDC ज्ञात कीजिए।
🟢 Answer
🔵 Step 1: ∠BAC = 180° − 69° − 31° = 80°.
🔵 Step 2: समान चाप BC पर स्थित अन्तःस्थित कोण समान ⇒ ∠BDC = ∠BAC.
✔️ निष्कर्ष: ∠BDC = 80°.

🔵 Question
Q 5. आकृति 9.26 में, एक वृत्त पर A, B, C और D चार बिन्दु हैं। AC और BD एक बिन्दु E पर इस प्रकार प्रतिछेद करते हैं कि ∠BEC = 130° तथा ∠ECD = 20° है। ∠BAC ज्ञात कीजिए।
🟢 Answer
💡 अवधारणा:
(क) वृत्त के भीतर प्रतिछेदित दो जीवाओं द्वारा बना कोण = 1/2 (उनके सम्मुख चापों के मापों का योग)।
(ख) किसी चाप का केन्द्र कोण = 2 × उसी चाप का अन्तःस्थित कोण।
🔵 Step 1: E, AC पर स्थित है ⇒ ∠ECD = ∠ACD = 20°.
🔵 Step 2: अतः चाप AD = 2 × 20° = 40°.
🔵 Step 3: ∠BEC = 130° ⇒ (चाप BC + चाप AD) = 2 × 130° = 260°.
🔵 Step 4: चाप BC = 260° − 40° = 220°.
🔵 Step 5: ∠BAC = 1/2 × (A को नहीं समेटने वाले चाप BC का माप) = 1/2 × (360° − 220°) = 140°/2 = 70°.
✔️ निष्कर्ष: ∠BAC = 70°.

🔵 Question
Q 6. ABCD एक चापीय चतुर्भुज है जिसके विकर्ण एक बिन्दु E पर प्रतिछेद करते हैं। यदि ∠DBC = 70° और ∠BAC = 30° हो, तो ∠BCD ज्ञात कीजिए। पुनः, यदि AB = BC हो, तो ∠ECD ज्ञात कीजिए।
🟢 Answer
(क) ∠BCD
🔵 Step 1: समान चाप BC पर अन्तःस्थित कोण समान ⇒ ∠BDC = ∠BAC = 30°.
🔵 Step 2: ΔBDC में, ∠BCD = 180° − ∠DBC − ∠BDC = 180° − 70° − 30° = 80°.
✔️ निष्कर्ष: ∠BCD = 80°.
(ख) ∠ECD (शर्त: AB = BC)
🔵 Step 1: AB = BC ⇒ ΔABC समद्विबाहु ⇒ ∠ACB = ∠BAC = 30°.
🔵 Step 2: C पर, ∠ACD = ∠BCD − ∠BCA = 80° − 30° = 50°.
🔵 Step 3: E, AC पर है ⇒ ∠ECD = ∠ACD.
✔️ निष्कर्ष: ∠ECD = 50°.

🔵 Question
Q 7. यदि एक चक्रीय चतुर्भुज के विकर्ण उसके शिखरों से जाने वाले वृत्त के व्यास हों, तो सिद्ध कीजिए कि वह एक आयत है।

🟢 Answer
💡 अवधारणा: व्यास पर बना कोई भी अन्तःस्थित कोण 90° होता है।
🔵 चरण 1: मानें AC और BD उसी वृत्त के व्यास हैं।
🔵 चरण 2: व्यास AC पर ⇒ ∠ABC = 90° तथा ∠ADC = 90°.
🔵 चरण 3: व्यास BD पर ⇒ ∠BAD = 90° तथा ∠BCD = 90°.
🔵 चरण 4: चतुर्भुज के चारों कोण 90° होने से सन्निकट भुजाएँ परस्पर लंब तथा विपरीत भुजाएँ समांतर होती हैं।
✔️ निष्कर्ष: यह चतुर्भुज आयत है।

🔵 Question
Q 8. यदि एक समलम्ब की असमान्तर भुजाएँ बराबर हों, तो सिद्ध कीजिए कि वह चक्रीय है।

🟢 Answer
💡 अवधारणा: समद्विबाहु समलम्ब में आधार कोण युग्म बराबर होते हैं; किसी चतुर्भुज के एक युग्म के विपरीत कोणों का योग 180° हो तो वह चक्रीय होता है।
🔵 चरण 1: समलम्ब ABCD में AB ∥ CD तथा AD = BC (असमान्तर भुजाएँ बराबर) दिए हैं।
🔵 चरण 2: CD पर A से AM ⟂ CD तथा B से BN ⟂ CD खींचें (M, N बिन्दु CD पर)।
🔵 चरण 3: समांतर रेखाओं के बीच दूरी समान ⇒ AM = BN.
🔵 चरण 4: समकोण त्रिभुज ADM और CBN में AD = BC (दिया), AM = BN (चरण 3), ∠ADM = ∠CBN = 90°.
🔵 चरण 5: अतः ΔADM ≅ ΔCBN (समकोण–कर्ण–एक-भुजा सर्वांगसमता नियम)।
🔵 चरण 6: सर्वांगसम त्रिभुजों के अनुरूप अंग बराबर ⇒ ∠A = ∠B तथा ∠C = ∠D.
🔵 चरण 7: AB ∥ CD ⇒ ∠B + ∠C = 180°.
🔵 चरण 8: चरण 6 से ∠A = ∠B ⇒ ∠A + ∠C = 180°.
✔️ निष्कर्ष: एक युग्म के विपरीत कोणों का योग 180° ⇒ ABCD चक्रीय है।

🔵 Question
Q 9. दो वृत्त दो बिन्दुओं B और C पर प्रतिच्छेद करते हैं। B से जाने वाले रेखाखण्ड ABD और PBQ क्रमशः दोनों वृत्तों को A, D तथा P, Q पर प्रतिच्छेद करते हैं (आकृति 9.27)। सिद्ध कीजिए कि ∠ACP = ∠QCD.

🟢 Answer
💡 मुख्य विचार: B पर बनी शीर्षाभिमुख कोण-समता से दोनों वृत्तों में कुछ चाप बराबर सिद्ध होंगे; उन्हीं चापों के आधे के रूप में C पर बने अन्तःस्थित कोणों का योग बराबर निकलेगा।
🔵 चरण 1: रेखाएँ ABD और PBQ, B पर प्रतिच्छेद करती हैं और AB ∥ BD (एक ही रेखा), PB ∥ BQ (एक ही रेखा) ⇒ शीर्षाभिमुख कोण: ∠ABD = ∠PBQ.
🔵 चरण 2: ∠ABD, बाएँ वृत्त में चाप AD का 1/2 है; ∠PBQ, दाएँ वृत्त में चाप PQ का 1/2 है।
🔵 चरण 3: अतः चाप AD = चाप PQ.
🔵 चरण 4: बाएँ वृत्त में चाप AD = चाप AB + चाप BD. दाएँ वृत्त में चाप PQ = चाप QB + चाप BP.
🔵 चरण 5: चरण 3 से ⇒ चाप AB + चाप BD = चाप QB + चाप BP.
🔵 चरण 6: दोनों ओर 1/2 लें: 1/2(चाप AB) + 1/2(चाप BD) = 1/2(चाप QB) + 1/2(चाप BP).
🔵 चरण 7: C पर बने अन्तःस्थित कोणों के रूप में लिखें:
 1/2(चाप AB) = ∠ACB, 1/2(चाप BD) = ∠BCD, 1/2(चाप QB) = ∠QCB, 1/2(चाप BP) = ∠BCP.
🔵 चरण 8: अतः ∠ACB + ∠BCP = ∠QCB + ∠BCD.
🔵 चरण 9: C पर कोण-योग: ∠ACP = ∠ACB + ∠BCP तथा ∠QCD = ∠QCB + ∠BCD.
✔️ निष्कर्ष: ∠ACP = ∠QCD.

🔵 Question
Q 10. यदि किसी त्रिभुज की दो भुजाओं को व्यास मानकर वृत्त खींचे जाएँ, तो सिद्ध कीजिए कि इन वृत्तों का प्रतिछेद बिन्दु तीसरी भुजा पर स्थित है।

🟢 Answer

💡 अवधारणा: व्यास पर बना अन्तःस्थित कोण 90° होता है (थेल्स का सिद्धान्त)।

🔵 चरण 1: ΔABC में AB और AC को व्यास मानकर दो वृत्त खींचें; उनका दूसरा प्रतिछेद बिन्दु P मानें (A के अतिरिक्त)।
🔵 चरण 2: AB व्यास ⇒ ∠APB = 90°.
🔵 चरण 3: AC व्यास ⇒ ∠APC = 90°.
🔵 चरण 4: ∠APB = 90° तथा ∠APC = 90° ⇒ PB ⟂ PA तथा PC ⟂ PA.
🔵 चरण 5: किसी बिन्दु से खींची गई एक ही लम्ब रेखा अद्वितीय होती है ⇒ B, P, C एक ही रेखा पर हैं।
✔️ निष्कर्ष: P, BC पर स्थित है; अर्थात प्रतिछेद बिन्दु तीसरी भुजा पर होता है।

🔵 Question
Q 11. उभयान्तिक कर्ण AC वाले दो समकोण त्रिभुज ABC और ADC हैं। सिद्ध कीजिए कि ∠CAD = ∠CBD है।

🟢 Answer

💡 अवधारणा: समान कर्ण AC पर बने समकोण त्रिभुजों के शीर्ष B और D उसी वृत्त पर स्थित होते हैं जिसका व्यास AC है; एक ही जीवा द्वारा अंतःस्थित कोण समान होते हैं।

🔵 चरण 1: ∠ABC = 90° तथा ∠ADC = 90° दिए हैं ⇒ A, B, C, D एक ही वृत्त पर स्थित हैं जिसका व्यास AC है।
🔵 चरण 2: इस वृत्त में जीवा CD पर विचार करें।
🔵 चरण 3: ∠CAD, जीवा CD द्वारा A पर अंतःस्थित कोण है।
🔵 चरण 4: ∠CBD, वही जीवा CD द्वारा B पर अंतःस्थित कोण है।
🔵 चरण 5: एक ही वृत्त में एक ही जीवा द्वारा अंतःस्थित कोण समान होते हैं।
✔️ निष्कर्ष: ∠CAD = ∠CBD.

🔵 Question
Q 12. सिद्ध कीजिए कि चक्रीय समांतर चतुर्भुज आयत होता है।

🟢 Answer

💡 अवधारणा:
(क) समांतर चतुर्भुज में विपरीत कोण बराबर होते हैं।
(ख) चक्रीय चतुर्भुज में विपरीत कोणों का योग 180° होता है।

🔵 चरण 1: ABCD समांतर चतुर्भुज है ⇒ ∠A = ∠C तथा ∠B = ∠D.
🔵 चरण 2: वही चतुर्भुज चक्रीय भी है ⇒ ∠A + ∠C = 180°.
🔵 चरण 3: चरण 1 और 2 से 2∠A = 180° ⇒ ∠A = 90°.
🔵 चरण 4: उसी प्रकार ∠B = 90°, ∠C = 90°, ∠D = 90°.
✔️ निष्कर्ष: चारों कोण 90° ⇒ चतुर्भुज आयत है।

————————————————————————————————————————————————————————————————————————————

अन्य महत्वपूर्ण प्रश्न

(कुल अंक: 80, समय: 3 घंटे)

🔵 Section A (प्रश्न 1–6) — (प्रत्येक 1 अंक)
🔵 प्रश्न 1
वृत्त की परिभाषा लिखिए।
🟢 उत्तर
➡️ समतल में स्थित वह बिन्दुपथ जिसकी प्रत्येक बिन्दु किसी नियत बिन्दु (केन्द्र) से समान दूरी पर होती है, वृत्त कहलाता है।

🔵 प्रश्न 2
वृत्त का व्यास और त्रिज्या में क्या सम्बन्ध है?
🟢 उत्तर
➡️ व्यास = 2 × त्रिज्या (d = 2r)

🔵 प्रश्न 3 (MCQ)
यदि किसी वृत्त की परिधि 44 सेमी है, तो उसकी त्रिज्या होगी—
🔴 7 सेमी
🟡 14 सेमी
🟢 21 सेमी
🔵 28 सेमी
🟢 उत्तर
➡️ परिधि = 2πr = 44
➡️ r = 44/(2 × 22/7) = 7 सेमी
✔️ सही विकल्प = 7 सेमी

🔵 प्रश्न 4
केन्द्र कोण 180° द्वारा बनी जीवा को क्या कहते हैं?
🟢 उत्तर
➡️ केन्द्र कोण 180° पर बनी जीवा को व्यास कहते हैं।

🔵 प्रश्न 5
स्पर्शरेखा की परिभाषा लिखिए।
🟢 उत्तर
➡️ वृत्त को केवल एक ही बिन्दु पर छूने वाली रेखा को स्पर्शरेखा कहते हैं।

🔵 प्रश्न 6 (MCQ)
यदि किसी वृत्त की त्रिज्या r है, तो उसका क्षेत्रफल होगा—
🔴 πr²
🟡 2πr
🟢 πd
🔵 πr
🟢 उत्तर
➡️ क्षेत्रफल = πr²
✔️ सही विकल्प = πr²

🟢 Section B (प्रश्न 7–12) — (प्रत्येक 2 अंक)
🟡 प्रश्न 7
वृत्त की परिधि का सूत्र लिखिए और 14 सेमी त्रिज्या वाले वृत्त की परिधि ज्ञात कीजिए।
🟢 उत्तर
➡️ परिधि = 2πr
➡️ = 2 × (22/7) × 14
➡️ = 88 सेमी

🟡 प्रश्न 8
त्रिज्या 7 सेमी वाले वृत्त का क्षेत्रफल ज्ञात कीजिए।
🟢 उत्तर
➡️ क्षेत्रफल = πr²
➡️ = (22/7) × 7²
➡️ = (22/7) × 49
➡️ = 154 सेमी²

🟡 प्रश्न 9
एक वृत्त का व्यास 28 सेमी है। उसका क्षेत्रफल ज्ञात कीजिए।
🟢 उत्तर
➡️ त्रिज्या r = 28/2 = 14 सेमी
➡️ क्षेत्रफल = πr²
➡️ = (22/7) × 14²
➡️ = (22/7) × 196
➡️ = 616 सेमी²

🟡 प्रश्न 10 (MCQ)
यदि किसी वृत्त की त्रिज्या दोगुनी कर दी जाए तो क्षेत्रफल—
🔴 दुगुना होगा
🟡 तीन गुना होगा
🟢 चार गुना होगा
🔵 आधा होगा
🟢 उत्तर
➡️ नया क्षेत्रफल = π(2r)² = 4πr²
➡️ क्षेत्रफल चार गुना होगा
✔️ सही विकल्प = चार गुना होगा

🟡 प्रश्न 11
एक वृत्त का क्षेत्रफल 154 सेमी² है। उसकी त्रिज्या ज्ञात कीजिए।
🟢 उत्तर
➡️ πr² = 154
➡️ (22/7)r² = 154
➡️ r² = (154 × 7)/22 = 49
➡️ r = √49 = 7 सेमी

🟡 प्रश्न 12
त्रिज्या 10 सेमी वाले वृत्त का व्यास और परिधि ज्ञात कीजिए।
🟢 उत्तर
➡️ व्यास = 2r = 20 सेमी
➡️ परिधि = 2πr = 2 × (22/7) × 10 = 440/7 ≈ 62.86 सेमी

🟡 Section C (प्रश्न 13–22) — (प्रत्येक 3 अंक)
🔵 प्रश्न 13
एक वृत्त की त्रिज्या 7 सेमी है। उसका क्षेत्रफल तथा परिधि ज्ञात कीजिए।
🟢 उत्तर
➡️ परिधि = 2πr = 2 × (22/7) × 7 = 44 सेमी
➡️ क्षेत्रफल = πr² = (22/7) × 7² = 154 सेमी²

🔵 प्रश्न 14
वृत्त की त्रिज्या 21 सेमी है। क्षेत्रफल और व्यास ज्ञात कीजिए।
🟢 उत्तर
➡️ व्यास = 2r = 42 सेमी
➡️ क्षेत्रफल = πr² = (22/7) × 21² = (22/7) × 441 = 1386 सेमी²

🔵 प्रश्न 15 (MCQ)
यदि किसी वृत्त का क्षेत्रफल 154 सेमी² है, तो उसकी परिधि होगी—
🔴 44 सेमी
🟡 66 सेमी
🟢 77 सेमी
🔵 88 सेमी
🟢 उत्तर
➡️ πr² = 154 ⇒ r = 7 सेमी
➡️ परिधि = 2πr = 2 × (22/7) × 7 = 44 सेमी
✔️ सही विकल्प = 44 सेमी

🔵 प्रश्न 16
किसी अर्धवृत्त की परिधि 72 सेमी है। उसकी त्रिज्या ज्ञात कीजिए।
🟢 उत्तर
➡️ अर्धवृत्त परिधि = πr + 2r
➡️ 72 = (22/7)r + 2r = (22r + 14r)/7 = (36r)/7
➡️ r = (72 × 7)/36 = 14 सेमी

🔵 प्रश्न 17
एक वृत्त का क्षेत्रफल 616 सेमी² है। उसकी परिधि ज्ञात कीजिए।
🟢 उत्तर
➡️ πr² = 616
➡️ (22/7)r² = 616
➡️ r² = (616 × 7)/22 = 196
➡️ r = 14 सेमी
➡️ परिधि = 2πr = 2 × (22/7) × 14 = 88 सेमी

🔵 प्रश्न 18
वृत्त की त्रिज्या 3.5 सेमी है। उसका क्षेत्रफल ज्ञात कीजिए।
🟢 उत्तर
➡️ क्षेत्रफल = πr² = (22/7) × (3.5)²
➡️ = (22/7) × 12.25
➡️ = 38.5 सेमी²

🔵 प्रश्न 19
यदि किसी वृत्त का क्षेत्रफल 616 सेमी² है, तो उसका व्यास ज्ञात कीजिए।
🟢 उत्तर
➡️ πr² = 616
➡️ (22/7)r² = 616
➡️ r² = 196 ⇒ r = 14 सेमी
➡️ व्यास = 2r = 28 सेमी

🔵 प्रश्न 20 (आन्तरिक विकल्प)
(क) एक अर्धवृत्त की परिधि 108 सेमी है। उसकी त्रिज्या ज्ञात कीजिए।
या
(ख) यदि किसी वृत्त की त्रिज्या 21 सेमी है, तो उसका क्षेत्रफल तथा परिधि ज्ञात कीजिए।
🟢 उत्तर
🔸 (क) के लिए
➡️ अर्धवृत्त परिधि = πr + 2r = 108
➡️ (22/7)r + 2r = 108
➡️ (22r + 14r)/7 = 108
➡️ 36r = 756
➡️ r = 21 सेमी
🔸 (ख) के लिए
➡️ परिधि = 2πr = 2 × (22/7) × 21 = 132 सेमी
➡️ क्षेत्रफल = πr² = (22/7) × 21² = 1386 सेमी²

🔵 प्रश्न 21
यदि किसी वृत्त का व्यास 14 सेमी है, तो उसका क्षेत्रफल और परिधि ज्ञात कीजिए।
🟢 उत्तर
➡️ r = 14/2 = 7 सेमी
➡️ परिधि = 2πr = 2 × (22/7) × 7 = 44 सेमी
➡️ क्षेत्रफल = πr² = (22/7) × 7² = 154 सेमी²

🔵 प्रश्न 22 (MCQ)
यदि किसी वृत्त की परिधि 132 सेमी है, तो उसकी त्रिज्या होगी—
🔴 14 सेमी
🟡 18 सेमी
🟢 21 सेमी
🔵 28 सेमी
🟢 उत्तर
➡️ 2πr = 132
➡️ r = 132/(2 × 22/7) = 21 सेमी
✔️ सही विकल्प = 21 सेमी

🔴 Section D (प्रश्न 23–30) — (प्रत्येक 4 अंक)
🔵 प्रश्न 23
एक वृत्त की त्रिज्या 14 सेमी है।
(क) उसकी परिधि तथा क्षेत्रफल ज्ञात कीजिए।
(ख) उतने ही क्षेत्रफल का एक आयत बनाया गया है जिसकी चौड़ाई 7 सेमी है। उस आयत की लम्बाई ज्ञात कीजिए।
🟢 उत्तर
✳️ सूत्र
➡️ परिधि = 2πr
➡️ क्षेत्रफल = πr²
➤ गणना (क)
➡️ r = 14
➡️ परिधि = 2πr = 2 × (22/7) × 14 = 88 सेमी
➡️ क्षेत्रफल = πr² = (22/7) × 14² = (22/7) × 196 = 616 सेमी²
➤ गणना (ख)
➡️ आयत का क्षेत्रफल = 616
➡️ चौड़ाई = 7
➡️ लम्बाई = क्षेत्रफल/चौड़ाई = 616/7 = 88 सेमी

🔵 प्रश्न 24 (आन्तरिक विकल्प)
(क) एक वृत्ताकार बगीचे की त्रिज्या 21 मी है। उसके चारों ओर 2 मी चौड़ी बाहरी पगडण्डी बनाई गई है। पगडण्डी का क्षेत्रफल ज्ञात कीजिए।
या
(ख) किसी वृत्त की परिधि 132 मी है। उसका क्षेत्रफल ज्ञात कीजिए।
🟢 उत्तर
🔸 (क) के लिए
दिया: r₁ = 21, r₂ = 23
➡️ पगडण्डी क्षेत्रफल = π(r₂² − r₁²) = π(23² − 21²) = π(529 − 441) = π × 88
➡️ = (22/7) × 88 = 1936/7 मी² ≈ 276.57 मी²
🔸 (ख) के लिए
➡️ 2πr = 132 ⇒ r = 132/(2 × 22/7) = 21
➡️ क्षेत्रफल = πr² = (22/7) × 21² = (22/7) × 441 = 1386 मी²

🔵 प्रश्न 25
एक पहिया जिसकी त्रिज्या 35 सेमी है, 100 चक्कर लगाता है। वह कितनी दूरी तय करेगा? साथ ही, यदि 1 कि.मी = 100000 सेमी हो, तो दूरी को कि.मी में भी लिखिए।
🟢 उत्तर
✳️ सूत्र
➡️ एक चक्कर की दूरी = परिधि = 2πr
➤ गणना
➡️ r = 35
➡️ परिधि = 2πr = 2 × (22/7) × 35 = 220 सेमी
➡️ 100 चक्कर की दूरी = 100 × 220 = 22000 सेमी
➡️ कि.मी में दूरी = 22000/100000 = 0.22 कि.मी

🔵 प्रश्न 26 (आन्तरिक विकल्प)
(क) एक अर्धवृतीय पार्क का व्यास 28 मी है। चारों ओर बाँस की घेराबन्दी केवल अर्धवृत्तीय भाग पर की जानी है (व्यास वाली सीधी भुजा पर नहीं)। कुल बाँस की लम्बाई ज्ञात कीजिए तथा यदि दर 120 रु/मी है तो कुल लागत ज्ञात कीजिए।
या
(ख) 176 सेमी लम्बाई की तार को मोड़कर एक वृत्त बनाया गया। उस वृत्त का क्षेत्रफल ज्ञात कीजिए।
🟢 उत्तर
🔸 (क) के लिए
➡️ व्यास = 28 ⇒ r = 14
➡️ अर्धवृत्त की परिधि (केवल चाप) = πr = (22/7) × 14 = 44 मी
➡️ लागत = 44 × 120 = 5280 रु
🔸 (ख) के लिए
➡️ तार की लम्बाई = परिधि = 2πr = 176
➡️ r = 176/(2 × 22/7) = 176 × 7/44 = 28
➡️ क्षेत्रफल = πr² = (22/7) × 28² = (22/7) × 784 = 2464 सेमी²

🔵 प्रश्न 27
दो वृत्तों की त्रिज्याएँ 7 सेमी और 14 सेमी हैं।
(क) उनकी परिधियों का अनुपात तथा क्षेत्रों का अनुपात ज्ञात कीजिए।
(ख) दोनों के क्षेत्रों का अन्तर ज्ञात कीजिए।
🟢 उत्तर
➤ अनुपात (क)
➡️ परिधि ∝ r ⇒ परिधि का अनुपात = 7 : 14 = 1 : 2
➡️ क्षेत्रफल ∝ r² ⇒ क्षेत्रफल का अनुपात = 7² : 14² = 49 : 196 = 1 : 4
➤ अन्तर (ख)
➡️ क्षेत्रफल₂ − क्षेत्रफल₁ = π(14² − 7²) = π(196 − 49) = π × 147
➡️ = (22/7) × 147 = 462 सेमी²

🔵 प्रश्न 28
एक गोल रस्सी को मोड़कर वृत्त बनाया गया है जिसका क्षेत्रफल 308 सेमी² है। उसी रस्सी से एक आयत बनाया जाता है जिसकी लम्बाई 22 सेमी है। आयत की चौड़ाई ज्ञात कीजिए।
🟢 उत्तर
➡️ πr² = 308 ⇒ r² = 308 × 7/22 = 98 ⇒ r = 7√2
➡️ रस्सी की कुल लम्बाई = परिधि = 2πr = 2 × (22/7) × 7√2 = 44√2 सेमी
➡️ आयत की परिमाप = 2(लम्बाई + चौड़ाई) = 44√2
➡️ 2(22 + चौड़ाई) = 44√2
➡️ 22 + चौड़ाई = 22√2
➡️ चौड़ाई = 22(√2 − 1) = 22√2 − 22 सेमी

🔵 प्रश्न 29 (आन्तरिक विकल्प)
(क) एक वृत्त का क्षेत्रफल 1540 सेमी² है। उसका व्यास ज्ञात कीजिए तथा यदि 5 सेमी × 5 सेमी के वर्ग फर्श-पट्टों से उसे पाटा जाए तो कितने फर्श-पट्टों की आवश्यकता होगी?
या
(ख) किसी वृत्त की परिधि 94.2 मी है। π = 22/7 मानकर त्रिज्या तथा क्षेत्रफल ज्ञात कीजिए।
🟢 उत्तर
🔸 (क) के लिए
➡️ πr² = 1540 ⇒ r² = 1540 × 7/22 = 490 ⇒ r = √490 = 7√10
➡️ व्यास = 2r = 14√10 सेमी
➡️ क्षेत्रफल = 1540 सेमी²
➡️ एक फर्श-पट्ट का क्षेत्रफल = 5 × 5 = 25 सेमी²
➡️ आवश्यक संख्या = 1540/25 = 61.6 ⇒ पूर्ण फर्श-पट्ट = 62
🔸 (ख) के लिए
➡️ दिया: 2πr = 94.2, π = 22/7
➡️ r = 94.2 / (2 × 22/7) = 94.2 × 7 / 44 = ≈ 14.99 मी
➡️ क्षेत्रफल = πr² = (22/7) × (14.99)²
➡️ (14.99)² ≈ 224.70
➡️ क्षेत्रफल ≈ (22/7) × 224.70 ≈ ≈ 706.1 मी²

🔵 प्रश्न 30
एक वृत्ताकार मैदान की त्रिज्या 50 मी है। उसके चारों ओर 2.5 मी चौड़ी बाहरी पगडण्डी बनानी है।
(क) पगडण्डी का क्षेत्रफल ज्ञात कीजिए।
(ख) यदि निर्माण की लागत 12 रु/मी² है, तो कुल लागत ज्ञात कीजिए।
🟢 उत्तर
➡️ r₁ = 50, r₂ = 50 + 2.5 = 52.5
➡️ पगडण्डी का क्षेत्रफल = π(r₂² − r₁²)
➡️ = π(52.5² − 50²) = π(2756.25 − 2500) = π × 256.25
➡️ = (22/7) × 256.25 = 5637.5/7 मी² ≈ 805.36 मी²
➡️ कुल लागत = 805.36 × 12 ≈ 9664.32 रु (लगभग)

————————————————————————————————————————————————————————————————————————————

मानचित्र

————————————————————————————————————————————————————————————————————————————
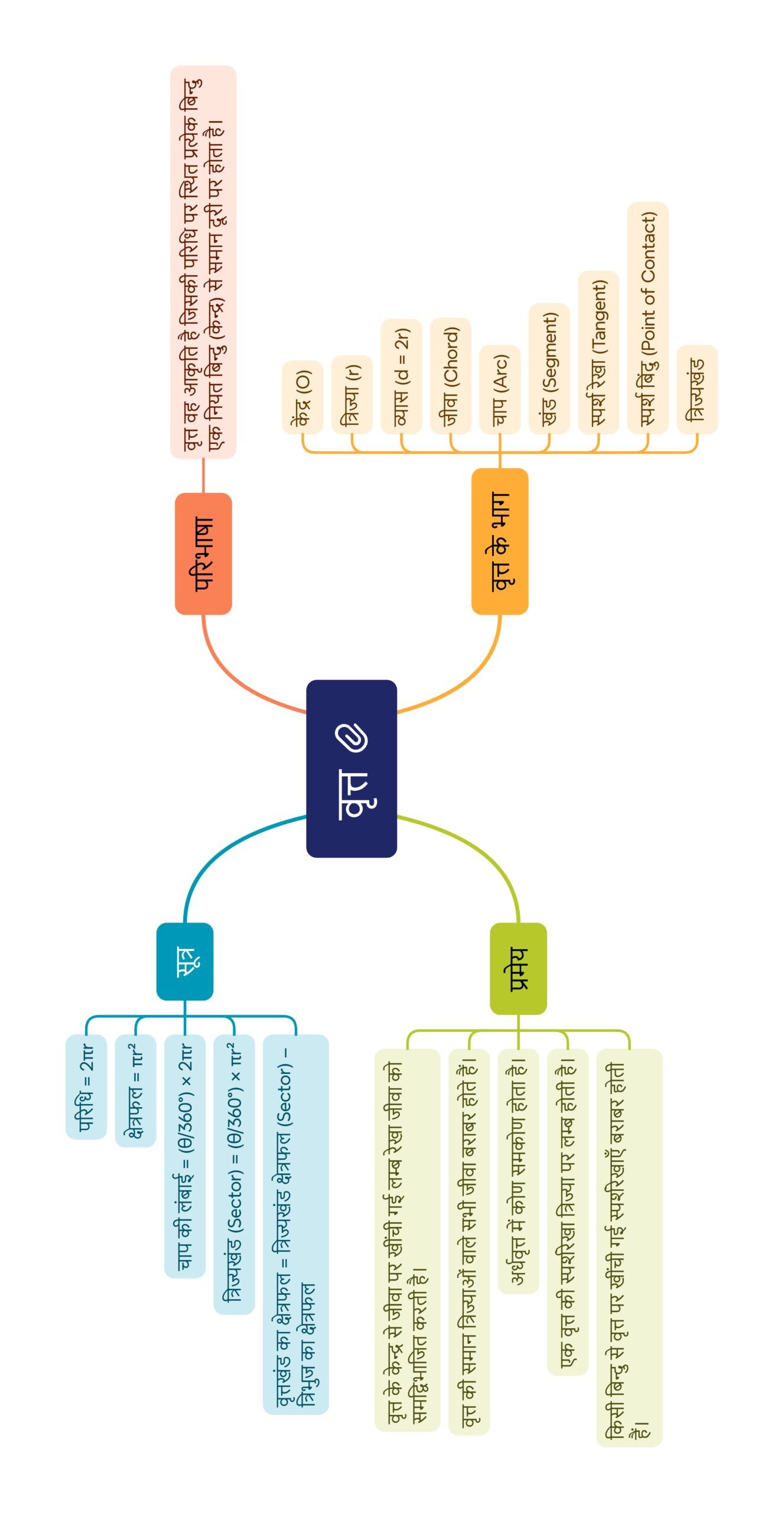