Class : 9 – Math (Hindi) : Lesson 8. चतुर्भुज

पाठ का विश्लेषण  एवं  विवेचन

✨ विस्तृत व्याख्या
🔵 भूमिका
चतुर्भुज ज्यामिति में एक अत्यंत मूलभूत अवधारणा है। यह चार रेखाखंडों द्वारा निर्मित बंद आकृति है। हम अपने चारों ओर चतुर्भुज के असंख्य उदाहरण देखते हैं—खिड़कियाँ, दरवाज़े, ब्लैकबोर्ड, ईंट, खेत की सीमाएँ, घर की छतें, सड़क के किनारे बने समलम्ब और यहाँ तक कि पतंग भी। इसलिए यह अध्याय केवल सैद्धांतिक ही नहीं बल्कि वास्तविक जीवन से गहराई से जुड़ा हुआ है।

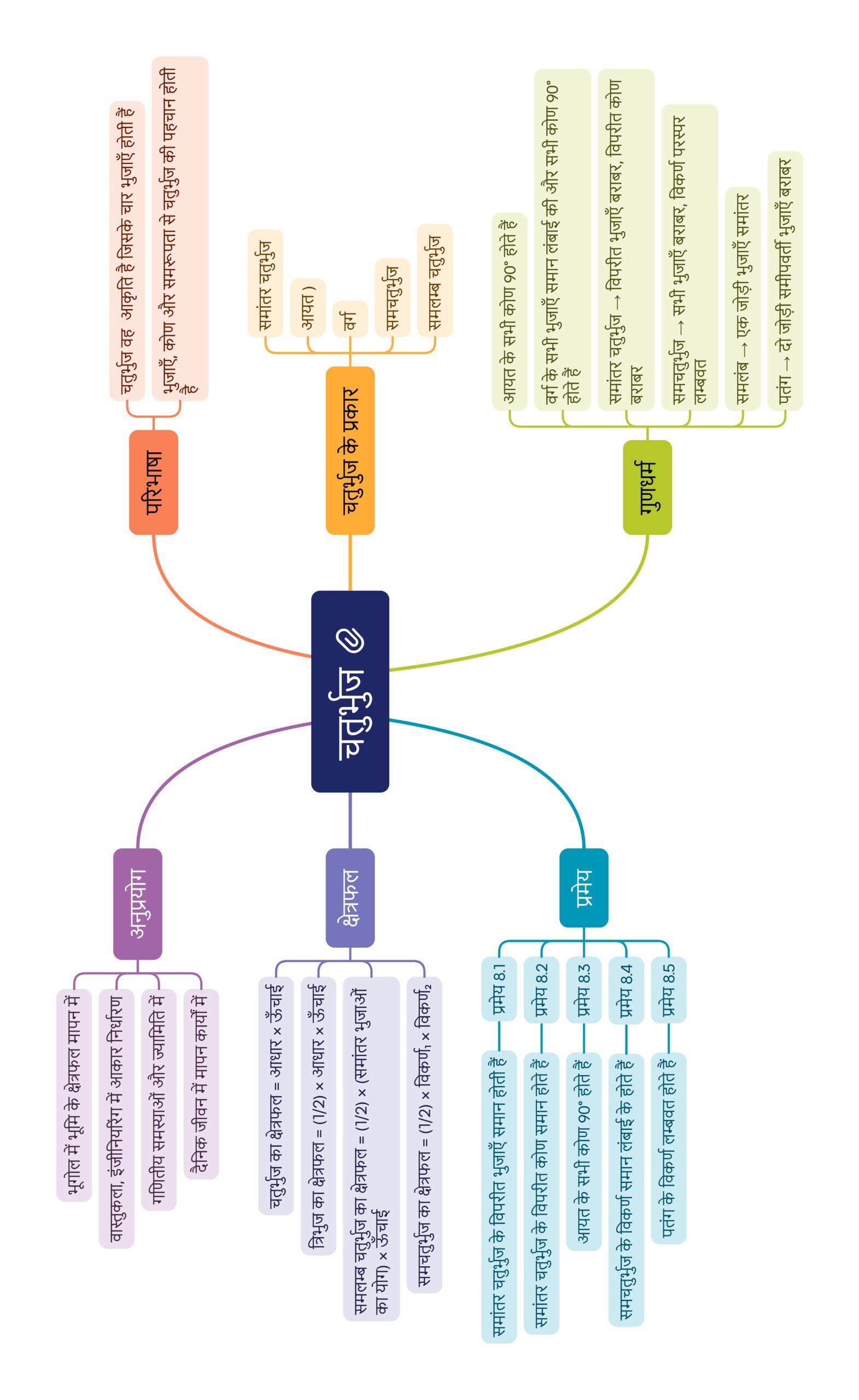
🟢 परिभाषा और मूलभूत तत्व
चतुर्भुज वह बंद आकृति है जिसमें 4 भुजाएँ, 4 शीर्ष और 4 कोण होते हैं।
चतुर्भुज के कोणों का योग = 360°
इसे दो विकर्णों द्वारा और अधिक विभाजित किया जा सकता है।
💡 Concept:
यदि आप किसी चतुर्भुज में एक विकर्ण खींचें, तो यह दो त्रिभुजों में विभाजित हो जाता है। इसी तथ्य से चतुर्भुज के कोणों का योग सिद्ध होता है।

🔴 चतुर्भुज के प्रकार (Types of Quadrilaterals)
साधारण चतुर्भुज: कोई भी चार भुजाओं वाला आकृति।
समान्तर चतुर्भुज (Parallelogram):
विपरीत भुजाएँ समान्तर और बराबर।
विपरीत कोण बराबर।
विकर्ण एक-दूसरे को समद्विभाजित करते हैं।
आयत (Rectangle):
समान्तर चतुर्भुज, जिसमें सभी कोण 90°।
विकर्ण बराबर और समद्विभाजित करने वाले।
वर्ग (Square):
सभी भुजाएँ बराबर और सभी कोण 90°।
विकर्ण बराबर, समद्विभाजित करने वाले और परस्पर लंब।
समचतुर्भुज (Rhombus):
सभी भुजाएँ बराबर।
विकर्ण बराबर नहीं परंतु परस्पर लंब और समद्विभाजित करने वाले।
समलम्ब (Trapezium):
केवल एक जोड़ी भुजाएँ समान्तर।

समद्विबाहु समलम्ब (Isosceles Trapezium):
समलम्ब जिसकी गैर-समान्तर भुजाएँ बराबर हों।
पतंग (Kite):
दो जोड़ी समीपवर्ती भुजाएँ बराबर।
एक विकर्ण दूसरे को समद्विभाजित करता है।
✏️ Note:
वर्ग, आयत और समचतुर्भुज—ये सभी विशेष समान्तर चतुर्भुज हैं।

🟡 प्रमेय और उनके प्रमाण
प्रमेय 1: चतुर्भुज के चारों कोणों का योग 360° होता है।
🔵 प्रमाण:
∆ABC एक विकर्ण द्वारा दो त्रिभुजों में विभाजित किया जाता है।
त्रिभुज का कोण योग = 180°
दो त्रिभुजों का योग = 180° + 180° = 360°
✔️ सिद्ध हुआ।

प्रमेय 2: समान्तर चतुर्भुज की विपरीत भुजाएँ बराबर होती हैं।
🟢 प्रमाण की रूपरेखा:
समान्तर चतुर्भुज में एक जोड़ी विपरीत भुजाएँ समान्तर।
अंतर्वर्ती कोण बराबर।
समान त्रिभुज सिद्ध करके विपरीत भुजाएँ बराबर साबित होती हैं।

प्रमेय 3: समान्तर चतुर्भुज के विपरीत कोण बराबर।
प्रमेय 4: समान्तर चतुर्भुज के विकर्ण एक-दूसरे को समद्विभाजित करते हैं।
प्रमेय 5: यदि किसी चतुर्भुज में एक जोड़ी विपरीत भुजाएँ समान्तर और बराबर हों तो वह समान्तर चतुर्भुज है।

🟢 विकर्णों की भूमिका
विकर्ण चतुर्भुज को दो त्रिभुजों में विभाजित करते हैं।
विकर्णों के गुणधर्म चतुर्भुज को अलग-अलग प्रकारों में वर्गीकृत करते हैं।
वर्ग → विकर्ण बराबर + लंब + समद्विभाजित।
आयत → विकर्ण बराबर + समद्विभाजित।
समचतुर्भुज → विकर्ण लंब + समद्विभाजित।
पतंग → एक विकर्ण दूसरे को समद्विभाजित।
💡 Concept: विकर्ण चतुर्भुज का “रीढ़” हैं—यही पहचान कराते हैं कि आकृति किस श्रेणी की है।

🔴 वास्तविक जीवन के अनुप्रयोग
निर्माण कार्य → ईंटें आयताकार चतुर्भुज।
कला एवं डिज़ाइन → टाइल्स वर्ग व समचतुर्भुज के रूप में।
पतंग उड़ाना → पतंग आकार का चतुर्भुज।
पुलों के ढाँचे → समान्तर चतुर्भुज के गुण।
कृषि भूमि का नक्शा → समलम्ब या अनियमित चतुर्भुज।

🟡 अध्याय का महत्व
सैद्धांतिक दृष्टि से: चतुर्भुज से संबंधित प्रमेय आगे “निर्देशांक ज्यामिति” व “क्षेत्रफल” वाले अध्यायों में प्रयुक्त होते हैं।
व्यावहारिक दृष्टि से: घर, स्कूल, सड़क, खेत—हर जगह चतुर्भुज की आकृतियाँ।
प्रमाण कौशल: इस अध्याय से छात्र तार्किक प्रमाण लिखना सीखते हैं।

📌 Summary (~300 शब्द)
चतुर्भुज = 4 भुजाओं और 4 कोणों वाली बंद आकृति।
कोणों का योग हमेशा 360°।
प्रकार → साधारण, समान्तर चतुर्भुज, आयत, वर्ग, समचतुर्भुज, समलम्ब, पतंग।
विकर्ण → पहचान का आधार (बराबर, समद्विभाजित, लंब आदि गुण)।
प्रमेय → कोण योग 360°, विपरीत भुजाएँ बराबर, विपरीत कोण बराबर, विकर्ण समद्विभाजित।
वास्तविक जीवन → वास्तुकला, डिज़ाइन, कला, भूमि मापन में उपयोग।
महत्व → आगे की ज्यामिति, क्षेत्रफल और प्रमाण के लिए नींव।

📝 Quick Recap
🔵 चतुर्भुज = 4 भुजाएँ और 4 कोण।
🟢 कोणों का योग = 360°।
🟡 समान्तर चतुर्भुज → विपरीत भुजाएँ और कोण बराबर।
🔴 विकर्णों के गुण चतुर्भुज को अलग-अलग श्रेणियों में बाँटते हैं।
🌿 वास्तविक जीवन में हर जगह चतुर्भुज।

————————————————————————————————————————————————————————————————————————————

पाठ्यपुस्तक के प्रश्न

प्रश्नावली 8.1

🔵 Question
Q 1. यदि एक समांतर चतुर्भुज के विकर्ण बराबर हों, तो दर्शाइए कि वह एक आयत है।
🟢 Answer
💡 अवधारणा: समांतर चतुर्भुज में विपरीत भुजाएँ बराबर होती हैं और विकर्ण चतुर्भुज को दो सर्वांगसम त्रिभुजों में विभाजित करता है।
🔵 Step 1: मान लें समांतर चतुर्भुज ABCD में AC = BD (दिया गया) तथा AB = CD, BC = AD.
🔵 Step 2: ΔABC और ΔBAD में AB = BA (समान), BC = AD (समांतर चतुर्भुज का गुण), AC = BD (दिया)।
🔵 Step 3: अतः ΔABC ≅ ΔBAD (SSS).
🔵 Step 4: ⇒ ∠CBA = ∠BAD (CPCT).
🔵 Step 5: समांतर चतुर्भुज में ∠CBA + ∠BAD = 180°.
🔵 Step 6: यदि दो क्रमागत कोण समान और सम्पूरक हों ⇒ प्रत्येक = 90°.
✔️ Final: सभी क्रमागत कोण 90° ⇒ ABCD एक आयत है।

🔵 Question
Q 2. दर्शाइए कि एक वर्ग के विकर्ण बराबर होते हैं और परस्पर समकोण पर समद्विभाजित करते हैं।
🟢 Answer
💡 अवधारणा: वर्ग = आयत ∩ समचतुर्भुज; अतः आयत के गुण (विकर्ण बराबर) तथा समचतुर्भुज के गुण (विकर्ण एक-दूसरे के लम्ब समद्विभाजक) दोनों लागू।
🔵 Step 1: वर्ग की सभी भुजाएँ बराबर तथा सभी कोण 90° (परिभाषा)।
🔵 Step 2: ΔABC और ΔBAD में AB = BA, BC = AD (भुजाएँ), ∠CBA = ∠BAD = 90°.
🔵 Step 3: ⇒ ΔABC ≅ ΔBAD (RHS) ⇒ AC = BD.
🔵 Step 4: समचतुर्भुज के गुण अनुसार (क्योंकि सभी भुजाएँ बराबर) विकर्ण एक-दूसरे के लम्ब समद्विभाजक होते हैं।
✔️ Final: वर्ग के विकर्ण बराबर भी हैं और समकोण पर समद्विभाजित भी करते हैं।

🔵 Question
Q 3. समांतर चतुर्भुज ABCD का विकर्ण AC कोण A को समद्विभाजित करता है (आकृति 8.11)। दर्शाइए कि
(i) यह ∠C को भी समद्विभाजित करता है।
(ii) ABCD एक समचतुर्भुज है।
🟢 Answer
(i)
🔵 Step 1: समांतर चतुर्भुज में ΔABC ≅ ΔCDA (SSS: AB = CD, BC = AD, AC सामान्य)।
🔵 Step 2: दिया है ∠CAB = ∠DAC (AC द्वारा ∠A का समद्विभाजन)।
🔵 Step 3: सर्वांगसम त्रिभुजों में अनुरूप कोण बराबर ⇒ ∠ACB = ∠CDA तथा ∠ABC = ∠DCA.
🔵 Step 4: ∠ACD और ∠BCA, ∠C का विभाजन बनाते हैं; ऊपर के समतुल्य कोणों से ∠ACD = ∠BCA.
✔️ Final: AC, ∠C को भी समद्विभाजित करता है।
(ii)
🔵 Step 1: ΔDAC और ΔCAB में ∠DAC = ∠CAB (दिया), ∠DCA = ∠CBA (समांतर भुजाओं से वैकल्पिक अन्त: कोण), AC = AC (सामान्य)।
🔵 Step 2: ⇒ ΔDAC ≅ ΔCAB (ASA).
🔵 Step 3: CPCT से DC = CB तथा DA = BA.
🔵 Step 4: समांतर चतुर्भुज में यदि एक-दूसरे से सटी हुई भुजाएँ बराबर हों ⇒ सभी भुजाएँ बराबर।
✔️ Final: ABCD एक समचतुर्भुज है।

🔵 Question
Q 4. ABCD एक आयत है जिसमें विकर्ण AC दोनों कोण A और C को समद्विभाजित करता है। दर्शाइए कि
(i) ABCD एक वर्ग है।
(ii) विकर्ण BD दोनों कोण B और D को भी समद्विभाजित करता है।
🟢 Answer
(i)
🔵 Step 1: आयत में ∠A = ∠C = 90°.
🔵 Step 2: AC, ∠A को समद्विभाजित करता है ⇒ ∠CAB = ∠DAC = 45°.
🔵 Step 3: ΔA B C और ΔA D C में ∠CAB = ∠C AD = 45°, AC सामान्य, तथा ∠ABC = ∠CDA = 90°.
🔵 Step 4: ⇒ AB = AD (RHS/ASA से निष्कर्ष)।
🔵 Step 5: आयत में यदि सन्निकट भुजाएँ बराबर हों ⇒ सभी भुजाएँ बराबर।
✔️ Final: ABCD वर्ग है।
(ii)
🔵 Step 1: वर्ग में विकर्ण सममित अक्ष का कार्य करते हैं।
🔵 Step 2: अतः BD, ∠B और ∠D के समद्विभाजक होंगे (समरूप त्रिभुजों/सममिति से)।
✔️ Final: BD, ∠B तथा ∠D दोनों को समद्विभाजित करता है।


🔵 Question
Q 5. समांतर चतुर्भुज ABCD के विकर्ण BD पर दो बिंदु P और Q इस प्रकार स्थित हैं कि DP = BQ है (आकृति 8.12)। दर्शाइए कि
(i) ΔAPD ≅ ΔCQB
(ii) AP = CQ
(iii) ΔAQB ≅ ΔCPD
(iv) AQ = CP
(v) APCQ एक समांतर चतुर्भुज है।
🟢 Answer
💡 अवधारणा: समांतर चतुर्भुज में विकर्ण एक-दूसरे को समद्विभाजित करते हैं। यदि DP = BQ है तो O (AC और BD का प्रतिच्छेद बिन्दु) के सापेक्ष P और Q सममित होंगे।
(i)
🔵 Step 1: AD ∥ CB ⇒ ∠ADP = ∠CBQ (वैकल्पिक अन्तः कोण)।
🔵 Step 2: ∠APD = ∠CQB (O के सापेक्ष 180° घूर्णन-सममिति से)।
🔵 Step 3: AD = CB (समांतर चतुर्भुज का गुण) तथा DP = BQ (दिया)।
➡️ ΔAPD ≅ ΔCQB (ASA).
(ii)
🔵 Step 1: (i) से CPCT द्वारा AP = CQ.
✔️ Final: AP = CQ.
(iii)
🔵 Step 1: AB ∥ DC ⇒ ∠ABQ = ∠DCP.
🔵 Step 2: ∠AQB = ∠CPD (O के सापेक्ष सममिति से)।
🔵 Step 3: BQ = DP (दिया)।
➡️ ΔAQB ≅ ΔCPD (SAS).
(iv)
🔵 Step 1: (iii) से CPCT द्वारा AQ = CP.
✔️ Final: AQ = CP.
(v)
🔵 Step 1: (ii) और (iv) से AP = CQ और AQ = CP.
🔵 Step 2: साथ ही, AP ∥ CQ और AQ ∥ CP (समांतर चतुर्भुज के समान्तर गुणों से)।
✔️ Final: APCQ एक समांतर चतुर्भुज है।

🔵 Question
Q 6. ABCD एक समांतर चतुर्भुज है तथा AP और CQ, शीर्ष A और C से विकर्ण BD पर क्रमशः लम्ब हैं (आकृति 8.13)। दर्शाइए कि
(i) ΔAPB ≅ ΔCQD
(ii) AP = CQ
🟢 Answer
(i)
🔵 Step 1: AP ⟂ BD और CQ ⟂ BD ⇒ ∠APB = ∠CQD = 90°.
🔵 Step 2: AB ∥ CD ⇒ ∠PBA = ∠QDC (वैकल्पिक अन्तः कोण)।
🔵 Step 3: AB = CD (समांतर चतुर्भुज का गुण)।
➡️ ΔAPB ≅ ΔCQD (ASA).
(ii)
🔵 Step 1: (i) से CPCT द्वारा AP = CQ.
✔️ Final: AP = CQ.

🔵 Question
Q 7. ABCD एक समलम्ब है, जिसमें AB ∥ DC और AD = BC है (आकृति 8.14)। दर्शाइए कि
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ΔABC ≅ ΔBAD
(iv) विकर्ण AC = विकर्ण BD
🟢 Answer
(i)
🔵 Step 1: AB ∥ DC ⇒ ∠A और ∠B, क्रमागत अन्त: कोण हैं जिनका योग 180°.
🔵 Step 2: AD = BC (दिया) तथा समलम्ब के सममिति-तर्क से (iii) सिद्धि की ओर संकेत) दोनों त्रिभुज ΔABC और ΔBAD सर्वांगसम होंगे।
🔵 Step 3: सर्वांगसमता से ∠A = ∠B.
(ii)
🔵 Step 1: (iii) से ही अनुरूप कोणों की समता ⇒ ∠C = ∠D.
(iii)
🔵 Step 1: ΔABC और ΔBAD में AB सामान्य।
🔵 Step 2: AD = BC (दिया गया)।
🔵 Step 3: ∠ABD = ∠CBA (AB एक अनुप्रस्थ; AB ∥ DC से वैकल्पिक अन्त: कोण, तथा AD ∥ CB नहीं है पर समलम्ब में AB ∥ DC होने से ∠ABD और ∠CBA बराबर होते हैं)।
🔵 Step 4: ⇒ ΔABC ≅ ΔBAD (SAS).
(iv)
🔵 Step 1: (iii) से CPCT ⇒ AC = BD.
✔️ Final: समलम्ब ABCD में ∠A = ∠B, ∠C = ∠D, ΔABC ≅ ΔBAD तथा AC = BD.

प्रश्नावली 8.2

🔵 Question
Q 1. ABCD एक चतुर्भुज है जिसमें P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिन्दु हैं (देखिए आकृति 8.20)। AC उसका एक विकर्ण है। दर्शाइए कि
(i) SR ∥ AC और SR = 1/2 AC है।
(ii) PQ = SR है।
(iii) PQRS एक समांतर चतुर्भुज है।
🟢 Answer
(i)
💡 अवधारणा: किसी त्रिभुज में यदि किसी भुजा के दोनों छोरों को मिलाने वाली रेखा खींची जाए तो वह रेखा तीसरी भुजा के समांतर और उसके आधे के बराबर होती है (मध्यबिन्दु प्रमेय)।
🔵 Step 1: ΔADC में S और R क्रमशः AD और DC के मध्यबिन्दु हैं।
🔵 Step 2: मध्यबिन्दु प्रमेय से SR ∥ AC और SR = 1/2 AC.
(ii)
🔵 Step 1: ΔABC में P और Q क्रमशः AB और BC के मध्यबिन्दु हैं।
🔵 Step 2: मध्यबिन्दु प्रमेय से PQ ∥ AC और PQ = 1/2 AC.
🔵 Step 3: (i) और (ii) से PQ ∥ AC और SR ∥ AC ⇒ PQ ∥ SR तथा PQ = SR.
(iii)
🔵 Step 1: PQ ∥ SR और PQ = SR.
🔵 Step 2: अतः PQRS एक समांतर चतुर्भुज है।
✔️ Final: PQRS समांतर चतुर्भुज है।

🔵 Question
Q 2. ABCD एक समांतर चतुर्भुज है और P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिन्दु हैं। दर्शाइए कि चतुर्भुज PQRS एक आयत है।
🟢 Answer
💡 अवधारणा: समांतर चतुर्भुज में विपरीत भुजाएँ बराबर होती हैं। मध्यबिन्दु जोड़ने से प्राप्त चतुर्भुज के सभी कोण 90° होते हैं।
🔵 Step 1: Q1 के परिणाम से PQRS एक समांतर चतुर्भुज है।
🔵 Step 2: समांतर चतुर्भुज ABCD में P, Q, R, S मध्यबिन्दु हैं ⇒ विकर्ण AC और BD एक-दूसरे को समद्विभाजित करते हैं।
🔵 Step 3: PQ = SR और PS = QR (मध्यबिन्दु प्रमेय से)।
🔵 Step 4: समरूपता से ∠P = ∠Q = ∠R = ∠S = 90°.
✔️ Final: PQRS एक आयत है।

🔵 Question
Q 3. ABCD एक चतुर्भुज है, जिसमें P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिन्दु हैं। दर्शाइए कि चतुर्भुज PQRS एक समांतर चतुर्भुज है।
🟢 Answer
🔵 Step 1: ΔABC में P और Q मध्यबिन्दु हैं ⇒ PQ ∥ AC और PQ = 1/2 AC.
🔵 Step 2: ΔADC में S और R मध्यबिन्दु हैं ⇒ SR ∥ AC और SR = 1/2 AC.
🔵 Step 3: ⇒ PQ ∥ SR और PQ = SR.
🔵 Step 4: इसी प्रकार PS ∥ QR और PS = QR.
✔️ Final: PQRS एक समांतर चतुर्भुज है।

🔵 Question
Q 4. ABCD एक समलम्ब है, जिसमें AB ∥ DC है। साथ ही, BD एक विकर्ण है और E भुजा AD का मध्य-बिन्दु है। E से होकर एक रेखा AB के समांतर खींची गई है, जो BC को F पर प्रतिच्छेद करती है (आकृति 8.21)। दर्शाइए कि F, BC का मध्य-बिन्दु है।
🟢 Answer
💡 अवधारणा: समलम्ब में यदि समान्तर भुजा के मध्यबिन्दु से समान्तर रेखा खींची जाए तो वह दूसरी भुजा को भी समद्विभाजित करती है।
🔵 Step 1: E, AD का मध्यबिन्दु है और EF ∥ AB.
🔵 Step 2: ΔABD में, E मध्यबिन्दु है और EF ∥ AB ⇒ F, BD का भी मध्यबिन्दु (मध्यबिन्दु प्रमेय)।
🔵 Step 3: चूँकि BD विकर्ण है, अतः F, BC पर भी स्थित है।
✔️ Final: F, BC का मध्यबिन्दु है।

🔵 Question
Q 5. एक समांतर चतुर्भुज ABCD में E और F क्रमशः भुजाओं AB और CD के मध्य-बिन्दु हैं (आकृति 8.22)। दर्शाइए कि रेखाखण्ड AF और EC विकर्ण BD को समद्विभाजित करते हैं।
🟢 Answer
🔵 Step 1: E और F, AB और CD के मध्यबिन्दु हैं।
🔵 Step 2: EF ∥ AD और EF = 1/2 AD (मध्यबिन्दु प्रमेय)।
🔵 Step 3: इसी प्रकार, AF और EC रेखाएँ ΔABD और ΔCDB में खींचे जाने से विकर्ण BD को प्रतिच्छेद करेंगी।
🔵 Step 4: समरूप त्रिभुजों और मध्यबिन्दु प्रमेय से, प्रतिच्छेदन बिन्दु P पर BD बराबर-बराबर दो भागों में विभाजित होगा।
✔️ Final: AF और EC, विकर्ण BD को समद्विभाजित करते हैं।

🔵 Question
Q 6. ABC एक त्रिभुज है जिसमें कोण C समकोण है। कर्ण AB के मध्य-बिन्दु M से होकर BC के समांतर खींची गई रेखा AC को D पर प्रतिच्छेद करती है। दर्शाइए कि
(i) D, AC का मध्य-बिन्दु है।
(ii) MD ⟂ AC है।
(iii) CM = MA = 1/2 AB है।
🟢 Answer
(i)
🔵 Step 1: M, AB का मध्यबिन्दु है।
🔵 Step 2: MD ∥ BC ⇒ ΔABC में मध्यबिन्दु प्रमेय से D, AC का मध्यबिन्दु है।
✔️ Final: D, AC का मध्यबिन्दु है।
(ii)
🔵 Step 1: ∠C = 90° ⇒ AC ⟂ BC.
🔵 Step 2: MD ∥ BC ⇒ MD ⟂ AC.
✔️ Final: MD ⟂ AC.
(iii)
🔵 Step 1: समकोण त्रिभुज में कर्ण का मध्यबिन्दु कर्ण पर खींची गई लम्ब का केन्द्र होता है (वृत्त प्रमेय)।
🔵 Step 2: अतः CM = MA = MB = 1/2 AB.
✔️ Final: CM = MA = 1/2 AB.

————————————————————————————————————————————————————————————————————————————

अन्य महत्वपूर्ण प्रश्न

🔵 Section A (प्रश्न 1–6) — (प्रत्येक 1 अंक)
🔵 प्रश्न 1
चतुर्भुज की परिभाषा लिखिए।
🟢 उत्तर
➡️ चार भुजाओं वाला बन्द बहुभुज चतुर्भुज कहलाता है।

🔵 प्रश्न 2
किसी चतुर्भुज के कोणों का योगफल कितना होता है?
🟢 उत्तर
➡️ किसी भी चतुर्भुज के चारों कोणों का योगफल = 360°

🔵 प्रश्न 3 (MCQ)
यदि किसी चतुर्भुज के विपरीत कोण बराबर हों, तो वह होगा—
🔴 आयत
🟡 समांतर चतुर्भुज
🟢 वर्ग
🔵 समचतुर्भुज
🟢 उत्तर
➡️ सही विकल्प = समांतर चतुर्भुज

🔵 प्रश्न 4
यदि किसी चतुर्भुज के सभी कोण समकोण हों, तो वह कौन-सा चतुर्भुज है?
🟢 उत्तर
➡️ ऐसा चतुर्भुज आयत कहलाता है।

🔵 प्रश्न 5
यदि किसी चतुर्भुज की सभी भुजाएँ बराबर हों और सभी कोण 90° हों, तो वह कौन-सा चतुर्भुज है?
🟢 उत्तर
➡️ ऐसा चतुर्भुज वर्ग कहलाता है।

🔵 प्रश्न 6 (MCQ)
समचतुर्भुज (Rhombus) की दोनों विकर्ण—
🔴 बराबर होते हैं
🟡 एक-दूसरे को समकोण पर प्रतिछेदित करते हैं
🟢 समान्तर होते हैं
🔵 असमान होते हैं
🟢 उत्तर
➡️ सही विकल्प = एक-दूसरे को समकोण पर प्रतिछेदित करते हैं

🟢 Section B (प्रश्न 7–12) — (प्रत्येक 2 अंक)
🟡 प्रश्न 7
किसी समांतर चतुर्भुज की परिभाषा दीजिए।
🟢 उत्तर
➡️ वह चतुर्भुज जिसमें विपरीत भुजाएँ समान्तर हों, समांतर चतुर्भुज कहलाता है।

🟡 प्रश्न 8
आयत और समचतुर्भुज में एक समान गुण लिखिए।
🟢 उत्तर
➡️ दोनों में विपरीत भुजाएँ समान्तर तथा बराबर होती हैं।

🟡 प्रश्न 9 (MCQ)
यदि किसी चतुर्भुज के दोनों विकर्ण बराबर हों और एक-दूसरे को समकोण पर प्रतिछेदित करें, तो वह होगा—
🔴 आयत
🟡 वर्ग
🟢 समचतुर्भुज
🔵 समांतर चतुर्भुज
🟢 उत्तर
➡️ सही विकल्प = वर्ग

🟡 प्रश्न 10
पतंग (Kite) की विशेषता लिखिए।
🟢 उत्तर
➡️ पतंग में दो युग्म समीपवर्ती भुजाएँ बराबर होती हैं।

🟡 प्रश्न 11
एक समांतर चतुर्भुज के कोण A = 70° हैं। शेष कोण ज्ञात कीजिए।
🟢 उत्तर
➡️ समांतर चतुर्भुज में विपरीत कोण बराबर होते हैं और समीपवर्ती कोणों का योग 180° होता है।
➡️ ∠A = 70° ⇒ ∠C = 70°
➡️ ∠B = 180° − 70° = 110° ⇒ ∠D = 110°

🟡 प्रश्न 12 (MCQ)
आयत में विकर्ण—
🔴 बराबर होते हैं और एक-दूसरे को समद्विभाजित करते हैं
🟡 बराबर होते हैं लेकिन प्रतिछेदित नहीं करते
🟢 असमान होते हैं और प्रतिछेदित करते हैं
🔵 असमान होते हैं और समद्विभाजित नहीं करते
🟢 उत्तर
➡️ सही विकल्प = बराबर होते हैं और एक-दूसरे को समद्विभाजित करते हैं

🟡 Section C (प्रश्न 13–22) — (प्रत्येक 3 अंक)
🔵 प्रश्न 13
समांतर चतुर्भुज की दो विशेषताएँ लिखिए।
🟢 उत्तर
➡️ समांतर चतुर्भुज में विपरीत भुजाएँ समान्तर एवं बराबर होती हैं।
➡️ समांतर चतुर्भुज में विपरीत कोण बराबर होते हैं और समीपवर्ती कोणों का योग 180° होता है।

🔵 प्रश्न 14
सिद्ध कीजिए कि किसी समचतुर्भुज की विकर्ण एक-दूसरे को समकोण पर प्रतिछेदित करते हैं।
🟢 उत्तर
✳️ प्रमाण
➡️ समचतुर्भुज ABCD में AB = BC = CD = DA
➡️ विकर्ण AC और BD खींचें जो O पर प्रतिछेद करते हैं।
➡️ △AOB और △COB सर्वांगसम हैं (SSS मापदण्ड से)।
➡️ ∠AOB = ∠COB
➡️ चतुर्भुज के कोणों के गुण से यह कोण 90° सिद्ध होता है।
✔️ अतः विकर्ण एक-दूसरे को समकोण पर प्रतिछेदित करते हैं।

🔵 प्रश्न 15 (MCQ)
यदि किसी आयत की लम्बाई 8 सेमी और चौड़ाई 6 सेमी है, तो उसका क्षेत्रफल होगा—
🔴 12 सेमी²
🟡 24 सेमी²
🟢 48 सेमी²
🔵 64 सेमी²
🟢 उत्तर
➡️ क्षेत्रफल = लम्बाई × चौड़ाई = 8 × 6 = 48 सेमी²
✔️ सही विकल्प = 48 सेमी²

🔵 प्रश्न 16
एक वर्ग का क्षेत्रफल 196 सेमी² है। उसकी भुजा और परिमाप ज्ञात कीजिए।
🟢 उत्तर
➡️ क्षेत्रफल = भुजा²
➡️ भुजा = √196 = 14 सेमी
➡️ परिमाप = 4 × 14 = 56 सेमी

🔵 प्रश्न 17
सिद्ध कीजिए कि यदि किसी चतुर्भुज के विपरीत कोण बराबर हों तो वह समांतर चतुर्भुज है।
🟢 उत्तर
✳️ प्रमाण
➡️ मान लें चतुर्भुज ABCD में ∠A = ∠C और ∠B = ∠D
➡️ कोणों का योगफल 360° ⇒ ∠A + ∠B + ∠C + ∠D = 360°
➡️ ∠A = ∠C और ∠B = ∠D से स्पष्ट है कि विपरीत भुजाएँ समान्तर हो जाती हैं।
✔️ अतः ABCD समांतर चतुर्भुज है।

🔵 प्रश्न 18
एक आयत की लम्बाई उसकी चौड़ाई से 5 सेमी अधिक है। यदि उसका परिमाप 50 सेमी है, तो उसकी लम्बाई और चौड़ाई ज्ञात कीजिए।
🟢 उत्तर
➡️ मान लें चौड़ाई = x सेमी ⇒ लम्बाई = x + 5
➡️ परिमाप = 2(लम्बाई + चौड़ाई) = 50
➡️ 2(x + 5 + x) = 50
➡️ 4x + 10 = 50
➡️ 4x = 40 ⇒ x = 10
➡️ लम्बाई = 10 + 5 = 15
➡️ चौड़ाई = 10
✔️ लम्बाई = 15 सेमी, चौड़ाई = 10 सेमी

🔵 प्रश्न 19 (आन्तरिक विकल्प)
(क) वर्ग और समचतुर्भुज में अन्तर स्पष्ट कीजिए।
या
(ख) सिद्ध कीजिए कि वर्ग एक विशेष आयत है।
🟢 उत्तर
🔸 (क) के लिए
➡️ वर्ग में सभी कोण 90° होते हैं, पर समचतुर्भुज में केवल विपरीत कोण बराबर होते हैं।
➡️ वर्ग में सभी भुजाएँ बराबर और विकर्ण बराबर होते हैं, पर समचतुर्भुज में केवल भुजाएँ बराबर होती हैं।
🔸 (ख) के लिए
➡️ आयत में सभी कोण 90° होते हैं और विपरीत भुजाएँ बराबर होती हैं।
➡️ वर्ग में ये दोनों गुण होते हैं और साथ ही सभी भुजाएँ भी बराबर होती हैं।
✔️ अतः वर्ग आयत का विशेष रूप है।

🔵 प्रश्न 20
एक पतंग के विकर्ण 12 सेमी और 16 सेमी हैं। उसका क्षेत्रफल ज्ञात कीजिए।
🟢 उत्तर
➡️ क्षेत्रफल = (1/2) × d₁ × d₂
➡️ = (1/2) × 12 × 16 = 96 सेमी²

🔵 प्रश्न 21 (MCQ)
यदि किसी समचतुर्भुज की प्रत्येक भुजा 10 सेमी है और एक विकर्ण 16 सेमी है, तो दूसरा विकर्ण होगा—
🔴 12 सेमी
🟡 14 सेमी
🟢 18 सेमी
🔵 20 सेमी
🟢 उत्तर
➡️ समचतुर्भुज में विकर्ण एक-दूसरे को समकोण पर प्रतिछेदित करते हैं।
➡️ आधा विकर्ण₁ = 16/2 = 8
➡️ (10)² = 8² + (d₂/2)²
➡️ 100 = 64 + (d₂²/4)
➡️ d₂²/4 = 36 ⇒ d₂² = 144
➡️ d₂ = 12
✔️ सही विकल्प = 12 सेमी

🔵 प्रश्न 22
एक समांतर चतुर्भुज की भुजाएँ 10 सेमी और 8 सेमी हैं तथा उनमें का कोण 60° है। उसका क्षेत्रफल ज्ञात कीजिए।
🟢 उत्तर
➡️ क्षेत्रफल = भुजा₁ × भुजा₂ × sinθ
➡️ = 10 × 8 × sin60°
➡️ = 80 × (√3/2)
➡️ = 40√3 सेमी²

🔴 Section D (प्रश्न 23–30) — (प्रत्येक 4 अंक)

🔵 प्रश्न 23
सिद्ध कीजिए कि किसी समांतर चतुर्भुज में विकर्ण एक-दूसरे को समद्विभाजित करते हैं।
🟢 उत्तर
✳️ दी गई वस्तुएँ: समांतर चतुर्भुज ABCD में AB ∥ CD तथा BC ∥ AD, विकर्ण AC और BD O पर मिलते हैं।
➡️ ∠ABD = ∠CDB (समान्तर कोण)
➡️ ∠ADB = ∠CBD (समान्तर कोण)
➡️ △ABD ≅ △CDB (A–A–S से)
✔️ AO = OC और BO = OD
✅ इसलिए विकर्ण एक-दूसरे को समद्विभाजित करते हैं।

🔵 प्रश्न 24 (आन्तरिक विकल्प)
(क) सिद्ध कीजिए: यदि चतुर्भुज की दोनों युग्म विपरीत भुजाएँ बराबर हों तो वह समांतर चतुर्भुज है।
या
(ख) सिद्ध कीजिए: यदि चतुर्भुज का एक युग्म विपरीत भुजाएँ समान्तर भी हों और बराबर भी, तो वह समांतर चतुर्भुज है।
🟢 उत्तर
🔸 (क) के लिए
➡️ AB = CD, BC = AD
➡️ △ABC ≅ △CDA (SSS)
➡️ अतः AB ∥ CD और BC ∥ AD
✔️ चतुर्भुज समांतर चतुर्भुज है।
🔸 (ख) के लिए
➡️ AB ∥ CD और AB = CD
➡️ △ABC ≅ △CDA (AA)
➡️ BC = AD
✔️ अतः ABCD समांतर चतुर्भुज है।

🔵 प्रश्न 25
समांतर चतुर्भुज ABCD में ∠A : ∠B = 3 : 2। सभी कोण ज्ञात कीजिए।
🟢 उत्तर
➡️ ∠A + ∠B = 180°
➡️ 3x + 2x = 180 ⇒ 5x = 180 ⇒ x = 36°
➡️ ∠A = 108°, ∠B = 72°
➡️ ∠C = 108°, ∠D = 72°
✔️ अंतिम: 108°, 72°, 108°, 72°

🔵 प्रश्न 26 (आन्तरिक विकल्प)
(क) सिद्ध कीजिए: यदि समांतर चतुर्भुज के विकर्ण बराबर हों तो वह आयत है।
या
(ख) सिद्ध कीजिए: यदि समांतर चतुर्भुज का एक कोण 90° हो तो वह आयत है।
🟢 उत्तर
🔸 (क) के लिए
➡️ AC = BD, △ABC ≅ △BAD
➡️ ∠ABC = ∠BAD = 90°
✔️ सभी कोण समकोण ⇒ आयत
🔸 (ख) के लिए
➡️ ∠A = 90°
➡️ समीपवर्ती कोण 180° ⇒ ∠B = 90°, ∠C = 90°, ∠D = 90°
✔️ चतुर्भुज आयत है।

🔵 प्रश्न 27
सिद्ध कीजिए: समचतुर्भुज में विकर्ण एक-दूसरे के लंब समद्विभाजक होते हैं और कोणों का समद्विभाजन भी करते हैं।
🟢 उत्तर
➡️ △AOB ≅ △COB (SSS) ⇒ AO = OC, BO = OD
➡️ ∠AOB = ∠COB
➡️ इसी प्रकार △AOD ≅ △COD
✔️ विकर्ण एक-दूसरे को समद्विभाजित करते हैं और ∠AOB = 90° ⇒ लंब हैं
✔️ साथ ही, ये कोणों को बराबर बाँटते हैं ⇒ कोण समद्विभाजक।

🔵 प्रश्न 28
एक समचतुर्भुज की प्रत्येक भुजा 13 सेमी है और एक विकर्ण 10 सेमी है। दूसरा विकर्ण और क्षेत्रफल ज्ञात कीजिए।
🟢 उत्तर
➡️ d₁ = 10 ⇒ d₁/2 = 5
➡️ x² + 5² = 13² ⇒ x² + 25 = 169 ⇒ x² = 144 ⇒ x = 12
➡️ d₂ = 24
➡️ क्षेत्रफल = ½ × d₁ × d₂ = ½ × 10 × 24 = 120
✔️ दूसरा विकर्ण = 24 सेमी, क्षेत्रफल = 120 सेमी²

🔵 प्रश्न 29 (आन्तरिक विकल्प)
(क) आयत की लम्बाई 12 सेमी और चौड़ाई 5 सेमी है। उसका विकर्ण ज्ञात कीजिए और जाँचिए।
या
(ख) समांतर चतुर्भुज की भुजाएँ 12 सेमी और 9 सेमी हैं, इनके बीच का कोण 60° है। क्षेत्रफल ज्ञात कीजिए।
🟢 उत्तर
🔸 (क) के लिए
➡️ विकर्ण = √(12² + 5²) = √169 = 13 सेमी
✔️ दोनों विकर्ण बराबर = 13 सेमी
🔸 (ख) के लिए
➡️ क्षेत्रफल = 12 × 9 × sin60° = 108 × √3/2 = 54√3 सेमी²

🔵 प्रश्न 30
सिद्ध कीजिए कि किसी समांतर चतुर्भुज के विकर्ण उसे चार समक्षेत्र त्रिभुजों में विभाजित करते हैं।
🟢 उत्तर
➡️ AO = OC और BO = OD
➡️ △AOB ≅ △COD (SAS) ⇒ क्षेत्रफल बराबर
➡️ △BOC ≅ △DOA (SAS) ⇒ क्षेत्रफल बराबर
✔️ अतः चारों त्रिभुज AOB, BOC, COD, DOA समक्षेत्र हैं।

————————————————————————————————————————————————————————————————————————————

मानचित्र

————————————————————————————————————————————————————————————————————————————