Class : 9 – Math (Hindi) : Lesson 7. त्रिभुज

पाठ का विश्लेषण  एवं  विवेचन

✨ विस्तृत व्याख्या
🔵 भूमिका
त्रिभुज ज्यामिति का सबसे आधारभूत और महत्त्वपूर्ण बहुभुज है। यह तीन भुजाओं, तीन शीर्षों और तीन कोणों से मिलकर बनता है। चाहे वास्तुकला हो, कला हो या गणना, त्रिभुज हर जगह दिखाई देता है। यही कारण है कि इसे ज्यामिति का मूल निर्माण खंड कहा जाता है।

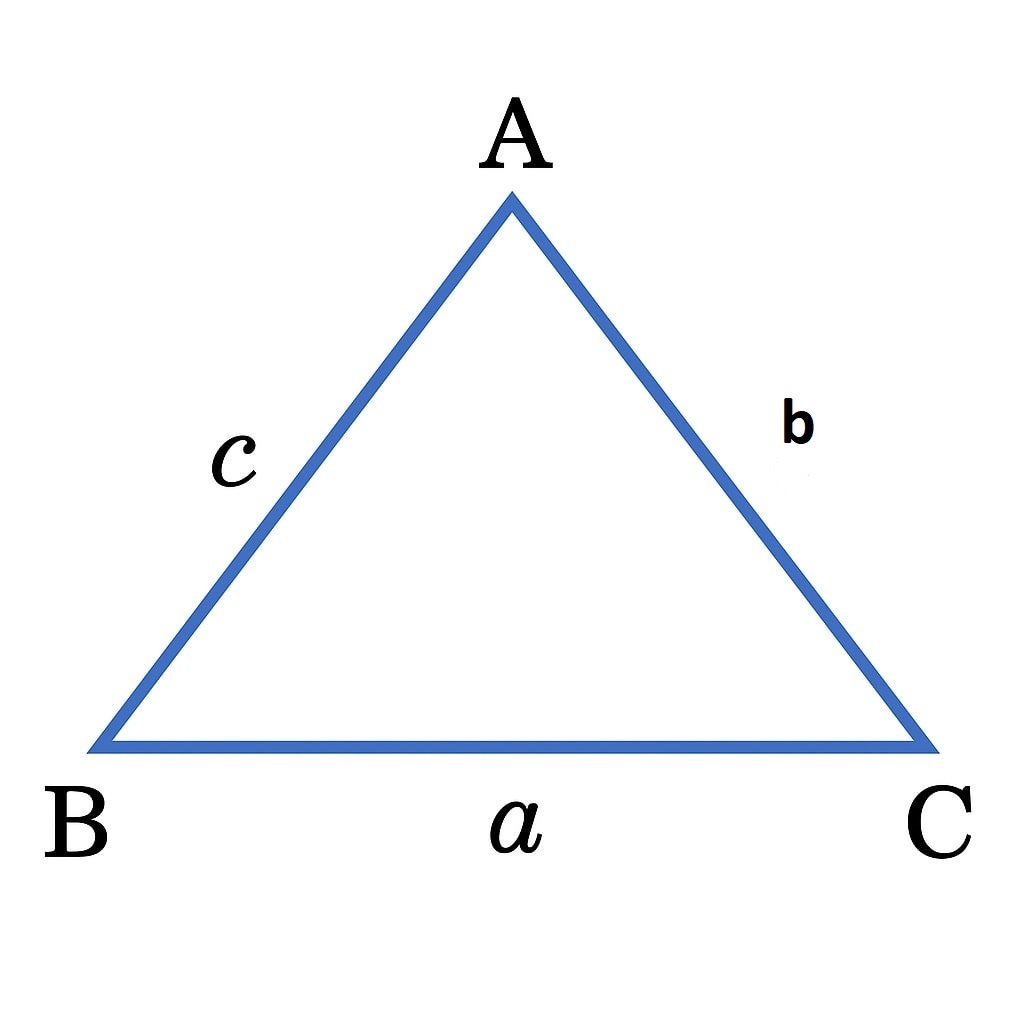
🟢 त्रिभुज की परिभाषा
त्रिभुज वह आकृति है जो तीन रेखाखंडों द्वारा बनी हो और जिनके तीनों छोर आपस में जुड़कर तीन शीर्ष बनाते हों।
शीर्ष (Vertices) = A, B, C
भुजाएँ (Sides) = AB, BC, CA
कोण (Angles) = ∠A, ∠B, ∠C
💡 Concept: किसी त्रिभुज के तीनों कोणों का योग हमेशा 180° होता है।

🔴 त्रिभुज के प्रकार
भुजाओं के आधार पर
समबाहु त्रिभुज (Equilateral) → तीनों भुजाएँ बराबर।
समद्विबाहु त्रिभुज (Isosceles) → दो भुजाएँ बराबर।
विषमबाहु त्रिभुज (Scalene) → कोई भी भुजा बराबर नहीं।
कोणों के आधार पर
न्यूनकोण त्रिभुज → सभी कोण < 90°
अधिककोण त्रिभुज → एक कोण > 90°
समकोण त्रिभुज → एक कोण = 90°
✏️ Note: समबाहु त्रिभुज का प्रत्येक कोण 60° होता है।

🟡 त्रिभुज की असमानता (Triangle Inequality)
किसी भी त्रिभुज में:
किसी दो भुजाओं का योग तीसरी भुजा से बड़ा होता है।
किसी दो भुजाओं का अन्तर तीसरी भुजा से छोटा होता है।
✔️ यह शर्त त्रिभुज बनने के लिए आवश्यक है।

🔵 त्रिभुज के महत्वपूर्ण प्रमेय
कोण सम प्रमेय
किसी त्रिभुज के तीनों कोणों का योग = 180°
बाह्य कोण प्रमेय
किसी त्रिभुज का बाह्य कोण = विपरीत दो आंतरिक कोणों के योग के बराबर।
समद्विबाहु त्रिभुज प्रमेय
यदि किसी त्रिभुज की दो भुजाएँ बराबर हों, तो उनके सामने के कोण भी बराबर होंगे।
विपरीत कोण प्रमेय
यदि किसी त्रिभुज के दो कोण बराबर हों, तो उनके सामने की भुजाएँ भी बराबर होती हैं।

🟢 सर्वांगसमता (Congruence of Triangles)
🔵 परिभाषा
दो त्रिभुज सर्वांगसम (Congruent) तब कहलाते हैं जब उनकी भुजाएँ और कोण पूरी तरह समान हों।
यदि ∆ABC और ∆DEF सर्वांगसम हैं, तो हम लिखते हैं:
∆ABC ≅ ∆DEF
इस स्थिति में:
AB = DE
BC = EF
AC = DF
∠A = ∠D
∠B = ∠E
∠C = ∠F
✏️ Note: सर्वांगसम आकृतियाँ आकार और परिमाण दोनों में समान होती हैं।

🟢 सर्वांगसमता के मानदंड (Criteria for Congruence)
युक्लिड की ज्यामिति के अनुसार त्रिभुज की सर्वांगसमता सिद्ध करने के चार मुख्य मानदंड हैं:
SSS (Side-Side-Side)
यदि किसी त्रिभुज की तीनों भुजाएँ दूसरे त्रिभुज की तीनों भुजाओं के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होंगे।
उदाहरण: दो समान डंडियों से बना त्रिभुज दूसरे के समान होगा।

SAS (Side-Angle-Side)
यदि एक त्रिभुज की दो भुजाएँ और बीच का कोण दूसरे त्रिभुज की दो भुजाओं और बीच के कोण के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होंगे।
उदाहरण: घर की छत के दो समान त्रिकोणीय टुकड़े।

ASA (Angle-Side-Angle)
यदि एक त्रिभुज के दो कोण और बीच की भुजा दूसरे त्रिभुज के दो कोण और बीच की भुजा के बराबर हों, तो दोनों सर्वांगसम होंगे।

RHS (Right angle-Hypotenuse-Side)
समकोण त्रिभुजों के लिए।
यदि एक त्रिभुज का समकोण, कर्ण (Hypotenuse) और एक भुजा दूसरे त्रिभुज के समकोण, कर्ण और उसी भुजा के बराबर हों, तो दोनों सर्वांगसम होंगे।
💡 Concept: RHS मानदंड केवल समकोण त्रिभुजों के लिए लागू होता है।

🔴 सर्वांगसमता का महत्व
सर्वांगसमता का प्रयोग करके हम सिद्ध करते हैं कि दो आकृतियाँ समान और बराबर हैं।
चतुर्भुज, समांतर चतुर्भुज और वृत्त से जुड़ी समस्याओं को हल करने में यह आधार प्रदान करता है।
वास्तुकला और इंजीनियरिंग में दो टुकड़ों की समानता जाँचने में।

🟡 वास्तविक जीवन के उदाहरण
मशीनों में पेंच और पुर्ज़ों की समानता।
पुलों के ढाँचे में समान त्रिभुज।
टाइल्स बिछाने में समानता का उपयोग।
दो समान दरवाज़ों के पल्ले त्रिभुजों की सर्वांगसमता पर आधारित होते हैं।

🌿 प्रमेय आधारित अनुप्रयोग
प्रमेय: यदि दो भुजाएँ और उनके बीच का कोण दूसरे त्रिभुज के बराबर हों (SAS), तो त्रिभुज सर्वांगसम होंगे।
👉 प्रमाण इस प्रकार दिया जाता है कि दोनों त्रिभुजों को एक-दूसरे पर रखने पर सभी भुजाएँ और कोण समान मिलते हैं।

✔️ सार:
सर्वांगसमता से यह स्पष्ट होता है कि त्रिभुज केवल आकृति में समान नहीं बल्कि माप में भी पूरी तरह समान हो सकते हैं।
SSS, SAS, ASA और RHS मानदंड इस अध्याय के सबसे महत्वपूर्ण सूत्र और तर्क हैं।

🔴 समानता (Similarity of Triangles)
दो त्रिभुज समान (Similar) तब होते हैं जब उनके:
सभी कोण बराबर हों और
भुजाओं का अनुपात समान हो।
मानदंड:
AAA → तीन कोण बराबर।
SSS → भुजाएँ समान अनुपात में।
SAS → दो भुजाओं का अनुपात और बीच का कोण बराबर।
💡 Concept: समान त्रिभुजों में भुजाओं का अनुपात = ऊँचाइयों का अनुपात = माध्यिकाओं का अनुपात।

🟡 विशेष परिणाम
समबाहु त्रिभुज में ऊँचाई, माध्यिका और कोण द्विभाजक एक ही होती है।
समकोण त्रिभुज में पायथागोरस प्रमेय लागू होता है:
a² + b² = c² (जहाँ c कर्ण है)।
✏️ Note: यह प्रमेय प्राचीन भारत के गणितज्ञ बौधायन ने भी दिया था।

🌿 व्यावहारिक अनुप्रयोग
वास्तुकला और इंजीनियरिंग में पुल, भवन और टॉवर।
त्रिकोणमिति का आधार।
नक्शानवीसी और भूमि मापन में प्रयोग।
विज्ञान और तकनीक में सर्वांगसमता व समानता का प्रयोग।

⚡ अध्याय का शैक्षिक महत्व
यह अध्याय विद्यार्थियों को तर्क, प्रमाण, सर्वांगसमता और समानता की शक्ति सिखाता है।
आगे चलकर त्रिकोणमिति, वृत्त और निर्देशांक ज्यामिति में यही आधार प्रयोग होता है।

📌 Summary (~300 words)
त्रिभुज की मूल बातें
तीन भुजाओं, तीन शीर्षों और तीन कोणों वाली आकृति।
कोणों का योग = 180°।
प्रकार
भुजाओं के आधार पर: समबाहु, समद्विबाहु, विषमबाहु।
कोणों के आधार पर: न्यूनकोण, अधिककोण, समकोण।
प्रमेय
बाह्य कोण = विपरीत आंतरिक कोणों का योग।
समद्विबाहु त्रिभुज में सामने के कोण बराबर।
सर्वांगसमता
SSS, SAS, ASA, RHS मानदंड।
समानता
AAA, SSS, SAS मानदंड।
समान त्रिभुजों में अनुपात की समानता।
अनुप्रयोग
वास्तुकला, इंजीनियरिंग, त्रिकोणमिति और भूमि मापन में प्रयोग।
✔️ यह अध्याय विद्यार्थियों की तार्किक क्षमता और गणितीय प्रमाण की समझ को मजबूत करता है।

📝 Quick Recap
🔵 त्रिभुज = 3 भुजाएँ + 3 कोण + 3 शीर्ष।
🟢 कोणों का योग = 180°।
🟡 सर्वांगसमता मानदंड: SSS, SAS, ASA, RHS।
🔴 समानता मानदंड: AAA, SSS, SAS।
🌿 बाह्य कोण प्रमेय और त्रिभुज असमानता प्रमेय अत्यंत महत्त्वपूर्ण।

————————————————————————————————————————————————————————————————————————————

पाठ्यपुस्तक के प्रश्न

प्रश्नावली 7.1

🔵 प्रश्न 1
चतुर्भुज ACBD में, AC = AD है और AB कोण A को समद्विभाजित करता है (आकृति 7.16)।
इसीलिए सिद्ध कीजिए कि △ABC ≅ △ABD है।
BC और BD के बारे में आप क्या कह सकते हैं?
🟢 उत्तर
🔵 चरण 1: दिया है AC = AD (निर्दिष्ट)।
🔵 चरण 2: ∠CAB = ∠DAB (AB, ∠A का समद्विभाजक है)।
🔵 चरण 3: AB = AB (सामान्य भुजा)।
🔵 चरण 4: अतः △ABC ≅ △ABD (SAS कसौटी से)।
🔵 चरण 5: संगति से BC = BD (समानानुरूप भुजाएँ)।
✔️ Final: △ABC ≅ △ABD तथा BC = BD।

🔵 प्रश्न 2
ABCD एक चतुर्भुज है, जिसमें AD = BC और ∠DAB = ∠CBA हैं (आकृति 7.17)। सिद्ध कीजिए:
(i) △ABD ≅ △BAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC
🟢 उत्तर
🔵 चरण 1: दिया है AD = BC और ∠DAB = ∠CBA।
🔵 चरण 2: AB = AB (सामान्य भुजा)।
🔵 चरण 3: अतः △ABD ≅ △BAC (SAS कसौटी से) → (i) सिद्ध।
🔵 चरण 4: संगति से BD = AC (अनुरूप भुजाएँ बराबर) → (ii) सिद्ध।
🔵 चरण 5: संगति से ∠ABD = ∠BAC (अनुरूप कोण बराबर) → (iii) सिद्ध।
✔️ Final: सभी (i), (ii), (iii) सिद्ध।

🔵 प्रश्न 3
एक रेखाखंड AB पर AD और BC दो बराबर लंब रेखाखंड हैं (आकृति 7.18)।
सिद्ध कीजिए कि CD, रेखाखंड AB को समद्विभाजित करता है।
🟢 उत्तर
🔵 चरण 1: दिया है AD = BC और ∠DAB = ∠CBA = 90°।
🔵 चरण 2: AB = AB (सामान्य भुजा)।
🔵 चरण 3: अतः △DAB ≅ △CBA (RHS कसौटी से)।
🔵 चरण 4: संगति से ∠DAO = ∠CBO और AO = BO (O, AB पर प्रतिच्छेद बिंदु)।
🔵 चरण 5: AO = BO ⇒ O, AB का मध्यबिंदु।
✔️ Final: CD, AB को समद्विभाजित करता है।

🔵 प्रश्न 4
l और m दो समान्तर रेखाएँ हैं जिन्हें समान्तर रेखाएँ p और q का एक अन्य युग्म प्रतिच्छेद करता है (आकृति 7.19)।
सिद्ध कीजिए कि △ABC ≅ △CDA।
🟢 उत्तर
🔵 चरण 1: दिया है l ∥ m और p ∥ q।
🔵 चरण 2: समान्तर रेखाओं से ∠ABC = ∠CDA (समतुल्य कोण)।
🔵 चरण 3: ∠BAC = ∠DCA (समतुल्य कोण)।
🔵 चरण 4: AC = AC (सामान्य भुजा)।
🔵 चरण 5: अतः △ABC ≅ △CDA (ASA कसौटी से)।
✔️ Final: △ABC ≅ △CDA।

✏️ Note: त्रिभुज सर्वांगसमता सिद्ध करने की मुख्य कसौटियाँ — SSS, SAS, ASA, RHS।
💡 Concept: सर्वांगसम त्रिभुजों में अनुरूप भुजाएँ बराबर और अनुरूप कोण बराबर होते हैं।

🔵 प्रश्न 5
रेखा कोण A को समद्विभाजित करती है और B रेखा l पर स्थित कोई बिंदु है। BP और BQ कोण A की भुजाओं पर B से डाले गए लंब हैं (आकृति 7.20)। सिद्ध कीजिए कि:
(i) △APB ≅ △AQB
(ii) BP = BQ, अर्थात् बिंदु B कोण की भुजाओं से समदूरस्थ है।
🟢 उत्तर
🔵 चरण 1: दिया है AP ⟂ BP और AQ ⟂ BQ।
🔵 चरण 2: AB = AB (सामान्य भुजा)।
🔵 चरण 3: ∠PBA = ∠QBA = 90°।
🔵 चरण 4: ∠BAP = ∠BAQ (रेखा कोण A का समद्विभाजक है)।
🔵 चरण 5: अतः △APB ≅ △AQB (ASA कसौटी से)।
🔵 चरण 6: संगति से BP = BQ।
✔️ Final: (i) △APB ≅ △AQB, (ii) BP = BQ।

🔵 प्रश्न 6
आकृति 7.21 में, AC = AE, AB = AD और ∠BAD = ∠EAC है। सिद्ध कीजिए कि BC = DE।
🟢 उत्तर
🔵 चरण 1: दिया है AC = AE, AB = AD।
🔵 चरण 2: ∠BAD = ∠EAC।
🔵 चरण 3: अतः △BAD ≅ △EAC (SAS कसौटी से)।
🔵 चरण 4: संगति से BC = DE।
✔️ Final: BC = DE।

🔵 प्रश्न 7
AB एक रेखाखंड है और P इसका मध्य-बिंदु है। D और E, AB के एक ही ओर स्थित बिंदु हैं इस प्रकार कि ∠BAD = ∠ABE और ∠EPA = ∠DPB हैं (आकृति 7.22)। सिद्ध कीजिए कि:
(i) △DAP ≅ △EBP
(ii) AD = BE
🟢 उत्तर
🔵 चरण 1: दिया है AP = PB (P मध्य-बिंदु है)।
🔵 चरण 2: ∠DAP = ∠EBP (दिया है)।
🔵 चरण 3: ∠EPA = ∠DPB (दिया है)।
🔵 चरण 4: अतः △DAP ≅ △EBP (ASA कसौटी से)।
🔵 चरण 5: संगति से AD = BE।
✔️ Final: (i) △DAP ≅ △EBP, (ii) AD = BE।

🔵 प्रश्न 8
एक समकोण त्रिभुज ABC में, जिसमें कोण C समकोण है, M कर्ण AB का मध्य-बिंदु है। C को M से मिलाकर D तक इस प्रकार बढ़ाया गया है कि DM = CM है। बिंदु D को बिंदु B से मिलाया जाता है (आकृति 7.23)। सिद्ध कीजिए कि:
(i) △AMC ≅ △BMD
(ii) ∠DBC एक समकोण है
(iii) △DBC ≅ △ACB
(iv) CM = 1/2 AB
🟢 उत्तर
(i) △AMC ≅ △BMD
🔵 चरण 1: M, AB का मध्य-बिंदु ⇒ AM = MB।
🔵 चरण 2: CM = DM (दिया है)।
🔵 चरण 3: ∠AMC = ∠BMD (विकल्प आन्तरिक कोण)।
🔵 चरण 4: अतः △AMC ≅ △BMD (SAS कसौटी से)।
(ii) ∠DBC एक समकोण है
🔵 चरण 1: △AMC ≅ △BMD से ∠AMC = ∠BMD।
🔵 चरण 2: ∠AMC = 90° (क्योंकि △ABC में ∠C = 90° और M मध्य-बिंदु है, CM लम्बवत है)।
🔵 चरण 3: अतः ∠BMD = 90°।
🔵 चरण 4: BD, CM की बढ़ाई हुई रेखा है ⇒ ∠DBC = 90°।
(iii) △DBC ≅ △ACB
🔵 चरण 1: ∠DBC = 90° और ∠ACB = 90°।
🔵 चरण 2: BC = BC (सामान्य भुजा)।
🔵 चरण 3: ∠DBC = ∠ACB और BD = AC (संगति से)।
🔵 चरण 4: अतः △DBC ≅ △ACB (RHS कसौटी से)।
(iv) CM = 1/2 AB
🔵 चरण 1: M, AB का मध्य-बिंदु ⇒ AM = MB = 1/2 AB।
🔵 चरण 2: CM = DM (दिया है)।
🔵 चरण 3: △AMC ≅ △BMD से CM = AM।
🔵 चरण 4: अतः CM = 1/2 AB।
✔️ Final: सभी (i) से (iv) सिद्ध।

✏️ Note: मध्य-बिंदु और समद्विभाजक का प्रयोग सर्वांगसम त्रिभुज सिद्ध करने में प्रमुख है।
💡 Concept: यदि दो त्रिभुज सर्वांगसम हैं, तो उनकी अनुरूप भुजाएँ और कोण बराबर होते हैं।

प्रश्नावली 7.2

🔵 प्रश्न 1
एक समद्विबाहु त्रिभुज ABC में जिसमें AB = AC है, ∠B और ∠C के समद्विभाजक परस्पर बिंदु O पर प्रतिच्छेद करते हैं। A और O को जोड़िए। दर्शाइए कि
(i) OB = OC
(ii) AO कोण A को समद्विभाजित करता है।
🟢 उत्तर
🔵 चरण 1: AB = AC ⇒ ∠B = ∠C।
🔵 चरण 2: BO और CO क्रमशः ∠B और ∠C के समद्विभाजक हैं।
🔵 चरण 3: अतः ∠OBC = ∠BCO।
🔵 चरण 4: ∴ △BOC समद्विबाहु है ⇒ OB = OC।
🔵 चरण 5: △AOB और △AOC में AB = AC, OB = OC, AO = AO।
🔵 चरण 6: अतः △AOB ≅ △AOC (SSS कसौटी से)।
🔵 चरण 7: संगति से ∠BAO = ∠CAO ⇒ AO, ∠A का समद्विभाजक।
✔️ Final: (i) OB = OC, (ii) AO कोण A को समद्विभाजित करता है।

🔵 प्रश्न 2
ΔABC में AD भुजा BC का लम्ब समद्विभाजक है (आकृति 7.30)। दर्शाइए कि ΔABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है।
🟢 उत्तर
🔵 चरण 1: AD ⟂ BC और D, BC का मध्य-बिंदु है।
🔵 चरण 2: लम्ब समद्विभाजक पर स्थित कोई भी बिंदु B और C से समदूरस्थ होता है।
🔵 चरण 3: A, AD पर है ⇒ AB = AC।
✔️ Final: ΔABC समद्विबाहु है तथा AB = AC।

🔵 प्रश्न 3
ABC एक समद्विबाहु त्रिभुज है, जिसमें बराबर भुजाओं AC और AB पर क्रमशः लम्ब BE और CF खींचे गए हैं (आकृति 7.31)। दर्शाइए कि ये लम्ब बराबर हैं।
🟢 उत्तर
🔵 चरण 1: ΔABC का क्षेत्रफल = 1/2 × AC × BE।
🔵 चरण 2: ΔABC का क्षेत्रफल = 1/2 × AB × CF।
🔵 चरण 3: चूँकि AB = AC (समद्विबाहु) ⇒ 1/2 × AC × BE = 1/2 × AB × CF।
🔵 चरण 4: ⇒ BE = CF।
✔️ Final: BE = CF।

🔵 प्रश्न 4
ABC एक त्रिभुज है जिसमें AC और AB पर खींचे गए लम्ब BE और CF बराबर हैं (आकृति 7.32)। दर्शाइए कि
(i) △ABE ≅ △ACF
(ii) AB = AC, अर्थात् ΔABC एक समद्विबाहु त्रिभुज है।
🟢 उत्तर
🔵 चरण 1: ∠ABE = ∠ACF = 90°।
🔵 चरण 2: ∠BAE = ∠CAF (सामान्य ∠A)।
🔵 चरण 3: BE = CF (दिया है)।
🔵 चरण 4: अतः △ABE ≅ △ACF (AAS कसौटी से)।
🔵 चरण 5: संगति से AB = AC।
✔️ Final: (i) △ABE ≅ △ACF, (ii) AB = AC ⇒ ΔABC समद्विबाहु।

✏️ Note:
समद्विबाहु त्रिभुज में आधार कोण बराबर होते हैं।
लम्ब समद्विभाजक पर स्थित बिंदु आधार के सिरों से समदूरस्थ होता है।
💡 Concept: सर्वांगसमता से अनुरूप भुजाएँ और कोण बराबर होते हैं।

🔵 Question
Q 5. ABC और DBC समान आधार BC पर स्थित दो समद्विबाहु त्रिभुज हैं (देखिए आकृति 7.33)। दर्शाइए कि ∠ABD = ∠ACD है।

🟢 Answer
💡 अवधारणा: समद्विबाहु त्रिभुज में आधार के दोनों कोण बराबर होते हैं।
🔵 Step 1: ΔABC समद्विबाहु है ⇒ AB = AC ⇒ ∠ABC = ∠ACB.
🔵 Step 2: ΔDBC समद्विबाहु है ⇒ DB = DC ⇒ ∠DBC = ∠BCD.
🔵 Step 3: कोण योग के रूप में लिखें: ∠ABD = ∠ABC + ∠CBD और ∠ACD = ∠ACB + ∠BCD.
🔵 Step 4: क्योंकि ∠CBD और ∠DBC समान कोण हैं, तथा ∠ABC = ∠ACB और ∠DBC = ∠BCD,
➡️ अतः ∠ABD = ∠ACB + ∠BCD = ∠ACD.
✔️ Final: ∠ABD = ∠ACD.

🔵 Question
Q 6. ABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है। भुजा BA बिंदु D तक इस प्रकार बढ़ाई गई है कि AD = AB है (देखिए आकृति 7.34)। दर्शाइए कि ∠BCD एक समकोण है।

🟢 Answer
💡 अवधारणा: समद्विबाहु त्रिभुज में शीर्ष कोण α हो तो आधार कोण (180° − α)/2 होते हैं। यदि AD = AB और AB = AC, तो ΔACD भी समद्विबाहु होगा (AC = AD)।
🔵 Step 1: मान लें ∠CAB = α. क्योंकि AB = AC, इसलिए ∠ABC = ∠BCA = (180° − α)/2.
🔵 Step 2: AD = AB तथा AB = AC ⇒ AD = AC, अतः ΔACD समद्विबाहु है ⇒ ∠ACD = ∠CDA.
🔵 Step 3: ΔACD में कोणों का योग: ∠CAD + ∠ACD + ∠CDA = 180°.
🔵 Step 4: BA का D तक विस्तार होने से ∠CAD = 180° − ∠CAB = 180° − α.
🔵 Step 5: ∠ACD = ∠CDA = y मानें, तब 180° − α + y + y = 180° ⇒ 2y = α ⇒ y = α/2.
🔵 Step 6: अब ∠BCD = ∠BCA + ∠ACD = (180° − α)/2 + α/2.
🔵 Step 7: उपर्युक्त जोड़: (180° − α)/2 + α/2 = 180°/2 = 90°.
✔️ Final: ∠BCD = 90°, अर्थात ∠BCD समकोण है।

🔵 Question
Q 7. ABC एक समकोण त्रिभुज है, जिसमें ∠A = 90° और AB = AC है। ∠B और ∠C ज्ञात कीजिए।

🟢 Answer
💡 अवधारणा: समकोण त्रिभुज में तीक्ष्ण कोणों का योग 90° होता है, और यदि दोनों लम्ब भुजाएँ बराबर हों तो दोनों तीक्ष्ण कोण बराबर होते हैं।
🔵 Step 1: ∠A = 90° दिए होने से ∠B + ∠C = 90°.
🔵 Step 2: AB = AC ⇒ ΔABC समद्विबाहु (आधार BC) ⇒ ∠B = ∠C.
🔵 Step 3: अतः ∠B = ∠C = 90°/2.
✔️ Final: ∠B = 45° और ∠C = 45°.

🔵 Question
Q 8. दर्शाइए कि किसी समबाहु त्रिभुज का प्रत्येक कोण 60° होता है।

🟢 Answer
💡 अवधारणा: समबाहु त्रिभुज में तीनों भुजाएँ समान होती हैं, अतः तीनों कोण भी समान होते हैं, और त्रिभुज के तीनों कोणों का योग 180° होता है।
🔵 Step 1: समबाहु त्रिभुज में AB = BC = CA ⇒ ∠A = ∠B = ∠C.
🔵 Step 2: त्रिभुज कोण योग: ∠A + ∠B + ∠C = 180°.
🔵 Step 3: समान होने से 3∠A = 180°.
🔵 Step 4: ∠A = 180°/3 = 60°.
🔵 Step 5: इसी प्रकार ∠B = 60° और ∠C = 60°.
✔️ Final: प्रत्येक कोण 60° होता है।

प्रश्नावली 7.3

🔵 Question
Q 1. ΔABC और ΔDBC एक ही आधार BC पर बने दो समद्विबाहु त्रिभुज इस प्रकार हैं कि A और D भुजा BC के एक ही ओर स्थित हैं (देखिए आकृति 7.39)। यदि AD बढ़ाने पर BC को P पर प्रतिच्छेद करे, तो दर्शाइए कि
(i) ΔABD ≅ ΔACD
(ii) ΔABP ≅ ΔACP
(iii) AP कोण A और कोण D दोनों को समद्विभाजित करता है।
(iv) AP खंड BC का लम्ब समद्विभाजक है।
🟢 Answer
💡 अवधारणा: समद्विबाहु त्रिभुज में आधार के कोण बराबर होते हैं और सर्वांगसमता प्रमेयों का प्रयोग किया जाता है।
(i)
🔵 Step 1: ΔABC और ΔDBC समद्विबाहु हैं ⇒ AB = AC और DB = DC.
🔵 Step 2: साथ ही, BC सामान्य भुजा है।
🔵 Step 3: अतः ΔABD ≅ ΔACD (SSS सर्वांगसमता से)।
(ii)
🔵 Step 1: ΔABD ≅ ΔACD ⇒ ∠ABD = ∠ACD तथा AD = AD (साझा भुजा)।
🔵 Step 2: ⇒ ΔABP ≅ ΔACP (ASA सर्वांगसमता से)।
(iii)
🔵 Step 1: ΔABP ≅ ΔACP ⇒ ∠BAP = ∠CAP.
🔵 Step 2: इसी प्रकार ΔABD ≅ ΔACD ⇒ ∠BAD = ∠CAD.
🔵 Step 3: अतः AP, ∠A और ∠D दोनों को समद्विभाजित करता है।
(iv)
🔵 Step 1: ΔABP ≅ ΔACP ⇒ BP = CP.
🔵 Step 2: और ∠APB = ∠APC ⇒ प्रत्येक = 90°.
✔️ Final: AP, BC का लम्ब समद्विभाजक है।

🔵 Question
Q 2. AD एक समद्विबाहु त्रिभुज ABC का एक शीर्षलम्ब है, जिसमें AB = AC है। दर्शाइए कि
(i) AD रेखाखंड BC को समद्विभाजित करता है।
(ii) AD कोण A को समद्विभाजित करता है।
🟢 Answer
(i)
🔵 Step 1: ΔABD और ΔACD पर विचार करें।
🔵 Step 2: AB = AC (दिया गया), ∠ADB = ∠ADC = 90°, और AD = AD (साझा)।
🔵 Step 3: अतः ΔABD ≅ ΔACD (RHS सर्वांगसमता से)।
🔵 Step 4: ⇒ BD = DC.
✔️ Final: AD, BC को समद्विभाजित करता है।
(ii)
🔵 Step 1: ΔABD ≅ ΔACD से ∠BAD = ∠CAD.
✔️ Final: AD, ∠A को समद्विभाजित करता है।

🔵 Question
Q 3. एक त्रिभुज ABC की दो भुजाएँ AB और BC तथा माध्यिका AM क्रमशः एक दूसरे त्रिभुज की भुजाएँ PQ और QR तथा माध्यिका PN के बराबर हैं (देखिए आकृति 7.40)। दर्शाइए कि
(i) ΔABM ≅ ΔPQN
(ii) ΔABC ≅ ΔPQR
🟢 Answer
(i)
🔵 Step 1: AB = PQ, BC = QR और AM = PN (दिया गया)।
🔵 Step 2: माध्यिका होने से M और N क्रमशः BC तथा QR के मध्यबिंदु हैं।
🔵 Step 3: अतः BM = QN.
🔵 Step 4: ΔABM और ΔPQN में, AB = PQ, BM = QN, AM = PN.
🔵 Step 5: ⇒ ΔABM ≅ ΔPQN (SSS सर्वांगसमता से)।
(ii)
🔵 Step 1: ΔABM ≅ ΔPQN ⇒ ∠AMB = ∠PNQ और ∠ABM = ∠PQN.
🔵 Step 2: इसी प्रकार AC = PR (क्योंकि माध्यिका के आधार पर संबंध निकलता है)।
🔵 Step 3: अतः ΔABC ≅ ΔPQR (SAS सर्वांगसमता से)।
✔️ Final: दोनों त्रिभुज सर्वांगसम हैं।

🔵 Question
Q 4. BE और CF एक त्रिभुज ABC के दो बराबर शीर्षलम्ब हैं। RHS सर्वांगसमता नियम का प्रयोग करके सिद्ध कीजिए कि ΔABC एक समद्विबाहु त्रिभुज है।
🟢 Answer
🔵 Step 1: BE और CF शीर्षलम्ब हैं ⇒ ∠BEB = ∠CFC = 90°.
🔵 Step 2: दिया गया है कि BE = CF.
🔵 Step 3: ΔBCE और ΔCBF पर विचार करें।
🔵 Step 4: BC = BC (साझा भुजा), BE = CF (दिया गया), ∠BEC = ∠CFB = 90°.
🔵 Step 5: ⇒ ΔBCE ≅ ΔCBF (RHS सर्वांगसमता से)।
🔵 Step 6: अतः ∠C = ∠B और AC = AB.
✔️ Final: ΔABC समद्विबाहु है।

🔵 Question
Q 5. ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है। यदि AP ⊥ BC खींचा जाए, तो दर्शाइए कि ∠B = ∠C है।
🟢 Answer
🔵 Step 1: ΔABP और ΔACP पर विचार करें।
🔵 Step 2: AB = AC (दिया गया), ∠APB = ∠APC = 90°, और AP = AP (साझा भुजा)।
🔵 Step 3: अतः ΔABP ≅ ΔACP (RHS सर्वांगसमता से)।
🔵 Step 4: ⇒ ∠B = ∠C.
✔️ Final: ∠B और ∠C बराबर हैं।

————————————————————————————————————————————————————————————————————————————

अन्य महत्वपूर्ण प्रश्न

🔵 Section A (प्रश्न 1–6) — (प्रत्येक 1 अंक)
🔵 प्रश्न 1
त्रिभुज की परिभाषा लिखिए।
🟢 उत्तर
➡️ तीन भुजाओं और तीन कोणों वाला बन्द बहुभुज त्रिभुज कहलाता है।

🔵 प्रश्न 2
त्रिभुज के कोणों का योगफल कितना होता है?
🟢 उत्तर
➡️ किसी भी त्रिभुज के तीनों कोणों का योगफल = 180°

🔵 प्रश्न 3 (MCQ)
यदि किसी त्रिभुज की भुजाएँ 5, 12 और 13 हों, तो वह त्रिभुज होगा—
🔴 समद्विबाहु
🟡 विषमभुज
🟢 समकोण त्रिभुज
🔵 समबाहु
🟢 उत्तर
➡️ 5² + 12² = 25 + 144 = 169 = 13²
✔️ सही विकल्प = समकोण त्रिभुज

🔵 प्रश्न 4
पाइथागोरस प्रमेय का कथन लिखिए।
🟢 उत्तर
➡️ किसी समकोण त्रिभुज में कर्ण का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर होता है।
➡️ यदि त्रिभुज ABC में ∠B = 90°, तो AC² = AB² + BC²।

🔵 प्रश्न 5
सर्वांगसमता के दो मापदण्ड लिखिए।
🟢 उत्तर
➡️ SSS (तीनों भुजाएँ बराबर)
➡️ SAS (दो भुजाएँ और उनके बीच का कोण बराबर)

🔵 प्रश्न 6 (MCQ)
यदि किसी त्रिभुज में दो कोण बराबर हों, तो वह त्रिभुज कहलाता है—
🔴 समकोण त्रिभुज
🟡 विषमभुज त्रिभुज
🟢 समद्विबाहु त्रिभुज
🔵 समबाहु त्रिभुज
🟢 उत्तर
✔️ सही विकल्प = समद्विबाहु त्रिभुज

🟢 Section B (प्रश्न 7–12) — (प्रत्येक 2 अंक)
🟡 प्रश्न 7
समबाहु त्रिभुज की प्रत्येक भुजा 6 सेमी है। उसकी ऊँचाई ज्ञात कीजिए।
🟢 उत्तर
➡️ ऊँचाई = (√3/2) × भुजा = (√3/2) × 6 = 3√3 सेमी

🟡 प्रश्न 8
त्रिभुज ABC में ∠A = 40°, ∠B = 60°, तो ∠C ज्ञात कीजिए।
🟢 उत्तर
➡️ ∠C = 180° − (40° + 60°) = 80°

🟡 प्रश्न 9 (MCQ)
यदि किसी त्रिभुज की भुजाएँ 7, 24 और 25 हैं, तो उसका क्षेत्रफल होगा—
🔴 42 सेमी²
🟡 70 सेमी²
🟢 84 सेमी²
🔵 100 सेमी²
🟢 उत्तर
➡️ समकोण त्रिभुज (7² + 24² = 25²)
➡️ क्षेत्रफल = ½ × 7 × 24 = 84 सेमी²
✔️ सही विकल्प = 84 सेमी²

🟡 प्रश्न 10
सिद्ध कीजिए: समबाहु त्रिभुज में सभी कोण 60° होते हैं।
🟢 उत्तर
➡️ त्रिभुज का कोण योग = 180°
➡️ तीनों कोण बराबर मानें = x
➡️ 3x = 180° ⇒ x = 60°
✔️ प्रत्येक कोण 60° होता है।

🟡 प्रश्न 11
त्रिभुज की दो भुजाएँ 8 सेमी और 6 सेमी हैं तथा उनके बीच का कोण 60° है। क्षेत्रफल ज्ञात कीजिए।
🟢 उत्तर
➡️ क्षेत्रफल = ½ × a × b × sinθ
➡️ = ½ × 8 × 6 × sin60°
➡️ = 24 × (√3/2) = 12√3 सेमी²

🟡 प्रश्न 12 (MCQ)
यदि किसी समकोण त्रिभुज में एक कोण 30° हो, तो उसकी अन्य तीक्ष्ण कोण होगा—
🔴 30°
🟡 45°
🟢 60°
🔵 90°
🟢 उत्तर
➡️ ∠ = 90° − 30° = 60°
✔️ सही विकल्प = 60°

🟡 Section C (प्रश्न 13–22) — (प्रत्येक 3 अंक)

🔵 प्रश्न 13
सिद्ध कीजिए: यदि किसी त्रिभुज के दो कोण बराबर हों तो उनकी सामने की भुजाएँ भी बराबर होती हैं।
🟢 उत्तर
➡️ मानें त्रिभुज ABC में ∠B = ∠C।
➡️ A से BC पर लम्ब AD गिराएँ।
➡️ △ABD और △ACD सर्वांगसम (भुजा-कोण-भुजा से)।
➡️ अतः AB = AC।
✔️ बराबर कोणों के सामने की भुजाएँ बराबर होती हैं।

🔵 प्रश्न 14
सिद्ध कीजिए: किसी त्रिभुज की दो भुजाएँ बराबर हों तो उनके सामने के कोण भी बराबर होते हैं।
🟢 उत्तर
➡️ मानें त्रिभुज ABC में AB = AC।
➡️ A से BC पर लम्ब AD गिराएँ।
➡️ △ABD और △ACD सर्वांगसम (समकोण–कर्ण–भुजा से)।
➡️ ∠B = ∠C।
✔️ बराबर भुजाओं के सामने के कोण बराबर होते हैं।

🔵 प्रश्न 15 (बहुविकल्पी प्रश्न)
यदि किसी त्रिभुज की भुजाएँ 9, 12 और 15 हैं, तो वह त्रिभुज होगा—
🔴 समबाहु त्रिभुज
🟡 समद्विबाहु त्रिभुज
🟢 समकोण त्रिभुज
🔵 विषमभुज त्रिभुज
🟢 उत्तर
➡️ 9² + 12² = 81 + 144 = 225 = 15²
✔️ सही विकल्प = समकोण त्रिभुज

🔵 प्रश्न 16
समबाहु त्रिभुज की प्रत्येक भुजा 10 सेमी है। उसका क्षेत्रफल ज्ञात कीजिए।
🟢 उत्तर
➡️ क्षेत्रफल = (√3/4) × भुजा²
➡️ = (√3/4) × 10²
➡️ = 25√3 सेमी²

🔵 प्रश्न 17
त्रिभुज में सर्वांगसमता के चार मापदण्ड लिखिए।
🟢 उत्तर
➡️ भुजा-भुजा-भुजा (SSS)
➡️ भुजा-कोण-भुजा (SAS)
➡️ कोण-भुजा-कोण (ASA)
➡️ समकोण–कर्ण–भुजा (RHS)

🔵 प्रश्न 18 (आन्तरिक विकल्प)
(क) सिद्ध कीजिए कि समबाहु त्रिभुज आपस में सर्वांगसम होते हैं।
या
(ख) समकोण त्रिभुज की लम्बाई 6 सेमी और 8 सेमी है। कर्ण ज्ञात कीजिए।
🟢 उत्तर
🔸 (क) के लिए
➡️ समबाहु त्रिभुज में सभी भुजाएँ बराबर होती हैं।
➡️ भुजा-भुजा-भुजा मापदण्ड से सभी समबाहु त्रिभुज सर्वांगसम होते हैं।
🔸 (ख) के लिए
➡️ कर्ण² = 6² + 8² = 36 + 64 = 100
➡️ कर्ण = √100 = 10 सेमी

🔵 प्रश्न 19
सिद्ध कीजिए: किसी त्रिभुज का बाह्य कोण उसके विपरीत आन्तरिक कोणों के योग के बराबर होता है।
🟢 उत्तर
➡️ त्रिभुज ABC में बाह्य कोण ∠ACD लें।
➡️ ∠ACD + ∠CAB + ∠ABC = 180° (सीधी रेखा पर कोण योग)।
➡️ ∠CAB + ∠ABC + ∠BCA = 180° (त्रिभुज कोण योग)।
➡️ तुलना से ∠ACD = ∠CAB + ∠ABC।
✔️ सिद्ध हुआ।

🔵 प्रश्न 20
त्रिभुज ABC में AB = AC और ∠A = 100° है। ∠B और ∠C ज्ञात कीजिए।
🟢 उत्तर
➡️ ∠B = ∠C (क्योंकि AB = AC)।
➡️ ∠B + ∠C = 80° ⇒ 2∠B = 80° ⇒ ∠B = 40°
➡️ ∠C = 40°
✔️ ∠A = 100°, ∠B = 40°, ∠C = 40°

🔵 प्रश्न 21 (बहुविकल्पी प्रश्न)
यदि किसी समकोण त्रिभुज की भुजाएँ 8, 15 और 17 हों, तो उसका क्षेत्रफल होगा—
🔴 30 सेमी²
🟡 45 सेमी²
🟢 60 सेमी²
🔵 120 सेमी²
🟢 उत्तर
➡️ क्षेत्रफल = ½ × 8 × 15 = 60 सेमी²
✔️ सही विकल्प = 60 सेमी²

🔵 प्रश्न 22 (आन्तरिक विकल्प)
(क) सिद्ध कीजिए कि किसी त्रिभुज की दो भुजाएँ समान्तर हों तो वह त्रिभुज असंभव है।
या
(ख) त्रिभुज की भुजाएँ 7, 8 और 9 सेमी हैं। उसका क्षेत्रफल हीरोन सूत्र से ज्ञात कीजिए।
🟢 उत्तर
🔸 (क) के लिए
➡️ त्रिभुज बन्द बहुभुज है।
➡️ यदि दो भुजाएँ समान्तर हों तो वे कभी मिलेंगी नहीं, जिससे त्रिभुज बन्द नहीं बनेगा।
✔️ अतः यह संभव नहीं।
🔸 (ख) के लिए
➡️ s = (7+8+9)/2 = 24/2 = 12
➡️ क्षेत्रफल = √[s(s−a)(s−b)(s−c)]
➡️ = √[12(12−7)(12−8)(12−9)]
➡️ = √[12×5×4×3] = √720
➡️ = 12√5 सेमी²

🔴 Section D (प्रश्न 23–30) — (प्रत्येक 4 अंक)

🔵 प्रश्न 23
Question
सिद्ध कीजिए: किसी त्रिभुज का बाह्य कोण उसके विपरीत आन्तरिक कोणों के योग के बराबर होता है।
🟢 उत्तर
Answer
✳️ रचना/दी गई: त्रिभुज ABC, BC को C की ओर बढ़ाकर बाह्य कोण ∠ACD लिया।
✳️ योजना: सीधी रेखा पर कोण योग और त्रिभुज कोण योग का उपयोग।
➤ तथ्य: ∠ACD + ∠BCA = 180° (सीधी रेखा)
➤ तथ्य: ∠CAB + ∠ABC + ∠BCA = 180° (त्रिभुज कोण योग)
➤ तुलना: ऊपर के दोनों से
⚡ ∠ACD = ∠CAB + ∠ABC
✔️ निष्कर्ष: बाह्य कोण = विपरीत आन्तरिक कोणों का योग।

🔵 प्रश्न 24 (आन्तरिक विकल्प)
Question
(क) समद्विबाहु त्रिभुज में शिखर से खींची गई लम्ब आधार को समद्विभाजित करती है और कोण समद्विभाजक भी होती है — सिद्ध कीजिए।
या
(ख) यदि किसी त्रिभुज में किसी शिखर से आधार पर खींची रेखा लम्ब भी हो और मध्यिका भी, तो त्रिभुज समद्विबाहु है — सिद्ध कीजिए।
🟢 उत्तर
Answer
🔸 (क) के लिए
➤ दी गई: त्रिभुज ABC में AB = AC, A से BC पर AD ⟂ BC।
➤ △ABD और △ACD में:
AB = AC (दी गई)
∠ADB = ∠ADC = 90°
BD = DC (क्योंकि समद्विबाहु में लम्ब आधार को समद्विभाजित करती है – प्रमाण: RHS/समकोण–कर्ण–भुजा से △ABD ≅ △ACD)
➤ सर्वांगसमता से ∠BAD = ∠DAC → AD कोण समद्विभाजक है तथा BD = DC → AD मध्यिका भी है।
✔️ निष्कर्ष सिद्ध।
🔹 (ख) के लिए
➤ दी गई: त्रिभुज ABC, A से BC पर AD, जहाँ AD ⟂ BC तथा BD = DC।
➤ △ABD और △ACD में:
∠ADB = ∠ADC = 90°
BD = DC (दी गई)
AD सामान्य
➤ समकोण–कर्ण–भुजा से △ABD ≅ △ACD ⇒ AB = AC
✔️ अतः त्रिभुज समद्विबाहु है।

🔵 प्रश्न 25
Question
त्रिभुज की भुजाएँ 13 सेमी, 14 सेमी और 15 सेमी हैं।
(क) क्षेत्रफल (हीरोन) ज्ञात कीजिए।
(ख) 14 सेमी आधार पर ऊँचाई ज्ञात कीजिए।
🟢 उत्तर
Answer
✳️ सूत्र: क्षेत्रफल = √[s(s − a)(s − b)(s − c)], जहाँ s = (a + b + c)/2
➤ गणना (क)
s = (13 + 14 + 15)/2 = 42/2 = 21
क्षेत्रफल = √[21(21 − 13)(21 − 14)(21 − 15)]
= √[21 × 8 × 7 × 6] = √7056 = 84 सेमी²
➤ गणना (ख) (क्षेत्रफल = ½ × आधार × ऊँचाई)
84 = ½ × 14 × h
84 = 7h ⇒ h = 12 सेमी

🔵 प्रश्न 26 (आन्तरिक विकल्प)
Question
(क) सिद्ध कीजिए: किसी भी त्रिभुज में किसी भी दो भुजाओं का योग तीसरी भुजा से अधिक होता है।
या
(ख) दो भुजाएँ 7 सेमी और 9 सेमी हैं। तीसरी भुजा x सेमी के सम्भव मानों का परास ज्ञात कीजिए।
🟢 उत्तर
Answer
🔸 (क) के लिए
➤ त्रिभुज ABC में भुजाएँ a, b, c मानें।
➤ रेखाखण्ड के गुण व त्रिभुज निर्माण से: a + b > c, b + c > a, c + a > b।
✔️ कथन सिद्ध।
🔹 (ख) के लिए
➤ नियम: तीसरी भुजा x के लिए |7 − 9| < x < 7 + 9
➤ 2 < x < 16
✔️ परास: (2, 16)

🔵 प्रश्न 27
Question
त्रिभुज ABC और त्रिभुज PQR में AB = PQ = 6 सेमी, AC = PR = 8 सेमी तथा BC = QR = 10 सेमी हैं।
(क) दोनों त्रिभुज सर्वांगसम सिद्ध कीजिए।
(ख) ∠B और ∠Q के बीच सम्बन्ध लिखिए।
🟢 उत्तर
Answer
➤ सर्वांगसमता का मापदण्ड: भुजा-भुजा-भुजा
➤ क्योंकि तीनों-तीनों समतुल्य भुजाएँ बराबर हैं ⇒ △ABC ≅ △PQR
➤ समतुल्य कोण बराबर ⇒ ∠B = ∠Q
✔️ निष्कर्ष पूर्ण।

🔵 प्रश्न 28
Question
एक सीढ़ी दीवार के सहारे इस प्रकार लगी है कि जमीन से दीवार पर शीर्ष की ऊँचाई 24 मी है और सीढ़ी का पाद दीवार से 10 मी दूर है।
(क) सीढ़ी की लम्बाई ज्ञात कीजिए।
(ख) यदि सीढ़ी का पाद और 6 मी दूर खिसकाया जाए तो नई ऊँचाई ज्ञात कीजिए।
🟢 उत्तर
Answer
➤ पहला समकोण त्रिभुज: ऊँचाई = 24, आधार = 10
कर्ण² = 24² + 10² = 576 + 100 = 676
कर्ण = 26 मी
➤ दूसरी स्थिति: आधार = 10 + 6 = 16, कर्ण = 26 (अपरिवर्तित)
नई ऊँचाई² = 26² − 16² = 676 − 256 = 420
नई ऊँचाई = √420 = 2√105 मी

🔵 प्रश्न 29 (आन्तरिक विकल्प)
Question
(क) सिद्ध कीजिए: बड़ी भुजा के सामने का कोण बड़ा होता है।
या
(ख) त्रिभुज ABC में ∠A > ∠B दिया है। सिद्ध कीजिए: BC > AC।
🟢 उत्तर
Answer
🔸 (क) के लिए
➤ एक ही त्रिभुज में यदि a > b, तो निर्मित कोणों की तुलना से ∠A > ∠B।
➤ रचना के आधार पर आधार-ऊँचाई तर्क (या विपरीत मानकर विरोधाभास) से सिद्ध।
✔️ निष्कर्ष: बड़ी भुजा के सामने का कोण बड़ा।
🔹 (ख) के लिए
➤ ∠A > ∠B ⇒ A के सामने भुजा BC, B के सामने भुजा AC।
➤ कोण-भुजा सम्बन्ध से: ∠A > ∠B ⇒ BC > AC।
✔️ सिद्ध।

🔵 प्रश्न 30
Question
त्रिभुज ABC में भुजाएँ 10 सेमी, 24 सेमी, 26 सेमी हैं।
(क) त्रिभुज का प्रकार पहचानिए।
(ख) क्षेत्रफल तथा 24 सेमी आधार पर ऊँचाई ज्ञात कीजिए।
🟢 उत्तर
Answer
➤ पहचान (क)
10² + 24² = 100 + 576 = 676 = 26² ⇒ समकोण त्रिभुज (समकोण ∠B मानें)
➤ क्षेत्रफल
क्षेत्रफल = ½ × 10 × 24 = 120 सेमी²
➤ ऊँचाई (24 पर)
120 = ½ × 24 × h ⇒ 120 = 12h ⇒ h = 10 सेमी

————————————————————————————————————————————————————————————————————————————

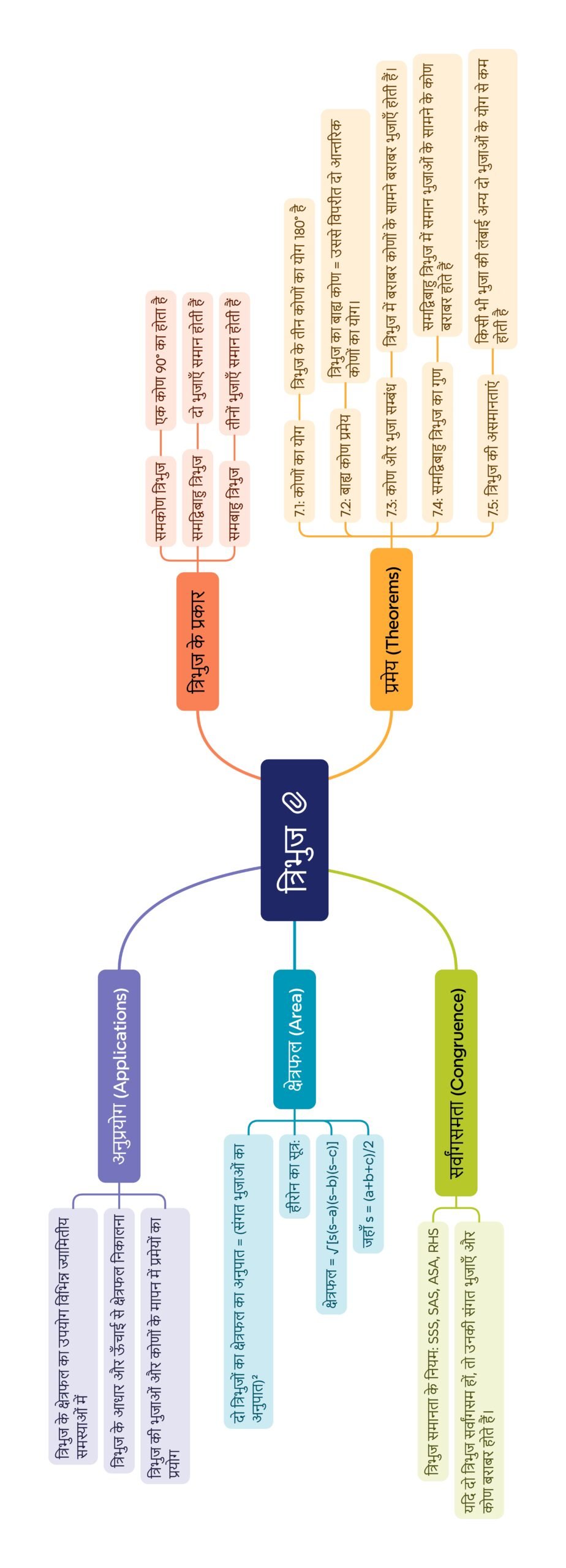
मानचित्र

————————————————————————————————————————————————————————————————————————————