Class : 9 – Math (Hindi) : Lesson 4. दो चरों वाले रैखिक समीकरण

पाठ का विश्लेषण  एवं  विवेचन

🔵 परिचय
बीजगणित और ज्यामिति दोनों ही गणित की महत्वपूर्ण शाखाएँ हैं। वास्तविक जीवन की समस्याओं को हल करने के लिए हम समीकरणों का प्रयोग करते हैं। कक्षा 9 में हम ऐसे समीकरणों का अध्ययन कर रहे हैं जिनमें दो चर होते हैं। इन समीकरणों को हम कहते हैं — दो चरों वाले रैखिक समीकरण।
👉 इनका महत्व इस कारण है कि ये रोज़मर्रा की समस्याओं (लागत–मूल्य, दूरी–समय, कार्य–दर, संख्याओं के संबंध) को गणितीय रूप में बदलने का सरल माध्यम प्रदान करते हैं।

🟢 1. दो चरों वाले रैखिक समीकरण की परिभाषा
परिभाषा: कोई भी समीकरण इस रूप का हो:
➡️ a x + b y + c = 0
जहाँ a, b, c वास्तविक संख्याएँ हों और a, b एक साथ शून्य न हों।
इसे दो चरों वाला रैखिक समीकरण कहते हैं।
उदाहरण:
2x + 3y − 6 = 0
x − y + 4 = 0
y = 2x + 1

🔴 2. हल (Solutions)
👉 किसी समीकरण का हल वह युग्म (x, y) है जो उसे संतुष्ट करता है।
✔️ उदाहरण: x + y = 7 के हल: (3, 4), (0, 7), (7, 0) आदि।
✔️ ऐसे अनन्त हल होते हैं क्योंकि हर वह बिन्दु जो समीकरण की रेखा पर स्थित है, उसका हल है।

🟡 3. एक चर और दो चरों वाले समीकरण में अंतर
एक चर (जैसे 2x + 3 = 0) का हल संख्या रेखा पर एक बिन्दु होता है।
दो चर (जैसे 2x + y − 6 = 0) का हल निर्देशांक तल पर एक सीधी रेखा होती है।
इसीलिए दो चर का समीकरण अनन्त हल रखता है।

🌿 4. समीकरण का ग्राफिक निरूपण
हर दो चरों वाला रैखिक समीकरण निर्देशांक तल पर एक सीधी रेखा को निरूपित करता है।
विधि:
समीकरण को ax + by + c = 0 रूप में लिखिए।
x या y को मान दीजिए और कम-से-कम 2–3 हल निकालिए।
प्राप्त बिन्दुओं को निर्देशांक तल पर चिन्हित कीजिए।
उन बिन्दुओं को मिलाइए।
✔️ यही समीकरण का ग्राफ है।

⚡ 5. प्रतिछेद (Intercept) विधि
यदि समीकरण ax + by + c = 0 है, तो
y = 0 रखने पर x-अवरोध (x-intercept) मिलता है।
x = 0 रखने पर y-अवरोध (y-intercept) मिलता है।
उदाहरण: 2x + 3y = 6
➡️ x = 0 ⇒ y = 2 → बिन्दु (0, 2)
➡️ y = 0 ⇒ x = 3 → बिन्दु (3, 0)
✔️ इन बिन्दुओं से रेखा खींची जाती है।

✳️ 6. अक्षों के समांतर रेखाएँ
x = a ⇒ y-अक्ष के समांतर ऊर्ध्व रेखा।
y = b ⇒ x-अक्ष के समांतर क्षैतिज रेखा।
✔️ ये भी दो चरों वाले रैखिक समीकरण हैं।

🟢 7. मान-सारिणी विधि (Tabular Method)

समीकरण 2x + 3y = 12 के लिए:

x = 0 ⇒ y = 4 → (0, 4)
x = 3 ⇒ y = 2 → (3, 2)
x = 6 ⇒ y = 0 → (6, 0)

✔️ तीनों बिन्दुओं (0,4), (3,2), (6,0) को मिलाकर सीधी रेखा प्राप्त होती है।

🔴 8. ढाल–अवरोध रूप (Slope-Intercept Form)
समीकरण ax + by + c = 0 को y = mx + c में लिखा जा सकता है।
यहाँ m = ढाल (slope) = −a/b
c = y-अवरोध।
उदाहरण: 2x + y − 6 = 0
➡️ y = −2x + 6
✔️ ढाल = −2, y-अवरोध = 6।

🌿 9. दो समीकरणों का युग्म (Pair of Linear Equations)
जब दो रेखाएँ साथ हों, तो संभावनाएँ:
प्रतिछेद करती हैं ⇒ एक हल।
समानांतर हैं ⇒ कोई हल नहीं।
एक-दूसरे पर अवस्थित हैं ⇒ अनन्त हल।

⚡ 10. सहरेखीयता (Collinearity)
यदि तीन बिन्दु एक ही सीधी रेखा पर हों, तो वे सहरेखीय कहलाते हैं।
👉 किसी समीकरण में रखने पर यदि सभी बिन्दु उसे संतुष्ट करें, तो वे सहरेखीय हैं।

✏️ 11. वास्तविक जीवन में अनुप्रयोग
लागत व मूल्य से सम्बंधित समस्याएँ।
गति–दूरी–समय के प्रश्न।
आयु, संख्याएँ या अनुपात से सम्बन्धित प्रश्न।
कार्य व समय संबंधी प्रश्न।

💡 12. अध्याय का महत्त्व
आगे चलकर “दो चरों वाले रैखिक समीकरणों के युग्म” (कक्षा 10) की नींव यही अध्याय है।
ग्राफिक विधि से समस्याओं को चित्रात्मक रूप से समझना सरल हो जाता है।

🟡 सारांश (~300 शब्द)
परिभाषा: ax + by + c = 0 दो चरों वाला रैखिक समीकरण है।
हल: (x, y) युग्म जो समीकरण को सत्य बनाए। हल अनन्त होते हैं।
एक चर बनाम दो चर: एक चर = संख्या रेखा पर बिन्दु; दो चर = निर्देशांक तल पर सीधी रेखा।
ग्राफ विधि: दो बिन्दु निकालकर रेखा खींची जाती है।
प्रतिछेद विधि: x और y-अवरोध द्वारा रेखा बनती है।
अक्ष-समांतर रेखाएँ: x = a और y = b रूप।
मान-सारिणी विधि: 2–3 मान रखकर बिन्दुओं की तालिका।
ढाल–अवरोध रूप: y = mx + c, जहाँ m = ढाल, c = y-अवरोध।
समीकरणों का युग्म: रेखाओं का प्रतिछेद = एक हल; समानांतर = कोई हल नहीं; एक-दूसरे पर = अनन्त हल।
सहरेखीयता: यदि तीन बिन्दु एक ही रेखा पर हों।
अनुप्रयोग: लागत–मूल्य, दूरी–समय, कार्य–समय जैसी समस्याओं का समाधान।

📝 Quick Recap
🔵 दो चरों वाला रैखिक समीकरण → ax + by + c = 0।
🟢 हल = अनन्त (x, y) युग्म।
🔴 ग्राफ → सीधी रेखा।
🟡 प्रतिछेद व मान-सारिणी विधि से ग्राफ आसानी से।
🌿 ढाल–अवरोध रूप = y = mx + c।
✔️ वास्तविक जीवन में उपयोग: लागत, दूरी, समय।

————————————————————————————————————————————————————————————————————————————

पाठ्यपुस्तक के प्रश्न

📄 प्रश्नावली 4.1

🔵 प्रश्न 1:
एक नोटबुक की कीमत एक कलम की कीमत से दो गुनी है। इस कथन को निरूपित करने के लिए दो चरों वाला एक रैखिक समीकरण लिखिए।
🟢 मान लीजिए:
नोटबुक की कीमत = x रु
कलम की कीमत = y रु
📘 कथन:
नोटबुक की कीमत = 2 × कलम की कीमत
✏️ अतः समीकरण:
➡ x = 2y
या
➡ x − 2y = 0 ✅

🔵 प्रश्न 2:
निम्नलिखित रैखिक समीकरणों को ax + by + c = 0 के रूप में व्यवस्थित कीजिए तथा प्रत्येक स्थिति में a, b और c के मान बताइए :

🟢 (i) 2x + 3y = 9.35
➡ रूपांतरण: 2x + 3y − 9.35 = 0
⇒ a = 2, b = 3, c = −9.35 ✅
🟢 (ii) x − (y / 5) − 10 = 0
➡ रूप पहले से ही समान है
⇒ a = 1, b = −1/5, c = −10 ✅
🟢 (iii) −2x + 3y = 6
➡ रूप: −2x + 3y − 6 = 0
⇒ a = −2, b = 3, c = −6 ✅
🟢 (iv) x = 3y
➡ रूपांतरण: x − 3y = 0
⇒ a = 1, b = −3, c = 0 ✅
🟢 (v) 2x = −5y
➡ रूपांतरण: 2x + 5y = 0
⇒ a = 2, b = 5, c = 0 ✅
🟢 (vi) 3x + 2 = 0
➡ रूप: 3x + 0y + 2 = 0
⇒ a = 3, b = 0, c = 2 ✅
🟢 (vii) y − 2 = 0
➡ रूप: 0x + y − 2 = 0
⇒ a = 0, b = 1, c = −2 ✅
🟢 (viii) 5 = 2x
➡ रूपांतरण: 2x − 5 = 0
⇒ a = 2, b = 0, c = −5 ✅

📄 प्रश्नावली 4.2

🔵 प्रश्न 1:
निम्नलिखित विकल्पों में कौन-सा विकल्प सत्य है और क्यों?
समीकरण: y = 3x + 5
🟢 उत्तर:
यह एक रैखिक समीकरण है जो x और y के बीच संबंध दर्शाता है।
इसका अपरिमित रूप से अनेक हल होते हैं क्योंकि x का कोई भी मान रखने पर y का एक मान प्राप्त होता है।
✅ अतः सही विकल्प है — (iii) अपरिमित रूप से अनेक हल हैं

🔵 प्रश्न 2:
निम्नलिखित समीकरणों में से प्रत्येक के चार हल लिखिए :
🟢 (i) 2x + y = 7
हल के लिए विभिन्न x मान रखिए :
यदि x = 0 ⇒ y = 7
यदि x = 1 ⇒ y = 5
यदि x = 2 ⇒ y = 3
यदि x = 3 ⇒ y = 1
✅ हल: (0, 7), (1, 5), (2, 3), (3, 1)

🟢 (ii) πx + y = 9
हल के लिए विभिन्न x मान रखिए :
यदि x = 0 ⇒ y = 9
यदि x = 1 ⇒ y = 9 − π
यदि x = 2 ⇒ y = 9 − 2π
यदि x = 3 ⇒ y = 9 − 3π
✅ हल: (0, 9), (1, 9−π), (2, 9−2π), (3, 9−3π)

🟢 (iii) x = 4y
हल के लिए विभिन्न y मान रखिए :
यदि y = 0 ⇒ x = 0
यदि y = 1 ⇒ x = 4
यदि y = 2 ⇒ x = 8
यदि y = 3 ⇒ x = 12
✅ हल: (0, 0), (4, 1), (8, 2), (12, 3)

🔵 प्रश्न 3:
बताइए कि निम्नलिखित हलों में कौन-सा समीकरण x − 2y = 4 का हल है और कौन-सा नहीं है :

🧮 समीकरण: x − 2y = 4

अब प्रत्येक बिंदु पर जाँच करते हैं —

1️⃣ (0, 2)
➡ x − 2y = 0 − 2(2) = 0 − 4 = −4 ≠ 4
❌ यह हल नहीं है

2️⃣ (2, 0)
➡ x − 2y = 2 − 2(0) = 2 − 0 = 2 ≠ 4
❌ यह हल नहीं है

3️⃣ (4, 0)
➡ x − 2y = 4 − 2(0) = 4 − 0 = 4 ✔
✅ यह हल है

4️⃣ (√2, 4√2)
➡ x − 2y = √2 − 2(4√2) = √2 − 8√2 = −7√2 ≠ 4
❌ यह हल नहीं है

5️⃣ (1, 1)
➡ x − 2y = 1 − 2(1) = 1 − 2 = −1 ≠ 4
❌ यह हल नहीं है

🟢 अतः केवल (4, 0) ही इस समीकरण का हल है। ✅

🔵 प्रश्न 4:

k का मान ज्ञात कीजिए जब (x = 2, y = 1) समीकरण 2x + 3y = k का एक हल हो।

📘 समीकरण: 2x + 3y = k
x = 2, y = 1 रखने पर:
➡ 2(2) + 3(1) = 4 + 3 = 7
✅ अतः k = 7

————————————————————————————————————————————————————————————————————————————

अन्य महत्वपूर्ण प्रश्न

प्रश्न 1 से 10: बहुविकल्पीय प्रश्न (MCQ) — उत्तर सहित
प्रश्न 1. दो चर वाले रेखीय समीकरण का सामान्य रूप होता है:
(a) ax² + by + c = 0
(b) ax + by = c
(c) ax + b = 0
(d) ax² + bx + c = 0
उत्तर: (b) ax + by = c

प्रश्न 2. समीकरण 2x + 3y = 6 में x और y का अधिकतम घातांक क्या है?
(a) 2
(b) 3
(c) 1
(d) 0
उत्तर: (c) 1

प्रश्न 3. यदि दो रेखाएँ एक-दूसरे को काटती हैं, तो रेखीय समीकरण युग्म के कितने हल होते हैं?
(a) कोई नहीं
(b) एक
(c) दो
(d) अनंत
उत्तर: (b) एक

प्रश्न 4. समीकरण x + y = 4 और x – y = 2 के हल क्या हैं?
(a) (1, 3)
(b) (2, 2)
(c) (3, 1)
(d) (4, 0)
उत्तर: (c) (3, 1)

प्रश्न 5. यदि दो समीकरण एक ही रेखा को दर्शाते हैं, तो उनके कितने हल होते हैं?
(a) कोई नहीं
(b) केवल एक
(c) दो
(d) अनंत
उत्तर: (d) अनंत

प्रश्न 6. यदि दो रेखाएँ समानांतर हैं, तो समीकरण युग्म के कितने हल होंगे?
(a) 1
(b) 0
(c) अनंत
(d) 2
उत्तर: (b) 0

प्रश्न 7. x + 2y = 6 के लिए, यदि x = 2 हो, तो y का मान क्या होगा?
(a) 1
(b) 2
(c) 3
(d) 4
उत्तर: (b) 2

प्रश्न 8. x – y = 0 रेखा किस बिंदु से होकर गुजरती है?
(a) (1, 0)
(b) (2, 3)
(c) (1, 1)
(d) (0, 1)
उत्तर: (c) (1, 1)

प्रश्न 9. यदि x + y = 5 और x – y = 1, तो x और y के मान हैं:
(a) x = 2, y = 3
(b) x = 3, y = 2
(c) x = 5, y = 0
(d) x = 1, y = 4
उत्तर: (b) x = 3, y = 2

प्रश्न 10. समीकरण 2x – y = 3 को ग्राफ पर दर्शाने के लिए कितने बिंदु न्यूनतम चाहिए?
(a) 1
(b) 2
(c) 3
(d) 4
उत्तर: (b) 2

प्रश्न 11 से 15: लघु उत्तर प्रश्न (1–2 पंक्तियों में)
प्रश्न 11. दो चर वाले रेखीय समीकरण का क्या रूप होता है?
उत्तर: इसका सामान्य रूप ax + by + c = 0 होता है, जहाँ a, b ≠ 0।

प्रश्न 12. रेखीय समीकरण का ग्राफ किस प्रकार की आकृति बनाता है?
उत्तर: यह समतल पर एक सीधी रेखा बनाता है।

प्रश्न 13. यदि दो रेखाएँ एक बिंदु पर मिलती हैं, तो युग्म के कितने हल होंगे?
उत्तर: एक अद्वितीय हल होगा।

प्रश्न 14. क्या दो समीकरणों के एक से अधिक हल हो सकते हैं?
उत्तर: हाँ, यदि दोनों रेखाएँ एक ही हों, तो अनंत हल होंगे।

प्रश्न 15. यदि दो रेखाएँ समानांतर हैं, तो क्या कोई हल होगा?
उत्तर: नहीं, तब युग्म का कोई हल नहीं होता।

प्रश्न 16 से 20: लघु उत्तर प्रश्न (1–2 पंक्तियों में)
प्रश्न 16. समीकरण 3x + 2y = 12 को संतुष्ट करने वाला कोई एक बिंदु बताइए।
उत्तर: (2, 3), क्योंकि 3(2) + 2(3) = 6 + 6 = 12

प्रश्न 17. रेखीय समीकरण युग्म का ग्राफ बनाने के लिए कितने बिंदु पर्याप्त होते हैं?
उत्तर: प्रत्येक रेखा के लिए दो बिंदु पर्याप्त होते हैं।

प्रश्न 18. यदि कोई युग्म असंगत है, तो ग्राफ पर रेखाओं की स्थिति क्या होगी?
उत्तर: रेखाएँ समानांतर होंगी और एक-दूसरे को नहीं काटेंगी।

प्रश्न 19. दो रेखाओं का प्रतिच्छेदन बिंदु क्या दर्शाता है?
उत्तर: वही युग्म का हल होता है (x, y) जो दोनों समीकरणों को संतुष्ट करता है।

प्रश्न 20. x = 3 और y = 2 की मदद से समीकरण x – y = 1 की सत्यता जाँचिए।
उत्तर: 3 – 2 = 1, समीकरण संतुष्ट होता है। अतः (3, 2) इसका हल है।

प्रश्न 21 से 25: मध्यम उत्तर प्रश्न (3–4 पंक्तियों में)
प्रश्न 21. x + y = 5 और x – y = 1 के हल को ग्राफ की सहायता से व्याख्या कीजिए।
उत्तर:
x + y = 5 की रेखा तथा x – y = 1 की रेखा ग्राफ पर एक बिंदु (3, 2) पर मिलती हैं।
यह बिंदु उन दोनों समीकरणों को संतुष्ट करता है, अतः यही युग्म का हल है।

प्रश्न 22. x – y = 2 को संतुष्ट करने वाले तीन बिंदु लिखिए।
उत्तर:
(i) (2, 0)
(ii) (3, 1)
(iii) (4, 2)
सभी बिंदुओं को समीकरण में रखकर संतुष्टि देखी जा सकती है।

प्रश्न 23. यह कैसे निर्धारित करेंगे कि कोई युग्म संगत है या नहीं?
उत्तर:
यदि रेखाएँ एक बिंदु पर मिलती हैं या एक ही रेखा होती हैं → संगत
यदि रेखाएँ समानांतर हैं और नहीं मिलती → असंगत

प्रश्न 24. दो रेखीय समीकरण कब अनंत हल देते हैं?
उत्तर:
जब दोनों रेखाएँ एक ही रेखा को दर्शाती हैं यानी दोनों समीकरण एक-दूसरे के गुणक होते हैं।
उदाहरण:
x + y = 2
2x + 2y = 4

प्रश्न 25. दो रेखीय समीकरणों के ग्राफ पर हल कैसे प्राप्त करते हैं?
उत्तर:
प्रत्येक समीकरण के लिए दो बिंदुओं का आलेखन करके ग्राफ पर रेखा खींची जाती है।
जहाँ दोनों रेखाएँ मिलती हैं, वही युग्म का हल होता है।


प्रश्न 26.
निम्नलिखित रेखीय समीकरण युग्म का हल निकालिए:
x + y = 6
x – y = 2
उत्तर:
चरण 1: पहले समीकरण को लिखें
x + y = 6 ……..(1)
चरण 2: दूसरे समीकरण को लिखें
x – y = 2 ……..(2)
चरण 3: समीकरण (1) और (2) को जोड़ें
(x + y) + (x – y) = 6 + 2
2x = 8
x = 4
चरण 4: x = 4 को समीकरण (1) में रखें
4 + y = 6
y = 6 – 4
y = 2
अतः हल है: x = 4, y = 2
अंतिम उत्तर: (4, 2)

प्रश्न 27.
रेखीय समीकरण युग्म का ग्राफ बनाकर हल निकालिए:
x + y = 4
x – y = 0
उत्तर:
समीकरण 1: x + y = 4
x = 0 ⇒ y = 4
x = 2 ⇒ y = 2
x = 4 ⇒ y = 0
तीन बिंदु: (0,4), (2,2), (4,0)
समीकरण 2: x – y = 0 ⇒ x = y
x = 0 ⇒ y = 0
x = 2 ⇒ y = 2
x = 3 ⇒ y = 3
तीन बिंदु: (0,0), (2,2), (3,3)
दोनों रेखाएँ (2,2) पर मिलती हैं।
अतः हल है: (2, 2)

प्रश्न 28.
निम्नलिखित युग्म के हल की प्रकृति बताइए:
x + y = 2
2x + 2y = 4
उत्तर:
दूसरे समीकरण को 2 से भाग दें:
2x + 2y = 4
⇒ x + y = 2
यह दोनों रेखाएँ एक ही रेखा दर्शाती हैं।
अतः हल: अनगिनत
प्रकृति: सहचर रेखाएँ, असंख्य हल

प्रश्न 29.
x + y = 5
x + y = 7
इस युग्म की हल की प्रकृति बताइए।
उत्तर:
बाईं ओर दोनों समीकरणों में x + y समान है, लेकिन दाईं ओर 5 ≠ 7
इसका अर्थ है कि रेखाएँ समानांतर हैं
अतः हल नहीं है
प्रकृति: असंगत युग्म, कोई हल नहीं

प्रश्न 30.
x – 2y = –2
–x + y = 1
का हल निकालिए।
उत्तर:
समीकरण 1: x – 2y = –2 ……..(1)
समीकरण 2: –x + y = 1 ……..(2)
अब (1) और (2) को जोड़ें:
x – 2y – x + y = –2 + 1
–y = –1
y = 1
अब y = 1 को समीकरण (1) में रखें:
x – 2(1) = –2
x – 2 = –2
x = 0
अंतिम उत्तर: (0, 1)

————————————————————————————————————————————————————————————————————————————

एक पृष्ठ में पुनरावृत्ति

────────────────────────────
📌 1. परिभाषा:
दो चर वाले रेखीय समीकरण का सामान्य रूप होता है:
ax + by + c = 0, जहाँ
a, b, c वास्तविक संख्याएँ हैं
x और y दो चर हैं
a और b में से कम से कम एक ≠ 0 होना चाहिए

📌 2. रेखीय समीकरण युग्म:
जब दो रेखीय समीकरण एक साथ दिए जाएँ और दोनों का एक साथ हल निकाला जाए, तो वह रेखीय समीकरण युग्म कहलाता है।
उदाहरण:
x + y = 5
x – y = 1

📌 3. हल की परिभाषा:
दोनों समीकरणों को संतुष्ट करने वाला (x, y) युग्म ही युग्म का हल होता है।

📌 4. हल की प्रकृति (तीन स्थितियाँ):
| रेखाओं की स्थिति | हल की संख्या | प्रकृति | |————————–|——————|——————–| | रेखाएँ एक बिंदु पर मिलें | 1 | अद्वितीय हल | | रेखाएँ एक ही हों | अनंत | अनंत हल | | रेखाएँ समानांतर हों | 0 | कोई हल नहीं |

📌 5. समाधान की विधियाँ:
✅ तालिका विधि: विभिन्न x के लिए y निकालें
✅ ग्राफ विधि: दोनों समीकरणों की रेखाएँ बनाकर प्रतिच्छेदन बिंदु खोजें
✅ बीजगणितीय विधियाँ (आगे की कक्षाओं में): प्रतिस्थापन, विलोपन

📌 6. ग्राफ बनाने के लिए:
प्रत्येक समीकरण के लिए दो या तीन बिंदु निकालें
उन्हें ग्राफ पेपर पर अंकित करें
रेखाएँ खींचें
जहाँ रेखाएँ मिलती हैं वही हल है

📌 7. ध्यान देने योग्य बातें:
🔹 समीकरणों का रूप ax + by + c = 0 में रखें
🔹 केवल दो रेखीय समीकरण होने चाहिए
🔹 चरों (x और y) का घात अधिकतम 1 होना चाहिए
🔹 हल (x, y) दोनों समीकरणों को संतुष्ट करे

📌 8. दैनिक जीवन में उपयोग:
✔ वस्तुओं की कीमतें ज्ञात करने में
✔ दो यात्रियों की मिलने की स्थिति
✔ दर–समय–दूरी से जुड़ी समस्याएँ
✔ साझेदारी और मिश्रण के प्रश्न

📌 9. अभ्यास सुझाव:
📍 ग्राफ पेपर पर दो समीकरण लेकर रेखाएँ बनाइए
📍 x = 0, x = 2, x = 4 आदि के लिए y निकालिए
📍 हल को दोनों समीकरणों में रखकर जाँच कीजिए

📌 10. सूत्र याद रखें:
x + y = c → सरल रेखा
x = y → विकर्ण रेखा
यदि दो समीकरण एक-दूसरे के गुणक हैं → अनंत हल
────────────────────────────

————————————————————————————————————————————————————————————————————————————

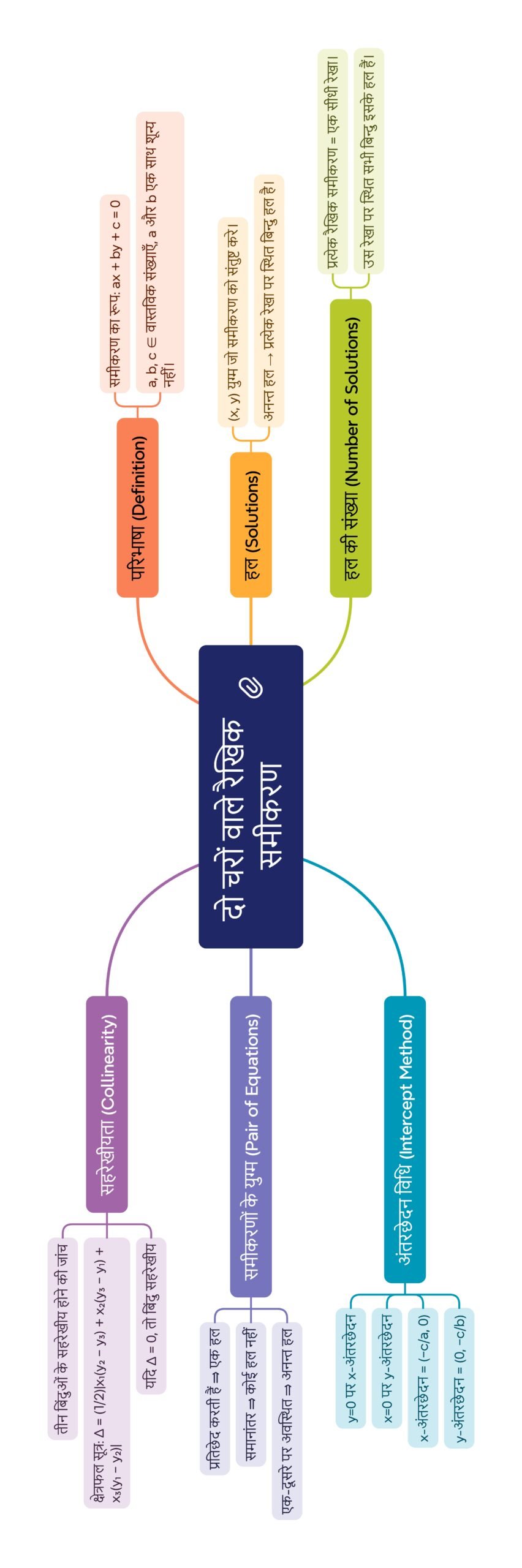
मानचित्र

————————————————————————————————————————————————————————————————————————————