Class : 9 – Math (Hindi) : Lesson 3. निर्देशांक ज्यामिति

पाठ का विश्लेषण  एवं  विवेचन

🔵 परिचय
निर्देशांक ज्यामिति (Coordinate Geometry) गणित की वह शाखा है जिसमें बीजगणित और ज्यामिति को जोड़ा जाता है। यह अवधारणा सबसे पहले रेने देकार्त (René Descartes) ने प्रस्तुत की थी।
👉 इसमें किसी बिन्दु की स्थिति को संख्याओं की सहायता से निर्धारित किया जाता है।
👉 संख्या रेखा पर एक बिन्दु की स्थिति एक संख्या से, जबकि तल (Plane) में किसी बिन्दु की स्थिति दो संख्याओं (x, y) से व्यक्त होती है।

🟢 1. निर्देशांक पद्धति (Coordinate System)
निर्देशांक तल (Coordinate Plane) दो लम्बवत संख्या रेखाओं से बनता है:
क्षैतिज रेखा = x-अक्ष
ऊर्ध्वाधर रेखा = y-अक्ष
👉 इन दोनों का प्रतिछेद बिन्दु = मूलबिन्दु (Origin O(0,0))

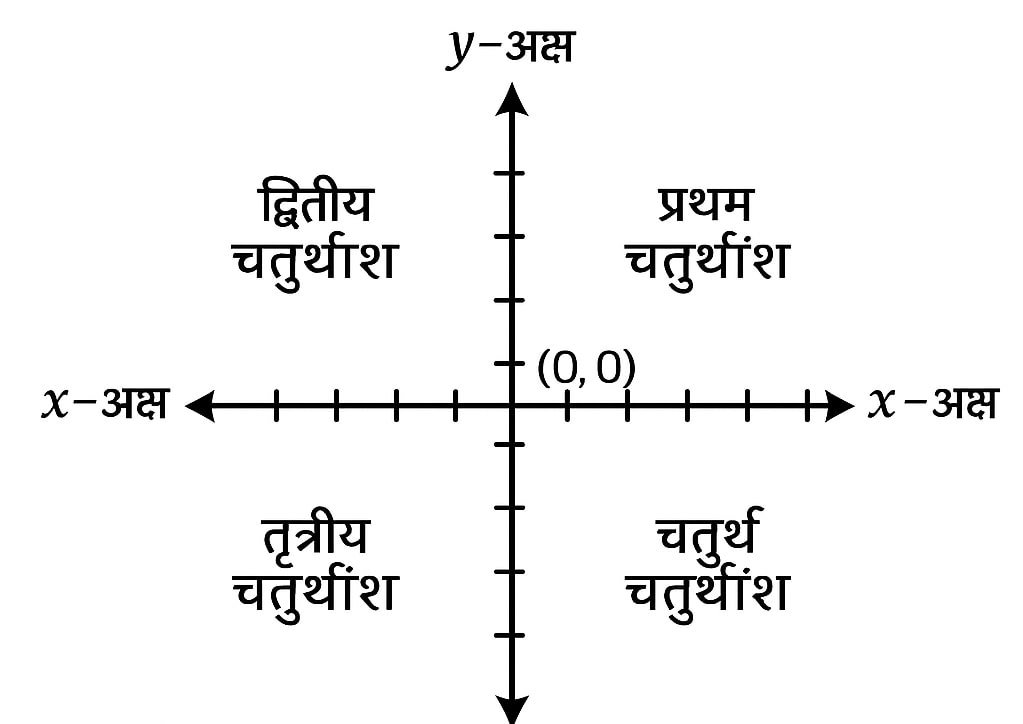
🔴 2. चतुर्थांश (Quadrants)
निर्देशांक तल को x और y अक्ष चार भागों में बाँटते हैं:
प्रथम चतुर्थांश (x > 0, y > 0)
द्वितीय चतुर्थांश (x < 0, y > 0)
तृतीय चतुर्थांश (x < 0, y < 0)
चतुर्थ चतुर्थांश (x > 0, y < 0)
✔️ प्रत्येक बिन्दु को क्रमबद्ध युग्म (x, y) द्वारा व्यक्त किया जाता है।

🟡 3. बिन्दु का निरूपण (Representation of a Point)
👉 बिन्दु P(a, b) का अर्थ है:
x = a → बिन्दु y-अक्ष से a इकाई दूर।
y = b → बिन्दु x-अक्ष से b इकाई दूर।
उदाहरण: P(3, 2) → मूल से 3 इकाई दाईं ओर और 2 इकाई ऊपर।

🌿 4. अक्षों पर बिन्दु
यदि बिन्दु x-अक्ष पर है → उसका y = 0 होगा।
यदि बिन्दु y-अक्ष पर है → उसका x = 0 होगा।
मूलबिन्दु O(0, 0) → दोनों अक्षों का प्रतिछेद।

⚡ 5. दूरी सूत्र (Distance Formula)
दो बिन्दु A(x₁, y₁), B(x₂, y₂) के बीच दूरी:
✔️ d = √((x₂ − x₁)² + (y₂ − y₁)²)
उदाहरण: A(1, 2), B(4, 6)
➡️ d = √((4 − 1)² + (6 − 2)²)
➡️ d = √(3² + 4²) = √(9 + 16)
➡️ d = √25 = 5
✔️ हल: दूरी = 5 इकाई

✳️ 6. मध्यबिन्दु सूत्र (Midpoint Formula)
यदि A(x₁, y₁), B(x₂, y₂) हों, तो AB का मध्यबिन्दु M:
✔️ M = ((x₁ + x₂)/2 , (y₁ + y₂)/2)
उदाहरण: A(2, 4), B(6, 8)
➡️ M = ((2 + 6)/2 , (4 + 8)/2)
➡️ M = (8/2 , 12/2)
➡️ M = (4, 6)

🟢 7. त्रिभुज के शीर्षों द्वारा क्षेत्रफल (Area of Triangle)
यदि A(x₁, y₁), B(x₂, y₂), C(x₃, y₃) हों, तो क्षेत्रफल:
✔️ Δ = (1/2)|x₁(y₂ − y₃) + x₂(y₃ − y₁) + x₃(y₁ − y₂)|
उदाहरण: A(0, 0), B(4, 0), C(0, 3)
➡️ Δ = (1/2)|0(0 − 3) + 4(3 − 0) + 0(0 − 0)|
➡️ Δ = (1/2)|0 + 12 + 0| = (1/2) × 12
➡️ Δ = 6 वर्ग इकाई

🔴 8. बिन्दुओं की सहरेखीयता (Collinearity)
यदि A, B, C बिन्दुओं का क्षेत्रफल = 0 हो → वे सहरेखीय हैं।
उदाहरण: A(1, 1), B(2, 2), C(3, 3)
➡️ Δ = (1/2)|1(2 − 3) + 2(3 − 1) + 3(1 − 2)|
➡️ Δ = (1/2)|−1 + 4 − 3| = (1/2)×0 = 0
✔️ अतः A, B, C सहरेखीय हैं।

🌿 9. वास्तविक जीवन में उपयोग
मानचित्र और GPS तकनीक → स्थान निर्धारण।
खगोल विज्ञान → ग्रहों–उपग्रहों की स्थिति।
इंजीनियरिंग → डिज़ाइन और मापन।
कम्प्यूटर ग्राफिक्स → चित्र और गेम डिज़ाइन।

✏️ टिप्पणी
निर्देशांक ज्यामिति = बीजगणित + ज्यामिति का मेल।
यह रेखाओं, आकृतियों और बिन्दुओं का गणितीय विश्लेषण करने की सशक्त विधि है।

🟡 सारांश (~300 शब्द)
निर्देशांक ज्यामिति = बीजगणित और ज्यामिति का संयोजन।
निर्देशांक तल = x-अक्ष (अभिक्षि-अक्ष) + y-अक्ष (अनुक्षि-अक्ष), प्रतिछेद = मूलबिन्दु (0,0)।
तल को 4 चतुर्थांशों में बाँटा जाता है।
बिन्दु (x, y) द्वारा व्यक्त।
सूत्र:
• दूरी = √((x₂ − x₁)² + (y₂ − y₁)²)
• मध्यबिन्दु = ((x₁ + x₂)/2 , (y₁ + y₂)/2)
• क्षेत्रफल = (1/2)|x₁(y₂ − y₃) + x₂(y₃ − y₁) + x₃(y₁ − y₂)|
सहरेखीयता: क्षेत्रफल = 0।
अनुप्रयोग: GPS, मानचित्र, खगोल विज्ञान, इंजीनियरिंग, कम्प्यूटर ग्राफिक्स।

📝 Quick Recap
🔵 निर्देशांक तल = x-अक्ष + y-अक्ष, मूल O(0,0)।
🟢 चतुर्थांश = 4 भाग (चिन्ह संयोजन द्वारा)।
🔴 दूरी सूत्र, 🟡 मध्यबिन्दु सूत्र।
🌿 क्षेत्रफल सूत्र = त्रिभुज के लिए।
⚡ सहरेखीयता → क्षेत्रफल = 0।
✔️ उपयोग → GPS, विज्ञान, इंजीनियरिंग।

————————————————————————————————————————————————————————————————————————————

पाठ्यपुस्तक के प्रश्न

प्रश्नावली 3.1

🔵 प्रश्न 1:
एक अन्य व्यक्ति को आप अपने अध्ययन मेज पर रखे टेबल लैम्प की स्थिति किस प्रकार बताएँगे?
🟢 उत्तर:
किसी वस्तु की स्थिति बताने के लिए हमें दो संख्याओं की आवश्यकता होती है —
1️⃣ एक दूरी, जो क्षैतिज दिशा (X-अक्ष) में होती है।
2️⃣ दूसरी दूरी, जो ऊर्ध्वाधर दिशा (Y-अक्ष) में होती है।
जैसे —
यदि टेबल लैम्प मेज के बाएँ कोने से 40 सेमी और सामने से 30 सेमी दूरी पर रखा है,
तो उसकी स्थिति को (40, 30) के रूप में व्यक्त किया जा सकता है।
इसे निर्देशांक युग्म (x, y) कहते हैं। ✅

🔵 प्रश्न 2 (सड़क योजना):
एक नगर में दो मुख्य सड़कें हैं, जो नगर के केन्द्र पर मिलती हैं।
ये सड़कें
एक उत्तर–दक्षिण दिशा में
दूसरी पूर्व–पश्चिम दिशा में हैं।
नगर की अन्य सड़कें इन मुख्य सड़कों के समान्तर हैं और प्रत्येक 200 मीटर की दूरी पर हैं।
मानक: 1 सेमी = 200 मीटर
📏 अतः कागज़ पर नगर का मॉडल बनाते समय प्रत्येक सड़क के बीच 1 सेमी का अंतर लिया जाएगा।
प्रत्येक क्रॉस-स्ट्रिट का निर्देशांक (x, y) इस प्रकार दिया जाएगा —
➡ यदि कोई सड़क उत्तर–दक्षिण दिशा में जाती है और वह चौथी सड़क है,
➡ तथा दूसरी सड़क पूर्व–पश्चिम दिशा में जाती है और वह पाँचवीं सड़क है,
तो उनका प्रतिच्छेदन बिंदु (4, 5) कहलाएगा।
उसी प्रकार,
➡ यदि दूसरी सड़क उत्तर–दक्षिण दिशा की हो और पाँचवीं सड़क पूर्व–पश्चिम दिशा की हो,
तो क्रॉस-स्ट्रिट को (2, 5) कहा जाएगा।

🔹 प्रश्नानुसार ज्ञात कीजिए —
🟢 (i) कितनी क्रॉस-स्ट्रिट को (4, 3) माना जा सकता है?
➡ चौथी सड़क (उत्तर-दक्षिण दिशा) और तीसरी सड़क (पूर्व-पश्चिम दिशा) का प्रतिच्छेदन।
✅ अतः एक ही क्रॉस-स्ट्रिट होगी — (4, 3)।
🟢 (ii) कितनी क्रॉस-स्ट्रिट को (3, 4) माना जा सकता है?
➡ तीसरी सड़क (उत्तर-दक्षिण दिशा) और चौथी सड़क (पूर्व-पश्चिम दिशा) का प्रतिच्छेदन।
✅ अतः एक ही क्रॉस-स्ट्रिट होगी — (3, 4)।

📘 निष्कर्ष:
✔ क्रॉस-स्ट्रिट का नामकरण क्रम (उत्तर–दक्षिण, पूर्व–पश्चिम) होता है।
✔ प्रत्येक युग्म अद्वितीय है।
✔ (4, 3) और (3, 4) दो अलग स्थान दर्शाते हैं।

प्रश्नावली 3.2

🔵 प्रश्न 1:
निम्नलिखित प्रश्नों में से प्रत्येक का उत्तर दीजिए :
🟢 (i) कार्तीय तल में किसी बिंदु की स्थिति निर्धारित करने वाली क्षैतिज और ऊर्ध्वाधर रेखाओं के क्या नाम हैं?
➡ क्षैतिज रेखा को X-अक्ष तथा ऊर्ध्वाधर रेखा को Y-अक्ष कहते हैं। ✅
🟢 (ii) इन दो रेखाओं से बने तल के प्रत्येक भाग का नाम बताइए।
➡ X-अक्ष और Y-अक्ष मिलकर तल को चार चतुर्थांशों में बाँटते हैं।
 • प्रथम चतुर्थांश (I)
 • द्वितीय चतुर्थांश (II)
 • तृतीय चतुर्थांश (III)
 • चतुर्थ चतुर्थांश (IV) ✅
🟢 (iii) उस बिंदु का नाम बताइए जहाँ ये दो रेखाएँ प्रतिच्छेदित होती हैं।
➡ दोनों रेखाएँ O (मूलबिंदु) पर प्रतिच्छेदित होती हैं। ✅

🔵 प्रश्न 2:
आकृति 3.14 देखकर निम्नलिखित को लिखिए :
🟢 (i) B के निर्देशांक :
➡ (−5, 2) ✅
🟢 (ii) C के निर्देशांक :
➡ (5, −5) ✅
🟢 (iii) निर्देशांक (−3, −5) द्वारा पहचाना गया बिंदु :
➡ E ✅
🟢 (iv) निर्देशांक (2, −4) द्वारा पहचाना गया बिंदु :
➡ G ✅
🟢 (v) D का अभिज्ञ :
➡ निर्देशांक = (6, 1) ✅
🟢 (vi) बिंदु H के निर्देशांक :
➡ (−3, −3) ✅
🟢 (vii) बिंदु L के निर्देशांक :
➡ (0, 5) ✅
🟢 (viii) बिंदु M के निर्देशांक :
➡ (−3, 0) ✅

————————————————————————————————————————————————————————————————————————————

अन्य महत्वपूर्ण प्रश्न

भाग 1: बहुविकल्पीय प्रश्न (MCQ) — उत्तर सहित
प्रश्न 1: निर्देशांक (3, –4) किस चतुर्थांश में स्थित है?
(a) प्रथम
(b) द्वितीय
(c) तृतीय
(d) चतुर्थ
उत्तर: (d) चतुर्थ

प्रश्न 2: निर्देशांक (0, –5) दर्शाता है –
(a) x-अक्ष पर बिंदु
(b) y-अक्ष पर बिंदु
(c) मूल बिंदु
(d) किसी चतुर्थांश में नहीं
उत्तर: (b) y-अक्ष पर बिंदु

प्रश्न 3: मूल बिंदु (Origin) का निर्देशांक होता है –
(a) (1, 1)
(b) (0, 0)
(c) (–1, –1)
(d) (1, 0)
उत्तर: (b) (0, 0)

प्रश्न 4: निर्देशांक (–2, 4) किस चतुर्थांश में आता है?
(a) प्रथम
(b) द्वितीय
(c) तृतीय
(d) चतुर्थ
उत्तर: (b) द्वितीय

प्रश्न 5: x-अक्ष पर स्थित बिंदु का y-अवयव होता है –
(a) धनात्मक
(b) ऋणात्मक
(c) शून्य
(d) अपरिभाषित
उत्तर: (c) शून्य

प्रश्न 6: बिंदु (–3, –5) किस चतुर्थांश में है?
(a) द्वितीय
(b) तृतीय
(c) चतुर्थ
(d) प्रथम
उत्तर: (b) तृतीय

प्रश्न 7: बिंदु (0, 0) को क्या कहते हैं?
(a) y-अक्ष
(b) x-अक्ष
(c) मूल बिंदु
(d) कोई नहीं
उत्तर: (c) मूल बिंदु

प्रश्न 8: निर्देशांक (4, 2) का x-अवयव है –
(a) 2
(b) 4
(c) 6
(d) 0
उत्तर: (b) 4

प्रश्न 9: निर्देशांक (–6, 0) का y-अवयव है –
(a) –6
(b) 6
(c) 0
(d) –12
उत्तर: (c) 0

प्रश्न 10: निर्देशांक (x, y) में x और y को क्रमशः कहते हैं –
(a) मूल और परिमाण
(b) क्षैतिज और ऊर्ध्वाधर अवयव
(c) अक्ष और कक्षा
(d) निर्देश और संकेत
उत्तर: (b) क्षैतिज और ऊर्ध्वाधर अवयव

भाग 2: लघु उत्तर प्रश्न (उत्तर 1–2 पंक्तियों में)
प्रश्न 11: निर्देशांक ज्यामिति की खोज किसने की थी?
उत्तर: रेने देकार्त (René Descartes) ने निर्देशांक ज्यामिति की खोज की थी।

प्रश्न 12: समतल में कुल कितने चतुर्थांश होते हैं?
उत्तर: चार चतुर्थांश होते हैं।

प्रश्न 13: बिंदु (0, –7) किस अक्ष पर स्थित है?
उत्तर: y-अक्ष पर।

प्रश्न 14: प्रथम चतुर्थांश में x और y के संकेत क्या होते हैं?
उत्तर: दोनों धनात्मक (+, +)।

प्रश्न 15: किसी बिंदु (x, y) में यदि x = 0 हो तो वह किस अक्ष पर होगा?
उत्तर: y-अक्ष पर।

प्रश्न 16: निर्देशांक (–3, –2) किस चतुर्थांश में आता है?
उत्तर: तृतीय चतुर्थांश।

प्रश्न 17: निर्देशांक (5, 0) में बिंदु किस अक्ष पर है?
उत्तर: x-अक्ष पर।

प्रश्न 18: निर्देशांक (–2, 5) में x और y के संकेत क्रमशः क्या हैं?
उत्तर: x ऋणात्मक, y धनात्मक।

प्रश्न 19: निर्देशांक (0, 0) को क्यों विशेष माना जाता है?
उत्तर: यह मूल बिंदु होता है, जहाँ x और y अक्ष मिलते हैं।

प्रश्न 20: समतल में किसी बिंदु की स्थिति कैसे दर्शाते हैं?
उत्तर: निर्देशांक (x, y) द्वारा।

भाग 3 (मध्यम उत्तर प्रश्न):
प्रश्न 21: निर्देशांक ज्यामिति से आप क्या समझते हैं?
उत्तर: निर्देशांक ज्यामिति गणित की वह शाखा है जिसमें बिंदुओं, रेखाओं और आकृतियों की स्थिति को समतल में दो संख्याओं (निर्देशांकों) द्वारा दर्शाया जाता है। इसमें बीजगणितीय विधियों से ज्यामितीय समस्याओं को हल किया जाता है।

प्रश्न 22: चतुर्थांशों को उनके संकेतों सहित समझाइए।
उत्तर:
प्रथम चतुर्थांश: (+x, +y)
द्वितीय चतुर्थांश: (–x, +y)
तृतीय चतुर्थांश: (–x, –y)
चतुर्थ चतुर्थांश: (+x, –y)

प्रश्न 23: समतल में बिंदु (–4, 3) को कैसे आलेखित करेंगे?
उत्तर:
x = –4 → मूल से बाईं ओर 4 इकाई
y = 3 → ऊपर की ओर 3 इकाई
इस बिंदु को द्वितीय चतुर्थांश में चिह्नित करेंगे।

प्रश्न 24: x-अक्ष और y-अक्ष में क्या अंतर है?
उत्तर:
x-अक्ष क्षैतिज रेखा होती है, जबकि y-अक्ष ऊर्ध्वाधर।
x-अक्ष पर y = 0 होता है, और y-अक्ष पर x = 0।

प्रश्न 25: निर्देशांक प्रणाली का दैनिक जीवन में एक उदाहरण दीजिए।
उत्तर: GPS प्रणाली में हम किसी स्थान की स्थिति को निर्देशांकों (देशांतर व अक्षांश) द्वारा खोजते हैं।

प्रश्न 26:
नीचे दिए गए निर्देशांकों के आधार पर बिंदुओं को चतुर्थांश सहित पहचानिए:
(i) A(4, 5), (ii) B(–3, 2), (iii) C(–2, –6), (iv) D(6, –4), (v) O(0, 0)
उत्तर:
(i) A(4, 5) — x > 0, y > 0 → प्रथम चतुर्थांश
(ii) B(–3, 2) — x < 0, y > 0 → द्वितीय चतुर्थांश
(iii) C(–2, –6) — x < 0, y < 0 → तृतीय चतुर्थांश (iv) D(6, –4) — x > 0, y < 0 → चतुर्थ चतुर्थांश
(v) O(0, 0) — मूल बिंदु (किसी चतुर्थांश में नहीं)

प्रश्न 27:
नीचे दिए गए बिंदुओं को समतल पर आलेखित (plot) कीजिए:
P(2, 3), Q(–4, 2), R(–3, –3), S(4, –2)
उत्तर (स्टेप-बाय-स्टेप):
सबसे पहले ग्राफ पेपर लें और x व y अक्ष खींचें।
मूल बिंदु O(0, 0) चिह्नित करें। 3.
P(2, 3): x = 2 (दाएँ), y = 3 (ऊपर) → प्रथम चतुर्थांश
Q(–4, 2): x = –4 (बाएँ), y = 2 (ऊपर) → द्वितीय चतुर्थांश
R(–3, –3): x = –3 (बाएँ), y = –3 (नीचे) → तृतीय चतुर्थांश
S(4, –2): x = 4 (दाएँ), y = –2 (नीचे) → चतुर्थ चतुर्थांश
सभी बिंदुओं को साफ़-साफ़ चिह्नित करें।

प्रश्न 28:
यदि किसी बिंदु का निर्देशांक (x, 0) है, तो वह बिंदु किस अक्ष पर स्थित होगा? उदाहरण सहित समझाइए।
उत्तर:
यदि निर्देशांक (x, 0) है, तो y-अवयव = 0
इसका अर्थ है कि बिंदु x-अक्ष पर स्थित होगा।
उदाहरण: (5, 0) → x-अक्ष पर 5 इकाई दाएँ
(–3, 0) → x-अक्ष पर 3 इकाई बाएँ
निष्कर्ष: y = 0 ⇒ बिंदु x-अक्ष पर होगा।

प्रश्न 29:
एक बिंदु के निर्देशांक (0, y) हों तो वह बिंदु कहाँ स्थित होता है? विभिन्न y के मान लेकर समझाइए।
उत्तर:
यदि x = 0, तो बिंदु y-अक्ष पर स्थित होगा।
उदाहरण:
(0, 4) → y-अक्ष पर ऊपर 4 इकाई
(0, –2) → y-अक्ष पर नीचे 2 इकाई
निष्कर्ष: x = 0 ⇒ बिंदु y-अक्ष पर होगा, चाहे y धनात्मक हो या ऋणात्मक।

प्रश्न 30:
नीचे दिए गए निर्देशांकों को देखकर यह बताइए कि कौन से बिंदु x-अक्ष, कौन से y-अक्ष, और कौन से चतुर्थांश में हैं:
(i) A(7, 0), (ii) B(0, –6), (iii) C(–3, 3), (iv) D(–4, –5), (v) E(5, –7)
उत्तर (वर्गीकरण सहित):
A(7, 0): x-अक्ष पर (y = 0)
B(0, –6): y-अक्ष पर (x = 0)
C(–3, 3): द्वितीय चतुर्थांश (x < 0, y > 0)
D(–4, –5): तृतीय चतुर्थांश (x < 0, y < 0)
E(5, –7): चतुर्थ चतुर्थांश (x > 0, y < 0)

————————————————————————————————————————————————————————————————————————————

एक पृष्ठ में पुनरावृत्ति

🟩 एक पृष्ठीय संशोधन पत्रक (One Page Revision Sheet)
अध्याय: निर्देशांक ज्यामिति (कक्षा 9 गणित)
────────────────────────────
📌 1. निर्देशांक ज्यामिति क्या है?
निर्देशांक ज्यामिति वह शाखा है जिसमें किसी बिंदु की स्थिति को दो संख्याओं (x, y) द्वारा समतल पर दर्शाया जाता है। इसे “डेकार्टियन ज्यामिति” भी कहा जाता है।

📌 2. समतल (Cartesian Plane)
दो लम्बवत रेखाएँ:
➤ क्षैतिज रेखा → x-अक्ष
➤ ऊर्ध्वाधर रेखा → y-अक्ष
मिलन बिंदु: मूल बिंदु (Origin) → निर्देशांक (0, 0)

📌 3. निर्देशांक (Coordinates)
बिंदु P के निर्देशांक: P(x, y)
➤ x = क्षैतिज दूरी
➤ y = ऊर्ध्वाधर दूरी
क्रम का ध्यान: (x, y) ही होगा, (y, x) नहीं।

📌 4. चतुर्थांश (Quadrants)
| चतुर्थांश | संकेत (x, y) | स्थिति | |———–|—————|———| | प्रथम | (+, +) | दाएँ-ऊपर
| द्वितीय | (–, +) | बाएँ-ऊपर
| तृतीय | (–, –) | बाएँ-नीचे
| चतुर्थ | (+, –) | दाएँ-नीचे

📌 5. विशेष निर्देशांक
मूल बिंदु: (0, 0)
x-अक्ष पर: (x, 0)
y-अक्ष पर: (0, y)

📌 6. आलेखन (Plotting Points)
बिंदु (3, –2) → दाएँ 3 इकाई, नीचे 2 इकाई
बिंदु (–4, 2) → बाएँ 4 इकाई, ऊपर 2 इकाई

📌 7. चिह्न पहचान शॉर्टकट
🟢 x > 0, y > 0 → प्रथम चतुर्थांश
🟢 x < 0, y > 0 → द्वितीय
🟢 x < 0, y < 0 → तृतीय 🟢 x > 0, y < 0 → चतुर्थ

📌 8. दैनिक जीवन में उपयोग
✔ GPS में स्थान का निर्धारण
✔ मानचित्रण (Mapping)
✔ गेम्स और ग्राफिक्स डिज़ाइन
✔ विज्ञान में मापन

📌 9. याद रखने योग्य बातें
✅ निर्देशांक = बिंदु की स्थिति
✅ क्रम = (x, y)
✅ मूल = (0, 0)
✅ केवल दो अक्ष होते हैं: x और y
✅ चतुर्थांश कुल 4

📌 10. अभ्यास सुझाव
🔹 ग्राफ पेपर पर 10 बिंदुओं का आलेखन करें
🔹 प्रत्येक चतुर्थांश से कम से कम 2 बिंदु चुनें
🔹 x और y अक्ष पर भी बिंदु चिह्नित करें
────────────────────────────

————————————————————————————————————————————————————————————————————————————

मानचित्र

————————————————————————————————————————————————————————————————————————————
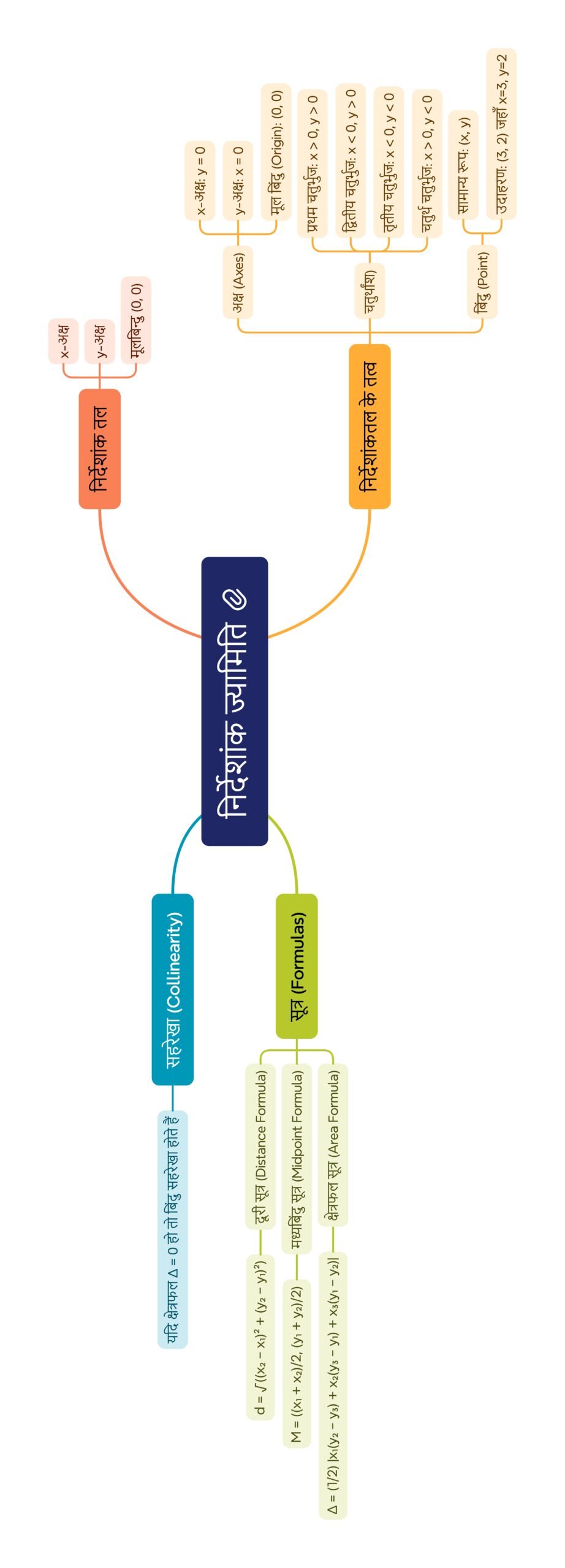