Class : 9 – Math (Hindi) : Lesson 11. पृष्ठीय क्षेत्रफल एवं आयतन
पाठ का विश्लेषण एवं विवेचन
✨ विस्तृत व्याख्या
🔵 भूमिका
ज्यामिति में त्रि-आयामी आकृतियाँ (3D figures) हमारे चारों ओर मौजूद हैं। घर, ईंट, बोतल, पानी की टंकी, फुटबॉल, बर्फ का गोला, सिलेंडर आदि सब त्रि-आयामी वस्तुएँ हैं। इन आकृतियों का अध्ययन करते समय दो मुख्य बातें आती हैं:
पृष्ठीय क्षेत्रफल (Surface Area) – वस्तु की सतह को ढकने के लिए आवश्यक क्षेत्रफल।
आयतन (Volume) – वस्तु में भरे जाने वाले स्थान का परिमाण।
यह अध्याय विद्यार्थियों को विभिन्न ठोस आकृतियों जैसे घन, घनाभ, बेलन, शंकु, गोला और अर्धगोला का पृष्ठीय क्षेत्रफल और आयतन निकालना सिखाता है।
🟢 घनाभ (Cuboid)
आयाम: लंबाई (l), चौड़ाई (b), ऊँचाई (h)
पृष्ठीय क्षेत्रफल:
कुल पृष्ठीय क्षेत्रफल (TSA) = 2(lb + bh + hl)
आयतन: V = l × b × h
✏️ Note: घनाभ एक डिब्बे जैसी आकृति होती है।
🔴 घन (Cube)
आयाम: सभी भुजाएँ समान (a)
पृष्ठीय क्षेत्रफल: TSA = 6a²
आयतन: V = a³
💡 Concept: पासे (Dice) और शक्कर की डली घन के उदाहरण हैं।
🟡 बेलन (Cylinder)
आयाम: त्रिज्या (r), ऊँचाई (h)
वक्र पृष्ठीय क्षेत्रफल (CSA): 2πrh
कुल पृष्ठीय क्षेत्रफल (TSA): 2πr(h + r)
आयतन: V = πr²h
✔️ उदाहरण: पाइप, ड्रम, स्तंभ।
🔵 शंकु (Cone)
आयाम: त्रिज्या (r), ऊँचाई (h), तिर्यक ऊँचाई (l = √(r² + h²))
वक्र पृष्ठीय क्षेत्रफल (CSA): πrl
कुल पृष्ठीय क्षेत्रफल (TSA): πr(l + r)
आयतन: V = 1/3 πr²h
✔️ उदाहरण: आइसक्रीम कोन, टेंट।
🟢 गोला (Sphere)
आयाम: त्रिज्या (r)
पृष्ठीय क्षेत्रफल: 4πr²
आयतन: 4/3 πr³
✔️ उदाहरण: फुटबॉल, बास्केटबॉल।
🔴 अर्धगोला (Hemisphere)
आयाम: त्रिज्या (r)
वक्र पृष्ठीय क्षेत्रफल (CSA): 2πr²
कुल पृष्ठीय क्षेत्रफल (TSA): 3πr²
आयतन: 2/3 πr³
✔️ उदाहरण: बर्फ का गोला, कटोरा।
🟡 पिरामिड (Pyramid) – (NCERT विस्तार में उल्लेखित)
आयतन: V = 1/3 × आधार क्षेत्रफल × ऊँचाई
🌿 संयोजित ठोस (Combination of Solids)
कभी-कभी वस्तुएँ दो या अधिक आकृतियों से मिलकर बनी होती हैं। जैसे:
आइसक्रीम = शंकु + अर्धगोला
सिलेंडर पर शंकु = टेंट
➡️ इनका पृष्ठीय क्षेत्रफल और आयतन अलग-अलग भागों का जोड़कर निकाला जाता है।
🔵 वास्तविक जीवन के अनुप्रयोग
भवन निर्माण → दीवारों का क्षेत्रफल व ईंटों की संख्या।
टंकी → पानी की क्षमता (आयतन)।
पैकेजिंग → डिब्बों का पृष्ठीय क्षेत्रफल।
खेल → गेंद, फुटबॉल, बास्केटबॉल का आयतन व क्षेत्रफल।
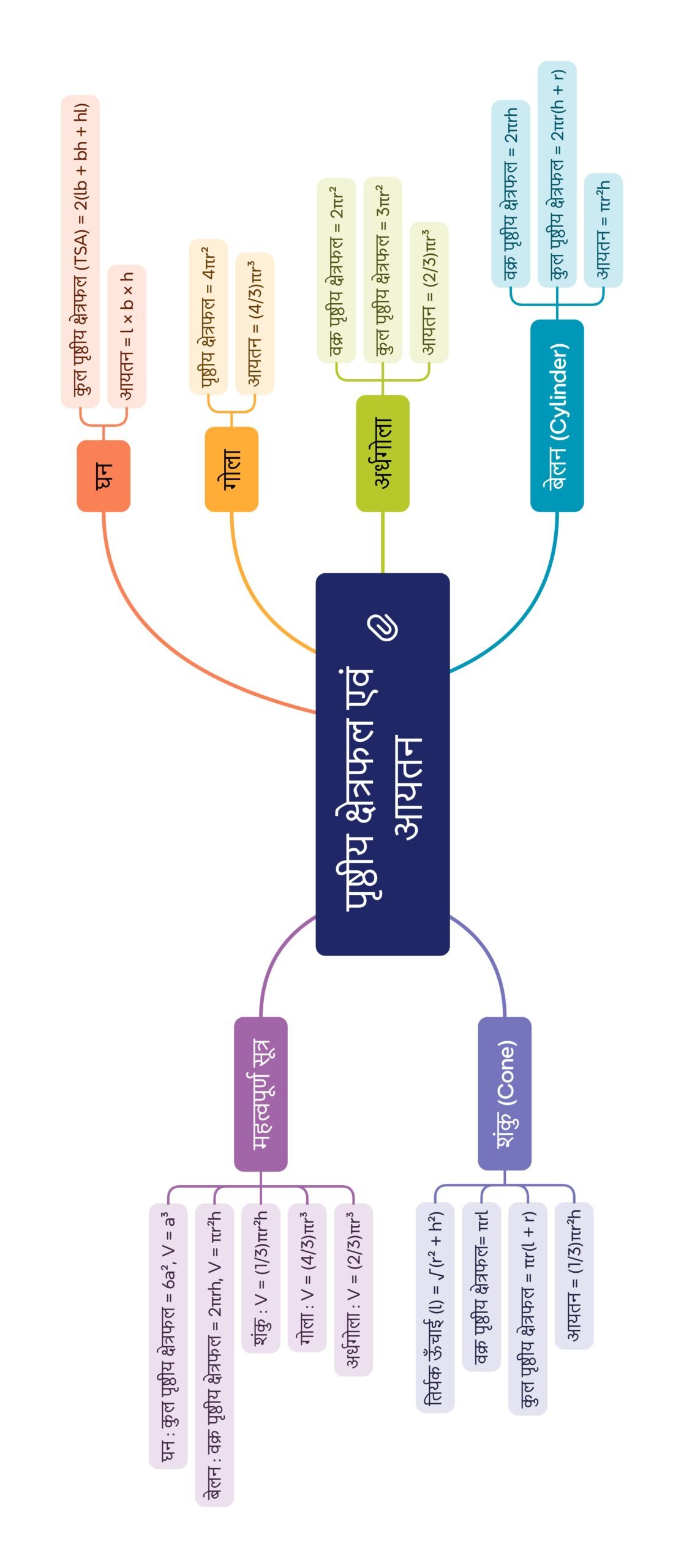
🟢 महत्वपूर्ण सूत्र सूची
घनाभ: TSA = 2(lb + bh + hl), V = lbh
घन: TSA = 6a², V = a³
बेलन: CSA = 2πrh, TSA = 2πr(h + r), V = πr²h
शंकु: CSA = πrl, TSA = πr(l + r), V = 1/3 πr²h
गोला: SA = 4πr², V = 4/3 πr³
अर्धगोला: CSA = 2πr², TSA = 3πr², V = 2/3 πr³
🔴 अध्याय का महत्व
विद्यार्थियों को त्रि-आयामी आकृतियों को समझने में मदद करता है।
भौतिकी, इंजीनियरिंग, वास्तुकला, दैनिक जीवन के कार्यों में इनका उपयोग होता है।
यह अध्याय गणना की व्यावहारिकता और गणित के वास्तविक उपयोग को दर्शाता है।
📌 Summary (~300 शब्द)
मुख्य अवधारणा: पृष्ठीय क्षेत्रफल = सतह को ढकने का क्षेत्र, आयतन = वस्तु में भरे स्थान का माप।
घनाभ: TSA = 2(lb + bh + hl), V = lbh
घन: TSA = 6a², V = a³
बेलन: CSA = 2πrh, TSA = 2πr(h + r), V = πr²h
शंकु: CSA = πrl, TSA = πr(l + r), V = 1/3 πr²h
गोला: SA = 4πr², V = 4/3 πr³
अर्धगोला: CSA = 2πr², TSA = 3πr², V = 2/3 πr³
संयोजित ठोस: अलग-अलग भागों के क्षेत्रफल/आयतन का जोड़।
अनुप्रयोग: पैकेजिंग, निर्माण, खेल, टंकी की क्षमता आदि।
✔️ यह अध्याय छात्रों को त्रि-आयामी आकृतियों की गहराई और उनके अनुप्रयोगों को समझाता है।
📝 Quick Recap
🔵 घनाभ: TSA = 2(lb + bh + hl), V = lbh
🟢 घन: TSA = 6a², V = a³
🟡 बेलन: CSA = 2πrh, V = πr²h
🔴 शंकु: V = 1/3 πr²h
🌿 गोला: SA = 4πr², V = 4/3 πr³
✔️ अर्धगोला: TSA = 3πr², V = 2/3 πr³
————————————————————————————————————————————————————————————————————————————
पाठ्यपुस्तक के प्रश्न
🔵 प्रश्नावली 11.1
🔹 जब तक अन्यथा न कहा जाए, π = 22/7 लीजिए।
🔵 प्रश्न 1. एक शंकु के आधार का व्यास 10.5 cm है और इसकी तिर्यक ऊँचाई 10 cm है। इसका वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
🟢 उत्तर:
💡 दिया: व्यास = 10.5 cm ⇒ त्रिज्या r = 10.5/2 = 5.25 cm, तिर्यक ऊँचाई l = 10 cm
➤ सूत्र: वक्र पृष्ठीय क्षेत्रफल (CSA) = π r l
➤ स्थापना: CSA = (22/7) × 5.25 × 10
➤ सरलीकरण: 5.25 = 21/4 ⇒ CSA = (22/7) × (21/4) × 10
➤ गणना: (21/7) = 3 ⇒ CSA = 22 × 3 × 10 / 4 = 660/4
✔️ अंतिम परिणाम: CSA = 165 cm²
🔵 प्रश्न 2. एक शंकु का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए, जिसकी तिर्यक ऊँचाई 21 m है और आधार का व्यास 24 m है।
🟢 उत्तर:
💡 दिया: व्यास = 24 m ⇒ r = 12 m, तिर्यक ऊँचाई l = 21 m
➤ सूत्र: कुल पृष्ठीय क्षेत्रफल (TSA) = π r (l + r)
➤ स्थापना: TSA = (22/7) × 12 × (21 + 12) = (22/7) × 12 × 33
➤ गणना: 22 × 12 × 33 = 8712 ⇒ TSA = 8712/7 m²
✔️ अंतिम परिणाम: TSA = 8712/7 m² ≈ 1244.571 m²
🔵 प्रश्न 3. एक शंकु का वक्र पृष्ठीय क्षेत्रफल 308 cm² है और इसकी तिर्यक ऊँचाई 14 cm है। ज्ञात कीजिए :
(i) आधार की त्रिज्या
(ii) शंकु का कुल पृष्ठीय क्षेत्रफल
🟢 उत्तर:
💡 दिया: CSA = 308 cm², l = 14 cm
➤ सूत्र (CSA): π r l = 308
➤ स्थापना: (22/7) × r × 14 = 308
➤ सरलीकरण: 14 × (22/7) = 44 ⇒ 44 r = 308
➤ गणना: r = 308/44 = 7 cm
➡️ (i) आधार की त्रिज्या r = 7 cm
अब कुल पृष्ठीय क्षेत्रफल:
➤ सूत्र (TSA): π r (l + r)
➤ स्थापना: TSA = (22/7) × 7 × (14 + 7) = 22 × 21
➤ गणना: 22 × 21 = 462
➡️ (ii) TSA = 462 cm²
✔️ अंतिम परिणाम: r = 7 cm, TSA = 462 cm²
🔵 प्रश्न 4. शंकु के आकार का एक तंबू 10 m ऊँचा है और उसके आधार की त्रिज्या 24 m है। ज्ञात कीजिए :
(i) तंबू की तिर्यक ऊँचाई
(ii) तंबू में लगे केनवास (canvas) की लागत, यदि 1 m² केनवास की लागत 70 रुपये है।
🟢 उत्तर:
💡 दिया: h = 10 m, r = 24 m, केनवास = वक्र पृष्ठीय आवरण (आधार खुला)
(i) तिर्यक ऊँचाई
➤ सूत्र: l = √(r² + h²)
➤ स्थापना: l = √(24² + 10²) = √(576 + 100)
➤ गणना: l = √676 = 26 m
➡️ तिर्यक ऊँचाई l = 26 m
(ii) केनवास की लागत
➤ वक्र पृष्ठीय क्षेत्रफल: CSA = π r l = (22/7) × 24 × 26
➤ गणना: 24 × 26 = 624 ⇒ CSA = (22 × 624)/7 = 13728/7 m²
➤ क्षेत्रफल (दशमलव): 13728/7 = 1961 1/7 m² (≈ 1961.142857 m²)
➤ लागत: = CSA × 70 = (13728/7) × 70 = 13728 × 10
✔️ अंतिम परिणाम: केनवास की लागत = ₹ 137280
🔵 प्रश्न 5.
8 m ऊँचाई और आधार की त्रिज्या 6 m वाले एक शंकु के आकार का तंबू बनाने में 3 m चौड़ी तिरपाल की कितनी लंबाई लगेगी? यह मान कर चलिए कि इसकी सिलाई और कटाई में 20 cm तिरपाल अतिरिक्त लगेगी। (π = 3.14 का प्रयोग कीजिए।)
🟢 उत्तर:
➡️ शंकु की तिर्यक ऊँचाई (l) = √(r² + h²)
= √(6² + 8²)
= √(36 + 64)
= √100
= 10 m
➡️ तंबू का वक्र पृष्ठीय क्षेत्रफल = πrl
= 3.14 × 6 × 10
= 188.4 m²
➡️ 3 m चौड़ी तिरपाल की आवश्यक लंबाई = (188.4 / 3)
= 62.8 m
➡️ सिलाई व कटाई हेतु अतिरिक्त तिरपाल = 0.20 m
तो कुल लंबाई = 62.8 + 0.20
= 63.0 m
✔️ अंतिम उत्तर: 63 m तिरपाल की आवश्यकता होगी।
🔵 प्रश्न 6.
शंकु के आधार पर एक गुम्बद की तिर्यक ऊँचाई और आधार व्यास क्रमशः 25 m और 14 m है। इसकी वक्र पृष्ठ पर ₹ 210 प्रति 100 m² की दर से सफेदी कराने का व्यय ज्ञात कीजिए।
🟢 उत्तर:
➡️ गुम्बद का त्रिज्या (r) = 14/2 = 7 m
➡️ तिर्यक ऊँचाई (l) = 25 m
➡️ वक्र पृष्ठीय क्षेत्रफल = πrl
= 3.14 × 7 × 25
= 549.5 m²
➡️ दर = ₹ 210 प्रति 100 m²
तो 1 m² की दर = 210/100 = ₹ 2.1
➡️ कुल व्यय = 549.5 × 2.1
= ₹ 1153.95
✔️ अंतिम उत्तर: ₹ 1154 (लगभग)।
🔵 प्रश्न 7.
गणेश जी की टोपी एक शंकु के आकार की है, जिसके आधार की त्रिज्या 7 cm और ऊँचाई 24 cm है। इसी प्रकार की 10 टोपियाँ बनाने के लिए आवश्यक गत्ते का क्षेत्रफल ज्ञात कीजिए।
🟢 उत्तर:
➡️ तिर्यक ऊँचाई (l) = √(r² + h²)
= √(7² + 24²)
= √(49 + 576)
= √625
= 25 cm
➡️ एक टोपी का वक्र पृष्ठीय क्षेत्रफल = πrl
= 3.14 × 7 × 25
= 549.5 cm²
➡️ 10 टोपियों का क्षेत्रफल = 10 × 549.5
= 5495 cm²
✔️ अंतिम उत्तर: 5495 cm² गत्ते की आवश्यकता होगी।
🔵 प्रश्न 8.
किसी बस स्टाप को पुरानी गत्ते से बने 50 खोखले शंकुओं द्वारा सड़क से अलग किया हुआ है। प्रत्येक शंकु के आधार का व्यास 40 cm है और ऊँचाई 1 m है। यदि इन शंकुओं की बाहरी पृष्ठों को पेंट करना है और पेंट की दर ₹ 12 प्रति m² है, तो इनको पेंट कराने में कितनी लागत आएगी? (π = 3.14 और √1.04 = 1.02 का प्रयोग कीजिए।)
🟢 उत्तर:
➡️ आधार त्रिज्या (r) = 40/2 = 20 cm = 0.2 m
➡️ ऊँचाई (h) = 1 m
➡️ तिर्यक ऊँचाई (l) = √(r² + h²)
= √(0.2² + 1²)
= √(0.04 + 1)
= √1.04
= 1.02 m
➡️ एक शंकु का वक्र पृष्ठीय क्षेत्रफल = πrl
= 3.14 × 0.2 × 1.02
= 0.64056 m²
➡️ 50 शंकुओं का क्षेत्रफल = 50 × 0.64056
= 32.028 m²
➡️ पेंट की लागत = 32.028 × 12
= ₹ 384.34
✔️ अंतिम उत्तर: ₹ 384 (लगभग)।
प्रश्नावली 11.2
🔵 प्रश्न 1.
निम्न त्रिज्या वाले गोलों का पृष्ठीय क्षेत्रफल ज्ञात कीजिए :
(i) 10.5 cm (ii) 5.6 cm (iii) 14 cm
🟢 उत्तर:
💡 सूत्र: गोले का पृष्ठीय क्षेत्रफल = 4πr² (यहाँ π = 22/7)
(i) r = 10.5 cm
➡️ पृष्ठीय क्षेत्रफल = 4 × (22/7) × 10.5²
➡️ = 4 × (22/7) × 110.25
➡️ = 1386 cm²
✔️ उत्तर: 1386 cm²
(ii) r = 5.6 cm
➡️ पृष्ठीय क्षेत्रफल = 4 × (22/7) × 5.6²
➡️ = 4 × (22/7) × 31.36
➡️ = 394.24 cm²
✔️ उत्तर: 394.24 cm²
(iii) r = 14 cm
➡️ पृष्ठीय क्षेत्रफल = 4 × (22/7) × 14²
➡️ = 4 × (22/7) × 196
➡️ = 2464 cm²
✔️ उत्तर: 2464 cm²
🔵 प्रश्न 2.
निम्न व्यास वाले गोलों का पृष्ठीय क्षेत्रफल ज्ञात कीजिए :
(i) 14 cm (ii) 21 cm (iii) 3.5 m
🟢 उत्तर:
💡 r = d/2, और पृष्ठीय क्षेत्रफल = 4πr²
(i) d = 14 cm ⇒ r = 7 cm
➡️ पृष्ठीय क्षेत्रफल = 4 × (22/7) × 7² = 616 cm²
✔️ उत्तर: 616 cm²
(ii) d = 21 cm ⇒ r = 10.5 cm
➡️ पृष्ठीय क्षेत्रफल = 4 × (22/7) × 10.5² = 1386 cm²
✔️ उत्तर: 1386 cm²
(iii) d = 3.5 m ⇒ r = 1.75 m
➡️ पृष्ठीय क्षेत्रफल = 4 × (22/7) × 1.75² = 38.5 m²
✔️ उत्तर: 38.5 m²
🔵 प्रश्न 3.
10 cm त्रिज्या वाले एक अर्धगोले का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए। (π = 3.14 लीजिए।)
🟢 उत्तर:
💡 अर्धगोले का कुल पृष्ठीय क्षेत्रफल = 3πr²
➡️ r = 10 cm, π = 3.14
➡️ कुल पृष्ठीय क्षेत्रफल = 3 × 3.14 × 10²
➡️ = 3 × 3.14 × 100 = 942 cm²
✔️ उत्तर: 942 cm²
🔵 प्रश्न 4.
एक गोलाकार गुब्बारे में हवा भरने पर, उसकी त्रिज्या 7 cm से 14 cm हो जाती है। इन दोनों स्थितियों में, गुब्बारे के पृष्ठीय क्षेत्रों का अनुपात ज्ञात कीजिए।
🟢 उत्तर:
💡 गोले का पृष्ठीय क्षेत्रफल ∝ r²
➡️ अनुपात = 7² : 14²
➡️ = 49 : 196
➡️ = 1 : 4
✔️ उत्तर: 1 : 4
🔵 प्रश्न 5.
पीतल से बने एक अर्धगोलाकार कटोरे का आंतरिक व्यास 10.5 cm है। ₹16 प्रति 100 cm² की दर से इसके आंतरिक पृष्ठ पर क्लैडिंग कराने का व्यय ज्ञात कीजिए।
🟢 उत्तर:
💡 आंतरिक त्रिज्या r = 10.5/2 = 5.25 cm, अर्धगोले का वक्र पृष्ठीय क्षेत्रफल = 2πr²
➡️ वक्र पृष्ठ = 2 × (22/7) × 5.25²
➡️ = 2 × (22/7) × 27.5625 = 173.25 cm²
➡️ लागत = (173.25/100) × ₹16 = ₹27.72 (लगभग)
✔️ उत्तर: ₹27.72 ≈ ₹28
🔵 प्रश्न 6.
उस गोले की त्रिज्या ज्ञात कीजिए जिसका पृष्ठीय क्षेत्रफल 154 cm² है।
🟢 उत्तर:
💡 4πr² = 154, π = 22/7
➡️ r² = 154/(4π) = 154/(4 × 22/7)
➡️ r² = 154 × 7 / 88 = 12.25
➡️ r = √12.25 = 3.5 cm
✔️ उत्तर: 3.5 cm
🔵 प्रश्न 7.
चन्द्रमा का व्यास पृथ्वी के व्यास का लगभग एक-चौथाई है। इन दोनों के पृष्ठीय क्षेत्रों का अनुपात ज्ञात कीजिए।
🟢 उत्तर:
💡 पृष्ठीय क्षेत्रफल ∝ (व्यास)²
➡️ अनुपात = (1/4)² : 1²
➡️ = 1/16 : 1
➡️ = 1 : 16 (चन्द्रमा : पृथ्वी)
✔️ उत्तर: 1 : 16
🔵 प्रश्न 8.
एक अर्धगोलाकार कटोरा 0.25 cm मोटी स्टील से बना है। इस कटोरे का आंतरिक त्रिज्या 5 cm है। इसकी बाहरी वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
🟢 उत्तर:
💡 बाहरी त्रिज्या R = 5 + 0.25 = 5.25 cm, वक्र पृष्ठीय क्षेत्रफल = 2πR²
➡️ बाहरी CSA = 2 × (22/7) × 5.25²
➡️ = 2 × (22/7) × 27.5625 = 173.25 cm²
✔️ उत्तर: 173.25 cm²
🔵 प्रश्न 9.
एक लंब वृत्तीय सिलेंडर त्रिज्या r वाले एक गोले को पूर्णतः घेरे हुए है (देखिए आकृति 11.10) ज्ञात कीजिए :
(i) गोले का पृष्ठीय क्षेत्रफल
(ii) बेलन का वक्र पृष्ठीय क्षेत्रफल
(iii) (i) और (ii) में प्राप्त क्षेत्रफलों का अनुपात
🟢 उत्तर:
(i) 💡 गोले का पृष्ठीय क्षेत्रफल = 4πr²
➡️ उत्तर: 4πr²
(ii) 💡 सिलेंडर का त्रिज्या = r, ऊँचाई = 2r ⇒ वक्र पृष्ठीय क्षेत्रफल = 2πrh
➡️ = 2πr × 2r = 4πr²
➡️ उत्तर: 4πr²
(iii) 💡 अनुपात = (4πr²) : (4πr²)
➡️ = 1 : 1
✔️ उत्तर: 1 : 1
प्रश्नावली 11.3
🔵 प्रश्न 1.
उस लंब वृत्तीय शंकु का आयतन ज्ञात कीजिए, जिसकी
(i) त्रिज्या 6 cm और ऊँचाई 7 cm है।
(ii) त्रिज्या 3.5 cm और ऊँचाई 12 cm है।
🟢 उत्तर:
💡 सूत्र: शंकु का आयतन = 1/3 πr²h
(i) r = 6 cm, h = 7 cm
➡️ आयतन = 1/3 × (22/7) × 6² × 7
➡️ = 1/3 × (22/7) × 36 × 7
➡️ = 1/3 × 792
➡️ = 264 cm³
✔️ उत्तर: 264 cm³
(ii) r = 3.5 cm, h = 12 cm
➡️ आयतन = 1/3 × (22/7) × (3.5)² × 12
➡️ = 1/3 × (22/7) × 12.25 × 12
➡️ = 1/3 × 462
➡️ = 154 cm³
✔️ उत्तर: 154 cm³
🔵 प्रश्न 2.
शंकु के आकार के उस बर्तन की लीटरों में धारिता ज्ञात कीजिए जिसकी
(i) त्रिज्या 7 cm और तिर्यक ऊँचाई 25 cm है।
(ii) ऊँचाई 12 cm और तिर्यक ऊँचाई 13 cm है।
🟢 उत्तर:
(i) r = 7 cm, l = 25 cm
➡️ h = √(l² – r²) = √(25² – 7²) = √(625 – 49) = √576 = 24 cm
➡️ आयतन = 1/3 × (22/7) × 7² × 24
➡️ = 1/3 × (22/7) × 49 × 24
➡️ = 1/3 × 3696
➡️ = 1232 cm³ = 1.232 L
✔️ उत्तर: 1.232 लीटर
(ii) h = 12 cm, l = 13 cm
➡️ r = √(l² – h²) = √(169 – 144) = √25 = 5 cm
➡️ आयतन = 1/3 × (22/7) × 5² × 12
➡️ = 1/3 × (22/7) × 25 × 12
➡️ = 314.3 cm³ = 0.314 L
✔️ उत्तर: 0.314 लीटर
🔵 प्रश्न 3.
एक शंकु की ऊँचाई 15 cm है। यदि उसका आयतन 1570 cm³ है, तो इसके आधार की त्रिज्या ज्ञात कीजिए। (π = 3.14 प्रयोग कीजिए)
🟢 उत्तर:
➡️ V = 1/3 πr²h
➡️ 1570 = 1/3 × 3.14 × r² × 15
➡️ 1570 = 15.7 r²
➡️ r² = 1570 ÷ 15.7
➡️ r² = 100
➡️ r = √100 = 10 cm
✔️ उत्तर: 10 cm
🔵 प्रश्न 4.
त्रिज्या 9 cm और ऊँचाई 24 cm वाले एक लंब वृत्तीय शंकु का आयतन 48π cm³ है, तो इसके आधार का व्यास ज्ञात कीजिए।
🟢 उत्तर:
➡️ दिया गया आयतन = 48π cm³
➡️ सूत्र: V = 1/3 πr²h
➡️ 48π = 1/3 × π × r² × 24
➡️ 48π = 8πr²
➡️ r² = 48π ÷ 8π = 6
➡️ r = √6 = 2.45 cm (लगभग)
➡️ व्यास = 2r = 4.9 cm
✔️ उत्तर: 4.9 cm (लगभग)
🔵 प्रश्न 5.
ऊपरी व्यास 3.5 m वाले शंकु के आकार का एक गड्ढा 12 m गहरा है। इसकी धारिता किलोलीटरों में कितनी है?
🟢 उत्तर:
💡 सूत्र: शंकु का आयतन
V = (1/3) × π × r² × h
➡️ व्यास = 3.5 m ⇒ r = 3.5 ÷ 2 = 1.75 m
➡️ ऊँचाई h = 12 m
➡️ r² = (1.75)² = 3.0625
➡️ π × r² × h = (22/7) × 3.0625 × 12
= (22/7) × 36.75
= 115.5
➡️ V = (1/3) × 115.5 = 38.5 m³
➡️ 1 m³ = 1000 L = 1 kL
✔️ अंतिम उत्तर: 38.5 किलोलीटर
🔵 प्रश्न 6.
एक लंब वृत्तीय शंकु का आयतन 9856 cm³ है। यदि इसके आधार का व्यास 28 cm है, तो ज्ञात कीजिए :
(i) शंकु की ऊँचाई
(ii) शंकु की तिर्यक ऊँचाई
(iii) शंकु का वक्र पृष्ठीय क्षेत्रफल
🟢 उत्तर:
(i) r = 28 ÷ 2 = 14 cm, V = 9856 cm³
➡️ सूत्र: V = (1/3) π r² h
➡️ 9856 = (1/3) × (22/7) × 14² × h
➡️ 9856 = (1/3) × (22/7) × 196 × h
➡️ 9856 = (1/3) × 616 × h = 205.33 h
➡️ h = 9856 ÷ 205.33 = 48 cm
(ii) तिर्यक ऊँचाई: l = √(r² + h²)
➡️ = √(14² + 48²)
➡️ = √(196 + 2304) = √2500
➡️ = 50 cm
(iii) वक्र पृष्ठीय क्षेत्रफल = π r l
➡️ = (22/7) × 14 × 50
➡️ = 2200 cm²
✔️ उत्तर: ऊँचाई = 48 cm, तिर्यक ऊँचाई = 50 cm, वक्र पृष्ठीय क्षेत्रफल = 2200 cm²
🔵 प्रश्न 7.
भुजाएँ 5 cm, 12 cm और 13 cm वाले एक समकोण त्रिभुज ABC को भुजा 12 cm के परित घुमाया जाता है। इस प्रकार प्राप्त ठोस का आयतन ज्ञात कीजिए।
🟢 उत्तर:
➡️ त्रिभुज समकोण है क्योंकि 5² + 12² = 13²
➡️ घुमाने पर शंकु बनेगा जिसमें r = 5 cm, h = 12 cm
➡️ आयतन V = (1/3) π r² h
➡️ = (1/3) × (22/7) × 25 × 12
➡️ = (1/3) × 942.86
➡️ = 314.3 cm³
✔️ उत्तर: 314.3 cm³
🔵 प्रश्न 8.
यदि प्रश्न 7 के त्रिभुज ABC को यदि भुजा 5 cm के परित घुमाया जाए, तो इस प्रकार प्राप्त ठोस का आयतन ज्ञात कीजिए। प्रश्न 7 और 8 में प्राप्त किए गए दोनों ठोसों के आयतनों का अनुपात भी ज्ञात कीजिए।
🟢 उत्तर:
➡️ अब r = 12 cm, h = 5 cm
➡️ V = (1/3) π r² h
➡️ = (1/3) × (22/7) × 144 × 5
➡️ = (1/3) × (22/7) × 720
➡️ = 754.3 cm³
➡️ अनुपात = 314.3 : 754.3 ≈ 1 : 2.4
✔️ उत्तर: 754.3 cm³ और अनुपात = 1 : 2.4
🔵 प्रश्न 9.
गेहूँ की एक ढेरी 10.5 m व्यास और ऊँचाई 3 m वाले एक शंकु के आकार की है। इसका आयतन ज्ञात कीजिए। इस ढेरी को वर्षा से बचाने के लिए कैनवास से ढक जाना है। ढकनेवाले कैनवास का क्षेत्रफल ज्ञात कीजिए।
🟢 उत्तर:
➡️ r = 10.5 ÷ 2 = 5.25 m, h = 3 m
➡️ आयतन = (1/3) π r² h
= (1/3) × (22/7) × (5.25)² × 3
= (1/3) × (22/7) × 27.5625 × 3
= (22/7) × 27.5625
= 86 m³
➡️ तिर्यक ऊँचाई l = √(r² + h²)
= √(5.25² + 3²)
= √(27.5625 + 9)
= √36.5625
≈ 6.05 m
➡️ वक्र पृष्ठीय क्षेत्रफल = π r l
= (22/7) × 5.25 × 6.05
≈ 99.6 m²
✔️ उत्तर: आयतन = 86 m³, कैनवास क्षेत्रफल = 99.6 m²
प्रश्नावली 11.4
🔵 प्रश्न 1.
उस गोले का आयतन ज्ञात कीजिए जिसकी त्रिज्या निम्न है :
(i) 7 cm
(ii) 0.63 m
🟢 उत्तर:
सूत्र: V = (4/3) × π × r³
(i) r = 7 cm
V = (4/3) × (22/7) × 7³
= (4/3) × (22/7) × 343
= (4/3) × 1078
= 1437.3 cm³
(ii) r = 0.63 m
V = (4/3) × (22/7) × (0.63)³
= (4/3) × (22/7) × 0.2500
= (4/3) × 0.7859
= 1.047 m³
✔️ उत्तर: (i) 1437.3 cm³, (ii) 1.047 m³
🔵 प्रश्न 2.
उस ठोस गोलाकार गेंद द्वारा हटाए गए (विस्थापित) पानी का आयतन ज्ञात कीजिए, जिसका व्यास निम्न है :
(i) 28 cm
(ii) 0.21 m
🟢 उत्तर:
सूत्र: V = (4/3) × π × r³
(i) d = 28 cm ⇒ r = 14 cm
V = (4/3) × (22/7) × 14³
= (4/3) × (22/7) × 2744
= 11419.3 cm³
(ii) d = 0.21 m ⇒ r = 0.105 m
V = (4/3) × (22/7) × (0.105)³
= (4/3) × (22/7) × 0.001157
= 0.00484 m³ = 4.84 L
✔️ उत्तर: (i) 11419.3 cm³, (ii) 4.84 L
🔵 प्रश्न 3.
धातु की एक गेंद का व्यास 4.2 cm है। यदि इस धातु का घनत्व 8.9 g/cm³ है, तो इस गेंद का भारमान ज्ञात कीजिए।
🟢 उत्तर:
सूत्र: V = (4/3) × π × r³
r = 4.2 ÷ 2 = 2.1 cm
V = (4/3) × (22/7) × (2.1)³
= (4/3) × (22/7) × 9.261
= 38.72 cm³
द्रव्यमान = आयतन × घनत्व
= 38.72 × 8.9 = 344.6 g
✔️ उत्तर: 344.6 g
🔵 प्रश्न 4.
चन्द्रमा का व्यास पृथ्वी के व्यास का लगभग एक-चौथाई है। चन्द्रमा का आयतन पृथ्वी के आयतन का कौन-सा भाग है?
🟢 उत्तर:
सूत्र: V ∝ d³
अनुपात = (1/4)³ : 1³
= 1/64 : 1
= 1 : 64
✔️ उत्तर: चन्द्रमा का आयतन पृथ्वी का 1/64 है।
🔵 प्रश्न 5.
व्यास 10.5 cm वाले एक अर्धगोलाकार कटोरे में कितने लीटर दूध आ सकता है?
🟢 उत्तर:
सूत्र: V = (1/2) × (4/3) × π × r³ = (2/3) × π × r³
r = 10.5 ÷ 2 = 5.25 cm
V = (2/3) × (22/7) × (5.25)³
= (2/3) × (22/7) × 144.7
= 302.7 cm³ = 0.303 L
✔️ उत्तर: 0.303 लीटर
🔵 प्रश्न 6.
एक बेलनाकार टंकी 1 cm मोटी लोहे की चादर से बनी है और यदि इसकी आंतरिक त्रिज्या 1 m है, तो टंकी की बाहरी त्रिज्या 1.01 m होगी। यदि टंकी की ऊँचाई 2.1 m है, तो प्रयुक्त लोहे का आयतन ज्ञात कीजिए।
🟢 उत्तर:
सूत्र: V = π × h × (R² – r²)
r = 1 m, R = 1.01 m, h = 2.1 m
V = (22/7) × 2.1 × (1.01² – 1²)
= (22/7) × 2.1 × (1.0201 – 1)
= (22/7) × 2.1 × 0.0201
= 0.1386 m³
रूपान्तरण: 1 m³ = 1000 L
= 138.6 L
✔️ उत्तर: 0.1386 m³ या 138.6 L
🔵 प्रश्न 7.
उस गोले का त्रिज्या ज्ञात कीजिए जिसका पृष्ठीय क्षेत्रफल 154 cm² है।
🟢 उत्तर:
सूत्र: A = 4 × π × r²
154 = 4 × (22/7) × r²
r² = (154 × 7) ÷ 88
r² = 12.25
r = √12.25 = 3.5 cm
✔️ उत्तर: 3.5 cm
🔵 प्रश्न 8.
किसी भवन का गुंबद एक अर्धगोले के आकार का है। अंदर से, इसमें सफेदी कराने में ₹498.96 व्यय हुआ। यदि सफेदी कराने की दर ₹2 प्रति वर्ग मीटर है, तो ज्ञात कीजिए :
(i) गुंबद का आंतरिक वक्र पृष्ठीय क्षेत्रफल
(ii) गुंबद के अंदर की हवा का आयतन
🟢 उत्तर:
(i)
सूत्र: वक्र पृष्ठीय क्षेत्रफल = 2 × π × r²
कुल व्यय = ₹498.96, दर = ₹2 प्रति m²
आंतरिक वक्र पृष्ठीय क्षेत्रफल = 498.96 ÷ 2 = 249.48 m²
तो, 2 × π × r² = 249.48
r² = 249.48 ÷ (2 × 22/7) = 249.48 ÷ (44/7) = 249.48 × 7 ÷ 44 = 39.7
r = √39.7 ≈ 6.3 m
✔️ आंतरिक वक्र पृष्ठीय क्षेत्रफल = 249.48 m²
(ii)
सूत्र: अर्धगोले का आयतन = (2/3) × π × r³
= (2/3) × (22/7) × (6.3)³
= (2/3) × (22/7) × 250.047
= (2/3) × 785.9 = 523.9 m³
✔️ हवा का आयतन = 523.9 m³
🔵 प्रश्न 10.
दवा की एक कैप्सूल (capsule) 3.5 mm व्यास का एक गोला (गोल्ली) है। इस कैप्सूल को भरने के लिए कितनी दवाई (mm³ में) की आवश्यकता होगी?
🟢 उत्तर:
सूत्र: V = (4/3) × π × r³
व्यास = 3.5 mm ⇒ r = 1.75 mm
V = (4/3) × (22/7) × (1.75)³
= (4/3) × (22/7) × 5.36
= (4/3) × 16.84
= 22.45 mm³
✔️ उत्तर: 22.45 mm³
🔵 प्रश्न 9.
लौह के सैकड़ों ठोस गोलों को पिघलाकर, जिनमें से प्रत्येक की त्रिज्या r है और पृष्ठीय क्षेत्रफल S है, एक बड़ा गोला बनाया जाता है जिसका पृष्ठीय क्षेत्रफल S′ है। ज्ञात कीजिए :
(i) नए गोले की त्रिज्या r′
(ii) S और S′ का अनुपात
🟢 उत्तर:
✨ (i) नए गोले की त्रिज्या
➡️ छोटे गोले का आयतन:
V = (4/3) × π × r³
➡️ n छोटे गोले पिघलाकर नया गोला:
n × (4/3) × π × r³ = (4/3) × π × r′³
➡️ r′³ = n × r³
➡️ r′ = n¹ᐟ³ × r
✔️ नए गोले की त्रिज्या: r′ = n¹ᐟ³ × r
✨ (ii) पृष्ठीय क्षेत्रफल का अनुपात
➡️ छोटे गोले का पृष्ठीय क्षेत्रफल:
S = 4 × π × r²
➡️ बड़े गोले का पृष्ठीय क्षेत्रफल:
S′ = 4 × π × r′²
= 4 × π × (n²ᐟ³ × r²)
➡️ अनुपात:
S : S′ = (4πr²) : (4πn²ᐟ³r²)
= 1 : n²ᐟ³
✔️ अनुपात: S : S′ = 1 : n²ᐟ³
————————————————————————————————————————————————————————————————————————————
अन्य महत्वपूर्ण प्रश्न
🔵 Section A (प्रत्येक 1 अंक, कुल 6 प्रश्न)
🔵 Question 1:
घन का कुल पृष्ठीय क्षेत्रफल का सूत्र लिखिए।
🟢 Answer:
कुल पृष्ठीय क्षेत्रफल = 6a² (जहाँ a = भुजा)
🔵 Question 2:
यदि किसी गोले का त्रिज्या r है, तो उसका पृष्ठीय क्षेत्रफल क्या होगा?
🟢 Answer:
पृष्ठीय क्षेत्रफल = 4πr²
🔵 Question 3:
किसी घनाभ का आयतन निकालने का सूत्र लिखिए।
🟢 Answer:
आयतन = l × b × h (लंबाई × चौड़ाई × ऊँचाई)
🔵 Question 4 (MCQ):
यदि शंकु की त्रिज्या r और ऊँचाई h है, तो उसका आयतन होगा:
1️⃣ πr²h
2️⃣ (1/2)πr²h
3️⃣ (1/3)πr²h
4️⃣ (4/3)πr³
🟢 Answer: 3️⃣
🔵 Question 5:
घन और घनाभ में पृष्ठीय क्षेत्रफल की दृष्टि से क्या अंतर है?
🟢 Answer:
घन: सभी फलक समान वर्गाकार।
घनाभ: फलक आयताकार और भिन्न आयामों के।
🔵 Question 6:
यदि किसी बेलन का व्यास 14 से.मी. और ऊँचाई 10 से.मी. हो, तो उसका वक्र पृष्ठीय क्षेत्रफल निकालिए।
🟢 Answer:
त्रिज्या r = 7 से.मी.
CSA = 2πrh = 2×(22/7)×7×10 = 440 से.मी.²
🟢 Section B (प्रत्येक 2 अंक, कुल 6 प्रश्न)
🔵 Question 7:
एक अर्द्धगोला (Hemisphere) की त्रिज्या 7 से.मी. है। उसका कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
🟢 Answer:
TSA = 3πr² = 3×(22/7)×7² = 462 से.मी.²
🔵 Question 8:
एक बेलनाकार पात्र की त्रिज्या 5 से.मी. और ऊँचाई 14 से.मी. है। इसका आयतन ज्ञात कीजिए।
🟢 Answer:
V = πr²h = (22/7)×25×14 = 1100 से.मी.³
🔵 Question 9:
एक घन की भुजा 4 से.मी. है। उसका पृष्ठीय क्षेत्रफल और आयतन ज्ञात कीजिए।
🟢 Answer:
TSA = 6a² = 6×16 = 96 से.मी.²
V = a³ = 64 से.मी.³
🔵 Question 10 (Assertion–Reason):
कथन (A): गोले का आयतन (4/3)πr³ होता है।
कारण (R): गोले का पृष्ठीय क्षेत्रफल 2πr² होता है।
विकल्प:
A. A और R दोनों सही हैं, और R सही व्याख्या है।
B. A सही है, R गलत है।
C. A गलत है, R सही है।
D. दोनों गलत हैं।
🟢 Answer: B
🔵 Question 11:
किसी शंकु का व्यास 14 से.मी. और तिर्यक ऊँचाई 10 से.मी. है। इसका वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
🟢 Answer:
r = 7, l = 10
CSA = πrl = (22/7)×7×10 = 220 से.मी.²
🔵 Question 12:
एक आयताकार टंकी 5 मीटर लंबी, 4 मीटर चौड़ी और 3 मीटर ऊँची है। इसमें कितना पानी समा सकता है?
🟢 Answer:
V = l×b×h = 5×4×3 = 60 मीटर³
✔️ पानी = 60 मीटर³
🟡 Section C (प्रत्येक 3 अंक, कुल 10 प्रश्न, 3–4 में आंतरिक विकल्प)
🔵 Question 13:
एक बेलनाकार टंकी की त्रिज्या 7 मीटर और ऊँचाई 10 मीटर है। इसमें कितना पानी समा सकता है?
🟢 Answer:
V = πr²h
= (22/7)×7²×10
= 1540 मीटर³
🔵 Question 14:
एक घनाभ का आयाम 12 से.मी. × 10 से.मी. × 8 से.मी. है। इसका कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
🟢 Answer:
TSA = 2(lb + bh + hl)
= 2(12×10 + 10×8 + 8×12)
= 2(120 + 80 + 96) = 592 से.मी.²
🔵 Question 15 (आंतरिक विकल्प):
(A) एक शंकु की त्रिज्या 7 से.मी. और ऊँचाई 24 से.मी. है। इसका तिर्यक ऊँचाई और वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
🟢 Answer:
l = √(r² + h²) = √(49 + 576) = 25 से.मी.
CSA = πrl = (22/7)×7×25 = 550 से.मी.²
OR
(B) एक अर्द्धगोले का पृष्ठीय क्षेत्रफल 462 से.मी.² है। त्रिज्या ज्ञात कीजिए।
TSA = 3πr²
462 = 3×(22/7)×r²
r² = 49 → r = 7 से.मी.
🔵 Question 16:
एक घन का पृष्ठीय क्षेत्रफल 600 से.मी.² है। घन की भुजा और आयतन ज्ञात कीजिए।
🟢 Answer:
TSA = 6a² = 600 → a² = 100 → a = 10 से.मी.
V = a³ = 1000 से.मी.³
🔵 Question 17 (आंतरिक विकल्प):
(A) एक बेलन का व्यास 14 से.मी. और ऊँचाई 20 से.मी. है। इसका कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
🟢 Answer:
r = 7, h = 20
CSA = 2πrh = 2×(22/7)×7×20 = 880
TSA = CSA + 2πr² = 880 + 2×(22/7)×49 = 1078 से.मी.²
OR
(B) एक घनाभ का आयतन 216 से.मी.³ है। यदि इसकी लंबाई, चौड़ाई और ऊँचाई बराबर हो, तो इसका पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
a³ = 216 → a = 6
TSA = 6a² = 6×36 = 216 से.मी.²
🔵 Question 18:
एक आइसक्रीम कोन का त्रिज्या 3.5 से.मी. और ऊँचाई 10 से.मी. है। इसका आयतन ज्ञात कीजिए।
🟢 Answer:
V = (1/3)πr²h = (1/3)×(22/7)×3.5²×10 = 128.33 से.मी.³
🔵 प्रश्न 19:
एक बेलन और एक शंकु की त्रिज्या समान 7 से.मी. है तथा ऊँचाई 24 से.मी. है। इनके आयतन का अनुपात ज्ञात कीजिए।
🟢 उत्तर:
बेलन का आयतन = πr²h = (22/7)×49×24 = 3696
शंकु का आयतन = (1/3)πr²h = 1232
अनुपात = 3696 : 1232 = 3 : 1
🔵 Question 20 (आंतरिक विकल्प):
(A) 14 से.मी. व्यास और 15 से.मी. ऊँचाई वाले बेलन का कुल पृष्ठीय क्षेत्रफल निकालिए।
🟢 Answer:
r = 7, h = 15
TSA = 2πrh + 2πr² = 2×(22/7)×7×15 + 2×(22/7)×49
= 660 + 308 = 968 से.मी.²
OR
(B) 7 से.मी. त्रिज्या वाले अर्द्धगोले का आयतन ज्ञात कीजिए।
V = (2/3)πr³ = (2/3)×(22/7)×343 = 718.67 से.मी.³
🔵 Question 21:
एक शंकु का आयतन 1232 से.मी.³ और ऊँचाई 24 से.मी. है। इसकी त्रिज्या ज्ञात कीजिए।
🟢 Answer:
V = (1/3)πr²h
1232 = (1/3)×(22/7)×r²×24
r² = 49 → r = 7 से.मी.
🔵 प्रश्न 22:
किसी ठोस वस्तु का घनत्व 8 ग्राम/से.मी.³ है और उसका आयतन 100 से.मी.³ है। उसका द्रव्यमान ज्ञात कीजिए।
🟢 उत्तर:
द्रव्यमान = घनत्व × आयतन
= 8 × 100 = 800 ग्राम
🔴 Section D (प्रत्येक 4 अंक, कुल 8 प्रश्न, 3 में आंतरिक विकल्प)
🔵 प्रश्न 23:
एक बेलन का व्यास 14 से.मी. और ऊँचाई 10 से.मी. है। इसका आयतन ज्ञात कीजिए।
🟢 उत्तर:
त्रिज्या r = 7 से.मी.
V = πr²h = (22/7)×7²×10 = 1540 से.मी.³
🔵 प्रश्न 24 (आंतरिक विकल्प):
(A) एक घनाभ का आयाम 15 से.मी. × 10 से.मी. × 8 से.मी. है। इसका कुल पृष्ठीय क्षेत्रफल निकालिए।
🟢 उत्तर:
TSA = 2(lb + bh + hl) = 2(150 + 80 + 120) = 700 से.मी.²
OR
(B) किसी घन का कुल पृष्ठीय क्षेत्रफल 600 से.मी.² है। उसकी भुजा और आयतन ज्ञात कीजिए।
6a² = 600 → a² = 100 → a = 10 से.मी.
V = a³ = 1000 से.मी.³
🔵 प्रश्न 25:
एक गोले की त्रिज्या 7 से.मी. है। उसका पृष्ठीय क्षेत्रफल और आयतन ज्ञात कीजिए।
🟢 उत्तर:
TSA = 4πr² = 4×(22/7)×49 = 616 से.मी.²
V = (4/3)πr³ = (4/3)×(22/7)×343 = 1436 से.मी.³
🔵 प्रश्न 26 (आंतरिक विकल्प):
(A) एक अर्द्धगोला जिसकी त्रिज्या 10.5 से.मी. है, उसका कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
🟢 उत्तर:
TSA = 3πr² = 3×(22/7)×10.5² = 1039.5 से.मी.²
OR
(B) एक शंकु की त्रिज्या 7 से.मी. और तिर्यक ऊँचाई 25 से.मी. है। इसका वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
CSA = πrl = (22/7)×7×25 = 550 से.मी.²
🔵 प्रश्न 27:
एक बेलनाकार टंकी का व्यास 3 मीटर और ऊँचाई 7 मीटर है। इसमें कितना पानी भरेगा? (1 मी³ = 1000 लीटर)
🟢 उत्तर:
r = 1.5 मीटर
V = πr²h = (22/7)×(1.5)²×7 = 49.5 मी³
पानी = 49.5 × 1000 = 49,500 लीटर
🔵 प्रश्न 28 (आंतरिक विकल्प):
(A) एक घनाभ का आयतन 1728 से.मी.³ है। यदि उसकी लंबाई = 12 से.मी., चौड़ाई = 12 से.मी. हो, तो ऊँचाई ज्ञात कीजिए।
🟢 उत्तर:
V = l×b×h → 1728 = 12×12×h → h = 12 से.मी.
OR
(B) एक बेलनाकार पाइप जिसकी लंबाई 7 मीटर, बाहरी त्रिज्या 14 से.मी. और मोटाई 2 से.मी. है, उसका आयतन ज्ञात कीजिए।
बाहरी r = 14 से.मी., आंतरिक r = 12 से.मी.
V = πh(R² − r²) = (22/7)×700×(196−144) = 11×700×52/7 = 57200 से.मी.³
🔵 प्रश्न 29:
एक आइसक्रीम कोन की त्रिज्या 7 से.मी. और ऊँचाई 24 से.मी. है, जिसके ऊपर 7 से.मी. त्रिज्या का अर्द्धगोला रखा है। इसका कुल आयतन ज्ञात कीजिए।
🟢 उत्तर:
V = (1/3)πr²h + (2/3)πr³
= (1/3)×(22/7)×49×24 + (2/3)×(22/7)×343
= 1232 + 686.67 = 1918.67 से.मी.³
🔵 प्रश्न 30 (आंतरिक विकल्प):
(A) एक शंकु की त्रिज्या 3.5 से.मी. और ऊँचाई 10 से.मी. है। उसका आयतन ज्ञात कीजिए।
🟢 उत्तर:
V = (1/3)πr²h = (1/3)×(22/7)×3.5²×10 = 128.33 से.मी.³
OR
(B) किसी धातु को पिघलाकर 5 से.मी. त्रिज्या वाले 9 गोलक बनाए गए। यदि धातु का कुल आयतन 4712.25 से.मी.³ था, तो जाँच कीजिए कि धातु पर्याप्त थी या नहीं।
एक गोलक का आयतन = (4/3)πr³ = (4/3)×(22/7)×125 = 523.33 से.मी.³
9 गोलक का कुल आयतन = 4710 से.मी.³ ≈ 4712.25 से.मी.³
✔️ धातु पर्याप्त थी।
————————————————————————————————————————————————————————————————————————————————————————————–
मानचित्र
————————————————————————————————————————————————————————————————————————————
