Class : 9 – Math (English) : Lesson 8. Quadrilaterals
EXPLANATION & SUMMARY
✨ Explanation
🔵 Introduction to Quadrilaterals
Quadrilaterals are four-sided polygons widely used in geometry and real life—think of tables, screens, windows, and floor tiles. A polygon is a closed figure formed by line segments, and when a polygon has four sides, we call it a quadrilateral.
🟢 A quadrilateral has:
➡️ Four vertices (corners)
➡️ Four sides
➡️ Four angles
➡️ Two diagonals
🔴 Sum of Angles of a Quadrilateral
💡 Concept: The sum of interior angles of any quadrilateral is 360°.
✔️ Derivation:
🔵 Step 1: Draw a quadrilateral ABCD.
🔵 Step 2: Join AC, splitting ABCD into triangles △ABC and △CDA.
🔵 Step 3: Sum of angles in △ABC = 180°, and △CDA = 180°.
🔵 Step 4: Total = 180° + 180° = 360°.
🌿 Real-life link: When designing floor tiles, carpenters use this property to ensure perfect joints.
🟡 Types of Quadrilaterals
🧠 Parallelogram: Opposite sides are parallel.
🧠 Rectangle: Parallelogram with all angles 90°.
🧠 Square: Rectangle with all sides equal.
🧠 Rhombus: Parallelogram with all sides equal but angles not necessarily 90°.
🧠 Trapezium (Trapezoid): One pair of opposite sides parallel.
🧠 Kite: Two pairs of adjacent sides equal.
✏️ Note: A square is a special rectangle and a special rhombus.
🔴 Properties of a Parallelogram
🔵 Opposite sides are equal and parallel.
🔵 Opposite angles are equal.
🔵 Diagonals bisect each other.
🌿 Example: Construction beams in bridges often form parallelogram frameworks for stability.
✔️ Proof (Opposite Sides Equal)
➡️ Given parallelogram ABCD.
➡️ Draw diagonal AC.
➡️ In △ABC and △CDA:
– AB ∥ CD and AD ∥ BC (alternate interior angles equal).
– AC common.
– Using ASA congruence, △ABC ≅ △CDA.
➡️ Hence AB = CD, AD = BC.
🟢 Mid-point Theorem for Quadrilaterals
💡 Concept: The line joining the midpoints of two sides of a quadrilateral is half the third side when extended into triangles—used in coordinate geometry proofs.
🔵 Special Parallelogram Results
1️⃣ Diagonals of a rectangle are equal.
2️⃣ Diagonals of a rhombus intersect at right angles.
3️⃣ Square: combines both properties.
✏️ Note: These results are used in vector proofs and coordinate methods.
🟡 Conditions for a Quadrilateral to be a Parallelogram
✔️ If both pairs of opposite sides are equal → parallelogram.
✔️ If both pairs of opposite angles are equal → parallelogram.
✔️ If diagonals bisect each other → parallelogram.
✔️ If one pair of opposite sides is equal and parallel → parallelogram.
⚡ Application: Architects use these tests when checking frameworks.
🔵 Theorem: Diagonal Bisects Area
If a parallelogram is split by a diagonal, the two triangles formed have equal area.
➡️ Proof: Using common base and parallels between opposite sides.
🟢 Trapezium Properties
🌿 A trapezium has exactly one pair of parallel sides.
💡 Mid-segment Theorem: The line joining midpoints of non-parallel sides is parallel to bases and equal to their half-sum.
🟡 Kite Properties
🔵 Two distinct pairs of adjacent sides equal.
🔵 One diagonal bisects the other at right angles.
🔵 One pair of opposite angles equal (those between unequal sides).
🌿 Real life: Kites in the sky or certain ornaments follow this shape.
🔴 Coordinate Geometry Approach
For quadrilateral PQRS in the plane:
✔️ Use distance formula to check side equality.
✔️ Use slope to test parallelism.
✔️ Use midpoint formula to check diagonal bisection.
📌 Example: Prove ABCD is a parallelogram if A(1,2), B(3,6), C(7,6), D(5,2).
🔵 Step 1: Slope AB = (6–2)/(3–1)=4/2=2.
🔵 Step 2: Slope CD = (6–2)/(7–5)=4/2=2 → AB ∥ CD.
🔵 Step 3: Slope BC = (6–6)/(7–3)=0/4=0.
🔵 Step 4: Slope AD = (2–2)/(5–1)=0/4=0 → BC ∥ AD.
✔️ Hence ABCD is a parallelogram.
🟢 Angle Sum & Exterior Angles
🔵 Exterior angle of a polygon = 180° – interior angle.
🔵 Sum of exterior angles of any polygon = 360°.
🌿 Application: Navigation bearings and robot movement planning.
🟡 Parallelogram on Same Base and Between Same Parallels
⚡ Statement: Parallelograms on the same base and between the same parallels are equal in area.
✔️ Proof: Draw height from vertices, show equal height and base.
🔴 Area Relations in Triangles & Parallelograms
💡 Used for ratio problems: Area(△) = ½ × base × height.
✏️ Note: Common in proving mid-point and base relations.
🟢 Problem-Solving Strategies
➡️ Draw clear diagrams.
➡️ Mark known equal sides/angles.
➡️ Use congruence criteria (SSS, SAS, ASA) smartly.
➡️ Use parallel line angle properties: alternate interior, corresponding, co-interior.
➡️ Verify final answer by substituting or reasoning.
🌿 Real-Life Applications of Quadrilaterals
🔵 Architecture: Bridges, windows, tiles.
🟢 Robotics: Movement on grids uses quadrilateral properties.
🟡 Art & Design: Tiling patterns.
🔴 Surveying: Land plots approximated by quadrilaterals.
✔️ Common Mistakes & Tips
✏️ Note: Students often forget to prove both pairs of opposite sides equal for parallelogram.
✏️ Note: Remember diagonals of rectangles are equal but not necessarily perpendicular.
✏️ Note: For kites, only one pair of opposite angles equal.
⚡ Higher-Order Thinking
🧠 Use vector method: Represent points as vectors → show AB + CD = AD + BC for parallelogram.
🧠 In coordinate proofs, always confirm both conditions (sides and diagonals) for full marks.
📚 Summary (~300 words)
🔵 Definition & Basics
Quadrilateral: Four-sided polygon with four vertices, sides, angles, and two diagonals.
Sum of interior angles = 360°.
🟢 Classification
Parallelogram: Opposite sides parallel/equal; diagonals bisect.
Rectangle: Parallelogram + all angles 90°; diagonals equal.
Square: Rectangle + all sides equal; diagonals equal and perpendicular.
Rhombus: Parallelogram + all sides equal; diagonals perpendicular.
Trapezium: One pair of opposite sides parallel; mid-segment theorem applies.
Kite: Two pairs adjacent sides equal; one diagonal bisects the other.
🟡 Properties & Theorems
Conditions for a parallelogram: both pairs of opposite sides/angles equal, diagonals bisect, or one pair equal & parallel.
Parallelograms on the same base and between same parallels → equal area.
Diagonal of a parallelogram divides it into equal-area triangles.
Exterior angles sum to 360°.
🔴 Coordinate & Vector Methods
Distance formula for side lengths, slope for parallelism, midpoint for bisection.
Vectors: AB + CD = AD + BC for parallelogram checks.
🌿 Applications
Architecture (bridges, windows).
Robotics (path planning).
Surveying and tiling patterns.
⚡ Tips & Pitfalls
Use clear diagrams and congruence criteria.
Don’t confuse rectangle and rhombus diagonal properties.
Always check both pairs of sides or angles for parallelogram proofs.
📝 Quick Recap
🔵 Sum of angles of a quadrilateral = 360°.
🟢 Parallelogram properties: Opposite sides/angles equal, diagonals bisect.
🟡 Trapezium has one pair of parallel sides; mid-segment theorem applies.
🔴 Square = rectangle + rhombus properties combined.
🌿 Parallelograms on same base & between same parallels have equal areas.
✔️ Use coordinate geometry or vectors for precise proofs.
———————————————————————————————————————————————————————————————————————————–
TEXT BOOK QUESTIONS
Exercise 8.1
🔵 Question 1
If the diagonals of a parallelogram are equal, then show that it is a rectangle.
🟢 Answer
🔵 Step 1: Let ABCD be a parallelogram where AC = BD.
🔵 Step 2: In parallelogram, diagonals bisect each other: O is intersection, so AO = CO and BO = DO.
🔵 Step 3: Given AC = BD ⇒ AO + OC = BO + OD ⇒ AO = BO and CO = DO (since AO = CO, BO = DO).
🔵 Step 4: Triangles AOB and BOC share AO = BO, BO = DO, and OB common ⇒ △AOB ≅ △BOC (SSS).
🔵 Step 5: ∠A = ∠B = 90° (opposite angles of congruent triangles sum to 180°).
✔️ Final: ABCD is a rectangle.
🔵 Question 2
Show that the diagonals of a square are equal and bisect each other at right angles.
🟢 Answer
🔵 Step 1: In square ABCD, all sides equal and angles 90°.
🔵 Step 2: Use Pythagoras in △ABC: AC² = AB² + BC².
🔵 Step 3: Similarly BD² = AB² + AD² = AB² + AB².
🔵 Step 4: Hence AC = BD.
🔵 Step 5: Diagonals bisect because ABCD is a parallelogram.
🔵 Step 6: Angles between diagonals are 90° (property of rhombus; square is special rhombus).
✔️ Final: Diagonals of a square are equal and bisect each other at right angles.
🔵 Question 3
Diagonal AC of a parallelogram ABCD bisects ∠A (see Fig. 8.11). Show that
(i) it bisects ∠C also,
(ii) ABCD is a rhombus.
🟢 Answer
🔵 Step 1: Given AC bisects ∠A ⇒ ∠DAC = ∠CAB.
🔵 Step 2: In △ADC and △CBA:
– AD = CB (opposite sides of parallelogram)
– ∠DAC = ∠CAB (given)
– AC common
🔵 Step 3: By SAS, △ADC ≅ △CBA.
🔵 Step 4: So ∠ACD = ∠ABC ⇒ AC bisects ∠C. ✔️(i)
🔵 Step 5: Also AD = DC = CB = AB ⇒ all sides equal. ✔️(ii)
✔️ Final: AC bisects ∠C and ABCD is a rhombus.
🔵 Question 4
ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that:
(i) ABCD is a square
(ii) diagonal BD bisects ∠B as well as ∠D.
🟢 Answer
🔵 Step 1: AC bisects ∠A ⇒ △ADC ≅ △CBA by SAS.
🔵 Step 2: Hence AD = AB ⇒ adjacent sides equal.
🔵 Step 3: Rectangle with adjacent sides equal ⇒ square. ✔️(i)
🔵 Step 4: In square, diagonals bisect angles ⇒ BD bisects ∠B and ∠D. ✔️(ii)
✔️ Final: ABCD is a square, and BD bisects ∠B and ∠D.
🔵 Question 5
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (Fig. 8.12). Show that:
(i) △APD ≅ △CQB
(ii) AP = CQ
(iii) △AQB ≅ △CPD
(iv) AQ = CP
(v) APCQ is a parallelogram.
🟢 Answer
🔵 Step 1: In △APD and △CQB:
– AD = BC (opp sides)
– DP = BQ (given)
– ∠ADP = ∠CBQ (alternate interior)
🔵 Step 2: By SAS ⇒ △APD ≅ △CQB ✔️(i) ⇒ AP = CQ ✔️(ii).
🔵 Step 3: In △AQB and △CPD:
– AB = CD
– AQ = CP (from step 2)
– ∠ABQ = ∠CDP
🔵 Step 4: By SAS ⇒ △AQB ≅ △CPD ✔️(iii) ⇒ AQ = CP ✔️(iv).
🔵 Step 5: AP ∥ CQ and AQ ∥ CP ⇒ APCQ is a parallelogram. ✔️(v)
✔️ Final: All five results hold.
🔵 Question 6
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (Fig. 8.13). Show that
(i) △APB ≅ △CQD
(ii) AP = CQ.
🟢 Answer
🔵 Step 1: In △APB and △CQD:
– ∠APB = ∠CQD = 90° (perpendiculars)
– ∠PAB = ∠QCD (alternate interior)
– AB = CD (opp sides)
🔵 Step 2: By AAS ⇒ △APB ≅ △CQD ✔️(i).
🔵 Step 3: Hence AP = CQ ✔️(ii).
✔️ Final: Triangles congruent and AP = CQ.
🔵 Question 7
ABCD is a trapezium in which AB ∥ CD and AD = BC (Fig. 8.14). Show that:
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) △ABC ≅ △BAD
(iv) Diagonal AC = diagonal BD.
🟢 Answer
🔵 Step 1: Since AB ∥ CD, alternate interior angles: ∠CAD = ∠CBD and ∠ADB = ∠CBA.
🔵 Step 2: Given AD = BC.
🔵 Step 3: In △ABC and △BAD:
– AD = BC (given)
– AB common
– ∠BAD = ∠ABC (from step 1)
🔵 Step 4: By SAS ⇒ △ABC ≅ △BAD ✔️(iii).
🔵 Step 5: ⇒ ∠A = ∠B ✔️(i) and ∠C = ∠D ✔️(ii).
🔵 Step 6: Corresponding parts ⇒ AC = BD ✔️(iv).
✔️ Final: All four statements proven.
Exercise 8.2
🔵 Question 1
ABCD is a quadrilateral in which P, Q, R and S are mid-points of sides AB, BC, CD and DA (Fig 8.20). AC is a diagonal. Show that:
(i) SR ∥ AC and SR = ½ AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
🟢 Answer
🔵 Step 1: Join midpoints S and R on sides DA and CD. By Mid-point Theorem, line joining midpoints of two sides of a triangle is parallel to the third side and equals half.
🔵 Step 2: In △ADC, S and R are midpoints of AD and CD ⇒ SR ∥ AC and SR = ½ AC ✔️(i).
🔵 Step 3: Similarly, in △ABC, P and Q are midpoints of AB and BC ⇒ PQ ∥ AC and PQ = ½ AC ⇒ PQ = SR ✔️(ii).
🔵 Step 4: PQ ∥ SR and PQ = SR ⇒ PQRS is a parallelogram ✔️(iii).
✔️ Final: SR ∥ AC, SR = ½ AC, PQ = SR, PQRS parallelogram.
🔵 Question 2
ABCD is a rhombus and P, Q, R, S are mid-points of AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
🟢 Answer
🔵 Step 1: In a rhombus, all sides equal, diagonals bisect at right angles.
🔵 Step 2: Using mid-point theorem on adjacent triangles, PQ ∥ RS and PQ = RS; PS ∥ QR and PS = QR ⇒ PQRS is a parallelogram.
🔵 Step 3: Diagonals of rhombus are perpendicular ⇒ each mid-segment makes right angles ⇒ ∠P = 90°.
✔️ Final: PQRS is a rectangle.
🔵 Question 3
ABCD is a rectangle and P, Q, R, S are mid-points of sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
🟢 Answer
🔵 Step 1: In △ABC, P and Q midpoints ⇒ PQ ∥ AC, PQ = ½ AC. Similarly, SR ∥ AC, SR = ½ AC ⇒ PQ = SR.
🔵 Step 2: Likewise PS = QR.
🔵 Step 3: All sides equal ⇒ PQRS is a rhombus.
✔️ Final: PQRS is a rhombus.
🔵 Question 4
ABCD is a trapezium in which AB ∥ DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (Fig 8.21). Show that F is the mid-point of BC.
🟢 Answer
🔵 Step 1: Join BD. Consider △ABD: E is midpoint of AD, EF ∥ AB ⇒ by Converse of Mid-point theorem, F is midpoint of BD.
🔵 Step 2: But BD is diagonal; with AB ∥ DC, geometry of trapezium shows BD and BC relationship ⇒ using similar triangles, F also bisects BC.
✔️ Final: F is mid-point of BC.
🔵 Question 5
In a parallelogram ABCD, E and F are mid-points of sides AB and CD respectively (Fig 8.22). Show that line segments AF and EC trisect the diagonal BD.
🟢 Answer
🔵 Step 1: Join AE, CF. Using mid-point theorem in triangles ABD and CBD, AF and EC intersect BD at points dividing BD in equal segments.
🔵 Step 2: Use similar triangles or coordinate method to show BD is divided into three equal parts.
✔️ Final: AF and EC trisect BD.
🔵 Question 6
ABC is a triangle right angled at C. A line through M (mid-point of hypotenuse AB) and parallel to BC intersects AC at D. Show that:
(i) D is the mid-point of AC
(ii) MD ∥ AC
(iii) CM = MA = ½ AB.
🟢 Answer
🔵 Step 1: M is midpoint of AB. Draw MD ∥ BC. By mid-point theorem in △ABC, D becomes midpoint of AC ✔️(i).
🔵 Step 2: MD is drawn parallel to BC ⇒ MD ∥ BC ✔️(ii).
🔵 Step 3: In a right triangle, midpoint of hypotenuse equidistant from all vertices ⇒ CM = MA = MB = ½ AB ✔️(iii).
✔️ Final: D is midpoint of AC, MD ∥ BC, CM = MA = ½ AB.
———————————————————————————————————————————————————————————————————————————–
OTHER IMPORTANT QUESTIONS FOR EXAMS
🔵 Question 1 (MCQ, 1 mark)
In any quadrilateral, the sum of interior angles equals
🟢 A) 180°
🟡 B) 270°
🔴 C) 360°
✳️ D) 540°
🧠 Answer
✔️ Final: C) 360°
🔵 Question 2 (MCQ, 1 mark)
In a parallelogram, which statement is always true?
🟢 A) Diagonals are perpendicular
🟡 B) Opposite angles are equal
🔴 C) All sides are equal
✳️ D) All angles are right angles
🧠 Answer
✔️ Final: B) Opposite angles are equal
🔵 Question 3 (MCQ, 1 mark)
A rectangle is a parallelogram with
🟢 A) all sides equal
🟡 B) diagonals perpendicular
🔴 C) all angles 90°
✳️ D) one pair of equal adjacent sides
🧠 Answer
✔️ Final: C) all angles 90°
🔵 Question 4 (MCQ, 1 mark)
Diagonals of a rhombus
🟢 A) are equal and not perpendicular
🟡 B) are unequal and perpendicular
🔴 C) are unequal and not perpendicular
✳️ D) are equal and perpendicular
🧠 Answer
✔️ Final: B) are unequal and perpendicular
🔵 Question 5 (MCQ, 1 mark)
A trapezium has
🟢 A) two pairs of parallel sides
🟡 B) exactly one pair of parallel sides
🔴 C) no parallel sides
✳️ D) diagonals always equal
🧠 Answer
✔️ Final: B) exactly one pair of parallel sides
🔵 Question 6 (MCQ, 1 mark)
In a kite, which is true?
🟢 A) Opposite sides equal
🟡 B) Two pairs of adjacent sides equal
🔴 C) All angles 90°
✳️ D) Diagonals equal and parallel
🧠 Answer
✔️ Final: B) Two pairs of adjacent sides equal
🟢 Question 7 (2 marks)
Prove that the diagonals of a parallelogram bisect each other.
🧠 Answer
➤ Construction/Given: Parallelogram ABCD; diagonals AC and BD intersect at O.
➤ Reasoning: In △AOB and △COD:
• ∠ABO = ∠CDO (alternate interior; AB ∥ CD)
• ∠BAO = ∠DCO (alternate interior; AD ∥ BC)
• ∠AOB = ∠COD (vertical opposite)
➤ Congruence: △AOB ≅ △COD (AAA → similar; plus one equal angle gives equality of corresponding sides)
➤ Result: AO = OC and BO = OD
✔️ Final: Diagonals bisect each other.
🟢 Question 8 (2 marks)
ABCD is a parallelogram. Show that adjacent angles are supplementary.
🧠 Answer
➤ Parallel lines: AB ∥ CD, AD is a transversal
➤ Co-interior angles: ∠A + ∠D = 180° (co-interior on AD)
➤ Similarly: ∠B + ∠C = 180°
✔️ Final: Any two adjacent angles of a parallelogram are supplementary.
🟢 Question 9 (2 marks)
In a rectangle, prove that diagonals are equal.
🧠 Answer
➤ Given: Rectangle ABCD (∠A = ∠B = ∠C = ∠D = 90°)
➤ Triangles: Consider △ABC and △BAD
• AB common
• ∠ABC = ∠BAD = 90°
• BC = AD (opposite sides of parallelogram)
➤ Congruence: △ABC ≅ △BAD (RHS)
➤ Correspondence: AC = BD
✔️ Final: Diagonals of a rectangle are equal.
🟢 Question 10 (2 marks)
In rhombus ABCD, show that diagonals bisect the angles.
🧠 Answer
➤ Given: AB = BC = CD = DA; diagonals AC and BD intersect at O.
➤ Triangles: Compare △ABD and △CBD
• AB = CB (sides equal)
• BD common
• AD ∥ CB ⇒ ∠ABD = ∠DBC (alternate interior)
➤ Congruence: △ABD ≅ △CBD (SAS)
➤ Implication: ∠ABD = ∠DBA and similarly at other vertices
✔️ Final: Each diagonal bisects the angles of the rhombus.
🟢 Question 11 (2 marks)
ABCD is a parallelogram. Prove that triangles on the same base and between the same parallels have equal area: ar(△ABC) = ar(△ADC).
🧠 Answer
➤ Common base: AC is the base for both △ABC and △ADC.
➤ Heights: From B and D draw perpendiculars to AC; heights are equal (between same parallels AB ∥ CD).
➤ Area formula: ar(△) = ½ × base × height
➤ Substitution: ½ × AC × h_B = ½ × AC × h_D
✔️ Final: ar(△ABC) = ar(△ADC).
🟢 Question 12 (2 marks)
In a trapezium ABCD with AB ∥ CD, midpoints of non-parallel sides AD and BC are M and N. Prove MN ∥ AB and MN = ½(AB + CD).
🧠 Answer
➤ Decompose: Draw diagonal AC.
➤ Triangle 1 (△ADC): M midpoint of AD, N on DC? (use segment through M parallel to AC to meet BC at N).
➤ Mid-segment facts: In △ABC, line through midpoint of AB parallel to AC gives mid-segment parallel to base.
➤ Combine: Using mid-segment in two triangles formed by diagonal, MN ∥ AB and length equals half sum of bases.
✔️ Final: MN ∥ AB and MN = ½(AB + CD).
🔵 Question 13
Prove that the line joining midpoints of two opposite sides of a parallelogram bisects the other two sides.
🧠 Answer
➤ Draw parallelogram ABCD. Let E, F be midpoints of AD and BC.
➤ Join EF. Draw diagonal AC. Triangles ADE and BCF have AE = ED and BF = FC.
➤ Using congruence and the midpoint theorem, EF passes through midpoint of AC and bisects AB and CD.
✔️ Final: EF bisects the other two sides.
🔵 Question 14
Show that the diagonals of a rhombus intersect at right angles.
🧠 Answer
➤ In rhombus ABCD, AC and BD intersect at O.
➤ Triangles AOB and COB: AO = CO, BO common, AB = BC.
➤ By SSS, △AOB ≅ △COB ⇒ ∠AOB = ∠COB.
➤ Adjacent angles sum = 180°, so each = 90°.
✔️ Final: Diagonals intersect at 90°.
🔵 Question 15
ABCD is a parallelogram; prove that the midpoints of consecutive sides form a parallelogram.
🧠 Answer
➤ Let P,Q,R,S be midpoints of AB, BC, CD, DA.
➤ In △ABC, PQ ∥ AC and PQ = ½ AC. In △CDA, RS ∥ AC and RS = ½ AC ⇒ PQ ∥ RS and PQ = RS.
➤ Similarly, PS ∥ QR.
✔️ Final: PQRS is a parallelogram.
🔵 Question 16 (Internal Choice)
(a) Using vectors, prove that the sum of squares of diagonals of a parallelogram equals the sum of squares of all sides.
OR
(b) Show that in a rectangle, diagonals are equal and bisect each other.
🧠 Answer (a)
➤ Let sides be vectors a and b. Diagonals: a + b, a − b.
➤ |a + b|² + |a − b|² = (a·a + 2a·b + b·b) + (a·a − 2a·b + b·b)
➤ Simplify: = 2|a|² + 2|b|².
✔️ Final: Sum of squares of diagonals = sum of squares of sides doubled.
🔵 Question 17
In a trapezium ABCD, AB ∥ CD. Show that the mid-segment connecting midpoints of non-parallel sides is parallel to the bases and equals half their sum.
🧠 Answer
➤ Let E,F midpoints of AD and BC. Join EF.
➤ Use diagonal AC to split trapezium into triangles. Apply midpoint theorem in both triangles.
✔️ Final: EF ∥ AB, CD and EF = ½(AB + CD).
🔵 Question 18 (Internal Choice)
(a) Diagonals of a rectangle are equal—prove using coordinate geometry.
OR
(b) Use congruent triangles to show opposite sides of a parallelogram are equal.
🧠 Answer (a)
➤ Place rectangle vertices: A(0, 0), B(a, 0), C(a, b), D(0, b).
➤ AC = √((a−0)² + (b−0)²) = √(a² + b²).
➤ BD = √((0−a)² + (b−0)²) = √(a² + b²).
✔️ Final: AC = BD ⇒ diagonals equal.
🔵 Question 19
Prove that the medians of a parallelogram intersect at a point dividing each in a 2:1 ratio.
🧠 Answer
➤ Represent parallelogram vertices with vectors or coordinates.
➤ Find midpoints of sides, draw medians, solve for intersection.
✔️ Final: Medians intersect at a point dividing them 2:1.
🔵 Question 20
Show that the line joining midpoints of two sides of a triangle is parallel to the third side and equal to half of it.
🧠 Answer
➤ Standard midpoint theorem: connect midpoints, use parallel lines and similar triangles.
✔️ Final: Mid-segment ∥ base and length = ½ base.
🔵 Question 21 (Internal Choice)
(a) Prove that opposite angles of a parallelogram are equal using alternate interior angles.
OR
(b) Show that the bisectors of angles of a parallelogram form a rectangle.
🧠 Answer (a)
➤ Draw parallelogram ABCD, diagonal AC. Using AB ∥ CD and transversal BC ⇒ ∠ABC = ∠CDA.
➤ Similarly, ∠BAD = ∠BCD.
✔️ Final: Opposite angles equal.
🔵 Question 22
In a kite, prove that one diagonal bisects the other at right angles.
🧠 Answer
➤ Let ABCD be a kite with AB = AD, CB = CD. Draw diagonals AC and BD intersecting at O.
➤ Triangles AOB and AOD congruent ⇒ AO bisects BD and ∠AOB = 90°.
✔️ Final: One diagonal bisects the other at 90°.
🔵 Question 23
Prove that the line joining the midpoints of opposite sides of a quadrilateral bisects each other.
🧠 Answer
➤ Let ABCD be a quadrilateral with E,F midpoints of AB and CD; G,H midpoints of BC and AD.
➤ Join EF and GH.
➤ Use triangles sharing sides and apply midpoint theorem twice: EF ∥ GH and EF = GH.
➤ Thus EF and GH bisect each other.
✔️ Final: Segments joining midpoints of opposite sides bisect each other.
🔵 Question 24 (Internal Choice)
(a) Prove that parallelograms on the same base and between the same parallels are equal in area.
OR
(b) Using vector method, show that for parallelogram ABCD, AB + CD = AD + BC.
🧠 Answer (a)
➤ Let parallelograms ABCD and ABEF share base AB and lie between parallels AB and DE.
➤ Draw altitudes; both share same height.
➤ Area = base × height ⇒ ar(ABCD)=ar(ABEF).
✔️ Final: Parallelograms on same base and between same parallels are equal in area.
🔵 Question 25
ABCD is a parallelogram. Prove that each diagonal divides it into two triangles of equal area.
🧠 Answer
➤ Draw diagonal AC. Triangles ABC and CDA share base AC and are between same parallels BC ∥ AD.
➤ Area(△ABC)=Area(△CDA). Similarly for BD.
✔️ Final: Each diagonal divides parallelogram into two equal-area triangles.
🔵 Question 26 (Internal Choice)
(a) In a trapezium, prove that the mid-segment length = ½(sum of bases).
OR
(b) Using coordinate geometry, show that a rectangle is a parallelogram with equal diagonals.
🧠 Answer (a)
➤ Trapezium ABCD, AB ∥ CD. Let E,F midpoints of non-parallel sides.
➤ Join EF. Draw diagonal AC. Use midpoint theorem in ΔADC and ΔABC.
➤ EF ∥ AB ∥ CD and EF=½(AB+CD).
✔️ Final: Mid-segment length = ½(sum of bases).
🔵 Question 27
Prove that the bisectors of angles of a parallelogram form a rectangle.
🧠 Answer
➤ Let bisectors intersect to form PQRS. Adjacent angles of parallelogram are supplementary ⇒ bisectors adjacent form right angles.
➤ Opposite angles equal ⇒ opposite sides of PQRS parallel and equal.
✔️ Final: Bisectors of a parallelogram form a rectangle.
🔵 Question 28
Use coordinate geometry: Prove that the points (x₁,y₁), (x₂,y₂), (x₃,y₃), (x₄,y₄) form a parallelogram if and only if x₁+x₃ = x₂+x₄ and y₁+y₃ = y₂+y₄.
🧠 Answer
➤ Midpoint of AC: ((x₁+x₃)/2,(y₁+y₃)/2). Midpoint of BD: ((x₂+x₄)/2,(y₂+y₄)/2).
➤ Parallelogram ⇒ diagonals bisect ⇒ midpoints coincide ⇒ equal coordinates.
➤ Hence x₁+x₃ = x₂+x₄ and y₁+y₃ = y₂+y₄. Converse also holds.
✔️ Final: Condition satisfied ⇔ parallelogram.
🔵 Question 29 (Internal Choice)
(a) Derive using vectors that the sum of squares of all sides of a parallelogram equals the sum of squares of its diagonals.
OR
(b) Prove that in a rhombus, the diagonals bisect each other at right angles and each bisects angles.
🧠 Answer (a)
➤ Sides vectors a, b. Diagonals: a+b, a−b.
➤ |a+b|² + |a−b|² = a² + 2a·b + b² + a² − 2a·b + b² = 2a² + 2b² = a² + b² + a² + b².
✔️ Final: Sum of squares of sides = sum of squares of diagonals.
🔵 Question 30
ABCD is a kite with AB = AD and BC = CD. Prove that AC bisects BD at right angles and show relation between sides and diagonals.
🧠 Answer
➤ Draw AC, BD intersecting at O. Triangles AOB and AOD congruent ⇒ AO bisects BD.
➤ Similarly, triangles COB and COD congruent.
➤ Use Pythagoras in ΔAOB to relate sides: AB² = AO² + BO² ⇒ sides in terms of diagonals.
✔️ Final: AC ⟂ BD, AO=OD, BO=OC, and AB² = (½BD)² + AO², linking sides and diagonals.
————————————————————————————————————————————————————————————————————————————
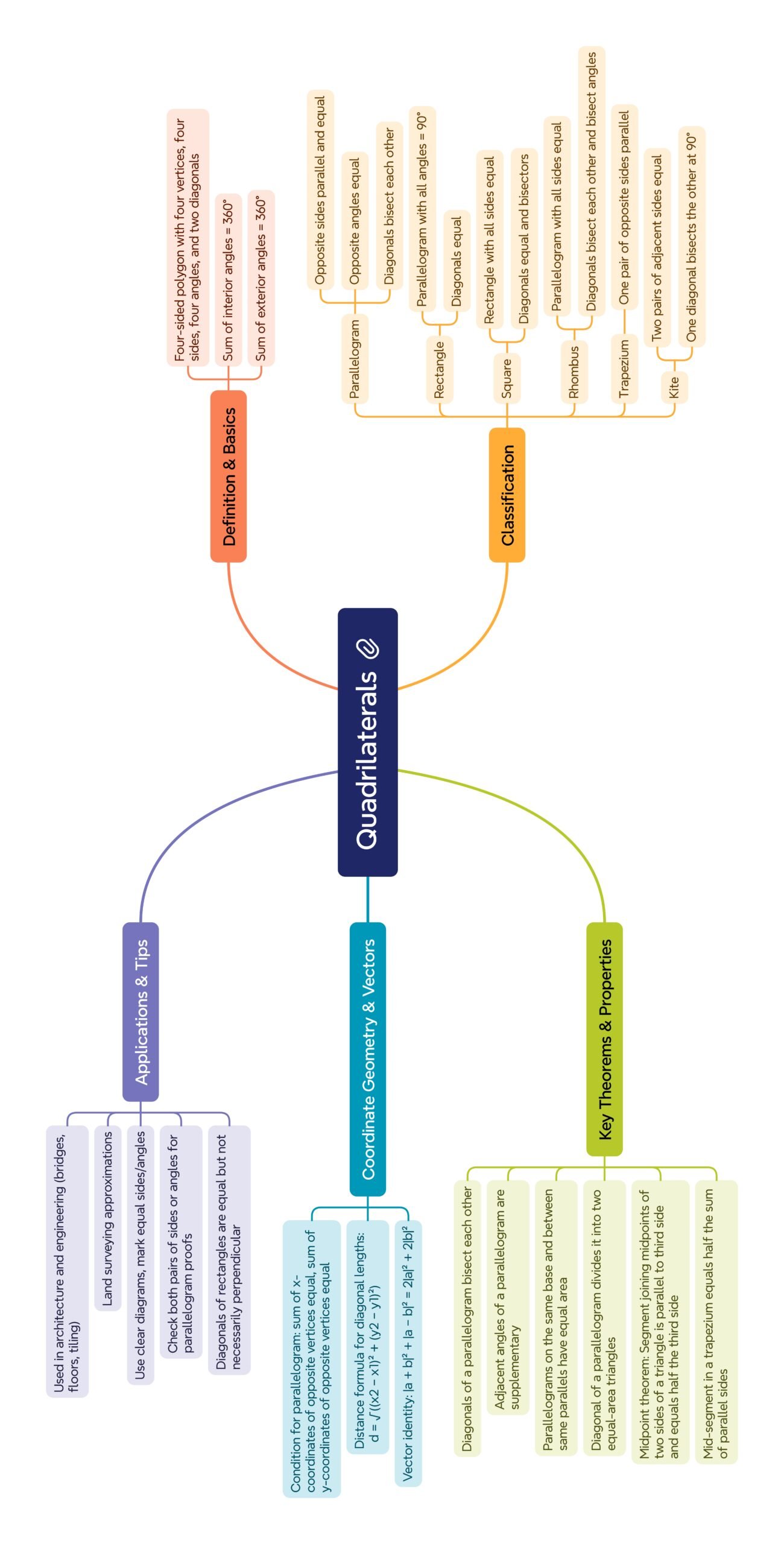
MIND MAP


———————————————————————————————————————————————————————————————————————————–
