Class : 9 – Math (English) : Lesson 5. Introduction to Euclid’s Geometry
EXPLANATION & SUMMARY
🔵 Overview
Euclid’s geometry is a deductive framework for two-dimensional mathematics. It starts with undefined terms, develops definitions, accepts axioms (common notions) and postulates, and from these proves theorems. This logical structure guarantees clarity and consistency for later topics like Lines & Angles and Triangles.
🟢 1. Structure of a Mathematical System
🔹 Undefined terms: point, line, plane.
🔹 Definitions:
• Line segment AB – part of a line between points A and B.
• Ray AB – starts at A, passes through B, extends infinitely.
• Angle ABC – opening between BA and BC.
• Circle – all points equidistant from a centre.
🔹 Axioms (common notions): truths valid for all quantities.
🔹 Postulates: truths specific to geometry.
🔹 Theorems: statements logically deduced from axioms and postulates.
💡 Concept: Imagine a pyramid—small base truths at the bottom, a huge structure of results built above.
🟡 2. Euclid’s Definitions
🌟 Point – has no length, breadth, or thickness.
🌟 Line – breadthless length extending infinitely in both directions.
🌟 Plane – flat, boundless surface.
🌟 Line segment AB – bounded by A and B.
🌟 Ray AB – begins at A and extends endlessly through B.
🌟 Angle ABC – figure formed by two rays sharing point B.
🌟 Right angle – 90°.
🌟 Circle – set of all points at a fixed distance (radius) from a fixed point (centre).
✏️ Note: Point, line, and plane remain undefined; we use their properties rather than formal definitions.
🔴 3. Euclid’s Axioms (Common Notions)
1️⃣ Things equal to the same thing are equal to one another.
2️⃣ If equals are added to equals, the wholes are equal.
• Example: If AB = CD and PQ = RS, then AB + PQ = CD + RS.
3️⃣ If equals are subtracted from equals, the remainders are equal.
• Example: If AB = CD and AP = CQ, then PB = QD.
4️⃣ Things which coincide with one another are equal to one another.
5️⃣ The whole is greater than the part.
6️⃣ Doubles of the same things are equal.
7️⃣ Halves of the same things are equal.
✏️ Tip: Always state which axiom or postulate you are using when justifying a step.
🟢 4. Euclid’s Postulates
1️⃣ A straight line may be drawn joining any two points.
2️⃣ A finite straight line can be extended indefinitely.
3️⃣ A circle can be drawn with any centre and any radius.
4️⃣ All right angles are equal to one another.
5️⃣ If a line intersects two lines so that the interior angles on one side sum to less than 180°, the two lines, if produced, meet on that side.
💡 Concept (Playfair’s Axiom): Through a point P not on a line l, at most one line can be drawn parallel to l.
🔵 5. Using Axioms and Postulates
✔ Drawing and extending: Use Postulate 1 to join points; Postulate 2 to extend.
✔ Constructing circles: Use Postulate 3.
✔ Comparing right angles: Use Postulate 4.
✔ Reasoning about parallels: Use Postulate 5 or Playfair’s Axiom.
🟡 6. First Deductions
🔹 Unique Line Through Two Points
• Postulate 1 ensures at least one line through A and B.
• Assume two distinct lines through A and B → contradiction.
• ✔ Therefore, exactly one line passes through two points.
🔹 Two Distinct Lines Meet at Most Once
• Suppose lines l₁ and l₂ meet at P and Q (P≠Q).
• Both contain P and Q → uniqueness violated.
• ✔ Hence, distinct lines intersect at most once.
🔴 7. Parallel Postulate Intuition
🔸 Let transversal t cut lines l and m.
🔸 Interior angles on one side: α and β.
🔸 If α + β < 180°, l and m meet on that side.
🔸 If α + β = 180°, l and m are parallel.
🔸 If α + β > 180°, they meet on the opposite side.
✏️ Tip: This angle condition underpins many angle-sum proofs later.
🟢 8. Playfair’s Axiom Detailed
✔ Through P not on l, draw candidate parallels.
✔ Any second candidate contradicts Postulate 5.
✔ Therefore, there is at most one parallel through P.
🔵 9. Real-World Connections
📐 Engineering – Bridges rely on parallels (Post. 5) and right angles (Post. 4).
🏗 Architecture – Stable corners use 90°.
🗺 Navigation – Shortest local paths approximate straight lines.
🖥 Computer Graphics – Coinciding figures ensure equal rendering (Axiom 4).
🟡 10. Proof Practice Guidelines
🧠 Format: Given → Reason → Statement.
🔹 Keep one calculation step per line.
🔹 Use math symbols: x², √x, A₁, A₂, fractions a/b.
🔹 Reference the axiom or postulate explicitly.
🔹 Never rely solely on a diagram’s appearance.
🔵 11. Deeper Reasoning Patterns
🔹 Direct Proof
• Begin with the given.
• Use known results (definitions, axioms, postulates).
• Deduce step-by-step until the desired statement is reached.
🔹 Proof by Contradiction
• Assume the opposite of what you want to prove.
• Combine this with known truths.
• Arrive at an impossible conclusion.
• ✔ Therefore, the original statement must be true.
🔹 Construction Method
• Add an auxiliary point, line, or circle.
• Use Postulate 1 or 3 to create new elements.
• Link them to known properties.
🔹 Parallel Logic
• Use Playfair’s Axiom or Postulate 5.
• Connect angle sums or alternate angles.
💡 Concept: Each proof is like a puzzle: small moves using Euclid’s tools create big results.
🟢 12. Mini-Examples for Practice
🔸 Addition Example (Axiom 2)
If AB = CD and PQ = RS,
then AB + PQ = CD + RS.
🔸 Subtraction Example (Axiom 3)
If AB = CD and AP = CQ,
then PB = QD.
🔸 Right Angles (Postulate 4)
If ∠ABC and ∠DEF are right angles,
then ∠ABC = ∠DEF.
🔸 Parallel Postulate Use
Let transversal t cut lines l and m.
If α + β = 180°,
then l ∥ m.
🟡 13. Common Pitfalls
🔴 Mistake: Assuming Diagrams Are Perfect
→ Drawings are not proofs; always cite an axiom or postulate.
🔴 Mistake: Confusing Figures with Measures
→ Write “length of AB = length of CD,” not “AB = CD” as objects.
🔴 Mistake: Skipping Justifications
→ Every step must mention the supporting axiom or postulate.
✏️ Tip: Keep a checklist of common notions and postulates nearby during practice.
🔵 14. Extended Real-Life Links
📐 Engineering and Architecture
• Parallel beams in bridges or roofs rely on Postulate 5.
• Perpendicular supports (90°) depend on Postulate 4.
🗺 Navigation and Surveying
• Straight lines approximate shortest distances locally.
🖥 Computer Graphics
• Coinciding objects (Axiom 4) ensure proper rendering.
🚀 Aerospace and Robotics
• Precise angles and parallels guarantee path calculations.
🟢 15. Building Your Reason Bank
🔹 Memorise Axioms 1–7.
🔹 Memorise Postulates 1–5.
🔹 Include Playfair’s Axiom.
🔹 Practise deriving:
• Unique line through two points.
• Distinct lines meet at most once.
💡 Concept: With this bank, you can justify nearly every step in basic geometry.
🟡 16. Linking to Future Chapters
🔸 Lines & Angles – Uses Postulate 5 for angle-sum properties.
🔸 Triangles – Congruence proofs depend on Axioms 2 and 3.
🔸 Circles – Postulate 3 is essential for constructions.
🔸 Coordinate Geometry – Translates Euclidean properties into algebraic form.
🔴 17. Practice Strategy
✔ Make small flashcards for each axiom/postulate.
✔ Rework mini-examples with your own segment names.
✔ Try to prove “two distinct lines meet at most once” without peeking.
✔ Draw different diagrams but always justify using reasons.
🔷 Summary (~300 words)
Euclid’s geometry is a deductive system that begins with undefined terms, definitions, axioms, and postulates, and from these builds all geometric truths. Points, lines, and planes remain undefined but describe all shapes. Definitions such as line segments, rays, angles, and circles arise from these primitives.
Axioms (common notions) apply universally:
• Things equal to the same thing are equal (Axiom 1).
• Adding equals to equals gives equal wholes (Axiom 2).
• Subtracting equals from equals gives equal remainders (Axiom 3).
• Coinciding things are equal (Axiom 4).
• The whole is greater than the part (Axiom 5).
• Doubles/halves of equals are equal (Axioms 6, 7).
Postulates are geometry-specific:
• Draw a straight line between any two points (Post. 1).
• Extend a finite line indefinitely (Post. 2).
• Draw a circle with any centre and radius (Post. 3).
• All right angles are equal (Post. 4).
• Parallel Postulate—if a transversal creates interior angles summing < 180°, the lines meet on that side (Post. 5).
Playfair’s Axiom restates Post. 5: through point P not on line l, at most one parallel to l exists.
From these, we deduce:
• Only one line passes through two points.
• Two distinct lines meet in at most one point.
These foundations guide constructions, proofs, and real-life applications in engineering, navigation, architecture, and graphics. Mastery of axioms/postulates and careful step-by-step reasoning ensures clarity and accuracy in all future geometry topics.
📝 Quick Recap
🌟 Axioms: universal truths (add/subtract equals, whole > part).
🌟 Postulates: geometry-specific rules (line, extend, circle, right angles, parallels).
🌟 Playfair’s Axiom: unique parallel through a point.
🌟 Theorems: one line through two points; two lines meet at most once.
🌟 Proof Practice: Given → Reason → Statement, one step per line.
🌟 Real-Life Use: bridges, CAD, surveying, graphics.
———————————————————————————————————————————————————————————————————————————–
TEXT BOOK QUESTIONS
EXERCISE 5.1
🔵 Question
Which of the following statements are true and which are false? Give reasons for your answers.
(i) Only one line can pass through a single point.
(ii) There are an infinite number of lines which pass through two distinct points.
(iii) A terminated line can be produced indefinitely on both the sides.
(iv) If two circles are equal, then their radii are equal.
(v) In Fig. 5.9, if AB = PQ and PQ = XY, then AB = XY.
🟢 Answer
🔵 (i) False
🔵 Step 1: Through a single point, infinitely many distinct lines can be drawn.
✔️ Final: False.
🔵 (ii) False
🔵 Step 1: Through any two distinct points, exactly one straight line passes (Euclid’s Postulate 1 and uniqueness).
✔️ Final: False.
🔵 (iii) True
🔵 Step 1: A finite straight line can be produced indefinitely on both sides (Euclid’s Postulate 2).
✔️ Final: True.
🔵 (iv) True
🔵 Step 1: If two circles are equal (coincide), then their radii are equal (definition of equal circles).
✔️ Final: True.
🔵 (v) True
🔵 Step 1: Given AB = PQ and PQ = XY.
🔵 Step 2: Things equal to the same thing are equal to one another (Axiom 1).
✔️ Final: AB = XY.
🔵 Question
2. Give a definition for each of the following terms. Are there other terms that need to be defined first? What are they, and how might you define them?
(i) parallel lines (ii) perpendicular lines (iii) line segment (iv) radius of a circle (v) square
🟢 Answer
(i) Parallel lines
🔵 Step 1: Two lines in the same plane that do not meet however far produced are called parallel lines.
🔵 Step 2: Needed first: point, line, plane (plane = flat surface extending without end).
(ii) Perpendicular lines
🔵 Step 1: Two lines that intersect to form a right angle (90 degrees) are perpendicular.
🔵 Step 2: Needed first: line, angle, right angle, plane.
(iii) Line segment
🔵 Step 1: Part of a line bounded by two endpoints A and B; written as AB.
🔵 Step 2: Needed first: point, line.
(iv) Radius of a circle
🔵 Step 1: A line segment joining the centre of a circle to any point on the circle.
🔵 Step 2: Needed first: circle, centre, point, line segment.
(v) Square
🔵 Step 1: A quadrilateral with four equal sides and four right angles (90 degrees each).
🔵 Step 2: Needed first: point, line segment, angle, right angle, quadrilateral.
💡 Concept: A square is both a rectangle (all angles 90 degrees) and a rhombus (all sides equal).
🔵 Question
3. Consider two ‘postulates’ given below:
(i) Given any two distinct points A and B, there exists a third point C which is in between A and B.
(ii) There exist at least three points that are not on the same line.
Do these postulates contain any undefined terms? Are these postulates consistent? Do they follow from Euclid’s postulates? Explain.
🟢 Answer
🔵 Step 1: Undefined terms present: point, line, and the relation “between”.
🔵 Step 2: Consistency: Yes. Both statements can be true together without contradiction.
🔵 Step 3: Do they follow from Euclid’s five postulates: No.
🟢 Reason (i): “Between” is not supplied by the five postulates; it is an additional assumption.
🟢 Reason (ii): Existence of at least three non-collinear points is independent of the five postulates.
✔️ Final: They contain undefined terms, are consistent, and do not follow directly from Euclid’s postulates.
🔵 Question
4. If a point C lies between two points A and B such that AC = BC, then prove that AC = 1/2 AB. Explain by drawing the figure.
🟢 Answer
🔵 Step 1: Since C lies between A and B, AB = AC + CB (segment addition).
🔵 Step 2: Given AC = BC.
🔵 Step 3: Substitute to get AB = AC + AC = 2*AC.
🔵 Step 4: Divide both sides by 2 to obtain AC = (1/2)AB.
🟡 Check: 2AC = AB holds; verified.
✔️ Final: AC = (1/2) AB.
🔵 Question
5. In Question 4, point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.
🟢 Answer
🔵 Existence
🔵 Step 1: With centres A and B and equal radius r, draw two circles (Postulate 3).
🔵 Step 2: Let them intersect at P and Q; join PQ.
🔵 Step 3: PQ meets AB at M; by equal radii, AP = BP and AQ = BQ.
🔵 Step 4: Points equidistant from A and B lie on the perpendicular bisector; hence AM = MB, so M is a mid-point.
🔵 Uniqueness
🔵 Step 5: Suppose C and D are both mid-points (C != D), so AC = CB and AD = DB.
🔵 Step 6: From AC = CB, AB = AC + CB = 2AC.
🔵 Step 7: From AD = DB, AB = AD + DB = 2AD.
🔵 Step 8: Hence 2AC = 2AD => AC = AD (Axiom 7: halves of equals are equal).
🔵 Step 9: Along AB, if C != D, then one of AC or AD is strictly smaller (Axiom 5: whole > part).
🔵 Step 10: Steps 8 and 9 contradict unless C = D.
✔️ Final: Every line segment has one and only one mid-point.
🔵 Question
6. In Fig. 5.10, if AC = BD, then prove that AB = CD.
🟢 Answer
🔵 Step 1: AC = AB + BC (segment addition).
🔵 Step 2: BD = BC + CD (segment addition).
🔵 Step 3: Given AC = BD.
🔵 Step 4: Substitute to get AB + BC = BC + CD.
🔵 Step 5: Subtract BC from both sides (Axiom 3) to obtain AB = CD.
🟡 Check: Replacing AB with CD in Step 4 gives equality; verified.
✔️ Final: AB = CD.
🔵 Question
7. Why is Axiom 5, in the list of Euclid’s axioms, considered a ‘universal truth’? (Note that the question is not about the fifth postulate.)
🟢 Answer
🔵 Step 1: Axiom 5 states “The whole is greater than the part.”
🔵 Step 2: This holds for all quantities (numbers, lengths, areas, masses, etc.), not only geometric figures.
🔵 Step 3: Because it applies across all contexts, it is called a universal truth.
✔️ Final: “Whole > part” is universally valid, hence Axiom 5 is a universal truth
———————————————————————————————————————————————————————————————————————————–
OTHER IMPORTANT QUESTIONS FOR EXAMS
🔵 Section A — Very Short / Objective (1 mark each)
🔵 Question
Which of the following is a common notion (axiom) in Euclid’s system?
🟢 A. Through two points, exactly one line passes
🟡 B. The whole is greater than the part
🔴 C. A circle can be drawn with any centre and radius
🔵 D. All right angles are equal
🟢 Answer
✔️ Correct option: B
🔵 Question
2) Euclid’s First Postulate states that:
🟢 A. A circle can be drawn with any centre and any radius
🟡 B. A straight line may be drawn from any one point to any other point
🔴 C. All right angles are equal
🔵 D. If a transversal makes interior angles less than two right angles, the lines meet on that side
🟢 Answer
✔️ Correct option: B
🔵 Question
3) Playfair’s Axiom states that through a point not on a line there are:
🟢 A. More than one parallels to the line
🟡 B. Exactly one parallel to the line
🔴 C. No parallels to the line
🔵 D. Infinitely many parallels to the line
🟢 Answer
✔️ Correct option: B
🔵 Question
4) Choose the false statement:
🟢 A. Two distinct lines can have at most one common point
🟡 B. There are infinitely many lines through a single point
🔴 C. Through two distinct points, infinitely many lines can pass
🔵 D. A finite straight line can be produced indefinitely
🟢 Answer
✔️ Correct option: C
🔵 Question
5) Which set lists traditional undefined terms in Euclid’s geometry?
🟢 A. point, line, plane
🟡 B. segment, ray, angle
🔴 C. triangle, circle, square
🔵 D. radius, diameter, chord
🟢 Answer
✔️ Correct option: A
🔵 Question
6) If AB = PQ and PQ = XY, then by a common notion we get:
🟢 A. AB > XY
🟡 B. AB < XY
🔴 C. AB = XY
🔵 D. AB and XY are not comparable
🟢 Answer
✔️ Correct option: C
🟢 Section B — Short Answer I (2 marks each)
🔵 Question
7) State Euclid’s Second Postulate and write one use of it.
🟢 Answer
🔵 Step 1: Euclid’s Second Postulate: a finite straight line can be produced indefinitely.
🔵 Step 2: Use: to extend a given segment AB beyond A or B during constructions/proofs.
✔️ Final: Postulate 2 lets us extend any finite line as needed.
🔵 Question
8) Define parallel lines and list the undefined terms required before defining them.
🟢 Answer
🔵 Step 1: Parallel lines are two lines in the same plane that do not meet however far produced.
🔵 Step 2: Required undefined terms: point, line, plane.
✔️ Final: Definition depends on accepting point, line, plane first.
🔵 Question
9) Show that if two angles are right angles, then they are equal.
🟢 Answer
🔵 Step 1: Let angle X and angle Y be right angles (each 90 degrees).
🔵 Step 2: Euclid’s Fourth Postulate: all right angles are equal to one another.
✔️ Final: angle X = angle Y.
🔵 Question
10) Prove that two distinct lines cannot have more than one common point.
🟢 Answer
🔵 Step 1: Assume distinct lines l and m share two different points A and B.
🔵 Step 2: Through two distinct points A and B, exactly one line passes (from Postulate 1 and uniqueness).
🔵 Step 3: Hence l = m, contradicting “distinct lines”.
✔️ Final: Distinct lines can have at most one common point.
🔵 Question
11) If C lies between A and B and AC = BC, prove that *AC = (1/2)AB.
🟢 Answer
🔵 Step 1: Since C is between A and B, AB = AC + CB.
🔵 Step 2: Given AC = BC, so AB = AC + AC.
🔵 Step 3: Therefore AB = 2*AC.
🔵 Step 4: Hence AC = (1/2)*AB.
✔️ Final: AC = (1/2)*AB.
🔵 Question
12) State whether the statement “Things which are equal to the same thing are equal to one another” is a postulate or an axiom, with reason.
🟢 Answer
🔵 Step 1: It is a common notion (axiom).
🔵 Step 2: Reason: it applies to all quantities (numbers, lengths, areas), not only to geometric figures.
✔️ Final: It is an axiom.
🟡 Section C – Short Answer II (3 marks each)
🔵 Question 13
State any three of Euclid’s postulates in your own words, and mention one use of each.
🟢 Answer
🔵 Step 1: Postulate 1: A straight line may be drawn joining any two points.
🔵 Step 2: Use of Postulate 1: join two points to form a segment for constructions/proofs.
🔵 Step 3: Postulate 2: A finite straight line can be produced indefinitely.
🔵 Step 4: Use of Postulate 2: extend a segment when needed in proofs.
🔵 Step 5: Postulate 3: A circle can be drawn with any centre and any radius.
🔵 Step 6: Use of Postulate 3: create loci at fixed distance from a point.
✔️ Final: Three postulates stated with one practical use each.
🔵 Question 14
Explain the difference between an axiom and a postulate with one example of each.
🟢 Answer
🔵 Step 1: Axiom: truth accepted for all quantities, not only geometry.
🔵 Step 2: Example axiom: things equal to the same thing are equal to one another.
🔵 Step 3: Postulate: geometry-specific assumption about points, lines, circles.
🔵 Step 4: Example postulate: through any two points, exactly one straight line can be drawn.
✔️ Final: Axioms are general; postulates are geometry-specific.
🔵 Question 15
Prove using Euclid’s common notions: if AB = CD and CD = EF, then AB = EF.
🟢 Answer
🔵 Step 1: Given AB = CD and CD = EF.
🔵 Step 2: By Axiom 1 (equal to the same), AB = EF.
✔️ Final: AB = EF by Axiom 1.
OR
Prove: if AB = CD, then AB + PQ = CD + PQ.
🟢 Answer
🔵 Step 1: Given AB = CD.
🔵 Step 2: Add equals to equals (Axiom 2) to get AB + PQ = CD + PQ.
✔️ Final: AB + PQ = CD + PQ by Axiom 2.
🔵 Question 16
Show that through two distinct points only one straight line can pass.
🟢 Answer
🔵 Step 1: By Postulate 1, a straight line can be drawn joining two distinct points A and B.
🔵 Step 2: Assume for contradiction there are two different lines through A and B.
🔵 Step 3: Two distinct lines through the same two points would violate uniqueness of line through two points.
🔵 Step 4: Therefore only one straight line passes through A and B.
✔️ Final: Unique line through two points is established.
🔵 Question 17
Using Playfair’s axiom, justify that through a point P not on line l there is at most one line parallel to l.
🟢 Answer
🔵 Step 1: Consider point P not on l.
🔵 Step 2: Suppose two different lines through P are both parallel to l.
🔵 Step 3: This contradicts Playfair’s axiom which allows at most one parallel through P.
🔵 Step 4: Hence, there is at most one parallel to l through P.
✔️ Final: Parallel through a given external point is unique.
OR
If a transversal cuts lines l and m with interior angles on the same side summing to 180 degrees, prove l || m.
🟢 Answer
🔵 Step 1: Let interior angles be alpha and beta with alpha + beta = 180 degrees.
🔵 Step 2: If l and m met on that side, Postulate 5 would require alpha + beta < 180 degrees.
🔵 Step 3: Given 180 degrees, meeting is impossible; lines do not meet on either side.
🔵 Step 4: Therefore l || m.
✔️ Final: l is parallel to m when interior angles sum to 180 degrees.
🔵 Question 18
If C lies between A and B and AC = (1/2)*AB, prove that C is the mid-point of AB.
🟢 Answer
🔵 Step 1: Since C is between A and B, AB = AC + CB.
🔵 Step 2: Given AC = (1/2)*AB.
🔵 Step 3: Substitute to get AB = (1/2)*AB + CB.
🔵 Step 4: Subtract (1/2)*AB from both sides to obtain (1/2)*AB = CB.
🔵 Step 5: Therefore AC = CB, and C lies on AB.
✔️ Final: AC = CB with C on AB implies C is the mid-point of AB.
🔵 Question 19
On a straight line A-B-C-D in that order, if AC = BD, prove that AB = CD.
🟢 Answer
🔵 Step 1: AC = AB + BC (segment addition).
🔵 Step 2: BD = BC + CD (segment addition).
🔵 Step 3: Given AC = BD, so AB + BC = BC + CD.
🔵 Step 4: Subtract BC from both sides (Axiom 3) to obtain AB = CD.
✔️ Final: AB = CD.
🔵 Question 20
Classify the following as undefined or defined terms and give one precise definition for a defined term you list: {point, line, plane, segment, ray, circle}.
🟢 Answer
🔵 Step 1: Undefined terms: point, line, plane.
🔵 Step 2: Defined terms: segment, ray, circle.
🔵 Step 3: Example definition (circle): set of all points at a fixed distance r from a fixed point called the centre.
✔️ Final: First three are undefined; the others are defined with standard definitions.
OR
State Postulate 3 and show one construction that uses it.
🟢 Answer
🔵 Step 1: Postulate 3: a circle can be drawn with any centre and any radius.
🔵 Step 2: Construction: given segment AB, draw a circle with centre A and radius AB to locate points at distance AB from A.
✔️ Final: Postulate 3 enables circle-based constructions.
🔵 Question 21
Two proposed postulates are:
(i) Given any two distinct points A and B, there exists a third point C between A and B.
(ii) There exist at least three points that are not on the same line.
Discuss undefined terms, consistency, and whether they follow from Euclid’s postulates.
🟢 Answer
🔵 Step 1: Undefined terms involved: point, line, and the relation “between”.
🔵 Step 2: Consistency: both can be true together without contradiction.
🔵 Step 3: Dependence: they do not follow directly from Euclid’s five postulates; they are independent assumptions.
✔️ Final: Contain undefined terms, are consistent, and are independent of Euclid’s five postulates.
🔵 Question 22
Show that if two angles are right angles, they are equal.
🟢 Answer
🔵 Step 1: Let angle X and angle Y be right angles.
🔵 Step 2: By Postulate 4, all right angles are equal to one another.
🔵 Step 3: Therefore angle X = angle Y.
✔️ Final: Any two right angles are equal by Postulate 4.
OR
Prove: if equals are subtracted from equals, the remainders are equal.
🟢 Answer
🔵 Step 1: Let a = b and let c be any quantity.
🔵 Step 2: Subtract c from both sides to get a – c and b – c.
🔵 Step 3: By Axiom 3, a – c = b – c.
✔️ Final: Remainders after subtracting equals are equal by Axiom 3.
🔴 Section D – Long Answer (4 marks each)
🔵 Question 23
Using Euclid’s postulates and common notions, prove that the perpendicular bisector of a segment AB is the set of all points equidistant from A and B.
🟢 Answer
🔵 Step 1: Let M be the midpoint of AB and let line p be perpendicular to AB at M.
🔵 Step 2: Take any point P on p. Then AM = MB by midpoint definition and PM is common.
🔵 Step 3: In triangles AMP and BMP, AM = MB, PM = PM, and angle AMP = angle BMP = 90 degrees.
🔵 Step 4: Therefore triangles AMP and BMP are congruent by RHS idea accepted in school geometry.
🔵 Step 5: Hence AP = BP (corresponding parts).
🔵 Step 6: Conversely, let a point Q satisfy QA = QB.
🔵 Step 7: Join QA and QB. If Q is not on the perpendicular at M, QA and QB would lie on different sides or not make equal right angles, contradicting equality via standard perpendicular bisector reasoning.
🔵 Step 8: Therefore Q must lie on the perpendicular through M.
✔️ Final: The perpendicular bisector of AB is exactly the locus of points equidistant from A and B.
🔵 Question 24
Prove that if two lines are each perpendicular to a third line, then they are parallel to each other.
🟢 Answer
🔵 Step 1: Let lines l and m be perpendicular to a line t at points P and Q respectively.
🔵 Step 2: Then angle between l and t at P is 90 degrees and angle between m and t at Q is 90 degrees (Postulate 4).
🔵 Step 3: Consider a transversal t across l and m. Interior angles on the same side are 90 degrees + 90 degrees = 180 degrees.
🔵 Step 4: By the parallel criterion consistent with Postulate 5, if interior angles on the same side sum to 180 degrees, lines do not meet on either side.
✔️ Final: Therefore l parallel m.
🔵 Question 25
Show that if two triangles coincide exactly when superposed, then their corresponding sides and angles are equal. Explain which axiom is used.
🟢 Answer
🔵 Step 1: Suppose triangle ABC superposes perfectly on triangle PQR.
🔵 Step 2: By Euclid’s common notion Axiom 4, things which coincide are equal to one another.
🔵 Step 3: Therefore AB = PQ, BC = QR, CA = RP.
🔵 Step 4: Also angle A = angle P, angle B = angle Q, angle C = angle R.
✔️ Final: Coincidence implies equality of all corresponding parts by Axiom 4.
🔵 Question 26
Using Euclid’s axioms, prove: if equals are added to equals and then equal parts are subtracted, the results remain equal. Formally, if a = b and c = d, then (a + c) – e = (b + d) – e for any e.
🟢 Answer
🔵 Step 1: Given a = b and c = d.
🔵 Step 2: By Axiom 2 (add equals to equals), a + c = b + d.
🔵 Step 3: Subtract equals from equals (Axiom 3) using the same e on both sides to get (a + c) – e = (b + d) – e.
✔️ Final: The stated equality holds by Axioms 2 and 3.
🔵 Question 27
Let a transversal cut lines l and m. If a pair of interior angles on the same side are supplementary, prove l parallel m. Also justify why the converse holds.
🟢 Answer
🔵 Step 1: Let the interior angles on the same side be alpha and beta with alpha + beta = 180 degrees.
🔵 Step 2: If l and m met on the side of these angles, Postulate 5 would require alpha + beta < 180 degrees.
🔵 Step 3: Since alpha + beta = 180 degrees, meeting is impossible on either side.
🔵 Step 4: Therefore l parallel m.
🔵 Step 5: Converse justification: If l parallel m, the interior angles on the same side are supplementary by the standard parallel angle result consistent with the non-meeting behavior of parallels.
✔️ Final: l parallel m iff interior angles on the same side sum to 180 degrees.
🔵 Question 28
Show that through a given point P not on a line l there is at most one line parallel to l. Use Playfair’s axiom and discuss why more than one parallel is impossible.
🟢 Answer
🔵 Step 1: Playfair’s axiom states: through P not on l, there is at most one line parallel to l.
🔵 Step 2: Suppose for contradiction two distinct lines p and q through P are both parallel to l.
🔵 Step 3: Consider transversal l crossing p and q. The interior angle relations would force distinct directions from P that both never meet l, contradicting Playfair’s axiom.
🔵 Step 4: Hence there cannot be two distinct parallels through P to l.
✔️ Final: Exactly one parallel through a given external point is possible, not more.
🔵 Question 29
Internal choice
A) Prove: If AC = (1/2)AB and C lies between A and B, then C is the unique midpoint of AB.
B) Prove: If AC = CD and A, C, D are collinear in that order with C between A and D, then AD = 2AC.
🟢 Answer A
🔵 Step 1: Since C is between A and B, AB = AC + CB.
🔵 Step 2: Given AC = (1/2)*AB.
🔵 Step 3: Substitute to get AB = (1/2)*AB + CB.
🔵 Step 4: Subtract (1/2)AB from both sides to obtain (1/2)AB = CB.
🔵 Step 5: Therefore AC = CB, so C is a midpoint.
🔵 Step 6: Uniqueness: If D were also a midpoint with D != C, then AC = CB and AD = DB imply AB = 2AC and AB = 2AD => AC = AD.
🔵 Step 7: Along AB, if C != D, one of AC or AD is smaller, contradicting equality with the same endpoints.
✔️ Final: C is the unique midpoint of AB.
🟢 Answer B
🔵 Step 1: Given A, C, D are collinear with C between A and D, so AD = AC + CD.
🔵 Step 2: Given AC = CD.
🔵 Step 3: Substitute to get AD = AC + AC = 2AC.
✔️ Final: AD = 2AC.
🔵 Question 30
Internal choice
A) From Euclid’s postulates, explain why a right angle is used as a standard unit for perpendicularity and show that any two perpendicular directions are equivalent.
B) Using common notions, show that if two segments are each double of a third segment, then they are equal.
🟢 Answer A
🔵 Step 1: By Postulate 4, all right angles are equal to one another.
🔵 Step 2: Perpendicularity is defined using a right angle at the point of intersection.
🔵 Step 3: Since any right angle equals any other right angle, any two constructions of perpendicular direction represent the same magnitude.
🔵 Step 4: Therefore the right angle serves as a standard unit and all perpendicular directions are equivalent in measure.
✔️ Final: Right angles form a universal unit for perpendicularity by Postulate 4.
🟢 Answer B
🔵 Step 1: Let segments AB and CD each be double of segment EF.
🔵 Step 2: Then AB = 2EF and CD = 2EF.
🔵 Step 3: By the common notion “doubles of the same are equal”, AB = CD.
✔️ Final: If two segments are doubles of the same segment, they are equal.
————————————————————————————————————————————————————————————————————————————
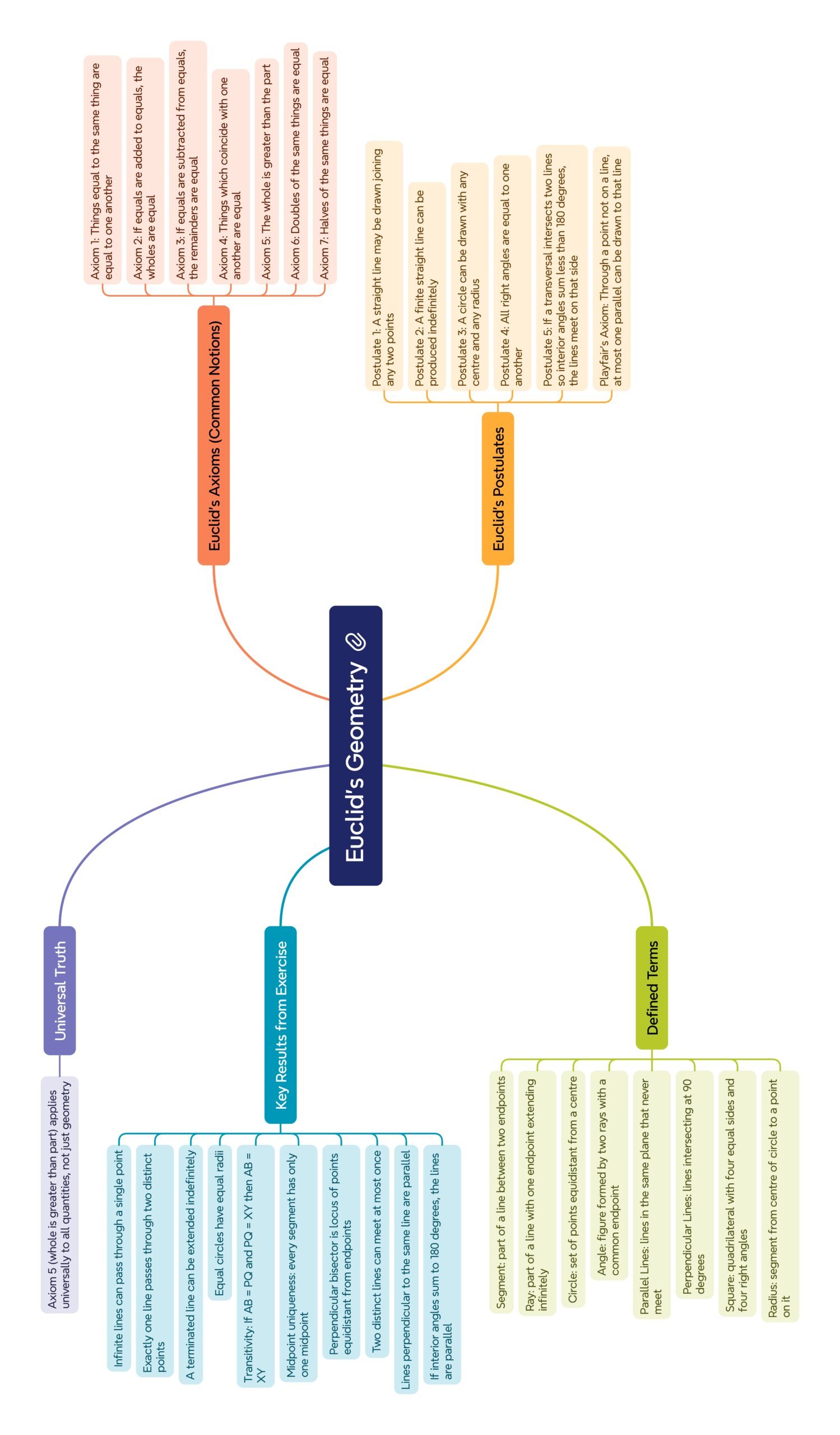
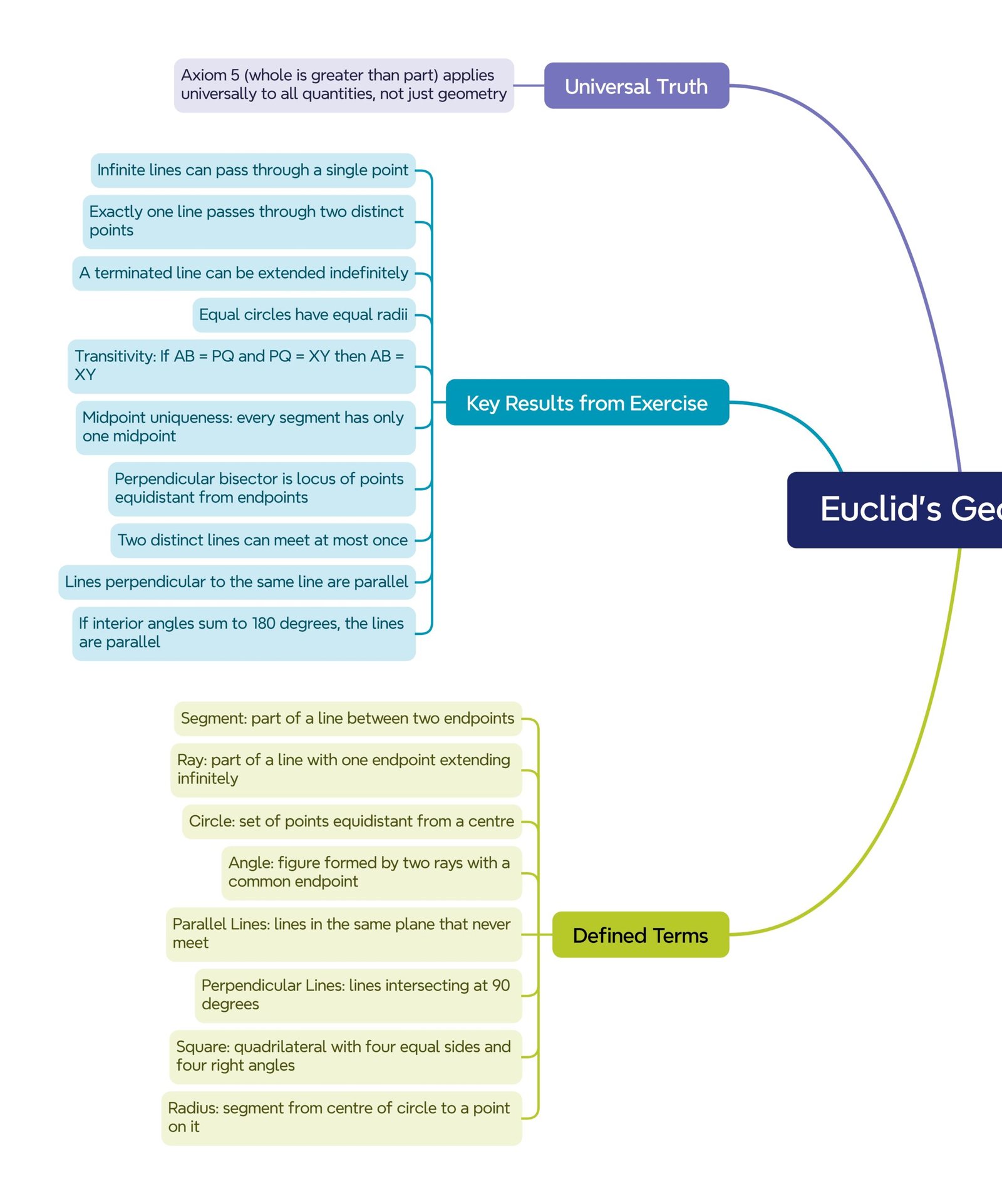
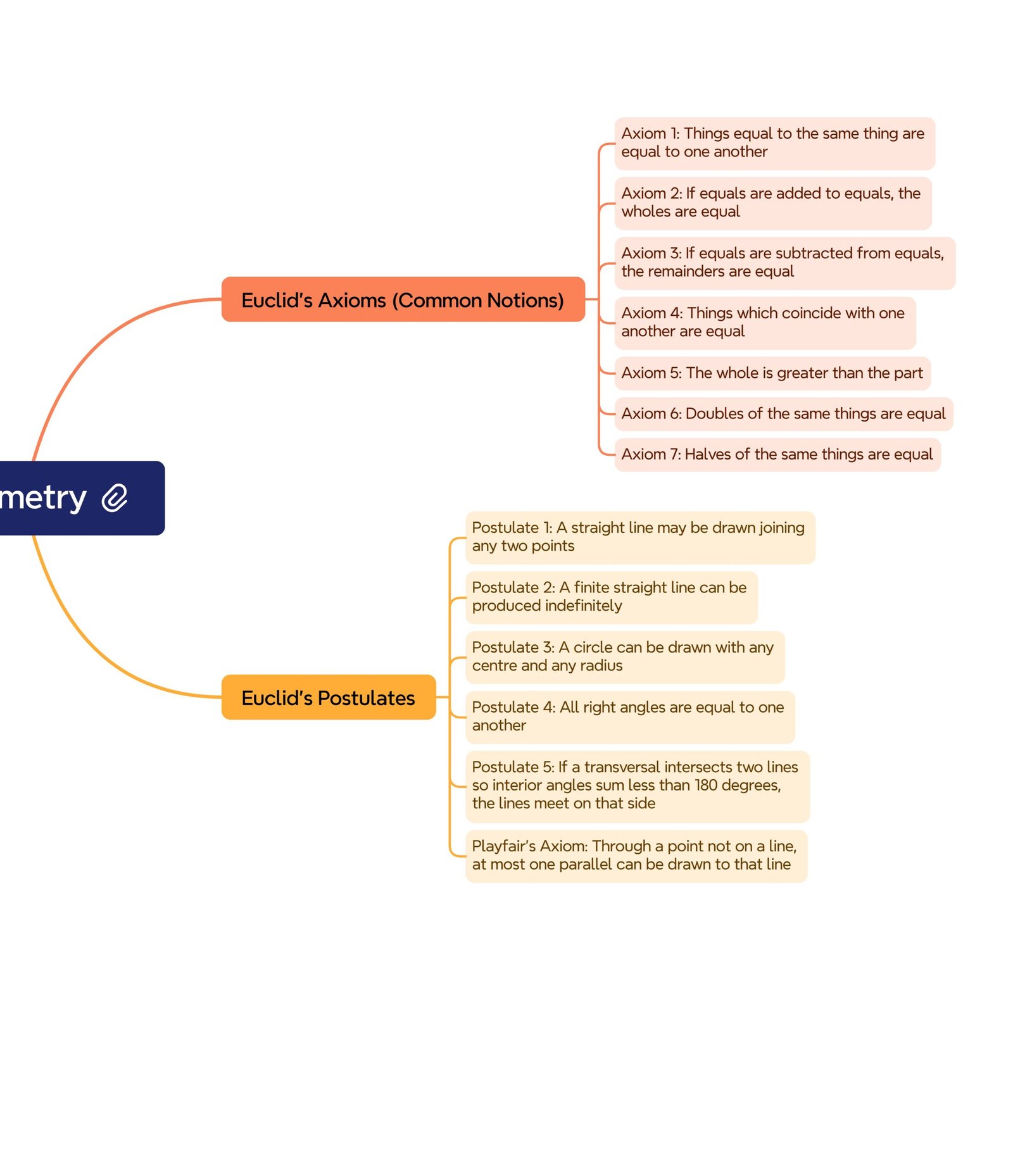
MIND MAP
———————————————————————————————————————————————————————————————————————————–
