Class : 9 – Maths (English) : Lesson 2. “Polynomials”
EXPLANATION & SUMMARY
🔵 Detailed Explanation
🔵 1) What is a Polynomial?
• ✨ Definition: A polynomial p(x) is an algebraic expression of the form a₀ + a₁x + a₂x² + … + aₙxⁿ where:
– Coefficients aᵢ ∈ ℝ (real numbers)
– Exponents n ∈ ℕ₀ (non-negative integers)
– Operations allowed: +, −, × only (no division by variable, no fractional or negative exponents).
• ✨ Examples: 3x³ − 5x² + 2x − 7; x² + x + 1.
• ✨ Non-examples: 3/x + 5 (division by variable), x⁻² + 7 (negative exponent), √x + 2 (radical exponent ≠ integer).
🟢 2) Terms, Coefficients, Variables, Degree
• Term: each part separated by + or − (e.g., 3x³, −5x²).
• Coefficient: numerical factor of a term (3 in 3x³).
• Variable: symbol like x.
• Degree of a term: exponent of variable (deg(−5x²)=2).
• Degree of polynomial: highest degree among terms (deg(3x³−5x²+2x−7)=3).
• Leading term: term with highest degree. Leading coefficient: coefficient of that term.
🟡 3) Classification by Degree
• Zero polynomial: all coefficients = 0 (degree undefined).
• Constant polynomial: degree 0 (e.g., 7).
• Linear: degree 1 (e.g., 4x − 3).
• Quadratic: degree 2 (e.g., x² + 5x + 6).
• Cubic: degree 3 (e.g., x³ − 7x + 2).
• Quartic: degree 4, Quintic: degree 5, etc.
🔴 4) Classification by Terms
• Monomial: one term (7x⁵).
• Binomial: two terms (x + 5).
• Trinomial: three terms (2x² + 3x − 1).
• Multinomial: more than three terms.
🔵 5) Standard Form and Ordering
• ✨ Standard form: arrange in descending powers of x. Example: 5 − 2x⁴ + 3x² becomes −2x⁴ + 3x² + 5.
• ✨ Two polynomials are equal ⇔ all corresponding coefficients equal.
🟢 6) Operations on Polynomials
➡️ (a) Addition/Subtraction
Combine like terms.
Example: (3x² + 4x − 7) + (x² − 2x + 5) = 4x² + 2x − 2.
➡️ (b) Multiplication
Use distributive property or identities.
Example: (2x + 3)(x − 4) = 2x² − 8x + 3x − 12 = 2x² − 5x − 12.
➡️ (c) Division Algorithm
Statement: For polynomials f(x) and g(x)≠0, ∃ unique q(x), r(x) s.t.
f(x) = g(x) × q(x) + r(x), deg(r)<deg(g).
Example: Divide 2x³ + 3x² + 2x + 5 by x² + 1.
Step 1: 2x³/x²=2x. Multiply: 2x³ + 2x.
Step 2: Subtract: (2x³ + 3x² + 2x + 5) − (2x³ + 2x)=3x² + 5.
Step 3: 3x²/x²=3. Multiply: 3x² + 3.
Step 4: Subtract: 3x² + 5 − (3x² + 3)=2.
So q(x)=2x+3, r(x)=2.
🟡 7) Remainder Theorem
• If p(x) divided by (x−a), remainder = p(a).
Example: Remainder of x³+3x²+3x+1 ÷ (x+1)?
Evaluate p(−1)= (−1)³+3(−1)²+3(−1)+1=−1+3−3+1=0 ⇒ remainder=0.
🔴 8) Factor Theorem
• x−a is factor of p(x) ⇔ p(a)=0.
Example: Check if x−2 is factor of x³−2x²−x+2.
p(2)=8−8−2+2=0 ⇒ factor confirmed.
🔵 9) Factorisation Methods
• Common factor: 5x²+10x=5x(x+2).
• Grouping: x³+3x²+3x+1=(x+1)³.
• Splitting middle term: x²+5x+6=(x+2)(x+3).
• Identities: a³+b³=(a+b)(a²−ab+b²).
🟢 10) Algebraic Identities (Important)
• (x+y)²=x²+2xy+y².
• (x−y)²=x²−2xy+y².
• x²−y²=(x+y)(x−y).
• (x+a)(x+b)=x²+(a+b)x+ab.
• (x+y+z)²=x²+y²+z²+2xy+2yz+2zx.
• (x+y)³=x³+y³+3xy(x+y).
• x³+y³=(x+y)(x²−xy+y²).
• x³−y³=(x−y)(x²+xy+y²).
🟡 11) Zeros of Polynomials
• Zero of p(x) is α such that p(α)=0.
• Linear polynomial ax+b has exactly one zero: −b/a.
• Quadratic may have 0,1, or 2 real zeros.
• Cubic may have 1 or 3 real zeros.
• Non-zero polynomial of degree n has ≤n zeros.
🔴 12) Graphical Meaning
• Plot y=p(x) on coordinate plane.
• Zeros correspond to x-intercepts.
• Example: y=x²−4 is a parabola crossing x-axis at x=±2.
🔵 13) Worked Examples
A) Add: (5x³−4x+7) + (3x³+2x²−7)=8x³+2x²−4x.
B) Multiply: (x−2)(x²+2x+4)=x³−8 (using a³−b³).
C) Divide: (x³−7x+6)/(x−1):
1. x³/x=x² ⇒ multiply x³−x².
2. Subtract: x²−7x+6.
3. x²/x=x ⇒ multiply x²−x.
4. Subtract: −6x+6.
5. −6x/x=−6 ⇒ multiply −6x+6.
6. Subtract: remainder=0 ⇒ quotient=x²+x−6.
D) Factorise: x³+27=(x+3)(x²−3x+9).
E) Use remainder theorem: remainder of 2x³+3x²−2x+5 ÷ (x−2)=29.
🟢 14) Common Mistakes
• Forgetting to arrange in descending order before division.
• Applying factor theorem wrongly (wrong value).
• Mixing up signs in identities.
• Assuming zero polynomial has degree 0 (it’s undefined).
🟡 15) Applications
• Physics: motion equations approximated by polynomials.
• Economics: profit/cost models.
• Computer graphics: Bézier curves.
• Engineering: structural analysis.
🔴 16) Higher-Order Ideas
• Polynomials form a ring under + and ×.
• Constant polynomial degree=0.
• Graphs are smooth—no breaks.
✨ 17) Mini-Exercise
Classify:7x⁵, x²+5, 3x³+2x²−x+1.
Find remainder of x³−2x²−x+2 ÷ (x−1).
Factorise x³−8.
Expand (2x−3y)³.
Verify (x+y+z)² identity.
🟣 Summary (≈ 300 words)
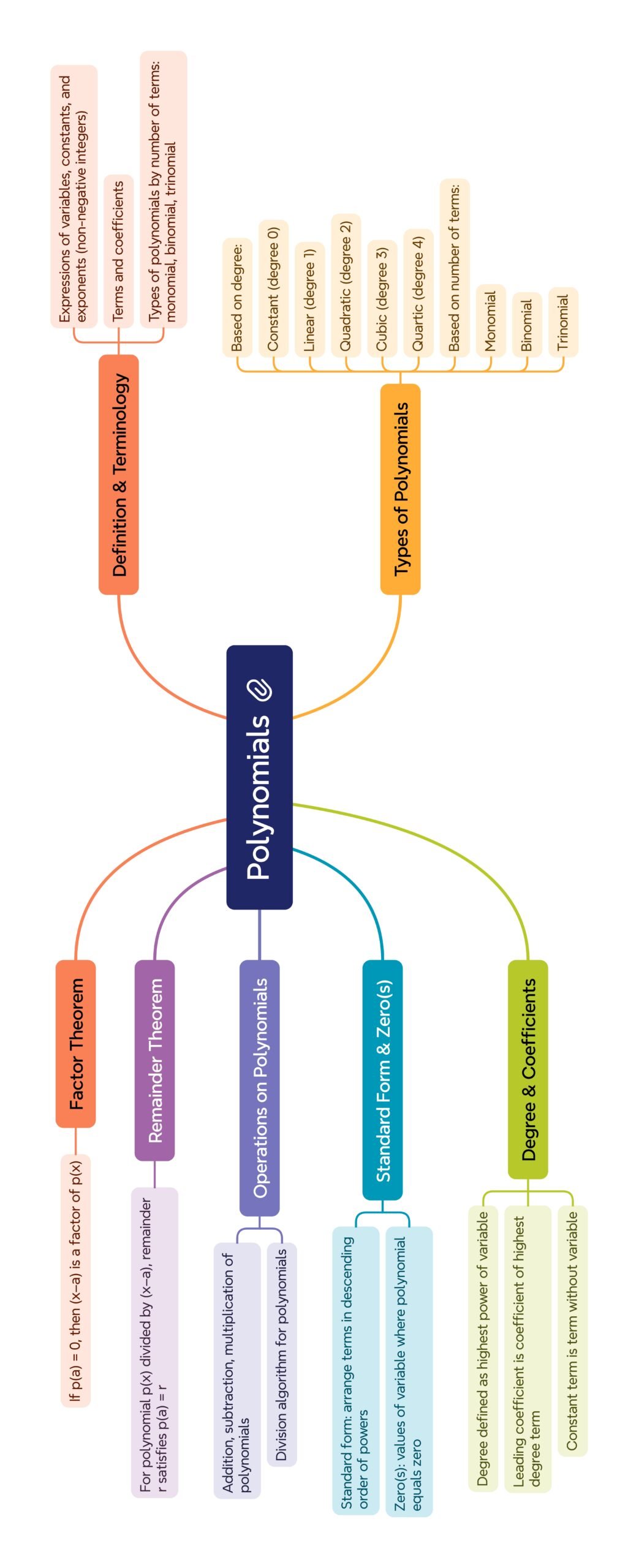
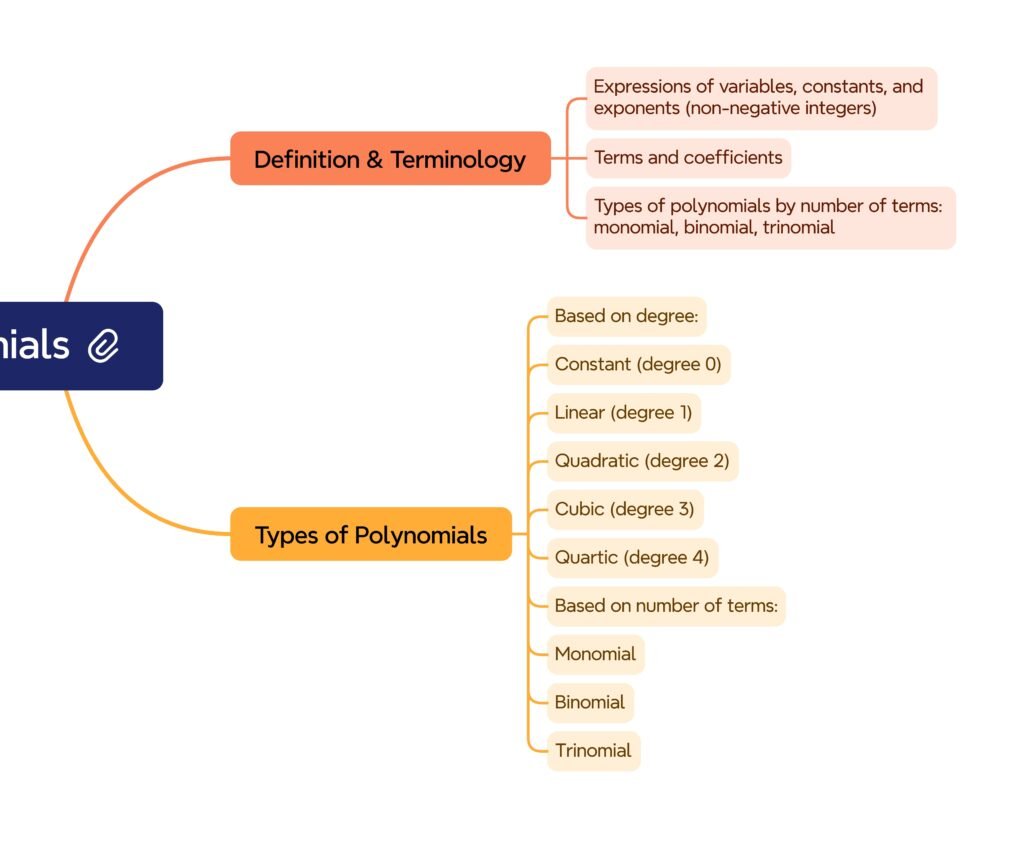
A polynomial p(x)=a₀+a₁x+a₂x²+…+aₙxⁿ is an algebraic expression with real coefficients, non-negative integer exponents, and only +, −, × operations. Its degree is the highest exponent. Classify polynomials by degree: constant (0), linear (1), quadratic (2), cubic (3), quartic (4)…; and by terms: monomial (1 term), binomial (2 terms), trinomial (3 terms), multinomial (>3).
Operations: addition and subtraction combine like terms; multiplication uses distributive law or identities. The Division Algorithm states f(x)=g(x)q(x)+r(x) with deg(r)<deg(g). Remainder Theorem: remainder when dividing by x−a is p(a). Factor Theorem: x−a is a factor ⇔ p(a)=0. Factorisation methods: common factors, grouping, splitting middle term, using identities, or factor theorem.
Important identities: (x±y)², x²−y², (x+a)(x+b), (x+y+z)², (x±y)³, x³±y³. Zeros of polynomials correspond to x-intercepts of graphs; a degree n polynomial has at most n zeros. Graphs of polynomials are continuous and smooth. Applications include modelling physical motion, cost/profit analysis, graphics, and engineering calculations.
Common errors: misordering terms before division, misapplying factor theorem, sign mistakes in identities, and confusing zero polynomial degree. Polynomials form a fundamental structure for algebra and calculus—mastering their properties ensures accurate problem-solving.
📝 Quick Recap
🔵 Definition: p(x)=a₀+a₁x+a₂x²+…+aₙxⁿ (aᵢ∈ℝ).
🟢 Types by degree: constant, linear, quadratic, cubic, quartic.
🟡 Types by terms: monomial, binomial, trinomial, multinomial.
🔴 Division Algorithm: f(x)=g(x)q(x)+r(x).
🔵 Remainder Theorem: remainder=p(a).
🟢 Factor Theorem: p(a)=0 ⇒ x−a is factor.
🟡 Identities: (x±y)², x²−y², (x+y+z)², x³±y³.
🔴 Graph: degree n ⇒ ≤ n zeros.
✨ Factorisation: grouping, splitting middle term, identities, factor theorem.

————————————————————————————————————————————————————————————————————————————–
TEXT BOOK QUESTIONS
Exercise 2.1
🔵 Question 1
Which of the following expressions are polynomials in one variable and which are not? State reasons for your answer.
(i) 4x² − 3x + 7 (ii) y² + √2 (iii) 3√t + √2 (iv) y + 2/y (v) x¹⁰ + y³ + t⁵⁰
🟢 Answer
🔵 (i) ✔ Polynomial in one variable x (all powers non-negative integers).
🔵 (ii) ✔ Polynomial in one variable y (powers non-negative integers, constant √2 allowed).
🔵 (iii) ❌ Not a polynomial: exponent of t is ½ (square root).
🔵 (iv) ❌ Not a polynomial: term 2/y has negative exponent (y⁻¹).
🔵 (v) ❌ Not a polynomial in one variable: involves three different variables (x, y, t).
✔ Final: (i) and (ii) are polynomials in one variable; (iii), (iv), (v) are not.
🔵 Question 2
Write the coefficients of x² in each of the following:
(i) 2 + x² + x (ii) 2 − x² + x³ (iii) (π/2) x² + x (iv) √2 x − 1
🟢 Answer
🔵 (i) Coefficient of x² = 1
🔵 (ii) Coefficient of x² = −1
🔵 (iii) Coefficient of x² = π/2
🔵 (iv) Coefficient of x² = 0 (no x² term)
✔ Final: (i) 1, (ii) −1, (iii) π/2, (iv) 0
🔵 Question 3
Give one example each of a binomial of degree 35, and a monomial of degree 100.
🟢 Answer
🔵 Binomial of degree 35: x³⁵ + 7
🔵 Monomial of degree 100: 5x¹⁰⁰
✔ Final: Examples: x³⁵ + 7 (binomial), 5x¹⁰⁰ (monomial).
🔵 Question 4
Write the degree of each of the following polynomials:
(i) 5x³ + 4x² + 7x (ii) 4 − y² (iii) 5t − √7 (iv) 3
🟢 Answer
🔵 (i) Highest power = 3 ⇒ degree = 3
🔵 (ii) Highest power = 2 ⇒ degree = 2
🔵 (iii) Highest power = 1 ⇒ degree = 1
🔵 (iv) Constant ⇒ degree = 0
✔ Final: Degrees: 3, 2, 1, 0
🔵 Question 5
Classify the following as linear, quadratic, and cubic polynomials:
(i) x² + x (ii) x − x³ (iii) y + y² + 4 (iv) 1 + x (v) 3t (vi) r² (vii) 7x³
🟢 Answer
🔵 (i) x² + x ⇒ Quadratic (highest power 2).
🔵 (ii) x − x³ ⇒ Cubic (highest power 3).
🔵 (iii) y + y² + 4 ⇒ Quadratic (highest power 2).
🔵 (iv) 1 + x ⇒ Linear (highest power 1).
🔵 (v) 3t ⇒ Linear (highest power 1).
🔵 (vi) r² ⇒ Quadratic (highest power 2).
🔵 (vii) 7x³ ⇒ Cubic (highest power 3).
✔ Final: Linear: (iv), (v); Quadratic: (i), (iii), (vi); Cubic: (ii), (vii).
Exercise 2.2
🔵 Question 1
Find the value of the polynomial 5x − 4x² + 3 at:
(i) x = 0 (ii) x = −1 (iii) x = 2
🟢 Answer
🔵 (i) x = 0: 5(0) − 4(0)² + 3 = 0 − 0 + 3 = 3
🔵 (ii) x = −1: 5(−1) − 4(−1)² + 3 = −5 − 4 + 3 = −9 + 3 = −6
🔵 (iii) x = 2: 5(2) − 4(2)² + 3 = 10 − 16 + 3 = −6 + 3 = −3
✔ Final: Values: 3, −6, −3
🔵 Question 2
Find p(0), p(1), p(2) for each of the following:
🟢 (i) p(y) = y² − y + 1
🔵 p(0) = 0² − 0 + 1 = 1
🔵 p(1) = 1² − 1 + 1 = 1 − 1 + 1 = 1
🔵 p(2) = 4 − 2 + 1 = 3
🟢 (ii) p(t) = 2 + t + 2t² − t³
🔵 p(0) = 2 + 0 + 0 − 0 = 2
🔵 p(1) = 2 + 1 + 2 − 1 = 4
🔵 p(2) = 2 + 2 + 8 − 8 = 4
🟢 (iii) p(x) = x³
🔵 p(0) = 0
🔵 p(1) = 1
🔵 p(2) = 8
🟢 (iv) p(x) = (x − 1)(x + 1)
🔵 p(0) = (0 − 1)(0 + 1) = (−1)(1) = −1
🔵 p(1) = (1 − 1)(1 + 1) = (0)(2) = 0
🔵 p(2) = (2 − 1)(2 + 1) = (1)(3) = 3
🔵 Question 3
Verify whether the following are zeroes of the polynomial:
🟢 (i) p(x) = 3x + 1, x = −1/3
🔵 p(−1/3) = 3(−1/3) + 1 = −1 + 1 = 0 ✔ Zero.
🟢 (ii) p(x) = 5x − π, x = 4/5
🔵 p(4/5) = 5(4/5) − π = 4 − π ≠ 0 ❌ Not a zero.
🟢 (iii) p(x) = x² − 1, x = 1, −1
🔵 p(1) = 1² − 1 = 0 ✔
🔵 p(−1) = (−1)² − 1 = 1 − 1 = 0 ✔
🟢 (iv) p(x) = (x + 1)(x − 2), x = −1, 2
🔵 p(−1) = (−1 + 1)(−1 − 2) = (0)(−3) = 0 ✔
🔵 p(2) = (2 + 1)(2 − 2) = (3)(0) = 0 ✔
🟢 (v) p(x) = x², x = 0
🔵 p(0) = 0 ✔ Zero.
🟢 (vi) p(x) = lx + m, x = −m/l
🔵 Substitute: l(−m/l) + m = −m + m = 0 ✔ Zero.
🟢 (vii) p(x) = 3x² − 1, x = −1/√3, 2/√3
🔵 For −1/√3: 3(1/3) − 1 = 1 − 1 = 0 ✔ Zero.
🔵 For 2/√3: 3(4/3) − 1 = 4 − 1 = 3 ≠ 0 ❌ Not a zero.
🟢 (viii) p(x) = 2x + 1, x = 1/2
🔵 p(1/2) = 2(1/2) + 1 = 1 + 1 = 2 ≠ 0 ❌ Not a zero.
🔵 Question 4
Find the zero of the polynomial in each case:
🟢 (i) p(x) = x + 5 ⇒ Zero when x + 5 = 0 ⇒ x = −5
🟢 (ii) p(x) = x − 5 ⇒ Zero ⇒ x = 5
🟢 (iii) p(x) = 2x + 5 ⇒ Zero ⇒ x = −5/2
🟢 (iv) p(x) = 3x − 2 ⇒ Zero ⇒ x = 2/3
🟢 (v) p(x) = 3x ⇒ Zero ⇒ x = 0
🟢 (vi) p(x) = ax, a ≠ 0 ⇒ Zero ⇒ x = 0
🟢 (vii) p(x) = cx + d, c ≠ 0 ⇒ Zero ⇒ x = −d/c
✔ Final: All zeroes listed correctly.
Exercise 2.3
🔵 Question 1
Determine which of the following polynomials has (x + 1) as a factor:
(i) x³ + x² + x + 1
(ii) x⁴ + x³ + x² + x + 1
(iii) x⁴ + 3x³ + 3x² + x + 1
(iv) x³ − x² − (2 + √2)x + √2
🟢 Answer
✏️ Factor Theorem: If p(−1) = 0, then (x + 1) is a factor.
🔵 (i) p(−1) = (−1)³ + (−1)² + (−1) + 1 = −1 + 1 −1 +1 = 0 ✔ Factor.
🔵 (ii) p(−1) = (−1)⁴ + (−1)³ + (−1)² + (−1) +1 =1 −1 +1 −1 +1 =1 ✔ Factor.
🔵 (iii) p(−1) =1 −3 +3 −1 +1 =1 ✔ Factor.
🔵 (iv) p(−1) = (−1)³ − (−1)² − (2+√2)(−1) + √2 = −1 −1 + (2+√2)+√2 = −2 +2 +2√2 =2√2 ≠0 ❌ Not a factor.
✔ Final: (i), (ii), (iii) have (x + 1) as a factor; (iv) does not.
🔵 Question 2
Use the Factor Theorem to determine whether g(x) is a factor of p(x):
(i) p(x) = 2x³ + x² − 2x − 1, g(x) = x + 1
(ii) p(x) = x³ + 3x² + 3x +1, g(x) = x + 2
(iii) p(x) = x³ −4x² + x + 6, g(x) = x −3
🟢 Answer
🔵 (i) Test x = −1: 2(−1)³ + (−1)² −2(−1) −1 = −2 +1 +2 −1 =0 ✔ Factor.
🔵 (ii) Test x = −2: (−2)³ +3(−2)² +3(−2)+1 = −8 +12 −6 +1 = −1 ≠0 ❌ Not a factor.
🔵 (iii) Test x = 3: 27 −36 +3 +6 =0 ✔ Factor.
✔ Final: Factors in (i) and (iii) only.
🔵 Question 3
Find the value of k if x −1 is a factor of p(x) in each:
(i) p(x) = x² + x + k
(ii) p(x) = 2x² + kx + √2
(iii) p(x) = kx² − √2 x +1
(iv) p(x) = kx² −3x + k
🟢 Answer
🔵 (i) Substitute x=1: 1 +1 +k=0 ⇒ k= −2.
🔵 (ii) Substitute x=1: 2 +k +√2=0 ⇒ k= −(2 +√2).
🔵 (iii) Substitute x=1: k −√2 +1=0 ⇒ k= √2 −1.
🔵 (iv) Substitute x=1: k −3 +k=0 ⇒2k=3 ⇒ k=3/2.
✔ Final: k values: −2, −(2 +√2), √2 −1, 3/2.
🔵 Question 4
Factorise:
(i) 12x² −7x +1
(ii) 2x² +7x +3
(iii) 6x² +5x −6
(iv) 3x² −x −4
🟢 Answer
🔵 (i) 12x² −7x +1 = 12x² −4x −3x +1 = 4x(3x −1) −1(3x −1) = (4x −1)(3x −1).
🔵 (ii) 2x² +7x +3 =2x² +6x +x +3 =2x(x+3)+1(x+3)=(2x+1)(x+3).
🔵 (iii) 6x² +5x −6 =6x² −4x +9x −6=2x(3x −2)+3(3x −2)=(2x+3)(3x −2).
🔵 (iv) 3x² −x −4 =3x² −4x +3x −4 = x(3x −4)+1(3x −4)=(x+1)(3x −4).
✔ Final: Factorisations above.
🔵 Question 5
Factorise:
(i) x³ −2x² −x +2
(ii) x³ +13x² +32x +20
(iii) x³ −3x² −9x −5
(iv) 2y³ + y² −2y −1
🟢 Answer
🔵 (i) Try factors of 2: x=1 ⇒1 −2 −1 +2=0 ⇒ factor (x−1). Divide: x³ −2x² −x +2 ÷ (x−1) ⇒ x² −x −2 ⇒ (x−2)(x+1). ✔ Final: (x−1)(x−2)(x+1).
🔵 (ii) Try x=−1: −1 +13 −32 +20=0 ⇒ factor (x+1). Synthetic division ⇒ x² +12x +20 ⇒ roots of 20:10,2: 10×2=20 sum=12 ⇒ (x+10)(x+2). ✔ Final: (x+1)(x+10)(x+2).
🔵 (iii) Try x=−1: −1 −3 +9 −5=0 ⇒ factor (x+1). Divide ⇒ x² −4x −5 ⇒ roots: (x−5)(x+1). ✔ Final: (x+1)(x−5)(x+1) = (x+1)²(x−5).
🔵 (iv) Try y=−1: −2 +1 +2 −1=0 ⇒ factor (y+1). Divide ⇒2y² −y −1 ⇒ roots: product=−2 sum=−1 ⇒ (2y+1)(y−1). ✔ Final: (y+1)(2y+1)(y−1).
Exercise 2.4
🔵 Question 1
Use suitable identities to find the following products:
(i) (x + 4)(x + 10) (ii) (x + 8)(x − 10) (iii) (3x + 4)(3x − 5) (iv) (y² + 3/2)(y² − 3/2) (v) (3 − 2x)(3 + 2x)
🟢 Answer
🔸 (i)
➤ x·x + 10x + 4x + 40
➤ = x² + 14x + 40
✔ Final: x² + 14x + 40
🔸 (ii)
➤ x² − 10x + 8x − 80
➤ = x² − 2x − 80
✔ Final: x² − 2x − 80
🔸 (iii)
➤ 9x² − 15x + 12x − 20
➤ = 9x² − 3x − 20
✔ Final: 9x² − 3x − 20
🔸 (iv) (Identity a² − b²)
➤ (y²)² − (3/2)²
✔ Final: y⁴ − 9/4
🔸 (v) (Identity a² − b²)
➤ 3² − (2x)²
✔ Final: 9 − 4x²
🔵 Question 2
Evaluate without multiplying directly:
(i) 103 × 107 (ii) 95 × 96 (iii) 104 × 96
🟢 Answer
🔸 (i)
➤ = 105² − 2²
➤ = 11025 − 4
✔ Final: 11021
🔸 (ii)
➤ = 95 × (100 − 4)
➤ = 9500 − 380
✔ Final: 9120
🔸 (iii)
➤ = 100² − 4²
➤ = 10000 − 16
✔ Final: 9984
🔵 Question 3
Factorise using appropriate identities:
(i) 9x² + 6xy + y² (ii) 4y² − 4y + 1 (iii) x² − y²/100
🟢 Answer
🔸 (i) (a² + 2ab + b²)
➤ (3x)² + 2(3x)(y) + y²
✔ Final: (3x + y)²
🔸 (ii) (a² − 2ab + b²)
➤ (2y)² − 2(2y)(1) + 1²
✔ Final: (2y − 1)²
🔸 (iii) (a² − b²)
➤ x² − (y/10)²
✔ Final: (x − y/10)(x + y/10)
🔵 Question 4
Expand using suitable identities:
(i) (x + 2y + 4z)² (ii) (2x − y + z)² (iii) (−2x + 3y + 2z)²
(iv) (3a − 7b − c)² (v) (−2x + 5y − 3z)² (vi) [(¼ a − ½ b + 1)]²
🟢 Answer
🔸 (i)
➤ x² + (2y)² + (4z)² + 2x(2y) + 2x(4z) + 2(2y)(4z)
✔ Final: x² + 4y² + 16z² + 4xy + 8xz + 16yz
🔸 (ii)
➤ (2x)² + (−y)² + z² + 2(2x)(−y) + 2(2x)(z) + 2(−y)(z)
✔ Final: 4x² + y² + z² − 4xy + 4xz − 2yz
🔸 (iii)
➤ (−2x)² + (3y)² + (2z)² + 2(−2x)(3y) + 2(−2x)(2z) + 2(3y)(2z)
✔ Final: 4x² + 9y² + 4z² − 12xy − 8xz + 12yz
🔸 (iv)
➤ (3a)² + (−7b)² + (−c)² + 2(3a)(−7b) + 2(3a)(−c) + 2(−7b)(−c)
✔ Final: 9a² + 49b² + c² − 42ab − 6ac + 14bc
🔸 (v)
➤ (−2x)² + (5y)² + (−3z)² + 2(−2x)(5y) + 2(−2x)(−3z) + 2(5y)(−3z)
✔ Final: 4x² + 25y² + 9z² − 20xy + 12xz − 30yz
🔸 (vi)
➤ (a/4)² + (−b/2)² + 1² + 2(a/4)(−b/2) + 2(a/4)(1) + 2(−b/2)(1)
✔ Final: a²/16 + b²/4 + 1 − ab/4 + a/2 − b
🔵 Question 5
Factorise:
(i) 4x² + 9y² + 16z² + 12xy − 24yz − 16xz
(ii) 2x² + y² + 8z² − 2√2 xy + 4√2 yz − 8xz
🟢 Answer
🔸 (i)
➤ Recognise as a perfect square.
➤ (2x + 3y − 4z)² = 4x² + 9y² + 16z² + 12xy − 16xz − 24yz.
✔ Final: (2x + 3y − 4z)²
🔸 (ii)
➤ Recognise pattern: (√2 x − y − 2√2 z)².
✔ Final: (√2 x − y − 2√2 z)²
🔵 Question 6
Write the following cubes in expanded form:
(i) (2x + 1)³ (ii) (2a − 3b)³ (iii) ((3/2)x + 1)³ (iv) (x − (2/3)y)³
🟢 Answer
🔸 (i)
➤ (u + v)³ = u³ + 3u²v + 3uv² + v³.
➤ u=2x,v=1 ⇒ 8x³ + 12x² + 6x + 1
🔸 (ii)
➤ u=2a,v=−3b ⇒ 8a³ − 36a²b + 54ab² − 27b³
🔸 (iii)
➤ u=3x/2,v=1 ⇒ 27x³/8 + 27x²/4 + 9x/2 + 1
🔸 (iv)
➤ u=x,v=−2y/3 ⇒ x³ − 2x²y + (4/3)xy² − 8y³/27
🔵 Question 7
Evaluate using suitable identities:
(i) 99³ (ii) 102³ (iii) 998³
🟢 Answer
🔸 (i)
➤ 99=100−1 ⇒ (100−1)³
➤ =100³−3·100²·1+3·100·1²−1
✔ Final: 970299
🔸 (ii)
➤ 102=100+2 ⇒ (100+2)³
➤ =100³+3·100²·2+3·100·4+8
✔ Final: 1061208
🔸 (iii)
➤ 998=1000−2 ⇒ (1000−2)³
➤ =1000³−3·1000²·2+3·1000·4−8
✔ Final: 994011992
🔵 Question 8
Factorise each of the following:
(i) 8a³ + b³ + 12a²b + 6ab²
(ii) 8a³ − b³ − 12a²b + 6ab²
(iii) 27 − 125a³ − 135a + 225a²
(iv) 64a³ − 27b³ − 144a²b + 108ab²
🟢 Answer
🔸 (i) (2a + b)³
🔸 (ii) (2a − b)³
🔸 (iii) Rewrite as (3 − 5a)³ ⇒ (3 − 5a)³
🔸 (iv) Recognise cube of (4a − 3b) ⇒ (4a − 3b)³
🔵 Question 9
Simplify: (2x + 3)³ − (2x − 3)³
🟢 Answer
✏️ Concept: a³ − b³ = (a − b)(a² + ab + b²)
🔸 Step 1: Let a = (2x + 3), b = (2x − 3).
🔸 Step 2: a − b = (2x + 3) − (2x − 3) = 6.
🔸 Step 3: a² + ab + b² = (2x + 3)² + (2x + 3)(2x − 3) + (2x − 3)².
🔸 Step 4: Expand:
(2x + 3)² = 4x² + 12x + 9
(2x + 3)(2x − 3) = 4x² − 9
(2x − 3)² = 4x² − 12x + 9
Sum = (4x² +12x +9) + (4x² −9) + (4x² −12x +9) = 12x² + 9.
🔸 Step 5: Multiply: 6(12x² + 9) = 72x² + 54.
✔ Final: 72x² + 54
🔵 Question 10
Factorise: x³ + 8 + 12x + 6x²
🟢 Answer
🔸 Step 1: Rewrite: x³ + 6x² + 12x + 8.
🔸 Step 2: Recognise as (x + 2)³ = x³ + 6x² +12x +8.
✔ Final: (x + 2)³
🔵 Question 11
Evaluate: (999)³ + (1)³ + (−1000)³
🟢 Answer
🔸 Step 1: Group: (999)³ + (−1000)³ + 1³.
🔸 Step 2: Use identity: a³ + b³ + c³ −3abc = (a+b+c)(a² + b² + c² −ab −bc −ca).
🔸 Step 3: a=999, b=−1000, c=1 ⇒ a+b+c=0 ⇒ sum=3abc.
🔸 Step 4: abc = 999(−1000)(1)=−999000.
3abc=−2997000.
✔ Final: −2997000
🔵 Question 12
Expand: (2x − 5y + 3z)³
🟢 Answer
✏️ Identity: (a + b + c)³
🔸 Step 1: (2x)³ + (−5y)³ + (3z)³ + 3[(2x)²(−5y) + (2x)²(3z) + (−5y)²(2x) + (−5y)²(3z) + (3z)²(2x) + (3z)²(−5y)] + 6(2x)(−5y)(3z).
🔸 Step 2: Expand cubes: 8x³ −125y³ +27z³.
🔸 Step 3: Squares: (2x)²=4x²; (−5y)²=25y²; (3z)²=9z².
Compute terms carefully:
3(4x²)(−5y)=−60x²y,
3(4x²)(3z)=36x²z,
3(25y²)(2x)=150xy²,
3(25y²)(3z)=225y²z,
3(9z²)(2x)=54xz²,
3(9z²)(−5y)=−135yz².
Triple product:6(2x)(−5y)(3z)=−180xyz.
✔ Final: 8x³ −125y³ +27z³ −60x²y +36x²z +150xy² +225y²z +54xz² −135yz² −180xyz
🔵 Question 13
Factorise: x³ + 3x² + 3x + 1
🟢 Answer
🔸 Step 1: Recognise (x + 1)³ = x³ +3x² +3x +1.
✔ Final: (x + 1)³
🔵 Question 14
Simplify: (x + 2)³ − (x − 2)³
🟢 Answer
🔸 Step 1: Use a³ − b³ = (a − b)(a² + ab + b²).
a − b = (x+2) − (x−2)=4.
a² + ab + b² = (x+2)² + (x+2)(x−2) + (x−2)².
(x+2)² = x²+4x+4, (x+2)(x−2)=x²−4, (x−2)²=x²−4x+4.
Sum= x²+4x+4 + x²−4 + x²−4x+4 = 3x²+4.
Multiply: 4(3x²+4)=12x²+16.
✔ Final: 12x² +16
🔵 Question 15
Factorise: 27x³ − 8y³
🟢 Answer
✏️ Difference of cubes: a³ − b³ = (a − b)(a² + ab + b²).
a=3x,b=2y.
➤ (3x −2y)(9x² +6xy +4y²).
✔ Final: (3x − 2y)(9x² + 6xy + 4y²)
🔵 Question 16
Factorise completely: x³ + 64
🟢 Answer
✏️ Sum of cubes: x³ +4³.
➤ (x +4)(x² −4x +16).
✔ Final: (x + 4)(x² − 4x +16)
————————————————————————————————————————————————————————————————————————————–
OTHER IMPORTANT QUESTIONS FOR EXAMS
🔵 Question 1 (Section A)
What is the degree of the polynomial p(x) = 7x³ − 4x² + 5?
🟢 Answer:
✳️ The highest power of x is 3.
✔️ Degree = 3
🔵 Question 2 (Section A)
Identify the type of polynomial: q(y) = 5y + 7.
🟢 Answer:
✳️ Number of terms = 2.
✔️ Two-term polynomial = Binomial
🔵 Question 3 (Section A)
Find p(2) if p(x) = x² − 3x + 2.
🟢 Answer:
➤ Substitute x = 2: p(2) = 2² − 3×2 + 2
➤ Simplify: 4 − 6 + 2 = 0
✔️ p(2) = 0
🔵 Question 4 (Section A)
State the value of k if x − 1 is a factor of x² + kx − 1.
🟢 Answer:
➤ By Factor Theorem: Substitute x=1.
➤ 1² + k(1) − 1 = 0 ⇒ 1 + k − 1 = 0
➤ k = 0
✔️ k = 0
🔵 Question 5 (Section A)
Write a monomial of degree 5.
🟢 Answer:
✳️ Example: 7x⁵
🔵 Question 6 (Section A)
If x = −2 is a zero of p(x) = x + 2, verify it.
🟢 Answer:
➤ p(−2) = −2 + 2 = 0
✔️ Hence, x = −2 is a zero.
🔴 Section B — Short Answer-I (2 marks each)
🔵 Question 7
Evaluate p(−1) for p(x) = x³ − 2x² + x − 5.
🟢 Answer:
➤ Substitute x = −1: (−1)³ − 2(−1)² + (−1) − 5
➤ = −1 − 2(1) − 1 − 5
➤ = −1 − 2 − 1 − 5
➤ = −9
✔️ p(−1) = −9
🔵 Question 8
If (x − 3) is a factor of x² + 2x − 15, find the other factor.
🟢 Answer:
➤ Use factorization: x² + 2x − 15
➤ Try factor pairs of −15 summing to 2 ⇒ 5 and −3.
➤ x² + 5x − 3x − 15
➤ = x(x + 5) − 3(x + 5)
➤ = (x − 3)(x + 5)
✔️ Other factor = (x + 5)
🔵 Question 9
Divide 2x³ + 3x² − 2x − 3 by x + 1.
🟢 Answer:
➤ Use synthetic division (x = −1): Coefficients 2, 3, −2, −3
➤ Bring down 2. Multiply −1×2 = −2; add to 3 → 1.
➤ Multiply −1×1 = −1; add to −2 → −3.
➤ Multiply −1×(−3) = 3; add to −3 → 0.
✔️ Quotient = 2x² + x − 3; Remainder = 0
🔵 Question 10
Find the zeros of p(x) = x² − 5x + 6.
🟢 Answer:
➤ Factorize: x² − 5x + 6 = x² − 2x − 3x + 6
➤ = x(x − 2) − 3(x − 2)
➤ = (x − 2)(x − 3)
✔️ Zeros: x = 2, x = 3
🔵 Question 11
Find a quadratic polynomial whose zeros are 3 and −2.
🟢 Answer:
➤ Sum of zeros = 3 + (−2) = 1.
➤ Product of zeros = 3×(−2) = −6.
➤ Form: x² − (sum)x + (product) = x² − 1x − 6.
✔️ Required polynomial = x² − x − 6
🔵 Question 12
The polynomial x³ + ax² + bx + c has (−2) as a zero. Perform division by x + 2 to express quotient and remainder in terms of a, b, c.
🟢 Answer:
➤ Using synthetic division (x = −2):
Coefficients: 1, a, b, c.
➤ Bring down 1. Multiply −2×1 = −2; add to a → (a − 2).
➤ Multiply −2×(a − 2) = (−2a + 4); add to b → (b − 2a + 4).
➤ Multiply −2×(b − 2a + 4) = (−2b + 4a − 8); add to c → (c − 2b + 4a − 8).
✔️ Quotient = x² + (a − 2)x + (b − 2a + 4)
✔️ Remainder = (c − 2b + 4a − 8)
🔵 Question 13 (Section C)
Using the Remainder Theorem, find the remainder when p(x) = 3x³ − 5x² + 2x − 7 is divided by (x − 2).
🟢 Answer:
✳️ ➤ Formula: Remainder on division by (x − a) = p(a).
✳️ ➤ Substitution: a = 2 ⇒ p(2) = 3(2)³ − 5(2)² + 2(2) − 7
✳️ ➤ Simplification: p(2) = 3(8) − 5(4) + 4 − 7 = 24 − 20 + 4 − 7 = 1
✔️ Final answer: Remainder = 1
🔵 Question 14 (Section C)
If x = 1 is a zero of p(x) = x³ + kx² − 4x − 4, find k.
🟢 Answer:
✳️ ➤ Factor Theorem: If x = 1 is a zero, then p(1) = 0.
✳️ ➤ Substitution: p(1) = 1³ + k·1² − 4·1 − 4 = 0
✳️ ➤ Simplification: 1 + k − 4 − 4 = 0 ⇒ k − 7 = 0
✔️ Final answer: k = 7
OR
🔵 Alternative Question 14
If (x − 2) is a factor of f(x) = 2x³ + ax² + bx + 4 and the remainder on division by (x + 1) is −3, find a and b.
🟢 Answer (Alternative):
✳️ ➤ From (x − 2) factor: f(2) = 0 ⇒ 2(8) + a(4) + b(2) + 4 = 0
✳️ ➤ Simplification: 16 + 4a + 2b + 4 = 0 ⇒ 4a + 2b + 20 = 0 … (1)
✳️ ➤ From remainder at x = −1: f(−1) = −3 ⇒ 2(−1)³ + a(1) + b(−1) + 4 = −3
✳️ ➤ Simplification: −2 + a − b + 4 = −3 ⇒ a − b + 2 = −3 ⇒ a − b = −5 … (2)
✳️ ➤ Solve (1) & (2): From (2), a = b − 5. Substitute in (1): 4(b − 5) + 2b + 20 = 0
✳️ ➤ 4b − 20 + 2b + 20 = 0 ⇒ 6b = 0 ⇒ b = 0 ⇒ a = −5
✔️ Final answer (Alt): a = −5, b = 0
🔵 Question 15 (Section C)
Find the factorization of x³ − 3x² − 4x + 12.
🟢 Answer:
✳️ ➤ Trial zero (by factor pairs of 12): Test x = 2 ⇒ 8 − 12 − 8 + 12 = 0 ✔
✳️ ➤ Divide by (x − 2): Synthetic with 2 on coefficients 1, −3, −4, 12 → quotient x² − x − 6
✳️ ➤ Factor the quotient: x² − x − 6 = (x − 3)(x + 2)
✔️ Final answer: x³ − 3x² − 4x + 12 = (x − 2)(x − 3)(x + 2)
🔵 Question 16 (Section C)
Given that 2 and −3 are zeros of the quadratic polynomial p(x), and p(0) = −12, find p(x).
🟢 Answer:
✳️ ➤ If zeros are 2 and −3: p(x) = k(x − 2)(x + 3)
✳️ ➤ Use p(0) = −12: −12 = k(−2)(3) = −6k
✳️ ➤ k = 2
✔️ Final answer: p(x) = 2(x − 2)(x + 3) = 2x² + 2x − 12
OR
🔵 Alternative Question 16
Construct a monic quadratic polynomial whose zeros are α and β with α + β = −5 and αβ = 6.
🟢 Answer (Alternative):
✳️ ➤ Monic quadratic: x² − (sum)x + (product)
✳️ ➤ Substitution: x² − (−5)x + 6 = x² + 5x + 6
✔️ Final answer (Alt): x² + 5x + 6
🔵 Question 17 (Section C)
If p(x) = 4x³ + 7x² − 5x + 6, find the remainder when divided by (x + 2) and by (x − 1). Hence, find the remainder when divided by (x + 2)(x − 1).
🟢 Answer:
✳️ ➤ R₁ = p(−2): 4(−8) + 7(4) − 5(−2) + 6 = −32 + 28 + 10 + 6 = 12
✳️ ➤ R₂ = p(1): 4(1) + 7(1) − 5(1) + 6 = 4 + 7 − 5 + 6 = 12
✳️ ➤ If divisor is (x + 2)(x − 1), remainder is linear: Ax + B.
✳️ ➤ Use A(−2) + B = 12 and A(1) + B = 12 ⇒ Solve:
From second: B = 12 − A. Substitute in first: −2A + (12 − A) = 12 ⇒ −3A = 0 ⇒ A = 0 ⇒ B = 12
✔️ Final answer: Remainder by (x + 2)(x − 1) is 12
🔵 Question 18 (Section C)
Find all zeros of f(x) = x³ − 6x² + 11x − 6.
🟢 Answer:
✳️ ➤ Trial zeros among factors of 6: Test x = 1 ⇒ 1 − 6 + 11 − 6 = 0 ✔
✳️ ➤ Divide by (x − 1): quotient x² − 5x + 6
✳️ ➤ Factor: x² − 5x + 6 = (x − 2)(x − 3)
✔️ Final answer: Zeros are x = 1, 2, 3
OR
🔵 Alternative Question 18
If one zero of g(x) = x² − (m + 3)x + (3m − 10) is 5, find m and the other zero.
🟢 Answer (Alternative):
✳️ ➤ Substitute x = 5: 25 − (m + 3)·5 + (3m − 10) = 0
✳️ ➤ 25 − 5m − 15 + 3m − 10 = 0 ⇒ (25 − 15 − 10) + (−5m + 3m) = 0 ⇒ 0 − 2m = 0
✳️ ➤ m = 0 ⇒ polynomial x² − 3x − 10 = 0
✳️ ➤ Other zero by factorization: (x − 5)(x + 2) ⇒ other zero = −2
✔️ Final answer (Alt): m = 0; other zero = −2
🔵 Question 19 (Section C)
Use the Division Algorithm to divide 3x³ − x² − 14x + 8 by x − 2. Write dividend = divisor×quotient + remainder.
🟢 Answer:
✳️ ➤ Synthetic with 2 on coefficients 3, −1, −14, 8 → bring down 3; 2·3=6; add → 5; 2·5=10; add → −4; 2·(−4)=−8; add → 0
✳️ ➤ Quotient = 3x² + 5x − 4; Remainder = 0
✔️ Final statement: 3x³ − x² − 14x + 8 = (x − 2)(3x² + 5x − 4) + 0
OR
🔵 Alternative Question 19
Factor completely: 2x³ + x² − 18x − 9.
🟢 Answer (Alternative):
✳️ ➤ Grouping: (2x³ + x²) + (−18x − 9) = x²(2x + 1) − 9(2x + 1)
✳️ ➤ Factor common: (2x + 1)(x² − 9) = (2x + 1)(x − 3)(x + 3)
✔️ Final answer (Alt): (2x + 1)(x − 3)(x + 3)
🔵 Question 20 (Section C)
For the quadratic h(x) = 5x² − 13x + 6, verify the relationship between zeros and coefficients.
🟢 Answer:
✳️ ➤ Factorize: 5x² − 13x + 6 = (5x − 3)(x − 2)
✳️ ➤ Zeros: α = 3/5, β = 2
✳️ ➤ Relationships: α + β = 3/5 + 2 = 13/5 = (−b)/a = 13/5 ✔
✳️ ➤ αβ = (3/5)·2 = 6/5 = c/a = 6/5 ✔
✔️ Final answer: Verified: α + β = (−b)/a and αβ = c/a
🔵 Question 21 (Section C)
Find a quadratic polynomial p(x) with integer coefficients such that one zero is 2 and the sum of zeros is −1.
🟢 Answer:
✳️ ➤ Let zeros be 2 and s with 2 + s = −1 ⇒ s = −3
✳️ ➤ Monic form: (x − 2)(x + 3) = x² + x − 6
✳️ ➤ Integer coefficients already satisfied.
✔️ Final answer: p(x) = x² + x − 6
OR
🔵 Alternative Question 21
If α and β are zeros of x² − 7x + 12, find a quadratic whose zeros are (α + 1) and (β + 1).
🟢 Answer (Alternative):
✳️ ➤ Given: α + β = 7, αβ = 12
✳️ ➤ New sum: (α + 1) + (β + 1) = (α + β) + 2 = 9
✳️ ➤ New product: (α + 1)(β + 1) = αβ + (α + β) + 1 = 12 + 7 + 1 = 20
✳️ ➤ Monic polynomial: x² − (new sum)x + (new product) = x² − 9x + 20
✔️ Final answer (Alt): x² − 9x + 20
🔵 Question 22 (Section C)
Find the value(s) of k such that the polynomial 2x² + kx + 18 has equal zeros.
🟢 Answer:
✳️ ➤ Condition for equal zeros (discriminant zero): Δ = b² − 4ac = 0
✳️ ➤ Substitution: a = 2, b = k, c = 18 ⇒ Δ = k² − 4(2)(18) = k² − 144
✳️ ➤ Solve: k² − 144 = 0 ⇒ k = ±12
✔️ Final answer: k = 12 or k = −12
OR
🔵 Alternative Question 22
If one zero of x² + (k − 3)x + (k − 2) is 1, find k and the other zero.
🟢 Answer (Alternative):
✳️ ➤ Substitute x = 1: 1 + (k − 3) + (k − 2) = 0
✳️ ➤ Simplify: 1 + k − 3 + k − 2 = 0 ⇒ 2k − 4 = 0 ⇒ k = 2
✳️ ➤ Polynomial becomes x² − x = x(x − 1)
✳️ ➤ Other zero = 0
✔️ Final answer (Alt): k = 2; other zero = 0
Question 23 (Section D)
Find the zeros of the cubic polynomial p(x) = 2x³ − 5x² − x + 6. Verify the relationships between zeros and coefficients.
🟢 Answer:
✳️ ➤ Trial zero by Factor Theorem: test x = −1 ⇒ 2(−1)³ − 5(−1)² − (−1) + 6 = −2 − 5 + 1 + 6 = 0 ✔
✳️ ➤ Divide by (x + 1): synthetic division with −1 on 2, −5, −1, 6 → quotient 2x² − 7x + 6.
✳️ ➤ Factor the quotient: 2x² − 7x + 6 = (2x − 3)(x − 2).
✳️ ➤ Zeros: x = −1, x = 3/2, x = 2.
✳️ ➤ Verification (for ax³ + bx² + cx + d with a = 2, b = −5, c = −1, d = 6):
➡️ Sum of zeros = (−b)/a = −(−5)/2 = 5/2.
➡️ Computed sum = (−1) + (3/2) + 2 = 5/2 ✔
➡️ Sum of pairwise products = c/a = (−1)/2 = −1/2.
➡️ Computed: (−1)(3/2) + (−1)(2) + (3/2)(2) = −3/2 − 2 + 3 = −1/2 ✔
➡️ Product of zeros = (−d)/a = −6/2 = −3.
➡️ Computed product = (−1)·(3/2)·2 = −3 ✔
✔️ Final answer: Zeros are −1, 3/2, 2; relationships verified.
🔵 Question 24 (Section D)
A cubic polynomial p(x) leaves remainders −6 and 2 when divided by (x − 2) and (x + 1), respectively. If (x − 3) is a factor of p(x), find one such p(x).
🟢 Answer:
✳️ Given:
➡️ p(2) = −6
➡️ p(−1) = 2
➡️ p(3) = 0 (since x − 3 is a factor)
✳️ Assume p(x) = (x − 3)(x² + u x + v)
➤ Step 1: Use p(2) = −6
p(2) = (2 − 3)(4 + 2u + v) = −1(4 + 2u + v) = −6
⇒ 4 + 2u + v = 6
⇒ 2u + v = 2 … (1)
➤ Step 2: Use p(−1) = 2
p(−1) = (−1 − 3)(1 − u + v) = −4(1 − u + v) = 2
⇒ 1 − u + v = −1/2
⇒ −u + v = −3/2
⇒ v = u − 3/2 … (2)
➤ Step 3: Substitute (2) into (1)
2u + (u − 3/2) = 2
3u − 3/2 = 2
3u = 2 + 3/2 = 7/2
u = 7/6
➤ Step 4: Find v
v = u − 3/2 = 7/6 − 9/6 = −2/6 = −1/3
➤ Step 5: Write p(x)
p(x) = (x − 3)(x² + (7/6) x − 1/3)
➤ Step 6 (Optional Expansion):
p(x) = x³ − 1.8333 x² − 3.8333 x + 1
✔️ Final Answer: p(x) = (x − 3)(x² + (7/6) x − 1/3)
🔵 Question 25 (Section D)
Show that x + 2 is a factor of x³ + 2x² − x − 2. Then factorise completely.
🟢 Answer:
✳️ ➤ Factor test at x = −2: (−2)³ + 2(−2)² − (−2) − 2 = −8 + 8 + 2 − 2 = 0 ⇒ (x + 2) is a factor.
✳️ ➤ Divide by (x + 2): quotient = x² − 1 (long/synthetic division).
✳️ ➤ Factor further: x² − 1 = (x − 1)(x + 1).
✔️ Final answer: x³ + 2x² − x − 2 = (x + 2)(x − 1)(x + 1)
OR
🔵 Alternative Question 25
Prove that x − 1 is a factor of x³ − 1 and factorise completely.
🟢 Answer (Alternative):
✳️ ➤ x³ − 1 = (x − 1)(x² + x + 1) (standard identity).
✔️ Final answer (Alt): x³ − 1 = (x − 1)(x² + x + 1)
🔵 Question 26 (Section D)
If the polynomial 2x³ + ax² + bx − 2 is divisible by both (x − 1) and (x + 1), find a and b.
🟢 Answer:
✳️ ➤ p(1) = 2 + a + b − 2 = 0 ⇒ a + b = 0.
✳️ ➤ p(−1) = −2 + a − b − 2 = 0 ⇒ a − b = 4.
✳️ ➤ Solve: from a + b = 0 ⇒ b = −a. Substitute in a − (−a) = 4 ⇒ 2a = 4 ⇒ a = 2, b = −2.
✔️ Final answer: a = 2, b = −2
OR
🔵 Alternative Question 26
Find a cubic polynomial whose zeros are −1, 0, and 2. Also find its value at x = 3.
🟢 Answer (Alternative):
✳️ ➤ p(x) = (x + 1)·x·(x − 2) = x³ − x² − 2x.
✳️ ➤ p(3) = 27 − 9 − 6 = 12.
✔️ Final answer (Alt): p(x) = x³ − x² − 2x; p(3) = 12
🔵 Question 27 (Section D)
Use the Factor Theorem to find k if (x − 1) is a factor of p(x) = kx³ + 3x² − kx − 3.
🟢 Answer:
✳️ ➤ Substitute x = 1: p(1) = k(1)³ + 3(1)² − k(1) − 3 = k + 3 − k − 3 = 0.
✳️ ➤ Identity 0 = 0 holds for every real k.
✔️ Final answer: Any real k (infinitely many solutions).
🔵 Question 28 (Section D)
If the zeros of 2x² + 5x + k are equal, find k. Also express the polynomial as a perfect square.
🟢 Answer:
✳️ ➤ Equal zeros condition: Δ = b² − 4ac = 0.
✳️ ➤ Substitution: a = 2, b = 5, c = k ⇒ 25 − 8k = 0 ⇒ k = 25/8.
✳️ ➤ Complete the square: 2x² + 5x + 25/8
➡️ 2x2+(5/2)x+25/16
x² + (5/2)x + 25/16x2+(5/2)x+25/16 = 2(x + 5/4)².
✔️ Final answer: k = 25/8; polynomial = 2(x + 5/4)²
OR
🔵 Alternative Question 28
Find m such that x² + (m − 4)x + (m − 5) has equal zeros. Write it as a perfect square.
🟢 Answer (Alternative):
✳️ ➤ Δ = (m − 4)² − 4(m − 5) = m² − 8m + 16 − 4m + 20 = m² − 12m + 36 = 0.
✳️ ➤ (m − 6)² = 0 ⇒ m = 6.
✳️ ➤ Polynomial: x² + 2x + 1 = (x + 1)².
✔️ Final answer (Alt): m = 6; polynomial = (x + 1)²
🔵 Question 29 (Section D)
Divide 4x³ − 12x² + 13x − 3 by 2x − 3 and verify the Division Algorithm.
🟢 Answer:
✳️ ➤ Synthetic division with 3/2 on coefficients 4, −12, 13, −3:
➡️ Bring down 4.
➡️ (3/2)·4 = 6; add to −12 → −6.
➡️ (3/2)·(−6) = −9; add to 13 → 4.
➡️ (3/2)·4 = 6; add to −3 → 3 (remainder).
✳️ ➤ Quotient = 2x² − 3x + 2; Remainder = 3.
✳️ ➤ Verification: (2x − 3)(2x² − 3x + 2) + 3
= 4x³ − 6x² − 6x² + 9x + 4x − 6 + 3
= 4x³ − 12x² + 13x − 3 ✔
✔️ Final answer: Quotient = 2x² − 3x + 2; Remainder = 3 (Division Algorithm verified).
🔵 Question 30 (Section D)
Construct a cubic polynomial whose sum of zeros is 2, sum of products of zeros taken two at a time is −3, and product of zeros is −4.
🟢 Answer:
✳️ ➤ For zeros α, β, γ:
➡️ α + β + γ = 2,
➡️ αβ + βγ + γα = −3,
➡️ αβγ = −4.
✳️ ➤ Standard form: x³ − (sum)x² + (sum of pairs)x − (product).
✳️ ➤ Substitute: x³ − 2x² − 3x + 4.
✔️ Final answer: x³ − 2x² − 3x + 4
————————————————————————————————————————————————————————————————————————————
MIND MAP

————————————————————————————————————————————————————————————————————————————-
