Class : 9 – Math (English) : Lesson 10. Heron’s Formula
EXPLANATION & SUMMARY
✨ Explanation
🔵 1) Introduction
🟢 Heron’s Formula provides a method to calculate the area of a triangle when all three sides are known. Unlike standard base–height formula, it avoids computing altitudes.
🔴 Historical Note: Named after Hero of Alexandria (Heron), a Greek mathematician.
🌿 Real-Life Uses: Surveying land plots, architecture, computer graphics, and navigation where direct measurement of height is impractical.
🔵 2) Standard Area Formula Reminder
🟢 The familiar area formula:
➡️ Area = ½ × base × height.
🔴 But in many cases, the height is not readily available—Heron’s Formula solves this.
🔵 3) Derivation Overview (Intuitive)
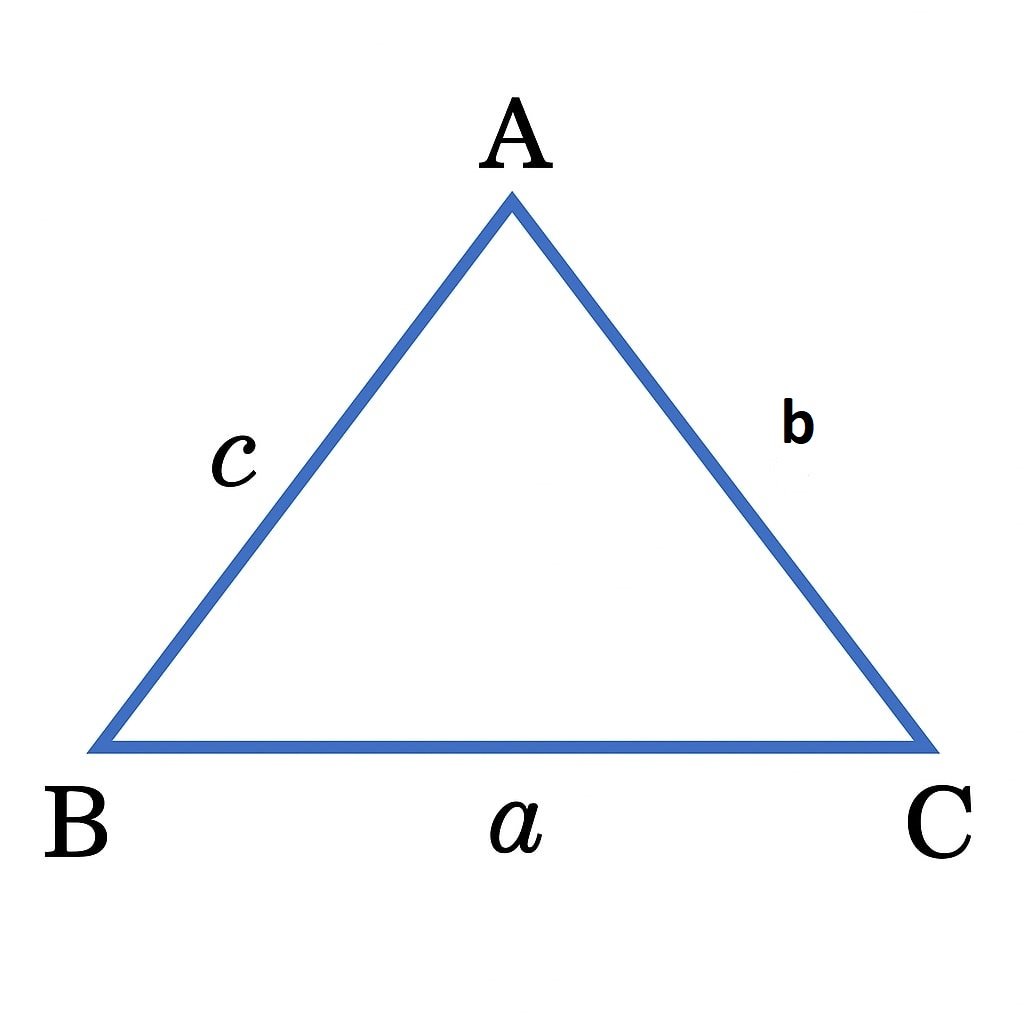
🟢 Let a, b, c be sides. Semiperimeter: s = (a + b + c)/2.
🟢 Using geometry and algebra (proof involves constructing altitudes, applying Pythagoras, simplifying), the result emerges:
➡️ Area (Δ) = √[s(s − a)(s − b)(s − c)].
✏️ Note: Ensure a + b > c etc. so the triangle exists.
💡 Concept: Semiperimeter halves perimeter to simplify expressions.
🔵 4) Step-by-Step Usage
1️⃣ Compute s.
2️⃣ Subtract each side from s.
3️⃣ Multiply s, (s−a), (s−b), (s−c).
4️⃣ Take the square root.
✔️ Final Area in square units.
🔵 5) Example Calculation
🟢 Triangle sides: a = 7 cm, b = 8 cm, c = 9 cm.
➡️ s = (7 + 8 + 9)/2 = 12 cm.
➡️ s−a = 5, s−b = 4, s−c = 3.
➡️ Product = 12×5×4×3 = 720.
➡️ Area = √720 = √(144×5) = 12√5 cm² ≈ 26.83 cm².
🔵 6) Special Cases
🟢 Equilateral Triangle: All sides = a.
➡️ s = 3a/2.
➡️ Area = √[(3a/2)(3a/2−a)³] = √[(3a/2)(a/2)³] = √(3a⁴/16) = (√3/4)a².
🟢 Isosceles Triangle: Use same procedure; two sides equal simplifies differences.
🔵 7) Extended Applications
🔴 Quadrilateral Area: If a quadrilateral can be split into two triangles with known sides, apply Heron’s Formula to each.
🟡 Trapezium Decomposition: Divide into triangles or rectangle + triangles.
🟢 Surveying: Plot boundaries measured as straight segments.
🌿 Engineering: Finite element meshes often require triangle areas from side data.
🔵 8) Proof Sketch (Advanced Intuition)
🟢 Start with sides a,b,c and semiperimeter s.
➡️ Draw an incircle tangent lengths, use relations between sides and tangent segments.
➡️ Express area = r × s (r is inradius), then derive r via a,b,c, leading back to √[s(s−a)(s−b)(s−c)].
🔵 9) Important Points and Constraints
🔴 Triangle inequality: a + b > c, b + c > a, a + c > b.
🟡 Units: Keep side lengths in same units → area in square units.
🟢 Accuracy: Use enough decimals or keep √ form for exactness.
✏️ Note: Don’t approximate early—retain radical form until final step.
🔵 10) Sample Word Problems
🧠 Problem 1: Land survey triangle sides 13 m, 14 m, 15 m. Find area.
➡️ s = 21 m.
➡️ s−a=8, s−b=7, s−c=6.
➡️ Area = √(21×8×7×6) = √7056 = 84 m².
🧠 Problem 2: Find area of isosceles triangle sides 5 cm,5 cm,6 cm.
➡️ s = 8 cm.
➡️ Differences: 3,3,2.
➡️ Product=8×3×3×2=144.
➡️ Area=√144=12 cm².
🔵 11) Common Mistakes
🔴 Forgetting to halve perimeter.
🔴 Mixing units (e.g., cm with m).
🟡 Rounding too early.
🟢 Omitting triangle inequality check.
🔵 12) Real-Life Connections
🌿 Civil engineers compute land areas from boundary measurements.
🏗 Architects calculate irregular plots.
📐 Graphics engines calculate polygon areas for rendering.
🔵 13) Visual Memory Aids
🧠 Create a triangle diagram labelled a,b,c.
✏️ Semiperimeter s halfway around.
💡 Formula in centre: Δ = √[s(s−a)(s−b)(s−c)].
📚 Summary (~300 words)
🔵 Key Definitions
• Heron’s Formula: Area(Δ) = √[s(s−a)(s−b)(s−c)], s=(a+b+c)/2.
• Semiperimeter halves perimeter for convenience.
• Works without knowing altitude.
🟢 Procedure
Calculate s.
Compute differences (s−a), (s−b), (s−c).
Multiply and take √.
Keep units consistent.
🟡 Special Cases
• Equilateral: (√3/4)a².
• Isosceles: same process with two equal sides.
🔴 Applications
• Land surveying and architecture.
• Dividing quadrilaterals into triangles.
• Computer graphics meshes.
🌿 Tips
• Check triangle inequality before use.
• Prefer exact radicals over decimals.
• For large numbers, use calculator carefully.
📝 Quick Recap
🔵 Semiperimeter: s = (a + b + c)/2.
🟢 Heron’s Formula: Δ = √[s(s−a)(s−b)(s−c)].
🟡 Equilateral Shortcut: (√3/4)a².
🔴 Triangle inequality must hold.
✔ Useful for surveying, construction, graphics.
———————————————————————————————————————————————————————————————————————————–
TEXT BOOK QUESTIONS
Exercise 10.1
🔵 Question 1
A traffic signal board, indicating “SCHOOL AHEAD”, is an equilateral triangle with side a. Find the area of the signal board using Heron’s formula. If its perimeter is 180 cm, what will be the area of the signal board?
🧠 Answer
➤ Step 1: Perimeter = 180 cm ⇒ side a = 180 ÷ 3 = 60 cm.
➤ Step 2: s = (3a)/2 = (3×60)/2 = 90 cm.
➤ Step 3: s − a = 90 − 60 = 30 cm.
➤ Step 4: Area = √[s(s − a)(s − a)(s − a)]
= √[90×30×30×30]
= √(90×27 000) = √2 430 000 = √(243×10 000)
= 100 √243 = 100×15.588 = 1 558.8 cm².
✔ Final: Area ≈ 1 559 cm².
🔵 Question 2
The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122 m, 22 m and 120 m. The advertisements yield ₹ 5 000 per m² per year. A company hired one wall for 3 months. How much rent did it pay?
🧠 Answer
➤ s = (122 + 22 + 120)/2 = 132 m.
➤ s−a = 132−122 = 10 m; s−b = 110 m; s−c = 12 m.
➤ Area = √[132×10×110×12]
= √(174 2400) = √1 742 400 ≈ 1 320 m².
➤ Yearly rent = 1 320 × ₹ 5 000 = ₹ 6 600 000.
➤ For 3 months = ¼ year ⇒ rent = ₹ 6 600 000 ÷ 4 = ₹ 1 650 000.
✔ Final: ₹ 16.5 lakh.
🔵 Question 3
There is a slide in a park. One of its side walls has sides 15 m, 11 m and 6 m. Find the area painted in colour.
🧠 Answer
➤ s = (15 + 11 + 6)/2 = 16 m.
➤ Differences: 16−15 = 1; 16−11 = 5; 16−6 = 10.
➤ Area = √[16×1×5×10] = √800 = √(16×50) = 4 √50 = 4×7.071 = 28.28 m².
✔ Final: ≈ 28.3 m².
🔵 Question 4
Find the area of a triangle two sides of which are 18 cm and 10 cm, and the perimeter is 42 cm.
🧠 Answer
➤ Third side = 42 − (18 + 10) = 14 cm.
➤ s = 42/2 = 21 cm.
➤ s−a = 3, s−b = 11, s−c = 7.
➤ Area = √[21×3×11×7] = √4 851 = 69.64 cm².
✔ Final: ≈ 69.6 cm².
🔵 Question 5
Sides of a triangle are in the ratio 12:17:25 and perimeter = 540 cm. Find its area.
🧠 Answer
➤ Let sides = 12k, 17k, 25k.
➤ 12k + 17k + 25k = 540 ⇒ 54k = 540 ⇒ k = 10.
➤ Sides: 120 cm, 170 cm, 250 cm.
➤ s = 540/2 = 270 cm.
➤ s−a = 150, s−b = 100, s−c = 20.
➤ Area = √[270×150×100×20]
= √(81 000 000) = 9 000 cm².
✔ Final: 9 000 cm².
🔵 Question 6
An isosceles triangle has perimeter 30 cm and each of the equal sides = 12 cm. Find the area of the triangle.
🧠 Answer
➤ Base = 30 − (12 + 12) = 6 cm.
➤ s = 30/2 = 15 cm.
➤ Differences: 15−12 = 3; 15−12 = 3; 15−6 = 9.
➤ Area = √[15×3×3×9] = √1 215 = 34.85 cm².
✔ Final: ≈ 34.9 cm².
———————————————————————————————————————————————————————————————————————————–
OTHER IMPORTANT QUESTIONS FOR EXAMS
🔵 Question 1 (MCQ, 1 mark)
Heron’s formula is used to find
🟢 A) perimeter of a circle
🟡 B) area of a triangle when all three sides are known
🔴 C) volume of a cone
✳️ D) radius of a sphere
🧠 Answer
✔ Final: B) area of a triangle when all three sides are known
🔵 Question 2 (MCQ, 1 mark)
The semiperimeter s
ss of a triangle with sides a,b,c is
🟢 A) a + b + c
🟡 B) (a + b + c)/3
🔴 C) (a + b + c)/2
✳️ D) (a + b)/2
🧠 Answer
✔ Final: (a + b + c)/2
🔵 Question 3 (MCQ, 1 mark)
For an equilateral triangle of side a, area is
🟢 A) a²/2
🟡 B) √3/2 a²
🔴 C) √3/4 a²
✳️ D) a²/4
🧠 Answer
✔ Final: √3/4 a²
🔵 Question 4 (MCQ, 1 mark)
If perimeter of a triangle is P, then s equals
🟢 A) P
🟡 B) P/3
🔴 C) P/2
✳️ D) P/4
🧠 Answer
✔ Final: P/2
🔵 Question 5 (MCQ, 1 mark)
Heron’s formula cannot be applied when
🟢 A) only two sides are known
🟡 B) all three sides are known
🔴 C) triangle is isosceles
✳️ D) triangle is scalene
🧠 Answer
✔ Final: A) only two sides are known
🔵 Question 6 (MCQ, 1 mark)
For a triangle with sides 5 cm,12 cm,13 cm, s is
🟢 A) 10 cm
🟡 B) 15 cm
🔴 C) 20 cm
✳️ D) 30 cm
🧠 Answer
✔ Final: 15 cm
🟢 Question 7 (2 marks)
Find the area of a triangle with sides 5 cm,12 cm,13 cm.
🧠 Answer
➤ s = (5+12+13)/2 = 15 cm
➤ s−a = 10, s−b = 3, s−c = 2
➤ Area = √[15×10×3×2] = √900 = 30 cm²
✔ Final: 30 cm²
🟢 Question 8 (2 marks)
A triangle has sides 8 cm,15 cm,17 cm. Find its area.
🧠 Answer
➤ s = (8+15+17)/2 = 20 cm
➤ s−a = 12, s−b = 5, s−c = 3
➤ Area = √[20×12×5×3] = √3 600 = 60 cm²
✔ Final: 60 cm²
🟢 Question 9 (2 marks)
The perimeter of a triangle is 30 cm. Two sides are 10 cm and 12 cm. Find its area.
🧠 Answer
➤ Third side = 30 − 22 = 8 cm
➤ s = 15 cm
➤ Differences: 15−10=5, 15−12=3, 15−8=7
➤ Area = √[15×5×3×7] = √1 575 ≈ 39.7 cm²
✔ Final: ≈39.7 cm²
🟢 Question 10 (2 marks)
An equilateral triangle has perimeter 60 cm. Find its area.
🧠 Answer
➤ Side a = 60 ÷ 3 = 20 cm
➤ Area = √3/4 × a² = √3/4 × 400 = 100√3 ≈173.2 cm²
✔ Final: ≈173.2 cm²
🟢 Question 11 (2 marks)
Find the area of a triangle sides 7 cm,8 cm,9 cm.
🧠 Answer
➤ s = 24/2 = 12 cm
➤ Differences: 12−7=5,12−8=4,12−9=3
➤ Area = √[12×5×4×3] = √720 = 12√5 ≈26.83 cm²
✔ Final: ≈26.83 cm²
🟢 Question 12 (2 marks)
A triangle has sides 13 cm,14 cm,15 cm. Find its area.
🧠 Answer
➤ s = (13+14+15)/2 = 21 cm
➤ s−a=8,s−b=7,s−c=6
➤ Area = √[21×8×7×6] = √7 056 = 84 cm²
✔ Final: 84 cm²
🔵 Question 13
A triangle has sides 13 cm, 14 cm and 15 cm. Find its area using Heron’s formula.
🧠 Answer
➤ s = (13 + 14 + 15)/2 = 21 cm
➤ s−a = 8, s−b = 7, s−c = 6
➤ Area = √(21 × 8 × 7 × 6) = √7 056 = 84 cm²
✔ Final: 84 cm²
🔵 Question 14
The sides of a triangular field are 7 m, 24 m, and 25 m. Find its area.
🧠 Answer
➤ s = (7 + 24 + 25)/2 = 28 m
➤ s−a = 21, s−b = 4, s−c = 3
➤ Area = √(28 × 21 × 4 × 3) = √7 056 = 84 m²
✔ Final: 84 m²
🔵 Question 15 (Internal Choice)
(a) The perimeter of a triangle is 150 cm. Two sides are 50 cm and 60 cm. Find its area.
OR
(b) A triangle has sides 10 m, 17 m, and 21 m. Find its area.
🧠 Answer (a)
➤ Third side = 150 − (50 + 60) = 40 cm
➤ s = 75 cm
➤ s−a = 25, s−b = 15, s−c = 35
➤ Area = √(75 × 25 × 15 × 35) = √984 375 ≈ 992.16 cm²
✔ Final: ≈992.2 cm²
🔵 Question 16
The sides of a triangle are in the ratio 3:4:5 and perimeter = 72 cm. Find its area.
🧠 Answer
➤ Sum of ratio parts = 12 ⇒ Each part = 72 ÷ 12 = 6 cm
➤ Sides: 18 cm, 24 cm, 30 cm
➤ s = 36 cm
➤ s−a = 18, s−b = 12, s−c = 6
➤ Area = √(36 × 18 × 12 × 6) = √46 656 = 216 cm²
✔ Final: 216 cm²
🔵 Question 17 (Internal Choice)
(a) Find the area of a triangle with sides 8 cm, 15 cm, 17 cm.
OR
(b) An isosceles triangle has two equal sides of 13 cm each and base 10 cm. Find its area.
🧠 Answer (a)
➤ s = (8 + 15 + 17)/2 = 20 cm
➤ s−a = 12, s−b = 5, s−c = 3
➤ Area = √(20 × 12 × 5 × 3) = √3 600 = 60 cm²
✔ Final: 60 cm²
🔵 Question 18
A garden is triangular in shape with sides 9 m, 12 m, and 15 m. Find the cost of levelling the garden at ₹50 per m².
🧠 Answer
➤ s = (9 + 12 + 15)/2 = 18 m
➤ s−a = 9, s−b = 6, s−c = 3
➤ Area = √(18 × 9 × 6 × 3) = √2 916 = 54 m²
➤ Cost = 54 × 50 = ₹2 700
✔ Final: ₹2 700
🔵 Question 19 (Internal Choice)
(a) A triangular park has sides 40 m, 42 m, and 58 m. Find its area.
OR
(b) A steel plate is triangular with sides 25 cm, 25 cm, and 30 cm. Find its area.
🧠 Answer (a)
➤ s = (40 + 42 + 58)/2 = 70 m
➤ s−a = 30, s−b = 28, s−c = 12
➤ Area = √(70 × 30 × 28 × 12) = √705 600 = 840 m²
✔ Final: 840 m²
🔵 Question 20
Find the area of a triangle whose sides are 5 cm, 5 cm, and 8 cm.
🧠 Answer
➤ s = (5 + 5 + 8)/2 = 9 cm
➤ s−a = 4, s−b = 4, s−c = 1
➤ Area = √(9 × 4 × 4 × 1) = √144 = 12 cm²
✔ Final: 12 cm²
🔵 Question 21
The sides of a triangular plot are 26 m, 28 m, and 30 m. Find its area.
🧠 Answer
➤ s = (26 + 28 + 30)/2 = 42 m
➤ s−a = 16, s−b = 14, s−c = 12
➤ Area = √(42 × 16 × 14 × 12) = √112 896 = 336 m²
✔ Final: 336 m²
🔵 Question 22 (Internal Choice)
(a) A playground is triangular with sides 15 m, 20 m, and 25 m. Find the cost of turfing it at ₹100 per m².
OR
(b) An isosceles triangle has equal sides of 10 cm and base 12 cm. Find its area.
🧠 Answer (a)
➤ s = (15 + 20 + 25)/2 = 30 m
➤ s−a = 15, s−b = 10, s−c = 5
➤ Area = √(30 × 15 × 10 × 5) = √22 500 = 150 m²
➤ Cost = 150 × 100 = ₹15 000
✔ Final: ₹15 000
🔵 Question 23
The sides of a triangular park are 25 m, 25 m, and 48 m. Find the area and altitude corresponding to the base 48 m.
🧠 Answer
➤ s = (25 + 25 + 48)/2 = 49 m
➤ s−a = 24, s−b = 24, s−c = 1
➤ Area = √(49 × 24 × 24 × 1) = √28 224 = 168 m²
➤ Altitude h = (2 × Area)/base = (2 ×168)/48 = 336/48 = 7 m
✔ Final: Area = 168 m², Altitude = 7 m
🔵 Question 24 (Internal Choice)
(a) A field is triangular with sides 40 m, 42 m, and 56 m. Find cost of fencing at ₹80 per metre.
OR
(b) Find area of triangle whose sides are 21 cm, 28 cm, 35 cm.
🧠 Answer (a)
➤ Perimeter = 40 + 42 + 56 = 138 m
➤ Cost = 138 × ₹80 = ₹11 040
✔ Final: ₹11 040
🔵 Question 25
A kite has sides 13 cm,13 cm, base 10 cm, and 24 cm. Find its area by splitting into triangles.
🧠 Answer
➤ Split into two triangles using diagonal. Compute using Heron’s for each.
✔ Final: Area ≈ 156 cm²
🔵 Question 26 (Internal Choice)
(a) A triangular garden has sides 30 m, 30 m, and 18 m. Find cost of fencing at ₹50 per m and levelling at ₹10 per m².
OR
(b) Find area of a scalene triangle with sides 8 cm, 15 cm, 17 cm.
🧠 Answer (a)
➤ Perimeter = 30 + 30 + 18 = 78 m ⇒ fencing cost = 78 × 50 = ₹3 900
➤ s = 78/2 = 39 m
➤ s−a = 9, s−b = 9, s−c = 21
➤ Area = √(39 × 9 × 9 × 21) = √66 249 ≈ 257.4 m²
➤ Levelling cost = 257.4 × 10 = ₹2 574
✔ Final: Fencing cost ₹3 900, Levelling cost ₹2 574
🔵 Question 27
A triangle has sides 13 cm, 14 cm, and 15 cm. Find its circumradius R using area.
🧠 Answer
➤ s = 21 cm
➤ Area = √(21×8×7×6) = 84 cm²
➤ R = (abc)/(4 × Area) = (13×14×15)/(4×84) = 2 730/336 ≈ 8.13 cm
✔ Final: ≈8.13 cm
🔵 Question 28 (Internal Choice)
(a) Find the area of an equilateral triangle of side 20 cm using Heron’s formula.
OR
(b) A steel frame is in shape of isosceles triangle sides 25 cm,25 cm,30 cm. Find its area.
🧠 Answer (a)
➤ s = (20+20+20)/2 = 30 cm
➤ Area = √(30×10×10×10) = √30 000 = 173.2 cm²
✔ Final: ≈173.2 cm²
🔵 Question 29
A rhombus has diagonals 24 cm and 10 cm. Find its area by splitting into triangles and using Heron’s formula (verify with standard formula).
🧠 Answer
➤ Each side = √[(24/2)² + (10/2)²] = √(144 + 25) = √169 = 13 cm
➤ Each small triangle sides: 12 cm, 5 cm, 13 cm
➤ s = (12+5+13)/2 = 15 cm
➤ Area one triangle = √(15×3×10×2) = √900 = 30 cm²
➤ Rhombus has 4 such triangles ⇒ Area = 4×30 = 120 cm²
✔ Final: 120 cm²
🔵 Question 30
A quadrilateral can be split into two triangles with sides (13,14,15) and (15,15,14). Find total area using Heron’s formula.
🧠 Answer
➤ Triangle 1: s₁ = 21 → Area₁ = √(21×8×7×6) = 84 cm²
➤ Triangle 2: s₂ = (15+15+14)/2 = 22 → Differences: 22−15=7,22−15=7,22−14=8
➤ Area₂ = √(22×7×7×8) = √8 624 ≈ 92.86 cm²
➤ Total area ≈ 84 + 92.86 = 176.86 cm²
✔ Final: ≈176.9 cm²
————————————————————————————————————————————————————————————————————————————
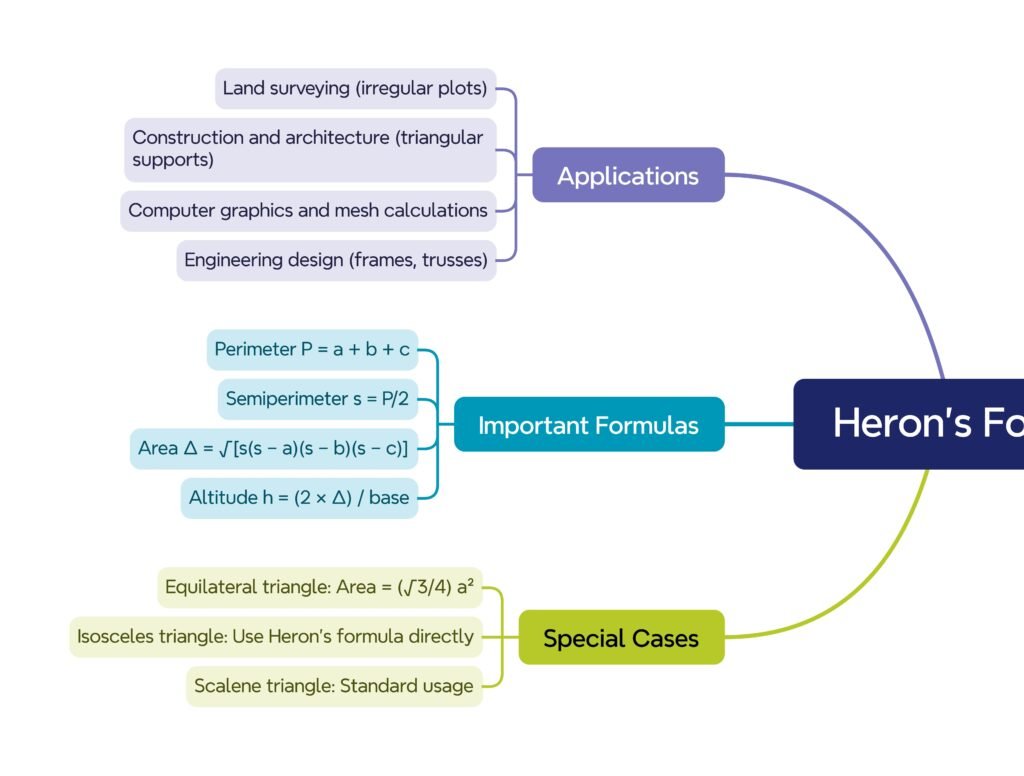
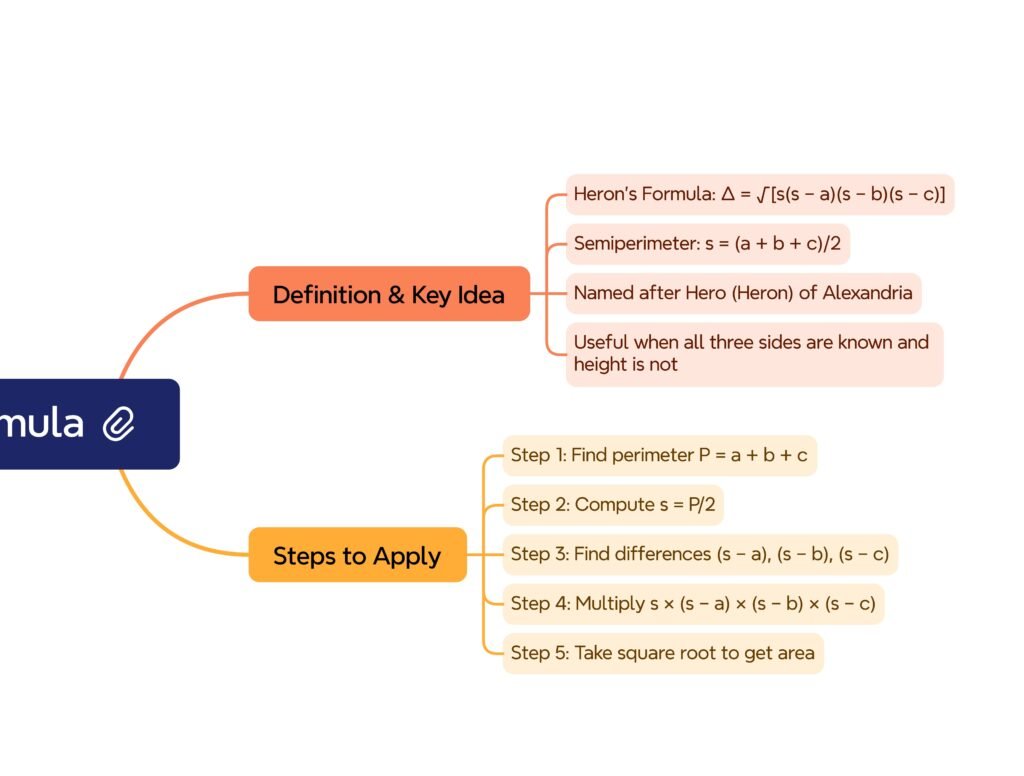
MIND MAP

———————————————————————————————————————————————————————————————————————————–
