Class : 9 – Math (English) : Lesson 1. Number Systems
EXPLANATION & SUMMARY
🔵 Detailed Explanation
🔵 1) Introduction: Why Number Systems?
• ✨ Numbers allow counting, measuring, labelling, and modelling.
• ✨ They form a hierarchy: natural → whole → integers → rationals → reals.
• ✨ A real number is any point on the number line.
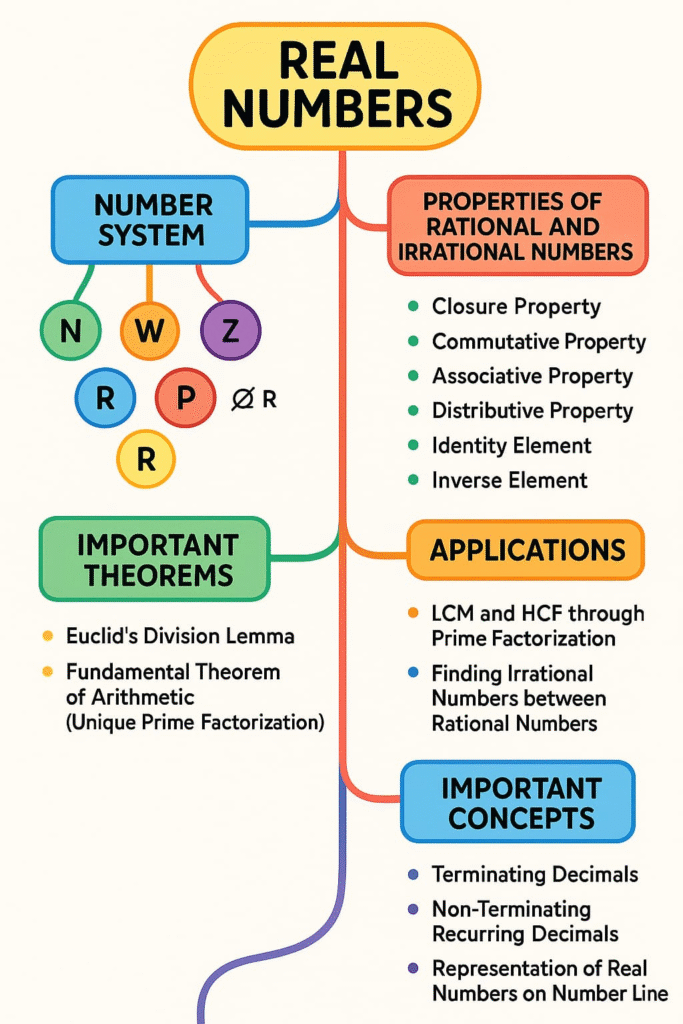
🟢 2) Sets of Numbers
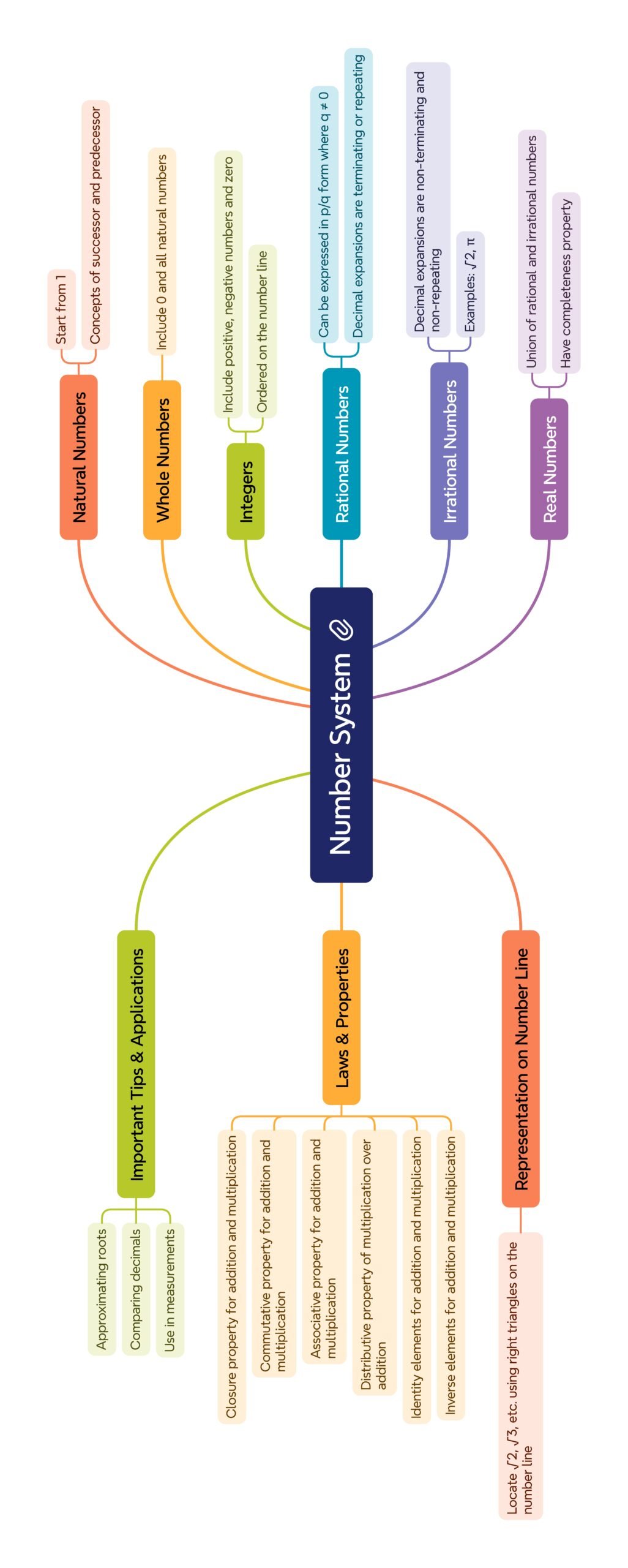
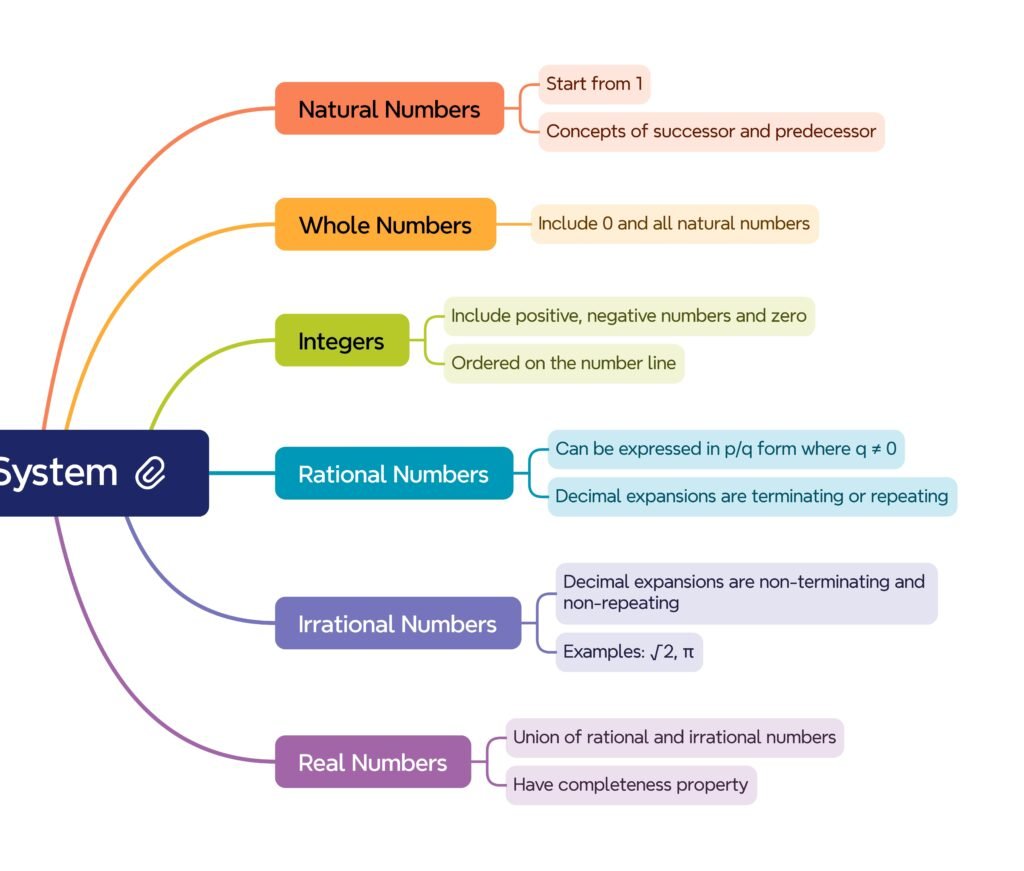
• Natural numbers (ℕ) = {1, 2, 3,…}.
• Whole numbers (𝕎) = {0, 1, 2, 3,…}.
• Integers (ℤ) = {…, −3, −2, −1, 0, 1, 2, 3,…}.
• Rationals (ℚ) = p/q, p, q ∈ ℤ, q≠0. Examples: 5=5/1, −7/3, 2.375=19/8.
• Irrationals (ℝ \ ℚ) = non-terminating, non-repeating decimals: √2, √3, π.
• Nesting: ℕ⊂𝕎⊂ℤ⊂ℚ⊂ℝ.
🟡 3) Decimal Expansions
• Terminating: stop after finite digits (e.g., 0.125).
• Non-terminating repeating: recurring block (e.g., 0.142857142857…).
• Non-terminating non-repeating: no pattern → irrational.
• ✏️ Key Fact: x ∈ ℚ ⇔ decimal is terminating or repeating.
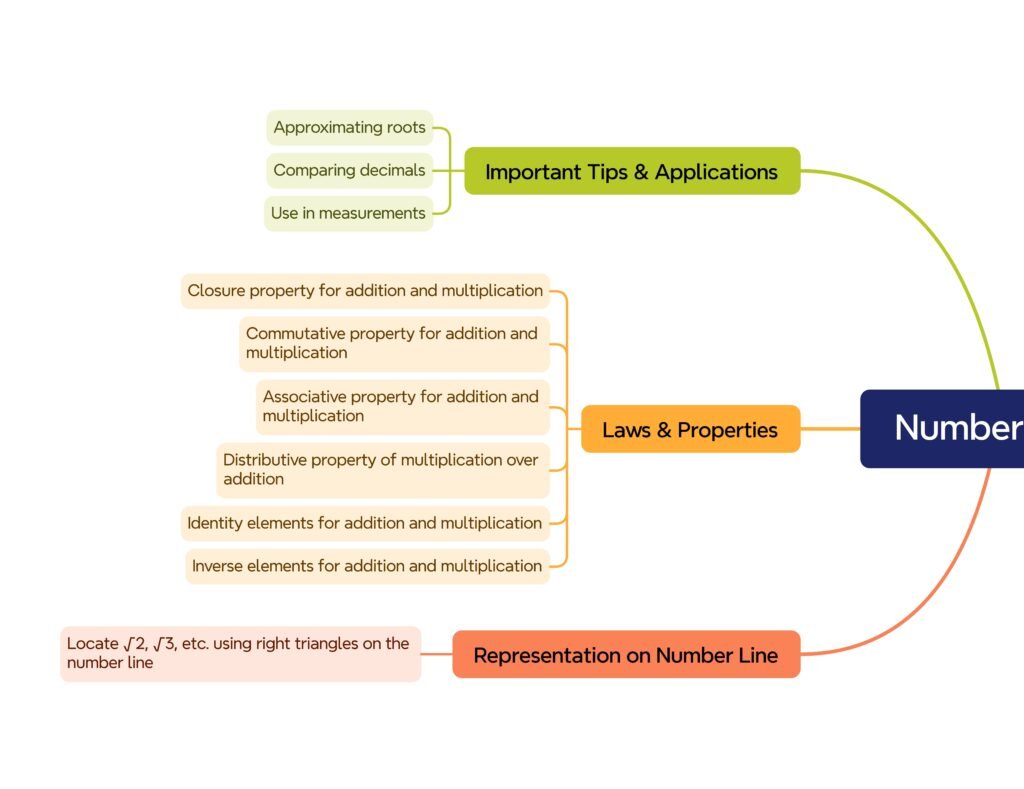
🔴 4) Placing √2 on the Number Line
Step 1: Draw OA=1 unit, AB=1 unit at right angles.
Step 2: Hypotenuse OB=√(1²+1²)=√2.
Step 3: With compass radius = OB, mark point on OA extension → √2.
Similarly, construct √3 using OB as a leg.
🔵 5) Proof of Irrationality of √2
Step 1: Assume √2=p/q (lowest terms).
Step 2: Square: 2=p²/q² ⇒ p²=2q².
Step 3: p² even ⇒ p even ⇒ p=2k.
Step 4: Substitute: 4k²=2q² ⇒ q²=2k² ⇒ q even.
Step 5: p,q both even contradicts lowest terms ⇒ √2 irrational.
🟢 6) 2ⁿ5ᵐ Test for Terminating Decimals
x=p/q (lowest terms) has terminating decimal ⇔ q=2ⁿ5ᵐ.
• Example: 13/40 → 40=2³×5 ⇒ terminating.
• Example: 7/12 → 12=2²×3 ⇒ factor 3 remains ⇒ repeating.
🟡 7) Convert Recurring Decimal to Rational
Example: x=0.35̅.
Step 1: 100x=35.35̅.
Step 2: 100x−x=35.
Step 3: 99x=35.
Step 4: x=35/99.
🔴 8) Operations on Real Numbers
• Closure: ℝ closed under +, −, ×, /.
• Commutativity: a+b=b+a; ab=ba.
• Associativity: (a+b)+c=a+(b+c).
• Distributivity: a(b+c)=ab+ac.
• Additive inverse: a+(−a)=0.
• Multiplicative inverse: a×(1/a)=1 (a≠0).
🔵 9) Rationalising Denominators
(i) 1/√3 = √3/3.
(ii) 1/(5−√2)=(5+√2)/(23).
(iii) (2+√5)/(3−√5)=(11+5√5)/4.
🟢 10) Laws of Exponents
• aᵐ×aⁿ=aᵐ⁺ⁿ.
• aᵐ/aⁿ=aᵐ⁻ⁿ.
• (aᵐ)ⁿ=aᵐⁿ.
• a⁰=1 (a≠0).
• a⁻ⁿ=1/aⁿ.
• a¹/ⁿ=ⁿ√a (a≥0).
• aᵐ/ⁿ=(ⁿ√a)ᵐ.
• (ab)ᵐ=aᵐbᵐ.
🟡 11) Comparing Real Numbers
• Use number line positions.
• Convert to decimals or common denominators.
• For roots, square carefully if both sides ≥0.
Example: compare √3 and 7/4. Square:3 vs 49/16=3.0625 ⇒ √3<1.75.
🔴 12) Worked Examples
A) Classify:
• 0.072=9/125 (terminating, rational).
• 0.18̅=2/11 (repeating, rational).
• √2 irrational.
• 2.050050005… irrational.
B) Use 2ⁿ5ᵐ test:
77/160 terminates (160=2⁵×5).
Decimal:77×625/100000=0.48125.
C) Rationalise:
5/(2√3)=5√3/6.
1/(√5−√2)=(√5+√2)/3.
(√7−√5)/(√7+√5)=(6−√35).
D) Exponents:
(2³/²)×(2¹/²)=2²=4.
27²/³=(³√27)²=9.
🔵 13) Successive Magnification
Zoom on 3.14–3.15 to locate π precisely; no gaps exist on the real line.
🟢 14) Common Mistakes
• Confusing recurring with non-recurring.
• Not reducing fractions before 2ⁿ5ᵐ test.
• Using wrong conjugate.
• Applying √a×√b when a,b<0.
🟡 15) Applications
Engineering, physics, computing, finance—real numbers are everywhere: measuring, coding decimals, modelling growth.
🔴 16) Self-Check Mini-Exercise
Classify:0.6̅, √11, 5/2, 0.1010010001… .
Use 2ⁿ5ᵐ test on 3/75 & 21/28.
Rationalise:(3+√2)/(2−√2).
Evaluate:16³/⁴,125⁻²/³.
Order:√3,19/11,1.72̅.
✨ 17) Big Idea — Completeness of ℝ
Between any two reals are infinitely many rationals and irrationals.
🟣 Summary (300 words)
The number system grows from counting numbers to all real numbers. Natural numbers ℕ include positive integers. Adding zero gives whole numbers 𝕎. Extending to negatives yields integers ℤ. Fractions and decimals form rationals ℚ=p/q. Non-terminating, non-repeating decimals like √2, π are irrationals. Together, ℚ and irrationals make reals ℝ. Every real number corresponds to a point on a continuous number line without gaps.
Decimal expansions classify numbers: terminating or repeating decimals are rational; non-terminating non-repeating decimals are irrational. To test termination, write p/q in lowest terms and factor q: if q=2ⁿ5ᵐ, the decimal terminates; otherwise it repeats. Recurring decimals convert to rationals via algebra: align repeating parts by multiplying by powers of 10, subtract, and solve for x.
Basic operations (+, −, ×, /) keep us inside ℝ. Properties like commutativity, associativity, and distributivity hold. Additive inverses (a+(−a)=0) and reciprocals (a×1/a=1) exist (except 0 has no reciprocal). Rationalising denominators simplifies radicals: multiply numerator and denominator by the conjugate. Exponents follow familiar rules: aᵐ×aⁿ=aᵐ⁺ⁿ, aᵐ/aⁿ=aᵐ⁻ⁿ, (aᵐ)ⁿ=aᵐⁿ, a⁰=1(a≠0), a⁻ⁿ=1/aⁿ, a¹/ⁿ=ⁿ√a(a≥0), aᵐ/ⁿ=(ⁿ√a)ᵐ.
Visualising irrationals uses the Pythagorean theorem. For √2, draw a right triangle with legs 1 and 1; its hypotenuse √2 locates on the number line. Successive magnification refines positions like π.
Errors to avoid: forgetting to reduce fractions before 2ⁿ5ᵐ test, misidentifying decimal types, or rationalising with wrong conjugates. Mastery of these rules underpins algebra, geometry, and analysis. Real numbers’ completeness—infinitely many values between any two—ensures accurate measurement and modelling.
📝 Quick Recap
🔵 N⊂𝕎⊂ℤ⊂ℚ⊂ℝ; irrationals=ℝ\ℚ.
🟢 Terminating test: q=2ⁿ5ᵐ ⇒ terminating decimal.
🟡 Recurring decimal → rational via subtraction trick.
🔴 Rationalise denominators using conjugates.
🔵 Exponents: aᵐ×aⁿ=aᵐ⁺ⁿ, aᵐ/aⁿ=aᵐ⁻ⁿ, (aᵐ)ⁿ=aᵐⁿ, aᵐ/ⁿ=(ⁿ√a)ᵐ.
————————————————————————————————————————————————————————————————————————————
TEXT BOOK QUESTIONS
📘 EXERCISE 1.1
🔵 Question 1
Is zero a rational number? Can you write it in the form p/q, where p and q are integers and q ≠ 0?
🟢 Answer
🔸 Step 1: A rational number can be expressed as p/q with p, q ∈ ℤ and q ≠ 0.
🔸 Step 2: Zero can be written as 0/1, 0/2, 0/(-7), etc.
✔ Final: Yes, zero is a rational number because 0/q (q ≠ 0) satisfies the definition.
🔵 Question 2
Find six rational numbers between 3 and 4.
🟢 Answer
🔸 Step 1: Convert to fractions with denominator 10 for easy selection.
🔸 Step 2: Examples between 3 and 4: 31/10, 32/10, 33/10, 34/10, 35/10, 36/10.
✔ Final: Six rational numbers are 31/10, 32/10, 33/10, 34/10, 35/10, 36/10.
🔵 Question 3
Find five rational numbers between 3/5 and 4/5.
🟢 Answer
🔸 Step 1: Express fractions with denominator 50 to create finer intervals:
3/5 = 30/50, 4/5 = 40/50.
🔸 Step 2: Choose values strictly between: 31/50, 32/50, 33/50, 34/50, 35/50.
✔ Final: Five rational numbers are 31/50, 32/50, 33/50, 34/50, 35/50.
🔵 Question 4
State whether the following statements are true or false. Give reasons.
(i) Every natural number is a whole number.
(ii) Every integer is a whole number.
(iii) Every rational number is a whole number.
🟢 Answer
🔸 (i) ✔ True — Natural numbers {1, 2, 3,…} are part of whole numbers {0, 1, 2, 3,…}.
🔸 (ii) ❌ False — Integers include negative numbers (e.g., −3), which are not whole numbers.
🔸 (iii) ❌ False — Rational numbers include fractions (e.g., 2/3) that are not whole numbers.
✔ Final: (i) True, (ii) False, (iii) False.
📘 EXERCISE 1.2
🔵 Question 1
State whether the following are true or false. Justify your answers.
(i) Every irrational number is a real number.
(ii) Every point on the number line is of the form √m, where m is a natural number.
(iii) Every real number is an irrational number.
🟢 Answer
🔸 (i) ✔ True — Irrational numbers are part of the real numbers.
🔸 (ii) ❌ False — Points on the number line can also be negative numbers, fractions, etc., not always √m.
🔸 (iii) ❌ False — Real numbers include both rationals and irrationals, so not all are irrational.
🔵 Question 2
Are the square roots of all positive integers irrational? If not, give an example of a square root of a number that is rational.
🟢 Answer
🔸 Step 1: Square roots of perfect squares are rational.
🔸 Step 2: Example: √9 = 3 (rational).
✔ Final: No, not all are irrational; √9 is rational.
🔵 Question 3
Show how √5 can be represented on the number line.
🟢 Answer
🔸 Step 1: Draw a number line, mark points O (0) and A (2).
🔸 Step 2: Extend OA to point B with AB = 1 unit, making OB = 2 +1 =3 units.
🔸 Step 3: Draw a semicircle with OB as diameter.
🔸 Step 4: Draw a perpendicular from A; let it meet the semicircle at C. AC = √5.
🔸 Step 5: Draw arc OC = √5 on the number line to represent √5.
✔ Final: √5 is represented by marking length AC on the number line.
🔵 Question 4
Classroom activity: Constructing the square root spiral.
🟢 Answer
🔸 Step 1: Draw a point O and line OP₁ of 1 unit.
🔸 Step 2: Draw P₁P₂ ⟂ OP₁ of 1 unit. Join OP₂ to get √2.
🔸 Step 3: Draw P₂P₃ ⟂ OP₂ of 1 unit. Join OP₃ to get √3.
🔸 Step 4: Continue this pattern: each new line segment is perpendicular to the previous radius and 1 unit long.
🔸 Step 5: Points P₁, P₂, P₃… joined give a spiral showing √2, √3, √4, …
✔ Final: A beautiful spiral represents successive square roots on the number line.
📘 EXERCISE 1.3
🔵 Question 1
Write in decimal form and state the type of decimal expansion:
(i) 36/100 (ii) 1/11 (iii) 4 1/8 (iv) 3/13 (v) 329/400 (vi) 11
🟢 Answer
🔸 (i) 36 ÷ 100 = 0.36 → terminating
🔸 (ii) 1 ÷ 11 = 0.09̄ → non-terminating repeating
🔸 (iii) 4 + 1/8 = 4.125 → terminating
🔸 (iv) 3 ÷ 13 = 0.230769̄ → non-terminating repeating
🔸 (v) 329 ÷ 400 = 0.8225 → terminating
🔸 (vi) 11 = 11.0 → terminating
🔵 Question 2
Predict decimal expansions of 2/7, 3/7, 4/7, 5/7, 6/7 using 1/7 = 0.142857̄.
🟢 Answer
✏️ Use cyclic permutations of 142857:
🔸 2/7 = 0.285714̄
🔸 3/7 = 0.428571̄
🔸 4/7 = 0.571428̄
🔸 5/7 = 0.714285̄
🔸 6/7 = 0.857142̄
🔵 Question 3
Express as p/q:
(i) 0.6̄ (ii) 0.47̄ (iii) 0.001̄
🟢 Answer
🔸 (i) Let x = 0.6̄.
➤ 10x = 6.6̄.
➤ 10x − x = 6.6̄ − 0.6̄ = 6.
➤ 9x = 6 ⇒ x = 2/3.
🔸 (ii) Let x = 0.47̄.
➤ 100x = 47.47̄.
➤ 100x − x = 47.47̄ − 0.47̄ = 47.
➤ 99x = 47 ⇒ x = 47/99.
🔸 (iii) Let x = 0.001̄.
➤ 1000x = 1.001̄.
➤ 1000x − x = 1.001̄ − 0.001̄ = 1.
➤ 999x = 1 ⇒ x = 1/999.
🔵 Question 4
Express 0.99999… in p/q form.
🟢 Answer
Let x = 0.9̄.
➤ 10x = 9.9̄.
➤ 10x − x = 9.
➤ 9x = 9 ⇒ x = 1.
🔵 Question 5
Maximum digits in repeating block of 1/17.
🟢 Answer
➤ The maximum length ≤ 16 for denominator 17.
✔ Final: 16 digits.
🔵 Question 6
Property of q for terminating decimals.
🟢 Answer
➤ In p/q (lowest terms), q’s prime factors must be only 2 and/or 5.
🔵 Question 7
Three numbers with non-terminating, non-recurring expansions.
🟢 Answer
Examples: √2, π, e.
🔵 Question 8
Three different irrationals between 5/7 (≈0.714) and 9/11 (≈0.818).
🟢 Answer
Possible choices: √0.72, √0.75, √0.8.
🔵 Question 9
Classify as rational or irrational:
(i) √23 (ii) √225 (iii) 0.3796̄ (iv) 7.478478…̄ (v) 1.10100100010000…
🟢 Answer
🔸 (i) √23 — Irrational.
🔸 (ii) √225 = 15 — Rational.
🔸 (iii) 0.3796̄ — Rational (repeating).
🔸 (iv) 7.478478…̄ — Rational (repeating block).
🔸 (v) 1.10100100010000… — Irrational (non-terminating, non-repeating).
📘 EXERCISE 1.4
🔵 Question 1
Classify the following numbers as rational or irrational:
(i) 2 − √5 (ii) (3 + √23) − √23 (iii) 2√7 / 7√7 (iv) 1/√2 (v) 2π
🟢 Answer
🔸 (i) 2 − √5 → Difference of a rational and an irrational ⇒ Irrational.
🔸 (ii) (3 + √23) − √23 = 3 ⇒ Rational.
🔸 (iii) 2√7 / 7√7 = 2/7 ⇒ Rational.
🔸 (iv) 1/√2 ⇒ Irrational.
🔸 (v) 2π ⇒ Irrational.
🔵 Question 2
Simplify each expression:
(i) (3 + √3)(2 + √2)
(ii) (3 + √3)(3 − √3)
(iii) (√5 + √2)²
(iv) (√5 − √2)(√5 + √2)
🟢 Answer
🔸 (i)
➤ = 3×2 + 3√2 + 2√3 + √3√2
➤ = 6 + 3√2 + 2√3 + √6
✔ Final: 6 + 3√2 + 2√3 + √6
🔸 (ii)
➤ = 3² − (√3)²
➤ = 9 − 3
✔ Final: 6
🔸 (iii)
➤ Use (a + b)² = a² + 2ab + b²
➤ = (√5)² + 2√5√2 + (√2)²
➤ = 5 + 2√10 + 2
✔ Final: 7 + 2√10
🔸 (iv)
➤ Use (a − b)(a + b) = a² − b²
➤ = (√5)² − (√2)²
➤ = 5 − 2
✔ Final: 3
🔵 Question 3
π is defined as c/d (ratio of circumference to diameter). This seems to contradict that π is irrational. Resolve.
🟢 Answer
🔸 Step 1: π = c/d is a definition, not an exact rational fraction.
🔸 Step 2: c and d themselves cannot be measured with perfect precision using rational numbers; π is not equal to any fraction exactly.
🔸 Step 3: Hence π remains irrational despite being defined as a ratio.
🔵 Question 4
Represent √9.3 on the number line.
🟢 Answer
🔸 Step 1: Draw line OA = 9.3 units on a number line.
🔸 Step 2: Extend OA by 1 unit to B (OB = 10.3).
🔸 Step 3: Mark midpoint M of OB and draw a semicircle on OB.
🔸 Step 4: Draw a perpendicular from A to intersect semicircle at C.
🔸 Step 5: AC = √9.3. Mark AC on the line from O to represent √9.3.
🔵 Question 5
Rationalise the denominators:
(i) 1/√7
(ii) 1/(√7 − √6)
(iii) 1/(√5 + √2)
(iv) 1/(√7 − 2)
🟢 Answer
🔸 (i)
➤ Multiply numerator and denominator by √7:
➤ (1×√7)/(√7×√7) = √7 / 7
✔ Final: √7 / 7
🔸 (ii)
➤ Multiply by conjugate (√7 + √6):
➤ (1×(√7 + √6)) / ((√7 − √6)(√7 + √6))
➤ = (√7 + √6) / (7 − 6)
➤ = (√7 + √6) / 1
✔ Final: √7 + √6
🔸 (iii)
➤ Multiply by conjugate (√5 − √2):
➤ (1×(√5 − √2)) / ((√5 + √2)(√5 − √2))
➤ = (√5 − √2) / (5 − 2)
➤ = (√5 − √2) / 3
✔ Final: (√5 − √2)/3
🔸 (iv)
➤ Multiply by conjugate (√7 + 2):
➤ (1×(√7 + 2)) / ((√7 − 2)(√7 + 2))
➤ = (√7 + 2) / (7 − 4)
➤ = (√7 + 2) / 3
✔ Final: (√7 + 2)/3
📘 EXERCISE 1.5
🔵 Question 1
Find:
(i) 64¹ᐟ² (ii) 32¹ᐟ⁵ (iii) 125¹ᐟ³
🟢 Answer
🔸 (i) 64¹ᐟ² = √64 = 8
🔸 (ii) 32¹ᐟ⁵ = ⁵√32 = 2
🔸 (iii) 125¹ᐟ³ = ³√125 = 5
🔵 Question 2
Find:
(i) 9³ᐟ² (ii) 32²ᐟ⁵ (iii) 16³ᐟ⁴ (iv) 125⁻¹ᐟ³
🟢 Answer
🔸 (i) 9³ᐟ² = (√9)³ = 3³ = 27
🔸 (ii) 32²ᐟ⁵ = (⁵√32)² = 2² = 4
🔸 (iii) 16³ᐟ⁴ = (⁴√16)³ = 2³ = 8
🔸 (iv) 125⁻¹ᐟ³ = 1 / 125¹ᐟ³ = 1/5 = 0.2
🔵 Question 3
Simplify:
(i) 2³ᐟ² × 2⁵ᐟ² (ii) (1 / 3³)⁷ (iii) 11² / 11⁴ (iv) 7¹ᐟ² ÷ 8¹ᐟ²
🟢 Answer
🔸 (i) Use aᵐ×aⁿ = aᵐ⁺ⁿ:
2³ᐟ² × 2⁵ᐟ² = 2³ᐟ²⁺⁵ᐟ² = 2⁸ᐟ² = 2⁴ = 16
🔸 (ii) (1 / 3³)⁷ = 1⁷ / (3³)⁷ = 1 / 3²¹
✔ Final: 1 / 3²¹
🔸 (iii) 11² / 11⁴ = 11²⁻⁴ = 11⁻² = 1 / 11²
✔ Final: 1 / 121
🔸 (iv) 7¹ᐟ² ÷ 8¹ᐟ² = (7/8)¹ᐟ² = √(7/8)
✔ Final: √(7/8)
————————————————————————————————————————————————————————————————————————————
OTHER IMPORTANT QUESTIONS FOR EXAMS
🔵 Section A (1 mark each — MCQs)
🔵 Question
Q1. The decimal expansion of 13/(2⁴×5²) will:
🔴 Options:
🔵 (A) Terminate after finite digits
🟢 (B) Be non-terminating recurring
🟡 (C) Be non-terminating non-recurring
🔴 (D) Not a rational number
🟢 Answer
✳️ Denominator = 2⁴×5² = 400 ⇒ of form 2ᵐ5ⁿ.
✔ Correct Option: 🔵 (A) Terminate after finite digits
🔵 Question
Q2. Which of these is irrational?
🔴 Options:
🔵 (A) √49
🟢 (B) 7/13
🟡 (C) 0.666…
🔴 (D) √3
🟢 Answer
✳️ √49 = 7 (rational), 7/13 rational, recurring decimal rational, √3 irrational.
✔ Correct Option: 🔴 (D) √3
🔵 Question
Q3. The product of two irrational numbers is:
🔴 Options:
🔵 (A) Always irrational
🟢 (B) Always rational
🟡 (C) Sometimes rational, sometimes irrational
🔴 (D) Never defined
🟢 Answer
✳️ Example: √2×√2=2 (rational), √2×√3 irrational.
✔ Correct Option: 🟡 (C) Sometimes rational, sometimes irrational
🔵 Question
Q4. The value of √2 ÷ √8 simplifies to:
🔴 Options:
🔵 (A) 1/2
🟢 (B) √2
🟡 (C) √8/√2
🔴 (D) 1/√4
🟢 Answer
✳️ √2 ÷ √8 = √(2/8)=√(1/4)=1/2.
✔ Correct Option: 🔵 (A) 1/2
🔵 Question
Q5. Express 0.001 in p/q form:
🔴 Options:
🔵 (A) 1/10
🟢 (B) 1/100
🟡 (C) 1/1000
🔴 (D) 10
🟢 Answer
✳️ 0.001=1/1000.
✔ Correct Option: 🟡 (C) 1/1000
🔵 Question
Q6. HCF(72,120) using Euclid’s lemma is:
🔴 Options:
🔵 (A) 12
🟢 (B) 24
🟡 (C) 18
🔴 (D) 6
🟢 Answer
✳️ 120=72×1+48;72=48×1+24;48=24×2+0 ⇒HCF=24.
✔ Correct Option: 🟢 (B) 24
🟢 Section B (2 marks each)
🔵 Question 7
Use Euclid’s algorithm to find HCF of 135 and 225.
🟢 Answer
✳️ 225=135×1+90
✳️ 135=90×1+45
✳️ 90=45×2+0
✔ Final: HCF=45
🔵 Question 8
Write three rational numbers between 1/5 and 1/4.
🟢 Answer
✳️ 1/5=0.2, 1/4=0.25.
✳️ Examples:21/100(0.21),22/100(0.22),23/100(0.23).
✔ Final: 21/100,22/100,23/100
🔵 Question 9
State whether √45 is rational or irrational. Justify.
🟢 Answer
✳️ √45=√(9×5)=3√5.
✳️ √5 is irrational ⇒ product is irrational.
✔ Final: Irrational
🔵 Question 10
Find the LCM and HCF of 60 and 48 and verify HCF×LCM=product.
🟢 Answer
✳️ 60=2²×3×5;48=2⁴×3.
✳️ HCF=2²×3=12.
✳️ LCM=2⁴×3×5=240.
✳️ Verify:12×240=2880=60×48.
✔ Final: HCF=12,LCM=240
🔵 Question 11
Find five rational numbers between √2 and √3.
🟢 Answer
✳️ √2≈1.414,√3≈1.732.
✳️ Choices:1.45,1.5,1.55,1.6,1.7.
✔ Final: 1.45,1.5,1.55,1.6,1.7
🔵 Question 12
Show that 3√7 is irrational.
🟢 Answer
✳️ Assume 3√7 rational⇒3√7=p/q.
✳️ Divide by3⇒√7=p/(3q) rational⇒contradiction.
✔ Final: 3√7 is irrational
🟡 Section C (3 marks each — Short Answer-II with internal choices)
🔵 Question 13
Use Euclid’s Division Lemma to find HCF of 867 and 255.
🟢 Answer
✳️ ➤ 867 = 255×3 + 102
✳️ ➤ 255 = 102×2 + 51
✳️ ➤ 102 = 51×2 + 0
✔ Final: HCF = 51
🔵 Question 14
Show that the cube of any even integer is divisible by 8.
🟢 Answer
✳️ Let n = 2k (even).
✳️ n³ = (2k)³ = 8k³.
✔ Final: Divisible by 8.
🔵 Question 15
Find the LCM and HCF of 84 and 90 and verify HCF × LCM = product.
🟢 Answer
✳️ 84 = 2²×3×7, 90 = 2×3²×5.
✳️ HCF = 2×3 = 6.
✳️ LCM = 2²×3²×5×7 = 420.
✳️ Check: 6×420 = 2520 = 84×90.
✔ Final: HCF = 6, LCM = 420.
🔵 Question 16
OR
Prove that there are infinitely many primes.
🟢 Answer
✳️ Assume finitely many primes p₁,p₂,…,pₙ.
✳️ Consider N = p₁p₂…pₙ + 1.
✳️ N not divisible by any listed primes ⇒ contradiction.
✔ Final: Infinitely many primes exist.
🔵 Question 17
Write three rational numbers between √3 and √5.
🟢 Answer
✳️ √3 ≈1.732, √5≈2.236.
✳️ Choices:1.8,1.9,2.0.
✔ Final: 1.8,1.9,2.0.
🔵 Question 18
Express 0.0016 as a fraction and say if it’s terminating or non-terminating.
🟢 Answer
✳️ 0.0016 = 16/10000 = 1/625.
✳️ 625=5⁴ ⇒ of form2ᵐ5ⁿ.
✔ Final: Terminating decimal.
🔵 Question 19
Show that 12ⁿ −1 is divisible by 11 for all natural numbers n.
🟢 Answer
✳️ Base: n=1 ⇒12−1=11 divisible.
✳️ Assume true for n=k ⇒12ᵏ=11m+1.
✳️ For k+1:12ᵏ⁺¹−1=12·12ᵏ−1=12(11m+1)−1=132m+12−1=132m+11.
✔ Final: Divisible by 11 for all n.
🔵 Question 20
Find HCF of 126 and 405 using Euclid’s algorithm.
🟢 Answer
✳️ 405=126×3+27.
✳️ 126=27×4+18.
✳️ 27=18×1+9.
✳️ 18=9×2+0.
✔ Final: HCF=9.
🔵 Question 21
State whether 0.101001000100001… is rational or irrational.
🟢 Answer
✳️ The decimal is non-terminating non-recurring.
✔ Final: Irrational.
🔵 Question 22
Use Euclid’s Division Lemma to show that the square of any positive integer is of the form 3m or 3m+1.
🟢 Answer
✳️ Let n=3q,3q+1 or3q+2.
➡ Case1: n=3q ⇒ n²=9q²=3(3q²)=3m.
➡ Case2: n=3q+1 ⇒ n²=9q²+6q+1=3(3q²+2q)+1=3m+1.
➡ Case3: n=3q+2 ⇒ n²=9q²+12q+4=3(3q²+4q+1)+1=3m+1.
✔ Final: n² is 3m or 3m+1.
🔴 Section D (4 marks each — Long Answer with internal choices)
🔵 Question 23
Prove that √2 + √5 is irrational.
🟢 Answer
✳️ Assume √2 + √5 = r (r ∈ ℚ).
✳️ Square: 2 + 5 + 2√10 = r² ⇒ 2√10 = r² − 7.
✳️ Divide: √10 = (r² − 7)/2 (rational) ⇒ contradiction.
✔ Final: √2 + √5 is irrational.
🔵 Question 24
Show that for any integer n, n³ − n is divisible by 6.
🟢 Answer
✳️ Factor: n³ − n = n(n² − 1) = n(n − 1)(n + 1).
✳️ Three consecutive integers ⇒ divisible by 2 and by 3.
✔ Final: Divisible by 6.
🔵 Question 25
Find HCF and LCM of 108 and 288 by prime factorisation and verify HCF×LCM = product.
🟢 Answer
✳️ 108 = 2² × 3³.
✳️ 288 = 2⁵ × 3².
✳️ HCF = 2² × 3² = 4 × 9 = 36.
✳️ LCM = 2⁵ × 3³ = 32 × 27 = 864.
✳️ Check: 36 × 864 = 31104 = 108 × 288.
✔ Final: HCF = 36, LCM = 864.
🔵 Question 26
OR Prove there are infinitely many primes of the form 4k + 3.
🟢 Answer
✳️ Assume finite primes of form 4k + 3: p₁,…,pₙ.
✳️ Consider N = 4(p₁p₂…pₙ) − 1 ≡ 3 (mod 4).
✳️ N not divisible by listed primes ⇒ contradiction.
✔ Final: Infinitely many primes of form 4k + 3.
🔵 Question 27
Represent √8 on a number line.
🟢 Answer
✳️ Draw OA = 2 (units). At A, draw AB = 2 (perpendicular).
✳️ OB = √(OA² + AB²) = √(4 + 4) = √8.
✳️ Draw arc centred at O with radius OB to locate √8.
✔ Final: OP = √8.
🔵 Question 28
Rationalise and simplify: 5 / (√5 + √3)
🟢 Answer
✳️ Multiply numerator and denominator by the conjugate:
5 / (√5 + √3) × (√5 − √3) / (√5 − √3)
= 5(√5 − √3) / (5 − 3)
= 5(√5 − √3) / 2
✔ Final: 5(√5 − √3) / 2
🔵 Question 29
Let x = √7 − √5. Form a polynomial with integer coefficients having x as a root.
🟢 Answer
✳️ Conjugate pair: √7 + √5 also a root.
✳️ (x − (√7 − √5))(x − (√7 + √5)) = x² − 2√7x + 7 − 5 = x² − 2√7x + 2.
✳️ Eliminate √7: Let y = x² + 2. Then y = 2√7x ⇒ square again to remove radicals.
✳️ After squaring and simplifying: x⁴ − 4x² − 20x² + 4 = x⁴ − 24x² + 4 = 0.
✔ Final: Polynomial is x⁴ − 24x² + 4 = 0.
🔵 Question 30
Prove that √3 is irrational.
🟢 Answer
✳️ Suppose √3 = a/b (gcd(a,b)=1).
✳️ Square: 3 = a²/b² ⇒ a² = 3b² ⇒ 3 divides a. Let a = 3k.
✳️ Substitute: 9k² = 3b² ⇒ b² = 3k² ⇒ 3 divides b.
✳️ Both divisible by 3 ⇒ contradiction.
✔ Final: √3 is irrational.
———————————————————————————————————————————————————————————————————————————–
MIND MAP
———————————————————————————————————————————————————————————————————————-
