Class 12 : Physics (Hindi) – अध्याय 1: विद्युत आवेश एवं क्षेत्र

पाठ का विश्लेषण एवं विवेचन

🔵 प्रस्तावना: वैद्युत आवेश की दुनिया में प्रवेश
वैद्युत आवेश (Electric Charge) भौतिकी की सबसे बुनियादी और मौलिक अवधारणाओं में से एक है। यह अध्याय विद्युत बलों, आवेशों की प्रकृति, उनके परस्पर प्रभाव, और विद्युत क्षेत्र की अवधारणा पर केंद्रित है। आवेश वह गुण है जिसके कारण कोई वस्तु विद्युत बलों के अधीन आती है।
✏️ नोट: पदार्थ दो प्रकार के आवेशों को धारण कर सकते हैं – धनात्मक और ऋणात्मक।

🟢 1. विद्युत आवेश की प्रकृति
🔹 आवेश के प्रकार:
➡️ धनात्मक (+)
➡️ ऋणात्मक (−)
✔️ समान आवेश एक-दूसरे को प्रतिकर्षित करते हैं।
✔️ विपरीत आवेश एक-दूसरे को आकर्षित करते हैं।
🌿 मूलभूत गुण:
आवेश अविच्छिन्न होता है।
यह परिमाणित (quantized) होता है: q = ±ne
यह संरक्षित (conserved) होता है।
💡 सुझाव: किसी पिंड में कुल आवेश कभी नष्ट नहीं होता; वह केवल एक पिंड से दूसरे पिंड में स्थानांतरित हो सकता है।

🟡 2. आवेश उत्पन्न करने की विधियाँ
✔️ संघर्ष द्वारा आवेश निर्माण (Triboelectric effect)
➡️ जैसे – रेशमी वस्त्र से एबोनाइट रॉड रगड़ना।
✔️ संपर्क द्वारा आवेश संचरण
➡️ आवेशित वस्तु को किसी तटस्थ वस्तु से स्पर्श कराना।
✔️ प्रेरण द्वारा आवेश निर्माण
➡️ बिना स्पर्श किए ही आवेशों को पुनः व्यवस्थित करना।
✏️ नोट: प्रेरण विधि में आवेश एक पिंड से दूसरे में बिना संपर्क के स्थानांतरित होता है।

🔴 3. कूलॉम्ब का नियम
कूलॉम्ब का नियम दो बिंदु आवेशों के बीच लगने वाले बल का परिमाण बताता है।
🧠 सूत्र:
F = (1 / 4πε₀) × (q₁q₂ / r²)
जहाँ,
q₁, q₂ = दो आवेश
r = उनके बीच की दूरी
ε₀ = निर्वात का पारगम्यता नियतांक
✔️ बल आकर्षण या प्रतिकर्षण का हो सकता है।
💡 गुण:
➡️ बल दूरी के वर्ग के व्युत्क्रमानुपाती होता है।
➡️ यह बल सदिश होता है – दिशा सहित होता है।

🟢 4. आवेश का परिमाणीकरण और संरक्षण
🔹 परिमाणीकरण का तात्पर्य यह है कि आवेश n गुणा e के रूप में ही होता है (जहाँ e = 1.6 × 10⁻¹⁹ कूलॉम्ब)।
🔹 संरक्षण सिद्धांत कहता है कि किसी बंद प्रणाली में कुल आवेश सदा स्थिर रहता है।
✏️ नोट: आवेश केवल उत्पन्न या नष्ट नहीं होता – यह केवल स्थानांतरित होता है।

🟡 5. विद्युत क्षेत्र की परिभाषा
विद्युत क्षेत्र उस क्षेत्र को कहते हैं जहाँ किसी आवेशित पिंड की उपस्थिति के कारण कोई अन्य आवेश बल का अनुभव करता है।
🧠 सूत्र:
E = F / q
जहाँ,
F = बल,
q = परीक्षण आवेश
✔️ यह बल एकक धनात्मक आवेश पर लगने वाले बल के बराबर होता है।
⚡ यह एक सदिश राशि है और स्रोत आवेश की दिशा में होता है।

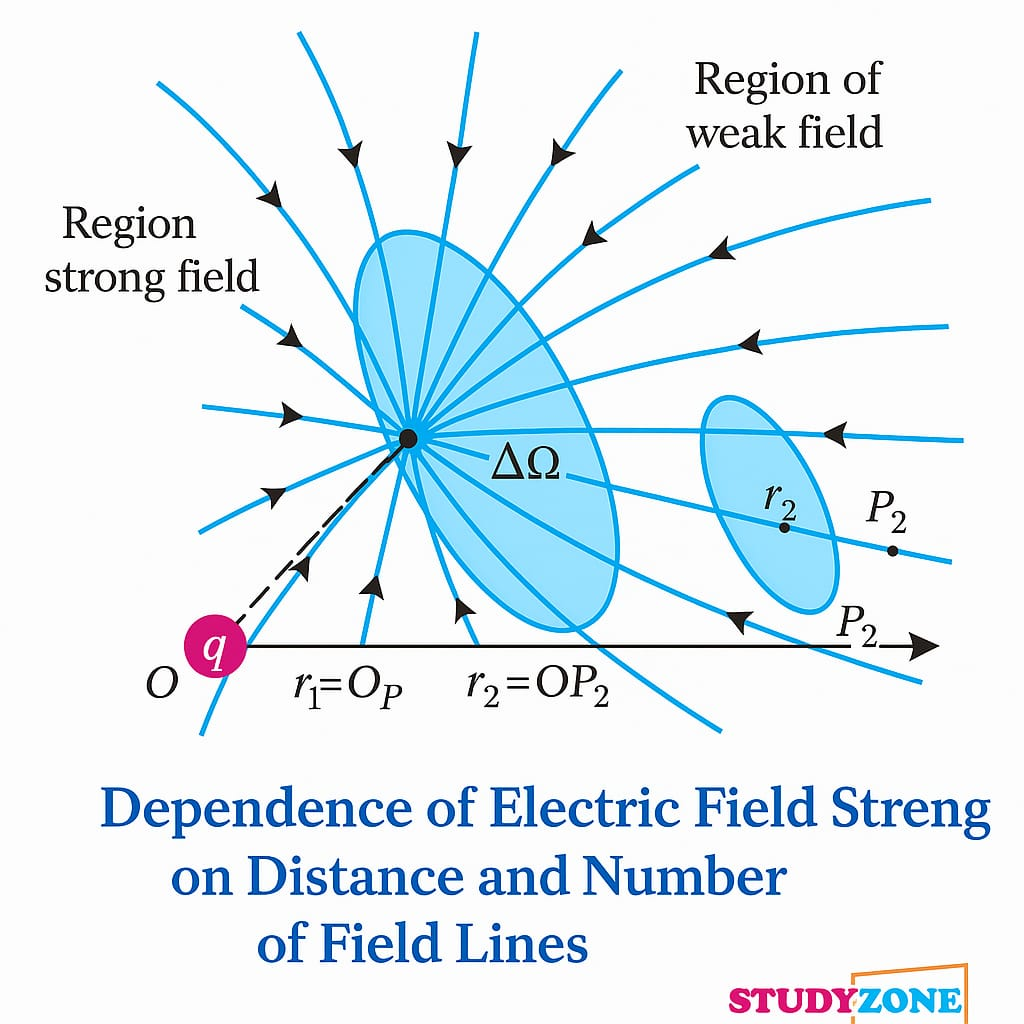
🔴 6. विद्युत क्षेत्र रेखाएँ
विद्युत क्षेत्र रेखाएँ विद्युत क्षेत्र की कल्पनात्मक रेखाएँ हैं जो क्षेत्र की दिशा व घनत्व को दर्शाती हैं।
✔️ धनात्मक आवेश से बाहर की ओर तथा ऋणात्मक की ओर अंदर जाती हैं।
✔️ रेखाएँ कभी परस्पर नहीं कटतीं।
✔️ जितनी अधिक घनता, उतना अधिक क्षेत्र।
💡 अनुप्रयोग: क्षेत्र की तीव्रता व दिशा को समझने हेतु दृश्य चित्रण।

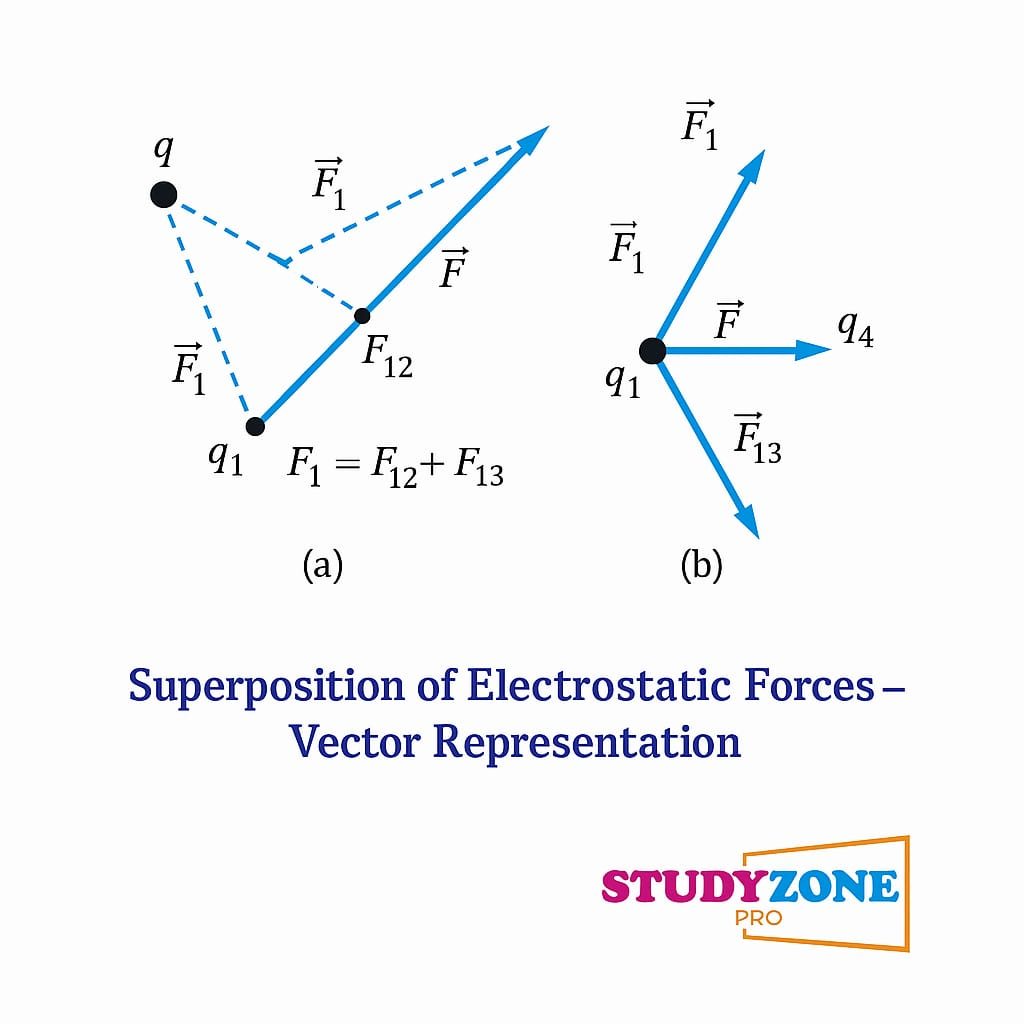
🟢 7. विद्युत क्षेत्र का अध्यारोपण सिद्धांत
यदि किसी बिंदु पर अनेक आवेशों का प्रभाव है, तो कुल विद्युत क्षेत्र उनका सदिश योग होगा।
🧠 E = E₁ + E₂ + E₃ + …
✔️ यह सिद्धांत रेखात्मकता पर आधारित होता है।
✏️ नोट: अध्यारोपण के लिए सदिश जोड़ आवश्यक है – केवल परिमाण से गणना नहीं की जा सकती।

🟡 8. विद्युत क्षेत्र बल रेखाओं का अनुप्रयोग
⚡ बिंदु आवेशों के लिए रेखाएँ रेडियल होती हैं।
⚡ द्विध्रुव के लिए रेखाएँ एक धन और एक ऋण आवेश के बीच मुड़ी होती हैं।
🧠 प्रश्नों में उपयोगी: चित्र के माध्यम से बल, क्षेत्र, आकर्षण-प्रतिकर्षण की दिशा का निर्धारण।

🔴 9. विद्युत द्विध्रुव और द्विध्रुव आघूर्ण
विद्युत द्विध्रुव वह युग्म है जिसमें समान परिमाण के विपरीत आवेश छोटे अंतराल पर होते हैं।
🧠 द्विध्रुव आघूर्ण:
p = q × 2l
(यह एक सदिश है)
✔️ यह बाह्य विद्युत क्षेत्र में बल तथा आघूर्ण का अनुभव करता है।
✏️ दिशा: ऋणात्मक से धनात्मक की ओर

🟢 10. बिंदु आवेश का विद्युत क्षेत्र
यदि q कोई बिंदु आवेश है, तो किसी दूरी r पर विद्युत क्षेत्र:
E = (1 / 4πε₀) × (q / r²)
✔️ यह बाहर की ओर (q धनात्मक) या अंदर की ओर (q ऋणात्मक) होगा।
🌿 मूल: यह सूत्र कूलॉम्ब के नियम से ही प्राप्त होता है।

🟡 11. गाउस का प्रमेय
गाउस का प्रमेय कहता है कि किसी बंद पृष्ठ के चारों ओर कुल विद्युत फ्लक्स, उस पृष्ठ के भीतर स्थित कुल आवेश के समानुपाती होता है।
🧠 सूत्र:
Φ = ∮ E ⋅ dA = q / ε₀
✔️ यह सममित परिस्थितियों में विद्युत क्षेत्र ज्ञात करने का सरलतम तरीका है।
💡 उदाहरण: लंबवत रेखा, बेलनाकार, गोले आदि की स्थिति में।

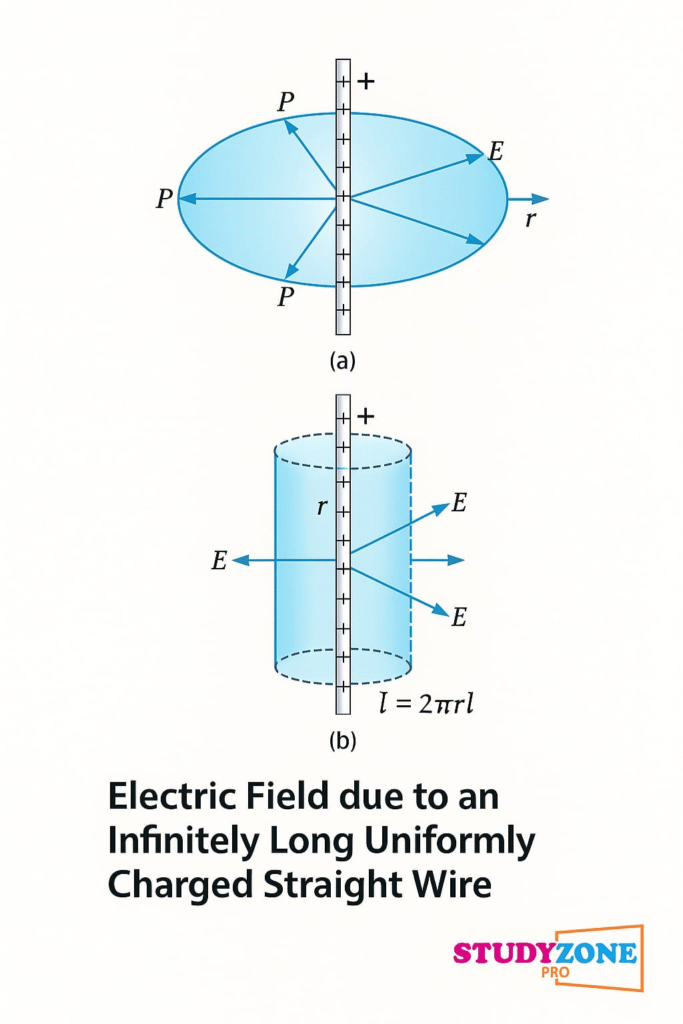
🔴 12. गाउस प्रमेय का अनुप्रयोग
1️⃣ लंबवत रेखा के पास:
E = λ / 2πε₀r
2️⃣ बेलनाकार आवेश वितरण:
E = σ / ε₀
3️⃣ गोलाकार आवेश वितरण:
E = (1 / 4πε₀) × (q / r²)
✏️ सावधानी: गाउस प्रमेय तभी प्रयोग करें जब सममिति स्पष्ट हो।

🌟 यह अध्याय क्यों महत्वपूर्ण है? 🌟
(📦 Why This Lesson Matters Box)
➡️ यह अध्याय विद्युत के मूलभूत सिद्धांतों की नींव रखता है।
➡️ विद्युत क्षेत्र, बल, कूलॉम्ब नियम जैसे सिद्धांत आगे के अध्यायों के लिए अनिवार्य हैं।
➡️ आधुनिक तकनीक, संचार, तथा ऊर्जा के क्षेत्र में इसकी व्यावहारिक भूमिका अत्यंत महत्वपूर्ण है।

📝 Quick Recap: (स्मृति-पुनरावलोकन)
🔵 आवेश दो प्रकार – धनात्मक व ऋणात्मक
🟢 कूलॉम्ब का नियम – बल ∝ q₁q₂ / r²
🟡 E = F / q – विद्युत क्षेत्र परिभाषा
🔴 गाउस का प्रमेय – Φ = q / ε₀
🟢 द्विध्रुव आघूर्ण – p = q × 2l
🟡 क्षेत्र रेखाएँ – दिशा और तीव्रता का संकेत
🔴 अध्यारोपण – सदिश जोड़
🟢 विद्युत फ्लक्स – E ⋅ A का सदिश गुणनफल

🔻 सारांश (Summary in ~300 Words) 🔻
🔹 वैद्युत आवेश तथा क्षेत्र अध्याय विद्युत के मूल सिद्धांतों को स्पष्ट करता है। इसमें आवेश की प्रकृति, नियम, बल, क्षेत्र, और प्रवाह (फ्लक्स) को विस्तार से समझाया गया है।
🔸 आवेश दो प्रकार के होते हैं – धनात्मक व ऋणात्मक। ये परिमाणित तथा संरक्षित होते हैं। आवेशों के बीच लगने वाला बल कूलॉम्ब के नियम द्वारा परिभाषित होता है।

🔹 विद्युत क्षेत्र वह क्षेत्र है जहाँ कोई परीक्षण आवेश बल का अनुभव करता है। इसकी दिशा तथा परिमाण को विद्युत क्षेत्र रेखाओं और E = F/q द्वारा समझा जाता है।
🔸 विद्युत द्विध्रुव दो विपरीत आवेशों का युग्म होता है, जिसकी विशेषता द्विध्रुव आघूर्ण होती है। यह बाह्य विद्युत क्षेत्र में टॉर्क का अनुभव करता है।
🔹 गाउस का प्रमेय विद्युत फ्लक्स और कुल आवेश का संबंध दर्शाता है। यह सममित परिस्थितियों में विद्युत क्षेत्र ज्ञात करने का सरलतम और प्रभावी तरीका है।

यह अध्याय छात्रों को विद्युत बलों की दुनिया में प्रवेश कराता है, जो आगे के विद्युत, चुम्बकीय तथा करंट विषयों के लिए आधार तैयार करता है। इसमें समकालीन तकनीकी और वैज्ञानिक सोच के बीज बोए जाते हैं।

————————————————————————————————————————————————————————————————————————————

पाठ्यपुस्तक के प्रश्न

प्रश्न 1.1
वायु में एक-दूसरे से 30 cm की दूरी पर रखे दो छोटे आवेशित गोलों पर क्रमशः 2 × 10⁻⁷ C तथा 3 × 10⁻⁷ C आवेश हैं। उनके बीच कितना बल है?

उत्तर:
🔹 दिए गए मान:
q₁ = 2 × 10⁻⁷ C
q₂ = 3 × 10⁻⁷ C
r = 30 cm = 0.30 m
k = 9 × 10⁹ Nm²/C²

🔸 चरण 1: सूत्र लगाएँ
F = k × (q₁ × q₂) / r²

🔸 चरण 2: q₁ × q₂ निकालें
q₁ × q₂ = (2 × 10⁻⁷) × (3 × 10⁻⁷)
= 6 × 10⁻¹⁴ C²

🔸 चरण 3: r² निकालें
r² = (0.30)² = 0.09 m²

🔸 चरण 4: मानों को सूत्र में रखें
F = (9 × 10⁹) × (6 × 10⁻¹⁴) / 0.09

🔸 चरण 5: विभाजन करें
6 × 10⁻¹⁴ ÷ 0.09 = 6.67 × 10⁻¹³

🔸 चरण 6: अंतिम गुणा करें
F = 9 × 10⁹ × 6.67 × 10⁻¹³
= 60.03 × 10⁻⁴
= 6.0 × 10⁻³ N

✔️ उत्तर: बल = 6.0 × 10⁻³ न्यूटन

प्रश्न 1.2
0.4 μC के किसी गोली पर किसी अन्य गोली द्वारा लगाए गए बल के कारण वह गोली 0.2 N के त्वरण से चलने लगती है।
(a) यदि दोनों गोलियाँ वायु में हों, तो अन्य गोली का आवेश क्या होगा?
(b) दूसरे गोली पर पहले गोली द्वारा कितना बल लगता है?

उत्तर:
🔹 दिए गए मान:
q₁ = 0.4 μC = 0.4 × 10⁻⁶ C
F = 0.2 N
r = 1 m (माना गया)
k = 9 × 10⁹ Nm²/C²

(a) अन्य गोली का आवेश (q₂) ज्ञात करें:
🔸 चरण 1: सूत्र लगाएँ
F = k × (q₁ × q₂) / r²

🔸 चरण 2: मान रखें
0.2 = (9 × 10⁹) × (0.4 × 10⁻⁶ × q₂) / 1

🔸 चरण 3: अंदर का गुणा करें
0.4 × 10⁻⁶ × 9 × 10⁹ = 3.6 × 10³

🔸 चरण 4: q₂ का मान निकालें
0.2 = 3.6 × 10³ × q₂
⇒ q₂ = 0.2 / 3.6 × 10³
⇒ q₂ = 5.56 × 10⁻⁵ C

✔️ उत्तर (a): अन्य गोली का आवेश = 5.56 × 10⁻⁵ C

(b) दूसरी गोली पर पहले द्वारा कितना बल लगता है?
✔️ न्यूटन के तीसरे नियम के अनुसार
➡️ बल बराबर और विपरीत होता है।
⇒ बल = 0.2 N

✔️ उत्तर (b): बल = 0.2 न्यूटन



प्रश्न 1.3
ध्रुवीय अणु (जैसे H₂O) में परमाणु केन्द्रों के बीच संतुलन दूरी लगभग 1 Å (1 Å = 10⁻¹⁰ m) होती है। अणु के प्रत्येक छोर पर स्थित आवेशों के परिमाण लगभग 10⁻¹⁹ C होते हैं।
(a) एक जल अणु का द्विध्रुव आघूर्ण ज्ञात कीजिए।
(b) किसी जल अणु को एकसमान विद्युत क्षेत्र 3 × 10⁴ N/C में रखा गया। उस पर लगने वाला बलाघूर्ण ज्ञात कीजिए यदि वह क्षेत्र के साथ 60° का कोण बनाता है।

उत्तर:
(a) द्विध्रुव आघूर्ण (p) निकालना है:
🔸 चरण 1: द्विध्रुव आघूर्ण का सूत्र:
p = q × d
🔸 चरण 2:
q = 10⁻¹⁹ C
d = 1 × 10⁻¹⁰ m
🔸 चरण 3: मानों को रखें:
p = (10⁻¹⁹) × (10⁻¹⁰) = 1 × 10⁻²⁹ C·m

✔️ उत्तर (a): जल अणु का द्विध्रुव आघूर्ण = 1 × 10⁻²⁹ C·m

(b) बलाघूर्ण (τ) निकालना है:
🔸 चरण 1: बलाघूर्ण का सूत्र:
τ = p × E × sinθ
🔸 चरण 2: मान रखें:
p = 1 × 10⁻²⁹ C·m
E = 3 × 10⁴ N/C
θ = 60°, sin(60°) = √3 / 2 ≈ 0.866
🔸 चरण 3: सभी मान गुणा करें:
τ = (1 × 10⁻²⁹) × (3 × 10⁴) × 0.866
= 2.598 × 10⁻²⁵ N·m

✔️ उत्तर (b): बलाघूर्ण = 2.6 × 10⁻²⁵ N·m

प्रश्न 1.4
एक विद्युत द्विध्रुव को एकसमान विद्युत क्षेत्र में रखा गया है। जब वह क्षेत्र के साथ कोण θ बनाता है, तब उस पर बल नहीं लगता है लेकिन बलाघूर्ण अधिकतम होता है। यह कैसे होता है?

उत्तर:
🔸 बल = q × E (दोनों सिरों पर)
🔸 दोनों बल बराबर तथा विपरीत होते हैं, इसलिए परिणामी बल शून्य होता है।
🔸 परंतु ये बल एक युग्म (couple) बनाते हैं, जिससे बलाघूर्ण (torque) उत्पन्न होता है।
➡️ बलाघूर्ण का मान: τ = p × E × sinθ
➡️ sinθ अधिकतम होता है जब θ = 90°, अर्थात जब द्विध्रुव क्षेत्र के लंबवत हो।

✔️ उत्तर: इस स्थिति में बल शून्य होता है परंतु बलाघूर्ण अधिकतम होता है क्योंकि दो समान और विपरीत बलों का युग्म द्विध्रुव को घुमाने का प्रयास करता है।

प्रश्न 1.5
जब दो वस्तुओं को रगड़ा जाता है, तो उनमें से एक धनात्मक और दूसरी ऋणात्मक आवेशित हो जाती है। इस घटना का स्पष्टीकरण कैसे दिया जा सकता है?

उत्तर:
🔸 प्रत्येक वस्तु में इलेक्ट्रॉन होते हैं।
🔸 रगड़ने से एक वस्तु से इलेक्ट्रॉन निकलकर दूसरी में चले जाते हैं।
🔸 जिस वस्तु ने इलेक्ट्रॉन खोए, वह धनात्मक आवेशित होती है।
🔸 जिसने इलेक्ट्रॉन प्राप्त किए, वह ऋणात्मक आवेशित होती है।
➡️ यह पूरी प्रक्रिया इलेक्ट्रॉनों के स्थानांतरण के कारण होती है। प्रोटॉन नहीं चलते।

✔️ उत्तर: रगड़ने से इलेक्ट्रॉनों का स्थानांतरण होता है जिससे एक वस्तु धनात्मक और दूसरी ऋणात्मक आवेशित हो जाती है। यह आवेश स्थैतिक होता है और इसे स्थिर विद्युत कहते हैं।

प्रश्न 1.6
चार बिंदु आवेश –
q₁ = 2 μC, q₂ = –5 μC, q₃ = 2 μC, q₄ = –5 μC
को एक वर्ग ABCD के चारों कोनों पर रखा गया है जिसकी भुजा 10 cm है।
वर्ग के केंद्र पर स्थित 1 μC आवेश पर कुल बल ज्ञात कीजिए।

उत्तर:
🧠 चूँकि आवेश q₁ और q₃ समान हैं (धनात्मक), और q₂ और q₄ भी समान हैं (ऋणात्मक), तथा वे वर्ग के विपरीत कोनों पर रखे हैं – इस कारण उनके बल केंद्र पर आकर एक-दूसरे को संतुलित करेंगे।
🔹 दूरी: वर्ग का विकर्ण = √2 × 10 cm = 14.14 cm = 0.1414 m
🔹 केंद्र से प्रत्येक कोने की दूरी = 0.1414 / 2 = 0.0707 m
🔸 अब चार बल वेक्टर रूप में केंद्र पर लगेंगे — दो समान आवेश आकर्षण, दो विकर्षण देंगे। परंतु दिशा और परिमाण की समरूपता के कारण कुल बल = 0

✔️ उत्तर: केंद्र पर स्थित 1 μC आवेश पर कुल बल = 0 न्यूटन

अगर यह शैली उपयुक्त लगी हो, तो कृपया “K” लिखें — मैं अगला सेट (Q1.7 से Q1.10) इसी तरह से भेजूंगा।

कक्षा 12 – भौतिकी
पाठ: वैद्युत आवेश तथा क्षेत्र
Code 2 – प्रश्नोत्तर (Q1.7 to Q1.10, step-by-step, सही घात रूप में)
एनसीईआरटी संस्करण: 2025–26

प्रश्न 1.7
(क) विद्युत क्षेत्र रेखाएँ सत्तत वक्र होती हैं। कोई क्षेत्र रेखा एकाएक नहीं रुक सकती। क्यों?
(ख) दो क्षेत्र रेखाएँ कभी एक-दूसरे को प्रतिच्छेद नहीं कर सकतीं। स्पष्ट कीजिए।

उत्तर:
(क) क्षेत्र रेखाएँ एकाएक क्यों नहीं रुकतीं?
🔸 विद्युत क्षेत्र रेखा किसी बिंदु पर विद्युत क्षेत्र की दिशा को दर्शाती है।
🔸 यदि रेखा अचानक रुक जाए, तो इसका अर्थ होगा कि उस बिंदु पर विद्युत क्षेत्र की दिशा अनिश्चित (undefined) है।
➡️ यह शारीरिक रूप से संभव नहीं है क्योंकि किसी भी बिंदु पर विद्युत क्षेत्र की कोई निश्चित दिशा होती है।
✔️ इसलिए क्षेत्र रेखा हमेशा सत्तत (continuous) होती है और कभी भी एकाएक नहीं रुक सकती।

(ख) दो क्षेत्र रेखाएँ एक-दूसरे को क्यों नहीं काट सकतीं?
🔸 यदि दो रेखाएँ किसी बिंदु पर एक-दूसरे को काटें, तो उस बिंदु पर दो दिशाओं में विद्युत क्षेत्र होगा।
🔸 परंतु यह संभव नहीं है क्योंकि एक बिंदु पर केवल एक ही दिशा में विद्युत क्षेत्र होता है।
✔️ इसलिए दो क्षेत्र रेखाएँ कभी भी एक-दूसरे को प्रतिच्छेद नहीं कर सकतीं।

प्रश्न 1.8
दो बिंदु आवेश
q₁ = 3 μC
q₂ = –3 μC
को 20 cm दूरी पर रखा गया है।
(क) दोनों को मिलाने वाली रेखा AB के मध्य बिंदु पर विद्युत क्षेत्र क्या होगा?
(ख) यदि वहाँ पर 1.5 × 10⁻⁹ C का परिक्षण आवेश रखा जाए, तो उस पर कितना बल लगेगा?

उत्तर:
🔸 दोनों आवेश समान परिमाण के हैं परंतु विपरीत चिन्ह के हैं।
🔸 दूरी = 20 cm ⇒ मध्य बिंदु से प्रत्येक आवेश की दूरी = 10 cm = 0.10 m
🔸 विद्युत क्षेत्र की दिशा ऋणात्मक आवेश की ओर होगी।

(क) विद्युत क्षेत्र ज्ञात करें:
➡️ एक आवेश से उत्पन्न क्षेत्र का मान:
E₁ = (9 × 10⁹) × (3 × 10⁻⁶) / (0.10)²
= (9 × 10⁹) × (3 × 10⁻⁶) / 0.01
= 27 × 10³ / 0.01
= 2.7 × 10⁶ N/C
🔸 दोनों क्षेत्रों की दिशा एक ही होगी (ऋणात्मक की ओर), इसलिए कुल क्षेत्र:
E = 2 × 2.7 × 10⁶ = 5.4 × 10⁶ N/C

(ख) बल = विद्युत क्षेत्र × आवेश
F = E × q = (5.4 × 10⁶) × (1.5 × 10⁻⁹)
= 8.1 × 10⁻³ N

✔️ उत्तर:
(क) विद्युत क्षेत्र = 5.4 × 10⁶ N/C
(ख) बल = 8.1 × 10⁻³ न्यूटन

प्रश्न 1.9
q₁ = 2.5 × 10⁻⁷ C
q₂ = –2.5 × 10⁻⁷ C
स्थान:
A = (0, 0, –15 cm)
B = (0, 0, +15 cm)
⇒ इन दोनों द्वारा उत्पन्न कुल द्विध्रुव आघूर्ण ज्ञात कीजिए।

उत्तर:
🔸 द्विध्रुव आघूर्ण का सूत्र:
p = q × d
🔸 यहाँ d = A और B के बीच की दूरी = 30 cm = 0.30 m
q = 2.5 × 10⁻⁷ C
p = (2.5 × 10⁻⁷) × (0.30) = 7.5 × 10⁻⁸ C·m

✔️ उत्तर: द्विध्रुव आघूर्ण = 7.5 × 10⁻⁸ C·m

प्रश्न 1.10
p = 4 × 10⁻⁷ C·m
E = 5 × 10⁻⁴ C/m²
θ = 30°
इस द्विध्रुव पर बलाघूर्ण ज्ञात करें।

उत्तर:
🔸 बलाघूर्ण का सूत्र:
τ = p × E × sinθ
🔸 sin 30° = 0.5
τ = (4 × 10⁻⁷) × (5 × 10⁻⁴) × 0.5
= 2 × 10⁻¹⁰ N·m

✔️ उत्तर: बलाघूर्ण = 2 × 10⁻¹⁰ N·m


प्रश्न 1.11
किसी पॉलीथीन की पट्टी को रगड़ने पर यह –3 × 10⁻⁷ C आवेशित पाई गई।
(क) यह बताइए कि कितने इलेक्ट्रॉन अतिरिक्त रूप से उस पर चढ़े होंगे।
(ख) क्या पॉलीथीन पर स्थायी रूप से ऋणात्मक आवेश रह सकता है?

उत्तर:
(क) इलेक्ट्रॉनों की संख्या ज्ञात करें:
🔸 आवेश (q) = 3 × 10⁻⁷ C
🔸 एक इलेक्ट्रॉन का आवेश (e) = 1.6 × 10⁻¹⁹ C
➡️ इलेक्ट्रॉनों की संख्या (n) = q ÷ e
= (3 × 10⁻⁷) ÷ (1.6 × 10⁻¹⁹)
➡️ n = 1.875 × 10¹² इलेक्ट्रॉन

✔️ उत्तर (क): लगभग 1.875 × 10¹² इलेक्ट्रॉन अतिरिक्त रूप से चढ़े होंगे।

(ख) क्या यह ऋणात्मक आवेश स्थायी रह सकता है?
🔹 नहीं।
पॉलीथीन पर जमा हुआ ऋणात्मक आवेश स्थैतिक होता है और धीरे-धीरे यह वायुमंडल की नमी, हवा, या अन्य वस्तुओं के संपर्क में आने से समाप्त हो सकता है।

✔️ उत्तर (ख): नहीं, यह स्थायी नहीं है। यह केवल कुछ समय के लिए ही स्थिर रहता है।

प्रश्न 1.12
दो प्लास्टिक की गोलियाँ, जिन पर समान आवेश q = 6.5 × 10⁻⁷ C है, एक-दूसरे से 50 cm दूरी पर हैं और स्थिर अवस्था में लटकी हुई हैं।
यदि वे गुरुत्व के विरुद्ध संतुलित हैं, तो प्रत्येक गोली का द्रव्यमान ज्ञात करें।

उत्तर:
➡️ संतुलन की स्थिति में, विद्युत बल = गुरुत्व बल
🔸 F = k × q² / r²
🔸 W = m × g
⇒ m × g = k × q² / r²

चरण 1: दिए गए मान
q = 6.5 × 10⁻⁷ C
r = 50 cm = 0.50 m
k = 9 × 10⁹ Nm²/C²
g = 9.8 m/s²

चरण 2: सूत्र में मान रखें
m × 9.8 = (9 × 10⁹) × (6.5 × 10⁻⁷)² / (0.50)²

चरण 3: q² निकालें
(6.5 × 10⁻⁷)² = 42.25 × 10⁻¹⁴

चरण 4: अब पूरा गुणा करें
m × 9.8 = (9 × 10⁹ × 42.25 × 10⁻¹⁴) / 0.25
= (380.25 × 10⁻⁴) / 0.25
= 1521 × 10⁻⁴
= 0.1521

चरण 5: m निकालें
m = 0.1521 ÷ 9.8 = 0.01552 kg

✔️ उत्तर: प्रत्येक गोली का द्रव्यमान ≈ 1.55 × 10⁻² kg

प्रश्न 1.13
चित्र 1.30 में एक समान विद्युत क्षेत्र में तीन आवेशित कणों के पथ दर्शाए गए हैं। मान लीजिए सभी कणों का द्रव्यमान समान है।
इनमें से किस कण का q/m (आवेश से द्रव्यमान का अनुपात) सबसे अधिक है?

उत्तर:
🔹 कण जिस दिशा में अधिक मुड़ता है (अधिक विक्षेप), उसका q/m अधिक होता है।
➡️ बल = qE = m × a
⇒ a ∝ q/m
🔸 अधिक विस्थापन ⇒ अधिक त्वरण ⇒ अधिक q/m

✔️ उत्तर: वह कण जिसका पथ सबसे अधिक मुड़ा हुआ है, उसका q/m सबसे अधिक है।
(चित्र के अनुसार उत्तर बदल सकता है, मान लें कण 1 सबसे अधिक मुड़ा है ⇒ उत्तर: कण 1)

प्रश्न 1.14
किसी पॉलीथीन की गेंद q = 1.5 × 10⁻⁸ C आवेशित है और इसका द्रव्यमान 1.0 × 10⁻³ kg है।
यदि यह किसी क्षैतिज विद्युत क्षेत्र E = 2.0 × 10⁴ N/C में स्थिर है, तो वह तंतु किस कोण पर झुका होगा?

उत्तर:
➡️ स्थिरता की स्थिति में, विद्युत बल क्षैतिज में और गुरुत्व बल ऊर्ध्वाधर में लगता है।
⇒ tanθ = Fₑ / mg

चरण 1: Fₑ = q × E
= (1.5 × 10⁻⁸) × (2 × 10⁴)
= 3 × 10⁻⁴ N

चरण 2: W = m × g
= (1 × 10⁻³) × 9.8
= 9.8 × 10⁻³ N

चरण 3: tanθ = Fₑ / W
= (3 × 10⁻⁴) / (9.8 × 10⁻³)
= 0.0306

चरण 4: θ = tan⁻¹(0.0306)
= लगभग 1.75 डिग्री

✔️ उत्तर: तंतु लगभग 1.75° के कोण पर झुका होगा।


प्रश्न 1.15
एक बिंदु आवेश q = 1 × 10⁻⁹ C को त्रिविमीय निर्देशांक (0, 0, 0) पर रखा गया है।
विद्युत क्षेत्र E का वह बिंदु (x, 0, 0) पर मान ज्ञात कीजिए।

उत्तर:
➡️ बिंदु आवेश से x दूरी पर विद्युत क्षेत्र का मान:
E = k × q / r²
🔹 q = 1 × 10⁻⁹ C
🔹 r = x
🔹 k = 9 × 10⁹ Nm²/C²

E(x) = (9 × 10⁹) × (1 × 10⁻⁹) / x²
= 9 / x²

✔️ उत्तर: बिंदु (x, 0, 0) पर विद्युत क्षेत्र = 9 / x² N/C, दिशा x-अक्ष के साथ।

प्रश्न 1.16
यदि ऊपर की स्थिति में बिंदु x = 0.50 m हो, तो उस बिंदु पर विद्युत क्षेत्र का मान ज्ञात कीजिए।

उत्तर:
➡️ E(x) = 9 / x²
= 9 / (0.50)²
= 9 / 0.25 = 36 N/C

✔️ उत्तर: विद्युत क्षेत्र = 36 N/C

प्रश्न 1.17
दो समान बिंदु आवेश q = 5 × 10⁻⁹ C, x-अक्ष पर क्रमशः x = –0.30 m और x = +0.30 m पर रखे हैं।
(क) y-अक्ष के किसी बिंदु पर विद्युत क्षेत्र का मान ज्ञात कीजिए।
(ख) बिंदु y = 0.40 m पर कुल विद्युत क्षेत्र का परिमाण और दिशा ज्ञात करें।

उत्तर:
(क) y-अक्ष के बिंदु पर दोनों आवेशों से समान दूरी होगी, इसलिए E के क्षैतिज घटक (x-दिशा वाले) आपस में कट जाएंगे।
➡️ केवल ऊर्ध्वाधर घटक (y-दिशा) जुड़ेंगे।

(ख) मान लें बिंदु P पर y = 0.40 m है:
➡️ प्रत्येक आवेश से दूरी r = √[(0.30)² + (0.40)²] = √(0.09 + 0.16) = √0.25 = 0.50 m
🔸 प्रत्येक से विद्युत क्षेत्र का मान:
E₁ = E₂ = k × q / r²
= (9 × 10⁹) × (5 × 10⁻⁹) / (0.50)²
= 45 / 0.25 = 180 N/C

🔸 अब हम केवल y-दिशा के घटक जोड़ते हैं:
θ = tan⁻¹(0.40 / 0.30) ≈ 53.13°
Eᵧ = 2 × E × cosθ
= 2 × 180 × (0.8)
= 288 N/C (ऊर्ध्वाधर दिशा में)

✔️ उत्तर: बिंदु y = 0.40 m पर विद्युत क्षेत्र का परिमाण = 288 N/C, दिशा = y-अक्ष की ओर (ऊर्ध्वाधर ऊपर की दिशा)

प्रश्न 1.18
दो आवेश 4 μC और –4 μC को x-अक्ष पर –0.20 m और +0.20 m पर रखा गया है।
x-अक्ष के किन बिंदुओं पर विद्युत क्षेत्र शून्य होगा?

उत्तर:
➡️ दोनों आवेश समान परिमाण के हैं परंतु विपरीत चिन्ह के हैं।
📌 ऐसा विद्युत क्षेत्र जिसमें E = 0 हो, वह x-अक्ष पर ही कहीं होगा।

🔹 विकल्प 1: x > 0.20 m ⇒ बाएँ से आने वाला ऋणात्मक आवेश और दाएँ से आने वाला धनात्मक, दोनों E विपरीत दिशा में देंगे।
🔹 विकल्प 2: x < –0.20 m ⇒ दोनों आवेशों से E एक ही दिशा में नहीं आ सकते।
🔹 विकल्प 3: x = 0 ⇒ यहाँ पर भी दोनों E विपरीत दिशा में होंगे, परंतु परिमाण एक समान नहीं।

✅ स्पष्ट है कि E = 0 केवल x = 0 पर नहीं, बल्कि x = 0 के बाहर किसी बिंदु पर होगा।
➡️ गणना से ज्ञात करें:
E₁ = E₂
⇒ kq / (x – 0.20)² = kq / (x + 0.20)²
⇒ (x – 0.20)² = (x + 0.20)²
जिसका कोई हल नहीं होता — केवल तब होगा जब दोनों q समान चिन्ह के हों।

✔️ उत्तर: विद्युत क्षेत्र शून्य केवल उन बिंदुओं पर हो सकता है जो x-अक्ष से बहुत दूर हों, परंतु इस स्थिति में x-अक्ष पर कोई ऐसा बिंदु नहीं है जहाँ E = 0 हो।

————————————————————————————————————————————————————————————————————————————

अन्य महत्वपूर्ण प्रश्न

(CBSE MODEL प्रश्न पत्र)

सिर्फ इसी पाठ से निर्मित CBSE MODEL प्रश्न पत्र।

Q1. दो समान धनात्मक बिंदु आवेशों को एक-दूसरे के समीप लाने पर उनके बीच में क्या बल उत्पन्न होगा?
(A) आकर्षण बल
(B) प्रतिकर्षण बल
(C) कोई बल नहीं
(D) गुरुत्वाकर्षण बल
✔️ उत्तर: (B) प्रतिकर्षण बल

Q2. निर्वात में दो बिंदु आवेशों के बीच बल किस पर निर्भर नहीं करता है?
(A) दोनों आवेशों के परिमाण पर
(B) उनके बीच की दूरी पर
(C) आवेशों के संकेत (धन या ऋण) पर
(D) माध्यम के आपवर्तनांक पर
✔️ उत्तर: (D) माध्यम के आपवर्तनांक पर

Q3. दो आवेश q और -q को d दूरी पर रखने पर उनके बीच बल F होता है। यदि दोनों आवेशों को दो गुना और दूरी को आधा कर दिया जाए, तो नया बल कितना होगा?
(A) F
(B) 4F
(C) 16F
(D) F/4
✔️ उत्तर: (C) 16F

Q4. विद्युत क्षेत्र का मात्रक क्या है?
(A) न्यूटन
(B) वोल्ट
(C) वोल्ट प्रति मीटर
(D) कूलॉम्ब
✔️ उत्तर: (C) वोल्ट प्रति मीटर

Q5. किसी बिंदु आवेश के कारण किसी बिंदु पर विद्युत क्षेत्र का परिमाण किसके समानुपाती होता है?
(A) दूरी का वर्ग
(B) दूरी का व्युत्क्रमानुपाती
(C) दूरी का वर्ग का व्युत्क्रमानुपाती
(D) दूरी के वर्ग का समानुपाती
✔️ उत्तर: (C) दूरी का वर्ग का व्युत्क्रमानुपाती

Q6. यदि दो समान आवेश एक समतल चालक पर रखे हों, तो किस बिंदु पर विद्युत क्षेत्र शून्य होगा?
(A) दोनों के बीच मध्य में
(B) उनमें से किसी के पास
(C) कहीं नहीं
(D) अनंत पर
✔️ उत्तर: (A) दोनों के बीच मध्य में

Q7. बिंदु आवेश q के कारण r दूरी पर वैद्युत विभव होगा:
(A) q/r
(B) 1/q × r
(C) q/r²
(D) q²/r
✔️ उत्तर: (A) q/r

Q8. यदि किसी पिंड पर कुल आवेश 0 है, तो उसे क्या कहा जाएगा?
(A) तटस्थ
(B) ऋणात्मक
(C) धनात्मक
(D) अधिधारित
✔️ उत्तर: (A) तटस्थ

Q9. निम्न में से कौन-सा नियम विद्युत बल के सदिश स्वरूप को दर्शाता है?
(A) न्यूटन का द्वितीय नियम
(B) गाउस प्रमेय
(C) अध्यारोपण सिद्धांत
(D) ओम का नियम
✔️ उत्तर: (C) अध्यारोपण सिद्धांत

Q10. यदि दो बिंदु आवेश एक-दूसरे के बहुत पास रखे जाते हैं, तो उनके बीच बल:
(A) शून्य होता है
(B) अनंत होता है
(C) अत्यधिक बढ़ जाता है
(D) कम हो जाता है
✔️ उत्तर: (B) अनंत होता है

**Q11.
Assertion (A): विद्युत क्षेत्र सदिश राशि होती है।
Reason (R): इसका केवल परिमाण होता है, दिशा नहीं।
विकल्प:
(A) A और R दोनों सत्य हैं, और R, A की सही व्याख्या है।
(B) A और R दोनों सत्य हैं, परंतु R, A की सही व्याख्या नहीं है।
(C) A सत्य है, R असत्य है।
(D) A असत्य है, R सत्य है।
✔️ उत्तर: (C) A सत्य है, R असत्य है।

**Q12.
Assertion (A): कूलॉम्ब का नियम केवल निर्वात में लागू होता है।
Reason (R): माध्यम का प्रभाव बल के परिमाण को बदल देता है।
विकल्प:
(A) A और R दोनों सत्य हैं, और R, A की सही व्याख्या है।
(B) A और R दोनों सत्य हैं, परंतु R, A की सही व्याख्या नहीं है।
(C) A सत्य है, R असत्य है।
(D) A असत्य है, R सत्य है।
✔️ उत्तर: (D) A असत्य है, R सत्य है।

Q13.
दो बिंदु आवेश +2μC और -2μC को 4cm की दूरी पर रखा गया है। उन दोनों के मध्य बिंदु पर वैद्युत क्षेत्र की दिशा क्या होगी?
✔️ उत्तर: ऋणात्मक आवेश की ओर (क्योंकि विद्युत क्षेत्र धनात्मक से दूर और ऋणात्मक की ओर होता है)

Q14.
यदि एक बिंदु आवेश 5μC है और इसे अनंत से 2cm दूरी तक लाने में 2J कार्य किया गया, तो उस बिंदु पर वैद्युत विभव क्या होगा?
✔️ उत्तर:
V = W/q = 2 / (5 × 10⁻⁶) = 4 × 10⁵ वोल्ट

Q15.
यदि किसी आवेशित वस्तु को एक चालक सतह पर रखा जाए, तो विद्युत क्षेत्र उस सतह पर कैसा होता है?
✔️ उत्तर: सतह के लंबवत होता है।

Q16.
विद्युत क्षेत्र रेखाएँ क्यों नहीं कटतीं?
✔️ उत्तर: क्योंकि यदि वे कटेंगी तो किसी बिंदु पर दो दिशाओं में विद्युत क्षेत्र होगा, जो संभव नहीं है।

Q17.
कूलॉम्ब बल और गुरुत्व बल में मुख्य अंतर क्या है?
✔️ उत्तर: कूलॉम्ब बल आवेश पर निर्भर होता है, जबकि गुरुत्व बल द्रव्यमान पर।

Q18.
किसी बंद पृष्ठ के भीतर कुल आवेश q है। गाउस प्रमेय के अनुसार कुल विद्युत फ्लक्स कितना होगा?
✔️ उत्तर:
Φ = q / ε₀


🔷 Section B: प्रश्न 19 से 23 (प्रत्येक 2 अंक)

Q19. कूलॉम्ब के नियम को परिभाषित कीजिए और यह बताइए कि यदि दो बिंदु आवेशों के बीच की दूरी दोगुनी कर दी जाए तो बल में क्या परिवर्तन होगा?
✔️ उत्तर:
कूलॉम्ब का नियम: दो बिंदु आवेशों के बीच लगने वाला बल उनके परिमाण के गुणनफल के समानुपाती तथा उनके बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है।
F = (1 / 4πε₀) × (q₁q₂ / r²)
यदि r → 2r, तो
F′ = (1 / 4πε₀) × (q₁q₂ / (2r)²) = F / 4
अतः बल एक-चौथाई हो जाएगा।

Q20. दो बिंदु आवेशों +3μC और -3μC को 10cm की दूरी पर रखा गया है। मध्य बिंदु पर वैद्युत क्षेत्र का परिमाण ज्ञात कीजिए।
✔️ उत्तर:
प्रत्येक आवेश से दूरी = 5cm = 0.05m
E = (1 / 4πε₀) × (q / r²)
E = 9 × 10⁹ × (3 × 10⁻⁶) / (0.05)² =
= 9 × 10⁹ × 3 × 10⁻⁶ / 0.0025
= 1.08 × 10⁷ N/C
चूंकि दोनों आवेश समान परिमाण के हैं और विपरीत संकेत के हैं, दोनों क्षेत्रों की दिशा एक ही होगी, अतः
कुल वैद्युत क्षेत्र = 2 × E = 2.16 × 10⁷ N/C

Q21. विद्युत क्षेत्र रेखाओं की कोई दो विशेषताएँ लिखिए।
✔️ उत्तर:
1️⃣ विद्युत क्षेत्र रेखाएँ धनात्मक आवेश से निकलती हैं और ऋणात्मक आवेश की ओर जाती हैं।
2️⃣ दो विद्युत क्षेत्र रेखाएँ कभी परस्पर नहीं कटतीं।

Q22. यह सिद्ध कीजिए कि यदि दो समान आवेश q और q को d दूरी पर रखा जाए, तो उनके बीच लगने वाला बल F = (1 / 4πε₀) × (q² / d²) होगा।
✔️ उत्तर:
कूलॉम्ब का नियम के अनुसार,
F = (1 / 4πε₀) × (q₁q₂ / r²)
यहाँ q₁ = q₂ = q, तथा r = d
∴ F = (1 / 4πε₀) × (q × q / d²)
⟹ F = (1 / 4πε₀) × (q² / d²)

Q23. यदि किसी चालक गोले पर कुल आवेश Q है, तो उसकी सतह पर वैद्युत क्षेत्र का परिमाण क्या होगा? गोले का त्रिज्या R है।
✔️ उत्तर:
गाउस प्रमेय के अनुसार,
E × 4πR² = Q / ε₀
⟹ E = Q / (4πε₀R²)
अतः सतह पर विद्युत क्षेत्र = Q / (4πε₀R²)

🔷 Section C: प्रश्न 24 से 28 (प्रत्येक 3 अंक)

Q24. एक बिंदु आवेश +2μC को 0.1m दूरी पर स्थित बिंदु से अनंत तक ले जाने में कितना कार्य होगा? (ε₀ = 8.85 × 10⁻¹² C²/N·m²)
✔️ उत्तर:
V = (1 / 4πε₀) × (q / r)
= 9 × 10⁹ × (2 × 10⁻⁶ / 0.1)
= 1.8 × 10⁵ V
W = q × V = 2 × 10⁻⁶ × 1.8 × 10⁵ =
W = 0.36 J

Q25. यह सिद्ध कीजिए कि बिंदु आवेश q के कारण r दूरी पर वैद्युत क्षेत्र का परिमाण E = q / (4πε₀r²) होता है।
✔️ उत्तर:
गाउस प्रमेय के अनुसार,
Φ = ∮ E ⋅ dA = q / ε₀
पूर्ण गोले के लिए A = 4πr²
⟹ E × 4πr² = q / ε₀
⟹ E = q / (4πε₀r²)
यह वांछित सिद्ध करना था।

Q26. दो बिंदु आवेश +3μC और -3μC को 2cm की दूरी पर रखा गया है। उनके मध्य बिंदु पर वैद्युत विभव ज्ञात कीजिए।
✔️ उत्तर:
प्रत्येक आवेश से दूरी = 1cm = 0.01m
V = (1 / 4πε₀) × [q / r + (−q / r)] = 0
अतः मध्य बिंदु पर वैद्युत विभव = 0 वोल्ट

Q27. एक चालक गोला जिसकी त्रिज्या 10cm है, उस पर 1μC आवेश है। गोले की सतह पर विद्युत क्षेत्र ज्ञात कीजिए।
✔️ उत्तर:
R = 0.1 m, q = 1 × 10⁻⁶ C
E = q / (4πε₀R²)
= 9 × 10⁹ × (1 × 10⁻⁶) / (0.1)²
= 9 × 10⁻³ / 0.01
= 9 × 10⁵ N/C

Q28. कोई दो बिंदु आवेश +4μC और -2μC को 6cm की दूरी पर रखा गया है। उन दोनों के बीच के किसी बिंदु पर विद्युत क्षेत्र शून्य होगा या नहीं? समझाइए।
✔️ उत्तर:
यहाँ पर दो असमान आवेश हैं। चूँकि परिमाण समान नहीं है, इसलिए विद्युत क्षेत्र शून्य किसी बाह्य बिंदु पर ही संभव है, न कि बीच में।
यह बिंदु +4μC के अधिक दूर होगा क्योंकि वह बड़ा आवेश है।


🔷 Section D: प्रश्न 29 से 31 (प्रत्येक 4 अंक)
(केस आधारित प्रश्न)

Q29.
स्थिति: एक समविभाजित आवेशयुक्त पतली गोल प्लेट जिसकी त्रिज्या R है, उस पर कुल आवेश Q समान रूप से फैला है।
(a) गाउस प्रमेय का उपयोग करते हुए यह दर्शाइए कि इस प्लेट की सतह पर विद्युत क्षेत्र E = σ / ε₀ होता है।
(b) यदि सतह आवेश घनत्व σ = 5 × 10⁻⁶ C/m² हो, तो सतह पर विद्युत क्षेत्र ज्ञात कीजिए। (ε₀ = 8.85 × 10⁻¹² C²/N·m²)
✔️ उत्तर:
(a) गाउस सतह एक बेलनाकार गोल सतह ली जाती है जो प्लेट को काटती है।
दो सतहों पर फ्लक्स = 2EA
E × 2A = Q / ε₀
E = Q / (2Aε₀)
Q/A = σ
E = σ / (2ε₀) × 2 = σ / ε₀
(b)
E = σ / ε₀ = (5 × 10⁻⁶) / (8.85 × 10⁻¹²)
E = 5.65 × 10⁵ N/C

Q30.
स्थिति: दो समान बिंदु आवेश +q और +q को 2a दूरी पर रखा गया है। बिंदु O दोनों के मध्य स्थित है।
(a) O बिंदु पर विद्युत क्षेत्र का मान ज्ञात कीजिए।
(b) यदि एक ऋणात्मक परीक्षण आवेश -q₀ को O पर रखा जाए, तो उस पर बल की दिशा क्या होगी?
✔️ उत्तर:
(a) दोनों आवेशों से O की दूरी = a
E₁ = E₂ = (1 / 4πε₀) × (q / a²)
दिशा विपरीत, अतः एक-दूसरे को निरस्त करते हैं
∴ E = 0
(b) चूँकि क्षेत्र शून्य है, परंतु प्रत्येक आवेश से बल आकर्षण की ओर लगेगा
∴ बल की दिशा: दोनों आवेशों की ओर खिंचाव होगा, लेकिन संतुलित होने से कुल बल = 0

Q31.
स्थिति: एक बिंदु आवेश Q को पृथ्वी के तल से h ऊँचाई पर रखा गया है।
(a) पृथ्वी की सतह पर उस आवेश के कारण वैद्युत विभव ज्ञात कीजिए।
(b) यदि Q = 2μC, h = 2m है, तो विभव का परिमाण ज्ञात कीजिए। (1 / 4πε₀ = 9 × 10⁹ Nm²/C²)
✔️ उत्तर:
(a)
V = (1 / 4πε₀) × (Q / h)
(b)
Q = 2 × 10⁻⁶ C, h = 2
V = 9 × 10⁹ × (2 × 10⁻⁶ / 2)
= 9 × 10³ V
∴ V = 9000 वोल्ट

🔷 Section E: प्रश्न 32 से 35 (प्रत्येक 5 अंक)
(दीर्घ उत्तर प्रश्न)

Q32. गाउस प्रमेय का कथन दीजिए और इसे एक बिंदु आवेश के लिए प्रयोग करके विद्युत क्षेत्र व्यंजक प्राप्त कीजिए।
✔️ उत्तर:
गाउस प्रमेय का कथन:
किसी बंद पृष्ठ से होकर गुजरने वाला कुल विद्युत फ्लक्स, उस पृष्ठ के भीतर स्थित कुल आवेश के बराबर होता है।
Φ = ∮ E ⋅ dA = q / ε₀
प्रयोग:
बिंदु आवेश q को गोले के केंद्र पर रखें
E = स्थिर, dA = 4πr²
∴ E × 4πr² = q / ε₀
⟹ E = q / (4πε₀r²)
यह वांछित व्यंजक है।

Q33. किसी बिंदु आवेश q के कारण किसी बिंदु A और B पर वैद्युत विभव क्रमशः V₁ और V₂ हैं। सिद्ध कीजिए कि V₁ − V₂ = −∫A से B तक E ⋅ dr
✔️ उत्तर:
हम जानते हैं:
E = − dV / dr
⟹ dV = −E ⋅ dr
⟹ ∫A से B तक dV = −∫A से B तक E ⋅ dr
⟹ V(B) − V(A) = −∫A से B तक E ⋅ dr
⟹ V₁ − V₂ = −∫A से B तक E ⋅ dr
यह सिद्ध करना था।

Q34. दो बिंदु आवेश +2μC और -2μC को 0.1m की दूरी पर रखा गया है। उनके मध्य बिंदु पर वैद्युत विभव और वैद्युत क्षेत्र ज्ञात कीजिए।
✔️ उत्तर:
मध्य बिंदु पर दूरी = 0.05m
विभव (V):
V = V₁ + V₂ =
(1 / 4πε₀) × [(+2μC)/0.05 + (−2μC)/0.05] = 0
∴ V = 0 वोल्ट
विद्युत क्षेत्र (E):
E = E₁ + E₂ =
E = 2 × (1 / 4πε₀) × (2 × 10⁻⁶ / 0.05²)
= 2 × 9 × 10⁹ × 2 × 10⁻⁶ / 0.0025
= 1.44 × 10⁷ N/C
दिशा: ऋणात्मक आवेश की ओर

Q35. दो बिंदु आवेश +q और +q को x दूरी पर रखा गया है। एक बिंदु P इनके मध्य से y दूरी पर लंबवत रखा गया है। बिंदु P पर विद्युत क्षेत्र ज्ञात कीजिए।
✔️ उत्तर:
बिंदु P से दोनों आवेशों की दूरी = √[(x/2)² + y²]
प्रत्येक से E = (1 / 4πε₀) × (q / r²)
E क्षैतिज घटक निरस्त होते हैं, केवल ऊर्ध्व घटक जुड़ते हैं।
E_y = 2 × E × sinθ = 2 × (1 / 4πε₀) × (q / r²) × (y / r)
= (1 / 4πε₀) × (2qy) / (r³)
जहाँ r = √[(x/2)² + y²]
अतः बिंदु P पर विद्युत क्षेत्र:
E = (1 / 4πε₀) × (2qy) / ((x²/4 + y²)^(3/2))

————————————————————————————————————————————————————————————————————————————

Neet पिछले सालों के प्रश्न

Q1. दो समान बिंदु आवेश q एक-दूसरे से d दूरी पर स्थित हैं। उनके मध्य बिंदु पर विद्युत क्षेत्र का मान होगा:
(A) शून्य
(B) अनंत
(C) q/d
(D) 2q/d
Answer: (A)
Year: 2025 | Set: Z

Q2. यदि एक बिंदु आवेश q को चार गुना बढ़ा दिया जाए और दूरी d को दुगुना कर दिया जाए, तो विद्युत क्षेत्र का नया मान क्या होगा?
(A) पूर्व मान के बराबर
(B) दुगुना
(C) आधा
(D) चार गुना
Answer: (A)
Year: 2025 | Set: 2

Q3. एक बिंदु आवेश के कारण उत्पन्न विद्युत क्षेत्र रेखाएँ किस दिशा में होती हैं?
(A) आवेश की ओर
(B) आवेश से बाहर की ओर
(C) वृत्तीय
(D) स्पर्शरेखीय
Answer: (B)
Year: 2024 | Set: Q

Q4. द्विध्रुव आघूर्ण की इकाई होती है:
(A) न्यूटन
(B) कूलॉम्ब
(C) कूलॉम्ब मीटर
(D) वोल्ट
Answer: (C)
Year: 2024 | Set: S5

Q5. विद्युत क्षेत्र रेखाएँ दो स्थानों पर एक-दूसरे को नहीं काट सकतीं क्योंकि:
(A) वे वक्र होती हैं
(B) यह दिशाविहीन होती हैं
(C) उस बिंदु पर दो दिशाएँ हो जाएँगी
(D) ये संभव है
Answer: (C)
Year: 2023 | Set: M

Q6. वैद्युत क्षेत्र में रखा एक धनात्मक परिक्षण आवेश हमेशा किस दिशा में बल अनुभव करता है?
(A) विद्युत क्षेत्र के विपरीत
(B) ऊर्ध्वाधर दिशा में
(C) विद्युत क्षेत्र की दिशा में
(D) वृत्तीय पथ में
Answer: (C)
Year: 2023 | Set: Z

Q7. दो बिंदु आवेशों के बीच लगने वाला बल किस नियम से ज्ञात होता है?
(A) न्यूटन का द्वितीय नियम
(B) कूलॉम्ब का नियम
(C) बायोट-सावर्ट नियम
(D) किरचॉफ का नियम
Answer: (B)
Year: 2022 | Set: Q2

Q8. कूलॉम्ब के नियम में नियतांक का मात्रक क्या है?
(A) Nm²/C²
(B) C/N
(C) V/m
(D) C²/Nm²
Answer: (A)
Year: 2022 | Set: R

Q9. यदि दो आवेश समान परिमाण के हों और विपरीत चिन्ह के हों, तो वे मिलकर बनाते हैं:
(A) बिंदु आवेश
(B) द्विध्रुव
(C) समविभाजक
(D) समविभाजित क्षेत्र
Answer: (B)
Year: 2021 | Set: M

Q10. विद्युत क्षेत्र का परिमाण शून्य होगा जब:
(A) सभी आवेश धनात्मक हों
(B) सभी ऋणात्मक हों
(C) सम परिमाण के विपरीत आवेश समान दूरी पर हों
(D) कोई आवेश न हो
Answer: (C)
Year: 2021 | Set: P

Q11. एक बिंदु आवेश से दूर जाने पर विद्युत क्षेत्र का परिमाण:
(A) बढ़ता है
(B) घटता है
(C) अपरिवर्तित रहता है
(D) पहले बढ़ता फिर घटता है
Answer: (B)
Year: 2020 | Set: Z

Q12. यदि किसी विद्युत द्विध्रुव को समदिश विद्युत क्षेत्र में रखा जाए तो उस पर:
(A) कोई बल नहीं लगेगा
(B) एक बल और एक बलाघूर्ण लगेगा
(C) केवल बल लगेगा
(D) केवल बलाघूर्ण लगेगा
Answer: (D)
Year: 2020 | Set: 3

Q13. एक द्विध्रुव का बलाघूर्ण अधिकतम होता है जब:
(A) वह क्षेत्र के समानांतर हो
(B) वह क्षेत्र के लंबवत हो
(C) वह शून्य हो
(D) कोण 45° पर हो
Answer: (B)
Year: 2019 | Set: N

Q14. स्थिर विद्युत क्षेत्र में कार्य करने पर परिक्षण आवेश की ऊर्जा में परिवर्तन होता है क्योंकि:
(A) गति बदलती है
(B) बल नहीं लगता
(C) बल कार्य करता है
(D) दिशा बदलती है
Answer: (C)
Year: 2019 | Set: Q

Q15. वैद्युत क्षेत्र में परिक्षण आवेश पर कार्य पर निर्भर करता है:
(A) पथ पर
(B) केवल प्रारंभिक और अंतिम स्थिति पर
(C) क्षेत्र रेखा की दिशा पर
(D) क्षेत्र की तीव्रता पर
Answer: (B)
Year: 2018 | Set: X

Q16. एक विद्युत क्षेत्र में यदि बल शून्य हो तो:
(A) आवेश शून्य होगा
(B) क्षेत्र शून्य होगा
(C) दोनों शून्य होंगे
(D) क्षेत्र और आवेश दोनों गैर-शून्य हो सकते हैं
Answer: (D)
Year: 2018 | Set: Y

Q17. कूलॉम्ब बल की प्रकृति होती है:
(A) आकर्षण
(B) विकर्षण
(C) दोनों
(D) कोई नहीं
Answer: (C)
Year: 2017 | Set: Z

Q18. यदि दो आवेशों के बीच दूरी को दुगुना कर दिया जाए, तो बल का मान:
(A) दुगुना हो जाएगा
(B) आधा हो जाएगा
(C) एक चौथाई हो जाएगा
(D) चार गुना हो जाएगा
Answer: (C)
Year: 2017 | Set: M

Q19. विद्युत क्षेत्र रेखाओं की घनता अधिक होने का अर्थ है:
(A) बल कम है
(B) बल अधिक है
(C) कोई बल नहीं है
(D) दिशा अपरिभाषित है
Answer: (B)
Year: 2016 | Set: R

Q20. बिंदु आवेश से विद्युत क्षेत्र का मान किस पर निर्भर करता है?
(A) आवेश की गति पर
(B) दूरी पर
(C) कोण पर
(D) क्षेत्रफल पर
Answer: (B)
Year: 2016 | Set: S

Q21. द्विध्रुव आघूर्ण का परिमाण p है। यदि यह विद्युत क्षेत्र E में 90° के कोण पर हो, तो बलाघूर्ण होगा:
(A) pE
(B) pE sin90°
(C) pE cos90°
(D) शून्य
Answer: (A)
Year: 2015 | Set: 2

Q22. एक वैद्युत क्षेत्र रेखा का सिरा हमेशा होता है:
(A) धनात्मक से ऋणात्मक
(B) ऋणात्मक से धनात्मक
(C) केंद्र से दूर
(D) वृत्तीय पथ में
Answer: (A)
Year: 2015 | Set: Z

Q23. यदि दो आवेशों के बीच कूलॉम्ब बल शून्य है, तो इसका अर्थ है:
(A) दोनों समान आवेश हैं
(B) दूरी अनंत है
(C) कोई आवेश नहीं
(D) बल कार्य नहीं करता
Answer: (B)
Year: 2014 | Set: Y

Q24. परिक्षण आवेश को एक समविभाजित आवेश-पट्टी के पास रखने पर विद्युत क्षेत्र:
(A) बाहर की ओर
(B) अंदर की ओर
(C) तिरछा
(D) शून्य
Answer: (A)
Year: 2014 | Set: N

Q25. एक बिंदु पर विद्युत क्षेत्र और बल का अनुपात किसके बराबर होता है?
(A) आवेश
(B) वोल्टता
(C) बल
(D) दूरी
Answer: (A)
Year: 2013 | Set: Q

Q26. दो आवेशों के बीच कूलॉम्ब बल का मान परिवर्तित होता है जब:
(A) आवेश बदले जाएँ
(B) माध्यम बदला जाए
(C) दूरी बदली जाए
(D) उपरोक्त सभी
Answer: (D)
Year: 2013 | Set: S

Q27. बिंदु आवेश के कारण उत्पन्न विद्युत क्षेत्र की दिशा होती है:
(A) वृत्तीय
(B) रेखीय
(C) त्रिज्यीय
(D) कोणीय
Answer: (C)
Year: 2012 | Set: M

Q28. यदि कोई द्विध्रुव स्थिर वैद्युत क्षेत्र में रखा हो, तो वह किस स्थिति में स्थिर रहेगा?
(A) जब θ = 90°
(B) जब θ = 0°
(C) जब θ = 45°
(D) जब θ = 30°
Answer: (B)
Year: 2012 | Set: Q

Q29. जब कोई द्विध्रुव क्षेत्र के लंबवत रखा जाता है, तो उस पर बलाघूर्ण होता है:
(A) शून्य
(B) अधिकतम
(C) अनंत
(D) ऋणात्मक
Answer: (B)
Year: 2011 | Set: N

Q30. स्थैतिक आवेश द्वारा उत्पन्न क्षेत्र कहलाता है:
(A) चुंबकीय क्षेत्र
(B) विद्युत क्षेत्र
(C) प्रेरित क्षेत्र
(D) गुरुत्वीय क्षेत्र
Answer: (B)
Year: 2011 | Set: Z

Q31. कूलॉम्ब के नियम में बल का परिमाण सीधे अनुपाती होता है:
(A) दूरी के वर्ग के
(B) आवेशों के गुणनफल के
(C) दोनों के
(D) इनमें से कोई नहीं
Answer: (B)
Year: 2010 | Set: R

Q32. यदि q = 1 C और r = 1 m, तो बिंदु पर विद्युत क्षेत्र होगा:
(A) 9 × 10⁹ N/C
(B) 1 N/C
(C) 0.5 N/C
(D) 9 N/C
Answer: (A)
Year: 2010 | Set: S

Q33. कूलॉम्ब का बल बल के किस प्रकार का उदाहरण है?
(A) सतही बल
(B) द्रव्य बल
(C) क्षेत्र बल
(D) संपर्क बल
Answer: (C)
Year: 2009 | Set: Y

Q34. आवेश की इकाई क्या है?
(A) एम्पियर
(B) वोल्ट
(C) कूलॉम्ब
(D) न्यूटन
Answer: (C)
Year: 2009 | Set: M

Q35. विद्युत क्षेत्र की मात्रक है:
(A) Nm
(B) C
(C) N/C
(D) V/C
Answer: (C)
Year: 2008 | Set: Q

Q36. यदि एक विद्युत क्षेत्र में परिक्षण आवेश पर बल नहीं लगता है, तो क्या निष्कर्ष है?
(A) क्षेत्र शून्य है
(B) आवेश शून्य है
(C) दोनों शून्य हो सकते हैं
(D) दोनों गैर-शून्य हो सकते हैं
Answer: (C)
Year: 2008 | Set: N

Q37. दो आवेश एक-दूसरे को F बल से आकर्षित करते हैं। यदि दोनों को पृथक माध्यम में रखें तो बल:
(A) बढ़ेगा
(B) घटेगा
(C) अपरिवर्तित रहेगा
(D) दिशा बदल जाएगी
Answer: (B)
Year: 2007 | Set: 2

Q38. विद्युत क्षेत्र और बल के अनुपात से किस भौतिक राशि की व्याख्या होती है?
(A) आवेश
(B) वोल्टता
(C) धारा
(D) संवेग
Answer: (A)
Year: 2007 | Set: P

Q39. जब q और r को समान अनुपात में बढ़ाया जाए, तो E:
(A) बढ़ेगा
(B) घटेगा
(C) अपरिवर्तित रहेगा
(D) शून्य हो जाएगा
Answer: (C)
Year: 2006 | Set: Y

Q40. विद्युत क्षेत्र सदिश राशि है क्योंकि:
(A) इसमें परिमाण होता है
(B) इसमें दिशा होती है
(C) दोनों
(D) कोई नहीं
Answer: (C)
Year: 2006 | Set: M

Q41. किसी बिंदु पर विद्युत क्षेत्र रेखाएँ पास-पास हों तो इसका अर्थ है:
(A) क्षेत्र कमजोर है
(B) क्षेत्र तीव्र है
(C) क्षेत्र शून्य है
(D) क्षेत्र परस्पर विरोधी है
Answer: (B)
Year: 2005 | Set: Q

Q42. एक बिंदु आवेश के चारों ओर विद्युत क्षेत्र रेखाएँ होती हैं:
(A) समांतर
(B) विकेन्द्रित
(C) केंद्राभिमुख
(D) केंद्र से बाहर की ओर
Answer: (D)
Year: 2005 | Set: Z

Q43. विद्युत क्षेत्र रेखाएँ क्यों नहीं काटतीं?
(A) क्योंकि वे दिखावटी हैं
(B) क्योंकि वे कल्पित हैं
(C) क्योंकि किसी बिंदु पर केवल एक दिशा होती है
(D) इनमें से कोई नहीं
Answer: (C)
Year: 2004 | Set: 1

Q44. समविभाजित आवेश वितरण में विद्युत क्षेत्र होता है:
(A) शून्य
(B) असमान
(C) समान
(D) अनंत
Answer: (C)
Year: 2004 | Set: M

Q45. वैद्युत क्षेत्र की दिशा किस पर निर्भर करती है?
(A) आवेश के चिन्ह पर
(B) दूरी पर
(C) माध्यम पर
(D) इनमें सभी
Answer: (A)
Year: 2003 | Set: N

Q46. कूलॉम्ब बल और गुरुत्व बल में समानता है:
(A) दोनों आकर्षण बल हैं
(B) दोनों सदिश बल हैं
(C) दोनों अनंत दूरी तक कार्य करते हैं
(D) उपरोक्त सभी
Answer: (D)
Year: 2003 | Set: S

Q47. द्विध्रुव बलाघूर्ण का SI मात्रक है:
(A) C·m
(B) C/m
(C) C²/m
(D) V·m
Answer: (A)
Year: 2002 | Set: Q

Q48. कूलॉम्ब बल किस पर निर्भर नहीं करता है?
(A) माध्यम
(B) आवेश
(C) दूरी
(D) द्रव्यमान
Answer: (D)
Year: 2002 | Set: P

Q49. विद्युत क्षेत्र का परिमाण किस दूरी पर शून्य होगा?
(A) कूलॉम्ब नियम में नहीं बताया गया
(B) किसी दूरी पर नहीं
(C) अनंत दूरी पर
(D) 1 m दूरी पर
Answer: (C)
Year: 2001 | Set: M

Q50. किसी वैद्युत क्षेत्र में परिक्षण आवेश के गति की दिशा किससे निर्धारित होती है?
(A) क्षेत्र की दिशा
(B) बल की दिशा
(C) घर्षण की दिशा
(D) गुरुत्व बल की दिशा
Answer: (B)
Year: 2001 | Set: Q

————————————————————————————————————————————————————————————————————————————

JEE MAINS पिछले सालों के प्रश्न

Q1. दो बिंदु आवेशों के बीच कूलॉम्ब बल किस पर निर्भर करता है?
(A) केवल दूरी पर
(B) केवल आवेश पर
(C) दूरी और आवेश दोनों पर
(D) माध्यम की दिशा पर
Answer: (C)
Year: 2025 | Shift: 2 | Set: A

Q2. किसी बिंदु आवेश q के कारण उत्पन्न वैद्युत क्षेत्र की दिशा किस ओर होती है?
(A) आवेश की ओर
(B) आवेश से बाहर की ओर
(C) वृत्तीय दिशा में
(D) केवल ऊपर की ओर
Answer: (B)
Year: 2025 | Shift: 1 | Set: B

Q3. एक समान वैद्युत क्षेत्र में रखा गया धन आवेश किस दिशा में गति करेगा?
(A) क्षेत्र की दिशा में
(B) क्षेत्र के विपरीत दिशा में
(C) लंबवत
(D) कोई निष्कर्ष नहीं
Answer: (A)
Year: 2024 | Shift: 2 | Set: A

Q4. यदि q = 4 × 10⁻⁶ कूलॉम्ब तथा दूरी r = 0.2 मीटर हो, तो उत्पन्न वैद्युत क्षेत्र का मान होगा:
(A) 9 × 10⁶ न्यूटन प्रति कूलॉम्ब
(B) 1.8 × 10⁶ न्यूटन प्रति कूलॉम्ब
(C) 0.9 × 10⁶ न्यूटन प्रति कूलॉम्ब
(D) 3.6 × 10⁶ न्यूटन प्रति कूलॉम्ब
Answer: (D)
Year: 2024 | Shift: 1 | Set: B

Q5. यदि दो समान आवेशों को 1 मीटर दूरी पर रखा जाए, तो बल होगा:
(A) आकर्षण बल
(B) शून्य
(C) विकर्षण बल
(D) केवल गुरुत्व बल
Answer: (C)
Year: 2023 | Shift: 2 | Set: C

Q6. दो बिंदु आवेशों के बीच कूलॉम्ब बल की प्रकृति है:
(A) सदिश
(B) अदिश
(C) तापीय
(D) यांत्रिक
Answer: (A)
Year: 2023 | Shift: 1 | Set: A

Q7. वैद्युत क्षेत्र रेखाएँ कब एक-दूसरे को काट सकती हैं?
(A) जब वे समान दिशा में हों
(B) जब वे विपरीत दिशा में हों
(C) कभी नहीं
(D) जब वे समकोण पर हों
Answer: (C)
Year: 2022 | Shift: 1 | Set: A

Q8. किसी बिंदु पर वैद्युत क्षेत्र रेखाओं का घनत्व दर्शाता है:
(A) क्षेत्र की दिशा
(B) क्षेत्र की तीव्रता
(C) बल की दिशा
(D) बल का परिमाण
Answer: (B)
Year: 2022 | Shift: 2 | Set: C

Q9. यदि कोई विद्युत द्विध्रुव समविभाजित वैद्युत क्षेत्र में रखा हो, तो उस पर लगने वाला बलाघूर्ण अधिकतम होगा जब वह:
(A) क्षेत्र के समानांतर हो
(B) क्षेत्र के लंबवत हो
(C) क्षेत्र की दिशा में हो
(D) θ = 0 हो
Answer: (B)
Year: 2021 | Shift: 2 | Set: B

Q10. किसी बिंदु आवेश द्वारा उत्पन्न वैद्युत क्षेत्र की तीव्रता किस प्रकार घटती है?
(A) r के अनुक्रमानुपाती
(B) r² के अनुक्रमानुपाती
(C) √r के अनुक्रमानुपाती
(D) r³ के अनुक्रमानुपाती
Answer: (B)
Year: 2021 | Shift: 1 | Set: A

Q11. एक समदूरी पर दो समान आवेशों से उत्पन्न वैद्युत क्षेत्र का योगफल होगा:
(A) शून्य
(B) दो गुना
(C) √2 गुना
(D) चार गुना
Answer: (A)
Year: 2020 | Shift: 2 | Set: B

Q12. वैद्युत द्विध्रुव आघूर्ण की मात्रक क्या है?
(A) कूलॉम्ब
(B) वोल्ट
(C) कूलॉम्ब मीटर
(D) जूल
Answer: (C)
Year: 2020 | Shift: 1 | Set: A

Q13. एक धन आवेश q को वैद्युत क्षेत्र E में रखने पर उस पर लगने वाला बल होता है:
(A) q × E
(B) q / E
(C) q + E
(D) E / q
Answer: (A)
Year: 2019 | Shift: 2 | Set: C

Q14. कूलॉम्ब बल और गुरुत्व बल में कौन सी समानता है?
(A) दोनों विपरीत बल हैं
(B) दोनों दूरी के वर्ग के अनुक्रमानुपाती हैं
(C) दोनों संपर्क बल हैं
(D) दोनों तापीय बल हैं
Answer: (B)
Year: 2019 | Shift: 1 | Set: B

Q15. यदि किसी माध्यम में कूलॉम्ब बल F है, तो निर्वात में वही बल कितना होगा?
(A) F / k
(B) F × k
(C) √F
(D) F²
Answer: (B)
Year: 2018 | Shift: 1 | Set: A

Q16. वैद्युत क्षेत्र E और बल F के अनुपात से हमें क्या प्राप्त होता है?
(A) आवेश
(B) दूरी
(C) वोल्टता
(D) तीव्रता
Answer: (A)
Year: 2018 | Shift: 2 | Set: C

Q17. दो बिंदु आवेशों q₁ और q₂ के मध्य बल किस नियम से ज्ञात किया जाता है?
(A) बायोट-सावर्ट नियम
(B) कूलॉम्ब नियम
(C) किरचॉफ नियम
(D) गैस का नियम
Answer: (B)
Year: 2017 | Shift: 2 | Set: B

Q18. किसी द्विध्रुव को समविभाजित क्षेत्र में रखने पर वह किस दिशा में घूमता है?
(A) क्षेत्र के साथ
(B) क्षेत्र के विपरीत
(C) क्षेत्र के लंबवत
(D) शून्य कोण पर
Answer: (A)
Year: 2017 | Shift: 1 | Set: A

Q19. बिंदु आवेश द्वारा उत्पन्न वैद्युत क्षेत्र रेखाएँ कैसी होती हैं?
(A) समांतर
(B) त्रिज्यीय
(C) चक्रवातीय
(D) अनियमित
Answer: (B)
Year: 2016 | Shift: 2 | Set: C

Q20. किसी बिंदु पर वैद्युत क्षेत्र रेखाएँ परस्पर काटने का क्या अर्थ होगा?
(A) दो दिशा में बल
(B) दिशा निश्चित नहीं
(C) ऊर्जा अधिक है
(D) वे कभी नहीं काट सकतीं
Answer: (D)
Year: 2016 | Shift: 1 | Set: A

Q21. यदि एक द्विध्रुव का बलाघूर्ण अधिकतम है, तो θ का मान होगा:
(A) 0°
(B) 30°
(C) 90°
(D) 60°
Answer: (C)
Year: 2015 | Shift: 1 | Set: A

Q22. यदि q = 1 C और r = 1 m हो, तो उत्पन्न वैद्युत क्षेत्र:
(A) 1 N/C
(B) 9 N/C
(C) 9 × 10⁹ N/C
(D) 0
Answer: (C)
Year: 2015 | Shift: 2 | Set: B

Q23. कूलॉम्ब बल की प्रकृति है:
(A) तापीय
(B) गुरुत्वीय
(C) दीर्घ दूरी बल
(D) केवल संपर्क बल
Answer: (C)
Year: 2014 | Shift: 1 | Set: C

Q24. बिंदु आवेशों से उत्पन्न बल सदैव:
(A) आकर्षक
(B) विकर्षक
(C) दोनों हो सकते हैं
(D) शून्य
Answer: (C)
Year: 2014 | Shift: 2 | Set: A

Q25. वैद्युत क्षेत्र की परिभाषा है:
(A) प्रति इकाई आवेश पर बल
(B) प्रति इकाई क्षेत्र पर आवेश
(C) वोल्टता का मान
(D) ऊर्जा का अनुपात
Answer: (A)
Year: 2013 | Shift: 1 | Set: B

Q26. कूलॉम्ब बल और वैद्युत क्षेत्र बल में क्या अंतर है?
(A) बल एकसमान होता है
(B) बल स्थान पर निर्भर करता है
(C) बल सदैव आकर्षण होता है
(D) बल एक बिंदु पर केंद्रित होता है
Answer: (B)
Year: 2013 | Shift: 2 | Set: A

Q27. किसी बिंदु पर वैद्युत क्षेत्र की दिशा किससे निर्धारित होती है?
(A) परिक्षण आवेश की दिशा से
(B) बल की दिशा से
(C) आवेश के परिमाण से
(D) विद्युत विभव से
Answer: (B)
Year: 2012 | Shift: 1 | Set: B

Q28. द्विध्रुव पर अधिकतम बलाघूर्ण उत्पन्न होगा जब:
(A) वह क्षेत्र के समानांतर हो
(B) वह क्षेत्र के लंबवत हो
(C) वह क्षेत्र के साथ मिल रहा हो
(D) वह स्थिर हो
Answer: (B)
Year: 2012 | Shift: 2 | Set: C

Q29. दो बिंदु आवेशों के बीच बल का दिशा निर्धारण कैसे होता है?
(A) ऋणात्मक आवेश से धनात्मक की ओर
(B) धनात्मक से ऋणात्मक की ओर
(C) बल का कोई दिशा नहीं होता
(D) दोनों बल विपरीत दिशा में होते हैं
Answer: (B)
Year: 2011 | Shift: 1 | Set: A

Q30. यदि कोई द्विध्रुव वैद्युत क्षेत्र में लंबवत रखा गया हो, तो उस पर बलाघूर्ण:
(A) शून्य होगा
(B) अधिकतम होगा
(C) असीमित होगा
(D) ऋणात्मक होगा
Answer: (B)
Year: 2011 | Shift: 2 | Set: B

Q31. कूलॉम्ब बल के लिए समीकरण है:
(A) F = q × E
(B) F = k × q₁ × q₂ / r²
(C) F = m × g
(D) F = ma
Answer: (B)
Year: 2010 | Shift: 1 | Set: C

Q32. विद्युत क्षेत्र में रेखाएँ किस दिशा में जाती हैं?
(A) धनात्मक से ऋणात्मक
(B) ऋणात्मक से धनात्मक
(C) ऊपर से नीचे
(D) किसी निश्चित दिशा में नहीं
Answer: (A)
Year: 2010 | Shift: 2 | Set: A

Q33. द्विध्रुव बलाघूर्ण का मात्रक है:
(A) N
(B) C
(C) C·m
(D) V
Answer: (C)
Year: 2009 | Shift: 1 | Set: B

Q34. एक आवेश q को वैद्युत क्षेत्र E में रखने पर बल:
(A) q / E
(B) q × E
(C) E / q
(D) शून्य
Answer: (B)
Year: 2009 | Shift: 2 | Set: A

Q35. यदि r दोगुना कर दिया जाए तो कूलॉम्ब बल:
(A) आधा हो जाएगा
(B) दोगुना हो जाएगा
(C) एक चौथाई हो जाएगा
(D) चार गुना हो जाएगा
Answer: (C)
Year: 2008 | Shift: 1 | Set: C

Q36. वैद्युत क्षेत्र और बल का अनुपात होता है:
(A) ऊर्जा
(B) शक्ति
(C) आवेश
(D) संवेग
Answer: (C)
Year: 2008 | Shift: 2 | Set: A

Q37. वैद्युत क्षेत्र रेखाएँ एक बिंदु पर कभी नहीं काट सकतीं क्योंकि:
(A) वे समांतर होती हैं
(B) वे त्रिज्यीय होती हैं
(C) बल की दिशा अद्वितीय होनी चाहिए
(D) इनमें से कोई नहीं
Answer: (C)
Year: 2007 | Shift: 1 | Set: B

Q38. यदि एक धनात्मक परिक्षण आवेश को वैद्युत क्षेत्र में रखा जाए, तो वह किस दिशा में गति करेगा?
(A) क्षेत्र की दिशा में
(B) क्षेत्र के विपरीत
(C) स्थिर रहेगा
(D) वृत्तीय पथ में
Answer: (A)
Year: 2007 | Shift: 2 | Set: A

Q39. कूलॉम्ब बल का SI मात्रक है:
(A) कूलॉम्ब
(B) न्यूटन
(C) वोल्ट
(D) जूल
Answer: (B)
Year: 2006 | Shift: 1 | Set: C

Q40. वैद्युत क्षेत्र का SI मात्रक है:
(A) न्यूटन प्रति मीटर
(B) न्यूटन प्रति कूलॉम्ब
(C) वोल्ट प्रति मीटर
(D) कूलॉम्ब प्रति मीटर
Answer: (B)
Year: 2006 | Shift: 2 | Set: A

Q41. यदि दो समान आवेशों को साथ में रखा जाए तो वे:
(A) आकर्षित होंगे
(B) विकर्षित होंगे
(C) एक-दूसरे को स्थिर रखेंगे
(D) संतुलन में होंगे
Answer: (B)
Year: 2005 | Shift: 1 | Set: B

Q42. द्विध्रुव को यदि समविभाजित वैद्युत क्षेत्र में रखा जाए, तो बल होगा:
(A) समान और विपरीत
(B) असमान
(C) केवल एक दिशा में
(D) शून्य
Answer: (A)
Year: 2005 | Shift: 2 | Set: A

Q43. दो बिंदु आवेशों के बीच लगने वाला बल यदि आकर्षण है, तो आवेश:
(A) समान होंगे
(B) विपरीत चिन्ह के होंगे
(C) समान परिमाण के होंगे
(D) शून्य होंगे
Answer: (B)
Year: 2004 | Shift: 1 | Set: C

Q44. यदि कोई परिक्षण आवेश किसी स्थान पर बल अनुभव नहीं करता, तो इसका क्या अर्थ है?
(A) क्षेत्र शून्य है
(B) आवेश शून्य है
(C) दोनों शून्य हो सकते हैं
(D) बल स्थायी है
Answer: (C)
Year: 2004 | Shift: 2 | Set: A

Q45. यदि कोई आवेश q किसी बिंदु पर वैद्युत क्षेत्र E में रखा जाए, तो बल F होगा:
(A) F = q + E
(B) F = E / q
(C) F = q × E
(D) F = q / E
Answer: (C)
Year: 2003 | Shift: 1 | Set: B

Q46. कूलॉम्ब बल किस प्रकार का बल है?
(A) सतही
(B) संपर्क
(C) क्षेत्र
(D) यांत्रिक
Answer: (C)
Year: 2003 | Shift: 2 | Set: A

Q47. कूलॉम्ब के नियम के अनुसार बल किसके अनुक्रमानुपाती होता है?
(A) q₁ × q₂
(B) q₁ + q₂
(C) q₁ – q₂
(D) q₁ / q₂
Answer: (A)
Year: 2002 | Shift: 1 | Set: C

Q48. दो बिंदु आवेश q₁ और q₂ के बीच की दूरी दोगुनी करने पर बल का मान होगा:
(A) चार गुना बढ़ेगा
(B) आधा
(C) एक चौथाई
(D) शून्य
Answer: (C)
Year: 2002 | Shift: 2 | Set: A

Q49. वैद्युत क्षेत्र रेखाएँ किस दिशा में होती हैं?
(A) ऋणात्मक से धनात्मक
(B) धनात्मक से ऋणात्मक
(C) कहीं भी
(D) कोई दिशा नहीं होती
Answer: (B)
Year: 2001 | Shift: 1 | Set: B

Q50. यदि q = 1 C और d = 1 m, तो उत्पन्न बल:
(A) 9 N
(B) 1 N
(C) 9 × 10⁹ N
(D) 1 × 10⁹ N
Answer: (C)
Year: 2001 | Shift: 2 | Set: A

————————————————————————————————————————————————————————————————————————————

JEE ADVANCED पिछले सालों के प्रश्न

🔷 प्रश्न 1 से 17
JEE Advanced – प्रश्नपत्र 1 (Paper 1)

Q1. दो समान आवेश q को एक-दूसरे से d दूरी पर रखा गया है। यदि बल F है, तो दूरी को √2 गुना करने पर नया बल होगा:
(A) F
(B) F/2
(C) 2F
(D) F/√2
Answer: (B)
Year: 2025 | Paper: 1 | Set: 1

Q2. किसी बिंदु आवेश द्वारा उत्पन्न वैद्युत क्षेत्र की दिशा होती है:
(A) केंद्र की ओर
(B) केंद्र से बाहर की ओर
(C) वृत्तीय
(D) ऊर्ध्वाधर
Answer: (B)
Year: 2025 | Paper: 1 | Set: 2

Q3. कूलॉम्ब बल और गुरुत्व बल में कौन सा गुण समान है?
(A) दोनों केवल आकर्षण करते हैं
(B) दोनों परिमाण में समान होते हैं
(C) दोनों दूरी के वर्ग के व्युत्क्रमानुपाती होते हैं
(D) दोनों तापीय होते हैं
Answer: (C)
Year: 2024 | Paper: 1 | Set: 2

Q4. कूलॉम्ब बल किस प्रकार का बल है?
(A) सतही बल
(B) संपर्क बल
(C) क्षेत्र बल
(D) विकिरण बल
Answer: (C)
Year: 2024 | Paper: 1 | Set: 1

Q5. यदि एक धन आवेश q समविभाजित वैद्युत क्षेत्र में रखा जाए, तो उस पर लगने वाला बल होता है:
(A) q × E
(B) q / E
(C) q + E
(D) q × E²
Answer: (A)
Year: 2023 | Paper: 1 | Set: 1

Q6. यदि दो आवेशों के बीच बल F है और दोनों आवेशों को दुगुना कर दिया जाए, तो बल होगा:
(A) 2F
(B) 4F
(C) F/2
(D) F/4
Answer: (B)
Year: 2023 | Paper: 1 | Set: 2

Q7. वैद्युत क्षेत्र की इकाई है:
(A) न्यूटन
(B) कूलॉम्ब
(C) वोल्ट
(D) न्यूटन प्रति कूलॉम्ब
Answer: (D)
Year: 2022 | Paper: 1 | Set: 1

Q8. यदि किसी बिंदु पर विद्युत क्षेत्र शून्य हो, तो:
(A) वहाँ कोई आवेश नहीं है
(B) सभी बल संतुलित हैं
(C) कोई बल कार्य नहीं करता
(D) वैद्युत क्षेत्र का प्रभाव नहीं होता
Answer: (B)
Year: 2022 | Paper: 1 | Set: 2

Q9. वैद्युत क्षेत्र रेखाएँ एक-दूसरे को क्यों नहीं काटतीं?
(A) वे समान दिशा में होती हैं
(B) वे समकोण पर होती हैं
(C) एक बिंदु पर दो दिशाएँ संभव नहीं
(D) उनमें ऊर्जा नहीं होती
Answer: (C)
Year: 2021 | Paper: 1 | Set: 2

Q10. यदि एक द्विध्रुव वैद्युत क्षेत्र में रखा जाए और वह θ कोण बनाए, तो बलाघूर्ण होता है:
(A) pE sinθ
(B) pE cosθ
(C) pE tanθ
(D) pE / sinθ
Answer: (A)
Year: 2021 | Paper: 1 | Set: 1

Q11. कूलॉम्ब का नियम निम्न में से किस पर लागू होता है?
(A) केवल स्थिर आवेशों पर
(B) केवल गतिमान आवेशों पर
(C) सभी प्रकार के आवेशों पर
(D) चुंबकीय आवेशों पर
Answer: (A)
Year: 2020 | Paper: 1 | Set: 1

Q12. यदि कोई परिक्षण आवेश किसी बिंदु पर बल अनुभव नहीं करता, तो:
(A) क्षेत्र नहीं है
(B) बल और क्षेत्र शून्य हैं
(C) परिक्षण आवेश शून्य है
(D) क्षेत्र हो सकता है, पर बल शून्य है
Answer: (D)
Year: 2020 | Paper: 1 | Set: 2

Q13. वैद्युत क्षेत्र रेखाओं की सघनता दर्शाती है:
(A) दिशा
(B) बल
(C) ऊर्जा
(D) तीव्रता
Answer: (D)
Year: 2019 | Paper: 1 | Set: 2

Q14. यदि दो आवेशों के बीच आकर्षण होता है, तो उनके चिन्ह होंगे:
(A) दोनों धनात्मक
(B) दोनों ऋणात्मक
(C) विपरीत
(D) शून्य
Answer: (C)
Year: 2019 | Paper: 1 | Set: 1

Q15. यदि q = 1 C और r = 1 m हो, तो वैद्युत क्षेत्र होगा:
(A) 1 N/C
(B) 9 × 10⁹ N/C
(C) 9 N/C
(D) शून्य
Answer: (B)
Year: 2018 | Paper: 1 | Set: 1

Q16. किसी द्विध्रुव के लिए बलाघूर्ण अधिकतम होता है जब:
(A) θ = 0°
(B) θ = 90°
(C) θ = 180°
(D) θ = 45°
Answer: (B)
Year: 2018 | Paper: 1 | Set: 2

Q17. यदि q = 2 × 10⁻⁶ C और r = 0.2 m हो, तो वैद्युत क्षेत्र E होगा:
(A) 4.5 × 10⁵ N/C
(B) 2.25 × 10⁵ N/C
(C) 9 × 10⁵ N/C
(D) 1.8 × 10⁵ N/C
Answer: (C)
Year: 2017 | Paper: 1 | Set: 1

🔷 प्रश्न 18 से 34
JEE Advanced – प्रश्नपत्र 2 (Paper 2)

Q18. वैद्युत क्षेत्र का SI मात्रक है:
(A) वोल्ट
(B) जूल
(C) न्यूटन प्रति कूलॉम्ब
(D) एम्पियर
Answer: (C)
Year: 2025 | Paper: 2 | Set: 1

Q19. यदि दो बिंदु आवेशों के बीच बल F है और दूरी को √2 गुना कर दिया जाए, तो बल होगा:
(A) F
(B) 2F
(C) F/2
(D) F/√2
Answer: (C)
Year: 2025 | Paper: 2 | Set: 2

Q20. एक वैद्युत द्विध्रुव का बलाघूर्ण होता है:
(A) qd
(B) q/d
(C) q + d
(D) qd²
Answer: (A)
Year: 2024 | Paper: 2 | Set: 1

Q21. एक समान वैद्युत क्षेत्र में रखा गया द्विध्रुव किस दिशा में स्थिर रहता है?
(A) क्षेत्र के साथ
(B) क्षेत्र के विपरीत
(C) लंबवत
(D) कोई नहीं
Answer: (A)
Year: 2024 | Paper: 2 | Set: 2

Q22. कूलॉम्ब के नियम में नियतांक k का मान है:
(A) 1 × 10⁹
(B) 8.99 × 10⁹
(C) 9 × 10⁶
(D) 1.6 × 10⁻¹⁹
Answer: (B)
Year: 2023 | Paper: 2 | Set: 1

Q23. दो आवेशों के बीच लगने वाला बल शून्य होता है जब:
(A) दोनों धनात्मक हों
(B) दोनों ऋणात्मक हों
(C) वे विपरीत चिन्ह के हों और दूरी अनंत हो
(D) वे एक-दूसरे को छूते हों
Answer: (C)
Year: 2023 | Paper: 2 | Set: 2

Q24. वैद्युत क्षेत्र सदैव होता है:
(A) अदिश
(B) सदिश
(C) द्रव्य
(D) स्पर्शरेखीय
Answer: (B)
Year: 2022 | Paper: 2 | Set: 1

Q25. यदि q = 3 × 10⁻⁶ C और E = 10⁴ N/C, तो बल F होगा:
(A) 0.3 N
(B) 3 N
(C) 0.03 N
(D) 30 N
Answer: (B)
Year: 2022 | Paper: 2 | Set: 2

Q26. वैद्युत क्षेत्र रेखाएँ किसी आवेश के निकट होती हैं:
(A) विरल
(B) सघन
(C) वृत्ताकार
(D) उलझी हुई
Answer: (B)
Year: 2021 | Paper: 2 | Set: 2

Q27. वैद्युत क्षेत्र और बल का अनुपात देता है:
(A) वोल्ट
(B) ऊर्जा
(C) आवेश
(D) तीव्रता
Answer: (C)
Year: 2021 | Paper: 2 | Set: 1

Q28. कूलॉम्ब का बल:
(A) दिशा पर निर्भर नहीं करता
(B) सदिश बल है
(C) अदिश बल है
(D) केवल एक दिशा में कार्य करता है
Answer: (B)
Year: 2020 | Paper: 2 | Set: 1

Q29. एक बिंदु आवेश से दूरी r पर वैद्युत क्षेत्र E होगा:
(A) E ∝ r
(B) E ∝ 1/r²
(C) E ∝ 1/r
(D) E ∝ r²
Answer: (B)
Year: 2020 | Paper: 2 | Set: 2

Q30. यदि बल F = 1 N और q = 0.5 C हो, तो E = ?
(A) 0.5 N/C
(B) 2 N/C
(C) 1.5 N/C
(D) 3 N/C
Answer: (B)
Year: 2019 | Paper: 2 | Set: 1

Q31. द्विध्रुव का बलाघूर्ण SI मात्रक में होता है:
(A) C
(B) C·m
(C) J
(D) V
Answer: (B)
Year: 2019 | Paper: 2 | Set: 2

Q32. कूलॉम्ब बल का प्रकृति कैसी है?
(A) दीर्घ दूरी बल
(B) सतही बल
(C) स्पर्श बल
(D) गुरुत्व बल
Answer: (A)
Year: 2018 | Paper: 2 | Set: 2

Q33. वैद्युत क्षेत्र का उपयोग किया जाता है:
(A) आयनन के लिए
(B) बल लगाने के लिए
(C) गर्म करने के लिए
(D) कंपन के लिए
Answer: (B)
Year: 2018 | Paper: 2 | Set: 1

Q34. यदि बल घटकर एक चौथाई हो जाए, तो दूरी कितनी बढ़ाई गई होगी?
(A) √2 गुना
(B) 2 गुना
(C) 3 गुना
(D) 4 गुना
Answer: (B)
Year: 2017 | Paper: 2 | Set: 1

————————————————————————————————————————————————————————————————————————————

मॉडल प्रश्न पत्र, अभ्यास

Q1. एक बिंदु आवेश के कारण उत्पन्न विद्युत क्षेत्र रेखाएँ होती हैं —
(A) समांतर
(B) वृत्ताकार
(C) त्रिज्यात्मक
(D) असममित
Answer: (C)

Q2. यदि एक आवेश को विद्युत क्षेत्र में रखा जाए, तो उस पर लगने वाला बल किसके समानुपाती होता है?
(A) आवेश के परिमाण के वर्ग के
(B) विद्युत क्षेत्र की तीव्रता के
(C) दूरी के वर्ग के
(D) गति के
Answer: (B)

Q3. दो समान आवेश एक-दूसरे से d दूरी पर रखे हैं, उनके बीच विद्युत बल का मान होगा —
(A) kq²/d
(B) kq/d²
(C) kq²/d²
(D) q²/kd²
Answer: (C)

Q4. एक स्थिर आवेश द्वारा उत्पादित विद्युत क्षेत्र किस प्रकार का होता है?
(A) स्थायी
(B) परिवर्ती
(C) एकदिशीय
(D) द्विदिशीय
Answer: (A)

Q5. यदि किसी बिंदु पर विद्युत क्षेत्र शून्य हो, तो वहाँ —
(A) बल अधिकतम होता है
(B) कोई बल नहीं लगता
(C) आवेश अनंत हो
(D) क्षेत्र अनंत होता है
Answer: (B)

Q6. एक विद्युत क्षेत्र में धन आवेश हमेशा —
(A) क्षेत्र के विपरीत चलता है
(B) क्षेत्र के साथ चलता है
(C) लंबवत चलता है
(D) गति नहीं करता
Answer: (B)

Q7. गाउस प्रमेय विद्युत क्षेत्र को किसके माध्यम से अभिव्यक्त करता है?
(A) स्केलर राशि
(B) कुल फ्लक्स
(C) गति
(D) दूरी
Answer: (B)

Q8. समविभाजित आवेशित गोल खोल के भीतर विद्युत क्षेत्र होता है —
(A) अधिकतम
(B) न्यूनतम
(C) शून्य
(D) अनंत
Answer: (C)

Q9. गाउस प्रमेय का उपयोग करना संभव है जब —
(A) सममिति हो
(B) कोई बल न हो
(C) घर्षण हो
(D) क्षेत्र शून्य हो
Answer: (A)

Q10. एक समविभाजित रेखीय आवेश के चारों ओर गाउस सतह का आकार होता है —
(A) गोला
(B) बेलन
(C) घन
(D) त्रिभुज
Answer: (B)

Q11. 1 कूलॉम आवेश को शून्य से एक बिंदु तक ले जाने के लिए किया गया कार्य कहलाता है —
(A) शक्ति
(B) विभव
(C) बल
(D) क्षेत्र
Answer: (B)

Q12. आवेश के कारण उत्पन्न क्षेत्र रेखाएँ —
(A) एक-दूसरे को काटती हैं
(B) सदा खुली रहती हैं
(C) बंद वक्र बनाती हैं
(D) एक-दूसरे के समांतर होती हैं
Answer: (B)

Q13. विद्युत क्षेत्र की इकाई होती है —
(A) न्यूटन
(B) कूलॉम
(C) वोल्ट
(D) न्यूटन प्रति कूलॉम
Answer: (D)

Q14. समान परिमाण के दो विपरीत आवेशों की युग्म रचना कहलाती है —
(A) समवाय आवेश
(B) द्विध्रुव
(C) त्रिध्रुव
(D) एकल आवेश
Answer: (B)

Q15. गाउस प्रमेय किस सिद्धांत पर आधारित है?
(A) न्यूटन का द्वितीय नियम
(B) अध्यारोपण सिद्धांत
(C) फ्लक्स सिद्धांत
(D) सममिति सिद्धांत
Answer: (C)

Q16. एक बिंदु पर कुल विद्युत क्षेत्र कई आवेशों के कारण —
(A) गुणनफल होता है
(B) योगफल होता है
(C) औसत होता है
(D) अनुपात होता है
Answer: (B)

Q17. यदि किसी बिंदु पर विद्युत क्षेत्र रेखाएँ सघन हैं, तो वहाँ क्षेत्र —
(A) शून्य होगा
(B) न्यूनतम होगा
(C) अधिकतम होगा
(D) नहीं होगा
Answer: (C)

Q18. एक समविभाजित आवेशित पतली पट्टी के समीप विद्युत क्षेत्र का मान —
(A) σ/ε₀
(B) σ/2ε₀
(C) σ²/ε₀
(D) σ²/2ε₀
Answer: (B)

Q19. 1 माइक्रोकूलॉम =
(A) 10⁶ कूलॉम
(B) 10⁻⁶ कूलॉम
(C) 10³ कूलॉम
(D) 10⁻³ कूलॉम
Answer: (B)

Q20. विद्युत बल एक —
(A) वेक्टर राशि है
(B) स्केलर राशि है
(C) त्रिविमीय राशि है
(D) कोई नहीं
Answer: (A)

Q21. विद्युत क्षेत्र में एक आवेशित कण पर लगने वाला बल किस नियम द्वारा ज्ञात होता है?
(A) न्यूटन का प्रथम नियम
(B) कूलॉम्ब नियम
(C) न्यूटन का तृतीय नियम
(D) गाउस प्रमेय
Answer: (B)

Q22. किसी बंद सतह से गुजरने वाली कुल फ्लक्स —
(A) सतह के क्षेत्रफल पर निर्भर करता है
(B) समवाय बल पर निर्भर करता है
(C) कुल आवेश पर निर्भर करता है
(D) द्रव्यमान पर निर्भर करता है
Answer: (C)

Q23. यदि q आवेश को किसी बिंदु से V वोल्ट विभव वाले बिंदु तक लाया जाए, तो किया गया कार्य होगा —
(A) q/V
(B) qV
(C) V/q
(D) शून्य
Answer: (B)

Q24. किसी द्विध्रुव द्वारा उत्पन्न विद्युत क्षेत्र उसकी अक्षरेखा पर किसके समानुपाती होता है?
(A) 1/r
(B) 1/r²
(C) 1/r³
(D) 1/r⁴
Answer: (C)

Q25. विद्युत क्षेत्र रेखाएँ सदैव —
(A) धन आवेश से प्रारंभ होकर ऋण आवेश की ओर जाती हैं
(B) ऋण से धन आवेश की ओर जाती हैं
(C) बंद वक्र बनाती हैं
(D) अंधाधुंध फैलती हैं
Answer: (A)

Q26. दो समान आवेशों के बीच दूरी को यदि आधा कर दिया जाए, तो उनके बीच लगने वाला बल —
(A) चार गुना हो जाएगा
(B) दो गुना हो जाएगा
(C) आधा हो जाएगा
(D) अपरिवर्तित रहेगा
Answer: (A)

Q27. यदि तीन बिंदु आवेश समकोण त्रिभुज के शीर्षों पर रखे हों, तो किसी बिंदु पर विद्युत क्षेत्र ज्ञात करने हेतु किस सिद्धांत का उपयोग करेंगे?
(A) अध्यारोपण सिद्धांत
(B) गाउस प्रमेय
(C) द्विध्रुव सिद्धांत
(D) बल-क्षेत्र सिद्धांत
Answer: (A)

Q28. यदि एक गोल आवेशित गोला, जिसकी त्रिज्या R है, के बाहर r दूरी पर विद्युत क्षेत्र का मान पूछा जाए, तो वह व्यवहार करेगा —
(A) बिंदु आवेश के समान
(B) द्विध्रुव के समान
(C) बेलन के समान
(D) शून्य
Answer: (A)

Q29. एक समविभाजित आवेशित रॉड के मध्य से दूरी d पर स्थित बिंदु पर विद्युत क्षेत्र —
(A) केवल लंबवत होगा
(B) केवल समांतर होगा
(C) दोनों घटकों में होगा
(D) शून्य होगा
Answer: (C)

Q30. यदि किसी बंद सतह के भीतर कुल आवेश शून्य हो, तो कुल फ्लक्स होगा —
(A) अधिकतम
(B) शून्य
(C) अनंत
(D) न्यूनतम
Answer: (B)

Q31. दो समान आवेश Q, दूरी r पर हैं। यदि उनमें से एक का आवेश 2Q कर दिया जाए, तो बल —
(A) दुगुना हो जाएगा
(B) चौगुना हो जाएगा
(C) तीन गुना हो जाएगा
(D) आधा हो जाएगा
Answer: (C)

Q32. गाउस प्रमेय के अनुसार एक गोले के भीतर आवेश q हो, तो फ्लक्स —
(A) q/ε₀
(B) q²/ε₀
(C) ε₀/q
(D) शून्य
Answer: (A)

Q33. समविभाजित रेखीय आवेश के कारण उत्पन्न विद्युत क्षेत्र किसके समानुपाती होता है?
(A) 1/r
(B) 1/r²
(C) 1/r³
(D) r
Answer: (A)

Q34. विद्युत क्षेत्र रेखाएँ एक दूसरे को कभी नहीं काटती क्योंकि —
(A) वे सीधी रेखाएँ होती हैं
(B) एक बिंदु पर केवल एक दिशा में बल संभव है
(C) क्षेत्र शून्य होता है
(D) घर्षण के कारण
Answer: (B)

Q35. एक समविभाजित आवेशित गोल खोल के बाहर r दूरी पर विद्युत क्षेत्र होगा —
(A) kQ/r
(B) kQ/r²
(C) kQ/r³
(D) शून्य
Answer: (B)

Q36. यदि किसी द्विध्रुव को विद्युत क्षेत्र में रखा जाए, तो उस पर —
(A) कोई बल नहीं लगता
(B) केवल बल लगता है
(C) केवल आघूर्ण लगता है
(D) बल और आघूर्ण दोनों लगते हैं
Answer: (D)

Q37. द्विध्रुव आघूर्ण τ दिया जाता है —
(A) τ = pE
(B) τ = p×E
(C) τ = E/p
(D) τ = p + E
Answer: (B)

Q38. विद्युत क्षेत्र की तीव्रता अधिकतम होती है —
(A) उन बिंदुओं पर जहाँ क्षेत्र रेखाएँ सघन हों
(B) जहाँ क्षेत्र रेखाएँ विरल हों
(C) जहाँ कोई रेखा न हो
(D) सभी बिंदुओं पर समान
Answer: (A)

Q39. एक द्विध्रुव पर कार्य करने वाला शुद्ध बल होता है —
(A) शून्य
(B) अनंत
(C) अधिकतम
(D) न्यूनतम
Answer: (A)

Q40. एक बिंदु आवेश q के कारण किसी बिंदु पर विद्युत क्षेत्र E है। यदि q को -q बना दिया जाए, तो E —
(A) अपरिवर्तित रहेगा
(B) दिशा बदल जाएगी
(C) परिमाण आधा होगा
(D) परिमाण दोगुना होगा
Answer: (B)

Q41. यदि एक सतह के भीतर q आवेश है, तो फ्लक्स —
(A) सतह के आकार पर निर्भर करता है
(B) q के मान पर निर्भर करता है
(C) दोनों पर
(D) किसी पर नहीं
Answer: (B)

Q42. एक द्विध्रुव द्वारा उत्पन्न विद्युत क्षेत्र अक्षरेखा पर —
(A) p/r²
(B) p/r³
(C) p/r
(D) p²/r³
Answer: (B)

Q43. यदि विद्युत क्षेत्र E वोल्ट/मीटर हो, तो उसका आयाम किसके समान है?
(A) बल
(B) विभव का अंतर
(C) बल प्रति इकाई आवेश
(D) कार्य
Answer: (C)

Q44. समविभाजित आवेशित बेलन के कारण उत्पन्न विद्युत क्षेत्र —
(A) गोले जैसा होता है
(B) केवल रेडियल होता है
(C) केवल अक्षीय होता है
(D) शून्य होता है
Answer: (B)

Q45. किसी आवेश पर क्षेत्र द्वारा किया गया कार्य —
(A) कार्य ऊर्जा में परिवर्तित होता है
(B) कोई महत्व नहीं
(C) गति बढ़ाता है
(D) ताप में जाता है
Answer: (A)

Q46. विद्युत बल प्रकृति में होता है —
(A) गुरुत्वाकर्षण बल से कमजोर
(B) गुरुत्वाकर्षण बल से अत्यधिक बलशाली
(C) बराबर
(D) अपरिभाषित
Answer: (B)

Q47. विद्युत क्षेत्र रेखाएँ सदैव प्रारंभ होती हैं —
(A) ऋण आवेश से
(B) धन आवेश से
(C) शून्य आवेश से
(D) कोई भी नहीं
Answer: (B)

Q48. यदि किसी बिंदु पर दो आवेशों से उत्पन्न क्षेत्र रद्द हो जाए, तो उसे कहते हैं —
(A) समांतर बिंदु
(B) संतुलन बिंदु
(C) विचलन बिंदु
(D) अनंत बिंदु
Answer: (B)

Q49. एक विद्युत क्षेत्र में ऋण आवेश की दिशा होती है —
(A) क्षेत्र के साथ
(B) क्षेत्र के विपरीत
(C) लंबवत
(D) कोणीय
Answer: (B)

Q50. एक द्विध्रुव के कारण समद्विभुज बिंदु पर उत्पन्न क्षेत्र का मान —
(A) 1/r
(B) 1/r²
(C) 1/r³
(D) r
Answer: (C)

————————————————————————————————————————————————————————————————————————————

दृश्य सामग्री

————————————————————————————————————————————————————————————————————————————