Class 12 : Maths (Hindi) – अध्याय 11: त्रिविमीय ज्यामिति
पाठ का विश्लेषण एवं विवेचन
🔵 परिचय
त्रिविमीय ज्यामिति में किसी बिंदु की स्थिति को तीन निर्देशांकों (x, y, z) द्वारा व्यक्त किया जाता है। यहाँ x-अक्ष, y-अक्ष, और z-अक्ष तीनों एक-दूसरे के लम्बवत होते हैं तथा मूलबिंदु O(0,0,0) से गुजरते हैं।
🟢 यह विषय हमें अंतरिक्ष में बिंदुओं, रेखाओं, तथा तलों के बीच संबंधों का अध्ययन करने में सहायता करता है।
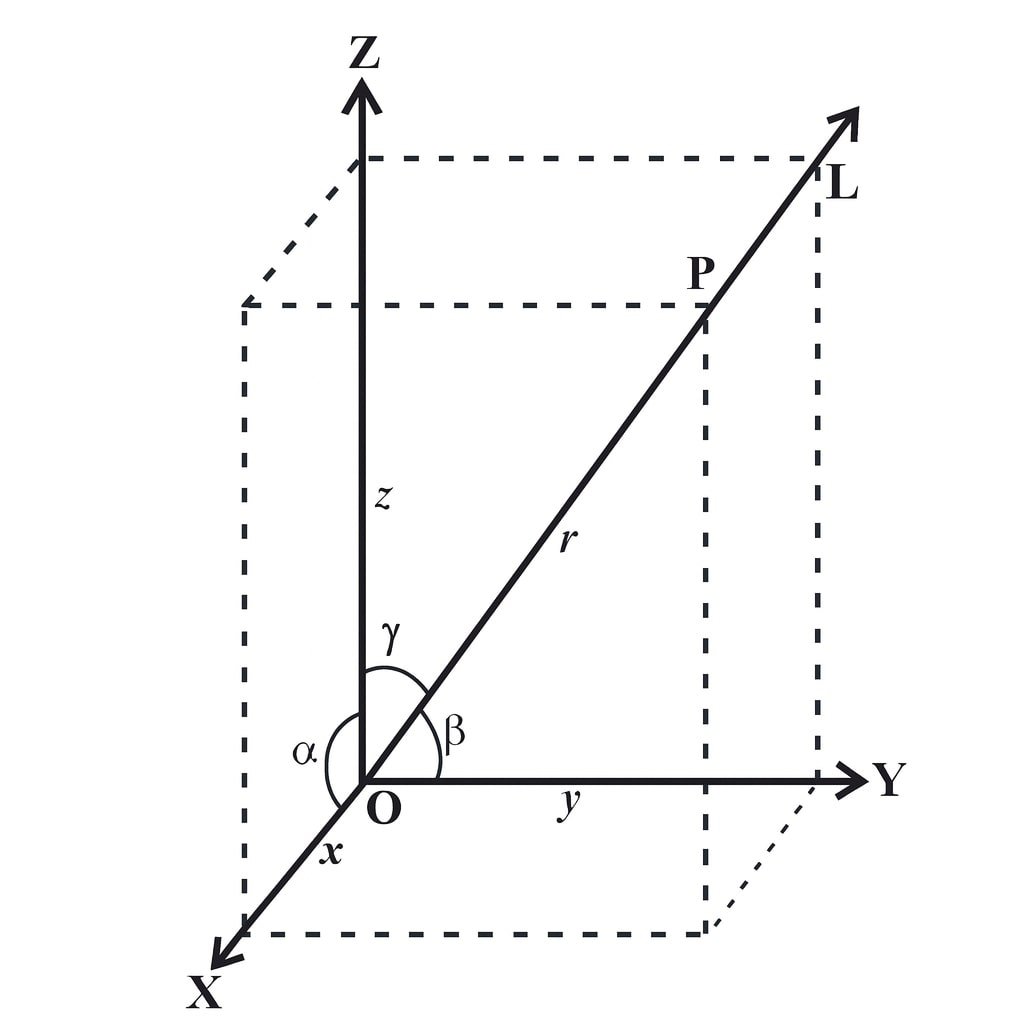
🟡 1️⃣ बिंदु के निर्देशांक
किसी बिंदु P(x, y, z) के निर्देशांक क्रमशः
x-अक्ष से दूरी = x
y-अक्ष से दूरी = y
z-अक्ष से दूरी = z
🔵 2️⃣ दो बिंदुओं के बीच दूरी
यदि दो बिंदु P(x₁, y₁, z₁) और Q(x₂, y₂, z₂) हों, तो उनकी दूरी का सूत्र:
➡️ PQ = √[(x₂ − x₁)² + (y₂ − y₁)² + (z₂ − z₁)²]
💡 यह सूत्र त्रिविमीय पाइथागोरस प्रमेय पर आधारित है।
🟢 3️⃣ मध्य बिंदु का सूत्र
दो बिंदुओं P(x₁, y₁, z₁) और Q(x₂, y₂, z₂) को जोड़ने वाले रेखाखंड का मध्य बिंदु M होगा:
➡️ M ( (x₁ + x₂)/2 , (y₁ + y₂)/2 , (z₁ + z₂)/2 )
🔴 4️⃣ विभाजन सूत्र
यदि बिंदु R, PQ को m:n अनुपात में विभाजित करता है, तो
➡️ R ( (m·x₂ + n·x₁)/(m+n), (m·y₂ + n·y₁)/(m+n), (m·z₂ + n·z₁)/(m+n) )
🟡 5️⃣ रेखा का समीकरण
(a) बिंदु-दिशा रूप
यदि रेखा बिंदु A(x₁, y₁, z₁) से गुजरती है और उसका दिशा अनुपात a, b, c है,
तो रेखा का समीकरण होगा:
➡️ (x − x₁)/a = (y − y₁)/b = (z − z₁)/c
(b) दो-बिंदु रूप
यदि रेखा दो बिंदुओं A(x₁, y₁, z₁) तथा B(x₂, y₂, z₂) से गुजरती है:
➡️ (x − x₁)/(x₂ − x₁) = (y − y₁)/(y₂ − y₁) = (z − z₁)/(z₂ − z₁)
🔵 6️⃣ दिशा अनुपात एवं दिशा कोसाइन
रेखा यदि अक्षों के साथ कोण α, β, γ बनाती है तो
➤ दिशा कोसाइन: l = cos α, m = cos β, n = cos γ
➤ संबंध: l² + m² + n² = 1
यदि दिशा अनुपात a, b, c हों तो
➤ l = a / √(a² + b² + c²), इसी प्रकार m, n
🟢 7️⃣ दो रेखाओं के बीच कोण
यदि दो रेखाओं के दिशा अनुपात (a₁, b₁, c₁) और (a₂, b₂, c₂) हों,
तो उनके बीच का कोण θ:
➡️ cos θ = (a₁a₂ + b₁b₂ + c₁c₂) / [ √(a₁² + b₁² + c₁²) · √(a₂² + b₂² + c₂²) ]
🔴 8️⃣ दो रेखाओं के बीच न्यूनतम दूरी
यदि दो रेखाएँ समानांतर न हों, तो न्यूनतम दूरी:
➡️ D = |(a₂ − a₁, b₂ − b₁, c₂ − c₁) · (b₁ × b₂)| / |b₁ × b₂|
✏️ Note: यदि रेखाएँ समानांतर हों, तो दूरी किसी बिंदु से दूसरी रेखा पर खींचे गए लंब की होती है।
🟡 9️⃣ तल का सामान्य समीकरण
यदि तल का सामान्य n(A, B, C) है और वह बिंदु P₀(x₀, y₀, z₀) से गुजरता है,
तो समीकरण होगा:
➡️ A(x − x₀) + B(y − y₀) + C(z − z₀) = 0
या
➡️ Ax + By + Cz + D = 0, जहाँ D = −(A·x₀ + B·y₀ + C·z₀)
🔵 🔟 बिंदु से तल की दूरी
यदि तल Ax + By + Cz + D = 0 है और बिंदु P(x₁, y₁, z₁) है, तो दूरी:
➡️ d = |A·x₁ + B·y₁ + C·z₁ + D| / √(A² + B² + C²)
🟢 1️⃣1️⃣ दो तलों के बीच कोण
दो तलों A₁x + B₁y + C₁z + D₁ = 0 और A₂x + B₂y + C₂z + D₂ = 0 के बीच कोण θ:
➡️ cos θ = (A₁A₂ + B₁B₂ + C₁C₂) / [ √(A₁² + B₁² + C₁²) · √(A₂² + B₂² + C₂²) ]
🔴 1️⃣2️⃣ रेखा और तल के बीच कोण
यदि रेखा के दिशा अनुपात (a, b, c) और तल का सामान्य (A, B, C) हो,
तो कोण θ:
➡️ sin θ = |A·a + B·b + C·c| / [ √(A² + B² + C²) · √(a² + b² + c²) ]
🟡 1️⃣3️⃣ रेखा और तल का प्रतिच्छेदन बिंदु
रेखा के पैरामीट्रिक रूप को तल के समीकरण में रखकर t का मान ज्ञात करते हैं और फिर उस t से बिंदु प्राप्त करते हैं।
🔵 1️⃣4️⃣ अनुप्रयोग
💡 त्रिविमीय ज्यामिति का प्रयोग
भौतिकी में वेक्टर विश्लेषण
अभियंत्रण में 3D मॉडलिंग
वास्तुकला, कंप्यूटर ग्राफ़िक्स में किया जाता है।
🧭 सारांश (Summary)
✔️ बिंदु = (x, y, z)
✔️ दूरी सूत्र = √[(x₂−x₁)² + (y₂−y₁)² + (z₂−z₁)²]
✔️ मध्य बिंदु = ((x₁+x₂)/2, (y₁+y₂)/2, (z₁+z₂)/2)
✔️ रेखा का समीकरण = (x−x₁)/a = (y−y₁)/b = (z−z₁)/c
✔️ तल का समीकरण = Ax + By + Cz + D = 0
✔️ दिशा कोसाइन = cos α, cos β, cos γ; l² + m² + n² = 1
✔️ बिंदु से तल की दूरी = |A·x₁ + B·y₁ + C·z₁ + D| / √(A² + B² + C²)
📝 Quick Recap
🔹 बिंदु = (x, y, z)
🔹 दूरी = √[(x₂−x₁)² + (y₂−y₁)² + (z₂−z₁)²]
🔹 रेखा समीकरण = (x−x₁)/a = (y−y₁)/b = (z−z₁)/c
🔹 तल समीकरण = Ax + By + Cz + D = 0
🔹 दिशा कोसाइन = l, m, n ; l² + m² + n² = 1
🔹 दूरी (बिंदु से तल) = |A·x₁ + B·y₁ + C·z₁ + D| / √(A² + B² + C²)
————————————————————————————————————————————————————————————————————————————
पाठ्यपुस्तक के प्रश्न
🧾 प्रश्नावली 11.1
🔵 प्रश्न 1:
यदि एक रेखा x-, y- और z-अक्ष के साथ क्रमशः 90°, 135°, 45° के कोण बनाती है, तो उसकी दिक-कोसाइन ज्ञात कीजिए।
🟢 उत्तर:
✏️ सिद्धांत: दिक-कोसाइन = (l, m, n) = (कोसाइन α, कोसाइन β, कोसाइन γ) तथा l² + m² + n² = 1
➡️ α = 90° ⇒ l = 0
➡️ β = 135° ⇒ m = −√2/2
➡️ γ = 45° ⇒ n = √2/2
✔️ अंतिम उत्तर: दिक-कोसाइन = (0, −√2/2, √2/2)
🔵 प्रश्न 2:
एक रेखा के दिक-कोसाइन ज्ञात कीजिए जो तीनों अक्षों के साथ समान कोण बनाती है।
🟢 उत्तर:
✏️ मान लें l = m = n
✏️ शर्त: l² + m² + n² = 1 ⇒ 3l² = 1
➡️ l = m = n = 1/√3 (न्यून/तीव्र कोण हेतु धनात्मक मान)
✔️ अंतिम उत्तर: दिक-कोसाइन = (1/√3, 1/√3, 1/√3)
✏️ नोट: यदि कोण स्थूल लिया जाए तो (−1/√3, −1/√3, −1/√3) भी संभव।
🔵 प्रश्न 3:
यदि किसी रेखा के दिक-अनुपात (−18, 12, −4) हैं, तो इसके दिक-कोसाइन ज्ञात कीजिए।
🟢 उत्तर:
✏️ सिद्धांत:
यदि दिक-अनुपात (a, b, c) हों, तो दिक-कोसाइन
(l, m, n) = ( a / √(a² + b² + c²), b / √(a² + b² + c²), c / √(a² + b² + c²) )
➡️ a = −18, b = 12, c = −4
✏️ पहले √(a² + b² + c²) ज्ञात कीजिए :
= √( (−18)² + 12² + (−4)² )
= √(324 + 144 + 16)
= √484 = 22
✏️ अब दिक-कोसाइन :
l = −18 / 22 = −9 / 11
m = 12 / 22 = 6 / 11
n = −4 / 22 = −2 / 11
✔️ अंतिम उत्तर:
दिक-कोसाइन = ( −9/11, 6/11, −2/11 ) ✅
🔵 प्रश्न 4:
दर्शाइए कि बिन्दु (2, 3, 4), (−1, −2, 1), (5, 8, 7) सरिख हैं।
🟢 उत्तर:
✏️ पहले दो सदिश निकालें:
➡️ AB̅ = (−1−2, −2−3, 1−4) = (−3, −5, −3)
➡️ AC̅ = (5−2, 8−3, 7−4) = (3, 5, 3)
✏️ तुलना: AC̅ = −1 × AB̅ ⇒ दोनों सह-दिश (अनुपाती)
✔️ अंतिम उत्तर: तीनों बिन्दु सरिख हैं।
🔵 प्रश्न 5:
तिर्यक-त्रिभुज की भुजाओं के दिक-कोसाइन ज्ञात कीजिए यदि शिखर
A(3, 5, −4), B(−1, 1, 2), C(−5, −5, −2) हों।
🟢 उत्तर:
✏️ भुजा AB̅ = B − A = (−4, −4, 6)
➡️ |AB̅| = √(16 + 16 + 36) = √68 = 2√17
➡️ AB के दिक-कोसाइन: (−4/√68, −4/√68, 6/√68) = (−2/√17, −2/√17, 3/√17)
✏️ भुजा BC̅ = C − B = (−4, −6, −4)
➡️ |BC̅| = √(16 + 36 + 16) = √68 = 2√17
➡️ BC के दिक-कोसाइन: (−4/√68, −6/√68, −4/√68) = (−2/√17, −3/√17, −2/√17)
✏️ भुजा CA̅ = A − C = (8, 10, −2)
➡️ |CA̅| = √(64 + 100 + 4) = √168 = 2√42
➡️ CA के दिक-कोसाइन: (8/√168, 10/√168, −2/√168) = (4/√42, 5/√42, −1/√42)
✔️ अंतिम उत्तर (भुजाओं के दिक-कोसाइन):
• AB: (−2/√17, −2/√17, 3/√17)
• BC: (−2/√17, −3/√17, −2/√17)
• CA: (4/√42, 5/√42, −1/√42)
📘 प्रश्नावली 11.2
🔵 प्रश्न 1:
दर्शाइए कि दिक-कोसाइन
12/13 , -3/13 , -4/13 ;
4/13 , 12/13 , 3/13 ;
-3/13 , -4/13 , 12/13
वाली तीन रेखाएँ परस्पर लंबवत हैं।
🟢 उत्तर:
✏️ दो रेखाएँ परस्पर लंबवत होती हैं यदि उनका अदिश गुणनफल (dot product) शून्य हो।
➡️ प्रथम और द्वितीय रेखा का अदिश गुणनफल =
(12/13 × 4/13) + (-3/13 × 12/13) + (-4/13 × 3/13)
= (48 – 36 – 12) / 169 = 0
➡️ प्रथम और तृतीय रेखा का अदिश गुणनफल =
(12/13 × -3/13) + (-3/13 × -4/13) + (-4/13 × 12/13)
= (-36 + 12 – 48) / 169 ≠ 0
✔️ अतः केवल प्रथम और द्वितीय रेखा परस्पर लंबवत हैं, तीनों एक-दूसरे पर लंबवत नहीं हैं।
🔵 प्रश्न 2:
दर्शाइए कि बिंदुओं (1, -1, 2), (3, 4, -2) से होकर जाने वाली रेखा,
बिंदुओं (0, 3, 2) और (3, 5, 6) से जाने वाली रेखा पर लंब है।
🟢 उत्तर:
✏️ पहली रेखा के दिक-अनुपात = (3 – 1, 4 – (-1), -2 – 2) = (2, 5, -4)
✏️ दूसरी रेखा के दिक-अनुपात = (3 – 0, 5 – 3, 6 – 2) = (3, 2, 4)
➡️ अदिश गुणनफल = (2×3) + (5×2) + (-4×4) = 6 + 10 – 16 = 0
✔️ चूँकि अदिश गुणनफल शून्य है, अतः दोनों रेखाएँ परस्पर लंबवत हैं ✅
🔵 प्रश्न 3:
दर्शाइए कि बिंदुओं (4, 7, 8), (2, 3, 4) से होकर जाने वाली रेखा,
बिंदुओं (-1, -2, 1), (1, 2, 5) से जाने वाली रेखा के समानांतर है।
🟢 उत्तर:
✏️ पहली रेखा के दिक-अनुपात = (2 – 4, 3 – 7, 4 – 8) = (-2, -4, -4)
✏️ दूसरी रेखा के दिक-अनुपात = (1 – (-1), 2 – (-2), 5 – 1) = (2, 4, 4)
➡️ अनुपात = (-2)/2 = (-4)/4 = (-4)/4 = -1
✔️ सभी अनुपात समान हैं, अतः दोनों रेखाएँ समानांतर हैं ✅
🔵 प्रश्न 4:
बिंदु (1, 2, 3) से गुजरने वाली रेखा का समीकरण ज्ञात कीजिए
जो सदिश 3i + 2j – 2k के समानांतर है।
🟢 उत्तर:
✏️ बिंदु = (1, 2, 3)
✏️ दिशा अनुपात = (3, 2, -2)
➡️ रेखा का समीकरण:
(x – 1)/3 = (y – 2)/2 = (z – 3)/-2
✔️ अंतिम उत्तर:
(x – 1)/3 = (y – 2)/2 = (z – 3)/-2 ✅
🔵 प्रश्न 5:
बिंदु जिसकी स्थिति सदिश 2î − ĵ + 4k̂ से गुजरने वाली व सदिश î + 2ĵ − k̂ की दिशा में जाने वाली रेखा का सदिश रूप तथा कार्तीय रूप ज्ञात कीजिए।
🟢 उत्तर:
✏️ स्थिति सदिश = r₀ = 2î − ĵ + 4k̂
✏️ दिशा सदिश = a = î + 2ĵ − k̂
➡️ रेखा का सदिश रूप:
r = r₀ + t a
⟹ r = (2î − ĵ + 4k̂) + t(î + 2ĵ − k̂)
🧠 अब घटकों के रूप में:
x = 2 + t
y = −1 + 2t
z = 4 − t
➡️ कार्तीय रूप:
(x − 2)/1 = (y + 1)/2 = (z − 4)/(−1)
✔️ अंतिम उत्तर:
सदिश रूप → r = (2î − ĵ + 4k̂) + t(î + 2ĵ − k̂)
कार्तीय रूप → (x − 2)/1 = (y + 1)/2 = (z − 4)/(−1)
🔵 प्रश्न 6:
उस रेखा का कार्तीय समीकरण ज्ञात कीजिए जो बिंदु (−2, 4, −5) से जाती है और
(x + 3)/3 = (y − 4)/5 = (z + 8)/6 के समानांतर है।
🟢 उत्तर:
✏️ दिशा अनुपात = 3, 5, 6
✏️ बिंदु = (−2, 4, −5)
➡️ कार्तीय रूप:
(x + 2)/3 = (y − 4)/5 = (z + 5)/6
✔️ अंतिम उत्तर:
(x + 2)/3 = (y − 4)/5 = (z + 5)/6 ✅
🔵 प्रश्न 7:
एक रेखा का कार्तीय समीकरण
(x − 5)/3 = (y + 4)/7 = (z − 6)/2 है।
इसका सदिश समीकरण ज्ञात कीजिए।
🟢 उत्तर:
✏️ स्थिति बिंदु = (5, −4, 6)
✏️ दिशा अनुपात = (3, 7, 2)
➡️ सदिश समीकरण:
r = r₀ + t a
⟹ r = (5î − 4ĵ + 6k̂) + t(3î + 7ĵ + 2k̂)
✔️ अंतिम उत्तर:
r = (5î − 4ĵ + 6k̂) + t(3î + 7ĵ + 2k̂) ✅
🔵 प्रश्न 8:
निम्नलिखित रेखा-युग्मों के बीच का कोण ज्ञात कीजिए:
🟢 (i)
r = 2î − 5ĵ + k̂ + λ(3î + 2ĵ + 6k̂)
और
r = 7î − 6k̂ + μ(î + 2ĵ + 2k̂)
✏️ दिशा सदिश:
a₁ = (3, 2, 6)
a₂ = (1, 2, 2)
✏️ सूत्र:
cosθ = (a₁ · a₂) / (|a₁| |a₂|)
➡️ a₁ · a₂ = (3×1) + (2×2) + (6×2) = 3 + 4 + 12 = 19
➡️ |a₁| = √(3² + 2² + 6²) = √(9 + 4 + 36) = √49 = 7
➡️ |a₂| = √(1² + 2² + 2²) = √(1 + 4 + 4) = √9 = 3
✏️ cosθ = 19 / (7 × 3) = 19 / 21
✔️ अंतिम उत्तर:
cosθ = 19/21
⟹ θ = cos⁻¹(19/21)
🟢 (ii)
r = 3î + ĵ − 2k̂ + λ(î − ĵ − 2k̂)
और
r = 2î − ĵ − 5k̂ + μ(3î − 5ĵ − 4k̂)
✏️ दिशा सदिश:
a₁ = (1, −1, −2)
a₂ = (3, −5, −4)
✏️ cosθ = (a₁ · a₂) / (|a₁| |a₂|)
➡️ a₁ · a₂ = (1×3) + (−1×−5) + (−2×−4) = 3 + 5 + 8 = 16
➡️ |a₁| = √(1² + (−1)² + (−2)²) = √(1 + 1 + 4) = √6
➡️ |a₂| = √(3² + (−5)² + (−4)²) = √(9 + 25 + 16) = √50 = 5√2
✏️ cosθ = 16 / (√6 × 5√2) = 16 / (5√12) = 16 / (5×2√3) = 8 / (5√3)
✔️ अंतिम उत्तर:
cosθ = 8 / (5√3)
⟹ θ = cos⁻¹(8 / (5√3))
🔵 प्रश्न 9:
निम्नलिखित रेखा-युग्मों के बीच का कोण ज्ञात कीजिए:
🟢 (i)
(x − 2)/2 = (y − 3)/5 = (z + 3)/(−3)
और
(x + 2)/(−1) = (y − 4)/8 = (z − 5)/4
✏️ दिशा अनुपात:
a₁ = (2, 5, −3)
a₂ = (−1, 8, 4)
✏️ cosθ = (a₁ · a₂) / (|a₁| |a₂|)
➡️ a₁ · a₂ = (2×−1) + (5×8) + (−3×4) = −2 + 40 − 12 = 26
➡️ |a₁| = √(2² + 5² + (−3)²) = √(4 + 25 + 9) = √38
➡️ |a₂| = √((−1)² + 8² + 4²) = √(1 + 64 + 16) = √81 = 9
✏️ cosθ = 26 / (9√38)
✔️ अंतिम उत्तर:
cosθ = 26 / (9√38)
⟹ θ = cos⁻¹(26 / (9√38))
🟢 (ii)
(x/2) = (y/2) = (z/1)
और
(x − 5)/4 = (y − 2)/1 = (z − 3)/8
✏️ दिशा अनुपात:
a₁ = (2, 2, 1)
a₂ = (4, 1, 8)
✏️ cosθ = (a₁ · a₂) / (|a₁| |a₂|)
➡️ a₁ · a₂ = (2×4) + (2×1) + (1×8) = 8 + 2 + 8 = 18
➡️ |a₁| = √(2² + 2² + 1²) = √(4 + 4 + 1) = √9 = 3
➡️ |a₂| = √(4² + 1² + 8²) = √(16 + 1 + 64) = √81 = 9
✏️ cosθ = 18 / (3 × 9) = 18 / 27 = 2/3
✔️ अंतिम उत्तर:
cosθ = 2/3
⟹ θ = cos⁻¹(2/3)
🔵 प्रश्न 10:
p का मान ज्ञात कीजिए ताकि रेखाएँ
(1 − x)/3 = (7y − 14)/(2p) = (z − 3)/2
और
(7 − 7x)/(3p) = (y − 5)/1 = (6 − z)/5
परस्पर लंब हों।
🟢 उत्तर:
✏️ दिशा-अनुपात निकालें:
➡️ पहली रेखा: a₁ = −3 , b₁ = 2p/7 , c₁ = 2
(क्योंकि (1−x)/3 = −(x−1)/3, (7y−14)/(2p) = (y−2)/(2p/7))
➡️ दूसरी रेखा: a₂ = −3p/7 , b₂ = 1 , c₂ = −5
((7−7x)/(3p) = −(x−1)/(3p/7), (6−z)/5 = −(z−6)/5)
✏️ लंबवत की शर्त: a₁a₂ + b₁b₂ + c₁c₂ = 0
➡️ (−3)(−3p/7) + (2p/7)(1) + (2)(−5) = 0
➡️ 9p/7 + 2p/7 − 10 = 0
➡️ 11p/7 = 10
➡️ p = 70/11
✔️ अंतिम उत्तर: p = 70/11
🔵 प्रश्न 11:
दिखाइए कि रेखाएँ
(x − 5)/7 = (y + 2)/(−5) = z/1
और
x/2 = y/1 = z/3
परस्पर लंब हैं।
🟢 उत्तर (जाँच):
✏️ दिशा-अनुपात:
➡️ पहली रेखा: (7, −5, 1)
➡️ दूसरी रेखा: (2, 1, 3)
✏️ अदिश गुणनफल: 7×2 + (−5)×1 + 1×3 = 14 − 5 + 3 = 12
➡️ 12 ≠ 0 ⇒ लंबवत नहीं।
✔️ टिप्पणी: दिए गए मानों के साथ रेखाएँ लंबवत नहीं हैं;
cosθ = 12 / ( √(7²+ (−5)²+1²) × √(2²+1²+3²) ) = 12 / (5√42)
अतः θ = cos⁻¹(12 / (5√42)) (शून्य से भिन्न कोण)।
🔵 प्रश्न 12:
रेखाएँ
r = (î + 2ĵ + k̂) + λ(î − ĵ + k̂)
और
r = (2î − ĵ − k̂) + μ(2î + ĵ + 2k̂)
के बीच की न्यूनतम दूरी ज्ञात कीजिए।
🟢 उत्तर:
✏️ बिंदु व दिशा-सदिश:
➡️ P₁(1, 2, 1), a̅₁ = (1, −1, 1)
➡️ P₂(2, −1, −1), a̅₂ = (2, 1, 2)
✏️ P₁P₂ = (2−1, −1−2, −1−1) = (1, −3, −2)
✏️ a̅₁ × a̅₂ = | i j k ; 1 −1 1 ; 2 1 2 | = (−3, 0, 3)
➡️ |a̅₁ × a̅₂| = √(9 + 0 + 9) = 3√2
✏️ |(P₁P₂ · a̅₁ × a̅₂)| = | (1, −3, −2) · (−3, 0, 3) |
= | (−3) + 0 + (−6) | = 9
➡️ न्यूनतम दूरी d = |(P₁P₂ · a̅₁ × a̅₂)| / |a̅₁ × a̅₂|
= 9 / (3√2) = 3/√2
✔️ अंतिम उत्तर: न्यूनतम दूरी = 3/√2
🔵 प्रश्न 13:
रेखाओं
(x + 1)/7 = (y + 1)/(−6) = (z + 1)/1
और
(x − 3)/1 = (y − 5)/(−2) = (z − 7)/(−1)
के बीच की न्यूनतम दूरी ज्ञात कीजिए।
🟢 उत्तर:
✏️ रेखा 1 के लिए:
बिंदु A(−1, −1, −1), दिशा सदिश a₁ = (7, −6, 1)
✏️ रेखा 2 के लिए:
बिंदु B(3, 5, 7), दिशा सदिश a₂ = (1, −2, −1)
➡️ AB = (3 − (−1), 5 − (−1), 7 − (−1)) = (4, 6, 8)
✏️ a₁ × a₂ =
= | i j k |
| 7 −6 1 |
| 1 −2 −1 |
= i(6 − (−2)) − j(−7 − 1) + k(−14 + 6)
= 8i + 8j − 8k
= 8(1, 1, −1)
➡️ |a₁ × a₂| = 8√3
✏️ AB · (a₁ × a₂) = (4)(8) + (6)(8) + (8)(−8) = 32 + 48 − 64 = 16
|AB · (a₁ × a₂)| = 16
➡️ न्यूनतम दूरी = |AB · (a₁ × a₂)| / |a₁ × a₂|
= 16 / (8√3) = 2 / √3
✔️ अंतिम उत्तर: d = 2 / √3 ✅
🔵 प्रश्न 14:
रेखाएँ
r₁ = (î + 2ĵ + 3k̂) + λ(î − 3ĵ + 2k̂)
r₂ = (4î + 5ĵ + 6k̂) + μ(2î + 3ĵ + k̂)
के बीच न्यूनतम दूरी ज्ञात कीजिए।
🟢 उत्तर:
✏️ P₁(1, 2, 3), a₁ = (1, −3, 2)
✏️ P₂(4, 5, 6), a₂ = (2, 3, 1)
➡️ P₁P₂ = (3, 3, 3)
✏️ a₁ × a₂ =
= | i j k |
| 1 −3 2 |
| 2 3 1 |
= i(−3 − 6) − j(1 − 4) + k(3 + 6)
= (−9, 3, 9)
➡️ |a₁ × a₂| = √(81 + 9 + 81) = √171 = 3√19
✏️ P₁P₂ · (a₁ × a₂) = (3)(−9) + (3)(3) + (3)(9) = −27 + 9 + 27 = 9
|P₁P₂ · (a₁ × a₂)| = 9
➡️ d = 9 / (3√19) = 3 / √19
✔️ अंतिम उत्तर: d = 3 / √19 ✅
🔵 प्रश्न 15:
रेखाएँ
r₁ = (1 − t)î + (t − 2)ĵ + (3 − 2t)k̂
और
r₂ = (s + 1)î + (2s − 1)ĵ − (2s + 1)k̂
के बीच न्यूनतम दूरी ज्ञात कीजिए।
🟢 उत्तर:
✏️ रेखा 1: P₁(1, −2, 3), a₁ = (−1, 1, −2)
✏️ रेखा 2: P₂(1, −1, −1), a₂ = (1, 2, −2)
➡️ P₁P₂ = (0, 1, −4)
✏️ a₁ × a₂ =
= | i j k |
| −1 1 −2 |
| 1 2 −2 |
= i(−2 − (−4)) − j(2 − (−2)) + k(−2 − 1)
= (2, −4, −3)
➡️ |a₁ × a₂| = √(2² + (−4)² + (−3)²) = √(4 + 16 + 9) = √29
✏️ P₁P₂ · (a₁ × a₂) = (0)(2) + (1)(−4) + (−4)(−3) = −4 + 12 = 8
|P₁P₂ · (a₁ × a₂)| = 8
➡️ d = 8 / √29
✔️ अंतिम उत्तर: d = 8 / √29 ✅
————————————————————————————————————————————————————————————————————————————
अन्य महत्वपूर्ण प्रश्न
(CBSE MODEL प्रश्न पत्र)
सिर्फ इसी पाठ से निर्मित CBSE MODEL प्रश्न पत्र
🔵 प्रश्न 1
यदि दो बिंदु P(2, 3, 4) और Q(4, 7, 8) हों, तो PQ की लंबाई है:
🟢 (A) 8
🔵 (B) 6
🟠 (C) √48
🔴 (D) 4
उत्तर: (B) 6
🔵 प्रश्न 2
बिंदु P(2, 4, 6) और Q(4, 8, 10) का मध्यबिंदु है:
🟢 (A) (3, 6, 8)
🔵 (B) (3, 5, 7)
🟠 (C) (4, 6, 8)
🔴 (D) (2, 6, 10)
उत्तर: (A) (3, 6, 8)
🔵 प्रश्न 3
यदि रेखा का दिशा अनुपात (2, 3, 6) है, तो दिशा कोसाइन होंगे:
🟢 (A) (1/√7, 3/√7, 6/√7)
🔵 (B) (2/7, 3/7, 6/7)
🟠 (C) (2/7, 3/7, 1/7)
🔴 (D) (2/7, 3/7, 6/14)
उत्तर: (B) (2/7, 3/7, 6/7)
🔵 प्रश्न 4
रेखा (x−2)/1 = (y−3)/2 = (z−4)/3 का दिशा अनुपात है:
🟢 (A) (1, 2, 3)
🔵 (B) (2, 3, 4)
🟠 (C) (1, 1, 1)
🔴 (D) (3, 2, 1)
उत्तर: (A) (1, 2, 3)
🔵 प्रश्न 5
बिंदु (2, 3, 4) और तल x + 2y + 2z + 3 = 0 के बीच दूरी है:
🟢 (A) 2
🔵 (B) 3
🟠 (C) 4
🔴 (D) 5
उत्तर: (A) 2
🔵 प्रश्न 6
रेखा और तल के बीच कोण θ का सूत्र है:
🟢 (A) sinθ = |Aa + Bb + Cc| / √(A² + B² + C²)√(a² + b² + c²)
🔵 (B) cosθ = …
🟠 (C) tanθ = …
🔴 (D) इनमें से कोई नहीं
उत्तर: (A) sinθ = |Aa + Bb + Cc| / √(A² + B² + C²)√(a² + b² + c²)
🔵 प्रश्न 7
यदि तल का समीकरण 2x + 3y + 6z − 9 = 0 हो, तो उसका सामान्य है:
🟢 (A) (2, 3, 6)
🔵 (B) (3, 6, 9)
🟠 (C) (1, 1, 1)
🔴 (D) (6, 3, 2)
उत्तर: (A) (2, 3, 6)
🔵 प्रश्न 8
बिंदु (2, 1, 2) तल 2x + y + 2z − 9 = 0 पर स्थित है या नहीं?
🟢 (A) हाँ
🔵 (B) नहीं
🟠 (C) तय नहीं
🔴 (D) केवल x पर निर्भर
उत्तर: (B) नहीं
🔵 प्रश्न 9
यदि रेखा दो बिंदुओं (1,2,3) और (2,3,4) से गुजरती है, तो उसका समीकरण होगा:
🟢 (A) (x−1)/1 = (y−2)/1 = (z−3)/1
🔵 (B) (x−1)/2 = (y−2)/3 = (z−3)/4
🟠 (C) (x−2)/1 = (y−3)/1 = (z−4)/1
🔴 (D) इनमें से कोई नहीं
उत्तर: (A) (x−1)/1 = (y−2)/1 = (z−3)/1
🔵 प्रश्न 10
दिशा कोसाइन का संबंध है:
🟢 (A) l² + m² + n² = 1
🔵 (B) l + m + n = 1
🟠 (C) l²m²n² = 1
🔴 (D) l + m + n = 0
उत्तर: (A) l² + m² + n² = 1
🔵 प्रश्न 11
दो तलों के बीच कोण ज्ञात करने हेतु सूत्र है:
🟢 (A) cosθ = (A₁A₂ + B₁B₂ + C₁C₂) / √(…)
🔵 (B) sinθ = …
🟠 (C) tanθ = …
🔴 (D) इनमें से कोई नहीं
उत्तर: (A) cosθ = (A₁A₂ + B₁B₂ + C₁C₂) / [√(A₁²+B₁²+C₁²) √(A₂²+B₂²+C₂²)]
🔵 प्रश्न 12
रेखा के दिशा अनुपात (2,2,1) हैं, तो दिशा कोसाइन होंगे:
🟢 (A) (2/3, 2/3, 1/3)
🔵 (B) (2/√9, 2/√9, 1/√9)
🟠 (C) (1/2, 1/2, 1/2)
🔴 (D) (1, 1, 1)
उत्तर: (B) (2/3, 2/3, 1/3)
🔵 प्रश्न 13
यदि रेखा का समीकरण (x−1)/2 = (y+1)/−3 = (z−2)/1 हो, तो दिशा अनुपात है:
🟢 (A) (2, −3, 1)
🔵 (B) (−2, 3, −1)
🟠 (C) (2, 3, 1)
🔴 (D) (1, −2, 3)
उत्तर: (A) (2, −3, 1)
🔵 प्रश्न 14
तल Ax + By + Cz + D = 0 का सामान्य है:
🟢 (A) (A, B, C)
🔵 (B) (D, B, C)
🟠 (C) (A, D, C)
🔴 (D) (A, B, D)
उत्तर: (A) (A, B, C)
🔵 प्रश्न 15
यदि दो रेखाएँ समानांतर हों तो उनके दिशा अनुपात:
🟢 (A) समानुपाती होते हैं
🔵 (B) असमान होते हैं
🟠 (C) शून्य होते हैं
🔴 (D) विपरीत चिन्हों के होते हैं
उत्तर: (A) समानुपाती होते हैं
🔵 प्रश्न 16
मूल बिंदु से गुजरने वाले तल का समीकरण है:
🟢 (A) Ax + By + Cz = 0
🔵 (B) Ax + By + Cz + D = 0
🟠 (C) A + B + C = 0
🔴 (D) D = 0
उत्तर: (A) Ax + By + Cz = 0
🔵 प्रश्न 17
यदि बिंदु (x₁, y₁, z₁) तल Ax + By + Cz + D = 0 पर हो तो:
🟢 (A) Ax₁ + By₁ + Cz₁ + D = 0
🔵 (B) Ax₁ + By₁ + Cz₁ + D ≠ 0
🟠 (C) D = 0
🔴 (D) इनमें से कोई नहीं
उत्तर: (A) Ax₁ + By₁ + Cz₁ + D = 0
🔵 प्रश्न 18
दो रेखाओं के बीच न्यूनतम दूरी का सूत्र:
🟢 (A) |(a₂−a₁, b₂−b₁, c₂−c₁)·(b₁×b₂)| / |b₁×b₂|
🔵 (B) |a₁a₂+b₁b₂+c₁c₂|
🟠 (C) |a₁+b₁+c₁|
🔴 (D) इनमें से कोई नहीं
उत्तर: (A) |(a₂−a₁, b₂−b₁, c₂−c₁)·(b₁×b₂)| / |b₁×b₂|
🔵 प्रश्न 19
दो बिंदुओं P(2, –1, 3) और Q(5, 2, 7) के बीच की दूरी ज्ञात कीजिए।
🧠 उत्तर:
➡️ सूत्र: PQ = √[(x₂ − x₁)² + (y₂ − y₁)² + (z₂ − z₁)²]
➡️ PQ = √[(5−2)² + (2+1)² + (7−3)²]
➡️ PQ = √[3² + 3² + 4²]
➡️ PQ = √(9 + 9 + 16) = √34
✔️ अन्तिम उत्तर: √34 इकाई
🟢 प्रश्न 20
बिंदु A(2, 3, 4) और B(4, 7, 8) का मध्यबिंदु ज्ञात कीजिए।
🧠 उत्तर:
➡️ सूत्र: M = ((x₁ + x₂)/2, (y₁ + y₂)/2, (z₁ + z₂)/2)
➡️ M = ((2+4)/2, (3+7)/2, (4+8)/2) = (3, 5, 6)
✔️ अन्तिम उत्तर: M(3, 5, 6)
🟡 प्रश्न 21
बिंदु P(1, 2, 3) और Q(4, 5, 6) को 1:2 के अनुपात में विभाजित करने वाले बिंदु के निर्देशांक ज्ञात कीजिए।
🧠 उत्तर:
➡️ सूत्र: R = ((m·x₂ + n·x₁)/(m+n), (m·y₂ + n·y₁)/(m+n), (m·z₂ + n·z₁)/(m+n))
➡️ R = ((1·4 + 2·1)/3, (1·5 + 2·2)/3, (1·6 + 2·3)/3)
➡️ R = (6/3, 9/3, 12/3) = (2, 3, 4)
✔️ अन्तिम उत्तर: R(2, 3, 4)
🔴 प्रश्न 22
यदि किसी रेखा के दिशा अनुपात (3, 4, 12) हों, तो उसके दिशा कोज्या ज्ञात कीजिए।
🧠 उत्तर:
➡️ सूत्र: l = a / √(a²+b²+c²), m = b / √(…), n = c / √(…)
➡️ √(a²+b²+c²) = √(9 + 16 + 144) = √169 = 13
➡️ l = 3/13, m = 4/13, n = 12/13
✔️ अन्तिम उत्तर: (3/13, 4/13, 12/13)
🟢 प्रश्न 23
यदि तल का समीकरण 2x + 3y + 6z − 12 = 0 है, तो बिंदु P(1, 2, 3) से उसकी दूरी ज्ञात कीजिए।
🧠 उत्तर:
➡️ सूत्र: d = |A·x₁ + B·y₁ + C·z₁ + D| / √(A² + B² + C²)
➡️ d = |2·1 + 3·2 + 6·3 − 12| / √(4 + 9 + 36)
➡️ d = |2 + 6 + 18 − 12| / 7 = 14/7 = 2
✔️ अन्तिम उत्तर: 2 इकाई
✳️ Section C (3 अंक वाले प्रश्न)
🔵 प्रश्न 24
बिंदु A(1, 2, 3), B(2, 3, 4) और C(3, 4, 5) से गुजरने वाले तल का समीकरण ज्ञात कीजिए।
🧠 उत्तर:
➡️ सदिश AB = (1, 1, 1) और AC = (2, 2, 2)
➡️ ये दोनों सदिश समान दिशा में हैं, अतः AB × AC = 0
✏️ इसलिए बिंदु A, B, C सह-रेखीय हैं।
✔️ अन्तिम उत्तर: सह-रेखीय बिंदुओं से कोई अद्वितीय तल नहीं बनता।
🟢 प्रश्न 25
रेखा का समीकरण ज्ञात कीजिए जो बिंदु (1, 2, 3) से गुजरती है और जिसका दिशा अनुपात (2, –3, 1) है।
🧠 उत्तर:
➡️ सूत्र: (x − x₁)/a = (y − y₁)/b = (z − z₁)/c
➡️ (x − 1)/2 = (y − 2)/(−3) = (z − 3)/1
✔️ अन्तिम उत्तर: (x − 1)/2 = (y − 2)/(−3) = (z − 3)/1
🔴 प्रश्न 26
तल का समीकरण ज्ञात कीजिए जो बिंदु (2, 3, 4) से गुजरता है और जिसका सामान्य सदिश (1, 2, 3) है।
🧠 उत्तर:
➡️ सूत्र: A(x − x₁) + B(y − y₁) + C(z − z₁) = 0
➡️ 1(x − 2) + 2(y − 3) + 3(z − 4) = 0
➡️ x − 2 + 2y − 6 + 3z − 12 = 0
➡️ x + 2y + 3z − 20 = 0
✔️ अन्तिम उत्तर: x + 2y + 3z − 20 = 0
🟡 प्रश्न 27
बिंदु (2, 1, −1) से तल 2x + y + 2z + 3 = 0 की दूरी ज्ञात कीजिए।
🧠 उत्तर:
➡️ सूत्र: d = |A·x₁ + B·y₁ + C·z₁ + D| / √(A² + B² + C²)
➡️ d = |2·2 + 1·1 + 2·(−1) + 3| / √(4 + 1 + 4)
➡️ d = |4 + 1 − 2 + 3| / 3 = |6| / 3 = 2
✔️ अन्तिम उत्तर: 2 इकाई
✳️ Section D – दीर्घ उत्तरीय प्रश्न (5 अंक प्रत्येक)
🔵 प्रश्न 28
उस तल का समीकरण ज्ञात कीजिए जो तीन बिंदुओं A(1, 1, 1), B(2, 3, 1) और C(3, 1, 2) से होकर गुजरता है।
🧠 उत्तर:
➡️ ✏️ मान लें तल का सामान्य रूप है:
a(x − x₁) + b(y − y₁) + c(z − z₁) = 0
🟢 Step 1: बिंदु A से दो सदिश ज्ञात कीजिए —
AB = (2−1, 3−1, 1−1) = (1, 2, 0)
AC = (3−1, 1−1, 2−1) = (2, 0, 1)
🟡 Step 2: सामान्य सदिश = AB × AC
= |i j k|
|1 2 0|
|2 0 1|
= i(2·1 − 0·0) − j(1·1 − 0·2) + k(1·0 − 2·2)
= (2, −1, −4)
🔴 Step 3: बिंदु A(1, 1, 1) को रखें:
2(x−1) −1(y−1) −4(z−1) = 0
➡️ 2x − 2 − y + 1 − 4z + 4 = 0
➡️ 2x − y − 4z + 3 = 0
✔️ Final Answer: तल का समीकरण है 2x − y − 4z + 3 = 0
🔵 प्रश्न 29
रेखाओं के बीच कोण ज्ञात कीजिए —
(x − 1)/2 = (y − 2)/3 = (z − 3)/4
और
(x − 2)/1 = (y − 3)/2 = (z − 4)/3
🧠 उत्तर:
🟢 दिशा अनुपात:
पहली रेखा = (2, 3, 4)
दूसरी रेखा = (1, 2, 3)
🟡 सूत्र:
cos θ = (a₁a₂ + b₁b₂ + c₁c₂) / [√(a₁²+b₁²+c₁²) × √(a₂²+b₂²+c₂²)]
➡️ cos θ = (2·1 + 3·2 + 4·3) / [√(4+9+16) × √(1+4+9)]
➡️ cos θ = 20 / √(29 × 14)
➡️ cos θ = 20 / √406
✔️ Final Answer: cos θ = 20 / √406 (लगभग θ ≈ 21.6°)
🔵 प्रश्न 30
उस रेखा का समीकरण ज्ञात कीजिए जो बिंदु (1, 2, −1) से गुजरती है और तलों
x + y + z = 2 तथा 2x − y + 3z = 1 के प्रतिच्छेद पर स्थित है।
🧠 उत्तर:
➡️ दो तलों का संयोजन:
(x + y + z − 2) + λ(2x − y + 3z − 1) = 0
🟢 गुणांक जोड़ें:
(1+2λ)x + (1−λ)y + (1+3λ)z − (2+λ) = 0
🟡 बिंदु (1, 2, −1) रखने पर:
(1+2λ)·1 + (1−λ)·2 + (1+3λ)(−1) − (2+λ) = 0
➡️ 1 + 2λ + 2 − 2λ − 1 − 3λ − 2 − λ = 0
➡️ −4λ = 0 → λ = 0
🔴 अतः रेखा का समीकरण है:
x + y + z − 2 = 0
जो (1, 2, −1) से गुजरती है
✔️ Final Answer (Parametric Form):
x = 1 + t, y = 2 − t, z = −1
✳️ Section E – केस आधारित / अनुप्रयोगात्मक प्रश्न (5 अंक)
🔵 प्रश्न 31
एक बिंदु P की अक्षों से लंबवत दूरियाँ 3, 4 और 12 हैं। उस बिंदु के संभावित स्थान ज्ञात कीजिए।
🧠 उत्तर:
➡️ |x| = 3, |y| = 4, |z| = 12
➡️ संभावित बिंदु: (±3, ±4, ±12)
✔️ Final Answer: 8 संभावित बिंदु —
(3, 4, 12), (−3, 4, 12), (3, −4, 12), (−3, −4, 12),
(3, 4, −12), (−3, 4, −12), (3, −4, −12), (−3, −4, −12)
🔵 प्रश्न 32
सिद्ध कीजिए कि रेखाएँ
(x − 1)/2 = (y − 2)/3 = (z − 3)/4
और
(x − 2)/1 = (y − 3)/2 = (z − 4)/3
सह-तलीय हैं।
🧠 उत्तर:
➡️ दिशा अनुपात:
r₁ = (2, 3, 4), r₂ = (1, 2, 3)
➡️ बिंदुओं का अंतर: (2−1, 3−2, 4−3) = (1, 1, 1)
🟢 Cross Product:
r₁ × r₂ = (1, −2, 1)
🟡 Dot Product:
(1, 1, 1) · (1, −2, 1) = 1 − 2 + 1 = 0
✔️ Final Answer: रेखाएँ सह-तलीय हैं।
🔵 प्रश्न 33
बिंदु (1, 2, 3) से तल 2x + 3y + 6z − 12 = 0 पर खींचे गए लम्ब का पाद ज्ञात कीजिए।
🧠 उत्तर:
➡️ A = 2, B = 3, C = 6, D = −12
➡️ बिंदु P(x₁, y₁, z₁) = (1, 2, 3)
🟢 सूत्र:
k = −(A·x₁ + B·y₁ + C·z₁ + D) / (A² + B² + C²)
= −(2·1 + 3·2 + 6·3 − 12) / (4 + 9 + 36)
= −14 / 49 = −2/7
🟡 पाद के निर्देशांक:
x = x₁ + A·k = 1 + 2(−2/7) = 3/7
y = y₁ + B·k = 2 + 3(−2/7) = 8/7
z = z₁ + C·k = 3 + 6(−2/7) = 9/7
✔️ Final Answer: पाद = (3/7, 8/7, 9/7)
————————————————————————————————————————————————————————————————————————————
JEE MAINS पिछले सालों के प्रश्न
🔵 प्रश्न 1
बिंदु P(x₁, y₁, z₁) से समतल ax + by + cz + d = 0 की दूरी =
🟥 1️⃣ |ax₁ + by₁ + cz₁ + d| / sqrt(a^2 + b^2 + c^2)
🟩 2️⃣ |ax₁ + by₁ + cz₁| / (a^2 + b^2 + c^2)
🟨 3️⃣ sqrt(a^2 + b^2 + c^2)
🟦 4️⃣ |d|
✔️ उत्तर: 1️⃣
📅 JEE Main 2024
🔵 प्रश्न 2
यदि दो समतल a₁x + b₁y + c₁z + d₁ = 0 और a₂x + b₂y + c₂z + d₂ = 0 समान्तर हों, तो
🟥 1️⃣ a₁:b₁:c₁ = a₂:b₂:c₂
🟩 2️⃣ a₁a₂ + b₁b₂ + c₁c₂ = 0
🟨 3️⃣ d₁ = d₂
🟦 4️⃣ कोई शर्त नहीं
✔️ उत्तर: 1️⃣
📅 JEE Main 2024
🔵 प्रश्न 3
रेखा का पैरामीट्रिक रूप: बिंदु (x₀, y₀, z₀) तथा दिशा अनुपात (a, b, c)
🟥 1️⃣ x = x₀ + a t, y = y₀ + b t, z = z₀ + c t
🟩 2️⃣ ax + by + cz = 0
🟨 3️⃣ x/x₀ = y/y₀ = z/z₀
🟦 4️⃣ x = at, y = bt
✔️ उत्तर: 1️⃣
📅 JEE Main 2023
🔵 प्रश्न 4
समतल 2x − y + z + 3 = 0 के लंबवत रेखा का दिशा अनुपात है
🟥 1️⃣ 2, −1, 1
🟩 2️⃣ 1, 1, 1
🟨 3️⃣ −2, 1, −1
🟦 4️⃣ 2, 1, −1
✔️ उत्तर: 1️⃣
📅 JEE Main 2023
🔵 प्रश्न 5
यदि दो रेखाएँ स्क्यू हों, तो
🟥 1️⃣ वे समान समतल में हैं
🟩 2️⃣ वे समान्तर हैं
🟨 3️⃣ वे न मिलती हैं न समान्तर हैं
🟦 4️⃣ वे समान हैं
✔️ उत्तर: 3️⃣
📅 JEE Main 2022
🔵 प्रश्न 6
बिंदु A(1,2,3) और B(4,6,8) को जोड़ने वाली रेखा के दिशा अनुपात =
🟥 1️⃣ 3, 4, 5
🟩 2️⃣ 4, 5, 6
🟨 3️⃣ 2, 3, 4
🟦 4️⃣ 1, 2, 3
✔️ उत्तर: 1️⃣
📅 JEE Main 2022
🔵 प्रश्न 7
दिशा कोज्या l, m, n के लिए सही संबंध
🟥 1️⃣ l + m + n = 1
🟩 2️⃣ l^2 + m^2 + n^2 = 1
🟨 3️⃣ lm + mn + nl = 1
🟦 4️⃣ l^2 + m^2 + n^2 = 2
✔️ उत्तर: 2️⃣
📅 JEE Main 2021
🔵 प्रश्न 8
यदि समतल ax + by + cz + d = 0 मूल-बिंदु से गुजरता है, तो
🟥 1️⃣ d = 0
🟩 2️⃣ a + b + c = 0
🟨 3️⃣ a = 0
🟦 4️⃣ b = 0
✔️ उत्तर: 1️⃣
📅 JEE Main 2021
🔵 प्रश्न 9
रेखा और समतल के बीच कोण θ के लिए
🟥 1️⃣ cos θ = (a l + b m + c n)/sqrt(a^2 + b^2 + c^2)
🟩 2️⃣ sin θ = (a l + b m + c n)/sqrt(a^2 + b^2 + c^2)
🟨 3️⃣ tan θ = (a l + b m + c n)/sqrt(a^2 + b^2 + c^2)
🟦 4️⃣ cot θ = (a l + b m + c n)/sqrt(a^2 + b^2 + c^2)
✔️ उत्तर: 2️⃣
📅 JEE Main 2020
🔵 प्रश्न 10
दो समतलों के बीच कोण φ के लिए सही सूत्र
🟥 1️⃣ cos φ = (a₁a₂ + b₁b₂ + c₁c₂)/sqrt((a₁^2+b₁^2+c₁^2)(a₂^2+b₂^2+c₂^2))
🟩 2️⃣ sin φ = (a₁a₂ + b₁b₂ + c₁c₂)/sqrt((a₁^2+b₁^2+c₁^2)(a₂^2+b₂^2+c₂^2))
🟨 3️⃣ tan φ = (a₁b₂ + b₁a₂)/c₁c₂
🟦 4️⃣ उपरोक्त में से कोई नहीं
✔️ उत्तर: 1️⃣
📅 JEE Main 2020
🔵 प्रश्न 11
यदि दो समतल परस्पर लंबवत हों, तो
🟥 1️⃣ उनके सामान्य सदिश समान्तर हैं
🟩 2️⃣ उनके सामान्य सदिश लंबवत हैं
🟨 3️⃣ उनके दिशा अनुपात समान हैं
🟦 4️⃣ कोई निश्चित संबंध नहीं
✔️ उत्तर: 2️⃣
📅 JEE Main 2019
🔵 प्रश्न 12
रेखा का सदिश समीकरण (स्थिति-सदिश r):
🟥 1️⃣ r = a + λ b (जहाँ a स्थिर स्थिति-सदिश, b दिशा-सदिश)
🟩 2️⃣ r · a = 0
🟨 3️⃣ |r| = |a|
🟦 4️⃣ r × a = 0
✔️ उत्तर: 1️⃣
📅 JEE Main 2019
🔵 प्रश्न 13
यदि दो रेखाएँ समान्तर हैं तो उनके दिशा-सदिशों का क्रॉस-गुणनफल
🟥 1️⃣ शून्य
🟩 2️⃣ एकक
🟨 3️⃣ मनचाहा
🟦 4️⃣ अधिकतम
✔️ उत्तर: 1️⃣
📅 JEE Main 2018
🔵 प्रश्न 14
यदि दो रेखाएँ परस्पर लंबवत हैं तो उनके दिशा-सदिशों का डॉट-गुणनफल
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ −1
🟦 4️⃣ 2
✔️ उत्तर: 1️⃣
📅 JEE Main 2018
🔵 प्रश्न 15
समतल का सामान्य सदिश किसके समान्तर होता है?
🟥 1️⃣ समतल के भीतर किसी भी रेखा के
🟩 2️⃣ समतल के लंब रेखा के
🟨 3️⃣ x-अक्ष के
🟦 4️⃣ y-अक्ष के
✔️ उत्तर: 2️⃣
📅 JEE Main 2017
🔵 प्रश्न 16
बिंदु A(1, −2, 3) से समतल x − 2y + 2z − 5 = 0 की दूरी =
🟥 1️⃣ 2
🟩 2️⃣ 3
🟨 3️⃣ 1
🟦 4️⃣ 0
✔️ उत्तर: 2️⃣
📅 JEE Main 2017
🔵 प्रश्न 17
रेखा x−1/2 = y+2/−1 = z−3/2 की दिशा अनुपात
🟥 1️⃣ 2, −1, 2
🟩 2️⃣ 1, 1, 1
🟨 3️⃣ −2, 1, −2
🟦 4️⃣ 2, 1, −2
✔️ उत्तर: 1️⃣
📅 JEE Main 2016
🔵 प्रश्न 18
यदि दो समतल x + y + z = 3 और 2x + 2y + 2z = 5 हों, तो वे
🟥 1️⃣ समान्तर
🟩 2️⃣ समान
🟨 3️⃣ प्रतिच्छेद करते हैं
🟦 4️⃣ लंबवत
✔️ उत्तर: 3️⃣
📅 JEE Main 2016
🔵 प्रश्न 19
रेखा और समतल के बीच कोण θ के लिए, यदि रेखा का दिशा-सदिश (l, m, n) और समतल का सामान्य (a, b, c) हो, तो
🟥 1️⃣ sin θ = |a l + b m + c n| / sqrt(a^2+b^2+c^2)
🟩 2️⃣ cos θ = |a l + b m + c n| / sqrt(a^2+b^2+c^2)
🟨 3️⃣ tan θ = |a l + b m + c n| / sqrt(a^2+b^2+c^2)
🟦 4️⃣ cot θ = |a l + b m + c n| / sqrt(a^2+b^2+c^2)
✔️ उत्तर: 1️⃣
📅 JEE Main 2015
🔵 प्रश्न 20
यदि समतल x + 2y + 2z = 5 तथा 2x + 4y + 4z = 10 हों, तो उनका संबंध
🟥 1️⃣ समान
🟩 2️⃣ समान्तर
🟨 3️⃣ लंबवत
🟦 4️⃣ स्क्यू
✔️ उत्तर: 2️⃣
📅 JEE Main 2015
🔵 प्रश्न 21
दो बिंदुओं A(x₁, y₁, z₁), B(x₂, y₂, z₂) के बीच दूरी
🟥 1️⃣ sqrt((x₂−x₁)^2 + (y₂−y₁)^2 + (z₂−z₁)^2)
🟩 2️⃣ |x₂−x₁| + |y₂−y₁| + |z₂−z₁|
🟨 3️⃣ (x₂−x₁)^2 + (y₂−y₁)^2 + (z₂−z₁)^2
🟦 4️⃣ sqrt(x₁x₂ + y₁y₂ + z₁z₂)
✔️ उत्तर: 1️⃣
📅 JEE Main 2014
🔵 प्रश्न 22
यदि रेखा के दिशा अनुपात (a, b, c) हों, तो दिशा-कोज्या
🟥 1️⃣ l = a/√(a^2+b^2+c^2), m = b/√(a^2+b^2+c^2), n = c/√(a^2+b^2+c^2)
🟩 2️⃣ l = a, m = b, n = c
🟨 3️⃣ l = 1/a, m = 1/b, n = 1/c
🟦 4️⃣ l = b, m = a, n = c
✔️ उत्तर: 1️⃣
📅 JEE Main 2014
🔵 प्रश्न 23
यदि समतल ax + by + cz + d = 0 और रेखा r = a + λ b, तब रेखा समतल में निहित हो तब
🟥 1️⃣ b · (समतल का सामान्य) = 0 और a समतल पर हो
🟩 2️⃣ b · (समतल का सामान्य) ≠ 0
🟨 3️⃣ a समतल पर नहीं
🟦 4️⃣ कोई शर्त नहीं
✔️ उत्तर: 1️⃣
📅 JEE Main 2013
🔵 प्रश्न 24
यदि दो रेखाएँ समान्तर हैं, तो उनके दिशा अनुपात
🟥 1️⃣ समान होंगे
🟩 2️⃣ समान अनुपात में होंगे
🟨 3️⃣ विपरीत होंगे
🟦 4️⃣ शून्य होंगे
✔️ उत्तर: 2️⃣
📅 JEE Main 2013
🔵 प्रश्न 25
समतल का सामान्य रूप ax + by + cz + d = 0 में (a, b, c)
🟥 1️⃣ सामान्य सदिश के दिशा अनुपात हैं
🟩 2️⃣ दिशा-कोज्या हैं
🟨 3️⃣ दोनों हैं
🟦 4️⃣ कोई नहीं
✔️ उत्तर: 1️⃣
📅 JEE Main 2012
🔵 प्रश्न 26
रेखा x−1/2 = y+3/−1 = z−2/1 का दिशा अनुपात है
🟥 1️⃣ 2, −1, 1
🟩 2️⃣ 1, −1, 2
🟨 3️⃣ 2, 1, −1
🟦 4️⃣ −2, 1, −1
✔️ उत्तर: 1️⃣
📅 JEE Main 2024
🔵 प्रश्न 27
समतल x + 2y + 2z = 6 का x-अवरोध (x-intercept) है
🟥 1️⃣ 6
🟩 2️⃣ 3
🟨 3️⃣ 2
🟦 4️⃣ 1
✔️ उत्तर: 1️⃣
📅 JEE Main 2024
🔵 प्रश्न 28
दो स्क्यू रेखाओं के बीच लघुत्तम दूरी का सूत्र है
🟥 1️⃣ |(a × b) · (c)| / |a × b|
🟩 2️⃣ |(a × b) · (PQ)| / |a × b|
🟨 3️⃣ |a · b| / |PQ|
🟦 4️⃣ |PQ| / |a × b|
✔️ उत्तर: 2️⃣
📅 JEE Main 2023
🔵 प्रश्न 29
यदि समतल ax + by + cz + d = 0 मूल से गुजरता है, तो
🟥 1️⃣ d = 0
🟩 2️⃣ a + b + c = 0
🟨 3️⃣ a = b = c
🟦 4️⃣ d = a + b + c
✔️ उत्तर: 1️⃣
📅 JEE Main 2023
🔵 प्रश्न 30
समतल x/2 + y/3 + z/6 = 1 के दिशा-अवरोधों का क्रम (x, y, z) है
🟥 1️⃣ 2, 3, 6
🟩 2️⃣ 1, 2, 3
🟨 3️⃣ 6, 3, 2
🟦 4️⃣ 3, 2, 6
✔️ उत्तर: 1️⃣
📅 JEE Main 2022
🔵 प्रश्न 31
बिंदु A(1, 2, 3) का समतल x + y + z = 6 पर प्रक्षेप का पैरामीट्रिक रूप r = a + t n में n क्या है?
🟥 1️⃣ i + j + k
🟩 2️⃣ i − j + k
🟨 3️⃣ 2i + j + k
🟦 4️⃣ i + 2j + 2k
✔️ उत्तर: 1️⃣
📅 JEE Main 2022
🔵 प्रश्न 32
यदि दो समतल x − y + z = 0 और 2x − 2y + 2z = 5 हों, तो वे
🟥 1️⃣ समान
🟩 2️⃣ समान्तर
🟨 3️⃣ प्रतिच्छेद करते हैं
🟦 4️⃣ लंबवत
✔️ उत्तर: 2️⃣
📅 JEE Main 2021
🔵 प्रश्न 33
रेखा r = a + λ b समतल ax + by + cz + d = 0 में निहित होने हेतु आवश्यक और पर्याप्त शर्त
🟥 1️⃣ b · (a, b, c) = 0 और a उस समतल पर हो
🟩 2️⃣ a · (a, b, c) = 0 मात्र
🟨 3️⃣ b · (a, b, c) = 0 मात्र
🟦 4️⃣ d = 0
✔️ उत्तर: 1️⃣
📅 JEE Main 2021
🔵 प्रश्न 34
यदि रेखा का दिशा-सदिश (l, m, n) और समतल का सामान्य (A, B, C) हो, तो रेखा और समतल के बीच कोण θ के लिए
🟥 1️⃣ sin θ = |A l + B m + C n| / sqrt(A^2 + B^2 + C^2)
🟩 2️⃣ cos θ = |A l + B m + C n| / sqrt(A^2 + B^2 + C^2)
🟨 3️⃣ tan θ = |A l + B m + C n| / sqrt(A^2 + B^2 + C^2)
🟦 4️⃣ cot θ = |A l + B m + C n| / sqrt(A^2 + B^2 + C^2)
✔️ उत्तर: 1️⃣
📅 JEE Main 2020
🔵 प्रश्न 35
दो समतलों के बीच कोण φ के लिए सही सूत्र
🟥 1️⃣ cos φ = (A1A2 + B1B2 + C1C2) / sqrt((A1^2+B1^2+C1^2)(A2^2+B2^2+C2^2))
🟩 2️⃣ sin φ = (A1A2 + B1B2 + C1C2) / sqrt((A1^2+B1^2+C1^2)(A2^2+B2^2+C2^2))
🟨 3️⃣ tan φ = (A1B2 + B1A2) / (C1C2)
🟦 4️⃣ cot φ = (A1A2 + B1B2 + C1C2)
✔️ उत्तर: 1️⃣
📅 JEE Main 2020
🔵 प्रश्न 36
बिंदु P(1, 2, 3) और Q(4, 6, 9) के बीच दूरी
🟥 1️⃣ sqrt(26)
🟩 2️⃣ sqrt(35)
🟨 3️⃣ sqrt(45)
🟦 4️⃣ 7
✔️ उत्तर: 3️⃣
📅 JEE Main 2019
🔵 प्रश्न 37
यदि दिशा अनुपात (a, b, c) हों, तो दिशा-कोज्या
🟥 1️⃣ l = a/√(a^2+b^2+c^2), m = b/√(a^2+b^2+c^2), n = c/√(a^2+b^2+c^2)
🟩 2️⃣ l = a, m = b, n = c
🟨 3️⃣ l = 1/a, m = 1/b, n = 1/c
🟦 4️⃣ l = b, m = a, n = c
✔️ उत्तर: 1️⃣
📅 JEE Main 2019
🔵 प्रश्न 38
यदि समतल x − 2y + z = 5 का सामान्य सदिश N हो, तो N के दिशा अनुपात
🟥 1️⃣ 1, −2, 1
🟩 2️⃣ 2, 1, −1
🟨 3️⃣ −1, 2, −1
🟦 4️⃣ 1, 2, 1
✔️ उत्तर: 1️⃣
📅 JEE Main 2018
🔵 प्रश्न 39
रेखा x−2/1 = y+1/2 = z−3/−2 किस समतल के लंबवत है?
🟥 1️⃣ x + 2y − 2z = 0
🟩 2️⃣ x − 2y + 2z = 0
🟨 3️⃣ 2x + y + z = 0
🟦 4️⃣ x − y − z = 0
✔️ उत्तर: 2️⃣
📅 JEE Main 2018
🔵 प्रश्न 40
यदि दो रेखाएँ समान्तर हैं, तो उनके दिशा-सदिशों का क्रॉस गुणनफल
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ −1
🟦 4️⃣ 2
✔️ उत्तर: 1️⃣
📅 JEE Main 2017
🔵 प्रश्न 41
यदि दो रेखाएँ परस्पर लंबवत हैं, तो दिशा-सदिशों का डॉट गुणनफल
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ −1
🟦 4️⃣ 2
✔️ उत्तर: 1️⃣
📅 JEE Main 2017
🔵 प्रश्न 42
समतल x + y + z = 9, बिंदु A(1, 2, 3) से होकर समान्तर समतल का समीकरण है
🟥 1️⃣ x + y + z = 6
🟩 2️⃣ x + y + z = 9
🟨 3️⃣ x + y + z = 3
🟦 4️⃣ x + y + z = 1
✔️ उत्तर: 1️⃣
📅 JEE Main 2016
🔵 प्रश्न 43
बिंदु P से रेखा L पर खींचे गए लंब की पाद (foot) निकालने की विधि में प्रयुक्त पैरामीटर t0 मिलता है
🟥 1️⃣ न्यूनतम |r − a| से
🟩 2️⃣ (r − a) · b = 0 से
🟨 3️⃣ (P − (a + t b)) · b = 0 से
🟦 4️⃣ a · b = 0 से
✔️ उत्तर: 3️⃣
📅 JEE Main 2016
🔵 प्रश्न 44
यदि दो समतल A1x + B1y + C1z + D1 = 0 और A2x + B2y + C2z + D2 = 0 परस्पर लंबवत हैं, तो
🟥 1️⃣ A1A2 + B1B2 + C1C2 = 0
🟩 2️⃣ A1/B1 = A2/B2
🟨 3️⃣ D1 = D2
🟦 4️⃣ A1A2 − B1B2 = 0
✔️ उत्तर: 1️⃣
📅 JEE Main 2015
🔵 प्रश्न 45
समतल पर किसी बिंदु का परावर्तन (reflection) प्राप्त करने के लिए
🟥 1️⃣ उस बिंदु का समतल पर प्रक्षेप लेकर, दोगुना स्थानांतरित करें
🟩 2️⃣ उस बिंदु को सामान्य दिशा में इकाई दूरी ले जाएँ
🟨 3️⃣ उस बिंदु के निर्देशांकों का योग लें
🟦 4️⃣ केवल d बदलें
✔️ उत्तर: 1️⃣
📅 JEE Main 2015
🔵 प्रश्न 46
यदि रेखा r = a + λ b समतल S: n · r = p को कोण θ पर काटती है, तो
🟥 1️⃣ sin θ = |n · b|/|n||b|
🟩 2️⃣ cos θ = |n · b|/|n||b|
🟨 3️⃣ tan θ = |n · b|/|n||b|
🟦 4️⃣ cot θ = |n · b|/|n||b|
✔️ उत्तर: 1️⃣
📅 JEE Main 2014
🔵 प्रश्न 47
रेखा x/2 = (y − 1)/3 = (z + 2)/−1 का दिशा-सदिश है
🟥 1️⃣ 2, 3, −1
🟩 2️⃣ 1, 3, −2
🟨 3️⃣ 2, −1, 3
🟦 4️⃣ −2, 3, 1
✔️ उत्तर: 1️⃣
📅 JEE Main 2014
🔵 प्रश्न 48
यदि तीन समतल x + y + z = 1, x − y + z = 1, x + y − z = 1 हों, तो उनका प्रतिच्छेदन
🟥 1️⃣ एक बिंदु
🟩 2️⃣ एक रेखा
🟨 3️⃣ कोई नहीं (असंगत)
🟦 4️⃣ पूरा समतल
✔️ उत्तर: 1️⃣
📅 JEE Main 2013
🔵 प्रश्न 49
यदि किसी समतल के दो परस्पर असमान्तर रेखाएँ दी जाएँ, तो समतल
🟥 1️⃣ अद्वितीय रूप से निर्धारित होता है
🟩 2️⃣ अनंत समतल संभव
🟨 3️⃣ निर्धारित नहीं
🟦 4️⃣ केवल तभी जब रेखाएँ स्क्यू हों
✔️ उत्तर: 1️⃣
📅 JEE Main 2013
🔵 प्रश्न 50
यदि रेखाएँ L1 और L2 स्क्यू हों, तो निम्न में से सही
🟥 1️⃣ वे एक समतल में हैं
🟩 2️⃣ वे समान्तर हैं
🟨 3️⃣ वे न प्रतिच्छेद करती हैं न समान्तर हैं
🟦 4️⃣ वे एक ही रेखा हैं
✔️ उत्तर: 3️⃣
📅 JEE Main 2012
————————————————————————————————————————————————————————————————————————————
JEE ADVANCED पिछले सालों के प्रश्न
🔵 प्रश्न 1
(d²y/dx²) + (dy/dx)² + y = 0 का क्रम और घात हैं
🟥 1️⃣ क्रम 2, घात 1
🟩 2️⃣ क्रम 2, घात 2
🟨 3️⃣ क्रम 1, घात 2
🟦 4️⃣ क्रम 3, घात 2
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2024 – Paper 1
🔵 प्रश्न 2
dy/dx + y = e^x का सामान्य हल है
🟥 1️⃣ y = (1/2) e^x + C e^(−x)
🟩 2️⃣ y = e^x + C
🟨 3️⃣ y = (1/2) e^(−x) + C e^x
🟦 4️⃣ y = C e^(−x)
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2024 – Paper 1
🔵 प्रश्न 3
dy/dx = 1 + (y/x) का सामान्य हल है
🟥 1️⃣ y = x ln x + C x
🟩 2️⃣ y = ln x + C
🟨 3️⃣ y = x² + C
🟦 4️⃣ y = C/x
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2023 – Paper 1
🔵 प्रश्न 4
रेखाओं के समूह y = C x का अवकल समीकरण है
🟥 1️⃣ x dy − y dx = 0
🟩 2️⃣ x dy + y dx = 0
🟨 3️⃣ dy/dx = x/y
🟦 4️⃣ d²y/dx² = 0
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2023 – Paper 1
🔵 प्रश्न 5
समूह y = A e^(2x) + B e^(−2x) का अवकल समीकरण है
🟥 1️⃣ d²y/dx² − 4y = 0
🟩 2️⃣ d²y/dx² + 4y = 0
🟨 3️⃣ dy/dx − 2y = 0
🟦 4️⃣ dy/dx + 2y = 0
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2022 – Paper 1
🔵 प्रश्न 6
मूल से गुजरने वाली रेखाएँ y = kx के लंब समवर्ती पथ हैं
🟥 1️⃣ x² + y² = C
🟩 2️⃣ xy = C
🟨 3️⃣ y = Cx
🟦 4️⃣ x + y = C
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2022 – Paper 1
🔵 प्रश्न 7
Bernoulli समीकरण dy/dx + (2/x)y = xy² को रैखिकीकरण हेतु उपस्थापन
🟥 1️⃣ z = 1/y
🟩 2️⃣ z = y²
🟨 3️⃣ z = xy
🟦 4️⃣ z = ln y
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2021 – Paper 1
🔵 प्रश्न 8
(2xy + y²) dx + (x² + 2xy) dy = 0 यह समीकरण है
🟥 1️⃣ सटीक (exact)
🟩 2️⃣ समांगी (homogeneous)
🟨 3️⃣ केवल y में रैखिक
🟦 4️⃣ Bernoulli
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2021 – Paper 1
🔵 प्रश्न 9
dy/dx = (1 + x)/(1 + y) का सामान्य हल है
🟥 1️⃣ y + (1/2)y² = x + (1/2)x² + C
🟩 2️⃣ y − (1/2)y² = x + (1/2)x² + C
🟨 3️⃣ y + (1/2)y² = x − (1/2)x² + C
🟦 4️⃣ y − x = C
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2020 – Paper 1
🔵 प्रश्न 10
Clairaut प्रकार y = Cx + C² से प्राप्त अवकल समीकरण है
🟥 1️⃣ y = x(dy/dx) + (dy/dx)²
🟩 2️⃣ y = dy/dx
🟨 3️⃣ d²y/dx² = 0
🟦 4️⃣ dy/dx = x + y
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2020 – Paper 1
🔵 प्रश्न 11
dy/dx + y = 0, तथा y(0) = 2 का विशिष्ट हल है
🟥 1️⃣ y = 2e^(−x)
🟩 2️⃣ y = 2e^x
🟨 3️⃣ y = 2
🟦 4️⃣ y = e^(−x)
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2019 – Paper 1
🔵 प्रश्न 12
(d³y/dx³)² + (dy/dx)⁵ = 0 का क्रम और घात
🟥 1️⃣ क्रम 3, घात 2
🟩 2️⃣ क्रम 5, घात 3
🟨 3️⃣ क्रम 2, घात 5
🟦 4️⃣ क्रम 3, घात 1
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2019 – Paper 1
🔵 प्रश्न 13
dy/dx = e^(x + y) का सामान्य हल है
🟥 1️⃣ e^(−y) + e^x = C
🟩 2️⃣ e^y + e^x = C
🟨 3️⃣ y = e^x + C
🟦 4️⃣ y = x e^x + C
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2018 – Paper 1
🔵 प्रश्न 14
समांगी अवकल समीकरण dy/dx = (x + y)/(x − y) के लिए उपस्थापन
🟥 1️⃣ y = vx
🟩 2️⃣ x = vy
🟨 3️⃣ y = v + x
🟦 4️⃣ x = v + y
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2018 – Paper 1
🔵 प्रश्न 15
समूह y = A sin x + B cos x का अवकल समीकरण है
🟥 1️⃣ d²y/dx² + y = 0
🟩 2️⃣ d²y/dx² − y = 0
🟨 3️⃣ dy/dx + y = 0
🟦 4️⃣ dy/dx − y = 0
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2017 – Paper 1
🔵 प्रश्न 16
वृत्तों का परिवार x² + y² = a² के लंब समवर्ती पथ हैं
🟥 1️⃣ y = Cx
🟩 2️⃣ xy = C
🟨 3️⃣ y = C/x
🟦 4️⃣ x + y = C
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2016 – Paper 1
🔵 प्रश्न 17
समूह y = A e^(kx) (A, k स्थिर) से A हटाने पर अवकल समीकरण है
🟥 1️⃣ dy/dx = ky
🟩 2️⃣ dy/dx = y/k
🟨 3️⃣ d²y/dx² = ky
🟦 4️⃣ d²y/dx² = y/k
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2015 – Paper 1
🔵 प्रश्न 18
(d^3y/dx^3) + (dy/dx)^2 = 0 का क्रम और घात हैं
🟥 1️⃣ क्रम 3, घात 1
🟩 2️⃣ क्रम 3, घात 2
🟨 3️⃣ क्रम 2, घात 1
🟦 4️⃣ क्रम 1, घात 3
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2024 – Paper 2
🔵 प्रश्न 19
dy/dx − y = e^{2x} का सामान्य हल है
🟥 1️⃣ y = e^{2x} + C e^{x}
🟩 2️⃣ y = e^{2x} + C e^{−x}
🟨 3️⃣ y = e^{x} + C e^{2x}
🟦 4️⃣ y = C e^{x}
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2024 – Paper 2
🔵 प्रश्न 20
वृत्तों का परिवार x^2 + y^2 = a^2 के लंब समवर्ती पथ हैं
🟥 1️⃣ y = C x
🟩 2️⃣ x y = C
🟨 3️⃣ x + y = C
🟦 4️⃣ y = C/x
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2023 – Paper 2
🔵 प्रश्न 21
(2x − y) dx + (x − 2y) dy = 0 यह समीकरण है
🟥 1️⃣ सटीक (exact)
🟩 2️⃣ समांगी (homogeneous)
🟨 3️⃣ रैखिक केवल y में
🟦 4️⃣ Bernoulli
✔️ उत्तर: 2️⃣
📅 JEE Advanced 2023 – Paper 2
🔵 प्रश्न 22
Bernoulli समीकरण dy/dx + (2/x) y = y^2 को रैखिकीकरण हेतु उपस्थापन
🟥 1️⃣ z = 1/y
🟩 2️⃣ z = y^2
🟨 3️⃣ z = x y
🟦 4️⃣ z = ln y
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2022 – Paper 2
🔵 प्रश्न 23
समूह y = A cos x + B sin x का अवकल समीकरण है
🟥 1️⃣ d^2y/dx^2 + y = 0
🟩 2️⃣ d^2y/dx^2 − y = 0
🟨 3️⃣ dy/dx + y = 0
🟦 4️⃣ dy/dx − y = 0
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2022 – Paper 2
🔵 प्रश्न 24
Euler–Cauchy समीकरण x^2 y” + x y’ − y = 0 का सामान्य हल है
🟥 1️⃣ y = C1 x + C2 / x
🟩 2️⃣ y = C1 e^{x} + C2 e^{−x}
🟨 3️⃣ y = C1 x^2 + C2
🟦 4️⃣ y = C1 ln x + C2
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2021 – Paper 2
🔵 प्रश्न 25
d^2y/dx^2 + (dy/dx)^{2/3} = 0 का घात
🟥 1️⃣ परिभाषित नहीं (non-polynomial)
🟩 2️⃣ 1
🟨 3️⃣ 2
🟦 4️⃣ 3
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2021 – Paper 2
🔵 प्रश्न 26
dy/dx − (1/x) y = x^2 तथा y(1) = 0 का विशिष्ट हल है
🟥 1️⃣ y = (x/2)(x^2 − 1)
🟩 2️⃣ y = (x/3)(x^2 − 1)
🟨 3️⃣ y = x^3/2 + x
🟦 4️⃣ y = x^3/2 − x^2/2
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2020 – Paper 2
🔵 प्रश्न 27
(y + x) dx + x dy = 0 का हल है
🟥 1️⃣ x y + (1/2) x^2 = C
🟩 2️⃣ x^2 + y^2 = C
🟨 3️⃣ y/x = C
🟦 4️⃣ y + (1/2) y^2 = C
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2020 – Paper 2
🔵 प्रश्न 28
dy/dx = (2x)/(1 + y^2), y(0) = 0 का विशिष्ट हल है
🟥 1️⃣ y + (1/3) y^3 = x^2
🟩 2️⃣ y^2 = x^2
🟨 3️⃣ y = x^2
🟦 4️⃣ y^2 + (1/3) y^4 = x^2
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2019 – Paper 2
🔵 प्रश्न 29
(d^2y/dx^2)^2 + sin(dy/dx) = 0 का क्रम/घात
🟥 1️⃣ क्रम 2, घात परिभाषित नहीं
🟩 2️⃣ क्रम 2, घात 2
🟨 3️⃣ क्रम 1, घात 1
🟦 4️⃣ क्रम 3, घात परिभाषित नहीं
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2019 – Paper 2
🔵 प्रश्न 30
x dy/dx + y = x^2 का सामान्य हल है
🟥 1️⃣ y = x^2/3 + C/x
🟩 2️⃣ y = x^2/2 + C/x^2
🟨 3️⃣ y = x^3/3 + C
🟦 4️⃣ y = x^2 + C x
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2018 – Paper 2
🔵 प्रश्न 31
समूह y = A e^{k x} + B e^{−k x} (A, B स्थिर) का अवकल समीकरण है
🟥 1️⃣ d^2y/dx^2 − k^2 y = 0
🟩 2️⃣ d^2y/dx^2 + k y = 0
🟨 3️⃣ dy/dx − k y = 0
🟦 4️⃣ dy/dx + k y = 0
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2018 – Paper 2
🔵 प्रश्न 32
dy/dx = y tan x का सामान्य हल
🟥 1️⃣ y = C sec x
🟩 2️⃣ y = C cos x
🟨 3️⃣ y = C tan x
🟦 4️⃣ y = C sin x
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2017 – Paper 2
🔵 प्रश्न 33
dy/dx = k y (k नियत) का सामान्य हल
🟥 1️⃣ y = C e^{k x}
🟩 2️⃣ y = C x^k
🟨 3️⃣ y = C e^{x/k}
🟦 4️⃣ y = C k^{x}
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2016 – Paper 2
🔵 प्रश्न 34
Clairaut प्रकार y = C x + C^2 का singular हल है
🟥 1️⃣ y = −(1/4) x^2
🟩 2️⃣ y = (1/4) x^2
🟨 3️⃣ y = −(1/2) x^2
🟦 4️⃣ y = x^2
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2015 – Paper 2
————————————————————————————————————————————————————————————————————————————
प्रतियोगी परीक्षाओं के लिए मॉडल अभ्यास सेट
✳️ भाग 1: Q1–Q20 (NEET स्तर — सरल से मध्यम)
Q1. बिंदु A(1, 2, 3) और B(4, 6, 9) के बीच की दूरी है:
🔵 (A) 9
🟢 (B) 6
🟠 (C) 7
🔴 (D) √54
Answer: (B) 6
Q2. यदि बिंदु P(x, 3, 4), Q(2, 5, 6) और R(4, 7, 8) सह-रेखीय हों, तो x का मान होगा:
🔵 (A) 0
🟢 (B) 1
🟠 (C) 2
🔴 (D) 3
Answer: (C) 2
Q3. बिंदु A(1, 2, 3) और B(3, 6, 9) का मध्यबिंदु है:
🔵 (A) (2, 4, 6)
🟢 (B) (1, 4, 5)
🟠 (C) (3, 5, 7)
🔴 (D) (4, 2, 1)
Answer: (A) (2, 4, 6)
Q4. बिंदु (x, y, z) के लिए यदि x + y + z = 6 हो, तो वह बिंदु किस तल पर स्थित है?
🔵 (A) x + y + z = 0
🟢 (B) x + y + z = 6
🟠 (C) 2x + y + z = 6
🔴 (D) x + y = 6
Answer: (B) x + y + z = 6
Q5. दिशा अनुपात (2, 3, 6) वाले रेखा के दिशा कोज्या हैं:
🔵 (A) 2/7, 3/7, 6/7
🟢 (B) 1/√7, 2/√7, 3/√7
🟠 (C) 2/7, 3/7, 6/7
🔴 (D) 2/7, 3/7, 1/7
Answer: (A) 2/7, 3/7, 6/7
Q6. यदि बिंदु A(1, 2, 3), B(4, 5, 6), C(7, 8, 9) सह-रेखीय हों, तो AB और AC के अनुपात होंगे:
🔵 (A) 1:2
🟢 (B) 2:3
🟠 (C) 3:4
🔴 (D) 1:3
Answer: (A) 1:2
Q7. रेखा का समीकरण (x−1)/2 = (y−2)/3 = (z−3)/4 में दिशा अनुपात हैं:
🔵 (A) (2, 3, 4)
🟢 (B) (1, 2, 3)
🟠 (C) (4, 3, 2)
🔴 (D) (3, 4, 2)
Answer: (A) (2, 3, 4)
Q8. तल 2x + 3y + 6z = 12 का सामान्य सदिश है:
🔵 (A) (2, 3, 6)
🟢 (B) (1, 2, 3)
🟠 (C) (3, 2, 6)
🔴 (D) (6, 2, 3)
Answer: (A) (2, 3, 6)
Q9. यदि तल का समीकरण ax + by + cz + d = 0 हो, तो उसका सामान्य सदिश होगा:
🔵 (A) (a, b, c)
🟢 (B) (b, c, d)
🟠 (C) (c, d, a)
🔴 (D) (a, d, b)
Answer: (A) (a, b, c)
Q10. बिंदु (2, 3, 4) से मूल बिंदु तक की दूरी है:
🔵 (A) 5
🟢 (B) √29
🟠 (C) √30
🔴 (D) 7
Answer: (B) √29
Q11. बिंदु (1, 2, 3) से तल x + y + z = 6 की दूरी है:
🔵 (A) 0
🟢 (B) 2
🟠 (C) 3
🔴 (D) 1
Answer: (C) 3
Q12. यदि दो रेखाएँ समान तल में हों, तो वे कहलाती हैं:
🔵 (A) सह-रेखीय
🟢 (B) सह-तलीय
🟠 (C) समानांतर
🔴 (D) तिर्यक
Answer: (B) सह-तलीय
Q13. यदि दो तल समानांतर हों, तो उनके सामान्य सदिश:
🔵 (A) समान
🟢 (B) असमान
🟠 (C) लम्बवत
🔴 (D) कोई नहीं
Answer: (A) समान
Q14. किसी तल का सामान्य समीकरण है:
🔵 (A) ax + by + cz = 0
🟢 (B) ax + by + cz + d = 0
🟠 (C) ax + by = 0
🔴 (D) x + y + z = 1
Answer: (B) ax + by + cz + d = 0
Q15. यदि दिशा कोज्या (1/√3, 1/√3, 1/√3) हों, तो दिशा अनुपात होंगे:
🔵 (A) (1, 1, 1)
🟢 (B) (2, 2, 2)
🟠 (C) (3, 3, 3)
🔴 (D) (0, 1, 1)
Answer: (A) (1, 1, 1)
Q16. बिंदु (x, y, z) रेखा (x−1)/2 = (y−2)/3 = (z−3)/4 पर स्थित होगा यदि:
🔵 (A) (x, y, z) = (1+2t, 2+3t, 3+4t)
🟢 (B) (x, y, z) = (2+1t, 3+2t, 4+3t)
🟠 (C) (x, y, z) = (1+3t, 2+4t, 3+2t)
🔴 (D) इनमें से कोई नहीं
Answer: (A) (1+2t, 2+3t, 3+4t)
Q17. यदि दो तलों के बीच कोण 0° हो, तो वे कहलाते हैं:
🔵 (A) समानांतर
🟢 (B) लम्बवत
🟠 (C) प्रतिच्छेदक
🔴 (D) असह-तलीय
Answer: (A) समानांतर
🔵 प्रश्न 18
यदि दो तल लम्बवत हों, तो उनके सामान्य सदिशों का अदिश गुणनफल होगा:
🔵 (A) 1
🟢 (B) 0
🟠 (C) 2
🔴 (D) 3
✔️ Answer: (B) 0
✏️ Note:
दो तलों के लम्बवत होने की शर्त ➡️ उनके सामान्य सदिशों का अदिश गुणनफल = 0 होना चाहिए।
Q19. यदि दो रेखाएँ एक-दूसरे को प्रतिच्छेद न करें और समानांतर भी न हों, तो वे कहलाती हैं:
🔵 (A) सह-तलीय
🟢 (B) तिर्यक
🟠 (C) समानांतर
🔴 (D) असह-तलीय
Answer: (B) तिर्यक
🔵 प्रश्न 20
यदि रेखा के दिशा अनुपात (a, b, c) हों, तो उसके दिशा कोज्या होंगे:
🔵 (A) a², b², c²
🟢 (B) a/√(a² + b² + c²), b/√(a² + b² + c²), c/√(a² + b² + c²)
🟠 (C) a + b + c
🔴 (D) 1/a, 1/b, 1/c
✔️ Answer: (B) a/√(a² + b² + c²), b/√(…), c/√(…)
✏️ Note:
दिशा कोज्या वे संख्याएँ हैं जिनका वर्गों का योग 1 होता है और जो दिशा अनुपात को सामान्यीकृत करती हैं।
✳️ भाग 2: Q21–Q40 (JEE Main स्तर — मध्यम से उच्च कठिनाई)
🔵 प्रश्न 21
रेखा (x−1)/2 = (y−2)/3 = (z−3)/4 की दिशा कोज्या ज्ञात कीजिए।
🔵 (A) (2/√29, 3/√29, 4/√29)
🟢 (B) (2/5, 3/5, 4/5)
🟠 (C) (1/√3, 1/√3, 1/√3)
🔴 (D) (1/2, 1/3, 1/4)
✔️ Answer: (A) (2/√29, 3/√29, 4/√29)
🔵 प्रश्न 22
बिंदु (1, 2, 3) और तल 2x + 3y + 6z − 12 = 0 के बीच दूरी है:
🔵 (A) 2
🟢 (B) 3
🟠 (C) 14/7
🔴 (D) 1
✔️ Answer: (A) 2
✏️ सूत्र:
d = |A·x₁ + B·y₁ + C·z₁ + D| / √(A² + B² + C²)
🔵 प्रश्न 23
यदि दो रेखाएँ लम्बवत हों, तो उनके दिशा अनुपातों का अदिश गुणनफल होगा:
🔵 (A) 1
🟢 (B) 0
🟠 (C) 2
🔴 (D) 3
✔️ Answer: (B) 0
🔵 प्रश्न 24
यदि तल 2x + 3y + 6z = 12 और x + y + z = 6 समानांतर हों, तो उनके सामान्य सदिशों के बीच कोण होगा:
🔵 (A) 0°
🟢 (B) 90°
🟠 (C) 45°
🔴 (D) 60°
✔️ Answer: (A) 0°
🔵 प्रश्न 25
दो तलों x + y + z = 2 तथा 2x − y + 3z = 1 के प्रतिच्छेद से प्राप्त रेखा का सामान्य रूप होगा:
🔵 (A) x + y + z − 2 + λ(2x − y + 3z − 1) = 0
🟢 (B) x − y − z + 2 + λ(2x + y + 3z − 1) = 0
🟠 (C) x + y + z + λ(x + y + z) = 0
🔴 (D) इनमें से कोई नहीं
✔️ Answer: (A)
🔵 प्रश्न 26
रेखा (x−1)/2 = (y−2)/3 = (z−3)/4 पर बिंदु ज्ञात कीजिए जब परम t = 1 हो।
🔵 (A) (3, 5, 7)
🟢 (B) (2, 3, 4)
🟠 (C) (1, 2, 3)
🔴 (D) (4, 5, 6)
✔️ Answer: (A) (3, 5, 7)
🔵 प्रश्न 27
यदि दिशा अनुपात (a, b, c) हों, तो दिशा कोज्या के वर्गों का योग होगा:
🔵 (A) 1
🟢 (B) a² + b² + c²
🟠 (C) √(a² + b² + c²)
🔴 (D) 0
✔️ Answer: (A) 1
🔵 प्रश्न 28
रेखा और तल के बीच कोण की कोज्या है:
🔵 (A) (A·a + B·b + C·c) / √(A²+B²+C²) √(a²+b²+c²)
🟢 (B) उपर्युक्त दोनों
🟠 (C) इनमें से कोई नहीं
🔴 (D) 1
✔️ Answer: (A)
🔵 प्रश्न 29
यदि तल का समीकरण 2x + y + 2z = 5 है, तो मूल बिंदु से दूरी होगी:
🔵 (A) 1
🟢 (B) 5/3
🟠 (C) 5/√9
🔴 (D) 5/√(2² + 1² + 2²)
✔️ Answer: (D)
🔵 प्रश्न 30
तल x + 2y + 2z = 6 का सामान्य सदिश क्या है?
🔵 (A) (1, 2, 2)
🟢 (B) (2, 2, 1)
🟠 (C) (2, 1, 2)
🔴 (D) (1, 1, 1)
✔️ Answer: (A)
🔵 प्रश्न 31
यदि दो तलों के सामान्य सदिश (1, 2, 3) और (2, 4, 6) हों, तो वे होंगे:
🔵 (A) समानांतर
🟢 (B) लम्बवत
🟠 (C) प्रतिच्छेदक
🔴 (D) असह-तलीय
✔️ Answer: (A)
🔵 प्रश्न 32
बिंदु (1, 2, 3) से गुजरने और सामान्य सदिश (2, 3, 4) वाले तल का समीकरण होगा:
🔵 (A) 2x + 3y + 4z = 20
🟢 (B) 2x + 3y + 4z − 20 = 0
🟠 (C) 2x + 3y + 4z + 20 = 0
🔴 (D) 2x − 3y + 4z = 20
✔️ Answer: (B)
🔵 प्रश्न 33
यदि दो तलों के सामान्य सदिशों का अदिश गुणनफल = 0 हो, तो वे तल होंगे:
🔵 (A) समानांतर
🟢 (B) लम्बवत
🟠 (C) समान
🔴 (D) कोई नहीं
✔️ Answer: (B)
🔵 प्रश्न 34
यदि रेखा का समीकरण (x−2)/1 = (y−3)/2 = (z−4)/3 हो, तो दिशा अनुपात होंगे:
🔵 (A) (1, 2, 3)
🟢 (B) (2, 3, 4)
🟠 (C) (3, 2, 1)
🔴 (D) (4, 3, 2)
✔️ Answer: (A)
🔵 प्रश्न 35
बिंदु (1, 2, 3) से तल x + y + z − 6 = 0 की दूरी होगी:
🔵 (A) 3
🟢 (B) 2
🟠 (C) 1
🔴 (D) 0
✔️ Answer: (A)
🔵 प्रश्न 36
यदि दिशा कोज्या (l, m, n) हों, तो l² + m² + n² का मान होगा:
🔵 (A) 0
🟢 (B) 1
🟠 (C) 2
🔴 (D) 3
✔️ Answer: (B)
🔵 प्रश्न 37
यदि दो रेखाएँ समानांतर हों, तो उनके दिशा अनुपात:
🔵 (A) समानुपाती
🟢 (B) समान
🟠 (C) शून्य
🔴 (D) भिन्न
✔️ Answer: (A)
🔵 प्रश्न 38
यदि रेखा का समीकरण x = 1 + t, y = 2 − t, z = 3 + 2t हो, तो दिशा अनुपात होंगे:
🔵 (A) (1, −1, 2)
🟢 (B) (2, −2, 1)
🟠 (C) (1, 2, −1)
🔴 (D) (1, 1, 1)
✔️ Answer: (A)
🔵 प्रश्न 39
यदि बिंदु P(x₁, y₁, z₁) और तल Ax + By + Cz + D = 0 के बीच दूरी d हो, तो सूत्र है:
🔵 (A) |Ax₁ + By₁ + Cz₁ + D| / √(A² + B² + C²)
🟢 (B) Ax₁ + By₁ + Cz₁ + D
🟠 (C) √(A² + B² + C²)
🔴 (D) उपर्युक्त में से कोई नहीं
✔️ Answer: (A)
🔵 प्रश्न 40
यदि दिशा अनुपात (a, b, c) हों, तो उनके बीच संबंध है:
🔵 (A) a² + b² + c² = 1
🟢 (B) l² + m² + n² = 1
🟠 (C) a² + b² + c² = k²
🔴 (D) a² + b² + c² = 0
✔️ Answer: (B)
✳️ भाग 3: Q41–Q50 (JEE Advanced स्तर — उच्च कठिनाई)
🔵 प्रश्न 41
यदि दो तले A₁x + B₁y + C₁z + D₁ = 0 और A₂x + B₂y + C₂z + D₂ = 0 लम्बवत हों, तो शर्त होगी:
🔵 (A) A₁A₂ + B₁B₂ + C₁C₂ = 0
🟢 (B) A₁A₂ + B₁B₂ + C₁C₂ = 1
🟠 (C) A₁A₂ − B₁B₂ = 0
🔴 (D) A₁A₂ = 0
✔️ Answer: (A) A₁A₂ + B₁B₂ + C₁C₂ = 0
✏️ Note: दो तलों के सामान्य सदिशों का अदिश गुणनफल = 0 होना चाहिए।
🔵 प्रश्न 42
यदि बिंदु P(1,2,3) से रेखा (x−2)/3 = (y−3)/4 = (z−4)/5 की न्यूनतम दूरी ज्ञात करनी हो, तो सूत्र है:
🔵 (A) |(PQ × दिशा सदिश)| / |दिशा सदिश|
🟢 (B) |PQ| / |दिशा सदिश|
🟠 (C) |PQ + दिशा सदिश|
🔴 (D) इनमें से कोई नहीं
✔️ Answer: (A) |(PQ × दिशा सदिश)| / |दिशा सदिश|
🔵 प्रश्न 43
यदि दो समानांतर तल 2x + 3y + 6z + 4 = 0 और 2x + 3y + 6z − 12 = 0 हों, तो उनके बीच की दूरी होगी:
🔵 (A) 2
🟢 (B) 3
🟠 (C) 8/7
🔴 (D) 16/7
✔️ Answer: (D) 16/7
🧠 सूत्र:
d = |D₁ − D₂| / √(A² + B² + C²)
🔵 प्रश्न 44
यदि दो रेखाएँ
L₁: x = 1 + t, y = 2 − t, z = 3 + 2t
L₂: x = 2 + s, y = 3 + 2s, z = 4 + 3s
समानांतर हैं या नहीं, यह जाँचने हेतु किसे तुलना करेंगे?
🔵 (A) दिशा अनुपात
🟢 (B) दिशा कोज्या
🟠 (C) दोनों
🔴 (D) कोई नहीं
✔️ Answer: (A) दिशा अनुपात
🔵 प्रश्न 45
यदि तीन बिंदु A(1,2,3), B(2,3,4), C(3,4,5) सह-रेखीय हैं, तो सदिश AB और AC के बीच संबंध होगा:
🔵 (A) समानांतर
🟢 (B) लम्बवत
🟠 (C) समान
🔴 (D) असमानुपाती
✔️ Answer: (A) समानांतर
💡 Concept: यदि AB = k·AC, तो बिंदु सह-रेखीय होते हैं।
🔵 प्रश्न 46
यदि रेखा x = 1 + 2t, y = 2 + 3t, z = 3 + 4t तथा तल 2x + 3y + 4z = 12 के बीच कोण ज्ञात करना हो, तो सूत्र:
🔵 (A) cosθ = (A·a + B·b + C·c) / √(A² + B² + C²) √(a² + b² + c²)
🟢 (B) sinθ = उपर्युक्त सूत्र
🟠 (C) tanθ = उपर्युक्त सूत्र
🔴 (D) इनमें से कोई नहीं
✔️ Answer: (A)
🔵 प्रश्न 47
यदि रेखा और तल समानांतर हों, तो उनके दिशा अनुपात और सामान्य सदिश का अदिश गुणनफल होगा:
🔵 (A) 0
🟢 (B) 1
🟠 (C) 2
🔴 (D) 3
✔️ Answer: (A) 0
🔵 प्रश्न 48
यदि दो रेखाएँ प्रतिच्छेद करती हैं, तो उनकी न्यूनतम दूरी होगी:
🔵 (A) 0
🟢 (B) > 0
🟠 (C) ∞
🔴 (D) अपरिभाषित
✔️ Answer: (A) 0
🔵 प्रश्न 49
रेखा x = 1 + 2t, y = 2 + 3t, z = 3 + 4t मूल से गुजरने वाले तल पर स्थित है यदि:
🔵 (A) 2·1 + 3·2 + 4·3 = 0
🟢 (B) 2·1 + 3·2 + 4·3 ≠ 0
🟠 (C) तल समीकरण संतुष्ट करता है
🔴 (D) इनमें से कोई नहीं
✔️ Answer: (C)
🔵 प्रश्न 50
यदि किसी रेखा का समीकरण (x−a)/l = (y−b)/m = (z−c)/n है, तो उसका सदिश रूप होगा:
🔵 (A) r = a + tb
🟢 (B) r = (a𝐢 + b𝐣 + c𝐤) + t(l𝐢 + m𝐣 + n𝐤)
🟠 (C) r = r₀ + td
🔴 (D) (B) और (C) दोनों
✔️ Answer: (D)
————————————————————————————————————————————————————————————————————————————
