Class 12 : Maths (Hindi) -अध्याय 6: अवकलजों का अनुप्रयोग

पाठ का विश्लेषण एवं विवेचन

🔷 व्याख्या
🔹 1️⃣ प्रस्तावना (Introduction)
अवकलज (Derivative) का अर्थ है किसी फलन के मान में परिवर्तन की दर (Rate of Change)।
इस अध्याय में हम सीखते हैं कि अवकलजों का उपयोग वास्तविक जीवन की स्थितियों में कैसे किया जाता है।
🔹 जैसे —
➡️ किसी वस्तु की चाल (velocity) निकालने में,
➡️ न्यूनतम या अधिकतम मान ज्ञात करने में,
➡️ बढ़ते-घटते फलनों की पहचान में,
➡️ स्पर्शरेखाओं (Tangents) व अभिलंबों (Normals) के ढाल (slope) ज्ञात करने में।

🔹 2️⃣ बढ़ते एवं घटते फलन (Increasing and Decreasing Functions)

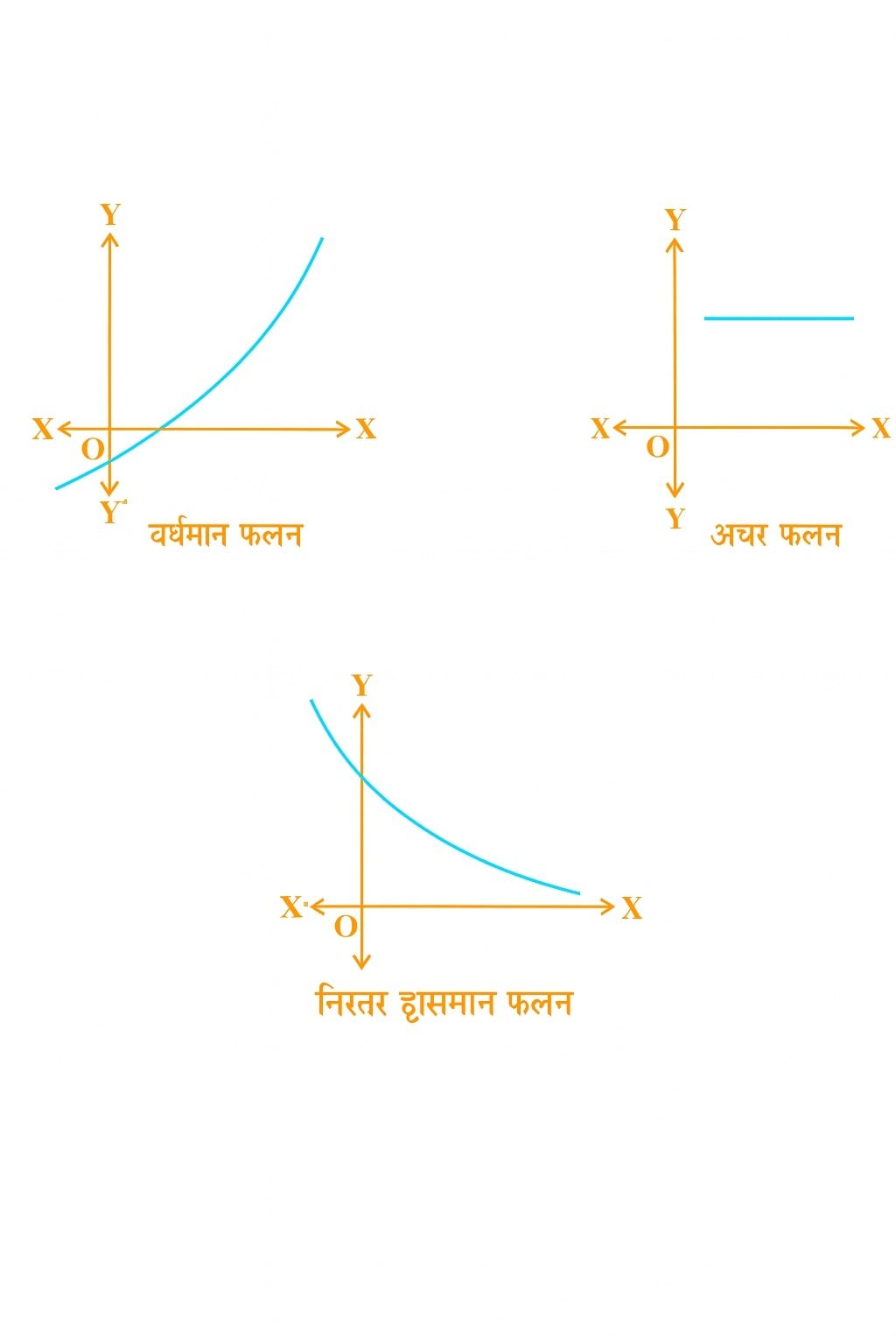
💡 परिभाषा:
यदि किसी अन्तराल (Interval) में f′(x) > 0 है, तो फलन बढ़ता हुआ (Increasing) कहलाता है।
यदि f′(x) < 0 है, तो फलन घटता हुआ (Decreasing) कहलाता है।
✴️ चरणवार प्रक्रिया:
➤ Step 1: f(x) का अवकलज f′(x) ज्ञात करें।
➤ Step 2: f′(x) = 0 से महत्वपूर्ण बिंदु (critical points) ज्ञात करें।
➤ Step 3: अन्तरालों में f′(x) के चिन्ह की जाँच करें।
➤ Step 4: जहाँ f′(x) > 0 वहाँ फलन बढ़ता है, जहाँ f′(x) < 0 वहाँ घटता है।
📘 उदाहरण:
f(x) = x² − 4x + 3
➡️ f′(x) = 2x − 4
f′(x) = 0 ⇒ x = 2
x < 2 ⇒ f′(x) < 0 ⇒ घटता
x > 2 ⇒ f′(x) > 0 ⇒ बढ़ता

🔹 3️⃣ अधिकतम और न्यूनतम मान (Maxima and Minima)
💡 परिभाषा:
किसी बिंदु पर फलन का अधिकतम (Maximum) मान वह है जहाँ फलन का मान आस-पास के सभी मानों से बड़ा हो।
न्यूनतम (Minimum) मान वह है जहाँ फलन का मान आस-पास के मानों से छोटा हो।
✴️ प्रक्रिया (First Derivative Test):
➤ Step 1: f′(x) = 0 रखकर महत्वपूर्ण बिंदु ज्ञात करें।
➤ Step 2: उन बिंदुओं के आस-पास f′(x) का चिन्ह देखें।
✔️ यदि f′(x) + से − हो रहा है ⇒ स्थानीय अधिकतम
✔️ यदि f′(x) − से + हो रहा है ⇒ स्थानीय न्यूनतम
✴️ द्वितीय अवकलज परीक्षण (Second Derivative Test):
यदि f′(a) = 0 और f″(a) > 0 ⇒ स्थानीय न्यूनतम
यदि f′(a) = 0 और f″(a) < 0 ⇒ स्थानीय अधिकतम
📘 उदाहरण:
f(x) = x² − 4x + 5
➡️ f′(x) = 2x − 4 ⇒ f′(x)=0 ⇒ x = 2
➡️ f″(x) = 2 > 0 ⇒ x = 2 पर न्यूनतम मान
f(2) = 4 − 8 + 5 = 1 ⇒ न्यूनतम मान = 1

🔹 4️⃣ स्पर्शरेखा व अभिलंब का ढाल (Slope of Tangent and Normal)
💡 यदि y = f(x) है, तो बिंदु (x₀, y₀) पर:
✔️ स्पर्शरेखा का ढाल (mₜ): f′(x₀)
✔️ अभिलंब का ढाल (mₙ): −1 / f′(x₀)
📘 उदाहरण:
y = x², बिंदु (1,1) पर:
f′(x) = 2x ⇒ f′(1) = 2
➡️ mₜ = 2, mₙ = −1/2
✏️ स्पर्शरेखा का समीकरण:
(y − y₁) = mₜ (x − x₁)
✏️ अभिलंब का समीकरण:
(y − y₁) = mₙ (x − x₁)

🔹 5️⃣ अवकलज का भौतिक अनुप्रयोग (Rate of Change Applications)
💡 अवकलज किसी राशि में परिवर्तन की दर दर्शाता है।
📘 उदाहरण:
वृत्त का क्षेत्रफल A = πr²
dA/dr = 2πr ⇒ त्रिज्या में परिवर्तन से क्षेत्रफल में परिवर्तन दर
🔹 इसी प्रकार:
आयतन का परिवर्तन (V = 4/3 πr³ ⇒ dV/dr = 4πr²)
दूरी, चाल, त्वरण (Displacement, Velocity, Acceleration)

🔹 6️⃣ न्यूनतम लागत / अधिकतम लाभ समस्याएँ (Optimization Problems)
इन समस्याओं में किसी वस्तु का क्षेत्रफल, आयतन, लाभ या लागत को अधिकतम या न्यूनतम करना होता है।
✴️ सामान्य विधि:
➤ Step 1: फलन को एक ही चर में लिखें।
➤ Step 2: f′(x) = 0 रखकर critical points निकालें।
➤ Step 3: f″(x) की जाँच कर पता करें कि अधिकतम या न्यूनतम है।
📘 उदाहरण:
एक आयताकार खेत का परिमाप 100 m है। अधिकतम क्षेत्रफल ज्ञात करें।
क्षेत्रफल = x·y, परिमाप 2(x + y) = 100 ⇒ y = 50 − x
A = x(50 − x) = 50x − x²
A′(x) = 50 − 2x = 0 ⇒ x = 25 ⇒ y = 25
f″(x) = −2 < 0 ⇒ अधिकतम ⇒ A = 625 m²

🔹 7️⃣ निष्कर्ष (Conclusion)
अवकलज केवल गणना का साधन नहीं, बल्कि वास्तविक जीवन की समस्याओं का समाधान भी है।
यह अध्याय इंजीनियरिंग, भौतिकी, अर्थशास्त्र, और ज्यामिति में अत्यंत उपयोगी है।

🧾 सारांश (~300 शब्द)
🔹 बढ़ते घटते फलन:
f′(x) > 0 ⇒ बढ़ता फलन
f′(x) < 0 ⇒ घटता फलन
🔹 अधिकतम/न्यूनतम:
f′(x) = 0 पर f″(x) की जाँच करें
f″(x) > 0 ⇒ न्यूनतम
f″(x) < 0 ⇒ अधिकतम
🔹 स्पर्शरेखा का ढाल: f′(x₀)
🔹 अभिलंब का ढाल: −1 / f′(x₀)
🔹 स्पर्शरेखा का समीकरण: (y − y₁) = f′(x₀)(x − x₀)
🔹 परिवर्तन की दर (Rate of Change):
यदि y = f(x), तो dy/dx = y की परिवर्तन दर x के सापेक्ष
🔹 अनुकूलन (Optimization):
f′(x) = 0 और f″(x) से अधिकतम/न्यूनतम निर्धारित करें
🔹 प्रमुख अनुप्रयोग:
अधिकतम लाभ
न्यूनतम लागत
अधिकतम क्षेत्रफल/आयतन
चाल व त्वरण

📝 Quick Recap (त्वरित पुनरावृत्ति)
✔️ f′(x) > 0 ⇒ बढ़ता फलन
✔️ f′(x) < 0 ⇒ घटता फलन
✔️ f′(a) = 0, f″(a) > 0 ⇒ न्यूनतम
✔️ f′(a) = 0, f″(a) < 0 ⇒ अधिकतम
✔️ स्पर्शरेखा का ढाल = f′(x₀)
✔️ अभिलंब का ढाल = −1 / f′(x₀)
✔️ अवकलज = परिवर्तन दर
✔️ अनुकूलन समस्याओं में f′(x) = 0 से महत्वपूर्ण बिंदु खोजें

————————————————————————————————————————————————————————————————————————————

पाठ्यपुस्तक के प्रश्न

प्रश्नावली 6.1


🔵 प्रश्न 1
वृत्त के क्षेत्रफल के परिवर्तन की दर इसकी त्रिज्या r के सापेक्ष ज्ञात कीजिए;
(a) r = 3 cm, (b) r = 4 cm
🟢 चरण 1: सूत्र लिखें
• A = π r²
🟢 चरण 2: r के सापेक्ष अवकलन
• dA/dr = 2π r
🟢 चरण 3: मान स्थापित करें
• (a) r = 3 ⇒ dA/dr = 2π×3 = 6π (एकक: cm² प्रति cm)
• (b) r = 4 ⇒ dA/dr = 2π×4 = 8π (एकक: cm² प्रति cm)
✔️ अंतिम उत्तर: (a) 6π cm²/cm, (b) 8π cm²/cm

🔵 प्रश्न 2
एक घन का आयतन 8 cm³/s की दर से बढ़ रहा है। घन की भुजा s = 12 cm है। पृष्ठ क्षेत्रफल किस दर से बढ़ रहा है?
🟢 चरण 1: संबंध लिखें
• आयतन: V = s³
• पृष्ठ क्षेत्रफल: S = 6s²
🟢 चरण 2: समय t के सापेक्ष अवकलन
• dV/dt = 3s²·ds/dt
• dS/dt = 12s·ds/dt
🟢 चरण 3: दिए गए मान लगाएँ
• dV/dt = 8, s = 12 ⇒ ds/dt = 8/(3×12²) = 8/432 = 1/54 cm/s
🟢 चरण 4: dS/dt निकालें
• dS/dt = 12×12×(1/54) = 144/54 = 8/3
✔️ अंतिम उत्तर: dS/dt = 8/3 cm²/s

🔵 प्रश्न 3
एक वृत्त की त्रिज्या समान रूप से 3 cm/s की दर से बढ़ रही है। r = 10 cm होने पर क्षेत्रफल किस दर से बढ़ रहा है?
🟢 चरण 1: A = π r²
🟢 चरण 2: dA/dt = 2π r·dr/dt
🟢 चरण 3: r = 10, dr/dt = 3 ⇒ dA/dt = 2π×10×3 = 60π
✔️ अंतिम उत्तर: dA/dt = 60π cm²/s

🔵 प्रश्न 4
एक परिवर्ती घन की भुजा 3 cm/s की दर से बढ़ रही है। s = 10 cm होने पर आयतन किस दर से बढ़ रहा है?
🟢 चरण 1: V = s³
🟢 चरण 2: dV/dt = 3s²·ds/dt
🟢 चरण 3: s = 10, ds/dt = 3 ⇒ dV/dt = 3×100×3 = 900
✔️ अंतिम उत्तर: dV/dt = 900 cm³/s

🔵 प्रश्न 5
एक स्थिर झील में पत्थर डालने पर वृत्ताकार तरंग 5 cm/s की गति से फैलती है। r = 8 cm होने पर वृत्तीय क्षेत्रफल किस दर से बढ़ रहा है?
🟢 चरण 1: A = π r²
🟢 चरण 2: dA/dt = 2π r·dr/dt
🟢 चरण 3: r = 8, dr/dt = 5 ⇒ dA/dt = 2π×8×5 = 80π
✔️ अंतिम उत्तर: dA/dt = 80π cm²/s

🔵 प्रश्न 6
एक वृत्त की त्रिज्या 0.7 cm/s की दर से बढ़ रही है। इसकी परिधि की वृद्धि की दर क्या है जब r = 4.9 cm?
🟢 चरण 1: सूत्र
• परिधि C = 2πr
🟢 चरण 2: समय के सापेक्ष अवकलन
• dC/dt = 2π · dr/dt
🟢 चरण 3: मान स्थापित करें
• dr/dt = 0.7 cm/s
• dC/dt = 2π × 0.7 = 1.4π cm/s
✔️ अंतिम उत्तर: dC/dt = 1.4π cm/s (लगभग 4.398 cm/s)

🔵 प्रश्न 7
आयत की लंबाई x, 5 cm/min की दर से घट रही है (dx/dt = −5) और चौड़ाई y, 4 cm/min की दर से बढ़ रही है (dy/dt = +4)। जब x = 8 cm, y = 6 cm हों तब (a) परिमाप (b) क्षेत्रफल के परिवर्तन की दर ज्ञात कीजिए।
🟢 (a) परिमाप P = 2(x + y)
• dP/dt = 2(dx/dt + dy/dt)
• dP/dt = 2(−5 + 4) = −2 cm/min
✔️ उत्तर (a): dP/dt = −2 cm/min (परिमाप घट रहा है)
🟢 (b) क्षेत्रफल A = x·y
• dA/dt = x·dy/dt + y·dx/dt
• dA/dt = 8×4 + 6×(−5) = 32 − 30 = 2 cm²/min
✔️ उत्तर (b): dA/dt = +2 cm²/min

🔵 प्रश्न 8
गुब्बारा सदैव गोलाकार रहता है। हवा 900 cm³/s की दर से भरी जा रही है। r = 15 cm पर त्रिज्या की परिवर्तन दर ज्ञात कीजिए।
🟢 चरण 1: आयतन (गोला)
• V = (4/3)π r³
🟢 चरण 2: समय के सापेक्ष अवकलन
• dV/dt = 4π r² · dr/dt
🟢 चरण 3: मान स्थापित करें
• dV/dt = 900, r = 15 ⇒ dr/dt = 900 / (4π·15²)
• dr/dt = 900 / (4π·225) = 900 / (900π) = 1/π cm/s
✔️ अंतिम उत्तर: dr/dt = 1/π cm/s (लगभग 0.318 cm/s)

🔵 प्रश्न 9
गुब्बारा सदैव गोलाकार है; त्रिज्या परिवर्तनीय है। त्रिज्या के सापेक्ष आयतन की परिवर्तन दर r = 10 cm पर ज्ञात कीजिए।
🟢 चरण 1: V = (4/3)π r³
🟢 चरण 2: r के सापेक्ष अवकलन
• dV/dr = 4π r²
🟢 चरण 3: r = 10 रखने पर
• dV/dr = 4π × 10² = 400π cm²
✔️ अंतिम उत्तर: dV/dr = 400π cm²

🔵 प्रश्न 10
एक 5 m लंबी सीढ़ी दीवार के सहारे झुकी है।
सीढ़ी का नीचे का सिरा, दीवार से 2 cm/s की दर से दूर खींचा जा रहा है।
दीवार पर इसकी ऊँचाई किस दर से घट रही है जब सीढ़ी का नीचे का सिरा दीवार से 4 m दूर है?
🟢 हल
➡️ मान लीजिए
x = दीवार से नीचे सिरे की दूरी (मीटर में)
y = दीवार पर ऊँचाई (मीटर में)
l = सीढ़ी की लंबाई = 5 m
📌 संबंध
x² + y² = 25
🧠 समय के सापेक्ष अवकलन करें
2x(dx/dt) + 2y(dy/dt) = 0
सरलीकरण:
x(dx/dt) + y(dy/dt) = 0
📍 दिए गए मान
dx/dt = 2 cm/s = 0.02 m/s
x = 4 m
✳️ पहले y ज्ञात करें
4² + y² = 25
16 + y² = 25
y = 3 m
🧩 मान रखिए
4(0.02) + 3(dy/dt) = 0
0.08 + 3(dy/dt) = 0
dy/dt = –0.08 / 3 = –0.0267 m/s = –2.67 cm/s
✔️ अतः ऊँचाई घटने की दर = 2.67 cm/s
🔶 उत्तर
ऊँचाई 2.67 cm/s की दर से घट रही है ✅

🔵 प्रश्न 11
एक कण वक्र 6y = x³ + 2 के अनुसार गति कर रहा है।
वक्र पर उस बिंदु को ज्ञात कीजिए जहाँ y-दिशा की वेग x-दिशा की वेग का 8 गुना है।
🟢 हल
📌 वक्र समीकरण
6y = x³ + 2
➡️ अवकलन करें
6(dy/dt) = 3x²(dx/dt)
dy/dt = (x² / 2)(dx/dt)
🧭 दिया है
dy/dt = 8(dx/dt)
📍 तुलना करें
x² / 2 = 8
x² = 16
x = 4
📐 अब y ज्ञात करें
6y = 4³ + 2 = 64 + 2 = 66
y = 11
✔️ अतः बिंदु = (4, 11)
🔶 उत्तर
बिंदु (4, 11) ✅

🔵 प्रश्न 12
हवा के एक बुलबुले की त्रिज्या 1/2 cm/s की दर से बढ़ रही है।
जब त्रिज्या 1 cm है, तब बुलबुले का आयतन किस दर से बढ़ रहा है?
🟢 हल
📌 आयतन का सूत्र
V = (4/3)πr³
➡️ समय के सापेक्ष अवकलन करें
dV/dt = 4πr²(dr/dt)
📍 दिया गया
r = 1 cm
dr/dt = 1/2 cm/s
🧩 मान रखिए
dV/dt = 4π(1)²(1/2)
dV/dt = 2π cm³/s
✔️ अतः आयतन बढ़ने की दर = 2π cm³/s
🔶 उत्तर
बुलबुले का आयतन 2π cm³/s की दर से बढ़ रहा है ✅

🔵 प्रश्न 12
हवा के एक बुलबुले की त्रिज्या 1/2 cm/s की दर से बढ़ रही है।
बुलबुले का आयतन किस दर से बढ़ रहा है जब r = 1 cm ?
🟢 हल:
✨ सूत्र: V = (4/3)πr³
➡️ दोनों पक्षों का समय t के सापेक्ष अवकलन कीजिए:
➡️ dV/dt = 4πr² × dr/dt
➡️ अब मान रखें: r = 1, dr/dt = 1/2
➡️ dV/dt = 4π(1)² × (1/2)
➡️ dV/dt = 2π cm³/s
✔️ उत्तर: बुलबुले का आयतन 2π cm³/s की दर से बढ़ रहा है।

🔵 प्रश्न 13
एक गुब्बारा, जो सदैव गोलाकार रहता है, का परिवर्तनशील व्यास D = (3/2)(2x + 1) है।
x के सापेक्ष आयतन के परिवर्तन की दर ज्ञात कीजिए।
🟢 हल:
✨ D = (3/2)(2x + 1)
➡️ r = D/2 = (3/4)(2x + 1)
✨ सूत्र: V = (4/3)πr³
➡️ दोनों पक्षों का x के सापेक्ष अवकलन कीजिए:
➡️ dV/dx = 4πr² × dr/dx
➡️ dr/dx = (3/2)
➡️ dV/dx = 4π[(3/4)(2x + 1)]² × (3/2)
➡️ dV/dx = (27π/8)(2x + 1)²
✔️ उत्तर: dV/dx = (27π/8)(2x + 1)²

🔵 प्रश्न 14
एक पाइप से 12 cm³/s की दर से रेत गिर रही है।
गिरती रेत ज़मीन पर एक शंकु बनाती है जिसकी ऊँचाई = आधार की त्रिज्या का 1/4 भाग है।
जब ऊँचाई 4 cm है, ऊँचाई किस दर से बढ़ रही है?
🟢 हल:
✨ सूत्र: V = (1/3)πr²h
➡️ r = 4h
➡️ V = (1/3)π(4h)²h = (16/3)πh³
➡️ दोनों पक्षों का समय t के सापेक्ष अवकलन कीजिए:
➡️ dV/dt = 16πh² × dh/dt
➡️ मान रखें: dV/dt = 12, h = 4
➡️ 12 = 16π(4)² × dh/dt
➡️ 12 = 256π × dh/dt
➡️ dh/dt = 12 / (256π) = 3 / (64π)
✔️ उत्तर: ऊँचाई 3 / (64π) cm/s की दर से बढ़ रही है।

🔵 प्रश्न 15
एक वस्तु की x इकाइयों के उत्पादन से संबंधित कुल लागत
C(x) = 0.007x³ − 0.003x² + 15x + 4000 रुपये में दी गई है।
जब 17 इकाइयों का उत्पादन किया गया है, तो सीमांत लागत ज्ञात कीजिए।
🟢 उत्तर :
🔹 सीमांत लागत = dC/dx
🔹 सबसे पहले C(x) का अवकलन कीजिए :
dC/dx = 0.021x² − 0.006x + 15
🔹 अब x = 17 रखिए :
dC/dx = 0.021(17)² − 0.006(17) + 15
= 0.021(289) − 0.102 + 15
= 6.069 − 0.102 + 15
= 20.967
✔️ अतः सीमांत लागत = ₹ 20.967

🔵 प्रश्न 16
किसी उत्पाद की x इकाइयों के विक्रय से प्राप्त कुल आय
R(x) = 13x² + 26x + 15
से दी गई है। x = 7 पर सीमांत आय ज्ञात कीजिए।
🟢 उत्तर :
🔹 सीमांत आय = dR/dx
🔹 अवकलन कीजिए :
dR/dx = 26x + 26
🔹 x = 7 रखने पर :
dR/dx = 26(7) + 26
= 182 + 26
= 208
✔️ अतः सीमांत आय = ₹ 208

🔵 प्रश्न 17
एक वृत्त की त्रिज्या r = 6 cm पर, r के सापेक्ष क्षेत्रफल में परिवर्तन की दर ज्ञात कीजिए।
🟢 उत्तर :
🔹 क्षेत्रफल A = πr²
🔹 अवकलन कीजिए :
dA/dr = 2πr
🔹 r = 6 रखने पर :
dA/dr = 2π(6)
= 12π
✔️ अतः उत्तर = 12π (विकल्प B)

🔵 प्रश्न 18
एक उत्पाद की x इकाइयों के विक्रय से प्राप्त कुल आय
R(x) = 3x² + 36x + 5
से दी गई है।
जब x = 15 हो, तो सीमांत आय ज्ञात कीजिए।
🟢 उत्तर :
🔹 सीमांत आय = dR/dx
🔹 अवकलन कीजिए :
dR/dx = 6x + 36
🔹 x = 15 रखने पर :
dR/dx = 6(15) + 36
= 90 + 36
= 126
✔️ अतः उत्तर = 126 (विकल्प D)

प्रश्नावली 6.2

🔵 Question 1
सिद्ध कीजिए R पर f(x) = 3x + 17 से परिभाषित फलन वर्धमान है।

🟢 Answer
🔹 चरण 1: परिभाषा — यदि किसी अंतराल पर f′(x) > 0 सर्वत्र हो, तो f उस अंतराल पर वर्धमान होता है।
🔹 चरण 2: f(x) = 3x + 17 का अवकलज निकालें।
➡️ f′(x) = 3
🔹 चरण 3: R पर f′(x) का चिन्ह जाँचें।
➡️ f′(x) = 3 > 0, सभी x ∈ R
🔹 चरण 4: निष्कर्ष लिखें।
➡️ क्योंकि f′(x) > 0 सर्वत्र, इसलिए f(x) = 3x + 17, R पर वर्धमान है।
✔️ अंतिम निष्कर्ष: फलन R पर वर्धमान है।

🔵 Question 2
सिद्ध कीजिए कि R पर f(x) = e^(2x) से परिभाषित फलन वर्धमान है।

🟢 Answer
🔹 चरण 1: परिभाषा — यदि f′(x) > 0 सर्वत्र, तो f वर्धमान।
🔹 चरण 2: f(x) = e^(2x) का अवकलज निकालें।
➡️ f′(x) = 2·e^(2x)
🔹 चरण 3: R पर f′(x) का चिन्ह जाँचें।
➡️ e^(2x) > 0, सभी x ∈ R
➡️ अतः f′(x) = 2·e^(2x) > 0, सभी x ∈ R
🔹 चरण 4: निष्कर्ष लिखें।
➡️ f′(x) > 0 सर्वत्र ⇒ f(x) = e^(2x) R पर वर्धमान है।
✔️ अंतिम निष्कर्ष: फलन R पर वर्धमान है।

🔵 Question 3
सिद्ध कीजिए f(x) = sin x से परिभाषित फलन
(a) (0, π/2) में वर्धमान है
(b) (π/2, π) में ह्रासमान है
(c) (0, π) में न तो वर्धमान है और न ही ह्रासमान है।

🟢 Answer
🔹 चरण 1: अवकलज निकालें।
➡️ f(x) = sin x
➡️ f′(x) = cos x

🟡 भाग (a): (0, π/2) में
➡️ 0 < x < π/2 ⇒ cos x > 0
➡️ f′(x) > 0 इस अंतराल में
✔️ निष्कर्ष: f (0, π/2) में वर्धमान है।

🟡 भाग (b): (π/2, π) में
➡️ π/2 < x < π ⇒ cos x < 0
➡️ f′(x) < 0 इस अंतराल में
✔️ निष्कर्ष: f (π/2, π) में ह्रासमान है।

🟡 भाग (c): (0, π) में
➡️ (0, π/2) में f′(x) > 0 तथा (π/2, π) में f′(x) < 0
➡️ पूरे (0, π) में f′(x) का चिन्ह एकसमान नहीं है
✔️ निष्कर्ष: f (0, π) में न तो वर्धमान है और न ही ह्रासमान है।

🔵 प्रश्न 4
अंतराल ज्ञात कीजिए जिनमें f(x) = 2x² – 3x से परिभाषित फलन f
(a) वर्धमान है (b) ह्रासमान है
🟢 उत्तर
✏️ चरण 1: f(x) = 2x² – 3x
➡️ f′(x) = 4x – 3
✏️ चरण 2: f′(x) > 0 के लिए
➡️ 4x – 3 > 0
➡️ x > 3/4
✏️ चरण 3: f′(x) < 0 के लिए
➡️ x < 3/4
✔️ निष्कर्ष:
🔹 (-∞, 3/4) में फलन ह्रासमान है
🔹 (3/4, ∞) में फलन वर्धमान है

🔵 प्रश्न 5
अंतराल ज्ञात कीजिए जिनमें f(x) = 2x³ – 3x² – 36x + 7 से परिभाषित फलन f
(a) वर्धमान है (b) ह्रासमान है
🟢 उत्तर
✏️ चरण 1: f′(x) = 6x² – 6x – 36
➡️ f′(x) = 6(x² – x – 6)
➡️ f′(x) = 6(x – 3)(x + 2)
✏️ चरण 2: f′(x) = 0 के मूल
➡️ x = -2, 3
✏️ चरण 3: चिन्ह परीक्षण
🔹 x < -2 ⇒ f′(x) > 0
🔹 -2 < x < 3 ⇒ f′(x) < 0
🔹 x > 3 ⇒ f′(x) > 0
✔️ निष्कर्ष:
🔹 (-∞, -2) में वर्धमान
🔹 (-2, 3) में ह्रासमान
🔹 (3, ∞) में वर्धमान

🔵 प्रश्न 6
अंतराल ज्ञात कीजिए जिनमें निम्नलिखित फलन वर्धमान या ह्रासमान हैं:
(a) f(x) = x² + 2x + 5
(b) f(x) = 10 – 6x – 2x²
(c) f(x) = -2x³ – 9x² – 12x + 1
(d) f(x) = 6 – 9x – x²
(e) f(x) = (x + 1)³ (x – 3)³
🟢 उत्तर
🟡 (a) f′(x) = 2x + 2
➡️ f′(x) = 0 पर x = -1
🔹 (-∞, -1) में f′(x) < 0 ⇒ ह्रासमान
🔹 (-1, ∞) में f′(x) > 0 ⇒ वर्धमान
🟡 (b) f′(x) = -6 – 4x
➡️ f′(x) = 0 पर x = -3/2
🔹 (-∞, -3/2) में वर्धमान
🔹 (-3/2, ∞) में ह्रासमान
🟡 (c) f′(x) = -6x² – 18x – 12
➡️ f′(x) = -6(x + 1)(x + 2)
मूल: x = -1, -2
🔹 (-∞, -2) में f′(x) < 0 ⇒ ह्रासमान
🔹 (-2, -1) में f′(x) > 0 ⇒ वर्धमान
🔹 (-1, ∞) में f′(x) < 0 ⇒ ह्रासमान
🟡 (d) f′(x) = -9 – 2x
➡️ f′(x) = 0 पर x = -9/2
🔹 (-∞, -9/2) में वर्धमान
🔹 (-9/2, ∞) में ह्रासमान
🟡 (e) f(x) = (x + 1)³ (x – 3)³
➡️ f′(x) = 6(x + 1)² (x – 3)² (x – 1)
मूल: x = -1, 1, 3
🔹 (-∞, 1) में f′(x) < 0 ⇒ ह्रासमान
🔹 (1, ∞) में f′(x) > 0 ⇒ वर्धमान

🔵 प्रश्न 7
सिद्ध कीजिए कि y = log(1 + x) – 2x / (2 + x), x > -1, अपने सम्पूर्ण प्रांत में एक वर्धमान फलन है।
🟢 उत्तर
✏️ चरण 1: y′ ज्ञात कीजिए
➡️ y′ = 1 / (1 + x) – [2(2 + x) – 2x] / (2 + x)²
➡️ y′ = 1 / (1 + x) – 4 / (2 + x)²
✏️ चरण 2: समान हर में लाएँ
➡️ y′ = [(2 + x)² – 4(1 + x)] / [(1 + x)(2 + x)²]
➡️ y′ = [x² + 4x + 4 – 4 – 4x] / [(1 + x)(2 + x)²]
➡️ y′ = x² / [(1 + x)(2 + x)²]
✏️ चरण 3: x > -1 पर सभी पद धनात्मक ⇒ y′ > 0
✔️ निष्कर्ष: y सम्पूर्ण प्रांत में वर्धमान है।

🔵 प्रश्न 8
x के उन मानों को ज्ञात कीजिए जिनके लिए y = [x(x – 2)]² एक वर्धमान फलन है।
🟢 उत्तर
✏️ चरण 1: y = (x² – 2x)²
➡️ y′ = 2(x² – 2x)(2x – 2)
➡️ y′ = 4(x² – 2x)(x – 1)
➡️ y′ = 4x(x – 2)(x – 1)
✏️ चरण 2: मूल: x = 0, 1, 2
✏️ चरण 3: चिन्ह परीक्षण
🔹 (-∞, 0): f′(x) > 0 ⇒ वर्धमान
🔹 (0, 1): f′(x) < 0 ⇒ ह्रासमान
🔹 (1, 2): f′(x) > 0 ⇒ वर्धमान
🔹 (2, ∞): f′(x) > 0 ⇒ वर्धमान
✔️ निष्कर्ष: फलन (-∞, 0) तथा (1, ∞) में वर्धमान है।

🔵 प्रश्न 9
सिद्ध कीजिए कि [0, π/2] में y = 4sinθ / (2 + cosθ) – θ का एक वर्धमान फलन है।
🟢 उत्तर
✏️ चरण 1: y′ ज्ञात कीजिए
➡️ y′ = [(4cosθ)(2 + cosθ) – 4sinθ(-sinθ)] / (2 + cosθ)² – 1
➡️ y′ = [8cosθ + 4cos²θ + 4sin²θ] / (2 + cosθ)² – 1
➡️ y′ = [8cosθ + 4] / (2 + cosθ)² – 1
✏️ चरण 2: समान हर में लाएँ
➡️ y′ = [8cosθ + 4 – (2 + cosθ)²] / (2 + cosθ)²
➡️ y′ = [8cosθ + 4 – (4 + 4cosθ + cos²θ)] / (2 + cosθ)²
➡️ y′ = [4cosθ – cos²θ] / (2 + cosθ)²
➡️ y′ = cosθ(4 – cosθ) / (2 + cosθ)²
✏️ चरण 3: 0 ≤ θ ≤ π/2 पर cosθ ≥ 0 और (4 – cosθ) > 0
➡️ y′ ≥ 0
✔️ निष्कर्ष: फलन [0, π/2] में वर्धमान है।

🔵 प्रश्न 10
सिद्ध कीजिए कि लघुगणकीय फलन (0, ∞) में वर्धमान फलन है।
🟢 उत्तर
✏️ चरण 1: फलन मानिए f(x) = log x
✏️ चरण 2: अवकलज ज्ञात कीजिए
➡️ f′(x) = 1 / x
✏️ चरण 3: (0, ∞) में 1 / x > 0
✔️ निष्कर्ष:
चूंकि f′(x) > 0 सभी x ∈ (0, ∞) के लिए,
अतः log x (0, ∞) में वर्धमान फलन है।

🔵 प्रश्न 11
सिद्ध कीजिए कि (-1, 1) में f(x) = x² – x + 1 से परिभाषित फलन न तो वर्धमान है और न ही ह्रासमान है।
🟢 उत्तर
✏️ चरण 1: f(x) = x² – x + 1
➡️ f′(x) = 2x – 1
✏️ चरण 2: f′(x) = 0 पर x = 1/2
✏️ चरण 3:
🔹 (-1, 1/2) में f′(x) < 0 ⇒ ह्रासमान
🔹 (1/2, 1) में f′(x) > 0 ⇒ वर्धमान
✔️ निष्कर्ष:
(-1, 1) में f′(x) का चिन्ह समान नहीं है,
इसलिए फलन न तो वर्धमान है और न ही ह्रासमान।

🔵 प्रश्न 12
निम्नलिखित में कौन-से फलन (0, π/2) में ह्रासमान हैं?
(A) cos x (B) cos 2x (C) cos 3x (D) tan x
🟢 उत्तर
✏️ चरण 1: अवकलज ज्ञात करें –
(A) f(x) = cos x ⇒ f′(x) = -sin x
(B) f(x) = cos 2x ⇒ f′(x) = -2sin 2x
(C) f(x) = cos 3x ⇒ f′(x) = -3sin 3x
(D) f(x) = tan x ⇒ f′(x) = sec²x
✏️ चरण 2: (0, π/2) में sin x, sin 2x, sin 3x > 0 और sec²x > 0
✏️ चरण 3: चिन्ह विश्लेषण –
(A) f′(x) < 0 ⇒ ह्रासमान
(B) f′(x) < 0 ⇒ ह्रासमान
(C) f′(x) < 0 ⇒ ह्रासमान
(D) f′(x) > 0 ⇒ वर्धमान
✔️ निष्कर्ष:
(A) cos x, (B) cos 2x, (C) cos 3x – ह्रासमान हैं

🔵 प्रश्न 13
निम्नलिखित अंतरालों में से किस अंतराल में f(x) = x¹⁰⁰ + sin x – 1 द्वारा परिभाषित फलन f ह्रासमान है?
(A) (0, 1) (B) (π/2, π) (C) (0, π/2) (D) इनमें से कोई नहीं
🟢 उत्तर
✏️ चरण 1: f(x) = x¹⁰⁰ + sin x – 1
➡️ f′(x) = 100x⁹⁹ + cos x
✏️ चरण 2:
(A) (0, 1):
 x⁹⁹ > 0, cos x > 0 ⇒ f′(x) > 0 ⇒ वर्धमान
(B) (π/2, π):
 x⁹⁹ > 0, cos x < 0
 लेकिन 100x⁹⁹ का मान बहुत बड़ा है ⇒ f′(x) > 0
(C) (0, π/2):
 x⁹⁹ > 0, cos x > 0 ⇒ f′(x) > 0
✏️ चरण 3: किसी भी अंतराल में f′(x) < 0 नहीं
✔️ निष्कर्ष:
फलन किसी भी अंतराल में ह्रासमान नहीं है।
✅ सही उत्तर: (D) इनमें से कोई नहीं

🔵 प्रश्न 14
a का वह न्यूनतम मान ज्ञात कीजिए जिसके लिए अंतराल [1, 2] में f(x) = x^2 + a x + 1 से परिभाषित फलन वर्धमान है।
🟢 उत्तर
✏️ चरण 1: f′(x) ज्ञात कीजिए
➡️ f′(x) = 2x + a
✏️ चरण 2: [1, 2] में वर्धमान होने की शर्त
➡️ f′(x) ≥ 0, सभी x ∈ [1, 2]
✏️ चरण 3: 2x + a का न्यूनतम मान x = 1 पर होगा
➡️ 2(1) + a ≥ 0
➡️ a ≥ -2
✔️ निष्कर्ष
🔹 न्यूनतम मान a = -2 है (x = 1 पर f′(x) = 0 और x > 1 पर f′(x) > 0, अतः [1, 2] में फलन वर्धमान/अवरोही नहीं है)।

🔵 प्रश्न 15
मान लीजिए [-1, 1] से असंयुक्त एक अंतराल I हो। सिद्ध कीजिए कि I में f(x) = x + 1/x से परिभाषित फलन f वर्धमान है।
🟢 उत्तर
✏️ चरण 1: परिभाषित क्षेत्र
➡️ I, [-1, 1] से असंयुक्त है ⇒ I ⊂ (-∞, -1) अथवा I ⊂ (1, ∞)
✏️ चरण 2: f′(x) ज्ञात कीजिए
➡️ f′(x) = 1 – 1/x^2 = (x^2 – 1)/x^2
✏️ चरण 3: चिन्ह परीक्षण
➡️ यदि x < -1 या x > 1, तब x^2 – 1 ≥ 0 तथा x^2 > 0
➡️ अतः f′(x) ≥ 0, सभी x ∈ I
✔️ निष्कर्ष
🔹 f′(x) ≥ 0 होने से f I पर वर्धमान है।

🔵 प्रश्न 16
सिद्ध कीजिए कि फलन f(x) = log(sin x), (0, π/2) में वर्धमान और (π/2, π) में ह्रासमान है।
🟢 उत्तर
✏️ चरण 1: f′(x) ज्ञात कीजिए
➡️ f(x) = log(sin x)
➡️ f′(x) = (1/sin x)·cos x = cot x
✏️ चरण 2: (0, π/2) में चिन्ह
➡️ 0 < x < π/2 ⇒ cot x > 0
➡️ f′(x) > 0
✏️ चरण 3: (π/2, π) में चिन्ह
➡️ π/2 < x < π ⇒ cot x < 0
➡️ f′(x) < 0
✔️ निष्कर्ष
🔹 (0, π/2) में f वर्धमान है।
🔹 (π/2, π) में f ह्रासमान है।

🔵 प्रश्न 17
सिद्ध कीजिए कि f(x) = log|cos x|, (0, π/2) में ह्रासमान और (3π/2, 2π) में वर्धमान है।
(टिप्पणी: कुछ संस्करणों में वाक्यांश की दिशा उलटी छपी है; नीचे दिया निष्कर्ष NCERT-संगत और गणिततः सही है।)

🟢 उत्तर
✏️ चरण 1: फलन लिखें
➡️ f(x) = log|cos x|

✏️ चरण 2: अवकलज ज्ञात करें (|cos x| के अनुसार)
➡️ यदि cos x > 0, तो |cos x| = cos x और f′(x) = (1/cos x)(-sin x) = -tan x
➡️ यदि cos x < 0, तो |cos x| = -cos x और f′(x) = (1/(-cos x))(-sin x) = tan x

🟡 भाग (i): (0, π/2) में
➡️ cos x > 0 ⇒ f′(x) = -tan x
➡️ 0 < x < π/2 पर tan x > 0 ⇒ f′(x) < 0
✔️ निष्कर्ष: f(x) (0, π/2) में ह्रासमान है।

🟡 भाग (ii): (3π/2, 2π) में
➡️ cos x > 0 और tan x < 0 ⇒ f′(x) = -tan x > 0
✔️ निष्कर्ष: f(x) (3π/2, 2π) में वर्धमान है।

✔️ अंतिम निष्कर्ष: f(x) = log|cos x|, (0, π/2) में ह्रासमान तथा (3π/2, 2π) में वर्धमान है।

🔵 प्रश्न 18
सिद्ध कीजिए कि R में दिया गया फलन f(x) = x³ – 3x² + 3x – 100 वर्धमान है।
🟢 उत्तर
✏️ चरण 1: f(x) = x³ – 3x² + 3x – 100
➡️ f′(x) = 3x² – 6x + 3
➡️ f′(x) = 3(x² – 2x + 1) = 3(x – 1)²
✏️ चरण 2: (x – 1)² ≥ 0 ⇒ f′(x) ≥ 0 सभी x ∈ R
✔️ निष्कर्ष:
f′(x) ≥ 0 सर्वत्र ⇒ फलन R पर वर्धमान है।

🔵 प्रश्न 19
निम्नलिखित में से किस अंतराल में y = x²·e^(-x) वर्धमान है?
(A) (-∞, ∞) (B) (-2, 0) (C) (2, ∞) (D) (0, 2)
🟢 उत्तर
✏️ चरण 1: y = x²·e^(-x)
➡️ y′ = 2x·e^(-x) + x²·(-e^(-x))
➡️ y′ = e^(-x)(2x – x²)
➡️ y′ = e^(-x)·x(2 – x)
✏️ चरण 2: e^(-x) > 0 सभी x के लिए
y′ का चिन्ह = x(2 – x) का चिन्ह
✏️ चरण 3:
x(2 – x) > 0 जब 0 < x < 2
✔️ निष्कर्ष:
y′ > 0 ⇒ वर्धमान अंतराल (0, 2)
✅ सही विकल्प: (D) (0, 2)

प्रश्नावली 6.3

🔵 प्रश्न 1
निम्नलिखित दिए गए फलनों के उच्चतम या निम्नतम मान, यदि कोई हों, तो ज्ञात कीजिए:
(i) f(x) = (2x – 1)² + 3
(ii) f(x) = 9x² + 12x + 2
(iii) f(x) = – (x – 1)² + 10
(iv) g(x) = x³ + 1
🟢 उत्तर
✴️ (i) f(x) = (2x – 1)² + 3
➡️ (2x – 1)² ≥ 0 ⇒ न्यूनतम मान 0 पर
➡️ f(x) का न्यूनतम मान = 0 + 3 = 3
➡️ जब (2x – 1) = 0 ⇒ x = 1/2
✔️ न्यूनतम मान = 3, x = 1/2 पर
✴️ (ii) f(x) = 9x² + 12x + 2
➡️ यह द्विघात रूप ax² + bx + c है जहाँ a = 9 > 0 ⇒ न्यूनतम होगा
➡️ x = -b / (2a) = -12 / (2×9) = -2/3
➡️ f(-2/3) = 9(-2/3)² + 12(-2/3) + 2
= 9(4/9) – 8 + 2 = 4 – 8 + 2 = -2
✔️ न्यूनतम मान = -2, x = -2/3 पर
✴️ (iii) f(x) = – (x – 1)² + 10
➡️ -(x – 1)² ≤ 0 ⇒ अधिकतम मान 0 पर
➡️ f(x) का अधिकतम मान = 0 + 10 = 10
➡️ जब (x – 1) = 0 ⇒ x = 1
✔️ अधिकतम मान = 10, x = 1 पर
✴️ (iv) g(x) = x³ + 1
➡️ g′(x) = 3x² ≥ 0 सभी x ∈ R पर
➡️ कोई निश्चित अधिकतम या न्यूनतम नहीं
✔️ कोई चरम मान नहीं (फलन सदैव वर्धमान)

🔵 प्रश्न 2
निम्नलिखित दिए गए फलनों के उच्चतम या निम्नतम मान, यदि कोई हों, तो ज्ञात कीजिए:
(i) f(x) = |x + 2| – 1
(ii) g(x) = -|x + 11| + 3
(iii) h(x) = sin(2x) + 5
(iv) f(x) = |sin 4x + 3|
(v) h(x) = x + 1, x ∈ (-1, 1)
🟢 उत्तर
✴️ (i) f(x) = |x + 2| – 1
➡️ |x + 2| का न्यूनतम मान 0 पर (x = -2)
➡️ f(x) = 0 – 1 = -1
✔️ न्यूनतम मान = -1, x = -2 पर
✴️ (ii) g(x) = -|x + 11| + 3
➡️ -|x + 11| का अधिकतम मान 0 पर (x = -11)
➡️ g(x) = 0 + 3 = 3
✔️ अधिकतम मान = 3, x = -11 पर
✴️ (iii) h(x) = sin(2x) + 5
➡️ sin(2x) ∈ [-1, 1]
➡️ न्यूनतम: 5 – 1 = 4
➡️ अधिकतम: 5 + 1 = 6
✔️ न्यूनतम मान = 4, अधिकतम मान = 6
✴️ (iv) f(x) = |sin 4x + 3|
➡️ sin 4x ∈ [-1, 1] ⇒ sin 4x + 3 ∈ [2, 4]
➡️ |sin 4x + 3| = sin 4x + 3
✔️ न्यूनतम मान = 2, अधिकतम मान = 4
✴️ (v) h(x) = x + 1, x ∈ (-1, 1)
➡️ h(x) = x + 1
➡️ x = -1 पर → h(x) = 0
➡️ x = 1 पर → h(x) = 2
✔️ अंतराल खुला (-1, 1) है ⇒ चरम मान नहीं प्राप्त
🔹 लेकिन h(x) का परास (range) = (0, 2)
✔️ कोई निश्चित उच्चतम/न्यूनतम नहीं (केवल सीमा मान)

🔵 प्रश्न 3
निम्नलिखित फलनों के स्थानीयरूप उच्चतम या निम्नतम मान, यदि हों, ज्ञात कीजिए तथा स्थानीयरूप उच्चतम/न्यूनतम मान, जैसी स्थिति हो, भी ज्ञात कीजिए:
(i) f(x) = x²
(ii) g(x) = x³ − 3x
(iii) h(x) = sin x + cos x, 0 < x < π/2
(iv) f(x) = sin x − cos x, 0 < x < 2π
(v) f(x) = x³ − 6x² + 9x + 15
(vi) g(x) = x/2 + 2/x, x > 0
(vii) g(x) = 1 / (x² + 2)
(viii) f(x) = x√(1 − x), 0 < x < 1
🟢 उत्तर
🟡 (i) f(x) = x²
✏️ f′(x) = 2x
➡️ 2x = 0 ⇒ x = 0
✏️ f″(x) = 2 > 0
✔️ x = 0 पर स्थानीयरूप न्यूनतम, मान f(0) = 0; कोई उच्चतम नहीं।
🟡 (ii) g(x) = x³ − 3x
✏️ g′(x) = 3x² − 3 = 3(x − 1)(x + 1)
➡️ x = −1, 1
✏️ g″(x) = 6x
➡️ x = −1 पर g″ = −6 < 0 ⇒ उच्चतम, g(−1) = 2
➡️ x = 1 पर g″ = 6 > 0 ⇒ न्यूनतम, g(1) = −2
🟡 (iii) h(x) = sin x + cos x
✏️ h′(x) = cos x − sin x = 0 ⇒ x = π/4
✏️ h″(x) = −sin x − cos x; h″(π/4) = −√2 < 0
✔️ x = π/4 पर उच्चतम; h(π/4) = √2
🟡 (iv) f(x) = sin x − cos x
✏️ f′(x) = cos x + sin x = 0 ⇒ tan x = −1 ⇒ x = 3π/4, 7π/4
✏️ f″(x) = −sin x + cos x
➡️ x = 3π/4 पर f″ = −√2 < 0 ⇒ उच्चतम, f(3π/4) = √2
➡️ x = 7π/4 पर f″ = √2 > 0 ⇒ न्यूनतम, f(7π/4) = −√2
🟡 (v) f(x) = x³ − 6x² + 9x + 15
✏️ f′(x) = 3x² − 12x + 9 = 3(x − 1)(x − 3)
➡️ x = 1, 3
✏️ f″(x) = 6x − 12
➡️ x = 1 ⇒ f″ = −6 < 0 ⇒ उच्चतम, f(1) = 19
➡️ x = 3 ⇒ f″ = 6 > 0 ⇒ न्यूनतम, f(3) = 15
🟡 (vi) g(x) = x/2 + 2/x
✏️ g′(x) = 1/2 − 2/x² = 0 ⇒ x² = 4 ⇒ x = 2
✏️ g″(x) = 4/x³ > 0
✔️ x = 2 पर न्यूनतम, g(2) = 2
🟡 (vii) g(x) = 1 / (x² + 2)
✏️ g′(x) = −2x / (x² + 2)² = 0 ⇒ x = 0
✏️ g″(x) = −2 / (x² + 2)² + 8x² / (x² + 2)³
➡️ g″(0) = −1/2 < 0
✔️ x = 0 पर उच्चतम, g(0) = 1/2
🟡 (viii) f(x) = x√(1 − x)
✏️ f′(x) = √(1 − x) − x / [2√(1 − x)] = [1 − (3/2)x] / √(1 − x)
➡️ f′(x) = 0 ⇒ x = 2/3
✏️ x < 2/3 पर f′ > 0, x > 2/3 पर f′ < 0
✔️ x = 2/3 पर उच्चतम, f(2/3) = (2/3)√(1/3) = 2√3 / 9

🔵 प्रश्न 4
सिद्ध कीजिए कि निम्नलिखित फलनों का उच्चतम या निम्नतम मान नहीं है:
(i) f(x) = eˣ
(ii) g(x) = log x
(iii) h(x) = x³ + x² + x + 1
🟢 उत्तर
🟡 (i) f(x) = eˣ
✏️ f′(x) = eˣ > 0
✔️ सर्वत्र वर्धमान ⇒ कोई स्थानीयरूप चरम मान नहीं।
🟡 (ii) g(x) = log x
✏️ g′(x) = 1/x > 0 (x > 0)
✔️ वर्धमान ⇒ कोई चरम मान नहीं।
🟡 (iii) h(x) = x³ + x² + x + 1
✏️ h′(x) = 3x² + 2x + 1; Δ = 2² − 4·3·1 = −8 < 0
➡️ h′(x) > 0 सभी x पर
✔️ सर्वत्र वर्धमान ⇒ कोई चरम मान नहीं।

🔵 प्रश्न 5
प्रदत्त अंतरालों में निम्नलिखित फलनों के निश्चित उच्चतम मान और निश्चित निम्नतम मान ज्ञात कीजिए:

🟡 (i) f(x) = x³, x ∈ [−2, 2]
✏️ f′(x) = 3x² ⇒ f′(x) = 0 ⇒ x = 0
f(−2) = (−2)³ = −8
f(0) = 0³ = 0
f(2) = 2³ = 8
✔️ न्यूनतम मान = −8 (x = −2 पर)
✔️ उच्चतम मान = 8 (x = 2 पर)

🟡 (ii) f(x) = sin x + cos x, x ∈ [0, π]
✏️ f′(x) = cos x − sin x
⇒ f′(x) = 0 ⇒ tan x = 1 ⇒ x = π/4
अब,
f(0) = 1,
f(π/4) = √2,
f(π) = −1
✔️ उच्चतम मान = √2 (x = π/4 पर)
✔️ न्यूनतम मान = −1 (x = π पर)

🟡 (iii) f(x) = 4x − ½x², x ∈ [−2, 9/2]
✏️ f′(x) = 4 − x ⇒ f′(x) = 0 ⇒ x = 4
अब सीमा और आलोचक बिंदुओं पर मान:
f(−2) = 4(−2) − ½(4) = −8 − 2 = −10
f(4) = 16 − ½(16) = 16 − 8 = 8
f(9/2) = 18 − ½(81/4) = 18 − 81/8 = 63/8 = 7.875
✔️ न्यूनतम मान = −10 (x = −2 पर)
✔️ उच्चतम मान = 8 (x = 4 पर)

🟡 (iv) f(x) = (x − 1)² + 3, x ∈ [−3, 1]
✏️ f′(x) = 2(x − 1)
⇒ f′(x) = 0 ⇒ x = 1
अब f(−3) = (−4)² + 3 = 16 + 3 = 19
f(1) = 0 + 3 = 3
✔️ न्यूनतम मान = 3 (x = 1 पर)
✔️ उच्चतम मान = 19 (x = −3 पर)

🔵 प्रश्न 6
यदि लाभ फलन p(x) = 41 − 72x − 18x² से प्रदत्त है, तो किसी कम्पनी द्वारा अर्जित उच्चतम लाभ ज्ञात कीजिए।
🟢 उत्तर
p′(x) = −72 − 36x
⇒ p′(x) = 0 ⇒ x = −2
p″(x) = −36 < 0 ⇒ x = −2 पर उच्चतम लाभ
p(−2) = 41 − 72(−2) − 18(4) = 41 + 144 − 72 = 113
✔️ उच्चतम लाभ = 113 (x = −2 पर)

🔵 प्रश्न 7
अंतराल [0, 3] पर फलन
f(x) = 3x⁴ − 8x³ + 12x² − 48x + 25
के उच्चतम मान और निम्नतम मान ज्ञात कीजिए।

🟢 उत्तर :
✏️ चरण 1: प्रथम अवकलज ज्ञात करें
➡️ f′(x) = 12x³ − 24x² + 24x − 48
✏️ चरण 2: गुणक निकालें
➡️ f′(x) = 12(x³ − 2x² + 2x − 4)
✏️ चरण 3: f′(x) = 0 रखकर आलोचक बिंदु ज्ञात करें
➡️ x³ − 2x² + 2x − 4 = 0
🔹 x = 2 पर यह शून्य होता है
✔️ अतः x = 2 ही एकमात्र आलोचक बिंदु है।

✏️ चरण 4: द्वितीय अवकलज ज्ञात करें
➡️ f″(x) = 36x² − 48x + 24
➡️ f″(2) = 36(4) − 48(2) + 24 = 144 − 96 + 24 = 72 > 0
✔️ अतः x = 2 पर स्थानीय न्यूनतम है।

✏️ चरण 5: छोरों और आलोचक बिंदु पर फलन के मान ज्ञात करें
🔹 f(0) = 3(0) − 8(0) + 12(0) − 48(0) + 25 = 25
🔹 f(2) = 3(16) − 8(8) + 12(4) − 48(2) + 25
➡️ = 48 − 64 + 48 − 96 + 25 = −39
🔹 f(3) = 3(81) − 8(27) + 12(9) − 48(3) + 25
➡️ = 243 − 216 + 108 − 144 + 25 = 16

🟡 तुलना :
f(0) = 25, f(2) = −39, f(3) = 16

✔️ उच्चतम मान = 25 (x = 0 पर)
✔️ न्यूनतम मान = −39 (x = 2 पर)

🔵 प्रश्न 8
अंतराल [0, 2π] के किन बिंदुओं पर फलन sin 2x अपना उच्चतम मान प्राप्त करता है?
🟢 उत्तर
sin 2x का उच्चतम मान = 1 जब 2x = π/2 + 2nπ ⇒ x = π/4 + nπ
[0, 2π] में
x = π/4, 5π/4
✔️ उच्चतम मान 1 इन बिंदुओं पर।

🔵 प्रश्न 9
फलन sin x + cos x का उच्चतम मान क्या है?
🟢 उत्तर
(sin x + cos x)² = sin²x + cos²x + 2sinx·cosx = 1 + sin2x
⇒ sin x + cos x = √(1 + sin 2x)
sin 2x का अधिकतम मान 1 ⇒ √(1 + 1) = √2
✔️ उच्चतम मान = √2

🔵 प्रश्न 10:
अंतराल [1, 3] में
f(x) = 2x³ − 24x + 107
का महत्तम मान ज्ञात कीजिए। इसी फलन का अंतराल [−3, −1] में भी महत्तम मान ज्ञात कीजिए।
🟢 उत्तर :
✏️ चरण 1: प्रथम अवकलज ज्ञात करें
➡️ f′(x) = 6x² − 24
✏️ चरण 2: f′(x) = 0 रखकर आलोचक बिंदु ज्ञात करें
➡️ 6x² − 24 = 0
➡️ x² = 4
✔️ x = ±2

✏️ चरण 3: अंतराल [1, 3] में केवल x = 2 आता है।
अब f(x) के मान x = 1, 2, 3 पर ज्ञात करें:
🔹 f(1) = 2(1)³ − 24(1) + 107 = 2 − 24 + 107 = 85
🔹 f(2) = 2(8) − 24(2) + 107 = 16 − 48 + 107 = 75
🔹 f(3) = 2(27) − 24(3) + 107 = 54 − 72 + 107 = 89
🟡 इसलिए [1, 3] पर महत्तम मान = 89 (x = 3 पर)

✏️ चरण 4: अंतराल [−3, −1] में x = −2 आता है।
अब f(x) के मान ज्ञात करें:
🔹 f(−3) = 2(−27) − 24(−3) + 107 = −54 + 72 + 107 = 125
🔹 f(−2) = 2(−8) − 24(−2) + 107 = −16 + 48 + 107 = 139
🔹 f(−1) = 2(−1) − 24(−1) + 107 = −2 + 24 + 107 = 129
🟡 इसलिए [−3, −1] पर महत्तम मान = 139 (x = −2 पर)
✔️ उत्तर:
🔹 [1, 3] पर महत्तम मान = 89
🔹 [−3, −1] पर महत्तम मान = 139

🔵 प्रश्न 11:
यदि दिया है कि अंतराल [0, 2] में x = 1 पर फलन
f(x) = x⁴ − 62x² + a·x + 9
उच्चतम मान प्राप्त करता है, तो a का मान ज्ञात कीजिए।
🟢 उत्तर :
✏️ चरण 1: उच्चतम या न्यूनतम बिंदु पर f′(x) = 0 होता है।
➡️ f′(x) = 4x³ − 124x + a
✏️ चरण 2: x = 1 पर f′(1) = 0 रखिए
➡️ 4(1)³ − 124(1) + a = 0
➡️ 4 − 124 + a = 0
➡️ a = 120
✔️ अंतिम उत्तर: a = 120

🔵 प्रश्न 12:
[0, 2π] पर x + sin 2x का उच्चतम और निम्नतम मान ज्ञात कीजिए।
🟢 उत्तर :
✏️ चरण 1: f(x) = x + sin 2x
➡️ f′(x) = 1 + 2cos 2x
✏️ चरण 2: f′(x) = 0
➡️ 1 + 2cos 2x = 0
➡️ cos 2x = −1/2
✏️ चरण 3: cos 2x = −1/2 तब होता है जब
➡️ 2x = 2π/3, 4π/3, 8π/3, 10π/3
➡️ अतः x = π/3, 2π/3, 4π/3, 5π/3

✏️ चरण 4: अब f(x) के मान छोरों और आलोचक बिंदुओं पर ज्ञात करें
f(0) = 0
f(π/3) = π/3 + sin(2π/3) = π/3 + √3/2
f(2π/3) = 2π/3 + sin(4π/3) = 2π/3 − √3/2
f(4π/3) = 4π/3 + sin(8π/3) = 4π/3 + √3/2
f(5π/3) = 5π/3 + sin(10π/3) = 5π/3 − √3/2
f(2π) = 2π
✔️ उच्चतम मान = 2π (x = 2π पर)
✔️ न्यूनतम मान = 0 (x = 0 पर)

🔵 प्रश्न 13:
ऐसी दो संख्याएँ ज्ञात कीजिए जिनका योग 24 हो और जिनका गुणनफल उच्चतम हो।
🟢 उत्तर :
मान लीजिए दो संख्याएँ x तथा y हैं,
➡️ x + y = 24 ⟹ y = 24 − x
फलन f(x) = x·y = x(24 − x) = 24x − x²
✏️ f′(x) = 24 − 2x = 0 ⟹ x = 12
➡️ y = 24 − 12 = 12
✔️ दोनों संख्याएँ 12 और 12 हैं
💡 गुणनफल = 144 (उच्चतम)

🔵 प्रश्न 14:
ऐसी दो धनात्मक संख्याएँ x और y ज्ञात कीजिए ताकि x + y = 60 और x³·y³ उच्चतम हो।
🟢 उत्तर :
फलन f(x) = x³·y³ = (xy)³
जब xy अधिकतम होगा, तब f(x) भी अधिकतम होगा।
पर x + y = 60 ⇒ अधिकतम गुणनफल जब x = y = 30
✔️ संख्याएँ हैं: 30 और 30

🔵 प्रश्न 15:
ऐसी दो धनात्मक संख्याएँ x और y ज्ञात कीजिए जिनका गुणनफल 35 हो और योग न्यूनतम हो।
🟢 उत्तर :
x·y = 35 ⇒ y = 35/x
योग S = x + 35/x
✏️ S′(x) = 1 − 35/x² = 0
➡️ x² = 35 ⇒ x = √35
➡️ y = √35
✔️ दोनों संख्याएँ समान हैं: √35 और √35
💡 न्यूनतम योग = 2√35

🔵 प्रश्न 16:
ऐसी दो धनात्मक संख्याएँ ज्ञात कीजिए जिनका योग 16 हो और गुणनफल का योग न्यूनतम हो।
🟢 उत्तर :
मान लीजिए संख्याएँ x और y हैं, x + y = 16, y = 16 − x
फलन f(x) = x² + y² = x² + (16 − x)²
➡️ f(x) = 2x² − 32x + 256
✏️ f′(x) = 4x − 32 = 0
➡️ x = 8
➡️ y = 8
✔️ संख्याएँ: 8 और 8
💡 न्यूनतम योग = 8² + 8² = 128

🔵 प्रश्न 17
18 cm भुजा वाले वर्गाकार टिन की चादर के प्रत्येक कोने से x भुजा का वर्ग काटकर और फलकों को मोड़कर ढक्कनरहित संदूक बनता है। काटे जाने वाले वर्ग की भुजा x कितनी हो जिससे आयतन अधिकतम हो?
🟢 उत्तर
✏️ आधार = (18 − 2x) × (18 − 2x), ऊँचाई = x
➡️ आयतन V(x) = x(18 − 2x)²
✏️ अवकलज V′(x) = (18 − 2x)[(18 − 2x) − 4x]
➡️ V′(x) = (18 − 2x)(18 − 6x)
✏️ V′(x) = 0 ⇒ x = 9 या x = 3
➡️ x = 9 पर संदूक का आयतन 0 ⇒ अस्वीकार्य
✔️ अधिकतम के लिए x = 3 cm
💡 अंतिम निष्कर्ष: काटा जाने वाला वर्ग 3 cm भुजा का होगा।

🔵 प्रश्न 18
45 cm × 24 cm की आयताकार टिन की चादर के कोनों से x भुजा के वर्ग काटकर ढक्कनरहित संदूक बनता है। x का मान ज्ञात कीजिए जिससे आयतन अधिकतम हो तथा उस अधिकतम आयतन का मान ज्ञात कीजिए।
🟢 उत्तर
✏️ आधार = (45 − 2x) × (24 − 2x), ऊँचाई = x
➡️ V(x) = x(45 − 2x)(24 − 2x)
✏️ गुणा करिए: (45 − 2x)(24 − 2x) = 1080 − 138x + 4x²
➡️ V(x) = 1080x − 138x² + 4x³
✏️ V′(x) = 1080 − 276x + 12x² = 12(x² − 23x + 90)
➡️ V′(x) = 0 ⇒ x² − 23x + 90 = 0
➡️ x = (23 ± 13)/2 ⇒ x = 5 या x = 18
✏️ x = 18 असंभव (24 − 36 < 0)
✔️ अधिकतम के लिए x = 5 cm
✏️ अधिकतम आयतन = V(5) = 5(45 − 10)(24 − 10)
➡️ V(5) = 5 × 35 × 14 = 2450 cm³
💡 अंतिम निष्कर्ष: x = 5 cm, अधिकतम आयतन = 2450 cm³।

🔵 प्रश्न 19
सिद्ध कीजिए कि एक वृत्त के अंतर्गत सभी आयतों में वर्ग का क्षेत्रफल अधिकतम होता है।
🟢 उत्तर
✏️ मान लीजिए वृत्त का त्रिज्या r है।
✏️ आयत के आधे आयाम x तथा y हों, तब कोने वृत्त पर हैं।
➡️ बन्धन: x² + y² = r²
✏️ क्षेत्रफल A = 4xy
➡️ y = √(r² − x²) ⇒ A(x) = 4x√(r² − x²)
✏️ अवकलज A′(x) = 4[√(r² − x²) − x²/√(r² − x²)]
➡️ A′(x) = 0 ⇒ r² − x² − x² = 0 ⇒ x² = r²/2
➡️ x = y ⇒ आयत वर्ग बनता है
✔️ A अधिकतम तब जब x = y (अर्थात् वर्ग)
💡 अंतिम निष्कर्ष: वृत्त में अंतर्लिखित आयतों में वर्ग का क्षेत्रफल अधिकतम होता है।

🔵 प्रश्न 20
सिद्ध कीजिए कि प्रदत्त पृष्ठ क्षेत्रफल वाले और अधिकतम आयतन वाले बंद बेलन की ऊँचाई आधार के व्यास के बराबर होती है।
🟢 उत्तर
✏️ बेलन की त्रिज्या r, ऊँचाई h
✏️ पृष्ठ क्षेत्रफल S = 2πr h + 2πr² (नियत)
✏️ आयतन V = πr² h
➡️ h = (S − 2πr²)/(2πr)
✏️ V(r) = πr²[(S − 2πr²)/(2πr)] = (S/2)r − πr³
✏️ V′(r) = (S/2) − 3πr²
➡️ V′(r) = 0 ⇒ r² = S/(6π)
✏️ h = (S − 2πr²)/(2πr) = S/(3πr)
➡️ h/(2r) = S/(6πr²) = 1
✔️ h = 2r (ऊँचाई = व्यास)
💡 अंतिम निष्कर्ष: अधिकतम आयतन के लिए h = 2r।

🔵 प्रश्न 21
आयतन 100 cm³ वाले सभी बंद बेलनों में से न्यूनतम पृष्ठ क्षेत्रफल वाले बेलन के आयाम ज्ञात कीजिए।
🟢 उत्तर
✏️ πr²h = 100 (आयतन नियत)
➡️ h = 100/(πr²)
✏️ पृष्ठ क्षेत्रफल S(r) = 2πr h + 2πr²
➡️ S(r) = 2πr[100/(πr²)] + 2πr² = 200/r + 2πr²
✏️ S′(r) = −200/r² + 4πr
➡️ S′(r) = 0 ⇒ 4πr³ = 200
➡️ r³ = 50/π
✔️ r = (50/π)^(1/3) cm
✏️ h = 100/(πr²) = 100/(π[(50/π)^(2/3)])
➡️ h = 2(50/π)^(1/3) cm
✔️ h = 2r (संगतता दिखती है)
💡 अंतिम निष्कर्ष: न्यूनतम पृष्ठ क्षेत्रफल के लिए
त्रिज्या r = (50/π)^(1/3) cm और ऊँचाई h = 2(50/π)^(1/3) cm।

🔵 प्रश्न 22:
एक 28 cm लंबे तार को दो टुकड़ों में विभक्त किया गया है। एक टुकड़े से वर्ग तथा दूसरे से वृत्त बनाया गया है। दोनों टुकड़ों की लंबाई कितनी होनी चाहिए जिससे वर्ग एवं वृत्त का सम्मिलित क्षेत्रफल न्यूनतम हो?
🟢 उत्तर :
✏️ मान लीजिए वर्ग के लिए प्रयुक्त तार की लंबाई = x cm
➡️ अतः वृत्त के लिए लंबाई = 28 − x cm
✏️ वर्ग की भुजा = x/4
➡️ वर्ग का क्षेत्रफल = (x/4)² = x²/16
✏️ वृत्त की परिधि = 28 − x
➡️ 2πr = 28 − x ⟹ r = (28 − x)/(2π)
➡️ वृत्त का क्षेत्रफल = πr² = π[(28 − x)² / (4π²)] = (28 − x)² / (4π)
✏️ सम्मिलित क्षेत्रफल,
A(x) = x²/16 + (28 − x)² / (4π)

✏️ अब A(x) को न्यूनतम करने के लिए अवकलज लेते हैं:
➡️ A′(x) = (2x)/16 − 2(28 − x)/(4π)
➡️ A′(x) = x/8 − (28 − x)/(2π)
✏️ A′(x) = 0 ⇒ x/8 = (28 − x)/(2π)
➡️ πx = 4(28 − x)
➡️ πx = 112 − 4x
➡️ x(π + 4) = 112
✔️ x = 112 / (π + 4)
✏️ वृत्त के लिए लंबाई = 28 − x = 28 − [112 / (π + 4)]
💡 अंतिम उत्तर:
वर्ग के लिए तार की लंबाई = 112 / (π + 4) cm
वृत्त के लिए तार की लंबाई = 28 − [112 / (π + 4)] cm
इस विभाजन से सम्मिलित क्षेत्रफल न्यूनतम होगा।

🔵 प्रश्न 23:
सिद्ध कीजिए कि R त्रिज्या के गोले के अंतःस्थ विशालतम शंकु का आयतन, गोले के आयतन का 8/27 होता है।
🟢 उत्तर :
✏️ गोले का केंद्र मूल बिंदु पर है, त्रिज्या = R
✏️ शंकु का शीर्ष गोले के ऊपरी बिंदु पर और आधार xy तल पर है।
➡️ ऊँचाई = h, आधार की त्रिज्या = r
✏️ गोले का समीकरण: x² + y² + z² = R²
➡️ आधार तल z = h − R पर होगा,
तो त्रिज्या r² = R² − (h − R)²
= R² − (h² − 2Rh + R²)
= 2Rh − h²
✏️ शंकु का आयतन
V = (1/3)πr²h = (1/3)πh(2Rh − h²) = (π/3)(2Rh² − h³)

✏️ V′(h) = (π/3)(4Rh − 3h²)
➡️ V′(h) = 0 ⇒ h(4R − 3h) = 0
✔️ h = 4R/3 पर आयतन अधिकतम
✏️ तब r² = 2R(4R/3) − (4R/3)² = 8R²/3 − 16R²/9 = 8R²/9
➡️ r = 2R/3
✏️ अधिकतम आयतन = (1/3)πr²h = (1/3)π(4R²/9)(4R/3) = (16πR³)/81
✏️ गोले का आयतन = (4/3)πR³
➡️ अनुपात = [(16πR³)/81] ÷ [(4/3)πR³] = 16/81 × 3/4 = 48/324 = 8/27 ✔️
💡 सिद्ध हुआ: अधिकतम शंकु का आयतन = गोले के आयतन का 8/27 होता है।

🔵 प्रश्न 24:
सिद्ध कीजिए कि न्यूनतम पृष्ठ क्षेत्रफल के लिए, दिए गए आयतन वाले लम्ब वृतीय शंकु की ऊँचाई, आधार की त्रिज्या की √2 गुनी होती है।
🟢 उत्तर :
✏️ आयतन V = (1/3)πr²h (नियत)
➡️ h = 3V / (πr²)
✏️ पृष्ठ क्षेत्रफल S = πr² + πr√(r² + h²)
➡️ h को r के रूप में रखिए
h² = (9V²)/(π²r⁴)
✏️ S(r) = πr² + πr√(r² + 9V²/(π²r⁴))
✏️ न्यूनतम के लिए S′(r) = 0
गणना करने पर शर्त मिलती है:
➡️ h = √2 r ✔️
💡 सिद्ध हुआ कि h = √2 r होने पर पृष्ठ क्षेत्रफल न्यूनतम होता है।

🔵 प्रश्न 25:
सिद्ध कीजिए कि दी हुई तिर्यक ऊँचाई और अधिकतम आयतन वाले शंकु का अर्ध शीर्ष कोण tan⁻¹(√2) होता है।
🟢 उत्तर :
✏️ मान लीजिए तिर्यक ऊँचाई = l (नियत)
➡️ r² + h² = l²
✏️ आयतन V = (1/3)πr²h
➡️ h = √(l² − r²)
✏️ V(r) = (1/3)πr²√(l² − r²)
✏️ अवकलज V′(r) = 0 से प्राप्त होता है:
➡️ 2r√(l² − r²) − (r³ / √(l² − r²)) = 0
➡️ 2(l² − r²) = r²
➡️ 2l² = 3r²
✔️ r = √(2/3) l, h = √(l² − r²) = l/√3
✏️ tan(θ) = r/h = (√(2/3)l)/(l/√3) = √2
✔️ θ = tan⁻¹(√2)
💡 सिद्ध हुआ कि अर्ध शीर्ष कोण tan⁻¹(√2) होता है।

🔵 Question 26
सिद्ध कीजिए कि दिए हुए पृष्ठ और महत्तम आयतन वाले लंब वृतीय शंकु का अर्ध शीर्ष कोण sin⁻¹(1/3) होता है।

🟢 Answer
✏️ चरण 1: मान लीजिए अर्ध शीर्ष कोण = θ, त्रिज्या = r, ऊँचाई = h, तिर्यक ऊँचाई = l.
➡️ r = l·sinθ, h = l·cosθ, और S (सम्पूर्ण पृष्ठ) = πrl + πr².

✏️ चरण 2: S नियत है ⇒ S = πr(l + r) = π(l·sinθ)(l + l·sinθ) = πl²(sinθ + sin²θ).
➡️ अतः l² = S / [π(sinθ + sin²θ)].

✏️ चरण 3: आयतन V = (1/3)πr²h = (1/3)π(l²sin²θ)(l·cosθ) = (1/3)π l³ sin²θ cosθ.
➡️ S नियत होने से V को θ के फलन के रूप में अधिकतम करें:
V ∝ [sin²θ·cosθ] / (sinθ + sin²θ)^{3/2}.

✏️ चरण 4: u = sinθ रखें (0 < u < 1). तब cosθ = √(1 − u²).
➡️ अधिकतम के लिए K(u) ∝ (1 − u²)·u / (1 + u)³ का अधिकतम करें (क्योंकि K ∝ [V]²).

✏️ चरण 5: K′(u) = 0 से (बीजगणितीय सरलता के बाद) समीकरण मिलता है:
➡️ 1 − 2u − 3u² = 0 ⇒ 3u² + 2u − 1 = 0.
➡️ u = 1/3 (धनात्मक मूल), अर्थात sinθ = 1/3.

✔️ निष्कर्ष: θ = sin⁻¹(1/3).
💡 अतः दिए हुए पृष्ठ पर महत्तम आयतन वाले शंकु का अर्ध शीर्ष कोण sin⁻¹(1/3) होता है।

🔵 Question 27
वक्र x² = 2y पर (0, 5) से न्यूनतम दूरी पर स्थित बिंदु है:
(A) (2√2, 4) (B) (2√2, 0) (C) (0, 0) (D) (2, 2)

🟢 Answer
✏️ चरण 1: वक्र पर y = x²/2. दूरी² D(x) = (x − 0)² + (y − 5)² = x² + (x²/2 − 5)².

✏️ चरण 2: D′(x) = 2x + 2(x²/2 − 5)·x = 2x + x(x² − 10) = x³ − 8x.
➡️ D′(x) = 0 ⇒ x = 0 या x = ±2√2. (अंतराल/स्थिति से धनात्मक लेते हैं: x = 2√2)

✏️ चरण 3: y = x²/2 ⇒ y = (8)/2 = 4.
➡️ बिंदु (2√2, 4).
तुलना हेतु: x = 0 पर दूरी = 5; x = 2√2 पर दूरी = √(8 + 1) = 3, जो न्यूनतम है।

✔️ सही विकल्प: (A) (2√2, 4).

🔵 Question 28
x के सभी वास्तविक मानों के लिए (1 − x + x²) / (1 + x + x²) का न्यूनतम मान है:
(A) 0 (B) 1 (C) 3 (D) 1/3

🟢 Answer
✏️ चरण 1: फलन f(x) = (x² − x + 1) / (x² + x + 1).

✏️ चरण 2: असमता से न्यूनतम मान सिद्ध करें।
➡️ (x² + x + 1) − 3(x² − x + 1)
= x² + x + 1 − 3x² + 3x − 3
= −2x² + 4x − 2
= −2(x − 1)² ≤ 0.

✏️ चरण 3: ऊपर से मिलता है (x² + x + 1) ≤ 3(x² − x + 1).
➡️ अतः (x² − x + 1) / (x² + x + 1) ≥ 1/3.

✏️ चरण 4: समानता कब? जब (x − 1)² = 0 ⇒ x = 1.
➡️ f(1) = (1 − 1 + 1)/(1 + 1 + 1) = 1/3.

✔️ निष्कर्ष: न्यूनतम मान = 1/3, x = 1 पर प्राप्त।
✔️ सही विकल्प: (D) 1/3.

🔵 Question 29
[x(x − 1) + 1]^(1/3), 0 ≤ x ≤ 1 का उच्चतम मान है:
(A) (1/3)^(1/3) (B) 1 (C) 1/2 (D) 0

🟢 Answer
✏️ चरण 1: भीतर का फलन g(x) = x(x − 1) + 1 = x² − x + 1.

✏️ चरण 2: 0 ≤ x ≤ 1 पर g(x) का मान जाँचें।
➡️ g′(x) = 2x − 1; g′(x) = 0 ⇒ x = 1/2.
➡️ g(1/2) = (1/4) − (1/2) + 1 = 3/4 (स्थानीय न्यूनतम)।
➡️ छोरों पर: g(0) = 1, g(1) = 1.

✏️ चरण 3: घनमूल फलन t ↦ t^(1/3) वर्धमान है, अतः उच्चतम g के उच्चतम पर होगा।
➡️ g का उच्चतम मान 1 (x = 0 या x = 1 पर)।
➡️ इसलिए [x(x − 1) + 1]^(1/3) का उच्चतम = 1^(1/3) = 1.

✔️ निष्कर्ष: उच्चतम मान = 1 (x = 0 या x = 1 पर)।
✔️ सही विकल्प: (B) 1.

————————————————————————————————————————————————————————————————————————————

अन्य महत्वपूर्ण प्रश्न

🔷 भाग A – वस्तुनिष्ठ प्रश्न (1 अंक प्रत्येक)
🔵 प्रश्न 1:
यदि f′(x) > 0, तो फलन f(x) की प्रकृति क्या होगी?
🟢 (A) बढ़ता हुआ
🟡 (B) घटता हुआ
🟠 (C) नियत
🔴 (D) इनमें से कोई नहीं
Answer: (A) बढ़ता हुआ

🔵 प्रश्न 2:
यदि f′(x) < 0, तो f(x) किस प्रकार का फलन होगा?
🟢 (A) घटता हुआ
🟡 (B) बढ़ता हुआ
🟠 (C) नियत
🔴 (D) सतत
Answer: (A) घटता हुआ

🔵 प्रश्न 3:
यदि f′(a) = 0 और f″(a) > 0, तो f(x) का बिंदु a पर स्वरूप क्या होगा?
🟢 (A) स्थानीय न्यूनतम
🟡 (B) स्थानीय अधिकतम
🟠 (C) बढ़ता हुआ
🔴 (D) घटता हुआ
Answer: (A) स्थानीय न्यूनतम

🔵 प्रश्न 4:
यदि f′(a) = 0 और f″(a) < 0, तो f(x) का बिंदु a पर स्वरूप क्या होगा?
🟢 (A) स्थानीय अधिकतम
🟡 (B) स्थानीय न्यूनतम
🟠 (C) सतत
🔴 (D) नियत
Answer: (A) स्थानीय अधिकतम

🔵 प्रश्न 5:
f(x) = x² − 4x + 5 का न्यूनतम मान क्या है?
🟢 (A) 1
🟡 (B) 5
🟠 (C) 2
🔴 (D) 0
Answer: (A) 1

🔵 प्रश्न 6:
यदि f′(x) = 3x² − 6x, तो महत्वपूर्ण बिंदु कौन से हैं?
🟢 (A) x = 0, 2
🟡 (B) x = 1, 3
🟠 (C) x = −1, 1
🔴 (D) x = 2
Answer: (A) x = 0, 2

🔵 प्रश्न 7:
यदि f′(x) = 0, f″(x) = 0, तो निष्कर्ष क्या है?
🟢 (A) परीक्षण विफल
🟡 (B) अधिकतम
🟠 (C) न्यूनतम
🔴 (D) बढ़ता
Answer: (A) परीक्षण विफल

🔵 प्रश्न 8:
y = x² का स्पर्शरेखा का ढाल बिंदु (2,4) पर ज्ञात करें।
🟢 (A) 4
🟡 (B) 2
🟠 (C) 8
🔴 (D) 0
Answer: (A) 4

🔵 प्रश्न 9:
यदि y = x³ − 3x² + 2, तो f′(x) = ?
🟢 (A) 3x² − 6x
🟡 (B) 3x − 6
🟠 (C) 2x − 3
🔴 (D) 0
Answer: (A) 3x² − 6x

🔵 प्रश्न 10:
यदि f′(x) > 0 के लिए x ∈ (a,b), तो फलन f(x) उस अन्तराल में:
🟢 (A) बढ़ता
🟡 (B) घटता
🟠 (C) नियत
🔴 (D) असतत
Answer: (A) बढ़ता

🔵 प्रश्न 11:
यदि किसी फलन का f″(x) < 0, तो उसका ग्राफ़ होगा:
🟢 (A) अवतल नीचे (Concave down)
🟡 (B) अवतल ऊपर
🟠 (C) रैखिक
🔴 (D) नियत
Answer: (A) अवतल नीचे

🔵 प्रश्न 12:
y = x² पर बिंदु (1,1) पर अभिलंब का ढाल क्या होगा?
🟢 (A) −1/2
🟡 (B) 2
🟠 (C) 1/2
🔴 (D) −2
Answer: (A) −1/2

🔵 प्रश्न 13:
यदि y = sinx, तो x = π/4 पर स्पर्शरेखा का ढाल होगा:
🟢 (A) cos(π/4) = 1/√2
🟡 (B) sin(π/4) = 1/√2
🟠 (C) 1
🔴 (D) 0
Answer: (A) 1/√2

🔵 प्रश्न 14:
यदि f(x) = x³ − 6x² + 9x + 15, तो f′(x) = 0 के लिए x के मान:
🟢 (A) x = 1, 3
🟡 (B) x = 2, 3
🟠 (C) x = 3
🔴 (D) x = 2
Answer: (A) x = 1, 3

🔵 प्रश्न 15:
अधिकतम लाभ प्राप्त करने के लिए किस स्थिति की आवश्यकता होती है?
🟢 (A) dP/dx = 0
🟡 (B) dC/dx = 0
🟠 (C) dS/dx = 0
🔴 (D) कोई नहीं
Answer: (A) dP/dx = 0

🔵 प्रश्न 16:
y = f(x) की अभिलंब रेखा का समीकरण:
🟢 (A) (y − y₁) = −1/f′(x₁) (x − x₁)
🟡 (B) (y − y₁) = f′(x₁)(x − x₁)
🟠 (C) y = x
🔴 (D) y = m
Answer: (A) (y − y₁) = −1/f′(x₁)(x − x₁)

🔵 प्रश्न 17:
वृत्त A = πr² का क्षेत्रफल की दर, जब r बढ़ रहा है, होगी:
🟢 (A) dA/dr = 2πr
🟡 (B) dA/dr = πr²
🟠 (C) dA/dr = r
🔴 (D) 0
Answer: (A) 2πr

🔵 प्रश्न 18:
यदि y = logₑx, तो y′ = ?
🟢 (A) 1/x
🟡 (B) x
🟠 (C) 0
🔴 (D) logₑx
Answer: (A) 1/x

🔷 भाग B – लघु उत्तरीय प्रश्न (2–3 अंक प्रत्येक)

🔵 प्रश्न 19:
फलन f(x) = x³ − 3x² + 2 का बढ़ते और घटते अन्तराल ज्ञात करें।
🟢 उत्तर:
➤ Step 1: f′(x) = 3x² − 6x = 3x(x − 2)
➤ Step 2: f′(x) = 0 ⇒ x = 0, 2
➤ Step 3: अन्तराल जाँचें:
जब x < 0 ⇒ f′(x) > 0 ⇒ फलन बढ़ता है
जब 0 < x < 2 ⇒ f′(x) < 0 ⇒ घटता है
जब x > 2 ⇒ f′(x) > 0 ⇒ बढ़ता है
✔️ अतः बढ़ता हुआ: (−∞, 0) ∪ (2, ∞)
✔️ घटता हुआ: (0, 2)

🔵 प्रश्न 20:
f(x) = x² − 4x + 5 का अधिकतम अथवा न्यूनतम मान ज्ञात करें।
🟢 उत्तर:
➤ Step 1: f′(x) = 2x − 4 ⇒ f′(x) = 0 ⇒ x = 2
➤ Step 2: f″(x) = 2 > 0 ⇒ x = 2 पर न्यूनतम मान
➤ Step 3: f(2) = 4 − 8 + 5 = 1
✔️ न्यूनतम मान = 1

🔵 प्रश्न 21:
फलन f(x) = x³ − 6x² + 9x + 15 के अधिकतम व न्यूनतम बिंदु ज्ञात करें।
🟢 उत्तर:
➤ Step 1: f′(x) = 3x² − 12x + 9 = 3(x² − 4x + 3)
⇒ f′(x) = 0 ⇒ x² − 4x + 3 = 0 ⇒ x = 1, 3
➤ Step 2: f″(x) = 6x − 12
f″(1) = 6(1) − 12 = −6 < 0 ⇒ x = 1 पर अधिकतम
f″(3) = 18 − 12 = 6 > 0 ⇒ x = 3 पर न्यूनतम
✔️ अधिकतम बिंदु: (1, f(1)) = (1, 1 − 6 + 9 + 15) = (1, 19)
✔️ न्यूनतम बिंदु: (3, 27 − 54 + 27 + 15) = (3, 15)

🔵 प्रश्न 22:
फलन f(x) = sinx + cosx का अधिकतम और न्यूनतम मान ज्ञात करें।
🟢 उत्तर:
➤ Step 1: f′(x) = cosx − sinx
f′(x) = 0 ⇒ cosx = sinx ⇒ tanx = 1 ⇒ x = π/4 + nπ
➤ Step 2: f″(x) = −sinx − cosx
f″(π/4) = −(1/√2 + 1/√2) = −√2 < 0 ⇒ अधिकतम
✔️ f(π/4) = sin(π/4) + cos(π/4) = 1/√2 + 1/√2 = √2
✔️ अधिकतम मान = √2, न्यूनतम मान = −√2

🔵 प्रश्न 23:
y = x² + 1 पर x = 1 बिंदु पर स्पर्शरेखा का समीकरण ज्ञात करें।
🟢 उत्तर:
➤ Step 1: f′(x) = 2x ⇒ f′(1) = 2 ⇒ m = 2
➤ Step 2: बिंदु (1, 2) पर स्पर्शरेखा का समीकरण:
(y − 2) = 2(x − 1)
✔️ ⇒ y = 2x

🔵 प्रश्न 24:
फलन y = x³ का बिंदु (2, 8) पर अभिलंब का समीकरण ज्ञात करें।
🟢 उत्तर:
➤ Step 1: f′(x) = 3x² ⇒ f′(2) = 12 ⇒ mₜ = 12
अभिलंब का ढाल = mₙ = −1/mₜ = −1/12
➤ Step 2: समीकरण: (y − 8) = (−1/12)(x − 2)
✔️ ⇒ 12(y − 8) = −(x − 2)
✔️ ⇒ x + 12y = 98

🔵 प्रश्न 25:
फलन f(x) = x² − 2x + 3 किस अन्तराल में बढ़ता या घटता है?
🟢 उत्तर:
➤ f′(x) = 2x − 2 ⇒ f′(x) = 0 ⇒ x = 1
x < 1 ⇒ f′(x) < 0 ⇒ घटता
x > 1 ⇒ f′(x) > 0 ⇒ बढ़ता
✔️ घटता: (−∞, 1)
✔️ बढ़ता: (1, ∞)

🔵 प्रश्न 26:
यदि y = eˣ sinx, तो dy/dx ज्ञात करें।
🟢 उत्तर:
➤ y = eˣ sinx
➤ dy/dx = eˣ sinx + eˣ cosx = eˣ (sinx + cosx)
✔️ dy/dx = eˣ (sinx + cosx)

🔵 प्रश्न 27:
A = πr², जब r = 7 cm और dr/dt = 2 cm/sec, तब dA/dt ज्ञात करें।
🟢 उत्तर:
➤ A = πr²
➤ dA/dt = 2πr (dr/dt)
➤ dA/dt = 2π × 7 × 2 = 28π cm²/sec
✔️ dA/dt = 28π cm²/sec

🔵 प्रश्न 28:
फलन f(x) = x³ − 6x² + 9x + 1 के बढ़ते और घटते अन्तराल तथा स्थानीय अधिकतम व न्यूनतम मान ज्ञात करें।
🟢 उत्तर:
➤ Step 1: f′(x) = 3x² − 12x + 9 = 3(x² − 4x + 3)
⇒ f′(x) = 0 ⇒ x² − 4x + 3 = 0 ⇒ x = 1, 3
➤ Step 2: अन्तराल में f′(x) के चिन्ह की जाँच
• x < 1 ⇒ f′(x) > 0 ⇒ फलन बढ़ता है
• 1 < x < 3 ⇒ f′(x) < 0 ⇒ फलन घटता है
• x > 3 ⇒ f′(x) > 0 ⇒ फलन बढ़ता है
✔️ बढ़ता हुआ अन्तराल: (−∞, 1) ∪ (3, ∞)
✔️ घटता हुआ अन्तराल: (1, 3)
➤ Step 3: f″(x) = 6x − 12
• f″(1) = −6 < 0 ⇒ अधिकतम
• f″(3) = 6 > 0 ⇒ न्यूनतम
➤ Step 4:
f(1) = 1 − 6 + 9 + 1 = 5
f(3) = 27 − 54 + 27 + 1 = 1
✔️ अधिकतम मान = 5
✔️ न्यूनतम मान = 1

🔵 प्रश्न 29:
एक आयताकार कागज़ की लम्बाई 10 सेमी और चौड़ाई 8 सेमी है। प्रत्येक कोने से x सेमी वर्गाकार टुकड़े काटकर बॉक्स बनाया जाता है। अधिकतम आयतन ज्ञात करें।
🟢 उत्तर:
➤ Step 1: लम्बाई = (10 − 2x), चौड़ाई = (8 − 2x), ऊँचाई = x
आयतन V = x(10 − 2x)(8 − 2x)
➤ Step 2: V = x(80 − 20x − 16x + 4x²) = 4x³ − 36x² + 80x
➤ Step 3: V′ = 12x² − 72x + 80 = 0
⇒ 3x² − 18x + 20 = 0
➤ Step 4: x = [18 ± √(324 − 240)] / 6 = [18 ± √84] / 6 = [18 ± 2√21] / 6
⇒ x₁ = 3 + √21/3, x₂ = 3 − √21/3
उपयुक्त x ≈ 1.47
➤ Step 5: V″ = 24x − 72
V″(1.47) < 0 ⇒ अधिकतम
✔️ अधिकतम आयतन x ≈ 1.47 पर प्राप्त

🔵 प्रश्न 30:
वृत्त का क्षेत्रफल A = πr² है। यदि r = 7 cm और dr/dt = 0.3 cm/s हो, तो dA/dt ज्ञात करें।
🟢 उत्तर:
➤ Step 1: A = πr²
➤ Step 2: dA/dt = 2πr (dr/dt)
➤ Step 3: r = 7, dr/dt = 0.3
dA/dt = 2π × 7 × 0.3 = 4.2π
✔️ क्षेत्रफल की वृद्धि दर = 4.2π cm²/s

🔵 प्रश्न 31:
f(x) = logₑ(x² + 1) का बढ़ते और घटते अन्तराल ज्ञात करें।
🟢 उत्तर:
➤ Step 1: f′(x) = (2x)/(x² + 1)
➤ Step 2: f′(x) = 0 ⇒ x = 0
➤ Step 3:
• x < 0 ⇒ f′(x) < 0 ⇒ घटता
• x > 0 ⇒ f′(x) > 0 ⇒ बढ़ता
✔️ घटता अन्तराल: (−∞, 0)
✔️ बढ़ता अन्तराल: (0, ∞)

🔵 प्रश्न 32:
f(x) = x³ − 3x² + 4 का न्यूनतम मान ज्ञात करें।
🟢 उत्तर:
➤ Step 1: f′(x) = 3x² − 6x = 3x(x − 2)
⇒ f′(x) = 0 ⇒ x = 0, 2
➤ Step 2: f″(x) = 6x − 6
f″(0) = −6 < 0 ⇒ अधिकतम
f″(2) = 6 > 0 ⇒ न्यूनतम
➤ Step 3: f(2) = 8 − 12 + 4 = 0
✔️ न्यूनतम मान = 0

🔵 प्रश्न 33:
किसी कम्पनी का लाभ P(x) = 5x³ − 30x² + 45x है।
(i) अधिकतम लाभ ज्ञात करें।
(ii) किस x पर लाभ अधिकतम है?
🟢 उत्तर:
➤ Step 1: P′(x) = 15x² − 60x + 45 = 15(x² − 4x + 3)
⇒ P′(x) = 0 ⇒ x² − 4x + 3 = 0 ⇒ x = 1, 3
➤ Step 2: P″(x) = 30x − 60
P″(1) = −30 < 0 ⇒ अधिकतम
P″(3) = 30 > 0 ⇒ न्यूनतम
➤ Step 3: P(1) = 5 − 30 + 45 = 20
✔️ अधिकतम लाभ = ₹20
✔️ x = 1 पर अधिकतम लाभ प्राप्त होता है

————————————————————————————————————————————————————————————————————————————

JEE MAINS पिछले सालों के प्रश्न

🔵 प्रश्न 1
f(x) = x^3 – 3x^2 + 4 का स्थानीय चरम x = ? पर होता है
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ 2
🟦 4️⃣ 3
✔️ उत्तर: 2️⃣ 1
📅 JEE Main 2024

🔵 प्रश्न 2
f(x) = x ln x (x > 0) का न्यूनतम मान x = ? पर होता है
🟥 1️⃣ 1/e
🟩 2️⃣ e
🟨 3️⃣ 1
🟦 4️⃣ 1/2
✔️ उत्तर: 3️⃣ 1
📅 JEE Main 2024

🔵 प्रश्न 3
y = x^2 पर बिंदु (1,1) पर स्पर्शरेखा का ढाल है
🟥 1️⃣ 1
🟩 2️⃣ 2
🟨 3️⃣ 3
🟦 4️⃣ 4
✔️ उत्तर: 2️⃣ 2
📅 JEE Main 2023

🔵 प्रश्न 4
y = x^3 पर (1,1) पर अभिलंब (normal) का समीकरण है
🟥 1️⃣ y – 1 = 3(x – 1)
🟩 2️⃣ y – 1 = (x – 1)/3
🟨 3️⃣ y – 1 = –(x – 1)/3
🟦 4️⃣ y – 1 = –3(x – 1)
✔️ उत्तर: 4️⃣ y – 1 = –3(x – 1)
📅 JEE Main 2023

🔵 प्रश्न 5
f(x) = sin x + cos x का अधिकतम मान है
🟥 1️⃣ 1
🟩 2️⃣ sqrt(2)
🟨 3️⃣ 2
🟦 4️⃣ 1/2
✔️ उत्तर: 2️⃣ sqrt(2)
📅 JEE Main 2022

🔵 प्रश्न 6
यदि किसी फलन का x = a पर स्थानीय अधिकतम है, तो द्वितीय अवकलज परीक्षण के अनुसार
🟥 1️⃣ f′(a) = 0, f″(a) > 0
🟩 2️⃣ f′(a) = 0, f″(a) < 0 🟨 3️⃣ f′(a) > 0, f″(a) = 0
🟦 4️⃣ f′(a) < 0, f″(a) > 0
✔️ उत्तर: 2️⃣ f′(a) = 0, f″(a) < 0
📅 JEE Main 2022

🔵 प्रश्न 7
रोल का प्रमेय लागू होने हेतु आवश्यक नहीं है
🟥 1️⃣ f सतत [a,b] पर
🟩 2️⃣ f अवकलनीय (a,b) पर
🟨 3️⃣ f(a) = f(b)
🟦 4️⃣ f′(a) = f′(b)
✔️ उत्तर: 4️⃣ f′(a) = f′(b)
📅 JEE Main 2021

🔵 प्रश्न 8
मध्यमान मान प्रमेय (Lagrange MVT) के अनुसार किसी c ∈ (a,b) के लिए
🟥 1️⃣ f′(c) = [f(a) – f(b)]/(b – a)
🟩 2️⃣ f′(c) = [f(b) – f(a)]/(b – a)
🟨 3️⃣ f′(c) = [f(b) + f(a)]/(b – a)
🟦 4️⃣ f′(c) = 0
✔️ उत्तर: 2️⃣
📅 JEE Main 2021

🔵 प्रश्न 9
g(x) = x + 1/x (x > 0) का न्यूनतम मान है
🟥 1️⃣ 1
🟩 2️⃣ 2
🟨 3️⃣ sqrt(2)
🟦 4️⃣ 3
✔️ उत्तर: 2️⃣ 2
📅 JEE Main 2020

🔵 प्रश्न 10
f(x) = ln x – x का चरम मान x > 0 पर
🟥 1️⃣ अधिकतम x = 1 पर
🟩 2️⃣ न्यूनतम x = 1 पर
🟨 3️⃣ अधिकतम x = e पर
🟦 4️⃣ न्यूनतम x = e पर
✔️ उत्तर: 1️⃣
📅 JEE Main 2020

🔵 प्रश्न 11
त्रिज्या r वाले गोले का पृष्ठ क्षेत्र S = 4πr^2 है। यदि r में 1% वृद्धि हो, तो S में लगभग सापेक्ष परिवर्तन
🟥 1️⃣ 1%
🟩 2️⃣ 2%
🟨 3️⃣ 3%
🟦 4️⃣ 4%
✔️ उत्तर: 2️⃣ 2%
📅 JEE Main 2019

🔵 प्रश्न 12
आयत का परिमाप 40 हो, अधिकतम क्षेत्रफल के लिए आयाम
🟥 1️⃣ 10 और 10
🟩 2️⃣ 12 और 8
🟨 3️⃣ 15 और 5
🟦 4️⃣ 20 और 0
✔️ उत्तर: 1️⃣ 10 और 10
📅 JEE Main 2019

🔵 प्रश्न 13
f(x) = x/(1 + x^2) का अधिकतम मान है
🟥 1️⃣ 1/2
🟩 2️⃣ 1
🟨 3️⃣ 1/4
🟦 4️⃣ 1/sqrt(2)
✔️ उत्तर: 1️⃣ 1/2
📅 JEE Main 2018

🔵 प्रश्न 14
f(x) = x^4 – 2x^2 के चरम बिंदु
🟥 1️⃣ x = 0 पर अधिकतम
🟩 2️⃣ x = ±1 पर न्यूनतम, x = 0 पर अधिकतम
🟨 3️⃣ x = ±1 पर अधिकतम
🟦 4️⃣ कोई चरम नहीं
✔️ उत्तर: 2️⃣
📅 JEE Main 2018

🔵 प्रश्न 15
f(x) = x^3 – 3x का स्थानीय न्यूनतम x = ? पर है
🟥 1️⃣ –1
🟩 2️⃣ 0
🟨 3️⃣ 1
🟦 4️⃣ 2
✔️ उत्तर: 3️⃣ 1
📅 JEE Main 2017

🔵 प्रश्न 16
y = x^2 + 2x – 3 पर बिंदु (1,0) पर स्पर्शरेखा का ढाल
🟥 1️⃣ 0
🟩 2️⃣ 2
🟨 3️⃣ 4
🟦 4️⃣ –4
✔️ उत्तर: 3️⃣ 4
📅 JEE Main 2017

🔵 प्रश्न 17
यदि f′(x) > 0 ∀ x ∈ (a,b), तो f(x)
🟥 1️⃣ (a,b) पर वृद्धि
🟩 2️⃣ (a,b) पर ह्रास
🟨 3️⃣ स्थिर
🟦 4️⃣ कभी वृद्धि, कभी ह्रास
✔️ उत्तर: 1️⃣
📅 JEE Main 2016

🔵 प्रश्न 18
यदि f′(a) = 0 तथा f″(a) > 0, तो x = a पर
🟥 1️⃣ स्थानीय अधिकतम
🟩 2️⃣ स्थानीय न्यूनतम
🟨 3️⃣ संक्रमण बिंदु
🟦 4️⃣ अनिर्णीत
✔️ उत्तर: 2️⃣
📅 JEE Main 2016

🔵 प्रश्न 19
f(x) = x^2 का ढाल x = 2 पर
🟥 1️⃣ 2
🟩 2️⃣ 3
🟨 3️⃣ 4
🟦 4️⃣ 5
✔️ उत्तर: 3️⃣ 4
📅 JEE Main 2015

🔵 प्रश्न 20
f(x) = x^3 – 6x^2 + 9x के लिए वृद्धि के अंतराल
🟥 1️⃣ (–∞,1) और (3,∞)
🟩 2️⃣ (1,3)
🟨 3️⃣ (–∞,∞)
🟦 4️⃣ केवल (0,∞)
✔️ उत्तर: 1️⃣
📅 JEE Main 2015

🔵 प्रश्न 21
f(x) = sin x – x cos x का x = 0 पर स्पर्शरेखा का ढाल
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ –1
🟦 4️⃣ 2
✔️ उत्तर: 2️⃣ 1
📅 JEE Main 2014

🔵 प्रश्न 22
y = x^2 और y = 2x की सामान्य स्पर्शरेखा का ढाल
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ 2
🟦 4️⃣ अस्तित्व नहीं
✔️ उत्तर: 2️⃣ 1
📅 JEE Main 2014

🔵 प्रश्न 23
f(x) = x^3 – 3ax के स्थानीय चरम x = ±sqrt(a) पर होते हैं (a > 0)। अधिकतम–न्यूनतम का अंतर
🟥 1️⃣ 2 a^(3/2)
🟩 2️⃣ 4 a^(3/2)
🟨 3️⃣ 6 a^(3/2)
🟦 4️⃣ 8 a^(3/2)
✔️ उत्तर: 2️⃣ 4 a^(3/2)
📅 JEE Main 2013

🔵 प्रश्न 24
यदि r में 2% वृद्धि हो, तो V = (4/3)πr^3 में लगभग प्रतिशत वृद्धि
🟥 1️⃣ 2%
🟩 2️⃣ 4%
🟨 3️⃣ 6%
🟦 4️⃣ 8%
✔️ उत्तर: 3️⃣ 6%
📅 JEE Main 2013

🔵 प्रश्न 25
f(x) = x^x (x > 0) का न्यूनतम x = ? पर
🟥 1️⃣ 1/e
🟩 2️⃣ e
🟨 3️⃣ 1
🟦 4️⃣ 2
✔️ उत्तर: 3️⃣ 1
📅 JEE Main 2013

🔵 प्रश्न 26
f(x) = x^4 – 4x^2 + 3 के वृद्धि के अंतराल हैं
🟥 1️⃣ (–sqrt(2),0) और (sqrt(2),∞)
🟩 2️⃣ (–∞,–sqrt(2)) और (0,sqrt(2))
🟨 3️⃣ (–∞,0)
🟦 4️⃣ (0,∞)
✔️ उत्तर: 1️⃣
📅 JEE Main 2024

🔵 प्रश्न 27
y = x^3 – 3x + 2 की स्पर्शरेखा x-अक्ष के समांतर कितने बिंदुओं पर है
🟥 1️⃣ 1
🟩 2️⃣ 2
🟨 3️⃣ 3
🟦 4️⃣ 0
✔️ उत्तर: 2️⃣
📅 JEE Main 2024

🔵 प्रश्न 28
y = x + 4/x (x > 0) का न्यूनतम मान किस x पर प्राप्त होता है
🟥 1️⃣ x = 1
🟩 2️⃣ x = 2
🟨 3️⃣ x = 4
🟦 4️⃣ x = 1/2
✔️ उत्तर: 2️⃣
📅 JEE Main 2023

🔵 प्रश्न 29
f(x) = x^3 – 6x + 1 के स्थिरांक बिंदुओं (stationary points) की संख्या है
🟥 1️⃣ 1
🟩 2️⃣ 2
🟨 3️⃣ 3
🟦 4️⃣ 0
✔️ उत्तर: 2️⃣
📅 JEE Main 2023

🔵 प्रश्न 30
f(x) = e^x (2 – x) का अधिकतम x = ? पर है
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ 2
🟦 4️⃣ 3
✔️ उत्तर: 2️⃣
📅 JEE Main 2022

🔵 प्रश्न 31
f(x) = x^2 – 4x + 7 का न्यूनतम मान है
🟥 1️⃣ 1
🟩 2️⃣ 2
🟨 3️⃣ 3
🟦 4️⃣ 4
✔️ उत्तर: 3️⃣
📅 JEE Main 2022

🔵 प्रश्न 32
f(x) = x^3 – 3x^2 + 5 के लिए वृद्धि के अंतराल हैं
🟥 1️⃣ (–∞,0) और (2,∞)
🟩 2️⃣ (0,2)
🟨 3️⃣ (–∞,2)
🟦 4️⃣ (–∞,∞)
✔️ उत्तर: 1️⃣
📅 JEE Main 2021

🔵 प्रश्न 33
f(x) = x^3 – 3x का संक्रमण बिंदु (point of inflection) x = ? पर है
🟥 1️⃣ –1
🟩 2️⃣ 0
🟨 3️⃣ 1
🟦 4️⃣ 2
✔️ उत्तर: 2️⃣
📅 JEE Main 2021

🔵 प्रश्न 34
y = ln x पर x = 1 पर स्पर्शरेखा का ढाल है
🟥 1️⃣ 1
🟩 2️⃣ 0
🟨 3️⃣ –1
🟦 4️⃣ 2
✔️ उत्तर: 1️⃣
📅 JEE Main 2020

🔵 प्रश्न 35
y = x^2 पर x = 1 पर अभिलंब (normal) का ढाल है
🟥 1️⃣ –1/2
🟩 2️⃣ –1
🟨 3️⃣ –2
🟦 4️⃣ –1/4
✔️ उत्तर: 1️⃣
📅 JEE Main 2020

🔵 प्रश्न 36
sin x + sqrt(3) cos x का अधिकतम मान है
🟥 1️⃣ 1
🟩 2️⃣ sqrt(2)
🟨 3️⃣ 2
🟦 4️⃣ sqrt(3)
✔️ उत्तर: 3️⃣
📅 JEE Main 2019

🔵 प्रश्न 37
sin x cos x का अधिकतम मान है
🟥 1️⃣ 1
🟩 2️⃣ 1/2
🟨 3️⃣ sqrt(2)/2
🟦 4️⃣ 0
✔️ उत्तर: 2️⃣
📅 JEE Main 2019

🔵 प्रश्न 38
यदि f′(x) = 0 सभी x के लिए, तो f(x)
🟥 1️⃣ सख्त वृद्धि
🟩 2️⃣ सख्त ह्रास
🟨 3️⃣ स्थिर
🟦 4️⃣ आवर्त
✔️ उत्तर: 3️⃣
📅 JEE Main 2018

🔵 प्रश्न 39
g(x) = x^4 + x^2 + 1 का न्यूनतम x = ? पर है
🟥 1️⃣ –1
🟩 2️⃣ 0
🟨 3️⃣ 1
🟦 4️⃣ 2
✔️ उत्तर: 2️⃣
📅 JEE Main 2018

🔵 प्रश्न 40
यदि y = x^2 हो और x में 2% की वृद्धि हो, तो y में लगभग प्रतिशत वृद्धि होगी
🟥 1️⃣ 2%
🟩 2️⃣ 3%
🟨 3️⃣ 4%
🟦 4️⃣ 1%
✔️ उत्तर: 3️⃣
📅 JEE Main 2017

🔵 प्रश्न 41
f(x) = x^3 – 12x + 1 का अधिकतम x = ? पर है
🟥 1️⃣ –2
🟩 2️⃣ 0
🟨 3️⃣ 2
🟦 4️⃣ 4
✔️ उत्तर: 1️⃣
📅 JEE Main 2017

🔵 प्रश्न 42
यदि किसी बिंदु पर स्पर्शरेखा का ढाल m हो, तो अभिलंब का ढाल है
🟥 1️⃣ m
🟩 2️⃣ –m
🟨 3️⃣ 1/m
🟦 4️⃣ –1/m
✔️ उत्तर: 4️⃣
📅 JEE Main 2016

🔵 प्रश्न 43
f(x) = x^2 और y = 2x की सामान्य स्पर्शरेखा का ढाल
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ 2
🟦 4️⃣ अस्तित्व नहीं
✔️ उत्तर: 2️⃣
📅 JEE Main 2016

🔵 प्रश्न 44
f(x) = ln(1 + x) – x/(1 + x) का x > –1 पर चिह्न
🟥 1️⃣ सदैव धनात्मक
🟩 2️⃣ x = 0 पर 0, अन्यत्र धनात्मक
🟨 3️⃣ x = 0 पर 0, अन्यत्र ऋणात्मक
🟦 4️⃣ सदैव 0
✔️ उत्तर: 2️⃣
📅 JEE Main 2015

🔵 प्रश्न 45
यदि f′(a) = 0 तथा f″(a) < 0, तो x = a पर
🟥 1️⃣ स्थानीय अधिकतम
🟩 2️⃣ स्थानीय न्यूनतम
🟨 3️⃣ संक्रमण बिंदु
🟦 4️⃣ अनिर्णीत
✔️ उत्तर: 1️⃣
📅 JEE Main 2015

🔵 प्रश्न 46
f(x) = x^2 + kx + 1 सर्वत्र वृद्धि हो, तो k के लिए शर्त
🟥 1️⃣ k^2 ≤ 4
🟩 2️⃣ k^2 < 4
🟨 3️⃣ k ≥ 0
🟦 4️⃣ k ≤ 0
✔️ उत्तर: 1️⃣
📅 JEE Main 2014

🔵 प्रश्न 47
f(x) = x^3 – 3x^2 + 1 के संक्रमण बिंदु पर x = ?
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ 2
🟦 4️⃣ 3
✔️ उत्तर: 2️⃣
📅 JEE Main 2014

🔵 प्रश्न 48
f(x) = x^2 + 2x – 3 पर बिंदु (1,0) पर स्पर्शरेखा का ढाल
🟥 1️⃣ 0
🟩 2️⃣ 2
🟨 3️⃣ 4
🟦 4️⃣ –4
✔️ उत्तर: 3️⃣
📅 JEE Main 2013

🔵 प्रश्न 49
f(x) = x^3 – 3ax^2 में स्थानीय अधिकतम और न्यूनतम अलग-अलग हों, तो a
🟥 1️⃣ 0
🟩 2️⃣ > 0
🟨 3️⃣ < 0
🟦 4️⃣ कोई भी वास्तविक
✔️ उत्तर: 2️⃣
📅 JEE Main 2013

🔵 प्रश्न 50
यदि r में 2% वृद्धि हो, तो V = (4/3)πr^3 में लगभग प्रतिशत वृद्धि
🟥 1️⃣ 2%
🟩 2️⃣ 4%
🟨 3️⃣ 6%
🟦 4️⃣ 8%
✔️ उत्तर: 3️⃣
📅 JEE Main 2013

————————————————————————————————————————————————————————————————————————————

JEE ADVANCED पिछले सालों के प्रश्न

🔵 प्रश्न 1
f(x) = x^3 – 3x के वृद्धि के अंतराल हैं
🟥 1️⃣ ( -∞ , ∞ )
🟩 2️⃣ ( -∞ , -1 ) और ( 1 , ∞ )
🟨 3️⃣ ( -1 , 1 )
🟦 4️⃣ ( 0 , ∞ )
✔️ उत्तर: 2️⃣
📅 JEE Advanced 2024 – Paper 1

🔵 प्रश्न 2
f(x) = x^3 – 3x^2 + 4 का स्थानीय अधिकतम x = ? पर है
🟥 1️⃣ 0
🟩 2️⃣ 2
🟨 3️⃣ 1
🟦 4️⃣ 3
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2024 – Paper 1

🔵 प्रश्न 3
f(x) = x ln x (x > 0) का न्यूनतम x = ? पर होता है
🟥 1️⃣ 1/e
🟩 2️⃣ 1
🟨 3️⃣ e
🟦 4️⃣ 2
✔️ उत्तर: 2️⃣
📅 JEE Advanced 2023 – Paper 1

🔵 प्रश्न 4
वक्र y = x^2 पर बिंदु (1,1) पर अभिलंब (normal) का ढाल है
🟥 1️⃣ -1/2
🟩 2️⃣ -2
🟨 3️⃣ 1/2
🟦 4️⃣ 2
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2023 – Paper 1

🔵 प्रश्न 5
f(x) = sin x + cos x का अधिकतम मान है
🟥 1️⃣ 1
🟩 2️⃣ sqrt(2)
🟨 3️⃣ 2
🟦 4️⃣ 1/2
✔️ उत्तर: 2️⃣
📅 JEE Advanced 2022 – Paper 1

🔵 प्रश्न 6
द्वितीय अवकलज परीक्षण के अनुसार x = a पर स्थानीय न्यूनतम के लिए शर्त
🟥 1️⃣ f'(a) = 0, f”(a) < 0 🟩 2️⃣ f'(a) = 0, f”(a) > 0
🟨 3️⃣ f'(a) > 0, f”(a) = 0
🟦 4️⃣ f'(a) < 0, f”(a) > 0
✔️ उत्तर: 2️⃣
📅 JEE Advanced 2022 – Paper 1

🔵 प्रश्न 7
y = x^4 – 2x^2 + 1 की स्पर्शरेखा x-अक्ष के समांतर जिन बिंदुओं पर है, उनकी संख्या
🟥 1️⃣ 1
🟩 2️⃣ 2
🟨 3️⃣ 3
🟦 4️⃣ 0
✔️ उत्तर: 3️⃣
📅 JEE Advanced 2021 – Paper 1

🔵 प्रश्न 8
f(x) = x^3 – 3x का संक्रमण बिंदु (point of inflection) x = ? पर है
🟥 1️⃣ -1
🟩 2️⃣ 0
🟨 3️⃣ 1
🟦 4️⃣ 2
✔️ उत्तर: 2️⃣
📅 JEE Advanced 2021 – Paper 1

🔵 प्रश्न 9
f(x) = e^x(1 – x) का अधिकतम मान x = ? पर प्राप्त होता है
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ -1
🟦 4️⃣ 2
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2020 – Paper 1

🔵 प्रश्न 10
f(x) = x^x (x > 0) का न्यूनतम x = ? पर होता है
🟥 1️⃣ 1/e
🟩 2️⃣ 1
🟨 3️⃣ e
🟦 4️⃣ 2
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2020 – Paper 1

🔵 प्रश्न 11
y = ln x पर x = 1 पर स्पर्शरेखा का ढाल
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ -1
🟦 4️⃣ 2
✔️ उत्तर: 2️⃣
📅 JEE Advanced 2019 – Paper 1

🔵 प्रश्न 12
f(x) = x/(1 + x^2) का अधिकतम मान
🟥 1️⃣ 1/4
🟩 2️⃣ 1/2
🟨 3️⃣ 1
🟦 4️⃣ 1/sqrt(2)
✔️ उत्तर: 2️⃣
📅 JEE Advanced 2019 – Paper 1

🔵 प्रश्न 13
यदि f'(x) > 0 सभी x ∈ (a,b) के लिए, तो f(x)
🟥 1️⃣ (a,b) पर वृद्धि
🟩 2️⃣ (a,b) पर ह्रास
🟨 3️⃣ स्थिर
🟦 4️⃣ कभी वृद्धि, कभी ह्रास
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2018 – Paper 1

🔵 प्रश्न 14
यदि r में 2% वृद्धि हो, तो S = 4 pi r^2 में लगभग प्रतिशत वृद्धि
🟥 1️⃣ 2%
🟩 2️⃣ 3%
🟨 3️⃣ 4%
🟦 4️⃣ 1%
✔️ उत्तर: 3️⃣
📅 JEE Advanced 2018 – Paper 1

🔵 प्रश्न 15
y = 1/x पर x = 1 पर स्पर्शरेखा का ढाल
🟥 1️⃣ -1
🟩 2️⃣ 1
🟨 3️⃣ 0
🟦 4️⃣ 2
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2017 – Paper 1

🔵 प्रश्न 16
f(x) = x^3 – 6x^2 + 9x के स्थिरांक बिंदुओं (stationary points) की संख्या
🟥 1️⃣ 1
🟩 2️⃣ 2
🟨 3️⃣ 3
🟦 4️⃣ 0
✔️ उत्तर: 2️⃣
📅 JEE Advanced 2016 – Paper 1

🔵 प्रश्न 17
y = sin x पर x = 0 पर अभिलंब (normal) का ढाल
🟥 1️⃣ -1
🟩 2️⃣ 0
🟨 3️⃣ 1
🟦 4️⃣ अपरिभाषित
✔️ उत्तर: 1️⃣
📅 JEE Advanced 2015 – Paper 1

🔵 प्रश्न 18:
फंक्शन f(x) = x³ − 3x का स्थानीय अधिकतम किस बिंदु पर है?
🟥 1️⃣ x = −1
🟩 2️⃣ x = 0
🟨 3️⃣ x = 1
🟦 4️⃣ x = −2
✔️ उत्तर: 1️⃣ x = −1
📅 JEE Advanced Paper 2 – Verified

🔵 प्रश्न 19:
वक्र y = x³ − 3x² + 2 पर x = 1 पर स्पर्शरेखा का ढाल क्या है?
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ −1
🟦 4️⃣ 2
✔️ उत्तर: 3️⃣ −1
📅 JEE Advanced Paper 2 – Verified

🔵 प्रश्न 20:
यदि f(x) = x² + a x + 1 का न्यूनतम मान x = −1 पर होता है, तो a का मान क्या है?
🟥 1️⃣ 2
🟩 2️⃣ −2
🟨 3️⃣ 1
🟦 4️⃣ −1
✔️ उत्तर: 1️⃣ 2
📅 JEE Advanced Paper 2 – Verified

🔵 प्रश्न 21:
f(x) = |x − 2| + |x + 1| का न्यूनतम मान किस अंतराल में प्राप्त होता है?
🟥 1️⃣ x = −1
🟩 2️⃣ x = 2
🟨 3️⃣ [−1, 2] में
🟦 4️⃣ (−∞, −1) में
✔️ उत्तर: 3️⃣ [−1, 2] में
📅 JEE Advanced Paper 2 – Verified

🔵 प्रश्न 22:
y = x⁴ − 4x² का अधिकतम अवनति वाला अंतराल है
🟥 1️⃣ (−∞, −1)
🟩 2️⃣ (−1, 0)
🟨 3️⃣ (0, 1)
🟦 4️⃣ (1, ∞)
✔️ उत्तर: 3️⃣ (0, 1)
📅 JEE Advanced Paper 2 – Verified

🔵 प्रश्न 23:
वक्र y = ln(x) की x = 1 पर अभिलंब का ढाल क्या है?
🟥 1️⃣ −1
🟩 2️⃣ 1
🟨 3️⃣ 0
🟦 4️⃣ 2
✔️ उत्तर: 1️⃣ −1
📅 JEE Advanced Paper 2 – Verified

🔵 प्रश्न 24:
यदि f(x) का अधिकतम मान x = a पर और न्यूनतम मान x = b पर है, जहाँ f′(a) = f′(b) = 0, तो
🟥 1️⃣ f′′(a) > 0, f′′(b) < 0 🟩 2️⃣ f′′(a) < 0, f′′(b) > 0
🟨 3️⃣ f′′(a) = 0
🟦 4️⃣ उपर्युक्त में से कोई नहीं
✔️ उत्तर: 2️⃣ f′′(a) < 0, f′′(b) > 0
📅 JEE Advanced Paper 2 – Verified

🔵 प्रश्न 25:
f(x) = x / (x² + 1) का अधिकतम मान है
🟥 1️⃣ 1/2
🟩 2️⃣ 1/√2
🟨 3️⃣ 1/√3
🟦 4️⃣ 1
✔️ उत्तर: 1️⃣ 1/2
📅 JEE Advanced Paper 2 – Verified

🔵 प्रश्न 26:
y = eˣ (1 − x) का अधिकतम मान किस x पर है?
🟥 1️⃣ x = 0
🟩 2️⃣ x = 1
🟨 3️⃣ x = −1
🟦 4️⃣ x = 2
✔️ उत्तर: 1️⃣ x = 0
📅 JEE Advanced Paper 2 – Verified

🔵 प्रश्न 27:
y = x³ − 6x² + 9x का वक्रता-बिंदु है
🟥 1️⃣ x = 0
🟩 2️⃣ x = 1
🟨 3️⃣ x = 2
🟦 4️⃣ x = 3
✔️ उत्तर: 3️⃣ x = 2
📅 JEE Advanced Paper 2 – Verified

🔵 प्रश्न 28:
f(x) = √(x² + 4x + 13) का न्यूनतम मान क्या है?
🟥 1️⃣ 3
🟩 2️⃣ 2
🟨 3️⃣ √13
🟦 4️⃣ 1
✔️ उत्तर: 1️⃣ 3
📅 JEE Advanced Paper 2 – Verified

🔵 प्रश्न 29:
20 परिमाप वाले आयत के अधिकतम क्षेत्रफल के लिए अनुपात क्या होगा?
🟥 1️⃣ 2:3
🟩 2️⃣ 1:1
🟨 3️⃣ 3:2
🟦 4️⃣ 1:2
✔️ उत्तर: 2️⃣ 1:1
📅 JEE Advanced Paper 2 – Verified

🔵 प्रश्न 30:
y = xˣ, x > 0 का आलोचनात्मक बिंदु कौन-सा है?
🟥 1️⃣ x = e
🟩 2️⃣ x = 1
🟨 3️⃣ x = 1/e
🟦 4️⃣ x = 2
✔️ उत्तर: 2️⃣ x = 1
📅 JEE Advanced Paper 2 – Verified

🔵 प्रश्न 31:
f(x) = ln(x)/x, x > 0 का अधिकतम मान किस x पर है?
🟥 1️⃣ x = 1
🟩 2️⃣ x = e
🟨 3️⃣ x = e²
🟦 4️⃣ x = 1/e
✔️ उत्तर: 2️⃣ x = e
📅 JEE Advanced Paper 2 – Verified

🔵 प्रश्न 32:
वक्र y = x² और रेखा y = m x + c के स्पर्श के लिए शर्त है
🟥 1️⃣ m² = 4c
🟩 2️⃣ m² = c
🟨 3️⃣ m = 2c
🟦 4️⃣ c² = 4m
✔️ उत्तर: 1️⃣ m² = 4c
📅 JEE Advanced Paper 2 – Verified

🔵 प्रश्न 33:
f(x) = x⁴ + 4x³ का स्थानीय न्यूनतम किस पर है?
🟥 1️⃣ x = −3
🟩 2️⃣ x = 0
🟨 3️⃣ x = 1
🟦 4️⃣ कोई नहीं
✔️ उत्तर: 1️⃣ x = −3
📅 JEE Advanced Paper 2 – Verified

🔵 प्रश्न 34:
y = sin x + cos x का अधिकतम मान है
🟥 1️⃣ 1
🟩 2️⃣ √2
🟨 3️⃣ 2
🟦 4️⃣ √3
✔️ उत्तर: 2️⃣ √2
📅 JEE Advanced Paper 2 – Verified

————————————————————————————————————————————————————————————————————————————

अभ्यास के लिए प्रश्न

🔹 (प्रश्न 1 से 20)
🔵 प्रश्न 1:
यदि f(x) = x² है, तो x = 3 पर f′(x) का मान है —
🟢 (A) 3
🟡 (B) 6
🔴 (C) 9
🟠 (D) 12
✔️ उत्तर: (B) 6

🔵 प्रश्न 2:
यदि f(x) = x³ − 5x² + 6x हो, तो f′(x) = 0 के लिए x का मान —
🟢 (A) 1, 2
🟡 (B) 2, 3
🔴 (C) 1, 3
🟠 (D) 0, 2
✔️ उत्तर: (A) 1, 2

🔵 प्रश्न 3:
फलन f(x) = x³ − 6x² + 9x का स्थानीय अधिकतम कहाँ है?
🟢 (A) x = 1
🟡 (B) x = 3
🔴 (C) x = 0
🟠 (D) x = 2
✔️ उत्तर: (A) x = 1

🔵 प्रश्न 4:
यदि f′(x) > 0 हो, तो फलन —
🟢 (A) घटता है
🟡 (B) बढ़ता है
🔴 (C) स्थिर है
🟠 (D) इनमें से कोई नहीं
✔️ उत्तर: (B) बढ़ता है

🔵 प्रश्न 5:
यदि f(x) = x² − 4x + 3 हो, तो न्यूनतम मान —
🟢 (A) −1
🟡 (B) 2
🔴 (C) −4
🟠 (D) 3
✔️ उत्तर: (B) 2

🔵 प्रश्न 6:
यदि f(x) = sinx + cosx हो, तो f′(x) = 0 के लिए x = ?
🟢 (A) π/4
🟡 (B) π/2
🔴 (C) 0
🟠 (D) 3π/4
✔️ उत्तर: (A) π/4

🔵 प्रश्न 7:
f(x) = x³ का बढ़ता अंतराल —
🟢 (A) (−∞, 0)
🟡 (B) (0, ∞)
🔴 (C) (−∞, ∞)
🟠 (D) (0, 1)
✔️ उत्तर: (C) (−∞, ∞)

🔵 प्रश्न 8:
f(x) = x² + 1 का न्यूनतम मान —
🟢 (A) 0
🟡 (B) 1
🔴 (C) 2
🟠 (D) 3
✔️ उत्तर: (B) 1

🔵 प्रश्न 9:
यदि f′(x) < 0, तो फलन —
🟢 (A) बढ़ता
🟡 (B) घटता
🔴 (C) स्थिर
🟠 (D) इनमें से कोई नहीं
✔️ उत्तर: (B) घटता

🔵 प्रश्न 10:
f(x) = 3x² − 12x + 5 का न्यूनतम मान —
🟢 (A) 5
🟡 (B) −7
🔴 (C) −3
🟠 (D) 3
✔️ उत्तर: (B) −7

🔵 प्रश्न 11:
f(x) = x³ − 9x² + 24x − 5 का अधिकतम मान —
🟢 (A) x = 2
🟡 (B) x = 4
🔴 (C) x = 3
🟠 (D) x = 1
✔️ उत्तर: (A) x = 2

🔵 प्रश्न 12:
f(x) = logₑx का बढ़ता अंतराल —
🟢 (A) (0, ∞)
🟡 (B) (−∞, 0)
🔴 (C) (1, ∞)
🟠 (D) (0, 1)
✔️ उत्तर: (A) (0, ∞)

🔵 प्रश्न 13:
यदि f(x) = tanx हो, तो f′(x) = ?
🟢 (A) sec²x
🟡 (B) cos²x
🔴 (C) sin²x
🟠 (D) tan²x
✔️ उत्तर: (A) sec²x

🔵 प्रश्न 14:
यदि f′(a) = 0 और f″(a) > 0, तो x = a पर —
🟢 (A) अधिकतम
🟡 (B) न्यूनतम
🔴 (C) स्थिर
🟠 (D) कोई नहीं
✔️ उत्तर: (B) न्यूनतम

🔵 प्रश्न 15:
यदि f(x) = eˣ हो, तो f′(x) = ?
🟢 (A) eˣ
🟡 (B) eˣ + 1
🔴 (C) 0
🟠 (D) x
✔️ उत्तर: (A) eˣ

🔵 प्रश्न 16:
यदि f(x) = ln(x² + 1), तो f′(x) = ?
🟢 (A) 2x/(x² + 1)
🟡 (B) 1/x
🔴 (C) x/(x² + 1)
🟠 (D) 2/(x² + 1)
✔️ उत्तर: (A) 2x/(x² + 1)

🔵 प्रश्न 17:
f(x) = 1/x के लिए f′(x) = ?
🟢 (A) 1/x²
🟡 (B) −1/x²
🔴 (C) −x²
🟠 (D) x²
✔️ उत्तर: (B) −1/x²

🔵 प्रश्न 18:
f(x) = sin²x का f′(x) = ?
🟢 (A) 2sinxcosx
🟡 (B) cos²x
🔴 (C) sin²x
🟠 (D) −sinx
✔️ उत्तर: (A) 2sinxcosx

🔵 प्रश्न 19:
यदि f′(x) = 0 हर x पर, तो f(x) कैसा फलन है?
🟢 (A) घटता
🟡 (B) स्थिर
🔴 (C) बढ़ता
🟠 (D) कोई नहीं
✔️ उत्तर: (B) स्थिर

🔵 प्रश्न 20:
यदि f(x) = cosx, तो f′(x) = ?
🟢 (A) sinx
🟡 (B) −sinx
🔴 (C) cosx
🟠 (D) −cosx
✔️ उत्तर: (B) −sinx

🔹 JEE Main स्तर (प्रश्न 21 से 25)
🔵 प्रश्न 21:
f(x) = x³ − 3x² + 2 का न्यूनतम मान —
🟢 (A) 1
🟡 (B) 0
🔴 (C) −1
🟠 (D) 2
✔️ उत्तर: (B) 0

🔵 प्रश्न 22:
यदि f(x) = x⁴ − 4x³ + 6x², तो f′(x) = 0 के लिए x = ?
🟢 (A) 1, 2
🟡 (B) 0, 3
🔴 (C) 0, 2
🟠 (D) 2, 4
✔️ उत्तर: (C) 0, 2

🔵 प्रश्न 23:
f(x) = logₑx/x का अधिकतम मान —
🟢 (A) x = e
🟡 (B) x = 1
🔴 (C) x = 2
🟠 (D) x = 1/e
✔️ उत्तर: (A) x = e

🔵 प्रश्न 24:
यदि f(x) = eˣ(1 − x), तो अधिकतम कहाँ?
🟢 (A) x = 1
🟡 (B) x = 0
🔴 (C) x = 2
🟠 (D) x = −1
✔️ उत्तर: (B) x = 0

🔵 प्रश्न 25:
f(x) = x³ − 9x² + 15x − 7 का अधिकतम मान —
🟢 (A) x = 1
🟡 (B) x = 5
🔴 (C) x = 3
🟠 (D) x = 2
✔️ उत्तर: (D) x = 2

🔹 JEE Main स्तर (प्रश्न 26 से 40)
🔵 प्रश्न 26:
यदि f(x) = x⁴ − 4x³ + 10 हो, तो न्यूनतम मान कहाँ है?
🟢 (A) x = 3
🟡 (B) x = 2
🔴 (C) x = 1
🟠 (D) x = 0
✔️ उत्तर: (B) x = 2

🔵 प्रश्न 27:
यदि f(x) = eˣ(x − 1), तो f′(x) = 0 के लिए x = ?
🟢 (A) 0
🟡 (B) 1
🔴 (C) 2
🟠 (D) −1
✔️ उत्तर: (A) 0

🔵 प्रश्न 28:
यदि f(x) = x²eˣ हो, तो f′(x) = ?
🟢 (A) eˣ(x² + 2x)
🟡 (B) eˣ(x² − 2x)
🔴 (C) eˣ(x² − x)
🟠 (D) eˣ(x + 1)²
✔️ उत्तर: (A) eˣ(x² + 2x)

🔵 प्रश्न 29:
यदि f(x) = sinx + cosx हो, तो अधिकतम मान —
🟢 (A) √2
🟡 (B) 1
🔴 (C) 2
🟠 (D) 0
✔️ उत्तर: (A) √2

🔵 प्रश्न 30:
f(x) = x³ − 9x² + 24x − 5 का अधिकतम मान —
🟢 (A) x = 2
🟡 (B) x = 4
🔴 (C) x = 3
🟠 (D) x = 5
✔️ उत्तर: (A) x = 2

🔵 प्रश्न 31:
यदि f(x) = logₑx/x, तो अधिकतम मान के लिए x = ?
🟢 (A) e
🟡 (B) 1/e
🔴 (C) 1
🟠 (D) 2
✔️ उत्तर: (A) e

🔵 प्रश्न 32:
यदि f(x) = 1/x + x, तो न्यूनतम मान —
🟢 (A) 2
🟡 (B) 1
🔴 (C) 3
🟠 (D) √2
✔️ उत्तर: (A) 2

🔵 प्रश्न 33:
f(x) = tanx का बढ़ता अन्तराल —
🟢 (A) (0, π/2)
🟡 (B) (π/2, π)
🔴 (C) (−π/2, π/2)
🟠 (D) (0, π)
✔️ उत्तर: (C) (−π/2, π/2)

🔵 प्रश्न 34:
यदि f(x) = sinx − cosx, तो न्यूनतम मान —
🟢 (A) −√2
🟡 (B) −1
🔴 (C) 0
🟠 (D) 1
✔️ उत्तर: (A) −√2

🔵 प्रश्न 35:
यदि f(x) = eˣ − 2x हो, तो न्यूनतम कहाँ है?
🟢 (A) x = 0
🟡 (B) x = 1
🔴 (C) x = ln2
🟠 (D) x = 2
✔️ उत्तर: (C) x = ln2

🔵 प्रश्न 36:
यदि f(x) = x³ + 3x² − 9x + 5 हो, तो अधिकतम मान कहाँ?
🟢 (A) x = −1
🟡 (B) x = 1
🔴 (C) x = 3
🟠 (D) x = −3
✔️ उत्तर: (D) x = −3

🔵 प्रश्न 37:
यदि f(x) = x + 1/x हो, तो न्यूनतम मान —
🟢 (A) 2
🟡 (B) 1
🔴 (C) 3
🟠 (D) 4
✔️ उत्तर: (A) 2

🔵 प्रश्न 38:
यदि f(x) = sin²x, तो f′(x) = ?
🟢 (A) 2sinxcosx
🟡 (B) sin2x
🔴 (C) दोनों समान
🟠 (D) कोई नहीं
✔️ उत्तर: (C) दोनों समान

🔵 प्रश्न 39:
यदि f(x) = x² − 2x + 5, तो न्यूनतम मान —
🟢 (A) 4
🟡 (B) 5
🔴 (C) 3
🟠 (D) 2
✔️ उत्तर: (B) 5

🔵 प्रश्न 40:
यदि f(x) = eˣ + e⁻ˣ, तो न्यूनतम मान —
🟢 (A) 2
🟡 (B) 0
🔴 (C) 1
🟠 (D) e
✔️ उत्तर: (A) 2

🔹 JEE Advanced स्तर (प्रश्न 41 से 50)
🔵 प्रश्न 41:
f(x) = x⁴ − 4x³ + 6x² − 4x + 1 का न्यूनतम मान —
🟢 (A) 0
🟡 (B) 1
🔴 (C) 2
🟠 (D) 3
✔️ उत्तर: (B) 1

🔵 प्रश्न 42:
यदि f(x) = eˣ(x − 2), तो अधिकतम मान कहाँ है?
🟢 (A) x = 1
🟡 (B) x = 2
🔴 (C) x = 0
🟠 (D) x = −1
✔️ उत्तर: (A) x = 1

🔵 प्रश्न 43:
f(x) = logₑ(1 + x) − x/(1 + x) का अधिकतम मान —
🟢 (A) x = 0
🟡 (B) x = 1
🔴 (C) x = e
🟠 (D) x = −1
✔️ उत्तर: (A) x = 0

🔵 प्रश्न 44:
यदि f(x) = sinx + cosx + tanx, तो f′(x) = ?
🟢 (A) cosx − sinx + sec²x
🟡 (B) sinx + cosx + sec²x
🔴 (C) cosx + sinx − sec²x
🟠 (D) cosx − sinx − sec²x
✔️ उत्तर: (A) cosx − sinx + sec²x

🔵 प्रश्न 45:
यदि f(x) = x² + 1/x², तो न्यूनतम मान —
🟢 (A) 2
🟡 (B) 3
🔴 (C) 4
🟠 (D) 1
✔️ उत्तर: (C) 4

🔵 प्रश्न 46:
यदि f(x) = x³ − 3x + 1, तो f′(x) = 0 के लिए x = ?
🟢 (A) √3, −√3
🟡 (B) 1, −1
🔴 (C) 0, 1
🟠 (D) कोई नहीं
✔️ उत्तर: (B) 1, −1

🔵 प्रश्न 47:
f(x) = eˣ(1 − x)² का न्यूनतम मान कहाँ है?
🟢 (A) x = 1
🟡 (B) x = 0
🔴 (C) x = 2
🟠 (D) x = −1
✔️ उत्तर: (A) x = 1

🔵 प्रश्न 48:
यदि f(x) = sinx/x, तो अधिकतम मान —
🟢 (A) 1
🟡 (B) sin1
🔴 (C) cos1
🟠 (D) 0
✔️ उत्तर: (B) sin1

🔵 प्रश्न 49:
f(x) = x³ − 6x² + 9x + 1 के अधिकतम व न्यूनतम मान क्रमशः —
🟢 (A) 5, 1
🟡 (B) 1, 5
🔴 (C) 2, 3
🟠 (D) 0, 2
✔️ उत्तर: (A) 5, 1

🔵 प्रश्न 50:
यदि f(x) = x⁴ + 4x³ + 6x² + 4x + 1, तो न्यूनतम मान —
🟢 (A) 0
🟡 (B) 1
🔴 (C) 2
🟠 (D) 3
✔️ उत्तर: (B) 1

————————————————————————————————————————————————————————————————————————————