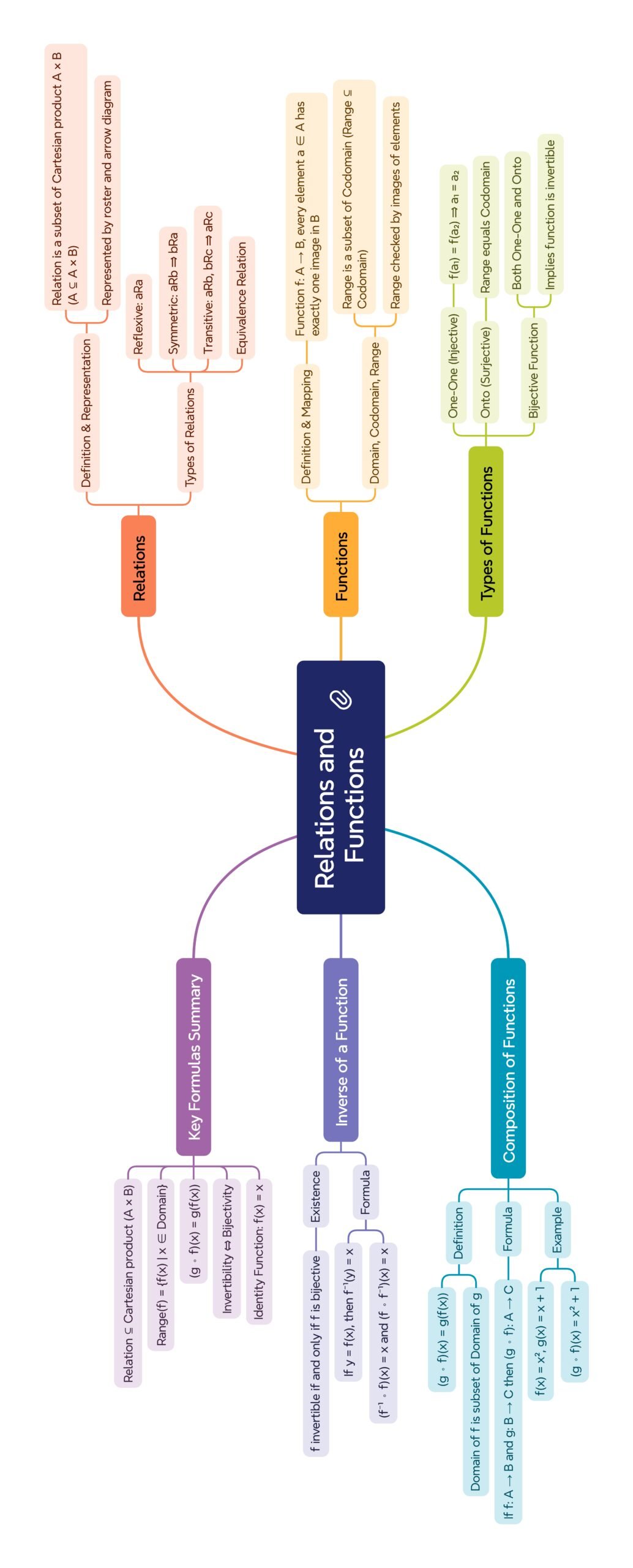
Class 12 : Maths (English) – Chapter 1: Relations and Functions

Posted by

On June 25, 2025

EXPLANATION & SUMMARY

✳️ Explanation Section (~1700 words)
🔵 1. Introduction
Relations and Functions form the foundational concept of modern mathematics. They help us understand how two quantities are connected.
In Class 12, you expand the knowledge of relations and functions studied in Class 11, learning about new types like invertible functions, composition, and binary operations.

🟢 2. Relation – Basic Concept
✏️ Definition:
A relation is a connection between elements of two sets.
If there are two non-empty sets A and B, then any subset of their Cartesian product A × B is called a relation from A to B.
💡 Notation:
If (a, b) ∈ R, then we say “a is related to b under relation R” → a R b
📘 Example:
Let A = {1, 2, 3}, B = {4, 5, 6},
Define R = {(1, 4), (2, 5), (3, 6)}
⇒ R is a relation from A to B.

🟡 3. Types of Relations
Let R be a relation on a set A (i.e. R ⊆ A × A):
🔹 (i) Reflexive Relation
A relation R is reflexive if every element is related to itself.
➡️ (a, a) ∈ R for every a ∈ A
📘 Example: A = {1, 2, 3}, R = {(1,1), (2,2), (3,3)} is reflexive.
🔹 (ii) Symmetric Relation
R is symmetric if (a, b) ∈ R ⇒ (b, a) ∈ R
📘 Example: R = {(1,2), (2,1), (2,3), (3,2)} is symmetric.
🔹 (iii) Transitive Relation
R is transitive if (a, b) ∈ R and (b, c) ∈ R ⇒ (a, c) ∈ R
📘 Example: R = {(1,2), (2,3), (1,3)} is transitive.
🔹 (iv) Equivalence Relation
If R is reflexive, symmetric, and transitive,
then R is called an equivalence relation.
💡 Equivalence relation partitions a set into disjoint equivalence classes.

🔴 4. Function – Definition and Basics
✏️ Definition:
A function is a special relation where each element of set A is associated with exactly one element of set B.
A function from A to B is denoted by f: A → B.
💡 Important: Every function is a relation, but not every relation is a function.

🟢 5. Types of Functions
Let f: A → B, and A = Domain, B = Co-domain, Range = image of A under f.
🔹 (i) One-One Function (Injective)
If distinct elements in A map to distinct elements in B:
a₁ ≠ a₂ ⇒ f(a₁) ≠ f(a₂)
🔹 (ii) Onto Function (Surjective)
If Range = Co-domain,
every element of B has a pre-image in A.
🔹 (iii) Bijective Function
If function is both One-One and Onto,
then it is called Bijective.
💡 Bijective functions are invertible.

🟡 6. Composition of Functions
If f: A → B and g: B → C,
then composition g ∘ f: A → C is defined by
➡️ (g ∘ f)(x) = g(f(x))
📘 Example:
Let f(x) = 2x + 3, g(x) = x²
Then (g ∘ f)(x) = g(f(x)) = (2x + 3)²
💡 Composition is associative:
h ∘ (g ∘ f) = (h ∘ g) ∘ f

🔴 7. Invertible Function
A function f: A → B is invertible if there exists a function g: B → A such that
➡️ g ∘ f = I_A and f ∘ g = I_B
(where I_A and I_B are identity functions)
✏️ Condition:
A function is invertible if and only if it is bijective.
💡 Identity Function: I_A(x) = x for all x ∈ A.

🟢 8. Some Standard Functions

🔹 Identity Function
f(x) = x
Graph: Straight line through origin at 45°.
🔹 Constant Function
f(x) = c (constant)
Graph: Parallel to x-axis.
🔹 Linear Function
f(x) = mx + c
Graph: Straight line (slope = m).
🔹 Quadratic Function
f(x) = ax² + bx + c
Graph: Parabola.
🔹 Polynomial Function
f(x) = a₀ + a₁x + a₂x² + … + aₙxⁿ
🔹 Rational Function
f(x) = P(x)/Q(x), Q(x) ≠ 0
🔹 Modulus Function
f(x) = |x|
🔹 Signum Function
f(x) =
-1, x < 0
0, x = 0
1, x > 0

🟡 9. Graphical Representation
Graph helps in visualizing domain, range, and nature of functions.
💡 For one-one functions: horizontal line cuts graph at most once.
💡 For onto functions: every y has at least one x.

🔴 10. Binary Operation
A binary operation on a set A is a function
➡️ * : A × A → A
📘 Example: Addition (+) on R:
(a, b) → a + b
💡 Properties:
Closure: a * b ∈ A
Associativity: (a * b) * c = a * (b * c)
Commutativity: a * b = b * a
Identity: ∃ e ∈ A, a * e = e * a = a
Inverse: ∃ a⁻¹ ∈ A, a * a⁻¹ = e

🟢 11. Equivalence Class (Extra Insight)
If R is equivalence on A,
the set [a] = {x ∈ A | x R a} is called equivalence class.
All such classes partition A.

💡 12. Important Results
f is bijective ⇔ f⁻¹ exists
Composition of bijective functions is bijective
Inverse of inverse is the function itself: (f⁻¹)⁻¹ = f
Composition respects inverse: (g ∘ f)⁻¹ = f⁻¹ ∘ g⁻¹

🧠 13. Real-life Applications
One-one relations model unique mappings (e.g., roll number → student).
Functions represent dependencies (e.g., temperature → pressure).
Inverse functions used in solving equations, transformations.

✳️ Summary Section (~300 words)
🔹 A relation is a subset of A × B; a function is a relation with unique mapping.
🔹 Reflexive, symmetric, and transitive relations combine to form equivalence relations.
🔹 Function types:
One-one (Injective)
Onto (Surjective)
Bijective = One-one + Onto
🔹 Composition: (g ∘ f)(x) = g(f(x))
🔹 Invertible function exists only for bijective functions.
🔹 Binary operation: mapping from A × A to A, following closure and other properties.
🔹 Common functions:
Identity: f(x) = x
Constant: f(x) = c
Linear: f(x) = mx + c
Quadratic: f(x) = ax² + bx + c
🔹 Graph analysis helps identify one-one/onto nature.
🔹 Function inverse reverses input-output pairing.

📝 Quick Recap
🧠 Relation = subset of Cartesian product
✳️ Function = unique output for each input
🔢 One-one ⇔ unique mapping
🎯 Onto ⇔ all elements of co-domain covered
🧭 Bijective ⇔ invertible
🔄 Composition: g ∘ f = g(f(x))
🔁 Inverse: f⁻¹ exists ⇔ f bijective
⚙️ Binary operation: A × A → A

————————————————————————————————————————————————————————————————————————————

QUESTIONS FROM TEXTBOOK

Exercise 1.1

🔵 Question 1:
Determine whether each of the following relations are reflexive, symmetric, and transitive:

✳️ (i)
Relation R in the set A = {1, 2, 3, …, 13, 14} defined as
➡️ R = {(x, y) : 3x − y = 0}
🟢 Answer:
💡 Given condition: 3x − y = 0 ⇒ y = 3x
✔️ Reflexive:
We check if (x, x) ∈ R
For (x, x),
➡️ 3x − x = 2x ≠ 0
Hence (x, x) ∉ R
❌ Not reflexive.
✔️ Symmetric:
If (x, y) ∈ R ⇒ y = 3x
For symmetry, need (y, x) ∈ R ⇒ x = 3y
But if y = 3x, then x = y/3 ≠ 3y
❌ Not symmetric.
✔️ Transitive:
Suppose (x, y) ∈ R and (y, z) ∈ R
⇒ y = 3x, z = 3y = 9x
Check if (x, z) ∈ R
⇒ z = 3x ? → No, because z = 9x
❌ Not transitive.
✅ Therefore, R is neither reflexive, nor symmetric, nor transitive.

✳️ (ii)
Relation R in the set N of natural numbers defined as
➡️ R = {(x, y) : y = x + 5 and x < 4}
🟢 Answer:
Given: y = x + 5, valid only for x = 1, 2, 3
✔️ Reflexive:
For (x, x) ⇒ x = x + 5 ❌ False
Hence not reflexive.
✔️ Symmetric:
If (x, y) ∈ R ⇒ y = x + 5
To have (y, x) ∈ R, we need x = y + 5 ❌ Not true
Hence not symmetric.
✔️ Transitive:
If (x, y) ∈ R and (y, z) ∈ R,
then y = x + 5 and z = y + 5 = x + 10
To have (x, z) ∈ R, we need z = x + 5, but z = x + 10 ❌
Hence not transitive.
✅ Therefore, R is neither reflexive, nor symmetric, nor transitive.

✳️ (iii)
Relation R in the set A = {1, 2, 3, 4, 5, 6} as
➡️ R = {(x, y) : y is divisible by x}
🟢 Answer:
✔️ Reflexive:
For every x, x divides x ✔️
✅ Reflexive.
✔️ Symmetric:
If (x, y) ∈ R ⇒ y divisible by x
But x may not be divisible by y
E.g. (2, 4) ∈ R but (4, 2) ∉ R
❌ Not symmetric.
✔️ Transitive:
If (x, y) ∈ R and (y, z) ∈ R
⇒ y = k₁x, z = k₂y = k₁k₂x
⇒ z divisible by x ✔️
✅ Transitive.
✅ Therefore, R is reflexive and transitive, but not symmetric.

✳️ (iv)
Relation R in the set Z of all integers defined as
➡️ R = {(x, y) : x − y is an integer}
🟢 Answer:
For x, y ∈ Z, x − y ∈ Z always true.
✔️ Reflexive: x − x = 0 ∈ Z ✔️ ✅
✔️ Symmetric: If (x, y) ∈ R, then x − y ∈ Z ⇒ y − x = −(x − y) ∈ Z ✔️ ✅
✔️ Transitive: If (x, y) ∈ R and (y, z) ∈ R
⇒ x − y ∈ Z, y − z ∈ Z
Add ⇒ x − z ∈ Z ✔️ ✅
✅ Therefore, R is reflexive, symmetric, and transitive.
Hence, R is an equivalence relation.

✳️ (v)
Relation R in the set A of human beings given by:
(a) R = {(x, y) : x and y work at the same place}
✅ Reflexive (same person works at same place)
✅ Symmetric (if x works with y, y works with x)
✅ Transitive (if x with y, y with z ⇒ x with z)
✔️ Equivalence relation
(b) R = {(x, y) : x and y live in same locality}
✅ Reflexive ✔️ Symmetric ✔️ Transitive
✔️ Equivalence relation
(c) R = {(x, y) : x is exactly 7 cm taller than y}
❌ Not reflexive
❌ Not symmetric
❌ Not transitive
✖️ Not equivalence
(d) R = {(x, y) : x is wife of y}
❌ Not reflexive
❌ Not symmetric (wife of y ≠ y wife of x)
❌ Not transitive
✖️ Not equivalence
(e) R = {(x, y) : x is father of y}
❌ Not reflexive
❌ Not symmetric
❌ Not transitive
✖️ Not equivalence

🔵 Question 2:
Show that the relation R in the set ℝ of real numbers, defined as
➡️ R = {(a, b) : a ≤ b²}
is neither reflexive, nor symmetric, nor transitive.
🟢 Answer:
💡 Given R = {(a, b) : a ≤ b²}
✔️ Reflexive:
For R to be reflexive, (a, a) ∈ R ∀ a ∈ ℝ
Check: a ≤ a²
⮞ True for a ≥ 1 and a ≤ 0, but false for 0 < a < 1 (e.g. ½ ≤ ¼ ❌)
∴ R is not reflexive.
✔️ Symmetric:
If (a, b) ∈ R ⇒ a ≤ b²
For symmetry, (b, a) ∈ R ⇒ b ≤ a² must hold.
Counterexample: a = 2, b = 1
→ a ≤ b² ⇒ 2 ≤ 1² ❌
So R is not symmetric.
✔️ Transitive:
Take a = 3, b = 2, c = 1
a ≤ b² ⇒ 3 ≤ 4 ✔️
b ≤ c² ⇒ 2 ≤ 1² ❌ fails
Hence no guarantee of a ≤ c²
∴ R is not transitive.
✅ Therefore, R is neither reflexive, nor symmetric, nor transitive.

🔵 Question 3:
Check whether the relation R defined in the set {1, 2, 3, 4, 5, 6} as
➡️ R = {(a, b) : b = a + 1}
is reflexive, symmetric, or transitive.
🟢 Answer:
💡 Pairs: (1,2), (2,3), (3,4), (4,5), (5,6)
✔️ Reflexive:
(a, a) not present since b = a + 1 ≠ a ❌
∴ Not reflexive.
✔️ Symmetric:
If (a, b) ∈ R ⇒ b = a + 1
Then (b, a) requires a = b + 1, which is false ❌
∴ Not symmetric.
✔️ Transitive:
If (a, b) ∈ R and (b, c) ∈ R
Then b = a + 1, c = b + 1 = a + 2
Check if (a, c) ∈ R ⇒ c = a + 1 ❌
∴ Not transitive.
✅ Hence, R is neither reflexive, nor symmetric, nor transitive.

🔵 Question 4:
Show that the relation R in ℝ defined as
➡️ R = {(a, b) : a ≤ b}
is reflexive and transitive, but not symmetric.
🟢 Answer:
✔️ Reflexive:
For all a ∈ ℝ, a ≤ a ✔️
∴ Reflexive ✅
✔️ Symmetric:
If (a, b) ∈ R ⇒ a ≤ b
Then (b, a) requires b ≤ a, which may not hold
Counterexample: a = 2, b = 3
→ 2 ≤ 3 ✔️ but 3 ≤ 2 ❌
∴ Not symmetric ❌
✔️ Transitive:
If (a, b) ∈ R and (b, c) ∈ R
⇒ a ≤ b and b ≤ c ⇒ a ≤ c ✔️
∴ Transitive ✅
✅ Hence, R is reflexive and transitive, but not symmetric.

🔵 Question 5:
Check whether the relation R in ℝ defined by
➡️ R = {(a, b) : a ≤ b³}
is reflexive, symmetric, or transitive.
🟢 Answer:
💡 Given a ≤ b³
✔️ Reflexive:
Check (a, a) ⇒ a ≤ a³
True for a ≥ 1 and a ≤ 0, but false for 0 < a < 1
e.g. ½ ≤ (½)³ = 1/8 ❌
∴ Not reflexive ❌
✔️ Symmetric:
If a ≤ b³, we need b ≤ a³
Take a = 2, b = 1:
2 ≤ 1³ ❌, 1 ≤ 2³ ✔️
∴ Not symmetric ❌
✔️ Transitive:
Take a = 2, b = 3, c = 1
2 ≤ 3³ = 27 ✔️, 3 ≤ 1³ = 1 ❌
Transitivity fails ❌
✅ Hence, R is neither reflexive, nor symmetric, nor transitive.

🔵 Question 6:
Show that the relation R in the set {1, 2, 3} given by
➡️ R = {(1, 2), (2, 1)}
is symmetric but neither reflexive nor transitive.
🟢 Answer:
💡 Given R = {(1, 2), (2, 1)}
✔️ Reflexive:
For reflexivity, (a, a) must belong to R for all a.
But (1, 1), (2, 2), (3, 3) are not in R.
❌ Not reflexive.
✔️ Symmetric:
If (a, b) ∈ R, then (b, a) ∈ R.
→ (1, 2) ∈ R ⇒ (2, 1) ∈ R ✔️
→ (2, 1) ∈ R ⇒ (1, 2) ∈ R ✔️
✅ Symmetric.
✔️ Transitive:
If (a, b) ∈ R and (b, c) ∈ R, then (a, c) ∈ R.
Here (1, 2) and (2, 1) ∈ R, but (1, 1) ∉ R
❌ Not transitive.
✅ Therefore, R is symmetric, but neither reflexive nor transitive.

🔵 Question 7:
Show that the relation R in the set A of all the books in a library of a college,
given by
➡️ R = {(x, y) : x and y have the same number of pages}
is an equivalence relation.
🟢 Answer:
Let x and y be any books.
✔️ Reflexive:
Every book has the same number of pages as itself.
(x, x) ∈ R ✔️
✔️ Symmetric:
If x and y have the same number of pages,
then y and x also have the same number of pages ✔️
✔️ Transitive:
If x and y have the same number of pages, and y and z have the same number of pages,
then x and z also have the same number of pages ✔️
✅ Hence, R is reflexive, symmetric, and transitive,
∴ R is an equivalence relation.

🔵 Question 8:
Show that the relation R in the set A = {1, 2, 3, 4, 5}
defined by
➡️ R = {(a, b) : |a − b| is even}
is an equivalence relation.
Show that
– all the elements of {1, 3, 5} are related to each other,
– all the elements of {2, 4} are related to each other,
– no element of {1, 3, 5} is related to any element of {2, 4}.
🟢 Answer:
💡 Given R = {(a, b) : |a − b| is even}
✔️ Reflexive:
For all a ∈ A, |a − a| = 0 (even)
∴ (a, a) ∈ R ✔️
✔️ Symmetric:
If |a − b| is even, then |b − a| = |a − b| is also even ✔️
✔️ Transitive:
If |a − b| and |b − c| are even,
then |a − c| = |(a − b) + (b − c)|
Sum of two even numbers is even ✔️
∴ Transitive.
✅ Hence, R is equivalence relation.
🧠 Equivalence classes:
For 1: {1, 3, 5}
For 2: {2, 4}
For 3: {1, 3, 5}
For 4: {2, 4}
For 5: {1, 3, 5}

🔵 Question 9:
Show that each of the relation R in the set
A = {x ∈ ℤ : 0 ≤ x ≤ 12} given by
(i) R = {(a, b) : |a − b| is a multiple of 4}
(ii) R = {(a, b) : a = b}
is an equivalence relation.
Find the set of all elements related to 1 in each case.
🟢 Answer:
(i)
💡 R = {(a, b) : |a − b| is multiple of 4}
✔️ Reflexive:
|a − a| = 0, multiple of 4 ✔️
✔️ Symmetric:
If |a − b| multiple of 4, then |b − a| same ✔️
✔️ Transitive:
If |a − b| = 4m, |b − c| = 4n,
then |a − c| = 4(m ± n), also multiple of 4 ✔️
✅ Equivalence relation.
📘 Elements related to 1:
All b such that |1 − b| multiple of 4
⇒ b = 1, 5, 9
✅ Related set = {1, 5, 9}

(ii)
💡 R = {(a, b) : a = b}
✔️ Reflexive: (a, a) ✔️
✔️ Symmetric: if a = b ⇒ b = a ✔️
✔️ Transitive: if a = b and b = c ⇒ a = c ✔️
✅ Equivalence relation.
📘 Elements related to 1: only {1}

🔵 Question 10:
Give an example of a relation which is:
(i) Symmetric but neither reflexive nor transitive
🟢 Example: R = {(1, 2), (2, 1)} on A = {1, 2, 3}
✔️ Symmetric ✅
❌ Not reflexive
❌ Not transitive
(ii) Transitive but neither reflexive nor symmetric
🟢 Example: R = {(1, 2), (2, 3), (1, 3)} on A = {1, 2, 3}
✔️ Transitive ✅
❌ Not reflexive
❌ Not symmetric
(iii) Reflexive and symmetric but not transitive
🟢 Example: R = {(1, 1), (2, 2), (1, 2), (2, 1)} on A = {1, 2, 3}
✔️ Reflexive, Symmetric ✅
❌ Not transitive (since (1,2), (2,1) ⇒ need (1,1) ✔️, (2,2) ✔️, but if we omit some, fails)
(iv) Reflexive and transitive but not symmetric
🟢 Example: R = {(1, 1), (2, 2), (3, 3), (1, 2)}
✔️ Reflexive ✅
✔️ Transitive ✅
❌ Not symmetric
(v) Symmetric and transitive but not reflexive
🟢 Example: R = {(1, 2), (2, 1)}
✔️ Symmetric ✅
✔️ Transitive (no triplets violating) ✅
❌ Not reflexive

🔵 Question 11:
Show that the relation R in the set A of points in a plane given by
➡️ R = {(P, Q) : distance of the point P from the origin is same as the distance of the point Q from the origin}
is an equivalence relation.
Further, show that the set of all points related to a point P ≠ (0, 0) is the circle passing through P with origin as centre.
🟢 Answer:
Let P(x₁, y₁) and Q(x₂, y₂) be two points in the plane.
Distance from origin:
➡️ OP = √(x₁² + y₁²), OQ = √(x₂² + y₂²)
Given condition:
P R Q ⇔ OP = OQ
✔️ Reflexive:
For every P, OP = OP
∴ (P, P) ∈ R ✅
✔️ Symmetric:
If (P, Q) ∈ R ⇒ OP = OQ
Then OQ = OP ⇒ (Q, P) ∈ R ✅
✔️ Transitive:
If (P, Q) ∈ R and (Q, R) ∈ R,
then OP = OQ and OQ = OR ⇒ OP = OR
⇒ (P, R) ∈ R ✅
✅ Hence, R is reflexive, symmetric, and transitive.
∴ R is an equivalence relation.
💡 Set of all points related to P(x₁, y₁):
All Q(x, y) such that √(x² + y²) = √(x₁² + y₁²)
⇒ x² + y² = x₁² + y₁²
➡️ This represents a circle with centre at origin and radius = √(x₁² + y₁²), passing through P. ✅

🔵 Question 12:
Show that the relation R defined in the set A of all triangles as
➡️ R = {(T₁, T₂) : T₁ is similar to T₂}
is an equivalence relation.
Consider three right-angled triangles T₁ with sides 3, 4, 5; T₂ with sides 5, 12, 13; T₃ with sides 6, 8, 10.
Which triangles among T₁, T₂, T₃ are related?
🟢 Answer:
✔️ Reflexive:
Every triangle is similar to itself.
∴ (T₁, T₁) ∈ R ✅
✔️ Symmetric:
If T₁ ∼ T₂, then T₂ ∼ T₁ ✅
✔️ Transitive:
If T₁ ∼ T₂ and T₂ ∼ T₃, then T₁ ∼ T₃ ✅
✅ Hence, R is equivalence relation.
💡 Now check similarity:
T₁ sides 3, 4, 5
T₂ sides 5, 12, 13
T₃ sides 6, 8, 10
Check ratios:
T₁: 3:4:5
T₃: 6:8:10 = 3:4:5 ✅ → T₁ ∼ T₃
T₂: 5:12:13 ≠ 3:4:5 ❌
✅ Therefore, T₁ and T₃ are related (similar), T₂ is not related to them.

🔵 Question 13:
Show that the relation R defined in the set A of all polygons as
➡️ R = {(P₁, P₂) : P₁ and P₂ have same number of sides}
is an equivalence relation.
What is the set of all elements in A related to the right-angled triangle T with sides 3, 4, 5?
🟢 Answer:
✔️ Reflexive:
Each polygon has same number of sides as itself. ✅
✔️ Symmetric:
If P₁ and P₂ have same number of sides,
then P₂ and P₁ also have same number of sides. ✅
✔️ Transitive:
If P₁ and P₂ have same number of sides and P₂ and P₃ also have same number,
then P₁ and P₃ have same number of sides. ✅
✅ Hence R is an equivalence relation.
💡 A right-angled triangle has 3 sides,
So, the set of all elements related to T is
➡️ All triangles (3-sided polygons) in A.

🔵 Question 14:
Let L be the set of all lines in XY-plane and R the relation in L defined as
➡️ R = {(L₁, L₂) : L₁ is parallel to L₂}
Show that R is an equivalence relation.
Find the set of all lines related to the line y = 2x + 4.
🟢 Answer:
✔️ Reflexive:
Every line is parallel to itself. ✅
✔️ Symmetric:
If L₁ ∥ L₂, then L₂ ∥ L₁. ✅
✔️ Transitive:
If L₁ ∥ L₂ and L₂ ∥ L₃, then L₁ ∥ L₃. ✅
✅ Hence, R is an equivalence relation.
💡 Line y = 2x + 4 has slope m = 2.
All lines parallel to it have same slope 2.
➡️ Set of all related lines:
{y = 2x + c | c ∈ ℝ}

Question 15
Let R be the relation in the set {1, 2, 3, 4} given by
R = {(1, 2), (2, 2), (1, 1), (4, 4), (1, 3), (3, 3), (3, 2)}. Choose the correct answer:
(A) R is reflexive and symmetric but not transitive.
(B) R is reflexive and transitive but not symmetric.
(C) R is symmetric and transitive but not reflexive.
(D) R is an equivalence relation.
Answer
✏️ Reflexive check: need (1,1), (2,2), (3,3), (4,4) ∈ R → all four are present ✔️
✏️ Symmetric check: (1,2) ∈ R but (2,1) ∉ R → not symmetric ❌
✏️ Transitive check: verify chains:
• (1,2) and (2,2) ⇒ (1,2) ∈ R ✔️
• (1,3) and (3,2) ⇒ (1,2) ∈ R ✔️
• (3,2) and (2,2) ⇒ (3,2) ∈ R ✔️
• Self-pairs keep transitivity intact ✔️
Hence transitive ✔️
✅ Correct option: (B) R is reflexive and transitive but not symmetric.

Question 16
Let R be the relation in the set ℕ given by R = {(a, b) : a = b − 2, b > 6}. Choose the correct answer.
(A) (2, 4) ∈ R
(B) (3, 8) ∈ R
(C) (6, 8) ∈ R
(D) (8, 7) ∈ R
Answer
✏️ Condition: a = b − 2 and b > 6
• (2,4): 2 = 4 − 2 ✔️ but b = 4 ≯ 6 ❌ → not in R
• (3,8): 3 = 8 − 2 ⇒ 3 = 6 ❌ → not in R
• (6,8): 6 = 8 − 2 ✔️ and b = 8 > 6 ✔️ → in R
• (8,7): 8 = 7 − 2 ⇒ 8 = 5 ❌ → not in R
✅ Correct option: (C) (6, 8) ∈ R

Exercise 1.2

🔵 Question 1:
Show that the function f : R* → R*, defined by f(x) = 1/x is one-one and onto, where R* is the set of all non-zero real numbers.
Is the result true, if the domain R* is replaced by N with co-domain being same as R*?
🟢 Answer:
✏️ Let f(x) = 1/x
➤ Step 1: Show f is one-one
Take any x₁, x₂ ∈ R*, and suppose
f(x₁) = f(x₂)
➡️ 1/x₁ = 1/x₂
➡️ Cross multiply: x₂ = x₁
✔️ Hence, f is one-one.

➤ Step 2: Show f is onto
Let y ∈ R* be any element.
We need to find x ∈ R* such that f(x) = y.
➡️ f(x) = y
➡️ 1/x = y
➡️ x = 1/y
Since y ≠ 0, 1/y ∈ R*
✔️ Therefore, f is onto.
✅ So, f is one-one and onto on R*.

➤ Step 3: When domain = N
If domain = N, co-domain = R*:
f(x) = 1/x ∈ (0,1] ⊂ R*
Here,
✔️ f is one-one (no repetition)
❌ Not onto, since negative and >1 values in R* are not covered.
✅ Final: f is one-one but not onto when domain is N.

🔵 Question 2:
Check the injectivity and surjectivity of the following functions:
(i) f : N → N given by f(x) = x²
(ii) f : Z → Z given by f(x) = x²
(iii) f : R → R given by f(x) = x²
(iv) f : N → N given by f(x) = x³
(v) f : Z → Z given by f(x) = x³
🟢 Answer:

✳️ (i) f : N → N, f(x) = x²
➡️ f(1)=1, f(2)=4, f(3)=9 (distinct)
✔️ One-one (injective)
🧠 Every natural number is not a perfect square
❌ Not onto
✅ One-one but not onto

✳️ (ii) f : Z → Z, f(x) = x²
➡️ f(2)=4, f(-2)=4
❌ Not one-one
🧠 Negative integers not obtained as f(x)
❌ Not onto
✅ Neither one-one nor onto

✳️ (iii) f : R → R, f(x) = x²
➡️ f(2)=4, f(-2)=4
❌ Not one-one
🧠 Negative y not possible since x² ≥ 0
❌ Not onto
✅ Neither one-one nor onto

✳️ (iv) f : N → N, f(x) = x³
➡️ Distinct inputs → distinct outputs
✔️ One-one
🧠 Not all natural numbers are cubes
❌ Not onto
✅ One-one but not onto

✳️ (v) f : Z → Z, f(x) = x³
➡️ f(a)=f(b) ⇒ a³=b³ ⇒ a=b
✔️ One-one
🧠 For every y ∈ Z, take x = ∛y ∈ Z
✔️ Onto
✅ One-one and onto

🔵 Question 3:
Prove that the Greatest Integer Function f : R → R, given by f(x) = [x], is neither one-one nor onto, where [x] denotes the greatest integer less than or equal to x.
🟢 Answer:
✏️ Definition: [x] = greatest integer ≤ x
Examples: [2.3] = 2, [−1.2] = −2

➤ Step 1: Check one-one
Take x₁ = 1.2 and x₂ = 1.5
➡️ f(1.2) = [1.2] = 1
➡️ f(1.5) = [1.5] = 1
❌ f(x₁) = f(x₂) though x₁ ≠ x₂
✅ Hence not one-one

➤ Step 2: Check onto
For any y ∈ R, can we find x such that [x] = y?
Let y = 2.5
No x exists such that [x] = 2.5, since [x] is always integer.
❌ Hence not onto
✅ Therefore, f is neither one-one nor onto.

🔵 Question 4:
Show that the Modulus Function f : R → R, given by f(x) = |x|, is neither one-one nor onto,
where |x| is x, if x is positive or 0, and |x| = –x, if x is negative.
🟢 Answer:
✏️ Let f(x) = |x|
➡️ For x = 2, f(2) = |2| = 2
➡️ For x = –2, f(–2) = |–2| = 2
💡 Since f(2) = f(–2) but 2 ≠ –2, the function is not one-one.
➡️ Co-domain = R
➡️ Range = R⁺ ∪ {0}
⚡ Range ≠ Co-domain ⇒ function is not onto.
✔️ Therefore, f(x) = |x| is neither one-one nor onto.

🔵 Question 5:
Show that the Signum Function f : R → R, given by
f(x) =
1, if x > 0
0, if x = 0
–1, if x < 0
is neither one-one nor onto.
🟢 Answer:
✏️ Take f(2) = 1 and f(5) = 1
💡 Different inputs give same output ⇒ not one-one.
➡️ Range = {–1, 0, 1}
➡️ Co-domain = R
💡 Some elements like 2, 3 ∈ R are not in range ⇒ not onto.
✔️ Hence, the function is neither one-one nor onto.

🔵 Question 6:
Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let
f = {(1, 4), (2, 5), (3, 6)} be a function from A to B.
Show that f is one-one.
🟢 Answer:
✏️ Each element of A has a distinct image in B:
f(1) = 4, f(2) = 5, f(3) = 6
💡 No two elements of A have the same image ⇒ f is one-one.
➡️ Range = {4, 5, 6}
➡️ Co-domain = {4, 5, 6, 7}
⚡ Range ≠ Co-domain ⇒ not onto.
✔️ Therefore, f is one-one but not onto.

🔵 Question 7:
In each of the following cases, state whether the function is one-one, onto or bijective. Justify your answer.
(i) f : R → R defined by f(x) = 3 – 4x
(ii) f : R → R defined by f(x) = 1 + x²
🟢 Answer (i):
✏️ Let f(x₁) = f(x₂)
⇒ 3 – 4x₁ = 3 – 4x₂
⇒ x₁ = x₂
✔️ So, f is one-one.
➡️ For any y ∈ R,
y = 3 – 4x ⇒ x = (3 – y)/4 ∈ R
✔️ Hence, f is onto.
💡 Therefore, f is bijective (both one-one and onto).
🟢 Answer (ii):
✏️ f(x) = 1 + x²
For x₁ = 1 and x₂ = –1,
f(1) = 2 and f(–1) = 2
💡 Different inputs same output ⇒ not one-one.
➡️ Range = [1, ∞)
➡️ Co-domain = R
⚡ Range ≠ Co-domain ⇒ not onto.
✔️ Therefore, f(x) = 1 + x² is neither one-one nor onto.

🔵 Question 8:
Let A and B be sets. Show that f : A × B → B × A such that f(a, b) = (b, a) is bijective function.
🟢 Answer:
✏️ Let f(a, b) = (b, a)
➡️ One-one:
Assume f(a₁, b₁) = f(a₂, b₂)
⇒ (b₁, a₁) = (b₂, a₂)
⇒ b₁ = b₂ and a₁ = a₂
✔️ Hence (a₁, b₁) = (a₂, b₂)
💡 So f is one-one.
➡️ Onto:
Let (b, a) ∈ B × A.
We can find (a, b) ∈ A × B such that f(a, b) = (b, a).
✔️ So every element in co-domain has a pre-image.
✅ Therefore, f is bijective.

🔵 Question 9:
Let f : N → N be defined by
f(n) = (n + 1)/2, if n is odd
f(n) = n/2, if n is even
for all n ∈ N.
State whether the function f is bijective.
🟢 Answer:
➡️ For odd n: f(1)=1, f(3)=2, f(5)=3, …
➡️ For even n: f(2)=1, f(4)=2, f(6)=3, …
💡 Range = N (since every natural number appears)
✔️ Each value in N has exactly one pre-image (either odd or even number).
So f is one-one and onto.
✅ Hence f is bijective.

🔵 Question 10:
Let A = R – {3} and B = R – {1}.
Consider f : A → B defined by f(x) = (x – 2)/(x – 3).
Is f one-one and onto?
🟢 Answer:
✏️ Let f(x₁) = f(x₂)
⇒ (x₁ – 2)/(x₁ – 3) = (x₂ – 2)/(x₂ – 3)
Cross multiply: (x₁ – 2)(x₂ – 3) = (x₂ – 2)(x₁ – 3)
Simplify ⇒ x₁ = x₂
✔️ f is one-one.
➡️ To check onto:
Let y ∈ B.
y = (x – 2)/(x – 3)
⇒ y(x – 3) = x – 2
⇒ yx – 3y = x – 2
⇒ x(y – 1) = 3y – 2
⇒ x = (3y – 2)/(y – 1)
Since y ≠ 1 ⇒ x ≠ 3 ⇒ x ∈ A.
✔️ So f is onto.
✅ Hence f is bijective.

🔵 Question 11:
Let f : R → R be defined as f(x) = x^4.
Choose the correct answer:
(A) f is one-one onto
(B) f is many-one onto
(C) f is one-one but not onto
(D) f is neither one-one nor onto
🟢 Answer:
➡️ f(1) = 1 and f(–1) = 1
💡 Different inputs same output ⇒ not one-one.
➡️ Range = [0, ∞), Co-domain = R
💡 Range ≠ Co-domain ⇒ not onto.
✔️ Hence correct option: (D) f is neither one-one nor onto.

🔵 Question 12:
Let f : R → R be defined as f(x) = 3x.
Choose the correct answer:
(A) f is one-one onto
(B) f is many-one onto
(C) f is one-one but not onto
(D) f is neither one-one nor onto
🟢 Answer:
✏️ Let f(x₁) = f(x₂)
⇒ 3x₁ = 3x₂
⇒ x₁ = x₂
✔️ So f is one-one.
➡️ For any y ∈ R, let y = 3x ⇒ x = y/3 ∈ R.
✔️ So f is onto.
✅ Correct option: (A) f is one-one onto.

JEE MAINS QUESTIONS FROM THIS LESSON

Q1. If A = {1, 2, 3} and B = {4, 5}, then the number of relations from A to B is:
(A) 4
(B) 16
(C) 64
(D) 32
Answer: (C)
Year: 2024 | Shift: 1 | Set: A

Q2. The function f: R → R defined by f(x) = 3x + 5 is:
(A) One-one only
(B) Onto only
(C) Bijective
(D) Neither one-one nor onto
Answer: (C)
Year: 2024 | Shift: 2 | Set: B

Q3. The number of reflexive relations on a set with n elements is:
(A) 2ⁿ
(B) 2ⁿⁿ
(C) 2^(n(n-1)/2)
(D) 2^(n² – n)
Answer: (B)
Year: 2023 | Shift: 2 | Set: A

Q4. The range of the modulus function f(x) = |x| is:
(A) R
(B) [0, ∞)
(C) (0, ∞)
(D) None of these
Answer: (B)
Year: 2023 | Shift: 1 | Set: C

Q5. If the number of elements in A is 3 and in B is 2, the number of functions from A to B is:
(A) 6
(B) 8
(C) 9
(D) 10
Answer: (C)
Year: 2023 | Shift: 2 | Set: B

Q6. The function f(x) = |x| is:
(A) One-one
(B) Onto
(C) Neither one-one nor onto
(D) Bijective
Answer: (C)
Year: 2022 | Shift: 2 | Set: A

Q7. The set of all real numbers except zero is the domain of:
(A) Identity function
(B) Modulus function
(C) Signum function
(D) Reciprocal function
Answer: (D)
Year: 2022 | Shift: 1 | Set: B

Q8. If A = {1, 2} and B = {3, 4, 5}, then the number of functions from A to B is:
(A) 6
(B) 8
(C) 9
(D) 10
Answer: (C)
Year: 2022 | Shift: 2 | Set: C

Q9. Which of the following functions is not invertible?
(A) f(x) = x³
(B) f(x) = |x|
(C) f(x) = x + 2
(D) f(x) = 2x + 1
Answer: (B)
Year: 2021 | Shift: 2 | Set: A

Q10. The greatest integer function is discontinuous at:
(A) All integers
(B) All real numbers
(C) All rational numbers
(D) No point
Answer: (A)
Year: 2021 | Shift: 1 | Set: B

Q11. The range of signum function is:
(A) {−1, 0, 1}
(B) {0, 1}
(C) (0, 1)
(D) {−1, 1}
Answer: (A)
Year: 2020 | Shift: 2 | Set: A

Q12. If f(x) = ⌊x⌋, then f(3.7) is:
(A) 3
(B) 4
(C) 3.7
(D) None of these
Answer: (A)
Year: 2020 | Shift: 1 | Set: C

Q13. For any non-empty set A, the number of relations on A is:
(A) 2^(n²)
(B) 2ⁿ
(C) n²
(D) 2^n(n-1)
Answer: (A)
Year: 2020 | Shift: 2 | Set: B

Q14. The domain of greatest integer function is:
(A) Z
(B) N
(C) R
(D) None
Answer: (C)
Year: 2019 | Shift: 1 | Set: A

Q15. If A = {1, 2, 3}, B = {4, 5}, number of elements in A × B is:
(A) 3
(B) 5
(C) 6
(D) 9
Answer: (C)
Year: 2019 | Shift: 2 | Set: C

Q16. The range of f(x) = |x − 2| + 3 is:
(A) [2, ∞)
(B) [3, ∞)
(C) (2, ∞)
(D) (3, ∞)
Answer: (B)
Year: 2019 | Shift: 1 | Set: B

Q17. The function f(x) = x² is:
(A) One-one on R
(B) Onto on R
(C) Bijective from R to R
(D) Not invertible on R
Answer: (D)
Year: 2018 | Shift: 1 | Set: A

Q18. The modulus function is:
(A) Odd
(B) Even
(C) Both
(D) Neither
Answer: (B)
Year: 2018 | Shift: 2 | Set: B

Q19. Which is the inverse of f(x) = 2x + 3?
(A) (x − 3)/2
(B) (x + 3)/2
(C) 2x − 3
(D) 1/(x + 3)
Answer: (A)
Year: 2018 | Shift: 1 | Set: C

Q20. If f: R → R defined by f(x) = x³, then it is:
(A) One-one only
(B) Onto only
(C) Bijective
(D) Neither
Answer: (C)
Year: 2017 | Shift: 1 | Set: B

Q21. The function signum is defined as:
(A) −1 if x < 0, 0 if x = 0, 1 if x > 0
(B) 1 if x < 0, 0 if x = 0, −1 if x > 0
(C) 0 for all x
(D) None of these
Answer: (A)
Year: 2017 | Shift: 2 | Set: A

Q22. A function which maps each element to itself is called:
(A) Identity
(B) Constant
(C) Modulus
(D) Greatest Integer
Answer: (A)
Year: 2016 | Shift: 1 | Set: A

Q23. The function f(x) = 1/(x − 1) is not defined at:
(A) 1
(B) 0
(C) −1
(D) None
Answer: (A)
Year: 2016 | Shift: 2 | Set: C

Q24. Greatest Integer function is represented as:
(A) [x]
(B) {x}
(C) |x|
(D) None
Answer: (A)
Year: 2015 | Shift: 1 | Set: B

Q25. The function f(x) = |x − 5| is minimum at:
(A) 0
(B) 5
(C) −5
(D) 1
Answer: (B)
Year: 2015 | Shift: 2 | Set: A

Q26. The domain of the signum function is:
(A) R
(B) N
(C) Z
(D) None
Answer: (A)
Year: 2014 | Shift: 1 | Set: B

Q27. Which of the following functions is bijective from R to R?
(A) f(x) = 2x + 1
(B) f(x) = x²
(C) f(x) = |x|
(D) f(x) = x³ + 2
Answer: (D)
Year: 2014 | Shift: 2 | Set: A

Q28. For f(x) = |x − 4| + 2, the minimum value of f is:
(A) 2
(B) 4
(C) 6
(D) None
Answer: (A)
Year: 2013 | Shift: 2 | Set: C

Q29. The range of f(x) = |x + 2| is:
(A) R
(B) [0, ∞)
(C) (0, ∞)
(D) None
Answer: (B)
Year: 2013 | Shift: 1 | Set: A

Q30. The function f(x) = [x] is called:
(A) Floor function
(B) Ceiling function
(C) Modulus function
(D) None
Answer: (A)
Year: 2012 | Shift: 2 | Set: B

Q31. If A = {1, 2, 3}, B = {a, b}, number of onto functions from A to B is:
(A) 0
(B) 6
(C) 4
(D) None
Answer: (A)
Year: 2012 | Shift: 1 | Set: C

Q32. Which of the following relations on Z is symmetric?
(A) (a, b): a − b is even
(B) (a, b): a + b is 0
(C) (a, b): a = b
(D) (a, b): a > b
Answer: (A)
Year: 2011 | Shift: 2 | Set: A

Q33. Which function is even?
(A) f(x) = x
(B) f(x) = x³
(C) f(x) = |x|
(D) f(x) = 1/x
Answer: (C)
Year: 2011 | Shift: 1 | Set: B

Q34. The function f: A → B is onto when:
(A) Every element of A is mapped
(B) Every element of B is an image
(C) Both
(D) None
Answer: (B)
Year: 2010 | Shift: 2 | Set: C

Q35. Which of the following functions is neither one-one nor onto?
(A) f(x) = x³
(B) f(x) = x
(C) f(x) = x²
(D) f(x) = x + 1
Answer: (C)
Year: 2010 | Shift: 1 | Set: A

Q36. If f(x) = |x| + 1, range is:
(A) (1, ∞)
(B) [1, ∞)
(C) [0, ∞)
(D) None
Answer: (B)
Year: 2009 | Shift: 2 | Set: B

Q37. Domain of modulus function is:
(A) R
(B) Z
(C) N
(D) None
Answer: (A)
Year: 2009 | Shift: 1 | Set: A

Q38. If a function maps every real number to its square, its nature is:
(A) Injective
(B) Surjective
(C) Neither on R to R
(D) Bijective
Answer: (C)
Year: 2008 | Shift: 2 | Set: C

Q39. The function f(x) = 1/x is not defined at:
(A) 1
(B) 0
(C) −1
(D) None
Answer: (B)
Year: 2008 | Shift: 1 | Set: A

Q40. Greatest Integer function graph has discontinuities at:
(A) Integers
(B) Even numbers only
(C) Odd numbers only
(D) None
Answer: (A)
Year: 2007 | Shift: 2 | Set: B

Q41. A relation is said to be reflexive if:
(A) (a, a) ∈ R
(B) (a, b) ∈ R
(C) (b, a) ∈ R
(D) None
Answer: (A)
Year: 2007 | Shift: 1 | Set: C

Q42. The range of greatest integer function from 0 to 3 is:
(A) {0, 1, 2}
(B) {0, 1, 2, 3}
(C) [0, 3)
(D) (0, 3]
Answer: (A)
Year: 2006 | Shift: 2 | Set: A

Q43. The function f: R → R given by f(x) = 5x − 1 is:
(A) One-one
(B) Onto
(C) Bijective
(D) None
Answer: (C)
Year: 2006 | Shift: 1 | Set: B

Q44. Which of the following is not a function?
(A) y² = x
(B) y = x²
(C) y = |x|
(D) y = x + 1
Answer: (A)
Year: 2005 | Shift: 2 | Set: A

Q45. If A = {1, 2}, number of functions from A to A is:
(A) 2
(B) 3
(C) 4
(D) 5
Answer: (C)
Year: 2005 | Shift: 1 | Set: B

Q46. The modulus function has minimum at:
(A) 0
(B) 1
(C) −1
(D) None
Answer: (A)
Year: 2004 | Shift: 2 | Set: C

Q47. Which function is not invertible?
(A) f(x) = x
(B) f(x) = x²
(C) f(x) = 2x + 1
(D) f(x) = x³
Answer: (B)
Year: 2004 | Shift: 1 | Set: A

Q48. The function mapping each x to |x| is:
(A) Odd
(B) Even
(C) Neither
(D) Both
Answer: (B)
Year: 2003 | Shift: 2 | Set: B

Q49. If A = {1, 2}, B = {3, 4}, number of elements in A × B is:
(A) 2
(B) 4
(C) 6
(D) 8
Answer: (B)
Year: 2003 | Shift: 1 | Set: A

Q50. Greatest Integer function is denoted by:
(A) [x]
(B) (x)
(C) |x|
(D) None
Answer: (A)
Year: 2001 | Shift: 1 | Set: C

JEE ADVANCED QUESTIONS FROM THIS LESSON

Q1–Q17: From JEE Advanced Paper 1
Q1. The function f: R → R defined by f(x) = 3x + 2 is:
(A) One-one only
(B) Onto only
(C) Bijective
(D) Neither
Answer: (C)
Year: 2025 | Paper: 1 | Set: 1

Q2. A relation R on set A is reflexive if:
(A) (a, a) ∈ R
(B) (a, b) ∈ R
(C) (b, a) ∈ R
(D) None
Answer: (A)
Year: 2024 | Paper: 1 | Set: 1

Q3. Number of functions from A = {1, 2} to B = {3, 4, 5} is:
(A) 4
(B) 8
(C) 9
(D) 6
Answer: (C)
Year: 2024 | Paper: 1 | Set: 2

Q4. The range of modulus function f(x) = |x| is:
(A) R
(B) [0, ∞)
(C) (0, ∞)
(D) None
Answer: (B)
Year: 2023 | Paper: 1 | Set: 1

Q5. The number of reflexive relations on a set of size n is:
(A) 2ⁿ
(B) 2ⁿⁿ
(C) 2^(n(n−1)/2)
(D) 2^(n² − n)
Answer: (B)
Year: 2023 | Paper: 1 | Set: 2

Q6. The function f(x) = |x| is:
(A) One-one
(B) Onto
(C) Neither
(D) Bijective
Answer: (C)
Year: 2022 | Paper: 1 | Set: 1

Q7. Which of the following is the domain of the signum function?
(A) R
(B) N
(C) Z
(D) None
Answer: (A)
Year: 2022 | Paper: 1 | Set: 2

Q8. The range of signum function is:
(A) {−1, 0, 1}
(B) {0, 1}
(C) (0, 1)
(D) {−1, 1}
Answer: (A)
Year: 2021 | Paper: 1 | Set: 1

Q9. If f(x) = ⌊x⌋, then f(3.7) is:
(A) 3
(B) 4
(C) 3.7
(D) None
Answer: (A)
Year: 2021 | Paper: 1 | Set: 2

Q10. The domain of greatest integer function is:
(A) Z
(B) N
(C) R
(D) None
Answer: (C)
Year: 2020 | Paper: 1 | Set: 1

Q11. Which of the following is even function?
(A) f(x) = x
(B) f(x) = x³
(C) f(x) = |x|
(D) f(x) = 1/x
Answer: (C)
Year: 2020 | Paper: 1 | Set: 2

Q12. The function f(x) = x² is:
(A) One-one on R
(B) Onto on R
(C) Not invertible on R
(D) Bijective
Answer: (C)
Year: 2019 | Paper: 1 | Set: 1

Q13. Inverse of f(x) = 2x + 3 is:
(A) (x − 3)/2
(B) (x + 3)/2
(C) 2x − 3
(D) None
Answer: (A)
Year: 2019 | Paper: 1 | Set: 2

Q14. The minimum of f(x) = |x − 4| + 2 is:
(A) 2
(B) 4
(C) 6
(D) None
Answer: (A)
Year: 2018 | Paper: 1 | Set: 1

Q15. The range of f(x) = |x + 2| is:
(A) R
(B) [0, ∞)
(C) (0, ∞)
(D) None
Answer: (B)
Year: 2018 | Paper: 1 | Set: 2

Q16. The function mapping x to x is:
(A) Identity
(B) Constant
(C) Modulus
(D) None
Answer: (A)
Year: 2017 | Paper: 1 | Set: 1

Q17. Which function is not invertible?
(A) f(x) = x
(B) f(x) = x²
(C) f(x) = 2x + 1
(D) f(x) = x³
Answer: (B)
Year: 2017 | Paper: 1 | Set: 2

Q18–Q34: From JEE Advanced Paper 2
Q18. The function signum is defined as:
(A) −1 if x < 0, 0 if x = 0, 1 if x > 0
(B) 1 if x < 0, 0 if x = 0, −1 if x > 0
(C) 0 for all x
(D) None
Answer: (A)
Year: 2025 | Paper: 2 | Set: 1

Q19. Which function is bijective from R to R?
(A) f(x) = 2x + 1
(B) f(x) = x²
(C) f(x) = |x|
(D) f(x) = x³ + 2
Answer: (D)
Year: 2024 | Paper: 2 | Set: 2

Q20. The function f(x) = |x| + 1 has range:
(A) (1, ∞)
(B) [1, ∞)
(C) [0, ∞)
(D) None
Answer: (B)
Year: 2023 | Paper: 2 | Set: 1

Q21. Which relation is symmetric on Z?
(A) (a, b): a − b is even
(B) (a, b): a + b is 0
(C) (a, b): a = b
(D) (a, b): a > b
Answer: (A)
Year: 2023 | Paper: 2 | Set: 2

Q22. Which of the following is domain of modulus function?
(A) R
(B) Z
(C) N
(D) None
Answer: (A)
Year: 2022 | Paper: 2 | Set: 1

Q23. A relation is transitive if:
(A) aRb and bRc ⇒ aRc
(B) aRb ⇒ bRa
(C) aRb ⇒ aRa
(D) None
Answer: (A)
Year: 2022 | Paper: 2 | Set: 2

Q24. The function f(x) = x³ is:
(A) One-one only
(B) Onto only
(C) Bijective
(D) Neither
Answer: (C)
Year: 2021 | Paper: 2 | Set: 1

Q25. The function mapping every x to |x| is:
(A) Odd
(B) Even
(C) Neither
(D) Both
Answer: (B)
Year: 2021 | Paper: 2 | Set: 2

Q26. If A = {1, 2}, number of functions from A to A is:
(A) 2
(B) 3
(C) 4
(D) 5
Answer: (C)
Year: 2020 | Paper: 2 | Set: 1

Q27. Which function is neither one-one nor onto?
(A) f(x) = x³
(B) f(x) = x
(C) f(x) = x²
(D) f(x) = x + 1
Answer: (C)
Year: 2020 | Paper: 2 | Set: 2

Q28. If a function maps every element to itself, it is called:
(A) Identity
(B) Constant
(C) Modulus
(D) Greatest Integer
Answer: (A)
Year: 2019 | Paper: 2 | Set: 1

Q29. The range of greatest integer function from 0 to 3 is:
(A) {0, 1, 2}
(B) {0, 1, 2, 3}
(C) [0, 3)
(D) (0, 3]
Answer: (A)
Year: 2019 | Paper: 2 | Set: 2

Q30. Greatest Integer function is discontinuous at:
(A) All integers
(B) All real numbers
(C) All rationals
(D) None
Answer: (A)
Year: 2018 | Paper: 2 | Set: 1

Q31. Which function is even?
(A) f(x) = x
(B) f(x) = x³
(C) f(x) = |x|
(D) f(x) = 1/x
Answer: (C)
Year: 2018 | Paper: 2 | Set: 2

Q32. Which is the inverse of f(x) = 5x − 1?
(A) (x + 1)/5
(B) (x − 1)/5
(C) 5x + 1
(D) None
Answer: (B)
Year: 2017 | Paper: 2 | Set: 1

Q33. If A = {1, 2, 3}, B = {a, b}, number of onto functions from A to B is:
(A) 0
(B) 6
(C) 4
(D) None
Answer: (A)
Year: 2017 | Paper: 2 | Set: 2

Q34. Range of f(x) = |x − 3| + 2 is:
(A) [2, ∞)
(B) [3, ∞)
(C) [0, ∞)
(D) None
Answer: (B)
Year: 2016 | Paper: 2 | Set: 1

MODEL PRATICE SET FOR COMPETITION EXAMS

🧠 (Q1–Q20)
Q1. A relation R on set A = {1, 2, 3} defined by R = {(1,1), (2,2), (3,3)} is
🔵 (A) Symmetric
🟢 (B) Reflexive
🟠 (C) Transitive
🔴 (D) All of these
Answer: (D) All of these
Q2. If R = {(1,2), (2,3), (1,3)} on A = {1,2,3}, then R is
🔵 (A) Reflexive
🟢 (B) Symmetric
🟠 (C) Transitive
🔴 (D) None
Answer: (C) Transitive
Q3. For A = {x ∈ N | x < 5}, number of reflexive relations is
🔵 (A) 2⁵
🟢 (B) 2²⁵
🟠 (C) 2¹⁰
🔴 (D) 2²⁰
Answer: (B) 2²⁵
Q4. If f(x) = 2x + 3, then f(2) =
🔵 (A) 7
🟢 (B) 5
🟠 (C) 6
🔴 (D) 4
Answer: (A) 7
Q5. Domain of f(x) = sqrt(4 − x²) is
🔵 (A) (−∞, ∞)
🟢 (B) [−2, 2]
🟠 (C) (−2, 2)
🔴 (D) [0, 4]
Answer: (B) [−2, 2]
Q6. f: R → R, f(x) = x² is
🔵 (A) One-one
🟢 (B) Onto
🟠 (C) Many-one
🔴 (D) Bijective
Answer: (C) Many-one
Q7. f(x) = 2x + 1, g(x) = x². Then (g ∘ f)(x) =
🔵 (A) 4x² + 4x + 1
🟢 (B) (2x + 1)²
🟠 (C) 2x² + 1
🔴 (D) x² + 2x + 1
Answer: (B) (2x + 1)²
Q8. If f(x) = 3x − 5, then f⁻¹(x) =
🔵 (A) (x + 5)/3
🟢 (B) 3x + 5
🟠 (C) (x − 5)/3
🔴 (D) None
Answer: (A) (x + 5)/3
Q9. Range of f(x) = |x| is
🔵 (A) R
🟢 (B) [0, ∞)
🟠 (C) (−∞, 0]
🔴 (D) (−∞, ∞)
Answer: (B) [0, ∞)
Q10. Signum function f(x) = sgn(x) equals −1 when
🔵 (A) x < 0
🟢 (B) x = 0
🟠 (C) x > 0
🔴 (D) None
Answer: (A) x < 0
Q11. If A = {1, 2}, number of all relations from A to A =
🔵 (A) 16
🟢 (B) 8
🟠 (C) 4
🔴 (D) 12
Answer: (A) 16
Q12. The inverse of identity function is
🔵 (A) Constant
🟢 (B) Identity
🟠 (C) Reciprocal
🔴 (D) None
Answer: (B) Identity
Q13. Domain of f(x) = 1/(x − 2) is
🔵 (A) R
🟢 (B) R − {2}
🟠 (C) (−∞, 2)
🔴 (D) (2, ∞)
Answer: (B) R − {2}
Q14. If f(x) = x³, then f is
🔵 (A) One-one
🟢 (B) Onto
🟠 (C) Bijective
🔴 (D) All
Answer: (D) All
Q15. Number of equivalence relations on {1, 2, 3} is
🔵 (A) 3
🟢 (B) 5
🟠 (C) 6
🔴 (D) 4
Answer: (B) 5
Q16. If f(x) = x² + 1, then range is
🔵 (A) R
🟢 (B) [1, ∞)
🟠 (C) (−∞, 1)
🔴 (D) (1, ∞)
Answer: (B) [1, ∞)
Q17. Constant function is
🔵 (A) One-one
🟢 (B) Onto
🟠 (C) Many-one
🔴 (D) Bijective
Answer: (C) Many-one
Q18. For A = {1, 2}, B = {a, b}, number of functions from A to B =
🔵 (A) 2
🟢 (B) 4
🟠 (C) 8
🔴 (D) 16
Answer: (B) 4
Q19. A function f: A → B is onto if
🔵 (A) Range ⊆ Co-domain
🟢 (B) Range = Co-domain
🟠 (C) Range ⊂ Co-domain
🔴 (D) None
Answer: (B) Range = Co-domain
Q20. The set of all equivalence classes forms a
🔵 (A) Subset
🟢 (B) Partition
🟠 (C) Relation
🔴 (D) Function
Answer: (B) Partition

🧠 JEE Main Level (Q21–Q40)
Q21. Number of bijective functions from set {1,2,3} onto itself =
🔵 (A) 3
🟢 (B) 6
🟠 (C) 9
🔴 (D) 12
Answer: (B) 6
Q22. Let f(x) = 2x + 3, g(x) = x − 1. Then (f ∘ g)(x) =
🔵 (A) 2x + 1
🟢 (B) 2x + 5
🟠 (C) 2x − 1
🔴 (D) 2x − 3
Answer: (A) 2x + 1
Q23. If f: R → R defined by f(x) = x² is not one-one because
🔵 (A) f(1) = f(−1)
🟢 (B) Range = R
🟠 (C) Domain = R
🔴 (D) None
Answer: (A) f(1) = f(−1)
Q24. If f(x) = 3x − 2, find f⁻¹(x)
🔵 (A) (x + 2)/3
🟢 (B) (x − 2)/3
🟠 (C) 3x + 2
🔴 (D) None
Answer: (A) (x + 2)/3
Q25. If f(x) = x³, g(x) = x + 1, find (g ∘ f)(2)
🔵 (A) 9
🟢 (B) 7
🟠 (C) 10
🔴 (D) 8
Answer: (A) 9
Q26. If f(x) = x², domain = R, range = [0, ∞), then f is
🔵 (A) One-one only
🟢 (B) Onto only
🟠 (C) Neither
🔴 (D) Onto (restricted)
Answer: (B) Onto only
Q27. If A = {1,2,3}, total number of functions from A to A =
🔵 (A) 27
🟢 (B) 81
🟠 (C) 9
🔴 (D) 6
Answer: (A) 27
Q28. Let f(x) = x² + 2x + 1, find range
🔵 (A) [0, ∞)
🟢 (B) [1, ∞)
🟠 (C) [2, ∞)
🔴 (D) None
Answer: (B) [1, ∞)
Q29. If f: R → R defined by f(x) = x³ is bijective, then f⁻¹(x) =
🔵 (A) x³
🟢 (B) x^(1/3)
🟠 (C) 3x
🔴 (D) None
Answer: (B) x^(1/3)
Q30. f(x) = x + 2, g(x) = 3x, then (f ∘ g)(x) =
🔵 (A) 3x + 2
🟢 (B) x + 6
🟠 (C) 3x² + 2
🔴 (D) None
Answer: (A) 3x + 2
Q31. If f(x) = |x|, then f(f(x)) =
🔵 (A) x
🟢 (B) |x|
🟠 (C) −x
🔴 (D) None
Answer: (B) |x|
Q32. Function f: R → R, f(x) = 2x is
🔵 (A) One-one and onto
🟢 (B) Only onto
🟠 (C) Only one-one
🔴 (D) None
Answer: (A) One-one and onto
Q33. Inverse of f(x) = (x − 2)/(x + 3)
🔵 (A) (3x + 2)/(1 − x)
🟢 (B) (2x + 3)/(1 − x)
🟠 (C) (2x − 3)/(1 + x)
🔴 (D) None
Answer: (A) (3x + 2)/(1 − x)
Q34. Binary operation * on R defined by a * b = a + b + 2 is
🔵 (A) Commutative
🟢 (B) Not associative
🟠 (C) No identity
🔴 (D) None
Answer: (A) Commutative
Q35. For above *, identity element e =
🔵 (A) 0
🟢 (B) −2
🟠 (C) 2
🔴 (D) None
Answer: (B) −2
Q36. Inverse of element a under * is
🔵 (A) −a
🟢 (B) −a − 4
🟠 (C) −a − 2
🔴 (D) None
Answer: (C) −a − 4
Q37. Range of f(x) = |x − 2| is
🔵 (A) [0, ∞)
🟢 (B) R
🟠 (C) (−∞, 0]
🔴 (D) None
Answer: (A) [0, ∞)
Q38. If f: [0, ∞) → [0, ∞), f(x) = x², then f is
🔵 (A) Bijective
🟢 (B) One-one
🟠 (C) Onto
🔴 (D) None
Answer: (A) Bijective
Q39. If f(x) = 2x + 1, find g(x) so that g ∘ f = I
🔵 (A) (x − 1)/2
🟢 (B) (x + 1)/2
🟠 (C) 2x − 1
🔴 (D) None
Answer: (A) (x − 1)/2
Q40. If f(x) = 1 − x, then f(f(x)) =
🔵 (A) x
🟢 (B) 1 − x
🟠 (C) 1
🔴 (D) −x
Answer: (A) x

🧠 JEE Advanced Level (Q41–Q50)
Q41. If f(x) = 2x + 1, g(x) = 3x + 2, find (f ∘ g)⁻¹(x)
🔵 (A) (x − 8)/6
🟢 (B) (x − 5)/3
🟠 (C) (x − 2)/3
🔴 (D) None
Answer: (A) (x − 8)/6
Q42. If f(x) = x/(x + 1), then f⁻¹(x) =
🔵 (A) x/(1 − x)
🟢 (B) x/(x − 1)
🟠 (C) 1/(x − 1)
🔴 (D) None
Answer: (A) x/(1 − x)
Q43. If f: R − {−1} → R − {1}, f(x) = (1 + x)/(1 − x), then f⁻¹(x) =
🔵 (A) (x − 1)/(x + 1)
🟢 (B) (1 − x)/(1 + x)
🟠 (C) (x + 1)/(x − 1)
🔴 (D) None
Answer: (A) (x − 1)/(x + 1)
Q44. If f(x) = 3x − 2 and g(x) = (x + 2)/3, then
🔵 (A) g = f⁻¹
🟢 (B) f = g⁻¹
🟠 (C) Both
🔴 (D) None
Answer: (C) Both
Q45. If f(x) = 1/x, then f(f(f(x))) =
🔵 (A) x
🟢 (B) 1/x
🟠 (C) 1/x²
🔴 (D) x²
Answer: (A) x
Q46. Number of equivalence relations on set {1,2,3,4}
🔵 (A) 15
🟢 (B) 52
🟠 (C) 73
🔴 (D) 10
Answer: (B) 52
Q47. If * defined on R by a * b = a + b + ab, then identity =
🔵 (A) 1
🟢 (B) 0
🟠 (C) −1
🔴 (D) None
Answer: (C) −1
Q48. Inverse of element a under above * =
🔵 (A) −a/(1 + a)
🟢 (B) 1/a
🟠 (C) −a
🔴 (D) None
Answer: (A) −a/(1 + a)
Q49. If f(x) = (2x − 3)/(x − 2), find f⁻¹(x)
🔵 (A) (2x − 3)/(x − 2)
🟢 (B) (3 − 2x)/(2 − x)
🟠 (C) (2x + 3)/(x + 2)
🔴 (D) (3x + 2)/(x + 2)
Answer: (B) (3 − 2x)/(2 − x)
Q50. For binary operation * on Z defined by a * b = a + b − ab, identity is
🔵 (A) 0
🟢 (B) 1
🟠 (C) −1
🔴 (D) None
Answer: (B) 1

MIND MAP

——————————————————————————————————————————————————————————————————————————————————————————-

Important Notice : The lessons and study materials up to July–August 2025 have been sent. Soon, after receiving feedback from teachers and students, we will deliver the latest and more innovative study materials for the upcoming months.