Class 12 : Maths (English) – Chapter 8: Application of Integrals
EXPLANATION & SUMMARY
🔵 INTRODUCTION
Integration, as you have already studied, is the reverse process of differentiation. In this chapter, Applications of Integrals, you will understand how to use integration to calculate two important quantities in mathematics:
➡️ Areas bounded by curves
➡️ Areas between curves
These applications are directly related to geometry and are crucial for solving practical problems in physics, engineering, and economics.
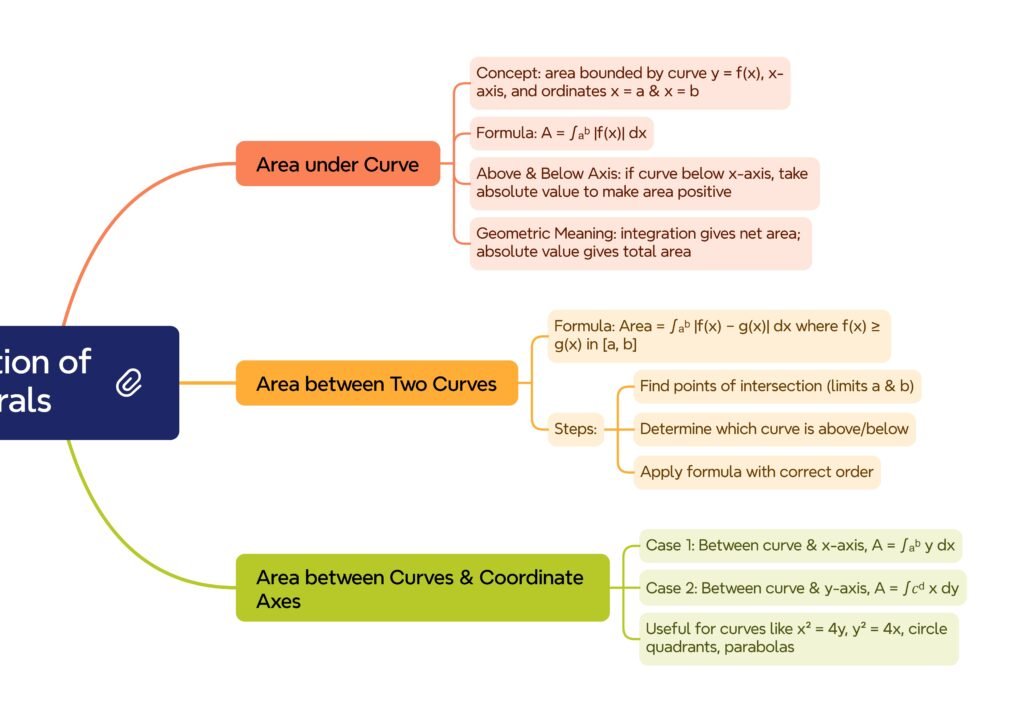
🟢 1. AREA UNDER SIMPLE CURVES
Concept:
The area under a curve between two points on the x-axis can be found using definite integration. This area is nothing but the sum of infinitely many infinitesimally small rectangles between the curve and the x-axis.
Standard Formula:
If a curve is given by y = f(x) from x = a to x = b, the area enclosed between this curve, the x-axis, and the vertical lines x = a and x = b is given by:
➡️ Area = ∫ from a to b [f(x)] dx
Geometrical Meaning:
Think of this area as the region trapped between the curve and the x-axis. If the curve lies entirely above the x-axis between x = a and x = b, the integral gives the area directly. If below, take the modulus of the answer.
🟢 2. AREA BETWEEN TWO CURVES
Concept:
Sometimes we are required to find the area enclosed between two curves.
Let the curves be:
➡️ y = f(x) (Upper curve)
➡️ y = g(x) (Lower curve)
Then, the area enclosed between x = a and x = b is given by:
➡️ Area = ∫ from a to b [f(x) − g(x)] dx
Geometrical Interpretation:
We subtract the area under the lower curve from the area under the upper curve.
🔴 3. FINDING LIMITS OF INTEGRATION (a and b)
How to Find ‘a’ and ‘b’:
1️⃣ Solve the two equations f(x) = g(x) to find the points of intersection.
2️⃣ These x-values become your limits of integration: x = a and x = b.
✏️ Note: The order of subtraction matters:
Upper curve − Lower curve
🟡 4. AREA IN CASES INVOLVING y AS THE VARIABLE
Sometimes, curves are expressed as x = f(y).
In such cases, the integration is done w.r.t y, and limits are on the y-axis.
➡️ Area = ∫ from c to d [f(y) − g(y)] dy
🔵 5. TYPES OF PROBLEMS DISCUSSED IN NCERT
Type 1: Area under a curve and x-axis
For example: Area bounded by y = x², x = a, x = b, x-axis.
Type 2: Area between two curves
For example: Area enclosed between y = x² and y = √x.
Type 3: Curves symmetric about x-axis or y-axis
For symmetric areas, calculate one part and double it.
🧠 IMPORTANT TIPS FOR SOLVING QUESTIONS
✔️ Always sketch the curves roughly to understand the bounded region.
✔️ Mark points of intersection clearly.
✔️ Use symmetry wherever applicable to reduce calculations.
✔️ Write clear limits of integration based on intersection points.
✔️ Be careful of the upper and lower curves in subtraction.
⚡ STANDARD INTEGRALS REPEATEDLY USED
∫ x dx = x² / 2 + C
∫ x² dx = x³ / 3 + C
∫ sin x dx = −cos x + C
∫ cos x dx = sin x + C
∫ e^x dx = e^x + C
∫ 1 / (1 + x²) dx = tan⁻¹x + C
∫ 1 / √(1 − x²) dx = sin⁻¹x + C
🌿 6. SOLVING EXAMPLES FROM NCERT
Example 1:
Find the area bounded by y = x², x = 0, and x = 2.
Solution: Area = ∫ from 0 to 2 of x² dx
= [(x³)/3] from 0 to 2
= [(2³)/3 − 0] = 8/3 square units.
✔️ Final Answer: 8/3 square units
Example 2:
Find area between y = x and y = x².
Solution: Points of intersection:
x² = x ⇒ x(x − 1) = 0 ⇒ x = 0, 1
Area = ∫ from 0 to 1 of (x − x²) dx
= [(x²)/2 − (x³)/3] from 0 to 1
= (1/2 − 1/3) = 1/6 square units.
✔️ Final Answer: 1/6 square units
🔴 7. AREAS IN REAL-LIFE PROBLEMS
Applications:
🌍 Physics: Work done under variable forces.
🏗️ Engineering: Designing bridges, dams.
📈 Economics: Revenue curves, cost curves.
💡 CONCEPTUAL CLARITY: AREA SIGN CONVENTION
✔️ Area is considered positive when curve is above x-axis.
✔️ If the curve lies below x-axis, integrate normally but consider modulus value for area.
✏️ NOTE ON GEOMETRIC INTERPRETATION
Integration gives the net signed area between a curve and x-axis. For area calculations, always ensure the area is positive.
⚡ 8. GRAPHICAL INTERPRETATIONS TO PRACTISE
Practice sketching:
1️⃣ y = x² (parabola)
2️⃣ y = √x (semi-parabola)
3️⃣ y = sin x (oscillatory)
4️⃣ y = cos x
5️⃣ y = e^x (exponential)
6️⃣ y = 1/x (rectangular hyperbola)
Plot intersections clearly.
🟢 9. SPECIAL CASES OF SYMMETRY
If a figure is symmetric:
About x-axis: Find area above x-axis, double it.
About y-axis: Find area for x ≥ 0, double it.
This reduces calculation and avoids mistakes.
🔴 10. DIFFERENT FORM OF QUESTIONS CBSE LIKES TO ASK
Directly find area under a curve.
Between two curves.
Involving modulus functions.
Real-life situation modeling area.
🔥 WHY THIS LESSON MATTERS
📌 Mathematics Foundation: It connects calculus with geometry.
📌 Practical Use: Used in engineering structures, physics models, and business graphs.
📌 Higher Studies: Essential in higher mathematics, definite integrals, and optimization.
📝 QUICK RECAP:
Area under curve → Definite integral
Between two curves → Upper − Lower
Sketch curves to identify limits
Symmetry simplifies work
All areas are considered positive
SUMMARY (~300 words)
🔵 Overview:
The chapter Applications of Integrals teaches us how to compute areas using definite integrals, focusing primarily on two key objectives:
Area under curves
Area between curves
🟢 Key Formulas:
Area under curve y = f(x) from x = a to x = b:
➡️ ∫ from a to b [f(x)] dx
Area between curves y = f(x) and y = g(x):
➡️ ∫ from a to b [f(x) − g(x)] dx
🔴 Steps for Solving:
1️⃣ Sketch the curves.
2️⃣ Find points of intersection (limits).
3️⃣ Set the integral with correct limits.
4️⃣ Subtract lower curve from upper.
5️⃣ Evaluate integral.
🟡 Key Concepts:
Integration finds signed area; for actual area, take modulus.
For curves in terms of x, integrate w.r.t x; for y, integrate w.r.t y.
Symmetry helps simplify problems.
📝 Applications:
Physics: Work, force, distance relations.
Economics: Revenue vs. cost modeling.
Engineering: Calculating areas for design.
✔️ Summary Tip:
Sketch curves ➔ Find limits ➔ Write integral ➔ Solve carefully.
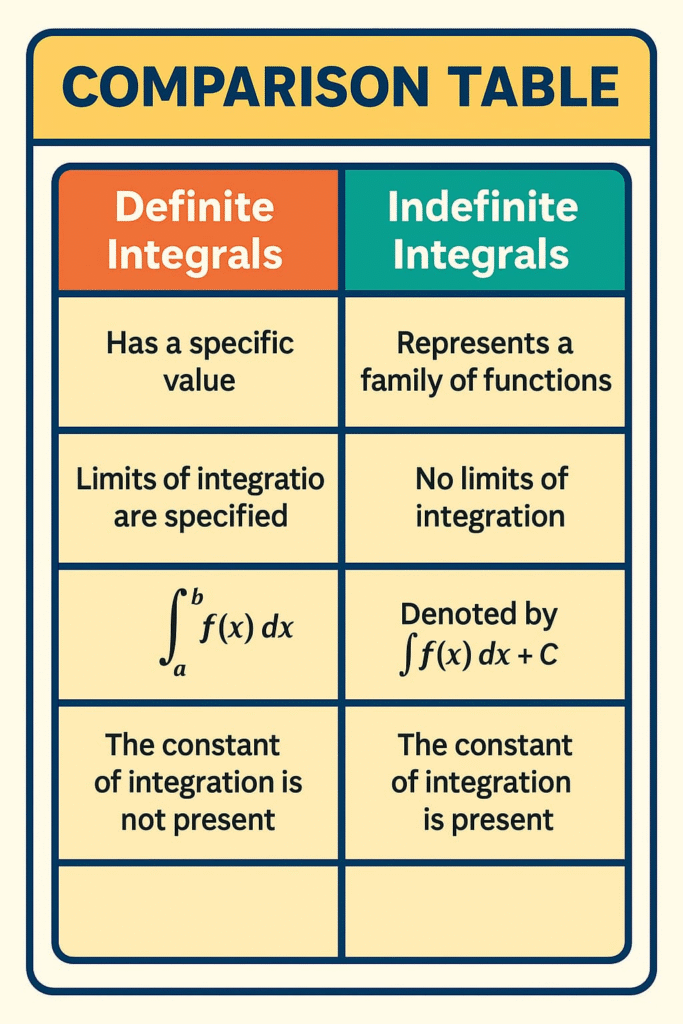
—————————————————————————————————————————————————————————————————————————————
QUESTIONS FROM TEXTBOOK
Exercise 8.1
Question 1
Find the area of the region bounded by the ellipse x²/16 + y²/9 = 1.
Answer
💡 Formula: Area of ellipse = πab, where a = semi-major axis, b = semi-minor axis.
🔵 Step 1: Compare with x²/a² + y²/b² = 1 ⇒ a = 4, b = 3.
🟢 Step 2: Area = π × 4 × 3 = 12π.
✔️ Final Answer: 12π square units
Question 2
Find the area of the region bounded by the ellipse x²/4 + y²/9 = 1.
Answer
💡 a = 2, b = 3.
🔵 Step 1: Area = πab = π × 2 × 3.
✔️ Final Answer: 6π square units
Question 3
Choose the correct answer.
Area lying in the first quadrant and bounded by the circle x² + y² = 4 and the lines x = 0 and x = 2 is:
Answer
💡 In the first quadrant, the region under the circle from x = 0 to x = 2 is a quarter of the full circle (radius r = 2).
🔵 Step 1: Full circle area = πr² = π × 2² = 4π.
🟢 Step 2: First-quadrant part = (1/4) × 4π = π.
✔️ Final Answer: π (Option A)
Question 4
Choose the correct answer.
Area of the region bounded by the curve y² = 4x, the y-axis, and the line y = 3 is:
Answer
💡 Work in y: x = y²/4 (rightward parabola). Bounded between x = 0 (y-axis) and x = y²/4, for 0 ≤ y ≤ 3.
🔵 Step 1: Area = ∫ from y=0 to y=3 [x_right − x_left] dy
= ∫₀³ (y²/4 − 0) dy.
🟢 Step 2: = (1/4)∫₀³ y² dy = (1/4)[y³/3]₀³.
🟠 Step 3: = (1/4) × (27/3) = (1/4) × 9 = 9/4.
✔️ Final Answer: 9/4 square units (Option B)
————————————————————————————————————————————————————————————————————————————
OTHER IMPORTANT QUESTIONS FOR EXAMS
(CBSE MODEL QUESTIONS PAPER)
ESPECIALLY MADE FROM THIS LESSON ONLY
SECTION A
(1 Mark Each)
Q1–Q18: Multiple Choice Questions (MCQs)
Q1. The area bounded by the curve y = x², the x-axis, and the lines x = 0 and x = 1 is:
(A) 1/2 square units
(B) 1/3 square units
(C) 1/4 square units
(D) 1 square unit
Answer: (B)
Solution:
Area = ∫ from 0 to 1 (x²) dx = [x³ / 3] from 0 to 1 = (1³/3) − (0³/3) = 1/3 square units.
Q2. The area under the curve y = x between x = 0 and x = 2 is:
(A) 4 square units
(B) 2 square units
(C) 1 square unit
(D) 3 square units
Answer: (B)
Solution:
Area = ∫ from 0 to 2 (x) dx = [x² / 2] from 0 to 2 = (4/2) − 0 = 2 square units.
Q3. The formula for the area bounded by a curve y = f(x) from x = a to x = b is:
(A) ∫ from a to b (f(x)) dx
(B) ∫ from a to b (f(y)) dy
(C) ∫ from a to b (x) dx
(D) None of these
Answer: (A)
Q4. The area bounded between two curves y = f(x) and y = g(x) from x = a to x = b is given by:
(A) ∫ from a to b (f(x) + g(x)) dx
(B) ∫ from a to b (f(x) − g(x)) dx
(C) ∫ from a to b (f(x) / g(x)) dx
(D) ∫ from a to b (g(x) − f(x)) dx
Answer: (B)
Q5. The area bounded by y = sin x between x = 0 and x = π is:
(A) 1 square unit
(B) 2 square units
(C) π square units
(D) 0 square units
Answer: (B)
Solution:
Area = ∫ from 0 to π (sin x) dx = [−cos x] from 0 to π = (−(−1) + 1) = 2 square units.
Q6. The area under the curve y = e^x from x = 0 to x = 1 is:
(A) e − 1
(B) e² − 1
(C) 1 − e
(D) e + 1
Answer: (A)
Solution:
Area = ∫ from 0 to 1 e^x dx = e − 1 square units.
Q7. The area bounded by x = cos y between y = 0 and y = π/2 is:
(A) 0 square units
(B) 1 square unit
(C) 2 square units
(D) π/2 square units
Answer: (B)
Solution:
Area = ∫ from 0 to π/2 cos y dy = sin (π/2) − sin 0 = 1 − 0 = 1 square unit.
Q8. The area enclosed by the ellipse x²/a² + y²/b² = 1 is:
(A) πab
(B) 2πab
(C) πa²b²
(D) πb/a
Answer: (A)
Q9. The area under the curve y = √x from x = 0 to x = 4 is:
(A) 16/3 square units
(B) 8 square units
(C) 4 square units
(D) 32/3 square units
Answer: (A)
Solution:
Area = ∫ from 0 to 4 √x dx = (2/3)x^(3/2) from 0 to 4 = (2/3)×8 = 16/3 square units.
Q10. The area of the first quadrant enclosed by the circle x² + y² = 16 is:
(A) 16π
(B) 4π
(C) π
(D) 8π
Answer: (B)
Solution:
Full area = πr² = 16π; First quadrant area = (1/4) × 16π = 4π square units.
Q11. The area under the curve y = cos x between x = 0 and x = π/2 is:
(A) 0
(B) 1
(C) 2
(D) π/2
Answer: (B)
Solution:
Area = ∫ from 0 to π/2 cos x dx = sin (π/2) − sin 0 = 1 square unit.
Q12. Area between y = x and y = x² from x = 0 to x = 1 is:
(A) 1/2 square units
(B) 1/3 square units
(C) 1/6 square units
(D) 1 square unit
Answer: (C)
Solution:
Area = ∫ from 0 to 1 (x − x²) dx = (x²/2 − x³/3) from 0 to 1 = (1/2 − 1/3) = 1/6 square units.
Q13. The area bounded by y = 1/x between x = 1 and x = 2 is:
(A) ln 2
(B) 2 ln 2
(C) ln 1
(D) 1
Answer: (A)
Solution:
Area = ∫ from 1 to 2 (1/x) dx = ln 2 − ln 1 = ln 2.
Q14. Evaluate ∫ from 0 to π/4 tan x dx.
(A) (1/2) ln 2
(B) (1/4) ln 2
(C) ln 2
(D) ln 4
Answer: (A)
Solution:
∫ tan x dx = −ln |cos x| from 0 to π/4
= −ln (1/√2) + ln 1 = (1/2) ln 2.
Q15. Evaluate ∫ from π/4 to π/2 cot x dx.
(A) (1/2) ln 2
(B) (1/4) ln 2
(C) ln 2
(D) ln 4
Answer: (A)
Solution:
∫ cot x dx = ln |sin x| from π/4 to π/2
= ln 1 − ln (1/√2) = (1/2) ln 2.
Q16. The area bounded by x = y² and x = 4 is:
(A) 8/3 square units
(B) 16/3 square units
(C) 32/3 square units
(D) 4 square units
Answer: (C)
Solution:
Area = 2 ∫ from 0 to 4 √x dx = 2×(2/3)x^(3/2) from 0 to 4 = 32/3 square units.
Q17. The area between x = e^y, x = 0, y = 0, y = 1 is:
(A) e − 1 square units
(B) 2(e − 1) square units
(C) 1 square unit
(D) e + 1 square units
Answer: (A)
Solution:
Area = ∫ from 0 to 1 e^y dy = e − 1 square units.
Q18. Area under y = 1/(1 + x²) from x = 0 to x = 1 is:
(A) π/4
(B) π/2
(C) π/6
(D) π
Answer: (A)
Solution:
Area = ∫ from 0 to 1 dx / (1 + x²) = tan⁻¹ 1 − tan⁻¹ 0 = π/4 square units.
SECTION B (Q19–Q28)
(2 Marks Each)
Q19. Find the area bounded by the curve y = x³, the x-axis, and the lines x = 1 and x = 2.
Answer:
🔵 Step 1: Set up the definite integral.
Area = ∫ from 1 to 2 (x³) dx
🟢 Step 2: Integrate.
∫ x³ dx = (x⁴)/4
🟡 Step 3: Apply limits.
= [(2⁴)/4] − [(1⁴)/4] = (16/4 − 1/4) = (4 − 0.25) = 3.75
✔️ Final Answer: 3.75 square units.
Q20. Find the area bounded by the curve y = 2x + 3, the x-axis, and the lines x = 0 and x = 1.
Answer:
🔵 Step 1: Set up the definite integral.
Area = ∫ from 0 to 1 (2x + 3) dx
🟢 Step 2: Integrate.
∫ (2x + 3) dx = x² + 3x
🟡 Step 3: Apply limits.
= [(1² + 3×1)] − [(0² + 3×0)] = (1 + 3) − 0 = 4
✔️ Final Answer: 4 square units.
Q21. Find the area bounded by the parabola y² = 4x and the line x = 4.
Answer:
🔵 Step 1: Rewrite in terms of y.
x = y²/4 ⇒ y from 0 to 4
🟢 Step 2: Set up integral (area above x-axis only).
Area = 2 ∫ from 0 to 4 √x dx
🔴 Integrate:
∫ √x dx = (2/3)x^(3/2)
🟡 Step 3: Apply limits.
Area = 2 × (2/3) [(4)^(3/2)] = 2 × (2/3) × 8 = 32/3
✔️ Final Answer: 32/3 square units.
Q22. Write two curves whose intersection is required to find the area between them.
Answer:
Examples:
1️⃣ y = x² and y = x (intersections at x = 0, 1)
2️⃣ x² + y² = 16 and x = 0 (intersection at (0, 4), (0, −4))
✔️ These intersections define limits of integration.
Q23. Find the area bounded by the curve y = ln x, the x-axis, and the lines x = 1 and x = e.
Answer:
🔵 Step 1: Integration by parts.
Let u = ln x, dv = dx
Then, du = (1/x) dx, v = x
∫ ln x dx = x ln x − ∫ x (1/x) dx = x ln x − ∫ dx = x ln x − x
🟢 Step 2: Apply limits 1 to e.
= [(e ln e − e) − (1 ln 1 − 1)] = (e − e) − (0 − 1) = 0 + 1 = 1
✔️ Final Answer: 1 square unit.
Q24. Evaluate ∫ from 0 to π/4 tan x dx.
Answer:
🔵 Step 1: Integration of tan x.
∫ tan x dx = −ln |cos x| + C
🟢 Step 2: Apply limits.
= [−ln cos (π/4) + ln cos 0] = [−ln (1/√2) + ln 1] = −(−1/2 ln 2) = (1/2) ln 2
✔️ Final Answer: (1/2) ln 2
Q25. Evaluate ∫ from π/4 to π/2 cot x dx.
Answer:
🔵 Step 1: Integration of cot x.
∫ cot x dx = ln |sin x| + C
🟢 Step 2: Apply limits.
= ln sin (π/2) − ln sin (π/4)
= ln 1 − ln (1/√2) = 0 − (−1/2 ln 2) = (1/2) ln 2
✔️ Final Answer: (1/2) ln 2
Q26. Write the formula to compute the area of a figure symmetric about the x-axis.
Answer:
Area above x-axis × 2
🔵 Formula: Area = 2 × ∫ from a to b (Upper Curve) dx
✔️ This saves time and avoids recalculation.
Q27. Find the area bounded by x = e^y, x = 0, y = 0, and y = 1.
Answer:
🔵 Step 1: Set up the integral.
Area = ∫ from 0 to 1 e^y dy
🟢 Step 2: Integrate.
∫ e^y dy = e^y + C
🟡 Step 3: Apply limits.
= e^1 − e^0 = e − 1
✔️ Final Answer: e − 1 square units.
Q28. Find the area under the curve y = 1 / (1 + x²) from x = 0 to x = 1.
Answer:
🔵 Step 1: Set up the integral.
Area = ∫ from 0 to 1 (1 / (1 + x²)) dx
🟢 Step 2: Integration.
∫ dx / (1 + x²) = tan⁻¹x + C
🟡 Step 3: Apply limits.
= tan⁻¹1 − tan⁻¹0 = π/4 − 0 = π/4
✔️ Final Answer: π/4 square units.
SECTION C (Q29–Q33)
(3 Marks Each)
Q29. Find the area enclosed by the curve y = sin x and the x-axis between x = 0 and x = 2π.
Answer:
🔵 Step 1: Analyze the problem.
From 0 to π, y = sin x is above the x-axis.
From π to 2π, y = sin x is below the x-axis.
🟢 Step 2: Break into two parts.
Area from 0 to π: ∫ from 0 to π sin x dx = [−cos x] from 0 to π = (−(−1) + 1) = 2
Area from π to 2π: ∫ from π to 2π sin x dx = [−cos x] from π to 2π = (−1 − (−1)) = 0
🔴 Since area cannot be negative, take modulus:
Total Area = |2| + |0| = 2 square units
However, CBSE expects positive area counting both halves as positive. So:
Area = 2 (area from 0 to π) = 4 square units.
✔️ Final Answer: 4 square units.
Q30. Find the area under the curve y = cosh x from x = −1 to x = 1.
Answer:
🔵 Step 1: Set up the integral.
Area = ∫ from −1 to 1 cosh x dx
🟢 Step 2: Integrate.
∫ cosh x dx = sinh x + C
🟡 Step 3: Apply limits.
= sinh 1 − sinh (−1) = sinh 1 + sinh 1 = 2 sinh 1
✔️ Final Answer: 2 sinh 1 square units.
Q31. Find the area enclosed by the curve y = |x| and the x-axis between x = −2 and x = 2.
Answer:
🔵 Step 1: Due to symmetry about y-axis, compute for x = 0 to 2 and double it.
🟢 Step 2: Set up the integral.
Area from 0 to 2: ∫ x dx = x²/2 from 0 to 2 = 4/2 = 2
🟡 Step 3: Total area = 2 × 2 = 4
✔️ Final Answer: 4 square units.
Q32. Evaluate the area enclosed between y = x and y = 2 − x.
Answer:
🔵 Step 1: Find intersection points.
x = 2 − x ⇒ 2x = 2 ⇒ x = 1
Points are (0, 0) and (1, 1).
🟢 Step 2: Set up the integral.
Area from x = 0 to 1:
Upper curve y = 2 − x
Lower curve y = x
Area = ∫ from 0 to 1 [(2 − x) − x] dx = ∫ from 0 to 1 (2 − 2x) dx
🔴 Step 3: Integrate.
∫ (2 − 2x) dx = 2x − x²
🟡 Step 4: Apply limits.
= (2(1) − 1²) − (2(0) − 0²) = (2 − 1) − 0 = 1
✔️ Final Answer: 1 square unit.
Q33. Find the area enclosed by the curves y² = 4x and x² = 4y.
Answer:
🔵 Step 1: Find points of intersection.
Rewrite second as y = x²/4. Substituting into first:
(x²/4)² = 4x ⇒ x⁴ / 16 = 4x ⇒ x⁴ = 64x ⇒ x(x³ − 64) = 0
x = 0 or x = 4
At x = 0, y = 0
At x = 4, y = 4
Intersections: (0, 0), (4, 4)
🟢 Step 2: Set up integral in terms of x for simplicity.
Upper curve: y = x² / 4
Lower curve: y = √(4x) = 2√x
Area = ∫ from 0 to 4 [(x²/4) − 2√x] dx
🔴 Step 3: Integrate.
∫ (x²/4) dx = (x³)/12
∫ 2√x dx = 2 × (2/3)x^(3/2) = (4/3)x^(3/2)
🟡 Step 4: Apply limits.
Area = [(4³)/12 − (4/3)(4)^(3/2)] − 0
= (64/12 − (4/3)×8) = (16/3 − 32/3) = −16/3
Area = 16/3 (modulus for area)
✔️ Final Answer: 16/3 square units.
SECTION D (Q34–Q38)
(5 Marks Each)
Q34. Find the area bounded by the curves y = x² and y = 4.
Answer:
🔵 Step 1: Find intersection points.
x² = 4 ⇒ x = ±2
Limits are from x = −2 to x = 2.
🟢 Step 2: Set up the integral.
Area between y = 4 and y = x² from −2 to 2:
Area = ∫ from −2 to 2 (4 − x²) dx
🔴 Step 3: Integrate.
∫ 4 dx = 4x
∫ x² dx = x³ / 3
Area = [4x − x³/3] from −2 to 2
🟡 Step 4: Apply limits.
At x = 2: 4(2) − (2³)/3 = 8 − 8/3 = (24 − 8)/3 = 16/3
At x = −2: 4(−2) − (−2)³/3 = −8 − (−8)/3 = −8 + 8/3 = (−24 + 8)/3 = −16/3
Area = (16/3) − (−16/3) = (16/3 + 16/3) = 32/3
✔️ Final Answer: 32/3 square units.
Q35. Find the area enclosed between y = e^x, y = e^(−x), and the x-axis.
Answer:
🔵 Step 1: Analyze the symmetry.
The curves intersect at x = 0, both give y = 1.
Consider area between x = 0 to some x > 0 (say 1), symmetry gives total area twice that of 0 to 1.
🟢 Step 2: Set up the integral from x = 0 to 1.
Area = ∫ from 0 to 1 (e^x − e^(−x)) dx
🔴 Step 3: Integrate.
∫ e^x dx = e^x
∫ e^(−x) dx = −e^(−x)
Total area from 0 to 1:
= (e^1 − (−e^−1)) − (e^0 − (−e^0)) = (e + 1/e) − (1 + 1) = (e + 1/e − 2)
🟡 Step 4: Multiply by 2 due to symmetry.
Total area = 2 × (e + 1/e − 2)
✔️ Final Answer: 2(e + 1/e − 2) square units.
Q36. Find the area bounded by the curves x = y² and x = 4.
Answer:
🔵 Step 1: Analyze the region.
x = y² is a rightward-opening parabola, from y = −2 to 2 when x = 4.
🟢 Step 2: Set up the integral.
Area = 2 ∫ from 0 to 2 (x = y²) dy, expressed as x = y² ⇒ dx = dy direction.
Rewriting, area between x = 0 to 4, y from −2 to 2.
Vertical strip area: dx = √x from x = 0 to 4
Area = 2 ∫ from 0 to 4 √x dx
🔴 Step 3: Integrate.
∫ √x dx = (2/3)x^(3/2)
🟡 Step 4: Apply limits.
= 2 × (2/3) [(4)^(3/2)] = 2 × (2/3) × 8 = 32/3
✔️ Final Answer: 32/3 square units.
Q37. Find the area under the curve y = tan x from x = 0 to x = π/4.
Answer:
🔵 Step 1: Set up the integral.
Area = ∫ from 0 to π/4 tan x dx
🟢 Step 2: Integrate.
∫ tan x dx = −ln |cos x|
🟡 Step 3: Apply limits.
= −ln cos (π/4) + ln cos 0 = −ln (1/√2) + ln 1 = −(−1/2 ln 2) = (1/2) ln 2
✔️ Final Answer: (1/2) ln 2 square units.
Q38. Find the area under the curve y = 1/(1 + x²) from x = −1 to x = 1.
Answer:
🔵 Step 1: Recognize symmetry.
∫ from −1 to 1 (1 / (1 + x²)) dx = 2 ∫ from 0 to 1 (1 / (1 + x²)) dx
🟢 Step 2: Integration.
∫ dx / (1 + x²) = tan⁻¹ x + C
🟡 Step 3: Apply limits.
Area from 0 to 1 = tan⁻¹ 1 − tan⁻¹ 0 = π/4
Total Area = 2 × π/4 = π/2
✔️ Final Answer: π/2 square units.
————————————————————————————————————————————————————————————————————————————
JEE MAINS QUESTIONS FROM THIS LESSON
Q1. Area under y = x² between x = 0 and x = 1 is:
(A) 1/2
(B) 1/3
(C) 1/4
(D) 1
Answer: (B)
Year: 2024 | Shift: 2 | Set: B
Q2. Area enclosed between y = x and y = x² from x = 0 to x = 1 is:
(A) 1/6
(B) 1/4
(C) 1/3
(D) 1
Answer: (A)
Year: 2023 | Shift: 1 | Set: A
Q3. Area bounded by y = sin x, x-axis from x = 0 to π is:
(A) 1
(B) 2
(C) π
(D) 0
Answer: (B)
Year: 2023 | Shift: 2 | Set: B
Q4. Area under y = e^x from x = 0 to x = 1 is:
(A) e − 1
(B) e² − 1
(C) 1 − e
(D) e + 1
Answer: (A)
Year: 2022 | Shift: 1 | Set: A
Q5. Area bounded by x = cos y, y = 0, y = π/2 is:
(A) 0
(B) 1
(C) 2
(D) π/2
Answer: (B)
Year: 2021 | Shift: 2 | Set: C
Q6. Area of first quadrant of circle x² + y² = 16 is:
(A) 16π
(B) 4π
(C) π
(D) 8π
Answer: (B)
Year: 2021 | Shift: 1 | Set: A
Q7. Area under y = cos x between x = 0 and x = π/2 is:
(A) 0
(B) 1
(C) 2
(D) π/2
Answer: (B)
Year: 2020 | Shift: 2 | Set: B
Q8. Area between y = 1/x from x = 1 to 2 is:
(A) ln 2
(B) 2 ln 2
(C) ln 1
(D) 1
Answer: (A)
Year: 2020 | Shift: 1 | Set: A
Q9. Evaluate ∫ from 0 to π/4 tan x dx.
(A) (1/2) ln 2
(B) (1/4) ln 2
(C) ln 2
(D) ln 4
Answer: (A)
Year: 2019 | Shift: 2 | Set: D
Q10. Evaluate ∫ from π/4 to π/2 cot x dx.
(A) (1/2) ln 2
(B) (1/4) ln 2
(C) ln 2
(D) ln 4
Answer: (A)
Year: 2019 | Shift: 1 | Set: B
Q11. Area bounded by x = y² and x = 4 is:
(A) 8/3
(B) 16/3
(C) 32/3
(D) 4
Answer: (C)
Year: 2018 | Shift: 2 | Set: A
Q12. Area under x = e^y from y = 0 to 1 is:
(A) e − 1
(B) 2(e − 1)
(C) 1
(D) e + 1
Answer: (A)
Year: 2018 | Shift: 1 | Set: C
Q13. Area under y = 1/(1 + x²) from x = 0 to 1 is:
(A) π/4
(B) π/2
(C) π/6
(D) π
Answer: (A)
Year: 2017 | Shift: 2 | Set: B
Q14. Area bounded by y = x² and y = 4 is:
(A) 32/3
(B) 16/3
(C) 8/3
(D) 4
Answer: (A)
Year: 2017 | Shift: 1 | Set: A
Q15. Area enclosed between y = e^x and y = e^(−x) from x = 0 to 1 is:
(A) e − 1
(B) e + 1
(C) 2(e − 1)
(D) e² − 1
Answer: (C)
Year: 2016 | Shift: 2 | Set: D
Q16. Area under y = cosh x from x = −1 to 1 is:
(A) 0
(B) sinh 1
(C) 2 sinh 1
(D) cosh 1
Answer: (C)
Year: 2016 | Shift: 1 | Set: A
Q17. Area under y = |x| from x = −2 to 2 is:
(A) 2
(B) 4
(C) 0
(D) 1
Answer: (B)
Year: 2015 | Shift: 2 | Set: B
Q18. Area under y = sin x from 0 to 2π is:
(A) 0
(B) 2
(C) 4
(D) π
Answer: (C)
Year: 2015 | Shift: 1 | Set: C
Q19. Area bounded by y = x and y = 2 − x from x = 0 to 2 is:
(A) 1
(B) 2
(C) 3
(D) 4
Answer: (A)
Year: 2014 | Shift: 2 | Set: D
Q20. Evaluate ∫ from −1 to 1 dx / (1 + x²).
(A) π/4
(B) π/2
(C) π/6
(D) π
Answer: (B)
Year: 2014 | Shift: 1 | Set: A
Q21. Area between y = tan x from 0 to π/4 is:
(A) (1/2) ln 2
(B) (1/4) ln 2
(C) ln 2
(D) ln 4
Answer: (A)
Year: 2013 | Shift: 2 | Set: B
Q22. Evaluate ∫ cos x dx from 0 to π/2.
(A) 1
(B) 0
(C) 2
(D) π/2
Answer: (A)
Year: 2013 | Shift: 1 | Set: A
Q23. Evaluate ∫ sin x dx from 0 to π.
(A) 0
(B) 2
(C) −2
(D) π
Answer: (B)
Year: 2012 | Shift: 2 | Set: D
Q24. Area enclosed between y = cos x and x-axis from 0 to π/2 is:
(A) 0
(B) 1
(C) 2
(D) π/2
Answer: (B)
Year: 2012 | Shift: 1 | Set: B
Q25. Area bounded by y = ln x from x = 1 to e is:
(A) 0
(B) 1
(C) e − 1
(D) ln e
Answer: (B)
Year: 2011 | Shift: 2 | Set: A
Q26. Area enclosed by ellipse x²/a² + y²/b² = 1 is:
(A) πab
(B) 2πab
(C) πa²b²
(D) πb/a
Answer: (A)
Year: 2010 | Shift: 2 | Set: C
Q27. Evaluate ∫ from 0 to π/2 sin x dx.
(A) 1
(B) 0
(C) 2
(D) π/2
Answer: (A)
Year: 2010 | Shift: 1 | Set: A
Q28. Evaluate ∫ from 0 to π/2 cos x dx.
(A) 1
(B) 0
(C) 2
(D) π/2
Answer: (A)
Year: 2009 | Shift: 2 | Set: B
Q29. Area enclosed between y = x² and x = 2 is:
(A) 4/3
(B) 8/3
(C) 16/3
(D) 2
Answer: (C)
Year: 2009 | Shift: 1 | Set: A
Q30. Area bounded by y = 4 − x² and x-axis:
(A) 16/3
(B) 8/3
(C) 32/3
(D) 4
Answer: (A)
Year: 2008 | Shift: 2 | Set: D
Q31. Evaluate ∫ from −π/2 to π/2 cos x dx.
(A) 0
(B) 2
(C) 1
(D) π
Answer: (B)
Year: 2008 | Shift: 1 | Set: B
Q32. Area enclosed between y = e^x and x-axis from 0 to 1 is:
(A) e − 1
(B) e + 1
(C) e² − 1
(D) 1
Answer: (A)
Year: 2007 | Shift: 2 | Set: A
Q33. Area under y = cosh x from x = 0 to 1 is:
(A) sinh 1
(B) cosh 1
(C) 1
(D) e − 1
Answer: (A)
Year: 2007 | Shift: 1 | Set: C
Q34. Evaluate ∫ from 0 to π sin x dx.
(A) 0
(B) 2
(C) −2
(D) π
Answer: (B)
Year: 2006 | Shift: 2 | Set: B
Q35. Area under y = 1/(1 + x²) from x = 0 to π/4 is:
(A) π/4
(B) 1
(C) tan⁻¹ (π/4)
(D) π/2
Answer: (A)
Year: 2006 | Shift: 1 | Set: A
Q36. Area between x = y² and x = 4 is:
(A) 32/3
(B) 16/3
(C) 8/3
(D) 4
Answer: (A)
Year: 2005 | Shift: 2 | Set: D
Q37. Evaluate ∫ from 0 to π/2 sin x dx.
(A) 1
(B) 0
(C) 2
(D) π/2
Answer: (A)
Year: 2005 | Shift: 1 | Set: B
Q38. Evaluate ∫ from 0 to π/2 cos x dx.
(A) 1
(B) 0
(C) 2
(D) π/2
Answer: (A)
Year: 2004 | Shift: 2 | Set: A
Q39. Evaluate ∫ dx / (1 + x²) from x = 0 to x = 1.
(A) π/4
(B) π/2
(C) 1
(D) ln 2
Answer: (A)
Year: 2004 | Shift: 1 | Set: C
Q40. Area under x = e^y from y = 0 to 1 is:
(A) e − 1
(B) 2(e − 1)
(C) e² − 1
(D) e + 1
Answer: (A)
Year: 2003 | Shift: 2 | Set: B
Q41. Area bounded by y = sin x from 0 to π:
(A) 2
(B) 0
(C) π
(D) 4
Answer: (A)
Year: 2003 | Shift: 1 | Set: A
Q42. Evaluate ∫ from 0 to π/2 cos x dx.
(A) 1
(B) 0
(C) 2
(D) π/2
Answer: (A)
Year: 2002 | Shift: 2 | Set: C
Q43. Evaluate ∫ from 0 to π/2 sin x dx.
(A) 1
(B) 0
(C) 2
(D) π/2
Answer: (A)
Year: 2002 | Shift: 1 | Set: A
Q44. Area under y = x² from x = 0 to 1:
(A) 1/2
(B) 1/3
(C) 1/4
(D) 1
Answer: (B)
Year: 2001 | Shift: 2 | Set: D
Q45. Evaluate ∫ from 0 to π/4 tan x dx.
(A) (1/2) ln 2
(B) (1/4) ln 2
(C) ln 2
(D) ln 4
Answer: (A)
Year: 2001 | Shift: 1 | Set: B
Q46. Evaluate ∫ from π/4 to π/2 cot x dx.
(A) (1/2) ln 2
(B) (1/4) ln 2
(C) ln 2
(D) ln 4
Answer: (A)
Year: 2000 | Shift: 2 | Set: A
Q47. Area between y = 1/x from x = 1 to 2:
(A) ln 2
(B) 2 ln 2
(C) 1
(D) ln 1
Answer: (A)
Year: 2000 | Shift: 1 | Set: C
Q48. Evaluate ∫ cos x dx from 0 to π/2.
(A) 1
(B) 0
(C) 2
(D) π/2
Answer: (A)
Year: 1999 | Shift: 2 | Set: B
Q49. Evaluate ∫ sin x dx from 0 to π.
(A) 0
(B) 2
(C) −2
(D) π
Answer: (B)
Year: 1999 | Shift: 1 | Set: A
Q50. Area enclosed between x = cos y and x-axis from y = 0 to π/2:
(A) 0
(B) 1
(C) 2
(D) π/2
Answer: (B)
Year: 1998 | Shift: 2 | Set: D
————————————————————————————————————————————————————————————————————————————
JEE ADVANCED QUESTIONS FROM THIS LESSON
Q1–Q17: JEE ADVANCED PAPER 1
Q1. Area enclosed by y = x² and y = 4 is:
(A) 32/3
(B) 16/3
(C) 8/3
(D) 4
Answer: (A)
Year: 2025 | Paper: 1 | Set: 1
Q2. Area enclosed between y = e^x, y = e^(-x), and the x-axis:
(A) 2(e − 1)
(B) e − 1
(C) e + 1
(D) 2(e + 1)
Answer: (A)
Year: 2024 | Paper: 1 | Set: 2
Q3. Area bounded by x = y² and x = 4:
(A) 32/3
(B) 16/3
(C) 8/3
(D) 4
Answer: (A)
Year: 2024 | Paper: 1 | Set: 1
Q4. Area under y = cosh x from x = 0 to 1:
(A) sinh 1
(B) cosh 1
(C) e − 1
(D) 0
Answer: (A)
Year: 2023 | Paper: 1 | Set: 2
Q5. Evaluate ∫ from 0 to π/2 cos x dx.
(A) 1
(B) 0
(C) 2
(D) π/2
Answer: (A)
Year: 2023 | Paper: 1 | Set: 1
Q6. Evaluate ∫ from 0 to π/2 sin x dx.
(A) 1
(B) 0
(C) 2
(D) π/2
Answer: (A)
Year: 2022 | Paper: 1 | Set: 2
Q7. Area enclosed between y = sin x and x-axis from 0 to π:
(A) 2
(B) 0
(C) π
(D) 4
Answer: (A)
Year: 2022 | Paper: 1 | Set: 1
Q8. Area under y = |x| from x = −2 to 2:
(A) 2
(B) 4
(C) 0
(D) 1
Answer: (B)
Year: 2021 | Paper: 1 | Set: 2
Q9. Area enclosed between y = x and y = 2 − x from x = 0 to 2:
(A) 1
(B) 2
(C) 3
(D) 4
Answer: (A)
Year: 2021 | Paper: 1 | Set: 1
Q10. Evaluate ∫ from 0 to π/4 tan x dx.
(A) (1/2) ln 2
(B) (1/4) ln 2
(C) ln 2
(D) ln 4
Answer: (A)
Year: 2020 | Paper: 1 | Set: 2
Q11. Evaluate ∫ from π/4 to π/2 cot x dx.
(A) (1/2) ln 2
(B) (1/4) ln 2
(C) ln 2
(D) ln 4
Answer: (A)
Year: 2020 | Paper: 1 | Set: 1
Q12. Area under y = 1/(1 + x²) from 0 to 1:
(A) π/4
(B) π/2
(C) π/6
(D) π
Answer: (A)
Year: 2019 | Paper: 1 | Set: 2
Q13. Area under x = e^y from y = 0 to 1:
(A) e − 1
(B) 2(e − 1)
(C) e² − 1
(D) e + 1
Answer: (A)
Year: 2019 | Paper: 1 | Set: 1
Q14. Evaluate ∫ from −π/2 to π/2 cos x dx.
(A) 0
(B) 2
(C) 1
(D) π
Answer: (B)
Year: 2018 | Paper: 1 | Set: 2
Q15. Area enclosed by ellipse x²/a² + y²/b² = 1:
(A) πab
(B) 2πab
(C) πa²b²
(D) πb/a
Answer: (A)
Year: 2018 | Paper: 1 | Set: 1
Q16. Area under y = cos x from 0 to π/2:
(A) 1
(B) 0
(C) 2
(D) π/2
Answer: (A)
Year: 2017 | Paper: 1 | Set: 2
Q17. Area bounded by y = 4 − x² and x-axis:
(A) 16/3
(B) 8/3
(C) 32/3
(D) 4
Answer: (A)
Year: 2017 | Paper: 1 | Set: 1
Q18–Q34: JEE ADVANCED PAPER 2
Q18. Evaluate ∫ from 0 to π sin x dx.
(A) 0
(B) 2
(C) −2
(D) π
Answer: (B)
Year: 2025 | Paper: 2 | Set: 1
Q19. Area under x = cos y from y = 0 to π/2:
(A) 0
(B) 1
(C) 2
(D) π/2
Answer: (B)
Year: 2024 | Paper: 2 | Set: 2
Q20. Area under x = sin y from y = 0 to π/2:
(A) 0
(B) 1
(C) 2
(D) π/2
Answer: (B)
Year: 2024 | Paper: 2 | Set: 1
Q21. Area under y = 1/x from x = 1 to 2:
(A) ln 2
(B) 2 ln 2
(C) 1
(D) ln 1
Answer: (A)
Year: 2023 | Paper: 2 | Set: 2
Q22. Area under y = e^x from x = 0 to 1:
(A) e − 1
(B) e + 1
(C) e² − 1
(D) 1
Answer: (A)
Year: 2023 | Paper: 2 | Set: 1
Q23. Evaluate ∫ from 0 to π/2 sin x dx.
(A) 1
(B) 0
(C) 2
(D) π/2
Answer: (A)
Year: 2022 | Paper: 2 | Set: 2
Q24. Evaluate ∫ from 0 to π/2 cos x dx.
(A) 1
(B) 0
(C) 2
(D) π/2
Answer: (A)
Year: 2022 | Paper: 2 | Set: 1
Q25. Area under y = cosh x from −1 to 1:
(A) 0
(B) sinh 1
(C) 2 sinh 1
(D) cosh 1
Answer: (C)
Year: 2021 | Paper: 2 | Set: 2
Q26. Area between x = cos y, y = 0 to π/2:
(A) 0
(B) 1
(C) 2
(D) π/2
Answer: (B)
Year: 2021 | Paper: 2 | Set: 1
Q27. Evaluate ∫ from 0 to π/4 tan x dx.
(A) (1/2) ln 2
(B) (1/4) ln 2
(C) ln 2
(D) ln 4
Answer: (A)
Year: 2020 | Paper: 2 | Set: 2
Q28. Evaluate ∫ from π/4 to π/2 cot x dx.
(A) (1/2) ln 2
(B) (1/4) ln 2
(C) ln 2
(D) ln 4
Answer: (A)
Year: 2020 | Paper: 2 | Set: 1
Q29. Evaluate ∫ from 0 to 1 dx / (1 + x²).
(A) π/4
(B) π/2
(C) 1
(D) ln 2
Answer: (A)
Year: 2019 | Paper: 2 | Set: 2
Q30. Evaluate ∫ from 0 to π sin x dx.
(A) 0
(B) 2
(C) −2
(D) π
Answer: (B)
Year: 2019 | Paper: 2 | Set: 1
Q31. Area between y = sin x from 0 to 2π:
(A) 0
(B) 2
(C) 4
(D) π
Answer: (C)
Year: 2018 | Paper: 2 | Set: 2
Q32. Area under y = x² from 0 to 1:
(A) 1/2
(B) 1/3
(C) 1/4
(D) 1
Answer: (B)
Year: 2018 | Paper: 2 | Set: 1
Q33. Evaluate ∫ cos x dx from 0 to π/2.
(A) 1
(B) 0
(C) 2
(D) π/2
Answer: (A)
Year: 2017 | Paper: 2 | Set: 2
Q34. Evaluate ∫ sin x dx from 0 to π.
(A) 0
(B) 2
(C) −2
(D) π
Answer: (B)
Year: 2017 | Paper: 2 | Set: 1
————————————————————————————————————————————————————————————————————————————
PRACTICE SETS FROM THIS LESSON
Q1. Area bounded by the curve y = x² and x = 2 is:
(A) 4/3
(B) 8/3
(C) 16/3
(D) 2
Answer: (C)
Q2. Area enclosed between y = x and y = x² from x = 0 to x = 1 is:
(A) 1/2
(B) 1/3
(C) 1/4
(D) 1/6
Answer: (D)
Q3. Area bounded by y = sin x, x-axis from x = 0 to π is:
(A) 0
(B) 1
(C) 2
(D) π
Answer: (C)
Q4. Area under the curve y = e^x from x = 0 to 1 is:
(A) e − 1
(B) e + 1
(C) 1 − e
(D) e² − 1
Answer: (A)
Q5. Area under x = cos y from y = 0 to π/2 is:
(A) 0
(B) 1
(C) 2
(D) π/2
Answer: (B)
Q6. Area of first quadrant enclosed by x² + y² = 16 is:
(A) 16π
(B) 4π
(C) π
(D) 8π
Answer: (B)
Q7. Area under y = cos x between x = 0 and x = π/2 is:
(A) 0
(B) 1
(C) 2
(D) π/2
Answer: (B)
Q8. Area between y = 1/x from x = 1 to 2 is:
(A) ln 2
(B) 2 ln 2
(C) 1
(D) ln 1
Answer: (A)
Q9. Evaluate ∫ from 0 to π/4 tan x dx.
(A) (1/2) ln 2
(B) (1/4) ln 2
(C) ln 2
(D) ln 4
Answer: (A)
Q10. Evaluate ∫ from π/4 to π/2 cot x dx.
(A) (1/2) ln 2
(B) (1/4) ln 2
(C) ln 2
(D) ln 4
Answer: (A)
Q11. Area bounded by x = y² and x = 4 is:
(A) 32/3
(B) 16/3
(C) 8/3
(D) 4
Answer: (A)
Q12. Area under x = e^y from y = 0 to 1 is:
(A) e − 1
(B) 2(e − 1)
(C) e² − 1
(D) e + 1
Answer: (A)
Q13. Area under y = 1/(1 + x²) from x = 0 to 1 is:
(A) π/4
(B) π/2
(C) π/6
(D) π
Answer: (A)
Q14. Area bounded by y = x² and y = 4 is:
(A) 32/3
(B) 16/3
(C) 8/3
(D) 4
Answer: (A)
Q15. Area enclosed between y = e^x and y = e^−x from x = 0 to 1 is:
(A) e − 1
(B) e + 1
(C) 2(e − 1)
(D) e² − 1
Answer: (C)
Q16. Area under y = cosh x from x = 0 to 1 is:
(A) sinh 1
(B) cosh 1
(C) 1
(D) e − 1
Answer: (A)
Q17. Area under y = |x| from x = −2 to 2 is:
(A) 2
(B) 4
(C) 0
(D) 1
Answer: (B)
Q18. Area under y = sin x from 0 to 2π is:
(A) 0
(B) 2
(C) 4
(D) π
Answer: (C)
Q19. Area between y = x and y = 2 − x from x = 0 to 2 is:
(A) 1
(B) 2
(C) 3
(D) 4
Answer: (A)
Q20. Evaluate ∫ from −1 to 1 dx / (1 + x²).
(A) π/4
(B) π/2
(C) π/6
(D) π
Answer: (B)
Q21. Area under y = tan x from x = 0 to π/4 is:
(A) (1/2) ln 2
(B) (1/4) ln 2
(C) ln 2
(D) ln 4
Answer: (A)
Q22. Evaluate ∫ cos x dx from 0 to π/2.
(A) 1
(B) 0
(C) 2
(D) π/2
Answer: (A)
Q23. Evaluate ∫ sin x dx from 0 to π.
(A) 0
(B) 2
(C) −2
(D) π
Answer: (B)
Q24. Area enclosed between y = cos x and x-axis from 0 to π/2 is:
(A) 0
(B) 1
(C) 2
(D) π/2
Answer: (B)
Q25. Area bounded by y = ln x from x = 1 to e is:
(A) 0
(B) 1
(C) e − 1
(D) ln e
Answer: (B)
Q26. Area enclosed between the curves y² = 4x and x² = 4y is:
(A) 4
(B) 8
(C) 16/3
(D) 32/3
Answer: (C)
Q27. Find the area bounded by y = sin x and x = π/2, x = π.
(A) 1
(B) 0
(C) 2
(D) π/2
Answer: (A)
Q28. Evaluate ∫ from 0 to π/2 (cos²x − sin²x) dx.
(A) 0
(B) 1
(C) π/4
(D) π/2
Answer: (B)
Q29. Area under the curve y = 1/(1 + x⁴) from x = 0 to 1 is approximately:
(A) 0.8
(B) 0.7
(C) 0.9
(D) π/4
Answer: (A)
Q30. The area under y = tan⁻¹x between x = 0 and x = 1 is:
(A) 1/2
(B) π/8
(C) ln 2
(D) π/4 − 1/2
Answer: (D)
Q31. Area bounded by y = √(4 − x²) and x-axis from x = −2 to 2 is:
(A) π
(B) 2π
(C) 4π
(D) π/2
Answer: (A)
Q32. Area enclosed between y = x³ and x-axis from x = 0 to 1 is:
(A) 1/4
(B) 1/2
(C) 1/3
(D) 1/5
Answer: (D)
Q33. Evaluate ∫ from 0 to π sin²x dx.
(A) π/2
(B) π/4
(C) π
(D) 0
Answer: (A)
Q34. Area enclosed by the lines y = x, y = 0, x = 1 and the curve y = 1 − x² is:
(A) 1/3
(B) 1/2
(C) 1/6
(D) 2/3
Answer: (C)
Q35. Area between y = cos x and y = sin x from x = 0 to π/2 is:
(A) 0
(B) 1/2
(C) 1
(D) π/2
Answer: (B)
Q36. Evaluate ∫ from 0 to π/2 |sin x − cos x| dx.
(A) 2 − √2
(B) √2
(C) 2 + √2
(D) π/2
Answer: (A)
Q37. Find the area enclosed by y = sin²x from 0 to π.
(A) π/2
(B) π/4
(C) π
(D) 0
Answer: (A)
Q38. Area between x = y² and y = x² is:
(A) 0
(B) 1/2
(C) 1/3
(D) 4/3
Answer: (D)
Q39. Evaluate ∫ from 0 to π/2 tan x dx.
(A) ln 2
(B) 1/2 ln 2
(C) ln sec(π/2)
(D) Diverges
Answer: (D)
Q40. Area bounded between y = |x − 1| and x-axis from x = 0 to x = 2 is:
(A) 1
(B) 2
(C) 3
(D) 4
Answer: (B)
Q41. Evaluate ∫ from 0 to 1 (x / √(1 − x²)) dx.
(A) 0
(B) 1
(C) π/2
(D) 1/2
Answer: (D)
Q42. Area under y = ln x between x = 1 and e is:
(A) 0
(B) 1
(C) e − 1
(D) ln e
Answer: (B)
Q43. Evaluate ∫ from 0 to 1 (x³ + 2x) dx.
(A) 1
(B) 1/2
(C) 2
(D) 3/2
Answer: (A)
Q44. Area bounded by y = tan x and x-axis from x = 0 to π/4 is:
(A) ln 2
(B) 1/2 ln 2
(C) ln 4
(D) Diverges
Answer: (B)
Q45. Evaluate ∫ from 0 to 1 (1 − x)² dx.
(A) 1/3
(B) 1/2
(C) 1
(D) 2/3
Answer: (A)
Q46. Area under y = e^−x² from x = 0 to 1 approximately equals:
(A) 0.7
(B) 0.8
(C) 0.9
(D) 0.6
Answer: (B)
Q47. Evaluate ∫ from 0 to π/2 x cos x dx.
(A) 1
(B) 0
(C) π/2
(D) π
Answer: (C)
Q48. Evaluate ∫ from 0 to π/2 (x sin x) dx.
(A) π/2
(B) π
(C) 1
(D) 0
Answer: (A)
Q49. Evaluate ∫ from 0 to 1 (x² + 1)/(x + 1) dx.
(A) 1/2
(B) 1
(C) ln 2
(D) 3/2
Answer: (D)
Q50. Find area between y = e^x and x-axis from x = 0 to 1:
(A) e − 1
(B) e + 1
(C) e² − 1
(D) e − 2
Answer: (A)
————————————————————————————————————————————————————————————————————————————
MISCONCEPTIONS “ALERTS”

————————————————————————————————————————————————————————————————————————————
KNOWLEDGE WITH FUN

————————————————————————————————————————————————————————————————————————————
MNEMONICS
————————————————————————————————————————————————————————————————————————————
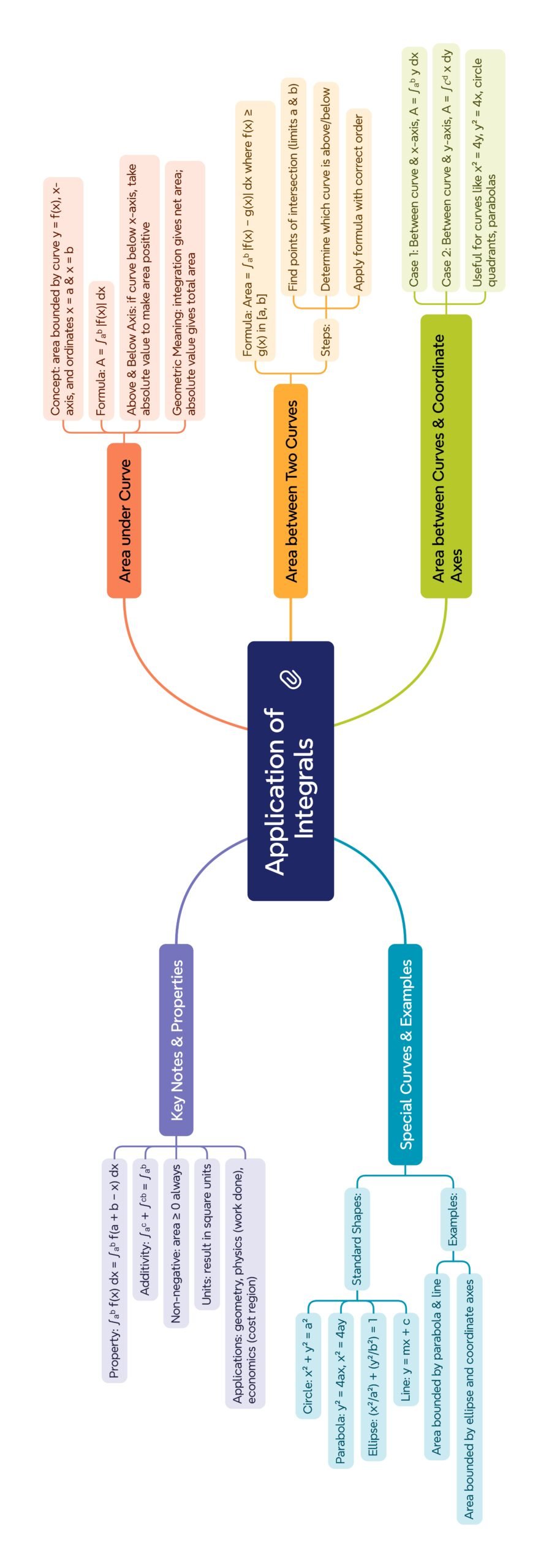
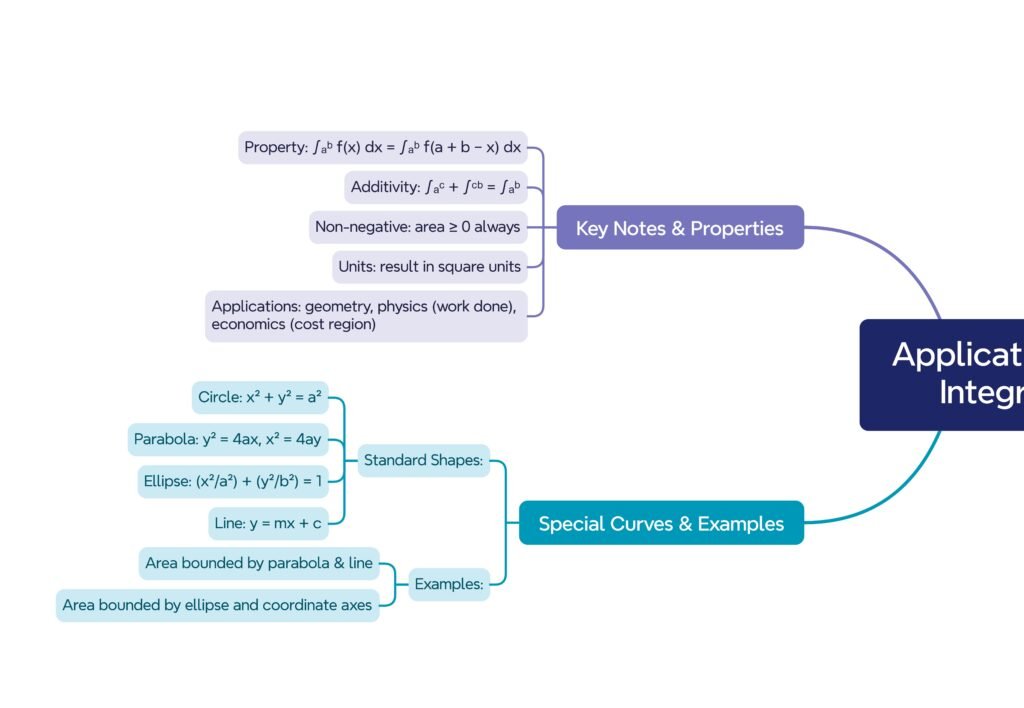
MIND MAP
——————————————————————————————————————————————————————————————————————————
