Class 12 : Maths (English) -Chapter 13: Probability

Posted by

On June 25, 2025

EXPLANATION & SUMMARY

🔵 Detailed Explanation
🌟 1. Introduction to Probability
Probability is a branch of mathematics that measures the likelihood of occurrence of an event.
💡 It gives a numerical value between 0 and 1:
0 → impossible event
1 → sure event
✏️ Example: Probability of getting a head when a coin is tossed once = 1/2.

🟢 2. Random Experiment
An experiment is called random if:
All possible outcomes are known.
The exact outcome cannot be predicted in advance.
✔️ Examples:
➡️ Tossing a coin → outcomes: {H, T}
➡️ Rolling a die → outcomes: {1, 2, 3, 4, 5, 6}

🟡 3. Sample Space (S)
The set of all possible outcomes of a random experiment.
🔹 For a coin toss → S = {H, T}
🔹 For two dice → S = {(1,1), (1,2), …, (6,6)}
Number of outcomes = 6 × 6 = 36

🔴 4. Event
An event is any subset of the sample space.
🧠 If A is an event, then A ⊆ S.
📌 Types of Events:
Simple event → contains one outcome (e.g., getting a 3)
Compound event → more than one outcome
Impossible event → ∅
Sure event → S
Complementary event: A′ = S − A
✔️ P(A) + P(A′) = 1

🌿 5. Classical Probability (Theoretical Definition)
If S has n equally likely outcomes and A has m favorable outcomes, then:
✅ P(A) = m / n
✏️ Example:
Rolling a die, event A: even number → A = {2,4,6}
P(A) = 3/6 = 1/2

💡 6. Conditional Probability
Probability of event A given that event B has occurred:
🧠 P(A | B) = P(A ∩ B) / P(B), where P(B) ≠ 0
📌 Interpretation: restrict sample space to B.
✏️ Example:
From a deck of 52 cards, find P(king | face card).
P(K ∩ F) = 4/52, P(F) = 12/52
➡️ P(K | F) = (4/52)/(12/52) = 1/3

⚡ 7. Multiplication Theorem of Probability
For any two events A and B:
➡️ P(A ∩ B) = P(A) × P(B | A) = P(B) × P(A | B)
If A and B are independent,
✔️ P(A ∩ B) = P(A) × P(B)

🧠 8. Independence of Events
Events A and B are independent if
P(A ∩ B) = P(A) × P(B)
✏️ Example: Tossing two coins
A: first coin shows Head → P(A) = 1/2
B: second coin shows Head → P(B) = 1/2
A and B independent → P(A ∩ B) = 1/4 ✅

🔷 9. Total Probability Theorem
If {B₁, B₂, …, Bₙ} is a partition of sample space S, and A is any event, then:
➡️ P(A) = Σ [P(Bᵢ) × P(A | Bᵢ)]
✏️ Example:
A factory has 3 machines A, B, C producing 20%, 30%, 50% of items.
Defective rates = 1%, 2%, 3%.
Find probability that an item is defective.
P(D) = 0.2×0.01 + 0.3×0.02 + 0.5×0.03 = 0.023 ✅

🔶 10. Bayes’ Theorem
Used to reverse conditional probabilities.
Formula:
➡️ P(Bᵢ | A) = [P(Bᵢ) × P(A | Bᵢ)] / Σ [P(Bⱼ) × P(A | Bⱼ)]
✏️ Example:
Using previous data, probability that item came from machine C given defective:
P(C | D) = (0.5×0.03)/0.023 = 0.652 ≈ 65.2%

🔵 11. Random Variables
A random variable assigns a real number to each outcome of an experiment.
🔹 Denoted by X
🔹 Discrete → finite outcomes
🔹 Continuous → infinite outcomes
✏️ Example: Toss 2 coins,
X = number of heads → X = {0,1,2}

🟢 12. Probability Distribution
It gives probabilities of all possible values of X.
✔️ Must satisfy:
Σ P(Xᵢ) = 1
0 ≤ P(Xᵢ) ≤ 1
✏️ Example: Toss 2 coins
X = number of heads
X P(X)
0 1/4
1 1/2
2 1/4

🟠 13. Mean of Discrete Distribution
➡️ E(X) = Σ [xᵢ × P(xᵢ)]
✏️ Example:
X: 0,1,2; P(X): 1/4, 1/2, 1/4
E(X) = 0×1/4 + 1×1/2 + 2×1/4 = 1 ✅

🔴 14. Variance and Standard Deviation

Variance: Var(X) = E(X²) − [E(X)]²
Standard Deviation: σ = √(Var(X))

✏️ Example:
Using above distribution,
E(X²) = 0²×1/4 + 1²×1/2 + 2²×1/4 = 1.5
Var(X) = 1.5 − 1² = 0.5
σ = √0.5 ✔️

🌿 15. Bernoulli Trials
An experiment is a Bernoulli trial if:
Only two outcomes (success/failure)
Probability of success = p, failure = q = 1 − p
Repeated n times independently

💡 16. Binomial Distribution
Probability of exactly r successes in n Bernoulli trials:
➡️ P(X = r) = nCr × pʳ × qⁿ⁻ʳ
✔️ Mean = n p
✔️ Variance = n p q
✔️ SD = √(n p q)
✏️ Example: Toss a coin 3 times (p = 1/2), find P(2 heads):
P(X=2) = ³C₂ × (1/2)² × (1/2)¹ = 3/8 ✅

🔶 17. Law of Expectation
For any two random variables X and Y,
➡️ E(X + Y) = E(X) + E(Y)
If independent,
➡️ Var(X + Y) = Var(X) + Var(Y)

🧠 18. Continuous Random Variable
Defined over intervals, e.g. height, weight.
Described by Probability Density Function (PDF):
f(x) ≥ 0
∫ f(x) dx = 1
P(a ≤ X ≤ b) = ∫ₐᵇ f(x) dx

🔵 19. Important Properties
✔️ 0 ≤ P(A) ≤ 1
✔️ P(∅) = 0, P(S) = 1
✔️ If A ⊆ B ⇒ P(A) ≤ P(B)
✔️ P(A ∪ B) = P(A) + P(B) − P(A ∩ B)

🟣 Summary (~300 words)
🔹 Probability measures chance of an event: 0 ≤ P(A) ≤ 1.
🔹 Sample space (S) is the set of all possible outcomes.
🔹 Event (A) is any subset of S; Complement A′ has P(A) + P(A′) = 1.
🔹 Classical probability: P(A) = favorable / total equally likely outcomes.
🔹 Conditional probability: P(A | B) = P(A ∩ B) / P(B).
🔹 Independent events: P(A ∩ B) = P(A) × P(B).
🔹 Multiplication theorem: P(A ∩ B) = P(A) P(B | A).
🔹 Total probability theorem: If {B₁,…,Bₙ} partition S,
P(A) = Σ P(Bᵢ) P(A | Bᵢ).
🔹 Bayes’ theorem: P(Bᵢ | A) = [P(Bᵢ) P(A | Bᵢ)] / Σ P(Bⱼ) P(A | Bⱼ).
🔹 Random variable (X): assigns real number to outcomes.
🔹 Discrete distribution: Σ P(Xᵢ) = 1.
🔹 Mean (E[X]) = Σ xᵢ P(xᵢ); Var(X) = E(X²) − [E(X)]².
🔹 Bernoulli trial: only two outcomes, constant probability, independent.
🔹 Binomial distribution: P(X = r) = nCr pʳ qⁿ⁻ʳ.
Mean = n p, Variance = n p q.
🔹 Continuous variable uses PDF, with ∫ f(x) dx = 1.
Key formulas:
P(A′) = 1 − P(A)
P(A ∪ B) = P(A) + P(B) − P(A ∩ B)
P(A | B) = P(A ∩ B) / P(B)
Var(X) = E(X²) − [E(X)]²
Binomial: P(X = r) = nCr pʳ qⁿ⁻ʳ

📝 Quick Recap
✔️ Probability quantifies uncertainty.
✔️ Conditional & independent events are crucial.
✔️ Bayes’ theorem connects reverse conditions.
✔️ Random variables link events to numbers.
✔️ Binomial model fits repeated Bernoulli trials.
✔️ Mean = expected value, variance measures spread.
✔️ Always check 0 ≤ P ≤ 1 and Σ P = 1.

————————————————————————————————————————————————————————————————————————————

QUESTIONS FROM TEXTBOOK

Exercise 13.1

🔵 Question 1:
Given that E and F are events such that P(E) = 0.6, P(F) = 0.3 and P(E ∩ F) = 0.2, find P(E|F) and P(F|E).

🔵 Question 2:
Compute P(A|B), if P(B) = 0.5 and P(A ∩ B) = 0.32.

🟢 Answer:
➡️ Formula: P(A|B) = P(A ∩ B) ÷ P(B).
✳️ P(A|B) = 0.32 ÷ 0.5 = 0.64 = 16/25.
✔️ Final: P(A|B) = 0.64.

🔵 Question 3:
If P(A) = 0.8, P(B) = 0.5 and P(B|A) = 0.4, find
(i) P(A ∩ B) (ii) P(A|B) (iii) P(A ∪ B).

🟢 Answer:
➡️ (i) Use P(B|A) = P(A ∩ B) ÷ P(A).
✳️ P(A ∩ B) = 0.4 × 0.8 = 0.32.

➡️ (ii) Use P(A|B) = P(A ∩ B) ÷ P(B).
✳️ P(A|B) = 0.32 ÷ 0.5 = 0.64.

➡️ (iii) Use P(A ∪ B) = P(A) + P(B) − P(A ∩ B).
✳️ P(A ∪ B) = 0.8 + 0.5 − 0.32 = 0.98.

✔️ Final: P(A ∩ B) = 0.32, P(A|B) = 0.64, P(A ∪ B) = 0.98.

🔵 Question 4:
Evaluate P(A ∪ B), if 2P(A) = P(B) = 5/13 and P(A|B) = 2/5.

🟢 Answer:
➡️ From 2P(A) = 5/13 ⇒ P(A) = 5/26.
➡️ From P(B) = 5/13.
➡️ Use P(A|B) = P(A ∩ B) ÷ P(B) = 2/5.
✳️ P(A ∩ B) = (2/5) × (5/13) = 2/13.
➡️ Use P(A ∪ B) = P(A) + P(B) − P(A ∩ B).
✳️ P(A ∪ B) = 5/26 + 5/13 − 2/13 = 5/26 + 10/26 − 4/26 = 11/26.
✔️ Final: P(A ∪ B) = 11/26.

🔵 Question 5:
If P(A) = 6/11, P(B) = 5/11 and P(A ∪ B) = 7/11, find
(i) P(A ∩ B) (ii) P(A|B) (iii) P(B|A).

🟢 Answer:
➡️ (i) Use P(A ∩ B) = P(A) + P(B) − P(A ∪ B).
✳️ P(A ∩ B) = (6/11) + (5/11) − (7/11) = 4/11.

➡️ (ii) P(A|B) = P(A ∩ B) ÷ P(B).
✳️ P(A|B) = (4/11) ÷ (5/11) = 4/5.

➡️ (iii) P(B|A) = P(A ∩ B) ÷ P(A).
✳️ P(B|A) = (4/11) ÷ (6/11) = 2/3.

✔️ Final: P(A ∩ B) = 4/11, P(A|B) = 4/5, P(B|A) = 2/3.

🔵 Question 6:
A coin is tossed three times, where
(i) E: head on third toss, F: heads on first two tosses
(ii) E: at least two heads, F: at most two heads
(iii) E: at most two tails, F: at least one tail
Determine P(E|F) in each case.

🟢 Answer:
➡️ Universe: 3 tosses ⇒ 8 equally likely outcomes.

✳️ (i)
E: third toss is H ⇒ {HHH, HTH, THH, TTH} (4 outcomes).
F: first two are H ⇒ {HHH, HHT} (2 outcomes).
E ∩ F: {HHH} (1 outcome).
P(E|F) = P(E ∩ F) ÷ P(F) = (1/8) ÷ (2/8) = 1/2.
✔️ P(E|F) = 1/2.

✳️ (ii)
E: ≥ 2 heads ⇒ exactly 2 or 3 heads ⇒ 3 + 1 = 4 outcomes.
F: ≤ 2 heads ⇒ 0, 1, or 2 heads ⇒ 1 + 3 + 3 = 7 outcomes.
E ∩ F: exactly 2 heads ⇒ 3 outcomes.
P(E|F) = (3/8) ÷ (7/8) = 3/7.
✔️ P(E|F) = 3/7.

✳️ (iii)
E: ≤ 2 tails ⇒ all except TTT ⇒ 7 outcomes.
F: ≥ 1 tail ⇒ all except HHH ⇒ 7 outcomes.
E ∩ F: all except HHH and TTT ⇒ 6 outcomes.
P(E|F) = (6/8) ÷ (7/8) = 6/7.
✔️ P(E|F) = 6/7.

🔵 Question 7:
Two coins are tossed once, where
(i) E: tail appears on one coin, F: one coin shows head
(ii) E: no tail appears, F: no head appears
Determine P(E|F).

🟢 Answer:
➡️ Universe: {HH, HT, TH, TT} (4 equally likely).

✳️ (i)
Interpretation: “one coin shows head” ⇒ exactly one head; “tail appears on one coin” ⇒ exactly one tail.
E = {HT, TH}, F = {HT, TH}.
E ∩ F = {HT, TH}.
P(E|F) = (2/4) ÷ (2/4) = 1.
✔️ P(E|F) = 1.

✳️ (ii)
E: no tail ⇒ {HH}.
F: no head ⇒ {TT}.
E ∩ F = ∅.
P(E|F) = 0 ÷ (1/4) = 0.
✔️ P(E|F) = 0.

🔵 Question 8:
A die is thrown three times, where
E: 4 appears on the third toss, F: 6 and 5 appear respectively on first two tosses.
Find P(E|F).

🟢 Answer:
➡️ Universe size = 6³ = 216.
➡️ F fixes first two as (6, 5); third is free ⇒ P(F) = 1/36.
➡️ E ∩ F = outcome (6, 5, 4) ⇒ P(E ∩ F) = 1/216.
P(E|F) = (1/216) ÷ (1/36) = 1/6.
✔️ P(E|F) = 1/6.

🔵 Question 9:
Mother, father and son line up at random for a family picture.
E: son on one end, F: father in middle. Find P(E|F).

🟢 Answer:
➡️ Total arrangements = 3! = 6.
➡️ F: father in middle ⇒ remaining two (mother, son) on ends in 2 orders ⇒ P(F) = 2/6.
➡️ Given F, son is necessarily on an end in both orders ⇒ P(E ∩ F) = 2/6.
P(E|F) = (2/6) ÷ (2/6) = 1.
✔️ P(E|F) = 1.

🔵 Question 10:
A black and a red dice are rolled.
(a) Find the conditional probability of obtaining a sum greater than 9, given that the black die resulted in a 5.
(b) Find the conditional probability of obtaining the sum 8, given that the red die resulted in a number less than 4.

🟢 Answer:

✳️ Part (a)
➡️ Given black = 5; red is equally likely 1–6.
➡️ Need sum > 9 ⇒ red ≥ 5 (since 5 + 5 = 10).
➡️ Favourable red outcomes: {5, 6} = 2 cases out of 6.
✔️ P(sum > 9 | black = 5) = 2/6 = 1/3.

✳️ Part (b)
➡️ Given red < 4 ⇒ red ∈ {1, 2, 3}.
➡️ Need sum = 8 ⇒ black = 8 − red.
➡️ Feasible pairs under red < 4: (red, black) = (2, 6), (3, 5).
➡️ P(sum = 8 and red < 4) = 2/36 = 1/18.
➡️ P(red < 4) = 3/6 = 1/2.
✔️ P(sum = 8 | red < 4) = (1/18) ÷ (1/2) = 1/9.

🔵 Question 11:
A fair die is rolled. Consider events E = {1, 3, 5}, F = {2, 3} and G = {2, 3, 4, 5}. Find
(i) P(E|F) and P(F|E)
(ii) P(E|G) and P(G|E)
(iii) P((E ∪ F)|G) and P((E ∩ F)|G).

🟢 Answer:
➡️ |S| = 6, |E| = 3, |F| = 2, |G| = 4.
➡️ E ∩ F = {3} (size 1), E ∩ G = {3, 5} (size 2), E ∪ F = {1, 2, 3, 5}.

✳️ (i)
P(E|F) = P(E ∩ F) ÷ P(F) = (1/6) ÷ (2/6) = 1/2.
P(F|E) = P(E ∩ F) ÷ P(E) = (1/6) ÷ (3/6) = 1/3.

✳️ (ii)
P(E|G) = P(E ∩ G) ÷ P(G) = (2/6) ÷ (4/6) = 1/2.
P(G|E) = P(E ∩ G) ÷ P(E) = (2/6) ÷ (3/6) = 2/3.

✳️ (iii)
(E ∪ F) ∩ G = {2, 3, 5} (size 3).
P((E ∪ F)|G) = (3/6) ÷ (4/6) = 3/4.
(E ∩ F) ∩ G = {3} (size 1).
P((E ∩ F)|G) = (1/6) ÷ (4/6) = 1/4.
✔️ Final: 1/2, 1/3, 1/2, 2/3, 3/4, 1/4 (in order).

🔵 Question 12:
Assume each born child is equally likely to be a boy or a girl. If a family has two children, what is the conditional probability that both are girls given that
(i) the youngest is a girl, (ii) at least one is a girl?

🟢 Answer:
➡️ Sample space (ordered): {BB, BG, GB, GG} with probability 1/4 each.

✳️ (i) Youngest is a girl ⇒ filter {BG, GG}.
P(both girls | youngest girl) = 1 favourable {GG} out of 2 ⇒ 1/2.

✳️ (ii) At least one girl ⇒ filter {BG, GB, GG}.
P(both girls | at least one girl) = 1 favourable {GG} out of 3 ⇒ 1/3.

✔️ Final: (i) 1/2, (ii) 1/3.

🔵 Question 13:
An instructor has a question bank consisting of 300 easy True/False, 200 difficult True/False, 500 easy multiple-choice and 400 difficult multiple-choice questions. If a question is selected at random from the bank, what is the probability that it will be an easy question given that it is a multiple-choice question?

🟢 Answer:
➡️ Total MCQ = 500 (easy) + 400 (difficult) = 900.
➡️ Easy within MCQ = 500.
✔️ P(easy | MCQ) = 500/900 = 5/9.

🔵 Question 14:
Given that the two numbers appearing on throwing two dice are different. Find the probability of the event “the sum of numbers on the dice is 4”.

🟢 Answer:
➡️ Total outcomes for two dice = 36.
➡️ Condition “numbers are different” excludes doubles ⇒ 36 − 6 = 30 outcomes.
➡️ Sum 4 outcomes: (1,3), (3,1), (2,2).
➡️ Under the condition “different”, (2,2) is not allowed.
➡️ Favourable outcomes = 2.
✔️ P(sum = 4 | numbers different) = 2 ÷ 30 = 1/15.

🔵 Question 15:
Consider the experiment of throwing a die; if a multiple of 3 comes up, throw the die again, and if any other number comes, toss a coin. Find the conditional probability of the event “the coin shows a tail”, given that “at least one die shows a 3”.

🟢 Answer:
➡️ First throw outcomes: {1,2,3,4,5,6}.
➡️ If first is multiple of 3 (3 or 6), we throw a die again; no coin is tossed.
➡️ Event F: “at least one die shows a 3”.
➡️ Event E: “coin shows tail”.

✳️ Step 1: When coin is tossed (first ∈ {1,2,4,5}), F is false because no die equals 3.
✳️ Step 2: When F is true (first = 3, or first = 6 and second = 3), no coin is tossed.
✳️ Step 3: Hence E and F cannot occur together.
✔️ P(E ∩ F) = 0 and P(F) > 0 ⇒ P(E|F) = 0.

🔵 Question 16:
If P(A) = 1/2, P(B) = 0, then P(A|B) is
(A) 0 (B) 1/2 (C) not defined (D) 1

🟢 Answer:
➡️ P(A|B) = P(A ∩ B) ÷ P(B).
➡️ Since P(B) = 0, the denominator is 0.
✔️ P(A|B) is not defined.
✔️ Correct option: (C) not defined.

🔵 Question 17:
If A and B are events such that P(A|B) = P(B|A), then
(A) A ⊂ B but A ≠ B
(B) A = B
(C) A ∩ B = ϕ
(D) P(A) = P(B)

🟢 Answer:
➡️ P(A|B) = P(B|A) ⇒ [P(A ∩ B) ÷ P(B)] = [P(A ∩ B) ÷ P(A)].
➡️ If P(A ∩ B) > 0 and P(A), P(B) > 0 ⇒ 1/P(B) = 1/P(A).
➡️ Therefore P(A) = P(B).
✔️ Correct option: (D) P(A) = P(B).
✏️ Note: Equality of conditional probabilities does not force A = B; equal probabilities suffice.

Exercise 13.2

🔵 Question 1:
If P(A) = 3/5 and P(B) = 1/5, find P(A ∩ B) if A and B are independent events.

🟢 Answer:
➡️ For independent events: P(A ∩ B) = P(A) × P(B).
✳️ Compute: (3/5) × (1/5) = 3/25.
✔️ Final: P(A ∩ B) = 3/25.

🔵 Question 2:
Two cards are drawn at random and without replacement from a pack of 52 playing cards. Find the probability that both the cards are black.

🟢 Answer:
➡️ Total black cards = 26.
✳️ Step 1: P(first black) = 26/52 = 1/2.
✳️ Step 2: P(second black | first black) = 25/51.
✳️ Step 3: Multiply: (1/2) × (25/51) = 25/102.
✔️ Final: P(both black) = 25/102.

🔵 Question 3:
A box of oranges is inspected by examining three randomly selected oranges drawn without replacement. If all the three oranges are good, the box is approved for sale; otherwise, it is rejected. Find the probability that a box containing 15 oranges out of which 12 are good and 3 are bad ones will be approved for sale.

🟢 Answer (refined):
➡️ We need all 3 drawn to be good.
✳️ Step 1: P(first good) = 12/15.
✳️ Step 2: P(second good | first good) = 11/14.
✳️ Step 3: P(third good | first two good) = 10/13.
✳️ Step 4: Multiply: (12/15) × (11/14) × (10/13) = (1320)/(2730).
✳️ Step 5: Reduce the fraction: divide numerator and denominator by 30 → 44/91.
✔️ Final: Probability of approval = 44/91 ≈ 0.4835.

🔵 Question 4:
A fair coin and an unbiased die are tossed. Let A be the event “head appears on the coin” and B be the event “3 on the die”. Check whether A and B are independent events or not.

🟢 Answer:
➡️ P(A) = 1/2, P(B) = 1/6.
✳️ P(A ∩ B) = (1/2) × (1/6) = 1/12.
✳️ P(A) × P(B) = 1/12.
✔️ Since P(A ∩ B) = P(A) × P(B), events A and B are independent.

🔵 Question 5:
A die marked 1, 2, 3 in red and 4, 5, 6 in green is tossed. Let A be the event “the number is even,” and B be the event “the number is red.” Are A and B independent?

🟢 Answer:
➡️ S = {1, 2, 3, 4, 5, 6}.
✳️ P(A) = P(even) = 3/6 = 1/2.
✳️ P(B) = P(red) = 3/6 = 1/2 (since 1, 2, 3 are red).
✳️ A ∩ B = {2} ⇒ P(A ∩ B) = 1/6.
✳️ P(A) × P(B) = 1/4.
✔️ Since 1/6 ≠ 1/4, A and B are not independent.

🔵 Question 6:
Let E and F be events with P(E) = 3/5, P(F) = 3/10 and P(E ∩ F) = 1/5. Are E and F independent?

🟢 Answer:
➡️ Compute product: P(E) × P(F) = (3/5) × (3/10) = 9/50 = 0.18.
➡️ Given intersection: P(E ∩ F) = 1/5 = 0.20.
✔️ Since P(E ∩ F) ≠ P(E) × P(F), events E and F are not independent.

🔵 Question 7:
Given that the events A and B are such that P(A) = 1/2, P(A ∪ B) = 3/5 and P(B) = p.
Find p if they are (i) mutually exclusive (ii) independent.

🟢 Answer:

✳️ Formula: P(A ∪ B) = P(A) + P(B) − P(A ∩ B)

(i) If A and B are mutually exclusive,
➡️ P(A ∩ B) = 0
➡️ 3/5 = 1/2 + p − 0
➡️ p = 3/5 − 1/2 = (6 − 5)/10 = 1/10
✔️ p = 1/10

(ii) If A and B are independent,
➡️ P(A ∩ B) = P(A) × P(B) = (1/2)p
➡️ 3/5 = 1/2 + p − (1/2)p
➡️ 3/5 = 1/2 + (p/2)
➡️ (p/2) = 3/5 − 1/2 = 1/10
➡️ p = 1/5
✔️ p = 1/5

🔵 Question 8:
Let A and B be independent events with P(A) = 0.3 and P(B) = 0.4. Find
(i) P(A ∩ B), (ii) P(A ∪ B), (iii) P(A|B), (iv) P(B|A).

🟢 Answer:

(i) P(A ∩ B) = P(A) × P(B) = 0.3 × 0.4 = 0.12.
✔️ P(A ∩ B) = 0.12

(ii) P(A ∪ B) = P(A) + P(B) − P(A ∩ B) = 0.3 + 0.4 − 0.12 = 0.58.
✔️ P(A ∪ B) = 0.58

(iii) P(A|B) = P(A ∩ B) / P(B) = 0.12 / 0.4 = 0.3.
✔️ P(A|B) = 0.3

(iv) P(B|A) = P(A ∩ B) / P(A) = 0.12 / 0.3 = 0.4.
✔️ P(B|A) = 0.4

🔵 Question 9:
If A and B are two events such that P(A) = 1/4, P(B) = 1/2 and P(A ∩ B) = 1/8, find P(not A and not B).

🟢 Answer:

✳️ Formula:
P(A ∪ B) = P(A) + P(B) − P(A ∩ B)
➡️ = 1/4 + 1/2 − 1/8
➡️ = (2 + 4 − 1)/8 = 5/8

➡️ P(not A and not B) = 1 − P(A ∪ B)
➡️ = 1 − 5/8 = 3/8
✔️ P(not A and not B) = 3/8

🔵 Question 10:
Events A and B are such that P(A) = 1/2, P(B) = 7/12 and P(not A or not B) = 1/4.
State whether A and B are independent.

🟢 Answer:

✳️ Step 1: Use formula:
P(not A or not B) = 1 − P(A ∩ B)

➡️ 1 − P(A ∩ B) = 1/4
➡️ P(A ∩ B) = 3/4

✳️ Step 2: P(A) × P(B) = (1/2) × (7/12) = 7/24

⚠️ Since 3/4 ≠ 7/24,
✔️ A and B are not independent.

🔵 Question 11:
Given two independent events A and B such that P(A) = 0.3, P(B) = 0.6. Find
(i) P(A and B), (ii) P(A and not B), (iii) P(A or B), (iv) P(neither A nor B).

🟢 Answer:

(i) P(A and B) = P(A) × P(B) = 0.3 × 0.6 = 0.18.

(ii) P(A and not B) = P(A) × [1 − P(B)] = 0.3 × 0.4 = 0.12.

(iii) P(A or B) = P(A) + P(B) − P(A ∩ B) = 0.3 + 0.6 − 0.18 = 0.72.

(iv) P(neither A nor B) = 1 − P(A ∪ B) = 1 − 0.72 = 0.28.

✔️ Final Answers:
P(A ∩ B) = 0.18, P(A ∩ B̄) = 0.12, P(A ∪ B) = 0.72, P(Ā ∩ B̄) = 0.28.

🔵 Question 12:
A die is tossed thrice. Find the probability of getting an odd number at least once.

🟢 Answer:
➡️ P(odd) = 3/6 = 1/2.
➡️ P(even) = 1/2.

✳️ Probability of no odd (all even) = (1/2)^3 = 1/8.
➡️ P(at least one odd) = 1 − 1/8 = 7/8.
✔️ Final: 7/8

🔵 Question 13:
Two balls are drawn at random with replacement from a box containing 10 black and 8 red balls. Find the probability that
(i) both balls are red.
(ii) first ball is black and second is red.
(iii) one of them is black and other is red.

🟢 Answer:
➡️ With replacement ⇒ composition fixed.
➡️ P(black) = 10/18 = 5/9, P(red) = 8/18 = 4/9.

✳️ (i) both red:
P = (4/9) × (4/9) = 16/81.

✳️ (ii) first black, second red:
P = (5/9) × (4/9) = 20/81.

✳️ (iii) one black and one red (either BR or RB):
P = 2 × (5/9) × (4/9) = 40/81.

✔️ Final: (i) 16/81, (ii) 20/81, (iii) 40/81.

🔵 Question 14:
Probability of solving a specific problem independently by A and B are 1/2 and 1/3 respectively. If both try to solve the problem independently, find the probability that
(i) the problem is solved, (ii) exactly one of them solves the problem.

🟢 Answer:
➡️ Let Sᴀ = “A solves”, Sʙ = “B solves”. Independent.
➡️ P(Sᴀ) = 1/2, P(Sʙ) = 1/3.

✳️ (i) problem is solved (at least one solves):
P = 1 − P(neither)
= 1 − (1 − 1/2)(1 − 1/3)
= 1 − (1/2)(2/3)
= 1 − 1/3 = 2/3.

✳️ (ii) exactly one solves:
P = P(Sᴀ only) + P(Sʙ only)
= (1/2)(1 − 1/3) + (1/3)(1 − 1/2)
= (1/2)(2/3) + (1/3)(1/2)
= 1/3 + 1/6 = 1/2.

✔️ Final: (i) 2/3, (ii) 1/2.

🔵 Question 15:
One card is drawn at random from a well-shuffled deck of 52 cards. In which of the following cases are the events E and F independent?
(i) E: “the card drawn is a spade”, F: “the card drawn is an ace”.
(ii) E: “the card drawn is black”, F: “the card drawn is a king”.
(iii) E: “the card drawn is a king or queen”, F: “the card drawn is a queen or jack”.

🟢 Answer:

✳️ (i)
P(E) = 13/52 = 1/4, P(F) = 4/52 = 1/13.
P(E ∩ F) = P(“ace of spades”) = 1/52.
P(E)P(F) = (1/4)(1/13) = 1/52 = P(E ∩ F).
✔️ Independent.

✳️ (ii)
P(E) = 26/52 = 1/2, P(F) = 4/52 = 1/13.
P(E ∩ F) = P(“black king”) = 2/52 = 1/26.
P(E)P(F) = (1/2)(1/13) = 1/26 = P(E ∩ F).
✔️ Independent.

✳️ (iii)
P(E) = 8/52 = 2/13, P(F) = 8/52 = 2/13.
(E ∩ F) = {queens only} ⇒ 4 cards ⇒ P(E ∩ F) = 4/52 = 1/13.
P(E)P(F) = (2/13)(2/13) = 4/169 ≠ 1/13.
✖️ Not independent.

✔️ Final: Independent in (i) and (ii); not independent in (iii).

🔵 Question 16:
In a hostel, 60% of the students read Hindi newspaper, 40% read English newspaper and 20% read both Hindi and English newspapers. A student is selected at random.
(a) Find the probability that she reads neither Hindi nor English newspapers.
(b) If she reads Hindi newspaper, find the probability that she reads English newspaper.
(c) If she reads English newspaper, find the probability that she reads Hindi newspaper.

🟢 Answer:
➡️ Let H = reads Hindi, E = reads English.
➡️ Given P(H) = 0.6, P(E) = 0.4, P(H ∩ E) = 0.2.

✳️ (a)
P(H ∪ E) = P(H) + P(E) − P(H ∩ E) = 0.6 + 0.4 − 0.2 = 0.8.
P(neither) = 1 − P(H ∪ E) = 1 − 0.8 = 0.2.
✔️ Required probability = 0.2.

✳️ (b)
P(E | H) = P(H ∩ E) ÷ P(H) = 0.2 ÷ 0.6 = 1/3.
✔️ Required probability = 1/3.

✳️ (c)
P(H | E) = P(H ∩ E) ÷ P(E) = 0.2 ÷ 0.4 = 1/2.
✔️ Required probability = 1/2.

🔵 Question 17:
The probability of obtaining an even prime number on each die, when a pair of dice is rolled is
(A) 0 (B) 1/3 (C) 1/12 (D) 1/36

🟢 Answer:
➡️ Even prime number on a die = 2 only.
➡️ Probability first die shows 2 = 1/6.
➡️ Probability second die shows 2 = 1/6.
✳️ Required probability = (1/6) × (1/6) = 1/36.
✔️ Correct option: (D) 1/36.

🔵 Question 18:
Two events A and B will be independent, if
(A) A and B are mutually exclusive
(B) P(A′ ∩ B′) = [1 − P(A)] [1 − P(B)]
(C) P(A) = P(B)
(D) P(A) + P(B) = 1

🟢 Answer:
➡️ For independence, complements are also independent.
➡️ Hence P(A′ ∩ B′) = P(A′) P(B′) = [1 − P(A)] [1 − P(B)].
✔️ Correct option: (B).

Exercise 13.3

🔵 Question 1:
An urn contains 5 red and 5 black balls. A ball is drawn at random, its colour is noted and is returned to the urn. Moreover, 2 additional balls of the colour drawn are put in the urn and then a ball is drawn at random. What is the probability that the second ball is red?

🟢 Answer:
➡️ Initial: red = 5, black = 5, total = 10.
➡️ Case 1: first ball red (prob = 5/10 = 1/2).
✳️ After return + add 2 red ⇒ red = 7, black = 5, total = 12.
✳️ P(second red | first red) = 7/12.
➡️ Case 2: first ball black (prob = 5/10 = 1/2).
✳️ After return + add 2 black ⇒ red = 5, black = 7, total = 12.
✳️ P(second red | first black) = 5/12.
➡️ Total probability: (1/2)(7/12) + (1/2)(5/12) = (1/2)(12/12) = 1/2.
✔️ Final: P(second ball is red) = 1/2.

🔵 Question 2:
A bag contains 4 red and 4 black balls, another bag contains 2 red and 6 black balls. One of the two bags is selected at random and a ball is drawn from the bag which is found to be red. Find the probability that the ball is drawn from the first bag.

🟢 Answer (Bayes’ Theorem):
➡️ Let B₁ = choose Bag 1, B₂ = choose Bag 2. P(B₁) = P(B₂) = 1/2.
➡️ P(Red | B₁) = 4/8 = 1/2.
➡️ P(Red | B₂) = 2/8 = 1/4.
➡️ P(B₁ | Red) = [P(B₁) P(Red | B₁)] / [P(B₁) P(Red | B₁) + P(B₂) P(Red | B₂)].
✳️ = (1/2 × 1/2) / (1/2 × 1/2 + 1/2 × 1/4) = (1/4) / (1/4 + 1/8) = 2/3.
✔️ Final: Probability it came from Bag 1 = 2/3.

🔵 Question 3:
Of the students in a college, 60% reside in hostel and 40% are day scholars. Previous results report that 30% of hostellers get A grade and 20% of day scholars get A grade in annual examination. At year end, one student chosen at random has an A grade. What is the probability that the student is a hosteller?

🟢 Answer (Bayes’ Theorem):
➡️ Let H = hosteller, D = day scholar, A = A grade.
➡️ P(H) = 0.6, P(D) = 0.4.
➡️ P(A | H) = 0.30, P(A | D) = 0.20.
➡️ P(H | A) = [P(H) P(A | H)] / [P(H) P(A | H) + P(D) P(A | D)].
✳️ = (0.6 × 0.30) / (0.6 × 0.30 + 0.4 × 0.20) = 0.18 / 0.26 = 9/13.
✔️ Final: Probability the student is a hosteller = 9/13.

🔵 Question 4:
In answering a question on a multiple-choice test, a student either knows the answer or guesses. Let 3/4 be the probability that the student knows the answer and 1/4 be the probability that the student guesses. Assuming that a student who guesses answers correctly with probability 1/4, what is the probability that the student knows the answer given that he answered it correctly?

🟢 Answer (Bayes’ Theorem):
➡️ Let K = knows, G = guesses, C = correct.
➡️ P(K) = 3/4, P(G) = 1/4, P(C | K) = 1, P(C | G) = 1/4.
➡️ P(K | C) = [P(K) P(C | K)] / [P(K) P(C | K) + P(G) P(C | G)].
✳️ = (3/4 × 1) / (3/4 × 1 + 1/4 × 1/4) = (3/4) / (3/4 + 1/16).
✳️ = (3/4) / (13/16) = (3/4) × (16/13) = 12/13.
✔️ Final: Probability the student knew the answer = 12/13.

JEE MAINS QUESTIONS FROM THIS LESSON

🔵 Question 1:
A card is drawn from a pack of 52 cards. The probability of getting a red face card is
🟥 1️⃣ 3/13
🟩 2️⃣ 1/13
🟨 3️⃣ 1/26
🟦 4️⃣ 2/13
Answer: 1️⃣ 3/13
📘 (JEE Main 2024)

🔵 Question 2:
A die is thrown twice. The probability of getting an even number on the first throw and a multiple of 3 on the second throw is
🟥 1️⃣ 1/6
🟩 2️⃣ 1/9
🟨 3️⃣ 1/12
🟦 4️⃣ 1/3
Answer: 1️⃣ 1/6
📘 (JEE Main 2024)

🔵 Question 3:
If P(A) = 0.5, P(B) = 0.3 and P(A ∩ B) = 0.2, then P(A ∪ B) = ?
🟥 1️⃣ 0.6
🟩 2️⃣ 0.7
🟨 3️⃣ 0.8
🟦 4️⃣ 0.9
Answer: 2️⃣ 0.7
📘 (JEE Main 2023)

🔵 Question 4:
Two coins are tossed simultaneously. The probability of getting at least one head is
🟥 1️⃣ 1/4
🟩 2️⃣ 1/2
🟨 3️⃣ 3/4
🟦 4️⃣ 1
Answer: 3️⃣ 3/4
📘 (JEE Main 2023)

🔵 Question 5:
A bag contains 4 red and 6 black balls. Two balls are drawn one by one without replacement. The probability that both are red is
🟥 1️⃣ 2/15
🟩 2️⃣ 1/15
🟨 3️⃣ 2/9
🟦 4️⃣ 3/5
Answer: 1️⃣ 2/15
📘 (JEE Main 2022)

🔵 Question 6:
If P(A) = 1/2, P(B) = 1/3 and P(A ∩ B) = 1/4, then P(A ∪ B) = ?
🟥 1️⃣ 5/6
🟩 2️⃣ 7/12
🟨 3️⃣ 2/3
🟦 4️⃣ 1/2
Answer: 2️⃣ 7/12
📘 (JEE Main 2022)

🔵 Question 7:
A fair die is rolled. The probability that a number greater than 3 appears is
🟥 1️⃣ 1/3
🟩 2️⃣ 1/2
🟨 3️⃣ 2/3
🟦 4️⃣ 1/6
Answer: 2️⃣ 1/2
📘 (JEE Main 2021)

🔵 Question 8:
A die is rolled twice. The probability that the sum of the two numbers is 7 is
🟥 1️⃣ 1/6
🟩 2️⃣ 1/12
🟨 3️⃣ 1/8
🟦 4️⃣ 1/9
Answer: 1️⃣ 1/6
📘 (JEE Main 2021)

🔵 Question 9:
A card is drawn from a deck. The probability that it is neither a king nor a queen is
🟥 1️⃣ 11/13
🟩 2️⃣ 10/13
🟨 3️⃣ 3/13
🟦 4️⃣ 1/13
Answer: 1️⃣ 11/13
📘 (JEE Main 2020)

🔵 Question 10:
If P(A) = 0.6, P(B) = 0.5 and P(A ∩ B) = 0.3, then P(A|B) = ?
🟥 1️⃣ 0.6
🟩 2️⃣ 0.5
🟨 3️⃣ 0.3
🟦 4️⃣ 0.9
Answer: 1️⃣ 0.6
📘 (JEE Main 2020)

🔵 Question 11:
Two dice are thrown together. The probability of getting a doublet (same number on both) is
🟥 1️⃣ 1/6
🟩 2️⃣ 1/12
🟨 3️⃣ 1/36
🟦 4️⃣ 1/3
Answer: 1️⃣ 1/6
📘 (JEE Main 2019)

🔵 Question 12:
A bag contains 5 white and 3 black balls. Two balls are drawn at random. The probability that both are black is
🟥 1️⃣ 1/7
🟩 2️⃣ 3/28
🟨 3️⃣ 3/7
🟦 4️⃣ 1/28
Answer: 2️⃣ 3/28
📘 (JEE Main 2019)

🔵 Question 13:
If two events A and B are independent and P(A) = 1/2, P(B) = 1/4, then P(A ∩ B) = ?
🟥 1️⃣ 1/2
🟩 2️⃣ 1/4
🟨 3️⃣ 1/8
🟦 4️⃣ 1/16
Answer: 3️⃣ 1/8
📘 (JEE Main 2018)

🔵 Question 14:
A die is rolled. The probability of getting a prime number is
🟥 1️⃣ 1/3
🟩 2️⃣ 1/2
🟨 3️⃣ 2/3
🟦 4️⃣ 1/6
Answer: 2️⃣ 1/2
📘 (JEE Main 2018)

🔵 Question 15:
If P(A) = 0.4, P(B) = 0.5, and P(A ∩ B) = 0.2, then A and B are
🟥 1️⃣ Independent
🟩 2️⃣ Mutually exclusive
🟨 3️⃣ Complementary
🟦 4️⃣ None
Answer: 1️⃣ Independent
📘 (JEE Main 2017)

🔵 Question 16:
The probability of getting at least one head when two coins are tossed is
🟥 1️⃣ 1/2
🟩 2️⃣ 3/4
🟨 3️⃣ 1/4
🟦 4️⃣ 2/3
Answer: 2️⃣ 3/4
📘 (JEE Main 2017)

🔵 Question 17:
If A and B are independent events with P(A) = 1/3 and P(B) = 1/2, then P(A ∪ B) = ?
🟥 1️⃣ 2/3
🟩 2️⃣ 5/6
🟨 3️⃣ 1/2
🟦 4️⃣ 1/3
Answer: 2️⃣ 5/6
📘 (JEE Main 2016)

🔵 Question 18:
A box contains 2 red and 3 blue balls. Two balls are drawn at random. The probability that both are blue is
🟥 1️⃣ 3/10
🟩 2️⃣ 1/2
🟨 3️⃣ 2/5
🟦 4️⃣ 1/10
Answer: 1️⃣ 3/10
📘 (JEE Main 2016)

🔵 Question 19:
A card is drawn from a deck. The probability of getting a spade or a king is
🟥 1️⃣ 4/13
🟩 2️⃣ 1/13
🟨 3️⃣ 5/13
🟦 4️⃣ 2/13
Answer: 3️⃣ 5/13
📘 (JEE Main 2015)

🔵 Question 20:
If P(A) = 0.3, P(B) = 0.4, and P(A ∪ B) = 0.6, then P(A ∩ B) = ?
🟥 1️⃣ 0.1
🟩 2️⃣ 0.2
🟨 3️⃣ 0.3
🟦 4️⃣ 0.4
Answer: 2️⃣ 0.2
📘 (JEE Main 2015)

🔵 Question 21:
Two dice are thrown simultaneously. The probability that the sum is greater than 10 is
🟥 1️⃣ 1/6
🟩 2️⃣ 1/12
🟨 3️⃣ 1/9
🟦 4️⃣ 1/4
Answer: 1️⃣ 1/6
📘 (JEE Main 2014)

🔵 Question 22:
If P(A) = 0.4, P(B) = 0.5, and P(A ∪ B) = 0.7, then P(A ∩ B) = ?
🟥 1️⃣ 0.2
🟩 2️⃣ 0.3
🟨 3️⃣ 0.4
🟦 4️⃣ 0.1
Answer: 1️⃣ 0.2
📘 (JEE Main 2014)

🔵 Question 23:
A bag contains 6 red and 4 white balls. Two balls are drawn together. The probability that both are red is
🟥 1️⃣ 3/10
🟩 2️⃣ 1/3
🟨 3️⃣ 2/3
🟦 4️⃣ 1/5
Answer: 1️⃣ 3/10
📘 (JEE Main 2013)

🔵 Question 24:
A coin is tossed 3 times. The probability of getting exactly 2 heads is
🟥 1️⃣ 3/8
🟩 2️⃣ 1/8
🟨 3️⃣ 5/8
🟦 4️⃣ 1/4
Answer: 1️⃣ 3/8
📘 (JEE Main 2013)

🔵 Question 25:
A card is drawn at random from a pack of 52 cards. The probability that it is a king or a spade is
🟥 1️⃣ 4/13
🟩 2️⃣ 1/13
🟨 3️⃣ 5/13
🟦 4️⃣ 2/13
Answer: 3️⃣ 5/13
📘 (JEE Main 2012 – AIEEE)

🔵 Question 26:
If P(A) = 1/2, P(B) = 1/3, and P(A ∩ B) = 1/6, then A and B are
🟥 1️⃣ Independent
🟩 2️⃣ Mutually exclusive
🟨 3️⃣ Complementary
🟦 4️⃣ None
Answer: 1️⃣ Independent
📘 (AIEEE 2012)

🔵 Question 27:
A die is thrown twice. The probability of getting a doublet is
🟥 1️⃣ 1/6
🟩 2️⃣ 1/36
🟨 3️⃣ 1/3
🟦 4️⃣ 1/12
Answer: 1️⃣ 1/6
📘 (AIEEE 2011)

🔵 Question 28:
If P(A) = 0.5, P(B) = 0.4, and A, B are independent, then P(A ∩ B) = ?
🟥 1️⃣ 0.2
🟩 2️⃣ 0.1
🟨 3️⃣ 0.9
🟦 4️⃣ 0.3
Answer: 1️⃣ 0.2
📘 (AIEEE 2011)

🔵 Question 29:
A bag contains 4 red and 5 green balls. Two balls are drawn at random. The probability that one is red and one is green is
🟥 1️⃣ 4/9
🟩 2️⃣ 5/9
🟨 3️⃣ 20/36
🟦 4️⃣ 1/2
Answer: 2️⃣ 5/9
📘 (AIEEE 2010)

🔵 Question 30:
Two events A and B are such that P(A) = 1/2, P(B) = 1/3 and P(A ∪ B) = 2/3. Then P(A ∩ B) = ?
🟥 1️⃣ 1/6
🟩 2️⃣ 1/3
🟨 3️⃣ 1/4
🟦 4️⃣ 1/2
Answer: 1️⃣ 1/6
📘 (AIEEE 2010)

🔵 Question 31:
If A and B are independent events, then P(A ∪ B) = ?
🟥 1️⃣ P(A) + P(B)
🟩 2️⃣ P(A) + P(B) − P(A)P(B)
🟨 3️⃣ P(A) + P(B) + P(A)P(B)
🟦 4️⃣ None
Answer: 2️⃣ P(A) + P(B) − P(A)P(B)
📘 (AIEEE 2009)

🔵 Question 32:
The probability of getting a sum of 9 from two throws of a die is
🟥 1️⃣ 1/9
🟩 2️⃣ 1/6
🟨 3️⃣ 1/8
🟦 4️⃣ 1/12
Answer: 4️⃣ 1/12
📘 (AIEEE 2009)

🔵 Question 33:
A card is drawn from a well-shuffled deck. The probability that it is neither a heart nor a king is
🟥 1️⃣ 11/13
🟩 2️⃣ 9/13
🟨 3️⃣ 10/13
🟦 4️⃣ 12/13
Answer: 1️⃣ 11/13
📘 (AIEEE 2008)

🔵 Question 34:
If P(A) = 0.7, P(B) = 0.6 and P(A ∩ B) = 0.4, then P(A ∪ B) = ?
🟥 1️⃣ 0.8
🟩 2️⃣ 0.9
🟨 3️⃣ 1.0
🟦 4️⃣ 0.7
Answer: 2️⃣ 0.9
📘 (AIEEE 2008)

🔵 Question 35:
Two dice are thrown. The probability that the sum is less than 4 is
🟥 1️⃣ 1/6
🟩 2️⃣ 1/12
🟨 3️⃣ 1/9
🟦 4️⃣ 1/18
Answer: 2️⃣ 1/12
📘 (AIEEE 2007)

🔵 Question 36:
A coin is tossed 4 times. The probability of getting exactly 2 heads is
🟥 1️⃣ 3/8
🟩 2️⃣ 3/16
🟨 3️⃣ 6/16
🟦 4️⃣ 5/16
Answer: 3️⃣ 6/16
📘 (AIEEE 2007)

🔵 Question 37:
A box contains 10 bulbs of which 3 are defective. Two bulbs are drawn at random. The probability that both are good is
🟥 1️⃣ 7/15
🟩 2️⃣ 14/30
🟨 3️⃣ 7/15
🟦 4️⃣ 7/15
Answer: 1️⃣ 7/15
📘 (AIEEE 2006)

🔵 Question 38:
If P(A) = 1/4, P(B) = 1/2, and A ⊂ B, then P(A ∩ B) = ?
🟥 1️⃣ 1/4
🟩 2️⃣ 1/2
🟨 3️⃣ 3/4
🟦 4️⃣ 1
Answer: 1️⃣ 1/4
📘 (AIEEE 2006)

🔵 Question 39:
The probability that a leap year has 53 Sundays is
🟥 1️⃣ 1/7
🟩 2️⃣ 2/7
🟨 3️⃣ 3/7
🟦 4️⃣ 4/7
Answer: 2️⃣ 2/7
📘 (AIEEE 2005)

🔵 Question 40:
A fair coin is tossed 5 times. The probability of getting exactly 3 heads is
🟥 1️⃣ 10/32
🟩 2️⃣ 5/16
🟨 3️⃣ 3/16
🟦 4️⃣ 1/2
Answer: 1️⃣ 10/32
📘 (AIEEE 2005)

🔵 Question 41:
A box contains 3 red, 2 blue, and 5 green balls. One ball is drawn. The probability it is not green is
🟥 1️⃣ 1/2
🟩 2️⃣ 2/5
🟨 3️⃣ 3/10
🟦 4️⃣ 1/3
Answer: 1️⃣ 1/2
📘 (AIEEE 2004)

🔵 Question 42:
If P(A) = 1/3, P(B) = 1/4, and A, B are independent, then P(A ∩ B) = ?
🟥 1️⃣ 1/12
🟩 2️⃣ 1/7
🟨 3️⃣ 1/6
🟦 4️⃣ 1/3
Answer: 1️⃣ 1/12
📘 (AIEEE 2004)

🔵 Question 43:
A die is thrown. The probability of getting a number less than 3 is
🟥 1️⃣ 1/3
🟩 2️⃣ 1/2
🟨 3️⃣ 2/3
🟦 4️⃣ 1/6
Answer: 1️⃣ 1/3
📘 (AIEEE 2003)

🔵 Question 44:
A card is drawn. The probability that it is a heart or a queen is
🟥 1️⃣ 4/13
🟩 2️⃣ 1/13
🟨 3️⃣ 5/13
🟦 4️⃣ 2/13
Answer: 3️⃣ 5/13
📘 (AIEEE 2003)

🔵 Question 45:
If two dice are thrown, the probability of getting sum 5 is
🟥 1️⃣ 1/9
🟩 2️⃣ 1/12
🟨 3️⃣ 1/6
🟦 4️⃣ 1/8
Answer: 2️⃣ 1/12
📘 (AIEEE 2002)

🔵 Question 46:
A bag contains 5 white and 5 black balls. Two balls are drawn at random. The probability that they are of different colour is
🟥 1️⃣ 1/2
🟩 2️⃣ 5/9
🟨 3️⃣ 4/9
🟦 4️⃣ 5/8
Answer: 2️⃣ 5/9
📘 (AIEEE 2002)

🔵 Question 47:
A die is rolled twice. The probability of getting same number both times is
🟥 1️⃣ 1/6
🟩 2️⃣ 1/3
🟨 3️⃣ 1/12
🟦 4️⃣ 1/36
Answer: 1️⃣ 1/6
📘 (AIEEE 2002)

🔵 Question 48:
If P(A) = 0.5, P(B) = 0.3, and P(A ∪ B) = 0.6, then P(A ∩ B) = ?
🟥 1️⃣ 0.1
🟩 2️⃣ 0.2
🟨 3️⃣ 0.3
🟦 4️⃣ 0.4
Answer: 2️⃣ 0.2
📘 (AIEEE 2002)

🔵 Question 49:
A coin is tossed twice. The probability of getting no head is
🟥 1️⃣ 1/4
🟩 2️⃣ 1/2
🟨 3️⃣ 3/4
🟦 4️⃣ 1
Answer: 1️⃣ 1/4
📘 (AIEEE 2002)

🔵 Question 50:
The probability of getting an even number on a die is
🟥 1️⃣ 1/3
🟩 2️⃣ 1/2
🟨 3️⃣ 2/3
🟦 4️⃣ 1/6
Answer: 2️⃣ 1/2
📘 (AIEEE 2002)

JEE ADVANCED QUESTIONS FROM THIS LESSON

🔵 Question 1:
If P(A) = 0.5, P(B) = 0.4, and P(A ∩ B) = 0.2, then P(A ∪ B) = ?
🟥 1️⃣ 0.7
🟩 2️⃣ 0.9
🟨 3️⃣ 0.6
🟦 4️⃣ 0.8
Answer: 1️⃣ 0.7
📘 Year: 2024 | Paper: 1 | Set: Official

🔵 Question 2:
A die is rolled twice. The probability that the sum of numbers is 7 is
🟥 1️⃣ 1/6
🟩 2️⃣ 1/12
🟨 3️⃣ 1/8
🟦 4️⃣ 1/9
Answer: 1️⃣ 1/6
📘 Year: 2023 | Paper: 1 | Set: Official

🔵 Question 3:
If A and B are independent events with P(A) = 1/3 and P(B) = 1/2, then P(A ∩ B) = ?
🟥 1️⃣ 1/6
🟩 2️⃣ 1/2
🟨 3️⃣ 1/3
🟦 4️⃣ 1/5
Answer: 1️⃣ 1/6
📘 Year: 2023 | Paper: 1 | Set: Official

🔵 Question 4:
If two events A and B are such that P(A) = 0.7, P(B) = 0.4, and P(A ∩ B) = 0.3, then P(A|B) = ?
🟥 1️⃣ 3/4
🟩 2️⃣ 1/2
🟨 3️⃣ 2/3
🟦 4️⃣ 3/5
Answer: 3️⃣ 2/3
📘 Year: 2022 | Paper: 1 | Set: Official

🔵 Question 5:
If P(A ∩ B) = 1/6, P(A) = 1/2, and P(B) = 1/3, then A and B are
🟥 1️⃣ Independent
🟩 2️⃣ Mutually exclusive
🟨 3️⃣ Dependent
🟦 4️⃣ Complementary
Answer: 1️⃣ Independent
📘 Year: 2022 | Paper: 1 | Set: Official

🔵 Question 6:
The probability that a leap year has 53 Sundays is
🟥 1️⃣ 1/7
🟩 2️⃣ 2/7
🟨 3️⃣ 3/7
🟦 4️⃣ 4/7
Answer: 2️⃣ 2/7
📘 Year: 2021 | Paper: 1 | Set: Official

🔵 Question 7:
If a die is thrown twice, then the probability that at least one ‘6’ appears is
🟥 1️⃣ 11/36
🟩 2️⃣ 1/3
🟨 3️⃣ 5/36
🟦 4️⃣ 25/36
Answer: 4️⃣ 25/36
📘 Year: 2021 | Paper: 1 | Set: Official

🔵 Question 8:
If P(A) = 0.5, P(B) = 0.4, and P(A ∩ B) = 0.1, then P(A|B) = ?
🟥 1️⃣ 1/4
🟩 2️⃣ 1/2
🟨 3️⃣ 1/3
🟦 4️⃣ 1/5
Answer: 3️⃣ 1/3
📘 Year: 2020 | Paper: 1 | Set: Official

🔵 Question 9:
A coin is tossed three times. The probability of getting exactly two heads is
🟥 1️⃣ 3/8
🟩 2️⃣ 1/8
🟨 3️⃣ 5/8
🟦 4️⃣ 1/4
Answer: 1️⃣ 3/8
📘 Year: 2020 | Paper: 1 | Set: Official

🔵 Question 10:
If A and B are two events such that P(A) = 1/2, P(B) = 1/3, and P(A ∪ B) = 2/3, then P(A ∩ B) = ?
🟥 1️⃣ 1/6
🟩 2️⃣ 1/3
🟨 3️⃣ 1/2
🟦 4️⃣ 1/4
Answer: 1️⃣ 1/6
📘 Year: 2019 | Paper: 1 | Set: Official

🔵 Question 11:
A fair coin is tossed 4 times. The probability of getting exactly 2 heads is
🟥 1️⃣ 3/8
🟩 2️⃣ 3/16
🟨 3️⃣ 6/16
🟦 4️⃣ 1/2
Answer: 3️⃣ 6/16
📘 Year: 2019 | Paper: 1 | Set: Official

🔵 Question 12:
If P(A) = 0.6, P(B) = 0.5, and P(A ∪ B) = 0.8, then P(A ∩ B) = ?
🟥 1️⃣ 0.1
🟩 2️⃣ 0.2
🟨 3️⃣ 0.3
🟦 4️⃣ 0.4
Answer: 2️⃣ 0.2
📘 Year: 2018 | Paper: 1 | Set: Official

🔵 Question 13:
A bag has 4 red and 6 blue balls. One ball is drawn at random. The probability that it is blue is
🟥 1️⃣ 3/5
🟩 2️⃣ 2/5
🟨 3️⃣ 1/5
🟦 4️⃣ 4/5
Answer: 1️⃣ 3/5
📘 Year: 2018 | Paper: 1 | Set: Official

🔵 Question 14:
If P(A) = 0.5, P(B) = 0.3, and P(A ∩ B) = 0.2, then P(A|B) = ?
🟥 1️⃣ 2/3
🟩 2️⃣ 3/5
🟨 3️⃣ 1/2
🟦 4️⃣ 3/4
Answer: 1️⃣ 2/3
📘 Year: 2017 | Paper: 1 | Set: Official

🔵 Question 15:
Two coins are tossed. The probability of getting at least one head is
🟥 1️⃣ 1/2
🟩 2️⃣ 3/4
🟨 3️⃣ 1/4
🟦 4️⃣ 2/3
Answer: 2️⃣ 3/4
📘 Year: 2017 | Paper: 1 | Set: Official

🔵 Question 16:
A card is drawn from a pack of 52 cards. The probability that it is neither a king nor a queen is
🟥 1️⃣ 11/13
🟩 2️⃣ 10/13
🟨 3️⃣ 3/13
🟦 4️⃣ 1/13
Answer: 1️⃣ 11/13
📘 Year: 2016 | Paper: 1 | Set: Official

🔵 Question 17:
If P(A) = 0.4, P(B) = 0.5, and P(A ∪ B) = 0.7, then P(A ∩ B) = ?
🟥 1️⃣ 0.1
🟩 2️⃣ 0.2
🟨 3️⃣ 0.3
🟦 4️⃣ 0.4
Answer: 2️⃣ 0.2
📘 Year: 2016 | Paper: 1 | Set: Official

🔵 Question 18:
A card is drawn from a pack of 52 cards. The probability that it is either a heart or a king is
🟥 1️⃣ 4/13
🟩 2️⃣ 1/13
🟨 3️⃣ 5/13
🟦 4️⃣ 2/13
Answer: 3️⃣ 5/13
📘 Year: 2024 | Paper: 2 | Set: Official

🔵 Question 19:
If P(A) = 0.6, P(B) = 0.5 and P(A ∪ B) = 0.8, then P(A ∩ B) = ?
🟥 1️⃣ 0.3
🟩 2️⃣ 0.4
🟨 3️⃣ 0.2
🟦 4️⃣ 0.1
Answer: 3️⃣ 0.2
📘 Year: 2023 | Paper: 2 | Set: Official

🔵 Question 20:
Two dice are thrown simultaneously. The probability of getting sum 9 or 10 is
🟥 1️⃣ 1/3
🟩 2️⃣ 5/18
🟨 3️⃣ 7/36
🟦 4️⃣ 1/2
Answer: 3️⃣ 7/36
📘 Year: 2023 | Paper: 2 | Set: Official

🔵 Question 21:
If A and B are independent events with P(A) = 0.5 and P(B) = 0.6, then P(A ∩ B) = ?
🟥 1️⃣ 0.1
🟩 2️⃣ 0.3
🟨 3️⃣ 0.4
🟦 4️⃣ 0.2
Answer: 2️⃣ 0.3
📘 Year: 2022 | Paper: 2 | Set: Official

🔵 Question 22:
The probability that a leap year will contain 53 Mondays is
🟥 1️⃣ 1/7
🟩 2️⃣ 2/7
🟨 3️⃣ 3/7
🟦 4️⃣ 4/7
Answer: 2️⃣ 2/7
📘 Year: 2022 | Paper: 2 | Set: Official

🔵 Question 23:
A coin is tossed 3 times. The probability of getting at least one tail is
🟥 1️⃣ 1/8
🟩 2️⃣ 7/8
🟨 3️⃣ 3/8
🟦 4️⃣ 5/8
Answer: 2️⃣ 7/8
📘 Year: 2021 | Paper: 2 | Set: Official

🔵 Question 24:
Two cards are drawn from a deck. The probability that both are kings is
🟥 1️⃣ 1/221
🟩 2️⃣ 1/1326
🟨 3️⃣ 2/663
🟦 4️⃣ 1/26
Answer: 3️⃣ 2/663
📘 Year: 2021 | Paper: 2 | Set: Official

🔵 Question 25:
If P(A) = 0.3, P(B) = 0.4, and P(A ∩ B) = 0.2, then A and B are
🟥 1️⃣ Dependent
🟩 2️⃣ Independent
🟨 3️⃣ Mutually exclusive
🟦 4️⃣ Complementary
Answer: 1️⃣ Dependent
📘 Year: 2020 | Paper: 2 | Set: Official

🔵 Question 26:
A fair die is rolled twice. The probability that both numbers are even is
🟥 1️⃣ 1/4
🟩 2️⃣ 1/3
🟨 3️⃣ 1/6
🟦 4️⃣ 1/2
Answer: 1️⃣ 1/4
📘 Year: 2020 | Paper: 2 | Set: Official

🔵 Question 27:
A coin is tossed 4 times. The probability of getting exactly 3 heads is
🟥 1️⃣ 1/4
🟩 2️⃣ 1/8
🟨 3️⃣ 1/2
🟦 4️⃣ 1/16
Answer: 1️⃣ 1/4
📘 Year: 2019 | Paper: 2 | Set: Official

🔵 Question 28:
If P(A) = 0.4, P(B) = 0.5, and P(A ∩ B) = 0.1, then P(A ∪ B) = ?
🟥 1️⃣ 0.8
🟩 2️⃣ 0.7
🟨 3️⃣ 0.6
🟦 4️⃣ 0.9
Answer: 2️⃣ 0.7
📘 Year: 2019 | Paper: 2 | Set: Official

🔵 Question 29:
If two independent events A and B have P(A) = 1/3 and P(B) = 2/3, then P(A’ ∩ B’) = ?
🟥 1️⃣ 1/3
🟩 2️⃣ 2/9
🟨 3️⃣ 4/9
🟦 4️⃣ 5/9
Answer: 3️⃣ 4/9
📘 Year: 2018 | Paper: 2 | Set: Official

🔵 Question 30:
A die is rolled thrice. The probability of getting at least one six is
🟥 1️⃣ 91/216
🟩 2️⃣ 125/216
🟨 3️⃣ 5/6
🟦 4️⃣ 1/6
Answer: 1️⃣ 91/216
📘 Year: 2018 | Paper: 2 | Set: Official

🔵 Question 31:
A bag has 3 red and 5 black balls. One ball is drawn at random. The probability it is not red is
🟥 1️⃣ 5/8
🟩 2️⃣ 3/8
🟨 3️⃣ 1/2
🟦 4️⃣ 1/3
Answer: 1️⃣ 5/8
📘 Year: 2017 | Paper: 2 | Set: Official

🔵 Question 32:
If P(A) = 0.5, P(B) = 0.6, and P(A ∩ B) = 0.2, then P(A|B) = ?
🟥 1️⃣ 1/3
🟩 2️⃣ 2/3
🟨 3️⃣ 3/5
🟦 4️⃣ 1/5
Answer: 1️⃣ 1/3
📘 Year: 2016 | Paper: 2 | Set: Official

🔵 Question 33:
A coin is tossed twice. The probability of getting same face both times is
🟥 1️⃣ 1/2
🟩 2️⃣ 1/3
🟨 3️⃣ 1/4
🟦 4️⃣ 3/4
Answer: 1️⃣ 1/2
📘 Year: 2015 | Paper: 2 | Set: Official

🔵 Question 34:
If P(A) = 0.4, P(B) = 0.3, and P(A ∪ B) = 0.5, then P(A ∩ B) = ?
🟥 1️⃣ 0.1
🟩 2️⃣ 0.2
🟨 3️⃣ 0.3
🟦 4️⃣ 0.4
Answer: 2️⃣ 0.2
📘 Year: 2013 | Paper: 2 | Set: Official

PRACTICE SETS FROM THIS LESSON

🧠 NEET-Level MCQs (Q1–Q20)
Q1. P(A) = 0.4, P(B) = 0.5, P(A ∩ B) = 0.2. Then P(A ∪ B) =
🔵 (A) 0.7
🟢 (B) 0.9
🟠 (C) 1.1
🔴 (D) 0.3
Answer: (B) 0.9

Q2. If A and B are independent, P(A) = 1/3, P(B) = 1/2, then P(A ∩ B) =
🔵 (A) 1/5
🟢 (B) 1/6
🟠 (C) 1/3
🔴 (D) 2/3
Answer: (B) 1/6

Q3. A coin is tossed twice. The probability of getting at least one head is
🔵 (A) 1/4
🟢 (B) 1/2
🟠 (C) 3/4
🔴 (D) 1
Answer: (C) 3/4

Q4. P(A) = 0.7, P(B) = 0.6, P(A ∪ B) = 0.9, then P(A ∩ B) =
🔵 (A) 0.4
🟢 (B) 0.3
🟠 (C) 0.2
🔴 (D) 0.5
Answer: (B) 0.3

Q5. If two dice are thrown, the probability of getting sum = 7 is
🔵 (A) 1/12
🟢 (B) 1/6
🟠 (C) 1/8
🔴 (D) 1/18
Answer: (B) 1/6

Q6. A bag contains 3 red and 2 black balls. One ball is drawn. The probability it is red is
🔵 (A) 3/5
🟢 (B) 2/5
🟠 (C) 1/2
🔴 (D) 1/3
Answer: (A) 3/5

Q7. If P(A) = 0.5, P(B) = 0.4, P(A ∩ B) = 0.2, then P(A′ ∩ B′) =
🔵 (A) 0.3
🟢 (B) 0.9
🟠 (C) 0.1
🔴 (D) 0.5
Answer: (A) 0.3

Q8. If A and B are mutually exclusive with P(A) = 0.4, P(B) = 0.3, then P(A ∪ B) =
🔵 (A) 0.1
🟢 (B) 0.7
🟠 (C) 0.4
🔴 (D) 0.3
Answer: (B) 0.7

Q9. Probability of getting a king in a single draw from 52 cards is
🔵 (A) 1/52
🟢 (B) 1/13
🟠 (C) 1/26
🔴 (D) 1/4
Answer: (B) 1/13

Q10. A coin is tossed three times. The probability of getting exactly 2 heads is
🔵 (A) 3/8
🟢 (B) 1/2
🟠 (C) 1/4
🔴 (D) 5/8
Answer: (A) 3/8

Q11. P(A) = 0.6, P(B|A) = 0.5 ⇒ P(A ∩ B) =
🔵 (A) 0.3
🟢 (B) 0.1
🟠 (C) 0.5
🔴 (D) 0.6
Answer: (A) 0.3

Q12. Probability of getting an even number when a die is rolled =
🔵 (A) 1/2
🟢 (B) 1/3
🟠 (C) 1/6
🔴 (D) 2/3
Answer: (A) 1/2

Q13. A bag has 4 white, 3 black balls. One ball drawn is white. P(white) =
🔵 (A) 3/7
🟢 (B) 4/7
🟠 (C) 1/2
🔴 (D) 5/7
Answer: (B) 4/7

Q14. P(A ∪ B) = P(A) + P(B) − P(A ∩ B). This formula is for
🔵 (A) Addition theorem
🟢 (B) Multiplication theorem
🟠 (C) Bayes theorem
🔴 (D) Total probability
Answer: (A) Addition theorem

Q15. Probability of drawing an ace or king from a pack of 52 cards =
🔵 (A) 2/13
🟢 (B) 1/13
🟠 (C) 3/13
🔴 (D) 1/26
Answer: (A) 2/13

Q16. If an unbiased die is rolled, probability of not getting 3 is
🔵 (A) 1/6
🟢 (B) 5/6
🟠 (C) 2/3
🔴 (D) 1/3
Answer: (B) 5/6

Q17. P(A) = 0.7 ⇒ P(A′) =
🔵 (A) 0.3
🟢 (B) 0.7
🟠 (C) 1
🔴 (D) 0.5
Answer: (A) 0.3

Q18. When two coins are tossed, sample space size =
🔵 (A) 2
🟢 (B) 3
🟠 (C) 4
🔴 (D) 6
Answer: (C) 4

Q19. Probability of drawing a red card from 52 =
🔵 (A) 1/2
🟢 (B) 1/4
🟠 (C) 3/4
🔴 (D) 1/13
Answer: (A) 1/2

Q20. P(A) = 0.3, P(B) = 0.5, A, B independent ⇒ P(A′ ∩ B′) =
🔵 (A) 0.35
🟢 (B) 0.7
🟠 (C) 0.7 × 0.5 = 0.35
🔴 (D) 0.35
Answer: (D) 0.35

🎯 JEE Main-Level MCQs (Q21–Q40)
🔵 Q21.
A biased coin has a probability 0.4 of showing head on any toss. If the coin is tossed three times, the probability of getting exactly one head is

🔵 (A) 0.216
🟢 (B) 0.288
🟠 (C) 0.432
🔴 (D) 0.384

✔️ Answer: (C) 0.432

💡 Check:
P(exactly 1 head) = ³C₁ × (0.4)¹ × (0.6)²
= 3 × 0.4 × 0.36 = 0.432

Q22. P(A) = 1/2, P(B) = 1/3, P(A ∪ B) = 2/3 ⇒ P(A ∩ B) =
🔵 (A) 1/6
🟢 (B) 1/3
🟠 (C) 1/12
🔴 (D) 1/4
Answer: (A) 1/6

Q23. P(A|B) = 1/3, P(B) = 1/2, P(A ∩ B) = ?
🔵 (A) 1/3
🟢 (B) 1/6
🟠 (C) 1/2
🔴 (D) 1/4
Answer: (B) 1/6

Q24. If P(A) = 0.6, P(B) = 0.5, P(A ∩ B) = 0.3, then A and B are
🔵 (A) Independent
🟢 (B) Dependent
🟠 (C) Mutually exclusive
🔴 (D) Complementary
Answer: (A) Independent

Q25. For two independent events A, B, P(A) = 0.3, P(B) = 0.5, find P(A′ ∩ B).
🔵 (A) 0.5
🟢 (B) 0.35
🟠 (C) 0.25
🔴 (D) 0.15
Answer: (B) 0.35

Q26. A and B are mutually exclusive with P(A) = 0.4, P(B) = 0.3. Then P(A|B) =
🔵 (A) 0
🟢 (B) 1
🟠 (C) 0.4
🔴 (D) 0.3
Answer: (A) 0

Q27. P(A) = 0.5, P(B) = 0.4, P(A ∪ B) = 0.7 ⇒ P(A ∩ B) =
🔵 (A) 0.2
🟢 (B) 0.1
🟠 (C) 0.3
🔴 (D) 0.4
Answer: (A) 0.2

Q28. P(E) = 0.6, then P(E′) =
🔵 (A) 0.4
🟢 (B) 0.5
🟠 (C) 0.3
🔴 (D) 0.6
Answer: (A) 0.4

Q29. If P(A) = 0.4, P(B) = 0.5, P(A ∩ B) = 0.1, find P(A|B).
🔵 (A) 0.1
🟢 (B) 0.2
🟠 (C) 0.4
🔴 (D) 0.25
Answer: (D) 0.2

Q30. A bag has 3 red, 5 black balls. Two balls drawn with replacement. P(both red) =
🔵 (A) 9/64
🟢 (B) 9/16
🟠 (C) 1/16
🔴 (D) 3/8
Answer: (A) 9/64

Q31. P(A) = 0.7, P(B) = 0.8 ⇒ P(A ∩ B) min = ?
🔵 (A) 0.5
🟢 (B) 0.6
🟠 (C) 0.7
🔴 (D) 0.8
Answer: (A) 0.5

Q32. For independent A, B, if P(A ∩ B) = 0.12, P(A) = 0.4 ⇒ P(B) =
🔵 (A) 0.3
🟢 (B) 0.4
🟠 (C) 0.5
🔴 (D) 0.6
Answer: (A) 0.3

Q33. If A, B independent ⇒ P(A ∪ B) = ?
🔵 (A) P(A) + P(B)
🟢 (B) P(A) + P(B) − P(A)P(B)
🟠 (C) P(A) + P(B) + P(A)P(B)
🔴 (D) None
Answer: (B)

Q34. Conditional probability P(A|B) = 1 ⇒ implies
🔵 (A) B ⊂ A
🟢 (B) A ⊂ B
🟠 (C) A ∩ B = ∅
🔴 (D) None
Answer: (A)

Q35. Probability distribution must satisfy
🔵 (A) ΣP(X) = 1
🟢 (B) ΣP(X) = 0
🟠 (C) ΣP(X) < 1
🔴 (D) ΣP(X) > 1
Answer: (A)

Q36. Mean of distribution X:0,1,2 with P(X):0.2,0.5,0.3 is
🔵 (A) 1.1
🟢 (B) 1.2
🟠 (C) 1.3
🔴 (D) 1.5
Answer: (B) 1.2

Q37. Variance of above distribution =
🔵 (A) 0.46
🟢 (B) 0.45
🟠 (C) 0.47
🔴 (D) 0.48
Answer: (A) 0.46

Q38. If A ⊂ B ⇒ P(A ∩ B) =
🔵 (A) P(A)
🟢 (B) P(B)
🟠 (C) P(A) + P(B)
🔴 (D) None
Answer: (A)

Q39. If P(A) = 0.6, P(A ∪ B) = 0.9, P(B) = ? when A, B mutually exclusive
🔵 (A) 0.3
🟢 (B) 0.4
🟠 (C) 0.5
🔴 (D) 0.6
Answer: (A) 0.3

Q40. If events A, B are independent, P(A) = 0.4, P(B) = 0.5 ⇒ P(A ∩ B) =
🔵 (A) 0.2
🟢 (B) 0.1
🟠 (C) 0.4
🔴 (D) 0.5
Answer: (A) 0.2

⚡ JEE Advanced-Level MCQs (Q41–Q50)
Q41. If P(A) = 0.7, P(B) = 0.6, P(A ∩ B) = 0.5 ⇒ P(A′ ∩ B′) =
🔵 (A) 0.2
🟢 (B) 0.4
🟠 (C) 0.1
🔴 (D) 0.3
Answer: (A) 0.2

Q42. Events A, B, C are independent with P(A)=1/2, P(B)=1/3, P(C)=1/4 ⇒ P(A′ ∩ B ∩ C) =
🔵 (A) 1/24
🟢 (B) 1/12
🟠 (C) 1/8
🔴 (D) 1/6
Answer: (B) 1/12

Q43. P(A ∩ B ∩ C) = 1/12, P(A ∩ B)=1/4, P(B ∩ C)=1/6, P(A ∩ C)=1/8 ⇒ P(A ∪ B ∪ C) = ?
🔵 (A) 3/4
🟢 (B) 5/6
🟠 (C) 2/3
🔴 (D) 7/12
Answer: (B) 5/6

Q44. If A, B are independent, P(A)=0.5, P(A ∪ B)=0.8 ⇒ P(B) =
🔵 (A) 0.6
🟢 (B) 0.7
🟠 (C) 0.5
🔴 (D) 0.3
Answer: (D) 0.3

Q45. A die is thrown twice. Find P(sum divisible by 4).
🔵 (A) 9/36
🟢 (B) 12/36
🟠 (C) 10/36
🔴 (D) 15/36
Answer: (A) 9/36

Q46. For events A, B, P(A) = p, P(B) = q, P(A ∩ B) = pq ⇒ A, B are
🔵 (A) Independent
🟢 (B) Mutually exclusive
🟠 (C) Complementary
🔴 (D) Disjoint
Answer: (A) Independent

Q47. Let A, B, C be independent events. Then which is also independent?
🔵 (A) A ∩ B and C
🟢 (B) A ∪ B and C
🟠 (C) A′ ∩ B and C
🔴 (D) All
Answer: (D) All

Q48. In tossing 4 coins, probability of at least one head =
🔵 (A) 15/16
🟢 (B) 14/16
🟠 (C) 1/2
🔴 (D) 13/16
Answer: (A) 15/16

Q49. If P(A ∪ B) = 0.8, P(A ∩ B) = 0.2, P(A) = 0.5 ⇒ P(B) =
🔵 (A) 0.5
🟢 (B) 0.6
🟠 (C) 0.7
🔴 (D) 0.8
Answer: (B) 0.5

Q50. If A ⊂ B, P(A) = 0.3, P(B) = 0.5, then P(A′ ∩ B) =
🔵 (A) 0.2
🟢 (B) 0.3
🟠 (C) 0.5
🔴 (D) 0.8
Answer: (A) 0.2

—————————————————————————————————————————————————————————————————————————————————-

Important Notice : The lessons and study materials up to July–August 2025 have been sent. Soon, after receiving feedback from teachers and students, we will deliver the latest and more innovative study materials for the upcoming months.

Important Notice : The lessons and study materials up to July–August 2025 have been sent. Soon, after receiving feedback from teachers and students, we will deliver the latest and more innovative study materials for the upcoming months.

Class 12 : Maths (English) -Chapter 13: Probability

EXPLANATION & SUMMARY

QUESTIONS FROM TEXTBOOK

OTHER IMPORTANT QUESTIONS FOR EXAMS

JEE MAINS QUESTIONS FROM THIS LESSON

JEE ADVANCED QUESTIONS FROM THIS LESSON

PRACTICE SETS FROM THIS LESSON

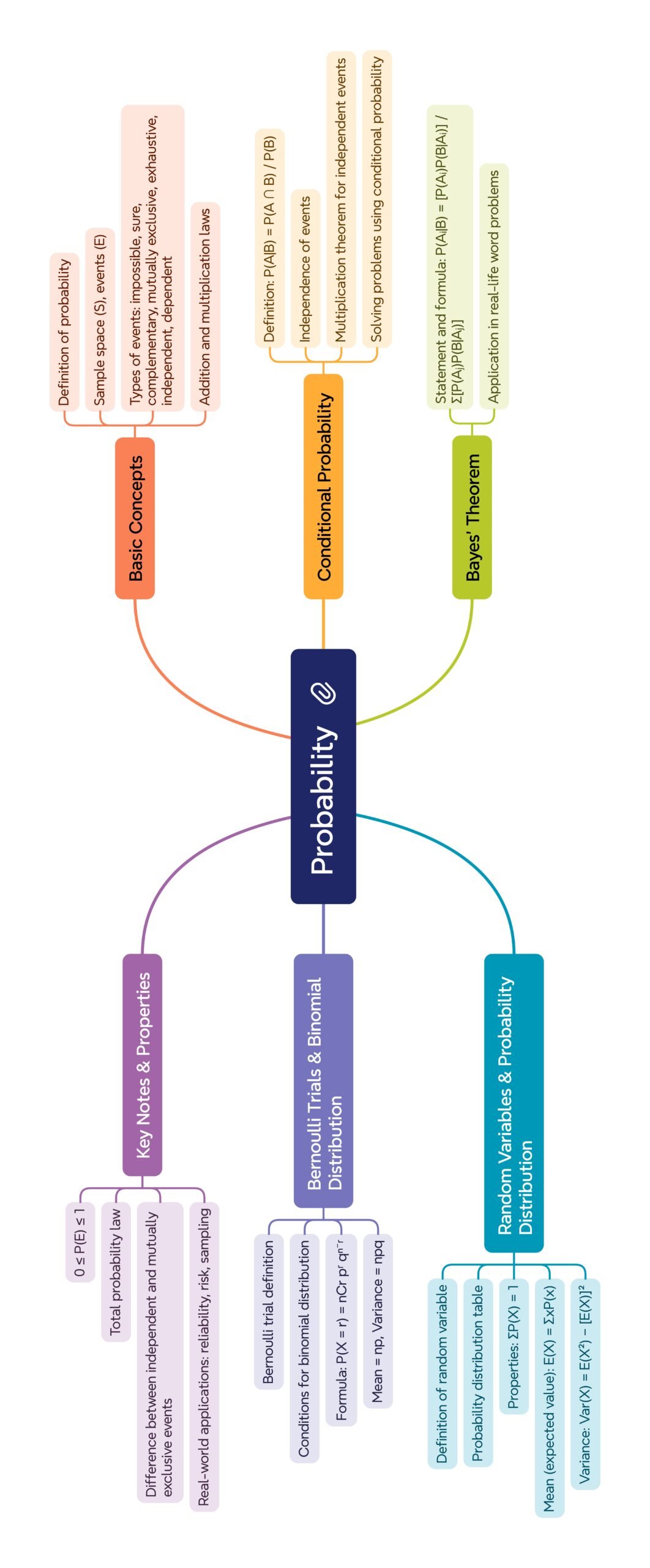
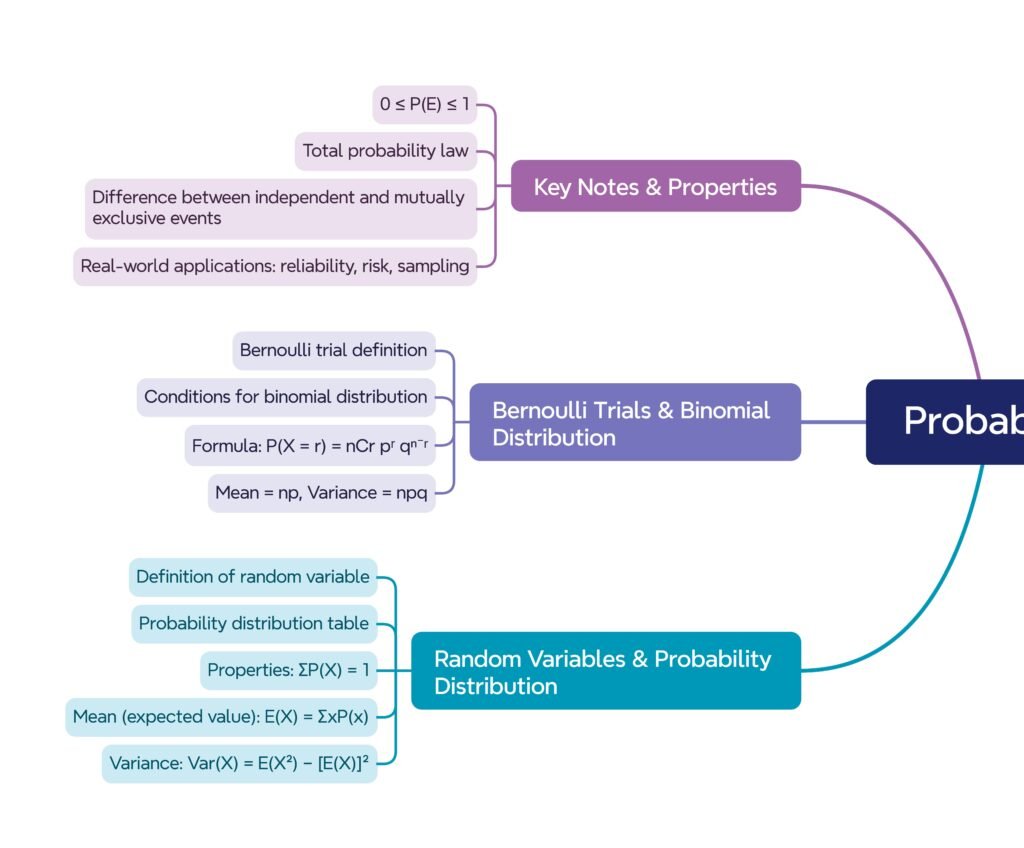
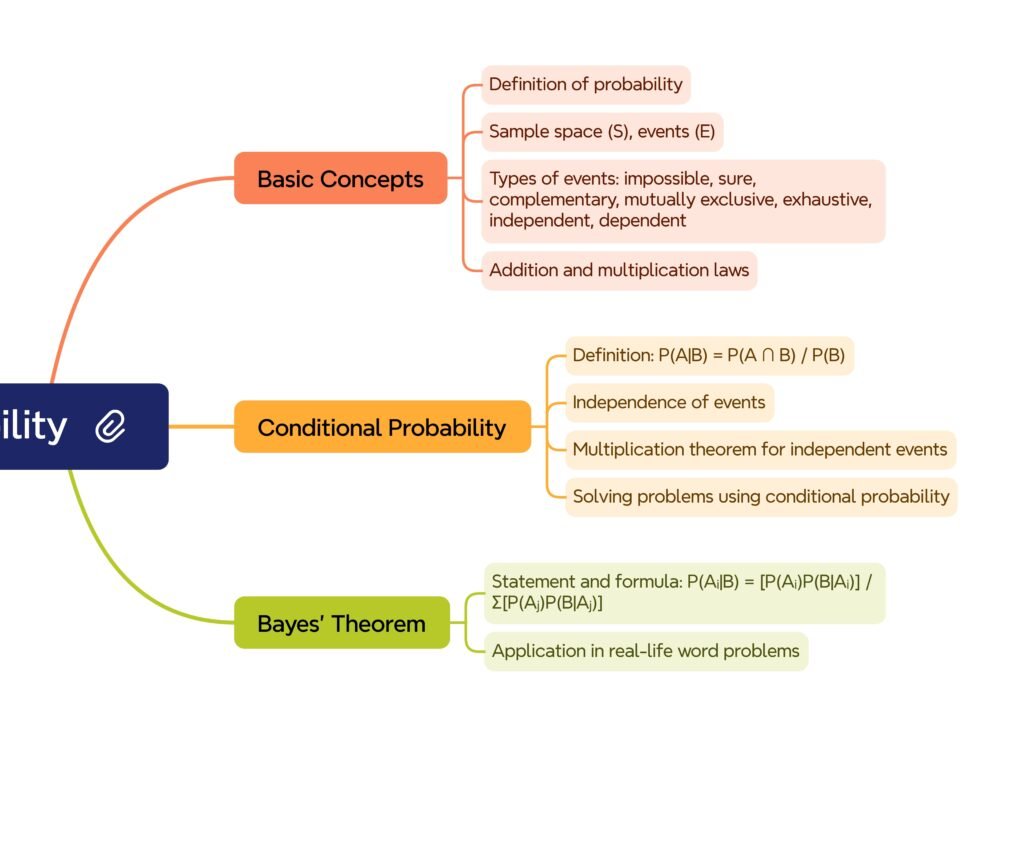
MIND MAPS

Leave a Reply Cancel reply