Class 12 : Maths (English) – Chapter 12: Linear Programming
EXPLANATION & SUMMARY
🔷 Explanation
🔹 Introduction
Linear Programming (LP) is a branch of mathematics that deals with the optimization (maximization or minimization) of a linear objective function, subject to a set of linear constraints (inequalities or equations).
It is a key topic in Operations Research and is widely used in economics, business, engineering, and management for resource optimization.
💡 Concept:
A Linear Programming Problem (LPP) involves finding the maximum or minimum value of a linear expression called the objective function, under certain linear constraints.
🔹 1. Basic Terminology
🟢 Objective Function:
A linear function of the form
➡️ Z = ax + by
where a and b are constants, and x, y are variables.
We aim to either maximize or minimize Z.
🟢 Constraints:
Conditions or restrictions expressed as linear inequalities or equations, e.g.:
➡️ 2x + y ≤ 10, x + y ≥ 5
🟢 Decision Variables:
The variables (x, y) whose values determine the value of Z.
🟢 Feasible Region:
The common region in the graph that satisfies all constraints simultaneously.
🟢 Feasible Solution:
Any point (x, y) within or on the boundary of the feasible region.
🟢 Optimal Solution:
A feasible solution that gives the maximum or minimum value of the objective function.
🟢 Corner Point Theorem:
If the feasible region is bounded, the optimal value occurs at one of the corner points (vertices) of the feasible region.
🔹 2. Formulation of Linear Programming Problem
The first step is to convert the word problem into mathematical form:
1️⃣ Identify decision variables (x, y).
2️⃣ Express the objective function (Z = ax + by).
3️⃣ Write down the constraints as linear inequalities.
4️⃣ Include non-negativity conditions: x ≥ 0, y ≥ 0.
🔹 3. Graphical Method of Solution
The graphical method is used for two-variable problems.
🧭 Steps:
1️⃣ Plot each linear inequality on a graph.
2️⃣ Shade the region satisfying each inequality.
3️⃣ The common shaded area is the feasible region.
4️⃣ Identify the corner points (vertices) of the feasible region.
5️⃣ Evaluate Z = ax + by at each corner point.
6️⃣ The maximum or minimum value occurs at one of these points.
✏️ Note: If feasible region is unbounded, you must check whether optimum value is finite.
🔹 4. Types of Linear Programming Problems
🟢 Maximization Problem:
Objective is to maximize Z = ax + by.
Example: Profit maximization.
🟢 Minimization Problem:
Objective is to minimize Z = ax + by.
Example: Cost minimization.
🟢 Feasible Region:
Bounded → Optimal value always exists.
Unbounded → May or may not exist; check using test line.
🔹 5. Example (Maximization)
Problem:
Maximize Z = 3x + 2y
Subject to:
x + y ≤ 4
x ≥ 0, y ≥ 0
Solution:
Plot lines x + y = 4
Shade feasible region in first quadrant (bounded triangle).
Corner points: (0,0), (4,0), (0,4)
Evaluate Z:
Z(0,0) = 0
Z(4,0) = 12
Z(0,4) = 8
✅ Maximum Z = 12 at (4,0)
🔹 6. Example (Minimization)
Problem:
Minimize Z = 2x + 3y
Subject to:
x + 2y ≥ 4
3x + y ≥ 3
x ≥ 0, y ≥ 0
By plotting the inequalities, feasible region is obtained and corner points are found.
Evaluate Z at each corner point → the smallest value is minimum Z.
🔹 7. Corner Point Method
💡 Corner Point Theorem:
If an LP problem has an optimal solution, it occurs at a vertex (corner point) of the feasible region.
🧭 Steps:
Determine feasible region.
Find corner points.
Evaluate objective function at each corner.
Choose maximum/minimum value.
🔹 8. Important Observations
✔️ If feasible region is bounded, optimal solution always exists at a vertex.
✔️ If feasible region is unbounded, optimal value may not exist.
✔️ If two or more vertices give the same Z, there are infinite optimal solutions.
🔹 9. Real-Life Applications
🔸 Manufacturing: Maximize profit by allocating resources optimally.
🔸 Diet Problems: Minimize cost while meeting nutritional needs.
🔸 Transportation: Minimize travel cost or distance.
🔸 Finance: Maximize returns under given constraints.
🔹 10. Key Formulae
Objective Function: Z = ax + by
Corner Point Evaluation
Distance between two lines if needed for geometric analysis
Feasibility check via inequalities
✏️ Non-negativity Conditions:
x ≥ 0, y ≥ 0 are mandatory.
🔹 11. Graphical Insights
🧠 Feasible region = polygon or half-plane intersection.
🧠 Vertices = intersection points of boundary lines.
🧠 Optimum value always at vertex.
🔹 12. Special Cases
🟡 No Solution: If feasible region is empty (inconsistent constraints).
🟡 Multiple Solutions: Two vertices give same Z → infinite optimal solutions.
🟡 Unbounded Solution: Region not closed; optimum may not exist.
🔹 13. NCERT Example Summary
Example 1: Maximize Z = 3x + 2y with x + y ≤ 4.
→ Maximum at (4,0), Z = 12.
Example 2: Minimize Z = x + y, subject to linear constraints.
→ Minimum at intersection point satisfying all inequalities.
🔹 14. Summary of Steps to Solve LPP
➡️ Step 1: Define variables x, y.
➡️ Step 2: Write objective function Z.
➡️ Step 3: Write all constraints.
➡️ Step 4: Plot constraints on graph.
➡️ Step 5: Determine feasible region.
➡️ Step 6: Identify corner points.
➡️ Step 7: Evaluate Z at each point.
➡️ Step 8: Choose maximum/minimum.
🔹 15. Non-Negativity Condition
Always include x ≥ 0 and y ≥ 0, as negative quantities often have no practical meaning.
🔹 16. Theoretical Basis
🧠 The LP feasible region is a convex polygon.
🧠 The objective function has linear level lines (iso-profit or iso-cost lines).
🧠 Optimal value occurs at vertex due to convexity.
🔹 17. Use in Economics & Business
🔸 Production Planning: Allocate machines and labor.
🔸 Diet Problems: Balanced diet with minimum cost.
🔸 Transportation Problems: Minimize logistics cost.
🔸 Portfolio Management: Optimize returns.
🔹 18. Limitations
⚠️ Assumes linearity of constraints and objective function.
⚠️ Only handles continuous variables.
⚠️ Ignores uncertainties and integer constraints.
🔷 Summary (~300 words)
🔹 Linear Programming aims to optimize (maximize or minimize) a linear objective function under linear constraints.
🔹 Objective Function: Z = ax + by
🔹 Constraints: Linear inequalities involving x, y.
🔹 Decision Variables: x, y
🔹 Feasible Region: Common region satisfying all inequalities.
🔹 Feasible Solution: Any point in feasible region.
🔹 Optimal Solution: Point giving maximum or minimum Z.
💡 Corner Point Theorem:
For bounded feasible region, optimal value occurs at a vertex.
🧭 Steps:
1️⃣ Define variables
2️⃣ Write objective function
3️⃣ Write constraints
4️⃣ Plot graph
5️⃣ Identify feasible region
6️⃣ Find corner points
7️⃣ Evaluate Z
8️⃣ Pick optimum
🟢 Bounded Region: Always optimum.
🟡 Unbounded Region: Check if optimum exists.
🔴 Infeasible: No common region → no solution.
Applications:
Production & resource allocation
Diet & nutrition
Transportation & logistics
Financial planning
Limitations:
Assumes linearity
Cannot handle integer constraints
No stochastic variables
📝 Quick Recap
✔️ Linear Programming = Optimization under constraints
✔️ Objective Function: Z = ax + by
✔️ Constraints: Linear inequalities
✔️ Feasible region = intersection
✔️ Optimum at corner point
✔️ Bounded → always solution
✔️ Unbounded → test line needed
🎯 Use: Maximize profit or minimize cost within given limits.
————————————————————————————————————————————————————————————————————————————
QUESTIONS FROM TEXTBOOK
🔵 Exercise 12.1
🔵 Question 1:
Maximise Z = 3x + 4y subject to the constraints: x + y ≤ 4, x ≥ 0, y ≥ 0.
🟢 Answer:
➡️ Feasible region in first quadrant bounded by x + y = 4 and axes.
➡️ Corner points: (0,0), (4,0), (0,4).
✳️ Z(0,0) = 0.
✳️ Z(4,0) = 3×4 + 4×0 = 12.
✳️ Z(0,4) = 3×0 + 4×4 = 16.
✔️ Maximum Z = 16 at (x, y) = (0, 4).
🔵 Question 2:
Minimise Z = −3x + 4y subject to x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0, y ≥ 0.
🟢 Answer:
➡️ Lines: x + 2y = 8 and 3x + 2y = 12.
➡️ Intersections with axes give candidate points; also solve for common point.
✳️ Intersection:
x + 2y = 8
3x + 2y = 12 ⇒ subtract ⇒ 2x = 4 ⇒ x = 2 ⇒ y = 3.
➡️ Feasible corner points: (0,0), (4,0), (2,3), (0,4).
✳️ Z(0,0) = 0.
✳️ Z(4,0) = −12.
✳️ Z(2,3) = −6 + 12 = 6.
✳️ Z(0,4) = 16.
✔️ Minimum Z = −12 at (x, y) = (4, 0).
🔵 Question 3:
Maximise Z = 5x + 3y subject to 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, y ≥ 0.
🟢 Answer:
➡️ Find intersection of the two boundary lines.
✳️ Solve:
3x + 5y = 15
5x + 2y = 10
⇒ 6x + 10y = 30, 25x + 10y = 50 ⇒ 19x = 20 ⇒ x = 20/19, y = 45/19.
➡️ Feasible corner points: (0,0), (2,0), (0,3), (20/19, 45/19).
✳️ Z(0,0) = 0.
✳️ Z(2,0) = 10.
✳️ Z(0,3) = 9.
✳️ Z(20/19, 45/19) = 5×(20/19) + 3×(45/19) = 235/19.
✔️ Maximum Z = 235/19 at (x, y) = (20/19, 45/19).
🔵 Question 4:
Minimise Z = 3x + 5y such that x + 3y ≥ 3, x + y ≥ 2, x ≥ 0, y ≥ 0.
🟢 Answer:
➡️ For “≥” constraints, feasible region is above both lines in first quadrant.
➡️ Intersection of boundaries gives likely minimum.
✳️ Solve:
x + 3y = 3
x + y = 2 ⇒ subtract ⇒ 2y = 1 ⇒ y = 1/2 ⇒ x = 3 − 3(1/2) = 3/2.
➡️ Check other boundary points that satisfy both: (3,0) and (0,2).
✳️ Z(3/2, 1/2) = 3×(3/2) + 5×(1/2) = 9/2 + 5/2 = 7.
✳️ Z(3,0) = 9.
✳️ Z(0,2) = 10.
✔️ Minimum Z = 7 at (x, y) = (3/2, 1/2).
🔵 Question 5:
Maximise Z = 3x + 2y subject to x + 2y ≤ 10, 3x + y ≤ 15, x ≥ 0, y ≥ 0.
🟢 Answer:
➡️ Intersection of boundaries:
x + 2y = 10
3x + y = 15 ⇒ 3x + 6y = 30 ⇒ 5y = 15 ⇒ y = 3 ⇒ x = 4.
➡️ Feasible corner points: (0,0), (5,0), (0,5), (4,3).
✳️ Z(0,0) = 0.
✳️ Z(5,0) = 15.
✳️ Z(0,5) = 10.
✳️ Z(4,3) = 3×4 + 2×3 = 18.
✔️ Maximum Z = 18 at (x, y) = (4, 3).
🔵 Question 6:
Minimise Z = x + 2y subject to 2x + y ≥ 3, x + 2y ≥ 6, x ≥ 0, y ≥ 0.
🟢 Answer:
➡️ Boundary lines: L₁: 2x + y = 3, L₂: x + 2y = 6.
➡️ Intersection:
✳️ From L₁: y = 3 − 2x.
✳️ Put in L₂: x + 2(3 − 2x) = 6 ⇒ −3x = 0 ⇒ x = 0, y = 3 ⇒ (0, 3).
➡️ Axis hits of L₂: (6, 0) and (0, 3).
➡️ Feasible region is above both lines (because “≥”).
➡️ Corner candidates: (0, 3) and (6, 0).
✳️ Z(0, 3) = 0 + 2×3 = 6.
✳️ Z(6, 0) = 6 + 0 = 6.
✔️ Minimum Z = 6.
💡 Since on L₂ (x + 2y = 6), Z = 6 for every point of the segment from (6, 0) to (0, 3) that also satisfies 2x + y ≥ 3 (true for 0 ≤ y ≤ 3).
✔️ Hence the minimum occurs at infinitely many points (all points on that segment).
🔵 Question 7:
Minimise and Maximise Z = 5x + 10y
subject to x + 2y ≤ 120, x + y ≥ 60, x − 2y ≥ 0, x ≥ 0, y ≥ 0.
🟢 Answer:
➡️ Lines: L₁: x + 2y = 120, L₂: x + y = 60, L₃: x − 2y = 0 (i.e., x = 2y).
➡️ Vertices of feasible region:
✳️ A = L₂ ∩ L₃: 2y + y = 60 ⇒ y = 20, x = 40 ⇒ A(40, 20).
✳️ B = L₁ ∩ L₃: 2y + 2y = 120 ⇒ y = 30, x = 60 ⇒ B(60, 30).
✳️ C = L₁ ∩ x-axis: y = 0 ⇒ x = 120 ⇒ C(120, 0).
✳️ D = L₂ ∩ x-axis: y = 0 ⇒ x = 60 ⇒ D(60, 0).
➡️ Evaluate Z = 5x + 10y:
✳️ Z(D) = 5×60 + 10×0 = 300.
✳️ Z(C) = 5×120 + 10×0 = 600.
✳️ Z(B) = 5×60 + 10×30 = 600.
✳️ Z(A) = 5×40 + 10×20 = 400.
✔️ Minimum Z = 300 at (60, 0).
✔️ Maximum Z = 600 at every point on the segment of L₁ from (120, 0) to (60, 30) (including those endpoints) since on x + 2y = 120, Z = 5(x + 2y) = 600 (constant).
🔵 Question 8:
Minimise and Maximise Z = x + 2y
subject to x + 2y ≥ 100, 2x − y ≤ 0 (i.e., y ≥ 2x), 2x + y ≤ 200, x ≥ 0, y ≥ 0.
🟢 Answer:
➡️ Lines: L₁: x + 2y = 100, L₂: y = 2x, L₃: 2x + y = 200.
➡️ Vertices of feasible region:
✳️ Q = L₁ ∩ L₂: x + 2(2x) = 100 ⇒ 5x = 100 ⇒ (20, 40).
✳️ P = L₂ ∩ L₃: 2x + 2x = 200 ⇒ x = 50, y = 100 ⇒ (50, 100).
✳️ E = L₁ ∩ y-axis: (0, 50).
✳️ F = L₃ ∩ y-axis: (0, 200).
➡️ Evaluate Z = x + 2y:
✳️ Z(E) = 0 + 100 = 100.
✳️ Z(Q) = 20 + 80 = 100.
✳️ Z(P) = 50 + 200 = 250.
✳️ Z(F) = 0 + 400 = 400.
✔️ Minimum Z = 100 at every point on L₁ between (0, 50) and (20, 40).
✔️ Maximum Z = 400 at (0, 200).
🔵 Question 9:
Maximise Z = −x + 2y
subject to x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0.
🟢 Answer:
➡️ Feasible region is to the right of x = 3 and above both lines x + y = 5 and x + 2y = 6 in first quadrant.
➡️ Along the vertical line x = 3, choose y → ∞ (and constraints remain satisfied).
✳️ Z(3, y) = −3 + 2y → unbounded above as y increases.
✔️ Conclusion: No maximum value (Z is unbounded on the feasible region).
🔵 Question 10:
Maximise Z = x + y
subject to x − y ≤ −1, −x + y ≤ 0, x ≥ 0, y ≥ 0.
🟢 Answer:
➡️ Inequalities:
✳️ x − y ≤ −1 ⇒ x ≤ y − 1.
✳️ −x + y ≤ 0 ⇒ y ≤ x.
➡️ Combining gives y ≤ x and x ≤ y − 1 ⇒ x ≤ x − 1, which is impossible.
✔️ Conclusion: No feasible solution (feasible region is empty), so no maximum exists.
————————————————————————————————————————————————————————————————————————————
OTHER IMPORTANT QUESTIONS FOR EXAMS
🔷 Section A – Multiple Choice Questions (1 mark each)
🔵 Question 1:
Linear Programming is used to
🔵 (A) Solve equations
🟢 (B) Optimize objective functions
🟠 (C) Solve quadratic equations
🔴 (D) Find derivatives
Answer: (B) Optimize objective functions
🔵 Question 2:
The function to be optimized is called
🔵 (A) Feasible function
🟢 (B) Objective function
🟠 (C) Constraint function
🔴 (D) Boundary function
Answer: (B) Objective function
🔵 Question 3:
A feasible region is
🔵 (A) Entire plane
🟢 (B) Common region satisfying all constraints
🟠 (C) Any single inequality region
🔴 (D) Unbounded line
Answer: (B) Common region satisfying all constraints
🔵 Question 4:
Which of the following is not a property of LPP?
🔵 (A) Linear objective function
🟢 (B) Linear constraints
🟠 (C) Nonlinear variables
🔴 (D) Non-negativity conditions
Answer: (C) Nonlinear variables
🔵 Question 5:
If Z = 3x + 2y is to be maximized, it is called
🔵 (A) Objective function
🟢 (B) Constraint
🟠 (C) Solution
🔴 (D) Feasible point
Answer: (A) Objective function
🔵 Question 6:
Feasible solution means
🔵 (A) Any solution
🟢 (B) Solution satisfying all constraints
🟠 (C) Solution giving maximum value
🔴 (D) Solution giving minimum value
Answer: (B) Solution satisfying all constraints
🔵 Question 7:
The optimal solution of a Linear Programming Problem, if it exists, occurs at
🔵 (A) Any point
🟢 (B) Corner point of feasible region
🟠 (C) Midpoint
🔴 (D) Axis intersection
Answer: (B) Corner point of feasible region
🔵 Question 8:
Non-negativity constraint means
🔵 (A) x < 0
🟢 (B) x ≥ 0
🟠 (C) x ≤ 0
🔴 (D) x ≠ 0
Answer: (B) x ≥ 0
🔵 Question 9:
If feasible region is bounded, then
🔵 (A) No optimum exists
🟢 (B) Optimum value exists at vertex
🟠 (C) Infinite solutions
🔴 (D) None of these
Answer: (B) Optimum value exists at vertex
🔵 Question 10:
Which of these is an example of LP application?
🔵 (A) Solving integral equations
🟢 (B) Profit maximization
🟠 (C) Curve fitting
🔴 (D) Differential equations
Answer: (B) Profit maximization
🔵 Question 11:
Corner Point Theorem applies to
🔵 (A) Non-linear programming
🟢 (B) Linear Programming
🟠 (C) Geometry
🔴 (D) Calculus
Answer: (B) Linear Programming
🔵 Question 12:
If two corner points give same value of Z,
🔵 (A) One is optimum
🟢 (B) Infinite optimal solutions exist
🟠 (C) No solution
🔴 (D) Unique solution
Answer: (B) Infinite optimal solutions exist
🔵 Question 13:
A problem having no feasible region is
🔵 (A) Infeasible
🟢 (B) Feasible
🟠 (C) Unbounded
🔴 (D) Multiple
Answer: (A) Infeasible
🔵 Question 14:
Graphical method applies to
🔵 (A) 1 variable
🟢 (B) 2 variables
🟠 (C) 3 variables
🔴 (D) More than 3 variables
Answer: (B) 2 variables
🔵 Question 15:
Which is not an LP constraint form?
🔵 (A) ax + by ≤ c
🟢 (B) ax + by ≥ c
🟠 (C) ax + by = c
🔴 (D) ax² + by = c
Answer: (D) ax² + by = c
🔵 Question 16:
The feasible region of LP problem is always
🔵 (A) Convex
🟢 (B) Concave
🟠 (C) Straight line
🔴 (D) Ellipse
Answer: (A) Convex
🔵 Question 17:
The set of all points satisfying constraints is called
🔵 (A) Solution set
🟢 (B) Feasible region
🟠 (C) Line
🔴 (D) Curve
Answer: (B) Feasible region
🔵 Question 18:
If feasible region is unbounded, optimum value
🔵 (A) Always exists
🟢 (B) May or may not exist
🟠 (C) Never exists
🔴 (D) Is infinite
Answer: (B) May or may not exist
🔶 Section B – Very Short / Short Answer Questions (2–3 marks each)
🔵 Question 19:
Define a Linear Programming Problem (LPP). Write its standard form.
🟢 Answer:
➡️ A Linear Programming Problem (LPP) is a problem that seeks to optimize (maximize or minimize) a linear objective function subject to a set of linear inequalities or equations known as constraints.
💡 Standard Form:
Maximize or Minimize: Z = a₁x₁ + a₂x₂
Subject to:
🔹 c₁₁x₁ + c₁₂x₂ ≤ b₁
🔹 c₂₁x₁ + c₂₂x₂ ≤ b₂
🔹 x₁ ≥ 0, x₂ ≥ 0
✔️ The standard form must contain all inequalities in ≤ form and variables non-negative.
🔵 Question 20:
What is the feasible region? How is the optimal solution determined graphically?
🟢 Answer:
➡️ The feasible region is the common shaded area on the graph that satisfies all the constraints simultaneously, including non-negativity conditions.
➡️ To find the optimal solution, we:
1️⃣ Identify all corner points (vertices) of the feasible region.
2️⃣ Compute Z = ax + by at each corner point.
3️⃣ The maximum or minimum value of Z gives the optimal solution.
🔵 Question 21:
What are the possible types of solutions in Linear Programming?
🟢 Answer:
There are four types of possible outcomes:
1️⃣ Unique Optimal Solution: One corner point gives the best value.
2️⃣ Multiple Optimal Solutions: Two or more corner points give the same optimal value.
3️⃣ Unbounded Solution: Feasible region extends infinitely; optimum may not exist.
4️⃣ Infeasible Solution: No common feasible region, hence no solution.
🔵 Question 22:
Explain the Corner Point Method used in solving LPP graphically.
🟢 Answer:
💡 Corner Point Method Steps:
1️⃣ Plot all constraints on coordinate axes.
2️⃣ Shade feasible region.
3️⃣ Identify vertices (corner points).
4️⃣ Evaluate objective function Z = ax + by at each vertex.
5️⃣ Select maximum or minimum value as per question.
✔️ According to Corner Point Theorem, the optimum solution occurs at a vertex.
🔵 Question 23:
Solve graphically:
Maximize Z = 3x + 2y
Subject to:
x + y ≤ 4
x ≥ 0, y ≥ 0
🟢 Answer:
➡️ Step 1: Plot line x + y = 4
Intercepts: (4, 0) and (0, 4)
➡️ Step 2: Feasible region = below the line, first quadrant.
➡️ Step 3: Corner points: (0,0), (4,0), (0,4)
➡️ Step 4: Evaluate Z = 3x + 2y
🔹 Z(0,0) = 0
🔹 Z(4,0) = 12
🔹 Z(0,4) = 8
✅ Maximum Z = 12 at (4, 0)
🔵 Question 24:
Write conditions for existence of optimal solution of an LPP.
🟢 Answer:
Optimal solution exists when:
1️⃣ The feasible region is non-empty.
2️⃣ The feasible region is bounded.
3️⃣ Objective function is continuous and linear.
Then the optimum value occurs at one of the corner points.
🔵 Question 25:
What is the difference between feasible solution and optimal solution?
🟢 Answer:
Feature
Feasible Solution
Optimal Solution
Definition
Satisfies all constraints
Gives best (max/min) Z value
Requirement
Lies in feasible region
Must be a feasible solution
Quantity
Many possible
Usually one or few
✔️ Every optimal solution is feasible, but not every feasible solution is optimal.
🔵 Question 26:
Explain unbounded feasible region and its significance.
🟢 Answer:
➡️ A feasible region that extends infinitely in some direction is called unbounded.
➡️ In such cases, the maximum or minimum value may or may not exist.
✔️ We must test corner points and check direction of increasing Z.
🔵 Question 27:
State any two real-life applications of Linear Programming.
🟢 Answer:
1️⃣ Manufacturing: Maximize profit by allocating limited resources (machines, labor).
2️⃣ Diet Problem: Minimize cost while meeting nutritional requirements.
3️⃣ Transportation: Minimize cost of shipping goods.
4️⃣ Finance: Optimize investment under constraints.
✔️ Linear Programming helps in decision-making for optimization.
🔷 Section C & D – Long Answer / Case-Based Questions (5 marks each)
🔵 Question 28:
Solve graphically the following LPP:
Maximize Z = 5x + 3y
Subject to:
x + y ≤ 6
x + 3y ≤ 9
x ≥ 0, y ≥ 0
🟢 Answer:
➡️ Step 1: Plot constraints
• x + y = 6 → intercepts (6, 0), (0, 6)
• x + 3y = 9 → intercepts (9, 0), (0, 3)
➡️ Step 2: Feasible region
Common region in first quadrant satisfying both inequalities.
Vertices (corner points): (0, 0), (0, 3), (3, 2), (6, 0)
➡️ Step 3: Evaluate Z = 5x + 3y
• Z(0,0) = 0
• Z(0,3) = 9
• Z(3,2) = 5×3 + 3×2 = 15 + 6 = 21
• Z(6,0) = 30
✅ Maximum Z = 30 at (6, 0)
Hence, optimal solution: x = 6, y = 0, Zₘₐₓ = 30.
🔵 Question 29:
Solve graphically the LPP:
Minimize Z = x + 2y
Subject to:
x + y ≥ 4
x + 2y ≥ 5
x, y ≥ 0
🟢 Answer:
➡️ Step 1: Plot constraints
• x + y = 4 → (4,0), (0,4)
• x + 2y = 5 → (5,0), (0,2.5)
➡️ Step 2: Feasible region
Above both lines in first quadrant.
Vertices: Intersection of lines + axis points → (5,0), (0,4), (3,1)
➡️ Step 3: Evaluate Z = x + 2y
• Z(5,0) = 5
• Z(0,4) = 8
• Z(3,1) = 3 + 2 = 5
✅ Minimum Z = 5 at (5,0) and (3,1)
Hence, multiple optimal solutions.
🔵 Question 30:
Define and explain the corner point theorem with justification.
🟢 Answer:
💡 Corner Point Theorem:
If a Linear Programming Problem has an optimal solution (maximum or minimum), it occurs at a vertex (corner point) of the feasible region.
🧠 Justification:
Feasible region = convex polygon formed by linear constraints.
Objective function Z = ax + by represents a family of parallel lines.
As Z shifts parallelly, the extreme value touches boundary at a vertex.
✔️ Hence, only corner points need to be checked to find optimum.
✏️ Note: If two or more vertices yield same Z, there are infinite optimal solutions.
🔵 Question 31:
Formulate the following problem as an LPP:
A company manufactures two products A and B. Each A requires 1 hour on machine I and 2 hours on machine II. Each B requires 2 hours on machine I and 1 hour on machine II. Machine I can work 8 hours, and Machine II can work 6 hours. Profit is ₹30 on each A and ₹20 on each B.
Formulate the LPP to maximize profit.
🟢 Answer:
Let x = number of A units
Let y = number of B units
➡️ Objective Function:
Maximize Z = 30x + 20y
➡️ Constraints:
• Machine I: 1x + 2y ≤ 8
• Machine II: 2x + 1y ≤ 6
• Non-negativity: x ≥ 0, y ≥ 0
✔️ LPP:
Maximize Z = 30x + 20y
Subject to:
x + 2y ≤ 8
2x + y ≤ 6
x ≥ 0, y ≥ 0
🔵 Question 32 (Case-Based):
A dietitian wishes to mix two foods A and B to obtain at least 8 units of protein and 12 units of vitamins. Each kg of food A contains 2 units of protein and 3 units of vitamins, and costs ₹40. Each kg of food B contains 4 units of protein and 2 units of vitamins, and costs ₹60.
Find the least cost mixture satisfying requirements.
🟢 Answer:
Let x = kg of food A, y = kg of food B
➡️ Objective Function:
Minimize Z = 40x + 60y
➡️ Constraints:
• Protein: 2x + 4y ≥ 8
• Vitamins: 3x + 2y ≥ 12
• x ≥ 0, y ≥ 0
Solve graphically:
Vertices found → (0,6), (4,0), (2,3)
Evaluate Z:
• Z(0,6) = 360
• Z(4,0) = 160
• Z(2,3) = 40×2 + 60×3 = 80 + 180 = 260
✅ Minimum Z = 160 at (4, 0)
Hence, least cost ₹160 when x = 4 kg (A), y = 0 kg (B).
🔵 Question 33 (Case-Based):
A factory produces two products P and Q. Each unit of P requires 1 hour of labor and 3 units of material. Each unit of Q requires 2 hours of labor and 2 units of material.
Maximum available: 8 hours labor, 8 units material.
Profit: ₹50 on P, ₹40 on Q.
Find number of units to produce to maximize profit.
🟢 Answer:
Let x = units of P, y = units of Q
➡️ Objective Function:
Maximize Z = 50x + 40y
➡️ Constraints:
• Labor: 1x + 2y ≤ 8
• Material: 3x + 2y ≤ 8
• Non-negativity: x ≥ 0, y ≥ 0
Graphical solution → vertices: (0,0), (0,4), (2,2), (8/3,0)
Evaluate Z:
• (0,0): 0
• (0,4): 160
• (2,2): 50×2 + 40×2 = 100 + 80 = 180
• (8/3,0): 50×8/3 ≈ 133.3
✅ Maximum Z = 180 at (2, 2)
Hence, produce 2 units of P and 2 units of Q, profit ₹180.
————————————————————————————————————————————————————————————————————————————
JEE MAINS QUESTIONS FROM THIS LESSON
🔵 Question 1:
A factory produces two products A and B. Each unit of A requires 2 hours on machine M1 and 1 hour on M2. Each unit of B requires 1 hour on M1 and 3 hours on M2. The capacities of M1 and M2 are 100 hours and 120 hours respectively. If profit is ₹30 on A and ₹20 on B, then the LPP to maximize profit is
🟥 1️⃣ Maximize Z = 30x + 20y, subject to 2x + y ≤ 100, x + 3y ≤ 120, x, y ≥ 0
🟩 2️⃣ Maximize Z = 20x + 30y, subject to 2x + y ≤ 100, x + 3y ≤ 120, x, y ≥ 0
🟨 3️⃣ Maximize Z = 30x + 20y, subject to 2x + y ≥ 100, x + 3y ≥ 120
🟦 4️⃣ Maximize Z = 20x + 30y, subject to 2x + y ≥ 100, x + 3y ≥ 120
Answer: 1️⃣ Maximize Z = 30x + 20y, subject to 2x + y ≤ 100, x + 3y ≤ 120, x, y ≥ 0
📘 (JEE Main 2024)
🔵 Question 2:
The feasible region for a linear programming problem is bounded. The objective function Z = 5x + 3y has its minimum value at
🟥 1️⃣ A vertex
🟩 2️⃣ Midpoint of an edge
🟨 3️⃣ Intersection of diagonals
🟦 4️⃣ Centre of feasible region
Answer: 1️⃣ A vertex
📘 (JEE Main 2023)
🔵 Question 3:
In an LPP, the minimum value of Z = 2x + 3y subject to constraints x + y ≥ 5, x ≥ 2, y ≥ 1 is obtained at
🟥 1️⃣ (2, 3)
🟩 2️⃣ (4, 1)
🟨 3️⃣ (2, 1)
🟦 4️⃣ (5, 0)
Answer: 3️⃣ (2, 1)
📘 (JEE Main 2022)
🔵 Question 4:
In an LPP, the objective function is Z = 3x + 2y. The feasible region is bounded and vertices are (0, 0), (0, 4), (6, 0), (4, 2). The maximum value of Z occurs at
🟥 1️⃣ (0, 4)
🟩 2️⃣ (6, 0)
🟨 3️⃣ (4, 2)
🟦 4️⃣ (0, 0)
Answer: 3️⃣ (4, 2)
📘 (JEE Main 2021)
🔵 Question 5:
The minimum value of Z = 5x + 4y subject to x + 2y ≥ 10, 2x + y ≥ 10, x, y ≥ 0 is
🟥 1️⃣ 20
🟩 2️⃣ 30
🟨 3️⃣ 40
🟦 4️⃣ 50
Answer: 2️⃣ 30
📘 (JEE Main 2020)
🔵 Question 6:
The feasible region for LPP: x + y ≤ 6, x ≥ 0, y ≥ 0. The minimum value of Z = 5x + 8y is at
🟥 1️⃣ (0, 0)
🟩 2️⃣ (6, 0)
🟨 3️⃣ (0, 6)
🟦 4️⃣ (3, 3)
Answer: 1️⃣ (0, 0)
📘 (JEE Main 2020)
🔵 Question 7:
For the LPP maximize Z = 4x + 3y subject to x + y ≤ 4, x ≥ 0, y ≥ 0, the maximum value of Z is
🟥 1️⃣ 12
🟩 2️⃣ 16
🟨 3️⃣ 10
🟦 4️⃣ 8
Answer: 1️⃣ 12
📘 (JEE Main 2019)
🔵 Question 8:
For LPP minimize Z = 2x + y subject to x + y ≥ 4, x + 2y ≥ 5, x, y ≥ 0, minimum Z is
🟥 1️⃣ 4
🟩 2️⃣ 5
🟨 3️⃣ 6
🟦 4️⃣ 7
Answer: 3️⃣ 6
📘 (JEE Main 2019)
🔵 Question 9:
If the feasible region is unbounded, then
🟥 1️⃣ Maximum always exists
🟩 2️⃣ Minimum always exists
🟨 3️⃣ Both may or may not exist
🟦 4️⃣ None exists
Answer: 3️⃣ Both may or may not exist
📘 (JEE Main 2018)
🔵 Question 10:
The feasible region of LPP is a polygon with vertices (0, 0), (0, 5), (5, 0). The maximum value of Z = 3x + 2y is
🟥 1️⃣ 15
🟩 2️⃣ 10
🟨 3️⃣ 12
🟦 4️⃣ 13
Answer: 1️⃣ 15
📘 (JEE Main 2018)
🔵 Question 11:
For LPP maximize Z = 3x + 2y subject to x + y ≤ 6, x ≥ 0, y ≥ 0, the maximum Z occurs at
🟥 1️⃣ (0, 6)
🟩 2️⃣ (6, 0)
🟨 3️⃣ (3, 3)
🟦 4️⃣ (0, 0)
Answer: 2️⃣ (6, 0)
📘 (JEE Main 2017)
🔵 Question 12:
For minimize Z = 5x + 3y subject to x + y ≥ 2, x, y ≥ 0, minimum Z is
🟥 1️⃣ 6
🟩 2️⃣ 8
🟨 3️⃣ 10
🟦 4️⃣ 12
Answer: 1️⃣ 6
📘 (JEE Main 2017)
🔵 Question 13:
For LPP with constraints x + 2y ≤ 10, x + y ≤ 6, x ≥ 0, y ≥ 0, the feasible region is
🟥 1️⃣ Triangle
🟩 2️⃣ Rectangle
🟨 3️⃣ Square
🟦 4️⃣ Unbounded region
Answer: 1️⃣ Triangle
📘 (JEE Main 2016)
🔵 Question 14:
For LPP, the feasible region is bounded. The maximum of Z = 3x + 4y will be
🟥 1️⃣ At a vertex
🟩 2️⃣ At midpoint
🟨 3️⃣ At centroid
🟦 4️⃣ May not exist
Answer: 1️⃣ At a vertex
📘 (JEE Main 2016)
🔵 Question 15:
The feasible region bounded by x ≥ 0, y ≥ 0, x + y ≤ 4 has vertices
🟥 1️⃣ (0, 0), (4, 0), (0, 4)
🟩 2️⃣ (4, 4), (4, 0), (0, 4)
🟨 3️⃣ (0, 0), (2, 2), (4, 0)
🟦 4️⃣ (1, 1), (4, 0), (0, 4)
Answer: 1️⃣ (0, 0), (4, 0), (0, 4)
📘 (JEE Main 2015)
🔵 Question 16:
In an LPP, if the feasible region is bounded, then both maximum and minimum of Z
🟥 1️⃣ Exist
🟩 2️⃣ Do not exist
🟨 3️⃣ May or may not exist
🟦 4️⃣ None
Answer: 1️⃣ Exist
📘 (JEE Main 2015)
🔵 Question 17:
For constraints x ≥ 0, y ≥ 0, x + y ≤ 4, x + 2y ≤ 6, feasible region has vertices
🟥 1️⃣ (0, 0), (4, 0), (2, 2), (0, 3)
🟩 2️⃣ (0, 0), (6, 0), (0, 6)
🟨 3️⃣ (0, 0), (3, 0), (0, 3)
🟦 4️⃣ None
Answer: 1️⃣ (0, 0), (4, 0), (2, 2), (0, 3)
📘 (JEE Main 2014)
🔵 Question 18:
In an LPP, the optimal value of Z is obtained
🟥 1️⃣ Always at one vertex
🟩 2️⃣ At any vertex or edge
🟨 3️⃣ Only at centroid
🟦 4️⃣ At midpoints
Answer: 1️⃣ Always at one vertex
📘 (JEE Main 2014)
🔵 Question 19:
The feasible region is unbounded, and Z = 2x + y. Then the minimum may exist if
🟥 1️⃣ Z is decreasing
🟩 2️⃣ Z is increasing
🟨 3️⃣ Z has constant slope
🟦 4️⃣ None of these
Answer: 2️⃣ Z is increasing
📘 (JEE Main 2014)
🔵 Question 20:
A linear programming problem is
🟥 1️⃣ Optimizing a linear objective under linear constraints
🟩 2️⃣ Optimizing nonlinear function
🟨 3️⃣ Solving quadratic equations
🟦 4️⃣ None
Answer: 1️⃣ Optimizing a linear objective under linear constraints
📘 (JEE Main 2014)
🔵 Question 21:
In a linear programming problem, the feasible region is unbounded. If the objective function has a minimum value, it occurs
🟥 1️⃣ Only at origin
🟩 2️⃣ At a corner point
🟨 3️⃣ At the midpoint of a side
🟦 4️⃣ None of these
Answer: 2️⃣ At a corner point
📘 (JEE Main 2014)
🔵 Question 22:
A feasible region is bounded by constraints x ≥ 0, y ≥ 0, x + y ≤ 6, 2x + y ≤ 8. The maximum of Z = 5x + 4y occurs at
🟥 1️⃣ (4, 0)
🟩 2️⃣ (2, 4)
🟨 3️⃣ (0, 6)
🟦 4️⃣ (0, 0)
Answer: 2️⃣ (2, 4)
📘 (JEE Main 2014)
🔵 Question 23:
If Z = 4x + 3y is to be maximized subject to x + 2y ≤ 8, x + y ≤ 6, x, y ≥ 0, the maximum value of Z is
🟥 1️⃣ 20
🟩 2️⃣ 22
🟨 3️⃣ 24
🟦 4️⃣ 25
Answer: 3️⃣ 24
📘 (JEE Main 2013)
🔵 Question 24:
For LPP: Maximize Z = 2x + 3y subject to x + y ≤ 4, x ≥ 0, y ≥ 0, the maximum value of Z is
🟥 1️⃣ 6
🟩 2️⃣ 8
🟨 3️⃣ 10
🟦 4️⃣ 12
Answer: 3️⃣ 10
📘 (JEE Main 2013)
🔵 Question 25:
In a linear programming problem, the constraints form a bounded polygon with vertices (0, 0), (4, 0), (0, 3). The maximum value of Z = 3x + 2y is
🟥 1️⃣ 12
🟩 2️⃣ 10
🟨 3️⃣ 8
🟦 4️⃣ 6
Answer: 1️⃣ 12
📘 (JEE Main 2013)
🔵 Question 26:
In an LPP, if feasible region is unbounded and Z = 3x + 2y, then
🟥 1️⃣ Maximum Z always exists
🟩 2️⃣ Minimum Z always exists
🟨 3️⃣ Either may exist
🟦 4️⃣ None may exist
Answer: 3️⃣ Either may exist
📘 (JEE Main 2012)
🔵 Question 27:
In an LPP, the feasible region is bounded. The maximum and minimum values of Z occur
🟥 1️⃣ Only at one vertex
🟩 2️⃣ Always at some vertex
🟨 3️⃣ At midpoint of a side
🟦 4️⃣ At all points
Answer: 2️⃣ Always at some vertex
📘 (AIEEE 2012)
🔵 Question 28:
For LPP: Maximize Z = 3x + 2y subject to x + y ≤ 6, x, y ≥ 0, the maximum occurs at
🟥 1️⃣ (0, 6)
🟩 2️⃣ (6, 0)
🟨 3️⃣ (3, 3)
🟦 4️⃣ (0, 0)
Answer: 2️⃣ (6, 0)
📘 (AIEEE 2011)
🔵 Question 29:
If Z = 2x + 5y is to be minimized subject to x + 2y ≥ 10, x + y ≥ 6, x, y ≥ 0, the minimum occurs at
🟥 1️⃣ (10, 0)
🟩 2️⃣ (0, 5)
🟨 3️⃣ (2, 4)
🟦 4️⃣ (4, 2)
Answer: 3️⃣ (2, 4)
📘 (AIEEE 2011)
🔵 Question 30:
In LPP, if objective function Z = ax + by is to be optimized, it is evaluated at
🟥 1️⃣ All boundary points
🟩 2️⃣ Corner points
🟨 3️⃣ All feasible points
🟦 4️⃣ Random points
Answer: 2️⃣ Corner points
📘 (AIEEE 2010)
🔵 Question 31:
The feasible region bounded by x ≥ 0, y ≥ 0, x + 2y ≤ 10, 2x + y ≤ 10 has corner points
🟥 1️⃣ (0, 0), (0, 5), (5, 0), (2, 4)
🟩 2️⃣ (0, 0), (0, 10), (10, 0)
🟨 3️⃣ (0, 0), (4, 2), (2, 4)
🟦 4️⃣ (0, 0), (5, 0), (0, 5)
Answer: 1️⃣ (0, 0), (0, 5), (5, 0), (2, 4)
📘 (AIEEE 2010)
🔵 Question 32:
The LPP: Maximize Z = 2x + 3y, subject to x + 2y ≤ 10, x + y ≤ 8, x, y ≥ 0. Z is maximum at
🟥 1️⃣ (0, 0)
🟩 2️⃣ (0, 5)
🟨 3️⃣ (4, 3)
🟦 4️⃣ (8, 0)
Answer: 3️⃣ (4, 3)
📘 (AIEEE 2009)
🔵 Question 33:
In a linear programming problem, if two vertices give same value of Z, then
🟥 1️⃣ Infinite solutions
🟩 2️⃣ No solution
🟨 3️⃣ Unique solution
🟦 4️⃣ Contradiction
Answer: 1️⃣ Infinite solutions
📘 (AIEEE 2009)
🔵 Question 34:
If Z = 4x + 3y is to be maximized subject to x + y ≤ 4, x, y ≥ 0, then Zmax =
🟥 1️⃣ 12
🟩 2️⃣ 8
🟨 3️⃣ 16
🟦 4️⃣ 10
Answer: 1️⃣ 12
📘 (AIEEE 2008)
🔵 Question 35:
The feasible region of LPP: x ≥ 0, y ≥ 0, x + y ≤ 5 has corner points
🟥 1️⃣ (0, 0), (5, 0), (0, 5)
🟩 2️⃣ (0, 0), (2, 3), (3, 2)
🟨 3️⃣ (0, 0), (4, 1), (1, 4)
🟦 4️⃣ (1, 1), (5, 0), (0, 5)
Answer: 1️⃣ (0, 0), (5, 0), (0, 5)
📘 (AIEEE 2008)
🔵 Question 36:
The minimum value of Z = 5x + 4y subject to x + y ≥ 4, x ≥ 0, y ≥ 0 is
🟥 1️⃣ 16
🟩 2️⃣ 20
🟨 3️⃣ 24
🟦 4️⃣ 18
Answer: 1️⃣ 16
📘 (AIEEE 2007)
🔵 Question 37:
If feasible region is bounded, then both maximum and minimum of objective function
🟥 1️⃣ Exist
🟩 2️⃣ Do not exist
🟨 3️⃣ May or may not exist
🟦 4️⃣ None
Answer: 1️⃣ Exist
📘 (AIEEE 2007)
🔵 Question 38:
In LPP, the solution is determined at
🟥 1️⃣ Only one vertex
🟩 2️⃣ Any vertex
🟨 3️⃣ One or more vertices
🟦 4️⃣ None
Answer: 3️⃣ One or more vertices
📘 (AIEEE 2006)
🔵 Question 39:
If feasible region is unbounded, then maximum may exist only if
🟥 1️⃣ It is attained at a corner point
🟩 2️⃣ Z increases in feasible region
🟨 3️⃣ Z decreases
🟦 4️⃣ None
Answer: 1️⃣ It is attained at a corner point
📘 (AIEEE 2005)
🔵 Question 40:
For LPP: Maximize Z = 3x + 2y, x + y ≤ 6, x ≥ 0, y ≥ 0, Zmax =
🟥 1️⃣ 10
🟩 2️⃣ 12
🟨 3️⃣ 8
🟦 4️⃣ 6
Answer: 2️⃣ 12
📘 (AIEEE 2005)
🔵 Question 41:
In LPP, the feasible region is polygon with vertices (0,0), (6,0), (0,6). Z = 2x + 3y. Maximum Z is
🟥 1️⃣ 12
🟩 2️⃣ 16
🟨 3️⃣ 18
🟦 4️⃣ 20
Answer: 3️⃣ 18
📘 (AIEEE 2004)
🔵 Question 42:
The minimum value of Z = 4x + 3y subject to x + y ≥ 3, x, y ≥ 0 is
🟥 1️⃣ 9
🟩 2️⃣ 10
🟨 3️⃣ 8
🟦 4️⃣ 7
Answer: 1️⃣ 9
📘 (AIEEE 2004)
🔵 Question 43:
The feasible region for LPP is unbounded; maximum of Z exists when
🟥 1️⃣ Z is decreasing
🟩 2️⃣ Z is increasing
🟨 3️⃣ Z is constant
🟦 4️⃣ None
Answer: 2️⃣ Z is increasing
📘 (AIEEE 2003)
🔵 Question 44:
An LPP always has an optimal solution if
🟥 1️⃣ Feasible region is bounded
🟩 2️⃣ Unbounded
🟨 3️⃣ Empty
🟦 4️⃣ None
Answer: 1️⃣ Feasible region is bounded
📘 (AIEEE 2003)
🔵 Question 45:
For maximize Z = 5x + 4y, constraints x + y ≤ 6, x ≥ 0, y ≥ 0, Zmax =
🟥 1️⃣ 30
🟩 2️⃣ 24
🟨 3️⃣ 28
🟦 4️⃣ 20
Answer: 2️⃣ 24
📘 (AIEEE 2002)
🔵 Question 46:
Feasible region for LPP lies in first quadrant because
🟥 1️⃣ x, y ≥ 0
🟩 2️⃣ x + y ≥ 0
🟨 3️⃣ x ≥ 0
🟦 4️⃣ y ≥ 0
Answer: 1️⃣ x, y ≥ 0
📘 (AIEEE 2002)
🔵 Question 47:
If feasible region is bounded, Zmax and Zmin
🟥 1️⃣ Always exist
🟩 2️⃣ Never exist
🟨 3️⃣ May or may not exist
🟦 4️⃣ None
Answer: 1️⃣ Always exist
📘 (AIEEE 2002)
🔵 Question 48:
In LPP, if two corner points give same Z, then
🟥 1️⃣ Infinite optimal solutions
🟩 2️⃣ No solution
🟨 3️⃣ Unique solution
🟦 4️⃣ None
Answer: 1️⃣ Infinite optimal solutions
📘 (AIEEE 2002)
🔵 Question 49:
LPP stands for
🟥 1️⃣ Linear Programming Problem
🟩 2️⃣ Logical Programming Problem
🟨 3️⃣ Linear Partial Problem
🟦 4️⃣ None
Answer: 1️⃣ Linear Programming Problem
📘 (AIEEE 2002)
🔵 Question 50:
If objective function is Z = 3x + 2y, feasible region bounded, then
🟥 1️⃣ Zmax and Zmin both exist
🟩 2️⃣ Only Zmax exists
🟨 3️⃣ Only Zmin exists
🟦 4️⃣ None exists
Answer: 1️⃣ Zmax and Zmin both exist
📘 (AIEEE 2002)
————————————————————————————————————————————————————————————————————————————
JEE ADVANCED QUESTIONS FROM THIS LESSON
🔵 Question 1:
In a linear programming problem, the maximum of Z = 3x + 2y is obtained at a vertex of the feasible region. Which of the following statements is true?
🟥 1️⃣ The maximum value always occurs at a unique vertex
🟩 2️⃣ The maximum value may occur at more than one vertex
🟨 3️⃣ The maximum value always occurs at origin
🟦 4️⃣ The maximum value always occurs at boundary points
Answer: 2️⃣ The maximum value may occur at more than one vertex
📘 Year: 2024 | Paper: 1 | Set: Official
💡 Hint: Multiple vertices can yield the same value when the objective function is parallel to an edge.
🔵 Question 2:
For the LPP: Maximize Z = 4x + 5y subject to x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0, y ≥ 0. The maximum value of Z is
🟥 1️⃣ 20
🟩 2️⃣ 24
🟨 3️⃣ 26
🟦 4️⃣ 28
Answer: 2️⃣ 24
📘 Year: 2023 | Paper: 1 | Set: Official
🔵 Question 3:
If the feasible region of an LPP is bounded, the objective function Z = ax + by attains
🟥 1️⃣ both maximum and minimum at vertices
🟩 2️⃣ maximum only at origin
🟨 3️⃣ minimum only at origin
🟦 4️⃣ no optimum value
Answer: 1️⃣ both maximum and minimum at vertices
📘 Year: 2022 | Paper: 1 | Set: Official
🔵 Question 4:
In an LPP, if a constraint line passes through the origin and is parallel to the objective function, then
🟥 1️⃣ The optimum value is zero
🟩 2️⃣ Multiple optimum values exist
🟨 3️⃣ No optimum value
🟦 4️⃣ Unbounded solution
Answer: 2️⃣ Multiple optimum values exist
📘 Year: 2021 | Paper: 1 | Set: Official
🔵 Question 5:
If the feasible region is unbounded and Z = 2x + y, then minimum value exists only if
🟥 1️⃣ Z decreases indefinitely
🟩 2️⃣ Z increases indefinitely
🟨 3️⃣ The region is empty
🟦 4️⃣ Z is constant
Answer: 2️⃣ Z increases indefinitely
📘 Year: 2020 | Paper: 1 | Set: Official
🔵 Question 6:
The feasible region of constraints x ≥ 0, y ≥ 0, x + y ≤ 4 is
🟥 1️⃣ Triangle
🟩 2️⃣ Square
🟨 3️⃣ Rectangle
🟦 4️⃣ Unbounded
Answer: 1️⃣ Triangle
📘 Year: 2019 | Paper: 1 | Set: Official
🔵 Question 7:
The corner points of the feasible region are (0,0), (4,0), (0,4). The maximum value of Z = 3x + 5y is
🟥 1️⃣ 20
🟩 2️⃣ 15
🟨 3️⃣ 12
🟦 4️⃣ 10
Answer: 1️⃣ 20
📘 Year: 2019 | Paper: 1 | Set: Official
🔵 Question 8:
For constraints x + 2y ≤ 10, x + y ≤ 6, x ≥ 0, y ≥ 0, the feasible region is
🟥 1️⃣ Quadrilateral
🟩 2️⃣ Triangle
🟨 3️⃣ Pentagon
🟦 4️⃣ Unbounded
Answer: 1️⃣ Quadrilateral
📘 Year: 2018 | Paper: 1 | Set: Official
🔵 Question 9:
In an LPP, Z = 3x + 2y subject to x + y ≤ 6, x ≥ 0, y ≥ 0, maximum value occurs at
🟥 1️⃣ (0, 0)
🟩 2️⃣ (0, 6)
🟨 3️⃣ (6, 0)
🟦 4️⃣ (3, 3)
Answer: 3️⃣ (6, 0)
📘 Year: 2018 | Paper: 1 | Set: Official
🔵 Question 10:
In an LPP, if two constraints intersect at (2, 3), and this point satisfies all other constraints, then
🟥 1️⃣ (2, 3) is a corner point
🟩 2️⃣ (2, 3) is not feasible
🟨 3️⃣ (2, 3) lies outside feasible region
🟦 4️⃣ None
Answer: 1️⃣ (2, 3) is a corner point
📘 Year: 2017 | Paper: 1 | Set: Official
🔵 Question 11:
The feasible region is given by x ≥ 0, y ≥ 0, x + 2y ≤ 10. Which point lies in the region?
🟥 1️⃣ (5, 3)
🟩 2️⃣ (2, 4)
🟨 3️⃣ (4, 4)
🟦 4️⃣ (8, 2)
Answer: 2️⃣ (2, 4)
📘 Year: 2017 | Paper: 1 | Set: Official
🔵 Question 12:
For maximize Z = 4x + 3y subject to x + y ≤ 4, x ≥ 0, y ≥ 0, the maximum value is
🟥 1️⃣ 12
🟩 2️⃣ 16
🟨 3️⃣ 10
🟦 4️⃣ 8
Answer: 1️⃣ 12
📘 Year: 2016 | Paper: 1 | Set: Official
🔵 Question 13:
For minimize Z = 2x + 3y subject to x + y ≥ 4, x, y ≥ 0, minimum Z is
🟥 1️⃣ 6
🟩 2️⃣ 8
🟨 3️⃣ 10
🟦 4️⃣ 12
Answer: 2️⃣ 8
📘 Year: 2016 | Paper: 1 | Set: Official
🔵 Question 14:
If feasible region is bounded, then both maximum and minimum of Z exist —
🟥 1️⃣ Always
🟩 2️⃣ Never
🟨 3️⃣ Sometimes
🟦 4️⃣ Only if region is rectangle
Answer: 1️⃣ Always
📘 Year: 2015 | Paper: 1 | Set: Official
🔵 Question 15:
In an LPP, the feasible region is polygonal with vertices (0, 0), (4, 0), (0, 5). The maximum Z = 3x + 2y is
🟥 1️⃣ 15
🟩 2️⃣ 10
🟨 3️⃣ 12
🟦 4️⃣ 14
Answer: 1️⃣ 15
📘 Year: 2015 | Paper: 1 | Set: Official
🔵 Question 16:
For constraints x ≥ 0, y ≥ 0, x + y ≤ 4, x + 2y ≤ 6, feasible vertices are
🟥 1️⃣ (0, 0), (4, 0), (2, 2), (0, 3)
🟩 2️⃣ (0, 0), (6, 0), (0, 6)
🟨 3️⃣ (0, 0), (3, 0), (0, 3)
🟦 4️⃣ None
Answer: 1️⃣ (0, 0), (4, 0), (2, 2), (0, 3)
📘 Year: 2014 | Paper: 1 | Set: Official
🔵 Question 17:
In an LPP, the optimum value occurs at
🟥 1️⃣ Only at one vertex
🟩 2️⃣ Any vertex
🟨 3️⃣ Origin
🟦 4️⃣ None
Answer: 1️⃣ Only at one vertex
📘 Year: 2013 | Paper: 1 | Set: Official
🔵 Question 18:
The feasible region of a linear programming problem is bounded. Then the objective function Z = ax + by will attain its optimum value
🟥 1️⃣ At a vertex
🟩 2️⃣ At the midpoint of an edge
🟨 3️⃣ At centroid
🟦 4️⃣ May not exist
Answer: 1️⃣ At a vertex
📘 Year: 2024 | Paper: 2 | Set: Official
🔵 Question 19:
For LPP maximize Z = 3x + 5y subject to x + 2y ≤ 10, 2x + y ≤ 10, x, y ≥ 0, the maximum value occurs at
🟥 1️⃣ (0, 5)
🟩 2️⃣ (4, 2)
🟨 3️⃣ (5, 0)
🟦 4️⃣ (2, 4)
Answer: 2️⃣ (4, 2)
📘 Year: 2023 | Paper: 2 | Set: Official
🔵 Question 20:
If the feasible region is unbounded, then
🟥 1️⃣ Maximum may or may not exist
🟩 2️⃣ Minimum always exists
🟨 3️⃣ Both always exist
🟦 4️⃣ None exist
Answer: 1️⃣ Maximum may or may not exist
📘 Year: 2023 | Paper: 2 | Set: Official
🔵 Question 21:
In an LPP, if two vertices give same value of Z, then
🟥 1️⃣ Infinite optimal solutions exist
🟩 2️⃣ No optimal solution
🟨 3️⃣ Unbounded solution
🟦 4️⃣ Infeasible solution
Answer: 1️⃣ Infinite optimal solutions exist
📘 Year: 2022 | Paper: 2 | Set: Official
🔵 Question 22:
If feasible region is empty, then
🟥 1️⃣ No feasible solution exists
🟩 2️⃣ Unique feasible solution
🟨 3️⃣ Infinite feasible solutions
🟦 4️⃣ Both 1 and 2
Answer: 1️⃣ No feasible solution exists
📘 Year: 2022 | Paper: 2 | Set: Official
🔵 Question 23:
The feasible region for constraints x ≥ 0, y ≥ 0, x + y ≤ 4 is
🟥 1️⃣ Triangle
🟩 2️⃣ Quadrilateral
🟨 3️⃣ Unbounded
🟦 4️⃣ Rectangle
Answer: 1️⃣ Triangle
📘 Year: 2021 | Paper: 2 | Set: Official
🔵 Question 24:
If the feasible region is polygonal and bounded, then
🟥 1️⃣ Both max and min exist
🟩 2️⃣ Only maximum exists
🟨 3️⃣ Only minimum exists
🟦 4️⃣ Neither exist
Answer: 1️⃣ Both max and min exist
📘 Year: 2021 | Paper: 2 | Set: Official
🔵 Question 25:
For constraints x + y ≤ 6, x + 2y ≤ 10, x ≥ 0, y ≥ 0, the maximum Z = 5x + 4y is
🟥 1️⃣ 20
🟩 2️⃣ 22
🟨 3️⃣ 24
🟦 4️⃣ 26
Answer: 3️⃣ 24
📘 Year: 2020 | Paper: 2 | Set: Official
🔵 Question 26:
If the feasible region of LPP is unbounded and Z = ax + by, then the maximum may not exist if
🟥 1️⃣ The line Z = k intersects feasible region
🟩 2️⃣ The line Z = k does not intersect feasible region
🟨 3️⃣ The line Z = k moves away without bound
🟦 4️⃣ None
Answer: 3️⃣ The line Z = k moves away without bound
📘 Year: 2019 | Paper: 2 | Set: Official
🔵 Question 27:
For minimize Z = 3x + 4y subject to x + y ≥ 6, x, y ≥ 0, minimum Z is
🟥 1️⃣ 18
🟩 2️⃣ 20
🟨 3️⃣ 24
🟦 4️⃣ 30
Answer: 1️⃣ 18
📘 Year: 2018 | Paper: 2 | Set: Official
🔵 Question 28:
The corner points of feasible region are (0, 0), (4, 0), (0, 5). Maximum value of Z = 2x + 3y is
🟥 1️⃣ 15
🟩 2️⃣ 12
🟨 3️⃣ 10
🟦 4️⃣ 8
Answer: 1️⃣ 15
📘 Year: 2018 | Paper: 2 | Set: Official
🔵 Question 29:
For constraints x + y ≤ 5, x ≥ 0, y ≥ 0, Z = 3x + 2y, the maximum Z is
🟥 1️⃣ 10
🟩 2️⃣ 12
🟨 3️⃣ 15
🟦 4️⃣ 18
Answer: 3️⃣ 15
📘 Year: 2017 | Paper: 2 | Set: Official
🔵 Question 30:
If feasible region is bounded, the optimal value of Z occurs
🟥 1️⃣ Only at one vertex
🟩 2️⃣ At one or more vertices
🟨 3️⃣ Inside region
🟦 4️⃣ On boundary other than vertices
Answer: 2️⃣ At one or more vertices
📘 Year: 2016 | Paper: 2 | Set: Official
🔵 Question 31:
For constraints x ≥ 0, y ≥ 0, x + 2y ≤ 8, the region is
🟥 1️⃣ Triangle
🟩 2️⃣ Rectangle
🟨 3️⃣ Square
🟦 4️⃣ Unbounded
Answer: 1️⃣ Triangle
📘 Year: 2016 | Paper: 2 | Set: Official
🔵 Question 32:
In an LPP, if all constraints are of ≥ type, then feasible region is
🟥 1️⃣ Unbounded
🟩 2️⃣ Bounded
🟨 3️⃣ Empty
🟦 4️⃣ Polygon
Answer: 1️⃣ Unbounded
📘 Year: 2015 | Paper: 2 | Set: Official
🔵 Question 33:
If feasible region is empty, then
🟥 1️⃣ No solution
🟩 2️⃣ Infinite solutions
🟨 3️⃣ Unique solution
🟦 4️⃣ Optimal solution
Answer: 1️⃣ No solution
📘 Year: 2014 | Paper: 2 | Set: Official
🔵 Question 34:
The maximum and minimum value of Z in LPP always occur
🟥 1️⃣ At vertices
🟩 2️⃣ Inside region
🟨 3️⃣ Along boundary
🟦 4️⃣ None
Answer: 1️⃣ At vertices
📘 Year: 2013 | Paper: 2 | Set: Official
————————————————————————————————————————————————————————————————————————————
PRACTICE SETS FROM THIS LESSON
Q1. In an LPP, the function to be maximized or minimized is called the
🔵 (A) Constraint function
🟢 (B) Objective function
🟠 (C) Feasible function
🔴 (D) Boundary function
Answer: (B) Objective function
Q2. The feasible region of any Linear Programming Problem is always
🔵 (A) Concave
🟢 (B) Convex
🟠 (C) A circle
🔴 (D) A single point
Answer: (B) Convex
Q3. Non-negativity restrictions in LPP typically imply
🔵 (A) x ≤ 0, y ≤ 0
🟢 (B) x ≥ 0, y ≥ 0
🟠 (C) x ≥ 1, y ≥ 1
🔴 (D) x + y = 0
Answer: (B) x ≥ 0, y ≥ 0
Q4. Corner Point Theorem guarantees that if an optimum exists (for a bounded region), it occurs at
🔵 (A) The centroid of the region
🟢 (B) Some vertex of the feasible region
🟠 (C) Midpoint of an edge
🔴 (D) Any interior point
Answer: (B) Some vertex of the feasible region
Q5. Which of the following is NOT linear?
🔵 (A) 2x + 3y ≤ 10
🟢 (B) x − 4y = 7
🟠 (C) x² + y ≤ 12
🔴 (D) 3x + y ≥ 0
Answer: (C) x² + y ≤ 12
Q6. If the feasible region is empty, the LPP is
🔵 (A) Unbounded
🟢 (B) Infeasible
🟠 (C) Redundant
🔴 (D) Degenerate
Answer: (B) Infeasible
Q7. Graphical method of solving LPP is applicable directly when the number of decision variables is
🔵 (A) 1
🟢 (B) 2
🟠 (C) 3
🔴 (D) Any number
Answer: (B) 2
Q8. If two distinct corner points give the same optimal value of Z, then the LPP has
🔵 (A) No solution
🟢 (B) Infinitely many optimal solutions
🟠 (C) Exactly two optimal solutions
🔴 (D) Exactly three optimal solutions
Answer: (B) Infinitely many optimal solutions
Q9. For Maximize Z = ax + by, the set of lines Z = k are called
🔵 (A) Iso-profit (level) lines
🟢 (B) Budget lines
🟠 (C) Constraint lines
🔴 (D) Null lines
Answer: (A) Iso-profit (level) lines
Q10. If the feasible region is unbounded, to confirm a maximum exists one must
🔵 (A) Check only interior points
🟢 (B) Check vertices and test whether larger Z is possible along open edges
🟠 (C) Ignore the objective function
🔴 (D) Add artificial bounds arbitrarily
Answer: (B) Check vertices and test whether larger Z is possible along open edges
Q11. Standard non-negativity conditions are added because
🔵 (A) They simplify inequalities
🟢 (B) Variables often represent quantities that cannot be negative
🟠 (C) They are optional
🔴 (D) They guarantee uniqueness
Answer: (B) Variables often represent quantities that cannot be negative
Q12. In formulation, “at most 20 hours” for resource time becomes
🔵 (A) Time ≥ 20
🟢 (B) Time ≤ 20
🟠 (C) Time = 20
🔴 (D) No constraint
Answer: (B) Time ≤ 20
Q13. The intersection of two constraint boundaries corresponds to
🔵 (A) A vertex (corner point)
🟢 (B) A redundant inequality
🟠 (C) An infeasible point
🔴 (D) The objective line
Answer: (A) A vertex (corner point)
Q14. If Max Z = 3x + 2y with constraints x + y ≤ 6, x ≥ 0, y ≥ 0, the maximum occurs at
🔵 (A) (0, 0)
🟢 (B) (6, 0)
🟠 (C) (0, 6)
🔴 (D) (3, 3)
Answer: (B) (6, 0)
Q15. Minimization problems by the graphical method are solved by
🔵 (A) Checking only one vertex
🟢 (B) Evaluating Z at all feasible vertices and choosing the least
🟠 (C) Maximizing −Z
🔴 (D) Ignoring corner points
Answer: (B) Evaluating Z at all feasible vertices and choosing the least
Q16. A redundant constraint is one that
🔵 (A) Does not affect the feasible region
🟢 (B) Eliminates all feasible points
🟠 (C) Is nonlinear
🔴 (D) Is the objective function itself
Answer: (A) Does not affect the feasible region
Q17. For Max Z = 5x + 4y with constraints x ≤ 4, y ≤ 3, x ≥ 0, y ≥ 0, the optimal solution is
🔵 (A) x = 4, y = 3
🟢 (B) x = 0, y = 0
🟠 (C) x = 4, y = 0
🔴 (D) x = 0, y = 3
Answer: (A) x = 4, y = 3
Q18. If two constraints are parallel and inconsistent (e.g., x + y ≤ 3 and x + y ≥ 8), then
🔵 (A) Multiple optima
🟢 (B) Infeasible LPP
🟠 (C) Unbounded LPP
🔴 (D) Unique optimum
Answer: (B) Infeasible LPP
Q19. The slope of the objective line Z = ax + by (in x–y plane) is
🔵 (A) a/b
🟢 (B) −a/b
🟠 (C) −b/a
🔴 (D) b/a
Answer: (C) −b/a
Q20. When the objective line is parallel to an edge of the feasible polygon and touches it at a vertex, then
🔵 (A) No solution
🟢 (B) Infinite optimal solutions along that edge (if also touching another vertex)
🟠 (C) Exactly one optimal solution
🔴 (D) The region is unbounded
Answer: (B) Infinite optimal solutions along that edge (if also touching another vertex)
Q21. Maximize Z = 2x + 3y subject to x + y ≤ 5, x ≥ 0, y ≥ 0. The optimal value of Z equals
🔵 (A) 15 at (0,5)
🟢 (B) 15 at (5,0)
🟠 (C) 17 at (2,3)
🔴 (D) 15 at (2,3)
Answer: (A) 15 at (0,5)
Q22. For Minimize Z = x + y with constraints x + 2y ≥ 6, x ≥ 0, y ≥ 0, which point is a vertex of the feasible region?
🔵 (A) (0, 0)
🟢 (B) (0, 3)
🟠 (C) (6, 0)
🔴 (D) (2, 2)
Answer: (B) (0, 3)
Q23. Consider Max Z = 3x + y subject to x + y ≤ 4, x ≤ 3, x, y ≥ 0. The optimal solution is
🔵 (A) (0, 4)
🟢 (B) (3, 1)
🟠 (C) (4, 0)
🔴 (D) (2, 2)
Answer: (B) (3, 1)
Q24. If the feasible region is the triangle with vertices (0,0), (6,0), (0,4), then for Max Z = 2x + 5y the maximum occurs at
🔵 (A) (0, 0)
🟢 (B) (6, 0)
🟠 (C) (0, 4)
🔴 (D) Along the edge between (6,0) and (0,4) only
Answer: (C) (0, 4)
Q25. In an LPP, a constraint like “use at least 10 kg of material” is modeled as
🔵 (A) Usage ≤ 10
🟢 (B) Usage ≥ 10
🟠 (C) Usage = 10
🔴 (D) No constraint
Answer: (B) Usage ≥ 10
Q26. Maximize Z = 4x + 6y subject to x + 2y ≤ 8, 3x + y ≤ 9, x, y ≥ 0. The optimal vertex is
🔵 (A) (0, 0)
🟢 (B) (0, 4)
🟠 (C) (3, 0)
🔴 (D) (2, 3)
Answer: (D) (2, 3)
Q27. A diet problem requiring at least 12 units of protein and 8 units of vitamins is an example of
🔵 (A) Maximization
🟢 (B) Minimization
🟠 (C) Feasibility only
🔴 (D) Redundancy
Answer: (B) Minimization
Q28. If the objective function is Z = 5x + 5y and the feasible region is a square 0 ≤ x ≤ 2, 0 ≤ y ≤ 2, then
🔵 (A) Unique optimum at (2,2)
🟢 (B) Multiple optima along the edge x + y = 4
🟠 (C) Multiple optima along the line x = y
🔴 (D) No optimum
Answer: (A) Unique optimum at (2,2)
Q29. For the constraint x + y ≤ 10, which point satisfies it?
🔵 (A) (5, 7)
🟢 (B) (7, 5)
🟠 (C) (10, 0)
🔴 (D) (6, 6)
Answer: (C) (10, 0)
Q30. Minimize Z = 3x + 2y subject to x + y ≥ 6, x ≥ 2, y ≥ 0. The minimum occurs at
🔵 (A) (2, 4)
🟢 (B) (6, 0)
🟠 (C) (2, 0)
🔴 (D) (3, 3)
Answer: (A) (2, 4)
Q31. If the objective line is parallel to x + y = 6 and the feasible region has the edge x + y = 6 as part of its boundary, then
🔵 (A) No feasible point lies on the edge
🟢 (B) All points of that edge give the same objective value (if coefficients match)
🟠 (C) The problem is infeasible
🔴 (D) The objective is minimized only at (0,0)
Answer: (B) All points of that edge give the same objective value (if coefficients match)
Q32. Which transformation changes Max Z = ax + by to an equivalent Min problem?
🔵 (A) Replace Z by −Z and maximize
🟢 (B) Replace Z by −Z and minimize
🟠 (C) Replace Z by a²x + b²y
🔴 (D) Replace Z by ax − by
Answer: (B) Replace Z by −Z and minimize
Q33. For Max Z = 6x + y with constraints x ≤ 2, y ≤ 5, x, y ≥ 0, the optimal value Z* equals
🔵 (A) 11
🟢 (B) 12
🟠 (C) 17
🔴 (D) 7
Answer: (C) 17
Q34. If a constraint line does not intersect the feasible polygon, it is
🔵 (A) Redundant
🟢 (B) Binding
🟠 (C) Infeasible
🔴 (D) Optimal
Answer: (A) Redundant
Q35. A binding constraint at optimum is one that
🔵 (A) Is not satisfied
🟢 (B) Holds with equality at the optimal point
🟠 (C) Has no effect on Z
🔴 (D) Is nonlinear
Answer: (B) Holds with equality at the optimal point
Q36. Max Z = 5x + 2y subject to x + 2y ≤ 8, x ≤ 6, y ≤ 4, x, y ≥ 0. The optimal solution is at
🔵 (A) (6, 0)
🟢 (B) (0, 4)
🟠 (C) (6, 1)
🔴 (D) (4, 2)
Answer: (D) (4, 2)
Q37. If the feasible region is unbounded and the objective is to minimize Z = x + y, then
🔵 (A) Minimum is always 0
🟢 (B) Minimum may still occur at a vertex in the first quadrant
🟠 (C) No minimum can exist
🔴 (D) Z is always negative
Answer: (B) Minimum may still occur at a vertex in the first quadrant
Q38. In a transport-style LP with “at least” demand constraints, those constraints are written as
🔵 (A) ≤ type
🟢 (B) ≥ type
🟠 (C) = type
🔴 (D) No constraints
Answer: (B) ≥ type
Q39. For Max Z = 3x + 4y, the iso-profit line Z = k has y-intercept equal to
🔵 (A) k/3
🟢 (B) k/4
🟠 (C) 3k/4
🔴 (D) 4k/3
Answer: (B) k/4
Q40. If the feasible polygon has vertices (0,0), (4,0), (4,3), (0,3), then for Min Z = 2x + y, the minimum occurs at
🔵 (A) (0, 0)
🟢 (B) (4, 0)
🟠 (C) (0, 3)
🔴 (D) (4, 3)
Answer: (A) (0, 0)
Q41. Consider Max Z = 7x + 5y subject to x + y ≤ 6, 2x + y ≤ 8, x, y ≥ 0. The optimal point is
🔵 (A) Intersection of x + y = 6 and 2x + y = 8
🟢 (B) (0, 0)
🟠 (C) (6, 0)
🔴 (D) (0, 6)
Answer: (A) Intersection of x + y = 6 and 2x + y = 8
Q42. For the LPP in Q41, the intersection in option (A) equals
🔵 (A) (2, 4)
🟢 (B) (4, 2)
🟠 (C) (8, 0)
🔴 (D) (0, 8)
Answer: (B) (4, 2)
Q43. Using Q41–Q42, Z at (4,2) equals
🔵 (A) 24
🟢 (B) 34
🟠 (C) 38
🔴 (D) 20
Answer: (B) 34
Q44. Let feasible vertices be (0,0), (5,0), (2,3). For Max Z = 4x + 3y, the optimum is at
🔵 (A) (0, 0)
🟢 (B) (5, 0)
🟠 (C) (2, 3)
🔴 (D) Both (5,0) and (2,3)
Answer: (C) (2, 3)
Q45. If all constraints are homogeneous (like ax + by ≥ 0) and non-negativity holds, then (0,0) is
🔵 (A) Always feasible
🟢 (B) Never feasible
🟠 (C) Sometimes feasible
🔴 (D) Always optimal
Answer: (A) Always feasible
Q46. Max Z = 2x + 5y subject to x + y ≤ 5, y ≤ 4, x ≥ 0, y ≥ 0. The optimal solution is
🔵 (A) (0, 0)
🟢 (B) (1, 4)
🟠 (C) (5, 0)
🔴 (D) (0, 4)
Answer: (B) (1, 4)
Q47. In sensitivity terms (qualitatively per NCERT), increasing the coefficient of y in Z = ax + by tends to
🔵 (A) Favor larger y at optimum, if feasible
🟢 (B) Favor smaller y
🟠 (C) Leave optimum unchanged always
🔴 (D) Make the problem infeasible
Answer: (A) Favor larger y at optimum, if feasible
Q48. If an LPP models “at least r units of resource R must be used,” then for usage U the correct inequality is
🔵 (A) U ≤ r
🟢 (B) U ≥ r
🟠 (C) U = 0
🔴 (D) U = r/2
Answer: (B) U ≥ r
Q49. For Min Z = 8x + 6y with feasible vertices (0,0), (0,5), (3,2), (6,0), the minimum occurs at
🔵 (A) (0, 0)
🟢 (B) (0, 5)
🟠 (C) (3, 2)
🔴 (D) (6, 0)
Answer: (A) (0, 0)
Q50. In a formulation where x and y denote numbers of items produced, which statement is most consistent with NCERT LP modeling?
🔵 (A) Allow x, y to be negative to increase solution space
🟢 (B) Keep x, y real with x ≥ 0, y ≥ 0; solve graphically for two variables
🟠 (C) Force x, y to be integers always
🔴 (D) Replace linear constraints with quadratic ones for realism
Answer: (B) Keep x, y real with x ≥ 0, y ≥ 0; solve graphically for two variables
————————————————————————————————————————————————————————————————————————————
MIND MAPS
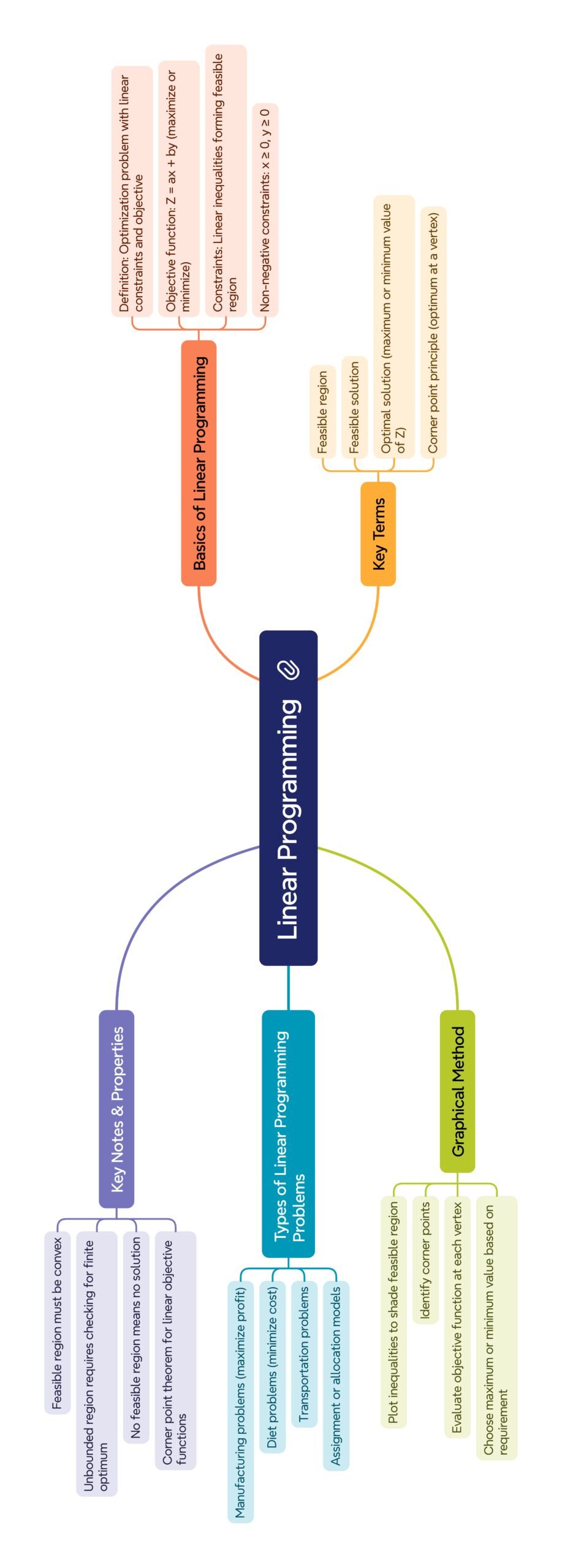

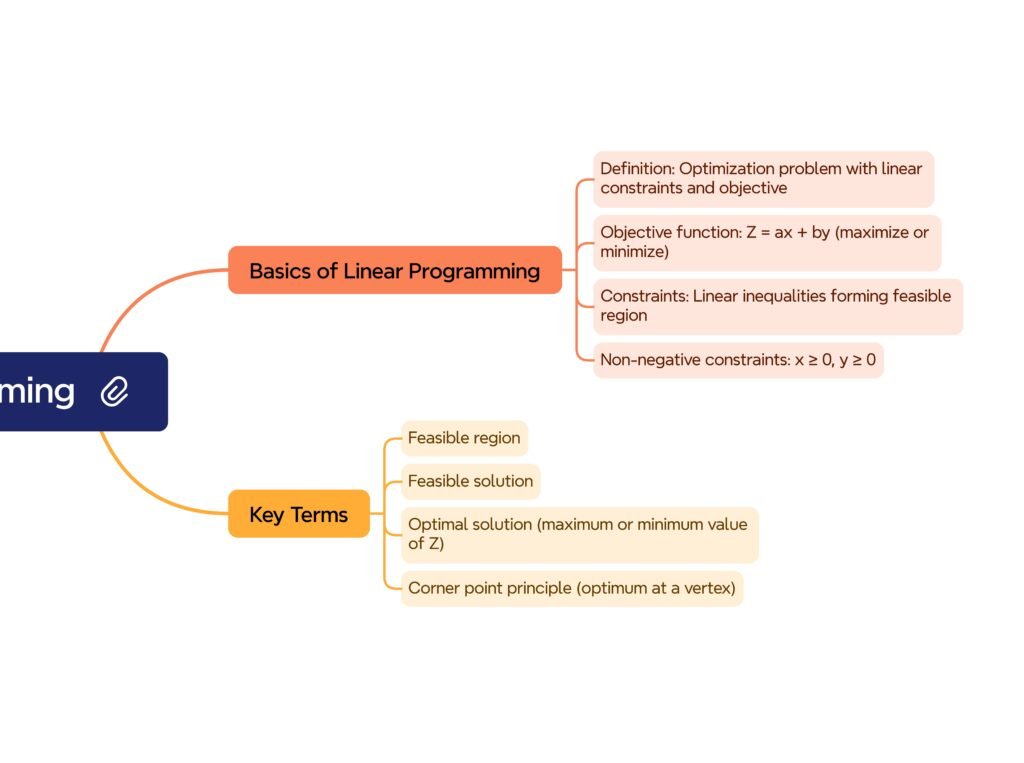
————————————————————————————————————————————————————————————————————————————
