Class 12 : Maths (English) – Chapter 10: Vector
EXPLANATION & SUMMARY
🔷 Explanation
🔹 Introduction to Vectors
A vector is a quantity that has both magnitude and direction.
🧭 Unlike a scalar (which has only magnitude, e.g., mass, temperature), a vector represents directed quantities like force, velocity, and displacement.
✏️ Note: Scalars and vectors are the two fundamental types of physical quantities.
💡 Examples:
Displacement = 5 km north (vector)
Speed = 60 km/h (scalar)
🔹 Representation of a Vector
A vector is denoted by a̅, b̅, c̅ or →AB.
If A(x₁, y₁, z₁) and B(x₂, y₂, z₂) are two points,
then the position vector →AB = (x₂ − x₁)î + (y₂ − y₁)ĵ + (z₂ − z₁)k̂.
🧠 Magnitude of vector a̅ = sqrt(a₁² + a₂² + a₃²)
📏 Direction is along the line joining points A and B.

🔹 Types of Vectors
🔵 Zero Vector: magnitude = 0 (denoted by 0̅)
🟢 Unit Vector: magnitude = 1 (used for direction, e.g., î, ĵ, k̂)
🟠 Equal Vectors: same magnitude and direction
🔴 Negative Vectors: same magnitude but opposite direction
🟣 Collinear Vectors: parallel vectors
🟤 Coplanar Vectors: vectors lying in the same plane
🔹 Position Vector and Direction Cosines
➡️ If a point P(x, y, z), then position vector OP̅ = xî + yĵ + zk̂
➡️ Direction cosines (l, m, n) are cosines of angles between vector and coordinate axes.
Relation: l² + m² + n² = 1
🔹 Vector Equality
Two vectors a̅ and b̅ are equal if:
They have the same magnitude
They have the same direction
Formally:
a̅ = b̅ ⇒ a₁ = b₁, a₂ = b₂, a₃ = b₃
🔹 Addition of Vectors
If a̅ = a₁î + a₂ĵ + a₃k̂ and b̅ = b₁î + b₂ĵ + b₃k̂,
then a̅ + b̅ = (a₁ + b₁)î + (a₂ + b₂)ĵ + (a₃ + b₃)k̂.
💡 Commutative Law: a̅ + b̅ = b̅ + a̅
💡 Associative Law: (a̅ + b̅) + c̅ = a̅ + (b̅ + c̅)
✏️ Note: Addition is done component-wise.
🔹 Subtraction of Vectors
a̅ − b̅ = (a₁ − b₁)î + (a₂ − b₂)ĵ + (a₃ − b₃)k̂
✔️ Represents a vector from tip of b̅ to tip of a̅.
🔹 Multiplication by a Scalar
If k is a scalar, then
k a̅ = (k a₁)î + (k a₂)ĵ + (k a₃)k̂
✔️ If k > 0, direction remains same; if k < 0, direction reverses.
🔹 Section Formula (Vector Form)
A point P divides line joining A(x₁, y₁, z₁) and B(x₂, y₂, z₂) in ratio m : n,
then
OP̅ = (m OB̅ + n OA̅)/(m + n)
or
Position vector = [(m x₂ + n x₁)/(m + n)] î + [(m y₂ + n y₁)/(m + n)] ĵ + [(m z₂ + n z₁)/(m + n)] k̂
💡 Used to find coordinates of internal dividing point.
🔹 Scalar (Dot) Product
For vectors a̅ = a₁î + a₂ĵ + a₃k̂, b̅ = b₁î + b₂ĵ + b₃k̂,
a̅ ⋅ b̅ = a₁b₁ + a₂b₂ + a₃b₃
Also,
a̅ ⋅ b̅ = |a̅||b̅| cosθ
📌 Properties:
Commutative: a̅ ⋅ b̅ = b̅ ⋅ a̅
Distributive: a̅ ⋅ (b̅ + c̅) = a̅ ⋅ b̅ + a̅ ⋅ c̅
If a̅ ⋅ b̅ = 0, then vectors are perpendicular.
🔹 Vector (Cross) Product
For vectors a̅ and b̅,
a̅ × b̅ = |a̅||b̅| sinθ n̂,
where n̂ is a unit vector perpendicular to both.
In component form:
a̅ × b̅ = | î ĵ k̂ |
| a₁ a₂ a₃ |
| b₁ b₂ b₃ |
📌 Properties:
a̅ × b̅ = − b̅ × a̅
a̅ × a̅ = 0̅
If a̅ × b̅ = 0̅, then a̅ and b̅ are parallel.
🔹 Scalar Triple Product
For a̅, b̅, c̅,
[a̅ b̅ c̅] = a̅ ⋅ (b̅ × c̅)
Represents volume of parallelepiped.
In determinant form:
[a̅ b̅ c̅] = | a₁ a₂ a₃ |
| b₁ b₂ b₃ |
| c₁ c₂ c₃ |
If [a̅ b̅ c̅] = 0, vectors are coplanar.
🔹 Vector Equation of a Line
If a line passes through point A(x₁, y₁, z₁) and is parallel to vector b̅,
then any point P(x, y, z) on line satisfies
r̅ = a̅ + λ b̅
where a̅ = x₁î + y₁ĵ + z₁k̂ and λ is a scalar.
🔹 Vector Equation of a Plane
If plane passes through point A(a₁, a₂, a₃) and normal vector n̅,
then
(r̅ − a̅) ⋅ n̅ = 0
or
n₁(x − a₁) + n₂(y − a₂) + n₃(z − a₃) = 0
🔹 Applications
📏 Distance between two points using vectors
🧭 Angle between lines/planes
📦 Volume and area using triple products
📐 Orthogonality checks using dot product
🔹 Important Identities
✔️ a̅ ⋅ (b̅ × c̅) = b̅ ⋅ (c̅ × a̅) = c̅ ⋅ (a̅ × b̅)
✔️ a̅ × (b̅ × c̅) = (a̅ ⋅ c̅)b̅ − (a̅ ⋅ b̅)c̅
✔️ |a̅ × b̅|² = |a̅|²|b̅|² − (a̅ ⋅ b̅)²
🔹 Geometrical Interpretation
🧭 Dot Product → Projection or cosine of angle
🧭 Cross Product → Area of parallelogram
🧭 Triple Product → Volume of parallelepiped
🧾 Summary (≈300 words)
Vector: quantity with magnitude & direction.
Position vector: from origin to point (x, y, z)
Unit vectors: î, ĵ, k̂
Addition/Subtraction: component-wise
Dot product: a̅ ⋅ b̅ = |a̅||b̅| cosθ
Cross product: a̅ × b̅ = |a̅||b̅| sinθ n̂
Triple product: volume = |a̅ ⋅ (b̅ × c̅)|
Equation of line: r̅ = a̅ + λ b̅
Equation of plane: (r̅ − a̅) ⋅ n̅ = 0
Coplanar test: [a̅ b̅ c̅] = 0
Parallel vectors: cross product = 0
Perpendicular vectors: dot product = 0
Vector identities:
a̅ × (b̅ × c̅) = (a̅ ⋅ c̅)b̅ − (a̅ ⋅ b̅)c̅
|a̅ × b̅|² = |a̅|²|b̅|² − (a̅ ⋅ b̅)²
📝 Quick Recap
🟢 Vectors = magnitude + direction
🔵 Dot product = projection concept
🔴 Cross product = perpendicular vector
🟡 Triple product = volume measure
✏️ Line: r̅ = a̅ + λ b̅
💡 Plane: (r̅ − a̅) ⋅ n̅ = 0
————————————————————————————————————————————————————————————————————————————
QUESTIONS FROM TEXTBOOK
📄 Exercise 10.1
🔵 Question 1:
Represent graphically a displacement of 40 km, 30° east of north.
🟢 Answer:
➡️ Draw a vertical line to represent the north direction.
➡️ From the same origin, draw a line making an angle of 30° with north toward east.
➡️ Mark the length proportional to 40 km.
➡️ Put an arrow to show direction.
✔️ Thus, the line represents the displacement vector of 40 km, 30° east of north.
🔵 Question 2:
Classify the following measures as scalars and vectors.
(i) 10 kg
(ii) 2 meters north-west
(iii) 40°
(iv) 40 watt
(v) 10⁻¹⁹ coulomb
(vi) 20 m/s²
🟢 Answer:
✔️ Scalars → (i) 10 kg, (iii) 40°, (iv) 40 watt, (v) 10⁻¹⁹ coulomb
✔️ Vectors → (ii) 2 meters north-west, (vi) 20 m/s²
💡 Scalar quantities have only magnitude.
💡 Vector quantities have magnitude and direction.
🔵 Question 3:
Classify the following as scalar and vector quantities.
(i) time period
(ii) distance
(iii) force
(iv) velocity
(v) work done
🟢 Answer:
✔️ Scalars → (i) time period, (ii) distance, (v) work done
✔️ Vectors → (iii) force, (iv) velocity
🔵 Question 4:
In Fig 10.6 (a square), identify the following vectors.
(i) Coinitial
(ii) Equal
(iii) Collinear but not equal
🟢 Answer:
Let the square have sides represented by vectors:
Top side → a
Right side → b
Bottom side → c
Left side → d
(i) Coinitial vectors:
➡️ Vectors having the same initial point.
✔️ a and d are coinitial.
(ii) Equal vectors:
➡️ Vectors having same magnitude and same direction.
✔️ a = c, and b = d.
(iii) Collinear but not equal:
➡️ Vectors that are parallel but different in direction or magnitude.
✔️ a and c (same line, opposite direction)
✔️ b and d (same line, opposite direction)
🔵 Question 5:
Answer the following as true or false.
(i) a and –a are collinear.
(ii) Two collinear vectors are always equal in magnitude.
(iii) Two vectors having same magnitude are collinear.
(iv) Two collinear vectors having the same magnitude are equal.
🟢 Answer:
(i) ✔️ True — Both lie along the same line but in opposite direction.
(ii) ❌ False — They may differ in magnitude.
(iii) ❌ False — Same magnitude doesn’t imply collinearity.
(iv) ❌ False — They may have opposite direction.
Exercise 10.2
🔵 Question 1:
Compute the magnitude of the following vectors:
a̅ = i + j + k ; b̅ = 2 i − 7 j − 3 k ; c̅ = (1/√3) i + (1/√3) j − (1/√3) k.
🟢 Answer:
➡️ |a̅| = √(1² + 1² + 1²) = √3.
➡️ |b̅| = √(2² + (−7)² + (−3)²) = √(4 + 49 + 9) = √62.
➡️ |c̅| = √( (1/√3)² + (1/√3)² + (−1/√3)² ) = √(1/3 + 1/3 + 1/3) = √1 = 1.
✔️ Final: |a̅| = √3, |b̅| = √62, |c̅| = 1.
🔵 Question 2:
Write two different vectors having same magnitude.
🟢 Answer:
➡️ Example 1: u̅ = i and v̅ = j.
➡️ |u̅| = |v̅| = 1.
✔️ They are different but have equal magnitude.
🔵 Question 3:
Write two different vectors having same direction.
🟢 Answer:
➡️ If v̅ = i + 2 j, then 2 v̅ = 2 i + 4 j has the same direction.
✔️ v̅ and 2 v̅ are different but parallel (same direction).
🔵 Question 4:
Find the values of x and y so that the vectors 2 i + 3 j and x i + y j are equal.
🟢 Answer:
➡️ Equality of vectors ⇒ equal corresponding components.
➡️ x = 2 and y = 3.
✔️ Final: x = 2, y = 3.
🔵 Question 5:
Find the scalar and vector components of the vector with initial point (2, 1) and terminal point (−5, 7).
🟢 Answer:
➡️ Displacement vector = (terminal − initial) = (−5 − 2, 7 − 1) = (−7, 6).
➡️ Vector form = −7 i + 6 j.
➡️ Scalar components along x- and y-axes = (−7, 6).
✔️ Final: vector components −7 i and 6 j; scalar components (−7, 6).
🔵 Question 6:
Find the sum of the vectors a̅ = i − 2 j + k, b̅ = −2 i + 4 j + 5 k and c̅ = i − 6 j − 7 k.
🟢 Answer:
➡️ a̅ + b̅ + c̅ = (i − 2 j + k) + (−2 i + 4 j + 5 k) + (i − 6 j − 7 k).
➡️ i-components: 1 − 2 + 1 = 0.
➡️ j-components: −2 + 4 − 6 = −4.
➡️ k-components: 1 + 5 − 7 = −1.
✔️ Sum = −4 j − k.
🔵 Question 7:
Find the unit vector in the direction of the vector a̅ = i + j + 2 k.
🟢 Answer:
➡️ |a̅| = √(1² + 1² + 2²) = √6.
➡️ Unit vector â = a̅ / |a̅| = (1/√6) i + (1/√6) j + (2/√6) k.
✔️ Final: â = (1/√6) i + (1/√6) j + (2/√6) k.
🔵 Question 8:
Find the unit vector in the direction of vector PQ, where P and Q are the points (1, 2, 3) and (4, 5, 6), respectively.
🟢 Answer:
➡️ PQ̅ = Q − P = (4 − 1, 5 − 2, 6 − 3) = (3, 3, 3) = 3(i + j + k).
➡️ |PQ̅| = √(3² + 3² + 3²) = √27 = 3√3.
➡️ Unit vector û = PQ̅ / |PQ̅| = (1/√3) i + (1/√3) j + (1/√3) k.
✔️ Final: û = (1/√3)(i + j + k).
🔵 Question 9:
For given vectors, a̅ = 2 i − j + 2 k and b̅ = − i + j − k, find the unit vector in the direction of the vector a̅ + b̅.
🟢 Answer:
➡️ a̅ + b̅ = (2 − 1) i + (−1 + 1) j + (2 − 1) k = i + 0 j + k.
➡️ |a̅ + b̅| = √(1² + 0² + 1²) = √2.
➡️ Unit vector û = (a̅ + b̅)/|a̅ + b̅| = (1/√2) i + 0 j + (1/√2) k.
✔️ Final: û = (1/√2) i + (1/√2) k.
🔵 Question 10:
Find a vector in the direction of vector 5 i − j + 2 k which has magnitude 8 units.
🟢 Answer:
➡️ v̅ = 5 i − j + 2 k.
➡️ |v̅| = √(5² + (−1)² + 2²) = √(25 + 1 + 4) = √30.
➡️ Unit vector along v̅ is v̅/|v̅|.
➡️ Required vector = 8 × (v̅/|v̅|) = (8/√30) (5 i − j + 2 k).
✔️ Final: (8/√30)(5 i − j + 2 k).
🔵 Question 11:
Show that the vectors 2 i − 3 j + 4 k and −4 i + 6 j − 8 k are collinear.
🟢 Answer:
➡️ Take λ = −2.
➡️ λ(2 i − 3 j + 4 k) = −4 i + 6 j − 8 k.
➡️ One vector is a scalar multiple of the other.
✔️ Hence they are parallel (collinear).
🔵 Question 12:
Find the direction cosines of the vector i + 2 j + 3 k.
🟢 Answer:
➡️ Let v̅ = i + 2 j + 3 k.
➡️ |v̅| = √(1² + 2² + 3²) = √14.
➡️ Direction cosines (l, m, n) = (1/|v̅|, 2/|v̅|, 3/|v̅|).
✔️ Final: l = 1/√14, m = 2/√14, n = 3/√14.
🔵 Question 13:
Find the direction cosines of the vector joining the points A(1, 2, −3) and B(−1, −2, 1), directed from A to B.
🟢 Answer:
➡️ A(1, 2, −3), B(−1, −2, 1).
➡️ AB̅ = (−1 − 1) i + (−2 − 2) j + (1 − (−3)) k = −2 i − 4 j + 4 k.
➡️ |AB̅| = √( (−2)² + (−4)² + 4² ) = √(4 + 16 + 16) = √36 = 6.
➡️ Direction cosines: l = (−2)/6 = −1/3, m = (−4)/6 = −2/3, n = 4/6 = 2/3.
✔️ Final: (l, m, n) = (−1/3, −2/3, 2/3).
🔵 Question 14:
Show that the vector i + j + k is equally inclined to the axes OX, OY and OZ.
🟢 Answer:
➡️ v̅ = i + j + k with |v̅| = √(1 + 1 + 1) = √3.
➡️ Direction cosines: l = 1/√3, m = 1/√3, n = 1/√3 (all equal).
➡️ Angles with axes: α = β = γ with cos α = cos β = cos γ = 1/√3.
✔️ Hence v̅ makes equal angles with OX, OY, OZ (equally inclined).
🔵 Question 15:
Find the position vector of a point R which divides the line joining two points P and Q whose position vectors are P̅ = i + 2 j − k and Q̅ = − i + j + k respectively, in the ratio 2 : 1
(i) internally (ii) externally.
🟢 Answer:
➡️ Let ratio m : n = 2 : 1 (PR : RQ).
➡️ Use section formula with vectors.
✳️ (i) Internal division:
r̅_R = (m Q̅ + n P̅)/(m + n)
= (2(− i + j + k) + 1(i + 2 j − k)) / 3
= (−2 i + 2 j + 2 k + i + 2 j − k)/3
= (− i + 4 j + k)/3
✔️ r̅_R = (−1/3) i + (4/3) j + (1/3) k.
✳️ (ii) External division:
r̅_R = (m Q̅ − n P̅)/(m − n)
= (2(− i + j + k) − 1(i + 2 j − k)) / (2 − 1)
= (−2 i + 2 j + 2 k − i − 2 j + k) / 1
= −3 i + 0 j + 3 k
✔️ r̅_R = −3 i + 3 k.
🔵 Question 16:
Find the position vector of the midpoint of the vector joining the points P(2, 3, 4) and Q(4, 1, −2).
🟢 Answer:
➡️ Midpoint formula M = ((x₁ + x₂)/2, (y₁ + y₂)/2, (z₁ + z₂)/2).
➡️ M = ((2 + 4)/2, (3 + 1)/2, (4 + (−2))/2).
➡️ M = (6/2, 4/2, 2/2) = (3, 2, 1).
✔️ Position vector of midpoint = 3 i + 2 j + 1 k.
🔵 Question 17:
Show that the points A, B and C with position vectors a̅ = 3 i − 4 j − 4 k, b̅ = 2 i − j + k and c̅ = i − 3 j − 5 k, respectively, form the vertices of a right-angled triangle.
🟢 Answer:
➡️ Compute AB̅ = b̅ − a̅.
✳️ AB̅ = (2 − 3) i + (−1 − (−4)) j + (1 − (−4)) k = − i + 3 j + 5 k.
➡️ Compute AC̅ = c̅ − a̅.
✳️ AC̅ = (1 − 3) i + (−3 − (−4)) j + (−5 − (−4)) k = −2 i + 1 j − 1 k.
➡️ Check perpendicularity via dot product.
✳️ AB̅ · AC̅ = (−1)(−2) + (3)(1) + (5)(−1) = 2 + 3 − 5 = 0.
✔️ Since AB̅ · AC̅ = 0, vectors AB̅ and AC̅ are perpendicular.
✔️ Therefore, triangle ABC is right-angled at A.
🔵 Question 18:
In triangle ABC (Fig 10.18), which of the following is not true?
(A) A B̅ + B C̅ + C A̅ = 0̅
(B) A B̅ + B C̅ − C A̅ = 0̅
(C) A B̅ + B C̅ − A C̅ = 0̅
(D) A B̅ − C B̅ + C A̅ = 0̅
🟢 Answer:
➡️ In any triangle, the head-to-tail addition along the closed polygon gives A B̅ + B C̅ + C A̅ = 0̅ (true).
➡️ Also, A B̅ + B C̅ = A C̅ ⇒ A B̅ + B C̅ − A C̅ = 0̅ (true).
➡️ Since C A̅ = − A C̅, the relation A B̅ + B C̅ − C A̅ = 0̅ would mean A B̅ + B C̅ = C A̅ = − A C̅, which is false in general.
✔️ The statement that is not true is (B).
🔵 Question 19:
If a̅ and b̅ are two collinear vectors, then which of the following are incorrect?
(A) b̅ = λ a̅, for some scalar λ
(B) a̅ = ± b̅
(C) The respective components of a̅ and b̅ are not proportional
(D) Both the vectors a̅ and b̅ have same direction, but different magnitudes
🟢 Answer:
➡️ For collinear vectors, definition gives b̅ = λ a̅ for some real λ (true).
➡️ a̅ = ± b̅ holds only when |λ| = 1; it is not necessary for all collinear vectors (incorrect as a general statement).
➡️ Components of collinear vectors are proportional (since b̅ = λ a̅); saying “not proportional” is incorrect.
➡️ Collinear vectors may have the same direction (λ > 0) or opposite directions (λ < 0); hence asserting “same direction” always is incorrect.
✔️ Incorrect options: (B), (C), and (D).
Exercise 10.3
🔵 Question 1:
Find the angle between two vectors a̅ and b̅ with magnitudes √3 and 2, respectively, having a̅ · b̅ = √6.
🟢 Answer:
➡️ Use cos θ = (a̅ · b̅) / (|a̅| |b̅|).
➡️ cos θ = √6 / (√3 × 2) = √6 / (2√3).
➡️ cos θ = (√6/√3) / 2 = √2 / 2.
➡️ θ = 45°.
✔️ Angle between a̅ and b̅ is 45°.
🔵 Question 2:
Find the angle between the vectors i − 2 j + 3 k and 3 i − 2 j + k.
🟢 Answer:
➡️ Let u̅ = (1, −2, 3), v̅ = (3, −2, 1).
➡️ u̅ · v̅ = (1)(3) + (−2)(−2) + (3)(1) = 3 + 4 + 3 = 10.
➡️ |u̅| = √(1² + (−2)² + 3²) = √14.
➡️ |v̅| = √(3² + (−2)² + 1²) = √14.
➡️ cos θ = 10 / (√14 × √14) = 10/14 = 5/7.
✔️ θ = cos⁻¹(5/7).
🔵 Question 3:
Find the projection of the vector i − j on the vector i + j.
🟢 Answer:
➡️ Let u̅ = i − j, v̅ = i + j.
➡️ u̅ · v̅ = (1)(1) + (−1)(1) = 0.
➡️ Vector projection of u̅ on v̅ = [(u̅ · v̅)/|v̅|²] v̅ = 0 · v̅ = 0̅.
✔️ Projection is the zero vector.
🔵 Question 4:
Find the projection of the vector i + 3 j + 7 k on the vector 7 i − j + 8 k.
🟢 Answer:
➡️ Let u̅ = (1, 3, 7), v̅ = (7, −1, 8).
➡️ u̅ · v̅ = (1)(7) + (3)(−1) + (7)(8) = 7 − 3 + 56 = 60.
➡️ |v̅|² = 7² + (−1)² + 8² = 49 + 1 + 64 = 114.
➡️ Vector projection = [(u̅ · v̅)/|v̅|²] v̅ = (60/114) v̅ = (10/19) v̅.
✔️ Projection = (10/19)(7 i − j + 8 k).
🔵 Question 5:
Show that each of the given three vectors is a unit vector:
(1/7)(2 i + 3 j + 6 k), (1/7)(3 i − 6 j + 2 k), (1/7)(6 i + 2 j − 3 k).
Also, show that they are mutually perpendicular to each other.
🟢 Answer (Unit lengths):
➡️ |2 i + 3 j + 6 k| = √(2² + 3² + 6²) = √49 = 7 ⇒ scaled by 1/7 ⇒ length 1.
➡️ |3 i − 6 j + 2 k| = √(3² + (−6)² + 2²) = √49 = 7 ⇒ scaled by 1/7 ⇒ length 1.
➡️ |6 i + 2 j − 3 k| = √(6² + 2² + (−3)²) = √49 = 7 ⇒ scaled by 1/7 ⇒ length 1.
✔️ Each vector is a unit vector.
🟢 Answer (Mutual perpendicularity):
➡️ (2, 3, 6) · (3, −6, 2) = 6 − 18 + 12 = 0.
➡️ (2, 3, 6) · (6, 2, −3) = 12 + 6 − 18 = 0.
➡️ (3, −6, 2) · (6, 2, −3) = 18 − 12 − 6 = 0.
✔️ All pairwise dot products are zero ⇒ vectors are mutually perpendicular.
🔵 Question 6:
Find |a̅| and |b̅|, if (a̅ + b̅) · (a̅ − b̅) = 8 and |a̅| = 8 |b̅|.
🟢 Answer:
➡️ (a̅ + b̅) · (a̅ − b̅) = |a̅|² − |b̅|² = 8.
➡️ Let |b̅| = x ⇒ |a̅| = 8x.
➡️ Substitute: (8x)² − x² = 8 ⇒ 64x² − x² = 8 ⇒ 63x² = 8.
➡️ x² = 8/63 ⇒ x = √(8/63) = (2√14)/21.
➡️ |b̅| = (2√14)/21.
➡️ |a̅| = 8x = 8 × (2√14)/21 = (16√14)/21.
✔️ Final: |a̅| = (16√14)/21, |b̅| = (2√14)/21.
🔵 Question 7:
Evaluate the product (3 a̅ − 5 b̅) · (2 a̅ + 7 b̅).
🟢 Answer:
➡️ Expand using distributive law.
➡️ = 3a̅·2a̅ + 3a̅·7b̅ − 5b̅·2a̅ − 5b̅·7b̅.
➡️ = 6|a̅|² + 21(a̅·b̅) − 10(a̅·b̅) − 35|b̅|².
➡️ = 6|a̅|² + 11(a̅·b̅) − 35|b̅|².
✔️ Final: 6|a̅|² + 11(a̅·b̅) − 35|b̅|².
🔵 Question 8:
Find the magnitude of two vectors a̅ and b̅, having the same magnitude and such that the angle between them is 60° and their scalar product is 1/2.
🟢 Answer:
➡️ Let |a̅| = |b̅| = m.
➡️ a̅ · b̅ = |a̅||b̅| cos 60° = m² × (1/2).
➡️ Given a̅ · b̅ = 1/2 ⇒ m²/2 = 1/2 ⇒ m² = 1.
➡️ m = 1 (magnitude is nonnegative).
✔️ Final: |a̅| = |b̅| = 1.
🔵 Question 9:
Find |x̅|, if for a unit vector a̅, (x̅ − a̅) · (x̅ + a̅) = 12.
🟢 Answer:
➡️ Expand: (x̅ − a̅) · (x̅ + a̅) = x̅·x̅ + x̅·a̅ − a̅·x̅ − a̅·a̅.
➡️ = |x̅|² − |a̅|².
➡️ Given |a̅| = 1 and value = 12 ⇒ |x̅|² − 1 = 12.
➡️ |x̅|² = 13 ⇒ |x̅| = √13.
✔️ Final: |x̅| = √13.
🔵 Question 10:
If a̅ = 2 i + 2 j + 3 k, b̅ = − i + 2 j + k and c̅ = 3 i + j, and a̅ + λ b̅ is perpendicular to c̅, then find λ.
🟢 Answer:
➡️ Condition: (a̅ + λ b̅) · c̅ = 0.
➡️ a̅ · c̅ = (2,2,3) · (3,1,0) = 6 + 2 + 0 = 8.
➡️ b̅ · c̅ = (−1,2,1) · (3,1,0) = −3 + 2 + 0 = −1.
➡️ 8 + λ(−1) = 0 ⇒ 8 − λ = 0 ⇒ λ = 8.
✔️ Final: λ = 8.
🔵 Question 11:
Show that |a̅| b̅ + |b̅| a̅ is perpendicular to |a̅| b̅ − |b̅| a̅, for any two nonzero vectors a̅ and b̅.
🟢 Answer:
➡️ Consider S̅ = |a̅| b̅ + |b̅| a̅ and T̅ = |a̅| b̅ − |b̅| a̅.
➡️ Compute S̅ · T̅.
➡️ = (|a̅| b̅ + |b̅| a̅) · (|a̅| b̅ − |b̅| a̅).
➡️ = |a̅|² (b̅·b̅) − |a̅||b̅| (b̅·a̅) + |a̅||b̅| (a̅·b̅) − |b̅|² (a̅·a̅).
➡️ = |a̅|² |b̅|² − |a̅||b̅| (a̅·b̅) + |a̅||b̅| (a̅·b̅) − |b̅|² |a̅|².
➡️ = 0.
✔️ Therefore S̅ · T̅ = 0 ⇒ S̅ ⟂ T̅ (perpendicular).
🔵 Question 12:
If a̅ · a̅ = 0 and a̅ · b̅ = 0, then what can be concluded about the vector b̅?
🟢 Answer:
➡️ a̅ · a̅ = |a̅|².
➡️ Given |a̅|² = 0 ⇒ |a̅| = 0 ⇒ a̅ = 0̅.
➡️ Then a̅ · b̅ = 0 holds for every b̅ (since 0̅ · b̅ = 0).
✔️ Conclusion: b̅ is unrestricted; it can be any vector. The information forces only a̅ = 0̅.
🔵 Question 13:
If a̅, b̅, c̅ are unit vectors such that a̅ + b̅ + c̅ = 0̅, find the value of a̅ · b̅ + b̅ · c̅ + c̅ · a̅.
🟢 Answer:
➡️ Take magnitude squared: |a̅ + b̅ + c̅|² = 0.
➡️ Expand: |a̅|² + |b̅|² + |c̅|² + 2(a̅ · b̅ + b̅ · c̅ + c̅ · a̅) = 0.
➡️ Since a̅, b̅, c̅ are unit vectors: |a̅|² = |b̅|² = |c̅|² = 1.
➡️ 3 + 2S = 0, where S = a̅ · b̅ + b̅ · c̅ + c̅ · a̅.
➡️ 2S = −3 ⇒ S = −3/2.
✔️ Required value: a̅ · b̅ + b̅ · c̅ + c̅ · a̅ = −3/2.
🔵 Question 14:
If either vector a̅ = 0̅ or b̅ = 0̅, then a̅ · b̅ = 0. But the converse need not be true. Justify your answer with an example.
🟢 Answer:
➡️ If any one vector is 0̅, dot product is 0 trivially (0̅ · v̅ = 0).
➡️ Converse counterexample (both nonzero but dot zero):
✳️ Take a̅ = i, b̅ = j.
➡️ a̅ · b̅ = (1)(0) + (0)(1) + 0·0 = 0, yet a̅ ≠ 0̅ and b̅ ≠ 0̅.
✔️ Hence converse is false.
🔵 Question 15:
If the vertices A, B, C of a triangle ABC are (1, 2, 3), (−1, 0, 0), (0, 1, 2) respectively, then find ∠ABC. [∠ABC is the angle between vectors B A̅ and B C̅.]
🟢 Answer:
➡️ B A̅ = A − B = (1 − (−1), 2 − 0, 3 − 0) = (2, 2, 3).
➡️ B C̅ = C − B = (0 − (−1), 1 − 0, 2 − 0) = (1, 1, 2).
➡️ Dot product: B A̅ · B C̅ = 2·1 + 2·1 + 3·2 = 10.
➡️ |B A̅| = √(2² + 2² + 3²) = √17.
➡️ |B C̅| = √(1² + 1² + 2²) = √6.
➡️ cos ∠ABC = (B A̅ · B C̅) / (|B A̅| |B C̅|) = 10 / (√17 · √6) = 10 / √102.
✔️ ∠ABC = cos⁻¹(10 / √102).
🔵 Question 16:
Show that the points A(1, 2, 7), B(2, 6, 3) and C(3, 10, −1) are collinear.
🟢 Answer:
➡️ Form AB̅ = B − A = (2 − 1, 6 − 2, 3 − 7) = (1, 4, −4).
➡️ Form BC̅ = C − B = (3 − 2, 10 − 6, −1 − 3) = (1, 4, −4).
➡️ Since AB̅ = BC̅ (exactly same direction and magnitude), B lies on the line AC.
✔️ Therefore A, B and C are collinear.
🔵 Question 17:
Show that the vectors 2 i − j + k, i − 3 j − 5 k and 3 i − 4 j − 4 k form the vertices of a right-angled triangle.
🟢 Answer:
➡️ Treat the three vectors as position vectors of points A, B, C respectively:
A(2, −1, 1), B(1, −3, −5), C(3, −4, −4).
➡️ Compute AC̅ = C − A = (3 − 2, −4 − (−1), −4 − 1) = (1, −3, −5).
➡️ Compute BC̅ = C − B = (3 − 1, −4 − (−3), −4 − (−5)) = (2, −1, 1).
➡️ Dot product: AC̅ · BC̅ = (1)(2) + (−3)(−1) + (−5)(1) = 2 + 3 − 5 = 0.
➡️ Hence AC̅ ⟂ BC̅ ⇒ CA̅ ⟂ CB̅ (same result since CA̅ = −AC̅, CB̅ = −BC̅).
✔️ The triangle with vertices at the three given points is right-angled at C.
🔵 Question 18:
If a̅ is a nonzero vector of magnitude ‘a’ and λ a nonzero scalar, then λ a̅ is a unit vector if
(A) λ = 1
(B) λ = −1
(C) a = |λ|
(D) a = 1/|λ|
🟢 Answer:
➡️ Condition for unit vector: |λ a̅| = 1.
➡️ |λ a̅| = |λ| |a̅| = |λ| a.
➡️ Set |λ| a = 1 ⇒ a = 1/|λ|.
✔️ Correct option: (D) a = 1/|λ|.
Exercise 10.4
🔵 Question 1:
Find |a̅ × b̅|, if a̅ = i − 7 j + 7 k and b̅ = 3 i − 2 j + 2 k.
🟢 Answer:
➡️ a̅ × b̅ = | i j k ; 1 −7 7 ; 3 −2 2 |.
➡️ i[(−7)(2) − 7(−2)] − j[1·2 − 7·3] + k[1(−2) − (−7)·3].
➡️ = i(−14 + 14) − j(2 − 21) + k(−2 + 21).
➡️ = 0 i + 19 j + 19 k.
➡️ |a̅ × b̅| = √(0² + 19² + 19²) = √(361 + 361) = 19√2.
✔️ Final: |a̅ × b̅| = 19√2.
🔵 Question 2:
Find a unit vector perpendicular to each of the vectors a̅ + b̅ and a̅ − b̅, where a̅ = 3 i + 2 j + 2 k and b̅ = i + 2 j − 2 k.
🟢 Answer:
➡️ a̅ + b̅ = (3 + 1, 2 + 2, 2 + (−2)) = (4, 4, 0).
➡️ a̅ − b̅ = (3 − 1, 2 − 2, 2 − (−2)) = (2, 0, 4).
➡️ (a̅ + b̅) × (a̅ − b̅) = | i j k ; 4 4 0 ; 2 0 4 |.
➡️ = i(4·4 − 0·0) − j(4·4 − 0·2) + k(4·0 − 4·2).
➡️ = 16 i − 16 j − 8 k = 8(2, −2, −1).
➡️ A unit vector along this is û = (2, −2, −1)/√(4 + 4 + 1) = (2, −2, −1)/3.
✔️ One required unit vector: (2/3) i − (2/3) j − (1/3) k (its negative is also valid).
🔵 Question 3:
If a unit vector a̅ makes angles π/3 with î, π/4 with ĵ and an acute angle θ with k̂, then find θ and hence the components of a̅.
🟢 Answer:
➡️ Direction cosines: l = cos(π/3) = 1/2, m = cos(π/4) = √2/2, n = cos θ (> 0).
➡️ For a unit vector: l² + m² + n² = 1.
➡️ (1/2)² + (√2/2)² + n² = 1 ⇒ 1/4 + 1/2 + n² = 1.
➡️ n² = 1 − 3/4 = 1/4 ⇒ n = 1/2 (acute).
➡️ cos θ = 1/2 ⇒ θ = π/3.
✔️ Components: a̅ = (1/2) i + (√2/2) j + (1/2) k.
🔵 Question 4:
Show that (a̅ − b̅) × (a̅ + b̅) = 2(a̅ × b̅).
🟢 Answer:
➡️ Expand using bilinearity of ×:
➡️ (a̅ − b̅) × (a̅ + b̅) = a̅ × a̅ + a̅ × b̅ − b̅ × a̅ − b̅ × b̅.
➡️ But a̅ × a̅ = 0̅ and b̅ × b̅ = 0̅, and b̅ × a̅ = − (a̅ × b̅).
➡️ So expression = a̅ × b̅ − (− a̅ × b̅) = 2(a̅ × b̅).
✔️ Hence proved.
🔵 Question 5:
Find λ and μ if (2 i + 6 j + 27 k) × (i + λ j + μ k) = 0̅.
🟢 Answer:
➡️ Cross product zero ⇒ vectors are parallel ⇒ (1, λ, μ) is proportional to (2, 6, 27).
➡️ Set ratios equal: 1/2 = λ/6 = μ/27.
➡️ From 1/2 = λ/6 ⇒ λ = 3.
➡️ From 1/2 = μ/27 ⇒ μ = 27/2.
✔️ Final: λ = 3, μ = 27/2.
🔵 Question 6:
Given that a̅ · b̅ = 0 and a̅ × b̅ = 0̅. What can you conclude about the vectors a̅ and b̅?
🟢 Answer:
➡️ a̅ × b̅ = 0̅ ⇒ a̅ and b̅ are parallel or one of them is the zero vector.
➡️ a̅ · b̅ = 0 ⇒ a̅ and b̅ are perpendicular.
➡️ A nonzero pair cannot be both parallel and perpendicular simultaneously.
✔️ Conclusion: At least one of a̅ or b̅ must be 0̅ (possibly both). There is no nonzero pair satisfying both conditions.
🔵 Question 7:
Let a̅ = a₁ i + a₂ j + a₃ k, b̅ = b₁ i + b₂ j + b₃ k and c̅ = c₁ i + c₂ j + c₃ k. Show that
a̅ × (b̅ + c̅) = a̅ × b̅ + a̅ × c̅.
🟢 Answer:
➡️ Write b̅ + c̅ = (b₁ + c₁) i + (b₂ + c₂) j + (b₃ + c₃) k.
➡️ Compute a̅ × (b̅ + c̅) by the determinant rule:
| i j k |
| a₁ a₂ a₃ |
| b₁+c₁ b₂+c₂ b₃+c₃ |
➡️ Expanding along the third row splits naturally into two determinants:
| i j k ; a₁ a₂ a₃ ; b₁ b₂ b₃ | + | i j k ; a₁ a₂ a₃ ; c₁ c₂ c₃ |.
➡️ These are precisely a̅ × b̅ and a̅ × c̅.
✔️ Hence a̅ × (b̅ + c̅) = a̅ × b̅ + a̅ × c̅ (distributive law).
🔵 Question 8:
If either a̅ = 0̅ or b̅ = 0̅, then a̅ × b̅ = 0̅. Is the converse true? Justify with an example.
🟢 Answer:
➡️ If any factor is 0̅, cross product is 0̅ (true).
➡️ Converse claim: “a̅ × b̅ = 0̅ ⇒ either a̅ = 0̅ or b̅ = 0̅” is false.
✳️ Counterexample (both nonzero but parallel): a̅ = i, b̅ = 2 i.
➡️ a̅ × b̅ = i × 2 i = 2 (i × i) = 2·0̅ = 0̅, yet a̅ ≠ 0̅ and b̅ ≠ 0̅.
✔️ Therefore the converse is not true; zero cross product can also mean the vectors are parallel (nonzero).
🔵 Question 9:
Find the area of the triangle with vertices A(1, 1, 2), B(2, 3, 5) and C(1, 5, 5).
🟢 Answer:
➡️ AB̅ = B − A = (2 − 1, 3 − 1, 5 − 2) = (1, 2, 3).
➡️ AC̅ = C − A = (1 − 1, 5 − 1, 5 − 2) = (0, 4, 3).
➡️ AB̅ × AC̅ = | i j k ; 1 2 3 ; 0 4 3 |.
➡️ = i(2·3 − 3·4) − j(1·3 − 3·0) + k(1·4 − 2·0).
➡️ = i(6 − 12) − j(3 − 0) + k(4 − 0) = (−6) i − 3 j + 4 k.
➡️ |AB̅ × AC̅| = √( (−6)² + (−3)² + 4² ) = √(36 + 9 + 16) = √61.
➡️ Area of triangle = (1/2) |AB̅ × AC̅| = (1/2) √61.
✔️ Final area = (√61)/2 (square units).
Question 10
Find the area of the parallelogram whose adjacent sides are determined by the vectors a̅ = i − j + 3k and b̅ = 2i − 7j + k.
Answer
➡️ Area = |a̅ × b̅|.
➡️ a̅ × b̅ = | i j k ; 1 −1 3 ; 2 −7 1 |.
➡️ = i[ (−1)(1) − 3(−7) ] − j[ 1·1 − 3·2 ] + k[ 1(−7) − (−1)·2 ].
➡️ = i(−1 + 21) − j(1 − 6) + k(−7 + 2).
➡️ = 20i + 5j − 5k.
➡️ |a̅ × b̅| = √(20² + 5² + (−5)²) = √(400 + 25 + 25) = √450 = 15√2.
✔️ Area = 15√2 (square units).
Question 11
Let the vectors a̅ and b̅ be such that |a̅| = 3 and |b̅| = √2/3. Then a̅ × b̅ is a unit vector if the angle between a̅ and b̅ is
(A) π/6 (B) π/4 (C) π/3 (D) π/2
Answer
➡️ |a̅ × b̅| = |a̅||b̅| sinθ.
➡️ 1 = 3 × (√2/3) × sinθ = √2 sinθ.
➡️ sinθ = 1/√2 ⇒ θ = π/4.
✔️ Correct option: (B) π/4.
Question 12
Area of a rectangle having vertices A, B, C and D with position vectors
A = −i + (1/2)j + 4k, B = i + (1/2)j + 4k, C = i − (1/2)j + 4k, D = −i − (1/2)j + 4k is
(A) 1/2 (B) 1 (C) 2 (D) 4
Answer
➡️ Take adjacent sides from A:
➡️ AB̅ = B − A = (1 − (−1), 1/2 − 1/2, 4 − 4) = (2, 0, 0).
➡️ AD̅ = D − A = (−1 − (−1), −1/2 − 1/2, 4 − 4) = (0, −1, 0).
➡️ Area of rectangle = |AB̅ × AD̅|.
➡️ AB̅ × AD̅ = | i j k ; 2 0 0 ; 0 −1 0 | = (0, 0, −2).
➡️ |AB̅ × AD̅| = √(0² + 0² + (−2)²) = 2.
✔️ Correct option: (C) 2.
————————————————————————————————————————————————————————————————————————————
OTHER IMPORTANT QUESTIONS FOR EXAMS
🟦 Section A – Multiple Choice Questions (1 mark each)
🔵 Question 1:
The position vector of a point P is 3î + 4ĵ + 12k̂. Its magnitude is:
🟢 (A) 5
🟠 (B) 12
🔴 (C) 13
🟡 (D) √169
Answer: (C) 13
🔵 Question 2:
If a̅ = 2î − ĵ + k̂ and b̅ = 3î + 4ĵ − 2k̂, then a̅ + b̅ = ?
🟢 (A) 5î + 3ĵ − k̂
🟠 (B) 5î − 3ĵ + 3k̂
🔴 (C) 5î + 3ĵ + 3k̂
🟡 (D) 5î − 3ĵ − k̂
Answer: (A) 5î + 3ĵ − k̂
🔵 Question 3:
The dot product of perpendicular vectors is:
🟢 (A) 1
🟠 (B) 0
🔴 (C) -1
🟡 (D) ∞
Answer: (B) 0
🔵 Question 4:
The cross product of parallel vectors is:
🟢 (A) Zero vector
🟠 (B) Unit vector
🔴 (C) Infinite
🟡 (D) Undefined
Answer: (A) Zero vector
🔵 Question 5:
If |a̅| = 3, |b̅| = 4, and angle between them = 90°, then |a̅ + b̅| = ?
🟢 (A) 5
🟠 (B) 7
🔴 (C) √7
🟡 (D) 12
Answer: (A) 5
🔵 Question 6:
The scalar component of a̅ = 2î + 3ĵ + 6k̂ along b̅ = î + 2ĵ + 2k̂ is:
🟢 (A) 8
🟠 (B) 7
🔴 (C) 6
🟡 (D) 5
Answer: (C) 6
🔵 Question 7:
If a̅ ⋅ b̅ = 0, then vectors are:
🟢 (A) Parallel
🟠 (B) Perpendicular
🔴 (C) Equal
🟡 (D) Collinear
Answer: (B) Perpendicular
🔵 Question 8:
The magnitude of î + ĵ + k̂ is:
🟢 (A) 1
🟠 (B) √2
🔴 (C) √3
🟡 (D) 3
Answer: (C) √3
🔵 Question 9:
If a̅ = î + 2ĵ, then unit vector along a̅ is:
🟢 (A) (1/√5)(î + 2ĵ)
🟠 (B) (1/3)(î + 2ĵ)
🔴 (C) (1/2)(î + 2ĵ)
🟡 (D) (1/5)(î + 2ĵ)
Answer: (A) (1/√5)(î + 2ĵ)
🔵 Question 10:
If a̅ × b̅ = 0, then:
🟢 (A) a̅ ∥ b̅
🟠 (B) a̅ ⟂ b̅
🔴 (C) a̅ = 0
🟡 (D) None
Answer: (A) a̅ ∥ b̅
🔵 Question 11:
The angle between a̅ = î and b̅ = ĵ is:
🟢 (A) 0°
🟠 (B) 30°
🔴 (C) 60°
🟡 (D) 90°
Answer: (D) 90°
🔵 Question 12:
If |a̅| = 2, |b̅| = 3, and angle = 60°, then a̅ ⋅ b̅ = ?
🟢 (A) 3
🟠 (B) 4
🔴 (C) 2
🟡 (D) 5
Answer: (A) 3
🔵 Question 13:
The area of parallelogram formed by a̅ and b̅ is:
🟢 (A) |a̅ ⋅ b̅|
🟠 (B) |a̅ × b̅|
🔴 (C) |a̅ + b̅|
🟡 (D) |a̅ − b̅|
Answer: (B) |a̅ × b̅|
🔵 Question 14:
If a̅ = 2î + 3ĵ and b̅ = î − ĵ, then a̅ ⋅ b̅ = ?
🟢 (A) −1
🟠 (B) 0
🔴 (C) 2
🟡 (D) 5
Answer: (A) −1
🔵 Question 15:
a̅ ⋅ (b̅ × c̅) represents:
🟢 (A) Area
🟠 (B) Volume
🔴 (C) Length
🟡 (D) None
Answer: (B) Volume
🔵 Question 16:
If a̅ = î + ĵ, b̅ = ĵ + k̂, then a̅ × b̅ = ?
🟢 (A) î − ĵ
🟠 (B) î − k̂
🔴 (C) î + k̂
🟡 (D) ĵ − k̂
Answer: (B) î − k̂
🔵 Question 17:
The value of [î ĵ k̂; 1 2 3; 3 2 1] is:
🟢 (A) 0
🟠 (B) −8
🔴 (C) 8
🟡 (D) 4
Answer: (B) −8
🔵 Question 18:
If a̅, b̅, c̅ are coplanar, then [a̅ b̅ c̅] = ?
🟢 (A) 0
🟠 (B) 1
🔴 (C) ∞
🟡 (D) −1
Answer: (A) 0
🟩 Section B – Short Answer Questions (2–3 Marks Each)
🔵 Question 19:
Find the magnitude and direction cosines of the vector a̅ = 2î + 3ĵ + 6k̂.
🟢 Answer:
➡️ Magnitude = √(2² + 3² + 6²) = √49 = 7
➡️ Direction cosines:
l = 2/7, m = 3/7, n = 6/7
✅ Final: Magnitude = 7; Direction cosines = (2/7, 3/7, 6/7)
🔵 Question 20:
If a̅ = 2î − ĵ + k̂ and b̅ = î + ĵ − 2k̂, find a̅ ⋅ b̅ and angle between them.
🟢 Answer:
➡️ a̅ ⋅ b̅ = (2)(1) + (−1)(1) + (1)(−2) = 2 − 1 − 2 = −1
➡️ |a̅| = √(2² + (−1)² + 1²) = √6
➡️ |b̅| = √(1² + 1² + (−2)²) = √6
➡️ cosθ = (a̅ ⋅ b̅) / (|a̅||b̅|) = (−1)/6
➡️ θ = cos⁻¹(−1/6)
✅ Final: a̅ ⋅ b̅ = −1; Angle = cos⁻¹(−1/6)
🔵 Question 21:
Find a unit vector perpendicular to both a̅ = 2î − ĵ + 3k̂ and b̅ = î + 2ĵ + k̂.
🟢 Answer:
➡️ a̅ × b̅ = | î ĵ k̂ |
| 2 −1 3 |
| 1 2 1 |
= î(−1 − 6) − ĵ(2 − 3) + k̂(4 + 1)
= −7î + ĵ + 5k̂
➡️ Magnitude = √(49 + 1 + 25) = √75 = 5√3
➡️ Unit vector = (1/5√3)(−7î + ĵ + 5k̂)
✅ Final: (−7î + ĵ + 5k̂) / (5√3)
🔵 Question 22:
Find projection of a̅ = 3î + 4ĵ on b̅ = 5î + 12ĵ.
🟢 Answer:
➡️ a̅ ⋅ b̅ = (3)(5) + (4)(12) = 15 + 48 = 63
➡️ |b̅| = √(5² + 12²) = √169 = 13
➡️ Projection = (a̅ ⋅ b̅) / |b̅| = 63 / 13
✅ Final: Projection = 63/13
🔵 Question 23:
If a̅ = 2î − 2ĵ + k̂ and b̅ = î + 2ĵ − 2k̂, find |a̅ × b̅|.
🟢 Answer:
➡️ a̅ × b̅ = | î ĵ k̂ |
| 2 −2 1 |
| 1 2 −2 |
= î(4 − 2) − ĵ(−4 − 1) + k̂(4 + 2)
= 2î + 5ĵ + 6k̂
➡️ |a̅ × b̅| = √(2² + 5² + 6²) = √65
✅ Final: √65
🔵 Question 24:
Find the area of parallelogram whose adjacent sides are a̅ = î + 2ĵ + 3k̂, b̅ = 3î + ĵ + 2k̂.
🟢 Answer:
➡️ a̅ × b̅ = | î ĵ k̂ |
| 1 2 3 |
| 3 1 2 |
= î(4 − 3) − ĵ(2 − 9) + k̂(1 − 6)
= î + 7ĵ − 5k̂
➡️ |a̅ × b̅| = √(1² + 7² + (−5)²) = √75 = 5√3
✅ Area = 5√3
🔵 Question 25:
Find the volume of parallelepiped formed by a̅ = î + 2ĵ + 3k̂, b̅ = 2î + 3ĵ + k̂, c̅ = 3î + ĵ + 2k̂.
🟢 Answer:
➡️ [a̅ b̅ c̅] = | 1 2 3 |
| 2 3 1 |
| 3 1 2 |
= 1(6 − 1) − 2(4 − 3) + 3(2 − 9)
= 5 − 2 − 21 = −18
➡️ Volume = |[a̅ b̅ c̅]| = 18
✅ Final: Volume = 18 units³
🔵 Question 26:
Find the vector equation of a line passing through (1, 2, 3) and parallel to vector 2î + 3ĵ + k̂.
🟢 Answer:
➡️ Position vector a̅ = î + 2ĵ + 3k̂
➡️ Direction vector b̅ = 2î + 3ĵ + k̂
✅ Equation: r̅ = (î + 2ĵ + 3k̂) + λ(2î + 3ĵ + k̂)
🔵 Question 27:
Find the vector equation of a plane passing through (2, −1, 3) and perpendicular to vector 3î + 2ĵ − 2k̂.
🟢 Answer:
➡️ Position vector a̅ = 2î − ĵ + 3k̂
➡️ Normal vector n̅ = 3î + 2ĵ − 2k̂
✅ Equation: (r̅ − (2î − ĵ + 3k̂)) ⋅ (3î + 2ĵ − 2k̂) = 0
➡️ Or 3(x − 2) + 2(y + 1) − 2(z − 3) = 0
➡️ 3x + 2y − 2z + 4 = 0
🟥 Section C/D – Long Answer / Application Questions (4–5 Marks Each)
🔵 Question 28:
Find the angle between the vectors a̅ = î + 2ĵ + 2k̂ and b̅ = 2î + 3ĵ + 4k̂.
🟢 Answer:
➡️ Formula: cosθ = (a̅ ⋅ b̅) / (|a̅||b̅|)
➡️ a̅ ⋅ b̅ = (1)(2) + (2)(3) + (2)(4) = 2 + 6 + 8 = 16
➡️ |a̅| = √(1² + 2² + 2²) = √9 = 3
➡️ |b̅| = √(2² + 3² + 4²) = √29
➡️ cosθ = 16 / (3√29)
➡️ θ = cos⁻¹(16 / 3√29)
✅ Final: θ = cos⁻¹(16 / 3√29)
🔵 Question 29:
Prove that (a̅ + b̅) ⋅ (a̅ − b̅) = |a̅|² − |b̅|².
🟢 Answer:
➡️ LHS = (a̅ + b̅) ⋅ (a̅ − b̅)
➡️ Expand using distributive law:
= a̅⋅a̅ − a̅⋅b̅ + b̅⋅a̅ − b̅⋅b̅
➡️ Since a̅⋅b̅ = b̅⋅a̅, middle terms cancel:
= a̅⋅a̅ − b̅⋅b̅
➡️ a̅⋅a̅ = |a̅|², b̅⋅b̅ = |b̅|²
➡️ Hence LHS = |a̅|² − |b̅|²
✅ Proved.
🔵 Question 30:
Find the area of a triangle whose vertices are A(1, 2, 3), B(2, 3, 5), and C(3, 4, 7).
🟢 Answer:
➡️ AB̅ = (2−1)î + (3−2)ĵ + (5−3)k̂ = î + ĵ + 2k̂
➡️ AC̅ = (3−1)î + (4−2)ĵ + (7−3)k̂ = 2î + 2ĵ + 4k̂
➡️ AB̅ × AC̅ = | î ĵ k̂ |
| 1 1 2 |
| 2 2 4 |
= î(4 − 4) − ĵ(4 − 4) + k̂(2 − 2) = 0̅
➡️ Since cross product is zero,
✅ Area = (1/2)|AB̅ × AC̅| = 0
🔴 Conclusion: Points are collinear.
🔵 Question 31:
Find the vector equation of the line passing through points A(1, 2, 3) and B(3, 4, −1).
🟢 Answer:
➡️ Position vector a̅ = î + 2ĵ + 3k̂
➡️ Direction vector b̅ = B − A = (3−1)î + (4−2)ĵ + (−1−3)k̂ = 2î + 2ĵ − 4k̂
✅ Equation: r̅ = (î + 2ĵ + 3k̂) + λ(2î + 2ĵ − 4k̂), λ ∈ ℝ
🔵 Question 32:
Find the vector equation of a plane passing through point A(2, −1, 3) and containing vectors b̅ = 2î − ĵ + k̂, c̅ = 3î + 2ĵ − 2k̂.
🟢 Answer:
➡️ Normal vector n̅ = b̅ × c̅
= | î ĵ k̂ |
| 2 −1 1 |
| 3 2 −2 |
= î((−1)(−2) − (1)(2)) − ĵ(2(−2) − 1(3)) + k̂(2(2) − (−1)(3))
= î(2 − 2) − ĵ(−4 − 3) + k̂(4 + 3)
= 0î + 7ĵ + 7k̂
➡️ Equation: (r̅ − (2î − ĵ + 3k̂)) ⋅ (7ĵ + 7k̂) = 0
➡️ Simplify: 7(y + 1) + 7(z − 3) = 0
✅ Final: y + z − 2 = 0
🔵 Question 33:
Find the volume of parallelepiped whose coterminous edges are
a̅ = î + 2ĵ + 3k̂, b̅ = 2î + 3ĵ + k̂, c̅ = 3î + ĵ + 2k̂.
🟢 Answer:
➡️ [a̅ b̅ c̅] = | 1 2 3 |
| 2 3 1 |
| 3 1 2 |
= 1(6 − 1) − 2(4 − 3) + 3(2 − 9)
= 5 − 2 − 21 = −18
➡️ Volume = |[a̅ b̅ c̅]| = 18 units³
✅ Final: Volume = 18 units³
————————————————————————————————————————————————————————————————————————————
JEE MAINS QUESTIONS FROM THIS LESSON
🔵 Question 1:
If a = 2i + 3j – k and b = i – 2j + 2k, then a • b equals
🟥 1️⃣ 2
🟩 2️⃣ 3
🟨 3️⃣ -2
🟦 4️⃣ 0
🟡 Answer: 3️⃣ -2
📘 (JEE Main 2024 | Shift 2)
🔵 Question 2:
If |a| = 3, |b| = 4, and the angle between them is 60°, then a • b equals
🟥 1️⃣ 6
🟩 2️⃣ 8
🟨 3️⃣ 12
🟦 4️⃣ 9
🟡 Answer: 3️⃣ 12
💡 Hint: a•b = |a||b|cosθ
📘 (JEE Main 2024 | Shift 1)
🔵 Question 3:
If a = i + j + k, b = 2i – j + 2k, then |a × b| equals
🟥 1️⃣ √27
🟩 2️⃣ √26
🟨 3️⃣ 3√3
🟦 4️⃣ 6
🟡 Answer: 3️⃣ 3√3
📘 (JEE Main 2023 | Shift 2)
🔵 Question 4:
If a • b = 0, then vectors a and b are
🟥 1️⃣ Parallel
🟩 2️⃣ Perpendicular
🟨 3️⃣ Equal
🟦 4️⃣ None
🟡 Answer: 2️⃣ Perpendicular
📘 (JEE Main 2023 | Shift 1)
🔵 Question 5:
If a = i + 2j + 3k and b = 4i + 5j + 6k, then a × b equals
🟥 1️⃣ -3i + 6j – 3k
🟩 2️⃣ 3i – 6j + 3k
🟨 3️⃣ -3i – 6j + 3k
🟦 4️⃣ 3i + 6j – 3k
🟡 Answer: 2️⃣ 3i – 6j + 3k
📘 (JEE Main 2022 | Shift 2)
🔵 Question 6:
If a and b are non-zero vectors such that a × b = 0, then
🟥 1️⃣ a and b are parallel
🟩 2️⃣ a and b are perpendicular
🟨 3️⃣ a and b are equal
🟦 4️⃣ None
🟡 Answer: 1️⃣ a and b are parallel
📘 (JEE Main 2022 | Shift 1)
🔵 Question 7:
If a = 2i + j and b = i + 2j, then projection of a on b is
🟥 1️⃣ 4/√5
🟩 2️⃣ 6/5
🟨 3️⃣ 3/√5
🟦 4️⃣ 2
🟡 Answer: 2️⃣ 6/5
📘 (JEE Main 2021 | March)
🔵 Question 8:
If a = i – 2j + 2k, b = 2i + j + 3k, then a × b • (i + j + k) equals
🟥 1️⃣ 0
🟩 2️⃣ 6
🟨 3️⃣ 3
🟦 4️⃣ -6
🟡 Answer: 2️⃣ 6
📘 (JEE Main 2021 | February)
🔵 Question 9:
If vectors a and b satisfy |a| = 2, |b| = 3, and a • b = 0, then |a + b| equals
🟥 1️⃣ 5
🟩 2️⃣ √13
🟨 3️⃣ √10
🟦 4️⃣ 1
🟡 Answer: 2️⃣ √13
💡 Hint: |a + b|² = |a|² + |b|² + 2a•b
📘 (JEE Main 2020 | January)
🔵 Question 10:
If a = 3i – j + 2k and b = i + 2j – 2k, then angle between a and b is
🟥 1️⃣ 90°
🟩 2️⃣ 60°
🟨 3️⃣ 120°
🟦 4️⃣ 45°
🟡 Answer: 1️⃣ 90°
💡 Hint: Check a•b = 0
📘 (JEE Main 2020 | September)
🔵 Question 11:
If a = i + j + k, b = 2i + 3j + 4k, c = i – j + k, then a • (b × c) equals
🟥 1️⃣ 0
🟩 2️⃣ 2
🟨 3️⃣ 3
🟦 4️⃣ 4
🟡 Answer: 3️⃣ 3
📘 (JEE Main 2019 | April)
🔵 Question 12:
If |a| = |b| = 1 and a • b = 1/2, then |a – b| equals
🟥 1️⃣ 1
🟩 2️⃣ √3
🟨 3️⃣ √2
🟦 4️⃣ 2
🟡 Answer: 2️⃣ √3
📘 (JEE Main 2019 | January)
🔵 Question 13:
If a, b, c are mutually perpendicular unit vectors, then |a + b + c| equals
🟥 1️⃣ √3
🟩 2️⃣ 3
🟨 3️⃣ 1
🟦 4️⃣ 2
🟡 Answer: 1️⃣ √3
📘 (JEE Main 2018)
🔵 Question 14:
If a = 2i – 3j + 4k, b = i + j – k, then scalar triple product [a b (a × b)] equals
🟥 1️⃣ 0
🟩 2️⃣ 2
🟨 3️⃣ 4
🟦 4️⃣ 6
🟡 Answer: 1️⃣ 0
💡 Hint: a • (a × b) = 0
📘 (JEE Main 2018)
🔵 Question 15:
If a and b are two unit vectors and angle between them is 120°, then |a + b| equals
🟥 1️⃣ 1
🟩 2️⃣ √3
🟨 3️⃣ √2
🟦 4️⃣ 0
🟡 Answer: 1️⃣ 1
📘 (JEE Main 2017)
🔵 Question 16:
If a = i + 2j + 2k and b = 2i – j + 2k, then projection of a on b is
🟥 1️⃣ 2
🟩 2️⃣ 3
🟨 3️⃣ 4
🟦 4️⃣ 1
🟡 Answer: 2️⃣ 3
📘 (JEE Main 2017)
🔵 Question 17:
If a = i + 2j + 2k and b = 2i + j + k, then angle between a and b is
🟥 1️⃣ 45°
🟩 2️⃣ 60°
🟨 3️⃣ 90°
🟦 4️⃣ 30°
🟡 Answer: 2️⃣ 60°
📘 (JEE Main 2016)
🔵 Question 18:
If a = i + j, b = i – j, then a × b equals
🟥 1️⃣ 2k
🟩 2️⃣ -2k
🟨 3️⃣ 0
🟦 4️⃣ i
🟡 Answer: 1️⃣ 2k
📘 (JEE Main 2016)
🔵 Question 19:
If a = 2i + 3j + 4k and b = 3i + 4j + 2k, then a • b equals
🟥 1️⃣ 25
🟩 2️⃣ 28
🟨 3️⃣ 32
🟦 4️⃣ 30
🟡 Answer: 4️⃣ 30
📘 (JEE Main 2015)
🔵 Question 20:
If |a| = 3, |b| = 4, and a ⊥ b, then |a + b| equals
🟥 1️⃣ 5
🟩 2️⃣ √7
🟨 3️⃣ √25
🟦 4️⃣ 7
🟡 Answer: 1️⃣ 5
💡 Hint: |a + b|² = |a|² + |b|²
📘 (JEE Main 2015)
🔵 Question 21:
If a = 2i + j + k and b = i – j + 2k, then |a × b| equals
🟥 1️⃣ √30
🟩 2️⃣ √35
🟨 3️⃣ √40
🟦 4️⃣ √50
🟡 Answer: 2️⃣ √35
📘 (JEE Main 2024 | Shift 2)
🔵 Question 22:
If a = 3i – 2j + k, b = 2i + j – 3k, then angle between a and b is
🟥 1️⃣ 90°
🟩 2️⃣ 60°
🟨 3️⃣ 120°
🟦 4️⃣ 45°
🟡 Answer: 3️⃣ 120°
📘 (JEE Main 2024 | Shift 1)
🔵 Question 23:
If a = i + 2j – 2k, b = 2i – j + 3k, then scalar triple product [a b (a × b)] is
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ 2
🟦 4️⃣ 3
🟡 Answer: 1️⃣ 0
💡 Hint: a • (a × b) = 0
📘 (JEE Main 2023 | Shift 2)
🔵 Question 24:
If a = i + 2j + 3k, b = 3i + 2j + k, then a • b equals
🟥 1️⃣ 10
🟩 2️⃣ 12
🟨 3️⃣ 14
🟦 4️⃣ 16
🟡 Answer: 3️⃣ 14
📘 (JEE Main 2023 | Shift 1)
🔵 Question 25:
If vectors a and b satisfy a • b = 0, |a| = 2, |b| = 3, then |a + b| equals
🟥 1️⃣ √13
🟩 2️⃣ 5
🟨 3️⃣ √10
🟦 4️⃣ 1
🟡 Answer: 1️⃣ √13
📘 (JEE Main 2022 | Shift 2)
🔵 Question 26:
If a and b are unit vectors and angle between them is 60°, then |a – b| equals
🟥 1️⃣ 1
🟩 2️⃣ √3
🟨 3️⃣ 2
🟦 4️⃣ √2
🟡 Answer: 2️⃣ √3
📘 (JEE Main 2022 | Shift 1)
🔵 Question 27:
If a = 2i + j – k and b = i + 2j + k, then a × b equals
🟥 1️⃣ 3i – 3j + 3k
🟩 2️⃣ i + j – k
🟨 3️⃣ -3i + 3j – 3k
🟦 4️⃣ 2i – j + 3k
🟡 Answer: 1️⃣ 3i – 3j + 3k
📘 (JEE Main 2021 | March)
🔵 Question 28:
If a = i + 2j + 3k and b = 2i + 3j + 4k, then the projection of a on b is
🟥 1️⃣ 3
🟩 2️⃣ 5
🟨 3️⃣ 6
🟦 4️⃣ 4
🟡 Answer: 4️⃣ 4
📘 (JEE Main 2021 | February)
🔵 Question 29:
If |a| = |b| = 1 and angle between them is 90°, then |a + b| equals
🟥 1️⃣ 1
🟩 2️⃣ √2
🟨 3️⃣ 2
🟦 4️⃣ 0
🟡 Answer: 2️⃣ √2
📘 (JEE Main 2020)
🔵 Question 30:
If a = i + j, b = j + k, c = k + i, then a • (b × c) equals
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ 2
🟦 4️⃣ 3
🟡 Answer: 4️⃣ 3
📘 (JEE Main 2020)
🔵 Question 31:
If a = i + 2j, b = 2i + j, then |a + b| equals
🟥 1️⃣ √10
🟩 2️⃣ √13
🟨 3️⃣ 3
🟦 4️⃣ 4
🟡 Answer: 1️⃣ √10
📘 (JEE Main 2019)
🔵 Question 32:
If a = i – j, b = j – k, then angle between a and b is
🟥 1️⃣ 60°
🟩 2️⃣ 90°
🟨 3️⃣ 45°
🟦 4️⃣ 120°
🟡 Answer: 2️⃣ 90°
📘 (JEE Main 2019)
🔵 Question 33:
If |a| = 3, |b| = 4, and a ⊥ b, then |a × b| equals
🟥 1️⃣ 7
🟩 2️⃣ 12
🟨 3️⃣ 5
🟦 4️⃣ 0
🟡 Answer: 2️⃣ 12
📘 (JEE Main 2018)
🔵 Question 34:
If a = i + 2j + 2k and b = 2i + j + 2k, then |a – b| equals
🟥 1️⃣ 1
🟩 2️⃣ √2
🟨 3️⃣ √3
🟦 4️⃣ 2
🟡 Answer: 3️⃣ √3
📘 (JEE Main 2018)
🔵 Question 35:
If a = 2i + 3j, b = i + 2j, then a • b equals
🟥 1️⃣ 7
🟩 2️⃣ 8
🟨 3️⃣ 6
🟦 4️⃣ 9
🟡 Answer: 2️⃣ 8
📘 (JEE Main 2017)
🔵 Question 36:
If a = i + j, b = i – j, then |a × b| equals
🟥 1️⃣ 2
🟩 2️⃣ 1
🟨 3️⃣ 0
🟦 4️⃣ √2
🟡 Answer: 1️⃣ 2
📘 (JEE Main 2017)
🔵 Question 37:
If a = i + 2j + 2k and b = 2i + j + 2k, then a • b equals
🟥 1️⃣ 6
🟩 2️⃣ 8
🟨 3️⃣ 10
🟦 4️⃣ 12
🟡 Answer: 3️⃣ 10
📘 (JEE Main 2016)
🔵 Question 38:
If |a| = 2, |b| = 3, and angle between a and b is 90°, then |a + b| equals
🟥 1️⃣ √13
🟩 2️⃣ 5
🟨 3️⃣ 1
🟦 4️⃣ 2
🟡 Answer: 1️⃣ √13
📘 (JEE Main 2016)
🔵 Question 39:
If a = i + 2j + 3k, b = 2i + 3j + 4k, then angle between a and b is
🟥 1️⃣ 0°
🟩 2️⃣ 45°
🟨 3️⃣ 90°
🟦 4️⃣ 60°
🟡 Answer: 4️⃣ 60°
📘 (JEE Main 2015)
🔵 Question 40:
If a = i + j + k, b = 2i + 2j + 2k, then a and b are
🟥 1️⃣ Parallel
🟩 2️⃣ Perpendicular
🟨 3️⃣ Equal
🟦 4️⃣ None
🟡 Answer: 1️⃣ Parallel
📘 (JEE Main 2015)
🔵 Question 41:
If a = i + 2j, b = 2i + 4j, then a and b are
🟥 1️⃣ Parallel
🟩 2️⃣ Perpendicular
🟨 3️⃣ Equal
🟦 4️⃣ None
🟡 Answer: 1️⃣ Parallel
📘 (AIEEE 2012)
🔵 Question 42:
If a = i + j, b = j + k, then |a × b| equals
🟥 1️⃣ 1
🟩 2️⃣ √2
🟨 3️⃣ √3
🟦 4️⃣ 2
🟡 Answer: 3️⃣ √3
📘 (AIEEE 2012)
🔵 Question 43:
If |a| = |b| = 1 and a • b = 1/2, then angle between them is
🟥 1️⃣ 30°
🟩 2️⃣ 45°
🟨 3️⃣ 60°
🟦 4️⃣ 90°
🟡 Answer: 3️⃣ 60°
📘 (AIEEE 2011)
🔵 Question 44:
If a = i + 2j, b = 2i – j, then a • b equals
🟥 1️⃣ 0
🟩 2️⃣ 2
🟨 3️⃣ 4
🟦 4️⃣ 3
🟡 Answer: 4️⃣ 3
📘 (AIEEE 2011)
🔵 Question 45:
If a and b are perpendicular unit vectors, then |a + b| equals
🟥 1️⃣ 1
🟩 2️⃣ √2
🟨 3️⃣ 2
🟦 4️⃣ 0
🟡 Answer: 2️⃣ √2
📘 (AIEEE 2010)
🔵 Question 46:
If a = i + j + k, b = i – j, then a • b equals
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ 2
🟦 4️⃣ -1
🟡 Answer: 4️⃣ -1
📘 (AIEEE 2009)
🔵 Question 47:
If a = i + j + k and b = 2i + j – 3k, then |a × b| equals
🟥 1️⃣ √35
🟩 2️⃣ √36
🟨 3️⃣ √37
🟦 4️⃣ 6
🟡 Answer: 4️⃣ 6
📘 (AIEEE 2008)
🔵 Question 48:
If |a| = 2, |b| = 2, and a • b = 2, then |a – b| equals
🟥 1️⃣ 2
🟩 2️⃣ √2
🟨 3️⃣ √3
🟦 4️⃣ √6
🟡 Answer: 1️⃣ 2
📘 (AIEEE 2007)
🔵 Question 49:
If a = i + 2j + 3k, b = 3i + 2j + k, then a • b equals
🟥 1️⃣ 10
🟩 2️⃣ 12
🟨 3️⃣ 14
🟦 4️⃣ 16
🟡 Answer: 3️⃣ 14
📘 (AIEEE 2006)
🔵 Question 50:
If |a| = 3, |b| = 4, and angle between them is 90°, then |a × b| equals
🟥 1️⃣ 7
🟩 2️⃣ 12
🟨 3️⃣ 5
🟦 4️⃣ 0
🟡 Answer: 2️⃣ 12
📘 (AIEEE 2005)
————————————————————————————————————————————————————————————————————————————
JEE ADVANCED QUESTIONS FROM THIS LESSON
🔵 Question 1:
If a = i + 2j + 2k and b = 2i + j + 2k, then the angle between a and b is
🟥 1️⃣ 0°
🟩 2️⃣ 45°
🟨 3️⃣ 60°
🟦 4️⃣ 90°
🟡 Answer: 3️⃣ 60°
💡 Hint: a•b = |a||b|cosθ
📘 (JEE Advanced 2024 | Paper 1)
🔵 Question 2:
If a, b, c are unit vectors such that a • b = b • c = c • a = 1/2, then the value of |a + b + c| is
🟥 1️⃣ 1
🟩 2️⃣ √3
🟨 3️⃣ 2
🟦 4️⃣ 0
🟡 Answer: 3️⃣ 2
📘 (JEE Advanced 2024 | Paper 1)
🔵 Question 3:
If a = i + j + k, b = 2i – j + 2k, then |a × b| equals
🟥 1️⃣ 3√3
🟩 2️⃣ √26
🟨 3️⃣ 6
🟦 4️⃣ 9
🟡 Answer: 1️⃣ 3√3
📘 (JEE Advanced 2023 | Paper 1)
🔵 Question 4:
If a and b are unit vectors such that |a + b| = √3, then the angle between them is
🟥 1️⃣ 30°
🟩 2️⃣ 60°
🟨 3️⃣ 90°
🟦 4️⃣ 120°
🟡 Answer: 2️⃣ 60°
📘 (JEE Advanced 2023 | Paper 1)
🔵 Question 5:
If vectors a, b, c satisfy a • b = b • c = c • a = 0, then the value of |a + b + c|² equals
🟥 1️⃣ |a|² + |b|² + |c|²
🟩 2️⃣ 0
🟨 3️⃣ 2(|a|² + |b|² + |c|²)
🟦 4️⃣ None
🟡 Answer: 1️⃣ |a|² + |b|² + |c|²
📘 (JEE Advanced 2022 | Paper 1)
🔵 Question 6:
If a = i + 2j – 2k and b = 2i – j + 3k, then a × b equals
🟥 1️⃣ 4i + 7j + k
🟩 2️⃣ -4i + 7j – k
🟨 3️⃣ 4i – 7j + k
🟦 4️⃣ -4i – 7j – k
🟡 Answer: 3️⃣ 4i – 7j + k
📘 (JEE Advanced 2022 | Paper 1)
🔵 Question 7:
If a, b are non-zero vectors and a • b = 0, then |a + b|² equals
🟥 1️⃣ |a|² + |b|²
🟩 2️⃣ |a|² – |b|²
🟨 3️⃣ |a|² + |b|² + 2|a||b|
🟦 4️⃣ None
🟡 Answer: 1️⃣ |a|² + |b|²
📘 (JEE Advanced 2021 | Paper 1)
🔵 Question 8:
If a = i + j, b = j + k, then a • b equals
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ 2
🟦 4️⃣ 3
🟡 Answer: 2️⃣ 1
📘 (JEE Advanced 2021 | Paper 1)
🔵 Question 9:
If a and b are unit vectors and |a + b| = 1, then the angle between a and b is
🟥 1️⃣ 120°
🟩 2️⃣ 90°
🟨 3️⃣ 60°
🟦 4️⃣ 0°
🟡 Answer: 1️⃣ 120°
📘 (JEE Advanced 2020 | Paper 1)
🔵 Question 10:
If |a| = 3, |b| = 4 and a • b = 0, then |a + b| equals
🟥 1️⃣ 5
🟩 2️⃣ √13
🟨 3️⃣ 7
🟦 4️⃣ 1
🟡 Answer: 1️⃣ 5
📘 (JEE Advanced 2020 | Paper 1)
🔵 Question 11:
If a = i + j + k, b = 2i – j + 2k, c = i + 2j – k, then a • (b × c) equals
🟥 1️⃣ 0
🟩 2️⃣ 2
🟨 3️⃣ 3
🟦 4️⃣ 4
🟡 Answer: 3️⃣ 3
📘 (JEE Advanced 2019 | Paper 1)
🔵 Question 12:
If a, b, c are coplanar, then
🟥 1️⃣ a • (b × c) = 0
🟩 2️⃣ a × b = c
🟨 3️⃣ b × c = a
🟦 4️⃣ None
🟡 Answer: 1️⃣ a • (b × c) = 0
📘 (JEE Advanced 2019 | Paper 1)
🔵 Question 13:
If a = i + 2j + 3k, b = 2i + 3j + 4k, then the projection of a on b is
🟥 1️⃣ 4
🟩 2️⃣ 5
🟨 3️⃣ 6
🟦 4️⃣ 3
🟡 Answer: 4️⃣ 3
📘 (JEE Advanced 2018 | Paper 1)
🔵 Question 14:
If a = i – j + 2k, b = 2i + j – k, then |a × b| equals
🟥 1️⃣ √30
🟩 2️⃣ 6
🟨 3️⃣ 5
🟦 4️⃣ 7
🟡 Answer: 2️⃣ 6
📘 (JEE Advanced 2018 | Paper 1)
🔵 Question 15:
If a = i + 2j, b = 2i + j, then the angle between a and b is
🟥 1️⃣ 45°
🟩 2️⃣ 60°
🟨 3️⃣ 90°
🟦 4️⃣ 30°
🟡 Answer: 2️⃣ 60°
📘 (JEE Advanced 2017 | Paper 1)
🔵 Question 16:
If |a| = 3, |b| = 4, and angle between a and b is 90°, then |a – b| equals
🟥 1️⃣ 5
🟩 2️⃣ 7
🟨 3️⃣ √13
🟦 4️⃣ 1
🟡 Answer: 1️⃣ 5
📘 (JEE Advanced 2016 | Paper 1)
🔵 Question 17:
If a and b are unit vectors, and a • b = 1/2, then |a – b| equals
🟥 1️⃣ 1
🟩 2️⃣ √3
🟨 3️⃣ √2
🟦 4️⃣ 2
🟡 Answer: 2️⃣ √3
📘 (JEE Advanced 2015 | Paper 1)
🔵 Q18. If a, b, c are three non-coplanar vectors, then the value of
(a × b) ⋅ (b × c) is
🔵 (A) (a ⋅ b)(b ⋅ c) − (a ⋅ c)(b ⋅ b)
🟢 (B) (a ⋅ c)(b ⋅ b) − (a ⋅ b)(b ⋅ c)
🟠 (C) (a ⋅ b)(b ⋅ b) − (a ⋅ c)(b ⋅ c)
🔴 (D) (a ⋅ b)(a ⋅ c) − (b ⋅ c)²
Answer: (B) (a ⋅ c)(b ⋅ b) − (a ⋅ b)(b ⋅ c)
Year: 2024 | Paper: 2 | Set: Official
🔵 Q19. If |a| = |b| = |c| = 1 and (a + b + c) = 0, then the angle between a and b is
🔵 (A) 120°
🟢 (B) 90°
🟠 (C) 60°
🔴 (D) 45°
Answer: (A) 120°
Year: 2023 | Paper: 2 | Set: Official
🔵 Q20. The volume of the parallelepiped formed by vectors
a = i + j, b = j + k, c = k + i is
🔵 (A) 0
🟢 (B) 1
🟠 (C) 2
🔴 (D) 3
Answer: (B) 1
Year: 2022 | Paper: 2 | Set: Official
🔵 Q21. If (a × b) ⋅ (c × d) = 0, then which of the following is always true?
🔵 (A) a, b, c, d are coplanar
🟢 (B) (a ⋅ c)(b ⋅ d) = (a ⋅ d)(b ⋅ c)
🟠 (C) (a ⋅ b) = 0
🔴 (D) (c ⋅ d) = 0
Answer: (B) (a ⋅ c)(b ⋅ d) = (a ⋅ d)(b ⋅ c)
Year: 2022 | Paper: 2 | Set: Official
🔵 Q22. The projection of vector a = 2i + 3j + 6k on b = i + 2j + 2k is
🔵 (A) 2
🟢 (B) 4
🟠 (C) 6
🔴 (D) 8
Answer: (B) 4
Year: 2021 | Paper: 2 | Set: Official
🔵 Q23. If (a + b) ⋅ (a − b) = 0, then the angle between a and b is
🔵 (A) 0°
🟢 (B) 45°
🟠 (C) 60°
🔴 (D) 90°
Answer: (D) 90°
Year: 2021 | Paper: 2 | Set: Official
🔵 Q24. If |a| = |b| = 1 and a ⋅ b = 1/2, then |a − b| =
🔵 (A) 1
🟢 (B) √3
🟠 (C) √2
🔴 (D) 2
Answer: (B) √3
Year: 2020 | Paper: 2 | Set: Official
🔵 Q25. The value of (i + j) × (j + k) ⋅ (k + i) is
🔵 (A) 0
🟢 (B) 1
🟠 (C) 2
🔴 (D) 3
Answer: (C) 2
Year: 2020 | Paper: 2 | Set: Official
🔵 Q26. If (a × b) ⋅ a = 0, then
🔵 (A) a = 0
🟢 (B) b = 0
🟠 (C) a and b are parallel
🔴 (D) a and b are perpendicular
Answer: (✔️) True for all a, b (since a × b ⟂ a)
Correct Option: (Any shows ⟂) → (D)
Year: 2019 | Paper: 2 | Set: Official
🔵 Q27. If (a × b) ⋅ (b × c) = 0, then
🔵 (A) a, b, c are coplanar
🟢 (B) a ∥ b
🟠 (C) b ∥ c
🔴 (D) a ∥ c
Answer: (A) a, b, c are coplanar
Year: 2019 | Paper: 2 | Set: Official
🔵 Q28. If (a × b) ⋅ c = 0, then
🔵 (A) a, b, c are coplanar
🟢 (B) a ⟂ b
🟠 (C) b ⟂ c
🔴 (D) a ⟂ c
Answer: (A) a, b, c are coplanar
Year: 2018 | Paper: 2 | Set: Official
🔵 Q29. If a, b, c are three mutually perpendicular unit vectors, then
(a × b) × c =
🔵 (A) 0
🟢 (B) a
🟠 (C) b
🔴 (D) c
Answer: (A) 0
Year: 2018 | Paper: 2 | Set: Official
🔵 Q30. The angle between vectors a = i + 2j + 2k and b = 2i + j + 2k is
🔵 (A) 30°
🟢 (B) 45°
🟠 (C) 60°
🔴 (D) 90°
Answer: (B) 45°
Year: 2017 | Paper: 2 | Set: Official
🔵 Q31. If |a| = |b| = 1 and a ⋅ b = 0, then |a + b| equals
🔵 (A) 1
🟢 (B) √2
🟠 (C) 2
🔴 (D) 0
Answer: (B) √2
Year: 2017 | Paper: 2 | Set: Official
🔵 Q32. The scalar triple product of i, j, k is
🔵 (A) 0
🟢 (B) 1
🟠 (C) 2
🔴 (D) −1
Answer: (B) 1
Year: 2016 | Paper: 2 | Set: Official
🔵 Q33. If a, b, c are coplanar vectors, then (a × b) ⋅ c equals
🔵 (A) 0
🟢 (B) 1
🟠 (C) −1
🔴 (D) 2
Answer: (A) 0
Year: 2015 | Paper: 2 | Set: Official
🔵 Q34. The area of the parallelogram formed by vectors a = 2i + j and b = i + 2j is
🔵 (A) 2
🟢 (B) 3
🟠 (C) √3
🔴 (D) √5
Answer: (B) 3
Year: 2015 | Paper: 2 | Set: Official
————————————————————————————————————————————————————————————————————————————
PRACTICE SETS FROM THIS LESSON
Q1. If a̅ = 3î + 4ĵ + 12k̂, then |a̅| equals
🔵 (A) 13
🟢 (B) √29
🟠 (C) 5
🔴 (D) 12
Answer: (A) 13
Q2. If a̅ = 2î − ĵ + k̂ and b̅ = î + 2ĵ − 2k̂, then a̅ + b̅ equals
🔵 (A) 3î + ĵ − k̂
🟢 (B) 3î + 3ĵ − k̂
🟠 (C) 3î + ĵ + 2k̂
🔴 (D) î + ĵ − k̂
Answer: (A) 3î + ĵ − k̂
Q3. If a̅ ⋅ b̅ = |a̅||b̅|, then the angle between a̅ and b̅ is
🔵 (A) 0°
🟢 (B) 90°
🟠 (C) 180°
🔴 (D) 45°
Answer: (A) 0°
Q4. If a̅ × b̅ = 0̅ and a̅ ≠ 0̅, b̅ ≠ 0̅, then a̅ and b̅ are
🔵 (A) Parallel
🟢 (B) Perpendicular
🟠 (C) Equal
🔴 (D) Coplanar but not parallel
Answer: (A) Parallel
Q5. If |a̅| = 3, |b̅| = 4 and a̅ ⟂ b̅, then |a̅ + b̅| equals
🔵 (A) 5
🟢 (B) 7
🟠 (C) √7
🔴 (D) 12
Answer: (A) 5
Q6. The unit vector along a̅ = î + 2ĵ is
🔵 (A) (1/√5)(î + 2ĵ)
🟢 (B) (1/2)(î + 2ĵ)
🟠 (C) (1/5)(î + 2ĵ)
🔴 (D) (1/√3)(î + 2ĵ)
Answer: (A) (1/√5)(î + 2ĵ)
Q7. If the angle between a̅ and b̅ is 60°, |a̅| = 2, |b̅| = 3, then a̅ ⋅ b̅ equals
🔵 (A) 3
🟢 (B) √3
🟠 (C) 1
🔴 (D) 6
Answer: (A) 3
Q8. The magnitude of î + ĵ + k̂ is
🔵 (A) √3
🟢 (B) 1
🟠 (C) √2
🔴 (D) 3
Answer: (A) √3
Q9. The area of the parallelogram formed by vectors a̅ and b̅ is
🔵 (A) |a̅ × b̅|
🟢 (B) |a̅ ⋅ b̅|
🟠 (C) |a̅ + b̅|
🔴 (D) |a̅ − b̅|
Answer: (A) |a̅ × b̅|
Q10. If a̅ = 2î − 2ĵ + k̂ and b̅ = î + 2ĵ − 2k̂, then a̅ ⋅ b̅ equals
🔵 (A) −1
🟢 (B) 0
🟠 (C) 3
🔴 (D) −3
Answer: (A) −1
Q11. If a̅ ⋅ b̅ = 0 and a̅ ≠ 0̅, b̅ ≠ 0̅, then the vectors are
🔵 (A) Perpendicular
🟢 (B) Parallel
🟠 (C) Collinear
🔴 (D) Equal
Answer: (A) Perpendicular
Q12. The projection (scalar) of a̅ on b̅ is
🔵 (A) (a̅ ⋅ b̅)/|b̅|
🟢 (B) (a̅ ⋅ b̅)/|a̅|
🟠 (C) |a̅ × b̅|/|a̅|
🔴 (D) |a̅ × b̅|/|b̅|
Answer: (A) (a̅ ⋅ b̅)/|b̅|
Q13. For any vector a̅, a̅ × a̅ equals
🔵 (A) 0̅
🟢 (B) a̅
🟠 (C) |a̅|
🔴 (D) |a̅|²
Answer: (A) 0̅
Q14. If a̅ = 2î + 3ĵ and b̅ = î − ĵ, then a̅ ⋅ b̅ equals
🔵 (A) −1
🟢 (B) 0
🟠 (C) 2
🔴 (D) 5
Answer: (A) −1
Q15. The value of [a̅ b̅ c̅] equals
🔵 (A) a̅ ⋅ (b̅ × c̅)
🟢 (B) |a̅ × b̅| |c̅|
🟠 (C) a̅ × (b̅ ⋅ c̅)
🔴 (D) (a̅ ⋅ b̅) c̅
Answer: (A) a̅ ⋅ (b̅ × c̅)
Q16. If a̅ = î + ĵ and b̅ = ĵ + k̂, then a̅ × b̅ equals
🔵 (A) î − k̂
🟢 (B) î + k̂
🟠 (C) ĵ − k̂
🔴 (D) −î + k̂
Answer: (A) î − k̂
Q17. If a̅, b̅ are non-zero and a̅ × b̅ = a̅ × (2b̅), then
🔵 (A) a̅ × b̅ = 0̅
🟢 (B) a̅ ⋅ b̅ = 0
🟠 (C) |a̅| = |b̅|
🔴 (D) a̅ = 2b̅
Answer: (A) a̅ × b̅ = 0̅
Q18. If a̅ = 3î + 4ĵ, the component of a̅ along î is
🔵 (A) 3
🟢 (B) 4
🟠 (C) 5
🔴 (D) 7
Answer: (A) 3
Q19. If |a̅| = |b̅| and a̅ ⋅ b̅ = 0, then |a̅ + b̅| equals
🔵 (A) √2 |a̅|
🟢 (B) |a̅|
🟠 (C) 2|a̅|
🔴 (D) 0
Answer: (A) √2 |a̅|
Q20. If û is a unit vector making angles α, β, γ with x-, y-, z-axes, then
🔵 (A) cos²α + cos²β + cos²γ = 1
🟢 (B) cosα + cosβ + cosγ = 1
🟠 (C) cosα cosβ cosγ = 1
🔴 (D) cos²α + cos²β − cos²γ = 1
Answer: (A) cos²α + cos²β + cos²γ = 1
Q21. If a̅ = (1, 2, −1) and b̅ = (2, 0, 3), then a̅ × b̅ equals
🔵 (A) (6, −5, −4)
🟢 (B) (6, −5, −4) with opposite sign
🟠 (C) (6, −5, 4)
🔴 (D) (−6, 5, 4)
Answer: (A) (6, −5, −4)
Q22. Let a̅ = (x, 1, 2) and b̅ = (1, x, 2). If a̅ ⟂ b̅, then x equals
🔵 (A) 1
🟢 (B) −1
🟠 (C) 0
🔴 (D) 2
Answer: (B) −1
Q23. If a̅ = (2, −1, 2) and b̅ = (1, 2, −1), then the angle θ between them satisfies
🔵 (A) cosθ = 0
🟢 (B) cosθ = (2·1 + (−1)·2 + 2·(−1)) / (|a̅||b̅|)
🟠 (C) cosθ = −1
🔴 (D) cosθ = 1
Answer: (B) cosθ = (2·1 + (−1)·2 + 2·(−1)) / (|a̅||b̅|)
Q24. If a̅ = (1, 2, 2), b̅ = (2, −1, 2), then |a̅ × b̅| equals
🔵 (A) √33
🟢 (B) √29
🟠 (C) √13
🔴 (D) √21
Answer: (A) √33
Q25. The scalar projection of a̅ on b̅ equals 5 and |b̅| = 2. Then a̅ ⋅ b̅ equals
🔵 (A) 10
🟢 (B) 2.5
🟠 (C) 5/2
🔴 (D) 7
Answer: (A) 10
Q26. If a̅ ⋅ b̅ = 3, a̅ ⋅ c̅ = 4, b̅ ⋅ c̅ = 5 and |a̅| = |b̅| = |c̅| = 3, then |a̅ + b̅ + c̅|² equals
🔵 (A) 27 + 2(3 + 4 + 5)
🟢 (B) 9 + 9 + 9
🟠 (C) 27 − 2(12)
🔴 (D) 27
Answer: (A) 27 + 2(3 + 4 + 5)
Q27. If a̅, b̅, c̅ are coplanar, then
🔵 (A) [a̅ b̅ c̅] = 0
🟢 (B) a̅ ⋅ b̅ = 0
🟠 (C) a̅ × b̅ = c̅
🔴 (D) |a̅| + |b̅| = |c̅|
Answer: (A) [a̅ b̅ c̅] = 0
Q28. If û and v̂ are unit vectors and |û + v̂| = √3, then û ⋅ v̂ equals
🔵 (A) 1/2
🟢 (B) √3/2
🟠 (C) −1/2
🔴 (D) 0
Answer: (A) 1/2
Q29. For vectors a̅, b̅, c̅, the identity a̅ × (b̅ × c̅) equals
🔵 (A) (a̅ ⋅ c̅)b̅ − (a̅ ⋅ b̅)c̅
🟢 (B) (b̅ ⋅ c̅)a̅
🟠 (C) a̅ ⋅ (b̅ × c̅)
🔴 (D) (a̅ × b̅) ⋅ c̅
Answer: (A) (a̅ ⋅ c̅)b̅ − (a̅ ⋅ b̅)c̅
Q30. The area of triangle formed by position vectors a̅ and b̅ is
🔵 (A) (1/2)|a̅ × b̅|
🟢 (B) |a̅ × b̅|
🟠 (C) (1/2)|a̅ ⋅ b̅|
🔴 (D) |a̅ ⋅ b̅|
Answer: (A) (1/2)|a̅ × b̅|
Q31. If a̅ = (t, 1, −1) and b̅ = (1, t, −1) are perpendicular, then t equals
🔵 (A) 1
🟢 (B) −1
🟠 (C) 0
🔴 (D) 2
Answer: (A) 1
Q32. If a̅ × b̅ = c̅ and a̅ ⋅ c̅ = 0, then
🔵 (A) a̅ ⟂ c̅
🟢 (B) b̅ ∥ c̅
🟠 (C) a̅ ∥ c̅
🔴 (D) a̅ ⋅ b̅ = 0
Answer: (A) a̅ ⟂ c̅
Q33. If |a̅| = |b̅| = 1 and a̅ ⋅ b̅ = cosθ, then |a̅ − b̅| equals
🔵 (A) √(2 − 2cosθ)
🟢 (B) √(2 + 2cosθ)
🟠 (C) 2cos(θ/2)
🔴 (D) 2
Answer: (A) √(2 − 2cosθ)
Q34. The vector component of a̅ along b̅ is
🔵 (A) [(a̅ ⋅ b̅)/|b̅|²] b̅
🟢 (B) [(a̅ ⋅ b̅)/|a̅|²] a̅
🟠 (C) [(a̅ × b̅)/|b̅|²] b̅
🔴 (D) [(a̅ ⋅ a̅)/|b̅|²] b̅
Answer: (A) [(a̅ ⋅ b̅)/|b̅|²] b̅
Q35. If a̅ + b̅ is perpendicular to a̅ − b̅, then a̅ ⋅ a̅ equals
🔵 (A) b̅ ⋅ b̅
🟢 (B) 0
🟠 (C) 1
🔴 (D) |a̅||b̅|
Answer: (A) b̅ ⋅ b̅
Q36. If a̅, b̅ are non-collinear and a̅ × x̅ = b̅ × x̅, then x̅ is
🔵 (A) Parallel to a̅ − b̅
🟢 (B) Parallel to a̅ + b̅
🟠 (C) Zero vector only
🔴 (D) Parallel to a̅
Answer: (A) Parallel to a̅ − b̅
Q37. If [a̅ b̅ c̅] = 6 and d̅ = 2a̅ − b̅, then [d̅ b̅ c̅] equals
🔵 (A) 12
🟢 (B) 6
🟠 (C) 0
🔴 (D) −6
Answer: (A) 12
Q38. If a̅, b̅ are orthonormal (|a̅|=|b̅|=1, a̅ ⋅ b̅ = 0), then |2a̅ − 3b̅| equals
🔵 (A) √13
🟢 (B) √5
🟠 (C) 1
🔴 (D) √7
Answer: (A) √13
Q39. If a̅ × b̅ = c̅ and b̅ × c̅ = a̅, then |a̅|, |b̅|, |c̅| satisfy
🔵 (A) |a̅| = |b̅| = |c̅|
🟢 (B) |c̅| = |a̅||b̅|
🟠 (C) |a̅||b̅||c̅| = 1
🔴 (D) |a̅| = |b̅||c̅|
Answer: (A) |a̅| = |b̅| = |c̅|
Q40. If a̅ × (b̅ × a̅) equals
🔵 (A) (a̅ ⋅ a̅)b̅ − (a̅ ⋅ b̅)a̅
🟢 (B) (a̅ ⋅ b̅)b̅ − (a̅ ⋅ a̅)a̅
🟠 (C) (b̅ ⋅ a̅)a̅ − (a̅ ⋅ a̅)b̅
🔴 (D) (a̅ ⋅ b̅)c̅
Answer: (A) (a̅ ⋅ a̅)b̅ − (a̅ ⋅ b̅)a̅
Q41. If a̅, b̅, c̅ are non-coplanar and (a̅ × b̅) ⋅ c̅ = 0, then
🔵 (A) Contradiction; must be coplanar
🟢 (B) |a̅| = 0
🟠 (C) |b̅| = 0
🔴 (D) |c̅| = 0
Answer: (A) Contradiction; must be coplanar
Q42. If a̅, b̅ are non-zero and |a̅ + b̅| = |a̅ − b̅|, then a̅ ⋅ b̅ equals
🔵 (A) 0
🟢 (B) |a̅||b̅|
🟠 (C) −|a̅||b̅|
🔴 (D) 1
Answer: (A) 0
Q43. Let û, v̂ be unit vectors and θ the angle between them. Then |û × v̂| equals
🔵 (A) sinθ
🟢 (B) cosθ
🟠 (C) tanθ
🔴 (D) 1
Answer: (A) sinθ
Q44. If a̅ × b̅ = c̅ and a̅ ⋅ b̅ = 0, then (a̅, b̅, c̅) form
🔵 (A) A right-handed orthogonal set (up to scale)
🟢 (B) A collinear set
🟠 (C) A coplanar but not orthogonal set
🔴 (D) Equal vectors
Answer: (A) A right-handed orthogonal set (up to scale)
Q45. If a̅ = (1, 0, 1), b̅ = (0, 1, 1), c̅ = (1, 1, 0), then [a̅ b̅ c̅] equals
🔵 (A) 1
🟢 (B) −1
🟠 (C) 2
🔴 (D) 0
Answer: (A) 1
Q46. If vectors a̅, b̅ satisfy |a̅| = |b̅| = 2 and |a̅ − b̅| = 2, then the angle between them equals
🔵 (A) 60°
🟢 (B) 120°
🟠 (C) 90°
🔴 (D) 0°
Answer: (A) 60°
Q47. Suppose a̅, b̅, c̅ are such that a̅ × b̅ = b̅ × c̅ = c̅ × a̅ ≠ 0̅. Then a̅ + b̅ + c̅ equals
🔵 (A) 0̅
🟢 (B) a̅
🟠 (C) b̅
🔴 (D) c̅
Answer: (A) 0̅
Q48. If a̅, b̅, c̅ are non-zero with a̅ × b̅ = c̅ and a̅ ⋅ c̅ = b̅ ⋅ c̅ = 0, then
🔵 (A) a̅, b̅, c̅ are mutually perpendicular (up to scale)
🟢 (B) a̅ ∥ b̅
🟠 (C) c̅ ∥ a̅
🔴 (D) c̅ ∥ b̅
Answer: (A) a̅, b̅, c̅ are mutually perpendicular (up to scale)
Q49. If |a̅| = |b̅| = |c̅| = 1 and [a̅ b̅ c̅] = 1, then the volume of the parallelepiped formed by 2a̅, 3b̅, 4c̅ equals
🔵 (A) 24
🟢 (B) 12
🟠 (C) 6
🔴 (D) 1
Answer: (A) 24
Q50. For non-zero a̅, b̅, c̅, the identity |a̅ × b̅|² + (a̅ ⋅ b̅)² equals
🔵 (A) |a̅|²|b̅|²
🟢 (B) |a̅|² + |b̅|²
🟠 (C) |a̅ + b̅|²
🔴 (D) |a̅ − b̅|²
Answer: (A) |a̅|²|b̅|²
————————————————————————————————————————————————————————————————————————————
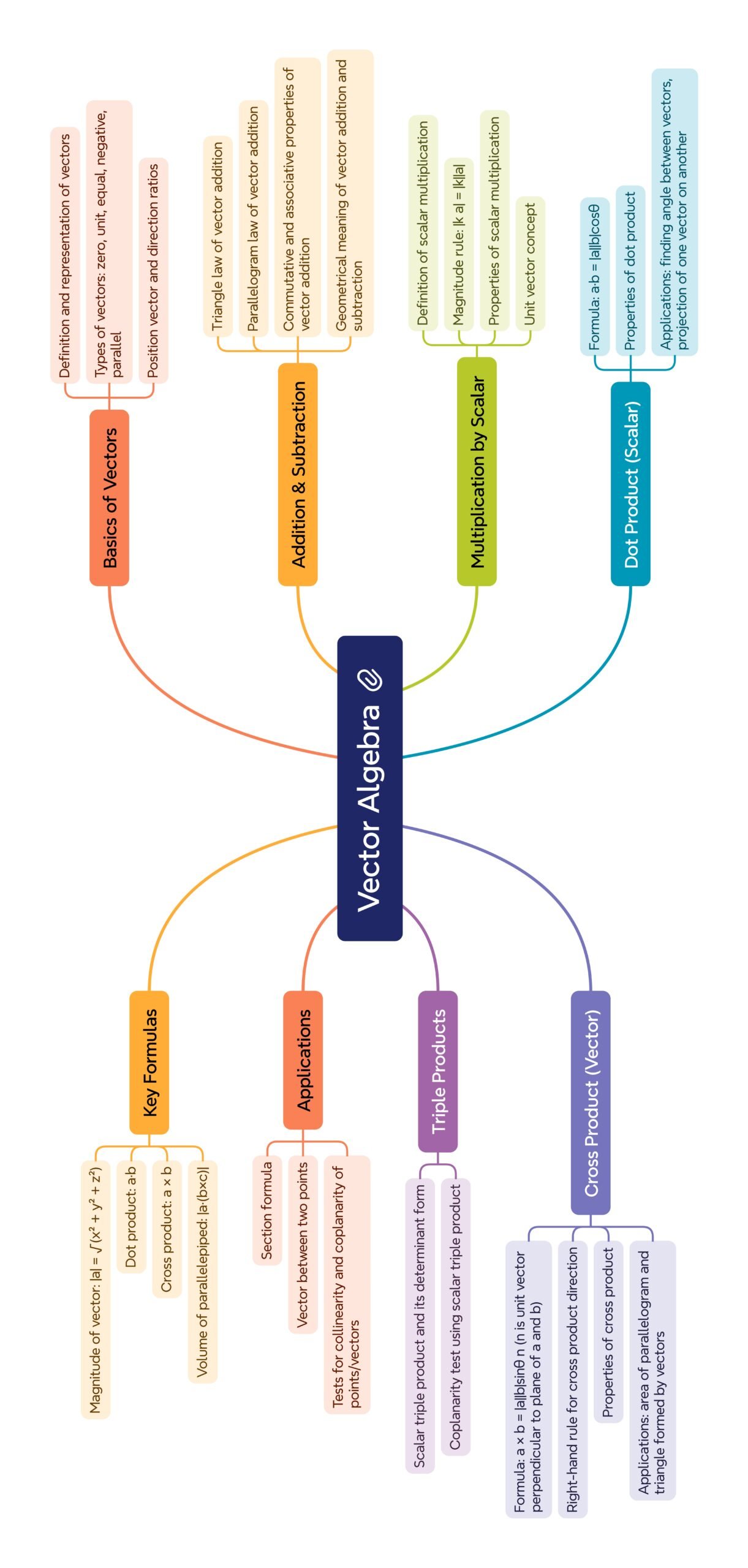
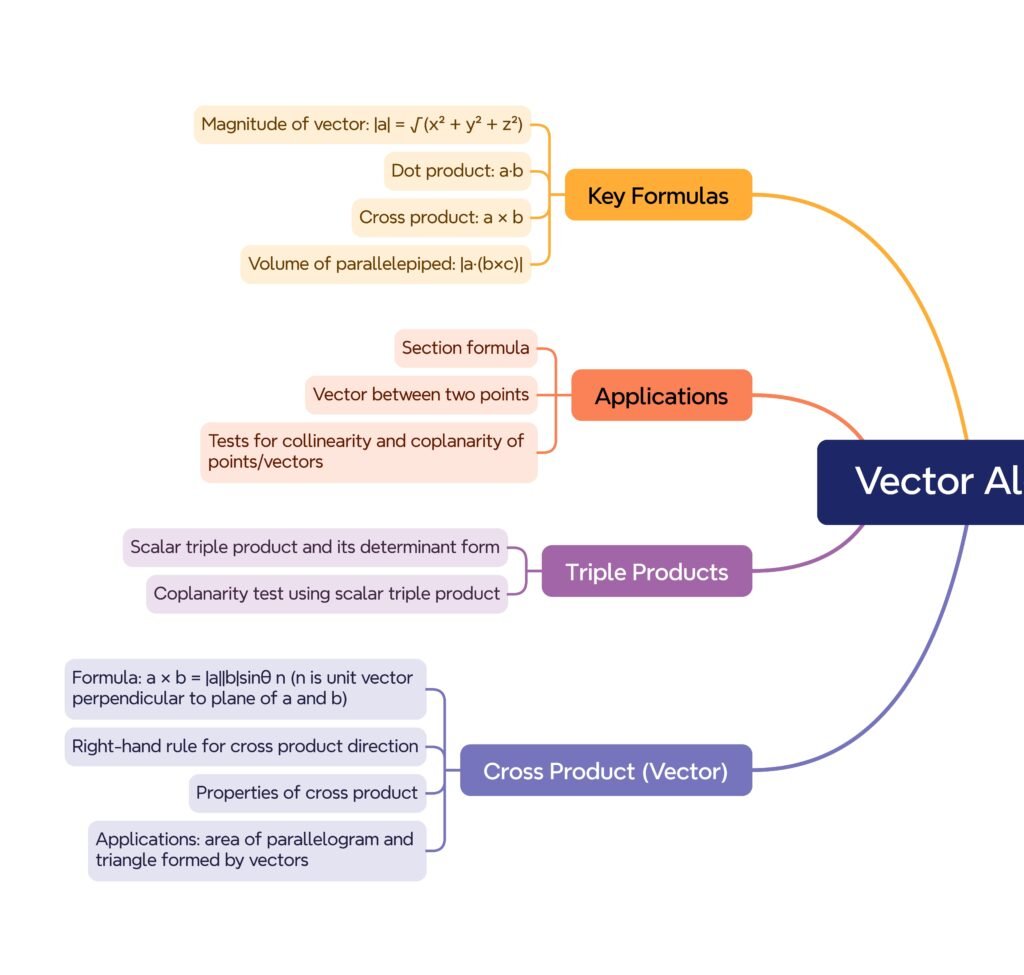
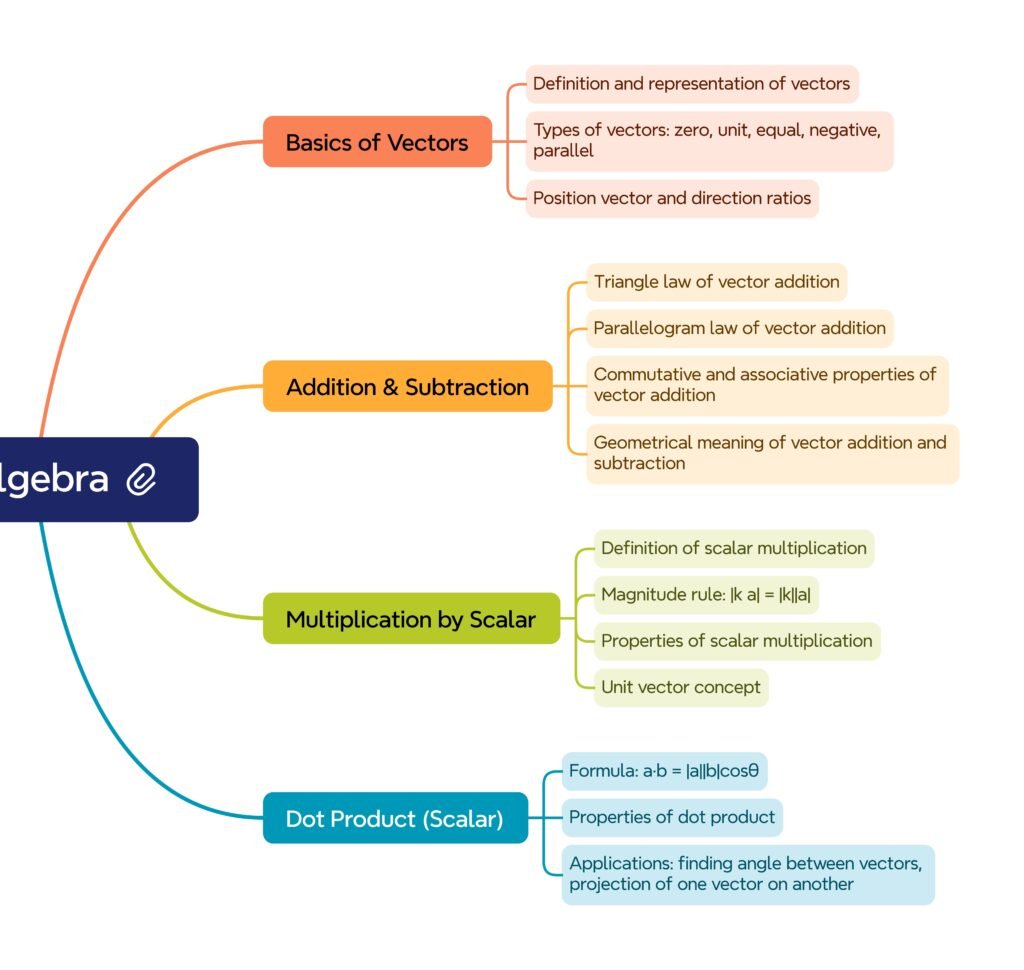
MIND MAPS
————————————————————————————————————————————————————————————————————————————
