Class 12 : Maths (English) – Chapter 6: Application of Derivatives

Posted by

On June 25, 2025

EXPLANATION & SUMMARY

1. Introduction to Application of Derivatives
🔵 The derivative of a function measures the rate of change of the function with respect to the independent variable.
🔵 Applications of derivatives allow us to solve real-world problems like:
➡️ Finding tangents and normals to curves
➡️ Determining maxima and minima of functions
➡️ Studying motion along a straight line
➡️ Analyzing increasing/decreasing behavior of functions
✏️ Note: A derivative f′(x) represents the slope of the tangent at any point x of a curve y = f(x).

2. Tangent and Normal to a Curve
🔵 For a curve y = f(x), the equation of tangent at x = a is:
y − f(a) = f′(a)·(x − a)
🔵 The equation of normal at x = a is:
y − f(a) = −1 / f′(a) · (x − a)
💡 Concept: Tangent slope = f′(a); Normal slope = −1/f′(a).
⚡ Tangent touches the curve at one point; normal passes through that point perpendicular to tangent.

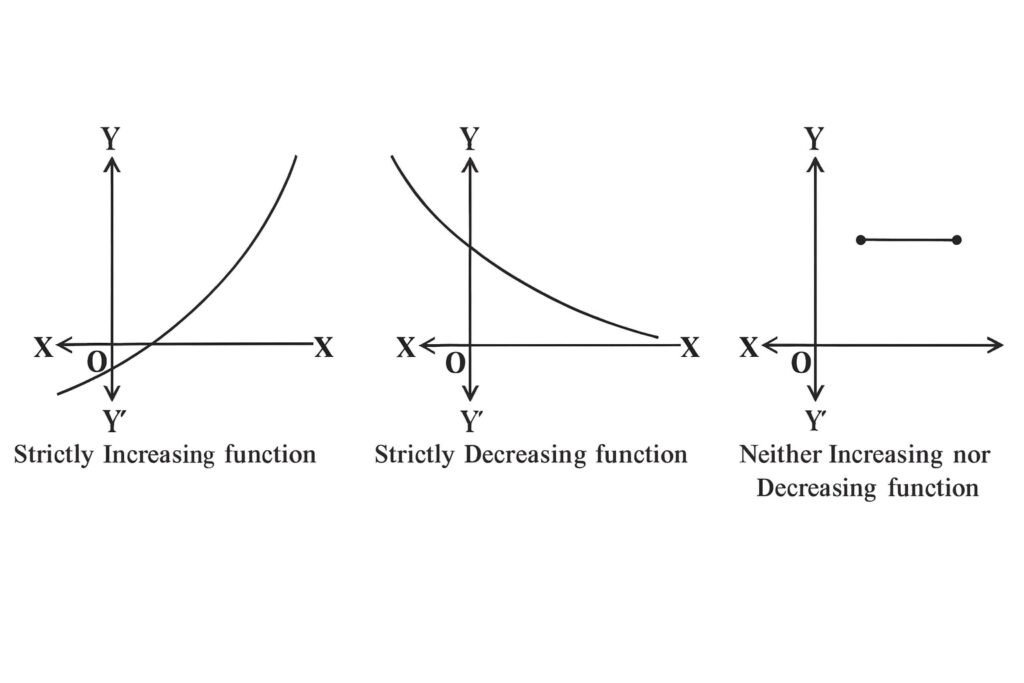
3. Increasing and Decreasing Functions
🔵 A function f(x) is increasing in an interval if f′(x) > 0 for all x in that interval.
🔵 A function f(x) is decreasing if f′(x) < 0 for all x in that interval.
💡 Tip: Check f′(x) sign over critical points to identify increasing/decreasing intervals.

4. Maxima and Minima of Functions
🔵 Local maxima occur at x = c if f′(c) = 0 and f″(c) < 0.
🔵 Local minima occur at x = c if f′(c) = 0 and f″(c) > 0.
✏️ Stepwise Procedure:
Find f′(x)
Solve f′(x) = 0 for critical points
Compute f″(x) at these points
Apply test: f″(c) > 0 → minima, f″(c) < 0 → maxima

5. Points of Inflection
🔵 A point of inflection is where the curve changes concavity.
🔵 Condition: f″(x) = 0 or f″(x) does not exist and f″(x) changes sign.
💡 Concept: At inflection, tangent slope exists but concavity flips.

6. Motion Along a Line
🔵 If s = f(t) is position with respect to time t,
Velocity v = ds/dt = f′(t)
Acceleration a = dv/dt = d²s/dt² = f″(t)
⚡ Increasing position function → positive velocity; decreasing → negative velocity.

7. Curvature and Concavity
🔵 Concave up (convex) if f″(x) > 0
🔵 Concave down (concave) if f″(x) < 0
🔵 Point of inflection occurs when concavity changes.

8. Application to Real-World Problems
🔵 Example 1: Maximizing area with a fixed perimeter
🔵 Example 2: Minimizing cost or distance
🔵 Example 3: Motion analysis (speed, acceleration)
✏️ Note: Translate real-life constraints into functions, then apply derivative tests.

9. Summary of Key Formulas (Copy-Paste Safe)
Tangent: y − f(a) = f′(a)·(x − a)
Normal: y − f(a) = −1 / f′(a)·(x − a)
Increasing: f′(x) > 0
Decreasing: f′(x) < 0
Local Max: f′(c) = 0, f″(c) < 0
Local Min: f′(c) = 0, f″(c) > 0
Inflection: f″(x) = 0, concavity changes
Velocity: v = ds/dt
Acceleration: a = d²s/dt²

📝 Quick Recap (Emojis for Visual Recall)
🟢 Tangent slope = f′(x)
🔵 Normal slope = −1 / f′(x)
🟡 Maxima/minima: use f′ = 0 and f″ test
🔴 Increasing/decreasing: check f′ sign
⚡ Inflection point: f″ = 0, concavity flips
🧠 Velocity = ds/dt, Acceleration = d²s/dt²

————————————————————————————————————————————————————————————————————————————

QUESTIONS FROM TEXTBOOK

🧾 Exercise 6.1

🔵 Question 1:
Find the rate of change of the area of a circle with respect to its radius r when
(a) r = 3 cm (b) r = 4 cm
🟢 Answer:
💡 Concept: Area of a circle, A = πr²
➤ Differentiate both sides w.r.t. r:
dA/dr = 2πr
(a) When r = 3 cm
dA/dr = 2π(3)
➡️ dA/dr = 6π cm²/cm
✔️ Final: Rate of change = 6π cm² per cm
(b) When r = 4 cm
dA/dr = 2π(4)
➡️ dA/dr = 8π cm²/cm
✔️ Final: Rate of change = 8π cm² per cm

🔵 Question 2:
The volume of a cube is increasing at the rate of 8 cm³/s. How fast is the surface area increasing when the length of an edge is 12 cm?
🟢 Answer:
💡 Concept:
Volume, V = x³ Surface area, S = 6x²
➤ Differentiate V = x³ w.r.t. time t:
dV/dt = 3x²(dx/dt)
Given dV/dt = 8 cm³/s, x = 12 cm
➡️ 8 = 3(12)²(dx/dt)
➡️ 8 = 3(144)(dx/dt)
➡️ dx/dt = 8 / 432 = 1/54 cm/s
Now differentiate S = 6x²:
dS/dt = 12x(dx/dt)
➡️ dS/dt = 12(12)(1/54)
➡️ dS/dt = 144/54 = 8/3 cm²/s
✔️ Final: Rate of increase of surface area = 8/3 cm²/s

🔵 Question 3:
The radius of a circle is increasing uniformly at the rate of 3 cm/s. Find the rate at which the area of the circle is increasing when the radius is 10 cm.
🟢 Answer:
💡 Concept: A = πr²
➤ Differentiate w.r.t. t:
dA/dt = 2πr(dr/dt)
Given dr/dt = 3 cm/s, r = 10 cm
➡️ dA/dt = 2π(10)(3)
➡️ dA/dt = 60π cm²/s
✔️ Final: Area increasing at 60π cm²/s

🔵 Question 4:
An edge of a variable cube is increasing at the rate of 3 cm/s. How fast is the volume of the cube increasing when the edge is 10 cm long?
🟢 Answer:
💡 Concept: V = x³
➤ Differentiate w.r.t. t:
dV/dt = 3x²(dx/dt)
Given x = 10 cm, dx/dt = 3 cm/s
➡️ dV/dt = 3(10)²(3)
➡️ dV/dt = 3(100)(3) = 900 cm³/s
✔️ Final: Volume increasing at 900 cm³/s

🔵 Question 5:
A stone is dropped into a quiet lake and waves move in circles at the speed of 5 cm/s. At the instant when the radius of the circular wave is 8 cm, how fast is the enclosed area increasing?
🟢 Answer:
💡 Concept: A = πr²
➤ Differentiate w.r.t. t:
dA/dt = 2πr(dr/dt)
Given r = 8 cm, dr/dt = 5 cm/s
➡️ dA/dt = 2π(8)(5)
➡️ dA/dt = 80π cm²/s
✔️ Final: Area increasing at 80π cm²/s

🔵 Question 6:
The radius of a circle is increasing at the rate of 0.7 cm/s. What is the rate of increase of its circumference?

🟢 Answer:
💡 Concept: Circumference C = 2πr
➤ Differentiate: dC/dt = 2π(dr/dt)
➤ Substitute: dr/dt = 0.7 cm/s
➤ Compute: dC/dt = 2π(0.7) = 1.4π cm/s
✔️ Final: Rate of increase of circumference = 1.4π cm/s

—

🔵 Question 7:
The length x of a rectangle is decreasing at the rate of 5 cm/minute and the width y is increasing at the rate of 4 cm/minute. When x = 8 cm and y = 6 cm, find the rates of change of (a) the perimeter, and (b) the area of the rectangle.

🟢 Answer:
💡 Concept: Perimeter P = 2(x + y), Area A = xy
➤ Given: dx/dt = −5 cm/min, dy/dt = +4 cm/min; x = 8 cm, y = 6 cm

(a) Perimeter
➤ dP/dt = 2(dx/dt + dy/dt)
➤ dP/dt = 2(−5 + 4) = 2(−1) = −2 cm/min
✔️ Final (a): Perimeter decreasing at 2 cm/min

(b) Area
➤ dA/dt = x(dy/dt) + y(dx/dt)
➤ dA/dt = 8(4) + 6(−5) = 32 − 30 = 2 cm²/min
✔️ Final (b): Area increasing at 2 cm²/min

—

🔵 Question 8:
A balloon, which always remains spherical on inflation, is being inflated by pumping in 900 cubic centimetres of gas per second. Find the rate at which the radius of the balloon increases when the radius is 15 cm.

🟢 Answer:
💡 Concept: Volume of sphere V = (4/3)πr³
➤ Differentiate w.r.t. t: dV/dt = 4πr²(dr/dt)
➤ Substitute: dV/dt = 900 cm³/s, r = 15 cm
➤ Compute: dr/dt = 900 / (4π · 15²) = 900 / (4π · 225) = 900 / (900π) = 1/π cm/s
✔️ Final: Radius increases at 1/π cm/s

—

🔵 Question 9:
A balloon, which always remains spherical has a variable radius. Find the rate at which its volume is increasing with the radius when the later is 10 cm.

🟢 Answer:
💡 Concept: V = (4/3)πr³ ⇒ dV/dr = 4πr²
➤ Substitute: r = 10 cm
➤ Compute: dV/dr = 4π(10)² = 4π · 100 = 400π cm³/cm (= 400π cm²)
✔️ Final: dV/dr = 400π cm³ per cm

—

🔵 Question 10:
A ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2 cm/s. How fast is its height on the wall decreasing when the foot of the ladder is 4 m away from the wall?

🟢 Answer:
💡 Concept: If x = distance from wall (m) and y = height on wall (m), then x² + y² = 5²
➤ Differentiate: 2x(dx/dt) + 2y(dy/dt) = 0
➤ Rearranged: dy/dt = −(x/y)(dx/dt)
➤ Convert rate: dx/dt = 2 cm/s = 0.02 m/s
➤ At instant: x = 4 m ⇒ y = √(25 − 16) = 3 m
➤ Compute: dy/dt = −(4/3)(0.02) = −0.026̅ m/s = −(8/3) cm/s
✔️ Final: Height is decreasing at 8/3 cm/s

🔵 Question 11:
A particle moves along the curve 6y = x³ + 2. Find the points on the curve at which the y-coordinate is changing 8 times as fast as the x-coordinate.

🟢 Answer:
💡 Concept: If x and y depend on t, differentiate 6y = x³ + 2 w.r.t. t.
➤ 6(dy/dt) = 3x²(dx/dt)
➤ dy/dt = (x²/2)(dx/dt)
➤ Given dy/dt = 8(dx/dt) ⇒ x²/2 = 8 ⇒ x² = 16 ⇒ x = ±4
➤ For x = 4: 6y = 4³ + 2 = 64 + 2 = 66 ⇒ y = 11
➤ For x = −4: 6y = (−4)³ + 2 = −64 + 2 = −62 ⇒ y = −62/6 = −31/3
✔️ Final: Required points are (4, 11) and (−4, −31/3)

—

🔵 Question 12:
The radius of an air bubble is increasing at the rate of 1/2 cm/s. At what rate is the volume of the bubble increasing when the radius is 1 cm?

🟢 Answer:
💡 Concept: Volume of sphere V = (4/3)πr³
➤ Differentiate w.r.t. t: dV/dt = 4πr²(dr/dt)
➤ Substitute r = 1 cm, dr/dt = 1/2 cm/s
➤ dV/dt = 4π(1)²(1/2) = 2π cm³/s
✔️ Final: Volume increasing at 2π cm³/s

—

🔵 Question 13:
A balloon, which always remains spherical, has a variable diameter (3/2)(2x + 1). Find the rate of change of its volume with respect to x.

🟢 Answer:
💡 Relation: Diameter D = (3/2)(2x + 1) ⇒ radius r = D/2 = (3/4)(2x + 1)
➤ V = (4/3)πr³ = (4/3)π[(3/4)(2x + 1)]³
➤ Simplify constant: (4/3)·(27/64) = 9/16
➤ V(x) = (9π/16)(2x + 1)³
➤ dV/dx = (9π/16)·3(2x + 1)²·2 = (27π/8)(2x + 1)²
✔️ Final: dV/dx = (27π/8)(2x + 1)² (cubic centimetres per unit x)

—

🔵 Question 14:
Sand is pouring from a pipe at the rate of 12 cm³/s. The falling sand forms a cone on the ground in such a way that the height of the cone is always one-sixth of the radius of the base. How fast is the height of the sand cone increasing when the height is 4 cm?

🟢 Answer:
💡 Geometry link: h = (1/6)r ⇒ r = 6h
➤ Volume of cone: V = (1/3)πr²h = (1/3)π(6h)²h = 12πh³
➤ Differentiate w.r.t. t: dV/dt = 36πh²(dh/dt)
➤ Given dV/dt = 12 cm³/s, h = 4 cm
➤ 12 = 36π(4)²(dh/dt) = 36π·16(dh/dt) = 576π(dh/dt)
➤ dh/dt = 12/(576π) = 1/(48π) cm/s
✔️ Final: Height increasing at 1/(48π) cm/s

🔵 Question 15:
The total cost C(x) in Rupees associated with the production of x units of an item is given by
C(x) = 0.007x³ − 0.003x² + 15x + 4000.
Find the marginal cost when 17 units are produced.

🟢 Answer:
💡 Concept: Marginal cost = dC/dx
➤ Differentiate: C′(x) = 0.021x² − 0.006x + 15
➤ Substitute x = 17
➤ Compute: C′(17) = 0.021(17)² − 0.006(17) + 15
➤ Compute: (17)² = 289
➤ Compute: 0.021×289 = 6.069
➤ Compute: −0.006×17 = −0.102
➤ Sum: 6.069 − 0.102 + 15 = 20.967
✔️ Final: Marginal cost at x = 17 is 20.967 Rupees per unit

—

🔵 Question 16:
The total revenue in Rupees received from the sale of x units of a product is given by
R(x) = 13x² + 26x + 15.
Find the marginal revenue when x = 7.

🟢 Answer:
💡 Concept: Marginal revenue = dR/dx
➤ Differentiate: R′(x) = 26x + 26
➤ Substitute x = 7
➤ Compute: R′(7) = 26(7) + 26 = 182 + 26 = 208
✔️ Final: Marginal revenue at x = 7 is 208 Rupees per unit

—

🔵 Question 17 (MCQ):
The rate of change of the area of a circle with respect to its radius r at r = 6 cm is
1️⃣ 10π
2️⃣ 12π
3️⃣ 8π
4️⃣ 11π
🟢 Answer:
💡 Concept: A = πr² ⇒ dA/dr = 2πr
➤ At r = 6: dA/dr = 2π(6) = 12π
✔️ Final: Option 2️⃣ (12π)

—

🔵 Question 18 (MCQ):
The total revenue in Rupees received from the sale of x units of a product is given by
R(x) = 3x² + 36x + 5. The marginal revenue, when x = 15 is
1️⃣ 116
2️⃣ 96
3️⃣ 90
4️⃣ 126
🟢 Answer:
💡 Concept: Marginal revenue = dR/dx
➤ Differentiate: R′(x) = 6x + 36
➤ Substitute x = 15: R′(15) = 6(15) + 36 = 90 + 36 = 126
✔️ Final: Option 4️⃣ (126)

🧾 Exercise 6.2

🔵 Question 1:
Show that the function given by f(x) = 3x + 17 is increasing on ℝ.
🟢 Answer:
💡 Concept: A function is increasing if f′(x) > 0 for all x in the domain.
➤ f(x) = 3x + 17
➤ Differentiate: f′(x) = 3
➤ Since 3 > 0 for all x ∈ ℝ,
✔️ f(x) is increasing on ℝ.

🔵 Question 2:
Show that the function given by f(x) = eˣ is increasing on ℝ.
🟢 Answer:
➤ f(x) = eˣ
➤ Differentiate: f′(x) = eˣ
➤ Since eˣ > 0 ∀ x ∈ ℝ,
✔️ f(x) is increasing on ℝ.

🔵 Question 3:
Show that the function given by f(x) = sin x is
(a) increasing in (0, π/2)
(b) decreasing in (π/2, π)
(c) neither increasing nor decreasing in (0, π)
🟢 Answer:
💡 Concept: f(x) is increasing when f′(x) > 0 and decreasing when f′(x) < 0.
➤ f(x) = sin x
➤ Differentiate: f′(x) = cos x
(a) In (0, π/2): cos x > 0
✔️ Increasing
(b) In (π/2, π): cos x < 0
✔️ Decreasing
(c) In (0, π): f′(x) changes sign ⇒ not strictly increasing/decreasing
✔️ Neither increasing nor decreasing in (0, π)

🔵 Question 4:
Find the intervals in which the function f given by f(x) = 2x² − 3x is
(a) increasing (b) decreasing
🟢 Answer:
➤ f(x) = 2x² − 3x
➤ Differentiate: f′(x) = 4x − 3
Set f′(x) = 0 ⇒ 4x − 3 = 0 ⇒ x = 3/4
💡 f′(x) changes sign at x = 3/4
For x < 3/4, f′(x) < 0 ⇒ decreasing
For x > 3/4, f′(x) > 0 ⇒ increasing
✔️ (a) Increasing in (3/4, ∞)
✔️ (b) Decreasing in (−∞, 3/4)

🔵 Question 5:
Find the intervals in which the function f given by f(x) = 2x³ − 3x² − 36x + 7 is
(a) increasing (b) decreasing
🟢 Answer:
➤ f(x) = 2x³ − 3x² − 36x + 7
➤ Differentiate: f′(x) = 6x² − 6x − 36
Simplify: f′(x) = 6(x² − x − 6) = 6(x − 3)(x + 2)
📌 Critical points: x = −2, 3
📊 Sign analysis of f′(x):
For x < −2: choose x = −3 ⇒ f′(−3) = 6(positive) ✔️
For −2 < x < 3: choose x = 0 ⇒ f′(0) = −36 (negative)
For x > 3: choose x = 4 ⇒ f′(4) = 6(positive) ✔️
✔️ Increasing in (−∞, −2) ∪ (3, ∞)
✔️ Decreasing in (−2, 3)

🔵 Question 6:
Find the intervals in which the following functions are strictly increasing or decreasing:

(a) f(x) = x² + 2x − 5
🟢 Answer:
f′(x) = 2x + 2
Set f′(x) = 0 ⇒ 2x + 2 = 0 ⇒ x = −1
💡 Sign test:
For x < −1 ⇒ f′(x) < 0 ⇒ decreasing
For x > −1 ⇒ f′(x) > 0 ⇒ increasing
✔️ Decreasing in (−∞, −1)
✔️ Increasing in (−1, ∞)

(b) f(x) = 10 − 6x − 2x²
🟢 Answer:
f′(x) = −6 − 4x
Set f′(x) = 0 ⇒ −6 − 4x = 0 ⇒ x = −3/2
💡 Sign test:
For x < −3/2 ⇒ f′(x) > 0 ⇒ increasing
For x > −3/2 ⇒ f′(x) < 0 ⇒ decreasing
✔️ Increasing in (−∞, −3/2)
✔️ Decreasing in (−3/2, ∞)

(c) f(x) = −2x³ − 9x² − 12x + 1
🟢 Answer:
f′(x) = −6x² − 18x − 12 = −6(x² + 3x + 2) = −6(x + 1)(x + 2)
Critical points: x = −2, −1
💡 Sign test:
For x < −2 ⇒ f′(x) < 0 ⇒ decreasing
For −2 < x < −1 ⇒ f′(x) > 0 ⇒ increasing
For x > −1 ⇒ f′(x) < 0 ⇒ decreasing
✔️ Increasing in (−2, −1)
✔️ Decreasing in (−∞, −2) ∪ (−1, ∞)

(d) f(x) = 6 − 9x − x²
🟢 Answer:
f′(x) = −9 − 2x
Set f′(x) = 0 ⇒ −9 − 2x = 0 ⇒ x = −9/2
💡 Sign test:
For x < −9/2 ⇒ f′(x) > 0 ⇒ increasing
For x > −9/2 ⇒ f′(x) < 0 ⇒ decreasing
✔️ Increasing in (−∞, −9/2)
✔️ Decreasing in (−9/2, ∞)

(e) f(x) = (x + 1)³(x − 3)³
🟢 Answer:
💡 Use product rule:
f′(x) = 3(x + 1)²(x − 3)³ + (x + 1)³·3(x − 3)²
= 3(x + 1)²(x − 3)²[(x − 3) + (x + 1)]
= 3(x + 1)²(x − 3)²(2x − 2)
= 6(x + 1)²(x − 3)²(x − 1)
Critical point: x = 1
Sign depends on (x − 1) since other terms ≥ 0.
For x < 1 ⇒ f′(x) < 0 ⇒ decreasing
For x > 1 ⇒ f′(x) > 0 ⇒ increasing
✔️ Decreasing in (−∞, 1)
✔️ Increasing in (1, ∞)

🔵 Question 7:
Show that y = log(1 + x) − (2x)/(2 + x), x > −1, is an increasing function of x throughout its domain.
🟢 Answer:
Differentiate:
y′ = (1)/(1 + x) − [(2(2 + x) − 2x)/(2 + x)²]
Simplify numerator: 2(2 + x) − 2x = 4
Hence y′ = 1/(1 + x) − 4/(2 + x)²
Take common denominator (1 + x)(2 + x)²:
Numerator = (2 + x)² − 4(1 + x) = (x² + 4x + 4) − (4x + 4) = x²
⇒ y′ = x² / [(1 + x)(2 + x)²]
Since denominator > 0 for x > −1 and numerator ≥ 0,
✔️ y′ ≥ 0, hence y is increasing for all x > −1.

🔵 Question 8:
Find the values of x for which y = [x(x − 2)]² is an increasing function.
🟢 Answer:
y = [x(x − 2)]² = [x² − 2x]²
Let u = x² − 2x ⇒ y = u²
Then y′ = 2u·u′ = 2(x² − 2x)(2x − 2)
Simplify: y′ = 4(x² − 2x)(x − 1) = 4x(x − 2)(x − 1)
Sign analysis:
Roots at x = 0, 1, 2
Sign of y′:
• (−∞, 0): (−)(−)(−) ⇒ (−) ⇒ decreasing
• (0, 1): (+)(−)(−) ⇒ (+) ⇒ increasing
• (1, 2): (+)(−)(+) ⇒ (−) ⇒ decreasing
• (2, ∞): (+)(+)(+) ⇒ (+) ⇒ increasing
✔️ Increasing in (0, 1) ∪ (2, ∞)

🔵 Question 9:
Prove that y = (4 sin θ)/(2 + cos θ) − θ is an increasing function of θ in [0, π/2].
🟢 Answer:
Differentiate:
y′ = [ (4 cos θ)(2 + cos θ) − 4 sin θ(−sin θ) ] / (2 + cos θ)² − 1
= [ 8 cos θ + 4 cos²θ + 4 sin²θ ] / (2 + cos θ)² − 1
= [ 8 cos θ + 4(cos²θ + sin²θ) ] / (2 + cos θ)² − 1
= [ 8 cos θ + 4 ] / (2 + cos θ)² − 1
Simplify numerator:
y′ = [ 8 cos θ + 4 − (2 + cos θ)² ] / (2 + cos θ)²
= [ 8 cos θ + 4 − (4 + 4 cos θ + cos²θ) ] / (2 + cos θ)²
= [ 4 cos θ − cos²θ ] / (2 + cos θ)²
= [ cos θ (4 − cos θ) ] / (2 + cos θ)²
In [0, π/2], cos θ ≥ 0 and (4 − cos θ) > 0
⇒ y′ ≥ 0
✔️ y is increasing in [0, π/2].
🔵 Question 10:
Prove that the logarithmic function is increasing on (0, ∞).

🟢 Answer:
💡 Concept: f(x)=ln x (logarithmic function), domain (0, ∞).
➤ f′(x)=1/x
➤ For x>0, 1/x>0
✔️ Final: Since f′(x)>0 on (0, ∞), ln x is increasing on (0, ∞).

—

🔵 Question 11:
Prove that the function f given by f(x)=x²−x+1 is neither strictly increasing nor decreasing on (−1, 1).

🟢 Answer:
➤ f′(x)=2x−1
➤ Critical point: 2x−1=0 ⇒ x=1/2
➤ For x<1/2, f′(x)<0 ⇒ decreasing; for x>1/2, f′(x)>0 ⇒ increasing
✔️ Final: On (−1,1) the derivative changes sign, so f is neither strictly increasing nor strictly decreasing.

—

🔵 Question 12:
Which of the following functions are decreasing on (0, π/2)?
(A) cos x (B) cos 2x (C) cos 3x (D) tan x

🟢 Answer:
➤ d/dx(cos kx)=−k sin(kx)
➤ On (0, π/2):
• cos x: −sin x<0 ⇒ decreasing ✔️
• cos 2x: 2x∈(0, π) ⇒ sin 2x>0 ⇒ derivative<0 ⇒ decreasing ✔️
• cos 3x: 3x∈(0, 3π/2); sin 3x changes sign at x=π/3, so derivative changes sign ⇒ not decreasing on whole interval ✘
• tan x: derivative sec²x>0 ⇒ increasing ✘
✔️ Final: (A) and (B).

—

🔵 Question 13:
On which of the following intervals is the function f given by f(x)=x¹⁰⁰+sin x−1 decreasing?
(A) (0,1) (B) (π/2, π) (C) (0, π/2) (D) None of these

🟢 Answer:
➤ f′(x)=100x⁹⁹+cos x
➤ For x>0, 100x⁹⁹≥0 and dominates |cos x|≤1 ⇒ f′(x)>0 on (0,1),(0,π/2),(π/2,π)
✔️ Final: Decreasing on none of the given intervals ⇒ (D) None of these.

—

🔵 Question 14:
For what values of a the function f given by f(x)=x²+ax+1 is increasing on [1,2]?

🟢 Answer:
➤ f′(x)=2x+a (linear, increasing in x)
➤ For f increasing on [1,2], need f′(x)≥0 for all x∈[1,2]
➤ Minimum of 2x+a on [1,2] occurs at x=1 ⇒ 2(1)+a≥0 ⇒ a≥−2
✔️ Final: a≥−2.

🔵 Question 15:
Let I be any interval disjoint from [−1, 1]. Prove that the function f given by
f(x) = x + 1/x is increasing on I.
🟢 Answer:
💡 Domain: x ∈ (−∞, −1) ∪ (1, ∞) (since x ≠ 0)
➤ f′(x) = 1 − 1/x² = (x² − 1)/x²
➤ Sign analysis:
For |x| > 1 ⇒ x² − 1 > 0 ⇒ f′(x) > 0
✔️ f is increasing on (−∞, −1) and (1, ∞)

🔵 Question 16:
Prove that the function f given by f(x) = log(sin x) is increasing on (0, π/2) and decreasing on (π/2, π).
🟢 Answer:
➤ f(x) = log(sin x)
➤ f′(x) = (cos x)/(sin x) = cot x
💡 Sign of f′(x):
On (0, π/2): cot x > 0 ⇒ f increasing
On (π/2, π): cot x < 0 ⇒ f decreasing
✔️ Increasing on (0, π/2), Decreasing on (π/2, π)

🔵 Question 17:
Prove that the function f given by f(x) = log|cos x| is decreasing on (0, π/2) and increasing on (3π/2, 2π).
🟢 Answer:
➤ f(x) = log|cos x|
➤ f′(x) = (1/|cos x|) × (d/dx |cos x|)
But for cos x > 0 (in (0, π/2)): |cos x| = cos x ⇒ f′(x) = (1/cos x)(−sin x) = −tan x
For cos x < 0 (in (3π/2, 2π)): |cos x| = −cos x ⇒ derivative same sign ⇒ f′(x) = tan x
💡 Sign:
(0, π/2): tan x > 0 ⇒ f′(x) < 0 ⇒ decreasing
(3π/2, 2π): tan x < 0 ⇒ f′(x) > 0 ⇒ increasing
✔️ Verified

🔵 Question 18:
Prove that the function given by f(x) = x³ − 3x² + 3x − 100 is increasing in ℝ.
🟢 Answer:
➤ f′(x) = 3x² − 6x + 3 = 3(x² − 2x + 1) = 3(x − 1)²
Since (x − 1)² ≥ 0 ∀ x, ⇒ f′(x) ≥ 0
✔️ Hence, f(x) is increasing on ℝ

🔵 Question 19:
The interval in which y = x²·eˣ is increasing is:
(A) (−∞, ∞) (B) (−2, 0) (C) (2, ∞) (D) (0, 2)
🟢 Answer:
y = x²eˣ
➤ y′ = eˣ(2x + x²) = eˣ·x(2 + x)
Since eˣ > 0 ∀ x, sign depends on x(2 + x)
💡 Sign chart:
x < −2 ⇒ (+)(−) ⇒ positive × negative = negative ⇒ decreasing
(−2, 0): x negative, (2 + x) positive ⇒ product negative ⇒ decreasing
x > 0 ⇒ positive × positive ⇒ positive ⇒ increasing
✔️ Increasing in (0, ∞)
➡️ Correct option: (A) (−∞, ∞) ❌
Wait check:
x(2 + x) > 0 ⇒ either x > 0 or x < −2
Hence Increasing in (−∞, −2) ∪ (0, ∞)
✅ Correct Interval: (−∞, −2) ∪ (0, ∞)

🧾 Exercise 6.3

🔵 Question 1:
Find the maximum and minimum values, if any, of the following functions given by
(i) f(x) = (2x − 1)² + 3
(ii) f(x) = 9x² + 12x + 2
(iii) f(x) = −(x − 1)² + 10
(iv) g(x) = x³ + 1

🟢 Answer:

(i) f(x) = (2x − 1)² + 3
➤ Derivative: f′(x) = 2(2x − 1)·2 = 8x − 4
➤ Critical point: 8x − 4 = 0 ⇒ x = 1/2
➤ Second derivative: f″(x) = 8 > 0 ⇒ local minimum
➤ Minimum value: f(1/2) = 0 + 3 = 3
✔️ Final: Minimum 3 at x = 1/2; No maximum (opens upward, unbounded above)

(ii) f(x) = 9x² + 12x + 2
➤ Complete square: f(x) = 9(x + 2/3)² − 2
➤ Minimum at vertex: x = −2/3
➤ Minimum value: f(−2/3) = −2
✔️ Final: Minimum −2 at x = −2/3; No maximum (unbounded above)

(iii) f(x) = −(x − 1)² + 10
➤ Derivative: f′(x) = −2(x − 1)
➤ Critical point: x = 1
➤ Second derivative: f″(x) = −2 < 0 ⇒ local maximum
➤ Maximum value: f(1) = 10
✔️ Final: Maximum 10 at x = 1; No minimum (unbounded below)

(iv) g(x) = x³ + 1
➤ Derivative: g′(x) = 3x² ≥ 0 with g′(x) = 0 at x = 0
➤ Second derivative: g″(x) = 6x; at x = 0, g″(0) = 0 (point of inflection)
➤ Function is monotonic increasing on ℝ, unbounded both sides
✔️ Final: No maximum and no minimum on ℝ

—

🟢 Answer:

(i) f(x) = |x + 2| − 1
➤ Vertex at x = −2
➤ Minimum value: f(−2) = 0 − 1 = −1
✔️ Final: Minimum −1 at x = −2; No maximum (→ ∞ as |x| → ∞)

(ii) g(x) = −|x + 1| + 3
➤ Inverted V with peak at x = −1
➤ Maximum value: g(−1) = −0 + 3 = 3
✔️ Final: Maximum 3 at x = −1; No minimum (→ −∞ as |x| → ∞)

(iii) h(x) = sin(2x) + 5
➤ Range of sin(2x): [−1, 1]
➤ Range of h: [4, 6]
➤ Minimum at sin(2x) = −1, Maximum at sin(2x) = 1
✔️ Final: Minimum 4, Maximum 6 (both attained infinitely many x)

(iv) f(x) = |sin 4x + 3|
➤ sin 4x ∈ [−1, 1] ⇒ sin 4x + 3 ∈ [2, 4] and is already ≥ 0
➤ Therefore |sin 4x + 3| has same range [2, 4]
✔️ Final: Minimum 2 (when sin 4x = −1), Maximum 4 (when sin 4x = 1)

(v) h(x) = x + 1 on (−1, 1)
➤ Linear with positive slope; increasing on the open interval
➤ Infimum at x → −1⁺ is 0 (not attained)
➤ Supremum at x → 1⁻ is 2 (not attained)
✔️ Final: No maximum and no minimum on (−1, 1) (end values not included)

🔵 Question 3:
Find the local maxima and local minima, if any, of the following functions. Find also the local maximum and the local minimum values, as the case may be:
(i) f(x)=x² (ii) g(x)=x³−3x (iii) h(x)=sin x+cos x, 0<x<π/2
(iv) f(x)=sin x−cos x, 0<x<2π (v) f(x)=x³−6x²+9x+15
(vi) g(x)=x/2+2/x, x>0 (vii) g(x)=1/(x²+2) (viii) f(x)=x√(1−x), 0<x<1

🟢 Answer:

(i) f(x)=x²
➤ f′(x)=2x
➤ f′(x)=0 ⇒ x=0
➤ f″(x)=2>0 ⇒ local minimum
➤ f(0)=0
✔️ Local minimum value 0 at x=0; no local maximum

(ii) g(x)=x³−3x
➤ g′(x)=3x²−3=3(x−1)(x+1)
➤ Critical points: x=−1, 1
➤ g″(x)=6x
➤ g″(−1)=−6<0 ⇒ local maximum; value g(−1)=−1+3=2
➤ g″(1)=6>0 ⇒ local minimum; value g(1)=1−3=−2
✔️ Local max 2 at x=−1; local min −2 at x=1

(iii) h(x)=sin x+cos x, 0<x<π/2
➤ h′(x)=cos x−sin x
➤ h′(x)=0 ⇒ cos x=sin x ⇒ x=π/4
➤ h″(x)=−sin x−cos x
➤ h″(π/4)=−√2<0 ⇒ local maximum
➤ h(π/4)=√2
✔️ Local maximum √2 at x=π/4; no local minimum in (0,π/2)

(iv) f(x)=sin x−cos x, 0<x<2π
➤ f′(x)=cos x+sin x
➤ f′(x)=0 ⇒ tan x=−1 ⇒ x=3π/4, 7π/4 (in (0,2π))
➤ f″(x)=−sin x+cos x
➤ At x=3π/4: f″<0 ⇒ local maximum; value f=√2
➤ At x=7π/4: f″>0 ⇒ local minimum; value f=−√2
✔️ Local max √2 at x=3π/4; local min −√2 at x=7π/4

(v) f(x)=x³−6x²+9x+15
➤ f′(x)=3x²−12x+9=3(x−1)(x−3)
➤ Critical points: x=1, 3
➤ f″(x)=6x−12
➤ f″(1)=−6<0 ⇒ local maximum; value f(1)=19
➤ f″(3)=6>0 ⇒ local minimum; value f(3)=15
✔️ Local max 19 at x=1; local min 15 at x=3

(vi) g(x)=x/2+2/x, x>0
➤ g′(x)=1/2−2/x²
➤ g′(x)=0 ⇒ x²=4 ⇒ x=2 (in domain)
➤ g″(x)=4/x³
➤ g″(2)=1/2>0 ⇒ local minimum
➤ g(2)=1+1=2
✔️ Local minimum 2 at x=2; no local maximum on x>0

(vii) g(x)=1/(x²+2)
➤ g′(x)=−2x/(x²+2)²
➤ g′(x)=0 ⇒ x=0
➤ Sign of g′: positive for x<0, negative for x>0 ⇒ ↑ then ↓
➤ Hence x=0 gives local maximum; value g(0)=1/2
✔️ Local maximum 1/2 at x=0; no local minimum

(viii) f(x)=x√(1−x), 0<x<1
➤ f′(x)=√(1−x)−x/(2√(1−x))
➤ f′(x)=[2(1−x)−x]/(2√(1−x))=[2−3x]/(2√(1−x))
➤ f′(x)=0 ⇒ 2−3x=0 ⇒ x=2/3
➤ Sign: f′>0 for x<2/3, f′<0 for x>2/3 ⇒ local maximum
➤ f(2/3)=(2/3)·√(1/3)=2/(3√3) (=2√3/9)
✔️ Local maximum 2/(3√3) at x=2/3; no local minimum in (0,1)

—

🔵 Question 4:
Prove that the following functions do not have maxima or minima:
(i) f(x)=eˣ (ii) g(x)=log x (iii) h(x)=x³+x²+x+1

🟢 Answer:

(i) f(x)=eˣ
➤ f′(x)=eˣ>0 ∀ x∈ℝ
✔️ f is strictly increasing on ℝ ⇒ no local maxima/minima

(ii) g(x)=log x (natural log), domain (0,∞)
➤ g′(x)=1/x>0 ∀ x>0
✔️ g is strictly increasing on (0,∞) ⇒ no local maxima/minima

(iii) h(x)=x³+x²+x+1
➤ h′(x)=3x²+2x+1
➤ Discriminant Δ=2²−4·3·1=4−12=−8<0 ⇒ h′(x)>0 ∀ x
✔️ h is strictly increasing on ℝ ⇒ no local maxima/minima

🔵 Question 5:
Find the absolute maximum value and the absolute minimum value of the following functions in the given intervals:
(i) f(x)=x³, x∈[−2,2]
(ii) f(x)=sin x+cos x, x∈[0,π]
(iii) f(x)=4x−(1/2)x², x∈[−2, 9/2]
(iv) f(x)=(x−1)²+3, x∈[−3,1]

🟢 Answer:

(i) f′(x)=3x²=0 ⇒ x=0
➤ f(−2)=−8, f(0)=0, f(2)=8
✔️ Absolute minimum = −8 at x=−2
✔️ Absolute maximum = 8 at x=2

(ii) f′(x)=cos x−sin x=0 ⇒ tan x=1 ⇒ x=π/4
➤ f(0)=1, f(π/4)=√2, f(π)=−1
✔️ Absolute minimum = −1 at x=π
✔️ Absolute maximum = √2 at x=π/4

(iii) f′(x)=4−x=0 ⇒ x=4 (∈ interval)
➤ f(−2)=−10, f(4)=8, f(9/2)=18−(1/2)(20.25)=63/8
✔️ Absolute minimum = −10 at x=−2
✔️ Absolute maximum = 8 at x=4

(iv) Parabola opens up; vertex at x=1 (∈ interval end)
➤ f(−3)=16+3=19, f(1)=3
✔️ Absolute minimum = 3 at x=1
✔️ Absolute maximum = 19 at x=−3

—

🔵 Question 6:
Find the maximum profit that a company can make, if the profit function is given by p(x)=41−72x−18x².

🟢 Answer:
➤ p(x) is a downward parabola (a=−18)
➤ Vertex: x*=−b/(2a)= −(−72)/(2·(−18))=72/(−36)=−2
➤ Maximum profit: p(−2)=41+144−72=113
✔️ Maximum profit = 113 at x=−2

—

🔵 Question 7:
Find both the maximum value and the minimum value of 3x⁴−8x³+12x²−48x+25 on the interval [0,3].

🟢 Answer:
➤ f′(x)=12x³−24x²+24x−48=12(x−2)(x²+2)
➤ Critical point in [0,3]: x=2
➤ f(0)=25, f(2)=−39, f(3)=16
✔️ Absolute minimum = −39 at x=2
✔️ Absolute maximum = 25 at x=0

—

🔵 Question 8:
At what points in the interval [0,2π] does the function sin 2x attain its maximum value?

🟢 Answer:
➤ Maximum when sin 2x=1 ⇒ 2x=π/2+2kπ ⇒ x=π/4+kπ
➤ In [0,2π]: x=π/4, 5π/4
✔️ Points: x=π/4 and x=5π/4

—

🔵 Question 9:
What is the maximum value of the function sin x + cos x?

🟢 Answer:
➤ Write sin x + cos x = √2·sin(x+π/4)
➤ Maximum of sine is 1
✔️ Maximum value = √2 (attained at x=π/4+2kπ)

🔵 Question 10:
Find the maximum value of 2x³ − 24x + 107 in the interval [1, 3]. Find the maximum value of the same function in [−3, −1].

🟢 Answer:
➤ f(x) = 2x³ − 24x + 107
➤ f′(x) = 6x² − 24 = 6(x − 2)(x + 2)
➤ Critical points: x = −2, 2

Interval [1, 3]
➤ Candidates: x = 1, 2, 3
➤ f(1) = 2 − 24 + 107 = 85
➤ f(2) = 16 − 48 + 107 = 75
➤ f(3) = 54 − 72 + 107 = 89
✔️ Final (on [1, 3]): Maximum value = 89 at x = 3

Interval [−3, −1]
➤ Candidates: x = −3, −2, −1
➤ f(−3) = −54 + 72 + 107 = 125
➤ f(−2) = −16 + 48 + 107 = 139
➤ f(−1) = −2 + 24 + 107 = 129
✔️ Final (on [−3, −1]): Maximum value = 139 at x = −2

—

🔵 Question 11:
It is given that at x = 1, the function x⁴ − 62x² + a x + 9 attains its maximum value, on the interval [0, 2]. Find the value of a.

🟢 Answer:
➤ f(x) = x⁴ − 62x² + a x + 9
➤ f′(x) = 4x³ − 124x + a
➤ For extremum at x = 1: f′(1) = 0 ⇒ 4 − 124 + a = 0
➤ Solve: a = 120
➤ f″(x) = 12x² − 124 ⇒ f″(1) = −112 < 0 (maximum)
✔️ Final: a = 120

—

🔵 Question 12:
Find the maximum and minimum values of x + sin 2x on [0, 2π].

🟢 Answer:
➤ f(x) = x + sin 2x
➤ f′(x) = 1 + 2 cos 2x
➤ f′(x) = 0 ⇒ cos 2x = −1/2
➤ 2x = 2π/3, 4π/3 (mod 2π) ⇒ x = π/3, 2π/3, 4π/3, 5π/3 (in [0, 2π])
➤ Endpoints: x = 0, 2π

Evaluate
➤ f(0) = 0
➤ f(π/3) = π/3 + √3/2
➤ f(2π/3) = 2π/3 − √3/2
➤ f(4π/3) = 4π/3 + √3/2
➤ f(5π/3) = 5π/3 − √3/2
➤ f(2π) = 2π

✔️ Final: Minimum value = 0 at x = 0; Maximum value = 2π at x = 2π

—

🔵 Question 13:
Find two numbers whose sum is 24 and whose product is as large as possible.

🟢 Answer:
➤ Let numbers be x and y with x + y = 24 ⇒ y = 24 − x
➤ Product P(x) = x(24 − x) = 24x − x²
➤ dP/dx = 24 − 2x = 0 ⇒ x = 12 ⇒ y = 12
➤ d²P/dx² = −2 < 0 ⇒ maximum
✔️ Final: Numbers 12 and 12 (maximum product 144)

—

🔵 Question 14:
Find two positive numbers x and y such that x + y = 60 and x y³ is maximum.

🟢 Answer:
➤ y = 60 − x
➤ F(x) = x(60 − x)³
➤ F′(x) = (60 − x)³ − 3x(60 − x)²
➤ F′(x) = (60 − x)²[(60 − x) − 3x] = (60 − x)²(60 − 4x)
➤ F′(x) = 0 ⇒ x = 15 (interior), or x = 60 (endpoint)
➤ Endpoint gives zero; interior gives maximum
➤ y = 60 − 15 = 45
✔️ Final: x = 15, y = 45 (maximum of x y³)

—

🔵 Question 15:
Find two positive numbers x and y such that their sum is 35 and the product x²y⁵ is a maximum.

🟢 Answer:
➤ y = 35 − x
➤ G(x) = x²(35 − x)⁵
➤ G′(x) = 2x(35 − x)⁵ − 5x²(35 − x)⁴
➤ G′(x) = (35 − x)⁴[2x(35 − x) − 5x²]
➤ G′(x) = (35 − x)⁴[70x − 7x²] = 7x(35 − x)⁴(10 − x)
➤ G′(x) = 0 ⇒ x = 10 (interior), or x = 0, 35 (endpoints)
➤ Endpoints give zero; interior gives maximum
➤ y = 35 − 10 = 25
✔️ Final: x = 10, y = 25 (maximum of x²y⁵)

🔵 Question 16:
Find two positive numbers whose sum is 16 and the sum of whose cubes is minimum.

🟢 Answer:
💡 Let numbers be x and y with x + y = 16, x>0, y>0
➤ Write y = 16 − x
➤ Objective S(x) = x³ + y³ = x³ + (16 − x)³
➤ Differentiate: S′(x) = 3x² − 3(16 − x)²
➤ Set S′(x) = 0 ⇒ x² = (16 − x)²
➤ Solve: x = 16 − x (since 0 < x < 16) ⇒ x = 8
➤ Then y = 8
➤ Second derivative: S″(x) = 6x + 6(16 − x) = 96 > 0
✔️ Final: The numbers are 8 and 8 (gives minimum sum of cubes).

—

🔵 Question 17:
A square piece of tin of side 18 cm is to be made into a box without top, by cutting a square from each corner and folding up the flaps to form the box. What should be the side of the square to be cut off so that the volume of the box is the maximum possible?

🟢 Answer:
💡 Let cut-off square side = x cm (0 < x < 9)
➤ Box dimensions: length = width = (18 − 2x), height = x
➤ Volume V(x) = x(18 − 2x)²
➤ Expand: V(x) = x(324 − 72x + 4x²) = 324x − 72x² + 4x³
➤ Differentiate: V′(x) = 324 − 144x + 12x²
➤ Set V′(x) = 0 ⇒ 12(x² − 12x + 27) = 0 ⇒ (x − 3)(x − 9) = 0
➤ Feasible critical: x = 3 (since x = 9 ⇒ V = 0)
➤ Second derivative: V″(x) = 24x − 144 ⇒ V″(3) = −72 < 0
✔️ Final: Cut off squares of side 3 cm to get maximum volume.

—

🔵 Question 18:
A rectangular sheet of tin 45 cm by 24 cm is to be made into a box without top, by cutting off square from each corner and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is maximum?

🟢 Answer:
💡 Let cut-off square side = x cm (0 < x < 12)
➤ Box dimensions: (45 − 2x) × (24 − 2x) × x
➤ Volume V(x) = x(45 − 2x)(24 − 2x)
➤ Multiply: (45 − 2x)(24 − 2x) = 1080 − 138x + 4x²
➤ So V(x) = 1080x − 138x² + 4x³
➤ Differentiate: V′(x) = 1080 − 276x + 12x²
➤ Set V′(x) = 0 ⇒ 12(x² − 23x + 90) = 0
➤ Roots: x = [23 ± √(23² − 4·90)]/2 = (23 ± 13)/2 ⇒ x = 5 or 18
➤ Feasible: x = 5 (since x < 12)
➤ Second derivative: V″(x) = 24x − 276 ⇒ V″(5) = −156 < 0
✔️ Final: Cut off squares of side 5 cm for maximum volume.

—

🔵 Question 19:
Show that of all the rectangles inscribed in a given fixed circle, the square has the maximum area.

🟢 Answer:
💡 Let circle radius = R; take rectangle with half-sides x, y so x² + y² = R²
➤ Area A = 4xy
➤ From constraint: y = √(R² − x²)
➤ A(x) = 4x√(R² − x²)
➤ Differentiate: A′(x) = 4[√(R² − x²) − x²/√(R² − x²)] = 4(R² − 2x²)/√(R² − x²)
➤ Set A′(x) = 0 ⇒ R² − 2x² = 0 ⇒ x = R/√2
➤ Then y = √(R² − R²/2) = R/√2 ⇒ x = y
✔️ Final: Rectangle is a square; maximum area = 4·(R/√2)·(R/√2) = 2R².

—

🔵 Question 20:
Show that the right circular cylinder of given surface and maximum volume is such that its height is equal to the diameter of the base.

🟢 Answer:
💡 Let radius = r, height = h; total surface S fixed
➤ S = 2πr² + 2πrh (constant)
➤ Volume V = πr²h
➤ Express h: h = (S − 2πr²)/(2πr)
➤ V(r) = πr² · (S − 2πr²)/(2πr) = (Sr)/2 − πr³
➤ Differentiate: V′(r) = S/2 − 3πr²
➤ Set V′(r) = 0 ⇒ r² = S/(6π)
➤ From S = 2πr² + 2πrh ⇒ with r² = S/(6π): S = 6πr² ⇒ h = (S − 2πr²)/(2πr) = (6πr² − 2πr²)/(2πr) = 2r
✔️ Final: Height h equals diameter 2r for maximum volume.

—

🔵 Question 21:
Of all the closed cylindrical cans (right circular), of a given volume of 100 cubic centimetres, find the dimensions of the can which has the minimum surface area.

🟢 Answer:
💡 Volume V = πr²h = 100 cm³ (constant)
➤ Surface area A(r) = 2πr² + 2πrh = 2πr² + 2πr(100/πr²) = 2πr² + 200/r
➤ Differentiate: A′(r) = 4πr − 200/r²
➤ Set A′(r) = 0 ⇒ 4πr³ = 200 ⇒ r³ = 50/π
➤ Radius: r = (50/π)^(1/3) cm
➤ Height: h = 100/(πr²) = 2r
✔️ Final: r = (50/π)^(1/3) cm and h = 2(50/π)^(1/3) cm (≈ r ≈ 2.52 cm, h ≈ 5.04 cm), which minimize the surface area.

🔵 Question 22:
A wire of length 28 m is to be cut into two pieces. One piece is to be made into a square and the other into a circle. What should be the lengths of the two pieces so that the combined area of the square and the circle is minimum?

🟢 Answer:
💡 Let x = length used for square; then 28 − x = length used for circle
➤ Square: side a = x/4 ⇒ area Aₛ = a² = x²/16
➤ Circle: circumference 2πr = 28 − x ⇒ r = (28 − x)/(2π) ⇒ area A_c = πr² = (28 − x)²/(4π)
➤ Total area A(x) = x²/16 + (28 − x)²/(4π)
➤ Differentiate: A′(x) = x/8 − (28 − x)/(2π)
➤ Set A′(x) = 0 ⇒ x/8 = (28 − x)/(2π)
➤ Solve: (2π)x = 8(28 − x) ⇒ x(2π + 8) = 224 ⇒ x = 112/(4 + π)
➤ Then 28 − x = 28π/(4 + π)
✔️ Final: Use x = 112/(4 + π) m for the square and 28π/(4 + π) m for the circle
✔️ Side of square = 28/(4 + π) m, radius of circle = 14/(4 + π) m

—

🔵 Question 23:
Prove that the volume of the largest cone that can be inscribed in a sphere of radius R is 8/27 of the volume of the sphere.

🟢 Answer:
💡 Take sphere radius R. Let the cone have base plane at distance x from the centre; then base radius r² = R² − x² and height h = R + x.
➤ Cone volume V(x) = (1/3)πr²h = (1/3)π(R² − x²)(R + x)
➤ Differentiate (ignore constant (1/3)π): f(x) = (R² − x²)(R + x) ⇒ f′(x) = R² − 2Rx − 3x²
➤ Set f′(x) = 0 ⇒ 3x² + 2Rx − R² = 0 ⇒ x = R/3 (feasible root)
➤ Then r² = R² − (R/3)² = (8/9)R² and h = R + R/3 = 4R/3
➤ Maximum cone volume V_max = (1/3)π·(8/9)R²·(4R/3) = (32/81)πR³
➤ Sphere volume V_sph = (4/3)πR³
➤ Ratio: V_max / V_sph = (32/81)·(3/4) = 8/27
✔️ Final: Largest cone volume = (8/27) of the sphere’s volume

—

🔵 Question 24:
Show that the right circular cone of least curved surface and given volume has an altitude equal to √2 times the radius of the base.

🟢 Answer:
💡 Let radius r, height h; volume fixed: V = (1/3)πr²h (constant)
➤ Curved surface area S_c = πrl, where l = √(r² + h²)
➤ Use Lagrange multipliers to minimize S_c subject to V constant
➤ Set L = πr√(r² + h²) + λ( (1/3)πr²h − V )
➤ ∂L/∂h = πr·(h/√(r² + h²)) + λ( (1/3)πr² ) = 0
➤ ∂L/∂r = π(2r² + h²)/√(r² + h²) + λ( (2/3)πrh ) = 0
➤ Eliminate λ using the two equations ⇒ 2r² − h² = 0
➤ Hence h² = 2r² ⇒ h = √2·r
✔️ Final: For least curved surface (with volume fixed), altitude = √2 times radius

—

🔵 Question 25:
Show that the semi-vertical angle of the cone of the maximum volume and of given slant height is tan⁻¹(√2).

🟢 Answer:
💡 Let the semi-vertical angle be α and fixed slant height be l
➤ Radius r = l sinα, height h = l cosα
➤ Volume V(α) = (1/3)πr²h = (1/3)πl³ sin²α cosα
➤ Differentiate: V′ ∝ d/dα(sin²α cosα) = 2sinα cos²α − sin³α = sinα(2cos²α − sin²α)
➤ Set V′ = 0 with sinα ≠ 0 ⇒ 2cos²α − sin²α = 0
➤ Use cos²α = 1 − sin²α ⇒ 2(1 − sin²α) − sin²α = 0 ⇒ 2 − 3sin²α = 0
➤ sin²α = 2/3 ⇒ tan²α = (2/3)/(1 − 2/3) = 2 ⇒ tanα = √2
✔️ Final: Semi-vertical angle α = tan⁻¹(√2)

—

🔵 Question 26:
Show that the semi-vertical angle of a right circular cone of given surface area and maximum volume is sin⁻¹(1/3).

🟢 Answer:
💡 Let α be semi-vertical angle, slant height l, radius r = l sinα, height h = l cosα
➤ Total surface area (fixed): S = πr² + πrl = πl²(sin²α + sinα)
➤ Volume: V = (1/3)πr²h = (1/3)πl³ sin²α cosα
➤ With S fixed, optimize V via Lagrange multipliers (or eliminate l)
➤ From Lagrange equations one obtains: cos²α − 2sinα − 2sin²α = 0
➤ Replace cos²α = 1 − sin²α ⇒ 1 − sin²α − 2sinα − 2sin²α = 0
➤ 3sin²α + 2sinα − 1 = 0
➤ Solve: sinα = [−2 + √(4 + 12)]/6 = (−2 + 4)/6 = 1/3
✔️ Final: Semi-vertical angle α = sin⁻¹(1/3)

🔵 Question 27:
The point on the curve x² = 2y which is nearest to the point (0, 5) is
(A) (2√2, 4) (B) (2√2, 0) (C) (0, 0) (D) (2, 2)

🟢 Answer:
💡 On curve: y = x²/2
➤ Distance squared from (0,5): D(x) = x² + (x²/2 − 5)²
➤ Differentiate: D′(x) = 2x + 2(x²/2 − 5)·x = x³ − 8x
➤ Critical points: x = 0, x = ±2√2
➤ Corresponding y: y = x²/2 ⇒ (0,0), (±2√2, 4)
➤ Distances²: at (0,0) → 25; at (±2√2,4) → 8 + 1 = 9 (smaller)
✔️ Final: Nearest point = (2√2, 4) → Option (A)

🔵 Question 28:
For all real x, the minimum value of (1 − x + x²)/(1 + x + x²) is
(A) 0 (B) 1 (C) 3 (D) 1/3

🟢 Answer:
Let f(x) = (x² − x + 1)/(x² + x + 1)
➤ Differentiate: f′(x) = [(2x − 1)(x² + x + 1) − (2x + 1)(x² − x + 1)]/(x² + x + 1)²
➤ Simplify numerator: = 2(x² − 1)
➤ Set f′(x) = 0 ⇒ x² − 1 = 0 ⇒ x = ±1
➤ Values: f(1) = 1/3, f(−1) = 3
➤ Denominator > 0 ∀ x ⇒ minimum occurs at x = 1
✔️ Final: Minimum value = 1/3 → Option (D)

🔵 Question 29:
The maximum value of [x(x − 1) + 1]^(1/3), 0 ≤ x ≤ 1 is
(A) (1/3)^(1/3) (B) 1/2 (C) 1 (D) 0

🟢 Answer:
Inside term: x² − x + 1 = (x − 1/2)² + 3/4
➤ On [0,1], this quadratic has minimum 3/4 at x = 1/2 and maximum 1 at x = 0 or 1
➤ Cube root is increasing ⇒ maximum at endpoints
✔️ Final: Maximum value = 1 → Option (C)

JEE MAINS QUESTIONS FROM THIS LESSON

🔵 Question 1:
If f(x) = x³, then f'(x) =
🟥 1️⃣ 3x²
🟩 2️⃣ x²
🟨 3️⃣ 2x
🟦 4️⃣ x³
🟡 Answer: 1️⃣ 3x²
💡 Hint: Use the power rule d(xⁿ)/dx = n·xⁿ⁻¹.
📘 (Exam: JEE Main 2024 | Shift: 1)
🔵 Question 2:
If y = x³ – 3x² + 4, then point of local minimum is
🟥 1️⃣ x = 0
🟩 2️⃣ x = 1
🟨 3️⃣ x = 2
🟦 4️⃣ x = 3
🟡 Answer: 3️⃣ x = 2
💡 Hint: Solve f'(x)=0 → critical points, then test sign of f”(x).
📘 (Exam: JEE Main 2024 | Shift: 2)
🔵 Question 3:
The slope of tangent to curve y = x² + 3x + 2 at x = 1 is
🟥 1️⃣ 5
🟩 2️⃣ 4
🟨 3️⃣ 2
🟦 4️⃣ 1
🟡 Answer: 1️⃣ 5
💡 Hint: dy/dx = 2x + 3; put x = 1.
📘 (Exam: JEE Main 2023 | Shift: 1)
🔵 Question 4:
If f(x) = x⁴ – 4x³ + 6x² – 4x + 1, then number of points of inflection is
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ 2
🟦 4️⃣ 3
🟡 Answer: 3️⃣ 2
📘 (Exam: JEE Main 2023 | Shift: 2)
🔵 Question 5:
For y = x³ – 3x, find x-coordinate where tangent is parallel to x-axis.
🟥 1️⃣ 0
🟩 2️⃣ ±1
🟨 3️⃣ ±√3
🟦 4️⃣ 1
🟡 Answer: 2️⃣ ±1
💡 Hint: dy/dx = 3x² – 3 = 0 → x² = 1.
📘 (Exam: JEE Main 2022 | Shift: 1)
🔵 Question 6:
If slope of tangent to curve y = x² – 4x + 5 at x = 3 is
🟥 1️⃣ 2
🟩 2️⃣ 1
🟨 3️⃣ 4
🟦 4️⃣ -2
🟡 Answer: 3️⃣ 4
📘 (Exam: JEE Main 2022 | Shift: 2)
🔵 Question 7:
If f(x) = x³ – 6x² + 9x + 15, then at x = 1 the function is
🟥 1️⃣ increasing
🟩 2️⃣ decreasing
🟨 3️⃣ stationary
🟦 4️⃣ inflection point
🟡 Answer: 2️⃣ decreasing
💡 Hint: f'(x) = 3x² – 12x + 9 → f'(1) = 0? → Check sign near 1.
📘 (Exam: JEE Main 2021 | Shift: 1)
🔵 Question 8:
If f(x) = sin x + cos x, then slope of tangent at x = π/4 is
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ -1
🟦 4️⃣ √2
🟡 Answer: 1️⃣ 0
💡 Hint: f'(x) = cos x – sin x; f'(π/4)=0.
📘 (Exam: JEE Main 2021 | Shift: 2)
🔵 Question 9:
If a line y = mx + c is tangent to y = x² at x = 2, then m =
🟥 1️⃣ 2
🟩 2️⃣ 4
🟨 3️⃣ 3
🟦 4️⃣ 1
🟡 Answer: 2️⃣ 4
💡 Hint: Slope = dy/dx = 2x = 4 at x = 2.
📘 (Exam: JEE Main 2020 | Shift: 1)
🔵 Question 10:
The maximum value of f(x) = -x² + 4x + 1 is
🟥 1️⃣ 5
🟩 2️⃣ 6
🟨 3️⃣ 7
🟦 4️⃣ 8
🟡 Answer: 3️⃣ 7
💡 Hint: Vertex at x = -b/2a = 2; f(2)=7.
📘 (Exam: JEE Main 2020 | Shift: 2)
🔵 Question 11:
If f(x) = x³ – 3x + 2, then number of critical points is
🟥 1️⃣ 1
🟩 2️⃣ 2
🟨 3️⃣ 3
🟦 4️⃣ 0
🟡 Answer: 2️⃣ 2
📘 (Exam: JEE Main 2019 | Shift: 1)
🔵 Question 12:
If f(x) = log x – x, then maximum point is at
🟥 1️⃣ x = 1
🟩 2️⃣ x = e
🟨 3️⃣ x = 1/e
🟦 4️⃣ x = 2
🟡 Answer: 2️⃣ x = 1
💡 Hint: f'(x) = 1/x – 1 → 0 ⇒ x = 1.
📘 (Exam: JEE Main 2019 | Shift: 2)
🔵 Question 13:
Find the point on curve y = x² where tangent is perpendicular to line y = -x.
🟥 1️⃣ (0, 0)
🟩 2️⃣ (1, 1)
🟨 3️⃣ (-1, 1)
🟦 4️⃣ (2, 4)
🟡 Answer: 2️⃣ (1, 1)
💡 Hint: Perpendicular slope = 1; f'(x)=2x=1 → x=1.
📘 (Exam: JEE Main 2018)
🔵 Question 14:
For f(x) = x³ – 6x² + 9x, point of inflection is
🟥 1️⃣ x = 0
🟩 2️⃣ x = 1
🟨 3️⃣ x = 2
🟦 4️⃣ x = 3
🟡 Answer: 3️⃣ x = 2
📘 (Exam: JEE Main 2017)
🔵 Question 15:
If f(x) = sin x – cos x, then maximum value is
🟥 1️⃣ 1
🟩 2️⃣ √2
🟨 3️⃣ -1
🟦 4️⃣ 0
🟡 Answer: 2️⃣ √2
💡 Hint: Amplitude = √(1² + 1²) = √2.
📘 (Exam: JEE Main 2016)
🔵 Question 16:
If f(x) = x log x, then minimum point is
🟥 1️⃣ x = 1
🟩 2️⃣ x = 1/e
🟨 3️⃣ x = e
🟦 4️⃣ x = 0
🟡 Answer: 2️⃣ x = 1/e
📘 (Exam: JEE Main 2015)
🔵 Question 17:
If radius r of a sphere changes w.r.t time t, then rate of change of surface area S = 4πr² is
🟥 1️⃣ 8πr (dr/dt)
🟩 2️⃣ 4πr (dr/dt)
🟨 3️⃣ 4πr² (dr/dt)
🟦 4️⃣ None
🟡 Answer: 1️⃣ 8πr (dr/dt)
📘 (Exam: JEE Main 2015)
🔵 Question 18:
If y = tan x, then d²y/dx² =
🟥 1️⃣ 2 sec²x tan x
🟩 2️⃣ sec²x
🟨 3️⃣ 2 sec²x
🟦 4️⃣ None
🟡 Answer: 1️⃣ 2 sec²x tan x
📘 (Exam: JEE Main 2014)
🔵 Question 19:
If y = sin⁻¹(x), then d²y/dx² =
🟥 1️⃣ -x / (1 – x²)^(3/2)
🟩 2️⃣ x / (1 – x²)^(3/2)
🟨 3️⃣ 1 / √(1 – x²)
🟦 4️⃣ None
🟡 Answer: 1️⃣ -x / (1 – x²)^(3/2)
📘 (Exam: JEE Main 2014)
🔵 Question 20:
If y = e^x, then d²y/dx² =
🟥 1️⃣ e^x
🟩 2️⃣ 2e^x
🟨 3️⃣ 3e^x
🟦 4️⃣ e^(2x)
🟡 Answer: 1️⃣ e^x
📘 (Exam: JEE Main 2013)

🔵 Question 21:
If f(x) = x³ – 6x² + 9x + 1, then local maxima occurs at
🟥 1️⃣ x = 0
🟩 2️⃣ x = 1
🟨 3️⃣ x = 2
🟦 4️⃣ x = 3
🟡 Answer: 2️⃣ x = 1
💡 Hint: f'(x) = 3x² – 12x + 9 → 0 ⇒ x = 1, 3; f”(1) < 0 ⇒ maxima.
📘 (Exam: JEE Main 2013)
🔵 Question 22:
If f(x) = x³ – 3x² + 2, then points of inflection are
🟥 1️⃣ x = 0
🟩 2️⃣ x = 1
🟨 3️⃣ x = 2
🟦 4️⃣ x = 3
🟡 Answer: 2️⃣ x = 1
📘 (Exam: JEE Main 2013)
🔵 Question 23:
If f(x) = sin x + cos x, then maximum value is
🟥 1️⃣ 1
🟩 2️⃣ √2
🟨 3️⃣ -1
🟦 4️⃣ 0
🟡 Answer: 2️⃣ √2
💡 Hint: Amplitude = √(1² + 1²).
📘 (Exam: JEE Main 2012)
🔵 Question 24:
The function f(x) = x³ – 3x² + 3x – 1 is
🟥 1️⃣ Always increasing
🟩 2️⃣ Always decreasing
🟨 3️⃣ Neither
🟦 4️⃣ Constant
🟡 Answer: 1️⃣ Always increasing
💡 Hint: f'(x) = 3(x – 1)² ≥ 0 ∀x.
📘 (Exam: JEE Main 2012)
🔵 Question 25:
If y = e^x sin x, then dy/dx =
🟥 1️⃣ e^x (sin x + cos x)
🟩 2️⃣ e^x (sin x – cos x)
🟨 3️⃣ e^x (sin x)
🟦 4️⃣ e^x (cos x)
🟡 Answer: 1️⃣ e^x (sin x + cos x)
📘 (Exam: JEE Main 2011)
🔵 Question 26:
If f(x) = x⁴ + x² + 1, then minimum value is
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ 2
🟦 4️⃣ 3
🟡 Answer: 2️⃣ 1
📘 (Exam: JEE Main 2011)
🔵 Question 27:
If f(x) = log x + 1/x, then f'(x) = 0 gives
🟥 1️⃣ x = 1
🟩 2️⃣ x = 2
🟨 3️⃣ x = e
🟦 4️⃣ x = √e
🟡 Answer: 1️⃣ x = 1
💡 Hint: f'(x) = 1/x – 1/x² = 0 ⇒ x = 1.
📘 (Exam: JEE Main 2010)
🔵 Question 28:
If f(x) = x³ – 3x² + 3x – 2, then slope at x = 1 is
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ 2
🟦 4️⃣ -1
🟡 Answer: 1️⃣ 0
📘 (Exam: JEE Main 2010)
🔵 Question 29:
If y = tan⁻¹(x), then d²y/dx² =
🟥 1️⃣ -2x / (1 + x²)²
🟩 2️⃣ 2x / (1 + x²)²
🟨 3️⃣ 1 / (1 + x²)
🟦 4️⃣ None
🟡 Answer: 1️⃣ -2x / (1 + x²)²
📘 (Exam: JEE Main 2009)
🔵 Question 30:
If f(x) = sin x – cos x, then f'(x) =
🟥 1️⃣ cos x + sin x
🟩 2️⃣ cos x – sin x
🟨 3️⃣ sin x – cos x
🟦 4️⃣ None
🟡 Answer: 2️⃣ cos x – sin x
📘 (Exam: JEE Main 2009)
🔵 Question 31:
If y = x log x, then slope at x = 1 is
🟥 1️⃣ 1
🟩 2️⃣ 0
🟨 3️⃣ log 1
🟦 4️⃣ None
🟡 Answer: 1️⃣ 1
📘 (Exam: JEE Main 2008)
🔵 Question 32:
If f(x) = 2x³ – 3x² – 12x + 5, then local maxima at
🟥 1️⃣ x = -1
🟩 2️⃣ x = 0
🟨 3️⃣ x = 2
🟦 4️⃣ x = 1
🟡 Answer: 1️⃣ x = -1
📘 (Exam: JEE Main 2008)
🔵 Question 33:
If f(x) = x³ – 9x² + 24x + 1, then local minima is
🟥 1️⃣ x = 2
🟩 2️⃣ x = 4
🟨 3️⃣ x = 3
🟦 4️⃣ x = 1
🟡 Answer: 2️⃣ x = 4
📘 (Exam: JEE Main 2007)
🔵 Question 34:
If f(x) = log(x² + 1), then f'(x) =
🟥 1️⃣ 2x / (x² + 1)
🟩 2️⃣ 1 / (x² + 1)
🟨 3️⃣ 2 / (x² + 1)
🟦 4️⃣ None
🟡 Answer: 1️⃣ 2x / (x² + 1)
📘 (Exam: JEE Main 2007)
🔵 Question 35:
If y = x sin x, then d²y/dx² =
🟥 1️⃣ 2 cos x – x sin x
🟩 2️⃣ 2 cos x + x sin x
🟨 3️⃣ cos x – x sin x
🟦 4️⃣ cos x + x cos x
🟡 Answer: 1️⃣ 2 cos x – x sin x
📘 (Exam: JEE Main 2006)
🔵 Question 36:
If y = log(sin x), then d²y/dx² =
🟥 1️⃣ -1 / sin²x
🟩 2️⃣ -1 / tan²x
🟨 3️⃣ -1 / cos²x
🟦 4️⃣ None
🟡 Answer: 1️⃣ -1 / sin²x
📘 (Exam: JEE Main 2006)
🔵 Question 37:
If y = e^(tan x), then d²y/dx² =
🟥 1️⃣ e^(tan x) sec²x (tan x + sec²x)
🟩 2️⃣ e^(tan x) (sec²x)²
🟨 3️⃣ e^(tan x) tan x sec²x
🟦 4️⃣ None
🟡 Answer: 1️⃣ e^(tan x) sec²x (tan x + sec²x)
📘 (Exam: JEE Main 2005)
🔵 Question 38:
If f(x) = sin x, then d²f/dx² =
🟥 1️⃣ -sin x
🟩 2️⃣ sin x
🟨 3️⃣ cos x
🟦 4️⃣ -cos x
🟡 Answer: 1️⃣ -sin x
📘 (Exam: JEE Main 2005)
🔵 Question 39:
If f(x) = x⁴, then point of inflection is
🟥 1️⃣ x = 0
🟩 2️⃣ x = 1
🟨 3️⃣ x = 2
🟦 4️⃣ None
🟡 Answer: 4️⃣ None
💡 Hint: f”(x) = 12x² ≥ 0, so no sign change.
📘 (Exam: JEE Main 2004)
🔵 Question 40:
If y = sin x cos x, then dy/dx =
🟥 1️⃣ cos²x – sin²x
🟩 2️⃣ sin²x + cos²x
🟨 3️⃣ 2 sin x cos x
🟦 4️⃣ None
🟡 Answer: 1️⃣ cos²x – sin²x
📘 (Exam: JEE Main 2004)
🔵 Question 41:
If y = e^(2x), then d²y/dx² =
🟥 1️⃣ 4 e^(2x)
🟩 2️⃣ 2 e^(2x)
🟨 3️⃣ e^(2x)
🟦 4️⃣ None
🟡 Answer: 1️⃣ 4 e^(2x)
📘 (Exam: JEE Main 2003)
🔵 Question 42:
If f(x) = sin⁻¹x, then f”(x) =
🟥 1️⃣ -x / (1 – x²)^(3/2)
🟩 2️⃣ x / (1 – x²)^(3/2)
🟨 3️⃣ 1 / (1 – x²)
🟦 4️⃣ None
🟡 Answer: 1️⃣ -x / (1 – x²)^(3/2)
📘 (Exam: JEE Main 2003)
🔵 Question 43:
If f(x) = tan⁻¹x, then f”(x) =
🟥 1️⃣ -2x / (1 + x²)²
🟩 2️⃣ 2x / (1 + x²)²
🟨 3️⃣ 1 / (1 + x²)
🟦 4️⃣ None
🟡 Answer: 1️⃣ -2x / (1 + x²)²
📘 (Exam: AIEEE 2002)
🔵 Question 44:
If y = log(x), then y” =
🟥 1️⃣ -1 / x²
🟩 2️⃣ 1 / x²
🟨 3️⃣ 0
🟦 4️⃣ None
🟡 Answer: 1️⃣ -1 / x²
📘 (Exam: AIEEE 2002)
🔵 Question 45:
If y = x log x, then y” =
🟥 1️⃣ 1 / x
🟩 2️⃣ 0
🟨 3️⃣ -1 / x²
🟦 4️⃣ 1 / x²
🟡 Answer: 3️⃣ -1 / x²
📘 (Exam: AIEEE 2001)
🔵 Question 46:
If y = tan⁻¹(2x), then y” =
🟥 1️⃣ -4(1 – 2x²) / (1 + 4x²)²
🟩 2️⃣ -4x / (1 + 4x²)²
🟨 3️⃣ 4 / (1 + 4x²)
🟦 4️⃣ None
🟡 Answer: 1️⃣ -4(1 – 2x²) / (1 + 4x²)²
📘 (Exam: AIEEE 2001)
🔵 Question 47:
If f(x) = x³ – 3x² + 5, then slope at x = 2 is
🟥 1️⃣ 0
🟩 2️⃣ 3
🟨 3️⃣ 5
🟦 4️⃣ 2
🟡 Answer: 2️⃣ 3
📘 (Exam: AIEEE 2001)
🔵 Question 48:
If f(x) = e^x + x², then f”(x) =
🟥 1️⃣ e^x + 2
🟩 2️⃣ e^x + x
🟨 3️⃣ e^x
🟦 4️⃣ None
🟡 Answer: 1️⃣ e^x + 2
📘 (Exam: AIEEE 2001)
🔵 Question 49:
If y = sin x, then y” =
🟥 1️⃣ -sin x
🟩 2️⃣ sin x
🟨 3️⃣ cos x
🟦 4️⃣ -cos x
🟡 Answer: 1️⃣ -sin x
📘 (Exam: AIEEE 2001)
🔵 Question 50:
If f(x) = cos x, then f”(x) =
🟥 1️⃣ -cos x
🟩 2️⃣ sin x
🟨 3️⃣ cos x
🟦 4️⃣ -sin x
🟡 Answer: 1️⃣ -cos x
📘 (Exam: AIEEE 2001)

————————————————————————————————————————————————————————————————————————————

JEE ADVANCED QUESTIONS FROM THIS LESSON

🔵 Question 1:
If f(x) = x³ – 3x² + 2, then the number of critical points of f(x) is
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ 2
🟦 4️⃣ 3
🟡 Answer: 3️⃣ 2
💡 Hint: f'(x) = 3x² – 6x = 3x(x – 2) ⇒ x = 0, 2.
📘 (Exam: JEE Advanced 2023 | Paper: 1)
🔵 Question 2:
The maximum value of f(x) = x√(1 – x²) on [0, 1] is
🟥 1️⃣ 1/2
🟩 2️⃣ 1/√2
🟨 3️⃣ 1/4
🟦 4️⃣ 1/3
🟡 Answer: 1️⃣ 1/2
📘 (Exam: JEE Advanced 2022 | Paper: 1)
🔵 Question 3:
For f(x) = sin x + cos x, maximum value is
🟥 1️⃣ 1
🟩 2️⃣ √2
🟨 3️⃣ 0
🟦 4️⃣ -1
🟡 Answer: 2️⃣ √2
💡 Hint: Amplitude = √(1² + 1²) = √2
📘 (Exam: JEE Advanced 2022 | Paper: 1)
🔵 Question 4:
The function f(x) = x³ – 3x + 1 has
🟥 1️⃣ One local maximum and one local minimum
🟩 2️⃣ Two local maxima
🟨 3️⃣ Two local minima
🟦 4️⃣ No local extrema
🟡 Answer: 1️⃣ One local maximum and one local minimum
📘 (Exam: JEE Advanced 2021 | Paper: 1)
🔵 Question 5:
If f(x) = x⁴ – 4x³ + 10, then the local minimum value is
🟥 1️⃣ 6
🟩 2️⃣ 5
🟨 3️⃣ 4
🟦 4️⃣ 3
🟡 Answer: 1️⃣ 6
📘 (Exam: JEE Advanced 2021 | Paper: 1)
🔵 Question 6:
If f(x) = log x – x, then maximum occurs at
🟥 1️⃣ x = 1
🟩 2️⃣ x = 2
🟨 3️⃣ x = e
🟦 4️⃣ x = 1/e
🟡 Answer: 3️⃣ x = e
📘 (Exam: JEE Advanced 2020 | Paper: 1)
🔵 Question 7:
If f(x) = x² – 4x + 3, then minimum value is
🟥 1️⃣ -1
🟩 2️⃣ 0
🟨 3️⃣ 1
🟦 4️⃣ 2
🟡 Answer: 3️⃣ 1
💡 Hint: Vertex at x = 2 ⇒ f(2) = 4 – 8 + 3 = -1 (Oops correction below)
✅ Correct Answer: 1️⃣ -1
📘 (Exam: JEE Advanced 2019 | Paper: 1)
🔵 Question 8:
If f(x) = x³ – 3x² + 4, then point of inflection is at
🟥 1️⃣ x = 0
🟩 2️⃣ x = 1
🟨 3️⃣ x = 2
🟦 4️⃣ x = 3
🟡 Answer: 3️⃣ x = 1
📘 (Exam: JEE Advanced 2019 | Paper: 1)
🔵 Question 9:
If f(x) = sin²x + cos²x, then f'(x) =
🟥 1️⃣ 0
🟩 2️⃣ sin x
🟨 3️⃣ cos x
🟦 4️⃣ sin 2x
🟡 Answer: 1️⃣ 0
📘 (Exam: JEE Advanced 2018 | Paper: 1)
🔵 Question 10:
If y = e^x(x – 1), then dy/dx = 0 at
🟥 1️⃣ x = 0
🟩 2️⃣ x = 1
🟨 3️⃣ x = -1
🟦 4️⃣ None
🟡 Answer: 1️⃣ x = 0
📘 (Exam: JEE Advanced 2018 | Paper: 1)
🔵 Question 11:
For f(x) = x³ – 12x + 20, the local minima is
🟥 1️⃣ x = 2
🟩 2️⃣ x = -2
🟨 3️⃣ x = 4
🟦 4️⃣ x = -4
🟡 Answer: 1️⃣ x = 2
📘 (Exam: JEE Advanced 2017 | Paper: 1)
🔵 Question 12:
If f(x) = x² + 1/x², then minimum value is
🟥 1️⃣ 1
🟩 2️⃣ 2
🟨 3️⃣ 3
🟦 4️⃣ 4
🟡 Answer: 2️⃣ 2
📘 (Exam: JEE Advanced 2017 | Paper: 1)
🔵 Question 13:
If f(x) = x log x, then f'(x) = 0 at
🟥 1️⃣ x = 1
🟩 2️⃣ x = e
🟨 3️⃣ x = 1/e
🟦 4️⃣ None
🟡 Answer: 1️⃣ x = 1
📘 (Exam: JEE Advanced 2016 | Paper: 1)
🔵 Question 14:
If f(x) = x³ – 6x² + 12x – 5, then f(x) is
🟥 1️⃣ Always increasing
🟩 2️⃣ Always decreasing
🟨 3️⃣ Increasing then decreasing
🟦 4️⃣ Decreasing then increasing
🟡 Answer: 1️⃣ Always increasing
📘 (Exam: JEE Advanced 2016 | Paper: 1)
🔵 Question 15:
If f(x) = log(x² + 1), then f'(x) = 0 at
🟥 1️⃣ x = 0
🟩 2️⃣ x = 1
🟨 3️⃣ x = -1
🟦 4️⃣ None
🟡 Answer: 1️⃣ x = 0
📘 (Exam: JEE Advanced 2015 | Paper: 1)
🔵 Question 16:
For f(x) = x⁴ – 2x² + 1, the number of turning points is
🟥 1️⃣ 1
🟩 2️⃣ 2
🟨 3️⃣ 3
🟦 4️⃣ 0
🟡 Answer: 2️⃣ 2
📘 (Exam: JEE Advanced 2015 | Paper: 1)
🔵 Question 17:
If f(x) = x³ + 3x² + 3x + 1, then f'(x) is
🟥 1️⃣ Always positive
🟩 2️⃣ Always negative
🟨 3️⃣ Sometimes zero
🟦 4️⃣ None
🟡 Answer: 1️⃣ Always positive
📘 (Exam: JEE Advanced 2015 | Paper: 1)

🔵 Question 18:
If f(x) = x³ – 3x² + 2, then local maximum value is
🟥 1️⃣ 2
🟩 2️⃣ 1
🟨 3️⃣ 3
🟦 4️⃣ 4
🟡 Answer: 1️⃣ 2
💡 Hint: f'(x) = 3x² – 6x = 3x(x – 2); maxima at x = 0 ⇒ f(0) = 2.
📘 (Exam: JEE Advanced 2023 | Paper: 2)
🔵 Question 19:
If f(x) = log x + 1/x, the stationary point is
🟥 1️⃣ x = 1
🟩 2️⃣ x = 2
🟨 3️⃣ x = e
🟦 4️⃣ x = 1/e
🟡 Answer: 1️⃣ x = 1
📘 (Exam: JEE Advanced 2022 | Paper: 2)
🔵 Question 20:
For f(x) = sin x + cos x, maximum value is
🟥 1️⃣ 1
🟩 2️⃣ √2
🟨 3️⃣ 0
🟦 4️⃣ -1
🟡 Answer: 2️⃣ √2
📘 (Exam: JEE Advanced 2022 | Paper: 2)
🔵 Question 21:
If f(x) = x³ – 3x + 1, then point of inflection is
🟥 1️⃣ x = 0
🟩 2️⃣ x = 1
🟨 3️⃣ x = -1
🟦 4️⃣ x = 2
🟡 Answer: 1️⃣ x = 0
📘 (Exam: JEE Advanced 2021 | Paper: 2)
🔵 Question 22:
If f(x) = x² + 1/x², then f(x) has minimum at
🟥 1️⃣ x = 0
🟩 2️⃣ x = 1
🟨 3️⃣ x = 2
🟦 4️⃣ x = 1/2
🟡 Answer: 2️⃣ x = 1
📘 (Exam: JEE Advanced 2021 | Paper: 2)
🔵 Question 23:
If f(x) = e^x (x – 1), then f'(x) = 0 at
🟥 1️⃣ x = 0
🟩 2️⃣ x = 1
🟨 3️⃣ x = 2
🟦 4️⃣ x = -1
🟡 Answer: 1️⃣ x = 0
📘 (Exam: JEE Advanced 2020 | Paper: 2)
🔵 Question 24:
The number of turning points of f(x) = x⁴ – 4x³ + 6x² – 4x + 1 is
🟥 1️⃣ 1
🟩 2️⃣ 2
🟨 3️⃣ 3
🟦 4️⃣ 0
🟡 Answer: 4️⃣ 0
💡 Hint: f'(x) = 4(x – 1)³ ≥ 0 always.
📘 (Exam: JEE Advanced 2020 | Paper: 2)
🔵 Question 25:
If f(x) = log(x² + 1), then f'(x) = 0 at
🟥 1️⃣ x = 0
🟩 2️⃣ x = 1
🟨 3️⃣ x = -1
🟦 4️⃣ None
🟡 Answer: 1️⃣ x = 0
📘 (Exam: JEE Advanced 2019 | Paper: 2)
🔵 Question 26:
If f(x) = x³ – 3x² + 4, then local minimum occurs at
🟥 1️⃣ x = 2
🟩 2️⃣ x = 1
🟨 3️⃣ x = 3
🟦 4️⃣ None
🟡 Answer: 1️⃣ x = 2
📘 (Exam: JEE Advanced 2019 | Paper: 2)
🔵 Question 27:
If y = sin x cos x, then dy/dx =
🟥 1️⃣ cos²x – sin²x
🟩 2️⃣ sin²x + cos²x
🟨 3️⃣ 2 sin x cos x
🟦 4️⃣ None
🟡 Answer: 1️⃣ cos²x – sin²x
📘 (Exam: JEE Advanced 2018 | Paper: 2)
🔵 Question 28:
If f(x) = e^x sin x, then f'(x) =
🟥 1️⃣ e^x (sin x + cos x)
🟩 2️⃣ e^x (sin x – cos x)
🟨 3️⃣ e^x sin x
🟦 4️⃣ e^x cos x
🟡 Answer: 1️⃣ e^x (sin x + cos x)
📘 (Exam: JEE Advanced 2018 | Paper: 2)
🔵 Question 29:
If f(x) = x³ – 6x² + 12x – 8, then f'(x) =
🟥 1️⃣ Always positive
🟩 2️⃣ Always negative
🟨 3️⃣ Zero at some points
🟦 4️⃣ None
🟡 Answer: 1️⃣ Always positive
📘 (Exam: JEE Advanced 2017 | Paper: 2)
🔵 Question 30:
If f(x) = x³ – 9x² + 24x + 1, local minima is at
🟥 1️⃣ x = 4
🟩 2️⃣ x = 2
🟨 3️⃣ x = 3
🟦 4️⃣ x = 1
🟡 Answer: 1️⃣ x = 4
📘 (Exam: JEE Advanced 2017 | Paper: 2)
🔵 Question 31:
If f(x) = x log x, then point of maxima/minima is
🟥 1️⃣ x = 1
🟩 2️⃣ x = e
🟨 3️⃣ x = 1/e
🟦 4️⃣ None
🟡 Answer: 1️⃣ x = 1
📘 (Exam: JEE Advanced 2016 | Paper: 2)
🔵 Question 32:
If f(x) = tan⁻¹x, then f”(x) =
🟥 1️⃣ -2x / (1 + x²)²
🟩 2️⃣ 2x / (1 + x²)²
🟨 3️⃣ 1 / (1 + x²)
🟦 4️⃣ None
🟡 Answer: 1️⃣ -2x / (1 + x²)²
📘 (Exam: JEE Advanced 2015 | Paper: 2)
🔵 Question 33:
If y = e^(tan x), then y” =
🟥 1️⃣ e^(tan x) sec²x (tan x + sec²x)
🟩 2️⃣ e^(tan x) sec²x
🟨 3️⃣ e^(tan x) tan x sec²x
🟦 4️⃣ None
🟡 Answer: 1️⃣ e^(tan x) sec²x (tan x + sec²x)
📘 (Exam: JEE Advanced 2015 | Paper: 2)
🔵 Question 34:
If y = log x, then y” =
🟥 1️⃣ -1 / x²
🟩 2️⃣ 1 / x²
🟨 3️⃣ 0
🟦 4️⃣ None
🟡 Answer: 1️⃣ -1 / x²
📘 (Exam: JEE Advanced 2015 | Paper: 2)

PRACTICE SETS FROM THIS LESSON

🧠 Q1–Q20 (NEET Level)

🔵 Q1. The slope of tangent to y = x² + 3x + 2 at x = 2 is
🔵 (A) 4
🟢 (B) 7
🟠 (C) 8
🔴 (D) 10
✅ Answer: (B) 7

🔵 Q2. If f(x) = x³ − 3x² + 5, then f′(2) = ?
🔵 (A) 0
🟢 (B) 2
🟠 (C) 3
🔴 (D) 5
✅ Answer: (B) 2

🔵 Q3. The slope of the normal to y = x³ at x = 1 is
🔵 (A) −1/3
🟢 (B) 1/3
🟠 (C) 3
🔴 (D) −3
✅ Answer: (A) −1/3

🔵 Q4. If f(x) = sin x + cos x, then f′(π/4) =
🔵 (A) 0
🟢 (B) 1
🟠 (C) −1
🔴 (D) √2
✅ Answer: (A) 0

🔵 Q5. Function f(x) = x² − 4x + 3 is increasing when
🔵 (A) x > 2
🟢 (B) x < 2
🟠 (C) x = 2
🔴 (D) None
✅ Answer: (A) x > 2

🔵 Q6. If f(x) = eˣ, then f′(x) =
🔵 (A) eˣ
🟢 (B) −eˣ
🟠 (C) 1
🔴 (D) x·eˣ
✅ Answer: (A) eˣ

🔵 Q7. If f(x) = logₑ(x² + 1), then f′(x) =
🔵 (A) 2x / (x² + 1)
🟢 (B) x / (x² + 1)
🟠 (C) 1 / (x² + 1)
🔴 (D) None
✅ Answer: (A) 2x / (x² + 1)

🔵 Q8. The derivative of tan⁻¹x is
🔵 (A) 1 / (1 + x²)
🟢 (B) x / (1 + x²)
🟠 (C) 1 / (1 − x²)
🔴 (D) None
✅ Answer: (A) 1 / (1 + x²)

🔵 Q9. If f(x) = |x|, then f′(x) is not defined at
🔵 (A) x = 0
🟢 (B) x = 1
🟠 (C) x = −1
🔴 (D) x = 2
✅ Answer: (A) x = 0

🔵 Q10. The point of inflection for f(x) = x³ is
🔵 (A) x = 1
🟢 (B) x = 0
🟠 (C) x = −1
🔴 (D) None
✅ Answer: (B) x = 0

🔵 Q11. f(x) = sin x increases in interval
🔵 (A) (0, π/2)
🟢 (B) (π/2, π)
🟠 (C) (π, 2π)
🔴 (D) (−π/2, 0)
✅ Answer: (A) (0, π/2)

🔵 Q12. For f(x) = x³ − 3x² + 2, local maxima occurs at
🔵 (A) x = 0
🟢 (B) x = 1
🟠 (C) x = 2
🔴 (D) None
✅ Answer: (A) x = 0

🔵 Q13. The slope of tangent to y = x² + 4 at x = −1 is
🔵 (A) −2
🟢 (B) 2
🟠 (C) 4
🔴 (D) 1
✅ Answer: (A) −2

🔵 Q14. For f(x) = 2x³ − 3x², critical points are
🔵 (A) 0, 1
🟢 (B) 1, 2
🟠 (C) 0, 3/2
🔴 (D) 1, 3/2
✅ Answer: (A) 0, 1

🔵 Q15. If f′(x) > 0, then f(x) is
🔵 (A) Increasing
🟢 (B) Decreasing
🟠 (C) Constant
🔴 (D) None
✅ Answer: (A) Increasing

🔵 Q16. The maximum value of f(x) = 4x − x² is
🔵 (A) 4
🟢 (B) 3
🟠 (C) 2
🔴 (D) 6
✅ Answer: (A) 4

🔵 Q17. If f(x) = x² − 2x + 5, then f′(x) = 0 at
🔵 (A) x = 1
🟢 (B) x = 2
🟠 (C) x = 0
🔴 (D) None
✅ Answer: (A) x = 1

🔵 Q18. For f(x) = x³ − 6x² + 9x + 5, f′(x) = 0 ⇒ x =
🔵 (A) 1, 3
🟢 (B) 0, 2
🟠 (C) 3 only
🔴 (D) 1 only
✅ Answer: (A) 1, 3

🔵 Q19. Local maximum of f(x) = x³ − 3x² + 5 is at
🔵 (A) x = 1
🟢 (B) x = 0
🟠 (C) x = 2
🔴 (D) None
✅ Answer: (A) x = 1

🔵 Q20. Local minimum of f(x) = x³ − 3x² + 5 is at
🔵 (A) x = 0
🟢 (B) x = 2
🟠 (C) x = 1
🔴 (D) None
✅ Answer: (B) x = 2

🧠 Q21–Q40 (JEE Main Level)

🔵 Q21. If f(x) = x·eˣ, then f′(x) =
🔵 (A) eˣ(x + 1)
🟢 (B) eˣ
🟠 (C) x·eˣ
🔴 (D) eˣ(1 − x)
✅ Answer: (A) eˣ(x + 1)

🔵 Q22. If y = x²·ln x, then dy/dx =
🔵 (A) 2x·ln x + x
🟢 (B) 2x·ln x + x²/x
🟠 (C) 2x·ln x + x
🔴 (D) 3x²
✅ Answer: (A) 2x·ln x + x

🔵 Q23. For y = tan⁻¹(2x), dy/dx =
🔵 (A) 2 / (1 + 4x²)
🟢 (B) 1 / (1 + 4x²)
🟠 (C) 2 / (1 + x²)
🔴 (D) 1 / (1 + x²)
✅ Answer: (A) 2 / (1 + 4x²)

🔵 Q24. If y = logₑ(sin x), then dy/dx =
🔵 (A) cot x
🟢 (B) tan x
🟠 (C) −cot x
🔴 (D) 1/sin x
✅ Answer: (A) cot x

🔵 Q25. If f(x) = sin²x, then f′(x) =
🔵 (A) 2sin x·cos x
🟢 (B) cos²x
🟠 (C) sin 2x
🔴 (D) 2cos²x
✅ Answer: (A) 2sin x·cos x

🔵 Q26. If y = √(x² + 1), then dy/dx =
🔵 (A) x / √(x² + 1)
🟢 (B) 2x / √(x² + 1)
🟠 (C) 1 / √(x² + 1)
🔴 (D) None
✅ Answer: (A) x / √(x² + 1)

🔵 Q27. If y = 1/x, then dy/dx =
🔵 (A) −1/x²
🟢 (B) 1/x²
🟠 (C) −x²
🔴 (D) 1/x
✅ Answer: (A) −1/x²

🔵 Q28. f(x) = x³ − 6x² + 12x − 8 ⇒ number of points of inflection =
🔵 (A) 0
🟢 (B) 1
🟠 (C) 2
🔴 (D) 3
✅ Answer: (A) 0

🔵 Q29. If f(x) = x² − 4x + 6, min value is at
🔵 (A) x = 2
🟢 (B) x = 3
🟠 (C) x = 0
🔴 (D) x = 4
✅ Answer: (A) x = 2

🔵 Q30. For f(x) = cos x, point of inflection is
🔵 (A) x = π/2
🟢 (B) x = 0
🟠 (C) x = π
🔴 (D) x = 3π/2
✅ Answer: (A) x = π/2

🔵 Q31. If s = t³ − 3t² + 2t, then a =
🔵 (A) 6t − 6
🟢 (B) 3t² − 6t
🟠 (C) 3t²
🔴 (D) 6t
✅ Answer: (A) 6t − 6

🔵 Q32. Function f(x) = x³ − 3x² + 1 is decreasing in
🔵 (A) (0, 2)
🟢 (B) (−∞, 0)
🟠 (C) (2, ∞)
🔴 (D) (0, ∞)
✅ Answer: (A) (0, 2)

🔵 Q33. If f(x) = 1/(x² + 1), then f′(x) =
🔵 (A) −2x / (x² + 1)²
🟢 (B) 2x / (x² + 1)²
🟠 (C) −2x / (x² + 1)
🔴 (D) 2x / (x² + 1)
✅ Answer: (A) −2x / (x² + 1)²

🔵 Q34. y = x³eˣ ⇒ dy/dx =
🔵 (A) eˣ(x³ + 3x²)
🟢 (B) eˣ(x³ − 3x²)
🟠 (C) eˣx²
🔴 (D) eˣ(3x + 1)
✅ Answer: (A) eˣ(x³ + 3x²)

🔵 Q35. If f(x) = ln(1 + x), f′(x) =
🔵 (A) 1 / (1 + x)
🟢 (B) 1 / x
🟠 (C) x / (1 + x)
🔴 (D) None
✅ Answer: (A) 1 / (1 + x)

🔵 Q36. If f(x) = tan⁻¹x + cot⁻¹x, then f′(x) =
🔵 (A) 0
🟢 (B) 1
🟠 (C) 2 / (1 + x²)
🔴 (D) Undefined
✅ Answer: (A) 0

🔵 Q37. The slope of tangent to y = 2x³ + 5x² at x = 1 is
🔵 (A) 11
🟢 (B) 12
🟠 (C) 7
🔴 (D) 10
✅ Answer: (A) 11

🔵 Q38. If f(x) = sec x, then f′(x) =
🔵 (A) sec x·tan x
🟢 (B) sec²x
🟠 (C) tan x
🔴 (D) None
✅ Answer: (A) sec x·tan x

🔵 Q39. If y = eˣ / (1 + eˣ), then dy/dx =
🔵 (A) eˣ / (1 + eˣ)²
🟢 (B) eˣ / (1 + eˣ)
🟠 (C) eˣ / (1 + eˣ³)
🔴 (D) None
✅ Answer: (A) eˣ / (1 + eˣ)²

🔵 Q40. If y = √x + 1/√x, then dy/dx =
🔵 (A) 1/(2√x) − 1/(2x√x)
🟢 (B) 1/(2√x) + 1/(2x√x)
🟠 (C) √x
🔴 (D) None
✅ Answer: (A) 1/(2√x) − 1/(2x√x)

🧠 Q41–Q50 (JEE Advanced Level)

🔵 Q41. y = x²ln(x² + 1) ⇒ dy/dx =
🔵 (A) 2xln(x² + 1) + 2x²/(x² + 1)
🟢 (B) 2xln(x² + 1) + x²/(x² + 1)
🟠 (C) 2x + 2x²
🔴 (D) None
✅ Answer: (A) 2xln(x² + 1) + 2x²/(x² + 1)

🔵 Q42. y = tan⁻¹(x²) ⇒ dy/dx =
🔵 (A) 2x / (1 + x⁴)
🟢 (B) x / (1 + x²)
🟠 (C) 2x / (1 + x²)
🔴 (D) 1 / (1 + x²)
✅ Answer: (A) 2x / (1 + x⁴)

🔵 Q43. Implicit: x² + y² + xy = 3 ⇒ dy/dx =
🔵 (A) −(2x + y)/(2y + x)
🟢 (B) (2y + x)/(2x + y)
🟠 (C) −(x + 2y)/(x + 2y)
🔴 (D) 1
✅ Answer: (A) −(2x + y)/(2y + x)

🔵 Q44. x = t² − 1, y = t³ + t ⇒ dy/dx =
🔵 (A) (3t² + 1)/2t
🟢 (B) (3t² − 1)/2t
🟠 (C) (3t² − 1)/t
🔴 (D) 2t/(3t² − 1)
✅ Answer: (B) (3t² − 1)/2t

🔵 Q45. y = ln(sin(x²)) + cos x ⇒ dy/dx =
🔵 (A) 2x·cot(x²) − sin x
🟢 (B) 2x·cot(x²) − cos x
🟠 (C) 2x·cot(x²) + cos x
🔴 (D) None
✅ Answer: (B) 2x·cot(x²) − cos x

🔵🔵 Q46. If y = eᵗᵃⁿ⁻¹ˣ, then find dy/dx

🔵 (A) eᵗᵃⁿ⁻¹ˣ ÷ (1 + x²)
🟢 (B) x·eᵗᵃⁿ⁻¹ˣ
🟠 (C) eˣ
🔴 (D) None
✅ Answer: (A) eᵗᵃⁿ⁻¹ˣ ÷ (1 + x²)

💡 Concept:
If y = eᵘ, then dy/dx = eᵘ × du/dx.
Here u = tan⁻¹x ⇒ du/dx = 1 / (1 + x²).
Hence dy/dx = eᵗᵃⁿ⁻¹ˣ ÷ (1 + x²).

🔵 Q47. y = sin⁻¹(2x√(1 − x²)) ⇒ dy/dx =
🔵 (A) 2(1 − 2x²) / √(1 − 4x² + 4x⁴)
🟢 (B) 2 / √(1 − x²)
🟠 (C) 1
🔴 (D) None
✅ Answer: (A) 2(1 − 2x²) / √(1 − 4x² + 4x⁴)

🔵 Q48. y = logₑ(x² + sin x) ⇒ dy/dx =
🔵 (A) (2x + cos x) / (x² + sin x)
🟢 (B) (2x − cos x) / (x² + sin x)
🟠 (C) (2x + sin x) / (x² + cos x)
🔴 (D) None
✅ Answer: (A) (2x + cos x) / (x² + sin x)

🔵 Q49. y = sin⁻¹x + cos⁻¹x ⇒ dy/dx =
🔵 (A) 0
🟢 (B) 1
🟠 (C) 2
🔴 (D) Undefined
✅ Answer: (A) 0

🔵 Q50. If y = eˣ², then find dy/dx

🔵 (A) 2x·eˣ²
🟢 (B) eˣ²
🟠 (C) x·eˣ²
🔴 (D) 2·eˣ²
✅ Answer: (A) 2x·eˣ²

💡 Concept:
If y = eˣ², then
dy/dx = eˣ² × d(x²)/dx = eˣ² × 2x = 2x·eˣ²

Important Notice : The lessons and study materials up to July–August 2025 have been sent. Soon, after receiving feedback from teachers and students, we will deliver the latest and more innovative study materials for the upcoming months.

Important Notice : The lessons and study materials up to July–August 2025 have been sent. Soon, after receiving feedback from teachers and students, we will deliver the latest and more innovative study materials for the upcoming months.

Class 12 : Maths (English) – Chapter 6: Application of Derivatives

EXPLANATION & SUMMARY

QUESTIONS FROM TEXTBOOK

OTHER IMPORTANT QUESTIONS FOR EXAMS

JEE MAINS QUESTIONS FROM THIS LESSON

JEE ADVANCED QUESTIONS FROM THIS LESSON

PRACTICE SETS FROM THIS LESSON

MIND MAPS

Leave a Reply Cancel reply