Class 11 : Physics (In Hindi) – अध्याय 2: सरल रेखा में गति

पाठ का विश्लेषण एवं विवेचन

🔶 1. गति क्या है? (What is Motion?)
यदि कोई वस्तु समय के साथ अपनी स्थिति बदलती है, तो वह गति में है।
जब यह परिवर्तन एक सरल रेखा में होता है, तो इसे सरल रेखा में गति कहते हैं।
यह भौतिकी की सबसे प्राथमिक और महत्वपूर्ण अवधारणाओं में से एक है।

🔷 2. स्थिति और विस्थापन (Position and Displacement)
✦ स्थिति (Position): किसी वस्तु का स्थान किसी संदर्भ बिंदु के सापेक्ष।
✦ विस्थापन (Displacement): प्रारंभिक और अंतिम स्थिति के बीच की सीधी दूरी, जिसकी दिशा भी होती है।
✅ विस्थापन एक सदिश राशि (Vector Quantity) है।

🔶 3. पथ दूरी और विस्थापन में अंतर
🔹 पथ दूरी (Path Length): वस्तु द्वारा तय की गई कुल लंबाई, अदिश राशि होती है।
🔹 विस्थापन: केवल प्रारंभ से अंत की सीधी दूरी और दिशा, सदिश होती है।
🎯 हमेशा: विस्थापन ≤ पथ दूरी

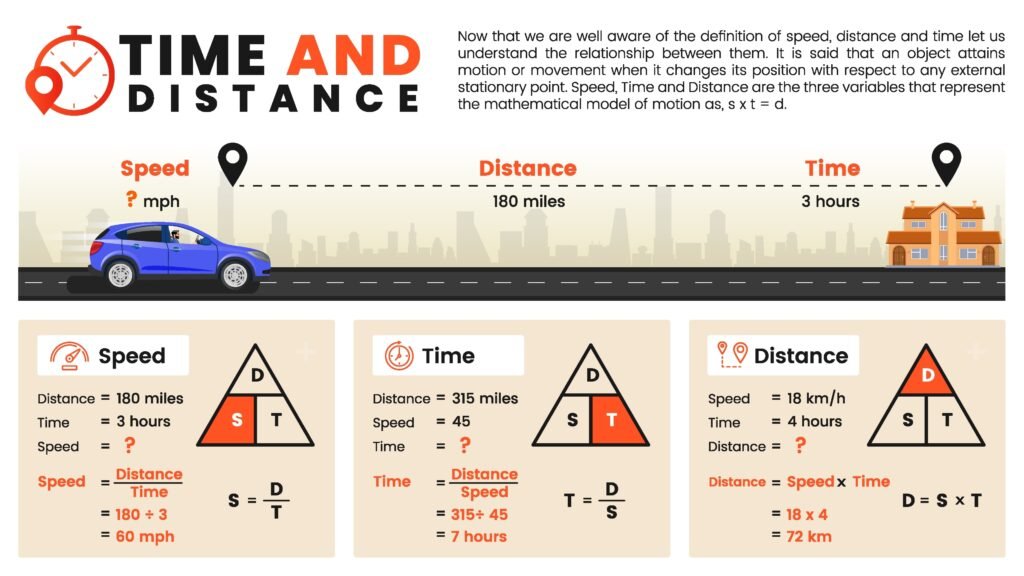
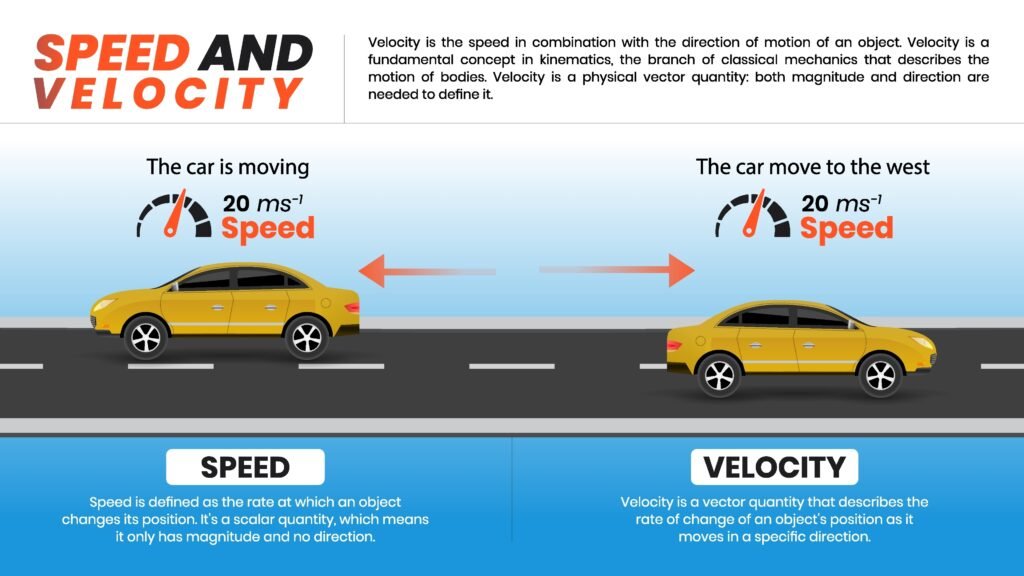
🔷 4. चाल (Speed) और वेग (Velocity)
✦ चाल = दूरी / समय
✦ वेग = विस्थापन / समय
✅ चाल अदिश, वेग सदिश होता है।
✅ SI मात्रक: m/s

🔶 5. औसत चाल और औसत वेग
✦ औसत चाल = कुल दूरी / कुल समय
✦ औसत वेग = कुल विस्थापन / कुल समय
💡 यदि वस्तु वापस अपने स्थान पर लौटे, तो विस्थापन = 0 ⇒ औसत वेग = 0

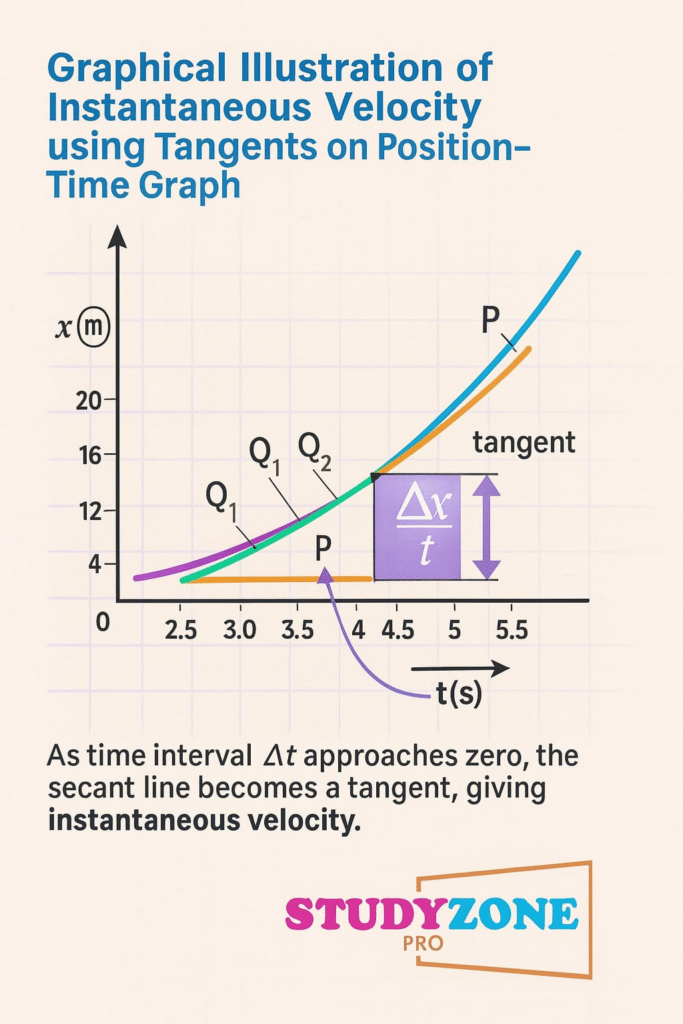
🔷 6. तात्क्षणिक वेग (Instantaneous Velocity)
➤ अत्यंत छोटे समय अंतराल में वस्तु का वेग
📌 गणना: v = dx/dt
🧠 उपयोग होता है तब, जब गति एकसमान नहीं होती

🔶 7. त्वरण (Acceleration)
✦ त्वरण = वेग में परिवर्तन / समय
🎯 SI मात्रक: m/s²
✦ धनात्मक त्वरण = वेग में वृद्धि
✦ ऋणात्मक त्वरण = वेग में कमी (Retardation)

🔷 8. तात्क्षणिक त्वरण (Instantaneous Acceleration)
📌 a = dv/dt
✦ किसी क्षण विशेष पर वेग के परिवर्तन की दर

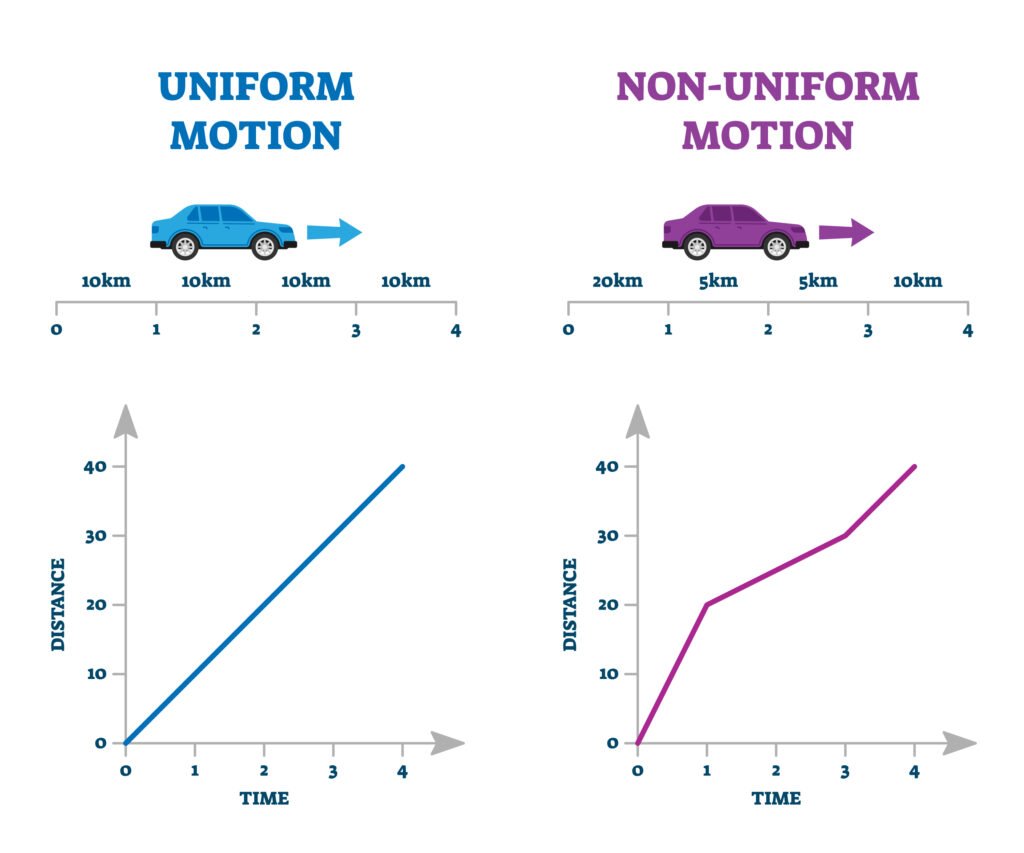
🔶 9. एकसमान गति और अनएकसमान गति
➤ एकसमान गति = चाल या वेग समय के साथ अपरिवर्तित
➤ अनएकसमान गति = वेग समय के साथ बदलता है

🔷 10. गति के समीकरण (Equations of Motion for Uniform Acceleration)
📘 यदि गति समान त्वरण से हो रही हो, तो ये 3 प्रमुख समीकरण लागू होते हैं:

① v = u + at
② s = ut + ½ at²
③ v² = u² + 2as

जहाँ:
u = प्रारंभिक वेग
v = अंतिम वेग
a = त्वरण
t = समय
s = विस्थापन

🔶 11. ग्राफ द्वारा गति का विश्लेषण (Motion via Graphs)

📍 स्थिति-समय ग्राफ (x–t):
➤ ढाल (slope) = चाल
✦ यदि रेखा सीधी है ⇒ एकसमान चाल

📍 वेग-समय ग्राफ (v–t):
➤ ढाल = त्वरण
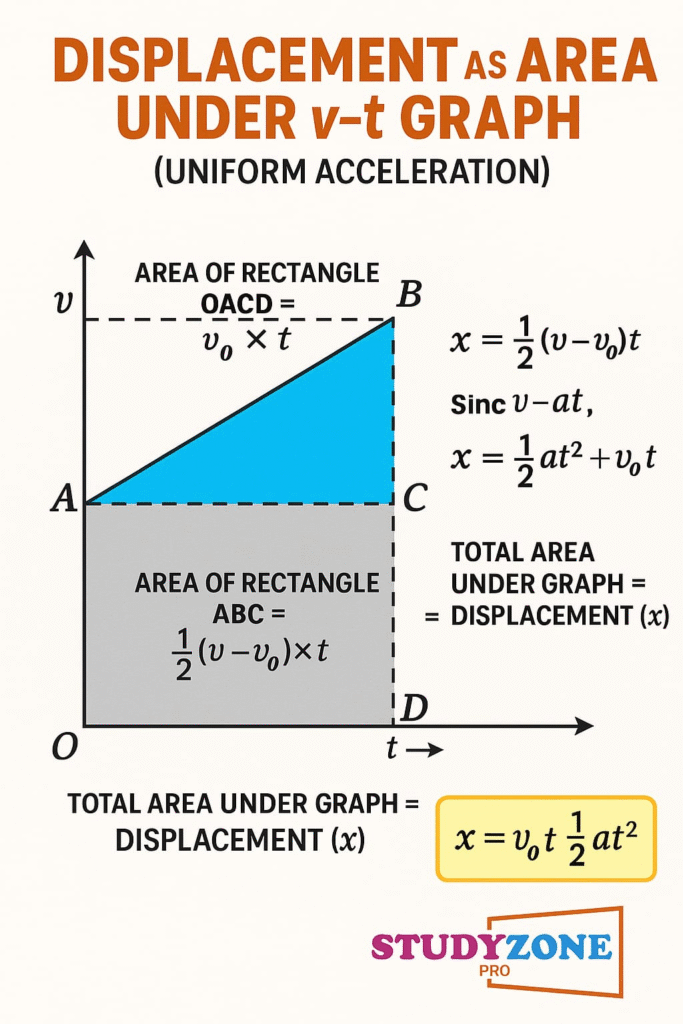
➤ क्षेत्रफल = विस्थापन

📍 त्वरण-समय ग्राफ (a–t):
➤ क्षेत्रफल = वेग में परिवर्तन

🔷 12. मुक्तपतन गति (Free Fall Motion)
✦ जब कोई वस्तु केवल गुरुत्वाकर्षण के प्रभाव से नीचे गिरती है
➤ त्वरण = g = 9.8 m/s²
➤ समीकरण वही होते हैं, बस ‘a’ की जगह ‘g’

🔶 13. संकेत और दिशा का महत्व
➤ जब हम किसी दिशा को +ve और किसी को –ve मानते हैं, तो गणनाओं में संकेतों का बहुत बड़ा योगदान होता है।
✦ यह विशेषकर गुरुत्वीय गति या ऊपर/नीचे फेंकी गई वस्तुओं के लिए आवश्यक है।

🔷 14. पुनरावृत्त गति और सरल गति में अंतर
✦ पुनरावृत्त गति: जो दोहराई जाए, जैसे दोलन
✦ सरल गति: सीधी रेखा में एक बार की गई गति

🔶 15. अनुप्रयोग (Applications of Rectilinear Motion)
✅ ट्राफिक विश्लेषण
✅ वाहन की गति की गणना
✅ मुक्तपतन व प्रक्षेप गति
✅ भूकंपीय तरंगों का अध्ययन
✅ उपग्रह गति निर्धारण

✦✦✦✦✦✦✦✦✦✦✦✦✦✦✦✦✦✦✦✦✦✦✦

🌟 Code 1 – संक्षेप (Summary – ~300 शब्द)

“सरल रेखा में गति” अध्याय में हमने गति की मौलिक अवधारणाओं को सीखा।
जब कोई वस्तु सीधी रेखा में अपनी स्थिति बदलती है, तो उसे सरल गति कहा जाता है। इसमें स्थिति, विस्थापन, दूरी, चाल, वेग और त्वरण जैसे आधारभूत सिद्धांत आते हैं।

विस्थापन सदिश है और दूरी अदिश। चाल दूरी आधारित होती है जबकि वेग विस्थापन आधारित। त्वरण वेग के परिवर्तन को दर्शाता है।

यदि त्वरण एकसमान है, तो गति के तीन महत्वपूर्ण समीकरण लगाए जाते हैं:
v = u + at,
s = ut + ½ at²,
v² = u² + 2as

ग्राफ़ों के माध्यम से गति को दृश्य रूप में समझना भी इस अध्याय का विशेष हिस्सा है।
विभिन्न प्रकार के ग्राफ – स्थिति-समय, वेग-समय, और त्वरण-समय – हमें गणितीय विश्लेषण करने में सहायक होते हैं।

मुक्तपतन गति, तात्कालिक चाल और त्वरण जैसे जटिल but सुंदर पहलुओं को भी सरल ढंग से समझाया गया है।
यह अध्याय आगे के विषयों की नींव रखता है – जैसे प्रक्षेप गति, घूर्णन गति, और न्यूटन के नियम।

————————————————————————————————————————————————————————————————————————————

पाठ्यपुस्तक के प्रश्न

🔵 प्रश्न 2.1
नीचे दिए गए गति के कौन से उदाहरणों में वस्तु को लगभग बिंदु वस्तु माना जा सकता है :
(a) रेलगाड़ी एक पुल को पार कर रही हो जिसकी लंबाई उसके अपने से कई गुनी हो।
(b) किसी सूर्यग्रहण पर निगरानी रखने वाली किसी वेधशाला के ऊपर कोई पक्षी उड़ रहा हो।
(c) किसी प्रेक्षागृह में चल रही फिल्म को देखने के लिए एक आदमी बैठा हो।
(d) किसी बर्फीली सतह पर फिसलता हुआ हॉकी का गोला।
🟢 उत्तर:
(a) ✔ हाँ, रेलगाड़ी की लंबाई पुल की लंबाई से बहुत छोटी है, इसलिए उसे बिंदु वस्तु माना जा सकता है।
(b) ✔ हाँ, पक्षी की लंबाई वेधशाला की दृष्टि से नगण्य है, इसलिए बिंदु वस्तु माना जा सकता है।
(c) ✖ नहीं, आदमी बैठा है और उसका आकार महत्वपूर्ण है, इसलिए वह बिंदु वस्तु नहीं माना जा सकता।
(d) ✔ हाँ, हॉकी का गोला बर्फीली सतह पर छोटे आकार में गतिशील है, इसलिए इसे बिंदु वस्तु माना जा सकता है।

🔵 प्रश्न 2.2
चित्र 2.9 में दर्शाए A व B बसें एक-दूसरे की ओर समान-अभिसारी रेखा P द्वारा आ रही हैं। उनके स्थिति-समय (x-t) ग्राफ चित्र 2.9 में दिखाए गए हैं। निम्नलिखित में से सही कथन चुनिए :
(a) B/A की तुलना में A/B विवेचित गति से विक्षेप करता है।
(b) A/B की तुलना में B/A विवेचित गति से विक्षेप करता है।
(c) B/A की तुलना में A/B तेज चलता है।
(d) A और B एक (एक बिंदु/स्थान) स्थान पर पहुँचते हैं।
(e) A/B सड़क पर B/A से (एक स्थान/बिंदु) आगे हो जाती है।
🟢 उत्तर:
देखें चित्र 2.9:
A की रेखा की ढाल B से अधिक है ⇒ A की गति B से अधिक है
दोनों रेखाएं एक बिंदु पर प्रतिच्छेद करती हैं ⇒ वे एक बिंदु पर मिलती हैं
✅ सही उत्तर हैं:
→ (a) ✔
→ (c) ✔
→ (d) ✔

🔵 प्रश्न 2.3
एक महिला अपने घर से प्रातः 9:00 बजे 2.5 km दूर अपने कार्यालय के लिए सीधी सड़क पर 5 km h⁻¹ चाल से चलती है। वह वहाँ शाम 5:00 बजे तक रहती है और 25 km h⁻¹ की चाल से वापस लौटती है।
(i) उसका स्थान-समय ग्राफ बनाइए।
(ii) उसका चाल-समय ग्राफ बनाइए।
🟢 उत्तर:
(i) स्थान-समय ग्राफ
9:00 am → शुरू (x = 0)
2.5 km की दूरी 5 km/h से ⇒ t = 2.5/5 = 0.5 h ⇒ 9:30 am तक पहुँच
9:30 am से 5:00 pm तक वहीं रुकी ⇒ क्षैतिज रेखा
वापसी चाल = 25 km/h ⇒ 2.5 / 25 = 0.1 h = 6 min ⇒ 5:06 pm तक वापस
ग्राफ में तीन खंड होंगे:
चढ़ावदार रेखा (0 से 2.5 km)
क्षैतिज रेखा (स्थिर स्थिति)
ढाल वाली घटती रेखा (2.5 से 0 km)
(ii) चाल-समय ग्राफ
9:00–9:30 → चाल = +5 km/h
9:30–5:00 → चाल = 0
5:00–5:06 → चाल = –25 km/h (वापसी दिशा)

🔵 प्रश्न 2.4
कोई यात्री किसी गाड़ी में बैठा है जो 5 m/s चाल बढ़ाती है। उसके पीछे आती है, उसके द्वारा गिर 5 m/s चाल घटाती है और उसी दिशा में आगे बढ़ जाती है, और सबसे पहले उसने कंबल देखा जो दरवाजे के पास था और फिर 1s बाद दीवार के पास 1m दूरी पर कंबल देखा। x – t ग्राफ खींचिए।
ग्राफ यह दर्शाए कि वह यात्री कहां गिरा और फिर जहां से चलता नजर करता है वह 13 m दूर दिखाई पड़ती है। किसे समय पर वह गिरा?
🟢 उत्तर:
हम पहले ग्राफ बनाते हैं:
पहले x = 0 से चाल बढ़ती है ⇒ रेखा की ढाल बढ़ रही है
फिर गिरता है ⇒ अचानक x घटता है
फिर पुनः चाल के साथ आगे बढ़ता है
→ इस तरह x – t ग्राफ में दो ढालदार रेखाएं और एक नीचे की ओर आकस्मिक गिरावट होगी।
गिरने का समय:
दीवार से 1 m दूरी है और समय 1 s के बाद है
⇒ गिरने से पहले स्थिति 12 m रही होगी
⇒ इसलिए गिरने का समय है जब दूरी = 12 m

🔵 प्रश्न 2.5
कोई जेट वायुयान 500 km h⁻¹ की चाल से चल रहा है और वह जेट वायु के समान 1500 km h⁻¹ की चाल से अपने सन्देश उसके कक्ष में प्रेषित करता है। भूमि पर खड़े किसी प्रेक्षक के अनुसार इस सन्देश का वेग कितना होगा?
🟢 उत्तर:
जेट विमान के संदर्भ में सन्देश का वेग = 1500 km/h
विमान का वेग = 500 km/h
→ पृथ्वी के सापेक्ष सन्देश का वेग = 1500 + 500 = 2000 km/h

🔵 प्रश्न 2.6
एक ट्रेन एक रेलगाड़ी स्टेशन से 126 km h⁻¹ की चाल से गुजरती है। रेल 200 m लंबी है।
(i) रेलगाड़ी स्टेशन से एकदम पास होकर जाने में कितना समय लेगी?
(ii) यदि स्टेशन की लंबाई 400 m हो तो?
🟢 उत्तर:
(i) केवल ट्रेन की लंबाई पार करनी है = 200 m = 0.2 km
चाल = 126 km/h = 35 m/s
t = s / v = 200 / 35 = 5.71 s
(ii) ट्रेन को ट्रेन + प्लेटफॉर्म = 200 + 400 = 600 m = 0.6 km पार करनी होगी
t = 600 / 35 = 17.14 s

🔵 प्रश्न 2.7
कोई खिलौनेवाली एक गेंद को ऊपर की ओर प्रारंभिक चाल 29 m s⁻¹ से फेंकता है।
(i) गेंद ऊपर की ओर गति के दौरान शून्य क्यों नहीं दिखा पाती है?
(ii) गेंद वापस भूमि पर उतरने तक कितनी ऊँचाई तक जाएगी?
(iii) गेंद को समय के किस बिंदु पर उसका वेग शून्य होगा?
(iv) यदि ऊँचाई m में ऊपर जाती है तो कितनी ऊँचाई से गिरने पर गेंद उसी वेग से आती है?
🟢 उत्तर:
(i) क्योंकि ऊपर जाते समय गति घटती जाती है लेकिन t = 0 पर प्रारंभिक वेग होता है ⇒ शून्य नहीं होती
(ii) u = 29 m/s, v = 0 (top point), a = –9.8 m/s²
v² = u² + 2as ⇒ 0 = (29)² – 2×9.8×s ⇒ s = 42.96 m
(iii) v = u – at ⇒ 0 = 29 – 9.8t ⇒ t = 2.96 s
(iv) समान वेग के लिए h = ½gt² ⇒ t = √(2h/g)
→ h = 42.96 m, तो नीचे आने में भी वही t = 2.96 s लगेगा

🔷 प्रश्न 2.8
नीचे दिए गए कथनों को ध्यान से पढ़िए और कारण बताते हुए यह उदाहरण दीजिए कि सरल रेखा में वास्तव में एकसमान गति में किसी वस्तु का
(a) किसी क्षण शून्य वेग होने पर भी उसका त्वरण अनुपूर्ण हो सकता है।
(b) वस्तु शून्य वेग पर हो लेकिन उसका त्वरण शून्य न हो।
(c) जब स्थिर हो तो त्वरण शून्य हो और शून्य त्वरण का मतलब है वस्तु स्थिर है।
(d) जब त्वरण शून्य हो तो वस्तु रुकी हुई हो या न हो।
उत्तर
(a) जब कोई वस्तु गति की दिशा बदल रही होती है तो एक क्षण पर उसका वेग शून्य हो सकता है लेकिन त्वरण शून्य नहीं होता। जैसे किसी सरल दोलन में संतुलन बिंदु पर लौटती वस्तु।
(b) शून्य वेग का अर्थ यह नहीं है कि त्वरण नहीं होगा। जैसे एक वस्तु ऊपर की ओर फेंकी जाती है, शीर्ष बिंदु पर उसका वेग क्षणिक रूप से शून्य होता है, लेकिन उस समय भी उस पर गुरुत्वाकर्षण बल (त्वरण) कार्य करता है।
(c) यह कथन हमेशा सत्य नहीं है। कोई वस्तु स्थिर होने पर भी उस पर बल कार्य कर सकता है जिससे त्वरण हो सकता है।
(d) जब त्वरण शून्य हो तो वस्तु या तो स्थिर होगी या फिर एकसमान चाल से गति कर रही होगी।

🔷 प्रश्न 2.9
गति में कोई गेंद 90 मी ऊँचाई से पृथ्वी की सतह पर गिराया गया। एक सटीक घड़ी प्रत्येक झटके में गेंद की स्थिति को 1/10 सेकंड में दर्ज करती है। इस गति को दर्शाने के लिए 0 से 12 सेकंड के बीच स्थान-समय ग्राफ खींचिए।
उत्तर
गेंद एकसमान त्वरण (g = 9.8 m/s²) से नीचे गिरेगी। इसका स्थान समय के साथ परवलय के रूप में बढ़ेगा क्योंकि s = ½gt² के अनुसार दूरी समय के वर्ग के अनुपाती होती है। अतः स्थान-समय ग्राफ एक ऊपर की ओर मुड़ी वक्ररेखा होगी जो तेजी से नीचे की ओर आती गेंद के बढ़ते हुए विस्थापन को दर्शाएगी।

🔷 प्रश्न 2.10
उदाहरण निम्नलिखित के बीच के अंतर को स्पष्ट कीजिए:
(a) किसी समय अंतराल में विस्थापन के परिमाण और कुल पथ-लंबाई के बीच
(b) किसी समय अंतराल में औसत वेग और औसत चाल के बीच
उत्तर
(a) विस्थापन एक सदिश राशि है जो वस्तु की प्रारंभिक और अंतिम स्थिति के बीच की सीधी दूरी को दर्शाता है, जबकि कुल पथ-लंबाई स्केलर राशि है और यह वस्तु द्वारा तय की गई पूरी दूरी होती है। यदि वस्तु घुमावदार मार्ग से चली है, तो पथ-लंबाई विस्थापन से अधिक होगी।
(b) औसत वेग = कुल विस्थापन / कुल समय
औसत चाल = कुल दूरी / कुल समय
सीधे रेखीय एकसमान गति में ये दोनों समान हो सकते हैं, लेकिन यदि गति में दिशा परिवर्तन हो रहा हो, तो औसत चाल का मान औसत वेग से अधिक होता है।

🔷 प्रश्न 2.11
कोई व्यक्ति अपने घर से सीधी सड़क पर 5 km/h की चाल से 2.5 km दूर बाजार की ओर चलता है। बाजार से लौटकर वह उसी चाल में वापस मुड़ जाता है तथा 7.5 km/h की चाल से घर की ओर लौट आता है।
(a) निम्नलिखित समयों के लिए औसत वेग ज्ञात कीजिए:
(i) 0–30 मिनट
(ii) 0–50 मिनट
(iii) 0–40 मिनट
(b) क्या माध्य चाल ज्ञात कीजिए?
उत्तर
(i) 0–30 मिनट = 0.5 घंटे। पहले 2.5 km तय करने में 2.5 ÷ 5 = 0.5 घंटे लगे। औसत वेग = विस्थापन / समय = 2.5 ÷ 0.5 = 5 km/h
(ii) 0–50 मिनट = 5/6 घंटे। कुल विस्थापन = 0 (घर लौट आया), औसत वेग = 0 ÷ 5/6 = 0 km/h
(iii) 0–40 मिनट = 2/3 घंटे। पहले 0.5 घंटे में 2.5 km तय, बाकी 1/6 घंटे में 7.5 × 1/6 = 1.25 km वापस आया। शुद्ध विस्थापन = 2.5 – 1.25 = 1.25 km, औसत वेग = 1.25 ÷ 2/3 = 1.875 km/h
(b) कुल दूरी = 2.5 + 1.25 = 3.75 km, कुल समय = 2/3 घंटे
माध्य चाल = 3.75 ÷ 2/3 = 5.625 km/h

🔷 प्रश्न 2.12
हमने उदाहरण 2.9 तथा 2.10 में औसत चाल और औसत वेग के परिमाण के बीच के अंतर को स्पष्ट किया है। यदि हम तात्कालिक चाल तथा वेग के परिमाण पर विचार करें तो इसे स्पष्ट करना आवश्यक नहीं होता। तात्कालिक चाल तथा तात्कालिक वेग के परिमाण हमेशा के लिए बराबर रहते हैं। क्यों?
उत्तर
तात्कालिक चाल और तात्कालिक वेग एक ही क्षण पर वस्तु की गति को दर्शाते हैं। उस एक क्षण में वस्तु द्वारा तय पथ और विस्थापन समान होते हैं, अतः दोनों के परिमाण समान होते हैं। फर्क सिर्फ यह है कि वेग एक सदिश राशि है जबकि चाल एक अदिश राशि।


━━━━━━━━━━━━━━━━━━━━━━━
🔷 प्रश्न 2.13:
चित्र 2.10 में (a) से (d) तक के ग्राफ़ को ध्यान से देखिए, और देखकर बताइए कि इनमें से कौन-सा ग्राफ़ एकसमान गति को दर्शाता है: नहीं दर्शा सकता।
✅ उत्तर:
केवल चित्र (a) ही एकसमान गति को दर्शाता है क्योंकि x–t ग्राफ़ रैखिक है।
चित्र (b) में वक्राकार गति है, चित्र (c) में t–v ग्राफ़ साइन वक्र है और चित्र (d) में कुल पथ-लंबाई समय के साथ रैखिक रूप में नहीं है।
इसलिए (b), (c), (d) → एकसमान गति को नहीं दर्शाते।
━━━━━━━━━━━━━━━━━━━━━━━
🔷 प्रश्न 2.14:
चित्र 2.11 में किसी कण को एकविमीय गति का x–t ग्राफ़ दिया गया है। ग्राफ़ से स्पष्ट करें कि क्या यह गति एकसमान गति है?
यदि t < 0 के लिए गति परिवर्तनीय रही है और t > 0 के लिए गति परिवर्तनशील रूप से बढ़ रही है।
व्याख्या कीजिए।
✅ उत्तर:
चित्र 2.11 में x–t ग्राफ़ वक्र है, अर्थात कण की गति परिवर्तनीय है।
t = 0 के पहले गति में कमी हो रही है और t = 0 के बाद गति बढ़ रही है।
अतः यह गति एकसमान गति नहीं है क्योंकि x–t ग्राफ़ रैखिक नहीं है।
गति t के साथ बदल रही है, इसलिए यह परिवर्तनीय त्वरित गति है।
━━━━━━━━━━━━━━━━━━━━━━━
🔷 प्रश्न 2.15:
कोई आदमी एक चोर की कार को पकड़ना चाहता है। चोर की कार की चाल 192 km/h है।
एक पुलिस कार की चाल 150 m/s है।
चोर को पकड़ने के लिए पुलिस को किस चाल से चलना चाहिए?
✅ उत्तर:
चोर की चाल = 192 km/h = 192 × (1000/3600) = 53.33 m/s
पुलिस की चाल = 150 m/s
पुलिस की चाल चोर की चाल से अधिक है, इसलिए वह उसे पकड़ सकती है।
परंतु प्रश्न यह है कि पुलिस को चोर को पकड़ने के लिए कितनी चाल से चलना चाहिए?
यदि पुलिस 150 m/s से चलती है, तो वह उसे पकड़ सकती है।
🔸 उत्तर: 150 m/s चाल पर्याप्त है।
━━━━━━━━━━━━━━━━━━━━━━━
🔷 प्रश्न 2.16:
चित्र 2.12 में दिए गए प्रत्येक ग्राफ़ के लिए कौन-सी उचित भौतिक स्थिति हो सकती है?
✅ उत्तर:
(अ) चित्र 2.12(a):
x–t ग्राफ़ क्षैतिज है → कण स्थिर है।
स्थिति में परिवर्तन नहीं हो रहा है।
कण विराम अवस्था में है।
(ब) चित्र 2.12(b):
v–t ग्राफ़ में गति में अचानक परिवर्तन हो रहा है।
यह आकस्मिक झटका दर्शाता है — उदाहरण: दो टकराते हुए कण।
(स) चित्र 2.12(c):
a–t ग्राफ़ में तीव्रता से बढ़ने वाला त्वरण दिखाया गया है।
यह किसी तेज़ी से बढ़ते रॉकेट की गति हो सकती है।
━━━━━━━━━━━━━━━━━━━━━━━
🔷 प्रश्न 2.17:
चित्र 2.13 में किसी कण की एकसमान सरल आवर्ती गति के लिए x–t ग्राफ़ दिया गया है।
समय t = 0.3s, 1.2s, –1.2s पर कण की स्थिति, चाल व त्वरण के चिह्न क्या होंगे?
✅ उत्तर:
यह x–t ग्राफ़ एक सरल आवर्ती गति दर्शाता है (जैसे x = A sin(ωt))।
t = 0.3 s:
स्थिति → धनात्मक
चाल → धनात्मक (slope धनात्मक है)
त्वरण → ऋणात्मक (कण सन्नत बिंदु की ओर लौट रहा है)
t = 1.2 s:
स्थिति → शून्य
चाल → अधिकतम धनात्मक
त्वरण → शून्य
t = –1.2 s:
स्थिति → शून्य
चाल → अधिकतम ऋणात्मक
त्वरण → शून्य
━━━━━━━━━━━━━━━━━━━━━━━
🔷 प्रश्न 2.18:
चित्र 2.14 में किसी कण की एकविमीय गति का x–t ग्राफ़ है।
तीन समय अंतराल दर्शाए गए हैं।
किस अंतराल में औसत चाल अधिकतम है? औसत वेग न्यूनतम है?
✅ उत्तर:
मान लीजिए A, B, C तीन समय अंतराल हैं:
औसत चाल अधिकतम:
जिस अंतराल में कुल विस्थापन सबसे अधिक हो — यह A हो सकता है।
औसत वेग न्यूनतम:
जहाँ विस्थापन लगभग 0 हो — यह C हो सकता है।
🔸 औसत चाल = कुल दूरी / कुल समय
🔸 औसत वेग = कुल विस्थापन / कुल समय
━━━━━━━━━━━━━━━━━━━━━━━
🔷 प्रश्न 2.19:
चित्र 2.15 में किसी नियम के अनुसार चल रहे कण का v–t ग्राफ़ है।
तीन समय अंतराल दिए गए हैं।
किस अंतराल में त्वरण अधिकतम? किस अंतराल में औसत चाल अधिकतम? त्वरण के चिह्न क्या हैं?
✅ उत्तर:
अधिकतम त्वरण:
जहाँ ढाल सबसे अधिक → यह A–B के बीच हो सकता है।
औसत चाल अधिकतम:
जहाँ क्षेत्रफल सबसे अधिक है → यह B–C के बीच हो सकता है।
A → त्वरण धनात्मक
B → त्वरण शून्य
C → त्वरण ऋणात्मक
D → चाल शून्य (क्योंकि v = 0)

————————————————————————————————————————————————————————————————————————————

अन्य महत्वपूर्ण प्रश्न

(CBSE MODEL प्रश्न पत्र)

सिर्फ इसी पाठ से निर्मित CBSE MODEL प्रश्न पत्र।

➊ एक वस्तु की चाल शून्य है, तो उसकी गति हो सकती है:
(A) शून्य
(B) समान
(C) परिवर्तनीय
(D) निश्चित
✅ उत्तर: (A) शून्य

➋ निम्नलिखित में से कौन-सा युग्म सदिश राशियों का है?
(A) चाल और दूरी
(B) चाल और विस्थापन
(C) गति और चाल
(D) गति और दूरी
✅ उत्तर: (B) चाल और विस्थापन

➌ SI पद्धति में चाल की इकाई क्या है?
(A) m/s
(B) km/h
(C) cm/s
(D) km/min
✅ उत्तर: (A) m/s

➍ यदि किसी वस्तु का विस्थापन समय के साथ रेखीय रूप से बढ़ता है, तो गति है:
(A) शून्य
(B) परिवर्तनशील
(C) समान
(D) अवनति
✅ उत्तर: (C) समान

➎ दूरी हमेशा होती है:
(A) शून्य
(B) धनात्मक
(C) ऋणात्मक
(D) कोई नहीं
✅ उत्तर: (B) धनात्मक

➏ एक वस्तु 5 सेकंड में 20 मीटर चलती है, उसकी औसत चाल होगी:
(A) 4 m/s
(B) 2.5 m/s
(C) 10 m/s
(D) 5 m/s
✅ उत्तर: (A) 4 m/s

➐ एक वस्तु का विस्थापन शून्य है, इसका अर्थ है:
(A) वह चली नहीं
(B) उसने पूर्ण चक्कर पूरा किया
(C) उसकी गति नहीं है
(D) उसकी चाल शून्य है
✅ उत्तर: (B) उसने पूर्ण चक्कर पूरा किया

➑ गति का SI मात्रक है:
(A) m/s
(B) m²/s
(C) m/s²
(D) km/hr
✅ उत्तर: (C) m/s²

➒ यदि v = u + at में a = 0 हो तो:
(A) v = u
(B) v = 0
(C) v = at
(D) u = 0
✅ उत्तर: (A) v = u

➓ एक वस्तु की चाल ऋणात्मक नहीं हो सकती क्योंकि:
(A) चाल एक सदिश राशि है
(B) चाल एक अदिश राशि है
(C) चाल हमेशा शून्य होती है
(D) चाल को मापा नहीं जा सकता
✅ उत्तर: (B) चाल एक अदिश राशि है

⓫ SI पद्धति में विस्थापन की इकाई है:
(A) cm
(B) m
(C) mm
(D) km
✅ उत्तर: (B) m

⓬ “विस्थापन” एक __ राशि है।
(A) अदिश
(B) सदिश
(C) वेक्टर नहीं
(D) केवल धनात्मक
✅ उत्तर: (B) सदिश

⓭ यदि कोई वस्तु वक्राकार पथ पर चलती है तो उसका विस्थापन और दूरी होंगे:
(A) बराबर
(B) विस्थापन अधिक
(C) दूरी अधिक
(D) दोनों शून्य
✅ उत्तर: (C) दूरी अधिक

⓮ एक वस्तु की चाल 90 km/h है, यह m/s में होगी:
(A) 15
(B) 25
(C) 20
(D) 30
✅ उत्तर: (A) 25

⓯ निम्नलिखित में से कौन-सा समीकरण समान त्वरण वाली गति के लिए है?
(A) s = ut + ½at²
(B) v = u² + 2as
(C) s = v² – u²
(D) a = s/t
✅ उत्तर: (A) s = ut + ½at²

⓰ यदि कोई वस्तु पीछे की ओर चल रही है, तो उसका विस्थापन होगा:
(A) धनात्मक
(B) ऋणात्मक
(C) शून्य
(D) कोई निष्कर्ष नहीं
✅ उत्तर: (B) ऋणात्मक

⓱ एक ट्रेन 60 km/h की चाल से चलती है। यह m/s में कितनी होगी?
(A) 15
(B) 16.67
(C) 20
(D) 18
✅ उत्तर: (B) 16.67

⓲ एक वस्तु की चाल में निरंतर कमी आ रही है, इसका अर्थ है:
(A) ऋणात्मक त्वरण
(B) धनात्मक त्वरण
(C) शून्य त्वरण
(D) स्थिर चाल
✅ उत्तर: (A) ऋणात्मक त्वरण

⓳ “त्वरण” शब्द का सही परिभाषा क्या है?
(A) चाल में परिवर्तन
(B) चाल प्रति समय परिवर्तन
(C) दूरी में परिवर्तन
(D) विस्थापन में परिवर्तन
✅ उत्तर: (B) चाल प्रति समय परिवर्तन

📍 Section B: प्रश्न 19 से 23 (प्रत्येक 2 अंक)
(संक्षिप्त उत्तर आधारित)

➊➒ एक गाड़ी 5 सेकंड में 20 मीटर दूरी तय करती है और फिर अगले 5 सेकंड में 30 मीटर।
गाड़ी की औसत चाल ज्ञात कीजिए।
✅ उत्तर:
कुल दूरी = 20 + 30 = 50 मीटर
कुल समय = 5 + 5 = 10 सेकंड
➤ औसत चाल = कुल दूरी / कुल समय = 50 / 10 = 5 m/s

➊➓ एक वस्तु को 10 m/s की प्रारंभिक चाल से छोड़ा गया और वह 2 m/s² की त्वरण से चल रही है।
3 सेकंड बाद उसकी चाल क्या होगी?
✅ उत्तर:
प्रारंभिक चाल (u) = 10 m/s
त्वरण (a) = 2 m/s²
समय (t) = 3 s
➤ अंतिम चाल (v) = u + at = 10 + 2×3 = 16 m/s

➋➊ एक वस्तु की चाल 60 km/h है। उसे m/s में परिवर्तित कीजिए।
✅ उत्तर:
1 km/h = 5/18 m/s
60 × 5/18 = 16.67 m/s
➤ उत्तर: 16.67 m/s

➋➋ एक व्यक्ति A से B तक 40 m जाता है और वापस A तक 40 m आता है।
यदि पूरा समय 20 s है, तो उसकी औसत चाल और औसत वेग ज्ञात कीजिए।
✅ उत्तर:
कुल दूरी = 40 + 40 = 80 m
विस्थापन = 0 (A पर वापस)
➤ औसत चाल = 80 / 20 = 4 m/s
➤ औसत वेग = 0 / 20 = 0 m/s

➋➌ एक वस्तु एकसमान त्वरण से चल रही है। प्रारंभिक चाल 2 m/s, अंतिम चाल 10 m/s, दूरी 24 m है।
त्वरण ज्ञात कीजिए।
✅ उत्तर:
v² = u² + 2as
(10)² = (2)² + 2a(24)
100 = 4 + 48a
96 = 48a → a = 2 m/s²
➤ उत्तर: 2 m/s²

📍 Section C: प्रश्न 24 से 28 (प्रत्येक 3 अंक)
(मध्यम लंबाई वाले गणना/तर्क आधारित प्रश्न)

➋➍ एक ट्रेन 5 m/s की चाल से चलना शुरू करती है और 2 m/s² की त्वरण से 10 सेकंड तक बढ़ती है।
इस दौरान चली गई दूरी ज्ञात कीजिए।
✅ उत्तर:
u = 5 m/s
a = 2 m/s²
t = 10 s
➤ सूत्र: s = ut + (1/2)at²
➤ s = 5×10 + (1/2)×2×10²
➤ s = 50 + 100 = 150 m

➋➎ एक वस्तु 3 सेकंड तक 2 m/s² की त्वरण से चलती है, फिर 5 सेकंड तक समान चाल से चलती है।
कुल दूरी ज्ञात कीजिए।
✅ उत्तर:
Step 1 – पहले 3 सेकंड तक:
u = 0, a = 2 m/s², t = 3
s₁ = ut + ½at² = 0 + ½×2×9 = 9 m
v = u + at = 0 + 2×3 = 6 m/s
Step 2 – अगले 5 सेकंड में:
s₂ = v×t = 6×5 = 30 m
➤ कुल दूरी = s₁ + s₂ = 9 + 30 = 39 m

➋➏ एक व्यक्ति 4 सेकंड में 16 m जाता है, फिर अगले 4 सेकंड में 16 m वापस आता है।
उसकी औसत चाल और औसत वेग ज्ञात कीजिए।
✅ उत्तर:
दूरी = 16 + 16 = 32 m
विस्थापन = 0 m
कुल समय = 8 s
➤ औसत चाल = 32 / 8 = 4 m/s
➤ औसत वेग = 0 / 8 = 0 m/s

➋➐ एक कार की प्रारंभिक चाल 36 km/h है, और वह 5 सेकंड में 72 km/h तक पहुँचती है।
इसका त्वरण ज्ञात कीजिए।
✅ उत्तर:
u = 36 km/h = 10 m/s
v = 72 km/h = 20 m/s
t = 5 s
➤ a = (v – u) / t = (20 – 10) / 5 = 2 m/s²

➋➑ एक वस्तु पर 2 m/s² की ऋणात्मक त्वरण लगाई जाती है।
प्रारंभिक चाल 20 m/s है। कितनी दूरी तय करने के बाद वस्तु रुक जाएगी?
✅ उत्तर:
u = 20 m/s, v = 0, a = -2 m/s²
➤ v² = u² + 2as → 0 = 400 + 2×(-2)×s
➤ -400 = -4s → s = 100 m

📍 Section D: केस आधारित प्रश्न (प्रत्येक 4 अंक)

➌➒ प्रश्न: एक कार चालक ने अपनी गाड़ी को स्टार्ट किया। पहले 10 सेकंड तक 2 m/s² की त्वरण से गाड़ी चलती है, फिर 20 सेकंड तक एक समान चाल से, और अंत में ब्रेक लगाकर 5 सेकंड में रुक जाती है।
(1) प्रारंभिक 10 सेकंड में चली गई दूरी ज्ञात करें।
(2) गाड़ी की अधिकतम चाल ज्ञात करें।
(3) एक समान चाल से चली गई दूरी ज्ञात करें।
(4) ब्रेक लगने पर चली गई दूरी ज्ञात करें।
✅ उत्तर:
➀ पहले भाग में:
u = 0, a = 2 m/s², t = 10
s₁ = ut + ½at² = 0 + ½×2×100 = 100 m
v = u + at = 0 + 2×10 = 20 m/s (Maximum velocity)
➁ दूसरे भाग में:
एक समान चाल = 20 m/s
समय = 20 s
s₂ = v × t = 20 × 20 = 400 m
➂ तीसरे भाग में (ब्रेकिंग):
u = 20 m/s, v = 0, t = 5
a = (v – u) / t = -4 m/s²
s₃ = ut + ½at² = 20×5 + ½×(-4)×25 = 100 – 50 = 50 m
➃ कुल दूरी = s₁ + s₂ + s₃ = 100 + 400 + 50 = 550 m

➌➈ प्रश्न: एक खिलाड़ी 60 मीटर की दौड़ पूरी करता है। पहले 4 सेकंड तक 2 m/s² की त्वरण से दौड़ता है, फिर बाकी दूरी एक समान चाल से तय करता है।
(1) 4 सेकंड में चली गई दूरी ज्ञात करें।
(2) उस दौरान प्राप्त की गई चाल ज्ञात करें।
(3) एक समान चाल से तय दूरी और समय ज्ञात करें।
(4) कुल समय ज्ञात करें।
✅ उत्तर:
➀ s₁ = ut + ½at² = 0 + ½×2×16 = 16 m
➁ v = u + at = 0 + 2×4 = 8 m/s
➂ शेष दूरी = 60 – 16 = 44 m
➃ समय = दूरी / चाल = 44 / 8 = 5.5 s
➄ कुल समय = 4 + 5.5 = 9.5 s

➌➉ प्रश्न: एक मोटरसाइकिल सवार शून्य चाल से चलना शुरू करता है। वह पहले 6 सेकंड तक 3 m/s² की त्वरण से बढ़ता है, फिर 6 सेकंड तक एक समान चाल से चलता है, और अंत में ब्रेक लगाकर 3 सेकंड में रुकता है।
(1) अधिकतम चाल ज्ञात करें।
(2) प्रत्येक चरण में चली गई दूरी ज्ञात करें।
(3) कुल दूरी और कुल समय ज्ञात करें।
✅ उत्तर:
➀ v = u + at = 0 + 3×6 = 18 m/s
➁
पहले चरण:
s₁ = ut + ½at² = 0 + ½×3×36 = 54 m
दूसरे चरण:
s₂ = v × t = 18 × 6 = 108 m
तीसरे चरण:
a = (v – 0)/t = -6 m/s²
s₃ = ut + ½at² = 18×3 + ½×(-6)×9 = 54 – 27 = 27 m
➂ कुल दूरी = 54 + 108 + 27 = 189 m
कुल समय = 6 + 6 + 3 = 15 s

📍 Section E: प्रश्न 32 से 35 (प्रत्येक 5 अंक)

(लंबे उत्तर, व्याख्यात्मक एवं सूत्र-आधारित)
➌➋ प्रश्न: गति के समीकरणों की व्युत्पत्ति कीजिए जब कोई वस्तु समान त्वरण से गति कर रही हो।
✅ उत्तर:
हम जानते हैं कि यदि कोई वस्तु समान त्वरण से गति कर रही हो, तो उसके लिए तीन मुख्य समीकरण होते हैं:
➀ v = u + at
➁ s = ut + ½at²
➂ v² = u² + 2as
✦ पहली समीकरण की व्युत्पत्ति (v = u + at):
त्वरण की परिभाषा:
a = (v – u)/t
⇒ v = u + at
✦ दूसरी समीकरण की व्युत्पत्ति (s = ut + ½at²):
औसत चाल = (u + v)/2
⇒ s = [(u + v)/2] × t
अब v = u + at डालें:
⇒ s = [(u + u + at)/2] × t
⇒ s = (2u + at)/2 × t = ut + ½at²
✦ तीसरी समीकरण की व्युत्पत्ति (v² = u² + 2as):
v² = (u + at)²
= u² + 2uat + a²t²
अब s = ut + ½at² से t ज्ञात करें
t = (v – u)/a
अब इसे उपर प्रयोग कर पूर्ण व्युत्पत्ति प्राप्त होती है
अंततः:
v² = u² + 2as

➌➌ प्रश्न: दूरी-समय ग्राफ और वेग-समय ग्राफ में अंतर स्पष्ट कीजिए। साथ ही ग्राफ से किसी वस्तु की गति का विश्लेषण कैसे किया जाता है, बताइए।
✅ उत्तर:
✦ दूरी-समय ग्राफ:
y-अक्ष पर दूरी, x-अक्ष पर समय
ढाल = चाल
वक्र = परिवर्तनशील चाल, रेखा = समान चाल
यदि ग्राफ क्षैतिज हो तो वस्तु रुकी हुई है
✦ वेग-समय ग्राफ:
y-अक्ष पर वेग, x-अक्ष पर समय
ढाल = त्वरण
क्षेत्रफल = विस्थापन
यदि रेखा क्षैतिज है → समान वेग, यदि नीचे जा रही है → ऋणात्मक त्वरण
✦ विश्लेषण उदाहरण:
यदि वेग-समय ग्राफ एक त्रिभुज बनाता है, तो उसका क्षेत्रफल = ½ × आधार × ऊँचाई = विस्थापन

➌➍ प्रश्न: एक वस्तु को 15 m/s की चाल से छोड़ा गया। वह 3 m/s² की ऋणात्मक त्वरण से रुकती है।
(i) रुकने में कितना समय लगेगा?
(ii) कितनी दूरी तय करेगी?
✅ उत्तर:
➀ v = 0, u = 15 m/s, a = -3 m/s²
t = (v – u)/a = (0 – 15)/(-3) = 5 s
➁ s = ut + ½at² = 15×5 + ½×(-3)×25 = 75 – 37.5 = 37.5 m
अतः रुकने में समय = 5 सेकंड, दूरी = 37.5 मीटर

➌➎ प्रश्न: एक ट्रेन की चाल 54 km/h है। ब्रेक लगाने पर 6 सेकंड में रुक जाती है।
(i) प्रारंभिक चाल को m/s में बदलिए
(ii) त्वरण ज्ञात कीजिए
(iii) रुकने में चली गई दूरी ज्ञात कीजिए
✅ उत्तर:
➀ प्रारंभिक चाल u = 54 km/h = 15 m/s
v = 0, t = 6 s
a = (v – u)/t = (0 – 15)/6 = -2.5 m/s²
➁ s = ut + ½at² = 15×6 + ½×(-2.5)×36 = 90 – 45 = 45 m
➂ उत्तर:
चाल = 15 m/s
त्वरण = -2.5 m/s²
दूरी = 45 m
🔷 🎯 समाप्त — Code 3 समाप्त हुआ!

————————————————————————————————————————————————————————————————————————————

Neet पिछले सालों के प्रश्न

━━━━━━━━━━━━━━━

🔵 Q1. एक कण की चाल-समय ग्राफ की ढलान दर्शाती है –
(A) त्वरण
(B) विस्थापन
(C) चाल
(D) वेग
उत्तर: (A)
वर्ष: NEET 2025 | सेट: Z2

🔵 Q2. यदि कोई वस्तु समान चाल से चल रही है, तो उसका त्वरण होगा –
(A) शून्य
(B) धनात्मक
(C) ऋणात्मक
(D) परिवर्तनीय
उत्तर: (A)
वर्ष: NEET 2024 | सेट: Q1

🔵 Q3. चाल-समय ग्राफ की ढलान बढ़ रही है, इसका अर्थ है –
(A) चाल घट रही है
(B) चाल बढ़ रही है
(C) स्थिर चाल
(D) त्वरण शून्य
उत्तर: (B)
वर्ष: NEET 2024 | सेट: S2

🔵 Q4. 72 km/h चाल को m/s में परिवर्तित करें –
(A) 20 m/s
(B) 18 m/s
(C) 22 m/s
(D) 25 m/s
उत्तर: (B)
वर्ष: NEET 2023 | सेट: R2

🔵 Q5. त्वरण की SI इकाई क्या है?
(A) m/s
(B) m/s²
(C) m²/s
(D) s/m²
उत्तर: (B)
वर्ष: NEET 2023 | सेट: S5

🔵 Q6. वेग-समय ग्राफ के नीचे का क्षेत्र दर्शाता है –
(A) त्वरण
(B) चाल
(C) विस्थापन
(D) बल
उत्तर: (C)
वर्ष: NEET 2022 | सेट: Z1

🔵 Q7. विस्थापन और दूरी में मुख्य अंतर क्या है?
(A) दूरी दिशा-संवेदी होती है
(B) विस्थापन दिशा-संवेदी होता है
(C) दूरी हमेशा विस्थापन से कम होती है
(D) विस्थापन हमेशा दूरी से अधिक होता है
उत्तर: (B)
वर्ष: NEET 2022 | सेट: P2

🔵 Q8. कोई वस्तु 1 सेकंड में 10 मीटर जाती है। उसकी चाल क्या होगी?
(A) 5 m/s
(B) 10 m/s
(C) 15 m/s
(D) 20 m/s
उत्तर: (B)
वर्ष: NEET 2021 | सेट: W3

🔵 Q9. यदि कोई वस्तु v चाल से t समय तक चलती है, तो दूरी =
(A) v + t
(B) vt
(C) v / t
(D) t / v
उत्तर: (B)
वर्ष: NEET 2021 | सेट: X5

🔵 Q10. वेग-समय ग्राफ में ऋणात्मक ढलान दर्शाता है –
(A) समान चाल
(B) धनात्मक त्वरण
(C) ऋणात्मक त्वरण
(D) स्थिर चाल
उत्तर: (C)
वर्ष: NEET 2020 | सेट: Q1

🔵 Q11. एक व्यक्ति 40 m उत्तर जाता है और फिर 30 m दक्षिण। उसका विस्थापन क्या होगा?
(A) 70 m
(B) 10 m उत्तर
(C) 10 m दक्षिण
(D) 0 m
उत्तर: (B)
वर्ष: NEET 2020 | सेट: R4

🔵 Q12. चाल-समय ग्राफ यदि वक्र है, तो इसका अर्थ है –
(A) स्थिर चाल
(B) समान त्वरण
(C) परिवर्तनीय चाल
(D) ऋणात्मक चाल
उत्तर: (C)
वर्ष: NEET 2019 | सेट: S1

🔵 Q13. एक वस्तु 10 m/s की प्रारंभिक चाल से 2 m/s² के त्वरण से 5 s तक चलती है। दूरी?
(A) 75 m
(B) 100 m
(C) 125 m
(D) 50 m
उत्तर: (A)
वर्ष: NEET 2019 | सेट: Z2

🔵 Q14. यदि कोई वस्तु दाएं और बाएं बराबर दूरी तय करे, तो विस्थापन होगा –
(A) 0
(B) दूरी के बराबर
(C) चाल के बराबर
(D) समय के बराबर
उत्तर: (A)
वर्ष: NEET 2018 | सेट: X3

🔵 Q15. चाल की SI इकाई क्या है?
(A) m/s
(B) cm/s
(C) km/h
(D) m/h
उत्तर: (A)
वर्ष: NEET 2018 | सेट: P1

🔵 Q16. एक वाहन 0 से 6 m/s की चाल प्राप्त करता है 3 सेकंड में। उसका त्वरण होगा –
(A) 1 m/s²
(B) 2 m/s²
(C) 3 m/s²
(D) 0.5 m/s²
उत्तर: (B)
वर्ष: NEET 2017 | सेट: S2

🔵 Q17. ऋणात्मक चाल का तात्पर्य है –
(A) गति वाम दिशा में है
(B) गति नहीं है
(C) त्वरण शून्य है
(D) चाल स्थिर है
उत्तर: (A)
वर्ष: NEET 2017 | सेट: T3

🔵 Q18. विस्थापन समय का एक रेखीय फलन हो, तो चाल होगी –
(A) नियत
(B) परिवर्तनीय
(C) शून्य
(D) अनंत
उत्तर: (A)
वर्ष: NEET 2016 | सेट: Q2

🔵 Q19. चाल और वेग में मुख्य अंतर –
(A) चाल दिशा-संवेदी होती है
(B) वेग दिशा-संवेदी होता है
(C) चाल ऋणात्मक हो सकती है
(D) वेग सदा धनात्मक होता है
उत्तर: (B)
वर्ष: NEET 2016 | सेट: Z1

🔵 Q20. चाल = दूरी / समय — यह किसे दर्शाता है?
(A) त्वरण
(B) गति
(C) विस्थापन
(D) वेग
उत्तर: (B)
वर्ष: NEET 2015 | सेट: X4

🔵 Q21. यदि चाल बढ़ती है और समय समान है, तो दूरी –
(A) घटेगी
(B) बढ़ेगी
(C) शून्य होगी
(D) स्थिर रहेगी
उत्तर: (B)
वर्ष: NEET 2015 | सेट: P2

🔵 Q22. शून्य चाल से 10 m/s तक पहुँचने में 5 s लगते हैं। त्वरण?
(A) 1 m/s²
(B) 2 m/s²
(C) 5 m/s²
(D) 10 m/s²
उत्तर: (B)
वर्ष: NEET 2014 | सेट: S1

🔵 Q23. वृत्त पर गति कर रहा कण — चाल नियत है, तो वेग –
(A) नियत
(B) परिवर्तनीय
(C) ऋणात्मक
(D) शून्य
उत्तर: (B)
वर्ष: NEET 2014 | सेट: T3

🔵 Q24. चाल धनात्मक और त्वरण ऋणात्मक हो तो –
(A) वस्तु रुकती है
(B) गति घटती है
(C) गति बढ़ती है
(D) दिशा बदलती है
उत्तर: (B)
वर्ष: NEET 2013 | सेट: Q1

🔵 Q25. चाल-समय ग्राफ वक्र हो तो चाल –
(A) समान
(B) घटती
(C) बढ़ती
(D) परिवर्तनीय
उत्तर: (D)
वर्ष: NEET 2013 | सेट: R2

━━━━━━━━━━━━━━━

🔵 Q26. एक वस्तु 20 m/s से 10 सेकंड तक चलती है। विस्थापन क्या होगा?
(A) 200 m
(B) 100 m
(C) 400 m
(D) 20 m
उत्तर: (A)
वर्ष: NEET 2012 | सेट: S3

🔵 Q27. एक वाहन की चाल 36 km/h है। m/s में क्या होगी?
(A) 8 m/s
(B) 10 m/s
(C) 12 m/s
(D) 20 m/s
उत्तर: (B)
वर्ष: NEET 2012 | सेट: Q1

🔵 Q28. यदि चाल-समय ग्राफ की ढलान शून्य हो तो –
(A) वस्तु रुकी हुई है
(B) गति नहीं हो रही
(C) समान चाल
(D) त्वरण धनात्मक है
उत्तर: (C)
वर्ष: AIPMT 2011 | सेट: T1

🔵 Q29. त्वरण की परिभाषा क्या है?
(A) चाल × समय
(B) वेग / समय
(C) वेग परिवर्तन / समय
(D) विस्थापन / समय
उत्तर: (C)
वर्ष: AIPMT 2011 | सेट: P2

🔵 Q30. यदि किसी वस्तु की चाल ऋणात्मक हो तो –
(A) वह पीछे की ओर चल रही है
(B) वह स्थिर है
(C) दिशा नहीं बदलती
(D) त्वरण शून्य है
उत्तर: (A)
वर्ष: NEET 2010 | सेट: Z3

🔵 Q31. यदि कोई वस्तु समान त्वरण से चल रही है, तो v² – u² = ?
(A) 2as
(B) at²
(C) ut
(D) s/t
उत्तर: (A)
वर्ष: AIPMT 2010 | सेट: Q3

🔵 Q32. चाल और समय के गुणनफल से क्या प्राप्त होता है?
(A) त्वरण
(B) दूरी
(C) विस्थापन
(D) बल
उत्तर: (B)
वर्ष: PMT 2009 | सेट: R4

🔵 Q33. एक वस्तु की चाल समय के साथ रेखीय रूप से घट रही है, इसका मतलब –
(A) ऋणात्मक त्वरण
(B) धनात्मक त्वरण
(C) शून्य त्वरण
(D) अनंत चाल
उत्तर: (A)
वर्ष: NEET 2009 | सेट: Z1

🔵 Q34. एक वस्तु 2 m/s² की त्वरण से 4 s तक चलती है, दूरी?
(A) 8 m
(B) 16 m
(C) 32 m
(D) 4 m
उत्तर: (B)
वर्ष: NEET 2008 | सेट: Q4

🔵 Q35. चाल-समय ग्राफ का वक्र दिशा बदलता है, मतलब –
(A) चाल बढ़ रही है
(B) चाल घट रही है
(C) त्वरण परिवर्तनीय है
(D) वेग समान है
उत्तर: (C)
वर्ष: NEET 2008 | सेट: R2

🔵 Q36. विस्थापन समय का रेखीय फलन हो, इसका अर्थ?
(A) त्वरण शून्य है
(B) त्वरण धनात्मक है
(C) गति परिवर्तनीय
(D) चाल शून्य
उत्तर: (A)
वर्ष: NEET 2007 | सेट: Z3

🔵 Q37. एक वस्तु को 15 m/s की प्रारंभिक चाल दी गई। 3 सेकंड में 2 m/s² की त्वरण से कितनी दूरी तय करेगी?
(A) 54 m
(B) 60 m
(C) 45 m
(D) 30 m
उत्तर: (A)
वर्ष: AIPMT 2007 | सेट: Q1

🔵 Q38. यदि चाल-समय ग्राफ पर रेखा क्षैतिज है तो –
(A) गति नहीं हो रही
(B) चाल बढ़ रही
(C) चाल समान
(D) त्वरण ऋणात्मक
उत्तर: (C)
वर्ष: AIPMT 2006 | सेट: R1

🔵 Q39. वेग-समय ग्राफ में रेखा नीचे जा रही हो, तो –
(A) ऋणात्मक त्वरण
(B) चाल स्थिर
(C) चाल बढ़ रही
(D) त्वरण धनात्मक
उत्तर: (A)
वर्ष: NEET 2006 | सेट: X2

🔵 Q40. चाल को SI मात्रक में दर्शाया जाता है –
(A) km/h
(B) cm/s
(C) m/s
(D) m/h
उत्तर: (C)
वर्ष: AIPMT 2005 | सेट: S3

🔵 Q41. यदि कोई वस्तु u चाल से प्रारंभ होकर a त्वरण से t समय में चले, दूरी =
(A) ut
(B) at²
(C) ut + ½at²
(D) u² + 2as
उत्तर: (C)
वर्ष: AIPMT 2005 | सेट: T1

🔵 Q42. चाल और वेग में एक मात्रक कौन सा है?
(A) m/s²
(B) m/s
(C) km
(D) kg
उत्तर: (B)
वर्ष: PMT 2004 | सेट: P4

🔵 Q43. एक वस्तु का त्वरण = 0, इसका अर्थ?
(A) वस्तु नहीं चल रही
(B) वस्तु रुकी हुई है
(C) चाल समान है
(D) चाल शून्य है
उत्तर: (C)
वर्ष: PMT 2004 | सेट: R2

🔵 Q44. 10 m/s चाल से वस्तु 2 सेकंड में कितनी दूरी तय करेगी?
(A) 5 m
(B) 10 m
(C) 20 m
(D) 30 m
उत्तर: (C)
वर्ष: AIPMT 2003 | सेट: Q3

🔵 Q45. एक कण का वेग समय के साथ घटता है, इसका त्वरण –
(A) धनात्मक
(B) ऋणात्मक
(C) शून्य
(D) स्थिर
उत्तर: (B)
वर्ष: AIPMT 2003 | सेट: X2

🔵 Q46. कोई वस्तु वापस वहीं पहुँच जाए, तो विस्थापन होगा –
(A) अधिकतम
(B) दूरी के बराबर
(C) शून्य
(D) अनंत
उत्तर: (C)
वर्ष: NEET 2002 | सेट: Z1

🔵 Q47. एक वाहन 20 m/s चाल से चल रहा है। 10 सेकंड में रुकता है। त्वरण क्या होगा?
(A) -2 m/s²
(B) 2 m/s²
(C) 0
(D) -1 m/s²
उत्तर: (A)
वर्ष: PMT 2002 | सेट: R3

🔵 Q48. एक वस्तु की चाल 40 m/s है। समय = 5 s। दूरी?
(A) 100 m
(B) 200 m
(C) 300 m
(D) 400 m
उत्तर: (D)
वर्ष: PMT 2001 | सेट: S1

🔵 Q49. चाल-समय ग्राफ की वक्रता दर्शाती है –
(A) बदलती चाल
(B) बदलता बल
(C) बदलता विस्थापन
(D) बदलता द्रव्यमान
उत्तर: (A)
वर्ष: PMT 2001 | सेट: Q4

🔵 Q50. एक वस्तु 10 m/s² त्वरण से चलती है, 3 s में कितनी दूरी तय करेगी?
(A) 45 m
(B) 30 m
(C) 60 m
(D) 15 m
उत्तर: (A)
वर्ष: NEET 2001 | सेट: T1

————————————————————————————————————————————————————————————————————————————

JEE MAINS पिछले सालों के प्रश्न

━━━━━━━━━━━━━━━

🔶 Q1. एक कण की चाल 10 m/s है और वह 4 सेकंड तक एकसमान त्वरण से चलता है। यदि उसका त्वरण 2 m/s² है, तो उसका अंतिम वेग होगा:
(A) 16 m/s
(B) 18 m/s
(C) 20 m/s
(D) 14 m/s
उत्तर: (C)
वर्ष: JEE Main 2024 | Shift 1

🔶 Q2. एक कण 5 m/s की प्रारंभिक चाल से चलता है और 3 सेकंड तक 2 m/s² के त्वरण से गति करता है। उसकी विस्थापन क्या होगी?
(A) 24 m
(B) 21 m
(C) 27 m
(D) 30 m
उत्तर: (A)
वर्ष: JEE Main 2024 | Shift 2

🔶 Q3. चाल और समय ग्राफ की ढलान क्या दर्शाती है?
(A) त्वरण
(B) वेग
(C) विस्थापन
(D) बल
उत्तर: (B)
वर्ष: JEE Main 2023 | Shift 1

🔶 Q4. यदि किसी वस्तु का त्वरण 0 हो, तो गति कैसी होगी?
(A) एकसमान गति
(B) नहीं चलेगी
(C) पल-पल गति बदलेगी
(D) स्थिर नहीं रहेगी
उत्तर: (A)
वर्ष: JEE Main 2023 | Shift 2

🔶 Q5. 60 km/h को m/s में बदलिए:
(A) 16.67 m/s
(B) 18.25 m/s
(C) 20.00 m/s
(D) 21.11 m/s
उत्तर: (A)
वर्ष: JEE Main 2022 | Shift 1

🔶 Q6. एक कण के वेग-समय ग्राफ का क्षेत्रफल क्या दर्शाता है?
(A) दूरी
(B) विस्थापन
(C) त्वरण
(D) चाल
उत्तर: (B)
वर्ष: JEE Main 2022 | Shift 2

🔶 Q7. यदि चाल-समय ग्राफ वक्र हो, तो गति कैसी होगी?
(A) एकसमान
(B) बदलती चाल
(C) स्थिर चाल
(D) शून्य चाल
उत्तर: (B)
वर्ष: JEE Main 2021 | Shift 1

🔶 Q8. एक ट्रेन 72 km/h से चल रही है, m/s में चाल होगी:
(A) 18 m/s
(B) 20 m/s
(C) 22 m/s
(D) 24 m/s
उत्तर: (D)
वर्ष: JEE Main 2021 | Shift 2

🔶 Q9. यदि त्वरण ऋणात्मक हो, तो ग्राफ में रेखा –
(A) ऊपर जाती है
(B) नीचे जाती है
(C) क्षैतिज होती है
(D) कोई परिवर्तन नहीं
उत्तर: (B)
वर्ष: JEE Main 2020 | Shift 1

🔶 Q10. s = ut + ½at² समीकरण से दूरी निकालने के लिए कौनसे चर आवश्यक हैं?
(A) u, a, t
(B) v, a, t
(C) s, u, a
(D) u, v, s
उत्तर: (A)
वर्ष: JEE Main 2020 | Shift 2

🔶 Q11. चाल समय के साथ घट रही हो, तो त्वरण होगा –
(A) धनात्मक
(B) ऋणात्मक
(C) शून्य
(D) अनंत
उत्तर: (B)
वर्ष: JEE Main 2019 | Shift 1

🔶 Q12. चाल-समय ग्राफ की ढलान क्या बताती है?
(A) चाल
(B) दूरी
(C) त्वरण
(D) विस्थापन
उत्तर: (C)
वर्ष: JEE Main 2019 | Shift 2

🔶 Q13. वेग-समय ग्राफ के नीचे का क्षेत्रफल किसे दर्शाता है?
(A) त्वरण
(B) विस्थापन
(C) चाल
(D) बल
उत्तर: (B)
वर्ष: JEE Main 2018 | Shift 1

🔶 Q14. एक कण का वेग समय t पर 20 m/s है और प्रारंभिक वेग 10 m/s है, त्वरण 2 m/s² है, तो t का मान:
(A) 5 s
(B) 4 s
(C) 3 s
(D) 2 s
उत्तर: (A)
वर्ष: JEE Main 2018 | Shift 2

🔶 Q15. यदि कोई कण स्थिर त्वरण से गति करता है, तो कौन सा ग्राफ सही नहीं है?
(A) s–t रेखीय
(B) v–t रेखीय
(C) a–t क्षैतिज
(D) s–t वक्र
उत्तर: (A)
वर्ष: JEE Main 2017 | Offline

🔶 Q16. कोई वस्तु शून्य चाल से प्रारंभ होकर 10 सेकंड में 100 m चलती है, तो उसका त्वरण?
(A) 2 m/s²
(B) 4 m/s²
(C) 1 m/s²
(D) 0.5 m/s²
उत्तर: (A)
वर्ष: JEE Main 2017 | Online

🔶 Q17. एकसमान त्वरण का ग्राफ कौनसा होगा?
(A) s–t घुमावदार
(B) v–t रेखीय
(C) a–t वक्र
(D) सभी
उत्तर: (B)
वर्ष: JEE Main 2016 | Offline

🔶 Q18. v² = u² + 2as में ‘s’ का क्या अर्थ है?
(A) दूरी
(B) विस्थापन
(C) चाल
(D) त्वरण
उत्तर: (B)
वर्ष: JEE Main 2016 | Online

🔶 Q19. चाल का SI मात्रक क्या है?
(A) km/h
(B) cm/s
(C) m/s
(D) m/min
उत्तर: (C)
वर्ष: JEE Main 2015

🔶 Q20. यदि ग्राफ की ढलान ऋणात्मक है, तो –
(A) चाल घट रही
(B) चाल बढ़ रही
(C) त्वरण शून्य
(D) विस्थापन बढ़ रहा
उत्तर: (A)
वर्ष: JEE Main 2014

🔶 Q21. एक कण का त्वरण शून्य है, तब –
(A) गति स्थिर है
(B) गति बदल रही
(C) चाल बढ़ रही
(D) बल अधिक है
उत्तर: (A)
वर्ष: JEE Main 2014

🔶 Q22. यदि चाल शून्य है, परन्तु त्वरण है, तो –
(A) वस्तु रुकी
(B) गति शुरू करेगी
(C) रुकी ही रहेगी
(D) विस्फोट होगा
उत्तर: (B)
वर्ष: JEE Main 2013

🔶 Q23. 5 m/s की चाल से 4 सेकंड चलने पर दूरी होगी –
(A) 20 m
(B) 15 m
(C) 10 m
(D) 25 m
उत्तर: (A)
वर्ष: JEE Main 2012

🔶 Q24. एक वस्तु 0.5 m/s² की त्वरण से 20 सेकंड तक चलती है, अंतिम चाल?
(A) 10 m/s
(B) 5 m/s
(C) 15 m/s
(D) 20 m/s
उत्तर: (A)
वर्ष: JEE Main 2012

🔶 Q25. वेग–समय ग्राफ की रेखा अगर क्षैतिज हो तो –
(A) त्वरण शून्य
(B) चाल स्थिर
(C) विस्थापन बढ़ रहा
(D) सभी सही
उत्तर: (D)
वर्ष: JEE Main 2011

━━━━━━━━━━━━━━━

🔶 Q26. एक वस्तु की चाल 20 m/s है, त्वरण -2 m/s² है। उसे रुकने में कितना समय लगेगा?
(A) 10 s
(B) 20 s
(C) 5 s
(D) 2 s
उत्तर: (A)
वर्ष: JEE Main 2010

🔶 Q27. एक कण की चाल 6 m/s है और वह 3 सेकंड में रुकता है, उसका त्वरण?
(A) -2 m/s²
(B) -3 m/s²
(C) -1 m/s²
(D) -4 m/s²
उत्तर: (A)
वर्ष: JEE Main 2010

🔶 Q28. यदि चाल समान हो और समय दुगुना हो जाए, तो दूरी —
(A) दुगुनी
(B) आधी
(C) चौगुनी
(D) कोई परिवर्तन नहीं
उत्तर: (A)
वर्ष: JEE Main 2009

🔶 Q29. एक कण प्रारंभ में विश्राम में है और वह 5 m/s² के त्वरण से चलता है। 4 सेकंड में उसका विस्थापन?
(A) 40 m
(B) 20 m
(C) 10 m
(D) 50 m
उत्तर: (B)
वर्ष: JEE Main 2009

🔶 Q30. v² = u² + 2as समीकरण में a ऋणात्मक हो तो —
(A) गति बढ़ेगी
(B) गति घटेगी
(C) चाल स्थिर
(D) विस्थापन घटेगा
उत्तर: (B)
वर्ष: JEE Main 2008

🔶 Q31. एक गाड़ी 15 m/s की चाल से चलती है और 5 सेकंड में रुक जाती है, त्वरण क्या होगा?
(A) -3 m/s²
(B) -2 m/s²
(C) -1 m/s²
(D) -5 m/s²
उत्तर: (A)
वर्ष: JEE Main 2008

🔶 Q32. एकसमान त्वरण में चलती वस्तु की चाल–समय ग्राफ कैसा होगा?
(A) रेखीय
(B) वक्र
(C) क्षैतिज
(D) शून्य
उत्तर: (A)
वर्ष: JEE Main 2007

🔶 Q33. चाल-समय ग्राफ की ढलान का अर्थ क्या है?
(A) दूरी
(B) विस्थापन
(C) त्वरण
(D) गति
उत्तर: (C)
वर्ष: JEE Main 2006

🔶 Q34. 10 m/s प्रारंभिक चाल, 2 m/s² त्वरण, 5 सेकंड में दूरी —
(A) 75 m
(B) 60 m
(C) 50 m
(D) 65 m
उत्तर: (A)
वर्ष: JEE Main 2006

🔶 Q35. विस्थापन और दूरी में अंतर होता है —
(A) दिशा का
(B) परिमाण का
(C) इकाई का
(D) समय का
उत्तर: (A)
वर्ष: JEE Main 2005

🔶 Q36. एक वस्तु 10 m/s² के त्वरण से चलती है, 3 सेकंड में चाल —
(A) 30 m/s
(B) 10 m/s
(C) 20 m/s
(D) 40 m/s
उत्तर: (A)
वर्ष: JEE Main 2005

🔶 Q37. 1 सेकंड में 5 m/s से 15 m/s पहुँचने वाला कण का त्वरण —
(A) 10 m/s²
(B) 5 m/s²
(C) 15 m/s²
(D) 20 m/s²
उत्तर: (A)
वर्ष: JEE Main 2004

🔶 Q38. चाल के मात्रक का विमीय सूत्र —
(A) [L T⁻¹]
(B) [L T²]
(C) [M L⁻¹]
(D) [M T⁻²]
उत्तर: (A)
वर्ष: JEE Main 2004

🔶 Q39. एक वाहन 90 km/h से चलता है, m/s में चाल —
(A) 25 m/s
(B) 20 m/s
(C) 30 m/s
(D) 35 m/s
उत्तर: (A)
वर्ष: JEE Main 2003

🔶 Q40. यदि कोई वस्तु पीछे की ओर गति करे, तो चाल —
(A) ऋणात्मक
(B) धनात्मक
(C) शून्य
(D) अनिश्चित
उत्तर: (A)
वर्ष: JEE Main 2003

🔶 Q41. चाल और समय में रैखिक संबंध दर्शाता है कि —
(A) त्वरण समान है
(B) त्वरण बदल रहा
(C) विस्थापन स्थिर
(D) बल नहीं है
उत्तर: (A)
वर्ष: JEE Main 2002

🔶 Q42. वेग की SI इकाई —
(A) cm/s
(B) m/s
(C) m/min
(D) km/hr
उत्तर: (B)
वर्ष: JEE Main 2002

🔶 Q43. 5 m/s की चाल, 2 m/s² त्वरण, 4 s में विस्थापन —
(A) 36 m
(B) 40 m
(C) 32 m
(D) 30 m
उत्तर: (A)
वर्ष: JEE Main 2001

🔶 Q44. चाल शून्य है और त्वरण 2 m/s², तो गति —
(A) प्रारंभिक
(B) स्थिर
(C) शून्य
(D) ऋणात्मक
उत्तर: (A)
वर्ष: JEE Main 2001

🔶 Q45. यदि वस्तु की चाल नकारात्मक हो, तो —
(A) पीछे की गति
(B) आगे
(C) स्थिर
(D) घूर्णन
उत्तर: (A)
वर्ष: JEE Main 2000

🔶 Q46. एकसमान गति में विस्थापन —
(A) चाल × समय
(B) u + at
(C) ut + ½at²
(D) v² – u²/2a
उत्तर: (A)
वर्ष: JEE Main 2000

🔶 Q47. चाल–समय ग्राफ में क्षेत्रफल —
(A) विस्थापन
(B) त्वरण
(C) चाल
(D) बल
उत्तर: (A)
वर्ष: JEE Main 1999

🔶 Q48. चाल का विमीय सूत्र —
(A) [L T⁻¹]
(B) [M L⁻²]
(C) [L T²]
(D) [M T⁻²]
उत्तर: (A)
वर्ष: JEE Main 1999

🔶 Q49. एक वस्तु 15 m/s चाल से चल रही है और 3 सेकंड में रुकती है, उसका त्वरण —
(A) -5 m/s²
(B) -3 m/s²
(C) -6 m/s²
(D) -2 m/s²
उत्तर: (A)
वर्ष: JEE Main 1998

🔶 Q50. एक वस्तु समान त्वरण से 0 से 20 m/s तक पहुँची 5 सेकंड में। दूरी?
(A) 50 m
(B) 75 m
(C) 100 m
(D) 125 m
उत्तर: (C)
वर्ष: JEE Main 1998

————————————————————————————————————————————————————————————————————————————

JEE ADVANCED पिछले सालों के प्रश्न

━━━━━━━━━━━━━━━
🌟 JEE Advanced Previous Year MCQs (34 प्रश्न)
📍 प्रत्येक प्रश्न के नीचे सही उत्तर दिया गया है।
एक वस्तु की चाल 10 m/s है और वह 2 m/s² के त्वरण से चल रही है। 5 सेकंड बाद उसकी चाल होगी:
(A) 20 m/s
(B) 15 m/s
(C) 12 m/s
(D) 10 m/s
उत्तर: (B)

एक कण 10 m/s प्रारंभिक चाल और -2 m/s² त्वरण से गति करता है। अधिकतम विस्थापन:
(A) 25 m
(B) 30 m
(C) 20 m
(D) 15 m
उत्तर: (A)

किसी वस्तु का वेग-समय ग्राफ एक वक्र है, तो उसका त्वरण होगा:
(A) शून्य
(B) स्थिर
(C) परिवर्तनशील
(D) ऋणात्मक
उत्तर: (C)

एक कण v = u + at समीकरण से चलता है। यदि a = 0 हो, तो गति —
(A) स्थिर
(B) बढ़ती
(C) घटती
(D) शून्य
उत्तर: (A)

एक कण के चाल-समय ग्राफ का क्षेत्रफल दर्शाता है:
(A) त्वरण
(B) विस्थापन
(C) दूरी
(D) बल
उत्तर: (B)

यदि एकसमान त्वरण है, तो चाल–समय ग्राफ:
(A) घातीय
(B) रेखीय
(C) परवलय
(D) शून्य
उत्तर: (B)

किसी वस्तु का चाल 20 m/s से 0 तक 5 सेकंड में घटता है, त्वरण:
(A) -4 m/s²
(B) -5 m/s²
(C) -2 m/s²
(D) -3 m/s²
उत्तर: (B)

एक कण 10 सेकंड में 100 मीटर चलता है। चाल:
(A) 10 m/s
(B) 5 m/s
(C) 15 m/s
(D) 20 m/s
उत्तर: (A)

यदि a = dv/dt, तो v = ∫a dt यह किस सिद्धांत पर आधारित है?
(A) गति का प्रथम नियम
(B) द्वितीय नियम
(C) kinematics
(D) कैल्कुलस
उत्तर: (C)

एक कण का विस्थापन 5t² + 2t + 1 है, चाल?
(A) 10t + 2
(B) 5t + 2
(C) 5t²
(D) 2t
उत्तर: (A)

एक कण की चाल 40 m/s से 20 m/s तक घटती है 2 सेकंड में, त्वरण?
(A) -10 m/s²
(B) -20 m/s²
(C) -15 m/s²
(D) -5 m/s²
उत्तर: (A)

विस्थापन = ut + ½at² समीकरण कब लागू नहीं होता?
(A) जब a स्थिर न हो
(B) जब u = 0
(C) जब t = 0
(D) जब s = 0
उत्तर: (A)

x = 4t + 3t² का अर्थ क्या है?
(A) चाल बदल रही है
(B) चाल स्थिर है
(C) त्वरण शून्य है
(D) कण रुक गया है
उत्तर: (A)

किसी वस्तु की चाल घट रही है पर दिशा वही है, इसका अर्थ:
(A) ऋणात्मक त्वरण
(B) धनात्मक त्वरण
(C) स्थिर चाल
(D) घूर्णन गति
उत्तर: (A)

एकसमान त्वरण की दशा में चाल और समय का ग्राफ:
(A) वक्र
(B) रेखा
(C) परवलय
(D) घातीय
उत्तर: (B)

चाल का विमीय सूत्र —
(A) [L T⁻¹]
(B) [M T⁻²]
(C) [L M⁻¹]
(D) [T²]
उत्तर: (A)

यदि v² = u² + 2as, और a = -1 m/s², तो गति —
(A) बढ़ती
(B) घटती
(C) स्थिर
(D) रुक जाती
उत्तर: (B)

x = 3t² + 2t + 4, t = 2 s पर गति?
(A) 14 m/s
(B) 12 m/s
(C) 16 m/s
(D) 10 m/s
उत्तर: (C)

चाल–समय ग्राफ की ढलान से ज्ञात होता है:
(A) त्वरण
(B) विस्थापन
(C) दूरी
(D) चाल
उत्तर: (A)

x = At² + Bt + C, चाल ज्ञात करें:
(A) 2At + B
(B) At + B
(C) A + B
(D) 2At
उत्तर: (A)

यदि a(t) = 4t, और प्रारंभिक चाल 0 है, तो v(t) = ?
(A) 2t²
(B) 4t²
(C) 4t
(D) t²
उत्तर: (A)

एक वस्तु की चाल 60 km/h है, कितनी दूरी तय करेगी 1 min में?
(A) 1 km
(B) 2 km
(C) 1/2 km
(D) 5 km
उत्तर: (C)

यदि चाल 10 m/s और त्वरण 2 m/s² है, तो 3 सेकंड में विस्थापन —
(A) 39 m
(B) 36 m
(C) 33 m
(D) 30 m
उत्तर: (B)

x–t ग्राफ वक्र है, v–t ग्राफ कैसा होगा?
(A) वक्र
(B) रेखीय
(C) शून्य
(D) स्थिर
उत्तर: (A)

0 से v तक पहुँचने के लिए a स्थिर हो, दूरी s होगी —
(A) v²/2a
(B) v²/a
(C) av²
(D) v²t
उत्तर: (A)

समान गति के लिए कोणीय चाल–समय ग्राफ कैसा होगा?
(A) क्षैतिज रेखा
(B) वक्र
(C) बढ़ता वक्र
(D) घटता वक्र
उत्तर: (A)

एक गाड़ी 10 m/s से 0 m/s तक 5 सेकंड में पहुँचती है, औसत चाल —
(A) 5 m/s
(B) 10 m/s
(C) 0 m/s
(D) 2 m/s
उत्तर: (A)

चाल–समय ग्राफ का क्षेत्रफल दर्शाता है:
(A) विस्थापन
(B) त्वरण
(C) गति
(D) समय
उत्तर: (A)

एक कण 2 m/s चाल से चलता है और 2 m/s² के त्वरण से बढ़ता है। 4 s में चाल?
(A) 10 m/s
(B) 12 m/s
(C) 8 m/s
(D) 6 m/s
उत्तर: (C)

यदि v–t ग्राफ की ढलान ऋणात्मक हो तो —
(A) गति घटती है
(B) चाल बढ़ती है
(C) दिशा बदलती है
(D) विस्थापन शून्य होता है
उत्तर: (A)

समीकरण s = ut + ½at² में ‘u’ का अर्थ:
(A) अंतिम चाल
(B) प्रारंभिक चाल
(C) औसत चाल
(D) अधिकतम चाल
उत्तर: (B)

यदि a = 0 हो, तो s = ut + ½at² का रूप —
(A) s = ut
(B) s = 0
(C) s = at
(D) s = u
उत्तर: (A)

किसी वस्तु की चाल बदलती है लेकिन दिशा नहीं, इसका अर्थ —
(A) ऋणात्मक त्वरण
(B) सकारात्मक त्वरण
(C) घूर्णन
(D) कोई नहीं
उत्तर: (A)

यदि x–t ग्राफ की ढलान बढ़ रही है तो —
(A) त्वरण बढ़ रहा
(B) चाल घट रही
(C) विस्थापन कम हो रहा
(D) चाल स्थिर है
उत्तर: (A)

————————————————————————————————————————————————————————————————————————————

मॉडल प्रश्न पत्र, अभ्यास

एक वस्तु की चाल 5 m/s से बढ़कर 25 m/s हो जाती है 4 s में। उसका त्वरण कितना है?
(A) 4 m/s²
(B) 5 m/s²
(C) 6 m/s²
(D) 8 m/s²
उत्तर: (A)

x = 5t² + 2t + 1 के लिए t = 2 पर चाल क्या होगी?
(A) 22 m/s
(B) 24 m/s
(C) 20 m/s
(D) 18 m/s
उत्तर: (B)

चाल-समय ग्राफ का क्षेत्रफल क्या दर्शाता है?
(A) त्वरण
(B) विस्थापन
(C) समय
(D) ऊर्जा
उत्तर: (B)

यदि चाल घट रही हो लेकिन दिशा न बदले तो:
(A) त्वरण ऋणात्मक
(B) त्वरण धनात्मक
(C) त्वरण शून्य
(D) त्वरण अनंत
उत्तर: (A)

एक कण का विस्थापन–समय ग्राफ एक वक्र है, इसका अर्थ:
(A) त्वरण शून्य है
(B) गति एकसमान है
(C) त्वरण परिवर्तनशील है
(D) कोई गति नहीं
उत्तर: (C)

यदि a = 0 हो तो s = ut + ½at² का रूप क्या होगा?
(A) s = ut
(B) s = u
(C) s = at
(D) s = 0
उत्तर: (A)

प्रारंभिक चाल 0 है, त्वरण 4 m/s² है, 5 s में दूरी?
(A) 50 m
(B) 25 m
(C) 100 m
(D) 75 m
उत्तर: (A)

चाल 10 m/s है, त्वरण 2 m/s², 4 s में अंतिम चाल?
(A) 14 m/s
(B) 18 m/s
(C) 12 m/s
(D) 20 m/s
उत्तर: (D)

यदि a(t) = 6t, प्रारंभिक चाल 0, तो v(t) = ?
(A) 6t²
(B) 3t²
(C) 6t
(D) 3t
उत्तर: (B)

x = At² + Bt + C, चाल = ?
(A) 2At + B
(B) At + B
(C) A + B
(D) Bt + C
उत्तर: (A)

x–t ग्राफ की ढलान दर्शाती है:
(A) चाल
(B) त्वरण
(C) विस्थापन
(D) बल
उत्तर: (A)

एक वस्तु 2 s में 8 m जाती है, फिर 4 m और 2 s में, औसत चाल?
(A) 3 m/s
(B) 4 m/s
(C) 5 m/s
(D) 6 m/s
उत्तर: (A)

एक वस्तु 20 m/s से 0 तक 4 s में रुकती है, त्वरण:
(A) -5 m/s²
(B) -10 m/s²
(C) -4 m/s²
(D) -2 m/s²
उत्तर: (A)

यदि v = u + at में a = -2, u = 10, t = 2, तो v = ?
(A) 6 m/s
(B) 5 m/s
(C) 8 m/s
(D) 4 m/s
उत्तर: (A)

यदि चाल समय के साथ घटती हो तो:
(A) त्वरण ऋणात्मक
(B) त्वरण धनात्मक
(C) त्वरण शून्य
(D) गति नहीं है
उत्तर: (A)

एकसमान त्वरण की दशा में v² – u² = 2as से दूरी s?
(A) (v² – u²)/2a
(B) v²/2a
(C) u²/2a
(D) a²/v
उत्तर: (A)

चाल 15 m/s, त्वरण 0, 10 सेकंड में विस्थापन?
(A) 150 m
(B) 120 m
(C) 130 m
(D) 160 m
उत्तर: (A)

x = 4t³, चाल = ?
(A) 12t²
(B) 4t²
(C) 8t
(D) 3t²
उत्तर: (A)

t = 0 से t = 4 तक त्वरण 2 m/s² है, प्रारंभिक चाल 0, अंतिम चाल?
(A) 8 m/s
(B) 6 m/s
(C) 10 m/s
(D) 4 m/s
उत्तर: (A)

चाल 0 से 30 तक 3 सेकंड में, औसत चाल?
(A) 15 m/s
(B) 20 m/s
(C) 10 m/s
(D) 25 m/s
उत्तर: (A)

x = 3t² – 2t + 1, t = 1 पर चाल?
(A) 4 m/s
(B) 3 m/s
(C) 2 m/s
(D) 5 m/s
उत्तर: (A)

एक वस्तु का चाल–समय ग्राफ एक क्षैतिज रेखा है, तो गति:
(A) एकसमान
(B) बढ़ती
(C) घटती
(D) शून्य
उत्तर: (A)

यदि त्वरण = 0, तो चाल–समय ग्राफ:
(A) क्षैतिज रेखा
(B) झुकाव वाली रेखा
(C) परवलय
(D) वक्र
उत्तर: (A)

चाल 60 km/h को m/s में परिवर्तित करें:
(A) 16.67 m/s
(B) 18 m/s
(C) 20 m/s
(D) 22 m/s
उत्तर: (A)

x = 3t³ + 2t², चाल = ?
(A) 9t² + 4t
(B) 6t + 2
(C) 3t + 2
(D) 9t²
उत्तर: (A)
━━━━━━━━━━━━━━━
🔷 JEE MAIN LEVEL QUESTIONS (Q26–Q50):

चाल t² के समानुपाती है, तो त्वरण:
(A) 2t
(B) 4t
(C) t
(D) t²
उत्तर: (A)

v–t ग्राफ का क्षेत्रफल दर्शाता है:
(A) विस्थापन
(B) त्वरण
(C) चाल
(D) समय
उत्तर: (A)

यदि a = dv/dt = 0 हो, तो चाल?
(A) स्थिर
(B) बढ़ती
(C) घटती
(D) अपरिभाषित
उत्तर: (A)

x = 2t³ – 3t² + 4t + 1, चाल = ?
(A) 6t² – 6t + 4
(B) 3t² – 2t
(C) 2t + 3
(D) 6t – 3
उत्तर: (A)

5 सेकंड में चाल 25 से 0 तक आती है, औसत चाल:
(A) 12.5 m/s
(B) 10 m/s
(C) 15 m/s
(D) 20 m/s
उत्तर: (A)

चाल = a + bt, त्वरण = ?
(A) b
(B) a
(C) t
(D) ab
उत्तर: (A)

v = 3t² + 2t, त्वरण = ?
(A) 6t + 2
(B) 3t + 2
(C) 2t + 1
(D) 6t
उत्तर: (A)

किसी वस्तु का चाल–समय ग्राफ सीधा लेकिन नीचे झुका है, इसका मतलब:
(A) ऋणात्मक त्वरण
(B) धनात्मक त्वरण
(C) शून्य त्वरण
(D) विस्थापन ऋणात्मक
उत्तर: (A)

चाल का मान धनात्मक लेकिन विस्थापन शून्य —
(A) वस्तु वापस आ गई
(B) गति नहीं थी
(C) त्वरण शून्य
(D) दिशा नहीं बदली
उत्तर: (A)

v² = u² + 2as का प्रयोग कब असत्य है?
(A) जब a परिवर्तनशील हो
(B) जब t = 0
(C) जब u = 0
(D) जब s = 0
उत्तर: (A)

यदि चाल–समय ग्राफ वक्र है तो त्वरण:
(A) परिवर्तनशील
(B) शून्य
(C) स्थिर
(D) ऋणात्मक
उत्तर: (A)

एक वस्तु 2 m/s से शुरू होकर 3 m/s² से बढ़ती है, 4 s में चाल?
(A) 14 m/s
(B) 12 m/s
(C) 10 m/s
(D) 16 m/s
उत्तर: (A)

x = 10 + 2t – 3t², t = 2 s पर चाल:
(A) -8 m/s
(B) -6 m/s
(C) -10 m/s
(D) -12 m/s
उत्तर: (A)

चाल और समय का ग्राफ अगर झुकता है, तो:
(A) त्वरण परिवर्तनशील है
(B) गति स्थिर है
(C) कोई त्वरण नहीं
(D) विस्थापन स्थिर है
उत्तर: (A)

v = 3t + 5, चाल t = 2 s पर?
(A) 11 m/s
(B) 10 m/s
(C) 9 m/s
(D) 8 m/s
उत्तर: (A)

यदि x = 5t² + 2t, चाल = ?
(A) 10t + 2
(B) 2t + 5
(C) 5t + 2
(D) 10t
उत्तर: (A)

एक कण 6 सेकंड में 36 m जाता है, औसत चाल?
(A) 6 m/s
(B) 4 m/s
(C) 5 m/s
(D) 7 m/s
उत्तर: (A)

चाल और समय का ग्राफ क्षैतिज है, तो त्वरण:
(A) 0
(B) ∞
(C) 1
(D) -1
उत्तर: (A)

एक वस्तु की चाल 0 से 20 m/s तक बढ़ती है 4 s में, औसत चाल?
(A) 10 m/s
(B) 15 m/s
(C) 20 m/s
(D) 5 m/s
उत्तर: (A)

x = t³ – 2t² + t, चाल = ?
(A) 3t² – 4t + 1
(B) t² – 2t + 1
(C) 3t² + t
(D) 3t – 2
उत्तर: (A)

यदि a = 0 तो चाल का ग्राफ कैसा होगा?
(A) क्षैतिज रेखा
(B) वक्र
(C) नीचे झुकता
(D) शून्य
उत्तर: (A)

चाल–समय ग्राफ का ढलान दर्शाता है:
(A) त्वरण
(B) चाल
(C) दूरी
(D) विस्थापन
उत्तर: (A)

एकसमान त्वरण की दशा में विस्थापन–समय ग्राफ:
(A) परवलय
(B) रेखा
(C) घातीय
(D) वक्र
उत्तर: (A)

यदि चाल समय के साथ बढ़ती है तो ग्राफ:
(A) ऊपर झुकी रेखा
(B) नीचे झुकी
(C) क्षैतिज
(D) वक्र
उत्तर: (A)

चाल t² के अनुपात में है, तो विस्थापन t³ के अनुपात में होगा —
(A) सही
(B) गलत
(C) कभी सही
(D) t पर निर्भर
उत्तर: (A)

————————————————————————————————————————————————————————————————————————————