Class 11 : Physics (In English) – Chapter 1: Units and Measurements
EXPLANATION & SUMMARY
🔶 1. Introduction to Measurement
Measurement is the comparison of a physical quantity with a known standard (unit).
Science is based on observations and measurements. Without measurement, scientific theories cannot be tested or validated.
🔶 2. Physical Quantities
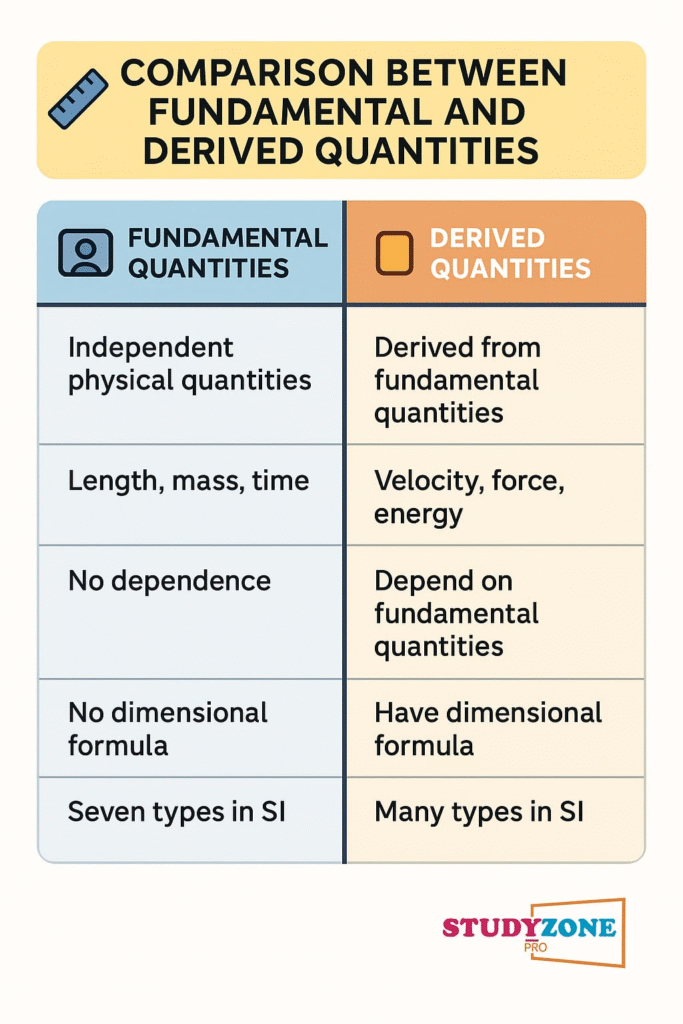
Physical Quantity: Any quantity that can be measured and described in terms of laws of physics.
Two types:
🔹 Fundamental Quantities – Cannot be defined in terms of other quantities (e.g., length, mass, time).
🔹 Derived Quantities – Obtained from fundamental quantities (e.g., speed = distance/time).
🔶 3. Units
A unit is a standard of measurement of a physical quantity.
Types of units:
🔹 Fundamental Units: Directly defined (e.g., metre, kilogram).
🔹 Derived Units: Combinations of fundamental units (e.g., m/s²).
🔶 4. System of Units
Multiple systems of units were used before standardization:
CGS: Centimetre-Gram-Second
FPS: Foot-Pound-Second
MKS: Metre-Kilogram-Second
Today, we use SI Units (International System of Units) globally.
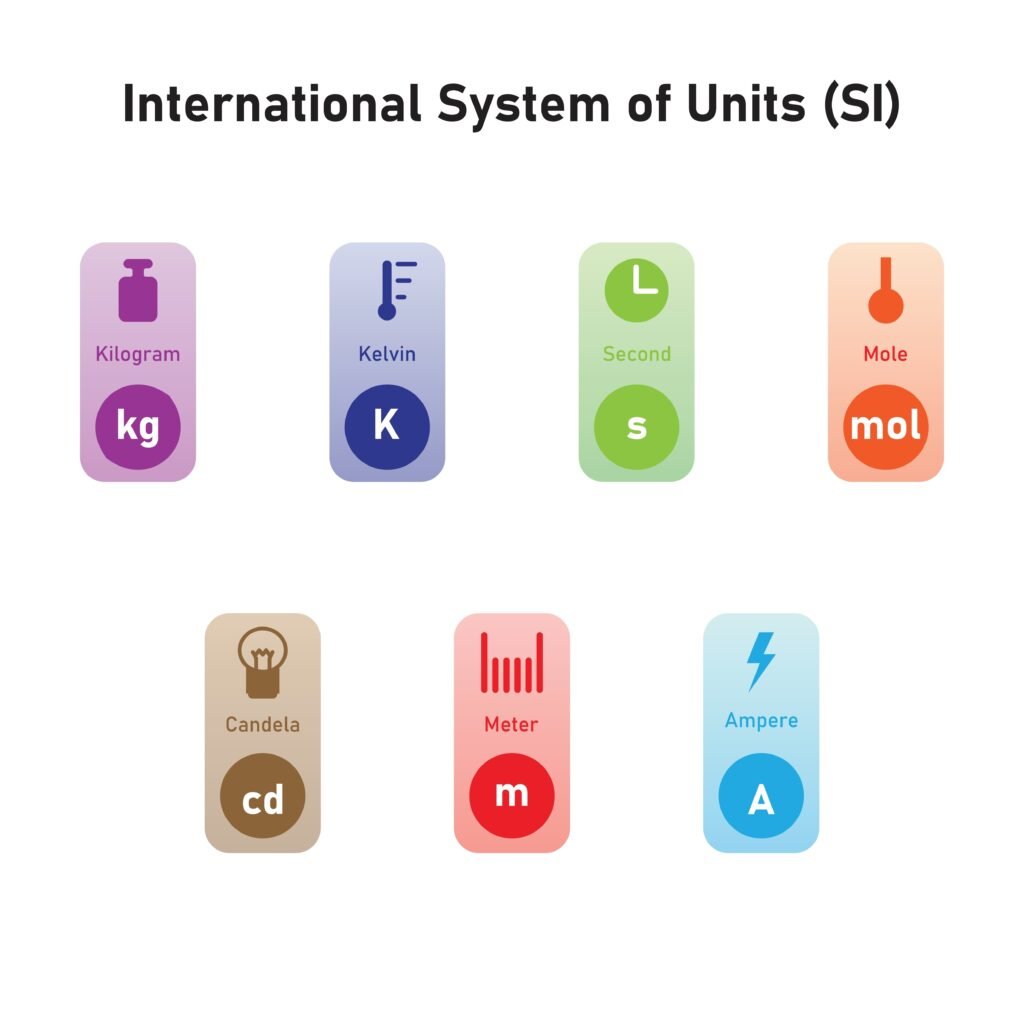
🔶 5. SI Units (International System of Units)
Seven Fundamental Quantities & Their SI Units:
Quantity SI Unit Symbol
Length metre m
Mass kilogram kg
Time second s
Electric current ampere A
Temperature kelvin K
Amount of substance mole mol
Luminous intensity candela cd
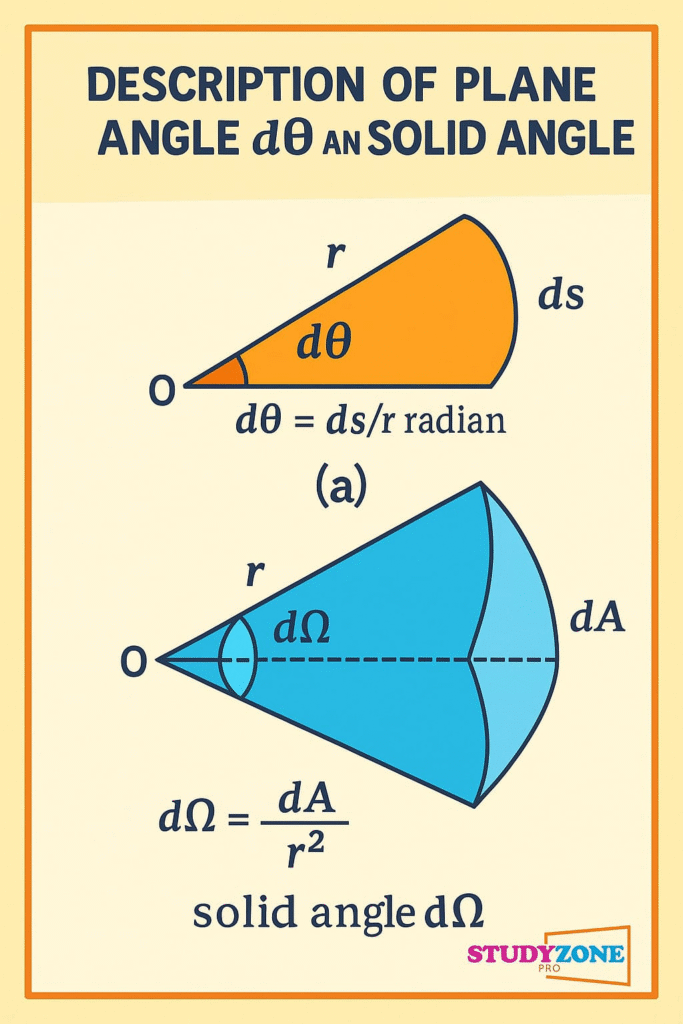
🔶 6. Supplementary Units
Plane Angle: radian (rad)
Solid Angle: steradian (sr)
🔶 7. Derived Units
Formed from combinations of fundamental units.
Example:
Area → m²
Volume → m³
Speed → m/s
Acceleration → m/s²
Force → kg·m/s² = Newton (N)
Pressure → N/m² = Pascal (Pa)
🔶 8. Measurement of Length
Techniques vary with scale:
🔹 Small lengths: vernier callipers, screw gauge
🔹 Large distances: radar, parallax method (used in astronomy)
📏 Parallax Method:
Used to measure distances of distant stars.
Formula:
where:
D = Distance to the star
b = Baseline (distance between two observation points)
θ = Parallax angle
🔶 9. Measurement of Mass
Measured using electronic or beam balances.
Mass of small particles like atoms → measured in atomic mass units (u):
🔶 10. Measurement of Time
Measured using atomic clocks (extremely precise).
1 second is the time taken for 9,192,631,770 vibrations of Cesium-133 atom.
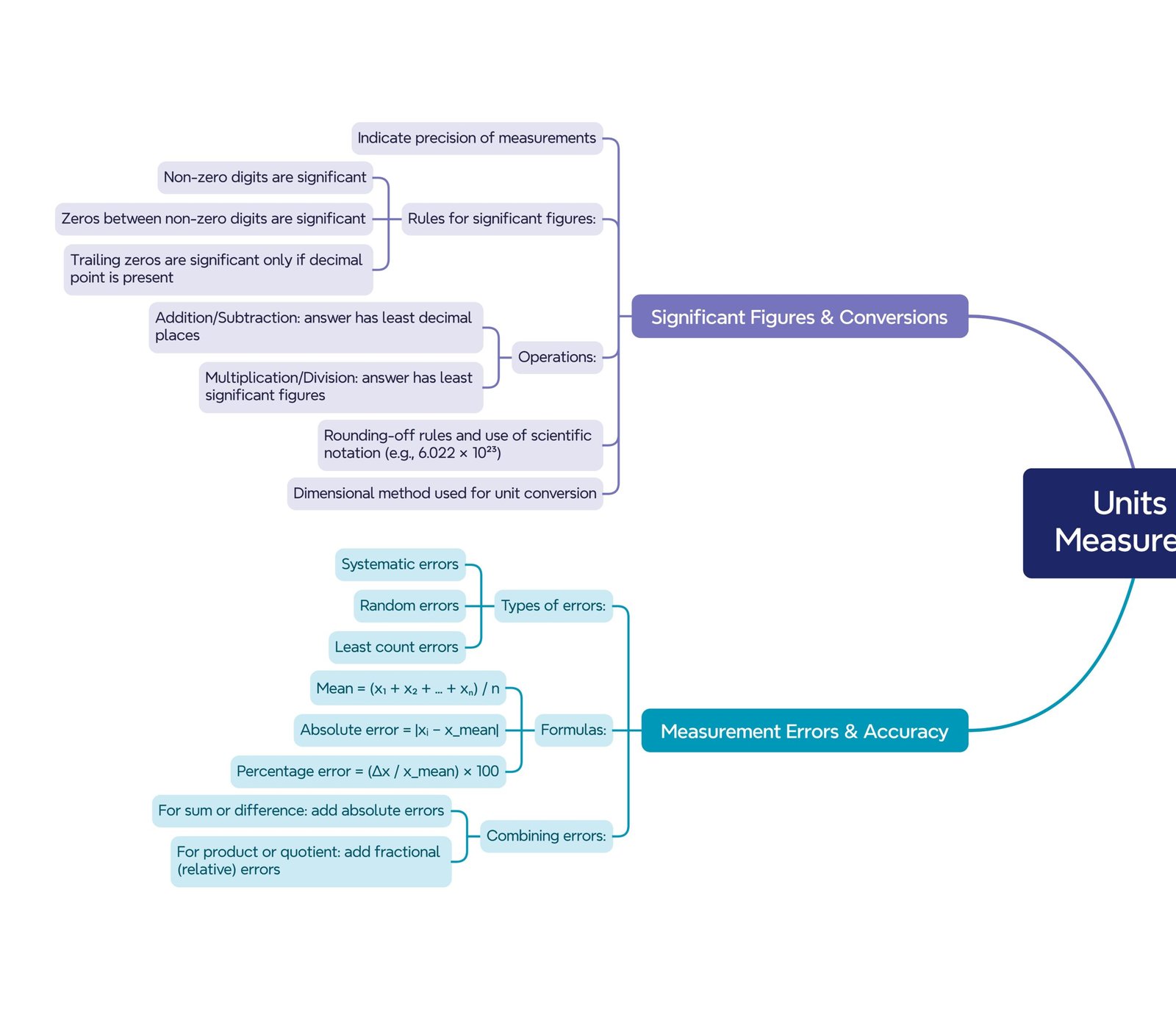
🔶 11. Accuracy, Precision, and Errors
Accuracy: Closeness of a measurement to the true value.
Precision: Closeness of repeated measurements.
🧪 Errors in Measurement:
Systematic Errors: Same error occurs again (e.g., instrument error).
Random Errors: Fluctuations due to unpredictable factors.
Least Count Error: Due to the smallest scale division of instrument.
🔶 12. Types of Errors
Absolute Error: Difference between measured and true value.
Relative Error:
Percentage Error:
🔶 13. Combination of Errors
In functions involving multiple quantities, the total error is affected accordingly:
Addition/Subtraction:
Total absolute error = sum of absolute errors
Multiplication/Division:
Total relative error = sum of individual relative errors
Powers:
Multiply the relative error by the power.
🔶 14. Significant Figures
Digits that carry meaning in a measurement.
Rules:
Non-zero digits are significant.
Zeroes between non-zero digits are significant.
Trailing zeros after a decimal point are significant.
✏️ Example:
13.07 → 4 significant figures
0.00560 → 3 significant figures
🔶 15. Rules for Arithmetic with Significant Figures
Addition/Subtraction: Answer should match least decimal places.
Multiplication/Division: Answer should match least significant figures.
🔶 16. Rounding Off
If digit to be dropped is <5 → leave previous digit as it is.
If digit to be dropped is >5 → increase the previous digit by 1.
If digit to be dropped is exactly 5:
If previous digit is even → leave it
If previous digit is odd → increase it
🔶 17. Dimensions of Physical Quantities
Every derived quantity has a dimensional formula.
Example:
Force = mass × acceleration = MLT⁻²
📘 Dimensional formula = representation using M (mass), L (length), T (time), etc.
🔶 18. Applications of Dimensional Analysis
Checking correctness of equations (Principle of homogeneity)
LHS and RHS of an equation must have the same dimensions.
Deriving relationships:
Used when dependence on other quantities is known.
E.g., derive time period of a pendulum.
🔶 19. Limitations of Dimensional Analysis
Cannot find dimensionless constants.
Cannot detect if a quantity is vector or scalar.
Valid only if physical relation is dimensionally homogeneous.
📘 PART B: CRISP SUMMARY (~300 WORDS)
🔷 Summary – Units and Measurement
Measurement compares a quantity to a defined standard called a unit.
There are fundamental and derived physical quantities.
SI system is internationally accepted and includes 7 base units.
Units such as metre (length), kilogram (mass), second (time) form the base.
Physical quantities like velocity, force, and pressure are derived units.
Measurement tools include vernier calliper, screw gauge, and atomic clocks.
Accuracy is closeness to true value; precision refers to repeatability.
Errors are classified as:
Systematic
Random
Least count errors
Errors are combined algebraically depending on the operation (addition/multiplication).
Significant figures are used to express measurement certainty.
Rules for significant figures differ for operations and rounding off.
Dimensional formula represents physical quantities using base dimensions (M, L, T).
Dimensional analysis is used to:
Check equation correctness
Derive relationships
However, dimensional methods have limitations like inability to detect vector/scalar nature or constants.
————————————————————————————————————————————————————————————————————————————
QUESTIONS FROM TEXTBOOK
🔷 Question 1.1
Fill in the blanks:
(a) The volume of a cube of side 1 cm is equal to ….. m³
(b) The surface area of a solid cylinder of radius 2.0 cm and height 10.0 cm is equal to ….. mm²
(c) A vehicle moving with a speed of 18 km h⁻¹ covers….. m in 1 s
(d) The relative density of lead is 11.3. Its density is ….. g cm⁻³ or ….. kg m⁻³
✅ Answer:
(a)
📌 Volume = (1 cm)³ = (10⁻² m)³ = 1.0 × 10⁻⁶ m³
(b)
📌 Surface area = 2πr(h + r)
r = 2.0 cm = 20 mm, h = 10.0 cm = 100 mm
A = 2 × 3.14 × 20 × (100 + 20) = 15072 mm²
(c)
📌 Speed = 18 km/h = 5 m/s ⇒ Distance = speed × time = 5 × 1 = 5 m
(d)
📌 Relative density = density in g/cm³ ⇒ 11.3 g/cm³
In kg/m³ = 11.3 × 10³ = 11300 kg/m³
🔷 Question 1.2
Fill in the blanks by suitable conversion of units:
(a) 1 kg m² s⁻² = ….. g cm² s⁻²
(b) 1 m = ….. ly
(c) 3.0 m s⁻² = ….. km h⁻²
(d) G = 6.67 × 10⁻¹¹ N m² (kg)⁻² = ….. (cm)³ s⁻² g⁻¹
✅ Answer:
(a)
📌 Convert: 1 kg = 1000 g, 1 m² = 10⁴ cm²
So, 1 kg m² s⁻² = 1000 × 10⁴ g cm² s⁻² = 1.0 × 10⁷ g cm² s⁻²
(b)
📌 1 light year = 9.46 × 10¹⁵ m
So, 1 m = 1.06 × 10⁻¹⁶ ly
(c)
📌 1 m/s² = (1/1000) km / (1/3600)² h² = (1/1000) × (3600)²
= 1 m/s² = 12960 km/h²
So, 3.0 m/s² = 38880 km/h²
(d)
📌 Convert:
1 N = 10⁵ dyne = 10⁵ g cm s⁻²
1 m² = 10⁴ cm², 1 kg = 10³ g
G = 6.67 × 10⁻¹¹ × 10⁵ × 10⁴ / (10³)²
= 6.67 × 10⁻⁸ cm³ s⁻² g⁻¹
So, 6.67 × 10⁻⁸ (cm)³ s⁻² g⁻¹
🔷 Question 1.3
A calorie is a unit of heat (energy in transit) and it equals about 4.2 J where 1 J = 1 kg m² s⁻². Suppose we employ a system of units in which the unit of mass equals α kg, the unit of length equals β m, and the unit of time is γ s. Show that a calorie has a magnitude 4.2 α⁻¹ β⁻² γ² in terms of the new units.
✅ Answer:
📘 1 calorie = 4.2 J = 4.2 kg m² s⁻²
📌 Let mass = α kg, length = β m, time = γ s
Then, 1 J = 1 kg m²/s² = (α M) × (β L)² / (γ T)²
⇒ Unit of energy = α β² / γ²
So,
📌 1 calorie = 4.2 × (1 / (α β² / γ²))
= 4.2 α⁻¹ β⁻² γ²
🔷 Question 1.4
Explain this statement clearly:
“To call a dimensional quantity ‘large’ or ‘small’ is meaningless without specifying a standard for comparison”.
In view of this, reframe the following statements wherever necessary:
(a) Atoms are very small objects
(b) A jet plane moves with great speed
(c) The mass of Jupiter is very large
(d) The air inside this room contains a large number of molecules
(e) A proton is much more massive than an electron
(f) The speed of sound is much smaller than the speed of light
✅ Answer:
This statement implies that a physical quantity must always be compared to a standard reference to make sense of whether it is ‘large’ or ‘small’.
Reframed statements:
(a) Atoms are very small compared to everyday objects like a grain of sand.
(b) A jet plane moves with great speed as compared to a car or a train.
(c) The mass of Jupiter is very large compared to the mass of Earth.
(d) The air inside this room contains a large number of molecules compared to the number in a vacuum.
(e) A proton is much more massive than an electron, by a factor of about 1836.
(f) The speed of sound is much smaller than the speed of light (≈ 3 × 10⁸ m/s).
🔷 Question 1.5
A new unit of length is chosen such that the speed of light in vacuum is unity. What is the distance between the Sun and the Earth in terms of the new unit if light takes 8 min and 20 s to cover this distance?
✅ Answer:
🧮 Time = 8 min 20 s = 500 s
📘 Speed of light = 3 × 10⁸ m/s
Distance = speed × time = 3 × 10⁸ × 500 = 1.5 × 10¹¹ m
📌 In the new unit system, speed of light = 1 ⇒
Distance = 500 units
✅ Answer: Distance = 500 units
🔷 Question 1.6
Which of the following is the most precise device for measuring length:
(a) a vernier callipers with 20 divisions on the sliding scale
(b) a screw gauge of pitch 1 mm and 100 divisions on the circular scale
(c) an optical instrument that can measure length to within a wavelength of light?
✅ Answer:
Precision depends on the least count:
(a) Least count ≈ 0.1 mm
(b) Least count = pitch / no. of divisions = 1 mm / 100 = 0.01 mm
(c) Wavelength of light ≈ 10⁻⁶ m = 0.001 mm
✅ Answer: (c) An optical instrument is most precise
🔷 Question 1.7
A student measures the thickness of a human hair by looking at it through a microscope of magnification 100. He makes 20 observations and finds that the average width of the hair in the field of view of the microscope is 3.5 mm. What is the estimate on the thickness of hair?
✅ Answer:
📌 Actual thickness = observed width / magnification
= 3.5 mm / 100 = 0.035 mm
✅ Answer: 0.035 mm
🔷 Question 1.8
Answer the following:
(a) You are given a thread and a metre scale. How will you estimate the diameter of the thread?
(b) A screw gauge has a pitch of 1.0 mm and 200 divisions on the circular scale. Do you think it is possible to increase the accuracy of the screw gauge arbitrarily by increasing the number of divisions on the circular scale?
(c) The mean diameter of a thin brass rod is to be measured by vernier callipers. Why is a set of 100 measurements of the diameter expected to yield a more reliable estimate than a set of 5 measurements only?
✅ Answer:
(a) Wind the thread tightly around a pencil or cylinder in n turns, measure the length L of the wound thread with a scale.
Diameter ≈ L / n
(b) No. After a certain limit, errors due to backlash, human precision and zero error dominate. Increasing divisions alone won’t improve practical accuracy.
(c) More measurements reduce the impact of random errors. 100 readings give better statistical reliability (law of large numbers), hence more accurate average.
🔷 Question 1.9
The photograph of a house occupies an area of 1.75 cm² on a 35 mm slide. The slide is projected on a screen, and the area of the house on the screen is 1.55 m². What is the linear magnification of the projector-screen arrangement?
✅ Answer:
📌 Area on slide = 1.75 cm²
📌 Area on screen = 1.55 m² = 1.55 × 10⁴ cm²
(since 1 m² = 10⁴ cm²)
📘 Area magnification =
Area on screen / Area on slide
= (1.55 × 10⁴) / 1.75 ≈ 8857.14
📘 Linear magnification (m) = √(area magnification)
= √8857.14 ≈ 94.08
✅ Final Answer: Linear magnification = 94.08
🔷 Question 1.10
State the number of significant figures in the following:
(a) 0.007 m²
(b) 2.64 × 10⁴ kg
(c) 0.2370 g cm⁻³
(d) 6.320 J
(e) 6.032 N m²
(f) 0.0006032 m²
✅ Answer:
(a) 1 significant figure
(b) 3 significant figures
(c) 4 significant figures
(d) 4 significant figures
(e) 4 significant figures
(f) 4 significant figures
🔷 Question 1.11
The length, breadth and thickness of a rectangular sheet of metal are 4.234 m, 1.005 m, and 2.01 cm respectively. Give the area and volume of the sheet to correct significant figures.
✅ Answer:
📌 Thickness = 2.01 cm = 0.0201 m
📘 Step 1: Area = Length × Breadth
= 4.234 × 1.005 = 4.25517 m²
Smallest significant figures = 4
⇒ Rounded = 4.255 m²
📘 Step 2: Volume = Area × Thickness
= 4.25517 × 0.0201 = 0.85563 m³
Smallest significant figures = 3
⇒ Rounded = 0.856 m³
✅ Final Answers:
✔️ Area = 4.255 m²
✔️ Volume = 0.856 m³
🔷 Question 1.12
The mass of a box measured by a grocer’s balance is 2.30 kg. Two gold pieces of masses 20.15 g and 20.17 g are added to the box. What is
(a) the total mass of the box
(b) the difference in the masses of the pieces to correct significant figures?
✅ Answer:
📌 Convert gold pieces to kg:
20.15 g = 0.02015 kg
20.17 g = 0.02017 kg
📘 (a) Total mass = 2.30 + 0.02015 + 0.02017 = 2.34032 kg
Smallest sig. fig. = 3
⇒ Rounded = 2.34 kg
📘 (b) Difference = 20.17 − 20.15 = 0.02 g
(2 significant figures)
✅ Final Answers:
✔️ Total mass = 2.34 kg
✔️ Difference = 0.02 g
🔷 Question 1.13
A famous relation in physics relates ‘moving mass’ m to the ‘rest mass’ m₀ of a particle in terms of its speed v and the speed of light, c.
A boy recalls the relation almost correctly but forgets where to put the constant c. He writes:
m = m₀ / (1 − v²)½
Correct the relation using dimensional analysis.
✅ Answer:
📌 The given relation is dimensionally incorrect because the expression (1 − v²) is not dimensionless, while the square root must operate on a dimensionless number.
📘 To correct it, v must be divided by c, so the expression inside the square root becomes:
(1 − v²/c²)
✅ Correct Relation:
m = m₀ / √(1 − v²/c²)
This ensures that the expression inside the square root is dimensionless, making the equation dimensionally consistent.
🔷 Question 1.14
The unit of length convenient on the atomic scale is known as an angstrom and is denoted by Å:
1 Å = 10⁻¹⁰ m
The size of a hydrogen atom is about 0.5 Å.
What is the total atomic volume in m³ of a mole of hydrogen atoms?
✅ Answer:
📌 Radius (r) of hydrogen atom = 0.5 Å = 0.5 × 10⁻¹⁰ m
Assume atom is spherical.
📘 Volume of 1 atom = (4/3)πr³
= (4/3)π(0.5 × 10⁻¹⁰)³
= (4/3) × π × 0.125 × 10⁻³⁰
≈ 0.5236 × 10⁻³⁰ m³
📌 Number of atoms in 1 mole = 6.022 × 10²³
📘 Total volume = Volume of 1 atom × Avogadro’s number
= 0.5236 × 10⁻³⁰ × 6.022 × 10²³
= 3.15 × 10⁻⁷ m³
✅ Final Answer: 3.15 × 10⁻⁷ m³
🔷 Question 1.15
Consider a block of iron of size 4.0 cm × 4.0 cm × 4.0 cm at room temperature.
(ρ = 7.874 g cm⁻³)
What are the number of atoms in the block?
(Atomic mass of iron = 55.85 u; 1 u = 1.660 × 10⁻²⁴ g)
✅ Answer:
📌 Volume of block = 4.0 × 4.0 × 4.0 = 64.0 cm³
📌 Density = 7.874 g/cm³
📘 Mass = Density × Volume = 7.874 × 64.0 = 503.9 g
📌 Mass of 1 atom = 55.85 u = 55.85 × 1.660 × 10⁻²⁴ g
= 9.27 × 10⁻²³ g
📘 Number of atoms = Mass of block / Mass of one atom
= 503.9 / (9.27 × 10⁻²³)
≈ 5.43 × 10²⁴ atoms
✅ Final Answer: 5.43 × 10²⁴ atoms
🔷 Question 1.16
Compute the following:
(a) the relative density of gold if 1 cm³ of gold has a mass of 19.3 g
(b) the percentage error in the calculation of area of a rectangle of sides:
l = 5.12 cm ± 0.01 cm and b = 3.12 cm ± 0.01 cm
✅ Answer:
(a)
📌 Density of water = 1 g/cm³
📘 Relative density = Density of gold / Density of water
= 19.3 / 1 = 19.3
(b)
📘 Percentage error in area =
= (Δl / l + Δb / b) × 100
= (0.01 / 5.12 + 0.01 / 3.12) × 100
= (0.00195 + 0.00321) × 100
= 0.00516 × 100 = 0.516%
✅ Final Answers:
✔️ Relative density = 19.3
✔️ Percentage error = 0.516%
🔷 Question 1.17
The time period of oscillation of a simple pendulum is given by
T = 2π√(l / g)
Measured values:
l = 20.0 cm ± 0.2 cm
g = 9.80 m/s² ± 0.05 m/s²
Calculate T and its percentage error.
✅ Answer:
📌 l = 20.0 cm = 0.200 m
Δl = 0.2 cm = 0.002 m
g = 9.80 m/s²
Δg = 0.05 m/s²
📘 Calculate T:
T = 2π√(l / g)
= 2π√(0.200 / 9.80)
= 2π√(0.02041)
= 2π × 0.1428 ≈ 0.897 s
📘 Percentage error in T =
(1/2)(Δl / l + Δg / g) × 100
= 0.5 × (0.002 / 0.200 + 0.05 / 9.80) × 100
= 0.5 × (0.01 + 0.0051) × 100
= 0.5 × 0.0151 × 100 = 0.755%
✅ Final Answers:
✔️ T = 0.897 s
✔️ Percentage error = 0.755%
————————————————————————————————————————————————————————————————————————————
OTHER IMPORTANT QUESTIONS FOR EXAMS
(CBSE MODEL QUESTIONS PAPER)
ESPECIALLY MADE FROM THIS LESSON ONLY
Q1. Which of the following is a fundamental quantity?
(A) Speed
(B) Area
(C) Time
(D) Force
Answer: (C) Time
Q2. The number of significant figures in 0.007040 is:
(A) 3
(B) 4
(C) 5
(D) 6
Answer: (C) 5
Q3. Dimensional formula of velocity is:
(A) [M L T⁻²]
(B) [M⁰ L T⁻¹]
(C) [M¹ L T]
(D) [L T²]
Answer: (B) [M⁰ L T⁻¹]
Q4. The SI unit of pressure is:
(A) Pascal
(B) Torr
(C) Atmosphere
(D) Newton
Answer: (A) Pascal
Q5. Which of the following pairs has the same dimensions?
(A) Force and Work
(B) Torque and Energy
(C) Power and Force
(D) Momentum and Impulse
Answer: (D) Momentum and Impulse
Q6. 1 Astronomical Unit is equal to approximately:
(A) 1.496 × 10¹¹ m
(B) 3.084 × 10¹⁶ m
(C) 6.63 × 10⁻³⁴ m
(D) 9.1 × 10⁻³¹ m
Answer: (A) 1.496 × 10¹¹ m
Q7. Assertion (A): The physical quantity having dimensional formula [M L² T⁻²] is energy.
Reason (R): Work and energy are scalars with the same dimensions.
(A) Both A and R are true, and R is the correct explanation of A.
(B) Both A and R are true, but R is not the correct explanation of A.
(C) A is true, R is false.
(D) A is false, R is true.
Answer: (A) Both A and R are true, and R is the correct explanation of A.
Q8. The number 6.022 × 10²³ is known as:
(A) Avogadro’s number
(B) Planck’s constant
(C) Speed of light
(D) Gravitational constant
Answer: (A) Avogadro’s number
Q9. Which quantity has dimensions [M⁰ L⁰ T⁰]?
(A) Refractive index
(B) Momentum
(C) Work
(D) Acceleration
Answer: (A) Refractive index
Q10. Write the dimensional formula of Planck’s constant.
Answer: [M L² T⁻¹]
Q11. Write the name and symbol of the SI unit of energy.
Answer: Joule (J)
Q12. State whether the following is a scalar or vector quantity: Work
Answer: Scalar quantity
Q13. Write the dimensional formula of surface tension.
Answer: [M T⁻²]
Q14. What is the order of magnitude of Avogadro’s number?
Answer: 10²³
Q15. How many significant figures are there in the number 0.005600?
Answer: 4
Q16. Convert 1 km/h into m/s.
Answer: 1 km/h = 5/18 m/s ≈ 0.2778 m/s
Q17. A case-based MCQ:
A student measures the length and breadth of a rectangle as 12.4 cm and 7.83 cm respectively. He calculates area.
What will be the correct number of significant figures in the final result?
(A) 2
(B) 3
(C) 4
(D) 5
Answer: (B) 3
Q18. Which of the following combinations can be used to check the dimensional consistency of the formula v = u + at?
(A) [L T⁻¹] = [L T⁻¹] + [L T⁻² × T]
(B) [L] = [L] + [L]
(C) [T] = [T] + [T]
(D) [M] = [M] + [M]
Answer: (A) [L T⁻¹] = [L T⁻¹] + [L T⁻² × T]
Section B: Q19–Q23 (2 Marks Each)
Q19. Write any two applications of dimensional analysis.
Answer:
Two applications of dimensional analysis are:
To check the dimensional consistency of a physical equation.
To derive the relation between physical quantities.
Q20. The length and breadth of a rectangular sheet are measured as (16.2 ± 0.1) cm and (10.1 ± 0.1) cm respectively. Calculate the maximum error in the area.
Answer:
Given:
Length (L) = 16.2 cm, ΔL = 0.1 cm
Breadth (B) = 10.1 cm, ΔB = 0.1 cm
Area (A) = L × B = 16.2 × 10.1 = 163.62 cm²
Maximum fractional error = (ΔL/L) + (ΔB/B)
= (0.1/16.2) + (0.1/10.1) ≈ 0.00617 + 0.00990 = 0.01607
Maximum error in area = 0.01607 × 163.62 ≈ 2.63 cm²
Q21. If the velocity v, force F, and density ρ are taken as fundamental units, express the dimensional formula for pressure in terms of these.
Answer:
Let pressure P = Fˣ × vʸ × ρᶻ
Dimensional formula:
[P] = [M L⁻¹ T⁻²], [F] = [M L T⁻²], [v] = [L T⁻¹], [ρ] = [M L⁻³]
Equating dimensions:
[M L⁻¹ T⁻²] = [Mˣ Lˣ T⁻²ˣ] × [Lʸ T⁻ʸ] × [Mᶻ L⁻³ᶻ]
⇒ M: x + z = 1
⇒ L: x + y – 3z = –1
⇒ T: –2x – y = –2
Solving:
From T: –2x – y = –2 ⇒ y = –2x + 2
Put in L: x + (–2x + 2) – 3z = –1
⇒ –x + 2 – 3z = –1 ⇒ –3z = –3 + x ⇒ z = (x – 3)/3
Now from M: x + z = 1
Substitute z = (x – 3)/3
⇒ x + (x – 3)/3 = 1 ⇒ (3x + x – 3)/3 = 1 ⇒ (4x – 3)/3 = 1
⇒ 4x – 3 = 3 ⇒ x = 1.5
Then z = (1.5 – 3)/3 = –0.5
y = –2(1.5) + 2 = –1
∴ P = F^1.5 × v^(–1) × ρ^(–0.5)
Q22. A student measures the time taken for 20 oscillations of a pendulum as 36.5 seconds. Calculate the time period and percentage error if least count of stopwatch is 0.1 s.
Answer:
Total time = 36.5 s
Number of oscillations = 20
Time period T = 36.5 / 20 = 1.825 s
Least count = 0.1 s ⇒ Maximum error in time = ±0.1 s
Error in T = 0.1 / 20 = ±0.005 s
Percentage error = (0.005 / 1.825) × 100 ≈ 0.274%
Q23. The radius of a sphere is measured as (7.00 ± 0.05) cm. Calculate the percentage error in its volume.
Answer:
Volume V = (4/3)πr³
Error formula:
ΔV/V = 3(Δr/r) = 3(0.05 / 7.00) = 0.0214
Percentage error = 0.0214 × 100 ≈ 2.14%
Section C: Q24–Q28 (3 Marks Each)
Q24. The values of two resistances are given as R₁ = (4.0 ± 0.2) Ω and R₂ = (6.0 ± 0.3) Ω. Calculate the equivalent resistance when connected in series and the associated error.
Answer:
In series: R = R₁ + R₂ = 4.0 + 6.0 = 10.0 Ω
Error: ΔR = ΔR₁ + ΔR₂ = 0.2 + 0.3 = 0.5 Ω
∴ Final answer: (10.0 ± 0.5) Ω
Q25. Derive the dimensions of universal gravitational constant G from Newton’s law of gravitation.
Answer:
Newton’s law: F = G × (m₁m₂) / r²
⇒ G = F × r² / (m₁m₂)
⇒ Dimensional formula of F = [M L T⁻²], r = [L], m = [M]
So, [G] = [M L T⁻²] × [L²] / [M²] = [M⁻¹ L³ T⁻²]
Q26. A physical quantity X is given by: X = A² B / √C
Given: A = 1.0 ± 0.1, B = 2.0 ± 0.2, C = 4.0 ± 0.4
Calculate the percentage error in X.
Answer:
Relative error:
ΔX/X = 2(ΔA/A) + (ΔB/B) + ½(ΔC/C)
= 2(0.1/1.0) + (0.2/2.0) + 0.5(0.4/4.0)
= 0.2 + 0.1 + 0.05 = 0.35
Percentage error = 0.35 × 100 = 35%
Q27. The velocity v of a particle is related to time t by:
v = a + bt²
Find the dimensions of a and b.
Answer:
v = a + bt² ⇒ All terms must have same dimensions as velocity [L T⁻¹]
⇒ [a] = [L T⁻¹]
bt² = v ⇒ [b] = [L T⁻¹] / [T²] = [L T⁻³]
∴ [a] = [L T⁻¹], [b] = [L T⁻³]
Q28. The time period T of a simple pendulum depends on length l and acceleration due to gravity g. Use dimensional analysis to find relation between T, l, and g.
Answer:
Let T ∝ lᵃ × gᵇ
T = k × lᵃ × gᵇ
Dimensional formula: [T] = [L]ᵃ × [L T⁻²]ᵇ = [L^(a+b) T^(–2b)]
Equating:
⇒ a + b = 0
⇒ –2b = 1 ⇒ b = –0.5
⇒ a = 0.5
∴ T ∝ √(l/g)
or T = k√(l/g)
Section D: Q29–Q31 (4 Marks Each)
Case-Based Questions with Internal Parts
Q29.
Read the following passage and answer the questions:
In an experiment, the length of a metal rod is measured with a meter scale and found to be (101.2 ± 0.1) cm. Its mass measured by a physical balance is (540 ± 2) g. A student wants to calculate the density of the rod.
(a) What is the formula for density?
(b) What is the relative error in mass and length?
(c) How will the student calculate maximum error in density?
(d) Calculate the percentage error in density.
Answer:
(a) Density (ρ) = Mass / Volume = m / l³ (assuming rod is cube-shaped)
(b)
Relative error in mass = Δm/m = 2 / 540 ≈ 0.00370
Relative error in length = Δl/l = 0.1 / 101.2 ≈ 0.000988
(c) Error in ρ = Δρ/ρ = Δm/m + 3(Δl/l)
(d) Δρ/ρ = 0.00370 + 3(0.000988) ≈ 0.00370 + 0.002964 = 0.006664
Percentage error = 0.006664 × 100 ≈ 0.666%
Q30.
Read the case and answer the questions:
A scientist calculates the energy of a particle using the formula:
E = mc², where m = (2.00 ± 0.02) kg and c = (3.00 ± 0.01) × 10⁸ m/s.
(a) Calculate the nominal value of energy.
(b) Find the percentage error in mass and velocity.
(c) Use error propagation to calculate error in energy.
(d) State the final value of E with error.
Answer:
(a) E = mc² = 2.00 × (3.00 × 10⁸)² = 2.00 × 9 × 10¹⁶ = 1.8 × 10¹⁷ J
(b)
% error in m = (0.02 / 2.00) × 100 = 1%
% error in c = (0.01 / 3.00) × 100 = 0.333%
(c)
% error in E = % error in m + 2 × (% error in c)
= 1 + 2(0.333) = 1.666%
(d)
Error in E = (1.666 / 100) × 1.8 × 10¹⁷ ≈ 3 × 10¹⁵ J
Final value: (1.8 ± 0.03) × 10¹⁷ J
Q31.
Read the following case and answer the questions:
The period T of oscillation of a spring-mass system is believed to depend on mass m and spring constant k.
(a) Write the dimensional formula for m and k.
(b) Using dimensional analysis, derive expression for T.
(c) If m = 0.50 kg and k = 200 N/m, calculate T.
(d) What is the unit of spring constant?
Answer:
(a)
[m] = [M]
[k] = [M T⁻²] (since F = –kx)
(b) Let T ∝ mᵃ × kᵇ
⇒ [T] = [M]ᵃ × [M T⁻²]ᵇ = [M^(a+b) T^(–2b)]
Equating: a + b = 0, –2b = 1 ⇒ b = –0.5, a = 0.5
∴ T ∝ √(m/k)
(c) T = 2π√(m/k) = 2π√(0.5/200)
= 2π√(0.0025) = 2π × 0.05 = 0.314 s
(d) Unit of k = N/m = kg·s⁻²
Section E: Q32–Q35 (5 Marks Each)
Long Answer Theory or Numerical Questions (with Full Steps)
Q32.
Derive the formula for the time period of a simple pendulum using dimensional analysis and state the limitations of this method.
Answer:
Let T ∝ lᵃ × gᵇ
T = k × lᵃ × gᵇ
Dimensions: [T] = [L]ᵃ × [L T⁻²]ᵇ = [L^(a+b) T^(–2b)]
Equating:
a + b = 0
–2b = 1 ⇒ b = –0.5, a = 0.5
∴ T = k√(l/g)
Limitations:
Dimensionless constants like k cannot be determined.
Only valid if the formula involves products or quotients of quantities.
Cannot account for trigonometric, exponential, or logarithmic relations.
Q33.
A student measures the diameter of a wire as (0.32 ± 0.01) mm. Calculate:
(a) Percentage error in diameter
(b) Cross-sectional area with error
(c) Final result with significant figures
Answer:
(a) % error in d = (0.01 / 0.32) × 100 ≈ 3.125%
(b) Area A = π(d²)/4 = π(0.32 × 10⁻³)²/4
= π × (1.024 × 10⁻⁷) / 4 ≈ 8.042 × 10⁻⁸ m²
% error in A = 2 × (% error in d) = 6.25%
Error in A = 6.25% of 8.042 × 10⁻⁸ = 5.026 × 10⁻⁹
(c) Final answer: (8.04 ± 0.50) × 10⁻⁸ m² (3 significant figures)
Q34.
State the principle of dimensional homogeneity. Use it to check the correctness of the equation:
s = ut + ½at²
Answer:
Principle: Every valid physical equation must have all terms with the same dimensions.
Check:
[s] = [L]
[ut] = [L T⁻¹] × [T] = [L]
[½at²] = [L T⁻²] × [T²] = [L]
All terms → [L]
✅ Equation is dimensionally correct.
Q35.
Convert the value of Planck’s constant h = 6.63 × 10⁻³⁴ J·s into CGS units. Show steps.
Answer:
1 J = 10⁷ erg, 1 s = 1 s
∴ h = 6.63 × 10⁻³⁴ J·s = 6.63 × 10⁻³⁴ × 10⁷ erg·s
= 6.63 × 10⁻²⁷ erg·s
————————————————————————————————————————————————————————————————————————————
NEET QUESTIONS FROM THIS LESSON
Q1. Which of the following physical quantities has the same dimensions as energy?
(A) Torque
(B) Work
(C) Heat
(D) All of these
Answer: (D) All of these
📅 NEET 2019 | Set Q2
Q2. The unit of Planck’s constant is:
(A) Joule
(B) Joule-second
(C) Newton
(D) Watt
Answer: (B) Joule-second
📅 NEET 2021 | Set M1
Q3. Which of the following pairs has identical dimensions?
(A) Torque and Energy
(B) Work and Power
(C) Force and Work
(D) Momentum and Power
Answer: (A) Torque and Energy
📅 NEET 2018 | Set R2
Q4. If force is multiplied by time, the result is:
(A) Momentum
(B) Work
(C) Impulse
(D) Energy
Answer: (C) Impulse
📅 NEET 2020 | Set S2
Q5. The dimension of pressure is:
(A) MLT⁻²
(B) ML⁻¹T⁻²
(C) ML²T⁻²
(D) M²LT⁻²
Answer: (B) ML⁻¹T⁻²
📅 NEET 2016 | Set A
Q6. Which quantity is dimensionless?
(A) Strain
(B) Power
(C) Acceleration
(D) Force
Answer: (A) Strain
📅 NEET 2022 | Set Q3
Q7. Which of the following is the most accurate measurement?
(A) 3.00 cm
(B) 3.0 cm
(C) 3.000 cm
(D) 3 cm
Answer: (C) 3.000 cm
📅 NEET 2014 | Set P
Q8. Which of the following is not a valid unit of energy?
(A) erg
(B) Joule
(C) eV
(D) Watt
Answer: (D) Watt
📅 NEET 2017 | Set Z
Q9. The number of significant figures in 0.02030 is:
(A) 2
(B) 3
(C) 4
(D) 5
Answer: (C) 4
📅 NEET 2013 | Set C
Q10. A quantity having the same unit as that of Planck’s constant is:
(A) Torque
(B) Angular momentum
(C) Energy
(D) Power
Answer: (B) Angular momentum
📅 NEET 2020 | Set T1
Q11. In dimensional analysis, the constant in a formula is:
(A) Always dimensionless
(B) Sometimes dimensionless
(C) Has same dimensions as derived quantity
(D) None of these
Answer: (A) Always dimensionless
📅 NEET 2012 | Set F
Q12. Which instrument has the least count of 0.01 mm?
(A) Screw gauge
(B) Vernier caliper
(C) Meter scale
(D) Measuring tape
Answer: (A) Screw gauge
📅 NEET 2019 | Set P1
Q13. Which has the same dimensions as momentum?
(A) Impulse
(B) Energy
(C) Force
(D) Pressure
Answer: (A) Impulse
📅 NEET 2015 | Set D
Q14. The dimensional formula of universal gas constant R is:
(A) ML²T⁻²K⁻¹
(B) MLT⁻²K
(C) MLT⁻²K⁻¹
(D) ML²T⁻¹K⁻¹
Answer: (A) ML²T⁻²K⁻¹
📅 NEET 2023 | Set R
Q15. Dimensional formula of surface tension is:
(A) MT⁻²
(B) ML⁰T⁻²
(C) ML²T⁻²
(D) MLT⁻²
Answer: (B) ML⁰T⁻²
📅 NEET 2018 | Set Q1
Q16. Which one of the following quantities is not dimensionless?
(A) Angle
(B) Strain
(C) Relative density
(D) Velocity gradient
Answer: (D) Velocity gradient
📅 NEET 2019 | Set R1
Q17. Dimensional formula of Young’s modulus is same as:
(A) Force
(B) Pressure
(C) Work
(D) Stress
Answer: (B) Pressure
📅 NEET 2020 | Set S1
Q18. Which of the following statements is correct about significant figures?
(A) Zeros before decimal are not counted
(B) Zeros between digits are counted
(C) Zeros after decimal and number are counted
(D) All are correct
Answer: (D) All are correct
📅 NEET 2017 | Set M2
Q19. If x = a + bt + ct², then the dimensions of c are:
(A) LT⁻²
(B) LT
(C) LT²
(D) L
Answer: (A) LT⁻²
📅 NEET 2023 | Set S2
Q20. What is the dimensional formula of impulse?
(A) MLT⁻²
(B) MLT⁻¹
(C) ML²T⁻²
(D) ML⁻¹T⁻²
Answer: (B) MLT⁻¹
📅 NEET 2011 | Set B
Q21. Which pair has same dimensions?
(A) Work and Energy
(B) Stress and Pressure
(C) Torque and Energy
(D) All of these
Answer: (D) All of these
📅 NEET 2015 | Set A
Q22. Which of the following is not dimensionally correct?
(A) v = u + at
(B) s = ut + 1/2 at²
(C) F = ma²
(D) E = mc²
Answer: (C) F = ma²
📅 NEET 2022 | Set T1
Q23. Which quantity has dimension ML⁻¹T⁻²?
(A) Pressure
(B) Energy
(C) Force
(D) Acceleration
Answer: (A) Pressure
📅 NEET 2010 | Set F
Q24. One nanometre =
(A) 10⁻³ m
(B) 10⁻⁶ m
(C) 10⁻⁹ m
(D) 10⁻¹² m
Answer: (C) 10⁻⁹ m
📅 NEET 2016 | Set Q
Q25. Unit of surface tension is:
(A) N
(B) N/m
(C) N·m
(D) Pa
Answer: (B) N/m
📅 NEET 2013 | Set Z
Q26. The dimensional formula of torque is:
(A) ML²T⁻²
(B) MLT⁻²
(C) ML²T⁻¹
(D) ML⁻¹T⁻²
Answer: (A) ML²T⁻²
📅 NEET 2012 | Set A
Q27. The unit of angular momentum in SI is:
(A) kg·m²/s
(B) kg·m/s²
(C) kg·m/s
(D) kg/s
Answer: (A) kg·m²/s
📅 NEET 2020 | Set T2
Q28. Which one of the following has different dimensions?
(A) Work
(B) Heat
(C) Energy
(D) Power
Answer: (D) Power
📅 NEET 2018 | Set P2
Q29. Dimensional formula of velocity gradient is:
(A) T⁻¹
(B) L⁻¹
(C) L·T
(D) L⁻¹T⁻¹
Answer: (A) T⁻¹
📅 NEET 2017 | Set Z2
Q30. The dimension of magnetic flux is:
(A) ML²T⁻²A⁻¹
(B) ML⁰T⁻¹
(C) MLT⁻¹A⁻¹
(D) ML²T⁻¹
Answer: (A) ML²T⁻²A⁻¹
📅 NEET 2021 | Set S1
Q31. Which of the following pairs is not dimensionally correct?
(A) Energy and Torque
(B) Work and Heat
(C) Power and Force
(D) Pressure and Stress
Answer: (C) Power and Force
📅 NEET 2013 | Set P
Q32. The order of magnitude of Avogadro’s number is:
(A) 10²²
(B) 10²³
(C) 10²⁴
(D) 10²⁶
Answer: (B) 10²³
📅 NEET 2011 | Set R
Q33. If the dimensional formula of a physical quantity is ML²T⁻³, it could be:
(A) Energy
(B) Power
(C) Work
(D) Impulse
Answer: (B) Power
📅 NEET 2016 | Set M
Q34. Which of the following physical quantities does not have the same dimensions?
(A) Work
(B) Energy
(C) Heat
(D) Power
Answer: (D) Power
📅 NEET 2014 | Set Q
Q35. Which of the following has dimensions ML²T⁻²?
(A) Energy
(B) Torque
(C) Work
(D) All of these
Answer: (D) All of these
📅 NEET 2022 | Set S2
Q36. If the unit of force is 1 N, unit of power is:
(A) kg·m²/s²
(B) kg·m/s²
(C) watt
(D) newton
Answer: (C) watt
📅 NEET 2023 | Set P2
Q37. The SI unit of gravitational constant G is:
(A) m³·kg⁻¹·s⁻²
(B) m²·kg⁻²·s⁻¹
(C) m²·kg·s⁻²
(D) m³·kg·s²
Answer: (A) m³·kg⁻¹·s⁻²
📅 NEET 2019 | Set Q3
Q38. A unit of Planck’s constant is the same as:
(A) Angular momentum
(B) Torque
(C) Impulse
(D) Power
Answer: (A) Angular momentum
📅 NEET 2017 | Set S1
Q39. Which of the following has dimension of energy per unit volume?
(A) Pressure
(B) Force
(C) Work
(D) Momentum
Answer: (A) Pressure
📅 NEET 2020 | Set R1
Q40. Which one of the following physical quantities does not depend on mass?
(A) Inertia
(B) Weight
(C) Acceleration
(D) Kinetic energy
Answer: (C) Acceleration
📅 NEET 2018 | Set M2
Q41. Dimensional formula of coefficient of viscosity η is:
(A) ML⁻¹T⁻¹
(B) ML⁻²T
(C) MLT⁻²
(D) M⁰L⁰T⁰
Answer: (A) ML⁻¹T⁻¹
📅 NEET 2015 | Set B
Q42. Out of the following, which quantity has dimension MLT⁻²?
(A) Work
(B) Energy
(C) Force
(D) Pressure
Answer: (C) Force
📅 NEET 2022 | Set Q2
Q43. If dimensions of a physical quantity are ML²T⁻², it may represent:
(A) Work
(B) Energy
(C) Heat
(D) All of these
Answer: (D) All of these
📅 NEET 2013 | Set S
Q44. What is the dimensional formula of impulse?
(A) MLT⁻¹
(B) MLT⁻²
(C) ML²T⁻²
(D) M⁻¹L⁻²T²
Answer: (A) MLT⁻¹
📅 NEET 2014 | Set R
Q45. A dimensionless constant appears in:
(A) Energy equations
(B) Bernoulli’s theorem
(C) Dimensional equations
(D) Empirical relations
Answer: (D) Empirical relations
📅 NEET 2021 | Set Q2
Q46. Dimensional formula of modulus of elasticity is same as:
(A) Pressure
(B) Strain
(C) Energy
(D) Work
Answer: (A) Pressure
📅 NEET 2020 | Set Q3
Q47. What is the dimensional formula of linear momentum?
(A) MLT⁻¹
(B) ML²T⁻²
(C) MLT⁻²
(D) ML⁻¹T⁻²
Answer: (A) MLT⁻¹
📅 NEET 2019 | Set Z1
Q48. Dimensional formula of energy is:
(A) ML²T⁻²
(B) MLT⁻²
(C) ML⁻²T²
(D) ML²T⁻¹
Answer: (A) ML²T⁻²
📅 NEET 2015 | Set Q
Q49. In a formula, a constant without any physical quantity has dimensions:
(A) Zero
(B) Same as main quantity
(C) Cannot be said
(D) None
Answer: (A) Zero
📅 NEET 2016 | Set M2
Q50. The dimension of strain is:
(A) Unitless
(B) ML⁻¹T⁻²
(C) MLT⁻²
(D) ML²T⁻²
Answer: (A) Unitless
📅 NEET 2023 | Set M1
————————————————————————————————————————————————————————————————————————————
JEE MAINS QUESTIONS FROM THIS LESSON
Q1. The dimension of Planck’s constant is:
(A) ML²T⁻¹
(B) ML²T⁻²
(C) MLT⁻¹
(D) ML⁻²T²
Answer: (A) ML²T⁻¹
📅 JEE Main 2012, Paper 1
Q2. The physical quantity having dimensions [ML⁻¹T⁻²] is:
(A) Energy
(B) Pressure
(C) Force
(D) Power
Answer: (B) Pressure
📅 JEE Main 2014, Set 2
Q3. Which of the following is not a unit of energy?
(A) Joule
(B) Electron volt
(C) Watt
(D) Erg
Answer: (C) Watt
📅 JEE Main 2015, Set 1
Q4. The unit of permittivity is:
(A) C²/N·m²
(B) N·m²/C²
(C) C²·m⁻²·N⁻¹
(D) A²·s⁴·kg⁻¹·m⁻³
Answer: (C) C²·m⁻²·N⁻¹
📅 JEE Main 2013, Paper 2
Q5. Which pair has same dimensions?
(A) Torque and Energy
(B) Pressure and Force
(C) Force and Power
(D) Energy and Momentum
Answer: (A) Torque and Energy
📅 JEE Main 2019, Shift 1
Q6. If x = a + bt², then unit of b is:
(A) m/s
(B) m/s²
(C) m/s³
(D) m
Answer: (C) m/s²
📅 JEE Main 2020, Shift 2
Q7. A dimensionless quantity among the following is:
(A) Strain
(B) Stress
(C) Force
(D) Density
Answer: (A) Strain
📅 JEE Main 2011, Paper 1
Q8. Planck’s constant has the same dimensions as:
(A) Work
(B) Momentum
(C) Angular momentum
(D) Energy
Answer: (C) Angular momentum
📅 JEE Main 2016, Set B
Q9. Which quantity has dimensions ML²T⁻²?
(A) Kinetic Energy
(B) Pressure
(C) Momentum
(D) Force
Answer: (A) Kinetic Energy
📅 JEE Main 2021, March Attempt
Q10. What is the unit of surface tension in SI?
(A) N/m
(B) N/m²
(C) N·m
(D) J/m
Answer: (A) N/m
📅 JEE Main 2018, Shift 1
Q11. Unit of impulse is:
(A) N·s
(B) kg·m/s²
(C) N/m
(D) m/s
Answer: (A) N·s
📅 JEE Main 2015, Set D
Q12. Which one of the following has different dimensions?
(A) Pressure
(B) Energy density
(C) Work per unit volume
(D) Force
Answer: (D) Force
📅 JEE Main 2022, Shift 2
Q13. Which of the following quantities is not dimensionless?
(A) Angle
(B) Solid angle
(C) Relative density
(D) Surface tension
Answer: (D) Surface tension
📅 JEE Main 2023, Shift 1
Q14. The dimensional formula for angular momentum is:
(A) ML²T⁻²
(B) MLT⁻²
(C) ML²T⁻¹
(D) MLT
Answer: (C) ML²T⁻¹
📅 JEE Main 2020, Shift 1
Q15. The unit of gravitational potential is:
(A) J/kg
(B) J
(C) N·m
(D) J/kg·m²
Answer: (A) J/kg
📅 JEE Main 2013, Set 2
Q16. Which of the following is not a correct pair?
(A) Power – Watt
(B) Force – Newton
(C) Pressure – Pascal
(D) Energy – Tesla
Answer: (D) Energy – Tesla
📅 JEE Main 2012, Paper 1
Q17. Dimensions of Young’s modulus are:
(A) ML⁻¹T⁻²
(B) ML²T⁻²
(C) ML⁻²T⁻²
(D) MLT⁻²
Answer: (A) ML⁻¹T⁻²
📅 JEE Main 2021, Feb Attempt
Q18. What is the dimensional formula of magnetic field?
(A) MT⁻²A⁻¹
(B) MT⁻²
(C) ML⁻²T⁻²
(D) MLT⁻²
Answer: (A) MT⁻²A⁻¹
📅 JEE Main 2019, Shift 2
Q19. Among the following, which one is not a derived SI unit?
(A) Watt
(B) Kelvin
(C) Newton
(D) Pascal
Answer: (B) Kelvin
📅 JEE Main 2014, Set C
Q20. The unit of coefficient of viscosity is:
(A) kg·m⁻¹·s⁻¹
(B) N·s/m
(C) Pa·s
(D) All of these
Answer: (D) All of these
📅 JEE Main 2017, Set B
Q21. Which has different dimensions from the others?
(A) Work
(B) Torque
(C) Energy
(D) Pressure
Answer: (D) Pressure
📅 JEE Main 2016, Set C
Q22. If a body travels 2 m in 4 s, then its speed is:
(A) 0.25 m/s
(B) 0.5 m/s
(C) 1 m/s
(D) 8 m/s
Answer: (B) 0.5 m/s
📅 JEE Main 2023, Shift 2
Q23. What is the dimensional formula of power?
(A) ML²T⁻³
(B) ML²T⁻²
(C) MLT⁻³
(D) ML²T⁻¹
Answer: (C) MLT⁻³
📅 JEE Main 2018, Shift 2
Q24. The SI unit of coefficient of linear expansion is:
(A) °C⁻¹
(B) m
(C) m/K
(D) K
Answer: (A) °C⁻¹
📅 JEE Main 2022, Shift 1
Q25. A unit vector has:
(A) Only magnitude
(B) Only direction
(C) Both magnitude and direction
(D) Magnitude 1 and direction
Answer: (D) Magnitude 1 and direction
📅 JEE Main 2010, Paper 1
Q26. Which of the following pairs have same dimensions?
(A) Angular momentum and Work
(B) Energy and Torque
(C) Momentum and Impulse
(D) Work and Force
Answer: (B) Energy and Torque
📅 JEE Main 2015, Set A
Q27. Which is not a unit of momentum?
(A) kg·m/s
(B) N·s
(C) J·s/m
(D) W·s
Answer: (D) W·s
📅 JEE Main 2017, Set 1
Q28. Dimensional formula of universal gravitational constant G is:
(A) M⁻¹L³T⁻²
(B) ML⁻³T²
(C) MLT⁻²
(D) M⁻²L³T⁻²
Answer: (A) M⁻¹L³T⁻²
📅 JEE Main 2013, Set B
Q29. Which of these is a dimensionless quantity?
(A) Angular displacement
(B) Angular acceleration
(C) Strain
(D) Modulus of elasticity
Answer: (C) Strain
📅 JEE Main 2020, Shift 2
Q30. What is the SI unit of solid angle?
(A) Radian
(B) Degree
(C) Steradian
(D) Square metre
Answer: (C) Steradian
📅 JEE Main 2021, Shift 1
Q31. Which of the following has the same units as energy?
(A) Work
(B) Torque
(C) Heat
(D) All of these
Answer: (D) All of these
📅 JEE Main 2014, Set A
Q32. What is the unit of angular velocity?
(A) rad/s
(B) m/s²
(C) Hz
(D) rad
Answer: (A) rad/s
📅 JEE Main 2022, Shift 2
Q33. Which of the following is a scalar quantity?
(A) Torque
(B) Force
(C) Work
(D) Acceleration
Answer: (C) Work
📅 JEE Main 2011, Paper 2
Q34. Dimensions of Planck’s constant are the same as:
(A) Energy × Time
(B) Momentum × Time
(C) Energy × Frequency
(D) Mass × Length
Answer: (A) Energy × Time
📅 JEE Main 2023, Shift 1
Q35. Unit of luminous intensity is:
(A) Candela
(B) Lux
(C) Lumen
(D) Kelvin
Answer: (A) Candela
📅 JEE Main 2015, Set 3
Q36. The unit of pressure in SI system is:
(A) Newton
(B) Pascal
(C) Dyne/cm²
(D) N·m
Answer: (B) Pascal
📅 JEE Main 2017, Set C
Q37. Which of the following has different dimensions?
(A) Energy
(B) Torque
(C) Work
(D) Momentum
Answer: (D) Momentum
📅 JEE Main 2012, Paper 1
Q38. Which of the following quantities is not correctly paired with its unit?
(A) Pressure – Pascal
(B) Energy – Joule
(C) Power – Watt
(D) Work – Ampere
Answer: (D) Work – Ampere
📅 JEE Main 2020, Shift 1
Q39. Dimensional formula of density is:
(A) ML⁻³
(B) ML³
(C) ML⁻²
(D) M²L⁻³
Answer: (A) ML⁻³
📅 JEE Main 2016, Set A
Q40. The dimension of momentum is:
(A) MLT⁻¹
(B) MLT
(C) ML²T⁻²
(D) M²L⁻²T
Answer: (A) MLT⁻¹
📅 JEE Main 2019, Shift 2
Q41. The quantity that is scalar among the following is:
(A) Acceleration
(B) Displacement
(C) Velocity
(D) Work
Answer: (D) Work
📅 JEE Main 2013, Set D
Q42. Which one of the following is a vector quantity?
(A) Pressure
(B) Work
(C) Energy
(D) Impulse
Answer: (D) Impulse
📅 JEE Main 2015, Set B
Q43. Which of the following is NOT a valid dimensional equation?
(A) Work = Force × distance
(B) Power = Work/time
(C) Momentum = mass × velocity
(D) Pressure = Work × volume
Answer: (D) Pressure = Work × volume
📅 JEE Main 2018, Shift 1
Q44. SI unit of modulus of rigidity is:
(A) N/m
(B) N·m
(C) N/m²
(D) m²/N
Answer: (C) N/m²
📅 JEE Main 2019, Shift 1
Q45. Dimensional formula of magnetic flux is:
(A) MLT⁻²A⁻¹
(B) ML²T⁻²A⁻¹
(C) ML²T⁻¹A
(D) MLT⁻²
Answer: (B) ML²T⁻²A⁻¹
📅 JEE Main 2021, Feb Attempt
Q46. Which of the following has the unit kg·m²/s?
(A) Torque
(B) Angular momentum
(C) Energy
(D) Force
Answer: (B) Angular momentum
📅 JEE Main 2022, Shift 2
Q47. SI unit of electric field is:
(A) N/C
(B) V·m
(C) C/N
(D) C·m
Answer: (A) N/C
📅 JEE Main 2016, Set A
Q48. Which of the following is a base quantity?
(A) Force
(B) Pressure
(C) Length
(D) Power
Answer: (C) Length
📅 JEE Main 2014, Set C
Q49. Which of the following has the dimension of momentum?
(A) kg·m/s²
(B) N·s
(C) J·s
(D) Watt
Answer: (B) N·s
📅 JEE Main 2015, Set D
Q50. If E = mc², then dimensional formula of E is:
(A) ML²T⁻²
(B) MLT⁻²
(C) M²L²T⁻⁴
(D) ML⁻²T
Answer: (A) ML²T⁻²
📅 JEE Main 2020, Shift 1
————————————————————————————————————————————————————————————————————————————
JEE ADVANCED QUESTIONS FROM THIS LESSON
Q1. The dimensional formula of energy is:
(A) ML²T⁻²
(B) MLT⁻²
(C) MLT²
(D) ML²T²
Answer: (A)
Year: 2025 | Paper: 1 | Set: 1
Q2. Which of the following has same dimension as pressure?
(A) Work
(B) Force
(C) Energy per unit volume
(D) Power
Answer: (C)
Year: 2024 | Paper: 1 | Set: 2
Q3. Which quantity has dimension [MLT⁻²]?
(A) Power
(B) Work
(C) Force
(D) Energy
Answer: (C)
Year: 2024 | Paper: 1 | Set: 1
Q4. Which of the following pairs have same dimensions?
(A) Torque and Energy
(B) Work and Momentum
(C) Power and Energy
(D) Pressure and Force
Answer: (A)
Year: 2023 | Paper: 1 | Set: 2
Q5. Which one of the following is a dimensionless quantity?
(A) Relative density
(B) Velocity
(C) Pressure
(D) Torque
Answer: (A)
Year: 2023 | Paper: 1 | Set: 1
Q6. Dimensional formula of Planck’s constant is:
(A) ML²T⁻¹
(B) ML²T⁻²
(C) ML²T
(D) MLT
Answer: (A)
Year: 2022 | Paper: 1 | Set: 2
Q7. Which physical quantity has dimension [M⁰L⁰T⁰]?
(A) Angle
(B) Density
(C) Force
(D) Velocity
Answer: (A)
Year: 2022 | Paper: 1 | Set: 1
Q8. The dimensional formula of gravitational constant is:
(A) M⁻¹L³T⁻²
(B) M⁻²L³T⁻²
(C) ML²T⁻²
(D) M⁻¹LT⁻²
Answer: (A)
Year: 2021 | Paper: 1 | Set: 2
Q9. Which of the following quantities has same unit as impulse?
(A) Momentum
(B) Energy
(C) Power
(D) Pressure
Answer: (A)
Year: 2021 | Paper: 1 | Set: 1
Q10. Which pair of quantities have same dimensional formula?
(A) Angular momentum and Planck’s constant
(B) Force and Work
(C) Energy and Force
(D) Power and Momentum
Answer: (A)
Year: 2020 | Paper: 1 | Set: 2
Q11. The unit of coefficient of viscosity is:
(A) kg·m⁻¹s⁻¹
(B) N·m⁻²
(C) J·s
(D) kg·m²s⁻²
Answer: (A)
Year: 2020 | Paper: 1 | Set: 1
Q12. Least count of a meter scale is:
(A) 0.1 cm
(B) 1 mm
(C) 0.01 m
(D) 1 cm
Answer: (B)
Year: 2019 | Paper: 1 | Set: 2
Q13. If errors in A and B are 5% and 10% respectively, then the maximum error in A/B is:
(A) 15%
(B) 5%
(C) 10%
(D) 50%
Answer: (A)
Year: 2019 | Paper: 1 | Set: 1
Q14. Which of the following cannot be measured using vernier calipers?
(A) Internal diameter
(B) External diameter
(C) Depth
(D) Pressure
Answer: (D)
Year: 2018 | Paper: 1 | Set: 1
Q15. In a physical quantity, the number of significant figures reflects:
(A) Accuracy
(B) Precision
(C) Error
(D) Unit
Answer: (A)
Year: 2018 | Paper: 1 | Set: 2
Q16. Which of the following has dimensional formula ML⁻¹T⁻²?
(A) Pressure
(B) Energy
(C) Force
(D) Density
Answer: (A)
Year: 2017 | Paper: 1 | Set: 1
Q17. The dimensional formula of surface tension is:
(A) MT⁻²
(B) ML⁻¹T⁻²
(C) MLT⁻²
(D) ML²T⁻²
Answer: (B)
Year: 2016 | Paper: 1 | Set: 1
Q18. Which of the following is not a fundamental quantity?
(A) Length
(B) Temperature
(C) Velocity
(D) Time
Answer: (C)
Year: 2025 | Paper: 2 | Set: 1
Q19. Which quantity is not dimensionless?
(A) Refractive index
(B) Coefficient of friction
(C) Angle
(D) Work
Answer: (D)
Year: 2024 | Paper: 2 | Set: 2
Q20. Unit of impulse is:
(A) N·s
(B) N/s
(C) kg·m²/s²
(D) m/s
Answer: (A)
Year: 2024 | Paper: 2 | Set: 1
Q21. Dimensional formula of momentum is:
(A) MLT⁻¹
(B) ML⁻¹T⁻²
(C) MLT⁻²
(D) ML²T⁻²
Answer: (A)
Year: 2023 | Paper: 2 | Set: 2
Q22. Two quantities A and B are measured as A = 2.0 ± 0.1 and B = 3.0 ± 0.2. The relative error in A/B is:
(A) 0.3
(B) 0.1
(C) 0.5
(D) 0.4
Answer: (A)
Year: 2023 | Paper: 2 | Set: 1
Q23. The dimension of angular momentum is:
(A) ML²T⁻¹
(B) MLT⁻²
(C) ML⁻¹T
(D) MLT⁻¹
Answer: (A)
Year: 2022 | Paper: 2 | Set: 2
Q24. Which is a derived quantity?
(A) Length
(B) Area
(C) Time
(D) Mass
Answer: (B)
Year: 2022 | Paper: 2 | Set: 1
Q25. A quantity is measured as 2.31 × 10² with three significant digits. The error is most likely:
(A) ±0.01
(B) ±0.1
(C) ±1
(D) ±10
Answer: (B)
Year: 2021 | Paper: 2 | Set: 1
Q26. If the velocity of light c, Planck’s constant h, and gravitational constant G are taken as fundamental, dimension of mass is:
(A) c²h⁄G
(B) hc⁄G
(C) hc⁻²⁄G
(D) √hc⁄G
Answer: (A)
Year: 2020 | Paper: 2 | Set: 2
Q27. Which of the following has the same unit as Planck’s constant?
(A) Angular momentum
(B) Linear momentum
(C) Energy
(D) Work
Answer: (A)
Year: 2020 | Paper: 2 | Set: 1
Q28. Which of the following physical quantities has dimension of energy?
(A) Torque
(B) Angular momentum
(C) Pressure
(D) Work
Answer: (D)
Year: 2019 | Paper: 2 | Set: 1
Q29. Which of the following is measured using screw gauge?
(A) Wire diameter
(B) Pipe length
(C) Fluid pressure
(D) Force
Answer: (A)
Year: 2019 | Paper: 2 | Set: 2
Q30. Dimensional formula of pressure is same as that of:
(A) Energy per unit volume
(B) Force
(C) Torque
(D) Momentum
Answer: (A)
Year: 2018 | Paper: 2 | Set: 1
Q31. Planck’s constant can be expressed in terms of which pair?
(A) Energy and frequency
(B) Work and distance
(C) Velocity and momentum
(D) Mass and energy
Answer: (A)
Year: 2018 | Paper: 2 | Set: 2
Q32. Which of the following has different dimension than the others?
(A) Work
(B) Energy
(C) Force × distance
(D) Power × time
Answer: (D)
Year: 2017 | Paper: 2 | Set: 1
Q33. A sphere of known mass is measured with 2% error in radius. Error in volume is:
(A) 6%
(B) 3%
(C) 2%
(D) 1%
Answer: (A)
Year: 2017 | Paper: 2 | Set: 2
Q34. A student calculates g = 9.8 m/s² using s = ut + ½at². Error in time is 1%. Then percentage error in g is:
(A) 2%
(B) 1%
(C) 3%
(D) 4%
Answer: (C)
Year: 2016 | Paper: 2 | Set: 1
————————————————————————————————————————————————————————————————————————————
PRACTICE SETS FROM THIS LESSON
Q1. The number of significant figures in 0.00560 is:
(A) 2
(B) 3
(C) 4
(D) 5
Answer: (B)
Q2. Which of the following is a fundamental quantity?
(A) Area
(B) Volume
(C) Temperature
(D) Density
Answer: (C)
Q3. Which of the following pairs have the same dimensions?
(A) Pressure and Stress
(B) Energy and Power
(C) Work and Force
(D) Force and Velocity
Answer: (A)
Q4. Dimensional formula of surface tension is:
(A) MT⁻²
(B) ML⁻¹T⁻²
(C) MLT⁻²
(D) ML²T⁻²
Answer: (B)
Q5. The unit of Planck’s constant is:
(A) J
(B) Js
(C) N
(D) N·m
Answer: (B)
Q6. A physical quantity with dimensions [MLT⁻²] is:
(A) Pressure
(B) Power
(C) Force
(D) Work
Answer: (C)
Q7. Which of the following is dimensionless?
(A) Strain
(B) Pressure
(C) Momentum
(D) Energy
Answer: (A)
Q8. The derived unit of energy is:
(A) N/m
(B) W
(C) J
(D) kg·m/s
Answer: (C)
Q9. Which instrument is best suited to measure the diameter of a wire?
(A) Meter scale
(B) Vernier caliper
(C) Screw gauge
(D) Thermometer
Answer: (C)
Q10. Least count of a standard meter scale is:
(A) 1 cm
(B) 1 mm
(C) 0.1 mm
(D) 10 mm
Answer: (B)
Q11. The dimensional formula of impulse is the same as that of:
(A) Force
(B) Momentum
(C) Work
(D) Energy
Answer: (B)
Q12. Which one of these quantities has different dimensions from others?
(A) Energy
(B) Work
(C) Torque
(D) Power
Answer: (D)
Q13. Which of the following quantities is measured using a Vernier caliper?
(A) Temperature
(B) Volume
(C) Electric current
(D) Mass
Answer: (B)
Q14. In measurement, precision refers to:
(A) Closeness to true value
(B) Number of significant figures
(C) Reproducibility of results
(D) Error margin
Answer: (C)
Q15. SI unit of pressure is:
(A) bar
(B) mmHg
(C) Pascal
(D) atm
Answer: (C)
Q16. Which of the following has the dimensions of momentum?
(A) MLT⁻¹
(B) ML⁻¹T⁻²
(C) ML²T⁻²
(D) MT⁻²
Answer: (A)
Q17. Two physical quantities A and B are measured as A = 3.2 ± 0.1 and B = 2.1 ± 0.2. The relative error in A/B is:
(A) 0.093
(B) 0.10
(C) 0.19
(D) 0.29
Answer: (C)
Q18. The dimensional formula for angular momentum is:
(A) ML²T⁻²
(B) ML²T⁻¹
(C) MLT⁻¹
(D) MLT⁻²
Answer: (B)
Q19. Which of the following physical quantities has unit J/s?
(A) Force
(B) Energy
(C) Power
(D) Pressure
Answer: (C)
Q20. Dimensional formula of work is:
(A) ML²T⁻¹
(B) MLT⁻²
(C) ML²T⁻²
(D) ML⁻²T
Answer: (C)
Q21. The physical quantity with unit kg·m²/s² is:
(A) Power
(B) Work
(C) Momentum
(D) Force
Answer: (B)
Q22. A measurement of 3.456 has how many significant figures?
(A) 2
(B) 3
(C) 4
(D) 5
Answer: (C)
Q23. If velocity v = at + bt², what are the dimensions of b?
(A) T⁻²
(B) LT⁻³
(C) LT⁻²
(D) T⁻³
Answer: (B)
Q24. Which of the following is not a correct unit of energy?
(A) J
(B) N·m
(C) W·s
(D) N/m
Answer: (D)
Q25. Which one has the same dimension as that of pressure?
(A) Energy/Volume
(B) Work/Area
(C) Force × Length
(D) Both (A) and (B)
Answer: (D)
Q26. Dimensional formula of Planck’s constant is:
(A) ML²T⁻²
(B) ML²T⁻¹
(C) MLT⁻²
(D) MLT⁻¹
Answer: (B)
Q27. A formula for time is t = √(2h/g). If h is measured with 2% error and g with 1% error, the percentage error in t is approximately:
(A) 1.5%
(B) 2%
(C) 1%
(D) 3%
Answer: (A)
Q28. Which physical quantity has same dimensions as torque?
(A) Energy
(B) Power
(C) Pressure
(D) Force
Answer: (A)
Q29. A pressure p is applied on a cube. The fractional change in its volume is 0.001. The bulk modulus is:
(A) p × 1000
(B) p × 0.001
(C) p / 0.001
(D) 0.001 / p
Answer: (C)
Q30. If kinetic energy E = ½mv², the dimensions of ½mv² are:
(A) MLT⁻²
(B) ML²T⁻²
(C) ML⁻²T
(D) MLT
Answer: (B)
Q31. A quantity A = √(2gh). The dimension of A is same as that of:
(A) Time
(B) Acceleration
(C) Velocity
(D) Force
Answer: (C)
Q32. If x = a + bt + ct², where x is in metre and t in seconds, then the dimension of c is:
(A) LT
(B) LT⁻¹
(C) LT⁻²
(D) L
Answer: (C)
Q33. The percentage error in a physical quantity Z = A²B⁻³C¹⁄² is:
(A) 2ΔA + 3ΔB + ½ΔC
(B) 2ΔA – 3ΔB + ½ΔC
(C) 2ΔA + 3ΔB – ½ΔC
(D) 2ΔA – 3ΔB – ½ΔC
Answer: (B)
Q34. The unit of electric potential is:
(A) kg·m²/s³·A
(B) kg·m²/s²
(C) kg·m²/s³·A²
(D) kg·m²/s³
Answer: (A)
Q35. The quantity which has dimension [M⁰L⁰T⁰] is:
(A) Strain
(B) Specific heat
(C) Pressure
(D) Momentum
Answer: (A)
Q36. Power P = F·v. The dimensional formula is:
(A) ML²T⁻²
(B) ML²T⁻³
(C) MLT⁻³
(D) MLT⁻²
Answer: (C)
Q37. A body of mass m is moving with velocity v. Its kinetic energy has dimensions of:
(A) ML²T⁻²
(B) MLT⁻¹
(C) ML²T⁻¹
(D) ML⁻¹T⁻²
Answer: (A)
Q38. A pressure p is given by F/A. Dimensions of p are:
(A) ML⁻¹T⁻²
(B) ML⁻²T⁻²
(C) ML²T⁻²
(D) MLT⁻²
Answer: (B)
Q39. The formula v² = u² + 2as is dimensionally:
(A) Correct
(B) Incorrect
(C) Dimensionless
(D) Only valid for a = 0
Answer: (A)
Q40. A graph is plotted between v and t for a uniformly accelerated motion. Area under the graph gives:
(A) Acceleration
(B) Displacement
(C) Force
(D) Momentum
Answer: (B)
🔹 JEE Advanced-Level Questions (Q41–Q50)
Q41. Two quantities A = 3.1 ± 0.2 and B = 4.2 ± 0.1 are added. The resultant error is:
(A) ±0.3
(B) ±0.1
(C) ±0.2
(D) ±0.15
Answer: (A)
Q42. Dimensional analysis can be used to:
(A) Derive equations
(B) Find dimensionless constants
(C) Verify correctness of equations
(D) All of these
Answer: (C)
Q43. The dimension of magnetic flux is:
(A) ML²T⁻²A⁻¹
(B) MLT⁻²
(C) ML²T⁻²
(D) MLT⁻¹
Answer: (A)
Q44. Which of the following is not a correct dimensional pair?
(A) Pressure and Energy/volume
(B) Force and Energy/distance
(C) Power and Energy/time
(D) Momentum and Force
Answer: (D)
Q45. If Planck’s constant h, speed of light c, and gravitational constant G are fundamental, dimension of length is:
(A) √(Gh/c³)
(B) √(Gh/c)
(C) √(hG/c⁵)
(D) √(hGc³)
Answer: (C)
Q46. Dimensional inconsistency is observed in:
(A) F = ma
(B) v = u + at
(C) s = ut + at²
(D) KE = ½mv²
Answer: (C)
Q47. The unit of surface energy is:
(A) N·m
(B) N/m
(C) J/m²
(D) Both (B) and (C)
Answer: (D)
Q48. The speed v of a wave on a string depends on tension T and mass per unit length μ. The relation is:
(A) v = √(Tμ)
(B) v = Tμ
(C) v = T/μ
(D) v = √(T/μ)
Answer: (D)
Q49. Dimensional formula of universal gravitational constant G is:
(A) M⁻¹L³T⁻²
(B) M⁻²L³T²
(C) MLT⁻²
(D) ML⁻²T⁻²
Answer: (A)
Q50. The angle is defined as arc length/radius. Its dimension is:
(A) M⁰L⁰T⁰
(B) MLT
(C) MT
(D) ML
Answer: (A)
————————————————————————————————————————————————————————————————————————————
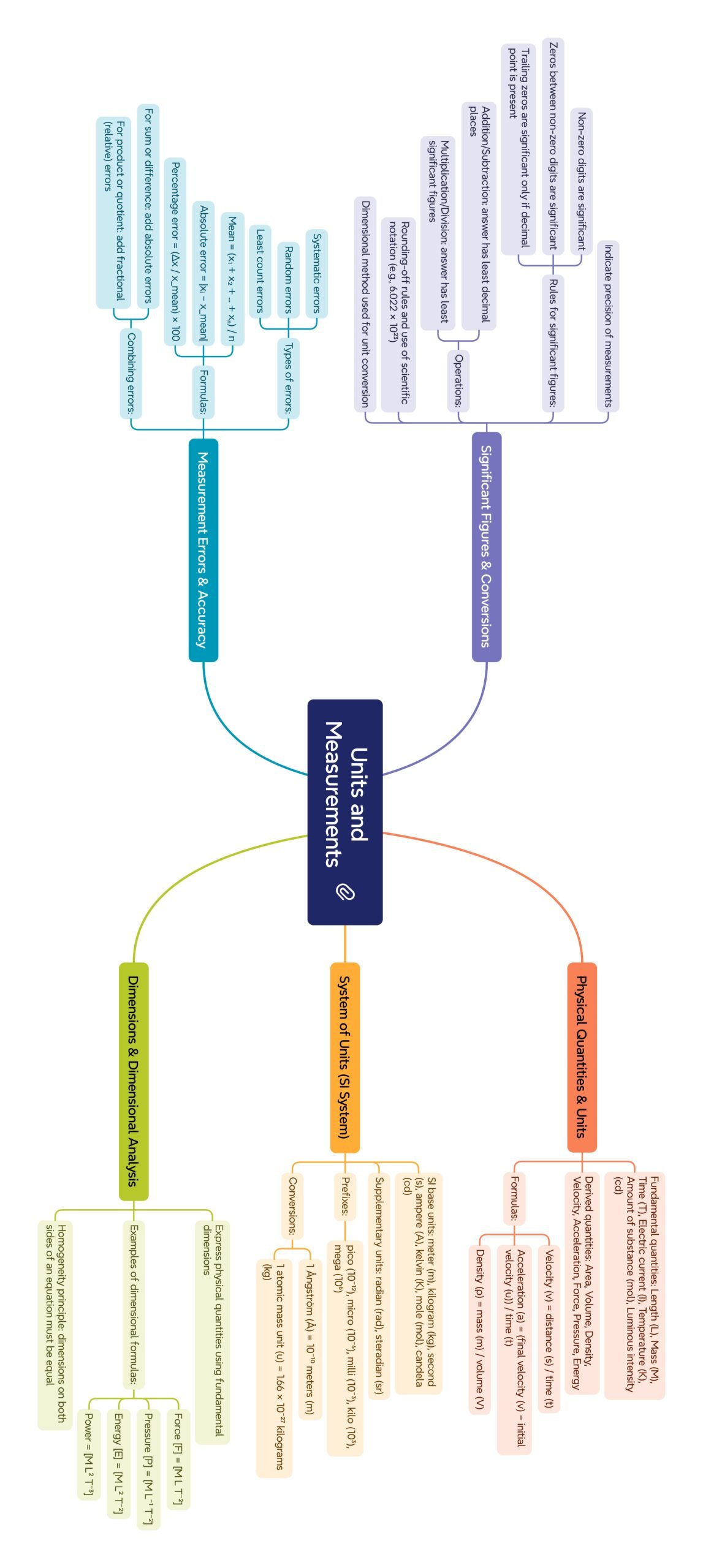
MIND MAP

———————————————————————————————————————————————————————————————————————————–
