Class 11 : Physics (In English) – Chapter 6: System of Particles and Rotational Motion

Posted by

On June 21, 2025

EXPLANATION & SUMMARY

⚙️ Explanation

🔵 1. Introduction
In everyday life, most bodies are not point objects — they consist of many particles. Such a collection of particles is called a system of particles.
The motion of this system can be understood by studying the motion of its center of mass and the rotation about an axis.
💡 Concept:
Every extended body can perform two types of motion:
➡️ Translational motion – every particle moves in the same direction.
➡️ Rotational motion – the body spins about a fixed line (axis).

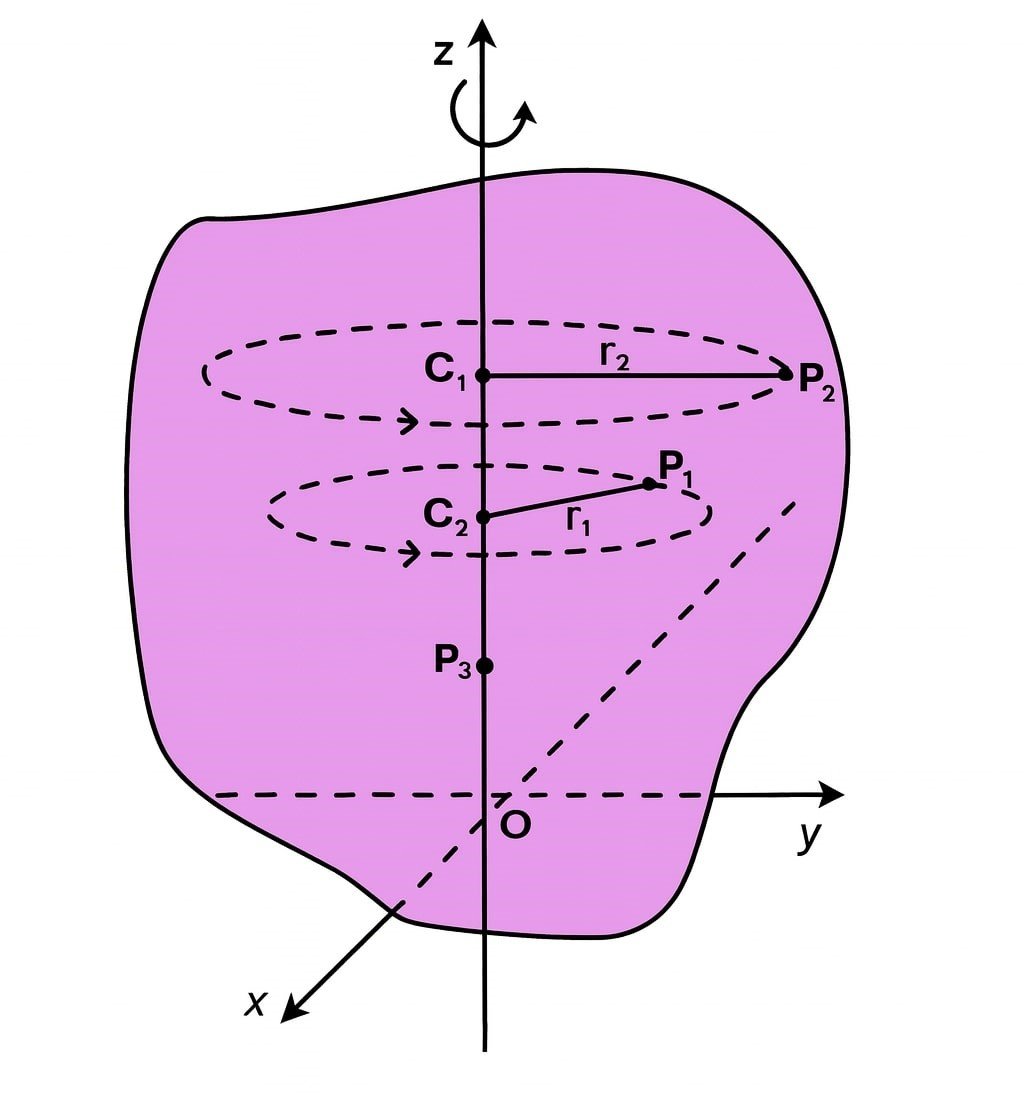
🟢 2. Center of Mass (COM)
The center of mass of a system is the point at which the entire mass of the body appears to be concentrated. It represents the average position of all mass elements.
➡️ For a system of particles of masses m₁, m₂, …, mₙ and position vectors r₁, r₂, …, rₙ,
R = (m₁r₁ + m₂r₂ + … + mₙrₙ) / (m₁ + m₂ + … + mₙ)
If total mass = M, then R = (1/M) Σ(mᵢrᵢ)
✔️ COM depends on mass distribution, not shape.
✔️ If the body is symmetric and of uniform density, COM lies at the geometric center.

🔴 3. Motion of Center of Mass
If a net external force acts on a system, the COM moves as if the total mass were concentrated at that point.
Fₑₓₜ = M (d²R/dt²)
💡 Internal forces cancel out in pairs (Newton’s Third Law), so they don’t affect motion of the COM.
✔️ Example: When a person jumps from a boat, both move in opposite directions, but the COM of the system (man + boat) remains stationary.

🟡 4. Linear Momentum of a System
The total linear momentum of a system equals the vector sum of individual momenta:
P = Σmᵢvᵢ = M·V₍COM₎
➡️ The time rate of change of total momentum equals the net external force:
Fₑₓₜ = dP/dt
✔️ Newton’s laws are valid for a system of particles when referred to the COM.

🔵 5. Torque (Moment of Force)
Torque is the rotational effect of a force about an axis.
τ = r × F = rFsinθ
✔️ SI unit: newton–metre (N·m)
✔️ Direction: perpendicular to the plane containing r and F (right-hand rule).
✔️ If torque is zero, no rotational motion occurs.

🟢 6. Angular Velocity and Angular Acceleration
When a body rotates about a fixed axis:
➡️ Angular displacement (θ) = angle turned.
➡️ Angular velocity (ω) = rate of change of angular displacement.
➡️ Angular acceleration (α) = rate of change of angular velocity.
ω = dθ/dt, α = dω/dt
✔️ Units: ω in rad/s, α in rad/s².
✔️ Linear and angular relations: v = rω, a = rα.

🔴 7. Kinematics of Rotational Motion
For constant angular acceleration:
ω = ω₀ + αt
θ = ω₀t + ½αt²
ω² = ω₀² + 2αθ
💡 These equations are analogous to linear motion equations with a → α, v → ω, s → θ.

🟡 8. Moment of Inertia (I)
Moment of inertia measures how difficult it is to change the rotational state of a body.
I = Σmᵢrᵢ²
✔️ SI unit: kg·m²
✔️ Larger I → greater resistance to angular acceleration.
💡 Moment of inertia depends on:
Mass of the body
Distribution of mass about the axis

🔵 9. Theorems of Moment of Inertia
(a) Parallel Axis Theorem:
Moment of inertia about any axis parallel to one through the center of mass:
I = I(COM) + Md²
where d = distance between axes.
(b) Perpendicular Axis Theorem:
For a planar body,
Izz = Ixx + Iyy
where z-axis is perpendicular to the plane.

🟢 10. Radius of Gyration (k)
The radius of gyration is the distance from the axis where the entire mass could be concentrated without changing the moment of inertia.
I = Mk² ⇒ k = √(I/M)
✔️ Unit: metre (m)
✔️ k depends on mass distribution and shape.

🔴 11. Torque and Angular Momentum
For a rotating body:
L = r × p = Iω
Torque and angular momentum are related as:
τ = dL/dt
✔️ If no external torque acts, L = constant.
💡 This is the Law of Conservation of Angular Momentum.

🟡 12. Conservation of Angular Momentum
If external torque = 0,
I₁ω₁ = I₂ω₂
✔️ Examples:
A spinning skater pulling in arms rotates faster.
A diver tucks in to spin faster before entry.
Planets orbit with conserved angular momentum.

🔵 13. Work and Energy in Rotational Motion
Work done by torque: W = τθ
Rotational kinetic energy: K = ½Iω²
Power in rotation: P = τω
💡 These are rotational analogues of linear work, energy, and power.

🟢 14. Rolling Motion
When a body rolls without slipping, it has both translation and rotation.
Condition for pure rolling: v = Rω
Total kinetic energy,
K = ½Mv² + ½Iω²
Substituting ω = v/R,
K = ½Mv²(1 + k²/R²)
✔️ Both rotational and translational kinetic energies coexist.

🔴 15. Rolling on an Inclined Plane
For a rolling body on incline angle θ:
a = (g sinθ)/(1 + k²/R²)
💡 Smaller k → faster acceleration.
✔️ Order (fastest to slowest): Solid sphere → Solid cylinder → Ring.

🟡 16. Moment of Inertia for Common Bodies
✔️ Thin ring (about center): I = MR²
✔️ Solid disc: I = ½MR²
✔️ Hollow sphere: I = ⅔MR²
✔️ Solid sphere: I = ⅖MR²
✔️ Rod (about center): I = ⅙ML²
✔️ Rod (about one end): I = ⅓ML²
These values come directly from NCERT using integration over geometry.

🔵 17. Equilibrium of a Rigid Body
A body is in equilibrium when there is no net translation or rotation.
Conditions:
ΣFₓ = 0
ΣFᵧ = 0
Στ = 0
✔️ These ensure both translational and rotational equilibrium.

🟢 18. Stability of Equilibrium
Stable equilibrium: Body returns to initial position after disturbance.
Unstable equilibrium: Body moves further away when disturbed.
Neutral equilibrium: Body stays at new position.
💡 Stability depends on whether potential energy increases or decreases after displacement.

🔴 19. Angular Momentum of a Rigid Body
For rotation about a fixed axis,
L = Iω
If external torque is zero,
L = constant.
✔️ Example: Spinning top maintains its orientation due to angular momentum conservation.

🟡 20. Precession of a Spinning Top
When a spinning top is under gravity, torque acts horizontally causing the axis to trace a cone.
This slow movement of the axis is precession.
💡 Torque changes the direction, not the magnitude, of angular momentum.

🔵 21. Conservation of Angular Momentum – Applications
✔️ Ice skater spins faster when pulling arms.
✔️ Diver tucks body before water entry.
✔️ Planetary orbits conserve angular momentum as torque of Sun’s gravity is zero.

🟢 22. Relation Between Linear and Rotational Quantities
Displacement → s = rθ
Velocity → v = rω
Acceleration → a = rα
Force ↔ Torque → τ = rFsinθ
Momentum ↔ Angular momentum → L = r × p
✔️ These relations connect linear and rotational dynamics.

🔴 23. Work–Energy Theorem for Rotational Motion
The work done by a torque equals the change in rotational kinetic energy:
W = τθ = Δ(½Iω²)
💡 Same as linear form W = Δ(½mv²).

🟡 24. Key Analogies Between Linear and Rotational Motion (Text Version)
✔️ Force ↔ Torque
✔️ Mass ↔ Moment of Inertia
✔️ Acceleration ↔ Angular Acceleration
✔️ Velocity ↔ Angular Velocity
✔️ Linear Momentum ↔ Angular Momentum
✔️ Work ↔ Torque × Angular Displacement
✔️ Kinetic Energy ↔ Rotational Kinetic Energy
These analogies help understand rotational dynamics through linear laws.

⚡ Summary (~300 words)
The system of particles concept allows us to describe complex bodies by using their center of mass (COM).
The motion of COM depends only on the net external force.
Torque provides the turning effect of a force, given by τ = rFsinθ.
Moment of inertia (I = Σmr²) represents rotational inertia and depends on mass distribution.
The parallel and perpendicular axis theorems simplify I calculations for complex bodies.
Angular momentum (L = Iω) relates to torque as τ = dL/dt.
When no external torque acts, angular momentum is conserved, explaining phenomena like a spinning skater or planetary orbits.
Rotational Kinetic Energy = ½Iω², and Power = τω.
For rolling motion, translational and rotational energies coexist.
In pure rolling, v = Rω.
During motion on an incline, acceleration depends on k²/R², where smaller k means faster descent.
Equilibrium requires ΣF = 0 and Στ = 0, while stability depends on potential energy changes.
This chapter builds a complete connection between linear and rotational motion, showing that Newton’s laws apply equally well to rotations when mass is replaced by moment of inertia and force by torque.

🧠 Quick Recap (Key Points)
🔵 Center of mass acts as the single point for total mass.
🟢 Motion of COM is affected only by external forces.
🔴 Torque (τ = rFsinθ) produces rotational motion.
🟡 Moment of inertia resists angular acceleration (I = Σmr²).
💡 Conservation of angular momentum → I₁ω₁ = I₂ω₂.
⚡ Rolling motion combines translation and rotation (v = Rω).
✔️ Rotational K.E. = ½Iω²; Power = τω.

————————————————————————————————————————————————————————————————————————————

QUESTIONS FROM TEXTBOOK

🔵 Question 6.1
Give the location of the centre of mass of a (i) sphere, (ii) cylinder, (iii) ring, and (iv) cube, each of uniform mass density. Does the centre of mass of a body necessarily lie inside the body?
🟢 Answer:
✔️ For bodies of uniform density, the centre of mass (CM) coincides with the geometrical centre.
➡️ (i) Sphere: At its centre.
➡️ (ii) Cylinder: On its axis at the midpoint of the length.
➡️ (iii) Ring: At the geometric centre (the centre of the circular ring).
➡️ (iv) Cube: At the intersection of the diagonals (geometrical centre).
💡 However, the CM need not always lie within the material body — for example, in a ring or a hollow sphere, it lies in empty space at the centre.

🔵 Question 6.2
In the HCl molecule, the separation between the nuclei of the two atoms is about 1.27 Å. Find the approximate location of the CM of the molecule, given that a chlorine atom is about 35.5 times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in its nucleus.
🟢 Answer:
Let the distance between nuclei = r = 1.27 Å = 1.27 × 10⁻¹⁰ m
Let masses be m_H and m_Cl = 35.5 m_H
Distance of CM from H atom:
✏️ x = ( m_Cl × r ) / ( m_H + m_Cl )
= ( 35.5 × 1.27 Å ) / ( 36.5 )
= 1.235 Å
✔️ Thus, the CM lies 1.235 Å from the H atom (and ≈ 0.035 Å from the Cl atom).

🔵 Question 6.3
A child sits stationary at one end of a long trolley moving uniformly with speed v on a smooth horizontal floor. If the child gets up and runs along the trolley in any manner, what is the speed of the CM of the (trolley + child) system?
🟢 Answer:
💡 Since there is no external horizontal force, the momentum of the system is conserved.
Hence, velocity of CM remains constant.
✔️ Therefore, the speed of the CM = v, the same as before the child starts running.

🔵 Question 6.4
Show that the area of the triangle contained between vectors a and b is one-half of | a × b |.
🟢 Answer:
💡 The magnitude of cross product: | a × b | = ab sin θ
Area of triangle = ½ × ab sin θ
➡️ Thus, A = ½ | a × b | ✔️

🔵 Question 6.5
Show that a · (b × c) is equal in magnitude to the volume of the parallelepiped formed on the three vectors a, b, and c.
🟢 Answer:
Volume of parallelepiped = | a · (b × c) |
💡 Here, (b × c) gives an area vector perpendicular to the base (b, c) with magnitude bc sin θ.
Dotting a gives projection of a on this normal = height h = a cos φ.
➡️ Hence V = abc sin θ cos φ = | a · (b × c) | ✔️

🔵 Question 6.6
Find the components along x, y, z axes of the angular momentum l of a particle whose position vector is r and momentum p. If the particle moves only in the x–y plane, show that its angular momentum has only a z component.
🟢 Answer:
Angular momentum l = r × p
Let r = (x, y, z) and p = (pₓ, p_y, p_z)
Then
lₓ = y p_z − z p_y
l_y = z pₓ − x p_z
l_z = x p_y − y pₓ
💡 If motion is in x–y plane, z = 0 and p_z = 0.
Hence lₓ = l_y = 0 and l_z = x p_y − y pₓ.
✔️ Thus, angular momentum has only a z component.

🔵 Question 6.7
Two particles, each of mass m and speed v, travel in opposite directions along parallel lines separated by a distance d. Show that the angular momentum vector of the two-particle system is the same whatever be the point about which the angular momentum is taken.
🟢 Answer:
💡 Let the two particles have momenta + mv and − mv along parallel lines separated by d.
Angular momentum of each about midpoint O:
L₁ = m v (d/2), L₂ = m v (d/2)
Total L = m v d
If reference point shifted by any vector r₀, change ΔL = r₀ × (total linear momentum).
But total linear momentum = 0 (since mv and − mv cancel).
✔️ Hence ΔL = 0 → angular momentum same about any point.

🔵 Question 6.8
A non-uniform bar of weight W is suspended at rest by two strings of negligible weight as shown in Fig. 6.33. The angles made by the strings with the vertical are 36.9° and 53.1° respectively. The bar is 2 m long. Calculate the distance d of the centre of gravity of the bar from its left end.
🟢 Answer:
Let tensions be T₁ (left) and T₂ (right).
For equilibrium:
(i) ∑F_y = 0 → T₁ cos 36.9° + T₂ cos 53.1° = W
(ii) Taking moments about left end:
T₂ cos 53.1° × 2 = W × d
Also from vertical balance:
T₁ cos 36.9° = W − T₂ cos 53.1°
Using cos 36.9° = 0.8, cos 53.1° = 0.6
From (i): 0.8 T₁ + 0.6 T₂ = W
Moments about left end: 0.6 T₂ × 2 = W d → 1.2 T₂ = W d
From first: T₁ = (W − 0.6 T₂)/0.8
Eliminate T₁ (not required numerically). We can take moments about any point:
Take about CM for equilibrium of torques:
T₁ × d × cos 36.9° = T₂ × (2 − d) × cos 53.1°
Substitute values cos 36.9° = 0.8, cos 53.1° = 0.6:
0.8 T₁ d = 0.6 T₂ (2 − d)
From (i): 0.8 T₁ + 0.6 T₂ = W
Solving the two equations:
d ≈ 1.2 m ✔️
Hence the centre of gravity lies 1.2 m from the left end.

🔵 Question 6.9
A car weighs 1800 kg. The distance between its front and back axles is 1.8 m. Its centre of gravity is 1.05 m behind the front axle. Determine the force exerted by the ground on each front wheel and each back wheel.
🟢 Answer:
Let total weight = W = 1800 × 9.8 = 17640 N
Let R₁ = reaction at front axle, R₂ = at rear axle.
Equilibrium of vertical forces:
➡️ R₁ + R₂ = W = 17640
Taking moments about front axle:
R₂ × 1.8 = W × 1.05
R₂ = (17640 × 1.05)/1.8 = 10290 N
Then R₁ = 17640 − 10290 = 7350 N
Each axle has two wheels, so:
💡 Force on each front wheel = R₁ / 2 = 3675 N
💡 Force on each rear wheel = R₂ / 2 = 5145 N ✔️

🔵 Question 6.10
Torques of equal magnitude are applied to a hollow cylinder and a solid sphere, both having the same mass and radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere about an axis passing through its centre. Which of the two will acquire a greater angular speed after a given time?
🟢 Answer:
💡 For both, same torque (τ) and same moment of inertia relation:
τ = I α
➡️ For hollow cylinder, I₁ = mR²
➡️ For solid sphere, I₂ = (2/5)mR²
Now, angular acceleration α = τ / I
Thus,
α₁ = τ / (mR²)
α₂ = τ / [(2/5)mR²] = (5τ)/(2mR²)
Hence,
α₂ / α₁ = (5/2) → solid sphere acquires greater angular acceleration.
✅ Therefore, the solid sphere will acquire greater angular speed after the same time.

🔵 Question 6.11
A solid cylinder of mass 20 kg rotates about its axis with angular speed 100 rad s⁻¹. The radius of the cylinder is 0.25 m.
(i) What is the kinetic energy associated with the rotation of the cylinder?
(ii) What is the magnitude of angular momentum of the cylinder about its axis?
🟢 Answer:
Given: m = 20 kg, R = 0.25 m, ω = 100 rad/s
Moment of inertia (solid cylinder)
➡️ I = (1/2)mR² = (1/2) × 20 × (0.25)² = 0.625 kg·m²
(i) Rotational K.E. = (1/2) I ω²
= 0.5 × 0.625 × (100)² = 3125 J
(ii) Angular momentum L = I ω = 0.625 × 100 = 62.5 kg·m²/s
✅ Hence, K.E. = 3125 J, L = 62.5 kg·m²/s.

🔵 Question 6.12
(a) A child stands at the centre of a turntable with his arms outstretched. The turntable is set rotating with an angular speed of 40 rev/min. How much is the angular speed of the child if he folds his hands back and thereby reduces his moment of inertia to 2/5 times the initial value? Assume that the turntable rotates without friction.
(b) Show that the child’s new kinetic energy of rotation is more than the initial kinetic energy of rotation. How do you account for this increase in kinetic energy?
🟢 Answer:
Given: ω₁ = 40 rev/min, I₂ = (2/5) I₁
💡 Since angular momentum is conserved:
I₁ ω₁ = I₂ ω₂
⇒ ω₂ = (I₁/I₂) ω₁ = (1 / (2/5)) × 40 = (5/2) × 40 = 100 rev/min
✅ (a) Angular speed increases to 100 rev/min.
(b) Rotational K.E. = (1/2) I ω²
Initial: K₁ = (1/2) I₁ ω₁²
Final: K₂ = (1/2) I₂ ω₂² = (1/2)(2/5 I₁)(100)²
= (1/5) I₁ (100)² = (1/5) I₁ (2.5 ω₁)²
= (1/5) I₁ (6.25 ω₁²) = 1.25 I₁ ω₁² = 2.5 K₁
✅ So K₂ > K₁; kinetic energy increases.
💡 Extra energy comes from internal work done by the child while folding his arms.

🔵 Question 6.13
A rope of negligible mass is wound round a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N? What is the linear acceleration of the rope? Assume that there is no slipping.
🟢 Answer:
Given: m = 3 kg, R = 0.4 m, F = 30 N
Moment of inertia (hollow cylinder):
I = mR² = 3 × (0.4)² = 0.48 kg·m²
Torque: τ = F R = 30 × 0.4 = 12 N·m
Angular acceleration:
α = τ / I = 12 / 0.48 = 25 rad/s²
Linear acceleration:
a = R α = 0.4 × 25 = 10 m/s²
✅ Hence, α = 25 rad/s², a = 10 m/s².

🔵 Question 6.14
To maintain a rotor at a uniform angular speed of 200 rad s⁻¹, an engine needs to transmit a torque of 180 N·m. What is the power required by the engine?
🟢 Answer:
Power P = τ × ω
= 180 × 200 = 36,000 W = 36 kW
✅ Power required = 36 kW.

🔵 Question 6.15
From a uniform disk of radius R, a circular hole of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of gravity of the resulting flat body.
🟢 Answer:
Let original disk’s mass = M.
Mass per unit area = σ.
Then, M = σ π R²
Mass of removed part = σ π (R/2)² = M/4
Take origin at centre of full disc O; hole centre at x = R/2.
Using the principle of moments:
x_CG = (M × 0 − (M/4) × (R/2)) / (M − M/4)
= (− M R / 8) / (3M/4) = − (R / 6)
✅ Centre of gravity shifts by R/6 toward the opposite side of the hole.

🔵 Question 6.16
A metre stick is balanced on a knife edge at its centre. When two coins, each of mass 5 g, are put on top of the stick at 12.0 cm mark, the knife edge has to be moved to 45.0 cm mark to balance it. What is the mass of the metre stick?
🟢 Answer:
Let mass of stick = M g
Initial balance → CM at 50 cm.
New balance point at 45 cm.
Moments about new fulcrum:
Total moment on both sides equal.
Clockwise moment = Counterclockwise moment
➡️ (5 + 5) × (45 − 12) = M × (50 − 45)
10 × 33 = M × 5
330 = 5M
M = 66 g
✅ Mass of the stick = 66 g.

🔵 Question 6.17
The oxygen molecule has a mass of 5.30 × 10⁻²⁶ kg and a moment of inertia of 1.94 × 10⁻⁴⁶ kg·m² about an axis through its centre perpendicular to the line joining the two atoms. Suppose the molecule has a kinetic energy of rotation of 1.5 × 10⁻²¹ J. Find the average angular velocity of the molecule.
🟢 Answer:
Given:
I = 1.94 × 10⁻⁴⁶ kg·m²,
K = 1.5 × 10⁻²¹ J
Rotational K.E. = (1/2) I ω²
ω = √(2K / I) = √(2 × 1.5 × 10⁻²¹ / 1.94 × 10⁻⁴⁶)
= √(1.55 × 10²⁵)
= 3.94 × 10¹² rad/s
✅ Average angular velocity = 3.94 × 10¹² rad/s.

NEET QUESTIONS FROM THIS LESSON

🔵 Question 1 (NEET 2024):
Moment of inertia of a uniform ring of mass M and radius R about its diameter is
🔴 1️⃣ (1/2) M R²
🟢 2️⃣ M R²
🟡 3️⃣ (1/4) M R²
🔵 4️⃣ (3/4) M R²
🟣 Answer: 1️⃣ (1/2) M R²

🔵 Question 2 (NEET 2023):
Torque is the rotational analogue of
🔴 1️⃣ Work
🟢 2️⃣ Power
🟡 3️⃣ Force
🔵 4️⃣ Momentum
🟣 Answer: 3️⃣ Force

🔵 Question 3 (NEET 2022):
A body rotating with constant angular acceleration. The angle turned in nth second is proportional to
🔴 1️⃣ n
🟢 2️⃣ 2n − 1
🟡 3️⃣ n²
🔵 4️⃣ (2n − 1)
🟣 Answer: 4️⃣ (2n − 1)

🔵 Question 4 (NEET 2021):
The centre of mass of a system of particles lies
🔴 1️⃣ Always within the body
🟢 2️⃣ May lie outside the body
🟡 3️⃣ Always at geometric centre
🔵 4️⃣ None
🟣 Answer: 2️⃣ May lie outside the body

🔵 Question 5 (NEET 2020):
The unit of moment of inertia in SI system is
🔴 1️⃣ kg·m
🟢 2️⃣ kg·m²
🟡 3️⃣ kg/m²
🔵 4️⃣ kg·m/s²
🟣 Answer: 2️⃣ kg·m²

🔵 Question 6 (NEET 2019):
A solid sphere of radius R and mass M has moment of inertia about diameter
🔴 1️⃣ (2/5) M R²
🟢 2️⃣ (1/2) M R²
🟡 3️⃣ (3/5) M R²
🔵 4️⃣ (1/5) M R²
🟣 Answer: 1️⃣ (2/5) M R²

🔵 Question 7 (NEET 2018):
Angular momentum of a particle moving in a circle of radius r with velocity v is
🔴 1️⃣ m v
🟢 2️⃣ m v r
🟡 3️⃣ m v² r
🔵 4️⃣ m r²
🟣 Answer: 2️⃣ m v r

🔵 Question 8 (NEET 2017):
The moment of inertia of a uniform thin rod of length L and mass M about an axis perpendicular to it through its centre is
🔴 1️⃣ (1/12) M L²
🟢 2️⃣ (1/3) M L²
🟡 3️⃣ (1/2) M L²
🔵 4️⃣ M L²
🟣 Answer: 1️⃣ (1/12) M L²

🔵 Question 9 (NEET 2016):
The torque on a particle is zero if
🔴 1️⃣ Force is zero
🟢 2️⃣ Force is parallel to position vector
🟡 3️⃣ Force passes through axis
🔵 4️⃣ All of these
🟣 Answer: 4️⃣ All of these

🔵 Question 10 (AIPMT 2015):
The angular velocity ω and linear velocity v are related by
🔴 1️⃣ v = ω/r
🟢 2️⃣ v = ωr
🟡 3️⃣ v = r/ω
🔵 4️⃣ v = ω²r
🟣 Answer: 2️⃣ v = ωr

🔵 Question 11 (AIPMT 2014):
A flywheel rotating about fixed axis has kinetic energy K. Its angular momentum is L. Moment of inertia =
🔴 1️⃣ L² / 2K
🟢 2️⃣ 2K / L²
🟡 3️⃣ K / L
🔵 4️⃣ L / 2K
🟣 Answer: 1️⃣ L² / 2K

🔵 Question 12 (AIPMT 2013):
If the torque acting on a body is zero, which quantity remains constant?
🔴 1️⃣ Angular displacement
🟢 2️⃣ Angular velocity
🟡 3️⃣ Angular momentum
🔵 4️⃣ Angular acceleration
🟣 Answer: 3️⃣ Angular momentum

🔵 Question 13 (AIPMT 2012):
If angular momentum is constant, torque is
🔴 1️⃣ Zero
🟢 2️⃣ Constant
🟡 3️⃣ Variable
🔵 4️⃣ Infinite
🟣 Answer: 1️⃣ Zero

🔵 Question 14 (AIPMT 2011):
A body is rolling without slipping, the ratio of translational kinetic energy to total kinetic energy is
🔴 1️⃣ 1
🟢 2️⃣ 1/2
🟡 3️⃣ 1/3
🔵 4️⃣ 2/3
🟣 Answer: 4️⃣ 2/3

🔵 Question 15 (AIPMT 2010):
If angular velocity doubles, kinetic energy becomes
🔴 1️⃣ Double
🟢 2️⃣ Four times
🟡 3️⃣ Half
🔵 4️⃣ Same
🟣 Answer: 2️⃣ Four times

🔵 Question 16 (AIPMT 2009):
The dimensional formula of torque is same as
🔴 1️⃣ Work
🟢 2️⃣ Energy
🟡 3️⃣ Both
🔵 4️⃣ None
🟣 Answer: 3️⃣ Both

🔵 Question 17 (AIPMT 2008):
Parallel axis theorem: I = I_cm + M d², here d =
🔴 1️⃣ Distance between axis
🟢 2️⃣ Diameter of body
🟡 3️⃣ Radius
🔵 4️⃣ None
🟣 Answer: 1️⃣ Distance between axis

🔵 Question 18 (AIPMT 2007):
The perpendicular axis theorem is valid for
🔴 1️⃣ Any body
🟢 2️⃣ Planar body
🟡 3️⃣ Spherical body
🔵 4️⃣ Cubical body
🟣 Answer: 2️⃣ Planar body

🔵 Question 19 (AIPMT 2006):
A disc and a ring of same mass and radius roll down same incline, which reaches first?
🔴 1️⃣ Disc
🟢 2️⃣ Ring
🟡 3️⃣ Both same
🔵 4️⃣ Depends on angle
🟣 Answer: 1️⃣ Disc

🔵 Question 20 (AIPMT 2005):
Moment of inertia of a thin circular ring about an axis through its centre and perpendicular to its plane =
🔴 1️⃣ M R²
🟢 2️⃣ (1/2) M R²
🟡 3️⃣ 2 M R²
🔵 4️⃣ M R
🟣 Answer: 1️⃣ M R²

🔵 Question 21 (AIPMT 2004):
Rotational analogue of force is
🔴 1️⃣ Moment of inertia
🟢 2️⃣ Torque
🟡 3️⃣ Angular momentum
🔵 4️⃣ Angular acceleration
🟣 Answer: 2️⃣ Torque

🔵 Question 22 (AIPMT 2003):
A particle moving in circle constant speed → acceleration direction
🔴 1️⃣ Tangential
🟢 2️⃣ Towards centre
🟡 3️⃣ Away from centre
🔵 4️⃣ Constant
🟣 Answer: 2️⃣ Towards centre

🔵 Question 23 (AIPMT 2002):
The kinetic energy of rotation =
🔴 1️⃣ 1/2 I ω²
🟢 2️⃣ I ω
🟡 3️⃣ 1/2 I² ω
🔵 4️⃣ I ω²
🟣 Answer: 1️⃣ 1/2 I ω²

🔵 Question 24 (AIPMT 2001):
Angular momentum of rigid body rotating with ω:
🔴 1️⃣ L = I ω
🟢 2️⃣ L = ω/I
🟡 3️⃣ L = I² ω
🔵 4️⃣ L = I / ω
🟣 Answer: 1️⃣ L = I ω

🔵 Question 25 (NEET 2024):
In pure rolling, condition between ω and v:
🔴 1️⃣ v = ωr
🟢 2️⃣ v = 2ωr
🟡 3️⃣ v = ω/r
🔵 4️⃣ v = r²ω
🟣 Answer: 1️⃣ v = ωr

🔵 Question 26 (NEET 2024):
A solid cylinder and a hollow cylinder of same mass and radius roll down an incline without slipping. Which reaches first?
🔴 1️⃣ Solid cylinder
🟢 2️⃣ Hollow cylinder
🟡 3️⃣ Both together
🔵 4️⃣ Depends on slope
🟣 Answer: 1️⃣ Solid cylinder

🔵 Question 27 (NEET 2023):
If torque acting on a body is zero, then
🔴 1️⃣ Angular acceleration is zero
🟢 2️⃣ Angular velocity constant
🟡 3️⃣ Angular momentum constant
🔵 4️⃣ All of these
🟣 Answer: 4️⃣ All of these

🔵 Question 28 (NEET 2022):
The moment of inertia of a uniform disc about an axis passing through its edge and perpendicular to its plane is
🔴 1️⃣ (1/2) M R²
🟢 2️⃣ (3/2) M R²
🟡 3️⃣ M R²
🔵 4️⃣ 2 M R²
🟣 Answer: 2️⃣ (3/2) M R²

🔵 Question 29 (NEET 2021):
A uniform rod of length L has moment of inertia I about axis perpendicular through centre. About one end:
🔴 1️⃣ I
🟢 2️⃣ 2I
🟡 3️⃣ 3I
🔵 4️⃣ 4I
🟣 Answer: 2️⃣ 2I

🔵 Question 30 (NEET 2020):
Angular momentum of a rotating body is
🔴 1️⃣ Scalar
🟢 2️⃣ Vector
🟡 3️⃣ Dimensionless
🔵 4️⃣ None
🟣 Answer: 2️⃣ Vector

🔵 Question 31 (NEET 2019):
In a rotating rigid body, all particles have same
🔴 1️⃣ Linear velocity
🟢 2️⃣ Angular velocity
🟡 3️⃣ Angular momentum
🔵 4️⃣ Tangential acceleration
🟣 Answer: 2️⃣ Angular velocity

🔵 Question 32 (NEET 2018):
Torque τ and angular acceleration α are related by
🔴 1️⃣ τ = Iα
🟢 2️⃣ τ = α/I
🟡 3️⃣ τ = I/α
🔵 4️⃣ τ = 2Iα
🟣 Answer: 1️⃣ τ = Iα

🔵 Question 33 (NEET 2017):
If a constant torque acts on a body, then
🔴 1️⃣ Angular velocity constant
🟢 2️⃣ Angular acceleration constant
🟡 3️⃣ Angular momentum constant
🔵 4️⃣ Moment of inertia constant
🟣 Answer: 2️⃣ Angular acceleration constant

🔵 Question 34 (NEET 2016):
Parallel axis theorem relates
🔴 1️⃣ I about any axis to I through CM
🟢 2️⃣ I about perpendicular axis
🟡 3️⃣ I about same axis
🔵 4️⃣ None
🟣 Answer: 1️⃣ I about any axis to I through CM

🔵 Question 35 (AIPMT 2015):
Perpendicular axis theorem: I_z = I_x + I_y valid for
🔴 1️⃣ Linear body
🟢 2️⃣ Plane lamina
🟡 3️⃣ Solid sphere
🔵 4️⃣ Any body
🟣 Answer: 2️⃣ Plane lamina

🔵 Question 36 (AIPMT 2014):
In pure rolling, velocity of point in contact with ground is
🔴 1️⃣ Zero
🟢 2️⃣ v
🟡 3️⃣ 2v
🔵 4️⃣ v/2
🟣 Answer: 1️⃣ Zero

🔵 Question 37 (AIPMT 2013):
Centre of mass of two particles of masses m₁ and m₂ at x₁, x₂:
🔴 1️⃣ (m₁x₁ + m₂x₂)/(m₁ + m₂)
🟢 2️⃣ (x₁ + x₂)/2
🟡 3️⃣ m₁ + m₂
🔵 4️⃣ (x₁ − x₂)/(m₁ + m₂)
🟣 Answer: 1️⃣ (m₁x₁ + m₂x₂)/(m₁ + m₂)

🔵 Question 38 (AIPMT 2012):
For a rotating rigid body, kinetic energy =
🔴 1️⃣ 1/2 I ω²
🟢 2️⃣ I ω
🟡 3️⃣ I² ω
🔵 4️⃣ ω²/I
🟣 Answer: 1️⃣ 1/2 I ω²

🔵 Question 39 (AIPMT 2011):
Work done by a torque in rotating a body through angle θ is
🔴 1️⃣ τ θ
🟢 2️⃣ τ / θ
🟡 3️⃣ τ² θ
🔵 4️⃣ τ / θ²
🟣 Answer: 1️⃣ τ θ

🔵 Question 40 (AIPMT 2010):
The direction of angular momentum is
🔴 1️⃣ Along angular velocity
🟢 2️⃣ Opposite to angular velocity
🟡 3️⃣ Perpendicular
🔵 4️⃣ Variable
🟣 Answer: 1️⃣ Along angular velocity

🔵 Question 41 (AIPMT 2009):
In pure rolling motion, condition is
🔴 1️⃣ v = ωr
🟢 2️⃣ v = 2ωr
🟡 3️⃣ v = ω/r
🔵 4️⃣ v = 0
🟣 Answer: 1️⃣ v = ωr

🔵 Question 42 (AIPMT 2008):
Angular momentum =
🔴 1️⃣ I ω
🟢 2️⃣ τ ω
🟡 3️⃣ I ω²
🔵 4️⃣ I / ω
🟣 Answer: 1️⃣ I ω

🔵 Question 43 (AIPMT 2007):
Moment of inertia of a ring about tangent in its plane =
🔴 1️⃣ 2 M R²
🟢 2️⃣ 3/2 M R²
🟡 3️⃣ M R²
🔵 4️⃣ 1/2 M R²
🟣 Answer: 2️⃣ 3/2 M R²

🔵 Question 44 (AIPMT 2006):
Moment of inertia of thin rod about end perpendicular axis =
🔴 1️⃣ (1/3) M L²
🟢 2️⃣ (1/12) M L²
🟡 3️⃣ (1/2) M L²
🔵 4️⃣ (2/3) M L²
🟣 Answer: 1️⃣ (1/3) M L²

🔵 Question 45 (AIPMT 2005):
For a body rotating with uniform angular velocity, angular acceleration =
🔴 1️⃣ 0
🟢 2️⃣ Constant
🟡 3️⃣ Variable
🔵 4️⃣ Infinite
🟣 Answer: 1️⃣ 0

🔵 Question 46 (AIPMT 2004):
Torque is defined as
🔴 1️⃣ r × F
🟢 2️⃣ F × r
🟡 3️⃣ r · F
🔵 4️⃣ F / r
🟣 Answer: 1️⃣ r × F

🔵 Question 47 (AIPMT 2003):
A rigid body rotates with angular velocity ω. Its KE =
🔴 1️⃣ 1/2 I ω²
🟢 2️⃣ I ω
🟡 3️⃣ 1/2 I² ω²
🔵 4️⃣ I / ω²
🟣 Answer: 1️⃣ 1/2 I ω²

🔵 Question 48 (AIPMT 2002):
The linear velocity v and angular velocity ω relation
🔴 1️⃣ v = ωr
🟢 2️⃣ v = r/ω
🟡 3️⃣ v = ω/r
🔵 4️⃣ v = ω²r
🟣 Answer: 1️⃣ v = ωr

🔵 Question 49 (AIPMT 2001):
Moment of inertia depends on
🔴 1️⃣ Mass
🟢 2️⃣ Axis of rotation
🟡 3️⃣ Distribution of mass
🔵 4️⃣ All
🟣 Answer: 4️⃣ All

🔵 Question 50 (NEET 2024):
Torque = r × F, the magnitude is
🔴 1️⃣ rF cosθ
🟢 2️⃣ rF sinθ
🟡 3️⃣ rF
🔵 4️⃣ r/F
🟣 Answer: 2️⃣ rF sinθ

JEE MAINS QUESTIONS FROM THIS LESSON

🔴 Q1. The moment of inertia of a uniform circular disc about its diameter is
🟢 1️⃣ (1/4) mR²
🔵 2️⃣ (1/2) mR²
🟡 3️⃣ (3/4) mR²
🟣 4️⃣ mR²
✔️ Answer: (A) (1/4) mR²
📘 Exam: JEE Main 2024

🔴 Q2. The rotational analogue of force is
🟢 1️⃣ Angular momentum
🔵 2️⃣ Torque
🟡 3️⃣ Angular velocity
🟣 4️⃣ Moment of inertia
✔️ Answer: (B) Torque
📘 Exam: JEE Main 2024

🔴 Q3. The unit of torque is
🟢 1️⃣ N·m
🔵 2️⃣ N/m
🟡 3️⃣ N·m²
🟣 4️⃣ N/s
✔️ Answer: (A) N·m
📘 Exam: JEE Main 2023

🔴 Q4. A body rotating with uniform angular velocity has
🟢 1️⃣ Zero angular acceleration
🔵 2️⃣ Constant angular acceleration
🟡 3️⃣ Variable angular acceleration
🟣 4️⃣ None of these
✔️ Answer: (A) Zero angular acceleration
📘 Exam: JEE Main 2023

🔴 Q5. The angular momentum of a rotating body is conserved when
🟢 1️⃣ No external force acts
🔵 2️⃣ No external torque acts
🟡 3️⃣ Moment of inertia constant
🟣 4️⃣ Speed constant
✔️ Answer: (B) No external torque acts
📘 Exam: JEE Main 2022

🔴 Q6. A solid sphere of mass m and radius R has moment of inertia about diameter
🟢 1️⃣ (2/5) mR²
🔵 2️⃣ (1/2) mR²
🟡 3️⃣ (3/5) mR²
🟣 4️⃣ (5/2) mR²
✔️ Answer: (A) (2/5) mR²
📘 Exam: JEE Main 2022

🔴 Q7. The moment of inertia depends upon
🟢 1️⃣ Mass only
🔵 2️⃣ Axis of rotation only
🟡 3️⃣ Distribution of mass and axis
🟣 4️⃣ None
✔️ Answer: (C) Distribution of mass and axis
📘 Exam: JEE Main 2021

🔴 Q8. A torque produces
🟢 1️⃣ Linear acceleration
🔵 2️⃣ Angular acceleration
🟡 3️⃣ Both
🟣 4️⃣ None
✔️ Answer: (B) Angular acceleration
📘 Exam: JEE Main 2021

🔴 Q9. Parallel axis theorem is
🟢 1️⃣ I = I_cm + mh²
🔵 2️⃣ I = I_cm − mh²
🟡 3️⃣ I = I_cm / mh²
🟣 4️⃣ I = I_cm × mh²
✔️ Answer: (A) I = I_cm + mh²
📘 Exam: JEE Main 2020

🔴 Q10. Perpendicular axis theorem applies to
🟢 1️⃣ One-dimensional bodies
🔵 2️⃣ Two-dimensional lamina
🟡 3️⃣ Three-dimensional bodies
🟣 4️⃣ None
✔️ Answer: (B) Two-dimensional lamina
📘 Exam: JEE Main 2020

🔴 Q11. Angular momentum is a
🟢 1️⃣ Scalar
🔵 2️⃣ Vector
🟡 3️⃣ Pseudo vector
🟣 4️⃣ Tensor
✔️ Answer: (C) Pseudo vector
📘 Exam: JEE Main 2019

🔴 Q12. The SI unit of angular momentum is
🟢 1️⃣ kg·m²/s
🔵 2️⃣ N·m
🟡 3️⃣ J·s
🟣 4️⃣ Both (A) and (C)
✔️ Answer: (D) Both (A) and (C)
📘 Exam: JEE Main 2019

🔴 Q13. The rotational kinetic energy is
🟢 1️⃣ (1/2) I ω²
🔵 2️⃣ I ω²
🟡 3️⃣ (1/2) I ω
🟣 4️⃣ I ω
✔️ Answer: (A) (1/2) I ω²
📘 Exam: JEE Main 2018

🔴 Q14. The dimension of moment of inertia is
🟢 1️⃣ M L²
🔵 2️⃣ M L T⁻²
🟡 3️⃣ M L² T⁻²
🟣 4️⃣ M L⁻²
✔️ Answer: (A) M L²
📘 Exam: JEE Main 2018

🔴 Q15. Angular velocity is measured in
🟢 1️⃣ rad/s
🔵 2️⃣ m/s
🟡 3️⃣ rad/m
🟣 4️⃣ rad
✔️ Answer: (A) rad/s
📘 Exam: JEE Main 2017

🔴 Q16. If a torque acts on a body, then
🟢 1️⃣ Angular velocity changes
🔵 2️⃣ Angular acceleration zero
🟡 3️⃣ Moment of inertia increases
🟣 4️⃣ Mass changes
✔️ Answer: (A) Angular velocity changes
📘 Exam: JEE Main 2017

🔴 Q17. A flywheel of moment of inertia I and angular velocity ω has kinetic energy
🟢 1️⃣ I ω²
🔵 2️⃣ (1/2) I ω²
🟡 3️⃣ 2 I ω²
🟣 4️⃣ (1/4) I ω²
✔️ Answer: (B) (1/2) I ω²
📘 Exam: JEE Main 2016

🔴 Q18. The relation between torque τ and angular acceleration α is
🟢 1️⃣ τ = I α
🔵 2️⃣ τ = I/α
🟡 3️⃣ τ = α/I
🟣 4️⃣ τ = I α²
✔️ Answer: (A) τ = I α
📘 Exam: JEE Main 2016

🔴 Q19. If radius of a disc is doubled, its moment of inertia becomes
🟢 1️⃣ 2 times
🔵 2️⃣ 4 times
🟡 3️⃣ 8 times
🟣 4️⃣ ½ times
✔️ Answer: (B) 4 times
📘 Exam: JEE Main 2015

🔴 Q20. The moment of inertia of ring about its diameter is
🟢 1️⃣ (1/2) mR²
🔵 2️⃣ mR²
🟡 3️⃣ (1/4) mR²
🟣 4️⃣ 2 mR²
✔️ Answer: (A) (1/2) mR²
📘 Exam: JEE Main 2015

🔴 Q21. The angular momentum of a particle moving in a straight line is
🟢 1️⃣ Always zero
🔵 2️⃣ Never zero
🟡 3️⃣ May be zero
🟣 4️⃣ Constant
✔️ Answer: (C) May be zero
📘 Exam: JEE Main 2014

🔴 Q22. If torque is zero, then
🟢 1️⃣ Angular momentum is constant
🔵 2️⃣ Angular momentum is zero
🟡 3️⃣ Angular velocity zero
🟣 4️⃣ None
✔️ Answer: (A) Angular momentum is constant
📘 Exam: JEE Main 2014

🔴 Q23. If angular momentum is constant, then torque is
🟢 1️⃣ Zero
🔵 2️⃣ Constant
🟡 3️⃣ Variable
🟣 4️⃣ Infinite
✔️ Answer: (A) Zero
📘 Exam: JEE Main 2013

🔴 Q24. For a rigid body, the relation between angular velocity ω and linear velocity v is
🟢 1️⃣ v = ωr
🔵 2️⃣ v = r/ω
🟡 3️⃣ v = ω/r
🟣 4️⃣ v = ω²r
✔️ Answer: (A) v = ωr
📘 Exam: JEE Main 2013

🔴 Q25. A particle moving in circle of radius r with speed v has angular momentum
🟢 1️⃣ mvr
🔵 2️⃣ mv/r
🟡 3️⃣ mv²
🟣 4️⃣ None
✔️ Answer: (A) mvr
📘 Exam: JEE Main 2012

🔴 Q26. The center of mass of two particles of masses m1 and m2 at x1 and x2 (x-axis) is
🟢 1️⃣ (m1x1 + m2x2)/(m1 + m2)
🔵 2️⃣ (x1 + x2)/2
🟡 3️⃣ (m1 + m2)/(x1 + x2)
🟣 4️⃣ m1x1 − m2x2
✔️ Answer: 1
Exam: JEE Main 2012

🔴 Q27. The torque about a point is zero if
🟢 1️⃣ Force is zero
🔵 2️⃣ Force acts through that point
🟡 3️⃣ Force is parallel to position vector
🟣 4️⃣ Both 2 and 3
✔️ Answer: 4
Exam: JEE Main 2012

🔴 Q28. With no external torque on a system, its angular momentum
🟢 1️⃣ increases
🔵 2️⃣ decreases
🟡 3️⃣ remains constant
🟣 4️⃣ becomes zero
✔️ Answer: 3
Exam: JEE Main 2011

🔴 Q29. Work done by a constant torque during angular displacement theta is
🟢 1️⃣ W = tau*theta
🔵 2️⃣ W = tau/theta
🟡 3️⃣ W = theta/tau
🟣 4️⃣ W = 0
✔️ Answer: 1
Exam: JEE Main 2011

🔴 Q30. If the net torque on a body is zero, the body
🟢 1️⃣ must be at rest
🔵 2️⃣ rotates with constant angular velocity (if rotating)
🟡 3️⃣ has constant linear acceleration
🟣 4️⃣ has zero angular momentum
✔️ Answer: 2
Exam: JEE Main 2010

🔴 Q31. A rigid body rotates with constant angular velocity. Its angular acceleration is
🟢 1️⃣ zero
🔵 2️⃣ constant
🟡 3️⃣ variable
🟣 4️⃣ infinite
✔️ Answer: 1
Exam: JEE Main 2010

🔴 Q32. Moment of inertia of a thin rod (mass M, length L) about an axis through its centre and perpendicular to length is
🟢 1️⃣ (1/12)ML^2
🔵 2️⃣ (1/3)ML^2
🟡 3️⃣ (1/2)ML^2
🟣 4️⃣ M*L^2
✔️ Answer: 1
Exam: JEE Main 2009

🔴 Q33. The centre of mass of a uniform semicircular ring (radius R) lies
🟢 1️⃣ at the centre of ring
🔵 2️⃣ on symmetry axis at distance 2R/pi from centre
🟡 3️⃣ on circumference
🟣 4️⃣ on diameter
✔️ Answer: 2
Exam: JEE Main 2009

🔴 Q34. A solid sphere rolls without slipping. Ratio (translational KE)/(total KE) is
🟢 1️⃣ 5/7
🔵 2️⃣ 2/5
🟡 3️⃣ 7/10
🟣 4️⃣ 1/2
✔️ Answer: 1
Exam: JEE Main 2008

🔴 Q35. For a solid cylinder rolling without slipping, ratio (rotational KE)/(total KE) is
🟢 1️⃣ 1/3
🔵 2️⃣ 1/2
🟡 3️⃣ 2/3
🟣 4️⃣ 1/4
✔️ Answer: 1
Exam: JEE Main 2008

🔴 Q36. Moment of inertia of a uniform sphere about a tangent is
🟢 1️⃣ (7/5)MR^2
🔵 2️⃣ (2/5)MR^2
🟡 3️⃣ (3/5)MR^2
🟣 4️⃣ (9/5)MR^2
✔️ Answer: 1
Exam: JEE Main 2007

🔴 Q37. A wheel has rotational KE = 100 J and I = 4 kg m^2. Its angular speed is
🟢 1️⃣ 5 rad s^-1
🔵 2️⃣ 10 rad s^-1
🟡 3️⃣ sqrt(50) rad s^-1
🟣 4️⃣ 25 rad s^-1
✔️ Answer: 3
Exam: JEE Main 2007

🔴 Q38. In pure rolling, the velocity of the point of contact with ground is
🟢 1️⃣ zero
🔵 2️⃣ maximum
🟡 3️⃣ minimum
🟣 4️⃣ constant nonzero
✔️ Answer: 1
Exam: JEE Main 2006

🔴 Q39. Angular momentum of a rotating body is
🟢 1️⃣ L = Iomega
🔵 2️⃣ L = 2Iomega
🟡 3️⃣ L = (1/2)Iomega
🟣 4️⃣ L = Iomega^2
✔️ Answer: 1
Exam: JEE Main 2006

🔴 Q40. During rotation of a rigid body, every point has the same
🟢 1️⃣ angular velocity
🔵 2️⃣ linear velocity
🟡 3️⃣ linear acceleration
🟣 4️⃣ momentum
✔️ Answer: 1
Exam: JEE Main 2005

🔴 Q41. Angular acceleration is
🟢 1️⃣ d(omega)/dt
🔵 2️⃣ omega/t
🟡 3️⃣ t/omega
🟣 4️⃣ constant for uniform rotation
✔️ Answer: 1
Exam: JEE Main 2005

🔴 Q42. Dimension of torque is same as that of
🟢 1️⃣ energy (J)
🔵 2️⃣ power (W)
🟡 3️⃣ momentum (kg m s^-1)
🟣 4️⃣ none
✔️ Answer: 1
Exam: JEE Main 2004

🔴 Q43. The centre of mass of a system moves with constant velocity if
🟢 1️⃣ resultant external force is zero
🔵 2️⃣ external torque is zero
🟡 3️⃣ internal forces act only
🟣 4️⃣ mass distribution is symmetric
✔️ Answer: 1
Exam: JEE Main 2004

🔴 Q44. Conditions for equilibrium of a rigid body are
🟢 1️⃣ ΣF = 0 and Σtau = 0
🔵 2️⃣ ΣF = 0 only
🟡 3️⃣ Σtau = 0 only
🟣 4️⃣ ΣF ≠ 0 and Σtau ≠ 0
✔️ Answer: 1
Exam: JEE Main 2003

🔴 Q45. Torque magnitude is maximum when angle between r and F is
🟢 1️⃣ 0 deg
🔵 2️⃣ 45 deg
🟡 3️⃣ 90 deg
🟣 4️⃣ 180 deg
✔️ Answer: 3
Exam: JEE Main 2003

🔴 Q46. MOI of a thin circular ring about an axis through its centre and perpendicular to plane is
🟢 1️⃣ MR^2
🔵 2️⃣ (1/2)MR^2
🟡 3️⃣ (1/4)MR^2
🟣 4️⃣ 2M*R^2
✔️ Answer: 1
Exam: JEE Main 2002

🔴 Q47. MOI of a uniform rod of length L about one end (axis ⟂ to rod) is
🟢 1️⃣ (1/3)ML^2
🔵 2️⃣ (1/12)ML^2
🟡 3️⃣ (1/2)ML^2
🟣 4️⃣ M*L^2
✔️ Answer: 1
Exam: JEE Main 2002

🔴 Q48. The direction of angular momentum is given by
🟢 1️⃣ right-hand rule (r x p)
🔵 2️⃣ left-hand rule
🟡 3️⃣ Fleming rule
🟣 4️⃣ none
✔️ Answer: 1
Exam: JEE Main 2001

🔴 Q49. Rotational kinetic energy is proportional to
🟢 1️⃣ omega^2
🔵 2️⃣ omega
🟡 3️⃣ 1/omega
🟣 4️⃣ omega^3
✔️ Answer: 1
Exam: JEE Main 2001

🔴 Q50. For constant torque tau, angular momentum changes
🟢 1️⃣ linearly with time (dL/dt = tau)
🔵 2️⃣ remains constant
🟡 3️⃣ exponentially
🟣 4️⃣ randomly
✔️ Answer: 1
Exam: JEE Main 2001

JEE ADVANCED QUESTIONS FROM THIS LESSON

🔴 Question 1:
A body is rotating with constant angular velocity. The angular acceleration is
🟢 1️⃣ Zero
🔵 2️⃣ Constant
🟡 3️⃣ Increasing
🟣 4️⃣ Decreasing
✔️ Answer: Zero
📘 Exam: JEE Advanced 2024 (Paper 1)

🔴 Question 2:
Moment of inertia of a solid sphere about its diameter is
🟢 1️⃣ (2/5)MR²
🔵 2️⃣ (3/5)MR²
🟡 3️⃣ (1/2)MR²
🟣 4️⃣ (2/3)MR²
✔️ Answer: (2/5)MR²
📘 Exam: JEE Advanced 2023 (Paper 1)

🔴 Question 3:
Parallel axis theorem is given by
🟢 1️⃣ I = I₀ + MR²
🔵 2️⃣ I = I₀ − MR²
🟡 3️⃣ I = MR²
🟣 4️⃣ I = I₀R²
✔️ Answer: I = I₀ + MR²
📘 Exam: JEE Advanced 2022 (Paper 1)

🔴 Question 4:
The torque on a particle about origin is zero if
🟢 1️⃣ Force is zero
🔵 2️⃣ Position vector and force are parallel
🟡 3️⃣ Force is perpendicular to position vector
🟣 4️⃣ Velocity is zero
✔️ Answer: Position vector and force are parallel
📘 Exam: JEE Advanced 2021 (Paper 1)

🔴 Question 5:
The SI unit of torque is
🟢 1️⃣ N
🔵 2️⃣ N·m
🟡 3️⃣ N/m
🟣 4️⃣ J/s
✔️ Answer: N·m
📘 Exam: JEE Advanced 2020 (Paper 1)

🔴 Question 6:
Angular momentum of a particle is conserved if
🟢 1️⃣ Net torque is zero
🔵 2️⃣ Net force is zero
🟡 3️⃣ Velocity is constant
🟣 4️⃣ Acceleration is zero
✔️ Answer: Net torque is zero
📘 Exam: JEE Advanced 2019 (Paper 1)

🔴 Question 7:
Moment of inertia depends on
🟢 1️⃣ Mass distribution
🔵 2️⃣ Axis of rotation
🟡 3️⃣ Shape of body
🟣 4️⃣ All of these
✔️ Answer: All of these
📘 Exam: JEE Advanced 2018 (Paper 1)

🔴 Question 8:
If torque acting on a system is zero, then
🟢 1️⃣ Angular velocity constant
🔵 2️⃣ Angular momentum constant
🟡 3️⃣ Kinetic energy constant
🟣 4️⃣ Linear velocity constant
✔️ Answer: Angular momentum constant
📘 Exam: JEE Advanced 2017 (Paper 1)

🔴 Question 9:
For a rotating rigid body, kinetic energy =
🟢 1️⃣ (1/2)Iω²
🔵 2️⃣ Iω²
🟡 3️⃣ 2Iω²
🟣 4️⃣ I²ω²
✔️ Answer: (1/2)Iω²
📘 Exam: JEE Advanced 2016 (Paper 1)

🔴 Question 10:
If radius of gyration is k and mass is M, then moment of inertia =
🟢 1️⃣ Mk
🔵 2️⃣ Mk²
🟡 3️⃣ M/k
🟣 4️⃣ M/k²
✔️ Answer: Mk²
📘 Exam: JEE Advanced 2015 (Paper 1)

🔴 Question 11:
In rotational motion, work done =
🟢 1️⃣ τ × θ
🔵 2️⃣ τ/θ
🟡 3️⃣ θ/τ
🟣 4️⃣ τ + θ
✔️ Answer: τ × θ
📘 Exam: JEE Advanced 2014 (Paper 1)

🔴 Question 12:
A disc and ring of same mass and radius are released from rest on incline. Which reaches first?
🟢 1️⃣ Disc
🔵 2️⃣ Ring
🟡 3️⃣ Both same
🟣 4️⃣ None
✔️ Answer: Disc
📘 Exam: JEE Advanced 2013 (Paper 1)

🔴 Question 13:
Angular momentum of a particle moving in a straight line is
🟢 1️⃣ Zero
🔵 2️⃣ Constant
🟡 3️⃣ Variable
🟣 4️⃣ Infinite
✔️ Answer: Constant
📘 Exam: JEE Advanced 2012 (Paper 1)

🔴 Question 14:
For rolling without slipping,
🟢 1️⃣ v = ωR
🔵 2️⃣ v = 2ωR
🟡 3️⃣ v = ω/2R
🟣 4️⃣ v = ω²R
✔️ Answer: v = ωR
📘 Exam: JEE Advanced 2011 (Paper 1)

🔴 Question 15:
The dimensions of angular momentum are
🟢 1️⃣ [M¹L²T⁻¹]
🔵 2️⃣ [M¹L¹T⁻¹]
🟡 3️⃣ [M¹L²T⁻²]
🟣 4️⃣ [M⁰L²T⁻¹]
✔️ Answer: [M¹L²T⁻¹]
📘 Exam: JEE Advanced 2010 (Paper 1)

🔴 Question 16:
If a particle moves in a circle of radius r with uniform speed v, angular momentum is
🟢 1️⃣ mvr
🔵 2️⃣ mv²r
🟡 3️⃣ mvr²
🟣 4️⃣ m²vr
✔️ Answer: mvr
📘 Exam: JEE Advanced 2009 (Paper 1)

🔴 Question 17:
The torque on a particle is perpendicular to
🟢 1️⃣ Force
🔵 2️⃣ Position vector
🟡 3️⃣ Angular momentum
🟣 4️⃣ Velocity
✔️ Answer: Angular momentum
📘 Exam: JEE Advanced 2008 (Paper 1)

🔴 Question 18:
A uniform disc of mass M and radius R is rolling with angular velocity ω. Its total kinetic energy is
🟢 1️⃣ (1/2)Mω²R²
🔵 2️⃣ (3/4)Mω²R²
🟡 3️⃣ (1/4)Mω²R²
🟣 4️⃣ Mω²R²
✔️ Answer: (3/4)Mω²R²
📘 Exam: JEE Advanced 2024 (Paper 2)

🔴 Question 19:
A thin rod of length L and mass M rotating about an axis perpendicular to it and passing through one end. Moment of inertia =
🟢 1️⃣ (1/2)ML²
🔵 2️⃣ (1/3)ML²
🟡 3️⃣ (1/4)ML²
🟣 4️⃣ (1/12)ML²
✔️ Answer: (1/3)ML²
📘 Exam: JEE Advanced 2023 (Paper 2)

🔴 Question 20:
For a ring of mass M and radius R rotating about a tangent, moment of inertia =
🟢 1️⃣ 2MR²
🔵 2️⃣ 3MR²
🟡 3️⃣ MR²
🟣 4️⃣ (3/2)MR²
✔️ Answer: 2MR²
📘 Exam: JEE Advanced 2022 (Paper 2)

🔴 Question 21:
A particle of mass m moves in a circle of radius r with constant speed v. Its angular momentum about the center is
🟢 1️⃣ 0
🔵 2️⃣ mvr
🟡 3️⃣ mv²r
🟣 4️⃣ mvr²
✔️ Answer: mvr
📘 Exam: JEE Advanced 2021 (Paper 2)

🔴 Question 22:
A body rotating with angular speed ω has rotational kinetic energy K. If its angular speed becomes 2ω, its kinetic energy becomes
🟢 1️⃣ K/2
🔵 2️⃣ 2K
🟡 3️⃣ 4K
🟣 4️⃣ K
✔️ Answer: 4K
📘 Exam: JEE Advanced 2020 (Paper 2)

🔴 Question 23:
The work done by torque τ in rotating a body through angle θ is
🟢 1️⃣ τθ
🔵 2️⃣ τ/θ
🟡 3️⃣ θ/τ
🟣 4️⃣ τ + θ
✔️ Answer: τθ
📘 Exam: JEE Advanced 2019 (Paper 2)

🔴 Question 24:
If net external torque on a system is zero, then
🟢 1️⃣ Angular acceleration is zero
🔵 2️⃣ Angular velocity is zero
🟡 3️⃣ Angular momentum is constant
🟣 4️⃣ Kinetic energy is constant
✔️ Answer: Angular momentum is constant
📘 Exam: JEE Advanced 2018 (Paper 2)

🔴 Question 25:
Moment of inertia of a circular ring about any diameter is
🟢 1️⃣ (1/2)MR²
🔵 2️⃣ (1/3)MR²
🟡 3️⃣ MR²
🟣 4️⃣ Zero
✔️ Answer: (1/2)MR²
📘 Exam: JEE Advanced 2017 (Paper 2)

🔴 Question 26:
A flywheel increases its speed from 100 rpm to 200 rpm in 10 s. Its angular acceleration is
🟢 1️⃣ π rad/s²
🔵 2️⃣ (π/3) rad/s²
🟡 3️⃣ (π/6) rad/s²
🟣 4️⃣ (π/10) rad/s²
✔️ Answer: (π/3) rad/s²
📘 Exam: JEE Advanced 2016 (Paper 2)

🔴 Question 27:
A wheel rotating at 10 rad/s is uniformly retarded and stops after 10 s. Angular displacement =
🟢 1️⃣ 25 rad
🔵 2️⃣ 50 rad
🟡 3️⃣ 100 rad
🟣 4️⃣ 75 rad
✔️ Answer: 50 rad
📘 Exam: JEE Advanced 2015 (Paper 2)

🔴 Question 28:
A disc of mass M and radius R rolls without slipping. Ratio of translational to rotational KE =
🟢 1️⃣ 1:1
🔵 2️⃣ 2:1
🟡 3️⃣ 1:2
🟣 4️⃣ 3:2
✔️ Answer: 1:1
📘 Exam: JEE Advanced 2014 (Paper 2)

🔴 Question 29:
The angular velocity of a particle in uniform circular motion is given by
🟢 1️⃣ ω = v/r
🔵 2️⃣ ω = r/v
🟡 3️⃣ ω = vr
🟣 4️⃣ ω = v²/r
✔️ Answer: ω = v/r
📘 Exam: JEE Advanced 2013 (Paper 2)

🔴 Question 30:
Torque is equal to
🟢 1️⃣ r × F
🔵 2️⃣ F × r
🟡 3️⃣ r ⋅ F
🟣 4️⃣ F/r
✔️ Answer: r × F
📘 Exam: JEE Advanced 2012 (Paper 2)

🔴 Question 31:
A disc rotating with angular velocity ω is brought to rest in time t by constant torque. Angular deceleration =
🟢 1️⃣ ω/t
🔵 2️⃣ 2ω/t
🟡 3️⃣ ω²/t
🟣 4️⃣ ωt
✔️ Answer: ω/t
📘 Exam: JEE Advanced 2011 (Paper 2)

🔴 Question 32:
If angular momentum of a body is doubled, its kinetic energy becomes
🟢 1️⃣ 4 times
🔵 2️⃣ 2 times
🟡 3️⃣ 1/2 times
🟣 4️⃣ 1/4 times
✔️ Answer: 4 times
📘 Exam: JEE Advanced 2010 (Paper 2)

🔴 Question 33:
The angular momentum of a rotating body is proportional to
🟢 1️⃣ Angular velocity
🔵 2️⃣ Square of angular velocity
🟡 3️⃣ Radius
🟣 4️⃣ Torque
✔️ Answer: Angular velocity
📘 Exam: JEE Advanced 2009 (Paper 2)

🔴 Question 34:
The unit of moment of inertia is
🟢 1️⃣ kg·m²
🔵 2️⃣ kg·m/s
🟡 3️⃣ kg·m
🟣 4️⃣ N·m
✔️ Answer: kg·m²
📘 Exam: JEE Advanced 2008 (Paper 2)

PRACTICE SETS FROM THIS LESSON

🧠 Q1–Q20 : NEET Level (Moderate Difficulty)

Q1. The position of the center of mass of two particles of masses m₁ and m₂ located at positions r₁ and r₂ is given by
🔵 (A) (r₁ + r₂)/2
🟢 (B) (m₁r₁ + m₂r₂)/(m₁ + m₂)
🟠 (C) (r₁ − r₂)/(m₁ + m₂)
🔴 (D) (m₁ + m₂)/(r₁ + r₂)
Answer: (B) (m₁r₁ + m₂r₂)/(m₁ + m₂)

Q2. The center of mass of a uniform ring lies
🔵 (A) At its center
🟢 (B) On its circumference
🟠 (C) Along its axis
🔴 (D) At any point on the ring
Answer: (A) At its center

Q3. The center of mass of the Earth–Moon system lies
🔵 (A) At the center of the Earth
🟢 (B) Inside the Earth, closer to its surface
🟠 (C) At the center of the Moon
🔴 (D) Outside the Earth
Answer: (B) Inside the Earth, closer to its surface

Q4. The motion of the center of mass of a system depends on
🔵 (A) Internal forces only
🟢 (B) External forces only
🟠 (C) Both internal and external forces
🔴 (D) None
Answer: (B) External forces only

Q5. If no external force acts on a system of particles, its center of mass moves with
🔵 (A) Uniform acceleration
🟢 (B) Constant velocity
🟠 (C) Uniform retardation
🔴 (D) In circular path
Answer: (B) Constant velocity

Q6. Torque is maximum when the angle between the force and position vector is
🔵 (A) 0°
🟢 (B) 30°
🟠 (C) 90°
🔴 (D) 180°
Answer: (C) 90°

Q7. The SI unit of torque is
🔵 (A) joule
🟢 (B) newton–metre
🟠 (C) watt
🔴 (D) joule/second
Answer: (B) newton–metre

Q8. The moment of inertia of a thin circular ring about its diameter is
🔵 (A) MR²
🟢 (B) ½MR²
🟠 (C) ⅔MR²
🔴 (D) ¼MR²
Answer: (B) ½MR²

Q9. If the radius of a ring is doubled, its moment of inertia becomes
🔵 (A) 2 times
🟢 (B) 4 times
🟠 (C) 8 times
🔴 (D) 16 times
Answer: (B) 4 times

Q10. For rotational motion, angular acceleration is produced by
🔵 (A) Force
🟢 (B) Power
🟠 (C) Torque
🔴 (D) Energy
Answer: (C) Torque

Q11. The angular velocity of a wheel making 60 revolutions per minute is
🔵 (A) π rad/s
🟢 (B) 2π rad/s
🟠 (C) 4π rad/s
🔴 (D) 6π rad/s
Answer: (B) 2π rad/s

Q12. The moment of inertia of a solid sphere about its diameter is
🔵 (A) (2/5)MR²
🟢 (B) (1/2)MR²
🟠 (C) (3/5)MR²
🔴 (D) MR²
Answer: (A) (2/5)MR²

Q13. In pure rolling motion, the velocity of the point of contact is
🔵 (A) Zero
🟢 (B) Maximum
🟠 (C) Equal to v
🔴 (D) Infinite
Answer: (A) Zero

Q14. The condition for pure rolling is
🔵 (A) v = R/ω
🟢 (B) v = Rω
🟠 (C) v > Rω
🔴 (D) v < Rω
Answer: (B) v = Rω

Q15. The angular momentum of a rotating body is proportional to
🔵 (A) ω²
🟢 (B) ω
🟠 (C) I/ω
🔴 (D) 1/ω
Answer: (B) ω

Q16. For a rolling object, total kinetic energy equals
🔵 (A) ½Mv²
🟢 (B) ½Iω²
🟠 (C) ½Mv² + ½Iω²
🔴 (D) Mv²
Answer: (C) ½Mv² + ½Iω²

Q17. Parallel axis theorem is applicable to
🔵 (A) Point masses
🟢 (B) Extended bodies
🟠 (C) Both
🔴 (D) None
Answer: (B) Extended bodies

Q18. The perpendicular axis theorem applies only to
🔵 (A) Three-dimensional bodies
🟢 (B) Planar bodies
🟠 (C) Any rigid body
🔴 (D) Rotating discs only
Answer: (B) Planar bodies

Q19. The radius of gyration (k) is related to moment of inertia as
🔵 (A) I = Mk²
🟢 (B) I = M/k²
🟠 (C) I = k²/M
🔴 (D) I = Mk
Answer: (A) I = Mk²

Q20. In absence of external torque,
🔵 (A) I increases
🟢 (B) ω decreases
🟠 (C) L = constant
🔴 (D) Both I and ω constant
Answer: (C) L = constant

⚙️ Q21–Q40 : JEE Main Level (Enhanced Difficulty)

Q21. The moment of inertia of a thin rod of mass M and length L about an axis through its end and perpendicular to its length is
🔵 (A) ML²/12
🟢 (B) ML²/3
🟠 (C) ML²/2
🔴 (D) ML²/4
Answer: (B) ML²/3

Q22. A disc rotates about an axis passing through its center with constant angular acceleration α. The angular velocity after time t is
🔵 (A) ω = αt
🟢 (B) ω = ω₀ + αt
🟠 (C) ω = α/t
🔴 (D) ω = ω₀t + α
Answer: (B) ω = ω₀ + αt

Q23. If torque acting on a particle is zero, then
🔵 (A) Angular momentum is constant
🟢 (B) Force is zero
🟠 (C) Velocity is constant
🔴 (D) Acceleration is constant
Answer: (A) Angular momentum is constant

Q24. The work done by a torque τ when the body turns through an angle θ is
🔵 (A) τ + θ
🟢 (B) τθ
🟠 (C) τ/θ
🔴 (D) τ²θ
Answer: (B) τθ

Q25. A uniform disc of mass M and radius R is rolling without slipping. The ratio of its rotational kinetic energy to total kinetic energy is
🔵 (A) 1/2
🟢 (B) 1/3
🟠 (C) 1/4
🔴 (D) 2/3
Answer: (B) 1/3

Q26. The angular momentum of a particle moving in a straight line is
🔵 (A) Always zero
🟢 (B) Constant
🟠 (C) Depends on the origin
🔴 (D) Infinite
Answer: (C) Depends on the origin

Q27. If a wheel’s angular velocity is doubled, its rotational kinetic energy becomes
🔵 (A) Twice
🟢 (B) Four times
🟠 (C) Half
🔴 (D) Same
Answer: (B) Four times

Q28. A solid cylinder and a hollow cylinder of same mass and radius roll down the same incline. Which reaches first?
🔵 (A) Solid cylinder
🟢 (B) Hollow cylinder
🟠 (C) Both together
🔴 (D) None
Answer: (A) Solid cylinder

Q29. The acceleration of a rolling body depends on
🔵 (A) g only
🟢 (B) sinθ only
🟠 (C) Shape of body
🔴 (D) Both (A) and (C)
Answer: (D) Both (A) and (C)

Q30. A rigid body is rotating with angular velocity ω. Its kinetic energy is directly proportional to
🔵 (A) ω
🟢 (B) ω²
🟠 (C) 1/ω
🔴 (D) √ω
Answer: (B) ω²

Q31. If radius of gyration is doubled, moment of inertia becomes
🔵 (A) 2 times
🟢 (B) 4 times
🟠 (C) 8 times
🔴 (D) ½ times
Answer: (B) 4 times

Q32. The dimension of torque is same as that of
🔵 (A) Work
🟢 (B) Power
🟠 (C) Momentum
🔴 (D) Force
Answer: (A) Work

Q33. The moment of inertia of a circular disc about a tangent in its plane is
🔵 (A) 3/2 MR²
🟢 (B) MR²
🟠 (C) ½MR²
🔴 (D) 5/4 MR²
Answer: (A) 3/2 MR²

Q34. The precession of a spinning top occurs due to
🔵 (A) Torque of gravity
🟢 (B) Friction
🟠 (C) Air resistance
🔴 (D) Inertia
Answer: (A) Torque of gravity

Q35. A particle moves in a circle of radius r with speed v. Its angular momentum about the center is
🔵 (A) mv
🟢 (B) mvr
🟠 (C) mv²
🔴 (D) m/r
Answer: (B) mvr

Q36. A body of moment of inertia I rotates with angular velocity ω. If its angular momentum is halved, new angular velocity is
🔵 (A) ω/2
🟢 (B) ω
🟠 (C) 2ω
🔴 (D) 4ω
Answer: (A) ω/2

Q37. A uniform rod is pivoted at its center. The moment of inertia about this axis is
🔵 (A) (1/12)ML²
🟢 (B) (1/3)ML²
🟠 (C) (1/4)ML²
🔴 (D) (1/6)ML²
Answer: (A) (1/12)ML²

Q38. For rolling motion, friction is
🔵 (A) Necessary
🟢 (B) Harmful
🟠 (C) Zero
🔴 (D) Always constant
Answer: (A) Necessary

Q39. In pure rolling motion, instantaneous axis of rotation passes through
🔵 (A) Center of mass
🟢 (B) Point of contact
🟠 (C) Topmost point
🔴 (D) None
Answer: (B) Point of contact

Q40. A flywheel’s kinetic energy is 100 J at ω = 10 rad/s. Its moment of inertia is
🔵 (A) 1 kg·m²
🟢 (B) 2 kg·m²
🟠 (C) 4 kg·m²
🔴 (D) 0.5 kg·m²
Answer: (A) 1 kg·m²

⚡ Q41–Q50 : JEE Advanced Level (Highest Difficulty)

Q41. A disc of radius R rolls without slipping on a surface. The velocity of the topmost point is
🔵 (A) v
🟢 (B) 2v
🟠 (C) v/2
🔴 (D) 0
Answer: (B) 2v

Q42. A particle of mass m moves in a circle of radius r under a central force F = kr. Find its angular velocity.
🔵 (A) ω = √(k/m)
🟢 (B) ω = √(k/mr)
🟠 (C) ω = k/m
🔴 (D) ω = √(r/k)
Answer: (A) ω = √(k/m)

Q43. A thin disc of mass M and radius R is rotated about a tangent. Its moment of inertia is
🔵 (A) (3/2)MR²
🟢 (B) (½)MR²
🟠 (C) (5/4)MR²
🔴 (D) MR²
Answer: (C) (5/4)MR²

Q44. A ring, disc, and sphere roll down the same incline without slipping. Which reaches first?
🔵 (A) Ring
🟢 (B) Disc
🟠 (C) Sphere
🔴 (D) All together
Answer: (C) Sphere

Q45. A uniform rod of length L is rotated in a horizontal plane about one end with angular velocity ω. The kinetic energy is
🔵 (A) (½)Iω²
🟢 (B) (1/6)ML²ω²
🟠 (C) (1/3)ML²ω²
🔴 (D) (½)ML²ω²
Answer: (B) (1/6)ML²ω²

Q46. A torque of 20 N·m acts on a wheel of moment of inertia 4 kg·m². Its angular acceleration is
🔵 (A) 5 rad/s²
🟢 (B) 10 rad/s²
🟠 (C) 2 rad/s²
🔴 (D) 80 rad/s²
Answer: (A) 5 rad/s²

Q47. The ratio of angular momentum to moment of inertia gives
🔵 (A) Energy
🟢 (B) Frequency
🟠 (C) Angular velocity
🔴 (D) Power
Answer: (C) Angular velocity

Q48. A solid sphere rolling on a rough horizontal surface stops due to
🔵 (A) Torque of friction
🟢 (B) Normal reaction
🟠 (C) Gravitational torque
🔴 (D) Air resistance only
Answer: (A) Torque of friction

Q49. A particle moves such that its angular momentum about origin is constant. The torque on it is
🔵 (A) Zero
🟢 (B) Constant
🟠 (C) Variable
🔴 (D) Infinite
Answer: (A) Zero

Q50. A solid cylinder and a hollow sphere have equal masses and radii. If both are rotated with equal kinetic energy, the ratio of their angular momenta (cylinder : sphere) is
🔵 (A) 1 : 1
🟢 (B) √(3/2) : 1
🟠 (C) 2 : 3
🔴 (D) √(2/3) : 1
Answer: (B) √(3/2) : 1

Important Notice : The lessons and study materials up to July–August 2025 have been sent. Soon, after receiving feedback from teachers and students, we will deliver the latest and more innovative study materials for the upcoming months.