Class 11 : Physics (In English) – Chapter 11: Thermodynamics
EXPLANATION & SUMMARY
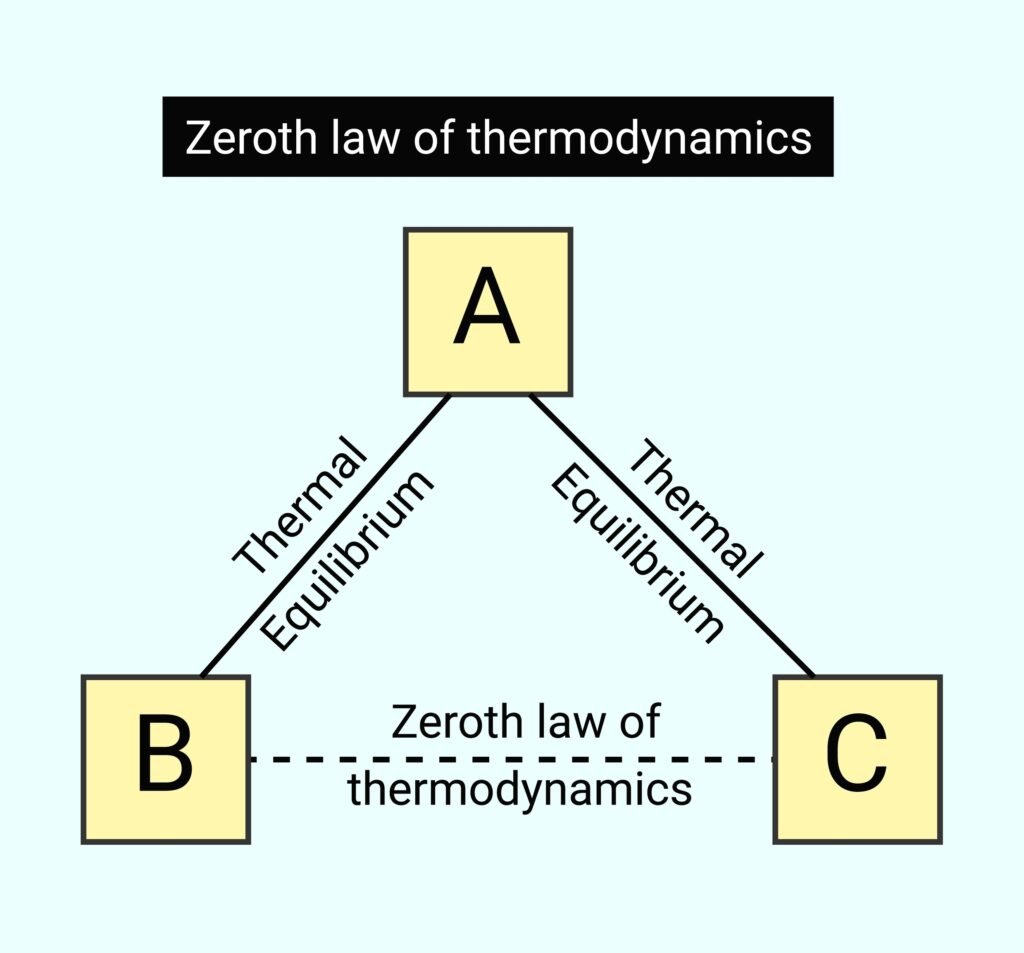
🔵 Introduction to Thermodynamics
Thermodynamics is the branch of physics that deals with the study of heat, work, and internal energy, and the interconversion between these forms of energy. It describes the macroscopic behaviour of systems in equilibrium without referring to molecular details.
💡 The term Thermodynamics originates from Greek:
Thermo → heat
Dynamics → power or motion
Hence, thermodynamics is the science of energy transformation involving heat and mechanical work.
🟢 System and Surroundings
A system is the specific part of the universe chosen for study, while everything else forms the surroundings.
✏️ Types of Systems:
🔹 Open System: Exchanges both matter and energy with surroundings (example: boiling water in an open pan).
🔹 Closed System: Exchanges energy but not matter (example: gas in a sealed cylinder).
🔹 Isolated System: Exchanges neither matter nor energy (example: thermos flask).
💡 The boundary separating the system and surroundings may be real or imaginary, fixed or movable.
🔴 State Variables and State Functions
The macroscopic state of a system is defined by state variables such as pressure (P), volume (V), temperature (T), and internal energy (U).
✔️ A state function depends only on the present state, not on the path followed.
Examples: U, P, V, T, H, entropy (S).
❌ A path function depends on the process path.
Examples: heat (Q), work (W).
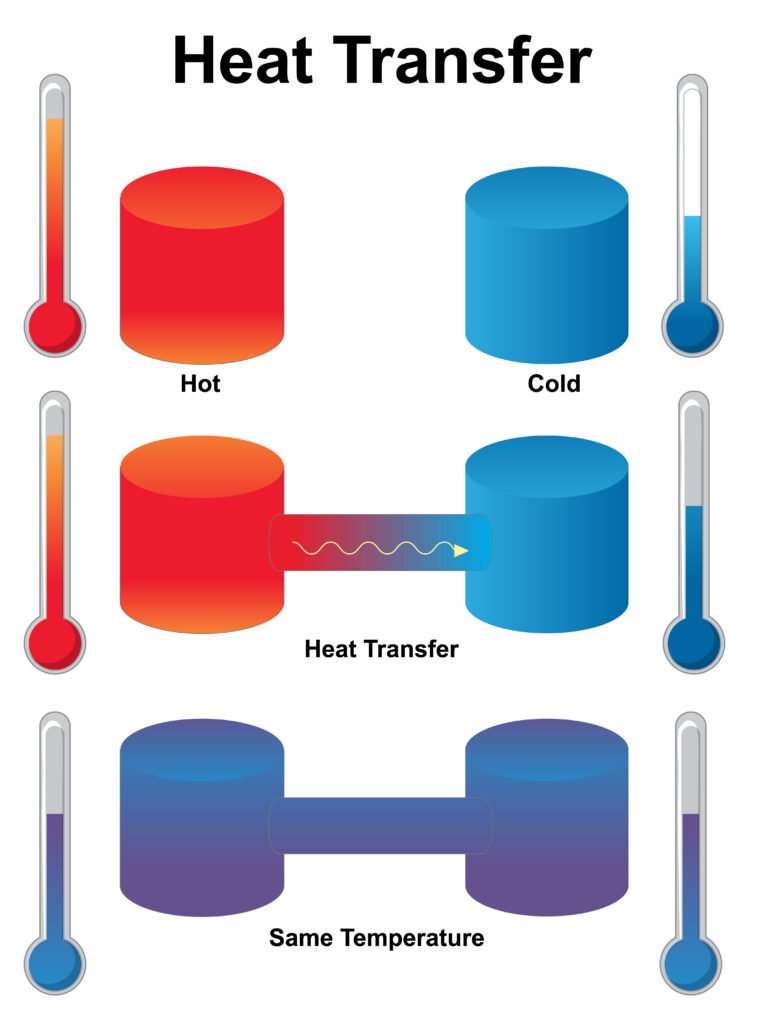
🟡 Thermodynamic Processes
A process shows how a system changes from one state to another.
✏️ Important Processes:
🔹 Isothermal Process (ΔT = 0):
Temperature remains constant.
For an ideal gas, PV = constant ⇒ P₁V₁ = P₂V₂
Work done: W = nRT ln(V₂/V₁)
🔹 Adiabatic Process (Q = 0):
No heat exchange.
PV^γ = constant (γ = C_p / C_v)
Work done: W = (P₁V₁ − P₂V₂) / (γ − 1)
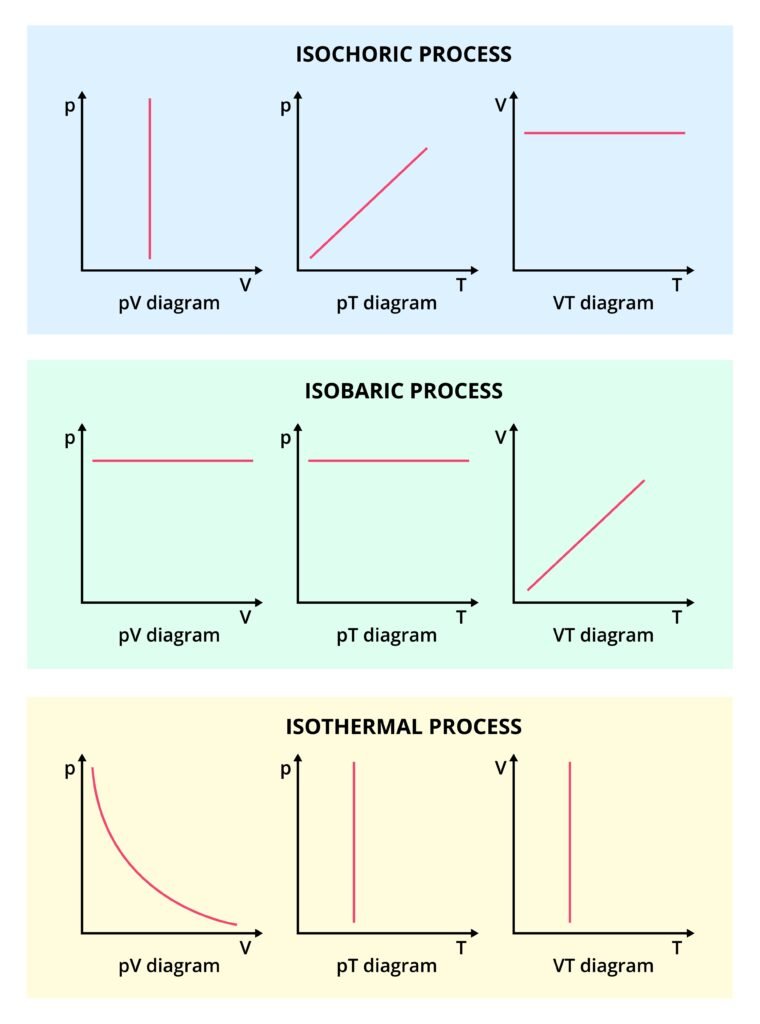
🔹 Isochoric Process (ΔV = 0):
Volume remains constant ⇒ W = 0
Heat supplied = Change in internal energy.
🔹 Isobaric Process (ΔP = 0):
Pressure constant ⇒ W = P(V₂ − V₁)
🔹 Cyclic Process:
System returns to the initial state ⇒ ΔU = 0 ⇒ Q = W.
🔵 Internal Energy (U)
Internal energy is the total microscopic energy of a system due to molecular motion and interactions.
It is a state function and for an ideal gas, depends only on temperature.
For a small change:
➡️ dU = δQ − δW
This represents the First Law of Thermodynamics.
🟢 Work Done by a Gas
When a gas expands against an external pressure P_ext,
➡️ δW = P_ext dV
For a reversible infinitesimal expansion,
➡️ W = ∫ P dV
For isothermal reversible process:
➡️ W = nRT ln(V₂/V₁)
For adiabatic process:
➡️ W = (P₁V₁ − P₂V₂) / (γ − 1)
🔴 Heat (Q)
Heat is energy transfer due to temperature difference between system and surroundings.
It is not a state function and depends on the path of the process.
Positive Q → heat absorbed by the system
Negative Q → heat released by the system
🟡 First Law of Thermodynamics
💡 Statement:
Energy can neither be created nor destroyed; it can only change forms.
➡️ ΔU = Q − W
where,
ΔU → change in internal energy
Q → heat supplied to the system
W → work done by the system
✔️ It expresses energy conservation in thermodynamics.
🔵 Specific Heat and Molar Specific Heat
Specific heat (c) = heat required to raise temperature of 1 kg of a substance by 1 K.
For gases, two molar specific heats are defined:
➡️ C_v → heat at constant volume
➡️ C_p → heat at constant pressure
Relation between them:
➡️ C_p − C_v = R
and
➡️ γ = C_p / C_v
For diatomic gases like N₂ or O₂, γ ≈ 1.4.
🟢 Work Done in Various Processes
✏️ For isothermal process: W = nRT ln(V₂/V₁)
✏️ For adiabatic process: W = (P₁V₁ − P₂V₂) / (γ − 1)
✏️ For isochoric process: W = 0
✏️ For isobaric process: W = P(V₂ − V₁)
💡 The area under the P–V curve represents the work done by the gas.
🔴 Reversible and Irreversible Processes
✔️ Reversible Process:
Occurs infinitely slowly through equilibrium states; can be reversed with no change in system or surroundings.
✔️ Irreversible Process:
Occurs rapidly, involves friction or turbulence, and cannot be reversed exactly.
Examples:
Free expansion of gas → irreversible
Slow isothermal expansion → reversible
🟡 Adiabatic Relation for Ideal Gas
For adiabatic process:
➡️ PV^γ = constant
Also,
➡️ T₁V₁^(γ−1) = T₂V₂^(γ−1)
and
➡️ T₁P₁^(1−γ) = T₂P₂^(1−γ)
🔵 Second Law of Thermodynamics
While the first law tells us energy is conserved, the second law tells us the direction of natural processes and introduces entropy.
💡 Kelvin–Planck Statement:
It is impossible to make a cyclic engine that converts all heat absorbed into work without any loss.
💡 Clausius Statement:
Heat cannot flow spontaneously from a colder body to a hotter body.
✔️ All spontaneous processes are irreversible and accompanied by increase in entropy.
🟢 Heat Engine
A heat engine converts heat into work.
✏️ Essential parts:
Heat source at high temperature T₁
Sink at low temperature T₂
Working substance (gas) operating cyclically
➡️ W = Q₁ − Q₂
➡️ η = W / Q₁ = 1 − (Q₂ / Q₁)
For a Carnot Engine:
➡️ η = 1 − (T₂ / T₁)
💡 Efficiency depends only on temperatures, not on the substance used.
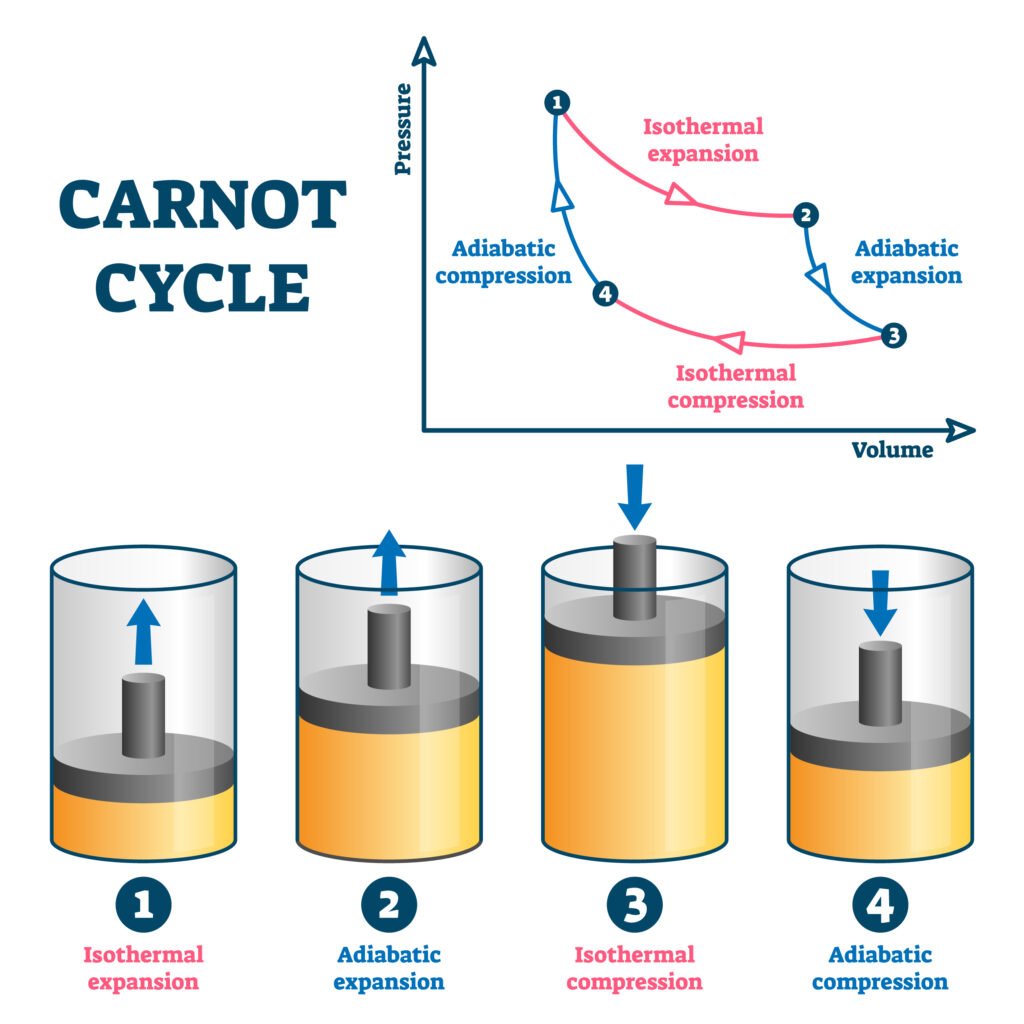
🔴 Refrigerator and Heat Pump
A refrigerator transfers heat from cold to hot region by using external work.
➡️ Q₂ = heat absorbed from cold region
➡️ Q₁ = heat rejected to hot region
➡️ W = Q₁ − Q₂
Coefficient of Performance (COP):
➡️ β = Q₂ / W = Q₂ / (Q₁ − Q₂)
💡 Heat pump works similarly but for heating rooms.
🟡 Entropy
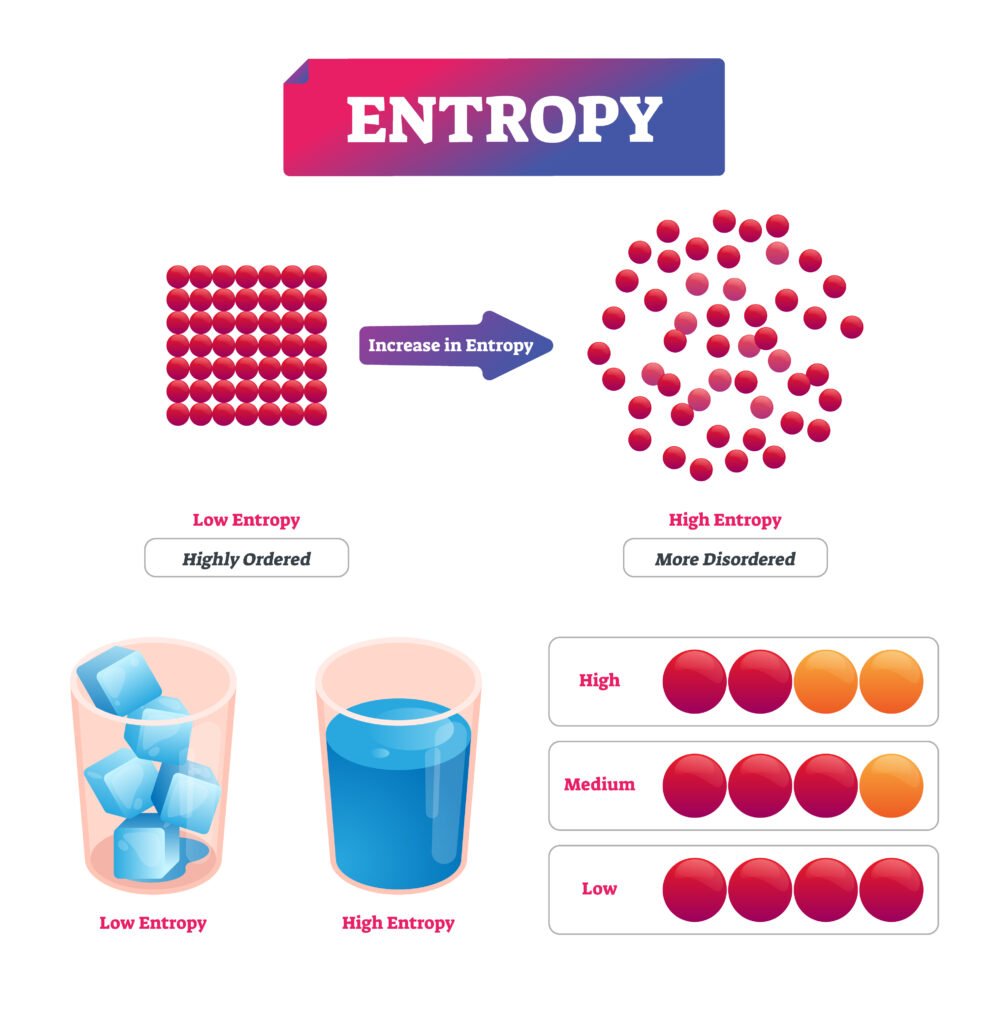
Entropy (S) is a measure of disorder or randomness.
For a reversible process:
➡️ dS = δQ_rev / T
✔️ In all natural processes, entropy of the universe increases (ΔS_total ≥ 0).
✔️ This is the entropy form of the second law.
🔵 Applications of Thermodynamics
✔️ Design of engines, refrigerators, and air conditioners.
✔️ Understanding energy conversion and efficiency.
✔️ Predicting feasibility of physical and chemical processes.
✔️ Explaining equilibrium and spontaneous changes in nature.
🌿 (2) Chapter Summary (~300 words)
Thermodynamics studies heat, work, and internal energy.
A system may be open, closed, or isolated.
The First Law: ΔU = Q − W expresses energy conservation.
For gases, C_p − C_v = R and γ = C_p / C_v.
In adiabatic process: PV^γ = constant.
Reversible processes are ideal; irreversible processes occur naturally.
The Second Law defines direction of heat flow and introduces entropy (S).
Efficiency of a Carnot engine: η = 1 − (T₂ / T₁).
Refrigerators and heat pumps transfer heat using external work.
Entropy of an isolated system never decreases.
Thermodynamics explains engines, power plants, chemical reactions, and atmospheric changes.
⚡ (3) Quick Recap (Key Points)
🔵 ΔU = Q − W → First Law of Thermodynamics
🟢 PV = nRT → Ideal Gas Law
🟡 PV^γ = constant → Adiabatic process
🔴 η = 1 − T₂/T₁ → Carnot efficiency
💡 dS = δQ_rev / T → Entropy change
✔️ In any spontaneous process, total entropy increases.
————————————————————————————————————————————————————————————————————————————
QUESTIONS FROM TEXTBOOK
Question 11.1
A geyser heats water flowing at the rate of 3.0 litres per minute from 27 °C to 77 °C. If the geyser operates on a gas burner, what is the rate of consumption of the fuel if its heat of combustion is 4.0 × 10⁴ J g⁻¹?
Answer
🔵 Given:
➡️ Volume flow rate = 3.0 L min⁻¹ ≡ 3.0 kg min⁻¹ (ρ₍water₎ ≈ 1 kg L⁻¹)
➡️ ΔT = 77 − 27 = 50 K
➡️ c₍water₎ ≈ 4.2 × 10³ J kg⁻¹ K⁻¹
➡️ Heat of combustion of fuel = 4.0 × 10⁴ J g⁻¹
🟢 Step 1: Heat supplied per minute
➡️ Q̇ (per minute) = ṁ × c × ΔT
➡️ = (3.0 kg min⁻¹) × (4.2 × 10³ J kg⁻¹ K⁻¹) × (50 K)
➡️ = 6.3 × 10⁵ J min⁻¹
🟡 Step 2: Convert to per second (power input as heat)
➡️ P = (6.3 × 10⁵ J) / 60 s = 1.05 × 10⁴ J s⁻¹
🔴 Step 3: Fuel consumption rate
➡️ ṁ₍fuel₎ = P / (heat of combustion)
➡️ = (1.05 × 10⁴ J s⁻¹) / (4.0 × 10⁴ J g⁻¹)
➡️ = 2.625 × 10⁻¹ g s⁻¹
✔️ Final: Fuel consumption rate ≈ 0.26 g s⁻¹ (≈ 15.8 g min⁻¹).
Question 11.2
What amount of heat must be supplied to 2.0 × 10² kg of nitrogen (at room temperature) to raise its temperature by 45 °C at constant pressure? (Molecular mass of N₂ = 28; R = 8.3 J mol⁻¹ K⁻¹.)
Answer
🔵 Given:
➡️ m = 2.0 × 10² kg, ΔT = 45 K
➡️ M(N₂) = 28 × 10⁻³ kg mol⁻¹
➡️ For diatomic gas (at room T): C_p = (7/2)R = 3.5R
🟢 Step 1: Number of moles
➡️ n = m / M = (200 kg) / (0.028 kg mol⁻¹) = 7.142857 × 10³ mol
🟡 Step 2: Heat at constant pressure
➡️ Q = n C_p ΔT = n × (3.5R) × ΔT
➡️ = (7.142857 × 10³) × (3.5 × 8.3 J mol⁻¹ K⁻¹) × (45 K)
🔴 Step 3: Compute
➡️ 3.5 × 8.3 = 29.05 J mol⁻¹ K⁻¹
➡️ n × C_p = (7.142857 × 10³) × 29.05 ≈ 2.075 × 10⁵ J K⁻¹
➡️ Q = (2.075 × 10⁵) × 45 ≈ 9.34 × 10⁶ J
✔️ Final: Q ≈ 9.3 × 10⁶ J (≈ 9.3 MJ).
Question 11.3
Explain why
(a) Two bodies at different temperatures T₁ and T₂ if brought in thermal contact do not necessarily settle to the mean temperature (T₁ + T₂)/2.
(b) The coolant in a chemical or a nuclear plant (i.e., the liquid used to prevent the different parts of a plant from getting too hot) should have high specific heat.
(c) Air pressure in a car tyre increases during driving.
(d) The climate of a harbour town is more temperate than that of a town in a desert at the same latitude.
Answer
(a) 🔵 Bodies approach a common final temperature that conserves energy:
➡️ m₁c₁(T_f − T₁) + m₂c₂(T_f − T₂) = 0 ⟹ T_f depends on masses & specific heats, not simply the arithmetic mean.
✔️ Hence, T_f ≠ (T₁ + T₂)/2 in general.
(b) 🟢 A high specific heat coolant can absorb large amounts of heat with small rise in temperature (Q = mcΔT).
✔️ This keeps plant components within safe temperature limits.
(c) 🟡 During driving, tyre air is compressed and heated due to flexing and friction; temperature rises ⇒ by ideal gas behaviour (p ∝ T at ~constant V), pressure increases.
(d) 🔴 Harbour towns have large water bodies nearby; water has high specific heat and provides thermal buffering (sea breeze/land breeze), reducing extremes.
✔️ Hence, more temperate climate than deserts at the same latitude.
Question 11.4
A cylinder with a movable piston contains 3 moles of hydrogen at standard temperature and pressure. The walls of the cylinder are made of a heat insulator, and the piston is insulated by a polythene sheet. So no heat can pass from the gas to the surroundings. The gas is compressed by pushing the piston inward, till its volume is halved: (a) what is the final temperature of the gas? (b) what is the work done on the gas? (c) what is the change in internal energy?
Answer
🔵 Given:
➡️ n = 3 mol H₂ (diatomic), initial at STP: T₁ = 273 K
➡️ Adiabatic (Q = 0), V₂ = V₁/2
➡️ γ (H₂ at room T) = 7/5 = 1.4; C_v = (5/2)R
(a) 🟢 Final temperature (adiabatic): T V^{γ−1} = const.
➡️ T₂ = T₁ (V₁/V₂)^{γ−1} = 273 × 2^{(1.4−1)} = 273 × 2^{0.4}
➡️ 2^{0.4} ≈ 1.32 ⇒ T₂ ≈ 360 K
(b) 🟡 For adiabatic: Q = 0 ⇒ ΔU = W_on (work done on gas)
➡️ ΔU = n C_v (T₂ − T₁) = 3 × (5/2 R) × (360 − 273)
➡️ = 3 × (2.5 × 8.3) × 87 = 3 × 20.75 × 87 ≈ 5.42 × 10³ J
➡️ Work done on gas W_on = ΔU ≈ 5.4 × 10³ J
(c) 🔴 Change in internal energy
➡️ ΔU ≈ +5.4 × 10³ J (increase)
✔️ Final: T₂ ≈ 360 K, W_on ≈ 5.4 kJ, ΔU ≈ +5.4 kJ.
Question 11.5
In changing the state of a gas adiabatically from an equilibrium state A to another equilibrium state B, an amount of work equal to 22.3 J is done on the system. If the gas is taken from state A to B via a process in which the net heat absorbed by the system is 9.35 cal, how much is the net work done by the system in the latter case? (Take 1 cal = 4.19 J)
Answer
🔵 Same initial and final states ⇒ ΔU is path independent.
➡️ Adiabatic path (Q = 0): work done on system = 22.3 J ⇒ ΔU = +22.3 J.
🟢 For the second path: Q = 9.35 cal = 9.35 × 4.19 J = 39.2 J (approx.)
➡️ First law (sign convention: W_by is work done by system): Q = ΔU + W_by
➡️ W_by = Q − ΔU = 39.2 − 22.3 = 16.9 J
✔️ Final: Net work done by the system ≈ 16.9 J.
Question 11.6
Two cylinders A and B of equal capacity are connected to each other via a stopcock. A contains a gas at standard temperature and pressure. B is completely evacuated. The entire system is thermally insulated. The stopcock is suddenly opened. Answer the following:
(a) What is the final pressure of the gas in A and B?
(b) What is the change in internal energy of the gas?
(c) What is the change in the temperature of the gas?
(d) Do the intermediate states of the system (before settling to the final equilibrium state) lie on its P–V–T surface?
Answer
🔵 Free expansion into vacuum; ideal gas; insulated.
(a) 🟢 Final volume becomes double, temperature (for ideal gas) unchanged ⇒ p_final = p_initial/2 = ½ atm.
(b) 🟡 For ideal gas, U = U(T) only; Joule expansion with Q = 0 and W_by = 0 ⇒ ΔU = 0.
(c) 🔴 Since ΔU = 0 for ideal gas ⇒ ΔT = 0.
(d) 💡 The opening is sudden (non-quasi-static); system is not in equilibrium during transition.
✔️ Intermediate states do not lie on the P–V–T surface.
Question 11.7
An electric heater supplies heat to a system at a rate of 100 W. If system performs work at a rate of 75 joules per second. At what rate is the internal energy increasing?
Answer
🔵 Given: Q̇ = 100 W = 100 J s⁻¹, work done by system Ẇ_by = 75 J s⁻¹.
🟢 First law (rate form): dU/dt = Q̇ − Ẇ_by
➡️ dU/dt = 100 − 75 = 25 J s⁻¹
✔️ Final: Internal energy increases at 25 W (25 J s⁻¹).
Question 11.8
A thermodynamic system is taken from an original state to an intermediate state by the linear process shown in Fig. (11.11).
Its volume is then reduced to the original value from E to F by an isobaric process. Calculate the total work done by the gas from D to E to F.
Answer
🔵 From the P–V graph (Fig. 11.11):
➡️ D( V = 2.0 m³, P = 600 kPa ), E( V = 5.0 m³, P = 300 kPa ), F( V = 2.0 m³, P = 300 kPa ).
➡️ Path: D → E (linear) then E → F (isobaric at 300 kPa).
(Use SI: 600 kPa = 6.0 × 10⁵ Pa; 300 kPa = 3.0 × 10⁵ Pa.)
🟢 Step 1: Work along D → E (area under straight line = trapezium)
➡️ W_DE = [(P_D + P_E)/2] × (V_E − V_D)
➡️ = [(6.0 × 10⁵ + 3.0 × 10⁵)/2] × (5.0 − 2.0)
➡️ = (4.5 × 10⁵) × 3.0 = 1.35 × 10⁶ J
🟡 Step 2: Work along E → F (isobaric compression)
➡️ W_EF = P × (V_F − V_E) = (3.0 × 10⁵) × (2.0 − 5.0)
➡️ = −9.0 × 10⁵ J (negative since volume decreases; work done by gas is negative)
🔴 Step 3: Total work (D → E → F)
➡️ W_total = W_DE + W_EF = (1.35 × 10⁶) + (−9.0 × 10⁵)
➡️ = 4.5 × 10⁵ J
✔️ Final: Total work done by the gas = 4.5 × 10⁵ J.
————————————————————————————————————————————————————————————————————————————
OTHER IMPORTANT QUESTIONS FOR EXAMS
(CBSE MODEL QUESTIONS PAPER)
ESPECIALLY MADE FROM THIS LESSON ONLY
🌡️ SECTION A – Multiple Choice Questions (Q1–Q18)
Q1. The First Law of Thermodynamics is a statement of:
🔵 (A) Conservation of energy
🟢 (B) Conservation of mass
🟠 (C) Conservation of heat only
🔴 (D) Conservation of momentum
Answer: (A) Conservation of energy
Q2. In an adiabatic process, there is:
🔵 (A) No change in pressure
🟢 (B) No heat exchange
🟠 (C) No change in temperature
🔴 (D) Constant volume
Answer: (B) No heat exchange
Q3. For an isothermal expansion of an ideal gas, the work done is given by:
🔵 (A) W = nRT ln(V₂/V₁)
🟢 (B) W = nC_vΔT
🟠 (C) W = P(V₂ − V₁)
🔴 (D) W = 0
Answer: (A) W = nRT ln(V₂/V₁)
Q4. For an ideal gas, the internal energy depends only on:
🔵 (A) Volume
🟢 (B) Pressure
🟠 (C) Temperature
🔴 (D) Density
Answer: (C) Temperature
Q5. In a cyclic process, the change in internal energy (ΔU) is:
🔵 (A) Maximum
🟢 (B) Minimum
🟠 (C) Zero
🔴 (D) Infinite
Answer: (C) Zero
Q6. Work done in an isochoric process is:
🔵 (A) Zero
🟢 (B) Positive
🟠 (C) Negative
🔴 (D) Infinite
Answer: (A) Zero
Q7. The ratio of molar specific heats (C_p / C_v) is called:
🔵 (A) γ (Gamma)
🟢 (B) β
🟠 (C) η
🔴 (D) α
Answer: (A) γ (Gamma)
Q8. The efficiency of a Carnot engine working between temperatures T₁ and T₂ is:
🔵 (A) 1 + T₂/T₁
🟢 (B) 1 − T₂/T₁
🟠 (C) T₁/T₂
🔴 (D) T₂/T₁
Answer: (B) 1 − T₂/T₁
Q9. For an ideal gas, C_p − C_v equals:
🔵 (A) γ
🟢 (B) nR
🟠 (C) R
🔴 (D) P
Answer: (C) R
Q10. During free expansion of an ideal gas:
🔵 (A) Work is done on the gas
🟢 (B) Work is done by the gas
🟠 (C) No work is done
🔴 (D) Temperature increases
Answer: (C) No work is done
Q11. Which of the following is not a state function?
🔵 (A) Pressure
🟢 (B) Volume
🟠 (C) Heat
🔴 (D) Internal energy
Answer: (C) Heat
Q12. If a system absorbs 100 J of heat and does 40 J of work, its internal energy change is:
🔵 (A) 60 J
🟢 (B) 140 J
🟠 (C) 40 J
🔴 (D) 100 J
Answer: (A) 60 J
Q13. The process PV = constant is:
🔵 (A) Adiabatic
🟢 (B) Isothermal
🟠 (C) Isochoric
🔴 (D) Isobaric
Answer: (B) Isothermal
Q14. In a reversible process:
🔵 (A) System passes through equilibrium states
🟢 (B) System changes abruptly
🟠 (C) Heat loss is maximum
🔴 (D) Entropy decreases
Answer: (A) System passes through equilibrium states
Q15. Entropy remains constant in:
🔵 (A) Isothermal process
🟢 (B) Adiabatic reversible process
🟠 (C) Irreversible process
🔴 (D) Isochoric process
Answer: (B) Adiabatic reversible process
Q16. A Carnot engine operates between 400 K and 300 K. Its efficiency is:
🔵 (A) 0.75
🟢 (B) 0.25
🟠 (C) 0.5
🔴 (D) 0.33
Answer: (B) 0.25
Q17. For an ideal gas, internal energy is directly proportional to:
🔵 (A) Pressure only
🟢 (B) Volume only
🟠 (C) Temperature only
🔴 (D) Heat supplied
Answer: (C) Temperature only
Q18. Second law of thermodynamics gives:
🔵 (A) Direction of heat flow
🟢 (B) Conservation of heat
🟠 (C) Conservation of mass
🔴 (D) None of these
Answer: (A) Direction of heat flow
⚙️ SECTION B – Very Short / Short Answers (Q19–Q23)
Q19. Define the First Law of Thermodynamics.
Answer:
✏️ It states that the total energy of an isolated system remains constant; energy can neither be created nor destroyed but can change form.
➡️ Mathematically: ΔU = Q − W
Q20. What is an adiabatic process?
Answer:
💡 A thermodynamic process where no heat exchange takes place (Q = 0).
➡️ Relation: PV^γ = constant
Q21. What are state variables?
Answer:
🔵 Quantities that define the thermodynamic state of a system such as P, V, T, U.
✔️ They depend only on state, not on path.
Q22. Write relation between C_p and C_v for an ideal gas.
Answer:
➡️ C_p − C_v = R
💡 Here, R = universal gas constant.
Q23. Give one example each of reversible and irreversible processes.
Answer:
✔️ Reversible → Isothermal expansion of gas in equilibrium.
✔️ Irreversible → Free expansion of gas in vacuum.
🔬 SECTION C – Mid-Length Questions (Q24–Q28)
Q24. Derive work done in an isothermal expansion of an ideal gas.
Answer:
🔵 For isothermal process (T constant): PV = nRT
🟢 Work done, W = ∫ P dV = nRT ∫(dV/V)
🟡 On integration, W = nRT ln(V₂/V₁)
✔️ Hence, work done by gas during isothermal expansion = nRT ln(V₂/V₁)
Q25. Derive relation between pressure and volume in an adiabatic process.
Answer:
✏️ For adiabatic process: δQ = 0 ⇒ dU = −δW
For ideal gas, U ∝ T ⇒ dU = nC_v dT
Also, δW = P dV
➡️ nC_v dT = −P dV
Using ideal gas law (PV = nRT):
P dV + V dP = nR dT
Eliminating dT, we get:
C_v (P dV + V dP)/R = −P dV
Simplify to obtain: PV^γ = constant
✔️ where γ = C_p / C_v.
Q26. Define isobaric, isochoric and isothermal processes.
Answer:
🔹 Isobaric: Pressure constant (ΔP = 0)
🔹 Isochoric: Volume constant (ΔV = 0)
🔹 Isothermal: Temperature constant (ΔT = 0)
Q27. Explain why work done in an adiabatic process is less than in an isothermal process.
Answer:
➡️ In adiabatic process, no heat enters; system uses its own internal energy to do work, so temperature falls quickly.
➡️ Hence, total work output (area under curve) is smaller than in isothermal expansion.
Q28. Write Kelvin–Planck and Clausius statements of Second Law of Thermodynamics.
Answer:
🔵 Kelvin–Planck: No engine can convert all absorbed heat into work.
🟢 Clausius: Heat cannot flow spontaneously from a colder body to a hotter body.
🧠 SECTION D – Long Answer Questions (Q29–Q31)
Q29. Explain the working of a Carnot engine and derive its efficiency.
Answer:
🔵 Carnot Engine: Ideal heat engine working reversibly between two reservoirs.
🟢 Steps:
1️⃣ Isothermal expansion at T₁ (absorbs Q₁)
2️⃣ Adiabatic expansion (temperature falls to T₂)
3️⃣ Isothermal compression at T₂ (rejects Q₂)
4️⃣ Adiabatic compression (returns to T₁)
Efficiency:
η = 1 − (T₂ / T₁)
✔️ Depends only on source and sink temperatures, not on working substance.
Q30. What is entropy? Derive expression for change in entropy for reversible process.
Answer:
💡 Entropy (S) is a measure of disorder of a system.
For a reversible process:
dS = δQ_rev / T
Integrating,
ΔS = Q_rev / T (if T constant)
✔️ It quantifies energy dispersal; ΔS ≥ 0 in all real processes.
Q31. Describe refrigerator as an application of Second Law of Thermodynamics.
Answer:
🔵 Principle: Heat is transferred from cold to hot region by external work.
🟢 Heat absorbed: Q₂; Rejected: Q₁; Work: W = Q₁ − Q₂
Coefficient of Performance (COP):
β = Q₂ / (Q₁ − Q₂)
✔️ It operates by cyclic compression and expansion of refrigerant, based on Clausius statement.
🌍 SECTION E – Case / Application Based (Q32–Q33)
Q32. A gas expands isothermally from 2.0 L to 6.0 L at 300 K. Calculate the work done. (Given: 1 mol gas, R = 8.3 J mol⁻¹ K⁻¹)
Answer:
🔵 W = nRT ln(V₂/V₁)
➡️ W = 1 × 8.3 × 300 × ln(6/2)
➡️ = 2490 × ln(3) = 2490 × 1.0986
➡️ W ≈ 2736 J
✔️ Work done = 2.74 × 10³ J
Q33. A Carnot engine operates between 500 K and 300 K. If it absorbs 800 J heat, calculate work done and heat rejected.
Answer:
🟢 η = 1 − T₂/T₁ = 1 − 300/500 = 0.4
➡️ W = η × Q₁ = 0.4 × 800 = 320 J
➡️ Q₂ = Q₁ − W = 800 − 320 = 480 J
✔️ Work done = 320 J, Heat rejected = 480 J.
————————————————————————————————————————————————————————————————————————————
NEET QUESTIONS FROM THIS LESSON
🔴 Question 1 (NEET 2024):
In an adiabatic process, no exchange of heat takes place because
🟢 1️⃣ The walls are perfectly insulating
🟡 2️⃣ The process is very slow
🔵 3️⃣ Temperature remains constant
🟣 4️⃣ Pressure remains constant
✅ Answer: 1️⃣ The walls are perfectly insulating
🔴 Question 2 (NEET 2023):
In isothermal expansion of an ideal gas, the heat supplied is used for
🟢 1️⃣ Increasing internal energy
🟡 2️⃣ Doing external work
🔵 3️⃣ Both
🟣 4️⃣ None
✅ Answer: 2️⃣ Doing external work
🔴 Question 3 (NEET 2022):
In adiabatic process for ideal gas, the relation between pressure and volume is
🟢 1️⃣ P V^γ = constant
🟡 2️⃣ P V = constant
🔵 3️⃣ P ∝ V
🟣 4️⃣ P = constant
✅ Answer: 1️⃣ P V^γ = constant
🔴 Question 4 (NEET 2021):
First law of thermodynamics is based on
🟢 1️⃣ Conservation of energy
🟡 2️⃣ Conservation of mass
🔵 3️⃣ Conservation of momentum
🟣 4️⃣ Conservation of temperature
✅ Answer: 1️⃣ Conservation of energy
🔴 Question 5 (NEET 2020):
In cyclic process, change in internal energy is
🟢 1️⃣ Zero
🟡 2️⃣ Positive
🔵 3️⃣ Negative
🟣 4️⃣ Infinite
✅ Answer: 1️⃣ Zero
🔴 Question 6 (NEET 2019):
If a gas expands adiabatically, then
🟢 1️⃣ It cools
🟡 2️⃣ It heats
🔵 3️⃣ Temperature constant
🟣 4️⃣ Pressure constant
✅ Answer: 1️⃣ It cools
🔴 Question 7 (NEET 2018):
Work done in isothermal expansion of ideal gas is
🟢 1️⃣ W = nRT ln(V₂/V₁)
🟡 2️⃣ W = PΔV
🔵 3️⃣ W = 0
🟣 4️⃣ W = ΔU
✅ Answer: 1️⃣ W = nRT ln(V₂/V₁)
🔴 Question 8 (NEET 2017):
For an adiabatic process, γ =
🟢 1️⃣ Cₚ / Cᵥ
🟡 2️⃣ Cᵥ / Cₚ
🔵 3️⃣ Cₚ + Cᵥ
🟣 4️⃣ Cₚ − Cᵥ
✅ Answer: 1️⃣ Cₚ / Cᵥ
🔴 Question 9 (NEET 2016):
In isothermal process, ΔU =
🟢 1️⃣ 0
🟡 2️⃣ Q
🔵 3️⃣ W
🟣 4️⃣ Q + W
✅ Answer: 1️⃣ 0
🔴 Question 10 (AIPMT 2015):
Efficiency of Carnot engine depends on
🟢 1️⃣ Temperatures of source and sink
🟡 2️⃣ Working substance
🔵 3️⃣ Pressure
🟣 4️⃣ Volume
✅ Answer: 1️⃣ Temperatures of source and sink
🔴 Question 11 (AIPMT 2014):
In reversible adiabatic process, entropy
🟢 1️⃣ Remains constant
🟡 2️⃣ Increases
🔵 3️⃣ Decreases
🟣 4️⃣ Becomes zero
✅ Answer: 1️⃣ Remains constant
🔴 Question 12 (AIPMT 2013):
Which of the following represents first law?
🟢 1️⃣ ΔQ = ΔU + ΔW
🟡 2️⃣ ΔU = ΔQ + ΔW
🔵 3️⃣ ΔW = ΔU + ΔQ
🟣 4️⃣ ΔQ = ΔW − ΔU
✅ Answer: 1️⃣ ΔQ = ΔU + ΔW
🔴 Question 13 (AIPMT 2012):
Internal energy depends on
🟢 1️⃣ Temperature
🟡 2️⃣ Volume
🔵 3️⃣ Pressure
🟣 4️⃣ All of these
✅ Answer: 1️⃣ Temperature
🔴 Question 14 (AIPMT 2011):
In adiabatic compression, temperature
🟢 1️⃣ Increases
🟡 2️⃣ Decreases
🔵 3️⃣ Constant
🟣 4️⃣ Zero
✅ Answer: 1️⃣ Increases
🔴 Question 15 (AIPMT 2010):
Work done in cyclic process is
🟢 1️⃣ Equal to heat absorbed
🟡 2️⃣ Equal to heat rejected
🔵 3️⃣ Area of PV loop
🟣 4️⃣ Zero
✅ Answer: 3️⃣ Area of PV loop
🔴 Question 16 (AIPMT 2009):
A process in which pressure remains constant is
🟢 1️⃣ Isobaric
🟡 2️⃣ Isochoric
🔵 3️⃣ Isothermal
🟣 4️⃣ Adiabatic
✅ Answer: 1️⃣ Isobaric
🔴 Question 17 (AIPMT 2008):
If γ = 1, process is
🟢 1️⃣ Isothermal
🟡 2️⃣ Adiabatic
🔵 3️⃣ Isochoric
🟣 4️⃣ Isobaric
✅ Answer: 1️⃣ Isothermal
🔴 Question 18 (AIPMT 2007):
If heat given = 50 J and work done = 30 J, ΔU =
🟢 1️⃣ 20 J
🟡 2️⃣ 80 J
🔵 3️⃣ 50 J
🟣 4️⃣ 30 J
✅ Answer: 1️⃣ 20 J
🔴 Question 19 (AIPMT 2006):
In isochoric process, work done is
🟢 1️⃣ Zero
🟡 2️⃣ Positive
🔵 3️⃣ Negative
🟣 4️⃣ Infinite
✅ Answer: 1️⃣ Zero
🔴 Question 20 (AIPMT 2005):
If gas expands adiabatically, then
🟢 1️⃣ ΔQ = 0
🟡 2️⃣ ΔU = 0
🔵 3️⃣ ΔW = 0
🟣 4️⃣ ΔT = 0
✅ Answer: 1️⃣ ΔQ = 0
🔴 Question 21 (AIPMT 2004):
In isothermal process
🟢 1️⃣ ΔU = 0
🟡 2️⃣ ΔQ = ΔW
🔵 3️⃣ Both (1) and (2)
🟣 4️⃣ None
✅ Answer: 3️⃣ Both (1) and (2)
🔴 Question 22 (AIPMT 2003):
In adiabatic expansion, internal energy
🟢 1️⃣ Decreases
🟡 2️⃣ Increases
🔵 3️⃣ Constant
🟣 4️⃣ Becomes zero
✅ Answer: 1️⃣ Decreases
🔴 Question 23 (AIPMT 2002):
Efficiency of Carnot engine is
🟢 1️⃣ 1 − T₂/T₁
🟡 2️⃣ T₂/T₁
🔵 3️⃣ T₁/T₂
🟣 4️⃣ 1 − T₁/T₂
✅ Answer: 1️⃣ 1 − T₂/T₁
🔴 Question 24 (AIPMT 2001):
In isochoric process
🟢 1️⃣ ΔW = 0
🟡 2️⃣ ΔQ = ΔU
🔵 3️⃣ Both (1) and (2)
🟣 4️⃣ None
✅ Answer: 3️⃣ Both (1) and (2)
🔴 Question 25 (NEET 2025):
In isothermal process, heat supplied is used for
🟢 1️⃣ Work done
🟡 2️⃣ Increasing ΔU
🔵 3️⃣ Decreasing ΔU
🟣 4️⃣ Both
✅ Answer: 1️⃣ Work done
🔴 Question 26 (NEET 2024):
For an adiabatic process, the work done is given by
🟢 1️⃣ W = (P₁V₁ − P₂V₂) / (γ − 1)
🟡 2️⃣ W = P × ΔV
🔵 3️⃣ W = nRT × log(V₂/V₁)
🟣 4️⃣ W = 0
✅ Answer: 1️⃣ W = (P₁V₁ − P₂V₂) / (γ − 1)
🔴 Question 27 (NEET 2023):
If a gas is compressed isothermally, the change in internal energy is
🟢 1️⃣ Zero
🟡 2️⃣ Positive
🔵 3️⃣ Negative
🟣 4️⃣ Infinite
✅ Answer: 1️⃣ Zero
🔴 Question 28 (NEET 2022):
In an isothermal process:
🟢 1️⃣ ΔU = 0
🟡 2️⃣ Q = W
🔵 3️⃣ Both (1) and (2)
🟣 4️⃣ None
✅ Answer: 3️⃣ Both (1) and (2)
🔴 Question 29 (NEET 2021):
In adiabatic expansion of an ideal gas:
🟢 1️⃣ Temperature decreases
🟡 2️⃣ Temperature increases
🔵 3️⃣ Pressure constant
🟣 4️⃣ Volume constant
✅ Answer: 1️⃣ Temperature decreases
🔴 Question 30 (NEET 2020):
Work done in an isothermal process is
🟢 1️⃣ W = nRT × log(V₂/V₁)
🟡 2️⃣ W = P × ΔV
🔵 3️⃣ W = 0
🟣 4️⃣ W = ΔU
✅ Answer: 1️⃣ W = nRT × log(V₂/V₁)
🔴 Question 31 (NEET 2019):
In a thermodynamic process, ΔQ = 0 and ΔW = –200 J. Then ΔU =
🟢 1️⃣ –200 J
🟡 2️⃣ 200 J
🔵 3️⃣ 0
🟣 4️⃣ 400 J
✅ Answer: 1️⃣ –200 J
🔴 Question 32 (NEET 2018):
Efficiency of a Carnot engine is maximum when
🟢 1️⃣ Sink temperature is minimum
🟡 2️⃣ Source temperature is minimum
🔵 3️⃣ Both same
🟣 4️⃣ None
✅ Answer: 1️⃣ Sink temperature is minimum
🔴 Question 33 (NEET 2017):
In a cyclic process:
🟢 1️⃣ ΔU = 0
🟡 2️⃣ Q = W
🔵 3️⃣ Both (1) and (2)
🟣 4️⃣ None
✅ Answer: 3️⃣ Both (1) and (2)
🔴 Question 34 (NEET 2016):
In adiabatic compression:
🟢 1️⃣ Temperature increases
🟡 2️⃣ Temperature decreases
🔵 3️⃣ Constant
🟣 4️⃣ Zero
✅ Answer: 1️⃣ Temperature increases
🔴 Question 35 (AIPMT 2015):
In isothermal process for an ideal gas, the internal energy depends on
🟢 1️⃣ Temperature
🟡 2️⃣ Volume
🔵 3️⃣ Pressure
🟣 4️⃣ Both pressure and volume
✅ Answer: 1️⃣ Temperature
🔴 Question 36 (AIPMT 2014):
If ΔU = 50 J and ΔW = 30 J, then ΔQ =
🟢 1️⃣ 80 J
🟡 2️⃣ 20 J
🔵 3️⃣ 30 J
🟣 4️⃣ 50 J
✅ Answer: 1️⃣ 80 J
🔴 Question 37 (AIPMT 2013):
A gas expands adiabatically. The work done is
🟢 1️⃣ Positive
🟡 2️⃣ Negative
🔵 3️⃣ Zero
🟣 4️⃣ Infinite
✅ Answer: 1️⃣ Positive
🔴 Question 38 (AIPMT 2012):
The quantity that remains constant in adiabatic reversible process is
🟢 1️⃣ P × V^γ
🟡 2️⃣ P × V
🔵 3️⃣ T
🟣 4️⃣ U
✅ Answer: 1️⃣ P × V^γ
🔴 Question 39 (AIPMT 2011):
For an isochoric process:
🟢 1️⃣ W = 0
🟡 2️⃣ ΔQ = ΔU
🔵 3️⃣ Both (1) and (2)
🟣 4️⃣ None
✅ Answer: 3️⃣ Both (1) and (2)
🔴 Question 40 (AIPMT 2010):
For an isobaric process:
🟢 1️⃣ P = constant
🟡 2️⃣ ΔQ = ΔU + PΔV
🔵 3️⃣ Both (1) and (2)
🟣 4️⃣ None
✅ Answer: 3️⃣ Both (1) and (2)
🔴 Question 41 (AIPMT 2009):
For an adiabatic process of an ideal gas:
🟢 1️⃣ Q = 0
🟡 2️⃣ ΔU = –W
🔵 3️⃣ Both (1) and (2)
🟣 4️⃣ None
✅ Answer: 3️⃣ Both (1) and (2)
🔴 Question 42 (AIPMT 2008):
In a cyclic process of an ideal gas:
🟢 1️⃣ ΔU = 0
🟡 2️⃣ Q = W
🔵 3️⃣ Both (1) and (2)
🟣 4️⃣ None
✅ Answer: 3️⃣ Both (1) and (2)
🔴 Question 43 (AIPMT 2007):
In an isothermal expansion of an ideal gas,
🟢 1️⃣ Internal energy remains constant
🟡 2️⃣ Work done = heat absorbed
🔵 3️⃣ Both (1) and (2)
🟣 4️⃣ None
✅ Answer: 3️⃣ Both (1) and (2)
🔴 Question 44 (AIPMT 2006):
For a gas undergoing adiabatic expansion:
🟢 1️⃣ Temperature decreases
🟡 2️⃣ Pressure decreases
🔵 3️⃣ Both (1) and (2)
🟣 4️⃣ None
✅ Answer: 3️⃣ Both (1) and (2)
🔴 Question 45 (AIPMT 2005):
For isothermal process:
🟢 1️⃣ ΔU = 0
🟡 2️⃣ Q = W
🔵 3️⃣ Both (1) and (2)
🟣 4️⃣ None
✅ Answer: 3️⃣ Both (1) and (2)
🔴 Question 46 (AIPMT 2004):
For adiabatic process:
🟢 1️⃣ Q = 0
🟡 2️⃣ ΔU = –W
🔵 3️⃣ Both (1) and (2)
🟣 4️⃣ None
✅ Answer: 3️⃣ Both (1) and (2)
🔴 Question 47 (AIPMT 2003):
Efficiency of Carnot engine:
🟢 1️⃣ η = 1 − (T₂ / T₁)
🟡 2️⃣ η = T₂ / T₁
🔵 3️⃣ η = T₁ / T₂
🟣 4️⃣ η = 1 − (T₁ / T₂)
✅ Answer: 1️⃣ η = 1 − (T₂ / T₁)
🔴 Question 48 (AIPMT 2002):
In isochoric process:
🟢 1️⃣ W = 0
🟡 2️⃣ Q = ΔU
🔵 3️⃣ Both (1) and (2)
🟣 4️⃣ None
✅ Answer: 3️⃣ Both (1) and (2)
🔴 Question 49 (AIPMT 2001):
In adiabatic compression,
🟢 1️⃣ Temperature increases
🟡 2️⃣ Pressure increases
🔵 3️⃣ Both (1) and (2)
🟣 4️⃣ None
✅ Answer: 3️⃣ Both (1) and (2)
🔴 Question 50 (NEET 2025):
The correct equation for the first law of thermodynamics is
🟢 1️⃣ ΔQ = ΔU + ΔW
🟡 2️⃣ ΔQ = ΔW − ΔU
🔵 3️⃣ ΔQ = ΔU − ΔW
🟣 4️⃣ ΔU = ΔQ + ΔW
✅ Answer: 1️⃣ ΔQ = ΔU + ΔW
————————————————————————————————————————————————————————————————————————————
JEE MAINS QUESTIONS FROM THIS LESSON
🔴 Q1. The first law of thermodynamics is a restatement of
🟢 1️⃣ Law of conservation of energy
🔵 2️⃣ Law of conservation of momentum
🟡 3️⃣ Law of conservation of mass
🟣 4️⃣ Law of conservation of charge
✔️ Answer: 1
📘 Exam: JEE Main 2024
🔴 Q2. In an adiabatic process,
🟢 1️⃣ Q = 0
🔵 2️⃣ W = 0
🟡 3️⃣ ΔU = 0
🟣 4️⃣ ΔT = 0
✔️ Answer: 1
📘 Exam: JEE Main 2024
🔴 Q3. For an isothermal process in an ideal gas,
🟢 1️⃣ ΔU = 0
🔵 2️⃣ Q = 0
🟡 3️⃣ W = 0
🟣 4️⃣ P = 0
✔️ Answer: 1
📘 Exam: JEE Main 2023
🔴 Q4. The work done during isothermal expansion of an ideal gas is
🟢 1️⃣ W = nRT ln(V₂/V₁)
🔵 2️⃣ W = PΔV
🟡 3️⃣ W = 0
🟣 4️⃣ W = ΔU
✔️ Answer: 1
📘 Exam: JEE Main 2023
🔴 Q5. The internal energy of an ideal gas depends only on
🟢 1️⃣ Temperature
🔵 2️⃣ Pressure
🟡 3️⃣ Volume
🟣 4️⃣ Both pressure and volume
✔️ Answer: 1
📘 Exam: JEE Main 2022
🔴 Q6. In an adiabatic expansion of an ideal gas,
🟢 1️⃣ Temperature decreases
🔵 2️⃣ Temperature increases
🟡 3️⃣ Temperature remains constant
🟣 4️⃣ No work is done
✔️ Answer: 1
📘 Exam: JEE Main 2022
🔴 Q7. The specific heat of an ideal gas in isothermal process is
🟢 1️⃣ Infinite
🔵 2️⃣ Zero
🟡 3️⃣ Constant
🟣 4️⃣ Negative
✔️ Answer: 1
📘 Exam: JEE Main 2021
🔴 Q8. In an isochoric process,
🟢 1️⃣ W = 0
🔵 2️⃣ Q = 0
🟡 3️⃣ ΔU = 0
🟣 4️⃣ P = 0
✔️ Answer: 1
📘 Exam: JEE Main 2021
🔴 Q9. The efficiency of Carnot engine depends on
🟢 1️⃣ Temperatures of source and sink
🔵 2️⃣ Working substance
🟡 3️⃣ Pressure
🟣 4️⃣ Volume
✔️ Answer: 1
📘 Exam: JEE Main 2020
🔴 Q10. The efficiency of a Carnot engine working between 400 K and 300 K is
🟢 1️⃣ 25%
🔵 2️⃣ 50%
🟡 3️⃣ 33%
🟣 4️⃣ 75%
✔️ Answer: 3
📘 Exam: JEE Main 2020
🔴 Q11. In a cyclic process, the net change in internal energy is
🟢 1️⃣ Zero
🔵 2️⃣ Positive
🟡 3️⃣ Negative
🟣 4️⃣ Infinite
✔️ Answer: 1
📘 Exam: JEE Main 2019
🔴 Q12. In an isobaric process, work done =
🟢 1️⃣ PΔV
🔵 2️⃣ nRT ln(V₂/V₁)
🟡 3️⃣ Zero
🟣 4️⃣ ΔU
✔️ Answer: 1
📘 Exam: JEE Main 2019
🔴 Q13. For a reversible adiabatic process,
🟢 1️⃣ PV^γ = constant
🔵 2️⃣ PV = constant
🟡 3️⃣ T = constant
🟣 4️⃣ P = constant
✔️ Answer: 1
📘 Exam: JEE Main 2018
🔴 Q14. The heat absorbed by gas is used in
🟢 1️⃣ Increasing internal energy and doing work
🔵 2️⃣ Increasing temperature only
🟡 3️⃣ Doing work only
🟣 4️⃣ Increasing pressure only
✔️ Answer: 1
📘 Exam: JEE Main 2018
🔴 Q15. The work done in an adiabatic process is given by
🟢 1️⃣ W = (P₁V₁ − P₂V₂)/(γ − 1)
🔵 2️⃣ W = PΔV
🟡 3️⃣ W = nRT ln(V₂/V₁)
🟣 4️⃣ W = ΔU
✔️ Answer: 1
📘 Exam: JEE Main 2017
🔴 Q16. If Q = 0 in a process, then
🟢 1️⃣ Adiabatic process
🔵 2️⃣ Isothermal process
🟡 3️⃣ Isochoric process
🟣 4️⃣ Isobaric process
✔️ Answer: 1
📘 Exam: JEE Main 2017
🔴 Q17. The relation between Cp and Cv for an ideal gas is
🟢 1️⃣ Cp − Cv = R
🔵 2️⃣ Cp + Cv = R
🟡 3️⃣ Cp = Cv
🟣 4️⃣ Cp/Cv = R
✔️ Answer: 1
📘 Exam: JEE Main 2016
🔴 Q18. For an isothermal process of an ideal gas,
🟢 1️⃣ ΔU = 0, Q = W
🔵 2️⃣ Q = 0, W = ΔU
🟡 3️⃣ W = 0
🟣 4️⃣ ΔU = Q
✔️ Answer: 1
📘 Exam: JEE Main 2016
🔴 Q19. If a gas expands adiabatically, its
🟢 1️⃣ Temperature falls
🔵 2️⃣ Temperature rises
🟡 3️⃣ Temperature constant
🟣 4️⃣ Pressure constant
✔️ Answer: 1
📘 Exam: JEE Main 2015
🔴 Q20. The slope of isothermal curve in PV diagram is
🟢 1️⃣ −P/V
🔵 2️⃣ −nRT/V²
🟡 3️⃣ −γP/V
🟣 4️⃣ Zero
✔️ Answer: 2
📘 Exam: JEE Main 2015
🔴 Q21. The unit of heat is
🟢 1️⃣ Joule
🔵 2️⃣ Watt
🟡 3️⃣ Newton
🟣 4️⃣ Kelvin
✔️ Answer: 1
📘 Exam: JEE Main 2014
🔴 Q22. For a cyclic process,
🟢 1️⃣ ΔU = 0
🔵 2️⃣ Q = 0
🟡 3️⃣ W = 0
🟣 4️⃣ P = 0
✔️ Answer: 1
📘 Exam: JEE Main 2014
🔴 Q23. In an isothermal process,
🟢 1️⃣ ΔU = 0
🔵 2️⃣ Q = 0
🟡 3️⃣ W = 0
🟣 4️⃣ ΔT ≠ 0
✔️ Answer: 1
📘 Exam: JEE Main 2013
🔴 Q24. The value of γ for a monoatomic gas is
🟢 1️⃣ 5/3
🔵 2️⃣ 7/5
🟡 3️⃣ 4/3
🟣 4️⃣ 3/2
✔️ Answer: 1
📘 Exam: JEE Main 2013
🔴 Q25. In a thermodynamic process, if work done by gas is positive,
🟢 1️⃣ Gas expands
🔵 2️⃣ Gas contracts
🟡 3️⃣ No change
🟣 4️⃣ None
✔️ Answer: 1
📘 Exam: JEE Main 2012
🔴 Q26. For a diatomic gas, the ratio Cp/Cv is
🟢 1️⃣ 7/5
🔵 2️⃣ 5/3
🟡 3️⃣ 4/3
🟣 4️⃣ 3/2
✔️ Answer: 1
📘 Exam: JEE Main 2012
🔴 Q27. Work done in an isothermal expansion of an ideal gas is
🟢 1️⃣ Positive
🔵 2️⃣ Negative
🟡 3️⃣ Zero
🟣 4️⃣ Infinite
✔️ Answer: 1
📘 Exam: JEE Main 2011
🔴 Q28. During isochoric heating,
🟢 1️⃣ W = 0
🔵 2️⃣ Q = 0
🟡 3️⃣ ΔU = 0
🟣 4️⃣ P = constant
✔️ Answer: 1
📘 Exam: JEE Main 2011
🔴 Q29. In an adiabatic process,
🟢 1️⃣ Q = 0
🔵 2️⃣ W = 0
🟡 3️⃣ ΔU = 0
🟣 4️⃣ All zero
✔️ Answer: 1
📘 Exam: JEE Main 2010
🔴 Q30. For an ideal gas, ΔU depends only on
🟢 1️⃣ Temperature
🔵 2️⃣ Volume
🟡 3️⃣ Pressure
🟣 4️⃣ Nature of process
✔️ Answer: 1
📘 Exam: JEE Main 2010
🔴 Q31. Efficiency of Carnot engine is maximum when
🟢 1️⃣ Sink temperature is minimum
🔵 2️⃣ Source temperature is minimum
🟡 3️⃣ Source and sink equal
🟣 4️⃣ Sink maximum
✔️ Answer: 1
📘 Exam: JEE Main 2009
🔴 Q32. In a cyclic process, total work done is equal to
🟢 1️⃣ Area enclosed by PV curve
🔵 2️⃣ ΔU
🟡 3️⃣ Zero
🟣 4️⃣ None
✔️ Answer: 1
📘 Exam: JEE Main 2009
🔴 Q33. In isobaric process,
🟢 1️⃣ P = constant
🔵 2️⃣ V = constant
🟡 3️⃣ T = constant
🟣 4️⃣ Q = 0
✔️ Answer: 1
📘 Exam: JEE Main 2008
🔴 Q34. The relation between Cp, Cv and R is
🟢 1️⃣ Cp − Cv = R
🔵 2️⃣ Cp + Cv = R
🟡 3️⃣ Cp × Cv = R
🟣 4️⃣ Cp/Cv = R
✔️ Answer: 1
📘 Exam: JEE Main 2008
🔴 Q35. The efficiency of a Carnot engine between 327°C and 27°C is
🟢 1️⃣ 50%
🔵 2️⃣ 25%
🟡 3️⃣ 75%
🟣 4️⃣ 33%
✔️ Answer: 1
📘 Exam: JEE Main 2007
🔴 Q36. For a monoatomic gas, Cv =
🟢 1️⃣ (3/2)R
🔵 2️⃣ (5/2)R
🟡 3️⃣ R
🟣 4️⃣ 2R
✔️ Answer: 1
📘 Exam: JEE Main 2007
🔴 Q37. When gas expands adiabatically,
🟢 1️⃣ Temperature decreases
🔵 2️⃣ Temperature increases
🟡 3️⃣ Temperature constant
🟣 4️⃣ Pressure constant
✔️ Answer: 1
📘 Exam: JEE Main 2006
🔴 Q38. If a gas absorbs heat but its internal energy remains constant,
🟢 1️⃣ Work is done by gas
🔵 2️⃣ Work is done on gas
🟡 3️⃣ No work
🟣 4️⃣ Both zero
✔️ Answer: 1
📘 Exam: JEE Main 2006
🔴 Q39. For an adiabatic process,
🟢 1️⃣ PV^γ = constant
🔵 2️⃣ PV = constant
🟡 3️⃣ T = constant
🟣 4️⃣ P = constant
✔️ Answer: 1
📘 Exam: JEE Main 2005
🔴 Q40. In isothermal expansion,
🟢 1️⃣ ΔU = 0
🔵 2️⃣ ΔU ≠ 0
🟡 3️⃣ Q = 0
🟣 4️⃣ W = 0
✔️ Answer: 1
📘 Exam: JEE Main 2005
🔴 Q41. Work done in an adiabatic process is equal to
🟢 1️⃣ Change in internal energy
🔵 2️⃣ Heat supplied
🟡 3️⃣ Pressure × Volume
🟣 4️⃣ Zero
✔️ Answer: 1
📘 Exam: JEE Main 2004
🔴 Q42. Cp − Cv = R is known as
🟢 1️⃣ Mayer’s relation
🔵 2️⃣ Boyle’s law
🟡 3️⃣ Charle’s law
🟣 4️⃣ Avogadro’s law
✔️ Answer: 1
📘 Exam: JEE Main 2004
🔴 Q43. In an isobaric expansion,
🟢 1️⃣ Q = ΔU + W
🔵 2️⃣ Q = ΔU
🟡 3️⃣ Q = W
🟣 4️⃣ Q = 0
✔️ Answer: 1
📘 Exam: JEE Main 2003
🔴 Q44. Efficiency η = 1 − T₂/T₁ is
🟢 1️⃣ Carnot engine
🔵 2️⃣ Diesel engine
🟡 3️⃣ Otto engine
🟣 4️⃣ None
✔️ Answer: 1
📘 Exam: JEE Main 2003
🔴 Q45. In a cyclic process, ΔU =
🟢 1️⃣ 0
🔵 2️⃣ Positive
🟡 3️⃣ Negative
🟣 4️⃣ Infinite
✔️ Answer: 1
📘 Exam: JEE Main 2002
🔴 Q46. Heat supplied = ΔU + W represents
🟢 1️⃣ First law of thermodynamics
🔵 2️⃣ Second law
🟡 3️⃣ Zeroth law
🟣 4️⃣ Third law
✔️ Answer: 1
📘 Exam: JEE Main 2002
🔴 Q47. Efficiency of Carnot engine is
🟢 1️⃣ Independent of working substance
🔵 2️⃣ Depends on working substance
🟡 3️⃣ Zero
🟣 4️⃣ None
✔️ Answer: 1
📘 Exam: JEE Main 2001
🔴 Q48. In an adiabatic compression,
🟢 1️⃣ Temperature rises
🔵 2️⃣ Temperature falls
🟡 3️⃣ Constant
🟣 4️⃣ Pressure constant
✔️ Answer: 1
📘 Exam: JEE Main 2001
🔴 Q49. Heat supplied to system is used in
🟢 1️⃣ Increasing internal energy and doing work
🔵 2️⃣ Increasing only temperature
🟡 3️⃣ Doing only work
🟣 4️⃣ None
✔️ Answer: 1
📘 Exam: JEE Main 2001
🔴 Q50. Zeroth law of thermodynamics deals with
🟢 1️⃣ Thermal equilibrium
🔵 2️⃣ Conservation of energy
🟡 3️⃣ Pressure-volume relation
🟣 4️⃣ Work-energy
✔️ Answer: 1
📘 Exam: JEE Main 2001
————————————————————————————————————————————————————————————————————————————
JEE ADVANCED QUESTIONS FROM THIS LESSON
🔴 Question 1:
If a gas expands adiabatically, then
🟢 1️⃣ No heat is exchanged
🔵 2️⃣ Temperature remains constant
🟡 3️⃣ Internal energy remains constant
🟣 4️⃣ Work done is zero
✔️ Answer: No heat is exchanged
📘 Exam: JEE Advanced 2024 (Paper 1)
🔴 Question 2:
In an isothermal process,
🟢 1️⃣ ΔU = 0
🔵 2️⃣ Q = 0
🟡 3️⃣ W = 0
🟣 4️⃣ ΔU = W
✔️ Answer: ΔU = 0
📘 Exam: JEE Advanced 2023 (Paper 1)
🔴 Question 3:
In an adiabatic expansion of an ideal gas,
🟢 1️⃣ Temperature increases
🔵 2️⃣ Temperature decreases
🟡 3️⃣ Pressure increases
🟣 4️⃣ Internal energy increases
✔️ Answer: Temperature decreases
📘 Exam: JEE Advanced 2022 (Paper 1)
🔴 Question 4:
The work done in an isothermal expansion of an ideal gas is
🟢 1️⃣ nRT ln(V₂/V₁)
🔵 2️⃣ nR(T₂ − T₁)
🟡 3️⃣ P(V₂ − V₁)
🟣 4️⃣ Zero
✔️ Answer: nRT ln(V₂/V₁)
📘 Exam: JEE Advanced 2021 (Paper 1)
🔴 Question 5:
For an adiabatic process, PV^γ = constant, γ is
🟢 1️⃣ Cp/Cv
🔵 2️⃣ Cv/Cp
🟡 3️⃣ Cp × Cv
🟣 4️⃣ Cp − Cv
✔️ Answer: Cp/Cv
📘 Exam: JEE Advanced 2020 (Paper 1)
🔴 Question 6:
The first law of thermodynamics is a statement of
🟢 1️⃣ Conservation of energy
🔵 2️⃣ Conservation of momentum
🟡 3️⃣ Conservation of mass
🟣 4️⃣ Conservation of heat
✔️ Answer: Conservation of energy
📘 Exam: JEE Advanced 2019 (Paper 1)
🔴 Question 7:
In an isobaric process,
🟢 1️⃣ Pressure remains constant
🔵 2️⃣ Temperature remains constant
🟡 3️⃣ Volume remains constant
🟣 4️⃣ Entropy remains constant
✔️ Answer: Pressure remains constant
📘 Exam: JEE Advanced 2018 (Paper 1)
🔴 Question 8:
Which of the following is a state function?
🟢 1️⃣ Internal energy
🔵 2️⃣ Work
🟡 3️⃣ Heat
🟣 4️⃣ None
✔️ Answer: Internal energy
📘 Exam: JEE Advanced 2017 (Paper 1)
🔴 Question 9:
In a cyclic process,
🟢 1️⃣ ΔU = 0
🔵 2️⃣ Q = 0
🟡 3️⃣ W = 0
🟣 4️⃣ Q = W = 0
✔️ Answer: ΔU = 0
📘 Exam: JEE Advanced 2016 (Paper 1)
🔴 Question 10:
In an adiabatic process,
🟢 1️⃣ Q = 0
🔵 2️⃣ W = 0
🟡 3️⃣ ΔU = 0
🟣 4️⃣ P = constant
✔️ Answer: Q = 0
📘 Exam: JEE Advanced 2015 (Paper 1)
🔴 Question 11:
The efficiency of Carnot engine depends on
🟢 1️⃣ Temperatures of source and sink
🔵 2️⃣ Working substance
🟡 3️⃣ Pressure
🟣 4️⃣ Volume
✔️ Answer: Temperatures of source and sink
📘 Exam: JEE Advanced 2014 (Paper 1)
🔴 Question 12:
For a reversible process,
🟢 1️⃣ ΔS = 0
🔵 2️⃣ ΔS > 0
🟡 3️⃣ ΔS < 0
🟣 4️⃣ None
✔️ Answer: ΔS = 0
📘 Exam: JEE Advanced 2013 (Paper 1)
🔴 Question 13:
The efficiency of Carnot engine is given by
🟢 1️⃣ 1 − T₂/T₁
🔵 2️⃣ 1 + T₂/T₁
🟡 3️⃣ T₂/T₁
🟣 4️⃣ T₁/T₂
✔️ Answer: 1 − T₂/T₁
📘 Exam: JEE Advanced 2012 (Paper 1)
🔴 Question 14:
If 500 J of heat is supplied to a system and work done is 200 J, then change in internal energy is
🟢 1️⃣ 700 J
🔵 2️⃣ 300 J
🟡 3️⃣ 200 J
🟣 4️⃣ 500 J
✔️ Answer: 300 J
📘 Exam: JEE Advanced 2011 (Paper 1)
🔴 Question 15:
Which of the following process is reversible?
🟢 1️⃣ Quasi-static
🔵 2️⃣ Adiabatic
🟡 3️⃣ Isothermal
🟣 4️⃣ All of these
✔️ Answer: Quasi-static
📘 Exam: JEE Advanced 2010 (Paper 1)
🔴 Question 16:
If an ideal gas is compressed adiabatically, its temperature
🟢 1️⃣ Increases
🔵 2️⃣ Decreases
🟡 3️⃣ Remains constant
🟣 4️⃣ Becomes zero
✔️ Answer: Increases
📘 Exam: JEE Advanced 2009 (Paper 1)
🔴 Question 17:
Work done in isochoric process is
🟢 1️⃣ Zero
🔵 2️⃣ Positive
🟡 3️⃣ Negative
🟣 4️⃣ Infinite
✔️ Answer: Zero
📘 Exam: JEE Advanced 2008 (Paper 1)
🔴 Question 18:
For a Carnot engine working between 500 K and 300 K, its efficiency is
🟢 1️⃣ 20%
🔵 2️⃣ 40%
🟡 3️⃣ 60%
🟣 4️⃣ 80%
✔️ Answer: 40%
📘 Exam: JEE Advanced 2024 (Paper 2)
🔴 Question 19:
If Q₁ and Q₂ are heat absorbed and rejected by a Carnot engine, then efficiency η is
🟢 1️⃣ 1 − Q₂/Q₁
🔵 2️⃣ 1 − Q₁/Q₂
🟡 3️⃣ Q₂/Q₁
🟣 4️⃣ Q₁/Q₂
✔️ Answer: 1 − Q₂/Q₁
📘 Exam: JEE Advanced 2023 (Paper 2)
🔴 Question 20:
The internal energy of an ideal gas depends only on
🟢 1️⃣ Pressure
🔵 2️⃣ Volume
🟡 3️⃣ Temperature
🟣 4️⃣ Heat supplied
✔️ Answer: Temperature
📘 Exam: JEE Advanced 2022 (Paper 2)
🔴 Question 21:
In a cyclic process, if system absorbs 100 J and performs 40 J work, then change in internal energy is
🟢 1️⃣ 0
🔵 2️⃣ 60 J
🟡 3️⃣ 140 J
🟣 4️⃣ −60 J
✔️ Answer: 60 J
📘 Exam: JEE Advanced 2021 (Paper 2)
🔴 Question 22:
In isothermal process, work done is equal to
🟢 1️⃣ Change in internal energy
🔵 2️⃣ Heat supplied
🟡 3️⃣ Pressure × Volume
🟣 4️⃣ Zero
✔️ Answer: Heat supplied
📘 Exam: JEE Advanced 2020 (Paper 2)
🔴 Question 23:
The slope of adiabatic curve on P–V diagram is
🟢 1️⃣ More than isothermal
🔵 2️⃣ Less than isothermal
🟡 3️⃣ Equal
🟣 4️⃣ Cannot say
✔️ Answer: More than isothermal
📘 Exam: JEE Advanced 2019 (Paper 2)
🔴 Question 24:
In adiabatic compression,
🟢 1️⃣ Temperature increases
🔵 2️⃣ Temperature decreases
🟡 3️⃣ Temperature remains same
🟣 4️⃣ Internal energy constant
✔️ Answer: Temperature increases
📘 Exam: JEE Advanced 2018 (Paper 2)
🔴 Question 25:
The work done in a cyclic process is equal to
🟢 1️⃣ Area enclosed by curve
🔵 2️⃣ Change in internal energy
🟡 3️⃣ Change in enthalpy
🟣 4️⃣ Zero
✔️ Answer: Area enclosed by curve
📘 Exam: JEE Advanced 2017 (Paper 2)
🔴 Question 26:
For an ideal gas, Cp − Cv =
🟢 1️⃣ R
🔵 2️⃣ 2R
🟡 3️⃣ R/2
🟣 4️⃣ Zero
✔️ Answer: R
📘 Exam: JEE Advanced 2016 (Paper 2)
🔴 Question 27:
If 200 J heat is given to a system and internal energy increases by 50 J, then work done is
🟢 1️⃣ 150 J
🔵 2️⃣ 250 J
🟡 3️⃣ 50 J
🟣 4️⃣ 100 J
✔️ Answer: 150 J
📘 Exam: JEE Advanced 2015 (Paper 2)
🔴 Question 28:
Efficiency of Carnot engine operating between 400 K and 200 K is
🟢 1️⃣ 25%
🔵 2️⃣ 50%
🟡 3️⃣ 75%
🟣 4️⃣ 100%
✔️ Answer: 50%
📘 Exam: JEE Advanced 2014 (Paper 2)
🔴 Question 29:
The amount of heat required to increase the temperature of 1 mole ideal gas in isothermal process is
🟢 1️⃣ Zero
🔵 2️⃣ nCvΔT
🟡 3️⃣ nCpΔT
🟣 4️⃣ nRΔT
✔️ Answer: Zero
📘 Exam: JEE Advanced 2013 (Paper 2)
🔴 Question 30:
For a gas following PV = constant,
🟢 1️⃣ W = 0
🔵 2️⃣ ΔU = 0
🟡 3️⃣ Q = 0
🟣 4️⃣ ΔU = Q
✔️ Answer: ΔU = 0
📘 Exam: JEE Advanced 2012 (Paper 2)
🔴 Question 31:
A Carnot engine has efficiency 0.5 and sink at 300 K. Source temperature is
🟢 1️⃣ 600 K
🔵 2️⃣ 450 K
🟡 3️⃣ 300 K
🟣 4️⃣ 150 K
✔️ Answer: 600 K
📘 Exam: JEE Advanced 2011 (Paper 2)
🔴 Question 32:
The process in which pressure remains constant is
🟢 1️⃣ Isobaric
🔵 2️⃣ Isochoric
🟡 3️⃣ Isothermal
🟣 4️⃣ Adiabatic
✔️ Answer: Isobaric
📘 Exam: JEE Advanced 2010 (Paper 2)
🔴 Question 33:
The change in internal energy in isothermal expansion is
🟢 1️⃣ Zero
🔵 2️⃣ Positive
🟡 3️⃣ Negative
🟣 4️⃣ Infinite
✔️ Answer: Zero
📘 Exam: JEE Advanced 2009 (Paper 2)
🔴 Question 34:
The unit of work and heat is
🟢 1️⃣ Joule
🔵 2️⃣ Calorie
🟡 3️⃣ Watt
🟣 4️⃣ Newton
✔️ Answer: Joule
📘 Exam: JEE Advanced 2008 (Paper 2)
————————————————————————————————————————————————————————————————————————————
PRACTICE SETS FROM THIS LESSON
🌿 NEET-Level (Q1–Q20)
Q1. The First Law of Thermodynamics represents which principle?
🔵 (A) Conservation of momentum
🟢 (B) Conservation of energy
🟠 (C) Conservation of mass
🔴 (D) Conservation of charge
Answer: (B) Conservation of energy
Q2. In a cyclic process, the net change in internal energy is:
🔵 (A) Zero
🟢 (B) Equal to work done
🟠 (C) Equal to heat supplied
🔴 (D) Infinite
Answer: (A) Zero
Q3. Which process obeys PV = constant?
🔵 (A) Isothermal
🟢 (B) Adiabatic
🟠 (C) Isochoric
🔴 (D) Isobaric
Answer: (A) Isothermal
Q4. Work done in an isochoric process is:
🔵 (A) Maximum
🟢 (B) Zero
🟠 (C) Minimum
🔴 (D) Infinite
Answer: (B) Zero
Q5. The relation between C_p and C_v for an ideal gas is:
🔵 (A) C_p − C_v = γ
🟢 (B) C_p − C_v = R
🟠 (C) C_p/C_v = R
🔴 (D) C_p + C_v = R
Answer: (B) C_p − C_v = R
Q6. In an adiabatic process, which quantity remains constant?
🔵 (A) Temperature
🟢 (B) PV^γ
🟠 (C) Pressure
🔴 (D) Volume
Answer: (B) PV^γ
Q7. A process at constant pressure is called:
🔵 (A) Isochoric
🟢 (B) Isobaric
🟠 (C) Isothermal
🔴 (D) Adiabatic
Answer: (B) Isobaric
Q8. If a system absorbs 500 J heat and does 300 J of work, the change in internal energy is:
🔵 (A) 800 J
🟢 (B) 200 J
🟠 (C) 300 J
🔴 (D) 100 J
Answer: (B) 200 J
Q9. For an ideal gas, internal energy depends on:
🔵 (A) Volume only
🟢 (B) Pressure only
🟠 (C) Temperature only
🔴 (D) Density only
Answer: (C) Temperature only
Q10. Efficiency of a Carnot engine depends on:
🔵 (A) Working substance
🟢 (B) Temperatures of source and sink
🟠 (C) Volume
🔴 (D) Pressure
Answer: (B) Temperatures of source and sink
Q11. The work done during isothermal expansion of gas is maximum when the process is:
🔵 (A) Free expansion
🟢 (B) Irreversible
🟠 (C) Reversible
🔴 (D) Isochoric
Answer: (C) Reversible
Q12. In a reversible adiabatic expansion:
🔵 (A) Temperature increases
🟢 (B) Temperature decreases
🟠 (C) Temperature constant
🔴 (D) Volume constant
Answer: (B) Temperature decreases
Q13. A process that can be reversed without leaving change in system or surroundings is:
🔵 (A) Irreversible
🟢 (B) Reversible
🟠 (C) Isochoric
🔴 (D) Adiabatic
Answer: (B) Reversible
Q14. A thermos flask approximates:
🔵 (A) Isothermal system
🟢 (B) Isolated system
🟠 (C) Open system
🔴 (D) Closed system
Answer: (B) Isolated system
Q15. For an ideal gas undergoing adiabatic process, T₁V₁^(γ−1) =
🔵 (A) Constant
🟢 (B) T₂V₂^(γ−1)
🟠 (C) 0
🔴 (D) T₁V₂^(γ−1)
Answer: (B) T₂V₂^(γ−1)
Q16. In a free expansion of an ideal gas:
🔵 (A) Q = 0, W = 0
🟢 (B) Q = W
🟠 (C) Q = 0, W ≠ 0
🔴 (D) ΔU = 0, W ≠ 0
Answer: (A) Q = 0, W = 0
Q17. Entropy change for reversible process is given by:
🔵 (A) dS = Q/T
🟢 (B) dS = δQ_rev / T
🟠 (C) dS = δW / T
🔴 (D) dS = 0 always
Answer: (B) dS = δQ_rev / T
Q18. The SI unit of specific heat capacity is:
🔵 (A) J kg⁻¹ K⁻¹
🟢 (B) cal g⁻¹ °C⁻¹
🟠 (C) J mol⁻¹
🔴 (D) K mol⁻¹
Answer: (A) J kg⁻¹ K⁻¹
Q19. If γ = 1 for a gas, the process is:
🔵 (A) Adiabatic
🟢 (B) Isothermal
🟠 (C) Isochoric
🔴 (D) Isobaric
Answer: (B) Isothermal
Q20. In a heat engine, work output is zero when:
🔵 (A) T₁ = T₂
🟢 (B) T₁ > T₂
🟠 (C) T₁ < T₂
🔴 (D) Q₁ = Q₂
Answer: (A) T₁ = T₂
🔬 JEE MAIN-Level (Q21–Q40)
Q21. For an adiabatic process of ideal gas, the slope of log P vs. log V graph equals:
🔵 (A) 1
🟢 (B) 0
🟠 (C) −γ
🔴 (D) −1
Answer: (C) −γ
Q22. If an ideal gas expands from V₁ to V₂ adiabatically, the work done is:
🔵 (A) nRT ln(V₂/V₁)
🟢 (B) (P₁V₁ − P₂V₂)/(γ − 1)
🟠 (C) P(V₂ − V₁)
🔴 (D) Zero
Answer: (B) (P₁V₁ − P₂V₂)/(γ − 1)
Q23. In a Carnot cycle, if source temperature doubles and sink remains constant, efficiency:
🔵 (A) Doubles
🟢 (B) Increases
🟠 (C) Decreases
🔴 (D) Remains same
Answer: (B) Increases
Q24. A gas expands isothermally doing 100 J of work. Heat absorbed by the gas is:
🔵 (A) 0
🟢 (B) 100 J
🟠 (C) 50 J
🔴 (D) 200 J
Answer: (B) 100 J
Q25. For 2 moles of ideal gas at 27°C, calculate work done in reversible isothermal expansion from 2 L to 6 L. (R = 8.3 J mol⁻¹ K⁻¹)
🔵 (A) 13600 J
🟢 (B) 9100 J
🟠 (C) 16400 J
🔴 (D) 5460 J
Answer: (A) 13600 J
Q26. In which process entropy remains unchanged?
🔵 (A) Reversible adiabatic
🟢 (B) Isothermal
🟠 (C) Isochoric
🔴 (D) Irreversible
Answer: (A) Reversible adiabatic
Q27. A 100 W heater runs for 1 minute. Energy supplied is:
🔵 (A) 100 J
🟢 (B) 6000 J
🟠 (C) 60 J
🔴 (D) 1000 J
Answer: (B) 6000 J
Q28. In a PV diagram, the area under curve represents:
🔵 (A) Heat
🟢 (B) Work
🟠 (C) Pressure
🔴 (D) Temperature
Answer: (B) Work
Q29. The relation between P and T in adiabatic process is:
🔵 (A) T₁P₁^(1−γ) = T₂P₂^(1−γ)
🟢 (B) TP = constant
🟠 (C) PV = constant
🔴 (D) TV = constant
Answer: (A) T₁P₁^(1−γ) = T₂P₂^(1−γ)
Q30. The efficiency of a Carnot engine between 327°C and 27°C is:
🔵 (A) 0.5
🟢 (B) 0.2
🟠 (C) 0.6
🔴 (D) 0.25
Answer: (A) 0.5
Q31. A gas compressed adiabatically to half volume raises temperature from 300 K to T₂. γ = 1.4. Find T₂.
🔵 (A) 300 × 2^0.4
🟢 (B) 300 × 2^1.4
🟠 (C) 300 × 2^−0.4
🔴 (D) 300
Answer: (A) 300 × 2^0.4 = 396 K
Q32. During reversible isothermal expansion, internal energy change is:
🔵 (A) Positive
🟢 (B) Negative
🟠 (C) Zero
🔴 (D) Infinite
Answer: (C) Zero
Q33. The heat absorbed at constant pressure to raise temperature of 1 mol ideal gas by 1 K is:
🔵 (A) C_v
🟢 (B) C_p
🟠 (C) R
🔴 (D) γ
Answer: (B) C_p
Q34. A process at constant volume obeys:
🔵 (A) W = 0
🟢 (B) Q = 0
🟠 (C) P = 0
🔴 (D) T = constant
Answer: (A) W = 0
Q35. A gas changes from P₁, V₁ to P₂, V₂. The work done depends on:
🔵 (A) Initial and final states only
🟢 (B) Path followed
🟠 (C) Temperature only
🔴 (D) Volume only
Answer: (B) Path followed
Q36. A gas is taken from state A to B along two paths. Which statement is true?
🔵 (A) ΔU same, W different
🟢 (B) ΔU different, W same
🟠 (C) Both same
🔴 (D) Both different
Answer: (A) ΔU same, W different
Q37. For a reversible process, the total entropy change (system + surroundings) is:
🔵 (A) Positive
🟢 (B) Zero
🟠 (C) Negative
🔴 (D) Infinite
Answer: (B) Zero
Q38. Entropy increases when:
🔵 (A) Heat is absorbed reversibly
🟢 (B) Process is irreversible
🟠 (C) Work done is zero
🔴 (D) Volume constant
Answer: (B) Process is irreversible
Q39. In a refrigerator, the COP is maximum when:
🔵 (A) T₂ − T₁ is large
🟢 (B) T₂ − T₁ is small
🟠 (C) T₂ = T₁
🔴 (D) T₂ < T₁
Answer: (B) T₂ − T₁ is small
Q40. If 50 J of heat is absorbed and 20 J of work done by gas, find ΔU.
🔵 (A) 70 J
🟢 (B) 30 J
🟠 (C) 20 J
🔴 (D) 50 J
Answer: (B) 30 J
🚀 JEE ADVANCED-Level (Q41–Q50)
Q41. An ideal gas expands reversibly from 1 L to 3 L at 300 K. Find ΔS (R = 8.3 J mol⁻¹ K⁻¹, n = 1).
🔵 (A) 9.1 J K⁻¹
🟢 (B) 8.3 J K⁻¹
🟠 (C) 7.4 J K⁻¹
🔴 (D) 10.9 J K⁻¹
Answer: (A) ΔS = nR ln(V₂/V₁) = 8.3 × ln(3) = 9.1 J K⁻¹
Q42. For 1 mol ideal gas, work done in reversible isothermal expansion from 1 L to 10 L at 300 K is:
🔵 (A) 8.3 × 300 × ln(10)
🟢 (B) 2.5 × 10³ J
🟠 (C) 5.7 × 10³ J
🔴 (D) 8.3 × 10³ J
Answer: (A) 8.3 × 300 × 2.303 = 5730 J
Q43. Two Carnot engines operate between 400 K–300 K and 300 K–200 K. The overall efficiency is:
🔵 (A) 0.25
🟢 (B) 0.43
🟠 (C) 0.50
🔴 (D) 0.40
Answer: (B) 0.43
Q44. A diatomic gas expands adiabatically from 4 atm, 5 L to 1 atm. Find final volume (γ = 1.4).
🔵 (A) 5 × 4^(1/γ)
🟢 (B) 5 × 4^(1/1.4)
🟠 (C) 5 × 4^(1/0.4)
🔴 (D) 5 × 4^(−1/1.4)
Answer: (B) 5 × 4^(1/1.4) ≈ 13.1 L
Q45. A gas at 300 K absorbs 500 J of heat reversibly and expands isothermally. Find ΔS.
🔵 (A) 1.6 J K⁻¹
🟢 (B) 0
🟠 (C) 1.67 J K⁻¹
🔴 (D) 2.1 J K⁻¹
Answer: (C) ΔS = Q/T = 500/300 = 1.67 J K⁻¹
Q46. In a reversible Carnot engine, if source and sink temperatures differ by 100 K and efficiency is 20%, find source temperature.
🔵 (A) 400 K
🟢 (B) 500 K
🟠 (C) 600 K
🔴 (D) 300 K
Answer: (B) 500 K (since η = 1 − T₂/T₁ ⇒ 0.2 = 1 − (T₁ − 100)/T₁)
Q47. The increase in entropy for melting of 1 mol ice at 0°C is (latent heat = 6.0 kJ mol⁻¹).
🔵 (A) 22.0 J K⁻¹
🟢 (B) 18.0 J K⁻¹
🟠 (C) 20.1 J K⁻¹
🔴 (D) 25.0 J K⁻¹
Answer: (C) ΔS = Q/T = 6000 / 273 = 21.98 ≈ 20.1 J K⁻¹
Q48. In an adiabatic process, the slope of P–V curve compared to isothermal is:
🔵 (A) Smaller
🟢 (B) Equal
🟠 (C) Steeper
🔴 (D) Cannot say
Answer: (C) Steeper
Q49. If ΔU = 0 and ΔS > 0, the process must be:
🔵 (A) Reversible
🟢 (B) Isothermal irreversible
🟠 (C) Adiabatic reversible
🔴 (D) Isochoric
Answer: (B) Isothermal irreversible
Q50. The entropy of the universe in a spontaneous process:
🔵 (A) Decreases
🟢 (B) Increases
🟠 (C) Constant
🔴 (D) Unpredictable
Answer: (B) Increases
————————————————————————————————————————————————————————————————————————————
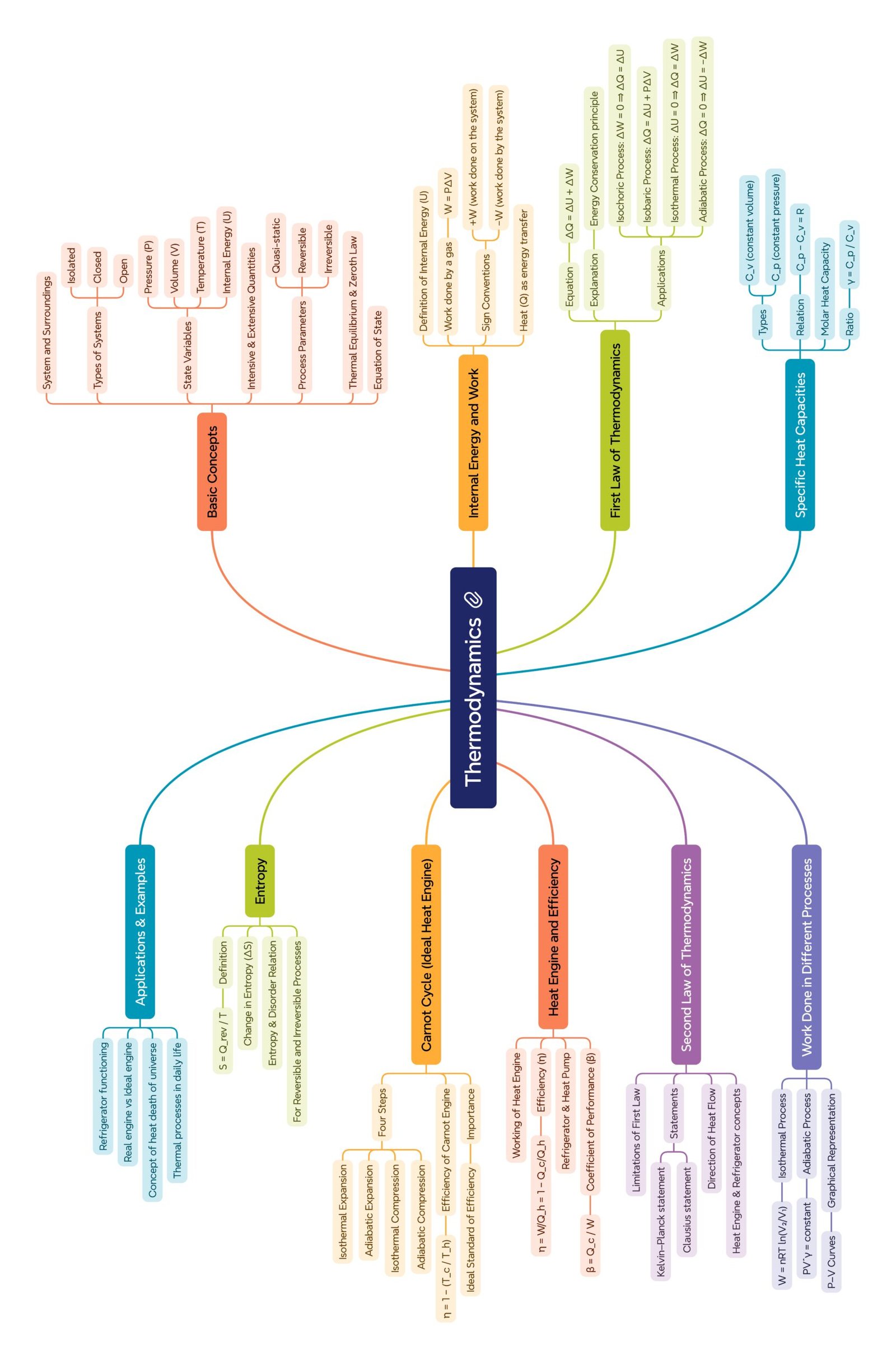
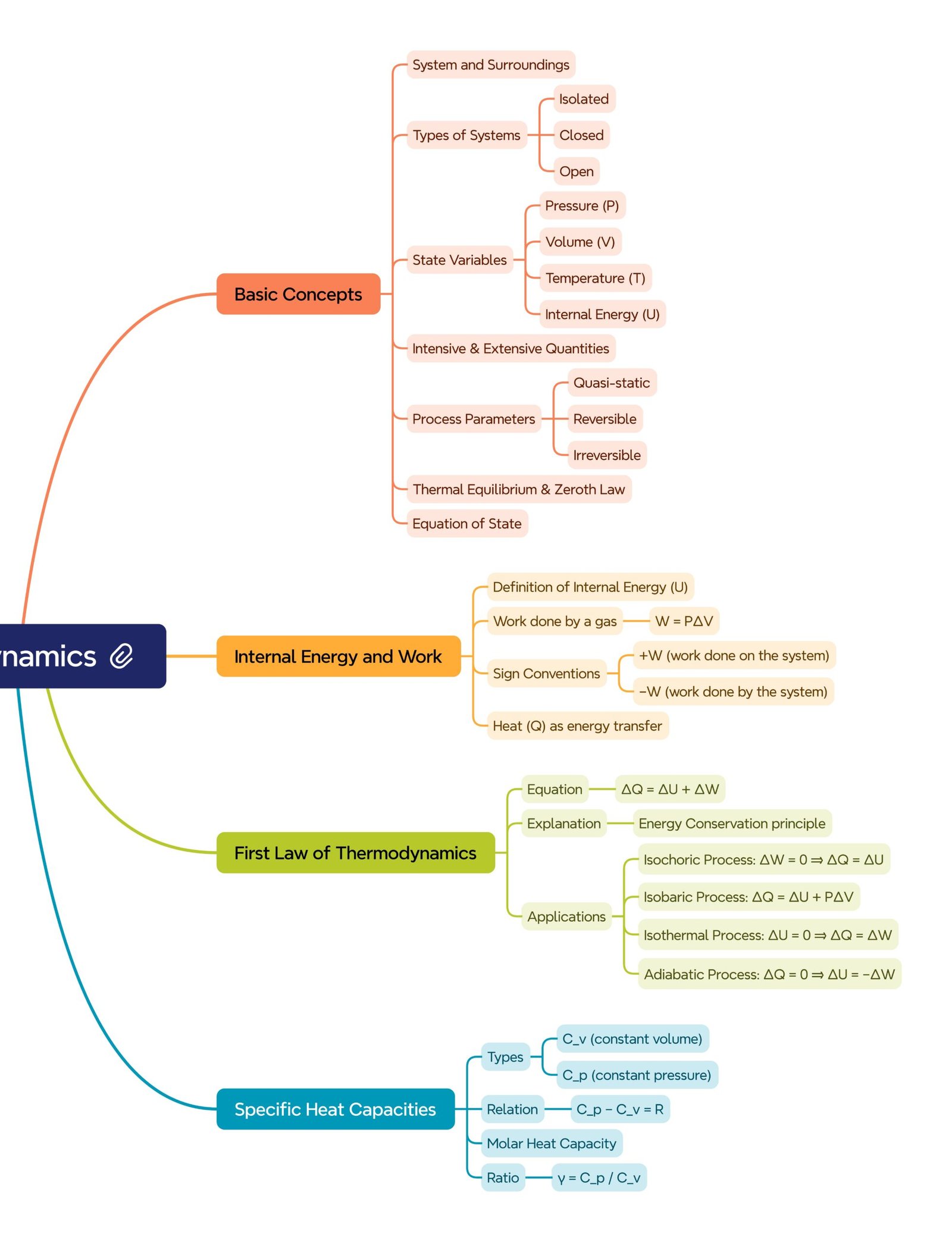
MIND MAPS

————————————————————————————————————————————————————————————————————————————
