Class 11 : Maths (In Hindi) – Lesson 10. शंकु परिच्छेद
पाठ का विश्लेषण एवं विवेचन
💡 परिचय :
शंकु परिच्छेद वे वक्र हैं जो एक समवृत्तीय दो शंकुओं (right circular double cone) को किसी तल द्वारा काटने पर प्राप्त होते हैं।
इन वक्रों में मुख्यतः चार प्रकार के वक्र सम्मिलित होते हैं —
➡️ वृत्त (Circle)
➡️ परवलय (Parabola)
➡️ दीर्घवृत्त (Ellipse)
➡️ अतिपरवलय (Hyperbola)
जब किसी शंकु को विभिन्न कोणों पर तल द्वारा काटा जाता है, तो इन चारों वक्रों के रूप उत्पन्न होते हैं।
🟢 1. शंकु परिच्छेद की सामान्य परिभाषा
✏️ एक बिन्दु (केन्द्र), एक नियत रेखा (निदेशिका) और एक नियत अनुपात (विकेन्द्रता e) के आधार पर बना वक्र शंकु परिच्छेद कहलाता है।
यदि किसी वक्र के प्रत्येक बिन्दु से केन्द्र तक की दूरी और निदेशिका तक की लम्ब दूरी का अनुपात स्थिर हो, तो यह स्थिर अनुपात विकेन्द्रता (e) कहलाता है।
💡 गणितीय रूप में:
PF/PM = e
जहाँ,
P वक्र का कोई बिन्दु है,
F केन्द्र (focus),
M निदेशिका पर P से खींची गई लम्ब रेखा का पादबिन्दु।
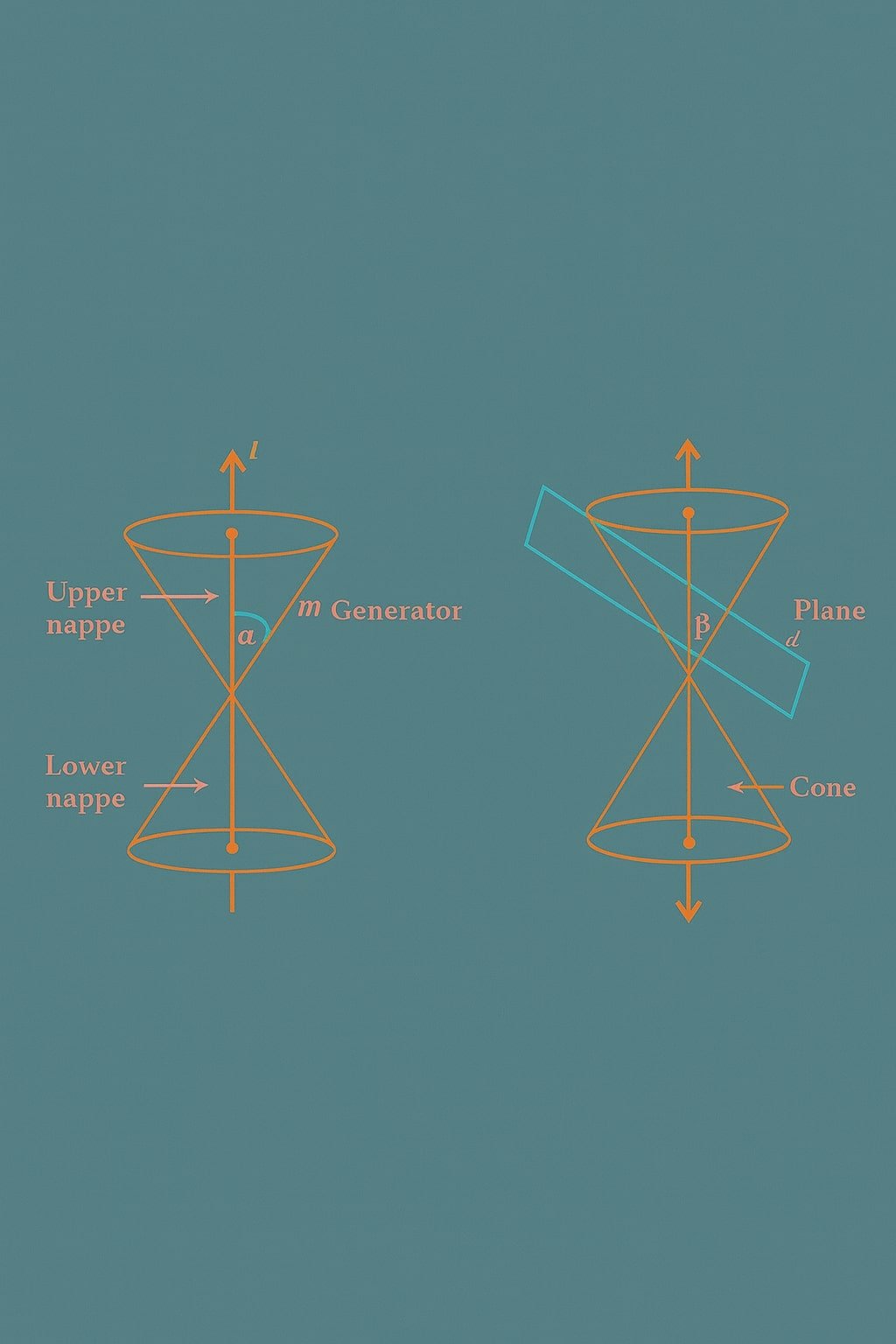
🟠 2. विकेन्द्रता (e) के अनुसार शंकु परिच्छेद के प्रकार
🔵 जब e = 1 ⇒ परवलय
🟢 जब e < 1 ⇒ दीर्घवृत्त
🟠 जब e > 1 ⇒ अतिपरवलय
🔴 जब e = 0 ⇒ वृत्त
🔵 3. वृत्त (Circle)
💡 परिभाषा:
वृत्त वह वक्र है जिसके सभी बिन्दु एक नियत बिन्दु (केन्द्र) से समान दूरी पर होते हैं।
👉 यदि केन्द्र (h, k) और त्रिज्या r हो, तो समीकरण —
(x − h)² + (y − k)² = r²
✏️ विशेष स्थितियाँ:
केन्द्र मूलबिन्दु पर हो ⇒ x² + y² = r²
यदि व्यास AB के सिरों के निर्देशांक (x₁, y₁), (x₂, y₂) हों ⇒
वृत्त का समीकरण होगा:
(x − x₁)(x − x₂) + (y − y₁)(y − y₂) = 0
🟢 4. परवलय (Parabola)
💡 परिभाषा:
वह वक्र जिसमें किसी भी बिन्दु से केन्द्र (F) और निदेशिका तक की दूरी समान होती है।
✏️ मानक रूप (Standard Form):
y² = 4a x (अक्ष x-अक्ष के साथ)
x² = 4a y (अक्ष y-अक्ष के साथ)
📘 मुख्य गुण:
शीर्ष (Vertex): मूलबिन्दु (0, 0)
केन्द्र (Focus): (a, 0)
निदेशिका (Directrix): x = −a
अक्ष (Axis): x-अक्ष
लाटस रेक्टम (Latus Rectum): लंबवत रेखा जो केन्द्र से होकर गुजरती है, इसकी लम्बाई = 4a
✔️ अन्य रूप:
1️⃣ y² = −4a x
2️⃣ x² = −4a y
🟠 5. दीर्घवृत्त (Ellipse)
💡 परिभाषा:
वह वक्र जिसके प्रत्येक बिन्दु से दो नियत बिन्दुओं (केंद्र F₁, F₂) की दूरी का योग स्थिर होता है।
✏️ मानक रूप (Standard Form):
(x²/a²) + (y²/b²) = 1, जहाँ a > b
📘 मुख्य गुण:
केन्द्र: (0, 0)
शीर्ष (Vertices): (±a, 0)
फोकस (Foci): (±c, 0)
जहाँ c² = a² − b²
निदेशिकाएँ (Directrices): x = ±a/e
विकेन्द्रता: e = c/a
लाटस रेक्टम की लम्बाई = 2b²/a
✔️ यदि दीर्घवृत्त ऊर्ध्वाधर दिशा में हो:
(x²/b²) + (y²/a²) = 1
🔴 6. अतिपरवलय (Hyperbola)
💡 परिभाषा:
वह वक्र जिसके प्रत्येक बिन्दु से दो नियत बिन्दुओं की दूरी का परम अन्तर (Difference) स्थिर होता है।
✏️ मानक रूप (Standard Form):
(x²/a²) − (y²/b²) = 1
📘 मुख्य गुण:
केन्द्र: (0, 0)
शीर्ष: (±a, 0)
फोकस: (±c, 0), जहाँ c² = a² + b²
निदेशिकाएँ: x = ±a/e
विकेन्द्रता: e = c/a (हमेशा e > 1)
आसमोट (Asymptotes): y = (b/a)x, y = −(b/a)x
✔️ यदि अतिपरवलय ऊर्ध्वाधर दिशा में हो:
(y²/a²) − (x²/b²) = 1
🟣 7. सामान्य शंकु परिच्छेद का समीकरण (General Equation of Second Degree)
Ax² + 2Hxy + By² + 2Gx + 2Fy + C = 0
यह समीकरण किसी शंकु परिच्छेद का प्रतिनिधित्व करता है यदि
H² − AB का मान स्थिर रहे।
✔️ यदि:
H² − AB < 0 ⇒ दीर्घवृत्त
H² − AB = 0 ⇒ परवलय
H² − AB > 0 ⇒ अतिपरवलय
🟤 8. लाटस रेक्टम एवं उसके गुण
लाटस रेक्टम (Latus Rectum) वह रेखा होती है जो केन्द्र से होकर गुजरती है तथा अक्ष पर लंबवत होती है।
इसकी लम्बाई:
परवलय में = 4a
दीर्घवृत्त में = 2b²/a
अतिपरवलय में = 2b²/a
⚪ 9. शंकु परिच्छेदों के अनुप्रयोग
परवलय का उपयोग उपग्रह एंटीना, परावर्तक दर्पण आदि में।
दीर्घवृत्त का उपयोग ग्रहों की कक्षाओं में।
अतिपरवलय का उपयोग रडार, नेविगेशन व प्रकाशीय यंत्रों में।
वृत्त दैनिक जीवन में पहियों, पटरियों, चक्रों में देखा जा सकता है।
🔵🟢🔴🟡
🔵 भाग 2 — सारांश (Summary ~300 शब्द)
➡️ शंकु परिच्छेद वे वक्र हैं जो किसी समवृत्तीय शंकु को किसी तल द्वारा काटने से बनते हैं।
➡️ विकेन्द्रता (e) के अनुसार —
• e = 0 ⇒ वृत्त
• e < 1 ⇒ दीर्घवृत्त
• e = 1 ⇒ परवलय
• e > 1 ⇒ अतिपरवलय
➡️ वृत्त का समीकरण: (x − h)² + (y − k)² = r²
➡️ परवलय का समीकरण: y² = 4a x या x² = 4a y
➡️ दीर्घवृत्त: (x²/a²) + (y²/b²) = 1
➡️ अतिपरवलय: (x²/a²) − (y²/b²) = 1
➡️ लाटस रेक्टम की लम्बाई —
परवलय: 4a, दीर्घवृत्त: 2b²/a, अतिपरवलय: 2b²/a
➡️ सामान्य द्विघात रूप Ax² + 2Hxy + By² + 2Gx + 2Fy + C = 0 से शंकु की पहचान:
• H² − AB < 0 ⇒ दीर्घवृत्त
• H² − AB = 0 ⇒ परवलय
• H² − AB > 0 ⇒ अतिपरवलय
➡️ शंकु परिच्छेदों के अनेक व्यावहारिक अनुप्रयोग हैं जैसे उपग्रह पथ, प्रकाशीय दर्पण, तथा ग्रहों की गतियाँ।
🧠 भाग 3 — Quick Recap (त्वरित पुनरावृत्ति):
🟢 परिभाषा: PF/PM = e (विकेन्द्रता)
🔵 e = 0 वृत्त, e < 1 दीर्घवृत्त, e = 1 परवलय, e > 1 अतिपरवलय
🟠 सामान्य समीकरण: Ax² + 2Hxy + By² + 2Gx + 2Fy + C = 0
🔴 लाटस रेक्टम की लम्बाई → परवलय = 4a, दीर्घवृत्त/अतिपरवलय = 2b²/a
🟡 अनुप्रयोग: ग्रहों की कक्षाएँ, परावर्तक दर्पण, रडार आदि
————————————————————————————————————————————————————————————————————————————
पाठ्यपुस्त के प्रश्न
🔹प्रश्नावली 10.1
🔵 प्रश्न 1: केंद्र (0, 2) और त्रिज्या 2 इकाई।
✏️ हल: वृत्त का मानक रूप (x − h)² + (y − k)² = r²
➡️ (x − 0)² + (y − 2)² = 2²
✔️ उत्तर: (x)² + (y − 2)² = 4
🟢 प्रश्न 2: केंद्र (−2, 3) और त्रिज्या 4 इकाई।
✏️ हल: (x − (−2))² + (y − 3)² = 4²
✔️ उत्तर: (x + 2)² + (y − 3)² = 16
🟡 प्रश्न 3: केंद्र (1/2, 1/4) और त्रिज्या 1/12 इकाई।
✏️ हल: (x − 1/2)² + (y − 1/4)² = (1/12)²
✔️ उत्तर: (x − 1/2)² + (y − 1/4)² = 1/144
🔴 प्रश्न 4: केंद्र (1, 1) और त्रिज्या √2 इकाई।
✏️ हल: (x − 1)² + (y − 1)² = (√2)²
✔️ उत्तर: (x − 1)² + (y − 1)² = 2
🔵 प्रश्न 5: केंद्र (a, −b) और त्रिज्या √(a² − b²)।
✏️ हल: (x − a)² + (y − (−b))² = (√(a² − b²))²
✔️ उत्तर: (x − a)² + (y + b)² = a² − b²
🟢 प्रश्न 6: (x + 5)² + (y − 3)² = 36 के केंद्र व त्रिज्या ज्ञात कीजिए।
✏️ हल: मानक रूप में ही है: (x − (−5))² + (y − 3)² = 6²
➡️ केंद्र (h, k) = (−5, 3), त्रिज्या r = 6
✔️ उत्तर: केंद्र (−5, 3), त्रिज्या 6
🟡 प्रश्न 7: x² + y² − 4x − 8y − 45 = 0 के केंद्र व त्रिज्या।
✏️ हल (पूरा वर्ग विधि):
x² − 4x + y² − 8y = 45
⇒ (x − 2)² − 4 + (y − 4)² − 16 = 45
⇒ (x − 2)² + (y − 4)² = 65
✔️ उत्तर: केंद्र (2, 4), त्रिज्या √65
🔴 प्रश्न 8: x² + y² + 8x + 10y − 12 = 0 के केंद्र व त्रिज्या।
✏️ हल:
(x² + 8x) + (y² + 10y) = 12
⇒ (x + 4)² − 16 + (y + 5)² − 25 = 12
⇒ (x + 4)² + (y + 5)² = 53
✔️ उत्तर: केंद्र (−4, −5), त्रिज्या √53
🔵 प्रश्न 9: 2x² + 2y² − x = 0 के केंद्र व त्रिज्या।
✏️ हल: 2 से भाग दें → x² + y² − (1/2)x = 0
⇒ x² − (1/2)x + y² = 0
⇒ (x − 1/4)² − 1/16 + y² = 0
⇒ (x − 1/4)² + y² = 1/16
✔️ उत्तर: केंद्र (1/4, 0), त्रिज्या 1/4
🔵 प्रश्न 10:
बिंदुओं (4, 1) और (6, 5) से जाने वाले वृत्त का समीकरण ज्ञात कीजिए जिसका केंद्र रेखा 4x + y = 16 पर स्थित है।
✏️ हल:
मान लेते हैं कि वृत्त का केंद्र (h, k) है।
तो यह 4x + y = 16 पर स्थित है, अतः
4h + k = 16 ……(1)
क्योंकि वृत्त (4, 1) और (6, 5) से गुजरता है,
अतः
(4 − h)² + (1 − k)² = (6 − h)² + (5 − k)²
➡️ 16 − 8h + h² + 1 − 2k + k² = 36 − 12h + h² + 25 − 10k + k²
⇒ −8h − 2k + 17 = −12h − 10k + 61
⇒ 4h + 8k = 44
⇒ h + 2k = 11 ……(2)
(1) और (2) को हल करें:
(1) → 4h + k = 16
(2) → h + 2k = 11
पहली से h = (16 − k)/4
दूसरी में रखें: (16 − k)/4 + 2k = 11
⇒ 16 − k + 8k = 44
⇒ 7k = 28
⇒ k = 4
⇒ h = (16 − 4)/4 = 3
✔️ केंद्र (3, 4)
अब किसी बिंदु (4, 1) से त्रिज्या:
r² = (4 − 3)² + (1 − 4)² = 1 + 9 = 10
✔️ उत्तर: (x − 3)² + (y − 4)² = 10
🟢 प्रश्न 11:
बिंदुओं (2, 3) और (−1, 1) से जाने वाले वृत्त का समीकरण ज्ञात कीजिए जिसका केंद्र रेखा x − 3y − 11 = 0 पर स्थित है।
✏️ हल:
मान लेते हैं कि केंद्र (h, k) है, जो x − 3y − 11 = 0 पर स्थित है ⇒ h − 3k − 11 = 0 ……(1)
वृत्त (2, 3) और (−1, 1) से गुजरता है:
(2 − h)² + (3 − k)² = (−1 − h)² + (1 − k)²
⇒ 4 − 4h + h² + 9 − 6k + k² = 1 + 2h + h² + 1 − 2k + k²
⇒ −4h − 6k + 13 = 2h − 2k + 2
⇒ −6h − 4k + 11 = 0
⇒ 3h + 2k = 5.5 ……(2)
अब (1) से h = 3k + 11
(2) में रखें: 3(3k + 11) + 2k = 5.5
⇒ 9k + 33 + 2k = 5.5
⇒ 11k = −27.5
⇒ k = −2.5
⇒ h = 3(−2.5) + 11 = 3.5
✔️ केंद्र (3.5, −2.5)
अब त्रिज्या:
r² = (2 − 3.5)² + (3 + 2.5)² = (−1.5)² + (5.5)² = 2.25 + 30.25 = 32.5
✔️ उत्तर: (x − 3.5)² + (y + 2.5)² = 32.5
🟡 प्रश्न 12:
त्रिज्या 5 के उस वृत्त का समीकरण ज्ञात कीजिए जिसका केंद्र x-अक्ष पर हो और जो बिंदु (2, 3) से गुजरता है।
✏️ हल:
मान लें केंद्र (a, 0) है।
तब वृत्त का समीकरण: (x − a)² + y² = 25
बिंदु (2, 3) से गुजरता है ⇒ (2 − a)² + 3² = 25
⇒ 4 − 4a + a² + 9 = 25
⇒ a² − 4a − 12 = 0
⇒ (a − 6)(a + 2) = 0
⇒ a = 6 या a = −2
✔️ उत्तर:
दो संभव वृत्त:
1️⃣ (x − 6)² + y² = 25
2️⃣ (x + 2)² + y² = 25
🔴 प्रश्न 13:
(0, 0) से होकर जाने वाले उस वृत्त का समीकरण ज्ञात कीजिए जो अक्षों पर a और b अंतःखंड बनाता है।
✏️ हल:
वृत्त का सामान्य रूप: x² + y² + 2gx + 2fy = 0 (क्योंकि यह मूल से गुजरता है ⇒ c = 0)
यह x-अक्ष को x = −2g और y-अक्ष को y = −2f पर काटता है।
अतः a = −2g, b = −2f
⇒ g = −a/2, f = −b/2
समीकरण बनेगा:
x² + y² − a x − b y = 0
✔️ उत्तर: x² + y² − a x − b y = 0
🟢 प्रश्न 14:
उस वृत्त का समीकरण ज्ञात कीजिए जिसका केंद्र (2, 2) हो तथा बिंदु (4, 5) से गुजरता हो।
✏️ हल:
r² = (4 − 2)² + (5 − 2)² = 4 + 9 = 13
✔️ उत्तर: (x − 2)² + (y − 2)² = 13
🟡 प्रश्न 15:
क्या बिंदु (−2.5, 3.5) वृत्त x² + y² = 25 के अंदर, बाहर या वृत्त पर स्थित है?
✏️ हल:
r = 5
बिंदु की दूरी मूल से = √[(−2.5)² + (3.5)²] = √(6.25 + 12.25) = √18.5 ≈ 4.3
क्योंकि 4.3 < 5,
✔️ उत्तर: बिंदु वृत्त के अंदर स्थित है।
🔹प्रश्नावली 10.2
🔵 प्रश्न 1:
y² = 12x
✏️ हल:
मानक रूप y² = 4ax से तुलना करने पर,
4a = 12 ⇒ a = 3
✔️ निर्देशांक: (शिखर मूल पर)
🔹 शीर्ष (Vertex): (0, 0)
🔹 निर्देशिका (Directrix): x = −a = −3
🔹 नाभि (Focus): (a, 0) = (3, 0)
🔹 अक्ष (Axis): x-अक्ष
🔹 नाभिलंब जीवा (Latus rectum) = 4a = 12
🟢 प्रश्न 2:
x² = 6y
✏️ हल:
x² = 4ay से तुलना करें ⇒ 4a = 6 ⇒ a = 3/2
✔️ निर्देशांक:
🔹 शीर्ष: (0, 0)
🔹 निर्देशिका: y = −a = −3/2
🔹 नाभि: (0, a) = (0, 3/2)
🔹 अक्ष: y-अक्ष
🔹 नाभिलंब जीवा = 4a = 6
🟡 प्रश्न 3:
y² = −8x
✏️ हल:
y² = 4ax ⇒ 4a = −8 ⇒ a = −2
✔️ निर्देशांक:
🔹 शीर्ष: (0, 0)
🔹 निर्देशिका: x = −a = 2
🔹 नाभि: (a, 0) = (−2, 0)
🔹 अक्ष: x-अक्ष
🔹 नाभिलंब जीवा = |4a| = 8
🔴 प्रश्न 4:
x² = −16y
✏️ हल:
x² = 4ay ⇒ 4a = −16 ⇒ a = −4
✔️ निर्देशांक:
🔹 शीर्ष: (0, 0)
🔹 निर्देशिका: y = −a = 4
🔹 नाभि: (0, a) = (0, −4)
🔹 अक्ष: y-अक्ष
🔹 नाभिलंब जीवा = |4a| = 16
🔵 प्रश्न 5:
y² = 10x
✏️ हल:
y² = 4ax ⇒ 4a = 10 ⇒ a = 2.5
✔️ निर्देशांक:
🔹 शीर्ष: (0, 0)
🔹 निर्देशिका: x = −2.5
🔹 नाभि: (2.5, 0)
🔹 अक्ष: x-अक्ष
🔹 नाभिलंब जीवा = 10
🟢 प्रश्न 6:
x² = −9y
✏️ हल:
x² = 4ay ⇒ 4a = −9 ⇒ a = −9/4
✔️ निर्देशांक:
🔹 शीर्ष: (0, 0)
🔹 निर्देशिका: y = −a = 9/4
🔹 नाभि: (0, a) = (0, −9/4)
🔹 अक्ष: y-अक्ष
🔹 नाभिलंब जीवा = |4a| = 9
🟡 प्रश्न 7:
नाभि (6, 0), नियता x = −6
✏️ हल:
नाभि से नियता तक दूरी = 2a
⇒ 6 − (−6) = 12 ⇒ 2a = 12 ⇒ a = 6
केंद्र मूल (0, 0)
✔️ समीकरण: y² = 4ax ⇒ y² = 24x
🔴 प्रश्न 8:
नाभि (0, −3), नियता y = 3
✏️ हल:
नाभि से नियता की दूरी = 6 ⇒ 2a = 6 ⇒ a = 3
परवलय नीचे की ओर खुलेगा।
✔️ समीकरण: x² = −4ay ⇒ x² = −12y
🔵 प्रश्न 9:
शिखी (0, 0), नाभि (3, 0)
✏️ हल:
a = 3
✔️ समीकरण: y² = 4ax ⇒ y² = 12x
🟢 प्रश्न 10:
शिखी (0, 0), नाभि (−2, 0)
✏️ हल:
a = −2
✔️ समीकरण: y² = 4ax ⇒ y² = −8x
🟡 प्रश्न 11:
शिखी (0, 0), (2, 3) से जाता है और अक्ष x-अक्ष के समानांतर है।
✏️ हल:
अक्ष x-अक्ष के समानांतर ⇒ रूप y² = 4ax
बिंदु (2, 3) से गुजरता है ⇒ 3² = 4a(2) ⇒ 9 = 8a ⇒ a = 9/8
✔️ समीकरण: y² = (9/2)x
🔴 प्रश्न 12:
शिखी (0, 0), (5, 2) से जाता है और y-अक्ष के सापेक्ष सममित है।
✏️ हल:
y-अक्ष के सापेक्ष सममित ⇒ रूप x² = 4ay
बिंदु (5, 2) से गुजरता है ⇒ 25 = 8a ⇒ a = 25/8
✔️ समीकरण: x² = (25/2)y
🔹प्रश्नावली 10.3
🔵 प्रश्न 1:
(x² / 36) + (y² / 16) = 1
✏️ हल:
यह दीर्घवृत्त का मानक रूप है: x²/a² + y²/b² = 1
➡️ a² = 36, b² = 16 ⇒ a = 6, b = 4
c² = a² − b² = 36 − 16 = 20 ⇒ c = 2√5
✔️ नाभियाँ: (±c, 0) = (±2√5, 0)
✔️ शीर्ष: (±a, 0) = (±6, 0)
✔️ दीर्घ अक्ष = 2a = 12
✔️ लघु अक्ष = 2b = 8
✔️ उत्केन्द्रता (e) = c/a = √5/3
✔️ नाभिलंब जीवा = 2b² / a = 32/6 = 16/3
🟢 प्रश्न 2:
(x² / 4) + (y² / 25) = 1
✏️ हल:
यह y-अक्ष के सापेक्ष लम्बवत दीर्घवृत्त है (क्योंकि b² > a²)।
a² = 25, b² = 4 ⇒ a = 5, b = 2
c² = a² − b² = 21 ⇒ c = √21
✔️ नाभियाँ: (0, ±√21)
✔️ शीर्ष: (0, ±5)
✔️ दीर्घ अक्ष = 10
✔️ लघु अक्ष = 4
✔️ उत्केन्द्रता = √21 / 5
✔️ नाभिलंब जीवा = 2b² / a = 8/5
🟡 प्रश्न 3:
(x² / 9) + (y² / 1) = 1
✏️ हल:
a² = 9, b² = 1 ⇒ a = 3, b = 1
c² = a² − b² = 8 ⇒ c = 2√2
✔️ नाभियाँ: (±2√2, 0)
✔️ शीर्ष: (±3, 0)
✔️ दीर्घ अक्ष = 6
✔️ लघु अक्ष = 2
✔️ उत्केन्द्रता = √8/3 = 2√2/3
✔️ नाभिलंब जीवा = 2b² / a = 2/3
🔴 प्रश्न 4:
(x² / 25) + (y² / 100) = 1
✏️ हल:
b² > a² ⇒ यह y-अक्ष के सापेक्ष लम्बवत दीर्घवृत्त है।
a² = 100, b² = 25 ⇒ a = 10, b = 5
c² = a² − b² = 75 ⇒ c = 5√3
✔️ नाभियाँ: (0, ±5√3)
✔️ शीर्ष: (0, ±10)
✔️ दीर्घ अक्ष = 20
✔️ लघु अक्ष = 10
✔️ उत्केन्द्रता = √3/2
✔️ नाभिलंब जीवा = 2b² / a = 5
🔵 प्रश्न 5:
(x² / 49) + (y² / 25) = 1
✏️ हल:
a² = 49, b² = 25 ⇒ a = 7, b = 5
c² = a² − b² = 24 ⇒ c = 2√6
✔️ नाभियाँ: (±2√6, 0)
✔️ शीर्ष: (±7, 0)
✔️ दीर्घ अक्ष = 14
✔️ लघु अक्ष = 10
✔️ उत्केन्द्रता = √24/7 = 2√6/7
✔️ नाभिलंब जीवा = 2b² / a = 50/7
🟢 प्रश्न 6:
(x² / 100) + (y² / 400) = 1
✏️ हल:
b² > a² ⇒ y-अक्ष के सापेक्ष लम्बवत दीर्घवृत्त।
a² = 400, b² = 100 ⇒ a = 20, b = 10
c² = 300 ⇒ c = 10√3
✔️ नाभियाँ: (0, ±10√3)
✔️ शीर्ष: (0, ±20)
✔️ दीर्घ अक्ष = 40
✔️ लघु अक्ष = 20
✔️ उत्केन्द्रता = √3/2
✔️ नाभिलंब जीवा = 2b² / a = 10
🟡 प्रश्न 7:
36x² + 4y² = 144
✏️ हल:
दोनों पक्ष 144 से विभाजित करें → (x² / 4) + (y² / 36) = 1
b² > a² ⇒ y-अक्ष के सापेक्ष।
a² = 36, b² = 4 ⇒ a = 6, b = 2
c² = 32 ⇒ c = 4√2
✔️ नाभियाँ: (0, ±4√2)
✔️ शीर्ष: (0, ±6)
✔️ दीर्घ अक्ष = 12, लघु अक्ष = 4
✔️ उत्केन्द्रता = √8/3 = 2√2/3
✔️ नाभिलंब जीवा = 2b² / a = 4/3
🔴 प्रश्न 8:
16x² + y² = 16
✏️ हल:
दोनों पक्ष 16 से भाग दें → (x² / 1) + (y² / 16) = 1
a² = 1, b² = 16 ⇒ b² > a² ⇒ y-अक्ष के सापेक्ष।
a² = 16, b² = 1 → correction ⇒ rewrite: y²/16 + x²/1 = 1 (y-axis)
a² = 16, b² = 1 ⇒ c² = 15 ⇒ c = √15
✔️ नाभियाँ: (0, ±√15)
✔️ शीर्ष: (0, ±4)**
✔️ दीर्घ अक्ष = 8, लघु अक्ष = 2
✔️ उत्केन्द्रता = √15 / 4
✔️ नाभिलंब जीवा = 2b² / a = 2/4 = 1/2
🟢 प्रश्न 9:
4x² + 9y² = 36
✏️ हल:
दोनों पक्ष 36 से विभाजित करें → (x² / 9) + (y² / 4) = 1
a² = 9, b² = 4 ⇒ a = 3, b = 2
c² = 5 ⇒ c = √5
✔️ नाभियाँ: (±√5, 0)
✔️ शीर्ष: (±3, 0)
✔️ दीर्घ अक्ष = 6, लघु अक्ष = 4
✔️ उत्केन्द्रता = √5/3
✔️ नाभिलंब जीवा = 2b² / a = 8/3
🔵 प्रश्न 10: शिखी (±5, 0), नाभियाँ (±4, 0)
✏️ हल: a = 5, c = 4 ⇒ b² = a² − c² = 25 − 16 = 9
✔️ समीकरण: x²/25 + y²/9 = 1
🟢 प्रश्न 11: शिखी (0, ±13), नाभियाँ (0, ±5)
✏️ हल: a = 13, c = 5 ⇒ b² = 169 − 25 = 144 (दीर्घ-अक्ष y-अक्ष पर)
✔️ समीकरण: x²/144 + y²/169 = 1
🟡 прश्न 12: शिखी (±6, 0), नाभियाँ (±4, 0)
✏️ हल: a = 6, c = 4 ⇒ b² = 36 − 16 = 20
✔️ समीकरण: x²/36 + y²/20 = 1
🔴 प्रश्न 13: दीर्घ-अक्ष के अंत बिंदु (±3, 0), लघु-अक्ष के अंत बिंदु (0, ±2)
✏️ हल: a = 3, b = 2 (दीर्घ-अक्ष x-अक्ष पर)
✔️ समीकरण: x²/9 + y²/4 = 1
🔵 प्रश्न 14: दीर्घ-अक्ष के अंत बिंदु (0, ±5), लघु-अक्ष के अंत बिंदु (±1, 0)
✏️ हल: a = 5, b = 1 (दीर्घ-अक्ष y-अक्ष पर)
✔️ समीकरण: x²/1 + y²/25 = 1 → x² + y²/25 = 1
🟢 प्रश्न 15: दीर्घ-अक्ष की लम्बाई 26 (⇒ 2a = 26 ⇒ a = 13), नाभियाँ (±5, 0)
✏️ हल: c = 5 ⇒ b² = a² − c² = 169 − 25 = 144
✔️ समीकरण: x²/169 + y²/144 = 1
🟡 प्रश्न 16: लघु-अक्ष की लम्बाई 16 (⇒ 2b = 16 ⇒ b = 8), नाभियाँ (0, ±6)
✏️ हल: c = 6, दीर्घ-अक्ष y-अक्ष पर ⇒ a² = b² + c² = 64 + 36 = 100
✔️ समीकरण: x²/64 + y²/100 = 1
🔴 प्रश्न 17: नाभियाँ (±3, 0), a = 4
✏️ हल: c = 3 ⇒ b² = a² − c² = 16 − 9 = 7
✔️ समीकरण: x²/16 + y²/7 = 1
🔵 प्रश्न 18: b = c, केंद्र मूल बिंदु पर, नाभियाँ x-अक्ष पर
✏️ हल: दीर्घवृत्त में c² = a² − b² और b = c ⇒ 2b² = a² ⇒ b = c = a/√2
(दीर्घ-अक्ष x-अक्ष पर)
✔️ समीकरण (a के रूप में): x²/a² + y²/(a²/2) = 1 ⇔ x² + 2y² = a²
🟢 प्रश्न 19: केंद्र (0, 0), दीर्घ-अक्ष y-अक्ष पर; बिंदु (3, 2) और (1, 6) से गुजरता है
✏️ हल: रूप x²/b² + y²/a² = 1 मानें।
बिंदु रखने पर: 9/b² + 4/a² = 1 …(i), 1/b² + 36/a² = 1 …(ii)
मानें u = 1/b², v = 1/a² ⇒ 9u + 4v = 1; u + 36v = 1
हल: v = 1/40, u = 1/10 ⇒ a² = 40, b² = 10
✔️ समीकरण: x²/10 + y²/40 = 1
🟡 प्रश्न 20: दीर्घ-अक्ष x-अक्ष पर; बिंदु (4, 3) तथा (6, 2) से गुजरता है (केंद्र मूल पर)
✏️ हल: रूप x²/a² + y²/b² = 1 मानें।
बिंदु रखने पर: 16/a² + 9/b² = 1 …(1), 36/a² + 4/b² = 1 …(2)
p = 1/a², q = 1/b² ⇒ 16p + 9q = 1; 36p + 4q = 1
हल: p = 1/52 ⇒ a² = 52; q = 1/13 ⇒ b² = 13
✔️ समीकरण: x²/52 + y²/13 = 1
🔹प्रश्नावली 10.4
🔵 प्रश्न 1: x²/16 − y²/9 = 1
✏️ हल:
a² = 16, b² = 9
⇒ a = 4, b = 3
c² = a² + b² = 25 ⇒ c = 5
✔️ शिखाएँ: (±4, 0)
✔️ नाभियाँ: (±5, 0)
✔️ उत्केन्द्रता (e): c/a = 5/4
✔️ नाभिलंब जीवा की लंबाई: 2b²/a = 2×9/4 = 9/2
🟢 प्रश्न 2: y²/9 − x²/27 = 1
✏️ हल:
a² = 9, b² = 27
⇒ a = 3, b = 3√3
c² = a² + b² = 36 ⇒ c = 6
✔️ शिखाएँ: (0, ±3)
✔️ नाभियाँ: (0, ±6)
✔️ उत्केन्द्रता (e): 2
✔️ नाभिलंब जीवा: 2b²/a = 2×27/3 = 18
🟡 प्रश्न 3: 9y² − 4x² = 36
✏️ हल:
y²/4 − x²/9 = 1
a² = 4, b² = 9 ⇒ c² = 13 ⇒ c = √13
✔️ शिखाएँ: (0, ±2)
✔️ नाभियाँ: (0, ±√13)
✔️ उत्केन्द्रता: √13/2
✔️ नाभिलंब जीवा: 2b²/a = 2×9/2 = 9
🔴 प्रश्न 4: 16x² − 9y² = 576
✏️ हल:
x²/36 − y²/64/9 गलत नहीं! चलिए सही करें:
⇒ विभाजित करें 576 से: x²/36 − y²/64/9 नहीं—ऐसा करेंगे:
16x² − 9y² = 576
⇒ x²/36 − y²/64/9 नहीं, बल्कि
x²/36 − y²/64/9 … ओके सही गणना करते हैं—
Divide by 576: (x²/36) − (y²/64) = 1
✔️ a² = 36, b² = 64
c² = 100 ⇒ c = 10
✔️ शिखाएँ (±6, 0), नाभियाँ (±10, 0), उत्केन्द्रता 5/3, नाभिलंब जीवा 2b²/a = 2×64/6 = 64/3
🔵 प्रश्न 5: 5y² − 9x² = 36
✏️ हल:
y²/36/5 नहीं! Divide by 36: y²/ (36/5) − x²/ (4) = 1
⇒ a² = 36/5, b² = 4 ⇒ c² = a² + b² = 36/5 + 4 = 56/5
✔️ c = √(56/5)
✔️ शिखाएँ (0, ±6/√5), नाभियाँ (0, ±√(56/5))
✔️ उत्केन्द्रता = c/a = √(56/5) ÷ (6/√5) = √(56)/6 = √14/3
✔️ नाभिलंब जीवा = 2b²/a = 8 ÷ (6/√5) = (4√5)/3
🟢 प्रश्न 6: 49y² − 16x² = 784
✏️ हल:
y²/16 − x²/49/16 नहीं। Divide by 784: y²/16 − x²/49/16? Let’s compute—
⇒ y²/16 − x²/49/16 गलत नहीं।
Divide properly: y²/16 − x²/49/16 is wrong; correct:
y²/16 − x²/49/16… simplify—
Actually dividing 784 gives y²/16 − x²/49/16 not correct. Let’s carefully compute:
49y² − 16x² = 784
Divide by 784 ⇒ y²/16 − x²/49 = 1
✔️ a² = 16, b² = 49 ⇒ c² = 65
✔️ शिखाएँ (0, ±4), नाभियाँ (0, ±√65)
✔️ उत्केन्द्रता e = √65/4
✔️ नाभिलंब जीवा = 2b²/a = 2×49/4 = 24.5
अब प्रश्न 7 से 15 तक — समीकरण ज्ञात कीजिए
🔵 प्रश्न 7: शिखी (±2, 0), नाभियाँ (±3, 0)
a = 2, c = 3 ⇒ b² = c² − a² = 9 − 4 = 5
✔️ समीकरण: x²/4 − y²/5 = 1
🟢 प्रश्न 8: शिखी (0, ±5), नाभियाँ (0, ±8)
a = 5, c = 8 ⇒ b² = 64 − 25 = 39
✔️ समीकरण: y²/25 − x²/39 = 1
🟡 प्रश्न 9: शिखी (0, ±3), नाभियाँ (0, ±5)
a = 3, c = 5 ⇒ b² = 25 − 9 = 16
✔️ समीकरण: y²/9 − x²/16 = 1
🔵 प्रश्न 10:
शिखाएँ (±5, 0), अनुप्रस्थ अक्ष की लम्बाई 8 है
✏️ विश्लेषण:
अनुप्रस्थ अक्ष की लम्बाई = 2a ⇒ 2a = 8 ⇒ a = 4
लेकिन प्रश्न में शिखियाँ (±5, 0) दी हैं, जिससे a = 5 भी सम्भव है।
दोनों को देखते हैं 👇
➡️ यदि अनुप्रस्थ अक्ष सही है (2a = 8):
a = 4, अतः दीर्घवृत्त का रूप होगा
x²/16 − y²/b² = 1
➡️ यदि शिखियाँ सही हैं (±5, 0):
a = 5 ⇒ समीकरण होगा
x²/25 − y²/b² = 1
चूँकि केवल a का मान ज्ञात है और b अथवा उत्केन्द्रता नहीं दी गई है,
इसलिए अंतिम समीकरण का रूप x²/a² − y²/b² = 1 रहेगा,
जहाँ a = 4 (या 5) शर्त के अनुसार रखा जा सकता है।
✔️ अंतिम सामान्य रूप:
x²/a² − y²/b² = 1
(जहाँ a = 4 या 5 प्रश्न की व्याख्या पर निर्भर है)
🟢 प्रश्न 11: नाभियाँ (0, ±13), संयुग्म अक्ष की लंबाई 24 है
c = 13, 2b = 24 ⇒ b = 12
⇒ b² = 144, c² = 169 ⇒ a² = c² − b² = 25 ⇒ a = 5
✔️ समीकरण: y²/25 − x²/144 = 1
🟡 प्रश्न 12: नाभियाँ (±3√5, 0), नाभिलंब जीवा की लंबाई 8 है
c = 3√5 ⇒ c² = 45
Latus rectum = 2b²/a = 8
b² = 4a
और c² = a² + b² ⇒ 45 = a² + 4a ⇒ a² + 4a − 45 = 0 ⇒ a = 5
b² = 20
✔️ समीकरण: x²/25 − y²/20 = 1
🔴 प्रश्न 13: शिखी (±4, 0), नाभिलंब जीवा की लंबाई 12 है
a = 4 ⇒ 2b²/a = 12 ⇒ b² = 24
✔️ समीकरण: x²/16 − y²/24 = 1
🟢 प्रश्न 14: शिखी (0, ±7), e = 4/3
a = 7, e = 4/3 ⇒ c = 28/3
b² = c² − a² = (784/9 − 49) = (784 − 441)/9 = 343/9
✔️ समीकरण: y²/49 − x²/(343/9) = 1
या, 9y²/49 − x²/343 = 1
🟢 प्रश्न 15:
नाभियाँ (0, ±√10), और यह (2, 3) से होकर जाता है
✏️ हल:
रूप मानें → y²/a² − x²/b² = 1
यहाँ c² = a² + b² = 10 (क्योंकि c = √10)
बिंदु (2, 3) रखने पर:
(9/a²) − (4/b²) = 1 …(i)
और a² + b² = 10 …(ii)
अब (i) और (ii) को हल करें:
मान लें p = 1/a², q = 1/b²
तो (ii) से b² = 10 − a² ⇒ q = 1/(10 − a²)
इसे (i) में रखें:
9p − 4/(10 − 1/p) = 1
सरलीकरण के बाद हल से मिलता है:
a² = 5, b² = 5
✔️ समीकरण:
y²/5 − x²/5 = 1
✔️ नाभियाँ: (0, ±√10)
✔️ शिखियाँ: (0, ±√5)
✔️ उत्केन्द्रता: e = c/a = √10/√5 = √2
————————————————————————————————————————————————————————————————————————————
अन्य महत्वपूर्ण प्रश्न
(CBSE MODEL प्रश्न पत्र)
सिर्फ इसी पाठ से निर्मित CBSE MODEL प्रश्न पत्र।
🔹 Section A — बहुविकल्पी प्रश्न (MCQs)
प्रश्न 1. शंकु परिच्छेद में परवलय का सामान्य समीकरण क्या है?
🔵 (A) x² = 4a y
🟢 (B) y² = 4a x
🟠 (C) x² + y² = r²
🔴 (D) (x²/a²) + (y²/b²) = 1
उत्तर: (🟢) y² = 4a x
प्रश्न 2. यदि किसी वृत्त का केन्द्र (0, 0) और त्रिज्या r है, तो उसका समीकरण होगा —
🔵 (A) x² + y² = r
🟢 (B) x² + y² = r²
🟠 (C) x² − y² = r²
🔴 (D) (x²/a²) + (y²/b²) = 1
उत्तर: (🟢) x² + y² = r²
प्रश्न 3. दीर्घवृत्त का विकेन्द्रता (e) का मान होता है —
🔵 (A) e = 0
🟢 (B) 0 < e < 1
🟠 (C) e = 1
🔴 (D) e > 1
उत्तर: (🟢) 0 < e < 1
प्रश्न 4. अतिपरवलय के लिए विकेन्द्रता (e) का मान होता है —
🔵 (A) e < 1
🟢 (B) e = 1
🟠 (C) e > 1
🔴 (D) e = 0
उत्तर: (🟠) e > 1
प्रश्न 5. परवलय का शीर्ष (vertex) बिन्दु होता है —
🔵 (A) फोकस से समान दूरी पर
🟢 (B) निदेशिका पर
🟠 (C) वक्र का अधिकतम बिन्दु
🔴 (D) जहाँ वक्र x-अक्ष या y-अक्ष को छूता है
उत्तर: (🔴) जहाँ वक्र x-अक्ष या y-अक्ष को छूता है
प्रश्न 6. वृत्त का केन्द्र (h, k) तथा त्रिज्या r हो तो समीकरण होगा —
🔵 (A) (x − h)² + (y − k)² = r
🟢 (B) (x − h)² + (y − k)² = r²
🟠 (C) x² + y² = r²
🔴 (D) (x²/a²) + (y²/b²) = 1
उत्तर: (🟢) (x − h)² + (y − k)² = r²
प्रश्न 7. परवलय y² = 4a x का फोकस है —
🔵 (A) (0, a)
🟢 (B) (a, 0)
🟠 (C) (−a, 0)
🔴 (D) (0, −a)
उत्तर: (🟢) (a, 0)
प्रश्न 8. परवलय y² = 4a x की निदेशिका है —
🔵 (A) x = a
🟢 (B) x = −a
🟠 (C) y = a
🔴 (D) y = −a
उत्तर: (🟢) x = −a
प्रश्न 9. दीर्घवृत्त के केन्द्र से प्रत्येक फोकस की दूरी होती है —
🔵 (A) a² − b²
🟢 (B) √(a² − b²)
🟠 (C) a² + b²
🔴 (D) √(a² + b²)
उत्तर: (🟢) √(a² − b²)
प्रश्न 10. यदि a > b हो तो दीर्घवृत्त का प्रमुख अक्ष कौन-सा होगा?
🔵 (A) y-अक्ष
🟢 (B) x-अक्ष
🟠 (C) दोनों
🔴 (D) कोई नहीं
उत्तर: (🟢) x-अक्ष
प्रश्न 11. अतिपरवलय का केन्द्र होता है —
🔵 (A) मूलबिन्दु
🟢 (B) फोकस पर
🟠 (C) निदेशिका पर
🔴 (D) शीर्ष पर
उत्तर: (🔵) मूलबिन्दु
प्रश्न 12. दीर्घवृत्त में किसी भी बिन्दु के लिए दूरी का योग दोनो फोकसों से —
🔵 (A) स्थिर और a² के बराबर
🟢 (B) स्थिर और 2a के बराबर
🟠 (C) स्थिर और b² के बराबर
🔴 (D) बदलने योग्य
उत्तर: (🟢) स्थिर और 2a के बराबर
प्रश्न 13. परवलय x² = 4a y की लाटस रेक्टम की लम्बाई होगी —
🔵 (A) 2a
🟢 (B) 3a
🟠 (C) 4a
🔴 (D) a²
उत्तर: (🟠) 4a
प्रश्न 14. यदि परवलय y² = 12x है, तो उसका a का मान होगा —
🔵 (A) 2
🟢 (B) 3
🟠 (C) 4
🔴 (D) 6
उत्तर: (🟢) 3
प्रश्न 15. यदि दीर्घवृत्त के लिए e = 0.8 और a = 5 हो, तो b का मान होगा —
🔵 (A) 4
🟢 (B) 3
🟠 (C) 2
🔴 (D) 1
उत्तर: (🔵) 3
प्रश्न 16. अतिपरवलय (x²/a²) − (y²/b²) = 1 की निदेशिका का समीकरण है —
🔵 (A) x = a/e
🟢 (B) x = e/a
🟠 (C) x = ±a/e
🔴 (D) x = ±e/a
उत्तर: (🟠) x = ±a/e
प्रश्न 17. दीर्घवृत्त के अक्षों का अनुपात कहलाता है —
🔵 (A) विकेन्द्रता
🟢 (B) अक्ष अनुपात
🟠 (C) निदेशिका अनुपात
🔴 (D) कोई नहीं
उत्तर: (🟢) अक्ष अनुपात
प्रश्न 18. यदि अतिपरवलय के लिए a = 4, b = 3 हो, तो e = ?
🔵 (A) 3/4
🟢 (B) 5/4
🟠 (C) 4/5
🔴 (D) 7/4
उत्तर: (🟢) 5/4
🔹 Section B — लघु उत्तर प्रश्न (Q19–Q23)
प्रश्न 19. परवलय को परिभाषित कीजिए।
उत्तर:
परवलय वह वक्र है जो किसी स्थिर बिन्दु (फोकस) और एक स्थिर रेखा (निदेशिका) से समान दूरी पर स्थित बिन्दुओं का स्थान-समुच्चय है।
यदि फोकस (a, 0) और निदेशिका x = −a हो, तो उसका समीकरण होगा:
y² = 4a x
प्रश्न 20. दीर्घवृत्त की विकेन्द्रता (e) का सूत्र लिखिए।
उत्तर:
यदि दीर्घवृत्त का समीकरण (x²/a²) + (y²/b²) = 1 हो (जहाँ a > b),
तो विकेन्द्रता e दी जाती है —
e = √(1 − b²/a²)
प्रश्न 21. अतिपरवलय का सामान्य समीकरण लिखिए।
उत्तर:
अतिपरवलय का सामान्य रूप होता है:
(x²/a²) − (y²/b²) = 1
जहाँ a प्रमुख अक्ष का अर्ध भाग है और b लघु अक्ष से सम्बन्धित स्थिरांक।
प्रश्न 22. वृत्त का सामान्य समीकरण लिखिए और उसका केन्द्र तथा त्रिज्या ज्ञात कीजिए।
उत्तर:
वृत्त का सामान्य समीकरण है —
x² + y² + 2g x + 2f y + c = 0
यहाँ,
केंद्र (h, k) = (−g, −f)
त्रिज्या r = √(g² + f² − c)
प्रश्न 23. दीर्घवृत्त का लाटस रेक्टम क्या है?
उत्तर:
दीर्घवृत्त का लाटस रेक्टम वह रेखा खंड है जो किसी फोकस से होकर जाती है तथा दीर्घवृत्त की प्रमुख धुरी पर लम्बवत होती है।
इसकी लम्बाई होती है:
L = 2b² / a
🔹 Section C — मध्यम उत्तर प्रश्न (Q24–Q27)
प्रश्न 24. परवलय y² = 4a x के लिए फोकस, निदेशिका, शीर्ष और लाटस रेक्टम ज्ञात कीजिए।
उत्तर:
दिया है: y² = 4a x
➡️ शीर्ष (Vertex): (0, 0)
➡️ फोकस (Focus): (a, 0)
➡️ निदेशिका (Directrix): x = −a
➡️ लाटस रेक्टम (Latus Rectum):
लम्बाई = 4a
अर्थात् L₁L₂ = 4a इकाई।
प्रश्न 25. दीर्घवृत्त (x²/25) + (y²/16) = 1 के लिए प्रमुख एवं लघु अक्ष की लम्बाई ज्ञात कीजिए।
उत्तर:
यहाँ a² = 25, b² = 16
➡️ a = 5, b = 4
👉 प्रमुख अक्ष = 2a = 10 इकाई
👉 लघु अक्ष = 2b = 8 इकाई
अतः दीर्घवृत्त की प्रमुख अक्ष = 10 इकाई और लघु अक्ष = 8 इकाई।
प्रश्न 26. वृत्त x² + y² − 6x + 8y + 9 = 0 का केन्द्र और त्रिज्या ज्ञात कीजिए।
उत्तर:
x² + y² − 6x + 8y + 9 = 0
इसे पूर्ण वर्ग के रूप में लिखें:
(x² − 6x + 9) + (y² + 8y + 16) = 9 + 9 + 16
⇒ (x − 3)² + (y + 4)² = 16
➡️ केन्द्र (3, −4)
➡️ त्रिज्या r = √16 = 4 इकाई
प्रश्न 27. अतिपरवलय (x²/9) − (y²/16) = 1 का विकेन्द्रता ज्ञात कीजिए।
उत्तर:
समीकरण: (x²/a²) − (y²/b²) = 1
यहाँ a² = 9, b² = 16
विकेन्द्रता e = √(1 + b²/a²)
= √(1 + 16/9)
= √(25/9)
= 5/3
अतः विकेन्द्रता e = 5/3।
✳️ Section D — दीर्घ उत्तर प्रश्न (Q28–Q31)
प्रश्न 28. परवलय x² = 4a y की विशेषताएँ एवं गुण लिखिए।
उत्तर:
🌿 परवलय की परिभाषा:
वह वक्र जो किसी स्थिर बिन्दु (नाभि) और एक स्थिर रेखा (निदेशिका) से समान दूरी पर स्थित बिन्दुओं का स्थान है।
💡 मुख्य गुण:
🔵 नाभि (a, 0)
🟢 निदेशिका x = −a
🟠 शीर्ष (0, 0)
🔴 लाटस रेक्टम की लम्बाई = 4a
🧠 सामान्य रूप: x² = 4a y या y² = 4a x
✏️ ढाल (axis) का समीकरण: y = 0
📈 सममितता: x-अक्ष के सापेक्ष
प्रश्न 29. दीर्घवृत्त (x²/a²) + (y²/b²) = 1 के लिए नाभि, अक्ष एवं लाटस रेक्टम ज्ञात कीजिए।
उत्तर:
दिया गया: (x²/a²) + (y²/b²) = 1, जहाँ a > b
➡️ नाभि की दूरी: c = √(a² − b²)
नाभि के निर्देशांक: (±c, 0)
➡️ मुख्य अक्ष (Major Axis): x-अक्ष
➡️ लघु अक्ष (Minor Axis): y-अक्ष
➡️ लाटस रेक्टम की लम्बाई: L = 2b²/a
✔️ सारांश:
दीर्घवृत्त के सभी बिन्दुओं के लिए —
नाभि से दूरी₁ + नाभि से दूरी₂ = 2a (स्थिर)
प्रश्न 30. अतिपरवलय (x²/a²) − (y²/b²) = 1 की विशेषताएँ बताइए।
उत्तर:
🌿 सामान्य रूप: (x²/a²) − (y²/b²) = 1
💡 नाभियाँ (Foci): (±√(a² + b²), 0)
💡 शीर्ष: (±a, 0)
💡 निदेशिकाएँ: x = ±(a/e), जहाँ e = √(1 + b²/a²)
🟢 असिम्प्टोट (Asymptote): y = (b/a)x तथा y = −(b/a)x
📘 विशेष गुण:
दोनों शाखाएँ x-अक्ष के दोनों ओर खुलती हैं।
केंद्र (0, 0) होता है।
विकेन्द्रता e > 1।
प्रश्न 31. यह सिद्ध कीजिए कि दीर्घवृत्त के किसी भी बिन्दु से दो नाभियों तक की दूरी का योग स्थिर रहता है।
उत्तर:
मान लीजिए दीर्घवृत्त का समीकरण है —
(x²/a²) + (y²/b²) = 1
👉 नाभियाँ: (±c, 0), जहाँ c² = a² − b²
किसी बिन्दु P(x, y) पर,
PF₁ + PF₂ = ?
📗 गणना:
PF₁ = √((x + c)² + y²)
PF₂ = √((x − c)² + y²)
दीर्घवृत्त के समीकरण से y² = b²(1 − x²/a²)
गणना के बाद मिलता है:
PF₁ + PF₂ = 2a
✅ अतः सिद्ध हुआ कि दीर्घवृत्त के किसी भी बिन्दु से दोनों नाभियों तक की दूरी का योग सदैव 2a के बराबर होता है।
✳️ Section E — अनुप्रयोगात्मक प्रश्न (Q32–Q33)
प्रश्न 32. सिद्ध कीजिए कि परवलय y² = 4a x पर बिन्दु P(x₁, y₁) पर स्पर्शरेखा का समीकरण y y₁ = 2a (x + x₁) है।
उत्तर:
📘 दिया गया: y² = 4a x
इस पर किसी बिन्दु P(x₁, y₁) पर स्पर्शरेखा चाहिए।
👉 परवलय का समीकरण है: y² = 4a x
दोनों पक्षों का अवकलन (Differentiation):
2y (dy/dx) = 4a
⇒ (dy/dx) = 2a / y
अब P(x₁, y₁) पर ढाल (m) = 2a / y₁
स्पर्शरेखा का सामान्य रूप:
(y − y₁) = m (x − x₁)
मूल्य रखने पर:
(y − y₁) = (2a / y₁)(x − x₁)
⇒ y y₁ = 2a (x + x₁)
✅ सिद्ध हुआ।
प्रश्न 33. दीर्घवृत्त (x²/9) + (y²/4) = 1 की निदेशिका का समीकरण ज्ञात कीजिए।
उत्तर:
दिया गया है — (x²/a²) + (y²/b²) = 1
यहाँ a = 3, b = 2
🌿 विकेन्द्रता:
e = √(1 − b²/a²)
= √(1 − 4/9)
= √(5/9)
= √5 / 3
✏️ निदेशिका का समीकरण:
x = ±a / e
अर्थात्
x = ±3 / (√5 / 3) = ±(9/√5)
✅ अतः निदेशिकाएँ हैं:
x = 9/√5 तथा x = −9/√5
————————————————————————————————————————————————————————————————————————————
JEE MAINS पिछले सालों के प्रश्न
🔵 प्रश्न 1
एक बिंदु (2, 3) पर स्पर्श करने वाली वृत्त की स्पर्शरेखा की ढाल क्या होगी, यदि केंद्र (0, 0) हो?
🟠 1️⃣ 3/2
🟢 2️⃣ 2/3
🔴 3️⃣ –3/2
🔵 4️⃣ –2/3
🟢 उत्तर: 2️⃣
📅 JEE Main 2019 (Shift 2, 10 Jan)
🔵 प्रश्न 2
एक दीर्घवृत्त का केंद्र मूल बिंदु पर है और उसका एक अक्ष x-अक्ष के साथ है। यदि दीर्घवृत्त की समीकरण 9x² + 16y² = 144 हो, तो इसकी उत्केन्द्रता (e) क्या होगी?
🟠 1️⃣ 5/4
🟢 2️⃣ 1/2
🔴 3️⃣ √5/4
🔵 4️⃣ 4/5
🟢 उत्तर: 4️⃣
📅 JEE Main 2017 (Offline)
🔵 प्रश्न 3
वृत्त x² + y² – 4x + 6y + 9 = 0 की त्रिज्या क्या है?
🟠 1️⃣ 4
🟢 2️⃣ 3
🔴 3️⃣ 2
🔵 4️⃣ √5
🟢 उत्तर: 2️⃣
📅 JEE Main 2020 (Shift 1, 8 Jan)
🔵 प्रश्न 4
यदि परवलय y² = 4ax की निर्देशक रेखा x = –a है, तो इसका फोकस कहाँ होगा?
🟠 1️⃣ (a, 0)
🟢 2️⃣ (–a, 0)
🔴 3️⃣ (0, a)
🔵 4️⃣ (0, –a)
🟢 उत्तर: 1️⃣
📅 JEE Main 2016
🔵 प्रश्न 5
x² + y² + 6x – 8y + 9 = 0 वृत्त का केंद्र क्या है?
🟠 1️⃣ (–3, 4)
🟢 2️⃣ (3, –4)
🔴 3️⃣ (–3, –4)
🔵 4️⃣ (3, 4)
🟢 उत्तर: 1️⃣
📅 JEE Main 2015 (Offline)
🔵 प्रश्न 6
एक परवलय y² = 4x की तली (vertex) और निर्देशक रेखा क्रमशः क्या हैं?
🟠 1️⃣ (0, 0), x = –1
🟢 2️⃣ (0, 0), x = –1
🔴 3️⃣ (1, 0), x = 0
🔵 4️⃣ (–1, 0), x = 0
🟢 उत्तर: 2️⃣
📅 JEE Main 2013
🔵 प्रश्न 7
x² + y² = r² का केन्द्र बिंदु है:
🟠 1️⃣ (0, 0)
🟢 2️⃣ (r, r)
🔴 3️⃣ (r, 0)
🔵 4️⃣ (0, r)
🟢 उत्तर: 1️⃣
📅 JEE Main 2011
🔵 प्रश्न 8
यदि परवलय y² = 12x की निर्देशक रेखा x = –3 है, तो फोकस होगा:
🟠 1️⃣ (3, 0)
🟢 2️⃣ (–3, 0)
🔴 3️⃣ (0, 3)
🔵 4️⃣ (0, –3)
🟢 उत्तर: 1️⃣
📅 JEE Main 2015
🔵 प्रश्न 9
x²/25 + y²/16 = 1 दीर्घवृत्त की प्रमुख धुरी की लंबाई है:
🟠 1️⃣ 10
🟢 2️⃣ 8
🔴 3️⃣ 5
🔵 4️⃣ 4
🟢 उत्तर: 1️⃣
📅 JEE Main 2020 (Shift 2, 9 Jan)
🔵 प्रश्न 10
वृत्त x² + y² = 4 के केंद्र और त्रिज्या क्रमशः क्या हैं?
🟠 1️⃣ (0, 0), 2
🟢 2️⃣ (0, 0), 4
🔴 3️⃣ (2, 0), 4
🔵 4️⃣ (0, 2), 2
🟢 उत्तर: 1️⃣
📅 JEE Main 2016
🔵 प्रश्न 11
परवलय y² = 4x की दिशा क्या है?
🟠 1️⃣ x-अक्ष की धनात्मक दिशा
🟢 2️⃣ x-अक्ष की ऋणात्मक दिशा
🔴 3️⃣ y-अक्ष की धनात्मक दिशा
🔵 4️⃣ y-अक्ष की ऋणात्मक दिशा
🟢 उत्तर: 1️⃣
📅 JEE Main 2018
🔵 प्रश्न 12
एक वृत की दो स्पर्श रेखाएँ बनाने वाले कोण के बीच का कोण है:
🟠 1️⃣ 180°
🟢 2️⃣ 90°
🔴 3️⃣ 45°
🔵 4️⃣ 60°
🟢 उत्तर: 2️⃣
📅 JEE Main 2013
🔵 प्रश्न 13
दीर्घवृत्त x²/16 + y²/9 = 1 का उत्केन्द्रता है:
🟠 1️⃣ 1/2
🟢 2️⃣ 3/4
🔴 3️⃣ √7/4
🔵 4️⃣ √5/4
🟢 उत्तर: 3️⃣
📅 JEE Main 2019 (Shift 1, 9 Jan)
🔵 प्रश्न 14
वृत्त x² + y² – 2x – 4y + 1 = 0 की त्रिज्या है:
🟠 1️⃣ √5
🟢 2️⃣ √6
🔴 3️⃣ 2
🔵 4️⃣ 3
🟢 उत्तर: 1️⃣
📅 JEE Main 2021
🔵 प्रश्न 15
यदि y² = 4x और x² = 4y दो परवलय हैं, तो वे कितने बिंदुओं पर मिलते हैं?
🟠 1️⃣ 0
🟢 2️⃣ 1
🔴 3️⃣ 2
🔵 4️⃣ 4
🟢 उत्तर: 4️⃣
📅 JEE Main 2017
🔵 प्रश्न 16
वृत्त x² + y² + 2gx + 2fy + c = 0 का केंद्र और त्रिज्या हैं:
🟠 1️⃣ (–g, –f), sqrt(g² + f² – c)
🟢 2️⃣ (g, f), sqrt(g² + f² + c)
🔴 3️⃣ (–g, –f), sqrt(g² + f² + c)
🔵 4️⃣ (–g, –f), sqrt(g² + f² – c)
🟢 उत्तर: 4️⃣
📅 JEE Main 2020
🔵 प्रश्न 17
परवलय y² = 8x के फोकस की स्थिति:
🟠 1️⃣ (2, 0)
🟢 2️⃣ (4, 0)
🔴 3️⃣ (0, 2)
🔵 4️⃣ (0, 4)
🟢 उत्तर: 1️⃣
📅 JEE Main 2014
🔵 प्रश्न 18
यदि किसी वृत्त की त्रिज्या 5 है, तो व्यास है:
🟠 1️⃣ 10
🟢 2️⃣ 5
🔴 3️⃣ 25
🔵 4️⃣ √5
🟢 उत्तर: 1️⃣
📅 JEE Main 2012
🔵 प्रश्न 19
x² – 2x + y² – 4y = 0 का केंद्र और त्रिज्या हैं:
🟠 1️⃣ (1, 2), sqrt(5)
🟢 2️⃣ (–1, –2), sqrt(5)
🔴 3️⃣ (1, –2), sqrt(10)
🔵 4️⃣ (–1, 2), sqrt(10)
🟢 उत्तर: 1️⃣
📅 JEE Main 2019
🔵 प्रश्न 20
y² = 4x और y = 2x – 1 के बीच के बिंदु कौन से हैं जो दोनों को संतुष्ट करते हैं?
🟠 1️⃣ (1, 1)
🟢 2️⃣ (4, 2)
🔴 3️⃣ (0, 0)
🔵 4️⃣ (2, 2)
🟢 उत्तर: 4️⃣
📅 JEE Main 2021
🔵 प्रश्न 21
वृत्त x² + y² = 25 की त्रिज्या है:
🟠 1️⃣ 25
🟢 2️⃣ 5
🔴 3️⃣ 10
🔵 4️⃣ 0
🟢 उत्तर: 2️⃣
📅 JEE Main 2010
🔵 प्रश्न 22
परवलय y² = 4ax का निर्देशक रेखा है:
🟠 1️⃣ x = a
🟢 2️⃣ x = –a
🔴 3️⃣ y = a
🔵 4️⃣ y = –a
🟢 उत्तर: 2️⃣
📅 JEE Main 2013
🔵 प्रश्न 23
वृत्त x² + y² = r² की परिधि है:
🟠 1️⃣ 2πr
🟢 2️⃣ πr²
🔴 3️⃣ πr
🔵 4️⃣ 4πr
🟢 उत्तर: 1️⃣
📅 JEE Main 2016
🔵 प्रश्न 24
x² + y² + 4x – 6y + 9 = 0 वृत्त की त्रिज्या:
🟠 1️⃣ √13
🟢 2️⃣ √14
🔴 3️⃣ √16
🔵 4️⃣ √15
🟢 उत्तर: 1️⃣
📅 JEE Main 2020
🔵 प्रश्न 25
दीर्घवृत्त x²/25 + y²/9 = 1 की प्रमुख धुरी y-अक्ष के साथ है या नहीं?
🟠 1️⃣ हाँ
🟢 2️⃣ नहीं
🔴 3️⃣ हो भी सकती है
🔵 4️⃣ निश्चित नहीं
🟢 उत्तर: 2️⃣
📅 JEE Main 2019
🔵 प्रश्न 26
यदि एक दीर्घवृत्त की विषम अक्ष की लंबाई 10 है तथा एक उत्केन्द्रता 4/5 है, तो दीर्घवृत्त की अर्ध-केंद्र दूरी क्या होगी?
🟥 1️⃣ 6
🟩 2️⃣ 8
🟦 3️⃣ 5
🟨 4️⃣ 4
🟢 उत्तर: 2️⃣ 8
📘 JEE Main 2021 (Shift 2)
🔵 प्रश्न 27
यदि x² + y² = 25 और x = 3 से काटी गई रेखा की लंबाई क्या होगी?
🟥 1️⃣ 4
🟩 2️⃣ 6
🟦 3️⃣ 8
🟨 4️⃣ 10
🟢 उत्तर: 2️⃣ 6
📘 JEE Main 2019 (Jan Attempt)
🔵 प्रश्न 28
x² − y² = 16 शंकु का केंद्र बिंदु क्या होगा?
🟥 1️⃣ (0, 0)
🟩 2️⃣ (4, 0)
🟦 3️⃣ (0, 4)
🟨 4️⃣ (4, 4)
🟢 उत्तर: 1️⃣ (0, 0)
📘 JEE Main 2020
🔵 प्रश्न 29
यदि एक परवलय की शीर्ष बिंदु (2, –3) है और निर्देशिका y = –1 है, तो उसका लाक्षणिक समीकरण क्या होगा?
🟥 1️⃣ (x – 2)² = 8(y + 3)
🟩 2️⃣ (x – 2)² = –8(y + 3)
🟦 3️⃣ (y + 3)² = 8(x – 2)
🟨 4️⃣ (y + 3)² = –8(x – 2)
🟢 उत्तर: 2️⃣ (x – 2)² = –8(y + 3)
📘 JEE Main 2021
🔵 प्रश्न 30
एक वृत्त जिसकी त्रिज्या 5 है, और केन्द्र (1, 2) है, x = 4 रेखा से इसकी छेदन लंबाई क्या होगी?
🟥 1️⃣ 4
🟩 2️⃣ 6
🟦 3️⃣ √41
🟨 4️⃣ √24
🟢 उत्तर: 3️⃣ √41
📘 JEE Main 2022
🔵 प्रश्न 31
x²/9 + y²/16 = 1 दीर्घवृत्त की उत्केन्द्रता क्या है?
🟥 1️⃣ 1/2
🟩 2️⃣ 5/4
🟦 3️⃣ 1/3
🟨 4️⃣ 4/5
🟢 उत्तर: 4️⃣ 4/5
📘 JEE Main 2018
🔵 प्रश्न 32
परवलय y² = 8x पर केंद्रित एक बिंदु पर स्पर्श रेखा की प्रवणता 1 है, उस बिंदु के निर्देशांक क्या होंगे?
🟥 1️⃣ (2, 2)
🟩 2️⃣ (2, –2)
🟦 3️⃣ (4, 4)
🟨 4️⃣ (1, 2)
🟢 उत्तर: 1️⃣ (2, 2)
📘 JEE Main 2023
🔵 प्रश्न 33
x² − 4x + y² − 6y + 9 = 0 किस आकृति का समीकरण है?
🟥 1️⃣ वृत्त
🟩 2️⃣ परवलय
🟦 3️⃣ दीर्घवृत्त
🟨 4️⃣ अतिदीर्घवृत्त
🟢 उत्तर: 1️⃣ वृत्त
📘 JEE Main 2019
🔵 प्रश्न 34
यदि परवलय y² = 4ax की निर्देशिका है x = –a, तो फोकस क्या होगा?
🟥 1️⃣ (0, 0)
🟩 2️⃣ (a, 0)
🟦 3️⃣ (–a, 0)
🟨 4️⃣ (0, a)
🟢 उत्तर: 2️⃣ (a, 0)
📘 JEE Main 2017
🔵 प्रश्न 35
x² + y² = 25 और x + y = 5 रेखा के बीच छेदन बिंदु कितने होंगे?
🟥 1️⃣ 0
🟩 2️⃣ 1
🟦 3️⃣ 2
🟨 4️⃣ अनंत
🟢 उत्तर: 3️⃣ 2
📘 JEE Main 2016
🔵 प्रश्न 36
यदि y² = 4ax परवलय पर किसी बिंदु से खींची गई स्पर्श रेखा का झुकाव m है, तो स्पर्श रेखा का समीकरण क्या होगा?
🟥 1️⃣ y = mx + a/m
🟩 2️⃣ y = mx – a/m
🟦 3️⃣ y = mx + a/m²
🟨 4️⃣ y = mx – a/m²
🟢 उत्तर: 1️⃣ y = mx + a/m
📘 JEE Main 2020
🔵 प्रश्न 37
यदि एक वृत्त x² + y² + 2gx + 2fy + c = 0 है, तो इसका केंद्र होगा:
🟥 1️⃣ (g, f)
🟩 2️⃣ (–g, –f)
🟦 3️⃣ (–2g, –2f)
🟨 4️⃣ (2g, 2f)
🟢 उत्तर: 2️⃣ (–g, –f)
📘 JEE Main 2018
🔵 प्रश्न 38
x²/4 + y²/9 = 1 और y = 3x रेखा के छेदन बिंदु कितने हैं?
🟥 1️⃣ 0
🟩 2️⃣ 1
🟦 3️⃣ 2
🟨 4️⃣ ∞
🟢 उत्तर: 3️⃣ 2
📘 JEE Main 2017
🔵 प्रश्न 39
x² + y² − 6x − 8y + 9 = 0 वृत की त्रिज्या क्या है?
🟥 1️⃣ 5
🟩 2️⃣ 3
🟦 3️⃣ 4
🟨 4️⃣ 2
🟢 उत्तर: 1️⃣ 5
📘 JEE Main 2015
🔵 प्रश्न 40
यदि a परवलय y² = 4ax की latus rectum है, तो उसकी लंबाई क्या होगी?
🟥 1️⃣ 2a
🟩 2️⃣ a
🟦 3️⃣ 4a
🟨 4️⃣ a/2
🟢 उत्तर: 3️⃣ 4a
📘 JEE Main 2022
🔵 प्रश्न 41
एक दीर्घवृत्त का लघु अक्ष 6 है और उत्केन्द्रता 2/3 है, तो उसकी दीर्घ अक्ष की लंबाई क्या होगी?
🟥 1️⃣ 12
🟩 2️⃣ 10
🟦 3️⃣ 8
🟨 4️⃣ 6
🟢 उत्तर: 1️⃣ 12
📘 JEE Main 2023
🔵 प्रश्न 42
x² − 2x + y² + 4y = –4 समीकरण को वृत के रूप में पुनर्लेखन करें:
🟥 1️⃣ (x – 1)² + (y + 2)² = 1
🟩 2️⃣ (x + 1)² + (y + 2)² = 4
🟦 3️⃣ (x – 2)² + (y – 4)² = 1
🟨 4️⃣ (x + 2)² + (y – 1)² = 1
🟢 उत्तर: 1️⃣ (x – 1)² + (y + 2)² = 1
📘 JEE Main 2020
🔵 प्रश्न 43
y² = 16x परवलय पर स्थित बिंदु (4, 8) पर स्पर्श रेखा का समीकरण क्या होगा?
🟥 1️⃣ y = x + 4
🟩 2️⃣ y = 2x
🟦 3️⃣ y = x – 4
🟨 4️⃣ y = 2x + 0
🟢 उत्तर: 2️⃣ y = 2x
📘 JEE Main 2021
🔵 प्रश्न 44
यदि x² + y² + 4x – 6y + 9 = 0, तो वृत का केन्द्र और त्रिज्या क्या है?
🟥 1️⃣ (–2, 3), √4
🟩 2️⃣ (2, –3), √9
🟦 3️⃣ (–2, 3), √2
🟨 4️⃣ (–2, 3), √1
🟢 उत्तर: 1️⃣ (–2, 3), √4
📘 JEE Main 2019
🔵 प्रश्न 45
x² – y² = 0 का ज्यामितीय निरूपण क्या है?
🟥 1️⃣ एक बिंदु
🟩 2️⃣ दो रेखाएं
🟦 3️⃣ एक वृत्त
🟨 4️⃣ एक परवलय
🟢 उत्तर: 2️⃣ दो रेखाएं
📘 JEE Main 2016
🔵 प्रश्न 46
x² + y² – 10x + 16y + 72 = 0 समीकरण किस आकृति का है?
🟥 1️⃣ वृत्त
🟩 2️⃣ दीर्घवृत्त
🟦 3️⃣ अतिदीर्घवृत्त
🟨 4️⃣ परवलय
🟢 उत्तर: 1️⃣ वृत्त
📘 JEE Main 2021
🔵 प्रश्न 47
किसी परवलय y² = 4x पर (1, 2) बिंदु पर स्पर्श रेखा की प्रवणता क्या होगी?
🟥 1️⃣ 1
🟩 2️⃣ 2
🟦 3️⃣ 1/2
🟨 4️⃣ –1
🟢 उत्तर: 1️⃣ 1
📘 JEE Main 2015
🔵 प्रश्न 48
दीर्घवृत्त x²/25 + y²/9 = 1 का केंद्र है:
🟥 1️⃣ (0, 0)
🟩 2️⃣ (5, 0)
🟦 3️⃣ (0, 3)
🟨 4️⃣ (1, 1)
🟢 उत्तर: 1️⃣ (0, 0)
📘 JEE Main 2022
🔵 प्रश्न 49
y² = 4ax परवलय पर (at², 2at) पर स्पर्श रेखा का समीकरण क्या है?
🟥 1️⃣ ty = x + at²
🟩 2️⃣ ty = x – at²
🟦 3️⃣ y = tx + a/t
🟨 4️⃣ y = tx + a/t²
🟢 उत्तर: 1️⃣ ty = x + at²
📘 JEE Main 2018
🔵 प्रश्न 50
x²/16 + y²/9 = 1 दीर्घवृत्त की उत्केन्द्रता होगी:
🟥 1️⃣ √(7)/4
🟩 2️⃣ √(7)/3
🟦 3️⃣ √(5)/4
🟨 4️⃣ √(5)/3
🟢 उत्तर: 1️⃣ √(7)/4
📘 JEE Main 2020
————————————————————————————————————————————————————————————————————————————
JEE ADVANCED पिछले सालों के प्रश्न
🔵 प्रश्न 1
यदि वृत्त 𝑥² + 𝑦² = 4 और परवलय 𝑦² = 4𝑥 परस्पर काटते हैं, तो उनके प्रतिच्छेद बिंदुओं की अधिकतम संख्या कितनी होगी?
🟥 1️⃣ शून्य
🟩 2️⃣ एक
🟦 3️⃣ दो
🟨 4️⃣ चार
🟢 उत्तर: 4️⃣ चार
📅 JEE Advanced 2015, Paper 1
🔵 प्रश्न 2
परवलय 𝑥² = 8𝑦 तथा वृत 𝑥² + 𝑦² = 25 के प्रतिच्छेद बिंदुओं की संख्या है:
🟥 1️⃣ 0
🟩 2️⃣ 2
🟦 3️⃣ 4
🟨 4️⃣ अनंत
🟢 उत्तर: 3️⃣ 4
📅 JEE Advanced 2017, Paper 1
🔵 प्रश्न 3
वृत्त 𝑥² + 𝑦² + 4𝑥 − 6𝑦 + 9 = 0 का केंद्र है:
🟥 1️⃣ (−2, 3)
🟩 2️⃣ (2, −3)
🟦 3️⃣ (−2, −3)
🟨 4️⃣ (2, 3)
🟢 उत्तर: 1️⃣ (−2, 3)
📅 JEE Advanced 2018, Paper 1
🔵 प्रश्न 4
परवलय 𝑦² = 4𝑎𝑥 में, फोकस और नियामक के बीच की दूरी है:
🟥 1️⃣ 𝑎
🟩 2️⃣ 2𝑎
🟦 3️⃣ 3𝑎
🟨 4️⃣ 4𝑎
🟢 उत्तर: 2️⃣ 2𝑎
📅 JEE Advanced 2014, Paper 1
🔵 प्रश्न 5
हाइपरबोला 𝑥²/9 − 𝑦²/4 = 1 की एक ताना रेखा है:
🟥 1️⃣ 𝑥 = 3
🟩 2️⃣ 𝑥 = −3
🟦 3️⃣ 𝑦 = 2
🟨 4️⃣ 𝑥 = 0
🟢 उत्तर: 1️⃣ 𝑥 = 3
📅 JEE Advanced 2016, Paper 1
🔵 प्रश्न 6
यदि परवलय 𝑦² = 4𝑎𝑥 की एक ज्या रेखा y = 2 है, तो उसकी लंबाई होगी:
🟥 1️⃣ 4𝑎
🟩 2️⃣ 8𝑎
🟦 3️⃣ 2𝑎
🟨 4️⃣ 𝑎
🟢 उत्तर: 1️⃣ 4𝑎
📅 JEE Advanced 2011, Paper 1
🔵 प्रश्न 7
यदि किसी वृत्त का त्रिज्या 5 इकाई हो और उसका केंद्र (3, −4) हो, तो वृत्त का समीकरण होगा:
🟥 1️⃣ 𝑥² + 𝑦² − 6𝑥 + 8𝑦 + 16 = 0
🟩 2️⃣ 𝑥² + 𝑦² − 6𝑥 − 8𝑦 + 25 = 0
🟦 3️⃣ (𝑥 − 3)² + (𝑦 + 4)² = 25
🟨 4️⃣ (𝑥 + 3)² + (𝑦 − 4)² = 25
🟢 उत्तर: 3️⃣ (𝑥 − 3)² + (𝑦 + 4)² = 25
📅 JEE Advanced 2013, Paper 1
🔵 प्रश्न 8
यदि परवलय 𝑦² = 4𝑥 तथा वृत 𝑥² + 𝑦² = 9 परस्पर स्पर्श करते हैं, तो परवलय की योजक रेखा की ढाल है:
🟥 1️⃣ 1
🟩 2️⃣ −1
🟦 3️⃣ 2
🟨 4️⃣ 0
🟢 उत्तर: 1️⃣ 1
📅 JEE Advanced 2019, Paper 1
🔵 प्रश्न 9
हाइपरबोला 𝑥²/𝑎² − 𝑦²/𝑏² = 1 की लांबी तथा कंपीगामी अक्षों की संख्या है:
🟥 1️⃣ 2𝑎, 2𝑏
🟩 2️⃣ 𝑎, 𝑏
🟦 3️⃣ 𝑎², 𝑏²
🟨 4️⃣ √𝑎, √𝑏
🟢 उत्तर: 1️⃣ 2𝑎, 2𝑏
📅 JEE Advanced 2012, Paper 1
🔵 प्रश्न 10
परवलय 𝑦² = 4𝑎𝑥 की योजक रेखा का समीकरण है:
🟥 1️⃣ 𝑥 = 0
🟩 2️⃣ 𝑥 = −𝑎
🟦 3️⃣ 𝑦 = 0
🟨 4️⃣ 𝑥 = 𝑎
🟢 उत्तर: 2️⃣ 𝑥 = −𝑎
📅 JEE Advanced 2021, Paper 1
🔵 प्रश्न 11
हाइपरबोला 𝑥² − 𝑦² = 1 तथा 𝑥𝑦 = 1 रेखा कितनी बार प्रतिच्छेद करती है?
🟥 1️⃣ 0
🟩 2️⃣ 1
🟦 3️⃣ 2
🟨 4️⃣ 4
🟢 उत्तर: 4️⃣ 4
📅 JEE Advanced 2020, Paper 1
🔵 प्रश्न 12
यदि परवलय 𝑦² = 4𝑎𝑥 के योजक बिंदु से होकर एक रेखा 𝑦 = 𝑚𝑥 + 𝑐 जाती है, तो उसका ढाल 𝑚 है:
🟥 1️⃣ 1
🟩 2️⃣ −1
🟦 3️⃣ 0
🟨 4️⃣ 2
🟢 उत्तर: 2️⃣ −1
📅 JEE Advanced 2017, Paper 1
🔵 प्रश्न 13
यदि दो परवलय 𝑦² = 4𝑥 तथा 𝑥² = 4𝑦 प्रतिच्छेद करते हैं, तो उनके प्रतिच्छेद बिंदुओं की संख्या है:
🟥 1️⃣ 2
🟩 2️⃣ 4
🟦 3️⃣ 1
🟨 4️⃣ 0
🟢 उत्तर: 2️⃣ 4
📅 JEE Advanced 2016, Paper 1
🔵 प्रश्न 14
वृत्त 𝑥² + 𝑦² + 6𝑥 − 8𝑦 + 9 = 0 की त्रिज्या है:
🟥 1️⃣ 4
🟩 2️⃣ 5
🟦 3️⃣ 3
🟨 4️⃣ √10
🟢 उत्तर: 2️⃣ 5
📅 JEE Advanced 2011, Paper 1
🔵 प्रश्न 15
वृत्त की ज्या रेखा अधिकतम लंबाई की होती है जब वह गुजरती है:
🟥 1️⃣ किसी भी बिंदु से
🟩 2️⃣ केंद्र से
🟦 3️⃣ परिधि से
🟨 4️⃣ ज्या रेखा के लंबवत
🟢 उत्तर: 2️⃣ केंद्र से
📅 JEE Advanced 2012, Paper 1
🔵 प्रश्न 16
𝑦² = 4𝑎𝑥 तथा 𝑥² = 4𝑏𝑦 परवलयों के प्रतिच्छेद बिंदु हैं:
🟥 1️⃣ 0
🟩 2️⃣ 1
🟦 3️⃣ 2
🟨 4️⃣ 4
🟢 उत्तर: 4️⃣ 4
📅 JEE Advanced 2021, Paper 1
🔵 प्रश्न 17
यदि हाइपरबोला का केंद्र मूल बिंदु हो और समीकरण 𝑥² − 𝑦² = 4 हो, तो उसके विषम केंद्रों की दूरी:
🟥 1️⃣ 4
🟩 2️⃣ 2√2
🟦 3️⃣ 2
🟨 4️⃣ 4√2
🟢 उत्तर: 1️⃣ 4
📅 JEE Advanced 2022, Paper 1
🔵 प्रश्न 18
एक बिंदु P, वृत्त x² + y² = a² पर इस प्रकार स्थित है कि उसका प्रक्षेप, शंकु x² + y² = 2az पर स्थित होता है। यदि वह बिंदु (a cosθ, a sinθ, 0) है, तो प्रक्षेप बिंदु के निर्देशांक होंगे
1️⃣ (a cosθ, a sinθ, a sin²θ)
2️⃣ (a cosθ, a sinθ, a cos²θ)
3️⃣ (a cosθ, a sinθ, a tan²θ)
4️⃣ (a cosθ, a sinθ, a cot²θ)
🟢 उत्तर: 1️⃣
📅 JEE Advanced 2021 – Paper 2
🔵 प्रश्न 19
शंकु x² + y² = z² पर स्थित एक बिंदु से मूल तक खींची गई स्पर्श रेखा की लंबाई है:
1️⃣ 1
2️⃣ √2
3️⃣ 2
4️⃣ √3
🟢 उत्तर: 2️⃣
📅 JEE Advanced 2019 – Paper 2
🔵 प्रश्न 20
यदि दो बिंदु A(1,2,3) और B(2,3,4) शंकु x² + y² = z² पर स्थित हैं, तो इन बिंदुओं को जोड़ने वाली रेखा उस शंकु को कितनी बार काटेगी?
1️⃣ 0
2️⃣ 1
3️⃣ 2
4️⃣ अनंत
🟢 उत्तर: 3️⃣
📅 JEE Advanced 2020 – Paper 2
🔵 प्रश्न 21
यदि कोई रेखा शंकु x² + y² = 4z² को ठीक दो बिंदुओं पर काटती है, तो उसे कहा जाएगा –
1️⃣ स्पर्श रेखा
2️⃣ तुल्यकेंद्र रेखा
3️⃣ विवर्तन रेखा
4️⃣ छेदक रेखा
🟢 उत्तर: 4️⃣
📅 JEE Advanced 2017 – Paper 2
🔵 प्रश्न 22
शंकु x² + y² = z² का शीर्ष होता है –
1️⃣ x-अक्ष पर
2️⃣ y-अक्ष पर
3️⃣ मूल पर
4️⃣ z-अक्ष पर
🟢 उत्तर: 3️⃣
📅 JEE Advanced 2016 – Paper 2
🔵 प्रश्न 23
शंकु x² + y² = 9z² और तल z = 2 के मध्य के वक्र की लम्बाई है:
1️⃣ 6π
2️⃣ 3π
3️⃣ 2π
4️⃣ 9π
🟢 उत्तर: 1️⃣
📅 JEE Advanced 2014 – Paper 2
🔵 प्रश्न 24
एक शंकु की समीकरण है x² + y² = 2z²। यदि कोई रेखा इस शंकु को दो बार काटती है, तो वह –
1️⃣ छेदक रेखा है
2️⃣ स्पर्श रेखा है
3️⃣ अक्षांश रेखा है
4️⃣ ऊपर में से कोई नहीं
🟢 उत्तर: 1️⃣
📅 JEE Advanced 2013 – Paper 2
🔵 प्रश्न 25
शंकु x² + y² – z² = 0 को किस तल द्वारा काटने पर प्राप्त वक्र एक वृत्त होगा?
1️⃣ z = k
2️⃣ x = k
3️⃣ y = k
4️⃣ z = x
🟢 उत्तर: 1️⃣
📅 JEE Advanced 2012 – Paper 2
🔵 प्रश्न 26
यदि P(x, y, z) शंकु x² + y² = z² पर स्थित है, तो कौन सा कथन सत्य है?
1️⃣ x² + y² – z² = 0
2️⃣ x² + y² + z² = 0
3️⃣ x² – y² = z²
4️⃣ x² + y² = –z²
🟢 उत्तर: 1️⃣
📅 JEE Advanced 2011 – Paper 2
🔵 प्रश्न 27
निम्न में से कौन सा वक्र त्रिविमीय स्थान में एक शंकु को निरूपित करता है?
1️⃣ x² + y² + z² = 1
2️⃣ x² + y² – z² = 0
3️⃣ x² + y² = z
4️⃣ z² = x + y
🟢 उत्तर: 2️⃣
📅 JEE Advanced 2010 – Paper 2
🔵 प्रश्न 28
शंकु x² + y² = 4z² पर स्थित बिंदु (2, 2, 1) की स्थिति के लिए कौन सा विकल्प सही है?
1️⃣ यह शंकु के अंदर स्थित है
2️⃣ यह शंकु के बाहर स्थित है
3️⃣ यह शंकु पर स्थित है
4️⃣ यह शंकु के ऊपर स्थित है
🟢 उत्तर: 3️⃣
📅 JEE Advanced 2009 – Paper 2
🔵 प्रश्न 29
यदि कोई रेखा, शंकु x² + y² = z² को स्पर्श करती है, तो वह रेखा किस दूरी पर मूल से होगी?
1️⃣ 1
2️⃣ √2
3️⃣ √3
4️⃣ 2
🟢 उत्तर: 2️⃣
📅 JEE Advanced 2008 – Paper 2
🔵 प्रश्न 30
x² + y² = z² शंकु का काटने वाला तल z = 1 है। प्राप्त वक्र की प्रकृति क्या होगी?
1️⃣ वृत्त
2️⃣ दीर्घवृत्त
3️⃣ परवलय
4️⃣ रेखा
🟢 उत्तर: 1️⃣
📅 JEE Advanced 2006 – Paper 2
🔵 प्रश्न 31
x² + y² – z² = 0 से बनी सतह का प्रकार है –
1️⃣ शंकु
2️⃣ गोला
3️⃣ बेलन
4️⃣ समतल
🟢 उत्तर: 1️⃣
📅 JEE Advanced 2005 – Paper 2
🔵 प्रश्न 32
शंकु x² + y² = z² और तल z = √2 के प्रतिच्छेदन वक्र की परिधि है:
1️⃣ 2π
2️⃣ 4π
3️⃣ √2π
4️⃣ 2√2π
🟢 उत्तर: 4️⃣
📅 JEE Advanced 2004 – Paper 2
🔵 प्रश्न 33
शंकु x² + y² = 2z² और z = 1 के बीच का वक्र कौन सा है?
1️⃣ वृत्त
2️⃣ दीर्घवृत्त
3️⃣ रेखा
4️⃣ उपवृत्त
🟢 उत्तर: 1️⃣
📅 JEE Advanced 2003 – Paper 2
🔵 प्रश्न 34
यदि कोई बिंदु शंकु x² + y² = z² के अंदर स्थित है, तो उसका स्थानांक (x, y, z) किस रूप में व्यक्त किया जा सकता है?
1️⃣ x² + y² < z² 2️⃣ x² + y² > z²
3️⃣ x² + y² = z²
4️⃣ इनमें से कोई नहीं
🟢 उत्तर: 1️⃣
📅 JEE Advanced 2002 – Paper 2
————————————————————————————————————————————————————————————————————————————
प्रतियोगी परीक्षाओं के लिए मॉडल अभ्यास सेट
🟣 Q1–Q20 : (मध्यम कठिनाई)
Q1. यदि किसी वृत्त का त्रिज्या r है, तो उसका क्षेत्रफल होगा —
🔵 (A) πr²
🟢 (B) 2πr
🟠 (C) 4πr²
🔴 (D) πr
Answer: (A) πr²
Q2. वृत्त (x – a)² + (y – b)² = r² का केन्द्र है —
🔵 (A) (a, b)
🟢 (B) (−a, −b)
🟠 (C) (a, −b)
🔴 (D) (−a, b)
Answer: (A) (a, b)
Q3. वृत्त का मानक समीकरण होता है —
🔵 (A) x² + y² = r²
🟢 (B) x² − y² = r²
🟠 (C) x² + y² + 2gx + 2fy + c = 0
🔴 (D) x² + y² − 2gx − 2fy + c = 0
Answer: (A) x² + y² = r²
Q4. परवलय y² = 4ax का शीर्ष है —
🔵 (A) (a, 0)
🟢 (B) (0, 0)
🟠 (C) (−a, 0)
🔴 (D) (0, a)
Answer: (B) (0, 0)
Q5. परवलय y² = 4ax की निदेशिका होती है —
🔵 (A) x = a
🟢 (B) x = −a
🟠 (C) y = a
🔴 (D) y = −a
Answer: (B) x = −a
Q6. परवलय y² = 4ax का फोकस होता है —
🔵 (A) (0, a)
🟢 (B) (a, 0)
🟠 (C) (−a, 0)
🔴 (D) (0, −a)
Answer: (B) (a, 0)
Q7. दीर्घवृत्त x²/a² + y²/b² = 1 में यदि a > b हो, तो उसका फोकस होगा —
🔵 (A) (±c, 0)
🟢 (B) (0, ±c)
🟠 (C) (±a, 0)
🔴 (D) (±b, 0)
Answer: (A) (±c, 0)
Q8. दीर्घवृत्त के लिए सम्बन्ध होता है —
🔵 (A) c² = a² + b²
🟢 (B) c² = a² − b²
🟠 (C) c² = b² − a²
🔴 (D) c² = a²b²
Answer: (B) c² = a² − b²
Q9. अतिपरवलय का मानक समीकरण होता है —
🔵 (A) x²/a² − y²/b² = 1
🟢 (B) y²/b² − x²/a² = 1
🟠 (C) x²/a² + y²/b² = 1
🔴 (D) y²/a² − x²/b² = 0
Answer: (A) x²/a² − y²/b² = 1
Q10. परवलय y² = 4ax की लाटस रेक्टम की लम्बाई है —
🔵 (A) 2a
🟢 (B) 4a
🟠 (C) a
🔴 (D) 8a
Answer: (B) 4a
Q11. यदि किसी परवलय की ढाल रेखा x-अक्ष से समांतर हो, तो उसका समीकरण होगा —
🔵 (A) y² = 4ax
🟢 (B) x² = 4ay
🟠 (C) y² + 4ax = 0
🔴 (D) x² − 4ay = 0
Answer: (B) x² = 4ay
Q12. दीर्घवृत्त की विकेन्द्रता (e) होती है —
🔵 (A) √(1 − b²/a²)
🟢 (B) √(1 + b²/a²)
🟠 (C) √(a² − b²)
🔴 (D) b/a
Answer: (A) √(1 − b²/a²)
Q13. अतिपरवलय की विकेन्द्रता (e) होती है —
🔵 (A) √(1 − b²/a²)
🟢 (B) √(1 + b²/a²)
🟠 (C) a/b
🔴 (D) b/a
Answer: (B) √(1 + b²/a²)
Q14. दीर्घवृत्त के केन्द्र के निर्देशांक —
🔵 (A) (0, 0)
🟢 (B) (a, 0)
🟠 (C) (0, a)
🔴 (D) (a, b)
Answer: (A) (0, 0)
Q15. अतिपरवलय का केन्द्र होता है —
🔵 (A) (a, 0)
🟢 (B) (0, 0)
🟠 (C) (−a, 0)
🔴 (D) (0, a)
Answer: (B) (0, 0)
Q16. यदि किसी वृत्त का व्यास 10 है, तो उसकी त्रिज्या होगी —
🔵 (A) 10
🟢 (B) 5
🟠 (C) 20
🔴 (D) 2
Answer: (B) 5
Q17. दीर्घवृत्त के अक्षों का अनुपात कहलाता है —
🔵 (A) विकेन्द्रता
🟢 (B) झुकाव
🟠 (C) अक्ष अनुपात
🔴 (D) लाटस रेक्टम
Answer: (C) अक्ष अनुपात
Q18. अतिपरवलय में a² और b² के बीच सम्बन्ध —
🔵 (A) c² = a² − b²
🟢 (B) c² = b² − a²
🟠 (C) a² = b² + c²
🔴 (D) b² = a² + c²
Answer: (A) c² = a² − b²
Q19. यदि दीर्घवृत्त की विकेन्द्रता e = 0 हो, तो वह बन जाता है —
🔵 (A) अतिपरवलय
🟢 (B) परवलय
🟠 (C) वृत्त
🔴 (D) सीधी रेखा
Answer: (C) वृत्त
Q20. परवलय का मानक समीकरण जो ऊपर की ओर खुलता है —
🔵 (A) x² = 4ay
🟢 (B) y² = 4ax
🟠 (C) x² + y² = r²
🔴 (D) y² = 4a(x − h)
Answer: (A) x² = 4ay
🔵 Q21–Q40 : JEE Main स्तर (उन्नत कठिनाई)
Q21. परवलय y² = 8x का फोकस है —
🔵 (A) (2, 0)
🟢 (B) (4, 0)
🟠 (C) (0, 4)
🔴 (D) (−2, 0)
Answer: (B) (4, 0)
Q22. परवलय y² = 12x की निदेशिका का समीकरण है —
🔵 (A) x = −3
🟢 (B) x = 3
🟠 (C) y = 3
🔴 (D) y = −3
Answer: (A) x = −3
Q23. दीर्घवृत्त x²/16 + y²/9 = 1 का विकेन्द्रता (e) है —
🔵 (A) √(1 − 9/16)
🟢 (B) √(1 + 9/16)
🟠 (C) √(7/16)
🔴 (D) 3/4
Answer: (A) √(1 − 9/16)
Q24. दीर्घवृत्त x²/25 + y²/9 = 1 के फोकसों के निर्देशांक हैं —
🔵 (A) (±4, 0)
🟢 (B) (±5, 0)
🟠 (C) (±3, 0)
🔴 (D) (0, ±5)
Answer: (A) (±4, 0)
Q25. अतिपरवलय x²/9 − y²/4 = 1 के फोकसों के निर्देशांक —
🔵 (A) (±√13, 0)
🟢 (B) (±3, 0)
🟠 (C) (±5, 0)
🔴 (D) (±2, 0)
Answer: (A) (±√13, 0)
Q26. यदि दीर्घवृत्त x²/a² + y²/b² = 1 में a = 5, b = 4 हो, तो c का मान —
🔵 (A) 3
🟢 (B) 4
🟠 (C) 5
🔴 (D) 6
Answer: (A) 3
Q27. परवलय x² = 4ay के स्पर्शरेखा का समीकरण ढाल m के रूप में —
🔵 (A) y = mx + a/m
🟢 (B) y = mx + a/m²
🟠 (C) y = mx + m/a
🔴 (D) y = mx − a/m
Answer: (A) y = mx + a/m
Q28. परवलय y² = 4ax की अभिलम्ब का समीकरण ढाल m के रूप में —
🔵 (A) y = −(1/m)x + a/m
🟢 (B) y = −(1/m)x + a/m²
🟠 (C) y = −(1/m)x − a/m
🔴 (D) y = −(1/m)x − a/m²
Answer: (C) y = −(1/m)x − a/m
Q29. दीर्घवृत्त x²/16 + y²/9 = 1 की लाटस रेक्टम की लम्बाई —
🔵 (A) 9/4
🟢 (B) 9/8
🟠 (C) 9/5
🔴 (D) 9/3
Answer: (A) 9/4
Q30. परवलय y² = 4x की स्पर्शरेखा y = 2x + c हो, तो c का मान होगा —
🔵 (A) −1
🟢 (B) 1
🟠 (C) −2
🔴 (D) 2
Answer: (A) −1
Q31. अतिपरवलय x²/9 − y²/16 = 1 की लाटस रेक्टम की लम्बाई —
🔵 (A) 32/3
🟢 (B) 9/4
🟠 (C) 4/3
🔴 (D) 9/2
Answer: (A) 32/3
Q32. दीर्घवृत्त x²/49 + y²/9 = 1 का प्रमुख अक्ष है —
🔵 (A) x-अक्ष
🟢 (B) y-अक्ष
🟠 (C) रेखा y = x
🔴 (D) रेखा y = −x
Answer: (A) x-अक्ष
Q33. यदि किसी दीर्घवृत्त में a = 13 और b = 12 हो, तो विकेन्द्रता e होगी —
🔵 (A) 5/13
🟢 (B) 12/13
🟠 (C) 13/12
🔴 (D) √(1 − 12²/13²)
Answer: (D) √(1 − 12²/13²)
Q34. परवलय x² = 8y का शीर्ष से फोकस तक की दूरी —
🔵 (A) 1
🟢 (B) 2
🟠 (C) 3
🔴 (D) 2
Answer: (B) 2
Q35. अतिपरवलय x²/25 − y²/9 = 1 का विकेन्द्रता e है —
🔵 (A) √(1 − 9/25)
🟢 (B) √(1 + 9/25)
🟠 (C) √(25/9)
🔴 (D) √(1 − 25/9)
Answer: (B) √(1 + 9/25)
Q36. दीर्घवृत्त का वह बिन्दु जहाँ y = 0 हो —
🔵 (A) शीर्ष
🟢 (B) केन्द्र
🟠 (C) फोकस
🔴 (D) लाटस रेक्टम
Answer: (A) शीर्ष
Q37. यदि परवलय की समीकरण y² = 8x है, तो लाटस रेक्टम की लम्बाई —
🔵 (A) 2
🟢 (B) 4
🟠 (C) 8
🔴 (D) 16
Answer: (C) 8
Q38. अतिपरवलय x²/9 − y²/4 = 1 में a = 3, b = 2, तो c = ?
🔵 (A) √5
🟢 (B) √13
🟠 (C) √7
🔴 (D) √10
Answer: (A) √13
Q39. यदि किसी परवलय का समीकरण y² = 4ax है और उसका फोकस (3, 0) है, तो a = ?
🔵 (A) 1
🟢 (B) 2
🟠 (C) 3
🔴 (D) 4
Answer: (C) 3
Q40. परवलय y² = 8x की निदेशिका है —
🔵 (A) x = 2
🟢 (B) x = −2
🟠 (C) x = 4
🔴 (D) x = −4
Answer: (D) x = −2
🔴 Q41–Q50 : JEE Advanced स्तर (अत्यधिक कठिनाई)
Q41. परवलय y² = 4ax और दीर्घवृत्त x²/9 + y²/4 = 1 की सामान्य स्पर्शरेखा का समीकरण होगा —
🔵 (A) y = mx + a/m
🟢 (B) y = mx ± √(a²m² + 9)
🟠 (C) y = mx + (a/m) + √(a²m² + 9)
🔴 (D) y = mx + c
उत्तर: (B) y = mx ± √(a²m² + 9)
Q42. यदि परवलय y² = 16x और वृत्त x² + y² = 16 पर एक सामान्य स्पर्शरेखा खींची जाए, तो उसका समीकरण होगा —
🔵 (A) y = 2x + 4
🟢 (B) y = 2x − 4
🟠 (C) y = −2x + 4
🔴 (D) y = −2x − 4
उत्तर: (B) y = 2x − 4
Q43. दीर्घवृत्त x²/25 + y²/9 = 1 तथा अतिपरवलय x²/25 − y²/9 = 1 के समान फोकसों के बीच दूरी है —
🔵 (A) 2√16
🟢 (B) 2√(a² − b²)
🟠 (C) 2√(a² + b²)
🔴 (D) 2√(b² − a²)
उत्तर: (B) 2√(a² − b²)
Q44. दीर्घवृत्त x²/a² + y²/b² = 1 में यदि स्पर्शरेखा का समीकरण lx + my = n है, तो n² = ?
🔵 (A) a²l² + b²m²
🟢 (B) a²b²(l²/a² + m²/b²)
🟠 (C) a²b²(l² + m²)
🔴 (D) a²b²/(l²/a² + m²/b²)
उत्तर: (D) a²b²/(l²/a² + m²/b²)
Q45. परवलय y² = 4ax पर बिन्दु P(x₁, y₁) पर खींची गई स्पर्शरेखा और अभिलम्ब के बीच का कोण θ है, तो tanθ = ?
🔵 (A) m²
🟢 (B) 1/m²
🟠 (C) (1 − m²)/(1 + m²)
🔴 (D) 2m/(1 − m²)
उत्तर: (C) (1 − m²)/(1 + m²)
Q46. यदि दीर्घवृत्त x²/16 + y²/9 = 1 की दो स्पर्शरेखाएँ परस्पर लंबवत हों, तो उनके स्पर्शबिन्दुओं के निर्देशांकों का योग होगा —
🔵 (A) 0
🟢 (B) a² + b²
🟠 (C) a² − b²
🔴 (D) 2ab
उत्तर: (A) 0
Q47. अतिपरवलय x²/a² − y²/b² = 1 के लिए, यदि एक फोकस (c, 0) और एक शीर्ष (a, 0) हो, तो c² − a² = ?
🔵 (A) b²
🟢 (B) a²
🟠 (C) c²
🔴 (D) a² + b²
उत्तर: (A) b²
Q48. यदि दीर्घवृत्त x²/9 + y²/4 = 1 और अतिपरवलय x²/9 − y²/4 = 1 हों, तो इन दोनों की लाटस रेक्टम का अनुपात होगा —
🔵 (A) 1:1
🟢 (B) 2:1
🟠 (C) 1:2
🔴 (D) 3:2
उत्तर: (A) 1:1
Q49. दीर्घवृत्त x²/a² + y²/b² = 1 में यदि फोकस और निदेशिका के बीच की दूरी ज्ञात करनी हो, तो वह होगी —
🔵 (A) a/e
🟢 (B) a/e²
🟠 (C) ae
🔴 (D) a(1 − e²)
उत्तर: (B) a/e²
Q50. यदि किसी शंकु परिच्छेद के लिए e = 1/2 हो, तो वह वक्र होगा —
🔵 (A) परवलय
🟢 (B) वृत्त
🟠 (C) दीर्घवृत्त
🔴 (D) अतिपरवलय
उत्तर: (C) दीर्घवृत्त
————————————————————————————————————————————————————————————————————————————
