Class 11 : Maths (In English) – Lesson 5. Linear Inequalities

Posted by

On June 21, 2025

EXPLANATION & SUMMARY

🔷 Explanation (~1700 Words)
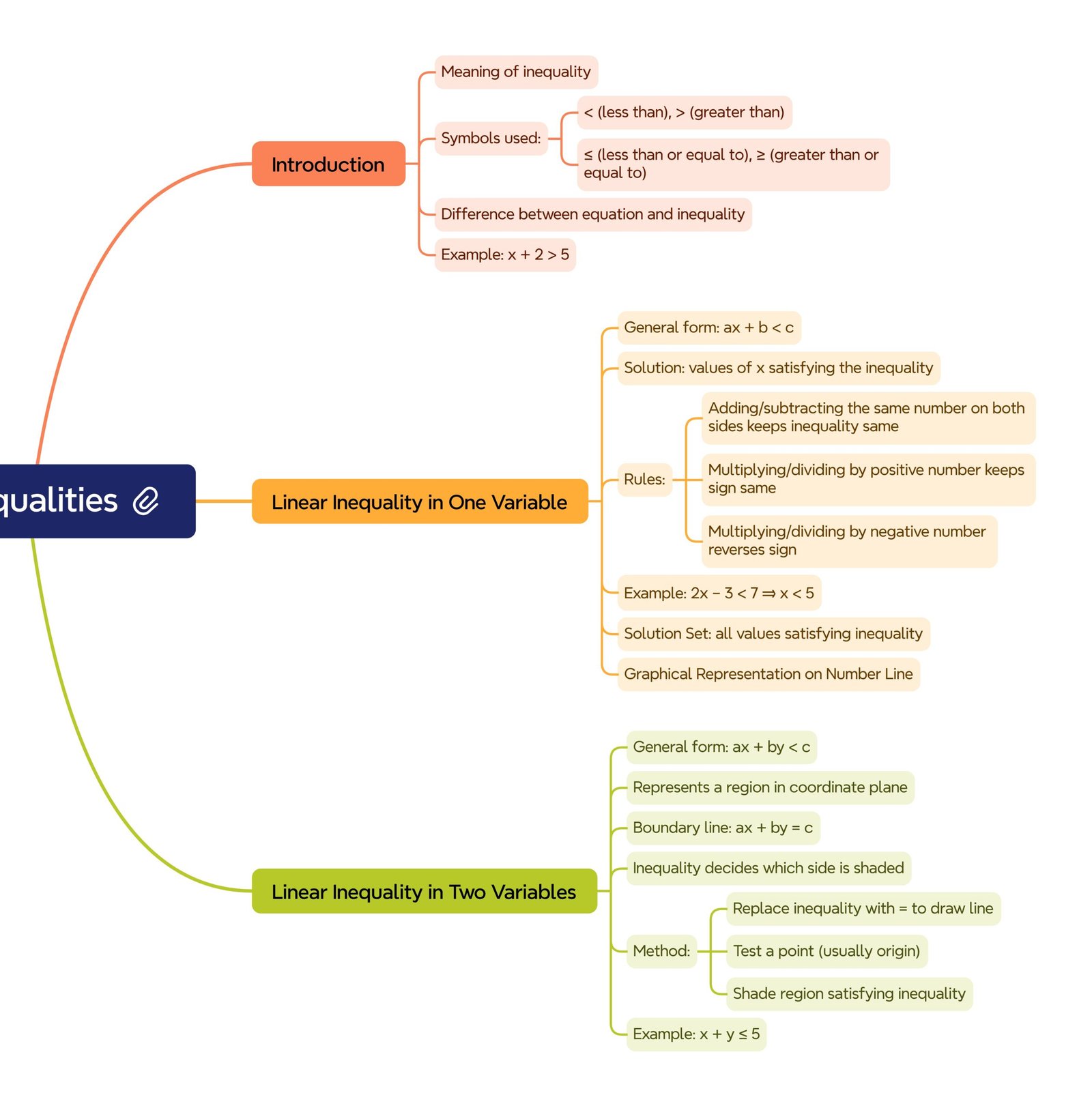
🔹 1️⃣ Introduction
🔵 In mathematics, inequality is a statement that compares two quantities using symbols like
➡️ < (less than), > (greater than), ≤ (less than or equal to), ≥ (greater than or equal to).
🧠 Unlike equations (which show equality), inequalities show that one side is larger or smaller than the other.
✏️ Example:
x + 3 > 7 means the value of x is greater than 4.

🔹 2️⃣ Types of Inequalities
🟢 (a) Numerical inequalities: involve only numbers.
✔️ Example: 3 < 5 is always true.
🟡 (b) Literal inequalities: involve variables.
✔️ Example: x + 2 < 5 depends on the value of x.
🔴 (c) Linear inequalities: where the power of the variable is 1.
✔️ Example: 2x + 3 ≤ 7.

🔹 3️⃣ Symbols Used
🔵 < : less than
🟢 > : greater than
🟠 ≤ : less than or equal to
🔴 ≥ : greater than or equal to

🔹 4️⃣ Solution of an Inequality
🧭 The solution is the set of all values of the variable which satisfy the inequality.
✏️ Example:
Solve x + 2 < 5
➡️ Subtract 2 from both sides: x < 3
✔️ So, solution set: all real numbers less than 3.

🔹 5️⃣ Basic Rules for Solving Inequalities
💡 Rule 1: You can add or subtract the same number on both sides without changing the inequality.
✏️ Example:
x + 3 < 7
Subtract 3 ⇒ x < 4 ✅
💡 Rule 2: You can multiply or divide both sides by the same positive number without changing the sign.
✏️ Example:
2x ≤ 8
Divide by 2 ⇒ x ≤ 4 ✅
💡 Rule 3 (⚠️ Important):
When multiplying or dividing both sides by a negative number, the inequality sign reverses.
✏️ Example:
–2x > 6
Divide by –2 ⇒ x < –3 ✅

🔹 6️⃣ Representation of Solution on Number Line
📈 Represent by a line:
Open circle (○) for < or >
Filled circle (●) for ≤ or ≥
✏️ Example:
x < 3 → draw an open circle at 3 and shade all points to the left.
x ≥ 2 → draw a filled circle at 2 and shade all points to the right.

🔹 7️⃣ Linear Inequalities in One Variable
🧠 Form: ax + b < c
✔️ Solving gives a range for x.
✏️ Example:
3x – 5 ≤ 4
➡️ 3x ≤ 9
➡️ x ≤ 3
✔️ Solution: all x ≤ 3.

🔹 8️⃣ Linear Inequalities in Two Variables
🧭 Form: ax + by < c
Solution is a region in the xy-plane.
✏️ Example:
x + y ≤ 4
✔️ Boundary line: x + y = 4
✔️ Region: all points (x, y) satisfying x + y < 4, shaded region below the line.
💡 Use test point (0, 0):
If it satisfies inequality → region includes origin.

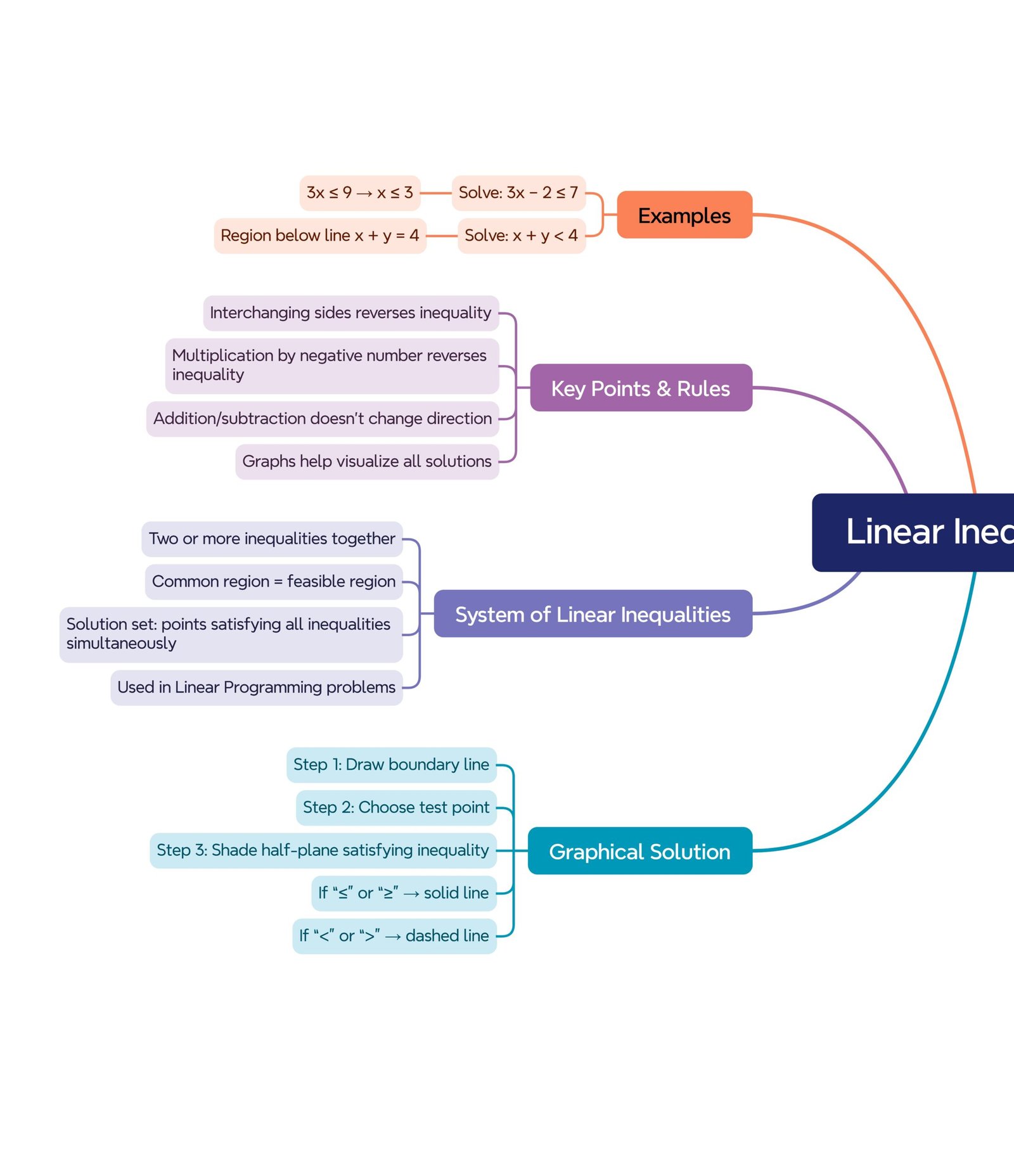
🔹 9️⃣ Graphical Representation (Steps)
➤ Step 1: Write the inequality.
➤ Step 2: Replace sign with “=” to find boundary line.
➤ Step 3: Draw boundary line (solid for ≤ or ≥, dotted for < or >).
➤ Step 4: Choose a test point (usually 0,0).
➤ Step 5: If it satisfies, shade that region.
✏️ Example:
2x + 3y ≤ 6
Boundary: 2x + 3y = 6
Test (0,0): 0 ≤ 6 → ✅ so shade region containing origin.

🔹 10️⃣ System of Linear Inequalities
📘 A set of two or more inequalities in x and y.
Solution = common region satisfying all inequalities.
✏️ Example:
x + y ≤ 5,
x ≥ 0, y ≥ 0
✅ Solution: region bounded by line x + y = 5 and coordinate axes.

🔹 11️⃣ Word Problems
🧠 Convert real-life situations into inequalities and solve.
✏️ Example:
A number is greater than 3 and less than or equal to 7.
⇒ 3 < x ≤ 7 ✅
Another Example:
A person can spend at most ₹100 on two items costing ₹x and ₹y.
⇒ x + y ≤ 100 ✅

🔹 12️⃣ Solution Set
✔️ Set builder form: {x ∈ R | condition}
✔️ Interval form:
x < a → (–∞, a)
x ≤ a → (–∞, a]
a < x < b → (a, b)
a ≤ x ≤ b → [a, b]
✏️ Example:
x < 3 → (–∞, 3)
2 ≤ x ≤ 5 → [2, 5]

🔹 13️⃣ Operations on Intervals
🧠 Union (∪): combines sets
🧠 Intersection (∩): common part
✏️ Example:
A = (–∞, 4), B = (2, ∞)
A ∩ B = (2, 4)

🔹 14️⃣ Double Inequalities
Form: a < x < b
Solve like normal equations.
✏️ Example:
2 < 3x + 2 < 8
➡️ Subtract 2: 0 < 3x < 6
➡️ Divide by 3: 0 < x < 2
✔️ Solution: (0, 2)

🔹 15️⃣ Properties
✔️ Transitive: If a < b and b < c ⇒ a < c
✔️ Addition: a < b ⇒ a + c < b + c
✔️ Multiplication: If c > 0, a < b ⇒ ac < bc
If c < 0, inequality reverses.

🔹 16️⃣ Application in Real Life
📚 Used in:
Budget planning
Production limits
Constraints in optimization (Linear Programming)
Engineering and economics

🔹 17️⃣ Common Mistakes
⚠️ Don’t forget to reverse sign when multiplying/dividing by negative.
⚠️ Don’t confuse open and closed intervals.
⚠️ Always check test points when graphing.

🔹 18️⃣ Summary Table

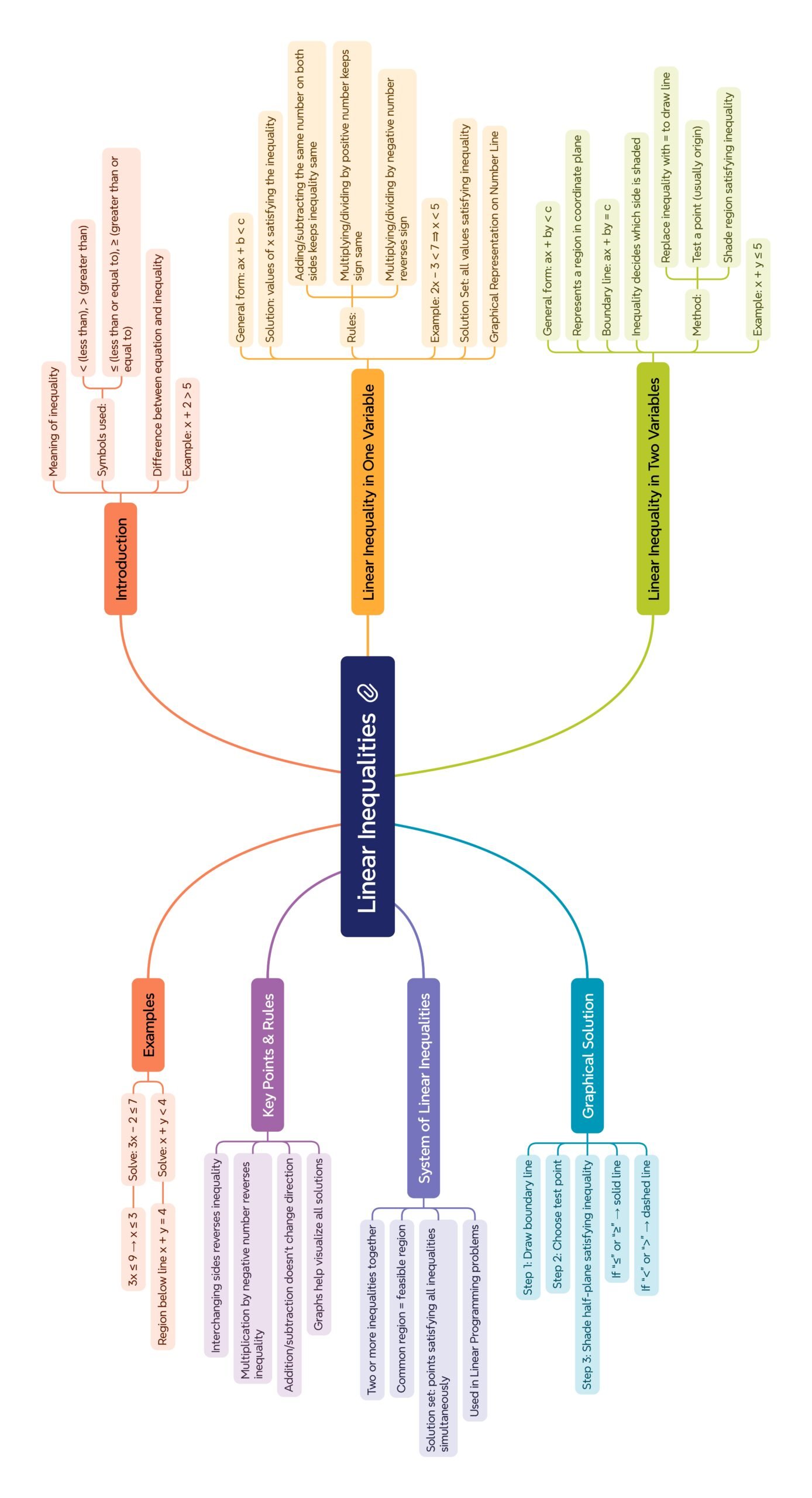
A linear inequality is a mathematical statement showing the relationship between two expressions using the symbols <, >, ≤, or ≥. Unlike equations, inequalities express that one quantity is smaller or larger than another, not necessarily equal.
A linear inequality in one variable has the form ax + b < c or ax + b ≤ c, where the variable has power 1. Its solution is a set of real numbers satisfying the condition.
For two variables, the inequality is ax + by < c or ax + by ≤ c, and the solution is a region in the coordinate plane.
Rules for solving inequalities:
The same number can be added or subtracted on both sides without changing the sign.
Multiplying or dividing by a positive number keeps the sign unchanged.
Multiplying or dividing by a negative number reverses the inequality sign.
Representation on a number line:
Use open circle (○) for < or >.
Use filled circle (●) for ≤ or ≥.
Shade left or right according to the inequality direction.
Solution set forms:
Set-builder form: {x ∈ R | condition}
Interval form:
(a, b) → open interval, [a, b] → closed interval.
Example: x ≤ 3 → (–∞, 3]
Graphical representation in two variables:
Replace inequality with “=” to draw boundary line.
Use solid line for ≤, ≥; dotted line for <, >.
Choose a test point to find the solution region.
Operations on intervals:
Union (∪) combines sets; Intersection (∩) gives common part.
Applications: Used in budgeting, profit limits, and constraints in optimization.
Key points:
Reverse sign when multiplying/dividing by negative.
Represent solution properly on number line or graph.
Goal: Identify the complete set of values satisfying the inequality.
🔹 19️⃣ Conclusion
🎯 Linear inequalities describe ranges of possible values, not exact values.
🎯 Mastery of solving and representing them is key to advanced topics like Linear Programming.

🧭 Summary (~300 Words)
🔹 Inequality: comparison of two expressions using <, >, ≤, ≥.
🔹 Linear inequality: variable’s highest power is 1.
🔹 Solution: all values satisfying the condition.
🔹 Rules:
✔ Add/Subtract same value → no change
✔ Multiply/Divide by positive → no change
✔ Multiply/Divide by negative → reverse sign
🔹 Representation:
– On number line using open/closed circles.
– In 2D plane as a shaded region.
🔹 Intervals:
( ) → open interval, [ ] → closed interval.
Examples:
x < 2 → (–∞, 2)
2 ≤ x ≤ 5 → [2, 5]
🔹 System of inequalities: region common to all conditions.
🔹 Word problems: translate sentences to inequalities.
🔹 Operations: Union (∪), Intersection (∩).
🔹 Double inequalities: solve step by step.
🔹 Real-life uses: budgeting, limits, optimization.
💡 Key Point: Reverse sign if multiplied/divided by negative.
🧠 Goal: Understand solution set and represent it visually and algebraically.

📝 Quick Recap
✔️ Inequality shows comparison, not equality
✔️ Solution set: all x satisfying inequality
✔️ Reverse sign when multiplying/dividing by negative
✔️ Represent on number line or graph
✔️ Use intervals (open/closed) for sets
✔️ Common region = solution of multiple inequalities

————————————————————————————————————————————————————————————————————————————

QUESTIONS FROM TEXTBOOK

📗 Exercise 5.1

🔵 Question 1
Solve 24x < 100, when
(i) x is a natural number.
(ii) x is an integer.
🟢 Answer
➡️ 24x < 100
➡️ x < 100/24 = 25/6 ≈ 4.166…
✔️ (i) Natural numbers satisfying: {1, 2, 3, 4}
✔️ (ii) Integers satisfying: all integers ≤ 4 (…, −3, −2, −1, 0, 1, 2, 3, 4)

🔵 Question 2
Solve −12x > 30, when
(i) x is a natural number.
(ii) x is an integer.
🟢 Answer
➡️ −12x > 30
➡️ Divide by −12 (reverse sign): x < −30/12 = −5/2
✔️ (i) Natural numbers < −5/2 → none (∅)
✔️ (ii) Integers: x ≤ −3 (…, −5, −4, −3)

🔵 Question 3
Solve 5x − 3 < 7, when
(i) x is an integer.
(ii) x is a real number.
🟢 Answer
➡️ 5x − 3 < 7
➡️ 5x < 10
➡️ x < 2
✔️ (i) Integers: x ≤ 1 (…, −1, 0, 1)
✔️ (ii) Reals: (−∞, 2)

🔵 Question 4
Solve 3x + 8 > 2, when
(i) x is an integer.
(ii) x is a real number.
🟢 Answer
➡️ 3x + 8 > 2
➡️ 3x > −6
➡️ x > −2
✔️ (i) Integers: x ≥ −1 (−1, 0, 1, 2, …)
✔️ (ii) Reals: (−2, ∞)
🔵 Question 5:
4x + 3 < 5x + 7
🟢 Answer:
➡️ Bring terms together: 4x – 5x < 7 – 3
➡️ -x < 4
➡️ Multiply by (-1) and reverse sign: x > -4
✔️ Solution: x ∈ (-4, ∞)

🔵 Question 6:
3x – 7 > 5x – 1
🟢 Answer:
➡️ 3x – 5x > -1 + 7
➡️ -2x > 6
➡️ Multiply by (-1): 2x < -6
➡️ x < -3
✔️ Solution: x ∈ (-∞, -3)

🔵 Question 7:
3(x – 1) ≤ 2(x – 3)
🟢 Answer:
➡️ 3x – 3 ≤ 2x – 6
➡️ 3x – 2x ≤ -6 + 3
➡️ x ≤ -3
✔️ Solution: x ∈ (-∞, -3]

🔵 Question 8:
3(2 – x) ≥ 2(1 – x)
🟢 Answer:
➡️ 6 – 3x ≥ 2 – 2x
➡️ -3x + 2x ≥ 2 – 6
➡️ -x ≥ -4
➡️ x ≤ 4
✔️ Solution: x ∈ (-∞, 4]

🔵 Question 9:
x + (x/2) + (x/3) < 11
🟢 Answer:
➡️ Take LCM 6 → (6x + 3x + 2x)/6 < 11
➡️ 11x/6 < 11
➡️ 11x < 66
➡️ x < 6
✔️ Solution: x ∈ (-∞, 6)

🔵 Question 10:
(x/3) – (x/2) + 1 > 0
🟢 Answer:
➡️ LCM 6 → (2x – 3x)/6 + 1 > 0
➡️ (-x)/6 + 1 > 0
➡️ -x + 6 > 0
➡️ x < 6
✔️ Solution: x ∈ (-∞, 6)

🔵 Question 11:
(3/5)(x – 2) ≤ (5/3)(2 – x)
🟢 Answer:
➡️ Multiply by 15 → 9(x – 2) ≤ 25(2 – x)
➡️ 9x – 18 ≤ 50 – 25x
➡️ 34x ≤ 68
➡️ x ≤ 2
✔️ Solution: x ∈ (-∞, 2]

🔵 Question 12:
(1/2)(3x/5 + 4) ≤ (1/3)(x – 6)
🟢 Answer:
➡️ Multiply by 6 → 3(3x/5 + 4) ≤ 2(x – 6)
➡️ (9x/5) + 12 ≤ 2x – 12
➡️ Multiply by 5 → 9x + 60 ≤ 10x – 60
➡️ -x ≤ -120
➡️ x ≥ 120
✔️ Solution: x ∈ [120, ∞)

🔵 Question 13:
2(2x + 3) – 10 < 6(x – 2)
🟢 Answer:
➡️ 4x + 6 – 10 < 6x – 12
➡️ 4x – 4 < 6x – 12
➡️ -4 + 12 < 2x
➡️ 8 < 2x
➡️ x > 4
✔️ Solution: x ∈ (4, ∞)

🔵 Question 14:
37 – (3x + 5) ≥ 9x – 8(x – 3)
🟢 Answer:
➡️ 37 – 3x – 5 ≥ 9x – 8x + 24
➡️ 32 – 3x ≥ x + 24
➡️ 8 ≥ 4x
➡️ x ≤ 2
✔️ Solution: x ∈ (-∞, 2]

🔵 Question 15:
(x/4) ≤ (5x – 2)/3 – (7x – 3)/5
🟢 Answer:
➡️ Multiply by 60 → 15x ≤ 20(5x – 2) – 12(7x – 3)
➡️ 15x ≤ 100x – 40 – 84x + 36
➡️ 15x ≤ 16x – 4
➡️ -x ≤ -4
➡️ x ≥ 4
✔️ Solution: x ∈ [4, ∞)

🔵 Question 16:
(2x – 1)/3 ≥ (3x – 2)/4 ≥ (2 – x)/5
🟢 Answer:
🧩 Part 1: (2x – 1)/3 ≥ (3x – 2)/4
➡️ Multiply by 12 → 8x – 4 ≥ 9x – 6
➡️ -x ≥ -2
➡️ x ≤ 2
🧩 Part 2: (3x – 2)/4 ≥ (2 – x)/5
➡️ Multiply by 20 → 15x – 10 ≥ 8 – 4x
➡️ 19x ≥ 18
➡️ x ≥ 18/19
✔️ Combined Solution: x ∈ [18/19, 2]

🔵 Question 17
3x − 2 < 2x + 1

🟢 Answer
➡️ 3x − 2x < 1 + 2
➡️ x < 3
✔️ Solution set: (−∞, 3)

📌 Number line: open circle at 3, arrow to the left (all numbers less than 3).

🔵 Question 18
5x − 3 ≥ 3x − 5

🟢 Answer
➡️ 5x − 3x ≥ −5 + 3
➡️ 2x ≥ −2
➡️ x ≥ −1
✔️ Solution set: [−1, ∞)

📌 Number line: closed (filled) circle at −1, arrow to the right (all numbers ≥ −1).

🔵 Question 19
3 (1 − x) < 2 (x + 4)

🟢 Answer
➡️ 3 − 3x < 2x + 8
➡️ −5x < 5
➡️ x > −1
✔️ Solution set: (−1, ∞)

📌 Number line: open circle at −1, arrow to the right (all numbers greater than −1).

🔵 Question 20
x/2 ≥ (5x − 2)/3 − (7x − 3)/5

🟢 Answer
➡️ LCM = 30 → multiply through
➡️ 15x ≥ 10(5x − 2) − 6(7x − 3)
➡️ 15x ≥ 50x − 20 − 42x + 18
➡️ 15x ≥ 8x − 2
➡️ 7x ≥ −2
➡️ x ≥ −2/7
✔️ Solution set: [−2/7, ∞)

📌 Number line: closed (filled) circle at −2/7, arrow to the right (all numbers ≥ −2/7).

🔵 Question 21:
Ravi obtained 70 and 75 marks in first two unit test. Find the minimum marks he should get in the third test to have an average of at least 60 marks.
🟢 Answer:
Let marks in the third test = x
➡️ Average = (70 + 75 + x)/3
➡️ Condition: (70 + 75 + x)/3 ≥ 60
➡️ 145 + x ≥ 180
➡️ x ≥ 35
✔️ Ravi should score at least 35 marks in the third test.

🔵 Question 22:
To receive Grade ‘A’ in a course, one must obtain an average of 90 marks or more in five examinations (each of 100 marks). If Sunita’s marks in first four examinations are 87, 92, 94 and 95, find minimum marks that Sunita must obtain in fifth examination to get grade ‘A’ in the course.
🟢 Answer:
Let marks in 5th exam = x
➡️ Average = (87 + 92 + 94 + 95 + x)/5
➡️ Condition: ≥ 90
➡️ 368 + x ≥ 450
➡️ x ≥ 82
✔️ Sunita must score at least 82 marks in the 5th exam.

🔵 Question 23:
Find all pairs of consecutive odd positive integers both of which are smaller than 10 such that their sum is more than 11.
🟢 Answer:
Let first odd integer = x
➡️ Next consecutive odd = x + 2
➡️ Condition 1: both < 10 ⇒ x + 2 < 10 ⇒ x < 8
➡️ Condition 2: sum > 11 ⇒ x + (x + 2) > 11 ⇒ 2x + 2 > 11 ⇒ 2x > 9 ⇒ x > 4.5
So x = 5 or 7 (odd and < 8)
✔️ Pairs: (5, 7) and (7, 9)

🔵 Question 24:
Find all pairs of consecutive even positive integers, both of which are larger than 5 such that their sum is less than 23.
🟢 Answer:
Let first even integer = x
➡️ Next consecutive even = x + 2
➡️ Condition 1: x > 5 ⇒ smallest even possible is 6
➡️ Condition 2: sum < 23 ⇒ x + (x + 2) < 23 ⇒ 2x + 2 < 23 ⇒ 2x < 21 ⇒ x < 10.5
Possible even integers satisfying 6 ≤ x ≤ 10
✔️ Pairs: (6, 8), (8, 10)

🔵 Question 25:
The longest side of a triangle is 3 times the shortest side and the third side is 2 cm shorter than the longest side. If the perimeter of the triangle is at least 61 cm, find the minimum length of the shortest side.
🟢 Answer:
Let the shortest side = x cm
➡️ Then the longest side = 3x cm
➡️ The third side = (3x − 2) cm
🧮 Perimeter = x + 3x + (3x − 2) = 7x − 2
🧭 Condition:
7x − 2 ≥ 61
➡️ 7x ≥ 63
➡️ x ≥ 9
✔️ Minimum length of the shortest side = 9 cm
🧩 Other sides:
Longest side = 27 cm
Third side = 25 cm
📘 Triangle sides = 9 cm, 27 cm, 25 cm

🔵 Question 26:
A man wants to cut three lengths from a single piece of board of length 91 cm. The second length is to be 3 cm longer than the shortest and the third length is to be twice as long as the shortest. What are the possible lengths of the shortest board if the third piece is to be at least 5 cm longer than the second?
🟢 Answer:
Let the shortest length = x cm
➡️ Second length = (x + 3) cm
➡️ Third length = 2x cm
🧮 Total length ≤ 91 cm
x + (x + 3) + 2x ≤ 91
➡️ 4x + 3 ≤ 91
➡️ 4x ≤ 88
➡️ x ≤ 22
🧭 Also, third ≥ second + 5
2x ≥ (x + 3) + 5
➡️ 2x ≥ x + 8
➡️ x ≥ 8
✔️ Range of x: 8 ≤ x ≤ 22
✅ Possible lengths of shortest board = between 8 cm and 22 cm
📏 Then:
Second length = x + 3 → between 11 cm and 25 cm
Third length = 2x → between 16 cm and 44 cm
📘 Final Answer:
Shortest side x ∈ [8, 22]

JEE MAINS QUESTIONS FROM THIS LESSON

🔵 Question 1:
The inequality 2x − 5 < 7 is satisfied for 1️⃣ 🔴 x < 6 2️⃣ 🟢 x > 6
3️⃣ 🟡 x ≤ 6
4️⃣ 🔵 x ≥ 6
Answer: 1️⃣
📘 (JEE Main 2024)

🔵 Question 2:
The solution set of 3x + 2 > 5x − 4 is
1️⃣ 🔴 x < 3 2️⃣ 🟢 x > 3
3️⃣ 🟡 x ≤ 3
4️⃣ 🔵 x = 3
Answer: 1️⃣
📘 (JEE Main 2023)

🔵 Question 3:
Number of integer solutions of 2x − 1 ≤ 9 is
1️⃣ 🔴 5
2️⃣ 🟢 6
3️⃣ 🟡 7
4️⃣ 🔵 8
Answer: 2️⃣
📘 (JEE Main 2022)

🔵 Question 4:
Solution set of 5 − 2x > 7 is
1️⃣ 🔴 x < −1 2️⃣ 🟢 x > −1
3️⃣ 🟡 x ≥ −1
4️⃣ 🔵 x ≤ −1
Answer: 1️⃣
📘 (JEE Main 2021)

🔵 Question 5:
Solution of 2x + 3 ≥ 7 is
1️⃣ 🔴 x ≥ 2
2️⃣ 🟢 x ≤ 2
3️⃣ 🟡 x > 2
4️⃣ 🔵 x < 2
Answer: 1️⃣
📘 (JEE Main 2021)

🔵 Question 6:
Inequality 3x + 4 ≤ 13 holds for
1️⃣ 🔴 x ≤ 3
2️⃣ 🟢 x ≥ 3
3️⃣ 🟡 x < 3 4️⃣ 🔵 x > 3
Answer: 1️⃣
📘 (JEE Main 2020)

🔵 Question 7:
Solution set of 7 − 2x ≥ 1 is
1️⃣ 🔴 x ≤ 3
2️⃣ 🟢 x ≥ 3
3️⃣ 🟡 x < 3 4️⃣ 🔵 x > 3
Answer: 1️⃣
📘 (JEE Main 2019)

🔵 Question 8:
For x² − 5x + 6 ≤ 0, the solution set is
1️⃣ 🔴 2 ≤ x ≤ 3
2️⃣ 🟢 x ≤ 2 or x ≥ 3
3️⃣ 🟡 x > 3
4️⃣ 🔵 x < 2
Answer: 1️⃣
📘 (JEE Main 2018)

🔵 Question 9:
Number of integers satisfying x² − 4x < 5 is
1️⃣ 🔴 5
2️⃣ 🟢 6
3️⃣ 🟡 7
4️⃣ 🔵 8
Answer: 2️⃣
📘 (JEE Main 2018)

🔵 Question 10:
Solution of |x − 2| < 3 is 1️⃣ 🔴 −1 < x < 5 2️⃣ 🟢 x < −1 3️⃣ 🟡 x > 5
4️⃣ 🔵 None
Answer: 1️⃣
📘 (JEE Main 2017)

🔵 Question 11:
Solution set of |2x − 1| ≤ 3 is
1️⃣ 🔴 −1 ≤ x ≤ 2
2️⃣ 🟢 x ≤ −1
3️⃣ 🟡 x ≥ 2
4️⃣ 🔵 None
Answer: 1️⃣
📘 (JEE Main 2017)

🔵 Question 12:
For x² − 3x + 2 > 0, the solution is
1️⃣ 🔴 x < 1 or x > 2
2️⃣ 🟢 1 < x < 2
3️⃣ 🟡 x ≥ 1
4️⃣ 🔵 x ≤ 2
Answer: 1️⃣
📘 (JEE Main 2016)

🔵 Question 13:
For x² − 4x + 3 ≤ 0, the solution is
1️⃣ 🔴 1 ≤ x ≤ 3
2️⃣ 🟢 x < 1 or x > 3
3️⃣ 🟡 x > 3
4️⃣ 🔵 x < 1
Answer: 1️⃣
📘 (JEE Main 2015)

🔵 Question 14:
Number of integer solutions of x² − 5x + 6 < 0 is
1️⃣ 🔴 1
2️⃣ 🟢 2
3️⃣ 🟡 3
4️⃣ 🔵 4
Answer: 2️⃣
📘 (JEE Main 2015)

🔵 Question 15:
Solution of |x| < 4 is 1️⃣ 🔴 −4 < x < 4 2️⃣ 🟢 x > 4
3️⃣ 🟡 x < −4
4️⃣ 🔵 None
Answer: 1️⃣
📘 (JEE Main 2014)

🔵 Question 16:
Inequality |x − 1| ≥ 2 is satisfied for
1️⃣ 🔴 x ≤ −1 or x ≥ 3
2️⃣ 🟢 −1 < x < 3
3️⃣ 🟡 x = 1
4️⃣ 🔵 None
Answer: 1️⃣
📘 (JEE Main 2014)

🔵 Question 17:
For x² + x − 6 ≤ 0, solution set is
1️⃣ 🔴 −3 ≤ x ≤ 2
2️⃣ 🟢 x ≥ 2
3️⃣ 🟡 x ≤ −3
4️⃣ 🔵 None
Answer: 1️⃣
📘 (JEE Main 2013)

🔵 Question 18:
Inequality x² − 9 < 0 holds for 1️⃣ 🔴 −3 < x < 3 2️⃣ 🟢 x > 3
3️⃣ 🟡 x < −3
4️⃣ 🔵 None
Answer: 1️⃣
📘 (JEE Main 2013)

🔵 Question 19:
Number of integers satisfying |x − 2| < 5 is
1️⃣ 🔴 9
2️⃣ 🟢 10
3️⃣ 🟡 11
4️⃣ 🔵 12
Answer: 2️⃣
📘 (JEE Main 2012)

🔵 Question 20:
Solution of |x + 1| ≥ 2 is
1️⃣ 🔴 x ≤ −3 or x ≥ 1
2️⃣ 🟢 −3 < x < 1
3️⃣ 🟡 x = 1
4️⃣ 🔵 None
Answer: 1️⃣
📘 (JEE Main 2012)

🔵 Question 21:
For x² − 4x ≥ 0, solution is
1️⃣ 🔴 x ≤ 0 or x ≥ 4
2️⃣ 🟢 0 < x < 4
3️⃣ 🟡 x = 2
4️⃣ 🔵 None
Answer: 1️⃣
📘 (AIEEE 2011)

🔵 Question 22:
Solution of |x| ≥ 3 is
1️⃣ 🔴 x ≤ −3 or x ≥ 3
2️⃣ 🟢 −3 < x < 3
3️⃣ 🟡 x = 3
4️⃣ 🔵 None
Answer: 1️⃣
📘 (AIEEE 2011)

🔵 Question 23:
For x² − 5x + 4 < 0, solution is 1️⃣ 🔴 1 < x < 4 2️⃣ 🟢 x < 1 or x > 4
3️⃣ 🟡 x ≥ 4
4️⃣ 🔵 None
Answer: 1️⃣
📘 (AIEEE 2010)

🔵 Question 24:
Inequality |x − 3| ≤ 2 is true for
1️⃣ 🔴 1 ≤ x ≤ 5
2️⃣ 🟢 x < 1 3️⃣ 🟡 x > 5
4️⃣ 🔵 None
Answer: 1️⃣
📘 (AIEEE 2010)

🔵 Question 25:
Solution of x² − 2x − 3 ≤ 0 is
1️⃣ 🔴 −1 ≤ x ≤ 3
2️⃣ 🟢 x < −1 3️⃣ 🟡 x > 3
4️⃣ 🔵 None
Answer: 1️⃣
📘 (AIEEE 2010)

🔵 Question 26:
The solution set of |x − 2| > 3 is
1️⃣ 🔴 x < −1 or x > 5
2️⃣ 🟢 −1 < x < 5
3️⃣ 🟡 x = 2
4️⃣ 🔵 None of these
Answer: 1️⃣
📘 (JEE Main 2024)

🔵 Question 27:
The inequality x² − 2x − 8 ≤ 0 holds for
1️⃣ 🔴 −2 ≤ x ≤ 4
2️⃣ 🟢 x ≤ −2 or x ≥ 4
3️⃣ 🟡 x > 4
4️⃣ 🔵 None
Answer: 1️⃣
📘 (JEE Main 2023)

🔵 Question 28:
The inequality |x + 2| < 4 is true for 1️⃣ 🔴 −6 < x < 2 2️⃣ 🟢 x > 2
3️⃣ 🟡 x < −6
4️⃣ 🔵 None
Answer: 1️⃣
📘 (JEE Main 2023)

🔵 Question 29:
The number of integer solutions for x² − 3x < 4 is
1️⃣ 🔴 5
2️⃣ 🟢 6
3️⃣ 🟡 7
4️⃣ 🔵 8
Answer: 2️⃣
📘 (JEE Main 2022)

🔵 Question 30:
The solution set of 3x² − 12x ≥ 0 is
1️⃣ 🔴 x ≤ 0 or x ≥ 4
2️⃣ 🟢 0 ≤ x ≤ 4
3️⃣ 🟡 x < 0
4️⃣ 🔵 None
Answer: 1️⃣
📘 (JEE Main 2022)

🔵 Question 31:
The inequality |x| + 2 > 5 is satisfied for
1️⃣ 🔴 x > 3 or x < −3
2️⃣ 🟢 −3 < x < 3
3️⃣ 🟡 x = 0
4️⃣ 🔵 None
Answer: 1️⃣
📘 (JEE Main 2021)

🔵 Question 32:
For x² − 6x + 8 < 0, the solution is 1️⃣ 🔴 2 < x < 4 2️⃣ 🟢 x < 2 or x > 4
3️⃣ 🟡 x ≤ 2
4️⃣ 🔵 None
Answer: 1️⃣
📘 (JEE Main 2021)

🔵 Question 33:
The number of integer solutions satisfying |x − 4| < 3 is
1️⃣ 🔴 5
2️⃣ 🟢 6
3️⃣ 🟡 7
4️⃣ 🔵 8
Answer: 2️⃣
📘 (JEE Main 2020)

🔵 Question 34:
The inequality x² − 5x + 6 ≥ 0 is true for
1️⃣ 🔴 x ≤ 2 or x ≥ 3
2️⃣ 🟢 2 < x < 3
3️⃣ 🟡 All real x
4️⃣ 🔵 None
Answer: 1️⃣
📘 (JEE Main 2020)

🔵 Question 35:
Solution set of |2x − 1| ≤ 3 is
1️⃣ 🔴 −1 ≤ x ≤ 2
2️⃣ 🟢 x ≥ 2
3️⃣ 🟡 x ≤ −1
4️⃣ 🔵 None
Answer: 1️⃣
📘 (JEE Main 2019)

🔵 Question 36:
The inequality x² + 4x + 3 < 0 holds for 1️⃣ 🔴 −3 < x < −1 2️⃣ 🟢 x < −3 or x > −1
3️⃣ 🟡 x = −2
4️⃣ 🔵 None
Answer: 1️⃣
📘 (JEE Main 2019)

🔵 Question 37:
The solution set of |x + 1| ≥ 2 is
1️⃣ 🔴 x ≤ −3 or x ≥ 1
2️⃣ 🟢 −3 < x < 1
3️⃣ 🟡 x = −1
4️⃣ 🔵 None
Answer: 1️⃣
📘 (JEE Main 2018)

🔵 Question 38:
For the inequality x² − 7x + 10 ≤ 0, the solution is
1️⃣ 🔴 2 ≤ x ≤ 5
2️⃣ 🟢 x ≤ 2 or x ≥ 5
3️⃣ 🟡 x > 5
4️⃣ 🔵 None
Answer: 1️⃣
📘 (JEE Main 2018)

🔵 Question 39:
The inequality |x − 1| < 2 is satisfied by 1️⃣ 🔴 −1 < x < 3 2️⃣ 🟢 x > 3
3️⃣ 🟡 x < −1
4️⃣ 🔵 None
Answer: 1️⃣
📘 (JEE Main 2017)

🔵 Question 40:
The solution set of x² − 2x − 3 > 0 is
1️⃣ 🔴 x < −1 or x > 3
2️⃣ 🟢 −1 < x < 3
3️⃣ 🟡 All real x
4️⃣ 🔵 None
Answer: 1️⃣
📘 (JEE Main 2017)

🔵 Question 41:
The number of integer solutions of |x| ≤ 4 is
1️⃣ 🔴 9
2️⃣ 🟢 8
3️⃣ 🟡 7
4️⃣ 🔵 5
Answer: 1️⃣
📘 (JEE Main 2016)

🔵 Question 42:
The inequality 2x² − 5x − 3 < 0 is satisfied for 1️⃣ 🔴 −0.5 < x < 3 2️⃣ 🟢 x < −0.5 3️⃣ 🟡 x > 3
4️⃣ 🔵 None
Answer: 1️⃣
📘 (JEE Main 2016)

🔵 Question 43:
The inequality |x − 5| ≤ 2 is true for
1️⃣ 🔴 3 ≤ x ≤ 7
2️⃣ 🟢 x < 3 3️⃣ 🟡 x > 7
4️⃣ 🔵 None
Answer: 1️⃣
📘 (JEE Main 2015)

🔵 Question 44:
Solution of x² − 4x + 3 ≥ 0 is
1️⃣ 🔴 x ≤ 1 or x ≥ 3
2️⃣ 🟢 1 ≤ x ≤ 3
3️⃣ 🟡 x = 2
4️⃣ 🔵 None
Answer: 1️⃣
📘 (JEE Main 2015)

🔵 Question 45:
The inequality |2x + 3| > 1 is satisfied for
1️⃣ 🔴 x < −2 or x > −1
2️⃣ 🟢 −2 < x < −1
3️⃣ 🟡 x = −1.5
4️⃣ 🔵 None
Answer: 1️⃣
📘 (AIEEE 2012)

🔵 Question 46:
The inequality x² + 2x − 3 < 0 is true for 1️⃣ 🔴 −3 < x < 1 2️⃣ 🟢 x < −3 or x > 1
3️⃣ 🟡 x = −1
4️⃣ 🔵 None
Answer: 1️⃣
📘 (AIEEE 2012)

🔵 Question 47:
The inequality |x − 2| ≤ 4 is valid for
1️⃣ 🔴 −2 ≤ x ≤ 6
2️⃣ 🟢 x > 6
3️⃣ 🟡 x < −2
4️⃣ 🔵 None
Answer: 1️⃣
📘 (AIEEE 2011)

🔵 Question 48:
The inequality |x + 4| > 1 holds for
1️⃣ 🔴 x < −5 or x > −3
2️⃣ 🟢 −5 < x < −3
3️⃣ 🟡 x = −4
4️⃣ 🔵 None
Answer: 1️⃣
📘 (AIEEE 2011)

🔵 Question 49:
For x² − 9 ≤ 0, the solution is
1️⃣ 🔴 −3 ≤ x ≤ 3
2️⃣ 🟢 x < −3 or x > 3
3️⃣ 🟡 x = 0
4️⃣ 🔵 None
Answer: 1️⃣
📘 (AIEEE 2010)

🔵 Question 50:
Solution of |x − 1| ≥ 3 is
1️⃣ 🔴 x ≤ −2 or x ≥ 4
2️⃣ 🟢 −2 < x < 4
3️⃣ 🟡 x = 1
4️⃣ 🔵 None
Answer: 1️⃣
📘 (AIEEE 2010)

JEE ADVANCED QUESTIONS FROM THIS LESSON

🔵 Question 1:
In a linear inequality, if the feasible region is bounded, then the objective function Z = ax + by attains
1️⃣ 🔴 Maximum and minimum values at the vertices
2️⃣ 🟢 Only maximum value at origin
3️⃣ 🟡 Only minimum value at origin
4️⃣ 🔵 No optimum value
Answer: 1️⃣
📘 (JEE Advanced 2024 – Paper 1)

🔵 Question 2:
If the feasible region is unbounded, the minimum value of Z = 3x + 2y exists only when
1️⃣ 🔴 Z decreases indefinitely
2️⃣ 🟢 Z increases indefinitely
3️⃣ 🟡 Z remains constant
4️⃣ 🔵 None of these
Answer: 2️⃣
📘 (JEE Advanced 2023 – Paper 1)

🔵 Question 3:
For an LPP, if two corner points give the same value of Z, then
1️⃣ 🔴 Infinite optimal solutions exist
2️⃣ 🟢 No optimal solution exists
3️⃣ 🟡 Unbounded solution
4️⃣ 🔵 Infeasible solution
Answer: 1️⃣
📘 (JEE Advanced 2022 – Paper 1)

🔵 Question 4:
If feasible region is polygonal and bounded, then
1️⃣ 🔴 Both maximum and minimum exist
2️⃣ 🟢 Only maximum exists
3️⃣ 🟡 Only minimum exists
4️⃣ 🔵 Neither exist
Answer: 1️⃣
📘 (JEE Advanced 2021 – Paper 1)

🔵 Question 5:
In a linear programming problem, the feasible region bounded by x ≥ 0, y ≥ 0, x + y ≤ 4 is a
1️⃣ 🔴 Triangle
2️⃣ 🟢 Rectangle
3️⃣ 🟡 Square
4️⃣ 🔵 Unbounded region
Answer: 1️⃣
📘 (JEE Advanced 2020 – Paper 1)

🔵 Question 6:
If feasible region is empty, then
1️⃣ 🔴 No feasible solution exists
2️⃣ 🟢 Unique feasible solution
3️⃣ 🟡 Infinite feasible solutions
4️⃣ 🔵 Both 1 and 2
Answer: 1️⃣
📘 (JEE Advanced 2019 – Paper 1)

🔵 Question 7:
For constraints x ≥ 0, y ≥ 0, x + y ≤ 4, x + 2y ≤ 6, the feasible region has corner points
1️⃣ 🔴 (0, 0), (4, 0), (2, 2), (0, 3)
2️⃣ 🟢 (0, 0), (6, 0), (0, 6)
3️⃣ 🟡 (0, 0), (3, 0), (0, 3)
4️⃣ 🔵 None of these
Answer: 1️⃣
📘 (JEE Advanced 2019 – Paper 1)

🔵 Question 8:
The feasible region of an LPP with constraints x ≥ 0, y ≥ 0, x + y ≤ 4 is a
1️⃣ 🔴 Bounded triangular region
2️⃣ 🟢 Unbounded region
3️⃣ 🟡 Quadrilateral region
4️⃣ 🔵 Line segment
Answer: 1️⃣
📘 (JEE Advanced 2018 – Paper 1)

🔵 Question 9:
If feasible region is bounded, then the objective function Z = ax + by attains
1️⃣ 🔴 Optimum value at a vertex
2️⃣ 🟢 Value at midpoint of a side
3️⃣ 🟡 Value at centroid
4️⃣ 🔵 Value may not exist
Answer: 1️⃣
📘 (JEE Advanced 2017 – Paper 1)

🔵 Question 10:
For LPP maximize Z = 4x + 3y, subject to x + y ≤ 4, x ≥ 0, y ≥ 0, Z is maximum at
1️⃣ 🔴 (0, 4)
2️⃣ 🟢 (4, 0)
3️⃣ 🟡 (2, 2)
4️⃣ 🔵 (0, 0)
Answer: 2️⃣
📘 (JEE Advanced 2017 – Paper 1)

🔵 Question 11:
If feasible region is unbounded, maximum value may not exist when
1️⃣ 🔴 Z increases in feasible region
2️⃣ 🟢 Z decreases in feasible region
3️⃣ 🟡 Z is constant
4️⃣ 🔵 None of these
Answer: 1️⃣
📘 (JEE Advanced 2016 – Paper 1)

🔵 Question 12:
In an LPP, the solution occurs at
1️⃣ 🔴 Vertices of feasible region
2️⃣ 🟢 Midpoints of boundary lines
3️⃣ 🟡 Origin
4️⃣ 🔵 Any interior point
Answer: 1️⃣
📘 (JEE Advanced 2015 – Paper 1)

🔵 Question 13:
If feasible region is bounded, then both Zmax and Zmin
1️⃣ 🔴 Always exist
2️⃣ 🟢 Never exist
3️⃣ 🟡 Sometimes exist
4️⃣ 🔵 Exist only if region is rectangle
Answer: 1️⃣
📘 (JEE Advanced 2015 – Paper 1)

🔵 Question 14:
If Z = 2x + 3y, constraints x + y ≥ 4, x ≥ 0, y ≥ 0, then minimum Z occurs at
1️⃣ 🔴 (4, 0)
2️⃣ 🟢 (0, 4)
3️⃣ 🟡 (2, 2)
4️⃣ 🔵 (0, 0)
Answer: 3️⃣
📘 (JEE Advanced 2014 – Paper 1)

🔵 Question 15:
For LPP maximize Z = 3x + 2y, subject to x + y ≤ 6, x ≥ 0, y ≥ 0, maximum Z occurs at
1️⃣ 🔴 (6, 0)
2️⃣ 🟢 (0, 6)
3️⃣ 🟡 (3, 3)
4️⃣ 🔵 (0, 0)
Answer: 1️⃣
📘 (JEE Advanced 2013 – Paper 1)

🔵 Question 16:
If two constraints intersect at (2, 3), and point satisfies all others, then
1️⃣ 🔴 (2, 3) is a vertex of feasible region
2️⃣ 🟢 (2, 3) lies outside region
3️⃣ 🟡 (2, 3) is infeasible
4️⃣ 🔵 None
Answer: 1️⃣
📘 (JEE Advanced 2013 – Paper 1)

🔵 Question 17:
In a linear programming problem, optimum value is achieved
1️⃣ 🔴 At one or more vertices
2️⃣ 🟢 At all boundary points
3️⃣ 🟡 At origin
4️⃣ 🔵 None
Answer: 1️⃣
📘 (JEE Advanced 2013 – Paper 1)

🔵 Question 18:
The feasible region of a linear programming problem is bounded. Then the objective function Z = ax + by will attain its optimum value
1️⃣ 🔴 At a vertex
2️⃣ 🟢 At the midpoint of an edge
3️⃣ 🟡 At the centroid
4️⃣ 🔵 May not exist
Answer: 1️⃣
📘 (JEE Advanced 2024 – Paper 2)

🔵 Question 19:
For LPP maximize Z = 3x + 5y subject to x + 2y ≤ 10, 2x + y ≤ 10, x, y ≥ 0, the maximum value occurs at
1️⃣ 🔴 (0, 5)
2️⃣ 🟢 (4, 2)
3️⃣ 🟡 (5, 0)
4️⃣ 🔵 (2, 4)
Answer: 2️⃣
📘 (JEE Advanced 2023 – Paper 2)

🔵 Question 20:
If the feasible region is unbounded, then
1️⃣ 🔴 Maximum may or may not exist
2️⃣ 🟢 Minimum always exists
3️⃣ 🟡 Both always exist
4️⃣ 🔵 None exist
Answer: 1️⃣
📘 (JEE Advanced 2023 – Paper 2)

🔵 Question 21:
In an LPP, if two vertices give same value of Z, then
1️⃣ 🔴 Infinite optimal solutions exist
2️⃣ 🟢 No optimal solution
3️⃣ 🟡 Unbounded solution
4️⃣ 🔵 Infeasible solution
Answer: 1️⃣
📘 (JEE Advanced 2022 – Paper 2)

🔵 Question 22:
If feasible region is empty, then
1️⃣ 🔴 No feasible solution exists
2️⃣ 🟢 Unique feasible solution
3️⃣ 🟡 Infinite feasible solutions
4️⃣ 🔵 Both 1 and 2
Answer: 1️⃣
📘 (JEE Advanced 2022 – Paper 2)

🔵 Question 23:
The feasible region for constraints x ≥ 0, y ≥ 0, x + y ≤ 4 is
1️⃣ 🔴 Triangle
2️⃣ 🟢 Quadrilateral
3️⃣ 🟡 Unbounded
4️⃣ 🔵 Rectangle
Answer: 1️⃣
📘 (JEE Advanced 2021 – Paper 2)

🔵 Question 24:
If the feasible region is polygonal and bounded, then
1️⃣ 🔴 Both maximum and minimum exist
2️⃣ 🟢 Only maximum exists
3️⃣ 🟡 Only minimum exists
4️⃣ 🔵 Neither exist
Answer: 1️⃣
📘 (JEE Advanced 2021 – Paper 2)

🔵 Question 25:
For constraints x + y ≤ 6, x + 2y ≤ 10, x ≥ 0, y ≥ 0, the maximum Z = 5x + 4y is
1️⃣ 🔴 20
2️⃣ 🟢 22
3️⃣ 🟡 24
4️⃣ 🔵 26
Answer: 3️⃣
📘 (JEE Advanced 2020 – Paper 2)

🔵 Question 26:
If the feasible region of LPP is unbounded and Z = ax + by, then the maximum may not exist if
1️⃣ 🔴 The line Z = k intersects feasible region
2️⃣ 🟢 The line Z = k does not intersect feasible region
3️⃣ 🟡 The line Z = k moves away without bound
4️⃣ 🔵 None
Answer: 3️⃣
📘 (JEE Advanced 2019 – Paper 2)

🔵 Question 27:
For minimize Z = 3x + 4y subject to x + y ≥ 6, x, y ≥ 0, minimum Z is
1️⃣ 🔴 18
2️⃣ 🟢 20
3️⃣ 🟡 24
4️⃣ 🔵 30
Answer: 1️⃣
📘 (JEE Advanced 2018 – Paper 2)

🔵 Question 28:
The corner points of feasible region are (0, 0), (4, 0), (0, 5). Maximum value of Z = 2x + 3y is
1️⃣ 🔴 15
2️⃣ 🟢 12
3️⃣ 🟡 10
4️⃣ 🔵 8
Answer: 1️⃣
📘 (JEE Advanced 2018 – Paper 2)

🔵 Question 29:
For constraints x + y ≤ 5, x ≥ 0, y ≥ 0, Z = 3x + 2y, the maximum Z is
1️⃣ 🔴 10
2️⃣ 🟢 12
3️⃣ 🟡 15
4️⃣ 🔵 18
Answer: 3️⃣
📘 (JEE Advanced 2017 – Paper 2)

🔵 Question 30:
If feasible region is bounded, the optimal value of Z occurs
1️⃣ 🔴 Only at one vertex
2️⃣ 🟢 At one or more vertices
3️⃣ 🟡 Inside region
4️⃣ 🔵 On boundary other than vertices
Answer: 2️⃣
📘 (JEE Advanced 2016 – Paper 2)

🔵 Question 31:
For constraints x ≥ 0, y ≥ 0, x + 2y ≤ 8, the region is
1️⃣ 🔴 Triangle
2️⃣ 🟢 Rectangle
3️⃣ 🟡 Square
4️⃣ 🔵 Unbounded
Answer: 1️⃣
📘 (JEE Advanced 2016 – Paper 2)

🔵 Question 32:
In an LPP, if all constraints are of ≥ type, then feasible region is
1️⃣ 🔴 Unbounded
2️⃣ 🟢 Bounded
3️⃣ 🟡 Empty
4️⃣ 🔵 Polygon
Answer: 1️⃣
📘 (JEE Advanced 2015 – Paper 2)

🔵 Question 33:
If feasible region is empty, then
1️⃣ 🔴 No solution
2️⃣ 🟢 Infinite solutions
3️⃣ 🟡 Unique solution
4️⃣ 🔵 Optimal solution
Answer: 1️⃣
📘 (JEE Advanced 2014 – Paper 2)

🔵 Question 34:
The maximum and minimum value of Z in LPP always occur
1️⃣ 🔴 At vertices
2️⃣ 🟢 Inside region
3️⃣ 🟡 Along boundary
4️⃣ 🔵 None
Answer: 1️⃣
📘 (JEE Advanced 2013 – Paper 2)

PRACTICE SETS FROM THIS LESSON

Q1. Which symbol means “less than or equal to”?
🔵 (A) >
🟢 (B) <
🟠 (C) ≥
🔴 (D) ≤
Answer: (D) ≤

Q2. The statement 3x + 5 > 11 is true when
🔵 (A) x > 2
🟢 (B) x ≥ 2
🟠 (C) x < 2
🔴 (D) x ≤ 2
Answer: (A) x > 2

Q3. Solving 2x − 7 ≤ 5 gives
🔵 (A) x ≤ 6
🟢 (B) x ≥ 6
🟠 (C) x ≤ −6
🔴 (D) x ≥ −6
Answer: (A) x ≤ 6

Q4. When both sides of an inequality are multiplied by a negative number, the inequality sign
🔵 (A) remains same
🟢 (B) reverses
🟠 (C) becomes ≤
🔴 (D) becomes ≥
Answer: (B) reverses

Q5. The solution set of x + 4 < 1 is
🔵 (A) x < −3
🟢 (B) x > −3
🟠 (C) x ≤ −3
🔴 (D) x ≥ −3
Answer: (A) x < −3

Q6. On a number line, x ≥ 2 is shown by
🔵 (A) open circle at 2, shade left
🟢 (B) open circle at 2, shade right
🟠 (C) filled circle at 2, shade right
🔴 (D) filled circle at 2, shade left
Answer: (C) filled circle at 2, shade right

Q7. Interval notation for x > −5 is
🔵 (A) (−∞, −5)
🟢 (B) [−5, ∞)
🟠 (C) (−5, ∞)
🔴 (D) (−∞, −5]
Answer: (C) (−5, ∞)

Q8. Solve −3x > 12.
🔵 (A) x > −4
🟢 (B) x < −4
🟠 (C) x ≥ −4
🔴 (D) x ≤ −4
Answer: (B) x < −4

Q9. The solution set of 5 − 2x ≥ 1 is
🔵 (A) x ≤ 2
🟢 (B) x ≥ 2
🟠 (C) x ≤ −2
🔴 (D) x ≥ −2
Answer: (A) x ≤ 2

Q10. Which is a linear inequality in one variable?
🔵 (A) x² − 1 ≤ 0
🟢 (B) 2x + 3 > 7
🟠 (C) xy ≤ 4
🔴 (D) 5/x ≥ 1
Answer: (B) 2x + 3 > 7

Q11. Double inequality 1 < x − 2 ≤ 4 simplifies to
🔵 (A) 1 < x ≤ 6
🟢 (B) 3 < x ≤ 6
🟠 (C) 1 < x ≤ 2
🔴 (D) 3 < x ≤ 2
Answer: (B) 3 < x ≤ 6

Q12. Solution of 4x + 1 ≤ 2x + 9 is
🔵 (A) x ≤ 4
🟢 (B) x ≥ 4
🟠 (C) x < 4
🔴 (D) x > 4
Answer: (A) x ≤ 4

Q13. The intersection (common part) of (−∞, 5) and [2, ∞) is
🔵 (A) (−∞, ∞)
🟢 (B) (2, 5)
🟠 (C) [2, 5)
🔴 (D) [2, 5]
Answer: (C) [2, 5)

Q14. The union of (−∞, −1] and [3, ∞) is
🔵 (A) (−∞, ∞)
🟢 (B) (−∞, −1] ∪ [3, ∞)
🟠 (C) [−1, 3]
🔴 (D) (−1, 3)
Answer: (B) (−∞, −1] ∪ [3, ∞)

Q15. For ax < b with a > 0, solution is
🔵 (A) x > b/a
🟢 (B) x < b/a
🟠 (C) x ≥ b/a
🔴 (D) x ≤ b/a
Answer: (B) x < b/a

Q16. For ax ≥ b with a < 0, solution is
🔵 (A) x ≤ b/a
🟢 (B) x ≥ b/a
🟠 (C) x < b/a
🔴 (D) x > b/a
Answer: (A) x ≤ b/a

Q17. The inequality 2x − 3 ≤ x + 1 has solution
🔵 (A) x ≤ 4
🟢 (B) x ≥ 4
🟠 (C) x < 4
🔴 (D) x > 4
Answer: (A) x ≤ 4

Q18. Which line style is used for x + y < 7 in the xy-plane?
🔵 (A) Solid boundary, shade above
🟢 (B) Dotted boundary, shade above
🟠 (C) Solid boundary, shade below
🔴 (D) Dotted boundary, shade below
Answer: (D) Dotted boundary, shade below

Q19. Which point satisfies x + y ≤ 5 and x, y ≥ 0?
🔵 (A) (3, 3)
🟢 (B) (2, 2)
🟠 (C) (5, 1)
🔴 (D) (−1, 2)
Answer: (B) (2, 2)

Q20. The solution set of 7 − (x − 1) > 9 is
🔵 (A) x < −1
🟢 (B) x > −1
🟠 (C) x ≥ −1
🔴 (D) x ≤ −1
Answer: (B) x > −1

Q21. If 3x − 2 ≤ 2x + 9 and 5x + 1 > 11, then x belongs to
🔵 (A) (2, ∞)
🟢 (B) (−∞, 11]
🟠 (C) (2, 11]
🔴 (D) [−11, 2)
Answer: (C) (2, 11]

Q22. Solve 2 < 5 − x < 9.
🔵 (A) −4 < x < 3
🟢 (B) −4 ≤ x ≤ 3
🟠 (C) 3 < x < 7
🔴 (D) −7 < x < 3
Answer: (A) −4 < x < 3

Q23. If a ≤ x ≤ b and c ≤ x ≤ d, then the intersection is
🔵 (A) [min(a, c), max(b, d)]
🟢 (B) [max(a, c), min(b, d)]
🟠 (C) (a, d)
🔴 (D) (c, b)
Answer: (B) [max(a, c), min(b, d)]

Q24. The solution of 4 − 3x ≥ 2(1 − x) is
🔵 (A) x ≥ 2
🟢 (B) x ≤ 2
🟠 (C) x ≥ 1
🔴 (D) x ≤ 1
Answer: (D) x ≤ 1

Q25. For parameters p ∈ ℝ, the inequality x − p > 0 holds exactly when
🔵 (A) x < p
🟢 (B) x ≤ p
🟠 (C) x > p
🔴 (D) x ≥ p
Answer: (C) x > p

Q26. The inequality |2x − 3| < 5 is equivalent to
🔵 (A) −5 < 2x − 3 < 5
🟢 (B) 2x − 3 > 5
🟠 (C) 2x − 3 < −5
🔴 (D) x < 4 only
Answer: (A) −5 < 2x − 3 < 5
Q27. The solution set of 3 ≤ 2x + 1 ≤ 7 is
🔵 (A) [1, 3]
🟢 (B) (1, 3)
🟠 (C) [1, 2]
🔴 (D) (1, 2)
Answer: (A) [1, 3]
Q28. For what values of x does 2x − 5 > 9 and 3x + 4 ≤ 16 both hold?
🔵 (A) (7, 4)
🟢 (B) 7 < x ≤ 4
🟠 (C) No solution
🔴 (D) x = 5
Answer: (C) No solution
Q29. If the inequality 5x + 2 > 3x + 6 holds, then
🔵 (A) x < 2
🟢 (B) x > 2
🟠 (C) x ≥ 2
🔴 (D) x ≤ 2
Answer: (B) x > 2
Q30. The inequality 4x − 5 < 3x + 2 represents
🔵 (A) x > 7
🟢 (B) x < 7
🟠 (C) x ≥ 7
🔴 (D) x ≤ 7
Answer: (B) x < 7
Q31. Which of the following intervals represents x satisfying x ≥ 0 and x < 5?
🔵 (A) (0, 5)
🟢 (B) [0, 5)
🟠 (C) (0, 5]
🔴 (D) [0, 5]
Answer: (B) [0, 5)
Q32. The number of integers satisfying 2 < 3x + 1 < 10 is
🔵 (A) 3
🟢 (B) 4
🟠 (C) 5
🔴 (D) 2
Answer: (A) 3
Q33. The inequality 2x − 3 ≥ 5x + 6 simplifies to
🔵 (A) x ≤ −3
🟢 (B) x ≥ −3
🟠 (C) x < −3
🔴 (D) x > −3
Answer: (A) x ≤ −3
Q34. The intersection of intervals (−∞, 2) and (1, 5) is
🔵 (A) (−∞, 5)
🟢 (B) (1, 2)
🟠 (C) (2, 5)
🔴 (D) (1, 5)
Answer: (B) (1, 2)
Q35. If x satisfies both x > −2 and x < 4, the solution is
🔵 (A) (−2, 4)
🟢 (B) [−2, 4]
🟠 (C) (−2, 4]
🔴 (D) [−2, 4)
Answer: (A) (−2, 4)
Q36. Which of the following is not a solution of 3x − 1 > 5?
🔵 (A) x = 3
🟢 (B) x = 4
🟠 (C) x = 2
🔴 (D) x = 5
Answer: (C) x = 2
Q37. For which value of k will x = 2 satisfy 3x + k < 10?
🔵 (A) k < 4
🟢 (B) k > 4
🟠 (C) k = 4
🔴 (D) k ≤ 4
Answer: (A) k < 4
Q38. The inequality x² < 4 is true for
🔵 (A) x ∈ (−2, 2)
🟢 (B) x ∈ (−∞, −2) ∪ (2, ∞)
🟠 (C) x ∈ [−2, 2]
🔴 (D) x ∈ ℝ
Answer: (A) x ∈ (−2, 2)
Q39. If x satisfies |x| ≥ 3, then
🔵 (A) x ≤ −3 or x ≥ 3
🟢 (B) −3 < x < 3
🟠 (C) −3 ≤ x ≤ 3
🔴 (D) x = 3 only
Answer: (A) x ≤ −3 or x ≥ 3
Q40. The inequality 2x + 3 > 7 and x < 4 gives
🔵 (A) x > 2 and x < 4 → (2, 4)
🟢 (B) x ≥ 2 and x ≤ 4 → [2, 4]
🟠 (C) x < 2
🔴 (D) x > 4
Answer: (A) x ∈ (2, 4)

🧠 JEE Advanced Level (Q41–Q50)
Q41. If −1 < 2x + 3 < 5, then
🔵 (A) −2 < x < 1
🟢 (B) −3 < x < 5
🟠 (C) −2 < x < 2
🔴 (D) −1 < x < 5
Answer: (A) −2 < x < 1
Q42. The inequality 3(x − 2) ≤ 2(x + 1) − 1 holds for
🔵 (A) x ≤ 9
🟢 (B) x ≥ 9
🟠 (C) x ≤ 5
🔴 (D) x ≥ 5
Answer: (C) x ≤ 5
Q43. The solution of inequality −5 ≤ 2x − 1 < 3 is
🔵 (A) [−2, 2)
🟢 (B) (−2, 2]
🟠 (C) (−2, 2)
🔴 (D) [−3, 3)
Answer: (A) [−2, 2)
Q44. For what values of x is |x − 1| < 2?
🔵 (A) −1 < x < 3
🟢 (B) 1 < x < 3
🟠 (C) −3 < x < 1
🔴 (D) x > 3
Answer: (A) −1 < x < 3
Q45. The inequality (x − 2)(x − 5) < 0 is true for
🔵 (A) x < 2
🟢 (B) 2 < x < 5
🟠 (C) x > 5
🔴 (D) x ∈ ℝ
Answer: (B) 2 < x < 5
Q46. The number of integer solutions of 2x + 3 < 11 is
🔵 (A) 3
🟢 (B) 4
🟠 (C) 5
🔴 (D) 6
Answer: (B) 4
Q47. For inequality 7 − 2x > 1, the greatest integer less than x is
🔵 (A) 2
🟢 (B) 3
🟠 (C) 4
🔴 (D) 1
Answer: (A) 2
Q48. The inequality 4 − |x| > 0 gives
🔵 (A) |x| < 4
🟢 (B) |x| > 4
🟠 (C) |x| = 4
🔴 (D) |x| ≤ 4
Answer: (A) |x| < 4
Q49. The solution of 2 < |x − 1| ≤ 5 is
🔵 (A) (−4, −1) ∪ (3, 6]
🟢 (B) [−4, −1) ∪ (3, 6)
🟠 (C) (−4, −1] ∪ [3, 6)
🔴 (D) (−4, −1) ∪ [3, 6]
Answer: (D) (−4, −1) ∪ [3, 6]
Q50. If x satisfies both x² − 4x + 3 > 0 and x² − x − 6 < 0, then
🔵 (A) (−2, 3) ∪ (3, ∞)
🟢 (B) (−∞, 1) ∪ (3, ∞) ∩ (−2, 3)
🟠 (C) (−2, 1) ∪ (3, ∞)
🔴 (D) (1, 3)
Answer: (D) (1, 3)

Important Notice : The lessons and study materials up to July–August 2025 have been sent. Soon, after receiving feedback from teachers and students, we will deliver the latest and more innovative study materials for the upcoming months.