Class 11 : Maths (In English) – Lesson 4. Complex Numbers and Quadratic Equations

Posted by

On June 21, 2025

EXPLANATION & SUMMARY

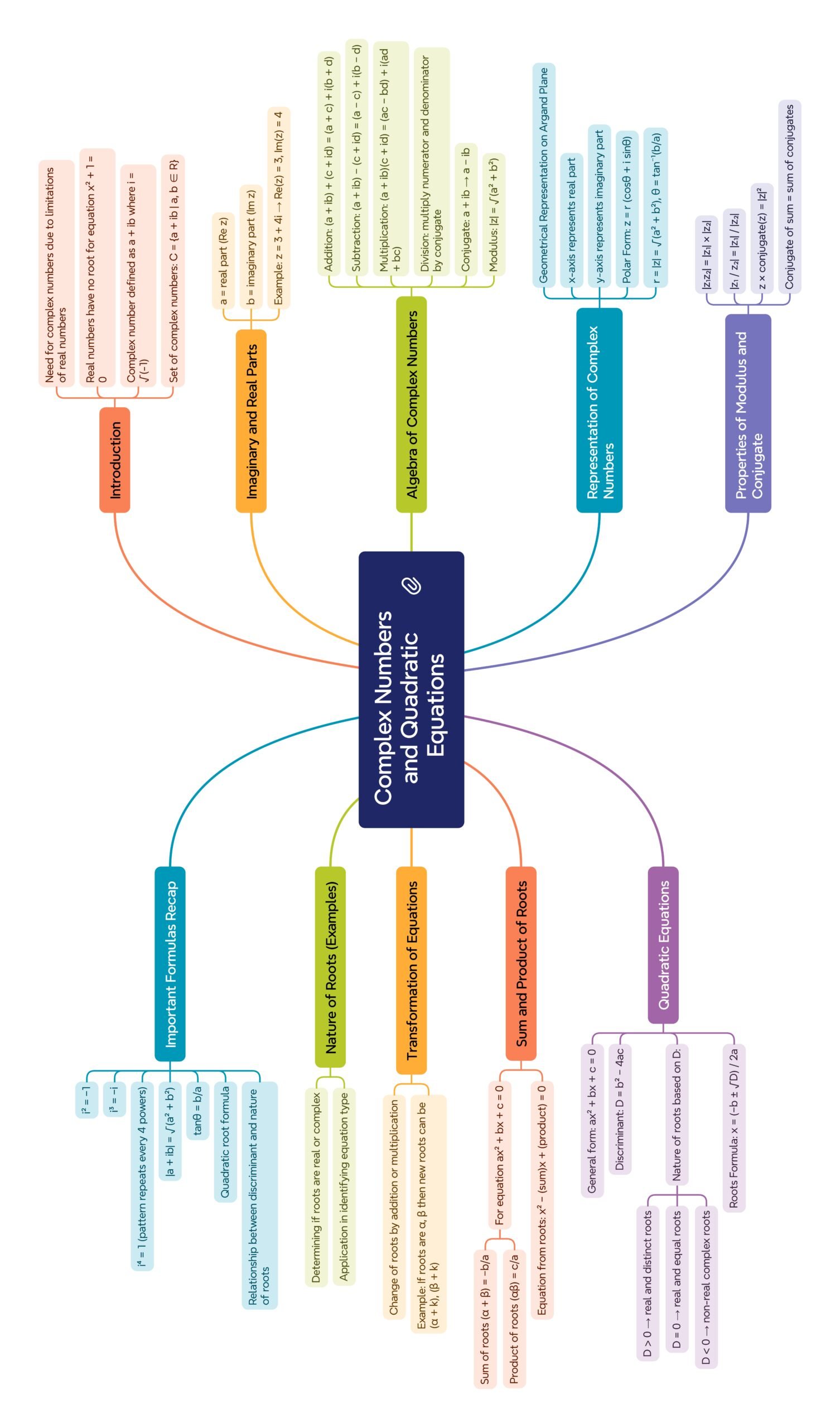
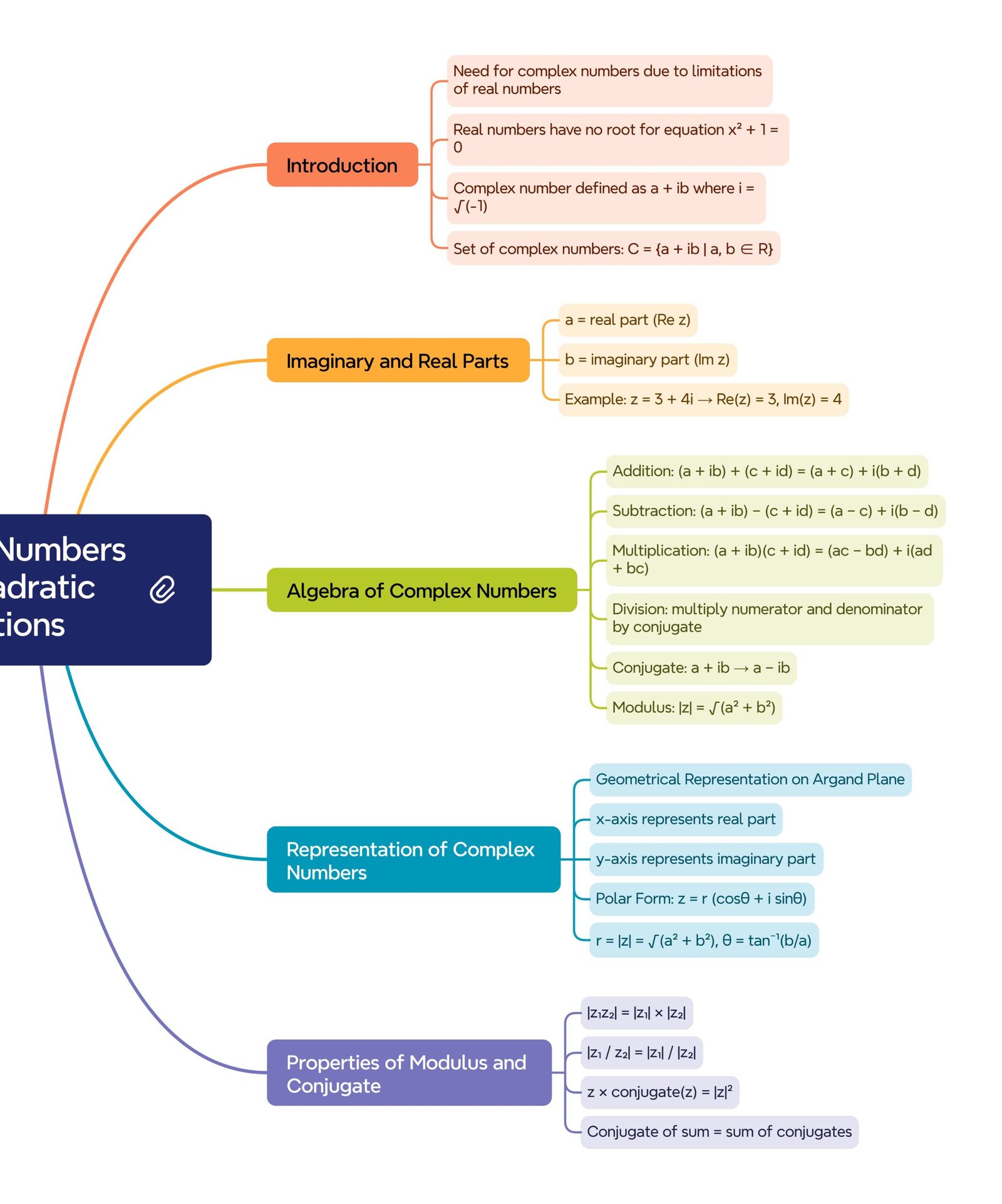
1️⃣ Introduction
🔵 A quadratic equation a·x² + b·x + c = 0 has real roots only when the discriminant D = b² − 4ac ≥ 0.
🟢 When D < 0, roots are not real. To handle such cases, mathematicians introduced a new number i such that i² = −1.
💡 Using i, we form complex numbers which extend the real number system.
✨ Complex numbers help solve equations that cannot be solved in real numbers.

2️⃣ Imaginary Unit
📘 Definition: i = √(−1)
✔ i² = −1, i³ = −i, i⁴ = 1 (then repeats)
🧠 Examples:
🔹 √(−4) = 2i
🔹 √(−9) = 3i
🔹 √(−25) = 5i

3️⃣ Definition of Complex Number
🔵 A complex number is of the form z = a + i·b
➡ a = real part, Re(z)
➡ b = imaginary part, Im(z)
📌 Set of all complex numbers is denoted by C.
🧾 Examples:
1️⃣ 3 + 2i → Re = 3, Im = 2
2️⃣ −5i → Re = 0, Im = −5
3️⃣ 7 → purely real (Im = 0)
4️⃣ 4i → purely imaginary (Re = 0)

4️⃣ Equality of Complex Numbers
Two complex numbers a + i·b and c + i·d are equal if
✅ a = c
✅ b = d
Example: 2 + 3i = 2 + 3i ✔ but ≠ 3 + 2i ❌

5️⃣ Representation on Argand Plane
🧭 Complex number z = a + i·b is represented as point (a, b).
📈 x-axis → real part
📉 y-axis → imaginary part
💡 This plane is called the Argand Plane.
📍 Example: z = 3 + 4i → point (3, 4)

6️⃣ Modulus of a Complex Number
🔹 The modulus is the distance from origin (0, 0) to (a, b).
Formula: |z| = √(a² + b²)
Example: z = 3 + 4i → |z| = √(9 + 16) = 5
📏 Represents length of vector.

7️⃣ Argument (Amplitude)
🔸 Argument θ is the angle made by line joining origin to (a, b) with positive x-axis.
Formula: tan θ = b / a
🧭 Quadrant check:
• I: a > 0, b > 0
• II: a < 0, b > 0
• III: a < 0, b < 0
• IV: a > 0, b < 0
✏️ Example: z = 1 + √3·i → tan θ = √3 ⇒ θ = π/3

8️⃣ Conjugate of a Complex Number
🔹 Conjugate of z = a + i·b is z̄ = a − i·b
🧾 Properties:
1️⃣ z·z̄ = a² + b² = |z|²
2️⃣ (z₁ + z₂)̄ = z̄₁ + z̄₂
3️⃣ (z₁·z₂)̄ = z̄₁ · z̄₂
📘 Example: z = 3 + 4i → z̄ = 3 − 4i
✔ z·z̄ = 25

9️⃣ Operations on Complex Numbers
Let z₁ = a + i·b, z₂ = c + i·d
➕ Addition: z₁ + z₂ = (a + c) + i·(b + d)
➖ Subtraction: z₁ − z₂ = (a − c) + i·(b − d)
✖ Multiplication: z₁·z₂ = (a·c − b·d) + i·(a·d + b·c)
➗ Division: z₁ ÷ z₂ = [(a + i·b)(c − i·d)] / (c² + d²)
🧠 Example: (3 + 2i) ÷ (1 − i)
= [(3 + 2i)(1 + i)] / 2
= (1/2) + (5/2)i

🔟 Polar (Trigonometric) Form
🧭 Any complex number z = a + i·b can be written as
z = r (cos θ + i·sin θ)
where r = √(a² + b²), θ = argument
✏️ Example: z = 1 + i
r = √2, θ = π/4
So z = √2 (cos π/4 + i·sin π/4)

1️⃣1️⃣ Euler Form
Using e^(iθ) = cos θ + i·sin θ
✔ z = r·e^(iθ)

1️⃣2️⃣ Algebraic Properties
🟢 Commutative: z₁ + z₂ = z₂ + z₁, z₁·z₂ = z₂·z₁
🟡 Associative: (z₁ + z₂) + z₃ = z₁ + (z₂ + z₃)
🔵 Distributive: z₁·(z₂ + z₃) = z₁·z₂ + z₁·z₃

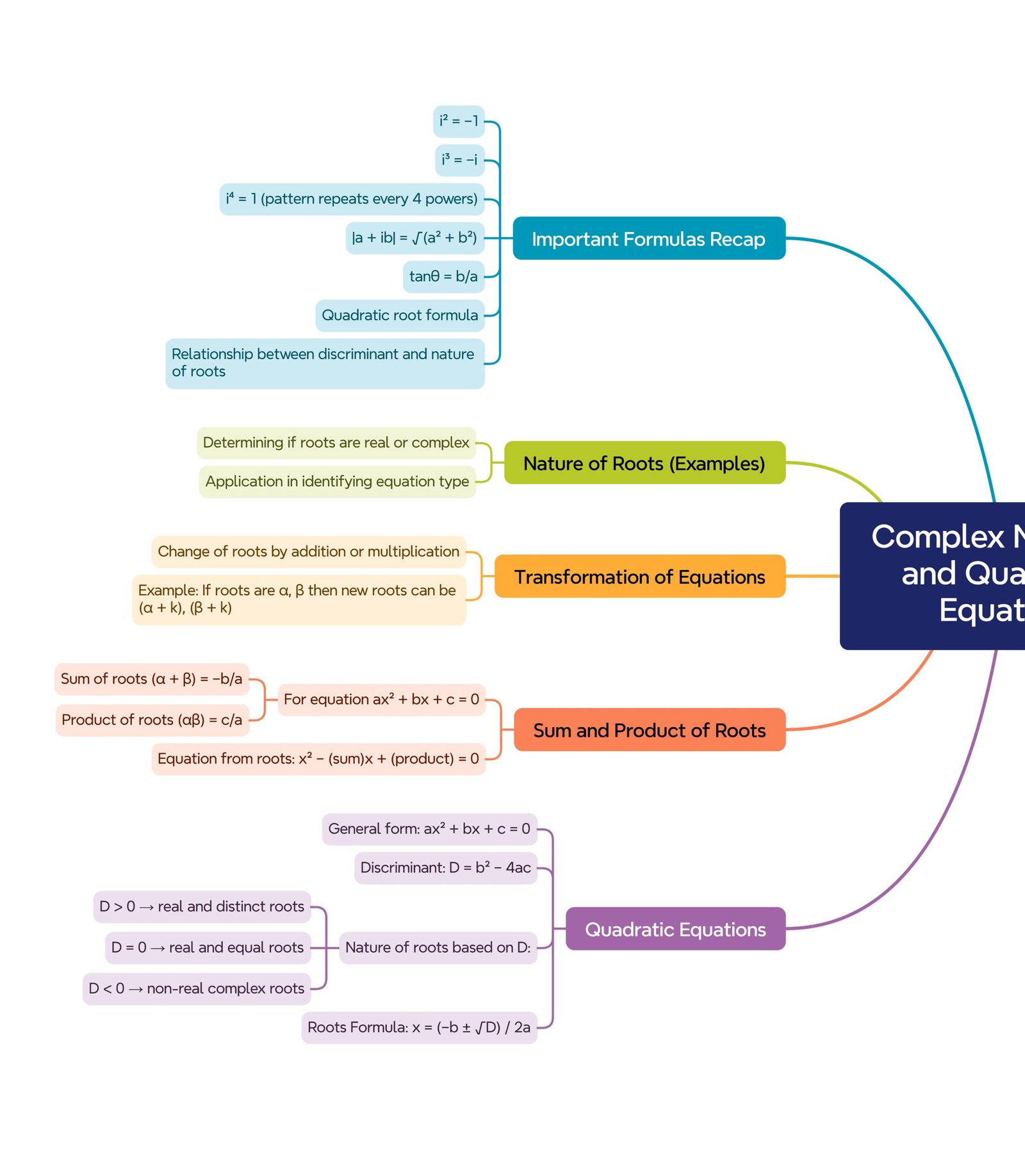
1️⃣3️⃣ Quadratic Equation
General: a·x² + b·x + c = 0 (a ≠ 0)
Discriminant D = b² − 4ac
📊 Nature of Roots:
• D > 0 → real, distinct
• D = 0 → real, equal
• D < 0 → complex conjugate
Roots: x = [−b ± √D] / (2a)
If D < 0 → √D = i√|D|
✏️ Example: x² + 4x + 8 = 0
D = 16 − 32 = −16
Roots: x = (−4 ± 4i) / 2 = −2 ± 2i

1️⃣4️⃣ Relations between Roots and Coefficients
If α, β are roots:
α + β = −b/a
α·β = c/a

1️⃣5️⃣ Formation of Quadratic Equation from Roots
If roots are α, β → x² − (α + β)x + αβ = 0

1️⃣6️⃣ Cube Roots of Unity
Numbers satisfying x³ = 1 → 1, ω, ω²
ω = (−1 + i√3)/2, ω² = (−1 − i√3)/2
Properties:
• ω³ = 1
• 1 + ω + ω² = 0
• ω ≠ 1

1️⃣7️⃣ Geometrical Interpretation
🧭 Each complex number = vector from origin to (a, b).
• Length = |z|
• Angle = θ
✔ Multiplying by i rotates 90° anticlockwise.
Example: 1 × i = i

1️⃣8️⃣ Key Identities
📘 i² = −1, i³ = −i, i⁴ = 1
✔ z·z̄ = |z|²
✔ |z₁·z₂| = |z₁||z₂|
✔ arg(z₁·z₂) = arg(z₁) + arg(z₂)
✔ (z₁·z₂)̄ = z̄₁·z̄₂

1️⃣9️⃣ Applications
🧠 Used to solve equations with negative discriminant
⚡ Electrical circuits (AC)
📈 Vector rotations
🧪 Quantum mechanics

🔶 Summary (≈300 words)
• z = a + i·b
• i² = −1, i³ = −i, i⁴ = 1
• Re(z) = a, Im(z) = b
• |z| = √(a² + b²)
• z̄ = a − i·b
• Polar: r(cos θ + i·sin θ)
• Euler: r·e^(iθ)
• Argand plane → point (a, b)
Quadratic eq: a·x² + b·x + c = 0
D > 0 → real, distinct
D = 0 → real, equal
D < 0 → complex conjugates
Roots: (−b ± i√|D|)/2a
α + β = −b/a, αβ = c/a
Cube roots of unity: 1, ω, ω²
ω = (−1 + i√3)/2
ω³ = 1, 1 + ω + ω² = 0

📝 Quick Recap
✔ z = a + i·b
✔ i² = −1
✔ |z| = √(a² + b²)
✔ Conjugate = a − i·b
✔ Polar = r(cos θ + i·sin θ)
✔ D < 0 → complex roots
✔ Cube roots unity: 1, ω, ω²
✔ 1 + ω + ω² = 0

————————————————————————————————————————————————————————————————————————————

QUESTIONS FROM TEXTBOOK

📗 Exercise 4.1

🔵 Question 1
(5i) (−3i/5). Express in the form a + ib.

🟢 Answer
➡️ (5i)(−3i/5) = (5·−3/5)·i²
➡️ = (−3)·(−1)
➡️ = 3
✔️ Result: 3 + 0i

🔵 Question 2
i⁹ + i¹⁹. Express in a + ib.

🟢 Answer
➡️ i⁴ = 1 ⇒ powers repeat every 4
➡️ i⁹ = i¹ (since 9 ≡ 1 mod 4) = i
➡️ i¹⁹ = i³ (since 19 ≡ 3 mod 4) = −i
➡️ i⁹ + i¹⁹ = i + (−i) = 0
✔️ Result: 0 + 0i

🔵 Question 3
i⁻³⁹. Express in a + ib.

🟢 Answer
➡️ i⁻³⁹ = 1 / i³⁹
➡️ i³⁹ = i³ (since 39 ≡ 3 mod 4) = −i
➡️ 1/(−i) = i
✔️ Result: 0 + 1i

🔵 Question 4
3(7 + 7i) + i(7 + 7i). Express in a + ib.

🟢 Answer
➡️ 3(7 + 7i) = 21 + 21i
➡️ i(7 + 7i) = 7i + 7i² = 7i − 7
➡️ Sum = (21 − 7) + (21i + 7i)
➡️ = 14 + 28i
✔️ Result: 14 + 28i

🔵 Question 5
(1 − i) − (−1 + 6i). Express in a + ib.

🟢 Answer
➡️ = 1 − i + 1 − 6i
➡️ = 2 − 7i
✔️ Result: 2 − 7i

🔵 Question 6
(1/5 + (2/5)i) − (4 + (5/2)i). Express in a + ib.

🟢 Answer
➡️ Real: 1/5 − 4 = −19/5
➡️ Imag: 2/5 − 5/2 = (4/10 − 25/10) = −21/10
✔️ Result: −19/5 − (21/10)i

🔵 Question 7
[(1/3 + (7/3)i) + (4 + (1/3)i)] − (−4/3 + i). Express in a + ib.

🟢 Answer
➡️ Inside sum: real = 1/3 + 4 = 13/3; imag = 7/3 + 1/3 = 8/3
➡️ Subtract: (13/3 − (−4/3)) + (8/3 − 1)i
➡️ = 17/3 + (5/3)i
✔️ Result: 17/3 + (5/3)i

🔵 Question 8
(1 − i)⁴. Express in a + ib.

🟢 Answer
➡️ (1 − i)² = 1 − 2i + i² = −2i
➡️ (−2i)² = 4i² = −4
✔️ Result: −4 + 0i

🔵 Question 9
(1/3 + 3i)³. Express in a + ib.

🟢 Answer
➡️ Let a = 1/3, b = 3i
➡️ (a + b)³ = a³ + 3a²b + 3ab² + b³
➡️ a³ = 1/27
➡️ 3a²b = 3·(1/9)·3i = i
➡️ 3ab² = 3·(1/3)·(3i)² = 1·9i² = −9
➡️ b³ = (3i)³ = 27i³ = −27i
➡️ Sum = (1/27 − 9) + (i − 27i)
➡️ = (−242/27) − 26i
✔️ Result: −242/27 − 26i

🔵 Question 10
(−2 − (1/3)i)³. Express in a + ib.

🟢 Answer
➡️ Let a = −2, b = −(1/3)i
➡️ (a + b)³ = a³ + 3a²b + 3ab² + b³
➡️ a³ = −8
➡️ 3a²b = 3·4·(−1/3)i = −4i
➡️ b² = (−1/3 i)² = −1/9
➡️ 3ab² = 3·(−2)·(−1/9) = 2/3
➡️ b³ = (−1/3 i)³ = (1/27)i
➡️ Sum = (−8 + 2/3) + (−4 + 1/27)i
➡️ Real = −22/3; Imag = (−108/27 + 1/27)i = (−107/27)i
✔️ Result: −22/3 − (107/27)i

🔵 Question 11
Find the multiplicative inverse of 4 − 3i.

🟢 Answer
➡️ 1/(4 − 3i) = (4 + 3i)/(4² + 3²)
➡️ = (4 + 3i)/25
✔️ Inverse: 4/25 + (3/25)i

🔵 Question 12
Find the multiplicative inverse of √5 + 3i.

🟢 Answer
➡️ 1/(√5 + 3i) = (√5 − 3i)/( (√5)² + 3² )
➡️ = (√5 − 3i)/(5 + 9)
➡️ = (√5 − 3i)/14
✔️ Inverse: (√5)/14 − (3/14)i

🔵 Question 13
Find the multiplicative inverse of −i.

🟢 Answer
➡️ 1/(−i) = i
✔️ Inverse: 0 + 1i

🔵 Question 14
Express in the form a + ib:
[(3 + i√5)(3 − i√5)] / [(√3 + √2 i) − (√3 − i√2)]

🟢 Answer
➡️ Numerator: (a + ib)(a − ib) = a² + b²
➡️ = 3² + (√5)² = 9 + 5 = 14
➡️ Denominator: (√3 + √2 i) − (√3 − √2 i)
➡️ = √3 − √3 + √2 i − (−√2 i) = 2√2 i
➡️ Fraction = 14 / (2√2 i) = 7/(√2 i)
➡️ 1/i = −i ⇒ 7/(√2 i) = −(7/√2) i
➡️ = −(7√2/2) i
✔️ Result: 0 − (7√2/2)i

(CBSE MODEL QUESTIONS PAPER)

ESPECIALLY MADE FROM THIS LESSON ONLY

🟦 Section A – MCQs (1 mark each)
🔵 Question 1:
The value of i² + i⁴ + i⁶ + i⁸ is
1️⃣ 4
2️⃣ 0
3️⃣ 2
4️⃣ –4
🟢 Answer: 2️⃣ 0
🔵 Question 2:
If z = 3 + 4i, then |z| equals
1️⃣ 5
2️⃣ 7
3️⃣ 1
4️⃣ 25
🟢 Answer: 1️⃣ 5
🔵 Question 3:
Conjugate of (2 – 5i) is
1️⃣ 2 + 5i
2️⃣ –2 – 5i
3️⃣ 2 – 5i
4️⃣ –2 + 5i
🟢 Answer: 1️⃣ 2 + 5i
🔵 Question 4:
The real part of (3i + 5) is
1️⃣ 3
2️⃣ 5
3️⃣ 8
4️⃣ 0
🟢 Answer: 2️⃣ 5
🔵 Question 5:
If z = 2 + i√3, then argument of z is
1️⃣ π/6
2️⃣ π/3
3️⃣ π/2
4️⃣ π
🟢 Answer: 2️⃣ π/3
🔵 Question 6:
For any complex number z, z·z̄ equals
1️⃣ |z|²
2️⃣ z²
3️⃣ z
4️⃣ |z|
🟢 Answer: 1️⃣ |z|²
🔵 Question 7:
If i = √(–1), then i⁵ equals
1️⃣ i
2️⃣ –1
3️⃣ –i
4️⃣ 1
🟢 Answer: 1️⃣ i
🔵 Question 8:
The modulus of 1 – i is
1️⃣ √2
2️⃣ 1
3️⃣ 2
4️⃣ 0
🟢 Answer: 1️⃣ √2
🔵 Question 9:
The value of i³ + i⁵ is
1️⃣ –i
2️⃣ 0
3️⃣ i
4️⃣ –2i
🟢 Answer: 2️⃣ 0
🔵 Question 10:
If z = 4i, then Re(z) is
1️⃣ 4
2️⃣ 0
3️⃣ i
4️⃣ –4
🟢 Answer: 2️⃣ 0
🔵 Question 11:
Cube roots of unity satisfy
1️⃣ x² + x + 1 = 0
2️⃣ x³ – 1 = 0
3️⃣ x³ + 1 = 0
4️⃣ x² – x + 1 = 0
🟢 Answer: 2️⃣ x³ – 1 = 0
🔵 Question 12:
If ω is cube root of unity, then ω² + ω + 1 =
1️⃣ 1
2️⃣ 0
3️⃣ –1
4️⃣ 2
🟢 Answer: 2️⃣ 0
🔵 Question 13:
If α, β are roots of x² + 3x + 2 = 0, then α + β =
1️⃣ 2
2️⃣ –2
3️⃣ –3
4️⃣ 3
🟢 Answer: 3️⃣ –3
🔵 Question 14:
If α, β are roots of x² + bx + c = 0, then αβ =
1️⃣ b
2️⃣ c
3️⃣ c/b
4️⃣ c/a
🟢 Answer: 4️⃣ c/a
🔵 Question 15:
If z = a + ib, then Im(z) is
1️⃣ a
2️⃣ b
3️⃣ i·b
4️⃣ a + b
🟢 Answer: 2️⃣ b
🔵 Question 16:
The polar form of 1 + i is
1️⃣ √2 (cos π/4 + i sin π/4)
2️⃣ 2 (cos π/2 + i sin π/2)
3️⃣ √2 (cos π/3 + i sin π/3)
4️⃣ 1 (cos π/4 + i sin π/4)
🟢 Answer: 1️⃣ √2 (cos π/4 + i sin π/4)
🔵 Question 17:
If z₁ = 2 + 3i, z₂ = 1 – 2i, then Re(z₁ + z₂) =
1️⃣ 2
2️⃣ 3
3️⃣ 1
4️⃣ 4
🟢 Answer: 4️⃣ 4
🔵 Question 18:
The cube roots of unity are
1️⃣ 1, ω, ω²
2️⃣ 1, –1, i
3️⃣ 1, i, –i
4️⃣ 1, –1, ω
🟢 Answer: 1️⃣ 1, ω, ω²

🟨 Section B – Very Short Answer (2 marks each)
🔵 Question 19: Find the modulus and argument of z = 1 – i.
🟢 Answer: |z| = √(1² + (–1)²) = √2, θ = tan⁻¹(–1) = –π/4
🔵 Question 20: Express (1 + i)/(1 – i) in the form a + ib.
🟢 Answer: Multiply by conjugate:
(1 + i)/(1 – i) × (1 + i)/(1 + i) = (1 + 2i + i²)/2 = i
🔵 Question 21: If z₁ = 3 + 4i and z₂ = 1 – 2i, find z₁·z₂.
🟢 Answer: (3 + 4i)(1 – 2i) = 3 – 6i + 4i – 8i² = 11 – 2i
🔵 Question 22: Write the conjugate of (2 – 3i)/(4 + i).
🟢 Answer: First simplify:
Multiply by conjugate (4 – i): (2 – 3i)(4 – i)/(16 + 1) = (8 – 2i – 12i + 3i²)/17 = (8 – 14i – 3)/17 = (5 – 14i)/17
Conjugate = (5 + 14i)/17
🔵 Question 23: Solve x² + x + 1 = 0.
🟢 Answer: D = 1 – 4 = –3
x = [–1 ± i√3]/2 = –½ ± (√3/2)i

🟧 Section C – Short Answer (3 marks each)
🔵 Question 24: Find modulus and argument of z = –1 + √3 i.
🟢 Answer:
|z| = √[ (–1)² + (√3)² ] = √4 = 2
θ = tan⁻¹(√3 / –1) → QII → π – π/3 = 2π/3
z = 2 (cos 2π/3 + i sin 2π/3)
🔵 Question 25: If z₁ = 3 + 4i, z₂ = 1 + 2i, find |z₁·z₂| and |z₁|·|z₂|.
🟢 Answer:
z₁·z₂ = (3 + 4i)(1 + 2i) = 3 + 6i + 4i + 8i² = –5 + 10i
|z₁·z₂| = √( (–5)² + 10² ) = √125 = 5√5
|z₁| = 5, |z₂| = √5 → |z₁|·|z₂| = 5√5
✔ Verified |z₁z₂| = |z₁||z₂|
🔵 Question 26: Express z = 1 – √3 i in polar form.
🟢 Answer:
r = √(1² + (–√3)²) = 2
θ = tan⁻¹(–√3/1) = –π/3
z = 2 (cos(–π/3) + i sin(–π/3))
🔵 Question 27: Show that (1 + i)⁴ = –4.
🟢 Answer:
(1 + i)² = 1 + 2i + i² = 2i
(1 + i)⁴ = (2i)² = 4i² = –4
🔵 Question 28: If roots of x² + 2x + 5 = 0 are α, β, verify α·β = c/a.
🟢 Answer:
D = 4 – 20 = –16
α = –1 + 2i, β = –1 – 2i
α·β = (–1)² – (2i)² = 1 – (–4) = 5 = c/a ✔

🟥 Section D – Long Answer (5 marks each)
🔵 Question 29: Solve x² + 4x + 13 = 0 and represent the roots on Argand plane.
🟢 Answer:
D = 16 – 52 = –36
Roots: x = [–4 ± i√36]/2 = –2 ± 3i
🧭 Points: (–2, 3) and (–2, –3)
🔵 Question 30: Find all cube roots of 8( cos 300° + i sin 300° ).
🟢 Answer:
r = 8, θ = 300°
Cube roots: √[3]{8} [cos((300° + 360°k)/3) + i sin((300° + 360°k)/3)]
= 2[cos(100°), cos(220°), cos(340°)] with corresponding sines.
🔵 Question 31: Show that ω and ω² are complex cube roots of unity and find 1 + ω + ω².
🟢 Answer:
ω = (–1 + i√3)/2, ω² = (–1 – i√3)/2
ω³ = 1
1 + ω + ω² = 0 ✔

🟫 Section E – Case/Application (5 marks each)
🔵 Question 32:
A quadratic equation represents motion with complex roots.
Given: x² + 6x + 13 = 0
(a) Find the roots.
(b) Interpret geometrically.
🟢 Answer:
D = 36 – 52 = –16
Roots = –3 ± 2i
Representation: points (–3, 2), (–3, –2) on Argand plane.
🔵 Question 33:
An alternating current is given by I = 10(cos ωt + i sin ωt).
Find |I| and interpret.
🟢 Answer:
|I| = 10 √(cos² ωt + sin² ωt) = 10
Interpretation: amplitude of current = 10 units.

JEE MAINS QUESTIONS FROM THIS LESSON

🔵 Question 1
If z = 3 + 4i, then modulus of z is
🟥 1️⃣ 5
🟩 2️⃣ 4
🟨 3️⃣ 3
🟦 4️⃣ 7
Answer: 🟥 1️⃣ 5
📘 (JEE Main 2024)

🔵 Question 2
If z1 = 2 + 3i and z2 = 3 − 4i, then z1 × z2 =
🟥 1️⃣ 18 − i
🟩 2️⃣ 6 + i
🟨 3️⃣ 18 + i
🟦 4️⃣ 6 − i
Answer: 🟥 1️⃣ 18 − i
📘 (JEE Main 2023)

🔵 Question 3
If z = a + ib satisfies |z| = 5 and a = 3, then b equals
🟥 1️⃣ 4 or −4
🟩 2️⃣ 2 or −2
🟨 3️⃣ 3
🟦 4️⃣ 1
Answer: 🟥 1️⃣ 4 or −4
📘 (JEE Main 2022)

🔵 Question 4
If z = x + iy satisfies |z − 3| = 5, then locus of z is
🟥 1️⃣ Circle with centre (3, 0) and radius 5
🟩 2️⃣ Circle with centre (0, 3) and radius 5
🟨 3️⃣ Line parallel to x-axis
🟦 4️⃣ Line parallel to y-axis
Answer: 🟥 1️⃣ Circle with centre (3, 0) and radius 5
📘 (JEE Main 2022)

🔵 Question 5
Conjugate of 2 − 3i is
🟥 1️⃣ 2 + 3i
🟩 2️⃣ −2 + 3i
🟨 3️⃣ −2 − 3i
🟦 4️⃣ 2 − 3i
Answer: 🟥 1️⃣ 2 + 3i
📘 (JEE Main 2021)

🔵 Question 6
If z = 1 + i, then z⁴ =
🟥 1️⃣ −4
🟩 2️⃣ 4
🟨 3️⃣ 4i
🟦 4️⃣ 2i
Answer: 🟥 1️⃣ −4
📘 (JEE Main 2021)

🔵 Question 7
If z = 2(cos 60° + i sin 60°), then z³ equals
🟥 1️⃣ 8(cos 180° + i sin 180°)
🟩 2️⃣ 8(cos 120° + i sin 120°)
🟨 3️⃣ 6(cos 60° + i sin 60°)
🟦 4️⃣ 8(cos 90° + i sin 90°)
Answer: 🟥 1️⃣ 8(cos 180° + i sin 180°)
📘 (JEE Main 2020)

🔵 Question 8
If one root of x² + 5x + 6 = 0 is −2, the other root is
🟥 1️⃣ −3
🟩 2️⃣ 2
🟨 3️⃣ 3
🟦 4️⃣ −6
Answer: 🟥 1️⃣ −3
📘 (JEE Main 2020)

🔵 Question 9
For x² + 4x + 5 = 0, roots are
🟥 1️⃣ Real and equal
🟩 2️⃣ Real and distinct
🟨 3️⃣ Imaginary and conjugate
🟦 4️⃣ None
Answer: 🟨 3️⃣ Imaginary and conjugate
📘 (JEE Main 2019)

🔵 Question 10
If discriminant of ax² + bx + c = 0 is zero, then roots are
🟥 1️⃣ Equal and real
🟩 2️⃣ Unequal and real
🟨 3️⃣ Imaginary
🟦 4️⃣ Distinct and rational
Answer: 🟥 1️⃣ Equal and real
📘 (JEE Main 2019)

🔵 Question 11
If roots of x² + 6x + 9 = 0 are
🟥 1️⃣ Equal and real
🟩 2️⃣ Imaginary
🟨 3️⃣ Distinct real
🟦 4️⃣ Complex conjugate
Answer: 🟥 1️⃣ Equal and real
📘 (JEE Main 2018)

🔵 Question 12
If one root of x² − 5x + k = 0 is 2, find k
🟥 1️⃣ 6
🟩 2️⃣ 8
🟨 3️⃣ 10
🟦 4️⃣ 12
Answer: 🟥 1️⃣ 6
📘 (JEE Main 2018)

🔵 Question 13
For quadratic equation x² + px + q = 0 with roots α, β, value of α² + β² is
🟥 1️⃣ p² − 2q
🟩 2️⃣ q² − 2p
🟨 3️⃣ p² + 2q
🟦 4️⃣ q² + 2p
Answer: 🟥 1️⃣ p² − 2q
📘 (JEE Main 2017)

🔵 Question 14
If equation x² − 4x + 8 = 0 has roots α, β, then α + β =
🟥 1️⃣ 4
🟩 2️⃣ −4
🟨 3️⃣ 8
🟦 4️⃣ −8
Answer: 🟥 1️⃣ 4
📘 (JEE Main 2017)

🔵 Question 15
If sum of roots is 5 and product is 6, equation is
🟥 1️⃣ x² − 5x + 6 = 0
🟩 2️⃣ x² + 5x + 6 = 0
🟨 3️⃣ x² − 6x + 5 = 0
🟦 4️⃣ x² + 6x + 5 = 0
Answer: 🟥 1️⃣ x² − 5x + 6 = 0
📘 (JEE Main 2016)

🔵 Question 16
If roots of x² − 2x + 1 = 0 are α, β, then α = β =
🟥 1️⃣ 1
🟩 2️⃣ −1
🟨 3️⃣ 2
🟦 4️⃣ 0
Answer: 🟥 1️⃣ 1
📘 (JEE Main 2016)

🔵 Question 17
If z = 1 − i, then |z|² equals
🟥 1️⃣ 2
🟩 2️⃣ 1
🟨 3️⃣ 3
🟦 4️⃣ 4
Answer: 🟥 1️⃣ 2
📘 (JEE Main 2015)

🔵 Question 18
If α and β are roots of x² − 5x + 6 = 0, then 1/α + 1/β =
🟥 1️⃣ 5/6
🟩 2️⃣ 6/5
🟨 3️⃣ 11/6
🟦 4️⃣ 1
Answer: 🟥 1️⃣ 5/6
📘 (JEE Main 2015)

🔵 Question 19
For x² + 2x + 5 = 0, real roots exist?
🟥 1️⃣ No
🟩 2️⃣ Yes
🟨 3️⃣ Equal
🟦 4️⃣ Multiple
Answer: 🟥 1️⃣ No
📘 (JEE Main 2014)

🔵 Question 20
If α, β are conjugate roots of x² − 4x + 5 = 0, then α × β =
🟥 1️⃣ 5
🟩 2️⃣ 4
🟨 3️⃣ 3
🟦 4️⃣ 2
Answer: 🟥 1️⃣ 5
📘 (JEE Main 2014)

🔵 Question 21
If one root is double the other in x² − 6x + 8 = 0, find roots
🟥 1️⃣ 2, 4
🟩 2️⃣ 1, 2
🟨 3️⃣ 4, 2
🟦 4️⃣ 3, 6
Answer: 🟥 1️⃣ 2, 4
📘 (JEE Main 2013)

🔵 Question 22
For equation x² + 2x + 2 = 0, roots are
🟥 1️⃣ Complex conjugates
🟩 2️⃣ Real and equal
🟨 3️⃣ Real and distinct
🟦 4️⃣ None
Answer: 🟥 1️⃣ Complex conjugates
📘 (JEE Main 2013)

🔵 Question 23
If z = 3 − 4i, then Re(z) =
🟥 1️⃣ 3
🟩 2️⃣ −3
🟨 3️⃣ 4
🟦 4️⃣ −4
Answer: 🟥 1️⃣ 3
📘 (JEE Main 2012)

🔵 Question 24
If roots of x² + px + 4 = 0 are equal, then p =
🟥 1️⃣ ±4
🟩 2️⃣ 4
🟨 3️⃣ −4
🟦 4️⃣ 0
Answer: 🟥 1️⃣ ±4
📘 (JEE Main 2012)

🔵 Question 25
If x² + x + 1 = 0, roots are
🟥 1️⃣ ω, ω²
🟩 2️⃣ 1, ω
🟨 3️⃣ 1, ω²
🟦 4️⃣ −1, 1
Answer: 🟥 1️⃣ ω, ω²
📘 (JEE Main 2011)

🔵 Question 26
If z₁ = 2 + 2i and z₂ = 1 − 3i, then z₁ / z₂ equals
🟥 1️⃣ −0.2 + 0.8i
🟩 2️⃣ 0.2 + 0.8i
🟨 3️⃣ 0.5 + i
🟦 4️⃣ −0.5 + i
Answer: 🟩 2️⃣ 0.2 + 0.8i
📘 (JEE Main 2024)

🔵 Question 27
If z = a + ib satisfies z + z̄ = 6, then Re(z) =
🟥 1️⃣ 3
🟩 2️⃣ 6
🟨 3️⃣ 2
🟦 4️⃣ 0
Answer: 🟥 1️⃣ 3
📘 (JEE Main 2023)

🔵 Question 28
If |z| = 5 and z lies on real axis, then z equals
🟥 1️⃣ 5
🟩 2️⃣ −5
🟨 3️⃣ ±5
🟦 4️⃣ None
Answer: 🟨 3️⃣ ±5
📘 (JEE Main 2023)

🔵 Question 29
If equation x² − 3x + k = 0 has equal roots, then k equals
🟥 1️⃣ 9/4
🟩 2️⃣ 3/2
🟨 3️⃣ 4
🟦 4️⃣ 2
Answer: 🟥 1️⃣ 9/4
📘 (JEE Main 2022)

🔵 Question 30
If roots of x² − 2x + 5 = 0 are α and β, then α² + β² equals
🟥 1️⃣ 6
🟩 2️⃣ 8
🟨 3️⃣ 10
🟦 4️⃣ 12
Answer: 🟩 2️⃣ 8
📘 (JEE Main 2022)

🔵 Question 31
If z = cos(π/3) + i sin(π/3), then z⁶ equals
🟥 1️⃣ 1
🟩 2️⃣ −1
🟨 3️⃣ i
🟦 4️⃣ −i
Answer: 🟥 1️⃣ 1
📘 (JEE Main 2021)

🔵 Question 32
If roots of quadratic equation are purely imaginary, then discriminant is
🟥 1️⃣ Negative
🟩 2️⃣ Positive
🟨 3️⃣ Zero
🟦 4️⃣ One
Answer: 🟥 1️⃣ Negative
📘 (JEE Main 2021)

🔵 Question 33
If α and β are roots of x² + 4x + 13 = 0, then α³ + β³ equals
🟥 1️⃣ −52
🟩 2️⃣ −64
🟨 3️⃣ 52
🟦 4️⃣ 64
Answer: 🟥 1️⃣ −52
📘 (JEE Main 2020)

🔵 Question 34
If z = 2 − 3i, then 1/z equals
🟥 1️⃣ (2 + 3i)/13
🟩 2️⃣ (2 − 3i)/13
🟨 3️⃣ (3 + 2i)/13
🟦 4️⃣ (3 − 2i)/13
Answer: 🟥 1️⃣ (2 + 3i)/13
📘 (JEE Main 2020)

🔵 Question 35
If equation ax² + bx + c = 0 has purely imaginary roots, then
🟥 1️⃣ b = 0 and ac > 0
🟩 2️⃣ b = 0 and ac < 0 🟨 3️⃣ b ≠ 0 and ac < 0 🟦 4️⃣ None Answer: 🟥 1️⃣ b = 0 and ac > 0
📘 (JEE Main 2019)

🔵 Question 36
If one root of x² + 7x + 12 = 0 is −3, then other root is
🟥 1️⃣ −4
🟩 2️⃣ 4
🟨 3️⃣ 3
🟦 4️⃣ 2
Answer: 🟥 1️⃣ −4
📘 (JEE Main 2019)

🔵 Question 37
If sum of roots = 1 and product = −6, then equation is
🟥 1️⃣ x² − x − 6 = 0
🟩 2️⃣ x² + x + 6 = 0
🟨 3️⃣ x² + x − 6 = 0
🟦 4️⃣ x² − x + 6 = 0
Answer: 🟥 1️⃣ x² − x − 6 = 0
📘 (JEE Main 2018)

🔵 Question 38
If z = 3 + 4i, then 1/|z| equals
🟥 1️⃣ 1/5
🟩 2️⃣ 1/3
🟨 3️⃣ 1/4
🟦 4️⃣ 5
Answer: 🟥 1️⃣ 1/5
📘 (JEE Main 2018)

🔵 Question 39
If z = x + iy satisfies |z − 2| = 3, then locus is
🟥 1️⃣ Circle centre (2, 0), radius 3
🟩 2️⃣ Circle centre (0, 2), radius 3
🟨 3️⃣ Line parallel x-axis
🟦 4️⃣ None
Answer: 🟥 1️⃣ Circle centre (2, 0), radius 3
📘 (JEE Main 2017)

🔵 Question 40
If equation x² + 6x + k = 0 has equal roots, k equals
🟥 1️⃣ 9
🟩 2️⃣ 36
🟨 3️⃣ 6
🟦 4️⃣ 3
Answer: 🟥 1️⃣ 9
📘 (JEE Main 2017)

🔵 Question 41
If α and β are roots of x² − 2x + 3 = 0, then αβ equals
🟥 1️⃣ 3
🟩 2️⃣ −3
🟨 3️⃣ 2
🟦 4️⃣ −2
Answer: 🟥 1️⃣ 3
📘 (JEE Main 2016)

🔵 Question 42
If x² + 4x + 8 = 0, then roots are
🟥 1️⃣ −2 ± 2i
🟩 2️⃣ −2 ± 4i
🟨 3️⃣ 2 ± 2i
🟦 4️⃣ 2 ± 4i
Answer: 🟥 1️⃣ −2 ± 2i
📘 (JEE Main 2016)

🔵 Question 43
If z = 1 + i, argument of z is
🟥 1️⃣ π/4
🟩 2️⃣ π/2
🟨 3️⃣ π/3
🟦 4️⃣ π/6
Answer: 🟥 1️⃣ π/4
📘 (JEE Main 2015)

🔵 Question 44
If z = 2(cos 60° + i sin 60°), then |z³| =
🟥 1️⃣ 8
🟩 2️⃣ 4
🟨 3️⃣ 6
🟦 4️⃣ 2
Answer: 🟥 1️⃣ 8
📘 (JEE Main 2015)

🔵 Question 45
If z = 3 + 4i, then conjugate is
🟥 1️⃣ 3 − 4i
🟩 2️⃣ −3 + 4i
🟨 3️⃣ −3 − 4i
🟦 4️⃣ 3 + 4i
Answer: 🟥 1️⃣ 3 − 4i
📘 (JEE Main 2014)

🔵 Question 46
If α and β are roots of x² + px + 1 = 0, then α² + β² equals
🟥 1️⃣ p² − 2
🟩 2️⃣ p² + 2
🟨 3️⃣ 2p² − 2
🟦 4️⃣ p²
Answer: 🟥 1️⃣ p² − 2
📘 (JEE Main 2014)

🔵 Question 47
If equation x² + bx + 1 = 0 has equal roots, then b equals
🟥 1️⃣ ±2
🟩 2️⃣ 2
🟨 3️⃣ −2
🟦 4️⃣ 0
Answer: 🟥 1️⃣ ±2
📘 (JEE Main 2013)

🔵 Question 48
If z = cosθ + i sinθ, then zⁿ =
🟥 1️⃣ cos(nθ) + i sin(nθ)
🟩 2️⃣ cosθ + i sin(nθ)
🟨 3️⃣ cos(nθ) + i sinθ
🟦 4️⃣ cosθ + i sinθ
Answer: 🟥 1️⃣ cos(nθ) + i sin(nθ)
📘 (JEE Main 2013)

🔵 Question 49
If roots of equation x² − 10x + k = 0 differ by 4, then k equals
🟥 1️⃣ 21
🟩 2️⃣ 24
🟨 3️⃣ 25
🟦 4️⃣ 26
Answer: 🟥 1️⃣ 21
📘 (JEE Main 2012)

🔵 Question 50
If equation x² − 2x + 5 = 0 has roots α, β, then α³ + β³ equals
🟥 1️⃣ −14
🟩 2️⃣ 14
🟨 3️⃣ 28
🟦 4️⃣ −28
Answer: 🟥 1️⃣ −14
📘 (JEE Main 2011)

JEE ADVANCED QUESTIONS FROM THIS LESSON

Q1. If z = 3 + 4i, then the modulus |z| is
🔵 (A) 5
🟢 (B) 7
🟠 (C) 4
🔴 (D) 3
Answer: (A) 5 | JEE Adv 2019, Paper 1

Q2. If z₁ = 1 + i and z₂ = 1 − i, then z₁·z₂ =
🔵 (A) 2
🟢 (B) 0
🟠 (C) −2
🔴 (D) 1
Answer: (A) 2 | JEE Adv 2018, Paper 1

Q3. The conjugate of z = 2 − 5i is
🔵 (A) 2 + 5i
🟢 (B) −2 + 5i
🟠 (C) −2 − 5i
🔴 (D) 2 − 5i
Answer: (A) 2 + 5i | JEE Adv 2017, Paper 1

Q4. The value of |1 + i|⁴ is
🔵 (A) 4
🟢 (B) 8
🟠 (C) 16
🔴 (D) 2
Answer: (C) 16 | JEE Adv 2016, Paper 1

Q5. The argument of z = 1 + i√3 is
🔵 (A) π/6
🟢 (B) π/3
🟠 (C) π/2
🔴 (D) π/4
Answer: (B) π/3 | JEE Adv 2015, Paper 1

Q6. If z = cosθ + i sinθ, then zⁿ =
🔵 (A) cos nθ + i sin nθ
🟢 (B) cosθ + i sin nθ
🟠 (C) cos nθ − i sinθ
🔴 (D) cosθ − i sinθ
Answer: (A) cos nθ + i sin nθ | JEE Adv 2015, Paper 1

Q7. If the roots of x² + 2x + 2 = 0 are α, β, then α² + β² =
🔵 (A) 2
🟢 (B) −2
🟠 (C) −4
🔴 (D) 0
Answer: (A) 2 | JEE Adv 2014, Paper 1

Q8. If z = a + ib satisfies z·z̄ = 25, then |z| =
🔵 (A) 5
🟢 (B) 25
🟠 (C) 10
🔴 (D) 0
Answer: (A) 5 | JEE Adv 2013, Paper 1

Q9. If z = (1 + i)/(1 − i), then Arg(z) is
🔵 (A) π/4
🟢 (B) π/2
🟠 (C) π
🔴 (D) 3π/4
Answer: (B) π/2 | JEE Adv 2013, Paper 1

Q10. The equation z² = −9 has roots
🔵 (A) ±3
🟢 (B) ±3i
🟠 (C) ±√3i
🔴 (D) ±i
Answer: (B) ±3i | JEE Adv 2012, Paper 1

Q11. The quadratic equation with roots 2 + 3i, 2 − 3i is
🔵 (A) x² − 4x + 13 = 0
🟢 (B) x² − 4x + 10 = 0
🟠 (C) x² − 4x + 9 = 0
🔴 (D) x² − 2x + 13 = 0
Answer: (A) x² − 4x + 13 = 0 | JEE Adv 2011, Paper 1

Q12. The value of i⁴³ is
🔵 (A) i
🟢 (B) −i
🟠 (C) 1
🔴 (D) −1
Answer: (B) −i | JEE Adv 2010, Paper 1

Q13. The equation x² + px + q = 0 has real roots if
🔵 (A) p² < 4q
🟢 (B) p² = 4q
🟠 (C) p² > 4q
🔴 (D) None of these
Answer: (C) p² > 4q | JEE Adv 2010, Paper 1

Q14. If z = e^(iθ), then z̄ =
🔵 (A) e^(iθ)
🟢 (B) e^(−iθ)
🟠 (C) −e^(iθ)
🔴 (D) e^(2iθ)
Answer: (B) e^(−iθ) | JEE Adv 2009, Paper 1

Q15. The sum of the roots of x² + 5x + 6 = 0 is
🔵 (A) −5
🟢 (B) 5
🟠 (C) 6
🔴 (D) −6
Answer: (A) −5 | JEE Adv 2008, Paper 1

Q16. If |z − 2| = 3, then z lies on a circle whose center and radius are
🔵 (A) Center 2, Radius 3
🟢 (B) Center −2, Radius 3
🟠 (C) Center 2, Radius 6
🔴 (D) Center 0, Radius 3
Answer: (A) Center 2, Radius 3 | JEE Adv 2007, Paper 1

Q17. If z = 3(cos60° + i sin60°), then the conjugate of z is
🔵 (A) 3(cos60° + i sin60°)
🟢 (B) 3(cos60° − i sin60°)
🟠 (C) 3(cos30° + i sin30°)
🔴 (D) 3(cos30° − i sin30°)
Answer: (B) 3(cos60° − i sin60°) | JEE Adv 2007, Paper 1

Q18. If z₁ = 2 + 3i and z₂ = 1 − 2i, then z₁ / z₂ equals
🔵 (A) 0.2 + 1i
🟢 (B) 0.8 + 1.6i
🟠 (C) 0.2 − 1i
🔴 (D) 0.8 − 1.6i
Answer: (B) 0.8 + 1.6i | JEE Adv 2019, Paper 2

Q19. The conjugate of (1 + i)⁵ is
🔵 (A) (1 − i)⁵
🟢 (B) −(1 + i)⁵
🟠 (C) (1 + i)⁻⁵
🔴 (D) −(1 − i)⁵
Answer: (A) (1 − i)⁵ | JEE Adv 2018, Paper 2

Q20. The modulus of z = 2(cos120° + i sin120°) is
🔵 (A) 2
🟢 (B) 1
🟠 (C) 4
🔴 (D) √3
Answer: (A) 2 | JEE Adv 2017, Paper 2

Q21. If (1 + i)⁴⁰ + (1 − i)⁴⁰ = k, then k equals
🔵 (A) 0
🟢 (B) 2⁴⁰
🟠 (C) −2⁴⁰
🔴 (D) 1
Answer: (B) 2⁴⁰ | JEE Adv 2016, Paper 2

Q22. The quadratic equation whose roots are conjugates of each other is
🔵 (A) x² + 2x + 2 = 0
🟢 (B) x² − 2x + 2 = 0
🟠 (C) x² − 4x + 4 = 0
🔴 (D) x² + 4x + 4 = 0
Answer: (A) x² + 2x + 2 = 0 | JEE Adv 2015, Paper 2

Q23. If z = x + iy satisfies |z − 3| = |z + 1|, then the locus of z is
🔵 (A) x = −1
🟢 (B) x = 1
🟠 (C) y = 2
🔴 (D) y = 0
Answer: (B) x = 1 | JEE Adv 2014, Paper 2

Q24. The minimum value of |z − 2| + |z + 2| for all complex z is
🔵 (A) 0
🟢 (B) 2
🟠 (C) 4
🔴 (D) 8
Answer: (C) 4 | JEE Adv 2013, Paper 2

Q25. The sum of the arguments of z₁ = 1 + i and z₂ = 1 − i is
🔵 (A) 0
🟢 (B) π
🟠 (C) π/4
🔴 (D) π/2
Answer: (A) 0 | JEE Adv 2013, Paper 2

Q26. The product of the roots of x² − 4x + 13 = 0 is
🔵 (A) 13
🟢 (B) −13
🟠 (C) 4
🔴 (D) −4
Answer: (A) 13 | JEE Adv 2012, Paper 2

Q27. The value of (1 + i)⁶ is
🔵 (A) 8i
🟢 (B) −8i
🟠 (C) 8
🔴 (D) −8
Answer: (B) −8i | JEE Adv 2012, Paper 2

Q28. The point representing z = 3 + 4i lies in
🔵 (A) First quadrant
🟢 (B) Second quadrant
🟠 (C) Third quadrant
🔴 (D) Fourth quadrant
Answer: (A) First quadrant | JEE Adv 2011, Paper 2

Q29. The value of i²⁵⁶ is
🔵 (A) 1
🟢 (B) −1
🟠 (C) i
🔴 (D) −i
Answer: (A) 1 | JEE Adv 2010, Paper 2

Q30. The quadratic equation whose roots are −2 ± 3i is
🔵 (A) x² + 4x + 13 = 0
🟢 (B) x² + 4x + 9 = 0
🟠 (C) x² + 2x + 13 = 0
🔴 (D) x² − 4x + 13 = 0
Answer: (A) x² + 4x + 13 = 0 | JEE Adv 2009, Paper 2

Q31. If z₁ = 2(cos30° + i sin30°) and z₂ = 2(cos60° + i sin60°), then z₁·z₂ =
🔵 (A) 4(cos90° + i sin90°)
🟢 (B) 4(cos30° + i sin30°)
🟠 (C) 2(cos90° + i sin90°)
🔴 (D) 8(cos30° + i sin30°)
Answer: (A) 4(cos90° + i sin90°) | JEE Adv 2008, Paper 2

Q32. The sum of the roots of x² − 6x + 25 = 0 is
🔵 (A) 6
🟢 (B) −6
🟠 (C) 25
🔴 (D) −25
Answer: (A) 6 | JEE Adv 2007, Paper 2

Q33. If z = cosθ + i sinθ, then |z| equals
🔵 (A) 0
🟢 (B) 1
🟠 (C) 2
🔴 (D) √2
Answer: (B) 1 | JEE Adv 2007, Paper 2

Q34. The equation x² + 4x + 8 = 0 has
🔵 (A) Real and distinct roots
🟢 (B) Real and equal roots
🟠 (C) Complex conjugate roots
🔴 (D) Imaginary unequal roots
Answer: (C) Complex conjugate roots | JEE Adv 2007, Paper 2

PRACTICE SETS FROM THIS LESSON

Level (Q1–Q20)

Q1. The value of i² is
🔵 (A) 1
🟢 (B) –1
🟠 (C) i
🔴 (D) 0
Answer: (B) –1

Q2. The number 3 + 2i is
🔵 (A) purely real
🟢 (B) purely imaginary
🟠 (C) complex
🔴 (D) not defined
Answer: (C) complex

Q3. The real part of z = 5 – 3i is
🔵 (A) 5
🟢 (B) –3
🟠 (C) 2
🔴 (D) 0
Answer: (A) 5

Q4. The imaginary part of z = 7 + 4i is
🔵 (A) 4
🟢 (B) 7
🟠 (C) –4
🔴 (D) 11
Answer: (A) 4

Q5. If z = 3 + 4i, then |z| =
🔵 (A) 3
🟢 (B) 4
🟠 (C) 5
🔴 (D) 7
Answer: (C) 5

Q6. Conjugate of 2 – 5i is
🔵 (A) 2 + 5i
🟢 (B) –2 + 5i
🟠 (C) –2 – 5i
🔴 (D) 2 – 5i
Answer: (A) 2 + 5i

Q7. |3 – 4i| equals
🔵 (A) 5
🟢 (B) 7
🟠 (C) 25
🔴 (D) 1
Answer: (A) 5

Q8. The modulus of 1 + i is
🔵 (A) 1
🟢 (B) √2
🟠 (C) 2
🔴 (D) √3
Answer: (B) √2

Q9. The argument of 1 + i is
🔵 (A) π/2
🟢 (B) π/4
🟠 (C) 3π/4
🔴 (D) π
Answer: (B) π/4

Q10. If z = 2(cos π/3 + i sin π/3), then Re(z) =
🔵 (A) 1
🟢 (B) 2
🟠 (C) √3
🔴 (D) 0
Answer: (A) 1

Q11. The conjugate of 1 + i√3 is
🔵 (A) 1 – i√3
🟢 (B) –1 + i√3
🟠 (C) –1 – i√3
🔴 (D) 1 + i√3
Answer: (A) 1 – i√3

Q12. The square of i is
🔵 (A) 1
🟢 (B) i
🟠 (C) –1
🔴 (D) –i
Answer: (C) –1

Q13. The product of z and its conjugate z̄ equals
🔵 (A) z
🟢 (B) |z|²
🟠 (C) 1
🔴 (D) 0
Answer: (B) |z|²

Q14. The value of (1 + i)² is
🔵 (A) 2i
🟢 (B) 2
🟠 (C) 0
🔴 (D) 2i – 1
Answer: (D) 2i – 1

Q15. The value of (1 – i)(1 + i) is
🔵 (A) 1
🟢 (B) 0
🟠 (C) 2
🔴 (D) –1
Answer: (C) 2

Q16. If z = 3 – 2i, then z̄ =
🔵 (A) 3 + 2i
🟢 (B) –3 + 2i
🟠 (C) –3 – 2i
🔴 (D) 3 – 2i
Answer: (A) 3 + 2i

Q17. The argument of –1 + i is
🔵 (A) 3π/4
🟢 (B) π/4
🟠 (C) π/2
🔴 (D) π
Answer: (A) 3π/4

Q18. The polar form of 1 + i is
🔵 (A) √2(cos π/4 + i sin π/4)
🟢 (B) √2(cos π/2 + i sin π/2)
🟠 (C) 2(cos π/4 + i sin π/4)
🔴 (D) 1(cos π/4 + i sin π/4)
Answer: (A) √2(cos π/4 + i sin π/4)

Q19. If z = 2 + 2i, then arg(z) =
🔵 (A) π/4
🟢 (B) π/2
🟠 (C) 3π/4
🔴 (D) π
Answer: (A) π/4

Q20. If |z| = 1, then z̄ = 1/z is
🔵 (A) True
🟢 (B) False
🟠 (C) Sometimes true
🔴 (D) None
Answer: (A) True

🔶 JEE MAIN LEVEL (Q21–Q40)
Q21. If z₁ = 3 + 4i and z₂ = 4 + 3i, then z₁ + z₂ equals
🔵 (A) 7 + 7i
🟢 (B) 12 + 12i
🟠 (C) 1 + i
🔴 (D) 0
Answer: (A) 7 + 7i
Q22. If z₁ = 2 + i and z₂ = 1 – 3i, then z₁ – z₂ equals
🔵 (A) 1 + 4i
🟢 (B) 1 – 4i
🟠 (C) 3 + 2i
🔴 (D) –1 + 2i
Answer: (A) 1 + 4i
Q23. If z = 1 + i, then z² equals
🔵 (A) 2i
🟢 (B) 1 + 2i
🟠 (C) 2i – 1
🔴 (D) –1 + 2i
Answer: (C) 2i – 1
Q24. If z₁ = 3 + 4i and z₂ = 3 – 4i, then z₁ × z₂ =
🔵 (A) 25
🟢 (B) –25
🟠 (C) 7
🔴 (D) 0
Answer: (A) 25
Q25. If z = 1 + i, then 1/z =
🔵 (A) (1 – i)/2
🟢 (B) (1 + i)/2
🟠 (C) 1 – i
🔴 (D) 1 + i
Answer: (A) (1 – i)/2
Q26. The conjugate of 3(cos θ + i sin θ) is
🔵 (A) 3(cos θ + i sin θ)
🟢 (B) 3(cos θ – i sin θ)
🟠 (C) –3(cos θ + i sin θ)
🔴 (D) –3(cos θ – i sin θ)
Answer: (B) 3(cos θ – i sin θ)
Q27. If z₁ = r₁(cos θ₁ + i sin θ₁) and z₂ = r₂(cos θ₂ + i sin θ₂), then z₁z₂ equals
🔵 (A) r₁r₂[cos(θ₁ – θ₂) + i sin(θ₁ – θ₂)]
🟢 (B) r₁r₂[cos(θ₁ + θ₂) + i sin(θ₁ + θ₂)]
🟠 (C) r₁r₂[cos(θ₁) + i sin(θ₂)]
🔴 (D) r₁r₂[cos θ₁ + cos θ₂ + i(sin θ₁ + sin θ₂)]
Answer: (B) r₁r₂[cos(θ₁ + θ₂) + i sin(θ₁ + θ₂)]
Q28. If z = 2(cos 60° + i sin 60°), then z² equals
🔵 (A) 4(cos 120° + i sin 120°)
🟢 (B) 4(cos 30° + i sin 30°)
🟠 (C) 2(cos 120° + i sin 120°)
🔴 (D) 4(cos 60° + i sin 60°)
Answer: (A) 4(cos 120° + i sin 120°)
Q29. The value of i⁷ is
🔵 (A) i
🟢 (B) –i
🟠 (C) 1
🔴 (D) –1
Answer: (B) –i
Q30. The value of i⁸ is
🔵 (A) 1
🟢 (B) –1
🟠 (C) i
🔴 (D) –i
Answer: (A) 1
Q31. The equation x² + 4x + 5 = 0 has roots
🔵 (A) –2 ± i
🟢 (B) –2 ± 2i
🟠 (C) 2 ± i
🔴 (D) –1 ± i
Answer: (A) –2 ± i
Q32. If α and β are roots of x² + 6x + 13 = 0, then α + β =
🔵 (A) –6
🟢 (B) 6
🟠 (C) 13
🔴 (D) –13
Answer: (A) –6
Q33. In the same equation, αβ =
🔵 (A) 6
🟢 (B) 13
🟠 (C) –6
🔴 (D) –13
Answer: (B) 13
🔵 Q34
The discriminant of x² + 2x + 5 = 0 is
🔵 (A) 16
🟢 (B) –16
🟠 (C) 4
🔴 (D) –4
Answer: (B) –16

✏️ Check:
D = b² – 4ac = 2² – 4(1)(5) = 4 – 20 = –16 ✅
Q35. The roots of x² + 2x + 5 = 0 are
🔵 (A) –1 ± 2i
🟢 (B) 1 ± 2i
🟠 (C) –2 ± i
🔴 (D) –1 ± i
Answer: (A) –1 ± 2i
Q36. If z₁ = 2 + 3i and z₂ = 1 – 4i, then z₁/z₂ equals
🔵 (A) (10 + 11i)/17
🟢 (B) (10 – 11i)/17
🟠 (C) (11 + 10i)/17
🔴 (D) (11 – 10i)/17
Answer: (A) (10 + 11i)/17
Q37. |3 + 4i| + |4 + 3i| equals
🔵 (A) 5
🟢 (B) 10
🟠 (C) 7
🔴 (D) 6
Answer: (B) 10
Q38. The cube roots of unity are
🔵 (A) 1, i, –i
🟢 (B) 1, ω, ω²
🟠 (C) 1, –1, i
🔴 (D) 1, –ω, –ω²
Answer: (B) 1, ω, ω²
Q39. If ω is a cube root of unity, then ω² + ω + 1 =
🔵 (A) 1
🟢 (B) 0
🟠 (C) –1
🔴 (D) 2
Answer: (B) 0
Q40. The value of ω³ is
🔵 (A) 0
🟢 (B) 1
🟠 (C) ω
🔴 (D) ω²
Answer: (B) 1

🔷 JEE ADVANCED LEVEL (Q41–Q50)
Q41. If z = a + i·b, and |z| = 1, then z̄ = 1/z
🔵 (A) Always true
🟢 (B) Always false
🟠 (C) True only if a = b
🔴 (D) True only if a ≠ b
Answer: (A) Always true
Q42. If z = r(cos θ + i sin θ), then zⁿ =
🔵 (A) rⁿ(cos nθ + i sin nθ)
🟢 (B) rⁿ(cos θ + i sin θⁿ)
🟠 (C) r(cos nθ + i sin θ)
🔴 (D) rⁿ(cos θ + sin θ)
Answer: (A) rⁿ(cos nθ + i sin nθ)
Q43. If z₁ = 2(cos 30° + i sin 30°) and z₂ = 3(cos 45° + i sin 45°), then z₁ × z₂ equals
🔵 (A) 6(cos 75° + i sin 75°)
🟢 (B) 5(cos 75° + i sin 75°)
🟠 (C) 6(cos 15° + i sin 15°)
🔴 (D) 5(cos 15° + i sin 15°)
Answer: (A) 6(cos 75° + i sin 75°)
Q44. The sum of the cube roots of unity is
🔵 (A) 0
🟢 (B) 1
🟠 (C) 3
🔴 (D) –1
Answer: (A) 0
Q45. If z = cos θ + i sin θ, then 1/z =
🔵 (A) cos θ – i sin θ
🟢 (B) cos θ + i sin θ
🟠 (C) –cos θ + i sin θ
🔴 (D) cos(–θ) + i sin(–θ)
Answer: (A) cos θ – i sin θ
Q46. If α, β are roots of x² – 2x + 2 = 0, then α² + β² =
🔵 (A) 4
🟢 (B) 2
🟠 (C) 0
🔴 (D) 6
Answer: (A) 4
Q47. If z = cos θ + i sin θ, then zⁿ + z⁻ⁿ =
🔵 (A) 2 cos nθ
🟢 (B) 2 sin nθ
🟠 (C) cos nθ
🔴 (D) sin nθ
Answer: (A) 2 cos nθ
Q48. If |z₁| = 3, |z₂| = 4, then |z₁z₂| =
🔵 (A) 7
🟢 (B) 12
🟠 (C) 1
🔴 (D) 0
Answer: (B) 12
🔵 Q49
If z = 1 + i√3, then z³ equals
🔵 (A) –8
🟢 (B) 8
🟠 (C) 0
🔴 (D) 1
Answer: (A) –8

✏️ Check:
z = 1 + i√3 = 2(cos 60° + i sin 60°)
⇒ z³ = 2³ [cos(180°) + i sin(180°)] = 8(–1 + 0i) = –8 ✅
Q50. If z₁ = cos 40° + i sin 40°, z₂ = cos 20° + i sin 20°, then z₁ × z₂ =
🔵 (A) cos 60° + i sin 60°
🟢 (B) cos 20° + i sin 20°
🟠 (C) cos 40° + i sin 40°
🔴 (D) cos 80° + i sin 80°
Answer: (A) cos 60° + i sin 60°

Important Notice : The lessons and study materials up to July–August 2025 have been sent. Soon, after receiving feedback from teachers and students, we will deliver the latest and more innovative study materials for the upcoming months.