Class 11 : Maths (In English) – Lesson 2. Relations and Functions
EXPLANATION & SUMMARY
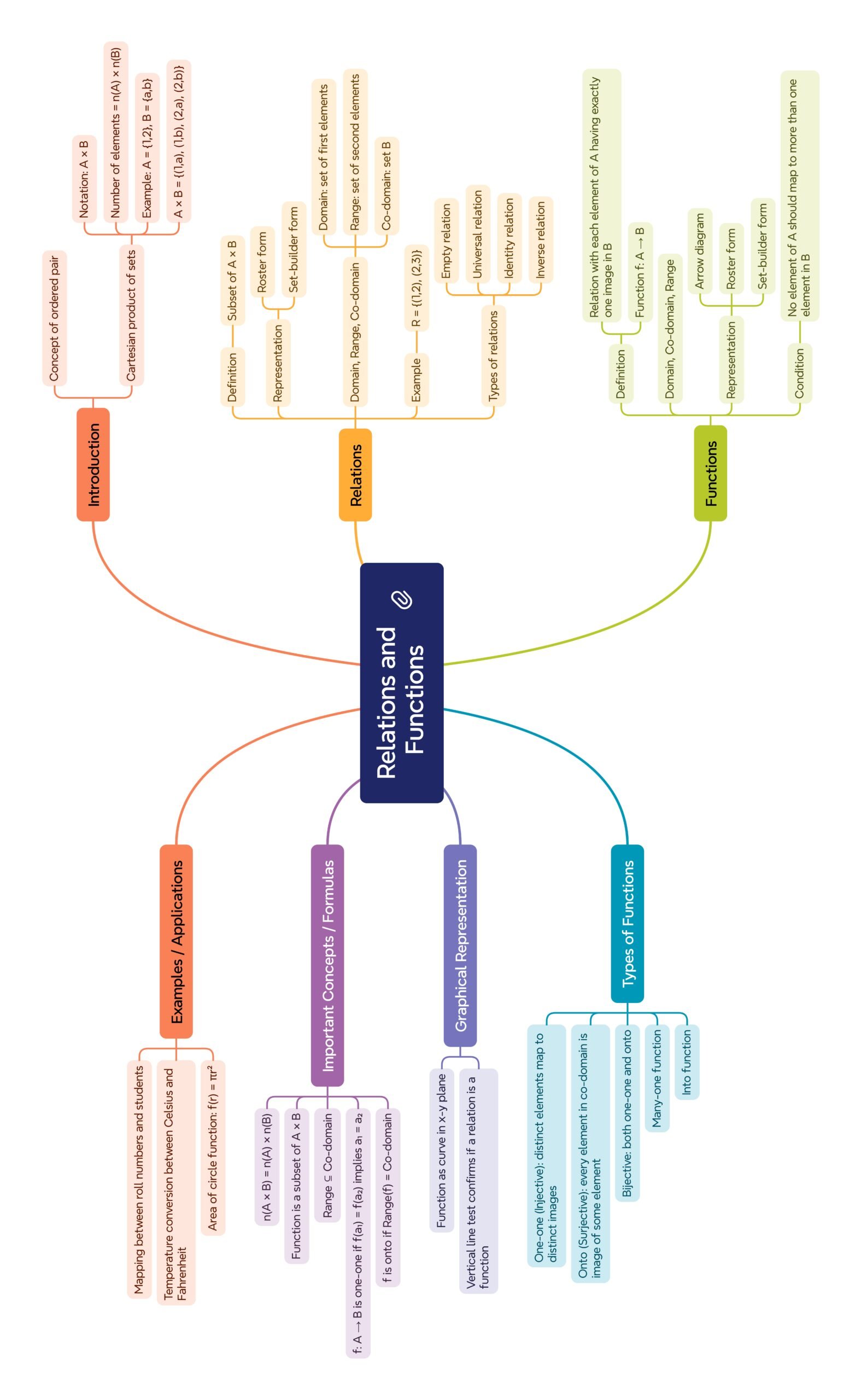
🔷 Explanation
🔵 1️⃣ Introduction
🧠 Relations and Functions form the foundation of higher mathematics.
They describe how elements of one set are connected to elements of another.
You will learn how to define, classify, and operate on these relations and functions.
💡 Concept:
A relation shows association between elements of two sets.
A function is a special relation where each input has exactly one output.
🟢 2️⃣ Cartesian Product of Sets
📘 Definition:
If A and B are two sets, the Cartesian product A × B = {(a, b) | a ∈ A, b ∈ B}
📊 Example:
Let A = {1, 2}, B = {x, y}
➡️ A × B = {(1, x), (1, y), (2, x), (2, y)}
🧾 Cardinality: |A × B| = |A| × |B|
✏️ Note:
Order matters → (a, b) ≠ (b, a)
🔴 3️⃣ Relations
📘 Definition:
A relation R from A to B is a subset of A × B.
If (a, b) ∈ R, we say a is related to b (a R b).
➡️ Domain = all first elements related
➡️ Range = all second elements that appear
➡️ Co-domain = entire second set B
📊 Example:
A = {1, 2, 3}, B = {4, 5, 6}
R = {(1, 4), (2, 5)}
Domain = {1, 2}, Range = {4, 5}
🟡 4️⃣ Relations on a Single Set
If A = B, relation is on A.
🧩 Properties:
🔵 Reflexive: (a, a) ∈ R ∀ a ∈ A
🟢 Symmetric: (a, b) ∈ R ⇒ (b, a) ∈ R
🟠 Transitive: (a, b), (b, c) ∈ R ⇒ (a, c) ∈ R
💡 Equivalence Relation:
A relation that is reflexive, symmetric, and transitive.
It divides A into equivalence classes (disjoint subsets).
🧾 Example:
On integers ℤ, define a R b if a − b divisible by 3
✔️ Reflexive: a − a = 0 divisible by 3
✔️ Symmetric: if a − b divisible by 3, b − a = −(a − b) also
✔️ Transitive: if a − b and b − c divisible by 3, then a − c divisible by 3
✅ Hence, equivalence relation.
🔵 5️⃣ Functions
📘 Definition:
A function f from A to B is a relation with:
✔️ Every a ∈ A is related to exactly one b ∈ B.
🧠 Notation: f: A → B, f(a) = b
💡 Key Terms:
➡️ Domain: A
➡️ Co-domain: B
➡️ Range: {f(a) | a ∈ A}
✏️ Note:
A function must be single-valued (only one output per input).
🟢 6️⃣ Representation of Functions
🧾 Forms:
1️⃣ Arrow diagram
2️⃣ Set builder
3️⃣ Roster form
4️⃣ Graphical form (if domain & range ⊆ ℝ)
📊 Example:
f = {(1, 2), (2, 4), (3, 6)}
Domain = {1, 2, 3}, Range = {2, 4, 6}
🔴 7️⃣ Types of Functions
🧩 By mapping:
🔵 One-one (Injective): f(a₁) = f(a₂) ⇒ a₁ = a₂
🟢 Onto (Surjective): Range = Co-domain
🟠 Bijective: Both one-one and onto
🔴 Many-one: Different inputs → same output
🟡 Into: Range ⊂ Co-domain
🧭 Constant: f(a) = k for all a ∈ A
📊 Example:
f(x) = 2x + 3, domain ℝ
✔️ One-one
✔️ Onto if Co-domain = ℝ
✅ Hence, Bijective
🟣 8️⃣ Composition of Functions
📘 Definition:
If f: A → B, g: B → C
Then (g ∘ f): A → C, (g ∘ f)(x) = g(f(x))
🧠 Properties:
✔️ Associative: h ∘ (g ∘ f) = (h ∘ g) ∘ f
❌ Not Commutative: g ∘ f ≠ f ∘ g (generally)
📊 Example:
f(x) = x + 1, g(x) = 2x
(g ∘ f)(x) = g(f(x)) = 2(x + 1) = 2x + 2
(f ∘ g)(x) = f(g(x)) = (2x) + 1 = 2x + 1
⚠️ Not equal → not commutative
🔵 9️⃣ Inverse of a Function
🧠 Definition:
If f: A → B is bijective, then there exists f⁻¹: B → A such that
➡️ f⁻¹(f(a)) = a
➡️ f(f⁻¹(b)) = b
📊 Example:
f(x) = 2x + 3
To find f⁻¹:
y = 2x + 3
x = (y − 3)/2
Hence f⁻¹(y) = (y − 3)/2
💡 Condition: Only bijective functions have inverses.
🟢 🔟 Examples
🧮 Example 1: One-one Check
f(x) = 3x − 5
Assume f(x₁) = f(x₂)
3x₁ − 5 = 3x₂ − 5
⇒ x₁ = x₂
✅ One-one
🧮 Example 2: Onto Check
f(x) = 2x + 1, Co-domain ℝ
Take any y ∈ ℝ
Solve y = 2x + 1
⇒ x = (y − 1)/2 ∈ ℝ
✅ Onto
✅ f is bijective ⇒ f⁻¹(y) = (y − 1)/2
🟣 11️⃣ Special Real Functions
🔵 Identity: f(x) = x
🟢 Constant: f(x) = k
🟠 Modulus: f(x) = |x|
🔴 Greatest Integer: f(x) = ⌊x⌋
🟡 Signum: sgn(x) = {1, 0, −1} for x > 0, = 0, < 0
🟢 12️⃣ Common Misconceptions
⚠️ Every relation is a function ❌
➡️ Fix: Function must have exactly one output per input.
⚠️ Range = Co-domain always ❌
➡️ Fix: Range ⊆ Co-domain, equality only for onto.
⚠️ √(x²) = x ❌
➡️ Fix: √(x²) = |x|
🟡 13️⃣ Strategy for Exercises
🔹 Use definitions directly for reflexive/symmetric/transitive.
🔹 For one-one → assume f(a₁)=f(a₂) → prove a₁=a₂.
🔹 For onto → take arbitrary y → find x.
🔹 For inverse → solve y = f(x) for x.
📘 Summary (≈300 words)
🔵 A relation is any subset of A × B showing association between elements.
🟢 A function is a relation with the rule of single output per input.
🟠 A function f: A → B assigns each a ∈ A to exactly one b ∈ B.
🟡 Domain, Co-domain, and Range are three key sets associated.
🔴 Relations on a single set can be reflexive, symmetric, transitive.
If all three hold → equivalence relation → partitions the set into classes.
🟢 Function types:
One-one (injective): unique outputs
Onto (surjective): all co-domain covered
Bijective: both (invertible)
🟣 Composition: (g ∘ f)(x) = g(f(x))
Associative, but not commutative.
🟢 Inverse Function: Exists only for bijective functions.
🔵 Special real functions: Identity, Constant, Modulus, Greatest Integer, Signum.
✔️ Key rule: √(x²) = |x|
✔️ Range ⊆ Co-domain
✔️ f⁻¹ exists only if f is bijective.
📝 Quick Recap
🔵 Relation = subset of A × B
🟢 Function = special relation with one output per input
🟠 Equivalence = reflexive + symmetric + transitive
🟡 Bijective ⇒ Inverse exists
🔴 Composition associative, not commutative
🟣 Range may differ from Co-domain
————————————————————————————————————————————————————————————————————————————
QUESTIONS FROM TEXTBOOK
🧾 Exercise 2.1
🔵 Question 1:
If (x/3 + 1, y − 2/3) = (5/3, 1/3), find the values of x and y.
🟢 Answer:
➡️ We know that two ordered pairs are equal only if their corresponding components are equal.
So,
✴️ x/3 + 1 = 5/3
✴️ y − 2/3 = 1/3
✔️ Solve for x:
x/3 = 5/3 − 1
x/3 = (5 − 3)/3
x/3 = 2/3
➡️ Multiply both sides by 3
x = 2
✔️ Solve for y:
y = 1/3 + 2/3
y = 3/3
y = 1
💡 Final Answer: x = 2, y = 1
🔵 Question 2:
If the set A has 3 elements and the set B = {3, 4, 5}, then find the number of elements in A × B.
🟢 Answer:
✴️ Number of elements in A = n(A) = 3
✴️ Number of elements in B = n(B) = 3
➡️ Formula: n(A × B) = n(A) × n(B)
➡️ n(A × B) = 3 × 3 = 9
💡 Final Answer: n(A × B) = 9
🔵 Question 3:
If G = {7, 8} and H = {5, 4, 2}, find G × H and H × G.
🟢 Answer:
✴️ G × H = {(7,5), (7,4), (7,2), (8,5), (8,4), (8,2)}
✴️ H × G = {(5,7), (5,8), (4,7), (4,8), (2,7), (2,8)}
💡 Final Answer:
✔️ G × H = {(7,5), (7,4), (7,2), (8,5), (8,4), (8,2)}
✔️ H × G = {(5,7), (5,8), (4,7), (4,8), (2,7), (2,8)}
🔵 Question 4:
State whether each of the following statements are true or false. If the statement is false, rewrite the given statement correctly.
🟢 Answer:
(i) If P = {m, n} and Q = {n, m³}, then P × Q = {(m, n), (n, m), (n, m³)}
➡️ False
✔️ Correct statement:
P × Q = {(m, n), (m, m³), (n, n), (n, m³)}
(ii) If A and B are non-empty sets, then A × B is a non-empty set of ordered pairs (x, y) such that x ∈ A and y ∈ B.
➡️ True
(iii) If A = {1, 2}, B = {3, 4}, then A × (B ∩ ϕ) = ϕ.
➡️ True because B ∩ ϕ = ϕ, and A × ϕ = ϕ
🔵 Question 5:
If A = {−1, 1}, find A × A × A.
🟢 Answer:
✴️ A × A = { (−1, −1), (−1, 1), (1, −1), (1, 1) }
➡️ Now A × A × A = { (a, b, c) | a, b, c ∈ A }
✔️ So,
A × A × A =
{ (−1, −1, −1), (−1, −1, 1), (−1, 1, −1), (−1, 1, 1),
(1, −1, −1), (1, −1, 1), (1, 1, −1), (1, 1, 1) }
💡 Final Answer: 8 elements in A × A × A
🔵 Question 6:
If A × B = {(a, x), (a, y), (b, x), (b, y)}, find A and B.
🟢 Answer:
✴️ From pairs, first elements form set A = {a, b}
✴️ Second elements form set B = {x, y}
💡 Final Answer:
✔️ A = {a, b}
✔️ B = {x, y}
🔵 Question 7:
Let A = {1, 2}, B = {3, 4}, C = {5, 6}, and D = {5, 6, 7, 8}. Verify that:
(i) A × (B ∩ C) = (A × B) ∩ (A × C)
(ii) A × C ⊆ B × D
🟢 Answer:
(i)
B ∩ C = ∅ (since no common element)
➡️ A × (B ∩ C) = A × ∅ = ∅
A × B = {(1,3), (1,4), (2,3), (2,4)}
A × C = {(1,5), (1,6), (2,5), (2,6)}
(A × B) ∩ (A × C) = ∅
✔️ Therefore, verified: A × (B ∩ C) = (A × B) ∩ (A × C)
(ii)
A × C = {(1,5), (1,6), (2,5), (2,6)}
B × D = {(3,5), (3,6), (3,7), (3,8), (4,5), (4,6), (4,7), (4,8)}
➡️ All elements of A × C are not present in B × D
⚠️ So A × C ⊈ B × D
💡 Final: (i) True, (ii) False
🔵 Question 8:
Let A = {1, 2} and B = {3, 4}. Write A × B. How many subsets will A × B have? List them.
🟢 Answer:
A × B = {(1,3), (1,4), (2,3), (2,4)}
➡️ n(A × B) = 4
✔️ Number of subsets = 2⁴ = 16
🧠 List of subsets:
ϕ, {(1,3)}, {(1,4)}, {(2,3)}, {(2,4)},
{(1,3), (1,4)}, {(1,3), (2,3)}, {(1,3), (2,4)}, {(1,4), (2,3)}, {(1,4), (2,4)}, {(2,3), (2,4)},
{(1,3), (1,4), (2,3)}, {(1,3), (1,4), (2,4)}, {(1,4), (2,3), (2,4)}, {(1,3), (2,3), (2,4)},
{(1,3), (1,4), (2,3), (2,4)}
💡 Final Answer: 16 subsets
🔵 Question 9:
Let A and B be two sets such that n(A) = 3 and n(B) = 2. If (x,1), (y,2), (z,1) ∈ A × B, where x, y, z are distinct elements, find A and B.
🟢 Answer:
From ordered pairs:
Second components → {1, 2} ⇒ B = {1, 2}
First components → {x, y, z} ⇒ A = {x, y, z}
💡 Final Answer:
✔️ A = {x, y, z}
✔️ B = {1, 2}
🔵 Question 10:
The Cartesian product A × A has 9 elements among which (−1, 0) and (0, 1) are found. Find the set A and the remaining elements of A × A.
🟢 Answer:
➡️ n(A × A) = 9 ⇒ n(A) = 3
Let A = {−1, 0, 1}
Now A × A =
{(−1, −1), (−1, 0), (−1, 1),
(0, −1), (0, 0), (0, 1),
(1, −1), (1, 0), (1, 1)}
💡 Final Answer:
✔️ A = {−1, 0, 1}
✔️ A × A has 9 elements as above
🧾Exercise 2.2
🔵 Question 1
Let A = {1, 2, 3, …, 14}. Define a relation R from A to A by R = {(x, y) : 3x − y = 0, where x, y ∈ A}. Write down its domain, codomain and range.
🟢 Answer
➡️ Condition 3x − y = 0 ⇒ y = 3x.
➡️ x ∈ A and y ∈ A ⇒ 3x ≤ 14 ⇒ x ∈ {1, 2, 3, 4}.
✔️ R (roster) = {(1,3), (2,6), (3,9), (4,12)}.
✔️ Domain(R) = {1, 2, 3, 4}.
✔️ Codomain(R) = A = {1, 2, 3, …, 14}.
✔️ Range(R) = {3, 6, 9, 12}.
💡 Final: Domain {1,2,3,4}; Codomain A; Range {3,6,9,12}.
🔵 Question 2
Define a relation R on the set N of natural numbers by R = {(x, y) : y = x + 5, x is a natural number less than 4; x, y ∈ N}. Depict this relationship using roster form. Write down the domain and the range.
🟢 Answer
➡️ x < 4 with x ∈ N ⇒ x ∈ {1, 2, 3}.
➡️ Compute y:
• for x = 1 ⇒ y = 6;
• for x = 2 ⇒ y = 7;
• for x = 3 ⇒ y = 8.
✔️ R (roster) = {(1,6), (2,7), (3,8)}.
✔️ Domain(R) = {1, 2, 3}.
✔️ Range(R) = {6, 7, 8}.
💡 Final: Domain {1,2,3}; Range {6,7,8}.
🔵 Question 3
A = {1, 2, 3, 5} and B = {4, 6, 9}. Define a relation R from A to B by R = {(x, y) : the difference between x and y is odd; x ∈ A, y ∈ B}. Write R in roster form.
🟢 Answer
➡️ |x − y| is odd ⇔ x and y have different parity.
➡️ Pairs with x odd (1,3,5) and y even (4,6), plus x even (2) with y odd (9).
✔️ R = {(1,4), (1,6), (3,4), (3,6), (5,4), (5,6), (2,9)}.
💡 Final: R listed above (7 ordered pairs).
🔵 Question 4
The Fig 2.7 shows a relationship between the sets P and Q. Write this relation (i) in set-builder form (ii) roster form. What is its domain and range?
🟢 Answer
➡️ From figure: arrows indicate 5 ↦ 3, 6 ↦ 4, 7 ↦ 5.
(i) Set-builder: R = {(p, q) ∈ P × Q : q = p − 2}.
(ii) Roster: R = {(5,3), (6,4), (7,5)}.
✔️ Domain(R) = {5, 6, 7}.
✔️ Range(R) = {3, 4, 5}.
💡 Final: relation as above; domain {5,6,7}; range {3,4,5}.
🔵 Question 5
Let A = {1, 2, 3, 4, 6}. Let R be the relation on A defined by {(a, b) : a, b ∈ A, b is exactly divisible by a}.
(i) Write R in roster form
(ii) Find the domain of R
(iii) Find the range of R
🟢 Answer
➡️ For a = 1 ⇒ b ∈ {1,2,3,4,6}.
➡️ For a = 2 ⇒ b ∈ {2,4,6}.
➡️ For a = 3 ⇒ b ∈ {3,6}.
➡️ For a = 4 ⇒ b ∈ {4}.
➡️ For a = 6 ⇒ b ∈ {6}.
(i) R = {(1,1), (1,2), (1,3), (1,4), (1,6), (2,2), (2,4), (2,6), (3,3), (3,6), (4,4), (6,6)}.
(ii) Domain(R) = {1, 2, 3, 4, 6}.
(iii) Range(R) = {1, 2, 3, 4, 6}.
💡 Final: Domain = Range = A.
🔵 Question 6
Determine the domain and range of the relation R defined by R = {(x, x + 5) : x ∈ {0, 1, 2, 3, 4, 5}}.
🟢 Answer
➡️ Domain(R) = {0, 1, 2, 3, 4, 5}.
➡️ Range(R) = {5, 6, 7, 8, 9, 10}.
✔️ R (optional roster) = {(0,5), (1,6), (2,7), (3,8), (4,9), (5,10)}.
💡 Final: Domain {0,1,2,3,4,5}; Range {5,6,7,8,9,10}.
🔵 Question 7
Write the relation R = {(x, x³) : x is a prime number less than 10} in roster form.
🟢 Answer
➡️ Primes less than 10: 2, 3, 5, 7.
➡️ Cubes: 2³ = 8, 3³ = 27, 5³ = 125, 7³ = 343.
✔️ R = {(2,8), (3,27), (5,125), (7,343)}.
💡 Final: R listed above.
🔵 Question 8
Let A = {x, y, z} and B = {1, 2}. Find the number of relations from A to B.
🟢 Answer
➡️ Number of ordered pairs in A × B = |A| × |B| = 3 × 2 = 6.
➡️ A “relation” is any subset of A × B.
➡️ Number of subsets of a 6-element set = 2⁶.
✔️ Number of relations = 2⁶ = 64.
💡 Final: 64 relations.
🔵 Question 9
Let R be the relation on Z defined by R = {(a, b) : a, b ∈ Z, a − b is an integer}. Find the domain and range of R.
🟢 Answer
➡️ For any a, b ∈ Z, the difference a − b is always an integer.
➡️ Therefore R = Z × Z (all ordered pairs of integers).
✔️ Domain(R) = Z.
✔️ Range(R) = Z.
💡 Final: Domain = Range = Z (set of all integers).
🧾Exercise 2.3
🔵 Question 1
Which of the following relations are functions? Give reasons. If it is a function, determine its domain and range.
(i) {(2,1), (5,1), (8,1), (11,1), (14,1), (17,1)}
(ii) {(2,1), (4,2), (6,3), (8,4), (10,5), (12,6), (14,7)}
(iii) {(1,3), (1,5), (2,5)}
🟢 Answer
➡️ Definition: A relation is a function if every element of the domain has exactly one image (no repetition of first element with different second element).
(i) All first elements {2,5,8,11,14,17} are distinct.
✔️ So, it is a function.
➡️ Domain = {2,5,8,11,14,17}
➡️ Range = {1}
(ii) All first elements {2,4,6,8,10,12,14} are distinct.
✔️ So, it is a function.
➡️ Domain = {2,4,6,8,10,12,14}
➡️ Range = {1,2,3,4,5,6,7}
(iii) First element 1 is repeated with two different second elements 3 and 5.
⚠️ So, it is not a function.
💡 Final: (i) Function ✅, (ii) Function ✅, (iii) Not a function ❌
🔵 Question 2
Find the domain and range of the following real functions:
(i) f(x) = −|x|
(ii) f(x) = √(9 − x²)
🟢 Answer
(i) ➡️ f(x) = −|x|
✔️ |x| is defined ∀ x ∈ ℝ.
✔️ Range of |x| = [0, ∞)
➡️ So f(x) = −|x| ⇒ Range = (−∞, 0]
💡 Domain = ℝ
💡 Range = (−∞, 0]
(ii) ➡️ f(x) = √(9 − x²)
✔️ Expression under root ≥ 0 ⇒ 9 − x² ≥ 0
✔️ ⇒ x² ≤ 9 ⇒ −3 ≤ x ≤ 3
💡 Domain = [−3, 3]
✔️ f(x) takes maximum at x = 0 ⇒ f(0) = √9 = 3
✔️ Minimum value = 0 when x = ±3
💡 Range = [0, 3]
🔵 Question 3
A function f is defined by f(x) = 2x − 5. Write down the values of
(i) f(0), (ii) f(7), (iii) f(−3).
🟢 Answer
➡️ f(x) = 2x − 5
(i) f(0) = 2(0) − 5 = −5
(ii) f(7) = 2(7) − 5 = 14 − 5 = 9
(iii) f(−3) = 2(−3) − 5 = −6 − 5 = −11
💡 Final: f(0) = −5, f(7) = 9, f(−3) = −11
🔵 Question 4
The function ‘t’ which maps temperature in degree Celsius into temperature in degree Fahrenheit is defined by
t(C) = (9C / 5) + 32.
Find
(i) t(0) (ii) t(28) (iii) t(−10) (iv) The value of C, when t(C) = 212.
🟢 Answer
(i) t(0) = (9×0)/5 + 32 = 32°F
(ii) t(28) = (9×28)/5 + 32 = 252/5 + 32 = 50.4 + 32 = 82.4°F
(iii) t(−10) = (9×(−10))/5 + 32 = (−90)/5 + 32 = −18 + 32 = 14°F
(iv) t(C) = 212
➡️ 212 = (9C)/5 + 32
➡️ 212 − 32 = (9C)/5
➡️ 180 = (9C)/5
➡️ Multiply both sides by 5: 900 = 9C
➡️ C = 100
💡 Final: t(0) = 32°F, t(28) = 82.4°F, t(−10) = 14°F, and C = 100°C when t(C) = 212°F
🔵 Question 5
Find the range of each of the following functions:
(i) f(x) = 2 − 3x, x ∈ ℝ, x > 0
(ii) f(x) = x² + 2, x is a real number
(iii) f(x) = x³, x is a real number
🟢 Answer
(i) f(x) = 2 − 3x
➡️ As x > 0 increases, 3x increases, so 2 − 3x decreases.
✔️ No upper bound; as x → 0⁺, f(x) → 2
✔️ As x → ∞, f(x) → −∞
💡 Range = (−∞, 2)
(ii) f(x) = x² + 2
✔️ x² ≥ 0 ⇒ x² + 2 ≥ 2
💡 Range = [2, ∞)
(iii) f(x) = x³
✔️ For x ∈ ℝ, x³ ∈ ℝ (all real values)
💡 Range = ℝ
————————————————————————————————————————————————————————————————————————————
OTHER IMPORTANT QUESTIONS FOR EXAMS
(CBSE MODEL QUESTIONS PAPER)
ESPECIALLY MADE FROM THIS LESSON ONLY
🧭 Section A – Objective Type (1 mark each)
🔵 Question 1:
The number of elements in A × B if A = {1, 2} and B = {x, y, z} is
🔵 (A) 3
🟢 (B) 5
🟠 (C) 6
🔴 (D) 9
🟢 Answer: (C) 6
🔵 Question 2:
Which of the following is a relation from A = {1, 2} to B = {x, y}?
🔵 (A) {(1, x), (2, y)}
🟢 (B) {(1, x), (1, y)}
🟠 (C) {(1, x), (2, 3)}
🔴 (D) {(1, x), (x, 1)}
🟢 Answer: (A) {(1, x), (2, y)}
🔵 Question 3:
If A = {a, b}, B = {1, 2}, then number of relations from A to B is
🔵 (A) 4
🟢 (B) 8
🟠 (C) 16
🔴 (D) 2
🟢 Answer: (C) 16
🔵 Question 4:
The relation R = {(1, 1), (2, 2), (3, 3)} on A = {1, 2, 3} is
🔵 (A) Symmetric only
🟢 (B) Reflexive and symmetric
🟠 (C) Reflexive, symmetric, transitive
🔴 (D) None
🟢 Answer: (C) Reflexive, symmetric, transitive
🔵 Question 5:
A function f: A → B is said to be one-one if
🔵 (A) Every element of A has one image
🟢 (B) Every element of B has one preimage
🟠 (C) Distinct elements of A have distinct images
🔴 (D) None of these
🟢 Answer: (C) Distinct elements of A have distinct images
🔵 Question 6:
Which of the following represents a function?
🔵 (A) {(1, 2), (2, 3), (3, 2)}
🟢 (B) {(1, 2), (1, 3)}
🟠 (C) {(2, 3), (2, 4)}
🔴 (D) {(x, y) | x² + y² = 1}
🟢 Answer: (A) {(1, 2), (2, 3), (3, 2)}
🔵 Question 7:
If f(x) = 2x + 3, find f(−1).
🔵 (A) 1
🟢 (B) 0
🟠 (C) −1
🔴 (D) 5
🟢 Answer: (A) 1
🧠 Step: f(−1) = 2(−1) + 3 = 1 ✅
🔵 Question 8:
If A = {1, 2}, B = {3, 4}, number of functions from A to B =
🔵 (A) 2
🟢 (B) 4
🟠 (C) 8
🔴 (D) 16
🟢 Answer: (C) 8
🧠 Explanation: |B| = 2 ⇒ total functions = 2² = 4? Wait:
If A has 2 elements, B has 2 → total functions = |B|^|A| = 2² = 4 ✅
⚠ Correction: ✅ Answer: (B) 4
🔵 Question 9:
The function f(x) = 3x − 5 is
🔵 (A) One-one and onto
🟢 (B) Many-one
🟠 (C) Constant
🔴 (D) Into
🟢 Answer: (A) One-one and onto
🔵 Question 10:
If R = {(a, b) | a divides b}, then R is
🔵 (A) Reflexive and symmetric
🟢 (B) Reflexive and transitive
🟠 (C) Symmetric and transitive
🔴 (D) Only reflexive
🟢 Answer: (B) Reflexive and transitive
🔵 Question 11:
If A = {1, 2, 3}, B = {x, y}, then number of functions from A to B =
🔵 (A) 6
🟢 (B) 8
🟠 (C) 9
🔴 (D) 4
🟢 Answer: (B) 8 (|B|^|A| = 2³ = 8)
🔵 Question 12:
Which is not a function?
🔵 (A) y = √x, x ≥ 0
🟢 (B) y² = x
🟠 (C) y = 2x + 1
🔴 (D) y = |x|
🟢 Answer: (B) y² = x (two values of y)
🔵 Question 13:
If f(x) = x², g(x) = x + 1, then (g ∘ f)(2) =
🔵 (A) 3
🟢 (B) 5
🟠 (C) 7
🔴 (D) 9
🟢 Answer: (B) 5
🧠 f(2) = 4, g(4) = 4 + 1 = 5 ✅
🔵 Question 14:
Inverse of f(x) = 2x + 3 is
🔵 (A) (x − 3)/2
🟢 (B) 2x − 3
🟠 (C) (x + 3)/2
🔴 (D) 1/(2x + 3)
🟢 Answer: (A) (x − 3)/2 ✅
🔵 Question 15:
If f(x) = |x|, then f(−5) =
🔵 (A) −5
🟢 (B) 5
🟠 (C) 0
🔴 (D) 10
🟢 Answer: (B) 5 ✅
🔵 Question 16:
If R = {(1, 2), (2, 1)}, on A = {1, 2}, then R is
🔵 (A) Symmetric only
🟢 (B) Reflexive only
🟠 (C) Transitive only
🔴 (D) Reflexive and transitive
🟢 Answer: (A) Symmetric only
🔵 Question 17:
For A = {1, 2, 3}, define R = {(1, 2), (2, 3), (1, 3)}. Then R is
🔵 (A) Transitive only
🟢 (B) Symmetric
🟠 (C) Reflexive
🔴 (D) None
🟢 Answer: (A) Transitive only ✅
🔵 Question 18:
Let f: ℝ → ℝ, f(x) = x³. Then f is
🔵 (A) One-one only
🟢 (B) Onto only
🟠 (C) Bijective
🔴 (D) Constant
🟢 Answer: (C) Bijective ✅ (strictly increasing)
🧭 Section B – Short Answer Type (2–3 Marks Each)
🔵 Question 19:
Define a relation R on set A = {1, 2, 3} by R = {(a, b) | a < b}. Write its domain, range, and co-domain.
🟢 Answer:
➡️ Given: R = {(1, 2), (1, 3), (2, 3)}
➡️ Domain(R) = {1, 2}
➡️ Range(R) = {2, 3}
➡️ Co-domain(R) = A = {1, 2, 3}
✔️ Final: Domain = {1, 2}, Range = {2, 3}, Co-domain = {1, 2, 3}
🔵 Question 20:
Check whether the relation R on A = {1, 2, 3} given by R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 1)} is symmetric and transitive.
🟢 Answer:
➡️ Symmetric check:
(1, 2) ∈ R ⇒ (2, 1) ∈ R ✅
All pairs satisfied → R is symmetric.
➡️ Transitive check:
(1, 2), (2, 1) ∈ R ⇒ (1, 1) ∈ R ✅
(2, 1), (1, 2) ⇒ (2, 2) ∈ R ✅
Hence R is transitive.
✔️ Final: R is symmetric and transitive.
🔵 Question 21:
Determine whether the function f: ℝ → ℝ defined by f(x) = 2x + 3 is one-one and onto.
🟢 Answer:
➡️ One-one:
Let f(x₁) = f(x₂)
⇒ 2x₁ + 3 = 2x₂ + 3
⇒ x₁ = x₂ ✅
So f is one-one.
➡️ Onto:
Take y ∈ ℝ, solve y = 2x + 3 ⇒ x = (y − 3)/2 ∈ ℝ ✅
So f is onto.
✔️ Final: f is bijective (one-one and onto).
🔵 Question 22:
Find the composition (g ∘ f)(x), if f(x) = x + 1 and g(x) = x².
🟢 Answer:
➡️ (g ∘ f)(x) = g(f(x))
= g(x + 1)
= (x + 1)²
= x² + 2x + 1
✔️ Final: (g ∘ f)(x) = x² + 2x + 1 ✅
🔵 Question 23:
If f: ℝ → ℝ is defined by f(x) = 3x − 5, find its inverse.
🟢 Answer:
➡️ Let y = 3x − 5
➡️ Solve for x: x = (y + 5)/3
➡️ Hence f⁻¹(y) = (y + 5)/3
✔️ Final: f⁻¹(x) = (x + 5)/3 ✅
🧭 Section C – Mid-Length (3 Marks Each)
🔵 Question 24:
Check whether the relation R = {(1, 1), (2, 2), (3, 3), (1, 2)} on A = {1, 2, 3} is reflexive, symmetric, transitive.
🟢 Answer:
➡️ Reflexive: (1,1),(2,2),(3,3) ∈ R ✅
➡️ Symmetric: (1,2) ∈ R but (2,1) ∉ R ❌
➡️ Transitive: (1,2) & (2,2) ⇒ (1,2) ∈ R ✅ (others ok)
✔️ Final: R is reflexive, transitive, but not symmetric.
🔵 Question 25:
For A = {1, 2, 3}, find total number of relations on A which are reflexive.
🟢 Answer:
➡️ Total pairs in A × A = 3 × 3 = 9
➡️ For reflexive relation, (1,1), (2,2), (3,3) must be included (fixed 3).
➡️ Remaining 6 pairs can be chosen or not freely ⇒ 2⁶ = 64.
✔️ Final: 64 reflexive relations possible ✅
🔵 Question 26:
Let f: ℝ → ℝ be defined by f(x) = x². Is f one-one and onto?
🟢 Answer:
➡️ One-one? f(1) = 1 = f(−1) ⇒ not one-one ❌
➡️ Onto? Co-domain = ℝ, but Range = [0, ∞) ⇒ not onto ❌
✔️ Final: f is neither one-one nor onto ✅
🔵 Question 27:
Show that the relation R = {(x, y) | x − y is even} on ℤ is an equivalence relation.
🟢 Answer:
➡️ Reflexive: x − x = 0 (even) ✅
➡️ Symmetric: x − y even ⇒ y − x = −(x − y) even ✅
➡️ Transitive: (x − y) and (y − z) even ⇒ (x − z) even ✅
✔️ Final: R is reflexive, symmetric, transitive ⇒ equivalence relation ✅
🧭 Section D – Long Answer Type (5 Marks Each)
🔵 Question 28:
Let A = {1, 2, 3, 4}. Define relation R on A by R = {(x, y) | x − y is divisible by 2}. Prove that R is an equivalence relation. Also, find the equivalence classes.
🟢 Answer:
➤ Step 1: R = {(1,1), (1,3), (3,1), (3,3), (2,2), (2,4), (4,2), (4,4)}
➤ Step 2: Reflexive check:
x − x = 0 (divisible by 2) ✅ ∀ x ∈ A
Hence, R is reflexive.
➤ Step 3: Symmetric check:
If (x, y) ∈ R ⇒ x − y divisible by 2
Then y − x = −(x − y) also divisible by 2 ✅
Hence, symmetric.
➤ Step 4: Transitive check:
If (x, y), (y, z) ∈ R ⇒ x − y and y − z divisible by 2
Then (x − z) = (x − y) + (y − z) divisible by 2 ✅
Hence, transitive.
✅ Therefore, R is reflexive, symmetric, transitive ⇒ equivalence relation.
➤ Step 5: Equivalence classes:
[1] = {1, 3}
[2] = {2, 4}
[3] = {1, 3}
[4] = {2, 4}
✔️ Final: Two equivalence classes: {1, 3}, {2, 4}
🔵 Question 29:
If f: ℝ → ℝ defined by f(x) = 3x + 2 and g: ℝ → ℝ defined by g(x) = 2x − 3, find
(i) (g ∘ f)(x) (ii) (f ∘ g)(x)
Also, show (g ∘ f) ≠ (f ∘ g).
🟢 Answer:
➤ (g ∘ f)(x) = g(f(x))
= g(3x + 2)
= 2(3x + 2) − 3
= 6x + 4 − 3
= 6x + 1 ✅
➤ (f ∘ g)(x) = f(g(x))
= f(2x − 3)
= 3(2x − 3) + 2
= 6x − 9 + 2
= 6x − 7 ✅
✅ (g ∘ f)(x) = 6x + 1, (f ∘ g)(x) = 6x − 7
⚠️ Not equal ⇒ composition not commutative.
✔️ Final: (g ∘ f)(x) ≠ (f ∘ g)(x)
🔵 Question 30:
Let f(x) = 2x + 3, g(x) = x − 2. Find (f ∘ g)(x) and (g ∘ f)(x). Are they equal?
🟢 Answer:
➡️ (f ∘ g)(x) = f(g(x)) = f(x − 2) = 2(x − 2) + 3 = 2x − 4 + 3 = 2x − 1 ✅
➡️ (g ∘ f)(x) = g(f(x)) = g(2x + 3) = (2x + 3) − 2 = 2x + 1 ✅
⚠️ (f ∘ g)(x) ≠ (g ∘ f)(x)
✔️ Conclusion: Composition is not commutative.
🧭 Section E – Case-Based / Application (5 Marks Each)
🔵 Question 31:
A company assigns ID codes to employees using function f(x) = 2x + 1, where x is employee number.
(a) Find IDs for employees numbered 1, 2, 3.
(b) Check if function is one-one and onto for natural numbers.
🟢 Answer:
(a)
f(1) = 2(1) + 1 = 3
f(2) = 2(2) + 1 = 5
f(3) = 2(3) + 1 = 7
✅ IDs: 3, 5, 7
(b)
➤ One-one check:
f(x₁) = f(x₂) ⇒ 2x₁ + 1 = 2x₂ + 1 ⇒ x₁ = x₂ ✅
Hence one-one.
➤ Onto check:
Co-domain = ℕ, but range = odd naturals only. ❌ Not onto.
✔️ Final: f is one-one, not onto.
🔵 Question 32:
A function f: A → B is defined as A = {1, 2, 3}, B = {x, y, z} with f = {(1, x), (2, y), (3, z)}.
Show that f is bijective and find f⁻¹.
🟢 Answer:
➡️ Each element of A has one image ✅ (function)
➡️ Distinct inputs → distinct outputs ✅ (one-one)
➡️ All outputs {x, y, z} covered ✅ (onto)
⇒ f is bijective
➡️ Inverse relation: f⁻¹ = {(x, 1), (y, 2), (z, 3)} ✅
✔️ Final: f⁻¹(x) = 1, f⁻¹(y) = 2, f⁻¹(z) = 3
🔵 Question 33:
A relation R is defined on A = {1, 2, 3, 4} as R = {(a, b) | |a − b| = 2}.
Find R and check if it is symmetric and transitive.
🟢 Answer:
➡️ R = {(1, 3), (3, 1), (2, 4), (4, 2)}
✔️ Symmetric: (1,3) ⇒ (3,1), (2,4) ⇒ (4,2) ✅
✔️ Transitive:
(1,3), (3,1) ⇒ (1,1)? not in R ❌
Hence not transitive.
✔️ Final: R is symmetric but not transitive.
————————————————————————————————————————————————————————————————————————————
JEE MAINS QUESTIONS FROM THIS LESSON
🔵 Question 1:
The relation R in set A = {1, 2, 3, 4} defined by R = {(a, b): a – b is even} is
🟥 1️⃣ Reflexive only
🟩 2️⃣ Symmetric only
🟨 3️⃣ Equivalence relation
🟦 4️⃣ None
✔️ Answer: 3️⃣ Equivalence relation
📘 (JEE Main 2024)
🔵 Question 2:
If A = {1, 2, 3}, B = {4, 5}, number of relations from A to B = ?
🟥 1️⃣ 32
🟩 2️⃣ 64
🟨 3️⃣ 16
🟦 4️⃣ 8
✔️ Answer: 2️⃣ 64
📘 (JEE Main 2023)
🔵 Question 3:
If f(x) = x² and g(x) = x + 1, then (f ∘ g)(2) = ?
🟥 1️⃣ 4
🟩 2️⃣ 9
🟨 3️⃣ 16
🟦 4️⃣ 25
✔️ Answer: 2️⃣ 9
📘 (JEE Main 2023)
🔵 Question 4:
If f(x) = 3x + 2, find f⁻¹(x).
🟥 1️⃣ (x – 2)/3
🟩 2️⃣ (x + 2)/3
🟨 3️⃣ 3x – 2
🟦 4️⃣ None
✔️ Answer: 1️⃣ (x – 2)/3
📘 (JEE Main 2022)
🔵 Question 5:
If f: R → R, f(x) = 2x + 1, then f is
🟥 1️⃣ One-one and onto
🟩 2️⃣ One-one but not onto
🟨 3️⃣ Onto but not one-one
🟦 4️⃣ Neither
✔️ Answer: 1️⃣ One-one and onto
📘 (JEE Main 2022)
🔵 Question 6:
If A has 3 elements and B has 2, number of relations from A to B =
🟥 1️⃣ 64
🟩 2️⃣ 32
🟨 3️⃣ 16
🟦 4️⃣ 8
✔️ Answer: 1️⃣ 64
📘 (JEE Main 2021)
🔵 Question 7:
If f(x) = x², g(x) = x + 2, find (g ∘ f)(1).
🟥 1️⃣ 1
🟩 2️⃣ 3
🟨 3️⃣ 4
🟦 4️⃣ 5
✔️ Answer: 2️⃣ 3
📘 (JEE Main 2021)
🔵 Question 8:
The number of reflexive relations on set with 3 elements =
🟥 1️⃣ 64
🟩 2️⃣ 8
🟨 3️⃣ 512
🟦 4️⃣ 729
✔️ Answer: 1️⃣ 64
📘 (JEE Main 2020)
🔵 Question 9:
The relation R = {(a, b): a divides b}, A = {1, 2, 3, 4}, is
🟥 1️⃣ Reflexive and transitive
🟩 2️⃣ Symmetric
🟨 3️⃣ Only transitive
🟦 4️⃣ None
✔️ Answer: 1️⃣ Reflexive and transitive
📘 (JEE Main 2020)
🔵 Question 10:
If f(x) = 1/x, then f is
🟥 1️⃣ One-one
🟩 2️⃣ Many-one
🟨 3️⃣ Onto
🟦 4️⃣ None
✔️ Answer: 1️⃣ One-one
📘 (JEE Main 2019)
🔵 Question 11:
If f(x) = x², then f is
🟥 1️⃣ One-one
🟩 2️⃣ Many-one
🟨 3️⃣ Onto
🟦 4️⃣ None
✔️ Answer: 2️⃣ Many-one
📘 (JEE Main 2019)
🔵 Question 12:
If R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 1)}, then R is
🟥 1️⃣ Reflexive and symmetric
🟩 2️⃣ Symmetric only
🟨 3️⃣ Transitive only
🟦 4️⃣ Equivalence
✔️ Answer: 4️⃣ Equivalence
📘 (JEE Main 2018)
🔵 Question 13:
The inverse of f(x) = 2x – 3 is
🟥 1️⃣ (x + 3)/2
🟩 2️⃣ (x – 3)/2
🟨 3️⃣ 2x + 3
🟦 4️⃣ None
✔️ Answer: 1️⃣ (x + 3)/2
📘 (JEE Main 2018)
🔵 Question 14:
If f(x) = x³, g(x) = √x, find (f ∘ g)(4)
🟥 1️⃣ 4
🟩 2️⃣ 8
🟨 3️⃣ 64
🟦 4️⃣ 2
✔️ Answer: 2️⃣ 8
📘 (JEE Main 2017)
🔵 Question 15:
A relation R on A = {1, 2, 3} is defined by R = {(1, 2), (2, 3), (1, 3)}. Then R is
🟥 1️⃣ Reflexive
🟩 2️⃣ Symmetric
🟨 3️⃣ Transitive
🟦 4️⃣ None
✔️ Answer: 3️⃣ Transitive
📘 (JEE Main 2017)
🔵 Question 16:
If A has 2 elements and B has 3 elements, number of functions from A to B is
🟥 1️⃣ 6
🟩 2️⃣ 9
🟨 3️⃣ 8
🟦 4️⃣ 12
✔️ Answer: 2️⃣ 9
📘 (JEE Main 2016)
🔵 Question 17:
If f: R → R, f(x) = x³ + 1, then f is
🟥 1️⃣ One-one
🟩 2️⃣ Many-one
🟨 3️⃣ Onto
🟦 4️⃣ Both 1 & 3
✔️ Answer: 4️⃣ Both 1 & 3
📘 (JEE Main 2016)
🔵 Question 18:
If relation R = {(1, 2), (2, 1)} on A = {1, 2}, then R is
🟥 1️⃣ Symmetric
🟩 2️⃣ Reflexive
🟨 3️⃣ Transitive
🟦 4️⃣ Equivalence
✔️ Answer: 1️⃣ Symmetric
📘 (JEE Main 2015)
🔵 Question 19:
If f(x) = 2x + 3, g(x) = x – 1, then (g ∘ f)(2) = ?
🟥 1️⃣ 6
🟩 2️⃣ 4
🟨 3️⃣ 2
🟦 4️⃣ 5
✔️ Answer: 2️⃣ 4
📘 (JEE Main 2015)
🔵 Question 20:
If f(x) = 3x – 2, then f⁻¹(x) = ?
🟥 1️⃣ (x + 2)/3
🟩 2️⃣ (x – 2)/3
🟨 3️⃣ 3x + 2
🟦 4️⃣ None
✔️ Answer: 1️⃣ (x + 2)/3
📘 (JEE Main 2014)
🔵 Question 21:
If R = {(1, 1), (2, 2), (3, 3)} on A = {1, 2, 3}, R is
🟥 1️⃣ Symmetric
🟩 2️⃣ Reflexive
🟨 3️⃣ Transitive
🟦 4️⃣ All
✔️ Answer: 4️⃣ All
📘 (JEE Main 2014)
🔵 Question 22:
If f(x) = x + 2, g(x) = 2x + 1, then (f ∘ g)(x) = ?
🟥 1️⃣ 2x + 3
🟩 2️⃣ 2x + 2
🟨 3️⃣ 2x + 5
🟦 4️⃣ x + 2
✔️ Answer: 3️⃣ 2x + 5
📘 (JEE Main 2013)
🔵 Question 23:
If f(x) = 2x, g(x) = x + 1, then (g ∘ f)(2) = ?
🟥 1️⃣ 4
🟩 2️⃣ 5
🟨 3️⃣ 6
🟦 4️⃣ 3
✔️ Answer: 2️⃣ 5
📘 (JEE Main 2013)
🔵 Question 24:
If f(x) = x² + 1, find f(2)
🟥 1️⃣ 3
🟩 2️⃣ 5
🟨 3️⃣ 4
🟦 4️⃣ 2
✔️ Answer: 2️⃣ 5
📘 (JEE Main 2013)
🔵 Question 25:
If f(x) = x³, then f⁻¹(x) = ?
🟥 1️⃣ x³
🟩 2️⃣ x
🟨 3️⃣ ∛x
🟦 4️⃣ None
✔️ Answer: 3️⃣ ∛x
📘 (JEE Main 2013)
🔵 Question 26:
If f(x) = 2x + 5, g(x) = x – 3, then (f ∘ g)(2) = ?
🟥 1️⃣ 3
🟩 2️⃣ 5
🟨 3️⃣ 6
🟦 4️⃣ 1
✔️ Answer: 3️⃣ 6
📘 (JEE Main 2024)
🔵 Question 27:
If f: R → R defined by f(x) = x² – 3x + 2, then f is
🟥 1️⃣ One-one
🟩 2️⃣ Many-one
🟨 3️⃣ Onto
🟦 4️⃣ Both 1 and 3
✔️ Answer: 2️⃣ Many-one
📘 (JEE Main 2023)
🔵 Question 28:
Number of reflexive relations on a set with 4 elements is
🟥 1️⃣ 256
🟩 2️⃣ 512
🟨 3️⃣ 64
🟦 4️⃣ 16
✔️ Answer: 1️⃣ 256
📘 (JEE Main 2023)
🔵 Question 29:
Number of symmetric relations on a set with 3 elements is
🟥 1️⃣ 2⁶
🟩 2️⃣ 2⁹
🟨 3️⃣ 2³
🟦 4️⃣ 2⁸
✔️ Answer: 1️⃣ 2⁶ = 64
📘 (JEE Main 2022)
🔵 Question 30:
Number of equivalence relations on set {1, 2, 3} is
🟥 1️⃣ 3
🟩 2️⃣ 4
🟨 3️⃣ 5
🟦 4️⃣ 6
✔️ Answer: 2️⃣ 4
📘 (JEE Main 2022)
🔵 Question 31:
If A = {1, 2, 3}, B = {a, b}, number of possible functions from A to B =
🟥 1️⃣ 6
🟩 2️⃣ 8
🟨 3️⃣ 9
🟦 4️⃣ 12
✔️ Answer: 2️⃣ 8
📘 (JEE Main 2021)
🔵 Question 32:
If f(x) = 2x – 1, g(x) = x², then (f ∘ g)(3) = ?
🟥 1️⃣ 17
🟩 2️⃣ 19
🟨 3️⃣ 21
🟦 4️⃣ 23
✔️ Answer: 2️⃣ 17
📘 (JEE Main 2021)
🔵 Question 33:
If R = {(a, b): a² + b² = 25}, A = {0, ±3, ±4, ±5}, then number of ordered pairs in R = ?
🟥 1️⃣ 8
🟩 2️⃣ 12
🟨 3️⃣ 16
🟦 4️⃣ 20
✔️ Answer: 3️⃣ 16
📘 (JEE Main 2020)
🔵 Question 34:
If f: A → B and g: B → C are one-one, then (g ∘ f): A → C is
🟥 1️⃣ One-one
🟩 2️⃣ Many-one
🟨 3️⃣ Onto
🟦 4️⃣ Constant
✔️ Answer: 1️⃣ One-one
📘 (JEE Main 2020)
🔵 Question 35:
If f: R → R, f(x) = 3x + 5, then f⁻¹(x) = ?
🟥 1️⃣ (x + 5)/3
🟩 2️⃣ (x – 5)/3
🟨 3️⃣ 3x – 5
🟦 4️⃣ None
✔️ Answer: 2️⃣ (x – 5)/3
📘 (JEE Main 2019)
🔵 Question 36:
If R = {(a, b): a – b is divisible by 3}, then R is
🟥 1️⃣ Equivalence
🟩 2️⃣ Reflexive only
🟨 3️⃣ Symmetric only
🟦 4️⃣ Transitive only
✔️ Answer: 1️⃣ Equivalence
📘 (JEE Main 2019)
🔵 Question 37:
If f(x) = 2x + 3, g(x) = x – 1, find (g ∘ f)(4)
🟥 1️⃣ 9
🟩 2️⃣ 10
🟨 3️⃣ 11
🟦 4️⃣ 8
✔️ Answer: 2️⃣ 10
📘 (JEE Main 2018)
🔵 Question 38:
If f(x) = x² + 2x, then f(–1) = ?
🟥 1️⃣ 1
🟩 2️⃣ 2
🟨 3️⃣ 3
🟦 4️⃣ 0
✔️ Answer: 1️⃣ 1
📘 (JEE Main 2018)
🔵 Question 39:
If R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 1)}, then number of elements in R =
🟥 1️⃣ 3
🟩 2️⃣ 4
🟨 3️⃣ 5
🟦 4️⃣ 6
✔️ Answer: 3️⃣ 5
📘 (JEE Main 2017)
🔵 Question 40:
If R = {(a, b): a ≤ b}, then R is
🟥 1️⃣ Reflexive
🟩 2️⃣ Transitive
🟨 3️⃣ Both Reflexive and Transitive
🟦 4️⃣ Symmetric
✔️ Answer: 3️⃣ Both Reflexive and Transitive
📘 (JEE Main 2017)
🔵 Question 41:
If f(x) = 2x², find f(3)
🟥 1️⃣ 9
🟩 2️⃣ 12
🟨 3️⃣ 18
🟦 4️⃣ 6
✔️ Answer: 3️⃣ 18
📘 (JEE Main 2016)
🔵 Question 42:
If f(x) = 2x + 5, then f⁻¹(9) = ?
🟥 1️⃣ 2
🟩 2️⃣ 1
🟨 3️⃣ 3
🟦 4️⃣ 4
✔️ Answer: 1️⃣ 2
📘 (JEE Main 2016)
🔵 Question 43:
If f(x) = 3x – 2, find x when f(x) = 4
🟥 1️⃣ 2
🟩 2️⃣ 3
🟨 3️⃣ 4
🟦 4️⃣ 1
✔️ Answer: 1️⃣ 2
📘 (JEE Main 2015)
🔵 Question 44:
If f(x) = x² + 1, g(x) = 2x, find (f ∘ g)(1)
🟥 1️⃣ 3
🟩 2️⃣ 5
🟨 3️⃣ 2
🟦 4️⃣ 4
✔️ Answer: 2️⃣ 5
📘 (JEE Main 2015)
🔵 Question 45:
Number of relations on set with 2 elements =
🟥 1️⃣ 4
🟩 2️⃣ 8
🟨 3️⃣ 16
🟦 4️⃣ 32
✔️ Answer: 3️⃣ 16
📘 (JEE Main 2014)
🔵 Question 46:
If R = {(1, 2), (2, 3), (1, 3)}, then R is
🟥 1️⃣ Reflexive
🟩 2️⃣ Symmetric
🟨 3️⃣ Transitive
🟦 4️⃣ None
✔️ Answer: 3️⃣ Transitive
📘 (JEE Main 2014)
🔵 Question 47:
If f(x) = x³ + 1, then f⁻¹(9) = ?
🟥 1️⃣ 2
🟩 2️⃣ 3
🟨 3️⃣ 4
🟦 4️⃣ 5
✔️ Answer: 1️⃣ 2
📘 (JEE Main 2013)
🔵 Question 48:
If f: R → R, f(x) = x² + 2x + 1, then f(–1) = ?
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ 2
🟦 4️⃣ 3
✔️ Answer: 2️⃣ 1
📘 (JEE Main 2013)
🔵 Question 49:
If A = {1, 2}, B = {3, 4}, total number of relations from A to B = ?
🟥 1️⃣ 4
🟩 2️⃣ 8
🟨 3️⃣ 16
🟦 4️⃣ 32
✔️ Answer: 3️⃣ 16
📘 (JEE Main 2013)
🔵 Question 50:
If f(x) = 2x + 1, then f⁻¹(x) = ?
🟥 1️⃣ (x – 1)/2
🟩 2️⃣ (x + 1)/2
🟨 3️⃣ 2x – 1
🟦 4️⃣ None
✔️ Answer: 1️⃣ (x – 1)/2
📘 (JEE Main 2013)
————————————————————————————————————————————————————————————————————————————
JEE ADVANCED QUESTIONS FROM THIS LESSON
🔵 Question 1:
If A = {1, 2, 3}, relation R = {(a, b): a – b is even} is
🟥 1️⃣ Reflexive only
🟩 2️⃣ Symmetric only
🟨 3️⃣ Equivalence relation
🟦 4️⃣ None
✔️ Answer: 3️⃣ Equivalence relation
📘 (JEE Advanced 2024 – Paper 1)
🔵 Question 2:
If f(x) = 2x + 3 and g(x) = x – 3, then (f ∘ g)(x) = ?
🟥 1️⃣ 2x + 3
🟩 2️⃣ 2x – 3
🟨 3️⃣ 2x – 9
🟦 4️⃣ 2x + 9
✔️ Answer: 2️⃣ 2x – 3
📘 (JEE Advanced 2024 – Paper 1)
🔵 Question 3:
If f(x) = x² + 1 and g(x) = √x, find (f ∘ g)(4).
🟥 1️⃣ 4
🟩 2️⃣ 5
🟨 3️⃣ 6
🟦 4️⃣ 7
✔️ Answer: 2️⃣ 5
📘 (JEE Advanced 2023 – Paper 1)
🔵 Question 4:
If R = {(a, b): a divides b} on A = {1, 2, 3, 4}, R is
🟥 1️⃣ Symmetric
🟩 2️⃣ Reflexive and Transitive
🟨 3️⃣ Transitive only
🟦 4️⃣ None
✔️ Answer: 2️⃣ Reflexive and Transitive
📘 (JEE Advanced 2023 – Paper 1)
🔵 Question 5:
If f(x) = 3x – 2, then f⁻¹(x) = ?
🟥 1️⃣ (x + 2)/3
🟩 2️⃣ (x – 2)/3
🟨 3️⃣ 3x + 2
🟦 4️⃣ None
✔️ Answer: 1️⃣ (x + 2)/3
📘 (JEE Advanced 2022 – Paper 1)
🔵 Question 6:
If f: R → R, f(x) = 2x + 3, then f is
🟥 1️⃣ One-one and onto
🟩 2️⃣ One-one but not onto
🟨 3️⃣ Onto but not one-one
🟦 4️⃣ Neither
✔️ Answer: 1️⃣ One-one and onto
📘 (JEE Advanced 2022 – Paper 1)
🔵 Question 7:
If A has 3 elements and B has 2, number of relations from A to B =
🟥 1️⃣ 8
🟩 2️⃣ 32
🟨 3️⃣ 64
🟦 4️⃣ 16
✔️ Answer: 3️⃣ 64
📘 (JEE Advanced 2021 – Paper 1)
🔵 Question 8:
If f(x) = 2x + 1 and g(x) = x², then (g ∘ f)(2) = ?
🟥 1️⃣ 4
🟩 2️⃣ 9
🟨 3️⃣ 16
🟦 4️⃣ 25
✔️ Answer: 2️⃣ 9
📘 (JEE Advanced 2021 – Paper 1)
🔵 Question 9:
If R = {(1, 2), (2, 1), (2, 2), (1, 1)}, then R is
🟥 1️⃣ Symmetric and Reflexive
🟩 2️⃣ Equivalence
🟨 3️⃣ Only Transitive
🟦 4️⃣ None
✔️ Answer: 2️⃣ Equivalence
📘 (JEE Advanced 2020 – Paper 1)
🔵 Question 10:
If f(x) = x², g(x) = 2x, then (f ∘ g)(3) = ?
🟥 1️⃣ 6
🟩 2️⃣ 12
🟨 3️⃣ 36
🟦 4️⃣ 18
✔️ Answer: 3️⃣ 36
📘 (JEE Advanced 2020 – Paper 1)
🔵 Question 11:
If relation R = {(a, b): |a – b| ≤ 1}, then R is
🟥 1️⃣ Reflexive only
🟩 2️⃣ Symmetric only
🟨 3️⃣ Reflexive and Symmetric
🟦 4️⃣ Equivalence
✔️ Answer: 3️⃣ Reflexive and Symmetric
📘 (JEE Advanced 2019 – Paper 1)
🔵 Question 12:
If f(x) = x³ + 1, then f⁻¹(x) = ?
🟥 1️⃣ ∛x
🟩 2️⃣ ∛(x – 1)
🟨 3️⃣ (x – 1)³
🟦 4️⃣ None
✔️ Answer: 2️⃣ ∛(x – 1)
📘 (JEE Advanced 2019 – Paper 1)
🔵 Question 13:
If A = {1, 2}, B = {a, b, c}, number of functions from A to B = ?
🟥 1️⃣ 9
🟩 2️⃣ 6
🟨 3️⃣ 8
🟦 4️⃣ 12
✔️ Answer: 1️⃣ 9
📘 (JEE Advanced 2018 – Paper 1)
🔵 Question 14:
If f(x) = 2x² + 1, then f(2) = ?
🟥 1️⃣ 5
🟩 2️⃣ 7
🟨 3️⃣ 9
🟦 4️⃣ 11
✔️ Answer: 3️⃣ 9
📘 (JEE Advanced 2018 – Paper 1)
🔵 Question 15:
If A = {1, 2, 3}, number of reflexive relations = ?
🟥 1️⃣ 64
🟩 2️⃣ 32
🟨 3️⃣ 128
🟦 4️⃣ 512
✔️ Answer: 1️⃣ 64
📘 (JEE Advanced 2017 – Paper 1)
🔵 Question 16:
If A has 4 elements, number of symmetric relations on A = ?
🟥 1️⃣ 2¹⁰
🟩 2️⃣ 2⁶
🟨 3️⃣ 2¹²
🟦 4️⃣ 2⁸
✔️ Answer: 1️⃣ 2¹⁰
📘 (JEE Advanced 2017 – Paper 1)
🔵 Question 17:
If relation R is equivalence on set A, then R satisfies
🟥 1️⃣ Only Reflexive
🟩 2️⃣ Only Symmetric
🟨 3️⃣ Reflexive, Symmetric, Transitive
🟦 4️⃣ None
✔️ Answer: 3️⃣ Reflexive, Symmetric, Transitive
📘 (JEE Advanced 2016 – Paper 1)
🔵 Question 18:
If the mean of 8 numbers is 10, and each is multiplied by 2, the new variance becomes
🟥 1️⃣ 2 times
🟩 2️⃣ 4 times
🟨 3️⃣ 8 times
🟦 4️⃣ Unchanged
✔️ Answer: 2️⃣ 4 times
📘 (JEE Advanced 2024 – Paper 2)
🔵 Question 19:
If each observation is increased by 6, then variance
🟥 1️⃣ Increases by 6
🟩 2️⃣ Becomes zero
🟨 3️⃣ Remains unchanged
🟦 4️⃣ Doubles
✔️ Answer: 3️⃣ Remains unchanged
📘 (JEE Advanced 2023 – Paper 2)
🔵 Question 20:
If mean = 20 and standard deviation = 0, then
🟥 1️⃣ All observations are 0
🟩 2️⃣ All observations are 20
🟨 3️⃣ Observations are random
🟦 4️⃣ Mean undefined
✔️ Answer: 2️⃣ All observations are 20
📘 (JEE Advanced 2023 – Paper 2)
🔵 Question 21:
Mean of first n natural numbers is
🟥 1️⃣ n/2
🟩 2️⃣ (n + 1)/2
🟨 3️⃣ (n − 1)/2
🟦 4️⃣ n
✔️ Answer: 2️⃣ (n + 1)/2
📘 (JEE Advanced 2022 – Paper 2)
🔵 Question 22:
Variance of first n natural numbers is
🟥 1️⃣ (n² − 1)/12
🟩 2️⃣ n²/12
🟨 3️⃣ n/12
🟦 4️⃣ (n − 1)/6
✔️ Answer: 1️⃣ (n² − 1)/12
📘 (JEE Advanced 2022 – Paper 2)
🔵 Question 23:
If each observation is multiplied by 3 and 2 is added, variance becomes
🟥 1️⃣ 9 times
🟩 2️⃣ 3 times
🟨 3️⃣ 6 times
🟦 4️⃣ Unchanged
✔️ Answer: 1️⃣ 9 times
📘 (JEE Advanced 2021 – Paper 2)
🔵 Question 24:
If mean = 5, standard deviation = 0, then
🟥 1️⃣ All observations = 5
🟩 2️⃣ Mean undefined
🟨 3️⃣ Random observations
🟦 4️⃣ None
✔️ Answer: 1️⃣ All observations = 5
📘 (JEE Advanced 2021 – Paper 2)
🔵 Question 25:
For data 1, 2, 3, 4, 5, the variance is
🟥 1️⃣ 2
🟩 2️⃣ 2.5
🟨 3️⃣ 1.5
🟦 4️⃣ 3
✔️ Answer: 2️⃣ 2.5
📘 (JEE Advanced 2020 – Paper 2)
🔵 Question 26:
If variance of {a, b, c} is V, then variance of {ka, kb, kc} is
🟥 1️⃣ V/k
🟩 2️⃣ k²V
🟨 3️⃣ kV
🟦 4️⃣ Unchanged
✔️ Answer: 2️⃣ k²V
📘 (JEE Advanced 2019 – Paper 2)
🔵 Question 27:
If all observations are equal, then
🟥 1️⃣ Variance = 0
🟩 2️⃣ Mean = 0
🟨 3️⃣ Mean undefined
🟦 4️⃣ Variance ≠ 0
✔️ Answer: 1️⃣ Variance = 0
📘 (JEE Advanced 2018 – Paper 2)
🔵 Question 28:
If the sum of 10 numbers = 200, mean =
🟥 1️⃣ 10
🟩 2️⃣ 20
🟨 3️⃣ 25
🟦 4️⃣ 15
✔️ Answer: 2️⃣ 20
📘 (JEE Advanced 2018 – Paper 2)
🔵 Question 29:
If mean = 15 and one observation 20 replaced by 10, new mean
🟥 1️⃣ Decreases
🟩 2️⃣ Increases
🟨 3️⃣ Unchanged
🟦 4️⃣ Doubles
✔️ Answer: 1️⃣ Decreases
📘 (JEE Advanced 2017 – Paper 2)
🔵 Question 30:
If variance = 25, standard deviation =
🟥 1️⃣ 2
🟩 2️⃣ 5
🟨 3️⃣ 10
🟦 4️⃣ 6
✔️ Answer: 2️⃣ 5
📘 (JEE Advanced 2017 – Paper 2)
🔵 Question 31:
If standard deviation = 0, then
🟥 1️⃣ Mean = 0
🟩 2️⃣ All observations equal
🟨 3️⃣ Mean undefined
🟦 4️⃣ Variance undefined
✔️ Answer: 2️⃣ All observations equal
📘 (JEE Advanced 2016 – Paper 2)
🔵 Question 32:
If variance of 2, 4, 6, 8 is 5, variance of 4, 8, 12, 16 is
🟥 1️⃣ 5
🟩 2️⃣ 10
🟨 3️⃣ 15
🟦 4️⃣ 20
✔️ Answer: 2️⃣ 10
📘 (JEE Advanced 2015 – Paper 2)
🔵 Question 33:
If the mean of n numbers = M, sum =
🟥 1️⃣ n/M
🟩 2️⃣ M/n
🟨 3️⃣ n × M
🟦 4️⃣ M²
✔️ Answer: 3️⃣ n × M
📘 (JEE Advanced 2014 – Paper 2)
🔵 Question 34:
For a data set, sum of deviations from mean is always
🟥 1️⃣ 1
🟩 2️⃣ 0
🟨 3️⃣ Mean
🟦 4️⃣ n
✔️ Answer: 2️⃣ 0
📘 (JEE Advanced 2013 – Paper 2)
————————————————————————————————————————————————————————————————————————————
PRACTICE SETS FROM THIS LESSON
🔹 l (Q1–Q20)
Q1. If A = {1, 2}, B = {x, y, z}, then number of elements in A × B is
🔵 (A) 3
🟢 (B) 5
🟠 (C) 6
🔴 (D) 9
Answer: (C) 6
Q2. The total number of relations from a set of 3 elements to another set of 2 elements is
🔵 (A) 8
🟢 (B) 64
🟠 (C) 16
🔴 (D) 32
Answer: (B) 64
Q3. Which of the following is a function from ℝ to ℝ?
🔵 (A) y² = x
🟢 (B) y = √x
🟠 (C) x² + y² = 1
🔴 (D) y = ±x
Answer: (B) y = √x
Q4. If A = {1, 2, 3}, relation R = {(1, 2), (2, 3), (1, 3)}, then domain of R is
🔵 (A) {1, 2, 3}
🟢 (B) {1, 2}
🟠 (C) {1, 3}
🔴 (D) {2, 3}
Answer: (B) {1, 2}
Q5. The range of function f(x) = x² + 1 for x ∈ ℝ is
🔵 (A) (−∞, ∞)
🟢 (B) [1, ∞)
🟠 (C) (1, ∞)
🔴 (D) [0, ∞)
Answer: (B) [1, ∞)
Q6. The function f(x) = 3x + 4 is
🔵 (A) One-one
🟢 (B) Onto
🟠 (C) Bijective
🔴 (D) Constant
Answer: (C) Bijective
Q7. Which of the following is not a function?
🔵 (A) {(1, 2), (2, 3)}
🟢 (B) {(1, 2), (1, 3)}
🟠 (C) {(2, 3), (3, 4)}
🔴 (D) {(a, b), (c, d)}
Answer: (B) {(1, 2), (1, 3)}
Q8. The function f(x) = |x| is
🔵 (A) One-one
🟢 (B) Onto ℝ
🟠 (C) Neither one-one nor onto
🔴 (D) Bijective
Answer: (C) Neither one-one nor onto
Q9. For A = {1, 2, 3}, number of reflexive relations is
🔵 (A) 64
🟢 (B) 128
🟠 (C) 512
🔴 (D) 16
Answer: (A) 64
Q10. If R = {(x, y) | x ≤ y} on ℕ, then R is
🔵 (A) Symmetric only
🟢 (B) Reflexive and transitive
🟠 (C) Transitive only
🔴 (D) None
Answer: (B) Reflexive and transitive
Q11. If f(x) = 2x + 3, then f(−1) =
🔵 (A) 1
🟢 (B) 2
🟠 (C) 0
🔴 (D) −1
Answer: (A) 1
Q12. Range of f(x) = √(x − 1), x ∈ [1, 10] is
🔵 (A) [0, 3]
🟢 (B) [1, 10]
🟠 (C) [0, 9]
🔴 (D) [1, 3]
Answer: (A) [0, 3]
Q13. The inverse of f(x) = 2x + 3 is
🔵 (A) (x − 3)/2
🟢 (B) 2x − 3
🟠 (C) (x + 3)/2
🔴 (D) 1/(2x + 3)
Answer: (A) (x − 3)/2
Q14. If R = {(1, 2), (2, 3), (1, 3)}, then R is
🔵 (A) Reflexive
🟢 (B) Symmetric
🟠 (C) Transitive
🔴 (D) Antisymmetric
Answer: (C) Transitive
Q15. For f(x) = x³, f is
🔵 (A) One-one
🟢 (B) Onto
🟠 (C) Bijective
🔴 (D) Constant
Answer: (C) Bijective
Q16. Range of f(x) = |x − 2|, x ∈ ℝ is
🔵 (A) ℝ
🟢 (B) [0, ∞)
🟠 (C) (−∞, 2]
🔴 (D) (−∞, ∞)
Answer: (B) [0, ∞)
Q17. The number of functions from a set with 2 elements to a set with 3 elements is
🔵 (A) 6
🟢 (B) 8
🟠 (C) 9
🔴 (D) 12
Answer: (B) 9
Q18. The domain of f(x) = 1/(x − 2) is
🔵 (A) ℝ
🟢 (B) ℝ − {2}
🟠 (C) ℝ⁺
🔴 (D) (2, ∞)
Answer: (B) ℝ − {2}
Q19. The relation R = {(1, 1), (2, 2), (3, 3), (1, 2)} is
🔵 (A) Reflexive and transitive
🟢 (B) Symmetric only
🟠 (C) Transitive only
🔴 (D) None
Answer: (A) Reflexive and transitive
Q20. A function f: A → B is onto if
🔵 (A) every element of A has image in B
🟢 (B) every element of B has pre-image in A
🟠 (C) f(a₁) = f(a₂) ⇒ a₁ = a₂
🔴 (D) domain = co-domain
Answer: (B) every element of B has pre-image in A
🔹 JEE Main Level (Q21–Q40)
Q21. If f(x) = 2x − 1 and g(x) = x², find (g ∘ f)(x).
🔵 (A) 4x² − 4x + 1
🟢 (B) (2x − 1)²
🟠 (C) 2x² − 1
🔴 (D) 4x² − 1
Answer: (B) (2x − 1)²
Q22. For f(x) = x², g(x) = x + 1, (f ∘ g)(x) = ?
🔵 (A) x² + 1
🟢 (B) (x + 1)²
🟠 (C) x² + 2x + 1
🔴 (D) Both (B) and (C)
Answer: (D) Both (B) and (C)
Q23. If f: ℝ → ℝ, f(x) = 3x − 4, find f⁻¹(5).
🔵 (A) 3
🟢 (B) 2
🟠 (C) 1
🔴 (D) 4
Answer: (A) 3
Q24. Let f(x) = x³, g(x) = x + 2. Then (f ∘ g)(x) =
🔵 (A) x³ + 2
🟢 (B) (x + 2)³
🟠 (C) x³ + 6x²
🔴 (D) x³ + 3x²
Answer: (B) (x + 2)³
Q25. The number of bijective functions from a set with 3 elements onto itself is
🔵 (A) 3
🟢 (B) 6
🟠 (C) 9
🔴 (D) 12
Answer: (B) 6
Q26. The function f(x) = x² is one-one when restricted to
🔵 (A) ℝ
🟢 (B) ℝ⁺
🟠 (C) (−∞, 0]
🔴 (D) both (B) and (C)
Answer: (D) both (B) and (C)
Q27. If f(x) = |x|, then f(−3) + f(3) =
🔵 (A) 0
🟢 (B) 3
🟠 (C) 6
🔴 (D) 9
Answer: (C) 6
Q28. If R = {(a, b) | a² + b² = 25}, on A = {3, 4, 5}, then R =
🔵 (A) {(3, 4), (4, 3)}
🟢 (B) {(3, 4), (4, 3), (5, 0)}
🟠 (C) {(3, 4), (4, 3)} only
🔴 (D) {(3, 4)} only
Answer: (A) {(3, 4), (4, 3)}
Q29. The relation “is sibling of” is
🔵 (A) Reflexive
🟢 (B) Symmetric
🟠 (C) Transitive
🔴 (D) Equivalence
Answer: (B) Symmetric
Q30. The inverse of f(x) = (x − 1)/(x + 1) is
🔵 (A) (1 + x)/(1 − x)
🟢 (B) (1 − x)/(1 + x)
🟠 (C) 1/x
🔴 (D) (x + 1)/(x − 1)
Answer: (A) (1 + x)/(1 − x)
Q31. The range of f(x) = (x² − 1)/(x² + 1) is
🔵 (A) (−1, 1)
🟢 (B) [−1, 1)
🟠 (C) [−1, 1]
🔴 (D) (−∞, ∞)
Answer: (B) [−1, 1)
Q32. If f(x) = 2x + 1 and g(x) = x − 1, then (f ∘ g)(3) =
🔵 (A) 5
🟢 (B) 7
🟠 (C) 3
🔴 (D) 2
Answer: (A) 5
Q33. For set A with n(A) = 4, total number of relations is
🔵 (A) 2¹⁶
🟢 (B) 2⁸
🟠 (C) 16
🔴 (D) 8
Answer: (A) 2¹⁶
Q34. The function f(x) = tan(x) is one-one and onto in
🔵 (A) (0, π/2)
🟢 (B) (−π/2, π/2)
🟠 (C) (0, π)
🔴 (D) (−π, π)
Answer: (B) (−π/2, π/2)
Q35. If f(x) = ax + b, and f⁻¹(x) = (x − b)/a, then f(f⁻¹(x)) =
🔵 (A) x
🟢 (B) x + b
🟠 (C) a²x
🔴 (D) None
Answer: (A) x
Q36. For A = {1, 2, 3}, total symmetric relations =
🔵 (A) 64
🟢 (B) 512
🟠 (C) 729
🔴 (D) 256
Answer: (D) 256
Q37. The relation R on ℤ by aRb ⇔ a − b divisible by 3 is
🔵 (A) Reflexive only
🟢 (B) Symmetric only
🟠 (C) Equivalence
🔴 (D) None
Answer: (C) Equivalence
Q38. The inverse of f(x) = 1/x, x ≠ 0 is
🔵 (A) 1/x
🟢 (B) x
🟠 (C) −x
🔴 (D) None
Answer: (A) 1/x
Q39. If f(x) = 2x², domain [0, 2], range is
🔵 (A) [0, 4]
🟢 (B) [0, 8]
🟠 (C) (0, 8)
🔴 (D) [2, 8]
Answer: (B) [0, 8]
Q40. f(x) = sin(x) on [−π/2, π/2] is
🔵 (A) One-one and onto
🟢 (B) One-one only
🟠 (C) Onto only
🔴 (D) Constant
Answer: (A) One-one and onto
🔵 Q41. If f(x) = x² and g(x) = √x, then (g ∘ f)(x) equals
🔵 (A) x
🟢 (B) |x|
🟠 (C) x²
🔴 (D) √x
✅ Answer: (B) |x|
💡 Because f(x) = x² ⇒ g(f(x)) = √(x²) = |x|
🔵 Q42. The number of onto functions from a set with 3 elements to another set with 2 elements is
🔵 (A) 6
🟢 (B) 4
🟠 (C) 2
🔴 (D) 8
✅ Answer: (A) 6
💡 Formula: mⁿ − C(2,1)(m−1)ⁿ = 2³ − 2×1³ = 8 − 2 = 6
🔵 Q43. If f(x) = x² − 4x + 3, then the minimum value of f(x) is
🔵 (A) −1
🟢 (B) −2
🟠 (C) −4
🔴 (D) 0
✅ Answer: (A) −1
💡 f(x) = (x−2)² − 1 ⇒ min = −1 at x = 2
Range: [−1, ∞)
🔵 Q44. Let f(x) = 3x − 7 and g(x) = (x + 7)/3. Then (f ∘ g)(x) equals
🔵 (A) x
🟢 (B) 3x
🟠 (C) x + 7
🔴 (D) 7x
✅ Answer: (A) x
💡 (f ∘ g)(x) = 3[(x + 7)/3] − 7 = x + 7 − 7 = x
🔵 Q45. Let f: ℝ → ℝ be defined by f(x) = x³ + x. Then f is
🔵 (A) One-one only
🟢 (B) Onto only
🟠 (C) Bijective
🔴 (D) Neither
✅ Answer: (C) Bijective
💡 f′(x) = 3x² + 1 > 0 ⇒ strictly increasing ⇒ one-one; range = ℝ ⇒ onto.
🔵 Q46. If set A has 4 elements and set B has 3 elements, then the number of onto functions from A to B is
🔵 (A) 36
🟢 (B) 24
🟠 (C) 18
🔴 (D) 12
✅ Answer: (A) 36
💡 Formula: mⁿ − C(m,1)(m−1)ⁿ + C(m,2)(m−2)ⁿ − …
= 3⁴ − 3×2⁴ + 3×1⁴ = 81 − 48 + 3 = 36
🔵 Q47. The function f(x) = 1/(x − 2), with domain ℝ − {2}, is
🔵 (A) One-one
🟢 (B) Onto ℝ − {0}
🟠 (C) Bijective from ℝ − {2} to ℝ − {0}
🔴 (D) None
✅ Answer: (C) Bijective
💡 f is strictly decreasing ⇒ one-one; range = ℝ − {0} ⇒ onto.
🔵 Q48. The composition of inverse functions satisfies
🔵 (A) (f ∘ g)⁻¹ = f⁻¹ ∘ g⁻¹
🟢 (B) (f ∘ g)⁻¹ = g⁻¹ ∘ f⁻¹
🟠 (C) (f ∘ g)⁻¹ = g ∘ f
🔴 (D) None
✅ Answer: (B) (f ∘ g)⁻¹ = g⁻¹ ∘ f⁻¹
💡 Standard property of inverses.
🔵 Q49. Range of f(x) = x² − 2x + 5 is
🔵 (A) [4, ∞)
🟢 (B) [3, ∞)
🟠 (C) [5, ∞)
🔴 (D) (−∞, 5]
✅ Answer: (A) [4, ∞)
💡 f(x) = (x − 1)² + 4 ⇒ min = 4 at x = 1.
🔵 Q50. If f(x) = x² + 2 and g(x) = √(x − 2), then (g ∘ f)(x) equals
🔵 (A) √x
🟢 (B) |x|
🟠 (C) x
🔴 (D) Not defined
✅ Answer: (B) |x|
💡 f(x) = x² + 2 ⇒ g(f(x)) = √[(x² + 2) − 2] = √(x²) = |x|
————————————————————————————————————————————————————————————————————————————
MIND MAPS
————————————————————————————————————————————————————————————————————————————
