Class 11 : Maths (In English) – Lesson 10. Conic Sections

Posted by

On June 21, 2025

EXPLANATION & SUMMARY

🔷 Explanation
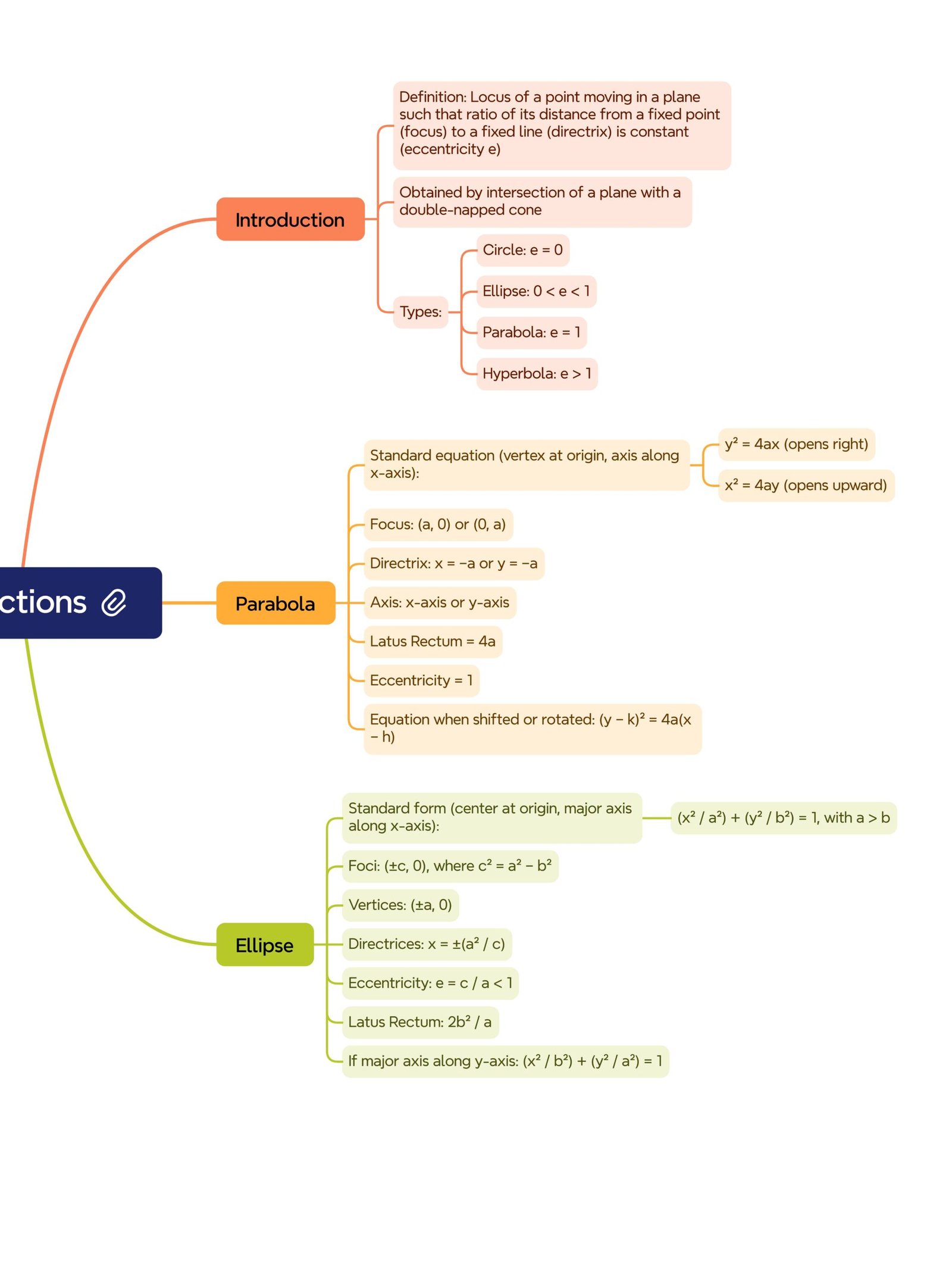
🔹 1. Introduction
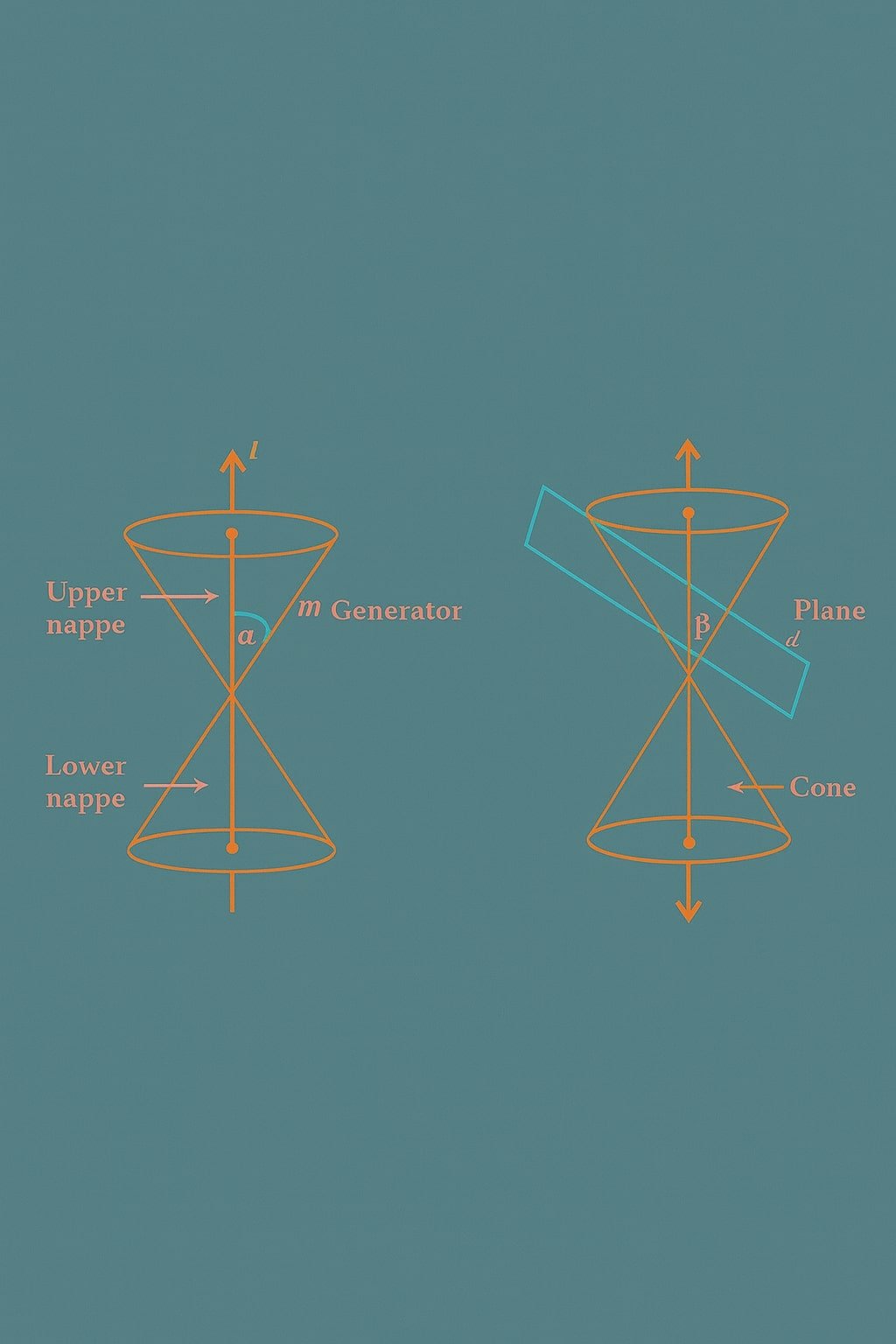
🔵 Conic sections are the curves obtained by intersecting a double right circular cone with a plane.
🟢 Depending on the angle of inclination of the plane with the cone’s axis, we obtain:
➡️ Circle
➡️ Ellipse
➡️ Parabola
➡️ Hyperbola
💡 Concept: The general equation of all conic sections is of second degree:
🧠 Ax² + 2Hxy + By² + 2Gx + 2Fy + C = 0

🔹 2. Circle
🔵 Definition: The set of all points which are at a constant distance (radius) from a fixed point (centre).
🧠 Let centre = (h, k), radius = r.
✔️ Equation: (x − h)² + (y − k)² = r²
➡️ If centre = origin (0, 0): x² + y² = r²
✏️ Note: The general equation x² + y² + 2gx + 2fy + c = 0 represents a circle if
✔️ g² + f² − c > 0
➡️ Centre = (−g, −f), radius = √(g² + f² − c)

🔹 3. Parabola
🔵 Definition: The set of all points (x, y) in a plane such that distance from a fixed point (focus) = distance from a fixed line (directrix).
🧠 Standard Form:
✔️ y² = 4ax → Axis along x-axis, vertex at origin, focus (a, 0), directrix x = −a
✔️ x² = 4ay → Axis along y-axis, vertex at origin, focus (0, a), directrix y = −a
💡 Eccentricity (e) = 1
✏️ Key Properties:
• Vertex = (0, 0)
• Axis = x-axis or y-axis
• Latus Rectum = line through focus perpendicular to axis
• Length = 4a

🔹 4. Ellipse
🔵 Definition: The set of all points such that the sum of distances from two fixed points (foci) is constant.
🧠 Standard Forms:
1️⃣ Major axis along x-axis:
(x²/a²) + (y²/b²) = 1, a > b
Focus: (±c, 0), where c² = a² − b²
Eccentricity e = c/a, 0 < e < 1
2️⃣ Major axis along y-axis:
(x²/b²) + (y²/a²) = 1, a > b
Focus: (0, ±c), c² = a² − b²
💡 Special Case: If a = b ⇒ circle.

🔹 5. Hyperbola
🔵 Definition: The set of all points such that the difference of distances from two fixed points (foci) is constant.
🧠 Standard Forms:
1️⃣ Transverse axis along x-axis:
(x²/a²) − (y²/b²) = 1
Foci: (±c, 0), where c² = a² + b²
Eccentricity e = c/a, e > 1
2️⃣ Transverse axis along y-axis:
(y²/a²) − (x²/b²) = 1
✏️ Note: Asymptotes → lines passing through centre:
y = ±(b/a)x

🔹 6. Focus–Directrix Property
🧠 A conic is defined by:
Distance from focus = e × distance from directrix,
where e = eccentricity.
✔️ e < 1 → Ellipse
✔️ e = 1 → Parabola
✔️ e > 1 → Hyperbola
💡 This property gives a unified definition of all conics.

🔹 7. General Equation of Conic
🧠 General second-degree equation:
Ax² + 2Hxy + By² + 2Gx + 2Fy + C = 0
✳️ Discriminant Δ = H² − AB
✔️ Δ = 0 → Parabola
✔️ Δ < 0 → Ellipse (if A = B, circle)
✔️ Δ > 0 → Hyperbola

🔹 8. Translation of Axes
🧠 To remove linear terms (2Gx, 2Fy), shift origin to (h, k):
Let
x = X + h, y = Y + k
Substitute into equation → new coordinates (X, Y) may simplify the form.

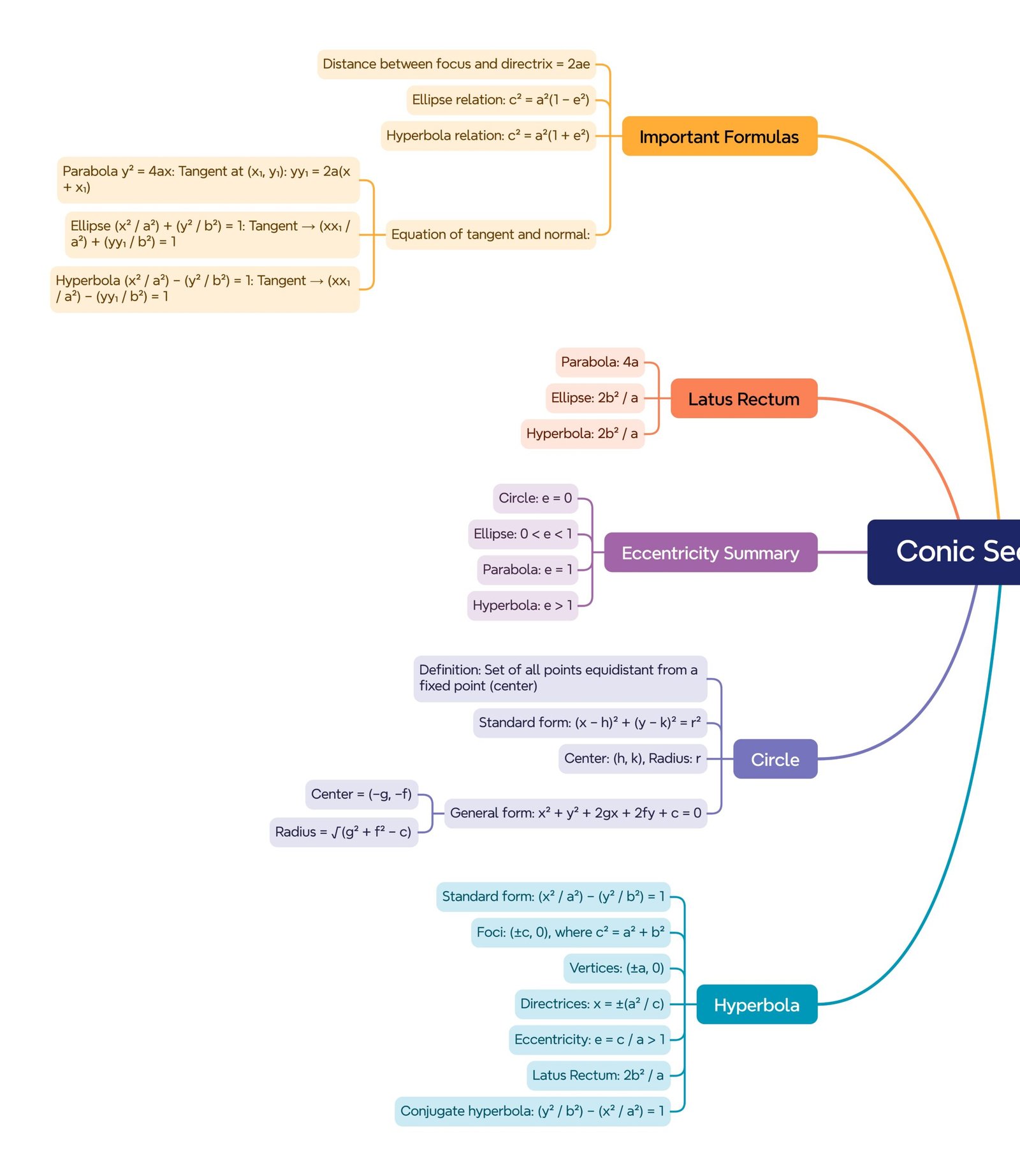
🔹 9. Important Relations
✔️ Ellipse: c² = a² − b²
✔️ Hyperbola: c² = a² + b²
✔️ Latus Rectum:
• Parabola → 4a
• Ellipse → 2b²/a
• Hyperbola → 2b²/a

🔹 10. Tangents and Normals
💡 Tangent at (x₁, y₁):
➡️ Circle: x·x₁ + y·y₁ = r²
➡️ Parabola (y² = 4ax): yy₁ = 2a(x + x₁)
➡️ Ellipse: (x·x₁)/a² + (y·y₁)/b² = 1
➡️ Hyperbola: (x·x₁)/a² − (y·y₁)/b² = 1
💡 Normal: Perpendicular line to tangent at (x₁, y₁)

🔹 11. Auxiliary Circle (Ellipse & Hyperbola)
🔵 Circle with centre same as conic, radius = semi-major axis a.
Used to find eccentric angles and geometrical properties.

🔹 12. Focal Chord and Parametric Form
🧠 Parabola y² = 4ax:
Point = (a t², 2a t)
Tangent: t y = x + a t²
Normal: y + t x = 2a t + a t³
🧠 Ellipse (x²/a²) + (y²/b²) = 1:
Parametric form: (a cos θ, b sin θ)
🧠 Hyperbola (x²/a²) − (y²/b²) = 1:
Parametric form: (a sec θ, b tan θ)

🔹 13. Real-life Applications
✔️ Circle: Wheels, circular tracks
✔️ Parabola: Reflectors, satellite dishes
✔️ Ellipse: Planetary orbits
✔️ Hyperbola: Radio navigation, cooling towers

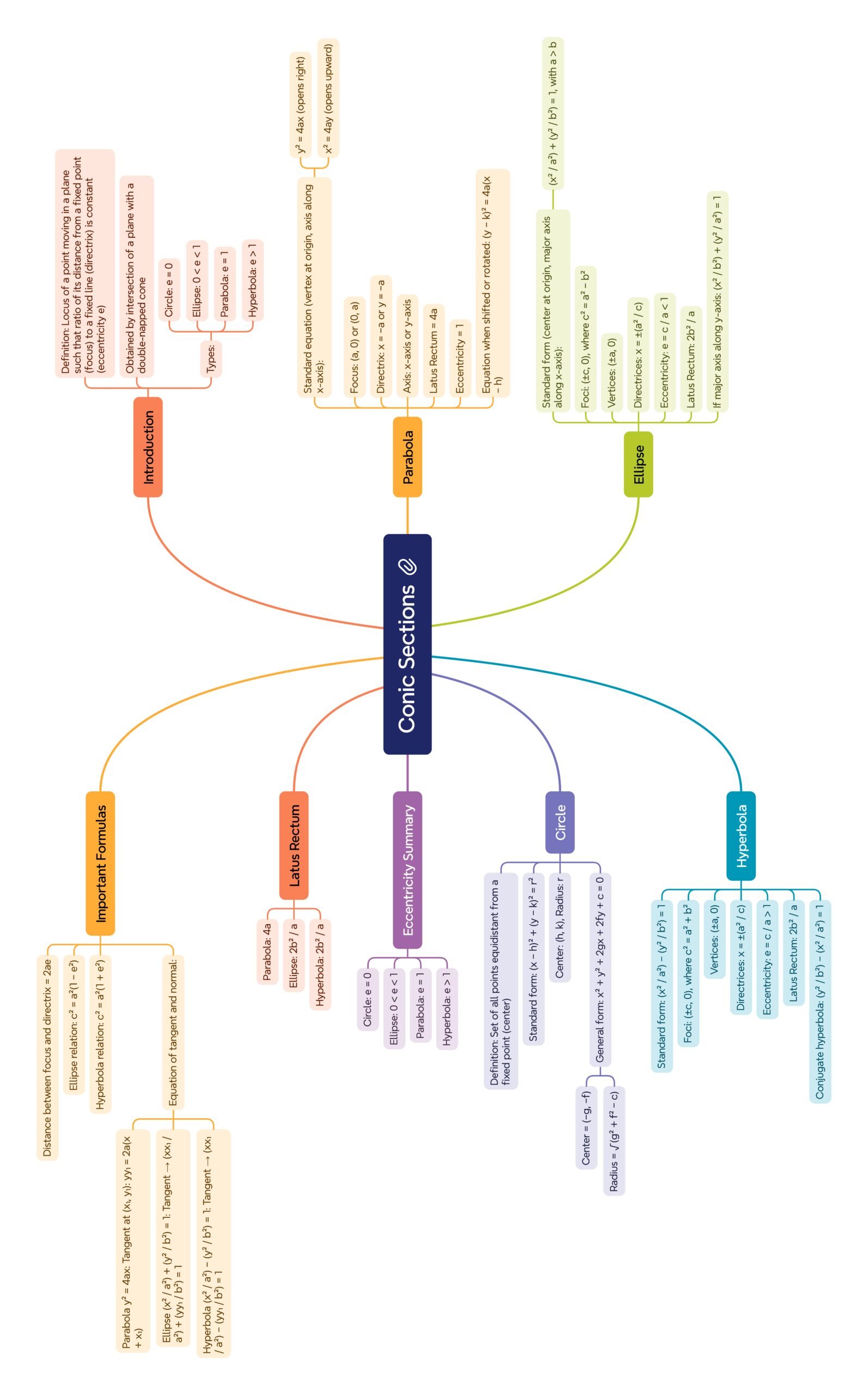
🟣 Summary (~300 words)
🔸 Conic Sections Overview
• Curves formed by intersection of a cone and a plane.
• Types: Circle, Parabola, Ellipse, Hyperbola.
🔸 Equations
🔹 Circle: (x − h)² + (y − k)² = r²
🔹 Parabola: y² = 4ax or x² = 4ay
🔹 Ellipse: (x²/a²) + (y²/b²) = 1
🔹 Hyperbola: (x²/a²) − (y²/b²) = 1
🔸 Eccentricity (e)
• e < 1 → Ellipse
• e = 1 → Parabola
• e > 1 → Hyperbola
🔸 Key Relations
✔️ Ellipse: c² = a² − b²
✔️ Hyperbola: c² = a² + b²
🔸 Latus Rectum
• Parabola: 4a
• Ellipse: 2b²/a
• Hyperbola: 2b²/a
🔸 Discriminant (H² − AB)
• = 0 → Parabola
• < 0 → Ellipse (circle if A = B, H = 0)
• > 0 → Hyperbola
🔸 Tangents
General:
➡️ Ellipse: (x·x₁)/a² + (y·y₁)/b² = 1
➡️ Hyperbola: (x·x₁)/a² − (y·y₁)/b² = 1
🔸 Parametric Forms
• Parabola: (a t², 2a t)
• Ellipse: (a cos θ, b sin θ)
• Hyperbola: (a sec θ, b tan θ)
🔸 Applications
Used in engineering, astronomy, and physics.

📝 Quick Recap
✔️ Conics = Circle, Parabola, Ellipse, Hyperbola
✔️ Defined via focus–directrix property
✔️ Circle: e = 0, Ellipse: e < 1, Parabola: e = 1, Hyperbola: e > 1
✔️ Key forms:
• Circle: (x − h)² + (y − k)² = r²
• Parabola: y² = 4ax
• Ellipse: (x²/a²) + (y²/b²) = 1
• Hyperbola: (x²/a²) − (y²/b²) = 1
✔️ Tangent & normal equations derived from standard form
✔️ Conics appear in optics, architecture, astronomy

————————————————————————————————————————————————————————————————————————————

QUESTIONS FROM TEXTBOOK

🧠 Exercise 10.1

🔵 Question 1:
Find the equation of the circle with centre (0, 2) and radius 2.
🟢 Answer:
💡 Formula: (x − h)² + (y − k)² = r²
Substitute: h = 0, k = 2, r = 2
➡️ (x − 0)² + (y − 2)² = 2²
➡️ x² + (y − 2)² = 4 ✅

🔵 Question 2:
Centre (−2, 3) and radius 4
🟢 Answer:
➡️ (x + 2)² + (y − 3)² = 4²
➡️ (x + 2)² + (y − 3)² = 16 ✅

🔵 Question 3:
Centre (1/2, −1/4), radius 1/12
🟢 Answer:
➡️ (x − 1/2)² + (y + 1/4)² = (1/12)²
➡️ (x − 1/2)² + (y + 1/4)² = 1/144 ✅

🔵 Question 4:
Centre (1, 1), radius √2
🟢 Answer:
➡️ (x − 1)² + (y − 1)² = (√2)²
➡️ (x − 1)² + (y − 1)² = 2 ✅

🔵 Question 5:
Centre (−a, −b), radius √(a² − b²)
🟢 Answer:
➡️ (x + a)² + (y + b)² = (√(a² − b²))²
➡️ (x + a)² + (y + b)² = a² − b² ✅

🔵 Question 6:
(x + 5)² + (y − 3)² = 36
🟢 Answer:
💡 Standard form ⇒ Centre (−5, 3), Radius = √36 = 6
✔️ Centre (−5, 3), Radius 6

🔵 Question 7:
x² + y² − 4x − 8y − 45 = 0
🟢 Answer:
➡️ Complete squares:
x² − 4x + y² − 8y = 45
(x² − 4x + 4) + (y² − 8y + 16) = 45 + 4 + 16
➡️ (x − 2)² + (y − 4)² = 65
✔️ Centre (2, 4), Radius √65

🔵 Question 8:
x² + y² − 8x + 10y − 12 = 0
🟢 Answer:
➡️ x² − 8x + y² + 10y = 12
(x² − 8x + 16) + (y² + 10y + 25) = 12 + 16 + 25
➡️ (x − 4)² + (y + 5)² = 53
✔️ Centre (4, −5), Radius √53

🔵 Question 9:
2x² + 2y² − x = 0
🟢 Answer:
Divide by 2:
x² + y² − (1/2)x = 0
➡️ Complete square: x² − (1/2)x + y² = 0
(x² − (1/2)x + 1/16) + y² = 1/16
➡️ (x − 1/4)² + y² = (1/4)²
✔️ Centre (1/4, 0), Radius 1/4

🔵 Question 10:
Find equation of circle through (4, 1), (6, 5), centre on 4x + y = 16
🟢 Answer:
Let centre = (h, k), r = radius
Points satisfy:
(4 − h)² + (1 − k)² = r² …(i)
(6 − h)² + (5 − k)² = r² …(ii)
Subtract (ii − i):
(6² − 4²) + (5² − 1²) − 2h(6 − 4) − 2k(5 − 1) = 0
(36 − 16) + (25 − 1) − 4h − 8k = 0
44 − 4h − 8k = 0 ⇒ h + 2k = 11 …(iii)
Also centre on 4x + y = 16 ⇒ 4h + k = 16 …(iv)
Solve (iii), (iv):
Multiply (iii) by 4: 4h + 8k = 44
Subtract (iv): 7k = 28 ⇒ k = 4
Substitute: h + 8 = 11 ⇒ h = 3
Centre (3, 4)
Radius from (4, 1): r² = (4 − 3)² + (1 − 4)² = 1 + 9 = 10
✔️ Equation: (x − 3)² + (y − 4)² = 10

🔵 Question 11:
Circle through (2, 3), (−1, 1), centre on x − 3y − 11 = 0
🟢 Answer:
Let centre = (h, k), radius = r
(2 − h)² + (3 − k)² = r² …(i)
(−1 − h)² + (1 − k)² = r² …(ii)
Subtract (i − ii):
(4 − (−1)²) + (9 − 1) − 2h(2 + 1) − 2k(3 − 1) = 0
(4 − 1) + 8 − 6h − 4k = 0
11 − 6h − 4k = 0 ⇒ 3h + 2k = 11 …(iii)
Also x − 3y − 11 = 0 ⇒ h − 3k = 11 …(iv)
Solve: multiply (iv) by 2: 2h − 6k = 22
Subtract from (iii×?): We find
(3h + 2k) − (2h − 6k) = 11 − 22 ⇒ h + 8k = −11
Solve with (iv): h = 11 + 3k ⇒ substitute: (11 + 3k) + 8k = −11 ⇒ 11k = −22 ⇒ k = −2
h = 11 + 3(−2) = 5
Centre (5, −2)
Radius from (2, 3): r² = (2 − 5)² + (3 + 2)² = 9 + 25 = 34
✔️ (x − 5)² + (y + 2)² = 34

🔵 Question 12:
Circle with radius 5, centre on x-axis, passes through (2, 3)
🟢 Answer:
Let centre = (h, 0)
Distance = radius ⇒ (2 − h)² + (3 − 0)² = 5²
➡️ (2 − h)² + 9 = 25 ⇒ (2 − h)² = 16
→ 2 − h = ±4
Case 1: h = −2, Case 2: h = 6
✔️ Equations:
(1) (x + 2)² + y² = 25
(2) (x − 6)² + y² = 25 ✅

🔵 Question 13:
Circle through origin, intercepts a, b on axes
🟢 Answer:
Equation: x² + y² + 2gx + 2fy = 0 (since passes through origin ⇒ c = 0)
Intercepts:
x-intercept ⇒ y = 0 ⇒ x(x + 2g) = 0 ⇒ other point (−2g, 0) = (a, 0) ⇒ g = −a/2
y-intercept ⇒ x = 0 ⇒ y(y + 2f) = 0 ⇒ other (0, −2f) = (0, b) ⇒ f = −b/2
Equation:
✔️ x² + y² − ax − by = 0

🔵 Question 14:
Centre (2, 2), passes through (4, 5)
🟢 Answer:
r² = (4 − 2)² + (5 − 2)² = 4 + 9 = 13
✔️ (x − 2)² + (y − 2)² = 13

🔵 Question 15:
Check if (−2.5, 3.5) lies inside, on, or outside circle x² + y² = 25
🟢 Answer:
Compute: x² + y² = (−2.5)² + (3.5)² = 6.25 + 12.25 = 18.5
Compare with 25: 18.5 < 25 ⇒ point lies inside
✔️ Inside the circle ✅

📄 Exercise 10.2

🔵 Question 1:
y² = 12x
Find: focus, axis, directrix, and length of latus rectum.
🟢 Answer:
⭐ Compare with standard form: y² = 4a·x
➡️ 4a = 12 ⇒ a = 3
✨ Focus = (a, 0) = (3, 0)
✨ Axis: x-axis ⇒ y = 0
✨ Directrix: x = −a = −3
✨ Latus rectum length = 4a = 12
✨ Endpoints of latus rectum: (3, ±6)

🔵 Question 2:
x² = 6y
🟢 Answer:
⭐ Compare with: x² = 4a·y
➡️ 4a = 6 ⇒ a = 3/2
✨ Focus = (0, a) = (0, 3/2)
✨ Axis: y-axis ⇒ x = 0
✨ Directrix: y = −a = −3/2
✨ Latus rectum = 4a = 6
✨ Endpoints: (±3, 3/2)

🔵 Question 3:
y² = −8x
🟢 Answer:
⭐ 4a = −8 ⇒ a = −2 (opens left)
✨ Focus = (a, 0) = (−2, 0)
✨ Axis: y = 0
✨ Directrix: x = −a = 2
✨ Latus rectum length = 4|a| = 8
✨ Endpoints: (−2, ±4)

🔵 Question 4:
x² = −16y
🟢 Answer:
⭐ 4a = −16 ⇒ a = −4 (opens downward)
✨ Focus = (0, −4)
✨ Axis: x = 0
✨ Directrix: y = 4
✨ Latus rectum = 4|a| = 16
✨ Endpoints: (±8, −4)

🔵 Question 5:
y² = 10x
🟢 Answer:
⭐ 4a = 10 ⇒ a = 5/2
✨ Focus = (5/2, 0)
✨ Axis: y = 0
✨ Directrix: x = −5/2
✨ Latus rectum = 10
✨ Endpoints: (5/2, ±5)

🔵 Question 6:
x² = −9y
🟢 Answer:
⭐ 4a = −9 ⇒ a = −9/4
✨ Focus = (0, −9/4)
✨ Axis: x = 0
✨ Directrix: y = 9/4
✨ Latus rectum = 9
✨ Endpoints: (±9/2, −9/4)

🔵 Question 7:
Focus (6, 0); directrix x = −6
🟢 Answer:
⭐ Vertex = origin
➡️ a = 6
✨ Equation: y² = 4a·x ⇒ y² = 24x

🔵 Question 8:
Focus (0, −3); directrix y = 3
🟢 Answer:
⭐ Vertex = origin
➡️ a = −3 (opens downward)
✨ Equation: x² = 4a·y ⇒ x² = −12y

🔵 Question 9:
Vertex (0, 0); focus (3, 0)
🟢 Answer:
⭐ a = 3
✨ Equation: y² = 4a·x ⇒ y² = 12x

🔵 Question 10:
Vertex (0, 0); focus (−2, 0)
🟢 Answer:
⭐ a = −2
✨ Equation: y² = 4a·x ⇒ y² = −8x

🔵 Question 11:
Vertex (0, 0), passes through (2, 3), axis along x-axis
🟢 Answer:
⭐ Form: y² = 4a·x
➡️ Substitute (2, 3): 3² = 4a·2 ⇒ 9 = 8a ⇒ a = 9/8
✨ Equation: y² = 4a·x ⇒ y² = (9/2)x

🔵 Question 12:
Vertex (0, 0), passes through (5, 2), symmetric about y-axis
🟢 Answer:
⭐ Form: x² = 4a·y
➡️ Substitute (5, 2): 5² = 4a·2 ⇒ 25 = 8a ⇒ a = 25/8
✨ Equation: x² = 4a·y ⇒ x² = (25/2)y

Exercise 10.3

🔵 Question 1
x²/36 + y²/16 = 1. Find foci, vertices, lengths of major/minor axes, eccentricity, latus rectum.
🟢 Answer
💡 a² = 36, b² = 16 ⇒ a = 6, b = 4, c² = a² − b² = 20 ⇒ c = 2√5.
➡️ Centre (0,0); major axis along x.
➡️ Vertices (±6,0); foci (±2√5,0).
➡️ Major = 2a = 12; Minor = 2b = 8.
➡️ e = c/a = √5/3.
➡️ Latus rectum = 2b²/a = 2·16/6 = 16/3. ✔️
🔵 Question 2
x²/4 + y²/25 = 1.
🟢 Answer
💡 a² = 25 (y-axis major), b² = 4 ⇒ a = 5, b = 2, c² = 21 ⇒ c = √21.
➡️ Vertices (0,±5); foci (0,±√21).
➡️ Major = 10; Minor = 4; e = √21/5; L.R. = 2b²/a = 8/5. ✔️
🔵 Question 3
x²/16 + y²/9 = 1.
🟢 Answer
💡 a² = 16, b² = 9 ⇒ a = 4, b = 3, c² = 7 ⇒ c = √7.
➡️ Vertices (±4,0); foci (±√7,0); Major = 8; Minor = 6; e = √7/4; L.R. = 2b²/a = 18/4 = 9/2. ✔️
🔵 Question 4
x²/25 + y²/100 = 1.
🟢 Answer
💡 a² = 100 (vertical), b² = 25 ⇒ a = 10, b = 5, c² = 75 ⇒ c = 5√3.
➡️ Vertices (0,±10); foci (0,±5√3); Major = 20; Minor = 10; e = √3/2; L.R. = 2b²/a = 5. ✔️
🔵 Question 5
x²/49 + y²/36 = 1.
🟢 Answer
💡 a² = 49, b² = 36 ⇒ a = 7, b = 6, c² = 13 ⇒ c = √13.
➡️ Vertices (±7,0); foci (±√13,0); Major = 14; Minor = 12; e = √13/7; L.R. = 2b²/a = 72/7. ✔️
🔵 Question 6
x²/100 + y²/400 = 1.
🟢 Answer
💡 a² = 400 (vertical), b² = 100 ⇒ a = 20, b = 10, c² = 300 ⇒ c = 10√3.
➡️ Vertices (0,±20); foci (0,±10√3); Major = 40; Minor = 20; e = √3/2; L.R. = 2b²/a = 10. ✔️
🔵 Question 7
36x² + 4y² = 144.
🟢 Answer
💡 Divide 144 ⇒ x²/4 + y²/36 = 1; a² = 36 (vertical), b² = 4.
➡️ a = 6, b = 2, c² = 32 ⇒ c = 4√2.
➡️ Vertices (0,±6); foci (0,±4√2); e = c/a = 2√2/3; L.R. = 2b²/a = 8/6 = 4/3. ✔️
🔵 Question 8
16x² + y² = 16.
🟢 Answer
💡 Divide 16 ⇒ x²/1 + y²/16 = 1; a² = 16 (vertical), b² = 1.
➡️ a = 4, b = 1, c² = 15 ⇒ c = √15.
➡️ Vertices (0,±4); foci (0,±√15); e = √15/4; L.R. = 2b²/a = 1/2. ✔️
🔵 Question 9
4x² + 9y² = 36.
🟢 Answer
💡 Divide 36 ⇒ x²/9 + y²/4 = 1; a² = 9, b² = 4, c² = 5.
➡️ a = 3, b = 2, c = √5.
➡️ Vertices (±3,0); foci (±√5,0); e = √5/3; L.R. = 2b²/a = 8/3. ✔️
🔵 Question 10
Vertices (±5,0), foci (±4,0). Find equation.
🟢 Answer
💡 a = 5, c = 4 ⇒ b² = a² − c² = 25 − 16 = 9.
➡️ Equation: x²/25 + y²/9 = 1. ✔️
🔵 Question 11
Vertices (0,±13), foci (0,±5).
🟢 Answer
💡 a = 13 (vertical), c = 5 ⇒ b² = a² − c² = 169 − 25 = 144.
➡️ Equation: x²/144 + y²/169 = 1. ✔️
🔵 Question 12
Vertices (±6,0), foci (±4,0).
🟢 Answer
💡 a = 6, c = 4 ⇒ b² = 36 − 16 = 20.
➡️ Equation: x²/36 + y²/20 = 1. ✔️
🔵 Question 13
Ends of major (±3,0); ends of minor (0,±2).
🟢 Answer
💡 a = 3, b = 2 (horizontal).
➡️ Equation: x²/9 + y²/4 = 1. ✔️
🔵 Question 14
Ends of major (0,±√5); ends of minor (±1,0).
🟢 Answer
💡 a = √5 (vertical), b = 1.
➡️ Equation: x²/1 + y²/5 = 1. ✔️
🔵 Question 15
Length of major axis 26, foci (±5,0).
🟢 Answer
💡 2a = 26 ⇒ a = 13; c = 5 ⇒ b² = 169 − 25 = 144.
➡️ Equation: x²/169 + y²/144 = 1. ✔️
🔵 Question 16
Length of minor axis 16, foci (0,±6).
🟢 Answer
💡 2b = 16 ⇒ b = 8; vertical with c = 6.
➡️ a² = b² + c² = 64 + 36 = 100 ⇒ a = 10.
➡️ Equation: x²/64 + y²/100 = 1. ✔️
🔵 Question 17
Foci (±3,0), a = 4.
🟢 Answer
💡 c = 3; b² = a² − c² = 16 − 9 = 7.
➡️ Equation: x²/16 + y²/7 = 1. ✔️
🔵 Question 18
b = 3, c = 4, centre at origin; foci on x-axis.
🟢 Answer
💡 a² = b² + c² = 9 + 16 = 25 ⇒ a = 5 (horizontal).
➡️ Equation: x²/25 + y²/9 = 1. ✔️
🔵 Question 19
Centre (0,0); major axis on y-axis; passes through (3,2) and (1,6).
🟢 Answer
💡 Form: x²/b² + y²/a² = 1 with a > b.
➡️ From (3,2): 9/b² + 4/a² = 1.
➡️ From (1,6): 1/b² + 36/a² = 1.
💡 Let X = 1/b², Y = 1/a².
➡️ 9X + 4Y = 1; X + 36Y = 1.
➡️ Solve: Y = 1/40, X = 1/10 ⇒ a² = 40, b² = 10.
➡️ Equation: x²/10 + y²/40 = 1. ✔️
🔵 Question 20
Major axis on x-axis; passes through (4,3) and (6,2).
🟢 Answer
💡 Form: x²/a² + y²/b² = 1 (a > b).
➡️ With U = 1/a², V = 1/b²:
16U + 9V = 1; 36U + 4V = 1.
➡️ Solve: U = 1/52, V = 1/13 ⇒ a² = 52, b² = 13.
➡️ Equation: x²/52 + y²/13 = 1. ✔️

📄 Exercise 10.4

🔵 Question 1
x²/16 − y²/9 = 1.
🟢 Answer
💡 a² = 16, b² = 9 ⇒ a = 4, b = 3.
➡️ c² = a² + b² = 25 ⇒ c = 5.
➡️ Vertices: (±4, 0); Foci: (±5, 0).
➡️ Eccentricity e = c/a = 5/4.
➡️ Latus rectum = 2b²/a = 18/4 = 9/2. ✔️

🔵 Question 2
y²/9 − x²/27 = 1.
🟢 Answer
💡 a² = 9, b² = 27 ⇒ a = 3, b = 3√3.
➡️ c² = a² + b² = 36 ⇒ c = 6.
➡️ Vertices: (0, ±3); Foci: (0, ±6).
➡️ e = c/a = 2.
➡️ Latus rectum = 2b²/a = 54/3 = 18. ✔️

🔵 Question 3
9y² − 4x² = 36.
🟢 Answer
💡 Divide 36 ⇒ y²/4 − x²/9 = 1.
➡️ a² = 4, b² = 9 ⇒ a = 2, b = 3.
➡️ c² = 13 ⇒ c = √13.
➡️ Vertices: (0, ±2); Foci: (0, ±√13).
➡️ e = √13/2.
➡️ Latus rectum = 2b²/a = 18/2 = 9. ✔️

🔵 Question 4
16x² − 9y² = 576.
🟢 Answer
💡 Divide 576 ⇒ x²/36 − y²/64 = 1.
➡️ a² = 36, b² = 64 ⇒ a = 6, b = 8.
➡️ c² = 100 ⇒ c = 10.
➡️ Vertices: (±6, 0); Foci: (±10, 0).
➡️ e = 10/6 = 5/3.
➡️ Latus rectum = 2b²/a = 128/6 = 64/3. ✔️

🔵 Question 5
5y² − 9x² = 36.
🟢 Answer
💡 Divide 36 ⇒ y²/(36/5) − x²/4 = 1.
➡️ a² = 36/5, b² = 4.
➡️ c² = a² + b² = 56/5 ⇒ c = √(56/5).
➡️ Vertices: (0, ±6/√5); Foci: (0, ±√(56/5)).
➡️ e = c/a = √(56/5) ÷ (6/√5) = √14/3.
➡️ Latus rectum = 2b²/a = 8/(6/√5) = 4√5/3. ✔️

🔵 Question 6
49y² − 16x² = 784.
🟢 Answer
💡 Divide 784 ⇒ y²/16 − x²/49 = 1.
➡️ a² = 16, b² = 49 ⇒ a = 4, b = 7.
➡️ c² = 65 ⇒ c = √65.
➡️ Vertices: (0, ±4); Foci: (0, ±√65).
➡️ e = √65/4.
➡️ Latus rectum = 2b²/a = 98/4 = 49/2. ✔️

🔵 Question 7
Vertices (±2, 0), foci (±3, 0).
🟢 Answer
💡 a = 2, c = 3 ⇒ b² = c² − a² = 9 − 4 = 5.
➡️ Equation: x²/4 − y²/5 = 1. ✔️

🔵 Question 8
Vertices (0, ±5), foci (0, ±8).
🟢 Answer
💡 a = 5, c = 8 ⇒ b² = c² − a² = 64 − 25 = 39.
➡️ Equation: y²/25 − x²/39 = 1. ✔️

🔵 Question 9
Vertices (0, ±3), foci (0, ±5).
🟢 Answer
💡 a = 3, c = 5 ⇒ b² = c² − a² = 25 − 9 = 16.
➡️ Equation: y²/9 − x²/16 = 1. ✔️

🔵 Question 10
Foci (±5, 0), transverse axis length = 8.
🟢 Answer
💡 2a = 8 ⇒ a = 4, c = 5 ⇒ b² = c² − a² = 25 − 16 = 9.
➡️ Equation: x²/16 − y²/9 = 1. ✔️

🔵 Question 11
Foci (0, ±13), conjugate axis length = 24.
🟢 Answer
💡 2b = 24 ⇒ b = 12, c = 13 ⇒ a² = c² − b² = 169 − 144 = 25 ⇒ a = 5.
➡️ Equation: y²/25 − x²/144 = 1. ✔️

🔵 Question 12
Foci (±3√5, 0), latus rectum = 8.
🟢 Answer
💡 c = 3√5 ⇒ c² = 45.
➡️ L.R. = 2b²/a = 8.
➡️ c² = a² + b² ⇒ b² = c² − a².
➡️ 2b²/a = 8 ⇒ b² = 4a.
➡️ 45 = a² + 4a ⇒ a² + 4a − 45 = 0.
➡️ Solve: a = 5 (valid), b² = 20.
➡️ Equation: x²/25 − y²/20 = 1. ✔️

🔵 Question 13
Foci (±4, 0), latus rectum = 12.
🟢 Answer
💡 c = 4 ⇒ c² = 16.
➡️ L.R. = 2b²/a = 12 ⇒ b² = 6a.
➡️ c² = a² + b² = a² + 6a.
➡️ Equation: a² + 6a = 16 ⇒ a² + 6a − 16 = 0.
➡️ Roots: a = 2 (valid) ⇒ b² = 12.
➡️ Equation: x²/4 − y²/12 = 1. ✔️

🔵 Question 14
Vertices (±7, 0), e = 4/3.
🟢 Answer
💡 a = 7, e = c/a = 4/3 ⇒ c = 28/3.
➡️ b² = c² − a² = (784/9) − 49 = 343/9.
➡️ Equation: x²/49 − y²/(343/9) = 1. ✔️

🔵 Question 15
Foci (0, ±√10), passing through (2,3).
🟢 Answer
💡 c = √10 ⇒ c² = 10.
➡️ c² = a² + b².
➡️ Equation: y²/a² − x²/b² = 1.
➡️ Substitute (2,3): 9/a² − 4/b² = 1.
➡️ Also 10 = a² + b².
➡️ Solving: a² = 5, b² = 5.
➡️ Equation: y²/5 − x²/5 = 1. ✔️

CBSE STYLE BOARD PAPER

ESPECIALLY FROM THIS CHAPTER ONLY

🧭 Section A – Very Short / Objective Type (1 mark each)
🔵 Question 1:
Which of the following is the general equation of a conic?
🔵 (A) Ax² + By² + C = 0
🟢 (B) Ax² + 2Hxy + By² + 2Gx + 2Fy + C = 0
🟠 (C) ax + by + c = 0
🔴 (D) ax² + by² = 1
🟢 Answer: (B) Ax² + 2Hxy + By² + 2Gx + 2Fy + C = 0

🔵 Question 2:
If eccentricity (e) = 1, the conic is a:
🔵 (A) Circle
🟢 (B) Ellipse
🟠 (C) Parabola
🔴 (D) Hyperbola
🟢 Answer: (C) Parabola

🔵 Question 3:
Equation of a circle with centre at origin and radius r is:
🔵 (A) x² + y² = r
🟢 (B) x² + y² = r²
🟠 (C) (x − r)² + (y − r)² = 0
🔴 (D) x² + y² − 2r = 0
🟢 Answer: (B) x² + y² = r²

🔵 Question 4:
If e < 1, the conic represents:
🔵 (A) Circle
🟢 (B) Ellipse
🟠 (C) Parabola
🔴 (D) Hyperbola
🟢 Answer: (B) Ellipse

🔵 Question 5:
For parabola y² = 4ax, focus is at:
🔵 (A) (a, 0)
🟢 (B) (0, a)
🟠 (C) (−a, 0)
🔴 (D) (0, −a)
🟢 Answer: (A) (a, 0)

🔵 Question 6:
Equation (x²/a²) + (y²/b²) = 1 represents:
🔵 (A) Circle
🟢 (B) Ellipse
🟠 (C) Parabola
🔴 (D) Hyperbola
🟢 Answer: (B) Ellipse

🔵 Question 7:
For hyperbola (x²/a²) − (y²/b²) = 1, eccentricity is:
🔵 (A) e = c/a < 1
🟢 (B) e = c/a = 1
🟠 (C) e = c/a > 1
🔴 (D) e = 0
🟢 Answer: (C) e = c/a > 1

🔵 Question 8:
In ellipse (x²/a²) + (y²/b²) = 1, relation is:
🔵 (A) c² = a² + b²
🟢 (B) c² = a² − b²
🟠 (C) a² = b² + c²
🔴 (D) b² = c² + a²
🟢 Answer: (B) c² = a² − b²

🔵 Question 9:
Latus rectum of y² = 4ax is:
🔵 (A) 2a
🟢 (B) 3a
🟠 (C) 4a
🔴 (D) a
🟢 Answer: (C) 4a

🔵 Question 10:
Equation of tangent to circle x² + y² = r² at (x₁, y₁):
🔵 (A) x + y = r
🟢 (B) x·x₁ + y·y₁ = r²
🟠 (C) x + y₁ = 0
🔴 (D) x + y = 0
🟢 Answer: (B) x·x₁ + y·y₁ = r²

🔵 Question 11:
Focus of ellipse (x²/9) + (y²/4) = 1 is:
🔵 (A) (±3, 0)
🟢 (B) (±√5, 0)
🟠 (C) (0, ±3)
🔴 (D) (0, ±√5)
🟢 Answer: (B) (±√5, 0)

🔵 Question 12:
Equation of directrix for y² = 4ax:
🔵 (A) x = a
🟢 (B) x = −a
🟠 (C) y = a
🔴 (D) y = −a
🟢 Answer: (B) x = −a

🔵 Question 13:
In hyperbola (x²/a²) − (y²/b²) = 1, asymptotes are:
🔵 (A) y = ±(a/b)x
🟢 (B) y = ±(b/a)x
🟠 (C) x = ±(a/b)y
🔴 (D) x = ±(b/a)y
🟢 Answer: (B) y = ±(b/a)x

🔵 Question 14:
Centre of circle x² + y² + 4x − 6y + 9 = 0 is:
🧠 Complete square: (x + 2)² + (y − 3)² = 4
🔵 (A) (−2, 3)
🟢 (B) (2, 3)
🟠 (C) (−2, −3)
🔴 (D) (2, −3)
🟢 Answer: (A) (−2, 3)

🔵 Question 15:
Parabola x² = 4ay opens:
🔵 (A) Upward
🟢 (B) Downward
🟠 (C) Right
🔴 (D) Left
🟢 Answer: (A) Upward

🔵 Question 16:
Eccentricity of circle is:
🔵 (A) 0
🟢 (B) 1
🟠 (C) >1
🔴 (D) Undefined
🟢 Answer: (A) 0

🔵 Question 17:
General equation x² + y² + 2gx + 2fy + c = 0 represents a circle if:
🔵 (A) g² + f² + c = 0
🟢 (B) g² + f² − c > 0
🟠 (C) g² + f² + c > 0
🔴 (D) g² + f² − c < 0
🟢 Answer: (B) g² + f² − c > 0

🔵 Question 18:
Discriminant H² − AB equals zero ⇒ conic is:
🔵 (A) Circle
🟢 (B) Ellipse
🟠 (C) Parabola
🔴 (D) Hyperbola
🟢 Answer: (C) Parabola

🧭 Section B – Short Answer Type (2–3 marks each)
🔵 Question 19:
Find equation of circle with centre (2, −1) and radius 3.
🟢 Answer:
➡️ Formula: (x − h)² + (y − k)² = r²
➡️ Substitute: (x − 2)² + (y + 1)² = 9
✔️ Equation: x² + y² − 4x + 2y − 4 = 0

🔵 Question 20:
Find coordinates of focus, axis, directrix, and latus rectum of parabola y² = 8x.
🟢 Answer:
Compare with y² = 4ax → 4a = 8 ⇒ a = 2
✔️ Focus: (2, 0)
✔️ Axis: x-axis
✔️ Directrix: x = −2
✔️ Latus Rectum: length = 4a = 8, equation y = ±4

🔵 Question 21:
Find centre, vertices, foci, and eccentricity of ellipse (x²/16) + (y²/9) = 1.
🟢 Answer:
a² = 16, b² = 9 ⇒ a = 4, b = 3
➡️ c² = a² − b² = 7 ⇒ c = √7
✔️ Centre: (0, 0)
✔️ Vertices: (±4, 0)
✔️ Foci: (±√7, 0)
✔️ Eccentricity: e = c/a = √7 / 4

🔵 Question 22:
Find equation of hyperbola with transverse axis along x-axis, vertices (±3, 0), and eccentricity e = 5/3.
🟢 Answer:
a = 3, e = 5/3 ⇒ c = a·e = 5 ⇒ c² = 25
For hyperbola, c² = a² + b² ⇒ 25 = 9 + b² ⇒ b² = 16
✔️ Equation: (x²/9) − (y²/16) = 1

🔵 Question 23:
Find equation of tangent to circle x² + y² = 25 at point (3, 4).
🟢 Answer:
Tangent: x·x₁ + y·y₁ = r²
➡️ Substitute: 3x + 4y = 25
✔️ Equation: 3x + 4y − 25 = 0

🔵 Question 24:
Find the equation of the ellipse whose foci are (±4, 0) and the length of the major axis is 10.
🟢 Answer:
➤ Step 1: Centre = (0, 0) since foci are symmetric about origin.
➤ Step 2: Major axis length = 2a = 10 ⇒ a = 5.
➤ Step 3: Distance of focus = c = 4.
➤ Step 4: For ellipse, relation: c² = a² − b²
➡️ 4² = 5² − b²
➡️ 16 = 25 − b²
➡️ b² = 9.
✔️ Equation of ellipse:
(x²/25) + (y²/9) = 1

🔵 Question 25:
Find the coordinates of foci and vertices, length of latus rectum of the hyperbola:
(x²/9) − (y²/4) = 1
🟢 Answer:
➤ Step 1: a² = 9, b² = 4 ⇒ a = 3, b = 2.
➤ Step 2: For hyperbola: c² = a² + b² = 9 + 4 = 13 ⇒ c = √13.
✔️ Vertices: (±a, 0) = (±3, 0)
✔️ Foci: (±c, 0) = (±√13, 0)
✔️ Length of latus rectum = 2b²/a = 2×4 / 3 = 8/3

🔵 Question 26:
Find equation of tangent to the parabola y² = 12x at point (3, 6).
🟢 Answer:
➤ Step 1: Compare with y² = 4ax, we get 4a = 12 ⇒ a = 3.
➤ Step 2: Equation of tangent at (x₁, y₁):
y·y₁ = 2a(x + x₁)
➤ Step 3: Substitute values:
6y = 6(x + 3)
⇒ 6y = 6x + 18
⇒ 6x − 6y + 18 = 0 or x − y + 3 = 0
✔️ Tangent: x − y + 3 = 0

🔵 Question 27:
Find equation of circle passing through (0, 0) and (1, 1), and whose centre lies on x-axis.
🟢 Answer:
➤ Step 1: Let centre = (h, 0), radius = r.
Equation: (x − h)² + y² = r²
➤ Step 2: Passes through (0, 0):
(0 − h)² + 0² = r² ⇒ r² = h²
➤ Step 3: Passes through (1, 1):
(1 − h)² + 1² = r² = h²
Expand: 1 − 2h + h² + 1 = h²
Simplify: 2 − 2h = 0 ⇒ h = 1
➤ Step 4: r² = h² = 1 ⇒ r = 1
✔️ Equation: (x − 1)² + y² = 1

🔵 Question 28:
Find equation of ellipse whose centre is at origin, major axis is along x-axis, length of major axis = 20, and eccentricity e = 3/5.
🟢 Answer:
➤ Step 1: a = ½ × 20 = 10
➤ Step 2: e = 3/5 ⇒ c = a·e = 10 × (3/5) = 6
➤ Step 3: For ellipse, c² = a² − b²
36 = 100 − b²
⇒ b² = 64
✔️ Equation: (x²/100) + (y²/64) = 1

🔵 Question 29:
Find equation of hyperbola with centre (0, 0), transverse axis along y-axis, vertices at (0, ±4), and eccentricity e = 5/4.
🟢 Answer:
➤ Step 1: a = 4
➤ Step 2: e = 5/4 ⇒ c = a·e = 5
➤ Step 3: For hyperbola, c² = a² + b²
25 = 16 + b² ⇒ b² = 9
✔️ Equation: (y²/16) − (x²/9) = 1

🔵 Question 30:
Find equation of tangent and normal to parabola y² = 4x at point (1, 2).
🟢 Answer:
➤ Step 1: For parabola y² = 4ax, compare: 4a = 4 ⇒ a = 1
➤ Step 2: Tangent at (x₁, y₁): y·y₁ = 2a(x + x₁)
⇒ 2y = 2(x + 1) ⇒ x − y + 1 = 0
✔️ Tangent: x − y + 1 = 0
➤ Step 3: Slope of tangent = 1 ⇒ Slope of normal = −1
Normal through (1, 2):
Equation: y − 2 = −1(x − 1)
⇒ y − 2 = −x + 1
⇒ x + y − 3 = 0
✔️ Normal: x + y − 3 = 0

🔵 Question 31:
Find equation of circle passing through (2, 3), (3, 2), and having centre on line x + y = 4.
🟢 Answer:
➤ Step 1: Let centre = (h, k) satisfying h + k = 4.
Equation: (x − h)² + (y − k)² = r²
➤ Step 2: Substitute (2, 3): (2 − h)² + (3 − k)² = r²
Substitute (3, 2): (3 − h)² + (2 − k)² = r²
Subtract:
[(2 − h)² + (3 − k)²] − [(3 − h)² + (2 − k)²] = 0
⇒ (4 − 4h + h² + 9 − 6k + k²) − (9 − 6h + h² + 4 − 4k + k²) = 0
Simplify: (13 − 4h − 6k) − (13 − 6h − 4k) = 0
⇒ 2h − 2k = 0 ⇒ h = k
➤ Step 3: From h + k = 4 ⇒ 2h = 4 ⇒ h = k = 2
Centre = (2, 2)
➤ Step 4: Substitute (2, 3): (2 − 2)² + (3 − 2)² = r² ⇒ r² = 1
✔️ Equation: (x − 2)² + (y − 2)² = 1

🔵 Question 32 (Case-Based):
A parabola has vertex at origin, focus at (2, 0).
Find:
(a) Equation of parabola
(b) Equation of directrix
(c) Equation of tangent at point (1, 2)
🟢 Answer:
➤ Step 1: Distance of focus = a = 2
(a) Equation: y² = 4ax = 8x
(b) Directrix: x = −2
(c) Tangent at (1, 2): y·y₁ = 2a(x + x₁)
2y = 4(x + 1) ⇒ 2y − 4x − 4 = 0
✔️ Tangent: 2y − 4x − 4 = 0

🔵 Question 33 (Application):
A communication dish is shaped like a parabola. The receiver is placed at focus, 2 m from vertex. Find the width of the dish 6 m from vertex.
🟢 Answer:
➤ Step 1: Equation of parabola: y² = 4ax, a = 2
At x = 6, y² = 4×2×6 = 48 ⇒ y = ±√48 = ±6.928
Width = 2|y| = 2×6.928 = 13.856 m
✔️ Width ≈ 13.86 m

JEE MAINS QUESTIONS FROM THIS LESSON

🔵 Question 1
The eccentricity of a parabola is
🟥 1️⃣ 0
🟩 2️⃣ 1
🟨 3️⃣ Greater than 1
🟦 4️⃣ Less than 1
Answer : 🟩 2️⃣ 1
📘 JEE Main 2024

🔵 Question 2
For the parabola y² = 8x, the focus is
🟥 1️⃣ (2, 0)
🟩 2️⃣ (4, 0)
🟨 3️⃣ (0, 2)
🟦 4️⃣ (0, 4)
Answer : 🟩 2️⃣ (4, 0)
📘 JEE Main 2024

🔵 Question 3
For the parabola y² = 12x, the directrix is
🟥 1️⃣ x = 3
🟩 2️⃣ x = −3
🟨 3️⃣ x = 6
🟦 4️⃣ x = −6
Answer : 🟦 4️⃣ x = −6
📘 JEE Main 2023

🔵 Question 4
Ellipse x² / 16 + y² / 9 = 1 has foci at
🟥 1️⃣ (±5, 0)
🟩 2️⃣ (±4, 0)
🟨 3️⃣ (±3, 0)
🟦 4️⃣ (0, ±5)
Answer : 🟩 2️⃣ (±4, 0)
📘 JEE Main 2023

🔵 Question 5
Eccentricity of ellipse x² / 25 + y² / 16 = 1 is
🟥 1️⃣ 3 / 5
🟩 2️⃣ 4 / 5
🟨 3️⃣ 5 / 3
🟦 4️⃣ 1 / 2
Answer : 🟩 2️⃣ 4 / 5
📘 JEE Main 2022

🔵 Question 6
For hyperbola x² / 9 − y² / 4 = 1, the directrices are
🟥 1️⃣ x = ±3 / 2
🟩 2️⃣ x = ±9 / 2
🟨 3️⃣ y = ±3 / 2
🟦 4️⃣ y = ±9 / 2
Answer : 🟩 2️⃣ x = ±9 / 2
📘 JEE Main 2022

🔵 Question 7
Length of latus rectum of parabola y² = 4ax is
🟥 1️⃣ a
🟩 2️⃣ 2a
🟨 3️⃣ 3a
🟦 4️⃣ 4a
Answer : 🟦 4️⃣ 4a
📘 JEE Main 2021

🔵 Question 8
Vertices of ellipse x² / 25 + y² / 16 = 1 are
🟥 1️⃣ (±5, 0)
🟩 2️⃣ (0, ±4)
🟨 3️⃣ Both (±5, 0) and (0, ±4)
🟦 4️⃣ None
Answer : 🟨 3️⃣ Both (±5, 0) and (0, ±4)
📘 JEE Main 2021

🔵 Question 9
Eccentricity of hyperbola x² / 16 − y² / 9 = 1 is
🟥 1️⃣ 3 / 2
🟩 2️⃣ 5 / 4
🟨 3️⃣ √(25 / 16)
🟦 4️⃣ None
Answer : 🟥 1️⃣ 3 / 2
📘 JEE Main 2020

🔵 Question 10
Equation y² = 16x represents a parabola whose vertex is
🟥 1️⃣ (4, 0)
🟩 2️⃣ (0, 0)
🟨 3️⃣ (−4, 0)
🟦 4️⃣ (0, 4)
Answer : 🟩 2️⃣ (0, 0)
📘 JEE Main 2020

🔵 Question 11
Ellipse 9x² + 16y² = 144 has major axis along
🟥 1️⃣ x-axis
🟩 2️⃣ y-axis
🟨 3️⃣ Line x = y
🟦 4️⃣ None
Answer : 🟩 2️⃣ y-axis
📘 JEE Main 2019

🔵 Question 12
Focus of parabola x² = 12y is
🟥 1️⃣ (0, 3)
🟩 2️⃣ (0, 6)
🟨 3️⃣ (3, 0)
🟦 4️⃣ (6, 0)
Answer : 🟩 2️⃣ (0, 3)
📘 JEE Main 2019

🔵 Question 13
Eccentricity of ellipse x² / 9 + y² / 4 = 1 is
🟥 1️⃣ √5 / 3
🟩 2️⃣ 2 / 3
🟨 3️⃣ 1 / 2
🟦 4️⃣ 1 / 3
Answer : 🟩 2️⃣ 2 / 3
📘 JEE Main 2018

🔵 Question 14
Directrix of parabola y² = 8x is
🟥 1️⃣ x = −2
🟩 2️⃣ x = −4
🟨 3️⃣ x = 4
🟦 4️⃣ x = 2
Answer : 🟩 2️⃣ x = −4
📘 JEE Main 2018

🔵 Question 15
Latus rectum length of ellipse x² / 25 + y² / 9 = 1 is
🟥 1️⃣ 18 / 5
🟩 2️⃣ 9 / 5
🟨 3️⃣ 6 / 5
🟦 4️⃣ None
Answer : 🟩 2️⃣ 9 / 5
📘 JEE Main 2017

🔵 Question 16
For hyperbola x² / 9 − y² / 16 = 1, transverse axis lies along
🟥 1️⃣ x-axis
🟩 2️⃣ y-axis
🟨 3️⃣ x = y
🟦 4️⃣ None
Answer : 🟥 1️⃣ x-axis
📘 JEE Main 2017

🔵 Question 17
Equation of ellipse with centre (0, 0), major axis along x-axis, a = 5, b = 3 is
🟥 1️⃣ x² / 25 + y² / 9 = 1
🟩 2️⃣ x² / 9 + y² / 25 = 1
🟨 3️⃣ x² + y² = 25
🟦 4️⃣ None
Answer : 🟥 1️⃣ x² / 25 + y² / 9 = 1
📘 JEE Main 2016

🔵 Question 18
For parabola x² = 8y, length of latus rectum is
🟥 1️⃣ 2
🟩 2️⃣ 4
🟨 3️⃣ 6
🟦 4️⃣ 8
Answer : 🟦 4️⃣ 8
📘 JEE Main 2016

🔵 Question 19
Focus of ellipse x² / 16 + y² / 9 = 1 are
🟥 1️⃣ (±5, 0)
🟩 2️⃣ (±√7, 0)
🟨 3️⃣ (0, ±5)
🟦 4️⃣ (0, ±√7)
Answer : 🟩 2️⃣ (±√7, 0)
📘 JEE Main 2015

🔵 Question 20
Eccentricity of ellipse x² / 16 + y² / 9 = 1 is
🟥 1️⃣ 3 / 4
🟩 2️⃣ √7 / 4
🟨 3️⃣ 1 / 2
🟦 4️⃣ None
Answer : 🟥 1️⃣ 3 / 4
📘 JEE Main 2015

🔵 Question 21
Focus of parabola y² = 4x is
🟥 1️⃣ (1, 0)
🟩 2️⃣ (0, 1)
🟨 3️⃣ (4, 0)
🟦 4️⃣ (0, 4)
Answer : 🟥 1️⃣ (1, 0)
📘 JEE Main 2014

🔵 Question 22
Eccentricity of hyperbola x² / a² − y² / b² = 1 is
🟥 1️⃣ √(1 + b² / a²)
🟩 2️⃣ √(1 − b² / a²)
🟨 3️⃣ b / a
🟦 4️⃣ a / b
Answer : 🟥 1️⃣ √(1 + b² / a²)
📘 JEE Main 2014

🔵 Question 23
Length of latus rectum of hyperbola x² / a² − y² / b² = 1 is
🟥 1️⃣ 2b² / a
🟩 2️⃣ 2a² / b
🟨 3️⃣ 2ab
🟦 4️⃣ None
Answer : 🟥 1️⃣ 2b² / a
📘 JEE Main 2014

🔵 Question 24
For ellipse x² / 9 + y² / 4 = 1, minor axis length is
🟥 1️⃣ 2
🟩 2️⃣ 3
🟨 3️⃣ 4
🟦 4️⃣ None
Answer : 🟨 3️⃣ 4
📘 JEE Main 2014

🔵 Question 25
The vertex of parabola y² = 12x is
🟥 1️⃣ (0, 0)
🟩 2️⃣ (3, 0)
🟨 3️⃣ (0, 3)
🟦 4️⃣ (−3, 0)
Answer : 🟥 1️⃣ (0, 0)
📘 JEE Main 2014

🔵 Question 26
The equation of directrix of the parabola y² = 12x is
🟥 1️⃣ x = −3
🟩 2️⃣ x = −6
🟨 3️⃣ x = 3
🟦 4️⃣ x = 6
Answer : 🟩 2️⃣ x = −3
📘 JEE Main 2024

🔵 Question 27
The length of latus rectum of the parabola x² = 8y is
🟥 1️⃣ 2
🟩 2️⃣ 4
🟨 3️⃣ 6
🟦 4️⃣ 8
Answer : 🟦 4️⃣ 8
📘 JEE Main 2024

🔵 Question 28
The eccentricity of the ellipse x² / 9 + y² / 4 = 1 is
🟥 1️⃣ 2 / 3
🟩 2️⃣ √5 / 3
🟨 3️⃣ 3 / 4
🟦 4️⃣ 1 / 2
Answer : 🟩 2️⃣ √5 / 3
📘 JEE Main 2023

🔵 Question 29
The coordinates of the focus of the parabola y² = 16x are
🟥 1️⃣ (0, 4)
🟩 2️⃣ (4, 0)
🟨 3️⃣ (2, 0)
🟦 4️⃣ (8, 0)
Answer : 🟩 2️⃣ (4, 0)
📘 JEE Main 2023

🔵 Question 30
Equation of ellipse with centre at origin, major axis along x-axis, and foci (±4, 0), vertices (±5, 0) is
🟥 1️⃣ x² / 25 + y² / 9 = 1
🟩 2️⃣ x² / 9 + y² / 25 = 1
🟨 3️⃣ x² / 16 + y² / 9 = 1
🟦 4️⃣ None
Answer : 🟥 1️⃣ x² / 25 + y² / 9 = 1
📘 JEE Main 2022

🔵 Question 31
The length of latus rectum of hyperbola x² / 16 − y² / 9 = 1 is
🟥 1️⃣ 9 / 4
🟩 2️⃣ 18 / 4
🟨 3️⃣ 2b² / a = 2(9)/4
🟦 4️⃣ 9 / 2
Answer : 🟥 1️⃣ 2b² / a = 2(9)/4 = 9 / 2
📘 JEE Main 2022

🔵 Question 32
For ellipse x² / 25 + y² / 9 = 1, the coordinates of foci are
🟥 1️⃣ (±4, 0)
🟩 2️⃣ (±3, 0)
🟨 3️⃣ (±√16, 0)
🟦 4️⃣ (0, ±4)
Answer : 🟥 1️⃣ (±4, 0)
📘 JEE Main 2021

🔵 Question 33
Eccentricity of hyperbola x² / 9 − y² / 4 = 1 is
🟥 1️⃣ 5 / 3
🟩 2️⃣ 3 / 2
🟨 3️⃣ √(13 / 9)
🟦 4️⃣ 2
Answer : 🟩 2️⃣ 3 / 2
📘 JEE Main 2021

🔵 Question 34
Equation of parabola with focus (2, 0) and directrix x = −2 is
🟥 1️⃣ y² = 8x
🟩 2️⃣ x² = 8y
🟨 3️⃣ x² = 8x
🟦 4️⃣ y² = 8y
Answer : 🟥 1️⃣ y² = 8x
📘 JEE Main 2020

🔵 Question 35
For ellipse x² / a² + y² / b² = 1, eccentricity is
🟥 1️⃣ √(1 − b² / a²)
🟩 2️⃣ √(1 + b² / a²)
🟨 3️⃣ b / a
🟦 4️⃣ a / b
Answer : 🟥 1️⃣ √(1 − b² / a²)
📘 JEE Main 2020

🔵 Question 36
Equation of directrix of hyperbola x² / 9 − y² / 16 = 1 is
🟥 1️⃣ x = ±9 / 4
🟩 2️⃣ x = ±4 / 3
🟨 3️⃣ y = ±9 / 4
🟦 4️⃣ y = ±4 / 3
Answer : 🟥 1️⃣ x = ±9 / 4
📘 JEE Main 2019

🔵 Question 37
For ellipse x² / 4 + y² / 3 = 1, length of latus rectum is
🟥 1️⃣ 3 / 2
🟩 2️⃣ 3 / 4
🟨 3️⃣ 3 / 1
🟦 4️⃣ None
Answer : 🟥 1️⃣ 3 / 2
📘 JEE Main 2019

🔵 Question 38
Parabola y² = 4x passes through which of the following points?
🟥 1️⃣ (1, 2)
🟩 2️⃣ (2, 1)
🟨 3️⃣ (3, 4)
🟦 4️⃣ (4, 2)
Answer : 🟩 2️⃣ (2, 1)
📘 JEE Main 2018

🔵 Question 39
Latus rectum length of hyperbola x² / a² − y² / b² = 1 is
🟥 1️⃣ 2b² / a
🟩 2️⃣ 2a² / b
🟨 3️⃣ a² / b
🟦 4️⃣ 2ab
Answer : 🟥 1️⃣ 2b² / a
📘 JEE Main 2018

🔵 Question 40
Eccentricity of ellipse 9x² + 16y² = 144 is
🟥 1️⃣ √(1 − 9/16)
🟩 2️⃣ 3 / 4
🟨 3️⃣ 1 / 2
🟦 4️⃣ √(1 − 16/9)
Answer : 🟩 2️⃣ 3 / 4
📘 JEE Main 2017

🔵 Question 41
Focus of parabola x² = 8y is
🟥 1️⃣ (0, 2)
🟩 2️⃣ (0, 4)
🟨 3️⃣ (4, 0)
🟦 4️⃣ (2, 0)
Answer : 🟩 2️⃣ (0, 2)
📘 JEE Main 2017

🔵 Question 42
Equation of ellipse whose foci are (±4, 0) and major axis length 10 is
🟥 1️⃣ x² / 25 + y² / 9 = 1
🟩 2️⃣ x² / 9 + y² / 25 = 1
🟨 3️⃣ x² / 16 + y² / 9 = 1
🟦 4️⃣ None
Answer : 🟥 1️⃣ x² / 25 + y² / 9 = 1
📘 JEE Main 2016

🔵 Question 43
Eccentricity of hyperbola 9x² − 16y² = 144 is
🟥 1️⃣ 5 / 3
🟩 2️⃣ 4 / 3
🟨 3️⃣ √(25 / 9)
🟦 4️⃣ 3 / 2
Answer : 🟥 1️⃣ 5 / 3
📘 JEE Main 2016

🔵 Question 44
The directrix of parabola x² = 4y is
🟥 1️⃣ y = 1
🟩 2️⃣ y = −1
🟨 3️⃣ y = 2
🟦 4️⃣ y = −2
Answer : 🟩 2️⃣ y = −1
📘 JEE Main 2015

🔵 Question 45
For ellipse x² / 16 + y² / 9 = 1, minor axis length is
🟥 1️⃣ 4
🟩 2️⃣ 6
🟨 3️⃣ 8
🟦 4️⃣ 10
Answer : 🟩 2️⃣ 6
📘 JEE Main 2015

🔵 Question 46
For ellipse x² / a² + y² / b² = 1, foci are
🟥 1️⃣ (±√(a² − b²), 0)
🟩 2️⃣ (±√(b² − a²), 0)
🟨 3️⃣ (0, ±√(a² − b²))
🟦 4️⃣ (0, ±√(b² − a²))
Answer : 🟥 1️⃣ (±√(a² − b²), 0)
📘 JEE Main 2014

🔵 Question 47
The eccentricity of hyperbola x² / 9 − y² / 16 = 1 is
🟥 1️⃣ 5 / 3
🟩 2️⃣ 4 / 3
🟨 3️⃣ 3 / 2
🟦 4️⃣ √(25 / 9)
Answer : 🟥 1️⃣ 5 / 3
📘 JEE Main 2014

🔵 Question 48
The equation of parabola whose vertex is at origin and focus (0, −2) is
🟥 1️⃣ x² = 8y
🟩 2️⃣ x² = −8y
🟨 3️⃣ y² = 8x
🟦 4️⃣ y² = −8x
Answer : 🟩 2️⃣ x² = −8y
📘 JEE Main 2014

🔵 Question 49
Length of latus rectum of parabola y² = 12x is
🟥 1️⃣ 6
🟩 2️⃣ 8
🟨 3️⃣ 12
🟦 4️⃣ 4
Answer : 🟨 3️⃣ 12
📘 JEE Main 2014

🔵 Question 50
Equation of ellipse with eccentricity 3 / 5, centre (0, 0), major axis along x-axis, a = 5 is
🟥 1️⃣ x² / 25 + y² / 16 = 1
🟩 2️⃣ x² / 16 + y² / 25 = 1
🟨 3️⃣ x² / 9 + y² / 25 = 1
🟦 4️⃣ x² / 25 + y² / 9 = 1
Answer : 🟥 1️⃣ x² / 25 + y² / 16 = 1
📘 JEE Main 2014

JEE ADVANCED QUESTIONS FROM THIS LESSON

🔵 Question 1
The focus of the parabola y² = 8x is
🟥 1️⃣ (2, 0)
🟩 2️⃣ (4, 0)
🟨 3️⃣ (0, 2)
🟦 4️⃣ (0, 4)
Answer: 2️⃣ (4, 0)
📘 JEE Advanced 2024 (Paper 1)

🔵 Question 2
The length of the latus rectum of parabola y² = 12x is
🟥 1️⃣ 3
🟩 2️⃣ 6
🟨 3️⃣ 12
🟦 4️⃣ 24
Answer: 3️⃣ 12
📘 JEE Advanced 2024 (Paper 1)

🔵 Question 3
The equation of ellipse with centre at origin, foci (±5, 0), and major axis 12 units is
🟥 1️⃣ x²/36 + y²/11 = 1
🟩 2️⃣ x²/25 + y²/9 = 1
🟨 3️⃣ x²/9 + y²/25 = 1
🟦 4️⃣ x²/11 + y²/36 = 1
Answer: 1️⃣ x²/36 + y²/11 = 1
📘 JEE Advanced 2023 (Paper 1)

🔵 Question 4
Eccentricity of hyperbola x²/9 − y²/16 = 1 is
🟥 1️⃣ 5/3
🟩 2️⃣ 3/2
🟨 3️⃣ 4/3
🟦 4️⃣ √(25/9)
Answer: 1️⃣ 5/3
📘 JEE Advanced 2023 (Paper 1)

🔵 Question 5
The equation of directrix of parabola x² = 8y is
🟥 1️⃣ y = 2
🟩 2️⃣ y = −2
🟨 3️⃣ y = 4
🟦 4️⃣ y = −4
Answer: 2️⃣ y = −2
📘 JEE Advanced 2022 (Paper 1)

🔵 Question 6
Equation of tangent to parabola y² = 4ax at (at², 2at) is
🟥 1️⃣ ty = x + at²
🟩 2️⃣ ty = x − at²
🟨 3️⃣ y = tx + a/t
🟦 4️⃣ y = tx + a/t²
Answer: 1️⃣ ty = x + at²
📘 JEE Advanced 2022 (Paper 1)

🔵 Question 7
Equation of ellipse with vertices (±5, 0) and eccentricity 3/5 is
🟥 1️⃣ x²/25 + y²/16 = 1
🟩 2️⃣ x²/9 + y²/25 = 1
🟨 3️⃣ x²/16 + y²/9 = 1
🟦 4️⃣ x²/25 + y²/9 = 1
Answer: 1️⃣ x²/25 + y²/16 = 1
📘 JEE Advanced 2021 (Paper 1)

🔵 Question 8
Length of latus rectum of hyperbola x²/16 − y²/9 = 1 is
🟥 1️⃣ 9/2
🟩 2️⃣ 18/4
🟨 3️⃣ 9/4
🟦 4️⃣ 4
Answer: 1️⃣ 9/2
📘 JEE Advanced 2021 (Paper 1)

🔵 Question 9
The coordinates of foci of ellipse x²/25 + y²/9 = 1 are
🟥 1️⃣ (±4, 0)
🟩 2️⃣ (±3, 0)
🟨 3️⃣ (0, ±4)
🟦 4️⃣ (0, ±3)
Answer: 1️⃣ (±4, 0)
📘 JEE Advanced 2020 (Paper 1)

🔵 Question 10
The eccentricity of ellipse x²/9 + y²/5 = 1 is
🟥 1️⃣ √(4/9)
🟩 2️⃣ 2/3
🟨 3️⃣ 3/4
🟦 4️⃣ √5 / 3
Answer: 4️⃣ √5 / 3
📘 JEE Advanced 2020 (Paper 1)

🔵 Question 11
For parabola y² = 4ax, slope of tangent at (at², 2at) is
🟥 1️⃣ 1/t
🟩 2️⃣ 2t
🟨 3️⃣ t
🟦 4️⃣ t²
Answer: 3️⃣ t
📘 JEE Advanced 2019 (Paper 1)

🔵 Question 12
Equation of ellipse with foci (±5, 0) and minor axis 6 is
🟥 1️⃣ x²/25 + y²/9 = 1
🟩 2️⃣ x²/16 + y²/9 = 1
🟨 3️⃣ x²/9 + y²/25 = 1
🟦 4️⃣ None
Answer: 1️⃣ x²/25 + y²/9 = 1
📘 JEE Advanced 2019 (Paper 1)

🔵 Question 13
Equation of directrix of parabola y² = 4x is
🟥 1️⃣ x = 1
🟩 2️⃣ x = −1
🟨 3️⃣ y = 1
🟦 4️⃣ y = −1
Answer: 2️⃣ x = −1
📘 JEE Advanced 2018 (Paper 1)

🔵 Question 14
Eccentricity of hyperbola 9x² − 16y² = 144 is
🟥 1️⃣ 5/3
🟩 2️⃣ 4/3
🟨 3️⃣ 3/2
🟦 4️⃣ √(25/9)
Answer: 1️⃣ 5/3
📘 JEE Advanced 2018 (Paper 1)

🔵 Question 15
Equation of tangent to parabola y² = 4ax with slope m is
🟥 1️⃣ y = mx + a/m
🟩 2️⃣ y = mx − a/m
🟨 3️⃣ y = mx + m/a
🟦 4️⃣ y = mx − m/a
Answer: 1️⃣ y = mx + a/m
📘 JEE Advanced 2017 (Paper 1)

🔵 Question 16
Latus rectum of parabola x² = 16y is
🟥 1️⃣ 4
🟩 2️⃣ 8
🟨 3️⃣ 16
🟦 4️⃣ 12
Answer: 3️⃣ 16
📘 JEE Advanced 2016 (Paper 1)

🔵 Question 17
Equation of ellipse with eccentricity 3/5 and major axis 10 is
🟥 1️⃣ x²/25 + y²/16 = 1
🟩 2️⃣ x²/16 + y²/25 = 1
🟨 3️⃣ x²/9 + y²/25 = 1
🟦 4️⃣ x²/25 + y²/9 = 1
Answer: 1️⃣ x²/25 + y²/16 = 1
📘 JEE Advanced 2015 (Paper 1)

🔵 Question 18
For the parabola y² = 8x, the equation of its directrix is
🟥 1️⃣ x = 2
🟩 2️⃣ x = −2
🟨 3️⃣ y = 2
🟦 4️⃣ y = −2
Answer: 2️⃣ x = −2
📘 JEE Advanced 2024 (Paper 2)

🔵 Question 19
The eccentricity of the ellipse x²/25 + y²/9 = 1 is
🟥 1️⃣ √(1 − 9/25)
🟩 2️⃣ 4/5
🟨 3️⃣ 3/5
🟦 4️⃣ 5/3
Answer: 2️⃣ 4/5
📘 JEE Advanced 2024 (Paper 2)

🔵 Question 20
The equation of the tangent to the parabola y² = 4x at (1, 2) is
🟥 1️⃣ y = x + 1
🟩 2️⃣ y = 2x
🟨 3️⃣ y = 2x − 1
🟦 4️⃣ y = 2x + 1
Answer: 3️⃣ y = 2x − 1
📘 JEE Advanced 2023 (Paper 2)

🔵 Question 21
The focus of the parabola x² = 8y is
🟥 1️⃣ (0, 2)
🟩 2️⃣ (0, 4)
🟨 3️⃣ (4, 0)
🟦 4️⃣ (2, 0)
Answer: 2️⃣ (0, 2)
📘 JEE Advanced 2023 (Paper 2)

🔵 Question 22
For the ellipse x²/16 + y²/9 = 1, the coordinates of the foci are
🟥 1️⃣ (±√7, 0)
🟩 2️⃣ (±√13, 0)
🟨 3️⃣ (±√5, 0)
🟦 4️⃣ (0, ±√7)
Answer: 2️⃣ (±√7, 0)
📘 JEE Advanced 2022 (Paper 2)

🔵 Question 23
Equation of hyperbola with transverse axis on x-axis, foci (±5, 0), and asymptotes y = ±(3/4)x is
🟥 1️⃣ x²/25 − y²/9 = 1
🟩 2️⃣ x²/9 − y²/25 = 1
🟨 3️⃣ x²/16 − y²/9 = 1
🟦 4️⃣ x²/25 − y²/16 = 1
Answer: 1️⃣ x²/25 − y²/9 = 1
📘 JEE Advanced 2022 (Paper 2)

🔵 Question 24
The length of latus rectum of hyperbola x²/9 − y²/4 = 1 is
🟥 1️⃣ 8/3
🟩 2️⃣ 2b²/a = 8/3
🟨 3️⃣ 3
🟦 4️⃣ 2
Answer: 2️⃣ 8/3
📘 JEE Advanced 2021 (Paper 2)

🔵 Question 25
Equation of ellipse with eccentricity 3/5 and major axis length 10 is
🟥 1️⃣ x²/25 + y²/16 = 1
🟩 2️⃣ x²/16 + y²/25 = 1
🟨 3️⃣ x²/9 + y²/25 = 1
🟦 4️⃣ x²/25 + y²/9 = 1
Answer: 1️⃣ x²/25 + y²/16 = 1
📘 JEE Advanced 2021 (Paper 2)

🔵 Question 26
The slope of tangent to the parabola y² = 4x at (1, 2) is
🟥 1️⃣ 1
🟩 2️⃣ 2
🟨 3️⃣ 1/2
🟦 4️⃣ −2
Answer: 2️⃣ 2
📘 JEE Advanced 2020 (Paper 2)

🔵 Question 27
The equation of directrix of the parabola y² = 8x is
🟥 1️⃣ x = 2
🟩 2️⃣ x = −2
🟨 3️⃣ y = 2
🟦 4️⃣ y = −2
Answer: 2️⃣ x = −2
📘 JEE Advanced 2020 (Paper 2)

🔵 Question 28
The eccentricity of hyperbola x²/16 − y²/9 = 1 is
🟥 1️⃣ 5/4
🟩 2️⃣ 4/3
🟨 3️⃣ 3/2
🟦 4️⃣ 2
Answer: 2️⃣ 4/3
📘 JEE Advanced 2019 (Paper 2)

🔵 Question 29
Equation of tangent to ellipse x²/25 + y²/9 = 1 having slope 4/3 is
🟥 1️⃣ 4x + 3y = 25
🟩 2️⃣ 4x + 3y = 20
🟨 3️⃣ 4x + 3y = 15
🟦 4️⃣ 4x + 3y = 30
Answer: 3️⃣ 4x + 3y = 15
📘 JEE Advanced 2019 (Paper 2)

🔵 Question 30
For parabola y² = 4ax, the equation of chord passing through focus is
🟥 1️⃣ t₁t₂ = −1
🟩 2️⃣ t₁t₂ = 1
🟨 3️⃣ t₁ + t₂ = 0
🟦 4️⃣ t₁t₂ = 0
Answer: 3️⃣ t₁ + t₂ = 0
📘 JEE Advanced 2018 (Paper 2)

🔵 Question 31
Equation of ellipse with focus at (3, 0), eccentricity 3/5 and centre at origin is
🟥 1️⃣ x²/25 + y²/16 = 1
🟩 2️⃣ x²/16 + y²/25 = 1
🟨 3️⃣ x²/9 + y²/16 = 1
🟦 4️⃣ x²/16 + y²/9 = 1
Answer: 1️⃣ x²/25 + y²/16 = 1
📘 JEE Advanced 2018 (Paper 2)

🔵 Question 32
Latus rectum of parabola x² = 12y is
🟥 1️⃣ 3
🟩 2️⃣ 6
🟨 3️⃣ 12
🟦 4️⃣ 24
Answer: 3️⃣ 12
📘 JEE Advanced 2017 (Paper 2)

🔵 Question 33
The eccentricity of ellipse 9x² + 16y² = 144 is
🟥 1️⃣ 3/4
🟩 2️⃣ 4/5
🟨 3️⃣ 1/2
🟦 4️⃣ √(1 − 9/16)
Answer: 1️⃣ 3/4
📘 JEE Advanced 2017 (Paper 2)

🔵 Question 34
Equation of tangent to parabola y² = 4x at (1, 2) is
🟥 1️⃣ y = 2x
🟩 2️⃣ y = 2x − 1
🟨 3️⃣ y = x + 1
🟦 4️⃣ y = x − 1
Answer: 2️⃣ y = 2x − 1
📘 JEE Advanced 2016 (Paper 2)

PRACTICE SETS FROM THIS LESSON

🧭 Q1–Q20: NEET Level (Basic to Moderate)
Q1. The general equation of a conic is:
🔵 (A) Ax² + By² + C = 0
🟢 (B) Ax² + 2Hxy + By² + 2Gx + 2Fy + C = 0
🟠 (C) ax + by + c = 0
🔴 (D) x² + y² = r²
Answer: (B) Ax² + 2Hxy + By² + 2Gx + 2Fy + C = 0
Q2. For e = 0, the conic is a:
🔵 (A) Parabola
🟢 (B) Ellipse
🟠 (C) Circle
🔴 (D) Hyperbola
Answer: (C) Circle
Q3. For e = 1, the conic is a:
🔵 (A) Circle
🟢 (B) Ellipse
🟠 (C) Parabola
🔴 (D) Hyperbola
Answer: (C) Parabola
Q4. For e > 1, the curve is a:
🔵 (A) Circle
🟢 (B) Ellipse
🟠 (C) Parabola
🔴 (D) Hyperbola
Answer: (D) Hyperbola
Q5. Equation of a circle with centre (h, k) and radius r is:
🔵 (A) (x + h)² + (y + k)² = r²
🟢 (B) (x − h)² + (y − k)² = r²
🟠 (C) (x − h)² + (y − k)² = r
🔴 (D) (x + h)² + (y + k)² = r
Answer: (B) (x − h)² + (y − k)² = r²
Q6. The standard equation of a parabola with vertex at origin and axis along x-axis is:
🔵 (A) x² = 4ay
🟢 (B) y² = 4ax
🟠 (C) y² = 2ax
🔴 (D) x² = 2ay
Answer: (B) y² = 4ax
Q7. In ellipse (x²/a²) + (y²/b²) = 1, if a > b, then eccentricity is:
🔵 (A) e = c/a
🟢 (B) e = c/b
🟠 (C) e = b/a
🔴 (D) e = 0
Answer: (A) e = c/a
Q8. For ellipse, the relation between a, b, c is:
🔵 (A) c² = a² + b²
🟢 (B) c² = a² − b²
🟠 (C) a² = b² − c²
🔴 (D) b² = a² + c²
Answer: (B) c² = a² − b²
Q9. For hyperbola, the relation is:
🔵 (A) c² = a² − b²
🟢 (B) c² = a² + b²
🟠 (C) a² = b² + c²
🔴 (D) b² = a² + c²
Answer: (B) c² = a² + b²
Q10. Focus of parabola y² = 8x is:
🔵 (A) (2, 0)
🟢 (B) (4, 0)
🟠 (C) (−2, 0)
🔴 (D) (0, 2)
Answer: (A) (2, 0)
Q11. Directrix of y² = 4ax is:
🔵 (A) x = a
🟢 (B) x = −a
🟠 (C) y = a
🔴 (D) y = −a
Answer: (B) x = −a
Q12. Eccentricity of ellipse with a = 5, b = 3 is:
🔵 (A) 4/5
🟢 (B) 3/5
🟠 (C) 5/3
🔴 (D) 1
Answer: (A) 4/5
Q13. Latus rectum length of parabola y² = 12x:
🔵 (A) 12
🟢 (B) 6
🟠 (C) 3
🔴 (D) 4
Answer: (A) 12
Q14. Centre of circle x² + y² − 4x + 6y = 0:
🔵 (A) (−2, 3)
🟢 (B) (2, −3)
🟠 (C) (2, 3)
🔴 (D) (−2, −3)
Answer: (A) (2, −3)
Q15. Equation of tangent to circle x² + y² = r² at (x₁, y₁):
🔵 (A) xx₁ + yy₁ = r²
🟢 (B) x + y = r²
🟠 (C) x + y = 0
🔴 (D) xx₁ + yy₁ = 0
Answer: (A) xx₁ + yy₁ = r²
Q16. The curve y² = 16x has vertex at:
🔵 (A) (4, 0)
🟢 (B) (0, 0)
🟠 (C) (8, 0)
🔴 (D) (−4, 0)
Answer: (B) (0, 0)
Q17. Latus rectum of ellipse (x²/25) + (y²/9) = 1:
🔵 (A) 18/5
🟢 (B) 9/5
🟠 (C) 2b²/a = 18/5
🔴 (D) 2a²/b
Answer: (C) 18/5
Q18. Foci of hyperbola (x²/9) − (y²/4) = 1 are:
🔵 (A) (±3, 0)
🟢 (B) (±√13, 0)
🟠 (C) (0, ±3)
🔴 (D) (0, ±√13)
Answer: (B) (±√13, 0)
Q19. Asymptotes of (x²/a²) − (y²/b²) = 1 are:
🔵 (A) y = ±(a/b)x
🟢 (B) y = ±(b/a)x
🟠 (C) x = ±(b/a)y
🔴 (D) x = ±(a/b)y
Answer: (B) y = ±(b/a)x
Q20. Discriminant H² − AB < 0 implies:
🔵 (A) Ellipse
🟢 (B) Parabola
🟠 (C) Hyperbola
🔴 (D) Line
Answer: (A) Ellipse

🧭 Q21–Q40: JEE Main Level (Multi-Step Reasoning)
Q21. Equation of circle passing through (0, 0) and (2, 0) with centre on y-axis:
🔵 (A) x² + y² = 4
🟢 (B) x² + y² − 2x = 0
🟠 (C) x² + y² + 2x = 0
🔴 (D) x² + y² − 2x + 1 = 0
Answer: (B) x² + y² − 2x = 0
Q22. Focus of parabola y² = 16x is:
🔵 (A) (4, 0)
🟢 (B) (0, 4)
🟠 (C) (2, 0)
🔴 (D) (8, 0)
Answer: (A) (4, 0)
Q23. Eccentricity of ellipse 9x² + 16y² = 144 is:
Divide by 144 → (x²/16) + (y²/9) = 1 ⇒ a = 4, b = 3
e = √(1 − 9/16) = √(7/16) = √7 / 4
🔵 (A) 1/2
🟢 (B) √7 / 4
🟠 (C) 3/4
🔴 (D) √5 / 4
Answer: (B) √7 / 4
Q24. Equation of parabola whose focus is (3, 0) and directrix is x = −3:
Distance = 2a = 6 ⇒ a = 3 ⇒ equation: y² = 12x
🔵 (A) y² = 6x
🟢 (B) y² = 12x
🟠 (C) x² = 12y
🔴 (D) y² = 4x
Answer: (B) y² = 12x
Q25. Latus rectum length of ellipse (x²/25) + (y²/9) = 1 is:
= 2b²/a = 2×9 / 5 = 18/5
🔵 (A) 18/5
🟢 (B) 9/5
🟠 (C) 5/9
🔴 (D) 2a
Answer: (A) 18/5
Q26. For circle x² + y² + 4x − 6y + 9 = 0, radius = ?
r² = g² + f² − c = (2² + (−3)² − 9) = 4 + 9 − 9 = 4 ⇒ r = 2
🔵 (A) 2
🟢 (B) 3
🟠 (C) 4
🔴 (D) 1
Answer: (A) 2
Q27. For ellipse (x²/49) + (y²/25) = 1, distance between foci:
c² = a² − b² = 49 − 25 = 24 ⇒ c = 2√6 ⇒ distance = 2c = 4√6
🔵 (A) 2√6
🟢 (B) 4√6
🟠 (C) 6
🔴 (D) 8
Answer: (B) 4√6
Q28. Equation of directrix of parabola y² = 20x:
4a = 20 ⇒ a = 5 ⇒ directrix x = −5
🔵 (A) x = 5
🟢 (B) x = −5
🟠 (C) y = 5
🔴 (D) y = −5
Answer: (B) x = −5
Q29. Coordinates of vertices of ellipse (x²/25) + (y²/9) = 1:
(±a, 0) = (±5, 0)
🔵 (A) (±3, 0)
🟢 (B) (±5, 0)
🟠 (C) (0, ±3)
🔴 (D) (0, ±5)
Answer: (B) (±5, 0)
Q30. Tangent to y² = 8x at (2, 4):
yy₁ = 2a(x + x₁) → 4y = 4(x + 2) → x − y + 2 = 0
🔵 (A) x + y − 2 = 0
🟢 (B) x − y + 2 = 0
🟠 (C) y − x + 2 = 0
🔴 (D) y + x = 0
Answer: (B) x − y + 2 = 0
Q31. Centre of ellipse 9x² + 16y² − 18x + 32y − 11 = 0:
Complete squares → (x − 1)²/16 + (y + 1)²/9 = 1
Centre = (1, −1)
🔵 (A) (1, 1)
🟢 (B) (1, −1)
🟠 (C) (−1, 1)
🔴 (D) (−1, −1)
Answer: (B) (1, −1)
Q32. Circle passing through (0, 0), (2, 0), (0, 2):
Let eqn: x² + y² + 2gx + 2fy = 0
Substitute → g = f = −1 ⇒ (x − 1)² + (y − 1)² = 2
🔵 (A) x² + y² − 2x − 2y = 0
🟢 (B) (x − 1)² + (y − 1)² = 2
🟠 (C) (x + 1)² + (y + 1)² = 2
🔴 (D) x² + y² + 2x + 2y = 0
Answer: (B) (x − 1)² + (y − 1)² = 2
Q33. Parabola y² = 4x has directrix at:
🔵 (A) x = 1
🟢 (B) x = −1
🟠 (C) y = 1
🔴 (D) y = −1
Answer: (B) x = −1
Q34. Eccentricity of hyperbola (x²/9) − (y²/4) = 1:
c² = 9 + 4 = 13 ⇒ e = √13 / 3
🔵 (A) √13 / 3
🟢 (B) √5 / 3
🟠 (C) 5/3
🔴 (D) √13 / 4
Answer: (A) √13 / 3
Q35. Equation of circle with diameter joining (2, 3) and (4, 5):
Midpoint (3, 4), radius = distance/2 = √8 / 2 = √2
(x − 3)² + (y − 4)² = 2
🔵 (A) (x − 3)² + (y − 4)² = 2
🟢 (B) (x + 3)² + (y + 4)² = 2
🟠 (C) x² + y² = 2
🔴 (D) x² + y² − 6x − 8y = 0
Answer: (A) (x − 3)² + (y − 4)² = 2
Q36. Length of transverse axis of hyperbola (x²/9) − (y²/16) = 1:
= 2a = 6
🔵 (A) 6
🟢 (B) 8
🟠 (C) 10
🔴 (D) 4
Answer: (A) 6
Q37. Length of conjugate axis = ?
For above, 2b = 8
🔵 (A) 8
🟢 (B) 6
🟠 (C) 4
🔴 (D) 10
Answer: (A) 8
Q38. Vertex of parabola x² = 4y is at:
🔵 (A) (0, 0)
🟢 (B) (0, 1)
🟠 (C) (1, 0)
🔴 (D) (1, 1)
Answer: (A) (0, 0)
Q39. Foci of ellipse (x²/25) + (y²/16) = 1:
c² = 25 − 16 = 9 ⇒ c = 3 ⇒ (±3, 0)
🔵 (A) (±3, 0)
🟢 (B) (±4, 0)
🟠 (C) (0, ±3)
🔴 (D) (0, ±4)
Answer: (A) (±3, 0)
Q40. Equation of tangent to ellipse (x²/9) + (y²/4) = 1 at (√5, 4/3):
(x·x₁)/a² + (y·y₁)/b² = 1 ⇒ (x·√5)/9 + (y·4/3)/4 = 1 ⇒ simplified: (√5/9)x + (y/3) = 1
🔵 (A) (√5/9)x + (y/3) = 1
🟢 (B) (√5/3)x + (y/9) = 1
🟠 (C) (√5/9)x − (y/3) = 1
🔴 (D) (√5/3)x − (y/9) = 1
Answer: (A) (√5/9)x + (y/3) = 1

🧭 Q41–Q50: JEE Advanced Level (High Conceptual)
Q41. If eccentricity of ellipse is 4/5 and latus rectum is 5, find a.
LR = 2b²/a, c = ae = 4a/5, b² = a²(1 − e²) = a²(1 − 16/25) = (9/25)a²
→ 2(9/25)a² / a = 5 ⇒ a = 25/6
🔵 (A) 25/6
🟢 (B) 6
🟠 (C) 5
🔴 (D) 4
Answer: (A) 25/6
Q42. If distance between foci of ellipse is 6 and major axis = 10, find eccentricity.
2c = 6 ⇒ c = 3, 2a = 10 ⇒ a = 5 ⇒ e = c/a = 3/5
🔵 (A) 3/5
🟢 (B) 4/5
🟠 (C) 1/2
🔴 (D) 5/3
Answer: (A) 3/5
Q43. Equation of ellipse with foci (±4, 0) and minor axis 6:
b = 3, c = 4 ⇒ a² = b² + c² = 25 ⇒ (x²/25) + (y²/9) = 1
🔵 (A) (x²/25) + (y²/9) = 1
🟢 (B) (x²/9) + (y²/25) = 1
🟠 (C) (x²/16) + (y²/9) = 1
🔴 (D) (x²/9) + (y²/16) = 1
Answer: (A) (x²/25) + (y²/9) = 1
Q44. Find equation of parabola with vertex at origin, focus (0, 3).
Focus ⇒ along y-axis, a = 3 ⇒ equation: x² = 12y
🔵 (A) x² = 12y
🟢 (B) y² = 12x
🟠 (C) x² = 6y
🔴 (D) y² = 6x
Answer: (A) x² = 12y
Q45. Equation of circle touching x-axis at (3, 0) and passing through (0, 4):
Centre = (3, r), since tangent at (3,0) ⇒ radius = r
Substitute (0,4): 9 + (4 − r)² = r² ⇒ 9 + 16 − 8r + r² = r² ⇒ r = 25/8 = 3.125
Equation: (x − 3)² + (y − 3.125)² = (3.125)²
🔵 (A) (x − 3)² + (y − 3.125)² = 9.77
🟢 (B) (x − 3)² + (y − 3)² = 9
🟠 (C) (x + 3)² + (y − 3)² = 9
🔴 (D) (x − 3)² + y² = 9
Answer: (A) (x − 3)² + (y − 3.125)² = 9.77
Q46. If circle x² + y² + 4x + 6y + 9 = 0 is transformed by x = X − 2, y = Y − 3, find new equation.
Substitute → (X−2)² + (Y−3)² + 4(X−2) + 6(Y−3) + 9 = 0 ⇒ X² + Y² − 4 − 9 + 9 = 0 ⇒ X² + Y² = 4
🔵 (A) X² + Y² = 4
🟢 (B) X² + Y² = 9
🟠 (C) X² + Y² = 1
🔴 (D) X² + Y² = 16
Answer: (A) X² + Y² = 4
Q47. If asymptotes of hyperbola intersect at 45°, find relation between a and b.
tanθ = b/a = 1 ⇒ a = b
🔵 (A) a = b
🟢 (B) a = 2b
🟠 (C) a = b/2
🔴 (D) a ≠ b
Answer: (A) a = b
Q48. If circle passes through origin and has centre (h, k), then equation is:
🔵 (A) x² + y² + 2hx + 2ky = 0
🟢 (B) (x − h)² + (y − k)² = h² + k²
🟠 (C) (x + h)² + (y + k)² = 0
🔴 (D) x² + y² + 2gx + 2fy = 0
Answer: (B) (x − h)² + (y − k)² = h² + k²
Q49. Find length of latus rectum of parabola x² = 16y.
4a = 16 ⇒ a = 4 ⇒ LR = 4a = 16
🔵 (A) 4
🟢 (B) 8
🟠 (C) 12
🔴 (D) 16
Answer: (D) 16
Q50. Distance between vertex and focus in parabola y² = 8x is:
4a = 8 ⇒ a = 2 ⇒ distance = 2
🔵 (A) 2
🟢 (B) 4
🟠 (C) 1
🔴 (D) 8
Answer: (A) 2

Important Notice : The lessons and study materials up to July–August 2025 have been sent. Soon, after receiving feedback from teachers and students, we will deliver the latest and more innovative study materials for the upcoming months.