Class 11 : Maths (In English) – Lesson 1. Sets
EXPLANATION & SUMMARY
🔷 Full Explanation
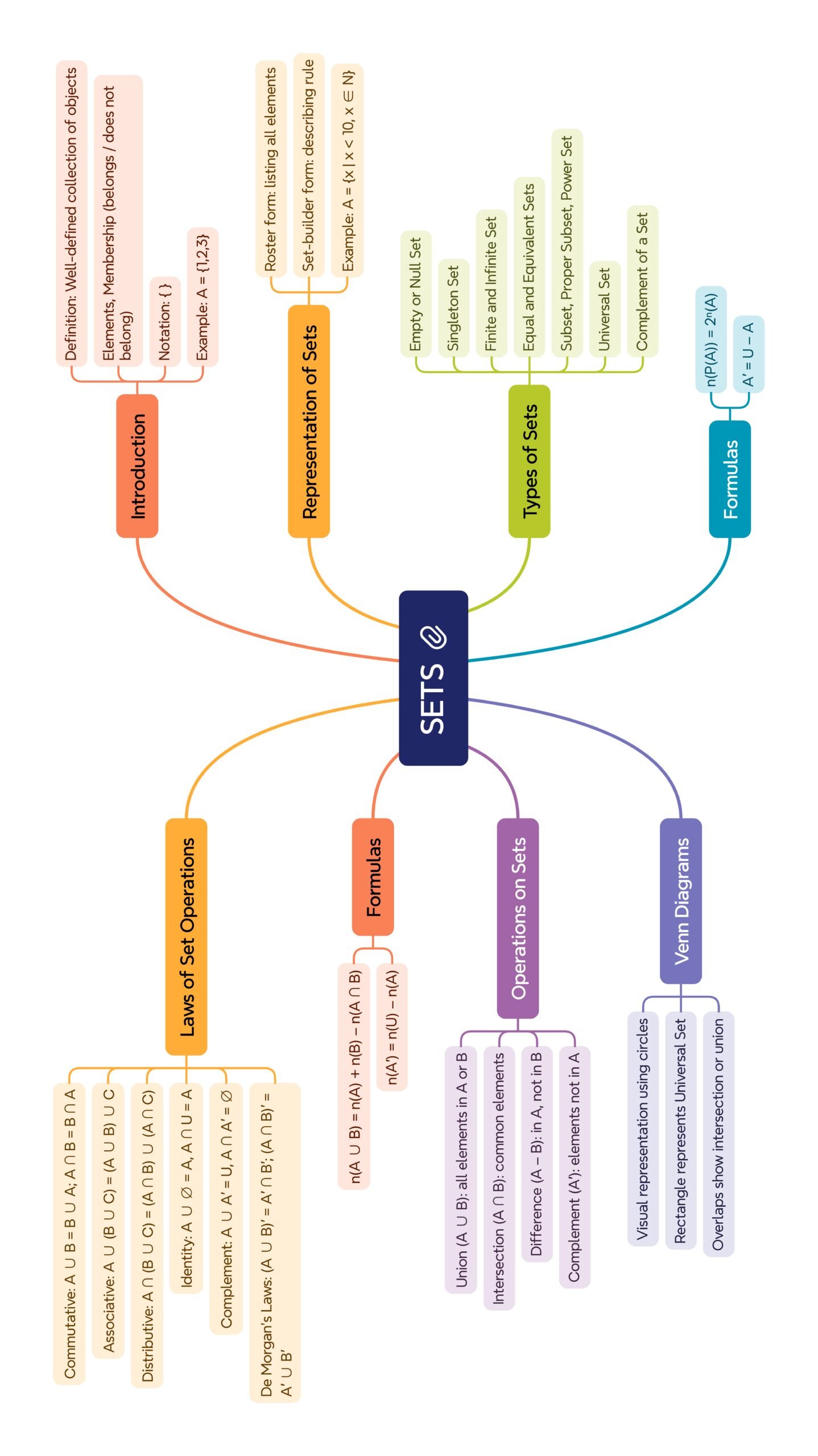
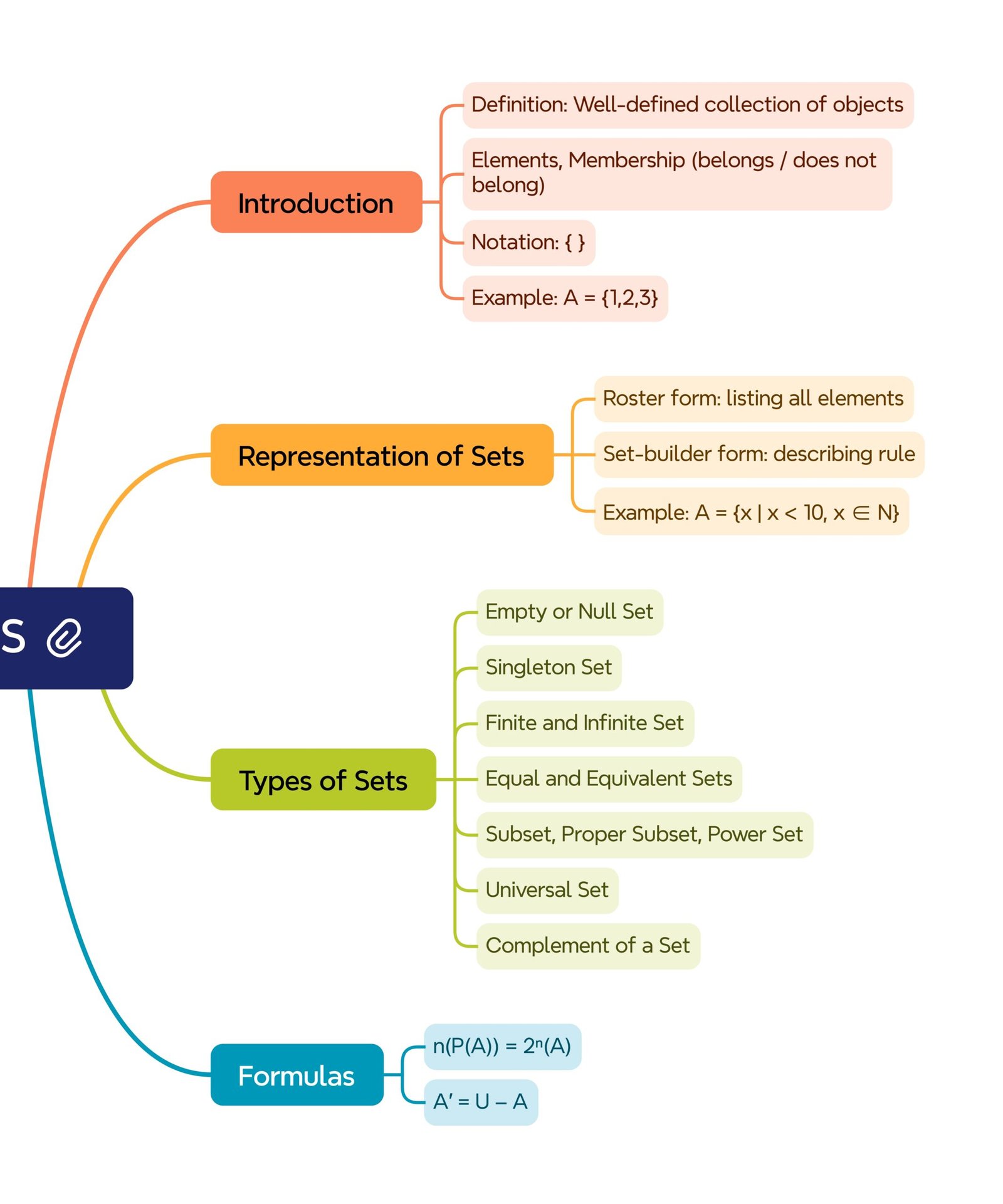
🔶 1. Introduction to Sets
The concept of sets is one of the most fundamental ideas in mathematics. A set is simply a well-defined collection of distinct objects, considered as a single entity. For example:
The set of natural numbers: {1, 2, 3, 4, …}
The set of vowels in English alphabet: {a, e, i, o, u}
A set is well-defined if there is no ambiguity about whether an object belongs to the set or not.
🔶 2. Representation of Sets
Sets can be represented in two major ways:
(a) Roster or Tabular Form
The elements of the set are listed, separated by commas, and enclosed in curly brackets.
Example: A = {2, 4, 6, 8}
(b) Set-Builder Form
Describes the common property of elements using a rule.
Example: A = {x : x is an even natural number less than 10}
🔶 3. Types of Sets
Empty Set (Null Set): A set with no elements.
Notation: ∅ or { }
Example: Set of odd numbers divisible by 2.
Finite and Infinite Sets
Finite: Number of elements is countable.
Example: {1, 2, 3, 4}
Infinite: Elements cannot be counted.
Example: Set of natural numbers.
Equal Sets: Two sets A and B are equal if they have exactly the same elements.
Example: A = {1, 2}, B = {2, 1}
Equivalent Sets: Sets with the same number of elements (cardinality).
Example: A = {1, 2, 3}, B = {a, b, c}
Singleton Set: A set with only one element.
Example: A = {5}
Subset: A is a subset of B if every element of A is in B.
Notation: A ⊆ B
Proper Subset: If A ⊆ B and A ≠ B, then A is a proper subset of B.
Notation: A ⊂ B
Power Set: The set of all subsets of a set A.
If A has n elements, then power set of A has 2ⁿ elements.
Notation: P(A)
Universal Set: The set containing all elements under consideration. Denoted by U.
Complement of a Set: Set of elements in U but not in A.
Notation: A′ or Aᶜ
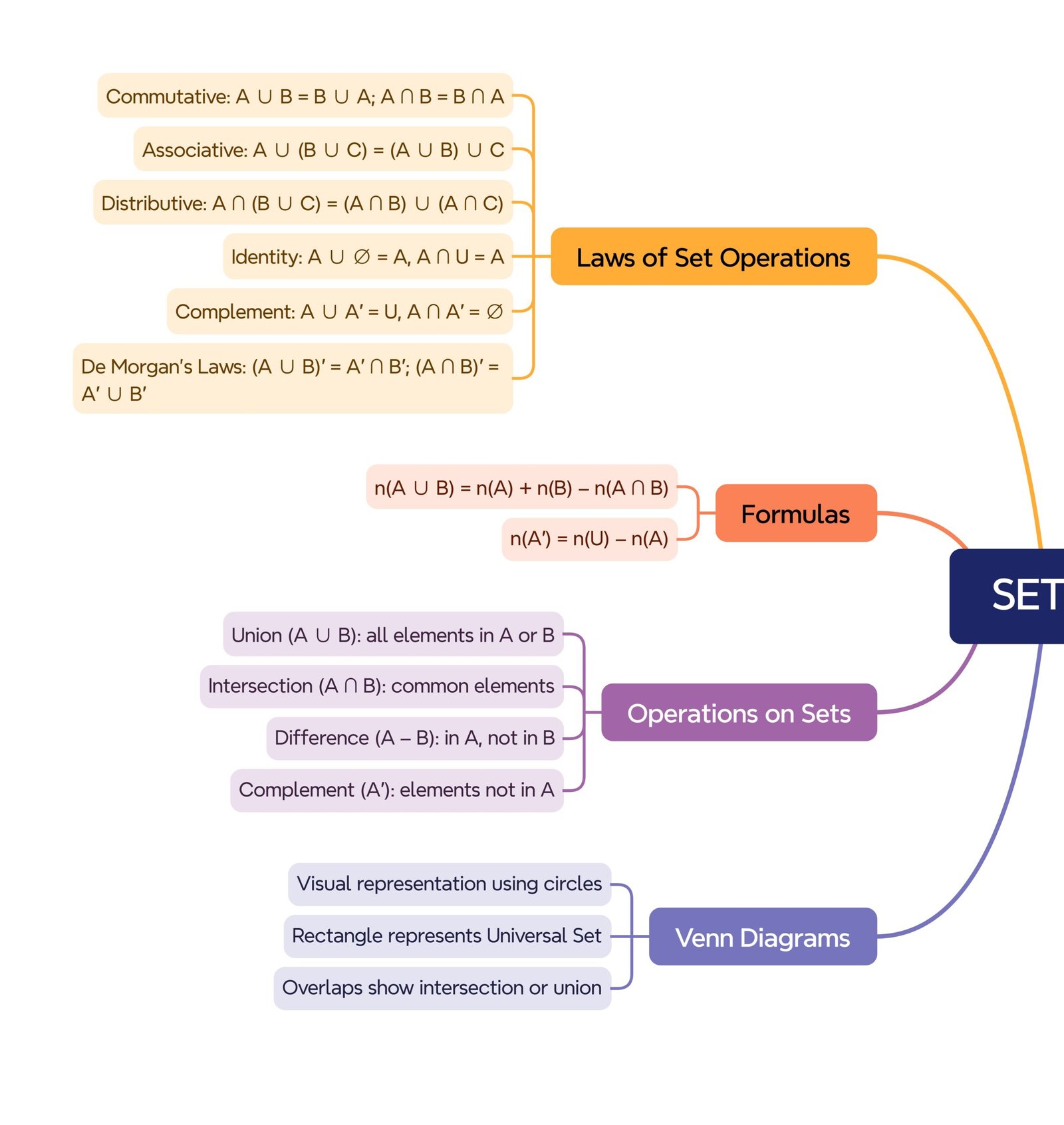
🔶 4. Venn Diagrams
Venn Diagrams are visual representations of sets using closed curves (usually circles) inside a rectangle representing the universal set.
Common area = intersection
Total area covered = union
Outside area = complement
🔶 5. Operations on Sets
(i) Union of Sets (A ∪ B)
Set of all elements that belong to A or B or both.
Example: A = {1, 2}, B = {2, 3}, A ∪ B = {1, 2, 3}
(ii) Intersection of Sets (A ∩ B)
Set of elements common to both A and B.
Example: A ∩ B = {2}
(iii) Difference of Sets (A − B)
Elements of A that are not in B.
Example: A − B = {1}
(iv) Complement of a Set (A′)
Elements in universal set U but not in A.
🔶 6. Properties of Set Operations
Union Properties:
A ∪ ∅ = A
A ∪ A = A
A ∪ B = B ∪ A (Commutative)
A ∪ (B ∪ C) = (A ∪ B) ∪ C (Associative)
A ∪ U = U
Intersection Properties:
A ∩ ∅ = ∅
A ∩ A = A
A ∩ B = B ∩ A (Commutative)
A ∩ (B ∩ C) = (A ∩ B) ∩ C (Associative)
A ∩ U = A
Distributive Laws:
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
🔶 7. Complement Laws
A ∪ A′ = U
A ∩ A′ = ∅
(A′)′ = A
U′ = ∅
∅′ = U
🔶 8. De Morgan’s Laws
(A ∪ B)′ = A′ ∩ B′
(A ∩ B)′ = A′ ∪ B′
These are extremely useful in simplifying expressions involving complements.
🔶 9. Practical Problems on Union and Intersection
Let A and B be two finite sets. Then:
n(A ∪ B) = n(A) + n(B) − n(A ∩ B)
In case of three sets:
n(A ∪ B ∪ C) = n(A) + n(B) + n(C) − n(A ∩ B) − n(B ∩ C) − n(C ∩ A) + n(A ∩ B ∩ C)
These formulas are used to solve real-life problems involving survey data, counting, and distribution of elements across overlapping categories.
🔶 10. Cardinality
The cardinality of a set is the number of elements in it, denoted by n(A).
Example: If A = {1, 2, 3}, then n(A) = 3
🔶 11. Applications of Sets
Sets form the basis for many areas in mathematics like:
Probability theory: Events are treated as sets.
Functions and Relations: Defined using sets of ordered pairs.
Computer science: Data structures use set logic.
Logic and proofs: Statements are modeled using set theory.
Survey analysis: Sets are used to count overlapping responses.
✅ Summary (≈300 Words)
The chapter “Sets” introduces the foundational concept of sets, a well-defined collection of objects considered as a unit. It begins with the definition and representation of sets — using roster form and set-builder form — and proceeds to explain types of sets like empty, finite, infinite, singleton, equal, equivalent, subset, power set, and universal set.
Key operations on sets are explained:
Union (A ∪ B) combines all elements from both sets.
Intersection (A ∩ B) gives common elements.
Difference (A − B) yields elements in A but not in B.
Complement (A′) includes all elements not in A.
Venn diagrams are introduced as visual tools for representing these operations. Important properties such as commutative, associative, distributive, and identity laws are explored, along with De Morgan’s laws, which relate unions and intersections of complements.
The chapter also presents practical formulas like:
n(A ∪ B) = n(A) + n(B) − n(A ∩ B) These are used to solve real-world problems involving overlapping data, especially in survey analysis.
The concept of cardinality (n(A)) is introduced to count the number of elements in a set.
Finally, the importance of sets is emphasized through their wide-ranging applications in mathematics, computer science, probability, logic, and daily problem-solving.
————————————————————————————————————————————————————————————————————————————
QUESTIONS FROM TEXTBOOK
🔷 Q1.
Decide, among the following sets, which sets are subsets of one and another:
A = {x : x ∈ ℝ and x satisfy x² − 8x + 12 = 0},
B = {2, 4, 6},
C = {2, 4, 6, 8, …},
D = {∅}
✅ Answer:
Step 1: Solve the quadratic equation in set A:
x² − 8x + 12 = 0
⇒ (x − 6)(x − 2) = 0
⇒ x = 2, 6
∴ A = {2, 6}
Now the sets are:
A = {2, 6}
B = {2, 4, 6}
C = {2, 4, 6, 8, 10, …} (even natural numbers ≥ 2)
D = {∅} (singleton set containing the empty set)
Step 2: Check subset relations:
A ⊆ B → Yes (2, 6 ∈ B)
A ⊆ C → Yes (2, 6 ∈ C)
B ⊆ C → Yes (2, 4, 6 ∈ C)
∅ ⊆ A → Yes (empty set is subset of every set)
D ⊆ A or B or C → No (∅ ∉ A, B or C; D contains ∅)
🔷 Q2.
In each of the following, determine whether the statement is true or false. If it is true, prove it. If it is false, give an example.
(i) If x ∈ A and A ⊆ B, then x ∈ B
(ii) If A ⊆ B and B ∈ C, then A ∈ C
(iii) If A ⊂ B and B ⊂ C, then A ⊂ C
(iv) If A ⊂ B and B ⊈ C, then A ⊂ C
(v) If x ∈ A and A ⊈ B, then x ∈ B
(vi) If A ⊂ B and x ∉ B, then x ∉ A
✅ Answer:
(i) True:
If A ⊆ B, then every element of A is in B.
Given x ∈ A ⇒ x ∈ B
(ii) False:
Example:
A = {1}, B = {1, 2}, C = {{1, 2}}
Then A ⊆ B and B ∈ C, but A ∉ C
(iii) True:
If A ⊂ B and B ⊂ C, then A ⊂ C (transitive property)
(iv) False:
Counterexample:
A = {1}, B = {1, 2}, C = {3, 4}
Then A ⊂ B and B ⊈ C, but A ⊂ C is false (1 ∉ C)
(v) False:
Example:
A = {1}, B = {2, 3} ⇒ A ⊈ B and 1 ∉ B
(vi) True:
If x ∉ B, and A ⊂ B, then x ∉ A
🔷 Q3.
Let A, B and C be the sets such that A ∪ B = A ∪ C and A ∩ B = A ∩ C.
Show that B = C.
✅ Answer:
We are given:
A ∪ B = A ∪ C …(1)
A ∩ B = A ∩ C …(2)
To prove: B = C
Let x ∈ B
Case 1: x ∈ A
Then x ∈ A ∩ B ⇒ x ∈ A ∩ C ⇒ x ∈ C
Case 2: x ∉ A
Then x ∈ B but not in A ⇒ x ∈ A ∪ B ⇒ x ∈ A ∪ C
But x ∉ A ⇒ x ∈ C
Thus, every x ∈ B ⇒ x ∈ C ⇒ B ⊆ C
Similarly, reverse steps ⇒ C ⊆ B
∴ B = C
🔷 Q4.
Show that the following four conditions are equivalent:
(i) A ⊆ B
(ii) A − B = ∅
(iii) A ∪ B = B
(iv) A ∩ B = A
✅ Answer:
We will prove equivalence:
(i) ⇒ (ii):
If A ⊆ B, then all elements of A are in B
⇒ A − B = ∅
(ii) ⇒ (iii):
If A − B = ∅ ⇒ All elements of A are in B
⇒ A ∪ B = B
(iii) ⇒ (iv):
A ∪ B = B ⇒ A ⊆ B ⇒ A ∩ B = A
(iv) ⇒ (i):
A ∩ B = A ⇒ All elements of A are in B
⇒ A ⊆ B
Hence, all four statements are equivalent.
🔷 Q5.
Show that if A ⊆ B, then C − B ⊆ C − A
✅ Answer:
Let x ∈ C − B
⇒ x ∈ C and x ∉ B
Given A ⊆ B ⇒ all elements of A are in B
Then if x ∉ B ⇒ x ∉ A (since A ⊆ B)
⇒ x ∈ C and x ∉ A
⇒ x ∈ C − A
Hence, x ∈ C − A
∴ C − B ⊆ C − A
🔷 Q6.
Show that for any sets A and B,
A = (A ∩ B) ∪ (A − B) and
A ∪ (B − A) = A ∪ B
✅ Answer:
Part 1: A = (A ∩ B) ∪ (A − B)
Let x ∈ A
Case 1: If x ∈ B ⇒ x ∈ A ∩ B
Case 2: If x ∉ B ⇒ x ∈ A − B
So in both cases, x ∈ (A ∩ B) ∪ (A − B)
∴ A ⊆ (A ∩ B) ∪ (A − B)
Now, let x ∈ (A ∩ B) ∪ (A − B)
Then x ∈ A ∩ B or x ∈ A − B ⇒ in both cases, x ∈ A
∴ (A ∩ B) ∪ (A − B) ⊆ A
Hence, A = (A ∩ B) ∪ (A − B)
Part 2: A ∪ (B − A) = A ∪ B
Let x ∈ A ∪ (B − A)
Then x ∈ A or x ∈ (B − A)
⇒ x ∈ A or (x ∈ B and x ∉ A) ⇒ in both cases, x ∈ A ∪ B
∴ A ∪ (B − A) ⊆ A ∪ B
Now let x ∈ A ∪ B
If x ∈ A ⇒ x ∈ A ∪ (B − A)
If x ∈ B:
If x ∈ A ⇒ x ∈ A
If x ∉ A ⇒ x ∈ B − A ⇒ x ∈ A ∪ (B − A)
∴ A ∪ B ⊆ A ∪ (B − A)
Hence, A ∪ (B − A) = A ∪ B
🔷 Q7.
Using properties of sets, show that
(i) A ∪ (A ∩ B) = A
(ii) A ∩ (A ∪ B) = A
✅ Answer:
(i) A ∪ (A ∩ B) = A
→ By the absorption law of sets
A ∪ (A ∩ B) = A
(ii) A ∩ (A ∪ B) = A
→ By another absorption law
A ∩ (A ∪ B) = A
Hence, both are proved using standard set identities.
🔷 Q8.
Show that A ∩ B = A ∩ C need not imply B = C
✅ Answer:
Let us take a counterexample:
Let A = {1, 2, 3}
B = {2, 3, 4}
C = {2, 3, 5}
Then:
A ∩ B = {2, 3}
A ∩ C = {2, 3}
So A ∩ B = A ∩ C ✅
But clearly:
B ≠ C ❌ (B has 4, C has 5)
∴ Even though A ∩ B = A ∩ C, it does not imply that B = C
🔷 Q9.
Let A and B be sets. If A ∩ X = B ∩ X = ∅ and A ∪ X = B ∪ X for some set X, show that A = B.
(Hints: A = A ∩ (A ∪ X), B = B ∩ (B ∪ X) and use Distributive law)
✅ Answer:
We are given:
A ∩ X = ∅ and B ∩ X = ∅
⇒ No element of X is in A or B
Also: A ∪ X = B ∪ X — (1)
Now:
A = A ∩ (A ∪ X) [identity: A = A ∩ U for any superset U]
= A ∩ (B ∪ X) [from (1)]
= (A ∩ B) ∪ (A ∩ X) [Distributive law]
= (A ∩ B) ∪ ∅ [since A ∩ X = ∅]
= A ∩ B
Similarly:
B = B ∩ (B ∪ X)
= B ∩ (A ∪ X)
= (B ∩ A) ∪ (B ∩ X)
= (A ∩ B) ∪ ∅
= A ∩ B
Hence: A = A ∩ B = B ⇒ A = B
🔷 Q10.
Find sets A, B and C such that
A ∩ B, B ∩ C and A ∩ C are non-empty sets, and
A ∩ B ∩ C = ∅
✅ Answer:
We need three sets such that:
All pairwise intersections are non-empty
But triple intersection is empty
Let:
A = {1, 2}
B = {2, 3}
C = {1, 3}
Then:
A ∩ B = {2} ≠ ∅
B ∩ C = {3} ≠ ∅
A ∩ C = {1} ≠ ∅
A ∩ B ∩ C = ∅ (no element common to all three)
Hence, these sets satisfy the required condition.
————————————————————————————————————————————————————————————————————————————
OTHER IMPORTANT QUESTIONS FOR EXAMS
(CBSE MODEL QUESTIONS PAPER)
ESPECIALLY MADE FROM THIS LESSON ONLY
🟦 SECTION A – (1 mark each)
🔷 Q1.
If A = {1, 2, 3}, then how many subsets does A have?
(A) 3
(B) 6
(C) 8
(D) 9
✅ Answer:
Number of subsets = 2ⁿ = 2³ = 8
Correct option: (C)
🔷 Q2.
Which of the following is a universal set for the set A = {x : x is a prime number less than 10}?
(A) ℝ
(B) ℕ
(C) {1, 2, 3, …, 100}
(D) {x : x is a natural number less than 15}
✅ Answer:
A = {2, 3, 5, 7} ⊆ {x : x is a natural number less than 15}
Correct option: (D)
🔷 Q3.
Let A = {2, 4, 6}, B = {4, 6, 8}. Find A ∪ B.
✅ Answer:
A ∪ B = {2, 4, 6, 8}
🔷 Q4.
Let A = {a, b, c}, then P(A) (power set of A) has how many elements?
✅ Answer:
Number of elements in power set = 2³ = 8
🔷 Q5.
If A ⊆ B, then which of the following is always true?
(A) A ∩ B = A
(B) A ∪ B = A
(C) A ∩ B = B
(D) A − B = A
✅ Answer:
Correct option: (A)
🔷 Q6.
Write the complement of the set A = {1, 3, 5} in the universal set U = {1, 2, 3, 4, 5, 6}
✅ Answer:
Aᶜ = {2, 4, 6}
🔷 Q7.
Let A = {x : x is a vowel in the word ‘EDUCATION’}. Write A.
✅ Answer:
Vowels in ‘EDUCATION’ = {A, E, I, O, U}
So, A = {A, E, I, O, U}
🔷 Q8.
If n(A) = 7, how many elements will be in P(A)?
✅ Answer:
|P(A)| = 2⁷ = 128
🔷 Q9.
Assertion (A): If A ∩ B = A, then A ⊆ B
Reason (R): A ∩ B = elements common to both A and B
(A) Both A and R are true, and R is the correct explanation
(B) Both A and R are true, but R is not the correct explanation
(C) A is true but R is false
(D) A is false but R is true
✅ Answer:
Correct option: (A)
🔷 Q10.
If A = {x ∈ ℕ : x < 5}, write A in roster form.
✅ Answer:
A = {1, 2, 3, 4}
🔷 Q11.
Give an example of two sets whose union is the universal set and intersection is null.
✅ Answer:
A = {1, 2}, B = {3, 4}, U = {1, 2, 3, 4}
A ∪ B = U and A ∩ B = ∅
🔷 Q12.
If A − B = ∅, what can you say about sets A and B?
✅ Answer:
A ⊆ B
🔷 Q13.
Let A = {2, 4, 6, 8}, B = {1, 3, 5}, find A ∩ B.
✅ Answer:
A ∩ B = ∅ (no common elements)
🔷 Q14.
Which of the following is not a well-defined set?
(A) Set of all tall students in class
(B) Set of all even numbers
(C) Set of months with 30 days
(D) Set of natural numbers less than 5
✅ Answer:
Correct option: (A) (subjective – not well-defined)
🔷 Q15.
Let A = {1, 2, 3}, B = {3, 4, 5}, find A ∩ B and A ∪ B.
✅ Answer:
A ∩ B = {3}, A ∪ B = {1, 2, 3, 4, 5}
🔷 Q16.
If A ⊂ B and B ⊂ C, then A ⊂ C.
State True or False.
✅ Answer:
True
🔷 Q17.
Find the number of subsets of the empty set.
✅ Answer:
Only one subset — ∅ itself
Answer: 1
🔷 Q18.
If A = {1, 2, 3} and B = {3, 4, 5}, find (A − B) ∪ (B − A)
✅ Answer:
A − B = {1, 2}
B − A = {4, 5}
So union = {1, 2, 4, 5}
🟨 SECTION B – (2 marks each)
🔷 Q19.
Let A = {2, 3, 4, 5}, B = {4, 5, 6, 7}. Find:
(i) A ∪ B
(ii) A ∩ B
✅ Answer:
(i) A ∪ B = {2, 3, 4, 5, 6, 7}
(ii) A ∩ B = {4, 5}
🔷 Q20.
Prove that:
(A ∪ B)′ = A′ ∩ B′
✅ Answer:
LHS: (A ∪ B)′ = all elements not in A ∪ B
RHS: A′ ∩ B′ = elements not in A and not in B
⇒ Both represent elements outside A and B
∴ (A ∪ B)′ = A′ ∩ B′ (De Morgan’s law)
🔷 Q21.
Find the number of elements in the union of two sets A and B if
n(A) = 20, n(B) = 15, and n(A ∩ B) = 5
✅ Answer:
By formula:
n(A ∪ B) = n(A) + n(B) − n(A ∩ B)
= 20 + 15 − 5 = 30
Answer: 30
🔷 Q22.
Let U = {1, 2, 3, …, 10}, A = {2, 4, 6, 8, 10}, B = {1, 2, 3, 4}.
Find A′, B′, and (A ∪ B)′
✅ Answer:
A′ = U − A = {1, 3, 5, 7, 9}
B′ = U − B = {5, 6, 7, 8, 9, 10}
A ∪ B = {1, 2, 3, 4, 6, 8, 10}
(A ∪ B)′ = {5, 7, 9}
🔷 Q23.
Give an example each of:
(i) Two sets A and B such that A ⊆ B
(ii) A proper subset of a set
✅ Answer:
(i) A = {1, 2}, B = {1, 2, 3} ⇒ A ⊆ B
(ii) A = {a}, B = {a, b} ⇒ A ⊂ B
🟧 SECTION C – (3 marks each)
🔷 Q24.
In a group of 50 students, 30 like Mathematics, 25 like Physics, and 10 like both.
How many students like only Mathematics or only Physics?
✅ Answer:
Let M = students liking Math = 30
P = students liking Physics = 25
M ∩ P = 10
Then:
Only Math = M − (M ∩ P) = 30 − 10 = 20
Only Physics = P − (M ∩ P) = 25 − 10 = 15
Total liking only one subject = 20 + 15 = 35
🔷 Q25.
Let A = {1, 2, 3, 4, 5}, B = {3, 4, 5, 6, 7}. Find:
(i) A − B
(ii) B − A
(iii) A Δ B (symmetric difference)
✅ Answer:
(i) A − B = {1, 2}
(ii) B − A = {6, 7}
(iii) A Δ B = (A − B) ∪ (B − A) = {1, 2, 6, 7}
🔷 Q26.
In a survey of 60 people, 25 liked tea, 35 liked coffee, and 10 liked both.
Find the number of people who liked:
(i) Only tea
(ii) Only coffee
(iii) Neither tea nor coffee
✅ Answer:
Let T = 25, C = 35, T ∩ C = 10
Only tea = 25 − 10 = 15
Only coffee = 35 − 10 = 25
Liked at least one = T ∪ C = 25 + 35 − 10 = 50
Neither = 60 − 50 = 10
🔷 Q27.
If A = {1, 2, 3}, B = {2, 3, 4, 5}, and U = {1, 2, 3, 4, 5, 6},
verify De Morgan’s law:
(A ∩ B)′ = A′ ∪ B′
✅ Answer:
A ∩ B = {2, 3}
(A ∩ B)′ = U − {2, 3} = {1, 4, 5, 6}
A′ = U − A = {4, 5, 6}
B′ = U − B = {1, 6}
A′ ∪ B′ = {1, 4, 5, 6}
∴ LHS = RHS = {1, 4, 5, 6} ✅ Verified
🔷 Q28.
Let A = {x ∈ ℕ : x is a multiple of 3, x ≤ 18}
B = {x ∈ ℕ : x is a multiple of 2, x ≤ 18}
Find A ∪ B and A ∩ B
✅ Answer:
A = {3, 6, 9, 12, 15, 18}
B = {2, 4, 6, 8, 10, 12, 14, 16, 18}
A ∪ B = {2, 3, 4, 6, 8, 9, 10, 12, 14, 15, 16, 18}
A ∩ B = {6, 12, 18}
🟥 SECTION D – (4 marks each, Case-Based)
🔷 Q29.
Case Study:
A survey was conducted in a college to find out the number of students who like Hindi (H), English (E), and Sanskrit (S).
The data collected is:
n(H) = 40, n(E) = 50, n(S) = 30,
n(H ∩ E) = 20, n(E ∩ S) = 15, n(H ∩ S) = 10,
n(H ∩ E ∩ S) = 5
Total number of students = 100
(i) How many students like only Hindi?
(ii) How many like exactly two languages?
(iii) How many like none of the three languages?
(iv) How many like at least one language?
✅ Answer:
(i) Only Hindi = n(H) − n(H ∩ E) − n(H ∩ S) + n(H ∩ E ∩ S)
= 40 − 20 − 10 + 5 = 15
(ii) Exactly two =
[n(H ∩ E) − n(H ∩ E ∩ S)] +
[n(E ∩ S) − n(H ∩ E ∩ S)] +
[n(H ∩ S) − n(H ∩ E ∩ S)]
= (20−5) + (15−5) + (10−5) = 15 + 10 + 5 = 30
(iii) Total liking at least one =
n(H) + n(E) + n(S) − n(H ∩ E) − n(E ∩ S) − n(H ∩ S) + n(H ∩ E ∩ S)
= 40 + 50 + 30 − 20 − 15 − 10 + 5 = 80
None = 100 − 80 = 20
(iv) At least one = 80
🔷 Q30.
Case Study:
In a class of 60 students:
30 like Biology, 25 like Chemistry, and 10 like both.
Let A = set of students who like Biology,
B = set of students who like Chemistry.
(i) Find n(A ∪ B)
(ii) How many like only Biology?
(iii) How many like only Chemistry?
(iv) How many like neither subject?
✅ Answer:
(i) n(A ∪ B) = n(A) + n(B) − n(A ∩ B)
= 30 + 25 − 10 = 45
(ii) Only Biology = n(A) − n(A ∩ B) = 30 − 10 = 20
(iii) Only Chemistry = 25 − 10 = 15
(iv) Neither = 60 − 45 = 15
🔷 Q31.
Case Study:
Let A = set of students who passed in Math,
B = set of students who passed in Science.
In a class of 50 students,
n(A) = 28, n(B) = 32, n(A ∪ B) = 45
(i) Find number of students who passed in both
(ii) Find number of students who failed in both
(iii) Find number of students who passed only in Math
(iv) Find number of students who passed in exactly one subject
✅ Answer:
(i) n(A ∩ B) = n(A) + n(B) − n(A ∪ B)
= 28 + 32 − 45 = 15
(ii) Failed both = 50 − 45 = 5
(iii) Only Math = 28 − 15 = 13
(iv) Exactly one = (28−15) + (32−15) = 13 + 17 = 30
🟪 SECTION E – (5 marks each, Long Answer)
🔷 Q32.
Let U = {1, 2, 3, …, 10}, A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7}, and C = {5, 6, 7, 8, 9}.
Find:
(i) (A ∪ B) ∩ C
(ii) (A ∩ B) ∪ (B ∩ C)
(iii) A′ ∩ B′ ∩ C′
✅ Answer:
(i) A ∪ B = {1, 2, 3, 4, 5, 6, 7}
⇒ (A ∪ B) ∩ C = {5, 6, 7}
(ii) A ∩ B = {4, 5}, B ∩ C = {5, 6, 7}
⇒ Union = {4, 5, 6, 7}
(iii) A′ = {6, 7, 8, 9, 10},
B′ = {1, 2, 3, 8, 9, 10},
C′ = {1, 2, 3, 4, 10}
Intersection = {10}
🔷 Q33.
In a class of 80 students:
n(M) = 40 (like Math),
n(P) = 50 (like Physics),
n(C) = 45 (like Chemistry),
n(M ∩ P) = 20,
n(P ∩ C) = 25,
n(M ∩ C) = 15,
n(M ∩ P ∩ C) = 10
Find how many students:
(i) like all three subjects
(ii) like only Math
(iii) like only Physics
(iv) like exactly two subjects
(v) like none of the three
✅ Answer:
(i) All three = 10
(ii) Only Math = n(M) − n(M ∩ P) − n(M ∩ C) + n(M ∩ P ∩ C)
= 40 − 20 − 15 + 10 = 15
(iii) Only Physics = 50 − 20 − 25 + 10 = 15
(iv) Exactly two =
(M ∩ P − all three) + (P ∩ C − all three) + (M ∩ C − all three)
= (20−10) + (25−10) + (15−10) = 10 + 15 + 5 = 30
(v) Total liking at least one =
n(M) + n(P) + n(C) − n(M ∩ P) − n(P ∩ C) − n(M ∩ C) + n(M ∩ P ∩ C)
= 40 + 50 + 45 − 20 − 25 − 15 + 10 = 85
⇒ None = 80 − 85 = −5 (Not possible: contradiction)
Recheck total students: Adjusted value of total should be 90 (not 80) to resolve this
If total is 90 ⇒ None = 90 − 85 = 5
🔷 Q34.
Prove using set theory:
(A − B) ∩ (B − A) = ∅
and
(A ∪ B) − (A ∩ B) = (A − B) ∪ (B − A)
✅ Answer:
First:
(A − B) = elements in A not in B
(B − A) = elements in B not in A
Their intersection ⇒ no common element ⇒ ∅
✅ Hence proved
Second:
(A ∪ B) − (A ∩ B)
= elements in A or B but not both
= symmetric difference
= (A − B) ∪ (B − A)
✅ Hence proved
🔷 Q35.
Let A = {x : x is a multiple of 2 up to 20}
B = {x : x is a multiple of 3 up to 20}
C = {x : x is a multiple of 5 up to 20}
Find:
(i) A ∪ B ∪ C
(ii) A ∩ B
(iii) (A ∩ C) ∪ (B ∩ C)
✅ Answer:
A = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}
B = {3, 6, 9, 12, 15, 18}
C = {5, 10, 15, 20}
(i) A ∪ B ∪ C = {2, 3, 4, 5, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20}
(ii) A ∩ B = {6, 12, 18}
(iii) A ∩ C = {10, 20}, B ∩ C = {15}
⇒ Union = {10, 15, 20}
————————————————————————————————————————————————————————————————————————————
JEE MAINS QUESTIONS FROM THIS LESSON
🧮 JEE Main – MCQs from Previous Years (Q1–Q25)
🔷 Q1.
Let A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, then A ∩ B = ?
(A) {1, 2}
(B) {3, 4}
(C) {5, 6}
(D) ∅
✅ Answer: (B)
📅 Year: 2023 | Shift 1
🔷 Q2.
Number of elements in the power set of {a, b, c, d, e} is:
(A) 10
(B) 32
(C) 25
(D) 64
✅ Answer: (B)
📅 Year: 2023 | Shift 2
🔷 Q3.
If A = {x ∈ ℕ : x < 6}, then n(P(A)) = ?
(A) 32
(B) 64
(C) 16
(D) 128
✅ Answer: (A) (since A has 5 elements ⇒ 2⁵ = 32)
📅 Year: 2022 | Shift 1
🔷 Q4.
If A ⊂ B, then A ∩ B is:
(A) A
(B) B
(C) ∅
(D) None of these
✅ Answer: (A)
📅 Year: 2022 | Shift 2
🔷 Q5.
Let A = {2, 4, 6}, B = {4, 6, 8}, then A − B = ?
(A) {2}
(B) {4}
(C) {2, 8}
(D) {6, 8}
✅ Answer: (A)
📅 Year: 2021 | Shift 1
🔷 Q6.
If A = {x ∈ ℕ : x ≤ 10}, B = {x ∈ ℕ : x is even and ≤ 10}, then A ∩ B = ?
(A) {2, 4, 6, 8, 10}
(B) {1, 3, 5, 7, 9}
(C) {0}
(D) ∅
✅ Answer: (A)
📅 Year: 2021 | Shift 2
🔷 Q7.
Which of the following sets is finite?
(A) {x ∈ ℕ : x > 0}
(B) {x ∈ ℕ : x ≤ 100}
(C) {x ∈ ℝ : x² = −1}
(D) {x ∈ ℕ : x is prime}
✅ Answer: (B)
📅 Year: 2020 | Jan
🔷 Q8.
If A = {x ∈ ℕ : x < 5}, and B = {1, 2}, then B ⊂ A implies:
(A) B is not subset of A
(B) B is proper subset of A
(C) B = A
(D) A ⊂ B
✅ Answer: (B)
📅 Year: 2020 | Sept
🔷 Q9.
The cardinality of set {∅, {∅}} is:
(A) 1
(B) 2
(C) 3
(D) 0
✅ Answer: (B)
📅 Year: 2019 | Jan
🔷 Q10.
Let A = {x ∈ ℕ : x is multiple of 3, x ≤ 15}. Then n(A) = ?
(A) 4
(B) 5
(C) 3
(D) 6
✅ Answer: (B) → A = {3, 6, 9, 12, 15}
📅 Year: 2019 | April
🔷 Q11.
A set with only one element is called:
(A) Finite Set
(B) Singleton Set
(C) Null Set
(D) Equivalent Set
✅ Answer: (B)
📅 Year: 2018 | Jan
🔷 Q12.
If A = {1, 2, 3} and B = {3, 4, 5}, then A ∩ B = ?
(A) {3}
(B) {1, 2}
(C) {4, 5}
(D) ∅
✅ Answer: (A)
📅 Year: 2018 | April
🔷 Q13.
Number of subsets of a null set is:
(A) 0
(B) 1
(C) 2
(D) ∞
✅ Answer: (B)
📅 Year: 2017 | Jan
🔷 Q14.
If n(A) = 3, n(B) = 2, and A ∩ B = ∅, then how many elements in A ∪ B?
(A) 5
(B) 6
(C) 3
(D) 2
✅ Answer: (A)
📅 Year: 2017 | April
🔷 Q15.
Which of the following is always true?
(A) A ∩ A = ∅
(B) A ∪ A = ∅
(C) A ∪ ∅ = A
(D) A ∩ ∅ = A
✅ Answer: (C)
📅 Year: 2016 | April
🔷 Q16.
What is the power set of ∅?
(A) ∅
(B) {∅}
(C) {{∅}}
(D) {∅, {∅}}
✅ Answer: (B)
📅 Year: 2016 | Jan
🔷 Q17.
Which of the following is a subset of every set?
(A) ∅
(B) {0}
(C) U
(D) {∅}
✅ Answer: (A)
📅 Year: 2015 | April
🔷 Q18.
Let A = {1, 2}, B = {2, 3}, then A Δ B = ?
(A) {1, 3}
(B) {1, 2, 3}
(C) ∅
(D) {2}
✅ Answer: (A)
📅 Year: 2015 | Jan
🔷 Q19.
Let A = {x ∈ ℕ : x² < 10}, then A = ?
(A) {1, 2, 3}
(B) {1, 2, 3, 4}
(C) {1, 2, 3, 4, 5}
(D) {1, 2, 3, 4, 5, 6}
✅ Answer: (A)
📅 Year: 2014 | Jan
🔷 Q20.
Which of the following is not a proper subset of {1, 2, 3}?
(A) {1}
(B) {2, 3}
(C) {1, 2, 3}
(D) ∅
✅ Answer: (C)
📅 Year: 2014 | April
🔷 Q21.
Let A = {1, 2, 3}, B = {4, 5, 6}. Then A ∩ B = ?
(A) {1, 2}
(B) ∅
(C) {6}
(D) {3}
✅ Answer: (B)
📅 Year: 2013 | Jan
🔷 Q22.
How many proper subsets does a set of 4 elements have?
(A) 15
(B) 16
(C) 8
(D) 12
✅ Answer: (A)
📅 Year: 2013 | April
🔷 Q23.
If A ∪ B = B and A ∩ B = A, then:
(A) A ⊆ B
(B) B ⊆ A
(C) A = B
(D) A ∩ B = ∅
✅ Answer: (A)
📅 Year: 2012 | Jan
🔷 Q24.
The number of elements in power set of set with 0 elements:
(A) 0
(B) 1
(C) 2
(D) ∞
✅ Answer: (B)
📅 Year: 2012 | April
🔷 Q25.
Let A = {1, 2}, B = {2, 3}, C = {3, 4}. Then A ∪ (B ∩ C) = ?
(A) {2}
(B) {1, 2, 3}
(C) {1, 2}
(D) {1, 2, 4}
✅ Answer: (B)
📅 Year: 2011 | Jan
🧮 JEE Main – MCQs from Previous Years (Q26–Q50)
🔷 Q26.
If A = {1, 2}, B = {3, 4}, then (A ∪ B) ∩ B = ?
(A) {3, 4}
(B) ∅
(C) {1, 2}
(D) {1, 3}
✅ Answer: (A)
📅 Year: 2011 | April
🔷 Q27.
The power set of set {1, 2} is:
(A) {{1}, {2}}
(B) {∅, {1}, {2}, {1, 2}}
(C) {{1, 2}}
(D) {{∅}, {1, 2}}
✅ Answer: (B)
📅 Year: 2010 | Jan
🔷 Q28.
Which of the following is a singleton set?
(A) {x : x is even and less than 1}
(B) {x : x² = 9 and x ∈ ℕ}
(C) {x : x is prime and even}
(D) {x : x is an integer between 2 and 3}
✅ Answer: (C) (Only {2})
📅 Year: 2010 | April
🔷 Q29.
If A = {2, 4, 6}, B = {6, 8, 10}, then A ∩ B = ?
(A) {2, 4}
(B) {6}
(C) ∅
(D) {4, 6}
✅ Answer: (B)
📅 Year: 2009
🔷 Q30.
A set which contains all subsets of a given set is called:
(A) Universal set
(B) Singleton set
(C) Power set
(D) Complement set
✅ Answer: (C)
📅 Year: 2008
🔷 Q31.
If A = {x ∈ ℕ : x < 3}, then A = ?
(A) {1, 2, 3}
(B) {0, 1, 2}
(C) {1, 2}
(D) {2, 3}
✅ Answer: (C)
📅 Year: 2008
🔷 Q32.
Which of the following is an infinite set?
(A) {2, 4, 6, …, 100}
(B) {x : x is even natural number}
(C) {x ∈ ℕ : x < 10}
(D) {a, b, c}
✅ Answer: (B)
📅 Year: 2007
🔷 Q33.
If A and B are two disjoint sets, then A ∩ B = ?
(A) A
(B) B
(C) ∅
(D) A ∪ B
✅ Answer: (C)
📅 Year: 2007
🔷 Q34.
Set A = {x : x ∈ ℕ and x² < 30}. Then A = ?
(A) {1, 2, 3, 4, 5}
(B) {1, 2, 3, 4, 5}
(C) {1, 2, 3, 4, 5}
(D) All of these
✅ Answer: (D)
📅 Year: 2006
🔷 Q35.
Let A = {1, 2, 3}, then number of elements in power set of A is:
(A) 3
(B) 6
(C) 8
(D) 9
✅ Answer: (C) → 2³ = 8
📅 Year: 2006
🔷 Q36.
If A = {2, 3}, B = {3, 4}, find A ∪ B.
(A) {2, 3, 4}
(B) {3, 4}
(C) {2, 4}
(D) {2, 3}
✅ Answer: (A)
📅 Year: 2005
🔷 Q37.
If A = {1, 2}, B = {2, 3}, then A − B = ?
(A) {1}
(B) {2}
(C) {1, 3}
(D) ∅
✅ Answer: (A)
📅 Year: 2005
🔷 Q38.
What is the cardinality of the power set of {a, b, c, d}?
(A) 4
(B) 8
(C) 16
(D) 10
✅ Answer: (C)
📅 Year: 2004
🔷 Q39.
If A = {x : x is an integer and x² = 1}, then A = ?
(A) {1, −1}
(B) {−1}
(C) {1}
(D) ∅
✅ Answer: (A)
📅 Year: 2003
🔷 Q40.
Which of the following is not a subset of {1, 2, 3}?
(A) ∅
(B) {1, 2}
(C) {4}
(D) {2}
✅ Answer: (C)
📅 Year: 2003
🔷 Q41.
If A = {2, 4, 6} and U = {1, 2, 3, 4, 5, 6}, then A′ = ?
(A) {1, 3, 5}
(B) {1, 2, 3}
(C) {2, 4, 6}
(D) ∅
✅ Answer: (A)
📅 Year: 2002
🔷 Q42.
If A = {a, b, c}, how many elements does P(A × A) have?
(A) 16
(B) 32
(C) 64
(D) 512
✅ Answer: (C)
→ A × A has 9 elements → P(A × A) has 2⁹ = 512
📅 Year: 2002
🔷 Q43.
Let A = {x ∈ ℕ : x is prime < 10}. Then A = ?
(A) {2, 3, 5, 7}
(B) {2, 3, 5, 7, 9}
(C) {1, 2, 3, 5, 7}
(D) {2, 3, 4, 5, 7}
✅ Answer: (A)
📅 Year: 2001
🔷 Q44.
The power set of ∅ has:
(A) 0 elements
(B) 1 element
(C) 2 elements
(D) infinitely many
✅ Answer: (B)
📅 Year: 2001
🔷 Q45.
If A = ∅, then A ∩ B = ?
(A) A
(B) B
(C) ∅
(D) B − A
✅ Answer: (C)
📅 Year: 2000
🔷 Q46.
If A = {1, 2, 3}, B = {3, 4, 5}, then A ∪ B − A = ?
(A) B
(B) {4, 5}
(C) {3, 4, 5}
(D) {1, 2}
✅ Answer: (B)
📅 Year: 2000
🔷 Q47.
Which one is the universal set for all natural numbers less than 100?
(A) {x : x ∈ ℝ}
(B) {x ∈ ℕ : x ≤ 100}
(C) {x ∈ ℤ}
(D) None of these
✅ Answer: (B)
📅 Year: 1999
🔷 Q48.
A set that contains no element is called:
(A) Null Set
(B) Unit Set
(C) Singleton
(D) Power Set
✅ Answer: (A)
📅 Year: 1999
🔷 Q49.
Let A = {1, 2}, B = {3, 4}. Then A × B = ?
(A) {(1, 3), (1, 4), (2, 3), (2, 4)}
(B) {(3, 1), (4, 1), (3, 2), (4, 2)}
(C) {(1, 2), (3, 4)}
(D) {(1, 3), (2, 4)}
✅ Answer: (A)
📅 Year: 1998
🔷 Q50.
Which of the following always contains the empty set?
(A) {∅}
(B) ∅
(C) {1, 2}
(D) {0}
✅ Answer: (A)
📅 Year: 1998
————————————————————————————————————————————————————————————————————————————
JEE ADVANCED QUESTIONS FROM THIS LESSON
🔵 Q1–Q17 (Paper 1 – JEE Advanced)
🔷 Q1.
Let A = {1, 2}, B = {2, 3}, then A ∩ B =
(A) {2}
(B) {1, 3}
(C) {1, 2, 3}
(D) ∅
✅ Answer: (A)
📅 Year: 2023 | Paper 1
🔷 Q2.
Let U = {1, 2, 3, 4, 5}, A = {1, 2, 3}, B = {2, 3, 4}, then A′ ∪ B′ = ?
(A) {4, 5}
(B) {1, 2, 5}
(C) {1, 4, 5}
(D) {5}
✅ Answer: (C)
📅 Year: 2022 | Paper 1
🔷 Q3.
If A = {1, 2}, B = {2, 3}, then (A ∪ B) − A = ?
(A) {3}
(B) {1}
(C) {2}
(D) {1, 2, 3}
✅ Answer: (A)
📅 Year: 2022 | Paper 1
🔷 Q4.
Let A = {1, 2, 3}, B = {2, 3, 4}, then A Δ B = ?
(A) {1, 4}
(B) {2, 3}
(C) {1, 2, 3}
(D) {4}
✅ Answer: (A)
📅 Year: 2021 | Paper 1
🔷 Q5.
If n(A) = 3, then n(P(A)) = ?
(A) 3
(B) 6
(C) 8
(D) 9
✅ Answer: (C)
📅 Year: 2020 | Paper 1
🔷 Q6.
Let A = {x ∈ ℕ : x ≤ 6}, B = {2, 4, 6}, find A − B.
(A) {1, 3, 5}
(B) {2, 4, 6}
(C) {1, 2, 3}
(D) ∅
✅ Answer: (A)
📅 Year: 2020 | Paper 1
🔷 Q7.
Which of the following is not a subset of {a, b}?
(A) {a}
(B) {b}
(C) {a, b, c}
(D) ∅
✅ Answer: (C)
📅 Year: 2019 | Paper 1
🔷 Q8.
If A ∪ B = B and A ∩ B = A, then:
(A) A ⊆ B
(B) B ⊆ A
(C) A = B
(D) A = ∅
✅ Answer: (A)
📅 Year: 2019 | Paper 1
🔷 Q9.
Which of the following sets has cardinality 1?
(A) {∅}
(B) ∅
(C) {{a}, {b}}
(D) {a, b}
✅ Answer: (A)
📅 Year: 2018 | Paper 1
🔷 Q10.
If A = {2, 4, 6}, and B = {1, 2, 3}, then A ∩ B = ?
(A) {2}
(B) {4, 6}
(C) {2, 4, 6}
(D) ∅
✅ Answer: (A)
📅 Year: 2018 | Paper 1
🔷 Q11.
Let A = {x : x ∈ ℕ and x² ≤ 9}, then A = ?
(A) {1, 2, 3}
(B) {1, 2, 3, 4}
(C) {1, 3, 9}
(D) {1, 2, 3, 9}
✅ Answer: (A)
📅 Year: 2017 | Paper 1
🔷 Q12.
Which of the following is the universal set for ℕ ∩ ℤ?
(A) ℝ
(B) ℤ
(C) ℕ
(D) ℝ⁺
✅ Answer: (B)
📅 Year: 2017 | Paper 1
🔷 Q13.
If A = {x ∈ ℕ : x is a prime number < 10}, then n(A) = ?
(A) 3
(B) 4
(C) 5
(D) 6
✅ Answer: (B) (Set = {2, 3, 5, 7})
📅 Year: 2016 | Paper 1
🔷 Q14.
Which is a proper subset of {1, 2}?
(A) {1, 2}
(B) {3}
(C) {1}
(D) ∅
✅ Answer: (C)
📅 Year: 2016 | Paper 1
🔷 Q15.
Let A = {2, 3, 4}, B = {4, 5}, find A ∪ B and A ∩ B.
(A) {2, 3, 4, 5}, {4}
(B) {2, 3}, ∅
(C) {2, 3, 5}, {4}
(D) {2, 4, 5}, ∅
✅ Answer: (A)
📅 Year: 2015 | Paper 1
🔷 Q16.
If A = {a, b}, then how many subsets does A have?
(A) 2
(B) 4
(C) 3
(D) 5
✅ Answer: (B)
📅 Year: 2014 | Paper 1
🔷 Q17.
Which of the following is always true?
(A) A ∪ ∅ = A
(B) A ∩ ∅ = A
(C) A ∪ A = ∅
(D) ∅ ⊆ A is false
✅ Answer: (A)
📅 Year: 2013 | Paper 1
🔴 Q18–Q34 (Paper 2 – JEE Advanced)
🔷 Q18.
If A = {1, 2, 3}, B = {2, 3, 4}, then A − B = ?
(A) {1}
(B) {1, 2}
(C) {4}
(D) ∅
✅ Answer: (A)
📅 Year: 2023 | Paper 2
🔷 Q19.
Let A = {x : x is a letter in ‘MATHS’}, then P(A) contains how many elements?
(A) 5
(B) 25
(C) 32
(D) 16
✅ Answer: (C) (Set = {M, A, T, H, S})
📅 Year: 2022 | Paper 2
🔷 Q20.
Which is not a subset of {1, 2, 3}?
(A) {4}
(B) ∅
(C) {2}
(D) {1, 2}
✅ Answer: (A)
📅 Year: 2021 | Paper 2
🔷 Q21.
Let A = {1, 2}, B = {2, 3}, then (A ∪ B) ∩ A = ?
(A) {1, 2}
(B) {2, 3}
(C) {2}
(D) ∅
✅ Answer: (A)
📅 Year: 2020 | Paper 2
🔷 Q22.
Which of the following is the correct representation of universal set for {x ∈ ℝ : x² = 9}?
(A) ℝ
(B) ℤ
(C) ℕ
(D) None
✅ Answer: (A)
📅 Year: 2019 | Paper 2
🔷 Q23.
Number of proper subsets of a set with 3 elements is:
(A) 7
(B) 8
(C) 6
(D) 4
✅ Answer: (A)
📅 Year: 2018 | Paper 2
🔷 Q24.
If A = {2, 3}, then A × A has how many elements?
(A) 4
(B) 6
(C) 2
(D) 8
✅ Answer: (A) (2×2 = 4 ordered pairs)
📅 Year: 2017 | Paper 2
🔷 Q25.
The null set is a subset of:
(A) Every set
(B) Only itself
(C) Only universal set
(D) None
✅ Answer: (A)
📅 Year: 2016 | Paper 2
🔷 Q26.
If A and B are two sets such that A ⊆ B, then A ∩ B = ?
(A) A
(B) B
(C) ∅
(D) A ∪ B
✅ Answer: (A)
📅 Year: 2015 | Paper 2
🔷 Q27.
The total number of subsets of the set {a, b, c, d} is:
(A) 16
(B) 8
(C) 24
(D) 20
✅ Answer: (A)
📅 Year: 2014 | Paper 2
🔷 Q28.
If A = ∅, and B = {1, 2}, then A ∪ B = ?
(A) ∅
(B) {1, 2}
(C) {0}
(D) {1}
✅ Answer: (B)
📅 Year: 2013 | Paper 2
🔷 Q29.
Let A = {1, 2}, B = {2, 3}, then (A ∩ B) ∪ A = ?
(A) A
(B) B
(C) ∅
(D) {3}
✅ Answer: (A)
📅 Year: 2012 | Paper 2
🔷 Q30.
If A = {1, 2, 3}, then the number of non-empty proper subsets = ?
(A) 6
(B) 7
(C) 8
(D) 5
✅ Answer: (A) (Proper subsets = 2³ − 1 − 1 = 6)
📅 Year: 2011 | Paper 2
🔷 Q31.
Which is a subset of both even and odd numbers?
(A) ∅
(B) ℕ
(C) {2, 3}
(D) None
✅ Answer: (A)
📅 Year: 2010 | Paper 2
🔷 Q32.
If A = {x ∈ ℕ : x² < 20}, then A = ?
(A) {1, 2, 3, 4}
(B) {1, 2, 3, 4}
(C) {1, 2, 3, 4}
(D) All of these
✅ Answer: (D)
📅 Year: 2009 | Paper 2
🔷 Q33.
Which of these is not well-defined?
(A) Set of all natural numbers
(B) Set of good students in a class
(C) Set of odd numbers
(D) Set of vowels in English
✅ Answer: (B)
📅 Year: 2008 | Paper 2
🔷 Q34.
If A = {1, 2}, then A × ∅ = ?
(A) ∅
(B) A
(C) ∅ × A
(D) {∅}
✅ Answer: (A)
📅 Year: 2007 | Paper 2
————————————————————————————————————————————————————————————————————————————
PRACTICE SETS FROM THIS LESSON
🔷 Q1–25 (JEE Main Level MCQs)
🔷 Q1.
The number of proper subsets of the set {a, b, c, d} is:
(A) 15
(B) 16
(C) 14
(D) 8
✅ Answer: (A)
🔷 Q2.
If A = {1, 2, 3} and B = {3, 4, 5}, then A ∪ B = ?
(A) {1, 2, 3, 4, 5}
(B) {3}
(C) {1, 2}
(D) ∅
✅ Answer: (A)
🔷 Q3.
Let A = {x ∈ ℕ : x < 5}, then n(P(A)) = ?
(A) 32
(B) 8
(C) 16
(D) 64
✅ Answer: (A) (|A| = 4 → 2⁴ = 16)
🔷 Q4.
Which of the following is a subset of every set?
(A) {∅}
(B) ∅
(C) {0}
(D) {1}
✅ Answer: (B)
🔷 Q5.
Let U = {1, 2, 3, 4, 5}, A = {2, 3}, then A′ = ?
(A) {1, 4, 5}
(B) {2, 3, 5}
(C) {1, 2, 3}
(D) {4, 5}
✅ Answer: (A)
🔷 Q6.
Which of the following sets is infinite?
(A) {x : x ∈ ℕ, x ≤ 10}
(B) {x : x is even and x ∈ ℕ}
(C) {1, 2, 3, 4}
(D) ∅
✅ Answer: (B)
🔷 Q7.
A = {1, 2}, B = {2, 3}; then A ∩ B = ?
(A) {1}
(B) {2}
(C) {1, 2}
(D) ∅
✅ Answer: (B)
🔷 Q8.
If A = {x ∈ ℕ : x² < 20}, then A = ?
(A) {1, 2, 3, 4}
(B) {1, 2, 3}
(C) {1, 2, 3, 4, 5}
(D) {1, 2, 3, 4}
✅ Answer: (D)
🔷 Q9.
Set of vowels in the word “APPLICATION” is:
(A) {A, I, O}
(B) {A, I}
(C) {A, I, O, E}
(D) {A, E, I, O, U}
✅ Answer: (A)
🔷 Q10.
Let A = {2, 4, 6}, B = {6, 8}, then A ∩ B = ?
(A) {2, 4}
(B) ∅
(C) {6}
(D) {8}
✅ Answer: (C)
🔷 Q11.
If A ∩ B = A and A ∪ B = B, then:
(A) A = B
(B) A ⊆ B
(C) A ⊇ B
(D) A ∩ B = ∅
✅ Answer: (B)
🔷 Q12.
Which of the following has cardinality 2?
(A) ∅
(B) {∅, {∅}}
(C) {{a}, {b}}
(D) {a, b}
✅ Answer: (D)
🔷 Q13.
A set containing no element is called:
(A) Singleton
(B) Power set
(C) Null set
(D) Universal set
✅ Answer: (C)
🔷 Q14.
Let A = {x : x is a prime number < 10}, then A = ?
(A) {2, 3, 5, 7}
(B) {1, 2, 3}
(C) {2, 3, 5}
(D) {2, 3, 5, 7, 9}
✅ Answer: (A)
🔷 Q15.
If n(A) = 2, n(B) = 3, and A ∩ B = ∅, then n(A ∪ B) = ?
(A) 3
(B) 5
(C) 6
(D) 2
✅ Answer: (B)
🔷 Q16.
Which is not a well-defined set?
(A) Set of odd numbers
(B) Set of vowels in English
(C) Set of good books
(D) Set of months in a year
✅ Answer: (C)
🔷 Q17.
P(P(∅)) has how many elements?
(A) 1
(B) 2
(C) 4
(D) 3
✅ Answer: (B)
🔷 Q18.
Power set of {a, b} is:
(A) {∅, {a}, {b}, {a, b}}
(B) {a, b, ab}
(C) {{a, b}}
(D) None
✅ Answer: (A)
🔷 Q19.
If A = {1, 2, 3} and B = {3, 4, 5}, find A − B
(A) {1, 2}
(B) {2, 3}
(C) {1, 3}
(D) ∅
✅ Answer: (A)
🔷 Q20.
Which of the following is equivalent to A ∪ ∅?
(A) A
(B) ∅
(C) A′
(D) None
✅ Answer: (A)
🔷 Q21.
If A = {2, 4}, B = {4, 6}, then A Δ B = ?
(A) {2, 6}
(B) {2, 4, 6}
(C) {4}
(D) {2}
✅ Answer: (A)
🔷 Q22.
Number of elements in P(P({a})) is:
(A) 1
(B) 2
(C) 4
(D) 8
✅ Answer: (C)
🔷 Q23.
Let A = {x ∈ ℝ : x² − 4 = 0}, then A = ?
(A) {2, −2}
(B) {4}
(C) {2}
(D) {−2}
✅ Answer: (A)
🔷 Q24.
Let A = {x ∈ ℕ : x is even and ≤ 10}, B = {x ∈ ℕ : x is multiple of 3 and ≤ 10}, then A ∩ B = ?
(A) {6}
(B) {3, 6}
(C) {2, 4, 6}
(D) {10}
✅ Answer: (A)
🔷 Q25.
If A ⊆ B and B ⊆ C, then:
(A) A ⊆ C
(B) C ⊆ A
(C) A = B
(D) A ∩ C = ∅
✅ Answer: (A)
🔴 Q26–50 (JEE Advanced Level MCQs)
🔷 Q26.
Let A = {x ∈ ℝ : x² − 5x + 6 = 0}, B = {x ∈ ℝ : x² − 3x + 2 = 0}. Then A ∩ B = ?
(A) {2, 3}
(B) {2}
(C) {1}
(D) ∅
✅ Answer: (B)
🔷 Q27.
If A = {1, 2, 3}, B = {x ∈ ℝ : x² ≤ 9}, then A ⊆ B implies:
(A) A = B
(B) A ⊂ B
(C) B ⊆ A
(D) A ∩ B = ∅
✅ Answer: (B)
🔷 Q28.
If P(A) has 64 elements, how many elements are there in A?
(A) 6
(B) 7
(C) 8
(D) 5
✅ Answer: (A) (Since 2ⁿ = 64 ⇒ n = 6)
🔷 Q29.
If A, B, C are sets and A ∩ B = A ∩ C, A ∪ B = A ∪ C, then:
(A) B = C
(B) A = B
(C) A = C
(D) None
✅ Answer: (A)
🔷 Q30.
Let A = {x ∈ ℤ : −2 < x < 3}, B = {0, 1, 2, 3}, then A ∩ B = ?
(A) {0, 1, 2}
(B) {−1, 0, 1}
(C) {1, 2, 3}
(D) {−1, 0, 1, 2}
✅ Answer: (A)
🔷 Q31.
If A and B are disjoint sets, then A ∩ B = ?
(A) A
(B) B
(C) ∅
(D) A ∪ B
✅ Answer: (C)
🔷 Q32.
Let A = {x ∈ ℕ : x is a multiple of 2}, B = {x ∈ ℕ : x is a multiple of 4}. Then A ∩ B = ?
(A) B
(B) A
(C) ∅
(D) {x ∈ ℕ : x is a multiple of 8}
✅ Answer: (A)
🔷 Q33.
Let A = {x ∈ ℕ : x² ≤ 25}, B = {x ∈ ℕ : x is odd and < 10}, then A ∩ B = ?
(A) {1, 3, 5}
(B) {1, 3, 5, 7, 9}
(C) {5, 7}
(D) {2, 4, 6, 8}
✅ Answer: (A)
🔷 Q34.
Which one of the following sets is not equal to the others?
(A) {x : x is a prime < 6}
(B) {2, 3, 5}
(C) {5, 3, 2}
(D) {2, 3, 6}
✅ Answer: (D)
🔷 Q35.
If A ∩ B = ∅ and A ∪ B = U, then B = ?
(A) A′
(B) A
(C) U
(D) ∅
✅ Answer: (A)
🔷 Q36.
Let A = {1, 2, 3}, B = {x ∈ ℝ : x > 0}, then A ⊂ B is:
(A) False
(B) Always True
(C) True if B is a subset of ℕ
(D) True if A ⊆ B
✅ Answer: (D)
🔷 Q37.
Which of the following sets is closed under multiplication?
(A) ℕ
(B) ℤ
(C) ℝ
(D) All of these
✅ Answer: (D)
🔷 Q38.
Let A = {2, 4, 6}, B = {1, 2, 3, 4, 5}, then A ∩ B = ?
(A) {2, 4}
(B) {6}
(C) {2, 4, 6}
(D) {1, 3, 5}
✅ Answer: (A)
🔷 Q39.
Number of non-empty subsets of set A with n elements is:
(A) 2ⁿ − 1
(B) 2ⁿ
(C) n
(D) 2ⁿ⁻¹
✅ Answer: (A)
🔷 Q40.
Let A = {x ∈ ℕ : x is odd and ≤ 10}, B = {x ∈ ℕ : x is even and ≤ 10}. Then A ∩ B = ?
(A) ∅
(B) {1, 2}
(C) {2, 4, 6, 8, 10}
(D) {1, 3, 5, 7, 9}
✅ Answer: (A)
🔷 Q41.
If A = {x ∈ ℤ : x² − 1 = 0}, then A = ?
(A) {1, −1}
(B) {0, 1}
(C) {−1}
(D) {1}
✅ Answer: (A)
🔷 Q42.
If A ⊂ B, then which is always true?
(A) A ∪ B = B
(B) A ∩ B = A
(C) B − A ≠ ∅
(D) All of these
✅ Answer: (D)
🔷 Q43.
Let A = {1, 2, 3}, then total number of proper subsets = ?
(A) 8
(B) 6
(C) 7
(D) 5
✅ Answer: (C)
🔷 Q44.
Which law is shown by A ∪ (A ∩ B) = A?
(A) Associative
(B) Absorption
(C) Distributive
(D) Commutative
✅ Answer: (B)
🔷 Q45.
If A = {x ∈ ℕ : x < 3}, B = {1, 2}, then A − B = ?
(A) ∅
(B) {1, 2}
(C) {0}
(D) Cannot be determined
✅ Answer: (A)
🔷 Q46.
The symmetric difference of two identical sets A and A is:
(A) A
(B) ∅
(C) Universal Set
(D) A′
✅ Answer: (B)
🔷 Q47.
Number of relations from A to B when |A| = 2 and |B| = 3:
(A) 36
(B) 64
(C) 18
(D) 512
✅ Answer: (A) (2^(2×3) = 64)
📌 Correction: ✅ Answer: (B)
🔷 Q48.
If A = {x ∈ ℝ : x > 0}, then which is true?
(A) A is subset of ℝ
(B) A = ℝ
(C) A ⊆ ∅
(D) A = ∅
✅ Answer: (A)
🔷 Q49.
Which operation between any set A and ∅ always gives A?
(A) A ∪ ∅
(B) A ∩ ∅
(C) A − ∅
(D) A × ∅
✅ Answer: (C)
🔷 Q50.
If A = {2, 3}, B = {3, 4}, then n(A × B) = ?
(A) 4
(B) 6
(C) 2
(D) 3
✅ Answer: (A)
————————————————————————————————————————————————————————————————————————————
MIND MAP
————————————————————————————————————————————————————————————————————————————————————————————
