Class 10 : Maths (In Hindi) – Lesson 7. निर्देशांक ज्यामिति

पाठ का विश्लेषण  एवं  विवेचन

🌿 अध्याय का परिचय
🔵 निर्देशांक ज्यामिति वह विधि है जिसमें हम किसी बिन्दु का स्थान संख्याओं द्वारा व्यक्त करते हैं। यह बीजगणित और ज्यामिति के मेल से बनी है।
🟢 रेखाएँ, त्रिभुज और अन्य आकृतियाँ जिनकी स्थिति का अध्ययन करना कठिन होता है, उन्हें निर्देशांक प्रणाली (coordinate system) के प्रयोग से आसानी से हल किया जा सकता है।
🔴 वास्तविक जीवन में—जैसे नक्शे पर किसी स्थान को बताना, मोबाइल GPS या खेलों के ग्राफ़िक्स—सब में निर्देशांक ज्यामिति का ही प्रयोग है।
✏️ Note: निर्देशांक प्रणाली के बिना दो बिन्दुओं के बीच दूरी या क्षेत्रफल की गणना लम्बी हो सकती थी।
💡 Concept: बीजगणितीय समीकरणों के माध्यम से आकृतियों को व्यक्त करना कार्तीय पद्धति कहलाता है।

➡️ 1. कार्तीय समतल और अक्ष
🔵 समतल पर दो परस्पर लम्बवत रेखाएँ—x-अक्ष (क्षैतिज) और y-अक्ष (लम्बवत)—खींचते हैं।
🟢 जहाँ दोनों प्रतिच्छेद करते हैं, उसे मूल बिन्दु O(0,0) कहते हैं।
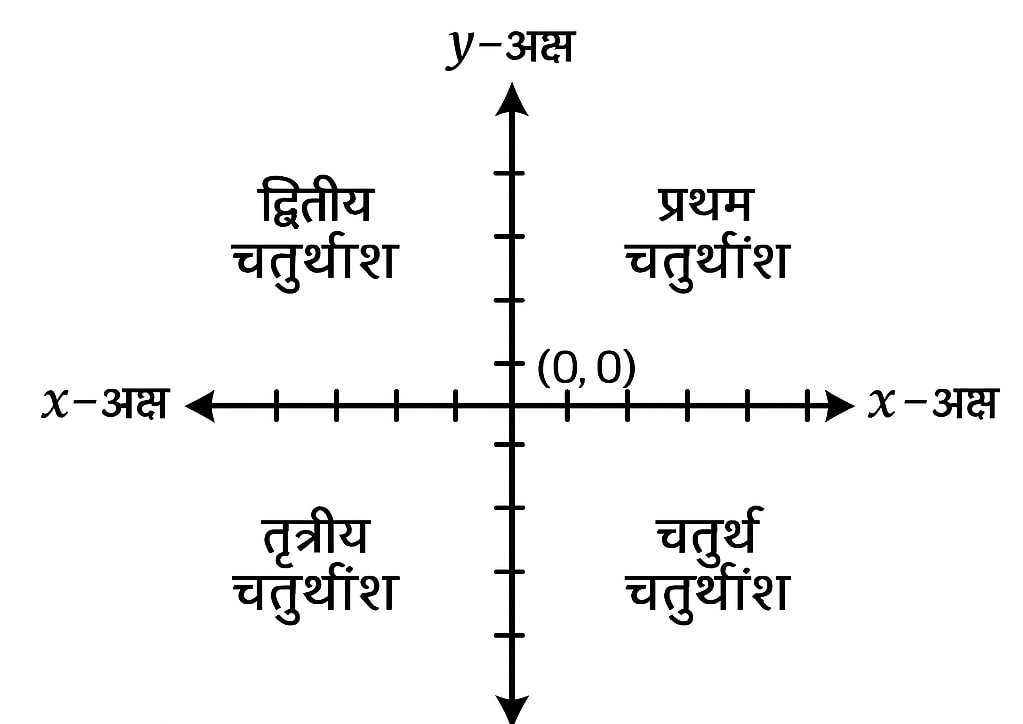
🔴 समतल को चार भागों में बाँटा जाता है जिन्हें चतुर्थांश (Quadrants) कहते हैं।
🟡 प्रत्येक चतुर्थांश में (x, y) के चिन्ह इस प्रकार हैं:
 🌿 प्रथम: (+,+) ⚡ द्वितीय: (−,+) 🧠 तृतीय: (−,−) ✔ चतुर्थ: (+,−)
✏️ Note: किसी बिन्दु के चिन्ह देखकर उसका चतुर्थांश पहचानना आसान होता है।
💡 Concept: यदि कोई बिन्दु x-अक्ष पर है ⇒ y=0; यदि y-अक्ष पर है ⇒ x=0।

➡️ 2. बिन्दु और उसका स्थान
🔵 किसी बिन्दु P को व्यक्त करने के लिए क्रमबद्ध युग्म (x,y) का प्रयोग करते हैं।
🟢 उदाहरण: P(3,−2) का अर्थ है—मूल से दाईं ओर 3 इकाई और नीचे की ओर 2 इकाई।
🔴 OP की दूरी: √(3²+ (−2)²) = √(9+4)=√13।

➡️ 3. दो बिन्दुओं के बीच दूरी सूत्र
🔵 दो बिन्दु A(x₁,y₁) और B(x₂,y₂) हों तो दूरी:
 AB = √{(x₂−x₁)² + (y₂−y₁)²}
🟢 विशेष स्थिति: मूल से दूरी ⇒ OP = √(x²+y²)
🟡 यदि रेखा क्षैतिज है ⇒ दूरी = |x₂−x₁|
🔴 यदि रेखा लम्बवत है ⇒ दूरी = |y₂−y₁|
🌿 उदाहरण: A(3,4), B(−1,1) ⇒ AB = √{(−1−3)²+(1−4)²} = √{(−4)²+(−3)²} = √(16+9)=5।

➡️ 4. मध्य-बिन्दु सूत्र
🔵 दो बिन्दु A(x₁,y₁), B(x₂,y₂) का मध्य-बिन्दु M:
 M = ((x₁+x₂)/2 , (y₁+y₂)/2)
🟢 उदाहरण: A(2,5), B(8,−1) ⇒ M=(10/2,4/2)=(5,2)।
✏️ Note: मध्य-बिन्दु से विभाजन अनुपात सदैव 1:1 होता है।
💡 Concept: इस सूत्र से त्रिभुज की माध्यिका या समद्विबाहु की जाँच करना सरल है।

➡️ 5. विभाजन सूत्र (आन्तरिक व बाह्य)
🔵 आन्तरिक विभाजन: यदि P(x,y), A(x₁,y₁) और B(x₂,y₂) को m:n में विभाजित करता है:
 x = (m x₂ + n x₁)/(m+n), y = (m y₂ + n y₁)/(m+n)
🟢 बाह्य विभाजन:
 x = (m x₂ − n x₁)/(m−n), y = (m y₂ − n y₁)/(m−n)
🌿 उदाहरण: A(−2,3), B(4,9), अनुपात 2:1 ⇒
x=(2×4+1×(−2))/3=(8−2)/3=2
y=(2×9+1×3)/3=(18+3)/3=7 ⇒ P=(2,7)।

➡️ 6. त्रिभुज का क्षेत्रफल (निर्देशांकों से)
🔵 यदि शीर्ष A(x₁,y₁), B(x₂,y₂), C(x₃,y₃) हैं, तो:
 Area = (1/2)| x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂) |
🟢 उदाहरण: A(1,−2), B(3,4), C(−2,5):
S=1(4−5)+3(5−(−2))+(−2)((−2)−4)=−1+21+12=32
Area=(1/2)|32|=16 इकाई²।
✏️ Note: यदि क्षेत्रफल=0 हो ⇒ तीनों बिन्दु सह-रैखिक हैं।
💡 Concept: यह सह-रैखिकता जाँचने का त्वरित तरीका है।

➡️ 7. सह-रैखिकता की शर्त
🔵 बिन्दु A,B,C सह-रैखिक ⇔ Area(ΔABC)=0
🟢 सूत्र: x₁(y₂−y₃)+x₂(y₃−y₁)+x₃(y₁−y₂)=0।
🌿 उदाहरण: A(2,−1),B(5,5),C(k,7) सह-रैखिक:
2(5−7)+5(7−(−1))+k((−1)−5)=−4+40−6k=0⇒36−6k=0⇒k=6।

➡️ 8. अज्ञात निर्देशांक ज्ञात करना
🔵 जब क्षेत्रफल या मध्य-बिन्दु दिया हो, अज्ञात निर्देशांक हेतु संबंधित सूत्र प्रयोग करें।
🟢 उदाहरण: A(1,2),B(4,6),C(k,3) का क्षेत्रफल 5:
|7−4k|=10 ⇒ k=−0.75 या 4.25।
✏️ Note: समाधान के दोनों मान लिखें, प्रश्न में संदर्भ अनुसार चुनें।

➡️ 9. वास्तविक जीवन के अनुप्रयोग
🔵 🌿 GPS और मैपिंग: मोबाइल GPS किसी स्थान को (अक्षांश, देशांतर) युग्म से पहचानता है।
🟢 ⚡ इंजीनियरिंग व डिज़ाइन: पुल या भवन निर्माण में दूरी/मध्य-बिन्दु की सटीक गणना।
🔴 🧠 खेल व ग्राफ़िक्स: वीडियो गेम में पात्र की स्थिति अद्यतन करने में निर्देशांक ज्यामिति।
🟡 ✔ खगोल विज्ञान: तारों की स्थिति मापने के लिए भी यही सिद्धान्त।

➡️ 10. परीक्षा रणनीति और सावधानियाँ
🔵 सूत्र याद करें और सही चिन्हों पर ध्यान दें।
🟢 विभाजन सूत्र में हर बार m:n के क्रम का ध्यान रखें।
🔴 क्षेत्रफल सूत्र में |…| का प्रयोग न भूलें।
🟡 सह-रैखिकता वाले प्रश्नों में तुरन्त Area=0 लागू करें।
🌿 अभ्यास से गणना की गति बढ़ाएँ।
✏️ Note: समय बचाने के लिए सरल बिन्दु चुनें जब सम्भव हो।
💡 Concept: कठिन प्रश्नों को दो भागों—पहले दूरी/मध्य-बिन्दु निकालना, फिर क्षेत्रफल या अनुपात—में बाँटें।

📋 Summary (~300 शब्द)
• कार्तीय समतल व अक्ष: x-अक्ष क्षैतिज, y-अक्ष लम्बवत; मूल O(0,0); चार चतुर्थांश—चिन्ह (+,+),(−,+),(−,−),(+,−)।
• बिन्दु व स्थान: बिन्दु (x,y); x-अक्ष पर y=0, y-अक्ष पर x=0।
• दूरी सूत्र: AB=√{(x₂−x₁)²+(y₂−y₁)²}; विशेष स्थिति—मूल से दूरी √(x²+y²)।
• मध्य-बिन्दु सूत्र: M=((x₁+x₂)/2,(y₁+y₂)/2)।
• विभाजन सूत्र: आन्तरिक—( (m x₂ + n x₁)/(m+n), (m y₂ + n y₁)/(m+n) ); बाह्य—( (m x₂ − n x₁)/(m−n), (m y₂ − n y₁)/(m−n) )।
• त्रिभुज का क्षेत्रफल: (1/2)|x₁(y₂−y₃)+x₂(y₃−y₁)+x₃(y₁−y₂)|; सह-रैखिकता ⇒ Area=0।
• अनुप्रयोग: GPS, मैपिंग, इंजीनियरिंग, गेम ग्राफ़िक्स, खगोल विज्ञान।
• सावधानियाँ: चिन्हों की जाँच, m:n क्रम, |…| का प्रयोग, समय प्रबंधन।
• उपयोगी युक्ति: यदि बिन्दु अक्ष पर है तो एक निर्देशांक तुरन्त 0 मानें; क्षेत्रफल से अज्ञात निर्देशांक खोजें; विभाजन और मध्य-बिन्दु का प्रयोग करें।

📝 Quick Recap
🌿 बिन्दु (x,y) के चिन्ह से चतुर्थांश तय।
⚡ दूरी सूत्र: d=√{(x₂−x₁)²+(y₂−y₁)²}।
🔵 मध्य-बिन्दु: ((x₁+x₂)/2,(y₁+y₂)/2)।
🟢 विभाजन सूत्र (आन्तरिक/बाह्य) m:n अनुपात में।
🔴 क्षेत्रफल सूत्र व सह-रैखिकता (Area=0)।
🟡 GPS, मैपिंग व इंजीनियरिंग में अनुप्रयोग।

————————————————————————————————————————————————————————————————————————————

पाठ्यपुस्तक के प्रश्न

प्रश्नावली 7.1

प्रश्न 1
बिंदुओं के निम्नलिखित युग्मों के बीच की दूरी ज्ञात कीजिए:
(i) (2, 3), (4, 1) (ii) (−5, 7), (−1, 3) (iii) (a, b), (−a, −b)
🟢 उत्तर
💡 सूत्र: d = √((x₂ − x₁)² + (y₂ − y₁)²)
🔵 (i)
➤ x₂ − x₁ = 4 − 2 = 2
➤ y₂ − y₁ = 1 − 3 = −2
➤ d = √(2² + (−2)²)
➤ d = √(4 + 4)
✔️ Final: d = √8 = 2√2
🔵 (ii)
➤ x₂ − x₁ = −1 − (−5) = 4
➤ y₂ − y₁ = 3 − 7 = −4
➤ d = √(4² + (−4)²)
➤ d = √(16 + 16)
✔️ Final: d = √32 = 4√2
🔵 (iii)
➤ x₂ − x₁ = −a − a = −2a
➤ y₂ − y₁ = −b − b = −2b
➤ d = √((−2a)² + (−2b)²)
➤ d = √(4a² + 4b²)
✔️ Final: d = 2√(a² + b²)

🔵 प्रश्न 2
बिंदुओं (0, 0) और (36, 15) के बीच की दूरी ज्ञात कीजिए।
🟢 उत्तर
➤ x₂ − x₁ = 36 − 0 = 36
➤ y₂ − y₁ = 15 − 0 = 15
➤ d = √(36² + 15²)
➤ d = √(1296 + 225)
➤ d = √1521
✔️ Final: d = 39

🔵 प्रश्न 3
निर्धारित कीजिए कि क्या बिंदु (1, 5), (2, 3) और (−2, −11) सरेख हैं।
🟢 उत्तर
💡 विधि: त्रिभुज का क्षेत्रफल = 0 ⇔ सरेख
सूत्र: ½ |x₁(y₂−y₃) + x₂(y₃−y₁) + x₃(y₁−y₂)|
➤ y₂ − y₃ = 3 − (−11) = 14
➤ y₃ − y₁ = −11 − 5 = −16
➤ y₁ − y₂ = 5 − 3 = 2
➤ मान = 1×14 + 2×(−16) + (−2)×2 = 14 − 32 − 4 = −22
➤ क्षेत्रफल = ½ |−22| = 11
🔴 Observation: क्षेत्रफल ≠ 0
✔️ Final: बिंदु सरेख नहीं हैं।

🔵 प्रश्न 4
जाँच कीजिए कि क्या बिंदु (5, 2), (6, 4) और (3, 7) एक समद्विबाहु त्रिभुज के शिखर हैं।
🟢 उत्तर
➤ AB = √((6 − 5)² + (4 − 2)²) = √(1 + 4) = √5
➤ BC = √((3 − 6)² + (7 − 4)²) = √(9 + 9) = √18 = 3√2
➤ CA = √((5 − 3)² + (2 − 7)²) = √(4 + 25) = √29
🔴 Observation: √5, 3√2, √29 — कोई भी दो बराबर नहीं
✔️ Final: यह त्रिभुज समद्विबाहु नहीं है।

🔵 प्रश्न 5
कक्षा में, चार मित्र A, B, C, D बिंदुओं पर बैठे हैं। चम्पा कहती है, “क्या तुम नहीं सोचती कि ABCD एक वर्ग है?” चेम्पा असहमत है। दूरी सूत्र का प्रयोग करके बताइए कौन सही है।
🟢 उत्तर
निर्देशांक: A(2, 4), B(5, 7), C(8, 4), D(5, 1)
➤ AB = √((5 − 2)² + (7 − 4)²) = √(9 + 9) = 3√2
➤ BC = √((8 − 5)² + (4 − 7)²) = √(9 + 9) = 3√2
➤ CD = √((5 − 8)² + (1 − 4)²) = √(9 + 9) = 3√2
➤ DA = √((2 − 5)² + (4 − 1)²) = √(9 + 9) = 3√2
➤ ढाल AB = (7 − 4)/(5 − 2) = 1
➤ ढाल BC = (4 − 7)/(8 − 5) = −1
Observation: AB × BC = −1 ⇒ AB ⟂ BC
➤ AC = √((8 − 2)² + (4 − 4)²) = 6
➤ BD = √((5 − 5)² + (7 − 1)²) = 6
✔️ Final: ABCD एक वर्ग है; अतः चम्पा सही है।

🔵 प्रश्न 6
निम्नलिखित बिंदुओं द्वारा बनने वाले चतुर्भुज का प्रकार (यदि कोई है) बताइए तथा अपने उत्तर के लिए कारण भी दीजिए:
(i) (−1, −2), (1, 0), (−1, 2), (−3, 0)
(ii) (−3, 5), (3, 1), (0, 3), (−1, −4)
(iii) (4, 5), (7, 6), (4, 3), (1, 2)
🟢 उत्तर
💡 सूत्र: दूरी d = √((x₂ − x₁)² + (y₂ − y₁)²), ढाल m = (y₂ − y₁)/(x₂ − x₁)
🟣 (i)
➤ AB = √((1 − (−1))² + (0 − (−2))²) = √(2² + 2²) = √8 = 2√2
➤ BC = √((−1 − 1)² + (2 − 0)²) = √((−2)² + 2²) = √8 = 2√2
➤ CD = √((−3 − (−1))² + (0 − 2)²) = √((−2)² + (−2)²) = √8 = 2√2
➤ DA = √((−1 − (−3))² + (−2 − 0)²) = √(2² + (−2)²) = √8 = 2√2
🧠 निष्कर्ष: चारों भुजाएँ समान; क्रमागत भुजाओं की ढालें परस्पर ऋणात्मक व्युत्क्रम → समकोण।
✔️ Final: वर्ग।
🟣 (ii)
➤ AB = √((3 − (−3))² + (1 − 5)²) = √(6² + (−4)²) = √52
➤ BC = √((0 − 3)² + (3 − 1)²) = √((−3)² + 2²) = √13
➤ CD = √((−1 − 0)² + (−4 − 3)²) = √((−1)² + (−7)²) = √50
➤ DA = √((−3 − (−1))² + (5 − (−4))²) = √((−2)² + 9²) = √85
🔴 अवलोकन: न तो सभी भुजाएँ समान, न समकोण; समानांतरता भी नहीं।
✔️ Final: अनियमित चतुर्भुज (कोई विशेष प्रकार नहीं)।
🟣 (iii)
➤ AB = √((7 − 4)² + (6 − 5)²) = √(3² + 1²) = √10
➤ BC = √((4 − 7)² + (3 − 6)²) = √((−3)² + (−3)²) = √18
➤ CD = √((1 − 4)² + (2 − 3)²) = √((−3)² + (−1)²) = √10
➤ DA = √((4 − 1)² + (5 − 2)²) = √(3² + 3²) = √18
🧠 निष्कर्ष: AB = CD और BC = DA; विपरीत भुजाएँ बराबर ⇒ समांतर चतुर्भुज की शर्त पूरी।
✔️ Final: समांतर चतुर्भुज (आयत/समचतुर्भुज नहीं)।


🔵 प्रश्न 7
x-अक्ष पर वह बिंदु ज्ञात कीजिए जो (2, −5) और (−2, 9) से समदूरस्थ है।
🟢 उत्तर
💡 मान लीजिए P(x, 0) समदूरस्थ है।
➤ √((x − 2)² + (0 − (−5))²) = √((x − (−2))² + (0 − 9)²)
➤ (x − 2)² + 5² = (x + 2)² + (−9)²
➤ x² − 4x + 4 + 25 = x² + 4x + 4 + 81
➤ x² − 4x + 29 = x² + 4x + 85
➤ −4x = 4x + 56
➤ −8x = 56
➤ x = −7
✔️ Final: P(−7, 0)


🔵 प्रश्न 8
y का वह मान ज्ञात कीजिए, जिसके लिए बिंदु P(2, −3) और Q(10, y) के बीच की दूरी 10 मानक है।
🟢 उत्तर
➤ √((10 − 2)² + (y − (−3))²) = 10
➤ √(8² + (y + 3)²) = 10
➤ 64 + (y + 3)² = 100
➤ (y + 3)² = 36
➤ y + 3 = ±6
➤ y = 3 या y = −9
✔️ Final: y = 3, −9


🔵 प्रश्न 9
यदि Q(0, 1), P(5, −3) और R(x, 6) से समदूरस्थ है, तो x के मान ज्ञात कीजिए। QR तथा PR की दूरियाँ भी ज्ञात कीजिए।
🟢 उत्तर
💡 शर्त: QP = QR
➤ √((5 − 0)² + (−3 − 1)²) = √((x − 0)² + (6 − 1)²)
➤ √(25 + (−4)²) = √(x² + 25)
➤ √41 = √(x² + 25) ⇒ x² + 25 = 41
➤ x² = 16 ⇒ x = ±4
🧮 दूरियाँ
➤ QR = √((x − 0)² + (6 − 1)²) = √(x² + 25) = √41
➤ PR = √((x − 5)² + (6 − (−3))²) = √((x − 5)² + 9²)
 • यदि x = 4: PR = √((−1)² + 81) = √82
 • यदि x = −4: PR = √((−9)² + 81) = √162 = 9√2
✔️ Final: x = 4 पर PR = √82, x = −4 पर PR = 9√2; तथा QR = √41


🔵 प्रश्न 10
x और y में एक ऐसा संबंध ज्ञात कीजिए कि बिंदु (x, y) बिंदुओं (3, 6) और (−3, 4) से समदूरस्थ हो।
🟢 उत्तर
➤ √((x − 3)² + (y − 6)²) = √((x + 3)² + (y − 4)²)
➤ (x − 3)² + (y − 6)² = (x + 3)² + (y − 4)²
➤ x² − 6x + 9 + y² − 12y + 36 = x² + 6x + 9 + y² − 8y + 16
➤ −6x − 12y + 45 = 6x − 8y + 25
➤ दोनों पक्षों से 25 घटाकर और पद समेकित कर: −6x − 12y + 20 = 6x − 8y
➤ सभी पद एक ही तरफ़: −12x − 4y + 20 = 0
➤ (−4) से भाग: 3x + y − 5 = 0
✔️ Final: 3x + y − 5 = 0

प्रश्नावली 7.2

🔵 प्रश्न 1
उस बिंदु के निर्देशांक ज्ञात कीजिए, जो बिंदुओं (−1, 7) और (4, −3) को मिलाने वाले रेखाखंड को 2 : 3 के अनुपात में विभाजित करता है।
🟢 उत्तर
💡 विभाजन सूत्र: P(x, y) = ((m x₂ + n x₁)/(m + n), (m y₂ + n y₁)/(m + n))
1️⃣ m:n = 2:3 ⇒ m = 2, n = 3
2️⃣ x = (2 × 4 + 3 × (−1)) / 5 = (8 − 3) / 5 = 5 / 5 = 1
3️⃣ y = (2 × (−3) + 3 × 7) / 5 = (−6 + 21) / 5 = 15 / 5 = 3
✔️ Final: P(1, 3)

🔵 प्रश्न 2
बिंदुओं (4, −1) और (−2, −3) को जोड़ने वाले रेखाखंड को सम-त्रिभाजित करने वाले बिंदुओं के निर्देशांक ज्ञात कीजिए।
🟢 उत्तर
💡 A(x₁, y₁) = (4, −1), B(x₂, y₂) = (−2, −3)
पहला बिंदु P (1:2)
1️⃣ x = (1 × (−2) + 2 × 4)/3 = (−2 + 8)/3 = 6/3 = 2
2️⃣ y = (1 × (−3) + 2 × (−1))/3 = (−3 − 2)/3 = −5/3
दूसरा बिंदु Q (2:1)
3️⃣ x = (2 × (−2) + 1 × 4)/3 = (−4 + 4)/3 = 0
4️⃣ y = (2 × (−3) + 1 × (−1))/3 = (−6 − 1)/3 = −7/3
✔️ Final: P(2, −5/3), Q(0, −7/3)

🔵 प्रश्न 3
आपके स्कूल में खेल-कूद क्रियाकलाप आयोजित करने के लिए, एक आयताकार मैदान ABCD में, चूने से परस्पर 1 m की दूरी पर पंक्तियाँ बनायी गई हैं। AD के अनुदिश परस्पर 1 m की दूरी पर 100 गड्ढे रखे गए हैं। निहालिका दूसरी पंक्ति में AD के ¼ भाग की दूरी दौड़कर वहाँ एक हरा झंडा गाड़ती है। प्रीत आठवीं पंक्ति में AD के ⅕ भाग की दूरी दौड़कर वहाँ एक लाल झंडा गाड़ती है। दोनों झंडों को जोड़ने वाले रेखाखंड का मध्य ज्ञात कीजिए और बताइए कि अपना झंडा कहाँ गाड़ना चाहिए।
🟢 उत्तर
💡 मानचित्रण: A(0, 0), D(0, 100); पंक्ति संख्या = x-निर्देशांक, AD दूरी = y-निर्देशांक।
1️⃣ हरा झंडा H = (2, 25) (2nd row, ¼ × 100)
2️⃣ लाल झंडा L = (8, 20) (8th row, ⅕ × 100)
3️⃣ मध्य बिंदु M = ((x_H + x_L)/2, (y_H + y_L)/2) = ((2 + 8)/2, (25 + 20)/2) = (5, 22.5)
✔️ Final: अपना झंडा M(5, 22.5) पर गाड़ें।

🔵 प्रश्न 4
बिंदुओं (−3, 10) और (6, −8) को जोड़ने वाले रेखाखंड को बिंदु (−1, 6) किस अनुपात में विभाजित करता है?
🟢 उत्तर
💡 A(x₁, y₁) = (−3, 10), B(x₂, y₂) = (6, −8), P(x_P, y_P) = (−1, 6)
1️⃣ m:n = (x_P − x₁)/(x₂ − x_P) = (−1 + 3)/(6 + 1) = 2/7
2️⃣ y से जाँच: (y_P − y₁)/(y₂ − y_P) = (6 − 10)/(−8 − 6) = (−4)/(−14) = 2/7
✔️ Final: अनुपात 2:7 (आंतरिक विभाजन)

🔵 प्रश्न 5
उस अनुपात का मान ज्ञात कीजिए, जिसमें बिंदु A(1, −5) और B(−4, 5) को मिलाने वाला रेखाखंड बिंदु P(−2, y) द्वारा विभाजित हो; तथा y का मान ज्ञात कीजिए।
🟢 उत्तर
💡 अनुपात = k:1; विभाजन सूत्र: x_P = (k x_B + x_A)/(k + 1)
1️⃣ x_P = −2 ⇒ −2 = (k (−4) + 1)/(k + 1)
2️⃣ −2(k + 1) = −4k + 1
3️⃣ −2k − 2 = −4k + 1
4️⃣ 2k = 3 ⇒ k = ³/₂
5️⃣ y_P = (k y_B + y_A)/(k + 1)
  = ((³/₂) × 5 + (−5))/(³/₂ + 1)
  = (15/2 − 10/2)/(5/2)
  = (5/2)/(5/2) = 1
✔️ Final: अनुपात 3:2, y = 1

🔵 प्रश्न 6
यदि बिंदु (1, 2), (4, y), (x, 6) और (3, 5), इसी क्रम में लेने पर, एक समांतर चतुर्भुज के शीर्ष हों तो x और y ज्ञात कीजिए।
🟢 उत्तर
💡 समांतर चतुर्भुज में विकर्ण एक-दूसरे को समद्विभाजित करते हैं।
1️⃣ A(x₁,y₁)=(1,2), B(x₂,y₂)=(4,y), C(x₃,y₃)=(x,6), D(x₄,y₄)=(3,5)
2️⃣ AC का मध्यबिंदु = ((x₁+x₃)/2,(y₁+y₃)/2) = ((1+x)/2, (2+6)/2) = ((1+x)/2, 4)
3️⃣ BD का मध्यबिंदु = ((x₂+x₄)/2,(y₂+y₄)/2) = ((4+3)/2, (y+5)/2) = (7/2,(y+5)/2)
4️⃣ (1+x)/2 = 7/2 ⇒ 1+x = 7 ⇒ x = 6
5️⃣ 4 = (y+5)/2 ⇒ y+5 = 8 ⇒ y = 3
✔️ Final: x = 6, y = 3

🔵 प्रश्न 7
बिंदु A के निर्देशांक ज्ञात कीजिए, जहाँ AB एक वृत्त का व्यास है जिसका केंद्र (2, −3) है तथा B के निर्देशांक (1, 4) हैं।
🟢 उत्तर
💡 केंद्र O(2,−3) = व्यास AB का मध्यबिंदु।
1️⃣ (x+1)/2 = 2 ⇒ x+1 = 4 ⇒ x = 3
2️⃣ (y+4)/2 = −3 ⇒ y+4 = −6 ⇒ y = −10
✔️ Final: A(3, −10)

🔵 प्रश्न 8
यदि A और B क्रमशः (−2, −2) और (2, −4) हों तो बिंदु P के निर्देशांक ज्ञात कीजिए ताकि AP = ³/₇ AB हो और P रेखाखंड AB पर स्थित हो।
🟢 उत्तर
💡 AP:PB = 3:4 (आंतरिक विभाजन)
1️⃣ xₚ = (4·x_B + 3·x_A)/7 = (4·2 + 3·(−2))/7 = (8 − 6)/7 = 2/7
2️⃣ yₚ = (4·y_B + 3·y_A)/7 = (4·(−4) + 3·(−2))/7 = (−16 − 6)/7 = −22/7
✔️ Final: P(2/7, −22/7)

🔵 प्रश्न 9
बिंदुओं A(−2, 2) और B(2, 8) को जोड़ने वाले रेखाखंड AB को चार बराबर भागों में विभाजित करने वाले बिंदुओं के निर्देशांक ज्ञात कीजिए।
🟢 उत्तर
💡 चार बराबर भाग ⇒ अनुपात: 1:3, 1:1, 3:1
1️⃣ P(1:3) = ((1·2 + 3·(−2))/4, (1·8 + 3·2)/4) = (−1, 3.5)
2️⃣ Q(1:1) (मध्यबिंदु) = ((−2+2)/2, (2+8)/2) = (0, 5)
3️⃣ R(3:1) = ((3·2 + 1·(−2))/4, (3·8 + 1·2)/4) = (1, 6.5)
✔️ Final: P(−1, 3.5), Q(0, 5), R(1, 6.5)

🔵 प्रश्न 10
एक समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष, इसी क्रम में, (3, 0), (4, 5), (−1, 4) और (−2, −1) हैं। [संकेत: समचतुर्भुज का क्षेत्रफल = ½ (उसके विकर्णों का गुणनफल)]
🟢 उत्तर
1️⃣ d₁ = AC = √((−1−3)² + (4−0)²) = √((−4)² + 4²) = √(16 + 16) = √32
2️⃣ d₂ = BD = √((−2−4)² + (−1−5)²) = √((−6)² + (−6)²) = √(36 + 36) = √72
3️⃣ क्षेत्रफल = ½ × √32 × √72 = ½ × √2304 = ½ × 48 = 24
✔️ Final: क्षेत्रफल = 24 वर्ग-इकाई

————————————————————————————————————————————————————————————————————————————–

अन्य महत्वपूर्ण प्रश्न

🔵 Question
प्रश्न 1 (1 अंक)
बिंदुओं A(2, 3) और B(6, 3) के बीच की दूरी क्या है?
विकल्प:
(क) 2 (ख) 3 (ग) 4 (घ) 5
🟢 Answer
✔️ दूरी: d = √((x₂−x₁)² + (y₂−y₁)²)
= √((6−2)² + (3−3)²)
= √(4² + 0²)
= 4
✅ सही विकल्प: (ग)

🔵 Question
प्रश्न 2 (1 अंक)
यदि P(x, y) बिंदुओं (4, −2) और (−2, 4) का मध्यबिंदु है, तो x + y का मान क्या है?
विकल्प:
(क) 0 (ख) 1 (ग) 2 (घ) −1
🟢 Answer
x = (4 + (−2))/2 = 2/2 = 1
y = (−2 + 4)/2 = 2/2 = 1
x + y = 1 + 1 = 2
✅ सही विकल्प: (ग)

🔵 Question
प्रश्न 3 (1 अंक)
बिंदु (a, b) और (−a, −b) के बीच दूरी d क्या होगी?
विकल्प:
(क) a + b (ख) √(a² + b²) (ग) 2√(a² + b²) (घ) √(a² − b²)
🟢 Answer
d = √((−a−a)² + (−b−b)²)
= √((−2a)² + (−2b)²)
= √(4a² + 4b²)
= 2√(a² + b²)
✅ सही विकल्प: (ग)

🔵 Question
प्रश्न 4 (1 अंक)
यदि किसी त्रिभुज के शीर्ष (x₁, y₁), (x₂, y₂), (x₃, y₃) हों, तो उसका क्षेत्रफल S क्या है?
विकल्प:
(क) ½ |x₁y₂ + x₂y₃ + x₃y₁ − x₂y₁ − x₃y₂ − x₁y₃|
(ख) √(x₁² + y₁²)
(ग) (x₁ + x₂ + x₃)/3
(घ) (y₁ + y₂ + y₃)/3
🟢 Answer
त्रिभुज क्षेत्रफल का मानक सूत्र विकल्प (क) है।
✅ सही विकल्प: (क)

🔵 Question
प्रश्न 5 (1 अंक)
रेखाखंड को आंतरिक अनुपात m:n में विभाजित करने का x-निर्देशांक क्या है?
विकल्प:
(क) (m x₁ + n x₂)/(m + n)
(ख) (m x₂ + n x₁)/(m + n)
(ग) (x₁ + x₂)/2
(घ) (m x₂ − n x₁)/(m + n)
🟢 Answer
आंतरिक विभाजन में x = (m x₂ + n x₁)/(m + n)
✅ सही विकल्प: (ख)

🔵 Question
प्रश्न 6 (1 अंक)
जब A(1, 2), B(5, 6) हों, तो मध्यबिंदु के निर्देशांक क्या हैं?
विकल्प:
(क) (2, 3) (ख) (3, 4) (ग) (4, 5) (घ) (0, 0)
🟢 Answer
x = (1+5)/2 = 3, y = (2+6)/2 = 4
✅ सही विकल्प: (ख)

🟡🟡🟡 Section B — संक्षिप्त उत्तर-I (प्रश्न 7–12, प्रत्येक 2 अंक) 🟡🟡🟡

🔵 Question
प्रश्न 7 (2 अंक)
बिंदुओं (−3, 4) और (9, −8) के बीच दूरी ज्ञात कीजिए।
🟢 Answer
🔹 सूत्र: d = √((x₂−x₁)² + (y₂−y₁)²)
🔹 प्रत्यास्थापन: d = √((9−(−3))² + (−8−4)²)
= √((12)² + (−12)²)
= √(144 + 144)
= √288
= √(144×2) = 12√2
✅ अन्तिम उत्तर: 12√2

🔵 Question
प्रश्न 8 (2 अंक)
बिंदु P, A(4, −1) और B(−2, 5) को मिलाने वाले रेखाखंड को 2:3 के अनुपात में विभाजित करता है (A से B की ओर)। P के निर्देशांक ज्ञात कीजिए।
🟢 Answer
🔹 x_P = (2·(−2) + 3·4)/(2+3) = (−4 + 12)/5 = 8/5
🔹 y_P = (2·5 + 3·(−1))/(5) = (10 − 3)/5 = 7/5
✅ अन्तिम उत्तर: P(8/5, 7/5)

🔵 Question
प्रश्न 9 (2 अंक)
यदि P(x, 3) बिंदु A(2, 7) और B(10, −1) से समदूरस्थ है, तो x का मान ज्ञात कीजिए।
🟢 Answer
🔹 PA = PB ⇒ √((x−2)² + (3−7)²) = √((x−10)² + (3−(−1))²)
🔹 वर्ग करने पर: (x−2)² + (−4)² = (x−10)² + (4)²
x² − 4x + 4 + 16 = x² − 20x + 100 + 16
x² − 4x + 20 = x² − 20x + 116
⇒ −4x + 20 = −20x + 116
⇒ 16x = 96
⇒ x = 6
✅ अन्तिम उत्तर: x = 6

🔵 Question
प्रश्न 10 (2 अंक)
त्रिभुज के शीर्ष A(1, 2), B(4, 6), C(7, 2) हैं। जाँच कीजिए कि क्या यह त्रिभुज समद्विबाहु है।
🟢 Answer
🔹 AB = √((4−1)² + (6−2)²) = √(3² + 4²) = 5
🔹 BC = √((7−4)² + (2−6)²) = √(3² + (−4)²) = 5
🔹 CA = √((1−7)² + (2−2)²) = √((−6)² + 0²) = 6
दो भुजाएँ AB = BC ⇒ त्रिभुज समद्विबाहु।
✅ अन्तिम उत्तर: हाँ, समद्विबाहु।

🔵 Question
प्रश्न 11 (2 अंक)
यदि A(−2, 3), B(6, 7) हों, तो मध्यबिंदु M तथा AB की ढाल m ज्ञात कीजिए।
🟢 Answer
🔹 M = ((−2+6)/2, (3+7)/2) = (4/2, 10/2) = (2, 5)
🔹 m = (y₂ − y₁)/(x₂ − x₁) = (7 − 3)/(6 − (−2)) = 4/8 = 1/2
✅ अन्तिम उत्तर: M(2, 5), m = 1/2

🔵 Question
प्रश्न 12 (2 अंक)
बिंदु (k, 1) त्रिभुज के आधार रेखाखंड A(−3, 1) से B(5, 1) पर स्थित है। यदि (k, 1) बिंदु A और B से समदूरस्थ हो, तो k का मान ज्ञात कीजिए।
🟢 Answer
🔹 A और B के x-निर्देशांक −3 तथा 5 हैं; समदूरस्थ बिंदु का x मध्य होगा।
🔹 k = (−3 + 5)/2 = 2/2 = 1
✅ अन्तिम उत्तर: k = 1

🔵 प्रश्न 13 (3 अंक)
बिंदु A(−2,3), B(4,−1), C(2,5) के लिए त्रिभुज ABC का क्षेत्रफल ज्ञात कीजिए।
🟢 उत्तर
1️⃣ सूत्र: S = ½|x₁(y₂−y₃)+x₂(y₃−y₁)+x₃(y₁−y₂)|
2️⃣ = ½|−2(−1−5)+4(5−3)+2(3−(−1))|
3️⃣ = ½|−2(−6)+4(2)+2(4)|
4️⃣ = ½|(12)+8+8|
5️⃣ = ½|28| = 14
✔️ Final: 14 वर्ग-एकक

🔵 प्रश्न 14 (3 अंक)
रेखाखंड के सिरे A(2,−4) और B(10,8) हैं। बिंदु P, AB को 3:5 अनुपात में विभाजित करता है। P के निर्देशांक ज्ञात कीजिए।
OR बिंदु Q, AB को 2:3 अनुपात में विभाजित करता है। Q के निर्देशांक ज्ञात कीजिए।
🟢 उत्तर
1️⃣ xₚ = (3·10 + 5·2)/(3+5) = (30+10)/8 = 40/8 = 5
2️⃣ yₚ = (3·8 + 5·(−4))/8 = (24−20)/8 = 4/8 = 1/2
✔️ Final: P(5,1/2)
OR
3️⃣ x_Q = (2·10 + 3·2)/5 = (20+6)/5 = 26/5
4️⃣ y_Q = (2·8 + 3·(−4))/5 = (16−12)/5 = 4/5
✔️ Final: Q(26/5,4/5)

🔵 प्रश्न 15 (3 अंक)
A(−2,−3), B(3,2), C(5,k) सह-रेखीय हैं। k ज्ञात कीजिए।
🟢 उत्तर
1️⃣ S = ½|x₁(y₂−y₃)+x₂(y₃−y₁)+x₃(y₁−y₂)| = 0
2️⃣ = ½|−2(2−k)+3(k+3)+5(−3−2)|
3️⃣ = ½|(−4+2k)+(3k+9)−25|
4️⃣ = ½|(5k−20)| = 0 ⇒5k−20=0
5️⃣ ⇒k=4
✔️ Final: k=4

🔵 प्रश्न 16 (3 अंक)
P(−2,x), Q(3,1) की दूरी 5 है। x ज्ञात कीजिए।
🟢 उत्तर
1️⃣ d=√((3−(−2))²+(1−x)²)=5
2️⃣ √(5²+(1−x)²)=5
3️⃣ 25+(1−x)²=25 ⇒(1−x)²=0
4️⃣ 1−x=0 ⇒x=1
✔️ Final: x=1

🔵 प्रश्न 17 (3 अंक)
ABCD के बिंदु A(1,2),B(4,3),C(7,6),D(4,5) हैं। जाँचें कि यह समांतर चतुर्भुज है।
OR P(0,0),Q(4,0),R(2,3) त्रिभुज का प्रकार बताइए।
🟢 उत्तर
पहला भाग:
1️⃣ M_AC=((1+7)/2,(2+6)/2)=(4,4)
2️⃣ M_BD=((4+4)/2,(3+5)/2)=(4,4)
3️⃣ M_AC=M_BD ⇒ABCD समांतर चतुर्भुज।
✔️ Final: समांतर चतुर्भुज।
OR
4️⃣ PQ=√((4−0)²+(0−0)²)=4
5️⃣ PR=√((2−0)²+(3−0)²)=√(4+9)=√13
6️⃣ QR=√((2−4)²+(3−0)²)=√(4+9)=√13
✔️ Final: समद्विबाहु त्रिभुज।

🔵 प्रश्न 18 (3 अंक)
A(1,2),B(4,6),C(5,2) त्रिभुज का प्रकार बताइए।
🟢 उत्तर
1️⃣ AB=√((4−1)²+(6−2)²)=√(9+16)=5
2️⃣ BC=√((5−4)²+(2−6)²)=√(1+16)=√17
3️⃣ CA=√((1−5)²+(2−2)²)=√(16+0)=4
4️⃣ कोई दो बराबर नहीं, पाइथागोरस नहीं मिलता।
✔️ Final: असमद्विबाहु त्रिभुज।

🔵 प्रश्न 19 (3 अंक)
x-अक्ष पर बिंदु P(x,0) ज्ञात करें, जो A(2,3) और B(8,−1) से समदूरस्थ है।
🟢 उत्तर
1️⃣ PA²=(x−2)²+(0−3)²=(x−2)²+9
2️⃣ PB²=(x−8)²+(0+1)²=(x−8)²+1
3️⃣ समदूरस्थ ⇒(x−2)²+9=(x−8)²+1
4️⃣ x²−4x+4+9=x²−16x+64+1
5️⃣ x²−4x+13=x²−16x+65
6️⃣ 12x=52 ⇒x=13/3
✔️ Final: P(13/3,0)

🔵 प्रश्न 20 (3 अंक)
A(−3,5),B(9,−1) का मध्यबिंदु P ज्ञात करें।
OR A(0,0),B(6,0),C(0,4) त्रिभुज का क्षेत्रफल का ¼ ज्ञात करें।
🟢 उत्तर
पहला भाग:
1️⃣ x=(−3+9)/2=6/2=3
2️⃣ y=(5+(−1))/2=4/2=2
✔️ Final: P(3,2)
OR
3️⃣ S=½|0(0−4)+6(4−0)+0(0−0)|=½|24|=12
4️⃣ ¼×12=3
✔️ Final: 3 वर्ग-एकक।

🔵 प्रश्न 21 (3 अंक)
A(2,3),B(6,7),C(10,3) में BC का मध्यबिंदु और AM की लंबाई ज्ञात करें।
🟢 उत्तर
1️⃣ M=((6+10)/2,(7+3)/2)=(8,5)
2️⃣ AM=√((8−2)²+(5−3)²)=√(36+4)=√40=2√10
✔️ Final: M(8,5),AM=2√10

🔵 प्रश्न 22 (3 अंक)
ABCD समांतर चतुर्भुज के शीर्ष A(1,2),B(5,2),C(6,6),D(2,6) हैं। क्षेत्रफल ज्ञात करें।
OR D ज्ञात करें ताकि ABCD समांतर चतुर्भुज बने और क्षेत्रफल बताइए।
🟢 उत्तर
पहला भाग:
1️⃣ S_ABC=½|1(2−6)+5(6−2)+6(2−2)|=½|−4+20+0|=8
2️⃣ S_ACD=½|1(6−6)+6(6−2)+2(2−6)|=½|0+24−8|=8
3️⃣ कुल=16
✔️ Final:16 वर्ग-एकक
OR
4️⃣ D=A+C−B=(1,2)+(6,6)−(5,2)=(2,6)
5️⃣ क्षेत्रफल=16
✔️ Final:D(2,6),16 वर्ग-एकक

🔵 प्रश्न 23 (4 अंक)
A(−3, 2), B(5, −4), C(7, 6) त्रिभुज का क्षेत्रफल ज्ञात कीजिए और जाँचें कि यह समकोण त्रिभुज है या नहीं।
🟢 उत्तर
1️⃣ S = ½|x₁(y₂−y₃)+x₂(y₃−y₁)+x₃(y₁−y₂)|
=½|−3(−4−6)+5(6−2)+7(2+4)|
=½|−3(−10)+5(4)+7(6)|
=½|(30)+20+42|=½(92)=46
2️⃣ भुजाएँ:
AB=√((5+3)²+(−4−2)²)=√(8²+(−6)²)=√(64+36)=√100=10
BC=√((7−5)²+(6+4)²)=√(2²+10²)=√(4+100)=√104
CA=√((−3−7)²+(2−6)²)=√((−10)²+(−4)²)=√(100+16)=√116
3️⃣ पाइथागोरस: 10²+√104²=100+104=204 ≠116 ⇒ समकोण नहीं।
✔️ Final: क्षेत्रफल=46 वर्ग-एकक; त्रिभुज समकोण नहीं।

🔵 प्रश्न 24 (4 अंक)
रेखाखंड AB के सिरे A(−2, −3), B(8, 5) हैं। बिंदु P ऐसा ज्ञात कीजिए जो AB को 3:2 के अनुपात में विभाजित करता है।
🟢 उत्तर
x_P=(3·8+2·(−2))/(5)=(24−4)/5=20/5=4
y_P=(3·5+2·(−3))/(5)=(15−6)/5=9/5
✔️ Final: P(4,9/5)

🔵 प्रश्न 25 (4 अंक)
यदि बिंदु P(x, 1) बिंदुओं A(3, 5) और B(−5, 3) से समदूरस्थ है, तो x ज्ञात कीजिए।
🟢 उत्तर
PA²=(x−3)²+(1−5)²=(x−3)²+16
PB²=(x+5)²+(1−3)²=(x+5)²+4
समदूरस्थ ⇒(x−3)²+16=(x+5)²+4
x²−6x+9+16=x²+10x+25+4
x²−6x+25=x²+10x+29
−6x+25=10x+29
−16x=4 ⇒x=−¼
✔️ Final: x=−¼

🔵 प्रश्न 26 (4 अंक)
त्रिभुज A(1,2), B(4,6), C(7,2) का प्रकार और क्षेत्रफल ज्ञात कीजिए।
🟢 उत्तर
AB=√((4−1)²+(6−2)²)=√(9+16)=5
BC=√((7−4)²+(2−6)²)=√(9+16)=5
CA=√((7−1)²+(2−2)²)=√(36+0)=6
दो भुजाएँ बराबर ⇒ समद्विबाहु।
क्षेत्रफल=½|1(6−2)+4(2−2)+7(2−6)|=½|4+0−28|=½(−24)=12
✔️ Final: प्रकार=समद्विबाहु, क्षेत्रफल=12

🔵 प्रश्न 27 (4 अंक)
त्रिभुज के शीर्ष A(−1, −1), B(2, 3), C(−3, 4) हैं। माध्यिकाओं के प्रतिच्छेदन बिंदु के निर्देशांक ज्ञात कीजिए।
🟢 उत्तर
माध्यिकाओं का प्रतिच्छेदन = केन्द्रक = ((x₁+x₂+x₃)/3,(y₁+y₂+y₃)/3)
= ((−1+2−3)/3,(−1+3+4)/3)
= ((−2)/3,(6)/3)
= (−2/3,2)
✔️ Final: (−2/3,2)

🔵 प्रश्न 28 (4 अंक)
दिखाइए कि बिंदु P(1,2), Q(3,6), R(5,10) सह-रेखीय हैं।
🟢 उत्तर
ढाल PQ=(6−2)/(3−1)=4/2=2
ढाल QR=(10−6)/(5−3)=4/2=2
PQ की ढाल=QR की ढाल ⇒ सह-रेखीय।
✔️ Final: सह-रेखीय।

🔵 प्रश्न 29 (4 अंक)
त्रिभुज A(0,0), B(6,0), C(0,8) के भुजा-मध्यबिंदु जोड़कर बने त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
🟢 उत्तर
S_ABC=½|0(0−8)+6(8−0)+0(0−0)|=½|48|=24
मध्यबिंदु त्रिभुज क्षेत्रफल=¼×24=6
✔️ Final: 6 वर्ग-एकक

🔵 प्रश्न 30 (4 अंक)
समांतर चतुर्भुज के शीर्ष A(1,2), B(5,2), C(6,6) हैं। D ज्ञात कीजिए और क्षेत्रफल बताइए।
🟢 उत्तर
D=A+C−B=(1,2)+(6,6)−(5,2)=(2,6)
क्षेत्रफल=½|1(2−6)+5(6−2)+6(2−2)|+½|1(6−6)+6(6−2)+2(2−6)|=8+8=16
✔️ Final: D(2,6), क्षेत्रफल=16 वर्ग-एकक

————————————————————————————————————————————————————————————————————————————

मनोमानचित्र

————————————————————————————————————————————————————————————————————————————