Class 10 : Maths (In Hindi) – Lesson 4. द्विघात समीकरण

पाठ का विश्लेषण  एवं  विवेचन

🔵 परिचय
गणित में समीकरण वह संबंध है जिसमें दो बीजीय अभिव्यक्तियाँ बराबर होती हैं।
द्विघात समीकरण (Quadratic Equation) बीजगणित का सबसे महत्त्वपूर्ण अध्याय है।
यह समीकरण चर (x) में दूसरे घात (x²) तक होता है और इसका हल (मूल) ढूँढना ही हमारा उद्देश्य है।
📌 परिभाषा:
ax² + bx + c = 0 (जहाँ a ≠ 0, a, b, c वास्तविक संख्याएँ) को द्विघात समीकरण कहते हैं।

🟢 1. द्विघात समीकरण की पहचान
यदि उच्चतम घात = 2 हो → द्विघात समीकरण।
यदि उच्चतम घात < 2 → रैखिक समीकरण।
यदि उच्चतम घात > 2 → उच्च घात समीकरण।
उदाहरण:
🔹 2x² + 3x + 5 = 0 → द्विघात
🔹 5y² – 7 = 0 → द्विघात
🔹 z² + √2z – 1 = 0 → द्विघात

🔴 2. द्विघात समीकरण बनाने की विधियाँ
🔹 शब्द समस्याओं (Word Problems) से द्विघात समीकरण बनाना।
उदाहरण: किसी संख्या का वर्ग उसके 5 गुना से 14 अधिक है।
➡️ मान लें संख्या = x
➡️ x² = 5x + 14
➡️ x² – 5x – 14 = 0 (द्विघात समीकरण)

🟡 3. द्विघात समीकरण हल करने की विधियाँ
✳️ (i) गुणनखण्ड विधि
उदाहरण: x² – 5x + 6 = 0
➡️ x² – 5x + 6 = (x – 2)(x – 3) = 0
➡️ हल: x = 2, x = 3

✳️ (ii) वर्ग पूर्ण करने की विधि
उदाहरण: x² + 6x – 7 = 0
➡️ x² + 6x = 7
➡️ x² + 6x + 9 = 7 + 9
➡️ (x + 3)² = 16
➡️ x + 3 = ±4
➡️ x = 1 या x = −7
✔️ हल: (1, −7)

✳️ (iii) सामान्य सूत्र विधि (Quadratic Formula)
यदि ax² + bx + c = 0 हो, तो
x = (−b ± √(b² − 4ac)) / 2a
उदाहरण: 2x² + 3x – 2 = 0
➡️ a = 2, b = 3, c = −2
➡️ D = b² − 4ac = 9 − (−16) = 25
➡️ x = (−3 ± √25) / 4
➡️ x = (−3 ± 5) / 4
➡️ x = (2/4) या (−8/4)
➡️ x = 1/2 या −2
✔️ हल: (1/2, −2)

🌿 4. विवर्तक (Discriminant)
परिभाषा: D = b² − 4ac
✔️ यह मूलों की प्रकृति बताता है।
यदि D > 0 और पूर्ण वर्ग हो → वास्तविक, भिन्न, परिमेय मूल।
यदि D > 0 और पूर्ण वर्ग न हो → वास्तविक, भिन्न, अपरिमेय मूल।
यदि D = 0 → वास्तविक, समान मूल।
यदि D < 0 → काल्पनिक मूल।

⚡ 5. द्विघात समीकरण के मूलों का गुण–नियम
यदि x₁ और x₂ मूल हैं:
x₁ + x₂ = −b/a
x₁ × x₂ = c/a
उदाहरण: x² − 5x + 6 = 0
➡️ मूल: 2 और 3
➡️ योग = 2 + 3 = 5 = −(−5)/1
➡️ गुणनफल = 2 × 3 = 6 = 6/1 ✔️

🟢 6. द्विघात समीकरण बनाना जब मूल दिए हों
यदि मूल x₁ और x₂ दिए हों, तो समीकरण:
x² − (x₁ + x₂)x + (x₁x₂) = 0
उदाहरण: मूल = 4 और 5
➡️ समीकरण = x² − 9x + 20 = 0

🔴 7. वास्तविक जीवन में उपयोग
क्षेत्रफल और परिमाप की समस्याएँ।
वेग–समय सम्बन्धी समस्याएँ।
वाणिज्य और लाभ–हानि।
भौतिकी में प्रक्षेप्य गति (Projectile Motion)।

✏️ Note:
द्विघात समीकरण हमेशा a ≠ 0 की शर्त पूरी करता है।
यदि a = 0 हो जाए तो समीकरण रैखिक हो जाएगा।

🟡 सारांश
द्विघात समीकरण का रूप: ax² + bx + c = 0, a ≠ 0।
पहचान: उच्चतम घात = 2।
बनाने की विधियाँ: शब्द समस्याओं से।
हल करने की विधियाँ:
• गुणनखण्ड विधि
• वर्ग पूर्ण करने की विधि
• सामान्य सूत्र विधि
विवर्तक (D = b² − 4ac):
• D > 0 (पूर्ण वर्ग) → वास्तविक, परिमेय, भिन्न मूल।
• D > 0 (पूर्ण वर्ग नहीं) → वास्तविक, अपरिमेय, भिन्न मूल।
• D = 0 → वास्तविक, समान मूल।
• D < 0 → काल्पनिक मूल।
मूलों के गुण–नियम:
• x₁ + x₂ = −b/a
• x₁x₂ = c/a
जब मूल दिए हों तो समीकरण बनाना: x² − (योग)x + गुणनफल = 0
अनुप्रयोग: क्षेत्रफल–परिमाप, गति–समय, लाभ–हानि, भौतिकी।

📝 Quick Recap
🔵 द्विघात समीकरण = ax² + bx + c = 0 (a ≠ 0)।
🟢 हल की विधियाँ = गुणनखण्ड, वर्ग पूर्ण करना, सामान्य सूत्र।
🔴 विवर्तक (D) मूलों की प्रकृति तय करता है।
🟡 मूलों के योग–गुणनफल के सूत्र याद रखें।
🌿 अनुप्रयोग = ज्यामिति, भौतिकी, वाणिज्य।

————————————————————————————————————————————————————————————————————————–

पाठ्यपुस्तक के प्रश्न

➤ प्रश्नावली 4.1

🔵 प्रश्न 1: जाँच कीजिए कि क्या निम्न द्विघात समीकरण हैं :
(i) (x+1)² = 2(x−3)
(ii) x² − 2x = (−2)(3 − x)
(iii) (x−2)(x+1) = (x−1)(x+3)
(iv) (x−3)(2x+1) = −(x+5)
(v) (2x−1)(x−3) = (x+5)(x−1)
(vi) x² + 3x + 1 = (x−2)²
(vii) (x+2)³ = 2x²(x² − 1)
(viii) x³ − 4x² − x + 1 = (x − 2)³

🟢 उत्तर 1 (एक-एक पद सरल करके, एक-एक पंक्ति में):

🟣 (i) (x+1)² = 2(x−3)
➡️ x² + 2x + 1 = 2x − 6
➡️ x² + 2x + 1 − 2x + 6 = 0
➡️ x² + 7 = 0 ⇒ ✔️ द्विघात

🟣 (ii) x² − 2x = (−2)(3 − x) = −6 + 2x
➡️ x² − 2x + 6 − 2x = 0
➡️ x² − 4x + 6 = 0 ⇒ ✔️ द्विघात

🟣 (iii) (x−2)(x+1) = (x−1)(x+3)
➡️ (x² − x − 2) = (x² + 2x − 3)
➡️ x² − x − 2 − x² − 2x + 3 = 0
➡️ −3x + 1 = 0 ⇒ ✖️ रैखिक (द्विघात नहीं)

🟣 (iv) (x−3)(2x+1) = −(x+5)
➡️ 2x² − 5x − 3 = −x − 5
➡️ 2x² − 5x − 3 + x + 5 = 0
➡️ 2x² − 4x + 2 = 0 ⇒ (भाग 2 से) x² − 2x + 1 = 0 ⇒ ✔️ द्विघात

🟣 (v) (2x−1)(x−3) = (x+5)(x−1)
➡️ (2x² − 7x + 3) = (x² + 4x − 5)
➡️ 2x² − 7x + 3 − x² − 4x + 5 = 0
➡️ x² − 11x + 8 = 0 ⇒ ✔️ द्विघात

🟣 (vi) x² + 3x + 1 = (x−2)² = x² − 4x + 4
➡️ x² + 3x + 1 − x² + 4x − 4 = 0
➡️ 7x − 3 = 0 ⇒ ✖️ रैखिक (द्विघात नहीं)

🟣 (vii) (x+2)³ = 2x²(x² − 1)
➡️ x³ + 6x² + 12x + 8 = 2x⁴ − 2x²
➡️ −2x⁴ + x³ + 8x² + 12x + 8 = 0
➡️ घात 4 ⇒ ✖️ द्विघात नहीं

🟣 (viii) x³ − 4x² − x + 1 = (x − 2)³ = x³ − 6x² + 12x − 8
➡️ x³ − 4x² − x + 1 − x³ + 6x² − 12x + 8 = 0
➡️ 2x² − 13x + 9 = 0 ⇒ ✔️ द्विघात

🧭 निष्कर्ष: ✔️ द्विघात — (i), (ii), (iv), (v), (viii) ; ✖️ द्विघात नहीं — (iii), (vi), (vii)

🔵 प्रश्न 2: निम्न स्थितियों का द्विघात समीकरणों के रूप में निरूपण कीजिए :
(i) एक आयताकार भूखण्ड का क्षेत्रफल 528 m² है। क्षेत्र की लंबाई (मीटर में) चौड़ाई के दूने से 4 m अधिक है। भूखण्ड की लंबाई और चौड़ाई ज्ञात करनी है।
(ii) दो क्रमागत धनात्मक पूर्णांकों का गुणनफल 306 है। दोनों पूर्णांकों का ज्ञात करना है।
(iii) रोहन की माँ उससे 26 वर्ष बड़ी है। उनकी आयु (वर्ष में) का गुणनफल अब से 3 वर्ष पश्चात 360 हो जाएगा। रोहन की वर्तमान आयु ज्ञात करनी है।
(iv) एक रेलगाड़ी 480 km की दूरी एक समान चाल से तय करती है। यदि इसकी चाल 8 km/h कम होती, तो वह उसी दूरी को तय करने में 3 h अधिक लेती। रेलगाड़ी की चाल ज्ञात करनी है।

🟢 उत्तर 2 (सिर्फ समीकरण बनाना; एक-एक पंक्ति):

🟣 (i) मान लें चौड़ाई = x m, तब लंबाई = 2x + 4 m
➡️ क्षेत्रफल: x(2x + 4) = 528
➡️ 2x² + 4x − 528 = 0 ⇒ (भाग 2 से) x² + 2x − 264 = 0 ⟵ ✔️ द्विघात

🟣 (ii) मान लें पहला पूर्णांक = n, दूसरा = n + 1
➡️ गुणनफल: n(n + 1) = 306
➡️ n² + n − 306 = 0 ⟵ ✔️ द्विघात

🟣 (iii) मान लें रोहन की वर्तमान आयु = x वर्ष, माँ की = x + 26 वर्ष
➡️ 3 वर्ष बाद आयुएँ: (x + 3) और (x + 29)
➡️ (x + 3)(x + 29) = 360
➡️ x² + 32x + 87 − 360 = 0 ⇒ x² + 32x − 273 = 0 ⟵ ✔️ द्विघात

🟣 (iv) मान लें चाल = x km/h, समय = 480/x h
➡️ नई चाल = x − 8, नया समय = 480/(x − 8) h
➡️ 480/(x − 8) = 480/x + 3
➡️ 480x − 480(x − 8) = 3x(x − 8)
➡️ 3840 = 3x² − 24x
➡️ 3x² − 24x − 3840 = 0 ⇒ (भाग 3 से) x² − 8x − 1280 = 0 ⟵ ✔️ द्विघात

➤ प्रश्नावली 4.2

🔵 प्रश्न 1: गुणनखंड विधि से निम्न द्विघात समीकरणों के मूल ज्ञात कीजिए :
🟣 (i) x² − 3x − 10 = 0
➡️ x² − 5x + 2x − 10 = 0
➡️ x(x − 5) + 2(x − 5) = 0
➡️ (x − 5)(x + 2) = 0
✔️ x = 5, −2
🟣 (ii) 2x² + x − 6 = 0
➡️ 2x² + 4x − 3x − 6 = 0
➡️ (2x² + 4x) − (3x + 6) = 0
➡️ 2x(x+2) − 3(x+2) = 0
➡️ (2x − 3)(x + 2) = 0
✔️ x = 3/2, −2
🟣 (iii) √2 x² + 7x + 5√2 = 0
➡️ √2 x² + 2x + 5x + 5√2 = 0
➡️ (√2 x² + 2x) + (5x + 5√2) = 0
➡️ x(√2 x + 2) + 5( x + √2) = 0
➡️ (√2 x + 2)(x + 5) = 0
✔️ x = −√2, −5
🟣 (iv) 2x² − x + 1/8 = 0
➡️ 16x² − 8x + 1 = 0 (भाजक हटाने हेतु 8 से गुणा)
➡️ (4x − 1)(4x − 1) = 0
➡️ (4x − 1)² = 0
✔️ x = 1/4 (दोहरा मूल)
🟣 (v) 100x² − 20x + 1 = 0
➡️ (10x − 1)(10x − 1) = 0
➡️ (10x − 1)² = 0
✔️ x = 1/10 (दोहरा मूल)

🔵 प्रश्न 2: उदाहरण 1 में दी गई समस्याओं को हल कीजिए।
✳️ उदाहरण 1 = Code 2 का प्रश्न 1 पहले ही हल हो चुका (मूल ज्ञात करना)। अतः प्रश्न 2 का आशय है – वही विधि अपनाकर समस्याएँ हल करें।

🔵 प्रश्न 3: ऐसी दो संख्याएँ ज्ञात कीजिए, जिनका योग 27 हो और गुणनफल 182 हो।
➡️ मान लें संख्याएँ = x और y
➡️ x + y = 27, xy = 182
➡️ समीकरण: t² − (x+y)t + xy = 0
➡️ t² − 27t + 182 = 0
➡️ (t − 13)(t − 14) = 0
✔️ संख्याएँ = 13 और 14

🔵 प्रश्न 4: दो क्रमागत धनात्मक पूर्णांक ज्ञात कीजिए जिनके वर्गों का योग 365 हो।
➡️ मान लें पहला पूर्णांक = n, दूसरा = n+1
➡️ n² + (n+1)² = 365
➡️ n² + n² + 2n + 1 = 365
➡️ 2n² + 2n + 1 − 365 = 0
➡️ 2n² + 2n − 364 = 0
➡️ n² + n − 182 = 0
➡️ (n − 13)(n + 14) = 0
✔️ n = 13 (धनात्मक)
➡️ पूर्णांक = 13, 14

🔵 प्रश्न 5 :
एक समकोण त्रिभुज की ऊँचाई इसके आधार से 7 cm कम है। यदि कर्ण 13 cm का हो, तो अन्य दो भुजाओं का ज्ञात कीजिए।
🟢 उत्तर 5 :
➡️ मान लें आधार = x cm
➡️ ऊँचाई = (x − 7) cm
➡️ कर्ण = 13 cm
✳️ पाइथागोरस प्रमेय:
कर्ण² = आधार² + ऊँचाई²
13² = x² + (x − 7)²
➡️ 169 = x² + (x² − 14x + 49)
➡️ 169 = 2x² − 14x + 49
➡️ 2x² − 14x + 49 − 169 = 0
➡️ 2x² − 14x − 120 = 0
➡️ x² − 7x − 60 = 0
✳️ गुणनखंड:
(x − 12)(x + 5) = 0
✔️ x = 12 (धनात्मक मान)
➡️ आधार = 12 cm
➡️ ऊँचाई = 12 − 7 = 5 cm
✔️ अन्य दो भुजाएँ = 12 cm और 5 cm

🔵 प्रश्न 6 :
एक कुटीर उद्योग एक दिन में कुछ बर्तन बनाता है। एक दिन यह पाया गया कि प्रत्येक नग की लागत उस दिन बनाए गए बर्तनों की संख्या के दुगुने से 3 अधिक थी और कुल लागत 90 रु. थी। प्रतिदिन बनाए गए बर्तनों की संख्या ज्ञात कीजिए।
🟢 उत्तर 6 :
➡️ मान लें प्रतिदिन बनाए गए बर्तन = x
➡️ प्रति नग लागत = 2x + 3 रु.
➡️ कुल लागत = x(2x + 3) = 90
✳️ समीकरण:
2x² + 3x − 90 = 0
✳️ गुणनखंड:
2x² + 15x − 12x − 90 = 0
(2x² + 15x) − (12x + 90) = 0
x(2x + 15) − 6(2x + 15) = 0
(2x + 15)(x − 6) = 0
✔️ x = 6 (धनात्मक मान)
➡️ प्रति नग लागत = 2(6) + 3 = 15 रु.
✔️ प्रतिदिन बनाए गए बर्तन = 6

➤ प्रश्नावली 4.3

🔵 प्रश्न 1.
निम्न द्विघात समीकरणों के मूलों की प्रकृति ज्ञात कीजिए। यदि मूलों का अस्तित्व हो तो उन्हें ज्ञात कीजिए :
🟣 (i) 2x² – 3x + 5 = 0
➡️ a = 2, b = −3, c = 5
➡️ D = b² − 4ac = (−3)² − 4(2)(5) = 9 − 40 = −31
✔️ D < 0 ⇒ वास्तविक मूल नहीं (केवल कल्पित मूल होंगे)
🟣 (ii) 3x² − 4√3 x + 4 = 0
➡️ a = 3, b = −4√3, c = 4
➡️ D = (−4√3)² − 4(3)(4) = 48 − 48 = 0
✔️ D = 0 ⇒ दो समान वास्तविक मूल
➡️ x = −b/2a = (4√3)/6 = 2√3/3
🟣 (iii) 2x² − 6x + 3 = 0
➡️ a = 2, b = −6, c = 3
➡️ D = b² − 4ac = (−6)² − 4(2)(3) = 36 − 24 = 12
✔️ D > 0 ⇒ दो भिन्न वास्तविक मूल
➡️ x = [6 ± √12] / 4
➡️ x = [6 ± 2√3] / 4
➡️ x = (3 ± √3)/2

🔵 प्रश्न 2.
निम्न प्रत्येक द्विघात समीकरण में k का ऐसा मान ज्ञात कीजिए कि उसके दो बराबर मूल हों :
🟣 (i) 2x² + kx + 3 = 0
➡️ दो समान मूल होने हेतु D = 0
➡️ D = k² − 4(2)(3) = k² − 24 = 0
✔️ k² = 24 ⇒ k = ±2√6
🟣 (ii) kx(x − 2) + 6 = 0
➡️ kx² − 2kx + 6 = 0
➡️ D = (−2k)² − 4(k)(6) = 4k² − 24k
➡️ 4k(k − 6) = 0
✔️ k = 0 या 6
➡️ k = 0 पर यह द्विघात नहीं रहेगा
✔️ अतः k = 6

🔵 प्रश्न 3.
क्या एक आयताकार बग़ीचा बनाना संभव है जिसकी लंबाई, चौड़ाई के दूने के बराबर हो और उसका क्षेत्रफल 800 m² हो? यदि हाँ, तो उसकी लंबाई और चौड़ाई ज्ञात कीजिए।
🟢 उत्तर:
➡️ मान लें चौड़ाई = x m ⇒ लंबाई = 2x m
➡️ क्षेत्रफल = x × 2x = 2x²
➡️ 2x² = 800 ⇒ x² = 400
➡️ x = 20 m
✔️ चौड़ाई = 20 m, लंबाई = 40 m

🔵 प्रश्न 4.
दो मित्रों की आयु का योग 20 वर्ष है। चार वर्ष पूर्व उनकी आयुओं का गुणनफल 48 था। उनकी वर्तमान आयु ज्ञात कीजिए।
🟢 उत्तर:
➡️ मान लें वर्तमान आयु = x और (20 − x)
➡️ 4 वर्ष पूर्व आयु = (x − 4) और (16 − x)
➡️ (x − 4)(16 − x) = 48
➡️ −x² + 20x − 64 = 48
➡️ −x² + 20x − 112 = 0
➡️ x² − 20x + 112 = 0
➡️ D = (−20)² − 4(1)(112) = 400 − 448 = −48 < 0
✔️ कोई वास्तविक हल नहीं ⇒ असंभव स्थिति

🔵 प्रश्न 5.
एक परिमाप 80 m तथा क्षेत्रफल 400 m² का एक पार्क बनाना संभव है? यदि हाँ, तो उसकी लंबाई और चौड़ाई ज्ञात कीजिए।
🟢 उत्तर:
➡️ मान लें लंबाई = x, चौड़ाई = y
➡️ 2(x + y) = 80 ⇒ x + y = 40 …(1)
➡️ xy = 400 …(2)
(1) से y = 40 − x
➡️ x(40 − x) = 400
➡️ 40x − x² = 400
➡️ x² − 40x + 400 = 0
➡️ D = (−40)² − 4(1)(400) = 1600 − 1600 = 0
✔️ समान वास्तविक मूल ⇒ x = 20
➡️ y = 40 − 20 = 20
✔️ लंबाई = 20 m, चौड़ाई = 20 m (पार्क वर्गाकार है)

————————————————————————————————————————————————————————————————————————–

अन्य महत्वपूर्ण प्रश्न

Section A (1 अंक वाले प्रश्न)
🔵 प्रश्न 1
समीकरण 2x² – 3x + 1 = 0 के गुणांकों (a, b, c) की पहचान कीजिए।
🟢 उत्तर
➡️ a = 2, b = –3, c = 1 ✔️

🔵 प्रश्न 2
द्विघात समीकरण का सामान्य रूप लिखिए।
🟢 उत्तर
➡️ सामान्य रूप है : ax² + bx + c = 0, जहाँ a ≠ 0 ✔️

🔵 प्रश्न 3
यदि किसी द्विघात समीकरण में विवर्तक (D) = 0 हो, तो उसके मूलों की प्रकृति क्या होगी?
🟢 उत्तर
➡️ मूल वास्तविक और समान होंगे ✔️

🔵 प्रश्न 4
समीकरण x² – 9 = 0 के मूल ज्ञात कीजिए।
🟢 उत्तर
➡️ x² – 9 = 0
➡️ x² = 9
➡️ x = ±3
✔️ मूल = 3, –3

🔵 प्रश्न 5
यदि किसी द्विघात समीकरण के मूल α और β हों, तो मूलों का गुणनफल क्या होगा?
🟢 उत्तर
➡️ αβ = c/a ✔️

🔵 प्रश्न 6
समीकरण x² + 5x + 6 = 0 के मूल ज्ञात कीजिए।
🟢 उत्तर
➡️ x² + 5x + 6 = 0
➡️ (x + 2)(x + 3) = 0
➡️ x = –2, –3 ✔️

Section B (2 अंक वाले प्रश्न)
🔵 प्रश्न 7
समीकरण x² – 7x + 10 = 0 के मूल ज्ञात कीजिए।
🟢 उत्तर
➡️ x² – 7x + 10 = 0
➡️ (x – 5)(x – 2) = 0
➡️ x = 5, 2 ✔️

🔵 प्रश्न 8
समीकरण 2x² – 4x + 3 = 0 के विवर्तक का मान ज्ञात कीजिए और मूलों की प्रकृति बताइए।
🟢 उत्तर
➡️ D = b² – 4ac
➡️ = (–4)² – 4(2)(3)
➡️ = 16 – 24
➡️ = –8
✔️ D < 0 ⇒ मूल वास्तविक नहीं, बल्कि काल्पनिक हैं।

🔵 प्रश्न 9
यदि किसी द्विघात समीकरण का एक मूल 2 है और समीकरण x² – 5x + k = 0 है, तो k का मान ज्ञात कीजिए।
🟢 उत्तर
➡️ एक मूल = 2
➡️ 2² – 5(2) + k = 0
➡️ 4 – 10 + k = 0
➡️ –6 + k = 0
➡️ k = 6 ✔️

🔵 प्रश्न 10
समीकरण 3x² – 2x – 1 = 0 को गुणनखण्ड विधि से हल कीजिए।
🟢 उत्तर
➡️ 3x² – 2x – 1 = 0
➡️ 3x² – 3x + x – 1 = 0
➡️ (3x² – 3x) + (x – 1) = 0
➡️ 3x(x – 1) + 1(x – 1) = 0
➡️ (3x + 1)(x – 1) = 0
➡️ x = –1/3, 1 ✔️

🔵 प्रश्न 11
यदि किसी द्विघात समीकरण के मूल α और β हों तथा α + β = 8 और αβ = 15 हो, तो समीकरण बनाइए।
🟢 उत्तर
➡️ सामान्य रूप : x² – (α + β)x + αβ = 0
➡️ x² – (8)x + 15 = 0
➡️ x² – 8x + 15 = 0 ✔️

🔵 प्रश्न 12
समीकरण x² – 2√2 x + 2 = 0 को हल कीजिए।
🟢 उत्तर
➡️ D = b² – 4ac
➡️ = (–2√2)² – 4(1)(2)
➡️ = 8 – 8 = 0
➡️ मूल = –b/2a
➡️ = –(–2√2) / 2(1)
➡️ = 2√2 / 2
➡️ = √2
✔️ दोनों मूल समान हैं = √2

Section C (3 अंक वाले प्रश्न)
🔵 प्रश्न 13
समीकरण 2x² – 5x + 3 = 0 के मूल ज्ञात कीजिए।
🟢 उत्तर
➡️ a = 2, b = –5, c = 3
➡️ D = b² – 4ac = (–5)² – 4(2)(3) = 25 – 24 = 1
➡️ मूल = [–b ± √D]/2a
➡️ = [5 ± √1]/4
➡️ = (5 ± 1)/4
➡️ x = 6/4 = 3/2, x = 4/4 = 1
✔️ मूल = 3/2, 1

🔵 प्रश्न 14
समीकरण 5x² – 6x – 2 = 0 को सूत्र विधि से हल कीजिए।
🟢 उत्तर
➡️ a = 5, b = –6, c = –2
➡️ D = b² – 4ac = (–6)² – 4(5)(–2) = 36 + 40 = 76
➡️ मूल = [–b ± √D]/2a
➡️ = [6 ± √76]/10
➡️ = [6 ± 2√19]/10
➡️ = (3 ± √19)/5
✔️ मूल = (3 + √19)/5, (3 – √19)/5

🔵 प्रश्न 15
एक द्विघात समीकरण का एक मूल –1 है और दूसरा 3 है। समीकरण लिखिए।
🟢 उत्तर
➡️ α = –1, β = 3
➡️ समीकरण = (x – α)(x – β) = 0
➡️ = (x + 1)(x – 3) = 0
➡️ = x² – 2x – 3 = 0 ✔️

🔵 प्रश्न 16
यदि किसी द्विघात समीकरण में मूलों का योग = 7 और गुणनफल = 12 हो, तो समीकरण ज्ञात कीजिए।
🟢 उत्तर
➡️ सामान्य रूप : x² – (α+β)x + αβ = 0
➡️ = x² – (7)x + 12 = 0
➡️ = x² – 7x + 12 = 0 ✔️

🔵 प्रश्न 17
समीकरण 6x² – x – 2 = 0 को हल कीजिए।
🟢 उत्तर
➡️ 6x² – x – 2 = 0
➡️ 6x² – 4x + 3x – 2 = 0
➡️ (6x² – 4x) + (3x – 2) = 0
➡️ 2x(3x – 2) + 1(3x – 2) = 0
➡️ (2x + 1)(3x – 2) = 0
➡️ x = –1/2, 2/3 ✔️

🔵 प्रश्न 18
x के लिए हल कीजिए :
(1/x²) – (5/x) + 6 = 0
🟢 उत्तर
➡️ मान लीजिए y = 1/x
➡️ तो समीकरण : y² – 5y + 6 = 0
➡️ (y – 2)(y – 3) = 0
➡️ y = 2, 3
➡️ 1/x = 2 ⇒ x = 1/2
➡️ 1/x = 3 ⇒ x = 1/3
✔️ हल = 1/2, 1/3

🔵 प्रश्न 19
समीकरण 4x² + 4√3 x + 3 = 0 के मूल ज्ञात कीजिए।
🟢 उत्तर
➡️ a = 4, b = 4√3, c = 3
➡️ D = b² – 4ac = (4√3)² – 4(4)(3)
➡️ = 48 – 48 = 0
➡️ मूल = –b/2a = –4√3 / 8 = –√3/2
✔️ दोनों मूल समान हैं = –√3/2

🔵 प्रश्न 20
यदि समीकरण x² + px + 16 = 0 के मूल वास्तविक एवं समान हों, तो p का मान ज्ञात कीजिए।
🟢 उत्तर
➡️ D = b² – 4ac
➡️ = p² – 4(1)(16)
➡️ = p² – 64
➡️ D = 0 ⇒ p² – 64 = 0
➡️ p² = 64
➡️ p = ±8 ✔️

🔵 प्रश्न 21 (आन्तरिक विकल्प)
(A) समीकरण x² – 2x – 15 = 0 को हल कीजिए।
या
(B) समीकरण 2x² – 7x + 3 = 0 के मूल ज्ञात कीजिए।
🟢 उत्तर (A)
➡️ x² – 2x – 15 = 0
➡️ (x – 5)(x + 3) = 0
➡️ x = 5, –3 ✔️
🟢 उत्तर (B)
➡️ 2x² – 7x + 3 = 0
➡️ D = (–7)² – 4(2)(3) = 49 – 24 = 25
➡️ x = [7 ± √25]/4
➡️ = (7 ± 5)/4
➡️ x = 12/4 = 3, x = 2/4 = 1/2
✔️ मूल = 3, 1/2

🔵 प्रश्न 22 (आन्तरिक विकल्प)
(A) यदि किसी द्विघात समीकरण का विवर्तक 0 से बड़ा हो, तो मूलों की प्रकृति बताइए।
या
(B) समीकरण 9x² – 12x + 4 = 0 के मूल ज्ञात कीजिए।
🟢 उत्तर (A)
➡️ यदि D > 0 ⇒ मूल वास्तविक एवं असमान होंगे ✔️
🟢 उत्तर (B)
➡️ 9x² – 12x + 4 = 0
➡️ D = (–12)² – 4(9)(4)
➡️ = 144 – 144 = 0
➡️ मूल = –b/2a = 12 / 18 = 2/3
✔️ दोनों मूल समान हैं = 2/3

🔴 Section D (4 अंक वाले प्रश्न)
🔵 प्रश्न 23
समीकरण 3x² – 4x – 5 = 0 को सूत्र विधि से हल कीजिए।
🟢 उत्तर
✳️ सूत्र: x = [-b ± √(b² – 4ac)] / 2a
➤ a = 3, b = –4, c = –5
➤ D = (–4)² – 4(3)(–5) = 16 + 60 = 76
➤ x = [4 ± √76] / 6
➤ = [4 ± 2√19] / 6
➤ = (2 ± √19)/3
✔️ Final: मूल = (2 + √19)/3 , (2 – √19)/3

🔵 प्रश्न 24 (आन्तरिक विकल्प)
(A) उन सभी k के मान ज्ञात कीजिए जिनके लिए समीकरण x² – 2(k+1)x + (k² + 2k) = 0 के मूल वास्तविक एवं असमान हों।
या
(B) सिद्ध कीजिए कि यदि किसी द्विघात ax² + bx + c = 0 में b² = 4ac हो, तो दोनों मूल समान होते हैं।
🟢 उत्तर (A)
➤ D = [–2(k+1)]² – 4(1)(k² + 2k)
➤ = 4(k+1)² – 4(k² + 2k)
➤ = 4[(k² + 2k + 1) – (k² + 2k)]
➤ = 4(1) = 4 > 0
✔️ Final: सभी वास्तविक k के लिए मूल वास्तविक एवं असमान हैं।
🟢 उत्तर (B)
➤ यदि b² = 4ac ⇒ D = 0
➤ D = 0 होने पर दोनों मूल समान।
✔️ Final: सिद्ध हुआ।

🔵 प्रश्न 25
यदि x² – 5x + 6 = 0 और x² – 7x + p = 0 का एक साझा मूल हो, तो p का मान तथा साझा मूल ज्ञात कीजिए।
🟢 उत्तर
➤ x² – 5x + 6 = (x – 2)(x – 3) ⇒ मूल = 2, 3
➤ साझा मूल 2 मानते हैं:
2² – 7(2) + p = 0
➤ 4 – 14 + p = 0
➤ p = 10
✔️ Final: p = 10 , साझा मूल = 2

🔵 प्रश्न 26 (आन्तरिक विकल्प)
(A) किसी संख्या से 3 कम और 4 अधिक का गुणनफल 77 है।
या
(B) दो क्रमागत पूर्णांकों का गुणनफल 156 है।
🟢 उत्तर (A)
➤ संख्या = x
➤ (x – 3)(x + 4) = 77
➤ x² + x – 89 = 0
➤ D = 357
➤ x = [–1 ± √357]/2
✔️ Final: x = (–1 + √357)/2 , (–1 – √357)/2
🟢 उत्तर (B)
➤ पूर्णांक = n , n+1
➤ n(n+1) = 156
➤ n² + n – 156 = 0
➤ (n+13)(n–12) = 0
➤ n = 12 या –13
✔️ Final: पूर्णांक = (12,13) या (–13,–12)

🔵 प्रश्न 27
यदि मूल α, β इस प्रकार हों कि α+β = 7/2 तथा αβ = –3/2, तो समीकरण एवं मूल ज्ञात कीजिए।
🟢 उत्तर
➤ समीकरण: x² – (7/2)x – 3/2 = 0
➤ 2x² – 7x – 3 = 0
➤ D = 73
➤ x = [7 ± √73]/4
✔️ Final: समीकरण = 2x² – 7x – 3 ; मूल = (7 ± √73)/4

🔵 प्रश्न 28 (आन्तरिक विकल्प)
(A) पूर्ण वर्ग विधि से x² – 8x + 5 = 0 हल कीजिए।
या
(B) 1/(x+1) + 1/(x–1) = 3/2 हल कीजिए।
🟢 उत्तर (A)
➤ x² – 8x + 5 = 0
➤ (x – 4)² = 11
➤ x = 4 ± √11
✔️ Final: x = 4 + √11 , 4 – √11
🟢 उत्तर (B)
➤ 1/(x+1) + 1/(x–1) = 3/2
➤ (2x)/(x² – 1) = 3/2
➤ 4x = 3x² – 3
➤ 3x² – 4x – 3 = 0
➤ D = 52 ⇒ √52 = 2√13
➤ x = (2 ± √13)/3
✔️ Final: x = (2 + √13)/3 , (2 – √13)/3

🔵 प्रश्न 29 (आन्तरिक विकल्प)
(A) वे m के मान ज्ञात कीजिए जिनके लिए mx² – 5x + 2 = 0 के मूल परिमेय हों।
या
(B) यदि x² + (k–3)x + (k–1) = 0 के मूल वास्तविक एवं असमान हों, तो k का मान-समुच्चय ज्ञात कीजिए।
🟢 उत्तर (A)
➤ D = 25 – 8m
➤ D = t² (पूर्ण वर्ग) ⇒ m = (25 – t²)/8
✔️ Final: m = (25 – t²)/8 जहाँ 25 – t² , 8 से विभाज्य हो।
🟢 उत्तर (B)
➤ D = (k–3)² – 4(k–1) = k² – 10k + 13
➤ D > 0 ⇒ k² – 10k + 13 > 0
➤ Critical points: k = 5 ± 2√3
✔️ Final: k < 5 – 2√3 या k > 5 + 2√3

🔵 प्रश्न 30
यदि x² – 4x + 1 = 0 के मूल α, β हों, तो α²+β² और 1/α + 1/β ज्ञात कीजिए।
🟢 उत्तर
➤ α+β = 4 , αβ = 1
➤ α²+β² = (α+β)² – 2αβ = 16 – 2 = 14
➤ 1/α + 1/β = (α+β)/αβ = 4/1 = 4
✔️ Final: α²+β² = 14 , 1/α + 1/β = 4

————————————————————————————————————————————————————————————————————————–

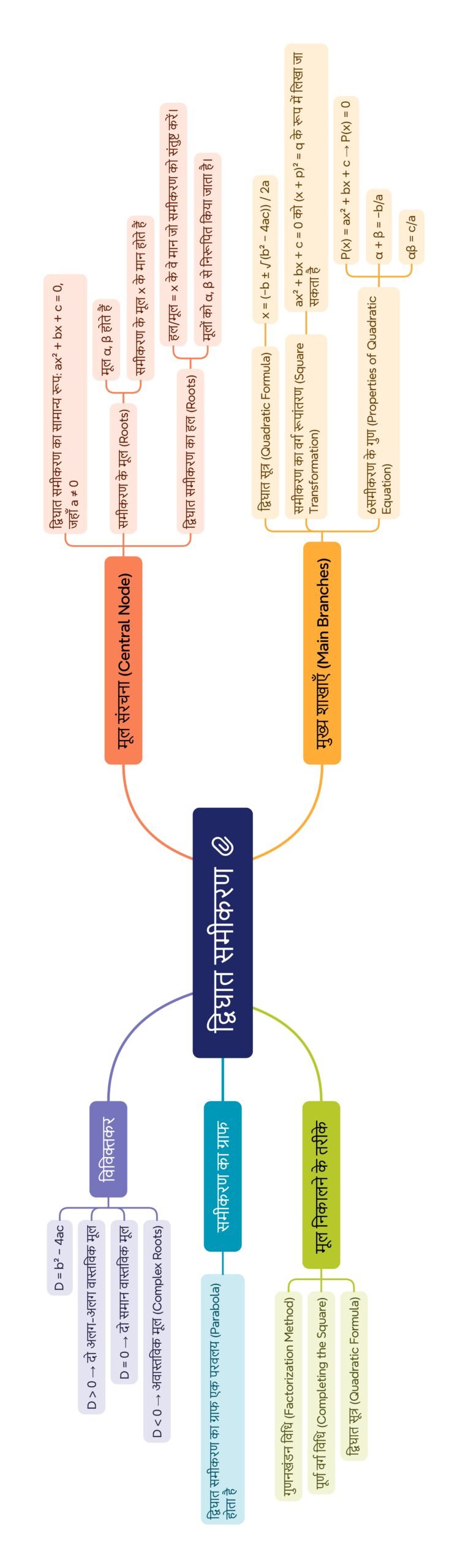
मानचित्र

————————————————————————————————————————————————————————————————————————–