Class 10 : Maths (In Hindi) – Lesson 2. बहुपद

पाठ का विश्लेषण  एवं  विवेचन

🔵 परिचय
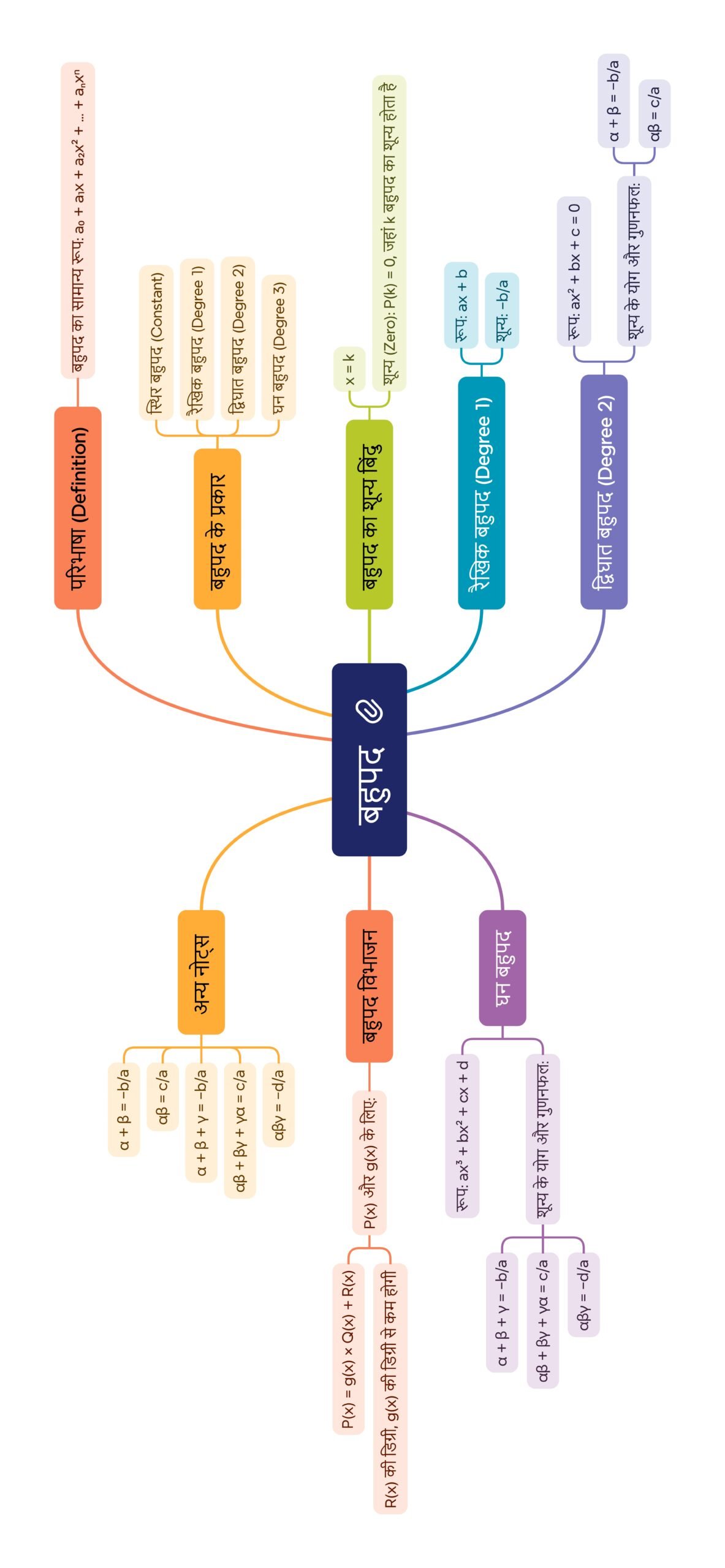
गणित में बहुपद (Polynomial) एक ऐसी बीजीय अभिव्यक्ति है जिसमें चर (x, y आदि) की घातें केवल पूर्णांक और अशून्य गुणांक के साथ होती हैं। बहुपद बीजगणित की रीढ़ हैं, क्योंकि इन्हीं से समीकरणों का निर्माण, हल और अनेक प्रमेयों की व्याख्या सम्भव होती है।
इस अध्याय का मुख्य उद्देश्य विद्यार्थियों को बहुपदों की परिभाषा, उनका वर्गीकरण, शून्यकों (Zeros) और गुणांकों (Coefficients) का संबंध, विभाजन एल्गोरिथ्म तथा व्यावहारिक उपयोग समझाना है।

🟢 1. बहुपद की परिभाषा
परिभाषा:
यदि p(x) = a₀ + a₁x + a₂x² + … + aₙxⁿ हो, जहाँ
a₀, a₁, …, aₙ वास्तविक संख्याएँ हैं,
n एक अशून्य पूर्णांक है,
तो इसे बहुपद कहते हैं।
✏️ टिप्पणी: x का उच्चतम घातांक बहुपद की घात (Degree) कहलाता है।

🔴 2. बहुपदों का वर्गीकरण
घात के आधार पर:
घात 1 → रैखिक बहुपद (Linear)
घात 2 → द्विघात बहुपद (Quadratic)
घात 3 → घन बहुपद (Cubic)
घात n → n घात का बहुपद
पदों की संख्या के आधार पर:
एकपद (Monomial) → जैसे 2x
द्विपद (Binomial) → जैसे x² + 3x
त्रिपद (Trinomial) → जैसे x² + 2x + 1

🟡 3. बहुपद के शून्यक (Zeros)
यदि p(x) किसी बहुपद का मान है और p(α) = 0 हो, तो α उस बहुपद का शून्यक कहलाता है।
उदाहरण:
p(x) = x² – 5x + 6
p(2) = 2² – 5×2 + 6 = 0
p(3) = 3² – 5×3 + 6 = 0
➡️ इस बहुपद के शून्यक 2 और 3 हैं।

🌿 4. बहुपद के शून्यकों और गुणांकों का संबंध
(i) द्विघात बहुपद
यदि p(x) = ax² + bx + c
और इसके शून्यक α, β हैं,
तो:
α + β = -b/a
αβ = c/a
(ii) घन बहुपद
यदि p(x) = ax³ + bx² + cx + d
और इसके शून्यक α, β, γ हैं,
तो:
α + β + γ = -b/a
αβ + βγ + γα = c/a
αβγ = -d/a
✔️ यह सम्बन्ध गणनाओं को सरल बनाते हैं।

⚡ 5. प्रमेय
(i) शेषफल प्रमेय (Remainder Theorem)
यदि p(x) किसी बहुपद को (x – a) से विभाजित किया जाए, तो शेषफल = p(a)।
उदाहरण:
p(x) = x² – 7x + 10
(x – 2) से विभाजित करने पर शेषफल = p(2) = 2² – 7×2 + 10 = 0।
✔️ अतः x – 2 एक गुणनखण्ड है।
(ii) गुणनखण्ड प्रमेय (Factor Theorem)
यदि p(a) = 0, तो (x – a) p(x) का गुणनखण्ड है।

🔵 6. बहुपदों का विभाजन एल्गोरिथ्म
विधि:
यदि p(x) और g(x) बहुपद हैं, और g(x) ≠ 0, तो बहुपद q(x) (भाजक) और r(x) (शेषफल) ऐसे मिलते हैं कि
p(x) = g(x) × q(x) + r(x),
जहाँ r(x) = 0 या r(x) की घात < g(x) की घात।
यह नियम संख्याओं के विभाजन जैसा ही है।

🟢 7. उदाहरण और प्रयोग
उदाहरण 1:
p(x) = x³ – 6x² + 11x – 6
p(1) = 0 ⇒ (x – 1) गुणनखण्ड
p(2) = 0 ⇒ (x – 2) गुणनखण्ड
p(3) = 0 ⇒ (x – 3) गुणनखण्ड
✔️ अतः p(x) = (x – 1)(x – 2)(x – 3)
प्रयोग:
बहुपदों से समीकरण हल करना।
शून्यकों से ग्राफ की आकृति बनाना।
इंजीनियरिंग और विज्ञान में गणनाएँ।

🌿 8. जीवन में उपयोग
आकाशीय पिंडों की गति का समीकरण बहुपद के रूप में।
क्षेत्रफल और आयतन की गणना।
उत्पादन–लागत–लाभ से जुड़े आँकड़े बहुपदों में।

✏️ टिप्पणी
बहुपदों में केवल पूर्णांक घातें आती हैं।
x^(-1), √x जैसी संख्याएँ बहुपद नहीं कहलातीं।

🟡 सारांश
बहुपद = बीजीय अभिव्यक्ति जिसमें चर की घातें पूर्णांक होती हैं।
वर्गीकरण:
• घात के आधार पर → रैखिक, द्विघात, घन, n-घात।
• पदों के आधार पर → एकपद, द्विपद, त्रिपद।
शून्यक: p(α) = 0 ⇒ α शून्यक।
शून्यक–गुणांक संबंध:
• द्विघात: α + β = -b/a, αβ = c/a।
• घन: α + β + γ = -b/a, αβ + βγ + γα = c/a, αβγ = -d/a।
शेषफल प्रमेय: (x – a) से भाग देने पर शेष = p(a)।
गुणनखण्ड प्रमेय: यदि p(a) = 0 तो (x – a) गुणनखण्ड है।
विभाजन एल्गोरिथ्म: p(x) = g(x)q(x) + r(x)।
प्रयोग: समीकरण हल, ग्राफ, विज्ञान और अर्थशास्त्र।

📝 Quick Recap
🔵 बहुपद = बीजीय अभिव्यक्ति, घात पूर्णांक।
🟢 वर्गीकरण = घात व पदों के आधार पर।
🔴 शून्यक–गुणांक सम्बन्ध महत्त्वपूर्ण।
🟡 शेषफल व गुणनखण्ड प्रमेय बहुपदों के हल में उपयोगी।
🌿 विभाजन एल्गोरिथ्म = संख्याओं जैसा।
⚡ अनुप्रयोग = विज्ञान, तकनीक, अर्थशास्त्र।

————————————————————————————————————————————————————————————————————————–

पाठ्यपुस्तक के प्रश्न

🔵प्रश्नावली 2.1

🔵 प्रश्न 1
किसी बहुपद p(x) के लिए, y = p(x) का ग्राफ नीचे आकृति 2.10 में दिया है। प्रत्येक स्थिति में, p(x) के शून्यों की संख्या ज्ञात कीजिए।

🟢 उत्तर
(i)
🔵 Step 1: ग्राफ x-अक्ष को नहीं छूता और न ही काटता है।
✔️ निष्कर्ष: शून्यों की संख्या = 0
(ii)
🔵 Step 1: ग्राफ x-अक्ष को एक बार काटता है।
✔️ निष्कर्ष: शून्यों की संख्या = 1
(iii)
🔵 Step 1: ग्राफ x-अक्ष को दो विभिन्न बिंदुओं पर काटता है।
✔️ निष्कर्ष: शून्यों की संख्या = 2
(iv)
🔵 Step 1: ग्राफ x-अक्ष को केवल एक बिंदु पर स्पर्श करता है (कटता नहीं)।
✔️ निष्कर्ष: शून्यों की संख्या = 1
(v)
🔵 Step 1: ग्राफ x-अक्ष को तीन विभिन्न बिंदुओं पर काटता है।
✔️ निष्कर्ष: शून्यों की संख्या = 3
(vi)
🔵 Step 1: ग्राफ x-अक्ष को चार विभिन्न बिंदुओं पर काटता है।
✔️ निष्कर्ष: शून्यों की संख्या = 4

🔵प्रश्नावली 2.2

🔵 प्रश्न 1
निम्न द्विघात बहुपदों के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के संबंध की सत्यता की जाँच कीजिए :
(i) x² − 2x − 8 (ii) 4s² − 4s + 1 (iii) 6x² − 3 − 7x
(iv) 4u² + 8u (v) t² − 15 (vi) 3x² − x − 4

(i) x² − 2x − 8
🟢 उत्तर
🔵 चरण 1: गुणनखंड = (x − 4)(x + 2)
🔵 चरण 2: शून्यक = 4, −2
🟡 जाँच (योग) = 4 + (−2) = 2 = −b/a
🟡 जाँच (गुणनफल) = 4 × (−2) = −8 = c/a
✔️ निष्कर्ष: संबंध सत्य

(ii) 4s² − 4s + 1
🟢 उत्तर
🔵 चरण 1: गुणनखंड = (2s − 1)²
🔵 चरण 2: शून्यक = 1/2, 1/2
🟡 जाँच (योग) = 1/2 + 1/2 = 1 = −b/a
🟡 जाँच (गुणनफल) = (1/2)(1/2) = 1/4 = c/a
✔️ निष्कर्ष: संबंध सत्य

(iii) 6x² − 3 − 7x
🟢 उत्तर
🔵 चरण 1: मानक रूप = 6x² − 7x − 3
🔵 चरण 2: विचिन्तक D = (−7)² − 4(6)(−3) = 49 + 72 = 121
🔵 चरण 3: शून्यक = (7 ± √121)/12 = 3/2, −1/3
🟡 जाँच (योग) = 3/2 + (−1/3) = 7/6 = −b/a
🟡 जाँच (गुणनफल) = (3/2)(−1/3) = −1/2 = c/a
✔️ निष्कर्ष: संबंध सत्य

(iv) 4u² + 8u
🟢 उत्तर
🔵 चरण 1: गुणनखंड = 4u(u + 2)
🔵 चरण 2: शून्यक = 0, −2
🟡 जाँच (योग) = 0 + (−2) = −2 = −b/a
🟡 जाँच (गुणनफल) = 0 × (−2) = 0 = c/a
✔️ निष्कर्ष: संबंध सत्य

(v) t² − 15
🟢 उत्तर
🔵 चरण 1: शून्यक = √15, −√15
🟡 जाँच (योग) = √15 + (−√15) = 0 = −b/a
🟡 जाँच (गुणनफल) = (√15)(−√15) = −15 = c/a
✔️ निष्कर्ष: संबंध सत्य

(vi) 3x² − x − 4
🟢 उत्तर
🔵 चरण 1: विचिन्तक D = (−1)² − 4(3)(−4) = 1 + 48 = 49
🔵 चरण 2: शून्यक = (1 ± √49)/6 = 4/3, −1
🟡 जाँच (योग) = 4/3 + (−1) = 1/3 = −b/a
🟡 जाँच (गुणनफल) = (4/3)(−1) = −4/3 = c/a
✔️ निष्कर्ष: संबंध सत्य

🔵 प्रश्न 2
एक द्विघात बहुपद ज्ञात कीजिए, जिसके शून्यों के योग तथा गुणनफल क्रमशः दी गई संख्याएँ हैं :
(i) 1/4, −1 (ii) √2, 1/3 (iii) 0, √5 (iv) 1, 1 (v) −1/4, 1/4 (vi) 4, 1
💡 रूप: यदि योग S तथा गुणनफल P हों, तो उचित बहुपद = x² − Sx + P
(भिन्न हो तो हर हटाकर पूर्णांकीय गुणांक बनाना उचित है)

(i) S = 1/4, P = −1
🔵 चरण 1: बहुपद = x² − (1/4)x − 1
🔵 चरण 2: हर हटाएँ → 4x² − x − 4
✔️ निष्कर्ष: अपेक्षित बहुपद = 4x² − x − 4

(ii) S = √2, P = 1/3
🔵 चरण 1: बहुपद = x² − √2 x + 1/3
🔵 चरण 2: हर हटाएँ → 3x² − 3√2 x + 1
✔️ निष्कर्ष: अपेक्षित बहुपद = 3x² − 3√2 x + 1

(iii) S = 0, P = √5
🔵 चरण 1: बहुपद = x² + √5
✔️ निष्कर्ष: अपेक्षित बहुपद = x² + √5

(iv) S = 1, P = 1
🔵 चरण 1: बहुपद = x² − x + 1
✔️ निष्कर्ष: अपेक्षित बहुपद = x² − x + 1

(v) S = −1/4, P = 1/4
🔵 चरण 1: बहुपद = x² − (−1/4)x + 1/4 = x² + 1/4 x + 1/4
🔵 चरण 2: हर हटाएँ → 4x² + x + 1
✔️ निष्कर्ष: अपेक्षित बहुपद = 4x² + x + 1

(vi) S = 4, P = 1
🔵 चरण 1: बहुपद = x² − 4x + 1
✔️ निष्कर्ष: अपेक्षित बहुपद = x² − 4x + 1

————————————————————————————————————————————————————————————————————————–

अन्य महत्वपूर्ण प्रश्न

🔵 खंड A (अत्यल्प/वस्तुनिष्ठ प्रश्न, 1 अंक प्रत्येक)
🔵 प्रश्न 1
यदि p(x) = x² − 5x + 6 है तो इसके शून्यकों का योग कितना होगा?
🟢 विकल्प:
🔹 1. 11
🔹 2. −5
🔹 3. 5
🔹 4. 6
🟢 उत्तर: 3 (योग = −b/a = 5)

🔵 प्रश्न 2
यदि p(x) = x² + 2x + 1 है तो इसके शून्यक हैं:
🟢 विकल्प:
🔹 1. 1, −1
🔹 2. 1, 1
🔹 3. −1, −1
🔹 4. 0, −1
🟢 उत्तर: 3 (−1, −1)

🔵 प्रश्न 3
यदि द्विघात बहुपद के शून्यक α, β हैं, तो बहुपद का रूप होगा:
🟢 विकल्प:
🔹 1. (x − α)(x − β)
🔹 2. x² + αx + β
🔹 3. (x + α)(x + β)
🔹 4. (x − α)(x + β)
🟢 उत्तर: 1

🔵 प्रश्न 4
यदि बहुपद 2x² + 5x + 3 = 0 के शून्यक α, β हैं, तो α + β का मान है:
🟢 विकल्प:
🔹 1. −5/2
🔹 2. 5/2
🔹 3. 2/5
🔹 4. −2/5
🟢 उत्तर: 1

🔵 प्रश्न 5
यदि α और β, x² − 3x + 2 = 0 के शून्यक हैं, तो αβ का मान है:
🟢 विकल्प:
🔹 1. 2
🔹 2. −2
🔹 3. 3
🔹 4. −3
🟢 उत्तर: 1

🔵 प्रश्न 6
कौन-सा बहुपद चार शून्यकों वाला है?
🟢 विकल्प:
🔹 1. 5x
🔹 2. x² + 1
🔹 3. x³ − 2
🔹 4. x⁴ − 1
🟢 उत्तर (स्पष्टीकरण सहित):
वास्तविक शून्यक गिनने पर x⁴ − 1 = (x − 1)(x + 1)(x² + 1) ⇒ केवल 2 वास्तविक शून्यक (±1) हैं।
पर यदि समिश्र शून्यकों को भी गिना जाए तो कुल 4 शून्यक हैं।
✔️ निष्कर्ष: कक्षा 10 में वास्तविक शून्यकों के सन्दर्भ में यह 2 शून्यक वाला है, पर समिश्र क्षेत्र में 4 शून्यक वाला।

🟢 खंड B (संक्षिप्त उत्तर-I, 2 अंक प्रत्येक)
🔵 प्रश्न 7
x² − 7x + 10 के शून्यक ज्ञात कीजिए।
🟢 उत्तर
🔵 चरण 1: गुणनखंड = (x − 5)(x − 2)
🔵 चरण 2: शून्यक = 5, 2
✔️ निष्कर्ष: शून्यक 5 और 2 हैं।

🔵 प्रश्न 8
4x² + 4x + 1 के शून्यक ज्ञात कीजिए।
🟢 उत्तर
🔵 चरण 1: गुणनखंड = (2x + 1)²
🔵 चरण 2: शून्यक = −1/2, −1/2
✔️ निष्कर्ष: शून्यक दोहराए हुए −1/2, −1/2 हैं।

🔵 प्रश्न 9
यदि α और β, बहुपद 2x² + 3x + 1 के शून्यक हैं तो α + β तथा αβ ज्ञात कीजिए।
🟢 उत्तर
🔵 चरण 1: α + β = −b/a = −3/2
🔵 चरण 2: αβ = c/a = 1/2
✔️ निष्कर्ष: योग = −3/2, गुणनफल = 1/2

🔵 प्रश्न 10
x² − 15 के शून्यक ज्ञात कीजिए।
🟢 उत्तर
🔵 चरण 1: x² − 15 = 0 ⇒ x² = 15
🔵 चरण 2: x = ±√15
✔️ निष्कर्ष: शून्यक √15, −√15

🔵 प्रश्न 11
यदि बहुपद x² − 2x − 8 के शून्यक α और β हैं, तो बहुपद α² + β² का मान ज्ञात कीजिए।
🟢 उत्तर
🔵 चरण 1: α + β = −b/a = 2
🔵 चरण 2: αβ = c/a = −8
🔵 चरण 3: α² + β² = (α + β)² − 2αβ
🔵 चरण 4: = (2)² − 2(−8) = 4 + 16 = 20
✔️ निष्कर्ष: α² + β² = 20

🔵 प्रश्न 12
x² + 7x + 10 के शून्यक ज्ञात कीजिए और यह दिखाइए कि उनका योग और गुणनफल गुणांकों के अनुपात के अनुसार हैं।
🟢 उत्तर
🔵 चरण 1: गुणनखंड = (x + 5)(x + 2)
🔵 चरण 2: शून्यक = −5, −2
🔵 चरण 3: योग = (−5) + (−2) = −7
🔵 चरण 4: −b/a = −7/1 = −7
🔵 चरण 5: गुणनफल = (−5)(−2) = 10
🔵 चरण 6: c/a = 10/1 = 10
✔️ निष्कर्ष: शून्यक और गुणांक का संबंध सत्य है।

🟡 खंड C (संक्षिप्त उत्तर-II, 3 अंक प्रत्येक)

🔵 प्रश्न 13
द्विघात बहुपद 2x² − 5x + 3 के शून्यक ज्ञात कीजिए और उनका योग तथा गुणनफल जाँचिए।
🟢 उत्तर
🔵 चरण 1: विचिन्तक D = (−5)² − 4(2)(3) = 25 − 24 = 1
🔵 चरण 2: शून्यक = (5 ± √1)/4 = (5 ± 1)/4
🔵 चरण 3: शून्यक = 3/2, 1
🔵 चरण 4: योग = 3/2 + 1 = 5/2 = −b/a
🔵 चरण 5: गुणनफल = 3/2 × 1 = 3/2 = c/a
✔️ निष्कर्ष: संबंध सत्य है।

🔵 प्रश्न 14
यदि बहुपद x² + 2x + k के शून्यक बराबर हों, तो k का मान ज्ञात कीजिए।
🟢 उत्तर
🔵 चरण 1: बराबर शून्यक होने की शर्त = D = 0
🔵 चरण 2: D = (2)² − 4(1)(k) = 4 − 4k
🔵 चरण 3: 4 − 4k = 0 ⇒ k = 1
✔️ निष्कर्ष: k = 1

🔵 प्रश्न 15
यदि बहुपद 3x² + kx + 1 के शून्यक विपरीत हों, तो k का मान ज्ञात कीजिए।
🟢 उत्तर
🔵 चरण 1: विपरीत शून्यक होने पर α + β = 0
🔵 चरण 2: α + β = −b/a = −k/3 = 0
🔵 चरण 3: ⇒ k = 0
✔️ निष्कर्ष: k = 0

🔵 प्रश्न 16
यदि बहुपद kx² − 14x + 8k के शून्यक बराबर हों, तो k का मान ज्ञात कीजिए।
🟢 उत्तर
🔵 चरण 1: बराबर शून्यक के लिए D = 0
🔵 चरण 2: D = (−14)² − 4(k)(8k) = 196 − 32k²
🔵 चरण 3: 196 − 32k² = 0 ⇒ 32k² = 196
🔵 चरण 4: k² = 49/8 ⇒ k = ±7/√8 = ±(7√2)/4
✔️ निष्कर्ष: k = ±(7√2)/4

🔵 प्रश्न 17
यदि किसी बहुपद के शून्यक 2 और −3 हैं, तो बहुपद ज्ञात कीजिए।
🟢 उत्तर
🔵 चरण 1: शून्यक 2 और −3 ⇒ बहुपद = (x − 2)(x + 3)
🔵 चरण 2: = x² + x − 6
✔️ निष्कर्ष: अपेक्षित बहुपद = x² + x − 6

🔵 प्रश्न 18
यदि किसी बहुपद के शून्यक √3 और −√3 हों, तो बहुपद ज्ञात कीजिए।
🟢 उत्तर
🔵 चरण 1: बहुपद = (x − √3)(x + √3)
🔵 चरण 2: = x² − 3
✔️ निष्कर्ष: अपेक्षित बहुपद = x² − 3

🔵 प्रश्न 19
यदि बहुपद 6x² + x − 2 के शून्यक α, β हैं, तो α² + β² का मान ज्ञात कीजिए।
🟢 उत्तर
🔵 चरण 1: α + β = −b/a = −1/6
🔵 चरण 2: αβ = c/a = −2/6 = −1/3
🔵 चरण 3: α² + β² = (α + β)² − 2αβ
🔵 चरण 4: = (−1/6)² − 2(−1/3)
🔵 चरण 5: = 1/36 + 2/3 = 1/36 + 24/36 = 25/36
✔️ निष्कर्ष: α² + β² = 25/36

🔵 प्रश्न 20
यदि बहुपद 2x² + 3x + 4 के शून्यक α, β हों, तो α³ + β³ का मान ज्ञात कीजिए।
🟢 उत्तर
🔵 चरण 1: α + β = −b/a = −3/2
🔵 चरण 2: αβ = c/a = 4/2 = 2
🔵 चरण 3: α³ + β³ = (α + β)³ − 3αβ(α + β)
🔵 चरण 4: = (−3/2)³ − 3(2)(−3/2)
🔵 चरण 5: = −27/8 + 9 = (−27 + 72)/8 = 45/8
✔️ निष्कर्ष: α³ + β³ = 45/8

🔵 प्रश्न 21
यदि किसी बहुपद के शून्यक α, β इस प्रकार हैं कि α + β = 1 और αβ = −2, तो बहुपद ज्ञात कीजिए।
🟢 उत्तर
🔵 चरण 1: बहुपद = x² − (α + β)x + αβ
🔵 चरण 2: = x² − (1)x − 2
🔵 चरण 3: = x² − x − 2
✔️ निष्कर्ष: अपेक्षित बहुपद = x² − x − 2

🔵 प्रश्न 22 (आन्तरिक विकल्प)
(i) यदि किसी बहुपद के शून्यक 3 और 4 हों, तो बहुपद ज्ञात कीजिए।
या
(ii) यदि किसी बहुपद के शून्यक −2 और 5 हों, तो बहुपद ज्ञात कीजिए।
🟢 उत्तर (i)
🔵 चरण 1: बहुपद = (x − 3)(x − 4) = x² − 7x + 12
🟢 उत्तर (ii)
🔵 चरण 1: बहुपद = (x + 2)(x − 5) = x² − 3x − 10
✔️ निष्कर्ष: अपेक्षित बहुपद या तो x² − 7x + 12 अथवा x² − 3x − 10 है।

🔴 खंड D (दीर्घ उत्तर प्रश्न, 4 अंक प्रत्येक)

🔵 प्रश्न 23
यदि किसी बहुपद के शून्यक 2 और 5 हों, तो बहुपद ज्ञात कीजिए तथा शून्यकों के योग और गुणनफल का सत्यापन कीजिए।
🟢 उत्तर
🔵 चरण 1: बहुपद = (x − 2)(x − 5) = x² − 7x + 10
🔵 चरण 2: शून्यक = 2, 5
🔵 चरण 3: योग = 2 + 5 = 7 = −b/a
🔵 चरण 4: गुणनफल = 2 × 5 = 10 = c/a
✔️ निष्कर्ष: बहुपद = x² − 7x + 10 और संबंध सत्य है।

🔵 प्रश्न 24 (आन्तरिक विकल्प)
(i) यदि बहुपद के शून्यक √2 और √3 हों, तो बहुपद ज्ञात कीजिए।
या
(ii) यदि बहुपद के शून्यक −√5 और √5 हों, तो बहुपद ज्ञात कीजिए।
🟢 उत्तर (i)
बहुपद = (x − √2)(x − √3)(x + √2)(x + √3) = (x² − 2)(x² − 3) = x⁴ − 5x² + 6
🟢 उत्तर (ii)
बहुपद = (x + √5)(x − √5) = x² − 5
✔️ निष्कर्ष: अपेक्षित बहुपद या तो x⁴ − 5x² + 6 अथवा x² − 5 है।

🔵 प्रश्न 25
यदि बहुपद p(x) = 6x² + 11x − 10 हो, तो इसके शून्यक ज्ञात कीजिए और उनका योग तथा गुणनफल कीजिए।
🟢 उत्तर
🔵 चरण 1: D = (11)² − 4(6)(−10) = 121 + 240 = 361
🔵 चरण 2: शून्यक = (−11 ± √361)/12 = (−11 ± 19)/12
🔵 चरण 3: शून्यक = (8/12, −30/12) = (2/3, −5/2)
🔵 चरण 4: योग = 2/3 + (−5/2) = (4 − 15)/6 = −11/6 = −b/a
🔵 चरण 5: गुणनफल = (2/3)(−5/2) = −5/3 = c/a
✔️ निष्कर्ष: शून्यक 2/3 और −5/2 हैं।

🔵 प्रश्न 26 (आन्तरिक विकल्प)
(i) यदि बहुपद का एक शून्यक 2 हो और दूसरा 1/3 हो, तो बहुपद ज्ञात कीजिए।
या
(ii) यदि बहुपद का एक शून्यक 0 हो और दूसरा −7 हो, तो बहुपद ज्ञात कीजिए।
🟢 उत्तर (i)
बहुपद = (x − 2)(x − 1/3) = x² − (7/3)x + 2/3 ⇒ 3x² − 7x + 2
🟢 उत्तर (ii)
बहुपद = x(x + 7) = x² + 7x
✔️ निष्कर्ष: अपेक्षित बहुपद 3x² − 7x + 2 अथवा x² + 7x है।

🔵 प्रश्न 27
यदि p(x) = 2x³ − 5x² − 4x + 3 हो और (x − 3) इसका एक गुणनखंड हो, तो अन्य शून्यक ज्ञात कीजिए।
🟢 उत्तर
🔵 चरण 1: (x − 3) से p(x) को भाग दीजिए।
🔵 चरण 2: 2x³ − 5x² − 4x + 3 ÷ (x − 3) = 2x² + x − 1
🔵 चरण 3: अब 2x² + x − 1 = 0 ⇒ शून्यक = (−1 ± √(1 + 8))/4 = (−1 ± 3)/4
🔵 चरण 4: शून्यक = 1/2, −1
✔️ निष्कर्ष: p(x) के शून्यक = 3, 1/2, −1

🔵 प्रश्न 28 (आन्तरिक विकल्प)
(i) यदि किसी घन बहुपद का एक शून्यक −1 हो और अन्य शून्यक 2 और 3 हों, तो बहुपद ज्ञात कीजिए।
या
(ii) यदि किसी घन बहुपद के शून्यक 0, 1 और −4 हों, तो बहुपद ज्ञात कीजिए।
🟢 उत्तर (i)
बहुपद = (x + 1)(x − 2)(x − 3) = x³ − 4x² + x + 6
🟢 उत्तर (ii)
बहुपद = x(x − 1)(x + 4) = x³ + 3x² − 4x
✔️ निष्कर्ष: अपेक्षित बहुपद या तो x³ − 4x² + x + 6 अथवा x³ + 3x² − 4x है।

🔵 प्रश्न 29
यदि किसी बहुपद के शून्यक 1, −1 और 2 हों, तो बहुपद ज्ञात कीजिए और शून्यकों का योग व गुणनफल की जाँच कीजिए।
🟢 उत्तर
🔵 चरण 1: बहुपद = (x − 1)(x + 1)(x − 2) = (x² − 1)(x − 2) = x³ − 2x² − x + 2
🔵 चरण 2: शून्यक = 1, −1, 2
🔵 चरण 3: योग = 1 + (−1) + 2 = 2 = −b/a
🔵 चरण 4: गुणनफल = (1)(−1)(2) = −2 = −d/a
✔️ निष्कर्ष: सत्यापन सही है।

🔵 प्रश्न 30 (आन्तरिक विकल्प)
(i) यदि किसी बहुपद का एक शून्यक 5 हो और अन्य शून्यक ±√2 हों, तो बहुपद ज्ञात कीजिए।
या
(ii) यदि किसी बहुपद का एक शून्यक 0 हो और अन्य शून्यक √3, −√3 हों, तो बहुपद ज्ञात कीजिए।
🟢 उत्तर (i)
बहुपद = (x − 5)(x − √2)(x + √2) = (x − 5)(x² − 2) = x³ − 5x² − 2x + 10
🟢 उत्तर (ii)
बहुपद = x(x − √3)(x + √3) = x(x² − 3) = x³ − 3x
✔️ निष्कर्ष: अपेक्षित बहुपद या तो x³ − 5x² − 2x + 10 अथवा x³ − 3x है।

————————————————————————————————————————————————————————————————————————–

मानचित्र

————————————————————————————————————————————————————————————————————————————