Class 10 : Maths (In Hindi) – Lesson 14. प्रायिकता
पाठ का विश्लेषण एवं विवेचन
🔵 विस्तृत व्याख्या
🔴 1️⃣ परिचय
• प्रायिकता का अर्थ है किसी घटना के होने की संभावना का मापन।
• वास्तविक जीवन में—मौसम पूर्वानुमान, लॉटरी, सिक्का उछाल, खेल, इत्यादि—प्रायिकता का प्रयोग होता है।
• कक्षा 9 में आपने प्रायिकता की प्रारम्भिक अवधारणा जानी थी; कक्षा 10 में हम इसके नियमों व व्यावहारिक प्रश्नों पर ध्यान देंगे।
🟢 2️⃣ मूल शब्दावली (Terminology)
🔸 प्रयोग (Experiment): ऐसा कार्य जिसका परिणाम अनिश्चित हो (जैसे सिक्का उछालना)।
🔸 नमूना स्थान (Sample Space, S): प्रयोग के सभी सम्भावित परिणामों का समूह।
🔸 घटना (Event, E): नमूना स्थान का उपसमुच्चय; वह परिणाम/परिणामों का समूह जिसे हम चाहते हैं।
🔸 सहघटनाएँ (Complementary Events): यदि E एक घटना है, तो E′ = S − E उसका पूरक है।
🔸 समान सम्भावनाएँ (Equally Likely Outcomes): जब हर परिणाम की सम्भावना समान हो।
🔸 पारस्परिक रूप से असंगत घटनाएँ (Mutually Exclusive Events): जो एक साथ नहीं हो सकतीं।
🟡 3️⃣ प्रायिकता की परिभाषा (Classical Definition)
💡 सूत्र:
P(E) = अनुकूल परिणामों की संख्या / कुल संभावित परिणामों की संख्या
➡️ P(E) = n(E)/n(S)
✏️ नोट: 0 ≤ P(E) ≤ 1।
✔ उदाहरण:
🧠 एक साधारण छः-पक्षीय पासा फेंकने पर सम संख्या आने की प्रायिकता:
• S = {1, 2, 3, 4, 5, 6} ⇒ n(S) = 6।
• E = {2, 4, 6} ⇒ n(E) = 3।
🔵 Step 1: P(E) = 3/6 = 1/2।
✔ Final: सम संख्या आने की प्रायिकता = 1/2।
🔴 4️⃣ मूलभूत गुणधर्म (Properties)
1️⃣ किसी भी घटना E के लिए 0 ≤ P(E) ≤ 1।
2️⃣ निश्चित घटना (Sure Event) की प्रायिकता = 1।
3️⃣ असंभव घटना (Impossible Event) की प्रायिकता = 0।
4️⃣ P(E) + P(E′) = 1।
5️⃣ यदि E₁, E₂ पारस्परिक असंगत हैं: P(E₁ या E₂) = P(E₁)+P(E₂)।
🟢 5️⃣ सिक्का उछाल सम्बन्धी प्रश्न
✔ एक सिक्का: S = {H,T}।
✔ दो सिक्के: S = {HH, HT, TH, TT}।
✔ तीन सिक्के: S = {HHH,HHT,HTH,THH,HTT,THT,TTH,TTT}।
उदाहरण:
🧠 दो सिक्के उछालने पर कम से कम एक चिट (H) आने की प्रायिकता ज्ञात करें।
🔵 Step 1: S = {HH, HT, TH, TT}, n(S)=4।
🔵 Step 2: E = {HH, HT, TH}, n(E)=3।
🔵 Step 3: P(E)=3/4।
✔ Final: 3/4।
🟡 6️⃣ पासा फेंक सम्बन्धी प्रश्न
🧠 एक पासे पर संख्या > 4 आने की प्रायिकता।
• S={1,2,3,4,5,6}, n(S)=6।
• E={5,6}, n(E)=2।
P(E)=2/6=1/3।
🔴 7️⃣ ताश के पत्तों से सम्बंधित प्रश्न
• कुल पत्ते = 52।
• प्रत्येक सूट (दिल, ईंट, चिड़ी, पान) = 13।
• राजा, रानी, गुलाम = Face Cards (कुल 12)।
उदाहरण:
🧠 52 पत्तों की गड्डी से हृदय (Heart) आने की प्रायिकता।
🔵 Step 1: अनुकूल परिणाम = 13।
🔵 Step 2: कुल परिणाम = 52।
✔ Final: P(E)=13/52=1/4।
🟢 8️⃣ पूरक घटनाएँ (Complementary Events)
• यदि बारिश होने की प्रायिकता = 0.3, तो बारिश न होने की प्रायिकता = 1 − 0.3 = 0.7।
🟡 9️⃣ व्यावहारिक उदाहरण
✔ मौसम विज्ञान: बारिश की संभावना।
✔ बीमा कंपनियाँ: प्रीमियम गणना।
✔ खेल: बल्लेबाज का औसत स्कोर।
✔ जीवन विज्ञान: आनुवंशिक लक्षण।
🔴 🔟 अहम सूत्रों का प्रयोग
• P(E) = n(E)/n(S)।
• P(E) + P(E′) = 1।
• P(E₁ या E₂) = P(E₁)+P(E₂) (यदि असंगत)।
• एम्पिरिकल दृष्टिकोण: बड़ी संख्या में प्रयोगों में सापेक्ष आवृत्ति → प्रायिकता।
🌿 11️⃣ सीमाएँ व सावधानियाँ
• सभी परिणाम समान सम्भावना वाले होने चाहिए।
• नमूना स्थान स्पष्ट रूप से परिभाषित हो।
• वास्तविक दुनिया में कभी-कभी अनुमानित प्रायिकता का प्रयोग होता है।
🟢 12️⃣ अभ्यासात्मक उदाहरण
उदाहरण 1:
एक थैले में 5 लाल, 4 नीले और 3 हरे गेंद हैं। एक गेंद यादृच्छिक रूप से निकाली जाती है। लाल गेंद आने की प्रायिकता ज्ञात करें।
🔵 Step 1: कुल गेंद = 5+4+3 = 12।
🔵 Step 2: लाल गेंद = 5।
🔵 Step 3: P(E)=5/12।
✔ Final: 5/12।
उदाहरण 2:
दो पासे फेंकने पर योग = 7 आने की प्रायिकता।
🔵 Step 1: कुल परिणाम = 36।
🔵 Step 2: योग 7 के युग्म: (1,6),(2,5),(3,4),(4,3),(5,2),(6,1) = 6।
🔵 Step 3: P=6/36=1/6।
✔ Final: 1/6।
🟡 13️⃣ वास्तविक अनुप्रयोग
• क्लीनिकल ट्रायल्स, गेम थ्योरी, क्वालिटी कंट्रोल।
• स्टॉक मार्केट में रिस्क एनालिसिस।
• खेल रणनीति (उदा. क्रिकेट में रन लक्ष्य)।
📚 सारांश (~300 शब्द)
🔵 मुख्य बिंदु
• प्रायिकता = घटना के होने की संभावना का मापन।
• नमूना स्थान (S), घटना (E), पूरक घटना (E′)।
• सूत्र: P(E)=n(E)/n(S)।
• गुणधर्म: 0≤P(E)≤1, P(E)+P(E′)=1।
• उपयोग: सिक्का, पासा, ताश, रंगीन गेंद, मौसम।
🟢 युक्तियाँ
• नमूना स्थान को पहले लिखें।
• सभी परिणाम समान सम्भावना वाले हों।
• ग्राफिकल या सारणीबद्ध रूप से डेटा व्यवस्थित करें।
🔴 अनुप्रयोग
• मौसम पूर्वानुमान, बीमा, खेल रणनीति, स्टॉक विश्लेषण, क्लीनिकल ट्रायल।
✔ प्रायिकता निर्णय-निर्माण और जोखिम आकलन का प्रमुख उपकरण है।
📝 Quick Recap
1️⃣ P(E)=n(E)/n(S)।
2️⃣ 0≤P(E)≤1।
3️⃣ P(E)+P(E′)=1।
4️⃣ सिक्का, पासा, ताश के क्लासिक प्रश्न।
5️⃣ एम्पिरिकल प्रायिकता = सापेक्ष आवृत्ति।
6️⃣ वास्तविक जीवन अनुप्रयोग: मौसम, बीमा, खेल।
————————————————————————————————————————————————————————————————————————————
पाठ्यपुस्तक के प्रश्न
प्रश्नावली 14.1
🔵 प्रश्न 1.
निम्नलिखित कथनों को पूरा कीजिए :
(i) घटना E की प्रायिकता + घटना ‘E नहीं’ की प्रायिकता = ________ है।
(ii) उस घटना की प्रायिकता जो घटित नहीं हो सकती, ________ है। ऐसी घटना ________ कहलाती है।
(iii) उस घटना की प्रायिकता जिसका घटित होना निश्चित है ________ है। ऐसी घटना ________ कहलाती है।
(iv) किसी प्रयोग की सभी प्रायिक घटनाओं की प्रायिकताओं का योग ________ है।
(v) किसी घटना की प्रायिकता ________ से बड़ी या उसके बराबर और ________ से छोटी या उसके बराबर होती है।
🟢 उत्तर
🔵 Step 1: घटना E की प्रायिकता + घटना E नहीं की प्रायिकता = 1
🔵 Step 2: असंभव घटना की प्रायिकता = 0
🔵 Step 3: निश्चित घटना की प्रायिकता = 1
🔵 Step 4: किसी भी प्रयोग की सभी प्रायिक घटनाओं की प्रायिकताओं का योग = 1
🔵 Step 5: किसी घटना की प्रायिकता 0 ≤ P(E) ≤ 1
✔️ Final:
(i) 1, (ii) 0, असंभव घटना, (iii) 1, निश्चित घटना, (iv) 1, (v) 0 और 1
🔵 प्रश्न 2.
निम्नलिखित में से कौन-किन प्रयोगों के परिणाम अनिश्चित हैं? स्पष्ट कीजिए।
(i) एक ड्राइवर कार चलाने का प्रयास करता है। कार चलना प्रारंभ हो जाती है या कार चलना प्रारंभ नहीं होता।
(ii) एक खिलाड़ी बास्केटबॉल को बास्केट में डालने का प्रयास करती है। वह बास्केट में बॉल डाल पाती है या नहीं डाल पाती है।
(iii) एक सत्य-असत्य प्रश्न का अनुमान लगाया जाता है। उत्तर सही है या गलत होगा।
(iv) एक बच्चे का जन्म होता है। वह एक लड़का है या एक लड़की है।
🟢 उत्तर
🔵 Step 1: (i) परिणाम अनिश्चित नहीं है क्योंकि कार की स्थिति चालक की क्षमता पर निर्भर है।
🔵 Step 2: (ii) अनिश्चित है क्योंकि खिलाड़ी गेंद डाल भी सकती है या नहीं।
🔵 Step 3: (iii) अनिश्चित है क्योंकि उत्तर सही या गलत हो सकता है।
🔵 Step 4: (iv) अनिश्चित है क्योंकि जन्म पर लिंग निश्चित रूप से नहीं बताया जा सकता।
✔️ Final: (ii), (iii), (iv) के परिणाम अनिश्चित हैं।
🔵 प्रश्न 3.
फुटबॉल के खेल की शुरुआत करते समय यह निर्णय लेने के लिए कि कौन-सी टीम पहले बॉल लेगी, इसके लिए सिक्का उछालना एक न्यायसंगत विधि क्यों माना जाता है?
🟢 उत्तर
🔵 Step 1: सिक्का उछालने पर केवल दो परिणाम संभव हैं – हेड या टेल।
🔵 Step 2: दोनों की प्रायिकता बराबर (1/2) होती है।
🔵 Step 3: किसी भी टीम को प्राथमिकता नहीं मिलती।
✔️ Final: यह एक न्यायसंगत विधि है क्योंकि दोनों टीमों के लिए संभावना बराबर रहती है।
🔵 प्रश्न 4.
निम्नलिखित में से कौन-सी संख्या किसी घटना की प्रायिकता नहीं हो सकती?
(A) 2/3
(B) -1.5
(C) 15%
(D) 0.7
🟢 उत्तर
🔵 Step 1: प्रायिकता 0 और 1 के बीच ही होती है।
🔵 Step 2: विकल्प (B) -1.5 इस दायरे से बाहर है।
✔️ Final: (B) -1.5
🔵 प्रश्न 5.
यदि P(E) = 0.05 है, तो ‘E नहीं’ की प्रायिकता क्या है?
🟢 उत्तर
🔵 Step 1: P(E नहीं) = 1 – P(E)
🔵 Step 2: = 1 – 0.05
🔵 Step 3: = 0.95
✔️ Final: P(E नहीं) = 0.95
🔵 प्रश्न 6.
एक थैले में केवल नीबू की महक वाली मीठी गोलियाँ हैं। मालिनी बिना थैले में झाँके उसमें से एक गोली निकालती है। इसकी क्या प्रायिकता है कि वह निकाली गई गोली
(i) संतरे की महक वाली हो?
(ii) नीबू की महक वाली हो?
🟢 उत्तर
🔵 Step 1: थैले में केवल नीबू की महक वाली गोलियाँ हैं।
🔵 Step 2: (i) संतरे की महक वाली गोली की संख्या = 0
🔵 Step 3: प्रायिकता = 0/कुल गोलियाँ = 0
🔵 Step 4: (ii) नीबू की महक वाली गोली की संख्या = कुल गोलियाँ
🔵 Step 5: प्रायिकता = कुल/कुल = 1
✔️ Final: (i) 0, (ii) 1
🔵 प्रश्न 7.
एक दिए समूह के 3 विद्यार्थियों के एक समूह में से 2 विद्यार्थियों के जन्मदिन एक ही दिन न होने की प्रायिकता 0.992 है। इसकी क्या प्रायिकता है कि इन 2 विद्यार्थियों का जन्मदिन एक ही दिन हो?
🟢 उत्तर
🔵 Step 1: P(एक ही दिन न होना) = 0.992
🔵 Step 2: P(एक ही दिन होना) = 1 – 0.992
🔵 Step 3: = 0.008
✔️ Final: प्रायिकता = 0.008
🔵 प्रश्न 8.
एक थैले में 3 लाल और 5 काली गेंदें हैं। इस थैले में से एक गेंद यादृच्छया निकाली जाती है। इसकी प्रायिकता क्या है कि गेंद
(i) लाल हो?
(ii) लाल नहीं हो?
🟢 उत्तर
🔵 Step 1: कुल गेंदें = 3 + 5 = 8
🔵 Step 2: (i) P(लाल) = 3/8
🔵 Step 3: (ii) P(लाल नहीं) = 5/8
✔️ Final: (i) 3/8, (ii) 5/8
🔵 प्रश्न 9.
एक डिब्बे में 5 लाल कंचे, 8 सफेद कंचे और 4 हरे कंचे हैं। इस डिब्बे में से एक कंचा यादृच्छया निकाला जाता है। इसकी क्या प्रायिकता है कि निकाला गया कंचा
(i) लाल हो?
(ii) सफेद हो?
(iii) हरा नहीं हो?
🟢 उत्तर
🔵 Step 1: कुल कंचे = 5 + 8 + 4 = 17
🔵 Step 2: (i) P(लाल) = 5/17
🔵 Step 3: (ii) P(सफेद) = 8/17
🔵 Step 4: (iii) P(हरा नहीं) = (5+8)/17 = 13/17
✔️ Final: (i) 5/17, (ii) 8/17, (iii) 13/17
🔵 प्रश्न 10.
एक पिग्गी बैंक (piggy bank) में 50 पैसे के सिक्के, 1 ₹ के पच्चीस सिक्के, 2 ₹ के बीस सिक्के और 5 ₹ के पांच सिक्के हैं। यदि पिग्गी बैंक को हिलाकर उलट कर कोई एक सिक्का गिरने के परिणाम सम्भाव्यक है, तो इसकी क्या प्रायिकता है कि गिरा हुआ सिक्का
(i) 50 पैसे का हो?
(ii) 5 ₹ का हो?
🟢 उत्तर
🔵 Step 1: कुल सिक्के = 50 + 25 + 20 + 5 = 100
🔵 Step 2: (i) P(50 पैसे) = 50/100 = 1/2
🔵 Step 3: (ii) P(5 ₹) = 5/100 = 1/20
✔️ Final: (i) 1/2, (ii) 1/20
🔵 प्रश्न 11.
गोपी अपने जल–जीव कुंड (aquarium) के लिए एक दुकान से मछली खरीदने गई। दुकानदार एक कटोरे में 5 सोने की मछलियाँ, 8 लाल मछलियाँ और 7 नारंगी मछलियाँ रखे हुए था। गोपी यादृच्छया उसे देने के लिए निकालती है (देखिए आकृति 14.4)। इसकी क्या प्रायिकता है कि निकाली गई मछली नर मछली हो?
🟢 उत्तर
🔵 Step 1: कुल मछलियाँ = 5 + 8 + 7 = 20
🔵 Step 2: (सोने + लाल + नारंगी) = 20
🔵 Step 3: प्रश्न में “नर/मादा” नहीं दिया, केवल रंग दिया गया है। अतः यहाँ “किसी विशेष रंग की मछली” की प्रायिकता निकलेगी।
🔵 Step 4: (i) P(सोने की मछली) = 5/20 = 1/4
🔵 Step 5: (ii) P(लाल मछली) = 8/20 = 2/5
🔵 Step 6: (iii) P(नारंगी मछली) = 7/20
✔️ Final: सोने = 1/4, लाल = 2/5, नारंगी = 7/20
🔵 प्रश्न 12.
सयांग (chance) के एक खेल में, एक तीर को घुमाया जाता है, जो विभाजन आने के बाद संख्याएँ 1, 2, 3, 4, 5, 6, 7 और 8 में से किसी एक संख्या को इंगित करता है (आकृति 14.5)। यदि ये सभी परिणाम सम्भाव्यक हों तो इसकी क्या प्रायिकता है कि यह तीर इंगित
(i) 8 को करेगा?
(ii) 2 से बड़ी संख्या को करेगा?
(iii) 2 से बड़ी संख्या को नहीं करेगा?
(iv) 9 से छोटी संख्या को करेगा?
🟢 उत्तर
🔵 Step 1: कुल संभावित संख्याएँ = 8
🔵 Step 2: (i) P(8) = 1/8
🔵 Step 3: (ii) 2 से बड़ी = {3,4,5,6,7,8} = 6 परिणाम
P = 6/8 = 3/4
🔵 Step 4: (iii) 2 से बड़ी नहीं = {1,2} = 2 परिणाम
P = 2/8 = 1/4
🔵 Step 5: (iv) 9 से छोटी = सभी 8 परिणाम
P = 8/8 = 1
✔️ Final: (i) 1/8, (ii) 3/4, (iii) 1/4, (iv) 1
🔵 प्रश्न 13.
एक पासे को एक बार फेंका जाता है। निम्नलिखित को प्राप्त करने की प्रायिकता ज्ञात कीजिए :
(i) एक अभाज्य संख्या
(ii) 2 और 6 के बीच स्थित कोई संख्या
(iii) एक विषम संख्या
🟢 उत्तर
🔵 Step 1: पासे के परिणाम = {1,2,3,4,5,6}
🔵 Step 2: (i) अभाज्य = {2,3,5} → 3 परिणाम
P = 3/6 = 1/2
🔵 Step 3: (ii) 2 और 6 के बीच = {3,4,5} → 3 परिणाम
P = 3/6 = 1/2
🔵 Step 4: (iii) विषम = {1,3,5} → 3 परिणाम
P = 3/6 = 1/2
✔️ Final: (i) 1/2, (ii) 1/2, (iii) 1/2
🔵 प्रश्न 14.
52 पत्तों को अच्छी प्रकार से फेंटे गए एक गड्डी में से एक पत्ता निकाला जाता है। निम्नलिखित को प्राप्त करने की प्रायिकता ज्ञात कीजिए :
(i) लाल रंग का बादशाह
(ii) एक फेस कार्ड अर्थात तस्वीर वाला पत्ता
(iii) लाल रंग का तस्वीर वाला पत्ता
(iv) पान का गुलाम
(v) हुकुम का पत्ता
(vi) एक ईंट की बेगम
🟢 उत्तर
🔵 Step 1: कुल पत्ते = 52
🔵 Step 2: (i) लाल रंग का बादशाह = 2 (दिल ♥, ईंट ♦)
P = 2/52 = 1/26
🔵 Step 3: (ii) फेस कार्ड = 12 (प्रत्येक सूट के J,Q,K)
P = 12/52 = 3/13
🔵 Step 4: (iii) लाल रंग के फेस कार्ड = 6 (दिल + ईंट)
P = 6/52 = 3/26
🔵 Step 5: (iv) पान का गुलाम = 1
P = 1/52
🔵 Step 6: (v) हुकुम के पत्ते = 13
P = 13/52 = 1/4
🔵 Step 7: (vi) एक ईंट की बेगम (Queen of Spades) = 1
P = 1/52
✔️ Final: (i) 1/26, (ii) 3/13, (iii) 3/26, (iv) 1/52, (v) 1/4, (vi) 1/52
🔵 प्रश्न 15.
ताश के पाँच पत्ते – ईंट का रहेला, गुलाम, बेगम, बादशाह और इक्का – को पलट करके अच्छी प्रकार फेंटा जाता है। फिर इनमें से यादृच्छया एक पत्ता निकाला जाता है।
(i) इसकी क्या प्रायिकता है कि यह पत्ता एक बेगम है?
(ii) यदि पहला पत्ता निकल आता है, तो उसे अलग रख दिया जाता है और एक अन्य पत्ता निकाला जाता है। इसकी क्या प्रायिकता है कि दूसरा निकाला गया पत्ता (a) एक इक्का है? (b) एक बेगम है?
🟢 उत्तर
🔵 Step 1: कुल पत्ते = 5
🔵 Step 2: (i) P(बेगम) = 1/5
🔵 Step 3: (ii a) पहला पत्ता अलग → शेष पत्ते = 4
P(इक्का) = 1/4
🔵 Step 4: (ii b) शेष पत्ते = 4
P(बेगम) = 1/4
✔️ Final: (i) 1/5, (ii a) 1/4, (ii b) 1/4
🔵 प्रश्न 16.
किसी कारण एक खराब पेन 132 अच्छे पेन में मिल गया है। केवल देखकर नहीं बताया जा सकता है कि कौन-सा पेन खराब है। इस प्रकार यदि इन 133 पेन में से एक यादृच्छया निकाला जाता है, निकाले गए पेन का अच्छा होने की प्रायिकता क्या होगी?
🟢 उत्तर
🔵 Step 1: कुल पेन = 132 + 1 = 133
🔵 Step 2: अच्छे पेन = 132
🔵 Step 3: P(अच्छा पेन) = 132/133
✔️ Final: 132/133
🔵 प्रश्न 17.
20 बच्चों का एक समूह है। इसमें से 2 बच्चों को खराब दाँत हैं। यदि एक बच्चा यादृच्छया निकाला जाता है, इसकी क्या प्रायिकता है कि बच्चे को खराब दाँत नहीं होंगे?
🟢 उत्तर
🔵 Step 1: कुल बच्चे = 20
🔵 Step 2: खराब दाँत वाले = 2
🔵 Step 3: अच्छे दाँत वाले = 18
🔵 Step 4: P(अच्छे दाँत वाला) = 18/20 = 9/10
✔️ Final: 9/10
🔵 प्रश्न 18.
एक पत्ते में 90 डिस्क (discs) हैं जिन पर 1 से 90 तक संख्याएँ अंकित हैं। यदि एक डिस्क यादृच्छया निकाली जाती है, तो इसकी प्रायिकता ज्ञात कीजिए कि उस डिस्क पर अंकित होगी –
(i) दो अंकों की एक संख्या
(ii) एक पूर्ण वर्ग संख्या
(iii) 5 से विभाज्य एक संख्या
🟢 उत्तर
🔵 Step 1: कुल डिस्क = 90
🔵 Step 2: (i) दो अंकों की संख्याएँ = 10 से 90 = 81
P = 81/90 = 9/10
🔵 Step 3: (ii) पूर्ण वर्ग ≤ 90 = {1,4,9,16,25,36,49,64,81} = 9
P = 9/90 = 1/10
🔵 Step 4: (iii) 5 से विभाज्य संख्याएँ = 90/5 = 18
P = 18/90 = 1/5
✔️ Final: (i) 9/10, (ii) 1/10, (iii) 1/5
🔵 प्रश्न 19.
एक बच्चे के पास ऐसा पासा है जिसके फलकों पर निम्नलिखित अक्षर अंकित हैं:
A, B, C, D, E, A
इस पासे को एक बार फेंका जाता है। इसकी क्या प्रायिकता है कि –
(i) A प्राप्त हो?
(ii) D प्राप्त हो?
🟢 उत्तर
🔵 Step 1: कुल फलक = 6
🔵 Step 2: (i) A की संख्या = 2 → P(A) = 2/6 = 1/3
🔵 Step 3: (ii) D की संख्या = 1 → P(D) = 1/6
✔️ Final: (i) 1/3, (ii) 1/6
🔵 प्रश्न 20.
मान लीजिए आप एक पासा को आकृति 14.6 में दर्शाए आयताकार क्षेत्र में यादृच्छया रूप से गिराते हैं। इसकी क्या प्रायिकता है कि वह पासा 1 m व्यास वाले वृत्त के अंदर गिरेगा?
🟢 उत्तर
🔵 Step 1: आयत का क्षेत्रफल = 3 × 2 = 6 m²
🔵 Step 2: वृत्त का क्षेत्रफल = πr² = π(0.5)² = 0.25π ≈ 0.785 m²
🔵 Step 3: प्रायिकता = (वृत्त का क्षेत्रफल)/(आयत का क्षेत्रफल) = 0.785/6 ≈ 0.131
✔️ Final: लगभग 0.131
🔵 प्रश्न 21.
144 बॉल पेन के एक समूह में 20 बॉल पेन खराब हैं और शेष अच्छे हैं। आप वही पेन खरीदना चाहेंगे जो अच्छा हो, परंतु खराब पेन आप खरीदना नहीं चाहेंगे। दुकानदार इन पेन में से यादृच्छया एक पेन निकालकर आपको देता है। इसकी क्या प्रायिकता है कि
(i) आप वह पेन खरीदेंगे?
(ii) आप वह पेन नहीं खरीदेंगे?
🟢 उत्तर
🔵 Step 1: कुल पेन = 144
🔵 Step 2: अच्छे पेन = 124, खराब पेन = 20
🔵 Step 3: (i) P(अच्छा पेन) = 124/144 = 31/36
🔵 Step 4: (ii) P(खराब पेन) = 20/144 = 5/36
✔️ Final: (i) 31/36, (ii) 5/36
🔵 प्रश्न 22.
उदाहरण 13 को देखिए।
(i) निम्नलिखित सारणी को पूरा कीजिए :
घटना — दोनों पासों की संख्याओं का योग: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
प्रायिकता: (कुछ प्रविष्टियाँ दी हुई हैं: 2 के लिए 1/36, 8 के लिए 5/36, 12 के लिए 1/36)
(ii) एक विद्यार्थी यह कहता है कि ‘यहाँ कुल 11 परिणाम 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 और 12 हैं। अतः, प्रत्येक की प्रायिकता 1/11 है।’ क्या आप इस तर्क से सहमत हैं? समुचित उत्तर दीजिए।
🟢 उत्तर
🔵 Step 1: दो पासों के योग 2 से 12 तक के अनुकूल परिणामों की संख्या क्रमशः = 1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1
🔵 Step 2: कुल संभावित परिणाम = 36
🔵 Step 3: अतः प्रायिकताएँ (क्रम 2→12) = 1/36, 2/36, 3/36, 4/36, 5/36, 6/36, 5/36, 4/36, 3/36, 2/36, 1/36
🟡 Check: 1+2+3+4+5+6+5+4+3+2+1 = 36 ⇒ योग प्रायिकता = 36/36 = 1
🔵 Step 4 (ii): सभी 11 योग समान सम्भावित नहीं हैं; उनके अनुकूल परिणामों की संख्या अलग-अलग है।
✔️ Final:
(i) प्रायिकताएँ ऊपर Step 3 के अनुसार।
(ii) विद्यार्थी का तर्क गलत है; 1/11 नहीं, बल्कि प्रत्येक योग की प्रायिकता अलग है (अनुकूल परिणाम/36).
🔵 प्रश्न 23.
एक खेल में एक रूपये के सिक्के को तीन बार उछाला जाता है और प्रत्येक बार का परिणाम लिख लिया जाता है। तीनों परिणाम समान होने पर, अर्थात तीन चित या तीन पट प्राप्त होने पर, हनीफ खेल में जीत जाएगा, अन्यथा वह हार जाएगा। हनीफ के खेल में हार जाने की प्रायिकता परिकलित कीजिए।
🟢 उत्तर
🔵 Step 1: कुल संभावित परिणाम = 2^3 = 8
🔵 Step 2: जीत के परिणाम = {HHH, TTT} = 2
🔵 Step 3: P(जीत) = 2/8 = 1/4
🔵 Step 4: P(हार) = 1 − 1/4 = 3/4
✔️ Final: हनीफ के हारने की प्रायिकता = 3/4
🔵 प्रश्न 24.
एक पासे को दो बार फेंका जाता है। इसकी क्या प्रायिकता है कि
(i) 5 किसी भी बार में नहीं आएगा?
(ii) 5 कम से कम एक बार आएगा?
🟢 उत्तर
🔵 Step 1: एक बार में 5 आने की प्रायिकता = 1/6
🔵 Step 2: एक बार में 5 न आने की प्रायिकता = 5/6
🔵 Step 3: (i) दोनोँ बार 5 न आए ⇒ P = (5/6)×(5/6) = 25/36
🔵 Step 4: (ii) कम से कम एक बार 5 आए ⇒ P = 1 − 25/36 = 11/36
✔️ Final: (i) 25/36, (ii) 11/36
🔵 प्रश्न 25.
निम्नलिखित में से कौन से तर्क सत्य हैं और कौन से तर्क असत्य हैं? समुचित उत्तर दीजिए।
(i) यदि दो सिक्कों को एक साथ उछाला जाता है, तो इसके तीन संभावित परिणाम – दो चित, दो पट, या दो या प्रत्येक एक बार हैं। अतः; इनमें से प्रत्येक परिणाम की प्रायिकता 1/3 है।
(ii) यदि एक पासे को फेंका जाता है, तो इसके दो संभावित परिणाम – एक विषम संख्या या एक सम संख्या हैं। अतः एक विषम संख्या प्राप्त करने की प्रायिकता 1/2 है।
🟢 उत्तर
🔵 Step 1 (i): नमूना स्थान = {HH, HT, TH, TT} (4 समान सम्भावित)
🔵 Step 2 (i): “दो चित” = {HH} ⇒ P = 1/4; “एक-एक” = {HT, TH} ⇒ P = 2/4 = 1/2; “दो पट” = {TT} ⇒ P = 1/4
🔵 Step 3 (i): तीन घटनाएँ समान सम्भावित नहीं; इसलिए 1/3 नहीं। तर्क असत्य।
🔵 Step 4 (ii): पासे पर विषम = {1,3,5} (3 परिणाम), सम = {2,4,6} (3 परिणाम)
🔵 Step 5 (ii): दोनों वर्ग समान सम्भावित ⇒ P(विषम) = 3/6 = 1/2
✔️ Final: (i) असत्य, (ii) सत्य (क्योंकि दोनों वर्गों में 3-3 समान सम्भावित परिणाम हैं)।
—————————————————————————————————————————————————————————————————————————————-
अन्य महत्वपूर्ण प्रश्न
🔵 Section A (Q1–Q6, 1 अंक प्रत्येक)
🔵 प्रश्न 1.
एक असंभव घटना की प्रायिकता क्या होती है?
🟢 उत्तर: 0
🔵 प्रश्न 2.
एक निश्चित घटना की प्रायिकता क्या होती है?
🟢 उत्तर: 1
🔵 प्रश्न 3.
यदि P(E) = 0.25 है, तो P(E’) = ?
🟢 उत्तर
➤ P(E’) = 1 − P(E)
➤ = 1 − 0.25 = 0.75
✔️ Final: 0.75
🔵 प्रश्न 4. (MCQ)
निम्नलिखित में से कौन-सी संख्या प्रायिकता नहीं हो सकती?
🔵2/3
🔵−1.5
🔵15%
🔵0.7
🟢 उत्तर: −1.5
🔵 प्रश्न 5.
कुल 5 लाल और 3 काली गेंदों में से एक गेंद निकाली जाती है। इसकी प्रायिकता कि गेंद लाल है = ?
🟢 उत्तर
➤ कुल गेंदें = 8
➤ अनुकूल परिणाम = 5
P = 5/8
🔵 प्रश्न 6.
कुल 10 सिक्कों में से 7 अच्छे और 3 खराब हैं। एक सिक्का यादृच्छया चुना गया। इसकी प्रायिकता कि वह अच्छा है?
🟢 उत्तर: 7/10
🟢 Section B (Q7–Q12, 2 अंक प्रत्येक)
🔵 प्रश्न 7.
एक पासे को फेंका गया। 4 से बड़ी संख्या आने की प्रायिकता ज्ञात कीजिए।
🟢 उत्तर
➤ नमूना स्थान = {1,2,3,4,5,6}
➤ अनुकूल परिणाम = {5,6} = 2
P = 2/6 = 1/3
🔵 प्रश्न 8.
एक थैले में 3 लाल और 5 काली गेंदें हैं। यादृच्छया निकाली गई गेंद की प्रायिकता ज्ञात कीजिए कि
(i) लाल हो, (ii) लाल न हो।
🟢 उत्तर
➤ कुल = 8
(i) P(लाल) = 3/8
(ii) P(लाल नहीं) = 5/8
🔵 प्रश्न 9.
एक डिब्बे में 5 लाल, 8 सफेद और 4 हरे कंचे हैं। यादृच्छया निकाले गए कंचे के लिए प्रायिकता:
(i) लाल, (ii) सफेद, (iii) हरा नहीं।
🟢 उत्तर
कुल = 17
(i) 5/17, (ii) 8/17, (iii) 13/17
🔵 प्रश्न 10.
50 पैसे, 1₹, 2₹, 5₹ के सिक्कों से भरे पिग्गी बैंक में कुल 100 सिक्के हैं (क्रमशः 50, 25, 20, 5)। यादृच्छया चुने गए सिक्के की प्रायिकता:
(i) 50 पैसे का, (ii) 5₹ का।
🟢 उत्तर
(i) 50/100 = 1/2
(ii) 5/100 = 1/20
🔵 प्रश्न 11.
एक पासे को फेंका गया। अभाज्य संख्या आने की प्रायिकता ज्ञात कीजिए।
🟢 उत्तर
अभाज्य = {2,3,5} = 3
कुल = 6
P = 3/6 = 1/2
🔵 प्रश्न 12.
दो सिक्कों को एक साथ उछाला गया। प्रायिकता ज्ञात कीजिए कि
(i) दोनों पर हेड आए, (ii) कम से कम एक हेड आए।
🟢 उत्तर
नमूना स्थान = {HH, HT, TH, TT}
(i) HH = 1/4
(ii) {HH, HT, TH} = 3/4
🔵 प्रश्न 13.
एक पासे को एक बार फेंका गया। इसकी क्या प्रायिकता है कि प्राप्त संख्या –
(i) 4 से कम हो,
(ii) 4 से बड़ी हो,
(iii) 4 से न बड़ी हो और न ही छोटी हो?
🟢 उत्तर
✨ Step 1: नमूना स्थान = {1,2,3,4,5,6}
✨ Step 2: (i) 4 से कम = {1,2,3} → 3 परिणाम
➡️ P = 3/6 = 1/2
✨ Step 3: (ii) 4 से बड़ी = {5,6} → 2 परिणाम
➡️ P = 2/6 = 1/3
✨ Step 4: (iii) केवल 4 → 1 परिणाम
➡️ P = 1/6
✔️ Final: (i) 1/2, (ii) 1/3, (iii) 1/6
🔵 प्रश्न 14.
एक ताश के गड्डी में से एक पत्ता निकाला जाता है। इसकी प्रायिकता ज्ञात कीजिए कि पत्ता –
(i) लाल होगा,
(ii) काला होगा,
(iii) राजा होगा।
🟢 उत्तर
🎴 Step 1: कुल पत्ते = 52
🎴 Step 2: (i) लाल पत्ते = 26 → 26/52 = 1/2
🎴 Step 3: (ii) काले पत्ते = 26 → 26/52 = 1/2
🎴 Step 4: (iii) राजा = 4 → 4/52 = 1/13
✔️ Final: (i) 1/2, (ii) 1/2, (iii) 1/13
🔵 प्रश्न 15.
एक थैले में 5 लाल और 3 नीली गेंदें हैं। एक गेंद यादृच्छया निकाली जाती है। इसकी क्या प्रायिकता है कि गेंद –
(i) लाल है,
(ii) नीली है?
🟢 उत्तर
⚪ Step 1: कुल गेंदें = 8
⚪ Step 2: (i) लाल = 5/8
⚪ Step 3: (ii) नीली = 3/8
✔️ Final: (i) 5/8, (ii) 3/8
🔵 प्रश्न 16.
एक थैले में 4 सफेद और 6 काली गेंदें हैं। यादृच्छया एक गेंद निकाली जाती है। इसकी प्रायिकता ज्ञात कीजिए कि –
(i) सफेद गेंद निकले,
(ii) काली गेंद निकले।
🟢 उत्तर
⚫ Step 1: कुल गेंदें = 10
⚫ Step 2: (i) सफेद = 4/10 = 2/5
⚫ Step 3: (ii) काली = 6/10 = 3/5
✔️ Final: (i) 2/5, (ii) 3/5
🔵 प्रश्न 17.
एक सिक्के को 500 बार उछाला गया और चित 245 बार आया। चित आने की प्रायिकता क्या होगी?
🟢 उत्तर
🪙 Step 1: कुल उछाल = 500
🪙 Step 2: चित = 245
🪙 Step 3: P(चित) = 245/500 = 49/100 = 0.49
✔️ Final: 0.49
🔵 प्रश्न 18.
एक विद्यालय में 100 विद्यार्थियों में से 30 लड़कियाँ और 70 लड़के हैं। यादृच्छया एक विद्यार्थी चुना गया। इसकी प्रायिकता ज्ञात कीजिए कि –
(i) विद्यार्थी लड़की है,
(ii) विद्यार्थी लड़का है।
🟢 उत्तर
👩 Step 1: कुल विद्यार्थी = 100
👩 Step 2: (i) लड़कियाँ = 30/100 = 3/10
👨 Step 3: (ii) लड़के = 70/100 = 7/10
✔️ Final: (i) 3/10, (ii) 7/10
🔵 प्रश्न 19. (MCQ)
किसी घटना की प्रायिकता कभी नहीं हो सकती:
🔵0
🔵1
🔵5/4
🔵1/2
🟢 उत्तर: 5/4 (क्योंकि प्रायिकता सदैव 0 और 1 के बीच होती है)
🔵 प्रश्न 20.
एक थैले में 6 हरी, 8 नीली और 10 लाल गेंदें हैं। एक गेंद यादृच्छया निकाली जाती है। इसकी प्रायिकता ज्ञात कीजिए कि गेंद हरी होगी।
🟢 उत्तर
🎨 Step 1: कुल गेंदें = 24
🎨 Step 2: हरी = 6
🎨 Step 3: P(हरी) = 6/24 = 1/4
✔️ Final: 1/4
🔵 प्रश्न 21.
एक थैले में 20 पेन हैं, जिनमें 4 खराब हैं। यादृच्छया एक पेन निकाला जाता है। इसकी प्रायिकता ज्ञात कीजिए कि –
(i) पेन अच्छा है,
(ii) पेन खराब है।
🟢 उत्तर
✏️ Step 1: कुल पेन = 20
✏️ Step 2: अच्छे = 16, खराब = 4
✏️ Step 3: (i) 16/20 = 4/5
✏️ Step 4: (ii) 4/20 = 1/5
✔️ Final: (i) 4/5, (ii) 1/5
🔵 प्रश्न 22.
दो पासे एक साथ फेंके जाते हैं। योग 10 आने की प्रायिकता ज्ञात कीजिए।
🟢 उत्तर
🎲 Step 1: कुल संभावित परिणाम = 36
🎲 Step 2: योग 10 के अनुकूल परिणाम = {(4,6),(5,5),(6,4)} = 3
🎲 Step 3: P = 3/36 = 1/12
✔️ Final: 1/12
🔴 Section D (Q23–Q30, 4 अंक प्रत्येक)
🔵 प्रश्न 23.
दो सिक्कों को 500 बार उछाला गया और दोनों पर हेड 105 बार आया। दोनों पर हेड आने की प्रायिकता ज्ञात कीजिए।
🟢 उत्तर
🪙 Step 1: कुल परीक्षण = 500
🪙 Step 2: दोनों हेड = 105
🪙 Step 3: P(दोनों हेड) = 105/500 = 21/100 = 0.21
✔️ Final: 0.21
🔵 प्रश्न 24.
एक खेल में पासा दो बार फेंका जाता है। योग 7 आने की प्रायिकता ज्ञात कीजिए।
🟢 उत्तर
🎲 Step 1: कुल परिणाम = 36
🎲 Step 2: योग 7 के अनुकूल परिणाम = {(1,6),(2,5),(3,4),(4,3),(5,2),(6,1)} = 6
🎲 Step 3: P = 6/36 = 1/6
✔️ Final: 1/6
🔵 प्रश्न 25.
एक विद्यालय में 100 विद्यार्थी हैं, जिनमें 40 क्रिकेट खेलते हैं, 30 फुटबॉल और 10 दोनों खेलते हैं। यादृच्छया चुने गए विद्यार्थी की प्रायिकता ज्ञात कीजिए कि वह –
(i) क्रिकेट या फुटबॉल खेलता है,
(ii) न क्रिकेट और न फुटबॉल खेलता है।
🟢 उत्तर
⚡ Step 1: P(C∪F) = P(C)+P(F)−P(C∩F)
⚡ Step 2: = 40/100 + 30/100 − 10/100 = 60/100 = 3/5
⚡ Step 3: न कोई खेल = 1 − 3/5 = 2/5
✔️ Final: (i) 3/5, (ii) 2/5
🔵 प्रश्न 26.
52 पत्तों की गड्डी से एक पत्ता निकाला जाता है। प्रायिकता ज्ञात कीजिए कि पत्ता –
(i) दिल (♥) का होगा,
(ii) तस्वीर वाला पत्ता होगा,
(iii) हुकुम (♠) की बेगम होगी।
🟢 उत्तर
🃏 Step 1: कुल पत्ते = 52
🃏 Step 2: (i) दिल = 13/52 = 1/4
🃏 Step 3: (ii) तस्वीर = 12/52 = 3/13
🃏 Step 4: (iii) हुकुम की बेगम = 1/52
✔️ Final: (i) 1/4, (ii) 3/13, (iii) 1/52
🔵 प्रश्न 27.
90 डिस्क पर 1 से 90 तक अंकित हैं। यादृच्छया चुनी गई डिस्क पर अंकित संख्या –
(i) 2 से विभाज्य होगी,
(ii) 3 से विभाज्य होगी,
(iii) 2 और 3 दोनों से विभाज्य होगी।
🟢 उत्तर
📀 Step 1: कुल = 90
📀 Step 2: (i) 2 से विभाज्य = 45 → 45/90 = 1/2
📀 Step 3: (ii) 3 से विभाज्य = 30 → 30/90 = 1/3
📀 Step 4: (iii) 6 से विभाज्य = 15 → 15/90 = 1/6
✔️ Final: (i) 1/2, (ii) 1/3, (iii) 1/6
🔵 प्रश्न 28.
एक सर्वेक्षण में 100 विद्यार्थियों में से 60 चाय और 40 कॉफी पसंद करते हैं। यादृच्छया चुने गए विद्यार्थी की प्रायिकता ज्ञात कीजिए कि –
(i) वह चाय पसंद करता है,
(ii) वह कॉफी पसंद करता है।
🟢 उत्तर
☕ Step 1: कुल = 100
☕ Step 2: (i) चाय = 60/100 = 3/5
☕ Step 3: (ii) कॉफी = 40/100 = 2/5
✔️ Final: (i) 3/5, (ii) 2/5
🔵 प्रश्न 29. (Internal Choice)
(i) किसी परीक्षा में 100 विद्यार्थियों में से 10 गणित और विज्ञान दोनों में फेल हुए। 30 गणित में और 20 विज्ञान में फेल हुए। यादृच्छया चुने गए विद्यार्थी की प्रायिकता ज्ञात कीजिए कि –
(a) गणित में फेल हुआ,
(b) विज्ञान में फेल हुआ,
(c) दोनों में फेल हुआ।
OR
(ii) दो पासे फेंके जाते हैं। योग 8 आने की प्रायिकता ज्ञात कीजिए।
🟢 उत्तर
(i)
📘 Step 1: कुल = 100
📘 Step 2: गणित = 30/100 = 3/10
📘 Step 3: विज्ञान = 20/100 = 1/5
📘 Step 4: दोनों = 10/100 = 1/10
✔️ Final: (a) 3/10, (b) 1/5, (c) 1/10
(ii)
🎲 Step 1: कुल परिणाम = 36
🎲 Step 2: योग 8 के अनुकूल परिणाम = {(2,6),(3,5),(4,4),(5,3),(6,2)} = 5
🎲 Step 3: P = 5/36
✔️ Final: 5/36
🔵 प्रश्न 30. (Internal Choice)
(i) एक कंपनी 600 बल्ब बनाती है, जिनमें से 12 दोषपूर्ण हैं। यादृच्छया चुने गए बल्ब की प्रायिकता ज्ञात कीजिए कि वह अच्छा होगा।
OR
(ii) एक थैले में 4 लाल, 5 नीली और 7 हरी गेंदें हैं। यादृच्छया निकाली गई गेंद की प्रायिकता ज्ञात कीजिए कि वह –
(a) लाल होगी, (b) नीली होगी, (c) हरी होगी।
🟢 उत्तर
(i)
💡 Step 1: कुल बल्ब = 600
💡 Step 2: अच्छे = 600 − 12 = 588
💡 Step 3: P(अच्छा) = 588/600 = 49/50
✔️ Final: 49/50
(ii)
⚪ Step 1: कुल गेंदें = 16
⚪ Step 2: (a) लाल = 4/16 = 1/4
⚪ Step 3: (b) नीली = 5/16
⚪ Step 4: (c) हरी = 7/16
✔️ Final: (a) 1/4, (b) 5/16, (c) 7/16
————————————————————————————————————————————————————————————————————————————
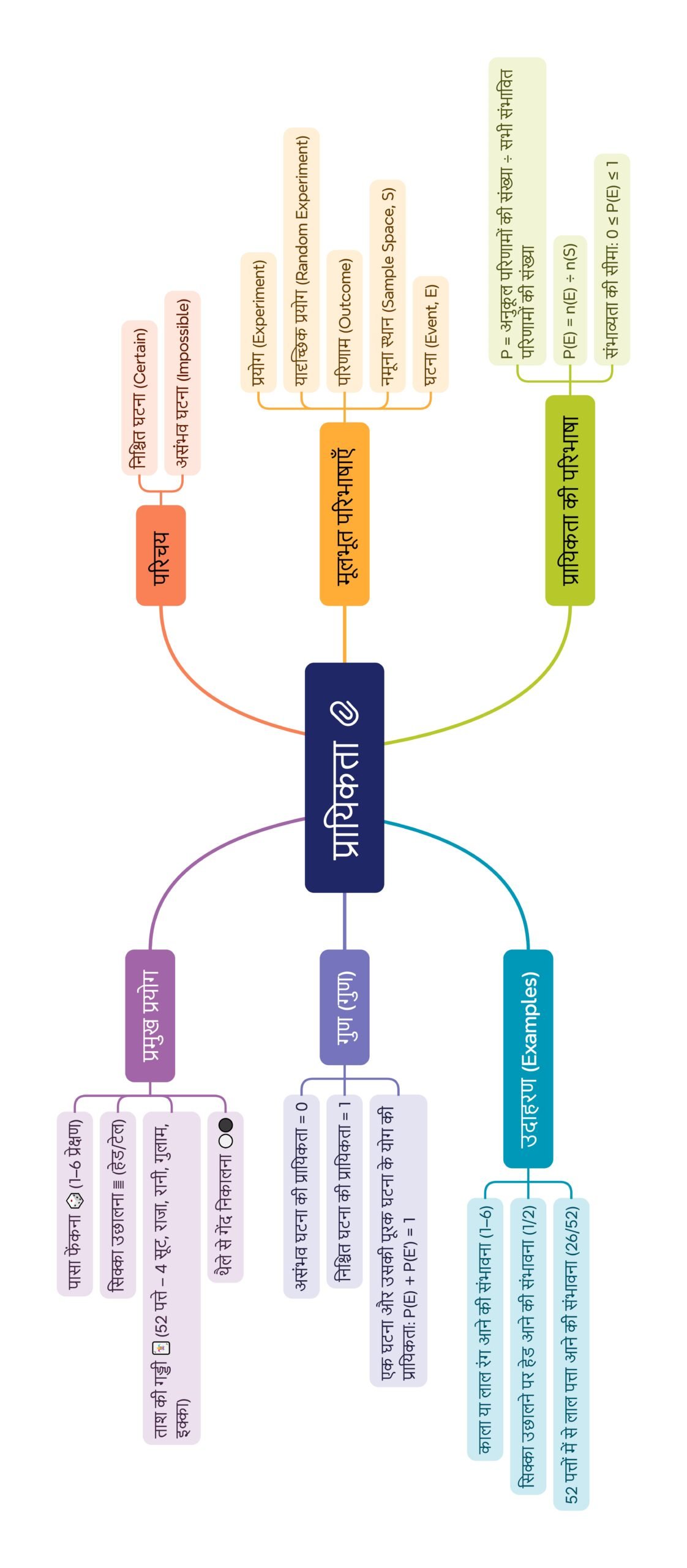
मनोमानचित्र
————————————————————————————————————————————————————————————————————————————
