Class 10 : Maths (In Hindi) – Lesson 12. पृष्ठीय क्षेत्रफल और आयतन

पाठ का विश्लेषण  एवं  विवेचन

🔵 विस्तृत व्याख्या (~1700 शब्द)
🔴 1️⃣ परिचय
 • इस अध्याय में हम विभिन्न ठोस आकृतियों (घन, घनाभ, बेलन, शंकु, गोला, अर्धगोला, खोखला बेलन आदि) के पृष्ठीय क्षेत्रफल (Surface Area) और आयतन (Volume) का अध्ययन करेंगे।
 • वास्तविक जीवन में पानी की टंकी, पाइप, आइसक्रीम कोन, गेंद, बेलनाकार ड्रम जैसी वस्तुओं के क्षेत्रफल व आयतन की गणना इसी अध्याय से होती है।

🟢 2️⃣ मूल परिभाषाएँ
 🔸 पृष्ठीय क्षेत्रफल (Surface Area): किसी ठोस आकृति की समस्त सतहों का कुल क्षेत्रफल।
 🔸 वक्र पृष्ठीय क्षेत्रफल (Curved Surface Area / Lateral Surface Area): केवल वक्र सतहों का क्षेत्रफल, आधार सतहें शामिल नहीं।
 🔸 आयतन (Volume): ठोस आकृति द्वारा घेरे गए स्थान की मात्रा।

🟡 3️⃣ घनाभ (Cuboid)
💡 गुणधर्म:
 • लंबाई = l, चौड़ाई = b, ऊँचाई = h।
🔵 सूत्र
 ➤ वक्र पृष्ठीय क्षेत्रफल = 2h(l + b)।
 ➤ कुल पृष्ठीय क्षेत्रफल = 2(lb + bh + hl)।
 ➤ आयतन V = l × b × h।
✔️ उदाहरण:
 l = 5 cm, b = 4 cm, h = 3 cm।
 CSA = 2×3(5+4) = 6×9 = 54 cm²।
 TSA = 2(20 + 12 + 15) = 2×47 = 94 cm²।
 V = 5×4×3 = 60 cm³।

🔴 4️⃣ घन (Cube)
💡 गुणधर्म:
 • सभी भुजाएँ समान = a।
🔵 सूत्र
 ➤ वक्र पृष्ठीय क्षेत्रफल = 4a²।
 ➤ कुल पृष्ठीय क्षेत्रफल = 6a²।
 ➤ आयतन = a³।

🟢 5️⃣ बेलन (Cylinder)
💡 गुणधर्म:
 • त्रिज्या = r, ऊँचाई = h।
🔵 सूत्र
 ➤ वक्र पृष्ठीय क्षेत्रफल = 2πrh।
 ➤ कुल पृष्ठीय क्षेत्रफल = 2πr(h + r)।
 ➤ आयतन = πr²h।
✏️ नोट: बेलनाकार वस्तुएँ: पाइप, ड्रम, पेन्सिल।

🟡 6️⃣ शंकु (Cone)
💡 गुणधर्म:
 • त्रिज्या = r, ऊँचाई = h, तिर्यक ऊँचाई = l = √(r² + h²)।
🔵 सूत्र
 ➤ वक्र पृष्ठीय क्षेत्रफल = πrl।
 ➤ कुल पृष्ठीय क्षेत्रफल = πr(l + r)।
 ➤ आयतन = (1/3)πr²h।
✔️ उदाहरण:
 r = 7 cm, h = 24 cm।
 l = √(7² + 24²) = √(49 + 576) = √625 = 25 cm।
 CSA = π×7×25 = 175π cm²।

🔴 7️⃣ गोला (Sphere)
🔵 सूत्र
 ➤ पृष्ठीय क्षेत्रफल = 4πr²।
 ➤ आयतन = (4/3)πr³।

🟢 8️⃣ अर्धगोला (Hemisphere)
🔵 सूत्र
 ➤ वक्र पृष्ठीय क्षेत्रफल = 2πr²।
 ➤ कुल पृष्ठीय क्षेत्रफल = 3πr²।
 ➤ आयतन = (2/3)πr³।

🟡 9️⃣ खोखला बेलन (Hollow Cylinder)
💡 गुणधर्म:
 • बाहरी त्रिज्या = R, भीतरी त्रिज्या = r, ऊँचाई = h।
🔵 सूत्र
 ➤ वक्र पृष्ठीय क्षेत्रफल = 2πh(R + r)।
 ➤ कुल पृष्ठीय क्षेत्रफल = 2πh(R + r) + 2π(R² − r²)।
 ➤ आयतन = πh(R² − r²)।

🔴 🔟 पिरामिड और फ्रस्टम (Frustum)
(हालाँकि मुख्य रूप से बेलन, शंकु, गोला पर जोर है, फ्रस्टम भी शामिल होता है)
🔵 फ्रस्टम का आयतन:
 V = (1/3)πh(R² + r² + Rr)।

🌿 11️⃣ संयुक्त ठोस आकृतियाँ (Combination of Solids)
 • कई प्रश्न ऐसे होते हैं जिनमें एक से अधिक ठोस आकृतियाँ जोड़ी जाती हैं।
 • तरीका: आवश्यक सतह क्षेत्रफल या आयतन जोड़ना या घटाना।
उदाहरण:
 🧠 एक बेलन के ऊपर शंकु लगा है। बेलन त्रिज्या = r, ऊँचाई = h₁, शंकु ऊँचाई = h₂।
 🔵 आयतन = πr²h₁ + (1/3)πr²h₂।

🟡 12️⃣ व्यावहारिक उदाहरण
 ✔️ पानी की टंकी, ड्रम, बर्फ के शंकु।
 ✔️ क्रिकेट गेंद और फुटबॉल – गोलाकार क्षेत्रफल व आयतन।
 ✔️ पिरामिड व गुम्बद – वास्तुकला।

🔴 13️⃣ उदाहरणात्मक समस्या 1
प्रश्न: त्रिज्या 7 cm व ऊँचाई 24 cm वाले शंकु का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
🔵 Step 1: l = √(r² + h²) = √(49 + 576) = √625 = 25 cm।
🔵 Step 2: CSA = πrl = π×7×25 = 175π cm²।
🔵 Step 3: TSA = πr(l + r) = π×7(25 + 7) = π×7×32 = 224π cm²।
✔️ Final: CSA = 175π cm², TSA = 224π cm²।

🟢 14️⃣ उदाहरणात्मक समस्या 2
प्रश्न: एक पाइप की भीतरी त्रिज्या 3 cm, बाहरी त्रिज्या 3.5 cm, लम्बाई 21 cm है। पाइप में प्रयुक्त धातु का आयतन ज्ञात करें।
🔵 Step 1: V = πh(R² − r²) = π×21(3.5² − 3²)।
🔵 Step 2: = π×21(12.25 − 9) = π×21×3.25।
🔵 Step 3: = 68.25π cm³ ≈ 214.4 cm³।
✔️ Final: ≈ 214.4 cm³।

🟡 15️⃣ वास्तविक जीवन अनुप्रयोग
 • टंकी निर्माण।
 • पाइपलाइन की क्षमता निर्धारण।
 • डिजाइन इंजीनियरिंग: कोन व बेलन संयुक्त मॉडल।
 • खेल उपकरण, पैकेजिंग, वास्तुकला।

📚 सारांश (~300 शब्द)
🔵 मुख्य सूत्र
 • घनाभ V = l×b×h, TSA = 2(lb+bh+hl)।
 • घन V = a³, TSA = 6a²।
 • बेलन V = πr²h, CSA = 2πrh, TSA = 2πr(h+r)।
 • शंकु V = (1/3)πr²h, CSA = πrl।
 • गोला V = (4/3)πr³, SA = 4πr²।
 • अर्धगोला V = (2/3)πr³, CSA = 2πr², TSA = 3πr²।
 • खोखला बेलन V = πh(R²−r²)।
🟢 युक्तियाँ
 • तिर्यक ऊँचाई l = √(r²+h²)।
 • मिश्रित ठोसों में जोड़ या घटाव का सही प्रयोग।
 • इकाइयाँ एक समान रखें (cm³, m³)।
🔴 अनुप्रयोग
 • पाइप, टंकी, ड्रम, पैकेजिंग।
 • वास्तुकला: गुम्बद, पिरामिड।
 • खेल उपकरण: गेंद, आइसक्रीम कोन।
✔️ यह अध्याय विभिन्न ठोस आकृतियों से जुड़े पृष्ठीय क्षेत्रफल व आयतन निकालने में सहायता करता है और वास्तविक जीवन समस्याओं को हल करने के लिए अत्यंत उपयोगी है।

📝 Quick Recap
1️⃣ CSA बेलन = 2πrh, TSA = 2πr(h+r)।
2️⃣ CSA शंकु = πrl, TSA = πr(l+r)।
3️⃣ गोला: SA = 4πr², V = (4/3)πr³।
4️⃣ अर्धगोला: CSA = 2πr², TSA = 3πr², V = (2/3)πr³।
5️⃣ घन: TSA = 6a², V = a³।
6️⃣ घनाभ: TSA = 2(lb+bh+hl), V = lbh।
7️⃣ संयुक्त ठोस = जोड़/घटाव से हल।

————————————————————————————————————————————————————————————————————————————

पाठ्यपुस्तक के प्रश्न

प्रश्नावली 12.1

🔵 Question 1
दो घन, जिनमें से प्रत्येक का आयतन 64 cm³ है, के संलयन फलकों को मिलाकर एक ठोस बनाया जाता है। इससे प्राप्त घनाभ का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
🟢 Answer
🔵 Step 1: प्रत्येक घन की भुजा a = ∛64 = 4 cm.
🔵 Step 2: दो घन मिलने पर घनाभ के आयाम: l = 8 cm, b = 4 cm, h = 4 cm.
🔵 Step 3: TSA = 2(lb + bh + hl)
➡️ = 2(8×4 + 4×4 + 8×4)
➡️ = 2(32 + 16 + 32)
➡️ = 2(80)
✔️ Final: 160 cm²

🔵 Question 2
कोई बर्तन एक खोखले अर्धगोले के आकार का है जिसके ऊपर एक खोखला बेलन अध्यारोपित है। अर्धगोले का त्रिज्या 14 cm है और इस बर्तन (पात्र) की कुल ऊँचाई 13 cm है। इस बर्तन का आन्तरिक पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
🟢 Answer
✏️ Note: दिए गये मान (r = 14 cm, कुल ऊँचाई = 13 cm) असंगत हैं; एनसीईआरटी के मानक संस्करण में r = 7 cm और कुल ऊँचाई 13 cm होती है, जिससे बेलन की ऊँचाई h = 13 − 7 = 6 cm मिलती है। आन्तरिक पृष्ठीय क्षेत्रफल = CSA(अर्धगोला) + CSA(बेलन) (ऊपर खुला है, इसलिए कोई वृत्तीय आधार नहीं जुड़ेगा)।
🔵 Step 1: r = 7 cm, h = 6 cm.
🔵 Step 2: CSA(अर्धगोला) = 2πr² = 2×22/7×7² = 308 cm².
🔵 Step 3: CSA(बेलन) = 2πrh = 2×22/7×7×6 = 264 cm².
🔵 Step 4: कुल आन्तरिक पृष्ठीय क्षेत्रफल = 308 + 264.
✔️ Final: 572 cm²

🔵 Question 3
एक खिलौना त्रिज्या 3.5 cm वाले एक शंकु के आकार का है, जो उसी त्रिज्या वाले एक अर्धगोले पर अध्यारोपित है। इस खिलौने की सम्पूर्ण ऊँचाई 15.5 cm है। इस खिलौने का संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
🟢 Answer
🔵 Step 1: r = 3.5 cm. कुल ऊँचाई = 15.5 cm ⇒ शंकु की ऊँचाई h = 15.5 − 3.5 = 12 cm.
🔵 Step 2: तिर्यक ऊँचाई l = sqrt(r² + h²) = sqrt(3.5² + 12²) = sqrt(12.25 + 144) = sqrt(156.25) = 12.5 cm.
🔵 Step 3: CSA(शंकु) = π r l = (22/7)×3.5×12.5 = 137.5 cm².
🔵 Step 4: CSA(अर्धगोला) = 2π r² = 2×22/7×(3.5)² = 77 cm².
🔵 Step 5: कुल पृष्ठीय क्षेत्रफल = 137.5 + 77.
✔️ Final: 214.5 cm²

🔵 Question 4
भुजा 7 cm वाले एक घनाकार ब्लॉक के ऊपर एक अर्धगोला रखा हुआ है। अर्धगोले का अधिकतम व्यास क्या हो सकता है? इस प्रकार बने ठोस का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
🟢 Answer
🔵 Step 1: अधिकतम व्यास = घन की भुजा = 7 cm ⇒ r = 3.5 cm.
🔵 Step 2: कुल पृष्ठीय क्षेत्रफल = (घन का TSA − शीर्ष के वृत्त का क्षेत्रफल) + CSA(अर्धगोला)
➡️ = (6a² − πr²) + 2πr² = 6a² + πr², जहाँ a = 7 cm.
🔵 Step 3: 6a² = 6×7² = 6×49 = 294 cm².
🔵 Step 4: πr² = (22/7)×(3.5)² = (22/7)×12.25 = 38.5 cm².
🔵 Step 5: कुल = 294 + 38.5.
✔️ Final: 332.5 cm² (और अधिकतम व्यास 7 cm)

🔵 Question 5
एक घनाकार ब्लॉक के एक फलक को अंदर की ओर से काट कर एक अर्धगोलीय गह्वर इस प्रकार बनाया गया है कि अर्धगोले का व्यास घन के एक किनारे के बराबर है। शेष बचे ठोस का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
🟢 Answer
🔵 Step 1: मान लें घन की भुजा a cm है ⇒ अर्धगोले का r = a/2.
🔵 Step 2: नया TSA = (घन का TSA − खुले वृत्त का क्षेत्रफल) + CSA(अर्धगोला)
➡️ = (6a² − πr²) + 2πr² = 6a² + πr².
🔵 Step 3: r = a/2 ⇒ πr² = π(a²/4).
🔵 Step 4: नया TSA = 6a² + π(a²/4).
✔️ Final: 6a² + (π a² / 4)

🔵 Question 6
दवा की एक कैप्सूल एक बेलन के आकार की है जिसके दोनों सिरों पर एक-एक अर्धगोला लगा हुआ है (देखिए आकृति 12.10)। पूरे कैप्सूल की लम्बाई 14 mm है और उसका व्यास 5 mm है। इसका पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
🟢 Answer
🔵 Step 1: त्रिज्या r = 5/2 = 2.5 mm। बेलन की ऊँचाई h = 14 − 2×2.5 = 9 mm।
🔵 Step 2: बेलन का वक्र पृष्ठीय क्षेत्रफल = 2πrh = 2×22/7×2.5×9 = 141.4 mm²।
🔵 Step 3: दोनों अर्धगोल = एक गोला ⇒ गोले का पृष्ठीय क्षेत्रफल = 4πr² = 4×22/7×6.25 = 78.6 mm²।
🔵 Step 4: कुल पृष्ठीय क्षेत्रफल = 141.4 + 78.6 = 220 mm²।
✔️ Final: 220 mm²

🔵 Question 7
कोई वस्तु एक बेलन के आकार का है जिस पर एक शंकु अध्यारोपित है। यदि बेलनाकार भाग की त्रिज्या और ऊँचाई क्रमशः 2.1 m और 4 m हैं तथा शंकु की ऊँचाई 2.8 m है, तब प्रति m² ₹500 की दर से इसमें प्रयुक्त कैनवास का क्षेत्रफल ज्ञात कीजिए। (ध्यान दीजिए कि वस्तु के आधार को कैनवास से नहीं ढका जाता है।)
🟢 Answer
🔵 Step 1: बेलन का CSA = 2πrh = 2×22/7×2.1×4 = 52.8 m²।
🔵 Step 2: शंकु की तिर्यक ऊँचाई l = √(2.1² + 2.8²) = √(4.41 + 7.84) = √12.25 = 3.5 m।
🔵 Step 3: शंकु का CSA = πrl = 22/7×2.1×3.5 = 22 m²।
🔵 Step 4: कुल पृष्ठीय क्षेत्रफल = 52.8 + 22 = 74.8 m²।
🔵 Step 5: लागत = 74.8 × 500 = ₹37,400।
✔️ Final: ₹37,400

🔵 Question 8
ऊँचाई 2.4 cm और व्यास 1.4 cm वाले एक ठोस बेलन में से उसी ऊँचाई और व्यास वाला एक बेलनाकार खाली (cavity) काट लिया जाता है। शेष बचे ठोस का न्यूनतम पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
🟢 Answer
🔵 Step 1: r = 1.4/2 = 0.7 cm, h = 2.4 cm।
🔵 Step 2: ठोस बेलन का TSA = 2πr(h + r) = 2×22/7×0.7×(2.4 + 0.7) = 4.4×3.1 = 13.64 cm²।
🔵 Step 3: हटाए गये बेलन के कारण दो वृत्त खुलते हैं ⇒ अतिरिक्त क्षेत्रफल = 2πr² = 2×22/7×0.49 = 3.08 cm²।
🔵 Step 4: कुल न्यूनतम पृष्ठीय क्षेत्रफल = 13.64 + 3.08 = 16.72 cm²।
✔️ Final: 16.72 cm²

🔵 Question 9
लकड़ी के एक ठोस बेलन के प्रत्येक सिरे पर एक अर्धगोला खोखलाकर निकालते हुए, एक वस्तु बनाई गई है (देखिए आकृति 12.11)। यदि बेलन की ऊँचाई 10 cm है और उसके आधार का त्रिज्या 3.5 cm है, तो इस वस्तु का संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
🟢 Answer
🔵 Step 1: बेलन का CSA = 2πrh = 2×22/7×3.5×10 = 220 cm²।
🔵 Step 2: दो अर्धगोल = एक गोला ⇒ गोले का पृष्ठीय क्षेत्रफल = 4πr² = 4×22/7×12.25 = 154 cm²।
🔵 Step 3: कुल पृष्ठीय क्षेत्रफल = 220 + 154 = 374 cm²।
✔️ Final: 374 cm²

प्रश्नावली 12.2

🔵 Question 1
एक ठोस एक अर्धगोले पर खड़े एक शंकु के आकार का है जिनकी त्रिज्याएँ 1 cm हैं तथा शंकु की ऊँचाई उसकी त्रिज्या के बराबर है। इस ठोस का आयतन π के पदों में ज्ञात कीजिए।
🟢 Answer
🔵 Step 1: r = 1 cm, शंकु की ऊँचाई h = 1 cm.
🔵 Step 2: आयतन = V(अर्धगोला) + V(शंकु).
🔵 Step 3: V(अर्धगोला) = (2/3)πr³ = (2/3)π(1³) = (2/3)π cm³.
🔵 Step 4: V(शंकु) = (1/3)πr²h = (1/3)π(1²)(1) = (1/3)π cm³.
🔵 Step 5: कुल आयतन = (2/3)π + (1/3)π = π cm³.
✔️ Final: π cm³

🔵 Question 2
एक इंजीनियरिंग के विद्यार्थी रजत से एक पतली एल्युमिनियम की शीट का प्रयोग करते हुए एक मॉडल बनाने को कहा गया जो एक ऐसे बेलन के आकार का हो जिसके दोनों सिरों पर दो शंकु जुड़े हुए हों। इस मॉडल का व्यास 3 cm है और इसकी लम्बाई 12 cm है। यदि प्रत्येक शंकु की ऊँचाई 2 cm है तो रजत द्वारा बनाए गए मॉडल में अन्तर्विष्ट हवा का आयतन ज्ञात कीजिए। (यह मान लीजिए कि मॉडल की आन्तरिक और बाहरी विमाएँ लगभग बराबर हैं।)
🟢 Answer
🔵 Step 1: व्यास = 3 cm ⇒ r = 1.5 cm. कुल लम्बाई = 12 cm.
🔵 Step 2: प्रत्येक शंकु की ऊँचाई = 2 cm ⇒ दो शंकु कुल = 4 cm. बेलन की ऊँचाई h = 12 − 4 = 8 cm.
🔵 Step 3: V(बेलन) = πr²h = π(1.5²)(8) = π(2.25)(8) = 18π cm³.
🔵 Step 4: V(एक शंकु) = (1/3)πr²h = (1/3)π(1.5²)(2) = (1/3)π(2.25)(2) = (4.5/3)π = 1.5π cm³.
🔵 Step 5: V(दो शंकु) = 2×1.5π = 3π cm³.
🔵 Step 6: कुल आयतन = 18π + 3π = 21π cm³.
✔️ Final: 21π cm³

🔵 Question 3
एक गुलाबजामुन में उसके आयतन की लगभग 30% चीनी की चाशनी होती है। 45 गुलाबजामुनों में लगभग कितनी चाशनी होगी, यदि प्रत्येक गुलाबजामुन एक बेलन के आकार का है, जिसके दोनों सिरे अर्धगोलीयाकार हैं तथा इसकी लम्बाई 5 cm और व्यास 2.8 cm है (देखिए आकृति 12.15)।

🟢 Answer
🔵 Step 1: व्यास = 2.8 cm ⇒ त्रिज्या r = 1.4 cm। कुल लम्बाई = 5 cm।
🔵 Step 2: बेलन भाग की ऊँचाई h = 5 − 2r = 5 − 2×1.4 = 2.2 cm।
🔵 Step 3: V_cyl = π r² h = (22/7)×(1.4)²×2.2 = (22/7)×1.96×2.2 = 13.552 cm³।
🔵 Step 4: दोनों अर्धगोल मिलकर एक गोला बनाते हैं ⇒ V_sphere = (4/3) π r³ = (4/3)×(22/7)×(1.4)³ = 11.498666… cm³।
🔵 Step 5: एक गुलाबजामुन का कुल आयतन V₁ = V_cyl + V_sphere = 13.552 + 11.498666… = 25.050666… cm³।
🔵 Step 6: चाशनी (30%) = 0.30 × V₁ = 0.30×25.050666… = 7.5152 cm³ (लगभग)।
🔵 Step 7: 45 गुलाबजामुनों के लिए चाशनी = 45 × 7.5152 = 338.184 cm³ (लगभग)।
🟡 Check: मात्रक cm³; मान यथार्थपरक (≈ 0.338 L)।
✔️ Final: लगभग 338.18 cm³ चाशनी

🔵 Question 4
एक कलमदान घनाभ के आकार की एक लकड़ी से बना है जिसमें कलम रखने के लिए चार शंखाकार गह्वर बने हुए हैं। घनाभ की विमाएँ 15 cm × 10 cm × 3.5 cm हैं। प्रत्येक गह्वर की त्रिज्या 0.5 cm है और गहराई 1.4 cm है। पूरे कलमदान में लकड़ी का आयतन ज्ञात कीजिए। (देखिए आकृति 12.16)

🟢 Answer
🔵 Step 1: घनाभ (लकड़ी) का आयतन V_cuboid = l × b × h
➡️ = 15 × 10 × 3.5
➡️ = 525 cm³

🔵 Step 2: एक शंख (शंकु) का आयतन V_cone = (1/3) π r² h
➡️ = (1/3) × (22/7) × (0.5)² × 1.4
➡️ = (1/3) × (22/7) × 0.25 × 1.4
➡️ = (1/3) × (22/7) × 0.35
➡️ = (1/3) × 1.1
➡️ = 0.3667 cm³

🔵 Step 3: चार शंखों का कुल आयतन = 4 × V_cone
➡️ = 4 × 0.3667
➡️ = 1.4668 cm³

🔵 Step 4: शेष ठोस का आयतन = V_cuboid − 4 × V_cone
➡️ = 525 − 1.4668
➡️ = 523.53 cm³

✔️ Final: पूरे कलमदान में लकड़ी का आयतन ≈ 523.53 cm³

🔵 Question 5
एक बर्तन एक उल्टे शंकु के आकार का है। इसकी ऊँचाई 8 cm है और इसके ऊपरी सिरे (जो खुला हुआ है) की त्रिज्या 5 cm है। यह ऊपर तक पानी से भरा हुआ है। जब इस बर्तन में सीसे की कुछ गोलियाँ जिनमें प्रत्येक 0.5 cm त्रिज्या वाला एक गोला है, डाली जाती हैं, तो इसमें से भरे हुए पानी का एक-चौथाई भाग बाहर निकल जाता है। बर्तन में डाली गई सीसे की गोलियों की संख्या ज्ञात कीजिए।
🟢 Answer
🔵 Step 1: शंकु का आयतन V_cone = (1/3)πr²h = (1/3)×3.14×5²×8 = (1/3)×3.14×25×8 = (1/3)×3.14×200 = (1/3)×628 = 209.33 cm³।
🔵 Step 2: बाहर निकला पानी = ¼ V_cone = 209.33/4 = 52.33 cm³।
🔵 Step 3: प्रत्येक गोली (गोला) का आयतन V_sphere = (4/3)πr³ = (4/3)×3.14×(0.5)³ = (4/3)×3.14×0.125 = (4/3)×0.3925 = 0.5233 cm³।
🔵 Step 4: आवश्यक गोलियों की संख्या = 52.33 / 0.5233 ≈ 100।
✔️ Final: लगभग 100 गोलियाँ

🔵 Question 6
ऊँचाई 220 cm और आधार व्यास 24 cm वाले एक बेलन, जिस पर ऊँचाई 60 cm और त्रिज्या 8 cm वाला एक अन्य बेलन आरोहित है, से लोहे का एक स्तंभ बना है। इस स्तंभ का आयतन ज्ञात कीजिए, जबकि दिया है 1 cm³ लोहे का द्रव्यमान लगभग 8 g होता है। (π=3.14 लीजिए।)
🟢 Answer
🔵 Step 1: पहले बेलन की त्रिज्या r₁ = 24/2 = 12 cm, ऊँचाई h₁ = 220 cm।
🔵 Step 2: V₁ = π r₁² h₁ = 3.14×12²×220 = 3.14×144×220 = 3.14×31680 = 99475.2 cm³।
🔵 Step 3: दूसरे बेलन की त्रिज्या r₂ = 8 cm, ऊँचाई h₂ = 60 cm।
🔵 Step 4: V₂ = π r₂² h₂ = 3.14×64×60 = 3.14×3840 = 12057.6 cm³।
🔵 Step 5: कुल आयतन V_total = V₁ + V₂ = 99475.2 + 12057.6 = 111532.8 cm³।
🔵 Step 6: लोहे का द्रव्यमान = 111532.8 × 8 = 892262.4 g ≈ 892.26 kg।
✔️ Final: आयतन ≈111533 cm³, द्रव्यमान ≈892.26 kg

🔵 Question 7
एक ठोस में, ऊँचाई 120 cm और त्रिज्या 60 cm वाला एक शंकु सम्मिलित है, जो 60 cm त्रिज्या वाले एक अर्धगोले पर अध्यारोपित है। इस ठोस को पानी से भरे हुए एक लम्ब वृत्तीय बेलन में इस प्रकार सीधा डाल दिया जाता है कि यह बेलन की तली को स्पर्श करे। यदि बेलन की त्रिज्या 60 cm है और ऊँचाई 180 cm है तो बेलन में शेष बचे पानी का आयतन ज्ञात कीजिए।
🟢 Answer
🔵 Step 1: बेलन का आयतन V_cyl = π r² h
= 3.14 × 60² × 180
= 3.14 × 3600 × 180
= 2,034,720 cm³
🔵 Step 2: शंकु का आयतन V_cone = (1/3) π r² h
= (1/3) × 3.14 × 60² × 120
= 452,160 cm³
🔵 Step 3: अर्धगोले का आयतन V_hemi = (2/3) π r³
= (2/3) × 3.14 × 60³
= 452,160 cm³
🔵 Step 4: ठोस का कुल आयतन V_solid = V_cone + V_hemi
= 452,160 + 452,160
= 904,320 cm³
🔵 Step 5: बेलन में शेष पानी = V_cyl − V_solid
= 2,034,720 − 904,320
= 1,130,400 cm³
✔️ Final: बेलन में शेष बचे पानी का आयतन ≈ 1,130,400 cm³

🔵 Question 8
एक गोलाकार काँच के बर्तन के एक बेलन के आकार की गर्दन है जिसकी लम्बाई 8 cm है और व्यास 2 cm है जबकि गोलाकार भाग का व्यास 8.5 cm है। इसमें भरे जा सकने वाली पानी की मात्रा ज्ञात कीजिए। यह भी ज्ञात कीजिए कि एक बच्चे ने इस बर्तन का आयतन 345 cm³ बताया है—जाँच कीजिए कि उक्त बच्चे का उत्तर सही है या नहीं, यह मानते हुए कि उपर्युक्त माप अन्तरिक मान्य हैं और π = 3.14।
🟢 Answer
🔵 Step 1: गोलाकार भाग की त्रिज्या r_s = 8.5/2 = 4.25 cm
🔵 Step 2: गोलाकार भाग का आयतन V_sphere = (4/3) π r³
= (4/3) × 3.14 × (4.25)³
= (4/3) × 3.14 × 76.765625
= 321.392 cm³ (लगभग)
🔵 Step 3: बेलन गर्दन की त्रिज्या r_c = 2/2 = 1 cm, ऊँचाई h_c = 8 cm
🔵 Step 4: बेलन गर्दन का आयतन V_cyl = π r² h
= 3.14 × 1² × 8
= 25.12 cm³
🔵 Step 5: कुल क्षमता V_total = V_sphere + V_cyl
= 321.392 + 25.12
= 346.512 cm³ (लगभग)
🟡 Check: बच्चे का उत्तर = 345 cm³
अन्तर = 346.512 − 345 = 1.512 cm³ (लगभग 0.4% त्रुटि)
✔️ Final: बर्तन की क्षमता ≈ 346.5 cm³ है। बच्चे का उत्तर 345 cm³ लगभग सही है, केवल थोड़ा कम।

—————————————————————————————————————————————————————————————————————————————–

अन्य महत्वपूर्ण प्रश्न

प्रश्न 1 (MCQ)
त्रिज्या 3 सेमी तथा ऊँचाई 5 सेमी वाले ठोस बेलन को गलाकर एक ठोस गोले में ढाला गया। गोले की त्रिज्या होगी:
🔵 (1) 3 सेमी
🟢 (2) √5 सेमी
🟡 (3) √(45/4) सेमी
🔴 (4) √(15/2) सेमी
🟢 उत्तर
➤ आयतन समान: πr²h = (4/3)πR³
➤ π×3²×5 = (4/3)πR³
➤ 45 = (4/3)R³ ⇒ R³ = 135/4
✔️ सही विकल्प: (3) √(45/4) सेमी

🔵 प्रश्न 2 (MCQ)
त्रिज्या r तथा ऊँचाई h वाले बेलन का वक्र पृष्ठीय क्षेत्रफल है:
🔵 (1) πr²h
🟢 (2) 2πrh
🟡 (3) 2πr(h + r)
🔴 (4) πr(h + r)
🟢 उत्तर
➡️ CSA(बेलन) = 2πrh
✔️ सही विकल्प: (2) 2πrh

🔵 प्रश्न 3 (MCQ)
त्रिज्या r वाले अर्धगोले (आधार सहित) का कुल पृष्ठीय क्षेत्रफल है:
🔵 (1) 2πr²
🟢 (2) 3πr²
🟡 (3) 4πr²
🔴 (4) (4/3)πr³
🟢 उत्तर
➡️ TSA = CSA(अर्धगोला) + आधार क्षेत्रफल = 2πr² + πr² = 3πr²
✔️ सही विकल्प: (2) 3πr²

🔵 प्रश्न 4 (MCQ)
त्रिज्याएँ R व r तथा तिर्यक ऊँचाई l वाले शंकुखंड का वक्र पृष्ठीय क्षेत्रफल है:
🔵 (1) π(R² − r²)l
🟢 (2) π(R + r)l
🟡 (3) 2π(R + r)l
🔴 (4) π(R − r)l
🟢 उत्तर
➡️ CSA = π(R + r)l
✔️ सही विकल्प: (2) π(R + r)l

🔵 प्रश्न 5
यदि किसी ठोस के सभी रैखिक आयाम दो गुना कर दिए जाएँ, तो उसका आयतन कितनी गुना हो जाएगा?
🟢 उत्तर
➡️ गुणक k = 2 ⇒ आयतन ∝ k³ ⇒ 8 गुना

🔵 प्रश्न 6
त्रिज्या 6 सेमी और ऊँचाई 7 सेमी वाले शंकु का आयतन ज्ञात कीजिए।
🟢 उत्तर
➡️ सूत्र: V = (1/3)πr²h
➡️ = (1/3)π×6²×7
➡️ = (1/3)π×36×7
➡️ = 84π सेमी³

🔵 प्रश्न 7
त्रिज्या 4 सेमी वाले ठोस अर्धगोले को गलाकर ऊँचाई 3 सेमी के बेलन में ढाला गया। बेलन की त्रिज्या ज्ञात कीजिए।
🟢 उत्तर
➡️ आयतन समान: V_hemi = V_cyl
➡️ (2/3)π(4³) = πR²(3)
➡️ (2/3)π×64 = 3πR²
➡️ 128/3 = 3R²
➡️ R² = 128/9
✔️ R = (8√2)/3 सेमी

🔵 प्रश्न 8
त्रिज्या 5 सेमी और तिर्यक ऊँचाई 13 सेमी वाले शंकु का वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
🟢 उत्तर
➡️ CSA = πrl = π×5×13
✔️ = 65π सेमी²

🔵 प्रश्न 9
एक खोखली बेलनाकार पाइप का बाहरी त्रिज्या 7 सेमी, भीतरी त्रिज्या 5 सेमी तथा लम्बाई 20 सेमी है। (i) प्रयुक्त धातु का आयतन तथा (ii) आन्तरिक व बाहरी वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
🟢 उत्तर
(i) आयतन = π(R² − r²)h
= π(7² − 5²)×20
= π(49 − 25)×20
= π×24×20
= 480π सेमी³
(ii) वक्र क्षेत्रफल = 2πRh + 2πrh
= 2π×7×20 + 2π×5×20
= 280π + 200π
= 480π सेमी²

🔵 प्रश्न 10
एक ठोस बेलन जिसके ऊपर अर्धगोला रखा है, दोनों की त्रिज्या 3.5 सेमी है। यदि कुल ऊँचाई 10.5 सेमी है, तो कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
🟢 उत्तर
➡️ बेलन की ऊँचाई h = 10.5 − 3.5 = 7 सेमी
➡️ TSA = CSA(अर्धगोला) + CSA(बेलन) + आधार
= 2πr² + 2πrh + πr²
= (2π×3.5²) + (2π×3.5×7) + (π×3.5²)
= (2π×12.25) + 49π + 12.25π
= 24.5π + 49π + 12.25π
✔️ = 85.75π सेमी²

🔵 प्रश्न 11
एक शंक्वाकार तम्बू में 15 व्यक्तियों को ठहराना है। प्रत्येक व्यक्ति को 1.2 मी² फर्श क्षेत्र की आवश्यकता है। यदि तम्बू का व्यास 7 मी है, तो जाँच कीजिए कि क्या यह पर्याप्त है।
🟢 उत्तर
➡️ आवश्यक क्षेत्रफल = 15×1.2 = 18 मी²
➡️ तम्बू का त्रिज्या r = 7/2 = 3.5 मी
➡️ उपलब्ध फर्श क्षेत्र = πr² = 3.14×(3.5)² = 38.48 मी²
➡️ 38.48 मी² > 18 मी²
✔️ निष्कर्ष: तम्बू का फर्श क्षेत्र पर्याप्त है।

🔵 प्रश्न 12
एक शंकुखंड की त्रिज्याएँ 6 सेमी व 4 सेमी तथा ऊँचाई 8 सेमी है। (i) उसकी तिर्यक ऊँचाई तथा (ii) कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
🟢 उत्तर
(i) तिर्यक ऊँचाई l = √(h² + (R − r)²)
= √(8² + (6 − 4)²)
= √(64 + 4)
= √68 = 2√17 सेमी
(ii) TSA = π(R + r)l + πR² + πr²
= π(6 + 4)(2√17) + π×36 + π×16
= 10π(2√17) + 52π
✔️ = (20√17 + 52)π सेमी²

🔵 प्रश्न 13
त्रिज्या 7 सेमी और ऊँचाई 20 सेमी वाले बेलन का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
🟢 उत्तर
➤ सूत्र: TSA(बेलन) = 2πr(h + r)
➤ प्रत्यारोपण: = 2π×7×(20 + 7)
➤ सरलीकरण: = 14π×27 = 378π
✔️ Final: 378π सेमी²

🔵 प्रश्न 14
त्रिज्या 3.5 सेमी तथा ऊँचाई 6 सेमी वाले शंकु का आयतन और वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए। (π = 22/7)
🟢 उत्तर
➤ तिर्यक ऊँचाई: l = √(r² + h²) = √(3.5² + 6²) = √(12.25 + 36) = √48.25
➤ CSA = π r l = (22/7)×3.5×√48.25 = 11√48.25 सेमी²
➤ आयतन V = (1/3)π r² h = (1/3)×(22/7)×(3.5)²×6
➤ गणना: (3.5)² = 12.25 ⇒ (22/7)×12.25×6 = 22×(12.25×6/7) = 22×10.5 = 231
➤ V = 231/3 = 77 सेमी³
✔️ Final: CSA = 11√48.25 सेमी² (≈ 76.45 सेमी²), V = 77 सेमी³

🔵 प्रश्न 15
त्रिज्या r वाले एक ठोस गोले को गलाकर उसी त्रिज्या r वाले एक अर्धगोले और एक बेलन (त्रिज्या r, ऊँचाई h) में ढाला गया। आयतन-संरक्षण मानते हुए h ज्ञात कीजिए।
🟢 उत्तर
➤ V(गोला) = (4/3)π r³
➤ V(अर्धगोला) = (2/3)π r³
➤ V(बेलन) = π r² h
➤ आयतन-समानता: (4/3)π r³ = (2/3)π r³ + π r² h
➤ सरलकरण: (4/3 − 2/3)π r³ = π r² h ⇒ (2/3)π r³ = π r² h
➤ r ≠ 0 ⇒ (2/3) r = h
✔️ Final: h = (2/3) r

🔵 प्रश्न 16
त्रिज्या 6 सेमी की धातु की अन्दर से रंगी जाने वाली अर्द्धगोलीय कटोरी की आन्तरिक सतह को रंगना है। यदि रंग की दर ₹0.80 प्रति सेमी² है, तो लागत ज्ञात कीजिए।
🟢 उत्तर
➤ आन्तरिक क्षेत्र = CSA(अर्द्धगोला) = 2π r² = 2π×6² = 72π सेमी²
➤ लागत = 72π × 0.80 = 57.6π रुपये
✔️ Final: ≈ ₹181.0 (π ≈ 3.14)

🔵 प्रश्न 17
एक खोखला बेलन: बाह्य त्रिज्या R = 10 सेमी, आन्तरिक त्रिज्या r = 8 सेमी, ऊँचाई h = 15 सेमी। प्रयुक्त धातु का आयतन ज्ञात कीजिए।
🟢 उत्तर
➤ V(सामग्री) = π(R² − r²)h
➤ = π(10² − 8²)×15 = π(100 − 64)×15 = π×36×15
➤ = 540π सेमी³
✔️ Final: 540π सेमी³

🔵 प्रश्न 18 (आन्तरिक विकल्प)
(A) एक पानी की टंकी बेलन (त्रिज्या 2 मी, ऊँचाई 3 मी) पर खड़े अर्द्धगोले (उसी त्रिज्या) की है। ऊपरी सतह खुली है। कुल आन्तरिक सतह क्षेत्र ज्ञात कीजिए।
या (OR)
(B) r = 3 सेमी, h = 4 सेमी वाले शंकु को गलाकर उसी त्रिज्या r के बेलन (ऊँचाई H) में ढाला गया। H ज्ञात कीजिए।
🟢 उत्तर (A)
➤ आन्तरिक क्षेत्र = CSA(बेलन) + CSA(अर्द्धगोला)
➤ = 2π r h + 2π r² = 2π×2×3 + 2π×2² = 12π + 8π
✔️ Final: 20π मी²
🟢 उत्तर (B)
➤ आयतन-समानता: (1/3)π r² h = π r² H
➤ (1/3)×π×3²×4 = π×3²×H
➤ (1/3)×9×4 = 9H ⇒ 12 = 9H
✔️ Final: H = 4/3 सेमी

🔵 प्रश्न 19 (आन्तरिक विकल्प)
(A) शंकुखंड: R = 12 सेमी, r = 8 सेमी, h = 15 सेमी। वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
या (OR)
(B) समान आकार के दो ठोसों का रैखिक अनुपात 3:5 है। उनके आयतनों का अनुपात ज्ञात कीजिए।
🟢 उत्तर (A)
➤ तिर्यक ऊँचाई: l = √(h² + (R − r)²) = √(15² + 4²) = √(225 + 16) = √241
➤ CSA = π(R + r) l = π(12 + 8)√241 = 20π√241
✔️ Final: 20π√241 सेमी²
🟢 उत्तर (B)
➤ रैखिक गुणक k = 3:5 ⇒ आयतन अनुपात = k³ = 3³ : 5³ = 27 : 125
✔️ Final: 27 : 125

🔵 प्रश्न 20 (आन्तरिक विकल्प)
(A) त्रिज्या 4.2 सेमी के ठोस गोले को गलाकर त्रिज्या 2.1 सेमी के छोटे-छोटे गोले बनाए जाते हैं। गोले की संख्या ज्ञात कीजिए।
या (OR)
(B) त्रिज्या r वाली लोहे की गोल गेंद पर 0.2 सेमी मोटाई की पेंट की परत चढ़ाई। प्रयुक्त पेंट का लगभग आयतन ज्ञात कीजिए (r ≫ 0.2 मान कर)।
🟢 उत्तर (A)
➤ संख्या n = V(बड़ा गोला) / V(छोटा गोला)
➤ = [(4/3)π(4.2)³] ÷ [(4/3)π(2.1)³] = (4.2/2.1)³ = 2³
✔️ Final: n = 8
🟢 उत्तर (B)
➤ पेंट आयतन ≈ पृष्ठ × मोटाई = 4π r² × 0.2
✔️ Final: 0.8π r² सेमी³ (लगभग)

🔵 प्रश्न 21 (आन्तरिक विकल्प)
(A) शंकुखंड-आकार की बाल्टी: R = 14 सेमी, r = 7 सेमी, h = 24 सेमी। सम्भरण आयतन ज्ञात कीजिए।
या (OR)
(B) 3:2:1 अनुपात की भुजाओं वाला घनाभ गलाकर घन बनाया गया। यदि घनाभ का आयतन 24a³ है, तो घन की भुजा ज्ञात कीजिए।
🟢 उत्तर (A)
➤ V(शंकुखंड) = (1/3)π h (R² + r² + Rr)
➤ = (1/3)π×24×(14² + 7² + 14×7)
➤ = 8π×(196 + 49 + 98) = 8π×343 = 2744π
✔️ Final: 2744π सेमी³
🟢 उत्तर (B)
➤ घनाभ आयतन = 24a³ = s³ (घन का आयतन)
➤ s = ∛(24a³) = ∛24 · a
✔️ Final: घन की भुजा = ∛24 · a

🔵 प्रश्न 22 (आन्तरिक विकल्प)
(A) त्रिज्या 3 मी व ऊँचाई 7 मी का कुआँ खोदा गया। निकली मिट्टी 22 मी × 2 मी के रास्ते पर समान मोटाई t में बिछाई गई। t ज्ञात कीजिए।
या (OR)
(B) त्रिज्या 10 सेमी और ऊँचाई 21 सेमी वाला बेलन गलाकर त्रिज्या 7 सेमी के ठोस गोले बनाए गए। गेंदों की संख्या ज्ञात कीजिए। (π = 22/7)
🟢 उत्तर (A)
➤ V(कुआँ) = π r² h = π×3²×7 = 63π m³
➤ क्षेत्रफल(रास्ता) = 22×2 = 44 m²
➤ मोटाई t = V/Area = (63π)/44 m
✔️ Final: t = (63π/44) m ≈ 4.50 m
🟢 उत्तर (B)
➤ V(बेलन) = π r² h = (22/7)×10²×21 = 6600 सेमी³
➤ V(एक गोला) = (4/3)π r³ = (4/3)×(22/7)×7³ = 4312/3 सेमी³ ≈ 1437.33 सेमी³
➤ संख्या n = 6600 ÷ (4312/3) = (6600×3)/4312 ≈ 4.59 ⇒ पूर्ण गोले = 4
✔️ Final: 4 गेंदें (थोड़ी सामग्री शेष)

🔵 Question 23
त्रिज्या 7 सेमी और ऊँचाई 24 सेमी वाला एक बेलन है। उसके ऊपर उसी त्रिज्या का एक शंकु अध्यारोपित है जिसकी ऊँचाई 25 सेमी है। ठोस का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
🟢 Answer
➤ दिए गए: r = 7 सेमी, h₁(बेलन) = 24 सेमी, h₂(शंकु) = 25 सेमी
➤ शंकु की तिर्यक ऊँचाई: l = √(r² + h₂²) = √(7² + 25²) = √(49 + 625) = √674
➤ TSA(ठोस) = CSA(बेलन) + CSA(शंकु) + नीचे का आधार क्षेत्रफल
➤ = 2π r h₁ + π r l + π r²
➤ = 2π×7×24 + π×7×√674 + π×7²
➤ = 336π + 7π√674 + 49π
✔️ Final: (385π + 7π√674) सेमी²

🔵 Question 24 (आन्तरिक विकल्प)
(A) एक घनाभ का आयतन 1386 सेमी³ है, जिसकी लम्बाई 21 सेमी और चौड़ाई 7 सेमी है। इसे गलाकर एक बेलन बनाया जाता है जिसकी ऊँचाई 12 सेमी है। बेलन की त्रिज्या ज्ञात कीजिए।
या (OR)
(B) त्रिज्या 3.5 सेमी वाले ठोस गोले को गलाकर 2:1 के अनुपात में दो बेलनों (उसी त्रिज्या r) की ऊँचाइयाँ बनायी जाती हैं। यदि दोनों बेलनों की त्रिज्या समान है और कुल आयतन संरक्षित है, तो सामान्य त्रिज्या r ज्ञात कीजिए (ऊँचाइयाँ 2h और h)।
🟢 Answer (A)
➤ V(घनाभ) = 21×7×h = 1386 ⇒ h = 1386/(147) = 9 सेमी (सत्यापन)
➤ पिघलाकर: V(बेलन) = V(घनाभ) ⇒ π r² (12) = 1386
➤ r² = 1386/(12π) = 115.5/π
➤ r = √(115.5/π)
✔️ Final: r = √(115.5/π) सेमी ≈ 6.06 सेमी (π ≈ 3.14)
🟢 Answer (B)
➤ V(गोला) = (4/3)π(3.5)³
➤ V(दोनों बेलन) = π r²(2h) + π r²(h) = 3π r² h
➤ आयतन-समानता: (4/3)π(3.5)³ = 3π r² h ⇒ (4/3)(42.875) = 3 r² h
➤ 57.166… = 3 r² h ⇒ r² h = 19.055…
✔️ Final: r² h = 19.055… सेमी³ (एकाधिक हल; r,h के संयुग्म मान संभव)

🔵 Question 25
त्रिज्या 4.2 सेमी वाले एक खोखले बेलन की मोटाई 0.2 सेमी है और ऊँचाई 20 सेमी है। (i) प्रयुक्त धातु का आयतन और (ii) कुल वक्र पृष्ठीय क्षेत्र (अंदर + बाहर) ज्ञात कीजिए।
🟢 Answer
➤ R = 4.2 सेमी, मोटाई t = 0.2 ⇒ r = R − t = 4.0 सेमी, h = 20 सेमी
➤ (i) V(सामग्री) = π(R² − r²)h = π(4.2² − 4.0²)×20
➤ = π(17.64 − 16.00)×20 = π(1.64)×20 = 32.8π
✔️ (i) Final: 32.8π सेमी³
➤ (ii) CSA(टोटल) = 2π R h + 2π r h = 2π h (R + r)
➤ = 2π×20×(4.2 + 4.0) = 40π×8.2 = 328π
✔️ (ii) Final: 328π सेमी²

🔵 Question 26 (आन्तरिक विकल्प)
(A) एक शंकुखंड की त्रिज्याएँ R = 12 सेमी, r = 8 सेमी और ऊँचाई h = 10 सेमी हैं। (i) तिर्यक ऊँचाई l तथा (ii) कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
या (OR)
(B) एक उल्टा शंक्वाकार टैंक (ऊपर खुला) की ऊँचाई 24 मी और ऊपरी त्रिज्या 7.5 मी है। उसमें पानी 18 मी गहराई तक है। टैंक में पानी का आयतन ज्ञात कीजिए।
🟢 Answer (A)
➤ l = √(h² + (R − r)²) = √(10² + 4²) = √(100 + 16) = √116 = 2√29
➤ CSA = π(R + r)l = π(12 + 8)(2√29) = 40π√29
➤ TSA = CSA + πR² + πr² = 40π√29 + π(144 + 64) = 40π√29 + 208π
✔️ Final: l = 2√29 सेमी, TSA = (40√29 + 208)π सेमी²
🟢 Answer (B)
➤ r(top) = 7.5 मी, H = 24 मी; पानी की गहराई h = 18 मी
➤ शंकु में समानता: r(h) / h = r(top) / H ⇒ r(h) = (7.5/24)×18 = 5.625 मी
➤ V(पानी) = (1/3)π r(h)² h = (1/3)π×(5.625)²×18
➤ = (1/3)π×31.640625×18 = 6π×31.640625 = 189.84375π
✔️ Final: लगभग 596.6 मी³ (π ≈ 3.14)

🔵 Question 27
एक काँच की बोतल का गोल भाग त्रिज्या 4 सेमी का गोला है और उसके ऊपर गर्दन 3 सेमी ऊँचाई और 1.5 सेमी त्रिज्या के बेलन की है। बोतल की कुल क्षमता ज्ञात कीजिए।
🟢 Answer
➤ V(गोला) = (4/3)π r³ = (4/3)π×4³ = (4/3)π×64 = 85.333…π
➤ V(गर्दन) = π r² h = π×1.5²×3 = π×2.25×3 = 6.75π
➤ V(कुल) = 85.333…π + 6.75π = 92.083…π
✔️ Final: ≈ 289.4 सेमी³ (π ≈ 3.14)

🔵 Question 28
एक ठोस बेलन (त्रिज्या 5 सेमी, ऊँचाई 10 सेमी) को गलाकर शंक्वाकार ठोस बनाया गया जिसकी ऊँचाई 12 सेमी है। नए शंकु की त्रिज्या ज्ञात कीजिए।
🟢 Answer
➤ V(बेलन) = π×5²×10 = 250π
➤ V(शंकु) = (1/3)π R²×12 = 4π R²
➤ आयतन-समानता: 250π = 4π R² ⇒ R² = 62.5 ⇒ R = √62.5
✔️ Final: R = √62.5 सेमी ≈ 7.91 सेमी

🔵 Question 29 (आन्तरिक विकल्प)
(A) एक आइसक्रीम कोन: शंकु की त्रिज्या 3.5 सेमी, ऊँचाई 12 सेमी; ऊपर अर्धगोलीय स्कूप (उसी r) रखा है। कुल आयतन ज्ञात कीजिए।
या (OR)
(B) त्रिज्या 7 सेमी वाला अर्द्धगोला बाहर से पेंट किया जाना है (आधार को छोड़कर)। 1 सेमी² पर ₹0.60 की दर से लागत ज्ञात कीजिए।
🟢 Answer (A)
➤ V(शंकु) = (1/3)π r² h = (1/3)π×3.5²×12 = (1/3)π×12.25×12 = 49π
➤ V(अर्धगोला) = (2/3)π r³ = (2/3)π×3.5³ = (2/3)π×42.875 = 28.583…π
➤ V(कुल) = 49π + 28.583…π = 77.583…π
✔️ Final: ≈ 243.8 सेमी³ (π ≈ 3.14)
🟢 Answer (B)
➤ बाहर पेंट क्षेत्र = CSA(अर्द्धगोला) = 2π r² = 2π×7² = 98π
➤ लागत = 98π × 0.60 = 58.8π
✔️ Final: ≈ ₹184.7 (π ≈ 3.14)

🔵 Question 30
एक आयताकार पानी की टंकी 2.5 मी × 1.6 मी × 1.2 मी (लम्बाई × चौड़ाई × ऊँचाई) तक पानी से भरी है। एक ठोस धातु का गोला त्रिज्या 0.4 मी इसमें पूरी तरह डुबोया जाता है। टंकी से बाहर निकला पानी और नया जल-स्तर (ऊँचाई) ज्ञात कीजिए।
🟢 Answer
➤ V(टंकी) = 2.5×1.6×1.2 = 4.8 मी³ (क्षमता)
➤ V(गोला) = (4/3)π r³ = (4/3)π×(0.4)³ = (4/3)π×0.064 = 0.08533…π
➤ निकला पानी = V(गोला) = 0.08533…π ≈ 0.268 मी³ (π ≈ 3.14)
➤ टंकी का आधार क्षेत्र A = 2.5×1.6 = 4.0 मी²
➤ जल-स्तर वृद्धि Δh = निकला_पानी / A = 0.268 / 4.0 = 0.067 मी = 6.7 सेमी
➤ प्रारम्भिक ऊँचाई = 1.2 मी ⇒ नया जल-स्तर = 1.2 + 0.067 = 1.267 मी
✔️ Final: निकला पानी ≈ 0.268 मी³, नया जल-स्तर ≈ 1.267 मी

————————————————————————————————————————————————————————————————————————————

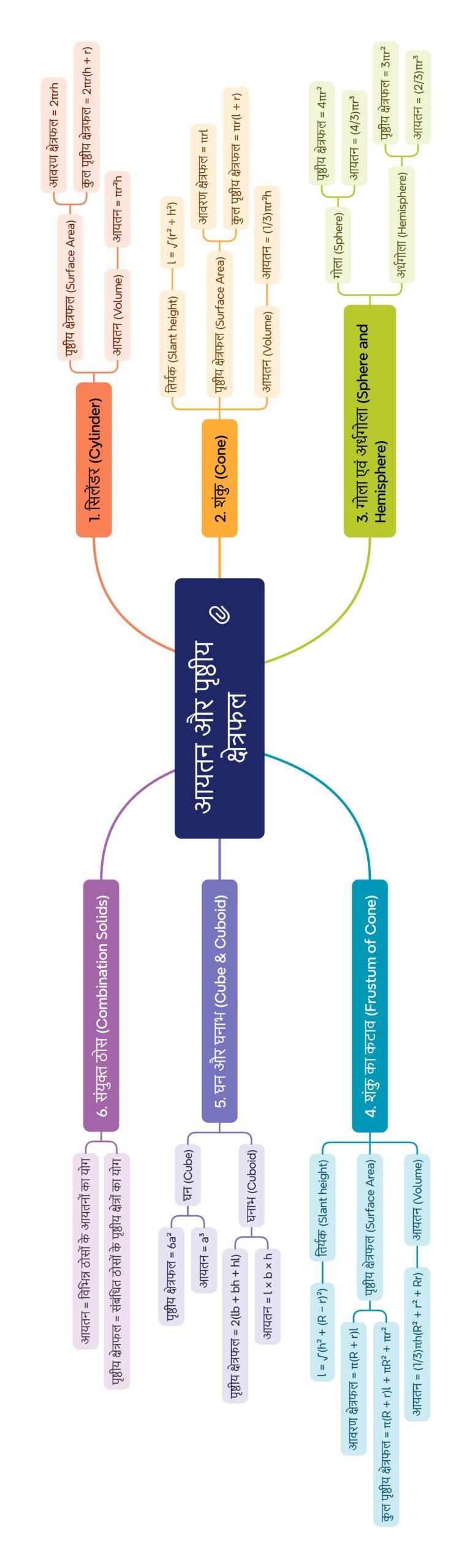
मनोमानचित्र

————————————————————————————————————————————————————————————————————————————