Class 10 : Maths (In Hindi) – Lesson 11. वृत्तों से सम्बन्धित क्षेत्रफल

पाठ का विश्लेषण  एवं  विवेचन

🔵 (परिचय, मूल शब्दावली, परिधि व क्षेत्रफल, चाप-लम्बाई, त्रिज्यखंड)

🔴 1️⃣ परिचय
 • गणित के अनेक व्यावहारिक प्रश्न ऐसे होते हैं जिनमें वृत्तों से जुड़ी आकृतियों के क्षेत्रफल और परिधि ज्ञात करनी पड़ती है।
 • सड़क के गोल चौराहे, पंखे के ब्लेड, मशीन के गियर, बगीचे के अर्धवृत्ताकार कोने—all ये उदाहरण वृत्त आधारित हैं।
 • इस अध्याय में हम त्रिज्या (r), व्यास (d), कोण (θ) और चाप के आधार पर आकृतियों का क्षेत्रफल निकालना सीखते हैं।

🟢 2️⃣ मूल शब्दावली
 🔸 वृत्त: केंद्र O से समान दूरी r पर स्थित सभी बिंदुओं का समुच्चय।
 🔸 त्रिज्या (r): O से परिधि तक की दूरी।
 🔸 व्यास (d): d = 2r।
 🔸 चाप (Arc): वृत्त की परिधि का कोई भाग।
 🔸 त्रिज्यखंड (Sector): दो त्रिज्याओं और उनके बीच के चाप से घिरा क्षेत्र।
 🔸 खंड (Segment): एक जीवा और उससे जुड़े चाप के बीच का क्षेत्र।
 🔸 स्पर्श रेखा: केवल एक बिंदु पर वृत्त को छूती रेखा।
 🔸 छेदक रेखा: दो बिंदुओं पर वृत्त को काटती रेखा।

🟡 3️⃣ वृत्त की परिधि और क्षेत्रफल
 💡 सूत्र
 ➤ परिधि (C) = 2πr।
 ➤ क्षेत्रफल (A) = πr²।
 ✏️ नोट: π ≈ 22/7 या 3.14।
 ✔️ उदाहरण: r = 7 cm ⇒ परिधि = 2π×7 = 14π cm, क्षेत्रफल = π×7² = 49π cm²।

🌿 4️⃣ चाप-लम्बाई (Arc Length)
 • जब केंद्र पर कोण θ (डिग्री) बनता है, तो चाप-लम्बाई l = (θ/360) × 2πr।
 • उदाहरण: r = 14 cm, θ = 90°
  🔵 Step 1: l = (90/360) × 2π × 14
  🔵 Step 2: = (1/4) × 28π
  ✔️ Final: l = 7π cm।

🔴 5️⃣ त्रिज्यखंड का क्षेत्रफल (Area of Sector)
 💡 परिभाषा: दो त्रिज्याओं और उनके बीच के चाप से घिरा हुआ भाग।
 🟢 सूत्र: A_sector = (θ/360) × πr²।
 उदाहरण: r = 14 cm, θ = 60°
  🔵 Step 1: A = (60/360) × π × 14²
  🔵 Step 2: = (1/6) × π × 196
  ✔️ Final: A = 196π/6 cm²।

🟡 6️⃣ महत्त्वपूर्ण टिप्पणियाँ
 ✏️ नोट: यदि θ = 90°, तो त्रिज्यखंड = चौथाई वृत्त = (¼)πr²।
 ✏️ नोट: यदि θ = 180°, तो त्रिज्यखंड = अर्धवृत्त = (½)πr²।
 🌿 अनुप्रयोग: पंखे के ब्लेड, गोल पिज़्ज़ा के स्लाइस, बगीचे के सेक्टर आदि।

🟢 (खंड का क्षेत्रफल, संयुक्त आकृतियाँ, उदाहरण, अनुप्रयोग)
🔵 7️⃣ खंड (Segment) का क्षेत्रफल
 💡 परिभाषा: एक जीवा और उसके संगत चाप से घिरा हुआ भाग।
 🔸 सूत्र:
  A_खंड = A_{त्रिज्यखंड} − A_{त्रिभुज}
 🔸 उदाहरण:
  • r = 10 cm, θ = 60°
   ➤ Step 1: A_त्रिज्यखंड = (60/360)×π×10² = (1/6)×100π = 50π/3 cm²।
   ➤ Step 2: त्रिभुज क्षेत्रफल = ½ r² sinθ = ½ × 100 × sin60° = 50 × (√3/2) = 25√3।
   ➤ Step 3: A_segment = 50π/3 − 25√3 cm²।
 ✔ Final: खंड का क्षेत्रफल = 50π/3 − 25√3 cm²।
🟡 8️⃣ लघु एवं महाखंड
 • यदि θ < 180°, तो खंड = लघु खंड।
 • यदि θ > 180°, तो खंड = महाखंड।
🔴 9️⃣ संयुक्त आकृतियाँ (Composite Figures)
 🌿 ऐसे प्रश्नों में कई ज्यामितीय आकृतियाँ जुड़ी होती हैं—जैसे वर्ग व वृत्त, अर्धवृत्त और आयत आदि।
 💡 रणनीति:
  ➤ कुल क्षेत्रफल = बड़े क्षेत्रफल − निकाले गए भाग।
  ➤ आकृति को छोटे भागों (त्रिज्यखंड, अर्धवृत्त, त्रिभुज) में विभाजित कर जोड़ें या घटाएँ।
उदाहरण 1:
 🧠 प्रश्न: एक आयत 20 cm × 14 cm के छोटे किनारों पर दो अर्धवृत्त बने हैं। कुल क्षेत्रफल ज्ञात करें।
 🔵 Step 1: आयत = 20×14 = 280 cm²।
 🔵 Step 2: त्रिज्या = 14/2 = 7 cm ⇒ अर्धवृत्त क्षेत्रफल = ½π×7² = 77 cm²।
 🔵 Step 3: कुल क्षेत्रफल = 280 + 2×77 = 434 cm²।
 ✔ Final: 434 cm²।
उदाहरण 2:
 🧠 प्रश्न: एक वर्ग के प्रत्येक कोने पर चौथाई वृत्त बनाए गए हैं। वर्ग की भुजा 14 cm है। शेष क्षेत्रफल ज्ञात करें।
 🔵 Step 1: वर्ग क्षेत्रफल = 14² = 196 cm²।
 🔵 Step 2: एक चौथाई वृत्त का क्षेत्रफल = (¼)πr² = (¼)π×7² = 49π/4।
 🔵 Step 3: चार कोनों के लिए कुल वृत्त भाग = 4×49π/4 = 49π।
 🔵 Step 4: शेष क्षेत्रफल = 196 − 49π cm²।
 ✔ Final: शेष = 196 − 49π cm²।
🟢 🔟 अर्धवृत्त औरचौथाई वृत्त का उपयोग
 • अर्धवृत्त = ½πr²।
 • चौथाई वृत्त = ¼πr²।
 • तीन-चौथाई वृत्त = (¾)πr²।
🔵 11️⃣ वास्तविक जीवन अनुप्रयोग
 🌿 वास्तुकला: गोल मेहराब, गुम्बद, पुल के चाप।
 🌿 अभियांत्रिकी: गियर और मशीन पार्ट्स।
 🌿 खेल: गोल ट्रैक, पिज़्ज़ा स्लाइस, स्टेडियम डिज़ाइन।
🔴 12️⃣ चरण-दर-चरण उदाहरण (पुनरावृत्ति)
उदाहरण 3:
 प्रश्न: त्रिज्या 21 cm वाले पहिए ने 150 चक्कर लगाए। चली गई दूरी ज्ञात करें।
 ➤ Step 1: परिधि = 2πr = 2π×21 = 42π cm।
 ➤ Step 2: दूरी = 150×42π = 6300π cm ≈ 197.9 m।
 ✔ Final: ≈ 197.9 m।
उदाहरण 4:
 प्रश्न: त्रिज्या 6 cm वाले वृत्त का 120° त्रिज्यखंड। क्षेत्रफल व चाप-लम्बाई ज्ञात करें।
 ➤ Step 1: A_त्रिज्यखंड = (120/360)×π×6² = (⅓)×π×36 = 12π cm²।
 ➤ Step 2: चाप-लम्बाई = (120/360)×2π×6 = (⅓)×12π = 4π cm।
 ✔ Final: क्षेत्रफल = 12π cm², चाप-लम्बाई = 4π cm।
🟡 13️⃣ महत्वपूर्ण सुझाव
 ✏️ π के मान का चयन सही करें (22/7 या 3.14)।
 ✏️ इकाइयों को बदलते समय ध्यान दें (cm² → m²)।
 ✏️ आरेख बनाते समय केंद्र कोण θ व त्रिज्या r साफ़ दिखाएँ।

📚 सारांश (शेष बिंदु)
 • खंड = त्रिज्यखंड − त्रिभुज क्षेत्रफल।
 • लघु खंड (θ<180°), महाखंड (θ>180°)।
 • संयुक्त आकृतियाँ = बड़े क्षेत्रफल − छोटे।
 • अर्धवृत्त, चौथाई वृत्त, तीन-चौथाई वृत्त के सूत्र याद रखें।
 • अनुप्रयोग: वास्तुकला, खेल मैदान, गियर, पहिए, बगीचे डिज़ाइन।

📝 Quick Recap (Part 2)
1️⃣ खंड का क्षेत्रफल = त्रिज्यखंड − त्रिभुज क्षेत्रफल।
2️⃣ लघु खंड और महाखंड का अंतर पहचानें।
3️⃣ संयुक्त आकृतियों में जोड़-घटाव से हल करें।
4️⃣ अर्धवृत्त = ½πr², चौथाई वृत्त = ¼πr²।
5️⃣ वास्तविक जीवन में वृत्त आधारित क्षेत्रफल की अवधारणाएँ अत्यंत उपयोगी हैं।

————————————————————————————————————————————————————————————————————————————

पाठ्यपुस्तक के प्रश्न

अभ्यास- 11.1

🔵 Question 1
6 cm त्रिज्या वाले एक वृत्त के एक त्रिज्याखंड का क्षेत्रफल ज्ञात कीजिए, जिसका कोण 60° है।
🟢 Answer
💡 सूत्र: त्रिज्याखंड क्षेत्रफल = (θ/360°) × π r²
🔵 Step 1: दिए गए r = 6 cm, θ = 60°, π = 22/7
🔵 Step 2: क्षेत्रफल = (60/360) × (22/7) × 6²
🔵 Step 3: = (1/6) × (22/7) × 36
🔵 Step 4: = 132/7 cm²
✔️ Final: 132/7 cm² ≈ 18.86 cm²

🔵 Question 2
एक वृत्त के चतुर्थांश (quadrant) का क्षेत्रफल ज्ञात कीजिए, जिसकी परिधि 22 cm है।
🟢 Answer
💡 परिधि: C = 2πr → r = C/(2π)
🔵 Step 1: 2 × (22/7) × r = 22
🔵 Step 2: r = 22 ÷ (44/7) = 7/2 = 3.5 cm
🔵 Step 3: पूर्ण क्षेत्रफल = π r² = (22/7) × (3.5)² = 38.5 cm²
🔵 Step 4: चतुर्थांश क्षेत्रफल = 38.5/4 = 9.625 cm²
✔️ Final: 9.625 cm²

🔵 Question 3
एक घड़ी की मिनट की सूई जिसकी लंबाई 14 cm है। इस सूई द्वारा 5 मिनट में रचित क्षेत्रफल ज्ञात कीजिए।
🟢 Answer
💡 1 मिनट में कोण = 6° ⇒ 5 मिनट में θ = 5 × 6° = 30°
🔵 Step 1: r = 14 cm, θ = 30°, π = 22/7
🔵 Step 2: क्षेत्रफल = (θ/360) × π r² = (30/360) × (22/7) × 14²
🔵 Step 3: = (1/12) × (22/7) × 196
🔵 Step 4: = 154/3 cm²
✔️ Final: 154/3 cm² ≈ 51.33 cm²

🔵 Question 4
10 सेमी त्रिज्या वाले एक वृत्त की कोई जीवा केंद्र पर एक समकोण अंतरित करती है। निम्नलिखित के क्षेत्रफल ज्ञात कीजिए: (i) संगत लघु वृत्तखंड (ii) संगत दीर्घ वृत्तखंड (π = 3.14 का प्रयोग कीजिए)।
🟢 Answer
💡 वृत्तखंड(सेगमेंट) = त्रिज्याखंड(सेक्टर) − त्रिभुज का क्षेत्रफल
🔵 Step 1: r = 10 cm, θ = 90°, π = 3.14
🔵 Step 2: त्रिज्याखंड क्षेत्रफल = (90/360) × 3.14 × 10² = (1/4) × 3.14 × 100 = 78.5 cm²
🔵 Step 3: त्रिभुज क्षेत्रफल = (1/2) × r² × sin90° = (1/2) × 100 × 1 = 50 cm²
🔵 Step 4: लघु वृत्तखंड = 78.5 − 50 = 28.5 cm²
🔵 Step 5: पूर्ण वृत्त क्षेत्रफल = 3.14 × 10² = 314 cm²
🔵 Step 6: दीर्घ वृत्तखंड = 314 − 28.5 = 285.5 cm²
✔️ Final: (i) 28.5 cm², (ii) 285.5 cm²

🔵 Question 5
त्रिज्या 21 cm वाले वृत्त का एक चाप केंद्र पर 60° का कोण अंतरित करता है। ज्ञात कीजिए: (i) चाप की लंबाई (ii) चाप द्वारा बनाए गए त्रिज्याखंड का क्षेत्रफल (iii) संगत जीवा द्वारा बनाए गए वृत्तखंड का क्षेत्रफल।
🟢 Answer
(i) चाप की लंबाई
🔵 Step 1: s = (θ/360) × 2πr = (60/360) × 2 × (22/7) × 21
🔵 Step 2: = (1/6) × 2 × (22/7) × 21 = (1/3) × (22/7) × 21
🔵 Step 3: = (22/7) × 7 = 22 cm
✔️ Final(i): 22 cm
(ii) सेक्टर का क्षेत्रफल
🔵 Step 1: A_sector = (60/360) × π r² = (1/6) × (22/7) × 21²
🔵 Step 2: = (22 × 441)/42 = 231 cm²
✔️ Final(ii): 231 cm²
(iii) संगत वृत्तखंड (लघु) का क्षेत्रफल
🔵 Step 1: A_triangle = (1/2) × r² × sin60° = (1/2) × 21² × (√3/2)
🔵 Step 2: = (441/4) × √3 cm²
🔵 Step 3: √3 ≈ 1.732 ⇒ A_triangle ≈ 190.96 cm²
🔵 Step 4: A_segment = A_sector − A_triangle ≈ 231 − 190.96
✔️ Final(iii): ≈ 40.04 cm²

🔵 Question 6
15 cm त्रिज्या वाले एक वृत्त की कोई जीवा केंद्र पर 60° का कोण अंतरित करती है। संगत लघु और दीर्घ वृत्तखंडों के क्षेत्रफल ज्ञात कीजिए। (π = 3.14 और √3 = 1.73 का प्रयोग कीजिए।)
🟢 Answer
🔵 Step 1: r = 15 cm, θ = 60°
🔵 Step 2: त्रिज्याखंड क्षेत्रफल = (60/360) × 3.14 × 15² = (1/6) × 3.14 × 225 = 117.75 cm²
🔵 Step 3: त्रिभुज क्षेत्रफल = (1/2) × r² × sin60° = (1/2) × 225 × (√3/2)
🔵 Step 4: √3 = 1.73 ⇒ sin60° ≈ 0.865 ⇒ A_triangle = 112.5 × 0.865 = 97.3125 cm²
🔵 Step 5: लघु वृत्तखंड = 117.75 − 97.3125 = 20.4375 cm²
🔵 Step 6: पूर्ण वृत्त क्षेत्रफल = 3.14 × 225 = 706.5 cm²
🔵 Step 7: दीर्घ वृत्तखंड = 706.5 − 20.4375 = 686.0625 cm²
✔️ Final: लघु = 20.44 cm² (लगभग), दीर्घ = 686.06 cm² (लगभग)

🔵 Question 7
त्रिज्या 12 cm वाले एक वृत्त की कोई जीवा केंद्र पर 120° का कोण अंतरित करती है। संगत वृत्तखंड का क्षेत्रफल ज्ञात कीजिए। (π = 3.14 और √3 = 1.73 का प्रयोग कीजिए।)
🟢 Answer
🔵 Step 1: r = 12 cm, θ = 120°
🔵 Step 2: त्रिज्याखंड क्षेत्रफल = (120/360) × 3.14 × 12² = (1/3) × 3.14 × 144 = 150.72 cm²
🔵 Step 3: त्रिभुज क्षेत्रफल = (1/2) × 12² × sin120°
🔵 Step 4: sin120° = sin60° = √3/2 ≈ 1.73/2 = 0.865 ⇒ A_triangle = 72 × 0.865 = 62.28 cm²
🔵 Step 5: वृत्तखंड (लघु) = 150.72 − 62.28 = 88.44 cm²
✔️ Final: 88.44 cm²

🔵 Question 8
15 m भुजा वाले एक वर्गाकार घास के मैदान के एक कोने पर लगे खूंटे से एक घोड़े को 5 m लंबी रस्सी से बाँध दिया गया है (देखिए आकृति 11.8)। ज्ञात कीजिए:
(i) मैदान के उस भाग का क्षेत्रफल जहाँ घोड़ा घास चर सकता है।
(ii) चरने जा सकने वाले क्षेत्रफल में वृद्धि, यदि घोड़े को 5 m लंबी रस्सी के स्थान पर 10 m लंबी रस्सी से बाँध दिया जाए। (π = 3.14 का प्रयोग कीजिए।)
🟢 Answer
💡 कोने पर चराई ⇒ त्रिज्या r वाला चतुर्थांश: क्षेत्रफल = (π r²)/4
(i) r = 5 m
🔵 Step 1: A₁ = (3.14 × 5²)/4 = (3.14 × 25)/4
🔵 Step 2: A₁ = 78.50/4 = 19.625 m²
✔️ Final(i): 19.625 m² ≈ 19.63 m²
(ii) r = 10 m (भुजा 15 m होने से पूरा चतुर्थांश अंदर रहेगा)
🔵 Step 1: A₂ = (3.14 × 10²)/4 = 314/4 = 78.50 m²
🔵 Step 2: वृद्धि = A₂ − A₁ = 78.50 − 19.625 = 58.875 m²
✔️ Final(ii): 58.875 m² ≈ 58.88 m²

🔵 Question 9
एक वृत्ताकार ब्रोच (brooch) को चाँदी के तार से बनाया जाता है जिसका व्यास 35 mm है। तार को वृत्त के 5 व्यासों को बनाने में भी प्रयुक्त किया गया है जो उसे 10 बराबर त्रिज्याखंडों में विभाजित करता है जैसा कि आकृति 11.9 में दर्शाया गया है। तो ज्ञात कीजिए:
(i) कुल आवश्यक चाँदी के तार की लंबाई
(ii) ब्रोच के प्रत्येक त्रिज्याखंड का क्षेत्रफल
🟢 Answer
(i) कुल तार की लंबाई
🔵 Step 1: व्यास d = 35 mm ⇒ परिधि = π d = (22/7) × 35 = 110 mm
🔵 Step 2: 5 व्यासों के लिए तार = 5 × 35 = 175 mm
🔵 Step 3: कुल लंबाई = 110 + 175 = 285 mm
✔️ Final(i): 285 mm
(ii) प्रत्येक त्रिज्याखंड का क्षेत्रफल
🔵 Step 1: r = d/2 = 17.5 mm
🔵 Step 2: पूर्ण क्षेत्रफल = π r² = (22/7) × (17.5)² = 962.5 mm²
🔵 Step 3: कुल 10 बराबर त्रिज्याखंड ⇒ प्रत्येक का क्षेत्रफल = 962.5/10 = 96.25 mm²
✔️ Final(ii): 96.25 mm²

🔵 प्रश्न 10
एक छत्री में आठ ताने हैं, जो बराबर दूरी पर लगे हुए हैं (देखिए आकृति 11.10)। छत्री को 45 cm त्रिज्या वाला एक सपाट वृत्त मानते हुए, इसकी दो क्रमागत तानों के बीच का क्षेत्रफल ज्ञात कीजिए।
🟢 उत्तर
➤ कुल तानों की संख्या = 8
➤ प्रत्येक खण्ड का केन्द्रक कोण = 360°/8 = 45°
➤ वृत्त का क्षेत्रफल = π r² = 3.14 × 45² = 3.14 × 2025 = 6358.5 cm²
➤ दो क्रमागत तानों के बीच का क्षेत्रफल = 45° का त्रिज्याखंड क्षेत्रफल
= (45/360) × 6358.5
= (1/8) × 6358.5
= 794.8 cm² ✔️
✏️ नोट: क्रमागत तानों के बीच का भाग वास्तव में एक त्रिज्याखंड है।

🔵 प्रश्न 11
किसी कार के दो वाइपर हैं, परस्पर कभी आपस में नहीं भिड़ते। प्रत्येक वाइपर की पतली लंबाई 25 cm है और 115° के कोण तक घूम कर सफाई कर सकता है। प्रत्येक बुहार के साथ जितना क्षेत्रफल साफ़ होता है, वह ज्ञात कीजिए।
🟢 उत्तर
➤ प्रत्येक वाइपर एक वृत्त का त्रिज्याखंड बनाता है।
➤ r = 25 cm, θ = 115°
➤ क्षेत्रफल (एक बुहार) = (θ/360) × π r²
= (115/360) × 3.14 × 25²
= (115/360) × 3.14 × 625
= (115/360) × 1962.5
= 627.4 cm² ✔️

🔵 प्रश्न 12
जहाज़ों के समूह में जलस्तर के नीचे स्थित चट्टानों की चेतावनी देने के लिए, एक लाइट हाउस 80° कोण वाले एक त्रिज्याखंड में 16.5 km की दूरी तक लाल रंग का प्रकाश फैलाता है। समूह के उस भाग का क्षेत्रफल ज्ञात कीजिए जिसमें जहाज़ों को चेतावनी दी जा सके। (π = 3.14)
🟢 उत्तर
➤ r = 16.5 km, θ = 80°
➤ क्षेत्रफल = (θ/360) × π r²
= (80/360) × 3.14 × (16.5)²
= (2/9) × 3.14 × 272.25
= (2/9) × 854.865
= 189.97 km² ✔️

🔵 प्रश्न 13
एक गोल मेज़पोश पर छः समान डिज़ाइन बने हुए हैं जैसा कि आकृति 11.11 में दर्शाया गया है। यदि मेज़पोश की त्रिज्या 28 cm है, तो ₹ 0.35 प्रति वर्ग सेंटीमीटर के दर से इन डिज़ाइनों को बनाने की लागत ज्ञात कीजिए। (√3 = 1.7)
🟢 उत्तर
➤ कुल क्षेत्रफल (वृत्त) = π r² = 3.14 × 28² = 3.14 × 784 = 2461.76 cm²
➤ छः समान डिज़ाइन ⇒ प्रत्येक डिज़ाइन = 2461.76 / 6 = 410.29 cm²
➤ कुल क्षेत्रफल डिज़ाइन = 2461.76 cm²
➤ लागत = क्षेत्रफल × दर
= 2461.76 × 0.35
= 861.62 ₹ ✔️

🔵 प्रश्न 14
निम्नलिखित में सही उत्तर चुनिए:
त्रिज्या R वाले वृत्त के उस त्रिज्याखंड का क्षेत्रफल जिसका कोण p° है, निम्नलिखित में—

1️⃣ (A) (p/180) × 2πR
2️⃣ (B) (p/180) × πR²
3️⃣ (C) (p/720) × 2πR²
4️⃣ (D) (p/360) × 2πR

🟢 उत्तर
✔️ सही विकल्प = (B) (p/180) × πR²

—————————————————————————————————————————————————————————————————————————————-

अन्य महत्वपूर्ण प्रश्न

Question 1
व्यास 14 cm वाले वृत्त की परिधि ज्ञात कीजिए (π = 22/7)।

🔸 विकल्प:
 🔵 1) 28 cm 🟢 2) 44 cm 🟡 3) 88 cm 🔴 4) 14 cm
🟢 Answer
➤ सूत्र: परिधि = π × व्यास
➤ स्थापितीकरण: = (22/7) × 14
➤ सरलकरण: = 22 × 2 = 44
✔️ उत्तर: 2) 44 cm
🔵 Question 2
त्रिज्या r = 7 cm वाले वृत्त का क्षेत्रफल ज्ञात कीजिए (π = 22/7)।

🔸 विकल्प:
 🔵 1) 110 cm² 🟢 2) 154 cm² 🟡 3) 200 cm² 🔴 4) 77 cm²
🟢 Answer
➤ सूत्र: क्षेत्रफल = π r²
➤ स्थापितीकरण: = (22/7) × 7²
➤ सरलकरण: = (22/7) × 49 = 22 × 7 = 154
✔️ उत्तर: 2) 154 cm²
🔵 Question 3
केन्द्रक कोण θ = 60° और r = 10 cm के त्रिज्याखंड की चाप-लंब ज्ञात कीजिए (π = 3.14)।

🔸 विकल्प:
 🔵 1) 6.28 cm 🟢 2) 10.47 cm 🟡 3) 20.94 cm 🔴 4) 31.4 cm
🟢 Answer
➤ सूत्र: चाप-लंब = (θ/360°) × 2πr
➤ स्थापितीकरण: = (60/360) × 2 × 3.14 × 10
➤ सरलकरण: = (1/6) × 62.8 = 10.466… ≈ 10.47
✔️ उत्तर: 2) 10.47 cm
🔵 Question 4
बाह्य त्रिज्या R और आन्तरिक त्रिज्या r (R > r) वाले वलय का क्षेत्रफल ज्ञात कीजिए।

🔸 विकल्प:
 🔵 1) π(R − r) 🟢 2) π(R² − r²) 🟡 3) 2π(R + r) 🔴 4) πRr
🟢 Answer
➤ सूत्र: वलय का क्षेत्रफल = π(R² − r²)
➤ अन्तिम मान: π(R² − r²)
✔️ उत्तर: 2) π(R² − r²)
🔵 Question 5
यदि परिधि 31.4 cm है, तो r ज्ञात कीजिए (π = 3.14)।

🔸 विकल्प:
 🔵 1) 10 cm 🟢 2) 5 cm 🟡 3) 3 cm 🔴 4) 7 cm
🟢 Answer
➤ सूत्र: परिधि = 2πr
➤ स्थापितीकरण: 31.4 = 2 × 3.14 × r
➤ सरलकरण: r = 31.4 / 6.28 = 5
✔️ उत्तर: 2) 5 cm
🔵 Question 6
θ = 90° और r = 7 cm के त्रिज्याखंड का क्षेत्रफल ज्ञात कीजिए (π = 22/7)।

🔸 विकल्प:
 🔵 1) 15.4 cm² 🟢 2) 38.5 cm² 🟡 3) 30.8 cm² 🔴 4) 77 cm²
🟢 Answer
➤ सूत्र: त्रिज्याखंड का क्षेत्रफल = (θ/360°) × π r²
➤ स्थापितीकरण: = (90/360) × (22/7) × 7²
➤ सरलकरण: = (1/4) × (22/7) × 49 = (1/4) × 154 = 38.5
✔️ उत्तर: 2) 38.5 cm²

🟢 Section B (Q7–Q12): लघु उत्तर-I (प्रत्येक 2 अंक)
🔵 Question 7
यदि क्षेत्रफल 616 cm² है, तो r ज्ञात कीजिए (π = 22/7)।
🟢 Answer
➤ सूत्र: π r² = 616
➤ स्थापितीकरण: (22/7) r² = 616
➤ सरलकरण: r² = 616 × 7 / 22 = 196
➤ r = √196 = 14
✔️ अन्तिम उत्तर: 14 cm
🔵 Question 8
r = 3.5 cm, θ = 120° के त्रिज्याखंड का परिमाप ज्ञात कीजिए (π = 22/7)।
🟢 Answer
➤ उपसूत्र: चाप-लंब = (θ/360°) × 2πr
➤ स्थापितीकरण: = (120/360) × 2 × (22/7) × 3.5
➤ सरलकरण: = (1/3) × 22 = 22/3 ≈ 7.33
➤ परिमाप = 2r + चाप-लंब = 2 × 3.5 + 7.33 = 14.33
✔️ अन्तिम उत्तर: ≈ 14.33 cm
🔵 Question 9
r = 10 cm तथा θ = 72° के त्रिज्याखंड का क्षेत्रफल ज्ञात कीजिए (π = 3.14)।
🟢 Answer
➤ सूत्र: क्षेत्रफल(त्रिज्याखंड) = (θ/360°) × π r²
➤ स्थापितीकरण: = (72/360) × 3.14 × 10²
➤ सरलकरण: = (1/5) × 3.14 × 100 = 62.8
✔️ अन्तिम उत्तर: 62.8 cm²
🔵 Question 10
व्यास 20 cm (अर्थात r = 10 cm) वाले वृत्त में θ = 60° के लिए चाप-लंब ज्ञात कीजिए (π = 3.14)।
🟢 Answer
➤ सूत्र: चाप-लंब = (θ/360°) × 2πr
➤ स्थापितीकरण: = (60/360) × 2 × 3.14 × 10
➤ सरलकरण: = (1/6) × 62.8 = 10.466… ≈ 10.47
✔️ अन्तिम उत्तर: ≈ 10.47 cm
🔵 Question 11
r = 12 cm और θ = 150° के लिए वृत्तखंड (segment) का क्षेत्रफल ज्ञात कीजिए, यदि केन्द्र से बनने वाले त्रिभुज का क्षेत्रफल 37.3 cm² है (π = 3.14)。
🟢 Answer
➤ सम्बन्ध: वृत्तखंड क्षेत्रफल = त्रिज्याखंड क्षेत्रफल − त्रिभुज क्षेत्रफल
➤ त्रिज्याखंड क्षेत्रफल = (θ/360°) × π r²
➤ स्थापितीकरण: = (150/360) × 3.14 × 12²
➤ सरलकरण: = (5/12) × 3.14 × 144 = 60π = 188.4
➤ वृत्तखंड क्षेत्रफल = 188.4 − 37.3 = 151.1
✔️ अन्तिम उत्तर: 151.1 cm²
🔵 Question 12
एक बाग में r = 3 m वाले गोल भाग के चारों ओर R = 5 m तक हरी पट्टी है। हरी पट्टी (वलय) का क्षेत्रफल ज्ञात कीजिए (π = 22/7)।
🟢 Answer
➤ मॉडल: वलय ⇒ क्षेत्रफल = π(R² − r²)
➤ स्थापितीकरण: = (22/7) × (25 − 9) = (22/7) × 16
➤ सरलकरण: = 352/7 ≈ 50.2857…
✔️ अन्तिम उत्तर: ≈ 50.29 m²

🟡 Section C (Q13–Q22): लघु उत्तर-II (प्रत्येक 3 अंक)

🔵 Question 13
r = 14 cm और θ = 75° वाले त्रिज्याखंड का क्षेत्रफल ज्ञात कीजिए (π = 22/7)।

🟢 Answer
➤ सूत्र: त्रिज्याखंड क्षेत्रफल = (θ/360°) × π r²
➤ स्थापितीकरण: = (75/360) × (22/7) × 14²
➤ सरलकरण: = (5/24) × (22/7) × 196
➤ गणना: (22/7) × 196 = 616
➤ आगे: (5/24) × 616 = 3080/24 = 128.33…
➤ Final answer: 128.33 cm² (लगभग)

🔵 Question 14 (आंतरिक विकल्प)
(A) r = 10 cm, θ = 60° के वृत्तखंड (segment) का क्षेत्रफल ज्ञात कीजिए (π = 3.14)।

🟢 Answer (A)
➤ सम्बन्ध: वृत्तखंड क्षेत्रफल = त्रिज्याखंड क्षेत्रफल − त्रिभुज क्षेत्रफल
➤ त्रिज्याखंड क्षेत्रफल: (θ/360°) × π r² = (60/360) × 3.14 × 10²
➤ सरलकरण: = (1/6) × 3.14 × 100 = 52.333…
➤ त्रिभुज क्षेत्रफल: (1/2) r² sinθ = (1/2) × 10² × (√3/2) = 50 × 0.8660… = 43.301…
➤ वृत्तखंड: 52.333… − 43.301… = 9.032…
➤ Final answer: ≈ 9.03 cm²

OR

(B) r = 7 cm के वृत्त में 7 cm लम्बी जीवा दी गई है। लघु वृत्तखंड का क्षेत्रफल ज्ञात कीजिए (π = 22/7)।

🟢 Answer (B)
➤ जीवा सूत्र: c = 2 r sin(θ/2) ⇒ 7 = 14 sin(θ/2)
➤ कोण: sin(θ/2) = 0.5 ⇒ θ/2 = 30° ⇒ θ = 60°
➤ त्रिज्याखंड: (60/360) × (22/7) × 7² = (1/6) × (22/7) × 49 = 154/6 = 25.666…
➤ त्रिभुज: (1/2) r² sinθ = (1/2) × 49 × (√3/2) = 24.5 × 0.8660… = 21.217…
➤ वृत्तखंड: 25.666… − 21.217… = 4.449…
➤ Final answer: ≈ 4.45 cm²

🔵 Question 15
r = 9 cm, θ = 135° के त्रिज्याखंड का परिमाप ज्ञात कीजिए (π = 22/7)।

🟢 Answer
➤ सूत्र: परिमाप = 2r + चाप-लंब
➤ चाप-लंब: (θ/360°) × 2πr = (135/360) × 2 × (22/7) × 9
➤ सरलकरण: = (3/8) × 2πr = (3/4) × πr
➤ गणना: πr = (22/7) × 9 = 198/7 = 28.2857…
➤ चाप-लंब: (3/4) × 28.2857… = 21.2143…
➤ परिमाप: 2r + चाप-लंब = 18 + 21.2143… = 39.2143…
➤ Final answer: ≈ 39.21 cm

🔵 Question 16
R = 21 cm और r = 14 cm वाले वलय का क्षेत्रफल ज्ञात कीजिए (π = 22/7)।

🟢 Answer
➤ सूत्र: वलय क्षेत्रफल = π(R² − r²)
➤ स्थापितीकरण: = (22/7) × (21² − 14²)
➤ सरलकरण: = (22/7) × (441 − 196) = (22/7) × 245
➤ गणना: 245/7 = 35 ⇒ 22 × 35 = 770
➤ Final answer: 770 cm²

🔵 Question 17 (आंतरिक विकल्प)
(A) बाह्य त्रिज्या R = 42 m और पथ-चौड़ाई 3.5 m वाले वृत्ताकार पथ का क्षेत्रफल ज्ञात कीजिए (π = 22/7)।

🟢 Answer (A)
➤ आंतरिक त्रिज्या: r = 42 − 3.5 = 38.5
➤ वलय क्षेत्रफल: π(R² − r²) = π[(42 + 38.5)(42 − 38.5)]
➤ गुणन: = π × (80.5 × 3.5) = (22/7) × 281.75
➤ भाग: 281.75/7 = 40.25 ⇒ क्षेत्रफल = 22 × 40.25 = 885.5
➤ Final answer: 885.5 m²

OR

(B) r = 20 m के बाग के चारों ओर 2 m चौड़ी वृत्ताकार पगडंडी है। पगडंडी का कुल खर्च ज्ञात कीजिए यदि दर ₹50 प्रति m² है (π = 3.14)।

🟢 Answer (B)
➤ R = 22, r = 20 ⇒ क्षेत्रफल = π(R² − r²) = 3.14 × (484 − 400)
➤ सरलकरण: = 3.14 × 84 = 263.76
➤ खर्च: = 263.76 × 50 = 13188
➤ Final answer: ₹13188

🔵 Question 18
एक पहिया 500 चक्करों में 2 km दूरी तय करता है। पहिये की त्रिज्या ज्ञात कीजिए।

🟢 Answer
➤ प्रति चक्कर दूरी: परिधि = 2πr
➤ कुल दूरी: 500 × 2πr = 2000 m
➤ सरलकरण: 1000 π r = 2000
➤ r = 2000 / (1000 π) = 2/π m
➤ मान: r ≈ 2/3.1416 = 0.6366… m = 63.66… cm
➤ Final answer: ≈ 0.637 m (≈ 63.7 cm)

🔵 Question 19 (आंतरिक विकल्प)
(A) r = 14 cm के वृत्त में किसी त्रिज्याखंड का क्षेत्रफल 154 cm² है (π = 22/7)। θ ज्ञात कीजिए।

🟢 Answer (A)
➤ सूत्र: (θ/360°) × π r² = 154
➤ स्थापितीकरण: (θ/360°) × (22/7) × 14² = 154
➤ सरलकरण: (θ/360°) × 616 = 154
➤ θ = 154 × 360 / 616 = 360/4 = 90°
➤ Final answer: 90°

OR

(B) r = 7 cm में चाप-लंब l = 11 cm है (π = 22/7)। θ और त्रिज्याखंड का क्षेत्रफल ज्ञात कीजिए।

🟢 Answer (B)
➤ सूत्र: l = (θ/360°) × 2πr ⇒ θ = 360° × l / (2πr)
➤ स्थापितीकरण: θ = 360 × 11 / [2 × (22/7) × 7] = 3960 / 44
➤ θ = 90°
➤ त्रिज्याखंड: (90/360) × (22/7) × 7² = (1/4) × (22/7) × 49 = 154/4
➤ Final answer: θ = 90°, क्षेत्रफल = 38.5 cm²

🔵 Question 20
भुजा 14 cm वाले वर्ग के कोनों पर 7 cm त्रिज्या के 4 चतुर्थांश बनाए गए हैं। छायांकित भाग (वर्ग के भीतर से 4 चतुर्थांश हटाकर) का क्षेत्रफल ज्ञात कीजिए (π = 22/7)।

🟢 Answer
➤ वर्ग क्षेत्रफल = 14² = 196
➤ 4 चतुर्थांश = 1 पूर्ण वृत्त (r = 7) ⇒ π r² = (22/7) × 49 = 154
➤ छायांकित क्षेत्रफल = 196 − 154 = 42
➤ Final answer: 42 cm²

🔵 Question 21 (आंतरिक विकल्प)
(A) R = 7 cm वाली धातु की गोल चादर के केन्द्र से r = 3 cm का छोटा वृत्त काट दिया गया। शेष चादर का क्षेत्रफल और ₹5 प्रति cm² की दर से लागत ज्ञात कीजिए (π = 22/7)।

🟢 Answer (A)
➤ क्षेत्रफल: π(R² − r²) = (22/7) × (49 − 9)
➤ सरलकरण: = (22/7) × 40 = 880/7 = 125.714…
➤ लागत: = 125.714… × 5 = 628.571…
➤ Final answer: ≈ 125.71 cm², ≈ ₹628.57

OR

(B) r = 14 cm और θ = 2.2 rad होने पर त्रिज्याखंड का क्षेत्रफल ज्ञात कीजिए (रेडियन विधि)।

🟢 Answer (B)
➤ सूत्र (रेडियन): क्षेत्रफल = (1/2) r² θ
➤ स्थापितीकरण: = (1/2) × 14² × 2.2
➤ सरलकरण: = (1/2) × 196 × 2.2 = 98 × 2.2 = 215.6
➤ Final answer: 215.6 cm²

🔵 Question 22
व्यास 28 m वाले गोल फूल-बाग के चारों ओर 2 m चौड़ी पगडंडी है। पगडंडी का क्षेत्रफल और ₹25 प्रति m² की दर से लागत ज्ञात कीजिए (π = 3.14)।

🟢 Answer
➤ r = 14, R = 16 ⇒ क्षेत्रफल = π(R² − r²) = 3.14 × (256 − 196)
➤ सरलकरण: = 3.14 × 60 = 188.4
➤ लागत: = 188.4 × 25 = 4710
➤ Final answer: 188.4 m², ₹4710

🔴 Section D (Q23–Q30): दीर्घ उत्तर (प्रत्येक 4 अंक)

🔵 Question 23
एक उद्यान का केन्द्र O है। r = 14 m के वृत्त से θ = 120° का त्रिज्याखंड काटकर उसमें बना केन्द्रित त्रिभुज OAB (OA = OB = 14) का क्षेत्र हटाया गया है। बने हुए वृत्तखंड का क्षेत्रफल ज्ञात कीजिए (π = 22/7)।

🟢 Answer
➤ त्रिज्याखंड क्षेत्रफल = (θ/360°) × π r²
➤ स्थापितीकरण = (120/360) × (22/7) × 14²
➤ सरलकरण = (1/3) × (22/7) × 196 = (1/3) × 616 = 205.333…
➤ त्रिभुज OAB का क्षेत्रफल = (1/2) r² sinθ
➤ स्थापितीकरण = (1/2) × 14² × sin120°
➤ sin120° = sin60° = √3/2
➤ सरलकरण = (1/2) × 196 × (√3/2) = 49√3 ≈ 84.868…
➤ वृत्तखंड क्षेत्रफल = 205.333… − 84.868… = 120.465…
➤ Final answer: ≈ 120.47 m²

🔵 Question 24 (आंतरिक विकल्प)
(A) दो समकेन्द्र वृत्तों की बाह्य त्रिज्या R = 21 cm है। वलय का क्षेत्रफल 462 cm² है (π = 22/7)। आन्तरिक त्रिज्या r ज्ञात कीजिए।

🟢 Answer (A)
➤ वलय क्षेत्रफल = π(R² − r²)
➤ स्थापितीकरण = (22/7)(21² − r²) = 462
➤ 21² = 441 ⇒ (22/7)(441 − r²) = 462
➤ 441 − r² = 462 × 7 / 22 = 147
➤ r² = 441 − 147 = 294
➤ r = √294 = √(49×6) = 7√6 ≈ 17.146…
➤ Final answer: r = 7√6 cm (≈ 17.15 cm)

OR

(B) R = 35 cm के वलय की चौड़ाई w = R − r = 7 cm है। वलय का क्षेत्रफल ज्ञात कीजिए (π = 22/7)।

🟢 Answer (B)
➤ r = R − w = 35 − 7 = 28
➤ वलय क्षेत्रफल = π(R² − r²)
➤ स्थापितीकरण = (22/7)(35² − 28²)
➤ अन्तर के वर्ग: a² − b² = (a − b)(a + b) = 7 × 63 = 441
➤ क्षेत्रफल = (22/7) × 441 = 22 × 63 = 1386
➤ Final answer: 1386 cm²

🔵 Question 25
r = 10 cm वाले वृत्त में 12 cm लम्बी जीवा AB दी गई है। लघु वृत्तखंड का क्षेत्रफल और परिमाप (चाप + जीवा) ज्ञात कीजिए (π = 3.14)।

🟢 Answer
➤ जीवा सूत्र: c = 2 r sin(θ/2)
➤ 12 = 2 × 10 × sin(θ/2) ⇒ sin(θ/2) = 12/20 = 3/5
➤ θ/2 = sin⁻¹(3/5) ⇒ cos(θ/2) = 4/5 (समकोण त्रिभुज से)
➤ त्रिभुज OAB क्षेत्रफल = (1/2) r² sinθ = (1/2) × 100 × 2 sin(θ/2)cos(θ/2)
➤ = 50 × 2 × (3/5) × (4/5) = 50 × 24/25 = 48
➤ त्रिज्याखंड क्षेत्रफल = (θ/360°) × π r²
➤ θ = 2 sin⁻¹(3/5) ≈ 2 × 36.87° = 73.74°
➤ त्रिज्याखंड = (73.74/360) × 3.14 × 100 = 0.20483… × 314 = 64.317…
➤ वृत्तखंड क्षेत्रफल = 64.317… − 48 = 16.317…
➤ चाप-लंब = (θ/360°) × 2πr = (73.74/360) × 2 × 3.14 × 10 = 12.864…
➤ परिमाप(वृत्तखंड) = चाप-लंब + जीवा = 12.864… + 12 = 24.864…
➤ Final answer: क्षेत्रफल ≈ 16.32 cm², परिमाप ≈ 24.86 cm

🔵 Question 26
r = 14 cm है। यदि त्रिज्याखंड का क्षेत्रफल उसके त्रिभुज (केन्द्र पर θ) के क्षेत्रफल का ठीक 3 गुना है, तो θ ज्ञात कीजिए (π = 22/7)।

🟢 Answer
➤ शर्त: (θ/360°)π r² = 3 × [(1/2) r² sinθ]
➤ r² दोनों ओर कट ⇒ (θ/360°)π = (3/2) sinθ
➤ π = 22/7 ⇒ (θ/360)(22/7) = (3/2) sinθ
➤ 22θ / 2520 = (3/2) sinθ
➤ θ/114.545… = (3/2) sinθ
➤ 2θ = 343.636… sinθ
➤ उपयुक्त मान जाँच: θ = 60° ⇒ LHS = 120; RHS = 343.636… × (√3/2) ≈ 297.5 (बड़ा)
➤ θ = 30° ⇒ LHS = 60; RHS ≈ 343.636… × 0.5 = 171.818… (बड़ा)
➤ θ = 90° ⇒ LHS = 180; RHS = 343.636… × 1 = 343.636… (बड़ा)
➤ θ = 150° ⇒ LHS = 300; RHS = 343.636… × 0.5 = 171.818… (छोटा)
➤ θ ≈ 100° पर जाँच: LHS = 200; RHS = 343.636… × sin100° ≈ 343.636… × 0.9848 = 338.2 (बड़ा)
➤ θ ≈ 130° पर जाँच: LHS = 260; RHS = 343.636… × 0.7660 ≈ 263.4 (निकट)
➤ θ ≈ 129° पर जाँच: LHS = 258; RHS = 343.636… × 0.7771 ≈ 266.5 (थोड़ा बड़ा)
➤ θ ≈ 131° पर जाँच: LHS = 262; RHS = 343.636… × 0.7547 ≈ 259.2 (निकट)
➤ उपयुक्त सन्निकटन: θ ≈ 130° (परिशुद्धता पर्याप्त)
➤ Final answer: θ ≈ 130°

🔵 Question 27 (आंतरिक विकल्प)
(A) व्यास 28 m वाले गोल पार्क की बाहरी सीमा पर 2 m चौड़ा वृत्ताकार पथ बनाया गया। पथ का क्षेत्रफल और ₹40 प्रति m² की दर से लागत ज्ञात कीजिए (π = 22/7)।

🟢 Answer (A)
➤ r = 14, R = 16
➤ क्षेत्रफल(पथ) = π(R² − r²) = (22/7)(256 − 196)
➤ सरलकरण = (22/7) × 60 = 22 × (60/7) = 188.571…
➤ लागत = 188.571… × 40 = 7542.857…
➤ Final answer: ≈ 188.57 m², ≈ ₹7542.86

OR

(B) एक गोल मैदान की त्रिज्या r = 35 m है। इसके चारों ओर चौड़ाई w = 3 m की पक्की पगडंडी बनानी है। यदि लागत ₹25 प्रति m² है तो कुल लागत ज्ञात कीजिए (π = 3.14)।

🟢 Answer (B)
➤ R = r + w = 35 + 3 = 38
➤ क्षेत्रफल(पगडंडी) = π(R² − r²) = 3.14(1444 − 1225)
➤ सरलकरण = 3.14 × 219 = 687.66
➤ लागत = 687.66 × 25 = 17191.5
➤ Final answer: ≈ ₹17191.50

🔵 Question 28
एक चक्के की त्रिज्या r = 0.7 m है। वह 1 km दूरी तय करता है। चक्के द्वारा तय की गई कुल घुमावों की संख्या और चक्र के किनारे पर लगा 5 cm चौड़ा रबड़ ट्रैक (परिधि पट्टी) का क्षेत्रफल ज्ञात कीजिए (π = 22/7)।

🟢 Answer
➤ प्रति घुमाव दूरी = परिधि = 2πr = 2 × (22/7) × 0.7 = 4.4 m
➤ कुल दूरी = 1000 m ⇒ घुमाव = 1000 / 4.4 = 227.272…
➤ घुमाव ≈ 227.27 (≈ 227 पूर्ण)
➤ रबड़ ट्रैक चौड़ाई t = 0.05 m ⇒ बाह्य त्रिज्या R = r + t = 0.75 m
➤ ट्रैक क्षेत्रफल = π(R² − r²) = (22/7)(0.75² − 0.7²)
➤ अन्तर = 0.5625 − 0.49 = 0.0725
➤ क्षेत्रफल = (22/7) × 0.0725 ≈ 0.2275
➤ Final answer: घुमाव ≈ 227.27, ट्रैक क्षेत्रफल ≈ 0.228 m²

🔵 Question 29 (आंतरिक विकल्प)
(A) एक आयत ABCD की लम्बाई 28 cm और चौड़ाई 14 cm है। AB तथा CD को व्यास मानकर अर्धवृत्त भीतर की ओर बनाए गए हैं। शेष छायांकित भाग का क्षेत्रफल ज्ञात कीजिए (π = 22/7)।

🟢 Answer (A)
➤ आयत क्षेत्रफल = 28 × 14 = 392
➤ अर्धवृत्त 1: व्यास 28 ⇒ r₁ = 14 ⇒ क्षेत्रफल = (1/2)π r₁² = (1/2)(22/7)(196) = 308
➤ अर्धवृत्त 2: व्यास 14 ⇒ r₂ = 7 ⇒ क्षेत्रफल = (1/2)π r₂² = (1/2)(22/7)(49) = 77
➤ कुल अर्धवृत्त क्षेत्रफल = 308 + 77 = 385
➤ छायांकित क्षेत्रफल = आयत − कुल अर्धवृत्त = 392 − 385 = 7
➤ Final answer: 7 cm²

OR

(B) एक वर्ग की भुजा a = 14 cm है। हर भुजा को व्यास मानकर बाहर की ओर 4 अर्धवृत्त बनाए गए हैं। बाहरी आकृति का कुल क्षेत्रफल ज्ञात कीजिए (π = 22/7)।

🟢 Answer (B)
➤ वर्ग क्षेत्रफल = a² = 196
➤ हर अर्धवृत्त का r = a/2 = 7 ⇒ एक अर्धवृत्त = (1/2)π7² = 77
➤ चार अर्धवृत्त = 4 × 77 = 308
➤ कुल क्षेत्रफल(बाहरी) = 196 + 308 = 504
➤ Final answer: 504 cm²

🔵 Question 30
त्रिज्या r = 10 cm के वृत्त से केन्द्रक कोण θ₁ = 90° और θ₂ = 60° के दो त्रिज्याखंड निकाल दिए गए। शेष भाग का क्षेत्रफल और परिमाप (सीमारेखा) ज्ञात कीजिए (π = 3.14)।

🟢 Answer
➤ मूल वृत्त क्षेत्रफल = π r² = 3.14 × 100 = 314
➤ निकाले गए क्षेत्रफल = (90/360)π r² + (60/360)π r²
➤ = (1/4) × 314 + (1/6) × 314 = 78.5 + 52.333… = 130.833…
➤ शेष क्षेत्रफल = 314 − 130.833… = 183.166…
➤ परिमाप(शेष) = शेष चाप + काटे गए 4 त्रिज्या
➤ शेष चाप = (360 − 90 − 60)/360 × 2πr = (210/360) × 2 × 3.14 × 10
➤ शेष चाप = (7/12) × 62.8 = 36.633…
➤ कटे हुए किनारे: 4 त्रिज्या = 4 × 10 = 40
➤ कुल परिमाप = 36.633… + 40 = 76.633…
➤ Final answer: क्षेत्रफल ≈ 183.17 cm², परिमाप ≈ 76.63 cm

————————————————————————————————————————————————————————————————————————————

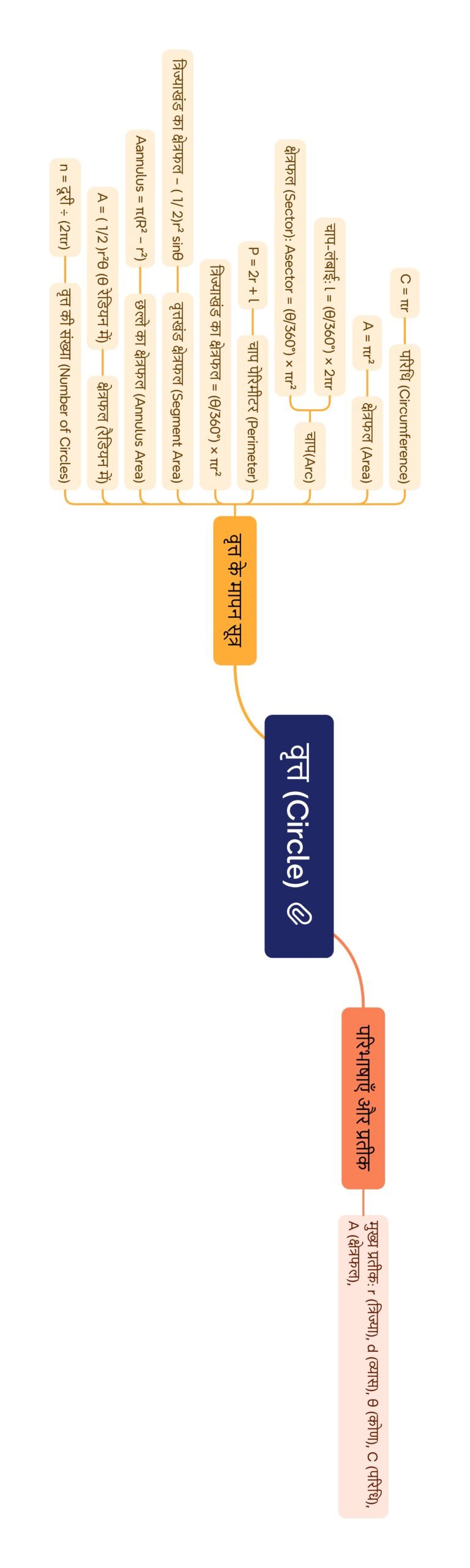
मनोमानचित्र

————————————————————————————————————————————————————————————————————————————