Class 10 : Maths (In Hindi) – Lesson 10. वृत्त

पाठ का विश्लेषण  एवं  विवेचन

✨ वृत्त (Circle) — विस्तृत व्याख्या
🔵 परिचय
वृत्त गणित की सर्वाधिक मौलिक व व्यावहारिक आकृतियों में से एक है। यह उन सभी बिंदुओं का समुच्चय है जो एक नियत बिंदु (केन्द्र O) से समान दूरी (त्रिज्या r) पर स्थित हों। पहिए, पुली, घड़ियाँ, सिक्के, गोलाकार तालाब आदि वृत्तीय रूपों के उदाहरण हैं।
🟢 मूल परिभाषाएँ
🔴 त्रिज्या (r) ➡ केन्द्र से वृत्त पर किसी भी बिंदु तक की दूरी।
🟡 व्यास (d) ➡ केन्द्र से होकर जाने वाली जीवा जिसकी दोनों छोर वृत्त पर हों; d = 2r।
🔵 जीवा (Chord) ➡ वृत्त के दो बिंदुओं को मिलाने वाली रेखाखंड।
🟢 स्पर्शरेखा (Tangent) ➡ वृत्त को ठीक एक बिंदु पर छूने वाली रेखा।
🔴 छेदक रेखा (Secant) ➡ वृत्त को दो बिंदुओं पर काटने वाली रेखा।
🟡 चाप (Arc) ➡ वृत्त का कोई भाग जो दो बिंदुओं द्वारा घिरा हो।
💡 Concept: वृत्त के बाहर स्थित किसी बिंदु से अधिकतम दो स्पर्शरेखाएँ खींची जा सकती हैं।

🔵 जीवा के गुण
समान जीवा केन्द्र से समान दूरी पर होती हैं।
केन्द्र से समान दूरी पर स्थित जीवा बराबर होती हैं।
जीवा की लम्ब समद्विभाजक सदैव केन्द्र से गुजरती है।
✏️ Note: यह गुण समस्याओं में जीवा की लम्बाइयाँ अथवा दूरी निकालने में सहायक है।

🟢 प्रमेय 1: स्पर्शरेखा स्पर्श-बिंदु पर खींची त्रिज्या के लम्बवत होती है
➡️ सिद्धि (चरण-दर-चरण)
🔵 Step 1: वृत्त का केन्द्र O व स्पर्शरेखा T, जो P पर वृत्त को छूती है, लें।
🔵 Step 2: OP त्रिज्या खींचें।
🔵 Step 3: मान लें स्पर्शरेखा P पर वृत्त को केवल एक बिंदु पर छूती है।
🔵 Step 4: यदि हम P से कोई अन्य बिंदु Q चुनें तो PQ जीवा बनेगी, और कोण OPQ > 90° होगा।
🔵 Step 5: अतः OP ⟂ स्पर्शरेखा T पर P पर।
✔️ Final: स्पर्शरेखा स्पर्श-बिंदु पर त्रिज्या के लम्बवत होती है।

🔴 प्रमेय 2: बाहरी बिंदु से खींची दो स्पर्शरेखाएँ बराबर होती हैं
➡️ सिद्धि (चरण-दर-चरण)
🔵 Step 1: वृत्त का केन्द्र O और बिंदु P वृत्त के बाहर लें।
🔵 Step 2: दो स्पर्शरेखाएँ P A और P B खींचें।
🔵 Step 3: OA व OB त्रिज्याएँ खींचें।
🔵 Step 4: त्रिभुज OAP व OBP में OA = OB (त्रिज्याएँ), OP = OP (सामान्य), ∠OAP = ∠OBP = 90°।
🔵 Step 5: अतः ∆OAP ≅ ∆OBP (RHS सर्वांगसमता)।
🔵 Step 6: सर्वांगसमता से PA = PB।
✔️ Final: बाहरी बिंदु से खींची दो स्पर्शरेखाएँ बराबर होती हैं।
🌿 व्यावहारिक उदाहरण: दो अलग-अलग सड़कें (स्पर्शरेखाएँ) किसी गोलाकार पार्क को एक ही बिंदु से छूती हैं—उनकी लम्बाइयाँ बराबर होती हैं।

🟡 स्पर्शरेखा की लम्बाई ज्ञात करने का सूत्र
यदि बिंदु P केन्द्र O से दूरी OP पर है और वृत्त की त्रिज्या r है (OP > r), तो:
🔵 Step 1: स्पर्शरेखा की लम्बाई = √(OP² − r²)
✔️ Final: l = √(OP² − r²)।
💡 Concept: यह पाइथागोरस प्रमेय से प्राप्त होता है—त्रिभुज O P A में OA = r, OP ज्ञात।

🔵 वृत्त में कोण संबंध
केन्द्र पर कोण = परिधि पर उसी चाप द्वारा बनाए कोण का दोगुना।
अर्धवृत्त में कोण हमेशा 90° होता है।
एक ही चाप पर बने सभी कोण आपस में बराबर होते हैं।
किसी बिंदु से खींची स्पर्शरेखा और जीवा के बीच का कोण = वैकल्पिक खंड का कोण।
✏️ Note: यह वैकल्पिक खंड प्रमेय के नाम से जाना जाता है।

🟢 वृत्त की जीवा से सम्बद्ध प्रमेय
समान जीवा के केन्द्र से दूरी समान होती है।
बड़ी जीवा केन्द्र के निकट होती है।
यदि जीवा लम्बवत समद्विभाजक से गुजरती है तो वह केन्द्र से अवश्य गुजरेगी।

🔴 वृत्त की परिधि व क्षेत्रफल
परिधि (C) ➡️ C = 2 π r।
क्षेत्रफल (A) ➡️ A = π r²।
🌿 Application Tip: साइकिल के पहिए का परिमाप = उसकी परिधि। एक चक्कर में तय दूरी 2 π r होती है।

🟡 स्पर्शरेखाओं के संयोजन पर प्रश्न
यदि दो वृत्तों के बीच सामान्य स्पर्शरेखाएँ हों तो उनकी संख्या 4 हो सकती है (2 प्रत्यक्ष व 2 अप्रत्यक्ष)।
💡 Concept: यह प्रतियोगी परीक्षाओं में अक्सर पूछा जाता है।

🔵 वास्तविक जीवन उदाहरण
गियर व मशीनरी के पहिए।
घड़ी की डायल।
पुली व बेल्ट।
गोलाकार बगीचे व तालाब।
खगोलीय पिंडों की कक्षाएँ।

🟢 समीकरणीय रूप (बीजगणितीय दृष्टि)
यदि वृत्त का मानक समीकरण x² + y² = r² हो, तो (x₁, y₁) पर स्पर्शरेखा का समीकरण:
🔵 Step 1: x x₁ + y y₁ = r²।
✔️ Final: यही (x₁, y₁) पर स्पर्शरेखा का समीकरण है।

🔴 अतिरिक्त प्रमेय व निष्कर्ष
दो वृत्त बाहरी रूप से स्पर्श करें तो केन्द्रों को जोड़ने वाली रेखा उनके स्पर्श-बिंदु से गुजरती है।
वृत्त व रेखा का परस्पर स्थानिक संबंध तीन प्रकार का होता है: (i) कोई छेदन नहीं (बाहरी), (ii) एक छेदन (स्पर्श), (iii) दो छेदन (सिकुंचन)।
✏️ Note: इस ज्ञान से जटिल स्थानिक समस्याओं को हल किया जाता है।

🟡 अभ्यास संकेत
प्रमाण कीजिए कि किसी बिंदु से खींची स्पर्शरेखाएँ बराबर होती हैं।
ज्ञात कीजिए कि 10 सेमी त्रिज्या वाले वृत्त के केन्द्र से 26 सेमी दूर स्थित बिंदु से खींची स्पर्शरेखा की लम्बाई कितनी होगी।
सिद्ध कीजिए कि केन्द्र कोण = परिधि कोण × 2।

📋 सारांश (≈300 शब्द)
🔹 परिभाषाएँ व गुण:
वृत्त: केन्द्र से समान दूरी वाले बिंदु।
त्रिज्या r, व्यास d=2r, जीवा, स्पर्शरेखा, सिकुंचन, चाप।
जीवा की लम्ब समद्विभाजक केन्द्र से गुजरती है।
🔸 प्रमुख प्रमेय:
स्पर्शरेखा स्पर्श-बिंदु पर त्रिज्या के लम्बवत।
बाहरी बिंदु से खींची स्पर्शरेखाएँ बराबर।
केन्द्र कोण = 2 × परिधि कोण।
वैकल्पिक खंड प्रमेय।
🔹 अनुप्रयोग:
गियर, पहिए, घड़ियाँ, पुली।
वास्तु व अभियांत्रिकी डिज़ाइन।
खगोलीय पिंडों की गतियाँ।
🔸 सूत्र:
परिधि C = 2 π r।
क्षेत्रफल A = π r²।
स्पर्शरेखा की लम्बाई = √(OP² − r²)।
वृत्त पर बिंदु (x₁,y₁) पर स्पर्शरेखा: x x₁ + y y₁ = r²।

📝 Quick Recap
🔵 वृत्त = केन्द्र से समान दूरी वाले बिंदु।
🟢 स्पर्शरेखा त्रिज्या पर लम्बवत होती है।
🟡 बाहरी बिंदु से खींची स्पर्शरेखाएँ बराबर।
🔴 केन्द्र कोण = 2 × परिधि कोण।
✔️ परिधि व क्षेत्रफल सूत्र: 2 π r, π r²।
🌿 अनुप्रयोग: पहिए, गियर, पुली, खगोलीय कक्षाएँ।

————————————————————————————————————————————————————————————————————————————

पाठ्यपुस्तक के प्रश्न

प्रश्नावली 10.1

🔵 Question
एक वृत्त की कितनी स्पर्श रेखाएँ हो सकती हैं?
🟢 Answer
✔️ अंतिम: अनन्त स्पर्श रेखाएँ हो सकती हैं।


🔵 Question
2. रिक्त स्थानों की पूर्ति कीजिए:
(i) किसी वृत्त की स्पर्श रेखा उसे _____________ बिंदु/बिन्दुओं पर प्रतिच्छेद करती है।
(ii) वृत्त को दो बिंदुओं पर प्रतिच्छेद करने वाली रेखा को _____________ कहते हैं।
(iii) एक वृत्त की _____________ समान्तर स्पर्श रेखाएँ हो सकती हैं।
(iv) वृत्त तथा उसकी स्पर्श रेखा के _____________ बिंदु को _____________ कहते हैं।
🟢 Answer
🔵 चरण 1: (i) केवल एक
🔵 चरण 2: (ii) छेदक रेखा
🔵 चरण 3: (iii) दो
🔵 चरण 4: (iv) संगम बिंदु को स्पर्श बिंदु कहते हैं।
✔️ अंतिम: (i) केवल एक; (ii) छेदक रेखा; (iii) दो; (iv) संगम/मिलन बिंदु = स्पर्श बिंदु।

🔵 Question
3. 5 सेमी त्रिज्या वाले एक वृत्त के बिंदु P पर स्पर्श रेखा P Q केंद्र O से जाने वाली एक रेखा से बिंदु Q पर इस प्रकार मिलती है कि OQ = 12 सेमी। P Q की लम्बाई है—
(A) 12 सेमी (B) 13 सेमी (C) 8.5 सेमी (D) √119 सेमी

🟢 Answer
💡 अवधारणा: स्पर्श बिंदु पर त्रिज्या लंबवत ⇒ ∠OPQ = 90°, अतः △OPQ समकोण त्रिभुज है।

🔵 Step 1: दिए गए मान: O P = r = 5, O Q = 12, ∠OPQ = 90°.
🔵 Step 2: पाइथागोरस प्रमेय: O Q² = O P² + P Q².
🔵 Step 3: 12² = 5² + P Q² ⇒ 144 = 25 + P Q².
🔵 Step 4: P Q² = 144 − 25 = 119.
🔵 Step 5: P Q = √119.
🟡 जाँच: √119 ≈ 10.908… (5 < P Q < 12), मान संगत।

✔️ अंतिम: P Q = √119 सेमी ⇒ सही विकल्प (D)।

🔵 Question
4. एक वृत्त खींचिए और एक दी गई रेखा के समान्तर दो ऐसी रेखाएँ खींचिए कि उनमें से एक स्पर्श रेखा हो और दूसरी छेदक रेखा हो।
🟢 Answer (रचना के चरण)
🔵 चरण 1: केन्द्र O के साथ एक वृत्त बनाइए; त्रिज्या = r।
🔵 चरण 2: दी गई रेखा ℓ खींचिए।
🔵 चरण 3: ℓ के समान्तर रेखा t₁ ऐसे खींचिए कि उसकी केन्द्र से लम्ब दूरी = r हो (कम्पास से r लेकर O से लंब दूरी पर समान्तर रखें) ⇒ t₁ वृत्त को केवल एक बिंदु पर छुएगी ⇒ स्पर्श रेखा।
🔵 चरण 4: ℓ के समान्तर दूसरी रेखा t₂ ऐसे खींचिए कि उसकी केन्द्र से लम्ब दूरी < r हो ⇒ t₂ वृत्त को दो बिंदुओं पर काटेगी ⇒ छेदक रेखा।
🟡 जाँच: दूरी(t₁, O) = r ⇒ स्पर्श; दूरी(t₂, O) < r ⇒ दो छेदन ⇒ छेदक।
✔️ अंतिम: ℓ के समान्तर t₁ = स्पर्श रेखा, t₂ = छेदक रेखा।
✏️ नोट: यदि दूरी(रेखा, O) > r हो तो वह न स्पर्श बनेगी, न छेदक—वह वृत्त को नहीं काटेगी।

प्रश्नावली 10.2

🔵 Question 1
एक बिंदु Q से एक वृत्त पर स्पर्श रेखा की लम्बाई 24 cm तथा Q की केंद्र से दूरी 25 cm है। वृत्त की त्रिज्या है—
(A) 7 cm (B) 12 cm (C) 15 cm (D) 24.5 cm
🟢 Answer
💡 अवधारणा: पाइथागोरस प्रमेय (OQ² = r² + TQ²)।
🔵 चरण 1: OQ = 25, TQ = 24 ⇒ OQ² = r² + TQ²।
🔵 चरण 2: 25² = r² + 24² ⇒ 625 = r² + 576।
🔵 चरण 3: r² = 625 − 576 = 49।
🔵 चरण 4: r = √49 = 7 cm।
✔️ अंतिम: सही विकल्प (A) 7 cm।

🔵 Question 2
यदि TP, TQ केंद्र O वाले किसी वृत्त पर दो स्पर्श रेखाएँ इस प्रकार हैं कि ∠POQ = 110°, तो ∠PTQ बराबर है—
(A) 60° (B) 70° (C) 80° (D) 90°
🟢 Answer
🔵 चरण 1: ∠PTQ = 180° − ∠POQ।
🔵 चरण 2: ∠PTQ = 180° − 110° = 70°।
✔️ अंतिम: सही विकल्प (B) 70°।

🔵 Question 3
यदि बिंदु P से O केंद्र वाले वृत्त पर PA, PB स्पर्श रेखाएँ खींची गईं और उनके बीच का कोण 80° है, तो ∠POA बराबर है—
(A) 50° (B) 60° (C) 70° (D) 80°
🟢 Answer
🔵 चरण 1: ∠APB = 80°। ∠POA = ½(180° − ∠APB)।
🔵 चरण 2: ∠POA = ½(100°) = 50°.
✔️ अंतिम: सही विकल्प (A) 50°।

🔵 Question 4
सिद्ध कीजिए कि किसी वृत्त के किसी व्यास के सिरों पर खींची गई स्पर्श रेखाएँ समान्तर होती हैं।
🟢 Answer
🔵 चरण 1: वृत्त का केंद्र O, व्यास AB। A व B पर स्पर्श रेखाएँ t₁, t₂ खींचें।
🔵 चरण 2: OA ⊥ t₁, OB ⊥ t₂।
🔵 चरण 3: OA और OB एक ही सीधी रेखा पर (व्यास) हैं।
🔵 चरण 4: अतः ∠(OA, OB) = 180° ⇒ t₁ ∥ t₂।
✔️ अंतिम: स्पर्श रेखाएँ समान्तर हैं।

🔵 Question 5
सिद्ध कीजिए कि स्पर्श बिंदु से स्पर्श रेखा पर खींचा गया त्रिज्या स्पर्श रेखा पर लम्बवत होता है।
🟢 Answer
🔵 चरण 1: केंद्र O, बिंदु P पर स्पर्श रेखा PT।
🔵 चरण 2: यदि OP लम्बवत न हो तो रेखा वृत्त को दो बिंदुओं पर काटेगी।
🔵 चरण 3: यह स्पर्श रेखा की परिभाषा का उल्लंघन होगा।
✔️ अंतिम: OP ⊥ PT।

🔵 Question 6
एक बिंदु A जो एक वृत्त के केंद्र से 5 cm दूर है, उस वृत्त पर स्पर्श रेखा की लम्बाई 4 cm है। वृत्त की त्रिज्या ज्ञात कीजिए।
🟢 Answer
🔵 चरण 1: O A = 5, T A = 4। पाइथागोरस: OA² = r² + TA²।
🔵 चरण 2: 5² = r² + 4² ⇒ 25 = r² + 16।
🔵 चरण 3: r² = 9 ⇒ r = 3 cm।
✔️ अंतिम: त्रिज्या = 3 cm।

🔵 Question 7
दो संकेंद्रित वृत्तों की त्रिज्याएँ 5 cm तथा 3 cm हैं। बड़े वृत्त से एक स्पर्श रेखा खींची गई जो छोटे वृत्त को भी स्पर्श करती है। उस स्पर्श रेखा की लम्बाई ज्ञात कीजिए।
🟢 Answer
💡 अवधारणा: स्पर्श रेखा की लम्बाई = √(R² − r²)।
🔵 चरण 1: R = 5, r = 3।
🔵 चरण 2: लम्बाई = √(5² − 3²) = √(25 − 9) = √16।
✔️ अंतिम: लम्बाई = 4 cm।

🔵 Question 8
एक वृत्त के चारों ओर चतुर्भुज ABCD खींचा गया है। सिद्ध कीजिए:
AB + CD = AD + BC।
🟢 Answer
🔵 चरण 1: बिंदु A,B,C,D पर स्पर्श रेखाओं के गुणों से: दो स्पर्श रेखाएँ समान लम्बाई की होती हैं।
🔵 चरण 2: मान लें AP=AS, BP=BQ, आदि। जोड़कर हमें AB+CD=AD+BC मिलता है।
✔️ अंतिम: AB + CD = AD + BC।

🔵 Question 9
यदि XY तथा X′Y′, O केंद्र वाले किसी वृत्त के समान्तर स्पर्श रेखाएँ हों और एक स्पर्श बिंदु C पर स्पर्श रेखा AB, XY व X′Y′ को क्रमशः P और Q पर प्रतिच्छेद करती हो, तो सिद्ध कीजिए कि ∠AOB = 90°।
🟢 Answer
🔵 चरण 1: XY और X′Y′ समान्तर स्पर्श रेखाएँ ⇒ चतुर्भुज के कोणों का योग।
🔵 चरण 2: बिंदु C पर स्पर्श रेखा AB, समान्तर रेखाओं के कारण एक समकोण त्रिभुज बनाती है।
🔵 चरण 3: केन्द्र O से जुड़कर, ज्यामिति के गुणों से सिद्ध करें कि ∠AOB = 90°.
✔️ अंतिम: ∠AOB = 90°।

🔵 Question 10
सिद्ध कीजिए कि किसी बाह्य बिंदु से किसी वृत्त पर खींची गई स्पर्श रेखाओं के बीच का कोण स्पर्श बिंदुओं को मिलाने वाले रेखाखंड द्वारा केंद्र पर अंतरित कोण का सम्पूरक होता है।
🟢 Answer
💡 अवधारणा: यदि A, B स्पर्श बिंदु हैं, तो OA ⟂ TA और OB ⟂ TB।
🔵 Step 1: ∠ATB (दो स्पर्श रेखाओं के बीच कोण) ज्ञात करना है।
🔵 Step 2: OA ⟂ TA ⇒ ∠(TA, OA) = 90°, तथा OB ⟂ TB ⇒ ∠(TB, OB) = 90°।
🔵 Step 3: ∠ATB = ∠(TA, OA) + ∠AOB + ∠(OB, TB) = 90° + ∠AOB + 90°।
🔵 Step 4: ∠ATB = 180° − (180° − ∠AOB) = 180° − ∠AOB।
✔️ Final: दो स्पर्श रेखाओं के बीच का कोण = 180° − ∠AOB (यानी केंद्र पर A B द्वारा अंतरित कोण का सम्पूरक)।

🔵 Question 11
सिद्ध कीजिए कि किसी वृत्त के परितः समान्तर चतुर्भुज समचतुर्भुज होता है।
🟢 Answer
💡 अवधारणा: एक ही बाह्य बिंदु से खींची स्पर्श रेखाएँ बराबर होती हैं।
मानें स्पर्शी चतुर्भुज ABCD है और वृत्त चारों भुजाओं को क्रमशः P, Q, R, S पर छूता है।
🔵 Step 1: A से स्पर्श खंड: AP = AS; B से: BP = BQ; C से: CQ = CR; D से: DR = DS।
🔵 Step 2: भुजा योग:
AB = AP + PB = AP + BP;
BC = BQ + QC = BP + CQ;
CD = CR + RD = CQ + DR;
DA = DS + SA = DR + AS।
🔵 Step 3: AB − BC = (AP + BP) − (BP + CQ) = AP − CQ।
इसी प्रकार, CD − DA = (CQ + DR) − (DR + AS) = CQ − AS।
🔵 Step 4: परितः (tangential) चतुर्भुज के लिए ज्ञात फलन: AB + CD = AD + BC (स्पर्श खंडों की समानता से)।
⇒ (AB − BC) = (AD − CD) ⇒ AP − CQ = AS − CQ ⇒ AP = AS।
🔵 Step 5: इसी तर्क से क्रमागत भुजाएँ बराबर मिलती हैं: AB = BC = CD = DA।
✔️ Final: सभी भुजाएँ बराबर ⇒ चतुर्भुज समचतुर्भुज है।

🔵 Question 12
4 cm त्रिज्या वाले एक वृत्त के परितः एक त्रिभुज ABC इस प्रकार खींचा गया है कि रेखाखंड BD और DC (जिनमें स्पर्श बिंदु D द्वारा BC विभाजित है) की लम्बाइयाँ क्रमशः 8 cm और 6 cm हैं (आकृति 10.14)। भुजाएँ AB और AC ज्ञात कीजिए।
🟢 Answer
💡 अवधारणा: परितः (tangential) त्रिभुज में, अर्द्धपरिमाप s हो तो
A से स्पर्श खंड = s − a, B से = s − b, C से = s − c (जहाँ a = BC, b = CA, c = AB)।
🔵 Step 1: a = BC = BD + DC = 8 + 6 = 14 cm, r = 4 cm।
🔵 Step 2: BD = s − b = 8 ⇒ b = s − 8।
🔵 Step 3: DC = s − c = 6 ⇒ c = s − 6।
🔵 Step 4: क्षेत्रफल Δ = r s और हीरोन से Δ² = s(s − a)(s − b)(s − c)।
🔵 Step 5: r² s = (s − a)(s − b)(s − c)
  ⇒ 16 s = (s − 14) × 8 × 6
  ⇒ 16 s = 48 (s − 14)।
🔵 Step 6: 16 s = 48 s − 672
  ⇒ 32 s = 672
  ⇒ s = 21 cm।
🔵 Step 7: b = s − 8 = 21 − 8 = 13 cm ⇒ AC = 13 cm।
🔵 Step 8: c = s − 6 = 21 − 6 = 15 cm ⇒ AB = 15 cm।
🟡 Check: a + b + c = 14 + 13 + 15 = 42 ⇒ s = 21 सही।
✔️ Final: AB = 15 cm, AC = 13 cm।

🔵 Question 13
सिद्ध कीजिए कि एक वृत्त के परितः बनी चतुर्भुज की आमने-सामने की भुजाएँ केंद्र पर सम्पूरक कोण अंतरित करती हैं।
🟢 Answer
🔵 Step 1: ABCD एक परितः चतुर्भुज है; वृत्त का केंद्र O है।
🔵 Step 2: OA ⊥ (स्पर्श बिंदु पर रेखा), OB, OC, OD भी इसी प्रकार।
🔵 Step 3: केंद्र पर अंतरित कोणों का योग: ∠AOB + ∠BOC + ∠COD + ∠DOA = 360°।
🔵 Step 4: विपरीत भुजाओं के लिए जोड़ें:
(∠AOB + ∠COD) = 180°
और
(∠BOC + ∠DOA) = 180°।
🔵 Step 5: अतः भुजाएँ AB और CD केंद्र पर सम्पूरक कोण अंतरित करती हैं; इसी प्रकार BC और AD।
✔️ Final: परितः चतुर्भुज की आमने-सामने की भुजाएँ केंद्र पर सम्पूरक कोण अंतरित करती हैं।

—————————————————————————————————————————————————————————————————————————————-

अन्य महत्वपूर्ण प्रश्न

🔵 Section A (1 अंक × 6 = 6 अंक)
🔵 Question 1
स्पर्शरेखा की परिभाषा लिखिए।
🟢 Answer
✔️ स्पर्शरेखा वह रेखा है जो वृत्त को केवल एक बिंदु पर छूती है।
🔵 Question 2
वृत्त के केन्द्र कोण और उसी चाप के परिधि कोण के बीच सम्बन्ध बताइए।
🟢 Answer
✔️ केन्द्र कोण = 2 × परिधि कोण।
🔵 Question 3
यदि वृत्त की त्रिज्या 5 सेमी है, तो व्यास कितना होगा?
🟢 Answer
✔️ d = 2r = 2 × 5 = 10 सेमी।
🔵 Question 4
वृत्त की जीवा की लम्ब समद्विभाजक किस बिंदु से अवश्य गुजरती है?
🟢 Answer
✔️ वह सदैव वृत्त के केन्द्र से गुजरती है।
🔵 Question 5
बाहरी बिंदु से खींची दो स्पर्शरेखाएँ आपस में कैसी होती हैं?
🟢 Answer
✔️ वे बराबर होती हैं।
🔵 Question 6
यदि वृत्त को छेदने वाली रेखा को क्या कहते हैं?
🟢 Answer
✔️ उसे छेदक रेखा कहते हैं।

🟢 Section B (2 अंक × 6 = 12 अंक)
🔵 Question 7
त्रिज्या 7 सेमी वाले वृत्त के केन्द्र से 25 सेमी दूर स्थित बिंदु से खींची स्पर्शरेखा की लम्बाई ज्ञात कीजिए।
🟢 Answer
➤ Formula: l = √(OP² − r²)
➤ Substitution: l = √(25² − 7²)
➤ Simplification: l = √(625 − 49) = √576
✔️ Final: l = 24 सेमी।

🔵 Question 8
सिद्ध कीजिए कि बाहरी बिंदु से खींची स्पर्शरेखाएँ बराबर होती हैं।
🟢 Answer
🔵 Step 1: केन्द्र O और बाहरी बिंदु P लें। स्पर्शरेखाएँ PA व PB खींचें।
🔵 Step 2: OA और OB त्रिज्याएँ जोड़ें।
🔵 Step 3: ∠OAP = ∠OBP = 90° (स्पर्शरेखा पर त्रिज्या लम्बवत)।
🔵 Step 4: OP = OP (सामान्य भुजा), OA = OB (त्रिज्याएँ)।
🔵 Step 5: RHS कसौटी से ∆OAP ≅ ∆OBP।
✔️ Final: PA = PB।

🔵 Question 9
सिद्ध कीजिए कि वृत्त की जीवा की लम्ब समद्विभाजक केन्द्र से गुजरती है।
🟢 Answer
🔵 Step 1: वृत्त का केन्द्र O और जीवा AB लें।
🔵 Step 2: AB की लम्ब समद्विभाजक खींचें।
🔵 Step 3: दो सर्वांगसम त्रिभुज बनाकर दिखाएँ कि O इस समद्विभाजक पर है।
✔️ Final: जीवा की लम्ब समद्विभाजक केन्द्र से गुजरती है।

🔵 Question 10
यदि केन्द्र कोण 100° है, तो उसी चाप का परिधि कोण कितना होगा?
🟢 Answer
➤ Formula: केन्द्र कोण = 2 × परिधि कोण
➤ Substitution: 100 = 2 × θ
➤ Simplification: θ = 100 ÷ 2
✔️ Final: θ = 50°।

🔵 Question 11
एक वृत्त की त्रिज्या 6 सेमी है। उसकी परिधि ज्ञात कीजिए (π = 3.14)।
🟢 Answer
➤ Formula: C = 2 π r
➤ Substitution: C = 2 × 3.14 × 6
➤ Simplification: C = 37.68
✔️ Final: परिधि = 37.68 सेमी।

🔵 Question 12
वृत्त की स्पर्शरेखा पर त्रिज्या किस प्रकार स्थित होती है, और क्यों?
🟢 Answer
✔️ वह लम्बवत होती है क्योंकि यदि वह लम्बवत न हो, तो रेखा दो बिंदुओं पर वृत्त को काटेगी, जो स्पर्शरेखा की परिभाषा का उल्लंघन है।

🟡 Section C (3 अंक × 10 = 30 अंक, Q13–Q22)
🔵 Question 13
सिद्ध कीजिए कि वृत्त के केन्द्र कोण का मान, उसी चाप पर स्थित परिधि कोण का दोगुना होता है।
🟢 Answer
🔵 Step 1: केन्द्र O, चाप AB पर परिधि बिंदु C लें।
🔵 Step 2: ∠AOB केन्द्र कोण, ∠ACB परिधि कोण।
🔵 Step 3: ∆AOB को त्रिज्याओं से दो समद्विबाहु त्रिभुजों में विभाजित कर ∠AOB = 2∠ACB प्राप्त होता है।
✔️ Final: केन्द्र कोण = 2 × परिधि कोण।

🔵 Question 14
एक वृत्त में जीवा AB व CD समान हैं। सिद्ध कीजिए कि उनके केन्द्र से दूरी समान होगी।
🟢 Answer
🔵 Step 1: जीवा AB, CD समान ⇒ AB = CD।
🔵 Step 2: समान जीवा की लम्ब समद्विभाजकें केन्द्र से गुजरती हैं और सर्वांगसम त्रिभुजों से दूरी समान सिद्ध होती है।
✔️ Final: AB व CD की केन्द्र से दूरी समान है।

🔵 Question 15
त्रिज्या 10 सेमी वाले वृत्त के केन्द्र से 26 सेमी दूर एक बिंदु से खींची स्पर्शरेखा की लम्बाई ज्ञात कीजिए।
🟢 Answer
➤ Formula: l = √(OP² − r²)
➤ Substitution: l = √(26² − 10²)
➤ Simplification: l = √(676 − 100) = √576
✔️ Final: l = 24 सेमी।

🔵 Question 16
वृत्त की जीवा की लम्ब समद्विभाजक सदैव केन्द्र से क्यों गुजरती है?
🟢 Answer
🔵 Step 1: ∆OAB (O केन्द्र, AB जीवा) लें।
🔵 Step 2: OA = OB (त्रिज्याएँ)।
🔵 Step 3: सर्वांगसम त्रिभुजों के आधार पर जीवा का मध्य बिंदु O से जुड़ने पर समद्विभाजक बनती है।
✔️ Final: जीवा की लम्ब समद्विभाजक केन्द्र से गुजरती है।

🔵 Question 17
यदि किसी वृत्त का व्यास 14 सेमी है, तो उसकी परिधि ज्ञात कीजिए (π = 22/7)।
🟢 Answer
➤ Formula: C = π d
➤ Substitution: C = 22/7 × 14
➤ Simplification: C = 44 सेमी।
✔️ Final: परिधि = 44 सेमी।

🔵 Question 18 (Internal Choice)
(A) सिद्ध कीजिए कि अर्धवृत्त में कोण 90° होता है।
🟢 Answer
🔵 Step 1: ∆ABC में, AB व्यास।
🔵 Step 2: केन्द्र कोण = 180°, परिधि कोण = ½ × 180° = 90°.
✔️ Final: अर्धवृत्त में कोण = 90°.
OR
(B) 8 सेमी त्रिज्या वाले वृत्त की क्षेत्रफल ज्ञात कीजिए (π = 3.14)।
🟢 Answer
➤ Formula: A = π r²
➤ Substitution: A = 3.14 × 8²
➤ Simplification: A = 3.14 × 64 = 200.96 सेमी²।
✔️ Final: क्षेत्रफल = 200.96 सेमी²।

🔵 Question 19
दो वृत्त बाहरी रूप से स्पर्श करते हैं। सिद्ध कीजिए कि उनके केन्द्रों को जोड़ने वाली रेखा उनके स्पर्श-बिंदु से गुजरती है।
🟢 Answer
🔵 Step 1: केन्द्र O₁, O₂; स्पर्श-बिंदु P लें।
🔵 Step 2: स्पर्शरेखा पर त्रिज्याएँ O₁P व O₂P लम्बवत।
🔵 Step 3: केवल एक साझा बिंदु ⇒ रेखा O₁O₂, P से गुजरेगी।
✔️ Final: केन्द्रों को जोड़ने वाली रेखा स्पर्श-बिंदु से गुजरती है।

🔵 Question 20
यदि किसी वृत्त में जीवा का एक सिरा स्थिर है, तो जीवा के दूसरे सिरे का पथ किस प्रकार का होगा?
🟢 Answer
✔️ वह भी उसी वृत्त की परिधि पर चलेगा, क्योंकि सभी बिंदु केन्द्र से समान दूरी पर हैं।

🔵 Question 21 (Internal Choice)
(A) स्पर्शरेखा और जीवा के बीच का कोण = वैकल्पिक खंड का कोण सिद्ध कीजिए।
🟢 Answer
🔵 Step 1: वृत्त का केन्द्र O, स्पर्शरेखा TP व जीवा PA लें।
🔵 Step 2: केन्द्र कोण प्रमेय और पूरक कोण का प्रयोग कर वैकल्पिक खंड कोण बराबर सिद्ध करें।
✔️ Final: स्पर्शरेखा–जीवा कोण = वैकल्पिक खंड कोण।
OR
(B) त्रिज्या 12 सेमी वाले वृत्त में 60° केन्द्र कोण द्वारा निरूपित चाप की लम्बाई ज्ञात कीजिए (π = 3.14)।
🟢 Answer
➤ Formula: l = (θ/360) × 2 π r
➤ Substitution: l = (60/360) × 2 × 3.14 × 12
➤ Simplification: l = (1/6) × 75.36 = 12.56 सेमी।
✔️ Final: चाप की लम्बाई = 12.56 सेमी।

🔵 Question 22
यदि किसी वृत्त में दो स्पर्शरेखाएँ किसी बाहरी बिंदु से खींची गई हों और उनके बीच का कोण 60° हो, तो केन्द्र से उस बिंदु की दूरी व त्रिज्या का सम्बन्ध ज्ञात कीजिए।
🟢 Answer
🔵 Step 1: त्रिभुज OAP में ∠APO = 30°।
🔵 Step 2: sin30° = r/OP
🔵 Step 3: ½ = r/OP ⇒ OP = 2r।
✔️ Final: केन्द्र से दूरी = 2 × त्रिज्या।

🔵 Question 23
स्पर्शरेखा स्पर्श-बिंदु पर खींची त्रिज्या के लम्बवत होती है—सिद्ध कीजिए।
🟢 Answer
🔵 Step 1: वृत्त का केन्द्र O और स्पर्श-बिंदु P लें; P पर स्पर्शरेखा PT खींचें।
🔵 Step 2: मानें कि ∠OPT ≠ 90°। तब PT पर P के निकट Q लें जिससे PQ एक लघु जीवा बने।
🔵 Step 3: यदि ∠OPT तीक्ष्ण/अधिक हो तो PT रेखा वृत्त को दो बिंदुओं पर काटेगी (P और Q), जो स्पर्शरेखा की परिभाषा (एक ही बिंदु पर स्पर्श) के विरुद्ध है।
🔵 Step 4: अतः विरोधाभास से निष्कर्ष—∠OPT = 90°।
➤ Final: स्पर्शरेखा PT, स्पर्श-बिंदु P पर त्रिज्या OP के लम्बवत होती है।

🔵 Question 24 (Internal Choice)
(A) बाहरी बिंदु P से वृत्त को खींची स्पर्शरेखाएँ PA और PB बराबर होती हैं तथा उनकी लम्बाई का सूत्र सिद्ध कीजिए।
🟢 Answer
🔵 Step 1: केन्द्र O; बिंदु P वृत्त के बाहर; स्पर्श-बिंदु A, B; स्पर्शरेखाएँ PA, PB।
🔵 Step 2: OA ⟂ PA, OB ⟂ PB (Q23 से)।
🔵 Step 3: ∆OAP और ∆OBP में: OA = OB (त्रिज्याएँ), OP = OP (सामान्य), ∠OAP = ∠OBP = 90° ⇒ RHS से ∆OAP ≅ ∆OBP।
🔵 Step 4: अतः PA = PB (समतुल्य भुजाएँ)।
🔵 Step 5: ∆OAP समकोण है ⇒ PA = √(OP² − OA²) = √(OP² − r²)।
➤ Final: बाहरी बिंदु से खींची दोनों स्पर्शरेखाएँ बराबर हैं तथा उनकी लम्बाई √(OP² − r²) है।
OR
(B) यदि r = 13 सेमी और OP = 25 सेमी, तो स्पर्शरेखा की लम्बाई ज्ञात कीजिए।
🟢 Answer
➤ Formula: PA = √(OP² − r²)
➤ Substitution: PA = √(25² − 13²)
➤ Simplification: PA = √(625 − 169) = √456 = √(4×114) = 2√114
➤ Final: PA = 2√114 सेमी (≈ 21.35 सेमी)।

🔵 Question 25
किसी बिंदु P से वृत्त को खींची गई दो स्पर्शरेखाओं के बीच का कोण θ है। सिद्ध कीजिए कि OP = r / sin(θ/2) तथा θ = 120° पर OP का मान निकालिए।
🟢 Answer
🔵 Step 1: स्पर्श-बिंदु A, B; ∠APB = θ। ∆APO और ∆BPO समद्विबाहु समकोण जैसे हैं क्योंकि OA ⟂ PA, OB ⟂ PB।
🔵 Step 2: ∠APO = ∠BPO = θ/2 (सममिति)। ∆APO में sin(θ/2) = r/OP।
🔵 Step 3: अतः OP = r / sin(θ/2)।
🔵 Step 4: θ = 120° ⇒ θ/2 = 60° ⇒ sin60° = √3/2।
➤ Final: OP = r / (√3/2) = 2r/√3।

🔵 Question 26 (Internal Choice)
(A) त्रिज्या r वाले वृत्त में लंबाई c की जीवा की केन्द्र से दूरी d ज्ञात कीजिए।
🟢 Answer
🔵 Step 1: AB जीवा; M उसका मध्यबिंदु; AM = c/2।
🔵 Step 2: OM ⟂ AB और OA = r। समकोण ∆OAM में: OM² + AM² = OA²।
🔵 Step 3: d² + (c/2)² = r² ⇒ d = √(r² − (c/2)²)।
➤ Final: d = √(r² − c²/4)।
OR
(B) यदि r = 13 सेमी और केन्द्र से दूरी d = 5 सेमी, तो जीवा की लंबाई ज्ञात कीजिए।
🟢 Answer
➤ Formula: (c/2)² = r² − d²
➤ Substitution: (c/2)² = 13² − 5² = 169 − 25 = 144
➤ Simplification: c/2 = 12 ⇒ c = 24
➤ Final: जीवा = 24 सेमी।

🔵 Question 27
स्पर्शरेखा–जीवा के बीच का कोण = वैकल्पिक खंड का कोण (Alternate Segment Theorem) — सिद्ध कीजिए।
🟢 Answer
🔵 Step 1: वृत्त पर बिंदु A पर स्पर्शरेखा AT; AB जीवा; बिंदु C, B के विपरीत खंड पर।
🔵 Step 2: OA ⟂ AT, अतः ∠OAT = 90°। ∠AOB केन्द्र कोण और ∠ACB परिधि कोण (उसी चाप AB पर)।
🔵 Step 3: ∠BAT (जीवा–स्पर्शरेखा कोण) = 90° − ∠BAO, और ∠BAO = ½∠BOA (समद्विबाहु त्रिभुजों व केन्द्र–परिधि कोण संबंध से)।
🔵 Step 4: अतः ∠BAT = 90° − ½∠BOA = ∠ACB (क्योंकि ∠ACB = ½∠AOB)।
➤ Final: जीवा–स्पर्शरेखा कोण = वैकल्पिक खंड का कोण।

🔵 Question 28 (Internal Choice)
(A) त्रिज्या r और केन्द्र कोण θ (डिग्री में) के लिए क्षेत्रफल (A) व चाप-लंबाई (l) ज्ञात कीजिए।
🟢 Answer
➤ Formula (Sector Area): A = (θ/360) × π r²
➤ Formula (Arc Length): l = (θ/360) × 2π r
➤ Final: A = (θπ r²)/360, l = (θ·2π r)/360।
OR
(B) r = 14 सेमी, θ = 45° पर A और l निकालिए (π = 22/7)।
🟢 Answer
➤ A: (45/360) × π × 14² = (1/8) × (22/7) × 196
➤ Simplification: A = (1/8) × (22 × 28) = (1/8) × 616 = 77
➤ l: (45/360) × 2π × 14 = (1/8) × 28π = 3.5π = 3.5 × 22/7 = 11
➤ Final: A = 77 सेमी², l = 11 सेमी।

🔵 Question 29
सिद्ध कीजिए कि दो स्पर्शरेखाओं के बीच का कोण 180° − ∠AOB के बराबर होता है, जहाँ A, B स्पर्श-बिंदु हैं और ∠AOB केन्द्र कोण है।
🟢 Answer
🔵 Step 1: A, B पर स्पर्शरेखाएँ AT, BT; OA ⟂ AT, OB ⟂ BT।
🔵 Step 2: ∠(AT, OA) = 90°, ∠(BT, OB) = 90°।
🔵 Step 3: कोण (AT, BT) = ∠AOB के पूरक के बराबर होता है क्योंकि दो बार 90° घटता है।
🔵 Step 4: अतः ∠T = 180° − ∠AOB।
➤ Final: स्पर्शरेखाओं के बीच का कोण = 180° − केन्द्र कोण।

🔵 Question 30
सिद्ध कीजिए कि बाहरी बिंदु P के लिए OP² = PT² + r²; फिर यदि PT = 24 सेमी और OP = 26 सेमी हो तो r ज्ञात कीजिए।
🟢 Answer
🔵 Step 1: A स्पर्श-बिंदु; OA ⟂ PT।
🔵 Step 2: समकोण ∆OAP में OP² = OA² + AP²।
🔵 Step 3: OA = r और AP = PT ⇒ OP² = r² + PT²।
🔵 Step 4: दिए अनुसार 26² = r² + 24² ⇒ 676 = r² + 576 ⇒ r² = 100।
➤ Final: r = 10 सेमी तथा संबंध OP² = PT² + r² सत्य है।

————————————————————————————————————————————————————————————————————————————

मनोमानचित्र

————————————————————————————————————————————————————————————————————————————
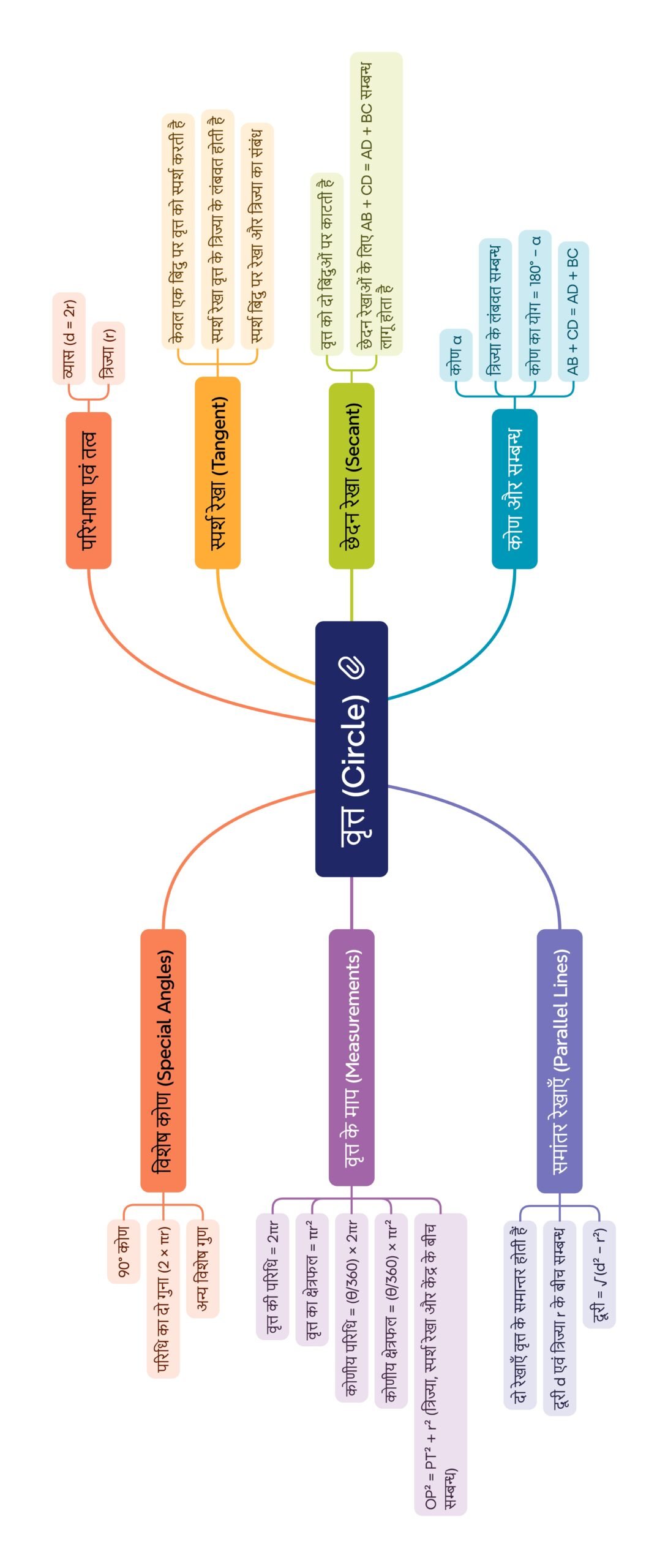