Class 10 : Maths (In Hindi) – Lesson 1. वास्तविक संख्याएँ
पाठ का विश्लेषण एवं विवेचन
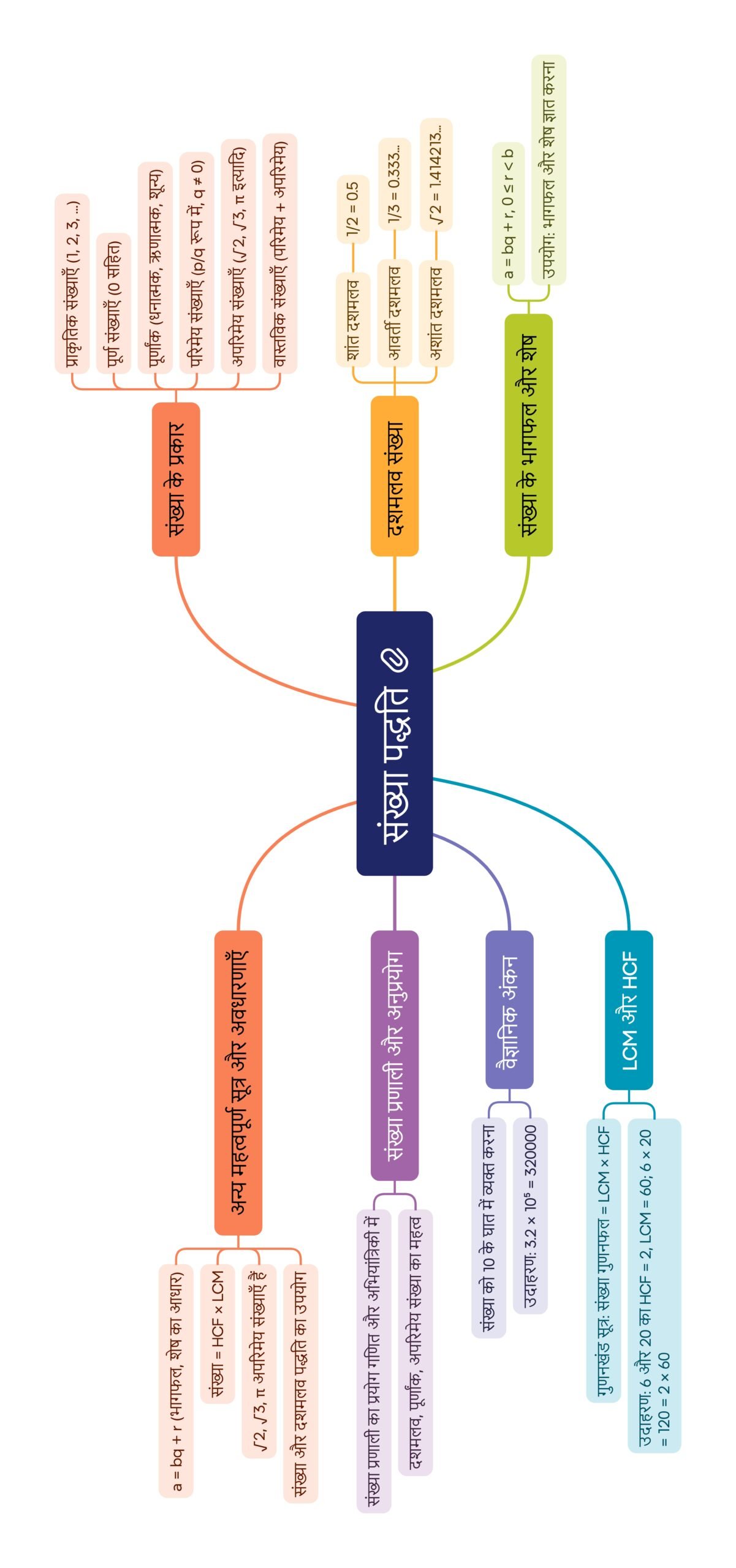
🔵 परिचय
मानव सभ्यता के आरम्भ से ही संख्याएँ जीवन का अभिन्न हिस्सा रही हैं। गिनती, मापन, व्यापार, वास्तुकला, विज्ञान और प्रौद्योगिकी—हर जगह संख्याओं का प्रयोग होता है। इस अध्याय “वास्तविक संख्याएँ” का उद्देश्य विद्यार्थियों को यह समझाना है कि गणित की पूरी नींव इन्हीं संख्याओं पर टिकी है।
वास्तविक संख्याएँ वे सभी संख्याएँ हैं जिन्हें संख्या रेखा पर निरूपित किया जा सकता है। इनमें परिमेय (जैसे 1/2, -3/4, 5) और अपरिमेय (जैसे √2, π) दोनों संख्याएँ आती हैं। यह अध्याय अंकगणित के मौलिक प्रमेय, HCF–LCM, परिमेय–अपरिमेय का वर्गीकरण, दशमलव प्रसार और जीवन में इनके अनुप्रयोगों पर केन्द्रित है।
🟢 1. संख्या पद्धति का विकास
प्रारम्भ में केवल प्राकृतिक संख्याएँ (1, 2, 3, …) प्रयोग में थीं।
शून्य और ऋणात्मक संख्याओं के आने से पूर्णांक बने।
p/q रूप की संख्याओं से परिमेय संख्याएँ बनीं।
√2, π, e जैसी संख्याएँ अपरिमेय कहलायीं।
➡️ परिमेय + अपरिमेय = वास्तविक संख्याएँ।
🔴 2. अंकगणित का मौलिक प्रमेय
👉 हर 1 से बड़ी प्राकृतिक संख्या या तो अभाज्य होती है या फिर अभाज्य संख्याओं के गुणनफल के रूप में केवल एक ही प्रकार से व्यक्त की जा सकती है (क्रम को छोड़कर)।
उदाहरण:
20 = 2² × 5
84 = 2² × 3 × 7
✏️ टिप्पणी: यह प्रमेय संख्या सिद्धान्त की नींव है।
🟡 3. HCF और LCM द्वारा अनुप्रयोग
दो संख्याएँ: 84 और 120
84 = 2² × 3 × 7
120 = 2³ × 3 × 5
➡️ HCF = 2² × 3 = 12
➡️ LCM = 2³ × 3 × 5 × 7 = 420
✔️ संबंध: HCF × LCM = 84 × 120
🌿 4. परिमेय एवं अपरिमेय संख्याएँ
परिमेय संख्या: p/q रूप में (q ≠ 0)।
अपरिमेय संख्या: जिन्हें p/q रूप में नहीं लिखा जा सकता (जैसे √2, √3, π)।
➡️ दोनों का संघटन वास्तविक संख्याएँ है।
⚡ 5. अपरिमेय का प्रमाण (√2)
🧠 विरोधाभास विधि:
मान लें √2 = p/q (p और q परस्पर अभाज्य)।
→ p² = 2q² ⇒ p सम है ⇒ p = 2r।
→ 4r² = 2q² ⇒ q² = 2r² ⇒ q भी सम।
लेकिन तब p और q दोनों सम होंगे, जबकि हमने परस्पर अभाज्य माना था।
➡️ विरोधाभास।
✔️ अतः √2 अपरिमेय है।
इसी विधि से √3, √5 आदि भी अपरिमेय सिद्ध किए जा सकते हैं।
🔵 6. दशमलव प्रसार
किसी संख्या का दशमलव रूप उसके परिमेय या अपरिमेय होने का संकेत देता है:
शांत दशमलव प्रसार → परिमेय।
आवर्ती दशमलव प्रसार → परिमेय।
अशांत दशमलव प्रसार → अपरिमेय।
उदाहरण:
1/2 = 0.5 (शांत)
1/3 = 0.333… (आवर्ती)
√2 = 1.414213… (अशांत)
🟢 7. परिमेय संख्या के दशमलव का प्रमेय
यदि p/q अपने सरलतम रूप में है:
यदि q के अभाज्य गुणनखंड केवल 2 और/या 5 हों → दशमलव शांत।
अन्य अभाज्य गुणनखंड हों → दशमलव आवर्ती।
उदाहरण:
1/8 = 0.125 (शांत)
1/6 = 0.1666… (आवर्ती)
🔴 8. संख्या रेखा पर अपरिमेय संख्याएँ
√2 को दर्शाने हेतु:
1 इकाई भुजाओं वाला समकोण त्रिभुज बनाएँ।
कर्ण = √2 होगा।
इसे संख्या रेखा पर चिह्नित करें।
🌿 9. अभाज्य संख्याएँ और 6k ± 1 रूप
6 से बड़ी प्रत्येक अभाज्य संख्या या तो (6k + 1) या (6k – 1) के रूप में होती है।
यह प्रमेय अभाज्य संख्याओं के वितरण के अध्ययन में महत्वपूर्ण है।
⚡ 10. जीवन में प्रयोग
HCF/LCM: समय सारिणी, घंटियों का एकसाथ बजना।
अपरिमेय: वास्तुकला, विकर्ण निकालना।
वास्तविक संख्याएँ: विज्ञान और गणित की आधारशिला।
✏️ टिप्पणी
वास्तविक संख्याओं में वे सब आती हैं जिन्हें संख्या रेखा पर दर्शाया जा सकता है।
काल्पनिक संख्या i (√-1) इनमें नहीं आती।
🟡 सारांश (~300 शब्द)
वास्तविक संख्याएँ = परिमेय + अपरिमेय।
अंकगणित का मौलिक प्रमेय: अद्वितीय अभाज्य गुणनखंडन।
HCF × LCM = गुणनफल।
√2, √3, √5 अपरिमेय (विरोधाभास विधि)।
दशमलव रूप:
• शांत → परिमेय।
• आवर्ती → परिमेय।
• अशांत → अपरिमेय।
संख्या रेखा पर √n निरूपण।
अभाज्य संख्याएँ 6k ± 1 रूप में।
अनुप्रयोग: गणना, वास्तुकला, विज्ञान।
📝 Quick Recap
🔵 वास्तविक = परिमेय + अपरिमेय।
🟢 मौलिक प्रमेय = अभाज्य गुणनखंडन।
🔴 HCF × LCM = गुणनफल।
🟡 अपरिमेय का प्रमाण = विरोधाभास।
🌿 दशमलव: शांत/आवर्ती → परिमेय; अशांत → अपरिमेय।
⚡ अभाज्य → 6k ± 1।
————————————————————————————————————————————————————————————————————————–
पाठ्यपुस्तक के प्रश्न
🟢 Exercise 1.1
🔵 प्रश्न 1
निम्नलिखित संख्याओं को अभाज्य गुणनखण्डों के गुणनफल के रूप में व्यवस्थित कीजिए :
(i) 140 (ii) 156 (iii) 3825 (iv) 5005 (v) 7429
🟢 उत्तर
(i) 140
🔵 Step 1: 140 ÷ 2 = 70
🔵 Step 2: 70 ÷ 2 = 35
🔵 Step 3: 35 ÷ 5 = 7
✔️ Final: 140 = 2² × 5 × 7
(ii) 156
🔵 Step 1: 156 ÷ 2 = 78
🔵 Step 2: 78 ÷ 2 = 39
🔵 Step 3: 39 ÷ 3 = 13
✔️ Final: 156 = 2² × 3 × 13
(iii) 3825
🔵 Step 1: 3825 ÷ 5 = 765
🔵 Step 2: 765 ÷ 5 = 153
🔵 Step 3: 153 ÷ 3 = 51
🔵 Step 4: 51 ÷ 3 = 17
✔️ Final: 3825 = 5² × 3² × 17
(iv) 5005
🔵 Step 1: 5005 ÷ 5 = 1001
🔵 Step 2: 1001 ÷ 7 = 143
🔵 Step 3: 143 ÷ 11 = 13
✔️ Final: 5005 = 5 × 7 × 11 × 13
(v) 7429
🔵 Step 1: 7429 ÷ 17 = 437
🔵 Step 2: 437 ÷ 19 = 23
✔️ Final: 7429 = 17 × 19 × 23
🔵 प्रश्न 2
पूर्णांकों के निम्नलिखित युग्मों के HCF और LCM ज्ञात कीजिए तथा इसकी जाँच कीजिए कि दो संख्याओं का गुणनफल = HCF × LCM है।
(i) 26 और 91 (ii) 510 और 92 (iii) 336 और 54
🟢 उत्तर
(i) 26 और 91
🔵 Step 1: 26 = 2 × 13, 91 = 7 × 13
🔵 Step 2: HCF = 13
🔵 Step 3: LCM = (26 × 91) ÷ 13 = 182
🟡 Check: 26 × 91 = 2366, HCF × LCM = 2366
✔️ Final: HCF = 13, LCM = 182
(ii) 510 और 92
🔵 Step 1: 510 = 2 × 3 × 5 × 17
🔵 Step 2: 92 = 2² × 23
🔵 Step 3: HCF = 2
🔵 Step 4: LCM = (510 × 92) ÷ 2 = 23460
🟡 Check: 510 × 92 = 46920, HCF × LCM = 46920
✔️ Final: HCF = 2, LCM = 23460
(iii) 336 और 54
🔵 Step 1: 336 = 2⁴ × 3 × 7
🔵 Step 2: 54 = 2 × 3³
🔵 Step 3: HCF = 6
🔵 Step 4: LCM = (336 × 54) ÷ 6 = 3024
🟡 Check: 336 × 54 = 18144, HCF × LCM = 18144
✔️ Final: HCF = 6, LCM = 3024
🔵 प्रश्न 3
अभाज्य गुणनखण्ड विधि द्वारा निम्नलिखित पूर्णांकों के HCF और LCM ज्ञात कीजिए :
(i) 12, 15 और 21 (ii) 17, 23 और 29 (iii) 8, 9 और 25
🟢 उत्तर
(i) 12 = 2² × 3, 15 = 3 × 5, 21 = 3 × 7
✔️ HCF = 3, LCM = 420
(ii) 17, 23 और 29 अभाज्य संख्याएँ हैं
✔️ HCF = 1, LCM = 17 × 23 × 29 = 11339
(iii) 8 = 2³, 9 = 3², 25 = 5²
✔️ HCF = 1, LCM = 2³ × 3² × 5² = 1800
🔵 प्रश्न 4
HCF (306, 657) = 9 दिया है। LCM (306, 657) ज्ञात कीजिए।
🟢 उत्तर
🔵 Step 1: 306 × 657 = 201042
🔵 Step 2: LCM = 201042 ÷ 9 = 22338
✔️ Final: LCM = 22338
🔵 प्रश्न 5
जाँच कीजिए कि क्या किसी प्राकृतिक संख्या n के लिए, संख्या 6n + 1 अंक 0 पर समाप्त हो सकती है।
🟢 उत्तर
🔵 Step 1: किसी भी संख्या का अंतिम अंक उसकी 10 से विभाज्यता पर निर्भर करता है।
🔵 Step 2: किसी भी प्राकृतिक संख्या n के लिए, 6n का अंतिम अंक केवल 0, 2, 4, 6 या 8 हो सकता है (क्योंकि 6 के गुणजों के अंतिम अंक यही आते हैं)।
🔵 Step 3: अतः 6n + 1 के अंतिम अंक होंगे:
➡️ 0 + 1 = 1
➡️ 2 + 1 = 3
➡️ 4 + 1 = 5
➡️ 6 + 1 = 7
➡️ 8 + 1 = 9
🔵 Step 4: देखा कि 6n + 1 के संभावित अंतिम अंक 1, 3, 5, 7 या 9 हैं।
🟡 जाँच: इनमें 0 शामिल नहीं है।
✔️ Final: किसी भी प्राकृतिक संख्या n के लिए 6n + 1 का अंतिम अंक 0 नहीं हो सकता।
🔵 प्रश्न 6
व्याख्या कीजिए कि 7×11×13+13 और 7×6×5×4×3×2×1+5 भाज्य संख्याएँ क्यों हैं।
🟢 उत्तर
🔵 Step 1: 7×11×13+13 = 1001+13 = 1014
🔵 Step 2: 1014 ÷ 13 = 78 (पूर्ण भाग)
🟡 जाँच: 1014, 13 का गुणज है → अभाज्य नहीं।
✔️ Final: 1014 भाज्य संख्या है।
🔵 Step 3: 7×6×5×4×3×2×1+5 = 5040+5 = 5045
🔵 Step 4: 5045 ÷ 5 = 1009 (पूर्ण भाग)
🟡 जाँच: 5045, 5 का गुणज है → अभाज्य नहीं।
✔️ Final: 5045 भाज्य संख्या है।
🔵 प्रश्न 7
किसी खेल के मैदान के चारों ओर एक वृत्ताकार पथ है। इस मैदान का एक चक्कर लगाने में सोनिया को 18 मिनट लगते हैं, जबकि इसी मैदान का एक चक्कर लगाने में रवि को 12 मिनट लगते हैं। मान लीजिए वे दोनों एक ही स्थान और एक ही समय पर चलना प्रारम्भ करके एक ही दिशा में चलते हैं। कितने समय बाद वे पुनः प्रारम्भिक स्थान पर मिलेंगे?
🟢 उत्तर
🔵 Step 1: सोनिया का समय = 18 मिनट, रवि का समय = 12 मिनट
🔵 Step 2: मिलने का समय = LCM(18, 12)
🔵 Step 3: 18 = 2×3², 12 = 2²×3
🔵 Step 4: LCM = 2²×3² = 36
🟡 जाँच: 36 ÷ 18 = 2, 36 ÷ 12 = 3 (दोनों पूर्णांक)
✔️ Final: वे 36 मिनट बाद पुनः प्रारम्भिक स्थान पर मिलेंगे।
🟢 Exercise 1.2
🔵 प्रश्न 1
सिद्ध कीजिए कि √5 एक अपरिमेय संख्या है।
🟢 उत्तर
🔵 Step 1: मान लीजिए √5 परिमेय है।
🔵 Step 2: तब इसे p/q के रूप में लिखा जा सकता है, जहाँ p और q परस्पर अभाज्य पूर्णांक हैं, q ≠ 0।
🔵 Step 3: ⇒ √5 = p/q
🔵 Step 4: दोनों ओर वर्ग करें → 5 = p²/q²
🔵 Step 5: ⇒ p² = 5q²
🔵 Step 6: इसका अर्थ है कि p² 5 से विभाज्य है ⇒ p भी 5 से विभाज्य होगा।
🔵 Step 7: मान लीजिए p = 5k
⇒ p² = 25k²
🔵 Step 8: समीकरण p² = 5q² में रखने पर → 25k² = 5q² ⇒ q² = 5k²
🔵 Step 9: इससे q² भी 5 से विभाज्य है ⇒ q भी 5 से विभाज्य होगा।
🔵 Step 10: इस प्रकार p और q दोनों 5 से विभाज्य हैं, जो p और q के परस्पर अभाज्य होने की शर्त का खण्डन है।
✔️ Final: अतः √5 अपरिमेय संख्या है।
🔵 प्रश्न 2
सिद्ध कीजिए कि 3 + 2√5 एक अपरिमेय संख्या है।
🟢 उत्तर
🔵 Step 1: मान लीजिए 3 + 2√5 परिमेय है।
🔵 Step 2: तब 2√5 = (3 + 2√5) − 3 होगा।
🔵 Step 3: चूँकि परिमेय संख्या में से परिमेय घटाने पर परिणाम परिमेय ही होता है, इसलिए 2√5 परिमेय होना चाहिए।
🔵 Step 4: लेकिन इसका अर्थ है कि √5 परिमेय है।
🔵 Step 5: यह विरोधाभास है क्योंकि पहले सिद्ध किया गया कि √5 अपरिमेय है।
✔️ Final: अतः 3 + 2√5 अपरिमेय संख्या है।
🔵 प्रश्न 3
सिद्ध कीजिए कि निम्नलिखित संख्याएँ अपरिमेय हैं :
(i) 1/√2 (ii) 7√5 (iii) 6 + √2
🟢 उत्तर
(i) 1/√2
🔵 Step 1: यदि 1/√2 परिमेय है, तो इसका व्युत्क्रम √2 भी परिमेय होगा।
🔵 Step 2: लेकिन √2 ज्ञात रूप से अपरिमेय है।
✔️ Final: 1/√2 अपरिमेय है।
(ii) 7√5
🔵 Step 1: 7 एक परिमेय संख्या है।
🔵 Step 2: √5 एक अपरिमेय संख्या है।
🔵 Step 3: परिमेय × अपरिमेय = अपरिमेय।
✔️ Final: 7√5 अपरिमेय है।
(iii) 6 + √2
🔵 Step 1: 6 परिमेय संख्या है।
🔵 Step 2: √2 अपरिमेय संख्या है।
🔵 Step 3: परिमेय + अपरिमेय = अपरिमेय।
✔️ Final: 6 + √2 अपरिमेय है।
————————————————————————————————————————————————————————————————————————–
अन्य महत्वपूर्ण प्रश्न
🔵 Section A (बहुविकल्पी/अल्प-उत्तरी, 1 अंक प्रत्येक) — Q1–Q6
🔵 Question 1
वक्तव्य: किसी भी दो धनात्मक पूर्णांकों a, b पर (a > b), यूक्लिड विभाजन अल्गोरिथ्म के अनुसार a = bq + r, जहाँ r का मान होता है
🟢 विकल्प:
🔹 1. r ≥ b
🔹 2. 0 ≤ r < b
🔹 3. r = b
🔹 4. r < 0
🟢 Answer: 2
🔵 Question 2
यदि किसी संख्या का अभाज्य गुणनखण्डन 2³×5² है, तो उसका दशमलव प्रसार होगा
🟢 विकल्प:
🔹 1. अनन्त परन्तु आवर्ती
🔹 2. समाप्ति वाला (टर्मिनेटिंग)
🔹 3. अनन्त एवं अनावर्ती
🔹 4. निश्चय नहीं किया जा सकता
🟢 Answer: 2
🔵 Question 3
किसी भी दो संख्याओं a, b के लिए गुणनफल = HCF(a, b) × LCM(a, b) — यह कथन
🟢 विकल्प:
🔹 1. सदैव सत्य
🔹 2. कभी-कभी सत्य
🔹 3. केवल अभाज्य संख्याओं के लिए
🔹 4. केवल सहाभाज्य संख्याओं के लिए
🟢 Answer: 1
🔵 Question 4
यदि p कोई अभाज्य है और p | a², तो यूक्लिड का लम्मा देता है
🟢 विकल्प:
🔹 1. p | a
🔹 2. p | 2a
🔹 3. p ∤ a
🔹 4. p | (a + 1)
🟢 Answer: 1
🔵 Question 5
निम्न में से कौन-सा परिमेय है?
🟢 विकल्प:
🔹 1. √5
🔹 2. 7√2
🔹 3. 3 + √3
🔹 4. 0
🟢 Answer: 4
🔵 Question 6
यदि किसी धनात्मक पूर्णांक n के लिए संख्या 6n + 1 है, तो यह अंतिम अंकों के किस समूह में आ सकती है?
🟢 विकल्प:
🔹 1. {0, 2, 4, 6, 8}
🔹 2. {1, 3, 5, 7, 9}
🔹 3. {2, 5, 8}
🔹 4. {0, 5}
🟢 Answer: 2
🟢 Section B (संक्षिप्त उत्तर-I, 2 अंक प्रत्येक) — Q7–Q12
🔵 Question 7
सिद्ध कीजिए कि √5 अपरिमेय है।
🟢 Answer
➤ मान लें √5 = p/q, जहाँ p, q परस्पर अभाज्य, q ≠ 0।
➤ वर्ग करें: 5 = p²/q² ⇒ p² = 5q²।
➤ 5 | p² ⇒ 5 | p; मानें p = 5k।
➤ तब 25k² = 5q² ⇒ q² = 5k² ⇒ 5 | q।
➤ p, q दोनों 5 से विभाज्य—परस्पर अभाज्य शर्त का खण्डन।
✔️ निष्कर्ष: √5 अपरिमेय।
🔵 Question 8
सिद्ध कीजिए कि 3 + 2√5 अपरिमेय है।
🟢 Answer
➤ मान लें 3 + 2√5 परिमेय है।
➤ तब 2√5 = (3 + 2√5) − 3 परिमेय होगा।
➤ ⇒ √5 परिमेय, जो Q7 से असत्य।
✔️ निष्कर्ष: 3 + 2√5 अपरिमेय।
🔵 Question 9
यदि किसी धनात्मक पूर्णांक का अभाज्य गुणनखण्डन 2ᵐ×5ⁿ (m, n पूर्णांक) हो, तो उसके दशमलव प्रसार का प्रकार लिखिए।
🟢 Answer
➤ हर हर (हर = denominator) केवल 2 और 5 के घात हों ⇒ भिन्न का दशमलव समाप्ति वाला होता है।
✔️ निष्कर्ष: 2ᵐ×5ⁿ रूप ⇒ समाप्ति वाला दशमलव।
🔵 Question 10
सहाभाज्य का परिभाषा तथा उदाहरण दीजिए।
🟢 Answer
➤ परिभाषा: दो पूर्णांकों का महत्तम समापवर्तक 1 हो तो वे सहाभाज्य कहलाते हैं।
➤ उदाहरण: 8 और 15; क्योंकि HCF(8, 15) = 1।
✔️ निष्कर्ष: 8, 15 सहाभाज्य।
🔵 Question 11
सिद्ध कीजिए कि 1/√2 अपरिमेय है।
🟢 Answer
➤ यदि 1/√2 परिमेय हो तो उसका व्युत्क्रम √2 भी परिमेय होगा।
➤ परन्तु √2 अपरिमेय है (प्रसिद्ध परिणाम)।
✔️ निष्कर्ष: 1/√2 अपरिमेय।
🔵 Question 12
दिखाइए कि 6n + 2 तथा 6n + 4 किसी भी n के लिए अभाज्य नहीं हैं।
🟢 Answer
➤ 6n + 2 = 2(3n + 1) ⇒ सदैव सम ⇒ 2 से विभाज्य ⇒ अभाज्य नहीं।
➤ 6n + 4 = 2(3n + 2) ⇒ सदैव सम ⇒ 2 से विभाज्य ⇒ अभाज्य नहीं।
✔️ निष्कर्ष: दोनों रूप भाज्य।
🟡 Section C (Q13–Q22, 3 अंक प्रत्येक, आन्तरिक विकल्प सम्मिलित)
🔵 प्रश्न 13
महत्तम समापवर्तक (306, 657) = 9 दिया है। लघुत्तम समापवर्त्य (306, 657) ज्ञात कीजिए।
🟢 उत्तर
🔵 Step 1: 306 × 657 = 201042
🔵 Step 2: लघुत्तम समापवर्त्य = (306 × 657) ÷ 9 = 22338
✔️ निष्कर्ष: ल.स. = 22338
🔵 प्रश्न 14
जाँच कीजिए कि क्या किसी प्राकृतिक संख्या n के लिए, संख्या 6n + 1 का अंतिम अंक 0 हो सकता है।
🟢 उत्तर
🔵 Step 1: 6n के संभावित अंतिम अंक = {0, 2, 4, 6, 8}
🔵 Step 2: 6n + 1 के अंतिम अंक = {1, 3, 5, 7, 9}
🟡 जाँच: इनमें 0 सम्मिलित नहीं है।
✔️ निष्कर्ष: 6n + 1 कभी 0 पर समाप्त नहीं हो सकती।
🔵 प्रश्न 15
व्याख्या कीजिए कि 7×11×13 + 13 और 7×6×5×4×3×2×1 + 5 भाज्य संख्याएँ क्यों हैं।
🟢 उत्तर
🔵 Step 1: 7×11×13 + 13 = 1001 + 13 = 1014
🔵 Step 2: 1014 ÷ 13 = 78 ⇒ 13 से विभाज्य
🔵 Step 3: 7×6×5×4×3×2×1 + 5 = 5040 + 5 = 5045
🔵 Step 4: 5045 ÷ 5 = 1009 ⇒ 5 से विभाज्य
✔️ निष्कर्ष: दोनों संख्याएँ भाज्य हैं।
🔵 प्रश्न 16
सिद्ध कीजिए कि 1/√3 अपरिमेय है।
🟢 उत्तर
🔵 Step 1: यदि 1/√3 परिमेय हो तो उसका व्युत्क्रम √3 परिमेय होगा।
🔵 Step 2: √3 ज्ञात रूप से अपरिमेय है।
✔️ निष्कर्ष: 1/√3 अपरिमेय है।
🔵 प्रश्न 17
सिद्ध कीजिए कि 5√2 अपरिमेय है।
🟢 उत्तर
🔵 Step 1: 5 परिमेय है।
🔵 Step 2: √2 अपरिमेय है।
🔵 Step 3: परिमेय × अपरिमेय = अपरिमेय।
✔️ निष्कर्ष: 5√2 अपरिमेय है।
🔵 प्रश्न 18
सिद्ध कीजिए कि 7 + √3 अपरिमेय है।
🟢 उत्तर
🔵 Step 1: 7 परिमेय है।
🔵 Step 2: √3 अपरिमेय है।
🔵 Step 3: परिमेय + अपरिमेय = अपरिमेय।
✔️ निष्कर्ष: 7 + √3 अपरिमेय है।
🔵 प्रश्न 19
एक संख्या लिखिए जो 2 तथा 3 दोनों से विभाज्य हो पर 6 से विभाज्य न हो।
🟢 उत्तर
🔵 Step 1: 2 और 3 का लघुत्तम समापवर्त्य = 6
🔵 Step 2: अतः यदि कोई संख्या 2 और 3 दोनों से विभाज्य है तो वह 6 से भी अवश्य विभाज्य होगी।
✔️ निष्कर्ष: ऐसी कोई संख्या सम्भव नहीं है।
🔵 प्रश्न 20
सिद्ध कीजिए कि √7 अपरिमेय है।
🟢 उत्तर
🔵 Step 1: मान लें √7 = p/q, (p, q परस्पर अभाज्य)
🔵 Step 2: वर्ग करने पर 7 = p²/q² ⇒ p² = 7q²
🔵 Step 3: 7 | p² ⇒ 7 | p ⇒ p = 7k
🔵 Step 4: रखने पर 49k² = 7q² ⇒ q² = 7k² ⇒ 7 | q
🔵 Step 5: p, q दोनों 7 से विभाज्य — विरोधाभास
✔️ निष्कर्ष: √7 अपरिमेय है।
🔵 प्रश्न 21 (आन्तरिक विकल्प)
(i) सिद्ध कीजिए कि √11 अपरिमेय है।
या
(ii) सिद्ध कीजिए कि 1/√7 अपरिमेय है।
🟢 उत्तर (i)
🔵 Step 1: मान लें √11 = p/q
🔵 Step 2: वर्ग करने पर 11 = p²/q² ⇒ p² = 11q²
🔵 Step 3: 11 | p² ⇒ 11 | p ⇒ p = 11k
🔵 Step 4: रखने पर q² = 11k² ⇒ 11 | q
🔵 Step 5: p, q दोनों 11 से विभाज्य — विरोधाभास
✔️ निष्कर्ष: √11 अपरिमेय है।
🟢 उत्तर (ii)
🔵 Step 1: यदि 1/√7 परिमेय है तो √7 भी परिमेय होगा।
🔵 Step 2: परन्तु √7 अपरिमेय है।
✔️ निष्कर्ष: 1/√7 अपरिमेय है।
🔵 प्रश्न 22 (आन्तरिक विकल्प)
(i) सिद्ध कीजिए कि 2 + √3 अपरिमेय है।
या
(ii) सिद्ध कीजिए कि 3√5 अपरिमेय है।
🟢 उत्तर (i)
🔵 Step 1: 2 परिमेय है।
🔵 Step 2: √3 अपरिमेय है।
🔵 Step 3: परिमेय + अपरिमेय = अपरिमेय।
✔️ निष्कर्ष: 2 + √3 अपरिमेय है।
🟢 उत्तर (ii)
🔵 Step 1: 3 परिमेय है।
🔵 Step 2: √5 अपरिमेय है।
🔵 Step 3: परिमेय × अपरिमेय = अपरिमेय।
✔️ निष्कर्ष: 3√5 अपरिमेय है।
🔴 Section D (Q23–Q30, 4 अंक प्रत्येक, आन्तरिक विकल्प लगभग 3 प्रश्नों में)
🔵 प्रश्न 23
सिद्ध कीजिए कि √3 अपरिमेय है।
🟢 उत्तर
🔵 Step 1: मान लें √3 = p/q (p, q परस्पर अभाज्य)।
🔵 Step 2: वर्ग करने पर 3 = p²/q² ⇒ p² = 3q²।
🔵 Step 3: 3 | p² ⇒ 3 | p ⇒ p = 3k।
🔵 Step 4: रखने पर 9k² = 3q² ⇒ q² = 3k² ⇒ 3 | q।
🔵 Step 5: p और q दोनों 3 से विभाज्य — परस्पर अभाज्य शर्त का खण्डन।
✔️ निष्कर्ष: √3 अपरिमेय है।
🔵 प्रश्न 24 (आन्तरिक विकल्प)
(i) सिद्ध कीजिए कि √2 अपरिमेय है।
या
(ii) सिद्ध कीजिए कि 1/√5 अपरिमेय है।
🟢 उत्तर (i)
🔵 Step 1: मान लें √2 = p/q।
🔵 Step 2: वर्ग करने पर 2 = p²/q² ⇒ p² = 2q²।
🔵 Step 3: 2 | p² ⇒ 2 | p ⇒ p = 2k।
🔵 Step 4: रखने पर q² = 2k² ⇒ 2 | q।
🔵 Step 5: p, q दोनों 2 से विभाज्य — विरोधाभास।
✔️ निष्कर्ष: √2 अपरिमेय।
🟢 उत्तर (ii)
🔵 Step 1: यदि 1/√5 परिमेय है तो √5 भी परिमेय होगा।
🔵 Step 2: लेकिन √5 अपरिमेय है।
✔️ निष्कर्ष: 1/√5 अपरिमेय।
🔵 प्रश्न 25
सिद्ध कीजिए कि 2√7 अपरिमेय है।
🟢 उत्तर
🔵 Step 1: 2 परिमेय संख्या है।
🔵 Step 2: √7 अपरिमेय है।
🔵 Step 3: परिमेय × अपरिमेय = अपरिमेय।
✔️ निष्कर्ष: 2√7 अपरिमेय है।
🔵 प्रश्न 26 (आन्तरिक विकल्प)
(i) सिद्ध कीजिए कि 4 + √2 अपरिमेय है।
या
(ii) सिद्ध कीजिए कि 5√11 अपरिमेय है।
🟢 उत्तर (i)
🔵 Step 1: 4 परिमेय है।
🔵 Step 2: √2 अपरिमेय है।
🔵 Step 3: परिमेय + अपरिमेय = अपरिमेय।
✔️ निष्कर्ष: 4 + √2 अपरिमेय।
🟢 उत्तर (ii)
🔵 Step 1: 5 परिमेय है।
🔵 Step 2: √11 अपरिमेय है।
🔵 Step 3: परिमेय × अपरिमेय = अपरिमेय।
✔️ निष्कर्ष: 5√11 अपरिमेय।
🔵 प्रश्न 27
यदि किसी भिन्न के हर (denominator) के अभाज्य गुणनखण्ड केवल 2 या 5 हों, तो उसका दशमलव प्रसार किस प्रकार का होगा? सिद्ध कीजिए।
🟢 उत्तर
🔵 Step 1: मान लें भिन्न = p/(2ᵐ×5ⁿ)।
🔵 Step 2: इसे (p×5ᵐ)/(10ᵐ×5ⁿ) या (p×2ⁿ)/(2ᵐ×10ⁿ) के रूप में लिखा जा सकता है।
🔵 Step 3: हर = 10ᵏ रूप में आ जाएगा।
🔵 Step 4: 1/10ᵏ का दशमलव प्रसार k स्थानों के बाद समाप्त हो जाता है।
✔️ निष्कर्ष: ऐसे भिन्न का दशमलव प्रसार समाप्ति वाला होता है।
🔵 प्रश्न 28 (आन्तरिक विकल्प)
(i) सिद्ध कीजिए कि √19 अपरिमेय है।
या
(ii) सिद्ध कीजिए कि 1/√13 अपरिमेय है।
🟢 उत्तर (i)
🔵 Step 1: मान लें √19 = p/q।
🔵 Step 2: वर्ग करने पर 19 = p²/q² ⇒ p² = 19q²।
🔵 Step 3: 19 | p² ⇒ 19 | p ⇒ p = 19k।
🔵 Step 4: रखने पर q² = 19k² ⇒ 19 | q।
🔵 Step 5: p और q दोनों 19 से विभाज्य — विरोधाभास।
✔️ निष्कर्ष: √19 अपरिमेय।
🟢 उत्तर (ii)
🔵 Step 1: यदि 1/√13 परिमेय है तो √13 भी परिमेय होगा।
🔵 Step 2: लेकिन √13 अपरिमेय है।
✔️ निष्कर्ष: 1/√13 अपरिमेय।
🔵 प्रश्न 29
सिद्ध कीजिए कि 8 + √5 अपरिमेय है।
🟢 उत्तर
🔵 Step 1: 8 परिमेय है।
🔵 Step 2: √5 अपरिमेय है।
🔵 Step 3: परिमेय + अपरिमेय = अपरिमेय।
✔️ निष्कर्ष: 8 + √5 अपरिमेय।
🔵 प्रश्न 30
सिद्ध कीजिए कि 9√2 अपरिमेय है।
🟢 उत्तर
🔵 Step 1: 9 परिमेय है।
🔵 Step 2: √2 अपरिमेय है।
🔵 Step 3: परिमेय × अपरिमेय = अपरिमेय।
✔️ निष्कर्ष: 9√2 अपरिमेय।
————————————————————————————————————————————————————————————————————————————-
मानचित्र
————————————————————————————————————————————————————————————————————————————
