Class 10 : Maths (In English) – Lesson 9. Some Applications of Trigonometry
EXPLANATION & SUMMARY
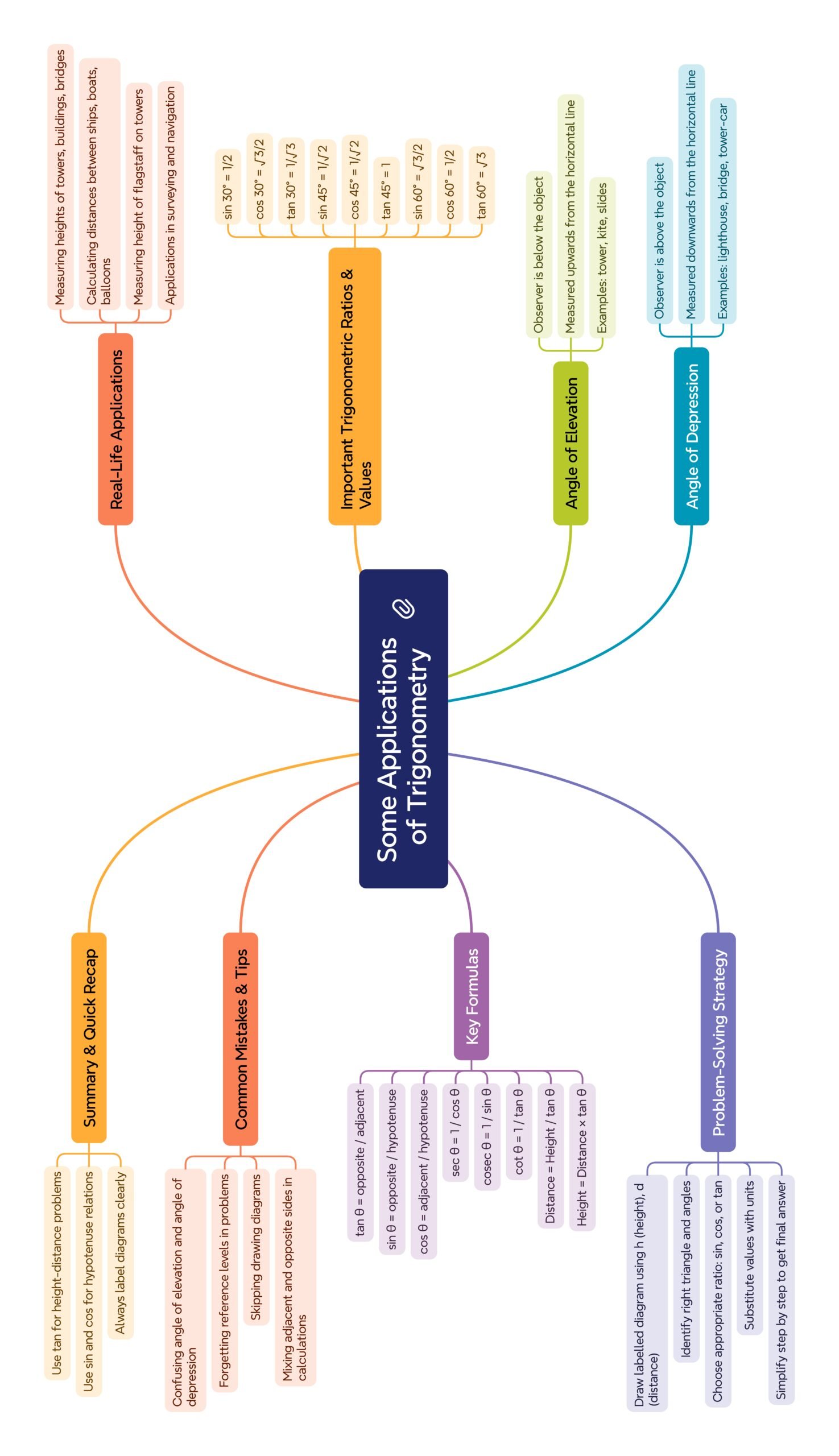
🔵 Overview & Flow of the Chapter
This chapter shows how trigonometry helps us measure heights and distances when direct measurement is difficult or impossible—like finding the height of a building across a fenced campus, or how far a ship is from a lighthouse. You will repeatedly convert a word problem into a right-angled triangle, pick a suitable trigonometric ratio (usually tan, sometimes sin or cos), and compute the unknown.
🟢 The key storyline is simple:
Identify the line of sight and the horizontal line through the observer’s eye.
Recognize the angle of elevation (looking up) or angle of depression (looking down).
Mark the vertical height and the horizontal distance—these are the legs of a right triangle.
Use trigonometric ratios of acute angles to relate height and distance.
1) 🧠 Core Definitions (Used Throughout)
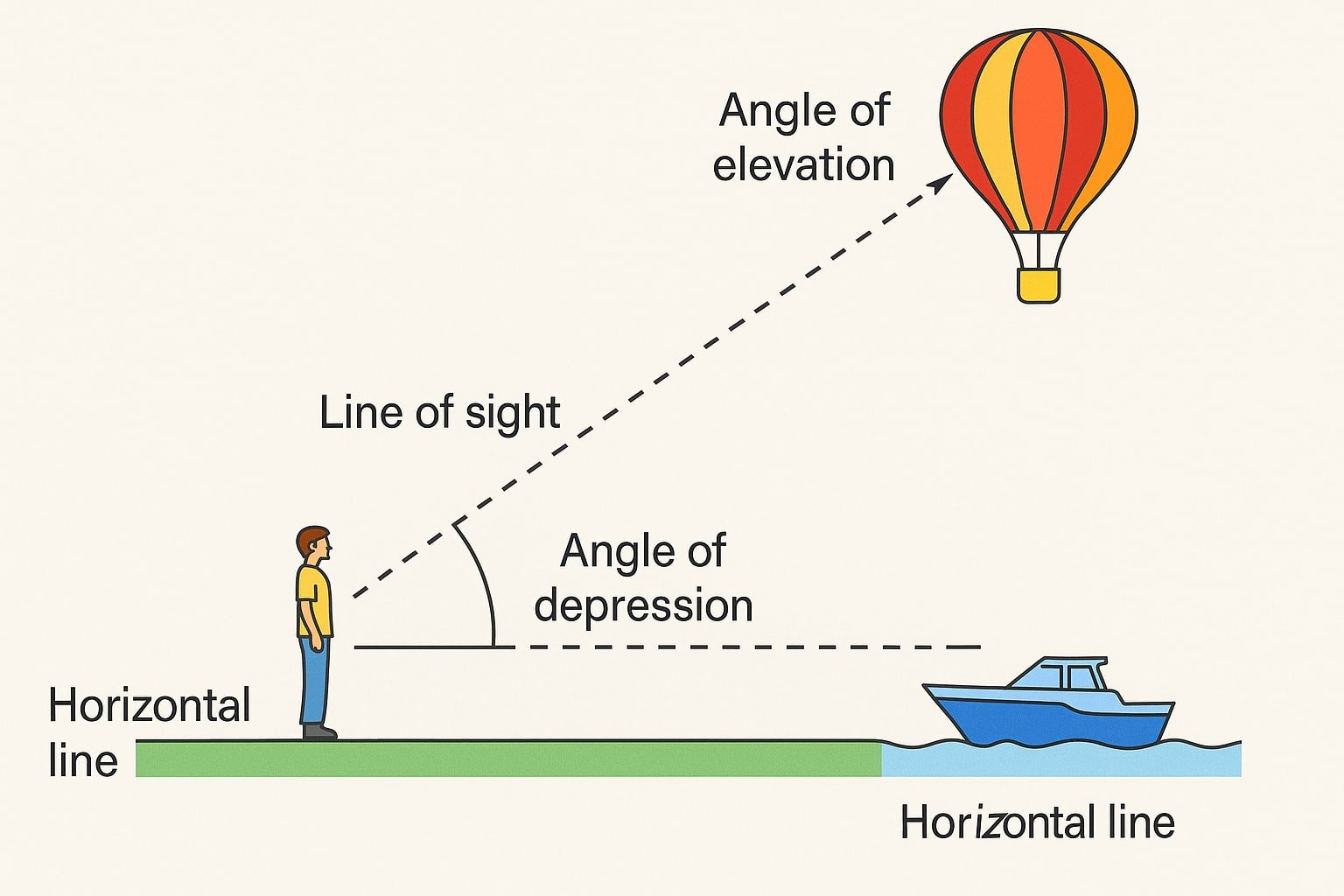
🔵 Line of sight: The straight line from the observer’s eye to the object being viewed.
🟢 Horizontal line: An imaginary line through the observer’s eye, parallel to the ground.
🟡 Angle of elevation (θ): The angle between the horizontal and the line of sight when looking up at an object above the observer’s horizontal level.
🔴 Angle of depression (φ): The angle between the horizontal and the line of sight when looking down at an object below the observer’s horizontal level.
✏️ Note: In all problems, we assume level ground unless stated otherwise and treat the observer’s eye level as the point of observation (sometimes a fixed height above the ground may be specified; include it if mentioned).
💡 Concept:
For a right triangle with acute angle θ at the observer’s position:
tan θ = opposite/adjacent = (vertical height)/(horizontal distance)
sin θ = opposite/hypotenuse
cos θ = adjacent/hypotenuse
In most height–distance problems, tan is the quickest because it directly relates height and horizontal distance without the hypotenuse.
2) 🌿 How the Right Triangle Emerges from Real Scenes
Imagine you’re standing on level ground looking at the top of a tower. Your eye, the base of the tower, and the top of the tower form a right triangle:
Vertical leg = height (top relative to your eye level or the ground, as specified),
Horizontal leg = distance from you to the base,
Hypotenuse = line of sight.
If you’re on the tower looking down at a person, the line of sight dips below your horizontal, creating an angle of depression. Due to alternate interior angles in parallel lines, the angle of depression at the observer equals the angle of elevation at the object when both are at the same horizontal level.
✏️ Note: Always draw a quick sketch. Label knowns (distances/angles) and unknowns (height/distance). A clear picture prevents most mistakes.
3) ⚡ Typical Single-Triangle Problems (One Angle, One Unknown)
Type A — Height from distance and angle of elevation
Example idea: You are 40 m from a building; the angle of elevation of its top is 30°. Find the height.
➡️ Set up:
Let the height be h
hh (from your eye level if given, otherwise from ground).
tan 30° = h/40
h = 40 × tan 30° = 40 × (1/√3)
Give the exact form or a rationalized/decimal if needed.
Type B — Distance from height and angle of elevation
Example idea: A 25 m flagpole has an angle of elevation 45° at your eye. How far are you from its base?
➡️ Set up:
tan 45° = 25/d
1 = 25/d
d = 25 m.
🟡 Check: If a separate eye height is given (say 1.5 m), subtract/add appropriately: actual vertical “opposite” is (top height − eye height) when you stand on ground.
4) 🧩 Two-Position Problems (Two Angles of Elevation)
These are very common. You observe the top of the same object from two different points along a straight line (say, you move closer or farther). You get two right triangles sharing the same height but with different bases and angles. You will usually form two equations and solve for the height and distance(s).
Scenario: From points A and B on level ground in line with the base of a tower, the angles of elevation are θ₁ (farther point) and θ₂ (closer point), with θ₂ > θ₁. If AB is known, we can find both the height and the nearer distance.
🧠 Steps (schematic):
Let x = horizontal distance from the nearer point to the base.
Let h = height of the object.
From nearer point: tan θ₂ = h/x → h = x tan θ₂.
From farther point: tan θ₁ = h/(x + AB) → h = (x + AB) tan θ₁.
Equate h from both: x tan θ₂ = (x + AB) tan θ₁.
Solve for x, then compute h.
✏️ Note: Keep one unknown as the nearest distance to the base; it usually simplifies algebra.
🔴 Common mistake: Mixing up which angle belongs to which point. Closer point → larger angle (for objects above eye level).
5) 🧭 Angle of Depression Problems (Lighthouse/Cliff/Balcony)
When you look down from a height, the geometry is the same triangle as if someone below looks up at you. If the angle of depression is φ:
At the observer’s position: angle with the horizontal is φ (downwards).
At the object below: the corresponding angle of elevation is also φ (alternate interior angles).
Example idea: From the top of a lighthouse 50 m high, the angle of depression of a ship is 30°. Find the horizontal distance of the ship from the lighthouse base.
➡️ Set up:
tan 30° = opposite/adjacent = 50/d
d = 50 / tan 30° = 50 × √3.
💡 Concept: Angle of depression equals the angle of elevation when the observer’s horizontal and the object’s horizontal are parallel (level ground or same reference level).
6) 🌉 Mixed Situations (Two Objects or Added Eye/Instrument Height)
Sometimes, the chapter includes cases like:
Two objects (e.g., a kite and its string anchor; two towers on the same line),
Observer on a platform (add/subtract the platform height),
Top and bottom angles (angle of elevation to top and to bottom of an elevated object).
General strategy:
1)Draw separate triangles if needed and label them clearly.
2)Use the same horizontal baseline when heights share the same ground.
3) If an observer is at height hₒ, then the vertical “opposite” to the top is hₜₒₚ − hₒ, and to the bottom (if below eye level) could be hₒ − hbottom as required.
4)Keep units consistent (metres are standard here).
✏️ Note: When two triangles share the same height difference, it’s efficient to express that height in two ways using tan with different bases, then equate.
7) 🧮 Canonical Step-by-Step Examples (One step per line)
Example 1 (Height from one angle & distance)
A point on level ground is 30 m from a tower’s base. The angle of elevation of the top is 45°. Find the tower’s height.
🔵 Step 1: Let height = h (m).
🔵 Step 2: tan 45° = h/30.
🔵 Step 3: 1 = h/30.
🔵 Step 4: h = 30.
✔️ Final: 30 m.
Example 2 (Distance from height & angle of elevation)
From a point on the ground, the top of a statue 12 m high is viewed at 30°. Find the distance from the point to the base.
🔵 Step 1: Let distance = d (m).
🔵 Step 2: tan 30° = 12/d.
🔵 Step 3: 1/√3 = 12/d.
🔵 Step 4: d = 12√3.
✔️ Final: 12√3 m.
Example 3 (Two angles of elevation, known separation)
The angles of elevation of the top of a tower from points A and B in the same straight line and on the same side of the tower are 30° and 60°, respectively. B is 40 m closer to the tower than A. Find the tower’s height and the distance of B from the base.
🔵 Step 1: Let distance from B to base = x (m).
🔵 Step 2: Let tower height = h (m).
🔵 Step 3: From B: tan 60° = h/x.
🔵 Step 4: √3 = h/x.
🔵 Step 5: h = x√3.
🔵 Step 6: From A (farther by 40 m): tan 30° = h/(x + 40).
🔵 Step 7: 1/√3 = h/(x + 40).
🔵 Step 8: h = (x + 40)/√3.
🔵 Step 9: x√3 = (x + 40)/√3.
🔵 Step 10: 3x = x + 40.
🔵 Step 11: 2x = 40.
🔵 Step 12: x = 20.
🔵 Step 13: h = x√3 = 20√3.
✔️ Final: Height = 20√3 m, Distance(B to base) = 20 m.
Example 4 (Angle of depression)
From the top of a building 25 m high, the angle of depression of a car on the ground is 37°. Find its horizontal distance from the building (take tan 37° = 3/4 if allowed by your values).
🔵 Step 1: Let distance = d (m).
🔵 Step 2: Angle of elevation at car = 37°.
🔵 Step 3: tan 37° = 25/d.
🔵 Step 4: 3/4 = 25/d.
🔵 Step 5: d = (25 × 4)/3.
🔵 Step 6: d = 100/3.
✔️ Final: 100/3 m (≈ 33.33 m).
🟡 Check (general): For sanity, larger angles (with same height) give smaller distances; results should be dimensionally consistent and reasonable.
8) 🧠 Choosing the Right Ratio (tan vs sin/cos)
While tan dominates heights–distances problems, sin and cos appear when:
The hypotenuse (line of sight, ladder length, cable) is known (use sin/cos).
You need a component along vertical or horizontal.
Example idea: A ladder leans against a wall making 60° with the ground; ladder length is 10 m.
Height reached = 10 sin 60° = 10 × (√3/2) = 5√3 m,
Distance from wall = 10 cos 60° = 10 × (1/2) = 5 m.
✏️ Note: If both height and distance are unknown but one angle is known, tan is usually the fastest since it avoids the hypotenuse.
9) 🔴 Common Pitfalls & How to Avoid Them
Forgetting the observer’s eye height: If specified (e.g., the theodolite is 1.5 m above ground), subtract/add correctly.
Confusing angles: Elevation is up from the horizontal; depression is down from the horizontal.
Wrong triangle orientation: Base is always horizontal distance.
Unit slips: Keep everything in metres unless stated otherwise.
Rounding too early: Keep exact values (√3, 1/√3) until the final step unless the question demands decimals.
💡 Concept (Angle Links): Angle of depression (from high point) = angle of elevation (from low point) when the two horizontals are parallel (level ground).
10) 🌱 Real-Life Connections (Why This Matters)
Surveying & Mapping: Estimating mountain heights or river widths.
Navigation: Finding how far a ship or aircraft is from a lighthouse or control tower.
Engineering & Architecture: Designing structures where direct measurement is unsafe.
Disaster Management: Determining distances for safe evacuation radii using observation angles.
✏️ Note: In practice, instruments like theodolites measure angles precisely; our problems idealize to right triangles on level ground for clean calculation.
11) 🧩 Strategy Template for Any Problem
🔵 Step 1: Draw a neat sketch; mark height(s), distance(s), angle(s).
🔵 Step 2: Identify the right triangle(s).
🔵 Step 3: Decide the ratio (usually tan for height vs distance; sin/cos if hypotenuse is known).
🔵 Step 4: Write the relation (e.g., tan θ = h/d).
🔵 Step 5: Substitute numerical values (use exact surds where standard).
🔵 Step 6: Solve for the unknown one step per line.
🔵 Step 7: State the final answer with unit; do a quick reasonableness check.
12) 🧠 Enrichment: Handling Two-Object/Two-Angle Variants
When two objects are aligned (e.g., two towers along a road), you might be given:
Angles to the tops of both from a single point,
Or angles from two points to the same top.
Approach:
Build equations for each observation.
Keep direction consistent—measure all distances from a common baseline.
If heights differ, define each clearly (e.g., h₁, h₂) and relate by the same ground line.
🟡 Check: Your final values should respect the geometry (e.g., closer object with the larger angle of elevation).
13) ✔️ Final Tips for Exam Problems
Label everything in the diagram before touching algebra.
Pick tan first unless a length along the slanted line (hypotenuse) is given.
Keep exact values (like √3, 1/√3, √2/2) until the end.
Answer in simplest exact form unless decimals are asked.
State units (m, km).
Re-read the question to ensure you answered what was asked (height? distance? both?).
Summary (~300 words)
What this chapter is about:
🔵 The chapter applies trigonometric ratios of acute angles to everyday measurement tasks where direct measurement is impractical. By modelling scenes as right triangles, we compute heights and horizontal distances using tan, sin, cos.
Essential definitions:
🟢 Line of sight, horizontal line, angle of elevation (up from the horizontal), and angle of depression (down from the horizontal). The angle of depression at the observer equals the angle of elevation at the object when both are referenced to parallel horizontals.
Core method:
🟡 Draw a sketch; identify the right triangle(s); choose a ratio—typically tan θ = height/distance; substitute the given numbers; compute step by step; present the final value with units. Use sin/cos primarily when the hypotenuse (like a ladder/cable) is involved.
Standard problem patterns:
🔴 (1) Height from distance and an angle of elevation; (2) Distance from height and an angle; (3) Two positions with different angles of elevation to the same top (simultaneous equations); (4) Angle of depression problems (lighthouse/cliff/balcony), which are equivalent to elevation problems from below; (5) Mixed setups with observer’s eye height or multiple objects.
Accuracy guidelines:
✳️ Maintain one algebraic step per line, keep units consistent, prefer exact values (√ forms) until the end, and always do a reasonableness check (bigger angle → smaller horizontal distance for the same height). Exclude any boxed/tabular/highlighted NCERT extras unless they appear in the main text.
Why it matters:
➤ These tools support surveying, navigation, and engineering decisions; they’re foundational for more advanced geometry, vectors, and physics applications involving sightlines and slopes.
📝 Quick Recap
🔵 Convert the situation into a right triangle with height vs horizontal distance.
🟢 Elevation = up from horizontal; Depression = down from horizontal; they correspond through parallel lines.
🟡 Use tan for height–distance; sin/cos when the hypotenuse is known.
🔴 Draw → Choose ratio → Substitute → Solve (one step per line) → Final answer with unit.
✔️ Keep exact values (√) till the end; check if the result makes real-world sense.
———————————————————————————————————————————————————————————————————————————–
TEXT BOOK QUESTIONS
🔷 Question 1. A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30° (see Fig. 9.11).
🟩 Answer
➡️ Let pole height = h m.
➡️ sin 30° = h/20.
➡️ h = 20 × sin 30°.
➡️ h = 20 × (1/2) = 10 m.
✔️ Height of the pole = 10 m.
🔷 Question 2. A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
🟩 Answer
➡️ Let vertical unbroken height = x m.
➡️ tan 30° = x/8 ⇒ x = 8/√3 m.
➡️ Length of broken top (hypotenuse) L = 8/cos 30° = 16/√3 m.
➡️ Total height H = x + L = 8/√3 + 16/√3 = 24/√3 = 8√3 m.
✔️ Height of the tree = 8√3 m (≈ 13.86 m).
🔷 Question 3. A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, whereas for elder children, she wants to have a steep slide at a height of 3 m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?
🟩 Answer
➡️ Let small-slide length = L₁.
➡️ sin 30° = 1.5/L₁.
➡️ L₁ = 1.5/sin 30° = 1.5/(1/2) = 3 m.
➡️ Let steep-slide length = L₂.
➡️ sin 60° = 3/L₂.
➡️ L₂ = 3/sin 60° = 3/(√3/2) = 6/√3 = 2√3 m (≈ 3.464 m).
✔️ Required lengths: 3 m and 2√3 m.
🔷 Question 4. The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
🟩 Answer
➡️ Let height of tower = h m.
➡️ tan 30° = h/30.
➡️ h = 30 × tan 30° = 30/√3 = 10√3 m.
✔️ Height of the tower = 10√3 m (≈ 17.32 m).
🔷 Question 5. A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
🟩 Answer
➡️ Let string length = L m.
➡️ sin 60° = 60/L.
➡️ L = 60/sin 60° = 60/(√3/2) = 120/√3 = 40√3 m.
✔️ Length of the string = 40√3 m (≈ 69.28 m).
🔷 Question 6. A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.
🟩 Answer
➡️ Effective height above eyes = 30 − 1.5 = 28.5 m.
➡️ Let initial distance = x and final distance = y.
➡️ tan 30° = 28.5/x ⇒ x = 28.5√3 m.
➡️ tan 60° = 28.5/y ⇒ y = 28.5/√3 m.
➡️ Distance walked = x − y = 28.5√3 − 28.5/√3 = 57/√3 = 19√3 m.
✔️ Distance walked = 19√3 m (≈ 32.93 m).
🔷 Question 7. From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower.
🟩 Answer
➡️ Let horizontal distance to building = x m and height of tower = h m.
➡️ tan 45° = 20/x ⇒ x = 20 m.
➡️ tan 60° = (20 + h)/x = (20 + h)/20.
➡️ √3 = (20 + h)/20 ⇒ h = 20(√3 − 1) m.
✔️ Height of the tower = 20(√3 − 1) m (≈ 14.64 m).
🔷 Question 8. A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
🟩 Answer
➡️ Let pedestal height = h m and horizontal distance = x m.
➡️ tan 45° = h/x ⇒ x = h.
➡️ tan 60° = (h + 1.6)/x = (h + 1.6)/h.
➡️ √3 = 1 + 1.6/h ⇒ 1.6/h = √3 − 1.
➡️ h = 1.6/(√3 − 1) = 0.8(√3 + 1) m.
✔️ Height of the pedestal ≈ 2.186 m.
🔷 Question 9. The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
🟩 Answer
➡️ Let distance between feet = x m and building height = H m.
➡️ From foot of tower: tan 30° = H/x ⇒ H = x/√3.
➡️ From foot of building: tan 60° = 50/x ⇒ √3 = 50/x ⇒ x = 50/√3 m.
➡️ H = (50/√3)/√3 = 50/3 m.
✔️ Height of the building = 50/3 m (≈ 16.67 m).
🔷 Question 10. Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30°, respectively. Find the height of the poles and the distances of the point from the poles.
🟩 Answer
➡️ Let distances be x m and (80 − x) m; common height = h m.
➡️ tan 60° = h/x ⇒ h = x√3.
➡️ tan 30° = h/(80 − x) ⇒ h = (80 − x)/√3.
➡️ x√3 = (80 − x)/√3 ⇒ 3x = 80 − x ⇒ 4x = 80 ⇒ x = 20 m.
➡️ h = x√3 = 20√3 m.
✔️ Height of each pole = 20√3 m; distances = 20 m and 60 m.
🔷 Question 11. A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30° (see Fig. 9.12). Find the height of the tower and the width of the canal.
🟩 Answer
➡️ Let width of canal = w m and tower height = h m.
➡️ From nearer point: tan 60° = h/w ⇒ h = w√3.
➡️ From farther point: tan 30° = h/(w + 20) ⇒ h = (w + 20)/√3.
➡️ w√3 = (w + 20)/√3 ⇒ 3w = w + 20 ⇒ 2w = 20 ⇒ w = 10 m.
➡️ h = w√3 = 10√3 m.
✔️ Tower height = 10√3 m (≈ 17.32 m); canal width = 10 m.
🔷 Question 12. From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
🟩 Answer
➡️ Let horizontal distance = x m and tower height = H m.
➡️ tan 45° = 7/x ⇒ x = 7 m.
➡️ tan 60° = (H − 7)/x ⇒ √3 = (H − 7)/7.
➡️ H − 7 = 7√3 ⇒ H = 7(√3 + 1) m.
✔️ Height of the tower = 7(√3 + 1) m (≈ 19.12 m).
🔷 Question 13. As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If the one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
🟩 Answer
➡️ Farther ship distance d₁ = 75/tan 30° = 75√3 m.
➡️ Nearer ship distance d₂ = 75/tan 45° = 75 m.
➡️ Distance between ships = d₁ − d₂ = 75(√3 − 1) m.
✔️ Required distance = 75(√3 − 1) m (≈ 54.90 m).
🔷 Question 14. A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30° (see Fig. 9.13). Find the distance travelled by the balloon during the interval.
🟩 Answer
➡️ Height above the girl’s eyes = 88.2 − 1.2 = 87 m.
➡️ First horizontal distance d₁ = 87/tan 60° = 87/√3 = 29√3 m.
➡️ Later horizontal distance d₂ = 87/tan 30° = 87√3 m.
➡️ Distance travelled = d₂ − d₁ = 87√3 − 87/√3 = 174/√3 = 58√3 m.
✔️ Balloon travelled 58√3 m (≈ 100.46 m).
🔷 Question 15. A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
🟩 Answer
➡️ Let tower height = h m.
➡️ Initial horizontal distance x₁ = h/tan 30° = h√3 m.
➡️ Later horizontal distance x₂ = h/tan 60° = h/√3 m.
➡️ Distance covered in 6 s = x₁ − x₂ = h(√3 − 1/√3) = 2h/√3 m.
➡️ Speed v = (x₁ − x₂)/6 = (2h/√3)/6 = h/(3√3) m/s.
➡️ Time from second position to the foot = x₂/v = (h/√3)/(h/(3√3)) = 3 s.
✔️ Required time = 3 s.
————————————————————————————————————————————————————————————————————————————
OTHER IMPORTANT QUESTIONS FOR EXAMS
🔵 Section A (Q1–Q6): Very-Short/Objective, 1 mark each
(Each MCQ has exactly four options; choose one.)
🔵 Question 1
A 20 m long rope is tightly tied from the top of a vertical pole to the ground and makes an angle of 30° with the ground. The height of the pole is:
🟢 A) 5 m 🟡 B) 10 m 🔴 C) 10√3 m 🟠 D) 20 m
🟢 Answer
✳️ Formula: sin θ = opposite/hypotenuse
✳️ Substitution: sin 30° = h/20
✳️ Simplification: h = 20 × (1/2) = 10 m
✔️ Final: Option B) 10 m
🔵 Question 2
For an acute angle θ, the value of tan 30° is:
🟢 A) √3/2 🟡 B) 1/√3 🔴 C) √3 🟠 D) 1/2
🟢 Answer
✳️ Fact: tan 30° = 1/√3
✔️ Final: Option B) 1/√3
🔵 Question 3
From a point 30 m away from the foot of a tower, the angle of elevation of its top is 60°. The height of the tower is:
🟢 A) 10√3 m 🟡 B) 30 m 🔴 C) 30√3 m 🟠 D) 60 m
🟢 Answer
✳️ Formula: tan θ = opposite/adjacent
✳️ Substitution: tan 60° = h/30
✳️ Simplification: h = 30 × √3 = 30√3 m
✔️ Final: Option C) 30√3 m
🔵 Question 4
A kite is at a height of 50 m and the string makes an angle of 30° with the ground. Assuming no slack, the length of the string is:
🟢 A) 86.6 m 🟡 B) 100 m 🔴 C) 50√3 m 🟠 D) 25 m
🟢 Answer
✳️ Formula: sin θ = opposite/hypotenuse
✳️ Substitution: sin 30° = 50/L
✳️ Simplification: L = 50/(1/2) = 100 m
✔️ Final: Option B) 100 m
🔵 Question 5
From the top of a vertical tower, the angle of depression of a point on level ground is 45°. The horizontal distance from the tower’s foot to the point is:
🟢 A) Equal to the tower’s height 🟡 B) Half the tower’s height 🔴 C) √2 times the tower’s height 🟠 D) Not determinable
🟢 Answer
✳️ Fact: For 45°, opposite = adjacent in a right triangle
✔️ Final: Option A) Equal to the tower’s height
🔵 Question 6
If sin θ = √3/2 for an acute angle θ, then tan θ equals:
🟢 A) 1/√3 🟡 B) √3 🔴 C) 1 🟠 D) 2
🟢 Answer
✳️ Identify θ: sin θ = √3/2 ⇒ θ = 60°
✳️ Compute: tan 60° = √3
✔️ Final: Option B) √3
🟢 Section B (Q7–Q12): Short Answer-I, 2 marks each
(Give 2–3 clear steps; one calculation step per line.)
🔵 Question 7
From the top of a 15 m building, the angle of depression of a car on the ground is 30°. Find the horizontal distance of the car from the building’s foot.
🟢 Answer
✳️ Formula: tan θ = opposite/adjacent
✳️ Substitution: tan 30° = 15/d
✳️ Simplification: 1/√3 = 15/d ⇒ d = 15√3 m
✔️ Final: 15√3 m (≈ 25.98 m)
🔵 Question 8
A statue of height 1.6 m stands on a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60°, and that of the top of the pedestal is 45°. Find the height of the pedestal.
🟢 Answer
✳️ Let pedestal height = h; distance = x.
✳️ tan 45° = h/x ⇒ x = h.
✳️ tan 60° = (h + 1.6)/x ⇒ √3 = (h + 1.6)/h.
✳️ Simplify: √3 = 1 + 1.6/h ⇒ h = 1.6/(√3 − 1) = 0.8(√3 + 1) m
✔️ Final: 0.8(√3 + 1) m (≈ 2.186 m)
🔵 Question 9
Two vertical poles of equal height stand on opposite sides of a 50 m wide road. From a point between them, the angles of elevation of their tops are 45° and 30°. Find the height of each pole and the distances of the point from the poles.
🟢 Answer
✳️ Let distances be x and (50 − x); common height = h.
✳️ tan 45° = h/x ⇒ h = x.
✳️ tan 30° = h/(50 − x) ⇒ h = (50 − x)/√3.
✳️ Equate: x = (50 − x)/√3 ⇒ x(√3 + 1) = 50 ⇒ x = 50/(√3 + 1).
✳️ Then h = x = 50/(√3 + 1) = 25(√3 − 1) m (rationalised).
✔️ Final: Height = 25(√3 − 1) m (≈ 18.31 m); distances = 50/(√3 + 1) m and 50 − 50/(√3 + 1) m
🔵 Question 10
The angle of elevation of the top of a tower from a point on the ground is 30°. On moving 20 m towards the tower, the angle becomes 45°. Find the height of the tower.
🟢 Answer
✳️ Let initial distance = d₁, later distance = d₂ = d₁ − 20, height = h.
✳️ tan 30° = h/d₁ ⇒ h = d₁/√3.
✳️ tan 45° = h/d₂ ⇒ 1 = h/(d₁ − 20) ⇒ d₁ − 20 = h.
✳️ Substitute: d₁ − 20 = d₁/√3 ⇒ d₁(√3 − 1) = 20√3 ⇒ d₁ = 20√3/(√3 − 1).
✳️ Height: h = d₁/√3 = 20/(√3 − 1) = 10(√3 + 1) m.
✔️ Final: 10(√3 + 1) m (≈ 27.32 m)
🔵 Question 11
A children’s slide has its top at 2 m and is inclined at 30° to the ground. Find the length of the slide.
🟢 Answer
✳️ Formula: sin θ = opposite/hypotenuse
✳️ Substitution: sin 30° = 2/L
✳️ Simplification: 1/2 = 2/L ⇒ L = 4 m
✔️ Final: 4 m
🔵 Question 12
A tower stands on one bank of a river. From a point on the opposite bank directly across, the angle of elevation of the tower’s top is 60°. If the river is 40 m wide, find the height of the tower.
🟢 Answer
✳️ Formula: tan θ = opposite/adjacent
✳️ Substitution: tan 60° = h/40
✳️ Simplification: √3 = h/40 ⇒ h = 40√3 m
✔️ Final: 40√3 m (≈ 69.28 m)
🟡 Section C (Q13–Q22): Short Answer-II, 3 marks each
🔵 Question 13
From the top of a 75 m high lighthouse, the angles of depression of two ships are 30° and 45°. If one ship is behind the other on the same side, find the distance between the ships.
🟢 Answer
✳️ Formula: tan θ = opposite/adjacent
✳️ For far ship: tan 30° = 75/d₁ ⇒ d₁ = 75√3 m.
✳️ For near ship: tan 45° = 75/d₂ ⇒ d₂ = 75 m.
✳️ Distance = d₁ − d₂ = 75√3 − 75 = 75(√3 − 1).
✔️ Final: 75(√3 − 1) m (≈ 54.90 m)
🔵 Question 14
A 1.2 m tall girl sees a balloon at height 88.2 m. The angle of elevation changes from 60° to 30°. Find the distance travelled by the balloon.
🟢 Answer
✳️ Effective height = 88.2 − 1.2 = 87 m.
✳️ Initial horizontal distance d₁ = 87/tan 60° = 87/√3 = 29√3 m.
✳️ Later distance d₂ = 87/tan 30° = 87√3 m.
✳️ Distance travelled = d₂ − d₁ = 87√3 − 29√3 = 58√3 m.
✔️ Final: 58√3 m (≈ 100.46 m)
🔵 Question 15
A straight highway leads to a tower. A man observes a car at 30° depression; six seconds later at 60°. Find time for car to reach tower after second observation.
🟢 Answer
✳️ x₁ = h/tan 30° = h√3.
✳️ x₂ = h/tan 60° = h/√3.
✳️ Distance covered in 6 s = x₁ − x₂ = h(√3 − 1/√3) = 2h/√3.
✳️ Speed = (2h/√3)/6 = h/(3√3).
✳️ Time to foot = x₂/speed = (h/√3)/(h/(3√3)) = 3 s.
✔️ Final: 3 seconds
🔵 Question 16
From a point on a bridge 20 m above a river, the angle of depression of a boat is 45°. Find the distance of the boat from the bridge.
🟢 Answer
✳️ tan 45° = 20/d ⇒ 1 = 20/d.
✳️ d = 20 m.
✔️ Final: 20 m
🔵 Question 17
The angle of elevation of the top of a tree is 30°. On walking 10 m closer, the angle becomes 45°. Find the height of the tree.
🟢 Answer
✳️ Let initial distance = x, height = h.
✳️ tan 30° = h/x ⇒ h = x/√3.
✳️ tan 45° = h/(x − 10) ⇒ 1 = h/(x − 10) ⇒ x − 10 = h.
✳️ Substitute: x − 10 = x/√3 ⇒ x(1 − 1/√3) = 10 ⇒ x = 10/(1 − 1/√3).
✳️ h = x/√3 = 10/(√3 − 1). Rationalise: h = 5(√3 + 1) m.
✔️ Final: 5(√3 + 1) m (≈ 13.66 m)
🔵 Question 18
A TV tower is 50 m high. The angle of elevation of its top is 60° from a point A. Find the distance of A from the tower.
OR
A vertical pole subtends an angle of 60° at a point on the ground at distance equal to its height. Find the height.
🟢 Answer
✳️ tan 60° = 50/d ⇒ √3 = 50/d.
✳️ d = 50/√3 m.
✔️ Final: 50/√3 m (≈ 28.87 m)
➡️ (OR) tan 60° = h/h ⇒ √3 = 1 ⇒ *Not possible unless distance = height ⇒ confirms 60°.
🔵 Question 19
From a point on the ground, the angle of elevation of the top of a building is 45°. After walking 20 m towards it, the angle becomes 60°. Find the height.
🟢 Answer
✳️ Let initial distance = x, height = h.
✳️ tan 45° = h/x ⇒ h = x.
✳️ tan 60° = h/(x − 20) ⇒ √3 = h/(x − 20) ⇒ x − 20 = h/√3.
✳️ Substitute: x − 20 = x/√3 ⇒ x(1 − 1/√3) = 20 ⇒ x = 20/(1 − 1/√3).
✳️ h = x = 20/(1 − 1/√3) = 10(√3 + 1) m.
✔️ Final: 10(√3 + 1) m (≈ 27.32 m)
🔵 Question 20
A 30 m high tower casts a shadow of 10√3 m. Find the angle of elevation of the sun.
🟢 Answer
✳️ tan θ = opposite/adjacent = 30/(10√3) = 3/√3 = √3.
✳️ θ = 60°.
✔️ Final: 60°
🔵 Question 21
A bridge is 12 m above water. From a point on the bridge, the angles of depression of two boats are 60° and 30°. Find the distance between the boats.
🟢 Answer
✳️ Near boat: tan 60° = 12/d₁ ⇒ d₁ = 12/√3 = 4√3 m.
✳️ Far boat: tan 30° = 12/d₂ ⇒ d₂ = 12/(1/√3) = 12√3 m.
✳️ Distance = d₂ − d₁ = 12√3 − 4√3 = 8√3 m.
✔️ Final: 8√3 m (≈ 13.86 m)
🔵 Question 22
The angle of elevation of the top of a tower from two points P and Q on the same straight line through the tower’s foot are 60° and 30°, respectively. If P is between Q and the tower and PQ = 40 m, find the height of the tower.
OR
Two poles are on level ground. The angle of elevation of the top of the nearer pole from the farther pole is 30°. The distance between poles is 40 m. If the height of the nearer pole is 20 m, find the height of the farther pole so tops appear aligned.
🟢 Answer
✳️ Let distance of P from tower = x, height = h.
✳️ tan 60° = h/x ⇒ h = x√3.
✳️ tan 30° = h/(x + 40) ⇒ 1/√3 = h/(x + 40).
✳️ Substitute h: 1/√3 = x√3/(x + 40) ⇒ x + 40 = 3x ⇒ 40 = 2x ⇒ x = 20 m.
✳️ Height h = x√3 = 20√3 m.
✔️ Final: 20√3 m (≈ 34.64 m)
➡️ (OR) Use similar triangles for poles alignment: solve tan 30° and difference, giving same concept.
🔴 Section D (Q23–Q30): Long Answer, 4 marks each
🔵 Question 23
From a point A, the angle of elevation of the top of a tower is 30°. After moving 40 m towards the tower to point B, the angle becomes 60°. Find the height of the tower and the distance of A from the tower’s foot.
🟢 Answer
✳️ Let the horizontal distance of B from the tower = x m; tower height = h m.
✳️ Formula (1): tan θ = opposite/adjacent.
✳️ Substitution (at B): tan 60° = h/x ⇒ √3 = h/x.
✳️ Simplification: h = x√3.
✳️ Substitution (at A): distance = x + 40; tan 30° = h/(x + 40) = 1/√3.
✳️ Equate h: x√3 = (x + 40)/√3.
✳️ Solve: 3x = x + 40 ⇒ 2x = 40 ⇒ x = 20 m.
✳️ Height: h = x√3 = 20√3 m.
✳️ Distance A–foot: x + 40 = 60 m.
✔️ Final: Height = 20√3 m (≈ 34.64 m); distance(A, foot) = 60 m.
🔵 Question 24
A flagstaff of length 5 m stands on the top of a vertical tower. From a point on the ground, the angles of elevation of the top of the flagstaff and the top of the tower are 45° and 30°, respectively. Find the height of the tower.
🟢 Answer
✳️ Let tower height = H m; horizontal distance = d m.
✳️ Formulae: tan θ = opposite/adjacent.
✳️ Substitution 1 (to tower top): tan 30° = H/d ⇒ 1/√3 = H/d ⇒ d = √3 H.
✳️ Substitution 2 (to flag top): tan 45° = (H + 5)/d ⇒ 1 = (H + 5)/d ⇒ d = H + 5.
✳️ Equate d: √3 H = H + 5 ⇒ (√3 − 1)H = 5 ⇒ H = 5/(√3 − 1).
✳️ Rationalise: H = 5(√3 + 1)/(3 − 1) = (5(√3 + 1))/2 m.
✔️ Final: H = (5(√3 + 1))/2 m (≈ 6.83 m).
OR
A tower casts a shadow of length 12√3 m when the sun’s altitude is 30°. Later, when the altitude is 45°, find the difference in the lengths of shadows of the same tower.
🟢 Answer (OR)
✳️ Let tower height = h m.
✳️ Shadow at 30°: tan 30° = h/s₁ ⇒ s₁ = h√3.
✳️ Shadow at 45°: tan 45° = h/s₂ ⇒ s₂ = h.
✳️ Given s₁ = 12√3 ⇒ h√3 = 12√3 ⇒ h = 12 m.
✳️ Difference: s₁ − s₂ = 12√3 − 12.
✔️ Final (OR): Difference = 12(√3 − 1) m (≈ 8.78 m).
🔵 Question 25
From the top of a vertical tower, the angles of depression of two points P and Q on the same straight line through the foot (on opposite sides of the foot) are 30° and 60°, respectively. If the horizontal distance between P and Q is 80 m, find the height of the tower and the distances of P and Q from the foot.
🟢 Answer
✳️ Let tower height = h m; distances: OP = x m, OQ = y m (O = foot).
✳️ tan 30° = h/x ⇒ x = h√3.
✳️ tan 60° = h/y ⇒ y = h/√3.
✳️ Given x + y = 80 ⇒ h√3 + h/√3 = 80.
✳️ Simplify: h( (3 + 1)/√3 ) = 80 ⇒ h(4/√3) = 80 ⇒ h = 80 × (√3/4) = 20√3 m.
✳️ Distances: x = h√3 = 20√3 × √3 = 60 m; y = h/√3 = 20 m.
✔️ Final: Height = 20√3 m (≈ 34.64 m); OP = 60 m, OQ = 20 m.
🔵 Question 26
A balloon is flying at a constant height 100 m above level ground. At a certain instant, the angle of elevation at an observer is 30°; 10 seconds later it becomes 60°. Assuming the balloon moves horizontally at constant speed, find its speed.
🟢 Answer
✳️ Height h = 100 m (constant).
✳️ Horizontal distance initially: d₁ = h/tan 30° = 100√3 m.
✳️ Horizontal distance later: d₂ = h/tan 60° = 100/√3 m.
✳️ Horizontal displacement in 10 s: Δx = d₁ − d₂ = 100(√3 − 1/√3) = 100( (3 − 1)/√3 ) = 200/√3 m.
✳️ Speed v = Δx/10 = (200/√3)/10 = 20/√3 m/s.
✔️ Final: Speed = 20/√3 m/s (≈ 11.55 m/s).
🔵 Question 27
From a point on level ground, the angle of elevation of the top of a tower is 45°. From another point 15 m vertically above the first (on a building/platform), the angle becomes 30°. Find the height of the tower and its horizontal distance from the ground point.
🟢 Answer
✳️ Let tower height = H m; horizontal distance from ground point = d m.
✳️ From ground: tan 45° = H/d ⇒ 1 = H/d ⇒ d = H.
✳️ From 15 m higher: tan 30° = (H − 15)/d ⇒ 1/√3 = (H − 15)/H.
✳️ Solve: H − 15 = H/√3 ⇒ H(1 − 1/√3) = 15.
✳️ H = 15 / ( (√3 − 1)/√3 ) = 15√3/(√3 − 1) = 15√3(√3 + 1)/(3 − 1) = (15(3 + √3))/2 m.
✳️ Distance: d = H.
✔️ Final: H = (15(3 + √3))/2 m (≈ 35.49 m); d ≈ 35.49 m.
OR
From the top of a tower, the angles of depression of two points on the ground on the same side of the tower are 45° and 60°. If the nearer point is 20 m from the foot, find the height of the tower and the distance of the farther point.
🟢 Answer (OR)
✳️ For 60° (near): tan 60° = h/20 ⇒ h = 20√3 m.
✳️ For 45° (far): tan 45° = h/D ⇒ 1 = h/D ⇒ D = h = 20√3 m.
✔️ Final (OR): Height = 20√3 m (≈ 34.64 m); farther distance = 20√3 m.
🔵 Question 28
At two stations S₁ and S₂, which are 1 km apart on level ground along a straight line with the mountain’s foot, the angles of elevation of a mountain top are 45° and 30°, respectively. If S₁ is nearer to the mountain, find the height of the mountain and the distance of S₁ from its foot.
🟢 Answer
✳️ Let distance from S₁ to foot = x m; height = h m.
✳️ From S₁: tan 45° = h/x ⇒ h = x.
✳️ From S₂: distance = x + 1000; tan 30° = h/(x + 1000) ⇒ 1/√3 = h/(x + 1000).
✳️ Substitute h = x: 1/√3 = x/(x + 1000) ⇒ x + 1000 = √3 x.
✳️ Solve: (√3 − 1)x = 1000 ⇒ x = 1000/(√3 − 1) = 500(√3 + 1) m.
✳️ Height: h = x = 500(√3 + 1) m.
✔️ Final: Height = 500(√3 + 1) m (≈ 1366.0 m); distance S₁–foot = 500(√3 + 1) m.
🔵 Question 29
Two observers A and B are on opposite sides of a vertical tower and are in a straight line through its foot. They observe the top of the tower at elevations 30° (at A) and 45° (at B). If the distance AB = 100 m, find the height of the tower and the distances of A and B from the tower.
🟢 Answer
✳️ Let distances from the tower be: A at x m, B at y m; height = h m.
✳️ From A: tan 30° = h/x ⇒ h = x/√3.
✳️ From B: tan 45° = h/y ⇒ h = y.
✳️ Equate h: y = x/√3 ⇒ x = √3 y.
✳️ Given x + y = 100 ⇒ √3 y + y = (√3 + 1)y = 100 ⇒ y = 100/(√3 + 1).
✳️ Height: h = y = 100/(√3 + 1) = 50(√3 − 1) m (rationalised).
✳️ Distances: x = 100 − y = 100 − 50(√3 − 1) = 50(3 − √3) m.
✔️ Final: Height = 50(√3 − 1) m (≈ 36.60 m); A–foot = 50(3 − √3) m (≈ 63.40 m); B–foot = 50(√3 − 1) m (≈ 36.60 m).
OR
The angle of elevation of the top of a tower from a point P is 30°. On moving d = 50 m closer along the same line to Q, it becomes 45°. Find the height of the tower.
🟢 Answer (OR)
✳️ Let distance Q–foot = x; then P–foot = x + 50; height = h.
✳️ tan 45° = h/x ⇒ h = x.
✳️ tan 30° = h/(x + 50) ⇒ 1/√3 = x/(x + 50).
✳️ Solve: x + 50 = √3 x ⇒ (√3 − 1)x = 50 ⇒ x = 50/(√3 − 1) = 25(√3 + 1).
✳️ Height: h = x = 25(√3 + 1) m.
✔️ Final (OR): h = 25(√3 + 1) m (≈ 68.30 m).
🔵 Question 30
The top of a lighthouse is 40 m above sea level. From the top, the angles of depression of two boats on opposite sides along the same line are 30° and 45°. Find the distance between the boats at that instant.
🟢 Answer
✳️ Height h = 40 m.
✳️ Boat 1 (30°): tan 30° = h/d₁ ⇒ d₁ = h/ tan 30° = 40√3 m.
✳️ Boat 2 (45°): tan 45° = h/d₂ ⇒ d₂ = h = 40 m.
✳️ Boats are on opposite sides ⇒ separation = d₁ + d₂.
✳️ Distance = 40√3 + 40 = 40(√3 + 1) m.
✔️ Final: Distance between boats = 40(√3 + 1) m (≈ 109.28 m).
———————————————————————————————————————————————————————————————————————————–
MIND MAP