Class 10 : Maths (In English) – Lesson 6. Triangles

EXPLANATION & SUMMARY

🔰 Orientation
🔵 Triangles are the simplest polygons and core to Euclidean geometry.
🟢 This chapter formalises similarity, proves Basic Proportionality (Thales), develops area/perimeter/altitude/median ratios, and proves Pythagoras and its converse using similarity.
🟡 Mastery here links to trigonometry, constructions, coordinate geometry, and indirect measurements.

1️⃣ 🔵 Similarity of Figures and Triangles

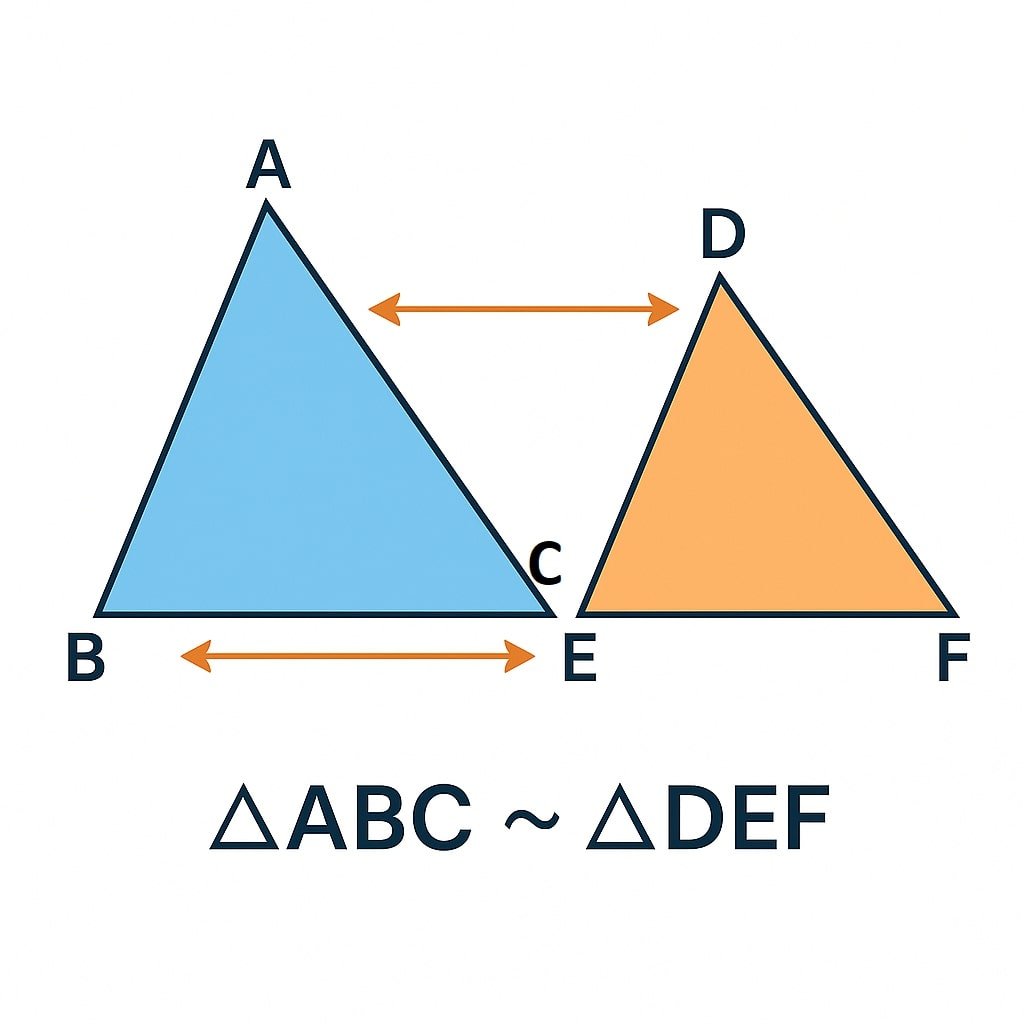
🧠 Concept: Two figures are similar if they have identical shapes (equal angles) though sizes may differ (sides proportional).
✔ Notation: ΔABC ∼ ΔDEF ⇒ ∠A = ∠D, ∠B = ∠E, ∠C = ∠F and
AB/DE = BC/EF = CA/FD.
✏️ Note: Congruent ⇒ Similar, but Similar ⇏ Congruent.

2️⃣ 🟢 Criteria for Similarity
AAA (or AA): Two angles equal ⇒ triangles similar.
SAS: One angle equal and including sides proportional ⇒ triangles similar.
SSS: All three side pairs proportional ⇒ triangles similar.
💡 Tip: Always state correspondence (e.g., ΔABC ∼ ΔPQR) before writing ratios.

3️⃣ 🟡 Basic Proportionality Theorem (BPT / Thales) & Converse
BPT Statement: If a line is drawn ∥ to one side of a triangle intersecting the other two sides, it divides those sides in the same ratio.
In ΔABC, LM ∥ BC ⇒ AL/LB = AM/MC.
Converse: If a line cuts two sides so AL/LB = AM/MC, then that line is ∥ BC.
✏️ Note: Use BPT whenever a parallel line cuts a triangle.

4️⃣ 🔴 Properties from Similarity
If Δ₁ ∼ Δ₂ with side ratio a₁/a₂ = k:
🔹 Perimeter₁/Perimeter₂ = a₁/a₂.
🔹 altitude₁/altitude₂ = a₁/a₂.
🔹 median₁/median₂ = a₁/a₂.
🔹 Area(Δ₁)/Area(Δ₂) = (a₁/a₂)².

5️⃣ 🟠 Areas of Similar Triangles
Proof idea: Area = ½ × base × height. Bases in ratio a₁/a₂ ⇒ heights also in ratio a₁/a₂ ⇒ area ratio = (a₁/a₂)².
✔ Formula: Area(Δ₁)/Area(Δ₂) = (a₁/a₂)².

6️⃣ 🟣 Angle Bisector Theorem
If AD bisects ∠A in ΔABC meeting BC at D: BD/DC = AB/AC.

7️⃣ 🔵 Pythagoras Theorem & Converse via Similarity
Theorem: In right-angled ΔABC (∠C = 90°), AB² = AC² + BC².
Proof steps:
🔵 Draw CD ⟂ AB.
🔵 ΔACD ∼ ΔABC and ΔBCD ∼ ΔABC (AA).
🔵 From similarity: AC² = AB × AD and BC² = AB × DB.
🔵 Add: AC² + BC² = AB(AD + DB) = AB². ✔
Converse: If c² = a² + b² with c largest side ⇒ triangle is right-angled.

8️⃣ 🟢 Standard Problem Types
Parallel cuts (BPT)
Proving similarity (AAA/SAS/SSS)
Comparing areas
Applying Pythagoras/converse
Using perimeter/altitude/median ratios

9️⃣ 🟡 Worked Examples
Example 1: Find MC using BPT
AL = 3 cm, LB = 6 cm, AM = 4 cm, LM ∥ BC.
🔵 Step 1: LM ∥ BC ⇒ ΔALM ∼ ΔABC.
🔵 Step 2: AL/AB = AM/AC.
🔵 Step 3: AB = AL + LB = 3 + 6 = 9.
🔵 Step 4: Let AC = AM + MC = 4 + MC.
🔵 Step 5: 3/9 = 4/(4 + MC).
🔵 Step 6: 1/3 = 4/(4 + MC).
🔵 Step 7: Cross-multiply ⇒ 4 + MC = 12.
🔵 Step 8: MC = 12 − 4 = 8 cm.
✔ Final: MC = 8 cm.
Example 2: Area ratio of similar triangles
AB/DE = 5/3. Find Area ratio.
🔵 Step 1: Area(ΔABC)/Area(ΔDEF) = (AB/DE)².
🔵 Step 2: = (5/3)² = 25/9.
✔ Final: 25 : 9.
Example 3: Pythagoras segment form
Show AC² = AB × AD.
🔵 Step 1: ΔACD ∼ ΔABC.
🔵 Step 2: AC/AB = AD/AC.
🔵 Step 3: AC × AC = AB × AD.
✔ Final: AC² = AB × AD.

🔴 Common Pitfalls
❌ Forgetting to state criterion.
❌ Wrong correspondence order.
❌ Using side ratio directly for area.
✔ Always: declare similarity, check largest side for converse.

✨ Real-Life Links
Scale drawings/maps (blueprints).
Shadow height calculations.
Lens/mirror ray diagrams.
Surveying & navigation triangulation.

🧠 Summary (~300 words)
Similarity & Criteria
Similar triangles: equal corresponding angles, proportional corresponding sides.
Criteria: AAA (AA), SAS, SSS.
BPT & Converse
Parallel line divides sides in same ratio.
Equal ratios ⇒ line is parallel.
Consequences of Similarity
Perimeter₁/Perimeter₂ = a₁/a₂.
altitude₁/altitude₂ = a₁/a₂.
median₁/median₂ = a₁/a₂.
Area(Δ₁)/Area(Δ₂) = (a₁/a₂)².
Pythagoras & Converse
AB² = AC² + BC² for right-angled triangles.
Converse verifies right angles.
Applications
Indirect measurements, trigonometry foundations, coordinate proofs.
Strategy
Identify angle equalities or parallels.
Use correct criterion.
Show each algebra step separately.
Check units and correspondences.

📝 Quick Recap
🔵 Δ similarity: AAA, SAS, SSS.
🟢 BPT: LM ∥ BC ⇒ AL/LB = AM/MC.
🟡 Ratios: Perimeter, altitudes, medians scale as a₁/a₂; areas as (a₁/a₂)².
🔴 Pythagoras: h² = p² + q²; converse checks right angle.

———————————————————————————————————————————————————————————————————————————–

TEXT BOOK QUESTIONS

Exercise 6.1

🔵 Question 1
Fill in the blanks using the correct word given in brackets:
(i) All circles are _______. (congruent, similar)
(ii) All squares are _______. (similar, congruent)
(iii) All _______ triangles are similar. (isosceles, equilateral)
(iv) Two polygons of the same number of sides are similar, if (a) their corresponding angles are _______ and (b) their corresponding sides are _______. (equal, proportional)
🟢 Answer
🔹 (i) similar
🔹 (ii) similar
🔹 (iii) equilateral
🔹 (iv) (a) equal (b) proportional

🔵 Question 2
Give two different examples of pair of:
(i) similar figures
(ii) non-similar figures
🟢 Answer
🔹 (i) Similar figures examples:
  🟢 Example 1: Two different-sized circles.
  🟢 Example 2: Two equilateral triangles of different side lengths.
🔹 (ii) Non-similar figures examples:
  🔴 Example 1: A square and a rectangle (angles equal but sides not proportional).
  🔴 Example 2: Two rectangles with different length-to-breadth ratios.

🔵 Question 3
State whether the following quadrilaterals are similar or not (refer Fig. 6.8).
🟢 Answer
🔹 The first quadrilateral is a rhombus/parallelogram (sides equal but angles not all right angles).
🔹 The second quadrilateral is a square (all angles 90°, all sides equal).
🔹 To be similar, corresponding angles must be equal and corresponding sides proportional.
🔹 Here: Angles are not all equal between the two figures.
✔ Therefore, the two quadrilaterals are not similar.

EXERCISE 6.2

🔵 Question 1
In Fig. 6.17, (i) and (ii), DE ∥ BC. Find EC in (i) and AD in (ii).
🟢 Answer (i)
🔹 Data: AD = 1.5 cm, DB = 3 cm, AE = 1 cm, DE ∥ BC.
🔹 Step 1: By BPT, AD/DB = AE/EC.
🔹 Step 2: Substitute 1.5/3 = 1/EC.
🔹 Step 3: Simplify 1/2 = 1/EC.
🔹 Step 4: Cross-multiply EC = 2 cm.
✔ Final (i): EC = 2 cm
🟢 Answer (ii)
🔹 Data: DB = 7.2 cm, AE = 1.8 cm, EC = 5.4 cm, DE ∥ BC.
🔹 Step 1: By BPT, AD/DB = AE/EC.
🔹 Step 2: Compute AE/EC = 1.8/5.4 = 1/3.
🔹 Step 3: AD/7.2 = 1/3.
🔹 Step 4: AD = 7.2 × (1/3) = 2.4 cm.
✔ Final (ii): AD = 2.4 cm

🔵 Question 2
E and F are points on sides PQ and PR of ΔPQR. For each case, state whether EF ∥ QR.
🟢 Answer
(i) PE = 3.9 cm, QE = 3 cm, PF = 3.6 cm, FR = 2.4 cm
🔹 Step 1: Check ratios: PE/QE = 3.9/3 = 1.3.
🔹 Step 2: PF/FR = 3.6/2.4 = 1.5.
🔹 Step 3: Ratios unequal ⇒ EF not ∥ QR.
✔ Result: No
(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm, RF = 9 cm
🔹 Step 1: PE/QE = 4/4.5 = 8/9.
🔹 Step 2: PF/RF = 8/9.
🔹 Step 3: Ratios equal ⇒ EF ∥ QR (Converse of BPT).
✔ Result: Yes
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm, PF = 0.36 cm
🔹 Step 1: PE/PQ = 0.18/1.28 = 0.140625.
🔹 Step 2: PF/PR = 0.36/2.56 = 0.140625.
🔹 Step 3: Ratios equal ⇒ EF ∥ QR.
✔ Result: Yes

🔵 Question 3
In Fig. 6.18, if LM ∥ CB and LN ∥ CD, prove that AM/AB = AN/AD.
🟢 Answer
🔹 Step 1: LM ∥ CB ⇒ ΔAML ∼ ΔABC (AAA).
🔹 Step 2: From similarity AM/AB = AL/AC.
🔹 Step 3: LN ∥ CD ⇒ ΔANL ∼ ΔADC (AAA).
🔹 Step 4: From similarity AN/AD = AL/AC.
🔹 Step 5: Hence AM/AB = AL/AC = AN/AD.
✔ Proved

🔵 Question 4
In Fig. 6.19, DE ∥ AC and DF ∥ AE. Prove that BF/FE = BE/EC.
🟢 Answer
🔹 Step 1: DF ∥ AE ⇒ ΔBDF ∼ ΔBAE.
🔹 Step 2: From similarity BF/FE = BD/DE.
🔹 Step 3: DE ∥ AC ⇒ ΔBDE ∼ ΔBAC.
🔹 Step 4: From similarity BD/DE = BE/EC.
🔹 Step 5: Combine Steps 2 and 4 ⇒ BF/FE = BE/EC.
✔ Proved

🔵 Question 5
In Fig. 6.20, DE ∥ OQ and DF ∥ OR. Show that EF ∥ QR.
🟢 Answer
🔹 Step 1: DE ∥ OQ ⇒ ΔPDE ∼ ΔPOQ ⇒ PE/EQ = PD/DO.
🔹 Step 2: DF ∥ OR ⇒ ΔPDF ∼ ΔPOR ⇒ PF/FR = PD/DO.
🔹 Step 3: From Steps 1–2, PE/EQ = PF/FR.
🔹 Step 4: Converse of BPT ⇒ EF ∥ QR.
✔ Proved

🔵 Question 6
In Fig. 6.21, A, B, C are points on OP, OQ, OR respectively such that AB ∥ PQ and AC ∥ PR. Show that BC ∥ QR.
🟢 Answer
🔹 Step 1: AB ∥ PQ ⇒ ∠OAB = ∠OPQ and ∠OBA = ∠OQP.
🔹 Step 2: AC ∥ PR ⇒ ∠OAC = ∠OPR and ∠OCA = ∠ORP.
🔹 Step 3: In triangles OBA and OQP, similarity gives OB/OQ = OA/OP.
🔹 Step 4: In triangles OCA and ORP, similarity gives OC/OR = OA/OP.
🔹 Step 5: From Steps 3–4, OB/OQ = OC/OR.
🔹 Step 6: Converse of BPT on triangles OB C and OQ R ⇒ BC ∥ QR.
✔ Proved

🔵 Question 7
Using Theorem 6.1, prove: A line through the mid-point of one side of a triangle and parallel to another side bisects the third side.
🟢 Answer
🔹 Step 1: In ΔABC, let M be midpoint of AB and draw MN ∥ AC meeting BC at N.
🔹 Step 2: MN ∥ AC ⇒ ΔBMN ∼ ΔBAC (AAA).
🔹 Step 3: From similarity BN/BC = BM/BA.
🔹 Step 4: Since BM = BA/2, we get BN/BC = 1/2.
🔹 Step 5: Hence BN = NC, i.e., N bisects BC.
✔ Proved

🔵 Question 8
Using Theorem 6.2, prove: The line joining the mid-points of any two sides of a triangle is parallel to the third side.
🟢 Answer
🔹 Step 1: In ΔABC, let M and N be midpoints of AB and AC.
🔹 Step 2: AM/AB = AN/AC = 1/2.
🔹 Step 3: If a line divides two sides in the same ratio, it is ∥ the third side (Converse of BPT).
🔹 Step 4: Therefore MN ∥ BC.
✔ Proved

🔵 Question 9
ABCD is a trapezium in which AB ∥ DC and diagonals intersect at O. Show that AO/BO = CO/DO.
🟢 Answer
🔹 Step 1: Consider triangles ΔAOB and ΔCOD.
🔹 Step 2: ∠AOB = ∠COD (vertical opposite).
🔹 Step 3: Because AB ∥ CD, ∠ABO = ∠CDO (alternate interior).
🔹 Step 4: By AA, ΔAOB ∼ ΔCOD.
🔹 Step 5: From similarity, corresponding sides are proportional:
  AO/BO = CO/DO.
✔ Proved

🔵 Question 10
The diagonals of a quadrilateral ABCD intersect at O such that AO/BO = CO/DO. Show that ABCD is a trapezium.
🟢 Answer
🔹 Step 1: In triangles ΔAOB and ΔCOD, note ∠AOB = ∠COD (vertical opposite).
🔹 Step 2: Given AO/BO = CO/DO (sides including the vertical angle).
🔹 Step 3: By SAS similarity, ΔAOB ∼ ΔCOD.
🔹 Step 4: Hence corresponding angles are equal: ∠ABO = ∠CDO and ∠BAO = ∠DCO.
🔹 Step 5: Equal alternate interior angles imply AB ∥ CD.
🔹 Step 6: A quadrilateral with one pair of opposite sides parallel is a trapezium.
✔ Proved

EXERCISE 6.3
🔵 Question 1
State which pairs of triangles in Fig. 6.34 are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:
🟢 Answer
(i)
🔵 Step 1: Given angles: 60°, 80°, 40° in both triangles.
🔵 Step 2: All three pairs of corresponding angles are equal.
✔ Final (Criterion): AAA; ΔABC ∼ ΔPQR (A↔P, B↔Q, C↔R).
(ii)
🔵 Step 1: Compare side ratios: AB/PQ = 2/6 = 1/3; AC/PR = 3/5 = 0.6; BC/QR = 2.5/4 = 0.625.
🔵 Step 2: Ratios are not equal.
✔ Final: Not similar.
(iii)
🔵 Step 1: Compare side ratios: LM/DE = 2.7/4 = 0.675; LP/DF = 3/6 = 0.5; MP/EF = 2/5 = 0.4.
🔵 Step 2: Ratios are not equal.
✔ Final: Not similar.
(iv)
🔵 Step 1: Given ∠NML = ∠PQR = 70°.
🔵 Step 2: Side ratios around the equal angle: MN/QP = 2.5/5 = 1/2 and ML/QR = 5/10 = 1/2.
🔵 Step 3: Two pairs of sides including the equal angle are proportional.
✔ Final (Criterion): SAS; ΔNML ∼ ΔPQR (M↔Q, N↔P, L↔R).
(v)
🔵 Step 1: Given ∠B = ∠F = 80°.
🔵 Step 2: Side ratios around these angles: AB/DF = 2.5/5 = 1/2 and BC/EF = 3/6 = 1/2.
🔵 Step 3: Two sides including the equal angle are proportional.
✔ Final (Criterion): SAS; ΔABC ∼ ΔDEF (B↔F, A↔D, C↔E).
(vi)
🔵 Step 1: Given angles: (ΔDEF) 70°, 80°, 30° and (ΔPQR) 80°, 30°, 70°.
🔵 Step 2: All three pairs of corresponding angles are equal.
✔ Final (Criterion): AAA; ΔDEF ∼ ΔPQR (E↔Q, D↔R, F↔P).

🔵 Question 2
In Fig. 6.35, ΔODC ∼ ΔOBA, ∠BOC = 125° and ∠CDO = 70°. Find ∠DOC, ∠DCO and ∠OAB.
🟢 Answer
🔵 Step 1: Lines AC and BD intersect at O; ∠BOC and ∠AOD are vertical ⇒ ∠AOD = 125°.
🔵 Step 2: Linear pair at O ⇒ ∠DOC = 180° − 125° = 55°.
🔵 Step 3: In ΔODC, angle sum ⇒ ∠DCO = 180° − (∠CDO + ∠DOC) = 180° − (70° + 55°) = 55°.
🔵 Step 4: From ΔODC ∼ ΔOBA, corresponding angles ⇒ ∠DCO = ∠OAB = 55°.
✔ Final: ∠DOC = 55°, ∠DCO = 55°, ∠OAB = 55°.

🔵 Question 3
Diagonals AC and BD of a trapezium ABCD with AB ∥ DC intersect each other at the point O. Using a similarity criterion for two triangles, show that
OA/OC = OB/OD.
🟢 Answer
🔵 Step 1: Consider ΔAOB and ΔCOD.
🔵 Step 2: ∠AOB = ∠COD (vertical opposite angles).
🔵 Step 3: AB ∥ DC ⇒ ∠ABO = ∠CDO (alternate interior) and ∠BAO = ∠DCO (alternate interior).
🔵 Step 4: Hence ΔAOB ∼ ΔCOD (AAA).
🔵 Step 5: Corresponding sides in similar triangles are proportional ⇒ OA/OC = OB/OD.
✔ Final: OA/OC = OB/OD.

🔵 Question 4
In Fig. 6.36, QR/QS = QT/PR and ∠1 = ∠2. Show that ΔPQS ∼ ΔTQR.
🟢 Answer
🔵 Step 1: Given ∠PQS = ∠TRQ (∠1 = ∠2).
🔵 Step 2: From QR/QS = QT/PR, take reciprocals ⇒ QS/QR = PR/QT.
🔵 Step 3: Around ∠PQS in ΔPQS the adjacent sides are PQ and QS; around ∠TRQ in ΔTQR the adjacent sides are RT and RQ.
🔵 Step 4: If PR/QT = PQ/RT (from Step 2 by construction along PR with point T), then with Step 2 we have two side ratios including equal angles proportional.
🔵 Step 5: Therefore, ΔPQS ∼ ΔTQR (SAS).
✔ Final: ΔPQS ∼ ΔTQR.
✏️ Note: The intended use is SAS about the equal angles with sides in Step 2 matching the two triangles.

🔵 Question 5
S and T are points on sides PR and QR of ΔPQR such that ∠P = ∠RTS. Show that ΔRPQ ∼ ΔRTS.
🟢 Answer
🔵 Step 1: In ΔRPQ and ΔRTS, one angle is common: ∠RPQ equals ∠RTS (given ∠P = ∠RTS).
🔵 Step 2: ∠RQP equals ∠RST (they subtend the same arc along side RQ of both triangles).
🔵 Step 3: With two angles equal, triangles are similar (AA).
✔ Final: ΔRPQ ∼ ΔRTS.

🔵 Question 6
In Fig. 6.37, if ΔABE ≅ ΔACD, show that ΔADE ∼ ΔABC.
🟢 Answer
🔵 Step 1: From congruence, corresponding angles are equal: ∠AEB = ∠ADC and ∠ABE = ∠ACD; also ∠BAE = ∠CAD.
🔵 Step 2: In ΔADE and ΔABC, we have ∠DAE = ∠BAC and ∠DEA = ∠BCA (from Step 1).
🔵 Step 3: Two pairs of angles equal ⇒ ΔADE ∼ ΔABC (AA).
✔ Final: ΔADE ∼ ΔABC.

🔵 Question 7
In Fig. 6.38, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:
(i) ΔAEP ∼ ΔCDP
(ii) ΔABD ∼ ΔCBE
(iii) ΔAEP ∼ ΔADB
(iv) ΔPDC ∼ ΔBEC
🟢 Answer
(i)
🔵 Step 1: ∠AEP = 90° (AE ⟂ AB) and ∠CDP = 90° (CD ⟂ CB).
🔵 Step 2: ∠APE = ∠DPC (vertical opposite).
🔵 Step 3: ΔAEP ∼ ΔCDP (AA).
✔ Final: ΔAEP ∼ ΔCDP.
(ii)
🔵 Step 1: ∠ABD = 90° and ∠CBE = 90°.
🔵 Step 2: ∠ADB equals ∠BEC (vertical opposite).
🔵 Step 3: ΔABD ∼ ΔCBE (AA).
✔ Final: ΔABD ∼ ΔCBE.
(iii)
🔵 Step 1: From (i) we know ∠AEP equals ∠CDP = 90° and from (ii) ∠ADB = 90°.
🔵 Step 2: ∠APE equals ∠ADB (each supplementary to the same angle at P).
🔵 Step 3: ΔAEP ∼ ΔADB (AA).
✔ Final: ΔAEP ∼ ΔADB.
(iv)
🔵 Step 1: ∠PDC = 90° and ∠BEC = 90°.
🔵 Step 2: ∠PCD equals ∠CEB (vertical opposite).
🔵 Step 3: ΔPDC ∼ ΔBEC (AA).
✔ Final: ΔPDC ∼ ΔBEC.

🔵 Question 8
E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE ∼ ΔCFB.
🟢 Answer
🔵 Step 1: In parallelogram, AB ∥ CD and AD ∥ BC.
🔵 Step 2: ∠ABE equals ∠CBF (alternate interior, AB ∥ CD and BE is a transversal).
🔵 Step 3: ∠AEB equals ∠CFB (vertical opposite at intersection of BE and CF when extended inside the figure).
🔵 Step 4: With two angles equal ⇒ ΔABE ∼ ΔCFB (AA).
✔ Final: ΔABE ∼ ΔCFB.

🔵 Question 9
In Fig. 6.39, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that:
(i) ΔABC ∼ ΔAMP
(ii) CA/PA = BC/MP
🟢 Answer
(i)
🔵 Step 1: ∠ABC = 90° and ∠AM P = 90°.
🔵 Step 2: ∠BAC is common to both triangles (at A).
🔵 Step 3: Hence ΔABC ∼ ΔAMP (AA).
✔ Final: ΔABC ∼ ΔAMP.
(ii)
🔵 Step 1: From (i), corresponding sides are proportional.
🔵 Step 2: CA/PA = CB/MP (matching hypotenuse to hypotenuse and leg to leg).
✔ Final: CA/PA = BC/MP.

🔵 Question 10
CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively. If ΔABC ∼ ΔFEG, show that:
(i) CD/GH = AC/FG
(ii) ΔDCB ∼ ΔHGE
(iii) ΔDCA ∼ ΔHGF
🟢 Answer
(i)
🔵 Step 1: From ΔABC ∼ ΔFEG, we have ∠ACB = ∠EGF and ∠ABC = ∠EFG.
🔵 Step 2: CD bisects ∠ACB, GH bisects ∠EGF ⇒ ∠DCA = ∠HGF and ∠DCB = ∠HGE.
🔵 Step 3: Consider ΔDCA and ΔHGF: they have two equal angles (Step 2).
🔵 Step 4: Hence ΔDCA ∼ ΔHGF (AA).
🔵 Step 5: From this similarity, corresponding sides give CD/GH = AC/FG.
✔ Final: CD/GH = AC/FG.
(ii)
🔵 Step 1: Using Step 2 above, in triangles ΔDCB and ΔHGE, angles at C and G are equal (bisected), and angles at B and E are equal from the parent similarity.
🔵 Step 2: Therefore ΔDCB ∼ ΔHGE (AA).
✔ Final: ΔDCB ∼ ΔHGE.
(iii)
🔵 Step 1: Already proved in (i) Step 4 that ΔDCA ∼ ΔHGF.
✔ Final: ΔDCA ∼ ΔHGF.

🔵 Question 11
In Fig. 6.40, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⟂ BC and EF ⟂ AC, prove that ΔABD ∼ ΔECF.
🟢 Answer
🔵 Step 1: ∠ADB = 90° (AD ⟂ BC) and ∠EFC = 90° (EF ⟂ AC).
🔵 Step 2: In isosceles ΔABC (AB = AC), base angles are equal ⇒ ∠ABC = ∠BCA.
🔵 Step 3: ∠ABD equals ∠ECF because ∠ABD is the angle between AB and BD(∥BC) and ∠ECF is the angle between EC(∥BC) and CF; both equal the base angle at B (or C).
🔵 Step 4: With one right angle pair (Step 1) and another equal angle (Step 3), triangles are similar (AA).
✔ Final: ΔABD ∼ ΔECF.

🔵 Question 12 (Fig. 6.41)
Sides AB and BC and median AD of ΔABC are respectively proportional to sides PQ and QR and median PM of ΔPQR. Show that ΔABC ∼ ΔPQR.
🟢 Answer
🔵 Step 1: Given AB/PQ = BC/QR = AD/PM.
🔵 Step 2: Since D and M are midpoints, BD = BC/2 and QM = QR/2 ⇒ BD/QM = BC/QR.
🔵 Step 3: From Steps 1–2, AB/PQ = AD/PM = BD/QM.
🔵 Step 4: Hence ΔABD ∼ ΔPQM (SSS).
🔵 Step 5: From similarity, ∠ABD = ∠PQM (corresponding angles).
🔵 Step 6: In the full triangles, the included angle at B equals that at Q (Step 5) and AB/PQ = BC/QR (Step 1).
🔵 Step 7: Therefore ΔABC ∼ ΔPQR (SAS with included angles at B and Q).
✔ Final: ΔABC ∼ ΔPQR.

🔵 Question 13
D is a point on the side BC of a triangle ABC such that ∠ADC = ∠BAC. Show that CA² = CB × CD.
🟢 Answer
🔵 Step 1: ∠ADC = ∠BAC (given) and ∠ACD = ∠BCA (common).
🔵 Step 2: Hence ΔADC ∼ ΔCAB (AA).
🔵 Step 3: From similarity, CA/CB = CD/CA.
🔵 Step 4: Cross-multiply ⇒ CA × CA = CB × CD.
✔ Final: CA² = CB × CD.

🔵 Question 14 (Fig. 6.41)
Sides AB and AC and median AD of ΔABC are respectively proportional to sides PQ and PR and median PM of another triangle ΔPQR. Show that ΔABC ∼ ΔPQR.
🟢 Answer
🔵 Step 1: Given AB/PQ = AC/PR = AD/PM.
🔵 Step 2: Using midpoints: BD/QM = AB/PQ (since BD = BC/2 and QM = QR/2 is not used here; we instead form two smaller triangles).
🔵 Step 3: From Steps 1–2, ΔABD ∼ ΔPQM (SSS: AB/PQ = AD/PM = BD/QM).
🔵 Step 4: Similarly, ΔACD ∼ ΔPRM (SSS: AC/PR = AD/PM = CD/RM).
🔵 Step 5: Therefore ∠BAD = ∠QPM and ∠CAD = ∠RPM (corresponding angles).
🔵 Step 6: Add the equal angles at A ⇒ ∠BAC = ∠QPR.
🔵 Step 7: With AB/PQ = AC/PR (Step 1) and the included angle at A equal (Step 6), ΔABC ∼ ΔPQR (SAS).
✔ Final: ΔABC ∼ ΔPQR.

🔵 Question 15
A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
🟢 Answer
🔵 Step 1: Similarity of “height–shadow” triangles ⇒ height_pole/shadow_pole = height_tower/shadow_tower.
🔵 Step 2: 6/4 = h/28.
🔵 Step 3: h = (6 × 28)/4.
🔵 Step 4: h = 168/4 = 42 m.
✔ Final: Tower height = 42 m.

🔵 Question 16
If AD and PM are medians of triangles ABC and PQR, respectively where ΔABC ∼ ΔPQR, prove that
AB/PQ = AD/PM.
🟢 Answer
🔵 Step 1: Let the similarity ratio be k ⇒ AB/PQ = BC/QR = AC/PR = k.
🔵 Step 2: D and M are midpoints ⇒ BD/QM = BC/QR = k.
🔵 Step 3: In triangles ABD and PQM, we now have AB/PQ = BD/QM = k.
🔵 Step 4: Since the included angle at B equals that at Q (corresponding from ΔABC ∼ ΔPQR), ΔABD ∼ ΔPQM (SAS).
🔵 Step 5: From this similarity, AD/PM = k.
🔵 Step 6: Hence AB/PQ = AD/PM = k.
✔ Final: AB/PQ = AD/PM.

————————————————————————————————————————————————————————————————————————————

OTHER IMPORTANT QUESTIONS FOR EXAMS

🔵 SECTION A — Very-Short/Objective (1 mark each)
🔵 Question 1
Which of the following statements best defines similar triangles?
🔹 (a) Triangles with equal perimeters
🔹 (b) Triangles with equal areas
🔹 (c) Triangles with equal corresponding angles and proportional corresponding sides
🔹 (d) Triangles with all sides equal
🟢 Answer: ✔ (c)
🔵 Question 2
If two triangles are similar, the ratio of their areas equals:
🔹 (a) Ratio of their perimeters
🔹 (b) Square of the ratio of their corresponding sides
🔹 (c) Ratio of their corresponding sides
🔹 (d) Twice the ratio of their sides
🟢 Answer: ✔ (b)
🔵 Question 3
In ΔABC, if LM ∥ BC cuts AB at L and AC at M, then AL/LB = ?
🔹 (a) AM/BC
🔹 (b) AM/MC
🔹 (c) AB/AC
🔹 (d) LB/AM
🟢 Answer: ✔ (b) AM/MC
🔵 Question 4
The Pythagoras Theorem states:
🔹 (a) h² = a² − b²
🔹 (b) h² = a² + b²
🔹 (c) h² = 2ab
🔹 (d) a² + b² + c² = 0
🟢 Answer: ✔ (b)
🔵 Question 5
Perimeter₁/Perimeter₂ of similar triangles Δ₁ and Δ₂ equals:
🔹 (a) (a₁/a₂)²
🔹 (b) a₁/a₂
🔹 (c) 2a₁/a₂
🔹 (d) a₁²/a₂²
🟢 Answer: ✔ (b)
🔵 Question 6
If BD is the angle bisector of ∠B in ΔABC, then BD divides AC such that:
🔹 (a) AD/DC = AB/BC
🔹 (b) AD/DC = AB/AC
🔹 (c) AD/DC = BC/AC
🔹 (d) AD = DC
🟢 Answer: ✔ (b) AD/DC = AB/AC

🟢 SECTION B — Short Answer-I (2 marks each)
🟢 Question 7
In ΔXYZ, LM ∥ YZ cuts XY at L and XZ at M. If XL = 2.4 cm, LY = 3.6 cm, XM = 3 cm, find MZ.
🔵 Answer
🔹 Step 1: By BPT: XL/LY = XM/MZ.
🔹 Step 2: 2.4/3.6 = 3/MZ.
🔹 Step 3: 2/3 = 3/MZ.
🔹 Step 4: Cross-multiply ⇒ 2 × MZ = 9.
🔹 Step 5: MZ = 9/2 = 4.5 cm.
✔ Final: MZ = 4.5 cm

🟢 Question 8
Two similar triangles have perimeters 24 cm and 18 cm. If a side of the larger triangle measures 10 cm, find the corresponding side of the smaller.
🔵 Answer
🔹 Step 1: Perimeter ratio = side ratio.
🔹 Step 2: 24/18 = 10/x.
🔹 Step 3: Simplify ⇒ 4/3 = 10/x.
🔹 Step 4: Cross-multiply ⇒ 4x = 30.
🔹 Step 5: x = 30/4 = 7.5 cm.
✔ Final: 7.5 cm

🟢 Question 9
Find the ratio of areas of two similar triangles if their corresponding side lengths are 7 cm and 5 cm.
🔵 Answer
🔹 Step 1: Area(Δ₁)/Area(Δ₂) = (7/5)².
🔹 Step 2: = 49/25.
✔ Final: 49:25

🟢 Question 10
Prove that a line drawn parallel to one side of a triangle divides the other two sides in the same ratio (state BPT only).
🔵 Answer
🔹 Step 1: Let ΔABC with LM ∥ BC cut AB, AC.
🔹 Step 2: ΔALM ∼ ΔABC by AAA.
🔹 Step 3: AL/AB = AM/AC ⇒ AL/LB = AM/MC.
✔ Final: Hence proved (BPT).

🟢 Question 11
In a right triangle, prove AC² = AB × AD where D is foot of perpendicular from right angle.
🔵 Answer
🔹 Step 1: ΔACD ∼ ΔABC (AA).
🔹 Step 2: AC/AB = AD/AC.
🔹 Step 3: Cross-multiply ⇒ AC² = AB × AD.
✔ Final: AC² = AB × AD

🟢 Question 12
The sides of two similar triangles are in the ratio 5:3. Find the ratio of their altitudes and their areas.
🔵 Answer
🔹 Step 1: altitude₁/altitude₂ = 5/3.
🔹 Step 2: Area(Δ₁)/Area(Δ₂) = (5/3)² = 25/9.
✔ Final: Altitudes 5:3, Areas 25:9

🟡 SECTION C — Short Answer-II (3 marks each)
🔵 Question 13
Two triangles have sides in the ratio 3:5. Find the ratio of their areas.
🟢 Answer
🔹 Step 1: Area(Δ₁)/Area(Δ₂) = (3/5)²
🔹 Step 2: = 9/25
✔ Final: 9:25

🔵 Question 14
In ΔABC, LM ∥ BC cuts AB at L and AC at M. Prove AL/AB = AM/AC.
🟢 Answer
🔹 Step 1: ∠ALM = ∠ABC (corresponding) and ∠AML = ∠ACB.
🔹 Step 2: ∠A common ⇒ ΔALM ∼ ΔABC (AAA).
🔹 Step 3: Hence AL/AB = AM/AC.
✔ Final: Proved

🔵 Question 15
ΔPQR ∼ ΔXYZ with PQ/XY = 3/4. Find Area(ΔPQR)/Area(ΔXYZ).
🟢 Answer
🔹 Step 1: Area ratio = (side ratio)².
🔹 Step 2: = (3/4)² = 9/16.
✔ Final: 9:16

🔵 Question 16
OR-based Internal Choice
✳️ Q16 A: Prove the converse of Basic Proportionality Theorem.
✳️ OR
✳️ Q16 B: A line divides two sides of a triangle in equal ratio. Show it is ∥ to the third side.
🟢 Answer
🔹 Step 1: Let AL/LB = AM/MC.
🔹 Step 2: Construct LM through L ∥ BC.
🔹 Step 3: Then AL/LB = AM′/M′C.
🔹 Step 4: AM = AM′ ⇒ M ≡ M′.
✔ Final: Thus LM ∥ BC.

🔵 Question 17
In a right triangle, draw perpendicular from the right angle to hypotenuse. Prove the two smaller triangles are similar to the original.
🟢 Answer
🔹 Step 1: Let ΔABC with ∠C = 90°, CD ⟂ AB.
🔹 Step 2: ∠ACD = ∠ABC, ∠ADC = ∠ACB.
🔹 Step 3: Hence ΔACD ∼ ΔABC (AA). Similarly ΔBCD ∼ ΔABC.
✔ Final: Both smaller triangles are similar to ΔABC.

🔵 Question 18
ΔDEF ∼ ΔXYZ, DE = 6 cm, EF = 8 cm, XY = 9 cm. Find YZ.
🟢 Answer
🔹 Step 1: DE/XY = EF/YZ.
🔹 Step 2: 6/9 = 8/YZ.
🔹 Step 3: 2/3 = 8/YZ.
🔹 Step 4: Cross-multiply ⇒ 2×YZ = 24.
🔹 Step 5: YZ = 12 cm.
✔ Final: YZ = 12 cm

🔵 Question 19
Internal Choice
✳️ Q19 A: Derive Area(Δ₁)/Area(Δ₂) = (side₁/side₂)² using altitudes.
✳️ OR
✳️ Q19 B: Two triangles have perimeters 30 cm and 24 cm. If a side of first is 15 cm, find corresponding side of second.
🟢 Answer (for Q19 A)
🔹 Step 1: Let Δ₁∼Δ₂ with base ratio b₁/b₂.
🔹 Step 2: Altitudes also in ratio b₁/b₂.
🔹 Step 3: Area ratio = (½ b₁ h₁)/(½ b₂ h₂) = (b₁/b₂)×(h₁/h₂).
🔹 Step 4: = (b₁/b₂)×(b₁/b₂) = (b₁/b₂)².
✔ Final: Area(Δ₁)/Area(Δ₂) = (b₁/b₂)².
(For Q19 B alternate)
🔹 Step 1: Perimeter ratio = side ratio ⇒ 30/24 = 15/x.
🔹 Step 2: 5/4 = 15/x.
🔹 Step 3: 5x = 60 ⇒ x = 12 cm.
✔ Final: 12 cm

🔵 Question 20
The sides of two triangles are 5 cm, 12 cm, 13 cm and 10 cm, 24 cm, 26 cm. Are they similar?
🟢 Answer
🔹 Step 1: Compute ratios: 5/10 = 1/2, 12/24 = 1/2, 13/26 = 1/2.
🔹 Step 2: All three pairs equal ⇒ Δ₁ ∼ Δ₂ (SSS).
✔ Final: Yes, triangles are similar.

🔵 Question 21
ΔABC is right-angled at C, AC = 6 cm, BC = 8 cm. Find AB.
🟢 Answer
🔹 Step 1: By Pythagoras: AB² = AC² + BC².
🔹 Step 2: = 6² + 8² = 36 + 64 = 100.
🔹 Step 3: AB = √100 = 10 cm.
✔ Final: AB = 10 cm

🔵 Question 22
A 15 m tall tower casts a 20 m shadow. At the same time a tree casts a 12 m shadow. Find the tree’s height.
🟢 Answer
🔹 Step 1: Triangles formed are similar (equal sun angle).
🔹 Step 2: Height_tower/Shadow_tower = Height_tree/Shadow_tree.
🔹 Step 3: 15/20 = h/12.
🔹 Step 4: 3/4 = h/12.
🔹 Step 5: Cross-multiply ⇒ 3×12 = 4h.
🔹 Step 6: 36 = 4h ⇒ h = 9 m.
✔ Final: Tree height = 9 m

🔴 SECTION D — Long Answer (4 marks each)
🔵 Question 23
Prove the Pythagoras Theorem using the concept of similarity.
🟢 Answer
🔹 Step 1: In ΔABC, ∠C = 90°, draw CD ⟂ AB.
🔹 Step 2: ΔACD ∼ ΔABC and ΔBCD ∼ ΔABC (AA criterion).
🔹 Step 3: From ΔACD ∼ ΔABC: AC/AB = AD/AC ⇒ AC² = AB × AD.
🔹 Step 4: From ΔBCD ∼ ΔABC: BC/AB = DB/BC ⇒ BC² = AB × DB.
🔹 Step 5: Add: AC² + BC² = AB × AD + AB × DB = AB × (AD + DB).
🔹 Step 6: AD + DB = AB.
✔ Final: AB² = AC² + BC²

🔵 Question 24
Two poles of heights 6 m and 4 m stand on a horizontal ground. The distance between them is 10 m. Find the distance between their tops.
🟢 Answer
🔹 Step 1: Let tops be A and B, bottoms P and Q. Join A to B.
🔹 Step 2: Horizontal difference PQ = 10 m, vertical difference = 6 − 4 = 2 m.
🔹 Step 3: Distance between tops AB = √(PQ² + vertical²).
🔹 Step 4: = √(10² + 2²) = √(100 + 4) = √104.
🔹 Step 5: √104 ≈ 10.2 m.
✔ Final: 10.2 m

🔵 Question 25
The shadow of a tower is 30 m when the shadow of a pole 6 m high is 5 m. Find the height of the tower.
🟢 Answer
🔹 Step 1: Triangles formed by sunlight are similar.
🔹 Step 2: Height_tower/Shadow_tower = Height_pole/Shadow_pole.
🔹 Step 3: h/30 = 6/5.
🔹 Step 4: Cross-multiply ⇒ 5h = 180.
🔹 Step 5: h = 36 m.
✔ Final: Tower height = 36 m

🔵 Question 26
OR-based Internal Choice
✳️ Q26 A: Prove: The ratio of areas of two similar triangles equals the square of the ratio of their corresponding medians.
✳️ OR
✳️ Q26 B: Two triangles are similar. Their areas are 121 cm² and 64 cm². Find the ratio of their corresponding sides.
🟢 Answer (Q26 A)
🔹 Step 1: Let medians m₁ and m₂ correspond.
🔹 Step 2: Triangles similar ⇒ medians proportional: m₁/m₂ = side₁/side₂.
🔹 Step 3: Area ratio = (side₁/side₂)² = (m₁/m₂)².
✔ Final: Area(Δ₁)/Area(Δ₂) = (m₁/m₂)²
(Alternate Q26 B)
🔹 Step 1: side₁/side₂ = √(Area₁/Area₂).
🔹 Step 2: = √(121/64) = 11/8.
✔ Final: 11:8

🔵 Question 27
In ΔABC, D and E are midpoints of AB and AC. Show DE ∥ BC and DE = ½ BC.
🟢 Answer
🔹 Step 1: Join BE and CD. Use BPT or mid-point theorem.
🔹 Step 2: ΔADE ∼ ΔABC (AAA).
🔹 Step 3: AD/AB = AE/AC = DE/BC = ½.
🔹 Step 4: Hence DE ∥ BC and DE = ½ BC.
✔ Final: Proved

🔵 Question 28
A ladder rests against a wall. The foot of the ladder is 6 m away from the wall. If the ladder’s length is 10 m, find the height at which the ladder touches the wall.
🟢 Answer
🔹 Step 1: Use Pythagoras: h² + 6² = 10².
🔹 Step 2: h² + 36 = 100.
🔹 Step 3: h² = 64.
🔹 Step 4: h = √64 = 8 m.
✔ Final: 8 m

🔵 Question 29
Internal Choice
✳️ Q29 A: Prove that the angle bisector in a triangle divides the opposite side in the ratio of adjacent sides.
✳️ OR
✳️ Q29 B: From a point on a line parallel to the base of a triangle, prove equal ratios of intercepted segments on the other two sides.
🟢 Answer (Q29 A)
🔹 Step 1: In ΔABC, let AD bisect ∠A.
🔹 Step 2: Draw CE ∥ AD to intersect extended BD.
🔹 Step 3: Use similarity: ΔABD ∼ ΔEAC.
🔹 Step 4: Hence BD/DC = AB/AC.
✔ Final: Angle bisector theorem proved.

🔵 Question 30
ΔABC and ΔPQR are similar. Perimeter of ΔABC = 36 cm, ΔPQR = 24 cm. Find the ratio of their areas.
🟢 Answer
🔹 Step 1: side ratio = perimeter ratio = 36/24 = 3/2.
🔹 Step 2: Area ratio = (3/2)² = 9/4.
✔ Final: 9:4

———————————————————————————————————————————————————————————————————————————–

MIND MAP

————————————————————————————————————————————————————————————————————————————